关于高等数学所有符的写法与读法

合集下载

高等数学中特殊符号读法及功能

常用高等数学符号的读法及含义表一、常用符号读法大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μμmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omikron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon 衣普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧米伽符号表符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作exa^x a的x次方；有理数x由反函数定义ln x exp x 的反函数ax 同a^xlogba 以b为底a的对数；blogba = acos x 在自变量x处余弦函数的值tan x 其值等于sin x/cos xcot x 余切函数的值或cos x/sin xsec x 正割含数的值，其值等于1/cos xcsc x 余割函数的值，其值等于1/sin xasin x y，正弦函数反函数在x处的值，即x = sin y acos x y，余弦函数反函数在x处的值，即x = cos y atan x y，正切函数反函数在x处的值，即x = tan y acot x y，余切函数反函数在x处的值，即x = cot y asec x y，正割函数反函数在x处的值，即x = sec y acsc x y，余割函数反函数在x处的值，即x = csc yθ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a?b a、b向量的点积(a?b) a、b向量的点积|v| 向量v的模符号含义|x| 数x的绝对值Σ表示求和，通常是某项指数。

高等数学中特殊符号读法及功能

常用高等数学符号的读法及含义表一、常用符号读法大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μμmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omikron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon 衣普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧米伽符号表符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作exa^x a的x次方；有理数x由反函数定义ln x exp x 的反函数ax 同a^xlogba 以b为底a的对数；blogba = acos x 在自变量x处余弦函数的值tan x 其值等于sin x/cos xcot x 余切函数的值或cos x/sin xsec x 正割含数的值，其值等于1/cos xcsc x 余割函数的值，其值等于1/sin xasin x y，正弦函数反函数在x处的值，即x = sin y acos x y，余弦函数反函数在x处的值，即x = cos y atan x y，正切函数反函数在x处的值，即x = tan y acot x y，余切函数反函数在x处的值，即x = cot y asec x y，正割函数反函数在x处的值，即x = sec y acsc x y，余割函数反函数在x处的值，即x = csc yθ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a?b a、b向量的点积(a?b) a、b向量的点积|v| 向量v的模符号表符号含义|x| 数x的绝对值Σ表示求和，通常是某项指数。

各种数学符号及读法大全

各种数学符号及读法大全数学是一门充满符号的科学，这些符号就像一种特殊的语言，帮助我们更简洁、准确地表达数学概念和进行运算。

下面就为大家介绍一些常见的数学符号及其读法。

一、基本运算符号1、加号（＋）：读作“加”，例如“2 ＋3”读作“二加三”。

2、减号（－）：读作“减”，比如“5 2”读作“五减二”。

3、乘号（×）：读作“乘”，像“4 × 5”读作“四乘五”。

在数学中，有时也会用“·”表示乘号，例如“3·2”，同样读作“三乘二”。

4、除号（÷）：读作“除以”，例如“6 ÷ 3”读作“六除以三”。

二、比较符号1、等于号（＝）：读作“等于”，比如“2 ＋ 3 ＝5”读作“二加三等于五”。

2、大于号（＞）：读作“大于”，例如“5 ＞3”读作“五大于三”。

3、小于号（＜）：读作“小于”，像“2 ＜4”读作“二小于四”。

4、大于等于号（≥）：读作“大于等于”，比如“x ≥ 5”读作“x 大于等于五”。

5、小于等于号（≤）：读作“小于等于”，例如“y ≤ 8”读作“y 小于等于八”。

三、括号1、小括号（）：通常读作“括号”，例如“（2 ＋ 3）× 4”读作“括号二加三括号乘四”。

2、中括号：读作“中括号”，像“ 5 （3 1）÷ 2”读作“中括号五减去括号三减一括号除以二”。

3、大括号｛｝：读作“大括号”，比如“｛ 2, 4, 6, 8 ｝”读作“大括号二，四，六，八”。

四、分数符号1、分数线（—）：例如“3/5”，读作“五分之三”。

分子在前，分母在后。

2、带分数：由整数部分和分数部分组成，例如“2 又1/3”，读作“二又三分之一”。

五、指数符号1、平方（²）：例如“5²”，读作“五的平方”。

2、立方（³）：像“2³”，读作“二的立方”。

3、多次方：比如“4 的 5 次方”写作“4^5”，读作“四的五次方”。

高数符号大全及读法

高数符号大全及读法
高数符号大全及读法如下：
符号：∑(读作西格玛)
含义：求和
符号：∫(读作拉个)
含义：不定积分
符号：dx (读作得克西)
含义：微分
符号：∫(读作拉个)
含义：定积分
符号：d (读作得)
含义：微分
符号：lim (读作林姆)
含义：极限
符号：f(z) (读作fai(z))
含义：关于z的m阶导函数
符号：C(n:m) (读作C艾克斯n:m)
含义：组合数，n中取m
符号：P(n:m) (读作P艾克斯n:m)
含义：排列数m|n m整除n m⊥n m与n互质
符号：a ∈A (读作艾塔属于A)
含义：a属于集合A
符号：#A (读作阿尔法艾塔)
含义：集合A中的元素个数
以上是高数中常用的一些符号及其读法，希望能够帮助到您。

数学符号读法大全高等数学中所有符号的读法

数学符号读法大全高等数学中所有符号的读法
1 Α α alpha a:lf 阿尔法角度；系数
2 Β β beta bet 贝塔磁通系数；角度；系数
3 Γ γ gamma ga:m 伽马电导系数（小写）
4 Δ δ delta delt 德尔塔变动；密度；屈光度
5 Ε ε epsilon ep`silon 伊普西龙对数之基数
6 Ζ ζ zeta zat截塔系数；方位角；阻抗；相对粘度；原子序数
7 Η η eta eit 艾塔磁滞系数；效率（小写）
8 Θ θ thet θit 西塔温度；相位角
9 Ι ι iot aiot 约塔微小,一点儿
10 Κ κ kappa kap 卡帕介质常数
11 ∧ λ lambda lambd 兰布达波长（小写）；体积
12 Μ μ mu mju 缪磁导系数；微（千分之一）；放大因数（小写）
13 Ν ν nu nju 纽磁阻系数
14 Ξ ξ xi ksi 克西
15 Ο ο omicron omik`ron 奥密克戎
16 ∏ π pi pai 派圆周率=圆周÷直径=3.1416
17 Ρ ρ rho rou 肉电阻系数（小写）
18 ∑ σ sigma `sigma 西格马总和（大写）,表面密度；跨导（小写）
19 Τ τ tau tau 套时间常数
20 Υ υ upsilon jup`silon 宇普西龙位移
21 Φ φ phi fai 佛爱磁通；角
22 Χ χ chi phai 西
23 Ψ ψ psi psai 普西角速；介质电通量（静电力线）；角
24 Ω ω omega o`miga 欧米伽欧姆（大写）；角速（小写）；角。

(完整)高等数学所有符号的写法与读法

高等数学所有符号的写法与读法￣hyphen 连字符' apostrophe 省略号；所有格符号— dash 破折号‘’single quotation marks 单引号“”double quotation marks 双引号( ) parentheses 圆括号[ ] square brackets 方括号Angle bracket{} Brace《》French quotes 法文引号；书名号... ellipsis 省略号¨ tandem colon 双点号" ditto 同上‖ parallel 双线号／virgule 斜线号＆ampersand = and～swung dash 代字号§ section; division 分节号→ arrow 箭号；参见号＋plus 加号；正号－minus 减号；负号± plus or minus 正负号× is multiplied by 乘号÷ is divided by 除号＝is equal to 等于号≠ is not equal to 不等于号≡ is equivalent to 全等于号≌ is equal to or approximately equal to 等于或约等于号≈ is approximately equal to 约等于号＜is less than 小于号＞is more than 大于号≮ is not less than 不小于号≯ is not more than 不大于号≤ is less than or equal to 小于或等于号≥ is more than or equal to 大于或等于号％per cent 百分之…‰ per mill 千分之…∞ infinity 无限大号∝ varies as 与…成比例√ (square) root 平方根∵ since; because 因为∴ hence 所以∷ equals, as (proportion) 等于，成比例∠ angle 角⌒ semicircle 半圆⊙ circle 圆○ circumference 圆周π pi 圆周率△ triangle 三角形⊥ perpendicular to 垂直于∪ union of 并，合集∩ intersection of 交，通集∫ the integral of …的积分∑ (sigma) summation of 总和° degree 度′ minute 分〃second 秒＃number …号℃ Celsius system 摄氏度＠at 单价x'是x prime(比如转置矩阵)x"是x double-prime常用数学符号读法大全以及主要数学符号含义-转载数学符号：（1）数量符号：如：i，2+i，a，x，自然对数底e，圆周率π。

高等数学中特殊符号的读法及功能

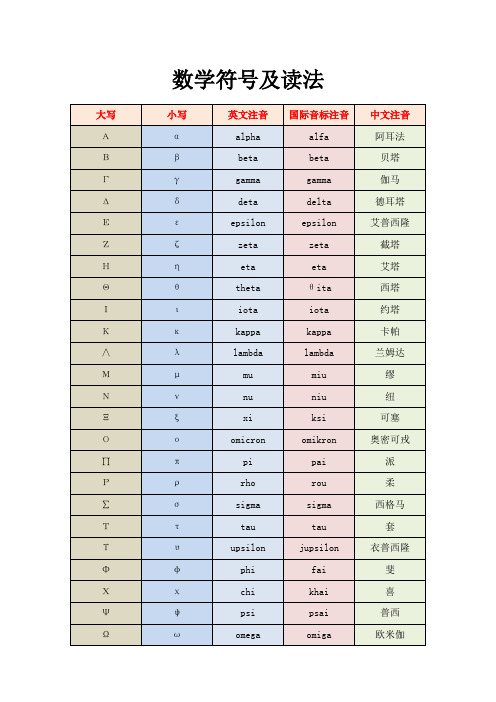
数学符号及读法符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作ex a^x a的x次方；有理数x由反函数定义ln x exp x 的反函数a x同a^xlog b a 以b为底a的对数；blog b a = acos x 在自变量x处余弦函数的值tan x 其值等于sin x/cos xcot x 余切函数的值或cos x/sin xsec x 正割含数的值，其值等于1/cos xcsc x 余割函数的值，其值等于1/sin x arcsin x y，正弦函数反函数在x处的值，即x = sin y arccos x y，余弦函数反函数在x处的值，即x = cos y arctan x y，正切函数反函数在x处的值，即x = tan y arccot x y，余切函数反函数在x处的值，即x = cot y arcsec x y，正割函数反函数在x处的值，即x = sec y arccsc x y，余割函数反函数在x处的值，即x = csc yθ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a?b a、b向量的点积(a?b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和，通常是某项指数。

下边界值写在其下部，上边界值写在其上部。

如j从1到100的和可以表示成：。

这表示 1 + 2 + …+ nM 表示一个矩阵或数列或其它|v> 列向量，即元素被写成列或可被看成k×1阶矩阵的向量<v| 被写成行或可被看成从1×k阶矩阵的向量dx 变量x的一个无穷小变化，dy, dz, dr等类似ds 长度的微小变化ρ变量(x2 + y2 + z2)1/2 或球面坐标系中到原点的距离r 变量(x2 + y2)1/2 或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式，其值是矩阵的行和列决定的平行区域的面积或体。

高等数学中符号的读法及功能(挺全的)

大写小写英文注音国际音标注音中文注音A a alpha alfa 阿耳法B3beta beta 贝塔r Y gamma gamma 伽马r5deta delta 德耳塔△£epsilon epsilon 艾普西隆E zeta zeta 截塔Z£eta eta 艾塔©z theta z ita 西塔H n iota iota 约塔K9kappa kappa 卡帕A i lambda lambda 兰姆达M K mu miu 缪N入nu niu 纽g xi ksi 可塞0V omicron omikron 奥密可戎n n pi pai 派p E rho rou 柔刀z sigma sigma 西格马T n tau tau 套Y u upsilon jupsilon 衣普西隆①9phi fai 斐①X chi khai 喜X I psi psai 普西omegaomiga欧米伽符号表符号含义i f(x)-1 的平方根函数f 在自变量x 处的值sin(x)在自变量x 处的正弦函数值exp(x)在自变量x 处的指数函数值，常被写作exa A x a 的x 次方；有理数x 由反函数定义ln x exp x 的反函数ax 同aAxlogba 以b 为底a 的对数；blogba = acos x 在自变量x 处余弦函数的值tan x 其值等于sin x/cos xcot x 余切函数的值或cos x/sin xsec x 正割含数的值，其值等于1/cos xcsc x 余割函数的值，其值等于1/sin xasin x y,正弦函数反函数在x处的值，即x = sin y acos x y,余弦函数反函数在x处的值，即x = cos y atan x y,正切函数反函数在x处的值，即x = tan y acot x y,余切函数反函数在x处的值，即x = cot y asec x y,正割函数反函数在x处的值，即x = sec y acsc x y，余割函数反函数在x处的值，即x = csc yZ 角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y ，当x、y、z 用于表示空间中的点时i, j, k分别表示x、y、z 方向上的单位向量(a, b, c) 以 a 、 b 、 c 为元素的向量(a, b) 以a、b 为元素的向量(a, b) a、b 向量的点积a?b a、b 向量的点积(a?b) a、b 向量的点积|v| 向量v 的模|x| 数x 的绝对值表示求和，通常是某项指数。

高数常见符号及读法

atan x
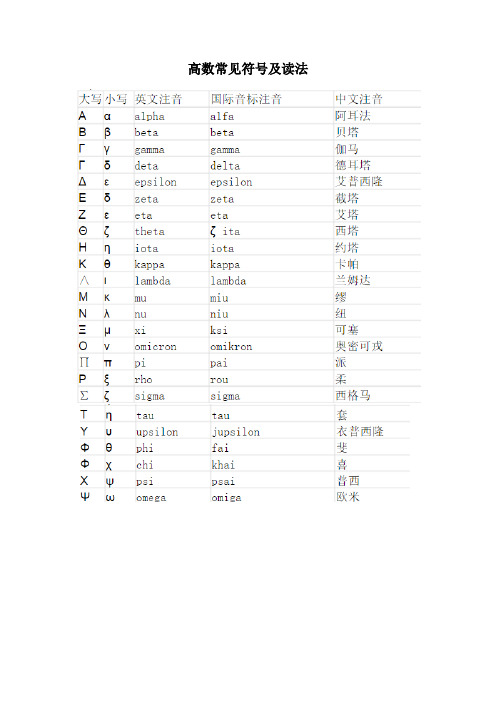
y，正切函数反函数在x处的值，即x = tan y
acot x
y，余切函数反函数在x处的值，即x = cot y
asec x
y，正割函数反函数在x处的值，即x = sec y
acsc x
y，余割函数反函数在x处的值，即x = csc y
θ
角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时
M
表示一个矩阵或数列或其它
|v>
列向量，即元素被写成列或可被看成k×1阶矩阵的向量
<v|
被写成行或可被看成从1×k阶矩阵的向量
dx
变量x的一个无穷小变化，dy, dz, dr等类似
ds
长度的微小变化
ρ
变量(x2 + y2 + z2)1/2或球面坐标系中到原点的距离
r
变量(x2 + y2)1/2或三维空间或极坐标中到z轴的距离
i, j, k
分别表示x、y、z方向上的单位向量
(a, b, c)
以a、b、c为元素的向量
(a, b)
以a、b为元素的向量
(a, b)
a、b向量的点积
a•b
a、b向量的点积
(a•b)
a、b向量的点积
|v|
向量v的模
|x|
数x的绝对值
Σ
表示求和，通常是某项指数。下边界值写在其下部，上边界值写在其上部。如j从1到100的和可以表示成：数学常用符号。这表示1 + 2 +…+ n
ds
沿曲线方向距离的导数
κ
曲线的曲率，单位切线向量相对曲线距离的导数的值：|dT/ds|
N

高数中的符号及读法

高数中的符号及读法
高数是数学的一个重要分支，它主要研究关于函数、空间等概念的数学原理，也是数学学习所必不可少的课程。

高数涉及到很多符号，如果不掌握它们的正确读法，就很难理解其蕴含的含义。

因此，了解高数中的符号及其读法对学习高数是至关重要的。

高数中的符号大致可分为两类：普通符号和特殊符号。

普通符号包括加减乘除等，它们的读法很容易记住，例如加号一般读作“加”，减号一般读作“减”，乘号一般读作“乘”，除号一般读作“除”。

特殊符号包括方程符号、函数符号、分数符号、数字符号、绝对值符号等。

方程符号一般读作“等于”，例如“2x+3=7”，一般读作“两个x再加上三等于七”；函数符号一般读作“对”，例如“y=f(x)”，一般读作“y对x的函数为f”；分数符号一般读作“分之”，例如“3/4”，一般读作“三分之四”；数字符号一般读作“的”，例如“x2”，一般读作“x的平方”；绝对值符号一般读作“绝对值”，例如“|x|”，一般读作“绝对值为x”。

另外，在高数中还有许多其他符号，包括∞、Σ、∫、γ、ω等。

其中，∞一般读作“无穷”，Σ一般读作“和”，∫一般读作“积分”，γ一般读作“伽玛”，ω一般读作“欧拉”。

为了更好地记忆高数中的符号及其读法，可以结合课本及其他书籍中的例题来多练习，以加深记忆。

此外，还可以跟随数学老师的讲解，对符号的读法进行探究，从而更好地理解高数中的符号及其读法。

总之，高数中的符号及其读法是高数学习中必不可少的一部分，
为了更好地学习高数，可以结合课本及其他书籍中的例题多练习，以加深记忆，还可以跟随数学老师的讲解，对符号的读法进行探究，从而更好地理解高数中的符号及其读法。

高等数学中符号的读法及功能 (挺全的)

大写小写英文注音国际音标注音中文注音Ααalpha alfa 阿耳法Ββbeta beta 贝塔Γγgamma gamma 伽马Δδdeta delta 德耳塔Εεepsilon epsilon 艾普西隆Ζζzeta zeta 截塔Ηηeta eta 艾塔Θθtheta θita西塔Ιιiota iota 约塔Κκkappa kappa 卡帕∧λlambda lambda 兰姆达Μμmu miu 缪Ννnu niu 纽Ξξxi ksi 可塞Οοomicron omikron 奥密可戎∏πpi pai 派Ρρrho rou 柔∑σsigma sigma 西格马Ττtau tau 套Υυupsilon jupsilon 衣普西隆Φφphi fai 斐Χχchi khai 喜Ψψpsi psai 普西Ωωomega omiga 欧米伽符号表符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作exa^x a的x次方；有理数x由反函数定义ln x exp x 的反函数ax 同a^xlogba 以b为底a的对数；blogba = acos x 在自变量x处余弦函数的值tan x 其值等于sin x/cos xcot x 余切函数的值或cos x/sin xsec x 正割含数的值，其值等于1/cos xcsc x 余割函数的值，其值等于1/sin xasin x y，正弦函数反函数在x处的值，即x = sin y acos x y，余弦函数反函数在x处的值，即x = cos y atan x y，正切函数反函数在x处的值，即x = tan y acot x y，余切函数反函数在x处的值，即x = cot y asec x y，正割函数反函数在x处的值，即x = sec y acsc x y，余割函数反函数在x处的值，即x = csc yθ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a?b a、b向量的点积(a?b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和，通常是某项指数。

高等数学中符号的读法及功能-(挺全的)

大写小写英文注音国际音标注音中文注音Αα alpha alfa阿耳法Ββ beta beta贝塔Γγ gamma gamma伽马Δδ deta delta德耳塔Εε epsilon epsilon 艾普西隆Ζζ zeta zeta截塔Ηη eta eta艾塔Θθ theta θita西塔Ιι iota iota约塔Κκ kappa kappa卡帕∧λ lambda lambda兰姆达Μμ mu miu缪Νν nu niu纽Ξξ xi k si 可塞Οο omicron omikron 奥密可戎∏π pi pai派Ρρ rho rou柔∑σ sigma sigma 西格马Ττ tau tau套Υυ upsilon jupsilon衣普西隆Φφ phi fai斐Χχ chi khai喜Ψψ psi psai 普西Ωω omega omiga欧米伽符号表符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作exa^x a的x次方；有理数x由反函数定义ln x exp x 的反函数ax 同 a^xlogba 以b为底a的对数； blogba = acos x 在自变量x处余弦函数的值符号含义tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值，其值等于 1/cos xcsc x 余割函数的值，其值等于 1/sin xasin x y，正弦函数反函数在x处的值，即 x = sin y acos x y，余弦函数反函数在x处的值，即 x = cos y atan x y，正切函数反函数在x处的值，即 x = tan y acot x y，余切函数反函数在x处的值，即 x = cot y asec x y，正割函数反函数在x处的值，即 x = sec y acsc x y，余割函数反函数在x处的值，即 x = csc yθ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a?b a、b向量的点积(a?b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和，通常是某项指数。

高等数学重要常用符号读法指南

大写小写英文注音国际音标注音中文注音Ααalpha alf a 阿耳法Ββbetabeta 贝塔Γγgamma gamma伽马Δδdetadelta 德耳塔Εεepsilon epsil on 艾普西隆Ζζzetazeta 截塔Ηηetaeta 艾塔Θθtheta θi ta 西塔Ιιiotaiota 约塔Κκkappa kappa卡帕∧λlambda lambda兰姆达Μμmumiu 缪Ννnuniu 纽Ξξxiksi 可塞Οοomicron omikron 奥密可戎∏πpipai 派Ρρrhorou 柔∑σsigma sigma西格马Ττtautau 套Υυupsilon jup silon 衣普西隆Φφphifai 斐Χχchikhai 喜Ψψpsipsai 普西Ωωomega omiga 欧米伽符号表符号含义i -1的平方根f(x) 函数f在自变量x处的值符号含义sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值，常被写作exa^x a的x次方；有理数x由反函数定义lnx expx的反函数ax 同a^xlogba 以b为底a的对数；blogba=acosx 在自变量x处余弦函数的值tanx 其值等于sinx/cosxcotx 余切函数的值或cosx/sinxsecx 正割含数的值，其值等于1/cosxcscx 余割函数的值，其值等于1/sinxasinx y，正弦函数反函数在x处的值，即x=sinyacosx y，余弦函数反函数在x处的值，即x=cosyatanx y，正切函数反函数在x处的值，即x=tanyacotx y，余切函数反函数在x处的值，即x=cotyasecx y，正割函数反函数在x处的值，即x=secyacscx y，余割函数反函数在x处的值，即x=cscyθ角度的一个标准符号，不注明均指弧度，尤其用于表示atanx/y，当x、y、z用于表示空间中的点时i,j,k 分别表示x、y、z方向上的单位向量(a,b,c) 以a、b、c为元素的向量(a,b) 以a、b为元素的向量(a,b) a、b向量的点积a?b a、b向量的点积(a?b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和，通常是某项指数。

高等数学中符号的读法及功能（挺全的）

⾼等数学中符号的读法及功能（挺全的）⼤写⼩写英⽂注⾳国际⾳标注⾳中⽂注⾳Ααalpha alfa 阿⽿法Ββbeta beta 贝塔Γγgamma gamma 伽马Γδdeta delta 德⽿塔Δεepsilon epsilon 艾普西隆Εδzeta zeta 截塔Ζεeta eta 艾塔Θζtheta ζita西塔Ηηiota iota 约塔Κθkappa kappa 卡帕∧ιlambda lambda 兰姆达Μκmu miu 缪Νλnu niu 纽Ξµxi ksi 可塞Ονomicron omikron 奥密可戎∏πpi pai 派Ρξrho rou 柔∑ζsigma sigma 西格马Τηtau tau 套Υυupsilon jupsilon ⾐普西隆Φθphi fai 斐Φχchi khai 喜Χψpsi psai 普西Ψωomega omiga 欧⽶伽符号表符号含义i -1的平⽅根f(x) 函数f在⾃变量x处的值sin(x) 在⾃变量x处的正弦函数值exp(x) 在⾃变量x处的指数函数值，常被写作exa^x a的x次⽅；有理数x由反函数定义ln x exp x 的反函数ax 同a^xlogba 以b为底a的对数；blogba = acos x 在⾃变量x处余弦函数的值tan x 其值等于sin x/cos xcot x 余切函数的值或cos x/sin xsec x 正割含数的值，其值等于1/cos xcsc x 余割函数的值，其值等于1/sin xasin x y，正弦函数反函数在x处的值，即x = sin y acos x y，余弦函数反函数在x处的值，即x = cos y atan x y，正切函数反函数在x处的值，即x = tan y acot x y，余切函数反函数在x处的值，即x = cot y asec x y，正割函数反函数在x处的值，即x = sec y acsc x y，余割函数反函数在x处的值，即x = csc yζ⾓度的⼀个标准符号，不注明均指弧度，尤其⽤于表⽰atan x/y，当x、y、z⽤于表⽰空间中的点时i, j, k 分别表⽰x、y、z⽅向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a?b a、b向量的点积(a?b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表⽰求和，通常是某项指数。

高数数学符号的读法

高数数学符号的读法一、运算符号1. “+”加号，可读作“加上”。

2. “-”减号，可读作“减”。

3. “×”乘号，可读作“乘”或“乘以”。

4. “÷”除号，可读作“除以”。

5. “=”等于号，可读作“等于”，另外，较大量的等于可以用“囿于篇幅原因，此处省略XXX 个字”代替。

6. “>”大于号，可读作“大于”。

7. “<”小于号，可读作“小于”。

8. “≥”大于或等于号，可读作“大于或等于”。

9. “≤”小于或等于号，可读作“小于或等于”。

10. “≠”不等于号，可读作“不等于”。

二、代数符号1. “n”表示正整数集。

2. “N+”表示正整数集内的所有正数。

3. “N”表示所有自然数。

4. “Z”表示整数集。

5. “Q”表示有理数集。

6. “R”表示实数集。

7. “0”表示零或常数。

8. “+”右上角小数字，代表幂，比如“x2”可读作“x的平方”。

9. “i”表示虚数单位。

10. “∞”表示无穷大。

三、函数符号1. “f(x)”，表示函数名，读作“f 括号x”，其中x为自变量。

2. “sin(x)”，正弦函数，读作“正弦括号x”。

3. “cos(x)”，余弦函数，读作“余弦括号x”。

4. “tan(x)”，正切函数，读作“正切括号x”。

5. “ln(x)”，自然对数函数，读作“自然对数括号x”。

6. “log(x)”，对数函数，读作“对数括号x”。

7. “π”，圆周率，读作“派”。

8. “e”，自然对数的底数，读作“e”。

9. “ρ”，总体密度函数的泊松分布参数，读作“rho”。

10. “σ”，标准差或均方差的正态分布参数，读作“sigma”。

四、集合符号1. “A”，“B”，“C”等大写字母表示集合。

例如，“A={1,2,3}”可以读作集合A包含元素1，2，3。

2. “a”，“b”，“c”等小写字母表示元素。

例如，“a∈A”可以读作元素a属于集合A。

3. “∈”表示集合的并运算。

常用数学符号读法大全以及主要数学符号含义

高等数学常用数学符号读法大全以及主要数学符号含义-转载大写小写英文注音国际音标注音中文注音Α α alpha alfa阿耳法Β β beta beta贝塔Γ γ gamma gamma伽马Γ δ deta delta德耳塔Δ ε epsilon epsilon艾普西隆Ε δ zeta zeta截塔Ζ ε eta eta艾塔Θ ζ theta ζita西塔Η η iota iota约塔Κ θ kappa kappa卡帕∧ι lambda lambda兰姆达Μ κmu miu缪Ν λ nu niu纽Ξ μ xi ksi可塞Ο ν omicro n omikron奥密可戎∏ π pi pai派Ρ ξ rho rou柔∑ ζ sigma sigma西格马Τ η tau tau套Υ υ upsilon jupsilon衣普西隆Φ θ phi fai斐Φ χ chi khai喜Χ ψ psi psai普西Ψ ω omega omiga欧米伽数学符号：（1）数量符号：如：i，2+i，a，x，自然对数底e，圆周率π。

（2）运算符号：如加号（＋），减号（－），乘号（×或·），除号（÷或／），两个集合的并集（∪），交集（∩），根号（√），对数（log，lg，ln），比（：），微分（dx），积分（∫）等。

（3）关系符号：如“＝”是等号，“≈”是近似符号，“≠”是不等号，“＞”是大于符号，“＜”是小于符号，“→ ”表示变量变化的趋势，“∽”是相似符号，“≌”是全等号，“∥”是平行符号，“⊥”是垂直符号，“∝”是反比例符号，“∈”是属于符号，“C”或“C下面加一横”是“包含”符号等。

（4）结合符号：如圆括号“（）”方括号“［］”，花括号“｛｝”括线“—”（5）性质符号：如正号“＋”，负号“－”，绝对值符号“‖”（6）省略符号：如三角形（△），正弦（sin），余弦（cos），x的函数（f(x)），极限（lim），因为（∵），所以（∴），总和（∑），连乘（∏），从n个元素中每次取出r个元素所有不同的组合数（C(r)(n) ），幂（A，Ac，Aq，x^n），阶乘（！）等。

关于高等数学所有符 的写法与读法

高等数学中特殊符号读法及功能

高等数学中特殊符号读法及功能

各种数学符号及读法大全

高数符号大全及读法

数学符号读法大全高等数学中所有符号的读法

(完整)高等数学所有符号的写法与读法

高等数学中特殊符号的读法及功能

高等数学中符号的读法及功能(挺全的)

高数常见符号及读法

高数中的符号及读法

高等数学中符号的读法及功能 (挺全的)

高等数学中符号的读法及功能-(挺全的)

高等数学重要常用符号读法指南

高等数学中符号的读法及功能（挺全的）

高数数学符号的读法

常用数学符号读法大全以及主要数学符号含义

关于高等数学所有符的写法与读法