江油中学2012级高二上期半期考试

合集下载

四川省南充市2024_2025学年高二英语上学期期中试题

2024－2024学年度上学期期中考试高2024级英语试题（时间：120 分钟总分：150分）第Ⅰ卷第一部分听力（共两节，满分20分）第一节（共5小题；每小题1分，满分5分）听下面5段对话。

每段对话下面有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. What’s wrong with Mark?A. He got a headache.B. He got a toothache.C. He got a backache.2. What may the weather be like now?A. Rainy.B. Sunny.C. Cloudy.3. What is the man going to do?A. Visit his friends.B. Fetch his luggage.C. Pick up the woman.4. How much is t he postage for the man’s parcel in total?A. $50.B. $90.C. $105.5. Where does the conversation probably take place?A. In a library.B. In a cinema.C. In a restaurant. 其次节（共15小题；每小题1分，满分15分）听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题给出5秒钟的作答时间。

每段对话或独白读两遍。

听第6段材料，回答第6、7题。

6. Where do the woman’s parents prefer to go in the summer holiday?A. London.B. Rome.C. Paris.7. Which attraction impressed the man most in Paris?A. The Louvre.B. The Seine.C. The Eiffel Tower.所第7段材料，回答第8至10题。

2023-2024学年四川省绵阳市高二上学期期末教学质量测试数学检测试卷(有解析)

EF F 两点，求 S△PAB 的最大值.
1．A
【分析】求出给定直线的斜率即可得该直线的一个方向向量 a ，再求与 a 共线的向量即可.
【详解】直线
2x
3
y
1
0
的斜率为
k
2 3
，则直线
2x
3
y
1
0
的一个方向向量
a
1,
2 3
，
对于
A，因
3
2 3
1
2
0
，即向量
(3,
2)
与
1,
2 3
共线，A
是；
对于Biblioteka 2 3rrr abc
r b
r c
2
3
rrr abc
1
r b
1
r c
2
r a
3 3 3.
故选：A.
7．C
【分析】连接 QA 、 OA ，由题意可得 QA QP ，所以 QA QO QP QO OP r ，根据双曲线的定义，即可得答案. 【详解】连接 QA 、 OA ，如图所示：
因为 l 为 PA 的垂直平分线，所以 QA QP ，
(1)求 a 的值； (2)估计家庭消费总支出的平均值及第 80 百分位数.（结果保留一位小数）
18．已知直线 l ： kx y 2k 1 0 （ k R ），圆 C ： x 12 y 12 9 . (1)试判断直线 l 与圆 C 的位置关系，并加以证明； (2)若直线 l 与圆 C 相交于 A ， B 两点，求 AB 的最小值及此时直线 l 的方程.
.
-3-
15．已知 F1 、 F2 是双曲线 C :
x2 a2
y2 b2

高二上学期期中考试数学试卷含答案

高二级上学期期中考试题数学本试卷共8页，22小题，满分150分，考试时间120分钟。

第一部分选择题（共60分）一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知直线l 1：2x ＋my ＝2，l 2：m 2x ＋2y ＝1，且l 1⊥l 2，则m 的值为( )A ．0B ．－1C ．0或1D ．0或－12．若一个圆锥的轴截面是面积为1的等腰直角三角形，则该圆锥的侧面积为( )A.2π B ．22π C ．2πD ．4π3．把正方形ABCD 沿对角线AC 折起，当以A ，B ，C ，D 四点为顶点的三棱锥体积最大时，直线BD 和平面ABC 所成角的大小为( )A ．90°B ．60°C ．45°D ．30°4．若过点（2，1）的圆与两坐标轴都相切，则圆心到直线230x y --=的距离为（）A B C D 5．下列命题中，正确的是( )A ．任意三点确定一个平面B ．三条平行直线最多确定一个平面C ．不同的两条直线均垂直于同一个平面，则这两条直线平行D ．一个平面中的两条直线与另一个平面都平行，则这两个平面平行6．已知M (3，23)，N (－1，23)，F (1，0)，则点M 到直线NF 的距离为( )A. 5 B ．23 C ． 22D ．3 37．已知各顶点都在一个球面上的正四棱柱(其底面是正方形，且侧棱垂直于底面)高为4，体积为16，则这个球的表面积是( )A ．20πB ．16πC ．32πD ．24π8．直线:20l x y ++=分别与x 轴、y 轴交于A 、B 两点，点P 在圆22(2)2x y -+=上，则ABP △面积的取值范围是（） A ．[]26，B ．[]48，C ．D ．⎡⎣二、多选题：本题共4小题，每小题5分，共20分.9．若220x x --<是2x a -<<的充分不必要条件，则实数a 的值可以是( ) A ．1B ．2C ．3D ．410．已知,αβ是两个不重合的平面，,m n 是两条不重合的直线，则下列命题正确的是（） A ．若//m n m α⊥，，则n α⊥ B ．若//,m n ααβ⋂=，则//m n C ．若m α⊥，m β⊥，则//αβ D ．若,//,m m n n αβ⊥⊥，则//αβ 11．若直线过点(1,2)A ，且在两坐标轴上截距的绝对值相等，则直线l 方程可能为( ) A ．10x y -+=B ．30x y +-=C ．20x y -=D ．10x y --=12．已知四棱锥P ABCD -，底面ABCD 为矩形，侧面PCD ⊥平面ABCD ，BC =CD PC PD ===.若点M 为PC 的中点，则下列说法正确的为（）A ．BM ⊥平面PCDB ．//PA 面MBDC ．四棱锥M ABCD -外接球的表面积为36π D ．四棱锥M ABCD -的体积为6第二部分非选择题（90分）三、填空题:本题共4小题,每小题5分，共20分.13．命题“20210x x x ∃<-->，”的否定是______________．14．已知直线l 1的方程为23y x =-+，l 2的方程为42y x =-，直线l 与l 1平行且与l 2在y 轴上的截距相同，则直线l 的斜截式方程为________________．15．若直线:l y kx =与曲线:1M y =+有两个不同交点，则k 的取值范围是________________．16．已知三棱锥S -ABC 的所有顶点都在球O 的球面上，SC 是球O 的直径．若平面SCA ⊥平面SCB ，SA ＝AC ，SB ＝BC ，三棱锥S -ABC 的体积为9，则球O 的体积为____________．四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.17．(本小题满分10分)已知直线l 1的方程为x ＋2y －4＝0，若l 2在x 轴上的截距为32，且l 1⊥l 2.(1)求直线l 1与l 2的交点坐标；(2)已知直线l 3经过l 1与l 2的交点，且在y 轴上的截距是在x 轴上的截距的2倍，求l 3的方程．18．(本小题满分12分)四棱锥P-ABCD 的底面ABCD 为直角梯形，AB ∥CD ，AB ⊥AD ，AB ＝12CD ＝1，P A ⊥平面ABCD ，P A ＝AD ＝ 3.(1)求证：PD ⊥AB ；(2)求四棱锥P-ABCD 的体积．19．(本小题满分12分)已知圆C 的圆心坐标为(a ，0)，且圆C 与y 轴相切． (1)已知a ＝1，M (4，4)，点N 是圆C 上的任意一点，求|MN |的最小值；(2)已知a ＜0，直线l 的斜率为43，且与y 轴交于点20,3⎛⎫- ⎪⎝⎭.若直线l 与圆C 相离，求a 的取值范围．20．(本小题满分12分)在直三棱柱ABC-A 1B 1C 1中，AB ＝5，AC ＝3，BC ＝4，点D 是线段AB 上的动点．(1)当点D 是AB 的中点时，求证：AC 1∥平面B 1CD ；(2)线段AB 上是否存在点D ，使得平面ABB 1A 1⊥平面CDB 1？若存在，试求出AD 的长度；若不存在，请说明理由．21. (本小题满分12分) 如图，多面体ABCDEF 中，四边形ABCD 是菱形，060ABC ∠=，FA ⊥平面ABCD ，//,2 2.FA ED AB FA ED ===求二面角F BC A --的大小的正切值；求点E 到平面AFC 的距离；求直线FC 与平面ABF 所成的角的正弦值.22. (本小题满分12分)已知圆22+=9：O x y ，过点()0,2P -任作圆O 的两条相互垂直的弦AB 、CD ，设M 、N 分别是AB 、CD 的中点，（1）直线MN 是否过定点? 若过，求出该定点坐标，若不过，请说明理由；（2）求四边形ACBD 面积的最大值，并求出对应直线AB 、CD 的方程.高二级上学期期中考试题数学答案及说明一、选择题：1.D ，2.A ，3.C ，4.B ，5.C ，6.B ，7.D ，8.A ，9.BCD ，10.ACD ，11.ABC ，12.BC.二、填空题：13.0x ∀<，2210x x --≤；14.y ＝－2x －2；15.13,24⎡⎫⎪⎢⎣⎭；16.36π.题目及详细解答过程：一、单选题(本题共8小题，每小题5分，共40分)1．已知直线l 1：2x ＋my ＝2，l 2：m 2x ＋2y ＝1，且l 1⊥l 2，则m 的值为( ) A ．0 B ．－1 C ．0或1 D ．0或－1 解析：因为l 1⊥l 2，所以2m 2＋2m ＝0，解得m ＝0或m ＝－1. 答案：D2．若一个圆锥的轴截面是面积为1的等腰直角三角形，则该圆锥的侧面积为( ) A.2π B ．22π C ．2π D ．4π 解析：设底面圆的半径为r ，高为h ，母线长为l ，由题可知，r ＝h ＝22l ，则12(2r )2＝1，r ＝1，l ＝2.所以圆锥的侧面积为πrl ＝2π. 答案：A3．把正方形ABCD 沿对角线AC 折起，当以A ，B ，C ，D 四点为顶点的三棱锥体积最大时，直线BD 和平面ABC 所成角的大小为( )A ．90°B ．60°C ．45°D ．30°解析：当三棱锥D ABC 体积最大时，平面DAC ⊥平面ABC .取AC 的中点O ，则∠DBO 即为直线BD 和平面ABC 所成的角．易知△DOB 是等腰直角三角形，故∠DBO ＝45°.答案：C4．若过点（2，1）的圆与两坐标轴都相切，则圆心到直线230x y --=的距离为（）A B C D 【答案】B【解析】由于圆上的点()2,1在第一象限，若圆心不在第一象限，则圆与至少与一条坐标轴相交，不合乎题意，所以圆心必在第一象限，设圆心的坐标为(),a a ，则圆的半径为a ，圆的标准方程为()()222x a y a a -+-=.由题意可得()()22221a a a -+-=，可得2650a a -+=，解得1a =或5a =，所以圆心的坐标为()1,1或()5,5，圆心到直线的距离均为121132555d ⨯--==；圆心到直线的距离均为22553255d ⨯--== 圆心到直线230x y --=的距离均为22555d -==；所以，圆心到直线230x y --=25. 故选：B ．5．下列命题中，正确的是( ) A ．任意三点确定一个平面 B ．三条平行直线最多确定一个平面C ．不同的两条直线均垂直于同一个平面，则这两条直线平行D ．一个平面中的两条直线与另一个平面都平行，则这两个平面平行解析：由线面垂直的性质，易知C 正确．答案：C6．已知M (3，23)，N (－1，23)，F (1，0)，则点M 到直线NF 的距离为( ) A. 5 B ．23 C ． 22D ．3 3解析：易知NF 的斜率k ＝－3，故NF 的方程为y ＝－3(x －1)，即3x ＋y －3＝0. 所以M 到NF 的距离为|33＋23－3|（3）2＋12＝2 3. 答案：B7．已知各顶点都在一个球面上的正四棱柱(其底面是正方形，且侧棱垂直于底面)高为4，体积为16，则这个球的表面积是( )A ．20πB ．16πC ．32πD ．24π解析：由题意知正四棱柱的底面积为4，所以正四棱柱的底面边长为2，正四棱柱的底面对角线长为22，正四棱柱的对角线为2 6.而球的直径等于正四棱柱的对角线，即2R ＝2 6.所以R ＝ 6.所以S 球＝4πR 2＝24π. 答案：D8．直线:20l x y ++=分别与x 轴、y 轴交于A 、B 两点，点P 在圆22(2)2x y -+=上，则ABP △面积的取值范围是（） A ．[]26，B ．[]48，C ．232⎡⎤⎣⎦，D ．2232⎡⎤⎣⎦，【答案】A 【解析】直线20x y ++=分别与x 轴，y 轴交于A ，B 两点，()()2,0,0,2A B ∴--,则22AB =.点P 在圆22(2)2x y -+=上，∴圆心为（2，0），则圆心到直线的距离1202222d ++==.故点P 到直线20x y ++=的距离2d 的范围为2,32⎡⎤⎣⎦，则[]22122,62ABP S AB d d ==∈△.故答案为A.二、多选题(每题5分，共20分)9．若220x x --<是2x a -<<的充分不必要条件，则实数a 的值可以是( ) A ．1B ．2C ．3D ．4【答案】BCD【解析】：由220x x --<，解得12x -<<．又220x x --<是2x a -<<的充分不必要条件，(1∴-，2)(2-，)a ，则2a ．∴实数a 的值可以是2，3，4．故选：BCD ．10．已知,αβ是两个不重合的平面，,m n 是两条不重合的直线，则下列命题正确的是（） A ．若//m n m α⊥，，则n α⊥ B ．若//,m n ααβ⋂=，则//m n C ．若m α⊥，m β⊥，则//αβ D ．若,//,m m n n αβ⊥⊥，则//αβ 【答案】ACD 【解析】若m α⊥，则,a b α∃⊂且a b P =使得m a ⊥，m b ⊥，又//m n ，则n a ⊥，n b ⊥，由线面垂直的判定定理得n α⊥，故A 对；若//m α，n αβ=，如图，设m AB =，平面1111D C B A 为平面α，//m α，设平面11ADD A 为平面β，11A D n αβ⋂==，则m n ⊥，故B 错；垂直于同一条直线的两个平面平行，故C 对；若,//m m n α⊥，则n α⊥，又n β⊥，则//αβ，故D 对；故选：ACD ．11．若直线过点(1,2)A ，且在两坐标轴上截距的绝对值相等，则直线l 方程可能为( ) A ．10x y -+= B ．30x y +-= C ．20x y -= D ．10x y --=【答案】ABC【解析】：当直线经过原点时，斜率为20210k -==-，所求的直线方程为2y x =，即20x y -=；当直线不过原点时，设所求的直线方程为x y k ±=，把点(1,2)A 代入可得12k -=，或12k +=，求得1k =-，或3k =，故所求的直线方程为10x y -+=，或30x y +-=；综上知，所求的直线方程为20x y -=、10x y -+=，或30x y +-=．故选：ABC ．12．已知四棱锥P ABCD -，底面ABCD 为矩形，侧面PCD ⊥平面ABCD ，23BC =，26CD PC PD ===.若点M 为PC 的中点，则下列说法正确的为（）A ．BM ⊥平面PCDB ．//PA 面MBDC ．四棱锥M ABCD -外接球的表面积为36π D ．四棱锥M ABCD -的体积为6 【答案】BC【解析】作图在四棱锥P ABCD -中：为矩形，由题：侧面PCD ⊥平面ABCD ，交线为CD ，底面ABCDBC CD ⊥，则BC ⊥平面PCD ，过点B 只能作一条直线与已知平面垂直，所以选项A错误；连接AC 交BD 于O ，连接MO ，PAC ∆中，OM ∥PA ，MO ⊆面MBD ，PA ⊄面MBD ，所以//PA 面MBD ，所以选项B 正确；四棱锥M ABCD -的体积是四棱锥P ABCD -的体积的一半，取CD 中点N ，连接PN ，PN CD ⊥，则PN平面ABCD ，32PN =，四棱锥M ABCD -的体积112326321223M ABCD V -=⨯⨯⨯⨯=所以选项D 错误.矩形ABCD 中，易得6,3,3AC OC ON ===，PCD 中求得：16,2NM PC ==在Rt MNO 中223MO ON MN =+=即： OM OA OB OC OD ====，所以O 为四棱锥M ABCD -外接球的球心，半径为3，所以其体积为36π，所以选项C 正确，故选：BC三、填空题(每题5分，共20分)13．命题“20210x x x ∃<-->，”的否定是______．【答案】0x ∀<，2210x x --≤【解析】因为特称命题的否定是全称命题，所以，命题20210x x x ∃<-->，，则该命题的否定是：0x ∀<，2210x x --≤ 故答案为：0x ∀<，2210x x --≤．14．已知直线l 1的方程为23y x =-+，l 2的方程为42y x =-，直线l 与l 1平行且与l 2在y 轴上的截距相同，则直线l 的斜截式方程为________________．解析：由斜截式方程知直线l 1的斜率k 1＝－2，又l ∥l 1，所以l 的斜率k ＝k 1＝－2.由题意知l 2在y 轴上的截距为－2，所以l 在y 轴上的截距b ＝－2.由斜截式方程可得直线l 的方程为y ＝－2x －2.答案：y ＝－2x －215．若直线:l y kx =与曲线()2:113M y x =+--有两个不同交点，则k 的取值范围是________________．解析：曲线M ：y ＝1＋1－（x －3）2是以(3，1)为圆心，1为半径的，且在直线y ＝1上方的半圆．要使直线l 与曲线M 有两个不同交点，则直线l 在如图所示的两条直线之间转动，即当直线l 与曲线M 相切时，k 取得最大值34；当直线l 过点(2，1)时，k 取最小值12.故k 的取值范围是13,24⎡⎫⎪⎢⎣⎭. 答案：13,24⎡⎫⎪⎢⎣⎭16．已知三棱锥S -ABC 的所有顶点都在球O 的球面上，SC 是球O 的直径．若平面SCA ⊥平面SCB ，SA ＝AC ，SB ＝BC ，三棱锥S -ABC 的体积为9，则球O 的体积为____________．解析：如图，连接OA ，OB .由SA ＝AC ，SB ＝BC ，SC 为球O 的直径，知OA ⊥SC ，OB ⊥SC .又由平面SCA ⊥平面SCB ，平面SCA ∩平面SCB ＝SC ，知OA ⊥平面SCB . 设球O 的半径为r ，则OA ＝OB ＝r ，SC ＝2r ，所以三棱锥S ABC 的体积为311323r V SC OB OA ⎛⎫=⨯⋅⋅= ⎪⎝⎭，即r 33＝9.所以r ＝3.所以3344336.33=O V r πππ=⨯=球答案：36π四、解答题(每题5分，共70分)17．(本小题满分10分)已知直线l 1的方程为x ＋2y －4＝0，若l 2在x 轴上的截距为32，且l 1⊥l 2.(1)求直线l 1与l 2的交点坐标；(2)已知直线l 3经过l 1与l 2的交点，且在y 轴上的截距是在x 轴上的截距的2倍，求l 3的方程．解：(1)设l 2的方程为2x －y ＋m ＝0，..........1分因为l 2在x 轴上的截距为32，所以3－0＋m ＝0，m ＝－3，即l 2：2x －y －3＝0.....3分联立⎩⎪⎨⎪⎧x ＋2y －4＝0，2x －y －3＝0，得⎩⎪⎨⎪⎧x ＝2，y ＝1.所以直线l 1与l 2的交点坐标为(2，1)．..........5分 (2)当l 3过原点时，l 3的方程为y ＝12x ..........6分当l 3不过原点时，设l 3的方程为12x y a a +=...........7分又直线l 3经过l 1与l 2的交点，所以2112a a+=，得52a =，l 3的方程为2x ＋y －5＝0...........8分综上，l 3的方程为y ＝12x 或2x ＋y －5＝0...........10分18．(本小题满分12分)四棱锥P-ABCD 的底面ABCD 为直角梯形，AB ∥CD ，AB ⊥AD ，AB ＝12CD ＝1，PA ⊥平面ABCD ，PA ＝AD ＝ 3.(1)求证：PD ⊥AB ；(2)求四棱锥P-ABCD 的体积．18.解：(1)证明：因为PA ⊥平面ABCD ，AB ⊂平面ABCD ，所以PA ⊥AB ，..........1分又因为AB ⊥AD ，AD ∩PA ＝A ，..........3分所以AB ⊥平面PAD ，..........4分又PD ⊂平面PAD ，..........5分所以AB ⊥PD ...........6分 (2)解：S 梯形ABCD ＝12(AB ＋CD )·AD ＝332，.......8分又PA ⊥平面ABCD ，..........9分所以V 四棱锥P-ABCD ＝13×S 梯形ABCD ·PA ＝13×332×3＝32...........12分19．(本小题满分12分)已知圆C 的圆心坐标为(a ，0)，且圆C 与y 轴相切． (1)已知a ＝1，M (4，4)，点N 是圆C 上的任意一点，求|MN |的最小值； (2)已知a ＜0，直线l 的斜率为43，且与y 轴交于点20,3⎛⎫- ⎪⎝⎭.若直线l与圆C 相离，求a 的取值范围．19.解：(1)由题意可知，圆C 的方程为(x －1)2＋y 2＝1...........2分又|MC |＝（4－1）2＋（4－0）2＝5，..........4分所以|MN |的最小值为5－1＝4...........5分(2)因为直线l 的斜率为43，且与y 轴相交于点20,3⎛⎫- ⎪⎝⎭，所以直线l 的方程为y ＝43x －23.即4x －3y －2＝0..........7分因为直线l 与圆C 相离，所以圆心C (a ，0)到直线l 的距离d ＞r . 则224243a a ->+.........9分又0a <，所以245a a ->-，解得2a >-..........11分所以a 的取值范围是(－2，0)．.........12分20．(本小题满分12分)在直三棱柱ABC-A 1B 1C 1中，AB ＝5，AC ＝3，BC ＝4，点D 是线段AB 上的动点． (1)当点D 是AB 的中点时，求证：AC 1∥平面B 1CD ；(2)线段AB 上是否存在点D ，使得平面ABB 1A 1⊥平面CDB 1？若存在，试求出AD 的长度；若不存在，请说明理由．20.解：(1)证明：如图，连接BC 1，交B 1C 于点E ，连接DE ，则点E 是BC 1的中点，又点D 是AB 的中点，由中位线定理得DE ∥AC 1，.........1分因为DE ⊂平面B 1CD ，.........2分AC 1⊄平面B 1CD ，.........3分所以AC 1∥平面B 1CD ..........4分(2)解：当CD ⊥AB 时，平面ABB 1A 1⊥平面CDB 1........5分证明：因为AA 1⊥平面ABC ，CD ⊂平面ABC ，所以AA 1⊥CD ..........6分又CD ⊥AB ，AA 1∩AB ＝A ，.........7分所以CD ⊥平面ABB 1A 1，因为CD ⊂平面CDB 1，.........8分所以平面ABB 1A 1⊥平面CDB 1，.........9分故点D 满足CD ⊥AB 时，平面ABB 1A 1⊥平面CDB 1......10分因为AB ＝5，AC ＝3，BC ＝4，所以AC 2＋BC 2＝AB 2，故△ABC 是以角C 为直角的三角形，又CD ⊥AB ，所以AD ＝95..........12分22. (本小题满分12分) 如图，多面体ABCDEF 中，四边形ABCD 是菱形，060ABC ∠=，FA ⊥平面ABCD ，//,2 2.FA ED AB FA ED ===求二面角F BC A --的大小的正切值；求点E 到平面AFC 的距离；求直线FC 与平面ABF 所成的角的正弦值.21.解：作于点G ，连接FG ，四边形ABCD 是菱形,,，为等边三角形,,-----1分平面ABCD ，平面ABCD ，，又，，平面AFG ，BC FG ∴⊥-----2分 G∴为二面角的平面角，------3分----------------------------4分连接AE ，设点E 到平面AFC 的距离为h ，则， ----------------------5分即，也就是，--------------------6分解得：； ------------------------------------------------7分(3)作CH AB ⊥于点H ，连接FH ，ABC ∆为等边三角形，H ∴为AB 的中点，221,3,5,AH CH FH FA AH ===+= FA ⊥平面ABCD ，CH ⊂平面ABCD ，FA CH ∴⊥，----8分又,CH AB AB AF A ⊥⋂=，CH ∴⊥平面ABF ，-----9分CFH ∴∠为直线FC 与平面ABF 所成的角，-------10分36sin 422CH CFH CF ∴∠===．-----------------12分 22.(本小题满分12分)已知圆22+=9：O x y ，过点()0,2P -任作圆O 的两条相互垂直的弦AB 、CD ，设M 、N 分别是AB 、CD 的中点，（1）直线MN 是否过定点?若过，求出该定点坐标，若不过，请说明理由；（2）求四边形ACBD 面积的最大值，并求出对应直线AB 、CD 的方程.22.解：（1）当直线AB CD 、的斜率存在且不为0，设直线AB 的方程为:()()()112220,,,,y kx k A x y B x y =-≠------------1分由2229+=y kx x y =-⎧⎨⎩得：()221450k x kx +--=--------------------2分点()0,2P -在圆内,故0∆>. 又 1212222422,21211M M Mx x k k x x x y kx k k k +∴+=∴===-=-+++ 即 2222,11kM k k ⎛⎫- ⎪++⎝⎭--------------------3分AB CD ⊥以1k -代换k 得22222,11k k N k k ⎛⎫-- ⎪++⎝⎭22222222111.22211MNk k k k k k k k k k -+-++∴==+++---------------4分∴直线MN 的方程为：222212121k k y x k k k -⎛⎫+=- ⎪++⎝⎭化简得2112k y x k-=-，故直线MN 恒过定点()01-，--------------------5分当直线AB CD 、的斜率不存在或为0时，显然直线MN 恒过定点()01-，综上，直线MN 恒过定点()01-，--------------------.6分 (2) 解法一:圆心O 到直线AB的距离1d =AB ==分（或由第（1）问得：21AB x =-==以1k -代换k 得CD =）AB CD ⊥∴以1k -代换k 得:CD =分12ACBD S AB CD ∴=⋅==分14=≤= 当且仅当221,1k k k==±时,取等号,故四边形ACBD 面积的最大值为14，--------------------11分对应直线AB 、CD 分别为2,2y x y x =-=--或2,2y x y x =--=-----------12分解法二：设圆心O 到直线AB 、CD 的距离分别为12,d d 、则22222211229,9AB r d d CD r d d =-=-=-=---------------------7分AB CD ⊥222124d d OP ∴+==--------------------8分()()()2222121221991821818414ACBD S AB CD d d d d OP ∴=⋅=≤-+-=-+=-=-=--------------------10分当且仅当12d d =，即1k =±时,取等号,故四边形ACBD 面积的最大值为14，--------------------11分对应直线AB 、CD 分别为2,2y x y x =-=--或2,2y x y x =--=---------12分。

2023-2024学年成四川省都七中2025届高二上半期考试英语试题(含答案)

2023-2024学年度上期高2025届半期考试英语试卷考试时间：120分钟满分：150分第一部分听力（共两节；每小题1. 5分，满分30分）做题时，先将答案标在试卷上。

录音结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节（共5小题；每小题1. 5分，共7. 5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1.Why is the man moving to New York?A. To start a new job.B. To go on a business trip.C. To look after his family.2.What does the woman mean?A. The backpack isn’t lost.B. The man is too careless.C. She’ll help find the backpack.3.What are they going to do first?A. Pickup Jim.B. Go back home.C. Stop by the cleaner’s.4.What is the relationship between the two speakers?A. Doctor and patient.B. Teacher and student.C. Boss and employee.5.What toppings will be on the pizza?A. Italian sausage.B. Pineapple.C. Black pepper.第二节（共15小题；每小题1. 5分，满分22. 5分）听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

四川省成都市2024-2025学年高二上学期月考(一)数学试题含答案

高二上数学月考（一）（答案在最后）一､单项选择题：本题共8个小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.某高校对中文系新生进行体测，利用随机数表对650名学生进行抽样，先将650名学生进行编号，001，002，…，649，650.从中抽取50个样本，下图提供随机数表的第4行到第6行，若从表中第5行第6列开始向右读取数据，则得到的第6个样本编号是（）32211834297864540732524206443812234356773578905642 84421253313457860736253007328623457889072368960804 32567808436789535577348994837522535578324577892345A.623B.328C.072D.457【答案】A【解析】【分析】按照随机数表提供的数据，三位一组的读数，并取001到650内的数，重复的只取一次即可【详解】从第5行第6列开始向右读取数据，第一个数为253，第二个数是313，第三个数是457，下一个数是860，不符合要求，下一个数是736，不符合要求，下一个是253，重复，第四个是007，第五个是328，第六个数是623，，故A正确.故选：A.2.某校高一共有10个班，编号1至10，某项调查要从中抽取三个班作为样本，现用抽签法抽取样本，每次抽取一个号码，共抽3次，设五班第二次被抽到的可能性为b，则（）A.19b= B.29b= C.310b= D.110b=【答案】D【解析】【分析】根据题意，在抽样过程中每个个体被抽到的概率相等即可求解.【详解】因为总体中共有10个个体，所以五班第一次没被抽到，第二次被抽到的可能性为91110910b=⨯=.故选：D.3.已知向量1,22AB ⎛⎫=- ⎪ ⎪⎝⎭，122BC ⎛⎫=- ⎪ ⎪⎝⎭，则ABC ∠=（）A.30°B.150°C.60°D.120°【答案】B 【解析】【分析】根据向量夹角的坐标表示求出向量夹角，进而求解几何角.【详解】因为向量13,22AB ⎛⎫=- ⎪ ⎪⎝⎭ ，31,22BC ⎛⎫=- ⎪ ⎪⎝⎭，所以13312222cos ,2AB BC AB BC AB BC⎛⎫⎛⎫⨯+-⨯- ⎪ ⎪⋅==⋅，又0,180AB BC ≤≤，所以,30AB BC =，所以,18030150BA BC =-= ，所以150ABC ∠=o .故选：B.4.已知,a b 为两条不同的直线，,αβ为两个不同的平面，则下列说法错误的是（）A.若//a b ，,b a αα⊂⊄，则//a αB.若,a b αα⊥⊥，则//a bC.若,,b a b αβαβ⊥⋂=⊥，则a β⊥D.若,a b 为异面直线，,a b αβ⊂⊂，//a β，//b α，则//αβ【答案】C 【解析】【分析】根据线面平行的判定定理判断A ，根据线面垂直的性质判断B ，当a α⊄时即可判断C ，根据异面直线的定义及线面平行的性质定理判断D.【详解】对于A ：若//a b ，,b a αα⊂⊄，根据线面平行的判定定理可知//a α，故A 正确；对于B ：若,a b αα⊥⊥，则//a b ，故B 正确；对于C ：当a α⊂时，,,b a b αβαβ⊥⋂=⊥，由面面垂直的性质定理可得a β⊥，当a α⊄时，,,b a b αβαβ⊥⋂=⊥，则//a β或a β⊂或a 与β相交，故C 错误；对于D ：因为a α⊂，//b α，所以存在b α'⊂使得//b b '，又b β⊂，b β'⊄，所以//b β'，又//a β且,a b 为异面直线，所以平面α内的两直线b '、a 必相交，所以//αβ，故D 正确.故选：C5.下列说法正确的是（）A.互斥的事件一定是对立事件，对立事件不一定是互斥事件B.若()()1P A P B +=，则事件A 与事件B 是对立事件C.从长度为1，3，5，7，9的5条线段中任取3条，则这三条线段能构成一个三角形的概率为25D.事件A 与事件B 中至少有一个发生的概率不一定比A 与B 中恰有一个发生的概率大【答案】D 【解析】【分析】根据互斥事件、对立事件和古典概型及其计算逐一判定即可．【详解】对于A ，由互斥事件和对立事件的关系可判断，对立事件一定是互斥事件，互斥事件不一定是对立事件，故A 错误;对于B ，由()()1P A P B +=，并不能得出A 与B 是对立事件，举例说明：现从a ，b ，c ，d 四个小球中选取一个小球，已知选中每个小球的概率是相同的，设事件A 表示选中a 球或b 球，则1()2P A =，事件B 表示选中b 球或c 球，则1()2P B =，所以()()1P A P B +=，但A ，B 不是对立事件，故B 错误;对于C ，该试验的样本空间可表示为：{(1,3,5),(1,3,7),(1,3,9),(1,5,7),(1,5,9),(1,7,9),(3,5,7),(3,5,9),(3,7,9)(5,7,9)}Ω=，共有10个样本点，其中能构成三角形的样本点有(3,5,7),(3,7,9),(5,7,9)，共3个，故所求概率310P =，故C 错误;对于D ，若A ，B 是互斥事件，事件A ，B 中至少有一个发生的概率等于A ，B 中恰有一个发生的概率，故D 正确．故选：D.6.一组数据：53，57，45，61，79，49，x ，若这组数据的第80百分位数与第60百分位数的差为3，则x =（）．A.58或64B.58C.59或64D.59【答案】A 【解析】【分析】先对数据从小到大排序，分57x ≤，79x ≥，5779x <<三种情况，舍去不合要求的情况，列出方程，求出答案,【详解】将已知的6个数从小到大排序为45，49，53，57，61，79．若57x ≤，则这组数据的第80百分位数与第60百分位数分别为61和57，他们的差为4，不符合条件；若79x ≥，则这组数据的第80百分位数与第60百分位数分别为79和61，它们的差为18，不符合条件；若5779x <<，则这组数据的第80百分位数与第60百分位数分别为x 和61（或61和x ），则613x -=，解得58x =或64x =故选：A7.如图，四边形ABCD 为正方形，ED ⊥平面,,2ABCD FB ED AB ED FB ==∥，记三棱锥,,E ACD F ABC F ACE ---的体积分别为123,,V V V ，则（）A.322V V =B.31V V =C.3123V V V =-D.3123V V =【答案】D 【解析】【分析】结合线面垂直的性质，确定相应三棱锥的高，求出123,,V V V 的值，结合选项，即可判断出答案.【详解】连接BD 交AC 于O ，连接,OE OF ，设22AB ED FB ===，由于ED ⊥平面,ABCD FB ED ∥，则FB ⊥平面ABCD ,则1211141112222,22133233323ACD ABC V S ED V S FB =⨯⨯=⨯⨯⨯⨯==⨯⨯=⨯⨯⨯⨯= ；ED ⊥平面,ABCD AC Ì平面ABCD ，故ED AC ⊥，又四边形ABCD 为正方形，则AC BD ⊥，而,,ED BD D ED BD =⊂ 平面BDEF ，故AC ⊥平面BDEF ，OF ⊂平面BDEF ，故AC OF ⊥，又ED ⊥平面ABCD ，FB ⊥平面ABCD ，BD ⊂平面ABCD ，故,ED BD FB BD ⊥⊥，222222,26,3,BD OD OB OE OD ED OF OB BF =∴===+==+=而()223EF BD ED FB =+-=，所以222EF OF OE +=，即得OE OF ⊥，而,,OE AC O OE AC =⊂ 平面ACE ，故OF ⊥平面ACE ，又22222AC AE CE ===+=，故(2231131323233434F ACE V V ACE S OF AC OF =-=⋅=⨯⋅=⨯= ，故323131231,2,,233V V V V V V V V V ≠≠≠-=，故ABC 错误，D 正确，故选：D8.已知平面向量a ，b ，e ，且1e = ，2a = .已知向量b 与e所成的角为60°，且b te b e -≥- 对任意实数t 恒成立，则12a e ab ++-的最小值为（）A.31+ B.23C.35 D.25【答案】B【解析】【分析】b te b e -≥-对任意实数t 恒成立，两边平方，转化为二次函数的恒成立问题，用判别式来解，算出||2b =r ，借助2a =，得到122a e a e +=+ ，12a e a b ++- 的最小值转化为11222a e a b++- 的最小值，最后用绝对值的三角不等式来解即可【详解】根据题意，1cos 602b e b e b ⋅=⋅︒=，b te b e -≥- ，两边平方22222||2||2b t e tb e b e b e +-⋅≥+-⋅ ，整理得到210t b t b --+≥ ，对任意实数t 恒成立，则()2Δ||410b b =--+≤ ，解得2(2)0b -≤ ，则||2b =r .由于2a =，如上图，122a e a e +=+ ，则111112(2)()22222a e a b a e a b a e a b ++-=++-≥+--222843e b e b b e =+=++⋅12a e ab ++- 的最小值为23当且仅当12,,2e b a -终点在同一直线上时取等号.故选：B ．二､多项选择题.本题共3个小题，每小题6分，共18分.在每个小题给出的选项中，有多项符合题目要求，部分选对的得部分，有选错的得0分.9.某保险公司为客户定制了5个险种：甲，一年期短期；乙，两全保险；丙，理财类保险；丁，定期寿险；戊，重大疾病保险．各种保险按相关约定进行参保与理赔．该保险公司对5个险种参保客户进行抽样调查，得到如图所示的统计图表．则（）A.丁险种参保人数超过五成B.41岁以上参保人数超过总参保人数的五成C.18－29周岁人群参保的总费用最少D.人均参保费用不超过5000元【答案】ACD 【解析】【分析】根据统计图表逐个选项进行验证即可.【详解】由参保险种比例图可知，丁险种参保人数比例10.020.040.10.30.54----=，故A 正确;由参保人数比例图可知，41岁以上参保人数超过总参保人数的45%不到五成，B 错误;由不同年龄段人均参保费用图可知，1829~周岁人群人均参保费用最少()3000,4000，但是这类人所占比例为15%，54周岁以上参保人数最少比例为10%，54周岁以上人群人均参保费用6000,所以18－29周岁人群参保的总费用最少，故C 正确．由不同年龄段人均参保费用图可知，人均参保费用不超过5000元,故D 正确;故选：ACD ．10.在发生公共卫生事件期间，有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天，每天新增疑似病例不超过7人”过去10日，甲､乙､丙､丁四地新增疑似病例数据信息如下：甲地：中位数为2，极差为5；乙地：总体平均数为2，众数为2；丙地：总体平均数为1，总体方差大于0；丁地：总体平均数为2，总体方差为3.则甲､乙､丙､丁四地中，一定没有发生大规模群体感染的有（）A.甲地B.乙地C.丙地D.丁地【答案】AD 【解析】【分析】假设最多一天疑似病例超过7人，根据极差可判断AD ；根据平均数可算出10天疑似病例总人数，可判断BC ．【详解】解：假设甲地最多一天疑似病例超过7人，甲地中位数为2，说明有一天疑似病例小于2，极差会超过5，∴甲地每天疑似病例不会超过7，∴选A ．根据乙、丙两地疑似病例平均数可算出10天疑似病例总人数，可推断最多一天疑似病例可能超过7人，由此不能断定一定没有发生大规模群体感染，∴不选BC ；假设丁地最多一天疑似病例超过7人，丁地总体平均数为2，说明极差会超过3，∴丁地每天疑似病例不会超过7，∴选D ．故选：AD ．11.勒洛四面体是一个非常神奇的“四面体”，它能像球一样来回滚动．勒洛四面体是以正四面体的四个顶点为球心，以正四面体的棱长为半径的四个球的相交部分围成的几何体．如图所示，设正四面体ABCD 的棱长为2，则下列说法正确的是（）A.勒洛四面体能够容纳的最大球的半径为22-B.勒洛四面体被平面ABC 截得的截面面积是(2π-C.勒洛四面体表面上交线AC 的长度为2π3D.勒洛四面体表面上任意两点间的距离可能大于2【答案】ABD 【解析】【分析】A 选项：求出正四面体ABCD 的外接球半径，进而得到勒洛四面体的内切球半径，得到答案；B 选项，作出截面图形，求出截面面积；C 选项，根据对称性得到交线AC 所在圆的圆心和半径，求出长度；D 选项，作出正四面体对棱中点连线，在C 选项的基础上求出长度.【详解】A 选项，先求解出正四面体ABCD 的外接球，如图所示：取CD 的中点G ，连接,BG AG ，过点A 作AF BG ⊥于点F ，则F 为等边ABC V 的中心，外接球球心为O ，连接OB ，则,OA OB 为外接球半径，设OA OB R ==，由正四面体的棱长为2，则1CG DG ==，BG AG ==133FG BG ==，233BF BG ==3AF ===，3OF AF R R =-=-，由勾股定理得：222OF BF OB +=，即22233R R ⎛⎫⎛-+= ⎪ ⎪ ⎪⎝⎭⎝⎭，解得：2R =，此时我们再次完整的抽取部分勒洛四面体，如图所示：图中取正四面体ABCD 中心为O ，连接BO 交平面ACD 于点E ，交 AD 于点F ，其中 AD 与ABD △共面，其中BO 即为正四面体外接球半径2R =，设勒洛四面体内切球半径为r ，则22r OF BF BO ==-=-，故A 正确；B 选项，勒洛四面体截面面积的最大值为经过正四面体某三个顶点的截面，如图所示：面积为(2221π333322222344⎛⎫⨯⨯⨯-⨯+⨯= ⎪ ⎪⎭⎝，B 正确；C 选项，由对称性可知：勒洛四面体表面上交线AC 所在圆的圆心为BD 的中点M ，故3MA MC ==2AC =，由余弦定理得：2221cos 23233AM MC AC AMC AM MC +-∠===⋅⨯⨯，故1arccos3AMC ∠=3AC 133，C 错误；D 选项，将正四面体对棱所在的弧中点连接，此时连线长度最大，如图所示：连接GH ，交AB 于中点S ，交CD 于中点T ，连接AT ，则22312ST AT AS =-=-=则由C 选项的分析知：3TG SH ==，所以323322GH =+=，故勒洛四面体表面上两点间的距离可能大于2，D 正确.故选：ABD.【点睛】结论点睛：勒洛四面体考试中经常考查，下面是一些它的性质：①勒洛四面体上两点间的最大距离比四面体的棱长大，是对棱弧中点连线，最大长度为232a a ⎫->⎪⎪⎭，②表面6个弧长之和不是6个圆心角为60︒的扇形弧长之和，其圆心角为1arccos 3，半径为32a .三､填空题：本题共3个小题，每小题5分，共15分.12.某工厂生产A 、B 、C 三种不同型号的产品，产品数量之比依次为3：4：7，现在用分层抽样的方法抽出容量为n 的样本，样本中的A 型号产品有15件，那么样本容量n 为________．【答案】70【解析】【分析】利用分层抽样的定义得到方程，求出70n =.【详解】由题意得315347n=++，解得70n =.故答案为：7013.平面四边形ABCD 中，AB =AD =CD =1，BD =BD ⊥CD ，将其沿对角线BD 折成四面体A ′﹣BCD ，使平面A ′BD ⊥平面BCD ，若四面体A ′﹣BCD 顶点在同一个球面上，则该球的表面积_____.【答案】3π【解析】【分析】根据BD ⊥CD ，BA ⊥AC ，BC 的中点就是球心，求出球的半径，即可得到球的表面积.【详解】因为平面A′BD ⊥平面BCD ，BD ⊥CD ，所以CD ⊥平面ABD ，∴CD ⊥BA ，又BA ⊥AD ，∴BA ⊥面ADC ，所以BA ⊥AC ，所以△BCD 和△ABC 都是直角三角形，由题意，四面体A ﹣BCD 顶点在同一个球面上，所以BC 的中点就是球心，所以BC =2所以球的表面积为：242π⋅=3π.故答案为：3π.【点睛】本题主要考查面面垂直的性质定理和球的外接问题，还考查空间想象和运算求解的能力，属于中档题.14.若一组样本数据12,,n x x x 的平均数为10，另一组样本数据1224,24,,24n x x x +++ 的方差为8，则两组样本数据合并为一组样本数据后的方差是__________.【答案】54【解析】【分析】计算出1n ii x =∑、21nii x=∑的值，再利用平均数和方差公式可求得合并后的新数据的方差.【详解】由题意可知，数据12,n x x x 的平均数为10，所以12)101(n x x x x n =+++= ，则110ni i x n ==∑，所以数据1224,24,,24n x x x +++ 的平均数为121(242424)210424n x x x x n'=++++++=⨯+= ，方差为()(()222221111444[24241010n n n i i i i i i s x x x x n n n n n ===⎤⎡⎤=+-+=-=-⨯⨯⎦⎣⎦∑∑∑2144008n i i x n ==-=∑，所以21102nii xn ==∑，将两组数据合并后，得到新数据1212,24,24,,24,n n x x x x x x +++ ，，则其平均数为11114)4)11113]4)[(2(3(222n i nn n i i i i i i i x x x x x n n n ====''=+=⨯+=⨯++∑∑∑∑()13104172=⨯⨯+=，方差为()()2222111111172417(586458)22n n n ni i i i i i i i s x x x x n n n ====⎡⎤=-++-=-+⎢⎥⎣⎦'∑∑∑∑1(51028610458)542n n n n=⨯-⨯+=.故答案为：54.四､解答题：本题共5个小题，共77分.解答应写出文字说明､证明过程或演算步骤.15.袋中有形状、大小都相同的4个小球，标号分别为1,2,3,4.（1）从袋中一次随机摸出2个球，求标号和为奇数的概率;（2）从袋中每次摸出一球，有放回地摸两次.甲、乙约定：若摸出的两个球标号和为奇数，则甲胜，反之，则乙胜.你认为此游戏是否公平?说明你的理由.【答案】（1）23（2）是公平的，理由见解析【解析】【分析】（1）利用列举法写出样本空间及事件的样本点，结合古典概型的计算公式即可求解;（2）利用列举法写出样本空间及事件的样本点，结合古典概型的计算公式及概率进行比较即可求解.【小问1详解】试验的样本空间{(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)}Ω=，共6个样本点，设标号和为奇数为事件B ，则B 包含的样本点为(1,2)，(1,4)，(2,3)，(3,4)，共4个，所以42().63P B ==【小问2详解】试验的样本空间Ω{(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)}=，共有16个，设标号和为奇数为事件C ，事件C 包含的样本点为(1,2)，(1,4)，(2,1)，(2,3)，(3,2)，(3,4)，(4,1)，(4,3)，共8个,故所求概率为81()162P C ==,即甲胜的概率为12，则乙胜的概率为12,所以甲、乙获胜的概率是公平的.16.（1）请利用已经学过的方差公式：()2211ni i s x xn ==-∑来证明方差第二公式22211n i i s x x n ==-∑；（2）如果事件A 与B 相互独立，那么A 与B 相互独立吗？请给予证明.【答案】（1）证明见解析；（2）独立，证明见解析【解析】【分析】（1）根据题意，对方差公式恒等变形，分析可得结论；（2）根据相互独立事件的定义，只需证明()()()P AB P A P B =即可.【详解】（1）()()()()2222212111n i n i s x xx x x x x x n n =⎡⎤=-=-+-++-⎢⎥⎣⎦∑ ()()2222121212n n x x x x x x x nx n ⎡⎤=+++-+++⎢⎥⎣⎦ ()22221212n x x x x nx nx n ⎡⎤=+++-⨯+⎢⎥⎣⎦ ()222121n x x x nx n ⎡⎤=+++-⎢⎥⎣⎦ 2211n i i x x n ==-∑；（2）因为事件A 与B 相互独立，所以()()()P AB P A P B =，因为()()()P AB P AB P A +=，所以()()()()()()P AB P A P AB P A P A P B =-=-()()()()()1P A P B P A P B =-=，所以事件A 与B 相互独立.17.如图，四棱锥P ABCD -的侧面PAD 是边长为2的正三角形，底面ABCD 为矩形，且平面PAD ⊥平面ABCD ，M ，N 分别为AB ，AD 的中点，二面角D PN C --的正切值为2.（1）求四棱锥P ABCD -的体积；（2）证明：DM PC⊥（3）求直线PM 与平面PNC 所成角的正弦值.【答案】（1）3（2）证明见解析（3）35【解析】【分析】（1）先证明DNC ∠为二面角D PN C --的平面角，可得底面ABCD 为正方形，利用锥体的体积公式计算即可；（2）利用线面垂直的判定定理证明DM ⊥平面PNC ，即可证明DM PC ⊥；（3）由DM⊥平面PNC 可得MPO ∠为直线PM 与平面PNC 所成的角，计算其正弦值即可.【小问1详解】解：∵PAD △是边长为2的正三角形，N 为AD 中点，∴PN AD ^，PN =又∵平面PAD ⊥平面ABCD ，平面PAD ⋂平面ABCD AD =∴PN ^平面ABCD又NC ⊂平面ABCD ，∴PN NC ⊥∴DNC ∠为二面角D PN C --的平面角，∴tan 2DC DNC DN∠==又1DN =，∴2DC =∴底面ABCD 为正方形.∴四棱P ABCD -的体积12233V =⨯⨯=.【小问2详解】证明：由（1）知，PN ^平面ABCD ，DM ⊂平面ABCD ，∴PN DM⊥在正方形ABCD 中，易知DAM CDN ≌△△∴ADM DCN ∠=∠而90ADM MDC ∠+∠=︒，∴90DCN MDC ∠+∠=︒∴DM CN ⊥∵PN CN N = ，∴DM ⊥平面PNC∵PC ⊂平面PNC ，∴DM PC ⊥.【小问3详解】设DM CN O ⋂=，连接PO ，MN .∵DM⊥平面PNC .∴MPO ∠为直线PM 与平面PNC 所成的角∵2,1AD AM ==，∴DM =5DO ==∴55MO ==又MN =PM ==∴35sin 5MO MPO PM ∠===∴直线PM 与平面PNC 所成角的正弦值为35.18.某市根据居民的月用电量实行三档阶梯电价，为了深入了解该市第二档居民用户的用电情况，该市统计局用比例分配的分层随机抽样方法，从该市所辖A ，B ，C 三个区域的第二档居民用户中按2：2：1的比例分配抽取了100户后，统计其去年一年的月均用电量（单位：kW h ⋅），进行适当分组后（每组为左闭右开的区间），频率分布直方图如下图所示.（1）求m 的值；（2）若去年小明家的月均用电量为234kW h ⋅，小明估计自己家的月均用电量超出了该市第二档用户中85%的用户，请判断小明的估计是否正确？（3）通过进一步计算抽样的样本数据，得到A 区样本数据的均值为213，方差为24.2；B 区样本数据的均值为223，方差为12.3；C 区样本数据的均值为233，方差为38.5，试估计该市去年第二档居民用户月均用电量的方差.（需先推导总样本方差计算公式，再利用数据计算）【答案】（1）0.016m =（2）不正确（3）78.26【解析】【分析】（1）利用频率和为1列式即可得解；（2）求出85%分位数后判断即可；（3）利用方差公式推导总样本方差计算公式，从而得解.【小问1详解】根据频率和为1，可知()0.0090.0220.0250.028101m ++++⨯=，可得0.016m =.【小问2详解】由题意，需要确定月均用电量的85%分位数，因为()0.0280.0220.025100.75++⨯=，()0.0280.0220.0250.016100.91+++⨯=，所以85%分位数位于[)230,240内，从而85%分位数为0.850.7523010236.252340.910.75-+⨯=>-.所以小明的估计不正确.【小问3详解】由题意，A 区的样本数为1000.440⨯=，样本记为1x ，2x ，L ，40x ，平均数记为x ；B 区的样本数1000.440⨯=，样本记为1y ，2y ，L ，40y ，平均数记为y ；C 区样本数为1000.220⨯=，样本记为1z ，2z ，L ，20z ，平均数记为z .记抽取的样本均值为ω，0.42130.42230.2233221ω=⨯+⨯+⨯=.设该市第二档用户的月均用电量方差为2s ，则根据方差定义，总体样本方差为()()()40402022221111100i j k i i i s x y z ωωω===⎡⎤=-+-+-⎢⎥⎣⎦∑∑∑()()()4040202221111100i j k i i i x x x y y y z z z ωωω===⎡⎤=-+-+-+-+-+-⎢⎥⎣⎦∑∑∑因为()4010ii x x =-=∑，所以()()()()404011220iii i x x x x x x ωω==--=--=∑∑，同理()()()()404011220jji i yyy y yy ωω==--=--=∑∑，()()()()202011220kki i zz z z zz ωω==--=--=∑∑，因此()()()()4040404022222111111100100i j i i i i s x x x y y y ωω====⎡⎤⎡⎤=-+-+-+-⎢⎥⎢⎥⎣⎦⎣⎦∑∑∑∑()()202022111100k i i z z z ω==⎡⎤+-+-⎢⎥⎣⎦∑∑，代入数据得()()222114024.2402132214012.340223221100100s ⎡⎤⎡⎤⎣⎦⎦=⨯+⨯-+⨯-⎣+⨯()212038.32023322178.26100⎡⎤+⨯+⨯-=⎣⎦.19.在世界杯小组赛阶段，每个小组内的四支球队进行循环比赛，共打6场，每场比赛中，胜、平、负分别积3，1，0分.每个小组积分的前两名球队出线，进入淘汰赛.若出现积分相同的情况，则需要通过净胜球数等规则决出前两名，每个小组前两名球队出线，进入淘汰赛.假定积分相同的球队，通过净胜球数等规则出线的概率相同（例如：若B ，C ，D 三支积分相同的球队同时争夺第二名，则每个球队夺得第二名的概率相同）.已知某小组内的A ，B ，C ，D 四支球队实力相当，且每支球队在每场比赛中胜、平、负的概率都是13，每场比赛的结果相互独立.（1）求A 球队在小组赛的3场比赛中只积3分的概率；（2）已知在已结束的小组赛的3场比赛中，A 球队胜2场，负1场，求A 球队最终小组出线的概率.【答案】（1）427（2）7981【解析】【分析】（1）分类讨论只积3分的可能情况，结合独立事件概率乘法公式运算求解；（2）由题意，若A 球队参与的3场比赛中胜2场，负1场，根据获胜的三队通过净胜球数等规则决出前两名，分情况讨论结合独立事件概率乘法公式运算求解.【小问1详解】A 球队在小组赛的3场比赛中只积3分，有两种情况.第一种情况：A 球队在3场比赛中都是平局，其概率为111133327⨯⨯=.第二种情况：A球队在3场比赛中胜1场，负2场，其概率为11113 3339⨯⨯⨯=.故所求概率为114 27927+=.【小问2详解】不妨假设A球队参与的3场比赛的结果为A与B比赛，B胜；A与C比赛，A胜；A与D比赛，A胜.此情况下，A积6分，B积3分，C，D各积0分.在剩下的3场比赛中：若C与D比赛平局，则C，D每队最多只能加4分，此时C，D的积分都低于A的积分，A可以出线；若B与C比赛平局，后面2场比赛的结果无论如何，都有两队的积分低于A，A可以出线；若B与D比赛平局，同理可得A可以出线.故当剩下的3场比赛中有平局时，A一定可以出线.若剩下的3场比赛中没有平局，则当B，C，D各赢1场比赛时，A可以出线.当B，C，D中有一支队伍胜2场时，若C胜2场，B胜1场，A，B，C争夺第一、二名，则A淘汰的概率为11111 333381⨯⨯⨯=；若D胜2场，B胜1场，A，B，D争夺第一、二名，则A淘汰的概率为11111 333381⨯⨯⨯=.其他情况A均可以出线.综上，A球队最终小组出线的概率为1179 1818181⎛⎫-+=⎪⎝⎭.【点睛】关键点点睛：解题的关键在于分类讨论获胜的三队通过净胜球数等规则决出前两名，讨论要恰当划分，做到不重不漏，从而即可顺利得解.。

四川省南充2024-2025学年高二上学期10月月考数学试题含答案

南充高中高2023级上期第一次月考数学试卷（答案在最后）考试时间：120分钟满分：150分注意事项：1.答题前，务必将自己的姓名、班级、考号填写在答题卡规定的位置上.2.答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其它答案标号.3.答非选择题时，将答案书写在答题卡相应位置上，写在本试卷上无效.4.考试结束后将答题卡交回.一、单选题（本题共8小题，每小题5分，共40分.在每小题给出的4个选项中，只有一项是符合题目要求的）1.“2sin 2θ=”是“π4θ=”的（）A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件【答案】C 【解析】【分析】判断“sin 2θ=”和“π4θ=”之间的逻辑推理关系，即可得答案.【详解】当2sin 2θ=时，π2π,Z 4k k θ=+∈或3π2π,Z 4k k θ=+∈，推不出π4θ=；当π4θ=时，必有2sin 2θ=，故“sin 2θ=”是“π4θ=”的必要不充分条件，故选：C2.设l ，m 是两条不同的直线，α，β，γ是三个不同的平面，下列说法正确的是（）A.若//l α，//m α，则//l mB.若//l α，//l β，则//αβC.若l α⊥，m α⊥，则//l mD.若αγ⊥，βγ⊥，则//αβ【答案】C【分析】根据直线与直线的位置关系、直线与平面的位置关系和平面与平面的位置关系依次判断选项即可.【详解】对选项A ，若//l α，//m α，则l 与m 的位置关系是平行，相交和异面，故A 错误.对选项B ，若//l α，//l β，则α与β的位置关系是平行和相交，故B 错误.对选项C ，若l α⊥，m α⊥，则根据线面垂直的性质得l 与m 的位置关系是平行，故C 正确.对选项D ，若αγ⊥，βγ⊥，则α与β的位置关系是平行和相交，故D 错误.故选：C3.若sin 2αα-+=，则tan(π)α-=（）A. B.C.3D.3-【答案】C 【解析】【分析】由sin 2αα-+=两边同时平方，从而利用sin tan cos =aa a可以实现角α的弦切互化，【详解】由sin 2αα-+=两边同时平方，可得22sin cos 3cos 4αααα-+=，∴222222sin cos 3cos tan 34sin cos tan 1ααααααααα-+-+==++，解得tan 3α=-.()tan tan 3παα∴-=-=.故选：C.4.如图，在正方体1111ABCD A B C D -中，,M N 分别为11,DB A C 的中点，则直线1A M 和BN 夹角的余弦值为（）A.23B.33C.23D.13【解析】【分析】以1,,DA DC DD 所在直线为,,x y z 轴，建立空间直角坐标系，根据向量夹角的余弦公式求解即可．【详解】分别以1,,DA DC DD 所在直线为,,x y z轴，建立如图所示空间直角坐标系，设正方体1111ABCD A B C D -的棱长为2，则()1(2,0,2),(1,1,0),(2,2,0),1,1,2A M B N ，所以()1(1,1,2),1,1,2MA BN =-=--设向量1MA 与BN的夹角为θ，则1142cos 63MA BN MA BNθ⋅===⋅，所以直线1A M 和BN 夹角的余弦值为23，故选：C ．5.在三棱锥S ABC -中，()()20SC SA BS SC SA ++⋅-=，则ABC V 是（）A.等边三角形B.直角三角形C.等腰三角形D.等腰直角三角形【答案】C 【解析】【分析】由向量的线性运算得到2,SC SA BS BC BA SC SA BC BA ++=+-=- ，从而说明22BC BA = ，即可求解.【详解】()()22,SC SA BS SC SA SB SC SB SA SB BC BA SC SA AC BC BA ++=+-=-+-=+-==- ，()()()()2220SC SA SB SC SA BC BA BC BA BC BA ∴+-⋅-=+⋅-=-= ，BC BA ∴=，即BC BA =，所以ABC V 是等腰三角形.故选：C6.杭州亚运会的三个吉祥物分别取名“琮琮”“宸宸”“莲莲”，如图，现将三张分别印有“琮踪”“宸宸”“莲莲”图案的卡片（卡片的形状､大小和质地完全相同）放入盒子中.若从盒子中依次有放回地取出两张卡片，则一张为“琮琮”，一张为“宸宸”的概率是（）A.38B.29C.59D.34【答案】B 【解析】【分析】记印有“琮琮”“宸宸”“莲莲”图案的卡片分别为,,A B C ，用列举法即可求解.【详解】记印有“琮琮”“宸宸”“莲莲”图案的卡片分别为,,A B C ，(),x y 代表依次摸出的卡片，{},,,x y A B C ∈，则基本事件分别为：()()()()()()()()(),,,,,,,,,,,,,,,,,A A A B A C B A B B B C C A C B C C ，其中一张为“琮琮”，一张为“宸宸”的共有两种情况：()(),,,A B B A ，所以从盒子中依次有放回地取出两张卡片，则一张为“琮琮”，一张为“宸宸”的概率是29.故选：B.7.已知函数()3f x x =，若正实数a ，b 满足()()490f a f b +-=，则11a b+的最小值为（）A.1B.3C.6D.9【答案】A 【解析】【分析】根据函数的奇偶性可得49a b +=，再结合基本不等式“1”的代换可得解.【详解】由已知()3f x x =，定义域为R ，且()()()33f x x x f x -=-=-=-，则()f x 是R 上的奇函数，且函数()3f x x =在R 上单调递增，又()()490f a f b +-=，即()()()499f a f b f b =--=-，则49a b =-，即49a b +=，且0a >，0b >，所以()1111114144415999a b a b a b a b a b b a b a ⎛⎫⎛⎫⎛⎫+=++=+++=++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭又44a b b a +≥=，即()11141554199a b a b b a ⎛⎫+=++≥+= ⎪⎝⎭，当且仅当4a b b a =，即32a =，3b =时，等号成立，即11a b+的最小值为1.故选：A.8.已知正三棱锥P ABC -的六条棱长均为6，S 是ABC V 及其内部的点构成的集合．设集合{}5T Q S PQ =∈=，则集合T 所表示的曲线长度为（）A.5πB.2πC.3D.π【答案】B 【解析】【分析】求出以P 为球心，5为半径的球与底面ABC 的截面圆的半径后即可求解.【详解】设顶点P 在底面上的投影为O ，连接BO ，则O 为三角形ABC 的中心，且23632BO =⨯⨯=，故PO ==因为5PQ =，故1OQ =，故S 的轨迹为以O 为圆心，1为半径的圆，集合T 所表示的曲线长度为2π故选：B二、多选题（本题共3小题，每小题6分，共18分.在每小题给出的4个选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部份分分，有选错的得0分.）9.函数()()sin 0,π2f x x ϕωϕω⎛⎫=+>< ⎪⎝⎭的部分图象如图所示，则（）A.2ω=B.π6ϕ=C.()f x 的图象关于点π,012⎛⎫⎪⎝⎭对称D.()f x 在区间5ππ,4⎛⎫⎪⎝⎭上单调递增【答案】ACD 【解析】【分析】根据三角函数的图象，先求得ω，然后求得ϕ，根据三角函数的对称性、单调性确定正确答案.【详解】()()5ππ2ππ,π,2,sin 22632T T f x x ωϕω=-=∴==∴==+，π2sin π133f ϕ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭，由于πππ2π7π,22636ϕϕ-<<<+<，所以2πππ,326ϕϕ+==-，所以A 选项正确，B 选项错误.()ππππsin 2,2π,,66122k f x x x k x k ⎛⎫=--==+∈ ⎪⎝⎭Z ，当0k =时，得π12x =，所以()f x 关于π,012⎛⎫⎪⎝⎭对称，C 选项正确，11111πππππ2π22π,ππ,26263k x k k x k k -+<-<+-+<<+∈Z ，当11k =时，得()f x 在54π,π63⎛⎫ ⎪⎝⎭上递增，则()f x 在区间5ππ,4⎛⎫⎪⎝⎭上单调递增，所以D 选项正确.故选：ACD10.对于随机事件A 和事件B ，()0.3P A =，()0.4P B =，则下列说法正确的是（）A.若A 与B 互斥，则()0.3P AB =B.若A 与B 互斥，则()0.7P A B ⋃=C.若A 与B 相互独立，则()0.12P AB =D.若A 与B 相互独立，则()0.7P A B ⋃=【答案】BC 【解析】【分析】根据互斥事件、相互独立事件的概率公式计算可得.【详解】对于A ：若A 与B 互斥，则()0P AB =，故A 错误；对于B ：若A 与B 互斥，则()()()0.7P A B P A P B =+= ，故B 正确；对于C ：若A 与B 相互独立，则()()()0.12P AB P A P B ==，故C 正确；对于D ：若A 与B 相互独立，则()()()()0.30.40.30.40.58P A B P A P B P AB ⋃=+-=+-⨯=，故D 错误.故选：BC11.如图，边长为1的正方形ABCD 所在平面与正方形ABEF 在平面互相垂直，动点,M N 分别在正方形对角线AC 和BF 上移动，且(0CM BN a a ==<<，则下列结论中正确的有（）A.(a ∃∈，使12MN CE=B.线段MN 存在最小值，最小值为23C.直线MN 与平面ABEF 所成的角恒为45°D.(a ∀∈，都存在过MN 且与平面BEC 平行的平面【分析】利用向量的线性运算可得()1MN a BC aBE =-+，结合向量的模的计算可判断B 的正误，结合向量夹角的计算可判断C 的正误，结合共面向量可判断D 的正误.【详解】因为四边形ABCD 正方形，故CB AB ⊥，而平面ABCD ⊥平面ABEF ，平面ABCD 平面ABEF AB =，CB ⊂平面ABCD ，故CB ⊥平面ABEF ，而BE ⊂平面ABEF ，故CB BE ⊥.设MC AC λ=，则= BN BF λ，其中()0,1λ=，由题设可得MN MC CB BN AC CB BF λλ=++=++，()()()1BC BA CB BA BE BC BE λλλλ=-+++=-+，对于A ，当12λ=即2a =时，111222MN BC BE CE =-+= ，故A 正确；对于B ，()22222111221222MN λλλλλ⎛⎫=-+=-+=-+ ⎪⎝⎭ ，故22MN ≥，当且仅当12λ=即2a =时等号成立，故min 22MN =，故B 错误；对于C ，由B 的分析可得()1MN BC BE λλ=-+，而平面ABEF 的法向量为BC 且()211MN BC BC λλ⋅=-=-，故cos ,MN BC =，此值不是常数，故直线MN 与平面ABEF 所成的角不恒为定值，故C 错误；对于D ，由B 的分析可得()1MN BC BE λλ=-+ ，故,,MN BC BE为共面向量，而MN ⊄平面BCE ，故//MN 平面BCE ，故D 正确；故选：AD三、填空题（本题共3小题，每小题5分，共15分.）12.复数2i12iz +=-的共轭复数z =______．【分析】根据复数的除法运算及共轭复数的概念可求解.【详解】因为2i 12i z +=-()()()()2i 12i 12i 12i ++=-+5i i 5==，所以z =i -.故答案为：i-13.已知向量()2,1,1a =- ，()1,,1b x = ，()1,2,1c =-- ，当a b ⊥ 时，向量b 在向量c上的投影向量为________．（用坐标表示）【答案】()1,2,1-【解析】【分析】先根据向量垂直得到方程，求出3x =，再利用投影向量公式求出答案.【详解】因为a b ⊥ ，所以210a b x ⋅=-+=，所以3x =．因为()1,3,1b = ，所以b 在c 上的投影向量为()1,2,1||||b c cc c c ⋅⋅=-=-．故答案为：()1,2,1-14.已知在ABC V 中，满足)34AB AC AB ACAB AC AB AC++=+,点M 为线段AB 上的一个动点，若MA MC ⋅ 取最小值3-时，则BC 边的中线长为______．【答案】1112【解析】【分析】设)34,,AB AC AB AC AD AN AE ABAC AB AC+===+，根据题意可推得||3,||4AD AN == ，2π3ADE ∠=，进一步根据MA MC ⋅ 取最小值3-时，求得对应的AC =AB =，由此即可得解.【详解】设)34,,AB AC AB AC AD AN AE ABAC AB AC+===+，则//,//AD EN AN DE ，四边形ADEN为平行四边形，||||3||3,||4,||4||||AB AD AD AN AE AC AN =====，22343712πcos 23423ADE ADE +-∴∠==-⇒∠=⨯⨯，又四边形ADEN 为平行四边形，3πBAC ∴∠=，设,,0,0MA AD AC AN λμλμ==≤≥，()()296MA MC MA MA AC AD AD AN λλμλλμ⋅=⋅+=⋅+=+，由题意2963λλμ+≥-即29630λλμ++≥恒成立，且存在,R λμ∈使得29630λλμ++=成立，其次29630λλμ++=当且仅当2296303Δ361080λλλμμμ⎧⎧=-++=⎪⇔⎨⎨=-=⎩⎪=⎩，此时AC ==AB ==所以BC边的中线长为122AB AC +===.故答案为：2.四、解答题（本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.）15.如图,四边形ABCD 为矩形,且2AD =,1AB =,PA ⊥平面ABCD ,1PA =,E 为BC 的中点．（1）求证：PE DE ⊥；（2）求四棱锥P ABCD -的外接球体积．【答案】（1）证明见解析（2【解析】【分析】（1）连接AE ，由线面垂直得到PA DE ⊥，再由线面垂直的判定定理得到DE ⊥平面PAE ，即可证明；（2）由底面为矩形利用长方体的性质可得四棱锥外接球的半径，再由体积公式计算体积.【小问1详解】连结,AE E 为BC 的中点,1EC CD ==，∴DCE △为等腰直角三角形,则45DEC ∠=︒，同理可得45AEB ∠=︒，∴90AED ∠=︒，∴DE AE ⊥，又PA ⊥平面ABCD ，且DE ⊂平面ABCD ，∴PA DE ⊥，又∵AE PA A = ，,AE PA ⊂平面PAE ，∴DE ⊥平面PAE ，又PE ⊂平面PAE ，∴DE PE ⊥．【小问2详解】∵PA ⊥平面ABCD ，且四边形ABCD 为矩形，∴P ABCD -的外接球直径2R =∴2R =，故：3344ππ332V R ⎛⎫=== ⎪ ⎪⎝⎭，∴四棱锥P ABCD -．16.ABC V 的内角,,A B C 的对边分别为,,a b c ，已知cos cos a B b A b c -=+.（1）求角A 的值；（2）若a ABC = ，求,b c .【答案】（1）2π3（2）2，2【解析】【分析】（1）由正弦定理及三角恒等变换化简即可得解；（2）由三角形面积公式及余弦定理求解即可.【小问1详解】cos cos a B b A b c -=+ ，由正弦定理可得：sin cos sin cos sin sin A B B A B C -=+，sin sin()sin cos cos sin C A B A B A B =+=+ ，sin cos sin cos sin sin cos cos sin A B B A B A B A B ∴-=++，即2sin cos sin B A B -=，sin 0B ≠ ，1cos 2A ∴=-，(0,π)A ∈ ，2π3A ∴=.【小问2详解】由题意，1sin 24ABC S bc A bc ===△，所以4bc =，由222222cos a b c bc A b c bc =+-=++，得()2216b c a bc +=+=，所以4b c +=，解得：2b c ==.17.全国执业医师证考试分实践技能考试与医学综合笔试两部分，每部分考试成绩只记“合格”与“不合格”，两部分考试都“合格”者，则执业医师考试“合格”，并颁发执业医师证书.甲、乙、丙三人在医学综合笔试中“合格”的概率依次为45，34，23，在实践技能考试中“合格”的概率依次为12，23，23，所有考试是否合格互不影响.（1）求甲没有获得执业医师证书的概率；（2）这三人进行实践技能考试与医学综合理论考试两项考试后，求恰有两人获得执业医师证书的概率.【答案】（1）35（2）13【解析】【分析】（1）先根据对立事件的概率公式结合独立事件概率乘积公式计算；（2）先应用对立事件的概率公式及独立事件概率乘积公式应用互斥事件求和计算；【小问1详解】记甲，乙，丙三人在医学综合笔试中合格依次为事件1A ，1B ，1C ，在实践考试中合格依次为2A ，2B ，2C ，设甲没有获得执业医师证书的概率为P124131()1525P P A A =-=-⨯=.【小问2详解】甲、乙、丙获得执业医师证书依次为12A A ，12B B ，12C C ，并且1A 与2A ，1B 与2B ，1C 与2C 相互独立，则()12412525P A A =⨯=，()12321432P B B =⨯=，()12224339P C C =⨯=,由于事件12A A ，12B B ，12C C 彼此相互独立，“恰有两人获得执业医师证书”即为事件：()()()()()()()()()121212121212121212A A B B C C A A B B C C A A B B C C ++，概率为212142141(1)(1)(1)52952952934P =⨯⨯-+⨯-⨯+-⨯⨯=.18.为深入学习贯彻习近平总书记关于禁毒工作重要指示精神，切实落实国家禁毒委员会《关于加强新时代全民禁毒宣传教育工作的指导意见》，巩固青少年毒品预防教育成果，大力推进防范青少年滥用涉麻精药品等成瘾性物质宣传教育活动，进一步增强青少年学生识毒防毒拒毒意识和能力，某市每年定期组织同学们进行禁毒知识竞赛活动，为了解同学们对禁毒知识的掌握情况，现从所有答卷中随机抽取100份作为样本，将样本的成绩（满分100分，成绩均为不低于40分的整数）分成六段：40,50，50,60，…，90,100得到如图所示的频率分布直方图．（1）求频率分布直方图中a 的值；（2）求样本成绩的第75百分位数；（3）已知落在50,60的平均成绩是56，方差是7，落在60,70的平均成绩为65，方差是4，求两组成绩的总平均数z 和总方差2s ．【答案】（1）0.030（2）84（3）平均数为62；方差为23【解析】【分析】（1）根据频率之和为1即可求解，（2）根据百分位数的计算公式即可求解，（3）根据平均数的计算公式可求得两组成绩的总平均数；再由样本方差计算总体方差公式可求得两组成绩的总方差，即可求解.【小问1详解】由每组小矩形的面积之和为1得，0.050.10.2100.250.11a +++++=，解得0.030a =．【小问2详解】成绩落在[)40,80内的频率为0.050.10.20.30.65+++=，落在[)40,90内的频率为0.050.10.20.30.250.9++++=，显然第75百分位数[)80,90m ∈，由()0.65800.0250.75m +-⨯=，解得84m =，所以第75百分位数为84；【小问3详解】由频率分布直方图知，成绩在[)50,60的市民人数为1000.110⨯=，成绩在[)60,70的市民人数为1000.220⨯=，所以10562065621020z ⨯+⨯==+；由样本方差计算总体方差公式，得总方差为()(){}222110756622046562231020s ⎡⎤⎡⎤=+-++-=⎣⎦⎣⎦+.19.如图，三棱柱111ABC A B C -中，2AB =，且ABC V 与1ABA △均为等腰直角三角形，1π2ACB AA B ∠=∠=．（1）若1A BC 为等边三角形，证明：平面1AAB ⊥平面ABC ；（2）若二面角1A AB C --的平面角为π3，求以下各值：①求点1B 到平面1A CB 的距离；②求平面11B A C 与平面1A CB 所成角的余弦值．【答案】（1）证明见解析（2）①2217，②277【解析】【分析】（1）根据等腰直角三角形及等边三角形的性质可得各边长，再根据勾股定理证明线线垂直，根据线线垂直可证线面垂直，进而可证面面垂直；（2）根据二面角的定义可值1CEA 为等边三角形，①利用等体积转化法可得点到平面距离；②根据二面角的定义可得两平面夹角.【小问1详解】设AB 的中点为E ，连接CE ，1A E ，如图所示，因为ABC V 与1ABA △均为等腰直角三角形，1π2ACB A AB ∠=∠=，故1cos 452BC A B AB ==⋅︒=CE AB ⊥，且112CE AB ==，1112A E AB ==，因为1A BC 为等边三角形，故12==AC BC ，故22211A C CE A E =+，即1CE A E ⊥，又AB ，1A E ⊂平面1AA B ，1A E AB E ⋂=，故CE ⊥平面1AA B ，且CE ⊂平面ABC ，故平面1AA B ⊥平面ABC ；【小问2详解】①由（1）知，CE AB ⊥，1A E AB ⊥，且平面1AA B ⋂平面ABC AB =，故1CEA ∠即二面角1A AB C --的平面角，即1π3CEA ∠=，故1CEA 为等边三角形，则111CA CE A E ===，因为CE AB ⊥，1A E AB ⊥，1A E CE E ⋂=，且CE ，1A E ⊂平面1CEA ，所以AB ⊥平面1CEA ，设线段1A E 中点为F ，则1CF A E ⊥，AB CF ⊥，又AB ，1A E ⊂平面11ABB A ，1AB A E E = ，CF ∴⊥平面11ABB A ，又在三角形1CEA中易知：2CF =，∴11111112133226C A BB A BB V CF S -=⋅=⨯⨯⨯⨯= ，又在三角形1A BC 中，由11AC =，1BC A B ==则22211113cos 24BC A B A CA BC BC AB +-∠==⋅，1sin 4A BC ∠=，则11117sin 24A BC S AB BC A BC =⋅⋅∠= ，设点1B 到平面1A CB 的距离为d ，又由1111113C A BB B A BC A BC V V S d --==⋅⋅△，可得7d =，即求点1B 到平面1A CB 的距离为2217；②由①知，AB ⊥平面1CEA ，而11//AB A B ，故11A B ⊥平面1CEA ，且1A C ⊂平面1CEA ，故111A B AC ⊥，则2211115B C A B AC =+=，设1AC 和1B C 的中点分别为M ，N ，连接MN ，BN ，BM，则11//MN A B ，11112MN A B ==，1MN AC ⊥，又因为12BC A B ==1BM A C ⊥，且MN ⊂平面11A B C ，BM ⊂平面1A BC ，故BMN ∠即二面角11B A C B --的平面角，且222211722BM BC CM BC A C ⎛⎫=-=-= ⎪⎝⎭，因为112BB AA BC ===，故1BN B C ⊥，则222211322BN BC CN BC B C ⎛⎫=-=-= ⎪⎝⎭，所以222731744cos 277212BM MN BN BMN BM MN +-+-∠==⋅⨯⨯，故平面11B A C 与平面1A CB 所成角的余弦值为277．。

四川省南充高级中学22024_2025学年高二英语上学期期中试题

四川省南充高级中学22024-2025学年高二英语上学期期中试题（试卷满分 150分，考试时间120分钟）第一部分听力（共两节，满分30分）第一节 (共5小题；每小题1.5分，满分7.5分)听下面 5 段对话。

每段对话后有一个小题，从题中所给的 A、B、C 三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有 10 秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. What is the woman going to do tomorrow?A. Go fishing.B. Go out with a friend.C. Go to the hospital.2. How will the woman get to the museum?A. By taking a shortcut.B. By taking the subway.C. By walking through the park.3. Where will the woman go on vacation?A. To New York City.B. To Los Angeles.C. To Burbank.4. Who is Mike?A. Miguel’s friend.B. Melvin’s friend.C. The girl’s brother.5. What do the speakers mainly talk about?A. The man’s hair.B. A photo of the man.C. The woman’s new hairstyle.其次节 (共15小题；每小题1.5分，满分22.5分)听下面 5 段对话或独白。

每段对话或独白后有几个小题，从题中所给的 A、B、C 三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题，每小题5 秒钟；听完后，各小题给出 5 秒钟的作答时间。

四川省成都市2023-2024学年高二上学期期中数学试题含解析

2023-2024学年度上期高2025届半期考试高二数学试卷（答案在最后）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷第1页至第2页，第Ⅱ卷第3页至第4页．注意事项：1．答题前，务必将自己的姓名、考籍号填写在答题卡规定的位置上．2．答选择题时，必须使用铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其他答案标号．3．答非选择题时，必须使用0.5毫米黑色墨迹签字笔，将答案书写在答题卡规定的位置上．4．所有题目必须在答题卡上作答，在试卷上作答无效．5．考试结束后，只将答题卡收回．第Ⅰ卷（选择题，共60分）一．单选题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知向量()(),2,2,3,4,2a x b =-=-，若a b ⊥，则x 的值为（）A.1B.4- C.4D.1-【答案】C 【解析】【分析】根据向量垂直的坐标运算即可求解.【详解】由()(),2,2,3,4,2a x b =-=- 得3840a b x ⋅=--= ，所以4x =，故选：C2.已知直线1:3410l x y --=与2:3430l x y -+=，则1l 与2l 之间的距离是（）A.45B.35C.25 D.15【答案】A 【解析】【分析】直接由两平行线之间的距离公式计算即可.【详解】因为已知直线1:3410l x y --=与2:3430l x y -+=，而()()34430⨯---⨯=，所以12l l //，所以由两平行线之间的距离公式可得1l 与2l 之间的距离是45d ==.故选：A.3.已知圆()()221:219C x y -++=与圆()()222:134C x y ++-=，则圆1C 与圆2C 的位置关系为（）A.相交B.外切C.内切D.内含【答案】B 【解析】【分析】根据两圆圆心距与半径的关系即可求解.【详解】()()221:219C x y -++=的圆心为()2,1,3r -=，()()222:134C x y ++-=的圆心为()1,3,2R -=，由于125C C ==,125C C r =+=R ，所以1C 与圆2C 外切，故选：B4.若直线()1:410l x a y +-+=与2:20l bx y +-=垂直，则a b +的值为（）A.2 B.45C.23D.4【答案】D 【解析】【分析】根据直线垂直的条件求解．【详解】由题意40b a +-=，∴4a b +=．故选：D ．5.已知事件,A B 相互独立，且()()0.3,0.7P A P B ==，则()P AB =（）A.1 B.0.79C.0.7D.0.21【答案】D 【解析】【分析】由独立事件的概率乘法公式计算．【详解】由题意()()()0.30.70.21P AB P A P B ==⨯=，故选：D ．6.如图，空间四边形OABC 中，,,OA a OB b OC c ===，点M 为BC 中点，点N 在侧棱OA 上，且2ON NA =，则MN =（）A.121232a b c--+B.211322a b c-++C.211322a b c --D.111222a b c +-【答案】C 【解析】【分析】由图形中线段关系，应用向量加减、数乘的几何意义用,,OA a OB b OC c === 表示出MN.【详解】1221()2332MN MB BO ON CB OB OA OA OB OC OB=++=-+=+-- 211211322322OA OB OC a b c =--=--.故选：C7.已知椭圆方程为()222210x y a b a b +=>>，长轴为12A A ，过椭圆上一点M 向x 轴作垂线，垂足为P ，若212||13MP A P A P =⋅，则该椭圆的离心率为（）A.3B.3C.13D.23【答案】B 【解析】【分析】根据题意，设()00,M xy ，表示出12,A P A P ，结合椭圆方程，代入计算，再由离心率公式，即可得到结果.【详解】设()00,M x y ，则2200221x y a b+=，()()()120,0,,0,,0A a A a P x -，则10A P x a =+，20A P x a =-，0MP y =所以222002201200||13a y y MP A P A x x a P x a+⋅=-==⋅-，且22x a <，所以22213y a x =-，即222003a x y -=，代入椭圆方程可得222002231a y y a b-+=，化简可得223a b =，则离心率为63e ===.故选：B8.现有一组数据不知道其具体个数，只知道该组数据平方后的数据的平均值是a ，该组数据扩大m 倍后的数据的平均值是b ，则原数据的方差、平方后的数据的方差、扩大m 倍后的数据的方差三个量中，能用,,a b m 表示的量的个数是（）A.0 B.1C.2D.3【答案】C 【解析】【分析】设出原始数据，逐个计算求解即可.【详解】设该组数据为123,,n x x x x ⋅⋅⋅，则12nx x x x n++⋅⋅⋅+=.所以22212n x x x a n++⋅⋅⋅+=，12n mx mx mx mx b n ++⋅⋅⋅+==，所以b x m =.原数据的方差()()()()2222221212221212n n n x x x x x x x x x x x x x s xnn n-+-+⋅⋅⋅+-++⋅⋅⋅+++⋅⋅⋅+==-+2222222b b a x x a x a a m m ⎛⎫=-+=-=-=- ⎪⎝⎭，可以用,,a b m 表示.扩大m 倍后的数据的方差：()()()()()()2222221212222n n mx mx mx mx mx mx x x x x x x s m nn ⎡⎤-+-+⋅⋅⋅+--+-+⋅⋅⋅+-==⎢⎥⎢⎥⎣⎦22222212b m s m a m a b m ⎛⎫==-=- ⎪⎝⎭，可以用,,a b m 表示.平方后的数据的方差：()()()()2222222224441212221232n n n x a x a x aa x x x x x x s a nn n-+-+⋅⋅⋅+-++⋅⋅⋅+++⋅⋅⋅+==-+44444422212122n n x x x x x x a a a n n++⋅⋅⋅+++⋅⋅⋅+=-+=-.不能用,,a b m 表示.故选：C.二．多选题：本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，至少有两个是符合题目要求的，全选对得5分，部分选对得2分，有错选得0分．9.我校举行党史知识竞赛，对全校参赛的1000名学生的得分情况进行了统计，把得分数据按照[)[)[)[)[]50,60,60,70,70,80,80,90,90,100分成5组，绘制了如图所示的频率分布直方图．根据图中信息，下列说法正确的是（）A.图中的x 值为0.020B.这组数据的极差为50C.得分在80分及以上的人数为400D.这组数据的众数的估计值为82【答案】AC 【解析】【分析】根据频率值和为1即可判断A ；根据由频率分布直方图无法求出这组数据得极差，即可判断B ；求出得分在80分及以上的频率，再乘以总人数，即可判断C ；根据频率分布直方图中众数即可判断D .【详解】解：()100.0050.0350.0300.0101x ⨯++++=，解得0.020x =，故A 正确；因为由频率分布直方图无法求出这组数据得极差，故B 错误；得分在80分及以上的频率为()100.0300.0100.4⨯+=，所以得分在80分及以上的人数为10000.4400⨯=，故C 正确；这组数据的众数的估计值为75，故D 错误.故选：AC .10.下列说法正确的是（）A.对任意向量,a b ，都有a b b a⋅=⋅B.若a b a c ⋅=⋅且0a ≠，则b c=C.对任意向量,,a b c，都有()()a b c a b c⋅⋅=⋅⋅ D.对任意向量,,a b c ，都有()+⋅=⋅+⋅ a b c a c b c【答案】AD 【解析】【分析】可由数量积的定义及运算律可逐一判定选项.【详解】cos ,a b a b a b ⋅=，cos ,b a a b a b ⋅= ，可得a b b a ⋅=⋅，故选项A 正确；由a b a c ⋅=⋅ 可得()0a b c ⋅-=，又0a ≠ ，可得b c = 或()a cb ⊥- ，故选项B 错误；()()cos ,R a b c a b a b c c λλ⋅⋅==∈,()()cos ,R a b c c b c b a a μμ⋅⋅==∈所以()()a b c a b c ⋅⋅=⋅⋅ 不一定成立，故选项C 错误；由向量数量积运算的分配律可知选项D 正确；故选：AD.11.甲､乙两支田径队队员的体重(单位：kg)信息如下：甲队体重的平均数为60，方差为200，乙队体重的平均数为68，方差为300，又已知甲､乙两队的队员人数之比为1：3，则关于甲､乙两队全部队员的体重的平均数和方差的说法正确的是（）A.平均数为67B.平均数为66C.方差为296D.方差为287【答案】BD 【解析】【分析】先利用比重计算全部队员体重的平均值，再利用平均值计算方差即可.【详解】依题意，甲的平均数160x =，乙的平均数268x =，而甲､乙两队的队员人数之比为1：3，所以甲队队员在所有队员中所占比重为14，乙队队员在所有队员中所占比重为34故甲、乙两队全部队员的体重的平均数为：1360686644x =⨯+⨯=；甲、乙两队全部队员的体重的方差为：()()22213200606630068665922828744s ⎡⎤⎡⎤=⨯+-+⨯+-=+=⎣⎦⎣⎦.故选：BD.12.已知四面体中三组对棱的中点间的距离都相等，则下列说法正确的是（）A.该四面体相对的棱两两垂直B.该四面体四个顶点在对面三角形的射影是对面三角形的外心C.该四面体的四条高线交于同一点（四面体的高线即为过顶点作底面的垂线）D.该四面体三组对棱平方和相等【答案】ACD 【解析】【分析】设,,AB b AC c AD d ===，利用向量法AD 选项，用几何法判断BC 选项．【详解】选项A ，如图，四面体ABCD 中，,,,,,E F G H I J 是所在棱中点，EF GH IJ ==，设,,AB b AC c AD d === ，则111()()222EF AF AE AD AB AC d b c =-=-+=-- ，111()()222GH AH AG AC AD AB c d b =-=+-=+- ，EF GH =，即EF GH = ，所以11()()22d b c c d b --=+-，所以222222222222d b c b d c d b c d b c c d b d b c++-⋅-⋅+⋅=+++⋅-⋅-⋅c d b c ⋅=⋅ ，即()0c b d ⋅-= ，所以()c b d ⊥- ，即AC DB ⊥，所以AC BD ⊥，同理,AB CD AD BC ⊥⊥，A 正确；选项B ，设1AH ⊥平面BCD ，1H 是垂足，CD ⊂平面BCD ，所以1AH CD ⊥，又AB CD ⊥，11,,AB AH A AB AH =⊂ 平面1ABH ，所以CD ⊥平面1ABH ，而1BH ⊂平面1ABH ，所以1CD BH ⊥，同理1BC DH ⊥，所以1H 是平面BCD 垂心，同理可得其它顶点在对面的射影是对面三角形的垂心，B 错；选项C ，如上图，1AH ⊥平面BCD ，2BH ⊥平面ACD ，3DH ⊥平面ABC ，123,,H H H 是垂足，先证明12,AH BH 相交，1AH ⊥平面BCD ，CD ⊂平面BCD ，所以1AH CD ⊥，又AB CD ⊥，11,,AB AH A AB AH =⊂ 平面1ABH ，所以CD ⊥平面1ABH ，同理CD ⊥平面2ABH ，所以平面1ABH 和平面2ABH 重合，即12,AH BH 共面，它们必相交，设12AH BH H ⋂=，下面证明DH ⊥平面ABC ，与证明CD ⊥平面1ABH 同理可证得BC ⊥平面1ADH ，又DH ⊂平面1ADH ，所以BC DH ⊥，同理由2BH ⊥平面ACD 可证得DH AC ⊥，而,AC BC 是平面ABC 内两相交直线，所以DH ⊥平面ABC ，因此DH 与3DH 重合，同理可证CH ⊥平面ABD ，C 正确；选项D ，由选项A 的讨论同理可得b c b d c d ⋅=⋅=⋅，222222222()2AB CD AB CD b d c b c d c d +=+=+-=++-⋅ ，222222222()2AC BD AC BD c d b b c d b d +=+=+-=++-⋅，所以2222AB CD AC BD +=+，同理222222AB CD AC BD AD BC +=+=+，D 正确．故选：ACD ．第Ⅱ卷（非选择题，共90分）三．填空题：本大题共4小题，每小题5分，共20分．13.经过()()0,2,1,0A B -两点的直线的方向向量为()1,k ，则k =______．【答案】2【解析】【分析】方向向量与BA平行，由此可得．【详解】由已知(1,2)BA =，()1,k 是直线AB 的方向向量，则2k =，故答案为：2.14.在一次篮球比赛中，某支球队共进行了8场比赛，得分分别为25，29，30，32，37，38，40，42，那么这组数据的第65百分位数为______．【答案】38【解析】【分析】根据百分位数的定义即可求解.【详解】865% 5.2⨯=,故这组数据的第65百分位数为第6个数38，故答案为：3815.写出与圆221:(1)(3)1C x y +++=和222:(3)(1)9C x y -++=都相切的一条直线的方程__________．【答案】0x =##4y =-##430x y -=##34100x y ++=【解析】【分析】判断两个圆是相离的，得到应该有四条公切线，画出图形易得0x =或4y =-为公切线，设切线方程为y kx b =+，根据圆心到直线的距离等于半径列出关于,k b 方程组，求解.【详解】因为圆1C 的圆心为()11,3C --，半径11r =圆2C 的圆心为()23,1C -，半径23r =又因为124C C =所以圆1C 与圆2C 相离，所以有4条公切线.画图为：易得:0a x =或:4n y =-是圆221:(1)(3)1C x y +++=和222:(3)(1)9C x y -++=的公切线设另两条公切线方程为：y kx b =+圆1C 到直线y kxb =+的距离为1=圆2C 到直线y kxb =+3=所以3133k b b k ++=-+所以31339k b b k ++=-+或31339k b b k ++=-+-34k b =+或52b =-当52b =-1==所以34k =-，切线方程为34100x y ++=当34k b =+3==所以()()225249b b +=++所以240b b +=所以0b =或4b =-当0b =时43k =，切线方程为430x y -=当4b =-时0k =，切线方程为4y =-故答案为：0x =或4y =-或430x y -=或34100x y ++=16.已知P 为直线=2y -上一动点，过点P 作圆221x y +=的两条切线，切点分别为,B C ，则点()2,1A 到直线BC 的距离的最大值为______．【答案】52【解析】【分析】首先设点00(,)P x y ，求过点BC 的直线方程，并判断直线BC 过定点，再利用几何关系求最大值.【详解】设00(,)P x y ，过点P 引圆221x y +=的两条切线，切点分别为,B C ，则切点在以OP 为直径的圆上，圆心00,22x y ⎛⎫ ⎪⎝⎭，半径r =，则圆的方程是22220000224x y x y x y +⎛⎫⎛⎫-+-=⎪ ⎪⎝⎭⎝⎭，整理为：22000x y x x y y +--=，又点,B C 在圆221x y +=上，两圆方程相减得到001x x y y +=，即直线BC 的方程是001x x y y +=，因为02y =-，代入001x x y y +=得021x x y -=，则直线BC 恒过定点10,2N ⎛⎫- ⎪⎝⎭，所以点()2,1A 到直线BC 的距离52d AN ≤==，所以点()2,1A 到直线BC 的距离的最大值为52.故答案为：52.【点睛】思路点睛：首先本题求以OP 为直径的圆，利用两圆相减，求得过两圆交点的直线方程，关键是发现直线BC 过定点，这样通过几何关系就容易求定点与动直线距离的最大值.四．解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17.已知ABC 的周长为()()14,3,0,3,0B C -．（1）求点A 的轨迹方程；（2）若AB AC ⊥，求ABC 的面积．【答案】（1）()2210167x y y +=≠（2）7【解析】【分析】（1）结合椭圆定义可得A 的轨迹方程.（2）利用AB AC ⊥及椭圆定义可列出方程，求解AC AB ⋅，即可算出ABC 的面积．【小问1详解】ABC 的周长为14且6,86BC AC AB BC =∴+=>=，根据椭圆的定义可知，点A 的轨迹是以()()3,0,3,0B C -为焦点，以8为长轴长的椭圆，即4,3,a c b ===A 的轨迹方程为221167x y+=，又A 为三角形的顶点，故所求的轨迹方程为()2210167x y y +=≠．【小问2详解】222,||||36AB AC AB AC BC ⊥∴+== ①．A 点在椭圆()2210167x y y +=≠上，且()()3,0,3,0B C -为焦点，8AC AB ∴+=，故22||264AC AB AC AB ++⋅=②．由①②可得，14AC AB ⋅=，故172S AC AB =⋅⋅=．ABC ∴ 的面积为7．18.如图，四面体OABC 的所有棱长都为1,,D E 分别是,OA BC 的中点，连接DE ．（1）求DE 的长；（2）求点D 到平面ABC 的距离．【答案】18.219.3【解析】【分析】（1）利用基底,,OA OB OC 表示出向量DE，再根据向量数量积求长度的方法即可求出；（2）由该几何体特征可知，点O 在平面ABC 的射影为ABC 的中心，即可求出．【小问1详解】因为四面体OABC 的所有棱长都是1，所以该四面体为正四面体，()1111122222DE DA AB BE OA OB OA OC OB OA OB OC =++=+-+-=-++，而且12OA OB OB OC OA OC ⋅=⋅=⋅= ，所以()()2211131442DE OA OB OC =--=-=，即2DE =，所以DE 的长为2．【小问2详解】因为四面体OABC 为正四面体，所以点O 在平面ABC 的射影O '为ABC 的中心，ABC 的外接圆半径为11sin6023︒⨯=，所以点O 到平面ABC 的距离为3d ==，由于D 点为线段OA 的中点，所以点D 到平面ABC 的距离为3．19.现从学校的800名男生中随机抽取50名测量身高，被测学生身高全部介于155cm 和195cm 之间，将测量结果按如下方式分成八组：第一组[)155160,，第二组[)160,165,⋅⋅⋅，第八组[]190195,．右图是按上述分组方法得到的频率分布直方图的一部分，已知第一组与第八组人数相同，第六组的人数为4人．（1）求第七组的频率并估计该校的800名男生的身高的中位数；（2）若从身高属于第六组和第八组的所有男生中随机抽取两名男生，记事件A 表示随机抽取的两名男生不．在同一组．．．．，求()P A ．【答案】（1）第七组的频率为0.06，中位数为174.5cm（2）815【解析】【分析】（1）根据频率为和1，可得第七组的频率为0.06，设学校的800名男生的身高中位数为m ，根据中位数的定义可得()0040080217000405...m ..+++-⨯=,求解即可；（2）用列举法写出基本事件的总数和两名男生不在同一组所包含的基本事件，即可得解.【小问1详解】（1）由直方图的性质，易知第七组的频率为415(0.008+0.016+0.04+0.04+0.06++0.008)=0.06505-⨯⨯．由于0.040.080.20.320.5,0.040.080.20.20.520.5++=<+++=>，设学校的800名男生的身高中位数为m ，则170175m <<，由()0040080217000405...m ..+++-⨯=,得1745m .=，所以学校的800名男生的身高的中位数为174.5cm ．【小问2详解】解：第六组[)180185,的人数为4，设为a b c d ,,,，第八组[]190195,的人数为0.0085502⨯⨯=，设为,A B ，则从中随机抽取两名男生有,,,,,,,,,,,,,dB,ab ac ad bc bd cd aA aB bA bB cA cB dA AB 共15种情况．事件A 表示随机抽取的两名男生不在同一组，所以事件A 包含的基本事件为,,,aA aB bA bB ，,,,cA cB dA dB 共8种情况．所以()815P A =．20.已知圆C 经过点()0,2A ，()6,4B ，且圆心在直线340x y --=上.（1）求圆C 的方程；（2）若平面上有两个点()6,0P -，()6,0Q ，点M 是圆C 上的点且满足2MP MQ=，求点M 的坐标.【答案】（1）()22420x y -+=（2）10,33⎛⎫ ⎪ ⎪⎝⎭或10,33⎛⎫-⎪ ⎪⎝⎭【解析】【分析】（1）设出圆心，利用点到直线的距离公式即可求得圆的方程.（2）根据已知条件求得M 满足的方程联立即可求得M 的坐标.【小问1详解】∵圆心在直线340x y --=上，设圆心()34,C a a +，已知圆C 经过点()0,2A ，()6,4B ，则由CA CB =，=解得0a =，所以圆心C 为()4,0，半径r CA ===所以圆C 的方程为()22420x y -+=；【小问2详解】设(),M x y ，∵M 在圆C 上，∴()22420x y -+=，又()6,0P -，()6,0Q ，由2MPMQ=可得：()()2222646x y x y ⎡⎤++=-+⎣⎦，化简得()221064x y -+=，联立()()22224201064x y x y ⎧-+=⎪⎨-+=⎪⎩解得10411,33M ⎛⎫ ⎪ ⎪⎝⎭或10411,33⎛⎫- ⎪ ⎪⎝⎭.21.如图，在直三棱柱111ABC A B C -中，1π,2,3,2BAC AB AC AA M ∠====是AB 的中点，N 是11B C 的中点，P 是1BC 与1B C 的交点，点Q 在线段1A N 上．（1）若//PQ 平面1A CM ，请确定点Q 的位置；（2）请在下列条件中任选一个，求11A QA N的值；①平面BPQ 与平面ABC的夹角余弦值为53；②直线AC 与平面BPQ所成角的正弦值为106．【答案】（1）Q 为1A N 靠近N 三等分点处（2）①1112A Q A N =；②1112A Q A N =【解析】【分析】（1）分别以1,,AC AB AA 所在直线为,,x y z 轴，建立空间直角坐标系，求出面1A CM 的法向量n，由//PQ 平面1A CM 得PQ n ⊥ ，即0PQ n ⋅= ，求解11A QA N即可；（2）设()1101A Q A Nλλ=<<，求出平面BPQ 的法向量为m，平面ABC 的法向量，若选择①，利用平面与平面的夹角的向量求法求解；若选择②，由直线与平面所成角的向量求法求解.【小问1详解】分别以1,,AC AB AA 所在直线为,,x y z轴，建立空间直角坐标系，()()()()()130,0,3,2,0,0,0,1,0,1,1,3,1,1,,,,32A C M N P Q a a ⎛⎫ ⎪⎝⎭，则()()1132,0,3,0,1,3,1,1,2A C A M PQ a a ⎛⎫=-=-=-- ⎪⎝⎭ ．设面1A CM 的法向量(),,n x y z =r ，则110A C n A M n ⎧⋅=⎪⎨⋅=⎪⎩ ，即23030x z y z -=⎧⎨-=⎩．令2z =，得()3,6,2n =．因为//PQ 平面1A CM ，所以PQ n ⊥ ，即0PQ n ⋅=．所以()()316130a a -+-+=，得23a =，122,,033A Q ⎛⎫= ⎪⎝⎭，所以13A Q = ．因为11123A Q A N A N ==，所以Q 为1A N 靠近N 三等分点处时，有//PQ 平面1A CM ．【小问2详解】设()1101A QA Nλλ=<<，则()11,,0A Q A N λλλ== ．所以1111331,1,,1,1,22PQ PA A Q PA A N PB λλλ⎛⎫⎛⎫=+=+=--=--⎪ ⎪⎝⎭⎝⎭．设平面BPQ 的法向量为()111,,m x y z =，则00PQ m PB m ⎧⋅=⎪⎨⋅=⎪⎩，即()()11111131102302x y z x y z λλ⎧-+-+=⎪⎪⎨⎪-+-=⎪⎩．令()141z λ=-，得()()()3,32,41m λλλ=--．注意到平面ABC 的法向量为()0,0,1，直线AC 的方向向量为()1,0,0，若选择①，平面BPQ 与平面ABC的夹角余弦值为53，则()10,0,1cos 53m mθ⋅==．即()2483001λλλ-+=<<，解得12λ=，即1112A Q A N =．若选择②，直线AC 与平面BPQ所成角的正弦值为106，则()21,0,0sin 106m mθ⋅==．即()2181713001λλλ+-=<<，解得12λ=，即1112A Q A N =．22.已知()()()2,3,2,0,2,0,A B C ABC -∠的内角平分线与y 轴相交于点E ．（1）求ABC 的外接圆的方程；（2）求点E 的坐标；（3）若P 为ABC 的外接圆劣弧 BC 上一动点，ABC ∠的内角平分线与直线AP 相交于点D ，记直线CD 的斜率为1k ，直线CP 的斜率为2k ，当1275k k =-时，判断点E 与经过,,P D C 三点的圆的位置关系，并说明理由．【答案】（1）2232524x y ⎛⎫+-=⎪⎝⎭（2）20,3⎛⎫ ⎪⎝⎭（3）点E 在经过,,P D C 三点的圆上，理由见解析【解析】【分析】（1）根据直角三角形的性质即可求解圆心和半径，从而得解；（2）根据等面积法或者利用角平分线的性质可得AB AF BCCF=，即可求解长度得斜率，进而可求解直线方程，得解；（3）联立方程可得22223234,11k k k P k k ⎛⎫--- ⎪++⎝⎭，6743,3131k k D k k --⎛⎫ ⎪--⎝⎭，根据1275k k =-可得1k =，即可求解点的坐标，由点的坐标求解圆的方程，即可判定.【小问1详解】易知ABC 为C 为直角的直角三角形，故外接圆的圆心为斜边AB 边的中点30,2⎛⎫ ⎪⎝⎭，半径为52，所以外接圆的方程为2232524x y ⎛⎫+-= ⎪⎝⎭．【小问2详解】设ABC ∠的内角平分线交AC 于点F ，根据角平分线性质定理，可知AB AF BCCF=，（利用11sin 22211sin 222ABFBCFABC AB BF AF BC S ABC S BC BF FC BC ∠⋅⋅==∠⋅⋅ 可得AB AF BC CF =）由结合3AF CF +=，5AB ==,4,3BC AC ==所以4133BD CF CF k BC =⇒==所以，ABC ∠的内角平分线方程为()123y x =+，令0x =，即可得点E 坐标20,3⎛⎫⎪⎝⎭．【小问3详解】点E 在经过,,P D C 三点的圆上，理由如下：由题意可知直线AP 的斜率存在，故设直线AP 的直线方程为()32y k x -=-，联立直线与圆的方程()223232524y k x x y ⎧-=-⎪⎨⎛⎫+-=⎪ ⎪⎝⎭⎩，可得()()22221344640kx k k x kk ++-+--=注意到,A P 两点是直线与圆的交点，所以2246421P k k x k --⋅=+222321P k k x k --∴=+，故22223234,11k k k P k k ⎛⎫--- ⎪++⎝⎭．联立直线AP 与ABC ∠的内角平分线方程()321233y k x y x ⎧-=-⎪⎨=+⎪⎩，可得6731k x k -=-6743,3131k k D k k --⎛⎫∴ ⎪--⎝⎭．此时221222243433434003443313111,6753423253422313111k k k k k k k k k k k k k k k k k k k k k ----------++======------+----++，12343475,1435534k k k k k k k -+∴==-=-∴=-+．此时，点31,22P ⎛⎫-- ⎪⎝⎭，点11,.22D P ⎛⎫- ⎪⎝⎭点满足在劣弧 BC 上．设经过,,P D C 三点的圆的方程为()2222040x y mx ny t m n t ++++=+->，则4205320120m t m n t m n t ++=⎧⎪--+=⎨⎪-++=⎩，解得5617673m n t ⎧=-⎪⎪⎪=⎨⎪⎪=-⎪⎩．所以，经过,,P D C 三点的圆的方程为2251770663x y x y +-+-=．将点20,3E ⎛⎫ ⎪⎝⎭代入圆的方程成立，所以点E 在经过,,P D C 三点的圆上.。

四川省江油中学2022-2023学年高二下学期第一阶段考试数学(理)试卷(PDF版)

江油中学2021级高二下期第一阶段考试数学（理）试题一、单选题（每小题5分，共60分）1．4i1i-的虚部为（）A ．2-B ．2C ．2iD ．2i-2．命题“0x ∀>，20x >”的否定是（）A ．0x ∃>，20x ≤B ．0x ∀≤，20x >C ．0x ∃≤，20x ≤D ．0x ∀≤，20x ≤3．若z 满足（1+i ）z =−4+2i ，则z =（）A ．10BC ．20D ．4．已知函数f （x ）=13x 3﹣f '（2）x 2+x ﹣3，则f '（2）＝（）A ．﹣1B ．1C ．﹣5D ．55．下列导数运算正确的是（）A ．()sin cos x x'=-B ．()33xx'=C ．()21log ln 2x x '=⋅D ．211x x'⎛⎫= ⎪⎝⎭6．“a<0”是“关于x 的不等式210ax ax +-<对任意实数x 恒成立”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件7．函数()2ln f x x =-2x 的单调递增区间为（）A ．(1∞--，)B ．(1，+∞)C ．(-1，1)D ．(0，1)8．已知一个圆柱形空杯，其底面直径为8cm ，高为20cm ，现向杯中注入溶液，已知注入溶液的体积V （单位：ml ）关于时间t （单位：s ）的函数为()()32π2π0V t t t t =+≥，不考虑注液过程中溶液的流失，则当4st =时杯中溶液上升高度的瞬时变化率为（）A ．2cm /sB ．4cm /sC ．6cm /sD ．8cm /s9．已知函数f （x ）的定义域为[﹣1，5]，其部分自变量与函数值的对应情况如表：x ﹣10245f （x ）312.513f （x ）的导函数f '（x ）的图象如图所示．给出下列四个结论：①f （x ）在区间[﹣1，0]上单调递增；②f （x ）有2个极大值点；③f （x ）的值域为[1，3]；④如果x ∈[t ，5]时，f （x ）的最小值是1，那么t 的最大值为4．其中，所有正确结论的序号是（）A ．③B ．①④C ．②③D ．③④10．已知命题:p 函数()()40f x x x x=+≠的最小值为4；命题:q 在ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，则“A B >”是“a b >”的充要条件.则下列命题为真命题的是（）A ．()p q⌝∧B ．()p q ∨⌝C ．p q∧D ．()()p q ⌝∧⌝11．若动点P 在直线1y x =+上，动点Q 在曲线22x y =-上，则|PQ |的最小值为（）A ．14B ．4C ．2D ．1812．已知函数()e 23ln x f x t x x x x ⎛⎫=++- ⎪⎝⎭有两个极值点，则t 的取值范围为（）A ．()3e ,+∞B ．{}31,e 2⎛⎫-∞- ⎪⎝⎭ C ．(){}31,e e,e 2⎛⎫-∞--- ⎪⎝⎭ D ．()1,e e,2⎛⎫-∞--- ⎪⎝⎭ 二、填空题（每小题5分，共20分）13．已知函数()cos2f x x =，则曲线()y f x =在点ππ,44f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭处的切线方程为__________．14．若z C ∈且22i 1z +-=，则22i z --的最大值为_______．15．已知函数()()212ln R 2f x x ax x a =--∈.若函数()f x 在区间[)1,+∞上单调递增，则实数a 的取值范围为__________．.16．已知函数()33f x x x =-，()e 22xx g x a =-+，对于任意[]12,0,2x x ∈，都有()()12f x g x ≤成立，则实数a的取值范围是________.三、解答题（17题10分，其余每题12分，共70分）17．复数(1)(1)()z m m m i m R =-+-∈.（Ⅰ）实数m 为何值时，复数z 为纯虚数；（Ⅱ）若m =2，计算复数1z z i-+．18．设集合{}23280A x x x =+-<，集合{}21B x m x m =-<<+．(1)已知p ：3B ∈，若p 为真命题，求实数m 的取值范围；(2)若“x A ∈”是“x B ∈”的必要不充分条件，求实数m 的取值范围．19．已知函数f(x)=e x (x −2)(1)求()f x '，()0f '，()1f '-﹔(2)求曲线()y f x =在点(0,-2)处的切线方程;(3)求函数f(x)的极值.20．已知p ：方程x 2+y 2﹣4x +a 2＝0表示圆：q ：方程1322=+ax y （a ＞0）表示焦点在y 轴上的椭圆．（1）若p 为真命题，求实数a 的取值范围；（2）若命题p Ⅴq 为真，p Λq 为假，求实数a 的取值范围．21．已知函数()323f x x mx nx =++在=1x -时有极值0.(1)求,m n 的值.(2)求g(x)=f(x)−x 3−3lnx 的单调区间.22．已知函数21()ln 2f x x ax x =-+.(1)讨论函数()f x 的单调性；(2)若()f x 有两个极值点1x ，2x ，且()()123ln 24f x f x -≥-，求a 的取值范围.江油中学2021级高二下期3月数学（理）试题参考答案1．B 2．A 3．B 4.B5．C 6．D 7．D 8．B 9．D10．A11．B12．【答案】D 【详解】函数()e 23ln x f x t x xx x ⎛⎫=++- ⎪的定义域为()0,∞+，13．202y x +-=14．515．1a ≤-.16．e ,2⎛⎤-∞ ⎥⎝⎦【详解】依题意得，对于任意[]12,0,2x x ∈，都有()()12f x g x ≤成立可等价为对于任意[]12,0,2x x ∈，都有()()max 12f x g x ≤成立，()33=- f x x x ，()()231f x x '∴=-，[]0,2x ∈，当01x <<时，()0f x '<，()f x 单调递减；当12x <<时，()0f x ¢>，()f x 单调递增；又()()00,22f f == ，()()max 22f x f ∴==，∴对于任意[]0,2x ∈，都有()2g x ≥成立，即对于任意[]0,2x ∈，都有2x e a x ≤成立，等价为mine 2x a x ⎛⎫≤ ⎪⎝⎭成立，令()e xh x x =，[]0,2x ∈，()()2e 1x x h x x -'∴=，当01x <<时，()0h x '<，()h x 单调递减；当12x <<时，()0h x '>，()h x 单调递增；()()min 1e h x h ∴==，2e a ∴≤，e 2a ∴≤，a ∴的取值范围是e ,2⎛⎤-∞ ⎥⎝⎦.17．【答案】（1）0m =（2）1122i -试题解析：（1）欲使z 为纯虚数，则须()10m m -=且10m -≠，所以得0m =18．【答案】(1)()2,5(2)[]5,3-【详解】（1）由题意得3B ∈，故231m m -<<+，解得：25m <<，故实数m 的取值范围是()2,5；19．【答案】(1))1()(-='x e x f x ，ef f 2)1(,1)0(-=-'-='，(2)02=++y x （3）极小值-e 20．【答案】（1）﹣2＜m ＜2．（2）（﹣2，0]∪[2，3）．21．【答案】(1),13m n ==；(2)函数g(x)=f(x)−x 3−3lnx 的单调减区间为(0,34)，单调增区间为(34,+∞).【详解】（1）由题可得2()36f x x mx n '=++，22．【答案】(1)答案见详解(2)32,2⎡⎫+∞⎪⎢⎪⎣⎭【详解】（1）因为函数21()ln 2f x x ax x =-+，则211()x ax f x x a x x -+'=-+=，0x >，令()21g x x ax =-+，则24a ∆=-，。

四川省江油中学2022-2023学年高二下学期第一阶段考试化学试卷(PDF版)

江油中学2021级高二下期第一阶段考试化学试题本试卷分为试题卷和答题卡两部分，其中试题卷由第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）组成，共6页；答题卡共2页。

满分100分，考试时间80分钟。

可能用到的相对原子质量：H1O16Na23第Ⅰ卷（选择题，共42分）一、选择题（本题包括14小题，每小题3分，共42分。

每小题只有一个选项符合题意）1．下列物质属于弱电解质的是A．氨水B．冰醋酸C．CaCO3D．C2H5OH2.四川柠檬品质上乘，若柠檬果汁pH＝2，则c(H＋)为A．0.1mol/L B．0.2mol/L C．0.01mol/L D．0.02mol/L3.下列物质在水中的电离方程式正确的是A．NaHCO3==Na＋＋H＋＋CO-23B．HClO H＋＋ClO－C．CuCl2==Cu2＋+Cl－D．CH 3COONH4CH3COO－+NH+44.某同学在实验报告中记录了下列数据，其中正确的是A．用托盘天平称取5.85g食盐B．用10mL量筒量取7.35mL盐酸C．用pH计测出某溶液pH为3.52D．从碱式滴定管放出酸性KMnO4溶液15.60mL 5.下列关于电离常数(K)的说法正确的是A．电离常数只与温度有关，升高温度，K值减小B．电离常数K与温度无关C．相同温度下，电离常数(K)越小，表示弱电解质的电离能力越弱D．多元弱酸各步电离常数大小关系为123K<K<K6.1909年，丹麦生理学家索仑生提出用pH表示水溶液的酸度：pH＝-lg[H+]，后来又定义pOH＝-lg[OH－]，p K W＝-lg K W。

对某水溶液的下列说法中错误的是A．pH＋pOH＝p K W B．若为酸性溶液则pH＞pOHC．常温下pH＋pOH＝14D．溶液pH＝7时未必呈中性7．食用白醋是生活中重要的调味品，其中含3%～5%的醋酸。

以下实验能证明醋酸为弱电解质的是A ．用食用白醋做导电实验，灯泡很暗B ．将水垢浸泡在白醋中，有CO 2气体放出C ．向白醋中滴入紫色石蕊试液，溶液呈红色D ．中和等pH 、等体积的盐酸和白醋，白醋消耗NaOH 多8．醋酸溶液中存在电离平衡：CH 3COOHH ＋＋CH 3COO －，下列叙述不正确的是A ．加水稀释，()()()3-+3c CH COOH c CH COO c H ⋅增大B ．0.10mol/L 的CH 3COOH 溶液加水稀释，溶液中c(OH -)增大C ．CH 3COOH 溶液中加少量的CH 3COONa 固体，平衡逆向移动D ．25℃时，欲使醋酸溶液的pH 和电离程度都减小，可加入少量冰醋酸9．向10mL 氨水中加入蒸馏水，将其稀释到1L 后，下列说法正确的是A ．+4NH 数目不变B ．)(23O H NH c ⋅增大C ．)()(423+⋅NH c O H NH c 减小D ．O H NH 23⋅的电离程度减小10．常温下，0.1mol·L -1的NaOH 溶液中由水电离出的OH -的物质的量浓度为A ．0.1mol·L -1B ．1.0×10-13mol·L -1C ．1.0×10-7mol·L -1D ．无法确定11．某课外活动小组对采集的酸雨样品进行化验，测得数据如下：c (Na +)＝5.0×10－6mol /L 、c (NH ＋4)＝2.0×10－5mol /L 、c (NO －3)＝2.0×10－4mol /L 、c (SO 2－4)＝4.0×10－4mol /L ，H +和OH －浓度未测定，则此酸雨的pH 约为A ．3B ．4C ．5D ．612．室温时，某溶液中由水电离生成的H ＋和OH －物质的量浓度的乘积为1×10－24，则在该溶液中一定不能大量共存的离子组是A ．Al 3＋、Na ＋、NO －3、Cl －B ．K ＋、Na ＋、Cl －、CO 2－3C ．Mg 2＋、Na ＋、Cl －、SO 2－4D ．NH ＋4、K ＋、SiO 2－3、NO －313．常温下，甲酸和乙酸的电离常数分别为1.8×10-4和1.8×10-5。

2023-2024学年四川省绵阳市江油市太白中学高二10月月考历史试题

2023-2024学年四川省绵阳市江油市太白中学高二10月月考历史试题1. 清代，督抚正式成为三司之上的地方大吏，但朝廷仍以中央官员差遣形式委派督抚任职，同时督抚之间职责又有交叠，互为监督。

这反映了（）A．清代地方官制冗杂B．中央权力下移C．地方治理效力提高D．监察制度发展2. 内廷指的是皇宫里面皇帝的私人随从组成的机构。

汉武帝时期，内廷的地位越来越高，内廷一开始是政府正式官署的下属机构，后来内廷的首领是“大司马”，大司马奉命可以领导尚书，他在政府里的实际权力就超过了丞相。

这反映出（）A．“汉承秦制”已被完全放弃B．相权削弱，皇权得到了加强C．完全破坏了三公九卿制D．新行政中枢确立3. 春秋战国时期有“师保”“辅贰”之制。

“天生民而立之君有君而为之式（卿佐），使师保之，勿使过度”，设“师氏”之官，“掌以诏王”，即“告王以善道”；又设“保氏”之官，“掌谏王恶”。

这些举措（）A．反映出分封制的渐趋瓦解B．说明中央尚未实现权力高度集中C．利于保障政治的正常运作D．折射出统治集团内部的权力争夺4. 亚里士多德记载当时希腊普遍流行的政体“正如人们谈论风向时，只有北风和南风，其他都是二者的变体，政体亦是只有两类，即民主制和寡头制”；在不同城邦之间，民主制和寡头制的深刻矛盾导致雅典和斯巴达斗争不止，并最终导致伯罗奔尼撒战争的爆发。

对此解读正确的是（）A．两种政体都建立在对奴隶专政的基础上B．斯巴达寡头政治下公民丧失参政的权力C．雅典鼠疫决定了伯罗奔尼撒战争的结果D．伯罗奔尼撒战争的本质是希腊政体之争5. 1296年，教皇卜尼法斯发布训令，未经教皇同意禁止任何国家的教士向君主纳税。

1301年，法国国王腓力四世首次召开法兰西三级会议，寻求民众的支持，宣称卜尼法斯是一名应该从教廷中开除的异教徒和罪犯。

据此可知（）A．工商业的发展推动法国权力结构发生异变B．法国由封君封臣制向议会制共和转变C．王权与教权的矛盾推动法国民族意识觉醒D．打破教会思想束缚引发欧洲宗教改革6. 1762年，英国议员约翰•威尔克斯创办了《苏格兰人》报。

四川省绵阳市南山中学双语学校2023-2024学年高二上学期12月月考英语真题卷

四川省绵阳市南山中学双语学校2023-2024学年高二上学期12月月考英语真题卷学校:___________姓名：___________班级：___________考号：___________一、阅读理解Heroes Stamp Design CompetitionWelcome to the Heroes Stamp Design Competition! Children aged 4-14 years are invited to design a stamp. Eight designs will be chosen for this stamp series from the Royal Mail. One of the designs could be yours. There are 120 great prizes on offer for area winners and runners-up. Plus, cash prizes for the winning school too.Stamp DesigningThe stamp design will be based on your hero or heroes of the coronavirus pandemic (新冠肺炎疫情). The past year has been very difficult for so many people. There are countless frontline workers and volunteers who have continued to work tirelessly to keep the country moving.Being a stamp designer is a very skilled job. One of the jobs of a stamp designer is to reduce the size of a picture to fit the stamp. When designing your stamp, have a think about what kind of image of your hero or heroes would make a good miniature (微生物) design for a stamp. The final stamps will be about 3.7cm wide×3.5cm high.Things to consider● Your stamp design must be drawn on the official competition entry form which your teacher will give you.● Your design must be your own original work.● Drawings must be flat, so please don’t stick any materials or textures (纹理) to your design.● Please use lots of colour (no black and white images) in your design.● Please avoid using highlighter pens.Good LuckThe closing date for the competition is 28th May. Please ask your teacher, or parent, for one of the official entry forms. You’re then ready to start designing! We can’t wait to see all of the amazing designs from gifted children across the country.Good Luck!1．Who would probably take part in the competition?A．Students B．DoctorsC．School teachers D．Professional designers2．What do we know about the competition?A．It will begin on 28th May.B．It is for a series of four stamps.C．It asks competitors to honor heroes on their stamps.D．It will provide each competing school with cash prizes.3．What is a requirement for the stamp design?A．It should be black and white.B．It should be drawn with highlight pens.C．It should be flat with textures.D．It should be drawn on a given formIn the 19th century, tuberculosis (肺结核) epidemics were spreading over Europe and the United States, killing an estimated one out of seven people. In ancient Greece, Hippocrates called it “the most considerable of the diseases.”The fight against tuberculosis reached a turning point on March 24, 1882, in a small meeting room of the German Physiological Society at Berlin. A doctor named Robert Koch used more than 200 microscopic preparations to identify the bacterium that causes tuberculosis: tubercle bacillus.In 1872, Koch took up the post of district physician in what is today Wolsztyn, Poland. His patients, many of them farmers, were dying from anthrax, an illness that destroyed their cows.Koch set out to solve the anthrax riddle. First, Koch visited anthrax-stricken farms to observe the cows. He witnessed how a healthy animal would die in a matter of days as its blood turned black. People in close contact with sick cows and sheep also fell ill. Examining drops of black blood from dead cows under his microscope, Koch spotted structures shaped like thin grains of rice, which blood from healthy animals did not have. These germs were Bacillus anthracis.To see if the bacteria were the cause of the illness, Koch designed his own testing methods. First, he soaked (浸泡) a wood splinter (碎片) with a sick animal’s blood; then he made a small cut at the base of each mouse’s tail and inserted (插入) the splinter into their bodies. The next morning, the mice were dead. When Koch checked their bodies, he found the same microscopic structures in their blood.In 1880, Koch’s team perfected his plate technique (技术) for generating pure cultures of bacteria, which was crucial in identifying the cause of tuberculosis. In 1890, he announced he had found the cure for tuberculosis. He called the medicine tuberculin, a substance taken from tubercle bacilli. The news gave rise to enormous hope around the world, but tuberculin turned out to be a major disappointment. More than ineffective, it even contributed to the death of some patients. To this day, no completely effective vaccine for tuberculosis has been found, but tuberculin has become a crucial part of testing for the disease.4．Why does the author mention Hippocrates in paragraph 1?A．To introduce the spread of tuberculosis.B．To show the huge impact of tuberculosis.C．To explain the concept of tuberculosis.D．To describe the history of tuberculosis.5．What did the turning point suggest?A．People found a cure for anthrax.B．Fewer people died from tuberculosis.C．Tuberculosis-causing bacteria were recognized.D．Anthrax stopped spreading beyond animals.6．How did Koch identify the cause of anthrax?A．He fed a mouse with a dead cow’s food.B．He inserted a wood splinter into a cow’s tail.C．He infected healthy mice with a sick animal’s blood.D．He examined a dead person’s blood under his microscope.7．What can we learn about the medicine Koch invented?A．It has cured many people.B．It was taken from healthy people.C．It was an effective tuberculosis vaccine.D．It has been used in testing for tuberculosis.Turning 18 is a big deal when you are a teenager. It means you are responsible for yourself and don’t need your parents’ permission any more. However, there are lots of opinions about when one becomes an adult. Some are based on science, while others are personal opinions. While currently the age is 18, science supports 25 as a more sensible agefor adulthood, and I agree.While studying the brain of teenagers, scientists have learned that when kids are around l8, their prefrontal cortex (前额皮层) is only halfway developed. The prefrontal-cortex helps people set and achieve goals by receiving signals from different regions of the brain to process information and adapting accordingly. That halfway development means that you still have things to learn and your brains still have time to develop until the age of 25.Some people think going off to college and living on your own qualify (使……具有资格) san adult, while others may believe having a steady income and being able to afford to live on your own are what make you an adult. Not everyone has a fortunate life where they have family that can provide support; there are situations where you are forced to become an “adult” whether you like it or not.In the foster care (寄养) system, once a child turns 18, he or she is considered an adult and can no longer receive state-sponsored support. These children are forced into a life where they have no family or anyone to support them other than those who were there for them in the system.Having a quality job will allow you to supply yourself with necessary things to live and help you become a more mature and responsible person. Also, going through difficult times and realizing life isn’t as easy as it seems, should qualify someone as an adult.8．What is the author’s attitude toward considering 25 as an age for adulthood?A．Cautious.B．Uncaring.C．Doubtful.D．Positive. 9．How does the prefrontal cortex work to help people set and achieve goals?A．By dealing with received signals and responding accordingly.B．By collecting information from other parts of the body.C．By sending instructions to different regions of the brainD．By transporting sensed emotions and making records10．What does the author intend to do in paragraph 3?A．Give a definition of adulthood.B．Stress the importance of family support.C．Prove not everyone lives a fortunate life.D．Show opinion on becoming an adult is divided11．What is one standard qualifying you as an adult according to the author?A．Setting up a family.B．Being responsible for your study.C．Accepting and learning from the low moments in life.D．Buying yourself quality things to live.Teenagers across the world eagerly await the day they become legal adults, to be free from the dependence of their parents and to practice the full rights of their citizenship. The situation is no different in South Korea. Here, the legal age of adulthood is 19. Ten years ago, the legal age was 20, but this was lowered by a year in 2013 based on recognition of the early maturity of modern teenagers. Now, from their 19th birthday onwards, South Korean teenagers can vote, get married and work full-time.Unlike most other countries, the South Korean government celebrates this transformation into adulthood with an official “Coming-of-Age Day”, which falls on every third Monday of May. Its first written record of celebrating adulthood dates back to the Goryeo Dynasty, where King Gwangjong gifted Prince Wang Juan outfit (服装) reserved for male adults in 965.By the late Jose on Dynasty, the ceremony marking adulthood developed into a full-grown event for the middle and upper classes, celebrated by their 15-year-olds. In this period, one of the most symbolic changes that adults-to-be went through was that boys would tie their long flowing (飘逸的) hair into a topknot (结) and cover it with at all black hat made of horsehair; likewise, girls put their hair, which they let fall as single braids (辫子) in youth, up into an eat knot and set it with a long hairpin (发簪).Today, the traditional coming-of-age ceremonies still live on, supported largely by government and public interests. But a set of very different customs has also been added. Unless they apply to participate in publicly-held ceremonies or attend schools that provide these series, 19-year-olds celebrate the third Monday of May the modem way, by having a nice meal with family or drinking with their friends.12．What led to the legal age of adulthood being lowered by a year in South Korea?A．The requirement for youth’s earlier practice of voting rights.B．The determination to satisfy teenagers’ expectations.C．The plan to reduce economic pressure on families.D．The realization of youth’s earlier maturity.13．Who received South Korea’s first recorded coming-of-age celebration according to thetext?A．Frince Wang Ju.B．King Gwangjong.C．An upper-class 15-year-old in the Jose on Dynasty.D．A middle-class 15-year-old in the Goryeo Dynasty.14．What marked the important change in celebrating adulthood during the Jose on Dynasty?A．A new type of hairstyle B．A specific birthday outfit.C．Making one’s own hat with horsehair.D．Replacing short hairpins with long ones. 15．What does the last paragraph suggest?A．Publicly-held ceremonies require group application.B．Traditional ceremonies should be more widely practiced.C．Teenagers nowadays prefer to celebrate adulthood at home.D．Society has seen broadening ways of adulthood celebration.Being “a grown-up” is a pretty unclear concept, even once you’re technically “grown-up”. My career has taken its fair share of twists and turns in the past three years sinceI graduated, and in some ways I feel like I’m still only starting to figure out what I want to do.16 . So if you’re still pondering the question, here’s my advice for making the best of it.17In some ways, in decision about the future allows you to have a much more open mind about various career choices than those who’ve always known exactly what they want to do. If you limit yourself too much, you could miss the opportunity to join an exciting new startup, develop a great business idea, or try something unexpected that you might love.Accept that the landscape is always changingWhile it may have once made sense to dream about being a doctor, lawyer, or professional ballet dancer, many of the jobs open to you now are ones you didn’t know about as a child. 18 . The job that fits you could be one you’d never even imagined at age 10, 25, or even 40.Redefine (重新定义) “grown-up”The concept of being a “grown-up” means that there’s a finish line to a personal and professional life that is, in reality, always changing. 19 this discovery will likely be the result of much trial and error, and you’ll probably find yourself fighting for new goalsthroughout much of your life.20 Being grown-up means being satisfed with the journey you’ve chosen and enjoying the many different roads you’ve followed.A．Do somethingB．Embrace uncertaintyC．Even if the job has its disadvantagesD．The Internet transformed the professional landscape in totally unexpected waysE．Truthfully, that grown-up person your childhood self once dreamed of might not exist F．And I’ve learned that it’s OK not to know what you want to be even at a grown-up ageG．While you can hope that you’ll one day find a hobby or career that you’re enthusiastic about二、完形填空The first time you make a speech is truly a special moment, and I will surely never21．A．smart B．shy C．honest D．impatient 22．A．planning B．choosing C．fearing D．promising 23．A．primary B．high C．art D．medical 24．A．list B．contribution C．note D．deal 25．A．along with B．as for C．except for D．instead of 26．A．give B．understand C．hear D．support 27．A．pain B．difference C．work D．fun 28．A．surprisingly B．proudly C．easily D．obviously 29．A．extremely B．increasingly C．occasionally D．hardly 30．A．political B．scary C．stupid D．emotional 31．A．recorded B．remembered C．shared D．taught 32．A．came across B．cared about C．applied for D．got through 33．A．pressure B．fortune C．confidence D．interest 34．A．arguing with B．depending on C．running for D．working against 35．A．thanks to B．regardless of C．in response to D．in exchange for三、语法填空rocks 45 order. If only more young people would understand that by putting away 20 percent of whatever they take in, they are creating something meaningful and lasting. We would see a generation of financially secure(经济有保障的), independent young people.四、书信写作46．假定你是李华，你的留学生好友Peter准备为本学期制定一个学习计划，于是发邮件询问你的建议。

四川省绵阳市江油中学高二语文上学期期中试题(含解析)

2018-2019学年四川省绵阳市江油中学高二（上）期中语文试卷一、现代文阅读（18分）阅读下面的文字，完成下列各题。

先秦儒家已形成比较立体、丰富的生态伦理思想。

这种思想首先体现为“乐”。

孔子非常擅长在观察自然现象时对自身社会经验进行审视和升华，自然之道和其处世之道在某个合适的时间节点产生共鸣，从而引发孔子深层的思考，其生态情怀也在类似的体悟中逐渐浓厚。

认知自然、体验自然、进而体悟人生哲理，让孔子得出“知者乐水，仁者乐山”这样的结论。

由“乐”而生“畏”。

孔子说：“天何言哉？四时行焉，百物生焉。

天何言哉！”在孔子看来，四季的轮回、万物的生长都有其运行轨迹和规律，这种力量非人力所能干涉，孔子对自然的敬畏之情也在这种感慨中毕现。

荀子则认为：“天行有常，不为尧存，不为桀亡。

”既然这种“常”的力量如此强大，非人力所能改变，聪明的做法就是顺应这种力量并对之合理利用，即荀子所讲的“制天命而用之”。

那么，该如何“制”呢？荀子较为强调见微知著、因循借力、顺时守天、因地制宜。

这种总结比起孔子体验式思维多了些理性，已试图对联系自然与人类社会的“道”进行理性阐释和总结。

在此基础上，“推人及物”的思想就产生了。

“人皆有不忍人之心”是孟子生态道德的基础，“不忍心”推广于自然万物就成了推人及物的生态道德。

如果说“老吾老以及人之老，幼吾幼以及人之幼，……故推恩足以保四海，不推恩无以保妻子”是简单适用于人类社会的推恩思维，是简单的换位思考、推己及人，那么，孟子的“亲亲而仁民，仁民而爱物”则已拓展为推人及物了。

荀子也说：“物也者，大共名也……推而别之，别则有别，至于无别然后至。

”他认为自然万物有着千丝万缕的联系，有共性，有同质性；同时，根据某种特质，又可在共性的基础上区分差异，剥离出异质性。

这种异质性基础上的同质性是推人及物的逻辑基石。

在生态实践中，先秦儒者非常强调“时禁”与适度消费。

孟子和荀子都注意到“时禁”的良好效益，可保证后续消费的“不可胜食”“不可胜用”。

四川省绵阳市江油中学2018-2019学年高二9月月考试题(语文)

第I卷一、现代文阅读(一)论述类文本阅读(本题共3小题，9分)阅读下文，完成1-3小题诸子之学，兴起于先秦，当时一大批富有创见的思想家喷涌而出，蔚为思想史之奇观。

在狭义上，诸子之学与先秦时代相联系；在广义上，诸子之学则不限于先秦而绵延于此后中国思想发展的整个过程，这一过程至今仍没有终结。

诸子之学的内在品格是历史的承继性以及思想的创造性和突破性。

“新子学”，即新时代的诸子之学，也应有同样的品格。

这可以从“照着讲”和“接着讲”两个方面来理解。

一般而言，“照着讲”，主要是从历史角度对以往经典作具体的实证性研究，诸如训诂、校勘、文献编纂等等。

这方面的研究涉及对以往思想的回顾、反思，既应把握历史上的思想家实际说了些什么，也应总结其中具有创造性和生命力的内容，从而为今天的思考提供重要的思想资源。

与“照着讲”相关的是“接着讲”。

从思想的发展与诸子之学的关联看，“接着讲”接近于诸子之学所具有的思想突破性的内在品格，它意味着延续诸子注重思想创造的传统。

以近代以来中西思想的互动为背景，“接着讲”无法回避中西思想之间的关系。

在中西之学已相遇的的背景下，“接着讲”同时展开为中西之学的交融，从更深的层次看，这种交融具体展开为世界文化的建构与发展过程。

中国思想传统与西方的思想传统都构成了世界文化的重要资源，而世界文化的发展，则以二者的互动为其重要前提。

这一意义上的“新子学”，同时表现为世界文化发展过程中创造性的思想系统。

相对于传统的诸子之学，“新子学”无疑获得了新的内涵与新的形态。

“照着讲”与“接着讲”二者无法分离，从逻辑上说，任何新思想的形成，都不能从“无”开始，它总是基于既有的思想演进过程，并需要对既有思想范围进行反思批判。

“照着讲”的意义，在于梳理以往的思想发展过程，打开前人思想的丰富内容，由此为后继思想提供理论之源，在此意义上，“照着讲”是“接着讲”的出发点。

然而，仅仅停留在“照着讲”，思想便容易止于过去，难以继续前行，可能无助于思想的创新。

四川省江油中学2022-2023学年高二下学期期中测试地理试卷(含答案)

四川省江油中学2022-2023学年高二下学期期中测试地理试卷学校：___________姓名：___________班级：___________考号：___________一、单选题下图为亚洲年均等降水量线示意图，图中①②③④为亚洲四个干旱中心。

读图完成下面小题。

1、据图可知，亚洲( )A.南部和东南部季风区降水丰富B.北部年均降水量小主要与地形有关C.年均降水量自东南向西北递减D.等降水量线的延伸方向与盛行风向一致2、图中a、b、c、d四箭头能正确表示冬季盛行风向的是( )A.aB.bC.cD.d3、下列关于干旱中心形成的主要原因的叙述，正确的是( )A.①地受索马里寒流减湿作用影响B.②地受高山阻挡，且远离海洋C.③地终年受副热带高气压带控制D.④地深居内陆，受海洋影响小读世界两区域图完成下面小题。

4、甲、乙两地冬季降水较多,共同的影响因素有( )①太阳辐射②大气环流③下垫面④暖流A.①②B.②③C.③④D.①④5、甲、乙两地所在区域的主要粮食作物相同,但耕作制度差异较大,主要影响因素是( )A.热量B.降水C.市场D.政策下图为日本北海道区域轮廓图。

读图，完成下面小题。

6、北海道东部海域为航行高风险区的最主要原因是( )A.海面冰山漂浮B.多地震，海啸频繁C.火山活动频繁D.多海雾，能见度差7、下列有关北海道的特征,叙述正确的是( )A.以山地为主,沿海多渔业资源B.东岸受季风影响,冬季降雪量大C.西岸受海洋影响,冬季气候温暖D.植被以亚寒带针叶林为主8、日本北海道与东北平原纬度大致相同，下列选项中，关于两地差异叙述正确的是( )A.北海道气候更寒冷B.北海道工业基础雄厚C.北海道降水量较小D.北海道旅游资源丰富日本东西两侧海岸冬季降雪量差距很大,靠近日本海一侧冬季降雪量远大于靠近太平洋一侧。

但据古气候学家研究发现,在距今2万年前的末次盛冰期,全球气温比现在低5-10℃,日本西侧的降雪量远小于现在。

四川省绵阳市2023-2024学年高二上学期语文期中考试试卷(含答案)1

四川省绵阳市2023-2024学年高二上学期语文期中考试试卷姓名：__________ 班级：__________考号：__________论述类文本阅读材料一小说作为一种文学形式，属于艺术之范畴，其终极旨归应为“诗”。

诗性当是小说作为一种文学形式的突出特征。

作家要艺术化地去处置现实，提升小说作为故事性文本的艺术含量，从而使其抵达更高层次的诗性彼岸。

过度地沉迷于故事性，便会遮蔽或者丧失其诗性，而堕入通俗性的歧途。

如何合理地掌握故事性和诗性之关系，应当成为小说家的第一要务。

综观中国当代小说的创作现状，诗性的缺失，正使其在背离葆有更高艺术含量的“纯文学”轨道上渐行渐远，而堕入了通俗性、庸俗化的平庸之境。

小说是当下最为繁荣的文学体裁，取得了不俗的成绩。

但一些作家似乎过多沉迷于叙述模式的借鉴和实验，陶醉于魔幻现实的营造，痴心于恢宏历史的展现，执着于玄妙故事的构思，却忽视或者漠视了小说诗性的构建。

在他们的作品中，难以找寻到诗化的现实、诗意的语言和充满诗魅的意象，而直露的现实、粗鄙的语言和意象的缺席，却占据了不小的空间。

而且，过度商业化的氛围造成了他们心态的浮躁和对利益的追逐，从而进一步加剧了小说的通俗性和庸俗化，使其几乎成了“快餐文化”的一分子。

这并不是对中国当代小说的全面否定。

中国当代小说中不乏富有诗性、艺术水准颇高的佳作，但这类作品似乎正在日益被通俗性的潮流冲刷、侵蚀。

（摘编自仕永波《小说亟待提升诗性品质》）材料二海德格尔认为，文学是人们在天地之间创造出来的崭新的诗意的世界，是借文字展示的诗意生存的生命。

日常生活是非诗意的，我们只有通过文学的引领才能到达诗意，感受无限，领悟神圣。

既然日常生活总是被非诗意遮蔽着，是庸常的、缺乏艺术质感的，而文学又必须是充满诗意的，那么，文学活动的第一步就应该是对生活进行异质化处理，也就是把客观生活改造成能够体现人生的普遍经验的、心灵化和情态化了的主客观相统一的诗意的生活。

四川省江油中学2013-2014学年高二物理上学期9月月考试题新人教版

江油中学2013—2014学年上学期高二九月月考物理试题（小英才班用）一．单项选择题（本题共12小题，每小题3分，共36分；在每小题给出的四个选项中，只有一个选项正确）1．电场中有一点P，下列说法正确的是【】A．若放在P点的点电荷的电荷量减半，则P点的场强减半B．若P点没有检验电荷，则P点的场强为零C．P点的场强越大，则同一电荷在P点受的电场力越大D．P点的场强方向为检验电荷在该点的受力方向2．把表头G改装成大量程电流表时，下列说法正确的是【】A．改装原理为并联电阻能增大通过G的电流B．改装成电流表后，表头G本身允许通过的最大电流并不改变C．改装后，表头G自身的电阻减小了D．改装后使用时，表头G的参量都发生改变，整个并联电路允许通过的电流增大了3、如图所示，有一弯管ab，其中心线是半径为R的一段圆弧，弧的圆心处有一个点电荷Q，有一束带负电的粒子流从a端的中点射入，恰能沿中心线通过弯管的粒子应为【】A、质量和速度均相同的粒子B、电量和动量均相同的粒子C、电量和动能均相同的粒子D、电量和速度均相同的粒子4．如图所示，a、b两点电势相同，电场强度也相同的是【】5．如图为竖起放置的光滑半圆孤绝缘细管的圆心O处放一点电荷，将质量为m，带电量为q的小球从圆弧管的水平直径端点由静止释放，小球沿细管滑到最低点B时，对管壁恰好无压力。

则放于圆心处的点电荷在AB弧中点处的场强大小为【】A、E=mg/qB、 E=2mg/qmg q D、不能确定C、E=3mg/q 3/6．如图所示，静止的电子在加速电压为U1的电场的作用下从O经P板的小孔射出，又垂直进入平行金属板间的电场，在偏转电压U2的作用下偏转一段距离。

现使U1加倍，要想使电子的运动轨迹不发生变化，应该使【】A．U2加倍 B．U2变为原来的4倍C．U2变为原来的2倍 D．U2变为原来的1/2倍7．有四个电源，电动势均为8V，内阻分别为1Ω、2Ω、4Ω、8Ω，今要对R = 2Ω的电阻供电，问选择内阻为多大的电源才能使R上获得的功率最大？【】A、1ΩB、2ΩC、4ΩD、8Ω8．右图是某种静电矿料分选器的原理示意图，带电矿粉经漏斗落入水平匀强电场后，分落在收集板中央的两侧．对矿粉分离的过程，下列表述正确的有【】A ．带正电的矿粉落在右侧B ．电场力对矿粉做正功C ．带负电的矿粉电势能变大D ．带电矿粉在运动过程中机械能守恒9．如图所示匀强电场E 的区域内，在O 点处放置一点电荷＋Q ， a 、b 、c 、d 、e 、f 为以O 为球心的球面上的点，aecf 平面与电场平行， bedf 平面与电场垂直，则下列说法中正确的是【】A ．b 、d 两点的电场强度相同B ．a 点的电势等于f 点的电势C ．点电荷＋q 在球面上任意两点之间移动时，电场力一定做功D ．将点电荷＋q 在球面上任意两点之间移动，从a 点移动到c 点电势能的变化量一定最大10．平行板电容器的两极板A 、B 接于电池两极，一带正电小球悬挂在电容器内部，闭合开关S ，电容器充电，这时悬线偏离竖直方向的夹角为θ，如图4所示，则【】A ．保持开关S 闭合，滑动变阻器触头P 向左移动，则θ角增大B ．保持开关S 闭合，带正电的A 极板向B 极板靠近，则θ角增大C ．开关S 断开，带正电的A 极板向B 极板靠近，则θ角增大D ．开关S 断开，同时剪断细绳，小球将做自由落体运动11．理发用的电吹风机中有电动机和电热丝，电动机带动风叶转动，电热丝给空气加热，直到热风将头发吹干．设电动机线圈电阻为R 1，它与电热丝的电阻R 2串联后接到直流电源上，电吹风机两端电压为U ，电流为I ，消耗的电功率为P ，则有【】①P ＝IU ②P ＝I 2(R 1＋R 2) ③P>IU ④P ＞I 2(R 1＋R 2)A ．①②B ．①④C ．②③D ．③④12．如图所示的电路中，灯泡A 和灯泡B 原来都是正常发光的，现在突然灯泡A 比原来变暗了些，灯泡B 比原来变亮了些，则电路中出现的故障可能是【】A ．R 3断路B ．R 1短路C ．R 2断路D ．R 1、R 2同时短路二．不定项选择题（本题共6小题，每小题3分，共18分；在每小题给出的四个选项中，有的只有一个选项正确，有的有多个选项正确，全部选对的得3分，选对但不全的得2分，有选错的得0分。

精品解析：四川省江油中学2022-2023学年高二上学期期中测试地理试题

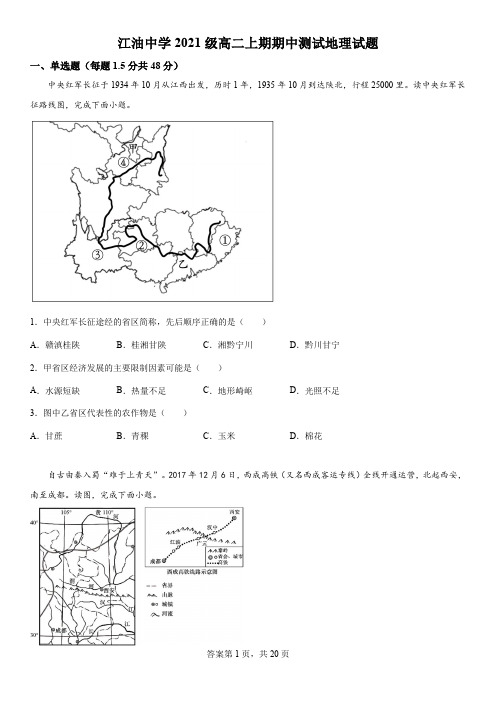
江油中学2021级高二上期期中测试地理试题一、单选题（每题1.5分共48分）中央红军长征于1934年10月从江西出发，历时1年，1935年10月到达陕北，行程25000里。

读中央红军长征路线图，完成下面小题。

1．中央红军长征途经的省区简称，先后顺序正确的是（）A．赣滇桂陕B．桂湘甘陕C．湘黔宁川D．黔川甘宁2．甲省区经济发展的主要限制因素可能是（）A．水源短缺B．热量不足C．地形崎岖D．光照不足3．图中乙省区代表性的农作物是（）A．甘蔗B．青稞C．玉米D．棉花自古由秦入蜀“难于上青天”。

2017年12月6日，西成高铁（又名西成客运专线）全线开通运营，北起西安，南至成都。

读图，完成下面小题。

4．西成高铁从西安向成都需要经过我国（）A．陕西省、甘肃省、四川省B．秦岭山区、汉江谷地、四川盆地C．内流区、外流区D．地势第一级阶梯、第二级阶梯5．西成高铁的全线贯通（）A．导致沿线地区生物多样性锐减B．进一步完善了我国西部高铁网络C．促进沿线地区矿产资源的开发D．消除了区域内地质灾害的影响6．地理环境的差异性造就了不同艺术风格的地方戏曲剧种。

西安所在的渭河平原区被称为关中地区，这里孕育了以“刚”和“粗狂”为主要艺术风格的（）A．秦腔B．越剧C．豫剧D．川剧兰州人喜面食，兰州牛肉面素有“一清、二白、三红、四绿、五黄”五大特点，即牛肉汤色清气香；萝卜片洁白纯净；辣椒油鲜红漂浮；香菜、蒜苗新鲜翠绿；面条则柔滑透黄。

下图为甘肃省年降水量分布图。

据此完成下面小题。

7．由年降水量和位置判断，兰州位于我国（）A．湿润区B．半湿润区C．干旱区D．半干旱区8．兰州人喜食面汤，除了牛肉面汤的味道鲜美外，当地气候特征可解释的是（）A．空气湿度大B．干燥多风C．暴雨天多D．阴雨天多9．当地形成牛肉和面食这种搭配。

地理角度可解释的是（）①当地环境特别适宜牦牛的生长①多民族聚居，食品种类兼具①位于农耕区和畜牧区过渡地带①当地只适合小麦生长A．①①B．①①C．①①D．①①西柏坡是河北省平山县一个马蹄形山弯中的小山村，村前是开阔而肥沃的土地，村后是群山峻岭。