高考倒计时复习第12天：三次函数

合集下载

三次函数专题(解析版)

三次函数专题一、定义：定义1、形如32(0)y ax bx cx d a =+++≠的函数，称为“三次函数”（从函数解析式的结构上命名）。

定义2、三次函数的导数232(0)y ax bx c a '=++≠，把2412b ac ∆=-叫做三次函数导函数的判别式。

由于三次函数的导函数是二次函数，而二次函数是高中数学中的重要内容，所以三次函数的问题，已经成为高考命题的一个新的热点和亮点。

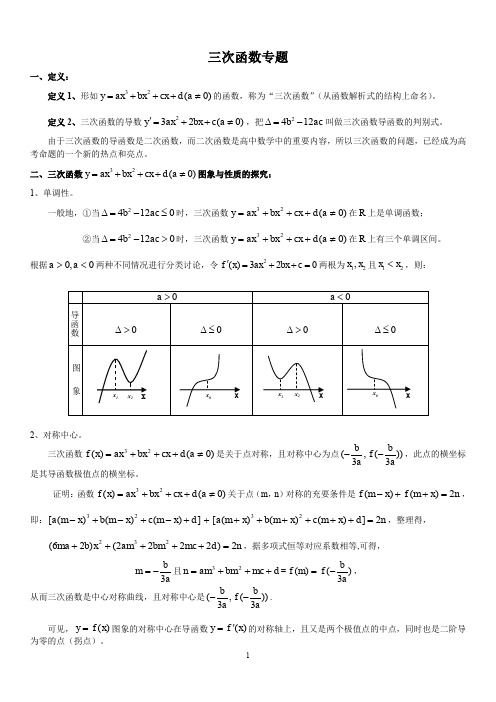
二、三次函数32(0)y ax bx cx d a =+++≠图象与性质的探究： 1、单调性。

一般地，①当24120b ac ∆=-≤时，三次函数)0(23≠+++=a d cx bx ax y 在R 上是单调函数； ②当24120b ac ∆=->时，三次函数)0(23≠+++=a d cx bx ax y 在R 上有三个单调区间。

根据0,0<>a a 两种不同情况进行分类讨论，令2()320f x ax bx c '=++=两根为12,x x 且12x x <，则：2、对称中心。

三次函数)0()(23≠+++=a d cx bx ax x f 是关于点对称，且对称中心为点))3(,3(abf a b --，此点的横坐标是其导函数极值点的横坐标。

证明：函数)0()(23≠+++=a d cx bx ax x f 关于点（m ，n ）对称的充要条件是n x m f x m f 2)()(=++-，即：])()()([23d x m c x m b x m a +-+-+-+n d x m c x m b x m a 2])()()([23=++++++，整理得，n d mc bm am x b ma 2)2222()26(232=+++++，据多项式恒等对应系数相等,可得， a b m 3-=且d mc bm am n +++=23=)3()(ab f m f -=，从而三次函数是中心对称曲线，且对称中心是))3(,3(ab f a b --. 可见，)(x f y =图象的对称中心在导函数)(x f y '=的对称轴上，且又是两个极值点的中点，同时也是二阶导为零的点（拐点）。

三次函数变化规律

三次函数的变化规律主要取决于函数的系数和自变量的值。

以下是一些可能影响三次函数变化规律的常见因素：
1.函数的系数：三次函数的系数决定了函数的开口方向、对称轴和顶点等基本性质。

例如，如果二次项系数为正，则函数图像开口向上；如果二次项系数为负，则函数图像开口向下。

2.自变量的值：自变量取不同的值时，函数值也会发生变化。

例如，当自变量取对称轴的值时，函数取得最值。

3.函数的导数：导数可以反映函数的变化速度和方向。

通过求导可以找到函数的极值点、拐点等关键点，从而更好地了解函数的变化规律。

4.函数的奇偶性：奇函数和偶函数的性质不同，奇函数关于原点对称，偶函数关于y轴对称。

这些对称性质也会影响函数的变化规律。

综上所述，三次函数的变化规律是一个复杂的问题，需要考虑多个因素的综合影响。

要了解更多关于三次函数的变化规律，建议查阅数学专业书籍或咨询数学专业人士。

专题14 三次函数(学生版) -2025年高考数学压轴大题必杀技系列导数

专题14 三次函数函数与导数一直是高考中的热点与难点, 我们知道二次函数是重要的且具有广泛应用的基本初等函数,学生对此已有较为全面、系统、深刻的认识,并在某些方面具备了把握规律的能力,由于三次函数的导数是二次函数,我们可以利用二次函数深入研究三次函数的图象与性质,这使得三次函数成为高考数学的一个热点.(一)三次函数的单调性由于三次函数()f x 的导数()f x ¢是二次函数,我们可以利用()0f x ¢=根的情况及根的分布来研究三次函数的单调性,特别是含有参数的三次函数的单调性通常要借助二次方程根的分布求解.【例1】（2024届青海省部分学校高三下学期联考）已知函数()()3211132f x x mx m x =+-+．(1)讨论()f x 的单调性；(2)若()f x 有3个不同的零点,求m 的取值范围．【解析】（1）()()()()2111f x x mx m x x m =+-+=-++¢,令()0f x ¢=,解得1x =或1x m =--,①当11m -->,即2m <-时,由()0f x ¢>得1x <或1x m >--；由()0f x ¢<得11x m <<--,所以()f x 在(),1¥-和()1,m ¥--+上单调递增；在()1,1m --上单调递减；②当11m --=,即2m =-时,()0f x ¢³恒成立,所以()f x 在R 上单调递增；③当11m --<,即2m >-时,由()0f x ¢>得1x >或1x m <--；由()0f x ¢<得11m x --<<,所以()f x 在(),1m ¥---和()1,¥+上单调递增；在()1,1m --上单调递减；综上,当2m <-时,()f x 在(),1¥-和()1,m ¥--+上单调递增；在()1,1m --上单调递减；当2m =-时,()f x 在R 上单调递增；当2m >-时,()f x 在(),1m ¥---和()1,¥+上单调递增；在()1,1m --上单调递减.（2）因为()f x 有3个零点,所以2m ¹-,当2m >-时,极大值()()221163m f m m æö--=++ç÷èø；极小值()12123f m =--,所以()22106312023m m m ìæö++>ç÷ïïèøíï--<ïî,解得43m >-且1m ¹-,当2m <-时,极大值()12123f m =--；极小值()()221163m f m m æö--=++ç÷èø,所以()22106312023m m m ìæö++<ç÷ïïèøíï-->ïî,解得4m <-,综上,m 的取值范围为()()4,4,11,3¥¥æö--È--È-+ç÷èø.(二)过平面上一点P 作三次函数图象的切线的条数1.此类问题一般是先设出切点Q ()(),t f t ,写出曲线()f x 在x t =处的切线方程,把点P 坐标代入,整理出一个关于t 的三次方程,该方程实根个数就是切线条数.2.以三次函数为 bx ax x f +=3)(为例,研究一下三次函数的切线问题：若M （x 1,y 1）是三次曲线bx ax x f +=3)(上的任一点,设过M 的切线与曲线y=f （x ）相切于（x 0,y 0）,则切线方程为))((000x x x f y y -¢=-,因点M 上此切线上,故))((01001x x x f y y -¢=-,又13110300,bx ax y bx ax y +=+=,所以))(3()(0120030131x x b ax bx ax bx ax -+=+-+,整理得：0)2()(10210=+-x x x x ,解得,10x x =或210x x -=.综上所述,当点M 是对称中心即01=x 时,过点M 作曲线的切线切点是惟一的,且为M ,故只有一条切线；当点M 不是对称中心即01¹x 时,过点M 作曲线的切线可产生两个不同的切点,故必有两条切线,其中一条就是以M 为切点（亦即曲线在点M 处）的切线. 由此可见,不仅切线与曲线的公共点可以多于一个,而且过曲线上点的切线也不一定惟一【例2】（2024届福建省泉州市高中毕业班5月适应性练习）已知函数()()32220f x ax x x a a =--+³．(1)当1a =时,若直线3y x b =-+与曲线()y f x =相切,求b ；(2)若直线22y x =--与曲线()y f x =恰有两个公共点,求a ．【解析】（1）当1a =时,()32221f x x x x =--+,()2342f x x x ¢=--,因为直线3y x b =-+与曲线()y f x =相切,设切点为()00,x y ,则切线斜率()2000342k f x x x ¢==--,可得2000032000034233221x x y x by x x x ì--=-ï=-+íï=--+î,解得00121x y b =ìï=-íï=î或00134273127x y b ì=ïïï=íïï=ïî,所以1b =或3127b =．（2）因为直线22y x =--与曲线()y f x =恰有两个公共点,所以方程322222ax x x a x --+=--,即方程()()321210a x x +--=有两个不等实根,因为=1x -是方程()()321210a x x +--=的一个根；当1x ¹-时,方程可化为()2220ax a x a -+++=（*）,依题意,方程（*）有不等于1-的唯一根,因为0a ³,若0a =,则（*）即220x -+=,1x =,满足条件；若0a >,则由()()22202420a a a a a a ++++¹ìïí=+-+=ïîV ,解得：23a =．综上所述,0a =或23a =．【例3】（2024届江苏省南通市高三上学期期初质量监测）已知函数()()320f x ax bx cx a =++>的极小值为2-,其导函数()f x ¢的图象经过()1,0A -,()10B ,两点.(1)求()f x 的解析式；(2)若曲线()y f x =恰有三条过点()1,P m 的切线,求实数m 的取值范围.【解析】（1）()232f x ax bx c ¢=++,因为0a >,且()f x ¢的图象经过()1,0A -,()10B ,两点.所以当(),1x Î-¥-时,()0f x ¢>,()f x 单调递增；当()1,1x Î-时,()0f x ¢<,()f x 单调递减；当()1,x Î+¥时,()0f x ¢>,()f x 单调递增.所以()f x 在1x =处取得极小值,所以()12f a b c =++=-,又因为()10f ¢-=,()10f ¢=,所以320a b c -+=,320a b c ++=,解方程组3203202a b c a b c a b c -+=ìï++=íï++=-î得1a =,0b =,3c =-,所以()33f x x x =-.（2）设切点为()00,x y ,则30003y x x =-,因为()233f x x ¢=-,所以()20033f x x ¢=-,所以切线方程为()()()320000333y x x x x x --=--,将()1,P m 代入上式,得32002330x x m -++=.因为曲线()y f x =恰有三条过点()1,P m 的切线,所以方程322330x x m -++=有三个不同实数解.记()32233g x x x m =-++,则导函数()()26661g x x x x x ¢=-=-,令()0g x ¢=,得0x =或1.列表：x(),0¥-0()0,11()1,+¥()g x ¢+0-+()g x ↗极大↘极小↗所以()g x 的极大值为()03g m =+,()g x 的极小值为()12g m =+,所以()()0010g g ì>ïí<ïî,解得32m -<<-.故m 的取值范围是()3,2--.(三)三次函数的极值三次函数()f x 的极值点就是二次函数()f x ¢的零点,所以与三次函数极值有关的问题常借助“三个二次”的关系求解.【例4】（2024届山东省实验中学高三二模）已知函数()()2()(,,)f x x a x b a b a b =--Î<R .(1)当1,2a b ==时,求曲线()y f x =在点()()22f ,处的切线方程；(2)设12,x x 是()f x 的两个极值点,3x 是()f x 的一个零点,且3132,x x x x ¹¹.是否存在实数4x ,使得1234,,,x x x x 按某种顺序排列后构成等差数列？若存在,求4x ；若不存在,说明理由.【解析】（1）当1,2a b ==时,()()2(1)2f x x x =--,则()()()()()()22121135f x x x x x x ¢=--+-=--,故()21f ¢=,又()20f =,所以曲线()y f x =在点()2,0处的切线方程为2y x =-；（2）()()()222()()33a b f x x a x b x a x a x +æö¢=--+-=--ç÷èø,由于a b <,故23a ba +<,令()0f x ¢>,解得x a <或23a b x +>；令()0f x ¢<,解得23a ba x +<<；可知()y f x =在2,3ab a +æöç÷èø内单调递减,在()2,,,3a b a +æö-¥+¥ç÷èø内单调递增,所以()f x 的两个极值点为2,3a b x a x +==,不妨设122,3a bx a x +==,因为3132,x x x x ¹¹,且3x 是()f x 的一个零点,故3x b =.又因为22233a b a b a b ++æö-=-ç÷èø,故4122233a b a b x a ++æö=+=ç÷èø,此时22,,,33a b a ba b ++依次成等差数列,所以存在实数4x 满足题意,且423a bx +=.(四)三次函数的零点1.若三次函数()f x 没有极值点,则()f x 有1个零点；2. 三次函数()f x 有2个极值点12,,x x ,则()()120f x f x >时()f x 有1个零点；()()120f x f x =时()f x 有2个零点；()()120f x f x <时()f x 有3个零点.【例5】（2023届江西省赣抚吉十一校高三第一次联考）已知函数322()432f x x mx m x =--+,其中0m ³.(1)若()f x 的极小值为－16,求m ；(2)讨论()f x 的零点个数.【解析】（1）由题得22()383(3)(3)f x x mx m x m x m ¢=--=-+,其中0m ³,当0m =时,()0f x ¢³,()f x 单调递增,()f x 无极值；当0m >时,令()0f x ¢>,解得3m x <-或3x m >；令()0f x ¢<,解得33mx m -<<,所以()f x 的单调递减区间为,33m m æö-ç÷èø,单调递增区间为,3m æö-¥-ç÷èø,()3,m +¥,所以当3x m =时,()f x 取得极小值()33218f m m =-,所以321816m -=-,解得1m =.（2）由（1）知当0m >时,()f x 的极小值为()33218f m m =-,()f x 的极大值为31420327m f m æö-=+>ç÷èø,当32180m -<,即m >时,()f x 有三个零点,如图①曲线；当32180m -=,即m =,()f x 有两个零点,如图②曲线；当32180m ->,即0<,()f x 有一个零点,如图③曲线；当0m =时,()32f x x =+,易知()f x 有一个零点. 综上,当0m £<()f x 有一个零点；当m ,()f x 有两个零点；当m >,()f x 有三个零点.(五)三次函数图象的对称性三次函数32()(0)f x ax bx cx d a =+++¹的图象有六种,如图：10010200200f x ()x10010200200f x ()x100102000200f x ()x对函数32()(0)f x ax bx cx d a =+++¹,原函数的极值点与单调性与导函数的正负有关,所以容易发现导函数中的参数当a 为正时,原函数的图象应为上图中的（1）、（3）、（5、（4）、（6）三种情况.当0D >时,二次方程()0f x ¢=有两相异实根1x ,故函数()f x 存在两个极值点,图象为上图中的（3）、（4,且在根的两边()f x ¢的符号相同,这时函数()f x 只存在驻点1）、（2）两种,当0D <时；方程()0f x ¢=无实根,()f x ¢）两种.仔细观察图象,我们还不难发现三次函数是中心对称曲线,这一点可以得到进一步的验证:设n x m f x m f 2)()(=++-,得n d x m c x m b x m a d x m c x m b x m a 2])()()([])()()([2323=++++++++-+-+-整理得,n d mc bm am x b ma 2)2222()26(232=+++++.据多项式恒等对应系数相等,可得ab m 3-=且d mc bm am n +++=23,从而三次函数是中心对称曲线,且由)(m f n =知其对称中心))(,(m f m 仍然在曲线上.而abm 3-=是否具有特殊的意义？对函数)(x f 进行两次求导,b ax x f 26)(+=¢¢再令等于0,得abx 3-=,恰好是对称中心的横坐标,这可不是巧合,因为满足0)(=¢¢m f 的m 正是函数拐点的横坐标,这一性质刚好与图象吻合.【例6】对于三次函数32()(0)f x ax bx cx d a =+++¹,给出定义：设()f x ¢是函数()y f x =的导数,()f x ¢¢是()f x ¢的导数,若方程()0f x ¢¢=有实数解0x ,则称点00(,())x f x 为函数()y f x =的“拐点”．某同学经过探究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心,且“拐点”就是对称中心．若32115()33212f x x x x =-+-,请你根据这一发现.（1）求函数()f x 的对称中心；（2）计算122020()(()()20212021202120213f f f f +++×××+.【解析】（1）2()3,()21f x x x f x x ¢¢¢=-+\=-Q ,令()0f x ¢¢=,即210x -=,解得12x =,321111115()(()3123222212f \=´-´+´-=,由题中给出的结论,可知函数()f x 的对称中心为1(,1)2.（2）由（1）知函数32115()33212f x x x x =-+-的对称中心为1(,1)2,所以11()()222f x f x ++-=,即()(1)2f x f x +-=,故120202201920201()()2,(()2,(()2202120212021202120212021f f f f f f +=+=×××+=,所以1220201()()((220202020202120212021202312f f f f +++×××+=´´=. (六)三次函数与韦达定理的交汇由于三次函数的导数是二次函数,而二次函数常与韦达定理交汇,故有时可以用定理交汇处理三次函数问题【例7】设21,x x 是函数)0(23)(223>-+=a x a xb x a x f 的两个极值点,且2||||21=+x x(1)求a 的取值范围； (2)求证：934||£b .【解析】(1)22')(a bx ax x f -+=,'12,()0x x f x =是的两个实根,又a ＞0a bx x a x x -=+<-=2121,0,a ab x x x x 4||||||222121+=-=+由2||||21=+x x 得22232244444(1)b a b a a a a a +==-=-，即1002£<\³a b Q (2)设,44)(322a a a gb -==则)32(4128)(2'a a a a a g -=-=22()(0)(1)33g a 在，在单调递增，在，上单调递增max 216[()](327g a g ==,934£\b 【例8】（2024年2月第二届“鱼塘杯”高考适应性练习）对三次函数()32,0f x ax bx cx d a =+++¹,如果其存在三个实根123,,x x x ,则有123122331123,,b c dx x x x x x x x x x x x a a a++=-++==-.称为三次方程根与系数关系.(1)对三次函数()32f x ax bx cx d =+++,设()()g x f x =¢,存在0x ÎR ,满足()()()0000f x g x g x =¹¢=.证明：存在10x x ¹,使得()()()210f x a x x x x =--；(2)称()f x 是[],m M 上的广义正弦函数当且仅当()f x 存在极值点()12,,x x m M Î,使得()(){}()(){}12,,f x f x f m f M =.在平面直角坐标系xOy 中,(),A a b 是第一象限上一点,设()()()2,()4bf x x a xg x x a x b x =-+=--.已知()g x 在()0,a 上有两根03x x <.（i ）证明：()f x 在()0,¥+上存在两个极值点的充要条件是327a b >；（ii ）求点A 组成的点集,满足()f x 是[]03,x x 上的广义正弦函数.【解析】（1）因为()00f x =,所以不妨设()()()()()012,0f x a x x x x x x a =---¹,所以()()()()()()()()()010212,0g x f x a x x x x a x x x x a x x x x a ¢==--+--+--¹,因为()()000g x g x =¢¹,所以()()()()()0001020,0g x f x a x x x x a ¢==--=¹,所以不妨取02x x =满足题意,且此时必有10x x ¹,否则若0x x =,则有()()30f x a x x =-,()()()203g x f x a x x ¢==-,()()06g x a x x ¢=-,而此时()()00060g x a x x ¢=-=与已知()()000g x g x =¢¹矛盾,综上所述,存在10x x ¹,使得()()()210f x a x x x x =--.（2）（i ）(),A a b 是第一象限上一点,所以0,0a b >>,因为()()b f x x a x x =-+,所以()()32222,0,0b x ax b f x a x a b x x-+-¢=--=>>,设()322h x x ax b =-+-,则()00h b =-<,而x ®-¥时,()h x ®+¥,x ®+¥时,()h x ®-¥,所以()3220h x x ax b =-+-=存在负根,因为()f x 在()0,¥+上存在两个极值点,等价于方程()3220x ax bf x x -+-¢==在()0,¥+上有两个根,等价于方程()3220h x x ax b =-+-=在()0,¥+上存在两个根,注意到三次方程最多有3个根,所以方程()3220h x x ax b =-+-=有一个负根,两个不同的正根,而()262h x x ax ¢=-+,当03a x <<时,()2620h x x ax ¢=-+>,()h x 单调递增,当3a x >时,()2620h x x ax ¢=-+<,()h x 单调递减,所以当且仅当33320327927a a a a h b b æö=-+-=->ç÷èø,即当且仅当327a b >,综上所述,命题（i ）得证；（ii ）容易验证,327a b >时,()0g x =也恰好有两个正根03,x x ,此时：由于对0x >来说,()0f x ¢=等价于3220x ax b -+=,()0g x =等价于()240x a x b --=,所以对0x >,如果()0g x =,那么()()()32202444a x a a x x a x a x f b b -----æö¢=-+=+=ç÷èø,这意味着3012,22a x a x x x --==,然后,对两个不相等的正数()()()(),,b u v f u f v u v a u v uv éù-=--+-êúëû,所以()()f u f v =当且仅当bu v a uv++=,那么如果1t x =或2x ,就有02a t x -=或3x ,故()()2f t g a t ¢=-,此时()()()()()()2322222222b t a t b b t at bt a t a t a a a t a t t a t t a t t a t ---++-+=-+=+=+=----,所以()()2f t f a t =-,这意味着()()()()0213,f x f x f x f x ==,最后,由于()()322m x h x x ax b =-=-+有一个极值点3a x =,所以12,x x 都不等于3a （12,x x 是不相等的正零点,同时该方程还有另一个负零点,但3a只要是根就是二重的,所以3a不可能是根）,这就说明1302,x x x x ¹¹,结合()f x 的单调性以及()()()()0213,f x f x f x f x ==,必有0123x x x x <<<,所以此时()f x 一定是广义正弦函数,综上所述,满足题意的(){}3,|27A a b ab =>.【例1】（2024届福建省泉州市高三5月适应性练习）已知函数()()32220f x ax x x a a =--+³．(1)当1a =时,若直线3y x b =-+与曲线()y f x =相切,求b ；(2)若直线22y x =--与曲线()y f x =恰有两个公共点,求a ．【解析】（1）当1a =时,()32221f x x x x =--+,()2342f x x x ¢=--,因为直线3y x b =-+与曲线()y f x =相切,设切点为()00,x y ,则切线斜率()2000342k f x x x ¢==--,可得2000032000034233221x x y x by x x x ì--=-ï=-+íï=--+î,解得00121x y b =ìï=-íï=î或00134273127x y b ì=ïïï=íïï=ïî,所以1b =或3127b =．（2）因为直线22y x =--与曲线()y f x =恰有两个公共点,所以方程322222ax x x a x --+=--,即方程()()321210a x x +--=有两个不等实根,因为=1x -是方程()()321210a x x +--=的一个根；当1x ¹-时,方程可化为()2220ax a x a -+++=（*）,依题意,方程（*）有不等于1-的唯一根,因为0a ³,若0a =,则（*）即220x -+=,1x =,满足条件；若0a >,则由()()22202420a a a a a a ++++¹ìïí=+-+=ïîV ,解得：23a =．综上所述,0a =或23a =．【例2】（2024届福建省泉州第五中学高考热身测试）已知函数()32,f x x ax a =-+ÎR .(1)若2x =-是函数()f x 的极值点,求a 的值,并求其单调区间；(2)若函数()f x 在1,33éùêúëû上仅有2个零点,求a 的取值范围．【解析】（1）()23f x x a =¢-,()2120f a =¢--=,得12a =,当12a =时,()23120f x x ¢=-=,得2x =-或2x =,()(),,x f x f x ¢的变化情况如下表所示,x(),2¥--2-()2,2-2()2,¥+()f x +0-+()f x ¢增区间极大值18减区间极小值14-增区间所以函数()f x 的增区间是(),2¥--和()2,¥+,减区间是()2,2-；（2）令()320f x x ax =-+=,1,33x éùÎêúëû,得3222x a x x x+==+,令()22g x x x =+,1,33x éùÎêúëû,()()32221220x g x x x x-=-==¢,得1x =,如下表,x131,13æöç÷èø1()1,33()g x ¢-0+()g x 559减区间极小值3增区间293因为函数()f x 在1,33éùêúëû上仅有2个零点,即y a =与()y g x =有2个交点,如图：即5539a <£.【例3】（2024届陕西省铜川市高三下学期模拟）已知函数()()322312R h x x x x m m =+-+Î的一个极值为2-．(1)求实数m 的值；(2)若函数()h x 在区间3,2k éùêúëû上的最大值为18,求实数k 与m 的值．【解析】（1）由()()322312R h x x x x m m =+-+Î,得()()()26612621h x x x x x ¢=+-=+-,令()0h x ¢=,得2x =-或1x =；令()0h x ¢<,得2<<1x -；令()0h x ¢>,得<2x -或1x >．所以函数()h x 有两个极值()2h -和()1h ．若()22h -=-,得()322(2)3(2)1222m ´-+´--´-+=-,解得22m =-；若()12h =-,得3221311212m ´+´-´+=-,解得5m =．综上,实数m 的值为－22或5．（2）由（1）得,()(),h x h x ¢在区间3,2æù-¥çúèû的变化情况如下表所示：x(),2-¥-2-()2,1-131,2æöç÷èø32()h x ¢+－+()h x Z 极大值20m +]极小值7m -Z92m -由表可知,①当312k £<时,函数()h x 在区间3,2k éùêëû上单调递增,所以最大值为3922h m æö=-ç÷èø,其值为253-或12,不符合题意；②当2k =-时,函数()h x 在()2,1-上单调递减,在31,2æöç÷èø上单调递增,因为()220h m -=+,3922h m æö=-ç÷èø,()322h h æö>ç÷èø,所以()h x 在3,2k éùêúëû上的最大值为()220h m -=+,其值为2-或25,不符合题意；③当2k <-时,函数()h x 在(),2k -上单调递增,在()2,1-上单调递减,在31,2æöç÷èø上单调递增,因为()220h m -=+,3922h m æö=-ç÷èø,()322h h æö>ç÷èø,所以()h x 在3,2k éùêúëû上的最大值为()220h m -=+,其值为2-或25,不符合题意；④当21k -<<时,()h x 在(),1k 上单调递减,在31,2æöç÷èø上单调递增,若()h x 在区间3,2k éùêúëû上的最大值为3922h m æö=-ç÷èø,其值为12或253-,不符合题意,又因为若22m =-,则()2202h m -=+=-．那么,函数()h x 在区间3,2k éùêúëû上的最大值只可能小于－2,不合题意,所以要使函数()h x 在区间3,2k éùêúëû上的最大值为18,必须使()32231218h k k k k m =+-+=,且5m =,即()322312518h k k k k =+-+=．所以322312130k k k +--=,所以3222213130k k k k k +++--=．所以()()()22111310kk k k k +++-+=,所以()()221310k k k +-+=．所以22130k k +-=或10k +=,所以k =10k +=．因为21k -<<,所以k =舍去．综上,实数k 的值为1,m -的值为5．【例4】（2023届江苏省徐州市睢宁县高三下学期5月模拟）已知函数32()2f x x mx =-+,R m Î,且()|()|g x f x =在(0,2)x Î上的极大值为1．(1)求实数m 的值；(2)若()b f a =,()c f b =,()a f c =,求,,a b c 的值．【解析】（1）2()|2|g x x x m =-,02x ££,① 0m £时,32()2g x x mx =-,∴2()620g x x mx ¢=-≥,无极值．② 4m ³时,32()2g x x mx =-+,∴()2(3)g x x m x ¢=-,当23m³,即6m ³时,()0g x ¢³,无极大值；当46m £<时,3m x <时,()0g x ¢>；23mx <<时,()0g x ¢<,∴()g x 在3m x =处取极大值,即3(1327m m g ==,∴3m =,舍去．③04m <<时,()32322,022,22m x mx x g x m x mx x ì-+££ïï=íï-<£ïî,∴()()()23,0223,22m x m x x g x m x x m x ì-££ïï=íï-<£î¢ï,03m x <<时,()0g x ¢>；32m m x <<时,()0g x ¢<；22mx <<时,()0g x ¢>．∴()g x 在3m x =处取极大值3127m =,∴3m =符合题意．综上,3m =．（2）由（1）可知,32()23f x x x =-+,()2()6661f x x x x x =-+=-+¢,令()0f x ¢>可得10x -<<,令()0f x ¢<可得1x >或0x <,如图所示．① 当0a <时,()0b f a =>,当302b <≤时,0()1c f b <=≤,则()0a f c =>,矛盾；当32b >时,()0c f b =<,∴()0a f c =>,矛盾．② 当0a =时,符合题意．③ 当102a <<时,102x <<时,()f x x <,∴10()2b f a a <=<<,则10()2c f b b <=<<,10()2a f c c <=<<,∴a cb a <<<,矛盾．④ 当12a =时,符合题意．⑤ 当112a <<时,112x <<时,()f x x >,∴11()2b f a a >=>>,则11()2c f b b >=>>,11()2a f c c >=>>,∴a cb a >>>,矛盾．⑥ 当1a =时,符合题意．⑦ 当312a <£时,0()1b f a =<≤,则0()1c f b =<≤,∴()1a f c =<,与1a >矛盾．⑧ 当32a >时,()0b f a =<,()0c f b =>,∴()1a f c =≤,与32a >矛盾．综上,0abc ===,或12a b c ===,或1a b c ===．【例5】（2023届重庆市第十一中学校高三上学期11月质量检测）已知函数()3233f x x x ax =-++,()f x 在1x 处取极大值,在2x 处取极小值.(1)若0a =,求函数()f x 的单调区间；(2)在方程()()1f x f x =的解中,较大的一个记为3x ,在方程()()2f x f x =的解中,较小的一个记为4x ,证明：4132x x x x --为定值.【解析】（1）当0a =时,()3233f x x x =-+,定义域为R,()236f x x x ¢=-,当()0f x ¢>时,2x >或0x <；当()0f x ¢<时,02x <<；即函数()f x 的单调增区间为(),0¥-,()2,+¥；单调减区间为(0,2).（2）由()236f x x x a ¢=-+,根据题意,得2360x x a -+=的两根为12,x x ,且12x x <,即36120a D =->,得3a <,122x x +=,所以121x x <<,因为()()1f x f x =,则32321113333x x ax x x ax -++=-++,可知323211133x x ax x x ax -+=-+,因为()10f x ¢=,即21163a x x =-,即()()()()233222211111111133323230x x x x ax ax x x x x x x x x x x x éù-+-+-=-+--+=-+-=ëû,可知3132x x =-,同理,由()()2f x f x =,可知()()()()233222222222222233323230x x x x ax ax x x x x x x x x x x x éù-+-+-=-+--+=-+-=ëû；得到4232x x =-,所以()1412123212111232113211x x x x x x x x x x x x ------====------.【例6】已知函数3211()(0)32f x ax bx cx a =++>．(1)若函数()f x 有三个零点分别为1x ,2x ,3x ,且1233x x x ++=-,129x x =-,求函数()f x 的单调区间；(2)若1(1)2f a ¢=-,322a c b >>,证明：函数()f x 在区间(0,2)内一定有极值点；(3)在（2）的条件下,若函数()f x求ba的取值范围．【解析】（1）因为函数3221111()()(0)3232f x ax bx cx x ax bx c a =++=++>,又1233x x x ++=-,129x x =-,则30x =,123x x +=-,129x x =-因为12,x x 是方程211032ax bx c ++=的两根,则332b a -=-,39c a =-,得2ba=,3c a =-,所以222()()(23)(1)(3)b c f x ax bx c a x x a x x a x x aa¢=++=++=+-=-+．令()0f x ¢=解得：1x =,3x =-当()0f x ¢>时,3x <-或1x >,当()0f x ¢<时,31x -<<,故()f x 的单调递减区间是(3,1)-,单调递增区间是(,3)-¥-,(1,)+¥．（2）因为2()f x ax bx c ¢=++,1(1)2f a ¢=-,所以12a b c a ++=-,即3220a b c ++=．又0a >,322a c b >>,所以30a >,20b <,即0a >．0b <．于是1(1)02f a ¢=-<,(0)f c ¢=, (2)424(32)f a b c a a c c a c ¢=++=-++=-．①当0c >时,因为(0)0f c ¢=>,1(1)02f a ¢=-<,而()f x ¢在区间(0,1)内连续,则()f x ¢在区间(0,1)内至少有一个零点,设为x m =,则在(0,)x m Î,()0f x ¢>,()f x 单调递增,在(,1)x m Î,()0f x ¢<,()f x 单调递减,故函数()f x 在区间(0,1)内有极大值点x m =； ②当0c £时,因为1(1)02f a ¢=-<, (2)0f a c ¢=->,则()f x ¢在区间(1,2)内至少有一零点．设为x n =,则在(1,)x n Î,()0f x ¢<,()f x 单调递减,在(,2)x n Î,()0f x ¢>,()f x 单调递增,故函数()f x 在区间(1,2)内有极小值点．综上得函数()f x 在区间(0,2)内一定有极值点．（3）设m ,n 是函数的两个极值点,则m ,n 也是导函数2()0f x ax bx c ¢=++=的两个零点,由（2）得3220a b c ++=,则b m n a +=-,32c bmn a a ==--．所以||m n -=由已知³,则两边平方得2(2)23b a ++³,得出21b a +³,或21b a +£-,即1b a ³-,或3ba£-,又232c a b =--,322a c b >>,所以3322a a b b >-->,即334a b a -<<-．因为0a >,所以334b a -<<-．综上分析,b a的取值范围是[1-,3)4-．1.（2024届江苏省连云港市高三下学期4月阶段测试）已知函数()32123f x x x mx n =-++在1x =时取得极值．(1)求实数m 的值；(2)存在[]2,4x Î,使得()2f x n >成立,求实数n 的取值范围．2.设函数()()()31f x x ax b x =---ÎR ,其中,a b 为实常数．(1)若3a =,求()f x 的单调区间；(2)若()f x 存在极值点0x ,且()()10f x f x =其中10x x ¹．求证：1023x x +=；3.（2024届海南省琼中县高三上学期9月全真模拟）已知函数()()24f x x x m =-,0m >．(1)当4m =时,求()f x 在[]1,1-上的值域；(2)若()f x 的极小值为2-,求m 的值．4.（2024届贵州省贵阳第一中学高三上学期适应性月考）已知函数()323f x x x =-.(1)求函数()y f x =在0x =处的切线方程；(2)若过点()1,P t -存在3条直线与曲线()y f x =相切,求t 的取值范围；(3)请问过点()0,0A ,()1,1B --,()1,3C -,()1,1D -,()1,2E -分别存在几条直线与曲线()y f x =相切？（请直接写出结论,不需要证明）5. （2024届内蒙古包头市高三上学期调研）已知函数3219()32f x x ax x =-++．(1)讨论()f x 的单调性；(2)若()()F x f x x =-有2个零点,求a 的值．（注：()3322()x a x a x ax a -=-++）6．（2024届江苏省南通市模拟预测）设0a >,函数3()21f x ax x =-+．(1)当1a =时,求过点(0,1)-且与曲线()y f x =相切的直线方程：(2)12,x x 是函数()f x 的两个极值点,证明：()()12f x f x +为定值．7．已知曲线()33f x x x l =-+在点()()A m f m ，处的切线与曲线的另外一个交点为B P ，为线段A B 的中点,O 为坐标原点．(1)求()f x 的极小值并讨论()f x 的奇偶性．(2)直线OP 的斜率记为k ,若()0,2m "Î,18k ³,求证：7l £-．8．设函数()321132f x x x ax =-+,a ÎR ．(1)若2x =是()f x 的极值点,求a 的值,并讨论()f x 的单调性．(2)已知函数()()21223g x f x ax =-+,若()g x 在区间()0,1内有零点,求a 的取值范围．(3)设()f x 有两个极值点1x ,2x ,试讨论过两点()()11,x f x ,()()22,x f x 的直线能否过点()1,1,若能,求a 的值；若不能,说明理由．9．已知函数()314f x x ax =++,()ln g x x =-,用{}min ,m n 表示m ,n 中的最小值,设函数()()(){}()min ,0h x f x g x x =>,讨论()h x 零点的个数．10．（2024届青海省部分学校高三下学期联考）已知函数()()3211132f x x mx m x =+-+．(1)讨论()f x 的单调性；(2)若()f x 有3个不同的零点,求m 的取值范围．11．（2023届上海市嘉定区高三三模）已知函数32()(R)f x x bx cx b c =++Î、,其导函数为()f x ¢,(1)若函数()f x 有三个零点123x x x 、、,且123133,9x x x x x ++==-,试比较(3)(0)f f -与3(2)f ¢的大小.(2)若(1)2f ¢=-,试判断()f x 在区间(0,2)上是否存在极值点,并说明理由.(3)在（1）的条件下,对任意的,R m n Î,总存在[0,3]x Î使得|()|f x mx n t ++³成立,求实数t 的最大值.12.设函数()3213f x x a x b =-+,其中a ,b 为常数．(1)讨论()f x 的单调性；(2)若函数()f x 有且仅有3个零点,求3b a 的取值范围．13．（2024届湖南省岳阳市高三教学质量监测三）已知ABC V 的三个角,,A B C 的对边分别为,,a bc 且2c b =,点D 在边BC 上,AD 是BAC Ð的角平分线,设AD kAC =（其中k 为正实数）．(1)求实数k 的取值范围；(2)设函数325()22b f x bx cx =-+-①当k =时,求函数()f x 的极小值；②设0x 是()f x 的最大零点,试比较0x 与1的大小．。

三次函数图像与性质(解析版)

专题2-2三次函数图像与性质【题型1】求三次函数的解析式【题型2】三次函数的单调性问题【题型3】三次函数的图像【题型4】三次函数的最值、极值问题【题型5】三次函数的零点问题【题型6】三次函数图像，单调性，极值，最值综合问题【题型7】三次函数对称中心【题型8】三次函数的切线问题【题型9】三次函数根与系数的关系1/342/34【题型1】求三次函数的解析式（1）一般式：()³²f x ax bx cx d =+++（a ≠0）（2）交点式：()123()()()f x a x x x x x x =---（a ≠0）1．若三次函数()f x 满足()()()()00,11,03,19f f f f ''====，则()3f =（）A ．38B ．171C ．460D ．965【解析】待定系数法，求函数解析式设()³²f x ax bx cx d =+++，则()232f x ax bx c '=++，由题意可得：()()()()0011031329f d f a b c d f c f a b c ⎧==⎪=+++=⎪⎨==⎪⎪=+'=⎩'+，解得101230a b c d =⎧⎪=-⎪⎨=⎪⎪=⎩，则()3210123f x x x x =-+，所以()32310312333171f =⨯-⨯+⨯=.【题型2】三次函数的单调性问题三次函数是高中数学中的一个重要内容，其考点广泛且深入，主要涉及函数的性质、图像、最值、零点以及与其他函数的综合应用等方面。

以下是对三次函数常见考点的详细分析：1.三次函数的定义与形式∙定义：形如f (x )=ax 3+bx 2+cx +d （其中a ≠=0）的函数称为三次函数。

∙形式：注意系数a ,b ,c ,d 的作用，特别是a 的正负决定了函数的开口方向（a >0开口向上，a <0开口向下）。

三次函数公式

三次函数公式三次函数是指变量x的次数最高为3的多项式函数，一般形式为y=ax^3+bx^2+cx+d，其中a、b、c、d是常数，且a不等于0。

这个函数是数学中的重要概念，在各个领域都有广泛的应用。

下面我们将从定义、图像、性质和应用等方面来介绍三次函数。

首先，让我们来看看三次函数的定义。

三次函数描述了一种非线性的关系，具有比一次函数和二次函数更为复杂的特性。

它的最高次数为3，表示函数中最高次幂的指数是3。

常数a决定了函数的开口方向，当a大于0时，函数开口向上，形成一个U形曲线；当a小于0时，函数开口向下，形成一个倒U形曲线。

而b、c、d则分别控制曲线的宽度和位置。

接下来，我们可以通过绘制三次函数的图像来更直观地理解它的特点。

图像的形状和走势可以帮助我们分析函数的增减性、极值点和拐点等重要信息，进而深入研究函数的性质。

根据系数a、b、c、d的取值，三次函数的图像可以呈现出各种不同的形态，例如上升曲线、下降曲线、S形曲线等。

这些图像展示了函数在不同定义域上的变化规律，为我们进一步研究函数提供了重要线索。

三次函数有许多重要的性质值得我们探究。

首先是函数的对称性。

根据函数的定义和三次项的指数特性，我们可以发现，当函数对称于y轴时，常数b和d的取值为0；当函数对称于原点时，常数c的取值为0。

这些对称性使得我们能够通过对称轴、对称点的分析，更加准确地确定函数图像的特征。

其次是函数的单调性。

通过求导，可以得到三次函数的导函数，进一步分析导函数的正负性，我们可以了解函数的增减情况，找到极值点和拐点。

这些性质对于函数的最值问题、优化问题等具有指导意义。

最后，三次函数在实际应用中有着广泛的应用。

在自然科学领域，它可以用来描述许多自然界现象的变化规律，如物体的运动轨迹、声音和光的传播等。

在经济学领域，三次函数可以用来建模经济增长、市场需求等经济现象。

在工程学领域，三次函数可以用来进行曲线拟合和数据预测，为各类工程问题提供解决思路。

三次函数的图像和性质以及在高考中的应用

函数的导函数为。我们不妨把方程称为原函数的导方程，其判别式。若，设其两根为，则可得到以下性质：
性质1：函数，
若，当时，y＝f(x)是增函数；当时，其单调递增区间是，单调递增区间是；
若，当时，是减函数；当时，其单调递减区间是，，单调递增区间是。
（证明略）
推论：函数，当时，不存在极大值和极小值；当时，有极大值、极小值。
（I）讨论f(1)和f(－1)是函数f(x)的极大值还是极小值；
（II）过点A（0，16）作曲线y＝f(x)的切线，求此切线方程。
解：（I）因为，所以导方程。
因为在x＝±1处取得极值，所以，是导方程的两根，
所以
解得a＝1，b＝0
所以
由推论得是f(x)的极大值；f(1)＝－2是f(x)的极小值。
下面仅选一些2004年高考中出现的部分试题，让我们来体会一下如何应用这些性质快速、准确地解答问题。
例1.（浙江）设是函数f(x)的导函数，的图象如图2所示，则y＝f(x)的图象最有可能是（）
图2
图3
解：根据图象特征，不妨设f(x)是三次函数。则的图象给出了如下信息：
① ；
②导方程两根是0，2，（f(x)对称中心的横坐标是1）；
③在（0，2）上；在（－，0）或（2，）上。
由①和性质1可排除B、D；由③和性质1确定选C。
例2.（江苏）函数在闭区间[－3，0]上的最大值、最小值分别是（）
A. 1，－1 B. 1，－17
C. 3，－17 D. 9，－19
解：函数的导方程是，两根为1和－1，由性质2得：
，
。
故选C。
例3.（天津）已知函数在x＝±1处取得极值。

高考数学专题复习：三次函数图像与性质及其应用

三次函数的图像与性质及应用一. 基本命题原理对于三次函数而言，其导函数为一个二次函数，那么根据其导函数的基本性质，可将三次函数的图象和性质梳理如下： 1.根的个数（0>a ）.对于三次函数，其导函数为二次函数:，二次函数的判别式化简为：△=，（1）若，则恰有一个实根；（2）若,且，则0)(=x f 恰有一个实根；（3）若,且，则0)(=x f 有两个不相等的实根；（4）若,且，则0)(=x f 有三个不相等的实根.注：由图像可知：①0)(=x f 含有一个实根的充要条件是曲线)(x f y =与x 轴只相交一次，即)(x f 在R 上为单调函数（或两极值同号），所以032≤−ac b （或032>−ac b ，且0)()(21>⋅x f x f ）.②0)(=x f 有两个相异实根的充要条件是曲线)(x f y =与x 轴有两个公共点且其中之一为切点，所以032>−ac b ，且0)()(21=⋅x f x f .③0)(=x f 有三个不相等的实根的充要条件是曲线)(x f y =与x 轴有三个公共点，即)(x f 有一个极大值，一个极小值，且两极值异号.故032>−ac b 且0)()(21<⋅x f x f .)0()(23≠+++=a d cx bx ax x f )0(23)(2'≠++=a c bx ax x f ()0f x =d cx bx ax x f +++=23)()0(23)('2≠++=a c bx ax x f )3(412422ac b ac b −=−032≤−ac b 0)(=x f 032>−ac b 0)()(21>⋅x f x f 032>−ac b 0)()(21=⋅x f x f 032>−ac b 0)()(21<⋅x f xf2.极值情况：三次函数（0>a ）,导函数为二次函数，二次函数的判别式化简为：△=，（1）若，则)(x f 在),(+∞−∞上为增函数；（2）若，则)(x f 在和上为增函数，)(x f 在),(21x x 上为减函数，其中. 证明：c bx ax x f ++=23)('2, △=)3(412422ac b ac b −=−，（1）当0≤∆ 即032≤−ac b 时，0)('≥x f 在 R 上恒成立，即)(x f 在),(+∞−∞为增函数.（2）当0>∆ 即032>−ac b 时，解方程0)('=x f ，得由0)('>x f 得1x x <或2x x >，)(x f 在),(1x −∞和),(2+∞x 上为增函数.由0)('<x f 得21x x x <<，)(x f 在),(21x x 上为减函数.总结以上得到结论:三次函数d cx bx ax x f +++=23)(（0>a ）（1）若032≤−ac b ，则)(x f 在R 上无极值；（2）若032>−ac b ，则)(x f 在R 上有两个极值；且)(x f 在1x x =处取得极大值，在2x x =处取得极小值.d cx bx ax x f +++=23)()0(23)(2'>++=a c bx ax x f )3(412422ac b ac b −=−032≤−ac b 032>−ac b ),(1x −∞),(2+∞x aacb b x a ac b b x 33,332221−+−=−−−=aacb b x a ac b b x 33,332221−+−=−−−=3.对称中心三次函数)0()(23≠+++=a d cx bx ax x f 的对称中心为点))3(,3(abf a b f −−，该点是三次函数的拐点，此点的横坐标也是二阶导数的零点.4.三次方程根与系数得关系（1）已知实系数多项式32()x ax bx cx d ϕ=+++有三个根,设为123,,.x x x123122331123,,.b c dx x x x x x x x x x x x a a a++=−++==−（2）由三次方程根与系数的关系：32()()()()().x a x b x c x a b c x ab bc ca x abc +++=+++++++5.对称中心处的切线拐点是函数凸凹性发生转换的点，即由凸转凹，或者由凹转凸，即0)(0''=x f ，当0x x <时，0)(''<x f 或0)(''>x f ，当0x x >时，0)(''>x f 或0)(''<x f .如图，点A 为函数)(x f 的拐点，做点A 处的切线，可以看到，具有单个拐点的函数)(x f y =可以看作是1个凸函数和1个凹函数通过拐点进行缝合，它们在缝合点处具有相同的切线l ，这条切线l 将平面分别两个半平面，一半包含一个凸函数，另一半包含一个凹函数二．典例应用★应用1.函数的性质考察.例 2.已知曲线3()3f x x x λ=−+在点(,())A m f m 处的切线与曲线的另外一个交点为,B P 为线段AB 的中点,O 为坐标原点.（1）求()f x 的极小值并讨论()f x 的奇偶性.（2）当函数()f x 为奇函数时,直线OP 的斜率记为k ,若34k −,求实数m 的取值范围. 解析：（1）2()333(1)(1)f x x x x '=−=+−，当11x −<<时,()0f x '<；当1x >时，()0f x '>.当0λ=时3()3f x x x =−,显然3()3()f x x x f x −=−+=−，所以()f x 为奇函数.当0λ≠时(1)2,(1)2f f λλ−=+=−+，显然(1)(1)f f −≠. 且(1)(1)20f f λ−+=≠，所以()f x 为非奇非偶函数.（2）2()33f x x '=−,所以曲线在点(,())A m f m 处的切线方程为()()32333()y m m m x m λ−−+=−−，其与原曲线方程33y x x λ=−+，联立化简得:2()(2)0x m x m −+=.从而()32,86(0)B m m m m λ−−++≠.所以3732,22m m m P λ⎛⎫−++− ⎪⎝⎭,3732m m k m λ−−=.由于(0,2),18m k ∀∈；即当(0,2)m ∈时，都有32721m m λ−.令3()721h m m m =−,则2()212121(1)(1)h m m m m '=−=+−，易知当01m <<时,()0h m '<；当12m <<时,()0h m '>.即()h m 在(0,1)上递减，在(1,2)上递增，所以当(0,2)m ∈时,min ()(1)14h m h ==−，所以2147λλ−⇔−，从而实数λ的取值范国为(,7]−∞−. 注：可以看到，切点的横坐标恰好便是方程①的二重根.例3.（切割线定理）如果我们将上述的内容再结合三次函数韦达定理，就可以得到更多有趣的结论.如图，过切点A ))(,(A A x f x 的切线与三次函数)(x f y =的图象交于B 点，同时，过))(,(00x f x 的割线AD 与三次函数)(x f y =的图象交于C A D ,,三点. 我们有以下结论：三次函数切割线定理. （1）abx x B A −=+2；（2）D C B A x x x x +=+；（3）A F E x x x 2=+.证明：显然，方程①整理可得：0)())((000'23=+−−+++x f x x x f d cx bx ax .结合上述重根个数定理以及韦达定理可得：abx x B A −=+2，结论（1）证毕. （2）设直线AD 的方程为m kx y +=，代入)(x f y =的表达式结合韦达定理可得：abx x x D C A −=++,再联立a b x x B A −=+2，可证得：D C B A x x x x +=+.（3）同理，如图a bx x x E E B −=++，再联立a b x x B A −=+2，可得：A F E x x x 2=+.练习1.（2016年天津卷）设函数R b a b ax x x f ∈−−−=,,)1()(3. （1）求)(x f 的单调区间；（2）若)(x f 存在极值点0x x =，且)()(10x f x f =，其中10x x ≠，求证：3201=+x x . 解析：（2）过极值点0x x =做函数)(x f 图象的切线)(0x f y =，其与)(x f y =交点横坐标为1x x =. 将函数b ax x x f −−−=3)1()(展开可得：)1()3(3)(23+−−+−=b x a x x x f 由上述切割线定理可知：3201=+x x ，证毕.练习2. 下列关于三次函数32()(0)()f x ax bx cx d a x R =+++≠∈叙述正确的是（） ①函数()f x 的图象一定是中心对称图形； ②函数()f x 可能只有一个极值点； ③当03bx a≠−时，()f x 在0x x =处的切线与函数()y f x =的图象有且仅有两个交点； ④当03bx a≠−时，则过点()()00,x f x 的切线可能有一条或者三条． A ．①③B ．②③C ．①④D ．②④由上述结论易得：A.★应用2.三次函数的切线个数例4．已知函数()33f x x x =−．（1）求()f x 在区间[]()0,0m m >上的最大值和最小值；（2）在曲线2yx 上是否存在点P ，使得过点P 可作三条直线与曲线()y f x =相切？若存在，求出其横坐标的取值范围；若不存在，请说明理由．解析：（2）假设存在符合条件的点()2,P a a，切点设为()300,3x xx −.所以，根据导数几何意义可得：()2300200333a x x x a x −−=−−即322002330x ax a a −++=①故问题转化为关于0x 的方程①存在三个不同实根．令()322233g x x ax a a =−++，则()()2666g x x ax x x a '=−=−；当0a =时，()260g x x ='≥，()g x 单调递增，不合题意；当0a >时，易知()g x 在(),0−∞单调递增，在()0,a 单调递减，在(),a +∞单调递增，从而()()000g g a ⎧>⎪⎨<⎪⎩，即2323030a a a a a ⎧+>⎨−++<⎩解得：a >0a <时，易知()g x 在(),a −∞单调递增，在(),0a 单调递减，在()0,+∞单调递增从而()()000g a g ⎧>⎪⎨<⎪⎩，即3223030a a a a a ⎧−++>⎨+<⎩解得：3a −<<，综上，存在符合条件的点()2,P a a，其横坐标的取值范围为⎛⎫−⋃+∞ ⎪ ⎪⎝⎭⎝⎭．注.三次函数的切线条数是三次函数中典型应用之一，其实质就是在讨论三次方程根的个数，是一类非常典型的函数与方程综合问题，颇受命题人青睐.★应用3.三次方程的根与韦达定理同样是2020年全国三卷23题，不等式选做题，依然以三次方程根与系数的关系命制而成，下面予以分析，希望各位读者在高三备考时重视对三次方程根与系数关系的认识程度，有备无患！例5．设直线y t =与曲线()23C y x x =−：的三个交点分别为()()()A a t B b t C c t ，，，，，，且a b c <<．现给出如下结论：①abc 的取值范围是()04，；②222a b c ++为定值；③6a b c ++=. 其中正确结论的为解析：设()()232369y f x x x x x x ==−=−+，则()23129f x x x '=+-，令()0f x '=，解得：1x =或3x =；当1x <或3x >时，0fx，当13x <<时，()0f x '<；∴()f x 在)1,(−∞上是增函数，在（1，3）上是减函数，在（3，+∞）上是增函数；当1x =时，()f x 取得极大值()14f =，当3x =时，()f x 取得极小值()30f =；作出函数()f x 的图象如图所示：∵直线y t =与曲线()23C y x x =−：有三个交点，由图象知04t ＜＜. 令()()232369g x x x t x x x t =−=+---，则a b c ，，是()0g x =的三个实根．∴()()()3269x x x t x a x b x c +=-----，即()()323269x x x t x a b c x ab ac bc x abc −+−=−+++++−，∴6a b c ++=，9ab bc ac ++=，abc t =，①③正确；∴()()2222218a b c a b c ab bc ac ++=++++=-，∴②正确；综上，正确的命题序号是①②③．故答案为：①②③．★应用4.三次方程根的分布下面这道题目是2020年三卷的导数压轴题，其实质考察了三次函数的零点分布.但其却具有非常丰厚的数学背景，即三次方程根的三角形式，也是此题的命题原理.为此，此题先用函数思想求解，再给出其命题背景.例6.（2020全国3卷）设函数c bx x x f ++=3)(，曲线)(x f y =在点))21(,21(f 处的切线与y 轴垂直. （1）求b ；（2）若)(x f 有一个绝对值不大于1的零点，证明:)(x f 所有的零点的绝对值都不大于1.解析：（1）因为'2()3f x x b =+，由题意，'1()02f =，即21302b ⎛⎫⨯+= ⎪⎝⎭,则34b =−.（2）由（1）可得33()4f x x x c =−+，故'2311()33()()422f x x x x =−=+−，令'()0f x >，得12x >或12x <−；令'()0f x <，得1122x −<<，所以()f x 在11(,)22−上单调递减，在1(,)2−∞−，1(,)2+∞上单调递增，且111111(1),(),(),(1)424244f c f c f c f c −=−−=+=−=+，若()f x 所有零点中存在一个绝对值大于1的零点0x ，则(1)0f −>或(1)0f <，即14c >或14c <−.当14c >时，111111(1)0,()0,()0,(1)0424244f c f c f c f c −=−>−=+>=−>=+>，又32(4)6434(116)0f c c c c c c −=−++=−<，由零点存在性定理知()f x 在(4,1)c −−上存在唯一一个零点0x ，即()f x 在(,1)−∞−上存在唯一一个零点，在(1,)−+∞上不存在零点，此时()f x 不存在绝对值不大于1的零点，与题设矛盾；当14c <−时，111111(1)0,()0,()0,(1)0424244f c f c f c f c −=−<−=+<=−<=+<，又32(4)6434(116)0f c c c c c c −=++=−>，由零点存在性定理知()f x 在(1,4)c −上存在唯一一个零点0'x ，即()f x 在(1,)+∞上存在唯一一个零点，在(,1)−∞上不存在零点，此时()f x 不存在绝对值不大于1的零点，与题设矛盾；综上，()f x 所有零点的绝对值都不大于1.应用5.三次函数的拐点切线例7.已知函数()321132f x x ax bx =++在区间[)(]1,1,1,3−内各有一个极值点. （1）求24a b −的最大值；（2）当248a b −=时，设函数()y f x =在点()()1,1A f 处的切线为l ，若在点A 处穿过()y f x =的图象（即动点在点A 附近沿曲线()y f x =运动，经过点A 时，从l 的一侧进入另一侧），求函数()f x 的表达式. 解析：（1）因为函数()321132f x x ax bx =++在区间[)(]1,1,1,3−内分别有一个极值点，所以b ax x x f ++='2)(在区间[)(]1,1,1,3−内分别有一个实根，设两实根为1x ，2x （1x <2x ），则b a x x 4212−=−，且4012≤−<x x ，于是4402≤−<b a ，16402≤−<b a ，且当11−=x ，32=x ，即2−=a ，3−=b 时等号成立，故24a b −的最大值是16（2）由b a f ++='1)1(知)(x f 在点()()1,1A f 处的切线l 的方程是)1)(1()1(−'=−x f f y ，即a x b a y 2132)1(−−++=，因为切线l 在点A 处穿过()y f x =的图象所以]2132)1[()()(a x b a x f x g −−++−=在1=x 两边附近的函数值异号，则1=x 不是)(x g 的极值点，而a x b a bx ax x x g 2132)1(2131)(23++++−++=，且)1)(1(1)1()(22a x x a ax xb a b ax x x g ++−=−−+=++−++='，若a −−≠11，则1=x 和a x −−=1都是)(x g 的极值点，所以a −−=11，即2−=a ，又由248a b −=得1−=b ，故x x x x f −−=2331)(.五．习题演练习题1．已知函数()()23f x x x =−，若()()()f a f b f c ==，其中a b c <<，则（）A ．12a <<B ．6a b c ++=C ．2a b +>D ．abc 的取值范围是()0,4 解析：因为()()23f x x x =−，所以()231293(3)(1)f x x x x x =−=−−'+，令()0f x '=，解得：1x =或3x =，当0f x 时，3x >或1x <，所以()f x 单调递增区间为(),1−∞和()3,+∞；当()0f x '<时，13x <<，所以()f x 单调递减区间为()1,3；且(3)0f =，(1)(4)4f f ==，如图：设()()()f a f b f c t ===，则04t <<，0134a b c <<<<<<，故选项A 错误；又()()()()f x t x a x b x b −=−−−，所以()23()()()x x t x a x b x c −−=−−−，即323269()()x x x t x a b c x ab ac bc x abc −+−=−+++++−，对照系数得6a b c ++=，故选项B 正确；(0,4)abc t =∈，故选项D 正确；因为34c <<，所以36()4a b <−+<，解得23a b <+<，故选项C 正确，综上，正确的选项为BCD.故选：BCD习题2.已知函数()313f x x tx t =++．（1）讨论函数()f x 的单调区间；（2）若函数()f x 有三个不同的零点1x 、2x 、3x ,求t 的取值范围,并证明：123x x x ++<解析：（1）2()f x x t =+'①当0t 时,()0f x ',则()f x 在R 上单调递增,无递减区间；②当0t <时, ()f x 在(上单调递减,在(,)∞∞−+上单调递增（2）由（1）知函数f (x )有三个零点,则0t <∵()f x 在(上单调递减,在(,)∞∞−+上单调递增∴()f x 的极大值为2(3f t =−且极大值大于0,极小值为23f t =+∵()f x 有三个不同的零点123,,x x x ,∴203f t =+< 解得94t <−,故t 的取值范围为9,4⎛⎫−∞− ⎪⎝⎭．又∵(0)0f t =<,当x →+∞时,有()f x →+∞,当x →−∞时,有()f x →−∞．∴设123x x x <<,由零点存在性定理知1230x x x <<<． ∴12x x +<又∵31233f t t t =++=−(0f => 3x <<因此123x x x ++习题3已知函数()3134f x x ax =−+,()lng x x =−．（1）讨论函数()f x 的单调性；（2）用{}min ,m n 表示,m n 中较小者,记函数()()(){}min ,h x f x g x =,（0x >）．若函数()h x 在0,上恰有3个零点,求实数a 的取值范围．解析：（1）()3134f x x ax =−+,x ∈R ,()233f x x a '=−当0a ≤时,0f x ,()f x 在R 上为单调递增，当0a >时,()(3f x x x '=,令0f x ,得x <x ()f x 单调递增令0f x ,得x <()f x 单调递减，综上：当0a ≤时,()f x 在(),−∞+∞为增函数当0a >时,()f x 在(,−∞和)+∞为增函数,在(为减函数（2）当(1,)x ∈+∞时,()ln 0g x x =−<,从而()min{(),()}()0h x f x g x g x =≤<,∴()h x 在（1,+∞）无零点.当x =1时,若512a ≤,则5(1)304f a =−≥,(1)min{(1),(1)}(1)0h f g g ===,故x =1是()h x 的零点；若512a >,则5(1)304f a =−<,(1)min{(1),(1)}(1)0h f g f ==<,故x =1不是()h x 的零点.当(0,1)x ∈时,()ln 0g x x =−>,所以只需考虑()f x 在)1,0(的零点个数.（ⅰ）若0a ≤或1a ≥,则()2()3f x x a '=−在)1,0(无零点,故()f x 在)1,0(单调,而1(0)4f =,5(1)34f a =−,所以当1a ≥时,()f x 在)1,0(有一个零点；当0a ≤时,()f x 在)1,0(无零点.（ⅱ）若01a <<,则()f x 在）单调递减,在单调递增,故当x ,()f x 取的最小值,最小值为124f =−.①若f ＞0,即0＜a ＜14,()f x 在)1,0(无零点.②若f =0,即14a =,则()f x 在)1,0(有唯一零点；③若f ＜0,即114a <<,由于1(0)4f =,5(1)34f a =−,所以当15412a <<时,()f x 在)1,0(有两个零点；当5112a <<时,()f x 在)1,0(有一个零点. 综上,当14a <或512a >时,()h x 由一个零点；当14a =或512a =时,()h x 有两个零点；当15412a <<时,()h x 有三个零点. 所以a 的取值范围是15,412⎛⎫ ⎪⎝⎭习题4．已知函数()()()32111032f x x a x ax a =+−−>．（1）求函数f （x ）的极值；（2）当a ＞1时，记f （x ）在区间[－1,2]的最大值为M ，最小值为m ．已知12,33M m ⎛⎫ ⎪⎝+⎭∈．设f （x ）的三个零点为x 1，x 2，x 3，求()122331f x x x x x x ++的取值范围．解析：（1）()()()()211f x x a x a x x a '=+−−=−+，令0f x ，解得x a <−或1x >，令()0f x '<，解得1a x −<<，所以()f x 在(),a −∞−，()1,+∞上单调递增，在(),1a −上单调递减，当x a =−时取得极大值，()3322321111132262f f a a a a a a a =−=−+−+=+极大值，当1x =时取得极小值，()11111132262f f a a a ==+−−=−−极小值，所以()f x 的极大值为321162a a +，极小值为1162a −−. （2）因为1a >，所以()f x 在()1,1−上单调递减，()1,2上单调递增，()11162m f a ==−−，因为()3521263f a −=−>，()222233f a =−<，所以()35126M f a =−=−， 111352362263a a <−−+−<，解得4533a <<，设123x x x <<，令()()2111032f x x x a x a ⎡⎤=+−−=⎢⎥⎣⎦，所以20x =，313x x a =−，()()3212233193322f x x x x x x f a a a ++=−=−−， 329322y a a =−−在45,33⎛⎫ ⎪⎝⎭上单调递减，当32934025,223a a ⎛⎫−−∈−− ⎪⎝⎭，所以()122331f x x x x x x ++的取值范围为4025,3⎛⎫−− ⎪⎝⎭.。

三次函数与高次函数

三次函数与高次函数在数学中，函数是一种映射关系，它将一个集合的元素对应到另一个集合的元素。

函数的种类很多，其中三次函数和高次函数是比较常见且重要的两种。

本文将介绍三次函数和高次函数的定义、性质以及它们在数学和实际问题中的应用。

一、三次函数的定义和性质三次函数是指次数为3的多项式函数。

一般形式为y = ax^3 + bx^2 + cx + d，其中a、b、c、d为实数且a不等于0。

三次函数的图像通常是曲线，部分可能会是“S”型曲线，也可能有一个或两个极值点。

三次函数的性质如下：1. 零点：三次函数的零点是使得函数值等于零的x值。

一个三次函数可能有1个、2个或3个零点。

2. 奇偶性：当a为奇数时，函数是奇函数；当a为偶数时，函数是偶函数。

3. 对称轴：对于奇函数来说，对称轴为y轴；对于偶函数来说，对称轴为y轴和x轴。

4. 极值点：三次函数的极值点可能有1个或2个。

当函数有极值点时，极值点处的斜率为0。

5. 增减性：三次函数的增减性根据导数来判断。

当导数大于0时，函数单调递增；当导数小于0时，函数单调递减。

二、高次函数的定义和性质高次函数是指次数大于3的多项式函数。

一般形式为y = a_nx^n +a_{n-1}x^{n-1} + ... + a_1x + a_0，其中n为大于3的整数，a_0, a_1, ..., a_n为实数且a_n不等于0。

高次函数的性质如下：1. 零点：高次函数可能有多个零点，其个数最多为n个，其中n为函数的次数。

2. 对称轴：对于奇次函数来说，对称轴为y轴；对于偶次函数来说，对称轴为y轴和x轴。

3. 极值点：高次函数的极值点可能有0个或多个。

当函数有极值点时，极值点处的斜率为0。

4. 增减性：高次函数的增减性同样可以根据导数来判断。

当导数大于0时，函数单调递增；当导数小于0时，函数单调递减。

三、三次函数与高次函数的应用1. 社会经济领域：三次函数和高次函数在社会经济领域中有广泛的应用，例如用于分析市场供求关系、经济增长模型等。

三次函数性质总结

三次函数性质总结三次函数是指函数的最高次项是3次的函数，一般的三次函数的函数表达式可以写成y=ax^3+bx^2+cx+d。

以下是关于三次函数的性质的总结：1.对称性：三次函数一般具有对称性，即关于y轴对称。

这是因为三次函数中只有偶次次项，所以具有对称性。

这可以通过函数图像来观察，如果一条曲线对称于y轴，则表示这个函数是一个三次函数。

2.零点：三次函数可能有一个或多个零点。

如果函数的零点为x=a，那么乘以(x-a)后，函数会变为二次函数，这是因为函数中的三次项会被消去，变成了二次项。

因此，三次函数的零点可以用来快速确定函数的根的个数。

3.单调性：三次函数的单调性与系数a有关。

当a>0时，三次函数是上凹的，即函数的曲线开口向上，为增函数；当a<0时，三次函数是下凹的，即函数的曲线开口向下，为减函数。

4.驻点：三次函数的导数是二次函数，因此导数为零的点称为驻点。

三次函数的驻点有最大值或最小值，可以通过求导数来求得驻点的位置。

5. 渐近线：三次函数可能有水平渐近线、垂直渐近线或斜渐近线。

水平渐近线是指当x趋于正无穷或负无穷时，函数值趋于一些常数；垂直渐近线是指当x等于一些常数时，函数值趋于正无穷或负无穷；斜渐近线是指当x趋于正无穷或负无穷时，函数值趋于ax^2+bx+c。

6.奇偶性：三次函数的奇偶性与系数b有关。

当b为奇数时，三次函数是奇函数，对称于原点，函数图像关于原点对称；当b为偶数时，三次函数是偶函数，对称于y轴，函数图像关于y轴对称。

7.映射性：三次函数的图像可以映射到整个坐标平面上，因为三次函数没有任何限制，所以可以取得任意的y值。

8.随着函数系数的变化，函数图象会发生相应的形变。

例如，当a的绝对值变大时，函数的曲线会变得更陡峭；当b的绝对值变大时，函数的曲线会向原点靠拢；当c的绝对值变大时，函数的曲线会上下平移；当d 的绝对值变大时，函数的曲线会上下平移。

总之，三次函数具有丰富的性质和特点，可以通过系数的变化来改变函数的图像和性质。

三次函数的图像和性质以及在高考中的应用

三次函数的性质以及在高考中的应用三次函数厂用+bF 七 +&（占0）已经成为中学阶段一个重要的函数，在高考和一些重大考试中频繁出现有关它的单独命题。

2004年高考，在江苏卷、浙江卷、天津卷、重庆卷、湖北卷中都出现了这个函数的单独命题，特别是湖北卷以压轴题的形式出现，更应该引起我们的重视。

单调性和对称性最能反映这个函数的特性。

下面我们就来探讨一下它的单调性、对称性以及图象变化规律。

函数厂卅4贰址沙验知）的导函数为八“+2卄。

我们不妨把方程2 I曲+称为原函数的导方程，其判别式色=4@一纸）。

若A >0，设其两根，则可得到以下性质:性质1：函数厂宀贰七+班尹）,若>0|,当A兰0时，y = f（x）是增函数；当|A >0|时，其单调递增区间是（-©无山［比+®）,单调递增区间是【冋，帀】；若口uD，当A < 0时，戸=/0）是减函数；当A >0时，其单调递减区间是（-□也］,［心！+侗），单调递增区间是［乃*心］。

（证明略）推论：函数厂用+用 F+辿#®,当怙£0|时，不存在极大值和极小值；当心时，有极大值41）、极小值•‘「。

根据a和「的不同情况，其图象特征分别为：图1性质2 :函数了何"F +M +滋+乳口尹5 ［耕*用］,若观E ［糾总］,且''■ ' 1 '，则：/何闷=msLX（f（m^ /（0）, /何）.（证明略）性质3 :函数’I .「一I是中心对称图形，其对称中心是证明：设函数7（工）=/亠曲4^+平知）的对称中心为（m, n）o—按向量住7-用、-冊将函数的图象平移，则所得函数》=/（兀+啊）一丹是奇函数，所以j（才+ wi） + 丁（一工+ - 2w = 0（纸诅+3）常-+a^ +助即+卍耕4£ 一理=0 上式对・L「恒成立，故化简得:3rna +占=0 ,得n - am1十占烧° +即耗+ d = /（------------ ）3aO__________________________ . 丄■ f （丄）所以，函数P =赤4” 5 T占°）的对称中心是（x 3a）o可见，y = f（x）图象的对称中心在导函数y ：I的对称轴上，且又是两个极值点的中点。

三次函数常见的性质及应用

三次函数常见的性质及应用在数学中，三次函数是把实数当做自变量的函数，其形式为： f(x)=ax+bx+cx+d其中，a≠0，b、c、d为常数。

三次函数是最常用的幂函数之一，也是处理数学实际问题的重要函数。

它可以通过它的性质及应用，来提高我们的数学认知水平。

二、三次函数的性质1、三次函数的一阶导数根据定义，一阶导数是指函数的斜率。

设f(x)=ax+bx+cx+d，其一阶导数为：f(x)=3ax+2bx+c综上所述，可以看出，三次函数的导数为二次函数。

2、三次函数的局部极值三次函数的局部极值问题可以使用一阶导数法来解决。

即求出f(x)=3ax+2bx+c的极值，再根据其值判断f(x)的极值情况。

也就是求出f(x)=0的解，即可找出f(x)的极大值和极小值。

3、三次函数的对称轴若令f(x)=0，即可得出f(x)的对称轴，它是函数图像的对称轴。

当b=0时，它可以是x轴，当b≠0时，它可以是一条直线。

三、三次函数的应用1、三次函数在求解复杂函数中的应用复杂函数是指有交叉部分的函数，如正弦函数、余弦函数等。

在求解这类复杂函数中，三次函数可以帮助我们把函数分解成几个子函数，并将其组合起来。

这样可以更方便地求解，也更容易理解。

2、三次函数在物理中的应用在物理学中，三次函数可以用来描述力学系统中物体的运动轨迹。

比如在动量定理中，物体在受外力作用时，其运动可以用三次函数来进行描述。

此外，三次函数还可以用于喷气发动机的设计中，是一种非常有效的工具。

四、总结以上就是三次函数的常见性质及应用。

它不仅可以把复杂的函数分解成若干个子函数，同时还可以在物理学中得到重要的应用。

只要我们熟悉三次函数的性质和应用，就可以更好地利用它来进行数学实际问题的解决，提高我们的数学认知水平。

三次函数的性质及应用

三次函数的性质及应用
1. 三次函数的定义
三次函数是指函数的最高次幂为3的代数函数，它的一般形式
为f(x) = ax^3 + bx^2 + cx + d，其中a、b、c、d为常数。

2. 三次函数的性质
- 零点：三次函数的零点是使得f(x) = 0的x值。

由于三次函数
是三次方程，理论上有三个实根或复根。

零点可以通过求解方程
f(x) = 0得到。

- 极值点：三次函数的极值点是函数达到最大值或最小值的点。

三次函数的极值点可能在实数轴上存在，也可能不存在。

可以通过
求解f'(x) = 0找到极值点。

- 函数图像：三次函数的图像通常呈现出一条平滑的曲线，称
为三次曲线。

根据三次函数的系数的取值范围不同，可以得到不同
形状的曲线，如上升曲线、下降曲线、拐点等。

3. 三次函数的应用
三次函数的性质在数学和实际问题中都有广泛应用，以下是一
些常见的应用领域：
- 物理学：三次函数可以用来描述物体的运动轨迹，如抛体运动、自由落体、弹性碰撞等。

- 经济学：三次函数可以用来描述经济模型中的供需曲线、成
本曲线等。

- 工程学：三次函数可以用来描述工程中的曲线形状，如桥梁
设计、道路设计等。

- 生物学：三次函数可以用来描述生物学中的生长曲线、代谢
曲线等。

三次函数的性质和应用对于理解和解决实际问题具有重要意义。

深入研究三次函数的数学特性和实际应用可以帮助我们更好地理解
和应用这一数学工具。

(简易版)三次函数的解题技巧

(简易版)三次函数的解题技巧三次函数是一种具有三次方程（三次多项式）形式的函数。

在解题时，我们可以使用以下技巧，以便更有效地求解三次函数的问题。

1. 寻找零点为了找到三次函数的解，我们需要找到函数的零点，即函数取值为零的点。

有几种方法可以帮助我们确定零点。

a. 因式分解如果三次函数可以进行因式分解，我们可以通过将函数表达式分解为一次、二次和一次多项式相乘的形式来找到零点。

通过令每个因式为零，我们可以解出方程并确定零点。

b. 二次函数技巧有时，三次函数可以通过将其转化为二次函数来解决。

这可以通过使用代换来实现，其中我们将一个新的变量代入三次函数中，使其变为二次函数。

解出二次函数后，我们可以获得原始问题的解。

c. 图像分析绘制函数的图像可以提供关于零点位置的有用信息。

通过观察图像，我们可以估计零点的大致位置，并使用数值方法进一步精确地确定它们。

2. 使用因式定理因式定理是一种能够找到多项式的因式的方法。

对于三次函数，我们可以使用因式定理找到其可能的因式，并进一步推导出零点。

通过将候选因式代入函数，我们可以测试其是否为零点，并进一步确定函数的解。

3. 使用综合定理综合定理是一种将函数的根与系数之间的关系联系起来的方法。

对于三次函数，我们可以使用综合定理来计算可能的根，并通过验证是否满足定理中的条件来确定它们是否是零点。

4. 数值解法如果以上方法无法找到解或求解过于复杂，我们可以使用数值解法来近似求解三次函数的根。

常见的数值解法包括二分法、牛顿法和二次插值法等。

这些方法可以利用计算机和计算工具进行计算，并给出函数的近似解。

以上是解决三次函数问题的一些简易技巧。

根据具体问题的不同，我们可以选择适合的方法来求解三次函数的根。

在解题过程中，我们可以结合使用不同的方法，以便更有效地解决问题。

参考资料：。

一个三次函数的解题方法与技巧

一个三次函数的解题方法与技巧引言三次函数是一种常见的数学函数形式，其方程为y = ax^3 + bx^2 + cx + d。

解三次函数可以帮助我们找到函数的根、极值以及曲线的行为。

本文将介绍一些解三次函数的方法与技巧，帮助读者更好地理解和解决相关问题。

方法一：因式分解当三次函数的形式比较简单，并且存在因式分解的可能时，我们可以尝试使用因式分解的方法来解题。

通过因式分解，我们可以将三次函数拆解成若干个一次因子与一个二次因子相乘的形式，从而更容易找到函数的根。

方法二：求导数与极值对于三次函数，我们可以通过求导数的方法找到函数的极值点。

通过求函数的一阶导数和二阶导数，并令导数等于零，我们可以求得函数的极值点和曲线的转折点。

方法三：图像分析与差值法利用数学软件或手绘曲线图，我们可以通过观察曲线的特征来了解函数的行为。

通过分析曲线的上升段、下降段以及拐点，我们可以推断函数的根和极值点的位置。

此外，还可以运用差值法，通过代入特定值来估算函数的零点。

方法四：牛顿法和二分法如果以上方法无法解决问题，我们可以尝试使用数值计算的方法。

牛顿法和二分法是两种常用的数值计算方法，可以较快地逼近函数的根。

牛顿法通过迭代计算函数的切线与x轴的交点，逐步逼近根的位置。

二分法则通过不断将区间一分为二，判断根位于哪一半区间内，逐步逼近根的位置。

总结解三次函数的方法与技巧多种多样，我们可以根据题目的不同特点和要求选择合适的方法来解决问题。

因式分解、求导数与极值、图像分析与差值法以及数值计算方法都是常用的解题手段，但需要根据具体情况选择合适的方法。

希望本文的介绍对读者在解题过程中有所帮助。

三次函数公式

三次函数公式（原创版）目录1.引言：介绍三次函数的定义和重要性2.三次函数的一般形式3.三次函数的图像特征4.三次函数的性质与应用5.结论：总结三次函数的公式及其作用正文1.引言三次函数是数学中的一种基本函数形式，它在各个领域的应用非常广泛，如物理、工程、生物学等。

了解和掌握三次函数的公式及性质，有助于我们更好地应对各种实际问题。

2.三次函数的一般形式三次函数是指形如 f(x) = ax^3 + bx^2 + cx + d（其中 a、b、c、d 为常数，且 a≠0）的函数。

在这个公式中，a、b、c、d 分别代表三次项系数、二次项系数、一次项系数和常数项。

3.三次函数的图像特征三次函数的图像通常具有以下特征：- 奇偶性：当 b=c=0 时，三次函数 f(x) = ax^3 + d 为奇函数或偶函数。

- 开口方向：当 a>0 时，函数图像开口向上；当 a<0 时，函数图像开口向下。

- 顶点位置：函数的顶点位于 x=-b/3a 处，其 y 值为 f(-b/3a) =d - b^2/27a。

4.三次函数的性质与应用三次函数具有以下性质：- 在一定区间内，三次函数最多有三个实根（包括重根）。

- 当 a<0 时，函数有一个局部极小值；当 a>0 时，函数有一个局部极大值。

三次函数在实际应用中的例子有很多，例如：- 经济学中的生产函数：描述生产过程中投入与产出之间的关系。

- 物理学中的运动方程：描述物体在重力作用下的运动状态。

- 生物学中的生长函数：描述生物体在一定条件下的生长过程。

5.结论三次函数是数学中非常重要的函数形式，它在各个领域的应用非常广泛。

三次函数知识点讲解全集高一

三次函数知识点讲解全集高一三次函数知识点讲解全集高一一、定义与基本性质1、三次函数的定义三次函数是指函数的最高次项是三次方的函数，通常表示为f(x) = ax^3 + bx^2 + cx + d，其中 a、b、c、d 是实数，且a ≠ 0。

2、三次函数的图像特点- 三次函数的图像是一条平滑的曲线，可能上升也可能下降；- 当 a > 0 时，图像开口向上，当 a < 0 时，图像开口向下；- 三次函数的图像可能有零点、极值点和拐点。

二、零点与方程1、零点的定义零点是使得函数值等于零的横坐标，即 f(x) = 0。

2、求解三次函数的零点- 当函数为 f(x) = ax^3 + bx^2 + cx + d，使用因式分解、配方法或求根公式可以解得零点；- 一般情况下，三次函数有3个零点。

3、三次函数的方程三次函数的方程形式为 f(x) = ax^3 + bx^2 + cx + d = 0。

三、极值点与单调性1、极值点的定义极值点是指函数在某一区间内取得最大值或最小值的点。

2、求解三次函数的极值点- 先求出导函数 f'(x) = 3ax^2 + 2bx + c；- 令 f'(x) = 0，解出 x 的值；- 根据得到的 x 值，代入原函数 f(x) 中求 y 值，即可得到极值点。

3、三次函数的单调性判断- 当 a > 0 时，函数递增，即左侧为负无穷趋向于正无穷；- 当 a < 0 时，函数递减，即左侧为正无穷趋向于负无穷；- 即当函数的导函数 f'(x) > 0 时，函数递增，f'(x) < 0 时，函数递减。

四、拐点与凹凸性1、拐点的定义拐点是指函数曲线由凹转凸或由凸转凹的点，具有 y 坐标的局部最大值或最小值。

2、求解三次函数的拐点- 先求出二阶导函数 f''(x) = 6ax + 2b；- 令 f''(x) = 0，解出 x 的值；- 根据得到的 x 值，代入原函数 f(x) 中求 y 值，即可得到拐点。

三次函数的图像与性质

三次函数的图像与性质形如f（x）=ax3+bx2+cx+d（a≠0）的函数叫做三次函数。

由于三次函数的导函数是二次函数，而二次函数是高中数学中的重要内容，所以三次函数的问题已经成为高考命题的一个新的热点和亮点，尤其是文科数学更是如此。

我们可以采用类比的方法，利用几何画板，较为深入地研究三次函数的图像与性质以及三次方程的解的个数的问题。

１三次函数的图像与性质设三次函数f（x）=ax3+bx2+cx+d（a≠0），其导函数f’（x）=3ax2+2bx+c，其判别式△=4b2-12ac=4（b2-3ac）。

当a>0时，若△>0，方程f’（x）=0有两个不相等的实数根，记作x1，x2，不妨令x1f（x2）。

结论1：f（x1）·f（x2）>0时，函数f（x）的图像与x轴有且仅有一个公共点；f（x1）·f（x2）=0时，函数f（x）的图像与x轴有且仅有两个公共点；f （x1）·f（x2）０，f（x2）0为例）：当a>0时，f（x）的四种图象３推论设三次函数f（x）＝ax3+bx2+cx+d（a>0），其导函数f’（x）=3ax2+2bx+c 的判别式△=4b2-12ac=4（b2-3ac）>0。

方程f’（x）=0有两个不相等的实数根，记作x1，x2，不妨令x1<x2，则函数f（x）在x=x1处取得极大值f（x1），函数f（x）在x=x2处取得极小值f（x2）。

类似可知a<0的情形（其余条件同前）：函数在x=x1处取得极小值f（x1），函数f（x）在x=x2处取得极大值f（x2）。

４例题例1.（湖南卷）用长为18 cm的钢条围成一个长方体形状的框架，要求长方体的长与宽之比为2：1，问该长方体的长、宽、高各为多少时，其体积最大？最大体积是多少？解：设长方体的宽为x（m），则长为2x（m），高为h==4.5-3x（m）（0<x<），故长方体的体积为V（x）=2x2（4.5-3x）＝９x2－６x３（m３）（0<x<），从而V’（x）=18x-18x2（4.5-3x）=18x（１－x）。

三次函数公式

三次函数公式（最新版）目录1.引言2.三次函数的定义和表示3.三次函数的性质4.三次函数的图像5.三次函数的实际应用6.结论正文【引言】在数学领域，函数是一种将一个数集中的数映射到另一个数集中的规则。

在函数中，三次函数是一个重要的概念，它是一种具有三个变量因子的函数。

本文将介绍三次函数的定义、性质、图像以及实际应用。

【三次函数的定义和表示】三次函数是指具有三个变量因子的函数，其一般形式为 f(x, y, z)。

其中，x、y、z 是自变量，f(x, y, z) 是因变量。

例如，f(x, y, z) = x^3 + 2xyz^2 - y^3z + 2xyz - 1 就是一个三次函数。

【三次函数的性质】1.三次函数具有三个变量因子，因此它具有更复杂的性质和行为。

2.三次函数的图像通常具有更多的拐点和极值点，这使得它在数学分析中具有挑战性。

3.三次函数的系数决定了它的图像形状。

例如，如果三次函数的系数为正，则其图像通常向上开口；如果系数为负，则其图像通常向下开口。

【三次函数的图像】为了更好地理解三次函数，我们可以通过绘制其图像来观察它的形状和特征。

通常，我们可以使用计算机图形软件或手工绘制的方法来完成。

三次函数的图像可以帮助我们理解其性质和行为，从而更好地理解这个函数。

【三次函数的实际应用】尽管三次函数在数学中具有重要的理论意义，但它在实际生活中的应用也非常广泛。

例如，它可以用于描述物理系统中的运动、化学反应中的浓度变化、生物学中的生长和繁殖等。

通过使用三次函数，我们可以更好地理解这些现象，并预测其未来的发展趋势。

【结论】总的来说，三次函数是一个重要的数学概念，它具有复杂的性质和行为，但其在实际生活中的应用也非常广泛。