平行四边形与三角形中位线练习题
中位线习题及答案

1.如图,在四边形ABCD中,BD⊥CD,AC⊥AB,E为BC的中点,∠EDA=60°,求证:AD=DE2.如图,在△ABC中,AD⊥CB、BE⊥AC,且相交于O点,N、M是CO、AB的中点,连接MN、ED,求证:MN是ED的中垂线证明:连接ME、MD、NE、ND(注:DE与MN交于P点)因AD⊥CB、BE⊥AC ,可得EM为直角△AEB斜边AB上的中线,EM=1/2 AB;MD为直角△ADB斜边AB上的中线,MD=1/2 AB∴EM=MDNE为直角△CEO斜边CO上的中线,NE=1/2 CO ND为直角△CDO斜边CO上的中线,ND=1/2 CO ∴NE=ND又MN=MN∴△MEN≌△MDN所以∠EMN=≌∠DMN又ME=MD,MP=MP∴△EMP≌△DMP∴EP=DP∠EPM = ∠DPM = 180°÷2 = 90°即:MN是ED的中垂线3、如图所示,BD、CE是三角形ABC的两条高,M、N分别是BC、DE的中点求证:MN⊥DE∵BD,CE为△ABC的两条高,∴BD⊥AC,CE⊥AB,∴∠BEC=∠BDC=90°,在Rt△BEC中,M为斜边BC的中点,∴EM=2分之一的BC,同理在Rt△BDC中,M为斜边BC的中点,可得DM=2分之一BC(不知可是这图?= =格式出了一点问题。
)∴EM=DM,∴M在线段ED的垂直平分线上,又N为ED的中点,∴N也在线段ED的垂直平分线上,∴MN垂直平分ED.M C4、如图,四边形ABCD中,∠DAB=∠DCB=90o,点M、N分别是BD、AC的中点。
MN、AC的位置关系如何?证明你的猜想。
DAB5、已知梯形ABCD中,∠B+∠C=90o,EF是两底中点的连线,试说明BC-AD =2EF解:作EM//AB,EN//CD,又AD//BC,则四边形AEMB,CDEN是平行四边形,AE=BM,ED=CN,∠EMN=∠B,∠ENM=角∠C∠B+∠C=90°,则△MEN是直角三角形。
三角形中位线专项训练(30道)(解析版)

三角形中位线专项训练(30道)(解析版)三角形中位线专项训练(30道)(解析版)1. 题目解析三角形中位线是指连接一个三角形的两个非邻边中点的线段。
在这个专项训练中,我们将解答30道关于三角形中位线的问题,并提供详细的解析,帮助你更好地理解和掌握相关概念和解题方法。
2. 题目设置2.1 第一类题目:中位线长度计算2.1.1 题目1:已知一个三角形的三边长度分别为a, b, c,求其中位线长度。
解析:根据中位线定义,连接三角形的两个非邻边中点可以得到一个平行四边形。
利用平行四边形的性质,可以计算出中位线长度为(c²+a²-0.5b²)/(2c)。
2.1.2 题目2:已知一个等边三角形的边长为a,求其中位线长度。
解析:等边三角形中位线长等于边长的一半,即中位线长度为a/2。
2.1.3 题目3:已知一个等腰三角形的底边长度为a,腰长为b,求其中位线长度。
解析:根据中位线定义,连接三角形的两个非邻边中点可以得到一个平行四边形。
利用平行四边形的性质,可以计算出中位线长度为(a²+b²)/(2a)。
2.2 第二类题目:中位线位置关系2.2.1 题目4:在一个等边三角形中,证明中位线与底边垂直且分割底边的比例为2:1。
解析:根据等边三角形的性质,中位线和底边垂直。
利用中位线定义和几何性质,可以证明中位线分割底边的比例为2:1。
2.2.2 题目5:已知在一个等腰三角形中,中位线长为x,底边长为y,求腰长。
解析:根据中位线定义,连接三角形的两个非邻边中点可以得到一个平行四边形。
利用平行四边形的性质,可以得到腰长为2x-y。
2.2.3 题目6:已知在一个一般三角形中,中位线等分了三角形的面积,证明这个三角形是等腰三角形。
解析:假设中位线等分了三角形的面积,利用三角形面积公式可以得到一个关于中位线和底边的方程。
通过求解这个方程,可以证明这个三角形是等腰三角形。
3. 题目变体上述题目只是针对三角形中位线的一部分问题进行了训练和解析。
2020-2021学年八年级数学人教版下册第18章《平行四边形》章末专题复习: 《中位线》相关训练

人教版八年级下册第18章《平行四边形》章末专题复习《中位线》相关训练一.选择题1.如图,△ABC中,D是AB的中点,E在AC上,且∠AED=90°+∠C,则BC+2AE 等于()A.AB B.AC C.AB D.AC2.如图所示,在△ABC中,AB=AC,D,E分别是AB,AC的中点,F,G为BC上的点,连接DG、EF,若AB=5cm,BC=8cm,FG=4cm,则△HFG的面积为()A.1cm2B.1.5cm2C.2cm2D.3cm23.如图,在四边形ABCD中,点P是边CD上的动点,点Q是边BC上的定点,连接AP,PQ,E,F分别是AP,PQ的中点,连接EF.点P在由C到D运动过程中,线段EF的长度()A.保持不变B.逐渐变小C.先变大,再变小D.逐渐变大4.如图,在三边互不相等的△ABC中,D、E、F分别是AB、AC、BC边的中点,连接DE,过点C作CM∥AB交DE的延长线于点M,连接CD、EF交于点N,则图中全等三角形共有()A.3对B.4对C.5对D.6对5.如图,在△ABC中,动点P在AB边上由点A向点B以3cm/s的速度匀速运动,则线段CP的中点Q运动的速度为()A.3cm/s B.2cm/s C.1.5cm/s D.1cm/s6.如图.在△ABC中,∠ACB=60°,AC=1,D是边AB的中点,E是边BC上一点.若DE平分△ABC的周长,则DE的长为()A.1B.C.D.7.如图,在△ABC中,点M为BC的中点,AD为△ABC的外角平分线,且AD⊥BD,若AB=6,AC=9,则MD的长为()A.3B.C.5D.8.如图,点B是直线l外一点,在l的另一侧任取一点K,以B为圆心,BK为半径作弧,交直线l于点M、N;再分别以M、N为圆心,以大于MN为半径作弧,两弧相交于点P;连接BP交直线l于点A;点C是直线l上一点,点D、E分别是线段AB、BC的中点;F在CA的延长线上,∠FDA=∠B,AC=8,AB=6,则四边形AEDF的周长为()A.8B.10C.16D.189.如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=8,BC=14,则线段EF的长为()A.2B.3C.5D.610.如图,在△ABC中,∠C=90°,E,F分别是AC,BC上两点,AE=16,BF=12,点P,Q,D分别是AF,BE,AB的中点,则PQ的长为()A.10B.8C.2D.2011.如图,BD、CE是△ABC的两条角平分线,AN⊥BD于点N,AM⊥CE于点M,连接MN,若△ABC的周长为17,BC=7,则MN的长度为()12.如图,四边形ABCD中,AB∥CD,AB=5,DC=11,AD与BC的和是12,点E、F、G分别是BD、AC、DC的中点,则△EFG的周长是()A.8B.9C.10D.1213.如图,△ABC的周长为32,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为()A.3B.4C.5D.614.如图,在△ABC中,AD是角平分线,AE是中线,CF⊥AD于点F,AC=5,AB=13,则EF的长为()A.B.C.3D.415.如图,四边形ABCD中,AC⊥BC,AD∥BC,BC=3,AC=4,AD=6.M是BD的中点,则CM的长为()二.填空题(共10小题)16.如图,在四边形ABCD中,AB∥CD,E,F分别是AC,BD的中点,已知AB=12,CD =6,则EF=.17.△ABC中,∠ACB=90°,BD=AC,M、N分别为CD、AB的中点,CD=2,MN=2,则CN=.18.如图,在四边形ABCD中,∠ADC+∠BCD=220°,E、F分别是AC、BD的中点,P 是AB边上的中点,则∠EPF=°.19.如图,已知在Rt△ABC中,∠ACB=90°,点D是AC延长线上的一点,AD=24,点E是BC上一点,BE=10,连接DE,M、N分别是AB、DE的中点,则MN=.20.如图,四边形ABCD中,∠BMF+∠CNF=90°,E、F分别是AD、BC的中点,AB=5,CD=12,则EF=.21.如图,∠MAN=90°,点C在边AM上,AC=2,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在的直线对称,点D,E分别为AB,BC的中点,连接DE 并延长交A′C所在直线于点F,连接A′E,当△A′EF为直角三角形时,AB的长为.22.如图,在△ABC中,D为BC边中点,P为AC边中点,E为BC上一点且BE=CE,连接AE,取AE中点Q并连接QD,取QD中点G,延长PG与BC边交于点H,若BC =6,则HE=.23.在四边形ABCD中,对角线AC⊥BD且AC=4,BD=8,E、F分别是边AB、CD的中点,则EF=.24.如图,△ABC的顶点落在两条平行线上,点D、E、F分别是△ABC三边中点,平行线间的距离是8,BC=6,移动点A,当CD=BD时,EF的长度是.25.如图,△ABC中,∠ACB=90°,AB边上的高线CD与△ABC的两条角平分线AE,BF分别交于H,G两点,点P,Q分别为HE,GF的中点,连接PQ,若AC=4,BC=6,则PQ的长为.三.解答题(共7小题)26.如图,在四边形ABCD中,AB=CD,点E、F分别是BC、AD的中点,连接EF并延长分别与BA、CD的延长线交于点M、N,∠BME与∠CNE的大小关系如何?试说明理由.27.已知:如图,四边形ABCD中,对角线AC=BD,E,F为AB、CD中点,连EF交BD、AC于P、Q求证:OP=OQ.28.(1)如图1,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F、G,连接FG.求证:FG=(AB+BC+AC).[提示:分别延长AF、AG与直线BC相交](2)如图2,若BD、CE分别是△ABC的内角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F、G,连接FG.线段FG与△ABC的三边又有怎样的数量关系?写出你的猜想,并给予证明.29.如图,在四边形ABCD中,AB=CD,E.F分别是BC.AD的中点,连接EF并延长,分别与BA,CD的延长线交于点M,N,则∠BME=∠CNE(不必证明)(温馨提示:在图(1)中,连接BD,取BD的中点H,连接HE.HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线的性质,可证明∠BME=∠CNE)(1)如图(2),在四边形ADBC中,AB与CD相交于点O,AB=CD,E.F分别是BC.AD 的中点,连接EF,分别交CD.BA于点M.N,判断△OMN的形状,请直接写出结论.(2)如图(3)中,在△ABC中,AC>AB,D点在AC上,AB=CD,E.F分别是BC.AD 的中点,连接EF并延长,与BA的延长线交于点G,若∠EFC=60°,连接GD,判断△AGD形状并证明.30.如图,在△ABC中,D为AC上一点,AB=CD,F是AD的中点,M为BC的中点,连接MF并延长交BA延长线于点E,G为EF的中点,求证:AG⊥ME.31.(1)如图1,在四边形ABCD中,AB=CD,E,F分别是AD,BC的中点,连接FE并延长,分别与BA,CD的延长线交于点M,N.求证:∠BME=∠CNE;(提示:取BD的中点H,连接FH,HE作辅助线)(2)如图2,在△ABC中,F是BC边的中点,D是AC边上一点,E是AD的中点,直线FE交BA的延长线于点G,若AB=DC=2,∠FEC=45°,求FE的长度.32.如图,在四边形ABCD中,BC、AD不平行,且∠BAD+∠ADC=270°,E、F分别是AD、BC的中点,已知EF=4,求AB2+CD2的值.参考答案一.选择题1.解:如图,过点B作BF∥DE交AC于点F.则∠BFC=∠DEF.又∵点D是AB的中点,∴EF=AE.∵∠DEF=∠BFC=180°﹣∠AED=180°﹣(90°+∠C)=90°﹣∠C,∴∠FBC=∠BFC,∴BC=FC,∴BC+2AE=AC.故选:B.2.解:连接,作AK⊥BC于K.∵AB=AC,∴BK=CK=BC=×8=4,在Rt△ABK中,AK===3,∵D、E分别是AB,AC的中点,∴DE是中位线,即平分三角形的高且DE=8÷2=4,∴DE=BC=FG,∴△DEH≌△GFH,H也是DG,EF的中点,∴△HFG的高是AK÷2=1.5÷2=0.75,∴S△HFG=4×0.75÷2=1.5.故选:B.3.解:连接AQ,∵点Q是边BC上的定点,∴AQ的大小不变,∵E,F分别是AP,PQ的中点,∴EF=AQ,∴线段EF的长度保持不变,故选:A.4.解:∵D、E分别是AB、AC边的中点,∴DE∥BC,DE=BC,∴∠EDC=∠FCD,∵F是BC边的中点,∴CF=BC,∴DE=CF,在△DNE和△CNF中,∴△DNE≌△CNF(AAS),同理△AED≌△CEM,∵E、F分别是AC、BC边的中点,∴EF∥AB,又CM∥AB,∴CM∥EF,∵DE∥BC,CM∥EF,∴四边形EFCM是平行四边形,∴△EFC≌△CME,△BCD≌△MDC,∴△EFC≌△ADE,∴图中全等三角形共有5对故选:C.5.解:取AC的中点H,连接QH,当点P与点A重合时,点Q与点H重合,∵点Q是线段CP的中点,点H为AC的中点,∴QH=AP,∵动点P在AB边上由点A向点B以3cm/s的速度匀速运动,∴点Q运动的速度为1.5cm/s,故选:C.6.解:延长BC至M,使CM=CA,连接AM,作CN⊥AM于N,∵DE平分△ABC的周长,∴ME=EB,又AD=DB,∴DE=AM,DE∥AM,∵∠ACB=60°,∴∠ACM=120°,∵CM=CA,∴∠ACN=60°,AN=MN,∴AN=AC•sin∠ACN=,∴AM=,∵BD=DA,BE=EM,∴DE=,故选:B.7.解:延长BD交CA的延长线于E,∵AD为∠BAE的平分线,BD⊥AD,∴∠EAD=∠BAD,∠ADE=∠ADB=90°,∵AD=AD,∴△ADE≌△ADB(ASA),∴BD=DE,AB=AE=6,∴CE=AC+AE=9+6=15,又∵M为△ABC的边BC的中点,∴DM是△BCE的中位线,∴MD=CE=×15=7.5.故选:D.8.解:由题意得,BA⊥MN,∴BC==10,∵∠BAC=90°,点E是线段BC的中点,∴AE=BE=BC=5,∴∠EAB=∠B,∵∠FDA=∠B,∴∠FDA=∠EAB,∴DF∥AE,∵点D、E分别是线段AB、BC的中点,∴DE∥AC,DE=AC=4,∴四边形AEDF是平行四边形,∴四边形AEDF的周长=2×(4+5)=18,故选:D.9.解:延长AF交BC于G,在△BF A和△BFG中,,∴△BF A≌△BFG(ASA)∴BG=AB=8,AF=FG,∴GC=BC﹣BG=6,∵AD=DB,AF=FG,∴DF∥BC,由AD=DB,∴AE=EC,∵AF=FG,AE=EC,∴EF=GC=3,故选:B.10.解:∵∠C=90°,∴∠CAB+∠CBA=90°,∵点P,D分别是AF,AB的中点,∴PD=BF=6,PD∥BC,∴∠PDA=∠CBA,同理,QD=AE=8,∠QDB=∠CAB,∴∠PDA+∠QDB=90°,即∠PDQ=90°,∴PQ==10,故选:A.11.解:∵△ABC的周长为17,BC=7.∴AB+AC=17﹣BC=10.如图,分别延长AM、AN交BC于点G,F.∵∠BNA=∠BNF=90°,BN=BN,∠NBA=∠NBF ∴△BNA≌△BNF(ASA)∴AN=FN,AB=FB同理,AM=MG,AC=GC,即MN为△AGF的中位线,∴MN=GF,而FB+GC=AB+AC,即BC+GF=AB+AC,∵BC=7,AB+AC=10,∴GF=3,∴MN=GF=,故选:A.12.解:连接AE,并延长交CD于K,∵AB∥CD,∴∠BAE=∠DKE,∠ABD=∠EDK,∵点E、F、G分别是BD、AC、DC的中点.∴BE=DE,在△AEB和△KED中,,∴△AEB≌△KED(AAS),∴DK=AB,AE=EK,EF为△ACK的中位线,∴EF=CK=(DC﹣DK)=(DC﹣AB),∵EG为△BCD的中位线,∴EG=BC,又FG为△ACD的中位线,∴FG=AD,∴EG+GF=(AD+BC),∵AD+BC=12,AB=5,DC=11,即DC﹣AB=6,∴EG+GF=6,FE=3,∴△EFG的周长是6+3=9.故选:B.13.解:∵BQ平分∠ABC,BQ⊥AE,∴∠ABQ=∠EBQ,∵∠ABQ+∠BAQ=90°,∠EBQ+∠BEQ=90°,∴∠BAQ=∠BEQ,∴AB=BE,同理:CA=CD,∴点Q是AE中点,点P是AD中点(三线合一),∴PQ是△ADE的中位线,∵BE+CD=AB+AC=32﹣BC=32﹣12=20,∴DE=BE+CD﹣BC=8,∴PQ=DE=4.故选:B.14.解:延长CF交AB于G,如图所示:∵AD是△ABC的角平分线,∴∠GAF=∠CAF,在△AGF和△ACF中,,∴△AGF≌△ACF(ASA),∴AG=AC=5,GF=CF,则BG=AB﹣AG=13﹣5=8.又∵AE是△ABC的中线,∴BE=CE,∴EF是△BCG的中位线,∴EF=BG=4.故选:D.15.解:延长BC到E使BE=AD,则四边形ABED是平行四边形,∵BC=3,AD=6,∴C是BE的中点,∵M是BD的中点,∴CM=DE=AB,∵AC⊥BC,∴AB===5,∴CM=,故选:C.二.填空题(共10小题)16.解:连接CF并延长交AB于G,∵AB∥CD,∴∠FDC=∠FBG,在△FDC和△FBG中,,∴△FDC≌△FBG(ASA)∴BG=DC=6,CF=FG,∴AG=AB﹣BG=12﹣6=6,∵CE=EA,CF=FG,∴EF=AG=3,故答案为:3.17.解:过点N作NE⊥BC于点E,则NE∥AC,又N是AB的中点,∴NE=AC,BE=(2+BD)=(2+AC)=1+AC,∴EM=MD+DE=1+BD﹣BE=AC,∴NE=ME,由勾股定理得,MN2=ME2+NE2,即(2)2=ME2+NE2,解得,NE=ME=2,∴CN===.故答案为:.18.解:∵四边形ABCD中,∠ADC+∠BCD=220°,∴∠BAD+∠ABC=360°﹣220°=140°,∵E、F分别是AC、BD的中点,P是AB边上的中点,∴PE是△ABC的中位线,PF是△ABD的中位线,∴PE∥BC,PF∥AD,∴∠BPF=∠BAD,∠APE=∠ABC,∴∠APE+∠BPF=∠BAD+∠ABC=140°,∴∠EPF=180°﹣140°=40°,故答案为:40.19.解:连接BD,取BD的中点F,连接MF、NF,如图所示:∵M、N、F分别是AB、DE、BD的中点,∴NF、MF分别是△BDE、△ABD的中位线,∴NF∥BE,MF∥AD,NF=BE=5,MF=AD=12,∵∠ACB=90°,∴AD⊥BC,∵MF∥AD,∴MF⊥BC,∵NF∥BE,∴NF⊥MF,在Rt△MNF中,由勾股定理得:MN===13;故答案为:13.20.解:连接BD,取BD的中点H,连接EH,HF,∵E、F分别是AD、BC的中点,∴EH∥AB,EH=AB=,HF∥CD,HF=CD=6,∴∠HEF=∠BMF,∠HFE=∠CNF,∵∠BMF+∠CNF=90°,∴∠HEF+∠HFE=90°,∴∠EHF=90°,∴EF===,故答案为:.21.解:当△A′EF为直角三角形时,存在两种情况:①当∠A'EF=90°时,如图1,∵△A′BC与△ABC关于BC所在直线对称,∴A'C=AC=2,∠ACB=∠A'CB,∵点D,E分别为AB,BC的中点,∴D、E是△ABC的中位线,∴DE∥AB,∴∠BDE=∠MAN=90°,∴∠BDE=∠A'EF,∴AB∥A'E,∴∠ABC=∠A'EB,∴∠A'BC=∠A'EB,∴A'B=A'E,Rt△A'CB中,∵E是斜边BC的中点,∴BC=2A'E,由勾股定理得:AB2=BC2﹣AC2,∴AE′=,∴AB=;②当∠A'FE=90°时,如图2,∵∠ADF=∠A=∠DFC=90°,∴∠ACF=90°,∵△A′BC与△ABC关于BC所在直线对称,∴∠ABC=∠CBA'=45°,∴△ABC是等腰直角三角形,∴AB=AC=2;综上所述,AB的长为或2;故答案为:或2.22.解:连接PQ.∵BD=DC=3,BE=BC=,EC=,∵AQ=QE,AP=PC,∴PQ∥EC,PQ=EC=,∵∠QPG=∠GHD,∠QGP=∠DGH,QG=GD,∴△PQG≌△HDG(AAS),∴PQ=HD=,BH=BD﹣DH=3﹣=,∴HE=BE﹣BH=﹣=,故答案为.23.解:如图,取BC的中点G,连接EG、FG,∵E、F分别是边AB、CD的中点,∴EG∥AC且EG=AC=×4=2,FG∥BD且FG=BD=×8=4,∵AC⊥BD,∴EG⊥FG,∴EF=.故答案为:224.解:如图,过点D作DH⊥BC于点H,∵过点D作DH⊥BC于点H,BC=6,∴BH=CH=3.又平行线间的距离是8,点D是AB的中点,∴DH=4,∴在直角△BDH中,由勾股定理知,BD===5.∵点D是AB的中点,∴AB=2BD=10.又点E、F分别是AC、BC的中点,∴EF是△ABC的中位线,∴EF=AB=5.故答案是:5.25.解:延长CP交AB于K,延长CQ交AB于L,△ABC中,∠ACB=90°,由勾股定理得:AB===2,∵BF是∠ABC的平分线,∴∠ABF=∠CBF,又∵CD⊥AB,∴∠CGF=∠BGD=90°﹣∠ABF=90°﹣∠CBF=∠CFB,∴CG=CF.又∵Q是GF的中点,∴CQ⊥GF,∴∠CQB=∠LQB=90°,∴∠BCQ=∠BLQ,∴BL=BC=6,∴CQ=LQ,同理得:CE=CH,∵P是EH的中点,∴CP⊥EH,∴AP⊥CK,同理得AK=AC=4,CP=PK,∵CP=PK,CQ=LQ,∴PQ=LK=(BL+AK﹣AB)=(6+4﹣2)=5﹣;故答案为:5﹣.三.解答题(共7小题)26.解:∠BME=∠CNE,理由如下:连接BD,取BD的中点H,连接HE、HF,∵点E、F分别是BC、AD的中点,∴HF∥BM.HF=AB,HE∥CD,HE=CD,∴∠1=∠BME,∠2=∠ENC,∵AB=CD,∴HF=HE,∴∠1=∠2,∴∠BME=∠CNE.27.证明:取BC中点G,连EG、FG,∵E,G为AB、BC中点,∴EG=AC,EG∥AC,∴∠FEG=∠OQP,同理,FG=BD,FG∥BD,∴∠EFG=∠OPQ,∵AC=BD,∴EG=FG,∴∠FEG=∠EFG,∴∠OPQ=∠OQP,∴OP=OQ.28.解:(1)如图1,∵AF⊥BD,∠ABF=∠MBF,∴∠BAF=∠BMF,在△ABF和△MBF中,,∴△ABF≌△MBF(ASA),∴MB=AB,∴AF=MF,同理:CN=AC,AG=NG,∴FG是△AMN的中位线,∴FG=MN,=(MB+BC+CN),=(AB+BC+AC).(2)猜想:FG=(AB+AC﹣BC),证明:如图2,延长AG、AF,与直线BC相交于M、N,∵由(1)中证明过程类似证△ABF≌△NBF,∴NB=AB,AF=NF,同理CM=AC,AG=MG,∴FG=MN,∴MN=2FG,∴BC=BN+CM﹣MN=AB+AC﹣2FG,∴FG=(AB+AC﹣BC).29.解:(1)取AC中点P,连接PF,PE,可知PE=,PE∥AB,∴∠PEF=∠ANF,同理PF=,PF∥CD,∴∠PFE=∠CME,又PE=PF,∴∠PFE=∠PEF,∴∠OMN=∠ONM,∴△OMN为等腰三角形.(2)判断出△AGD是直角三角形.证明:如图连接BD,取BD的中点H,连接HF、HE,∵F是AD的中点,∴HF∥AB,HF=AB,同理,HE∥CD,HE=CD,∵AB=CD∴HF=HE,∴∠HEF=∠HFE,∵∠EFC=60°,∴∠HEF=60°,∴∠HEF=∠HFE=60°,∴△EHF是等边三角形,∴∠3=∠EFC=∠AFG=60°,∴△AGF是等边三角形.∵AF=FD,∴GF=FD,∴∠FGD=∠FDG=30°∴∠AGD=90°即△AGD是直角三角形.30.证明:连接BD,取BD的中点为O,连接FO,MO,∵F是AD的中点,M为BC的中点,∴MO是△BCD的中位线,FO是△ABD的中位线,∴MO=CD,FO=AB,MO∥AC,OF∥AB,∵AB=CD,∴MO=FO,∴∠OFM=∠OMF,∵OF∥AB,∴∠OFM=∠AEF,∵OM∥AC,∴∠OMF=∠CFM=∠AFE,∴∠AEF=∠AFE,∴AE=AF,∵G为EF的中点,∴AG⊥ME.31.(1)证明:连接BD,取DB的中点H,连接EH,FH,∵E,H分别是AD,BD的中点,∴EH∥AB,EH=AB,∴∠BME=∠HEF,∵F,H分别是BC,BD的中点,∴FH∥CD,FH=CD,∴∠CNE=∠HFE,∵AB=CD∴HE=FH,∴∠HEF=∠HFE∴∠BME=∠CNE;(2)连接BD,取DB的中点H,连接EH,FH,∵E,F分别是AD,BC的中点,∴EH=AB,FH=CD,FH∥AC,∴∠HFE=∠FEC=45°,∵AB=CD=2,∴HF=HE=1,∴∠HEF=∠HFE=45°,∴∠EHF=180°﹣∠HFE﹣HEF=90°,∴.32.解:连接BD,取BD的中点M,连接EM并延长交BC于N,连接FM,∵∠BAD+∠ADC=270°,∴∠ABC+∠C=90°,∵E、F、M分别是AD、BC、BD的中点,∴EM∥AB,FM∥CD,EM=AB,FM=CD,∴∠MNF=∠ABC,∠MFN=∠C,∴∠MNF+∠MFN=90°,即∠NMF=90°,由勾股定理得,ME2+MF2=EF2=16,∴AB2+CD2=(2ME)2+(2MF)2=64.。
八年级数学下册第6章平行四边形6.4三角形的中位线定理

第6章6.4三角形的中位线定理一.选择题(共10小题)1.(2020•魏县二模)如图,△ABC中,D,E分别上边AB,AC的中点,若DE=3,则BC=()A.B.9 C.6 D.5(1题图)(2题图)(3题图)(4题图)2.(2020•山西)如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是()A.8 B.10 C.12 D.143.(2020•怀柔区二模)如图所示,A,B两点分别位于一个池塘的两端,小聪想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为10m,则A,B间的距离为()A.15m B.25m C.30m D.20m4.(2020•南漳县模拟)如图,▱ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3cm,则AB 的长为()A.12cm B.9cm C.6cm D.3cm5.(2020•莆田模拟)如图,△ABC的中线BD、CE交于点O,连接OA,点G、F分别为OC、OB的中点,BC=8,AO=6,则四边形DEFG的周长为()A.12 B.14 C.16 D.18(5题图)(6题图)(7题图)(8题图)6.(2020春•宁城县期末)如图,已知矩形ABCD的对角线AC的长为10cm,连接各边中点E,F,G,H得四边形EFGH,则四边形EFGH的周长为()A.20cm B.20cm C.20cm D.25cm7.(2020春•抚州期末)如图,在△ABC中,AB=5,BC=6,AC=7,点D,E,F分别是△ABC三边的中点,则△DEF的周长为()A.9 B.10 C.11 D.128.(2020春•山亭区期末)如图,已知△ABC的周长是1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2020个三角形的周长为()A.B.C.D.9.(2020•泰安)如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为()A.6 B.7 C.8 D.10(9题图)(10题图)(11题图)(12题图)10.(2020•邢台二模)如图,四边形ABCD的两条对角线AC、BD互相垂直,A1B1C1D1是四边形ABCD的中点四边形,如果AC=8,BD=10,那么四边形A1B1C1D1的面积为()A.20 B.40 C.36 D.10二.填空题(共10小题)11.(2020•河池)如图,在△ABC中,D、E分别是AB、AC的中点,若BC=10,则DE= .12.(2020•泰安)如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.若AB=8,AD=12,则四边形ENFM的周长为.13.(2020•盐城)如图,点D、E、F分别是△ABC各边的中点,连接DE、EF、DF.若△ABC的周长为10,则△DEF的周长为.(13题图)(14题图)(15题图)(16题图)14.(2020•衡阳)如图所示,小明为了测量学校里一池塘的宽度AB,选取可以直达A、B两点的点O处,再分别取OA、OB的中点M、N,量得MN=20m,则池塘的宽度AB为m.15.(2020•龙岩校级质检)如图,在△ABC中,∠ACB=60°,点D,E分别是AB,AC的中点,点F在线段DE上,连结AF,CF.若CF恰好平分∠ACB,则∠FAC的度数为.16.(2020•昌平区二模)已知:如图,在△A BC中,点D为BC上一点,CA=CD,CF平分∠ACB,交AD于点F,点E为AB的中点.若EF=2,则BD= .17.(2020春•南长区期末)如图,在△ABC中,点D在BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连接MN.若AB=5,BC=8,则MN= .18.(2020春•薛城区期末)如图,四边形ABCD中,AD=BC,F、E、G分别是AB、CD、AC的中点,若∠DAC=20°,∠ACB=60°,则∠FEG=.(17题图)(18题图)(19题图)(20题图)19.(2020春•昌乐县期末)如图,在△ABC中,点M为BC的中点,AD平分∠BAC,且BD⊥AD于点D,延长BD交AC于点N.若AB=12,AC=18,则MD的长为.20.(2020春•胶州市期末)如图,△ABC中,D,E分别是AB,AC的中点,F是DE上一点,且AF⊥FC,若BC=9,DF=1,则AC的长为.三.解答题(共5小题)21.(2020秋•龙口市期末)如图,D、E分别是△ABC的边AB、AC的中点,点O是△ABC内部任意一点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.求证:四边形DGFE是平行四边形.22.(2020•邵阳)如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=BC,连接CD和EF.(1)求证:DE=CF;(2)求EF的长.23.(2020春•临清市期中)已知如图:在△ABC中,AB、BC、CA的中点分别是E、F、G,AD是高.求证:∠EDG=∠EFG.24.(2020春•泗阳县期末)如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.(1)试判断线段DE与FH之间的数量关系,并说明理由;(2)求证:∠DHF=∠DEF.25.(2020春•工业园区期中)如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,垂足为N,且AB=6,BC=10,MN=1.5,求△ABC的周长.青岛版八年级数学下册第6章6.4三角形的中位线定理同步训练题参考答案一.选择题(共10小题)1.C 2.C 3.D 4.C 5.B 6.A 7.A 8.D 9.C 10.A二.填空题(共10小题)11.5 12.20 13.5 14.40 15.60°16.4 17.18.20°19.3 20.7三.解答题(共5小题)21.证明:∵D、E分别是AB、AC边的中点,∴DE∥BC,且DE=BC,同理,GF∥BC,且GF=BC,∴DE∥GF且DE=GF,四边形DGFE是平行四边形.22.(1)证明:∵D、E分别为AB、AC的中点,∴DE BC,∵延长BC至点F,使CF=BC,∴DE FC,即DE=CF;(2)解:∵DE FC,∴四边形DEFC是平行四边形,∴DC=EF,∵D为AB的中点,等边△ABC的边长是2,∴AD=BD=1,CD⊥AB,BC=2,∴DC=EF=.23.证明:连接EG,∵E、F、G分别是AB、BC、CA的中点,∴EF为△ABC的中位线,EF=AC.(三角形的中位线等于第三边的一半)又∵AD⊥BC,∴∠ADC=90°,DG为直角△ADC斜边上的中线,∴DG=AC.(直角三角形斜边上的中线等于斜边的一半)∴DG=EF.同理DE=FG,EG=GE,∴△EFG≌△GDE(SSS).∴∠EDG=∠EFG.(23题图)(24题图)(25题图)24.解:(1)DE与FH相等.理由如下:∵D、E分别是AB、BC边的中点.∴ED∥AC,DE=AC,∵AH⊥BC,垂足为H,F是AC的中点,∴HF=AC,∴DE=FH.(2)∵DH=AB,AD=AB,∴AD=DH,∴∠DAH=∠DHA,同理可证:∠FAH=∠FHA,∴∠DHF=∠DAF,∵AD∥EF,D E∥AF,∴四边形ADEF是平行四边形,∴∠DEF=∠DAF,∴∠DHF=∠DEF.25.解:延长线段BN交AC于E.∵AN平分∠BAC,在△ABN和△AEN中,∴△ABN≌△AEN(SAS),∴AE=AB=6,BN=NE,又∵M是△ABC的边BC的中点,∴CE=2MN=2×1.5=3,∴△ABC的周长是AB+BC+AC=6+10+6+3=25.八年级上学期期末数学试卷一、选择题(每题只有一个答案正确)1.如图,在ABC 中,AB AC =,D 是BC 的中点,P 是AD 上任意一点,连接BP 、CP 并延长分别交AC 、AB 于点E 、F ,则图中的全等三角形共有( )A .7对B .6对C .5对D .4对【答案】A 【分析】根据等腰三角形的性质,全等三角形的判断及性质可知有以下7对三角形全等:△ABD ≌△ACD 、△ABP ≌△ACP 、△ABE ≌△ACF 、△APF ≌△APE 、△PBD ≌△PCD 、△BPF ≌△CPE 、△BCF ≌△CBE .【详解】①∵AB AC =,D 是BC 的中点,由等腰三角形三线合一可知:BAD CAD ∠=∠,AD BC ⊥,∴()ABD ACD AAS ≌②由AB AC =,BAD CAD ∠=∠,AP AP =,∴(ABP ACP SSS ≌)③由②可知,ABE ACF ∠=∠,∵ABE ACF ∠=∠,AB AC =,BAE CAF ∠=∠,∴()ABE ACF ASA ≌④由③可知,AFP AEP ∠=∠,∵AFP AEP ∠=∠,BAD CAD ∠=∠,AP AP =∴()APF APE AAS ≌⑤由①可知,ADB ADC ∠=∠,BD CD =,又∵PD PD =,∴()PBD PCD SAS ≌⑥由③⑤可知,AFP AEP ∠=∠,BP CP =,∴BFP CEP ∠=∠ ,又∵BPF CPE ∠=∠ ,()BPF CPE AAS ≌⑦由⑤可知BCF CBE ∠=∠,由⑥可知BFP CEP ∠=∠,又∵BC CB =∴()BCF CBE AAS ≌∴共7对全等三角形,故选A .【点睛】本题主要考查等腰三角形的性质,全等三角形的性质及判定,熟练掌握全等三角形的判定定理(SSS SAS AAS ASA HL 、、、、)是解题的关键.2.周长38cm 的三角形纸片ABC (如图甲),AB AC =,将纸片按图中方式折叠,使点A 与点B 重合,折痕为DE (如图乙),若DBC ∆的周长为25cm ,则BC 的长为( )A .10 cmB .12cmC .15cmD .13cm【答案】B【分析】由折叠的性质可得AD=BD ,由△ABC 的周长为38cm ,△DBC 的周长为25cm ,可列出两个等式,可求解.【详解】∵将△ADE 沿DE 折叠,使点A 与点B 重合,∴AD=BD ,∵△ABC 的周长为38cm ,△DBC 的周长为25cm ,∴AB+AC+BC=38cm ,BD+CD+BC=AD+CD+BC=AC+BC=25cm ,∴AB=13cm=AC∴BC=25-13=12cm故选:B .【点睛】本题考查了翻折变换,熟练运用折叠的性质是本题的关键.32…,,按下列方式进行排列:24,…若2的位置记为(1,2),2,1)A.(5,4)B.(4,4)C.(4,5)D.(3,5)【答案】B…∵19×2=38,4行,第4个数字.故选:B.【点睛】此题考查的是数字的变化规律,找出其中的规律是解题的关键.4.下列算式中,正确的是()A.a4•a4=2a4B.a6÷a3=a2C.(a﹣b)2=a2﹣b2D.(﹣3a2b)2=9a4b2【答案】D【分析】根据同底数相乘(或相除),底数不变指数相加(或相减);幂的乘方:底数不变,指数相乘;完全平方公式,对各选项分析判断后利用排除法即可求解.【详解】解:A、原式=a8,故A错误.B、原式=a3,故B错误.C、原式=a2﹣2ab+b2,故C错误.D、原式=9a4b2,故D正确故选:D.【点睛】本题考查同底数幂的乘法,同底数幂的除法,完全平方公式,幂的乘方,解题的关键是熟练掌握运算法则和公式.5.如图,在OAB 和OCD 中,,,,40OA OB OC OD OA OC AOB COD ==>∠=∠=︒,连接,AC BD 交于点M ,连接OM .下列结论:①AC BD =;②40AMB ∠=︒;③OM 平分BOC ∠;④MO 平分BMC ∠.其中正确的个数为( ).A .4B .3C .2D .1【答案】B【分析】根据题意逐个证明即可,①只要证明()AOC BOD SAS ≌,即可证明AC BD =; ②利用三角形的外角性质即可证明; ④作OG MC ⊥于G ,OH MB ⊥于H ,再证明()OCG ODH AAS ≌即可证明MO 平分BMC ∠.【详解】解:∵40AOB COD ∠=∠=︒,∴AOB AOD COD AOD ∠+∠=∠+∠,即AOC BOD ∠=∠,在AOC △和BOD 中,OA OBAOC BOD OC OD=⎧⎪∠=∠⎨⎪=⎩,∴()AOC BOD SAS ≌,∴,OCA ODB AC BD ∠=∠=,①正确;∴OAC OBD ∠=∠,由三角形的外角性质得:,AMB OAC AOB OBD ∠+∠=∠+∠∴40AMB AOB ∠=∠=°,②正确;作OG MC ⊥于G ,OH MB ⊥于H ,如图所示:则90OGC OHD ∠=∠=°,在OCG 和ODH 中,OCA ODB OGC OHD OC OD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()OCG ODH AAS ≌,∴OG OH =,∴MO 平分BMC ∠,④正确;正确的个数有3个;故选B .【点睛】本题是一道几何的综合型题目,难度系数偏上,关键在于利用三角形的全等证明来证明线段相等,角相等. 6.用科学记数法表示0.0000018=( )A .61.810-⨯B .61.810⨯C .51.810-⨯D .71810-⨯【答案】A【分析】绝对值小于1的数可以利用科学记数法表示,一般形式为a ×10-n ,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【详解】0.0000018=61.810-⨯.故选A.【点睛】此题考查了科学记数法的表示方法,科学记数法的表示形式为a ×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.7.如图,在ABC 中,点D 是BC 延长线上一点,70A ∠=︒,120ACD ∠=︒,则B 等于( ).A .60°B .80°C .70°D .50°【答案】D 【分析】利用外角的性质解答即可.【详解】∵ ∠ACD =∠B +∠A ,∴∠B =∠ACD -∠A =120°-70°=50°,故选:D .【点睛】本题考查外角的性质,属于基础题型.8.如图,为了弘扬中华民族的传统文化,我校开展了全体师生学习“弟子规”活动.对此学生会就本校“弟子规学习的重要性”对1000名学生进行了调查,将得到的数据经统计后绘制成如图所示的扇形统计图,可知认为“很重要”的人数是( )A .110B .290C .400D .600【答案】D 【分析】利用1000ד很重要”的人数所占的百分率,即可得出结论.【详解】解:1000×(1-11%-29%)=600故选D .【点睛】此题考查的是扇形统计图,掌握百分率和部分量的求法是解决此题的关键.9.关于函数24y x =-的图像,下列结论正确的是( )A .必经过点(1,2)B .与x 轴交点的坐标为(0,-4)C .过第一、三、四象限D .可由函数2y x =-的图像平移得到【答案】C【分析】根据一次函数的性质对各选项进行逐一分析即可.【详解】解:A 、∵当x=1时,y=2-4=-2≠2,∴图象不经过点(1,2),故本选项错误;B 、点(0,-4)是y 轴上的点,故本选项错误;C 、∵k=2>0,b=-4<0,∴图象经过第一、三、四象限,故本选项正确;D 、函数y=-2x 的图象平移得到的函数系数不变,故本选项错误.故选:C .【点睛】本题考查的是一次函数的性质,熟知一次函数y=kx+b (k≠0),当k >0,b <0时函数图象经过一、三、四象限是解答此题的关键.10.下列长度的三条线段能组成三角形的是( )A .1,2,3B .2,2,4C .2,3,4D .2,4,8【答案】C【分析】根据三角形的三边关系进行分析判断.【详解】根据三角形任意两边的和大于第三边,得A 中,1+2=3,不能组成三角形;B 中,2+2<4,不能组成三角形;C 中,3+2>4,能够组成三角形;D 中,2+4<8,不能组成三角形.故选:C .【点睛】此题主要考查三角形的构成条件,解题的关键是熟知三角形任意两边的和大于第三边.二、填空题11.科学家发现一种病毒的直径为0.0043微米,则用科学记数法表示为__________微米.【答案】4.1×10﹣1 【解析】0.0041=4.1×10﹣1. 点睛:本题考查用科学记数法表示较小的数,一般形式为a×10﹣n ,其中1≤|a|<10,n 为由原数左边起第一个不为零的数字前面的0的个数所决定(包括小数点前面的0).12.因式分解:3x 2-6xy+3y 2=______.【答案】3(x ﹣y )1【解析】试题分析:原式提取3,再利用完全平方公式分解即可,得到3x 1﹣6xy+3y 1=3(x 1﹣1xy+y 1)=3(x ﹣y )1.考点:提公因式法与公式法的综合运用13.如图,将一块直角三角板DEF 放置在锐角ABC ∆上,使得该三角板的两条直角边DE 、DF 恰好分别经过B 、C ,若40A ∠=︒,则ABD ACD ∠+∠=_________.【答案】50°【分析】根据三角形的内角和定理求出∠ABC+∠ACB 的度数,再根据直角三角形两锐角互余的关系得到∠DBC+∠DCB=90°,由此即可得到答案.【详解】∵∠A+∠ABC+∠ACB=180°,40A ∠=︒,∴∠ABC+∠ACB=140°,∵∠BDC=90°,∴∠DBC+∠DCB=90°,∴ABD ACD ∠+∠=(∠ABC+∠ACB)-(∠DBC+∠DCB)=50°,故答案为:50°. 【点睛】此题考查三角形的内角和定理,直角三角形两锐角互余的关系,所求角度不能求得每个角的度数时,可将两个角度的和求出,这是一种特殊的解题方法.14.分式11x +有意义的条件是__________. 【答案】x ≠﹣1【分析】根据分式有意义,分母不等于零,列不等式求解即可.【详解】解:由题意得:x +1≠0,解得:x ≠﹣1,故答案为:x ≠﹣1【点睛】本题考查分式有意义的条件,解题的关键是从以下三方面透彻理解分式的概念:分式无意义时,分母为零;分式有意义时,分母不为零;分式的值为零时,分子为零且分母不为零.15.如图,C 为线段AE 上一动点(不与点A ,E 重合),在AE 同侧分别作等边ABC 和等边CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连接PQ .则下列结论:①AD =BE ;②PQ ∥AE ;③AP =BQ ;④DE =DP .其中正确的有________.(填序号)【答案】①②③【分析】根据等边三角形的三边都相等,三个角都是60°,可以证明ACD 与BCE 全等,根据全等三角形对应边相等可得AD =BE ,所以①正确,对应角相等可得∠CAD =∠CBE ,然后证明ACP 与BCQ 全等,根据全等三角形对应边相等可得PC =PQ ,从而得到CPQ 是等边三角形,再根据等腰三角形的性质可以找出相等的角,从而证明PQ ∥AE ,所以②正确;根据全等三角形对应边相等可以推出AP =BQ ,所以③正确,根据③可推出DP =EQ ,再根据DEQ 的角度关系DE ≠DP . 【详解】解:∵等边ABC 和等边CDE ,∴AC =BC ,CD =CE ,∠ACB =∠ECD =60°,∴180°﹣∠ECD =180°﹣∠ACB ,即∠ACD =∠BCE , 在ACD 与BCE 中,AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩, ∴ACD ≌BCE (SAS ),∴AD =BE ,故①小题正确; ∵ACD ≌BCE (已证),∴∠CAD =∠CBE ,∵∠ACB =∠ECD =60°(已证),∴∠BCQ =180°﹣60°×2=60°,∴∠ACB =∠BCQ =60°, 在ACP 与BCQ 中,CAD CBE AC BCACB BCQ ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴ACP ≌BCQ (ASA ),∴AP =BQ ,故③小题正确;PC =QC ,∴PCQ是等边三角形,∴∠CPQ=60°,∴∠ACB=∠CPQ,∴PQ∥AE,故②小题正确;∵AD=BE,AP=BQ,∴AD﹣AP=BE﹣BQ,即DP=QE,∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,∴∠DQE≠∠CDE,故④小题错误.综上所述,正确的是①②③.故答案为:①②③.【点睛】本题考查了等边三角形的性质,全等三角形的判定与性质,以及平行线的判定,需要多次证明三角形全等,综合性较强,但难度不是很大,是热点题目,仔细分析图形是解题的关键.16.一个大型商场某天销售的某品牌的运动鞋的数量和尺码如下表:这些鞋的尺码组成的一组数据的中位数是_______.【答案】23.1【分析】根据中位数的定义分析,即可得到答案.【详解】鞋的销售量总共12双,鞋的尺码从小到大排列后中间两个数为:23,24∴中位数为:23.1故答案为:23.1.【点睛】本题考查了中位数的知识,解题的关键是熟练掌握中位数的定义,从而完成求解.17.分解因式:41a-=___________.【答案】2(1)(1)(1)a a a ++-【分析】原式利用平方差公式分解即可.【详解】42221(1)(1)(1)(1)(1)a a a a a a -=+-=++-,故答案为2(1)(1)(1)a a a ++-.【点睛】此题考查了因式分解-运用公式法,熟练掌握因式分解的方法是解本题的关键.三、解答题18.象山红美人柑橘是我省农科院研制的优质品种,宁波市某种植基地2017年种植“象山红美人”100亩,到2019年“象山红美人”的种植面积达到196亩.(1)求该基地这两年“象山红美人”种植面积的平均增长率;(2)市场调查发现,当“象山红美人”的售价为45元/千克时,每天能售出200千克,售价每降价1元,每天可多售出50千克,为了推广宣传,基地决定降价促销,同时减少库存,已知该基地“象山红美人”的平均成本价为33元/千克,若使销售“象山红美人”每天获利3150元,则售价应降低多少元?【答案】(1)平均增长率为40%;(2)售价应降低5元.【分析】(1)设该基地这两年种植面积的平均增长率为x ,增长两次后种植面积为21001()x +,达到196亩即可列出方程2100(1)196x +=求解;(2)设售价应降低m 元,则每天的销量为(20050)m +千克,每千克的利润为(45-m-33)元,再根据总利润=单个利润×数量即可列出方程求解.【详解】解:(1)设该基地这两年种植面积的平均增长率为x ,根据题意可得:2100(1)196x +=,两边同时除以100,解得0.4x =或-2.4(舍去),∴平均增长率为40%,故答案为:40%;(2)设售价应降低m 元,则每天的销量为(20050)m +千克,根据题意可得:(4533)(20050)3150m m --+=解得13m =或25m =,当13m =时,每天的销量为:200+50×3=350千克,当25m =时,每天的销量为:200+50×5=450千克,∵要减少库存,故每天的销量越多越好,∴售价应降低5元,故答案为:售价应降低5元.【点睛】本题考查了一元二次方程在增长率问题和销售问题中的应用,根据题目正确列出方程是解题的关键. 19.某电器公司计划装运甲、乙两种家电到农村销售(规定每辆汽车按规定满载,且每辆汽车只能装同一种家电),已知每辆汽车可装运甲种家电20台,乙种家电30台.(1)若用8辆汽车装运甲、乙两种家电共190台到A 地销售,问装运甲、乙两种家电的汽车各有多少辆? (2)如果每台甲种家电的利润是180元,每台乙种家电的利润是300元,那么该公司售完这190台家电后的总利润是多少?【答案】(1)装运甲种家电的汽车有5辆,装运乙种家电的汽车有3辆;(2)该公司售完这190台家电后的总利润是45000元.【分析】(1)设装运甲种家电的汽车有x 辆,装运乙种家电的汽车有y 辆,根据用8辆汽车装运甲、乙两种家电共190台即可求得x 、y 的值;(2)根据总利润=甲种家电的利润+乙种家电的利润,列出算式计算即可求解.【详解】解:(1)设装运甲种家电的汽车有x 辆,装运乙种家电的汽车有y 辆,依题意有82030190x y x y +=⎧⎨+=⎩ , 解得53x y =⎧⎨=⎩. 故装运甲种家电的汽车有5辆,装运乙种家电的汽车有3辆;(2)20×5×180+30×3×300=45000(元). 答:该公司售完这190台家电后的总利润是45000元.【点睛】本题考查二元一次方程组的应用,利润的计算,本题中解关于x 、y 的方程组是解题关键.20.如图,在平面直角坐标系xOy 中,A(-3,4),B(-4,1),C(-1,1).(1)在图中作出△ABC 关于x 轴的轴对称图形△A′B′C′;(2)直接写出A ,B 关于y 轴的对称点A″,B″的坐标.【答案】(1)见解析;(2)A″(3,4),B″(4,1).【分析】(1)正确找出对应点A′,B′,C′即可得出△ABC关于x轴的轴对称图形△A′B′C′;(2)根据关于y轴对称的点,纵坐标不变,横坐标改变符号直接写出即可.【详解】(1)如图所示;(2)点A(﹣3,4)、B(﹣4,1)关于y轴的对称点A″、B″的坐标分别为:A″(3,4),B″(4,1).【点睛】本题考查轴对称图形的作法以及关于坐标轴对称的点的坐标特点,灵活应用关于坐标轴对称的点的性质是解题的关键.21.已知:如图,AD垂直平分BC,D为垂足,DM⊥AB,DN⊥AC,M、N分别为垂足.求证:DM=DN.【答案】见解析.【分析】根据垂直平分线的性质得到AC=AB,再利用等腰三角形的性质得到AD是角平分线,最后利用角平分线的性质即可得到结论.【详解】证明:∵AD垂直平分BC,∴AC=AB,即ABC是等腰三角形,∴AD平分∠BAC,∵DM⊥AB,DN⊥AC,∴DM=DN.【点睛】本题考查了垂直平分线的性质,等腰三角形的判定与性质,角平分线的性质,熟练掌握各性质判定定理是解题的关键.22.甲、乙两工程队合作完成一项工程,需要12天完成,工程费用共36000元,若甲、乙两工程队单独完成此项工程,乙工程队所用的时间是甲工程队的1.5倍,乙工程队每天的费用比甲工程队少800元. (1)问甲、乙两工程队单独完成此项工程各需多少天?(2)若让一个工程队单独完成这项工程,哪个工程队的费用较少?【答案】 (1)甲单独完成需要20天,则乙单独完成需要30天;(2) 选择乙比较划算【解析】(1)设甲单独完成需要x天,则乙单独完成需要1.5x天,根据甲、乙两工程队合作完成一项工程,需要12天完成列方程求解即可.x-元,根据甲、乙两工程队合作完成一项工程,工(2)设甲每天费用为x元,则乙每天费用为(800)程费用共36000元列方程求解,然后计算出费用比较即可.【详解】解:(1)设甲单独完成需要x天,则乙单独完成需要1.5x天,由题意得1212+=,1x x1.5x天,解得20x符合题意,经检验20所以乙:30天;x-元;(2)设甲每天费用为x元,则乙每天费用为(800)+-=,解得190012(800)36000x xx=;所以甲:1900元/天,乙:1100元/天;所以甲单独完成此项工程所需费用为:1900×20=38000元;乙单独完成此项工程所需费用为:1100×30=33000元;所以选择乙比较划算;【点睛】本题考查分式方程在工程问题中的应用以及一元一次方程的应用.分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.工程问题的基本关系式:工作总量=工作效率×工作时间.23.某公司开发的960件新产品必须加工后才能投放市场,现有甲、乙两个工厂都想加工这批产品,已知甲工厂单独加工48件产品的时间与乙工厂单独加工72件产品的时间相等,而且乙工厂每天比甲工厂多加工8件产品,在加工过程中,公司需每天支付50元劳务费请工程师到厂进行技术指导.(1)甲、乙两个工厂每天各能加工多少件产品?(2)该公司要选择既省时又省钱的工厂加工产品,乙工厂预计甲工厂将向公司报加工费用为每天800元,请问:乙工厂向公司报加工费用每天最多为多少元时,有望加工这批产品?【答案】(1)甲工厂每天加工16件产品,则乙工厂每天加工24件;(2)乙工厂向公司报加工费用每天最多为1225元时,有望加工这批产品.【分析】(1)此题的等量关系为:乙工厂每天加工产品的件数=甲工厂每天加工产品的件数+8;甲工厂单独加工48件产品的时间=乙工厂单独加工72件产品的时间,设未知数,列方程求出方程的解即可;(2)先分别求出甲乙两工厂单独加工这批新产品所需时间,再求出甲工厂所需费用,然后根据乙工厂所需费用要小于甲工厂所需费用,设未知数,列不等式,再求出不等式的最大整数解即可.【详解】(1)设甲工厂每天加工x件产品,则乙工厂每天加工(x+8)件产品,根据题意得:48728x x=+,解得:x=16,检验:x(x+8)=16(16+8)≠0,∴x=16是原方程的解,∴x+8=16+8=24,答:甲工厂每天加工16件产品,则乙工厂每天加工24件.(2)解:甲工厂单独加工这批新产品所需时间为:960÷16=60,所需费用为:60×800+50×60=51000,乙工厂单独加工这批新产品所需时间为:960÷24=40,解:设乙工厂向公司报加工费用每天最多为y元时,有望加工这批产品则:40y+40×50≤51000解之y≤1225∴y的最大整数解为:y=1225答:乙工厂向公司报加工费用每天最多为1225元时,有望加工这批产品.【点睛】本题考查分式方程的应用,涉及到的公式:工作总量=工作效率×工作时间;分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.24.已知:如图,把ABC ∆向上平移3个单位长度,再向右平移2个单位长度,得到'''A B C ∆; (1)写出',','A B C 的坐标;(2)求出ABC ∆的面积;(3)点P 在y 轴上,且BCP ∆与ABC ∆的面积相等,求点P 的坐标.【答案】(1)A ′(0,4)、B′(-1,1)、C′(3,1);(2)6;(3)P (0,1)或(0,-5).【分析】(1)观察图形可得△ABC 的各顶点坐标,继而根据上加下减,左减右加即可得到平移后对应点A′、B′、C′的坐标;即可得到△A ′B ′C ′;(2)直接利用三角形面积公式根据BC 以及BC 边上的高进行求解即可;(3)由△BCP 与△ABC 的面积相等可知点P 到BC 的距离等于点A 到BC 的距离,据此分情况求解即可.【详解】(1)观察图形可得A (-2,1),B (-3,-2),C (1,-2),因为把△ABC 向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′,所以A′(-2+2,1+3)、B′(-3+2,-2+3)、C′(1+2,-2+3),即A′(0,4)、B′(-1,1)、C′(3,1);(2)S△ABC=12BC AD=1432⨯⨯=6;(3)设P(0,y),∵△BCP与△ABC同底等高,∴|y+2|=3,即y+2=3或y+2=-3,解得y1=1,y2=-5,∴P(0,1)或(0,-5).【点睛】本题考查了图形的平移,三角形的面积,熟练掌握平移的规律“上加下减,左减右加”是解题的关键.25.如图,在等边△ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E(点E不与点A重合).(1)若∠CAP=20°.①求∠AEB=°;②连结CE,直接写出AE,BE,CE之间的数量关系.(2)若∠CAP=α(0°<α<120°).①∠AEB的度数是否发生变化,若发生变化,请求出∠AEB度数;②AE,BE,CE之间的数量关系是否发生变化,并证明你的结论.【答案】(1)①1;②CE+AE=BE;(2)①1°;②结论不变:CE+AE=BE,证明见解析【分析】(1)①证明AB=AD,推出∠ABD=∠D=40°,再利用三角形的外角的性质即可解决问题.②结论:CE+AE=BE.在BE上取点M使ME=AE,证明△BAM≌△CAE(SAS),推出BM=EC可得结论.(2)①结论:∠AEB的度数不变,∠AEB=1°.证明方法类似(1).②结论不变:CE+AE=BE.证明方法同(1).【详解】解:(1)①在等边△ABC中,AC=AB,∠BAC=1°,由对称可知:AC=AD,∠PAC=∠PAD,∴AB=AD,∴∠ABD=∠D,∵∠PAC=20°,∴∠PAD=20°,∴∠BAD=∠BAC+∠PAC+∠PAD=100°,∴∠D=12(180°﹣∠BAD)=40°,∴∠AEB=∠D+∠PAD=1°.故答案为:1.②结论:CE+AE=BE.理由:在BE上取点M使ME=AE,∵EM=EA,∠AEM=1°,∴△AEM是等边三角形,∴AM=AE,∠MAE=∠BAC=1°,∴∠MAB=∠CAE,∵AB=AC,∴△BAM≌△CAE(SAS),∴BM=EC,∴CE+AE=BM+EM=BE.(2)①结论:∠AEB的度数不变,∠AEB=1°.理由:在等边△ABC中,AC=AB,∠BAC=1°由对称可知:AC=AD,∠EAC=∠EAD,∵∠EAC=∠DAE=α,∵AD=AC=AB,∴∠D=12(180°﹣∠BAC﹣2α)=1°﹣α,∴∠AEB=1﹣α+α=1°.②结论不变:CE+AE=BE.理由:在BE上取点M使ME=AE,∵EM=EA,∠AEM=1°,∴△AEM是等边三角形,∴AM=AE,∠MAE=∠BAC=1°,∴∠MAB=∠CAE,∵AB=AC,∴△BAM≌△CAE(SAS),∴BM=EC,∴CE+AE=BM+EM=BE.【点睛】本题属于三角形综合题,考查了等边三角形的判定和性质,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.八年级上学期期末数学试卷一、选择题(每题只有一个答案正确)1.已知x 2+2(m ﹣1)x+9是一个完全平方式,则m 的值为( )A .4B .4或﹣2C .±4D .﹣2【答案】B【分析】利用完全平方公式的结构特征判断即可确定出m 的值.【详解】∵x 2+2(m ﹣1)x+9是一个完全平方式,∴2(m ﹣1)=±6,解得:m =4或m =﹣2,故选:B .【点睛】本题考查了完全平方公式的应用,掌握完全平方公式的结构特征是解题的关键.2.函数2y ax b =+-的图象如图所示,则函数y ax b =--的大致图象是( )A .B .C .D .【答案】B【分析】根据一次函数的图象的性质确定a 和b 的符号,进而解答即可.【详解】解:由函数y=ax+b-2的图象可得:a <0,b-2=0,∴a <0,b=2>0,所以函数y=-ax-b 的大致图象经过第一、四、三象限,故选:B .【点睛】本题考查了一次函数的性质,关键是根据一次函数的图象的性质确定a 和b 的符号.3.如图,在△ABC 中,∠ABC 和∠ACB 的平分线交于点O ,过O 点作EF ∥BC ,交AB 于E ,交AC 于F ,若BE=3,CF=2,则线段EF 的长为( )A .5B .6C .7D .8【答案】A 【分析】利用角平分线性质结合平行线性质,可以证出∠EBO=∠BOE ,∠COF=∠OCF ,由等角对等边可得线段相等,等量代换即可得.【详解】∵BO 平分∠ABC ,CO 平分∠ACB ,∴∠ABO=∠CBO ,∠ACO=∠BCO ,又∵EF ∥BC ,∴∠CBO=∠BOE ,∠BCO=∠COF ,∴∠EBO=∠BOE , ∠OCF=∠COF ,∴BE=EO ,FO=CF ,∴EF=EO+FO=BE+CF=3+2=5,故选:A .【点睛】本题考查了角平分线的定义,等腰三角形的判定和性质,平行线的性质,线段相等的等量代换,熟记图形的性质是解题的关键.4.下列条件中,不能..判断一个三角形是直角三角形的是 ( ) A .三个角的比是2∶3∶5B .三条边,,a b c 满足关系222a c b =-C .三条边的比是2∶4∶5D .三边长为1,2,3【答案】C【分析】根据直角三角形的判定方法,对选项进行一一分析,排除错误答案.【详解】A 、三个角的比为2:3:5,设最小的角为2x ,则2x+3x+5x=180°,x=18°,5x=90°,能组成直角三角形,故不符合题意;B 、三条边满足关系a 2=c 2-b 2,能组成直角三角形,故不符合题意;C 、三条边的比为2:4:5,22+42≠52,不能组成直角三角形,故正确;D 、12+32=22,能组成直角三角形,故此选项不符合题意;故选C.。
八年级数学下册第6章平行四边形6.4三角形的中位线定理

第6章6.4三角形的中位线定理一.选择题(共10小题)1.(2020•魏县二模)如图,△ABC中,D,E分别上边AB,AC的中点,若DE=3,则BC=()A.B.9 C.6 D.5(1题图)(2题图)(3题图)(4题图)2.(2020•山西)如图,在△ABC中,点D、E分别是边AB,BC的中点.若△DBE的周长是6,则△ABC的周长是()A.8 B.10 C.12 D.143.(2020•怀柔区二模)如图所示,A,B两点分别位于一个池塘的两端,小聪想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为10m,则A,B间的距离为()A.15m B.25m C.30m D.20m4.(2020•南漳县模拟)如图,▱ABCD中,对角线AC,BD交于点O,点E是BC的中点.若OE=3cm,则AB 的长为()A.12cm B.9cm C.6cm D.3cm5.(2020•莆田模拟)如图,△ABC的中线BD、CE交于点O,连接OA,点G、F分别为OC、OB的中点,BC=8,AO=6,则四边形DEFG的周长为()A.12 B.14 C.16 D.18(5题图)(6题图)(7题图)(8题图)6.(2020春•宁城县期末)如图,已知矩形ABCD的对角线AC的长为10cm,连接各边中点E,F,G,H得四边形EFGH,则四边形EFGH的周长为()A.20cm B.20cm C.20cm D.25cm7.(2020春•抚州期末)如图,在△ABC中,AB=5,BC=6,AC=7,点D,E,F分别是△ABC三边的中点,则△DEF的周长为()A.9 B.10 C.11 D.128.(2020春•山亭区期末)如图,已知△ABC的周长是1,连接△ABC三边的中点构成第二个三角形,再连接第二个三角形三边的中点构成第三个三角形…依此类推,则第2020个三角形的周长为()A.B.C.D.9.(2020•泰安)如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为()A.6 B.7 C.8 D.10(9题图)(10题图)(11题图)(12题图)10.(2020•邢台二模)如图,四边形ABCD的两条对角线AC、BD互相垂直,A1B1C1D1是四边形ABCD的中点四边形,如果AC=8,BD=10,那么四边形A1B1C1D1的面积为()A.20 B.40 C.36 D.10二.填空题(共10小题)11.(2020•河池)如图,在△ABC中,D、E分别是AB、AC的中点,若BC=10,则DE= .12.(2020•泰安)如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.若AB=8,AD=12,则四边形ENFM的周长为.13.(2020•盐城)如图,点D、E、F分别是△ABC各边的中点,连接DE、EF、DF.若△ABC的周长为10,则△DEF的周长为.(13题图)(14题图)(15题图)(16题图)14.(2020•衡阳)如图所示,小明为了测量学校里一池塘的宽度AB,选取可以直达A、B两点的点O处,再分别取OA、OB的中点M、N,量得MN=20m,则池塘的宽度AB为m.15.(2020•龙岩校级质检)如图,在△ABC中,∠ACB=60°,点D,E分别是AB,AC的中点,点F在线段DE上,连结AF,CF.若CF恰好平分∠ACB,则∠FAC的度数为.16.(2020•昌平区二模)已知:如图,在△A BC中,点D为BC上一点,CA=CD,CF平分∠ACB,交AD于点F,点E为AB的中点.若EF=2,则BD= .17.(2020春•南长区期末)如图,在△ABC中,点D在BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连接MN.若AB=5,BC=8,则MN= .18.(2020春•薛城区期末)如图,四边形ABCD中,AD=BC,F、E、G分别是AB、CD、AC的中点,若∠DAC=20°,∠ACB=60°,则∠FEG=.(17题图)(18题图)(19题图)(20题图)19.(2020春•昌乐县期末)如图,在△ABC中,点M为BC的中点,AD平分∠BAC,且BD⊥AD于点D,延长BD交AC于点N.若AB=12,AC=18,则MD的长为.20.(2020春•胶州市期末)如图,△ABC中,D,E分别是AB,AC的中点,F是DE上一点,且AF⊥FC,若BC=9,DF=1,则AC的长为.三.解答题(共5小题)21.(2020秋•龙口市期末)如图,D、E分别是△ABC的边AB、AC的中点,点O是△ABC内部任意一点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.求证:四边形DGFE是平行四边形.22.(2020•邵阳)如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=BC,连接CD和EF.(1)求证:DE=CF;(2)求EF的长.23.(2020春•临清市期中)已知如图:在△ABC中,AB、BC、CA的中点分别是E、F、G,AD是高.求证:∠EDG=∠EFG.24.(2020春•泗阳县期末)如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.(1)试判断线段DE与FH之间的数量关系,并说明理由;(2)求证:∠DHF=∠DEF.25.(2020春•工业园区期中)如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,垂足为N,且AB=6,BC=10,MN=1.5,求△ABC的周长.青岛版八年级数学下册第6章6.4三角形的中位线定理同步训练题参考答案一.选择题(共10小题)1.C 2.C 3.D 4.C 5.B 6.A 7.A 8.D 9.C 10.A二.填空题(共10小题)11.5 12.20 13.5 14.40 15.60°16.4 17.18.20°19.3 20.7三.解答题(共5小题)21.证明:∵D、E分别是AB、AC边的中点,∴DE∥BC,且DE=BC,同理,GF∥BC,且GF=BC,∴DE∥GF且DE=GF,四边形DGFE是平行四边形.22.(1)证明:∵D、E分别为AB、AC的中点,∴DE BC,∵延长BC至点F,使CF=BC,∴DE FC,即DE=CF;(2)解:∵DE FC,∴四边形DEFC是平行四边形,∴DC=EF,∵D为AB的中点,等边△ABC的边长是2,∴AD=BD=1,CD⊥AB,BC=2,∴DC=EF=.23.证明:连接EG,∵E、F、G分别是AB、BC、CA的中点,∴EF为△ABC的中位线,EF=AC.(三角形的中位线等于第三边的一半)又∵AD⊥BC,∴∠ADC=90°,DG为直角△ADC斜边上的中线,∴DG=AC.(直角三角形斜边上的中线等于斜边的一半)∴DG=EF.同理DE=FG,EG=GE,∴△EFG≌△GDE(SSS).∴∠EDG=∠EFG.(23题图)(24题图)(25题图)24.解:(1)DE与FH相等.理由如下:∵D、E分别是AB、BC边的中点.∴ED∥AC,DE=AC,∵AH⊥BC,垂足为H,F是AC的中点,∴HF=AC,∴DE=FH.(2)∵DH=AB,AD=AB,∴AD=DH,∴∠DAH=∠DHA,同理可证:∠FAH=∠FHA,∴∠DHF=∠DAF,∵AD∥EF,D E∥AF,∴四边形ADEF是平行四边形,∴∠DEF=∠DAF,∴∠DHF=∠DEF.25.解:延长线段BN交AC于E.∵AN平分∠BAC,在△ABN和△AEN中,∴△ABN≌△AEN(SAS),∴AE=AB=6,BN=NE,又∵M是△ABC的边BC的中点,∴CE=2MN=2×1.5=3,∴△ABC的周长是AB+BC+AC=6+10+6+3=25.2019-2020学年中考数学模拟试卷一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知x1,x2是关于x的方程x2+ax-2b=0的两个实数根,且x1+x2=-2,x1·x2=1,则b a的值是( ) A.B.-C.4 D.-12.如图是由5个大小相同的正方体搭成的几何体,这个几何体的俯视图是()A.B.C.D.3.如图,下列条件不能判定△ADB∽△ABC的是()A.∠ABD=∠ACB B.∠ADB=∠ABCC.AB2=AD•AC D.AD AB AB BC4.在如图的2016年6月份的日历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是()A.27 B.51 C.69 D.725.在下面的四个几何体中,左视图与主视图不相同的几何体是()A.B.C.D.6.如图,桌面上放着1个长方体和1个圆柱体,按如图所示的方式摆放在一起,其左视图是()A.B.C.D.7.如图,在三角形ABC中,∠ACB=90°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC、A′B′交于点O,则∠COA′的度数是()A.50°B.60°C.70°D.80°8.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中相似三角形共有()A.1对B.2对C.3对D.4对9.在同一坐标系中,反比例函数y=kx与二次函数y=kx2+k(k≠0)的图象可能为()A.B.C.D.10.如图,正方形ABCD的对角线AC与BD相交于点O,∠ACB的角平分线分别交AB,BD于M,N 两点.若AM=2,则线段ON的长为( )A.22B.32C.1 D.6211.若关于x的一元二次方程x2﹣2x+m=0有两个不相等的实数根,则m的取值范围是()A.m<﹣1 B.m<1 C.m>﹣1 D.m>112.某品牌的饮水机接通电源就进入自动程序:开机加热到水温100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,水温从100℃降到35℃所用的时间是()A.27分钟B.20分钟C.13分钟D.7分钟二、填空题:(本大题共6个小题,每小题4分,共24分.)13.写出一个大于3且小于4的无理数:___________.14.对于二次函数y=x2﹣4x+4,当自变量x满足a≤x≤3时,函数值y的取值范围为0≤y≤1,则a的取值范围为__.15.如图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m.水面下降2.5m,水面宽度增加_____m.16.如图,Y ABCD的周长为36,对角线AC,BD相交于点O.点E是CD的中点,BD=12,则△DOE 的周长为.17.将两张三角形纸片如图摆放,量得∠1+∠2+∠3+∠4=220°,则∠5=__.18.如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E 在OB的延长线上,当正方形CDEF的边长为4时,阴影部分的面积为_____.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(6分)如图,已知A(3,0),B(0,﹣1),连接AB,过B点作AB的垂线段BC,使BA=BC,连接AC.如图1,求C点坐标;如图2,若P点从A点出发沿x轴向左平移,连接BP,作等腰直角△BPQ,连接CQ,当点P在线段OA上,求证:PA=CQ;在(2)的条件下若C、P,Q三点共线,求此时∠APB 的度数及P点坐标.20.(6分)有A、B两组卡片共1张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,1.它们除了数字外没有任何区别,随机从A组抽取一张,求抽到数字为2的概率;随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?21.(6分)手机下载一个APP、缴纳一定数额的押金,就能以每小时0.5到1元的价格解锁一辆自行车任意骑行,共享单车为解决市民出行的“最后一公里”难题帮了大忙,人们在享受科技进步、共享经济带来的便利的同时,随意停放、加装私锁、推车下河、大卸八块等毁坏共享单车的行为也层出不穷•某共享单车公司一月投入部分自行车进入市场,一月底发现损坏率不低于10%,二月初又投入1200辆进入市场,使可使用的自行车达到7500辆.一月份该公司投入市场的自行车至少有多少辆?二月份的损坏率为20%,进入三月份,该公司新投入市场的自行车比二月份增长4a%,由于媒体的关注,毁坏共享单车的行为点燃了国民素质的大讨论,三月份的损坏率下降为14a%,三月底可使用的自行车达到7752辆,求a的值.22.(8分)先化简,再求值:2231422a a aa a a-÷--+-,其中a与2,3构成ABC∆的三边,且a为整数.23.(8分)小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B、C两点的俯角分别为45°、35°.已知大桥BC与地面在同一水平面上,其长度为100m,求热气球离地面的高度.(结果保留整数)(参考数据:sin35°=0.57,cos35°=0.82,tan35°=0.70)24.(10分)孔明同学对本校学生会组织的“为贫困山区献爱心”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:10:8,又知此次调查中捐款30元的学生一共16人.孔明同学调查的这组学生共有_______人;这组数据的众数是_____元,中位数是_____元;若该校有2000名学生,都进行了捐款,估计全校学生共捐款多少元?25.(10分)如图,在▱ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:△ADE≌△CBF;求证:四边形BFDE为矩形.26.(12分)已知抛物线y=ax2﹣bx.若此抛物线与直线y=x只有一个公共点,且向右平移1个单位长度后,刚好过点(3,1).①求此抛物线的解析式;②以y轴上的点P(1,n)为中心,作该抛物线关于点P对称的抛物线y',若这两条抛物线有公共点,求n的取值范围;若a>1,将此抛物线向上平移c个单位(c>1),当x=c时,y=1;当1<x<c时,y>1.试比较ac与1的大小,并说明理由.27.(12分)为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+1.设这种产品每天的销售利润为w元.求w与x之间的函数关系式.该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?参考答案一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.A【解析】【分析】根据根与系数的关系和已知x1+x2和x1•x2的值,可求a、b的值,再代入求值即可.【详解】解:∵x1,x2是关于x的方程x2+ax﹣2b=0的两实数根,∴x1+x2=﹣a=﹣2,x1•x2=﹣2b=1,解得a=2,b=,∴b a=()2=.故选A.2.A【解析】分析:根据从上面看得到的图形是俯视图,可得答案.详解:从上面看第一列是两个小正方形,第二列是一个小正方形,第三列是一个小正方形,故选:A.点睛:本题考查了简单组合体的三视图,从上面看得到的图形是俯视图.3.D【解析】【分析】根据有两个角对应相等的三角形相似,以及根据两边对应成比例且夹角相等的两个三角形相似,分别判断得出即可.【详解】解:A、∵∠ABD=∠ACB,∠A=∠A,∴△ABC∽△ADB,故此选项不合题意;B、∵∠ADB=∠ABC,∠A=∠A,∴△ABC∽△ADB,故此选项不合题意;C、∵AB2=AD•AC,∴AC ABAB AD,∠A=∠A,△ABC∽△ADB,故此选项不合题意;D、ADAB=ABBC不能判定△ADB∽△ABC,故此选项符合题意.故选D.【点睛】点评:本题考查了相似三角形的判定,利用了有两个角对应相等的三角形相似,两边对应成比例且夹角相等的两个三角形相似.4.D【解析】设第一个数为x,则第二个数为x+7,第三个数为x+1.列出三个数的和的方程,再根据选项解出x,看是否存在.解:设第一个数为x,则第二个数为x+7,第三个数为x+1故三个数的和为x+x+7+x+1=3x+21当x=16时,3x+21=69;当x=10时,3x+21=51;当x=2时,3x+21=2.故任意圈出一竖列上相邻的三个数的和不可能是3.故选D.“点睛“此题主要考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.5.B【解析】【分析】由几何体的三视图知识可知,主视图、左视图是分别从物体正面、左面看所得到的图形,细心观察即可求解.【详解】A、正方体的左视图与主视图都是正方形,故A选项不合题意;B、长方体的左视图与主视图都是矩形,但是矩形的长宽不一样,故B选项与题意相符;C、球的左视图与主视图都是圆,故C选项不合题意;D、圆锥左视图与主视图都是等腰三角形,故D选项不合题意;故选B.【点睛】本题主要考查了几何题的三视图,解题关键是能正确画出几何体的三视图.6.C【解析】【分析】根据左视图是从左面看所得到的图形进行解答即可.【详解】从左边看时,圆柱和长方体都是一个矩形,圆柱的矩形竖放在长方体矩形的中间.故选:C.【点睛】本题考查了三视图的知识,左视图是从物体的左面看得到的视图.7.B【解析】试题分析:∵在三角形ABC中,∠ACB=90°,∠B=50°,∴∠A=180°﹣∠ACB﹣∠B=40°.由旋转的性质可知:BC=B′C,∴∠B=∠BB′C=50°.又∵∠BB′C=∠A+∠ACB′=40°+∠ACB′,∴∠ACB′=10°,∴∠COA′=∠AOB′=∠OB′C+∠ACB′=∠B+∠ACB′=60°.故选B.考点:旋转的性质.8.C【解析】∵∠ACB=90°,CD⊥AB,∴△ABC∽△ACD,△ACD∽CBD,△ABC ∽CBD ,所以有三对相似三角形.故选C .9.D【解析】【分析】根据k >0,k <0,结合两个函数的图象及其性质分类讨论.【详解】分两种情况讨论:①当k <0时,反比例函数y=k x ,在二、四象限,而二次函数y=kx 2+k 开口向上下与y 轴交点在原点下方,D 符合;②当k >0时,反比例函数y=k x ,在一、三象限,而二次函数y=kx 2+k 开口向上,与y 轴交点在原点上方,都不符.分析可得:它们在同一直角坐标系中的图象大致是D .故选D .【点睛】本题主要考查二次函数、反比例函数的图象特点.10.C【解析】【分析】作MH ⊥AC 于H ,如图,根据正方形的性质得∠MAH=45°,则△AMH 为等腰直角三角形,所以,再根据角平分线性质得,则,于是利用正方形的性质得到+2,OC=12+1,所以△CON ∽△CHM ,再利用相似比可计算出ON 的长.【详解】试题分析:作MH ⊥AC 于H ,如图,∵四边形ABCD为正方形,∴∠MAH=45°,∴△AMH为等腰直角三角形,∴AH=MH=22AM=22×2,∵CM平分∠ACB,∴2,∴2,∴22(2)2,∴OC=122+1,CH=AC﹣2+222,∵BD⊥AC,∴ON∥MH,∴△CON∽△CHM,∴ON OCMH CH=21222+=+∴ON=1.故选C.【点睛】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了角平分线的性质和正方形的性质.11.B【解析】【分析】根据方程有两个不相等的实数根结合根的判别式即可得出△=4-4m>0,解之即可得出结论.【详解】∵关于x的一元二次方程x2-2x+m=0有两个不相等的实数根,∴△=(-2)2-4m=4-4m>0,解得:m<1.故选B.【点睛】本题考查了根的判别式,熟练掌握“当△>0时,方程有两个不相等的两个实数根”是解题的关键.12.C【解析】【分析】先利用待定系数法求函数解析式,然后将y=35代入,从而求解.【详解】解:设反比例函数关系式为:kyx=,将(7,100)代入,得k=700,∴700yx =,将y=35代入700yx =,解得20x=;∴水温从100℃降到35℃所用的时间是:20-7=13,故选C.【点睛】本题考查反比例函数的应用,利用数形结合思想解题是关键.二、填空题:(本大题共6个小题,每小题4分,共24分.)13π等,答案不唯一.【解析】【详解】本题考查无理数的概念.无限不循环小数叫做无理数.介于3和4之间的无理数有无穷多个,因为2239,416==,故而9和16L都是无理数.14.1≤a≤1【解析】【分析】根据y的取值范围可以求得相应的x的取值范围.【详解】解:∵二次函数y=x1﹣4x+4=(x﹣1)1,∴该函数的顶点坐标为(1,0),对称轴为:x=﹣42 22ba-=-=,把y=0代入解析式可得:x=1,把y=1代入解析式可得:x1=3,x1=1,所以函数值y的取值范围为0≤y≤1时,自变量x的范围为1≤x≤3,故可得:1≤a≤1,故答案为:1≤a≤1.【点睛】此题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质和数形结合的思想解答.15.1.【解析】【分析】根据已知建立平面直角坐标系,进而求出二次函数解析式,再通过把y=-1.5代入抛物线解析式得出水面宽度,即可得出答案【详解】解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O 为原点,抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半1米,抛物线顶点C坐标为(0,1),设顶点式y=ax1+1,把A点坐标(-1,0)代入得a=-0.5,∴抛物线解析式为y=-0.5x1+1,当水面下降1.5米,通过抛物线在图上的观察可转化为:当y=-1.5时,对应的抛物线上两点之间的距离,也就是直线y=-1与抛物线相交的两点之间的距离,可以通过把y=-1.5代入抛物线解析式得出:-1.5=-0.5x1+1,解得:x=±3,1×3-4=1,所以水面下降1.5m,水面宽度增加1米.故答案为1.【点睛】本题考查了二次函数的应用,根据已知建立坐标系从而得出二次函数解析式是解决问题的关键,学会把实际问题转化为二次函数,利用二次函数的性质解决问题,属于中考常考题型.16.1.【解析】∵ABCD的周长为33,∴2(BC+CD)=33,则BC+CD=2.∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,∴OD=OB=BD=3.又∵点E是CD的中点,∴OE是△BCD的中位线,DE=CD.∴OE=BC.∴△DOE的周长="OD+OE+DE=" OD +12(BC+CD)=3+9=1,即△DOE的周长为1.17.40°【解析】【分析】直接利用三角形内角和定理得出∠6+∠7的度数,进而得出答案.【详解】如图所示:∠1+∠2+∠6=180°,∠3+∠4+∠7=180°,∵∠1+∠2+∠3+∠4=220°,∴∠1+∠2+∠6+∠3+∠4+∠7=360°,∴∠6+∠7=140°,∴∠5=180°-(∠6+∠7)=40°.故答案为40°.【点睛】主要考查了三角形内角和定理,正确应用三角形内角和定理是解题关键.18.4π﹣1【解析】分析:连结OC,根据勾股定理可求OC的长,根据题意可得出阴影部分的面积=扇形BOC的面积-三角形ODC 的面积,依此列式计算即可求解.详解:连接OC ∵在扇形AOB 中∠AOB=90°,正方形CDEF 的顶点C 是»AB 的中点,∴∠COD=45°,∴22,∴阴影部分的面积=扇形BOC 的面积-三角形ODC 的面积 =22451(42)43602π⨯⨯-⨯=4π-1. 故答案是:4π-1.点睛:考查了正方形的性质和扇形面积的计算,解题的关键是得到扇形半径的长度.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤. 19.(1)C (1,-4).(2)证明见解析;(3)∠APB=135°,P (1,0).【解析】【分析】(1)作CH ⊥y 轴于H ,证明△ABO ≌△BCH ,根据全等三角形的性质得到BH=OA=3,CH=OB=1,求出OH ,得到C 点坐标;(2)证明△PBA ≌△QBC ,根据全等三角形的性质得到PA=CQ ;(3)根据C 、P ,Q 三点共线,得到∠BQC=135°,根据全等三角形的性质得到∠BPA=∠BQC=135°,根据等腰三角形的性质求出OP ,得到P 点坐标.【详解】(1)作CH ⊥y 轴于H ,则∠BCH+∠CBH=90°,∵AB ⊥BC ,∴∠A BO+∠CBH=90°,∴∠ABO=∠BCH ,在△ABO 和△BCH 中,ABO BCHAOB BHC AB BC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABO ≌△BCH ,∴BH=OA=3,CH=OB=1,∴OH=OB+BH=4,∴C 点坐标为(1,﹣4);(2)∵∠PBQ=∠ABC=90°,∴∠PBQ ﹣∠ABQ=∠ABC ﹣∠ABQ ,即∠PBA=∠QBC , 在△PBA 和△QBC 中,BP BQPBA QBC BA BC=⎧⎪∠=∠⎨⎪=⎩,∴△PBA ≌△QBC ,∴PA=CQ ;(3)∵△BPQ 是等腰直角三角形,∴∠BQP=45°,当C 、P ,Q 三点共线时,∠BQC=135°, 由(2)可知,△PBA ≌△QBC ,∴∠BPA=∠BQC=135°,∴∠OPB=45°,∴OP=OB=1,∴P点坐标为(1,0).【点睛】本题考查的是全等三角形的判定和性质、三角形的外角的性质,掌握全等三角形的判定定理和性质定理是解题的关键.20.(1)P(抽到数字为2)=13;(2)不公平,理由见解析.【解析】试题分析:(1)根据概率的定义列式即可;(2)画出树状图,然后根据概率的意义分别求出甲、乙获胜的概率,从而得解.试题解析: (1)P=13;(2)由题意画出树状图如下:一共有6种情况,甲获胜的情况有4种,P=42 63 =,乙获胜的情况有2种,P=21 63 =,所以,这样的游戏规则对甲乙双方不公平.考点:游戏公平性;列表法与树状图法.21.(1)7000辆;(2)a的值是1.【解析】【分析】(1)设一月份该公司投入市场的自行车x辆,根据损坏率不低于10%,可得不等量关系:一月初投入的自行车-一月底可用的自行车≥一月损坏的自行车列不等式求解;(2)根据三月底可使用的自行车达到7752辆,可得等量关系为:(二月份剩余的可用自行车+三月初投入的自行车)×三月份的损耗率=7752辆列方程求解.【详解】解:(1)设一月份该公司投入市场的自行车x辆,x﹣(7500﹣110)≥10%x,解得x≥7000,答:一月份该公司投入市场的自行车至少有7000辆;(2)由题意可得,[7500×(1﹣1%)+110(1+4a%)](1﹣14a%)=7752, 化简,得a 2﹣250a+4600=0,解得:a 1=230,a 2=1, ∵1%20%4a <,解得a <80,∴a=1,答:a 的值是1.【点睛】本题考查了一元一次不等式和一元二次方程的实际应用,根据一月底的损坏率不低于10%找出不等量关系式解答(1)的关键;根据三月底可使用的自行车达到7752辆找出等量关系是解答(2)的关键. 22.1【解析】试题分析:先进行分式的除法运算,再进行分式的加减法运算,根据三角形三边的关系确定出a 的值,然后代入进行计算即可.试题解析:原式=()()()()()()()()()2113212232323233aa a a a a a a a a a a a a a a +--⋅+=+==+--------- , ∵a 与2、3构成△ABC 的三边,∴3−2<a<3+2,即1<a<5,又∵a 为整数,∴a=2或3或4,∵当x=2或3时,原分式无意义,应舍去,∴当a=4时,原式=14-3=1 23.热气球离地面的高度约为1米.【解析】【分析】作AD ⊥BC 交CB 的延长线于D ,设AD 为x ,表示出DB 和DC ,根据正切的概念求出x 的值即可.【详解】解:作AD ⊥BC 交CB 的延长线于D ,设AD 为x ,由题意得,∠ABD=45°,∠ACD=35°,在Rt △ADB 中,∠ABD=45°,∴DB=x ,在Rt △ADC 中,∠ACD=35°,∴tan ∠ACD=AD CD, ∴ 100x x = 710 , 解得,x≈1.答:热气球离地面的高度约为1米.【点睛】考查的是解直角三角形的应用,理解仰角和俯角的概念、掌握锐角三角函数的概念是解题的关键,解答时,注意正确作出辅助线构造直角三角形.24.(1)60;(2)20,20;(3)38000【解析】【分析】(1)利用从左到右各长方形高度之比为3:4:5:10:8,可设捐5元、10元、15元、20元和30元的人数分别为3x 、4x 、5x 、10x 、8x ,则根据题意得8x=1,解得x=2,然后计算3x+4x+5x++10x+8x 即可; (2)先确定各组的人数,然后根据中位数和众数的定义求解;(3)先计算出样本的加权平均数,然后利用样本平均数估计总体,用2000乘以样本平均数即可.【详解】(1)设捐5元、10元、15元、20元和30元的人数分别为3x 、4x 、5x 、10x 、8x ,则8x=1,解得:x=2,∴3x+4x+5x+10x+8x=30x=30×2=60(人);(2)捐5元、10元、15元、20元和30元的人数分别为6,8,10,20,1.∵20出现次数最多,∴众数为20元;∵共有60个数据,第30个和第31个数据落在第四组内,∴中位数为20元;(3)5610815102020301660⨯+⨯+⨯+⨯+⨯⨯2000=38000(元),∴估算全校学生共捐款38000元. 【点睛】本题考查了条形统计图:条形统计图是用线段长度表示数据,根据数量的多少画成长短不同的矩形直条,然后按顺序把这些直条排列起来.也考查了样本估计总体、中位数与众数.25.(1)证明见解析;(2)证明见解析.【解析】【分析】(1)由DE 与AB 垂直,BF 与CD 垂直,得到一对直角相等,再由ABCD 为平行四边形得到AD=BC ,对角相等,利用AAS 即可的值;(2)由平行四边形的对边平行得到DC 与AB 平行,得到∠CDE 为直角,利用三个角为直角的四边形为矩形即可的值.【详解】解:(1)∵DE ⊥AB ,BF ⊥CD ,∴∠AED=∠CFB=90°,∵四边形ABCD 为平行四边形,∴AD=BC ,∠A=∠C ,在△ADE 和△CBF 中,{AED CFBA CAD BC ∠=∠∠=∠=,∴△ADE ≌△CBF (AAS );(2)∵四边形ABCD 为平行四边形,∴CD ∥AB ,∴∠CDE+∠DEB=180°,∵∠DEB=90°,∴∠CDE=90°,∴∠CDE=∠DEB=∠BFD=90°,则四边形BFDE 为矩形.【点睛】本题考查1.矩形的判定;2.全等三角形的判定与性质;3.平行四边形的性质.26.(1)①212y x x =-+;②n≤1;(2)ac≤1,见解析. 【解析】【分析】(1)①△=1求解b =1,将点(3,1)代入平移后解析式,即可;②顶点为(1,12)关于P (1,n )对称点的坐标是(﹣1,2n ﹣12),关于点P 中心对称的新抛物线y'=12(x+1)2+2n ﹣12=12x 2+x+2n ,联立方程组即可求n 的范围; (2)将点(c ,1)代入y =ax 2﹣bx+c 得到ac ﹣b+1=1,b =ac+1,当1<x <c 时,y >1. b 2a≥c ,b≥2ac ,ac+1≥2ac ,ac≥1;【详解】解:(1)①ax 2﹣bx =x ,ax 2﹣(b+1)x =1,△=(b+1)2=1,b =﹣1,平移后的抛物线y =a (x ﹣1)2﹣b (x ﹣1)过点(3,1),∴4a ﹣2b =1,∴a =﹣12,b =﹣1,原抛物线:y =﹣12x 2+x ,②其顶点为(1,12)关于P (1,n )对称点的坐标是(﹣1,2n ﹣12),∴关于点P 中心对称的新抛物线y'=12(x+1)2+2n ﹣12=12x 2+x+2n . 由221y=x +x+2n21y=-x +x2⎧⎪⎪⎨⎪⎪⎩得:x 2+2n =1有解,所以n≤1.(2)由题知:a >1,将此抛物线y =ax 2﹣bx 向上平移c 个单位(c >1),其解析式为:y =ax 2﹣bx+c 过点(c ,1),∴ac 2﹣bc+c =1 (c >1),∴ac ﹣b+1=1,b =ac+1,且当x =1时,y =c ,对称轴:x =b2a ,抛物线开口向上,画草图如右所示.由题知,当1<x <c 时,y >1. ∴b2a ≥c ,b≥2ac ,∴ac+1≥2ac ,ac≤1;【点睛】本题考查二次函数的图象及性质;掌握二次函数图象平移时改变位置,而a 的值不变是解题的关键. 27. (1)2w 2x 120x 1600=-+-;(2) 该产品销售价定为每千克30元时,每天销售利润最大,最大销售利润2元;(3)该农户想要每天获得150元的销售利润,销售价应定为每千克25元.【解析】【分析】(1)根据销售额=销售量×销售价单x ,列出函数关系式.(2)用配方法将(2)的函数关系式变形,利用二次函数的性质求最大值.(3)把y=150代入(2)的函数关系式中,解一元二次方程求x ,根据x 的取值范围求x 的值.【详解】解:(1)由题意得:()()()2w x 20y x 202x 802x 120x 1600=-⋅=--+=-+-,∴w 与x 的函数关系式为:2w 2x 120x 1600=-+-.(2)()22w 2x 120x 16002x 30200=-+-=--+,∵﹣2<0,∴当x=30时,w 有最大值.w 最大值为2.答:该产品销售价定为每千克30元时,每天销售利润最大,最大销售利润2元.(3)当w=150时,可得方程﹣2(x ﹣30)2+2=150,解得x 1=25,x 2=3.∵3>28,∴x 2=3不符合题意,应舍去.答:该农户想要每天获得150元的销售利润,销售价应定为每千克25元.。
初中数学北师大版八年级下册第六章 平行四边形3.三角形的中位线-章节测试习题(3)

章节测试题1.【答题】如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点.连接AF,BF,∠AFB=90°,且AB=8,BC=14,则EF的长是()A. 2B. 3C. 4D. 5【答案】B【分析】本题考查三角形的中位线.【解答】∵点D,E分别是边AB,AC的中点,∴DE是△ABC的中位线,∵BC=14,∴DE BC=7,∵∠AFB=90°,AB=8,∴DF AB=4,∴EF=DE﹣DF=7﹣4=3,选B.2.【答题】如图,在四边形ABCD中,P是对角线BD的中点,点E、F分别是AB、CD 的中点,AD=BC,∠EPF=140°,则∠EFP的度数是()A. 50°B. 40°C. 30°D. 20°【答案】D【分析】本题考查三角形的中位线.【解答】∵P是BD的中点,E是AB的中点,∴PE是△ABD的中位线,∴PE AD,同理,PF BC,∵AD=BC,∴PE=PF,∴∠EFP(180°﹣∠EPF)(180°﹣140°)=20°,选D.3.【答题】如图,在△ABF中,点C在中位线DE上,且CE CD,连接AC,BC,∠ACB=90°,若BF=20,则AB的长为()A. 10B. 12C. 14D. 16【答案】D【分析】本题考查三角形的中位线.【解答】∵DE是△ABC的中位线,BF=20,∴DE BF=10,∵CE CD,∴CD DE=8,∵∠ACB=90°,∴AB=2CD=16,选D.4.【答题】如图,△ABC中,N是BC边上的中点,AM平分∠BAC,BM⊥AM于点M,若AB=8,MN=2.则AC的长为()A. 10B. 11C. 12D. 13【答案】C【分析】本题考查三角形的中位线.【解答】延长BM交AC于D,如图所示:∵BM⊥AM于点M,∴∠AMB=∠AMD=90°,∵AM平分∠BAC,∴∠BAM=∠DAM,在△BAM和△DAM中,,∴△BAM≌△DAM(ASA).∴AD=AB=8,BM=MD,∵N是BC边上的中点,∴MN为△BCD的中位线,∴DC=2MN=4,∴AC=AD+DC=8+4=12.选C.5.【答题】如图,在△ABC中,∠A=90°,D是AB的中点,过点D作BC的平行线交AC于点E,作BC的垂线交BC于点F,若AB=CE,且△DFE的面积为1,则BC的长为()A. 2B. 5C. 4D. 10【答案】A【分析】本题考查三角形的中位线.【解答】如图,过A作AH⊥BC于H.∵D是AB的中点,∴AD=BD,∵DE∥BC,∴AE=CE,∴DE BC,∵DF⊥BC,∴DF∥AH,DF⊥DE,∴BF=HF,∴DF AH,∵△DFE的面积为1,∴DE•DF=1,∴DE•DF=2,∴BC•AH=2DE•2DF=4×2=8,∴AB•AC=8,∵AB=CE,∴AB=AE=CE AC,∴AB•2AB=8,∴AB=2(负值舍去),∴AC=4,∴BC.选A.6.【答题】如图,∠MAN=90°,点C在边AM上,AC=2,点B为边AN上一动点,连接BC,△A'BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A'B于点F,连接A'E.当△A'EF为直角三角形时,AB的长为______.【答案】或2【分析】本题考查三角形的中位线.【解答】当△A'EF为直角三角形时,存在两种情况:①当∠A'EF=90°时,如图,∵△A'BC与△ABC关于BC所在直线对称,∴A'C=AC=2,∠ACB=∠A'CB,∵点D,E分别为AC,BC的中点,∴DE是△ABC的中位线,∴DE∥AB,∴∠CDE=∠MAN=90°,∴∠CDE=∠A'EF,∴∠ACB=∠A'EC,∴∠A'CB=∠A'EC,∴A'C=A'E=2,在Rt△A'CB中,E是斜边BC的中点,∴BC=2AE'=4,由勾股定理可得AB2=BC2﹣AC2,∴AB;②当∠A'FE=90°时,如图,∵∠ADF=∠A=∠DFB=90°,∴∠ABF=90°,∵△A'BC与△ABC关于BC所在直线对称,∴∠ABC=∠CBA'=45°,∴△ABC为等腰直角三角形,∴AB=AC=2.综上,AB的长为或2.故答案为或2.7.【答题】如图,在△ABC中,M,N分别是AB和AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D.若BC=4,则CD的长为______.【答案】2【分析】本题考查三角形的中位线.【解答】∵M,N分别是AB和AC的中点,∴MN是△ABC的中位线,∴MN BC=2,MN∥BC,∴∠NME=∠D,∠MNE=∠DCE,∵点E是CN的中点,∴NE=CE,∴△MNE≌△DCE(AAS),∴CD=MN=2.故答案为2.8.【答题】如图,△ABC的周长为16,D,E,F分别为AB,BC,AC的中点,M,N,P分别为DE,EF,DF的中点,则△MNP的周长为______.如果△ABC,△DEF,△MNP分别为第1个,第2个,第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是______.【答案】4;【分析】本题考查三角形的中位线.【解答】∵△ABC的周长为16,D、F、E分别为AB、AC、BC的中点,∴EF、DF、DE为三角形中位线,∴EF AB,DE AC,DF BC,∴EF+DE+DF(AB+AC+BC),即△DEF的周长是△ABC周长的一半,同理,△MNP的周长是△DEF的周长的一半,即△MNP的周长=△ABC的周长的16=4,以此类推,第n个小三角形的周长是第一个三角形周长的16=,故答案为4;.9.【题文】如图,在△ABC中,AB=AC,点D是边AB的点,DE∥BC交AC于点E,连接BE,点F、G、H分别为BE、DE、BC的中点.(1)求证:FG=FH;(2)当∠A为多少度时,FG⊥FH?并说明理由.【答案】(1)见解答;(2)当∠A=90°时,FG⊥FH.理由见解答. 【分析】本题考查三角形的中位线.【解答】(1)证明:∵AB=AC.∴∠ABC=∠ACB,∵DE∥BC,∴∠ADE=∠ABC,∠AED=∠ACB,∴∠ADE=∠AED,∴AD=AE,∴DB=EC,∵点F、G、H分别为BE、DE、BC的中点,∴FG是△EDB的中位线,FH是△BCE的中位线,∴FG BD,FH CE,∴FG=FH;(2)解:如图,延长FG交AC于N,∵FG是△EDB的中位线,FH是△BCE的中位线,∴FH∥AC,FN∥AB,∵FG⊥FH,∴∠A=90°,∴当∠A=90°时,FG⊥FH.10.【题文】如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.(1)如图1,BE的延长线与AC边相交于点D,求证:EF(AC﹣AB);(2)如图2,△ABC中,AB=9,AC=5,求线段EF的长.【答案】(1)见解答;(2)2.【分析】本题考查三角形的中位线.【解答】(1)证明:在△AEB和△AED中,,∴△AEB≌△AED(ASA),∴BE=ED,AD=AB,∵BE=ED,BF=FC,∴EF CD(AC﹣AD)(AC﹣AB);(2)解:如图,分别延长BE、AC交于点H,在△AEB和△AEH中,,∴△AEB≌△AED(ASA),∴BE=EH,AH=AB=9,∵BE=EH,BF=FC,∴EF CH(AH﹣AC)=2.11.【答题】如图,在中,,分别是,的中点,,是上一点,连接,,.若,则的长度为()A. B. C. D.【答案】B【分析】本题考查的是三角形中位线定理和直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.根据直角三角形的性质求出FE,根据三角形中位线定理计算即可.【解答】,,,;,分别是,的中点,为的中位线,,选B.12.【答题】如图,的周长为,点,都在边上,的平分线垂直于,垂足为,的平分线垂直于,垂足为,若,则的长为()A. B. C. D.【答案】C【分析】本题考查了三角形的中位线定理,解答本题的关键是判断出△BAE、△CAD是等腰三角形,利用等腰三角形的性质确定PQ是△ADE的中位线.首先判断△BAE、△CAD是等腰三角形,从而得出BA=BE,CA=CD,由△ABC的周长为32,及BC=12,可得DE=8,利用中位线定理可求出PQ.【解答】平分,,.,,,,同理,点是的中点,点是中点(三线合一),是的中位线,,,.选C.13.【答题】如图,在四边形ABCD中,已知AB=CD,M、N、P分别是AD、BC、BD的中点∠ABD=20°,∠BDC=70°,则∠NMP的度数为()A. 50°B. 25°C. 15°D. 20°【答案】B【分析】本题考查了三角形中位线定理及等腰三角形的判定和性质,解题时要善于根据已知信息,确定应用的知识.根据中位线定理和已知,易证明△PMN是等腰三角形,根据等腰三角形的性质和已知条件即可求出∠PMN的度数.【解答】在四边形ABCD中,∵M、N、P分别是AD、BC、BD的中点,∴PN,PM分别是△CDB与△DAB的中位线,∴PM AB,PN DC,PM∥AB,PN∥DC.∵AB=CD,∴PM=PN,∴△PMN是等腰三角形,∴∠PMN=∠PNM.∵PM∥AB,PN∥DC,∴∠MPD=∠ABD=20°,∠BPN=∠BDC=70°,∴∠MPN=∠MPD+∠NPD=20°+(180﹣70)°=130°,∴∠PMN25°.选B.14.【答题】已知,四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是()A. 1<MN<5B. 1<MN≤5C. <MN<D. <MN≤【答案】D【分析】本题考查了三角形的中位线,解答此题的关键是根据题意作出辅助线,利用三角形的中位线定理和三角形的三边关系求解.当AB∥CD时,MN最短,利用中位线定理可得MN的最长值,作出辅助线,利用三角形中位线及三边关系可得MN的其他取值范围.【解答】连接BD,过M作MG∥AB,连接NG.∵M是边AD的中点,AB=2,MG∥AB,∴MG是△ABD的中位线,BG=GD,MG=AB=×2=1;∵N是BC的中点,BG=GD,CD=3,∴NG是△BCD的中位线,NG=CD=×3=,在△MNG中,由三角形三边关系可知MG-NG<MN<MG+NG,即-1<MN<+1,∴<MN<,当MN=MG+NG,即MN=时,四边形ABCD是梯形,故线段MN长的取值范围是<MN≤.选D.15.【答题】如图,点、、分别是的边、、的中点,连接、、得,如果的周长是,那么的周长是()A. B. C. D.【答案】B【分析】本题考查了三角形中位线定理.解题的关键是根据中位线定理得出边之间的数量关系.由于D、E分别是AB、BC中点,则DE是△ABC的中位线,那么DE=AC,同理有EF=AB,DF=BC,于是易求△DEF的周长.【解答】、分别是的边、的中点,,同理,,.选B.16.【答题】如图,中,是的中点,平分,于点,若,,则等于()A. B. C. D.【答案】C【分析】本题考查的是三角形中位线定理、全等三角形的判定和性质,三角形的中位线平行于第三边,且等于第三边的一半.延长BD交AC于H,证明△ADB≌△ADH,根据全等三角形的性质得到AH=AB=12,BD=DH,求出HC,根据三角形中位线定理计算即可.【解答】延长交于,平分,,,,,是中点,,,选C.17.【答题】如图,在四边形中,,,,分别是,,的中点,若,,则等于()A. B. C. D.【答案】A【分析】本题考查了三角形中位线定理和等腰三角形的判定与性质.中位线是三角形中的一条重要线段,由于它的性质与线段的中点及平行线紧密相连,因此,它在几何图形的计算及证明中有着广泛的应用.根据三角形中位线定理和等腰三角形等边对等角的性质求解即可.【解答】,,,分别是,,中点,是的中位线,是的中位线,,,,.又,,,,,,.选A.18.【答题】已知△ABC的周长为1,连接其三边中点构成第二个三角形,再连接第二个三角形的中点构成第三个三角形,以此类推,则第2012个三角形的周长为()A. B. C. D.【答案】C【分析】本题考查相似三角形的性质.【解答】∵连接△ABC三边中点构成第二个三角形,∴新三角形的三边与原三角形的三边的比值为1:2,∴它们相似,且相似比为1:2,同理:第三个三角形与第二个三角形的相似比为1:2,即第三个三角形与第一个三角形的相似比为1:22,以此类推:第2012个三角形与原三角形的相似比为1:22011,∵周长为1,∴第2012个三角形的周长为1:22011.选C.19.【答题】如图,▱ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为()A. 3cmB. 6cmC. 9cmD. 12cm【答案】B【分析】本题考查三角形的中位线.【解答】∵四边形ABCD是平行四边形,∴OA=OC;又∵点E是BC的中点,∴BE=CE,∴AB=2OE=2×3=6(cm),选B.20.【答题】如图,在中,,分别是,的中点,是线段上一点,连接,,若,,,则的长为______.【答案】18【分析】本题考查是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.根据直角三角形的性质得到DF=8,根据EF=1,得到DE=9,根据三角形中位线定理解答即可.【解答】,点是的中点,,,,、分别是,的中点,,故答案为.。
三角形中位线经典测试题

三角形中位线经典测试题1、已知三角形ABC,其中AC与BD交于点O,BC边中点为E,OE=1,求AB的长。
2、已知三角形ABC,其中DE是BC边的中位线,DE=2cm,求BC的长。
3、已知三角形ABC,要测量A、B两点间的距离,取OA的中点C,OB的中点D,测得CD=30米,求AB的长。
4、顺次连结任意四边形各边中点所得到的四边形一定是平行四边形。
5、以三角形的三个顶点及三边中点为顶点的平行四边形共有4个。
6、已知四边形ABCD中,R、P分别是BC、CD上的点,E、F分别是AP、RP的中点,当点P在CD上从C向D移动而点R不动时,线段EF的长不变。
7、已知三角形三边长分别为6、8、10,则它的中位线构成的三角形的面积为24.8、已知△ABC中,AD=11/44AB,AE=AC,BC=16,求DE的长。
9、已知四边形ABCD中,M、N、P、Q分别为AB、BD、CD、AC的中点,证明四边形MNPQ是平行四边形。
10、已知四边形ABCD中,AD∥BC,BC=3AD,E、F分别是对角线AC、BD的中点,证明四边形ADEF是平行四边形。
11、已知四边形ABCD中,AB=CD,E、F分别为BC、AD的中点,BA、EF的延长线交于点M,CD、EF的延长线交于点N,证明∠AME=∠XXX。
12、已知△ABC中,P是中线AD的中点,连接BP并延长交AC于E,F为BE的中点,证明AF∥DE。
13、已知四边形ABCD中,M是OB的中点,连接AM并延长至P,使MP=AM,连接DP交AC于N,证明(1)MN∥AD;(2)S四边形MPNQ=S△XXX。
14、已知△ABC中,AD是外角平分线,CD⊥AD于D,E是BC的中点,证明(1)DE∥AB;(2)DE=1/2(AB+AC)。
15、已知等腰梯形ABCD中,AB∥CD,AB>CD,AD=BC,对角线相交于点O,∠AOB=60°,且E、F、M分别是OD、OA、BC的中点,证明△EFM是等边三角形。
三角形中位线定理专练

三角形中位线定理专练1.如图,在△ ABC中,D是AB上一点,且AD=AC,AE⊥ CD,垂足是E,F 是CB的中点.求证:BD=2EF.2.如图所示,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点.求证:△ EFG是等腰三角形.3.在△ ABC中,中线BE、CF交于点O,M、N分别是BO、CO中点,则四边形MNEF是什么特殊四边形?并说明理由.4.如图,BE,CF是△ ABC的角平分线,AN⊥ BE于N,AM⊥ CF于M,求证:MN∥ BC.5.如图,BM、CN分别平分△ABC的外角∠ ABD、∠ ACE,过A分别作BM、CN的垂线,垂足分别为M、N,交CB、BC的延长线于D、E,连结MN.求证:MN=(AB+BC+AC)6.如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.(1)求证:四边形ADEF是平行四边形;(2)求证:∠ DHF=∠ DEF.7.如图,在四边形ABCD中,对角线AC、BD交于点O,E、F分别是AB、CD 的中点,且AC=BD.求证:OM=ON.8.如图,M是△ ABC的边BC的中点,AN平分∠ BAC,BN⊥ AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3(1)求证:BN=DN;(2)求△ ABC的周长.三角形中位线定理专练参考答案与试题解析一.解答题(共8小题)1.(2014?山东模拟)如图,在△ABC中,D是AB上一点,且AD=AC,AE⊥CD,垂足是E,F是CB的中点.求证:BD=2EF.【考点】三角形中位线定理.菁优网版权所有【专题】常规题型.【分析】根据三角形的中位线定理,在三角形中准确应用,并且求证E为CD 的中点,再求证EF为△BCD的中位线.【解答】证明:在△ACD中,因为AD=AC 且AE⊥CD,所以根据等腰三角形中底边的垂线与底边的交点即中点,可以证明:E为CD的中点,又因为F是CB的中点,所以,EF∥BD,且EF为△BCD的中位线,因此EF=BD,即BD=2EF.【点评】此题主要是中位线定理在三角形中的应用,考查在三角形中位线为对应边长的的定理.2.(2015春?天津校级期中)如图所示,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点.求证:△EFG是等腰三角形.【考点】三角形中位线定理;等腰三角形的判定.菁优网版权所有【专题】证明题.【分析】由于E,F,G分别是AB,CD,AC的中点,利用中位线定理,GF=AD,GE=BC,又因为AD=BC,所以GF=GE.【解答】证明:∵E,F,G分别是AB,CD,AC的中点.∴GF=AD,GE=BC.又∵AD=BC,∴GF=GE,即△EFG是等腰三角形.【点评】本题通过给出的中点,利用中位线定理,证得边相等,从而证明等腰三角形,是一道基础题.3.(2015秋?青岛校级月考)在△ABC中,中线BE、CF交于点O,M、N分别是BO、CO中点,则四边形MNEF是什么特殊四边形?并说明理由.【考点】三角形中位线定理;平行四边形的判定.菁优网版权所有【分析】根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC,MN∥BC且MN=BC,从而得到EF∥MN且EF=MN,再根据一组对边平行且相等的四边形是平行四边形判断.【解答】解:四边形MNEF是平行四边形.理由如下:∵BE、CF是中线,∴E、F分别是AC、AB的中点,∴EF是△ABC的中位线,∴EF∥BC且EF=BC,∵M、N分别是BO、CO中点,∴MN是△OBC的中位线,∴MN∥BC且MN=BC,∴EF∥MN且EF=MN,∴四边形MNEF是平行四边形.【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行四边形的判定,熟记定理并准确识图是解题的关键.4.(2015春?泗洪县校级期中)如图,BE,CF是△ABC的角平分线,AN⊥BE 于N,AM⊥CF于M,求证:MN∥BC.【考点】三角形中位线定理;等腰三角形的判定与性质.菁优网版权所有【专题】证明题.【分析】延长AN、AM分别交BC于点D、G,根据BE为∠ABC的角平分线,BE⊥AG可知∠BAN=∠BGN故△ABG为等腰三角形,所以BN也为等腰三角形的中线,即AM=GN.同理AM=DM,根据三角形中位线定理即可得出结论.【解答】证明:延长AN、AM分别交BC于点D、G.∵BE为∠ABC的角平分线,BE⊥AG,∴∠BAG=∠BGA,∴△ABG为等腰三角形,∴BN也为等腰三角形的中线,即AN=GN.同理AM=DM,∴MN为△ADG的中位线,∴MN∥BC.【点评】本题考查的是三角形中位线定理,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.5.(2015春?富顺县校级月考)如图,BM、CN分别平分△ABC的外角∠ABD、∠ACE,过A分别作BM、CN的垂线,垂足分别为M、N,交CB、BC的延长线于D、E,连结MN.求证:MN=(AB+BC+AC)【考点】三角形中位线定理;等腰三角形的判定与性质.菁优网版权所有【专题】证明题.【分析】首先通过△ABM≌△DBM,得到AB=DB,AM=DM,同理:AN=EN,AC=CE,再根据三角形的中位线定理即可得到结果.【解答】证明:∵AM⊥BM,∴∠AMB=∠DMB=90°,∵BM平分∠ABD,∴∠ABM=∠DBM,在△ABM与△DBM中,,∴△ABM≌△DBM(asa),∴AB=DB,AM=DM,同理:AN=EN,AC=CE,∴MN=DE=(DB+BC+CE)=(AB+BC+AC).【点评】本题考查了三角形的中位线定理,全等三角形的判定与性质,证明三角形全等是解题的关键.6.(2014?宿迁)如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.(1)求证:四边形ADEF是平行四边形;(2)求证:∠DHF=∠DEF.【考点】三角形中位线定理;直角三角形斜边上的中线;平行四边形的判定.菁优网版权所有【专题】证明题;几何综合题.【分析】(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥AB,DE∥AC,再根据平行四边形的定义证明即可;(2)根据平行四边形的对角相等可得∠DEF=∠BAC,根据直角三角形斜边上的中线等于斜边的一半可得DH=AD,FH=AF,再根据等边对等角可得∠DAH=∠DHA,∠FAH=∠FHA,然后求出∠DHF=∠BAC,等量代换即可得到∠DHF=∠DEF.【解答】证明:(1)∵点D,E,F分别是AB,BC,CA的中点,∴DE、EF都是△ABC的中位线,∴EF∥AB,DE∥AC,∴四边形ADEF是平行四边形;(2)∵四边形ADEF是平行四边形,∴∠DEF=∠BA C,∵D,F分别是AB,CA的中点,AH是边BC上的高,∴DH=AD,FH=AF,∴∠DAH=∠DHA,∠FAH=∠FHA,∵∠DAH+∠FAH=∠BAC,∠DHA+∠FHA=∠DHF,∴∠DHF=∠BAC,∴∠DHF=∠DEF.【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,等腰三角形的性质,直角三角形斜边上的中线等于斜边的一半的性质,平行四边形的判定与性质,熟记各性质并准确识图是解题的关键.7.(2014?丹阳市校级模拟)如图,在四边形ABCD中,对角线AC、BD交于点O,E、F分别是AB、CD的中点,且AC=BD.求证:OM=ON.【考点】三角形中位线定理;平行线的性质;等腰三角形的判定与性质.菁优网版权所有【专题】证明题.【分析】取AD的中点G,连接EG,FG,构造三角形的中位线,根据三角形的中位线定理进行证明即可.【解答】证明:取AD的中点G,连接EG,FG,∵G、F分别为AD、CD的中点,∴GF是△ACD的中位线,∴GF=AC,同理可得,GE=BD,∵AC=BD,∴GF=GE=AC=BD.∴∠GFN=∠GEM,又∵EG∥OM,FG∥ON,∴∠OMN=∠GEM=∠GFN=∠ONM,∴OM=ON.【点评】本题考查了三角形的中位线性质定理,解题的关键是构造三角形的中位线.运用三角形的中位线的数量关系和位置关系进行分析证明.8.(2013?永州)如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN 于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3(1)求证:BN=DN;(2)求△ABC的周长.【考点】三角形中位线定理;等腰三角形的判定与性质.菁优网版权所有【分析】(1)证明△ABN≌△ADN,即可得出结论;(2)先判断MN是△BDC的中位线,从而得出CD,由(1)可得AD=AB=10,从而计算周长即可.【解答】(1)证明:在△ABN和△ADN中,∵,∴△ABN≌△ADN(ASA),∴BN=DN.(2)解:∵△ABN≌△ADN,∴AD=AB=10,又∵点M是BC中点,∴MN是△BDC的中位线,∴CD=2MN=6,故△ABC的周长=AB+BC+CD+AD=10+15+6+10=41.【点评】本题考查了三角形的中位线定理及等腰三角形的判定,注意培养自己的敏感性,一般出现高、角平分线重合的情况,都需要找到等腰三角形.。
八年级数学人教版下册第十八章练习平行四边形

20.我们把依次连接任意一个四边形各边中点得到的四边形叫做中点四边形.
(1)这个中点四边形EFGH的形状是___________;
求证:四边形AECF是平行四边形.
③平行四边形四边中点的连线所形成的四边形是平行四边形.
连接三角形两边的________的线段叫做三角形的中位线,三角形的中位线________于三角形的第三边,并且等于第三边的________
又∵AF=CE,
∵AB∥DC,DE、CF ∴Rt△DAE≌Rt△CBF 求证AD=BC;
6.如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为( ) (2)已知AD=BC,
分别与AB、CD垂直, ∴∠A=∠B. 17 如图所示,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点.
1 题 平行四边形
2题
解:连接 AC,由三角形中位线性质得,EF∥AC 且 EF=12AC,
GH∥AC 且 GH=12AC,
∴EF 綊 GH,
∴四边形 EFGH 是平行四边形
21.如图,在梯形ABCD中,AB∥DC.
(1)已知∠A=∠B, 求证AD=BC;
(2)已知AD=BC, 求证∠A=∠B.
20.我们把依次连接任意一个四边形各边中点得到的四边 形叫做中点四边形.
如图,在四边形ABCD中,E,F,G,H分别是边AB,BC , CD , DA 的 中 点 , 依 次 连 接 各 边 中 点 得 到 中 点 四 边 形 EFGH.
(1)这个中点四边形EFGH的形状是___________; (2)请证明你的结论.
平行四边形与三角形中位线练习题汇编

1.如图,已知四边形ABCD 中,点E ,F ,G ,H 分别是AB 、CD 、AC 、BD 的中点,并且点E 、F 、G 、H 有在同一条直线上.求证:EF 和GH 互相平分.2.如图,在ABC ∆中,oBAC 90=∠,BC AD ⊥,BE 、AF 分别是ABC ∠、DAC ∠的平分线,且相交于点O ,BE 交AD 于G ,求证:GF//AC.3.如图所示.DE ⊥AC ,BF ⊥AC ,DE=BF ,∠ADB=∠DBC .求证:四边形ABCD 是平行四边形.F4.如图2-39所示.在平行四边形ABCD中,△ABE和△BCF都是等边三角形.求证:△DEF是等边三角形.5.如图2-40所示.ABCD中,AF平分∠BAD交BC于F,DE⊥AF交CB于E.求证:BE=CF.6.如图2-41所示.矩形ABCD中,F在CB延长线上,AE=EF,CF=CA.求证:BE⊥DE.7.如图,矩形ABCD 中,∠AOB =60°,DE 平分∠ADC ,交BC 于E ,求∠OED 度数. D C B AEO8.Rt △ABC 中,∠ABC =90°,∠C =60°,BC =2,D 是AC 的中点,从D 作DE ⊥AC 与CB 的延长线交于点E ,以AB 、BE 为邻边作矩形ABEF ,连结DF ,则DF 的长.F E DC B A9. 如图,BD =AC ,M 、N 分别为AD 、BC 的中点,AC 、BD 交于E ,MN 与BD 、AC 分别交于点F 、G ,求证:EF =EG .N M G F EDC B A10.(2007•黑龙江)在△ABC 中,AB=AC ,点P 为△ABC 所在平面内一点,过点P 分别作PE ∥AC 交AB 于点E ,PF ∥AB 交BC 于点D ,交AC 于点F .若点P 在BC 边上(如图1),此时PD=0,可得结论:PD+PE+PF=AB .请直接应用上述信息解决下列问题:当点P 分别在△ABC 内(如图2),△ABC 外(如图3)时,上述结论是否成立?若成立,请给予证明;若不成立,PD ,PE ,PF 与AB 之间又有怎样的数量关系,请写出你的猜想,不需要证明.11.如图,在△ABC 中,点O 是AC 边上的一个动点,过点O 作直线MN ∥BC ,设MN 交∠BCA 的角平分线于点E ,交∠BCA 的外角平分线于点F .(1)求证:EO =FO ;(2)当点O 运动到何处时,四边形AECF 是矩形?并证明你的结论. AB C E F MN O (第19题图)。
(完整版)三角形的中位线经典练习题及其答案

八年级三角形的中位线练习题及其答案1.连结三角形___________的线段叫做三角形的中位线. 2.三角形的中位线______于第三边,并且等于_______. 3.一个三角形的中位线有_________条. 4。
如图△ABC 中,D 、E 分别是AB 、AC 的中点,则线段CD 是△ABC 的___, 线段DE 是△ABC _______5、如图,D 、E 、F 分别是△ABC 各边的中点 (1)如果EF =4cm ,那么BC =__cm 如果AB =10cm ,那么DF =___cm(2)中线AD 与中位线EF 的关系是___6.如图1所示,EF 是△ABC 的中位线,若BC=8cm ,则EF=_______cm .(1) (2) (3) (4)7.三角形的三边长分别是3cm ,5cm ,6cm ,则连结三边中点所围成的三角形的周长是_________cm . 8.在Rt △ABC 中,∠C=90°,AC=•5,•BC=•12,•则连结两条直角边中点的线段长为_______. 9.若三角形的三条中位线长分别为2cm ,3cm,4cm,则原三角形的周长为( ) A .4。
5cm B .18cm C .9cm D .36cm10.如图2所示,A ,B 两点分别位于一个池塘的两端,小聪想用绳子测量A ,B 间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A ,B 的点C ,找到AC ,BC 的中点D,E ,并且测出DE 的长为10m ,则A ,B 间的距离为( )A .15mB .25mC .30mD .20m11.已知△ABC 的周长为1,连结△ABC 的三边中点构成第二个三角形,•再连结第二个三角形的三边中点构成第三个三角形,依此类推,第2010个三角形的周长是( ) A 、20081 B 、20091 C 、220081 D 、22009112.如图3所示,已知四边形ABCD ,R ,P 分别是DC ,BC 上的点,E ,F 分别是AP ,RP 的中点,当点P 在BC上从点B 向点C 移动而点R 不动时, 那么下列结论成立的是( ) A .线段EF 的长逐渐增大 B .线段EF 的长逐渐减少 C .线段EF 的长不变 D .线段EF 的长不能确定13.如图4,在△ABC 中,E ,D ,F 分别是AB ,BC ,CA 的中点,AB=6,AC=4,则四边形AEDF•的周长是( ) A .10 B .20 C .30 D .4014.如图所示,□ ABCD 的对角线AC ,BD 相交于点O ,AE=EB ,求证:OE ∥BC .15.已知矩形ABCD 中,AB =4cm ,AD =10cm ,点P 在边BC 上移动,点E 、F 、G 、H 分别是AB 、AP 、DP 、DC 的中点。
人教版初中数学八年级下册同步练习题18.1.2平行四边形的判定(4)——三角形的中位线

18.1.2平行四边形的判定(4)一一三角形的中位线课堂学习检测一、填空题:1.(1)三角形的中位线的定义:连结三角形两边叫做三角形的中位线.(2)三角形的中位线定理是三角形的中位线三边,并且等于2.如图,△43。
的周长为64,E、F、G分别为WA AC.■的中点,』'、6'、C分别为研EG、GF的中点,△/'B'C的周长为.如果及7、4EFG、△』'B'C分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第〃个三角形的周长是•3.中,D、E分别为45、"。
的中点,若座=4,AD=3,AE=2,则■的周长为—二、解答题4.已知:如图,四边形/列中,E、F、G、日分别是/以Ba CD、以的中点.求证:四边形麽诳是平行四边形.5.已知:网的中线初、堡交于点。
F、G分别是缪、%的中点.求证:四边形力碰是平行四边形.综合、运用、诊断6.已知:如图,E为6BCD中庞'边的延长线上的一点,代CE=DC,连结如'分别交应;刃于点尺G,连结4C交初于。
连结必求证:AB=20F.7.已知:如图,在曲时中,£是⑦的中点,尸是/的中点,FC与BE交于G.求证:GF=GC.E CAD.8.已知:如图,在四边形曲%中,AD=BC, E 、尸分别是力C 、/边的中点,死'的延长线分别与如、BC的延长线交于〃、G 点.求证:/AHF=/BGF.拓展、探究、思考9.已知:如图,网中,力是此'边的中点,北'平分ZBAC, BELAE 于E 点,若AB=5, AC=7,求应Z 10.如图在中,D 、E 分别为』弥上的点,巨BD=CE, < "分别是庞、,的中点.过刎的直线交AB 于P,交如于。
线段#、40相等吗?为什么?A参考答案1.(1)中点的线段;(2)平行于三角形的,第三边的一半.2.16,64X(-)71-1.3.18.24.提示:可连结刃(或AC).5.略.6.连结庞CE』ABnUABECnBF=FC.DABCD=>AO=OC,:.AB=20F.7.提示:取座的中点R证明四边形庭烈'是平行四边形.8.提示:连结』G取』C的中点M再分别连结依MF,可得£¥=成9.ED=\,提示:延长冏?,交/C于尸点.10.提示:AP^AQ,取网的中点&连接洌NH.证明zMW是等腰三角形,进而证明/AP4ZAQP.最新人教版八年级数学下册期中综合检测卷考试用时:120分钟,试卷满分:120分一、选择题(每小题3分,共30分)1.若式子后3在实数范围内有意义,则x的取值范围是()A.xN3B.xW3C.x>3D.x<32.下列各组数中,能构成直角三角形的是()A.4,5,6B.l,1,a/2C.6,8,11D.5,12,233.下列各式是最简二次根式的是()A.炯B.V7C.a/20D,V034.下列运算正确的是()A.yfs-=B.=2?C.-'Jl=^2D.』(2一赃V=2-sf55.方程I 4x-8 I +Jx-y-m=O,当y>0时,m 的取值范围是()A.O<m<lB.mN2C.mW2D.m<26.若一个三角形的三边长为6,8, x,则此三角形是直角三角形时,x 的值是()A.8 B.10 C.2a /7 D.10 或 2妗7. 将直角三角形的各边都缩小或扩大同样的倍数后,得到的三角形( )A.可能是锐角三角形B.不可能是直角三角形C.仍然是直角三角形D.可能是钝角三角形8. 能判定四边形ABCD 为平行四边形的题设是( )A.AB〃CD, AD=BCB.AB=CD, AD=BCC.ZA=ZB, ZC=ZDD.AB=AD, CB=CD 9.如图,已知四边形ABCD 是平行四边形,下列结论中不正确的是()A.当AB=BC 时,它是菱形C.当ZABC=90°时,它是矩形 B.当ACLBD 时,它是菱形D.当AC=BD 时,它是正方形第9题图 第10题图第13题图 第15题图10.如图,E 、F 分别是正方形ABCD 的边CD 、AD 上的点,且CE=DF, AE 、BF 相交于点O, 下列结论:(1)AE=BF ; (2) AE±BF ; (3) AO=OE ; (4)S aaob =S 四边形 deof 中正确的有( )A.4个B.3个C.2个D.1个二、填空题(每小题3分,共24分)11.已知最简二次根式』4a+3b与'刈2a-b+6可以合并,则ab=.12.若直角三角形的两直角边长为a、b,且满足V«2-6a+9+I b-4I=0,则该直角三角形的斜边长为.2513.如图所示,分别以直角三角形的三边为直径作半圆,其中两个半圆的面积S1=—n,8S2=2n,则S3=.14.四边形ABCD的对角线AC,BD相交于点O,AC±BD,且OB=OD,请你添加一个适当的条件,使四边形ABCD成为菱形(只需添加一个即可).15.如图,^ABC在正方形网格中,若小方格边长为1,则^ABC的形状是16.已知菱形ABCD中,对角线AC与BD相交于点O,ZBAD=120°,AC=4,则该菱形的面积是•17.AABC中,若AB=15,AC=13,高AD=12,则AABC的周长是.18.如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P为线段BC上的点.小明同学写出了一个以OD为腰的等腰三角形ODP的顶点P的坐标(3,4),请你写出其余所有符合这个条件的P 点坐标■三、解答题(共66分)19.(8分)计算下列各题:(1)(a/48-4J-)-(3J--2^5);(2)(2—迅严比•(2+V3)2016-2X|-^|-(-V3)°.220.(8分)如图是一块地,已知AD=4m,CD=3m,AB=13m,BC=12m,且CD±AD,求这块地的面积.21.(8分)已知9+血与9—应的小数部分分别为a,b,试求ab~3a+4b~7的值.22.(10分)如图,在等腰直角三角形ABC中,ZABC=90°,D为AC边上中点,过D点作DEXDF,交AB于E,交BC于F,若AE=4,FC=3,求EF的长.23.(10分)如图,^ABC是直角三角形,且ZABC=90°,四边形BCDE是平行四边形, E为AC的中点,BD平分ZABC,点F在AB上,且BF=BC.求证:(1)DF=AE;(2)DF±AC.24.(10分)如图,四边形ABCD是一个菱形绿地,其周长为402m,ZABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/r^,请问需投资金多少元?(结果保留整数)25.(12分)(1)如图①,已知△ABC,以AB、AC为边向^ABC外作等边AABD和等边△ACE,连接BE,CD,请你完成图形,并证明:BE=CD;(尺规作图,不写作法,保留作图痕迹)(2)如图②,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,BE 和CD有什么数量关系?简单说明理由;(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:如图③,要测量池塘两岸相对的两点B,E的距离,已经测得ZABC=45°CAE=90°,AB=BC=100米,AC=AE,求BE的长.最新人教版八年级数学下册期末综合检测卷一、选择题(每小题3分,共30分)1.二次根式而i 、屈、应、Jx + 2、j40f 、J/ +》2中,最简二次根式有()A.1个B.2个C.3个D.4个2.若式子目有意义,则x 的取值范围为()A.xN4B.x 尹 3C.x34 或 x 乂3D.x34 且 x 尹33.下列计算正确的是( )A.a /4 X ^/6=4a /6B 疝+痴=应C.何:屁22 D.J(-15)2=-154.在 RtAABC 中,ZACB=90° , AC=9, BC=12,则点 C 到 AB 的距离是( )A 36「12A,—— B.—5 25厂 9、30C. — D.----4 45.平行四边形ABCD 中,ZB=4ZA,则ZC=()A.18° B.36° C.72° D.144°6.如图,菱形ABCD 的两条对角线相交于O,菱形的周长是20 cm, AC : BD=4 : 3,则菱形的面积是()A.12 cm 2 B.24 cm 2 C.48 cm 2 D.96 cm 2第6题图第8题图第10题图X =-17.若方程组(2工+*=3的解是.贝I直线y=—2x+b与y=x—a\x-y=a的交点坐标是()A.(-l,3)B.(l,-3)C.(3,-1)D.(3,1)8.甲、乙两人在一次百米赛跑中,路程s(m)与赛跑时间t(s)的关系如图所示,则下列说法正确的是()A.甲、乙两人的速度相同B.甲先到达终点C.乙用的时间短D.乙比甲跑的路程多9.在我市举行的中学生春季田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:成绩(m) 1.50 1.60 1.65 1.70 1.75 1.80人数124332这些运动员跳高成绩的中位数和众数分别是()A.1.70, 1.65B.1.70, 1.70C.1.65, 1.70D.3,410.如图,在^ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE±AB于E,PF±AC 于F,M为EF中点,则AM的最小值为()二、填空题(每小题3分,共24分)11.当x=时,二次根式x+1有最小值,最小值为12.已知a,b,c是^ABC的三边长,且满足关系式yjc2-a2-b2+\a-b\=O,则Z^ABC的形状为13.平行四边形ABCD的两条对角线AC、BD相交于点O,AB=13,AC=10,DB=24,则四边形ABCD的周长为.14.如图,一次函数"灯x+bi y2=k2x+b2的图象相交于A(3,2),则不等式(k2—/ci)x+b2 -bi>0的解集为第14题图第16题图第18题图15.在数据一1,0,3,5,8中插入一个数据X,使得该组数据的中位数为3,则x的值为16.如图,3XBCD中,E、F分别在CD和BC的延长线上,ZECF=60°,AE〃BD,EF1BC, EF=2,则AB的长是.17.(山东临沂中考)某中学随机抽查了50名学生,了解他们一周的课外阅读时间,结果如下表所示:时间(小时)4567人数1020155则这50名学生一周的平均课外阅读时间是小时.18.如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD 上,下列结论:①CE=CF,②ZAEB=75°,③BE+DF=EF,④S正方形ABCD=2+0,其中正确的序号是.(把你认为正确的都填上)三、解答题(共66分)19.(8分)计算下列各题:(1)12V2-31-+a/18(2)先化简,再求值:"+。
三角形的中位线基础题30道解答题

9.5 三角形的中位线基础题汇编(3)BCBC=3DE=6中点重合)EF=EF=CE=,求BCD=EM=(9.5 三角形的中位线基础题汇编(3)参考答案与试题解析一.解答题(共30小题)1.如图,在四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点.四边形EGFH是平行四边形吗?请证明你的结论.2.请写出“如图,在△ABC中,若DE是△ABC的中位线,则DE=BC”的逆命题.判断逆命题的真假,并说明你的理由?BC3.在四边形ABCD中,BD、AC相交于点O,AC=BD,E、F分别是AB、CD的中点,连接EF,分别交AC、BD 于点M、N.判断△MON的形状,并说明理由.EG=4.如图,在△ABC中,AD⊥BC于点D,E、F、G分别是BC、AC、AB的中点,若AB=BC=3DE=6,求四边形DEFG的周长.BC=3DE=6BC=3DE=6EF=×BC=×,AB=×=GF+DG+DE+EF=+3+2+3=.5.如图,在△ABC中(AB≠AC),M为BC的中点,AD平分∠BAC交BC于D,BE⊥AD于E,CF⊥AD于F,求证:ME=MF.MF=ME=GBME=6.△ABC中,D为BC中点,E为AD中点,直线BE交AC于F,求证:AC=3AF.7.如图,已知△XYZ中,MY=NZ,A、B分别是YN、MZ的中点,延长AB、BA分别交XZ、XY于点D、C,求证:XC=XD.BE=NZ BE=MY8.如图,AB为⊙O的一条弦,CD为直径(C不与A、B及中点重合),作CE⊥AB于E,DF⊥AB于F,问CE﹣DF的值是否变化?为什么?9.△ABC中,D为CB的延长线上一点,BE是∠ABD的角平分线,AE⊥BE,F是AC的中点,试说明:EF∥BC,且EF=(AB+BC).EF=10.如图,在四边形ABCD中,E、F分别是AD、BC的中点,连接FE并延长,分别交CD的延长线于点M、N,∠BME=∠CNE,求证:AB=CD.GE=GF=CDAB GF=CD11.已知,如图,AB=AC=BE,CD为△ABC中AB边上的中线,求证:CE=2CD.12.如图,在△ABC中,∠ACB=90°,点D在AB上,AC=AD,DE⊥CD交BC于点E,AF平分∠BAC交BC于F点.(1)求证:AF∥DE;(2)当AC=6,AB=10时,求BE的长.==,,BE=13.在四边形ABCD中,AB∥CD,E、F是AD、BC中点.求证:EF=(AB+CD),EF∥CD.EF=DM=14.如图,已知△ABC中,点D是BA上一点,BD=AC,E,F分别是BC,DA的中点,EF和CA的延长线相交于点G.求证:AG=AF.15.如图,AD是△ABC的中线,E,F,G分别是AB,AD,DC的中点,求证:EG与DF互相平分.ACED=16.已知:如图,点B是AD的中点,点E是AB的中点,AB=AC 求证:CE=CD.ACBE=CDCE=17.在△ABC中,AD⊥BC于D点,BE为中线,且∠CBE=30°.求证:AD=BE.EF=EF=EF=18.如图,在△ABC中,D、E、F分别是AB、BC、AC的中点,AB=6,AC=8,DF=5,求AE的长.BC=519.已知如图,△ABC中,AD为BC的中线,E为AD的中点,延长CE交AB于点F,求的值.(用多种方法解答);或过BF=DM==20.在△ABC中,D是AB的中点,DC⊥AC且tan∠BCD=,求tanA的值.BCD=,设,即BCD==ABBE=CE=AC.21.已知在△ABC中,M是BC的中点,AN平分∠BAC,AN⊥BN,求证:MN∥AC.22.已知:如图,在△ABC中,AB>AC,AD平分∠BAC,BE垂直AD延长线于E,M是BC中点.求证:EM=(AB﹣AC).CF=CF23.如图,在△ABC中,若∠B=2∠C,AD⊥BC,E为BC边中点,求证:AB=2DE.24.如图,在四边形ABCD中,AD=BC,P是对角线BD的中点,M是DC的中点,N是AB的中点.求证:∠PMN=∠PNM.PM=PN=ADBC PN=AD25.如图,△ABC中,BM平分∠ABC,AM⊥BM,垂足M点,点N为AC的中点,AB=10,BC=6,求MN长度.MN=26.已知:△ABC,用刻度尺量出△ABC的各边的长度,并取各边的中点,画出△ABC的三条中线,你发现了什么?27.如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为E,F是BC中点,探究BD与EF的关系.并说明理由.EF=28.如图,平行四边形ABCD的对角线AC,BD相交于点O,AE=EB.求证:OE∥BC.29.△ABC中,AD是∠BAC的平分线,G是BC的中点,过G作直线FG平行于AD,分别交AB和CA的延长线于点E和点F,求证:BE=CF=(AB+AC).BF=CE=30.如图,在△ABC中,AD=DE=EF=FB,AG=GH=HI=IC,已知BC=8,则DG+EH+FI的长是多少?BCBC BCDG+EH+FI=BC+BC=。
中考数学总复习《构造三角形中位线模型解题》专项提升练习题(附答案)

中考数学总复习《构造三角形中位线模型解题》专项提升练习题(附答案)学校:___________班级:___________姓名:___________考号:___________一、三角形中位线的概念和性质1.连接三角形两边中点的线段叫做三角形的中位线2.三角形中位线定理:三角形的中位线平行于第三遍,且等于第三边的一半3.隐含中点的条件:等腰三角形三线合一(顶角的角平分线底边的中垂线),平行四边形对角线的交点。
例1.如图,点D、E分别为△ABC的边AB、AC的中点,点F在DE的延长线上,CF∥BA,若BC=8,则EF=( ) A.4 B.8 C.5 D.3例2.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠EPF=136°,则∠EFP的度数是( ) A.68° B.34° C.22° D.44°二、连接两点构造三角形的中位线例3.如图,在四边形ABCD中,∠A=90°,AB=12,AD=5.点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF的最大值是.4例4.如图1,已知点E ,F ,G ,H 分别是四边形ABCD 的边AB ,BC ,CD ,DA 的中点,根据以下思路可以证明四边形EFGH 是平行四边形:如图2,将图1中的点C 移动至与点E 重合的位置,F ,G ,H 仍是BC ,CD ,DA 的中点,求证:四边形CFGH 是平行四边形.三.已知角平分线+垂直构造中位线例5.如图,AD 为ABC 中BAC ∠的外角平分线,BD AD ⊥于D ,E 为BC 中点5DE =,3AC =则AB 长为( )A .8.5B .8C .7.5D .7例6.如图,在△ABC 中,∠ABC =90°,在边AC 上截取AD =AB ,连接BD ,过点A 作AE ⊥BD 于点E ,F 是边BC 的中点,连接EF.若AB =5,BC =12,求EF 的长度.例7.如图,在△ABC中,已知AB=6,AC=10,AD平分∠BAC,BD⊥AD于点D,点E为BC的中点,求DE的长.四.倍长法构造三角形的中位线例8.如图,在△ABC中,∠ABC=90°,BA=BC,△BEF为等腰直角三角形,∠BEF=90°,M为AF的中点.求证ME=12CF.例9.如图,在△ABC中,∠ABC=90°,AB=BC,BD⊥AC于点D,CE平分∠ACB,交AB于点E,交BD于点F.求证:(1)△BEF是等腰三角形;(2)BD=12(BC+BF).五.已知一边中点,取另一边中点构造三角形的中位线例10.如图,四边形ABCD中,点E,F分别是边AB,CD的中点,且AD=6,BC=10,则线段EF的长可能为( )A.7B.8.5C.9D.10六.已知两边中点,取第三边中点构造三角形的中位线例11.如图,菱形ABCD 的对角线AC BD ,相交于点O .E ,F 分别是AD OC ,的中点,若1207BAD EF ∠=︒=,ABCD 的周长为( )A .8B .16C .3D .3例12.如图,已知四边形ABCD 中AC BD ⊥,AC=6,8BD =点E 、F 分别是边AD 、BC 的中点,连接EF ,则EF 的长是 __.强化训练题一.选择题1.如图 在△ABC 中 AB =4 BC =5 AC =8.点D E F 分别是相应边上的中点 则四边形DFEB 的周长等于( )A .8B .9C .12D .132.如图 △ABC 中 AB =AC =12 BC =10 AD 平分∠BAC 交BC 于点D 点E 为AC 的中点 连接DE 则△CDE 的周长为( )A .11B .17C .18D .163.如图 在ABC 中 45B ∠=︒ 60C ∠=︒ AD BC ⊥于点D 6BD = 若E F 分别为AB BC 的中点 则EF 的长为( )A 2B 6C 6D 34.如图 ABCD 的对角线AC BD 交于点O AE 平分BAD ∠交BC 于点E且60ADC ∠=︒ 12AB BC = 连接OE .下列结论中不成立的是( )A .30CAD ∠=︒B .ABCD S AB AC =⋅ C .OB AB =D .14OE BC =5.如图 四边形ABCD 中 ∠B =90° AB =8 BC =6 点M 是对角线AC 的中点 点N 是AD 边的中点 连结BM MN 若BM =3MN 则线段CD 的长是( )A .53B .3C .103D .56.已知三角形三边长分别为7cm 8cm 9cm 作三条中位线组成一个新的三角形 同样方法作下去 一共做了五个新的三角形 则这五个新三角形的周长之和为( )A .46.5cmB .22.5cmC .23.25cmD .以上都不对7.如图 在ABC 中 AE 平分BAC ∠ BE AE ⊥于点E 点F 是BC 的中点 若10AB = 6AC = 则EF 的长为( )A .2B .3C .4D .58.如图 在四边形ABCD 中 点E F 分别为AD DC 的中点 连接EB BF EF △EBF 的面积为 S 1 .点G 为四边形ABCD 外一点 连接AG BG EG FG 使得AG =BC ∠GAB =∠ABC △EGF 的面积为 S 2 则 S 1 与 S 2 满足的关系是( )A .S 1 = S 2B .2 S 1 =3 S 2C .3 S 1 =4 S 2D .3 S 1 =2 S 29.如图 平行四边形ABCD 中 O 为对角线交点 DP 平分ADC ∠ CP 平分BCD ∠ 7AB = 10AD = 则OP 的长为( )A .1.5B .2C .2.5D .310.如图 ▱ABCD 的顶点A D 分别在直角∠MON 的两边OM ON 上运 动(不与点O 重合) ▱ABCD 的对角线AC BD 相交于点P 连接OP 若OP=5 则▱ABCD 的周长最小值是( )A .20B .25C .10D .15二 填空题11.如图 在平行四边形ABCD 中 E 是CD 的中点 F 是AE 的中点 CF 交BE 于点G 若BE =8 则GE = .12.如图 DE 为△ABC 的中位线 点F 在DE 上 且∠AFC 为直角 若AC =6cm BC =8cm 则DF 的长为 .13.如图已知三角形纸片ABC第1次折叠使点B落在BC边上的点B'处折痕AD交BC于点D;第2次折叠使点A落在点D处折痕MN交AB'于点P.若12BC=则MP与MN的和是_________.14.如图在▱ABCD中AC是对角线∠ACD=90°点E是BC的中点AF平分∠BAC CF⊥AF于点F连接EF.已知AB=5BC=13则EF的长为.15.如图在Rt△ABC中∠ACB=90°AC=BC=6 点D是AC边上的一点且AD=2 以AD为直角边作等腰直角三角形ADE连接BE并取BE的中点F连接CF则CF的长为.16.如图 EF是△ABC的中位线 O是EF上一点且满足OE=2OF.则△ABC的面积与△AOC的面积之比为.17.如图□ABCD的顶点C在等边△BEF的边BF上点E在AB的延长线上 G为DE的中点连接CG.若AD=5 AB=CF=3 则CG的长为.三.解答题18.如图△ABC的中线BE CF相交于G且AB=12 AC=16 BC=20 求GC的长.19.如图在平行四边形ABCD中对角线AC BD、相交于点O点E是边BC中点连接OE并延长至点F使EF OE、.连接BF CF(1)求证:四边形OBFC是平行四边形;(2)求证:OF CD∥.20.如图四边形ABCD为平行四边形 E为AD上的一点连接EB并延长使BF=BE 连接EC并延长使CG=CE连接FG H为FG的中点连接DH(1)求证:四边形AFHD为平行四边形;(2)若CB=CE∠EBC=75°∠DCE=10°求∠DAB的度数.21.如图,点B为AC上一点,分别以AB,BC为边在AC同侧作等边三角形ABD和等边三角形BCE,点P,M,N分别为AC,AD,CE的中点.(1)求证:PM=PN;(2)求∠MPN的度数.22.如图,在△ABC中,AB=AC,AD⊥BC于点D,点P是AD的中点,延长BP交AC于点N,求证:AN=13AC.23.(1)如图1 在四边形ABCD中AB=CD E F分别是AD BC的中点连接FE 并延长分别与BA CD的延长线交于点M N.求证:∠BME=∠CNE;(提示:取BD的中点H连接FH HE作辅助线)(2)如图2 在△ABC中F是BC边的中点D是AC边上一点E是AD的中点直线FE交BA的延长线于点G若AB=DC=2 ∠FEC=45°求FE的长度.24.【发现与证明】如图在四边形ABCD中 E F G H是各边中点对角线AC BD相交于点O I J是AC BD的中点连接EF EH HG GF EI GI EJ FJ IJ GJ IH.结论1:四边形EFGH是平行四边形;结论2:四边形EJGI是平行四边形;结论3:S四边形EFGH =12S四边形ABCD;……(1)请选择其中一个结论加以证明(只需证明一个结论).(2)【探究与应用】(★温馨提示:以下问题可以直接使用上述结论)①如图1 在四边形ABCD中 F H分别为边AB DC的中点连结HF.已知AD=6 BC=4线段HF的取值范围是 .②如图2 在四边形ABCD中点E F G H分别是AB BC CD DA的中点连接EG FH交于点O EG=8cm FH=6cm ∠EOF=60°求S四边形ABCD.答案部分:例1.A ∵点D E 分别为△ABC 的边AB AC 的中点 ∴DE 是△ABC 的中位线 ∴DE ∥BC ,DE =12BC =4.∴DF ∥BC ∵DF ∥BC ,CF ∥BA∴四边形BCFD 是平行四边形 ∴DF =BC =8,∴EF =DF -DE =4.例2.C ∵P 是BD 的中点,E 是AB 的中点 ∴PE =12AD ,同理,PF =12BC ∵AD =BC ,∴PE =PF∴∠EFP =12×(180°-∠EPF )=22°. 故选C.例3.答案 6.5解:如图,连接DN DB∵点E F 分别为DM MN 的中点 ∴EF 是△MDN 的中位线 ∴EF =12DN当N与点B重合时,DN最大,此时EF的值最大∵∠A=90°,AB=12,AD=5∴DB=√AD2+AB2=13,∴EF的最大值为6.5 故答案为6.5.例4.证明如图,连接BD∵C,H分别是AB,DA的中点∴CH是△ABD的中位线BD∴CH∥BD,CH=12BD同理,FG∥BD,FG=12∴CH∥FG,CH=FG∴四边形CFGH是平行四边形.例5.D解:延长BD CA交于点F∠的外角平分线∵AD为ABC中BAC∴FAD BAD∠=∠∵BD AD⊥∴90∠=∠=︒ADF ADB在ABD△和AFD△中FAD BAD AD ADADF ADB ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ABD AFD △≌△ ∴AB AF = BD DF = 又E 为BC 中点 5DE = ∴210CF DE == 又3AC =∴7AF CF AC AB =-==. 故选:D .例6.解: 在△ABC 中,∠ABC =90°,AB =5,BC =12 则AC =√AB 2+BC 2=√52+122=13 ∵AD =AB =5∴DC =AC -AD =13-5=8 ∵AD =AB ,AE ⊥BD ,∴BE =ED ∵BF =FC ,∴EF =12DC =4.解:如图,延长BD 交AC 于点F ,∵AD 平分∠BAC ,∴∠BAD =∠CAD .∵BD ⊥AD ∴∠ADB =∠ADF又∵AD =AD ,∴△ADB ≌△ADF (ASA ).∴AF =AB =6,BD =FD .∵AC =10,∴CF =AC -AF =10-6=4.∵E 为BC 的中点,∴DE 是△BCF 的中位线.∴DE =12CF =12×4=2.例8.证明:如图,延长FE 至N ,使EN =EF ,连接BN ,AN ,则ME =12AN . ∵EF =EN ,∠BEF =90°,∴BE 垂直平分FN . ∴BF =BN .∴∠BNF =∠BFN . ∵△BEF 为等腰直角三角形,∠BEF =90°,∴∠BFN =45°.∴∠BNF =45°. ∴∠FBN =90°,即∠FBA +∠ABN =90°.又∠FBA +∠CBF =90° ∴∠CBF =∠ABN .在△BCF 和△BAN 中,∵BF =BN ,∠CBF =∠ABN ,BC =BA∴△BCF ≌△BAN (SAS ).∴CF =AN .∴ME =12AN =12CF .例9.(1)证明:在△ABC 中,∵AB =BC ,∠ABC =90°,∴∠ACB =45°. ∵CE 平分∠ACB ,∴∠ECB =∠ACE =22.5°.∴∠BEF =∠CFD =∠BFE =67.5°.∴BE =BF ,即△BEF 是等腰三角形. (2)解:如图,延长AB 至点M ,使得BM =AB ,连结CM .易知D 是AC 的中点∴BD ∥MC ,BD =12MC .∴∠BFE =∠MCE .由(1)得∠BEF =∠BFE ,BE =BF ,∴∠BEF =∠MCE .∴ME =MC .∵BM =AB =BC ,∴BD =12MC =12ME =12(MB +BE )=12(BC +BF ).例10.A 如图,连接BD ,取BD 的中点H ,连接HF ,HE∵点E ,H 分别是AB ,BD 的中点,∴EH 是△ABD 的中位线,∴EH =12AD =3 同理可得FH =12BC =5,∴EF ≤FH +EH =8,故选A .例11.B 解:取CD 的中点G 连接EG FG点E 为AD 的中点 点F 为OC 的中点12EG AC ∴=EG AC ∥ 12FG OD = //FG OD四边形ABCD 是菱形 120BAD ∠=︒AC BD ∴⊥ 60ADC ∠=︒ 1302ODC ADC ∠=∠=︒EG GF ∴⊥ AD DC AC ==设CD x = 则12EG x = 3FG 7EF =22213()()(7)2x ∴+= 解得4x =4CD ∴=∴菱形ABCD的周长为:44416CD=⨯=故选:B.例12解:如图取AB的中点G连接EG FG∵E F分别是边AD CB的中点∴EG BD∥且118422EG BD==⨯=FG AC且116322FG AC==⨯=∵AC BD⊥∴EG FG⊥∴2222435EF EG FG=++=.故答案为:5.强化训练题一.选择题1.如图在△ABC中AB=4 BC=5 AC=8.点D E F分别是相应边上的中点则四边形DFEB的周长等于()A.8 B.9 C.12 D.13解:∵点D F分别是AB AC的中点∴DF=BC=2.5同理EF=AB=2∴四边形DFEB的周长=EF+FD+DB+BE=9故选:B .2.解:∵AB =AC AD 平分∠BAC ∴BD =DC =BC =5 ∵点E 为AC 的中点∴CE =AC =6 DE =AB =6 ∴△CDE 的周长=CD +CE +DE =17 故选:B . 3.A 解:45B ∠=︒ AD BC ⊥ABD ∴是等腰直角三角形 6AD BD ∴=60C ∠=︒30DAC ∴∠=︒12DC AC ∴=2233AD AC DC DC AC ∴-=36AC =22AC ∴=E F 分别为AB BC 的中点1122222EF AC ∴==⨯=故选:A . 4.C解:四边形ABCD 是平行四边形60ABC ADC ∴∠=∠=︒ 120BAD ∠=︒AE 平分BAD ∠60BAE EAD ∴∠=∠=︒ABE ∴是等边三角形AE AB BE ∴==AB =12BC AE ∴=12BC90BAC ∴∠=︒30CAD ∴∠=︒ 故A 正确; AC AB ⊥∴ABCDSAB AC =⋅ 故B 正确AB =12BC OB =12BDBD BC >AB OB ∴≠ 故C 错误; CE BE = CO OA = OE ∴=12ABOE ∴=14BC 故D 正确. 故选:C . 5.【答案】C6.已知三角形三边长分别为7cm 8cm 9cm 作三条中位线组成一个新的三角形 同样方法作下去 一共做了五个新的三角形 则这五个新三角形的周长之和为( ) A .46.5cmB .22.5cmC .23.25cmD .以上都不对解:由△ABC 三边长分别为7cm 8cm 9cm 三条中位线组成一个新的三角形 可知新三角形与原三角形相似 相似比是1:2 即:后一个三角形的周长都是前一个三角形周长的∵原三角形的周长=7+8+9=24 ∴这个新三角形的周长=×24=12 ∴这个五个新三角形的周长之和=24+×24+×24+×24+×24=23.25故选:C .7.A解:延长AC BE 交于点M∵AE 平分BAC ∠ BE AE ⊥∴90AEB AEM ∠=∠=︒ CAE BAE ∠=∠∵AE AE =∴ABE AME ≌∴10AB AM == BE EM =∵6AC =∴4CM AM AC =-=∵点F 是BC 的中点 BE EM =∴EF 为BCM 中位线 ∴122EF CM ==.故选:A .8.【答案】A解:连接 AC∵∠GAB =∠ABC∴AG ∥BC .又 AG = BC可知四边形 AGBC 是平行四边形∴AC ∥BG点 E F 分别为 AD DC 的中点∴EF 是△ ADC 的中位线∴EF ∥AC∴ EF ∥BG .∴点 B 与点 G 到 EF 的距离相等△EBF 与△ EGF 是同底等高的关系∴ S △ EBF = S △ EGF 即S1=S2故选: A9.A解:如图 延长DP 交BC 于点F四边形ABCD 是平行四边形AD BC ∴∥ OD OB = 7AB CD == 10BC AD ==180ADC BCD ∴∠+∠=︒ ADF CFD ∠=∠ DP 平分ADC ∠ CP 平分BCD ∠ADF CDF ∠=∠∴ FCP DCP ∠=∠90CDP DCP ∴∠+∠=︒ CDF CFD ∠=∠7DC CF ∴== DP PF =OP ∴是DBF 的中位线()()111107 1.5222OP BF BC CF ∴==-=-= 故选:A .10.解:如图 取 AD 的中点 H ,连接 PH , OH∵四边形 ABCD 是平行四边形 ∴AP = PC又∵点 H 是 AD 中点 LAOD =90°∴PH =- AB , OH =- AD∴OH + PH ≥ OP∴AB + AD ≥2OP∴四边形 ABCD 的周长最小值为20故选: A .二.填空题11.解:取 BE 的中点 M 连接 FM , CM∵F 为AE 的中点 M 为 BE 的中点∴MF =AB , FM // AB∵四边形 ABCD 是平行四边形∴DC = AB , DC // AB∵E 为 CD 的中点∴CE =DC∴ CE = FM , CE // FM .∴四边形 EFMC 是平行四边形∴EG = GM∵BM = EM = BE =x8=4∴ EG =x4=2故答案为:212.如图 DE 为△ABC 的中位线 点F 在DE 上 且∠AFC 为直角 若AC =6cmBC =8cm则DF 的长为 1cm .解:∵DE 为△ABC 的中位线∴DE =BC =4(cm )∵∠AFC 为直角 E 为AC 的中点∴FE =AC =3(cm )∴DF =DE ﹣FE =1(cm )故答案为:1cm .13.6解:如图2 由折叠得:AM MD = MN AD ⊥ AD BC ⊥ 连接GD∴GN BC∥GN是AD的垂直平分线∴AG DG=∴GAD GDA∠=∠∵90GBD GAD GDB GDA∠+∠=︒=∠+∠∴GBD GDB∠=∠∴GB GD=∴AG BG=同理可得:AN CN=∴GN是ABC的中位线而12BC=∴162GN BC==∵PM GM=∴6 MP MN GM MN GN+=+==.故答案为:6.14.【答案】7215.解:延长AE BC交于点H∵△ADE是等腰直角三角形∴∠HAC=45°AE=AD=2∴CH=AC=BC AH=AC=6∴EH=AH﹣AE=4∵BC=CH BF=FE∴FC=EH=2故答案为:2.16.【答案】3 (或3:1)】解: EF 是△ ABC 的中位线.. EF / BC , EF = BCOE =20F: OE =BC =BC设点 A 到 BC 的距离为 h则 S △ ABC = BC · h , S △ aoc =OE · h =BC · h =BC · h:△ ABC 的面积与△ AOC 的面积之比=3:1.故选: D .17.【答案】52解答】解:∵四边形 ABCD 是平行四边形∴AD = BC , CD = AB , DC / AB∵AD =5, AB = CF =3.∴CD =3, BC =5∴BF = BC + CF =8∵△ BEF 是等边三角形 G 为 DE 的中点∴BF = BE =8, DG = EG延长 CG 交 BE 于点 H∵DC / AB∴∠CDG=∠HEG在△ DCG 和△ EHG 中∠CDG=∠HEGDG = EG∠DGC =∠ EGH∴△ DCGR △ EHG ( ASA ).∴DC = EH , CG = HG∵ CD =3, BE =8∴HE =3, BH =5∵ LCBH =60°, BC = BH =5∴△CBH 是等边三角形∴CH = BC =5∴CG = CH =52故答案为:52三.解答题18.如图△ABC的中线BE CF相交于G且AB=12 AC=16 BC=20 求GC的长.解:∵AB=12 AC=16 BC=20∴AB2+AC2=BC2∴△ABC是直角三角形∴∠A=90°∵F是AB中点∴AF=6∴CF===2∵中线BE CF相交于G∴G是△ABC重心∴CG:GF=2:1∴CG=.19.(1)证明见解析(2)证明见解析(1)证明:∵点E是边BC中点∴BE CE=又∵EF OE=∴四边形OBFC是平行四边形;(2)证明:∵四边形ABCD是平行四边形对角线AC BD、相交于点O ∴点O是BD的中点又∵点E是边BC中点∴OE是BCD△的中位线∴OE CD即OF CD∥.20.【答案】(1)证明:∵BF=BE CG=CE∴BC为△FEG的中位线FG∴BC//FG BC=12又∵H是FG的中点∴FH=1FG2∴BC=FH .又∵四边形ABCD是平行四边形∴AD//BC AD=BC∴AD//FH AD=FH∴四边形AFHD是平行四边形;(2)解:∵四边形ABCD是平行四边形∴∠DAB=∠DCB∵CE=CB∴∠BEC=∠EBC=75°∴∠BCE=180°−75°−75°=30°∴∠DCB=∠DCE+∠BCE=10°+30°=40°∴∠DAB=40° .21.解:(1)如图,连接CD,AE.由三角形中位线定理可得PM∥12CD,PN∥12AE.∵△ABD和△BCE是等边三角形,∴AB=DB,BE=BC,∠ABD=∠CBE=60°∴∠ABE=∠DBC.∴△ABE≌△DBC,∴AE=DC.∴PM=PN.(2)如图,设PM交AE于F,PN交CD于G,AE交CD于H,AE交BD于Q.由(1)知△ABE≌△DBC,∴∠BAE =∠BDC.又∵∠DQH=∠BQA,∴∠AHD=∠ABD=60°,∴∠FHG=120°.22.证明:如图,取NC的中点H,连接DH过点H作HE∥AD,交BN的延长线于E.∵AB=AC,AD⊥BC,∴D为BC的中点.∵H为NC的中点,∴DH∥BN.又∵PD∥EH,∴四边形PDHE是平行四边形.∴HE=PD.∵P为AD的中点,∴AP=PD. ∴AP=EH.又∵HE∥AD,∴∠PAN=∠EHN,∠APN=∠HEN.∴△APN≌△HEN(ASA).∴AN=NH. ∴AN=NH=HC. ∴AN=13AC.23.(1)证明:连接BD取DB的中点H连接EH FH ∵E H分别是AD BD的中点∴EH∥AB EH=AB∴∠BME=∠HEF∵F H分别是BC BD的中点∴FH∥CD FH=CD∴∠CNE=∠HFE∵AB=CD∴HE=FH∴∠HEF=∠HFE∴∠BME=∠CNE;(2)连接BD取DB的中点H连接EH FH∵E F分别是AD BC的中点∴EH=AB FH=CD FH∥AC∴∠HFE=∠FEC=45°∵AB=CD=2∴HF=HE=1∴∠HEF=∠HFE=45°∴∠EHF=180°﹣∠HFE﹣HEF=90°∴.24.【答案】(1)解:结论1:四边形EFGH是平行四边形;证明:∵在四边形ABCD中 E F G H是各边中点∴EF为∆ABD的中位线∴EF∥BD EF=12BD同理可得GH∥BD GH=12BD∴GH∥EF GH=EF∴四边形EFGH是平行四边形;结论2:四边形EJGI是平行四边形;证明:∵E J G I分别为DA DB BC AC中点∴EJ为∆ABD的中位线∴EJ∥AB EJ=12AB同理可得IG∥AB IG=12AB∴EJ∥IG EJ=IG∴四边形EJGI是平行四边形;结论3:S四边形EFGH=12S四边形ABCD;证明:由结论1证明可得 EF=12BD GH=12BD∴∆AEF的高为∆ADB高的一半∆CHG的高为∆BCD高的一半∴S�AEF=14S�ADB S�CHG=14S�CDB同理:S�DEH=14S�DAC S�BFG=14S�BCA∴S四边形EFGH=S四边形ABCD−S�AEF−S�CHG−S�DEH−S�BFG=12S四边形ABCD;(2)解:①连接AC 取AC的中点E 连接FE HE∵点E F为AC AB的中点∴EF=12BC=2同理:EH=12AD=3第 31 页 共 31 页 ∴EH-EF<FH<EF+EH即1<EH<5故答案为:1<FH<5;②如图所示 连接EFGH 由结论1可得四边形EFGH 为平行四边形如图所示 过点E 作EM ∥FH 交GH 延长线于点M 过点G 作GN ⊥EM∵EF ∥GM EM ∥FH∴四边形FHME 为平行四边形∴FH=EM=6 ∠EOF=∠GEM=60° FE=HM∴∠EGN=30°∴EN=12EG =4∴GN =√EG 2−EN 2=4√3∴S �EGM =12EM ×GN =12√3由图可得S 四边形EFGH =S �EGM =12√3由结论3可得:S 四边形ABCD =2S 四边形EFGH =24√3.。
三角形的中位线(专项练习)-2020-2021学年八年级数学下册基础知识专项讲练(华东师大版)
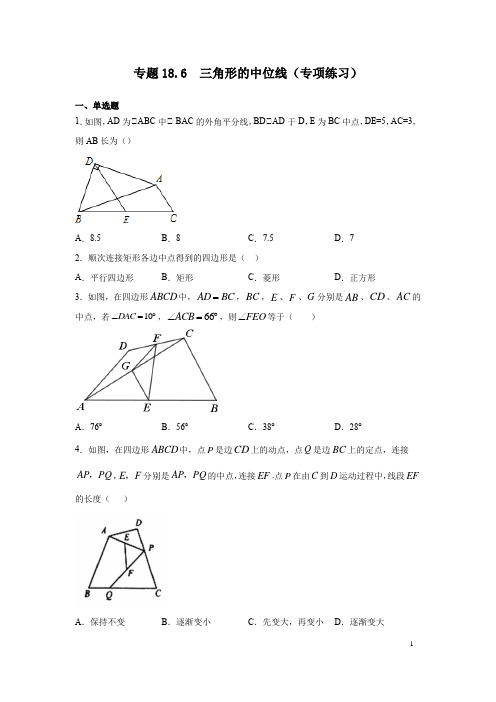
专题18.6 三角形的中位线(专项练习)一、单选题1.如图,AD 为△ABC 中△ BAC 的外角平分线,BD△AD 于D ,E 为BC 中点,DE=5,AC=3,则AB 长为()A .8.5B .8C .7.5D .72.顺次连接矩形各边中点得到的四边形是( )A .平行四边形B .矩形C .菱形D .正方形 3.如图,在四边形ABCD 中,AD BC =,BC ,E 、F 、G 分别是AB 、CD 、AC 的中点,若10DAC ∠=︒,66ACB ∠=︒,则FEO ∠等于( )A .76°B .56°C .38°D .28° 4.如图,在四边形ABCD 中,点P 是边CD 上的动点,点Q 是边BC 上的定点,连接AP PQ ,,EF ,分别是AP PQ ,的中点,连接EF .点P 在由C 到D 运动过程中,线段EF 的长度( )A .保持不变B .逐渐变小C .先变大,再变小D .逐渐变大5.ABC 中,D 、E 分别为AB 、AC 边的中点,若BC=8cm ,则DE 为( ) A .16cm B .8cm C .4cm D .2cm6.在Rt ABC △中,90,13,5ACB AB AC ︒∠===,点D 是AB 上一动点,作//DE AC ,且2DE =,连结,BE CD P Q ,,分别是BE DC 、的中点连结PQ ,则PQ 长为( )A B .C .6 D .6.57.如图,已知△ABC 中,点M 是BC 边上的中点,AN 平分△BAC ,BN△AN 于点N ,若AB =8,MN =2,则AC 的长为( )A .12B .11C .10D .98.如图,将三角形纸片ABC 沿过,AB AC 边中点D 、E 的线段DE 折叠,点A 落在BC 边上的点F 处,下列结论中,一定正确的个数是( )△BDF 是等腰三角形 △12DE BC = △四边形ADFE 是菱形 △2BDF FEC A ∠+∠=∠A .1B .2C .3D .4二、填空题9.如图,在Rt ABC 中,90ACB ∠=︒,30A ∠=︒,点D ,E 分别是AB 和AC 边的中点,若4CD =,则DE =__________.10.如图,,,D E F 分别是ABC ∆各边的中点,AH 是高,,5AB AC ED ≠=,判断AD ________AH (大小),FHC ∆是___________(类别),四边形AEDF 是______________________(类别)11.如图,在Rt △ABC 中,△ACB =90°,点D 、E 、F 分别为AB 、AC 、AD 的中点,若AB =12,则EF 的长为__________.12.如图,CD 是ABC ∆的中线,点E 、F 分别是AC 、DC 的中点,3BD =,则EF =_________.13.如图,在ABC中,AB=AC,AM BC⊥,延长AC到点D,连接BD,取BD的中点N,连接MN.若AB=3,AD=5,则MN=_______________.14.如图,在△ABC中,D是AC边的中点,且BD△AC,ED△BC,ED交AB于点E,若AC=4,BC=6,则△ADE的周长为______.15.如图,△ABC的中位线DE=6cm,把△ABC沿DE折叠,使点A落在边BC上的点F处,若A、F两点间的距离是8cm,则△ABC的面积为_____cm2.16.如图,在ABC中,△ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD=13BD,连接DM、DN、MN.若AB=4,则DN=_____.17.如图,在ABC∆中,D、E分别为BC、AC的中点,且ABC的面积为16,则ADE 的面积是______.18.如图,面积为16的菱形ABCD 中,点O 为对角线的交点,点E 是边BC 的中点,过点E 作EF BD ⊥ 于点F ,EG AC ⊥于点G ,则四边形EFOG 的面积为__.19.如图,在菱形ABCD 中,45B ∠=︒,BC =E ,F 分别是边CD ,BC 上的动点,连接AE ,EF ,G ,H 分别为AE ,EF 的中点,连接GH ,则GH 的最小值为________.20.如图,有一块形状为Rt △ABC 的斜板余料,△A =90°,AB =6cm ,AC =8cm ,要把它加工成一个形状为□DEFG 的工件,使GF 在边BC 上,D 、E 两点分别在边AB 、AC 上,若点D 是边AB 的中点,则DEFG 的面积为_________2cm .21.如图,在平行四边形纸片ABCD 中,2cm AB =,将纸片沿对角线AC 对折至CF ,交AD 边于点E ,此时BCF △恰为等边三角形,则图中折叠重合部分的面积是________.22.如图,在ABC 中,点D E 、分别在边AB 、 AC 上,//DE BC ,将ADE 沿直线DE 翻折后与 FDE 重合,DF 、EF 分别与边BC 交于点M 、N ,如果 8DE =,23AD AB =,那么MN 的长是 _____ .23.如图,△ABC 是边长为1的等边三角形,取BC 边中点E ,作ED △AB ,EF △AC ,得到四边形EDAF ,它的周长记作C 1;取BE 中点E 1,作E 1D 1△FB ,E 1F 1△EF ,得到四边形E 1D 1FF 1,它的周长记作C 2.照此规律作下去,则C 2020=__.24.如图,在Rt ABC △中,90A ︒∠=,2AB =,点D 是BC 边的中点,点E 在AC 边上,若45DEC ︒∠=,那么DE 的长是__________.三、解答题25.在正方形ABCD 中,点E 是边CD 的中点,点P 是边AD 上一点(与点A 、D 不重合),射线PE 与BC 的延长线交于点Q .(1)如图,求证:PE QE =;(2)如图,连接PB ,PB PQ =,过点E 作//EF BC 交PB 于点F ,连接AF ,在不添加任何辅助线的情况下,请直接写出与线段AF 相等的所有线段.26.如图,在ABC 中,AB AC =,E ,F 分别是BC ,AC 的中点,连接EF ,以AC 为斜边作直角三角形ADC ,连接DE 、DF .(1)求证:FE FD =.(2)若24CAD CAB ∠=∠=︒,求EDF ∠的度数.27.如图,在△ABC 中,点D ,E 分别是BC ,AC 的中点,延长BA 至点F ,使得AF =12AB ,连接DE ,AD ,EF ,DF .(1)求证:四边形ADEF 是平行四边形;(2)若AB =6,AC =8,BC =10,求EF 的长.28.如图,等边ABC ∆中,D ,E 分别是AB ,AC 的中点,延长BC 到点F ,使12CF BC =,连结DE ,CD ,EF .(1)求证:四边形DCFE 是平行四边形;(2)若等边ABC ∆的边长为6,求EF 的长.29.如图,在ABC 中,D E 、分别是AB AC 、的中点,延长DE 到点,F 使得,EF BE =连接CF .若EC 平分BEF ∠.(1)求证:四边形BCFE 是菱形;(2)若8,120AC BCF =∠=︒,求菱形BCFE 的面积.参考答案1.D【分析】延长BD、CA交于点F,易证△ADF≌△ADB(ASA),则BD=DF,AB=AF,得到点D为BF中点,即DE为△BCF的中位线,再根据已知线段的长度,即可顺利求得AB的长.【详解】解:如图,分别延长BD、AC交于点F,△AD为△ABC中△BAC的外角平分线,△△FAD=△BAD,△BD△AD,△△FDA=△BDA=90°,在△BDA和△FDA中,FAD BAD AD ADFDA BDA ∠=∠⎧⎪=⎨⎪∠=∠⎩,△△BDA≌△FDA(ASA),△AB=AF,BD=FD,即D为BF的中点,△E为BC中点,△DE为△BCF的中位线,△DE=5,AC=3,△CF=2DE=2⨯5=10,△AF=CF-AC=10-3=7.△AB=AF=7.故选D.【点拨】本题考查三角形的综合,涉及的知识点有全等三角形的判定,中位线定理等,难度一般,是中考的常考知识点,正确作出辅助线并证明全等是顺利解题的关键.2.C【分析】根据三角形的中位线定理,得新四边形各边都等于原四边形的对角线的一半,进而可得连接对角线相等的四边形各边中点得到的四边形是菱形.【详解】解:如图,矩形ABCD 中,,AC BD ∴=,,,E F G H 分别为四边的中点,1//,,2EF BD EF BD ∴=1//,,2GH BD GH BD = 1,2FG AC = //,,EF GH EF GH ∴=∴ 四边形ABCD 是平行四边形, 11,,,22AC BD EF BD FG AC === ,EF FG ∴=∴ 四边形EFGH 是菱形.故选C .【点拨】本题主要考查了矩形的性质、菱形的判定,以及三角形中位线定理,关键是掌握三角形的中位线定理及菱形的判定.3.D 【分析】利用EG 、FG 分别是ABC ∆和ADC ∆两个三角形的中位线,求出EG FG =,从而得出FGC ∠和EGC ∠,再根据EG FG =,利用三角形内角和定理即可求出FEG ∠的度数.【详解】解:△E 、F 、G 分别是AB 、CD 、AC 的中点, △EG 、FG 分别是ABC ∆和ADC ∆两个三角形的中位线, △//EG BC ,//FG AD ,且22AD BCEG FG ===, △10FGC DAC ∠=∠=︒,180114EGC ACB ∠=︒-∠=︒, △124EGF FGC EGC ∠=∠+∠=︒, 又△EG FG =, △()()111801801242822FEG EGF ∠=-∠=-︒=︒︒︒. 故本题答案为:D . 【点拨】本题考查了三角形内角和定理,等腰三角形的判定与性质,三角形中位线定理.解决本题的关键是正确理解题意,熟练掌握三角形中位线定理,通过等腰三角形的性质找到相等的角. 4.A 【分析】连接AQ ,则可知EF 为△PAQ 的中位线,可知EF =12AQ ,可知EF 不变. 【详解】 如图,连接AQ ,△E 、F 分别为PA 、PQ 的中点, △EF 为△PAQ 的中位线, △EF =12AQ , △Q 为定点,△AQ 的长不变, △EF 的长不变, 故选:A .【点拨】本题主要考查三角形中位线定理,掌握三角形中位线平行第三边且等于第三边的一半是解题的关键. 5.C 【分析】先画出图形,再根据三角形的中位线定理即可得. 【详解】由题意,画出图形如下:点D 、E 分别为AB 、AC 边的中点,DE ∴是ABC 的中位线, 1184()22DE BC cm ∴==⨯=, 故选:C . 【点拨】本题考查了三角形的中位线定理,熟记三角形的中位线定理是解题关键. 6.A 【分析】由勾股定理得出,取BD 中点F ,连接PF 、QF ,证出PF 是△BDE的中位线,FQ是△BCD的中位线,由三角形中位线定理得出PF△ED,PF=12DE=1,FQ△BC,FQ=12BC=6,证出PF△FQ,再由勾股定理求出PQ即可.【详解】解:△△ACB=90°,AB=13,AC=5,,取BD中点F,连接PF、QF,如图所示:△P、Q分别是BE、DC的中点,△PF是△BDE的中位线,FQ是△BCD的中位线,△PF△ED,PF=12DE=1,FQ△BC,FQ=12BC=6,△DE△AC,AC△BC,△PF△FQ,==故选:A.【点拨】本题考查了三角形中位线定理、勾股定理、平行线的性质;熟练掌握勾股定理,由三角形中位线定理得出PF△ED,FQ△BC是解题的关键.7.A【分析】延长BN交AC于D,证明△ANB△△AND,根据全等三角形的性质、三角形中位线定理计算即可.【详解】解:延长BN交AC于D,在△ANB 和△AND 中,90NAB NAD AN ANANB AND ∠∠⎧⎪⎨⎪∠∠︒⎩====, △△ANB△△AND , △AD=AB=8,BN=ND , △M 是△ABC 的边BC 的中点, △DC=2MN=4, △AC=AD+CD=12, 故选:A . 【点拨】本题考查的是三角形中位线定理,三角形的中位线平行于第三边,并且等于第三边的一半. 8.C 【分析】根据菱形的判定和等腰三角形的判定,采用排除法,逐条分析判断. 【详解】 解:△△DE △BC ,△△ADE =△B ,△EDF =△BFD , 又△△ADE △△FDE ,△△ADE =△EDF ,AD =FD ,AE =CE , △△B =△BFD ,△△BDF 是等腰三角形,故△正确; 同理可证,△CEF 是等腰三角形, △BD =FD =AD ,CE =FE =AE , △DE 是△ABC 的中位线,△DE =12BC ,故△正确; △△B =△BFD ,△C =△CFE ,又△△A +△B +△C =180°,△B +△BFD +△BDF =180°,△C +△CFE +△CEF =180°, △△BDF +△FEC =2△A ,故△正确.而无法证明四边形ADFE 是菱形,故△错误. 所以一定正确的结论个数有3个, 故选:C . 【点拨】本题考查了菱形的判定,中位线定理,等腰三角形的判定和性质,菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:△定义;△四边相等;△对角线互相垂直平分.具体选择哪种方法需要根据已知条件来确定. 9.2 【分析】由直角三角形斜边上的中线等于斜边的一半可得出28AB CD ==,又因为30A ∠=︒,所以4BC =,由三角形的中位线定理可得出122DE BC ==. 【详解】解:△CD 是Rt ABC 中斜边上的中线,4CD = △28AB CD ==△90ACB ∠=︒,30A ∠=︒ △4BC =△点D ,E 分别是AB 和AC 边的中点 △122DE BC == 故答案为:2. 【点拨】本题考查的知识点是三角形的中位线定理,由直角三角形斜边上的中线等于斜边的一半可得出28AB CD ==,是解此题的关键. 10.> 等腰三角形 平行四边形 【分析】(1)连接AD 可知,在Rt ADH 中,AH 为直角边,AD 为斜边,可得AH 与AD 大小关系;(2)在Rt AHC 中,11,22HF AC FC AC ==,可得HF FC =,可得FHC 为等腰三角形;(3)根据中位线的性质,可得//,//DE AF AE DF ,可得AEDF 的形状 【详解】(1)连接AD ,在Rt ADH 中,AH 为直角边,AD 为斜边,得AD AH >; 故答案为:>(2)在Rt ADC 中,F 为AC 中点 △11,22HF AC FC AC ==, △HF FC =,△FHC 为等腰三角形; 故答案为:等腰三角形(3)△,,D E F 分别是ABC ∆各边的中点 △//,//DE AF AE DF△四边形AEDF 为平行四边形 故答案为:平行四边形 【点拨】本题考查了直角三角形的边角关系,以及中点的应用,熟知中点的作用是解题的关键. 11.3 【分析】根据直角三角形的性质求出CD ,根据三角形中位线定理计算即可. 【详解】在Rt△ABC中,△ACB=90°,D为AB的中点,△CD12=AB=6△E,F分别为AC,AD的中点,△EF12=CD=3.故答案为:3【点拨】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.12.1.5【分析】先由中线知BD=AD,求出AD,再利用三角形中位线是性质即可解答.【详解】解:△CD是ABC的中线,3BD=△AD=BD= 3△点E、F分别是AC、DC的中点,△EF是ACD的中位线,△EF=12AD=1.5,故答案为:1.5.【点拨】本题考查了三角形的中线和中位线,熟练掌握三角形中位线的性质是解答的关键.13.1【分析】由题意易得BM=MC,则有MN△CD,12MN CD=,进而可求解.【详解】解:AB=AC,AM BC⊥,∴BM=MC,BN=ND,∴MN△CD,12MN CD=,AB=3,AD=5,∴CD=2,∴MN=1;故答案为1.【点拨】本题主要考查等腰三角形的性质及三角形中位线,熟练掌握等腰三角形的性质及三角形中位线是解题的关键.14.8【分析】根据线段垂直平分线的性质得到AB=BC=6,根据三角形中位线定理求出DE,根据直角三角形的性质求出AE,根据三角形的周长公式计算,得到答案.【详解】△D是AC边的中点,BD△AC,△BD是线段AC的垂直平分线,AD12=AC=2,△AB=BC=6,△D是AC边的中点,ED△BC,△点E是AB的中点,DE12=BC=3,在Rt△ADB中,点E是AB的中点,△DE12=AB=3,△△ADE的周长=AE+DE+AD=8,故答案为:8.【点拨】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.15.48【分析】根据对称轴垂直平分对应点连线,可得AF即是△ABC的高,再由中位线的性质求出BC,继而可得△ABC的面积.【详解】解:连接AF,△DE是△ABC的中位线,△DE△BC,BC=2DE=12cm;由折叠的性质可得:AF△DE,△AF△BC,△S△ABC=12BC×AF=12×12×8=48cm2.故答案为:48.【点拨】本题考查了翻折变换的性质及三角形的中位线定理,解答本题的关键是得出AF是△ABC的高.16.2【分析】连接CM,根据直角三角形的性质求出CM,根据三角形中位线定理得到MN=12BC,MN//BC,证明四边形NDCM是平行四边形,根据平行四边形的性质解答.【详解】解:连接CM,△△ACB=90°,M是AB的中点,△CM=12AB=2,△M、N分别是AB、AC的中点,△MN=12BC,MN//BC,△CD=13 BD,△CD=12 BC,△MN=CD,又MN//BC,△四边形NDCM是平行四边形,△DN=CM=2,故答案为:2.【点拨】本题考查直角三角形斜边的中线定理、三角形中位线定理、平行四边形的判定与性质等知识,是重要考点,难度较易,掌握相关知识是解题关键.17.4【分析】先根据D点是BC的中点,E点是AC的中点,得出S△ADE=14×S△ABC,即可得出答案.【详解】△D点是BC的中点,△S△ABD=S△ADC=12S△ABC,△E点是AC的中点,△S△ADE=S△DCE=12S△ADC=14×S△ABC△S△ABC=16,△S△ADE=4,故答案为:4.【点拨】本题考查了三角形中线的性质,得出S△ADE=14×S△ABC是解题关键.18.2【分析】由菱形的性质得出OA=OC,OB=OD,AC△BD,面积=12AC×BD,证出四边形EFOG是矩形,EF//OC,EG//OB,得出EF、EG都是△OBC的中位线,则EF=12OC=14AC,EG =12OB =14BD ,由矩形面积即可得出答案. 【详解】解:△四边形ABCD 是菱形,△OA =OC ,OB =OD ,AC△BD ,面积=12AC×BD=16, △AC×BD=32△EF△BD 于F ,EG△AC 于G ,△四边形EFOG 是矩形,EF//OC ,EG//OB ,△点E 是线段BC 的中点,△EF 、EG 都是△OBC 的中位线,△EF =12OC =14AC ,EG =12OB =14BD , △矩形EFOG 的面积=EF×EG =14AC×14BD =116×32=2; 故答案为:2.【点拨】本题考查了菱形的性质、矩形的判定与性质、三角形中位线定理等知识;熟练掌握菱形的性质和矩形的性质是解题的关键.19.2【分析】连结AF ,利用中位线的性质GH=12AF ,要使GH 最小,只要AF 最小,由点F 在BC ,当AF△BC 时,AF 最小,利用菱形性质求出AB =45B ∠=︒确定△ABF 为等腰直角三角形,得出AF=BF ,由勾股定理得:22222AB BF AF AF =+=求出AF 即可.【详解】连结AF ,△G ,H 分别为AE ,EF 的中点,△GH△AF ,且GH=12AF , 要使GH 最小,只要AF 最小,由点F 在BC ,当AF△BC 时,AF 最小,在菱形ABCD 中,BC = △AB =在Rt△ABF 中,45B ∠=︒,△△ABF 为等腰直角三角形,△AF=BF ,由勾股定理得:22222AB BF AF AF =+=,△(22=2AF ,△AFGH 最小=12【点拨】本题考查动点图形中的中位线,菱形的性质,等腰直角三角形的性质,勾股定理应用问题,掌握中位线的性质,菱形性质,等腰直角三角形的性质, 点F 在BC 上,AF 最短,点A 到BC 直线的距离最短时由点A 向直线BC 作垂线,垂线段AF 为最短是解题关键. 20.12【分析】作AH BC ⊥交BC 于H 点,交DE 于I 点,根据90,6,8A AB cm AC cm 可得BC 10cm =,根据D 是边AB 的中点可知DE 是ABC 的中位线,得12AIIH AH ,利用三角形面积1122ABC S AC AB BC AH ,可得245AH =,11225IH AH ,则根据DEFG S DE IH ,计算可得结果.【详解】如图示,作AH BC ⊥交BC 于H 点,交DE 于I 点,△90,6,8A AB cm AC cm△BC 10cm =△D 是边AB 的中点,//DE BC ,△DE 是ABC 的中位线,5DE cm = △12AIIH AH , 又△1122ABCS AC AB BC AH , 即有6810AH , △245AH =, △1124122255IHAH , △2125125DEFG S DE IHcm , 故答案为:12.【点拨】本题考查了三角形中位线的应用,勾股定理,三角形的面积和平行四边形的面积,熟悉相关性质定理是解题的关键.中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.212cm【分析】BCF △为等边三角形,点A 为BF 的中点,可得90BAC ∠=︒,求得12ACD S AC CD =,再证明出点E 为AD 的中点,得到12ACE ACD S S =,可求出面积. 【详解】解:ABC 折叠至ACF 处,∴AB=AF=2cm ,BC=BF=CF=4cm ,BCF △为等边三角形,AC BF ∴⊥,90BAC ∠=︒, 又四边形ABCD 为平行四边形,∴//AB CD ,90ACD ∴∠=︒,AC ==,CD=AB=2cm ,12ACD S AC CD ∴==212⨯=2cm , 点A 为BF 的中点,//AE BC ,∴AE 为BCF △的中位线,1122AE BC AD ∴==, ∴点E 为AD 的中点, 12ACE ACD S S ∴==12⨯2cm 为折叠重合部分的面积,2cm .【点拨】本题考查了折叠问题以及等边三角形和平行四边形的综合问题,还涉及勾股定理,需要有一定的推理论证能力,熟练掌握等边三角形和平行四边形的性质是解题的关键.22.4【分析】设3AB a =,从而可得2,a AD a BD ==,先根据平行线的性质可得,ADE B EDM BMD ∠=∠∠=∠,再根据翻折的性质可得,2ADE EDM DF AD a ∠=∠==,从而可得B BMD ∠=∠,然后根据等腰三角形的判定可得DM BD a ==,从而可得FM a =,最后根据三角形的中位线定理即可得.【详解】设3AB a =,则2,BD D a A a A AB D =-==,//DE BC ,,ADE B EDM BMD ∠=∠∠=∠∴,由翻折的性质得:,2ADE EDM DF AD a ∠=∠==,B BMD ∴∠=∠,DM BD a ∴==,FM DF DM a DM ∴=-==,即点M 是DF 的中点,又//DE BC ,MN ∴是FDE 的中位线,118422MN DE ∴==⨯=, 故答案为:4.【点拨】本题考查了翻折的性质、等腰三角形的判定、三角形的中位线定理等知识点,熟练掌握翻折的性质是解题关键.23.201812【分析】先计算出C 1、C 2的长,进而得到规律,最后求出C 2020的长即可.【详解】解:△E 是BC 的中点,ED △AB ,△DE 是△ABC 的中位线,△DE =12AB =12,AD =12AC =12, △EF △AC ,△四边形EDAF 是菱形,△C 1=4×12, 同理C 2=4×12×12=4×212, …C n =4×12n , △20202020201811422C =⨯=. 故答案为:201812.【点拨】本题考查了中位线的性质,菱形的判定与性质,根据题意得到规律是解题关键.24【分析】过D作DF△AC于F,得到AB△DF,求得AF=CF,根据三角形中位线定理得到DF=12 AB=1,根据等腰直角三角形的性质即可得到结论.【详解】解:过D作DF△AC于F,△△DFC=△A=90°,△AB△DF,△点D是BC边的中点,△BD=DC,△AF=CF,△DF=12AB=1,△△DEC=45°,△△DEF是等腰直角三角形,△DE DF,【点拨】本题考查了三角形的中位线定理,平行线的判定和性质,等腰直角三角形的性质,正确的作出辅助线构造等腰直角三角形是解题的关键.25.(1)见解析;(2)BF、PF、PE、QE.【分析】(1)根据正方形的性质及对顶角相等利用ASA即可证明PDE QCE≌,再利用全等三角形的性质即可得证;(2)根据三角形中位线的判定及性质定理、直角三角形斜边上的中线即可得出答案.【详解】(1)证明:如图,△四边形ABCD 是正方形△90D ECQ ∠=∠=︒,△E 是CD 的中点△DE CE =,又△DEP CEQ ∠=∠△()PDE QCE ASA ≌△△△PE QE =(2)如图,BF 、PF 、PE 、QE,//PB PQ EF BC =,PE QE =∴EF 为PBQ △的中位线PF FB PE EQ ∴===,四边形ABCD 为正方形,90BAP ∴∠=︒,∴AF 为BAP Rt △斜边的中线12AF BP BF PF ∴=== ∴与线段AF 相等的所有线段为:BF 、PF 、PE 、QE .【点拨】本题考查了正方形的性质、三角形中位线的判定及性质定理、直角三角形斜边上的中线、全等三角形的判定及性质,熟练掌握性质定理是解题的关键.26.(1)见解析;(2)54︒【分析】(1)根据三角形中位线定理推出12FE AB =,根据直角三角形斜边上的中线等于斜边的一半推出12FD AC =,即可证明FE FD =; (2)根据三角形中位线定理推出24EFC BAC ∠=∠=︒,根据直角三角形斜边上的中线的性质结合三角形的外角性质推出48DFC ∠=︒,利用(1)的结论结合三角形内角和定理即可求得EDF ∠的度数.【详解】(1)△E ,F 分别是BC ,AC 的中点, △12FE AB =, △F 是AC 的中点,90ADC ∠=︒, △12FD AC =, △AB AC =,△FE FD =;(2)△E ,F 分别是BC ,AC 的中点,△//FE AB ,△24EFC BAC ∠=∠=︒,△F 是AC 的中点,90ADC ∠=︒,△FD AF =,△24ADF CAD ︒∠=∠=,△48DFC ∠=︒,△72EFD ∠=︒,△FE FD=,△18072542FED EDF︒-︒∠=∠==︒.【点拨】本题考查了三角形中位线定理,直角三角形斜边上的中线等于斜边一半,平行线的性质,三角形的外角性质等,灵活运用有关定理来分析、判断、推理或解答是解题的关键.27.(1)见解析;(2)EF=5.【分析】(1)利用三角形的中位线的性质与等量代换得出DE=AF,DE△AF,从而得出结论.(2)先利用(1)中的结论得出EF=AD,再利用勾股定理的逆定理,求出△ABC是直角三角形,再利用直角三角形斜边上的中线等于斜边的一半求出。
平行四边形及中位线2

平行四边形与中位线2一.填空题(共2小题)1.(2013•泉州)如图,顺次连结四边形ABCD四边的中点E、F、G、H,则四边形EFGH 的形状一定是.2.如图,已知E、F、G、H是四边形ABCD四边的中点,则四边形EFGH的形状为;如四边形ABCD的对角线AC与BD的和为40,则四边形EFGH的周长为.二.解答题(共16小题)3.(2014•宁夏)在平行四边形ABCD中,将△ABC沿AC对折,使点B落在B′处,A B′和CD相交于点O.求证:OA=OC.4.(2014•江岸区模拟)已知:如图,在▱ABCD中,E、F是对角线AC上的两点,且AE=CF.求证:四边形BFDE是平行四边形.5.如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,(1)求证:AE=AF;(2)求证:△ABE≌△AGF.6.(2015春•平顶山期末)已知:如图,在平行四边形ABCD中,E,F分别是AB,CD上的两点,且AE=CF,AF、DE相交于点M,BF、CE相交于点N.求证:四边形EMFN是平行四边形.7.如图,在▱ABCD中,E,F分别为AD,BC上两点,且BF=DE,连AF,CE,BE,DF,AF与BE交于M,DF与CE交于N,求证:四边形FMEN为平行四边形.8.(2015春•召陵区期末)如图,已知在平行四边形ABCD中,E、F分别是边AD、BC上的点,且DE=BF,过E、F两点作直线,分别与CD、AB的延长线相交于点M、N,连接CE、AF.求证:(1)四边形AFCE是平行四边形;(2)△MEC≌△NFA.9.如图,AF与BE互相平分,EC与DF互相平分,求证:四边形ABCD是平行四边形.10.(2006•湛江)如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点,试判断四边形EFGH的形状,并证明你的结论.11.(2011秋•XX区校级期末)如图,B、C、D三点在同一直线上,分别以BC、CD为边在同侧作两个正三角形△ABC和△ECD,P为BD边中点,M、N分别为AB、ED的中点,连接PM、PN,探求PM与PN的数量关系与∠MPN的度数,并证明.12.如图,点P是四边形ABCD的对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠CBD=45°.∠ADB=105°,试探究EF与PF之间的数量关系,并证明.13.已知,如图,点E、F分别为四边形ABCD的对角线AC、BD的中点,求证:EF<(AB+CD).14.在△ABC中,点M为BC的中点,AD为△ABC的角平分线,且BD⊥AD,若AB=12,AC=18,求MD的长.15.如图,在△ABC中,AB=BC,∠ABC=90°,F为BC上一点,M为AF的中点,BE平分∠ABC,且EF⊥BE,求证:CF=2ME.16.如图,△ABC中,∠ABC=90°,BA=BC,△BEF为等腰直角三角形,∠BEF=90°,M 为AF的中点,求证:ME=CF.17.四边形ABCD中,AB=a,CD=b(a>b),M、N分别是AD、BC的中点,求MN的取值范围.18.如图,△ABC中,∠C=90°,CA=CB,E、F分别为CA、CB上一点,CE=CF,M、N 分别为AF、BE的中点.求证:AE=MN.平行四边形与中位线2参考答案与试题解析一.填空题(共2小题)1.(2013•泉州)如图,顺次连结四边形ABCD四边的中点E、F、G、H,则四边形EFGH 的形状一定是平行四边形.【考点】中点四边形.【分析】顺次连接任意四边形四边中点所得的四边形,一组对边平行并且等于原来四边形某一对角线的一半,说明新四边形的对边平行且相等.所以是平行四边形.【解答】解:如图,连接AC,∵E、F、G、H分别是四边形ABCD边的中点,∴HG∥AC,HG=AC,EF∥AC,EF=AC;∴EF=HG且EF∥HG;∴四边形EFGH是平行四边形.故答案是:平行四边形.【点评】本题考查了平行四边形的判断与三角形的中位线定理的应用,三角形的中位线平行于第三边,并且等于第三边的一半.2.如图,已知E、F、G、H是四边形ABCD四边的中点,则四边形EFGH的形状为平行四边形;如四边形ABCD的对角线AC与BD的和为40,则四边形EFGH的周长为40.【考点】平行四边形的判定;三角形中位线定理.【专题】证明题.【分析】利用三角形的中位线定理求出四边形EFGH的两组对边相等,即可证得四边形EFGH是平行四边形,继而即可求得EFGH的周长.【解答】解:连接AC、BD,∵E、F、G、H分别为四边形ABCD四边的中点,∴EH=BD,FG=BD,HG=AC,EF=AC,∴EH=FG,EF=HG,∴四边形EFGH是平行四边形.∴四边形EFGH的周长=EH+HG+FG+EF=×2×AC×BD=AC+BD=40.故答案为:平行四边形;40.【点评】本题考查了平行四边形的判定与三角形中位线定理,三角形中位线性质应用比较广泛,尤其是在三角形、四边形方面起着非常重要作用,本题解题的关键是将四边形分为四个三角形,然后利用中位线定理解答.二.解答题(共16小题)3.(2014•宁夏)在平行四边形ABCD中,将△ABC沿AC对折,使点B落在B′处,A B′和CD相交于点O.求证:OA=OC.【考点】平行四边形的性质;等腰三角形的判定与性质;翻折变换(折叠问题).【专题】证明题.【分析】由在平行四边形ABCD中,将△ABC沿AC对折,使点B落在B′处,即可求得∠DCA=∠B′AC,则可证得OA=OC.【解答】证明:∵△AB′C是由△ABC沿AC对折得到的图形,∴∠BAC=∠B′AC,∵在平行四边形ABCD中,AB∥CD,∴∠BAC=∠DCA,∴∠DCA=∠B′AC,∴OA=OC.【点评】此题考查了平行四边形的性质、等腰三角形的判定与性质以与折叠的性质.此题难度不大,注意掌握折叠前后图形的对应关系,注意掌握数形结合思想的应用.4.(2014•江岸区模拟)已知:如图,在▱ABCD中,E、F是对角线AC上的两点,且AE=CF.求证:四边形BFDE是平行四边形.【考点】平行四边形的判定与性质;全等三角形的判定与性质.【专题】证明题.【分析】先连接BD,交AC于O,由于四边形ABCD是平行四边形,易知OB=OD,OA=OC,而AE=CF,根据等式性质易得OE=OF,再根据两组对角线互相平分的四边形是平行四边形可证之.【解答】证明:连接BD,交AC于O,∵四边形ABCD是平行四边形,∴OB=OD,OA=OC,∵AE=CF,∴OA﹣AE=OC﹣CF,∴OE=OF,∴四边形BFDE是平行四边形.【点评】本题考查了平行四边形的判定和性质,解题的关键是作辅助线,使其中出现对角线相交的情况.5.如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,(1)求证:AE=AF;(2)求证:△ABE≌△AGF.【考点】翻折变换(折叠问题).【专题】证明题.【分析】(1)根据折叠的性质可得∠CEF=∠AEF,根据平行线的性质可得∠CEF=∠EFA,根据等量关系可得∠AEF=∠EFA,根据等角对等边即可求解;(2)根据平行四边形的性质,可得AB=CD,∠BAD=∠BCD,根据折叠的性质,可得AG=CD,∠EAG=∠BCD,所以AB=AG,∠BAD=∠EAG,由等量代换可得∠BAE=∠GAF,得到AB∥CD,AE∥GF,AD∥BC,得到∠BEA=∠EAF=∠GFA,AAS可证△ABE≌△AGF.【解答】(1)证明:由折叠的性质可得∠CEF=∠AEF,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠CEF=∠EFA,∴∠AEF=∠EFA,∴AE=AF;(2)证明:∵四边形ABCD是平行四边形,∴AB=CD,∠BAD=∠BCD,又根据题意得:AG=CD,∠EAG=∠BCD,∴AB=AG,∠BAD=∠EAG,∴∠BAE=∠GAF,又∵AB∥CD,AE∥GF,AD∥BC,∴∠BEA=∠EAF=∠GFA,在△ABE与△AGF中,,∴△ABE≌△AGF(AAS).【点评】此题是折叠问题,是中考中的常见题目.解此题首先要注意折叠前后的部分全等,即对应角与对应边都相等.解此题还要注意平行四边形的性质的求解方法.6.(2015春•平顶山期末)已知:如图,在平行四边形ABCD中,E,F分别是AB,CD上的两点,且AE=CF,AF、DE相交于点M,BF、CE相交于点N.求证:四边形EMFN是平行四边形.【考点】平行四边形的判定.【专题】证明题.【分析】由平行四边形的性质得出AB∥CD,AB=CD,再由AE=CF,得出BE=DF,证出四边形AECF、四边形BEDF是平行四边形,得出对边平行AF∥EC,DE∥BF,即可得出结论.【解答】证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴AE∥CF,BE∥DF,∵AE=CF,∴BE=DF,∴四边形AECF、四边形BEDF是平行四边形,∴AF∥EC,DE∥BF,∴四边形EMFN是平行四边形.【点评】本题考查了平行四边形的判定与性质;熟练掌握平行四边形的性质与判定方法,并能进行推理论证是解决问题的关键.7.如图,在▱ABCD中,E,F分别为AD,BC上两点,且BF=DE,连AF,CE,BE,DF,AF与BE交于M,DF与CE交于N,求证:四边形FMEN为平行四边形.【考点】平行四边形的判定与性质.【专题】证明题.【分析】先证明四边形BEDF是平行四边形,得出BE∥DF,再证明四边形AECF是平行四边形,得出FM∥EN,根据平行四边形的定义即可得出结论.【解答】证明:∵四边形ABCD是平行四边形,则AD∥BC,∴BF∥DE,∵BF=DE,∴四边形BEDF是平行四边形,∴BE∥DF,即ME∥FN,∵BF=DE,∴AE=CF,又∵AE∥CF,∴四边形AECF是平行四边形,∴FM∥EN,∴四边形FMEN是平行四边形.【点评】本题考查平行四边形的判定和性质定理;通过证明平行四边形得出对边平行是解决问题的关键关键.8.(2015春•召陵区期末)如图,已知在平行四边形ABCD中,E、F分别是边AD、BC上的点,且DE=BF,过E、F两点作直线,分别与CD、AB的延长线相交于点M、N,连接CE、AF.求证:(1)四边形AFCE是平行四边形;(2)△MEC≌△NFA.【考点】平行四边形的判定与性质;全等三角形的判定与性质.【分析】(1)由平行四边形的性质可证得AE=CF且AE∥CF,可证得结论;(2)由(1)结合平行四边形的性质可得到EC=AF,∠ECF=∠EAF,可证∠MCE=∠NAF,则可证明△MEC≌△NFA.【解答】证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC且AD=BC,又∵DE=BF,∴AE=CF,∴四边形AFCE是平行四边形;(2)∵四边形ABCD是平行四边形,∴∠MCB=∠NAD,且CD∥AB,∴∠M=∠N,∵四边形AFCE是平行四边形,∴EC=AF,∠ECF=∠EAF,∴∠MCE=∠NAF,在△MEC和△NFA中∴△MEC≌△NFA(AAS).【点评】本题主要考查平行四边形的性质和判定,掌握平行四边形的对边平行且相等、对角相等和对角线互相平分是解题的关键.9.如图,AF与BE互相平分,EC与DF互相平分,求证:四边形ABCD是平行四边形.【考点】平行四边形的判定.【专题】证明题.【分析】连接AE、DE、EF、BF、CF,根据AF与BE互相平分,EC与DF互相平分,得到四边形AEFB和四边形EFCD是平行四边形,从而得到AB∥CD,AB=CD,利用一组对边平行且相等的四边形是平行四边形判定四边形ABCD是平行四边形即可.【解答】证明:连接AE、DE、EF、BF、CF,∵AF与BE互相平分,EC与DF互相平分,∴四边形AEFB和四边形EFCD是平行四边形,∴AB∥EF∥CD,AB=EF=CD,∴AB∥CD,AB=CD,∴四边形ABCD是平行四边形.【点评】本题考查了平行四边形的判定,解题的关键是正确的作出辅助线,并利用平行四边形的判定定理进行判定.10.(2006•湛江)如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点,试判断四边形EFGH的形状,并证明你的结论.【考点】平行四边形的判定;三角形中位线定理.【专题】压轴题;探究型.【分析】四边形EFGH是平行四边形,连接AC,根据中位线定理,可证得EF∥AC,且EF=AC.GH∥AC,且GH=AC,∴EF GH.∴四边形EFGH是平行四边形.【解答】解:四边形EFGH是平行四边形证明:连接AC,如图.∵E,F分别是AB,BC的中点,∴EF是△ABC的中位线,∴EF∥AC,且EF=AC.同理:GH∥AC,且GH=AC,∴EF GH.∴四边形EFGH是平行四边形.【点评】此题主要考查平行四边形的判定,综合运用了中位线定理,作辅助线是关键.11.(2011秋•XX区校级期末)如图,B、C、D三点在同一直线上,分别以BC、CD为边在同侧作两个正三角形△ABC和△ECD,P为BD边中点,M、N分别为AB、ED的中点,连接PM、PN,探求PM与PN的数量关系与∠MPN的度数,并证明.【考点】全等三角形的判定与性质;等边三角形的性质;三角形中位线定理.【专题】探究型.【分析】通过△ACD≌△BCE的对应边相等知AD=BE;然后由三角形中位线定理求得PM=PN;由平行线的性质、等量代换以与三角形外角定理来求∠MPN的度数.【解答】解:PM=PN,∠MPN=120°;理由如下:连接AD、BE.∵△ABC和△ECD是等边三角形,∴AC=BC,∠BCA=60°,CD=CE,∠ECD=60°;∴∠ECD+∠ACE=∠BCA+∠ACE,即∠ACD=∠BCE,∴在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴AD=BE(全等三角形的对应角相等),∠CAD=∠CBE(全等三角形的对应角相等);又∵P为BD边中点,M、N分别为AB、ED的中点,∴PM=AD,PN=BE,∴PM=PN;∵MP∥AD(中位线的性质),∴∠BPM=∠CDA;同理,得∠NPD=∠EBC=∠CAD,∴∠MPN=180°﹣∠BPM﹣∠NPD=180°﹣∠CDA﹣∠CAD=∠ACD(等量代换),∵∠ACD=∠ABC+∠BAC=120°,即∠MPN=120°.【点评】本题考查了全等三角形的判定与性质、三角形中位线定理以与等边三角形的性质.本题中利用三角形中位线定理将所求线段与已知线段联系了起来.12.如图,点P是四边形ABCD的对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠CBD=45°.∠ADB=105°,试探究EF与PF之间的数量关系,并证明.【考点】三角形中位线定理.【分析】连接PE,由三角形中位线定理可知PF=PE,且∠EPF=120°,过点P作PG⊥EF,由直角三角形的性质可求得FG=PF,可求得EF=PF.【解答】解:EF=PF.证明如下:如图,连接PE,∵P、E分别为BD、AB的中点,∴PE∥AD,且PE=AD,∴∠ADP+∠EPD=180°,∴∠EPD=75°,∵F、P为CD、BD中点,∴PF∥BC,且PF=BC,∴∠DPF=∠DBC=45°,∵AD=BC,∴PF=PE,且∠EPF=75°+45°=120°,过P作PG⊥EF于点G,则EF=2FG,在Rt△PFG中,由勾定理可得FG=PF,∴EF=PF.【点评】本题主要考查三角形中位线定理,掌握三角形中位线平行且等于第三边的一半是解题的关键.13.已知,如图,点E、F分别为四边形ABCD的对角线AC、BD的中点,求证:EF<(AB+CD).【考点】三角形中位线定理;三角形三边关系.【专题】证明题.【分析】设BC中点为G,连接EG、FG.由中位线的性质得FG=DC,EG=AB,再根据三角形的三边关系可得EF<EG+FG,再利用等量代换可得EF<(AB+CD).【解答】证明:设BC中点为G,连接EG、FG.∵点E、F分别为四边形ABCD的对角线AC、BD的中点,∴FG=DC,EG=AB,∵在△EFG中,EF<EG+FG,∴EF<(AB+CD).【点评】此题主要考查了三角形中位线的性质,关键是掌握三角形的中位线平行于第三边,并且等于第三边的一半.14.在△ABC中,点M为BC的中点,AD为△ABC的角平分线,且BD⊥AD,若AB=12,AC=18,求MD的长.【考点】三角形中位线定理;等腰三角形的判定与性质.【分析】首先延长BD,交AC于E,利用ASA得出△ABD≌△AED,进而得出DM为△BCE 的中位线,进而得出答案.【解答】解:如图,延长BD,交AC于E,∵AD⊥BD,∴∠EDA=∠BDA,∵AD为△ABC的角平分线,∴∠BAD=∠EAD,在△ABD和△AED中,,∴△ABD≌△AED(ASA),∴AB=AE=12,DB=DE,∴EC=AC﹣AE=18﹣12=6,∵DB=DE,M为BC中点∴DM=EC=3.【点评】此题主要考查了全等三角形的判定以与三角形中位线定理,得出BD=DE是解题关键.15.如图,在△ABC中,AB=BC,∠ABC=90°,F为BC上一点,M为AF的中点,BE平分∠ABC,且EF⊥BE,求证:CF=2ME.【考点】三角形中位线定理;等腰直角三角形.【专题】证明题.【分析】延长FE,交AB于F',可证明CF=AF′,进一步可证明△FME∽△AFF′,可求得AF′=2ME,可证得结论.【解答】解:如图,延长FE,交AB于F',∵BE为∠ABC的平分线,且EF⊥BE,∴BE为FF′的垂直平分线,BF=BF',EF=EF'又∵AB=BC,BF=BF',∴CF=AF',∵M为AF的中点,AM=MF,在△FME和△FAF'中,∠MFE=∠AFF',FM:FA=FE:FF'=1:2,∴△FME∽△FAF',∴FM:FA=ME:AF'=1:2,即AF'=2ME,又∵CF=AF',∴CF=2ME.【点评】本题主要考查相似三角形的判定和性质,延长FE交AB于F'证明CF=AF′是解题的关键.16.如图,△ABC中,∠ABC=90°,BA=BC,△BEF为等腰直角三角形,∠BEF=90°,M 为AF的中点,求证:ME=CF.【考点】全等三角形的判定与性质;三角形中位线定理.【专题】证明题.【分析】延长EF到D,使DE=EF,连接AD、BD,判断出△BDF是等腰直角三角形,根据等腰直角三角形的性质可得BD=BF,再求出∠CBF=∠ABD,然后利用“边角边”证明△ABD和△CBF全等,根据全等三角形对应边相等可得AD=CF,再根据三角形的中位线平行于第三边并且等于第三边的一半可得ME=AD,从而得到ME=CF.【解答】证明:如图,延长EF到D,使DE=EF,连接AD、BD,∵△BEF为等腰直角三角形,∠BEF=90°,∴∠BFE=45°,BE⊥DF,∴BE垂直平分DF,∴∠BDE=45°,∴△BDF是等腰直角三角形,∴BD=BF,∠DBF=90°,∵∠CBF+∠ABF=∠ABC=90°,∠ABD+∠ABF=∠DBF=90°,∴∠CBF=∠ABD,在△ABD和△CBF中,,∴△ABD≌△CBF(SAS),∴AD=CF,∵M为AF的中点,DE=EF,∴ME是△ADF的中位线,∴ME=AD,∴ME=CF.【点评】本题考查了全等三角形的判定与性质,三角形的中位线平行于第三边并且等于第三边的一半,同角的余角相等的性质,作辅助线构造出全等三角形和等腰直角三角形是解题的关键,也是本题的难点.17.四边形ABCD中,AB=a,CD=b(a>b),M、N分别是AD、BC的中点,求MN的取值范围.【考点】三角形中位线定理;三角形三边关系.【专题】证明题.【分析】先取BD的中点E,连接ME、NE,由三角形的中位线性质得:ME=a,NE=b,再由三角形的两边之和大于第三边,求出MN的取值范围.【解答】解:取BD的中点E,连接ME、NE,由三角形的中位线性质可得:ME=AB=a,NE=CD=b,∵ME+NE>MN,∴MN<(a+b)【点评】本题考查了三角形的中位线定理,以与三角形的三边关系定理.18.如图,△ABC中,∠C=90°,CA=CB,E、F分别为CA、CB上一点,CE=CF,M、N 分别为AF、BE的中点.求证:AE=MN.【考点】三角形中位线定理;等腰直角三角形.【专题】证明题.【分析】取AB的中点G,连接MG、NG,根据三角形的中位线平行于第三边并且等于第三边的一半可得NG=AE,NG∥AE,MG=BF,MG∥BF,再求出AE=BF,∠MGN=90°,判断出△MNG是等腰直角三角形,根据等腰直角三角形的性质可得NG=MN,再表示出AE即可得证.【解答】证明:如图,取AB的中点G,连接MG、NG,∵M、N分别为AF、BE的中点,∴NG=AE,NG∥AE,MG=BF,MG∥BF,∵CE=CF,∠C=90°,∴AE=BF,∠MGN=∠C=90°,∴MG=NG,∴△MNG是等腰直角三角形,∴NG=MN,∴AE=2NG=NG=×2MN=MN,即AE=MN.【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,等腰直角三角形的判定与性质,熟记定理并作辅助线构造成等腰直角三角形是解题的关键.考点卡片1.三角形三边关系(1)三角形三边关系定理:三角形两边之和大于第三边.(2)在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式,只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.(3)三角形的两边差小于第三边.(4)在涉与三角形的边长或周长的计算时,注意最后要用三边关系去检验,这是一个隐藏的定时炸弹,容易忽略.2.全等三角形的判定与性质(1)全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.(2)在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.3.等腰三角形的判定与性质1、等腰三角形提供了好多相等的线段和相等的角,判定三角形是等腰三角形是证明线段相等、角相等的重要手段.2、在等腰三角形有关问题中,会遇到一些添加辅助线的问题,其顶角平分线、底边上的高、底边上的中线是常见的辅助线,虽然“三线合一”,但添加辅助线时,有时作哪条线都可以,有时不同的做法引起解决问题的复杂程度不同,需要具体问题具体分析.3、等腰三角形性质问题都可以利用三角形全等来解决,但要注意纠正不顾条件,一概依赖全等三角形的思维定势,凡可以直接利用等腰三角形的问题,应当优先选择简便方法来解决.4.等边三角形的性质(1)等边三角形的定义:三条边都相等的三角形叫做等边三角形,等边三角形是特殊的等腰三角形.①它可以作为判定一个三角形是否为等边三角形的方法;②可以得到它与等腰三角形的关系:等边三角形是等腰三角形的特殊情况.在等边三角形中,腰和底、顶角和底角是相对而言的.(2)等边三角形的性质:等边三角形的三个内角都相等,且都等于60°.等边三角形是轴对称图形,它有三条对称轴;它的任意一角的平分线都垂直平分对边,三边的垂直平分线是对称轴.5.等腰直角三角形(1)两条直角边相等的直角三角形叫做等腰直角三角形.(2)等腰直角三角形是一种特殊的三角形,具有所有三角形的性质,还具备等腰三角形和直角三角形的所有性质.即:两个锐角都是45°,斜边上中线、角平分线、斜边上的高,三线合一,等腰直角三角形斜边上的高为外接圆的半径R,而高又为内切圆的直径(因为等腰直角三角形的两个小角均为45°,高又垂直于斜边,所以两个小三角形均为等腰直角三角形,则两腰相等);(3)若设等腰直角三角形内切圆的半径r=1,则外接圆的半径R=+1,所以r:R=1:+1.6.三角形中位线定理(1)三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.(2)几何语言:如图,∵点D、E分别是AB、AC的中点∴DE∥BC,DE=BC.7.平行四边形的性质(1)平行四边形的概念:有两组对边分别平行的四边形叫做平行四边形.(2)平行四边形的性质:①边:平行四边形的对边相等.②角:平行四边形的对角相等.③对角线:平行四边形的对角线互相平分.(3)平行线间的距离处处相等.(4)平行四边形的面积:①平行四边形的面积等于它的底和这个底上的高的积.②同底(等底)同高(等高)的平行四边形面积相等.8.平行四边形的判定(1)两组对边分别平行的四边形是平行四边形.符号语言:∵AB∥DC,AD∥BC∴四边行ABCD是平行四边形.(2)两组对边分别相等的四边形是平行四边形.符号语言:∵AB=DC,AD=BC∴四边行ABCD是平行四边形.(3)一组对边平行且相等的四边形是平行四边形.符号语言:∵AB∥DC,AB=DC∴四边行ABCD是平行四边形.(4)两组对角分别相等的四边形是平行四边形.符号语言:∵∠ABC=∠ADC,∠DAB=∠DCB∴四边行ABCD是平行四边形.(5)对角线互相平分的四边形是平行四边形.符号语言:∵OA=OC,OB=OD∴四边行ABCD是平行四边形.9.平行四边形的判定与性质平行四边形的判定与性质的作用平行四边形对应边相等,对应角相等,对角线互相平分与它的判定,是我们证明直线的平行、线段相等、角相等的重要方法,若要证明两直线平行和两线段相等、两角相等,可考虑将要证的直线、线段、角、分别置于一个四边形的对边或对角的位置上,通过证明四边形是平行四边形达到上述目的.运用定义,也可以判定某个图形是平行四边形,这是常用的方法,不要忘记平行四边形的定义,有时用定义判定比用其他判定定理还简单.凡是可以用平行四边形知识证明的问题,不要再回到用三角形全等证明,应直接运用平行四边形的性质和判定去解决问题.10.中点四边形中点四边形.11.翻折变换(折叠问题)1、翻折变换(折叠问题)实质上就是轴对称变换.2、折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.3、在解决实际问题时,对于折叠较为复杂的问题可以实际操作图形的折叠,这样便于找到图形间的关系.首先清楚折叠和轴对称能够提供给我们隐含的并且可利用的条件.解题时,我们常常设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.我们运用方程解决时,应认真审题,设出正确的未知数..。
考点22 空间几何平行问题(练习)(解析版)

考点22 空间几何平行问题【题组一 三角形中位线】1.如图,点E 和点F 分别是BC ,1A C 的中点,求证://EF 平面11A B BA【答案】见解析【解析】证明如图,连接1A B .在1A BC 中,因为E 和F 分别是BC ,1A C 的中点,所以1//EF BA .又因为EF ⊄11A B BA ,1BA ⊂平面1AB BA ,所以//EF 平面11A B BA .2.如图,四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥面ABCD ,E 为PD 的中点,证明://PB 平面AEC ;【答案】证明见解析【解析】设BD 交AC 于点O ,连结EO .因为ABCD 为矩形,所以O 为BD 的中点.又E 为PD 的中点,所以EO ∥PB又EO 平面AEC ,PB 平面AEC 所以PB ∥平面AEC .3.如图所示,在三棱锥P ABC -中,F 为BC 的中点,DE 垂直平分PC ,且DE 分别交AC PC ,于点,D E ,证明://EF ABP 平面【答案】见解析【解析】证明:DE 垂直平分PC E ∴为PC 的中点 又F 为BC 的中点 EF ∴为BCP 的中位线 //EF BP ∴ 又,EF ABP BP ABP ⊄⊂平面平面 //EF ABP ∴平面4.如图,12AB AD CD ==,若M 为EA 中点,求证:AC ∥平面MDF【答案】证明见解析【解析】设EC 与DF 交于点N ,连结MN ,在矩形CDEF 中,点N 为EC 中点,如图:M 为EA 中点,∴MN ∥AC 又AC ⊄平面MDF ,MN ⊂平面MDF ∴AC ∥平面MDF .5.已知四棱锥P ABCD -中,侧面PAD ABCD ⊥底面,PB AD ⊥,PAD △是边长为2的正三角形,底面ABCD 是菱形,点M 为PC 的中点,求证:PA MDB ∥平面【答案】证明见解析【解析】连结AC ,交BD 于O ,由于底面ABCD 为菱形,∴O 为AC 中点又M 为PC 的中点,//MO PA ,又MO MDB PA MDB ⊂⊄平面,平面//PA MDB ∴平面6.如图所示,在三棱柱ABC -A 1B 1C 1中,AC =BC ,点D 是AB 的中点,求证:BC 1∥平面CA 1D .【答案】略【解析】证明:如图所示,连接AC 1交A 1C 于点O ,连接OD ,则O 是AC 1的中点.∵点D 是AB 的中点, ∴OD ∥BC 1.又∵OD ⊂平面CA 1D ,BC 1⊄平面CA 1D ,∴BC 1∥平面CA 1D.【题组二 构造平行四边形证线面平行】1.如图,四棱锥P ABCD -中侧面P AB 为等边三角形且垂直于底面ABCD ,12AB BC AD ==, E 是PD 的中点,证明:直线CE ∥平面PAB【答案】见解析【解析】取PA 的中点F ,连FE FB 、, E 是PD 的中点, ∴FE //=12AD , 又BC //=12AD ∴FE //=BC ∴四边形EFBC 是平行四边形 CE ∴∥BF 又CE ⊄平面PAB ,BF ⊂平面PAB CE ∥平面PAB2.如图,菱形ABCD ,,E F 分别是,AB PD 的中点,求证://EF 平面PBC ;【答案】证明见解析【解析】解法一:(1)取PC 中点H ,连接FH ,BH .因为,E F 分别是,AB PD 的中点,所以////FH DC BE ,且12FH DC BE ==, 所以四边形EFHB 为平行四边形,所以//EF BH ,因为BH ⊂平面PBC ,EF ⊄平面PBC ,所以//EF 平面PBC .3.由四棱柱1111ABCD A B C D -截去三棱锥111C B CD -,后得到的几何体如图所示.四边形ABCD 为正方形,O 为AC 与BD 的交点,E 为AD 的中点,证明:1//AO 平面11B CD【答案】证明见解析【解析】如图②所示,取11B D 的中点1O ,连接111CO ,AO 由于多面体1111ABCD A B C D -是四棱柱,所以11//A O OC ,11A O OC =, 因此四边形11AOCO 为平行四边形,所以11//A O O C .又1O C ⊂平面11B CD ,1AO ⊄平面11B CD ,所以1//AO 平面11B CD . 4.在如图所示的五面体ABCDEF 中,四边形ABCD 为菱形,且60,22,//,DAB EA ED AB EF EF AB M ∠=︒====为BC 中点,求证:FM ∕∕平面BDE【答案】见解析【解析】取BD 中点O ,连接,OM OE ,因为,O M 分别为,BD BC 的中点,所以//OM CD ,且12OM CD =, 因为四边形ABCD 为菱形,所以//,CD AB CD ⊄又平面,ABFE AB ⊂平面ABFE ,所以//CD 平面ABFE .因为平面ABFE平面,CDEF EF CD =⊂平面CDEF ,所以CD EF ∕∕.又2AB CD ==,所以12EF CD =. 所以四边形OMFE 为平行四边形,所以//MF OE .又OE ⊂平面BDE ,且MF ⊄平面BDE ,所以//MF 平面BDE .【题组三 线面垂直证线面平行】1.如图所示,在正方体1111ABCD A B C D -中,M 是AB 上一点,N 是1A C 的中点,MN ⊥平面1A DC .求证:1//MN AD .【答案】证明见解析【解析】因为四边形11ADD A 为正方形,所以11AD A D ⊥.又CD ⊥平面11ADD A ,1AD ⊂平面11ADD A ,所以1CD AD ⊥.因为1A D CD D =,所以1AD ⊥平面1A DC .又MN ⊥平面1A DC ,所以1∥MN AD .2.已知正方体1111ABCD A B C D -,,E F 分别为AC 和1A D 上的点,且EF AC ⊥,1EF A D ⊥.(1)求证:1//EF BD ;(2)求证:1,,BE D F DA 三条直线交于一点.【答案】(1)详见解析;(2)详见解析【解析】证明:(1)如图,连结1AB 和1B C ,在正方体1111ABCD A B C D -中,11//A D B C ,∵1EF A D ⊥,∴1EF B C ⊥,又EF AC ⊥,1AC B C C ⋂=,∴1EF AB C ⊥平面.又在正方体1111ABCD A B C D -中,11B C BC ⊥,111B C D C ⊥,1111BC D C C ⋂=∴111B C BC D ⊥平面,又111BD BC D ⊂平面,∴11B C BD ⊥.同理可得11B A BD ⊥,又111B A B C B ⋂=,∴11BD AB C ⊥平面.∴EF ∥1BD .(2)由题意可得1EF BD <(或者1D F 和BE 不平行),又由(1)知EF ∥1BD ,所以直线1D F 和BE 必相交,不妨设1BE D F G ⋂=,则1G D F ∈,又111D F AA D D 平面⊂,所以11G AA D D ∈平面,同理G ABCD ∈平面.因为11AA D D ABCD AD ⋂=平面平面,所以G AD ∈,所以BE 、1D F 、DA 三条直线交于一点.【题组四 三角形相似比证线线平行】1.如图,在四面体A BCD -中,M 是AD 的中点,P 是BM 的中点,点Q 在线段AC 上,且3AQ QC =求证://PQ 平面BCD .【答案】证明见解析【解析】如下图所示,取BD 的中点O ,在线段CD 上取点F ,使得3DF FC =,连接OP 、OF 、FQ .3AQ QC =,3AQ DF QC FC ∴==,//QF AD ∴,且14QF AD =.O 、P 分别为BD 、BM 的中点,//OP AD ∴,且12OP DM =. M 为AD 的中点,14OP AD ∴=. //OP QF ∴且OP QF =,四边形OPQF 是平行四边形,//PQ OF ∴.PQ ⊄平面BCD ,OF ⊂平面BCD ,//PQ ∴平面BCD .2.如图,三棱锥P ABC -中,PA ⊥底面ABC ,PA AB =,点E 、F 分别为P A 、AB 的中点,点D 在PC 上,且2PD DC =,明://CF 平面BDE ;【答案】见解析【解析】设AE 中点为G ,连结GF ,GC ,则//GF EB ,//GF 平面EBD .32PG PC PE PD ==,∴//ED GC ,//GC 平面EBD , ∴平面//GFC 平面EBD ,∴//FC 平面1EBD ;【题组五 线面平行性质证线线平行】1.如图,在三棱柱111ABC A B C -中,D 是BC 的中点,E 是11A C 上一点,但1//A B 平面1B DE ,则11A E EC 的值为_______. 【答案】12【解析】如下图所示,连接1BC 交1B D 于点F ,连接EF .在三棱柱111ABC A B C -中,11//BC B C ,11BDF C B F ∴∆∆, D 为BC 的中点,111122BD BC B C ∴==,11112BF BD FC B C ∴==. 1//A B 平面1B DE ,1A B ⊂平面11A BC ,平面11A BC ⋂平面1B DE EF =,1//A B EF ∴,11112A E BF EC FC ∴==,故答案为12. 2.如图,在多面体ABCDEF 中,DE ⊥平面ABCD ,AD ∥BC ,平面BCEF ⋂平面ADEF EF =,60BAD ︒∠=,2AB =,1DE EF ==,求证:BC ∥EF;【答案】证明见解析【解析】证明:∵AD ∥BC ,AD ⊂平面ADEF ,BC ⊄平面ADEF ,∴BC ∥平面ADEF .又BC ⊂平面BCEF ,平面BCEF 平面ADEF EF =,∴BC ∥EF .3.如图所示,三棱柱111ABC A B C -中,点M ,N 分别是线段11A C ,1A B 的中点,设平面1MNB 与平面11BCC B 的交线为l ,求证://MN l .【答案】证明见解析【解析】证明:如图所示,连接1C B ,在11A BC 中,点M ,N 分别为11A C ,1A B 的中点,所以1MN //C B . 又MN ⊄平面11BCC B ,1BC ⊂平面11BCC B ,所以//MN 平面11BCC B .又MN ⊂平面1MNB ,平面1MNB ⋂平面11BCC B l =,所以//MN l .4.如图所示,已知三棱锥A BCD -中,E ,F 分别是边AB ,AD 的中点,过EF 的平面截三棱锥得到的截面为EFHG ,求证://EF GH .【答案】证明见解析【解析】证明:在ABD △中,因为E ,F 分别是边AB ,AD 的中点,所以由三角形的中位线定理可知//EF BD .又因为EF ⊄面BCD ,BD ⊂面BCD ,所以由线面平行的判定定理可知//EF 面BCD .又因为EF ⊂面EFHG ,面EFHG ⋂面BCD GH =,所以由线面平行的性质定理可知//EF GH .【题组六 面面平行性质证线线平行】1.在如图所示的五面体 ABCDEF 中,四边形ABCD 为平行四边形,//EF 平面ABCD ,2EA ED AB EF ===,M 为BC 的中点.求证://FM 平面BDE .【答案】证明见解析【解析】取CD 的中点N ,连接MN 、FN .因为N 、M 分别为CD 、BC 的中点,所以//MN BD .又BD ⊂平面BDE ,且MN ⊄平面BDE ,所以//MN 平面BDE ,因为//EF 平面ABCD ,EF ⊂平面ABFE ,平面ABCD 平面ABFE AB =,所以//EF AB .又22AB CD DN EF ===,//AB CD ,所以//EF DN ,EF DN =,所以四边形EFND 为平行四边形,所以//FN ED .又ED ⊂平面BDE ,且FN ⊄平面BDE ,以//FN 平面BDE .又FN MN N ⋂=,所以平面//MNF 平面BDE .又FM ⊂平面MFN ,所以//FM 平面BDE .2.如图,在正四棱锥P ABCD -中,点F 在棱PA 上,且2PF FA =,点E 为棱PD 的中点,求证:CE //平面BDF【答案】见详解【解析】如图取PF 的中点M ,又2PF FA =,所以F 为MA 的中点,连接AC 交BD 于点O因为四边形ABCD 正方形,所以O 为AC 的中点又点E 为棱PD 的中点,所以ME //DF OF //MC ,又,OF FD F MC ME M ⋂=⋂=且,OF FD ⊂平面BDF ,,MC ME ⊂平面MCE所以平面BDF //平面MCE ,又CE ⊂平面MCE所以CE //平面BDF .3.如图,在四棱柱1111ABCD A B C D -中,底面ABCD 为梯形,//AD BC ,平面1A DCE 与1B B 交于点E .求证:1//EC A D .【答案】证明见解析【解析】因为BE ∥AA 1,AA 1⊂平面AA 1D ,BE ⊄平面AA 1D ,所以BE ∥平面AA 1D .因为BC ∥AD ,AD ⊂平面AA 1D ,BC ⊄平面AA 1D ,所以BC ∥平面AA 1D .又BE ∩BC =B ,BE ⊂平面BCE ,BC ⊂平面BCE ,所以平面BCE ∥平面AA 1D .又平面A 1DCE ∩平面BCE =EC ,平面A 1DCE ∩平面AA 1D =A 1D ,所以EC ∥A 1D .4.如图,已知四棱锥P ABCD -的底面为直角梯形,//AB CD ,90DAB ︒∠=,PA ⊥底面ABCD ,且112PA AD DC AB ====,M ,N 分别是PB ,PC 的中点.求证://DN 平面AMC .【答案】证明见解析【解析】如图,连接DB 交AC 于点F . ∵12DC AB =,//DC AB ,∴12DF FB =. 取PM 的中点G ,连接DG ,FM ,则1122GM PM BM ==,GM DF BM BF ∴=, //DG FM ∴.又DG ⊄平面AMC ,FM ⊂平面AMC ,∴//DG 平面AMC .连接GN ,则//GN MC .又GN 平面AMC ,MC ⊂平面AMC ,∴//GN 平面AMC .又GN DG G ⋂=,∴平面//DNG 平面AMC .又DN ⊂平面DNG ,∴//DN 平面AMC .5.如图,在四棱柱''''ABCD A B C D -中,点M 和N 分别为1B C 和1D D 的中点、求证://MN 平面ABCD .【答案】证明见解析.【解析】证明:如图, 设E 为棱1CC 的中点,连接NE ME ,.M N ,分别为1B C ,1DD 的中点,11////ME C B CB ∴,//NE CD .又ME NE ,在平面ABCD 的外部,//ME ∴平面ABCD ,NE ∥平面ABCD .又ME NE E ⋂=, ∴平面//MNE 平面ABCD .又MN ⊂平面MNE ,//MN ∴平面ABCD .【题组七 面面平行】1.如图,在正方体1111ABCD A B C D -中,,,M N P 分别是1AD ,1BD B C ,的中点. 求证:(1)MN ∥平面11CC D D ;(2)平面MNP 平面11CC D D .【答案】证明见解析【解析】(1)如图,连接1,AC CD .∵四边形ABCD 是正方形,N 是BD 的中点,∴N 是AC 的中点. 又∵M 是1AD 的中点,∴1//MN CD .∵MN ⊄平面11CC D D ,1CD ⊂平面11CC D D ,∴//MN 平面11CC D D .(2)连接1BC ,1C D ,∵四边形11B BCC 是正方形,P 是1B C 的中点,∴P 是1BC 的中点.又∵N 是BD 中点,∴1PN C D .∵PN ⊄平面111,CC D D C D ⊂平面11CC D D ,∴PN 平面11CC D D .由(1)知MN ∥平面11CC D D ,且MN PN N ⋂=, ∴平面//MNP 平面11CC D D .2.如图,在三棱柱111ABC A B C -中,E ,F ,G 分别为11B C ,11A B ,AB 的中点. ()1求证:平面11//A C G 平面BEF ;()2若平面11AC G BC H ⋂=,求证:H 为BC 的中点.【答案】(1)见解析(2)见解析【解析】 () 1如图, E ,F 分别为11B C ,11A B 的中点,11//EF A C ∴, 11A C ⊂平面11AC G ,EF ⊄平面11AC G ,//EF ∴平面11AC G , 又F ,G 分别为11A B ,AB 的中点,1A F BG ∴=, 又1//A F BG ,∴四边形1A GBF 为平行四边形,则1//BF A G , 1A G ⊂平面11AC G ,BF ⊄平面11AC G ,//BF ∴平面11AC G , 又EF BF F ⋂=,∴平面11//A C G 平面BEF ; ()2平面//ABC 平面111A B C ,平面11A C G ⋂平面11111A B C A C =, 平面11AC G 与平面ABC 有公共点G ,则有经过G 的直线,设交BC H =, 则11//AC GH ,得//GH AC , G 为AB 的中点,H ∴为BC 的中点.。
2022年全国数学中考真题(江苏河南广东四川湖南等)汇编专题12 平行四边形与中位线(解析版)

专题12 平行四边形与中位线一.选择题1.(2022·四川乐山)如图,在平行四边形ABCD 中,过点D 作DE ⊥AB ,垂足为E ,过点B 作BF ⊥AC ,垂足为F .若AB =6,AC =8,DE =4,则BF 的长为( )A .4B .3C .52D .2【答案】B【分析】利用平行四边形ABCD 的面积公式即可求解.【详解】解:⊥DE ⊥AB ,BF ⊥AC ,⊥S 平行四边形ABCD =DE ×AB =2×12×AC ×BF , ⊥4×6=2×12×8×BF ,⊥BF =3,故选:B . 【点睛】本题考查了平行四边形的性质,利用平行四边形ABCD 的面积公式求垂线段的长是解题的关键. 2.(2022·浙江宁波)如图,在Rt ABC 中,D 为斜边AC 的中点,E 为BD 上一点,F 为CE 中点.若AE AD =,2DF =,则BD 的长为( )A .22B .3C .23D .4【答案】D【分析】根据三角形中位线可以求得AE 的长,再根据AE =AD ,可以得到AD 的长,然后根据直角三角形斜边上的中线和斜边的关系,可以求得BD 的长.【详解】解:⊥D 为斜边AC 的中点,F 为CE 中点,DF =2,⊥AE =2DF =4,⊥AE =AD ,⊥AD =4,在Rt ⊥ABC 中,D 为斜边AC 的中点,⊥BD =12AC =AD =4,故选:D .【点睛】本题考查直角三角线斜边上的中线和斜边的关系、三角形的中位线,解答本题关键是求出AD 的长. 3.(2022·四川眉山)在ABC 中,4AB =,6BC =,8AC =,点D ,E ,F 分别为边AB ,AC ,BC 的中点,则DEF 的周长为( )A .9B .12C .14D .16【答案】A【分析】根据三角形的中位线平行于第三边,并且等于第三边的一半,可得出△ABC 的周长=2△DEF 的周长.【详解】⊥D ,E ,F 分别为各边的中点,⊥DE 、EF 、DF 是△ABC 的中位线, ⊥DE =12BC =3,EF =12AB =2,DF =12AC =4,⊥△DEF 的周长=3+2+4=9.故选:A . 【点睛】本题考查了三角形中位线定理.解题的关键是根据中位线定理得出边之间的数量关系. 4.(2022·浙江绍兴)如图,在平行四边形ABCD 中,22AD AB ==,60ABC ∠=︒,E ,F 是对角线BD 上的动点,且BE DF =,M ,N 分别是边AD ,边BC 上的动点.下列四种说法:①存在无数个平行四边形MENF ;②存在无数个矩形MENF ;③存在无数个菱形MENF ;④存在无数个正方形MENF .其中正确的个数是( )A .1B .2C .3D .4【答案】C【分析】根据题意作出合适的辅助线,然后逐一分析即可.【详解】如图,连接AC 、与BD 交于点O ,连接ME,MF,NF,EN,MN ,⊥四边形ABCD 是平行四边形⊥OA =OC ,OB =OD⊥BE =DF ⊥OE =OF ⊥点E,F 时BD 上的点,⊥只要M,N 过点O ,那么四边形MENF 就是平行四边形⊥存在无数个平行四边形MENF ,故①正确;只要MN =EF ,MN 过点O ,则四边形MENF 是矩形,⊥点E 、F 是BD 上的动点,⊥存在无数个矩形MENF ,故②正确;只要MN ⊥EF ,MN 过点O ,则四边形MENF 是菱形;⊥点E 、F 是BD 上的动点,⊥存在无数个菱形MENF ,故③正确;只要MN =EF ,MN ⊥EF ,MN 过点O ,则四边形MENF 是正方形,而符合要求的正方形只有一个,故④错误;故选:C【点睛】本题考查正方形的判定、菱形的判定、矩形的判定、平行四边形的判定、解答本题的关键时明确题意,作出合适的辅助线.5.(2022·浙江嘉兴)如图,在ABC 中,8AB AC ==,点E ,F ,G 分别在边AB ,BC ,AC 上,EF AC ∥,GF AB ∥,则四边形AEFG 的周长是( )A .32B .24C .16D .8【答案】C【分析】根据EF AC ∥,GF AB ∥,可得四边形AEFG 是平行四边形,从而得到FG =AE ,AG =EF ,再由EF AC ∥,可得⊥BFE =⊥C ,从而得到⊥B =⊥BFE ,进而得到BE =EF ,再据四边形AEFG 的周长是2(AE +EF ),即可求解.【详解】解⊥⊥EF AC ∥,GF AB ∥,⊥四边形AEFG 是平行四边形,⊥FG =AE ,AG =EF ,⊥EF AC ∥,⊥⊥BFE =⊥C ,⊥AB =AC ,⊥⊥B =⊥C ,⊥⊥B =⊥BFE ,⊥BE =EF ,⊥四边形AEFG 的周长是2(AE +EF )=2(AE +BE )=2AB =2×8=16.故选:C【点睛】本题主要考查了平行四边形的判定和性质,等腰三角形的性质,熟练掌握平行四边形的判定和性质,等腰三角形的性质是解题的关键.6.(2022·四川达州)如图,在ABC 中,点D ,E 分别是AB ,BC 边的中点,点F 在DE 的延长线上.添加一个条件,使得四边形ADFC 为平行四边形,则这个条件可以是( )A .B F ∠=∠ B .DE EF =C .AC CF=D .AD CF =【答案】B【分析】利用三角形中位线定理得到DE ⊥AC 且DE =12AC ,结合平行四边形的判定定理进行选择.【详解】解:⊥在⊥ABC 中,D ,E 分别是AB ,BC 的中点,⊥DE 是⊥ABC 的中位线,⊥DE ⊥AC 且DE =12AC ,A 、根据⊥B =⊥F 不能判定CF ⊥AD ,即不能判定四边形ADFC 为平行四边形,故本选项错误.B 、根据DE =EF 可以判定DF =AC ,由“一组对边平行且相等的四边形是平行四边形”得到四边形ADFC 为平行四边形,故本选项正确.C 、根据AC =CF 不能判定AC ⊥DF ,即不能判定四边形ADFC 为平行四边形,故本选项错误.D 、根据AD =CF ,FD ⊥AC 不能判定四边形ADFC 为平行四边形,故本选项错误.故选:B .【点睛】本题主要考查了三角形的中位线的性质和平行四边形的判定.三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半.7.(2022·浙江丽水)如图,在ABC 中,D ,E ,F 分别是BC ,AC ,AB 的中点.若6AB =,8BC =,则四边形BDEF 的周长是( )A .28B .14C .10D .7【答案】B 【分析】首先根据D ,E ,F 分别是BC ,AC ,AB 的中点,可判定四边形BDEF 是平行四边形,再根据三角形中位线定理,即可求得四边形BDEF 的周长. 【详解】解:D ,E ,F 分别是BC ,AC ,AB 的中点,EF ∴、ED 分别是ABC △的中位线,EF BC ∴∥,ED AB ∥且11==8=422EF BC ⨯,11==6=322ED AB ⨯, ∴四边形BDEF 是平行四边形,=4BD EF ∴=,3BF ED ==,∴四边形BDEF 的周长为:=3434=14BF BD ED EF ++++++,故选:B .【点睛】本题考查了平行四边形的判定及性质,三角形中位线定理,判定出四边形BDEF 是平行四边形是解决本题的关键.8.(2022·湖南怀化)一个多边形的内角和为900°,则这个多边形是( )A .七边形B .八边形C .九边形D .十边形【答案】A【分析】根据n 边形的内角和是(n ﹣2)•180°,列出方程即可求解.【详解】解:根据n 边形的内角和公式,得(n ﹣2)•180°=900°,解得n =7,⊥这个多边形的边数是7,故选:A .【点睛】本题考查了多边形的内角和,解题的关键是熟记内角和公式并列出方程.9.(2022·四川南充)如图,在正五边形ABCDE 中,以AB 为边向内作正ABF ,则下列结论错误的是( )A .AE AF =B .EAF CBF ∠=∠C .F EAF ∠=∠D .CE ∠=∠【答案】C 【分析】利用正多边形各边长度相等,各角度数相等,即可逐项判断.【详解】解:⊥多边形ABCDE 是正五边形,⊥该多边形内角和为:5218540(0)-⨯︒=︒,AB AE =, ⊥5401085C E EAB ABC ︒∠=∠=∠=∠==︒,故D 选项正确; ⊥ABF 是正三角形,⊥60FAB FBA F ∠=∠=∠=︒,AB AF FB ==,⊥1086048EAF EAB FAB ∠=∠-∠=︒-︒=︒,1086048CBF ABC FBA ∠=∠-∠=︒-︒=︒,⊥EAF CBF ∠=∠,故B 选项正确;⊥AB AE =,AB AF FB ==,⊥AE AF =,故A 选项正确;⊥60F ∠=︒,48EAF ∠=︒,⊥F EAF ∠≠∠,故C 选项错误,故选:C .【点睛】本题考查正多边形的性质以及多边形内角和公式,熟练掌握正多边形“各边长度相等,各角度数相等”是解题的关键.10.(2022·湖南湘潭)在ABCD 中(如图),连接AC ,已知40BAC ∠=︒,80ACB ∠=︒,则BCD ∠=( )A .80︒B .100︒C .120︒D .140︒【答案】C【分析】根据平行四边形的对边平行和两直线平行内错角相等的性质,再通过等量代换即可求解.【详解】解:⊥四边形ABCD 为平行四边形,⊥AB ∥CD ⊥⊥DCA =⊥CAB ,⊥BCD ∠=⊥DCA +⊥ACB ,40BAC ∠=︒,80ACB ∠=︒⊥BCD ∠=40º+80º=120º,故选:C .【点睛】此题考查了平行四边形的性质和平行线的性质,解题的关键是熟记性质并熟练运用.11.(2022·河北)依据所标数据,下列一定为平行四边形的是( )A .B .C .D .【答案】D【分析】根据平行四边形的判定及性质定理判断即可;【详解】解:平行四边形对角相等,故A 错误;一组对边平行不能判断四边形是平行四边形,故B 错误;三边相等不能判断四边形是平行四边形,故C 错误;一组对边平行且相等的四边形是平行四边形,故D 正确;故选:D .【点睛】本题主要考查平行四边形的判定及性质,掌握平行四边形的判定及性质是解题的关键. 12.(2022·湖南岳阳)下列命题是真命题的是( )A .对顶角相等B .平行四边形的对角线互相垂直C .三角形的内心是它的三条边的垂直平分线的交D .三角分别相等的两个三角形是全等三角形【答案】A【分析】根据对顶角性质判断A ,根据平行四边形的性质判断B ,根据三角形的内心定义判断C ,根据全等三角形的判定定理判断D .【详解】A.对顶角相等是一个正确的命题,是真命题,故A 符合题意;B.菱形的对角线互相垂直,非菱形的平行四边形的对角线不垂直,所以平行四边形的对角线互相垂直是一个假命题,故B 不符合题意;C.三角形的内心是三角形内角平分线的交点,不一定是三边的垂直平分线的交点,则三角形的内心是它的三条边的垂直平分线的交点是一个假命题,故C 不符合题意;D.三角分别相等的两个三角形不一定全等,故D 不符合题意;故选:A .【点睛】本题考查了真命题与假命题的判断,对顶角的性质,平行四边形的性质,三角形的内心定义,全等三角形的判定,熟练掌握这些性质、定义、定理是解决问题的关键.13.(2022·河北)如图,将三角形纸片剪掉一角得四边形,设△ABC 与四边形BCDE 的外角和的度数分别为α,β,则正确的是( )A .0αβ-=B .0αβ-<C .0αβ->D .无法比较α与β的大小【答案】A【分析】多边形的外角和为360︒,△ABC 与四边形BCDE 的外角和均为360︒,作出选择即可.【详解】解:⊥多边形的外角和为360︒,⊥△ABC 与四边形BCDE 的外角和α与β均为360︒,⊥0αβ-=,故选:A .【点睛】本题考查多边形的外角和定理,注意多边形的外角和为360︒是解答本题的关键.14.(2022·河南)如图,在菱形ABCD 中,对角线AC ,BD 相交于点O ,点E 为CD 的中点.若OE =3,则菱形ABCD 的周长为( )A .6B .12C .24D .48【答案】C【分析】由菱形的性质可得出BO =DO ,AB =BC =CD =DA ,再根据中位线的性质可得26BC OE ==,结合菱形的周长公式即可得出结论.【详解】解:⊥四边形ABCD 为菱形,⊥BO =DO ,AB =BC =CD =DA ,⊥OE =3,且点E 为CD 的中点,OE ∴是BCD △的中位线,⊥BC =2OE =6.⊥菱形ABCD 的周长为:4BC =4×6=24.故选:C .【点睛】本题考查了菱形的性质以及中位线的性质,解题的关键是求出AD =6.15.(2022·山东泰安)如图,平行四边形ABCD 的对角线AC ,BD 相交于点O .点E 为BC 的中点,连接EO 并延长交AD 于点F ,60ABC ∠=︒,2BC AB =.下列结论:①AB AC ⊥;②4AD OE =;③四边形AECF是菱形;④14BOE ABC S S =△△.其中正确结论的个数是( ) A .4B .3C .2D .1【答案】A 【分析】通过判定ABE ∆为等边三角形求得60=︒∠BAE ,利用等腰三角形的性质求得30EAC ∠=︒,从而判断①;利用有一组邻边相等的平行四边形是菱形判断③,然后结合菱形的性质和含30直角三角形的性质判断②;根据三角形中线的性质判断④.【详解】解:点E 为BC 的中点,22BC BE CE ∴==,又2BC AB =,AB BE ∴=,60ABC ∠=︒,ABE ∴∆是等边三角形,60BAE BEA ∴∠=∠=︒,30EAC ECA ∴∠=∠=︒,90BAC BAE EAC ∴∠=∠+∠=︒,即AB AC ⊥,故①正确;在平行四边形ABCD 中,//AD BC ,AD BC =,AO CO =,CAD ACB ∴∠=∠,在AOF ∆和COE ∆中,CAD ACB OA OC AOF COE ∠=∠⎧⎪=⎨⎪∠=∠⎩,()AOF COE ASA ∴∆≅∆,AF CE ∴=,∴四边形AECF 是平行四边形,又AB AC ⊥,点E 为BC 的中点,AE CE ∴=,∴平行四边形AECF 是菱形,故③正确;AC EF ∴⊥,在Rt COE ∆中,30ACE ∠=︒,111244OE CE BC AD ∴===,故②正确; 在平行四边形ABCD 中,OA OC =,又点E 为BC 的中点,ΔΔΔ1124BOE BOC ABC S S S ∴==,故④正确; 综上所述:正确的结论有4个,故选:A .【点睛】本题考查平行四边形的性质,等边三角形的判定和性质,菱形的判定和性质,含30的直角三角形的性质,掌握菱形的判定是解题关键.16.(2022·山东滨州)下列命题,其中是真命题的是( )A .对角线互相垂直的四边形是平行四边形B .有一个角是直角的四边形是矩形C .对角线互相平分的四边形是菱形D .对角线互相垂直的矩形是正方形【答案】D【分析】分别根据平行四边形,矩形,菱形及正方形的判定定理进行判断即可.【详解】对角线互相平分的四边形是平行四边形,故A 错误,不符合题意;有三个角是直角的四边形是矩形,故B 错误,不符合题意;对角线互相垂直平分的四边形是菱形,故C 错误,不符合题意;对角线互相垂直的矩形是正方形,故D 正确,符合题意;故选:D .【点睛】本题考查了平行四边形,矩形,菱形及正方形的判定定理,熟练掌握知识点是解题的关键.二、填空题17.(2022·江苏扬州)“做数学”可以帮助我们积累数学活动经验.如图,已知三角形纸片ABC ,第1次折叠使点B 落在BC 边上的点B '处,折痕AD 交BC 于点D ;第2次折叠使点A 落在点D 处,折痕MN 交AB '于点P .若12BC =,则MP MN +=_____________. 【答案】6【分析】根据第一次折叠的性质求得12BD DB BB ''==和AD BC ⊥,由第二次折叠得到AM DM =,MN AD ⊥,进而得到MN BC ,易得MN 是ADC 的中位线,最后由三角形的中位线求解.【详解】解:⊥已知三角形纸片ABC ,第1次折叠使点B 落在BC 边上的点B '处,折痕AD 交BC 于点D ,⊥12BD DB BB ''==,AD BC ⊥. ⊥第2次折叠使点A 落在点D 处,折痕MN 交AB '于点P ,⊥AM DM =,AN ND =,⊥MN AD ⊥,⊥MN BC .⊥AM DM =,⊥MN 是ADC 的中位线,⊥12MP DB '=,12MN DC =. ⊥12BC =,2BD DC CB BD BC +=+'=,⊥()111162222MP MN DB DC DB DB B C BC +=+=+='+''='. 故答案为:6.【点睛】本题主要考查了折叠的性质和三角形中位线的性质,理解折叠的性质,三角形的中位线性质是解答关键.18.(2022·江苏连云港)如图,在ABCD 中,150ABC ∠=︒.利用尺规在BC 、BA 上分别截取BE 、BF ,使BE BF =;分别以E 、F 为圆心,大于12EF 的长为半径作弧,两弧在CBA ∠内交于点G ;作射线BG 交DC于点H .若1AD =,则BH 的长为_________. 【答案】2【分析】如图所示,过点H 作HM ⊥BC 于M ,由作图方法可知,BH 平分⊥ABC ,即可证明⊥CBH =⊥CHB ,得到1CH BC ==,从而求出HM ,CM 的长,进而求出BM 的长,即可利用勾股定理求出BH 的长.【详解】解:如图所示,过点H 作HM ⊥BC 于M ,由作图方法可知,BH 平分⊥ABC ,⊥⊥ABH =⊥CBH ,⊥四边形ABCD 是平行四边形,⊥1BC AD AB CD ==∥,,⊥⊥CHB =⊥ABH ,⊥C =180°-⊥ABC =30°,⊥⊥CBH =⊥CHB ,⊥1CH BC ==,⊥12HM CH ==⊥CM ==,⊥BM BC CM =-=⊥BH ==【点睛】本题主要考查了角平分线的尺规作图,平行四边形的性质,含30度角的直角三角形的性质,勾股定理,等腰三角形的性质与判定等等,正确求出CH 的长是解题的关键.19.(2022·四川南充)数学实践活动中,为了测量校园内被花坛隔开的A ,B 两点的距离,同学们在AB 外选择一点C ,测得,AC BC 两边中点的距离DE 为10m (如图),则A ,B 两点的距离是_______________m .【答案】20【分析】根据题意得出DE 为∆ABC 的中位线,然后利用其性质求解即可.【详解】解:⊥点D 、E 为AC ,BC 的中点,⊥DE 为∆ABC 的中位线,⊥DE =10,⊥AB =2DE =20,故答案为:20.【点睛】题目主要考查三角形中位线的判定和性质,熟练掌握三角形中位线的性质是解题关键. 20.(2022·湖南株洲)如图所示,已知60MON ∠=︒,正五边形ABCDE 的顶点A 、B 在射线OM 上,顶点E 在射线ON 上,则AEO ∠=_________度.【答案】48【分析】EAO ∠是正五边形的一个外角,利用多边形外交和360°算出一个外角EAO ∠,再利用OAE △的内角和180°,即可算出【详解】⊥四边形ABCDE 是正五边形,EAO ∠是一个外角 ⊥360725EAO ︒∠==︒ 在OAE △中:180180726048AEO EAO MON ∠=︒-∠-∠=︒-︒-︒=︒故答案为:48【点睛】本题考查多边形外角和和三角形内角和,注意多边形外角和均为360°21.(2022·四川遂宁)如图,正六边形ABCDEF 的顶点A 、F 分别在正方形BMGH 的边BH 、GH 上.若正方形BMGH 的边长为6,则正六边形ABCDEF 的边长为______.【答案】4【分析】连接BE ,根据正六边形的特点可得//BE AF ,根据含30度角的直角三角形的性质即可求解.【详解】如图,连接BE ,正六边形ABCDEF 的顶点A 、F 分别在正方形BMGH 的边BH 、GH 上 正六边形每个内角为360180=1202︒-︒,BE 为对称轴 180ABE BAF ∴∠+∠=︒//AF BE ∴则60ABE HAF ∠=∠=︒=FEB ∠则30AFH ∠=︒,正方形BMGH 的边长为66BH ∴=, 12AH AF =设AH x =,则26x x += 解得2x =24BA x ∴==故答案为:4 【点睛】本题考查了正多边形的性质,正方形的性质,含30度角的直角三角形的性质,掌握以上知识是解题的关键.22.(2022·浙江舟山)正八边形的一个内角的度数是____ 度.【答案】135【分析】根据多边形内角和定理:(n﹣2)•180°(n≥3且n为正整数)求出内角和,然后再计算一个内角的度数即可.【详解】正八边形的内角和为:(8﹣2)×180°=1080°,每一个内角的度数为:1080°÷8=135°,故答案为135.23.(2022·江西)正五边形的外角和等于_______◦.【答案】360【详解】试题分析:任何n边形的外角和都等于360度.考点:多边形的外角和.24.(2020·湖南湘西)一个正多边形的内角和是外角和的2倍,则这个多边形的边数是______.【答案】6【分析】利用正多边形的外角和以及正多边形的内角和定理即可解决问题.【详解】解:∵正多边形的外角和是360度,正多边形的内角和是外角和的2倍,则内角和是720度,720÷180+2=6,∴这个多边形的边数为6.故答案为:6.【点睛】本题主要考查了正多边形的内角和定理与外角和定理,熟练掌握定理是解题的关键.25.(2022·湖南常德)剪纸片:有一张长方形的纸片,用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片;从这2张中任选一张,再用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片,这样共有3张纸片:从这3张中任选一张,再用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片,这样共有4张纸片;……;如此下去,若最后得到10张纸片,其中有1张五边形纸片,3张三角形纸片,5 张四边形纸片,则还有一张多边形纸片的边数为________.【答案】6【分析】根据多边形的内角和进行即可求解.【详解】解:根据题意用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片,则每剪一次,所有的多边形的内角和增加360°,10张纸片,则剪了9次,其中有1张五边形纸片,3张三角形纸片,5 张四边形纸片,设还有一张多边形纸片的边数为n,()()()∴-⨯︒+⨯︒+-⨯︒⨯+-⨯︒=︒+︒⨯,52180318042180521803603609n解得6n =.故答案为:6.【点睛】本题考查了多边形内角和公式,理解题意是解题的关键.26.(2022·浙江台州)如图,在ABC 中,90ACB ∠=︒,D ,E ,F 分别为AB ,BC ,CA 的中点.若EF 的长为10,则CD 的长为________.【答案】10【分析】根据三角形中位线定理求出AB ,根据直角三角形的性质解答.【详解】解:∵E 、F 分别为BC 、AC 的中点,∴AB =2EF =20,∵∠ACB =90°,点D 为AB 的中点, ∴1102CD AB ==, 故答案为:10.【点睛】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.27.(2022·湖北荆州)如图,点E ,F 分别在□ABCD 的边AB ,CD 的延长线上,连接EF ,分别交AD ,BC 于G ,H .添加一个条件使⊥AEG ⊥⊥CFH ,这个条件可以是______.(只需写一种情况)【答案】AE CF =(答案不唯一)【分析】由平行四边形的性质可得:,A C ∠=∠ 证明,E F ∠=∠ 再补充两个三角形中的一组相对应的边相等即可. 【详解】解: ABCD ,,,AB CD A C ∥,F E 所以补充:,AE CF =∴ ⊥AEG ⊥⊥CFH ,故答案为:AE CF =(答案不唯一)【点睛】本题考查的是全等三角形的判定与性质,平行四边形的性质,掌握“平行四边形的性质与利用ASA证明三角形全等”是解本题的关键.28.(2022·江苏苏州)如图,在平行四边形ABCD 中,AB AC ⊥,3AB =,4AC =,分别以A ,C 为圆心,大于12AC 的长为半径画弧,两弧相交于点M ,N ,过M ,N 两点作直线,与BC 交于点E ,与AD 交于点F ,连接AE ,CF ,则四边形AEC F 的周长为______.【答案】10【分析】根据作图可得MN AC ⊥,且平分AC ,设AC 与MN 的交点为O ,证明四边形AECF 为菱形,根据平行线分线段成比例可得AE 为ABC 的中线,然后勾股定理求得BC ,根据直角三角形中斜边上的中线等于斜边的一半可得AE 的长,进而根据菱形的性质即可求解.【详解】解:如图,设AC 与MN 的交点为O ,根据作图可得MN AC ⊥,且平分AC ,AO OC ∴=,四边形ABCD 是平行四边形,AD BC ∴∥,FAO OCE ∴∠=∠,又AOF COE ∠=∠,AO CO = ,AOF COE ∴≌,AF EC ∴=,AF CE ∥,∴四边形AECF 是平行四边形, MN 垂直平分AC ,EA EC ∴=,∴四边形AECF 是菱形,AB AC ⊥,MN AC ⊥,EF AB ∴∥,1BE OCEC AO∴==,E ∴为BC 的中点,Rt ABC △中, 3AB =,4AC =,5BC ∴,1522AE BC ==, ∴四边形AEC F 的周长为410AE =.故答案为:10.【点睛】本题考查了垂直平分线的性质,菱形的性质与判定,勾股定理,平行线分线段成比例,平行四边形的性质与判定,综合运用以上知识是解题的关键.29.(2022·湖南邵阳)如图,在等腰ABC 中,120A ∠=︒,顶点B 在ODEF 的边DE 上,已知140∠=︒,则2∠=_________.【答案】110º【分析】先根据等腰三角形的性质求出⊥ABC 的度数;再根据平行四边形对边平行和两直线平行同旁内角互补的性质,得出⊥2+⊥ABE =180º,代入求解即可.【详解】解:⊥ABC 是等腰三角形,⊥A =120º,⊥⊥ABC =⊥C =(180º-⊥A )÷2=30º,⊥四边形ODEF 是平行四边形,⊥OF ∥DE ,⊥⊥2+⊥ABE =180º,即⊥2+30º+40º=180º,⊥⊥2=110º.故答案为:110º.【点睛】此题考查了等腰三角形的性质和平行四边形的性质,解题的关键是数形结合,熟练运用上述知识求解.30.(2022·甘肃武威)如图,在四边形ABCD 中,AB DC ,AD BC ∥,在不添加任何辅助线的前提下,要想四边形ABCD 成为一个矩形,只需添加的一个条件是_______________.【答案】90A ∠=︒(答案不唯一)【分析】】先证四边形ABCD 是平行四边形,再由矩形的判定即可得出结论.【详解】解:需添加的一个条件是⊥A =90°,理由如下:⊥AB ⊥DC ,AD ⊥BC ,⊥四边形ABCD 是平行四边形,又⊥⊥A =90°,⊥平行四边形ABCD 是矩形,故答案为:⊥A =90°(答案不唯一).【点睛】本题考查了矩形的判定、平行四边形的判定与性质等知识,熟练掌握矩形的判定和平行四边形的判定与性质是解题的关键.31.(2022·山东滨州)如图,在矩形ABCD 中,5,10AB AD ==.若点E 是边AD 上的一个动点,过点E 作EF AC ⊥且分别交对角线AC ,直线BC 于点O 、F ,则在点E 移动的过程中,AF FE EC ++的最小值为________. 【答案】25552+ 【分析】过点D 作BM EF ∥交BC 于M ,过点A 作AN EF ∥,使AN EF =,连接NE ,当N 、E 、C 三点共线时,AF FE EC CN AN ++≥+,分别求出CN 、AN 的长度即可.【详解】过点D 作DM EF ∥交BC 于M ,过点A 作AN EF ∥,使AN EF =,连接NE ,∴四边形ANEF 是平行四边形,∴,AN EF AF NE ==,∴当N 、E 、C 三点共线时,AF CE +最小,四边形ABCD 是矩形,5,10AB AD ==,10,5,,90AD BC AB CD AD BC ABC ∴====∠=︒∥,AC ∴=∴四边形EFMD 是平行四边形,DM EF ∴=,DM EF AN ∴==,EF AC ⊥,,DM AC AN AC ∴⊥⊥,90CAN ∴∠=︒,90MDC ACD ACD ACB ∴∠+∠=︒=∠+∠,MDC ACB ∴∠=∠,tan tanMDC ACB∴∠=∠,即MC ABCD BC=,52MC∴=,在Rt CDM中,由勾股定理得DM AN===,在Rt ACN中,由勾股定理得252CN==,AF FE EC CN AN ++≥+,∴AF FE EC++≥,AF FE EC ∴++【点睛】本题考查了利用轴对称求最短距离问题,勾股定理,矩形的性质,解直角三角形,平行四边形的判定和性质,熟练掌握知识点,准确作出辅助线是解题的关键.三、解答题32.(2022·浙江嘉兴)小惠自编一题:“如图,在四边形ABCD中,对角线AC,BD交于点O,AC⊥BD,OB=OD.求证:四边形ABCD是菱形”,并将自己的证明过程与同学小洁交流.若赞同小惠的证法,请在第一个方框内打“√”;若赞成小洁的说法,请你补充一个条件,并证明.【答案】赞成小洁的说法,补充,OA OC=证明见解析【分析】先由OB=OD,,OA OC=证明四边形ABCD是平行四边形,再利用对角线互相垂直,从而可得结论.【详解】解:赞成小洁的说法,补充.OA OC=证明:⊥OB=OD,,OA OC=∴四边形ABCD是平行四边形,AC⊥BD,⊥四边形ABCD是菱形.【点睛】本题考查的是平行四边形的判定,菱形的判定,掌握“菱形的判定方法”是解本题的关键. 33.(2022·浙江温州)如图,在ABC 中,AD BC ⊥于点D ,E ,F 分别是,AC AB 的中点,O 是DF 的中点,EO 的延长线交线段BD 于点G ,连结DE ,EF ,FG .(1)求证:四边形DEFG 是平行四边形.(2)当5AD =,5tan 2EDC ∠=时,求FG 的长. 【答案】(1)见解析【分析】(1)根据E ,F 分别是AC ,AB 的中点,得出EF BC ∥,根据平行线的性质,得出FEO DGO ∠=∠,EFO GDO ∠=∠,结合O 是DF 的中点,利用“AAS”得出EFO GDO △≌△,得出EF GD =,即可证明DEFG 是平行四边形;(2)根据AD BC ⊥,E 是AC 中点,得出12DE AC EC ==,即可得出5tan tan 2C EDC =∠=,即52AD DC =,根据5AD =,得出CD =2,根据勾股定理得出AC 的长,即可得出DE ,根据平行四边形的性,得出FG DE ==(1)解:(1)⊥E ,F 分别是AC ,AB 的中点,⊥EF BC ∥,⊥FEO DGO ∠=∠,EFO GDO ∠=∠,⊥O 是DF 的中点,⊥FO DO =,⊥()EFO GDO AAS ≌,⊥EF GD =,⊥四边形DEFG 是平行四边形.(2)⊥AD BC ⊥,E 是AC 中点, ⊥12DE AC EC ==,⊥EDC C ∠=∠, ⊥5tan tan 2C EDC =∠=, ⊥52AD DC =, ⊥5AD =,⊥2CD =,⊥1122DE AC ====. ⊥四边形DEFG 为平行四边形,⊥FG DE == 【点睛】本题主要考查了平行线四边形的判定和性质,勾股定理,直角三角形斜边上的中线,三角形全等的判定和性质,三角函数的定义,平行线的性质,中位线的性质,根据题意证明EFO GDO △≌△,是解题的关键.34.(2022·云南)如图,在平行四边形ABCD 中,连接BD ,E 为线段AD 的中点,延长BE 与CD 的延长线交于点F ,连接AF ,⊥BDF =90°(1)求证:四边形ABDF 是矩形;(2)若AD =5,DF =3,求四边形ABCF 的面积S .【答案】(1)见解析;(2)18.【分析】(1)根据平行四边形的性质及全等三角形的判定证得ABE △⊥DFE △,即可得到AB =DF ,从而证明四边形ABDF 是平行四边形,再根据⊥BDF =90°即可证明四边形ABDF 是矩形;(2)根据全等的性质、矩形性质及勾股定理得到AB =DF =3,AF =4,由平行四边形性质求得CF =6,最后利用梯形的面积公式计算即可.(1)证明:⊥四边形ABCD 是平行四边形,⊥AB ⊥CD ,即AB ⊥CF ,⊥⊥BAE =⊥FDE ,⊥E 为线段AD 的中点,⊥AE =DE ,又⊥⊥AEB =⊥DEF ,⊥ABE △⊥DFE △(ASA ),⊥AB =DF ,又⊥AB ⊥DF ,⊥四边形ABDF 是平行四边形,⊥⊥BDF =90°,⊥四边形ABDF 是矩形;(2)解:由(1)知,四边形ABDF 是矩形,⊥AB =DF =3,⊥AFD =90°,⊥在Rt ADF 中,4AF =,⊥四边形ABCD 是平行四边形,⊥AB =CD =3,⊥CF =CD +DF =3+3=6, ⊥()()113641822S AB CF AF =+=⨯+⨯=. 【点睛】本题考查了全等三角形的判定与性质,平行四边形的判定与性质,矩形的判定与性质,勾股定理等知识,熟练掌握各性质及判定定理进行推理是解题的关键.35.(2022·四川凉山)在Rt ⊥ABC 中,⊥BAC =90°,D 是BC 的中点,E 是AD 的中点,过点A 作AF ⊥BC 交CE 的延长线于点F .(1)求证:四边形ADBF 是菱形;(2)若AB =8,菱形ADBF 的面积为40,求AC 的长.【答案】(1)见解析(2)10【分析】(1)证△AEF ⊥⊥DEC (AAS ),得△AEF ⊥⊥DEC (AAS ),再证四边形ADBF 是平行四边形,然后由直角三角形斜边中线等于斜边的一半得证AD =BD =12BC ,即可由菱形判定定理得出结论;(2)连接DF 交AB 于O ,由菱形面积公式S 菱形ADBF =12AB DF ⋅=40,求得OD 长,再由菱形性质得OA =OB ,证得OD 是三角形的中位线,由中位线性质求解可.(1)证明:⊥E 是AD 的中点,⊥AE =DE⊥AF ∥BC ,⊥⊥AFE =⊥DCE ,在△AEF 和△DEB 中,AFE DCE AEF DEC AE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,⊥⊥AEF ⊥⊥DEC (AAS ),⊥AF =CD ,⊥D 是BC 的中点,⊥CD =BD ,⊥AF =BD ,⊥四边形ADBF 是平行四边形,⊥⊥BAC =90°,⊥D 是BC 的中点,⊥AD =BD =12BC ,⊥四边形ADBF 是菱形;(2)解:连接DF 交AB 于O ,如图 由(1)知:四边形ADBF 是菱形,⊥AB ⊥DF ,OA =12AB =12×8=4, S 菱形ADBF =12AB DF ⋅=40,⊥182DF ⨯=40, ⊥DF =10,⊥OD =5,⊥四边形ADBF 是菱形,⊥O 是AB 的中点,⊥D 是BC 的中点,⊥OD 是⊥BAC 的中位线,⊥AC =2OD =2×5=10.答:AC 的长为10.【点睛】本题考查平行四边形的判定,菱形的判定与性质,三角形全等的判定与性质,直角三角形斜边中线的性质,三角形中位线的性质,熟练掌握菱形的判定与性质是解题的关键.36.(2022·四川自贡)如图,用四根木条钉成矩形框ABCD ,把边BC 固定在地面上,向右推动矩形框,矩形框的形状会发生改变(四边形具有不稳定性).(1)通过观察分析,我们发现图中线段存在等量关系,如线段EB 由AB 旋转得到,所以EB AB =.我们还可以得到FC = , EF = ;(2)进一步观察,我们还会发现EF ⊥AD ,请证明这一结论;(3)已知BC 30,DC 80==cm cm ,若BE 恰好经过原矩形DC 边的中点H ,求EF 与BC 之间的距离.【答案】(1)CD ,AD ;(2)见解析;(3)EF 于BC 之间的距离为64cm .【分析】(1)由推动矩形框时,矩形ABCD 的各边的长度没有改变,可求解;(2)通过证明四边形BEFC 是平行四边形,可得结论;(3)由勾股定理可求BH 的长,再证明△BCH ⊥⊥BGE ,得到BH CH BE EG=,代入数值求解EG ,即可得到答案. (1)解:⊥ 把边BC 固定在地面上,向右推动矩形框,矩形框的形状会发生改变(四边形具有不稳定性).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.如图,已知四边形ABCD 中,点E ,F ,G ,H 分别是AB 、CD 、AC 、BD 的中点,并且点E 、F 、G 、H 有在同一条直线上.
求证:EF 和GH 互相平分.
2.如图,在ABC ∆中,o
BAC 90=∠,BC AD ⊥,BE 、AF 分别是ABC ∠、DAC ∠的平分线,且相交于点O ,BE 交AD 于G ,求证:GF//AC.
3.如图所示.DE ⊥AC ,BF ⊥AC ,DE=BF ,∠ADB=∠DBC .求证:四边形ABCD 是平行四边形.
A
B D F E
O G
4.如图2-39所示.在平行四边形ABCD中,△ABE和△BCF都是等边三角形.求证:△DEF是等边三角形.
5.如图2-40所示.ABCD中,AF平分∠BAD交BC于F,DE⊥AF交CB于E.求证:BE=CF.
6.如图2-41所示.矩形ABCD中,F在CB延长线上,AE=EF,CF=CA.求证:BE⊥DE.
7.如图,矩形ABCD 中,∠AOB =60°,DE 平分∠ADC ,交BC 于E ,求∠OED 度数. D C B A
E
O
8.Rt △ABC 中,∠ABC =90°,∠C =60°,BC =2,D 是AC 的中点,从D 作DE ⊥AC 与CB 的延长线交于点E ,以AB 、BE 为邻边作矩形ABEF ,连结DF ,则DF 的长.
F E D
C B A
9. 如图,BD =AC ,M 、N 分别为AD 、BC 的中点,AC 、BD 交于E ,MN 与BD 、AC 分别交
于点F、G,求证:EF=EG.
N
M
G
F
E
D
C
B
A
10.(2007•黑龙江)在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.若点P在BC边上(如图1),此时PD=0,可得结论:PD+PE+PF=AB.
请直接应用上述信息解决下列问题:
当点P分别在△ABC内(如图2),△ABC外(如图3)时,上述结论是否成立?若成立,请给予证明;若不成立,PD,PE,PF与AB之间又有怎样的数量关系,请写出你的猜想,不需要证明.
11.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
A
B C E F M
N O (第19题图)。
