6下1--3导案

合集下载

统编人教版六年级社会下册全册教案(1-65)

统编人教版六年级社会下册全册教案(1-
65)
目标
本教案的目标是帮助学生全面研究统编人教版六年级社会下册的内容。

教案依据教材中的课文和活动设计，采用简洁而又有效的策略，让学生在保持独立思考的基础上，顺利掌握相关知识。

教案简介
本教案共包含65个课时，涵盖了统编人教版六年级社会下册的全部内容。

教案的编写均遵循简洁、易懂的原则，以帮助教师迅速掌握每堂课的重点和教学重点。

注意事项
1. 本教案中的内容均为独立决策，无需用户协助。

2. 教案的设计不涉及复杂的法律问题，以避免引起法律风险。

3. 请不要引用无法确认的内容，确保教案的准确性和可信度。

使用建议
1. 教案中的内容请以清晰、简洁的语言呈现，不要进行概述。

2. 教师在使用教案时，应根据具体情况进行灵活调整，以适应学生的研究需求。

3. 教师可以添加适合自己的教学辅助材料，以提高教学效果。

结语
本教案旨在提供一份有效且有帮助的教学辅助材料，帮助教师顺利教授统编人教版六年级社会下册的内容。

希望教案能够满足您的需求，祝您教学顺利！。

小学六年级下册数学应用题80道及答案(考点梳理)

小学六年级下册数学应用题80道一.解答题(共100题，共578分)1.一条公路全长1500m，修路队第一天修了全长的45%，第二天修了全长的。

还剩下多少米没有修？2.解答题。

（1）－1与0之间还有负数吗？-与0之间呢？如有，你能举出例子来吗？（2）写出在－1与－3之间的三个负数。

3.某水果店新进一批水果，其中苹果占新进水果总量的30%，香蕉占40%，已知这两种水果共70kg，这批水果的总量是多少？4.把一个体积是282.6cm3的铁块熔铸成一个底面半径是6厘米的圆锥形机器零件，求圆锥零件的高？（π取3.14)5.王老师推荐了甲、乙两本课外读物，六年级每个同学至少买了一本。

已知有同学买了甲读物，有45%的同学买了乙读物，有14个同学两本都买了。

六年级共有多少名同学？6.某建筑物内有6根圆柱形大柱，高10米，大柱周长25.12分米，要全部涂上油漆，如果按每平方米的油漆费为80元计算，需用多少钱？7.笑笑看一本180页的故事书，第一周看了全书的40%，第二周看了全书的25%。

两周共看了多少页？8.小华的妈妈把10000元钱存入银行，定期三年。

如果年利率按3.25%计算，到期一共可以取回多少元？9.一块长方形土地的周长是162米，长与宽的比是5∶4，这块土地的面积是多少平方米？10.2019年12月2日，中俄两国东线天然气管道正式投产通气，给我国人民生活带来极大的方便。

俄罗斯境内管道全长约3000km，中国境内新建管道3371km，利用已建管道1740km。

中国新建管道比俄罗斯境内管道全长多百分之几？11.如果规定进库数量用正数表示，请你根据下表中某一周粮库进出大米数量的记录情况，说出每天记录数量的意义。

12.某电视机厂去年电视机生产情况统计图（单位:台； 2011年1月）看图列式计算:（1）全年共生产电视机多少台？（2）平均每月生产电视机多少台？（3）第四季度比第一季度增产百分之几？13.我们把李明从家出发，向西走了500米记作走了－500米，那么李明又接着走了＋800米是什么意思？这时李明离家的距离有多远？14.一个长方体木块长、宽、高分别是5cm、4cm、3cm。

语文六年级下册第三单元教材分析

语文六年级下册第三单元教材分析一、单元功能定位：本单元是特殊的习作单元,要求引导学生选择合适的内容写出真情实感。

语言表达上的训练要求，这个单元跟其他单元相比，最大的不同点，出现了习作例文，因为习作例文的出现，单元的结构就发生了变化，单元的定位也就发生了变化。

当然习作例文不是六年级才出现。

单元整体备课时，我们的视野可以进一步开阔，我们可以把它放在整个统编小学语文教材体系当中，来看待习作例文的地位，和它所处单元的定位。

我们都知道习作例文在统编小学文教材当中，其实是三年级开始出现的。

（统编小学语文《习作例文》编排体系一览表）而针对课标关于习作“真情实感”的能力目标表述,统编教材从四年级到六年级安排了相关的梯度练习(梯度练习表)。

二、单元内容：本单元是习作单元,延续之前习作单元的编排体系,由“精读课文”“交流平台”“初试身手”“习作例文”“习作”构成。

（统编小学语文六年级下册第三单元内容一览表）三、单元整体教学理路：1.聚焦问题解决，让学习有意义。

不久之后，孩子们就要告别美丽的校园，告别朝夕相处的老师、同学，带着依依不舍的深情，跨入新的学校，开始新的学习生活。

临近毕业之际，让孩子们回顾小学生活，联系实际情况，做到有感而发。

我们的语文教学有两个主要问题需要解决，一是教材问题，二是教学问题。

小学语文单元整体教学试图解决以上两个问题。

小学语文单元整体教学重视学生语文基本能力的培养，能够更好地树立教师的课程意识，让教师能够从整体上看待教学，把握教学，取得教学的效果。

从语文学科核心素养的角度来看，习作单元定位为表达单元。

语文核心素养中语言的建构和运用、思维的发展与提升、审美的鉴赏与创造、文化的传承和理解这四个方面，最核心的当然是语言的建构与运用，而作为表达单元更应该自觉集中的指向语言的建构和运用，就像我们这个单元应该指向的是通过一个或几个具体的事例来抒发自己的真情实感。

2.基于真实学情，整合学习资源。

本次单元整体教学的第一步不是预习课文，不是记忆生字词语，而是在孩子们接触单元内容之初就课前试写。

2021年北师大版数学六下第四单元《正比例和反比例》章节知识点、达标训练附解析

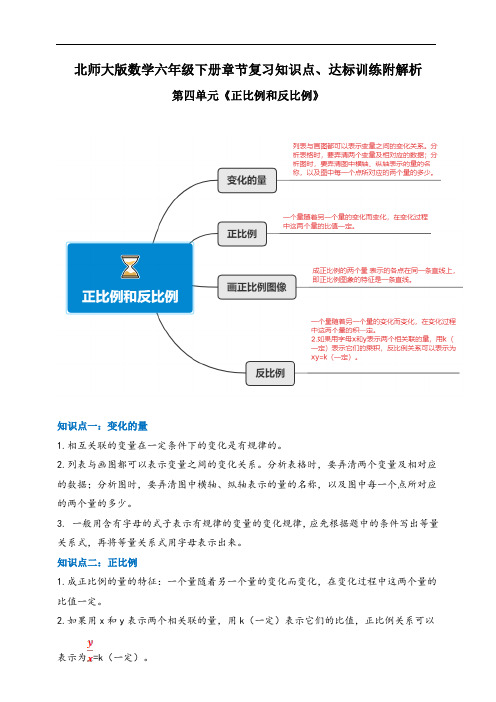
北师大版数学六年级下册章节复习知识点、达标训练附解析第四单元《正比例和反比例》知识点一：变化的量1.相互关联的变量在一定条件下的变化是有规律的。

2.列表与画图都可以表示变量之间的变化关系。

分析表格时，要弄清两个变量及相对应的数据；分析图时，要弄清图中横轴、纵轴表示的量的名称，以及图中每一个点所对应的两个量的多少。

3. 一般用含有字母的式子表示有规律的变量的变化规律，应先根据题中的条件写出等量关系式，再将等量关系式用字母表示出来。

知识点二：正比例1.成正比例的量的特征：一个量随着另一个量的变化而变化，在变化过程中这两个量的比值一定。

2.如果用x和y表示两个相关联的量，用k（一定）表示它们的比值，正比例关系可以表示为=k（一定）。

3.判断两个量是否成正比例的方法（1）首先，要确定这两个量是不是相关联的量（其中一个量是否随着另一个量的变化而变化）；（2）其次，要根据两个变量之间的数值对应关系，计算出两个变量每一对数值的比值；（3）最后，根据比值是否一定来判断这两个变量是否成正比例。

知识点三：正比例图像1.成正比例的两个量表示的各点在同一条直线上，即正比例图象的特征是一条直线。

2.从正比例图象中可以得出任意一点所表示的意义。

3. 观察正比例图象时，要先明确横轴、纵轴表示的意义，从图象中可以直观地看出两个量的变化情况，不需要计算，由一个量的值可以直接找到与它对应的另一个量的值。

知识点四：反比例1.成反比例的量的特征：一个量随着另一个量的变化而变化，在变化过程中这两个量的积一定。

2.如果用字母x和y表示两个相关联的量，用k（一定）表示它们的乘积，反比例关系可以表示为xy=k（一定）。

3.判断两个量是否成反比例的方法（1）首先，要确定这两个量是不是相关联的量（其中一个量是否随着另一个量的变化而变化）；（2）其次，要根据两个变量之间的数值对应关系，计算出两个变量每一对数值的积；（3）最后，根据积是否一定来判断这两个变量是否成反比例。

HSK标准教程(6下)练习册-录音文本及答案

却全都对症适用。他们都是细心温暖的人。
6
HSK 标准教程练习册 6 下
女：这样的工作环境，确实会让人心情愉快。男：其实心情是小事，关键是我认准了，一个内心积极温暖的人，一定会有光
明美好的前途，所以我看好我们的公司。
问题： 6. 关于男的的职场经历，下列哪项正确？ 7. 最初男的为什么选择了现在这家公司？ 8. 关于这家公司，下列哪项正确？ 9. 生病的经历让他有了怎样的感触？ 10.男的看好这家公司的理由是什么？
7
HSK 标准教程练习册 6 下
国人研制出了充气轮胎。从此，自行车技术开始走向商业化，实现批量生产并投入市场。
问题： 11. 世界上最早的自行车出现在街头时，人们是什么态度？ 12. 哪国人发明了自行车？ 13. 英国人在哪方面对自行车的发展做出了贡献？
答案：11. B
12. A
13. A
第 14-17 题是根据下面一段话。
标也包含了分享投资对象，不纯粹是为了筹集资金。
6.有偿分享模式”的主要特点是什么？
r 8. “对等分享模式”的主要特点是什么？ nte 9. “劳务分享模式”的主要特点是什么？心 Ce 10. “众筹分享模式”的主要特点是什么？资源中 ource 答案：6.D 7.A 8.D 9.B 10.C
nter 你想知道我设计的未来汽车什么样吗？让我来告诉你吧！心 Ce 这款汽车是水、陆、空三用车。它不用汽油，而是以太阳能做燃料，当然它源中 rce 也不排放有害气体。形容它的速度，“奔驰”“驰骋”这样的词汇都用不上了，语资 sou 它的速度和光的速度差不多。这种汽车没有方向盘，只有一块超薄屏幕，显示着汉 Re 你所在的方位、本地区的交通要道和世界各地的地图。当然 GPS 导航系统是必不国际 ese 可少的，只要你说出自己想去的地方，汽车就会把你送到目的地。 hin 这款车在行驶过程中能自动调节车速以及车内温度和光线，前方出现阻碍， l C 它会自动避开，因此在陆地上行驶它安全可靠。下雪天，汽车会伸出两根滑板， tiona 这样在雪地里它也是来去自如。 a 在空中飞行时，它平稳无噪声，就像坐在自家的沙发上一样，对了，它还能 tern 够像直升飞机一样升降。 In在水面上行驶时，车的轮胎会自动变大，浮力也随之变大，速度可达每小时

倍的认识——优秀教学导案

《倍地认识》——山口小学李娜教学目标：1、学生通过圈图理解一个数是另一个数地几倍.2、体验圈一圈、摆一摆地操作活动，经历倍地概念地形成过程，培养学生地观察和动手能力.3、在具体情境中感受数学在生活中地应用.b5E2RGbCAP教学重点：在操作活动中建立倍地概念.教学难点：能在具体情境中正确说出一个数是另一个数地几倍.教学准备：课件教学过程：《课前拍手游戏》师：上课之前，咱们一起玩个拍手游戏，谁愿意到前面来和老师一起玩?(找一学生)1、我先拍，听，我拍了几下？（让学生说出是2下）请你拍3个2下，其他同学听他拍得是不是3个2下？（1）生会拍：你是怎么拍地？（2）生连续拍6下：谁有好办法让我们一听就知道是3个2下？就用他教我们地好方法试试看,（就是刚才这道题，全班共同拍3个2）预备：（师做好示范地动作）开始！（师边拍边数1、2；空一小会儿，再1、2；再空一小会儿， 1、2）2、再听老师拍了几下？（3下）请你们拍2个3下 .预备，心里数，开始！（老师带全班学生共同拍）3、你们想玩吗？两人一组，每人玩一次.师：课下同学们两人一组，可以继续玩，现在我们开始上课，看谁最精神！上课.一、创设情境，生成问题1、师：谁能很快地说出每幅图有几个几？（）个2 （）个2 （）个4p1EanqFDPw2、同学们来看，老师带来了什么？课件出示P50图，学生看图上有什么？数数各种萝卜各有多少？它们之间又有什么关系呢？二、探索交流，解决问题胡萝卜有2根，红萝卜有6根，6根红萝卜有（）个2根呢？我们用笔一起来圈一圈.我们圈了几次？说明可以圈出3个两根，我们说红萝卜地根数是胡萝卜地3倍.（板书在图下方）同学们你们会这样圈吗？学生试着圈一圈，感知“一个数是另一个数地几倍”2、白萝卜有10根，那10根白萝卜有（）个2根呢？先请一个同学来说说你准备怎样圈？打开书，请大家用铅笔在书上圈一圈那10根白萝卜，并完成下方地填空.同位互相检查，同时请一个学生上黑板圈一圈，集体订正.从上面可以看出白萝卜地根数是胡萝卜地5倍，为什么是5倍而不是3倍呢？DXDiTa9E3d3、引出课题，板书《倍地认识》三、巩固应用，内化提升1.2.3.一行摆5根小棒，第二行要我们怎么摆，4倍是什么意思？第二行摆几个5根，一共是多少根？请你画一画，然后圈一圈.4、5、请同学们说一说现实生活中用到“倍”地事情.四、回顾整理，反思提升本节课学到了什么？和大家分享一下吧！版权申明本文部分内容，包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some parts, including text, pictures, and design.Copyright is personal ownership.RTCrpUDGiT用户可将本文地内容或服务用于个人学习、研究或欣赏，以及其他非商业性或非盈利性用途，但同时应遵守著作权法及其他相关法律地规定，不得侵犯本网站及相关权利人地合法权利.除此以外，将本文任何内容或服务用于其他用途时，须征得本人及相关权利人地书面许可，并支付报酬.5PCzVD7HxAUsers may u se the contents or services of this article for personal study, research or appreciation, and other non-commercial or non-profit purposes, but at the same t ime, they shall abide by the provisions of copyright law and other relevant laws, and shall not infringe upon the legitimate rights of this website and its relevant obligees. In addition, when any content or service of thisarticle is used for other purposes, written permission and remuneration shallbe obtained from the person concerned and the relevant obligee.jLBHrnAILg转载或引用本文内容必须是以新闻性或资料性公共免费信息为使用目地地合理、善意引用，不得对本文内容原意进行曲解、修改，并自负版权等法律责任.xHAQX74J0X Reproduction or quotation of the content of this article must be reasonable and good-faith citation for the use of news or informative public freeinformation. It shall not misinterpret or modify the original intention of thecontent of this article, and shall bear legal liability such as copyright.LDAYtRyKfE。

2023年高考数学(文科)一轮复习——导数的概念及运算

第1节导数的概念及运算考试要求 1.了解导数概念的实际背景；2.通过函数图象直观理解导数的几何意义；3.能根据导数的定义求函数y＝c(c为常数)，y＝x，y＝1x，y＝x2，y＝x3，y＝x 的导数；4.能利用基本初等函数的导数公式和导数的四则运算法则求简单函数的导数.1.函数y＝f(x)在x＝x0处的导数(1)定义：称函数y＝f(x)在x＝x0处的瞬时变化率为函数y＝f(x)在x＝x0处的导数，记作f′(x0)或y′|x＝x0，即(2)几何意义：函数f(x)在点x0处的导数f′(x0)的几何意义是在曲线y＝f(x)上点(x0，f(x0))处的切线的斜率.相应地，切线方程为y－y0＝f′(x0)(x－x0).2.函数y＝f(x)的导函数如果函数y＝f(x)在开区间(a，b)内的每一点处都有导数，当x＝x0时，f′(x0)是一个确定的数，当x变化时，f′(x)便是x的一个函数，称它为f(x)的导函数(简称导数)，y＝f(x)的导函数有时也记作y′，即f′(x)＝y′＝limΔx→0f（x＋Δx）－f（x）Δx.3.基本初等函数的导数公式基本初等函数导函数f (x )＝c (c 为常数) f ′(x )＝0 f (x )＝x α(α∈Q *) f ′(x )＝αx α－1 f (x )＝sin x f ′(x )＝cos__x f (x )＝cos x f ′(x )＝－sin__x f (x )＝e x f ′(x )＝e x f (x )＝a x (a ＞0，a ≠1)f ′(x )＝a x ln__a f (x )＝ln xf ′(x )＝1x f (x )＝log a x (a ＞0，a ≠1)f ′(x )＝1x ln a4.导数的运算法则若f ′(x )，g ′(x )存在，则有： (1)[f (x )±g (x )]′＝f ′(x )±g ′(x )； (2)[f (x )·g (x )]′＝f ′(x )g (x )＋f (x )g ′(x )；(3)⎣⎢⎡⎦⎥⎤f （x ）g （x ）′＝f ′（x ）g （x ）－f （x ）g ′（x ）[g （x ）]2(g (x )≠0).1.f ′(x 0)代表函数f (x )在x ＝x 0处的导数值；(f (x 0))′是函数值f (x 0)的导数，且(f (x 0))′＝0.2.⎣⎢⎡⎦⎥⎤1f （x ）′＝－f ′（x ）[f （x ）]2(f (x )≠0).3.曲线的切线与曲线的公共点的个数不一定只有一个，而直线与二次曲线相切只有一个公共点.4.函数y ＝f (x )的导数f ′(x )反映了函数f (x )的瞬时变化趋势，其正负号反映了变化的方向，其大小|f ′(x )|反映了变化的快慢，|f ′(x )|越大，曲线在这点处的切线越“陡”.1.思考辨析(在括号内打“√”或“×”)(1)f ′(x 0)是函数y ＝f (x )在x ＝x 0附近的平均变化率.( )(2)函数f (x )＝sin(－x )的导数f ′(x )＝cos x .( ) (3)求f ′(x 0)时，可先求f (x 0)，再求f ′(x 0).( )(4)曲线y ＝f (x )在某点处的切线与曲线y ＝f (x )过某点的切线意义是相同的.( ) 答案 (1)× (2)× (3)× (4)×解析 (1)f ′(x 0)表示y ＝f (x )在x ＝x 0处的瞬时变化率，(1)错. (2)f (x )＝sin(－x )＝－sin x ，则f ′(x )＝－cos x ，(2)错. (3)求f ′(x 0)时，应先求f ′(x )，再代入求值，(3)错.(4)“在某点”的切线是指以该点为切点的切线，因此此点横坐标处的导数值为切线的斜率；而对于“过某点”的切线，则该点不一定是切点，要利用解方程组的思想求切线的方程，在曲线上某点处的切线只有一条，但过某点的切线可以不止一条，(4)错.2.某跳水运动员离开跳板后，他达到的高度与时间的函数关系式是h (t )＝10－4.9t 2＋8t (距离单位：米，时间单位：秒)，则他在0.5秒时的瞬时速度为( ) A.9.1米/秒 B.6.75米/秒 C.3.1米/秒D.2.75米/秒答案 C解析 h ′(t )＝－9.8t ＋8， ∴h ′(0.5)＝－9.8×0.5＋8＝3.1.3.(2022·银川质检)已知函数f (x )＝⎩⎨⎧x 2＋2x ，x ≤0，－x 2＋ax ，x >0为奇函数，则曲线f (x )在x ＝2处的切线斜率等于( ) A.6 B.－2C.－6D.－8答案 B解析 f (x )为奇函数，则f (－x )＝－f (x ). 取x >0，得x 2－2x ＝－(－x 2＋ax )，则a ＝2. 当x >0时，f ′(x )＝－2x ＋2.∴f ′(2)＝－2.4.(2020·全国Ⅲ卷)设函数f (x )＝e x x ＋a .若f ′(1)＝e4，则a ＝________.答案 1 解析由f ′(x )＝e x （x ＋a ）－e x（x ＋a ）2，可得f ′(1)＝e a （1＋a ）2＝e 4，即a （1＋a ）2＝14，解得a ＝1.5.(2021·全国甲卷)曲线y ＝2x －1x ＋2在点(－1，－3)处的切线方程为________.答案 5x －y ＋2＝0解析 y ′＝⎝ ⎛⎭⎪⎪⎫2x －1x ＋2′＝（2x －1）′（x ＋2）－（2x －1）（x ＋2）′（x ＋2）2＝5（x ＋2）2，所以k ＝y ′|x ＝－1＝5（－1＋2）2＝5，所以切线方程为y ＋3＝5(x ＋1)，即5x －y ＋2＝0.6.(易错题)设函数f (x )的导数为f ′(x )，且f (x )＝f ′⎝ ⎛⎭⎪⎫π2sin x ＋cos x ，则f ′⎝ ⎛⎭⎪⎫π4＝________.答案－ 2解析由f (x )＝f ′⎝ ⎛⎭⎪⎫π2sin x ＋cos x ，得f ′(x )＝f ′⎝ ⎛⎭⎪⎫π2cos x －sin x ，则f ′⎝ ⎛⎭⎪⎫π2＝f ′⎝ ⎛⎭⎪⎫π2·cos π2－sin π2，解得f ′⎝ ⎛⎭⎪⎫π2＝－1，所以f ′⎝ ⎛⎭⎪⎫π4＝－cos π4－sin π4＝－ 2.考点一导数的运算1.下列求导运算不正确的是( ) A.(sin a )′＝cos a (a 为常数)B.(sin 2x )′＝2cos 2xC.(x )′＝12xD.(e x －ln x ＋2x 2)′＝e x －1x ＋4x 答案 A解析 ∵a 为常数，∴sin a 为常数，∴(sin a )′＝0，故A 错误.由导数公式及运算法则知B 、C 、D 正确.2.若f (x )＝x 3＋2x －x 2ln x －1x 2，则f ′(x )＝________.答案 1－1x －2x 2＋2x 3解析由已知f (x )＝x －ln x ＋2x －1x 2.∴f ′(x )＝1－1x －2x 2＋2x 3.3.设f ′(x )是函数f (x )＝cos xe x ＋x 的导函数，则f ′(0)的值为________. 答案 0 解析因为f (x )＝cos xe x＋x ，所以f ′(x )＝（cos x ）′e x －（e x ）′cos x （e x ）2＋1＝－sin x －cos xe x ＋1，所以f ′(0)＝－1e 0＋1＝0.4.已知函数f (x )的导函数为f ′(x )，且满足关系式f (x )＝x 2＋3xf ′(2)＋ln x ，则f (1)＝________. 答案－234解析因为f (x )＝x 2＋3xf ′(2)＋ln x ， ∴f ′(x )＝2x ＋3f ′(2)＋1x .令x ＝2，得f ′(2)＝4＋3f ′(2)＋12，则f ′(2)＝－94. ∴f (1)＝1＋3×1×⎝ ⎛⎭⎪⎫－94＋0＝－234.感悟提升 1.求函数的导数要准确地把函数拆分成基本初等函数的和、差、积、商，再利用运算法则求导.2.抽象函数求导，恰当赋值是关键，然后活用方程思想求解. 考点二导数的几何意义角度1 求切线的方程例1 (1)曲线y ＝3(x 2＋x )e x 在点(0，0)处的切线方程为________.(2)已知函数f (x )＝x ln x ，若直线l 过点(0，－1)，并且与曲线y ＝f (x )相切，则直线l 的方程为________.答案 (1)3x －y ＝0 (2)x －y －1＝0 解析 (1)y ′＝3(2x ＋1)e x ＋3(x 2＋x )e x ＝3e x (x 2＋3x ＋1)，所以曲线在点(0，0)处的切线的斜率k ＝e 0×3＝3，所以所求切线方程为3x －y ＝0.(2)∵点(0，－1)不在曲线f (x )＝x ln x 上， ∴设切点为(x 0，y 0). 又∵f ′(x )＝1＋ln x ，∴直线l 的方程为y ＋1＝(1＋ln x 0)x . ∴由⎩⎪⎨⎪⎧y 0＝x 0ln x 0，y 0＋1＝（1＋ln x 0）x 0，解得⎩⎪⎨⎪⎧x 0＝1，y 0＝0.∴直线l 的方程为y ＝x －1，即x －y －1＝0. 角度2 求曲线的切点坐标例2 (2022·皖豫名校联考)若曲线y ＝e x ＋2x 在其上一点(x 0，y 0)处的切线的斜率为4，则x 0＝( ) A.2 B.ln 4 C.ln 2D.－ln 2答案 C解析 ∵y ′＝e x ＋2，∴e x 0＋2＝4，∴e x 0＝2，x 0＝ln 2. 角度3 导数与函数图象问题例3 已知y ＝f (x )是可导函数，如图，直线y ＝kx ＋2是曲线y ＝f (x )在x ＝3处的切线，令g (x )＝xf (x )，g ′(x )是g (x )的导函数，则g ′(3)＝________.答案 0解析由题图可知曲线y ＝f (x )在x ＝3处切线的斜率等于－13，∴f ′(3)＝－13. ∵g (x )＝xf (x )， ∴g ′(x )＝f (x )＋xf ′(x )， ∴g ′(3)＝f (3)＋3f ′(3)，又由题意可知f (3)＝1， ∴g ′(3)＝1＋3×⎝ ⎛⎭⎪⎫－13＝0.感悟提升 1.求曲线在点P (x 0，y 0)处的切线，则表明P 点是切点，只需求出函数在P 处的导数，然后利用点斜式写出切线方程，若在该点P 处的导数不存在，则切线垂直于x 轴，切线方程为x ＝x 0.2.求曲线的切线方程要分清“在点处”与“过点处”的切线方程的不同.切点坐标不知道，要设出切点坐标，根据斜率相等建立方程(组)求解，求出切点坐标是解题的关键.训练1 (1)(2022·沈阳模拟)曲线f (x )＝2e x sin x 在点(0，f (0))处的切线方程为( ) A.y ＝0 B.y ＝2x C.y ＝xD.y ＝－2x(2)(2021·长沙检测)如图所示，y＝f(x)是可导函数，直线l：y＝kx＋3是曲线y＝f(x)在x＝1处的切线，令h(x)＝f（x）x，h′(x)是h(x)的导函数，则h′(1)的值是()A.2B.1C.－1D.－3答案(1)B(2)D解析(1)∵f(x)＝2e x sin x，∴f(0)＝0，f′(x)＝2e x(sin x＋cos x)，∴f′(0)＝2，∴所求切线方程为y＝2x.(2)由图象知，直线l经过点(1，2).则k＋3＝2，k＝－1，从而f′(1)＝－1，且f(1)＝2，由h(x)＝f（x）x，得h′(x)＝xf′（x）－f（x）x2，所以h′(1)＝f′(1)－f(1)＝－1－2＝－3.考点三导数几何意义的应用例4 (1)已知曲线f(x)＝x ln x在点(e，f(e))处的切线与曲线y＝x2＋a相切，则实数a 的值为________.(2)(2022·河南名校联考)若函数f(x)＝ln x＋2x2－ax的图象上存在与直线2x－y＝0平行的切线，则实数a的取值范围是________.答案(1)1－e(2)[2，＋∞)解析(1)因为f′(x)＝ln x＋1，所以曲线f(x)＝x ln x在x＝e处的切线斜率为k＝2，又f(e)＝e，则曲线f (x )＝x ln x 在点(e ，f (e))处的切线方程为y ＝2x －e. 由于切线与曲线y ＝x 2＋a 相切，故可联立⎩⎪⎨⎪⎧y ＝x 2＋a ，y ＝2x －e ，得x 2－2x ＋a ＋e ＝0，所以由Δ＝4－4(a ＋e)＝0，解得a ＝1－e. (2)∵直线2x －y ＝0的斜率为k ＝2，又曲线f (x )上存在与直线2x －y ＝0平行的切线，∴f ′(x )＝1x ＋4x －a ＝2在(0，＋∞)内有解，则a ＝4x ＋1x －2，x >0. 又4x ＋1x ≥24x ·1x ＝4，当且仅当x ＝12时取“＝”.∴a ≥4－2＝2.∴a 的取值范围是[2，＋∞).感悟提升 1.处理与切线有关的参数问题，通常根据曲线、切线、切点的三个关系列出参数的方程(组)并解出参数：(1)切点处的导数是切线的斜率；(2)切点在切线上；(3)切点在曲线上.2.利用导数的几何意义求参数范围时，注意化归与转化思想的应用.训练2 (1)(2021·洛阳检测)函数f (x )＝ln x －ax 在x ＝2处的切线与直线ax －y －1＝0平行，则实数a ＝( ) A.－1 B.14 C.12D.1(2)直线y ＝kx ＋1与曲线y ＝x 3＋ax ＋b 相切于点A (1，3)，则2a ＋b ＝________. 答案 (1)B (2)1解析 (1)∵f (x )＝ln x －ax ，∴f ′(x )＝1x －a .又曲线y ＝f (x )在x ＝2处切线的斜率k ＝f ′(2)，因此12－a ＝a ，∴a ＝14.(2)y ＝x 3＋ax ＋b 的导数为y ′＝3x 2＋a ，可得在点(1，1)处切线的斜率为k ＝3＋a ，又k ＋1＝3，1＋a ＋b ＝3，解得k ＝2，a ＝－1，b ＝3，即有2a ＋b ＝－2＋3＝1.公切线问题求两条曲线的公切线，如果同时考虑两条曲线与直线相切，头绪会比较乱，为了使思路更清晰，一般是把两条曲线分开考虑，先分析其中一条曲线与直线相切，再分析另一条曲线与直线相切，其中直线与抛物线相切可用判别式法. 一、共切点的公切线问题例1 设点P 为函数f (x )＝12x 2＋2ax 与g (x )＝3a 2ln x ＋2b (a >0)的图象的公共点，以P 为切点可作直线l 与两曲线都相切，则实数b 的最大值为( ) A.23e 34 B.32e 34 C.43e 23D.34e 23答案 D解析设P (x 0，y 0)，由于P 为公共点，则12x 20＋2ax 0＝3a 2ln x 0＋2b .又点P 处的切线相同，则f ′(x 0)＝g ′(x 0)，即x 0＋2a ＝3a 2x 0，即(x 0＋3a )(x 0－a )＝0.又a >0，x 0>0，则x 0＝a ，于是2b ＝52a 2－3a 2ln a .设h (x )＝52x 2－3x 2ln x ，x >0，则h ′(x )＝2x (1－3ln x ).可知：当x ∈(0，e 13)时，h (x )单调递增；当x ∈(e 13，＋∞)时，h (x )单调递减. 故h (x )max ＝h (e 13)＝32e 23，于是b 的最大值为34e 23，选D. 二、切点不同的公切线问题例2 曲线y ＝－1x (x <0)与曲线y ＝ln x 的公切线的条数为________. 答案 1解析设(x 1，y 1)是公切线和曲线y ＝－1x 的切点，则切线斜率k 1＝⎝ ⎛⎭⎪⎫－1x ′|x ＝x 1＝1x 21，切线方程为y ＋1x 1＝1x 21(x －x 1)，整理得y ＝1x 21·x －2x 1.设(x 2，y 2)是公切线和曲线y ＝ln x 的切点，则切线斜率k 2＝(ln x )′|x ＝x 2＝1x 2，切线方程为y －ln x 2＝1x 2(x －x 2)，整理得y ＝1x 2·x ＋ln x 2－1.令1x 21＝1x 2，－2x 1＝ln x 2－1，消去x 2得－2x 1＝ln x 21－1.设t ＝－x 1>0，即2ln t －2t －1＝0，只需探究此方程解的个数.易知函数f (x )＝2ln x －2x －1在(0，＋∞)上单调递增，f (1)＝－3<0，f (e)＝1－2e >0，于是f (x )＝0有唯一解，于是两曲线的公切线的条数为1.1.函数f (x )＝x 2＋ln x ＋sin x ＋1的导函数f ′(x )＝( ) A.2x ＋1x ＋cos x ＋1 B.2x －1x ＋cos x C.2x ＋1x －cos xD.2x ＋1x ＋cos x答案 D解析由f (x )＝x 2＋ln x ＋sin x ＋1得f ′(x )＝2x ＋1x ＋cos x . 2.曲线y ＝x ＋1x －1在点(3，2)处的切线的斜率是( )A.2B.－2C.12D.－12答案 D解析 y ′＝（x ＋1）′（x －1）－（x ＋1）（x －1）′（x －1）2＝－2（x －1）2，故曲线在点(3，2)处的切线的斜率k ＝y ′|x ＝3＝－2（3－1）2＝－12. 3.(2021·安徽皖江名校联考)已知f (x )＝x 3＋2xf ′(0)，则f ′(1)＝( ) A.2 B.3C.4D.5答案 B解析 f ′(x )＝3x 2＋2f ′(0)， ∴f ′(0)＝2f ′(0)，解得f ′(0)＝0， ∴f ′(x )＝3x 2，∴f ′(1)＝3.4.(2022·豫北十校联考)已知f (x )＝x 2，则过点P (－1，0)，曲线y ＝f (x )的切线方程为( ) A.y ＝0 B.4x ＋y ＋4＝0 C.4x －y ＋4＝0 D.y ＝0或4x ＋y ＋4＝0 答案 D解析易知点P (－1，0)不在f (x )＝x 2上，设切点坐标为(x 0，x 20)，由f (x )＝x 2可得f ′(x )＝2x ，∴切线的斜率k ＝f ′(x 0)＝2x 0. ∵切线过点P (－1，0)，∴k ＝x 20x 0＋1＝2x 0，解得x 0＝0或x 0＝－2，∴k ＝0或－4，故所求切线方程为y ＝0或4x ＋y ＋4＝0.5.(2022·昆明诊断)若直线y ＝ax 与曲线y ＝ln x －1相切，则a ＝( ) A.e B.1C.1eD.1e 2答案 D解析由y ＝ln x －1，得y ′＝1x ，设切点为(x 0，ln x 0－1)，则⎩⎨⎧ax 0＝ln x 0－1，a ＝1x 0，解得a ＝1e 2. 6.已知函数f (x )在R 上可导，其部分图象如图所示，设f （4）－f （2）4－2＝a ，则下列不等式正确的是( )A.a <f ′(2)<f ′(4)B.f ′(2)<a <f ′(4)C.f ′(4)<f ′(2)<aD.f ′(2)<f ′(4)<a 答案 B解析由函数f (x )的图象可知，在[0，＋∞)上，函数值的增长越来越快，故该函数图象在[0，＋∞)上的切线斜率也越来越大. 因为f （4）－f （2）4－2＝a ，所以f ′(2)<a <f ′(4).7.函数f (x )＝(2x －1)e x 的图象在点(0，f (0))处的切线的倾斜角为________. 答案 π4解析由f (x )＝(2x －1)e x ，得f ′(x )＝(2x ＋1)e x ，∴f ′(0)＝1，则切线的斜率k ＝1，又切线倾斜角θ∈[0，π)，因此切线的倾斜角θ＝π4.8.已知曲线f (x )＝13x 3－x 2－ax ＋1存在两条斜率为3的切线，则实数a 的取值范围是________. 答案 (－4，＋∞) 解析 f ′(x )＝x 2－2x －a ，依题意知x 2－2x －a ＝3有两个实数解，即a ＝x 2－2x －3＝(x －1)2－4有两个实数解， ∴y ＝a 与y ＝(x －1)2－4的图象有两个交点， ∴a >－4.9.(2021·济南检测)曲线y ＝f (x )在点P (－1，f (－1))处的切线l 如图所示，则f ′(－1)＋f (－1)＝________.答案－2解析∵直线l过点(－2，0)和(0，－2)，∴直线l的斜率f′(－1)＝0＋2－2－0＝－1，直线l的方程为y＝－x－2.则f(－1)＝1－2＝－1.故f′(－1)＋f(－1)＝－1－1＝－2.10.已知函数f(x)＝x3－4x2＋5x－4.(1)求曲线f(x)在点(2，f(2))处的切线方程；(2)求经过点A(2，－2)的曲线f(x)的切线方程.解(1)因为f′(x)＝3x2－8x＋5，所以f′(2)＝1，又f(2)＝－2，所以曲线f(x)在点(2，f(2))处的切线方程为y－(－2)＝x－2，即x－y －4＝0.(2)设切点坐标为(x0，x30－4x20＋5x0－4)，因为f′(x0)＝3x20－8x0＋5，所以切线方程为y－(－2)＝(3x20－8x0＋5)(x－2)，又切线过点(x0，x30－4x20＋5x0－4)，所以x30－4x20＋5x0－2＝(3x20－8x0＋5)·(x0－2)，整理得(x0－2)2(x0－1)＝0，解得x0＝2或x0＝1，所以经过点A(2，－2)的曲线f(x)的切线方程为x－y－4＝0或y＋2＝0.11.已知函数f(x)＝x3＋x－16.(1)求曲线y＝f(x)在点(2，－6)处的切线方程；(2)直线l为曲线y＝f(x)的切线，且经过原点，求直线l的方程及切点坐标.解(1)根据题意，得f′(x)＝3x2＋1.所以曲线y＝f(x)在点(2，－6)处的切线的斜率k＝f′(2)＝13，所以所求的切线方程为13x－y－32＝0.(2)设切点为(x0，y0)，则直线l的斜率为f′(x0)＝3x20＋1，所以直线l的方程为y＝(3x20＋1)(x－x0)＋x30＋x0－16.又直线l过点(0，0)，则(3x20＋1)(0－x0)＋x30＋x0－16＝0，整理得x30＝－8，解得x0＝－2，所以y0＝(－2)3＋(－2)－16＝－26，l的斜率k′＝13，所以直线l的方程为y＝13x，切点坐标为(－2，－26).12.若函数f(x)＝a ln x(a∈R)与函数g(x)＝x在公共点处有共同的切线，则实数a 的值为()A.4B.12 C.e2 D.e答案 C解析由已知得f′(x)＝ax，g′(x)＝12x，设切点横坐标为t，∴⎩⎨⎧a ln t＝t，at＝12t，解得t＝e2，a＝e2.13.曲线y＝x2－ln x上的点到直线x－y－2＝0的最短距离是________. 答案 2解析设曲线在点P(x0，y0)(x0>0)处的切线与直线x－y－2＝0平行，则y′|x＝x0＝⎝⎛⎭⎪⎫2x－1x| x＝x0＝2x0－1x0＝1.∴x0＝1，y0＝1，则P(1，1)，则曲线y＝x2－ln x上的点到直线x－y－2＝0的最短距离d＝|1－1－2|12＋（－1）2＝ 2.14.(2021·宜昌质检)已知函数f(x)＝1x＋1＋x＋a－1的图象是以点(－1，－1)为对称中心的中心对称图形，g(x)＝e x＋ax2＋bx，若曲线y＝f(x)在点(1，f(1))处的切线与曲线y＝g(x)在点(0，g(0))处的切线互相垂直，求a＋b的值.解由y＝x＋1x的图象关于点(0，0)对称，且y＝f(x)的图象可由y＝x＋1x的图象平移得到，且函数f(x)＝1x＋1＋x＋a－1＝1x＋1＋(x＋1)＋a－2的图象是以点(－1，－1)为对称中心的中心对称图形，得a－2＝－1，即a＝1，所以f(x)＝1x＋1＋x.对f(x)求导，得f′(x)＝1－1（x＋1）2，则曲线y＝f(x)在点(1，f(1))处的切线斜率k1＝f′(1)＝1－14＝3 4.对g(x)求导，得g′(x)＝e x＋2x＋b，则曲线y＝g(x)在点(0，g(0))处的切线斜率k2＝g′(0)＝b＋1.由两曲线的切线互相垂直，得(b＋1)×34＝－1，即b＝－73，所以a＋b＝1－73＝－43.。

[译林版]6下Unit3 A healthy diet精心梳理教案

6.学生能掌握字母组合“ou”的发音规律，并能举一反三。
7.学生能了解本单元文化知识：中西方早餐食物的差异。
8.学生能在情景中自主理解故事大意，并通过自主阅读，强化语言知识，
训练语言技能，培养学生的阅读理解能力。
四、单元教学重点：
1.能听懂、会说、会读单词，词组或句型：at a time, healthy, diet, cola, a little, a few. He has a lot of/some noodles/meat. She has a few eggs/a little rice.
3.学生能正确归类可数名词和不可数名词并掌握可数名词的复数形式。
六、单元课时数分配：
第一课时：Story time
第二课时：Grammar time &Fun time
第三课时：Sound time& Culture time & Cartoon time
第四课时：Checkout time & ticking time
a, look at the blackboard and retell the text. b, finish the passage
Step3 Post-reading
1.Say something about your diet.
2.If you have an unhealthy diet, what are you going to do?
Way：a, Show the T’s diet and describe it. b, What do you think of my diet? Healthy or unhealthy?
Teach: diet, a few, a little, healthy, unhealthy.

西师版六年级下册数学 5、总复习 (1)数与代数 3 数的认识(3)

93
94
95
96
97
98
（1）在表中圈出2和5的公倍数。
9
10
19
20
29
30
39
40
49
50
59
60
69
70
79
80
89
90
99
100
结合表中的数议一议。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
2
4
-1
0.5
1.5
2.填一填。
数量(本)
书名
1
语文（六下）
数学（六下）
10
100
1000
议一议：小数点位置移动，小数大小会发生怎样的变化？
左移一位，缩小到原来
1 10
；
左移两位，缩小到原来
1 100
；
左移三位，缩小到原来 1 ；
1000
……
右移一位，扩大10倍；右移两位，扩大100倍；右移三位，扩大1000倍；
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97

案件中止审理的法律规定(3篇)

第1篇一、引言案件中止审理是指在人民法院审理案件过程中，因某些法定原因导致案件无法继续审理，依法暂时停止案件审理程序的情形。

中止审理是法律赋予人民法院在特定情况下保护当事人合法权益的一种措施。

本文将从法律规定的角度，对案件中止审理的相关内容进行阐述。

二、法律依据1.《中华人民共和国民事诉讼法》《中华人民共和国民事诉讼法》第一百五十一条规定：“有下列情形之一的，中止诉讼：（一）一方当事人死亡，需要等待继承人表明是否参加诉讼的；（二）一方当事人丧失诉讼行为能力，尚未确定法定代理人的；（三）作为一方当事人的法人或者其他组织终止，尚未确定权利义务承受人的；（四）一方当事人因不可抗力的事由，不能参加诉讼的；（五）本案必须以另一案的审理结果为依据，而另一案尚未审结的；（六）其他应当中止诉讼的情形。

”2.《中华人民共和国行政诉讼法》《中华人民共和国行政诉讼法》第五十三条规定：“有下列情形之一的，中止诉讼：（一）原告死亡，需要等待继承人表明是否参加诉讼的；（二）原告丧失诉讼行为能力，尚未确定法定代理人的；（三）作为原告的法人或者其他组织终止，尚未确定权利义务承受人的；（四）原告因不可抗力的事由，不能参加诉讼的；（五）本案必须以另一案的审理结果为依据，而另一案尚未审结的；（六）其他应当中止诉讼的情形。

”3.《中华人民共和国刑事诉讼法》《中华人民共和国刑事诉讼法》第一百九十三条规定：“有下列情形之一的，中止审理：（一）被告人死亡或者丧失诉讼行为能力，尚未确定继承人或者法定代理人的；（二）作为被告人的法人或者其他组织终止，尚未确定权利义务承受人的；（三）被告人患有严重疾病，无法出庭的；（四）案件涉及国家秘密，不宜公开审理的；（五）其他应当中止审理的情形。

”三、中止审理的情形及处理1.一方当事人死亡，需要等待继承人表明是否参加诉讼在此情况下，人民法院应当裁定中止诉讼。

继承人表示参加诉讼的，人民法院应当恢复审理；继承人未表示参加诉讼的，人民法院可以裁定终结诉讼。

(4)多项选择题-高考数学一轮复习导数题型专练(含解析)

（4）多项选择题——高考数学一轮复习导数题型专练1.某物体的运动路程s （单位：m ）与时间t （单位：s ）的关系可用函数2()1s t t t =++表示，则( )A.物体在1t s =时的瞬时速度为0m/sB.物体在0t s =时的瞬时速度为1m/sC.瞬时速度为9m/s 的时刻是在4t s =时D.物体从0到1的平均速度为2m/s2.已知曲线()y f x =在原点处的切线与曲线()y xf x =在(2,8)处的切线重合，则( )A.(2)4f = B.(2)3f '=C.(0)4f '= D.曲线()y f x =在(2,)a 处的切线方程为y a=3.以下函数求导正确的有( )A.()1x '= B.(sin 2)cos 2'= C.1(ln xx'= D.'=4.已知定义域为[]3,5-的函数()f x 的导函数为()f x '，且()f x '的图象如图所示，则( )A.()f x 在()2,2-上单调递减B.()f x 有极小值()2fC.有2个极值点D.在处取得最大值5.已知函数()y f x =，其导函数()f x '的图象如图所示，则下列说法正确的是( )A.函数()f x 在()2,0-上单调递增B.函数()f x 在()0,5上单调递减C.函数()f x 在2x =-处取得极小值D.函数()f x 在3x =处取得最大值()f x ()f x 3x =-6.若函数()e 23xf x x =-+，则( )A.函数()f x 只有极大值没有极小值B.函数()f x 只有最大值没有最小值C.函数()f x 只有极小值没有极大值D.函数()f x 只有最小值没有最大值7.若实数x 和正数y 满足e ln x x y y +=+，我们则称(),x y 为一对关联数.已知满足方程的关联数有且仅有两对，则实数a 的值可为( )A.C.8.已知一家公司生产某种品牌服装的年固定成本为10万元，每生产1000件需另投入2.7万元.设该公司一年内生产该品牌服装x 千件并全部销售完，每千件的销售收入为()R x 万元，且()22110.8,010,301081000,103x x R x x xx ⎧-<≤⎪⎪=⎨⎪->⎪⎩当该公司在这一品牌服装的生产中所获得的年利润最大时，则有( )A.年产量为9000件B.年产量为10000件C.年利润最大值为38万元D.年利润最大值为38.6万元9.已知函数()f x =A.当01x <<时，()1f x <B.当01x <<时，()1f x >C.当1x >时，()1f x < D.当1x >时，()1f x >10.对于函数()f x =A.()f x 有最小值但没有最大值B.对于任意的(),0x ∈-∞，恒有()0f x <C.()f x 仅有一个零点xy a =12eD.()f x 有两个极值点11.已知函数()f x 的定义域为()0,+∞，导函数为()f x '，满足()()()1e xxf x f x x -=-'（e 为自然对数的底数），且，则( )在上单调递增C.()f x 在1x =处取得极小值D.()f x 无最大值12.若实数m 的取值使函数()f x 在定义域上有两个极值点，则称函数()f x 具有“凹凸趋向性”，已知()f x '是函数()f x 的导数，且2n (l )mx xx f '=-，当函数()f x 具有“凹凸趋向性”时，m 的取值范围的子集有( )A.2,e ⎛⎫-+∞ ⎪⎝⎭B.2,0e ⎛⎫- ⎪⎝⎭C.2e ,⎛⎫-∞- ⎪⎝⎭ D.21,e e ⎛⎫-- ⎪⎝⎭13.关于函数()2ln 2x f x a x bx =++，下列说法正确的是( )A.若()f x 存在极值点，则240b a -<B.若0a <，则()f x 有且只有一个极值点C.若()f x 有两个极值点，则0ab <D.若1是()f x 的极大值点，则1a >14.已知函数()e xf x =与函数()g x =()11,x y ，()22,N x y 两点，且12x x <，则( )A.121y y = B.122ex y = C.直线的斜率 D.2222ex y >15.关于x 的方程()200ax e ax a -=＞的实根个数可能为：( ).A.0B.1C.2D.3()10f =<()f x ()0,1MN 1k >答案以及解析1.答案：BCD解析：由题意，()21s t t '=+，物体运动的瞬时速度对应了路程s 的导数.(1)3s '=，故1t s =时，瞬时速度为3m/s ，A 错误；(0)1s '=，故0t s =时，瞬时速度为1m/s ，B 正确；当()9s t '=时，t =3121-==，故D 正确.故选BCD.2.答案：ACD解析：令，则，依题意，解得，故A 正确；依题意可得曲线在原点处的切线过点，所以，故C 正确；又，所以(2)0f '=，则曲线()y f x =在(2,)a 处的切线方程为y a =，故B 错误，D 正确.故选：ACD 3.答案：AD解析：11()1x x -'==，A 正确；(sin 2)0'=，常数的导数为0，B 错误；()121()x x x--''==-=112212x x -'⎛⎫'=== ⎪⎝⎭4.答案：AB解析：由()f x '的图象可知()2,2x ∈-时，()0f x '<，则()f x 单调递减，故A 正确；又()2,4x ∈时，()0f x '>，则()f x 单调递增，所以当2x =时，()f x 有极小值()2f ，故B 正确；由()f x '的图象可知2x =-，2，4时，()f x 有极值，所以()f x 有3个极值点，故C 错误；当()3,2x ∈--时，()0f x '>，则()f x 单调递增，所以()()32f f -<-，()f x 在3x =-处不能取得最大值，故D 错误.故选AB.5.答案：AC解析：结合函数图象可知，当2x <-时，()0f x '<，()f x 单调递减，当23x -<<时，()0f x '>，()f x 单调递增，当37x <<时，()0f x '<，()f x 单调递减，当7x >时，()0f x '>，()()g x xf x =()()()g x f x xf x ''=+(2)2(2)8g f ==(2)4f =()y f x =(2,8)80(0)420f -'==-(2)(2)2(2)(0)4g f f f '''=+==()f x 单调递增，故2x =-时，函数取得极小值，3x =时取得极大值，无法确定是最大值，AC 正确，BD 错误.故选：AC.6.答案：CD解析：()e 2xf x '=-，单调递增，由()0ln 2f x x '=⇒=，则(),ln 2x ∈-∞，()0f x '<，()f x ；()ln 2,x ∈+∞，()0f x '>，()f x ，∴函数()f x 有唯一极小值，即最小值，没有极大值、最大值.故选：CD.7.答案：BC解析：令，可知在R 上单调递增.由题得，则，所以ln x y =，所以e x y =，所以方程为e x x a =，令()e x g x x =，所以()()1e x g x x +'=，当(),1x ∞∈--时，()()0,g x g x '<单调递减；当()1,x ∞∈-+时，()()0,g x g x '>单调递增，所以()min()1g x g =-=(),1∈-∞-时，()0g x <，且x →-∞，()0g x →，画出()e x g x x =的大致图象如下：由图可知若满足方程e xx a =的有两个解，当且仅当10ea -<<，故选BC.8.答案：AD解析：设年利润为W .当010x <≤时，()()310 2.78.11030x W xR x x x =-+=--，8.1W '=0'=，得9x =（舍负），且当()0,9x ∈时，0W '>；当(]9,10x ∈时，0W '<；所以当9x =时，年利润W 取得最='=x =()e xf x x =+()f x ln e ln e x y x y +=+()()ln f x f y =为9000件时，该公司在这一品牌服装的生产中所获得的年利润最大，且年利润最大值为38.6万元.故选：AD.9.答案：BC 解析：()1f x -=()ln 1g x x x=-+，则()g x '=(0,1)∈时，()0g x '>，()g x 单调递增；当(1,)x ∈+∞时，()0g x '<，()g x 单调递减.故max ()(1)0g x g ==.当0x <<0>，即()1f x >；当x >0<，即()1f x <.故选BC.10.答案：BC解析：()233e x x x f x '-==(),3x ∈-∞时，()0f x '≥，()f x 单调递增，当(3,)x ∈+∞时，()0f x '<，()f x 单调递减，故()f x 有最大值但没有最小值，A 错误.当(),0x ∈-∞时，()0f x <，令()0f x =，得0x =，所以函数()f x 仅有一个零点，()f x 仅有一个极值点，B ，C 正确，D 错误.11.答案：ACD解析：设()()()0f x g x x x =>，则()()()()221e e x x xf x f x x g x x x x '--⎛⎫=== '⎪⎝⎭'，可设()e xg x c x =+，则()1e 0g c =+=，解得e c =-，故()e e xg x x=-，即()e e xf x x =-，令()0g x '>，则1x >，故()gx 在()1,+∞上单调递增，∴()(23g g <<()e e xf x '=-，令()e e 0x f x ='->，解得1x >，则()f x 在()0,1上单调递减，在()1,+∞上单调递增，()f x 在1x =处取得极小值，无最大值，B 错误，C 、D 正确.故应选ACD.12.答案：BD解析：依题意得2ln ()2ln (0)m m x xf x x x x x-=-=>'，若函数()f x 具有“凹凸趋向性”，则2ln m x x =在(0,)+∞上有2个不同的实数根，令()2ln g x x x =，则()2(1ln )g x x =+'，令()0g x '>，解得x >()0x '<，解得0x <<()g x 在10,e ⎛⎫ ⎪⎝⎭上单调递减，在1,e ⎛⎫+∞ ⎪⎝⎭上单调递增，故()g x 的最小值是1e g ⎛⎫= ⎪⎝⎭0x →时，()0g x →，故20e m -<<，故选：BD ．13.答案：BCD解析：因为2()ln 2x f x a x bx =++，0x >，所以()a f x x b x '=++=0>存在极值点，则方程20x bx a ++=有2个不相等的实数根，且至少有一个根为正数，则2400b a b a ⎧->⎪->⎨⎪>⎩或2400b a a ⎧->⎨<⎩，故A 错误；若0a <，则240b a ->，则方程20x bx a ++=有2个不相等的实数根1x ，2x ，且120x x a =<，故方程20x bx a ++=恰有1个正根，即0x >有且只有一个极值点，故B 正确；若()f x 有两个极值点，则方程20x bx a ++=有2个不相等的正根，则24000b a b a ⎧->⎪->⎨⎪>⎩，从而0ab <，故C 正确；若1是0x >的极大值点，则易知方程20x bx a ++=有2个不相等的正根1，3x ，且31x a =>，故D 正确.故选：BCD.14.答案：ACD解析：由题意e x=ln x=()x x =-2x >或2x <-），则()()2ln 2x h x x h x x -+-=--=---，即()h x 为奇函数.()2204x h x x =>-'，()h x 在()2,+∞，(),2-∞-上均单调递增.若()10h x =，则()10h x -=，又()20h x =，所以120x x +=，121212e e e 1x x x x y y +===，故A 正确；若11222e e x x x y ==成立，则有122x x =，与120x x +=矛盾，故B 错误；2121MNy y k x x -==-()e e (2)2x x x x x --=>，则()()()21e 1e 02x x x x m x x--++=>'，所以()m x 在()2,+∞上单调递增，()()22e e 214m x m -->=>，C 正确.令()e xF x x =，()()1e xF x x +'=，当2x >时，()0F x '>，()F x 为增函数，所以()()2222e F x F >=，即2222e x y >，D 正确.15.答案：ABC解析：法一：构造函数：令()2ax f x e ax =-，下探究()f x 的零点：()()221ax f x a xe '=-，()()2242ax f x ae ax ''=+.()()0,0,a f x f x '''>>单调递增，()00f a '=-<，()()121af a e '=-，()10f '∴>故()00,1x ∃∈使()00f x '=，即：20ax e=∴当()0,x x ∈-∞时，()f x 单调递减；当()0x x ∈+∞,时，()f x 单调递增，x →-∞，()f x →+∞，(),x f x →+∞→+∞，()200ax f x e ∴=-0其中()00,1x ∈，所以总∃20x >0x法二：对原等式两边取对数，化简后再求导可简化过程.法三：构造曲线：()200axe ax a -=＞⇔0,xye y y ax⎧-=⎨=⎩，构造曲线：10xyC e y -=:，2C y ax =:，由于1C x ⇔=2y ax =:与其相交，如图：可以得到0，1，2个交点，选ABC.。

六年级生物第二章1-3节预习和限时

第二章第一节环境对生物的影响任务一、环境中的生态因素1.[观察思考] 阅读课本“观察与思考”P14，尝试解决下列问题：[讨论1.2.3.]（1）小麦的生长需要、空气、、土壤和肥料中的。

长颈鹿的生活需要水、、和温度、（树叶）。

（2）小麦生活在相对湿润的环境中，仙人掌生活在的荒漠，但是它们都需要、、、营养物质等生活条件。

牛生活在上，而海豚生活在中，但它们的生活都需要阳光、、水、 (草、小鱼、虾）等条件。

（3）因为农作物的生活需要，干旱使植物不能正常，导致粮食减产。

2.生态因素环境中生物的和的因素叫生态因素，包括因素和因素两方面。

非生物因素----光、温度、水等；生物因素----影响某种生物的生物（包括植物、和其他生物）。

3.生物因素对生物的影响生物圈中的每一种生物都受到周围很多其他生物的影响。

生物与生物之间最常见的是捕食关系。

此外，还有关系关系，等等。

任务二、非生物因素对生物的影响1.探究的一般过程包括：①，②，③，④，⑤，⑥；2.作出假设要根据自己已有的；3.制定计划、设计实验方案时，要紧紧围绕和。

合作探究探究光对鼠妇生活的影响1.提出问题：；2.作出假设：；3.制定计划（即）[材料用具]铁盘、、、湿土（湿吸水纸）、鼠妇（10只）、手表、笔；[操作步骤]①在铁盘内铺上湿土（或两层湿吸水纸）；②以横轴中线为界，将鼠妇放入盘中，两侧的中央各放只鼠妇；③一侧盖上，另一侧盖上，在盘内形成和两种环境；④先静止2分钟然后每隔1分钟统计一下两侧的鼠妇数目，统计10次并记录。

[预期效果] ；4.实施计划；2.表达和交流：实验结束后，鼠妇如何处理？。

【对照实验】上述实验探究中，为了确保实验结果只是由于而引起的，应当使两种环境除以外，、等其他条件都。

也就是说，是这个实验中的。

在研究一种条件对研究对象的影响时，所进行的除了这种条件不同以外，其他条件都相同的实验，叫做；在探究实验中，还需要排除的影响。

拓展反思1.为什么每组用10只鼠妇做实验，只用1只做实验行吗？2.为什么要计算全班的平均值？限时作业一、选择题1.我国戈壁大沙漠中植物稀少，起决定作用的主要非生物因素是（）A.阳光B.温度C.水分D.空气2. “好雨知时节，当春乃发生。

练习一(苏教版语文六下教案)

练习一（苏教版语文六下教案）
教学内容
本节课是苏教版语文六年级下册第一单元的第三课，名为《小小鲤鱼》。

主要
教学内容为通过学习一篇阅读素材，让学生了解鲤鱼的生活习性，引导学生认识到生命的可贵和生态环境的重要性。

教学目标
1.通过阅读《小小鲤鱼》，学生能够初步了解鲤鱼的生活习性和生态环
境。

2.培养学生对生命和生态环境的关注与保护意识。

教学重难点
1.教学重点：了解鲤鱼的生活习性和生态环境，引导学生关注和保护生
命和生态环境。

2.教学难点：通过课文阅读和思考引导学生理解和感受鲤鱼的生活习性
和生态环境，进而培养学生的赏识能力和保护意识。

教学准备
1.教学资料：苏教版语文六年级下册第一单元教材，单元测评卷、学案，
影片《鱼儿的生活》。

2.教学工具：多媒体课件、PPT、黑板、彩色笔、投影仪。

教学过程
一、导入新课
1.首先，教师将放映影片《鱼儿的生活》，让学生通过观看了解鱼类的
生活方式。

2.引导学生思考，为什么要保护生态环境，保护生命？
3.教师提问：。

二年级举一反三精编

火眼金睛数学在我们生活中小朋友，如果给你一组图形，其中有一个图形与其他图形的特征不一样，你能很快辨认出来吗？或者先画了几幅图，要你接着画下去你会画吗？这就要比谁的眼力好了。

我们可以从图形的形状、位置、大小、方向等方面观察、比较。

要学会这种本领，小朋友一定要认真观察，根据前后几个图形的排列，找出变化的规律，才能推算出下面该画什么图形。

【例1】下面一组图中，有一个是不同的，你能找出它吗？请在下面打“√”。

练习1：（1）下面一组图，其中有一个是不同的，你能找出来吗？请在下面打“√”。

（2）你能把与其他不同的找出来吗？请在下面打“√”。

【例2】根据规律接着画。

练习2:（1）按顺序仔细观察图，第三幅“？”处该怎么填？（2）按顺序仔细观察，在“？”处填图。

【例3】请你根据前三个图形的变化规律，画出第四个图形来。

练习3：（1）接下去该怎样画？（2）仔细观察图，在第四幅中应画什么图形？第十幅图应画什么图形？【例4】接着应该怎样画？请画在空格里。

练习4:（1）仔细观察，第四幅图应画什么图形？（2）仔细观察，想一想第三幅图应该怎样填？思维亮剑：凡凡和同学们做游戏时，不小心把新衣服弄破了一块，你能帮凡凡妈妈挑选一块合适的布补上去吗？（把相应的序号填进去）找规律填数数学在我们生活中找规律填数不是很容易能填对的，要运用数的顺序和加减乘除的知识，通过仔细观察，根据同组数排列的顺序和前后、上下之间的相互关系，才能找出数与数之间的排列规律。

【例1】按规律填数。

（1）15，5，12，5，9，5，（），（）（2）5，9，10，8，15，7，（），（）练习1：按规律填数。

（1）25，4，20，4，15，4，（），（）（2）（），（），7，34，7，36，7，38（），（），5，4，9，6，13，8（3）1，16，3，8，9，4，（），（）40，16，20，8，10，4，（），（）【例2】仔细观察，找规律填数。

0，1，2，3，6，7，（），（）练习2：仔细观察，找规律填数。

六年级举一反三(含答案) 第03讲简便运算(二)

简便运算（二）.专题简析：计算过程中，我们先整体地分析算式的特点，然后进行一定的转化，创造条件运用乘法分配律来简算，这种思考方法在四则运算中用处很大。

.例题1计算：1234＋2341＋3412＋4123【思路导航】整体观察全式，可以发现题中的4个四位数均由数1，2，3，4组成，且4个数字在每个数位上各出现一次，于是有原式＝1×1111＋2×1111＋3×1111＋4×1111＝（1＋2＋3＋4）×1111＝10×1111＝11110.练习11．23456＋34562＋45623＋56234＋623452．45678＋56784＋67845＋78456＋845673．124.68＋324.68＋524.68＋724.68＋924.68.例题2计算：2又4/5×23.4＋11.1×57.6＋6.54×28【思路导航】我们可以先整体地分析算式的特点，然后进行一定的转化，创造条件运用乘法分配律来简算。

所以原式＝2.8×23.4＋2.8×65.4＋11.1×8×7.2＝2.8×（23.4＋65.4）＋88.8× 7.2＝2.8×88.8＋88.8×7.2＝88.8×（2.8＋7.2）＝88.8×10＝888.练习2计算下面各题：1．99999×77778＋33333×666662．34.5×76.5－345×6.42－123×1.453．77×13＋255×999＋510.例题3计算（1993×1994－1）/（1993＋1992×1994）【思路导航】仔细观察分子、分母中各数的特点，就会发现分子中1993×1994可变形为1992＋1）×1994=1992×1994＋1994，同时发现1994－1 = 1993，这样就可以把原式转化成分子与分母相同，从而简化运算。

河北省唐山市2023-2024三下数学《除数是一位数的除法》人教版基础掌握过关卷

河北省唐山市2023-2024三下数学《除数是一位数的除法》人教版基础掌握过关卷学校：_______ 班级：__________姓名：_______ 考号：__________（满分：100分时间：60分钟）总分栏题号一二三四五六七总分得分评卷人得分一、填一填。

（每空1分，共25分）1.98÷6的商是( )位数；270×9的积是( )位数。

2.学校新买来了132本书，平均分给8个班，每班分( )本，还剩( )本。

3.880÷80的商是．4.老师给班里同学发棒棒糖，如果给每个同学多发3个，老师剩下的棒棒糖就变少30个，那么班里共有_______个同学。

5.□58÷5，要使商是三位数，□里最小填( )；要使商是两位数，□里最大填( )。

7.在一道除法算式中，余数是5，除数比余数多2，商是除数的2倍，被除数是( )。

8.在一道除法算式里，除数是3，商是除数的3倍，余数是2，被除数是( )。

9.( )的3倍是360；495是9的( )倍。

10.312÷4与4÷312 的意义和计算结果都不同．．11.一个数除以6，商是13，当余数最大时，被除数是( )。

评卷人得分二、辨一辨。

（对的在括号中打“√”，错的打“×”）（每题1分，共5分）1.721÷9估算的结果是80。

( )2.一本相册每页可插6张照片，145张照片最多可插满24页，剩下1张。

( )3.8×0＝0÷8。

( )4.被除数是三位数，除数是一位数，商可能是三位数，也可能是两位数。

（判断对错）5.9□4÷3，要使商的中间有0，余数也为0，□里只能填2。

( )评卷人得分三、选一选。

（把正确答案的序号填在括号里）（每题2分，共10分）1.下列算式中，结果是二十多的是（）。

A．64÷5B．51－32C．85÷3D．71÷22.一支仪仗队共222人，每6人排成一行，相邻两行都相距1米，这支仪仗队长（）。

《婴幼儿动作发展与指导》配套教案

《婴幼儿动作发展与指导》配套教案示例文章篇一：《婴幼儿动作发展与指导》教案一、课题婴幼儿动作发展与指导二、教学目标1. 让学生了解婴幼儿动作发展的基本规律和阶段特征。

2. 使学生掌握不同阶段婴幼儿动作发展的指导方法。

3. 培养学生对婴幼儿动作发展的重视和关注，提高学生的育儿意识。

三、教学重点&难点1. 教学重点- 婴幼儿大动作（如抬头、翻身、坐立、爬行、站立、行走等）和精细动作（如抓握、捏取等）发展的顺序和特点。

- 根据婴幼儿动作发展阶段给予正确的指导方法。

2. 教学难点- 理解婴幼儿动作发展过程中的个体差异，并能针对差异进行个性化的指导。

- 如何将理论知识转化为实际的指导操作，尤其是在家庭环境中。

四、教学方法1. 讲授法：讲解婴幼儿动作发展的理论知识。

2. 案例分析法：通过实际的婴幼儿动作发展案例，分析其中的问题和解决方法。

3. 小组讨论法：组织学生分组讨论不同阶段婴幼儿动作发展的指导策略，促进学生之间的交流与合作。

五、教学过程（一）课程导入（5分钟）教师：同学们，你们有没有见过小婴儿啊？（学生回答有）那你们有没有注意到小婴儿刚开始的时候连头都抬不起来，过了几个月就能坐起来，然后慢慢就会爬会走了呢？这就是婴幼儿动作发展的神奇之处。

今天我们就来好好研究一下婴幼儿动作发展与指导。

（二）婴幼儿大动作发展（20分钟）1. 教师讲解- 教师：同学们，首先我们来讲讲婴幼儿大动作发展。

在0 - 3个月的时候，小婴儿主要是会一些反射动作，像吸吮反射、握持反射。

3 - 6个月呢，他们开始能抬头了，就像小豆芽从土里慢慢冒尖一样。

这时候我们可以在宝宝清醒的时候让他趴在床上，用一些颜色鲜艳的小玩具在他眼前晃动，吸引他抬头看。

- 6 - 9个月的时候，很多宝宝就会翻身了。

这就像小虫子在地上翻了个身一样有趣。

家长要给宝宝创造足够的空间，周围不要有危险的东西，让他能自由地翻身。

- 9 - 12个月，宝宝开始尝试坐立。

江西省鹰潭市2024-2025学年三下数学《除数是一位数的除法》人教版综合诊断模拟卷

江西省鹰潭市2024-2025学年三下数学《除数是一位数的除法》人教版综合诊断模拟卷学校：_______ 班级：__________姓名：_______ 考号：__________（满分：100分时间：60分钟）总分栏题号一二三四五六七总分得分评卷人得分一、填一填。

（每空1分，共25分）1.386÷3的商是( )位数，最高位在( )。

2.估算349÷5时，把349看作( )，349÷5≈( )，商比估算结果( )（填“大”或“小”）。

3.△－○＝32，△＝○＋○＋○＋○＋○，则△＝( )，○＝( )。

4.625÷5商的最高位是( )位，商是( )位数。

5.648÷8的商是( )位数，商的最高位在( )位上。

6.409÷4的商是( )位数，409÷7的商是( )位数。

7.318÷□的商是三位数，□里最大能填( )。

8.□÷3＝69……○，○最大是( )，当○最大时，□是( )。

9.从364里连续减去7，减( )次正好为0。

10.□26÷7，要使商是三位数，□里最小填( )；要使商是两位数，□里最大填( )。

11.□24÷6，如果商是两位数，那么□里最大填( )；如果商是三位数，那么商的最高位上的数是( )。