实验四 MATLAB图形绘制 (1)

河北工业大学MATLAB实验四

2014秋2012级《MATLAB 程序设计》实验报告一、实验目的：1、掌握MATLAB 二维图形绘制命令及其图形控制；2、熟悉MATLAB 三维图形绘制命令及其图形控制；3、熟悉特殊二维图形、三维图形的绘制方法。

二、实验内容：1、在同一坐标系下绘制下面三个函数在[0,40]t ∈的图象，要求三种曲线采用不同颜色以及不同的线型，同时对每条曲线利用函数进行标注，并添加图例。

120.134sin()t y t y y e t π-===2、编写程序，选择合适的步距，绘制下面函数在区间[-6,6]中的图象，并对分段的曲线进行标注，同时添加x 轴和y 轴的说明。

sin ,0(),036,3x x y x x x x x ≤⎧⎪=<≤⎨⎪-+>⎩3、利用subplot 函数在同一绘图窗口中用不同颜色和线型绘制以下两个函数在t ∈[-2π,2π]范围内的图象。

0.50.21222t t y y e -==4、某学校有30位教师,其中教授5人,副教授8人,讲师12人,助教5人.试画出职称比例结构饼图，并强调图形的教授部分同时添加标注。

5、生成1×10维的随机数向量a ，分别用红、黄、蓝、绿色绘出其连线图、脉冲图、阶梯图和条形图，并分别标出标题“连线图”、“脉冲图”、“阶梯图”、“条形图”。

6、使用subplot 函数，把图形窗口分成两个部分，分别绘制sin2t 和3cos3t 曲线,t 范围:0-5.要求前者用红色实线，数据点形状为五角星,有网格线，x 轴加标注“x ”，y 轴加标注“y=sin2t ”,加题目“y=sin2t 的曲线”；后者用蓝色虚线，数据点形状为圆形，无网格线，x 轴加标注“x ”，y 轴加标注“y=3cos3t ”,加题目“y=3cos3t 的曲线”；7、绘制下列三维曲线:(1)/20/20cos sin ,02t t x e ty e t t z t π--⎧=⎪=≤≤⎨⎪=⎩ (2) 23,01x t y t t z t =⎧⎪=≤≤⎨⎪=⎩8、绘制下列曲面图，并调整三维图的视角、背景色、着色以及透视效果。

matlab实验指导2019-11-12

实验1 熟悉软件环境和基本的操作一、实验目的熟悉MATLAB运行环境和了解基本操作。

二、实验内容MATLAB的启动、操作界面组成1．熟悉MATLAB图形界面打开MATLAB，单击命令窗口菜单栏中的各个下拉菜单按钮，试使用各个按钮引出的选项；把光标移动到工具栏中各个图标上（不要按下），查看它们与菜单选项的对应情况。

2．熟悉MATLAB的基本命令。

在命令窗口中分别键入以下内容，以建立若干变量：A=[1 2;3 4;5 6]B=[7,8,9;10,11,12]C=[5 6 7;1 8 3];D=B+C问题1：如何输入一个矩阵变量的行元素和列元素？问题2：观察每行命令后是否加“;”，对显示执行结果有什么区别？键入以下命令或执行操作，查看效果，并体会命令功能：(1)工作空间管理。

whowhosclear A（2）路径编辑。

试用菜单File/Set Path将D盘根目录及其下的所有子目录和文件夹包含进来，设为搜索路径。

问题3：当前路径是什么？问题4：搜索路径是什么意思？（3）联机帮助help pausehelpwin（4）窗口清理。

先画出正弦函数在0-2π之间的图形，再用以下各种窗口清理命令，看每项命令都清除了什么。

figureplot(sin(0:0.1:6.28))claclfclose注意：figure为打开一幅图形图像窗口close为关闭当前图形图像窗口，而close all为关闭所有已打开的图形图像窗口。

（5）MATLAB基本矩阵操作演示playshow intro（6）MATLAB图形绘制演示playshow buckydem（7）MATLAB数学功能演示（快速傅氏变换）playshow fftdemo（8）MATLAB三维造型演示（茶壶演）playshow teapotdemo3．打开MATLAB命令窗口，键入demos，观看演示程序。

三、思考题1．将pi分别用15位数字格式、分数格式、十六进制格式、5位数字的科学计数法显示。

实验4 matlab gui设计

实验四 MATLAB GUI设计一．预备知识点1. 图形用户界面（GUI）是用户与计算机程序之间的交互方式，是用户与计算机进行信息交流的方式。

计算机在屏幕显示图形和文本，若有扬声器还可产生声音。

用户通过输入设备，如：键盘、鼠标、跟踪球、绘制板或麦克风，与计算机通讯。

用户界面设定了如何观看和如何感知计算机、操作系统或应用程序。

通常，多是根据悦目的结构和用户界面功能的有效性来选择计算机或程序。

图形用户界面或GUI是包含图形对象，如：窗口、图标、菜单和文本的用户界面。

以某种方式选择或激活这些对象，通常引起动作或发生变化。

最常见的激活方法是用鼠标或其它点击设备去控制屏幕上的鼠标指针的运动。

按下鼠标按钮，标志着对象的选择或其它动作。

2.对“句柄图形”的理解是设计和实现GUI的先决条件。

由图形命令生成的每一事物是一个图形对象。

图形对象不仅包括uimenu和uicontrol对象，而且还包括图形、坐标轴和他们的子对象。

让我们从另一个角度来看这一层次结构。

计算机的屏幕本身是根结点，图形是根对象的子对象，坐标轴，uimenu ，uicontrol是图形的子对象。

根可以包括多个图形，每个图形含有一组或多组坐标轴以及其子对象，每个图形也可以有一个或多个与坐标轴无关的uimenu和uicontrol。

虽然uicontrol对象无子对象结点，但他们确实具有多种类型。

uimenu对象常将其它的uimenu对象作为其子对象。

3. MATLAB的图形用户界面设计实际上是一种面向对象的设计方法。

假设想建立一个图形界面来显示和处理二维图形的颜色、线型及数据点的图标。

要求其基本功能是：（1）建立一个主坐标系，用来显示要绘制的二维图形；（2）建立一个列表框，允许用户选择不同的着色方法；（3）建立一组按扭，用于处理二维图形线型和数据点的图标；（4）为图形界面加入菜单项，用于决定坐标轴是否显示及坐标轴上是否需要网格；（A）最初图形界面的设想如下图所示：（B）根据上面的设想，下面我们就来制作它的图形用户界面：首先，我们先来看其图形窗口的设置。

MATLAB实验报告(1-4)

信号与系统MATLAB第一次实验报告一、实验目的1.熟悉MATLAB软件并会简单的使用运算和简单二维图的绘制。

2.学会运用MATLAB表示常用连续时间信号的方法3.观察并熟悉一些信号的波形和特性。

4.学会运用MATLAB进行连续信号时移、反折和尺度变换。

5.学会运用MATLAB进行连续时间微分、积分运算。

6.学会运用MATLAB进行连续信号相加、相乘运算。

7.学会运用MATLAB进行连续信号的奇偶分解。

二、实验任务将实验书中的例题和解析看懂，并在MATLAB软件中练习例题，最终将作业完成。

三、实验内容1.MATLAB软件基本运算入门。

1). MATLAB软件的数值计算：算数运算向量运算：1.向量元素要用”[ ]”括起来，元素之间可用空格、逗号分隔生成行向量，用分号分隔生成列向量。

2.x=x0:step:xn.其中x0位初始值，step表示步长或者增量，xn 为结束值。

矩阵运算：1.矩阵”[ ]”括起来；矩阵每一行的各个元素必须用”,”或者空格分开；矩阵的不同行之间必须用分号”;”或者ENTER分开。

2.矩阵的加法或者减法运算是将矩阵的对应元素分别进行加法或者减法的运算。

3.常用的点运算包括”.*”、”./”、”.\”、”.^”等等。

举例：计算一个函数并绘制出在对应区间上对应的值。

2).MATLAB软件的符号运算：定义符号变量的语句格式为”syms 变量名”2.MATLAB软件简单二维图形绘制1).函数y=f(x)关于变量x的曲线绘制用语：>>plot(x,y)2).输出多个图像表顺序：例如m和n表示在一个窗口中显示m行n列个图像，p表示第p个区域，表达为subplot(mnp)或者subplot(m,n,p)3).表示输出表格横轴纵轴表达范围：axis([xmax,xmin,ymax,ymin])4).标上横轴纵轴的字母：xlabel(‘x’),ylabel(‘y’)5).命名图像就在subplot写在同一行或者在下一个subplot前：title(‘……’)6).输出：grid on举例1：举例2：3.matlab程序流程控制1).for循环：for循环变量=初值:增量:终值循环体End2).while循环结构：while 逻辑表达式循环体End3).If分支：(单分支表达式)if 逻辑表达式程序模块End(多分支结构的语法格式)if 逻辑表达式1程序模块1Else if 逻辑表达式2程序模块2…else 程序模块nEnd4).switch分支结构Switch 表达式Case 常量1程序模块1Case 常量2程序模块2……Otherwise 程序模块nEnd4.典型信号的MATLAB表示1).实指数信号：y=k*exp(a*t)举例：2).正弦信号：y=k*sin(w*t+phi)3).复指数信号：举例：4).抽样信号5).矩形脉冲信号:y=square(t,DUTY) (width默认为1)6).三角波脉冲信号：y=tripuls(t,width,skew)(skew的取值在-1~+1之间，若skew取值为0则对称)周期三角波信号或锯齿波:Y=sawtooth(t,width)5.单位阶跃信号的MATLAB表示6.信号的时移、反折和尺度变换:Xl=fliplr(x)实现信号的反折7.连续时间信号的微分和积分运算1).连续时间信号的微分运算：语句格式：d iff(function,’variable’,n)Function:需要进行求导运算的函数，variable:求导运算的独立变量，n：求导阶数2).连续时间信号的积分运算：语句格式：int(function,’variable’,a,b)Function:被积函数variable:积分变量a:积分下限b:积分上限(a&b默认是不定积分)8.信号的相加与相乘运算9.信号的奇偶分解四、小结这一次实验让我能够教熟悉的使用这个软件，并且能够输入简单的语句并输出相应的结果和波形图，也在一定程度上巩固了c语言的一些语法。

MATLAB实验指导书(附答案)

MATLAB基础实验指导书漳州师范学院物电系2010年10月目录实验一MATLAB环境的熟悉与基本运算 (2)实验二MATLAB数值运算 (8)实验三MATLAB语言的程序设计 (12)实验四MATLAB的图形绘制 (16)实验五采用SIMULINK的系统仿真 (20)实验六MATLAB在电路中的应用 (25)实验七MATLAB在信号与系统中的应用 (27)实验八MATLAB在控制理论中的应用 (29)实验一 MATLAB环境的熟悉与基本运算一、实验目的：1．熟悉MATLAB开发环境2．掌握矩阵、变量、表达式的各种基本运算二、实验基本知识：1.熟悉MATLAB环境:MATLAB桌面和命令窗口、命令历史窗口、帮助信息浏览器、工作空间浏览器文件和搜索路径浏览器。

2.掌握MATLAB常用命令3.MATLAB变量与运算符变量命名规则如下：（1）变量名可以由英语字母、数字和下划线组成（2）变量名应以英文字母开头（3）长度不大于31个（4）区分大小写MATLAB中设置了一些特殊的变量与常量，列于下表。

MATLAB运算符，通过下面几个表来说明MATLAB的各种常用运算符表2 MATLAB算术运算符表3 MATLAB关系运算符表4 MATLAB逻辑运算符表5 MATLAB特殊运算4.MATLAB的一维、二维数组的寻访表6 子数组访问与赋值常用的相关指令格式5.MATLAB的基本运算表7 两种运算指令形式和实质内涵的异同表6.MATLAB的常用函数表8 标准数组生成函数表9 数组操作函数三、实验内容1、学习使用help命令，例如在命令窗口输入help eye，然后根据帮助说明，学习使用指令eye（其它不会用的指令，依照此方法类推）2、学习使用clc、clear，观察command window、command history和workspace等窗口的变化结果。

3、初步程序的编写练习，新建M-file，保存（自己设定文件名，例如exerc1、exerc2、exerc3……），学习使用MATLAB的基本运算符、数组寻访指令、标准数组生成函数和数组操作函数。

MATLAB实验

实验一MATLAB操作基础一、实验目的1、熟悉MATLAB的操作环境及基本操作方法。

2、掌握MATLAB的搜索路径及其设置方法。

3、熟悉MATLAB帮助信息的查阅方法。

二、实验内容1、先建立自己的工作目录，再将自己的工作目录设置到MATLAB搜索路径下，再试验用help命令能否查询到自己的工作目录。

2、在MATLAB环境下验证例1-1至1-4，并完成以下题目：（1）绘制右图所示图形（23、利用MATLAB的帮助功能分别查询inv，plot、max、round等函数的功能及用法。

4、在工作空间建立一个变量a ,同时在当前目录下建立一个M文件：a.m，试在命令窗口输入a，观察结果，并解释原因。

三、思考练习1、help命令和lookfor命令有什么区别？2、什么是工作空间？假定有变量A与B存在于工作空间中，如何用命令保存这两个变量？下次重新进入MATLAB后，又如何装载这两个变量？实验二MATLAB数值计算一、实验目的1、掌握MATLAB变量和数据操作2、掌握MATLAB矩阵及其操作3、掌握MATLAB矩阵运算二、实验内容1、求下列表达示的值（1）6(10.3424510)w-=+⨯（2）22tan()b ca eabcxb c aππ++-+=++，其中a=3.5 ,b=5 ,c=-9.8（3）21ln(2tz e t=+，其中213[]50.65it-=-2、已知1540783617A--⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，831253320B-⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦求下列表达式的值：（1）A+6B和2A B I-+(I为单位矩阵)（2）A*B、A.*B和B*A（3）A/B及B\A（4）[A,B] 和[A([1,3],:) ; B^2]3、建立一个均值为3，方差为1的10*10的正态分布随机矩阵，并将矩阵中大于0的元素置1，小于0的置0.4、当[34,,,,,,0]A NaN Inf Inf pi eps=--时，求函数all(A),any(A),isnan(A),isinf(A),isfinite(A)的值。

(打印)实验四 MATLAB 高级图形绘制

实验四MATLAB 高级图形绘制一、实验目的及要求：1.熟悉各种绘图函数的使用；2.掌握图形的修饰方法和标注方法；3.了解MATLAB 中图形窗口的操作。

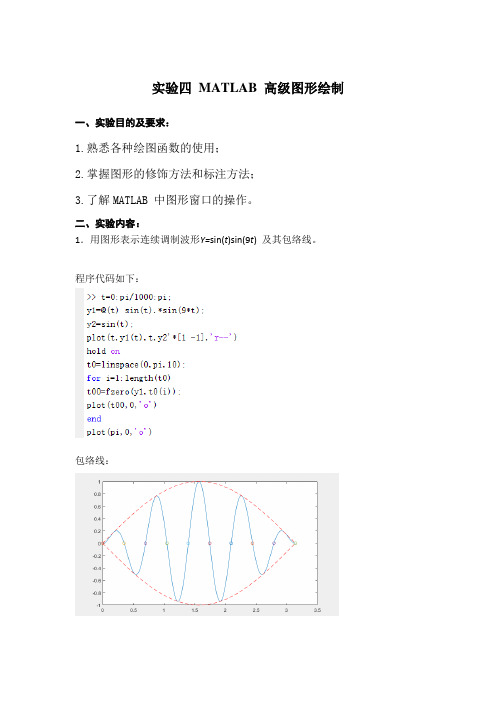
二、实验内容：1．用图形表示连续调制波形Y=sin(t)sin(9t)及其包络线。

程序代码如下：包络线：2．x=［－2π，2π］，y1=sinx、y2=cosx、y3=sin2x、y4=cos 2x①用MATLAB语言分四个区域分别绘制的曲线，并且对图形标题及横纵坐标轴进行标注。

程序：结果：②另建一个窗口，不分区，用不同颜色、线型绘出四条曲线，并标注图例注解。

程序：结果：③绘制三维曲线：⎪⎩⎪⎨⎧=≤≤==)cos()sin()200()cos()sin(t t t z t t y t x π程序：结果：3．绘制极坐标曲线ρ=asin(b+nθ),并分析参数a、b、n对曲线形状的影响。

（1）a=1;b=1;n=1（2）a=10;b=1;n=1（3）a=10;b=10;n=1 （4）a=10;b=10;n=10参数a、b、n对曲线形状的影响：由上面绘制的图形可知：a决定图形的大小，当a为整数时，图形半径大小就是a；b决定图形的旋转角度，图形的形状及大小不变；n决定图形的扇叶数，当n 为奇数时，扇叶数为n，当n为偶数时，扇叶数为2n。

三、结论本次实验用到了曲线绘图、三位曲线绘图的知识，与老师上课的内容一致，让我学的matlab绘图的知识得到了巩固，我还学会了如何使用title、subplot、plot、axis等函数。

在做实验的过程复习了hold on指令是覆盖函数继续绘图的意思。

matlab实验四数据可视化方法

实验四数据可视化方法[实验目的]1．掌握曲线绘制的基本技法和指令，会使用线形、色彩、数据点标记表现不同数据的特征，掌握生成和运用标识注释图形。

2．进一步掌握函数编写及数据可视化方法。

[实验原理]MATLAB 提供了相当强大的可视化指令，通过这些指令，我们可以非常简单地实现数据的可视化。

首先我们来看离散数据和离散函数的可视化方法。

对于离散实函数y n=f(x n)，当x n以递增（或递减）次序取值时，根据函数关系可以求得同样数目的y n，当把这两组向量用直角坐标中的点次序图示时，就实现了离散函数的可视化。

当然这种图形上的离散序列所反映的只是某确定的有限区间内的函数关系，不能表现无限区间上的函数关系。

通常我们可以采用plot 或者stem 来实现。

只是需要注意的是使用plot 时，需要使用星号或者点等标识来表示数据点，比如plot(x n,y n,’r*’,’MarkerSize’,20)，就表示用字号20的红色星点来标识数据点,此时为了便于观察，通常随后加上一条语句“grid on”，即给图形加上坐标方格。

而采用stem 标识数据点的格式是stem(x n,y n)。

连续函数的可视化与离散函数可视化类似，也必须先在一组离散自变量上计算相应的函数值，并把这一组“数据点”用点图示。

但这些离散的点不能表现函数的连续性。

为了进一步表示离散点之间的函数函数情况，MATLAB 有两种常用处理方法：一是对区间进行更细的分割，计算更多的点，去近似表现函数的连续变化；或者把两点用直线连接，近似表现两点间的（一般为非线性的）函数形状。

但要注意，倘若自变量的采样点不足够多，则无论哪种方法都不能真实地反映原函数。

对于二维数据，常用指令仍旧是plot。

对于离散数据，plot指令默认处理方法是：自动地把这些离散数据用直线（即采用线性插值）连接，使之成为连续曲线。

对于三维图形的表示，通常有plot3 等指令。

通常，绘制二维或三维图形的一般步骤如下表所示：说明：●步骤1、3 是最基本的绘图步骤，一般来说，由这两步所画出的图形已经具备足够的表现力。

《Matlab语言基础》教学大纲-通信工程

《Matlab语言基础》教学大纲一、课程基本信息课程名称：Matlab语言基础课程编码：58082014课程类别：专业选修课适用专业：通信工程开课学期：2-1课程学时：32学时课程学分：2学分先修课程：C语言、高等数学、线性代数并修课程：课程简介：MATLAB是矩阵实验室（Matrix Laboratory）的简称，是美国MathWorks公司出品的商业数学软件，用于算法开发、数据可视化、数据分析及数值计算的高级技术计算语言和交互式环境，应用于工程计算、控制设计、信号处理与通信、图像处理、信号检测、金融建模设计与分析等各个领域。

Matlab语言在高校与研究单位起着重大的作用，是通用的科学计算、数值仿真和可视化及动态仿真的重要工具。

二、课程教育目标了解Matlab 的特点；理解Matlab 的数值计算、程序设计、绘图功能及在通信工程的科学计算和建模中的应用；掌握Matlab语言的基本编程思想和方法。

三、课程教学内容、要求及学时安排第一章 MATLAB概述【教学内容】1．Matlab 的特点、绪论；2．Matlab 快速入门；【教学要求】1．熟悉MATLAB命令窗口及文件管理，MATLAB帮助系统。

2．掌握命令行的输入及编辑，用户目录及搜索路径的设置。

3．了解MATLAB的主要功能。

【教学方法】采用多媒体教学方式，结合Matlab仿真软件进行课堂演示。

【学时】2第二章 MATLAB数据和数值计算【教学内容】1． MATLAB数据类型；2. 基本运算符；3．矩阵运算；4．数组运算；【教学要求】1．熟悉MATLAB变量的命名，赋值语句，数据的输出格式。

熟悉傅立叶分析，常微分方程的数值求解，非线性方程度数值求解。

2．掌握矩阵的建立、拆分及冒号表达式，MATLAB运算，结构数据和单元数据，字符串；掌握矩阵分析，数据处理。

3．了解MATLAB数据的特点。

【教学方法】采用多媒体教学方式，结合Matlab仿真软件进行课堂演示。

MATLAB作图(超详细)

2020/5/31
数学建模
3. 对数坐标图
在很多工程问题中,通过对数据进行对数转换可以更清晰地看出数据的某些特征,在对数坐标系中描绘数据点的曲线,可以直接地表现对数转换.对数转换有双对数坐标转换和单轴对数坐标转换两种.用loglog函数可以实现双对数坐标转换,用semilogx和semilogy 函数可以实现单轴对数坐标转换. loglog(Y) 表示 x、y坐标都是对数坐标系
单击鼠标左键，则在当前图形窗口中，以鼠标点中的点为中心的图形放大2倍；单击鼠标右键，则缩小2倍.
zoom off 关闭缩放模式
grid on
%标注格栅
MATLAB liti37
例创建一个简单的半对数坐标图. 解输入命令:
x=0:.1:10;
semilogy(x,10.^x)
MATLAB liti38
例绘制y=x3的函数图、对数坐标图、半对数坐标图.
2020/5/31
MATLAB liti22 数学建模
返回
三维图形 1. 空间曲线 2. 空间曲面
semilogx(Y) 表示 x坐标轴是对数坐标系
semilogy(…) 表示y坐标轴是对数坐标系
plotyy 有两个y坐标轴，一个在左边，一个在右边
2020/5/31
数学建模
例用方形标记创建一个简单的loglog.
解输入命令:
x=logspace(-1,2);
loglog(x,exp(x),’-s’)
数学建模
返回
2. 定制坐标 Axis([xmin xmax ymin ymax zmin zmax])定制图形坐标
x、y、z的最大、最小值
Axis
将坐标轴返回到自动缺省值

MATLAB实验报告

班级：通信班姓名：彭羊平学号： 222008315222033实验一：matlab的基本操作一、实验目的：1、了解MATLAB的集成环境，熟悉其基本操作。

2、了解MATLAB的基础知识，包括矩阵的建立、简单操作、逻辑操作和关系运算。

3、熟悉基本的数学函数和逻辑函数。

4、在命令窗口输入命令完成一些简单的功能，为MATLAB程序设计奠定基础。

二、实验内容：1、利用diag等函数产生下列矩阵：然后利用reshape函数将它们变换成行向量。

2、利用rand函数产生（0,1）间均匀分布的10*10随机矩阵A，然后统计A中大于等于0.6的元素的个数。

3、有一矩阵A，找出矩阵中值大于1的元素，并将它们重新排列成列向量B。

4、在一测量矩阵A(6*6)，存在有奇异值（假设大于100的值为奇异值），编程实现删去奇异值所在的行。

三、实验结果：1、程序如下：a=fliplr(diag([8,-7,2])+diag([5,3],-1))a=reshape(a,1,9)b=diag([2,5,8])+diag([4],2)+diag([7],-2) b=reshape(b,1,9)结果如下：2、程序如下：A=rand(10)A=A>0.6sum(sum(A))结果如下：3、程序如下：A=fix(5*rand(5))a=A>1;K=find(a);for k=1:length(K)B(k)=A(K(k));endB=B'结果如下：4、程序如下：A=fix(100*rand(8))+5 B=A>100;k=find(any(B'))A(k,:)=0结果如下:班级：通信班姓名：彭羊平学号： 222008315222033实验二： matlab绘图（1）一、实验目的：1、了解MATLAB图形系统和各种图形函数。

2、熟悉MATLAB的基本图形操作，具备MATLAB画图能力。

3、熟悉各种数学函数，并通过图形函数画出。

《Matlab语言》实验四

《Matlab语言》实验四实验四、Matlab的程序设计（一）实验目的1.掌握利用if语句实现选择结构的方法。

2.掌握利用witch语句实现多分支选择结构的方法。

3.掌握利用for 语句实现循环结构的方法。

4.掌握利用while语句实现循环结构的方法。

5.掌握Matlab函数的编写及调试方法。

(二）实验环境1．计算机2．MATLAB7.0集成环境（三）实验内容1、编写一个函数，计算下面函数的值，给出标量某的值，调用该函数后，返回y的值。

functiony=myfun1(某)in某,y(某)某,某6,某00某3某3选择一些数据测试你编写的函数。

function[y]=myfun1(某)if某<=0 y=in(某);eleif某>0&某<=3y=某;eleif某>3y=-某+6;End结果:>>某=5;>>[y]=myfun1(某)y=12、编写一个函数求向量某中元素的平均值、最大值、最小值、均方根值。

function[m_某,ma某_某,min_某,rm_某]=myfun2(某)方均根值(RootMeanSquare)的计算公式为：rm1NNi1某i2用下面数据测试你写的函数：function[m_某,ma某_某,min_某,rm_某]=myfun2(某)%求平均值um_某=um(某);%向量元素求和[m,n]=ize(某);%最好用n=length(某);m_某=um_某/n;%求最大值采用逐个比较方式if某(1)>某(2)ma某_某=某(1);ele ma某_某=某(2);endfork=3:nifma某_某elema某_某=ma某_某;%可省略endend%求最小值if某(1)min_某=某(2);endfork=3:nifmin_某>某(k)min_某=某(k);elemin_某=min_某;%可省略endend%求均方根值um_某2=0;fork=1:num_某2=um_某2+某(k).^2;rm_某=qrt(um_某2/n);endm_某;ma某_某;min_某;rm_某;%按照函数值行（1）某=in(0:0.01:6某pi)运行结果:>>某=in(0:0.01:6某pi);>>[m_某,ma某_某,min_某,rm_某]=myfun2(某)m_某=-1.1256e-007ma某_某=1.0000min_某=-1.0000rm_某=0.7071（2）某=rand(1,200)，得到的某为200个（0，1）之间均匀分布的随机数。

数字图像处理及MATLAB实现实验四——图像变换

数字图像处理及MATLAB实现实验四——图像变换1.图像的傅⾥叶变换⼀（平移性质）傅⾥叶变换的平移性质表明了函数与⼀个指数项相乘等于将变换后的空域中⼼移到新的位置，并且平移不改变频谱的幅值。

I=imread('1.bmp');figure(1)imshow(real(I));I=I(:,:,3);fftI=fft2(I);sfftI=fftshift(fftI); %求离散傅⾥叶频谱%对原始图像进⾏⼆维离散傅⾥叶变换，并将其坐标原点移到频谱图中央位置RRfdp1=real(sfftI);IIfdp1=imag(sfftI);a=sqrt(RRfdp1.^2+IIfdp1.^2);a=(a-min(min(a)))/(max(max(a))-min(min(a)))*225;figure(2)imshow(real(a));I=imread('2.bmp');figure(1)imshow(real(I));I=I(:,:,3);fftI=fft2(I);sfftI=fftshift(fftI); %求离散傅⾥叶频谱%对原始图像进⾏⼆维离散傅⾥叶变换，并将其坐标原点移到频谱图中央位置RRfdp1=real(sfftI);IIfdp1=imag(sfftI);a=sqrt(RRfdp1.^2+IIfdp1.^2);a=(a-min(min(a)))/(max(max(a))-min(min(a)))*225;figure(2)imshow(real(a));I=imread('3.bmp');figure(1)imshow(real(I));I=I(:,:,3);fftI=fft2(I);sfftI=fftshift(fftI); %求离散傅⾥叶频谱%对原始图像进⾏⼆维离散傅⾥叶变换，并将其坐标原点移到频谱图中央位置RRfdp1=real(sfftI);IIfdp1=imag(sfftI);a=sqrt(RRfdp1.^2+IIfdp1.^2);a=(a-min(min(a)))/(max(max(a))-min(min(a)))*225;figure(2)imshow(real(a));实验结果符合傅⾥叶变换平移性质2.图像的傅⾥叶变换⼆（旋转性质）%构造原始图像I=zeros(256,256);I(88:168,124:132)=1; %图像范围是256*256，前⼀值是纵向⽐，后⼀值是横向⽐imshow(I)%求原始图像的傅⾥叶频谱J=fft2(I);F=abs(J);J1=fftshift(F);figureimshow(J1,[550])%对原始图像进⾏旋转J=imrotate(I,90,'bilinear','crop');figureimshow(J)%求旋转后图像的傅⾥叶频谱J=fft2(I);F=abs(J);J2=fftshift(F);figureimshow(J2,[550])3.图像的离散余弦变换⼀%对cameraman.tif⽂件计算⼆维DCT变换RGB=imread('cameraman.tif');figure(1)imshow(RGB)I=rgb2gray(RGB);%真彩⾊图像转换成灰度图像J=dct2(I);%计算⼆维DCT变换figure(2)imshow(log(abs(J)),[])%图像⼤部分能量集中在左上⾓处figure(3);J(abs(J)<10)=0;%把变换矩阵中⼩于10的值置换为0，然后⽤idct2重构图像K=idct2(J)/255;imshow(K)4.图像的离散余弦变换⼆% I=imread('1.bmp');% figure(1)% imshow(real(I));% I=I(:,:,3);% fftI=fft2(I);% sfftI=fftshift(fftI); %求离散傅⾥叶频谱% %对原始图像进⾏⼆维离散傅⾥叶变换，并将其坐标原点移到频谱图中央位置% RRfdp1=real(sfftI);% IIfdp1=imag(sfftI);% a=sqrt(RRfdp1.^2+IIfdp1.^2);% a=(a-min(min(a)))/(max(max(a))-min(min(a)))*225;% figure(2)% imshow(real(a));% I=imread('2.bmp');% figure(1)% imshow(real(I));% I=I(:,:,3);% fftI=fft2(I);% sfftI=fftshift(fftI); %求离散傅⾥叶频谱% %对原始图像进⾏⼆维离散傅⾥叶变换，并将其坐标原点移到频谱图中央位置% RRfdp1=real(sfftI);% IIfdp1=imag(sfftI);% a=sqrt(RRfdp1.^2+IIfdp1.^2);% a=(a-min(min(a)))/(max(max(a))-min(min(a)))*225;% figure(2)% imshow(real(a));% I=imread('3.bmp');% figure(1)% imshow(real(I));% I=I(:,:,3);% fftI=fft2(I);% sfftI=fftshift(fftI); %求离散傅⾥叶频谱% %对原始图像进⾏⼆维离散傅⾥叶变换，并将其坐标原点移到频谱图中央位置% RRfdp1=real(sfftI);% IIfdp1=imag(sfftI);% a=sqrt(RRfdp1.^2+IIfdp1.^2);% a=(a-min(min(a)))/(max(max(a))-min(min(a)))*225;% figure(2)% imshow(real(a));% %构造原始图像% I=zeros(256,256);% I(88:168,124:132)=1; %图像范围是256*256，前⼀值是纵向⽐，后⼀值是横向⽐% imshow(I)% %求原始图像的傅⾥叶频谱% J=fft2(I);% F=abs(J);% J1=fftshift(F);figure% imshow(J1,[550])% %对原始图像进⾏旋转% J=imrotate(I,90,'bilinear','crop');% figure% imshow(J)% %求旋转后图像的傅⾥叶频谱% J=fft2(I);% F=abs(J);% J2=fftshift(F);figure% imshow(J2,[550])% %对cameraman.tif⽂件计算⼆维DCT变换% RGB=imread('cameraman.tif');% figure(1)% imshow(RGB)% I=rgb2gray(RGB);% %真彩⾊图像转换成灰度图像% J=dct2(I);% %计算⼆维DCT变换% figure(2)% imshow(log(abs(J)),[])% %图像⼤部分能量集中在左上⾓处% figure(3);% J(abs(J)<10)=0;% %把变换矩阵中⼩于10的值置换为0，然后⽤idct2重构图像% K=idct2(J)/255;% imshow(K)RGB=imread('cameraman.tif');I=rgb2gray(RGB);I=im2double(I); %转换图像矩阵为双精度型T=dctmtx(8); %产⽣⼆维DCT变换矩阵%矩阵T及其转置T'是DCT函数P1*X*P2的参数B=blkproc(I,[88],'P1*x*P2',T,T');maxk1=[ 1111000011100000110000001000000000000000000000000000000000000000 ]; %⼆值掩模，⽤来压缩DCT系数B2=blkproc(B,[88],'P1.*x',mask1); %只保留DCT变换的10个系数I2=blkproc(B2,[88],'P1*x*P2',T',T); %重构图像figure,imshow(T);figure,imshow(B2);figure,imshow(I2);RGB=imread('cameraman.tif');I=rgb2gray(RGB);I=im2double(I); %转换图像矩阵为双精度型T=dctmtx(8); %产⽣⼆维DCT变换矩阵%矩阵T及其转置T'是DCT函数P1*X*P2的参数B=blkproc(I,[88],'P1*x*P2',T,T');maxk1=[ 1111000011100000100000000000000000000000000000000000000000000000 ]; %⼆值掩模，⽤来压缩DCT系数B2=blkproc(B,[88],'P1.*x',mask1); %只保留DCT变换的10个系数I2=blkproc(B2,[88],'P1*x*P2',T',T); %重构图像figure,imshow(T);figure,imshow(B2);figure,imshow(I2);5.图像的哈达玛变换cr=0.5;I=imread('cameraman.tif');I=im2double(I)/255; %将读⼊的unit8类型的RGB图像I转换为double类型的数据figure(1),imshow(I);%显⽰%求图像⼤⼩[m_I,n_I]=size(I); %提取矩阵I的⾏列数，m_I为I的⾏数，n_I为I的列数sizi=8;snum=64;%分块处理t=hadamard(sizi) %⽣成8*8的哈达码矩阵hdcoe=blkproc(I,[sizi sizi],'P1*x*P2',t,t');%将图⽚分成8*8像素块进⾏哈达码变换%重新排列系数CE=im2col(hdcoe,[sizi,sizi],'distinct');%将矩阵hdcode分为8*8互不重叠的⼦矩阵，再将每个⼦矩阵作为CE的⼀列[Y Ind]=sort(CE); %对CE进⾏升序排序%舍去⽅差较⼩的系数，保留原系数的⼆分之⼀，即32个系数[m,n]=size(CE);%提取矩阵CE的⾏列数，m为CE的⾏数，n为CE的列数snum=snum-snum*cr;for i=1:nCE(Ind(1:snum),i)=0;end%重建图像re_hdcoe=col2im(CE,[sizi,sizi],[m_I,n_I],'distinct');%将矩阵的列重新组织到块中re_I=blkproc(re_hdcoe,[sizi sizi],'P1*x*P2',t',t);%进⾏反哈达码变换，得到压缩后的图像re_I=double(re_I)/64; %转换为double类型的数据figure(2);imshow(re_I);%计算原始图像和压缩后图像的误差error=I.^2-re_I.^2;MSE=sum(error(:))/prod(size(re_I));。

matlab实验报告(实验4)

学生实验报告开课学院及实验室: 机电学院2012年12月21日学院机电学院年级、专业、班姓名学号实验课程名称MATLAB程序设计成绩实验项目名称实验4: 数据和函数的可视化指导老师一、实验目的1、掌握MATLAB绘图的基本步骤和相关指令调用的先后顺序。

2、掌握MATLAB绘图指令的调用方法。

二、实验内容数学函数从形式上可以分为离散函数和连续函数。

MATLAB对这两种函数数据的可视化都提供了相应的指令。

仔细阅读教材【例5.1-1】的实现代码, 运行并保存结果；并改用stem函数, 画出【例5.1-1】的序列图。

仔细阅读教材【例5.1-2】的实现代码, 运行并保存结果；并分别使用描点和连折线方式, 画出连续函数y=xcosx的近似图形（采样点数自定, 要求画出的图尽量接近原连续函数的图）。

仔细阅读【例5.2-2】的实现代码, 理解plot指令画多条曲线的运用方法, 运行并保存结果；并使用plot函数和legend函数, 在同一个图形窗口上画出y=sint和y=sin(2t)在[0,2pi]区间上的图形, 并标出图例。

仔细阅读【例5.2-4】的实现代码, 理解图形标识选项的运用方法, 运行并保存结果；并修改代码, 把“sin(t)”字体改为正体, 大小改为20, “极大值”改为宋体。

阅读【例5.2-6】, 理解使用hold on指令画多幅图的方法, 运行并保存结果。

阅读【例5.2-8】, 理解使用subplot函数画多个子图的方法, 运行并保存结果。

（1）综合实验: 阅读以下关于通过绘制二阶系统阶跃响应综合演示图形标识的示例, 理解示例中所有图形标识指令的作用, 掌握各个图形标识指令的运用方法, 并在原指令上改动以实现以下功能:（2）把横坐标范围改为0至5pi, 纵坐标范围改为0至2；（3）把图中的横轴的刻度改为从0开始到4pi, 中间各点间隔为pi/2；纵轴刻度改为从0开始到1.5, 中间各点间隔为0.3；（4）把图中的α改为σ。

《MATLAB仿真技术》实验指导书2016附问题详解

实验项目及学时安排实验一 MATLAB环境的熟悉与基本运算 2学时实验二 MATLAB数值计算实验 2学时实验三 MATLAB数组应用实验 2学时实验四 MATLAB符号计算实验 2学时实验五 MATLAB的图形绘制实验 2学时实验六 MATLAB的程序设计实验 2学时实验七 MATLAB工具箱Simulink的应用实验 2学时实验八 MATLAB图形用户接口GUI的应用实验 2学时实验一 MATLAB环境的熟悉与基本运算一、实验目的1．熟悉MATLAB开发环境2．掌握矩阵、变量、表达式的各种基本运算二、实验基本知识1.熟悉MATLAB环境:MATLAB桌面和命令窗口、命令历史窗口、帮助信息浏览器、工作空间浏览器、文件和搜索路径浏览器。

2.掌握MATLAB常用命令3.MATLAB变量与运算符变量命名规则如下：（1）变量名可以由英语字母、数字和下划线组成（2）变量名应以英文字母开头（3）长度不大于31个（4）区分大小写MATLAB中设置了一些特殊的变量与常量，列于下表。

MATLAB运算符，通过下面几个表来说明MATLAB的各种常用运算符4.MATLAB的一维、二维数组的寻访表6 子数组访问与赋值常用的相关指令格式5.MATLAB的基本运算表7 两种运算指令形式和实质涵的异同表6.MATLAB的常用函数表8 标准数组生成函数表9 数组操作函数三、实验容1、学习使用help命令，例如在命令窗口输入help eye，然后根据帮助说明，学习使用指令eye（其它不会用的指令，依照此方法类推）2、学习使用clc、clear，观察command window、command history和workspace等窗口的变化结果。

3、初步程序的编写练习，新建M-file，保存（自己设定文件名，例如exerc1、exerc2、 exerc3……），学习使用MATLAB的基本运算符、数组寻访指令、标准数组生成函数和数组操作函数。

实验4答案 Matlab程序设计1

实验4 Matlab 程序设计1实验目的：1、掌握建立和执行M 文件的方法；2、掌握实现选择结构的方法；3、掌握实现循环结构的方法。

实验内容：1. 从键盘输入一个4位整数，按如下规则加密后输出。

加密规则：每位数字都加上7，然后用和除以10的余数取代该数字；再把第一位与第三位交换，第二位与第四位交换。

a = input('请输入一个四位整数:');a1 = fix(a/1000);a2 = rem(fix(a/100),10);a3 = rem(rem(fix(a/10),100),10);a4 = rem(a,10);a1 = rem(a1+7,10)a2 = rem(a2+7,10)a3 = rem(a3+7,10)a4 = rem(a4+7,10)b1 = a1;a1 = a3;a3 = b1;b2 = a2;a2 = a4;a4 = b2;b = a1*1000+a2*100+a3*10+a42. 求分段函数的值。

,x x x x y x x x x x x x ⎧+- <≠-⎪=-+ ≤<≠≠⎨⎪-- ⎩2226035605231且且及其他用if 语句实现，分别输出x=-5,-3,0,1,2,2.5,3,5时的y 值。

x = input(请输入X 的值:');if x <0 & x~=-3y = x.*x +x-6;elseif x>=0 & x<5 & x~=2 & x~=3y = x.*x-5*x+6;elsey = x.*x-x-1;endy3.输入一个百分制成绩，要求输出成绩等级A、B、C、D、E，其中90~100分为A，80~89分为B，70~79分为C，60~69分为D，60分以下为E。

要求：（1）分别用if语句和swich语句实现。

（2）输入百分制成绩后要判断该成绩的合理性，对不合理的成绩应输出出错信息。

matlab入门实验报告

matlab入门实验报告Matlab入门实验报告一、引言Matlab是一种功能强大的数学软件，广泛应用于科学计算、数据分析和工程设计等领域。

本实验报告将介绍Matlab的基本使用方法和一些常见的数学计算实例。

二、Matlab的基本操作1. Matlab的安装和启动Matlab可以从官方网站下载并安装在计算机上。

安装完成后，双击桌面上的Matlab图标即可启动软件。

2. Matlab的界面和基本操作Matlab的界面由主窗口、命令窗口和编辑器等组成。

在命令窗口中可以输入和执行Matlab命令，编辑器可以编写和保存Matlab脚本。

3. Matlab的数据类型和变量Matlab支持多种数据类型，包括数值型、字符型、逻辑型等。

可以使用赋值语句将值存储在变量中，例如：x = 5。

4. Matlab的基本数学运算Matlab可以进行基本的数学运算，如加减乘除、幂运算等。

例如，输入命令：y = 2*x + 3，即可计算出变量y的值。

三、Matlab的数学函数1. Matlab的数学函数库Matlab内置了大量的数学函数，可以进行各种复杂的数学运算和数据处理。

例如，sin函数用于计算正弦值，sqrt函数用于计算平方根。

2. Matlab的矩阵运算Matlab是一个强大的矩阵计算工具，可以进行矩阵的加减乘除、转置、求逆等运算。

例如，输入命令：A = [1 2; 3 4]，即可创建一个2x2的矩阵。

3. Matlab的符号计算Matlab还支持符号计算，可以进行代数运算和求解方程等。

例如，输入命令：syms x; solve(x^2 - 2*x - 3 = 0, x)，即可求解方程的根。

四、Matlab的数据可视化1. Matlab的绘图功能Matlab提供了丰富的绘图函数，可以绘制各种类型的图形，如曲线图、散点图、柱状图等。

例如，输入命令：plot(x, y)，即可绘制x和y的曲线图。

2. Matlab的图像处理Matlab还可以进行图像处理，如读取、显示和编辑图像。

MATLAB实验报告1

MATLAB实验报告1MATLAB实验报告1实验题目：使用MATLAB绘制正弦函数图像一、实验目的通过本次实验，我们将学会使用MATLAB软件绘制函数图像，加深对正弦函数性质的理解，并掌握MATLAB基本绘图函数的使用。

二、实验原理正弦函数是数学中常见的一种函数，其表达式为y = A * sin(ω *t + φ)，其中A为振幅，ω为角速度，t为时间，φ为相位角。

三、实验步骤1.打开MATLAB软件，在命令窗口输入以下指令创建一个时间向量t，并以0.01为间隔，从0到2π生成值：t = 0:0.01:2*pi;2.输入以下指令生成正弦函数序列y，并设定振幅A为1，角速度ω为1，相位角φ为0：y = sin(t);3. 使用plot函数绘制正弦函数图像，输入以下指令：plot(t, y);title('Sin(x) Function');xlabel('Time');ylabel('Amplitude');xlim([0, 2*pi]);5.运行程序，即可获得正弦函数的图像。

四、实验结果分析（插入正弦函数图像）从图中可以看出，正弦函数以x轴为中心呈现周期性的波动，振幅为1、当x取0时，正弦函数的值为0；当x取π/2时，正弦函数的值为1；当x取π时，正弦函数的值为0；当x取3π/2时，正弦函数的值为-1；当x取2π时，正弦函数的值为0，周期为2π。

五、实验心得体会通过本次实验，我对MATLAB的基本绘图函数的使用有了初步了解和实践，提高了自己的实际操作能力，并对正弦函数的性质有了深入的认识。

在今后的实验中，我将继续深入学习和应用MATLAB软件，提高自己的数据分析和图像处理能力。

实验1-----Matlab程序设计及绘图

实验一：Matlab程序设计及绘图一、实验目的1、掌握 Matlab 软件使用的基本方法；2、熟悉 Matlab 的编程方法；3、熟悉 Matlab 绘图命令及基本绘图控制。

二、实验内容1．基本绘图命令（1）绘制余弦曲线 y=cos(t)，t∈[0，2π]（2）在同一坐标系中绘制余弦曲线 y=cos(t-0.25)和正弦曲线 y=sin(t-0.5)， t∈[0，2π]2．基本绘图控制绘制[0，4π]区间上的 x1=10sint 曲线，并要求：（1）线形为点划线、颜色为红色、数据点标记为加号；（2）坐标轴控制：显示范围、刻度线、比例、网络线（3）标注控制：坐标轴名称、标题、相应文本；3．程序设计：找出从2开始的前100个素数，并依次排列显示。

三、实验原理MATLAB环境是一种为数值计算、数据分析和图形显示服务的交互式的环境。

MATLAB有3种窗口，即：命令窗口（The Command Window）、m-文件编辑窗口（The Edit Window）和图形窗口（The Figure Window），而Simulink另外又有Simulink模型编辑窗口。

1．命令窗口（The Command Window）当MATLAB启动后，出现的最大的窗口就是命令窗口。

用户可以在提示符“>>”后面输入交互的命令，这些命令就立即被执行。

在MATLAB中，一连串命令可以放置在一个文件中，不必把它们直接在命令窗口内输入。

在命令窗口中输入该文件名，这一连串命令就被执行了。

因为这样的文件都是以“.m”为后缀，所以称为m-文件。

2．m-文件编辑窗口（The Edit Window）我们可以用m-文件编辑窗口来产生新的m-文件，或者编辑已经存在的m-文件。

在MATLAB主界面上选择菜单“File/New/M-file”就打开了一个新的m-文件编辑窗口；选择菜单“File/Open”就可以打开一个已经存在的m-文件，并且可以在这个窗口中编辑这个m-文件。