大学物理II知识点
大学物理2 复习重点

各章重点§8库仑定律F 12=k q 1q 2r 123r 12 k=9.0*109N.m 2/C 2ε0=8.85×10−12C 2/(N ∙m 2)真空中库仑定律F 21=−F 12=14πεq 1q 2r 213r 21电场强度E =Fq 0F =14πεqq 0r 3rE =q4πε0r 3rE = qi4πε0r i3r i n i =1§9静电场中的电介质D =E0ε真空中E rεε0介质中高斯定理⎰∑=∙Si q S d D电容电容器孤立导体uqC=电容器BA u u qC -=电场能量电容器Qu Cu C Q W 2121222===电场⎰=VwdV W 电场能量密度:221E w ε=求C 的方法定义法AB AB U C U E q q =→→→能量法W qC W w E q 22=→→→→§10&11 电流强度、电流密度dt dq I =n dS dI j⊥=l d E l d E kl k⋅=⋅=⎰⎰内ε(E K 为非静电场强)磁通量⎰⋅=Φs m S d B 磁场的计算34r rl Id B d⨯=πμ⎰⨯=34r r l Id Bπμ⎰=B d B∑⎰=⋅il I l d B0μ304rr q B⨯=υπμ磁场方程⎰=⋅S S d B 0 ⎰∑=⋅l i I l d B 0μ 载流线圈的磁矩n NIS P m=电磁相互作用B l Id f d ⨯=⎰⨯=lB l Id f B P M m ⨯=B q F⨯=υ⎰ΦΦΦ=21m m m Id A 霍耳电压b IB R U H H =霍耳系数)1(nqR H =直电流的磁场)cos (cos 4210ααπμ-=a I B 无限长载流直导线aIB πμ20=半无限长载流直导线a I B πμ40=直导线延长线上0=B 2. 圆电流轴线上某点的磁场大小232220)(2x R IR B +=μ右手螺旋法则载流圆环圆心处的B 圆心角R I B 20μ=载流圆弧圆心角R I R I B πθμπθμ42200=∙=长直载流螺线管⎩⎨⎧=外0内0nI B μ无限大载流导体薄板0nI B μ=环形载流螺线管⎪⎩⎪⎨⎧=外内20rNIB πμ2121、R R R R ->>12R Nn π=nI B 0μ≈ §13自感系数IL mψ=自感电动势dt dI Ll -=ε互感系数12121I M ψ=21212I M ψ=M M M ==1221互感电动势dt dI M 121-=εdtdI M 212-=ε动生电动势⎰⋅⨯=l d B v iε电磁感应定律dtd mi Φ-=ε 感生电动势S d tBl d Es l i⋅∂∂-=⋅=⎰⎰涡ε课本例题电流的功率PPT 例题※在截面半径为R 的圆柱形空间充满磁感应强度为B 的均匀磁场, B 的方向沿圆柱形轴线 , B 的大小随时间按dB /dt = k 的规律均匀增加 , 有一长L =2R 的金属棒abc 位于图示位置,求金属棒中的感生电动势.解: 作辅助线oa 、oc 构== 成闭合回路oabco 。
大学物理2深刻复习归纳

p-V图几何意义
(2) 内能变化
(3) 功和热量是过程量,内能是状态量。 2. 热力学第一定律
Q E W 对微小的变化过程 dQ dE dW
28 / 30
3. 摩尔热容 定体摩尔热容量 定压摩尔热容量
热容比
自由度i
29 / 30
3. 等值过程
过 程
特征
过程 能量转换 方程 方式
内能增量ΔE
25 / 30
7. 麦克斯韦速率分布函数 8. 下列各式的物理意义:
26 / 30
9. 三种特征速率 (1) 最概然速率 (2) 平均速率 (3) 方均根速率
10. 气体分子平均碰撞频率及平均自由程
27 / 30
第13章 热力学基础
1. 功、热量、内能
(1) 准静态过程的功 W V2 pdV V1
暗明 纹纹
明纹 暗纹
dk dk+1
15 / 30
● 条纹间距b (明纹或暗纹)
2n D (大小三角形) bL
b
LБайду номын сангаас
n1
n
D
/ 2n
16 / 30
四、单缝衍射 1.单缝衍射条件
很小
b
· P x
0 f
bsin 0
中央明纹
bsin k bsin (2k 1)
2
暗纹 明纹
(k 1, 2,3, )
驻波的形成:沿相反方向传播的两相干简谐波的相互 叠加形成驻波
波节 y
波腹
x o
11 / 30
相邻波腹(波节)的距离: 驻波的位相: 若相邻波节之间为一段,则同一段中各点的振动
位相相同,而相邻段振动的位相相反
大学物理II-2总结

k 固有角频率: J l 固有周期: T 2 g
mgl 2 ml
g l
14.25 设摆偏离平衡位置的微小角度为,则摆受力矩
1 3 M ( mgl mgl ) sin mgl k 2 2 3 其中 k mgl 2
力矩为正比回复力矩,摆动为谐振。
0
v v f (v)dv
0
平均速率
例:那些速率大于 v0
的分子的平均速率
v
v0
v dN N
2
v0
v Nf (v)dv
v0
v f (v)dv
v0
Nf (v)dv
v0
f (v)dv
方均根速率
v Βιβλιοθήκη 0v f (v)dv
2
最概然速率
vp
六 、理想气体的麦克斯韦速率分布函数
准静态过程的曲线表示
(1) p-V图
•图中的一个点表示一个平衡 态。 •图中的一条曲线表示一个准 静态过程。 •过程方程为:p=p(V) (2) p-T图
T
b
T
(3) T-V图
V
第二节
热力学第一定律
一、热力学第一定律
在热运动过程中,系统从外界吸收的热量等 于系统内能的增量与系统对外界所做的功之和。 这个结论叫热力学第一定律。
是t=0 时刻简谐振动的相位,叫初相。
相位变化: 3、周期与频率
d 叫角频率,且 dt 表示相位变化的速率。
t
周期
T
2
频率
1 T 2
曲线表述和旋转矢量法 解: 振幅A=2cm 初位相:=/3
大二物理知识点及公式大全

大二物理知识点及公式大全在大二物理学习中,掌握物理知识点和公式是非常重要的。
下面将为您整理大二物理知识点及公式大全,帮助您更好地理解和应用这些概念。
一、力和运动1. 牛顿第一定律:物体在不受力的作用下保持静止或匀速直线运动。
2. 牛顿第二定律:F = m·a,力等于物体质量乘以加速度。
3. 牛顿第三定律:任何两个物体之间的相互作用力大小相等、方向相反。
二、力学1. 动量:p = m·v,动量等于物体质量乘以速度。
2. 冲量:J = F·Δt,冲量等于力乘以时间。
3. 动能:KE = 1/2·m·v^2,动能等于物体质量乘以速度的平方再除以2。
4. 功:W = F·s,功等于力乘以位移。
5. 功率:P = W/Δt,功率等于功除以时间。
6. 机械能守恒定律:在只受重力和弹力做功的情况下,机械能守恒。
三、振动与波动1. 振动周期:T,振动周期是一个完整振动所用的时间。
2. 频率:f,频率是单位时间内振动次数的倒数。
3. 简谐振动:受力方向与位移方向成正比的振动。
4. 波长:λ,波长是相邻波峰或波谷之间的距离。
5. 频率与波长的关系:v = f·λ,波速等于频率乘以波长。
四、光学1. 光的折射定律:n1·sinθ1 = n2·sinθ2,入射角的正弦与折射角的正弦成比例。
2. 焦距公式:1/f = 1/v + 1/u,其中f为焦距,v为像距,u为物距。
3. 成像公式:1/v + 1/u = 1/f,根据成像公式可以求得物体成像的位置和大小。
4. 光的干涉与衍射:光通过两个或多个狭缝或物体时产生的干涉或衍射现象。
5. 光的颜色和频率:光的颜色与频率有关,红光的频率低,紫光的频率高。
五、电学1. 电流:I,电荷通过导体的速率。
2. 电压:V,单位电荷在电场中的势能。
3. 电阻:R,电流在电路中遇到的阻碍。
4. 欧姆定律:I = V/R,电流等于电压除以电阻。
大学物理2复习总结

大学物理2复习总结一、知识点回顾大学物理2是物理学的一个重要分支,它涵盖了力学、电磁学、光学、热学等多个方面的知识。
在复习过程中,我首先对各个知识点进行了回顾,包括:牛顿运动定律、动量守恒定律、能量守恒定律、电场强度、电势、磁场、光的干涉和衍射、波动等。
通过对这些知识点的复习,我巩固了基础,为后续的解题打下了坚实的基础。
二、重点难点解析在复习过程中,我发现有一些知识点是特别重要的,也是我在学习中遇到的难点。
比如,牛顿运动定律的综合应用、电磁场的理解、光的干涉和衍射的原理和计算等。
对于这些重点难点,我进行了深入的分析和理解,通过大量的例题和练习题来加深对这些知识点的理解和掌握。
三、解题方法总结大学物理2的解题方法非常重要,掌握了解题方法,才能更好地解决各种问题。
在复习过程中,我总结了一些常用的解题方法,如:牛顿运动定律的矢量表示、动量守恒定律的代数表示、能量守恒定律的综合应用、电场强度的计算、电势的计算、磁场的计算、光的干涉和衍射的计算等。
通过这些方法的掌握,我能够更好地解决各种问题。
四、错题总结与反思在复习过程中,我发现自己在一些问题上容易出错,比如:对牛顿运动定律的理解不够深入、对电磁场的理解不够准确、对光的干涉和衍射的计算不够熟练等。
对于这些问题,我进行了总结和反思,分析了出错的原因,并通过大量的练习来避免类似的错误再次发生。
五、知识框架构建在复习结束后,我构建了大学物理2的知识框架,将各个知识点有机地在一起。
通过这个知识框架,我能够更好地理解和掌握大学物理2的知识点,也能够更好地应用这些知识点解决实际问题。
六、备考策略优化在备考过程中,我还优化了自己的备考策略。
我制定了详细的复习计划,将每个知识点都安排在合理的复习时间内。
我注重了课堂听讲和笔记整理的结合,确保自己对每个知识点都有深入的理解。
我注重了练习和反思的结合,通过大量的练习来提高自己的解题能力,同时不断反思自己的解题方法和思路。
通过这次复习总结,我对大学物理2有了更深入的理解和掌握,同时也提高了自己的解题能力和思维能力。
大二下学期物理知识点总结

大二下学期物理知识点总结一、力学1. 动力学动力学研究物体的运动规律,是力学的一个重要分支。
在大二下学期的物理课程中,我们学习了牛顿运动定律、平抛运动、圆周运动以及万有引力等内容。
牛顿第一定律(惯性定律):物体在外力作用下保持静止或匀速直线运动,直至外力作用终止。
牛顿第二定律(运动定律):物体在外力作用下会发生加速,其加速度大小与外力成正比,与物体的质量成反比,且在同一直线上与外力方向相同。
牛顿第三定律(作用-反作用定律):两个物体相互作用时,彼此之间的作用力与反作用力大小相等、方向相反。
平抛运动是指物体在水平方向做匀速直线运动的同时,竖直方向存在匀加速直线运动的情况。
在学习中,我们掌握了平抛运动的位移、速度、加速度等相关计算方法。
圆周运动是指物体在圆周运动过程中的运动规律,包括圆周运动速度、圆周运动加速度以及向心力等相关内容。
通过学习,我们了解了圆周运动的加速度计算方法,以及向心力与离心力的区别与计算方法。
万有引力是由牛顿在《自然哲学的数学原理》中提出的重要物理学定律。
在大二下学期的物理课程中,我们系统学习了万有引力的大小计算、万有引力与万有引力势能的关系,以及地球表面引力的计算等内容。
2. 动能与功率动能是物体由于运动而具有的能量,其大小与物体的质量以及运动速度有关。
在课程中,我们学习了动能的计算公式,以及与势能的转化关系等内容。
功率是描述单位时间内对物体所做的功或能量转换速率的物理量。
我们学习了功率的计算公式,以及功率与动能、动力的关系,掌握了功率的单位和量纲等内容。
3. 质点系与刚体运动在学习动力学的过程中,我们还系统学习了质点系与刚体运动的相关知识。
质点系的运动规律涉及到多个物体的运动相互影响,我们学习了质点系的动量守恒定律、机械能守恒定律,以及弹性碰撞和非弹性碰撞等内容。
在刚体运动方面,我们学习了刚体的平动运动和转动运动规律,掌握了刚体的绕定轴转动的运动方程、角动量守恒定律等内容。
二、热学1. 热力学基本概念热力学是研究热现象和热能转换的学科,我们在大二下学期的物理课程中系统学习了热力学的基本概念。
大学物理知识点汇总二
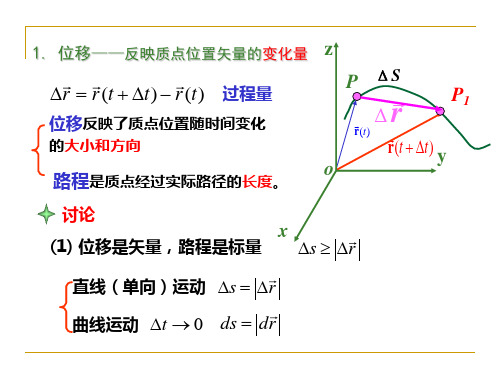
4. 角量与线量的关系
角量
角位置、角速度、角加速度
线量
位矢、速度、加速度
s R
v lim s lim R R d R
t0 t t0 t
dt
an
v2 R
(R)2
R
R 2
at
dv dt
R
d
dt
R
P(t t)
P(t) o
x
第二章 质点力学的运动定律
本章内容
——动力学
§2.1 质点力学的基本定律 力的瞬时作用效果
三 动量守恒定律
t F exdt t0x 0
n
n
pi pi0 p = 常矢量
i1
i1
动量守恒定律:在某时间内,如果质点组所受外力矢量和为始终为 零,则在该时间内质点组的总动量守恒.
➢ 单个质点 ➢ 两个质点系统 ➢ n个质点组系统
mv mv0
m1v1 m2v2 m1v10 m2v20
定义: Ek
i
1 2
mi vi 2
1 2
i
mi ri 2
2
1 2
J2
注意: 刚体是一个特殊的质点组,同样服从功能转换关系
质点组的功能原理
W
ex
W in 非保
Ek Ep
Ek 0 Ep0
刚体转动的功能关系
W in 非保
0
W ex
ex
M d
Ek Ep
Ek 0 Ep0
特点: 各质元在转动平面内作半径不同的圆周运动;
且角位移、角速度、角加速度均相同。
一、刚体定轴转动的运动学描述
角位置: (t) rad 角速度: d
dt
角加速度: d d2
大学物理2期末考试重点及复习

s1 s2
r1 r2
*
2 1 2π
r2 r1
P
对空间不同的位置,都有恒定的,因而合强 度在空间形成稳定的分布,即有干涉现象。
定值
讨 论
A
A1 A2 2 A1 A2 cos
2 2
可看出A是与时间无关的稳定值 ,其大小取决于该 点处两分振动的相位差
上式代表x1 处质点在其平衡位置附近以角频率w 作简谐运动。
x 2 1 2 2 t 一定。令t=t1,则质点位移y 仅是x 的函数。
x2 x1
2 x y A cos t1 即
同一波线上任意两点的振动位相差:
x A cos t u
由于 P 为波传播方向上任一点,因此上 述方程能描述波传播方向上任一点的振动, 具有一般意义,即为沿 x 轴正方向传播的平 面简谐波的波函数,又称波动方程.
2π 2πν 和 uT 利用 T 可得波动方程的几种不同形式:
干涉的位相差条件 当 2kπ时k 0,1,2,3... 合振幅最大 当
2k 1π
Amax A1 A2
合振幅最小
Amin A1 A2
干涉的波程差条件 当 r1 r2 k 时(半波长偶数倍)
合振幅最大
Amax A1 A2
然后确定三个特征量:、A、 旋转矢量法确定: 先在X轴上找到相应x0,有 两个旋转矢量,由的正 负来确定其中的一个
A
O
x0 A
X
v 0 0, 上半圆, 0 v 0 0, 下半圆, 2或 0 v 0 0, x0 A, 0, x0 A,
大二物理知识点总结

大二物理知识点总结一、力学力学是物理学的一个重要分支,研究物体的运动规律和相互作用关系。
大二力学主要包括以下知识点:1. 运动学运动学研究物体的运动状态和运动规律,主要包括位移、速度、加速度等概念。
重要知识点包括:(1)位移:物体在运动过程中位置的变化量。
(2)速度:物体单位时间内所经过的路程。
(3)加速度:速度的变化率,即单位时间内速度的变化量。
(4)匀速直线运动和变速直线运动:物体在运动过程中速度是否恒定的情况。
2. 动力学动力学研究物体受力作用时的运动规律,主要包括牛顿三定律、动量定理、动能定理等概念。
重要知识点包括:(1)牛顿三定律:第一定律(惯性定律)、第二定律(运动定律)、第三定律(作用—反作用定律)。
(2)动量定理:物体受力作用时,动量的变化率等于所受合外力。
(3)动能定理:物体的动能变化等于所受合外力做功。
(4)万有引力定律:两个物体之间的引力与它们的质量和距离的平方成正比。
3. 转动力学转动力学研究物体绕轴的旋转运动规律,主要包括角度、角速度、角加速度等概念。
重要知识点包括:(1)角度:物体在圆周上所对的角。
(2)角速度:物体单位时间内绕轴旋转的角度。
(3)角加速度:角速度的变化率,即单位时间内角速度的变化量。
(4)转动惯量:物体对围绕着的轴的转动难易程度。
(5)角动量:物体绕轴旋转时的动量大小。
二、电磁学电磁学是研究电荷的相互作用和电磁场的性质的学科。
大二电磁学主要包括以下知识点:1. 静电学静电学研究带电物体之间的相互作用和电场的性质,主要包括库仑定律、电场强度、电势等概念。
重要知识点包括:(1)库仑定律:两个带电物体之间的电力与它们之间的距离的平方成反比、与它们的电量乘积成正比。
(2)电场强度:在某一点的电场力与单位正电荷所受到的力。
(3)电势:单位正电荷在电场中具有的电势能。
2. 电动力学电动力学研究带电粒子在电场和磁场中的运动规律,主要包括洛伦兹力、磁感应强度、磁场能量等概念。
大学物理第二章知识点

(Ek 2 EP2)(Ek1 EP1) E2 E1
当A外 A非保内 0
—系统的功能原理
则:E2 E1 C --机械能守恒定律
A外 A非 保 内 E2 E1
X. J. Feng
—系统的功能原理
当A外 A非保内 0 E2 E1 C ---机械能守恒
3. 一对滑动摩擦力的功恒小于零。
(摩擦生热是一对滑动摩擦力作功的结果)
2.2 保守力和势能 1.重力的功 A(xa ya za )B(xb yb zb )
z
X. J. Feng
B
F mgk
dr dxi dy j dzk
y A xo
A
F dr
例2.1 :作用在质点的力F (2 yi 4x2 j)(N),质点从X. J. Feng
原点运动到坐标为x (2 m),y (1 m)的C点(如图所示),
计算力F分别沿下列路径所作的功:
y( j)
(1)沿路径oac; (2)沿路径oc。
解: (1).A Aoa Aac16(J )
0
dy 16
(2yi
(J)
4x2
j)
(dxi
dyj )
x 2 y
2ydx
4x2dy
2 2( x )dx
1
4(2
y)2
dy
7.3(J )
02
0
例2.2: 质点 m=0.5Kg, 运动方程 x= 5t, y = 0.5t2 (SI) , X. J. Feng
rm地
N
大学物理2知识点总结
1 2
LI
2
1 B 2
2
1 2
H
2
1 2
BH
V
w m dV
Maxwell方程组和电磁辐射概要
D dS q
S
0
1、Maxwell方程组:
E dl
L
i
B dS 0
H d l
B t
dS
非稳恒
L
L
H d l Ic Id
(全电流定律)
4、铁磁质的特性: r;磁化饱和;剩磁;磁滞;居里点 μ
5、磁滞回线:
BS
0
BS ——饱和磁感应强度 Br ——剩余磁感应强度 Hc——矫顽力
磁滞损耗∝回线包围的面积
6、铁磁质的分类: 类别 软磁材料 特点 Hc小,回线“瘦”; 易磁化;“铁损”小 用途 铁芯
ˆ 夹角) n 、B
3、感生电动势: (1)导体回路: 一段导体:
L
E i dl
B
S
t
dS
L
E i dl
(2)圆柱形区域(均匀B∥柱轴且 B 空间分布均匀) t ① E i 线是以区域中心为圆心的一组同心圆,
点电荷q在外电场中受力: F q E (2) Gauss定理: 电通量: Φ e d e E d
S
S
S
E d S
q
0
i
高斯面内所有 电荷的代数和
3、求场强 (1)利用场强叠加原理 点电荷
大学大学物理II2总结.ppt

u
y(x,t) Acos[(t x) ]
u
O
y(x,t) Acos(t 2 x )
x
x
波沿x轴负向传播的波动方程:y( x, t )
A cos[t
2
x
]
波的能量
Wk
Wp
1 2
VA2 2
sin2 (t
x) u
结论:质元在参与波动的过程中,内部的动能和
22
多普勒效应
观察者运动
接收到的波的范围变化
波源运动
波长变化
R
u vR u vs
s
两者相向运动: vR > 0, vS 0 两者背离运动: vR < 0, vS 0
第十六章 电磁振荡和电磁波
电磁波
1、电磁波的特点: •速度: u 1
真空中:c 1
2.998108 m / s
u
·····················u·T···x
u
T
平面简谐波的波动方程
平面简谐波的特点:介质中各质点振动频率、振 幅相同。只有相位在波的传播方向上依次落后。
设已知O(x=0)处质点的振动方程为:
y0 (t) Acos(t )
沿x正方向传播的波动方程
y
4( /d ) 8( /d )sin
当
d a
k k
时, 会出现缺级现象。
光栅衍射的特点:
(1)衍射角较大,光栅衍射条纹间距大,易于实现 精密测量。衍射的级次有限。
由于:
sink
k
ab
1
光栅衍射主极大的最高级次:k a b
大一大学物理二知识点

大一大学物理二知识点物理作为一门自然科学,研究的是自然界中各种物质和能量的运动规律。
大一大学物理二是物理学专业的一门重要课程,它深入探讨了电磁学和热学等领域的知识,为学生提供了扎实的物理基础,为以后的学习和研究打下了坚实基础。
一、电场与电势电场与电势是物理学中非常重要的概念。
电荷周围都会形成电场,它的强度与电荷的数量和距离有关。
电势则是描述电场的物理量,它表示单位正电荷在电场中的势能。
根据库仑定律,电势与电荷的乘积成正比,与距离的倒数成反比。
学生需要掌握电场和电势之间的数学关系,能够计算电场和电势的数值。
二、电容和电容器电容是描述电路中储存电荷能力的物理量。
电容器则是实现电路中电荷储存的设备。
电容器由两个导体板和介质组成,当加上电压时,电荷会在导体板之间储存。
学生需要了解电容器的定义和常见的电容电压关系。
此外,他们还需要学会计算电容器的等效电容、串并联电容的计算,并了解RC电路的特性。
三、磁场与电磁感应磁场是物理学中的另一个重要概念,它描述电荷或电流周围的磁性力。
根据安培环路定律,磁场的强度与电流成正比,与距离成反比。
学生需要了解磁场的计算方法和磁场对电荷和电流的力的作用。
另外,电磁感应也是大一大学物理二课程中的重要内容,它描述了磁场对电流的感应作用。
学生需要掌握法拉第电磁感应定律和左手定则,能够计算感应电动势的大小和方向。
四、交变电流和电磁波交变电流是电路中的一种特殊现象,它的方向和大小随着时间的变化而变化。
学生需要了解交变电流的特性和计算方法,能够计算交变电流的幅值和频率。
此外,电磁波也是物理学中的重要概念,它是由交变电场和交变磁场组成的一种能量传播形式。
学生需要了解电磁波的特性和计算方法,熟悉电磁波的产生和传播机制。
五、光学和几何光学光学是研究光的传播和现象的物理学分支。
几何光学是光学中的重要课题,它研究的是光在接触透明介质表面时的传播规律。
学生需要了解折射和反射的定律,掌握镜面成像和透镜成像的计算方法。
大学物理2内容小结

1.磁通量:
2.磁场高斯定理:(无源场)
3.安培环路定理
载流长直螺线管内磁场
螺绕环内磁场
无限长载流圆柱面
无限长载流圆柱体
四.磁场对电流及运动电荷的作用
1.安培定律
2.均匀磁场对载流线圈的作用
所受合力:,所受力矩:
磁矩的定义
3.洛伦兹力公式:
洛伦兹力:
带电粒子在均匀磁场中的运动:
,圆周运动,半径,周期
1.电容器中的能量:
2.电介质中电场的能量密度:
,(真空)
静电场总能量:
第十一章 电流和恒磁场
一.电流及导电规律
1.电流
电流密度 关系
2.电流连续性方程:
恒定电流
3.欧姆定律的微分形式
4.电动势:,为非静电性电场强度
二.毕奥——萨伐尔定律
无限长直电流磁场
载流圆环圆心磁场
匀速运动点电荷磁场
三.磁场高斯定理和安培环路定理
不,螺旋运动,周期,螺距
4.霍耳效应
第十二章 电磁感应
1. 法拉第电磁感应定律:
楞次定律:判断感应电流的方向
2. 动生电动势:
特例:
3. 感生电场和感生电动势
4.互感和自感
互感 互感电动势
自感 自感电动势
自感磁能
第十四章 波动光学
1.光程和获得相干光的方法
光程的定义:
获得相干光的方法:把光源上同一点发出的光分成两部分,有分波前法
能与关系,(3)存在截止频率(即红限),当时,逸出光电子的初动
能随入射光的频率的增加而线性增加,与入射光的强度无关;(4)光
电效应具有瞬时性。
爱因斯坦的光子论
光波是由一个一个的光子组成,光子的能量为
大学物理2总结

旋转振幅矢量 —要能正确确定 φ 要能正确确定
2.简谐振动的能量
1 1 2 2 2 动能: 动能: Ek = m υ = kA sin (ω t +ϕ) 2 2 1 2 = 1 kA2cos2 (ω t +ϕ) 势能: 势能: Ep = k x 2 2
1 2 机械能: 机械能: E = kA 2
简谐振动的总机械能守恒! 简谐振动的总机械能守恒! 的总机械能守恒
ε动 = ∫ dε动 = ∫v× B⋅ d l
L L
产生动生电动势的非静电力是洛仑兹力 任意小段的导线: 任意小段的导线: d ε 动 = v × B ⋅ d l 感生电动势
ε感
∂B = E 涡 ⋅ dl = −∫∫ ⋅ dS ∂t L S
∫
产生感生电动势的非静电力是涡旋电场力
2. 自感 互感
ψ =LI
λ
2. 平面简谐波的波函数(表达式,波动方程) 平面简谐波的波函数(表达式,波动方程) x y( x, t ) = Acos[ω(t ± ) +ϕo ] u 或
t x y( x, t ) = Acos[2π( ± ) +ϕo ] T λ
x0 点的简谐振动方程 t0 时刻的波形表达式
(1) 当 x= x0 (2) 当 t = t0
1 ms = ± 2
Lz = ml ℏ
Sz = msℏ
不同的量子态的数目: 不同的量子态的数目 一定时, 当 n、l、ml 一定时,为 2 ; 一定时, 当 n、l 一定时,为 2 (2l+1) ; 一定时, 当 n一定时,为 2n2 。 一定时
1 Ek = E p = E 2
3. 简谐振动的合成 同方向、同频率 同方向、同频率: 合振动 : x = A cos(ω t + φ )
《大学物理II》知识点

《大学物理II 》知识点1.热学(1)统计物理初步【掌握】热力学系统:热学研究的由大量微观粒子组成的宏观物体。
平衡态:系统的宏观性质不随时间发生变化,且系统的内部也不存在能量或质量的任何宏观流动。
一个系统在不受外界影响的条件下,如果它的宏观性质不再随时间变化,我们就说这个系统处于热力学平衡态。
状态参量:平衡态的宏观性质的量称为状态参量(几何、力学、化学、电磁) 理想气体状态方程:PV=νRT (普适气体恒量R=8.31 [ J.mol -1.K -1])理想气体的压强和温度及其统计意义:221v m w = w n p 32= kT w 23= R=8.31[J·mol -1·K -1] k=1.38×10-23[J·K -1] N A = 6.02×1023[mol] R=k ·N A 能量均分定理:分子的每一个可能的自由度都有相同的平均动能kT 21 分子的平均平动能kT 23 分子的平均总动能kT i 2i 自由度(刚性:单原子3、双原子5、多原子6)特殊CO 2理想气体的内能:N kT i 2 (1mol RT i 2) 麦克斯韦速率分布律:公式,图像,物理意义 ()2223224v e kT m v f kT mv −⎟⎠⎞⎜⎝⎛=ππ 0d ()d N N f N ∞==∫∫v v v v v220()d f ∞=∫v v v v 三种常见的气体分子速率是:最概然速率 p ≈v平均速率 ≈v==[9章]气体分子的平均碰撞次数Z 和平均自由程λ:2Z d n =vZ λ===v [了解]玻耳兹曼分布律。
(2)热力学【掌握】准静态过程:一个过程,如果任意时刻的中间态都无限接近于一个平衡态,则此过程为准静态过程。
功:dA=p ·dV热量:热力学第一定律:Q=(E 2-E 1)+A用于三个过程:等体,吸热全部用于增加内能 C V ,m =R i 2 等温,吸热全部用于对外做功等压,吸热一部分用于增加内能,一部分用于对外做功C P,m =R+R i 2热容量:理想气体的绝热过程:PV γ=consTV γ-1=consp γ-1T -γ=cons绝热线与等温线的区别(p285)循环过程:经历一系列变化又回到初始状态。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、 质点运动量的描述(1) 位置矢量r:运动方程: k t z j t y i t x t r )()()()(++=;模为 222z y x r ++=位移矢量:)()(t r t t r r -∆+=∆;注意:一般r r ∆≠∆(2) 速度:x y z dr v v i v j v k dt ==++,分量式:x y z v ,v ,v dx dy dzdt dt dt===; 速度的大小:222x y z dr ds v v v v v dt dt==++=≡,v 为速率。
速度方向沿曲线切线指向运动的前方。
平均速度:x y z r v v i v j v k t ∆==++∆,分量式:,,x y z x y zv v v t t t∆∆∆===∆∆∆ (3) 加速度:22x y z dv d r a a i a j a k dt dt===++,加速度大小:222xy z a a a a =++ 分量式:222222,,y x z x y z dv dv dv d x d y d za a a dt dt dt dt dt dt ======; 自然坐标系:t e v v =,n n t t e a e a a+=,t dv a dt =(有正负!),2n v a ρ=,此处v 为速率,ρ为曲率半径。
2、 圆周运动:角位置θ,角速度d dt θω=,角加速度:d dtωα=; 角量与线量的关系:θR s =,R v ω=,t dv a R dt α==,22n va R Rω==3、 抛体运动:0000200000cos 1sin 2x x x x y y y y a v v v x v ta g v v gt v gt y v t gt θθ=→==→=⎧⎪⎨=-→=-=-→=-⎪⎩其中0θ为起抛角。
22t n a a g += 4、 相对运动速度变换: AB AC CB v v v =+ 或表示为 AB AC BC v v v =- 加速度变换:AB AC CB a a a =+ 或 AB AC BC a a a =-(注意:这是矢量加法,用平行四边形作图或分解为分量计算;注意下标的规律。
)★小结:两类题型:已知r ,求导得到a v ,;已知a ,分离变量积分得到r v,已知θ,求导得到ω,β;已知β,分离变量积分得ω,θ(1)常力作用下的连接体:隔离体法,分别画受力图;设加速度的正方向,分别列方程;然后找拉力和加速度之间的关系。
(2)圆周运动时,按照切向和法向分解: 2,t t n n dv v F ma m F ma m dt R====, 注意t F 和n F 的正负。
(3) 非惯性系: 'F F ma →→→+=惯, 其中0=F m a →→-惯, 'a →为物体在非惯性中的加速度。
第三章 动量和角动量(1)平动问题,,()F p m v →→→描述,d pF dt→→=; 若0F →=,动量守恒。
(2)转动问题,,M r F L r p →→→→→→=⨯=⨯描述,d LM dt→→=; 若0M →=,角动量守恒。
(3) 冲量:2121,t t I F dt I P P →→→→→==-⎰(4) 质心(对于由多个质点构成的系统而言):22;i i CCiC im r d rr F M Ma mdt →→→→===∑∑∑ 其中i F →∑合外力,i M m =∑(5)变质量物体问题 :()d v dmF m v u dt dt→→→→=+- 其中F →为系统受的合外力,m 为主体的质量,v →主体的速度,u →客体的速度。
第四章 功与能(1) 力对质点的功: d baA F r =⋅⎰功率:P F v →→=⋅(2) 动能定理 对于质点: 2211d ,22bb a k aA F r mv mv E =⋅=-=∆⎰其中212k E mv = 为质点动能,A 为外力对质点做的功对于质点系: e i k A A E +=∆ 其中e A 为外力的功,i A 系统内力的功 (3) 保守力和势能若d 0F r ⋅≡⎰, 则F 为保守力(F保的做功与路径无关,只与初末态有关)常用势能:2p p p 1E ,E ,E 2Mm Gmgh kx r =-== (注意零势能点的选取)结论: ()p E d rr F r =⋅⎰参考点保保守力: ()p p p p dE dE dE F E i j k dxdydz→→→→=-∇=-++(4)质点系的功能原理和机械能守恒e id A A E +=∆ 其中k p E E E =+为系统的机械能,id A 为非保守内力的功若0e id A A +=,则0E ∆= 即系统的机械能守恒第五章 刚体力学参考答案平动描述刚体转动r →− 位矢θ − 角位置d rv dt→→=− 速度d dtθω=− 角速度 d va dt→→=− 加速度d dtωα=− 角加速度 F →− 力M r F →→→=⨯ − 力矩p m v →→= − 动量L r p →→→=⨯ − 角动量 (定轴转动:z L J ω=) m − 质量22i i J r m r dm =∆=∑⎰ − 转动惯量d pF m a dt →→→== − 牛顿第二定律z z dL d M J J dt dtωα=== − 定轴转动定理 2121t t I F dt p p →→→→==-⎰ − 动量定理2121t z t M dt J J ωω=-⎰− 角动量定理若0F →=, 质点或质点系的动量守恒若0z M =, 定轴转动的角动量守恒b aA F d s →→=⋅⎰ − 功21z A M d θθθ=⎰ − 功212k E mv =− 动能212k E J ω=− 动能 2221211122k k A E E mv mv =-=- − 动能定理2221211122k k A E E J J ωω=-=- − 动能定理k p E E E =+ − 机械能k p E E E =+ − 刚体的机械能若=0,=0A A 外非保内,机械能守恒若除重力外的其他外力矩不做功,刚体系统机械能 守恒第六章 狭义相对论基础1、 两个基本假设:(1) 光速不变原理:在任何惯性系中,光在真空中的速率都相等,等于c 。
(2) 狭义相对性原理:一切物理定律在所有惯性系中都具有相同的形式。
2、 洛仑兹时空间隔变换式: (P 点为被观察的某一事件)'22''2'2211x vt x v cy y z zv t x c t v c -=-==-=-''22''''22211x vt x v c y y z z v t x c t v c +=-==+=-3、 速度变换式:21x x x u vu v u c -'=-, 22211y y xu v c u vu c-'=-, 22211z z x u v c u v u c -'=-, 4、 狭义相对论的时空观:(1) 同时的相对性:∑系中不同地点同时发生........的两件事,在'∑系中观察,必不同时。
(2) 运动的物体沿x 轴方向的长度收缩:22001/l l v c l =-<0l 是静止..长度,称为固有长度。
(测量l 的两端是同时进行的;对于斜杆,分解为分量讨论) (3) 时间膨胀:0221v cττ=-,0τ是参考系中同一地点....(.即物体静止在该处........).不同时刻发生的两事件的时间间隔,称为固有时间。
5、 ★ 质量与速度的关系:0221m m v c=-,★ 静止能量:200E m c =; ★总能量:20221E E mc v c==-,★ 动能: ()2200021/k E E mc m c E v c =-=--,★ 动能定理:12k k E E A -=外,★ 动量 ()021/m v p mv v c ==-6、 光子:20000, E m E E mc h p mc cν======,, 7、 两个粒子碰撞,复合成一个新的粒子:满足系统的能量守恒,动量守恒。
第七章 气体动理论1、 宏观 (理想气体状态方程)molmpV RT M =或 p n k T= 分子数密度/n N V =,/A k R N =,R=8.31J/(mol·K),k=1.38×10-23J/K 2、 微观压强:23k p n ε=(宏观量是微观量的统计平均) 2012k m v ε= ——分子的平均平动动能平均平动动能:32k kT ε=T 的微观本质:气体的温度是气体分子平均平动动能的量度,反映了分子热运动的剧烈程度。
3、 能量均分原理:在平衡态下,物质分子的每个自由度都具有相同的平均动能,大小都为/2kT 。
(1) 分子的平均动能:2k i kT ε=其中总自由度i = t+r 。
单原子分子:i =3;双原子分子:i =5,(平动自由度t =3,转动自由度r =2);多原子分子:i =6,(平动自由度t =3,转动自由度r =3)。
(2) 质量为m 的理想气体的内能:()222A mol mol m i i m iE N kT RT pV M M === 4、 速率分布函数 f (v )(1) ()dNf v dv N=表示速率取值在v — v+ dv 区间内的分子数dN 占总分子数N 的百分比,也称为概率。
(2) 归一化条件:()1f v dv ∞=⎰(即()f v ~v 曲线下的面积等于1)(3) 最概然速率:022p mol kT RTv m M ==平均速率:088molkT RTv m M ππ==方均根速率:2033molkT RTv m M == 计算平均值的方法: ()0v vf v dv ∞=⎰★速率在v 1—v 2区间的分子的平均速率 =22112211()()()()v v v v v v v v vNf v dv vf v dvNf v dvf v dv=⎰⎰⎰⎰5、 分子的平均碰撞频率:22 Z v d n π=⋅⋅平均自由程:22122v kTZ d n d pλππ=== (p nkT =) 第八章 热力学1、 热力学第一定律Q A E =+∆,其中Q 、A 与过程有关,是过程量;E 是状态量,ΔE 与过程无关。
(1) 气体对外做功:21V V A pdV =⎰气体膨胀,A>0;气体压缩,A<0; A 为p-V 图上过程曲线下的面积 (2) 内能的变化: 21()22i m i mE R T R T T M M∆=∆=- 内能只与温度的变化有关,所以,该公式适用于任意过程。
