山东省潍坊市2021年3月一模考试数学试卷 (1)
山东省潍坊市2021年中考数学试卷(含解析)
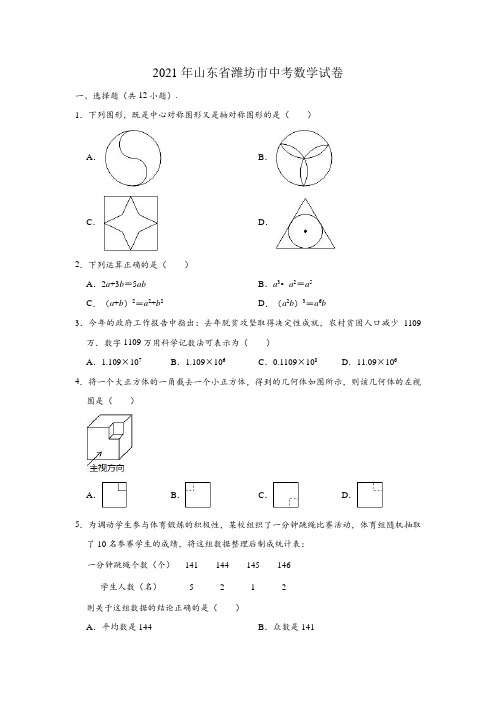
2021年山东省潍坊市中考数学试卷一、选择题(共12小题).1.下列图形,既是中心对称图形又是轴对称图形的是()A.B.C.D.2.下列运算正确的是()A.2a+3b=5ab B.a3•a2=a5C.(a+b)2=a2+b2D.(a2b)3=a6b3.今年的政府工作报告中指出:去年脱贫攻坚取得决定性成就,农村贫困人口减少1109万.数字1109万用科学记数法可表示为()A.1.109×107B.1.109×106C.0.1109×108D.11.09×106 4.将一个大正方体的一角截去一个小正方体,得到的几何体如图所示,则该几何体的左视图是()A.B.C.D.5.为调动学生参与体育锻炼的积极性,某校组织了一分钟跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成统计表:一分钟跳绳个数(个)141144145146学生人数(名)5212则关于这组数据的结论正确的是()A.平均数是144B.众数是141C.中位数是144.5D.方差是5.46.若m2+2m=1,则4m2+8m﹣3的值是()A.4B.3C.2D.17.如图,点E是▱ABCD的边AD上的一点,且,连接BE并延长交CD的延长线于点F,若DE=3,DF=4,则▱ABCD的周长为()A.21B.28C.34D.428.关于x的一元二次方程x2+(k﹣3)x+1﹣k=0根的情况,下列说法正确的是()A.有两个不相等的实数根B.有两个相等的实数根C.无实数根D.无法确定9.如图,函数y=kx+b(k≠0)与y=(m≠0)的图象相交于点A(﹣2,3),B(1,﹣6)两点,则不等式kx+b>的解集为()A.x>﹣2B.﹣2<x<0或x>1C.x>1D.x<﹣2或0<x<110.如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=4,以点O为圆心,2为半径的圆与OB交于点C,过点C作CD⊥OB交AB于点D,点P是边OA上的动点.当PC+PD 最小时,OP的长为()A.B.C.1D.11.若关于x的不等式组有且只有3个整数解,则a的取值范围是()A.0≤a≤2B.0≤a<2C.0<a≤2D.0<a<212.若定义一种新运算:a⊗b=,例如:3⊗1=3﹣1=2;5⊗4=5+4﹣6=3.则函数y=(x+2)⊗(x﹣1)的图象大致是()A.B.C.D.二、填空题(本大题共6小题,共18分.只要求填写最后结果,每小题填对得3分.)13.因式分解:x2y﹣9y=.14.若|a﹣2|+=0,则a+b=.15.如图,在Rt△ABC中,∠C=90°,∠B=20°,PQ垂直平分AB,垂足为Q,交BC 于点P.按以下步骤作图:①以点A为圆心,以适当的长为半径作弧,分别交边AC,AB于点D,E;②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧相交于点F;③作射线AF.若AF与PQ的夹角为α,则α=°.16.若关于x的分式方程+1有增根,则m=.17.如图,矩形ABCD中,点G,E分别在边BC,DC上,连接AC,EG,AE,将△ABG 和△ECG分别沿AG,EG折叠,使点B,C恰好落在AE上的同一点,记为点F.若CE =3,CG=4,则sin∠DAE=.18.如图,四边形ABCD是正方形,曲线DA1B1C1D1A2…是由一段段90度的弧组成的.其中:的圆心为点A,半径为AD;的圆心为点B,半径为BA1;的圆心为点C,半径为CB1;的圆心为点D,半径为DC1;…,…的圆心依次按点A,B,C,D循环.若正方形ABCD的边长为1,则的长是.三、解答题(本大题共7小题,共66分.解答应与出文字说明、证明过程或演算步骤.)19.先化简,再求值:(1﹣)÷,其中x是16的算术平方根.20.某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度.如图,桥AB是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥AB的上方120米的点C处悬停,此时测得桥两端A,B两点的俯角分别为60°和45°,求桥AB的长度.21.在4月23日“世界读书日”来临之际,某校为了了解学生的课外阅读情况,从全校随机抽取了部分学生,调查了他们平均每周的课外阅读时间t(单位:小时).把调查结果分为四档,A档:t<8;B档:8≤t<9;C档:9≤t<10;D档:t≥10.根据调查情况,给出了部分数据信息:①A档和D档的所有数据是:7,7,7.5,10,7,10,7,7.5,7,7,10.5,10.5;②图1和图2是两幅不完整的统计图.根据以上信息解答问题:(1)求本次调查的学生人数,并将图2补充完整;(2)已知全校共1200名学生,请你估计全校B档的人数;(3)学校要从D档的4名学生中随机抽取2名作读书经验分享,已知这4名学生1名来自七年级,1名来自八年级,2名来自九年级,请用列表或画树状图的方法,求抽到的2名学生来自不同年级的概率.22.如图,AB为⊙O的直径,射线AD交⊙O于点F,点C为劣弧的中点,过点C作CE⊥AD,垂足为E,连接AC.(1)求证:CE是⊙O的切线;(2)若∠BAC=30°,AB=4,求阴影部分的面积.23.因疫情防控需要,消毒用品需求量增加.某药店新进一批桶装消毒液,每桶进价50元,每天销售量y(桶)与销售单价x(元)之间满足一次函数关系,其图象如图所示.(1)求y与x之间的函数表达式;(2)每桶消毒液的销售价定为多少元时,药店每天获得的利润最大,最大利润是多少元?(利润=销售价﹣进价)24.如图1,在△ABC中,∠A=90°,AB=AC=+1,点D,E分别在边AB,AC上,且AD=AE=1,连接DE.现将△ADE绕点A顺时针方向旋转,旋转角为α(0°<α<360°),如图2,连接CE,BD,CD.(1)当0°<α<180°时,求证:CE=BD;(2)如图3,当α=90°时,延长CE交BD于点F,求证:CF垂直平分BD;(3)在旋转过程中,求△BCD的面积的最大值,并写出此时旋转角α的度数.25.如图,抛物线y=ax2+bx+8(a≠0)与x轴交于点A(﹣2,0)和点B(8,0),与y 轴交于点C,顶点为D,连接AC,BC,BC与抛物线的对称轴l交于点E.(1)求抛物线的表达式;(2)点P是第一象限内抛物线上的动点,连接PB,PC,当S△PBC=S△ABC时,求点P 的坐标;(3)点N是对称轴l右侧抛物线上的动点,在射线ED上是否存在点M,使得以点M,N,E为顶点的三角形与△OBC相似?若存在,求点M的坐标;若不存在,请说明理由.参考答案一、选择题(本大题共12小题,共36分.在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对得3分,错选、不选或选出的答案超过一个均记0分.)1.下列图形,既是中心对称图形又是轴对称图形的是()A.B.C.D.【分析】根据轴对称图形与中心对称图形的概念依次对各项进行判断即可.解:A.不是轴对称图形,是中心对称图形,故此选项不符合题意;B.是轴对称图形,不是中心对称图形,故此选项不符合题意;C.是轴对称图形,也是中心对称图形,故此选项符合题意;D.是轴对称图形,不是中心对称图形,故此选项不符合题意;故选:C.2.下列运算正确的是()A.2a+3b=5ab B.a3•a2=a5C.(a+b)2=a2+b2D.(a2b)3=a6b【分析】根据合并同类项、幂的乘方,同底数幂乘法以及完全平方公式,逐项判断即可.解:A、不是同类项,不能合并,故选项A计算错误;B、a3•a2=a5,故选项B计算正确;C、(a+b)2=a2++2ab+b2,故选项C计算错误;D、(a2b)3=a6b3,故选项D计算错误.故选:B.3.今年的政府工作报告中指出:去年脱贫攻坚取得决定性成就,农村贫困人口减少1109万.数字1109万用科学记数法可表示为()A.1.109×107B.1.109×106C.0.1109×108D.11.09×106【分析】科学记数法的表示形式为a×10n,其中1≤|a|<10,n为整数,故先将1109万换成11090000,再按照科学记数法的表示方法表示即可得出答案.解:∵1109万=11090000,∴11090000=1.109×107.故选:A.4.将一个大正方体的一角截去一个小正方体,得到的几何体如图所示,则该几何体的左视图是()A.B.C.D.【分析】找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.解:从几何体的左边看可得到一个正方形,正方形的右上角处有一个看不见的小正方形画为虚线,故选:D.5.为调动学生参与体育锻炼的积极性,某校组织了一分钟跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成统计表:一分钟跳绳个数(个)141144145146学生人数(名)5212则关于这组数据的结论正确的是()A.平均数是144B.众数是141C.中位数是144.5D.方差是5.4【分析】根据平均数,众数,中位数,方差的性质分别计算出结果,然后判判断即可.解:根据题目给出的数据,可得:平均数为:,故A选项错误;众数是:141,故B选项正确;中位数是:,故C选项错误;方差是:=4.4,故D选项错误;故选:B.6.若m2+2m=1,则4m2+8m﹣3的值是()A.4B.3C.2D.1【分析】把变形为4m2+8m﹣3=4(m2+2m)﹣3,再把m2+2m=1代入计算即可求出值.解:∵m2+2m=1,∴4m2+8m﹣3=4(m2+2m)﹣3=4×1﹣3=1.故选:D.7.如图,点E是▱ABCD的边AD上的一点,且,连接BE并延长交CD的延长线于点F,若DE=3,DF=4,则▱ABCD的周长为()A.21B.28C.34D.42【分析】根据平行四边形的性质得AB∥CD,再由平行线得相似三角形,根据相似三角形求得AB,AE,进而根据平行四边形的周长公式求得结果.解:∵四边形ABCD是平行四边形,∴AB∥CF,AB=CD,∴△ABE∽△DFE,∴,∵DE=3,DF=4,∴AE=6,AB=8,∴AD=AE+DE=6+3=9,∴平行四边形ABCD的周长为:(8+9)×2=34.故选:C.8.关于x的一元二次方程x2+(k﹣3)x+1﹣k=0根的情况,下列说法正确的是()A.有两个不相等的实数根B.有两个相等的实数根C.无实数根D.无法确定【分析】先计算判别式,再进行配方得到△=(k﹣1)2+4,然后根据非负数的性质得到△>0,再利用判别式的意义即可得到方程总有两个不相等的实数根.解:△=(k﹣3)2﹣4(1﹣k)=k2﹣6k+9﹣4+4k=k2﹣2k+5=(k﹣1)2+4,∴(k﹣1)2+4>0,即△>0,∴方程总有两个不相等的实数根.故选:A.9.如图,函数y=kx+b(k≠0)与y=(m≠0)的图象相交于点A(﹣2,3),B(1,﹣6)两点,则不等式kx+b>的解集为()A.x>﹣2B.﹣2<x<0或x>1C.x>1D.x<﹣2或0<x<1【分析】结合图象,求出一次函数图象在反比例函数图象上方所对应的自变量的范围即可.解:∵函数y=kx+b(k≠0)与的图象相交于点A(﹣2,3),B(1,﹣6)两点,∴不等式的解集为:x<﹣2或0<x<1,故选:D.10.如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=4,以点O为圆心,2为半径的圆与OB交于点C,过点C作CD⊥OB交AB于点D,点P是边OA上的动点.当PC+PD 最小时,OP的长为()A.B.C.1D.【分析】延长CO交⊙O于点E,连接EP,交AO于点P,则PC+PD的值最小,利用平行线份线段成比例分别求出CD,PO的长即可.解:如图,延长CO交⊙O于点E,连接ED,交AO于点P,此时PC+PD的值最小.∵CD⊥OB,∴∠DCB=90°,又∠AOB=90°,∴∠DCB=∠AOB,∴CD∥AO∴∵OC=2,OB=4,∴BC=2,∴,解得,CD=;∵CD∥AO,∴,即,解得,PO=故选:B.11.若关于x的不等式组有且只有3个整数解,则a的取值范围是()A.0≤a≤2B.0≤a<2C.0<a≤2D.0<a<2【分析】先求出不等式组的解集(含有字母a),利用不等式组有三个整数解,逆推出a 的取值范围即可.解:解不等式3x﹣5≥1得:x≥2,解不等式2x﹣a<8得:x<,∴不等式组的解集为:2≤x<,∵不等式组有三个整数解,∴三个整数解为:2,3,4,∴4<≤5,解得:0<a≤2,故选:C.12.若定义一种新运算:a⊗b=,例如:3⊗1=3﹣1=2;5⊗4=5+4﹣6=3.则函数y=(x+2)⊗(x﹣1)的图象大致是()A.B.C.D.【分析】根据a⊗b=,可得当x+2≥2(x﹣1)时,x≤4,分两种情况:当x≤4时和当x>4时,分别求出一次函数的关系式,然后判断即可得出结论.解:∵当x+2≥2(x﹣1)时,x≤4,∴当x≤4时,(x+2)⊗(x﹣1)=(x+2)﹣(x﹣1)=x+2﹣x+1=3,即:y=3,当x>4时,(x+2)⊗(x﹣1)=(x+2)+(x﹣1)﹣6=x+2+x﹣1﹣6=2x﹣5,即:y=2x﹣5,∴k=2>0,∴当x>4时,y=2x﹣5,函数图象向上,y随x的增大而增大,综上所述,A选项符合题意.故选:A.二、填空题(本大题共6小题,共18分.只要求填写最后结果,每小题填对得3分.)13.因式分解:x2y﹣9y=y(x+3)(x﹣3).【分析】先提取公因式y,再对余下的多项式利用平方差公式继续分解.解:x2y﹣9y,=y(x2﹣9),=y(x+3)(x﹣3).14.若|a﹣2|+=0,则a+b=5.【分析】根据非负数的性质列式求出a、b的值,然后代入代数式进行计算即可得解.解:根据题意得,a﹣2=0,b﹣3=0,解得a=2,b=3,∴a+b=2+3=5.故答案为:5.15.如图,在Rt△ABC中,∠C=90°,∠B=20°,PQ垂直平分AB,垂足为Q,交BC 于点P.按以下步骤作图:①以点A为圆心,以适当的长为半径作弧,分别交边AC,AB于点D,E;②分别以点D,E为圆心,以大于DE的长为半径作弧,两弧相交于点F;③作射线AF.若AF与PQ的夹角为α,则α=55°.【分析】根据直角三角形两锐角互余得∠BAC=70°,由角平分线的定义得∠2=35°,由线段垂直平分线可得△AQM是直角三角形,故可得∠1+∠2=90°,从而可得∠1=55°,最后根据对顶角相等求出α.解:如图,∵△ABC是直角三角形,∠C=90°,∴∠B+∠BAC=90°,∵∠B=20°,∴∠BAC=90°﹣∠B=90°﹣20°=70°,∵AM是∠BAC的平分线,∴,∵PQ是AB的垂直平分线,∴△AMQ是直角三角形,∴∠AMQ+∠2=90°,∴∠AMQ=90°﹣∠2=90°﹣35°=55°,∵∠α与∠AMQ是对顶角,∴∠α=∠AMQ=55°.故答案为:55°.16.若关于x的分式方程+1有增根,则m=3.【分析】先把分式方程去分母转化为整式方程,然后由分式方程有增根求出x的值,代入到转化以后的整式方程中计算即可求出m的值.解:去分母得:3x=m+3+(x﹣2),整理得:2x=m+1,∵关于x的分式方程有增根,即x﹣2=0,∴x=2,把x=2代入到2x=m+1中得:2×2=m+1,解得:m=3;故答案为:3.17.如图,矩形ABCD中,点G,E分别在边BC,DC上,连接AC,EG,AE,将△ABG 和△ECG分别沿AG,EG折叠,使点B,C恰好落在AE上的同一点,记为点F.若CE =3,CG=4,则sin∠DAE=.【分析】根据折叠的性质结合勾股定理求得GE=5,BC=AD=8,证得Rt△EGF∽Rt△EAG,求得,再利用勾股定理得到DE的长,即可求解.解:矩形ABCD中,GC=4,CE=3,∠C=90°,∴GE=,根据折叠的性质:BG=GF,GF=GC=4,CE=EF=3,∠AGB=∠AGF,∠EGC=∠EGF,∠GFE=∠C=90°,∠B=∠AFG=90°,∴BG=GF=GC=4,∠AFG+∠EFG=90°,∴BC=AD=8,点A,点F,点E三点共线,∵∠AGB+∠AGF+∠EGC+∠EGF=180°,∴∠AGE=90°,∴Rt△EGF∽Rt△EAG,∴,即,∴,∴DE=,∴,故答案为:.18.如图,四边形ABCD是正方形,曲线DA1B1C1D1A2…是由一段段90度的弧组成的.其中:的圆心为点A,半径为AD;的圆心为点B,半径为BA1;的圆心为点C,半径为CB1;的圆心为点D,半径为DC1;…,…的圆心依次按点A,B,C,D循环.若正方形ABCD的边长为1,则的长是4039π.【分析】曲线DA1B1C1D1A2…是由一段段90度的弧组成的,半径每次比前一段弧半径+1,到AD n﹣1=AA n=4(n﹣1)+1,BA n=BB n=4(n﹣1)+2,再计算弧长.解:由图可知,曲线DA1B1C1D1A2…是由一段段90度的弧组成的,半径每次比前一段弧半径+1,AD=AA1=1,BA1=BB1=2,……,AD n﹣1=AA n=4(n﹣1)+1,BA n=BB n=4(n﹣1)+2,故的半径为BA2021=BB2021=4(2021﹣1)+2=8078,的弧长=.故答案为:4039π.三、解答题(本大题共7小题,共66分.解答应与出文字说明、证明过程或演算步骤.)19.先化简,再求值:(1﹣)÷,其中x是16的算术平方根.【分析】先将括号里的进行通分运算,然后再计算括号外的除法,把除法运算转化为乘法运算,进行约分,得到最简分式,最后把x值代入运算即可.解:原式=,=,=,=.∵x是16的算术平方根,∴x=4,当x=4时,原式=.20.某校“综合与实践”小组采用无人机辅助的方法测量一座桥的长度.如图,桥AB是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥AB的上方120米的点C处悬停,此时测得桥两端A,B两点的俯角分别为60°和45°,求桥AB的长度.【分析】过点C作CD⊥AB,垂足为D,根据在C处测得桥两端A,B两点的俯角分别为60°和45°,可得∠CAD=∠MCA=60°,∠CBD=∠NCB=45°,利用特殊角懂得三角函数求解即可.解:如图示:过点C作CD⊥AB,垂足为D,由题意得,∠MCA=∠A=60°,∠NCB=∠B=45°,CD=120,在Rt△ACD中,AD===40(米),在Rt△BCD中,∵∠CBD=45°,∴BD=CD=120(米),∴AB=AD+BD=(40+120)(米).答:桥AB的长度为(40+120)米.21.在4月23日“世界读书日”来临之际,某校为了了解学生的课外阅读情况,从全校随机抽取了部分学生,调查了他们平均每周的课外阅读时间t(单位:小时).把调查结果分为四档,A档:t<8;B档:8≤t<9;C档:9≤t<10;D档:t≥10.根据调查情况,给出了部分数据信息:①A档和D档的所有数据是:7,7,7.5,10,7,10,7,7.5,7,7,10.5,10.5;②图1和图2是两幅不完整的统计图.根据以上信息解答问题:(1)求本次调查的学生人数,并将图2补充完整;(2)已知全校共1200名学生,请你估计全校B档的人数;(3)学校要从D档的4名学生中随机抽取2名作读书经验分享,已知这4名学生1名来自七年级,1名来自八年级,2名来自九年级,请用列表或画树状图的方法,求抽到的2名学生来自不同年级的概率.【分析】(1)用A档和D档所有数据数减去D档人数即可得到A档人数,用A档人数除以所占百分比即可得到总人数;用总人数减去A档,B档和D档人数,即可得到C档人数,从而可补全条统计图;(2)先求出B档所占百分比,再乘以1200即可得到结论;(3)分别用A,B,C,D表示四名同学,然后通过画树状图表示出所有等可能的结果数,再用概率公式求解即可.解:(1)由于A档和D档共有12个数据,而D档有4个,因此A档共有:12﹣4=8人,8÷20%=40人,补全图形如下:(2)1200×=480(人),答:全校B档的人数为480.(3)用A表示七年级学生,用B表示八年级学生,用C和D分别表示九年级学生,画树状图如下,因为共有12种等可能的情况数,其中抽到的2名学生来自不同年级的有10种,所以P(2名学生来自不同年级)==.22.如图,AB为⊙O的直径,射线AD交⊙O于点F,点C为劣弧的中点,过点C作CE⊥AD,垂足为E,连接AC.(1)求证:CE是⊙O的切线;(2)若∠BAC=30°,AB=4,求阴影部分的面积.【分析】(1)连接BF,证明BF∥CE,连接OC,证明OC⊥CE即可得到结论;(2)连接OF,求出扇形FOC的面积即可得到阴影部分的面积.解:(1)连接BF,∵AB是⊙O的直径,∴∠AFB=90°,即BF⊥AD,∵CE⊥AD,∴BF∥CE,连接OC,∵点C为劣弧的中点,∴OC⊥BF,∵BF∥CE,∴OC⊥CE,∵OC是⊙O的半径,∴CE是⊙O的切线;(2)连接OF,∵OA=OC,∠BAC=30°,∴∠BOC=60°,∵点C为劣弧的中点,∴,∴∠FOC=∠BOC=60°,∵AB=4,∴FO=OC=OB=2,∴S扇形FOC=,即阴影部分的面积为:.23.因疫情防控需要,消毒用品需求量增加.某药店新进一批桶装消毒液,每桶进价50元,每天销售量y(桶)与销售单价x(元)之间满足一次函数关系,其图象如图所示.(1)求y与x之间的函数表达式;(2)每桶消毒液的销售价定为多少元时,药店每天获得的利润最大,最大利润是多少元?(利润=销售价﹣进价)【分析】(1)设y与x之间的函数表达式为y=kx+b,将点(60,100)、(70,80)代入一次函数表达式,即可求解;(2)根据利润等于每桶的利润乘以销售量得w关于x的二次函数,根据二次函数的性质即可求解.解:(1)设y与销售单价x之间的函数关系式为:y=kx+b,将点(60,100)、(70,80)代入一次函数表达式得:,解得:,故函数的表达式为:y=﹣2x+220;(2)设药店每天获得的利润为W元,由题意得:w=(x﹣50)(﹣2x+220)=﹣2(x﹣80)2+1800,∵﹣2<0,函数有最大值,∴当x=80时,w有最大值,此时最大值是1800,故销售单价定为80元时,该药店每天获得的利润最大,最大利润1800元.24.如图1,在△ABC中,∠A=90°,AB=AC=+1,点D,E分别在边AB,AC上,且AD=AE=1,连接DE.现将△ADE绕点A顺时针方向旋转,旋转角为α(0°<α<360°),如图2,连接CE,BD,CD.(1)当0°<α<180°时,求证:CE=BD;(2)如图3,当α=90°时,延长CE交BD于点F,求证:CF垂直平分BD;(3)在旋转过程中,求△BCD的面积的最大值,并写出此时旋转角α的度数.【分析】(1)利用“SAS”证得△ACE≌△ABD即可得到结论;(2)利用“SAS”证得△ACE≌△ABD,推出∠ACE=∠ABD,计算得出AD=BC=,利用等腰三角形“三线合一”的性质即可得到结论;(3)观察图形,当点D在线段BC的垂直平分线上时,△BCD的面积取得最大值,利用等腰直角三角形的性质结合三角形面积公式即可求解.【解答】(1)证明:如图2中,根据题意:AB=AC,AD=AE,∠CAB=∠EAD=90°,∵∠CAE+∠BAE=∠BAD+∠BAE=90°,∴∠CAE=∠BAD,在△ACE和△ABD中,,∴△ACE≌△ABD(SAS),∴CE=BD;(2)证明:如图3中,根据题意:AB=AC,AD=AE,∠CAB=∠EAD=90°,在△ACE和△ABD中,,∴△ACE≌△ABD(SAS),∴∠ACE=∠ABD,∵∠ACE+∠AEC=90°,且∠AEC=∠FEB,∴∠ABD+∠FEB=90°,∴∠EFB=90°,∴CF⊥BD,∵AB=AC=,AD=AE=1,∠CAB=∠EAD=90°,∴BC=AB=,CD=AC+AD=,∴BC=CD,∵CF⊥BD,∴CF是线段BD的垂直平分线;(3)解:△BCD中,边BC的长是定值,则BC边上的高取最大值时△BCD的面积有最大值,∴当点D在线段BC的垂直平分线上时,△BCD的面积取得最大值,如图4中:∵∵AB=AC=,AD=AE=1,∠CAB=∠EAD=90°,DG⊥BC于G,∴AG=BC=,∠GAB=45°,∴DG=AG+AD=,∠DAB=180°﹣45°=135°,∴△BCD的面积的最大值为:,旋转角α=135°.25.如图,抛物线y=ax2+bx+8(a≠0)与x轴交于点A(﹣2,0)和点B(8,0),与y 轴交于点C,顶点为D,连接AC,BC,BC与抛物线的对称轴l交于点E.(1)求抛物线的表达式;(2)点P是第一象限内抛物线上的动点,连接PB,PC,当S△PBC=S△ABC时,求点P 的坐标;(3)点N是对称轴l右侧抛物线上的动点,在射线ED上是否存在点M,使得以点M,N,E为顶点的三角形与△OBC相似?若存在,求点M的坐标;若不存在,请说明理由.【分析】(1)直接将A(﹣2,0)和点B(8,0)代入y=ax2+bx+8(a≠0),解出a,b的值即可得出答案;(2)先求出点C的坐标及直线BC的解析式,再根据图及题意得出三角形PBC的面积;过点P作PG⊥x轴,交x轴于点G,交BC于点F,设,根据三角形PBC的面积列关于t的方程,解出t的值,即可得出点P的坐标;(3)由题意得出三角形BOC为等腰直角三角形,然后分MN=EM,MN=NE,NE=EM 三种情况讨论结合图形得出边之间的关系,即可得出答案.解:(1)∵抛物线y=ax2+bx+8(a≠0)过点A(﹣2,0)和点B(8,0),∴,解得,∴抛物线解析式为:;(2)当x=0时,y=8,∴C(0,8),∴直线BC解析式为:y=﹣x+8,∵,∴,过点P作PG⊥x轴,交x轴于点G,交BC于点F,设,∴F(t,﹣t+8),∴,∴,即,∴t1=2,t2=6,∴P1(2,12),P2(6,8);(3)∵C(0,8),B(8,0),∠COB=90°,∴△OBC为等腰直角三角形,抛物线的对称轴为,∴点E的横坐标为3,又∵点E在直线BC上,∴点E的纵坐标为5,∴E(3,5),设,①当MN=EM,∠EMN=90°,当△NME~△COB时,则,解得或(舍去),∴此时点M的坐标为(3,8),②当ME=EN,当∠MEN=90°时,则,解得:或(舍去),∴此时点M的坐标为;③当MN=EN,∠MNE=90°时,连接CM,故当N为C关于对称轴l的对称点时,△MNE~△COB,此时四边形CMNE为正方形,∴CM=CE,∵C(0,8),E(3,5),M(3,m),∴,∴,解得:m1=11,m2=5(舍去),此时点M的坐标为(3,11);故在射线ED上存在点M,使得以点M,N,E为顶点的三角形与△OBC相似,点M的坐标为:(3,8),或(3,11).。
第一次月考(考试范围:第一、二章)【单元测试】年七年级数学上册尖子生选拔卷(人教版)(解析版)

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!第一次月考(考试范围:第一、二章)(人教版)选拔卷(考试时间:90分钟试卷满分:120分)一、选择题:本题共10个小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2021·重庆市实验学校)下列由四舍五入得到的近似数说法正确的是()A.0.720精确到百分位B.4´精确到千分位5.07810C.3.6万精确到十分位D.2.90精确到0.01【答案】D【分析】根据近似数的精确度对各选项进行判断.【详解】解:A、0.720精确到千分位,故A选项错误;B、5.078×104精确到十位,故B选项错误;C、3.6万精确到千位,故C选项错误;D、2.90精确到0.01,故D选项正确.故选:D.【点睛】本题考查了近似数和有效数字:从一个数的左边第一个不是0的数字起到末位数字止,所有的数字都是这个数的有效数字.近似数与精确数的接近程度,可以用精确度表示.一般有,精确到哪一位,保留几个有效数字等说法.2.(2021·河南初一期中)如图,关于A、B、C这三部分数集的个数,下列说法正确的是()A.A、C两部分有无数个,B部分只有一个0B.A、B、C三部分有无数个C.A、B、C三部分都只有一个D.A部分只有一个,B、C两部分有无数个【答案】A【分析】根据有理数的分类可以看出A指的是负整数,B指的是整数中除了正整数与负整数外的部分整数,C指的是正整数,最后根据各数性质进一步判断即可.【解析】由图可得:A指的是负整数,B指的是整数中除了正整数与负整数外的部分整数,C指的是正整数,∵整数中除了正整数与负整数外的部分整数只有0、负整数与正整数都有无数个,∴A、C两部分有无数个,B只有一个.故选:A.【点睛】本题主要考查了有理数的分类,熟练掌握相关概念是解题关键.)2015A答案.2)=【点睛】此题考查有理数的混合运算,掌握有理数乘方的逆运算是解题的关键.a,1B的正负,然后根据绝对值的意义去掉绝对值符号后可以得到答案.,.判断出式子的正负是解题关键.p,14C的值,代入原式计算即可求出值.,.【点睛】此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.210B积和即可.nB.形的面积等于总面积减去最后一个空白的小长方形的面积是解答此题的关键.1,2021C【分析】原式利用题中的新定义化简,约分即可得到结果..【点睛】此题考查有理数的混合运算,熟练掌握运算法则是解题的关键.)①②③……个D.个顶点;顶点,.【点睛】本题考查图形类规律,解题的关键是通过观察得出规律.)5B的意义,从而得出结论.距离之和.,.【点睛】本题考查绝对值的意义,解题的关键是学会利用数形结合的思想解决问题.,第三个数记2A.19900B.1991519934 C,从而可求得结果.C察并找出规律,这对学生的归纳能力提出了更高的要求.分。
2021-2022学年山东省东营市广饶县高一年级下册学期3月月考(线上)数学试题【含答案】

2021-2022学年山东省东营市广饶县第一中学高一下学期3月月考(线上)数学试题一、单选题1.的值为( )()sin 600-︒A B .C .D .1212-【答案】A【分析】根据任意角的周期性,结合诱导公式求的值.()sin 600-︒【详解】由题设,()sin 600sin(2360120)sin120-︒=-⨯︒-︒=︒=故选:A2.化简以下各式:①;②;③;④AB BC CA ++ AB AC BD CD -+- OA OD AD -+,结果为零向量的个数是( )NQ QP MN MP ++-A .1B .2C .3D .4【答案】D【分析】由向量的加法三角形法则和向量加法三角形法则可得.【详解】;;0AB BC CA ++= 0AB AC BD CD CB BD DC -+-=++=;.0OA OD AD DA AD -+=+= 0NQ QP MN MP NQ QP PM MN ++-=+++=故选:D3.已知,则等于( )1cos ,,0222ππαα⎛⎫⎛⎫+=∈- ⎪ ⎪⎝⎭⎝⎭tan αA .BC .D 【答案】C【分析】利用诱导化简,再利用同角公式计算作答.【详解】由得:,即,因,则1cos 22πα⎛⎫+= ⎪⎝⎭1sin 2α-=1sin 2α=-,02πα⎛⎫∈- ⎪⎝⎭cos α==所以sin tan cos ααα==故选:C4.已知在平行四边形中,,,对角线与相交于ABCD (2,6)AD = (4,4)AB =-AC BD 点( ),M BM = A .B .C .D .(2,5)--()3,1(2,5)-(1,5)-【答案】B【分析】根据向量减法的运算法则即可计算:.()1122BM BD AD AB==-【详解】.()()113,122BM BD AD AB ==-=故选:B.5.已知,,则( )1sin cos 5αα+=-()0,απ∈tan α=A .B .C .D .344343-34-【答案】D【分析】根据已知条件可得出关于、的方程组,解出、的值,可sin αcos αsin αcos α求得的值.tan α【详解】因为,则,由已知可得,解得()0,απ∈sin 0α>221sin cos 5sin cos 1sin 0ααααα⎧+=-⎪⎪+=⎨⎪>⎪⎩,3sin 54cos 5αα⎧=⎪⎪⎨⎪=-⎪⎩因此,.sin 3tan cos 4ααα==-故选:D.6.二十四节气是中华民族上古农耕文明的产物,是中国农历中表示季节变迁的24个特定节令.现行的二十四节气是根据地球在黄道(即地球绕太阳公转的轨道)上的位置变化而制定的.每个节气对应地球在黄道上运动所到达的一个位置.根据描述,从冬15︒至到雨水对应地球在黄道上运动的弧度数为 ( )A .B .C .D .3π-512π-512π3π【答案】D【解析】根据条件,得到从夏至到立秋对应地球在黄道上运动的角度,即可求415⨯解.【详解】根据题意,立秋时夏至后的第三个节气,故从从夏至到立秋对应地球在黄道上运行了.41560⨯=故选:D7.直角三角形中,是斜边上一点,且满足,点、在过点ABC P BC 2BP PC =M N 的直线上,若,,,则下列结论错误的是P AM mAB = AN nAC =()0,0m n >>( )A .为常数B .的最小值为12m n +m n +169C .的最小值为D .、的值可以为,2m n +3m n 12m =2n =【答案】B【分析】作出图形,由可得出,根据三点共线的结论得出2BP PC = 1233AP AB AC =+,结合基本不等式可判断出各选项的正误,即可得出结论.123m n +=【详解】如下图所示:由,可得,2BP PC = ()2AP AB AC AP -=-,1233AP AB AC∴=+ 若,,,AM mAB = AN nAC =()0,0m n >>则,,1AB AM m = 1AC ANn =,1233AP AM ANm n ∴=+ 、、三点共线,M P N ,,12133m n ∴+=123m n ∴+=故A 正确;所以,时,也满足,则D 选项正确;12m =2n =123m n +=,当且仅当时,()122255223333333n m m n m n m n m n ⎛⎫+=++=++≥= ⎪⎝⎭ m n =等号成立,C 选项成立;,当且仅当()1221113333n m m n m n m n m n ⎛⎫+=++=++≥= ⎪⎝⎭时,即,B 选项错误.n =m =n =故选:B8.是所在平面上一点,满足:,的面积是,P ABC 2PA PB PC AB ++=ABC 1S 的面积是,则( )PAB △2S A .B .C .D .124S S =123S S =122S S =12S S =【答案】B【分析】根据得出,所以∥并且方向一样,由2PA PB PC AB ++= 3AP BC = AP BC此可得出三角形面积关系.【详解】解:由题意得:22()PA PB PC AB AP PB ++==+ 3AP BC∴= ∥并且方向一样AP ∴ BC设与的距离为AP BC h11,22PAB ABC S AP h S BC h=⋅=⋅又3BC AP = 121,33PAB ABC S S S S ∴==故选:B 二、多选题9.下列说法错误的是( )A .与735°终边相同的角是15°B .若一扇形的圆心角为15°,半径为3cm ,则扇形面积为23cm 4πC .设是锐角,则角为第一或第二象限角α2αD .设是第一象限,则为第一或第三象限角α2α【答案】ABC【分析】令终边相同的角的关系可判断A ,利用角的范围或特例可判断CD 的正误,利用公式计算扇形的面积后可判断B.【详解】对于A ,,故与终边也相同,故A 错误.735375360︒-︒=︒375︒735︒对于B ,扇形面积为,故B 错误.221812m 323c ππ⨯⨯=对于C ,如果,则,此时为轴线角,故C 错误.4πα=22πα=2α对于D ,因为是第一象限,故,α22,2k k k Zππαπ<<+∈故,故为第一或第三象限角,故D 正确.,24k k k Zαπππ<<+∈2α故选:ABC.10.有下列说法其中正确的说法为A .若,,则:a b b c a c B .若,,分别表示,的面积,则230OA OB OC ++=AOC S ∆ABC S ∆AOC ∆ABC ∆;:1:6AOC ABC S S ∆∆=C .两个非零向量,,若,则与共线且反向;a b a b a b-=+ a b D .若,则存在唯一实数使得a b λa b =λ【答案】BC【解析】A 选项错误,例如,推不出,B 选项利用向量可确定O 点位置,可0b =a c ∥知O 到AC 的距离等于B 到AC 距离的,故正确,C 选项两边平方根据向量的数量积16的性质可知夹角为,结论正确,D 选项错误,例如.π0b =【详解】A 选项错误,例如,推不出,B 选项,设AC 的中点为M, BC 的中点0b =a c ∥为D, 因为,所以,即,所以O 是MD 230OA OB OC ++=2220OM OD ⨯+= 2OM OD =- 的三等分点,可知O 到AC 的距离等于D 到AC 距离的,而B 到AC 的距离等于D13到AC 距离的2倍,故可知O 到AC 的距离等于B 到AC 距离的,根据三角形面积16公式可知正确,C 选项两边平方可得 ,所以,即夹角22||||a b a b -⋅= cos ,1a b <>=-为,结论正确,D 选项错误,例如. 故选B C.π0b =【点睛】本题主要考查了向量共线,向量的夹角,向量的数量积,向量的线性运算,属于中档题.11.下面的命题正确的有( )A .方向相反的两个非零向量一定共线B .单位向量都相等C .若,满足且与同向,则a b ||||a b > a b a b> D .“若A 、B 、C 、D 是不共线的四点,且”“四边形ABCD 是平行四边形”AB DC =⇔【答案】AD【分析】根据向量的定义和性质,逐项判断正误即可.【详解】对于A ,由相反向量的概念可知A 正确;对于B ,任意两个单位向量的模相等,其方向未必相同,故B 错误;对于C ,向量之间不能比较大小,只能比较向量的模,故C 错误;对于D ,若A 、B 、C 、D 是不共线的四点,且,AB DC =可得,且,故四边形ABCD 是平行四边形;//AB DC AB DC =若四边形ABCD 是平行四边形,可知,且,//AB DC AB DC =此时A 、B 、C 、D 是不共线的四点,且,故D 正确.AB DC =故选:AD.12.已知角和都是任意角,若满足,则称与“广义互余”θϕ2,2k k Z πθϕπ+=+∈θϕ若,则下列角中,可能与角“广义互余”的有( ).()1sin 4πα+=-βαA .B .C .D .sin β=()1cos 4πβ+=tan β=tan β【答案】AC 【分析】由题可得,根据诱导公式化简计算判断每个选项即可.1sin 4α=【详解】若与广义互余,则,即.αβ2()2k k Z παβπ+=+∈2()2k k Z πβπα=+-∈又由,可得.()1sin 4πα+=-1sin 4α=对于A ,若与广义互余,则αβsin sin(2)cos 2k πβπαα=+-===由可得与可能广义互余,故A 正确;sin β=αβ对于B ,若与广义互余,则,由αβ1cos cos(2)sin 24k πβπαα=+-==可得 ,故B 错误;()1cos 4πβ+=1cos 4β=-对于C ,综上可得,所以Csin β=1cos 4β=sin tan cos βββ==正确,D 错误.故选:AC .三、填空题13.若,则与同方向的单位向量是______.(1,1),(1,2)a b ==- a b -【答案】【分析】用除以它的模可得.a b - 【详解】由已知,(2,1)a b -=- a b -=所以与同方向的单位向量是.a b- a ba b-=-故答案为:14.,则 ________1cos 123πθ⎛⎫-= ⎪⎝⎭5sin 12πθ⎛⎫+= ⎪⎝⎭【答案】13【分析】因为= ,所以结合三角函数的诱导公式求值;51212ππθθ-++2π【详解】因为=,由诱导公式得:51212ππθθ-++2πsin =5sin 12πθ⎛⎫+= ⎪⎝⎭--212ππθ⎡⎤⎢⎥⎣⎦()1 cos 123πθ⎛⎫-=⎪⎝⎭故答案为13【点睛】本题考查三角函数的化简求值,考查三角函数中的恒等变换应用,关键是“拆角配角”思想的应用,是中档题.15.已知,,点P 在线段AB 的延长线上,且,则点P 的()2,3A ()4,3B -32AP PB = 坐标为___________.【答案】()8,15-【分析】由题 可得,可得,即求.12AB BP=2OP OB AB =+ 【详解】点在线段的延长线上,且,P AB 3||||2AP PB = ,∴12AB BP= ,,,.∴2(4OP OB AB =+= 3)2(2-+6)(8-=15)-所以点P 的坐标为.()8,15-故答案为:.()8,15-16.已知为第二象限角,则______.αcos sin =【答案】sin cos αα-【分析】先由题意,得到,,再根据同角三角函数基本关系化简,sin 0α>cos 0α<即可得出结果.【详解】因为为第二象限角,所以,,αsin 0α>cos 0α<因此cos sin cos sin =+.1sin 1cos cos sin 1sin 1cos sin cos cos sin αααααααααα--=⋅+⋅=-++-=-故答案为:.sin cos αα-【点睛】本题主要考查三角函数的化简问题,熟记同角三角函数基本关系即可,属于常考题型.四、解答题17.已知,分别求下列各式的值.tan 3α=(1)4sin 2cos 5cos 3sin αααα-+(2)sin cos αα(3)222sin sin cos 3cos αααα+-【答案】(1);57(2);310(3).95【分析】(1)(2)(3)根据给定条件,将关于正余弦的齐次式化成正切,再代值计算作答.【详解】(1)因为,所以.tan 3α=4sin 2cos 4tan 243255cos 3sin 53tan 5337αααααα--⨯-===+++⨯(2)因为,所以.tan 3α=2222sin cos tan 33sin cos sin cos tan 13110αααααααα====+++(3)因为,所以tan 3α=2222222sin sin cos 3cos sin 2sin sin cos co 3c s os αααααααααα+--+=+.22222tan tan 323339tan 1315ααα+-⨯+-===++18.已知扇形的圆心角为,所在圆的半径为.αr(1)若, ,求扇形的弧长;120α=6r =(2)若扇形的周长为,当为多少弧度时,该扇形面积最大?并求出最大面积.24αS 【答案】(1);(2),.4π2rad 36【详解】试题分析:(1)由已知利用弧长公式即可计算得解.(2)根据扇形的弧长与半径的关系,建立等式,然后根据面积公式转化成关于r 的二次函数,通过解二次函数最值即可得到结论.试题解析:(1)∵, ,∴021********3a ππ==⨯=6r =2•643l r παπ==⨯=(2)设扇形的弧长为,则,即(),l 224l r +=242l r =-012r <<扇形的面积,()()2211•242•1263622S l r r r r r r ==-=-+=--+所以当且仅当时, 有最大值36,6r =S 此时,∴242612l =-⨯=1226l r α===.rad 19.如图所示,△中,,,.线段相交ABC ,AB a AC b == 2AE AB =3AF AC = ,BF CE 于点.P(1)用向量与表示及;a b BF CE (2)若,试求实数的值.AP xAB y AC =+ ,x y 【答案】(1),;13BF b a =- 12CE a b=-(2),.25x =15y =【分析】(1)根据向量加法、数乘、相反向量的几何意义,将、用表BF CE,AB AC 示即可.(2)由题图知,,结合已知条件求得,根(1)AP AB AF λλ=+-(1)AP AC AE μμ=+- ,λμ据平面向量的基本定理可得的值.,x y 【详解】(1)由题设,,1133BF BA AF AC AB b a=+=-=-.1122CA AE AB AC a b CE =+=-=- (2)设,FP FB λ= EP EC μ=所以,且,(1)AP AB AF λλ=+- (1)AP AC AE μμ=+- 0,1λμ<<所以,则,可得,1132AB AC AC AB λμλμ--+=+ 1213μλλμ-⎧=⎪⎪⎨-⎪=⎪⎩2515λμ⎧=⎪⎪⎨⎪=⎪⎩所以,故,.2155AP AB AC =+ 25x =15y =20.已知为第三象限角,且.α3sin()cos()tan()22()sin()tan(2)2f ππαααπαπαπα---+=+-(1) 化简;()f α(2) 若,求的值.323απ=-()f α(3) 若,求的值.()f α=cos()πα+【答案】(1);(23)sin α-15【详解】试题分析:(1)由诱导公式可化简得到;(2)因为()sin ,f αα=-∴;(3)由题意可得32322()()()sin()333f f sin απππ=-===sin α=三角函数基本关系式可得1cos 5α==-试题解析:(1)(cos )(sin )(tan )()(cos )(tan )f αααααα-⋅⋅-=⋅-;sin α=-(2)3232322()()sin()sin()sin()3333f f αππππ=-=--===(3),()sin f αα=-=∴sin α=又为第三象限角,α,∴1cos 5α===-.∴1cos()cos 5παα+=-=【解析】1. 诱导公式;2. 同角三角函数基本关系式21.已知,是平面内两个不共线的非零向量,,,1e →2e →122AB e e →→→=+12BE e e λ→→→=-+,且三点共线.122EC e e →→→=-+,,A E C (1)求实数的值;λ(2)若,,求的坐标;()12,1e →=()22,2e →=-BC →(3)已知,在(2)的条件下,若四点按顺时针顺序构成平行四边形,()3,5D ,,,A B C D 求点A 的坐标.【答案】(1);(2);(3).32-()7,2--(10,7)【分析】(1)根据平面向量的加法运算,得出,再利用,12(1)AE AB BE e e λ→→→→→=+=++A ,三点共线,利用向量的共线定理可知存在实数,使得,解出的值,E C k AE k EC →→=λ即可得出结果;(2)根据平面向量坐标的加法运算,得出,可求出的坐标;12132BC BE EC e e →→→→→=+=--BC →(3)由平行四边形的性质,可知,设,则,计算得出AD BC →→=(,)A x y (3,5)AD x y →=--点的坐标.A 【详解】解:(1)由题可知,,,,122AB e e →→→=+12BE e e λ→→→=-+122EC e e →→→=-+,121212(2)()(1)AE AB BE e e e e e e λλ→→→→→→→→→∴=+=++-+=++,,三点共线,A E C 存在实数,使得,∴k AE k EC →→=即,1212(1)(2)e e k e e λ→→→→++=-+得.12(12)(1)k e k e λ→→+=--,是平面内两个不共线的非零向量, 1e →2e →,解得:,.∴1201k k λ+=⎧⎨=-⎩12k =-32λ=-(2)已知,,()12,1e →=()22,2e →=-.()()()12136,31,17,22BC BE EC e e →→→→→=+=--=--+-=--(3)四点按逆时针顺序构成平行四边形,且,,,,A B C D ()3,5D ,∴AD BC →→=设,则,(,)A x y (3,5)AD x y →=--, (7,2)BC →=--,解得,即点的坐标为.∴3752x y -=-⎧⎨-=-⎩107x y =⎧⎨=⎩A (10,7)22.已知:关于的方程的两根为和,.求:x 221)0x x m -+=sin θcos θ(0,2)θπ∈(1)的值;tan sin cos tan 11tan θθθθθ+--(2)的值;m (3)方程的两根及此时的值.θ【答案】(1;(2);(3)方程的两个根分别为,对应的m =12θ值为 或..6π3π【分析】(1)由题意得,再根据三角函数的恒等变换化简sin cos sin cos 2mθθθθ⎧+=⎪⎪⎨⎪=⎪⎩,从而求得结果.tan sin cos tan 11tan θθθθθ+--sin cos θθ+(2)由、 以及同角三角函数的基本关系可得sin cos θθ+=sin cos 2m θθ=,由此解得21m +=m (3)由以上可得,和 的值,sin cos θθ+=sin cos θθ=sin θcos θ从而求得故此时方程的两个根及的值.θ【详解】解:(1)由于关于的方程的两根为和,故x 221)0x x m -++=sin θcos θ有,sin cos sin cos 2mθθθθ⎧+=⎪⎪⎨⎪=⎪⎩∴22tan sin cos sin cos (sin cos )(sin cos )sin cos tan 11tan sin cos cos sin sin cos θθθθθθθθθθθθθθθθθθθ+-+=+==+=-----(2)由、sin cos θθ+=,,即,解得sin cos 2m θθ=222sin 2sin cos cos θθθθ∴++=21m +=m =(3)由以上可得,,sin cos θθ+=sin cos θθ=1sin 2θ=或者.cos θ=sin θ=1cos 2θ=故此时方程的两个根分别为的值为 或.12θ6π3π【点睛】本题主要考查一元二次方程根与系数的关系,同角三角函数的基本关系的应用,三角函数的恒等变换,根据三角函数的值求角,属于中档题.。
数学丨山东省潍坊市2025届高三9月开学调研监测考试数学试卷及答案

5. 已知圆 C:x2 + y2 - 2x = 0,则过点 P3,0 的圆 C 的切线方程是
A.
y
=±
1 2
(x - 3)
C.
y =±
3 3
(x - 3)
B. y =±2(x - 3) D. y =± 3 (x - 3)
6. 数列 an 中,a1 = 2,an+1 = an + 2, 若 ak + ak+1 +⋯+ak+9 = 270, 则 k =
高三开学调研监测考试
试卷类型:A
数学试题
本试卷共 4 页.满分 150 分.考试时间 120 分钟。
2024.09
注意事项:
1. 答题前,考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名。
2. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改
动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上.写在
Pí + 3## QQQQQQQQQQQQQQQQQQQQQQQQQQQQQ , + MUé8Lí 5! 3+! /4! -!+4BC;&3)5 /+5 -!# 3!,# QQQQQQQQQ )) +
S 53! 槡7#S&"#&9Ñ + /4/53# /5 /! 槡7 3)% /! 槡7!QQQQ )+ + )5!P(M$Vy#
S
1!%#%#%"
#*!%#%
#+"
##!%#+#%"
#&!
+
山东省潍坊市2023-2024学年人教版小学数学三年级上学期《期末试卷》(含答案)

2023-2024学年山东省潍坊市三年级(上)期末数学试卷一、判断题。
1.把一张正方形纸分成4份,每份是这张正方形纸的. .2.一箱带鱼398元,李华想带3000元钱一定能买回7箱带鱼。
3.用两个相同的正方形拼成一个长方形,这个长方形的周长是两个正方形周长的和. .4.汽车在笔直的公路上行驶,车轮和车身的运动都是平移现象。
5.一个乘数的末尾有2个0,积的末尾也只有2个0。
二、选择题。
6.(3分)李华有2件上衣和2条裤子,要配成一套衣服,有( )种不同的搭配方法.A.2B.4C.6D.87.(3分)一块蛋糕,爸爸吃了它的,妈妈吃了它的,这块蛋糕( )A.还剩它的B.吃了它的C.已经被吃完了D.不确定8.(3分)□96是一个三位数,□96×6的积最接近3000,方框里是( )A.2B.3C.4D.59.(3分)小美妈妈买了3盒草莓共重24千克,平均每盒重( )A.800克B.8000克C.800千克D.8000千克10.(3分)如图,把一张边长6cm的正方形纸从中间对折成两个长方形,再剪开,每个长方形的周长是( )cm。
A.9B.12C.18D.20三、填空题。
11.(3分)在横线上填上合适的单位名称。
①踢5个毽子用10 ②一双轮滑鞋约重1000 ③小朋友洗一次澡需要40 ④小刚同学的体重约是30 12.(3分)在横线上填上“>”“<”或“=”。
3005克 3千克2吨 303千克3分40秒 300秒400 71×6 1 13.(3分)一节课是40分钟,第三节上课时间10:30,下课时间是 。
14.(3分)钟面上秒针走了6个大格,时间经过了 秒,秒针的运动是 。
15.(3分)如果△+☆=20,☆=△+△+△,那么☆= ,△= 。
16.(3分)光明小学的教学楼在操场的西南方向,小明在操场上完体育课要回教学楼,应往 方向走。
17.(3分)三年级2班同学去唠山北宅樱桃采摘园采摘,请根据要求完成题目。
2023-2024学年山东省潍坊市高一(上)期中数学试卷【答案版】

2023-2024学年山东省潍坊市高一(上)期中数学试卷一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A ={﹣1,1,2},B ={x |x 2=x },则A ∩B =( ) A .{﹣1}B .{1}C .{﹣1,1}D .{﹣1,0,1,2}2.命题“∃x ∈Z ,x ∈N ”的否定为( ) A .∃x ∈Z ,x ∉NB .∃x ∉Z ,x ∈NC .∀x ∈Z ,x ∉ND .∀x ∈Z ,x ∈N3.与函数y =√x 3为同一函数的是( ) A .y =x √xB .y =−x √xC .y =x √−xD .y =|x |4.函数f (x )=√−x 2+2x +3的单调递减区间是( ) A .(﹣∞,1]B .[1,3]C .(﹣1,3)D .[1,+∞)5.已知a >b >0,下列不等式中正确的是( ) A .a ﹣1<b ﹣1B .ab <b 2C .1a+1<1b+1D .c a>cb6.已知函数f(x)={x +a ,x >0,|x|+1,x <0,且f (f (﹣1))=4,则a =( )A .2B .1C .0D .﹣17.已知函数f (x )为奇函数,且对任意的x 1,x 2∈R ,当x 1<x 2时,f(x 1)−f(x 2)x 1−x 2<0,则关于x 的不等式f (x 2﹣x )<0的解集为( ) A .(0,1) B .(﹣∞,0)∪(1,+∞) C .(﹣1,0)D .(﹣∞,﹣1)∪(0,+∞)8.某人分两次购买同一种物品,因价格有变动,两次购买时物品的单价分别为a 1,a 2且a 1≠a 2.若他每次购买数量一定,其平均价格为b 1;若他每次购买的费用一定,其平均价格为b 2,则( ) A .b 1<b 2 B .b 1>b 2C .b 1=b 2D .b 1,b 2不能比较大小二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分. 9.下列函数值域为[1,+∞)的是( ) A .y =x +1 B .y =x 2+2x +2 C .y =1−x1+xD .y =x −1x +1(x ≥1)10.已知关于x 的不等式ax 2+bx +c <0的解集为{x |x <﹣4或x >3},则( ) A .a >0B .12a +c =0C .a +b +c >0D .不等式ax−b ax−c≤0的解集为{x |﹣12<x ≤1}11.若a >0,b >0,a +b =1,则( ) A .ab ≤14B .1a+1b≥4C .|a −12|+|b −14|≤14D .a 2+b ≥3412.对于任意实数x ,函数f (x )满足:当n −12<x ≤n +12(n ∈Z)时,f (x )=x ﹣n ,则( ) A .f (2023)=0B .f (x )的值域为(−12,12]C .f (x )在区间(−12,52]上单调递增D .f (x )的图象关于点(k ,0)(k ∈Z )对称三、填空题:本题共4小题,每小题5分,共20分.13.已知集合M ={x ,x +2,2},若0∈M ,则x = . 14.已知函数y =f (x )的定义域为[﹣2,5],则函数y =f(2x−1)x−1的定义域为 . 15.已知f (x ),g (x )是分别定义在R 上的奇函数和偶函数,且f (x )﹣g (x )=x 3+x 2+1,则f (1)+g (2)= .16.已知函数f(x)={|x −1|,0≤x <2,2(x −3)2−1,x ≥2,则函数y =f(f(x))−12的零点个数为 .四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(10分)设全集U =R ,集合A ={x |1<x <4},B ={x |m ﹣1≤x ≤m +1}. (1)当m =4时,求A ∪B ,A ∩(∁U B );(2)若“x ∈A ”是“x ∈B ”的必要条件,求实数m 的取值范围.18.(12分)已知f (x )是定义在R 上的偶函数,当x ≤0时,f (x )=x 2+2x . (1)求函数f (x )的解析式;(2)在给出的坐标系中画出f (x )的图象,并写出f (x )的单调增区间.19.(12分)已知函数f (x )=ax 2+(a ﹣2)x +14(a ∈R).(1)若关于x 的不等式f (x )≥0的解集是实数集R ,求a 的取值范围; (2)当a <0时,解关于x 的不等式f (x )−94≤0.20.(12分)为改善生态环境,某企业对生产过程中产生的污水进行处理.已知该企业污水日处理量为x 百吨(70≤x ≤120),日处理污水的总成本y 元与x 百吨之间的函数关系可近似地表示为y =12x 2+40x +5000.(1)该企业日污水处理量为多少百吨时,平均成本最低?(平均成本=y x)(2)若该企业每处理1百吨污水获收益100元,为使该企业可持续发展,政府决定对该企业污水处理进行财政补贴,补贴方式有两种方案:方案一:每日进行定额财政补贴,金额为4200元;方案二:根据日处理量进行财政补贴,处理x 百吨获得金额为40x +1700元.如果你是企业的决策者,为了获得每日最大利润,你会选择哪个方案进行补贴?并说明原因. 21.(12分)已知函数f (x )对于任意实数x ,y ∈R ,都有f (x +y )+2=f (x )+f (y ),且f (2)=4. (1)求f (1)的值;(2)令g (x )=f (x )﹣2,求证:函数g (x )为奇函数;(3)求f (﹣2023)+f (﹣2022)+…+f (﹣1)+f (0)+f (1)+…+f (2022)+f (2023)的值. 22.(12分)已知函数f (x ),g (x )满足g (x )=f (x )+a 2f(x)(a >0). (1)设f (x )=x ,求证:函数g (x )在区间(0,a )上为减函数,在区间(a ,+∞)上为增函数; (2)设f (x )=√1−x1+x. ①当a =1时,求g (x )的最小值;②若对任意实数r ,s ,t ∈[−35,35],|g (r )﹣g (s )|<g (t )恒成立,求实数a 的取值范围.2023-2024学年山东省潍坊市高一(上)期中数学试卷参考答案与试题解析一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={﹣1,1,2},B={x|x2=x},则A∩B=()A.{﹣1}B.{1}C.{﹣1,1}D.{﹣1,0,1,2}解:集合A={﹣1,1,2},B={x|x2=x}={0,1},则A∩B={1}.故选:B.2.命题“∃x∈Z,x∈N”的否定为()A.∃x∈Z,x∉N B.∃x∉Z,x∈N C.∀x∈Z,x∉N D.∀x∈Z,x∈N解:因为特称命题的否定是全称命题,所以“∃x∈Z,x∈N”的否定是:“∀x∈Z,x∉Z”.故选:C.3.与函数y=√x3为同一函数的是()A.y=x√x B.y=−x√x C.y=x√−x D.y=|x|解:∵函数y=√x3中x3≥0可得x≥0,故函数y=√x3的定义域为[0,+∞),排除CD,又y=√x3=x√x,排除B.故选:A.4.函数f(x)=√−x2+2x+3的单调递减区间是()A.(﹣∞,1]B.[1,3]C.(﹣1,3)D.[1,+∞)解:由﹣x2+2x+3≥0,解得﹣1≤x≤3,设t=﹣x2+2x+3,由二次函数的性质可知:t在x∈[﹣1,1]上单调递增,在x∈[1,3]上单调递减,又因为y=√t在定义上为增函数,由复合函数的性质可得:函数f(x)=√−x2+2x+3的单调递减区间是[1,3].故选:B.5.已知a>b>0,下列不等式中正确的是()A.a﹣1<b﹣1B.ab<b2C.1a+1<1b+1D.ca>cb解:因为a>b>0,所以a﹣1>b﹣1,A错误;因为a>b>0,所以ab>b2,B错误;因为a+1>b+1>0,所以0<1a+1<1b+1,C正确;因为1a<1b,所以c a<cb,D 错误.故选:C .6.已知函数f(x)={x +a ,x >0,|x|+1,x <0,且f (f (﹣1))=4,则a =( )A .2B .1C .0D .﹣1解:∵函数f(x)={x +a ,x >0,|x|+1,x <0,∴f (﹣1)=|﹣1|+1=2, f (f (﹣1))=2+a =4, ∴a =2. 故选:A .7.已知函数f (x )为奇函数,且对任意的x 1,x 2∈R ,当x 1<x 2时,f(x 1)−f(x 2)x 1−x 2<0,则关于x 的不等式f (x 2﹣x )<0的解集为( ) A .(0,1) B .(﹣∞,0)∪(1,+∞) C .(﹣1,0)D .(﹣∞,﹣1)∪(0,+∞)解:因为对任意的x 1,x 2∈R ,当x 1<x 2时,f(x 1)−f(x 2)x 1−x 2<0,所以f (x )在R 上单调递减, 因为f (x )为奇函数,即f (0)=0, 因为f (x 2﹣x )<0=f (0), 所以x 2﹣x >0, 解得x >1或x <0. 故选:B .8.某人分两次购买同一种物品,因价格有变动,两次购买时物品的单价分别为a 1,a 2且a 1≠a 2.若他每次购买数量一定,其平均价格为b 1;若他每次购买的费用一定,其平均价格为b 2,则( ) A .b 1<b 2 B .b 1>b 2C .b 1=b 2D .b 1,b 2不能比较大小解:设每次购买数量为x ,平均价格为b 1=a 1x+a 2x 2x=a 1+a 22, 设每次购买的费用为y ,平均价格为b 2=2y y a 1+ya 2=2a 1a2a 1+a 2,∵a 1≠a 2,∴(a 1+a 2)2>4a 1a 2⇒a 1+a 22>2a 1a 2a 1+a 2⇒b 1>b 2.故选:B .二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分. 9.下列函数值域为[1,+∞)的是( ) A .y =x +1 B .y =x 2+2x +2 C .y =1−x1+xD .y =x −1x +1(x ≥1)解:y =x +1的值域为R ,A 错误;y =x 2+2x +2=(x +1)2+1≥1,B 符合题意; y =1−x1+x =−x−1x+1=−1+2x+1≠−1,C 不符合题意; 当x ≥1时,y =x −1x +1单调递增,故y ≥1,D 符合题意. 故选:BD .10.已知关于x 的不等式ax 2+bx +c <0的解集为{x |x <﹣4或x >3},则( ) A .a >0B .12a +c =0C .a +b +c >0D .不等式ax−b ax−c≤0的解集为{x |﹣12<x ≤1}解:已知关于x 的不等式ax 2+bx +c <0的解集为{x |x <﹣4或x >3}, 可得﹣4,3是方程ax 2+bx +c =0的两个根,且a <0,则{−ba =−4+3c a =−4×3,即b =a ,c =﹣12a ,所以c +12a =0,故A 错误,B 正确;因为1∉{x |x <﹣4或x >3},所以a ×12+b ×1+c >0,即a +b +c >0,故C 正确; 又不等式ax−b ax−c≤0等价于{(ax −b)(ax −c)≤0ax −c ≠0,即{(ax −a)(ax +12a)≤0ax +12a ≠0,即{(x −1)(x +12)≤0x ≠−12,解得﹣12<x ≤1,故D 正确. 故选:BCD .11.若a >0,b >0,a +b =1,则( )A .ab ≤14B .1a+1b≥4C .|a −12|+|b −14|≤14D .a 2+b ≥34解:因为a +b =1≥2√ab ,解得ab ≤14,当且仅当a =b =12时,等号成立,故A 正确;由1a+1b=(a +b)(1a+1b)=2+b a+a b≥2+2√b a ⋅ab=4,当且仅当a =b =12时,等号成立,可得B 正确;当a =15,b =45时,|a −12|+|b −14|=1720>14,故|a −12|+|b −14|≤14不成立,故C 错误;根据题意,可得a 2+b =a 2−a +1=(a −12)2+34≥34,当且仅当a =b =12时,a 2+b 的最小值为34,故D 正确. 故选:ABD .12.对于任意实数x ,函数f (x )满足:当n −12<x ≤n +12(n ∈Z)时,f (x )=x ﹣n ,则( ) A .f (2023)=0B .f (x )的值域为(−12,12]C .f (x )在区间(−12,52]上单调递增D .f (x )的图象关于点(k ,0)(k ∈Z )对称解:由题意得f (x )={⋯x +1,−32<x ≤−12x ,−12<x ≤12x −1,12<x ≤32,x −2,32<x ≤52⋯,其大致图象如图所示,故f (2023)=f (2022)=f (2021)=…=f (0)=0,A 正确; 由函数的图象可知,函数的值域为(−−12,12],B 正确; 根据函数图象可知,f (x )在区间(−12,52]上不单调,C 错误; 根据函数的图象可知,f (x )的图象关于(k 2,0)对称,D 错误.故选:AB .三、填空题:本题共4小题,每小题5分,共20分. 13.已知集合M ={x ,x +2,2},若0∈M ,则x = ﹣2 . 解:集合M ={x ,x +2,2},若0∈M ,则x =0或x +2=0, 所以x =0或x =﹣2,当x =0时,x +2=2,不满足元素的互异性,舍去, 当x =﹣2时,集合M ={﹣2,0,2},符合题意, 综上所述,x =﹣2. 故答案为:﹣2.14.已知函数y =f (x )的定义域为[﹣2,5],则函数y =f(2x−1)x−1的定义域为 {x |−12≤x ≤3且x ≠1} . 解:数y =f (x )的定义域为[﹣2,5],则{−2≤2x −1≤5x −1≠0,解得−12≤x ≤3且x ≠1,故函数y 的定义域为{x |−12≤x ≤3且x ≠1}. 故答案为:{x |−12≤x ≤3且x ≠1}.15.已知f (x ),g (x )是分别定义在R 上的奇函数和偶函数,且f (x )﹣g (x )=x 3+x 2+1,则f (1)+g (2)= ﹣4 .解:因为f (x ),g (x )分别是定义在R 上的奇函数和偶函数, 且f (x )﹣g (x )=x 3+x 2+1,①所以f (﹣x )﹣g (﹣x )=(﹣x )3+(﹣x )2+1=﹣x 3+x 2+1,即﹣f (x )﹣g (x )=﹣x 3+x 2+1,变形可得:f (x )+g (x )=x 3﹣x 2﹣1,② 由①②解得:f (x )=x 3,g (x )=﹣x 2﹣1, 则f (1)=1,g (2)=﹣5, 故f (1)+g (2)=﹣4. 故答案为:﹣4.16.已知函数f(x)={|x −1|,0≤x <2,2(x −3)2−1,x ≥2,则函数y =f(f(x))−12的零点个数为 7 .解:令f (x )=t ,则有y =f(f(x))−12=f (t )−12, 令f (t )−12=0,得f (t )=12,当0≤t <2时,由|t ﹣1|=12,解得t 1=12或t 2=32;当t ≥2时,由2(t ﹣3)2﹣1=12,解得t 3=3−√32,t 4=3+√32, 作出y =f (x )的图象,如图所示:由此可得当f (x )=12时,有4个根(y =f (x )的图象与y =12的图象有4个交点); 当f (x )=32时,有1根(y =f (x )的图象与y =32的图象有1交点); 当f (x )=3−√32时,有1根(y =f (x )的图象与y =3−√32的图象有1交点); 当f (x )=3+√32时,有1根(y =f (x )的图象与y =3+√32的图象有1交点);所以一共有4+1+1+1=7个零点. 故答案为:7.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(10分)设全集U =R ,集合A ={x |1<x <4},B ={x |m ﹣1≤x ≤m +1}. (1)当m =4时,求A ∪B ,A ∩(∁U B );(2)若“x ∈A ”是“x ∈B ”的必要条件,求实数m 的取值范围.解:(1)m =4时,A ={x |1<x <4},B ={x |m ﹣1≤x ≤m +1}={x |3≤x ≤5}, 则∁U B ={x |x >5或x <3},A ∪B ={x |1<x ≤5},A ∩(∁U B )={x |1<x <3}; (2)若“x ∈A ”是“x ∈B ”的必要条件, 则B ⊆A ,则{m −1>1m +1<4,解得:2<m <3,即实数a 的取值范围是(2,3).18.(12分)已知f (x )是定义在R 上的偶函数,当x ≤0时,f (x )=x 2+2x . (1)求函数f (x )的解析式;(2)在给出的坐标系中画出f (x )的图象,并写出f (x )的单调增区间.解:(1)设x>0,则﹣x<0,所以f(﹣x)=x2﹣2x,因为f(x)是定义在R上的偶函数,所以f(﹣x)=f(x),所以当x>0 时,f(x)=f(﹣x)=x2﹣2x,综合可得:f(x)={x2+2x,x≤0 x2−2x,x>0;(2)根据题意,由(1)的结论,f(x)={x2+2x,x≤0 x2−2x,x>0,其图象为:该函数的单调递增区间为(﹣1,0),(1,+∞).19.(12分)已知函数f(x)=ax2+(a﹣2)x+14(a∈R).(1)若关于x的不等式f(x)≥0的解集是实数集R,求a的取值范围;(2)当a<0时,解关于x的不等式f(x)−94≤0.解:(1)若关于x的不等式f(x)≥0的解集是实数集R,即ax2+(a−2)x+14≥0在实数集R上恒成立,当a =0时,x ≤18,不符合题意;当a ≠0时,要使关于x 的不等式f (x )≥0的解集是实数集R , 则要满足{a >0(a −2)2−4a ×14≤0,解得1≤a ≤4, 综上可得,实数l 的取值范围是{a |1≤a ≤4}.(2)由题意f(x)−94≤0 可变为ax 2+(a ﹣2)x ﹣2≤0, 可得ax 2+(a ﹣2)x ﹣2=(ax ﹣2)(x +1),当a <0时,方程(ax ﹣2)(x +1)=0的两根为−1,2a, ①当a <﹣2时,因为−1<2a ,解不等式得x ≤﹣1或x ≥2a ; ②当a =﹣2时,因为−1=2a ,此时不等式的解集为R ; ③当﹣2<a <0时,因为−1>2a,解不等式得x ≤2a或x ≥﹣1; 综上所述,不等式的解集为:当﹣2<a <0时,不等式的解集为{x|x ≤2a 或≥−1}; 当a =﹣2时,不等式的解集为R ;当a <﹣2时,不等式的解集为{x|x ≤−1或x ≥2a}.20.(12分)为改善生态环境,某企业对生产过程中产生的污水进行处理.已知该企业污水日处理量为x 百吨(70≤x ≤120),日处理污水的总成本y 元与x 百吨之间的函数关系可近似地表示为y =12x 2+40x +5000.(1)该企业日污水处理量为多少百吨时,平均成本最低?(平均成本=yx )(2)若该企业每处理1百吨污水获收益100元,为使该企业可持续发展,政府决定对该企业污水处理进行财政补贴,补贴方式有两种方案:方案一:每日进行定额财政补贴,金额为4200元;方案二:根据日处理量进行财政补贴,处理x 百吨获得金额为40x +1700元.如果你是企业的决策者,为了获得每日最大利润,你会选择哪个方案进行补贴?并说明原因. 解:(1)∵y =12x 2+40x +5000, ∴yx =x 2+5000x+40,又x ∈[70,120],则y x=x 2+5000x+40≥2√x 2⋅5000x +40=140,当且仅当x 2=5000x,即x =100百吨时,平均成本最低;(2)选择方案一:设每日获利为y 1,∴y 1=100x ﹣(12x 2+40x +5000)+4200=−12x 2+60x ﹣800=−12(x ﹣60)2+1000,∵x ∈[70,120],∴当x =70百吨时,获得最大利润为950元; 选择方案二:设每日获利为y 2,则y 2=100x +40x +1700﹣(12x 2+40x +5000)=−12x 2+100x ﹣3300=−12(x ﹣100)2+1700,∵x ∈[70,120],∴当x =100百吨时,获得最大利润为1700元, 又1700>950,故选择方案二进行补贴.21.(12分)已知函数f (x )对于任意实数x ,y ∈R ,都有f (x +y )+2=f (x )+f (y ),且f (2)=4. (1)求f (1)的值;(2)令g (x )=f (x )﹣2,求证:函数g (x )为奇函数;(3)求f (﹣2023)+f (﹣2022)+…+f (﹣1)+f (0)+f (1)+…+f (2022)+f (2023)的值. 解:(1)∵对于任意实数x ,y ∈R ,都有f (x +y )+2=f (x )+f (y ),且f (2)=4. ∴f (1+1)+2=f (1)+f (1),∴4+2=2f (1),∴f (1)=3; (2)证明:∵f (0+0)+2=f (0)+f (0),∴f (0)=2,又x ∈R ,∴g (﹣x )+g (x )=f (﹣x )﹣2+f (x )﹣2=f (﹣x )+f (x )﹣4=f (﹣x +x )+2﹣4=f (0)﹣2=0, ∴g (x )为奇函数;(3)由(2)知g (﹣x )+g (x )=0,f (x )=g (x )+2, ∴f (﹣x )+f (x )=4,又f (0)=2,∴f (﹣2023)+f (﹣2022)+…+f (﹣1)+f (0)+f (1)+…+f (2022)+f (2023) =2023×4+2=8094.22.(12分)已知函数f (x ),g (x )满足g (x )=f (x )+a 2f(x)(a >0).(1)设f (x )=x ,求证:函数g (x )在区间(0,a )上为减函数,在区间(a ,+∞)上为增函数; (2)设f (x )=√1−x1+x .①当a =1时,求g (x )的最小值;②若对任意实数r ,s ,t ∈[−35,35],|g (r )﹣g (s )|<g (t )恒成立,求实数a 的取值范围.解:(1)证明:由题意,可得g(x)=x +a 2x ,令0<x 1<x 2,则g(x 2)−g(x 1)=x 2+a 2x 2−(x 1+a 2x 1)=(x 2−x 1)+a 2⋅x 1−x 2x 1x 2=(x 2−x 1)(1−a 2x 1x 2)=(x 2−x 1)x 1x 2−a 2x 1x 2,当0<x 1<x 2<a 时,x 2﹣x 1>0,x 1x 2>0且x 1x 2−a 2<0, 故g (x 2)﹣g (x 1)<0,故g (x )在区间(0,a )上为减函数; 当x 2>x 1>a 时,x 2﹣x 1>0,x 1x 2>0且x 1x 2−a 2>0,所以g (x 2)﹣g (x 1)>0,所以g (x )在区间(a ,+∞)上为增函数. (2)①令1−x 1+x>0⇔(1+x)(1−x)>0,解得﹣1<x <1,由g(x)=f(x)+a 2f(x)中f (x )可知, f(x)=√1−x 1+x 的定义域为(﹣1,1),且f(x)=√21+x−1, 因为x ∈(﹣1,1],所以x +1∈(0,2],所以2x+1−1∈(0,+∞),所以f (x )∈(0,+∞),令t =f (x ),则p(t)=t +1t, 所以p(t)=t +1t≥2,当且仅当t =1时取等号, 所以g (x )min =g (0)=2,②因为|g (r )﹣g (s )|<g (t )恒成立,所以g (x )max ﹣g (x )min <g (x )min ,所以g (x )max <2g (x )min , 由①可知,x ∈[−35,35]时,f(x)∈[12,2], 令t =f(x)∈[12,2],令ℎ(t)=t +a 2t, 由(1)知,h (t )在(0,a )上为减函数,在(a ,+∞)上为增函数, 所以当a ≥2时,h (t )在[12,2]上为减函数, 所以g(x)max =ℎ(t)max =ℎ(12)=12+2a 2,g(x)min =ℎ(t)min =ℎ(2)=2+a 22, 所以12+2a 2<2(2+a 22),所以−√142<a <√142,与a ≥2矛盾,当12<a <2时,h (t )在[12,a]上为减函数,h (t )在[a ,2]上为增函数,所以{ℎ(12)<2ℎ(a)ℎ(2)<2ℎ(a),所以{12+2a 2<4a 2+a 22<4a,解得4−2√3<a <2+√32,当a≤12时,h(t)在[12,2]上为增函数,所以2+a22<2(12+2a2),所以a2>27,所以a>√147或a<−√147,由a≤12,得a<−√147,又a>0,所以a∈∅,综上,a的取值范围为{a|4−2√3<a<2+√32}.。
【中考冲刺】2021年山东省潍坊市中考数学模拟试卷(附答案)

∵ >0,
∴x>0时,y>0,y随着x的增大而减小,
x<0时,y<0,y随着x的增大而减小,
∵−6<0,
∴y1<0,
∵0<2<3,
∴
∴ ,
故选:A.
【点睛】
本题考查了反比例函数图象上点的坐标特征,正确掌握反比例函数的性质和反比例函数的增减性是解题的关键.
4.B
【分析】
根据圆内接四边形的性质得到∠DAB,进而求出∠EAB,根据圆周角定理得到∠EBA=90°,根据直角三角形两锐角互余即可得出结论.
【详解】
解:设OA1=A1A2=A2A3=…=A2010A2021=t,则P1(t, ),P2(2t, ),P3(3t, ),…,P2021(2021t, ),
所以S2021= .
故选:A.
【点睛】
本题考查了反比例函数系数k的几何意义:在反比例函数y= 的图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.也考查了反比例函数图象上点的坐标特征.
三、解答题
19.解下列方程:
(1)
(2)
20.如图,一次函数 的图象交反比例函数 的图象于 两点,交 轴于点 .
(1)求反比例函数与一次函数的关系式.
(2)求 的面积.
(3)根据图象回答:当 为何值时,一次函数的值大于反比例函数的值?
21.如图,某中学依山而建,校门 处有一坡度 的斜坡 ,长度为 米,在坡顶 处看教学楼 的楼顶 的仰角 ,离 点 米远的 处有一个花台,在 处仰望 的仰角是 , 的延长线交校门处的水平面于点 .(提示: )
【点睛】
本题考查了函数自变量取值范围的求法.函数自变量的范围一般从三个方面考虑:
2021年普通高等学校招生全国统一考试数学试题理(全国卷1,含答案)

2021年普通高等学校招生全国统一考试数学试题 理(全国卷1)注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设1i2i 1iz -=++,则||z = A .0B .12C .1D .22.已知集合{}220A x x x =-->,则A =RA .{}12x x -<< B .{}12x x -≤≤ C .}{}{|1|2x x x x <->D .}{}{|1|2x x x x ≤-≥3.某地域通过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地域农村的经济收入转变情况,统计了该地域新农村建设前后农村的经济收入组成比例,取得如下饼图:建设前经济收入组成比例 建设后经济收入构成比例则下面结论中不正确的是 A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半 4.设n S 为等差数列{}n a 的前n 项和,若3243S S S =+,12a =,则=5a A .12-B .10-C .10D .125.设函数32()(1)f x x a x ax =+-+,若()f x 为奇函数,则曲线()y f x =在点(0,0)处的切线方程为A .2y x =-B .y x =-C .2y x =D .y x =6.在ABC △中,AD 为BC 边上的中线,E 为AD 的中点,则EB = A .3144AB AC - B .1344AB AC - C .3144AB AC + D .1344AB AC + 7.某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A .172B .52C .3D .28.设抛物线C :y 2=4x 的核心为F ,过点(–2,0)且斜率为23的直线与C 交于M ,N 两点,则FM FN ⋅= A .5B .6C .7D .89.已知函数e 0()ln 0x x f x x x ⎧≤=⎨>⎩,,,,()()g x f x x a =++.若g (x )存在2个零点,则a 的取值范围是 A .[–1,0)B .[0,+∞)C .[–1,+∞)D .[1,+∞)10.下图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆组成,三个半圆的直径别离为直角三角形ABC 的斜边BC ,直角边AB ,AC .△ABC 的三边所围成的区域记为I ,黑色部份记为II ,其余部份记为III .在整个图形中随机取一点,此点取自I ,II ,III 的概率分别记为p 1,p 2,p 3,则A .p 1=p 2B .p 1=p 3C .p 2=p 3D .p 1=p 2+p 311.已知双曲线C :2213x y -=,O 为坐标原点,F 为C 的右核心,过F 的直线与C 的两条渐近线的交点别离为M 、N .若△OMN 为直角三角形,则|MN |= A .32B .3 C. D .412.已知正方体的棱长为1,每条棱所在直线与平面α所成的角相等,则α截此正方体所得截面面积的最大值为 ABCD二、填空题:本题共4小题,每小题5分,共20分。
2021年中考一模考试《数学卷》含答案解析

数学中考综合模拟检测试题学校________ 班级________ 姓名________ 成绩________一、选择题(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个选项是正确的)1.实数4的相反数是( ) A. 14-B. -4C.14D. 42.如图是由4个相同的小正方体组成的一个立体图形,其主视图是( )A. B. C. D.3.2019年1月3日10时26分,“嫦娥四号”探测器飞行约380000千米,实现人类探测器首次在月球背面软着陆.数据380000用科学记数法表示为( ) A. 38×104B. 3.8×104C. 3.8×105D. 0.38×1064.(2018乌鲁木齐)在平面直角坐标系xOy 中,将点()12N --,绕点O 旋转180°,得到的对应点的坐标是( )A. ()12, B. ()12-, C. ()12--, D. ()12-, 5.不等式组12220360x x -<⎧⎨-≤⎩的解集是( )A. 46x -<≤B. 4x ≤-或2x >C. 42x -<≤D. 24x ≤<6.下列图形,既是轴对称图形又是中心对称图形的是( ) A 正三角形B. 正五边形C. 等腰直角三角形D. 矩形7.化简()22x 的结果是( ) A. x 4B. 2x 2C. 4x 2D. 4x8.在同一副扑克牌中抽取2张“方块”,3张“梅花”,1张“红桃”.将这6张牌背面朝上,从中任意抽取1张,是“红桃”的概率为( ) A.16B.13C.12D.239.如图,将矩形纸片ABCD 沿直线EF 折叠,使点C 落在AD 边的中点C′处,点B 落在点B′处,其中AB=9,BC=6,则FC′的长为( )A.103B. 4C. 4.5D. 510.二次函数2y ax bx c =++的图象如图,且,OA OC =则( )A. 1ac b +=B. 1ab c += C. 1bc a +=D. 以上都不是二、填空题(本题共6小题,每小题3分,共18分)11.如图,EABC ∆边CA 延长线上一点,过点E 作//ED BC .若070BAC ∠=,050CED ∠=,则B ∠=________°.12.如图,∠AOE =∠BOE =15°,EF ∥OB ,EC ⊥OB 于C ,若EC =1,则OF =_____.13.为了建设“书香校园”,某校七年级的同学积极捐书,下表统计了七(1)班40名学生的捐书情况: 捐书(本) 3 4 5 7 10 人数 5710117该班学生平均每人捐书______本.14.中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹x 两,牛每头y 两,根据题意可列方程组为_____________.15.如图,无人机于空中A 处测得某建筑顶部B 处的仰角为45,测得该建筑底部C 处的俯角为17.若无人机的飞行高度AD 为62m ,则该建筑的高度BC 为__m .(参考数据:sin170.29≈,cos170.96≈,tan170.31≈)16.甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步1500米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示,则乙到终点时,甲距终点的距离是______米.三.解答下列各题(本题共4小题,其中17、18、19题9分、20题12分,共39分)17.计算:1332)182+18.化简: 2212(1)244x x xx x x +--÷--+ 19.如图,EF=BC ,DF=AC ,DA=EB .求证:∠F=∠C .20.某校为了解九年级学生每天参加体育锻炼的时间,从该校九年级学生中随机抽取20名学生进行调查,得到如下数据(单位:分钟):306070103011570607590,,,,,,,,,,157040751058060307045,,,,,,,,,对以上数据进行整理分析,得到下列表一和表二:根据以上提供的信息,解答下列问题:()1填空:①a=,b=;②c=,d=;()2如果该校现有九年级学生200名,请估计该校九年级学生每天参加体育锻炼的时间达到平均水平及以上的学生人数.四、解答题(本题共3小题,其中21、22题各9分,23题10分,共28分)21.改善小区环境,争创文明家园.如图所示,某社区决定在一块长(AD)16m,宽(AB)9m的矩形场地ABCD上修建三条同样宽的小路,其中两条与AB平行,另一条与AD平行,其余部分种草.要使草坪部分的总面积为1122m,则小路的宽应为多少?22.如图,函数12y x=的图象与函数kyx=(x>0)的图象相交于点P(4,m).(1)求m,k的值;(2)直线y=3与函数12y x =的图象相交于点A ,与函数k y x=(x >0)的图象相交于点B ,求线段AB 长.23.如图,△ABC 中,AB =AC ,以AC 为直径的⊙O 交BC 于点D ,点E 为AC 延长线上一点,且DE 是⊙O 的切线.(1)求证:∠CDE =12∠BAC ; (2)若AB =3BD ,CE =4,求⊙O 的半径.五、解答题(本题共3小题,其中24题11分,25、26题各12分,共35分)24.如图,在平面直角坐标系xOy 中,直线112y x =+与y 轴,x 轴分别相交于点A B 、.点D 是x 轴上动点,点D 从点B 出发向原点O 运动,点E 在点D 右侧,2DE BD =.过点D 作DH AB ⊥于点,H 将DBH △沿直线DH 翻折,得到,DCH 连接CE .设,BD t =DCH 与AOB 重合部分面积为.S 求:(1)求线段BC 的长(用含t 的代数式表示);(2)求S 关于t 的函数解析式,并直接写出自变量t 的取值范围. 25.阅读下面材料,完成()()13-题. 数学课上,老师出示了这样一道题:如图1,在ABC 中,,.BA BC AB kAC ==点F 在AC 上,点E 在BF 上,2BE EF =.点D 在BC 延长线上,连接,180AD AE ACD DAE ∠+∠=、.探究线段AD 与AE 的数量关系并证明.同学们经过思考后,交流了自己的想法:小明:“通过观察和度量,发现CAD ∠与EAB ∠相等.” 小亮:“通过观察和度量,发现FAE ∠与D ∠也相等.”小伟:“通过边角关系构造辅助线,经过进一步推理, 可以得到线段AD 与AE数量关系.”老师:“保留原题条件,延长图1中的,AE 与BC 相交于点H (如图2),若知道DH 与AH 的数量关系,可以求出ABCH的值.”(1)求证:CAD EAB ∠=∠; (2)求ADAE的值(用含k 的式子表示); (3)如图2,若,DH AH =则ABCH的值为 (用含k 的式子表示). 26.已知抛物线2y x bx c =++过点A(m-2,n), B (m+4,n ),C (m ,53n -). (1)b=__________(用含m 的代数式表示); (2)求△ABC 的面积; (3)当1222m x m ≤≤+时,均有6y m -≤≤,求m 的值.答案与解析一、选择题(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个选项是正确的)1.实数4的相反数是()A.14B. -4C.14D. 4【答案】B【解析】【分析】根据相反数的定义即可解答.【详解】∵符号相反,绝对值相等的两个数互为相反数,∴4的相反数是﹣4;故选B.【点睛】本题考查了相反数的定义,熟知只有符号不同的两个数互为相反数是解决问题的关键.2.如图是由4个相同的小正方体组成的一个立体图形,其主视图是()A. B. C. D.【答案】A【解析】【分析】根据三视图的概念即可快速作答.【详解】解:立体图形的主视图,即正前方观察到的平面图,即选项A符合题意;故答案为A.【点睛】本题考查了三视图的概念及正确识别主视图,解题的关键在于良好的空间想象能力.3.2019年1月3日10时26分,“嫦娥四号”探测器飞行约380000千米,实现人类探测器首次在月球背面软着陆.数据380000用科学记数法表示为()A. 38×104B. 3.8×104C. 3.8×105D. 0.38×106【答案】C 【解析】 【分析】对于一个绝对值较大的数,用科学记数法写成10n a ⨯ 的形式,其中110a ≤<,n 是比原整数位数少1的数.【详解】380000=3.8×105. 故选C.【点睛】此题考查了科学记数法的表示方法.科学记数法的表示形式为a ×10n 的形式,其中1≤|a |<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.4.(2018乌鲁木齐)在平面直角坐标系xOy 中,将点()12N --,绕点O 旋转180°,得到的对应点的坐标是( )A. ()12, B. ()12-, C. ()12--, D. ()12-, 【答案】A 【解析】【详解】点N 绕着点O 旋转180°,恰好关于原点对称,点(1,2)N --的中心对称点为(1,2),故选A .5.不等式组12220360x x -<⎧⎨-≤⎩的解集是( )A. 46x -<≤B. 4x ≤-或2x >C. 42x -<≤D. 24x ≤<【答案】C 【解析】 【分析】分别求出每一个不等式的解集,再确定出解集的公共部分即可得解. 【详解】解不等式12220x -<,得:4x >-, 解不等式360x -≤,得:2x ≤, 则不等式组的解集为42x -<≤, 故选C .【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键. 6.下列图形,既是轴对称图形又是中心对称图形的是( )A. 正三角形B. 正五边形C. 等腰直角三角形D. 矩形【答案】D【解析】【分析】根据轴对称图形与中心对称图形的概念逐一进行分析判断即可得.【详解】A.正三角形是轴对称图形,不是中心对称图形;B.正五边形是轴对称图形,不是中心对称图形;C.等腰直角三角形是轴对称图形,不是中心对称图形;D.矩形是轴对称图形,也是中心对称图形,故选D.【点睛】本题考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后两部分重合.7.化简()22x的结果是()A. x4B. 2x2C. 4x2D. 4x【答案】C【解析】【分析】利用积的乘方法则:把每一个因式分别乘方,再把所得的幂相乘即可.【详解】(2x)²=2²·x²=4x²,故选C.【点睛】本题考查了积的乘方,解题的关键是掌握积的乘方的运算法则.8.在同一副扑克牌中抽取2张“方块”,3张“梅花”,1张“红桃”.将这6张牌背面朝上,从中任意抽取1张,是“红桃”的概率为()A. 16B.13C.12D.23【答案】A【解析】【分析】直接利用概率公式计算可得.【详解】解:从中任意抽取1张,是“红桃”的概率为16,故选A.【点睛】本题主要考查概率公式,随机事件A 的概率P (A )=事件A 可能出现的结果数÷所有可能出现的结果数.9.如图,将矩形纸片ABCD 沿直线EF 折叠,使点C 落在AD 边的中点C′处,点B 落在点B′处,其中AB=9,BC=6,则FC′的长为( )A. 103B. 4C. 4.5D. 5【答案】D【解析】【分析】设FC ′=x ,则FD=9-x ,根据矩形的性质结合BC=6、点C ′为AD 的中点,即可得出C ′D 的长度,在Rt △FC ′D 中,利用勾股定理即可找出关于x 的一元一次方程,解之即可得出结论.【详解】设FC′=x ,则FD=9﹣x ,∵BC=6,四边形ABCD 为矩形,点C′为AD 的中点,∴AD=BC=6,C′D=3,在Rt △FC′D 中,∠D=90°,FC′=x ,FD=9﹣x ,C′D=3,∴FC′2=FD 2+C′D 2,即x 2=(9﹣x )2+32,解得:x=5,故选D .【点睛】本题考查了矩形的性质以及勾股定理,在Rt △FC′D 中,利用勾股定理找出关于FC′的长度的一元二次方程是解题的关键.10.二次函数2y ax bx c =++的图象如图,且,OA OC =则( )A. 1ac b +=B. 1ab c +=C. 1bc a +=D. 以上都不是【答案】A【解析】【分析】 根据题意可知,本题考察二次函数图像与系数的关系,根据图像与坐标轴的交点,运用两边相等求出交点坐标,代入坐标进行求解.【详解】∵OA OC =∴点A 、C 的坐标为(-c ,0),(0,c)∴把点A 的坐标代入2y ax bx c =++得∴2=0ac bc c -+∴()10c ac b -+=∵0c ≠∴10ac b -+=∴1ac b +=故选A【点睛】本题考察二次函数图像与系数关系,解题关键是根据图像得出系数取值范围,再代入点的坐标进行解决. 二、填空题(本题共6小题,每小题3分,共18分)11.如图,E 为ABC ∆边CA 延长线上一点,过点E 作//ED BC .若070BAC ∠=,050CED ∠=,则B ∠=________°.【答案】60【解析】【分析】利用平行线的性质,即可得到∠CED=∠C=50°,再根据三角形内角和定理,即可得到∠B 的度数.【详解】解:∵ED ∥BC ,∴∠CED=∠C=50°,又∵∠BAC=70°,∴△ABC中,∠B=180°-50°-70°=60°,故答案为60.【点睛】本题主要考查了平行线的性质,解题时注意运用两直线平行,内错角相等.12.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF=_____.【答案】2【解析】【分析】作EH⊥OA于H,根据角平分线的性质求出EH,根据直角三角形的性质求出EF,根据等腰三角形的性质解答即可.【详解】作EH⊥OA于H.∵∠AOE=∠BOE=15°,EC⊥OB,EH⊥OA,∴EH=EC=1,∠AOB=30°.∵EF∥OB,∴∠EFH=∠AOB=30°,∠FEO=∠BOE,∴EF=2EH=2,∠FEO=∠FOE,∴OF=EF=2.故答案2.【点睛】本题考查了等腰三角形的判定、角平分线的性质、平行线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.13.为了建设“书香校园”,某校七年级的同学积极捐书,下表统计了七(1)班40名学生的捐书情况:捐书(本) 3 4 5 7 10人数 5 7 10 11 7该班学生平均每人捐书______本.【答案】6【解析】【分析】利用加权平均数公式进行求解即可得. 【详解】该班学生平均每人捐书3547510711107640⨯+⨯+⨯+⨯+⨯=(本), 故答案为6.【点睛】本题考查了加权平均数,熟练掌握加权平均数的计算公式是解题的关键.14.中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹x 两,牛每头y 两,根据题意可列方程组为_____________.【答案】46483538x y x y +=⎧⎨+=⎩【解析】【分析】直接利用“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两”,分别得出方程得出答案.【详解】解:设马每匹x 两,牛每头y 两,根据题意可列方程组为: 46483538x y x y +=⎧⎨+=⎩ 故答案是:46483538x y x y +=⎧⎨+=⎩【点睛】此题主要考查了二元一次方程组的应用,正确得出等式是解题关键.15.如图,无人机于空中A 处测得某建筑顶部B 处的仰角为45,测得该建筑底部C 处的俯角为17.若无人机的飞行高度AD 为62m ,则该建筑的高度BC 为__m .(参考数据:sin170.29≈,cos170.96≈,tan170.31≈)【答案】262【解析】【分析】作AE BC ⊥于E ,根据正切的定义求出AE ,根据等腰直角三角形的性质求出BE ,结合图形计算即可.【详解】作AE BC ⊥于E ,则四边形ADCE 为矩形,62EC AD ∴==,在Rt AEC ∆中,tan EC EAC AE ∠=, 则62200tan 0.31EC AE EAC =≈=∠, 在Rt AEB ∆中,45BAE ∠=,200BE AE ∴==,20032262()BC m ∴=+=,则该建筑的高度BC 为262m ,故答案为262.【点睛】本题考查的是解直角三角形的应用﹣仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.16.甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步1500米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示,则乙到终点时,甲距终点的距离是______米.【答案】175【解析】试题解析:根据题意得,甲的速度为:75÷30=2.5米/秒,设乙的速度为m 米/秒,则(m -2.5)×(180-30)=75,解得:m =3米/秒,则乙的速度为3米/秒, 乙到终点时所用的时间为:15003=500(秒), 此时甲走的路程是:2.5×(500+30)=1325(米),甲距终点的距离是1500-1325=175(米).【点睛】本题考查了一次函数的应用,读懂题目信息,理解并得到乙先到达终点,然后求出甲、乙两人所用的时间是解题的关键.三.解答下列各题(本题共4小题,其中17、18、19题9分、20题12分,共39分)17.计算:2)+【答案】-1.【解析】【分析】先利用平方差公式简便运算乘法,同时化简二次根式,再合并同类二次根式即可.【详解】解:2)+=3-4+=-1.【点睛】本题考查的是二次根式的混合运算,二次根式的化简,掌握利用平方差公式进行简便运算是解题的关键.18.化简: 2212(1)244x x x x x x +--÷--+ 【答案】3x . 【解析】【分析】先通分,计算括号内的减法,把除法转化为乘法,约分后得到结论. 【详解】解:原式=212(2)122()22(2)2x x x x x x x x x x x x+--+-+--÷=•----323.2x x x x-=•=- 【点睛】本题考查的是分式的化简,考查了分式的加减法,分式的除法,掌握以上运算是解题的关键. 19.如图,EF=BC ,DF=AC ,DA=EB .求证:∠F=∠C .【答案】见解析.【解析】【分析】欲证明∠F =∠C ,只要证明△ABC ≌△DEF(SSS)即可.【详解】证明:DA BE =,DE AB ∴=,在ABC ∆和DEF ∆中,AB DE AC DF BC EF =⎧⎪=⎨⎪=⎩,()ABC DEF SSS ∴∆≅∆,C F ∴∠=∠.【点睛】本题主要考查全等三角形的判定与性质.20.某校为了解九年级学生每天参加体育锻炼的时间,从该校九年级学生中随机抽取20名学生进行调查,得到如下数据(单位:分钟):306070103011570607590,,,,,,,,,,157040751058060307045,,,,,,,,,对以上数据进行整理分析,得到下列表一和表二:根据以上提供的信息,解答下列问题:()1填空:①a=,b=;②c=,d=;()2如果该校现有九年级学生200名,请估计该校九年级学生每天参加体育锻炼的时间达到平均水平及以上的学生人数.【答案】(1)①5,3;②65,70;(2)130人.【解析】【分析】(1)①根据数据统计出a、b;②根据中位数和众数的定义求出c,d即可;(2)先求出样本用样本达到平均水平及以上的学生的概率,然后用九年级学生数×样本达到平均水平及以上的学生的概率即可.【详解】解:()1①经统计:该组数据处于30≤t<60的数据有5个, 处于90≤t<120的数据有3个,∴a=5;b=3故答案为:5;3②将这组数据从小到大排序,位于第10个的数据是60,第11个的数据是70∴中位数为(60+70)÷2=65这组数据中出现次数最多的是70 ∴众数为70 ∴6570,c d==故答案为:65;70.()132********⨯=(人),答:估计该校九年级学生每天参加体育锻炼的时间达到平均水平及以上的学生人数为130人.【点睛】本题考查中位数、众数、平均数、样本估计总体的思想等知识,掌握中位数、众数、平均数等基本知识是解答本题的关键.四、解答题(本题共3小题,其中21、22题各9分,23题10分,共28分)21.改善小区环境,争创文明家园.如图所示,某社区决定在一块长(AD)16m,宽(AB)9m的矩形场地ABCD上修建三条同样宽的小路,其中两条与AB平行,另一条与AD平行,其余部分种草.要使草坪部分的总面积为1122m,则小路的宽应为多少?【答案】小路的宽应为1m .【解析】【分析】设小路的宽应为x 米,那么草坪的总长度和总宽度应该为(16-2x ),(9-x );那么根据题意得出方程,解方程即可.【详解】解:设小路的宽应为x 米,根据题意得:(162)(9)112x x --=,解得:11x =,216x =.∵169>,∴16x =不符合题意,舍去,∴1x =.答:小路的宽应为1米.【点睛】本题考查一元二次方程的应用,弄清“草坪的总长度和总宽度”是解决本题的关键. 22.如图,函数12y x =的图象与函数k y x=(x >0)的图象相交于点P (4,m ). (1)求m ,k 的值;(2)直线y=3与函数12y x =的图象相交于点A ,与函数k y x=(x >0)的图象相交于点B ,求线段AB 长.【答案】(1)m=2,k=8;(2)103.【解析】【分析】(1)将点P(4,m)代入y=x,求出m=2,再将点P(4,2)代入kyx=即可求出k的值;(2) 分别求出A、B两点的坐标,即可得到线段AB的长.【详解】(1)∵函数12y x=的图象过点P(4,m),∴m=2,∴P(4,2),∵函数kyx=(x>0)的图象过点P,∴k=4×2=8;(2)将y=3代入12y x=,得x=6,∴点A(6,3).将y=3代入8yx=,得x=83,∴点B(83,3).∴AB=6﹣83=103.【点睛】本题主要考查了利用待定系数法求函数解析式以及函数图象上点的坐标特征,解题时注意:点在图象上,点的坐标就一定满足函数的解析式.23.如图,△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,点E为AC延长线上一点,且DE是⊙O 的切线.(1)求证:∠CDE=12∠BAC;(2)若AB=3BD,CE=4,求⊙O的半径.【答案】(1)见解析;(2)14.【解析】【分析】(1)根据圆周角定理得出∠ADC=90°,按照等腰三角形的性质和已知的2倍角关系,证明∠ODE为直角即可得到答案;(2)通过证得△CDE∽△DAE,根据相似三角形的性质即可求得.【详解】(1)如图,连接OD,AD,∵AC是直径,∴∠ADC=90°,-∴AD⊥BC,∵AB=AC,∴∠CAD=∠BAD=12∠BAC,∵DE是⊙O的切线;∴OD⊥DE∴∠ODE=90°∴∠ADC=∠ODE∴∠CDE=∠ADO ∵OA=OD,∴∠CAD=∠ADO,∴∠CDE=∠CAD,∠CAD=12∠BAC,∴∠CDE=12∠BAC.(2)解:∵AB=AC,AD⊥BC,∴BD=CD,∵AB=3BD,∴AC=3DC,设DC=x,则AC=3x,∴AD2222,AC DC x-=∵∠CDE=∠CAD,∠DEC=∠AED,∴△CDE∽△DAE,∴CE DC DE DE AD AE∴==,即43422DE DE xx==+∴DE=82,,x=283,∴AC=3x=28,∴⊙O的半径为14.【点睛】本题考查了圆的切线的判定定理、圆周角定理、等腰三角形的性质、三角形相似的判定和性质,解题的关键是作出辅助线构造直角三角形或等腰三角形.五、解答题(本题共3小题,其中24题11分,25、26题各12分,共35分)24.如图,在平面直角坐标系xOy 中,直线112y x =+与y 轴,x 轴分别相交于点A B 、.点D 是x 轴上动点,点D 从点B 出发向原点O 运动,点E 在点D 右侧,2DE BD =.过点D 作DH AB ⊥于点,H 将DBH △沿直线DH 翻折,得到,DCH 连接CE .设,BD t =DCH 与AOB 重合部分面积为.S 求:(1)求线段BC 的长(用含t 的代数式表示);(2)求S 关于t 的函数解析式,并直接写出自变量t 的取值范围.【答案】(1)55t BC =;(2)222420536224825357734288523334t t S t t t t t t ⎧⎛⎫<≤ ⎪⎪⎝⎭⎪⎪⎛⎫=-+-<≤⎨ ⎪⎝⎭⎪⎪⎛⎫-+<≤⎪ ⎪⎝⎭⎩ 【解析】【分析】(1)先根据直线112y x =+求得点A 、B 的坐标,利用勾股定理求得AB 的长,进而可求得5555sin ABO cos ABO ∠=∠=,由翻折知DB DC t ==,12BH CH BC ==,最后根据255BH cos ABO BD ∠==求得55t BH =,即可求得BC 的长; (2)分类讨论:当203t <≤时,当2534t <≤时,当524t <≤时,分别画出相应图形,然后利用相似三角形的性质分别表示出对应的底和高,进而可得S 关于t 的函数解析式即可. 【详解】解:()1∵直线112y x =+与y 轴,x 轴分别相交于点A B 、, ∴点()()012,0A B -,,,∴由勾股定理得22125AB =+=∴在直角AOB 中,525,55sin ABO cos ABO ∠=∠=, 由翻折知:DB DC t ==,12BH CH BC ==, 255BH cos ABO BD∠==, 255t BH ∴=, 455t BC ∴=, ()2当203t <≤时, 过点C 做CG BO ⊥于点G ,45CG t ∴=, 55CG sin ABO BC∴∠==, 45GC t ∴=, 14225S t t ∴=⨯⨯ 245t = 当2534t <≤时, 设OA 交CE 于点F ,45CD BD t GC t ===,, ∴由勾股定理得35GD t =,37255GE t t t ∴=-=, 382255GO t t t =--=-, 78 23255OE EG OG t t t ∴=-=-+=-, //OF CG ,EOFCGE ∴, OF OE CG OG∴=, ()4327OF t ∴=-, 12OFE S OE OF =⋅ ()()14323227t t =⋅-⋅- 222(73)t -= , DCE OFE S S S =-∴2622483577t t =-+-, 当524t <≤时, 设CD 交OA 于点P ,//,OP CG,DOP DGC ∴OP OD CG DG∴=, 2OD t =-,()423OP OP t ∴==-,12S OD OP =⋅⋅∴ 2288333t t =-+, ∴综上所述,222420536224825357734288523334t t S t t t t t t ⎧⎛⎫<≤ ⎪⎪⎝⎭⎪⎪⎛⎫=-+-<≤⎨ ⎪⎝⎭⎪⎪⎛⎫-+<≤⎪ ⎪⎝⎭⎩ 【点睛】本题考查了一次函数的图像与性质,解直角三角形、相似三角形的判定及性质,根据点D 的位置画出相应的图形然后运用分类讨论思想以及相似三角形的性质是解决本题的关键.25.阅读下面材料,完成()()13-题.数学课上,老师出示了这样一道题:如图1,在ABC 中,,.BA BC AB kAC ==点F 在AC 上,点E 在BF 上,2BE EF =.点D 在BC 延长线上,连接,180AD AE ACD DAE ∠+∠=、.探究线段AD 与AE 的数量关系并证明.同学们经过思考后,交流了自己的想法:小明:“通过观察和度量,发现CAD ∠与EAB ∠相等.”小亮:“通过观察和度量,发现FAE ∠与D ∠也相等.”小伟:“通过边角关系构造辅助线,经过进一步推理, 可以得到线段AD 与AE 的数量关系.” 老师:“保留原题条件,延长图1中的,AE 与BC 相交于点H (如图2),若知道DH 与AH 的数量关系,可以求出AB CH的值.”(1)求证:CAD EAB ∠=∠;(2)求AD AE的值(用含k 的式子表示); (3)如图2,若,DH AH =则AB CH 的值为 (用含k 的式子表示). 【答案】(1)证明见解析;(2)3AD AE k =;(3)2115AB k CH ++= 【解析】【分析】(1)由BA BC =可知BAC BCA ∠=∠,再通过180ACD DAE ∠+∠=以及平角为180°,可以得到CAD EAB ∠=∠;(2)方法一:过点C 做ACM ABE ∠=∠,交AD 于点M ,通过AEB AMC 可知AC AM CM AB AE BE ==,通过DCM AFE 可知DM CM AE EF =,通过比例关系可推导出AD AE的值;方法二:过点B 做//BN AC 交AE 延长线于点N ,通过AHC DHA 和ACD ABN 相似得到的比例关系即可可推导出AD AE的值; (3)同方法二辅助线,通过证明AHC DHA ,AFE NBE ,然后由对应边成比例即可推导出结论.【详解】()1BA BC =,BAC BCA ∴∠=∠180,ACD DAE ∠+∠=180,ACD ACB ∠+∠=∴∠=∠ADE ACB,∴∠=∠DAE BAC,∴∠=∠DAC BAE,()2方法一:∠=∠,交AD于点M 过点C做ACM ABE∠=∠,DAC BAE∴AEB AMCAC AM CM∴==AB AE BE=AB kAC1∴=AM AEk1=CM BEk=2BE EF2∴=CM FEk∠=∠+∠AEF EAB ABE∠=∠+∠DMC MAC ACM∴∠=∠DMC AEFACB D DAC∠=∠+∠∠=∠+∠DAE DAC FAEDAE ACB∠=∠∴∠=∠D FAE∴DCM AFEDM CM∴=AE EF2∴=DM AEk3∴=+=AD AM DM AEkAD3∴=AE k方法二:BN AC交AE延长线于点,N 过点B做//,∴∠=∠N FAE∠=∠,AFE EBN∴,AFE NBEAE EF∴=NE BE=BE EF2,∴=NE EA2,NA EA∴=3,∠=∠+∠ACB D DAC,DAE DAC FAE∠=∠+∠,DAE ACB∠=∠,∴∠=∠,D FAE,DAC BAE ∴∠=∠ ACD ABN ∴ AC AD AB AN ∴= ,AB kAC = ,AN kAD ∴= 3,AE kAC ∴= 3AD AE k ∴= ()3同方法二辅助线,D CAH ∠=∠ ,AHC DHA ∠=∠ AHC DHA ∴ 2AH HC DH ∴=⋅ 23AH AC DH AD == 23AD AC ∴= AB kAC = 32AD AB k ∴= 3AD AE k =12AE AB ∴= 设2AH a AB BC b ===,13,2DH a AE b ∴== 2NE AE =NE b ∴=EH AH AE EN NH =-=-322NH b a ∴=- 2AH HC DH =⋅43CH a ∴= 53CD a ∴= ∴由方法二相似得53BN ak = ADHNBH ' AD DH NB NH∴= 33253232b a k ak b a ∴=- 222912200b ab a k ∴--=(123a b -∴=(舍),(223ab +=12AB CH +∴= 【点睛】本题考查了相似三角形的判定和性质,正确作出辅助线是解题的关键.26.已知抛物线2y x bx c =++过点A(m-2,n), B (m+4,n ),C (m ,53n -).(1)b=__________(用含m 的代数式表示);(2)求△ABC 的面积;(3)当1222m x m ≤≤+时,均有6y m -≤≤,求m 的值.【答案】(1)b=-2m-2;(2)24;(3)m =. 【解析】【分析】(1)根据A(m-2,n), B (m+4,n )纵坐标一致,结合对称轴即可求解;(2)先用含m 的代数式表示c ,再带入A 点坐标即可求出n=3,最后利用铅锤法即可求出△ABC 的面积; (3)先用只含m 的代数式表示二次函数解析式,再结合带取值范围的二次函数最值求法分类讨论即可.【详解】(1)∵2y x bx c =++过点A(m-2,n), B (m+4,n ), ∴对称轴2422b m m x -++=-= ∴22b m =--(2)∵22b m =--∴2(22)y x m x c =-++把C (m ,53n -)代入2(22)y x m x c =-++ ∴2523c m m n =+-∴225(22)23y x m x m m n =-+++-把A(m-2,n)代入225(22)23y x m x m m n =-+++-得583n n =-∴n=3∴A(m-2,3), B (m+4,3),C (m ,5-)∴AB=6C 点到x 轴的距离为:3﹣(-5)=8,∴S △ABC=12×6×8=24 (3)∵n=3∴22(22)25y x m x m m =-+++-∴2(1)6y x m =---∴当1x m =+时-6y =最小∵6y m -≤≤ ∴由函数增减性知11222m m m ≤+≤+ 即1m ≥-∴当10m -≤<时 由函数增减性知12x m =时,y m =最大 ∴21(1)62m m m =---∴m =±当0m ≥时由函数增减性知22x m =+时,y m =最大∴2(221)6m m m =+---∴1m =(舍)2m =∴12m -+=【点睛】本题考查二次函数综合运用,当参数比较多时可以带入解析式,利用解方程消元法消去多余的参数,在最后一问中对于带取值范围的二次函数最值需要根据对称轴与取值范围的关系确定范围内的最值.。
2021年3月山东省潍坊市高三英语一模试题(含答案解析)

High school students coming from across the globe are offered the unique opportunity to gain hands-on research experience in mathematics field while working one on one with teaching staff over four intense weeks. Everything is free for chosen applicants except their meals.
第一部分阅读(共两节,满分50分)
第一节(共15小题;每小题2.5分,满分37.5分)
阅读下列短文,从每题所给的A、B、C、D四个选项中选出最佳选项。
A
To improve a high schooler’s chance of getting into a top university, the summer programs allow young students to explore fields of interest and get a taste of college life.
D. It awards students advanced technical degrees.
1.【答案】B
【解析】细节理解题。根据算三段中'This week-long program aimed at all US high school students can help them develop the skills necessary for future job in engineering while learning about the value and reward of acquiring advanced technical degrees.(这个为期一周的项目针对所有美国高中生,可以帮助他们发展未来工程工作所需的技能,同时了解获得高级技术学位的价值和回报)“可知,MITES有望为职业前景打下基础。故选B.
2025届山东省潍坊市高三第一次调研测试数学试卷含解析
2025届山东省潍坊市高三第一次调研测试数学试卷请考生注意:1.请用2B 铅笔将选择题答案涂填在答题纸相应位置上,请用0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。
写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.函数f (x )=21xx e -的图象大致为()A .B .C .D .2.如图所示的程序框图,若输入4a =,3b =,则输出的结果是( )A .6B .7C .5D .83.根据最小二乘法由一组样本点(),i i x y (其中1,2,,300i =),求得的回归方程是ˆˆˆybx a =+,则下列说法正确的是( )A .至少有一个样本点落在回归直线ˆˆˆybx a =+上 B .若所有样本点都在回归直线ˆˆˆybx a =+上,则变量同的相关系数为1 C .对所有的解释变量i x (1,2,,300i =),ˆˆibx a +的值一定与i y 有误差 D .若回归直线ˆˆˆybx a =+的斜率ˆ0b >,则变量x 与y 正相关 4.阅读下侧程序框图,为使输出的数据为,则①处应填的数字为A .B .C .D .5.小张家订了一份报纸,送报人可能在早上6:307:30-之间把报送到小张家,小张离开家去工作的时间在早上7.008:00-之间.用A 表示事件:“小张在离开家前能得到报纸”,设送报人到达的时间为x ,小张离开家的时间为y ,(,)x y 看成平面中的点,则用几何概型的公式得到事件A 的概率()P A 等于( )A .58B .25C .35D .786.把函数()sin 2(0)6f x A x A π⎛⎫=-≠ ⎪⎝⎭的图象向右平移4π个单位长度,得到函数()g x 的图象,若函数()()0g x m m ->是偶函数,则实数m 的最小值是( )A .512πB .56π C .6π D .12π7.已知椭圆2222:19x y C a a +=+,直线1:30l mx y m ++=与直线2:30l x my --=相交于点P ,且P 点在椭圆内恒成立,则椭圆C 的离心率取值范围为( ) A .2⎛ ⎝⎭B .2⎫⎪⎪⎝⎭C .10,2⎛⎫ ⎪⎝⎭D .1,12⎛⎫ ⎪⎝⎭8.已知函数()ln f x x =,若2()()3F x f x kx =-有2个零点,则实数k 的取值范围为( )A .21,06e ⎛⎫-⎪⎝⎭B .1,06e ⎛⎫-⎪⎝⎭C .10,6e ⎛⎫ ⎪⎝⎭D .210,6e ⎛⎫ ⎪⎝⎭9.设函数()22cos 23sin cos f x x x x m =++,当0,2x π⎡⎤∈⎢⎥⎣⎦时,()17,22f x ⎡⎤∈⎢⎥⎣⎦,则m =( ) A .12B .32C .1D .7210.设等差数列{}n a 的前n 项和为n S ,若495,81a S ==,则10a =( ) A .23B .25C .28D .2911.已知||3a =,||2b =,若()a ab ⊥-,则向量a b +在向量b 方向的投影为( ) A .12B .72C .12-D .72-12.已知抛物线2:4(0)C y px p =>的焦点为F ,过焦点的直线与抛物线分别交于A 、B 两点,与y 轴的正半轴交于点S ,与准线l 交于点T ,且||2||FA AS =,则||||FB TS =( ) A .25B .2C .72D .3二、填空题:本题共4小题,每小题5分,共20分。
潍坊市重点中学2021-2022学年中考试题猜想数学试卷含解析

2021-2022中考数学模拟试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。
选择题必须用2B铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,D,E,F分别为AB,AC,AD的中点,若BC=2,则EF的长度为()A.B.1 C.D.2.如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )A.13B.23C.34D.453.一个多边形的每个内角都等于120°,则这个多边形的边数为()A.4 B.5 C.6 D.74.如图,下列四个图形是由已知的四个立体图形展开得到的,则对应的标号是()A.①②③④B.②①③④C.③②①④D.④②①③5.如图,AB是O的直径,弦CD AB,垂足为点E,点G是AC上的任意一点,延长AG交DC的延长线于点F ,连接,,GC GD AD .若25BAD ∠=︒,则AGD ∠等于( )A .55︒B .65︒C .75︒D .85︒6.如图,点A ,B 在双曲线y=3x (x >0)上,点C 在双曲线y=1x(x >0)上,若AC ∥y 轴,BC ∥x 轴,且AC=BC ,则AB 等于( )A .2B .22C .4D .327.图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A ,B 在围成的正方体中的距离是( )A .0B .1C .2D .38.如图,在平面直角坐标系中,P 是反比例函数ky x=的图像上一点,过点P 做PQ x ⊥轴于点Q ,若OPQ △的面积为2,则k 的值是( )A .-2B .2C .-4D .49.在一次男子马拉松长跑比赛中,随机抽取了10名选手,记录他们的成绩(所用的时间)如下: 选手 1 2 3 4 5 6 7 8 9 10 时间(min)129136140145146148154158165175由此所得的以下推断不正确...的是( ) A .这组样本数据的平均数超过130 B .这组样本数据的中位数是147C .在这次比赛中,估计成绩为130 min 的选手的成绩会比平均成绩差D .在这次比赛中,估计成绩为142 min 的选手,会比一半以上的选手成绩要好10.如图,在▱ABCD 中,对角线AC 的垂直平分线分别交AD 、BC 于点E 、F ,连接CE ,若△CED 的周长为6,则▱ABCD 的周长为( )A .6B .12C .18D .2411.二次函数y =ax 2+bx +c (a ≠0)的图象如图,下列结论正确的是( )A .a <0B .b 2-4ac <0C .当-1<x <3时,y >0D .-2ba=1 12.如图,等腰三角形ABC 底边BC 的长为4 cm ,面积为12 cm 2,腰AB 的垂直平分线EF 交AB 于点E ,交AC 于点F ,若D 为BC 边上的中点,M 为线段EF 上一点,则△BDM 的周长最小值为( )A .5 cmB .6 cmC .8 cmD .10 cm二、填空题:(本大题共6个小题,每小题4分,共24分.)13.分解因式:m 3–m=_____. 14.如图,正△的边长为,点、在半径为的圆上,点在圆内,将正绕点逆时针针旋转,当点第一次落在圆上时,旋转角的正切值为_______________15.如图,矩形OABC 的边OA ,OC 分别在轴、轴上,点B 在第一象限,点D 在边BC 上,且∠AOD=30°,四边形OA′B′D 与四边形OABD 关于直线OD 对称(点A′和A ,B′和B 分别对应),若AB=1,反比例函数(0)ky k x=≠的图象恰好经过点A′,B ,则的值为_________.16.若点M (k ﹣1,k+1)关于y 轴的对称点在第四象限内,则一次函数y=(k ﹣1)x+k 的图象不经过第 象限.17.从长度分别是3,4,5的三条线段中随机抽出一条,与长为2,3的两条线段首尾顺次相接,能构成三角形的概率是_______.18.如图,在平行四边形ABCD 中,E 为边BC 上一点,AC 与DE 相交于点F ,若CE=2EB ,S △AFD =9,则S △EFC 等于_____.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(6分)如图,在⊙O 中,弦AB 与弦CD 相交于点G ,OA ⊥CD 于点E ,过点B 的直线与CD 的延长线交于点F ,AC ∥BF .(1)若∠FGB=∠FBG ,求证:BF 是⊙O 的切线; (2)若tan ∠F=34,CD=a ,请用a 表示⊙O 的半径; (3)求证:GF 2﹣GB 2=DF•GF .20.(6分)如图,已知矩形 OABC 的顶点A 、C 分别在 x 轴的正半轴上与y 轴的负半轴上,二次函数228255y x x =--的图像经过点B 和点C .(1)求点 A 的坐标;(2)结合函数的图象,求当 y<0 时,x 的取值范围.21.(6分)如图,某人站在楼顶观测对面的笔直的旗杆AB ,已知观测点C 到旗杆的距离CE=83m ,测得旗杆的顶部A 的仰角∠ECA=30°,旗杆底部B 的俯角∠ECB=45°,求旗杆AB 的髙.22.(8分)已知平行四边形.尺规作图:作的平分线交直线于点,交延长线于点(要求:尺规作图,保留作图痕迹,不写作法);在(1)的条件下,求证:.23.(8分)某商城销售A,B两种自行车.A型自行车售价为2 100元/辆,B型自行车售价为1 750元/辆,每辆A型自行车的进价比每辆B型自行车的进价多400元,商城用80 000元购进A型自行车的数量与用64 000元购进B型自行车的数量相等.()1求每辆A,B两种自行车的进价分别是多少?()2现在商城准备一次购进这两种自行车共100辆,设购进A型自行车m辆,这100辆自行车的销售总利润为y元,要求购进B型自行车数量不超过A型自行车数量的2倍,总利润不低于13 000元,求获利最大的方案以及最大利润.24.(10分)如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC,CF平分∠DCE.求证:CF⊥DE于点F.25.(10分)我国南水北调中线工程的起点是丹江口水库,按照工程计划,需对原水库大坝进行混凝土培厚加高,使坝高由原来的162米增加到176.6米,以抬高蓄水位,如图是某一段坝体加高工程的截面示意图,其中原坝体的高为BE,背水坡坡角∠BAE=68°,新坝体的高为DE,背水坡坡角∠DCE=60°.求工程完工后背水坡底端水平方向增加的宽度AC.(结果精确到0.1米,参考数据:sin 68°≈0.93,cos 68°≈0.37,tan 68°≈2.5,3≈1.73)26.(12分)如图,在△ABC中,∠ACB=90°,点D是AB上一点,以BD为直径的⊙O和AB相切于点P.(1)求证:BP平分∠ABC;(2)若PC=1,AP=3,求BC的长.27.(12分)深圳某书店为了迎接“读书节”制定了活动计划,以下是活动计划书的部分信息:“读书节“活动计划书书本类别科普类文学类进价(单位:元)18 12备注(1)用不超过16800元购进两类图书共1000本;科普类图书不少于600本;…(1)已知科普类图书的标价是文学类图书标价的1.5倍,若顾客用540元购买的图书,能单独购买科普类图书的数量恰好比单独购买文学类图书的数量少10本,请求出两类图书的标价;经市场调査后发现:他们高估了“读书节”对图书销售的影响,便调整了销售方案,科普类图书每本标价降低a(0<a<5)元销售,文学类图书价格不变,那么书店应如何进货才能获得最大利润?参考答案一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、B【解析】根据题意求出AB的值,由D是AB中点求出CD的值,再由题意可得出EF是△ACD的中位线即可求出.【详解】∠ACB=90°,∠A=30°,BC=AB.BC=2,AB=2BC=22=4, D 是AB 的中点,CD=AB= 4=2.E,F 分别为AC,AD 的中点, EF 是△ACD 的中位线.EF=CD= 2=1. 故答案选B. 【点睛】本题考查的知识点是三角形中位线定理,解题的关键是熟练的掌握三角形中位线定理. 2、C 【解析】易证△DEF ∽△DAB ,△BEF ∽△BCD ,根据相似三角形的性质可得EF AB= DF DB ,EF CD =BFBD ,从而可得EF AB +EF CD =DF DB +BFBD=1.然后把AB=1,CD=3代入即可求出EF 的值. 【详解】∵AB 、CD 、EF 都与BD 垂直, ∴AB ∥CD ∥EF ,∴△DEF ∽△DAB,△BEF ∽△BCD ,∴EF AB= DF DB ,EF CD =BFBD , ∴EF AB +EF CD =DF DB +BF BD =BD BD=1. ∵AB=1,CD=3, ∴1EF +3EF=1, ∴EF=34. 故选C. 【点睛】本题考查了相似三角形的判定及性质定理,熟练掌握性质定理是解题的关键.3、C【解析】试题解析:∵多边形的每一个内角都等于120°,∴多边形的每一个外角都等于180°-120°=10°,∴边数n=310°÷10°=1.故选C.考点:多边形内角与外角.4、B【解析】根据常见几何体的展开图即可得.【详解】由展开图可知第一个图形是②正方体的展开图,第2个图形是①圆柱体的展开图,第3个图形是③三棱柱的展开图,第4个图形是④四棱锥的展开图,故选B【点睛】本题考查的是几何体,熟练掌握几何体的展开面是解题的关键.5、B【解析】连接BD,利用直径得出∠ABD=65°,进而利用圆周角定理解答即可.【详解】连接BD,∵AB是直径,∠BAD=25°,∴∠ABD=90°-25°=65°,∴∠AGD=∠ABD=65°,故选B.【点睛】此题考查圆周角定理,关键是利用直径得出∠ABD=65°.6、B【解析】【分析】依据点C在双曲线y=1x上,AC∥y轴,BC∥x轴,可设C(a,1a),则B(3a,1a),A(a,3a),依据AC=BC,即可得到3a﹣1a=3a﹣a,进而得出a=1,依据C(1,1),B(3,1),A(1,3),即可得到AC=BC=2,进而得到Rt△ABC中,AB=22.【详解】点C在双曲线y=1x上,AC∥y轴,BC∥x轴,设C(a,1a),则B(3a,1a),A(a,3a),∵AC=BC,∴3a﹣1a=3a﹣a,解得a=1,(负值已舍去)∴C(1,1),B(3,1),A(1,3),∴AC=BC=2,∴Rt△ABC中,AB=22,故选B.【点睛】本题主要考查了反比例函数图象上点的坐标特征,注意反比例函数图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.7、C【解析】试题分析:本题考查了勾股定理、展开图折叠成几何体、正方形的性质;熟练掌握正方形的性质和勾股定理,并能进行推理计算是解决问题的关键.由正方形的性质和勾股定理求出AB的长,即可得出结果.解:连接AB,如图所示:根据题意得:∠ACB=90°,由勾股定理得:AB==;故选C.考点:1.勾股定理;2.展开图折叠成几何体.8、C【解析】根据反比例函数k 的几何意义,求出k 的值即可解决问题【详解】解:∵过点P 作PQ ⊥x 轴于点Q ,△OPQ 的面积为2,∴|2k |=2, ∵k <0,∴k=-1.故选:C .【点睛】本题考查反比例函数k 的几何意义,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型. 9、C【解析】分析:要求平均数只要求出数据之和再除以总个数即可;对于中位数,因图中是按从小到大的顺序排列的,所以只要找出最中间的一个数(或最中间的两个数)即可求解.详解:平均数=(129+136+140+145+146+148+154+158+165+175)÷10=149.6(min),故这组样本数据的平均数超过130,A 正确,C 错误;因为表中是按从小到大的顺序排列的,一共10名选手,中位数为第五位和第六位的平均数,故中位数是(146+148)÷2=147(min),故B 正确,D 正确.故选C. 点睛:本题考查的是平均数和中位数的定义.要注意,当所给数据有单位时,所求得的平均数和中位数与原数据的单位相同,不要漏单位.10、B【解析】∵四边形ABCD 是平行四边形,∴DC=AB ,AD=BC ,∵AC 的垂直平分线交AD 于点E ,∴AE=CE ,∴△CDE 的周长=DE+CE+DC=DE+AE+DC=AD+DC=6,∴▱ABCD 的周长=2×6=12,故选B .11、D试题分析:根据二次函数的图象和性质进行判断即可.解:∵抛物线开口向上,∴0a>∴A选项错误,∵抛物线与x轴有两个交点,∴240b ac->∴B选项错误,由图象可知,当-1<x<3时,y<0∴C选项错误,由抛物线的轴对称性及与x轴的两个交点分别为(-1,0)和(3,0)可知对称轴为1x=即-=1,∴D选项正确,故选D.12、C【解析】连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再根据EF是线段AB的垂直平分线可知,点B关于直线EF的对称点为点A,故AD的长为BM+MD的最小值,由此即可得出结论.【详解】如图,连接AD.∵△ABC是等腰三角形,点D是BC边的中点,∴AD⊥BC,∴S△ABC=12BC•AD=12×4×AD=12,解得:AD=6(cm).∵EF是线段AB的垂直平分线,∴点B关于直线EF的对称点为点A,∴AD的长为BM+MD的最小值,∴△BDM的周长最短=(BM+MD)+BD=AD+12BC=6+12×4=6+2=8(cm).故选C.本题考查的是轴对称﹣最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.二、填空题:(本大题共6个小题,每小题4分,共24分.)13、m (m+1)(m-1)【解析】根据因式分解的一般步骤:一提(公因式)、二套(平方差公式()()22a b a b a b -=+-,完全平方公式()2222a ab b a b ±+=±)、三检查(彻底分解),可以先提公因式,再利用平方差完成因式分解 【详解】解:()()()32111m m m m m m m -=-=+- 故答案为:m (m+1)(m-1).【点睛】本题考查因式分解,掌握因式分解的技巧是解题关键.14、【解析】作辅助线,首先求出∠DAC 的大小,进而求出旋转的角度,即可得出答案.【详解】如图,分别连接OA 、OB 、OD ;∵OA=OB= ,AB=2,∴△OAB 是等腰直角三角形,∴∠OAB=45°;同理可证:∠OAD=45°,∴∠DAB=90°;∵∠CAB=60°,∴旋转角的正切值是,故答案为:.【点睛】此题考查等边三角形的性质,旋转的性质,点与圆的位置关系,解直角三角形,解题关键在于作辅助线. 1543【解析】解:∵四边形ABCO是矩形,AB=1,∴设B(m,1),∴OA=BC=m,∵四边形OA′B′D与四边形OABD关于直线OD对称,∴OA′=OA=m,∠A′OD=∠AOD=30°,∴∠A′OA=60°,过A′作A′E⊥OA于E,∴OE=12m,3,∴A′(12m3),∵反比例函数y=kx(k≠0)的图象恰好经过点A′,B,∴12m•3,∴43∴k=43.【点睛】本题考查反比例函数图象上点的坐标特征;矩形的性质,利用数形结合思想解题是关键.16、一【解析】试题分析:首先确定点M所处的象限,然后确定k的符号,从而确定一次函数所经过的象限,得到答案.∵点M(k﹣1,k+1)关于y轴的对称点在第四象限内,∴点M(k﹣1,k+1)位于第三象限,∴k﹣1<0且k+1<0,解得:k<﹣1,∴y=(k﹣1)x+k经过第二、三、四象限,不经过第一象限考点:一次函数的性质17、2 3【解析】共有3种等可能的结果,它们是:3,2,3;4, 2, 3;5, 2, 3;其中三条线段能够成三角形的结果为2,所以三条线段能构成三角形的概率=23.故答案为23.18、1【解析】由于四边形ABCD是平行四边形,所以得到BC∥AD、BC=AD,而CE=2EB,由此即可得到△AFD∽△CFE,它们的相似比为3:2,最后利用相似三角形的性质即可求解.【详解】解:∵四边形ABCD是平行四边形,∴BC∥AD、BC=AD,而CE=2EB,∴△AFD∽△CFE,且它们的相似比为3:2,∴S△AFD:S△EFC=(32)2,∴S△EFC=1.故答案为1.【点睛】此题主要考查了相似三角形的判定与性质,解题首先利用平行四边形的构造相似三角形的相似条件,然后利用其性质即可求解.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19、(1)证明见解析;(2)25r a48;(3)证明见解析.【解析】(1)根据等边对等角可得∠OAB=∠OBA,然后根据OA⊥CD得到∠OAB+∠AGC=90°,从而推出∠FBG+∠OBA=90°,从而得到OB⊥FB,再根据切线的定义证明即可.(2)根据两直线平行,内错角相等可得∠ACF=∠F,根据垂径定理可得CE=12CD=12a,连接OC,设圆的半径为r,表示出OE,然后利用勾股定理列式计算即可求出r.(3)连接BD,根据在同圆或等圆中,同弧所对的圆周角相等可得∠DBG=∠ACF,然后求出∠DBG=∠F,从而求出△BDG和△FBG相似,根据相似三角形对应边成比例列式表示出BG2,然后代入等式左边整理即可得证.【详解】解:(1)证明:∵OA=OB,∴∠OAB=∠OBA.∵OA⊥CD,∴∠OAB+∠AGC=90°.又∵∠FGB=∠FBG,∠FGB=∠AGC,∴∠FBG+∠OBA=90°,即∠OBF=90°.∴OB⊥FB.∵AB是⊙O的弦,∴点B在⊙O上.∴BF是⊙O的切线.(2)∵AC∥BF,∴∠ACF=∠F.∵CD=a,OA⊥CD,∴CE=12CD=12a.∵tan∠F=34,∴AE 3tan ACF CE 4∠==, 即AE 314a 2=. 解得3AE a 8=. 连接OC ,设圆的半径为r ,则3OE r a 8=-,在Rt △OCE 中,222CE OE OC +=,即22213a r a r 28⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭, 解得25r a 48=. (3)证明:连接BD ,∵∠DBG=∠ACF ,∠ACF=∠F (已证),∴∠DBG=∠F .又∵∠FGB=∠FGB ,∴△BDG ∽△FBG .∴DG GB GB GF=,即GB 2=DG•GF . ∴GF 2﹣GB 2=GF 2﹣DG•GF=GF (GF ﹣DG )=GF•DF ,即GF 2﹣GB 2=DF•GF .20、(1)(40),;(2)15x -<<【解析】(1)当0x =时,求出点C 的坐标,根据四边形OABC 为矩形,得出点B 的坐标,进而求出点A 即可; (2)先求出抛物线图象与x 轴的两个交点,结合图象即可得出.【详解】解:(1)当0x =时,函数228255y x x =--的值为-2, ∴点C 的坐标为(0,2)-∵四边形OABC 为矩形, ,2OA CB AB CO ∴=== 解方程2282255x x --=-,得120,4x x ==. ∴点B 的坐标为(4)2-,. ∴点A 的坐标为(40),. (2)解方程2282055x x --=,得121,5x x =-=. 由图象可知,当0y <时,x 的取值范围是15x -<<.【点睛】本题考查了二次函数与几何问题,以及二次函数与不等式问题,解题的关键是灵活运用几何知识,并熟悉二次函数的图象与性质.21、 .【解析】利用∠ECA 的正切值可求得AE ;利用∠ECB 的正切值可求得BE ,由AB=AE+BE 可得答案.【详解】在Rt △EBC 中,有BE=EC×tan45°m , 在Rt △AEC 中,有AE=EC×tan30°=8m ,∴+8(m ).【点睛】本题考查了解直角三角形的应用-俯角、仰角问题,要求学生能借助其关系构造直角三角形并解直角三角形.22、(1)见解析;(2)见解析.【解析】试题分析:(1)作∠BAD 的平分线交直线BC 于点E ,交DC 延长线于点F 即可;(2)先根据平行四边形的性质得出AB ∥DC ,AD ∥BC ,故∠1=∠2,∠3=∠1.再由AF 平分∠BAD 得出∠1=∠3,故可得出∠2=∠1,据此可得出结论.(2)∵四边形ABCD是平行四边形,∴AB∥DC,AD∥BC,∴∠1=∠2,∠3=∠1.∵AF平分∠BAD,∴∠1=∠3,∴∠2=∠1,∴CE=CF.考点:作图—基本作图;平行四边形的性质.23、(1)每辆A型自行车的进价为2 000元,每辆B型自行车的进价为1 600元;(2)当购进A型自行车34辆,B型自行车66辆时获利最大,最大利润为13300元.【解析】(1)设每辆B型自行车的进价为x元,则每辆A型自行车的进价为(x+10)元,根据题意列出方程,求出方程的解即可得到结果;(2)由总利润=单辆利润×辆数,列出y与x的关系式,利用一次函数性质确定出所求即可.【详解】(1)设每辆B型自行车的进价为x元,则每辆A型自行车的进价为(x+10)元,根据题意,得=,解得x=1600,经检验,x=1600是原方程的解,x+10=1 600+10=2 000,答:每辆A型自行车的进价为2 000元,每辆B型自行车的进价为1 600元;(2)由题意,得y=(2100﹣2000)m+(1750﹣1600)(100﹣m)=﹣50m+15000,根据题意,得,解得:33≤m≤1,∵m为正整数,∴m=34,35,36,37,38,39,1.∵y=﹣50m+15000,k=﹣50<0,∴y随m的增大而减小,∴当m=34时,y有最大值,最大值为:﹣50×34+15000=13300(元).【点睛】本题主要考查一次函数的应用、分式方程的应用及一元一次不等式组的应用.仔细审题,找出题目中的数量关系是解答本题的关键.24、证明见解析.【解析】根据平行线性质得出∠A=∠B,根据SAS证△ACD≌△BEC,推出DC=CE,根据等腰三角形的三线合一定理推出即可.【详解】∵AD∥BE,∴∠A=∠B.在△ACD和△BEC中∵,∴△ACD≌△BEC(SAS),∴DC=CE.∵CF平分∠DCE,∴CF⊥DE(三线合一).【点睛】本题考查了全等三角形的性质和判定,平行线的性质,等腰三角形的性质等知识点,关键是求出DC=CE,主要考查了学生运用定理进行推理的能力.25、工程完工后背水坡底端水平方向增加的宽度AC约为37.3米.【解析】解:在Rt△BAE中,∠BAE=680,BE=162米,∴(米).在Rt△DEC中,∠DGE=600,DE=176.6米,∴DECE102.08tan DGE3==≈∠(米).∴AC CE AE102.0864.8037.2837.3=-≈-=≈(米).∴工程完工后背水坡底端水平方向增加的宽度AC约为37.3米.在Rt△BAE和Rt△DEC中,应用正切函数分别求出AE和CE的长即可求得AC的长.26、(1)证明见解析;(2)2BC=【解析】试题分析:(1)连接OP,首先证明OP∥BC,推出∠OPB=∠PBC,由OP=OB,推出∠OPB=∠OBP,由此推出∠PBC=∠OBP;(2)作PH⊥AB于H.首先证明PC=PH=1,在Rt△APH中,求出AH,由△APH∽△ABC,求出AB、BH,由Rt△PBC≌Rt△PBH,推出BC=BH即可解决问题.试题解析:(1)连接OP,∵AC是⊙O的切线,∴OP⊥AC,∴∠APO=∠ACB=90°,∴OP∥BC,∴∠OPB=∠PBC,∵OP=OB,∴∠OPB=∠OBP,∴∠PBC=∠OBP,∴BP平分∠ABC;(2)作PH⊥AB于H.则∠AHP=∠BHP=∠ACB=90°,又∵∠PBC=∠OBP,PB=PB,∴△PBC≌△PBH ,∴PC=PH=1,BC=BH,在Rt△APH中,AH=2222-=,AP PH在Rt△ACB中,AC2+BC2=AB2∴(AP+PC)2+BC2=(AH+HB)2,即42+BC2=(22+BC)2,解得2BC=.27、(1)A类图书的标价为27元,B类图书的标价为18元;(2)当A类图书每本降价少于3元时,A类图书购进800本,B类图书购进200本,利润最大;当A类图书每本降价大于等于3元,小于5元时,A类图书购进600本,B类图书购进400本,利润最大.【解析】(1)先设B类图书的标价为x元,则由题意可知A类图书的标价为1.5x元,然后根据题意列出方程,求解即可.(2)先设购进A类图书t本,总利润为w元,则购进B类图书为(1000-t)本,根据题目中所给的信息列出不等式组,求出t的取值范围,然后根据总利润w=总售价-总成本,求出最佳的进货方案.【详解】解:(1)设B类图书的标价为x元,则A类图书的标价为1.5x元,根据题意可得540540101.5x x-=,化简得:540-10x=360,解得:x=18,经检验:x=18是原分式方程的解,且符合题意,则A类图书的标价为:1.5x=1.5×18=27(元),答:A类图书的标价为27元,B类图书的标价为18元;(2)设购进A类图书t本,总利润为w元,A类图书的标价为(27-a)元(0<a<5),由题意得,() 1812100016800600t tt+-≤⎧≥⎨⎩,解得:600≤t≤800,则总利润w=(27-a-18)t+(18-12)(1000-t)=(9-a)t+6(1000-t)=6000+(3-a)t,故当0<a<3时,3-a>0,t=800时,总利润最大,且大于6000元;当a=3时,3-a=0,无论t值如何变化,总利润均为6000元;当3<a<5时,3-a<0,t=600时,总利润最大,且小于6000元;答:当A类图书每本降价少于3元时,A类图书购进800本,B类图书购进200本时,利润最大;当A类图书每本降价大于等于3元,小于5元时,A类图书购进600本,B类图书购进400本时,利润最大.【点睛】本题考查了一次函数的应用,分式方程的应用、一元一次不等式组的应用、一次函数的最值问题,解答本题的关键在于读懂题意,设出未知数,找出合适的等量关系,列出方程和不等式组求解.。
2024-2025学年山东省潍坊市高三(上)开学数学试卷(含答案)

2024-2025学年山东省潍坊市高三(上)开学数学试卷一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.复数1−2i1+2i 的虚部是( )A. 45B. −45C. 35D. −352.设集合A ={1,2,4},B ={x|x 2−5x +m =0},若A ∩B ={2},则B =( )A. {2,−3}B. {2,−6}C. {2,3}D. {2,6}3.已知向量a ,b ,c 在正方形网格中的位置如图所示,若网格纸上小正方形的边长为2,则(a +b )⋅c +a ⋅b =( )A. 0B. 3C. 6D. 124.坡屋顶是我国传统建筑造型之一,蕴含着丰富的数学元素.如图,某坡屋顶可视为一个五面体,其中两个面是全等的等腰梯形,还有两个面是全等的等腰三角形,若AB =25m ,BC =10m ,且等腰梯形所在平面、等腰三角形所在平面与平面ABCD 的夹角均为45°,则该五面体的体积为( )A. 375m 3B. 16253m 3C. 545m 3D. 625m 35.已知圆C :x 2+y 2−2x =0,则过点P(3,0)的圆C 的切线方程是( )A. y =±12(x−3)B. y =±2(x−3)C. y =±33(x−3) D. y =±3(x−3)6.数列{a n }中,a 1=2,a n +1=a n +2,若a k +a k +1+⋯+a k +9=270,则k =( )A. 7B. 8C. 9D. 107.设10≤x 1<x 2<x 3<x 4≤104,随机变量ξ1取值x 1,x 2,x 3,x 4的概率均为14,随机变量ξ2取值x 1+x 2+x 33,x 2+x 3+x 43,x 3+x 4+x 13,x 4+x 1+x 23,x 2+x 3+x 43的概率也均为14,若记D(ξ1),D(ξ2)分别是ξ1,ξ2的方差,则( )A. D(ξ1)>D(ξ2)B. D(ξ1)=D(ξ2)C. D(ξ1)<D(ξ2)D. D(ξ1)与D(ξ2)的大小不确定8.已知定义在实数集R 上的函数f(x),其导函数为f′(x),且满足f(x +y)=f(x)+f(y)+xy ,f(1)=0,f′(1)=12,则f′(2)=( )A. 0B. 34C. 1D. 32二、多选题:本题共3小题,共18分。
2021年山东省潍坊市诸城市中考数学一模试卷(解析版)

2021年山东省潍坊市诸城市中考数学一模试卷一、选择题(本题共8小题,每小题3分,共24分.在每个小题给出的四个选项中,只有一项是符合题目要求的)1.如图,数轴上的A,B,C三点所表示的数分别为a,b,c,且原点为O,根据图中各点位置,下列数值最大的是()A.a B.b C.|c|D.﹣b2.下列计算正确的是()A.a3•a4=a12B.(a2)3=a6C.(2a)2=2a2D.2a4÷a4=a4 3.下列几何体是由5个相同的小正方体搭成的,其俯视图是()A.B.C.D.4.21世纪以来我国经济总量规模扩大了10倍,取得了举世瞩目的成就,2020年我国国内生产总值首次突破1000000亿元,达到1016000亿元.数据1016000用科学记数法表示为()A.1.016×106B.1.016×105C.10.16×105D.1016×1035.如图,是小明绘制的他在一周内每天跑步圈数的折线统计图.下列结论不正确的是()A.众数是10B.中位数是9C.平均数是9D.方差是86.已知关于x的分式方程+2=的解为正数,则正整数m的取值可能是()A.6B.5C.4D.37.如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中剩余的小正方形中任意一个涂黑,则三个被涂黑的小正方形构成轴对称图形的概率是()A.B.C.D.8.如图,半圆O的直径AB=8,将半圆O绕点B顺时针旋转45°得到半圆O′,与AB交于点P,则图中阴影部分的面积为()A.4π+8B.4π﹣8C.8πD.8π+8二、选择题(本题共4小题,每小题3分,共12分.在每小题给出的选项中,有多项符合题目要求,全部选对的得3分,有选错的得0分,部分选对的得2分)9.若直线y=kx﹣b沿y轴平移3个单位得到新的直线y=kx﹣1,则b的值为.(多选)A.2B.﹣2C.4D.﹣410.如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A′B′C′,以下说法正确是.(多选)A.S△ABC:S△A′B′C′=1:2B.AB:A′B′=1:2C.点A,O,A′三点在同一条直线上D.BC∥B′C′11.已知抛物线y=ax2+bx+c上部分点的横坐标x与纵坐标y的对应值如右表,则下列结论正确的是.(多选)x…﹣4﹣3﹣2﹣1…y…﹣3010…A.对称轴为直线x=﹣2B.abc>0C.a+b+c<0D.关于x的一元二次方程ax2+bx+c﹣1=0有两个不相等的实数解12.如图,已知∠AOB,按以下步骤作图:①在射线OA上取一点C,以点O为圆心,OC 长为半径作,交射线OB于点D;②连接CD,分别以点C、D为圆心,CD长为半径作弧,交于点M、N;③连接OM,MN.根据以上作图过程及所作图形,下列结论中正确的是.(多选)A.∠COM=∠CODB.点M与点D关于直线OA对称C.若∠AOB=20°,则OM=MND.MN∥CD三、填空题(本大题共6小题,共18分,只要求填写最后结果,每小题填对得3分)13.因式分解:a3b3+2a2b2+ab=.14.使有意义的x的取值范围是.15.如图,在6×6的正方形网格中,每个小正方形的边长都是1,点A,B,C均在网格交点上,⊙O是△ABC的外接圆,则tan∠BAC的值为.16.对于实数x,我们[x]表示不大于x的最大整数,例如[1.2]=1,[3]=3,[﹣2.5]=﹣3,若[]=5,则x的取值范围是.17.如图,在矩形ABCD中,将△DEC沿DE折叠得到△DEC',点C'恰好为对角线AC的中点,则的值等于.18.如图,正方形ABCD边长为2,点G在以AB为直径的半圆上的一个动点,点F是边CD上的一个动点,点E是AD的中点,则EF+FG的最小值为.四、解答题(本大题共7小题,共66分.解答要写出必要的文字说明、证明过程或演算步骤)19.国家“十四五”规划明确强化实施“健康中国”战略.为了引导学生积极参与体育运动,增强身体素质,某校举办了一分钟跳绳比赛,随机抽取了m名学生一分钟跳绳的次数(x 次)进行调查统计,按照以下标准划分为四档:100≤x<120,不合格;120≤x<140,合格;140≤x<160,良好;160≤x<180,优秀.并根据统计结果绘制了如下条形统计图和扇形统计图:请结合上述信息完成下列问题:(1)m=,a=;(2)在扇形统计图中,“良好”等级对应的圆心角的度数是;(3)若该校有1200名学生,根据抽样调查结果,请估计该校学生一分钟跳绳次数达到合格及以上的人数.20.如图,一次函数y1=﹣2x+b的图象分别交x轴,y轴于D,C两点,交反比例函数y2=图象于A(﹣1,6),B(m,﹣2)两点.(1)求k,b的值;(2)点E是y轴上点C下方一点,若S△AEB=,求E点的坐标;(3)当y1>y2时,x的取值范围是.21.如图所示,某建筑物楼顶有信号设备EF,小明同学为了测量信号设备EF的高度,沿直线AD出发,在A点时观测到设备最低点F的仰角∠A=30°;向前走8米到达B点时,测得最高点E的仰角∠EBC=60°,若设备EF=4米,求信号设备EF的最高点的离地高度(结果保留根号).22.如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,直线AB与⊙O相切于点B,连接BP并延长,交直线l于点C.(1)求证:AB=AC;(2)若PC=2,OA=5,求线段PB的长.23.某蔬菜基地种植的某种绿色蔬菜,根据今年的市场行情,预计从5月1日起的50天内,第x天上市的该种蔬菜每千克的市场售价为y1元,y1是关于x的一次函数,其中部分对应数据如下表;第x天上市的该种蔬菜每千克的种植成本为y2元,y2与x满足关系y2=(x﹣25)2+2.x123…y1 5.04 4.98 4.92…(1)求市场售价y1与上市时间x的函数表达式,并写出x的取值范围;(2)若市场售价减去种植成本为利润,自5月1日起的50天内,第几天上市的该种蔬菜每千克的利润最大,最大利润是多少?24.如图1,已知∠MBN=90°,四根长度相等的木棒AB,BC,CD,DA首尾相接组成四边形ABCD,点F是AB的中点,连接BD,CF交于点E,BE的垂直平分线GH交AB 于点G,交BD于点H,连接GE.(1)如图1,若BC,BA分别在BM,BN上,求证:GE⊥AB;(2)如图2,将木棒BA固定在射线BN上,当木棒BC绕着点B由BM开始顺时针旋转时,求证:AD=3GE;(3)在(2)的旋转过程中,设∠MBC=α,且α满足0°<α<90°.若△GEF是直角三角形,请直接写出α的值.25.如图,直线与坐标轴交于A,G两点,经过B(2,0)、C(6,0)两点的抛物线y=ax2+bx+2与直线交于A,D两点.(1)求抛物线的解析式及点D的坐标;(2)点M是抛物线上位于直线AD下方上的一个动点,当点M运动到什么位置时△MDA 的面积最大?最大值是多少?(3)在x轴上是否存在点P,使以A、P、D为顶点的三角形是直角三角形?若存在,直接写出满足条件的点P的坐标;若不存在,请说明理由.参考答案一、选择题(本题共8小题,每小题3分,共24分.在每个小题给出的四个选项中,只有一项是符合题目要求的)1.如图,数轴上的A,B,C三点所表示的数分别为a,b,c,且原点为O,根据图中各点位置,下列数值最大的是()A.a B.b C.|c|D.﹣b【分析】在数轴上分别找到|c|和﹣b,利用数轴比较大小,数轴上的数越往右右越大,越往左越小.解:由数轴可知,|c|=﹣c,在数轴上分别表示|c|和﹣b,∴b<c<a<|c|<﹣b,故最大数值是﹣b.故选:D.2.下列计算正确的是()A.a3•a4=a12B.(a2)3=a6C.(2a)2=2a2D.2a4÷a4=a4【分析】A.利用同底数幂的运算法则,底数不变,指数相加可得;B.根据幂的乘方,底数不变,指数相乘可得结果;C.根据积的乘方等于乘方的积,可计算结果;D.根据单项式除单项式的运算法则进行计算即可.解:A.a3•a4=a7≠a12,计算结果错误,不符合题意;B.(a2)3=a6,计算结果正确,符合题意;C.(2a)2=4a2,计算结果错误,不符合题意;D.2a4÷a4=2,计算结果错误,不符合题意;故选:B.3.下列几何体是由5个相同的小正方体搭成的,其俯视图是()A.B.C.D.【分析】找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.解:从上面看,是一行3个小正方形,故选:B.4.21世纪以来我国经济总量规模扩大了10倍,取得了举世瞩目的成就,2020年我国国内生产总值首次突破1000000亿元,达到1016000亿元.数据1016000用科学记数法表示为()A.1.016×106B.1.016×105C.10.16×105D.1016×103【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.解:将1016000用科学记数法表示为:1.016×106.故选:A.5.如图,是小明绘制的他在一周内每天跑步圈数的折线统计图.下列结论不正确的是()A.众数是10B.中位数是9C.平均数是9D.方差是8【分析】由折线图得到一周内每天跑步圈数的数据,计算这组数据的平均数、中位数、众数、方差,然后判断得结论.解:A.数据10出现的次数最多,即众数是10,故本选项正确,不符合题意;B.排序后的数据中,最中间的数据为9,即中位数为9,故本选项正确,符合题意;C.平均数为:(7+8+9+9+10+10+10)=9,故本选项正确,不符合题意;D.方差为[(7﹣9)2+(8﹣9)2+(9﹣9)2+(9﹣9)2+(10﹣9)2+(10﹣9)2+(10﹣9)2]=,故本选项不正确,符合题意;故选:D.6.已知关于x的分式方程+2=的解为正数,则正整数m的取值可能是()A.6B.5C.4D.3【分析】解分式方程+2=,得.因为分式方程的解是正数,所以且,进而推断出m<5且m≠3.那么,C符合题意.解:+2=.方程两边同乘(x﹣1),得m+2(x﹣1)=3.解得:.∵关于x的分式方程+2=的解为正数,∴且.∴m<5且m≠3.故选:C.7.如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中剩余的小正方形中任意一个涂黑,则三个被涂黑的小正方形构成轴对称图形的概率是()A.B.C.D.【分析】分别将7个空白处涂黑,判断出所得图案是轴对称图形的个数,再根据概率公式进行计算.解:如图①②③④⑤任意一处涂黑时,图案为轴对称图形,∵共有7个空白处,将①②③④⑤处任意一处涂黑,图案为轴对称图形,共5处,∴构成轴对称图形的概率是,故选:D.8.如图,半圆O的直径AB=8,将半圆O绕点B顺时针旋转45°得到半圆O′,与AB交于点P,则图中阴影部分的面积为()A.4π+8B.4π﹣8C.8πD.8π+8【分析】根据题意和扇形面积计算公式、三角形的面积公式,可以计算出图中阴影部分的面积,本题得以解决.解:由已知可得,AB=8,∠OBO′=45°,弓形PB的面积是:﹣=4π﹣8,阴影部分的面积是:﹣(4π﹣8)=8π﹣4π+8=4π+8,故选:A.二、选择题(本题共4小题,每小题3分,共12分.在每小题给出的选项中,有多项符合题目要求,全部选对的得3分,有选错的得0分,部分选对的得2分)9.若直线y=kx﹣b沿y轴平移3个单位得到新的直线y=kx﹣1,则b的值为BC.(多选)A.2B.﹣2C.4D.﹣4【分析】根据上加下减的原则可知,将直线y=kx﹣b沿y轴平移3个单位得到直线y=kx﹣b±3,即直线y=kx﹣1,那么﹣b±3=﹣1,即可求出b的值.解:根据上加下减的原则可得:﹣b±3=﹣1,解得b=﹣2或4.故答案是:BC.10.如图,以点O为位似中心,把△ABC放大为原图形的2倍得到△A′B′C′,以下说法正确是BCD.(多选)A.S△ABC:S△A′B′C′=1:2B.AB:A′B′=1:2C.点A,O,A′三点在同一条直线上D.BC∥B′C′【分析】根据位似图形的概念相似三角形的性质判断即可.解:以点O为位似中心,把△ABC放大为原图形的2倍得到△A′B′C′,则△ABC∽△A′B′C′,且相似比为1:2,∴S△ABC:S△A′B′C′=1:4,故A选项说法错误;∴AB:A′B′=1:2,点A,O,A′三点在同一条直线上,BC∥B′C′,B、C、D说法正确;故答案为:BCD.11.已知抛物线y=ax2+bx+c上部分点的横坐标x与纵坐标y的对应值如右表,则下列结论正确的是AC.(多选)x…﹣4﹣3﹣2﹣1…y…﹣3010…A.对称轴为直线x=﹣2B.abc>0C.a+b+c<0D.关于x的一元二次方程ax2+bx+c﹣1=0有两个不相等的实数解【分析】根据二次函数的性质和表格中的数据,可以判断各个小题中的结论是否成立,本题得以解决.解:A.由表格可知,抛物线的对称轴是直线x=﹣2,故A正确;B.抛物线的顶点坐标(﹣2,1),有最大值,故抛物线的开口向下,∴a<0,∵对称轴x=﹣2,∴b<0,当x=﹣4和x=2时,函数值相等,故c=﹣3<0,∴abc<0,故B错误;C.当x=1时,y=a+b+c,∵开口向下,∴当x=1时,y<0,故C正确;D.关于x的一元二次方程ax2+bx+c﹣1=0,即ax2+bx+c=1,当x=﹣2时,等号成立,但只有1个实数根,故D错误.故答案为:AC.12.如图,已知∠AOB,按以下步骤作图:①在射线OA上取一点C,以点O为圆心,OC长为半径作,交射线OB于点D;②连接CD,分别以点C、D为圆心,CD长为半径作弧,交于点M、N;③连接OM,MN.根据以上作图过程及所作图形,下列结论中正确的是ABD.(多选)A.∠COM=∠CODB.点M与点D关于直线OA对称C.若∠AOB=20°,则OM=MND.MN∥CD【分析】根据等弧所对圆周角相等可以判断A;根据平行线的判定可以判断D;根据CM =CD,OM=OD,可得OA垂直平分MD,可以判断B;根据∠AOB=∠AOM=∠BON =20°,得∠MON=60°,由OM=ON,可得△OMN为等边三角形,进而可以判断C.解:由作法得CM=CD,∴=,∴∠COM=∠COD,所以A选项的结论正确;连接MD,∵=,∴∠DMN=∠MDC,∴CD∥MN,所以D选项的结论正确;∵CM=CD,OM=OD,∴OA垂直平分MD,∴点M与点D关于OA对称,所以B选项的结论正确;∵∠AOB=∠AOM=∠BON=20°,∴∠MON=60°,∵OM=ON,∴△OMN为等边三角形,∴OM=MN,所以C选项的结论错误.∴正确的是ABD.故答案为:ABD.三、填空题(本大题共6小题,共18分,只要求填写最后结果,每小题填对得3分)13.因式分解:a3b3+2a2b2+ab=ab(ab+1)2.【分析】直接提取公因式ab,再利用公式法分解因式得出答案.解:a3b3+2a2b2+ab=ab(a2b2+2ab+1)=ab(ab+1)2.故答案为:ab(ab+1)2.14.使有意义的x的取值范围是x>2020,且x≠2021.【分析】根据零指数幂的底数不等于0,二次根式的被开方数非负,分母不等于0即可得出答案.解:根据题意得:x﹣2021≠0,x﹣2020≥0,x﹣2020≠0,∴x>2020,且x≠2021,故答案为:x>2020,且x≠2021.15.如图,在6×6的正方形网格中,每个小正方形的边长都是1,点A,B,C均在网格交点上,⊙O是△ABC的外接圆,则tan∠BAC的值为.【分析】延长CO交⊙O于点D,连接BD,根据正切的定义求出tan D,根据圆周角定理得到∠A=∠D,得到答案.解:延长CO交⊙O于点D,连接BD,在Rt△BCD中,tan∠BDC===,由圆周角定理得:∠BAC=∠BDC,∴tan∠BAC=,故答案为:.16.对于实数x,我们[x]表示不大于x的最大整数,例如[1.2]=1,[3]=3,[﹣2.5]=﹣3,若[]=5,则x的取值范围是46≤x<56.【分析】先根据[x]表示不大于x的最大整数,列出不等式组,再求出不等式组的解集即可.解:根据题意得:5≤<5+1,解得:46≤x<56,故答案为46≤x<56.17.如图,在矩形ABCD中,将△DEC沿DE折叠得到△DEC',点C'恰好为对角线AC的中点,则的值等于.【分析】根据折叠的性质可得DC=DC′,C′E=CE,,根据矩形性质及直角三角形中线性质可得△C′DC是等边三角形,然后根据三角形函数关系可得答案.解:∵将△DEC沿DE折叠得到△DEC',∴△DCE≌△DC′E,∴DC=DC′,C′E=CE,∵C'为对角线AC的中点,∴在矩形ABCD中,CC′=DC′,∵四边形ABCD是矩形,∴DC=DC′=CC′,∴△C′DC是等边三角形,∴C′DC=60°,∴∠EDC=×60°=30°,∵tan∠DCE==,∴=,∵C′E=CE,∴,∴=.故答案为:.18.如图,正方形ABCD边长为2,点G在以AB为直径的半圆上的一个动点,点F是边CD上的一个动点,点E是AD的中点,则EF+FG的最小值为.【分析】作E点关于CD的对称点E',连接E'O,交CD于F,交半圆O于G,此时EF+FG 的值最小,在Rt△AE'O中,E'O=,即可求EF+FG的最小值为﹣1.解:作E点关于CD的对称点E',连接E'O,交CD于F,交半圆O于G,此时EF+FG 的值最小,∵EF=E'F,∴EF+FG=E'F+FG,∴EF+FG的最小值为E'O﹣GO,∵正方形边长为2,∴AO=GO=1,∵E是AD的中点,∴DE=DE'=1,∴EE'=2,在Rt△AE'O中,E'O===,∴E'O﹣GO=﹣1,∴EF+FG的最小值为﹣1,故答案为:﹣1.四、解答题(本大题共7小题,共66分.解答要写出必要的文字说明、证明过程或演算步骤)19.国家“十四五”规划明确强化实施“健康中国”战略.为了引导学生积极参与体育运动,增强身体素质,某校举办了一分钟跳绳比赛,随机抽取了m名学生一分钟跳绳的次数(x 次)进行调查统计,按照以下标准划分为四档:100≤x<120,不合格;120≤x<140,合格;140≤x<160,良好;160≤x<180,优秀.并根据统计结果绘制了如下条形统计图和扇形统计图:请结合上述信息完成下列问题:(1)m=40,a=14;(2)在扇形统计图中,“良好”等级对应的圆心角的度数是108°;(3)若该校有1200名学生,根据抽样调查结果,请估计该校学生一分钟跳绳次数达到合格及以上的人数.【分析】(1)根据优秀的人数和所占的百分比,求出抽取的总人数,再用总人数减去其他人数求出a即可;(2)用360°乘以“良好”等级所占的百分比即可;(3)用该校的总人数乘以一分钟跳绳次数达到合格及以上的人数所占的百分比即可.解:(1)m=10÷25%=40,a=40﹣4﹣12﹣10=14;故答案为:40,14;(2)在扇形统计图中,“良好”等级对应的圆心角的度数是360°×=108°;故答案为:108°;(3)估计该校一分钟跳绳次数达到合格及以上的人数为1200×=1080(人).20.如图,一次函数y1=﹣2x+b的图象分别交x轴,y轴于D,C两点,交反比例函数y2=图象于A(﹣1,6),B(m,﹣2)两点.(1)求k,b的值;(2)点E是y轴上点C下方一点,若S△AEB=,求E点的坐标;(3)当y1>y2时,x的取值范围是x<﹣1或0<x<3.【分析】(1)先把A点坐标分别代入y1=﹣2x+b和y2=中利用待定系数法即可求得k、b;(2)设E(a,0),先求得B(3,﹣2),然后根据三角形面积公式得到)=2CE=2(4﹣a)=,解方程求得a;(3)观察图象求得即可.解:(1)将A(﹣1,6)代入一次函数y=﹣2x+b,得b=4;将A(﹣1,6)代入,得k=﹣6.(2)设E(a,0),将B(m,﹣2)代入,得m=3,∴B(3,﹣2)∴)=2CE=2(4﹣a)=,∴E(0,);(3)观察图象,当y1>y2时,x的取值范围是x<﹣1或0<x<3,故答案为:x<﹣1或0<x<3.21.如图所示,某建筑物楼顶有信号设备EF,小明同学为了测量信号设备EF的高度,沿直线AD出发,在A点时观测到设备最低点F的仰角∠A=30°;向前走8米到达B点时,测得最高点E的仰角∠EBC=60°,若设备EF=4米,求信号设备EF的最高点的离地高度(结果保留根号).【分析】设FD的长为x,在Rt△ACF中,根据三角函数的定义得到AD=,在Rt △ABE中,根据三角函数的定义得到BD=,于是得到﹣=8,解方程求得FD,进而即可求得ED.解:设FD的长为x,依据题意得在Rt△ADF中,∠A=30°,∴AD=,在Rt△EDB中,∠EBD=60°,EF=4,∴BD=,∵AB=8,∴AD﹣BD=8,即﹣=8,解得x=,∴ED==+6.22.如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,直线AB与⊙O相切于点B,连接BP并延长,交直线l于点C.(1)求证:AB=AC;(2)若PC=2,OA=5,求线段PB的长.【分析】(1)根据切线的性质得到∠ABO=90°,然后证明∠ABC=∠ACB,从而得到AB=AC;(2)设⊙O的半径为r,则OB=OP=r,PA=5﹣r,利用勾股定理得到52﹣r2=(2)2﹣(5﹣r)2,解得r=3,所以OP=3,PA=2,过O点作OH⊥PB,如图,根据垂径定理得到PH=BH,再证明△OPH∽△CPA,利用相似比求出PH,从而得到BP的长.【解答】(1)证明:∵直线AB与⊙O相切于点B,∴OB⊥AB,∴∠ABO=90°,∵OA⊥AC,∴∠OAC=90°,∵∠OBC+∠ABC=90°,∠ACP+∠APC=90°,而∠APC=∠OPB=∠OBP,∴∠ABC=∠ACB,∴AB=AC;(2)解:设⊙O的半径为r,则OB=OP=r,PA=5﹣r,在Rt△OAB中,AB2=52﹣r2,在Rt△PAC中,AC2=(2)2﹣(5﹣r)2,∵AB=AC,∴52﹣r2=(2)2﹣(5﹣r)2,解得r=3,∴OP=3,PA=2,过O点作OH⊥PB,如图,则PH=BH,∵∠OPH=∠APC,∠OHP=∠CAP,∴△OPH∽△CPA,∴=,即=,解得PH=,∴PB=2PH=.23.某蔬菜基地种植的某种绿色蔬菜,根据今年的市场行情,预计从5月1日起的50天内,第x天上市的该种蔬菜每千克的市场售价为y1元,y1是关于x的一次函数,其中部分对应数据如下表;第x天上市的该种蔬菜每千克的种植成本为y2元,y2与x满足关系y2=(x﹣25)2+2.x123…y1 5.04 4.98 4.92…(1)求市场售价y1与上市时间x的函数表达式,并写出x的取值范围;(2)若市场售价减去种植成本为利润,自5月1日起的50天内,第几天上市的该种蔬菜每千克的利润最大,最大利润是多少?【分析】(1)y1函数是分段函数,写出各定义域的解析式,y2是二次函数,(2)由市场售价减去种植成本为纯利润列出函数关系式,求出最大值.解:(1)设y1=kx+b,∵函数图象过点(1,5.04),(2,4.98),∴,解得:,∴y1=﹣x+5.1(0<x≤50,x取正整数);(2)设纯利润为w,由题意得:w=y1﹣y2==,∵a=<0,且0≤x≤50,∴x=22时(符合题意),每千克利润最大,最大值为1.69元;∴第22天上市的该种蔬菜每千克的利润最大,最大利润是1.69元.24.如图1,已知∠MBN=90°,四根长度相等的木棒AB,BC,CD,DA首尾相接组成四边形ABCD,点F是AB的中点,连接BD,CF交于点E,BE的垂直平分线GH交AB 于点G,交BD于点H,连接GE.(1)如图1,若BC,BA分别在BM,BN上,求证:GE⊥AB;(2)如图2,将木棒BA固定在射线BN上,当木棒BC绕着点B由BM开始顺时针旋转时,求证:AD=3GE;(3)在(2)的旋转过程中,设∠MBC=α,且α满足0°<α<90°.若△GEF是直角三角形,请直接写出α的值.【分析】(1)先证明四边形ABCD是正方形,推得∠ABD=∠ADB=45°,再由HG垂直平分BE,得∠GEB=∠GBE=45°,则∠BGE=90°,推导出GE⊥AB;(2)由菱形对边平行的性质证明△BFE∽△DCE,由F是AB的中点,可得到=,再证明△GEB∽△ADB,由相似三角形的性质即可证得结论;(3)连接AC,在0°<α<90°的范围内,△GEF是直角三角形只存在∠EFG=90°一种情况,根据线段垂直平分线的性质证明△ABC是等边三角形,即可求出α的值.【解答】(1)证明:如图1,∵AB=BC=CD=DA,∴四边形ABCD是菱形,∵∠MBN=90°,BC,BA分别在BM,BN上,∴∠CBA=90°,四边形ABCD是正方形,∴∠BAD=90°,∴∠ABD=∠ADB=45°,∵HG垂直平分BE,∴GE=GB,∴∠GEB=∠GBE=45°,∴∠BGE=90°,∴GE⊥AB.(2)证明:如图2,由(1)得,四边形ABCD是菱形,∴AB∥CD,∴FB∥CD,∴△BFE∽△DCE,∴,∵点F是AB的中点,∴FB=AB=CD,∴=,∴=;∵HG垂直平分BE,∴GE=GB,∴∠GEB=∠ABD,∵∠ADB=∠ABD,∴∠GEB=∠ADB,∴GE∥AD,∴△GEB∽△ADB,∴=,∴AD=3GE.(3)如图3,连接AC,∵∠MBC=α,且0°<α<90°,△GEF是直角三角形,∴∠EFG=90°,∵AF=BF,CF⊥AB,∴AC=BC,∴AB=AC=BC,∴△ABC是等边三角形,∴∠ABC=60°,∴∠MBC=90°﹣∠ABC=30°,∴α=30°.25.如图,直线与坐标轴交于A,G两点,经过B(2,0)、C(6,0)两点的抛物线y=ax2+bx+2与直线交于A,D两点.(1)求抛物线的解析式及点D的坐标;(2)点M是抛物线上位于直线AD下方上的一个动点,当点M运动到什么位置时△MDA 的面积最大?最大值是多少?(3)在x轴上是否存在点P,使以A、P、D为顶点的三角形是直角三角形?若存在,直接写出满足条件的点P的坐标;若不存在,请说明理由.【分析】(1)由待定系数法可求出抛物线解析,联立直线和抛物线解析式可得出点D的坐标;(2)如图1,过点M作y轴的平行线交线段AD于点N,设点N坐标为N(x,x+2),设M坐标为M(x,x2﹣x+2),可求出△MAD的面积,由二次函数的性质可得出答案;(3)分三种情况:①当点P为直角顶点时,②当点A为直角顶点时,③当点D为直角顶点时,由直角三角形的性质及相似三角形的性质可得出答案.解:(1)∵抛物线y=ax2+bc+2经过B(2,0)、C(6,0)两点,∴,解得,∴抛物线的解析式,∵当x=0时,y=2,∴点A的坐标为(0,2),∴m=2,即直线解析式为:,∴抛物线与直线交于A、D两点,∴,解得,,∴D(12,10);(2)如图1,过点M作y轴的平行线交线段AD于点N,设点M的坐标为,则点N的坐标为(x,),∴=﹣,∴S=,∵a=﹣1<0,∴S有最大值,∵当M运动到M(6,0)时,S有最大值为36;(3)①当点P为直角顶点时,设P(x,0),过点D作DH⊥x轴,垂足为H,则△PDH∽△APO,∴,∴,∴x2﹣12x+20=0,∴x1=2,x2=10,∴点P的坐标为(2,0)或(10,0).②当点A为直角顶点时,如图,过点A作AP⊥AD,交x轴与点P,设P(x,0),则△OPA∽△AOG.∴,∴,∴x=,∴点P的坐标为(,0);③当点D为直角顶点时,过点D作DP⊥AD,交x轴于点P,设P(x,0),过点D作DH⊥x轴于点H,则△PDH∽△DGH,∴,∴=,∴x=∴点P的坐标为(,0),∴满足条件的点P的坐标为(2,0)或(10,0)或(,0)或(,0).。
山东省潍坊市2021年中考数学真题试卷

2021年山东省潍坊市中考数学试卷一、单项选择题(共8小题,每小题3分,共24分.每小题四个选项只有一项正确.)1.下列各数的相反数中,最大的是()A.2B.1C.﹣1D.﹣22.如图,一束水平光线照在有一定倾斜角度的平面镜上,若入射光线与出射光线的夹角为60°()A.15°B.30°C.45°D.60°3.第七次全国人口普查数据显示,山东省常住人口约为10152.7万人,将101 527 000用科学记数法(精确到十万位)()A.1.02×108B.0.102×109C.1.015×108D.0.1015×1094.若菱形两条对角线的长度是方程x2﹣6x+8=0的两根,则该菱形的边长为()A.B.4C.25D.55.如图,某机器零件的三视图中,既是轴对称图形()A.主视图B.左视图C.俯视图D.不存在6.不等式组的解集在数轴上表示正确的是()A.B.C.D.7.如图为2021年第一季度中国工程机械出口额TOP10国家的相关数据(同比增速是指相对于2020年第一季度出口额的增长率),下列说法正确的是()A.对10个国家出口额的中位数是26201万美元B.对印度尼西亚的出口额比去年同期减少C.去年同期对日本的出口额小于对俄罗斯联邦的出口额D.出口额同比增速中,对美国的增速最快8.记实数x1,x2,…,x n中的最小数为min|x1,x2,…,x n|=﹣1,则函数y=min|2x﹣1,x,4﹣x|的图象大致为()A.B.C.D.二、多项选择题(共4小题,每小题3分,共12分.每小题四个选项有多项正确,全部选对得3分,部分选对得2分,有选错的即得0分.)9.下列运算正确的是.A.(a﹣)2=a2﹣a+B.(﹣a﹣1)2=C.=D.=210.如图,在直角坐标系中,点A是函数y=﹣x图象上的动点,1为半径作⊙A.已知点B(﹣4,0),连接AB,当⊙A与两坐标轴同时相切时,tan∠ABO的值可能为.A.3B.C.5D.11.古希腊数学家欧几里得在《几何原本》中记载了用尺规作某种六边形的方法,其步骤是:①在⊙O上任取一点A,连接AO并延长交⊙O于点B,BO为半径作圆孤分别交⊙O于C,D两点,DO并延长分交⊙O于点E,F;④顺次连接BC,F A,AE,DB,得到六边形AFCBDE.连接AD,交于点G,则下列结论正确的是.A.△AOE的内心与外心都是点GB.∠FGA=∠FOAC.点G是线段F的三等分点D.EF=AF12.在直角坐标系中,若三点A(1,﹣2),B(2,﹣2),C(2,0)中恰有两点在抛物线y=ax2+bx﹣2(a >0且a,b均为常数)的图象上,则下列结论正确是.A.抛物线的对称轴是直线x=B.抛物线与x轴的交点坐标是(﹣,0)和(2,0)C.当t>﹣时,关于x的一元二次方程ax2+bx﹣2=t有两个不相等的实数根D.若P(m,n)和Q(m+4,h)都是抛物线上的点且n<0三、填空题(共4小题,每小题4分,共16分.只填写最后结果.)13.甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:甲:函数的图象经过点(0,1);乙:y随x的增大而减小;丙:函数的图象不经过第三象限.根据他们的叙述,写出满足上述性质的一个函数表达式为.14.若x<2,且+|x﹣2|+x﹣1=0,则x=.15.在直角坐标系中,点A1从原点出发,沿如图所示的方向运动,到达位置的坐标依次为:A2(1,0),A3(1,1),A4(﹣1,1),A5(﹣1,﹣1),A6(2,﹣1),A7(2,2),….若到达终点A n(506,﹣505),则n的值为.16.如图,在直角坐标系中,O为坐标原点与y=(a>b>0)在第一象限的图象分别为曲线C1,C2,点P为曲线C1上的任意一点,过点P作y轴的垂线交C2于点A,作x轴的垂线交C2于点B,则阴影部分的面积S△AOB=_____.(结果用a,b表示)四、解答题(共7小题,共68分.解答要写出必要的文字说明、证明过程或演算步骤)17.(1)计算:(﹣2021)0+3+(1﹣3﹣2×18);(2)先化简,再求值:•﹣xy(+)(x,y)是函数y=2x与y=的图象的交点坐标.18.如图,某海岸线M的方向为北偏东75°,甲、乙两船同时出发向C处海岛运送物资.甲船从港口A 处沿北偏东45°方向航行,其中乙船的平均速度为v.若两船同时到达C处海岛,求甲船的平均速度.(结果用v表示.参考数据:≈1.4,≈1.7)19.从甲、乙两班各随机抽取10名学生(共20人)参加数学素养测试,将测试成绩分为如下的5组(满分为100分),B组:60≤x<70,C组:70≤x<80,E组:90≤x≤100,分别制成频数分布直方图和扇形统计图如图.(1)根据图中数据,补充完整频数分布直方图并估算参加测试的学生的平均成绩(取各组成绩的下限与上限的中间值近似的表示该组学生的平均成绩);(2)参加测试的学生被随机安排到4个不同的考场,其中小亮、小刚两名同学都参加测试;用树状图或列表法求小亮、小刚两名同学被分在不同考场的概率;(3)若甲、乙两班参加测试的学生成绩统计如下:甲班:62,64,66,76,77,83,83;乙班:51,52,69,71,71,89,99则可计算得两班学生的样本平均成绩为x甲=76,x乙=76;样本方差为s甲2=80,s乙2=275.4.请用学过的统计知识评判甲、乙两班的数学素养总体水平并说明理由.20.某山村经过脱贫攻坚和乡村振兴,经济收入持续增长.经统计,近五年该村甲农户年度纯收入如表所示:年度(年)2016201720182019202020211.52.5 4.57.511.3年度纯收入(万元)若记2016年度为第1年,在直角坐标系中用点(1,15),(2,2.5),(3,4.5),(4,7.5),(5,11.3)表示近五年甲农户纯收入的年度变化情况.如图所示(m>0),y=x+b(k>0),y=ax2﹣0.5x+c(a>0),以便估算甲农户2021年度的纯收入.(1)能否选用函数y =(m>0)进行模拟,请说明理由;(2)你认为选用哪个函数模拟最合理,请说明理由;(3)甲农户准备在2021年底购买一台价值16万元的农机设备,根据(2)中你选择的函数表达式21.如图,半圆形薄铁皮的直径AB=8,点O为圆心(不与A,B重合),连接AC并延长到点D,使AC=CD,AB于点E,F,连接OC,θ随点C的移动而变化.(1)移动点C,当点H,B重合时(2)当θ<45°时,求证:BH•AH=DH•FF;(3)当θ=45°时,将扇形OAC剪下并卷成一个圆锥的侧面,求该圆锥的底面半径和高.22.如图,在直角坐标系中,O为坐标原点(2,﹣),抛物线与轴的一个交点为A(4,0),点B(2,2)(1)判断点C是否在该抛物线上,并说明理由;(2)顺次连接AB,BC,CO;(3)设点P是抛物线上的动点,连接PM、PC、AC,△P AC的面积S随点P的运动而变化;当S的值为②时,求点P的横坐标的值.直线AC的函数表达式S取的一个特殊值满足条件的P点的个数S的可能取值范围①64个③②3个102个④23.如图1,在△ABC中,∠C=90°,AC=1,D为△ABC内部的一动点(不在边上),将线段BD绕点D 逆时针旋转60°,使点B到达点F的位置,使点A到达点E的位置,连接AD,AE,AF,EF.(1)求证:△BDA≌△BFE;(2)①CD+DF+FE的最小值为;②当CD+DF+FE取得最小值时,求证:AD∥BF.(3)如图2,M,N,P分别是DF,AF,连接MP,NP,请判断∠MPN的大小是否为定值.若是,求出其度数,请说明理由.。
2021年-有答案-山东省潍坊市诸城市林家村镇四年级(上)第三次月考数学试卷

2021学年山东省潍坊市诸城市林家村镇四年级(上)第三次月考数学试卷一、仔细审题,我来填.(每空1分,共24)1. 第五次人口普查结果公布:中国总人口1295330000人,改写成以“万”为单位的数是________人,省略“亿”后面的尾数约是________人。
2. 一个八位数,最高位上是8,十万位上是5,万位是6,百位上是2,其它数位都是0,这个数写作________读作________.3. 在横线里填上“>”,“<”或“=”.54070800000________5470800000 48万________480001900000000________9亿1000000________999999.4. 线段有________个端点,射线有________个端点,直线________端点。
5. 6930÷21,可以把除数看作________去试商比较简便,商是________位数。
6. A÷21=20…(),在括号里最大能填________,这个被除数最大是________.7. 一个数和25相乘的积是15000,如果这个数缩小100倍,积变成________.8. 与最小的六位数相邻的两个数分别是________和________.9. 你认为,过一点可以画________条直线,过两点可以画________条直线。
10. 一个除法算式,除数是28,商是20,被除数是________,如果被除数和除数同时乘2,商是________.11. 在3、15、20、60、7、28、120中,60的因数有________,7的倍数有________.二、判断.(对的在括号里打√,错的打×)(每小题1分共计8分)射线有一个端点,直线没有端点,所以直线比射线长。
________.520÷30=170...10________.(判断对错)在同一平面内,不重合的两条直线,不相交就平行。
潍坊市寿光市2021年3月初二下月考数学试卷含答案解析

潍坊市寿光市2021年3月初二下月考数学试卷含答案解析一.选择题(3分×12=36分)1.下列各数中,无理数的个数有()﹣0.101001,,,,,0,.A.1个B.2个C.3个D.4个2.下列说法正确的是()A.﹣4是﹣16的平方根B.4是(﹣4)2的平方根C.(﹣6)2的平方根是﹣6 D.的平方根是±43.设的小数部分为b,那么(4+b)b的值是()A.1 B.是一个有理数 C.3 D.无法确定4.下列各式表示正确的是()A.B.C.D.5.已知x、y为正数,且|x2﹣4|+(y2﹣3)2=0,假如以x、y的长为直角边作一个直角三角形,那么以那个直角三角形的斜边为边长的正方形的面积为()A.5 B.25 C.7 D.156.若m>n,则下列不等式中成立的是()A.m+a<n+b B.ma<nb C.ma2>na2D.a﹣m<a﹣n7.不等式组的解集在数轴上表示为()A.B.C.D.8.假如不等式组无解,那么m的取值范畴是()A.m>8 B.m≥8 C.m<8 D.m≤89.如图,数轴上表示1、的对应点分别为点A、点B.若点A是BC的中点,则点C所表示的数为()A.B.C.D.10.有一个数值转换器,原理如下:当输入的x为64时,输出的y是()A.8 B.C.D.11.如图所示为一种“羊头”形图案,其作法是:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②,…,依此类推,若正方形①的面积为64,则正方形⑤的面积为()A.2 B.4 C.8 D.1612.如图,矩形纸片ABCD中,点E是AD的中点,且AE=1,BE的垂直平分线MN恰好过点C.则矩形的一边AB的长度为()A.1 B.C.D.2二.填空题(4分×6=24分)13.﹣27的立方根与的平方根的和是.14.某商品进价200元,标价300元,商场规定能够打折销售,但其利润不能低于5%,该商品最多能够折.15.已知a>5,不等式(5﹣a)x>a﹣5解集为.16.如图所示,折叠长方形的一边AD,使点D落在边BC的点F处,已知AB=8cm,BC=10cm,则EC的长为cm.17.若关于x的不等式组有解,则实数a的取值范畴是.18.若不等式组的解集为x>3,则a的取值范畴是.三.解答题(8+8+12+12=40分)19.分析探究题:细心观看如图,认真分析各式,然后解答问题.OA22=()2+1=2 S1=;OA32=()2+1=3 S2=;OA42=()2+1=4 S3=…(1)请用含有n(n为正整数)的等式S n=;(2)推算出OA10=.(3)求出S12+S22+S32+…+S102的值.20.解不等式组,把它的解集在数轴上表示出来,并求该不等式组所有整数解的和..21.某企业新增了一个化工项目,为了节约资源,爱护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情形如下表:A型B型价格(万元/台)12 10月污水处理能力(吨/月)200 160经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.(1)该企业有几种购买方案?(2)哪种方案更省钱,说明理由.22.问题背景:在△ABC中,AB、BC、AC三边的长分别为、、,求那个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.如此不需求△ABC的高,而借用网格就能运算出它的面积.(1)请你将△ABC的面积直截了当填写在横线上.(2)画△DEF,DE、EF、DF三边的长分别为、、①判定三角形的形状,说明理由.②求那个三角形的面积.山东省潍坊市寿光市世纪学校2020~2021学年度八年级下学期月考数学试卷(3月份)参考答案与试题解析一.选择题(3分×12=36分)1.下列各数中,无理数的个数有()﹣0.101001,,,,,0,.A.1个B.2个C.3个D.4个【考点】无理数.【专题】应用题.【分析】依照有理数包括整数和分数,无理数包括无限不循环小数和开方开不尽的数,找出其中无理数即可解答.【解答】解:∵﹣0.101001是有理数,是无理数,是有理数,是无理数,是无理数,0是有理数,﹣=﹣4是有理数;∴无理数的个数为:3.故选C.【点评】本题要紧考查了无理数,把握无理数包括无限不循环小数和开方开不尽的数,能快速准确的找出无理数.2.下列说法正确的是()A.﹣4是﹣16的平方根B.4是(﹣4)2的平方根C.(﹣6)2的平方根是﹣6 D.的平方根是±4【考点】平方根.【专题】存在型.【分析】依照平方根的定义进行解答即可.【解答】解:A、因为﹣16<0,因此﹣16没有平方根,故A选项错误;B、因为(﹣4)2,=16,42,=16,因此4是(﹣4)2的平方根,故B选项正确;C、因为(﹣6)2=36,因此(﹣6)2的平方根是±6,故C选项错误;D、因为=4,因此的平方根是±2,故D选项错误.故选:B.【点评】本题考查的是平方根的定义,即假如一个数的平方等于a,那个数就叫做a的平方根,也叫做a的二次方根.一个正数有两个平方根,这两个平方根互为相反数,零的平方根是零,负数没有平方根.3.设的小数部分为b,那么(4+b)b的值是()A.1 B.是一个有理数 C.3 D.无法确定【考点】估算无理数的大小.【分析】第一确定的整数部分,然后即可确定小数部分b,由题意可知b=﹣2,把它代入所求式子运算即可.【解答】解:∵的小数部分为b,∴b=﹣2,把b=﹣2代入式子(4+b)b中,原式=(4+b)b=(4+﹣2)×(﹣2)=3.故选C.【点评】本题既考查了代数式求值的方法,也考查了无理数的估算,同时还隐含了整体的数学思想和正确运算的能力.4.下列各式表示正确的是()A.B.C.D.【考点】平方根.【专题】运算题.【分析】利用平方根的定义化简各项,即可做出判定.【解答】解:A、=5,本选项错误;B、±=±5,本选项错误;C、±=±5,本选项正确;D、±=±5,本选项错误.故选C.【点评】此题考查了平方根,熟练把握平方根的定义是解本题的关键.5.已知x、y为正数,且|x2﹣4|+(y2﹣3)2=0,假如以x、y的长为直角边作一个直角三角形,那么以那个直角三角形的斜边为边长的正方形的面积为()A.5 B.25 C.7 D.15【考点】勾股定理;非负数的性质:绝对值;非负数的性质:偶次方.【分析】本题可依照“两个非负数相加和为0,则这两个非负数的值均为0”解出x、y的值,然后运用勾股定理求出斜边的长.斜边长的平方即为正方形的面积.【解答】解:依题意得:x2﹣4=0,y2﹣3=0,∴x=2,y=,斜边长==,因此正方形的面积=()2=7.故选C.【点评】本题综合考查了勾股定理与非负数,解这类题的关键是利用直角三角形,用勾股定理来寻求未知系数的等量关系.6.若m>n,则下列不等式中成立的是()A.m+a<n+b B.ma<nb C.ma2>na2D.a﹣m<a﹣n【考点】不等式的性质.【分析】看各不等式是加(减)什么数,或乘(除以)哪个数得到的,用不用变号.【解答】解:A、不等式两边加的数不同,错误;B、不等式两边乘的数不同,错误;C、当a=0时,错误;D、不等式两边都乘﹣1,不等号的方向改变,都加a,不等号的方向不变,正确;故选D.【点评】不等式的性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变;(2)不等式两边乘(或除以)同一个正数,不等号的方向不变;(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.7.不等式组的解集在数轴上表示为()A.B.C.D.【考点】在数轴上表示不等式的解集;解一元一次不等式组.【分析】解不等式组,求出不等式组的解集,即可解答.【解答】解:不等式组的解集为:﹣3<x≤1,故选:A.【点评】本题考查了在数轴上表示不等式的解集,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,假如数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段确实是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.8.假如不等式组无解,那么m的取值范畴是()A.m>8 B.m≥8 C.m<8 D.m≤8【考点】解一元一次不等式组.【专题】运算题.【分析】依照不等式取解集的方法,大大小小无解,可知m和8之间的大小关系,求出m的范畴即可.【解答】解:因为不等式组无解,即x<8与x>m无公共解集,利用数轴可知m≥8.故选:B.【点评】本题考查不等式解集的表示方法,依照大大小小无解,也确实是没有中间来确定m的范畴.做题时注意m=8时也满足不等式无解的情形.9.如图,数轴上表示1、的对应点分别为点A、点B.若点A是BC的中点,则点C所表示的数为()A.B.C.D.【考点】实数与数轴.【分析】设点C表示的数是x,再依照中点坐标公式即可得出x的值.【解答】解:设点C表示的数是x,∵数轴上表示1、的对应点分别为点A、点B,点A是BC的中点,∴=1,解得x=2﹣.故选D.【点评】本题考查的是实数与数轴,熟知数轴上的点与实数是一一对应关系是解答此题的关键.10.有一个数值转换器,原理如下:当输入的x为64时,输出的y是()A.8 B.C.D.【考点】算术平方根.【专题】图表型.【分析】把64按给出的程序逐步运算即可.【解答】解:由题中所给的程序可知:把64取算术平方根,结果为8,因为8是有理数,因此再取算术平方根,结果为为无理数,故y=.故选B.【点评】此类题目比较简单,解答此类题目的关键是弄清题目中所给的运算程序.11.如图所示为一种“羊头”形图案,其作法是:从正方形①开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形②和②,…,依此类推,若正方形①的面积为64,则正方形⑤的面积为()A.2 B.4 C.8 D.16【考点】勾股定理.【专题】规律型.【分析】依照题意可知第一个正方形的面积是64,则第二个正方形的面积是32,…,进而可找出规律得出第n个正方形的面积,即可得出结果.【解答】解:第一个正方形的面积是64;第二个正方形的面积是32;第三个正方形的面积是16;…第n个正方形的面积是,∴正方形⑤的面积是4.故选:B.【点评】本题考查了正方形的性质、等腰直角三角形的性质、勾股定理.解题的关键是找出第n个正方形的面积.12.如图,矩形纸片ABCD中,点E是AD的中点,且AE=1,BE的垂直平分线MN恰好过点C.则矩形的一边AB的长度为()A.1 B.C.D.2【考点】勾股定理;线段垂直平分线的性质;矩形的性质.【分析】本题要依靠辅助线的关心,连接CE,第一利用线段垂直平分线的性质证明BC=EC.求出EC后依照勾股定理即可求解.【解答】解:如图,连接EC.∵FC垂直平分BE,∴BC=EC(线段垂直平分线的性质)又∵点E是AD的中点,AE=1,AD=BC,故EC=2,利用勾股定理可得AB=CD==.故选:C.【点评】本题考查的是勾股定理、线段垂直平分线的性质以及矩形的性质,本题的关键是要画出辅助线,证明BC=EC后易求解.本题难度中等.二.填空题(4分×6=24分)13.﹣27的立方根与的平方根的和是0或﹣6.【考点】立方根;平方根.【分析】分别利用平方根、立方根的定义求解即可.解题注意=9,因此求的算术平方根确实是求9的平方根.【解答】解:∵﹣27的立方根是﹣3,的平方根是±3,因此它们的和为0或﹣6.故答案:0或﹣6.【点评】此题要紧考查了立方根、算术平方根的定义,其中求一个数的立方根,应先找出所要求的那个数是哪一个数的立方.由开立方和立方是互逆运算,用立方的方法求那个数的立方根.注意一个数的立方根与原数的性质符号相同,一个正数的平方根有两个且互为相反数.14.某商品进价200元,标价300元,商场规定能够打折销售,但其利润不能低于5%,该商品最多能够7折.【考点】一元一次不等式的应用.【分析】利润率不能低于5%,意思是利润率大于或等于5%,相应的关系式为:(利润﹣进价)÷进价≥5%,把相关数值代入即可求解.【解答】解:售价为300×0.1x,那么利润为300×0.1x﹣200,因此相应的关系式为300×0.1x﹣200≥200×5%,解得:x≥7.答:该商品最多能够7折.故答案为:7.【点评】此题要紧考查了一元一次不等式的应用,解决本题的关键是得到利润率的相关关系式,注意“不能低于”用数学符号表示为“≥”;利润率是利润与进价的比值.15.已知a>5,不等式(5﹣a)x>a﹣5解集为x<﹣1.【考点】不等式的性质.【分析】先由a>5,得出5﹣a<0,由不等式的差不多性质得出答案.【解答】解:∵a>5,∴5﹣a<0,∴解不等式(5﹣a)x>a﹣5,得x<﹣1.故答案为:x<﹣1.【点评】本题要紧考查了不等式的性质,解题的关键是注意不等号的方向是否改变.16.如图所示,折叠长方形的一边AD,使点D落在边BC的点F处,已知AB=8cm,BC=10cm,则EC的长为3cm.【考点】勾股定理;翻折变换(折叠问题).【分析】能够依照轴对称的性质得到相关的线段之间的关系.再依照勾股定理进行运算.【解答】解:∵D,F关于AE对称,因此△AED和△AEF全等,∴AF=AD=BC=10,DE=EF,设EC=x,则DE=8﹣x.∴EF=8﹣x,在Rt△ABF中,BF==6,∴FC=BC﹣BF=4.在Rt△CEF中,由勾股定理得:CE2+FC2=EF2,即:x2+42=(8﹣x)2,解得x=3.∴EC的长为3cm.【点评】专门注意轴对称的性质以及熟练运用勾股定理.17.若关于x的不等式组有解,则实数a的取值范畴是a>﹣1.【考点】解一元一次不等式组;解一元一次不等式.【专题】运算题.【分析】求出不等式①的解集,依照题意得出a>﹣1,即得到答案.【解答】解:,解不等式①得:x>﹣1,∵不等式组有解,∴a>﹣1.故答案为:a>﹣1.【点评】本题要紧考查对解一元一次不等式(组)的明白得和把握,能依照题意和不等式的解集得出a>﹣1是解此题的关键.18.若不等式组的解集为x>3,则a的取值范畴是a≥3.【考点】不等式的解集.【分析】依照求不等式组的解集的方法:同大取较大可知a≥3.【解答】解:不等式组的解集为x>3,则a≥3.故答案为:a≥3.【点评】解答此题要依照不等式组解集的求法解答.求不等式组的解集,应注意:同大取较大,同小取较小,小大大小中间找,大大小小解不了.三.解答题(8+8+12+12=40分)19.分析探究题:细心观看如图,认真分析各式,然后解答问题.OA22=()2+1=2 S1=;OA32=()2+1=3 S2=;OA42=()2+1=4 S3=…(1)请用含有n(n为正整数)的等式S n=;(2)推算出OA10=.(3)求出S12+S22+S32+…+S102的值.【考点】勾股定理;算术平方根.【专题】规律型.【分析】(1)此题要利用直角三角形的面积公式,观看上述结论,会发觉,第n个图形的一直角边确实是,然后利用面积公式可得.(2)由同述OA2=,0A3=…可知OA10=.(3)S12+S22+S32+…+S102的值确实是把面积的平方相加就可.【解答】解:(1)+1=n+1Sn=(n是正整数);故答案是:;(2)∵OA12=1,OA22=()2+1=2,OA32=()2+1=3,OA42=()2+1=4,∴OA12=,OA2=,OA3=,…∴OA 10=;故答案是:;(3)S12+S22+S32+…+S102=()2+()2+()2+…+()2=(1+2+3+ (10)=.即:S12+S22+S32+…+S102=.【点评】此题考查了勾股定理、算术平方根.解题的关键是观看,观看题中给出的结论,由此结论找出规律进行运算.千万不可盲目运算.20.解不等式组,把它的解集在数轴上表示出来,并求该不等式组所有整数解的和..【考点】解一元一次不等式组;不等式的性质;在数轴上表示不等式的解集;解一元一次不等式;一元一次不等式组的整数解.【专题】运算题.【分析】求出每个不等式的解集,依照找不等式组解集的规律找出不等式组的解集,找出不等式组的整数解,相加即可.【解答】解:,∵解不等式①得:x≥﹣1,解不等式②得:x<2,∴不等式组的解集为:﹣1≤x<2,在数轴上表示不等式组的解集为:,∵不等式组的整数解为﹣1,0,1,∴不等式组所有整数解的和是:﹣1+0+1=0.【点评】本题考查了不等式的性质,解一元一次不等式(组),在数轴上表示不等式组的解集,不等式组的整数解等知识点的应用,关键是求出不等式组的解集,题目具有一定的代表性,是一道比较好的题目.21.某企业新增了一个化工项目,为了节约资源,爱护环境,该企业决定购买A、B两种型号的污水处理设备共8台,具体情形如下表:A型B型价格(万元/台)12 10月污水处理能力(吨/月)200 160经预算,企业最多支出89万元购买设备,且要求月处理污水能力不低于1380吨.(1)该企业有几种购买方案?(2)哪种方案更省钱,说明理由.【考点】一元一次不等式组的应用.【专题】应用题.【分析】(1)设购买污水处理设备A型号x台,则购买B型号(8﹣x)台,依照企业最多支出89万元购买设备,要求月处理污水能力不低于1380吨,列出不等式组,然后找出最合适的方案即可.(2)运算出每一方案的花费,通过比较即可得到答案.【解答】解:设购买污水处理设备A型号x台,则购买B型号(8﹣x)台,依照题意,得,解那个不等式组,得:2.5≤x≤4.5.∵x是整数,∴x=3或x=4.当x=3时,8﹣x=5;当x=4时,8﹣x=4.答:有2种购买方案:第一种是购买3台A型污水处理设备,5台B型污水处理设备;第二种是购买4台A型污水处理设备,4台B型污水处理设备;(2)当x=3时,购买资金为12×3+10×5=86(万元),当x=4时,购买资金为12×4+10×4=88(万元).因为88>86,因此为了节约资金,应购污水处理设备A型号3台,B型号5台.答:购买3台A型污水处理设备,5台B型污水处理设备更省钱.【点评】本题考查了一元一次不等式组的应用,本题是“方案设计”问题,一样可把它转化为求不等式组的整数解问题,通过表格猎取相关信息,在实际问题中抽象出不等式组是解决这类问题的关键.22.问题背景:在△ABC中,AB、BC、AC三边的长分别为、、,求那个三角形的面积小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.如此不需求△ABC的高,而借用网格就能运算出它的面积.(1)请你将△ABC的面积直截了当填写在横线上. 3.5(2)画△DEF,DE、EF、DF三边的长分别为、、①判定三角形的形状,说明理由.②求那个三角形的面积.【考点】勾股定理;三角形的面积.【专题】运算题;作图题.【分析】(1)利用恰好能覆盖△ABC的边长为3的小正方形的面积减去三个小直角三角形的面积即可解答;(2)①利用勾股定理的逆定理进行解答,②利用(1)方法解答就能够解决问题.【解答】解:(1)如图,S△ABC=3×3﹣×3×1﹣×2×1﹣×3×2=3.5;(2)①△DEF为直角三角形;因为+=,因此△DEF为直角三角形;②S△DEF=3×2﹣×3×1﹣×2×2﹣×1×1=2;答:△DEF的面积为2.【点评】此题考查勾股定理,勾股定理的逆定理以及三角形面积的运算.。
2021-2022学年山东省潍坊市潍城区青岛版五年级上册期末质量检测数学试卷

潍坊市潍城区2021~2022学年度第一学期期末质量检测五年级数学试题时间:90分钟满分:100分一、反复比较,正确选择。
(把正确答案序号填在括号里)(9分)1.我国陆地面积约960万()。
A.平方分米B.公顷C.平方米D.平方千米2. 2.503503…的小数部分的第100位数字是()。
A.0B.3C.53.下面图形中,对称轴最多的是()。
A. B. C. D.4.下列属于方程的是()。
A.8+2b=2B.8-2.4=5.6C.24-2x<55.如图,甲和乙的面积关系是()。
A.甲>乙B.甲<乙C.甲=乙6.长方形的周长是24米,它的长和宽的米数是两个质数,这个长方形的面积是()。
A.11m²B.27m²C.35m²7.张洋、王欣、李刚和赵亮4人排成一行照相,张洋固定在左起第二的位置上,王欣、李刚和赵亮3人随意排。
有()种不同的排法。
A.25B.30C.24D.68.在学校的展示课上,小芳把一个平行四边形木框拉成了长方形,它的面积()。
A.不变B.变大C.变小9.盒子里有36个球,丁丁要按下面的要求拿球:不许一次拿完,也不许一个一个地拿,每次拿的个数要相同,拿到最后一个也不剩。
丁丁一共有()种拿法。
A.7B.8C.9二、动脑思考,细心填写。
(每空1分,共24分)10.0.8+0.8+0.8+0.8=()×()=()。
11.一个三位小数,保留两位小数是1.80,这个三位数最大是(),最小是()。
12.11.705705705…是()小数,循环节是(),用简便写法记作(),这个小数保留两位是()。
13.60平方千米=()公顷0.6公顷=()平方米14.三位数26□,如果它是5的倍数,□里可以填();如果它既是5的倍数又是2的倍数,□里可以填()。
15.在括号里填上“>”“<”或“=”。
7.3÷0.3()73÷3 1.55×0.9() 1.550.86÷0.9()0.86 4.5×1.1() 4.5÷1.116.各举1例:生活中的平移现象();生活中的旋转现象()。
2021届山东省潍坊市高三一模考试数学试题(解析版)

2021届山东省潍坊市高三一模考试数学试题一、单选题1.已知集合{}{}22,0,20A B x x x =-=-=,则以下结论正确的是( )A .AB = B .{}0A B ⋂=C .A B A ⋃=D .A B ⊆【答案】B【分析】由题得{0,2}B =, 再判断得解.【详解】由题得{0,2}B =, 所以A B ≠,{}0A B ⋂=,A B A ≠,A 不是B 的子集, 故选:B2.已知复数cos sin z i θθ=+(i 为虚部单位),则1z -的最大值为( )A .1BC .2D .4【答案】C【分析】由复数模的几何含义,知1z -=,即可求其最大值.【详解】由题意知:1|cos 1sin |z i θθ-=-+== ∴当cos 1θ=-时,1z -的最大值为2. 故选:C3.在一次数学实验中,某同学运用图形计算器采集到如下一组数据:在以下四个函数模型(,a b 为待定系数)中,最能反映,x y 函数关系的是( ) A .y a bx =+ B .by a x=+C .log b y a x =+D .x y a b =+【答案】D【分析】在坐标系中画出点,根据点的特征进行判断即可.【详解】根据点在坐标系中的特征可以知道,当自变量每增加1时,y 的增加是不相同的,所以不是线性增加,排除A ; 由图象不具有反比例函数特征,排除B ; 因为自变量有负值,排除C ;当自变量增加到3时,y 增加的很多,所以符合指数的增加特征,D 正确, 故选:D.4.在空间中,下列命题是真命题的是( ) A .经过三个点有且只有一个平面 B .平行于同一平面的两直线相互平行C .如果两个角的两条边分别对应平行,那么这两个角相等D .如果两个相交平面垂直于同一个平面,那么它们的交线也垂直于这个平面 【答案】D【分析】由三点共线判断A ;由线面、线线位置关系判断B ;根据等角定理判断C ;由线面平行和垂直的判定以及性质判断D.【详解】当三点在一条直线上时,可以确定无数个平面,故A 错误; 平行于同一平面的两直线可能相交,故B 错误;由等角定理可知,如果两个角的两条边分别对应平行,那么这两个角相等或互补,故C 错误;如果两个相交平面,αβ垂直于同一个平面γ,且l αβ=,则在平面α、β内分别存在直线,m n 垂直于平面γ,由线面垂直的性质可知//n m ,再由线面平行的判定定理得//m β,由线面平行的性质得出//m l ,则l γ⊥,故D 正确; 故选:D5.接种疫苗是预防和控制传染病最经济、有效的公共卫生干预措施.根据实验数据,人在接种某种病毒疫苗后,有80%不会感染这种病毒,若有4人接种了这种疫苗,则最多1人被感染的概率为( )A .512625B .256625C .113625D .1625【答案】A【分析】最多1人被感染即4人没有人感染和4人中恰好有1人被感染,利用独立重复试验的概率和互斥事件的概率求解.【详解】由题得最多1人被感染的概率为041344414256256512()()()555625625C C ++==. 故选:A【点睛】方法点睛:求概率常用的方法:先定性(确定所求的概率是六种概率(古典概型的概率、几何概型的概率、互斥事件的概率、独立事件的概率、独立重复试验的概率、条件概率)的哪一种),再定量.6.多项式()()())2112(3x x x x ++++展开式中 3x 的系数为A .6B .8C .12D .13【答案】C【分析】首先原式()()()()()()2123123x x x x x x x =+++++++,分两部分求3x的系数.【详解】原式()()()()()()2123123xx x x x x x =+++++++,所以展开式中含3x的项包含()()()123x x x +++中x 项为12231311x x x x ⋅⋅+⋅⋅+⋅⋅= ,和()()()123x x x +++中3x的项为3x ,这两项的系数和为11112+=.故选:C7.已知20202021,20212020,ln 2a b c ===,则( ) A .log log a b c c > B .log log c c a b >C .c c a b <D .a b c c <【答案】D【分析】由题意知01,01b a c <<<<<,根据各选项并结合对应函数的区间单调性,即可判断指对数式的大小关系.【详解】由题意知:20202021log 20211log 20200a b =>>=>,而 0ln21c <=<, ∴log c y x =在定义域内单调减,故log 0log c c a b <<,则B 错误;11log 0log log log a b c c c c a b=<<=,故A 错误; c y x =在第一象限的单调递增知c c a b >,故C 错误;x y c =定义域内单调递减,即a b c c <,故D 正确;故选:D8.某中学开展劳动实习,学习加工制作食品包装盒.现有一张边长为6的正六边形硬纸片,如图所示,裁掉阴影部分,然后按虚线处折成高为3的正六棱柱无盖包装盒,则此包装盒的体积为( )A .144B .72C .36D .24【答案】B【分析】利用正六边形的性质求出正六棱柱的底边周长,再根据棱柱的体积:V S h =⋅底即可求解.【详解】如图:由正六边形的每个内角为23π, 33BF = 所以1tan 60BFBE ==可得正六棱柱底边边长6214AB =-⨯=, 所以正六棱柱体积:1364437222V =⨯⨯⨯⨯. 故选:B二、多选题9.已知双曲线()222:109x y C a a -=>的左,右焦点分别为12,F F ,一条渐近线方程为34y x =,P 为C 上一点,则以下说法正确的是( ) A .C 的实轴长为8 B .C 的离心率为53C .218PF PF -=D .C 的焦距为10【答案】AD【分析】根据双曲线方程及一条渐近线求出4a =,写出双曲线方程,根据双曲线的定义、性质即可判断各项的正误.【详解】由双曲线方程知:渐近线方程为3y x a=±,而一条渐近线方程为34y x =,∴4a =,故22:1169x y C -=,∴双曲线:实轴长28a =,离心率为544c e a ===,由于P 可能在C 不同分支上则有21||8PF PF -=,焦距为210c ==.∴A 、D 正确,B 、C 错误. 故选:AD10.已知函数21,0()cos ,0x x f x x x ⎧+=⎨<⎩,,则下列结论正确的是( )A .()f x 是偶函数B .312f f π⎛⎫⎛⎫-= ⎪ ⎪⎝⎭⎝⎭ C .()f x 是增函数 D .()f x 的值域为[1,)-+∞【答案】BD【分析】利用反例可判断AC 错误,结合函数的解析式可判断BD 为正确,从而可得正确的选项.【详解】()12f =,而()()1cos11f f -=<,故()f x 不是偶函数,故A 错误. 因为77cos cos 3333f f ππππ⎛⎫⎛⎫⎛⎫⎛⎫-=-=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,故()f x 不是增函数,故C 错误.()3012f f f π⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭,故B 正确.当0x <时,()[]1,1f x ∈-,当0x ≥时,()[)1,f x ∈+∞, 故()f x 的值域为[1,)-+∞,故D 正确. 故选:BD.11.南宋数学家杨辉所著的《详解九章算法·商功》中出现了如图所示的形状,后人称为“三角垛”.“三角垛”的最上层有1个球,第二层有3个球,第三层有6个球,…,设各层球数构成一个数列{}n a ,则( )A .412a =B .11n n a a n +=++C .1005050a =D .122n n n a a a ++=⋅【答案】BC【分析】根据示意图,结合题意找到各层球的数量与层数的关系,可得1(1)2n n n n a a n -+=+=,即可判断各项的正误. 【详解】由题意知:12311,3,6,...,n n a a a a a n -====+,故(1)2n n n a +=, ∴44(41)102a ⨯+==,故A 错误; 11n n a a n +=++,故B 正确;100100(1001)50502a ⨯+==,故C 正确;12(1)n a n n +=+,2(1)(2)(3)4n n n n n n a a ++++=⋅,显然122n n n a a a ++≠⋅,故D 错误;故选:BC12.已知实数,,x y z 满足1x y z ++=,且2221x y z ++=,则下列结论正确的是( )A .0xy yz xz ++=B .z 的最大值为12C .z 的最小值为13- D .xyz 的最小值为427-【答案】ACD【分析】将1x y z ++=两边平方后结合2221x y z ++=可得A 正确,利用基本不等式可判断BC 的正误,利用导数求出xyz 的最小值后可判断D 的正误. 【详解】因为1x y z ++=,故()21x y z ++=,所以2222221x y z xy yz xz +++++=,因为2221x y z ++=,故0xy yz xz ++=,故A 正确.又2221x y z ++=可化为()2221x y xy z +-+=即()22121z xy z --+=,所以2xy z z =-,而22x y xy +⎛⎫≤ ⎪⎝⎭,故2212z z z -⎛⎫-≤ ⎪⎝⎭,整理得到23210z z --≤,故113z -≤≤, 当且仅当23x y ==时13z =-;当且仅当0x y ==时1z =;故z 的最小值为13-,z 的最大值为1,故B 错误,C 正确.又()232xyz z z z z z =-=-,其中113z -≤≤.令()32f z z z =-,113z -≤≤,故()()23232f z z z z z '=-=-,当103z -<<时,()0f z '>,当203z <<时,()0f z '<, 当213z <<时,()0f z '>, 故()f z 在1,03⎡⎤-⎢⎥⎣⎦为增函数,在20,3⎛⎫ ⎪⎝⎭为减函数,2,13⎡⎤⎢⎥⎣⎦为增函数,故()min 124min ,3327f z f f ⎧⎫⎛⎫⎛⎫=-=-⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎩⎭,故D 正确. 故选:ACD.【点睛】方法点睛:多元不等式的最值的问题,可利用基本不等式构建目标变量的不等式,从而可求目标变量的取值范围或最值(注意检验),也可以利用消元法结合导数求最值.三、填空题13.已知正方形ABCD 的边长为1,AB a =,BC b =,AC c =,则a b c ++=________.【答案】【分析】由向量的加法可得AB BC AC +=,再求解正方形的对角线即可. 【详解】由题意可得,AC 是正方形的对角线长,故2AC =又AB BC AC +=所以222a b c AC ++==故答案为:【点睛】本题考查向量的加法,以及模长的求解,属向量基础题. 14.写出一个存在极值的奇函数()f x =_______________________. 【答案】sin x (不唯一) 【分析】举出正弦函数即可.【详解】由于正弦函数()sin f x x =为奇函数,且存在极值 故答案为:sin x15.已知抛物线2:4C y x =的焦点为F ,准线为l ,点P 在抛物线C 上,PQ 垂直l 于点Q ,QF 与y 轴交于点,T O 为坐标原点,且2OT =,则PF =_______________________.【答案】5【分析】依题意TMQ TOF ≌,即可得到T 为OM 的中点,从而求出P 的纵坐标,再代入抛物线方程求出P 的横坐标,最后根据焦半径公式计算可得;【详解】解:依题意可得()1,0F ,:1l x =-,根据抛物线的定义可知PQ PF =,设PQ 与y 轴相交于点M ,因为2OT =,又OF QM =,所以TMQ TOF ≌,所以T 为OM 的中点,所以4OM =即P 的纵坐标为4,在24y x =中令4y =,得4x =,所以4152pPQ x =+=+=,所以5PF =故答案为:516.某市为表彰在脱贫攻坚工作中做出突出贡献的先进单位,制作了一批奖杯,奖杯的剖面图形如图所示,其中扇形OAB 的半径为10,60,PBA QAB AQ QP PB ∠=∠===,若按此方案设计,工艺制造厂发现,当OP 最长时,该奖杯比较美观,此时AOB ∠=_______________________.【答案】2π【分析】作OM QP ⊥交QP 于M ,交AB 于C ,且OC AB ⊥,设AOC θ∠=,求出AB 、OC ,设AQ QP BP x ===,作⊥QE AB 交AB 于E ,PF AB ⊥交AB 于F ,可得出10sin x θ=,10cos 53OM OC CM θθ=+=+,由勾股定理可得()()2222210cos 535sin OP OM MP θθθ=+=++然后求最值可得答案.【详解】作OM QP ⊥交QP 于M ,交AB 于C ,且OC AB ⊥,设AOC θ∠=, 则20sin θ=AB ,10cos OC θ=,设AQ QP BP x ===,作⊥QE AB 交AB 于E ,PF AB ⊥交AB 于F , 因为60PBA QAB ∠=∠=,所以12AE BF x ==,3CM PF x ==, EF QP x ==,所以2AB x =,所以20sin 2AB x θ==,即10sin x θ=,310cos 10cos 53OM OC CM x θθθ=+=+=+, 所以()()2222210cos 35sin OP OM MP θθθ=+=++222100cos 75sin 1003cos 25sin 1005032θθθθθθ=+++=+,因为[]sin 21,1θ∈-,所以当sin 21θ=即4πθ=时2OP 最大,也就是OP 最长时2AOB π∠=.故答案为:2π. 【点睛】本题考查了用三角函数解决几何问题,关键点是作出辅助线利用勾股定理求出2OP ,考查了学生分析问题、解决问题的能力.四、解答题17.在①函数()y f x =的图象关于直线3x π=对称,②函数()y f x =的图象关于点,06P π⎛⎫ ⎪⎝⎭对称,③函数()y f x =的图象经过点2,13Q π⎛⎫- ⎪⎝⎭这三个条件中任选一个,补充在下面问题中并解答.问题:已知函数()sin cos cos sin 0,||2f x x x πωϕωϕωϕ⎛⎫=+><⎪⎝⎭最小正周期为π,且 ,判断函数()f x 在,62ππ⎛⎫⎪⎝⎭上是否存在最大值?若存在,求出最大值及此时的x 值;若不存在,说明理由. 注:如果选择多个条件分别解答,按第一个解答计分. 【答案】答案不唯一,具体见解析【分析】先对函数化简得()sin()f x x ωϕ=+,由函数的最小正周期为π,可得2ω=,则()sin(2)f x x ϕ=+,若选①,则有2()32k k ππϕπ⨯+=+∈Z ,从而可求出ϕ的值,进而可求出函数的解析式,再利用换元法可求得最值;若选②,则有2()6k k πϕπ⨯+=∈Z ,从而可求出ϕ的值,然后利用换元法可求得最值;若选③,则有222()32k k ππϕπ⨯+=-∈Z ,从而可求出ϕ的值,再利用换元法可求最值即可 【详解】解:()sin cos cos sin sin()f x x x x ωϕωϕωϕ=+=+, 由已知函数()f x 的周期2T ππω==,求得2ω=,所以()sin(2)f x x ϕ=+, 若选①,则有2()32k k ππϕπ⨯+=+∈Z ,解得()6k k πϕπ=-∈Z ,又因为2πϕ<,所以,0,6k πϕ==-,所以()sin 26f x x π⎛⎫=-⎪⎝⎭, 当,62x ππ⎛⎫∈⎪⎝⎭时,52,666t x πππ⎛⎫=-∈ ⎪⎝⎭, 所以当2t π=,即3x π=时,函数()f x 取得最大值,最大值为1.若选②,则有2()6k k πϕπ⨯+=∈Z ,解得()3k k πϕπ=-∈Z ,又因为2πϕ<,所以0,3k πϕ==-,所以()sin 23f x x π⎛⎫=-⎪⎝⎭,当,62x ππ⎛⎫∈ ⎪⎝⎭时,220,33t x ππ⎛⎫=-∈ ⎪⎝⎭, 所以当2t π=,即512x π=时,函数()f x 取得最大值,最大值为1.若选③,则有222()32k k ππϕπ⨯+=-∈Z ,解得112()6k k πϕπ=-∈Z , 又因为2πϕ<,所以1,6k πϕ==,所以()sin 26f x x π⎛⎫=+⎪⎝⎭, 当,62x ππ⎛⎫∈⎪⎝⎭时,72,626t x πππ⎛⎫=+∈ ⎪⎝⎭, 显然,函数()f x 在该区间上没有最大值.【点睛】关键点点睛:此题考查利用三角函数的性质求函数解析式,考查求三角函数的最值,考查计算能力,解题的关键是根据题意正确的求出函数的解析式,再利用换元法求函数的最值,属于中档题18.已知数列{}n a 的前n 项和为211,6,12n n n S a S a +==+. (1)证明:数列1n S 为等比数列,并求出n S .(2)求数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和n T .【答案】(1)证明见解析;31nn S =+;(2)111243n n T -=-⨯. 【分析】(1)根据递推关系及等比数列的定义证明;(2)由(1)可得31nn S =+,根据,n n S a 关系求解通项,根据等比数列求和公式计算即可.【详解】(1)由已知()1112n n n S S S +=-+, 整理得132n n S S +=-, 所以()1131n n S S +-=-, 令1n =,得121142S a =+=,所以113S -=, 所以1n S 是以3为首项,3为公比的等比数列, 所以()111133n n n S S --=-⨯=,所以31nn S =+;(2)由(1)知,31nn S =+,当2n 时,()111313123nn n n n n a S S ---=-=+-+=⨯,当1n =时,114a S ==, 所以14,1,23,2,n n n a n -=⎧=⎨⨯⎩ 所以11,1,4111,2,23n n n a n -⎧=⎪⎪=⎨⎛⎫⎪⨯ ⎪⎪⎝⎭⎩ 所以1112111111111631424313n n n n T a a a --⎛⎫- ⎪⎝⎭=+++=+=-⨯-. 19.如图,在四棱锥P ABCD -中,侧面PAD 为等边三角形且垂直于底面ABCD ,//AD BC ,AB AD ⊥, 24AB BC ==,E 是棱PD 上的动点(除端点外),F ,M分别为AB ,CE 的中点.(1)求证://FM 平面PAD ;(2)若直线EF 与平面PAD 所成的最大角为30,求平面CEF 与平面PAD 所成锐二面角的余弦值.【答案】(1)证明见解析;(2)9331. 【分析】(1)取CD 的中点N ,连结FN ,MN ,证明平面//MFN 平面PAD ,再用面面平行的性质定理证明即可;(2)作出直线EF 与平面PAD 所成角的平面角,通过最大角为30,确定AD 长度,建立空间直角坐标系,用向量法计算二面角余弦值. 【详解】(1)证明:取CD 的中点N ,连结FN ,MN , 因为F ,N 分别为AB ,CD 的中点, 所以//FN AD ,又因为FN ⊄平面PAD ,AD ⊂平面PAD , 所以//FN 平面PAD , 同理,//MN 平面PAD , 又因为FN MN N ⋂=, 所以平面//MFN 平面PAD , 又因为FM ⊂平面MFN , 所以//FM 平面PAD .(2)因为平面PAD ⊥平面ABCD ,AB AD ⊥, 所以AB ⊥平面PAD ,所以AEF ∠即为直线EF 与平面PAD 所成的角, 且2tan AF AEF AE AE∠==, 当AE 最小,即E 为PD 中点时,AE PD ⊥, 此时AEF ∠最大为30, 又因为2AF =,所以23AE =4=AD . 取AD 的中点O ,连结PO ,OC , 易知PO ⊥平面ABCD , 因为//AO BC 且AO BC =, 所以四边形ABCO 为平行四边形,所以AO OC ⊥,以O 为坐标原点,OC 的方向为x 轴正方向,建立如图所示的空间直角坐标系O xyz -. 则(0,0,0)O ,(4,0,0)C ,(0,2,0)D ,(0,0,23)P ,(0,1,3)E ,(2,2,0)F -,(4,1,3)CE =-,(2,2,0)FC =,设1(,,)n x y z =为平面CEF 的法向量,则1100C FC n E n ⎧⋅=⎪⎨⋅=⎪⎩, 即220,430,x y x y z +=⎧⎪⎨-++=⎪⎩可取1(3,3,5)n =-.设平面PAD 的法向量为()21,0,0n =, 所以121212393cos ,3131n n n n n n ⋅===⋅,所以平面CEF 与平面PAD 所成锐二面角的余弦值为9331.【点睛】求直线与平面所成的角的一般步骤:①找直线与平面所成的角,即通过找直线在平面上的射影来完成; ②计算,要把直线与平面所成的角转化到一个三角形中求解.20.在对人体的脂肪含量和年龄之间的关系的研究中,科研人员获得了一些年龄和脂肪含量的简单随机样本数据()(),1,2,,20,2565i i i x y i x =<<,其中i x 表示年龄,i y 表示脂肪含量,并计算得到202148280ii x==∑,202021115480,27220,48,27 4.7ii i i i yx y x y ======≈∑∑.(1)请用相关系数说明该组数据中y 与x 之间的关系可用线性回归模型进行拟合,并求y 关于x 的线性回归方程y a bx =+(,a b 的计算结果保留两位小数);(2)科学健身能降低人体脂肪含量,下表是甲,乙两款健身器材的使用年限(整年)统计表:某健身机构准备购进其中--款健身器材,以使用年限的频率估计概率,请根据以上数据估计,该机构选择购买哪一款健身器材,才能使用更长久?参考公式:相关系数()()nniii ix x y y x y nxyr ---==∑∑对于一组具有线性相关关系的数据()(),1,2,...,i i x y i n =,其回归直线y bx a =+的斜率和截距的最小二乘估计分别为:()()()121ˆˆˆ,niii nii x x y y bay bx x x ==--==--∑∑. 【答案】(1)答案见解析;ˆ0.59 1.37y x =-;(2)该机构购买甲款健身器材更划算.【分析】(1)根据提供数据,计算相关系数,确定相关性,求线性回归方程即可; (2)以频率估计概率,列出甲、乙款的分布列,计算期望,比较大小即可. 【详解】(1)222304,729x y ==,201201300i ii x yxy =-=∑,20221202200ii xx =-=∑,22120900ni i y y =-=∑,2020 0.92i ix y x yr -=≈∑,因为y 与x 的相关系数接近1,所以y 与x 之间具有较强的线性相关关系,可用线性回归模型进行拟合;由题可得,()()()20201120202221120 130.5912220iii ii i iii i x x y y x y x yb x x xx ====---===≈--∑∑∑∑, ˆˆ270.59148 1.37ay bx =-=-⨯≈-, 所以ˆ0.59 1.37yx =-, (2)以频率估计概率,设甲款健身器使用年限为X (单位:年)()50.160.470.380.2 6.6E X =⨯+⨯+⨯+⨯=,设乙款健身器使用年限为Y (单位:年)()50.360.470.280.1 6.1E Y =⨯+⨯+⨯+⨯=,因为()()E X E Y >,所以该机构购买甲款健身器材更划算.21.已知函数()()22sin x af x a x-=-∈R .(1)若曲线()y f x =在点,22f ππ⎛⎫⎛⎫ ⎪⎪⎝⎭⎝⎭处的切线经过坐标原点,求实数a ;(2)当0a >时,判断函数()f x 在(0,)x π∈上的零点个数,并说明理由.【答案】(1)224a π=--;(2)答案不唯一,具体见解析. 【分析】(1)求出函数的导数,根据导数几何意义求斜率,由切线方程求a ;(2)原问题转化为2()2sin g x x a x =--的零点问题,求导,利用导数可得()g x 单调性,结合零点存在性即可求解. 【详解】(1)()222sin cos (),sin 2x x x a xf x f xππ--⎛⎫'== ⎪⎝⎭, 所以()f x 在点,22f ππ⎛⎫⎛⎫ ⎪⎪⎝⎭⎝⎭处的切线方程为y x π=, 所以222f ππ⎛⎫= ⎪⎝⎭,即2222,2424a a πππ--==--;(2)因为()0,x π∈, 所以sin 0x >,所以220sin x ax--=可转化为22sin 0x a x --=,设2()2sin g x x a x =--, 则()22cos g x x x '=- 当,2x ππ⎡⎫∈⎪⎢⎣⎭时,()0g x '>, 所以()g x 在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递增. 当0,2x π⎛⎫∈ ⎪⎝⎭时,设()()22cos h x g x x x '==-, 此时()22sin 0h x x '=+>,所以()'g x 在0,2x π⎛⎫∈ ⎪⎝⎭时单调递增,又(0)20g '=-<,02g ππ⎛⎫'=>⎪⎝⎭,所以存在00,2x π⎛⎫∈ ⎪⎝⎭使得()0g x '=且()00,x x ∈时()g x 单调递减,0,2x x π⎡⎫∈⎪⎢⎣⎭时()g x 单调递增.综上,对于连续函数()g x ,在()00,x x ∈时,()g x 单调递减, 在()0,x x π∈时,()g x 单调递增. 又因为(0)0g a =-<,所以当20()g a ππ=->,即2a π<时,函数()g x 有唯一零点在区间0(,)x π上,当20()g a ππ=-≤,即2a π≥时,函数()g x 在区间(0,)π上无零点,综上可知,当20a π<<时,函数()f x 在(0,)π上有1个零点; 当2a π≥时,函数()f x 在(0,)π上没有零点.【点睛】关键点点睛:由题意可转化为2()2sin g x x a x =--在区间(0,)π上的零点个数问题,求导,利用导数可得函数单调性,在()00,x x ∈时,()g x 单调递减,在()0,x x π∈时,()g x 单调递增,分类讨论(0)g a =-的正负即可.22.在平面直角坐标系中,12,A A 两点的坐标分别为()()2,0,2,0-,直线12,A M A M 相交于点M 且它们的斜率之积是34-,记动点M 的轨迹为曲线E . (1)求曲线E 的方程;(2)过点()1,0F 作直线l 交曲线E 于,P Q 两点,且点P 位于x 轴上方,记直线12,AQ A P 的斜率分别为12,k k .①证明:12k k 为定值; ②设点Q 关于x 轴的对称点为1Q ,求1PFQ △面积的最大值.【答案】(1)221(2)43x y x +=≠±;(2)①证明见解析;②4. 【分析】(1)根据条件列出方程化简即可求出曲线方程;(2)设直线l 的方程为()()()1122121,,,,0,0x my P x y Q x y y y =+><,直接表示出斜率12,k k ,消元为关于12,y y 的式子,再根据直线与椭圆联立可得12,y y 的和、积,代入化简即可求证12k k 为定值;由题意1Q 坐标为()22,x y -,可得直线1PQ 恒过点D (4,0),11PFQ PFD Q FD S S S =-△△△,化简后利用均值不等式求最值. 【详解】(1)设点M 坐标为(),x y , 则直线12,A M A M 的斜率分别为,,222y yx x x ≠±+-, 依题意知3224y y x x ⋅=-+-, 化简得221(2)43x y x +=≠±;(2)①设直线l 的方程为()()()1122121,,,,0,0x my P x y Q x y y y =+><,则()()()()()212121212111222122121121121121223332y x y my y my y y y y k my y y x y k x y my y my y y my y y x ---++-+=====++++-,又221143x my x y =+⎧⎪⎨+=⎪⎩,消x 得()2234690m y my ++-=,得122122634934m y y m y y m ⎧+=-⎪⎪+⎨⎪=-⎪+⎩,, 因此112221211229631343434993333434m m my y k m m m m m k y y m m -++-++++===-+-+++, 故12k k 为定值13; ②1Q 坐标为()22,x y -,则直线1PQ 方程为()121112y y y y x x x x +-=--,令0y =解得()()()21121122112121121212121121x x y my y my y x y x y my y x xy y y y y y y y -++++=+===+++++第 21 页 共 21 页 22923414634m m m m ⎛⎫- ⎪+⎝⎭=+=-+, 即直线1PQ 恒过()4,0D 点, 故11PFQ PFD Q FD S S S =-△△△12113322y y =⨯-⨯ 123||||||2y y =- 1232y y =+ 236||234m m =⨯+ 943||||m m =+94212=, 当243m =,即3m =±时,等号成立, 此时1PFQ△. 【点睛】关键点点睛:求1PFQ △面积的最大值,首先要表示出三角形面积,根据本题条件,转化为11PFQ PFD Q FD S S S =-△△△是解题的关键,表示出三角形面积236||234m S m =⨯+后,选择合适的方法求最大值,是解题的一个难点,本题可采用分子分母同除以||m 后,利用均值不等式求解.。
