MATLAB进行等倾干涉动态模拟仿真
MATLAB进行等倾干涉动态模拟仿真

5.使用MATLAB进行等倾干涉动态模拟仿真5.1. 界面设计GUI界面设计]6[主要包括以下几个步骤:第一步构思草图,编排控件的布局。
打开MATLAB程序,在FILE菜单中选择NEW GUI,打开guide设计界面模板,界面模板左边的各个控件可以直接用鼠标拖到编辑框。
第二步设置各控件的属性。
如设置各个控件的标识(Tag),字体等。
第三步各个控件代码的设计。
关键是OpeningFcn(初始界面函数)和控件的CallBack(回调函数)代码的设计。
初始界面函数即设定各参数的初始值,可根据实际情况设定。
回调函数是核心,是对界面控件触发时的事件响应函数。
根据需要,等倾干涉条纹的动态模拟图形用户界面使用了2个按钮(Push Button),标识为绘图和退出,用鼠标点击任一项目,则会执行相应的功能;4个静态文本框(Static Text)用于输入波长,厚度及各自的单位;2个滑动条(Slider),用鼠标拖动相应的滑动条就可以改变波长和厚度的大小;1个坐标轴对象(Axes)用于显示仿真结果。
界面如图4。
图 4 仿真界面5.2 演示控件的回调函数演示控件的功能是通过其回调程序来实现的,用户界面设计完成之后,选中控件用鼠标双击,在弹出的菜单中选择Viewbacks,在其子菜单中选择CallBack,就可以进入回调程序编辑器中,在编辑器中编写控件代码,使图形界面完成约定的功能。
演示控件的回调函数代码为:lambda=get(handles.slider1,'value');d=get(handles.slider2,'value');f=200;n=1;N=300;xmax=10;ymax=10;x=linspace(-xmax,xmax,N);y=linspace(-ymax,ymax,N);for i=1:Nfor j=1:Nr(i,j)=sqrt(x(i)^2+y(j)^2);B(i,j)=cos(pi*(2*n*d*cos(asin(n*sin(atan(r(i,j)/f)))))/lambda).^2;endendNCLevels=255;Br=4*B*NCLevels;colormap(gray(NCLevels));image(x,y,Br);axes(handles.axes1)5.3改变参数对比相邻亮条纹间距变化规律用户通过调节平台的滑动条,分别改变入射波长,厚度影响等倾干涉的两个参数,可以分别得到不同的干涉图样。
基于Matlab的光学实验仿真

基于Matlab的光学实验仿真基于Matlab的光学实验仿真一、引言光学是研究光的传播、反射、折射和干涉等现象的学科,广泛应用于光学器件、光通信等领域。
在光学实验中,通过搭建实验装置来观察和研究光的行为,以验证光学理论并深入理解光的特性。
然而,传统的光学实验不仅设备复杂,成本高昂,而且需要大量的实验时间和实验设计。
因此,基于计算机仿真的方法成为了一种重要的补充和替代。
Matlab作为一种强大的数值计算和仿真工具,具有强大的数学运算能力和友好的图形界面,被广泛应用于科学研究和工程设计。
在光学实验中,Matlab可以模拟光的传播、折射、干涉等各种光学现象,使得研究人员可以在计算机上进行光学实验,加速实验过程并提高实验效率。
二、光的传播仿真在光学实验中,光的传播是一项重要的研究内容。
通过Matlab的计算能力,我们可以模拟光线在不同介质中的传播情况,并观察其光程差、折射等现象。
光的传播可以用波动光学的理论来描述,其中最经典的是亥姆霍兹方程。
在Matlab中,我们可以利用波动光学的相关工具箱,通过求解亥姆霍兹方程来模拟光的传播。
例如,我们可以模拟光在一特定系统中的衍射效应。
在Matlab中,衍射效应可以通过菲涅尔衍射和弗雷涅尔衍射来模拟。
我们可以设定特定的光源和障碍物,通过Matlab的计算能力计算光的传播、衍射和干涉等现象,得到不同条件下的衍射效应,并可视化展示。
三、光的折射仿真光的折射是光学领域中的另一个重要现象,研究光的折射对于理解光在不同介质中的传播行为至关重要。
通过Matlab的仿真,我们可以模拟光的折射行为,并研究不同介质对光的影响。
在Matlab中,我们可以利用光学工具箱中的折射相关函数,输入光线的入射角度、折射率等参数,模拟光线在不同介质中的折射行为。
通过改变不同介质的折射率、入射角度等参数,我们可以观察到光的全反射、折射偏折等现象,并进行定量分析和比较。
四、光的干涉仿真光的干涉是光学领域的重要研究课题之一,通过模拟光的干涉行为,可以深入理解光的相干性、波动性质等特性。
如何通过MATLAB进行模拟与仿真

如何通过MATLAB进行模拟与仿真MATLAB是一种用于科学计算、数据分析和可视化的强大工具,它也是进行模拟和仿真的理想选择。
通过MATLAB,用户可以编写脚本或函数来描述和模拟各种现象,并通过可视化结果来验证和分析模拟过程。
在本文中,我们将介绍如何使用MATLAB进行模拟和仿真,包括建模、求解、可视化和分析。
首先,建立一个模型是进行模拟和仿真的第一步。
在MATLAB中,可以使用符号计算工具箱或数值计算方法来建立模型。
符号计算工具箱提供了一种使用符号表达式而不是数值进行计算的方法,这对于一些复杂系统的建模非常有用。
数值计算方法则使用数值解来近似求解模型。
在MATLAB中,可以通过定义变量和方程来建立模型。
例如,假设我们要建立一个简单的弹簧振动系统的模型,可以使用如下的方程:m*x''+k*x=0其中,m是质量,x是位移,k是弹簧常数。
我们可以使用MATLAB的符号计算工具箱来定义这个方程:syms x(t) m keqn = m * diff(x, t, t) + k * x == 0这样,我们就建立了一个描述弹簧振动系统的方程。
接下来,我们需要求解这个方程。
在MATLAB中,可以使用ode45函数来求解常微分方程。
例如,使用ode45函数求解上面的方程,并绘制振动的位移随时间的变化曲线:tspan = [0 10]; % 时间范围x0=1;%初始位移v0=0;%初始速度parameters = {m, k}; % 参数figure;plot(t, x(:, 1))xlabel('时间')ylabel('位移')title('弹簧振动')function dxdt = spring_ode(t, x, m, k)dxdt = [x(2); -k/m * x(1)];end在上面的代码中,我们定义了一个名为spring_ode的函数来描述弹簧振动的常微分方程。
如何利用Matlab进行模拟和仿真实验

如何利用Matlab进行模拟和仿真实验Matlab是一种功能强大的数学计算和数据可视化软件。
它不仅可以进行数学模拟和仿真实验,还可以处理数据、绘制图表和实施算法。
在工程、物理学、生物学等领域,Matlab被广泛用于解决各种实际问题。
本文将介绍如何利用Matlab进行模拟和仿真实验,并探讨其在实验设计和结果分析中的应用。
一. Matlab的基本功能Matlab具有很多基本功能,如矩阵操作、数值计算、符号计算等。
这些功能使得Matlab成为进行模拟和仿真实验的理想选择。
在Matlab中,可以定义和操作矩阵,进行线性代数运算,如求解方程组、矩阵求逆等。
此外,Matlab还提供了许多内置函数,可以进行数值计算和符号计算,如求解微分方程、积分、数值优化等。
二. 模拟实验的设计在进行模拟实验之前,首先需要设计实验方案。
实验设计包括选择合适的模型和参数设置,确定实验变量和观测指标等。
在Matlab中,可以使用函数或脚本来定义模型和参数,通过修改参数值来观察实验结果的变化。
比如,可以使用Matlab的模型库来选择合适的模型,然后使用函数传入参数值进行求解。
此外,Matlab还提供了绘图功能,可以绘制实验结果的图表,以便更直观地分析数据。
三. 仿真实验的实施在设计好实验方案后,就可以开始进行仿真实验了。
在Matlab中,可以使用已定义的模型和参数进行仿真计算。
可以通过Matlab的编程功能来实现计算过程的自动化。
比如,可以使用循环语句来迭代计算,以观察参数变化对结果的影响。
此外,Matlab还提供了随机数生成和统计分析函数,可以用于生成随机变量和分析实验数据。
四. 实验结果的分析在完成仿真实验后,需要对实验结果进行分析。
Matlab提供了丰富的数据处理和分析工具,可以对实验数据进行统计分析、绘图和可视化展示。
可以使用Matlab的数据处理函数来计算均值、标准差、相关系数等统计指标。
此外,Matlab还可以通过绘图函数来绘制直方图、散点图、线图等图形,以便更好地理解和展示数据。
在Matlab中进行模拟和仿真

在Matlab中进行模拟和仿真Matlab是一种功能强大的数学软件,广泛应用于科学研究、工程设计和数据分析等领域。
它不仅拥有丰富的数学函数库和绘图工具,还提供了一套强大的仿真和模拟功能,使用户能够更加方便地进行系统建模和性能评估。
本文将以Matlab中的模拟和仿真为主题,介绍其应用和原理,希望能为读者提供一些有用的参考和指导。
一、模拟与仿真的基本概念模拟和仿真是现代科学和工程中常用的研究方法,通过对实际系统进行数学建模和计算机模拟,可以在不进行实际试验的情况下,预测和评估系统的性能和行为。
模拟和仿真能够节省时间和成本,提高研究效率,使得科学家和工程师能够更快地了解和优化系统。
在Matlab中,模拟和仿真一般包括以下几个步骤:首先,确定系统的数学模型,即建立数学方程或差分方程描述系统的动态行为。
其次,选择仿真方法和算法,根据系统的特点和需求,确定合适的模拟算法,如欧拉法、龙格-库塔法等。
然后,设定仿真参数,包括仿真时间、步长等,这些参数将影响仿真结果的准确性和计算效率。
最后,执行仿真,并对仿真结果进行分析和评估。
二、Matlab中的模拟功能在Matlab中,模拟功能是通过内置的仿真工具和函数库来实现的。
Matlab提供了一系列用于数学建模和仿真分析的函数、工具箱和工具。
例如,Simulink是Matlab中最常用的仿真工具之一,它基于图形化仿真模型,可以快速搭建各种系统的模型,并进行仿真和分析。
Simulink提供了丰富的模块和工具箱,能够满足不同系统的建模和仿真需求。
用户可以通过拖放模块、连接信号线的方式,构建系统模型,并设置参数、仿真时间等。
Simulink还支持自定义模块和函数,用户可以根据具体需要,编写自己的模块和函数,以满足特定的仿真需求。
除了Simulink之外,Matlab还提供了其他一些实用的仿真函数和工具,如ode45函数用于解非刚性系统的常微分方程,ode15s函数用于解刚性系统的常微分方程等。
matlab的几个干涉实验模拟

基于matlab 的几个干涉实验模拟------------吴旭普摘要:根据干涉原理对牛顿环,杨氏双缝和迈克尔逊干涉仪原理进行分析得到各种参数的关系,采用计算机模拟方法并通过软件matlab 编程并运行得到干涉图样 关键词:干涉 matlab 牛顿环 杨氏干涉 迈克尔逊干涉仪 一.牛顿环干涉模拟 1.建模如图,牛顿环是一种分振幅法产生干涉的装置,由一光平玻璃和一曲率很大的平凸透镜构成,平玻璃和平凸透镜之间形成了一个空气劈尖,且其等厚轨迹是以接触点为圆心的一系列同心圆,所以干涉条纹的形状也是明暗相间的同心圆。
在编制程序之前,我们需要对决定干涉条纹特征的光程差、相位差与干涉条纹半径r ,光波波长和平凸透镜的曲率半径R 之间的曲率半径R 之间的关系。
对于形成牛顿环干涉处的空气层厚度e ,两相干光的光程差为: 22e λ∆=+由几何关系:因为R>>e ,所以略去故得:所以两相干光的相位差为:=两相干光的干涉光强为:其中分别是反射光1和反射光2的光强,为使问题简单化设平凸透镜和平板玻璃的反射率均为15%,并且设两反射光的光强近似相等,均设为最终牛顿环干涉的光强为2.程序编写Clear all %清除内存lamd=600e-9; %设定入射光波长 R=10; %设定牛顿环曲率 rm=1e-2; %设定干涉条纹区域 x=0:0.0001:rm; y=rm:-0.0001:0; [X,Y]=meshgrid(x,y); r2=X.^2+Y.^2;phi=2*pi*(r2/R+lamd/2)/lamd; %相位差I=4*cos(phi./2).^2; %第一象限干涉光强 N=255; %设定灰度等级Ir2=(I/4.0)*N; %最大光强为最大灰度Ir1=fliplr(Ir2); %矩阵对称操作Ir3=flipud(Ir1);Ir4=flipud(Ir2);Ir=[Ir1 Ir2;Ir3 Ir4]; %构造图像矩阵figureimage(Ir,'XData',[-0.02,0.02],'YData',[0.02,-0.02]); %画干涉条纹colormap(gray(N));axis squareTitle(“牛顿环干涉光强”)3.运行程序与结果分析如图2,模拟结果与实验一致,通过以上推倒可知牛顿环条纹与相位差有很大联系。
光的干涉和衍射的matlab模拟

光的干涉和衍射的matlab模拟单缝夫琅和费衍射是光的衍射现象之一,如图2所示。
当单色光波通过一个狭缝时,光波会向周围扩散,形成一系列同心圆环。
这些圆环的亮度分布是由夫琅和费衍射公式描述的,即。
其中为入射光波长,为狭缝宽度,为衍射角。
夫琅和费衍射公式表明,随着衍射角的增大,圆环的半径会减小,而亮度则会逐渐减弱。
在MATLAB中,可以通过输入实验参数,如光波长和狭缝宽度,来观察圆环的亮度分布和半径随衍射角的变化情况。
同时,还可以探讨不同波长和狭缝宽度对圆环亮度和半径的影响。
4双缝衍射双缝衍射是光的干涉和衍射现象的结合,如图3所示。
当一束单色光波通过两个狭缝时,光波会在屏幕上形成一系列干涉条纹和衍射环。
干涉条纹的亮度分布与___双缝干涉相同,而衍射环的亮度分布则由夫琅和费衍射公式描述。
在MATLAB中,可以通过输入实验参数,如光波长、双缝间距和双缝宽度,来观察干涉条纹和衍射环的亮度分布和条纹间距、环半径随实验参数的变化情况。
同时,还可以探讨不同实验参数对干涉条纹和衍射环的影响。
5衍射光栅衍射光栅是一种利用衍射现象制成的光学元件,如图4所示。
当一束单色光波通过光栅时,光波会被分为多个衍射光束,形成一系列亮度不同的衍射条纹。
衍射条纹的亮度分布与夫琅和费衍射公式描述的圆环类似,但是条纹间距和亮度分布会受到光栅常数的影响。
在MATLAB中,可以通过输入实验参数,如光波长和光栅常数,来观察衍射条纹的亮度分布和条纹间距随实验参数的变化情况。
同时,还可以探讨不同实验参数对衍射条纹的影响。
总之,通过MATLAB模拟光的干涉和衍射现象,可以更加直观地理解和掌握这些重要的光学现象,同时也可以为实验设计和数据分析提供有力的工具和支持。
本文介绍了___双缝干涉、单缝夫琅禾费衍射和衍射光栅光谱的计算机模拟。
当一束单色平行光通过宽度可调的狭缝,射到其后的光屏上时,形成一系列亮暗相间的条纹。
单缝夫琅禾费衍射的光强分布可以通过惠更斯-费涅耳原理计算。
如何在Matlab中进行模拟和仿真

如何在Matlab中进行模拟和仿真引言:模拟和仿真是数字化时代不可替代的工具,在众多领域具有广泛的应用。
Matlab作为一种强大的数学计算软件,提供了丰富的工具和函数,可以帮助我们进行各种模拟和仿真分析。
本文将介绍如何在Matlab中进行模拟和仿真,以及一些常用的技巧和注意事项。
一、Matlab中的模拟和仿真工具1. Matlab的基本特性Matlab具有高效的计算能力和友好的用户界面,支持多种数学运算、绘图和数据处理功能。
它提供了丰富的工具箱,可以满足不同领域的模拟和仿真需求。
2. Matlab SimulinkMatlab Simulink是Matlab中的一款强大的系统仿真工具,可用于建立各种复杂的动态系统模型。
通过使用Simulink中的模块和线路连接,可以直观地建立并仿真各种系统,如电路、机械系统、控制系统等。
3. Matlab中的其他工具箱除了Simulink,Matlab还提供了许多其他工具箱,如Signal Processing Toolbox、Control System Toolbox、Communication Toolbox等,可以用于处理和分析特定领域的信号、控制和通信问题。
这些工具箱提供了丰富的函数和算法,大大简化了模拟和仿真的过程。
二、Matlab模拟和仿真的基本步骤1. 建立模型在进行模拟和仿真之前,首先需要明确模型的目标和要求。
然后,根据模型的特点和公式,使用Matlab提供的函数和工具箱,建立相应的数学模型。
可以根据需要将模型分为多个子系统,以便更好地组织和管理模型。
2. 参数设置模型建立完成后,需要设置各个参数的数值。
这些参数可能包括模型的物理特性、控制参数等。
根据具体情况,可以通过手工输入、数据拟合或对已有数据的分析来确定参数的取值。
3. 运行仿真参数设置完成后,即可运行仿真。
Matlab提供了多种仿真方法,如连续仿真、离散仿真、Monte Carlo仿真等。
基于Matlab的波的干涉实验仿真研究

第32卷第4期大学物理实验Vol.32No.42019年8月PHYSICALEXPERIMENTOFCOLLEGEAug.2019收稿日期:2019 ̄03 ̄22∗通讯联系人文章编号:1007 ̄2934(2019)04 ̄0076 ̄03基于Matlab的波的干涉实验仿真研究史㊀严∗ꎬ牛宽宽(石家庄铁道大学数理系ꎬ河北石家庄㊀050043)摘要:利用计算机和Matlab方法对大学物理实验中的波的干涉实验进行了仿真研究ꎬ并进行了适当的计算和作图ꎬ此方法可以大大简化实验条件ꎬ并能加深学生对物理实验内涵的理解ꎮ关键词:计算机技术ꎻMatlab软件ꎻ波的干涉实验中图分类号:O4 ̄39文献标志码:ADOI:10.14139/j.cnki.cn22 ̄1228.2019.04.021㊀㊀在传统的大学物理实验中ꎬ通常需要使用大量的实验仪器㊁装置ꎬ需要在特定的物理实验室中进行操作ꎬ并且需要一定的环境条件ꎬ如:温度㊁湿度㊁压力㊁外场等[1]ꎮ随着计算机技术的发展ꎬ越来越多的新技术㊁新方法被引入到大学物理实验的科研和教学环节中[2]ꎬ其中使用Matlab程序方法进行大学物理和实验的仿真研究是一个热点[3 ̄7]ꎬ利用这个方法既可以使学生深刻理解物理实验的内涵ꎬ又可以减少对实验条件的依赖ꎬ有很大的发展空间ꎮ本文使用Matlab方法详细研究了波的干涉实验ꎮ1㊀波的干涉实验的强度和图样研究1.1㊀物理模型及分析设空间中两个相干波源ꎬ其角频率都为wꎬ初相位分别是φ1和φ2ꎬ两个波源之间的距离是2aꎬ假设空间任意一点Pꎬ两列波在P点产生的振动是u1=A1cos(wt+φ1-2πr1/λ)u2=A2cos(wt+φ2-2πr2/λ)其中ꎬA1和A2分别是两列波在P点的振幅ꎻr1和r2是两个波源到P点的距离ꎮ则P点的合振动是u=u1+u2=Acos(wt+φ)其中A=A21+A22+2A1A2cosΔφφ=arctanA1sin(φ1-2πr1/λ)+A2sin(φ2-2πr2/λ)A1cos(φ1-2πr1/λ)+A2cos(φ2-2πr2/λ)Δφ称为相位差Δφ=φ2-φ1-2πr2-r1λ其中ꎬδ=r2-r1称为波程差ꎮ波的强度与振幅的平方成正比ꎬ所以波的强度是I=I1+I2+2I1I2cosΔφ当Δφ=2κπ时(k=0ꎬ1ꎬ-1ꎬ )满足这样条件的点干涉振幅最大ꎬ称为干涉相长ꎻ当Δφ=(2κ+1)π时(k=0ꎬ1ꎬ-1ꎬ )ꎬ满足这样条件的点干涉振幅最小ꎬ称为干涉相消ꎮ1.2㊀编程思想取A1为振幅单位ꎬ则合振幅可表示如下A=A11+A∗22+2A∗2cosΔφ其中ꎬA∗2=A2/A1ꎬ取I1=A21为波的强度单位ꎬ则波的总强度可表示如下I=I1(1+I∗22I∗2cosΔφ)其中ꎬI∗2=I2/I1=A∗22ꎮ可限定0<A∗2<1ꎬ或者取A2为振幅单位ꎮ波的振幅和强度随A∗2值不同而不同ꎮ取分振幅之比为参数向量ꎬ取相差为自变量向量ꎬ形成矩阵ꎬ即可计算相对合振幅和相对强度ꎮ1.3㊀作图及分析取干涉相长的级数为2ꎬ则有5个干涉相长位置ꎬ4个干涉相消位置ꎬ取四个不同的分振幅之比0.1㊁0.4㊁0.7㊁1ꎬ绘制相对合振幅如图1ꎮ图1㊀两列相干波干涉的振幅分布同样的数据ꎬ绘制两列波干涉的相对强度ꎬ如图2所示ꎮ图2㊀两列相干波干涉的强度分布根据图1可知ꎬ随着振幅比的增大ꎬ相对振幅的大小范围急剧变化ꎬ但整体上还是有余弦函数的趋势ꎮ由图2可以看出ꎬ相对强度是相差的余弦函数ꎬ随着振幅比增大ꎬ干涉相长增强ꎬ干涉相消减弱ꎮ2㊀水波的干涉实验图样研究2.1㊀物理模型及分析两列相干的水波相遇ꎬ仿真模拟其形成的干涉图样ꎮ假设两列相干水波的振幅都为A0ꎬ频率相同ꎬ振动方向相同ꎬ令它们的初相位均是零ꎬ则它们在P点叠加的合振幅和初相位分别是A=2A0cos(πr1-r2λ)φ=arctan-sin(2πr1/λ)-sin(2πr2/λ)cos(2πr1/λ)+cos(2πr2/λ)由此可得ꎬ在干涉相长线上ꎬ不同的点的相位一般也是不同的ꎮ根据振动方程可以确定各点的位移值ꎮ2.2㊀编程思想取波长为单位ꎬ则水波的合振幅可表示如下A∗=A∗02cosπ(r∗2-r∗1)[]初相位可表示为φ=arctan-sin(2πr∗1)+sin(2πr∗2)[]cos(2πr∗1)+cos(2πr∗2)其中ꎬA∗0=A0/λꎬA∗=A/λꎬ波程r∗1=x∗2+(y∗-a∗)2r∗2=x∗2+(y∗+a∗)2其中ꎬx∗=x/λꎬy∗=y/λꎮP点的振动方程可表示如下u∗=A∗cos(t∗+φ)其中t∗=wt表示无量纲的时间ꎮ2.3㊀作图根据各点位移的大小ꎬ用曲面surf指令画出水波的初始干涉图样ꎬ变换各点的坐标数值ꎬ连续扫描ꎬ形成波的传播的动画ꎬ显示稳定的干涉图样ꎬ设置俯视角即可得两列水波的干涉图样ꎮ如图3所示图3㊀水波的干涉图样效果图3㊀总㊀结在大学物理实验的教学和科研中ꎬ计算机技77基于Matlab的波的干涉实验仿真研究术都提供了很大的帮助ꎬ在科研中主要进行数值分析和模拟㊁复杂的演算和推导ꎬ在教学中是重要的辅助工具ꎬ可以帮助学生处理实验数据㊁解决物理问题和作图等ꎮ对于大学物理和实验中的问题ꎬ应用计算机程序解决物理问题是一个新的思想ꎬ未来有很大的应用前景ꎮ参考文献:[1]㊀王振彪ꎬ刘虎ꎬ郑乔ꎬ等.大学物理实验[M].中国铁道出版社ꎬ2009.[2]㊀隋成华ꎬ魏高尧ꎬ等.大学物理实验[M].高等教育出版社ꎬ2016.[3]㊀李海涛ꎬ苏艳丽ꎬ等.MATLABGUI在光学实验教学中的应用[J].大学物理实验ꎬ2017ꎬ30(6). [4]㊀周群益.MATLAB可视化大学物理学[M].清华大学出版社ꎬ2001.[5]㊀彭芳麟.理论力学计算机模拟[M].清华大学出版社ꎬ2002.[6]㊀张志涌.精通matlab[M].北京航空航天大学出版社ꎬ2000.[7]㊀NicholasJ.GiordanoꎬComputationalPhysics[M].清华大学出版社ꎬ2011.SimulationResearchonInterferenceExperimentofWaveBasedonMatlabSHIYan∗ꎬNIUKuankuan(DepartmentofMathsandPhysicsꎬShijiazhuangTiedaoUniversityꎬShijiazhuang050043ꎬChina)Abstract:UsingMatlabmethodꎬwesimulatedandstudiedtheinterferenceexperimentofwaveincollegephys ̄icsexperiment.Thismethodcansimplifytheexperimentconditionanddeepenthestudents'understandingofphysicscontent.Keywords:computertechnologyꎻMatlabsoftwareꎻinterferenceexperimentofwave87基于Matlab的波的干涉实验仿真研究。
基于matlab的等倾干涉实验仿真

输入理论2
输入理论3
我们得到干涉加强或减弱的条件为:
等倾干涉
2 建模与仿真
二维图像程序
3 仿真结果及分析 等倾干涉:设波长500nm,薄膜厚度系数为2500,屏距为0.2m。程序运行结果如下:
干涉条纹图
输入理论1 输输入入理理论论22 输入理论3
干涉三维图
3 仿真结果及分析 现在我们改变薄膜厚度系数:设波长500nm,薄膜厚度系数为4000,屏距为0.2m。程序 运行结果如下图: 假如上次间距是d中心为j级,这次间距为比d小的数级数肯定也小,则间距就大。 说明:薄膜厚度越薄,条纹间距越大。结合两次实验仿真结果可以很明显看出薄膜厚度增 加,单位面积内得到干涉环越多,即干涉输环入越理密论集1 ,仿真结果和理论分析吻合。
输输入入理理论论22
输入理论3
干涉条纹图
干涉三维图
3 仿真结果及分析
等倾干涉:等倾干涉干涉条纹是由一组内疏外密输的入同理心论1圆环组成的。其干涉图样与球面波 干涉光源垂直观察屏的干涉图样很相似。由理论可知,平行平板厚度增加时,干涉条纹变 得密集;离干涉中心越远,条纹越密集。实际仿真中,增加薄膜厚度系数,可以看到条纹
入射光的振幅分为两部分,两部分光波相遇形成干涉现象。等倾干涉是光波照射在厚度相同的薄膜上,入射角不
同造成广播之间存在光程差,进而产生干涉条纹,每一级条纹对应不同的角度。等倾干涉模型如下图。
输入理论1 如右图所示等倾干涉光程差图,我们可以得到光路1和 2的光程差公式:
' 2d n22 n12 sin2 i
基于matlab的等倾干涉实 验仿真
黄强煌
2017.12.25
目录 Content
如何在Matlab中进行模拟仿真

如何在Matlab中进行模拟仿真在科学和工程领域中,模拟仿真是一种非常重要的工具,可以帮助实现对现实世界复杂问题的理解和分析。
而在这方面,Matlab是一个功能强大且广泛使用的软件平台,它提供了丰富的工具和函数,便于进行模拟仿真。
本文将介绍如何在Matlab中进行模拟仿真,并探讨其中的一些关键技巧和注意事项。
首先,要进行模拟仿真,我们需要有一个模型。
模型是对待研究问题的一种简化和抽象,它可以是数学方程、系统方程或者演化规则等形式。
在Matlab中,可以使用符号计算工具箱对模型进行推导和建立。
通过定义变量、方程和初始条件,可以将实际问题转化为计算机可以处理的形式。
一旦建立了模型,就可以开始进行仿真了。
在Matlab中,可以使用数值计算工具箱中的函数来求解微分方程、差分方程和代数方程等。
例如,ode45函数可以用于求解常微分方程,而ode15s函数则适合求解刚性方程。
此外,还有丰富的工具函数可以用于求解常微分方程组、偏微分方程和随机过程等。
除了求解方程,Matlab还提供了许多其他的工具和函数,用于分析和处理仿真结果。
例如,可以使用绘图函数来可视化仿真结果,帮助我们更好地理解问题。
Matlab中的绘图函数可以实现各种类型的图形,包括线图、散点图、柱状图、等高线图等。
此外,还可以使用统计工具箱中的函数进行数据分析和参数估计。
在进行模拟仿真时,我们还需要注意一些技巧和注意事项。
首先,要注意选择合适的数值方法和精度。
不同的问题可能需要不同的数值方法,而选择适当的数值方法可以提高求解效率和准确性。
此外,要注意数值方法的稳定性和收敛性。
有时候,仿真结果可能会出现数值误差,这时可以考虑使用更高精度的方法或者增加计算步长来改善结果。
其次,要注意仿真中的参数选择和设置。
参数的选择会影响仿真结果的准确性和可靠性。
有时候,我们需要进行参数敏感性分析,即通过改变参数的值来观察仿真结果的变化情况。
这可以帮助我们了解模型的行为和性质,并指导进一步的研究和设计。
基于Matlab的光学干涉现象仿真

21 年 8 01 月第 2 期 3
科 技 视 界
项目 与课题
r xft ( e /) Ma=* nt t2; a ha
N= 01 5 ; f r 1N o :
xi ( 1 2r a/ 一 )r a ; (=i ) M x( 1 M x ) 一 N 一
fr= : oj1 N
yj ( 1 2 r a/ — )r a ; (=j ) M x( 1 M x ) 一 N 一 r,= qt ('+ ( ) ( )srx) y ; i j (i2 j C dh (j 2 dsr1r , ̄f ) e ai = / t +(j2 ' ; , ) q ( i) /2 '  ̄
通讯作者 : 吴平辉 ( 8. 一) 福建泉 州人, 1 3O , 9 1 男, 硕士 , 主要从事光 电检测技 术与光学设计方面的研究工作 。 为主要成员参加 国家自然科 学基 作 金和浙江省 自然科 学基金各一项 , ( u a oM dmO ts、O t l t n s ee )《 已在(or lf oe pi>< p e coi tr 、中国激光》 国内 Jn c>( o e r c L ts 等 外核心刊物上发表论文 1 篇 。 0多
设光源波长 为 50a 薄膜 厚度 为 O2 m, 0 m, . m 透镜焦距为 02 5 . m。通过 Ma a t b编程 、 l 计算 , 获得等倾干涉 二维 和三维光强分 布 图, 分别 如图 2 图 3所示 。程序源代码如下 : 、 f02 = .;
l d = 0 * f(9; a a 50 l ' ) mb 一
P i,= idl (jlm d ; h( )2 p eti)a b a i j a ,/ Bi)4 cs h( ) ) ; ( = *o( i, 2 ̄ , j P i/ 2 j
matlab的几个干涉实验模拟

基于matlab 的几个干涉实验模拟------------吴旭普摘要:根据干涉原理对牛顿环,杨氏双缝和迈克尔逊干涉仪原理进行分析得到各种参数的关系,采用计算机模拟方法并通过软件matlab 编程并运行得到干涉图样 关键词:干涉 matlab 牛顿环 杨氏干涉 迈克尔逊干涉仪 一.牛顿环干涉模拟 1.建模如图,牛顿环是一种分振幅法产生干涉的装置,由一光平玻璃和一曲率很大的平凸透镜构成,平玻璃和平凸透镜之间形成了一个空气劈尖,且其等厚轨迹是以接触点为圆心的一系列同心圆,所以干涉条纹的形状也是明暗相间的同心圆。
在编制程序之前,我们需要对决定干涉条纹特征的光程差、相位差与干涉条纹半径r ,光波波长和平凸透镜的曲率半径R 之间的曲率半径R 之间的关系。
对于形成牛顿环干涉处的空气层厚度e ,两相干光的光程差为: 22e λ∆=+由几何关系:因为R>>e ,所以略去故得:所以两相干光的相位差为:=两相干光的干涉光强为:其中分别是反射光1和反射光2的光强,为使问题简单化设平凸透镜和平板玻璃的反射率均为15%,并且设两反射光的光强近似相等,均设为最终牛顿环干涉的光强为2.程序编写Clear all %清除内存lamd=600e-9; %设定入射光波长 R=10; %设定牛顿环曲率 rm=1e-2; %设定干涉条纹区域 x=0:0.0001:rm; y=rm:-0.0001:0; [X,Y]=meshgrid(x,y); r2=X.^2+Y.^2;phi=2*pi*(r2/R+lamd/2)/lamd; %相位差I=4*cos(phi./2).^2; %第一象限干涉光强 N=255; %设定灰度等级Ir2=(I/4.0)*N; %最大光强为最大灰度Ir1=fliplr(Ir2); %矩阵对称操作Ir3=flipud(Ir1);Ir4=flipud(Ir2);Ir=[Ir1 Ir2;Ir3 Ir4]; %构造图像矩阵figureimage(Ir,'XData',[-0.02,0.02],'YData',[0.02,-0.02]); %画干涉条纹colormap(gray(N));axis squareTitle(“牛顿环干涉光强”)3.运行程序与结果分析如图2,模拟结果与实验一致,通过以上推倒可知牛顿环条纹与相位差有很大联系。
牛顿环干涉实验的 Matlab模拟

3.2 波长 对牛顿环的影响
改变波长 情况下,保持 R=2m , =500nm,如图 5 所示:
图5
R=2m , =500nm
保持 R=2m , =400nm,如图 6 所示:
图6
R=2m , =400nm
通过图 2、图 5、图 6 的比较发现,波长对牛顿环干涉的影响,随着波长的减小,牛顿环向内收 缩,条纹也变的越来越窄。
2d / 2
(1)
k 1,2, k 1,2,
(2k 1 ) / 2 产生暗纹的条件是: (2k) / 2 产生亮纹的条件是:
(2) (3)
对于间隙厚度 d 与条纹半径 r 的关系,由几何关系得:
r 2 R2 (R d )2
1.牛顿环干涉的原理
在编制程序之前, 我们需要对决定干涉条纹特征的光程差、 相位差与干涉条纹半径 r, 光波波长 和平凸透镜的曲率半径 R 之间的关系。装置如图 1 所示:
图1
牛顿环装置图
将一块曲率半径为 R 的平凸透镜凸面朝下放在一块平面透镜上,以平行单色光垂直照射,则经 空气层上下表面反射的两束光线有一光程差,在平凸透镜凸面相遇后,将发生干涉。 当透镜凸面的曲率半径 R 很大时, 相遇时的两反射光线的几何程差为该处空气间隙厚度 d 的两倍, 即 2d。又因这两条相干光线中一条光线来自光密媒质面上的反射,另一条光线来自光疏媒质上的反 射,它们之间有一附加的半波损失,所以在 P 点处得两相干光的总光程差为:
(12)
2.编写程序
为了得到明暗相间的牛顿环干涉条纹,我们需要用 matlab 模拟出光强变化过程,也就是说,我
们编程的重点在于实现对公式 (12)的模拟。设光强的系数 4 I 0 =1,波长 =600nm ,凸透镜曲率半径 R=2m。建立一个大小为 8mm*8mm 具有 400*400 个像素点的视场,视场各点(x,y)到视场中心的距 离可以表示为: r= x 2 y 2 根据公式(12),利用 matlab 编程: R=2; Lamda=632.8e-9; [x,y]=meshgrid(linspace(-0.004,0.004,400)); r2=(x.^2+y.^2); delta=pi*r2/(R*lamda)+pi/2; I=cos(delta).^2; Imshow(I); %牛顿环曲率半径 %波长 %视场范围 %各点到中心的距离 %相位差 %干涉光强 %画图 (13)
实验6 干涉的Matlab模拟
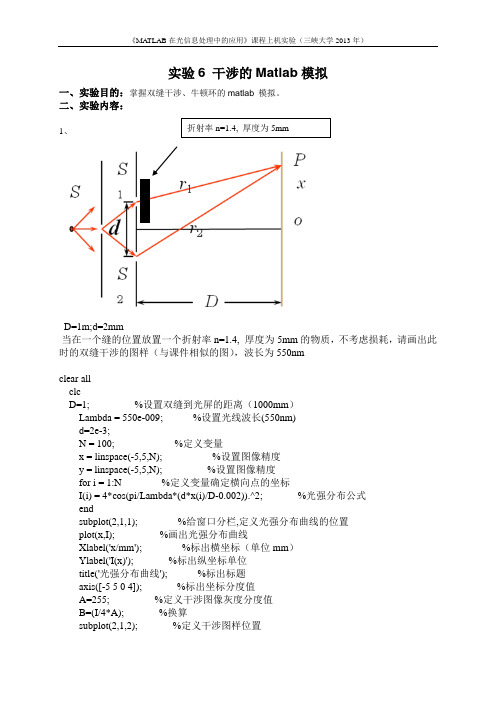
实验6 干涉的Matlab模拟一、实验目的:掌握双缝干涉、牛顿环的matlab 模拟。
二、实验内容:折射率n=1.4, 厚度为5mm1、D=1m;d=2mm当在一个缝的位置放置一个折射率n=1.4, 厚度为5mm的物质,不考虑损耗,请画出此时的双缝干涉的图样(与课件相似的图),波长为550nmclear allclcD=1; %设置双缝到光屏的距离(1000mm)Lambda = 550e-009; %设置光线波长(550nm)d=2e-3;N = 100; %定义变量x = linspace(-5,5,N); %设置图像精度y = linspace(-5,5,N); %设置图像精度for i = 1:N %定义变量确定横向点的坐标I(i) = 4*cos(pi/Lambda*(d*x(i)/D-0.002)).^2; %光强分布公式endsubplot(2,1,1); %给窗口分栏,定义光强分布曲线的位置plot(x,I); %画出光强分布曲线Xlabel('x/mm'); %标出横坐标(单位mm)Ylabel('I(x)'); %标出纵坐标单位title('光强分布曲线'); %标出标题axis([-5 5 0 4]); %标出坐标分度值A=255; %定义干涉图像灰度分度值B=(I/4*A); %换算subplot(2,1,2); %定义干涉图样位置image(x,y,B); %画出干涉图像原形 colormap(gray(A)); %将图样转化为灰度图 Xlabel('x/mm'); %标出横坐标(单位mm ) Ylabel('y/mm'); %标出纵坐标(单位mm ) title('干涉图样'); %标出标题axis([-5 5 0 5]); %标出坐标分度值-5-4-3-2-101234501234x/mm I (x )光强分布曲线x/mmy /m m干涉图样-5-4-3-2-10123450123452、请画出d, D, 波长分别变化(假如对不同波长折射率一样)时候的双缝干涉的强度分布的2维图形。
基于matlab干涉系统仿真

成绩:《工程光学》综合性练习一题目:基于matlab的干涉系统仿真学院精密仪器与光电子工程学院专业测控技术与仪器年级 20**级班级 *班姓名 **学号20**年**月综合练习大作业一一、要求3—4人组成小组,对下面给出的各题目利用Matlab等工具进行仿真。
二、仿真题目1、对于杨氏双缝干涉,改变双缝的缝宽和缝间距,观察干涉图样变化①原理图图中参数光线波长:lam=500纳米;双缝距离:d=0。
1毫米;(可调)双缝距接收屏距离:D=1米;接收屏范围:xs:-0.005~0.005ys:—0。
005~0。
005光源振幅:AI=A2=1;(单位振幅,可调)②matlab代码:clear;lam=500e-9;%设定波长lam(500纳米)d=0。
5e—3;%设定两缝之间距离d(0。
5毫米)D=1; %双缝到接收屏距离D(1米)A1=1; %初始两光源均为单位振幅A2=1;xm=0.005;ym=xm;%接受屏的范围ym,xm(0.01*0。
01矩形)n=1001;xs=linspace(—xm,xm,n);%用线性采样法生成两个一位数组xs,ys%(n为总点数)ys=linspace(—ym,ym,n);L1=sqrt((xs-d/2).^2+ys。
^2+D^2);%光屏上点(xs,ys)距光源1距离r1L2=sqrt((xs+d/2)。
^2+ys。
^2+D^2);%光屏上点(xs,ys)距光源2距离r2E1=A1。
/sqrt(L1)。
*exp(1i*L1*2*pi/lam);%光源1在接受屏上复振幅E1E2=A2。
/sqrt(L2)。
*exp(1i*L2*2*pi/lam);%光源2在接受屏上复振幅E2E=E1+E2; %复振幅叠加为合成振幅EI=abs(E).^2;%和振幅光强nc=255; %灰度br=(I/4)*nc; %灰度强度image(xs,ys,br); %生成干涉图样colormap(gray(nc));③初始干涉仿真图样④改变参数后的仿真图样(缝宽即光振幅A1、A2,缝间距d)A1=1。
基于Matlab的迈克尔逊干涉仪仿真模拟

基于 Matlab的迈克尔逊干涉仪仿真模拟 一、原理
迈克尔逊干涉仪结构示意图如下:
二、仿真结果
仿真参数如下:
1)模拟光束传播至透镜(焦距为40cm) 2)传播至分束镜,分光比设置为50% 3)一束光传播至倾斜反射镜2,并对反射镜2进行倾斜,在返回至分束镜 4) 模拟参考光,传播至反射镜1,并从反射镜1反射回分束镜 5) 物光与参考光传播至屏幕,并进行叠加,求其强度。
最后仿真结果如下:
上述仿真matlab程序可从以下链接处获取:
迈克尔逊干涉仿Βιβλιοθήκη 结果
Matlab光学仿真设计

用Matlab光学仿真设计关于光学中等倾干涉的现象光电11401 刘兴伟17号光线以倾角i入射,上下两条反射光线经过透镜作用汇聚一起,形成干涉。
由于入射角相同的光经薄膜两表面反射形成的反射光在相遇点有相同的光程差,也就是说,凡入射角相同的就形成同一条纹,故这些倾斜度不同的光束经薄膜反射所形成的干涉花样是一些明暗相间的同心圆环.这种干涉称为等倾干涉。
基本理论:薄膜干涉中两相干光的光程差公式(表示为入射角的函数形式)为式中n 为薄膜的折射率;n0为空气的折射率;h为入射点的薄膜厚度;i0为薄膜的入射角;+λ/2为由于两束相干光在性质不同的两个界面(一个是光疏-光密界面,另一是光密-光疏界面)上反射而引起的附加光程差;λ为真空中波长。
薄膜干涉原理广泛应用于光学表面的检验、微小的角度或线度的精密测量、减反射膜和干涉滤光片的制备等。
当光程差为波长整数倍时,形成亮条纹,为半波长奇数倍时是暗条纹。
等倾条纹是内疏外密的同心圆环。
如图所示:设计程序如下:为了方便计算,这里假设光波为垂直入射到薄膜上,并且设光源波长为450nm。
薄膜的厚度魏0。
35nm,透镜焦距为0.25m。
通过matlab编程计算获得等倾干涉二维和三维光强分别如图所示。
二维图像三维图像设计程序如下:F=0。
25;Lambda=450*10e-9;d=3。
5*10e—4;Theta=0。
15;rMax=f*tan(theta/2);N=451;For i=1:Nx(i)=(i-1)*rMax/(N—1)—rMax;For j=1:Ny(i)=(i-1)*rMax/(N-1)—rMax;r(i,j)=sqrt(x(i)^2+y(j)^2;delta(i,j)=2*d/sqrt(1+r(i,j)^2/f^2);Phi(i,j)=2*pi*delta(i,j)/lambda;B(i,j)=4*cos(Phi(i,j)/2)^2;endendNCLevels=255;Br=(B/4.0)*NCLevels; figure(1);image(x,y,Br);Colormap(gray(NCLevels));axis sqare;Figure(2);mesh(x,y,Br);Calormap(gray(NCLevels));Axis square;。
Unity内嵌Matlab子程序实现迈克尔逊干涉仪虚拟仿真实验中的干涉动态演示

Unity内嵌Matlab子程序实现迈克尔逊干涉仪虚拟仿真实
验中的干涉动态演示
邓莉;孙可;刘金梅;吴平颐;景培书;刘梓谊;李成渊
【期刊名称】《大学物理实验》
【年(卷),期】2022(35)3
【摘要】利用MATLAB软件对实验过程中的等倾干涉、等厚干涉的动态演变进行了动态仿真模拟。
采用Unity软件创建迈克尔逊干涉仪虚拟仿真实验场景,内嵌MATLAB子程序,通过调节动臂实现迈克尔逊干涉仪虚拟仿真实验中等倾干涉条纹的吞吐,等倾干涉转化为等厚干涉以及白光干涉等动态实验过程。
该干涉变化的演示过程直观、形象,增强了使用者与迈克尔逊干涉虚拟仿真实验间的交互性。
【总页数】7页(P124-130)
【作者】邓莉;孙可;刘金梅;吴平颐;景培书;刘梓谊;李成渊
【作者单位】华东师范大学物理与电子科学学院;华东师范大学教师教育实验教学中心
【正文语种】中文
【中图分类】O4-39
【相关文献】
1.基于Matlab的迈克尔逊干涉仪测液体折射率仿真研究
2.基于Labview的迈克尔逊干涉仪测量空气折射率虚拟实验研究
3.迈克尔逊干涉仪上演示杨氏干涉
4.基
于MATLAB的迈克尔逊干涉仪干涉视频处理5.基于LabVIEW的迈克尔逊干涉仪虚拟仿真实验系统设计
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.使用MATLAB进行等倾干涉动态模拟仿真
5.1. 界面设计
GUI界面设计]6[主要包括以下几个步骤:
第一步构思草图,编排控件的布局。
打开MATLAB程序,在FILE菜单中选择NEW GUI,打开guide设计界面模板,界面模板左边的各个控件可以直接用鼠标拖到编辑框。
第二步设置各控件的属性。
如设置各个控件的标识(Tag),字体等。
第三步各个控件代码的设计。
关键是OpeningFcn(初始界面函数)和控件的CallBack(回调函数)代码的设计。
初始界面函数即设定各参数的初始值,可根据实际情况设定。
回调函数是核心,是对界面控件触发时的事件响应函数。
根据需要,等倾干涉条纹的动态模拟图形用户界面使用了2个按钮(Push Button),标识为绘图和退出,用鼠标点击任一项目,则会执行相应的功能;4个静态文本框(Static Text)用于输入波长,厚度及各自的单位;2个滑动条(Slider),用鼠标拖动相应的滑动条就可以改变波长和厚度的大小;1个坐标轴对象(Axes)用于显示仿真结果。
界面如图4。
图 4 仿真界面
5.2 演示控件的回调函数
演示控件的功能是通过其回调程序来实现的,用户界面设计完成之后,选中控件用鼠标双击,在弹出的菜单中选择Viewbacks,在其子菜单中选择CallBack,就可以进入回调程序编辑器中,在编辑器中编写控件代码,使图形界面完成约定的功能。
演示控件的回调函数代码为:
lambda=get(handles.slider1,'value');
d=get(handles.slider2,'value');
f=200;
n=1;
N=300;
xmax=10;
ymax=10;
x=linspace(-xmax,xmax,N);
y=linspace(-ymax,ymax,N);
for i=1:N
for j=1:N
r(i,j)=sqrt(x(i)^2+y(j)^2);
B(i,j)=cos(pi*(2*n*d*cos(asin(n*sin(atan(r(i,j)/f)))))/lambda).^2;
end
end
NCLevels=255;
Br=4*B*NCLevels;
colormap(gray(NCLevels));
image(x,y,Br);
axes(handles.axes1)
5.3改变参数对比相邻亮条纹间距变化规律
用户通过调节平台的滑动条,分别改变入射波长,厚度影响等倾干涉的两个参数,可以分别得到不同的干涉图样。
5.3.1 改变入射波长
图6 厚度d=0.0049405mm不变,波长为λ=0.00045mm时,等倾干涉图
图7 厚度d=0.0049405mm不变,波长为λ=0.0005mm时,等倾干涉图
图8 厚度d=0.0049405mm不变,波长为λ=0.0006mm时,等倾干涉图
条纹变化特征:从图6到图8的调节过程中,随着参数λ的增加,相邻的亮条纹之间的距离越来越大。
5.3.2 改变薄膜厚度
图9厚度为d=0.6mm波长,为λ=0.0005mm时,等倾干涉图
图10 厚度为d=0.7mm,波长为λ=0.0005mm时,等倾干涉图
图11厚度为d=0.8mm,波长为λ=0.0005mm时,等倾干涉图从图中可以看出条纹变化特征:薄膜的厚度d越大,即相邻的亮条纹之间的距离越小,条纹越密,越不易辨认。
6 结束语
在光学领域里,计算机仿真技术也在发挥着越来越重要的作用,特别是在光学教学过程中,对光学现象的理解离不开光学实验。
本文对等倾干涉实验理论进行了分析,应用MATLAB指令,采用计算机模拟仿真技术对其干涉条纹进行了模拟仿真,得到了光学实验的仿真图像。
利用matlab来开发光学信息处理实验仿真系统,提高了实验的效率,快速实现研究中的新构想,这为光学的理论分析与实验提供了方便,并为相关课件设计提供了新的途径。
因此,推广应用类似于matlab这样功能强大的编程软件来进行仿真实验的开发,将给教学和科研带来便利。
参考文献
[1] 张平.matlab基础与应用简明教程[M].电子工业出版社.2001
[2] 曲伟娟.基于Matlab的光学实验仿真[J].西北工业大学学报,2004,21(3):21-24.
[3] 姚启均.光学教程[M].北京:高等教育出版社,2002.
[4] 谢谦.关于等倾干涉的讨论[J].商洛师范专科学校学报,2002,16(2):71-73.
[5] 张智星.Matlab程序设计与应用[M].电子工业出版社,2001.
[6] 李季军.matlab GUI在光学仿真中的应用[J]通化师范学院学报,2012 31(2):52-54.。
