2014电子测量技术3
电力电子技术实验指导(2014下)

《电力电子技术》实验指导书自动化教研室二○一四年八月实验一单项桥式半控整流电路实验实验性质:验证性实验实验日期:一、实验目的1.加深对单相桥式半控整流电路带电阻性、电阻电感性负载时各工作情况的理解。
2.了解单相桥式半控整流电路的工作原理,学会对实验中出现的问题加以分析和解决。
二、实验设备三、实验线路及原理本实验电路图如图1-1 所示,实验线路图如图1-2 所示。
两组锯齿波同步移相触发电路均在TK-12挂件上,触发信号加到两个晶闸管(锯齿波触发脉冲G1,K1加到VT1的控制极和阴极,G3,K3加到VT3控制极和阴极),图中的R电阻900Ω,电感L d用100mH,直流电压表、电流表从电源控制屏获得。
四、实验内容1.锯齿波同步触发电路的调试。
2.单相桥式半控整流电路带电阻性负载。
3.单相桥式半控整流电路带电阻电感性负载。
图1-1 电路图图1-2 接线路图五、预习要求1.阅读电力电子技术教材中有关单相桥式半控整流电路的有关内容。
2.了解单相桥式半控整流电路的工作原理。
六、思考题1.单相桥式半控整流电路在什么情况下会发生失控现象?七、实验方法1.用两根导线将220V将TKDD-2电源控制屏的交流电压接到TK-12的“外接220V”端,按下“启动”按钮,打开TK-12电源开关,用双踪示波器观察“锯齿波同步触发电路”各观察孔的波形。
2.锯齿波同步移相触发电路调试。
令U ct=0时(RP2电位器顺时针转到底),α=170o。
3.单相桥式半控整流电路带电阻性负载:按原理图1-2接线,主电路接可调电阻R,将电阻器调到最大阻值位置,按下“启动”按钮,用示波器观察负载电压U d、晶闸管两端电压U VT,调节锯齿波同步移相触发电路上的移相控制电位器RP2,观察并记录在不同α角时U d的波形,测量相应电源电压U2、负载电压U d、电流I d计算公式: U d = 0.9U2(1+cosα)/24.单相桥式半控整流电路带电阻电感性负载①断开主电路后,将负载换成将平波电抗器L d(10OmH)与电阻R串联。
电子测量技术作业答案3

正确答案:说法正确 解答参考:
14. 直流双电桥用于中值电阻的精密测量。 你选择的答案: 未选择 [错误] 正确答案:说法错误 解答参考:
15. 直流双电桥用于精密测量大电阻。 你选择的答案: 未选择 [错误] 正确答案:说法错误 解答参考:
16. 电桥的收敛性越好,表明其达到平衡的速度越慢。 你选择的答案: 未选择 [错误] 正确答案:说法错误 解答参考:
二、不定项选择题(有不定个选项正确,共2道小题) 10. 下列哪些参数是阻抗测量的范畴? [不选全或者选错,不算完成]
(A) 电阻 (B) 电感 (C) 电容 (D) 品质因数 (E) 损耗因数
你选择的答案: 未选择 [错误] 正确答案:A B C D E 解答参考:
11. 通用电子计数器包括 [不选全或者选错,不算完成] (A) 时基信号产生电路 (B) A输入通道和B输入通道 (C) 主门电路 (D) 控制电路 (E) 计数及显示电路
你选择的答案: 未选择 [错误] 正确答案:D 解答参考:
6. 采用电子计数器直接测频,不管计数量N为何值,最大的量化绝对误 差总是等于( )。
(A) +1个计数单位 (B) -1个计数单位 (C) ±1个计数单位 (D) N个计数单位 你选择的答案: 未选择 [错误] 正确答案:C 解答参考:
7. 在用计数式频率计测量频率比N=fA/fB时,选用的门控信号由( )产生。 (A) fA信号放大整形后的信号 (B) fB信号放大整形后的信号 (C) 晶体振荡器产生的信号 (D) 晶体振荡器产生的信号分频后的信号
你选择的答案: 未选择 [错误] 正确答案:A B C D E 解答参考:
三、判断题(判断正误,共9道小题) 12. 在直流单电桥中,电源与指零仪互换位置,电桥平衡状态不变。 你选择的答案: 未选择 [错误] 正确答案:说法正确 解答参考:
电子测量技术题库及答案

电子测量技术题库及答案特点:(1)测量频率范围宽(2)侧脸量程宽(3)测量准确度高度相差悬殊(4)测量速度快(5)可以进行遥测(6)易于实现测试智能化和测试自动化(7)影响因素众多,误差处理复杂一般方法:(1)偏差式;在测量过程中,用仪器仪表指针的位移表示被测量大小的测量方法称为偏差式(2)零位式:测量时将被测量与标准量相比较,用指零仪表指示被测量与标准量相等。
(3)微差式:偏差与零点相结合测量仪表的主要性能指标:(1)精度:测量结果与被测量真值相一致的程度。
①精密度(测量结果的分散程度)测量值之间《=0.1v②正确度(测量结果与真值的接近程度)丨测量值-真值丨《=0.1v③准确度(1.2结合反应)(2)稳定性{稳定度:指在规定的时间区间,其他外界条件恒定不变的情况下,仪器示值变化的大小。
影响量:由于电源电压、频率、环境温度、湿度、气压、震动等外界条件变化搞成仪器表示值的变化量。
(3)输入阻抗(4)灵敏度(分辨力、分辨率):灵敏度表示测量仪器对被测量变化的敏感程度。
偏转灵敏度的倒数被称为偏转因数。
示波管荧光屏上光电偏移的距离就定义为他的偏转灵敏度cm/v cm/mv(5)线性度(y=f(x)为过度点直线)。
(6)动态特性:测量仪表的动态特性表示仪表的输出响应随输入变化的能力。
计量的基本概念:计量是利用技术和法制手段实现单位同意和量值准确可靠的测量。
(1)单位制:任何测量都要有一个体现计量单位的量作为标准,这样的量称作计量标准。
(2)基准:指用当代最先进的科学技术和工艺水平,以最高的准确度和稳定性建立起来的专门用以规定、保持和复现物理量计量单位的特殊量具或仪器装置等。
①主基准:主基准也成原始基准,是用来复现和八寸计量单位,具有现代科学技术所能达到的最高准确度的计量器具。
也叫国家基准②副基准:副基准是通过直接或间接与国家基准比对,确定其量值并经过国家鉴定批准的计量器具。
③工作基准:工作基准是经过主基准和副基准校准或比对,并经过国家鉴定批准,实际用以鉴定下属计量彼岸准的计量器具。
任务 3 使用数字式存储示波器测量波形(电子测量技术)

任务3 使用数字式存储示波器测量波形【任务目标】1.熟悉数字式存储示波器的面板结构和功能。
2.掌握使用数字式存储示波器测量波形的方法。
【任务内容】使用数字式存储示波器测量常规波形的参数。
【任务分析】具有存储功能的示波器称为存储示波器,而将信号以数字形式存储的示波器,称为数字式存储示波器。
数字式存储示波器主要是以数字存储器为核心,配以模数和数模转换器构成的。
数字式存储示波器通常采用大规模集成电路和微处理器,在微处理器统一控制下工作。
与模拟式通用示波器相比,该示波器具有以下优点:①可用数字、字符显示测量结果。
②测量波形可以存储在存储器中,便于数据计算、交换与处理。
③便于程控和多种方式输出。
④便于进行功能扩展。
1. TDS1012B型示波器外形图TDS1012B型示波器外形图如图3-3-1 所示。
图3-3-1 TDS1012B型示波器外形图2. TDS1012B型示波器面板功能TDS1012B型示波器面板如图3-3-2 所示。
屏幕侧菜单功能菜单触发部分水平系统垂直系统图3-3-2 TDS1012B型示波器面板3. TDS1012B型示波器面板功能(1)垂直系统各部件功能(见表3-3-1)【认识仪器】表3-3-1 垂直系统各部件功能垂直移位旋钮垂直菜单按键垂直偏转因数旋钮输入端子(2)水平系统各部件功能(见表3-3-2)表3-3-2 水平系统各部件功能水平移位旋钮水平菜单按键设置为零按键扫描时间因数旋钮外触发输入端子(3)触发部分各部件功能(见表3表3表3)表3-3-3 触发部分各部件功能触发电平设置旋钮触发菜单按键设置为50%按键续表强制触发按键触发视图按键(4)功能菜单各部件功能(见表3-3-4)表3-3-4 功能菜单各部件功能多用途旋钮保存按键自动量程按键参考波形按键保存/调出按键辅助功能按键测量按键光标按键采集按键显示按键帮助按键续表默认设置按键自动设置按键单次序列按键运行/停止按键(5)其他前面板部件功能(见表3-3-5)表3-3-5 其他前面板部件功能USB闪存驱动器接口探头补偿及校准信号接口探头检测按键屏幕显示区域除显示波形外,也会显示测量过程中关于波形的参数和数字存储示波器控制设置、菜单等信息。
任务 3 使用函数信号发生器(电子测量技术)

任务3 使用函数信号发生器函数信号发生器是一种多波形信号源,能够输出正弦波、方波、三角波、锯齿波等多种波形的信号,其输出波形均可用数学函数来描述,所以称为函数信号发生器。
函数信号发生器的输出频率范围很宽,一般可从几赫至几十兆赫。
由于函数信号发生器具有以上特点,它在很多情况下能够替代正弦信号发生器、脉冲信号发生器等,在生产、测试、维修和实验等工作中得到越来越广泛的应用。
本任务分别要求输出三种不同频率、幅度的波形,可采用函数信号发生器来实现。
EE1641C型函数信号发生器是一款广泛使用的函数信号发生器。
1. EE1641C型函数信号发生器的外形EE1641C型函数信号发生器的外形如图2-3-1 所示。
图2-3-1 EE1641C型函数信号发生器的外形【任务分析】【认识仪器】2. EE1641C型函数信号发生器的面板EE1641C型函数信号发生器的面板如图2-3-2 所示,各部件的功能见表2-3-1。
输入输出端子频率与幅度显示窗口选择按键与调节旋钮图2-3-2 EE1641C型函数信号发生器的面板表2-3-1 EE1641C型函数信号发生器面板各部件的功能部件功能频率显示窗口显示输出信号或外测信号的频率,其中,左侧显示信号波形,右侧显示信号频率的单位,下方为当前所选的频段指示灯幅度显示窗口显示输出信号的幅度,右侧显示输出信号的幅度单位和类型,下方为当前所选的输出衰减指示灯频率微调旋钮改变输出频率的 1 个频程内的频率范围占空比旋钮改变输出信号的对称性。
当此旋钮处在中心位置或关闭位置时,输出对称信号直流电平旋钮幅度调节旋钮扫描宽度/调制度旋钮扫描速率旋钮CMOS 电平调节旋钮频挡选择按键续表波形选择按键衰减选择按键幅值选择按键方式选择按键单脉冲按键电源开关按键外部输入端子函数输出端子同步输出端子单次脉冲端子点频输出端子(选件)功率输出端子(选件)3. EE1641C型函数信号发生器的性能指标EE1641C型函数信号发生器的性能指标见表2-3-2。
电子测量技术课后习题答案

2.4 有一个100V 的被测电压,若用0.5 级、量程为0-300V 和1.0 级、量程为0-100V 的两只电压表测量,问哪只电压表测得更准些?为什么?答:要判断哪块电压表测得更准确,即判断哪块表的测量准确度更高。
(1)对量程为0-300V、±0.5 级电压表,根据公式有% 100 % % 100 1x s x x x m x % 5 . 1 % 100 100 % 5 . 0 300 (2)对量程为0-100V、±1.0 级电压表,同样根据公式有% 100 % % 100 2 x s x x x m x % 0 . 1 % 100 100 % 0 . 1 100 从计算结果可以看出,用量程为0-100V、±1.0 级电压表测量所产生的示值相对误差小,所以选用量程为0-100V、±1.0 级电压表测量更准确。
2.9 测量上限为500V 的电压表,在示值450V 处的实际值为445V,求该示值的:(1)绝对误差(2)相对误差(3)引用误差(4)修正值答:(1)绝对误差V V V A x x 5 450 445 (2)相对误差% 12 . 1 % 100 445 5 % 100x x x (3)引用误差% 0 . 1 % 100 500 5 % 100m m x x (4)修正值V x c 5 2.10 对某电阻进行等精度测量10 次,数据如下(单位kΩ):0.992、0.993、0.992、0.991、0.993、0.994、0.997、0.994、0.991 、0.998。
试给出包含误差值的测量结果表达式。
答:1).将测量数据按先后次序列表。
n )(V V i )(V i )( 2 2 V i n )(V V i )(Vi )(2 2 V i 1 0.992 -0.0015 0.00000225 6 0.9940.0005 0.00000025 2 0.993 -0.0005 0.00000025 7 0.997 0.0035 0.00001225 3 0.992 -0.0015 0.00000225 8 0.994 0.0005 0.00000025 4 0.991 -0.0025 0.00000625 9 0.991 -0.0025 0.00000625 5 0.993 -0.0005 0.00000025 10 0.998 0.0045 0.00002025 2).用公式 n i i x n x 1 求算术平均值。
2014级课程表
机械设计基础A 陈智文 西教学楼424(217)[7-8节]
钳工实习 和运 钳工(2-16)[7-8节]
电工技术 宋涌利 西教学楼124(217)[7-8节]
电工技术 宋涌利 西教学楼400(217)[1-2节] 高等数学B 李铁光 西教学楼400(1017)[3-4节]
工程力学 陈智 西教学楼224(217)[3-4节]
大学英语B 彭书勤 西教学楼304(217)[1-2节] 机械设计基础A 钟彦西教学楼200 2节/单周(2-17)[3-4 节]
高等数学B 李铁光 西教学楼224(1017)[1-2节] 钳工实习 陈昌云 钳工(2-16)[3-4节]
高等数学B 李铁光 西教学楼224(1017)[1-2节] 大学英语B 彭书勤 西教学楼308(217)[3-4节] 钳工实习 陈昌云 钳工(2-16)[5-6节]
数控技术1401
大学英语B 胡晓明 西教学楼309(217)[3-4节] 计算机绘图 王欣 西教学楼200(217)[5-6节]
钳工实习 陈昌云 钳工(2-16)[3-4节] 计算机绘图 王欣 西教学楼200(217)[5-6节]
体育
体育
女生体育
女生体育
大学英语B 杨宏丽 西教学楼409(217)[1-2节] 工程力学 陈智 西教学楼224(217)[3-4节]
金属工艺学 张芙丽 西教学楼124(217)[5-6节] 机械设计基础A 张芙丽西教学楼124 2节/单周(2-17)[7-8 节]
大学铁道技术学院2014-2015学年第2学期总课表
铁道机车车辆1401
计算机绘图 王欣 西教学楼200(217)[1-2节]
铁道机车车辆1402
计算机绘图 王欣 西教学楼200(217)[1-2节] 大学英语B 王玉玲 西教学楼216(217)[3-4节] 钳工实习 和运 钳工2(2-16)[5-6节]
电子测量技术第三版 第5章 练习题及答案
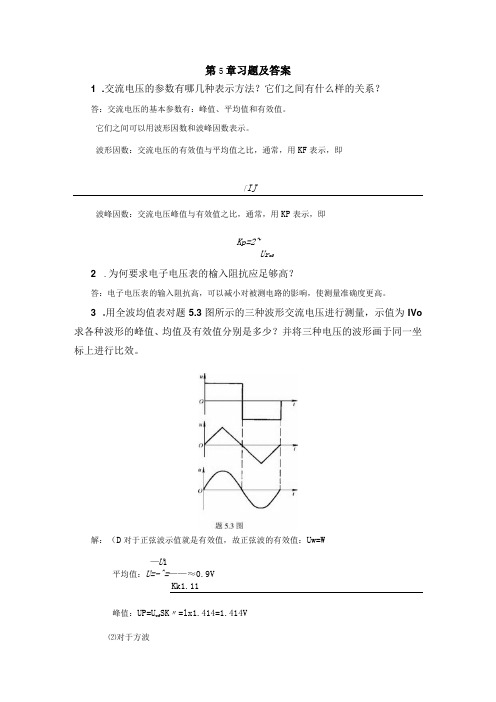
第5章习题及答案1 .交流电压的参数有哪几种表示方法?它们之间有什么样的关系?答:交流电压的基本参数有:峰值、平均值和有效值。
它们之间可以用波形因数和波峰因数表示。
波形因数:交流电压的有效值与平均值之比,通常,用KF表示,即「IJ波峰因数:交流电压峰值与有效值之比,通常,用KP表示,即Kp=2~Ur mS2 .为何要求电子电压表的榆入阻抗应足够高?答:电子电压表的输入阻抗高,可以减小对被测电路的影响,使测量准确度更高。
3 .用全波均值表对题5.3图所示的三种波形交流电压进行测量,示值为IVo 求各种波形的峰值、均值及有效值分别是多少?并将三种电压的波形画于同一坐标上进行比效。
解:(D对于正弦波示值就是有效值,故正弦波的有效值:Uw=W—U1平均值:U=-^=——≈0.9VKk1.11峰值:UP=U wf SK〃=lx1.414=1.414V⑵对于方波・・・方波电压的有效值 U nns =0.9K F U a =0.9X1×1=0.9V—U 1平均值:t/=—三-=-=ιv KF I峰值:UP=U WW K 产IXl=W⑶对于三角波 V 三角波的波形因数K 产1.15,示值Ua=W・・・三角波电压的有效值U rmS =09KFUa =0.9×1.15×1=1.35V-U 1平均值:U=-^=——≈0.87VK F 1.15峰值:UF=U ZW SK 产lxl.73=1.73V4.用峰值电压表对题5.3图所示三种波形电压进行测量,示值为1V,试分别求出其有效值、平均值、峰值各为多少?并将三种电压波形画于同一坐标上加以比较。
解:⑴对于正弦波,示值就是有效值,故正弦波的有效值UW=IV 峰值:UP=y∣2U a =√2×1=1.4IV—U 1平均值:U=-^=——≈0.9V KF 1.11⑵对于方波・・•方波的波峰因数为KP=1.示值τj∖∣2V2U=——Ua =——×1≈1.41VWW K p a 1 峰值:^=^=√2×1=1.41VKp=^J3Ua =IVV 三角波的波峰因数为 ,号值・・・三角波的有效值:U zW s=性Ua=,xl ≈0.82VV 方波的波形因数 =1,示值 Ua=W平均值:U=U 「1 KF T =IV ⑶对于三角波峰值:UP=E=亚×l=14W5.用一台5位半的DVM 进行电压测量,已知固有误差为±0.003%读数土 Qoo2%满度。
霍尔传感器误差原因及补偿措施

2 影响测量精确度的因素
2.1 温度误差
霍尔传感器的材料一般是半导体,随温 度变化较为明显,尤其是输入输出电阻和灵敏 度随温度变化而变化,导致对测量的精度有着 很大的影响。
3.1 温度误差补偿措施
(1)使用温度系数较小的半导体作为材 料,如 InAs。
(2)使用恒流源供电且输入回路并联电 阻补偿方法。
文/章程
摘
本文介绍了霍尔传感器在应
用过程中存在的测量精度误差原 要 因,并且有针对性的提出了补偿
方 法。 霍 尔 传 感 器 的 材 料 一 般 是
半 导 体, 因 此 容 易 受 温 度 变 化 的
干 扰, 且 制 造 过 程 中 由 于 霍 尔 电
极 位 置 影 响, 会 产 生 温 度 误 差 和
按照n型半导体的导电规律自由电子将会向着和电流i相反的方向移动产生一个速度v当磁场中的自由电子受到洛伦兹力f的作用后正负电荷将分别沿着垂直于磁场和电流的方向往导体两侧移动最终汇集在导体两侧形成一个稳定的电动势uh即霍尔电动势称这种现象霍尔效应
• 电子技术 Electronic Technology
霍尔传感器误差原因及补偿措施
4 结束语
随着科技的进步,我们更加重视传感器 的精度问题。霍尔传感器有着广泛的应用,但 由于测量精度随温度变化明显,并且存在不等 位电势等原因,霍尔传感器的精确性存在局限。
图 2:零位误差补偿电路
针对各种误差列举出了相应误差补偿措施,其 中温度误差补偿措施有 5 点,零位误差补偿措 施有 2 点,较为广泛的是采用补偿电路。使用 以上补偿措施对霍尔传感器进行改进,将会极 大的提高霍尔传感器精度并且对其未来的使用 和发展具有积极的意义。
1 霍尔效应原理
电子测量技术课后答案(赵会兵版)

电子测量技术的应用领域
电力领域
电力设备的电气参 数测量、电网运行 监测等。
医疗电子
医疗设备的电气性 能测试、生命体征 监测等。
通信领域
通信设备的性能测 试、网络质量监测 等。
汽车电子
汽车电子控制系统 的故障诊断、排放 控制等。
科研领域
03 电子测量仪器及其应用
信号发生器及其应用
正弦波信号发生器
用于产生稳定的正弦波信号,常用于测试电子设 备的性能和测量基本参数。
脉冲信号发生器
能产生各种宽度、幅度和重复频率的脉冲信号, 用于测试数字电路的时序和逻辑功能。
函数信号发生器
能产生三角波、方波、正弦波等周期信号,常用 于模拟电路的测试和校准。
03
电子测量的基本原理基于电磁 感应定律、欧姆定律等物理学 原理,通过电子元件和电路实 现测量。
电子测量的基本方法
直接测量
直接读取被测量的数值,如使用万用表测量电压或电流。
比较测量
通过比较器将被测信号与标准信号进行比较,从而得出被测信号 的数值。
间接测量
通过测量与被测物理量相关的其他量,再经过计算得出被测物理 量。
故障诊断与排除
根据测量结果,诊断设备故障原因,提出相应的维修和排除故障方 案。
05 电子测量技术的发展趋势 与挑战
电子测量技术的发展趋势
智能化 数字化 微型化 集成化
随着人工智能和机器学习技术的快速发展,电子测量技术正朝 着智能化方向发展,实现自动识别、自动测量和自动分析等功
能。
数字化技术使得电子测量更加精确和可靠,同时也提高了测量 效率,降低了测量误差。
通信信号的测量与分析
《电子测量技术》实验指导书2014(DOC)

《电子测量技术》实验指导书(试用版)适用专业:电子信息工程通信工程安徽建筑工业学院电子与信息工程学院2007年09月目录前言 .......................................................................................... 错误!未定义书签。
实验一:误差分析与数据处理 .. (1)实验二:示波器的原理及应用 (5)实验三:电压的测量 (9)实验四:频谱分析仪原理及应用研究 (12)实验一:误差分析与数据处理实验学时:3实验类型:演示实验要求:必修一、实验目的1、学习万用表等测量工具的使用方法2、掌握测量数据的处理方法二、实验内容1、用万用表测量电阻R值及交流电压值,各测量20个数据,然后进行数据处理,分析测量误差。
(1)电阻R的测量先从电阻色环上读取电阻阻值大小,再用万用表的欧姆档测量电阻R值,看与读取数值是否相符。
共测20次,得到20个数据,求出在置信概率95%时被测元件的估计值、方差及测量结果,测量及计算过程如下表所示:表1-1(2)交流电压的测量利用信号发生器产生一个频率为50Hz,振幅为20V以内的低频正弦信号,利用数字万用表交流电压档测量信号电压,测量20次,获得20个数据,求出该信号的估计值,方差及测量结果。
表1-2三、实验原理、方法和手段一个物理量在一定条件下所呈现的客观大小或真实数值称作它的真值,而真值必须利用理想的量具或者测量一起进行无误差的测量,因而是无法测到的。
在实际测量中所得到的都是利用各中测量器具所测得的测量值,由于测量器具不准确,测量手段不完善,环境影响等等原因,必然导致产生测量误差,测量误差具有普遍性和必然性,人们只能将误差限制在一定的范围内而不可能消除。
测量的绝对误差定义为:△x =x -A 0 ,其中x 为测得值,A 0为被测量的真值,而A 0一般无法获得,只能利用实际值A 去代替,由在对被测量的多次测量值中,剔除了系统误差及粗大误差后,剩下的随机误差具有抵偿性,因而为获得比较接近A 的测量结果提供了可能。
现代电子测量(三)

1V -3db=0.707V 带宽
频率
Risetime(ns) =350/bandwidth(MHz) Measured risetime(tr)2 = (tr signal)2+(tr scope)2
如需精确测量: 示波器带宽 > 3 × 信号频率
示波器基本参数
Sample Rate/Bandwidth vs. Risetime Error 示波器采样率( S/s ,点 /秒)的选择
位置,可以采集触发事件以前的信号。
模拟示波器在垂直系统中由延迟线提供了小量的预触
发。
示波器的基本控制
触发系统和控制——触发电平和斜率 斜率控制决定触发点是位于信号的上升沿还是下降沿。上
升沿具有正斜率,而下降沿是负斜率; 电平控制决定触发点在边缘的何处发生。
示波器的基本控制
触发系统和控制——触发源 任何一个输入通道; 不同于输入通道的外部源; 电源信号;
现代电子测量(三)
示波器基本知识
本节课的主要内容
示波器发展、分类与特点 示波器原理 示波器的基本控制 示波器基本参数 示波器使用实例介绍
示波器的发展
第 一 代 —— 模 拟 示 波 器 ( ART-Analog Real Time
Oscilloscope)
廿世纪四十年代——电子示波器兴起的时代; 廿世纪六十年代——出现了带宽6GHz的取样示波器;
Oscilloscope)
1978年——出现了数字储存示波器,它是公认的第二代示波
器产品;
进入九十年代——数字示波器除了提高带宽到 1GHz以上,更
重要的是它的全面性能超越模拟示波器。
示波器的分类
电子测量技术

电子测量技术新形势下,随着现代化科技的蓬勃发展,电子测量技术在实际生活中的发展及应用越来越受到人们的广泛关注和重视。
电子测量技术,作为大多数电子产品精密及准确测量的重要技术,广泛应用于测量电能量、信号特性及其所受干扰、元件及电路参数等电学专业的测量。
就目前的电子技术市场来看,可以说,电子测量技术的应用早已进入了一个较为理想和成熟的发展环境。
电子测量仪器是知识密集、技术密集、高速发展中的行业。
由于微电子技术、计算机技术的高速发展及其在电子测量技术与仪器中的应用,新的测试理论、测试方法、测试领域以及新的仪器结构不断涌现,在电子、电力、航空、航天、能源、交通、广播、电视、通信及其信息系统、微电子及电子元器件测试等方面已冲破了传统仪器的概念。
电子测量主要应用于电学专业的测量,例如,电信号传输特性的测量。
电子测量也广泛的应用于非电学专业的测量,例如,它通过各种类型的传感器,能量转化器把非电量(如热力学、光学、机械学的物理量)转换为电量(如电流、电压、频率等)进行研究,而后得出反映出非电量的测量结果。
随着电子技术的不断发展,测量的内容愈来愈广泛,通常包括以下几个方面:(1)电能量的测量,包括对于电流、电压、电功率的测量。
(2)信号的特性及所受干扰的测量,例如信号的失真度、频率相位、脉冲参数、调制度、信号频谱、信噪比等。
(3)元件和电路参数的测量,例如电限、电感、电容、电子器件(电子管、晶体管、扬效应管等)的测量,集成电路的测量,电路频率响应、通频带宽度、品质因数、相位移、延时、衰减和增益等的测量。
然而目前国际上著名仪器公司电子仪器销售额所占比例不断下降,国内电子仪器厂所处的状况大致类同。
因而研究我国当前电子测量仪器行业发展战略决策,已成为仪器行业专家们共同关注的问题电子测量技术的测量频率范围广相对于以往的测量技术来说,电子测量技术具有测量频率范围宽、量程大等优势。
通过电子测量技术的实际应用,能够利用电子测量仪器,进行深海压力、高温炉温度等特殊环境下的测量工作,一定程度上降低了测量人员的工作强度,同时也有效保证了测量结果的准确性和客观性。
电子测量技术课后习题答案1-8章

《电子测量技术》------课后习题第一章1.1解释名词:①测量;②电子测量。
答:测量是为确定被测对象的量值而进行的实验过程。
在这个过程中,人们借助专门的设备,把被测量与标准的同类单位量进行比较,从而确定被测量与单位量之间的数值关系,最后用数值和单位共同表示测量结果。
从广义上说,凡是利用电子技术进行的测量都可以说是电子测量;从狭义上说,电子测量是指在电子学中测量有关电的量值的测量。
1.2叙述直接测量、间接测量、组合测量的特点,并各举一两个测量实例。
答:直接测量:它是指直接从测量仪表的读数获取被测量量值的方法。
如:用电压表测量电阻两端的电压,用电流表测量电阻中的电流。
间接测量:利用直接测量的量与被测量之间的函数关系,间接得到被测量量值的测量方法。
如:用伏安法测量电阻消耗的直流功率P,可以通过直接测量电压U,电流I,而后根据函数关系P=UI,经过计算,间接获得电阻消耗的功耗P;用伏安法测量电阻。
组合测量:当某项测量结果需用多个参数表达时,可通过改变测试条件进行多次测量,根据测量量与参数间的函数关系列出方程组并求解,进而得到未知量,这种测量方法称为组合测量。
例如,电阻器电阻温度系数的测量。
1.3解释偏差式、零位式和微差式测量法的含义,并列举测量实例。
答:偏差式测量法:在测量过程中,用仪器仪表指针的位移(偏差)表示被测量大小的测量方法,称为偏差式测量法。
例如使用万用表测量电压、电流等。
零位式测量法:测量时用被测量与标准量相比较,用零示器指示被测量与标准量相等(平衡),从而获得被测量从而获得被测量。
微差式测量法:通过测量待测量与基准量之差来得到待测量量值。
如用微差法测量直流稳压源的稳定度。
1.4叙述电子测量的主要内容。
答:电子测量内容包括:(1)电能量的测量如:电压,电流电功率等;(2)电信号的特性的测量如:信号的波形和失真度,频率,相位,调制度等;(3)元件和电路参数的测量如:电阻,电容,电感,阻抗,品质因数,电子器件的参数等;(4)电子电路性能的测量如:放大倍数,衰减量,灵敏度,噪声指数,幅频特性,相频特性曲线等。
14级电子测量与仪器答案

周口职业技术学院期末考试试卷答案考试科目:电子测量与仪器试卷适用专业:14级应用电子技术考核方式:开卷()闭卷(√)2014~2015学年度二学期套别:Ⅰ套一、填空题(每空2分,共30分)1、RC桥式振荡电路;电压和功率2、频率比;周期3、4 ;41/2;4、电子枪;偏转系统;5、等幅扫频信号;幅度6、电桥平衡原理;7、软件;采集硬件;现代仪器技术与计算机技术8、0.25二、判断题(每题1分,共10分)1√2×3×4√5√6×7√8×9√10×三、简答题(每题5分,共30分)1、虚拟仪器(Virtual Instrument简称VI)也叫计算机仪器,是以计算机为基础,配以相应测试功能的硬件作为信号输人输出的接口,利用虚拟仪器软件开发平台(如LabVIEW Lab Windows/CVI )在计算机的屏幕上虚拟出仪器的面板(包括显示器、指示灯、旋钮、开关、按键等)并实现相应的功能,人们可以通过鼠标或键盘操作虚拟仪器面板上的旋钮、开关和按键,去选用仪器功能,设置各种工作参数,启动或停止一台识器的工作 .2、低频信号发生器的基本组成包括主振级、主振输出调节电位器、电压放大器、输出衰减器、功率放大器、阻抗变换器(输出变压器)和指示电压表。
主振级产生低频正弦振荡信号,经电压放大器放大,达到电压输出幅度的要求,经输出衰减器可直接输出电压,用主振输出调节电位器调节输出电压的大小。
电压输出端的负载能力很弱,只能供给电压,故为电压输出。
振荡信号再经功率放大器放大后,才能输出较大的功率。
阻抗变换器用来匹配不同的负载阻抗,以便获得最大的功率输出。
电压表通过开关换接,测量输出电压或输出功率3、通用电子计数器具有测量频率、频率比、周期、时间间隔、累加计数以及自检等功能。
电子计数器由输入通道、计数显示电路、标准时间产生电路和逻辑控制电路等部分组成。
它的测量原理是闸门开启时间等于计数脉冲周期与计数脉冲计数值之积4、 用数字万用表测量直流电压;用模拟式万用表测量直流电压用零示法测量直流电压;用电子电压表测量直流电压用示波器测量直流电压微差法测量直流电压含交流成分的直流电压的测量5、通用示波器是由主机、垂直通道(Y 通道)、水平通道(X 通道)三大部分组成。
《电子测量技术》习题(三)答案

《电子测量技术》习题(三)答案一、填空题(每空1分,共25分)1.电子测量的内容包括(电能量的测量)、(电子元器件参数的测量)、(电信号的特性和质量的测量)、(电路性能的测量)和(特性曲线的测量)五个方面。
2.相对误差定义为(绝对误差)与(真值)的比值,通常用百分数表示。
3.电子测量按测量的方法分类为(直接测量)、(间接测量)和(组合测量)三种。
4.为保证在测量80V电压时,误差≤±1%,应选用等于或优于(±0.5)级的100V量程的电压表。
5.用四位半的DVM测量15V的稳压电源电压为15.125V,取四位有效数字时,其值为(15.13V)。
6.示波器为保证输入信号波形不失真,在Y轴输入衰减器中采用(RC分压电路)电路。
7.电子示波器的心脏是阴极射线示波管,它主要由(电子枪)、(偏转系统)和(荧光屏)三部分组成。
8.示波器的“聚焦”旋钮具有调节示波器中(第一阳或A1 )极与(第二阳或A2、G2)极之间电压的作用。
9.没有信号输入时,仍有水平扫描线,这时示波器工作在(连续扫描)状态,若工作在(触发扫描)状态,则无信号输入时就没有扫描线。
10.电压表的基本组成形式为(检波—放大)式。
11.电子计数器的测周原理与测频相反,即由(被测输入信号)信号控制主门开通,而用(晶体震荡器信号)脉冲进行计数。
12.数字电压表的最大计数容量为19999,通常称该表为(4 或四位半)位数字电压表;若其最小量程为0.2V,则其分辨力为(10μV)。
二、改错题1.双踪示波器中电子开关的转换频率远大于被测信号的频率时,双踪显示工作在“交替”方式( 交替改成断续)2.示波器扫描信号频率是被测信号频率的倍时,屏幕上显示的波形向左跑动。
( 左改成右)3.常用电工仪表分为±0.1、±0.2、±0.5、±1.0、±1.5、±2.5、±4.0七级。
《电子测量技术》模拟试题一

《电子测量技术》模拟试题一一、填空题(共10空,每空2分,共20分)1.电子测量的内容包括电信号能量参数的测量、___________、电路元件参数的测量及电子设备的性能指标测量。
答案:电信号特性参数的测量解析:电子测量的内容即为电子测量的对象,电信号的特性参数是电子测量重要的方面。
2.按测量的手续分类,电子测量的技术方法有:直接测量、__________和组合式测量。
答案:间接测量解析:直接测量、间接测量及组合测量属于电子测量技术在测量手续上的技术分类,大多数的测量实质上是间接测量。
3.测量的过程也是信号变换的过程,电子测量常用的几种变换有:量值变换、__________、参量变换、能量变换和波形变换等。
答案:频率变换解析:将信号(信息)进行变换是为了更好的测量,甚至是将一般不能测量的对象经过信号变换后而实现测量,频率变换就是将一种频率大小的信号转换为另一频率大小的信号。
4.用 1.5级、50mA的电流表测量某个电流值,则有可能产生的最大电流绝对误差为__________mA。
答案:±0.75解析:告诉了仪表的等级及量程,就可以根据引用相对误差的定义计算出量程内可能产生的最大绝对误差。
5.用电子计数器测量交流信号的频率,为了提高测量的准确度,对于高频信号应采用测频率的方法,对于低频信号应采用__________的方法。
答案:测周解析:使用哪种测量方法好,是按照±1误差的大小比较而确定的,±1误差的大小按各自的误差计算公式进行分析。
6.在交流电压模拟式测量中,根据电压表和被测信号参数的对应关系,常用的交流电压表有峰值电压表、__________和有效值电压表。
答案:均值电压表解析:确定是什么类型的交流电压表,是按照电压表内部检波方式决定的。
7.若两个交流电压的峰值相同,当用正弦波有效值刻度的峰值电压表分别测量时,电压表的读数__________。
答案:相等解析:正弦波有效值刻度的峰值电压表内部峰值检波器的输出正比于被测信号的峰值,表做好了,其检波系数就确定了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
29
G99 (15) s (T ) = 2.70 × 0.033 = 0.089C υ8 = 0.104 > G99 (15) s(T )
可判断 T8 是异常值,应予以剔除。再对 剔除后的14个数据重新进行判断。 剔除T8后,剩余数据的算术平均值为:
1 n 1 14 T ' = ∑ Ti = ∑ Ti = 20.411 C n i =1 14 i =1
对于第i项测量值xi,若有
x xi <
x − ks ( x)
xi 或 x
> x + ks ( x)
25
则xi 被视为异常值。
② 常用的判别准则
莱特准则
适用条件 测量数据为正态分布或近似 正态分布,且测量次数较多 (一般 n ≥ 20 )的情况。 在一组重复测量结果中,对于第i 项测量值 xi ,若满足 υi > 3s ( x ) 则视该测量值xi为异常值。 注意:不能用于非正态分布数据或测 量次数较少的情况。
1 s( x ) = s ( xk ) n
19
2.系统误差
(1)系统误差的概念
在重复性条件下,对同一被测量进行 无限多次测量所得结果的平均值与被测量 真值之差,称为系统误差。 系统误差实际反 映了被测量的数学期 望偏离真值的程度。
x
A0
ε
0 1 2 3 4 … i i+1 … n
20
(2)系统误差产生的原因
10
随机误差的定义式:
δi = xi − x
无穷次测量的 算术平均值
x
A0
δi
0 1 2 3 4 …
i i+1
…
∞
残差的定义:
υi = xi − x
有限次测量的 算术平均值
当测量次数趋于无穷时,残差的性质就反 映了随机误差的的性质。
11
(3)随机误差的性质
根据中心极限定理可知,当一个量受多 种随机因素的共同影响而随机取值时,则它 的分布就近似服从正态分布,因此,测量中 的随机误差的分布大多接近正态分布。
xi yi f(xi) Bi
1 1.1 1.12 0.02
2 1.9 1.92 0.02
3 3.2 3.24 0.04
4 3.8 3.84 0.04
5 5.2 5.26 0.06
检测装置的非线性度为: 0.06 Bmax ×100% = 5.2 − 1.1 100% = 1.4% A
若本测量系统为线性系统,则其静态灵敏度可看成是 拟合直线的斜率,即S=1.01( 0C/V)
26
格拉布斯准则
适用条件 适用于各种分布,测量次数多 或少均可。 格拉布斯准则系数 在一组重复测量结果中,对于第i项测 量值 xi ,若满足 υi > G p (n) s ( x) 则视该测量值xi为异常值。 格拉布斯准则系数不仅和测量次数有 关,而且和置信概率有关。其数值可通过 查表得到。
27
例 对温度进行了15次重复测量,测得的温度值 Ti及残差vi列于表1,试检查测量数据中有无异常 值。 表1 测得的温度值及残差
可疑数据-- 与其它数据有明显差异的测 量数据。 可疑数据或为异常值,或为正常值。
可疑数据
p( x)
x
A0
x
u x − 3σ
ux
u x + 3σ
0 1 2 3 4 …
i i+1
…
n
24
利用统计学方法来判断异常值
① 基本思想
给定一个置信概率P,按一定的分布确定相 应的置信区间 [ x − ks ( x ), x + ks ( x ) ] , 凡在此置信区间之外的测量数据就被视为异常值。
6
2、测量误差的表示
⑴ 绝对误差 定义
被测量的测量结果 x 与其真值A0之差。
∆x = x − A0
实际计算式
不可能准 确获知
约定真值 ∆x = x − x0 (实际值) 约定真值:用高一级的标准仪器或计量 标准比对所测得的量值,或已修正过的 多次测量的算术平均值。
7
⑵ 相对误差
绝对误差与被测量的真值之比。 ∆x γA = × 100% A0
12
随机误差δ的概率 密度函数
p (δ ) = 1 2π σ (δ ) e
δ2 − 2σ 2 (δ )
分布曲线
p (δ )
δ
o
随机误差的四个性质:
①单峰性 ②有界性
绝对值小的误差出现的机会比绝对 值大的误差出现的机会多。 多次测量中,误差绝对值的波动有 一定的范围。
13
随机误差δ的概率 密度函数
5 ∑ ������������������������������������������������ − ∑ ������������������������ ∑ ������������������������ ������������0 = 5 ∑ ������������������������2 − (∑ ������������������������ ) 2
������������������������0 ������������ɸ ������������ɸ
=0
且
������������������������0
=0
即
解上述方程组得
带入数据后得
∑ ������������������������2 ∑ ������������������������ − ∑ ������������������������ ∑ ������������������������������������������������ ������������0 = 5 ∑ ������������������������2 − (∑ ������������������������ ) 2 ������������0 =1.01 ������������0 =0.01
p (δ ) = 1 2π σ (δ ) e
δ2 − 2σ 2 (δ )
分布曲线
p (δ )
δ
o
随机误差的四个性质:
③对称性 当测量次数足够多时,绝对值相等的 正、负误差出现的机会几乎相同。 ④抵偿性 当测量次数足够多时,随机误差的 算术平均值趋于零。
14
根据随机误差的性质,在实际测量中,可 通过多次测量取平均值的办法来减小随机误差 对测量结果的影响。
第二章 测量误差与测量不确定度
§ 2.1 测量误差 § 2.2 测量不确定度 § 2.3 标准不确定度的评定 § 2.4 合成标准不确定度的评定 § 2.5 扩展不确定度的评定 § 2.6 测量不确定度的报告
5
2.1
测量误差
2.1.1 测量误差的基本概念及表示
1.基本概念
测量误差:测量结果与被测量真值之间的差异。 测量结果——由测量赋予的被测量之值。可 以是单次测量时仪器的示值、也可以是多次 重复测量的平均值。 真值——指一个物理量在一定条件下所呈现 的客观大小或真实数值。
p( x) = 1
分布曲线
p( x)
[ x − µ x ]2 − 2σ 2 ( x )
σ ( x) 2π
e
x
ux
16
被测量的表征
被测量X的数学期望E ( X ) = u x 2 ( x) D ( X ) = σ 方差 标准差 D( X ) = σ ( x) 注意: 在有限次测量中,通常采用测量值的算术 平均值来作为被测量数学期望的估计值;采用 实验标准差来作为被测量标准差的估计值。
17
① 测量值的算术平均值 --数学期望的估计值
1 n x = ∑ xk n k =1
② 测量值的实验标准差 --标准差的估计值 贝塞尔公式
s ( xk ) =
1 n 2 ( xk − x ) = ∑ n − 1 k =1
1 n 2 υk ∑ n − 1 k =1
18
③ 算术平均值的实验标准差 --算术平均值标准差的估计值
例:1.5级的仪表即 a = 1.5 则 γ m ≤ 1.5% 或 γ m 测量误差的分类 1.随机误差
(1)随机误差的概念
在同一测量条件下多次重复测量同一量时, 由多种对测量观测值影响微小、相互独立且 无确定规律的随机因素的影响所导致的、每 次测量中其绝对值和符号都以不可预知的方 式变化的测量误差。
测量设备的缺陷 测量环境条件不合要求 测量方法不完善 测量人员的不良习惯及生理条件限制
(3)系统误差的修正
利用修正值对测量结果中的系统误差进行修正
修正值
c = x0 − x
被测量的实际值 x0 = x + c
21
注意:修正值具有一定的不确定度,因此 在进行不确定度评定时,修正值的测量 不确定度应作为一个分量来考虑。
序号i 1 2 3 4 5 6 7 8 Ti (℃) 20.42 20.43 20.40 20.43 20.42 20.43 序号i 9 10 11 12 13 14 20.39 20.30 15
vi(℃) 0.016 0.026 -0.004 0.026 0.016 0.026 -0.014 -0.104 Ti(℃) 20.40 20.43 20.42 20.41 20.39 20.39 20.40 vi(℃) -0.004 0.026 0.016 0.006 -0.014 -0.014 -0.004
∑ ������������������������2 ∑ ������������������������ − ∑ ������������������������ ∑ ������������������������������������������������ ������������0 = ������������ ∑ ������������������������2 − (∑ ������������������������ ) 2
