ANSYS常用压电陶瓷的材料系数
用ANSYS软件分析压电陶瓷的振动状态

第30卷第1期2008年3月湖北大学学报(自然科学版)Journal of Hubei University (Natural Science )Vol.30 No.1 Mar.,2008 收稿日期:2006206202作者简介:雷辉(19812 ),男,硕士生文章编号:100022375(2008)0120029205用ANSYS 软件分析压电陶瓷的振动状态雷辉,周双娥(湖北大学数学与计算机学院,湖北武汉430062)摘 要:近年来,压电陶瓷的应用日趋广泛.但是由于压电陶瓷片的边界条件和应力状况比较复杂,利用传统实验手段对其研究不仅耗时费力,而且其结果具有很强的局部性,因此利用大型通用仿真软件ANSYS 8.0来进行计算机仿真.通过对压电陶瓷片中的耦合效应进行计算机模拟分析,得出压电陶瓷的振动状态图.实验结果表明ANSYS 8.0在处理压电耦合场这方面有很强的处理能力,大大简化了建模和计算,强大的后处理功能更是让研究者能够很直观地获得数据结果和模拟图像. 关键词:仿真;压电陶瓷;振动状态 中图分类号:TP302 文献标志码:A1 引言计算机仿真技术是以多种学科和理论为基础,以计算机及其相应构件为工具,通过虚拟试验的方法来分析和解决问题的一门综合性技术[1].近年来,压电陶瓷的应用日趋广泛,而在实际应用中,特别是将压电陶瓷技术应用于混凝土结构的监测中,由于压电陶瓷片的边界条件和应力状况比较复杂,利用传统实验手段对其研究不仅耗时费力,而且其结果具有很强的局部性[2].因此利用计算机仿真技术对压电陶瓷进行研究具有较好的理论与实际意义.本文中利用大型通用有限元分析软件ANS YS 8.0,对压电陶瓷片中的耦合效应进行模拟分析,并得出其模态和谐振态,实验表明ANS YS 8.0能很好地解决压电陶瓷片的压电耦合问题.图1 处理器模型2 ANSYS 仿真原理ANS YS 软件是融结构、流体、电场、磁场、声场分析于一体的大型通用有限元分析软件,由世界上最大的有限元分析软件公司之一的美国ANS YS 开发,它能与多数CAD 软件接口,实现数据的共享和交换.20世纪90年代该软件开始在我国的机械制造、航空航天、汽车交通、铁道、石油化工、能源等领域得到应用,为各领域中产品设计、科学研究作出了很大的贡献[3].ANS YS 软件使用统一的集中式数据库来存储所有模型数据和求解结果(见图1)[4].模型数据(包括实体模型和有限元模型、材料等)通过前处理器写入数据库;载荷和求解结果通过求解器写入数据库;后处理结果通过后处理器写入数据库.3 处理过程3.1 定义材料参数 材料参数包括定义单元类型,这里选取了solid226,并在它的option 选项里选择压 湖北大学学报(自然科学版)第30卷30电这个选项.然后定义压电陶瓷的密度、介电常数、刚度系数和压电常数,后两个参数是用矩阵的形式来表示的.为了方便后期的网格划分处理,添加了一个单元类型mesh200,它主要用来进行面划分,下一节将详细介绍.定义材料参数的部分代码及注释如下所示:ET,1,SOL ID226,101 !定义solid226单元类型KEYOP T,1,1,1001!在solid226选项中选择压电选项ET,2,M ESH200!3!定义mesh200单元类型KEYOP T,2,1,7KEYOP T,2,2,0MPTEMP,,,,,,,,MPTEMP,1,0MPDA TA,DENS,1,7600!定义压电陶瓷密度TB,AN EL,1,1,21,0!定义压电陶瓷的刚度系数TB TEMP,0TBDA TA,,1.32e11,7.1e10,7.3e10,,,TBDA TA,,1.32e11,7.3e10,,,,1.15e11TBDA TA,,,,,3.0e10,,TBDA TA,,2.6e10,,2.6e10,,,MPTEMP,,,,,,,,!定义压电陶瓷的介电常数MPTEMP,1,0MPDA TA,PERX,1,,7.124e-9MPDA TA,PER Y,1,,7.124e-9MPDA TA,PERZ,1,,5.841e-9TB,PIEZ,1,,,0!定义压电陶瓷的压电系数TBMODIF,1,1,TBMODIF,1,2,TBMODIF,1,3,-4.1TBMODIF,2,1,TBMODIF,2,2,TBMODIF,2,3,-4.1TBMODIF,3,1,TBMODIF,3,2,TBMODIF,3,3,14.1TBMODIF,4,1,TBMODIF,4,2,TBMODIF,4,3,TBMODIF,5,1,TBMODIF,5,2,10.5TBMODIF,5,3,TBMODIF,6,1,10.5TBMODIF,6,2,TBMODIF,6,3,3.2 建立模型及网格划分 首先新建一个长为0.005m,宽为0.001m的矩形.然后选取单元类型为mesh200,对该矩形进行面划分,其中长和宽分别划分8份和10份,结果如图2所示.然后用操作选项中的Ext rude命令将其扩展成一个已划分好的圆盘体,其中要在Extrude选项中将单元类型选择为solid226,并在要划分的数目中填入10.接着用Extrude命令将其扩展成一个圆盘,其扩展结果如图3所示.第1期雷辉等:用ANSYS 软件分析压电陶瓷的振动状态31 图2 面划分图 图3 体划分图3.3 添加约束条件和负载 添加的约束条件是在上、下表面的圆心处分别添加位移约束,使其只能沿纵向方向移动.具体代码及注释如下:nsel ,s ,loc ,y ,0nsel ,r ,loc ,z ,0nsel ,r ,loc ,x ,0!选取下表面圆心上的点d ,all ,ux ,0!使其不能沿x 方向运动d ,all ,uz ,0!使其不能沿y 方向运动nsel ,s ,loc ,y ,0.001!选取上表面圆心上的点nsel ,r ,loc ,z ,0!同理nsel ,r ,loc ,x ,0d ,all ,ux ,0d ,all ,uz ,0给圆盘添加的电压负载是在圆盘的上下表面的两个电极上加上耦合电压,其电压值分别为5伏和0伏.这样使得圆盘上下电势差为5伏.其代码及注释如下:nsel ,s ,loc ,y ,0!选取下表面所有节点cp ,1,volt ,all !为下表面添加耦合电压3get ,n_bot ,node ,0,num ,min !定义下表面的电极节点nsel ,s ,loc ,y ,0.001!选取上表面所有节点cp ,2,volt ,all !为上表面添加耦合电压3get ,n_top ,node ,0,num ,min !定义上表面的电极节点nsel ,all !选取所有节点d ,n_bot ,volt ,0!下表面加0伏电压d ,n_top ,volt ,5!上表面加5伏电压3.4 静态和模态下的处理 首先选择处理状态为静态,并在此状态下得出其静态电容,代码及注释如下:/SOL !进入处理环节AN T YPE ,0!选择静态处理/STA TUS ,SOL U SOL V E !求解3get ,cs ,node ,n_top ,rf ,chrg !得到上电极电量值fini !处理结束3SET ,cs ,abs (cs )/5!得到静态电容接着进行模态分析,设定它有20个子步,频率范围为02200000Hz ,并且将上表面短路,代码及注释如下:/SOL U !进入处理环节AN T YPE ,2!选择模态处理MODOPT ,L ANB ,20!定义处理方法和子步数EQSL V ,SPAR !选择处理器MXPAND ,20,,,1!要显示的子步数L UMPM ,0PSTRES ,0MODOPT ,L ANB ,20,0,2000000,,OFF !定义频率范围32 湖北大学学报(自然科学版)第30卷d ,n_top ,volt ,0!上表面短路nsel ,all!选择所有节点/STA TUS ,SOL USOL V E !求解3.5 后处理 后处理是指检查并分析求解的结果的相关操作.这是分析中最重要的环节之一,因为任何分析的最终目的都是为了研究作用在模型上的的载荷是如何影响设计的[5].检查分析结果可使用两个后处理器:POST1(通用后处理器)和POST26(时间历程后处理器).POST1允许检查整个模型在某一载荷步和子步(或对某一特定时间点或频率)的结果.POST26可以检查模型的指定节点的某一结果项相对于时间、频率或其它结果项的变化.在求解时,ANS YS 将结果写入结果文件,进行后处理时,结果文件必须存在且可用.结果文件名的后缀取决于分析类型,对于结构分析的结果文件的后缀为RST [6].本次实验只用到了POST1.在后处理中利用一个循环语句可以得出不同频率下的动态电容、动态电感、电量以及阻抗值.其代码和注释如下:/POST13SET ,nmodes ,20!定义nmodes =203dim ,C ,array ,nmodes!定义电容数组3dim ,L ,array ,nmodes!定义电感数组3SET ,PI2,233.14159!定义PI2=233.14159set ,first!设定第一个子步/com ,3do ,i ,1,nmodes !定义一个循环,从1到20步3get ,Fi ,mode ,i ,freq !得到该步的频率值3get ,Qi ,node ,n_top ,rf ,chrg !得到该步的电量值3SET ,Omi ,Pi23Fi !将线速度转化为角速度3SET ,C (i ),(Qi/Omi )332!计算相关的动态电容3SET ,L (i ),1/(Omi 3323C (i ))!计算相关的动态电感/com ,Mode %i %!在输出窗口中显示第几步/com ,Resonant f requency F =%Fi %Hz !在输出窗口中显示频率值/com ,Dynamic capacitance C =%C (i )%F !在输出窗口中显示动态电容值/com ,Dynamic inductance L =%L (i )%H !在输出窗口中显示动态电感值/com ,charge Q =%Qi %C!在输出窗口中显示电量值/com ,Impedance R =%5/(233.141593Fi 3Qi )%!在输出窗口中显示阻抗值/com ,set ,next !进入下一个子步3enddo!循环结束FINISH同时可以在主菜单的Animation 选项下看一下压电圆盘在各个不同频率下的振动状态,这里截取了几个振动图,如图4所示:(a )频率为29728Hz (b )频率为65741Hz (c )频率为53476Hz图4 振动状态图第1期雷辉等:用ANSYS软件分析压电陶瓷的振动状态33 4 结束语本文对压电陶瓷圆盘添加了约束和对称负载,解决了压电陶瓷压电场与结构场的耦合问题,并且最终得到了压电圆盘在静态下的电容值,以及它在模态下的动态电容、动态电感、电量和阻抗,而且还可以观察圆盘在各个不同频率下的振动状态,以便于今后对材料性能的研究以及对材料的改进.同时,不难发现Ansys8.0在处理压电耦合场这方面有很强的处理能力,像Solid226就是专门针对压电分析而定义的,而且Ansys8.0在其材料库中建立了相关的压电材料,因此大大简化了有限元的建模和计算,强大的后处理功能更是让研究者能够很直观的获得数据结果和模拟图像.参考文献:[1]林书玉,张福成.压电陶瓷圆片振子的多模耦合振动[J].电子学报,1994,12:43249.[2]姜德义,郑拯宇.压电陶瓷片耦合振动模态的ANSYS模拟分析[J].传感技术学报,2003,12:9216.[3]陈大任.压电陶瓷微位移驱动器概述[J].电子元件与材料,1994,2:33240.[4]邵蕴秋.ANSYS8.0有限元分析实例导航[M].北京:中国铁道出版社,2004.[5]刘涛.精通ANSYS[M].北京:清华大学出版社,2002.[6]任重.ANSYS实用分析教程[M].北京:北京大学出版社,2003.Using ANSYS to analyze the vibration state of piezoelectric ceramicL EI Hui,ZHOU Shuang2e(School of Mathematics and Computer Science,Hubei University,Wuhan430062,China) Abstract:The application of piezoelect ric ceramic becomes more and more extensive,However,it needs to take much more time to st udy it by t raditional experiment s and t he result s are often unilateral for complex prezoelect ric ceramics boundary co ndition and st ress state.In t his view,we use big2scale general piezoelect ric ceramic’s boundary condition and st ress state simulating software ANS YS8.0to carry t hrough comp uter simulation.We gain t he pict ure of piezoelect ric ceramic’s vibration state by using comp uter to analyze t he coupling effect of piezoelect ric ceramic.The experiment result indicates t hat ANS YS8.0can competently deal wit h p roblems about piezoelectric coupling field.It optimizes t he time of creating model and comp uting largly,and it s st rong f unction of post dealing makes researchers can directly obtain data result s and simulating images.K ey w ords:simulation;piezoelect ric ceramic;vibratio n state(责任编辑肖铿,胡小洋)。
(完整版)ansysworkbench常见材料设置

Ansys workbench常用材料属性
1. isotropic secant coefficient of expansion 各向同性的热胀系数
需要输入基准温度、热膨胀系数。
基准温度,默认22度热膨胀系数
2. orthotropic secant coefficient of expansion 各向异性的热胀系数
需要输入基准温度、三个方向的热膨胀系数。
3. isotropic instantaneous coefficient of expansion 各向同性的热胀系数(随温度变化)需要输入基准温度、热膨胀系数。
(随温度变化)
4. orthotropic instantaneous coefficient of expansion 各向异性的热胀系数(随温度变化)需要输入基准温度、三个方向的热膨胀系数。
(随温度变化)
5. 阻尼系数、质量阻尼、刚度阻尼
6.Isotropic elasticity 各项同性的线弹性材料
需要输入弹性模量与泊松比
7.orthotropic elasticity 各项异性的线弹性材料
需要输入各方向的弹性模量与泊松比
8 Bilinear isotropic/kinematic hardening 双线性材料(非线性材料)需要输入屈服强度及切向模量,需要配合isotropic elasticity使用。
9.multilinear isotropic/kinematic hardening 多线性材料(非线性材料,应力应变曲线)需要配合isotropic elasticity使用,输入应力应变曲线。
压电陶瓷振动的有限元分析ansys

廖火生压电陶瓷悬臂板振动的参数化研究第一章绪论1.1压电材料概述1.1.1压电效应1880年法国物理学家皮埃尔和雅各居里兄弟在研究石英晶体的物理性质时发现:当沿着晶片的某些方向施加作用力使晶片发生变形后,晶片上相对的两个表面会出现等量的正负电荷,电荷的密度与施加的力的大小有关,这种现象称为压电现象,具有压电现象的介质称为压电体。
压电效应反应了晶体的弹性性能与介电性能之间的耦合。
当对压电陶瓷施加一个与极化方向平行的压力F,如图1.1(a)所示,陶瓷片将产生压缩变形,片内的正、负束缚电荷之间的距离变小,极化强度也变小。
因此,原来吸附在电极上的自由电荷,有一部分被释放,片内的正、负电荷之间的距离变大,极化强度也变大,因此电极上又吸附一部分自由电荷而出现充电现象。
这种由机械效应转变为电效应的现象就是压电效应。
压电效应包括正压电效应和逆压电效应。
如图所示:图1.1 压电效应示意图:(a)正压电效应(b)负压电效应正压电效应:当压电晶体在外力作用下发生形变时,在它的某些相对应的面上产生异号电荷,这种没有电场作用,只是由于形变产生的极化现象称为正压电效应。
1廖火生压电陶瓷悬臂板振动的参数化研究逆压电效应:当压电晶体施加一电场时,不仅产生了极化,同时还产生了形变,这种由电场产生形变的现象称为逆压电效应。
1.1.2压电陶瓷的诞生与发展具有压电效应性能的陶瓷称为压电陶瓷,1942年美国麻省理工学院绝缘研究室发现,在钛酸钡铁电陶瓷上施加直流高压电场,使其自发极化沿电场方向择优取向,除去电场后仍能保持一定的剩余极化,使它具有压电效应,从此诞生了压电陶瓷。
钛酸钡()陶瓷的发现促进了压电材料的发展,BaTiO3它不但使压电材料从一些单晶体材料发展到压电陶瓷等多晶体材料,而且在压电性能上也有了大幅度提高。
??OTiZrPb,压电陶瓷,其压电效应强,当今广泛应用的压电陶瓷是PZT,即3PbZrO?PbTiO二元系年发现的它是由美国学者B.贾菲等人于1954稳定性好。
压电陶瓷材料测试需要知道的13个基本参数

压电陶瓷材料测试需要知道的13个基本参数压电陶瓷材料是一种具有压电效应的材料,可将机械的压力或应力转化为电能,同时也可以将电能转化为机械的压力或应力。
因此,对于压电陶瓷材料的测试,需要关注以下13个基本参数。
1.介电常数(Dielectric constant):介电常数是指材料在电场作用下的电极化能力,是压电陶瓷材料的一个重要指标。
介电常数越大,材料的电极化能力越强。
2.电容(Capacitance):电容是指单位电压下存储的电荷量,通常以法拉(F)为单位。
对于压电陶瓷材料,电容可以用来判断材料的电性能。
3.压电系数(Piezoelectric coefficient):压电系数是指压电材料产生的电荷与施加在材料上的应力或压力之间的比例关系。
压电系数可以分为压电应力系数和压电应变系数。
4.机械耦合系数(Electromechanical coupling coefficient):机械耦合系数是指压电陶瓷材料在机械和电学特性之间的耦合程度。
该参数描述了材料将电能转化为机械能或将机械能转化为电能的能力。
5.压电应用温度范围(Operating temperature range):压电陶瓷材料在不同温度下的性能是不同的,因此需要确定材料的工作温度范围。
过高或过低的温度可能会影响材料的性能。
6.力常数(Force constant):力常数是指压电材料在单位面积上所承受的力与电压或电荷之间的比例关系。
力常数可以用来描述材料的力学特性。
7.色散(Dispersion):色散是指压电陶瓷材料的压电性能随着频率的变化而产生的变化。
了解材料的色散特性可以优化材料的应用。
8.应力-应变曲线(Stress-strain curve):应力-应变曲线描述了在施加外力或压力时,材料的应力和应变之间的关系。
通过绘制应力-应变曲线,可以获得材料的力学性能。
9.电化学稳定性(Electrochemical stability):压电陶瓷材料应具有良好的电化学稳定性,以确保其在一定电压或电流下不发生电化学反应。
压电陶瓷ANSYS

tbdata,19,1.786e10,0
tbdata,21,1.786e10
tb,piez,3 ! Piezoelectric matrix 72A??? 99.3.4
tbdata,1,0,0,-12.3082
tbdata,4,0,0,-12.3082
*get,ntop,node,,num,min
nsel,s,loc,z,0
cp,21,volt,all
*get,nbot,node,,num,min
ALLS
finish
/eof
!-------------------------------------------
NUMSTR,KP,1
NUMSTR,LINE,1
NUMSTR,AREA,1
block,0,10,0,5,0,1
type,3
mat,3
esize,0.5
vmesh,all
!------------boundary condition-----------------------
nsel,s,loc,x,0
d,all,ux
d,all,uy
d,all,uz
! -------------COUPLE THE TWO FACE OF ELECTRODE -------------
nsel,s,loc,x,10
cp,11,volt,all
tbdata,16,1.786e10,0,0
tbdata,19,1.786e10,0
tbdata,21,1.786e10
tb,piez,3 ! Piezoelectric matrix 72A??? 99.3.4
ansys耦合场 压电梁的模态分析

压电梁的模态分析几何尺寸:梁的长度L1=300mm 宽度W=30mm 厚度 H1=2mm 压电片长度 L=50mm 宽度W=30mm 厚度 H=1mm 采用pzt-5H 压电陶瓷片模态分析结果一阶振型(f=23.144Hz ) ++- -箭头为压电陶瓷的极化方向二阶振型(f=137.52Hz)/prep7! PZT-5H 材料特性参数mp,DENS,1,7700 ! 密度, kg/m**3mp,perx,1,1700 ! 介电常数mp,pery,1,1700mp,perz,1,1470tb,ANEL,1 ! 弹性劲度系数, N/m^2 tbdata,1,12.6E10,7.95E10,8.41E10 ! c11,c12,c13tbdata,7,12.6E10,8.41E10 ! c11,c33tbdata,12,11.7E10 ! c33tbdata,16,2.30E10 ! c44tbdata,19,2.30E10 ! c44tbdata,21,2.35E10 ! c66tb,PIEZ,1 ! 压电(应力)常数, C/m^2 tbdata,3,-6.5 ! e31tbdata,6,-6.5 ! e31tbdata,9,23.3 ! e33tbdata,11,17.0 ! e15tbdata,13,17.0 ! e15!定义主结构的材料参数mp,dens,2,7800EX,2,209e9nuxy,2,0.3! 定义压电复合梁几何模型(L=50mm W=30mm H = 1 mm)L=50e-3W=30e-3H =1e-3 !压电片几何尺寸L1=300e-3H1=2e-3 !主结构几何尺寸local,11 ! 建立下层局部坐标+Z 方向local,12,,,,,,,180 ! 建立上层局部坐标-Z 方向csys,11 ! 激活局部坐标系11 +y 方向block,0,L1,0,W,O,H1block,0,L,0,W,0,-Hblock,0,L,0,W,H1,H1+Hvglue,all !将梁同压电片粘结et,1,solid5,3 !定义压电单元et,2,solid45 !定义主结构单元!采用映射划分网格连接相邻面asel,s,loc,z,0cm,CM_1,areacmplot,CM_1accat,CM_1asel,s,loc,z,H1cm,CM_2,areaaccat,CM_2!进行网格划分LESIZE,ALL,5e-3, , , ,1, , ,1,mat,1 $ type,1 $ esys,11 !对下层压电片网格划分Vmesh,4mat,2 $ type,2 $ esys,11 !对中间结构网格划分Vmesh,6mat,1 $ type,1 $ esys,12 !对上层压电片网格划分vmesh,5nsel,s,loc,z,-H !定义下层电极cp,1,volt,all*get,n_bot,node,0,num,minnsel,s,loc,z,H+H1 !定义上层电极cp,2,volt,all*get,n_top,node,0,num,minnsel,s,loc,z,0 !压电片中间面电压耦合nsel,r,loc,x,0,Lcm,CM_3,nodensel,s,loc,z,H1nsel,r,loc,x,0,Lcm,Cm_4,nodecmsel,s,cm_3,nodecmsel,a,cm_4,nodecp,3,volt,allfini/soluantype,modalmodopt,lanb,3mxpand,3nsel,s,loc,x,0d,all,ux,0,,,,uy,uzd,n_top,volt,0 !上下层电极短路d,n_bot,volt,0nsel,allsolvefini。
压电陶瓷材料测试需要知道的13个基本参数

压电陶瓷材料测试需要知道的13个基本参数压电陶瓷材料是一种能够通过施加电压或应力来产生机械变形,或者通过施加机械压力或应变来产生电荷分离的材料。
在压电陶瓷材料测试中,以下是13个基本参数,用于评估和分析材料的性能和特性。
1.压电系数(Piezoelectric Coefficient):表示压电陶瓷材料在单位电场下产生的机械应变或单位应变下产生的电荷。
具体包括压电应变系数和压电电荷系数。
2.介电常数(Dielectric Constant):指材料在外加电场下的电容率。
介电常数决定了材料的电介质性能。
3.机械质量密度(Mechanical Density):表示单位体积内材料的质量。
机械质量密度影响材料的力学性能。
4.晶体结构(Crystal Structure):描述压电陶瓷材料的晶体结构,如立方晶系、四方晶系等。
5.绝缘电阻(Insulation Resistance):表示材料对电流的阻抗能力。
绝缘电阻高表示材料的绝缘性能好。
6.介电损耗因子(Dielectric Loss Factor):表示压电材料在交变电源下的能量损耗。
7.压电耦合因子(Piezoelectric Coupling Factor):表示材料电能到机械能的转换效率。
该参数对于传感器和执行器的性能至关重要。
8.矢量震荡模式(Vector Resonance Mode):表示压电材料在特定频率下的最佳工作模式。
根据应用的需要,不同的矢量震荡模式可以选择。
9.饱和电压(Saturation Voltage):指材料在电场作用下的饱和电压值。
在此电压下,材料的压电响应达到最大。
10.功率密度(Power Density):表示材料转换电能到机械能的能力。
高功率密度表示材料具有更高的工作效率。
11.主谐波(Fundamental Resonance):表示材料在特定频率下的共振点。
主谐波频率是设计和优化压电材料应用的重要参考。
12.稳定性(Stability):指材料在温度、湿度和外界环境变化下的稳定性能。
基于ANSYS模态分析的压电陶瓷参数数据的转换及其输入

面向 分析时压电材料 � 可以进行下面的处理 参数输入与转换 � � � +
�
� � � 首先列出了压电陶瓷的基本压电方程 , 为下面的
�
-1 -1 � � 讨论提供了一个框架 . 然后详细讨论了把制造商提供 . (7 ) � � � � 的数据转换为 A 需要的数据的方法 , 这些数据 由于方程 (2 ) 反映的是应力与电位移而不是应变 包括了刚度矩阵 ,介电常数矩阵和压电常数矩阵 . � 与电位移的关系,所以把方程(7 )代入方程 (2 )可得 压电方程组 � � � � + � , (8 ) 压电 体是结构与电学的耦合体 , 具有压电效应 � � 和 逆压电 效应 , 是一 些材料 (� 例 如 , 石英 ,压 电陶 瓷 ) � � � � � ( ) + � , (9 ) � � 的 天然属 性. 压电体具有机电转换功能 , 可以把力效 -1 -1 � � � � � . (10 ) � � � � + (� ) � � 应转换为电效应 . 对于压电体来说 ,电场作用能使它 把方程 ( 7) 和 (10) 组成方 程组与方程 (3),( 4) 对 产生电 位移 ,一些 力也能在某些方向产生电 位移 同 -1 -1
收 稿日 期� 2 009-0 7-10 基 金项 目� 国 家自 � 然科 学基金 项目 " � 基于 压电 转换 的振 动能 量回 收及 整流 变换 技术 的研 究" (N . 50 57702 3) 作� 者简 介� 罗 平 � (1983-), 男, 安徽 亳 州市人 , 广东 技术 师范 学院 教务 处科 员 研 究方 向 计 算机 测试 与控 制, 数字 资源 建设 及自 动化 技术
引
言
O3 ,19 55 年 ,
基于Ansys的压电陶瓷材料振动特性仿真与研究

基于Ansys的压电陶瓷材料振动特性仿真与研究【摘要】本文以智能材料中压电陶瓷为研究对象,对其进行的主动振动控制。
本论文总结分析了压电陶瓷的特性和相关的物理学方程,依据理论分析的结果,确定PZT材料的具体参数的选择,分析压电陶瓷特性和力学模型。
利用Ansys 仿真软件对梁进行模态分析得到各阶模态下的振动频率,观察振动情况。
并分析PZT在静态、动态电压下的电致伸缩特性。
然后给梁上的压电陶瓷一个激振,观察和分析梁的振动情况。
最后在梁的某个位置粘贴第二片压电陶瓷,对其施加与第一片相反的电压,抑制梁的振动,观察分析抑制情况。
【关键词】压电陶瓷;Ansys仿真;PZT1.引言压电材料是指具有压电效应,能够实现电能与机械能相互转换的晶体材料,受到压力作用时会在两端面间出现电压,进而表现出压电效应[1]。
压电效应的机理是:具有压电性的晶体对称性较低,当受到外力作用发生形变时,晶胞中正负离子的相对位移使正负电荷中心不再重合,导致晶体发生宏观极化,而晶体表面电荷面密度等于极化强度在表面法向上的投影,所以压电材料受压力作用形变时两端面会出现异号电荷[2]。
反之,压电材料在电场中发生极化时,会因电荷中心的位移导致材料变形[3]。
压电陶瓷具有价格低廉、易于批量生产等优点,已被广泛应用于社会生产的各个领域,尤其是在超声领域及电子科学技术领域中,压电陶瓷材料已逐渐处于绝对的优势支配地位,如医学及工业超声检测、水声探测、压电换能器、超声马达、显示器件、电控多色滤波器等[4]。
随着现代高科技的迅猛发展,智能结构和器件广泛应用于信息技术、新材料技术和航天等高技术领域,并日益显示出其巨大的优越性[5]。
近年来,各国都在积极研究功能陶瓷,研究的重点大都是从老材料中发掘新效应,开拓新应组织和结构入手,寻找新的压电材料。
特别值得重视的是随着材料展,目前国际上对压电材料的应用研究十分活跃[6]。
2.压电陶瓷材料的仿真与分析选取了solid226 ,Solid226单元需要介电常数ε,压电常数数(压电应力矩阵[e]或者压电应变矩阵[d]),弹性常数(柔度矩阵[S]或刚度矩阵[C]),以及密度。
压电陶瓷热胀系数表

压电陶瓷热胀系数表1. 引言压电陶瓷是一种具有压电效应的材料,其在应用中需要考虑到其热胀系数。
本文将详细介绍压电陶瓷的概念、特性以及相关的热胀系数表。
2. 压电陶瓷的概念与特性2.1 概念压电陶瓷是一种能够在机械力作用下产生电荷分离现象,并且在外加电场作用下发生形变的材料。
其具有良好的机械性能、化学稳定性和高温稳定性,因此被广泛应用于传感器、换能器、滤波器等领域。
2.2 特性•压电效应:当施加机械力时,压电陶瓷会产生极化现象,即正负电荷分离。
这种效应使得压电陶瓷可用于传感器和换能器等设备。
•热胀系数:压电陶瓷在温度变化时会发生尺寸变化,这与其内部结构和晶格有关。
因此,了解压电陶瓷的热胀系数对于应用中的温度补偿和设计至关重要。
3. 压电陶瓷热胀系数表下表是一份压电陶瓷常见材料的热胀系数表:压电陶瓷材料热胀系数 (10^-6/℃)PZT-4 3.5PZT-5H 4.0PZT-8 4.2PZT-9 3.8PZT-12 4.5以上表格列出了几种常见的压电陶瓷材料及其对应的热胀系数。
这些数据可以作为工程设计和制造过程中的参考。
4. 压电陶瓷热胀系数的影响因素压电陶瓷的热胀系数受多种因素影响,包括材料成分、晶体结构、温度变化等。
4.1 材料成分不同压电陶瓷材料由于其成分不同,其晶格结构和化学键强度也会有所差异,从而导致热胀系数的差异。
4.2 晶体结构压电陶瓷的晶体结构也会对其热胀系数产生影响。
例如,钙钛矿结构的压电陶瓷具有较高的热胀系数,而酒石酸盐结构的压电陶瓷则具有较低的热胀系数。
4.3 温度变化温度变化是导致压电陶瓷发生尺寸变化的主要因素之一。
随着温度的升高或降低,压电陶瓷材料会发生膨胀或收缩,从而导致其尺寸发生变化。
5. 结论本文介绍了压电陶瓷及其特性,并提供了一份常见压电陶瓷材料的热胀系数表。
了解和掌握压电陶瓷材料的特性和热胀系数对于工程设计和制造过程至关重要。
在实际应用中,需要根据具体情况选择合适的材料,并考虑温度补偿等因素,以确保设备和器件能够正常工作。
基于ANSYS的含缺陷压电陶瓷材料有限元仿真分析

福州大学学报( 自然科学版)
J o u r n a l o f F u z h o uU n i v e r s i t y ( N a t u r a l S c i e n c eE d i t i o n )
V o l . 4 2N o . 5 O c t . 2 0 1 4
{
E S T E ( i ,j =1 , 2 ,…, 6 ) i =s i j j +d i n n T D T E ( m ,n=1 , 2 , 3 ) m =d m j j +ε n n m
E T 为应力张量;S 为应变张量;E D s 为常电场柔度系数;d 式中: i j j i n为电场矢量; m 为电位移; i n为常应力压 T 电应变系数;ε m n 为常应力介电常数 . 1 . 3 压电陶瓷材料
压电陶瓷是一种压电多晶材料,其成分多为金属氧化物,通过掺杂其他物质成分的方式可得到适合 不同器件性能要求的各种压电换能器材料.压电陶瓷材料因其能耗低、响应快、刚度大、易于控制,可粘
7 ] 贴于本体结构表面或可嵌入本体结构内部,生产工艺较成熟等优点,在智能结构中得到了广泛的应用 [ .
2 压电陶瓷材料微观组织结构设计仿真
( 1 .S c h o o l o f M a t e r i a l s S c i e n c ea n dE n g i n e e r i n g ,L a n z h o uU n i v e r s i t yo f T e c h n o l o g y ,G a n s u ,L a n z h o u7 3 0 0 5 0 ,C h i n a ; 2 .S t a t eK e yL a b o r a t o r yo f A d v a n c e dP r o c e s s i n ga n dR e c y c l i n go f N o n - F e r r o u s M e t a l s ,L a n z h o uU n i v e r s i t y ,G a n s u ,L a n z h o u7 3 0 0 5 0 ,C h i n a ; o f T e c h n o l o g y 3 .S c h o o l o f E l e c t r o n i ca n dI n f o r m a t i o nE n g i n e e r i n g ,L a n z h o uJ i a o t o n gU n i v e r s i t y ,G a n s u ,L a n z h o u7 3 0 0 7 0 ,C h i n a )
压电陶瓷振动的有限元分析ansys

压电陶瓷振动的有限元分析ansys第⼀章绪论1.1压电材料概述1.1.1压电效应1880年法国物理学家⽪埃尔和雅各居⾥兄弟在研究⽯英晶体的物理性质时发现:当沿着晶⽚的某些⽅向施加作⽤⼒使晶⽚发⽣变形后,晶⽚上相对的两个表⾯会出现等量的正负电荷,电荷的密度与施加的⼒的⼤⼩有关,这种现象称为压电现象,具有压电现象的介质称为压电体。
压电效应反应了晶体的弹性性能与介电性能之间的耦合。
当对压电陶瓷施加⼀个与极化⽅向平⾏的压⼒F,如图1.1(a)所⽰,陶瓷⽚将产⽣压缩变形,⽚内的正、负束缚电荷之间的距离变⼩,极化强度也变⼩。
因此,原来吸附在电极上的⾃由电荷,有⼀部分被释放,⽚内的正、负电荷之间的距离变⼤,极化强度也变⼤,因此电极上⼜吸附⼀部分⾃由电荷⽽出现充电现象。
这种由机械效应转变为电效应的现象就是压电效应。
压电效应包括正压电效应和逆压电效应。
如图所⽰:图1.1 压电效应⽰意图:(a)正压电效应(b)负压电效应正压电效应:当压电晶体在外⼒作⽤下发⽣形变时,在它的某些相对应的⾯上产⽣异号电荷,这种没有电场作⽤,只是由于形变产⽣的极化现象称为正压电效应。
逆压电效应:当压电晶体施加⼀电场时,不仅产⽣了极化,同时还产⽣了形变,这种由电场产⽣形变的现象称为逆压电效应。
1.1.2压电陶瓷的诞⽣与发展具有压电效应性能的陶瓷称为压电陶瓷,1942年美国⿇省理⼯学院绝缘研究室发现,在钛酸钡铁电陶瓷上施加直流⾼压电场,使其⾃发极化沿电场⽅向择优取向,除去电场后仍能保持⼀定的剩余极化,使它具有压电效应,从此诞⽣了压电陶瓷。
钛酸钡(3BaTiO )陶瓷的发现促进了压电材料的发展,它不但使压电材料从⼀些单晶体材料发展到压电陶瓷等多晶体材料,⽽且在压电性能上也有了⼤幅度提⾼。
当今⼴泛应⽤的压电陶瓷是PZT ,即()3,O Ti Zr Pb 压电陶瓷,其压电效应强,稳定性好。
它是由美国学者B.贾菲等⼈于1954年发现的33PbTiO PbZrO -⼆元系固溶体压电陶瓷,其机械品质因数约为钛酸钡(3BaTiO )陶瓷的两倍。
压电材料ansys建模需要输入的属性
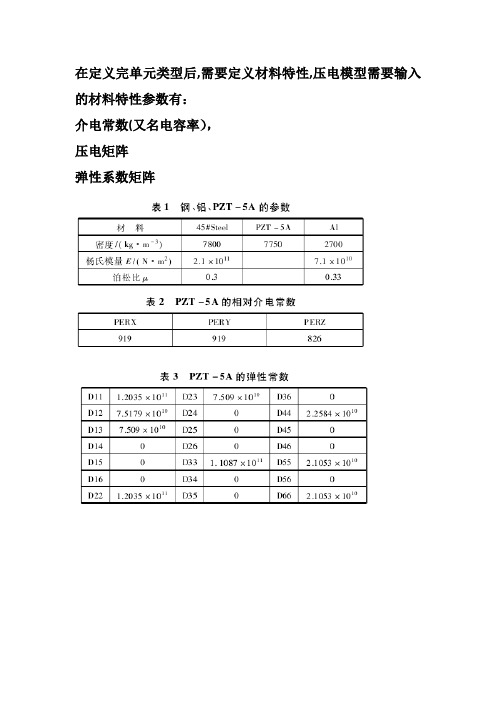
在定义完单元类型后,需要定义材料特性,压电模型需要输入的材料特性参数有:介电常数(又名电容率),压电矩阵弹性系数矩阵弹性基底材料及属性1、介电系数矩阵对于SOLID98 单元,可用MP 命令确定相对介电系数值作为PERX、PERY 和PERZ。
介电系数值分别代表介电系数矩阵的对角分量,即用MP 命令输入的介电系数总认为是常应变下的介电系数.2、压电矩阵可以用[ e ]形式-压电应力矩阵或用[ d ]形式—压电应变矩阵定义压电矩阵。
[ e ]矩阵通常与以刚度矩阵[ c ]形式表示各向异性弹性输入有关,而[ d ]矩阵和柔度矩阵相关.ANSYS 使用第一次界定温度下的弹性矩阵将压电应变矩阵[ d ]矩阵转换成压电应力矩阵[ e ]。
为确定这种变化所需要的弹性矩阵,可用TB,ANEL 命令.使用TB,PIEZ 和TBDATA 命令定义压电矩阵。
对于大多数已经公布的压电材料,压电矩阵数据都是按照x,y,z,yz,xz,xy 顺序的,基于IEEE 标准之上,而ANSYS 的输入数据是按照以上所示的x,y,z,xy,yz,xz 顺序。
也就是说,输入该参数是必须通过改变剪切项的行数据以转换到ANSYS 数据格式。
因此需将IEEE 常数61 62 63 [ e e e ]输入为ANSYS 的xy 行;将IEEE 常数41 42 43 [e e e]输入为ANSYS 的yz 行;将IEEE 常数51 52 53 [ e e e ]输入为ANSYS 的xz 行。
具体形式如矩阵(5.2)所示:3、弹性系数矩阵该矩阵为6 ×6对称矩阵(对于2-D 模型为4 ×4矩阵),它确定刚度系数([ c ]矩阵)或柔度系数([ s ]矩阵).弹性系数矩阵使用以下的数据表输入:使用TB,ANEL 和TB,DATA 命令定义系数矩阵[ c ]。
和压电矩阵的情况类似,大多数压电材料的[ c ]矩阵使用不同的参数顺序,需要通过如下方式改变剪切项的行和列数据以将IEEE矩阵转换到ANSYS 输入顺序。
ansys压电分析实例Ansys压电分析

ansys压电分析实例Ansys压电分析导读:就爱阅读网友为您分享以下“Ansys压电分析”的资讯,希望对您有所帮助,感谢您对的支持! ansys压电分析压电效应分析是一种结构-电场耦合分析。
当给石英和陶瓷等压电材料加电压时,它们会产生位移,反之若使之振动,则会产生电压。
压力传感器就是压电效应的一种典型的应用。
压电分析(ANSYS/Multiphysics或ANSYS /Mechanical软件包提供这种分析)类型可以是静力、模态、预应力模态、谐波、预应力谐波和瞬态分析。
压电分析只能用下列单元类型之一:PLANE13, KEYOPT(1)=7,耦合场四边形实体单元SOLID5, KEYOPT(1)=0或3,耦合场六面体单元SOLID98, KEYOPT(1)=0或3,耦合场四面体单元KEYOPT选项激活压电自由度:位移和电压。
对于SOLID5和SOLID98,KEYOPT(1)=3仅激活压电选项。
注意:如果模型中激活了至少一个带有压电自由度(位移和VOLT)的单元,则需要用到VOLT自由度的所有单元必须是上面三种压电单元其中之一。
而且,所有的这些单元均需激活压电自由度。
如果不希望在这些单元中存在压电效应,则需给材料定义非常小的压电特性。
压电KEYOPT用NLGEOM,SSTIF,PSTRES命令可用大挠度和应力刚化作用(参见《ANSYS Commands Reference》对这些命令的更多信息,参见《ANSYS Structural Analysis Guide》及《ANSYS,Inc. Theory Reference》的第三章关于大挠度及应力刚化功能的更多信息)。
对PLANE13,通过设置KEYOPT(1)=7可用大挠度及应力刚化功能。
对SOLID5及SOLID98通过设置KEYOPT(1)=3可用大挠度及应力刚化功能。
而且小挠度及应力刚化选项可以通过KEYOPT (1)=0使用。
注意-对压电分析不能使用自动求解控制。
压电陶瓷材料的主要性能及参数

压电陶瓷材料的主要性能及参数自由介电常数εT33(free permittivity)电介质在应变为零(或常数)时的介电常数,其单位为法拉/米。
相对介电常数εTr3(relative permittivity)介电常数εT33与真空介电常数ε0之比值,εTr3=εT33/ε0,它是一个无因次的物理量。
介质损耗(dielectric loss)电介质在电场作用下,由于电极化弛豫过程和漏导等原因在电介质内所损耗的能量。
损耗角正切tgδ(tangent of loss angle)理想电介质在正弦交变电场作用下流过的电流比电压相位超前90 0,但是在压电陶瓷试样中因有能量损耗,电流超前的相位角ψ小于900,它的余角δ(δ+ψ=900)称为损耗角,它是一个无因次的物理量,人们通常用损耗角正切tgδ来表示介质损耗的大小,它表示了电介质的有功功率(损失功率)P与无功功率Q之比。
即:电学品质因数Qe(electrical quality factor)电学品质因数的值等于试样的损耗角正切值的倒数,用Qe表示,它是一个无因次的物理量。
若用并联等效电路表示交变电场中的压电陶瓷的试样,则Qe=1/ tgδ=ωCR机械品质因数Qm(mechanical quanlity factor)压电振子在谐振时储存的机械能与在一个周期内损耗的机械能之比称为机械品质因数。
它与振子参数的关系式为:泊松比(poissons ratio)泊松比系指固体在应力作用下的横向相对收缩与纵向相对伸长之比,是一个无因次的物理量,用δ表示:δ= - S 12 /S11串联谐振频率fs(series resonance frequency)压电振子等效电路中串联支路的谐振频率称为串联谐振频率,用f s 表示,即并联谐振频率fp(parallel resonance frequency)压电振子等效电路中并联支路的谐振频率称为并联谐振频率,用f p 表示,即f p =谐振频率fr(resonance frequency)使压电振子的电纳为零的一对频率中较低的一个频率称为谐振频率,用f r 表示。
