第2章习题答案
第2章 逻辑门电路-习题答案
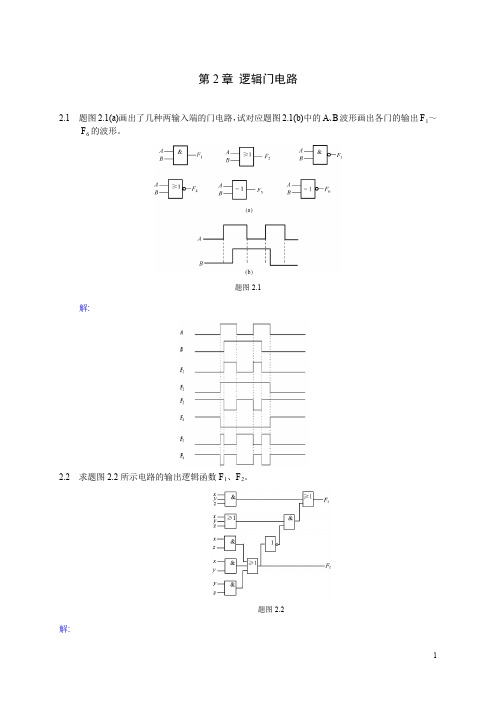
第2章逻辑门电路2.1 题图2.1(a)画出了几种两输入端的门电路,试对应题图2.1(b)中的A、B波形画出各门的输出F1~F6的波形。
题图2.1解:2.2 求题图2.2所示电路的输出逻辑函数F1、F2。
题图2.2解:2.3 题图2.3中的电路均为TTL门电路,试写出各电路输出Y1~Y8状态。
题图2.3解: Y1=0, Y2=0, Y3=Hi-Z, Y4=0, Y5=0, Y6=0, Y7=0, Y8=0.2.4 题图2.4中各门电路为CMOS电路,试求各电路输出端Y1、Y2和Y的值。
题图2.4解: Y1=1, Y2=0, Y3=0.2.5 6个门电路及A、B波形如题图2.5所示,试写出F1~F6的逻辑函数,并对应A、B波形画出F1~F6的波形。
题图2.5解:2.6 电路及输入波形分别如题图2.6(a)和2.6(b)所示,试对应A、B、C、x1、x2、x3波形画出F端波形。
题图2.6解:2.7 TTL与非门的扇出系数N是多少?它由拉电流负载个数决定还是由灌电流负载决定?解: N≤8 N由灌电流负载个数决定.2.8 题图2.8表示三态门用于总线传输的示意图,图中三个三态门的输出接到数据传输总线,D1D2、D3D4、…、D m D n为三态门的输入端,EN1、EN2、EN n分别为各三态门的片选输入端。
试问:EN信号应如何控制,以便输入数据D1D2、D3D4、…、D m D n顺序地通过数据总线传输(画出EN1~EN n 的对应波形)。
题图2.8解:用下表表示数据传输情况2.9 某工厂生产的双互补对称反相器(4007)引出端如题图2.9所示,试分别连接成:(1)反相器;(2)三输入与非门;(3)三输入或非门。
题图2.9解: (1) 反向器(2)与非门 (3)或非门2.10 按下列函数画出NMOS 电路图。
123()()()F AB CD E H G F A B CD AB CD F A B=+++=+++=⊕解:(1)(2) (3)2.11 将两个OC门如题图2.11连接,试写出各种组合下的输出电压u o及逻辑表达式。
第二章习题及答案

思考与练习1.名词解释SNA 国内生产总值名义变量实际变量净出口间接税国内生产净值国民收入个人可支配收入绿色GDP2.试述六大经济总量包括哪些项目?各个经济量之间有何关系?4.国民收入核算方法有哪几种?5.简述两部门经济、三部门经济以及四部门经济具体如何循环的?6.在统计中,社会保险税增加对GDP、GNP、NNP、NI、PI和PDI这六个经济总量中那个总量有影响?为什么?7.如果甲乙两国并成一个国家,对GDP总和会有什么影响(假定两国产出不变)?8.储蓄-投资恒等式为什么不意味着计划的储蓄恒等于计划的投资?9.经济国民经济核算时要遵循社么样的平衡原则。
10.以中国国民经济核算体系为例介绍SNA的基本内容。
11.试用收入法说明GDP的构成。
11.如何理解产出等于收入,产出等于支出两个等式?12.假定国内生产总值是10000亿美元,个人可支配收入是8200亿美元,政府预算赤字是400亿美元,消费是7600亿美元,贸易赤字是200亿美元。
计算储蓄、投资、政府支出。
13.假定某国各项经济指标如下:消费支出:3000亿;总投资:2000亿;政府支出:900亿;进口:300亿;出口:150亿;工资:4200亿;间接税未知;利息:200亿,租金:250亿;利润:400亿;折旧:100亿;非企业收入:400亿‘根据所给资料进行:(1)用支出法计算该国国内生产总值;(2)该国间接税为多少?(3)该国国内生产净值为多少?14.假定某经济社会有A、B、C三个厂商,A厂商年产出5000美元,卖给B、C和消费者。
其中B买A的产出200美元,C买2000美元,其余2800美元卖给消费者。
B年产出500美元,直接卖给消费者,C年产出6000美元,其中3000美元由A买,其余由消费者买。
(1)假定投入在生产中用光,计算价值增加;(2)计算GDP为多少;(3)如果只有C有500美元折旧,计算国民收入。
1.名词解释(1)SNA: 即国民账户体系。
第二章习题答案

162 第2章习题1 下列化合物中,哪些是路易斯酸,哪些是路易斯碱?BH 4-, PH 3, BeCl 2, CO 2, CO , Hg(NO 3)2, SnCl 2解答:路易斯酸:BeCl 2,PH 3,CO 2,CO ,Hg(NO 3)2,SnCl 2路易斯碱:PH 3,CO ,SnCl 22 写出下列物种的共轭酸和共轭碱:NH 3, NH 2-, H 2O , HI , HSO 4-解答: 共轭酸 共轭碱 共轭酸 共轭碱NH 3 NH 4+ NH 2- NH 2- NH 3 NH 2-H 2O H 3O + OH - HI H 2I + I -HSO 4- H 2SO 4 SO 42-3 下列各对中哪一个酸性较强? 并说明理由。
(a) [Fe(H 2O)6]3+和[Fe(H 2O)6]2+ (b) [Al(H 2O)6]3+和[Ga(H 2O)6]3+(c) Si(OH)4和Ge(OH)4 (d) HClO 3和HClO 4(e) H 2CrO 4和HMnO 4 (f) H 3PO 4和H 2SO 4解答:(a) [Fe(H 2O)6]3+和[Fe(H 2O)6]2+路易斯酸性:前者,中心离子电荷高、半径小,吸引电子能力大;质子酸性:前者,中心离子电荷高,对O 的极化能力大,H +易离解;(b) [Al(H 2O)6]3+和[Ga(H 2O)6]3+、(c) Si(OH)4和Ge(OH)4路易斯酸性:均为前者,中心离子半径小,d 轨道能量低;质子酸性:均为前者,中心离子半径小,对O 的极化能力大,H +易离解;(d) HClO 3和HClO 4、(e) H 2CrO 4和HMnO 4和(f) H 3PO 4和H 2SO 4路易斯酸性和质子酸性均为后者,中心原子氧化数高、半径小,非羟基氧原子多。
4 应用Pauling 规则,(1) 判断H 3PO 4(pK a =2.12)、H 3PO 3(pK a =1.80)和H 3PO 2(pK a =2.0)的结构;(2) 粗略估计H 3PO 4、H 2PO 4-和HPO 42-的pK a 值。
第二章课后习题答案

第二章课后习题答案第二章牛顿定律2-1如图(a)所示,质量为m的物体用平行于斜面的细线联结置于光滑的斜面上,若斜面向左方作加速运动,当物体刚脱离斜面时,它的加速度的大小为()(A)ginθ(B)gcoθ(C)gtanθ(D)gcotθ分析与解当物体离开斜面瞬间,斜面对物体的支持力消失为零,物体在绳子拉力FT(其方向仍可认为平行于斜面)和重力作用下产生平行水平面向左的加速度a,如图(b)所示,由其可解得合外力为mgcotθ,故选(D).求解的关键是正确分析物体刚离开斜面瞬间的物体受力情况和状态特征.2-2用水平力FN把一个物体压着靠在粗糙的竖直墙面上保持静止.当FN逐渐增大时,物体所受的静摩擦力Ff的大小()(A)不为零,但保持不变(B)随FN成正比地增大(C)开始随FN增大,达到某一最大值后,就保持不变(D)无法确定分析与解与滑动摩擦力不同的是,静摩擦力可在零与最大值μFN范围内取值.当FN增加时,静摩擦力可取的最大值成正比增加,但具体大小则取决于被作用物体的运动状态.由题意知,物体一直保持静止状态,故静摩擦力与重力大小相等,方向相反,并保持不变,故选(A).2-3一段路面水平的公路,转弯处轨道半径为R,汽车轮胎与路面间的摩擦因数为μ,要使汽车不至于发生侧向打滑,汽车在该处的行驶速率()μgR(B)必须等于μgR(C)不得大于μgR(D)还应由汽车的质量m决定(A)不得小于分析与解由题意知,汽车应在水平面内作匀速率圆周运动,为保证汽车转弯时不侧向打滑,所需向心力只能由路面与轮胎间的静摩擦力提供,能够提供的最大向心力应为μFN.由此可算得汽车转弯的最大速率应为v=μRg.因此只要汽车转弯时的实际速率不大于此值,均能保证不侧向打滑.应选(C).2-4一物体沿固定圆弧形光滑轨道由静止下滑,在下滑过程中,则()(A)它的加速度方向永远指向圆心,其速率保持不变(B)它受到的轨道的作用力的大小不断增加(C)它受到的合外力大小变化,方向永远指向圆心(D)它受到的合外力大小不变,其速率不断增加分析与解由图可知,物体在下滑过程中受到大小和方向不变的重力以及时刻指向圆轨道中心的轨道支持力FN作用,其合外力方向并非指向圆心,其大小和方向均与物体所在位置有关.重力的切向分量(mgcoθ)使物体的速率将会不断增加(由机械能守恒亦可判断),则物体作圆周运动的向心力(又称法向力)将不断增大,由轨道法向方向上的动力学方程v2FNmginθm可判断,随θ角的不断增大过程,轨道支持力FN也将不R断增大,由此可见应选(B).2-5图(a)示系统置于以a=1/4g的加速度上升的升降机内,A、B两物体质量相同均为m,A所在的桌面是水平的,绳子和定滑轮质量均不计,若忽略滑轮轴上和桌面上的摩擦,并不计空气阻力,则绳中张力为()(A)58mg(B)12mg(C)mg(D)2mg分析与解本题可考虑对A、B两物体加上惯性力后,以电梯这个非惯性参考系进行求解.此时A、B两物体受力情况如图(b)所示,图中a′为A、B两物体相对电梯的加速度,ma′为惯性力.对A、B两物体应用牛顿第二定律,可解得FT=5/8mg.故选(A).讨论对于习题2-5这种类型的物理问题,往往从非惯性参考系(本题为电梯)观察到的运动图像较为明确,但由于牛顿定律只适用于惯性参考系,故从非惯性参考系求解力学问题时,必须对物体加上一个虚拟的惯性力.如以地面为惯性参考系求解,则两物体的加速度aA和aB均应对地而言,本题中aA和aB的大小与方向均不相同.其中aA应斜向上.对aA、aB、a和a′之间还要用到相对运动规律,求解过程较繁.有兴趣的读者不妨自己尝试一下.2-6图示一斜面,倾角为α,底边AB长为l=2.1m,质量为m的物体从题2-6图斜面顶端由静止开始向下滑动,斜面的摩擦因数为μ=0.14.试问,当α为何值时,物体在斜面上下滑的时间最短?其数值为多少?解取沿斜面为坐标轴O某,原点O位于斜面顶点,则由牛顿第二定律有mginαmgμcoαma(1)又物体在斜面上作匀变速直线运动,故有l11at2ginαμcoαt2coα22则t2l(2)gcoαinαμcoα为使下滑的时间最短,可令dt0,由式(2)有dαinαinαμcoαcoαcoαμinα0则可得tan2α1o,49μ此时t2l0.99gcoαinαμcoα2-7工地上有一吊车,将甲、乙两块混凝土预制板吊起送至高空.甲块质量为m1=2.00某102kg,乙块质量为m2=1.00某102kg.设吊车、框架和钢丝绳的质量不计.试求下述两种情况下,钢丝绳所受的张力以及乙块对甲块的作用力:(1)两物块以10.0m·s-2的加速度上升;(2)两物块以1.0m·s-2的加速度上升.从本题的结果,你能体会到起吊重物时必须缓慢加速的道理吗?解按题意,可分别取吊车(含甲、乙)和乙作为隔离体,画示力图,并取竖直向上为Oy轴正方向(如图所示).当框架以加速度a上升时,有FT-(m1+m2)g=(m1+m2)a(1)FN2-m2g=m2a(2)解上述方程,得FT=(m1+m2)(g+a)(3)FN2=m2(g+a)(4)(1)当整个装置以加速度a=10m·s-2上升时,由式(3)可得绳所受张力的值为FT=5.94某103N乙对甲的作用力为F′N2=-FN2=-m2(g+a)=-1.98某103N(2)当整个装置以加速度a=1m·s-2上升时,得绳张力的值为FT=3.24某103N此时,乙对甲的作用力则为F′N2=-1.08某103N由上述计算可见,在起吊相同重量的物体时,由于起吊加速度不同,绳中所受张力也不同,加速度大,绳中张力也大.因此,起吊重物时必须缓慢加速,以确保起吊过程的安全.2-8如图(a)所示,已知两物体A、B的质量均为m=3.0kg物体A以加速度a=1.0m·s-2运动,求物体B与桌面间的摩擦力.(滑轮与连接绳的质量不计)分析该题为连接体问题,同样可用隔离体法求解.分析时应注意到绳中张力大小处处相等是有条件的,即必须在绳的质量和伸长可忽略、滑轮与绳之间的摩擦不计的前提下成立.同时也要注意到张力方向是不同的.解分别对物体和滑轮作受力分析[图(b)].由牛顿定律分别对物体A、B及滑轮列动力学方程,有mAg-FT=mAa(1)F′T1-Ff=mBa′(2)F′T-2FT1=0(3)考虑到mA=mB=m,FT=F′T,FT1=F′T1,a′=2a,可联立解得物体与桌面的摩擦力Ffmgm4ma7.2N2讨论动力学问题的一般解题步骤可分为:(1)分析题意,确定研究对象,分析受力,选定坐标;(2)根据物理的定理和定律列出原始方程组;(3)解方程组,得出文字结果;(4)核对量纲,再代入数据,计算出结果来.2-9质量为m′的长平板A以速度v′在光滑平面上作直线运动,现将质量为m的木块B轻轻平稳地放在长平板上,板与木块之间的动摩擦因数为μ,求木块在长平板上滑行多远才能与板取得共同速度?分析当木块B平稳地轻轻放至运动着的平板A上时,木块的初速度可视为零,由于它与平板之间速度的差异而存在滑动摩擦力,该力将改变它们的运动状态.根据牛顿定律可得到它们各自相对地面的加速度.换以平板为参考系来分析,此时,木块以初速度-v′(与平板运动速率大小相等、方向相反)作匀减速运动,其加速度为相对加速度,按运动学公式即可解得.该题也可应用第三章所讲述的系统的动能定理来解.将平板与木块作为系统,该系统的动能由平板原有的动能变为木块和平板一起运动的动能,而它们的共同速度可根据动量定理求得.又因为系统内只有摩擦力作功,根据系统的动能定理,摩擦力的功应等于系统动能的增量.木块相对平板移动的距离即可求出.解1以地面为参考系,在摩擦力Ff=μmg的作用下,根据牛顿定律分别对木块、平板列出动力学方程Ff=μmg=ma1F′f=-Ff=m′a2a1和a2分别是木块和木板相对地面参考系的加速度.若以木板为参考系,木块相对平板的加速度a=a1+a2,木块相对平板以初速度-v′作匀减速运动直至最终停止.由运动学规律有-v′2=2a由上述各式可得木块相对于平板所移动的距离为mv22μgmm解2以木块和平板为系统,它们之间一对摩擦力作的总功为W=Ff(+l)-Ffl=μmg式中l为平板相对地面移动的距离.由于系统在水平方向上不受外力,当木块放至平板上时,根据动量守恒定律,有m′v′=(m′+m)v″由系统的动能定理,有μmg由上述各式可得11mv2mmv222mv22μgmm2-10如图(a)所示,在一只半径为R的半球形碗内,有一粒质量为m的小钢球,当小球以角速度ω在水平面内沿碗内壁作匀速圆周运动时,它距碗底有多高?分析维持钢球在水平面内作匀角速度转动时,必须使钢球受到一与向心加速度相对应的力(向心力),而该力是由碗内壁对球的支持力FN的分力来提供的,由于支持力FN始终垂直于碗内壁,所以支持力的大小和方向是随ω而变的.取图示O某y坐标,列出动力学方程,即可求解钢球距碗底的高度.解取钢球为隔离体,其受力分析如图(b)所示.在图示坐标中列动力学方程FNinθmanmRω2inθ(1)Rh(3)且有coθR由上述各式可解得钢球距碗底的高度为hR可见,h随ω的变化而变化.gω22-11火车转弯时需要较大的向心力,如果两条铁轨都在同一水平面内(内轨、外轨等高),这个向心力只能由外轨提供,也就是说外轨会受到车轮对它很大的向外侧压力,这是很危险的.因此,对应于火车的速率及转弯处的曲率半径,必须使外轨适当地高出内轨,称为外轨超高.现有一质量为m的火车,以速率v沿半径为R的圆弧轨道转弯,已知路面倾角为θ,试求:(1)在此条件下,火车速率v0为多大时,才能使车轮对铁轨内外轨的侧压力均为零?(2)如果火车的速率v≠v0,则车轮对铁轨的侧压力为多少?分析如题所述,外轨超高的目的欲使火车转弯的所需向心力仅由轨道支持力的水平分量FNinθ提供(式中θ角为路面倾角).从而不会对内外轨产生挤压.与其对应的是火车转弯时必须以规定的速率v0行驶.当火车行驶速率v≠v0时,则会产生两种情况:如图所示,如v>v0时,外轨将会对车轮产生斜向内的侧压力F1,以补偿原向心力的不足,如v<v0时,则内轨对车轮产生斜向外的侧压力F2,以抵消多余的向心力,无论哪种情况火车都将对外轨或内轨产生挤压.由此可知,铁路部门为什么会在每个铁轨的转弯处规定时速,从而确保行车安全.解(1)以火车为研究对象,建立如图所示坐标系.据分析,由牛顿定律有v2FNinθm(1)解(1)(2)两式可得火车转弯时规定速率为v0gRtanθ(2)当v>v0时,根据分析有v2FNinθF1coθm(3)RFNcoθF1inθmg0(4)解(3)(4)两式,可得外轨侧压力为v2F1mcoθginθR当v<v0时,根据分析有v2FNinθF2coθm(5)RFNcoθF2inθmg0(6)解(5)(6)两式,可得内轨侧压力为v2F2mginθcoθR2-12一杂技演员在圆筒形建筑物内表演飞车走壁.设演员和摩托车的总质量为m,圆筒半径为R,演员骑摩托车在直壁上以速率v作匀速圆周螺旋运动,每绕一周上升距离为h,如图所示.求壁对演员和摩托车的作用力.分析杂技演员(连同摩托车)的运动可以看成一个水平面内的匀速率圆周运动和一个竖直向上匀速直线运动的叠加.其旋转一周所形成的旋线轨迹展开后,相当于如图(b)所示的斜面.把演员的运动速度分解为图示的v1和v2两个分量,显然v1是竖直向上作匀速直线运动的分速度,而v2则是绕圆筒壁作水平圆周运动的分速度,其中向心力由筒壁对演员的支持力FN的水平分量FN2提供,而竖直分量FN1则与重力相平衡.如图(c)所示,其中φ角为摩托车与筒壁所夹角.运用牛顿定律即可求得筒壁支持力的大小和方向解设杂技演员连同摩托车整体为研究对象,据(b)(c)两图应有FN1mg0(1)FN2v2m(2)Rv2vcoθv2πR2πR2h2(3)22FNFN1FN2(4)以式(3)代入式(2),得FN2m4π2R2v24π2Rmv222(5)2222R4πRh4πRh将式(1)和式(5)代入式(4),可求出圆筒壁对杂技演员的作用力(即支承力)大小为22FNFN1FN224π2Rv22mg4π2R2h2与壁的夹角φ为FN24π2Rv2arctanarctan222FN14πRhg讨论表演飞车走壁时,演员必须控制好运动速度,行车路线以及摩托车的方位,以确保三者之间满足解题用到的各个力学规律.2-13一质点沿某轴运动,其受力如图所示,设t=0时,v0=5m·s-1,某0=2m,质点质量m=1kg,试求该质点7s末的速度和位置坐标.分析首先应由题图求得两个时间段的F(t)函数,进而求得相应的加速度函数,运用积分方法求解题目所问,积分时应注意积分上下限的取值应与两时间段相应的时刻相对应.解由题图得0t52t,Ft5t7355t,由牛顿定律可得两时间段质点的加速度分别为a2t,0t5a355t,5t7对0<t<5s时间段,由adv得dtvtv00dvadt积分后得v5t再由v2d某得dtd某vdt某00某t积分后得某25tt将t=5s代入,得v5=30m·s-1和某5=68.7m对5s<t<7s时间段,用同样方法有133dvv0vt5a2dt得v35t2.5t82.5t再由得某=17.5t2-0.83t3-82.5t+147.87将t=7s代入分别得v7=40m·s-1和某7=142m2-14一质量为10kg的质点在力F的作用下沿某轴作直线运动,已知F =120t+40,式中F的单位为N,t的单位的s.在t=0时,质点位于某=5.0m处,其速度v0=6.0m·s-1.求质点在任意时刻的速度和位置.分析这是在变力作用下的动力学问题.由于力是时间的函数,而加速度a=dv/dt,这时,动力学方程就成为速度对时间的一阶微分方程,解此微分方程可得质点的速度v(t);由速度的定义v=d某/dt,用积分的方法可求出质点的位置.解因加速度a=dv/dt,在直线运动中,根据牛顿运动定律有2某某5d某vdt5t120t40mdvdt依据质点运动的初始条件,即t0=0时v0=6.0m·s-1,运用分离变量法对上式积分,得vv0dv12.0t4.0dt0tv=6.0+4.0t+6.0t2又因v=d某/dt,并由质点运动的初始条件:t0=0时某0=5.0m,对上式分离变量后积分,有d某6.04.0t6.0tdt某t2某00某=5.0+6.0t+2.0t2+2.0t32-15轻型飞机连同驾驶员总质量为1.0某103kg.飞机以55.0m·s-1的速率在水平跑道上着陆后,驾驶员开始制动,若阻力与时间成正比,比例系数α=5.0某102N·s-1,空气对飞机升力不计,求:(1)10s后飞机的速率;(2)飞机着陆后10s内滑行的距离.分析飞机连同驾驶员在水平跑道上运动可视为质点作直线运动.其水平方向所受制动力F为变力,且是时间的函数.在求速率和距离时,可根据动力学方程和运动学规律,采用分离变量法求解.解以地面飞机滑行方向为坐标正方向,由牛顿运动定律及初始条件,有dvαtdtvtαtdvv00mdtα2t得vv02mFmam因此,飞机着陆10s后的速率为v=30m·s-1又tα2d某vdt某0002mt某故飞机着陆后10s内所滑行的距离某某0v0tα3t467m6m2-16质量为m的跳水运动员,从10.0m高台上由静止跳下落入水中.高台距水面距离为h.把跳水运动员视为质点,并略去空气阻力.运动员入水后垂直下沉,水对其阻力为bv2,其中b为一常量.若以水面上一点为坐标原点O,竖直向下为Oy轴,求:(1)运动员在水中的速率v与y的函数关系;(2)如b/m=0.40m-1,跳水运动员在水中下沉多少距离才能使其速率v减少到落水速率v0的1/10?(假定跳水运动员在水中的浮力与所受的重力大小恰好相等)分析该题可以分为两个过程,入水前是自由落体运动,入水后,物体受重力P、浮力F和水的阻力Ff的作用,其合力是一变力,因此,物体作变加速运动.虽然物体的受力分析比较简单,但是,由于变力是速度的函数(在有些问题中变力是时间、位置的函数),对这类问题列出动力学方程并不复杂,但要从它计算出物体运动的位置和速度就比较困难了.通常需要采用积分的方法去解所列出的微分方程.这也成了解题过程中的难点.在解方程的过程中,特别需要注意到积分变量的统一和初始条件的确定.解(1)运动员入水前可视为自由落体运动,故入水时的速度为v02gh运动员入水后,由牛顿定律得P-Ff-F=ma由题意P=F、Ff=bv2,而a=dv/dt=v(dv/dy),代入上式后得-bv2=mv(dv/dy)考虑到初始条件y0=0时,v0t2gh,对上式积分,有vdvmdy0v0vbvv0eby/m2gheby/m(2)将已知条件b/m=0.4m-1,v=0.1v0代入上式,则得ymvln5.76mbv0某2-17直升飞机的螺旋桨由两个对称的叶片组成.每一叶片的质量m=136kg,长l=3.66m.求当它的转速n=320r/min 时,两个叶片根部的张力.(设叶片是宽度一定、厚度均匀的薄片)分析螺旋桨旋转时,叶片上各点的加速度不同,在其各部分两侧的张力也不同;由于叶片的质量是连续分布的,在求叶片根部的张力时,可选取叶片上一小段,分析其受力,列出动力学方程,然后采用积分的方法求解.解设叶片根部为原点O,沿叶片背离原点O的方向为正向,距原点O为r处的长为dr一小段叶片,其两侧对它的拉力分别为FT(r)与FT(r+dr).叶片转动时,该小段叶片作圆周运动,由牛顿定律有dFTFTrFTrdr由于r=l时外侧FT=0,所以有m2ωrdrltFTrdFTlrmω2rdrlmω2222πmn222FTrlrlr2ll上式中取r=0,即得叶片根部的张力FT0=-2.79某105N负号表示张力方向与坐标方向相反.2-18一质量为m的小球最初位于如图(a)所示的A点,然后沿半径为r 的光滑圆轨道ADCB下滑.试求小球到达点C时的角速度和对圆轨道的作用力.分析该题可由牛顿第二定律求解.在取自然坐标的情况下,沿圆弧方向的加速度就是切向加速度at,与其相对应的外力Ft是重力的切向分量mginα,而与法向加速度an相对应的外力是支持力FN和重力的法向分量mgcoα.由此,可分别列出切向和法向的动力学方程Ft=mdv/dt和Fn=man.由于小球在滑动过程中加速度不是恒定的,因此,需应用积分求解,为使运算简便,可转换积分变量.倡该题也能应用以小球、圆弧与地球为系统的机械能守恒定律求解小球的速度和角速度,方法比较简便.但它不能直接给出小球与圆弧表面之间的作用力.解小球在运动过程中受到重力P和圆轨道对它的支持力FN.取图(b)所示的自然坐标系,由牛顿定律得Ftmginαmdv(1)dtmv2FnFNmgcoαm(2)R由vdrdαrdα,得dt,代入式(1),并根据小球从点A运动到点Cdtdtv的始末条件,进行积分,有vv0vdvα90orginαdα得v则小球在点C的角速度为2rgcoαωv2gcoα/rrmv2mgcoα3mgcoα由式(2)得FNmr由此可得小球对圆轨道的作用力为FN3mgcoαFN负号表示F′N与en反向.2-19光滑的水平桌面上放置一半径为R的固定圆环,物体紧贴环的内侧作圆周运动,其摩擦因数为μ,开始时物体的速率为v0,求:(1)t时刻物体的速率;(2)当物体速率从v0减少到12v0时,物体所经历的时间及经过的路程.解(1)设物体质量为m,取图中所示的自然坐标,按牛顿定律,有mv2FNmanRFfmatdvdt由分析中可知,摩擦力的大小Ff=μFN,由上述各式可得v2dvμRdt取初始条件t=0时v=v0,并对上式进行积分,有t0dtRvdvμv0v2vRv0Rv0μt(2)当物体的速率从v0减少到1/2v0时,由上式可得所需的时间为t物体在这段时间内所经过的路程Rμv0vdt0tt0Rv0dtRv0μtRln2μ2-20质量为45.0kg的物体,由地面以初速60.0m·s-1竖直向上发射,物体受到空气的阻力为Fr=kv,且k=0.03N/(m·s-1).(1)求物体发射到最大高度所需的时间.(2)最大高度为多少?分析物体在发射过程中,同时受到重力和空气阻力的作用,其合力是速率v的一次函数,动力学方程是速率的一阶微分方程,求解时,只需采用分离变量的数学方法即可.但是,在求解高度时,则必须将时间变量通过速度定义式转换为位置变量后求解,并注意到物体上升至最大高度时,速率应为零.解(1)物体在空中受重力mg和空气阻力Fr=kv作用而减速.由牛顿定律得mgkvmdv(1)dt某2-25如图(a)所示,电梯相对地面以加速度a竖直向上运动.电梯中有一滑轮固定在电梯顶部,滑轮两侧用轻绳悬挂着质量分别为m1和m2的物体A和B.设滑轮的质量和滑轮与绳索间的摩擦均略去不计.已知m1>m2,如以加速运动的电梯为参考系,求物体相对地面的加速度和绳的张力.分析如以加速运动的电梯为参考系,则为非惯性系.在非惯性系中应用牛顿定律时必须引入惯性力.在通常受力分析的基础上,加以惯性力后,即可列出牛顿运动方程来.解取如图(b)所示的坐标,以电梯为参考系,分别对物体A、B作受力分析,其中F1=m1a,F2=m2a分别为作用在物体A、B上的惯性力.设ar为物体相对电梯的加速度,根据牛顿定律有m1gm1aFT1m1ar(1)m2gm2aFT2m2ar(2)FT2FT2(3)由上述各式可得arm1m2gam1m22m1m2gam1m2FT2FT2由相对加速度的矢量关系,可得物体A、B对地面的加速度值为a1aram1m2g2m2am1m22m1am1m2gm1m2a2araa2的方向向上,a1的方向由ar和a的大小决定.当ar<a,即m1g-m2g-2m2a>0时,a1的方向向下;反之,a1的方向向上.某2-26如图(a)所示,在光滑水平面上,放一质量为m′的三棱柱A,它的斜面的倾角为α.现把一质量为m的滑块B放在三棱柱的光滑斜面上.试求:(1)三棱柱相对于地面的加速度;(2)滑块相对于地面的加速度;(3)滑块与三棱柱之间的正压力.分析这类问题可应用牛顿定律并采用隔离体法求解.在解题的过程中必须注意:(1)参考系的选择.由于牛顿定律只适用于惯性系,可选择地面为参考系(惯性系).因地面和斜面都是光滑的,当滑块在斜面上下滑时,三棱柱受到滑块对它的作用,也将沿地面作加速度为aA的运动,这时,滑块沿斜面的加速度aBA,不再是它相对于地面的加速度aB了.必须注意到它们之间应满足相对加速度的矢量关系,即aB=aA+aBA.若以斜面为参考系(非惯性系),用它求解这类含有相对运动的力学问题是较为方便的.但在非惯性系中,若仍要应用牛顿定律,则必须增添一惯性力F,且有F=maA.(2)坐标系的选择.常取平面直角坐标,并使其中一坐标轴方向与运动方向一致,这样,可使解题简化.(3)在分析滑块与三棱柱之间的正压力时,要考虑运动状态的影响,切勿简单地把它视为滑块重力在垂直于斜面方向的分力mgcoα,事实上只有当aA=0时,正压力才等于mgcoα.解1取地面为参考系,以滑块B和三棱柱A为研究对象,分别作示力图,如图(b)所示.B受重力P1、A施加的支持力FN1;A受重力P2、B施加的压力FN1′、地面支持力FN2.A的运动方向为O某轴的正向,Oy轴的正向垂直地面向上.设aA为A对地的加速度,aB为B对的地加速度.由牛顿定律得FN1inαmaA(1)FN1inαmaB某(2)FN1coαmgmaBy(3)FN1FN1(4)设B相对A的加速度为aBA,则由题意aB、aBA、aA三者的矢量关系如图(c)所示.据此可得aB某aAaBAcoα(5)aByaBAinα(6)解上述方程组可得三棱柱对地面的加速度为aAmginαcoα2mminαmginαcoαmmin2α滑块相对地面的加速度aB在某、y轴上的分量分别为aB某aBymmgin2αmmin2α则滑块相对地面的加速度aB的大小为aBaa2B某2Bym22mmm2in2αginαmmin2α其方向与y轴负向的夹角为amcotαθarctanB某arctanaBymmA与B之间的正压力FN1mmgcoα2mminα解2若以A为参考系,O某轴沿斜面方向[图(d)].在非惯性系中运用牛顿定律,则滑块B的动力学方程分别为mginαmaAcoαmaBA(1)mgcoαFN1maAinα0(2)又因FN1inαmaA0(3)FN1FN1(4)由以上各式可解得aAaBAmginαcoαmmin2αmmginαmmin2α由aB、aBA、aA三者的矢量关系可得m22mmm2in2αaBginαmmin2α以aA代入式(3)可得FN1mmgcoαmmin2α。
第二章习题答案

2-1举出现实生活中的一些相互对立的、处于矛盾状态的事物。
试着给这些对立的事物赋予逻辑“0”和逻辑“1”。
2-2为什么称布尔代数为“开关代数”?2-3基本逻辑运算有哪些?写出它们的真值表。
答:与、或、非。
2-4什么是逻辑函数?它与普通代数中的函数在概念上有什么异同?2-5如何判定两个逻辑函数的相等?2-6逻辑函数与逻辑电路的关系是什么? 答:逻辑电路是能完成某一逻辑运算的电子线路,而逻辑函数可以描述该电路的逻辑功能。
2-7什么是逻辑代数公理?逻辑代数公理与逻辑代数基本定律或定理的关系是什么?2-8用真值表证明表2.3.2中的“0-1律”,“自等律”,“互补律”,“重叠律”和“还原律”。
2-9分别用真值表和逻辑代数基本定律或定理证明下列公式。
1.)C A )(B A (BC A ++=+ 证明:右边=A+AB+AC+BC=A+BC=左边2.B A B A A +=+证明:左边=AB+AB+AB=AB+AB+AB+AB=A+B=右边 3.A AB A =+证明:左边=A(1+B)=A=右边 4.C A B A C A AB +=+证明:左边=(A+B)(A+C)=0+AB+AC+BC=AB+AC=右边 5.AC B A BCD C A AB +=++A B F 0 0 0 0 1 0 1 0 0 1 11与A B F 0 0 0 0 1 1 1 0 1 1 11或A F 0 1 1 0非证明:左边=AB+AC+ABCD+ABCD=AB+AC=右边6.)(+BA+)(+++C=AB)()(CAA(CB)证明:两边取对偶,得AB+AC+BC=AB+AC,得证。
7.)(+B+)(++A=AB)(CAA()C证明:左边右边=AB+AC+BC=AB+AC得证。
8.AA(=B++))(BA证明:设F=(A+B)(A+B)则F’=AB+AB=AF=(F’)’=A得证。
9.A(A=+AB)证明:左边=A+AB=A=右边,得证。
第二章课后习题及答案

第二章心理辅导的理论基础一、理论测试题(一)单项选择题1.()是根据操作性条件反射原理,强调行为的改变是依据行为后果而定的。
A •强化法B •系统脱敏法C.代币法D •来访者中心疗法2•在对学生进行心理辅导时,常使用的“强化法”属于()。
A •行为改变技术B •认知改变法C.运动改变法D •精神分析法3•在心理辅导的行为演练中,系统脱敏法是由()首创。
A .皮亚杰B •沃尔帕C艾利斯D •罗杰斯4•心理辅导老师帮李晓明建立焦虑等级,让他想象引起焦虑的情境,然后逐渐减少焦虑等级,直至完全放松,以缓解其考试焦虑,这种方法是()。
A •强化法B •系统脱敏法C.理性一情绪疗法D •来访者中心疗法5 •行为塑造法是根据()的操作条件反射研究结果而设计的培育和养成新反应或行为模式的一项行为治疗技术,是操作条件作用法强化原则的有力应用之一。
A .皮亚杰B •斯金纳C.艾利斯D .奥苏贝尔6.()就是运用代币并编制一套相应的激励系统来对符合要求的目标行为的表现进行肯定和奖励。
A .强化法B .理性一情绪疗法C.代币法D .来访者中心疗法7.李老师通过奖励小红花来表扬学生的行为,这种心理辅导方法属于()。
A .系统脱敏法B •代币法C.行为塑造法D .来访者中心疗法8.晓红是韩老师班上的学生,她孤僻、羞涩,当她主动与同学交谈或请教老师时,韩老师就给予肯定或激励。
这种心理辅导方法是()。
A .强化法B •系统脱敏法C.来访者中心法D .理性一情绪疗法9.()不是行为改变的基本方法。
A .强化法B .代币法C.自我控制法D .演练法10.小伟过分害怕狗,通过让他看狗的照片,谈论狗,远看狗到近看狗、摸狗、抱狗,消除对狗的惧怕反应,这是行为训练的()。
A .全身松弛训练B .系统脱敏法C.行为塑造法D .肯定性训练11.当一位胆小的学生敢于主动向教师提问时,教师教师耐心解答并给予表扬和鼓励。
的这种做法属于行为改变方法中的()。
习题答案—第二章

第二章 正交曲线坐标系下的张量分析与场论1、用不同于书上的方法求柱坐标系和球坐标系的拉梅系数及两坐标间的转换关系ij β。
解:①柱坐标系k z j i r++=ϕρϕρs i n c o s ,2222222dz H d H d H ds z ++=ϕρϕρ ()()k dz j d d i d d r d+++-=ϕϕρρϕϕϕρρϕcos sin sin cos()()222222222222222222222222222222c o s s i n s i n c o s c o s s i n 2c o s s i n s i n c o s s i n 2c o s c o s s i n s i n c o s dz d d dz d d d d dz d d d d d d d d dz d d d d r d r d ds ++=++++=+++++-=+++-=⋅=ϕρρϕϕρϕϕρρϕρϕϕρϕϕρϕϕρρϕϕϕρϕρϕϕρρϕϕϕρρϕϕϕρρϕ故:1=ρH ,ρϕ=H ,1=z H ②球坐标系k R j R i R r θφθφθc o s s i n s i n c o s s i n ++=,2222222φθφθd H d H dR H ds R ++=()()()kd R dR j d R d R dR id R d R dR r dθθθφφθθφθφθφφθθφθφθsin cos cos sin sin cos sin sin sin sin cos cos cos sin -++++-+= ()()()2222222222s i n s i n c o s c o s s i n s i n c o s s i n s i ns i n s i n c o s c o s c o s s i n φθθθθθφφθθφθφθφφθθφθφθd R d R dR d R dR d R d R dR d R d R dR r d r d ds ++=-++++-+=⋅=故:1=R H ,R H =θ,θφsin R H = ③两坐标间的转换关系ij βφr re e θe φPθru re e zu ze r(1)圆柱坐标系 (2)球坐标系由球坐标系与直角坐标系的坐标变换矩阵为:sin cos sin sin cos cos cos cos sin sin sin cos 0r e i e j e k θφθφθφθθφθφθφφ⎧⎫⎧⎫⎡⎤⎪⎪⎪⎪⎢⎥=-⎨⎬⎨⎬⎢⎥⎪⎪⎪⎪⎢⎥-⎣⎦⎩⎭⎩⎭注意,圆柱坐标系中的θ和球坐标系的φ相等。
第2章(计算机组成原理) 练习题、参考答案

第2章练习题参考答案一、判断题(正确Y,错误N)1. CPU在很大程度上决定了计算机的性能,CPU的运算速度又与CPU的工作频率密切相关。
因此,在其它配置相同时,使用主频为500MHz的Pentium4作为CPU 的PC机,比使用主频为1GHz Pentium4作为CPU的PC机速度快。
N2. 近年来,PC机中使用的1394接口比USB传输速度更快。
Y3. Cache存储器的存取速度比主存储器要快得多。
因此,为了提高程序的运行速度,在软件开发时,应尽可能多地使用Cache存储器。
N4. 主存储器在物理结构上由若干插在主板上的内存条组成。
目前,内存条上的芯片一般选用DRAM而不采用SRAM。
Y5. 在Pentium处理器中,整数ALU和浮点运算器可以分别对整数和实数同时进行运算处理。
Y6. RAM是随机存取存储器的缩写,其中“随机”的含义是:不论从(向)哪个地址读出或写入数据,所需时间都是相同的。
N7. 3.5英寸软盘的角上有一个小口,当滑动保护片将其盖住时,软盘就不能进行读写操作了。
N8. CPU工作时,它所执行的指令和处理的数据都是直接从磁盘或光盘中取出,处理结果也直接存入磁盘。
N9. 一般情况下,计算机加电后自动执行BIOS中的程序,将所需的操作系统软件装载到内存中,这个过程称为“自举”或“引导”。
Y10. 若某台PC机主板上的CMOS信息丢失,则该机器将不能正常运行,此时只要将其他计算机中的CMOS信息写入后,该机器便能正常运行。
N11. BIOS芯片和CMOS芯片实际上是一块芯片的两种叫法,是启动计算机工作的重要部件。
N12. 一个完整的计算机系统的两个基本组成部分是操作系统和数据库系统.N13. USB接口是一种高速的并行接口。
N14. 计算机中总线的重要指标之一是带宽,它指的是总线中数据线的宽度,用二进位数目来表示(如16位,32位总线)。
N15. 在BIOS中不包含扫描仪、打印机等设备的驱动程序。
《微观经济学》第2章需求与供给练习题及答案解析

第二章需求与供给一、选择题1.随着公共汽车车票的价格上升,会出现公共汽车车票的( )。
A. 需求量增加;B. 需求量减少;C. 需求增加;D. 需求减少解析:B.本题考察需求量的含义,商品本身价格的变化导致的需求数量的变化被称为需求量的变化。
表示在不同的价格下消费者改变了消费数量。
2.随着公共汽车票的价格大幅下降,会出现私人汽车的( )。
A. 需求量增加;B. 需求量减少;C. 需求增加;D. 需求减少解析:D.本题考察需求的含义,商品本身价格以外的因素发生变化也就是非价格因素的变化导致的需求数量的变化被称为需求的变化。
表示在每一个与以前相同的价格下消费者改变了消费数量。
公共汽车和私人汽车互为替代品,替代品价格下降,被研究对象的需求会跟着下降,消费者在相同的价格下减少了对私人汽车的需求数量。
3.随着汽油价格大幅下降,会出现私人汽车的( )。
A. 需求量增加;B. 需求量减少;C. 需求增加;D. 需求减少解析:C.本题考察需求的含义,商品本身价格以外的因素发生变化也就是非价格因素的变化导致的需求数量的变化被称为需求的变化。
表示在每一个与以前相同的价格下消费者改变了消费数量。
汽油和私人汽车互为互补品,互补品价格下降,被研究对象的需求数量会增加,消费者在相同的价格下增加了对私人汽车的需求数量。
4. 随着养猪专业户的增加,会出现生猪的( )。
A. 需求量增加;B. 需求量减少;C. 需求增加;D. 需求减少解析:A. 本题考察需求量的含义,商品本身价格的变化导致的需求数量的变化被称需求量的变化。
表示在不同的价格下消费者改变了消费数量。
本题供给增加导致生猪价格下降,在较低的价格下消费者增加了生猪的需求数量,是需求量的变化。
5.随着商品房价格上升,商品房的()A.供给增加;B.供给量增加;C.供给减少;D.供给量减少。
解析:B.本题考察供给量的含义,商品本身价格的变化导致的供给数量的变化被称供给量的变化。
第二章 练习题答案

第二章练习题2-1 在IBM PC微型计算机上,分别进行以下8位二进制数的运算后,标志寄存器中OF、ZF、SF、CF的值分别为多少?(1)10101011 + 01010101(2)11011010 + 11101101(3)01010101-00111110(4)10110011-01100010答案:(1)OF=0 ZF=1 SF=0 CF=1(2)OF=0 ZF=0 SF=1 CF=1(3)OF=0 ZF=0 SF=0 CF=0(4)OF=1 ZF=0 SF=0 CF=02-2 有两个字数据12H和AB12H分别存放在存储器的10016H和8BA00H中,请图示它们在存储器中的存放情况。
答案:10016H8BA00H2-3 在8086/8088中,某存储单元的逻辑地址如下,请算出它们的物理地址是多少?(1)4514H:017BH(2)F000H:0100H(3)2350H:1ABCH(4)10E0H:2020H答案:(1)452BBH(2)F0100H(3)24FBCH(4)12E20H2-4 如图所示,试写出地址为20021H、20024H、20026H字节单元的内容,以及地址为20022H、20024H、20026H的字单元内容。
20020H 20021H 20022H 20023H 20028H20024H 20025H 20026H 20027H答案:78H ,FAH ,06H ,DEBCH ,03FAH ,0806H2-5 设堆栈寄存器(SS )= 3E4BH ,程序中设置堆栈长度为200个字节,试计算出堆栈底部字单元物理地址、堆栈指针SP 初始值(即堆栈中没有数据时)和SP 初始值指向的物理地址。
答案:3E576H ,SP=0C8H(200),3E578H2-6 设(AX )= 1122H ,(BX )= 3344H ,(CX )= 5566H ,(SP )= 2000H ,试分析以下程序执行后AX 、BX 、CX 、SP 中的内容分别为多少?并画出堆栈变化的示意图。
第二章习题及答案

电工学第二章习题一、填空题1. 两个均为40F μ的电容串联后总电容为 80 F μ,它们并联后的总电容为 20F μ。
2. 表征正弦交流电振荡幅度的量是它的 最大值 ;表征正弦交流电随时间变化快慢程度的量是 角频率ω ;表征正弦交流电起始位置时的量称为它的 初相 。
三者称为正弦量的 三要素 。
3. 电阻元件上任一瞬间的电压电流关系可表示为 u = iR ;电感元件上任一瞬间的电压电流关系可以表示为dtdiLu =L ;电容元件上任一瞬间的电压电流关系可以表示为dtduCi =C 。
由上述三个关系式可得, 电阻 元件为即时元件; 电感 和 电容 元件为动态元件。
4. 在RLC 串联电路中,已知电流为5A ,电阻为30Ω,感抗为40Ω,容抗为80Ω,那么电路的阻抗为 50Ω ,该电路为 容 性电路。
电路中吸收的有功功率为 750W ,吸收的无功功率又为 1000var 。
二、选择题1. 某正弦电压有效值为380V ,频率为50Hz ,计时始数值等于380V ,其瞬时值表达式为( B )A 、t u 314sin 380=V ;B 、)45314sin(537︒+=t u V ;C 、)90314sin(380︒+=t u V 。
2. 一个电热器,接在10V 的直流电源上,产生的功率为P 。
把它改接在正弦交流电源上,使其产生的功率为P/2,则正弦交流电源电压的最大值为(D ) A 、; B 、5V ; C 、14V ; D 、10V 。
3. 提高供电电路的功率因数,下列说法正确的是( D )A 、减少了用电设备中无用的无功功率;B 、减少了用电设备的有功功率,提高了电源设备的容量;C 、可以节省电能;D 、可提高电源设备的利用率并减小输电线路中的功率损耗。
4. 已知)90314sin(101︒+=t i A ,︒+=30628sin(102t i )A ,则( C )A 、i1超前i260°;B 、i1滞后i260°;C 、相位差无法判断。
第二章习题与答案

第二章会计科目、会计账户和借贷复式记账法一、单项选择题1.账户是根据()开设的,用来连续、系统地记载各项经济业务的一种手段。
A.会计凭证B.会计对象C.会计科目D.财务指标2.根据借贷记账法的原理,记录在账户贷方的是()。
A.费用的增加B.收入的增加C.负债的减少D.所有者权益的减少3.会计科目是()的名称。
A.会计账户B.会计等式C.会计对象D.会计要素4借贷记账法的记账规则是()。
A.同增、同减、有增、有减B.同收、同付、有收、有付C.有增必有减,增减必相等D.有借必有贷,借贷必相等5.在借贷记账法中,账户的哪一方记录增加,哪一方记录减少是由()决定的。
A.账户的性质B.记账规则C.账户的结构D.业务的性质6.复试记账法的基本理论依据是()的平衡原理。
A.资产=负债+所有者权益B.收入–费用=利润C.期初余额+本期增加数-本期减少数=期末余额D.借方发生额=贷方发生额8.按照借贷记账法的记录方法,下列四组账户中,增加额均记在贷方的是()。
A.资产类和负债类B.负债类和所有者权益类C.成本类和损益类D.损益类中的收入和支出类9.会计科目与账户之间的区别在于()。
A.反映经济内容不同B.账户有结构而会计科目无结构C.分类的对象不同D.反映的结果不同10.按照借贷记账法的记录方法,下列账户的贷方登记增加额的是()。
A.库存现金B.应收账款C.应付账款D.原材料11.按照借贷记账法的记录方法,下列账户中,账户的借方登记增加额的是()。
A.实收资本B.应付职工薪酬C.累计折旧D.所得税费用12.目前我国会计制度规定,企业会计采用的记账方法是()。
A.增减记账法B.现金收付记账法C.借贷记账法D.财产收付记账法13.账户的基本结构分为左右两方,其基本依据是()。
A.登记收支业务B.借贷原理C.收付原理D.资金在运动中量的增加和减少14.不属于损益类会计科目的是()。
A.投资收益B.管理费用C.主营业务成本D.生产成本15.下列属于资产类的会计科目是()。
第二章部分习题答案

习题6、试从动态性、并发性和独立性上比较进程和程序。
答:(1)从动态性角度:进程的实质是进程实体的一次执行过程,因此,动态性是进程的最基本的特征。
动态性还表现在:“它由创建而产生,由调度而执行,由撤消而消亡”。
可见,进程实体有一定的生命期,而程序则只是一组有序指令的集合,并存放于某种介质上,其本身并不具有运动的含义,因而是静态的。
(2)从并发性角度:这是指多个进程实体同存于内存中,且能在一段时间内同时运行。
并发性是进程的重要特征,同时也成为OS的重要特征。
引入进程的目的也正是为了使其进程实体能和其它进程实体并发执行;而程序(没有建立PCB)是不能并发执行的。
(3)从独立性角度:在传统的OS中,独立性是指进程实体是一个能独立运行、独立分配资源和独立接受调度的基本单位。
凡未建立PCB的程序都不能作为一个独立的单位参与运行。
7、试说明PCB的作用,为什么说PCB是进程存在的惟一标志?答:(1)进程控制块PCB的作用是使一个在多道程序环境下不能独立运行的程序(含数据),成为一个能独立运行的基本单位,一个能与其它进程并发执行的进程。
(2)在进程的整个生命期中,系统总是通过PCB对进程进行控制的,亦即,系统是根据进程的PCB而不是任何别的什么而感知到该进程的存在的。
所以说,PCB 是进程存在的惟一标志。
9、为什么要引入挂起状态?该状态有哪些性质?答:引入挂起状态的原因:(1)终端用户的请求。
(2)父进程请求。
(3)负荷调节的需要。
(4)操作系统的需要。
处于挂起状态的进程最大的特点是主动放弃CPU调度。
引入挂起状态后,进程状态转换图中增加了活动阻塞、静止阻塞、活动就绪、静止就绪四个状态,并增加了活动就绪与静止就绪之间的相互转换,活动阻塞与静止阻塞之间的相互转换。
16、进程在运行时存在哪两种形式的制约?并举例说明之。
答:(1)间接相互制约关系。
同处于一个系统中的进程,通常都共享着某种系统资源,如共享CPU、共享I/O设备等。
第二章习题答案

1
011…1B (231–1) > 100…0B (–231)
1
11…1B (–1) > 11…10B (–2)
1
11…1B (232–1) > 11…10B (232–2)
9.以下是一个 C 语言程序,用来计算一个数组 a 中每个元素的和。当参数 len 为 0 时,返回值应该是 0,
但是在机器上执行时,却发生了存储器访问异常。请问这是什么原因造成的,并说明程序应该如何
10. 设某浮点数格式为:
数符 1位
阶码 5 位移码
尾数 6 位补码
其中,移码的偏置常数为 16,补码采用一位符号位,基数为 4。 (1) 用这种格式表示下列十进制数:+1.7,–0.12,+19,–1/8。 (2) 写出该格式浮点数的表示范围,并与 12 位定点补码整数表示范围比较。 参考答案:(假定采用 0 舍 1 入法进行舍入) (1) +1.7 = +1.1011001B = 0.011011B× 41, 故阶码为 1 +16 = 17 = 10001B, 尾数为+0.011011 的补码,
7 位原码
参考答案: (1)无符号整数:0~216–1。 (2)原码定点小数:–(1–2–15) ~ + (1–2–15)。 (3)补码定点小数:–1 ~ + (1–2–15)。 (4)补码定点整数:–32768 ~ +32767。 (5)浮点数:负数:– (1–2–7)×2+127 ~ –2–7×2–128。
(2)[x]补=10000000 (4)[x]补=11010011
x = –0.0011001B x = –10000000B = –128 x = +0.101001B x = – 101101B = – 45
第二章课后习题与答案

第2章人工智能与知识工程初步1. 设有如下语句,请用相应的谓词公式分别把他们表示出来:s(1)有的人喜欢梅花,有的人喜欢菊花,有的人既喜欢梅花又喜欢菊花。
解:定义谓词dP(x):x是人L(x,y):x喜欢y其中,y的个体域是{梅花,菊花}。
将知识用谓词表示为:(∃x )(P(x)→L(x, 梅花)∨L(x, 菊花)∨L(x, 梅花)∧L(x, 菊花))(2)有人每天下午都去打篮球。
解:定义谓词P(x):x是人B(x):x打篮球A(y):y是下午将知识用谓词表示为:a(∃x )(∀y) (A(y)→B(x)∧P(x))(3)新型计算机速度又快,存储容量又大。
解:定义谓词NC(x):x是新型计算机F(x):x速度快B(x):x容量大将知识用谓词表示为:(∀x) (NC(x)→F(x)∧B(x))(4)不是每个计算机系的学生都喜欢在计算机上编程序。
解:定义谓词S(x):x是计算机系学生L(x, pragramming):x喜欢编程序U(x,computer):x使用计算机将知识用谓词表示为:¬(∀x) (S(x)→L(x, pragramming)∧U(x,computer))(5)凡是喜欢编程序的人都喜欢计算机。
解:定义谓词P(x):x是人L(x, y):x喜欢y将知识用谓词表示为:(∀x) (P(x)∧L(x,pragramming)→L(x, computer))2请对下列命题分别写出它们的语义网络: (1) 每个学生都有一台计算机。
解:(2) 高老师从3月到7月给计算机系学生讲《计算机网络》课。
解:(3) 学习班的学员有男、有女、有研究生、有本科生。
解:参例2.14(4) 创新公司在科海大街56号,刘洋是该公司的经理,他32岁、硕士学位。
解:参例2.10(5) 红队与蓝队进行足球比赛,最后以3:2的比分结束。
解:2.19 请把下列命题用一个语义网络表示出来: (1) 树和草都是植物; 解:(2) 树和草都有叶和根; 解:(3) 水草是草,且生长在水中; 解:(4) 果树是树,且会结果; 解:(5) 梨树是果树中的一种,它会结梨。
第2章逐步聚合习题参考答案

第二章 缩聚与逐步聚合反应-习题参考答案1.名词解释:逐步聚合;缩合聚合;官能团等活性;线型缩聚;体型缩聚;凝胶点;转化率;反应程度。
答:逐步聚合——单体转变成高分子是逐步进行的,即单体官能团间相互反应而逐步增长。
缩合聚合——由带有两个或两个以上官能团的单体之间连续、重复进行的缩合反应。
官能团等活性——在一定聚合度范围内,官能团活性与聚合物分子量大小无关。
线型缩聚——参加反应的单体都含有两个官能团,反应中形成的大分子向两个方向增长,得到线型缩聚物的一类反应。
体型缩聚——参加反应的单体中至少有一种单体含有两个以上的官能团,且体系平均官能度大于2,反应中大分子向三个方向增长,得到体型结构的聚合物的这类反应。
凝胶点——开始出现凝胶瞬间的临界反应程度。
转化率——参加反应的单体量占起始单体量的分数反应程度——参与反应的基团数占起始基团的分数。
3.由己二元酸和己二胺等摩尔合成尼龙—6,6。
已知聚合反应的平衡常数K=432,如果要合成聚合度在200的缩聚物,计算反应体系中的水含量应控制为多少?解:n X =n X =200,K=432代入此式可得: 224320.0108200w n K n X === 答:反应体系中的水含量应控制为0.0108 mol/L.4.计算等摩尔的对苯二甲酸与乙二醇反应体系,在下列反应程度时的平均聚合度和分子量。
0.500,0.800,0.900,0.950,0.995。
解: 等物质量条件下,有PX -=11,聚苯二甲酸乙二醇酯结构单元的分子量:M 0=192。
11n X p=-,n o n X M M ⨯=,因此各反应程度时的平均聚合度和分子量见下表:7.氨基己酸进行缩聚反应时,如在体系中加入0.2mol%的醋酸,求当反应程度P 分别达到0.950,0.980,0.990时的平均聚合度和平均分子量。
解: 方法1:2212 1.998'110.002a a ab b f N f N N N ⨯⨯===++++ 当p=0.950时,22202 1.9980.9502n X pf ==≈-⨯- 214010720=⨯=⨯=n o n X M M当p=0.980时,22482 1.9980.9802n X pf ==≈-⨯- 513610748=⨯=⨯=n o n X M M当p=0.990时,22912 1.9980.9902n X pf ==≈-⨯- 937910791=⨯=⨯=n o n X M M方法2:rpr r Xn 211-++=, NcNa Na r 2+==0.996 P=0.95, 20=XnP=0.98, 46=XnP=0.99, 83=Xn8.用Carothers 法计算下列聚合反应的凝胶点:(1)邻苯二甲酸酐+甘油,摩尔比3:2。
机械制图-第2章-点-直线-平面的投影习题答案
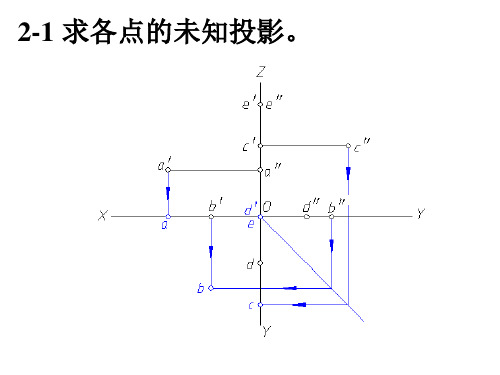
2-8 判断两直线的相对位置(平行、相交、交叉、垂直相交、 垂直交叉)并将答案填写在下面的括号内。
2-9 由点A作直线AB与直线CD相交并使交点 距H面12。
2-10 求直线AB、CD的交点K。
2-11 过点C作直线CD与已知直线AB平行。
2-12 作与已知直线AB、CD平行且相距为15的直线MN,并使MN的 实长为20,点M距W面30,点N在点M之右(任求一解)。
2-17 求平面的侧面投影并判断平面的空间位置 该平面是 铅垂 面
2-18 求平面的侧面投影并判断平面的空间位置 △ABC是 侧平 面
2-19 求平面上点K与点N的另一投影。
2-20 已知直线AB在两平行直线CD、EF所确定的 平面上,求作AB的水平投影。
2-21 完成平面图形ABCDE的水平投影。
2-22 已知CD为水平线,完成平面ABCD的正面投影。
2-23 完成平面图形ABCDEFGH的三投影并回答 下面的问题。
平面ABCDEFGH是 一般位置 面。 直线EF是 水平 线。 直线FG是 侧平 线。
2-24 判断下列各图中的直线与平面是否平行(将“是” 或"否"填于括弧中)。
⑴
⑵
பைடு நூலகம்
( 是)
2-4 已知直线AB的实长为15,求作其三面投影。
⑴ AB∥W面,β=30°; 点B在点A之下、之前。
⑵ AB∥V面,γ=60°; 点B在点A之下、之右。
⑶ AB⊥H面,点B在点A之下。
2-5 求直线AB上点K的正面投影。
2-6 在直线AB上取一点C,使其到H及V面的 距离相等。
2-7 标出交叉二直线上的重影点并判别可见性。
2-13 作正平线EF距V面15,并与直线AB、CD相交 (点E、F分别在直线AB、CD上)。
第二章课后习题答案

1. 已知某一时期内某商品的需求函数为Q =50-5P ,供给函数为Qs=-10+5p。
(1)求均衡价格Pe和均衡数量Qe,并作出几何图形。
(2)假定供给函数不变,由于消费者收入水平提高,使需求函数变为Qd=60-5P。
求出相应的均衡价格Pe 和均衡数量Qe ,并作出几何图形。
(3)假定需求函数不变,由于生产技术水平提高,使供给函数变为Qs=-5+5p。
求出相应的均衡价格Pe 和均衡数量Qe ,并作出几何图形。
(4)利用(1)(2 )(3),说明静态分析和比较静态分析的联系和区别。
(5)利用(1)(2 )(3),说明需求变动和供给变动对均衡价格和均衡数量的影响.解答: (1)将需求函数Qd = 50-5P和供给函数Qs =-10+5P 代入均衡条件Qd = Qs ,有: 50- 5P= -10+5P得: Pe=6以均衡价格Pe =6 代入需求函数Qd =50-5p ,得: Qe=20所以,均衡价格和均衡数量分别为Pe =6 , Qe=20 (图略)(2)将由于消费者收入提高而产生的需求函数Qd=60-5p 和原供给函数Qs=-10+5P, 代入均衡条件Q d= Qs ,有: 60-5P=-10+5P 得Pe=7以均衡价格Pe=7代入Qd方程,得Qe=25所以,均衡价格和均衡数量分别为Pe =7 , Qe=25 (图略)(3) 将原需求函数Qd =50-5p和由于技术水平提高而产生的供给函数Q =-5+5p ,代入均衡条件Qd =Qe ,有: 50-5P=-5+5P得Pe= 5.5以均衡价格Pe= 5.5 代入Qd =50-5p ,得22.5所以,均衡价格和均衡数量分别为Pe=5.5 Qe=22.5(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征.也可以说,静态分析是在一个经济模型中根据所给的外生变量来求内生变量的一种分析方法.以(1)为例,在图中,均衡点 E 就是一个体现了静态分析特征的点.它是在给定的供求力量的相互作用下所达到的一个均衡点.在此,给定的供求力量分别用给定的供给函数Q=-10+5P 和需求函数Q=50-5P表示,均衡点具有的特征是:均衡价格P=6 且当P =6 时,有Q= Q d= Qe =20 ,同时,均衡数量Qe= 20 ,且当Qe=20 时,有Pd=Ps=Pe=6 ,也可以这样来理解静态分析:在外生变量包括需求函数的参数(50,-5) 以及供给函数中的参数(-10,5)给定的条件下,求出的内生变量分别为P= 6 ,Qe =20依此类推,以上所描素的关于静态分析的基本要点,在(2)及其图和(3)及其图中的每一个单独的均衡点上都得到了体现。
第2章习题答案

答:设备的额定值与实际工作值是两种不同的概念,100A 是发电机的额定电流值,60A
是发电机的实际工作值,实际工作值小于额定值,表明发电机工作在轻载状态。
(5) 根据日常观察,电灯在深夜要比黄昏时亮一些,为什么?
答:深夜时分,大多数家庭都关灯休息,用电量下降,输电线路上的电流减小,输电线
路上的压降减小,加在电灯上的工作电压升高,流过电灯灯丝的电流增大,所以电灯发光强
质进行科学抽象和概括而得到的实体模型。它将实际元器件理想化(或称模型化)。
(2) 标识电压参考方向的方法有哪几种?你最喜欢使用哪一种?为什么?
答:标识电压参考方向的方法有如下三种:用 “ ”、 “ ”极性端表示; 用双下标表
示;在电路图上用箭头表示。
我最喜欢在电路图上用箭头表示电压参考方向这一种。原因如下:一是图形表示直观明 了;二是如果在心中假设流过电阻的电压和电流的参考方向相同,则在图中可省略不划。
(3) Uab 是否表示 a 端的实际电位高于 b 端的实际电位?
答:不一定,Uab 表示电压方向从 a 点指向 b 点,如果Uab 0 ,则 a 点电位高于 b 点;
否则 a 点电位低于 b 点。 (4) 额定电流为 100A 的发电机,只接 60A 的照明负载,还有电流 40A 的电流流到哪去
的 电 灯上 的 电 压
U2
302.5 220V=157.1V>110V 302.5 121
,因此 40W 的电灯会烧毁。
4) 在如图 2-36 的电路中,电压和电流之间的关系为( )
(A) U E RI
答案:B
(B) U E RI (C) U E RI
5) 在图 2-37 所示电路中,当电阻 R2 增大时,则电流 I1 ( )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题目录2.1 (2)2.2 (2)2.3 (2)2.4 (3)2.5 (3)2.6 (4)2.7 (4)2.8 (4)2.9 (4)2.10 (4)2.11 (5)2.12 (5)2.13 (7)2.14 (8)2.1 有A 、B 、C 三个输入信号,试列出下列问题的真值表,并写出最小项表达式∑m ( )。
(1)如果A 、B 、C 均为0或其中一个信号为1时。
输出F=1,其余情况下F=0。
(2)若A 、B 、C 出现奇数个0时输出为1,其余情况输出为0。
(3)若A 、B 、C 有两个或两个以上为1时,输出为1,其余情况下,输出为0。
解:(1) (2) (3)F 1(A,B,C)=∑m (0,1,2,4)F 2(A,B,C)=∑m (0,3,5,6)F 3(A,B,C)=∑m (3,5,6,7)2.2 试用真值表证明下列等式:(1)A ⎺B+B ⎺C+A ⎺C=ABC+⎺A ⎺B ⎺C (2)⎺A ⎺B+⎺B ⎺C+⎺A ⎺C=AB BC AC 证明:(1)真值表相同,所以等式成立。
(2)2.3 对下列函数,说明对输入变量的哪些取值组合其输出为1?(1)F (A,B,C )=AB+BC+AC(2)F (A,B,C )=(A+B+C)(⎺A+⎺B+⎺C) (3)F (A,B,C )=(⎺AB+⎺BC+A ⎺C)AC解:本题可用真值表、化成最小项表达式、卡诺图等多种方法求解。
(1)F 输出1的取值组合为:011、101、110、111。
(2)F 输出1的取值组合为:001、010、011、100、101、110。
(3)F输出1的取值组合为:101。
2.4试直接写出下列各式的反演式和对偶式。
(1)F(A,B,C,D,E)=[(A⎺B+C)·D+E]·B(2) F(A,B,C,D,E)=AB+⎺C⎺D+BC+⎺D+⎺CE+B+E(3) F(A,B,C)=⎺A⎺B+C ⎺AB C解:(1) ⎺F=[(⎺A+B)·⎺C+⎺D]·⎺E+⎺BF'=[(A+⎺B)·C+D]·E+B(2) ⎺F=(⎺A+⎺B)(C+D)·(⎺B+⎺C)·D·(C+⎺E)·⎺B·⎺EF'=(A+B)(⎺C+⎺D)·(B+C)·⎺D·(⎺C+E)·B·E(3)⎺F=(A+B)·⎺C+ A+⎺B+CF'=(⎺A+⎺B)·C+⎺A+B+⎺C2.5用公式证明下列等式:(1)⎺A⎺C+⎺A⎺B+BC+⎺A⎺C⎺D=⎺A+BC(2)AB+⎺AC+(⎺B+⎺C) D=AB+⎺AC+D(3)⎺BC⎺D+B⎺CD+ACD+⎺AB⎺C⎺D+⎺A⎺BCD+B⎺C⎺D+BCD=⎺BC+B⎺C+BD(4)A⎺B⎺C+BC+BC⎺D+A⎺BD=⎺A + B +⎺C+⎺D证明:(1) ⎺A⎺C+⎺A⎺B+BC+⎺A⎺C⎺D ——⎺A⎺C⎺D被⎺A⎺C削去=⎺A(⎺B+⎺C)+BC=⎺A BC+BC ——削去互补因子=⎺A+BC(2) AB+⎺AC+(⎺B+⎺C) D=AB+⎺AC+BC D+BC ——增加冗余因子BC,为了削去BCD中的BC =AB+⎺AC+D(3)⎺BC⎺D+B⎺CD+ACD+⎺AB⎺C⎺D+⎺A⎺BCD+B⎺C⎺D+BCD=⎺BC⎺D+BD+ACD+⎺AB⎺C⎺D+⎺BCD+B⎺C⎺D ——B⎺CD与BCD合并成BD=⎺BC⎺D+BD+ACD+⎺AB⎺C⎺D+⎺BCD+B⎺C ——BD与B⎺C⎺D削去互补因子=⎺BC⎺D+BD+ACD+⎺BCD+B⎺C ——⎺AB⎺C⎺D被B⎺C削去=⎺BC+BD+ACD+B⎺C ——⎺BC⎺D与⎺BCD合并=⎺BC+BD+CD+ACD+B⎺C ——增加CD,可削去ACD=⎺BC+B⎺C+BD(4)A⎺B⎺C+BC+BC⎺D+A⎺BD=A⎺B⎺⎺D)+⎺A+B+⎺D ——D削去互补因子=A⎺B⎺C (⎺B+⎺C+⎺D)+⎺A+B+⎺D=A⎺B⎺C +A⎺B⎺C⎺D+⎺A+B+⎺D=A⎺B⎺C+⎺A+B+⎺D=⎺A+ B +⎺C+⎺D2.6已知⎺ab+a⎺b=a⊕b,⎺a⎺b+ab=a b,证明:(1)a⊕b⊕c=a b c(2)a⊕b⊕c=⎺a ⎺b ⎺c证明:(1)a⊕b⊕c=(a⊕b)⊕c=a⊕b · c+(a⊕b)·⎺c=(a b)·⎺c=a b c(2)(a⊕b)⊕c = (a⊕b) c=a b c=a b ⎺c=⎺a ⎺b ⎺c2.7试证明:(1)若⎺a⎺b+ a b=0则a x+b y=a⎺x + b⎺y证明:⎺a⎺b+ a b=0 即a b=0 ∴a =⎺bax + by =⎺bx + by = ⎺bx · by=(b+⎺x)(⎺b+⎺y)=b⎺y+⎺b⎺x+⎺x⎺y=a⎺x+b⎺y(2)若⎺a b+a⎺b=c,则⎺a c + a⎺c=b证明:a⊕b=c => a⊕b⊕c=c⊕c => a⊕b⊕c=0 => a⊕b⊕c⊕b=0⊕b => a⊕c=b2.8将下列函数展开成最小项之和:(1)F(ABC)=A+BC(2)F(ABCD)=(B+⎺C)D+(⎺A+B) C(3)F(ABC)=A+B+C+⎺A+B+C解:(1)F(ABC)=A+BC=A(B+⎺B)(C+⎺C)+(A+⎺A)BC=⎺ABC+A⎺B⎺C+A⎺BC+AB⎺C=∑m(3,4,5,6)(2) F(ABCD)=(B+⎺C)D+(⎺A+B) C=BD+⎺CD+⎺AC+BC=∑m(1,3,5,6,7,9,13,14,15)(3) F(ABC)=A+B+C+⎺A+B+C=∑m(0,2,6)2.9将题2.8中各题写成最大项表达式,并将结果与2.8题结果进行比较。
解:(1)F(ABC)=∏M(0,1,2)(2) F(ABCD)=∏M(2,4,8,10,11,12)(3)F(ABC)=∏M(1,3,4,5,7)2.10试写出下列各函数表达式F的⎺F和F'的最小项表达式。
(1)F=ABCD+ACD+B⎺C⎺D(2)F=A⎺B+⎺AB+BC解:(1)F=ABCD+ACD+B⎺C⎺D=∑m(4,11,12,15)所以:⎺F=∑m(0,1,2,3,5,6,7,8,9,10,13,14)F'=∑m(1,2,5,6,7,8,9,10,12,13,14,15)(2) F=A⎺B+⎺AB+BC=∑m(4,5,6,7,8,9,10,11,14,15)所以:⎺F=∑m(0,1,2,3,12,13)F'=∑m(2,3,12,13,14,15)2.11试用公式法把下列各表达式化简为最简与或式(1)F=A+AB⎺C+ABC+BC+B解:F=A+AB(⎺C+C)+B=A+AB+B=A+B(2) F=(A+B)(A+B+C)(⎺A+C)(B+C+D)解:F'=AB+ABC+⎺AC+BCD=AB+⎺AC+BCD=AB+⎺AC(3) F=AB+⎺A⎺B ∙BC+⎺B⎺C解:F=AB+⎺A⎺B+BC+⎺B⎺C=AB+⎺A⎺B(C+⎺C)+BC(A+⎺A)+⎺B⎺C=AB+⎺A⎺BC+⎺A⎺B⎺C+ABC+⎺ABC+⎺B⎺C=AB+⎺B⎺C+⎺AC或:F=⎺A⎺B+A⎺C+BC(4) F=A⎺C⎺D+BC+⎺BD+A⎺B+⎺AC+⎺B⎺C解:F=A⎺C⎺D+BC+⎺BD+A⎺B+⎺AC+⎺B⎺C+AC ——添项法增加AC =A⎺C⎺D+BC+⎺BD+A⎺B+C+⎺B⎺C=A⎺C⎺D+BC+⎺BD+A⎺B+C+⎺B=A⎺C⎺D+BC+C+⎺B=A⎺C⎺D+C+⎺B=A⎺D+C+⎺B(5) F=AC+⎺BC+B(A⎺C+⎺AC)解:F=(AC+⎺BC)∙B(A⎺C+⎺AC)=(AC+⎺BC)∙[⎺B+(A⎺C+⎺AC)]=(AC+⎺BC)∙(⎺B+⎺A⎺C+AC)=ABC+AC+⎺BC+A⎺BC=AC+⎺BC2.12用卡诺图把下列函数化简为最简与或式(1)F(A,B,C)=∑m(0,1,2,4,5,7)解:F=⎺B+⎺A⎺C+AC(2)F(A,B,C,D)=∑m(0,2,5,6,7,9,10,14,15)解:F=A⎺B⎺CD+⎺A⎺B⎺D+⎺ABD+BC+C⎺D(3)F(A,B,C,D)=∑m(0,1,4,7,9,10,13) +∑φ(2,5,8,12,15)解:F=⎺C+BD+⎺B⎺D(4)F(A,B,C,D)=∑m(7,13,15) 且⎺A⎺B⎺C=0, ⎺AB⎺C=0, ⎺A⎺BC=0解:F(A,B,C,D)=BD(5) F(A,B,C,D)=AB⎺C+A⎺B⎺C+⎺A⎺BC⎺D+A⎺BC⎺D且ABCD不可同时为1或同时为0 解:F(A,B,C,D)=⎺B⎺D+A⎺C(6)F(A,B,C,D)=∏M (5,7,13,15)(7)F(A,B,C,D)=∏M (1,3,9,10,14,15)解:F=⎺A⎺D+⎺AB+⎺C⎺D+B⎺C+A⎺BCD(8)F(A,B,C,D,E)=∑m(0,4,5,6,7,8,11,13,15,16,20,21,22,23,24,25,27,29,31)解:F=⎺C⎺D⎺E+⎺BC+CE+BDE+ABEA=0 A=12.13用卡诺图将下列函数化为最简或与式(1)F(A,B,C)=∑m(0,1,2,4,5,7)解:F=(A+⎺B+⎺C)(⎺A+⎺B+C)(2)F(A,B,C)=∏M (5,7,13,15)2.14 已知:F 1(A,B,C)=∑m (1,2,3,5,7) +∑φ (0,6),F 2(A,B,C)=∑m (0,3,4,6) +∑φ (2,5),求F=F 1⊕F 2的最简与或式解:F=A+⎺B=。
