清华大学毕业设计论文遗传算法
遗传算法的研究及应用毕业设计

毕业设计遗传算法的研究及应用摘要本文分为三部分:第一部分:遗传算法的概述。
主要介绍了遗传算法的基本思想、遗传算法的构成要素、遗传算法的特点、遗传算法的基本模型、遗传算法的应用情况及今后的研究方向等等的内容。
第二部分:基于Matlab 7.0下的遗传算法求解函数最值问题。
遗传算法作为一种新的优化方法,广泛地用于计算科学、模式识别和智能故障诊断等方面,它适用于解决复杂的非线性和多维空间寻优问题,近年来也得到了较为广阔的应用。
本人选择了函数优化这个应用领域,按照遗传算法的步骤,即编码、解码、计算适应度(函数值)、选择复制运算、交叉运算和变异运算,对函数进行求解最值。
第三部分:对遗传算法求函数最值问题的改进。
这部分主要针对本文第二部分进行改进,通过改变基本遗传算法运行参数值,如改变交叉概率Pc值和变异概率Pm值,从而使最优值更加接近相对标准下函数的最值。
关键词:遗传算法适应度交叉概率变异概率目录1 前言 (1)2 遗传算法概述 (1)2.1生物进化理论和遗传学的基本知识 (1)2.2遗传算法的基本思想 (3)2.3遗传算法的构成要素 (3)2.3.1 染色体编码方法 (3)2.3.2 适应度函数 (4)2.3.3 遗传算子 (4)2.3.4 基本遗传算法运行参数 (5)2.4遗传算法的特点 (6)2.5遗传算法的基本模型 (7)2.6遗传算法的应用 (8)2.7遗传算法今后的研究方向 (10)3 基于MATLAB 7.0下的遗传算法求解函数最值问题 (11)3.1遗传算法的标准函数 (11)3.2解题步骤说明 (12)3.2.1 编码问题 (12)3.2.2 选择运算 (12)3.2.3 交叉运算 (13)3.2.4 变异运算 (13)3.3运行参数说明 (14)3.4对遗传算法求得的最值的分析 (14)3.5运行程序以及对其解释 (14)3.6从数学的角度求解函数最优值 (18)3.6.1 自变量x以0.2为步进单位 (18)3.6.2 自变量x以0.1为步进单位 (19)3.6.3 自变量x以更精确的数为步进单位 (21)4 对遗传算法求解函数最值问题的改进 (21)4.1寻找求得最优解的运行参数值 (22)4.1.1 当Pc=0.9和Pm=0.0001 (22)4.1.2 当Pc=0.9和Pm=0.001 (23)4.1.3 当Pc=0.9和Pm=0.01 (24)4.1.4 当Pc=0.9和Pm=0.1 (26)4.1.5 当Pc=0.4和Pm=0.1 (27)5 结论 (29)参考文献 (30)ABSTRACT (31)附录 (32)致谢 (38)仲恺农业工程学院毕业论文(设计)成绩评定表 (39)1 前言生命科学与工程科学的相互交叉、相互渗透和相互促进是近代科学技术发展的一个显著特点,而遗传算法的蓬勃发展正体现了科学发展的这一特征和趋势。
数学建模遗传算法与优化问题【精品毕业设计】(完整版)
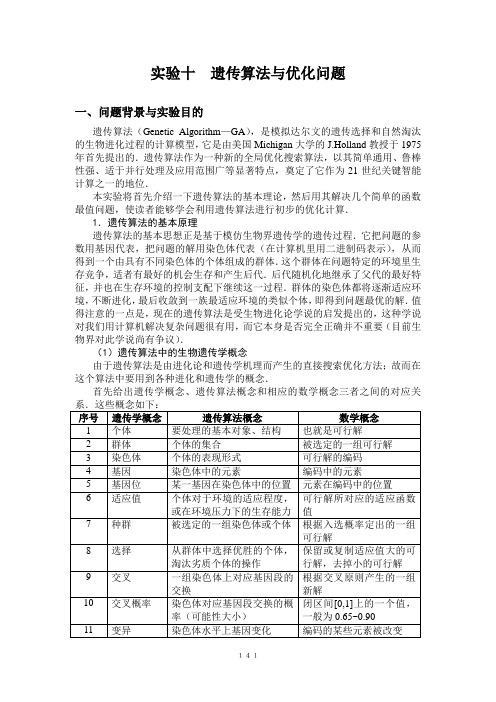
实验十遗传算法与优化问题一、问题背景与实验目的遗传算法(Genetic Algorithm—GA),是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型,它是由美国Michigan大学的J.Holland教授于1975年首先提出的.遗传算法作为一种新的全局优化搜索算法,以其简单通用、鲁棒性强、适于并行处理及应用范围广等显著特点,奠定了它作为21世纪关键智能计算之一的地位.本实验将首先介绍一下遗传算法的基本理论,然后用其解决几个简单的函数最值问题,使读者能够学会利用遗传算法进行初步的优化计算.1.遗传算法的基本原理遗传算法的基本思想正是基于模仿生物界遗传学的遗传过程.它把问题的参数用基因代表,把问题的解用染色体代表(在计算机里用二进制码表示),从而得到一个由具有不同染色体的个体组成的群体.这个群体在问题特定的环境里生存竞争,适者有最好的机会生存和产生后代.后代随机化地继承了父代的最好特征,并也在生存环境的控制支配下继续这一过程.群体的染色体都将逐渐适应环境,不断进化,最后收敛到一族最适应环境的类似个体,即得到问题最优的解.值得注意的一点是,现在的遗传算法是受生物进化论学说的启发提出的,这种学说对我们用计算机解决复杂问题很有用,而它本身是否完全正确并不重要(目前生物界对此学说尚有争议).(1)遗传算法中的生物遗传学概念由于遗传算法是由进化论和遗传学机理而产生的直接搜索优化方法;故而在这个算法中要用到各种进化和遗传学的概念.首先给出遗传学概念、遗传算法概念和相应的数学概念三者之间的对应关遗传算法计算优化的操作过程就如同生物学上生物遗传进化的过程,主要有三个基本操作(或称为算子):选择(Selection)、交叉(Crossover)、变异(Mutation).遗传算法基本步骤主要是:先把问题的解表示成“染色体”,在算法中也就是以二进制编码的串,在执行遗传算法之前,给出一群“染色体”,也就是假设的可行解.然后,把这些假设的可行解置于问题的“环境”中,并按适者生存的原则,从中选择出较适应环境的“染色体”进行复制,再通过交叉、变异过程产生更适应环境的新一代“染色体”群.经过这样的一代一代地进化,最后就会收敛到最适应环境的一个“染色体”上,它就是问题的最优解.下面给出遗传算法的具体步骤,流程图参见图1:第一步:选择编码策略,把参数集合(可行解集合)转换染色体结构空间;第二步:定义适应函数,便于计算适应值;第三步:确定遗传策略,包括选择群体大小,选择、交叉、变异方法以及确定交叉概率、变异概率等遗传参数;第四步:随机产生初始化群体;第五步:计算群体中的个体或染色体解码后的适应值;第六步:按照遗传策略,运用选择、交叉和变异算子作用于群体,形成下一代群体;第七步:判断群体性能是否满足某一指标、或者是否已完成预定的迭代次数,不满足则返回第五步、或者修改遗传策略再返回第六步.图1 一个遗传算法的具体步骤遗传算法有很多种具体的不同实现过程,以上介绍的是标准遗传算法的主要步骤,此算法会一直运行直到找到满足条件的最优解为止.2.遗传算法的实际应用例1:设2()20.5f x x x =-++,求 max (), [1,2]f x x ∈-.注:这是一个非常简单的二次函数求极值的问题,相信大家都会做.在此我们要研究的不是问题本身,而是借此来说明如何通过遗传算法分析和解决问题.在此将细化地给出遗传算法的整个过程.(1)编码和产生初始群体首先第一步要确定编码的策略,也就是说如何把1-到2这个区间内的数用计算机语言表示出来.编码就是表现型到基因型的映射,编码时要注意以下三个原则:完备性:问题空间中所有点(潜在解)都能成为GA 编码空间中的点(染色体位串)的表现型;健全性:GA 编码空间中的染色体位串必须对应问题空间中的某一潜在解; 非冗余性:染色体和潜在解必须一一对应.这里我们通过采用二进制的形式来解决编码问题,将某个变量值代表的个体表示为一个{0,1}二进制串.当然,串长取决于求解的精度.如果要设定求解精度到六位小数,由于区间长度为2(1)3--=,则必须将闭区间 [1,2]-分为6310⨯等分.因为216222097152231024194304=<⨯<= 所以编码的二进制串至少需要22位.将一个二进制串(b 21b 20b 19…b 1b 0)转化为区间[1,2]-内对应的实数值很简单,只需采取以下两步(Matlab 程序参见附录4):1)将一个二进制串(b 21b 20b 19…b 1b 0)代表的二进制数化为10进制数:21212019102100()(2)'i i i b b b b b b x =⋯=⋅=∑2)'x 对应的区间[1,2]-内的实数:12)1(2'122---⋅+-=x x 例如,一个二进制串a=<1000101110110101000111>表示实数0.637197.'x =(1000101110110101000111)2=2288967637197.01232288967122=-⋅+-=x 二进制串<0000000000000000000000>,<1111111111111111111111>,则分别表示区间的两个端点值-1和2.利用这种方法我们就完成了遗传算法的第一步——编码,这种二进制编码的方法完全符合上述的编码的三个原则.首先我们来随机的产生一个个体数为4个的初始群体如下:pop(1)={<1101011101001100011110>, %% a1<1000011001010001000010>, %% a2<0001100111010110000000>, %% a3<0110101001101110010101>} %% a4(Matlab 程序参见附录2)化成十进制的数分别为:pop(1)={ 1.523032,0.574022 ,-0.697235 ,0.247238 }接下来我们就要解决每个染色体个体的适应值问题了.(2)定义适应函数和适应值由于给定的目标函数2()20.5f x x x =-++在[1,2]-内的值有正有负,所以必须通过建立适应函数与目标函数的映射关系,保证映射后的适应值非负,而且目标函数的优化方向应对应于适应值增大的方向,也为以后计算各个体的入选概率打下基础.对于本题中的最大化问题,定义适应函数()g x ,采用下述方法:min min (), ()0()0,f x F f x F g x -->⎧=⎨⎩若其他 式中min F 既可以是特定的输入值,也可以是当前所有代或最近K 代中()f x 的最小值,这里为了便于计算,将采用了一个特定的输入值.若取min 1F =-,则当()1f x =时适应函数()2g x =;当() 1.1f x =-时适应函数()0g x =.由上述所随机产生的初始群体,我们可以先计算出目标函数值分别如下(Matlab 程序参见附录3):f [pop(1)]={ 1.226437 , 1.318543 , -1.380607 , 0.933350 }然后通过适应函数计算出适应值分别如下(Matlab 程序参见附录5、附录6): 取min 1F =-,g[pop(1)]= { 2.226437 , 2.318543 , 0 , 1.933350 }(3)确定选择标准这里我们用到了适应值的比例来作为选择的标准,得到的每个个体的适应值比例叫作入选概率.其计算公式如下:对于给定的规模为n 的群体pop={123,,,,n a a a a },个体i a 的适应值为()i g a ,则其入选概率为1()(),1,2,3,,()i s i n ii g a P a i n g a ===⋯∑由上述给出的群体,我们可以计算出各个个体的入选概率.首先可得 41() 6.478330ii g a ==∑, 然后分别用四个个体的适应值去除以41()i i g a =∑,得:P (a 1)=2.226437 / 6.478330 = 0.343675 %% a 1P (a 2)=2.318543 / 6.478330 = 0.357892 %% a 2P (a 3)= 0 / 6.478330 = 0 %% a 3P (a 4)=1.933350 / 6.478330 = 0.298433 %% a 4(Matlab 程序参见附录7)(4)产生种群计算完了入选概率后,就将入选概率大的个体选入种群,淘汰概率小的个体,并用入选概率最大的个体补入种群,得到与原群体大小同样的种群(Matlab 程序参见附录8、附录11).要说明的是:附录11的算法与这里不完全相同.为保证收敛性,附录11的算法作了修正,采用了最佳个体保存方法(elitist model),具体内容将在后面给出介绍.由初始群体的入选概率我们淘汰掉a3,再加入a2补足成与群体同样大小的种群得到newpop(1)如下:newpop(1)={<1101011101001100011110>,%% a1<1000011001010001000010>,%% a2<1000011001010001000010>,%% a2<0110101001101110010101>} %% a4(5)交叉交叉也就是将一组染色体上对应基因段的交换得到新的染色体,然后得到新的染色体组,组成新的群体(Matlab程序参见附录9).我们把之前得到的newpop(1)的四个个体两两组成一对,重复的不配对,进行交叉.(可以在任一位进行交叉)<110101110 1001100011110>,<1101011101010001000010>交叉得:<100001100 1010001000010>,<1000011001001100011110><10000110010100 01000010>,<1000011001010010010101>交叉得:<01101010011011 10010101>,<0110101001101101000010>通过交叉得到了四个新个体,得到新的群体jchpop (1)如下:jchpop(1)={<1101011101010001000010>,<1000011001001100011110>,<1000011001010010010101>,<0110101001101101000010>}这里采用的是单点交叉的方法,当然还有多点交叉的方法,不过有些烦琐,这里就不着重介绍了.(6)变异变异也就是通过一个小概率改变染色体位串上的某个基因(Matlab程序参见附录10).现把刚得到的jchpop(1)中第3个个体中的第9位改变,就产生了变异,得到了新的群体pop(2)如下:pop(2)= {<1101011101010001000010>,<1000011001001100011110>,<1000011011010010010101>,<0110101001101101000010> }然后重复上述的选择、交叉、变异直到满足终止条件为止.(7)终止条件。
遗传算法简介及sga流程【精品毕业设计】(完整版)

遗传算法:遗传算法(Genetic Algorithm)是一类借鉴生物界的进化规律(适者生存,优胜劣汰遗传机制)演化而来的随机化搜索方法。
遗传算法(Genetic Algorithms简称GA)是由美国Michigan大学的John Holland教授于20世纪60年代末创建的。
它来源于达尔文的进化论和孟德尔、摩根的遗传学理论,通过模拟生物进化的机制来构造人工系统。
遗传算法作为一种全局优化方法,提供了一种求解复杂系统优化问题的通用框架,它不依赖于问题的具体领域,对优化函数的要求很低并且对不同种类的问题具有很强的鲁棒性,所以广泛应用于计算机科学、工程技术和社会科学等领域。
John Holland教授通过模拟生物进化过程设计了最初的遗传算法,我们称之为标准遗传算法。
标准遗传算法流程如下:1)初始化遗传算法的群体,包括初始种群的产生以及对个体的编码。
2)计算种群中每个个体的适应度,个体的适应度反映了其优劣程度。
3)通过选择操作选出一些个体,这些个体就是母代个体,用来繁殖子代。
4)选出的母代个体两两配对,按照一定的交叉概率来进行交叉,产生子代个体。
5)按照一定的变异概率,对产生的子代个体进行变异操作。
6)将完成交叉、变异操作的子代个体,替代种群中某些个体,达到更新种群的目的。
7)再次计算种群的适应度,找出当前的最优个体。
8)判断是否满足终止条件,不满足则返回第3)步继续迭代,满足则退出迭代过程,第7)步中得到的当前最优个体,通过解码,就作为本次算法的近似最优解。
早熟收敛:一般称之为“早熟”,是遗传算法中的一种现象。
指在遗传算法早期,在种群中出现了超级个体,该个体的适应值大大超过当前种群的平均个体适应值。
从而使得该个体很快在种群中占有绝对的比例,种群的多样性迅速降低,群体进化能力基本丧失,从而使得算法较早收敛于局部最优解的现象。
早熟收敛的本质特征是指群体中的各个个体非常相似,群体的多样性急剧减少,当前群体缺乏有效等位基因(最优解位串上的等位基因),在遗传算子作用下不能生成高阶竞争模式。
遗传算法解决TSP问题【精品毕业设计】(完整版)

GA(Fitness,Fitness_threshold,p,r,m)
Fitness:适应度评分函数,为给定假设赋予一个评估分数
Fitness_threshold:指定终止判据的阈值
p:群体中包含的假设数量
r:每一步中通过交叉取代群体成员的比例
m:变异率
初始化群体:P←随机产生的p个假设
在本程序的TSP问题中一共有20个城市,也就是在图模型中有20个顶点,因此一个染色体的长度为20。
3.3适应函数f(i)
对具有n个顶点的图,已知各顶点之间( , )的边长度d( , ),把 到 间的一条通路的路径长度定义为适应函数:
对该最优化问题,就是要寻找解 ,使f( )值最小。
3.4选择操作
选择作为交叉的双亲,是根据前代染色体的适应函数值所确定的,质量好的个体,即从起点到终点路径长度短的个体被选中的概率较大。
(2)交叉(Crossover):对于选中进行繁殖的两个染色体X,Y,以X,Y为双亲作交叉操作,从而产生两个后代X1,Y1.
(3)变异(Mutation):对于选中的群体中的个体(染色体),随机选取某一位进行取反运算,即将该染色体码翻转。
用遗传算法求解的过程是根据待解决问题的参数集进行编码,随机产生一个种群,计算适应函数和选择率,进行选择、交叉、变异操作。如果满足收敛条件,此种群为最好个体,否则,对产生的新一代群体重新进行选择、交叉、变异操作,循环往复直到满足条件。
3.变异:使用均匀的概率从Ps中选择m%的成员.对于选出的每个成员,在它表示中随机选择一个为取反
4.更新:P←Ps
5.评估:对于P中的每个h计算Fitness(h)
从P中返回适应度最高的假设
3.
3.1 TSP问题的图论描述
毕业设计论文基于遗传算法的BP神经网络的优化问题研究.doc

编号:审定成绩:重庆邮电大学毕业设计(论文)设计(论文)题目:基于遗传算法的BP神经网络的优化问题研究学院名称:学生姓名:专业:班级:学号:指导教师:答辩组负责人:填表时间:2010年06月重庆邮电大学教务处制摘要本文的主要研究工作如下:1、介绍了遗传算法的起源、发展和应用,阐述了遗传算法的基本操作,基本原理和遗传算法的特点。
2、介绍了人工神经网络的发展,基本原理,BP神经网络的结构以及BP算法。
3、利用遗传算法全局搜索能力强的特点与人工神经网络模型学习能力强的特点,把遗传算法用于神经网络初始权重的优化,设计出混合GA-BP算法,可以在一定程度上克服神经网络模型训练中普遍存在的局部极小点问题。
4、对某型导弹测试设备故障诊断建立神经网络,用GA直接训练BP神经网络权值,然后与纯BP算法相比较。
再用改进的GA-BP算法进行神经网络训练和检验,运用Matlab软件进行仿真,结果表明,用改进的GA-BP算法优化神经网络无论从收敛速度、误差及精度都明显高于未进行优化的BP神经网络,将两者结合从而得到比现有学习算法更好的学习效果。
【关键词】神经网络BP算法遗传算法ABSTRACTThe main research work is as follows:1. Describing the origin of the genetic algorithm, development and application, explain the basic operations of genetic algorithm, the basic principles and characteristics of genetic algorithms.2. Describing the development of artificial neural network, the basic principle, BP neural network structure and BP.3. Using the genetic algorithm global search capability of the characteristics and learning ability of artificial neural network model with strong features, the genetic algorithm for neural network initial weights of the optimization, design hybrid GA-BP algorithm, to a certain extent, overcome nerves ubiquitous network model training local minimum problem.4. A missile test on the fault diagnosis of neural network, trained with the GA directly to BP neural network weights, and then compared with the pure BP algorithm. Then the improved GA-BP algorithm neural network training and testing, use of Matlab software simulation results show that the improved GA-BP algorithm to optimize neural network in terms of convergence rate, error and accuracy were significantly higher than optimized BP neural network, a combination of both to be better than existing learning algorithm learning.Key words:neural network back-propagation algorithms genetic algorithms目录第一章绪论 (1)1.1 遗传算法的起源 (1)1.2 遗传算法的发展和应用 (1)1.2.1 遗传算法的发展过程 (1)1.2.2 遗传算法的应用领域 (2)1.3 基于遗传算法的BP神经网络 (3)1.4 本章小结 (4)第二章遗传算法 (5)2.1 遗传算法基本操作 (5)2.1.1 选择(Selection) (5)2.1.2 交叉(Crossover) (6)2.1.3 变异(Mutation) (7)2.2 遗传算法基本思想 (8)2.3 遗传算法的特点 (9)2.3.1 常规的寻优算法 (9)2.3.2 遗传算法与常规寻优算法的比较 (10)2.4 本章小结 (11)第三章神经网络 (12)3.1 人工神经网络发展 (12)3.2 神经网络基本原理 (12)3.2.1 神经元模型 (12)3.2.2 神经网络结构及工作方式 (14)3.2.3 神经网络原理概要 (15)3.3 BP神经网络 (15)3.4 本章小结 (21)第四章遗传算法优化BP神经网络 (22)4.1 遗传算法优化神经网络概述 (22)4.1.1 用遗传算法优化神经网络结构 (22)4.1.2 用遗传算法优化神经网络连接权值 (22)4.2 GA-BP优化方案及算法实现 (23)4.3 GA-BP仿真实现 (24)4.3.1 用GA直接训练BP网络的权值算法 (25)4.3.2 纯BP算法 (26)4.3.3 GA训练BP网络的权值与纯BP算法的比较 (28)4.3.4 混合GA-BP算法 (28)4.4 本章小结 (31)结论 (32)致谢 (33)参考文献 (34)附录 (35)1 英文原文 (35)2 英文翻译 (42)3 源程序 (47)第一章绪论1.1 遗传算法的起源从生物学上看,生物个体是由细胞组成的,而细胞则主要由细胞膜、细胞质、和细胞核构成。
遗传算法详解范文

遗传算法详解范文
一、什么是遗传算法
遗传算法(Genetic Algorithm,简称GA)是一种基于自然选择和遗传的算法,是由John Holland于1960年提出的,它是为了解决复杂的全局优化问题而设计的全局优化算法。
在计算机科学中,遗传算法是一种利用遗传进化的思想,模拟生物进化的过程,通过繁殖、淘汰,以及多样性和变异的原理,在有效的空间中,不断改进解决方案,以得到最优解的一种方法。
二、遗传算法工作原理
遗传算法是一种仿生的全局优化方法,它基于自然选择和遗传进化中的基本概念,通过模拟和改进自然选择和遗传,对问题进行全局优化。
其工作原理是模拟生物进化过程,将生物进化中求解能力最强的种群变化适应度最大的种群,优胜劣汰,交叉繁殖,变异演化,以期望获得全局最优解。
在遗传算法中,种群通过遗传演算,数次进化,演化出适应环境最优的解决方案。
遗传算法会先初始化一组解决方案,称为“种群”,然后不断的进行繁殖、交叉、突变、选择等运算,逐渐将种群中的个体演化为最优的解决方案。
遗传算法的具体操作步骤如下:
(1)初始化:为了使遗传算法发挥作用,首先要求用户提供一组初始解(个体)。
基于遗传算法的优化设计论文[5篇]
![基于遗传算法的优化设计论文[5篇]](https://img.taocdn.com/s3/m/cad20e2c974bcf84b9d528ea81c758f5f61f2985.png)
基于遗传算法的优化设计论文[5篇]第一篇:基于遗传算法的优化设计论文1数学模型的建立影响抄板落料特性的主要因素有:抄板的几何尺寸a和b、圆筒半径R、圆筒的转速n、抄板安装角β以及折弯抄板间的夹角θ等[4,9]。
在不同的参数a、β、θ下,抄板的安装会出现如图1所示的情况。
图1描述了不同参数组合下抄板的落料特性横截面示意图。
其中,图1(a)与图1(b)、图1(c)、图1(d)的区别在于其安装角为钝角。
当安装角不为钝角且OB与OC的夹角σ不小于OD与OC夹角ψ时(即σ≥ψ),会出现图1(b)所示的安装情况;当σ<ψ时,又会出现图1(c)与图1(d)所示的情况,而两者区别在于,η+θ是否超过180°,若不超过,则为图1(c)情况,反之则为图1(d)情况。
其中,点A为抄板上物料表面与筒壁的接触点或为物料表面与抄板横向长度b边的交点;点B为抄板的顶点;点C为抄板折弯点;点D为抄板边与筒壁的交点;点E为OB连线与圆筒内壁面的交点;点F为OC连线与圆筒内壁面的交点。
1.1动力学休止角(γ)[4,10]抄板上的物料表面在初始状态时保持稳定,直到物料表面与水平面的夹角大于物料的休止角(最大稳定角)时才发生落料情况。
随着转筒的转动,抄板上物料的坡度会一直发生改变。
当物料的坡度大于最大稳定角时,物料开始掉落。
此时,由于物料的下落,物料表面重新达到最大稳定角开始停止掉落。
然而,抄板一直随着转筒转动,使得抄板内物料的坡度一直发生改变,物料坡度又超过最大休止角。
这个过程一直持续到抄板转动到一定位置(即抄板位置处于最大落料角δL时),此时抄板内的物料落空。
通常,在计算抄板持有量时,会采用动力学休止角来作为物料发生掉落的依据,即抄板内的物料坡度超过γ时,物料开始掉落。
该角主要与抄板在滚筒中的位置δ、动摩擦因数μ和弗劳德数Fr等有关。
1.2抄板持有量的计算随着抄板的转动,一般可以将落料过程划分为3部分(R-1,R-2,R-3),如图1(a)所示。
自然计算遗传算法【精品毕业设计】(完整版)

自然计算大作业一.二进制编码在遗传算法中,首先要将数据进行编码,这里采用二进制的方式进行编码。
第一步,我们根据题目的介绍可以得知该函数含有两个变量,以及各自的定义域。
在二进制编码中,我们首先要先计算它的编码长度。
计算公式如下: $${2^{{m_j} - 1}} < ({b_j} - {a_j})*precision \le {2^{{m_j}}} - 1$$其中precision为精度,如小数点后5位,则precision=10^5,mj为编码长度,${x_j} \in [{a_j},{b_j}]$二.二进制解码解码即编码的逆过程:$${x_j} = {a_j} + {\rm{decimal}}(substrin{g_j}) \times \frac{{{b_j} - {a_j}}}{{{2^{{m_j}}} - 1}}$$三.种群初始化编码完成后,开始对种群初始化,为了简便采用随机地方式进行初始化。
初始群体的生成:随机产生N个初始串结构数据,每个串结构数据称为一个个体,N个个体构成了一个群体。
GA以这N个串结构数据作为初始点开始进化。
def rand_init(self):for i in range(self.code_x1_length):self.code_x1 += str(random.randint(0, 1))for i in range(self.code_x2_length):self.code_x2 += str(random.randint(0, 1))四.适应度评估适应度表明个体或解的优劣性。
不同的问题,适应度函数的定义方式也不同。
def decoding(self, code_x1, code_x2):self.x1 = self.bounds[0][0] + int(code_x1, 2) * (self.bounds[0][1] - self.bounds[0][0]) / (2 ** self.code_x1_length - 1)self.x2 = self.bounds[1][0] + int(code_x2, 2) * (self.bounds[1][1] - self.bounds[1][0]) / (2 ** self.code_x2_length - 1)五.选择选择的目的是为了从当前群体中选出优良的个体,使它们有机会作为父代为下一代繁殖子孙。
遗传算法新论文【精品毕业设计】(完整版)

学校代码 10126 学号 00708037 分类号密级本科毕业论文基于遗传算法的图像阈值分割学院、系数学科学学院计算数学系专业名称信息与计算科学年级 2007级学生姓名刘家祥指导教师曹军2011年 5月 20 日内容摘要图像分割就是指把图像分成各具特性的区域并提取出感兴趣目标的技术和过程。
图像的分割是以灰度值作为分割的依据,通过各个像素的灰度值和事先确定的阈值的比较来分割图像。
如何确定最合适的阈值是处理好图像分割的关键,这自然成为一直以来分割算法研究的焦点。
遗传算法是对生物进化论中自然选择和遗传学机理中生物进化过程的模拟来计算最优解的方法。
遗传算法具有众多的优点,如鲁棒性、并行性、自适应性和快速收敛,可以应用在图像处理技术领域中图像分割技术来确定分割阈值。
本文主要介绍基于遗传算法的最小误差阈值法、最大类间方差法(Otsu法)以及最佳直方图熵法(KSW熵法)等三种方法分割图像。
关键词:图像分割,遗传算法,阈值分割AbstractImage segmentation refers to the image into regions each with characteristics and goals of the technology to extract and process of interest. Segmentation is a segmentation based on gray value, gray value of each pixel through the predetermined threshold value and comparing the image segmentation. How to determine the most appropriate threshold is the key to handling image segmentation, which has naturally become the focus of segmentation algorithms.Genetic algorithm is a biological theory of evolution and genetic mechanism of natural selection in biological evolution simulation method to calculate the optimal solution. Genetic algorithm has many advantages, such as robustness, parallel, adaptive, and fast convergence, can be used in the field of image processing image segmentation technique to determine the split threshold.In this paper, genetic algorithm based on minimum error threshold, the largest class variance (Otsu method) and the best histogram entropy (KSW entropy method) are three ways to split the image.Keywords : Image segmentation, genetic algorithms, threshold目录第一章绪论 .................................................. - 1 - 第二章遗传算法概述 ........................................ . - 2 -2.1遗传算法的研究历史....................................... - 2 -2.2生物背景................................................. - 2 -2.3遗传算法的基本思想....................................... - 3 -2.4遗传算法的几个概念....................................... - 4 -2.4.1适应度函数......................................... - 4 -2.4.2遗传算法最常用的算子............................... - 4 -2.5遗传算法运算的基本流程................................... - 5 - 第三章图像分割的现状 ........................................ - 7 -3.1图像分割简介............................................. - 7 -3.2图像分割方法............................................. - 8 -3.2.1基于边缘检测的分割................................. - 8 -3.2.2基于区域的分割..................................... - 8 -3.2.3边缘与区域相结合的分割............................. - 9 -3.3阈值选取................................................. - 9 - 第四章基于遗传算法的图像阈值分割 ........................... - 10 -4.1图像阈值................................................ - 10 -4.2阈值分割的原理.......................................... - 10 -4.3最小误差阈值法.......................................... - 11 -4.3.1最小误差法图像阈值分割............................ - 11 -4.3.2 利用遗传算法来改进最小误差法...................... - 12 -4.4 最大类间方差法(Otsu法)............................... - 13 -4.4.1最大类间方差法(Otsu法)阈值分割.................. - 13 -4.4.2 Otsu阈值分割的遗传算法设计........................ - 15 -4.5 KSW熵法................................................ - 17 -4.5.1 KSW熵阈值分割................................... - 17 -4.5.2 KSW单阈值分割的遗传算法设计..................... - 18 -4.5.3 KSW双阈值分割的遗传算法设计..................... - 19 - 第五章基于新的遗传算法的图像分割 ........................... - 25 -5.1混沌遗传算法............................................ - 25 -5.2量子遗传算法............................................ - 25 -5.3免疫遗传算法............................................ - 25 - 结论 .......................................................... - 26 - 致谢 .......................................................... - 27 - 参考文献: ..................................................... - 28 -内蒙古大学本科学年论文第- 1 - 页基于遗传算法的图像阈值分割第一章绪论图像分割是图像处理与计算机视觉的基本问题之一,是图像处理到图像分析的关键步骤。
关于遗传算法的研究毕业论文

摘要:在本篇论文主要讨论的是通过介绍生物的遗传问题,什么是遗传算法(genetic Algorithm),遗传算法的性质,应用,传统遗传算法的基本步骤和遗传算法的目前的发展趋向等等内容,使大家得到关于遗传算法的比较深厚的了解。
中文关键词:遗传;遗传算法;染色体;基因;基因地点;基因特征值;适应度英文关键词:Genetic;Genetic Algorithm;Chronmosome;Gene;Locus;Gene Feature;Fitness1、生物的遗传问题与自然选择:众所周知,生命的出现,变化以及其消亡是必然的。
在地球上最早的生命出现以来,在自然界中多种多样的生物一起存在着并且生命的形式与物种不断发生着变化。
由于不同原因,一些物种相继消亡,有一些物种得以生存到现在且还有一些生物改变到另一种生物。
那么到底是什么原因导致这种情况呢?我们先看一下达尔文的自然选择学说的主要内容。
达尔文的自然选择学说是一种被人们广泛接受的生物进化学说。
这种学说认为,生物要生存下去,就必须进行生存斗争。
生存斗争包括种内斗争、种间斗争以及生物跟无机环境之间的斗争三个方面。
在生存斗争中,具有有利变异的个体容易存活下来,并且有更多的机会将有利变异传给后代;具有不利变异的个体就容易被淘汰,产生后代的机会也少的多。
因此,凡是在生存斗争中获胜的个体都是对环境适应性比较强的。
达尔文把这种在生存斗争中适者生存,不适者淘汰的过程叫做自然选择。
它表明,遗传和变异是决定生物进化的内在因素。
自然界中的多种生物之所以能够适应环境而得以生存进化,是和遗传和变异生命现象分不开的。
总之,在这个问题中,我们把主要原因概括在下列两个方面:一个是自然界为生命存在方式所提供的条件即有些生物由于对自然界的适应能力比较强,它们都能适应自然环境的各种变化,反而,还有一些生物的适应能力比较弱,所以它们不能适应自然环境和资源的变化并且很容易就被自然界淘汰。
原因之二是生物自身的遗传与变异功能。
遗传算法论文

数学建模论文基本遗传算法的MATLAB实现一、问题的提出遗传算法是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法,它借鉴了达尔文的进化论和孟德尔的进化学说。
其本质是一种高效、并行、全局搜索的方法,它能在搜索过程中自动获取和积累有关搜索空间的知识,并自适应的控制过程以求的最优解。
遗传算法操作使用适者生存的原则,在潜在的解决方案中逐次产生一个近似最优方案。
在遗传算法的每一代中,根据个体在问题域中的适应度值和从自然遗传中借鉴来的再造方法进行个体选择,产生一个新的近似解。
这个过程导致种群中个体的进化,得到新个体比原来个体更适应环境,就像自然界中的改造一样。
基本遗传算法,最重要的是产生随机数的过程,已知目标函数max f(x1,x2)=21.5+x1*sin(4*pi*x1)+x2*sin(20*pi*x2)其中约束条件为:-3.0<=x1<=12.14.1<=x2<=5.8 编程用matlab实现基本遗传算法。
二、问题的分析与模型的建立:遗传算法是一种基于生物进化原理构想出来的搜索最优解的仿真算法,它模拟基因重组与进化的自然过程,把待解决问题的参数编成二进制码或十进制码即基因,若干基因组成一个染色体个体许多染色体进行类似于自然选择配对交叉和变异的运算,经过多次重复迭代直到得到最后的优化结果。
习惯上,适应度值越大,表示解的质量越好。
对于求解最小值问题,可通过变换转为求解最大值问题。
遗传算法以群体为基础,不以单点搜索为基础,能同时从不同点获得多具极值,因此不易陷入局部最优;遗传算法是对问题变量的编码集进行操作,而不是变量本身,有效地避免了对变量的微分操作运算;遗传算法只是利用目标函数来区别群体中的个体好坏而不必对其进行过多的附加操作。
基本遗传算法定义:基本遗传算法是一种群体型操作,该操作以群体中的所有个体为对象只使用基本遗传算子:选择算子,交叉算子,变异算子其遗传操作过程简单,容易理解,是其他一些遗传算法的基础。
遗传算法及其应用实例【精品毕业设计】(完整版)

遗传算法及其应用实例遗传算法(Genetic Algorithm)是由美国Michigan大学的Holland 教授(1969)提出,后经由De Jong(1975),Goldberg(1989)等归纳总结所形成的一类模拟进化算法。
遗传算法搜索最优解的方法是模仿生物的进化过程,即通过选择与染色体之间的交叉和变异来完成的。
遗传算法主要使用选择算子、交叉算子与变异算子来模拟生物进化,从而产生一代又一代的种群X (t )。
(1)选择算子:是模拟自然选择的操作,反映“优胜劣汰”原理。
它根据每一个个体的适应度,按照一定规则或方法,从t代种群X (t )中选择出一些优良的个体(或作为母体,或让其遗传到下一代种群X (t 1))。
(2)交叉算子:是模拟有性繁殖的基因重组操作,它将从种群X (t )所选择的每一对母体,以一定的交叉概率交换它们之间的部分基因。
(3)变异算子:是模拟基因突变的遗传操作,它对种群X (t )中的每一个个体,以一定的变异概率改变某一个或某一些基因座上的基因值为其他的等位基因。
交叉算子与变异算子的作用都在于重组染色体基因,以生成新的个体。
遗传算法的运算过程如下:步1(初始化)确定种群规模N,交叉概率P c,变异概率P m和终止进化准则;随机生成N个个体作为初始种群X (0);置t ← 0。
步2(个体评价)计算评估X (t )中各个体的适应度。
步3(种群进化)3.1.选择(母体)从X (t )中运用选择算子选择出M / 2对母体(M ≥ N)。
3.2.交叉对所选择的M / 2对母体,以概率P c执行交叉,形成M 个中间个体。
3.3.变异对M个中间个体分别独立以概率P m执行变异,形成M 个候选个体。
3.4.选择(子代)从上述所形成的M个候选个体中依据适应度选择出N个个体组成新一代种群X (t +1)。
步4(终止检验)如已满足终止准则,则输出X (t +1)中具有最大适应度的个体作为最优解,终止计算,否则置t ← t +1并转步2。
遗传算法论文【精品毕业设计】(完整版)

论文名称:遗传算法姓名:***学号:***********班级:计算机科学与技术1班院系:信息与电气工程学院日期:2014年6月18日摘要 (2)第一章引言 (3)1.1搜索法 (3)1.2遗传算法 (3)第二章遗传算法(Genetic Algorithms,GA) (4)2.1遗传算法的基本概念 (4)2.2遗传算法的实现步骤 (6)第三章遗传算法的特点及应用 (9)3.1遗传算法的特点 (9)3.2遗传算法的应用 (9)第四章遗传算法的缺点及发展 (12)4.1遗传算法的缺点 (12)第五章遗传算法代码实现 (13)附录遗传算法代码(GA Code) (14)摘要智能搜索算法包括遗传算法、禁忌算法、模拟退火算法等。
其中遗传算法(GA)是人类从基因遗传的生物进化思想的启发下提出的,它是一种进化计算,进化计算实质上是自适应的机器学习方法,遗传算法根据基因遗传时候的变化,它在运算的时候也分为选择、交叉、变异三种行为。
它比盲目的搜索效率高的多,又比专门的针对特定问题的算法通用性强,它是一种于问题无关的求解模式。
但是遗传算法又有很大的不确定性,以及过早的收敛性,所以可以和其他算法一起使用来对问题求解。
关键词:遗传算法;GA;实现;应用;改进第一章引言1.1搜索法人工智能问题广义地说,都可以看作是一个问题求解问题,在问题的求解过程中,人们所面临的大多数现实问题往往没有确定性的算法,通常需要用搜索算法来解决。
搜索法是人工智能中问题的求解的基本方法,搜索法可大致分为有信息搜索和无信息搜索,约束满足问题和博弈问题的求解均可表述为搜索过程。
搜索法的本质是再状态空间中从问题的初始状态搜索到通向目标状态的路径。
当前的智能搜索算法本质上也是搜索法,如遗传算法、蚁群算法、神经网络等。
一般搜索可以根据是否使用启发式信息分为盲目搜素和启发式搜索,也可以根据问题的表示方式分为状态空间搜索和与/或树搜索。
盲目搜索一般是指从当前状态到目标状态需要走多少步或者并不知道每条路径的花费,所能做的只是可以区分出哪个是目标状态。
遗传算法毕业论文[管理资料]
![遗传算法毕业论文[管理资料]](https://img.taocdn.com/s3/m/f1a76ba0767f5acfa0c7cda5.png)
遗传算法毕业论文【摘要】遗传算法(Genetic Algorithm, GA)是近年来迅速发展起来的一种全新的随机搜索与优化算法,其基本思想基于Darwin的进化论和Mendel的遗传学。
遗传算法的广泛应用和发展潜能使很多学者深入研究遗传算法,并出版了很多关于它的书籍。
TSP问题是古老的经典的问题,有关的研究有几百年的时间。
TSP旅行商问题是一类典型的NP完全问题,遗传算法是解决NP问题的一种较理想的方法。
论文首先介绍了遗传算法的基本原理、遗传算法的特点,遗传算法的发展方向和它的主要应用领域;接着针对TSP 问题论述了遗传算法在编码表示和遗传算子(包括选择算子,交叉算子,变异算子这三种算子)等方面的应用情况,简单讨论几种编码方法,并改进了交叉算子。
接着对改进的遗传算法做了实验,得出结果并分析了数据。
最后我做了一个TSP 简单应用。
【关键词】遗传算法;TSP;遗传算子;编码【Abstract】Genetic Algorithm (Genetic Algorithm, GA) is a new random search and optimization algorithm ,develop rapidly in recent years, the basic idea of the theory is Darwin and Mendel's genetics. Extensive use of genetic algorithms and development potential make many scholars in-depth study of genetic algorithms, and published many books about it.TSP problem is the old classic question and about its research have hundreds of years of time. "TSP" Traveling Salesman Problem is a kind of a typical NP-complete problem, genetic algorithms to solve NP problems is a more desirable method.Paper first introduces the characteristics, development direction and major applications of basic genetic algorithms, and then discussed for the TSP problem of genetic algorithms and genetic coding that operator (including the selection operator, crossover operator, mutation operator of these three operator) and other aspects of the application, make a brief discussion about several coding methods, and improved crossover operator. Then use improved genetic algorithm to do the experiment, get the outcome and analyze the data. Finally, I do a simple suing about TSP.【Keywords】genetic algorithm; TSP; genetic operator; coding目录第一章遗传算法理论 (4) (4) (6)遗传算法的原理 (7) (8) (9) (10) (11) (13)第二章.遗传算法的基本原理和实现技术 (15)模式定理 (15)编码技术 (16)群体设定 (16) (17)遗传操作 (17) (19)第三章TSP问题描述与实算 (20)旅行商问题描述 (20) (21) (21)适应函数度 (21)选择算子的设计 (21)交叉算子的设计 (22) (23)对TSP遗传算法的改进: (25)TSP遗传算法参数实验 (25)改进的交叉算子:产生多个个体的部分映射与顺序交叉结合的算子. (28)TSP算法实例 (38)附录(求51个城市最短距离算法) (42)总结 (54)参考文献 (55)致谢 (55)第一章遗传算法理论当前科学技术正进入多学科互相交叉、互相渗透、互相影响的时代,生命科学与工程科学的交叉、渗透和相互促进是其中一个典型例子,也是近代科学技术发展的一个显著特点。
遗传算法 (1)【精品毕业设计】(完整版)

遗传算法定义遗传算法(Genetic Algorithm)是模拟达尔文的遗传选择和自然淘汰的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法,它是有美国Michigan大学J.Holland教授于1975年首先提出来的,并出版了颇有影响的专著《Adaptation in Natural and Artificial Systems》,GA这个名称才逐渐为人所知,J.Holland教授所提出的GA通常为简单遗传算法(SGA)。
遗传算法是从代表问题可能潜在的解集的一个种群(population)开始的,而一个种群则由经过基因(gene)编码的一定数目的个体(individual)组成。
每个个体实际上是染色体(chromosome)带有特征的实体。
染色体作为遗传物质的主要载体,即多个基因的集合,其内部表现(即基因型)是某种基因组合,它决定了个体的形状的外部表现,如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。
因此,在一开始需要实现从表现型到基因型的映射即编码工作。
由于仿照基因编码的工作很复杂,我们往往进行简化,如二进制编码,初代种群产生之后,按照适者生存和优胜务汰的原理,逐代(generation)演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度(fitness)大小选择(selection)个体,并借助于自然遗传学的遗传算子(genetic operators)进行组合交叉(crossover)和变异(mutation),产生出代表新的解集的种群。
这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境,末代种群中的最优个体经过解码(decoding),可以作为问题近似最优解。
遗传算法特点遗传算法是一类可用于复杂系统优化的具有鲁棒性的搜索算法,与传统的优化算法相比,主要有以下特点:1、遗传算法以决策变量的编码作为运算对象。
传统的优化算法往往直接决策变量的实际植本身,而遗传算法处理决策变量的某种编码形式,使得我们可以借鉴生物学中的染色体和基因的概念,可以模仿自然界生物的遗传和进化机理,也使得我们能够方便的应用遗传操作算子。
遗传算法及其应用-毕业论文

摘要遗传算法是一种模拟自然界生物进化的搜索算法,由于它的简单易行、鲁棒性强,尤其是其不需要专门的领域知识而仅用适应度函数作评价来指导搜索过程,从而使它的应用范围极为广泛,并且己在众多领域得到了实际应用,取得了许多令人瞩目的成果,引起了广大学者和工程人员的关注。
在简要的介绍了遗传算法的发展历史和研究现状及其生物学、数学基础后,文中引出了遗传算法的基本概念和原理、分析了遗传算法的基本实现技术。
如:编码、适应度函数、遗传算法的三大遗传操作、参数规则等。
最后在介绍了遗传算法程序设计原则的基础上,编程实现了遗传算法在图像识别中的应用,在实践中检验了遗传算法的实际效果。
关键词:遗传算法,适应度函数,图像识别ABSTRACTThe gen etic algorithm is a kind of search ing method which simulates thenatural evolution. It is simple and easy to implement, especially it do not needthe special field kno wledge, so it has bee n using in very broad fields. Now thegen etic algorithm has got a lot of fruits, and more and more scholars beg in to pay atte ntio n on it.After brief in troducted the gen etic algorithm and studyed the history ofthe development status and biology, mathematical basis, webrought out the basic genetic algorithm concepts and principles, analysised the genetic algorithm to achieve the basic tech no logy. Such as: cod ing, fit ness function, gen etic algorithm of the three major genetic manipulation, and other parameters of the rules. Fin ally, in troduceda gen etic algorithm procedures based on theprinciples of design, programming a genetic algorithm in the application of image recog niti on, in practice, we test the practical effects of gen etic algorithm.Key word : genetic algorithm , Fitness function , image recognition引言当前科学技术正进入多学科互相交叉、互相渗透、互相影响的时代,生命科学与工程科学的交叉、渗透和相互促进是其中的一个典型例子,也是近代科学技术发展的一个显著特点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
iii
清华大学毕业设计论文
Furthermore, with best local minimum broadcast to every node at certain frequency, convergence time is remarkably reduced. To enhance the convergence speed of a sub-population, Hybrid Genetic Algorithm (such as genetic algorithm embedded with Downhill method) is introduced. It has been very important in the application domain of function optimization because it can greatly reduce the possibility of pre-mature. Two different downhill method are implemented. Depth first downhill and width first downhill. This paper basically deals with two important applications of the Genetic Algorithm. One is function optimization by Hybrid Parallel Genetic Algorithm (HPGA) running under the MPI environment. Selection of genetic factors is discussed and comparison with traditional GA is made to illustrate the effectiveness of the algorithm. The other is Travelling Salesman Problem by Parallel Genetic Algorithm. Keywords: Genetic Algorithm; Hybrid Genetic Algorithm; Parallel Genetic Algorithm; Downhill Method; Optimization; TSP;
ii
清华大学毕业设计论文
Abstract
It has always been a compelling task to develop a universal algorithm that can automatically gain and accumulate the knowledge of a search space during the searching process and then find the best solution or approximately the best solution. The Genetic Algorithm is such a kind of algorithm which turn out to be very effective. Genetic Algorithm is a part of evolutionary computing originally invented by Dr J.Holland in the year 1975 and developed by him and his students and colleges. As can be seen literally, Genetic Algorithm is inspired by Darwins theory about evolution. GAs are inherently parallel optimization procedures, which utilize a "survival of the fittest" approach. A basic GA employs selection, crossover and mutation operators. The whole process can be referred to as "reproduction". Algorithm is started with a set of solution (represented by chromosomes) called sub-population. Solutions from one sub-populations are taken and used to form a new sub-population by a hope that the new population will be better, at least not worse than the old one. Solutions are selected according to their fitness. The more suitable they are the more chances they have to reproduce. The main characteristic of the GA is that it is simple, universal and robust. After about 20 year’s development, GA has been successfully used in a lot of fields such as the Travelling Salesman Problem, Scheduling, Function Optimization, Machine Learning etc. Traditional simple GAs have their own drawbacks. First, by mutation and crossover, good sub-solution might be disrupted. Besides, maintaining diversity seems to be prominent considerations. Because of these reasons, the Parallel Genetic Algorithm (PGA) is taken into account. The parallel genetic algorithm is an adaptation of the genetic algorithm to parallel computers. Parallel search greatly overcome the problems in population diversity.
iv
清华大学毕业设计论文
目
摘
录
要 ······························································································CT ····································································································· III 目 录 ······································································································· V
清华大学毕业设计论文
摘 要
研究能在搜索过程中自动获取和积累有关搜索空间的知识,并自适应的控 制搜索过程,从而得到最优解或准最优解的通用搜索算法一直是令人瞩目的课 题。遗传算法就是这种特别有效的算法。 遗传算法(Genetic Algorithm——GA) ,是模拟达尔文的遗传选择和自然 淘汰的生物进化过程的计算模型,它是由美国 Michigan 大学的 J.Holland 教授 于 1975 年首先提出的。 J.Holland 教授和它的研究小组围绕遗传算法进行研究的 宗旨有两个:抽取和解释自然系统的自适应过程以及设计具有自然系统机理的 人工系统。遗传算法的大致过程是这样的:将每个可能的解看作是群体中的一 个个体或染色体,并将每个个体编码成字符串的形式,根据预定的目标函数对 每个个体进行评价,即给出一个适应度值。开始时,总是随机的产生一些个体, 根据这些个体的适应度利用遗传算子——选择(Selection) 、交叉(Crossover) 、 变异(Mutation)对它们重新组合,得到一群新的个体。这一群新的个体由于 继承了上一代的一些优良特性,明显优于上一代,以逐步向着更优解的方向进 化。遗传算法主要的特点在于:简单、通用、鲁棒性强。经过二十多年的发展, 遗传算法已经在旅行商问题、生产调度、函数优化、机器学习等领域得到成功 的应用。 传统的遗传算法虽然具有隐含的并行性,但其实实现方法在本质上仍然是 串行的。这种串行的遗传算法在解决一些实际问题时,由于需要较多的个体数 量和大量的计算,使得进化过程比较缓慢,难以达到实时的要求。因此并行遗 传算法(Parallel Genetic Alogrithm——PGA)就受到了较大的重视,并且已经 成为目前遗传算法研究的主要课题。遗传算法与并行计算机相结合,能把并行 机的高速性和遗传算法固有的并行性两者的长处彼此结合起来。 尽管遗传算法比其他传统搜索方法有更强的鲁棒性,但它更擅长全局搜索, 而局部搜索能力却不足。有研究证明,GA 可以用极快的速度达到最优解的 90% 左右,但要达到真正的最优解则要花费相当长的时间。实验表明,如果兼顾收 敛速度和解的质量两个指标,单纯的遗传算法未必能比其他搜索算法快很多。 目前较为活跃的研究领域是将遗传算法于传统的、基于问题知识的启发式搜索
第一章 简单遗传算法 ························································································ 1 1.1 遗传算法的生物学基础 ············································································ 1 1.1.1 遗传和变异 ······················································································ 1 1.1.2 进化 ································································································ 2 1.2 简单遗传算法简介 ··················································································· 2 1.2.1 算法概要 ························································································· 2 1.2.2 遗传算法的手工模拟 ········································································· 6 1.3 简单遗传算法的特点 ··············································································· 7 1.4 简单遗传算法的应用以及发展方向·························································· 10 1.4.1 遗传算法的应用 ············································································· 10 1.4.2 遗传算法的发展方向 ······································································· 11 第二章 遗传算法的基本原理和实现技术 ··························································· 13 2.1 模式定理(schemata theorem) ···························································· 13 2.1.1 模式 ······························································································ 13 2.1.2 模式定理 ······················································································· 13 2.2 编码方法 ······························································································ 16 2.2.1 编码问题 ······················································································· 16 2.2.2 编码技术 ······················································································· 16 2.3 群体设定 ······························································································ 17 2.4 适应度函数··························································································· 18 2.4.1 目标函数到适应度函数的映射 ·························································· 18 v
