理力答案_第四章
人教版八年级物理《第四章物态变化》知识点+习题(含答案)打印版

第四章 物态变化一、温度1、 定义:温度表示物体的冷热程度。
2、 单位:① 国际单位制中采用热力学温度。
② 常用单位是摄氏度(℃) 规定:在一个标准大气压下冰水混合物的温度为0度,沸水的温度为100度,它们之间分成100等份,每一等份叫1摄氏度 某地气温-3℃读做:零下3摄氏度或负3摄氏度 ③ 换算关系T=t + 273K3、测量——温度计(常用液体温度计)① 温度计构造:下有玻璃泡,里盛水银、煤油、酒精等液体;内有粗细均匀的细玻璃管,在外面的玻璃管上均匀地刻有刻度。
② 温度计的原理:利用液体的热胀冷缩进行工作。
③ 分类及比较: ④ 常用温度计的使用方法:使用前:观察它的量程,判断是否适合待测物体的温度;并认清温度计的分度值,以便准确读数。
使用时:温度计的玻璃泡全部浸入被测液体中,不要碰到容器底或容器壁;温度计玻璃泡浸入被测液体中稍候一会儿,待温度计的示数稳定后再读数;读数时玻璃泡要继续留在被测液体中,视线与温度计中液柱的上表面相平。
◇温度计的玻璃泡要做大目的是:温度变化相同时,体积变化大,上面的玻璃管做细的目的是:液体体积变化相同时液柱变化大,两项措施的共同目的是:读数准确。
二、物态变化填物态变化的名称及吸热放热情况: 1、熔化和凝固 ① 熔化:定义:物体从固态变成液态叫熔化。
晶体物质:海波、冰、石英水晶、 非晶体物质:松香、石蜡玻璃、沥青、蜂蜡食盐、明矾、奈、各种金属 熔化图象:熔化特点:固液共存,吸热,温度不变 熔化特点:吸热,先变软变稀,最后变为液态,温度不断上升。
熔点 :晶体熔化时的温度。
熔化的条件:⑴ 达到熔点。
⑵ 继续吸热。
② 凝固 :定义 :物质从液态变成固态 叫凝固。
固液升华 吸热 凝华 放热凝固图象:凝固特点:固液共存,放热,温度不变 凝固特点:放热,逐渐变稠、变黏、变硬、最后成固体,温度不断降低。
凝固点 :晶体凝固时的温度。
同种物质的熔点、凝固点相同。
凝固的条件:⑴ 达到凝固点。
经济学原理第四章课后题答案

第四章供给与需求的市场力量复习题:1、什么是市场竞争?简单描述除了完全竞争市场之外的市场类型。
答:竞争市场是有许多买者与卖者,以至于每个人对市场价格的影响都微乎其微的市场。
除了完全竞争市场之外,还有垄断市场。
在这个市场上只有一个卖者,他决定价格。
这个卖者被称为垄断者。
还有寡头市场,在这个市场上有几个并不总是主动竞争的卖者,他们提供相似或相同的产品。
通常情况下,寡头们会尽力联合起来,防止剧烈的竞争,收取较高的市场价格。
还有垄断竞争市场,这是一个有许多提供相似但不相同产品的企业的市场结构。
由于各自提供的产品不同,每个企业对产品的价格有一定的影响力。
2、什么因素决定买者对一种物品的需求量?答:物品的价格、买者的收入、相关物品的价格、买者的嗜好、预期决定买者对一种物品的需求量。
3、什么是需求表和需求曲线?它们如何相关联?为什么需求曲线向右下方倾斜?答:需求表是表示一种物品价格与需求量之间关系的表格,需求曲线是表示一种物品价格与需求量之间关系的图形。
需求曲线将需求表用图形的形式表现出来,需求表是需求曲线上假设干个点的坐标的数字表格排列。
需求曲线向右下方倾斜是因为在其他条件不变的情况下,随着价格上升,需求量会减少。
4.消费者嗜好的变化引起了沿着需求曲线的变动,还是需求曲线的移动?价格的变化引起了沿着需求曲线的变动,还是需求曲线的移动?答:消费者嗜好的变化引起了需求曲线的移动,价格的变化引起了沿着需求曲线的变动。
5、波匹的收入减少了,结果他买了更多的菠菜。
菠菜是低档物品还是正常物品?波匹菠菜的需求曲线是什么样的?答:菠菜对波匹来说是低档物品。
因为波匹的收入减少了,他对菠菜的需求量反而增大。
波匹菠菜的需求曲线是向右下方倾斜的。
6、什么因素决定了卖者对一种物品的供给量?答:价格、投入价格、技术、预期决定了卖者对一种物品的供给量。
7、什么是供给表和供给曲线?它们如何相关联?为什么供给曲线向右上方倾斜?答:供给表是表示一种物品价格与供给量之间关系的表格,供给曲线是表示一种物品价格与供给量之间关系的图形。
大学物理学课后习题4第四章答案
k
m1g x1
1.0 103 9.8 4.9 102
0.2
N m1
而 t 0 时, x0 1.0 102 m,v0 5.0 102 m s-1 ( 设向上为正)
又
k m
0.2 8 103
5,即T
2
1.26s
A
x02
(
v0
)2
(1.0 102 )2 (5.0 102 )2 5
(7)两列波叠加产生干涉现象必须满足的条件
是
,
和
。
[答案:频率相同,振动方向相同,在相遇点的位相差恒定。]
4.3 质量为10 103 kg 的小球与轻弹簧组成的系统,按
x 0.1cos(8t 2 ) (SI) 的规律作谐振动,求: 3
(1)振动的周期、振幅和初位相及速度与加速度的最大值; (2)最大的回复力、振动能量、平均动能和平均势能,在哪些位置上动能与 势能相等?
习题 4.2(2) 图 [答案:b、f; a、e]
(3)一质点沿 x 轴作简谐振动,振动范围的中心点为 x 轴的原点,已知周 期为 T,振幅为 A。
( a ) 若 t=0 时 质 点 过 x=0 处 且 朝 x 轴 正 方 向 运 动 , 则 振 动 方 程 为 x=___________________。
[答案: 2 s ] 3
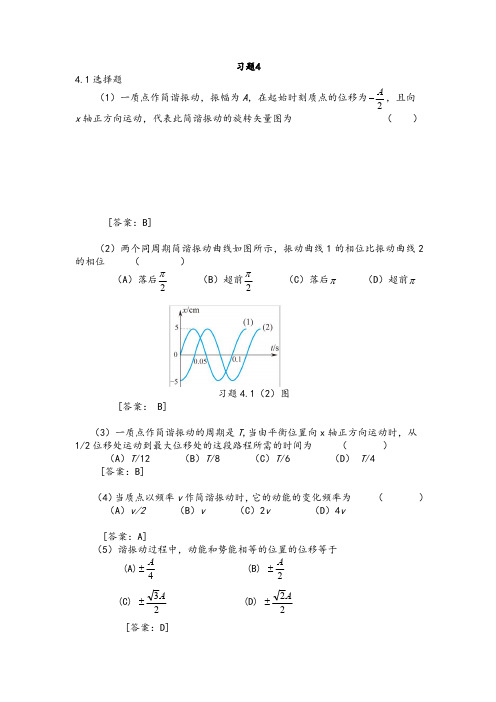
(2)一水平弹簧简谐振子的振动曲线如题 4.2(2)图所示。振子在位移为零, 速度为-A、加速度为零和弹性力为零的状态,对应于曲线上的____________ 点。振子处在位移的绝对值为 A、速度为零、加速度为-2A 和弹性力为-KA 的 状态,则对应曲线上的____________点。
103
(
)2
大学物理学课后习题4第四章答案

[答案:D]
4.2 填空题 (1)一质点在 X 轴上作简谐振动,振幅 A=4cm,周期 T=2s,其平衡位置
取作坐标原点。若 t=0 时质点第一次通过 x=-2cm 处且向 x 轴负方向运动,则 质点第二次通过 x=-2cm 处的时刻为__ __s。
(3) t2 5s 与 t1 1s 两个时刻的位相差;
解:(1)设谐振动的标准方程为 x Acos(t 0 ) ,相比较厚则有:
A 0.1m,
8 ,T
2
1 4
s,
0
2
/3
又
vm A 0.8 m s1 2.51 m s1
am 2 A 63.2 m s2
(2)
Fm mam 0.63N
(1) x0 A ;
(2)过平衡位置向正向运动; (3)过 x A 处向负向运动;
2
(4)过 x A 处向正向运动. 2
试求出相应的初位相,并写出振动方程.
解:因为
v
x0 A cos0 0 Asin
0
将以上初值条件代入上式,使两式同时成立之值即为该条件下的初位相.故有
1
x Acos( 2 t ) T
103
(
)2
0.17
4.2
103
N
2
方向指向坐标原点,即沿 x 轴负向.
(2)由题知, t 0 时,0 0 ,
t t时
x0
A ,且v 2
0, 故 t
3
∴
t
3
/
2
2s 3
化工原理答案传热

第四章 传热热传导【4-1】有一加热器,为了减少热损失,在加热器的平壁外表面,包一层热导率为0.16W/(m·℃)、厚度为300mm 的绝热材料。
已测得绝热层外表面温度为30℃,另测得距加热器平壁外表面250mm 处的温度为75℃,如习题4-1附图所示。
试求加热器平壁外表面温度。
解 2375℃, 30℃t t ==计算加热器平壁外表面温度1t ,./()W m λ=⋅016℃ (1757530025005016016)t --= ..145025********t =⨯+=℃ 【4-2】有一冷藏室,其保冷壁是由30mm 厚的软木做成的。
软木的热导率λ=0.043 W/(m·℃)。
若外表面温度为28℃,内表面温度为3℃,试计算单位表面积的冷量损失。
解 已知.(),.123℃, 28℃, =0043/℃ 003t t W m b m λ==⋅=,则单位表面积的冷量损失为【4-3】用平板法测定材料的热导率,平板状材料的一侧用电热器加热,另一侧用冷水冷却,同时在板的两侧均用热电偶测量其表面温度。
若所测固体的表面积为0.02m 2,材料的厚度为0.02m 。
现测得电流表的读数为2.8A ,伏特计的读数为140V ,两侧温度分别为280℃和100℃,试计算该材料的热导率。
解 根据已知做图热传导的热量 .28140392Q I V W =⋅=⨯=.().()12392002002280100Qb A t t λ⨯==-- 【4-4】燃烧炉的平壁由下列三层材料构成:耐火砖层,热导率λ=1.05W/(m·℃),厚度230b mm =;绝热砖层,热导率λ=0.151W/(m·℃);普通砖层,热导率λ=0.93W/(m·℃)。
耐火砖层内侧壁面温度为1000℃,绝热砖的耐热温度为940℃,普通砖的耐热温度为130℃。
(1) 根据砖的耐热温度确定砖与砖接触面的温度,然后计算绝热砖层厚度。
物理化学第四章课后答案完整版

第四章多组分系统热力学4.1有溶剂A与溶质B形成一定组成的溶液。
此溶液中B的浓度为c B,质量摩尔浓度为b B,此溶液的密度为。
以M A,M B分别代表溶剂和溶质的摩尔质量,若溶液的组成用B的摩尔分数x B表示时,试导出x B与c B,x B与b B之间的关系。
解:根据各组成表示的定义4.2D-果糖溶于水(A)中形成的某溶液,质量分数,此溶液在20℃时的密度。
求:此溶液中D-果糖的(1)摩尔分数;(2)浓度;(3)质量摩尔浓度。
解:质量分数的定义为4.3在25℃,1 kg水(A)中溶有醋酸(B),当醋酸的质量摩尔浓度b B介于和之间时,溶液的总体积求:(1) 把水(A )和醋酸(B )的偏摩尔体积分别表示成b B 的函数关系。
(2)时水和醋酸的偏摩尔体积。
解:根据定义当时4.4 60℃时甲醇的饱和蒸气压是84.4 kPa ,乙醇的饱和蒸气压是47.0 kPa 。
二者可形成理想液态混合物。
若混合物的组成为二者的质量分数各50 %,求60℃时此混合物的平衡蒸气组成,以摩尔分数表示。
解:甲醇的摩尔分数为58980049465004232500423250....x B =+=4.5 80℃时纯苯的蒸气压为100 kPa ,纯甲苯的蒸气压为38.7 kPa 。
两液体可形成理想液态混合物。
若有苯-甲苯的气-液平衡混合物,80℃时气相中苯的摩尔分数,求液相的组成。
解:4.6在18℃,气体压力101.352 kPa下,1 dm3的水中能溶解O2 0.045 g,能溶解N2 0.02 g。
现将1 dm3被202.65 kPa空气所饱和了的水溶液加热至沸腾,赶出所溶解的O2和N2,并干燥之,求此干燥气体在101.325 kPa,18℃下的体积及其组成。
设空气为理想气体混合物。
其组成体积分数为:,解:显然问题的关键是求出O2和N2的亨利常数。
4.7 20℃下HCl 溶于苯中达平衡,气相中HCl 的分压为101.325 kPa 时,溶液中HCl 的摩尔分数为0.0425。
人教版八年级年级物理上册第四章经典例题4.1光的直线传播专项训练含答案

人教版八年级年级物理第四章经典例题4.1光的直线传播专项训练含答案一、单选题1.野外生存能力是户外运动者的必备技能。
下列生存技能与物理知识相对应的是()A.影长辨向﹣光的折射现象B.削竹为刀﹣减面积增压力C.融冰取水﹣固体升华现象D.钻木取火﹣做功改变内能2.设光在真空中的传播速度为v1,在水中的传播速度为v2,在普通玻璃中的传播速度为v3,则它们之间的大小关系是()A.v1<v2<v3B.v1>v2=v3C.v1>v2>v3D.v1=v2=v33.2020年6月21日下午,包括郴州在内的很多地区都能观察到罕见的天文现象﹣﹣日食。
下列关于日食现象的分析正确的是()A.日食现象是由于地球运动到了太阳和月球之间而发生的B.日食的形成原理与镜中花、水中月的原理相同C.日食的形成原理与小孔成像的原理相同D.日食的形成原理与照相机的工作原理相同4.2020年6月21日在我国部分地区观察到日环食现象。
日环食现象是由于()A.月球表面反射太阳光形成的B.月球挡住太阳光形成的C.太阳光经过小孔后形成的D.太阳光经过地球大气层折射后形成的5.下列成语涉及到的物理知识与光的直线传播无关的是()A.立竿见影B.一叶障目C.鱼翔浅底D.管中窥豹6.北京时间2019 年4 月10日21时,首张黑洞照片全球发布,露出真容的黑洞,距离地球5500万光年,质量约为太阳的65 亿倍,黑洞是一种质量极大的密实天体,具有非常强的引力,在它周围的一定区域内,连光也无法逃逸出去。
下列说法中错误的是()A.光年是长度单位B.黑洞的密度非常大C.黑洞强大的引力是分子间的引力D.人眼无法直接看见黑洞内部二、填空题7.在模拟日食、月食的实验中,王老师画了图示。
如果地球上观察到日食,这些人应该是位于__________(选填“甲”或“乙”)处,此时月亮在__________处(选填“A”、“B”或“C”)。
8.为了探究树荫下光斑的成因,小明设计了开有菱形状孔(边长约为5cm)的卡片甲正对太阳光如图,并用另一张卡片乙紧贴在甲上沿箭头方向水平移动,观察距卡片50cm 且与甲平行放置的光屏上光斑的变化情况,发现光斑开始是菱形的,然后逐渐变小,但形状与孔一样,亮度______(填“变亮”、“变暗”或“不变”)。
生理第四章血液循环试题及答案

生理第四章血液循环试题及答案第四章血液循环二、填空题1、内分泌2、缩短,舒张期缩短3、等容收缩期,快速射血期,减慢射血期4、关闭,关闭5、关闭,关闭+-1.心脏除了有循环功能外,还有____________功能。
2.心率减慢时,心动周期_____________,其中以_________更为明显。
3.心室收缩期包括_____________,___________和____________。
4.等容收缩期时,房室瓣处在___________状态,半月瓣处在___________状态。
5.等容舒张期时,房室瓣处于___________状态,半月瓣处于___________状态。
三、单项选择题(a型题)1.e2.b3.b4.b5.e1.心动周期中,占到时间最久的就是()a.心房收缩期b.等容收缩期c.等容舒张期d.射血期e.充盈期2.心动周期中,心室血液的蓄积主要依赖于()a.心房收缩的挤压作用b.心室舒张时造成负压的“抽吸”作用c.胸内负压促进静脉血回心d.血液依赖地心引力而回流e.骨骼肌的挤压作用促进静脉血回心3.在一次心动周期中,左心室压力增高速度最快的就是()a.心房收缩期b.等容收缩期c.快速射血期d.减慢射血期e.等容舒张期4.在一次心动周期中,室内甩最低的时期就是()a.等容收缩期b.快速射血期c.减慢射血期d.等容舒张期e.快速充盈期5.心动周期中,心室容积最小就是()a.等容舒张期末b.快速充盈期末c.快速射血期末d.减慢充盈期e.心房收缩期末四、多项选择题(x型题)1.ac2.abc3.bd4.cd5.acd1.等容收缩期的特点就是()a.心室容积不发生改变b.心室内压下降速度最快c.房室瓣膜和半月瓣都关闭d.心室内甩低于动脉压e.心房内压低于心室内压2.左心室泵血时()a.心室肌的收缩和舒张是造成室内压力变化的原因b.压力梯度是推动血液在腔室之间流动的主要动力c.瓣膜的活动可以掌控血流方向d.瓣膜的活动与室内甩的变化毫无关系e.心室容积不出现发生改变3.心房和心室在心脏泵血活动中的作用()a.房室压力梯度的构成主要源自心房膨胀b.心室等容舒张期内,室内压力大幅度上升c.心房收缩对于心室充盈起主要作用d.心房收缩进入心室的血量约占心室充盈总量的30%e.房室压力梯度的形成主要来自心房舒张4.关于搏出量正确的叙述有()a.等同于每分输出量与心率的乘积b.左心室大于右心室c.指一次眩晕一侧心室射向的血量d.正常人安静时为60-80mle.5~6l/min5.关于心音正确的叙述有()a.第一心音出现在心缩期,持续时间较长b.第二心音出现在心舒期,持续时间较长c.第一心音产生标志着心室收缩开始d.第二心音产生标志着心室舒张开始e.第一心音调高、持续时间长五、是非题(恰当的填上“t”,错误的填上“f”)1.t2.t3.f4.t5.t()1.血液循环的主要功能就是顺利完成体内的物质运输。
大学物理课后习题答案第四章

第四章机械振动4.1一物体沿x 轴做简谐振动,振幅A = 0.12m ,周期T = 2s .当t = 0时,物体的位移x = 0.06m ,且向x 轴正向运动.求:(1)此简谐振动的表达式;(2)t = T /4时物体的位置、速度和加速度;(3)物体从x = -0.06m ,向x 轴负方向运动第一次回到平衡位置所需的时间. [解答](1)设物体的简谐振动方程为x = A cos(ωt + φ),其中A = 0.12m ,角频率ω = 2π/T = π.当t = 0时,x = 0.06m ,所以cos φ = 0.5,因此φ = ±π/3. 物体的速度为v = d x /d t = -ωA sin(ωt + φ).当t = 0时,v = -ωA sin φ,由于v > 0,所以sin φ< 0,因此:φ = -π/3.简谐振动的表达式为:x = 0.12cos(πt – π/3).(2)当t = T /4时物体的位置为;x = 0.12cos(π/2 – π/3) = 0.12cosπ/6 = 0.104(m). 速度为;v = -πA sin(π/2 – π/3) = -0.12πsinπ/6 = -0.188(m·s -1).加速度为:a = d v /d t = -ω2A cos(ωt + φ)= -π2A cos(πt - π/3)= -0.12π2cosπ/6 = -1.03(m·s -2). (3)方法一:求时间差.当x = -0.06m 时,可得cos(πt 1 - π/3) = -0.5, 因此πt 1 - π/3 = ±2π/3.由于物体向x 轴负方向运动,即v < 0,所以sin(πt 1 - π/3) > 0,因此πt 1 - π/3 = 2π/3,得t 1 = 1s .当物体从x = -0.06m 处第一次回到平衡位置时,x = 0,v > 0,因此cos(πt 2 - π/3) = 0, 可得 πt 2 - π/3 = -π/2或3π/2等.由于t 2> 0,所以πt 2 - π/3 = 3π/2, 可得t 2 = 11/6 = 1.83(s).所需要的时间为:Δt = t 2 - t 1 = 0.83(s).方法二:反向运动.物体从x = -0.06m ,向x 轴负方向运动第一次回到平衡位置所需的时间就是它从x = 0.06m ,即从起点向x 轴正方向运动第一次回到平衡位置所需的时间.在平衡位置时,x = 0,v < 0,因此cos(πt - π/3) = 0,可得 πt - π/3 = π/2,解得t = 5/6 = 0.83(s).[注意]根据振动方程x = A cos(ωt + φ),当t = 0时,可得φ = ±arccos(x 0/A ),(-π<φ<= π), 初位相的取值由速度决定.由于v = d x /d t = -ωA sin(ωt + φ),当t = 0时,v = -ωA sin φ,当v > 0时,sin φ< 0,因此 φ = -arccos(x 0/A );当v < 0时,sin φ> 0,因此φ = arccos(x 0/A )π/3.可见:当速度大于零时,初位相取负值;当速度小于零时,初位相取正值.如果速度等于零,当初位置x 0 = A 时,φ = 0;当初位置x 0 = -A 时,φ = π.4.2已知一简谐振子的振动曲线如图所示,试由图求:(1)a ,b ,c ,d ,e 各点的位相,及到达这些状态的时刻t 各是多少?已知周期为T ; (2)振动表达式; (3)画出旋转矢量图. [解答]方法一:由位相求时间.(1)设曲线方程为x = A cos Φ,其中A 表示振幅,Φ = ωt + φ表示相位. 由于x a = A ,所以cos Φa = 1,因此Φa = 0.由于x b = A /2,所以cos Φb = 0.5,因此Φb = ±π/3;由于位相Φ随时间t 增加,b 点位相就应该大于a 点的位相,因此Φb = π/3.由于x c = 0,所以cos Φc = 0,又由于c 点位相大于b 位相,因此Φc = π/2.同理可得其他两点位相为:Φd = 2π/3,Φe = π.c 点和a 点的相位之差为π/2,时间之差为T /4,而b 点和a 点的相位之差为π/3,时间之差应该为T /6.因为b 点的位移值与O 时刻的位移值相同,所以到达a 点的时刻为t a = T /6. 到达b 点的时刻为t b = 2t a = T /3.图4.2到达c 点的时刻为t c = t a + T /4 = 5T /12. 到达d 点的时刻为t d = t c + T /12 = T /2. 到达e 点的时刻为t e = t a + T /2 = 2T /3.(2)设振动表达式为:x = A cos(ωt + φ),当t = 0时,x = A /2时,所以cos φ = 0.5,因此φ =±π/3; 由于零时刻的位相小于a 点的位相,所以φ = -π/3, 因此振动表达式为. 另外,在O 时刻的曲线上作一切线,由于速度是位置对时间的变化率,所以切线代表速度的方向;由于其斜率大于零,所以速度大于零,因此初位相取负值,从而可得运动方程.(3)如图旋转矢量图所示.方法二:由时间求位相.将曲线反方向延长与t 轴 相交于f 点,由于x f = 0,根据运动方程,可得所以:.显然f 点的速度大于零,所以取负值,解得t f = -T /12.从f 点到达a 点经过的时间为T /4,所以到达a 点的时刻为:t a = T /4 + t f = T /6, 其位相为:. 由图可以确定其他点的时刻,同理可得各点的位相.4.3 有一弹簧,当其下端挂一质量为M 的物体时,伸长量为9.8×10-2m .若使物体上下振动,且规定向下为正方向.(1)t = 0时,物体在平衡位置上方8.0×10-2m 处,由静止开始向下运动,求运动方程;(2)t = 0时,物体在平衡位置并以0.60m·s -1速度向上运动,求运动方程. [解答]当物体平衡时,有:Mg – kx 0 = 0, 所以弹簧的倔强系数为:k = Mg/x 0, 物体振动的圆频率为:s -1). 设物体的运动方程为:x = A cos(ωt + φ).(1)当t = 0时,x 0 = -8.0×10-2m ,v 0 = 0,因此振幅为:=8.0×10-2(m);由于初位移为x 0 = -A ,所以cos φ = -1,初位相为:φ = π. 运动方程为:x = 8.0×10-2cos(10t + π).(2)当t = 0时,x 0 = 0,v 0 = -0.60(m·s -1),因此振幅为:v 0/ω|=6.0×10-2(m);由于cos φ = 0,所以φ = π/2;运动方程为:x = 6.0×10-2cos(10t +π/2).4.4 质量为10×10-3kg 的小球与轻弹簧组成的系统,按的规律作振动,式中t 以秒(s)计,x 以米(m)计.求: (1)振动的圆频率、周期、振幅、初位相; (2)振动的速度、加速度的最大值;(3)最大回复力、振动能量、平均动能和平均势能;cos(2)3t x A T ππ=-cos(2)03t T ππ-=232f t Tπππ-=±203a a t T πΦπ=-=ω==0||A x ==A =20.1cos(8)3x t ππ=+(4)画出这振动的旋转矢量图,并在图上指明t 为1,2,10s 等各时刻的矢量位置. [解答](1)比较简谐振动的标准方程:x = A cos(ωt + φ),可知圆频率为:ω =8π,周期T = 2π/ω = 1/4 = 0.25(s),振幅A = 0.1(m),初位相φ = 2π/3.(2)速度的最大值为:v m = ωA = 0.8π = 2.51(m·s -1); 加速度的最大值为:a m = ω2A = 6.4π2 = 63.2(m·s -2). (3)弹簧的倔强系数为:k = mω2,最大回复力为:f = kA = mω2A = 0.632(N); 振动能量为:E = kA 2/2 = mω2A 2/2 = 3.16×10-2(J), 平均动能和平均势能为:= kA 2/4 = mω2A 2/4 = 1.58×10-2(J). (4)如图所示,当t 为1,2,10s 等时刻时,旋转矢量的位置是相同的.4.5 两个质点平行于同一直线并排作同频率、同振幅的简谐振动.在振动过程中,每当它们经过振幅一半的地方时相遇,而运动方向相反.求它们的位相差,并作旋转矢量图表示.[解答]设它们的振动方程为:x = A cos(ωt + φ), 当x = A /2时,可得位相为:ωt + φ = ±π/3.由于它们在相遇时反相,可取Φ1 = (ωt + φ)1 = -π/3,Φ2 = (ωt + φ)2 = π/3,它们的相差为:ΔΦ = Φ2 – Φ1 = 2π/3,或者:ΔΦ` = 2π –ΔΦ = 4π/3.矢量图如图所示.4.6一氢原子在分子中的振动可视为简谐振动.已知氢原子质量m = 1.68×10-27kg ,振动频率v = 1.0×1014Hz ,振幅A = 1.0×10-11m .试计算:(1)此氢原子的最大速度; (2)与此振动相联系的能量.[解答](1)氢原子的圆频率为:ω = 2πv = 6.28×1014(rad·s -1), 最大速度为:v m = ωA = 6.28×103(m·s -1).(2)氢原子的能量为:= 3.32×10-20(J).4.7 如图所示,在一平板下装有弹簧,平板上放一质量为1.0kg 的重物,若使平板在竖直方向上作上下简谐振动,周期为0.50s ,振幅为2.0×10-2m ,求:(1)平板到最低点时,重物对平板的作用力;(2)若频率不变,则平板以多大的振幅振动时,重物跳离平板? (3)若振幅不变,则平板以多大的频率振动时,重物跳离平板? [解答](1)重物的圆频率为:ω = 2π/T = 4π,其最大加速度为:a m = ω2A ,合力为:F = ma m ,方向向上.重物受到板的向上支持力N 和向下的重力G ,所以F = N – G . 重物对平板的作用力方向向下,大小等于板的支持力: N = G + F = m (g +a m ) = m (g +ω2A ) = 12.96(N).(2)当物体的最大加速度向下时,板的支持为:N = m (g - ω2A ). 当重物跳离平板时,N = 0,频率不变时,振幅为:A = g/ω2 = 3.2×10-2(m).(3)振幅不变时,频率为:3.52(Hz).4.8 两轻弹簧与小球串连在一直线上,将两弹簧拉长后系在固定点A 和B 之间,整个系统放在光滑水平面上.设两弹簧的原长分别为l 1和l 2,倔强系统分别为k 1和k 2,A和B 间距为L ,小球的质量为m .(1)试确定小球的平衡位置;k pE E =212m E mv=2ωνπ==(2)使小球沿弹簧长度方向作一微小位移后放手,小球将作振动,这一振动是否为简谐振动?振动周期为多少?[解答](1)这里不计小球的大小,不妨设L > l 1 + l 2,当小球平衡时,两弹簧分别拉长x 1和x 2,因此得方程:L = l 1 + x 1 + l 2 + x 2;小球受左右两边的弹簧的弹力分别向左和向右,大小相等,即k 1x 1 = k 2x 2. 将x 2 = x 1k 1/k 2代入第一个公式解得:.小球离A 点的距离为:.(2)以平衡位置为原点,取向右的方向为x 轴正方向,当小球向右移动一个微小距离x 时,左边弹簧拉长为x 1 + x ,弹力大小为:f 1 = k 1(x 1 + x ), 方向向左;右边弹簧拉长为x 1 - x ,弹力大小为:f 2 = k 2(x 2 - x ), 方向向右.根据牛顿第二定律得:k 2(x 2 - x ) - k 1(x 1 + x ) = ma ,利用平衡条件得:,即小球做简谐振动.小球振动的圆频率为:.4.9如图所示,质量为10g 的子弹以速度v = 103m·s -1水平射入木块,并陷入木块中,使弹簧压缩而作简谐振动.设弹簧的倔强系数k = 8×103N·m -1,木块的质量为4.99kg ,不计桌面摩擦,试求:(1)振动的振幅;(2)振动方程.[解答](1)子弹射入木块时,由于时间很短,木块还来不及运动,弹簧没有被压缩,它们的动量守恒,即:mv = (m + M)v 0.解得子弹射入后的速度为:v 0 = mv/(m + M) = 2(m·s -1),这也是它们振动的初速度.子弹和木块压缩弹簧的过程机械能守恒,可得:(m + M ) v02/2 = kA 2/2, 所以振幅为:10-2(m). (2)振动的圆频率为:= 40(rad·s -1).取木块静止的位置为原点、向右的方向为位移x 的正方向,振动方程可设为:x = A cos(ωt + φ).当t = 0时,x = 0,可得:φ = ±π/2;由于速度为正,所以取负的初位相,因此振动方程为:x = 5×10-2cos(40t - π/2).4.10如图所示,在倔强系数为k 的弹簧下,挂一质量为M 的托盘.质量为m 的物体由距盘底高h 处自由下落与盘发生完全非弹性碰撞,而使其作简谐振动,设两物体碰后瞬时为t = 0时刻,求振动方程.[解答]物体落下后、碰撞前的速度为:物体与托盘做完全非弹簧碰撞后,根据动量守恒定律可得它们的共同速度为,这也是它们振动的初速度.设振动方程为:x = A cos(ωt + φ),211212()k x L l l k k =--+211111212()k L l x l L l l k k =+=+--+2122d ()0d xm kk x t++=ω=22T πω==A v =ω=v =0m v v m M ==+图4.9 图4.10其中圆频率为:物体没有落下之前,托盘平衡时弹簧伸长为x 1,则:x 1 = Mg/k .物体与托盘磁盘之后,在新的平衡位置,弹簧伸长为x 2,则:x 2= (M + m )g/k . 取新的平衡位置为原点,取向下的方向为正,则它们振动的初位移为x 0 = x 1 - x 2 = -mg/k .因此振幅为:初位相为:4.11 装置如图所示,轻弹簧一端固定,另一端与物体m 间用细绳相连,细绳跨于桌边定滑轮M 上,m 悬于细绳下端.已知弹簧的倔强系数为k = 50N·m -1,滑轮的转动惯量J = 0.02kg·m 2,半径R = 0.2m ,物体质量为m = 1.5kg ,取g = 10m·s -2.(1)试求这一系统静止时弹簧的伸长量和绳的张力;(2)将物体m 用手托起0.15m ,再突然放手,任物体m 下落而整个系统进入振动状态.设绳子长度一定,绳子与滑轮间不打滑,滑轮轴承无摩擦,试证物体m 是做简谐振动; (3)确定物体m 的振动周期;(4)取物体m 的平衡位置为原点,OX 轴竖直向下,设振物体m 相对于平衡位置的位移为x ,写出振动方程.[解答](1)在平衡时,绳子的张力等于物体的重力T = G = mg = 15(N).这也是对弹簧的拉力,所以弹簧的伸长为:x 0 = mg/k = 0.3(m).(2)以物体平衡位置为原点,取向下的方向为正,当物体下落x 时,弹簧拉长为x 0 + x ,因此水平绳子的张力为:T 1 = k (x 0+ x ).设竖直绳子的张力为T 2,对定滑轮可列转动方程:T 2R – T 1R = Jβ, 其中β是角加速度,与线加速度的关系是:β = a/R .对于物体也可列方程:mg - T 2 = ma . 转动方程化为:T 2 – k (x 0 + x ) = aJ/R 2,与物体平动方程相加并利用平衡条件得:a (m + J/R 2) = –kx ,可得微分方程:,故物体做简谐振动. (3)简谐振动的圆频率为:s -1). 周期为:T 2 = 2π/ω = 1.26(s).(4)设物体振动方程为:x = A cos(ωt + φ),其中振幅为:A = 0.15(m). 当t = 0时,x = -0.15m ,v 0 = 0,可得:cos φ = -1,因此φ = π或-π, 所以振动方程为:x = 0.15cos(5t + π),或x = 0.15cos(5t - π).4.12一匀质细圆环质量为m ,半径为R ,绕通过环上一点而与环平面垂直的水平光滑轴在铅垂面内作小幅度摆动,求摆动的周期.[解答]通过质心垂直环面有一个轴,环绕此轴的转动惯量为:I c = mR 2.根据平行轴定理,环绕过O 点的平行轴的转动惯量为I = I c + mR 2 = 2mR 2.当环偏离平衡位置时,重力的力矩为:M = mgR sin θ, 方向与角度θ增加的方向相反.ω=A ==00arctan v x ϕω-==222d 0d /x kx t m J R +=+ω=根据转动定理得:Iβ = -M ,即,由于环做小幅度摆动,所以sin θ≈θ,可得微分方程:. 摆动的圆频率为:周期为:4.13 重量为P 的物体用两根弹簧竖直悬挂,如图所示,各弹簧的倔强系数标明在图上.试求在图示两种情况下,系统沿竖直方向振动的固有频率.[解答](1)前面已经证明:当两根弹簧串联时,总倔强系数为k = k1k 2/(k 1 + k 2),因此固有频率为(2)前面还证明:当两根弹簧并联时,总倔强系数等于两个弹簧的倔强系数之和,因此固有频率为.4.14质量为0.25kg 的物体,在弹性力作用下作简谐振动,倔强系数k = 25N·m -1,如果开始振动时具有势能0.6J ,和动能0.2J ,求:(1)振幅;(2)位移多大时,动能恰等于势能?(3)经过平衡位置时的速度.[解答]物体的总能量为:E = E k + E p = 0.8(J).(1)根据能量公式E = kA2/2,得振幅为:.(2)当动能等于势能时,即E k = E p ,由于E = E k + E p ,可得:E = 2E p ,即,解得:= ±0.179(m). (3)再根据能量公式E = mv m2/2,得物体经过平衡位置的速度为: 2.53(m·s -1).4.15 两个频率和振幅都相同的简谐振动的x-t 曲线如图所示,求: (1)两个简谐振动的位相差;(2)两个简谐振动的合成振动的振动方程. [解答](1)两个简谐振动的振幅为:A = 5(cm), 周期为:T = 4(s),圆频率为:ω =2π/T = π/2,它们的振动方程分别为:x 1 = A cos ωt =5cosπt /2, x 2 = A sin ωt =5sinπt /2 =5cos(π/2 - πt /2)即x 2=5cos(πt /2 - π/2).位相差为:Δφ = φ2 - φ1 = -π/2. (2)由于x = x 1 + x 2 = 5cosπt /2 +5sinπt /2 = 5(cosπt /2·cosπ/4 +5sinπt /2·sinπ/4)/sinπ/4 合振动方程为:(cm).22d sin 0d I mgR tθθ+=22d 0d mgRt Iθθ+=ω=222T πω===2ωνπ===2ωνπ===A =2211222kA kx =⨯/2x =m v =cos()24x t ππ=- (b)图4.134.16 已知两个同方向简谐振动如下:,.(1)求它们的合成振动的振幅和初位相; (2)另有一同方向简谐振动x 3 = 0.07cos(10t +φ),问φ为何值时,x 1 + x 3的振幅为最大?φ为何值时,x 2 + x 3的振幅为最小?(3)用旋转矢量图示法表示(1)和(2)两种情况下的结果.x 以米计,t 以秒计.[解答](1)根据公式,合振动的振幅为:=8.92×10-2(m). 初位相为:= 68.22°.(2)要使x 1 + x 3的振幅最大,则:cos(φ– φ1) = 1,因此φ– φ1 = 0,所以:φ = φ1 = 0.6π. 要使x 2 + x 3的振幅最小,则 cos(φ– φ2) = -1,因此φ– φ2 = π,所以φ = π + φ2 = 1.2π.(3)如图所示.4.17质量为0.4kg 的质点同时参与互相垂直的两个振动:, .式中x 和y 以米(m)计,t 以秒(s)计.(1)求运动的轨道方程;(2)画出合成振动的轨迹;(3)求质点在任一位置所受的力.[解答](1)根据公式:,其中位相差为:Δφ = φ2 – φ1 = -π/2,130.05cos(10)5x t π=+210.06cos(10)5x t π=+A =11221122sin sin arctancos cos A A A A ϕϕϕϕϕ+=+0.08cos()36x t ππ=+0.06cos()33y t ππ=-2222212122cos sin x y xyA A A A ϕϕ+-∆=∆所以质点运动的轨道方程为:. (2)合振动的轨迹是椭圆.(3)两个振动的圆频率是相同的ω = π/3,质点在x 方向所受的力为,即F x = 0.035cos(πt /3 + π/6)(N).在y 方向所受的力为,即F y = 0.026cos(πt /3 - π/3)(N).用矢量表示就是,其大小为,与x 轴的夹角为θ = arctan(F y /F x ).4.18 将频率为384Hz 的标准音叉振动和一待测频率的音叉振动合成,测得拍频为3.0Hz ,在待测音叉的一端加上一小块物体,则拍频将减小,求待测音叉的固有频率.[解答]标准音叉的频率为v 0 = 384(Hz), 拍频为Δv = 3.0(Hz), 待测音叉的固有频率可能是v 1 = v 0 - Δv = 381(Hz), 也可能是v 2 = v 0 + Δv = 387(Hz).在待测音叉上加一小块物体时,相当于弹簧振子增加了质量,由于ω2 = k/m ,可知其频率将减小.如果待测音叉的固有频率v 1,加一小块物体后,其频率v`1将更低,与标准音叉的拍频将增加;实际上拍频是减小的,所以待测音叉的固有频率v 2,即387Hz .4.19示波器的电子束受到两个互相垂直的电场作用.电子在两个方向上的位移分别为x = A cos ωt 和y = A cos(ωt +φ).求在φ = 0,φ = 30º,及φ = 90º这三种情况下,电子在荧光屏上的轨迹方程.[解答]根据公式,其中Δφ = φ2 – φ1 = -π/2,而φ1 = 0,φ2 = φ.(1)当Δφ = φ = 0时,可得,质点运动的轨道方程为y = x ,轨迹是一条直线.(2)当Δφ = φ = 30º时,可得质点的轨道方程, 即,轨迹是倾斜的椭圆.(3)当Δφ = φ = 90º时,可得, 即x 2 + y 2 = A 2,质点运动的轨迹为圆.4.20三个同方向、同频率的简谐振动为,,.222210.080.06x y +=22d d x x x F ma m t==20.08cos()6m t πωω=-+22d d y y y F ma m t==20.06cos()3m t ωω=--πi+j x y F F F =F =2222212122cos sin x y xyA A A A ϕϕ+-∆=∆2222220x y xyA A A+-=222214x y A+=222/4x y A +=22221x y A A +=10.08cos(314)6x t π=+20.08cos(314)2x t π=+350.08cos(314)6x t π=+求:(1)合振动的圆频率、振幅、初相及振动表达式; (2)合振动由初始位置运动到所需最短时间(A 为合振动振幅). [解答]合振动的圆频率为:ω = 314 = 100π(rad·s -1). 设A 0 = 0.08,根据公式得:A x = A 1cos φ1 + A 2cos φ2 + A 3cos φ3 = 0,A y = A 1sin φ1 + A 2sin φ2 + A 3sin φ3 = 2A 0 = 0.16(m), 振幅为:,初位相为:φ = arctan(A y /A x ) = π/2.合振动的方程为:x = 0.16cos(100πt + π/2).(2)当时,可得:,解得:100πt + π/2 = π/4或7π/4.由于t > 0,所以只能取第二个解,可得所需最短时间为t = 0.0125s .x A =A =/2x =cos(100/2)2t ππ+。
在职研究生-心理学-第四章-感觉和知觉练习题(含答案)

第四章感觉与知觉一、填空题1关系。
23、观察的品质包括:4、运动知觉是指个体对物体空间位移的反应,可分为567.89觉。
10.观察的品质有观察的目的性、二、单项选择题1、知觉条件在一定的范围内发生变化,而知觉对象的影响仍然相对不变的特性称为知觉的()。
A选择性B整体性C理解性D恒常性2、两个静态的物体按一定的时间依次出现,使人觉得是一个动态的物体,这种知觉称为()。
A真动知觉B似动知觉C幻觉D时间错觉3、月朗星稀是感觉的()现象。
A适应现象B对比C后象征D视觉障碍4、胃的剧烈收缩所引起的疼痛属于()。
A内受感觉B本受感觉C外受感觉D运动觉5、入芝兰之室久而不闻其香,属于感觉的()。
A继进对比B回想C适应D继时对比6、对事物的各种属性,各个部分以及它们之间的关系的综合的整体的直接反映称为()。
A思维B感觉C知觉D概括7、个体对同一物体的凹凸或对不同物体的远近的反应称为()知觉。
A深度B大小C形状D面积8、视觉属于()。
A内受感觉B本受感觉C机体觉D外受感觉9、个体对客观现象的延续性和顺序性的反应是()知觉。
A运动B空间C方位D时间10、机体位置运动状态的反应是()感觉。
A外受B内受C本受D皮肤11、费希纳指出符合对数定律的是()。
A 心理量和物理量的关系B心理量变化和物理量C物理量的变化和心理量D感觉和感觉阈限12、最简单最低级的心理现象是()A 感觉B知觉C记忆D注意13、内脏痛觉属于()A外受感觉B本受感觉C内受感觉D感受性14、从黑暗处到明亮处感受性降低的过程叫()A嗅觉B皮肤觉C暗适应D明适应15、没有适应现象的感觉是()A嗅觉B皮肤温度觉C触压觉D痛觉16.人脑对直接作用于感觉器官的客观事物的整体属性的反映是( ):A.感觉B.反应c.知觉D.阈限17.人对最小的客观刺激量的感觉能力是( ):A.感觉阈限B.绝对感觉阈限C绝对感受性D.差别感受性18.闻到苹果香味,看到苹果红色外观出磨苹果感到光滑等引起的心理活动是( )。
《物理学基本教程》课后答案_第四章__刚体的转动

第五章 刚体的转动5-13 如图5-13(a)所示,滑轮转动惯量为0.012m kg ⋅,半径为7 cm ,物体质量为5 kg ,由一绳与倔强系数k=200 N/m 的弹簧相连,若绳与滑轮间无相对滑动,滑轮轴上的摩擦忽略不计,求:(1)当绳拉直弹簧无伸长时,使物体由静止而下落的最大距离;(2)物体速度达最大值的位置及最大速率.分析 下面的5-17题中将证明,如果绕定轴转动的刚体除受到轴的支承力外仅受重力作用,则由刚体和地球组成的系统机械能守恒.如果将滑轮、地球和物体与弹簧组成一个弹性系统和重力系统合成的系统,当无重力和弹性力以外的力作功的情况下,整个系统的机械能守恒,可以应用机械能守恒定律.下面的解则仅应用功能原理和力矩所作的功与刚体转动动能的关系进行计算.解 (1) 物体由静止而下落到最低点时,速度为零,位移为1x ,在此期间重力所作的功完全转换为弹簧弹性势能的增量,即21121kx mgx = m 0.49m 2008.95221=⨯⨯==k mg x (2)物体与滑轮受力如图5-13(b)所示,设物体的最大速率为0v ,此时的位移为0x ,加速度00=a ,滑轮的角加速度000==R a α,分别应用牛顿第二定律和转动定律T1aF ’T1m m g(a) (b)图5-13ma F mg =-T1αJ R F F =-)(T2T1可得此时T1F mg =,F T1= F T2,又因对于轻弹簧有0T2kx F =,则得m 0.245m 2008.950=⨯==k mg x 在此过程中,重力所作之功等于弹性势能的增量、物体动能和滑轮转动动能的增量的和,即2020200212121ωJ m kx mgx ++=v 因R 00v =ω,得 m/s 31.1m/s 9.85)07.001.05(2001)(122=⨯⨯+⨯=+=mg R J m k v5-7 如图5-7(a )所示的系统中,m 1 = 50 kg ,m 2 = 40 kg ,圆盘形滑轮质量m = 16 kg ,半径R = 0.1 m ,若斜面是光滑的,倾角为30°,绳与滑轮间无相对滑动,不计滑轮轴上的摩擦,(1)求绳中张力;(2)运动开始时,m 1距地面高度为1 m ,需多少时间m 1到达地面?分析 由于存在物体运动和滑轮定轴转动,而且必须考虑圆盘形滑轮的质量,这是一个质点动力学和刚体动力学的综合问题,应该采用隔离物体法,分别m αF ’T1 F T1 m 2 m 1 F F T2a︒30m 2g m 1g(a ) (b )图5-7对运动物体作受力分析,对转动的滑轮作所受力矩的分析,然后分别应用牛顿第二定律和转动定律.解 (1)各物体与滑轮受力情况如图5-7(b )所示,其中F T1= F ’T1,F T2= F ’T2,轴对滑轮的支承力F N 不产生力矩,选取物体运动方向为坐标轴正向,分别应用牛顿第二定律和转动定律,可得22121rad/s 3021)(30sin =++︒-=g mR R m m m m α N 340)(1T1=-=αR g m FN 316)30sin (2T2=+︒=αR g m F2m/s 3==αR a(2) m 1到达地面的时间为s 0.816s 3122=⨯==a h t 、5-1 一个匀质圆盘由静止开始以恒定角加速度绕过中心而垂直于盘面的定轴转动.在某一时刻,转速为10 r/s ,再转60转后,转速变为15 r/s ,试计算:(1)角加速度;(2)由静止达到10 r/s 所需时间;(3)由静止到10 r/s 时圆盘所转的圈数.分析 绕定轴转动的刚体中所有质点都绕轴线作圆周运动,并具有相同的角位移、角速度和角加速度,因此描述运动状态的物理量与作圆周运动的质点的相似.当角加速度恒定时,绕定轴转动的刚体用角量表示的运动学公式与匀加速直线运动的公式类似.解 (1) 根据题意,转速由rad/s 1021⨯=πω变为rad/s 1522⨯=πω期间的角位移rad 260πθ⨯=,则角加速度为22222122rad/s 54.6rad/s 2602)102()152(2=⨯⨯⨯-⨯=-=πππθωωα (2) 从静止到转速为rad/s 1021⨯=πω所需时间为s 9.61s 54.61021=⨯==παωt (3) t 时间内转的圈数为48261.91022122121=⨯⨯⨯===ππωππθt N 5-2 唱片在转盘上匀速转动,转速为78 r/min ,由开始到结束唱针距转轴分别为15 cm 和7.5 cm ,(1)求这两处的线速度和法向加速度;(2)在电动机断电以后,转盘在15 s 内停止转动,求它的角加速度及转过的圈数.分析 绕定轴转动的刚体中所有质点具有相同的角位移、角速度和角加速度,但是线速度、切向加速度和法向加速度等线量则与各质点到转轴的距离有关.角量与线量的关系与质点圆周运动的相似.解 (1) 转盘角速度为rad/s 8.17rad/s 60278=⨯=πω,唱片上m 15.01=r 和m 075.02=r 处的线速度和法向加速度分别为m /s 1.23m /s 15.017.811=⨯==r ωv222121n m /s 10.0m /s 15.017.8=⨯==r ωam /s .6130m /s 075.017.822=⨯==r ωv222222n m /s .015m /s 075.017.8=⨯==r ωa(2) 电动机断电后,角加速度为22rad/s 545.0rad/s 1517.800-=-=-=t ωα 转的圈数为 75.921517.8212212=⨯⨯===πωππθt N 5-3 如图5-3所示,半径r 1 = 30 cm 的A 轮通过皮带被半径为r 2 = 75 cm 的B 轮带动,B 轮以π rad/s 的匀角加速度由静止起动,轮与皮带间无滑动发生,试求A 轮达到3000 r/min 所需要的时间. 分析 轮与皮带间无滑动,则同一时刻,两轮边缘的线速度相同,均等于皮带的传送速度;两轮边缘的切向加速度也相同,均等于皮带的加速度.解 设A 、B 轮的角加速度分别为A α、B α,由于两轮边缘与皮带连动,切向加速度相同,即2B 1A r r αα=则 B 12A ααr r = A 轮角速度达到rad/s 6030002⨯=πω所需要的时间为 s 40s 75.06030.0300022B 1A =⨯⨯⨯⨯===ππαωαωr r tB A r 1 r 2图5-35-4 在边长为b 的正方形的顶点上,分别有质量为m 的四个质点,求此系统绕下列转轴的转动惯量:(1)通过其中一质点A ,平行于对角线BD 的转轴,如图5-4所示.(2)通过A 垂直于质点所在平面的转轴.分析 由若干质点组成的质点系对某转轴的转动惯量等于各质点对该转轴转动惯量的叠加.每一质点对转轴的转动惯量等于它的质量与其到转轴的垂直距离平方的乘积. 解 (1)因质点B 和D 到转轴的垂直距离A 2B 和A 1D 为a 22,质点C 到转轴的垂直距离AC 为a 2,而质点A 位于转轴上,则系统对通过A 点平行于BD 的转轴的转动惯量为()222132222ma am a m J =+⎪⎪⎭⎫ ⎝⎛=(2) 因质点B 和D 到转轴的垂直距离AB 和AD 为a ,质点C 到转轴的垂直距离AC 为a 2,而质点A 位于转轴上,则系统对通过A 垂于质点所在平面转轴的转动惯量为()2222422ma a m ma J =+=5-5 求半径为R ,质量为m 的均匀半圆环相对于图5-5中所示轴线的转动惯量.分析 如果刚体的质量连续分布在一细线上,可用质量线密度描述其分布情况,如果分布是均匀的,则质量线密度λ为常量.在刚体上取一小段线元l d ,质量为l d λ,对转轴的转动惯量为l r d 2λ,其中该线元AA 2B图5-4 R图5-5到转轴的距离r 与线元在刚体上的位置有关.整个刚体的转动惯量就是刚体上所有线元转动惯量的总和,即所取线元的转动惯量对刚体分布的整个区域积分的结果.解 均匀半圆环的质量线密度为Rm πλ=,在半圆环上取一小段圆弧作为线元θd d R l =,质量为θπθπλd d d d m R R m l m === 此线元到转轴的距离为θsin R r =,对轴线的转动惯量为m r d 2,则整个半圆环的转动惯量为2022221d sin d mR m R m r J =⋅==⎰⎰θπθπ 5-6 一轻绳跨过滑轮悬有质量不等的二物体A 、B ,如图5-6(a)所示,滑轮半径为20 cm ,转动惯量等于2m kg 50⋅,滑轮与轴间的摩擦力矩为m N 198⋅.,绳与滑轮间无相对滑动,若滑轮的角加速度为2rad/s 362.,求滑轮两边绳中张力之差. 分析 由于定轴转动的刚体的运动规律遵从转动定律,因此对于一个定轴转动的滑轮来说,仅当其质量可以忽略,转动惯量为零,滑轮加速转动时跨越滑轮的轻绳两边的张力才相等.这就是在质点动力学问题中通常采用的简化假设.在掌握了转动定律后,不应该再忽略滑轮质量,通常将滑轮考虑为质量均匀分布的圆盘,则跨越滑轮的轻绳两边的张力对转轴的合力矩是滑轮产生角加速度的原因.解 滑轮所受力和力矩如图5-6(b)所示,其中跨越滑轮的轻绳两边的张力分别为F T1和F T2,轴的支承力F N 不产生力矩,由转动定律可得fF T1 F T2(a) (b)图5-6αJ M R F F =--f T2T1)()(1f T2T1M J R F F +=-α N 101.08N )1.9836.250(2.01 3⨯=+⨯⨯= 5-7 如图5-7(a )所示的系统中,m 1 = 50 kg ,m 2 = 40 kg ,圆盘形滑轮质量m = 16 kg ,半径R = 0.1 m ,若斜面是光滑的,倾角为30°,绳与滑轮间无相对滑动,不计滑轮轴上的摩擦,(1)求绳中张力;(2)运动开始时,m 1距地面高度为1 m ,需多少时间m 1到达地面?分析 由于存在物体运动和滑轮定轴转动,而且必须考虑圆盘形滑轮的质量,这是一个质点动力学和刚体动力学的综合问题,应该采用隔离物体法,分别对运动物体作受力分析,对转动的滑轮作所受力矩的分析,然后分别应用牛顿第二定律和转动定律.解 (1)各物体与滑轮受力情况如图5-7(b )所示,其中F T1= F ’T1,F T2= F ’T2,轴对滑轮的支承力F N 不产生力矩,选取物体运动方向为坐标轴正向,分别应用牛顿第二定律和转动定律,可得m αF ’T1 F T1 m 2 m 1 F F T2a︒30m 2g m 1g(a ) (b )图5-7由于物体的加速度等于滑轮边缘的线速度,则αR a =,与以上各式联立解得22121rad/s 3021)(30sin =++︒-=g mR R m m m m α N 340)(1T1=-=αR g m FN 316)30sin (2T2=+︒=αR g m F2m/s 3==αR a(2) m 1到达地面的时间为s 0.816s 3122=⨯==a h t 5-8 飞轮质量为60 kg ,半径为0.25 m ,当转速为1000 r/min 时,要在5 s 内令其制动,求制动力F ,设闸瓦与飞轮间摩擦系数μ=0.4,飞轮的转动惯量可按匀质圆盘计算,闸杆尺寸如图5-8所示.分析 制动力F 作用在闸杆上,闸杆在制动力和飞轮的正压力的力矩作用下达到平衡,转动轴在墙上,这是刚体在力矩作用下的平衡问题.由于二力的力臂已知,应该求出闸杆与飞轮之间的正压力.飞轮受到闸杆的正压力、闸瓦与飞轮间摩擦力和轴的支承力作用,其中闸杆的正压力和轴的支承力的力矩为零,在闸瓦与飞轮间摩擦力的力矩作用下制动,应用转动定律可以求出摩擦力矩,然后由摩擦力与正压力关系可以求出闸杆与飞轮之间的正压力.F图5-8解 以飞轮为研究对象,飞轮的转动惯量为221mR J =,制动前角速度为rad/s 6010002⨯=πω,制动时角加速度为tωα-=.制动时闸瓦对飞轮的压力为F N ,闸瓦与飞轮间的摩擦力N f F F μ=,应用转动定律,得αα2f 21mR J R F ==- 则 t mR F μω2N =以闸杆为研究对象.在制动力F 和飞轮对闸瓦的压力-F N 的力矩作用下闸杆保持平衡,两力矩的作用力臂分别为m )75.050.0(+=l 和m 50.01=l ,则有01N =-l F FlN 157N 6054.021000225.06075.050.050.021N 1=⨯⨯⨯⨯⨯⨯⨯+===πμωt mR l l F l l F 5-9 一风扇转速为900 r/min ,当马达关闭后,风扇均匀减速,止动前它转过了75转,在此过程中制动力作的功为44.4 J ,求风扇的转动惯量和摩擦力矩.分析 合外力矩对刚体所作的功等于刚体的转动动能的增量.制动过程中风扇只受摩擦力矩作用,而且由于风扇均匀减速,表明摩擦力矩为恒定值,与风扇角位移的乘积就是所作的功.解 设制动摩擦力矩为M ,风扇转动惯量为J ,止动前风扇的角位移N πθ2=,摩擦力矩所作的功为N M M W πθ2⋅-=-=摩擦力矩所作的功应等于风扇转动动能的增量,即2210ωJ W -= 则 2222m kg 01.0m kg )60/2900()4.44(22⋅=⋅⨯-⨯-=-=πωW J m N 0.0942m N 7524.442⋅=⋅⨯--=-=ππN W M5-10 如图5-10(a )所示,质量为24 kg 的鼓形轮,可绕水平轴转动,一绳缠绕于轮上,另一端通过质量为5 kg 的圆盘形滑轮悬有10 kg 的物体,当重物由静止开始下降了0.5 m 时,求:(1)物体的速度;(2)绳中张力.设绳与滑轮间无相对滑动.分析 这也是一个质点动力学和刚体动力学的综合问题,鼓形轮和滑轮都视为圆盘形定轴转动的刚体,应该采用隔离物体法,分别对运动物体作受力分析,对刚体作所受力矩的分析,然后分别应用牛顿第二定律和转动定律.解 各物体受力情况如图5-10(b )所示,其中F T1= F ’T1,F T2= F ’T2,鼓形轮的转动惯量为2121R m ,圆盘形滑轮的转动惯量为2221r m ,分别应用牛顿第二定律和转动定律,可得ma F mg =-T2222T1T221)(αr m r F F =- 121T121αR m R F =(1) 绳与滑轮间无相对滑动,物体的加速度等于鼓形轮和滑轮边缘的切向加速度,即12ααR r a ==.重物由静止开始下降了h = 0.5 m 时,速度ah 2=v ,由以上各式得αT1 F 2α ’T2 a F T2m g(a ) (b )图5-10m/s 2m/s )524(21105.08.9102)(212221=+⨯+⨯⨯⨯=++==m m m mgh ah v (2)绳中张力为N 48N 5241028.924102211T1=++⨯⨯⨯=++=m m m g mm F N 85N 5241028.9)524(102)(2121T2=++⨯⨯+⨯=+++=m m m g m m m F 5-11 一蒸汽机的圆盘形飞轮质量为200 kg ,半径为1 m ,当飞轮转速为120 r/min 时关闭蒸汽阀门,若飞轮在5 min 内停下来,求在此期间飞轮轴上的平均摩擦力矩及此力矩所作的功.分析 制动过程中飞轮只受摩擦力矩作用,该摩擦力矩不一定为恒定值,但是由于只需求平均摩擦力矩,因此可以假设飞轮均匀减速,由已知条件求出平均角加速度,再应用转动定律求出平均摩擦力矩.解 飞轮转动惯量为221mR J =,关闭蒸汽阀门后t = 5 min 内的平均角加速度为t00ωα-=,应用转动定律,平均摩擦力矩 m N 194m N 60560/212012002121202⋅-=⋅⨯⨯⨯⨯⨯-=-==.t mR J M πωα 在此期间平均摩擦力矩所作的功等于飞轮转动动能的增量J 7896J )60/2120(12002121 21212102220220-=⨯⨯⨯⨯⨯-=⋅-=-=πωωmR J W 负号表示平均摩擦力矩作负功,方向与飞轮旋转方向相反.5-12 长为85 cm 的均匀细杆,放在倾角为45°的光滑斜面上,可以绕过上端点的轴在斜面上转动,如图5-12(a)所示,要使此杆实现绕轴转动一周,至少应给予它的下端多大的初速度?分析 细杆在斜面上转动,斜面的支承力与转轴平行,转轴的支承力通过转轴,它们的力矩都为零,只有重力在转动平面内分量的力矩作功.解 如图5-12(b)所示,杆所受重力在转动平面内的分量为︒45sin mg ,当杆与初始位置的夹角为θ时,重力分量对转轴的力矩为θsin 2145sin l mg ⋅︒,此时若杆有角位移θd ,则重力矩所作的元功为θθd sin 2145sin d ⋅⋅︒=l mg W 杆从最低位置到最高位置重力矩所作的功为︒-=⋅⋅︒-==⎰⎰45sin d sin 2145sin d 0mgl l mg W W πθθ 重力矩所作的功等于此期间杆的转动动能的增量2021045sin ωJ mgl -=︒- 其中231ml J =,t 00v =ω,则 m/s 5.94m/s 45sin 85.08.9645sin 60=︒⨯⨯⨯=︒=gl v5-13 如图5-13(a)所示,滑轮转动惯量为0.012m kg ⋅,半径为7 cm ,物体质量为5 kg ,由一绳与倔强系数k=200 N/m 的弹簧相连,若绳与滑轮间无相对滑动,滑轮轴上的摩擦忽略不计,求:(1)当绳拉直弹簧无伸长时,使物体由静止而下落的最大距离;(2)物体速度达最大值的位置及最大速率.v 0 ︒45 (a) (b) 图5-12分析 下面的5-17题中将证明,如果绕定轴转动的刚体除受到轴的支承力外仅受重力作用,则由刚体和地球组成的系统机械能守恒.如果将滑轮、地球和物体与弹簧组成一个弹性系统和重力系统合成的系统,当无重力和弹性力以外的力作功的情况下,整个系统的机械能守恒,可以应用机械能守恒定律.下面的解则仅应用功能原理和力矩所作的功与刚体转动动能的关系进行计算.解 (1) 物体由静止而下落到最低点时,速度为零,位移为1x ,在此期间重力所作的功完全转换为弹簧弹性势能的增量,即21121kx mgx = m 0.49m 2008.95221=⨯⨯==k mg x (2)物体与滑轮受力如图5-13(b)所示,设物体的最大速率为0v ,此时的位移为0x ,加速度00=a ,滑轮的角加速度000==R a α,分别应用牛顿第二定律和转动定律ma F mg =-T1αJ R F F =-)(T2T1可得此时T1F mg =,F T1= F T2,又因对于轻弹簧有0T2kx F =,则得m 0.245m 2008.950=⨯==k mg x 在此过程中,重力所作之功等于弹性势能的增量、物体动能和滑轮转动动能T1aF ’T1m m g(a) (b)图5-13的增量的和,即2020200212121ωJ m kx mgx ++=v 因R 00v =ω,得 m/s 31.1m/s 9.85)07.001.05(2001)(122=⨯⨯+⨯=+=mg R J m k v5-14 圆盘形飞轮A 质量为m ,半径为r ,最初以角速度ω0转动,与A 共轴的圆盘形飞轮B 质量为4m ,半径为2r ,最初静止,如图5-14所示,两飞轮啮合后,以同一角速度ω转动,求ω及啮合过程中机械能的损失.分析 当物体系统所受的合外力矩为零时,系统的角动量守恒,在此过程中,由于相互作用的内力作功,机械能一般不守恒.解 以两飞轮组成的系统为研究对象,由于运动过程中系统无外力矩作用,角动量守恒,有 ωωω2202)2(4212121r m mr mr += 得 0171ωω= 初始机械能为2022021412121ωωmr mr W =⋅=啮合后机械能为 2022222241171)2(421212121ωωωmr r m mr W =⋅+⋅=则机械能损失为 1202211716411716W mr W W W ==-=∆ω 5-15 一人站在一匀质圆板状水平转台的边缘,转台的轴承处的摩擦可忽略A图5-14不计,人的质量为m ’,转台的质量为10 m ’,半径为R .最初整个系统是静止的,这人把一质量为m 的石子水平地沿转台的边缘的切线方向投出,石子的速率为v (相对于地面).求石子投出后转台的角速度与人的线速度.分析 应用角动量守恒定律,必须考虑定律的适用条件,即合外力矩为零.此外还应该注意到,定律表达式中的角动量和角速度都必须是对同一惯性参考系选取的,而转动参考系不是惯性参考系.解 以人、转台和石子组成的系统为研究对象,由于系统无外力矩作用,角动量守恒,设转台角速度ω的转向与投出的石子速度v 方向一致,初始时系统角动量为零,得0=+v mR J ω 人和转台的转动惯量为221021R m R m J '+'=,代入上式后得 Rm m '-=6v ω 人的线速度 mm R '-=='6v v ω 其中负号表示转台角速度转向和人的线速度方向与假设方向相反.5-16 一人站立在转台上,两臂平举,两手各握一个m = 4 kg 的哑铃,哑铃距转台轴r 0 = 0.8 m ,起初,转台以ω0 = 2π rad/s 的角速度转动,然后此人放下两臂,使哑铃与轴相距r = 0.2 m ,设人与转台的转动惯量不变,且J = 52m kg ⋅,转台与轴间摩擦忽略不计,求转台角速度变为多大?整个系统的动能改变了多少?分析 角动量守恒定律是从定轴转动的刚体导出的,却不但适用与刚体,而且适用于绕定轴转动的任意物体和物体系统.解 以人、转台和哑铃组成的系统为研究对象,由于系统无外力矩作用,角动量守恒,有ωω)2()2(2020mr J mr J +=+rad/s 12.0rad/s 22.04258.042522220220=⨯⨯⨯+⨯⨯+=++=πωωmr J mr J 动能的增量为J183 J )2()8.0425(21J 12)2.0425(21 )2(21)2(2122222020220=⨯⨯⨯+⨯-⨯⨯⨯+⨯=+-+=-=∆πωωmr J mr J W W W 5-17 证明刚体中任意两质点相互作用力所作之功的和为零.如果绕定轴转动的刚体除受到轴的支承力外仅受重力作用,试证明它的机械能守恒.分析 在刚体动力学中有很多涉及重力矩作功的问题,如果能证明当只有重力矩作功时刚体和地球组成的系统机械能守恒,就能应用机械能守恒定律,而且还可以用刚体的质心的势能代替整个刚体中所有质点势能的总和,使求解过程大大简化. 证 刚体中任意两质点相互作用力沿转轴方向的分量对定轴转动不起作用,而在垂直于转轴的平面内的分量F 和-F 大小相等,方向相反,作用在一条直线上,如图5-17所示.设F 与转轴的垂直距离为ϕsin r ,则当刚体有微小角位移θd 时,力F 所作的功为θϕd sin Fr ,而其反作用力-F 所作的功为θϕd sin Fr -,二者之和为零,即刚体中任意两质点相互作用力所作之功的和为零.绕定轴转动的刚体除受到轴的支承力外仅受重力作用,刚体中任意质点则受到内力和重力作用,当刚体转动时,因为已经证明了任意两质点相互作用内力所作之功的和为零,则刚体中各质点相互作用力所作的总功为零,而且轴的支承力-F图5-17也不作功,就只有重力作功,因此机械能守恒.5-18 一块长m 50.0=L ,质量为m '=3.0 kg 的均匀薄木板竖直悬挂,可绕通过其上端的水平轴无摩擦地自由转动,质量m =0.1kg 的球以水平速度m/s 500=v 击中木板中心后又以速度m/s 10=v 反弹回去,求木板摆动可达到的最大角度.木板对于通过其上端轴的转动惯量为231L m J '= . 分析 质点的碰撞问题通常应用动量守恒定律求解,有刚体参与的碰撞问题则通常应用角动量守恒定律求解.质点对一点的角动量在第四章中已经讨论过,当质点作直线运动时,其角动量的大小是质点动量和该点到质点运动直线的垂直距离的乘积.解 对球和木板组成的系统,在碰撞瞬间,重力对转轴的力矩为零,且无其他外力矩作用,系统角动量守恒,碰撞前后球对转轴的角动量分别为021v mL 和v mL 21-,设碰后木板角速度为ω,则有 ωJ mL mL +-=v v 21210 设木板摆动可达到的最大角度为θ,如图5-18所示,木板摆动过程中只有重力矩作功,重力矩所作的功应等于木板转动动能的增量,即)1(cos 21d sin 2121002-'=⋅'-=-⎰θθθωθgL m L g m J (1) 由以上两式得388.050.08.90.34)1050(1.0314)(31cos 2222202=⨯⨯⨯+⨯⨯-='+-=gL m m v v θ ︒==19.67)388.0arccos(θ根据5-17的结果,由于木板在碰撞后除受到轴的支承力外仅受重力作用,v mm ’g图5-18它的机械能守恒,取木板最低位置为重力势能零点,达到最高位置时它的重力势能应等于碰撞后瞬间的转动动能,也可以得到(1)式.5-19 半径为R 质量为m '的匀质圆盘水平放置,可绕通过圆盘中心的竖直轴转动.圆盘边缘及R /2处设置了两条圆形轨道,质量都为m 的两个玩具小车分别沿二轨道反向运行,相对于圆盘的线速度值同为v .若圆盘最初静止,求二小车开始转动后圆盘的角速度.分析 当合外力矩为零时,应用角动量守恒定律应该注意到表达式中的角动量和角速度都是对同一惯性参考系选取的.转动参考系不是惯性参考系,所以小车对圆盘的速度和角动量必须应用相对运动速度合成定理转换为对地面的速度和角动量.解 设两小车和圆盘的运动方向如图5-19所示,以圆盘的转动方向为正向,外轨道上小车相对于地面的角动量为)(v -ωR mR ,内轨道上小车相对于地面的角动量为)21(21v +ωR R m ,圆盘的角动量为ωω221R m J '=.对于两小车和圆盘组成的系统,外力对转轴的力矩为零,角动量守恒,得ωωω221)21(21)(R m R R m R mR '+++-v v Rm m m )25(2'+=v ω vωv图5-19。
高中物理必修一第四章《运动和力的关系》检测题(包含答案解析)(20)

一、选择题、、,用两根轻弹簧和一根轻绳相连,挂在天1.如图所示,三个质量均为m的物块a b c、之间的轻绳剪断,下列说法正确的是()花板上,处于静止状态。
现将b cA.在刚剪断轻绳的瞬间,b的加速度大小为gB.在刚剪断轻绳的瞬间,c的加速度大小为2gC.在刚剪断轻绳的瞬间,a的加速度大小为g、下落过程中,两者一直保持相对静止D.剪断轻绳后,a b2.如图所示,吊篮A、物体B、物体C的质量分别为m、6m、2m,B和C分别固定在轻质弹簧的两端,B和C在吊篮的水平底板上处于静止状态,将悬挂吊篮的轻绳剪断的瞬间()A.吊篮A的加速度大小为gB.物体B的加速度大小为gC.物体C的加速度大小为2gD.A和C的加速度大小都为3g3.在房顶的底部宽度一定情况下,为了使雨滴能尽快地淌离房顶,要设计好房顶的高度,设雨滴沿房顶下淌时做无初速度无摩擦的运动。
那么如图所示的四种情况中符合要求的是()A .图AB .图BC .图CD .图D4.从地面上以初速度v 0竖直上抛一质量为m 的小球,若运动过程中受到的空气阻力与其速率成正比,球运动的速率随时间变化的规律如图所示,t 1时刻到达最高点,再落回地面,落地速率为v 1,且落地前小球已经做匀速运动,则下列说法中正确的是( )A .小球加速度在上升过程中逐渐减小,在下降过程中也逐渐减小B .小球抛出瞬间的加速度大小为011g v v ⎛⎫+ ⎪⎝⎭C .小球被抛出时的加速度值最大,最高点的加速度值最小D .小球上升过程的平均速度等于02v 5.如图所示,质量为m 的三角形木楔A 置于倾角为θ的固定斜面上,它与斜面间的动摩擦因数μ,一水平力F 作用在木楔A 的竖直平面上,在力F 的推动下,木楔A 以恒定的速度向上滑动,则F 的大小为( )A .()sin cos cos mg θμθθ+ B .()sin cos cos cos mg θμθθμθ+- C .()sin cos mg θμθ+ D .()sin cos cos cos mg θμθθμθ++ 6.磁性车载支架(图甲)使用方便,它的原理是将一个引磁片贴在手机背面,再将引磁片对准支架的磁盘放置,手机就会被牢牢地吸附住(图乙)。
物理化学答案——第四章_化学平衡习题解答[1]
![物理化学答案——第四章_化学平衡习题解答[1]](https://img.taocdn.com/s3/m/995f0e3383c4bb4cf7ecd1f7.png)
第四章 化学平衡一、基本公式和内容提要 1. 化学反应的方向和限度(1)反应系统的吉布斯自由能和反应进度反应进行过程中,A 和B 均各以纯态存在而没有相互混合,则在反应进度为ξ时反应体系的总吉布斯自由能G *为:G * = n A μA * + n B μB * = (1-ξ)μA * +ξμB * = μA * +ξ(μB * -μA *)对于封闭体系在定温定压下在反应实际进行过程中,A 和B 是不可能以纯态存在的。
它们是混合在一起的,因此还存在混合吉布斯自由能△mix G 。
△mix G = RT (n A lnX A + n B lnX B ) = RT [(1-ξ)ln(1-ξ) + ξlnξ](2)化学反应标准平衡常数理想气体的化学反应()()()()aA g bB g gG g hH g −−→++←−− bB a A hH gG P P P P P P P P )/()/()/()/(θθθθ= e )--(1θθθθμμμμB A H G b a h g RT-+= 常数 = K θK θ称为标准平衡常数。
(3)化学反应的等温方程式(a )对任意反应达平衡时:△r G m θ = -RTlnK θ△r G m θ是指产物和反应物均处于标准态时,产物的吉布斯自由能和反 应物的吉布斯自由能总和之差,称为反应的“标准吉布斯自由能变化”。
(b )反应在定温定压条件下△r G m = △r G m θ+ RT ln Q p上式称为范特霍夫(Vait Hoff) 等温方程。
(c )依据吉布斯自由能函数可判断反应进行的方向,在温度、压力一定的条件下:RT ln Q a < RTlnK θ Q a <K θ △r G m <0 反应正向自发进行 若 RT ln Q a >RTlnK θ Q a >K θ △r G m >0 反应逆向自发进行若 RT ln Q a = RTlnK θ Q a = K θ △r G m =0 反应达平衡 2. 反应的标准吉布斯自由能变化 (1)化学反应的△r G m 与△r G m θ(a )在一定温度和压力为p θ下,任何物质的标准态化学势μi θ都有确定值,所以任何化学反应的△r G m θ都是常数;(b )△r G m 不是常数,在一定T ,p 下,它与各物质的活度(分压、浓度)等有关,即与Q a 有关;(c )在定温定压条件下0W '=时,△r G m 的正负可以指示化学反应自发进行的方向,在定温下△r G m θ的正负通常不能指示反应进行的方向,根据公式△r G m = △r G m θ+ RT ln Q p ,但当△r G m θ的数值很大时,也可用其值估计反应的方向。
高中物理必修一第四章《运动和力的关系》测试题(含答案解析)

一、选择题1.如图所示,倾角为θ的足够长传送带以恒定的速率0v 沿逆时针方向运行。
0t =时,将质量1kg m =的小物块(可视为质点)轻放在传送带上,物块速度随时间变化的图象如图所示。
设沿传送带向下为正方向,取重力加速度210m/s g =则( )A .1~2s 内,物块的加速度为21m/sB .小物块受到的摩擦力的方向始终沿传送带向下C .传送带的倾角30θ=︒D .小物块与传送带之间的动摩擦因数0.5μ=2.2020年7月20日消息,近日俄军最新型的图-160M 战略轰炸机首飞,飞行过程持续34分钟,飞行高度为1500米,能搭载多达40吨的各型炸药。
在这则新闻中涉及了质量、长度和时间及其单位,在国际单位制中,下列说法中正确的是( )A .新闻中涉及的“34分钟、1500米和40吨”中,只有米是国际单位制中的基本单位B .“千克米每二次方秒”被定义为“牛顿”,所以“牛顿”是国际单位制中的基本单位C .秒是国际单位制中力学三个基本物理量之一,而天只是时间的单位D .两个或更多的符号表示的单位一定是导出单位3.在真空的牛顿管里的羽毛和铁片下落的快慢相同,在有空气的牛顿管里的羽毛下落的慢、铁片下落的快,这其中最主要的原因是( )A .铁钉比鸡毛重B .铁钉比鸡毛密度大C .鸡毛受到的空气阻力大D .铁钉下落的加速度比鸡毛下落的加速度大4.如图,箱子内,一物体静止在倾斜固定的木板上。
现将箱子轻放到弹性安全气垫上并由静止释放,在箱子从A 向下压缩气垫至最低点B 的过程中,物体始终相对木板静止。
设木板对物体的支持力和摩擦力分别为N 和f ,则从A 到B 的过程中( )A .N 先增大后减小,f 先减小后增大B .N 先减小后增大,f 先增大后减小C .N 和f 都是一直减小D .N 和f 都是一直增大5.一质量为m 的乘客在高楼内乘坐竖直电梯下楼,其位移s 与时间t 的关系图像如图所示。
乘客所受支持力的大小用F N 表示、速度用v 表示,重力加速度大小为g 。
《管理学原理》:试题及答案第四章

一、单项选择题1.在决策时有一定自由处置权指的是()。
A.规则B.政策C.程序D.标准2.管理中居于主导地位的是()。
A.计划B.组织C.人员配备D.领导3.计划的效率是指()。
A.编制计划要快B.计划的预期目标保证实现C.投入与产出比例高D.计划指标既先进又可行4.计划工作的核心是()。
A.制定目标B.制定方案C.做出决策D.选择方案5.在决策或处理问题时指导及沟通思想活动的方针和一般规定是()。
A.规则B.程序C.规划D.政策考试论坛6.按具体情况采取或不采取某个特殊的行动指的是()。
A.政策B.程序C.规则D.规划二、多项选择题1.计划工作的特点是()。
A.目的性B.主导性C.经济性D.统一性E.普遍性2.计划按其范围划分,可分为()。
A.战略计划B.战术计划C.上层计划D.中层计划E.基层计划3.广义的计划工作是指()。
A.制订计划B.拟定方案C.执行计划D.检查计划的执行情况E.选择方案三、填空题1.程序规定了处理问题的______方法、步骤。
2.______也被称之为数字化的计划。
3.狭义的计划工作是指______.4.______是在目的或任务指导下,提出整个组织所要达到的具体目标。
四、简答题:1.简述计划工作的基本特征。
2.简述计划工作的步骤。
五、论述题:1.试论计划工作的重要性。
2.试述计划的表现形式。
管理学原理跟踪复习答案(第四章)一、单项选择题1.B;2.A;3.C;4.C;5.D;6.C.二、多项选择题1.ABCE;2.CDE;3.ACD.三、填空题1.例行;2.预算;3.制订计划;4.目标四、简答题1.计划工作的基本特征是:PPkao 考试网 (1)目的性。
组织是通过精心安排的合作去实现目标而得以生存和发展的。
计划工作旨在促使组织目标的实现。
计划工作的一个主要方面就是确立目标。
(2)主导性。
计划工作须在组织工作、人员配备、指导与领导工作和控制工作之前进行,是进行其它各项管理工作的基础,并贯穿于整个管理过程。
生理学试题及答案第四章-血液循环

第四章血液循环参考答案在后面!一、名词解释1、心动周期2、心音3、搏出量4、射血分数5、心输出量6、心指数7、心力储藏8、自律性9、窦性心律10、有效不应期11、期前收缩/期前兴奋12、代偿间歇13、房室延搁14、血压15、中心静脉压二、填空题1、根据电生理特性及功能的不同,心肌细胞可分为两大类:和。
2、根据去极化速度的快慢和机制的不同,心肌细胞可分为:和。
两者去极相主要开放的离子通道分别为:和。
3、心肌细胞有4种生理特性,分别为:、、和。
4、心室肌细胞动作电位可分为五期,分别称为、、、和。
5、心肌细胞兴奋性的周期性变化依次为:、和。
6、心脏的正常起搏点是,除此之外的各个部位统称为。
由窦房结细胞所控制的心律称为,假设为窦房结以外各个点控制的心律称为。
7、心电图的P波代表过程,QRS综合波代表过程,T波代表过程。
8、在一个心动周期中,心室的射血是由于的作用,心室充盈主要依靠的作用,心房起着的作用。
9、第一心音标志着的开场,第二心音标志着的开场。
10、调节或影响心输出量的因素有、、、。
11、心室肌的前负荷是,后负荷是。
12、心力储存由和两局部构成。
13、分配血管一般是指,毛细血管前阻力血管是指和。
14、正常成年人安静状况下,收缩压一般为mmHg,舒X压一般为mmHg。
15、中心静脉压的上下取决于和之间的相互关系。
16、在微循环中,迂回通路的作用是,直捷通路的作用是,动-静脉短路的作用是。
17、组织液生成与回流取决于四种力量的比照,其中动力是和,阻力是和。
18、在临床上,肾上腺素常用于,而去甲肾上腺素常用于。
三、选择题1、关于心动周期的论述,以下哪项是错误的" 〔〕A、舒X期比收缩期长B、房、室有共同收缩的时期C、房室有共同的舒X期D、心率加快时,心动周期缩短E、心率对舒X期的影响更明显2、在每一个心动周期中,左心室压力升高速度最快的是:〔〕A、心房收缩朗B、等容收缩期C、快速射血期D、减慢射血期E、等容舒X期3、心室内压力达最高值在〔〕A、心房收缩期末B、等容收缩期末C、快速射血期D、等容舒X期末E、心室充盈期末4、心动周期中,在以下那个时期主动脉压最低?〔〕A、等容收缩期未B、等容收缩期末C、减慢射血期末D、快速充盈期末E、减慢充盈期末5、在心室等容收缩期时:〔〕A、房内压>室内压>主动脉压B、房内压<室内压>主动脉压C、房内压=室内压>主动脉压D、房内压<室内压<主动脉压E、房内压>室内压<主动脉压6、在心室等容舒X期时:〔〕A、房内压>室内压>主动脉压B、房内压<室内压>主动脉压C、房内压=室内压>主动脉压D、房内压<室内压<主动脉压E、房内压>室内压<主动脉压7、主功脉瓣关闭见于:〔〕A、快速射血期开场时B、快速充盈期开场时C、等容收缩期开场时D、等容舒X期开场时E、减慢充盈期开场时8、房室瓣开放见于:〔〕A、等容收缩期未B、心室收缩期初C、等容舒X朗初D、等容收缩期初E、等容舒X期末9、从房室瓣关闭到半月瓣关闭之间的间隔相当于:〔〕A、心房收缩期B、心房舒X期C、心室收缩期D、心室舒X期E、等容收缩期10、从动脉瓣关闭到下一次动脉瓣开放的时间相当于心动周期中的〔〕A、心室舒X期B、心室射血期C、等容收缩期D、心室舒X期+等容收缩期E、等容舒X期+等容收缩期11、心室容积最小在〔〕A、等容收缩期末B、快速射血期末C、减慢射血期末D、等容舒X期初E、心室充盈期初12、心室容积达最大值在〔〕A、心房收缩期末B、等容收缩期末C、射血期D、等容舒X期末E、心室充盈期末13、心动周期中,心室血液充盈主要是出于:〔〕A、血液依赖地心引力而回流B、骨骼肌的挤压作用加速静脉回流C、心房收缩的挤压作用D、心室舒X的抽吸作用E、胸内负压促进静脉回流14、心房收缩挤入心室的血液量约占心室总充盈量的〔〕A、5%B、10%C、30%D、50%E、80%15、第一心音产生主要是由于〔〕A、半月瓣关闭B、半月瓣开放C、房室瓣关闭D、房室瓣开放E、心房肌收缩16、第二心音产生主要是由于〔〕A、主动脉瓣和肺动脉瓣开放B、主动脉瓣和肺动脉瓣关闭C、房室瓣突然开放D、房室瓣突然关闭E、心房肌收缩17、XX成年男性静息状态下每搏量约为:〔〕A、30m1B、50m1C、70mlD、90mlE、110ml18、每搏输出量占以下哪个容积的百分数称为射血分数?〔〕A、回心血量B、心输出量C、等容舒X期容积D、心室收缩末期容积E、心空舒X末期容积19、心输出量是指:〔〕A、每分钟由一侧心房射出的血量B、每分钟由一侧心室射出的血量C、每分钟由左、右心室射出的血量之和D、一次心跳一侧心室射出的血量E、一次心跳两侧心室同时射出的血量20、XX成年人静息状态下,心输出量约为:〔〕A、2-3L/minB、4-6L/minC、6-8L/minD、9-10L/minE、11-12L/min21、心指数等于:〔〕A、每搏输出量×体外表积B、每搏输出量/体外表积C、心输出量×体外表积D、心率×每搏输出量×体外表积E、心率×每搏输出量/体外表积22、影响心博出量的因素不包括:〔〕A、心室舒X末期充盈量B、动脉血压C、心肌收缩能力D、心率E、心室肌细胞动作电位跨膜离子流动的种类23、心室肌的前负荷是指〔〕A、心室舒X末期容积或压力B、心室收缩末期容积或压力C、心室等容收缩期的容积或压力D、心室等容舒X期的容积或压力E、大动脉血压24、心室肌的前负荷可以用以下哪项来间接表示" 〔〕A、收缩末期容积或压力B、舒X末期容积或压力C、等容收缩期容积或压力D、等容舒X期容积或压力E、舒X末期动脉压25、心室肌的后负荷是指:〔〕A、心房压力B、大动脉血压C、快速射血期心室内压D、减慢射血期心室内压E、等容收缩期初心室内压26、在心率、前负荷和收缩力不变的情况下,增加心肌的后负荷,会使〔〕A、等容收缩期延长,射血速度加快,每搏输出量增加B、等容收缩期延长,射血速度减慢,每搏输出量增加C、等容收缩期延长,射血速度减慢,每搏输出量减少D、等容收缩期缩短,射血速度加快,每搏输出量增加E、等容收缩期缩短,射血速度减慢,每搏输出量减少27、在心肌的前负荷和收缩能力不变的情况下,增加后负荷可使:〔〕A、等容收缩期延长B、射血期延长C、等容舒X期延长D、心室充盈期延长E、每搏输出量增加28、心肌的异长调节是指心脏每搏输出量取决于:〔〕A、平均动脉压上下B、心率贮备大小C、心力贮备大小D、心室收缩末期容积大小E、心室舒X末期容积大小29、心肌的等长调节是通过改变以下哪个因素来调节心脏的泵血功能?〔〕A、心肌初长度B、肌小节的初长度C、横桥联结的数目D、心肌收缩能力E、心室舒X末期容积30、以下哪项使心室舒X末期充盈量减少〔〕A、心率一定程度减慢时B、外周静脉压与心房压之差加大C、心房压与心室压之差加大D、心肌收缩加强E、心房收缩能力加大31、正常人心率超过去180次/分时,主要影响以下哪些变化〔〕A、心动周期缩短B、收缩期缩短C、舒X期缩短D、收缩期缩短明显E、舒X期缩短明显32、正常人心率超过去180次/min时,心输出量减少的主要原因〔〕A、快速充盈期缩短B、减慢充盈期缩短C、等容收缩期缩短D、快速射血期缩短E、减慢射血期缩短33、强体力劳动时,心输出量可以增加到静息时的:〔〕A、2—3倍B、5—6倍C、10一15倍D、15—20倍E、20倍以上34、有关心力贮备以下哪项说法是错误的" 〔〕A、XX者与某种心脏病人假设在静息时心输出量无差异,那么他们的心力贮备也应一致B、收缩期贮备大于舒X期贮备C、心力贮备能力取决于心率及每博输出量D、心力贮备也称泵功能贮备E、心力贮备是指心输出量随机体代谢需要而增加的35、区分心肌快、慢反响细胞的依据是:〔〕A、静息电位的大小B、0期去极化的速率C、平台期的长短D、3期复极化的快慢E、4期自动去极化的速度36、心室肌细胞动作电位0期去极是由于〔〕A、Na+ 电导降低B、Na+ 电导增加C、Ca2+ 电导降低D、Ca2+ 电导增加E、K+ 电导增加37、心室肌动作电位1期复极是由于以下哪种离子流动的结果〔〕A、K+ 外流B、K+ 内流C、Na+ 内流D、Ca2+ 内流E、Cl- 内流38、心室肌细胞动作电位平台期是以下哪能离子跨膜流动的综合结果〔〕A、Na+ 内流,Cl- 外流B、Na+ 外流,Cl- 内流C、Ca2+ 内流,K+ 外流D、K+ 内流Ca2+ 外流E、Na+ 内流,K2+ 外流39、以下哪项不是心肌细胞平台期的特点〔〕A、膜电位处于零电位水平B、是区别神经细胞和骨骼肌细胞动作电位的主要特征C、心肌动作电位时程较长的主要原因之一D、它与心室肌不会产生强直收缩有关E、形成的离子是Na+缓慢内流40、心室肌细胞动作电位的特点是:〔〕A、持续时间短B、去极幅度小C、复极速度与去极速度相等D、升支与降支对称E、复极有平台期41、心室肌细胞动作电位4期恢复细胞内外离子正常浓度梯度靠〔〕A、细胞膜渗漏B、单纯扩散C通道易化扩散D、载体易化扩散E、钠-钾泵主动转运42、以下关于心室肌细胞动作电位离子根底的表达,哪一项为哪一项错误的" 〔〕A、0期主要是Na+内流B、1期主要是Cl-内流C、2期主要是Ca2+内流与K+外流D、3期主要是K+外流E、1期主要是K+外流43、下面关于心室肌细胞Na+通道的描述,哪一项为哪一项错误的?〔〕A.是电压依从性的B、激活和失活的速度都很快C、可被河豚毒所阻断D.选择性较强,只有Na+可以通过E.在去极化到-40mV时被激活44、关于心室肌细胞Ca2+通道的表达,下面哪一项为哪一项错误的?〔〕A、激话、失活以及再复活所需时间均比Na+通道长B、选择性高,只允许Ca2+通透C、电压依从性D、激活的阈电位水平为-50—-35mVE、可被异搏定及Mn2+所阻断45、自律细胞区别于非自律细胞的生物电活动主要特征是〔〕A、0期除极速度快B、平台期较明显C、1期复极速度慢D、3期复极速度慢E、4期有自动除极46、窦房结细胞动作电位0期去极大是由于〔〕A、Na+ 电导增加B、Na+ 电导降低C、Ca2+ 电导增加D、Ca2+ 电导降低E、K+ 电导增加47、下面关于窦房结细胞动作电位的描述,哪项是不正确的" 〔〕A、最大复极电位为-70mVB、阈电位为-40mVC、无明显的复极1期和平台期D、除极幅度小于普肯耶细胞E、0期除极时程比普肯耶细胞短得多48、窦房结细胞的起搏活动是由于:〔〕A、K+递减性外流B、Na+递增性内流C、K-递减性外流与Na+递增性内流D、Ca2+递增性内流E、K+递减性外流与Ca2+递增性内流49、浦肯野细胞和心室肌细胞动作电位的区别主要是〔〕A、4期自动除极有无B、3期复极速度不同C、平台期持续时间相差较大D、1期形成机制不同E、0期除极速度不同50、关于普肯野细胞起搏电流If,错误的表达是〔〕A、主要离子成分为Na离子B、充分激活的膜电位为-100MvC、是一种超极化激活的电流D、可被铯离子所阻断E、可被河豚毒所阻断51、衡量心肌自律性上下的主要指标是:〔〕A、动作电位的幅值B、最大复极电位水平C、4期膜电位自动去极化速率D、阈电位水平E、0期去极化速度52、自律性最高的是〔〕A、窦房结B、心房肌C、房室交界D、普肯耶纤维E、房室束53、在无神经和体液因素影响下,窦房结自动兴奋的频率为:〔〕A、90/minB、80/minC、75/minD、100/minE、150/min54、心脏的潜在起搏点有:〔〕A、窦房结B、心房肌C、房室交界区D、心室肌E、普肯耶纤维55、窦房结能成为心脏正常起搏点的原因是:〔〕A、静息电位仅为-70mVB、阈电位为-40mVC、0期去极速度快D、动作电位没有明显的平台期E、4期电位去极速率快56、下述关于超速压抑的描述,哪一项为哪一项不正确的" 〔〕A.高频起搏点驱使低频起搏点进展低频率搏动B、频率差异愈大,抑制效应愈强C、窦房结停搏后,首先由受压抑程度铰小的房室交界起搏D.窦房结对心室的控制中断后,可出现一段时间的心室停搏E、为防止撤去超速抑制时诱发的心脏停博,中断人工起搏器使应逐步减慢其驱动频率57、轻度高血钾引起心肌兴奋性升高的原因是:〔〕A、静息电位绝对值减小导致距阈电位水平的差距缩小B、静息电位绝对值增大导致距阈电位水平的差距增大C.细胞膜对钾的通透性减小D.细脑膜对钙的通透性增大E.细胞膜对钠的通透性增大58、当血钾逐步升高时,心肌的兴奋性:〔〕A.逐步升高B、逐步降低C、先升高后降低D、先降低后升高E、不变59、细胞外Ca2+浓度降低对心肌生理特性的影响,以下哪项是错误的?〔〕A、快反响细胞阈电位下移,兴奋性升高B、细胞膜对Na+内流的抑制作用减弱C、0期去极速度增快D、0期去极幅度增高E、4期自动去极速度减慢,自律性降低60、心室肌有效不应期的长短主要取决于〔〕A、动作电位0期去极的速度B、动作电位复极末期的长短C、阈电位水平的上下D、钠-钾泵功能E、动作电位2期的长短61、心室肌的有效不应期较长,一直持续到:〔〕A、收缩期开场B、收缩期中间C、舒X期开场D、舒X中后期E、舒X期完毕62、对心室肌细胞有效不应期特征的表达,错误的选项是〔〕A、可产生局部兴奋B、阈上刺激能产生动作电位C、Na+通道失活D、此期相当于心室全收缩期舒X早期E、此期时间较长远63、心肌不会产生强直收缩的原因是〔〕A、心肌有自律性B、心肌呈"全或无〞收缩C、心肌肌浆网不兴旺D、心肌对胞外Ca2+依赖性大E、心肌的有效不应期特别长64、心室肌出现相对不应期原因是:〔〕A、膜电位绝对值仍低于静息电位,Na+通道的开放能力尚未恢复正常B、Ca2+通道已逐渐复活C、0期去极速度高于正常D、0期去极幅度高于正常E、兴奋传导速度高于正常65、心肌细胞超常期内兴奋性高于正常,所以:〔〕A、兴奋传导速度高于正常B、动作电位幅度大于正常C、动作电位0期去极速度快于正常D、刺激阈值低于正常E、自动节律性高于正常66、室性期前收缩之后出现代偿性间歇的原因是:〔〕A、窦房结的节律性兴奋延迟发放B、窦房结的节律件兴奋少发放一次C、窦房结的节律性兴奋传出速度大大减慢D、室性期前收缩的有效不应期特别长E、窦房结一次节律兴奋落在室性期前收缩的有效不应期内67、心脏内兴奋传导的顺序是:〔〕A、窦房结—房室交界—心房肌—心室肌B、窦房结—房室交界—心室肌—普肯耶纤维C、窦房结—心房肌—心室肌—普肯耶纤维D、窦房结—心房肌—左右束支—普耶纤维E、窦房结—心房肌—房室交界—房室束和左右束支—普肯耶纤维—心室肌68、兴奋在心脏内传导时,速度最慢的是〔〕A、心室肌B、心房肌C、房室交界D、结希束E、浦肯野纤维69、房室延搁的生理意义〔〕A、使P波增宽B、使QRS波增宽C、使心室肌有效不应期延长D、使心室肌不会产生强直收缩E、使心房、心室不会产生收缩重叠70、房室延搁的生理意义是:〔〕A、使心室肌不会产生完全强直收缩B、增强心肌收缩力C、使心室肌有效不应期延长D、使心房、心室不会同时收缩E、使心室肌动作电位幅度增加71、在下述关于心肌传导性的描述中,哪—项是错误的?〔〕A、心肌细胞直径细小,传导速度慢B.动作电位幅度大,传导速度快C、动作电位0期去极速率慢,传导速度慢D.阈电位水平下移,传导速度快E、心肌处在超常期内,传导速度快72、以下哪项对心肌兴奋传导影响不大〔〕A、细胞直径B、0期除极速度和幅度C、邻近部位细胞膜静息电位与阈电位差距D、邻近部位膜0期除极时钠或钙通道性状E、胞外Ca2+浓度73、正常心电图描述,错误的选项是:〔〕A、P波代表两心房去极化B、QRS波代表两心室去极化C.P-R间期表示兴奋从心房传到心室的时间D.S-T段说明心室各部位间没有电位差存在E、心电图是心肌兴奋与收缩过程的反响74、关于心电图的描述,下面哪一项为哪一项错误的?〔〕A、心电图反映心脏兴奋的产生、传导和恢复过程中的生物电变化B、心电图与心脏的机械收缩活动无直接关系C、心肌细胞的生物电变化是心电图的来源D、电极放置位置不同,记录出来的心电图曲线根本一样E、心电图曲线与单个心肌细胞的生物电变化曲线有明显区别75、弹性贮器血管指的是〔〕A、大动脉B、微动脉C、肺动脉和主动脉D、微静脉E、静脉76、阻力血管主要是指:〔〕A、大动脉B、小动脉及微动脉C、毛细血管D、小静脉E、大静脉77、关于微动脉,以下哪一项为哪一项错误的" 〔〕A、在调节动脉压中起主要作用B、在调节器官血流量中起主要作用C、其管壁厚度和管腔直径的比值比中动脉的大D、收缩时组织液的生成量减少E、其管壁平滑肌的X力主要受局部代谢产物调节78、总截面积最大的血管〔〕A、毛细血管B、小动脉C、小静脉D、大静脉E、大动脉79、容量血管是指〔〕A、动脉B、静脉C、毛细血管D、肺血管E、皮肤血管80、血量分配比例最高的部位是:〔〕A、心脏及动脉B、毛细血管C、静脉D、皮肤血管床E、肝脏及脾脏81、静脉系统成为外周的血液贮存库,主要是由于:〔〕A、静脉管壁有可扩X性B、静脉管壁平滑肌少C、许多静脉位于皮下组织中D、静脉系统的容积大E、静脉血液的氧饱和度低82、关于静脉,以下表达中哪—项是错误的" 〔〕A、承受交感缩血管纤维支配B、管壁平滑肌在静脉被扩X时发生收缩C、容纳了全身血量的一半以上D、回心血量不受体位变化的影响E、回心血量取决于外周静脉压和中心静脉压之差83、以下关于各类血管功能特点的表达,哪一项为哪一项正确的" 〔〕A、毛细血管前括约肌肉属于毛细血管前阻力局部,交感缩血管纤维的分布极少B、主动脉和大动脉有弹性贮器的作用,使血液能在血管系统内匀速流动C、微静脉口径不变时,微动脉舒X有利于组织液进入血液D、静脉的舒缩活动是促使静脉血回流入心脏的主要动力E、毛细血管分支多,总的截面积大,容纳了循环血量的60%以上84、对血流速度表达,错误的选项是:〔〕A、各类血管中各段的总血流量一样,血流速度那么不一样B、毛细血管中血流速度较快C.主动脉中血流速度最快D.在封闭的循环管道系统,血流速度与血管总横截面积成反比E、心缩期动脉中血流速度比心舒期快85、血液在血管内流动时,血流阻力〔〕A、与血管的半径成正比B、与血管半径的立方成反比C、与血管半径的平方成正比D、与血管半径的四次方成反比E、与血管半径的平方成反比86、血流阻力主要来自〔〕A、毛细血管B、微静脉C、微动脉和小动脉D、中动脉E、大动脉87、关于血流阻力,以下哪项表达是错误的" 〔〕A、与血管的长度成正比B、与血液的粘滞度成正比C、与血流量成反比D、与血管半径的平方成反比E、是由于血液流动时发生的摩擦造成的88、当血流通过以下哪一部位时,血压的降落最大?〔〕A、主动脉和大动脉B、小动脉和微动脉C、毛细血管D、微静脉和小静脉E、大静脉和腔静脉89、收缩压相当于以下心动周期中哪期时的动脉内压力" 〔〕A、等容收缩期B、快速射血朔C、减慢射血期D、快速充盈期E、减慢充盈期90、收缩压为100mmHg,舒X压为70mmHg,其平均动脉压均为〔〕A、70mmHgB、75mmHgC、80mmHgD、85mmHgE、90mmHg91、循环系统平均充盈压可以反映:〔〕A、血管容积和循环血量之间的关系B、体循环和肺循环容量之间的关系C、心脏射血与外周阻力之间的关系D、静脉血压与动脉血压之间的关系E、血流与血流阻力之间的关系92、外周阻力和心率不变而每搏输出量增大时,动脉血压的变化主要是〔〕A、收缩压升高B、舒X压升高C、收缩压和舒X压升高幅度一样D、收缩压降低,舒X压升高E、收缩压升高,舒X压降低93、影响正常人舒X压的主要因素是:〔〕A、大动脉弹性B、心输出量C、阻力血管口径的变化D、血液粘滞性E、血管长度94、主动脉在维持舒X压中起重要作用,主要是由于主动脉〔〕A、口径大B、管壁厚C、管壁有可扩X性和弹性D、血流速度快E、对血流的摩擦阻力小95、老年人,主动脉弹性减退时,动脉血压的变化是〔〕A、收缩压降低,舒X压升高B、收缩压升高,舒X压升高C、收缩压升高,舒X压降低D、收缩压变化不大,舒X压升高E、收缩压降低,舒X压变化不大96、老年人的脉压比年轻人大,这主要是由于:〔〕A、老年人的心输出量较小B、老年人的循环血量较少C、老年人的主动脉和大动脉弹性降低D、老年人的小动脉硬化E、老年人的血液粘滞性高97、老年人,主动脉弹性减退,并伴有小动脉硬化时,动脉血压的变化是:〔〕A、收缩压降低,舒X压升高B、收缩压升高,舒X压降低C、收缩压升高,舒X压升高D、收缩压变化不大,舒X压升高E、收缩压升高,舒X压变化不大98、生理情况下对动脉血压影响不大的因素是:〔〕A、外周阻力B、心率C、动脉弹性D、心输出量E、血液粘滞性99、中心静脉压的正常值为:〔〕A、4-12kPaB、0.4-12kPaC、0.4-1.2kPaD、1.2-4.0kPaE、0-0.4kPa 100、使中心静脉压升高的是:〔〕A、血容量增加B、周身血管舒XC、静脉回心血量减少D、心脏射血能力增强E、循环血量减少101、以下关于中心静脉压的表达,哪一项为哪一项错误的" 〔〕A、是指胸腔大静脉和右心房的血压B、心脏射血能力减弱时,中心静脉压较低C、其正常变动范围为0.4—12kPa(4—12cmH2O)D、是反映心血管功能状态的一个指标E、外周静脉广泛收缩时中心静脉压升高102、心脏收缩力增强时,静脉回心血量增加,这是因为:〔〕A、动脉血压升高B、血流速度加快C、心输出量增加D、舒X期室内压低E、静脉压增高103、下肢肌肉运动时节律性地压迫下肢静脉〔〕A、可驱使静脉内的血液向心脏和毛细血管两个方向流动B、是人在立位是下肢静脉回流的唯一动力C、可增加下肢组织的生成D、可减少动脉和静脉之间的压力差E、加速静脉回流,减少组织液的生成104、以下因素中促进静脉回心血量增加的是〔〕A、心输出量增加B、外周阻力增C、动脉血压升高D、体循环平均充盈压降低E、心舒期室内压降低105、真毛细血管不具有以下哪一项特点" 〔〕A、管壁很薄B、血流缓慢C、管壁的通道性大D、是血液和组织液进展物质交换的场所E、安静时,骨骼肌中大约有80%的真毛细血管处于开放状态106、关于微循环直捷通路功能的表达,正确的选项是〔〕A、血流速度较慢B、是血液和组织之间进展物质交换的主要部位C、经常处于开放状态D、在骨骼肌组织中较少见E、在体温调节中发挥作用107、关于微循环直捷通路,以下述中错误的选项是〔〕A、直捷通路经常处于开放状态B、直捷通路血流速度较快C、直捷通路主要功能不是进展物质交换D、直捷通路在皮肤中较多见E、直捷通路主要功能是使一局部血液迅速通过微循环而进入静脉108、影响毛细血管前括约肌舒缩活动的主要因素是〔〕A、交感舒血管神经纤维末梢释放的乙酰胆碱B、副交感神经末梢释放的乙酰胆碱C、局部代谢产物增多D、肾上腺髓质释放的肾上腺素E、交感神经末梢释放的去甲肾上腺素109、肌肉运动时,其血流量增加的主要原因是:〔〕A、动脉血压升高B、未活动的肌肉内血管收缩C、肌肉收缩时,局部代谢产物增多D、交感缩血管纤维活动减弱E、心输出量增加110、生成组织液的有效滤过压等于〔〕A、(毛细血管血压+组织液胶体渗透压〕-〔血浆胶体渗透压+组织液静水压〕B、(毛细血管血压+血浆胶体渗透压〕-〔组织液胶体渗透压+组织液静水压〕C、(毛细血管血压+组织液静水压〕-〔毛细血管血压+组织液胶体渗透压〕D、(血浆胶体渗透压+组织液胶体渗透压〕-〔毛细血管血压+组织液静水压〕E、(组织液静水压+组织液胶体渗透压〕-〔毛细血管血压+血浆胶体渗透压〕111、组织液生成主要取决于:〔〕A、毛细血管血压B、有效滤过压C、血浆胶体渗透压D、血浆晶体渗透压E、组织液静水压112、当血浆蛋白显著减少时,引起水肿的主要原因是:〔〕A、血浆晶体渗透压下降B.血浆胶体渗透压下降C、毛细血管壁通透性增加D、醛固酮分泌减少E.有效滤过压下降113、右心衰竭时所引起的组织水肿,其主要原因是:〔〕A、毛细血管压升高B、淋巴回流受阻C、血浆胶体渗透压降低D、组织液静水压降低E、组织液胶体渗透压升高114、以下情况下,能使组织液生成减少的是:〔〕A、大量血浆蛋白丧失B、毛细血管前阻力减小C、淋巴回流受阻D、右心衰竭,静脉回流受阻E、血浆胶体渗透压升高115、迷走神经对心脏的作用是:〔〕A、心率减慢,传导加快,而不应期缩短B、心率减慢,传导慢,而不应期延长C、心率减慢,传导慢,而不应期缩短D、心率快,传导慢,而不应期缩短E、心率快,传导加快,而不应期缩短116、留神迷走神经兴奋时〔〕A、可使心率加快B、心房肌收缩缩力加强C、心房肌不应期缩短。
人教版地理七年级上册综合能力训练___第四章居民与聚落(含参考答案)

第四章:世界的居民第一节:人口与人种知识导学:18世纪之前:缓慢18世纪以后:加快世界人口的增长决定因素:出生率、死亡率<0 减少>0 增加表示方法人口增长柱状折线图=0 停止表示方法:人口密度稠密:中低纬度近海的平原地区世界人口的分布不均匀稀疏:沙漠、雨林、高纬度、高原和山区影响因素:海陆位置、纬度位置、地形、气候等人口增长过快人口问题乡村人口大规模迁入城市人口增长过慢白种人:欧洲西部、北美洲、大洋洲主要人种及分布黄种人:亚洲东部不同的人种黑种人:非洲、大洋洲、美国境内人种分布的原因:环境影响、人口迁移等种族平等本节的重点是世界人口的增长、人口的分布、人口问题和人种的分布。
在学习时,要充分利用课本上的图、表、照片。
通过分析世界人口增长曲线和世界人口增长示意图,很容易得出世界人口增长速度的逐渐加快的结论。
再结合生活中的实际问题,讨论人口问题产生的原因、危害和解决措施。
世界人口和人种的分布也都要以充分阅读分析分布图为基础展开。
综合能力训练:一、填空:1、18世纪以前,人口增长的十分,18世纪以后,特别是20世纪以来,世界人口增长速度。
2、山东省1997年总人口8785万,出生率为1.128%,自然增长率为0.463%,则山东省本年的死亡率为,约新增人口人。
3、人口增长速度的快慢,可以用来表示,人口分布的疏密程度可以用来表示。
4、人口稠密的地区多分布在纬度近海的地区。
5、山东省土地面积约15万平方千米,2000年全省总人口约9079万人,那么2000年山东省人口密度约为人/平方千米,人口分布的比较。
6、为了解决人口增长过快带来的问题,人类必须控制自己,做到有计划的生育,使人口的增长与、经济的发展相适应,与、资源相协调,提高人口素质。
7、、欧洲以及是世界上人口最稠密的地区。
8、世界人口每增加10亿人,所用的时间越来越,说明世界人口增长速度逐渐。
二、选择:1、世界上黑种人的故乡是。
A、非洲B、欧洲C、拉丁美洲D、亚洲2、我国的新疆维吾尔族和哈萨克族属于种人。
大学生心理素质训练第四章答案

大学生心理素质训练第四章答案1. 以下对于情绪的描述不正确的是: [单选题] *怒是由于事物或对象再三妨碍和干扰,使个人的愿望不能达到或产生与愿望相违背的情景时,紧张感逐渐积累而产生的情绪体验。
哀是指所热爱对象的遗失、破裂以及与所盼望东西的幻灭相联系的情绪体验。
惧往往是由于缺乏准备,不能处理、驾驭或不能摆脱某种可怕或危险情景时所表现的情绪体验。
惊是指盼望的目标达到和需要得到满足之后,随之而来的紧张感解除时的情绪体验。
(正确答案)2. 战国策云:“天子之怒,伏尸百万,流血千里。
布衣之怒,免冠徒跌,以头抢地。
志土之怒,流血五步,天下缟素。
”林冲上梁山,岳飞要“饥餐胡虏肉”、“渴饮匈奴血”.皆为怒。
这些论述是对于愤怒情绪的描述,对于愤怒这一情绪,以下描述不正确的是: [单选题] *愤怒是一种富于冲动性的情感,它是由于遇到与愿望相违背或愿望不能达到,并一再的受到妨碍而逐渐积累起来的紧张爆发的情绪。
大脑中有一个分管情绪的中枢,叫“杏仁核”。
理性中枢叫“大脑皮质”。
愤怒的同时,杏仁核激动过久,容易让人失去理智。
题项中的描述,是由于愤怒过久,而失去理智的表现。
(正确答案)3. 寻寻觅觅,冷冷清清,凄凄惨惨戚戚。
乍暖还寒时候,最难将息。
三杯两盏淡酒,怎敌它晚来风急?雁过也,正伤心,却是旧时相识。
对悲哀情绪的描述: [单选题] *悲哀作为一种负性基本情绪,通常指是由分离、丧失和失败引起的情绪反应。
悲伤程度取决于失去的东西的重要性和价值大小;也依赖于主体的意识倾向和个体特征。
悲伤包含沮丧、失望、气馁、意志消沉、孤独和孤立等情绪体验。
悲伤根据其程度不同,可细分为遗憾、失望、难过、悲伤、极度悲痛。
以上描述都正确(正确答案)4. 俗谓“胆战心惊”、“腿灌了铅”,更为准确的是指 [单选题] *一种恐惧情绪人们企图摆脱、逃避某种情景而又苦于无力的情绪恐惧往往欠缺处理或摆脱可怕情景的力量和知识而造成的人们在恐惧状态下,身心过程的特征是:血管收缩、忽急忽缓、战栗。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:为求 ,首先解除A处约束,并建立如图(a)所示的力和虚位移图。由虚位移原理
于是
KN·m
4-19均质杆AB的长为l,重为P,搁置在宽为a的槽内,如图所示。设A、D处光滑接触,试求平衡位置的 角,并讨论其平衡的稳定性。
解:建立如图所示的坐标系,以杆为研究对象,约束是理想的,主动力只有重力,系统的势能为:
由约束知:
(1)
主动力的虚功为:
(2)
将(8在曲柄OA上作用力矩为M=6 的力偶。OA=150mm,OO1=200mm,O1B=500mm,BC=780mm,略去摩擦及自重。当OA⊥OO1时(如图所示),为了使机构处于平衡,求作用在滑块C上的水平力P。
解:
如图,OA杆速度为 ,其中
所以:
(1)
CB杆的速度瞬心为E点, , ,所以:
(2)
利用虚位移原理可得:
将(1)、(2)代入,得:
由 的任意性,可得:
4-15平台钢架由一个 形框架带中间铰 构成。框架的上端刚性地插在混凝土墙内,下端则搁在圆柱滚动支座上。求当 和 两力作用时,插入端A处的铅直反作用力。
解:欲求 端铅直方向力,解除 端铅直方向约束,代之以约束力 ,则 只能上下平动, 和 点的虚位移大小相同 ,方向可知沿铅直方向, 点虚位移方向沿水平方向,由此可以确定 的速度瞬心即为 的折角处点 。可以求出 作用点D的虚位移 满足:
将(2)式代入,并由 可得:
4-6两等长杆AB与BC在B点用铰链接,又在杆的D和E两点连一弹簧,如图所示。弹簧系数为k,当距离AC等于a时,弹簧的拉力为零。如在C点作用一水平力F,杆系处于平衡。设AB=l,BD=b,杆重及摩擦略去不计,求距离AC之值。
解:解除弹簧DE的约束,代之以约束反力 和 。
因为当AC等于a时,弹簧的拉力为零,从而当AC等于 时,弹簧弹力:
解:如图所示,以A为原点建立坐标系。则D点坐标:
对上式进行变分可得:
(1)
此时弹簧的弹力为:
(2)
以杆AB、滑套D和杆CD为研究对象,约束为理想约束。将弹簧去除,代之以作用在D和B上的弹簧力。弹簧力在 上所做的虚功为零,在 上做的虚功为 ,利用虚位移原理有:
(3)
将(1)式代入得:
由 的任意性可得:
以EF中点为坐标原点建立坐标系,则有
则有:
因为系统质系平衡,由虚位移原理有:
由此解得:
4-14已知AD=DB=6m,CD=3m,在节点D的载荷为P,各杆自重不计。试用虚位原理求图示桁架中杆3的内力。
解:将杆3解除,并代之以相应的内力S。这样,结构ACD可以绕A点定轴转动,CB做平面运动,B、C、D点的虚位移如图所示。根据运动学中定轴转动的知识可知:
对BC杆,有 ,其中 , ,
由以上式子可得
则A点的虚位移rA与滑块C的虚位移rC的关系同速度之间的关系,即
由虚位移原理 ,代入rA与rC的关系
得P = 125N.
4-9两相同的均质杆,长度均为l,质量均匀为m,其上作用力偶如图。试求在平衡状态时,杆与水平线之间的夹角 , 。
解:假设上面杆的质心为A点,下面质心为B点。
于是
4-2图示机构的在C处铰接,在D点上作用水平力P,已知AC=BC=EC=FC=DE=DF=l,求保持机构平衡的力Q的值。
解:建立如图所示的坐标系,由几何关系得:
,
由虚位移原理得:
所以:
4-4反平行四边形机构 中的杆 和 用铰链 和 互相连接,同时又用铰链 和 连在机架 上。在杆 的铰链 处作用着水平力 。在铰链 沿垂直于杆 的方向作用有力 ,机构在图示位置处于平衡。设 , , , 。求 的大小。
而 ,平衡时有:
代入 可得:
答:
4-17图示三铰拱的自重不计,求在水平力P作用下支座A和B的约束反力。
解:解除B点Y方向上的约束,假设B点Y方向上的力为 ,有:
所以:
根据力平衡原理有:
然后解除C点的约束,假设A点X和Y方向的力为 和 。对C点,根据力矩平衡,可以得到:
所以:
再根据X方向上的力平衡,可以得到:
所以:
4-18图示组合梁上作用有载荷P1=5kN,P2=4kN,P3=3kN,以及M=2kN·m的力偶。不计摩擦及梁的质量。试用虚位移原理求固定端A的约束反力偶之矩MA。
解:如图所示,重力 , , 的坐标分别为 , , 。
易知
, ,
由几何关系有
变分得
解得
主动力 的虚功为0,即
带入 便得
4-12图示平面平衡系统,在列其整体的平衡方程时,不需计入弹簧内力;而用虚位移原理求力F1和F2之间的关系时,必需计入弹簧的虚功,二者矛盾吗?简要说明理由。
解:这二者并不矛盾。
在列其整体的平衡方程时,弹簧力是属于内力,不计入平衡方程。
解:根据题意,选三根杆组成的整体为研究对象,约束均为理想约束,主动力为 。质系平衡,则由虚位移原理,有
又由运动学知识,
其中 是沿CB杆方向的分量。
联立上述两式可得,
4-5滑套D套在光滑直杆AB上,并带动CD杆在铅垂滑道上滑动,如图所示。已知当 时,弹簧等于原长,且弹簧系数为5kN/m。若系统的自重不计,求在任意位置 角平衡时,在AB杆上应加多大力偶矩M。
虚位移原理求力F1和F2之间的关系时,弹簧力是主动力,必须计入。
4-13长度均为l的轻棒四根,由光滑铰链联成一菱形ABCD;AB、AD两边支于同一水平线的两个钉E,F上,相距为2a,BD间用一细绳连接,C点作用一铅直力P,如图所示。设A点的顶角为2 ,试用虚功原理求绳中张力T。
解:根据题意,以四根杆组成的整体为研究对象,约束为理想约束,主动力为 。
假设 不动, 有一个小的转角 ,
那么 ,那么两根杆所做的功为
而力偶所做的功为:
而根据虚位移原理,
现假设 不动, 有一个小的转角 ,
那么 , ,两根杆所做的功为
而力偶所做的功为:
而根据虚位移原理,
4-10三均质细杆以铰链相联,其A端和B端另以铰链联接在固定水平直线AB上,如图所示。已知各杆的重量与其长度成正比,AC=a,CD=DB=2a,AB=3a。设铰链为理想约束,求杆系平衡时 和 间的关系。
4-1图示为一轧纸钳,其尺寸如图所示。工作时上、下钳口保持平行,设手握力为P,求作用于纸片上的力Q的大小。
解:
1)取整个轧纸钳为研究对象。
2)系统约束为理想约束。
3)主动力P和Q分别作用在B点和A点。
4)取A点和B点的无穷小真实位移为虚位移 和 。
5)建立虚位移和的关系。由几何关系得
6)主动力的虚功为
由虚功原理列方程可得:
解得: 为插入端A铅直反作用力。
4-16试用虚位原理求图标桁架1、2两杆的内力。
解:如左图去掉1杆,代以作用力F,设F点虚位移为(方向向下),则点E,G,H的虚位移分别为 ,
由虚位移原理有 可得 ;
如右图,分析机构左半部分。设E点虚位移为(方向向下),则点G的虚位移为 ,由虚位移原理有 可得 ;
