2018天府新区数学二诊

合集下载

2018年四川省成都市中考数学二诊试卷((有答案))

2018年四川省成都市中考数学二诊试卷一、选择题（本大题共10小题，共30.0分）1.化简的结果是A. 3B.C.D. 9【答案】A【解析】解：，故A正确，故选：A．根据算术平方根是非负数，可得答案．本题考查了二次根式的化简，算术平方根是非负数．2.下列运算正确的是A. B. C. D.【答案】C【解析】解：A、，此选项计算错误；B、，此选项计算错误；C、，此选项计算正确；D、，此选项计算错误；故选：C．根据合并同类项法则、同底数幂的除法、同底数幂的乘法和幂的乘方分别计算即可判断．本题主要考查幂的运算，解题的关键是熟练掌握同底数幂的除法、同底数幂的乘法、幂的乘方及积的乘方运算的法则．3.如图是由六个相同的小正方体搭成的几何体，这个几何体的主视图是A.B.C.D.【答案】B【解析】解：从正面看第一层是三个小正方形，第二层左边一个小正方形，第三层左边一个小正方形，故选：B．根据从正面看得到的图形是主视图，可得答案．本题考查了简单组合体的三视图，从正面看得到的图形是主视图．4.把写成n为整数的形式，则n为A. 1B.C. 2D.【答案】B【解析】解：把写成n为整数的形式为，则n为．故选：B．绝对值小于1的正数也可以利用科学记数法表示，一般形式为，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．本题考查用科学记数法表示较小的数，一般形式为，其中，n为由原数左边起第一个不为零的数字前面的0的个数所决定．5.谜语：干活两腿脚，一腿勤，一腿懒，一脚站，一脚转打一数学学习用具，谜底为A. 量角器B. 直尺C. 三角板D. 圆规【答案】D【解析】解：圆规有两只脚，一铁脚固定，另一脚旋转，故选：D．利用圆规的特点直接得到答案即可．本题考查了简单的数学知识，稍有点数学常识的同学就会做出正确的回答，难度不大．6.在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示：A. 、B. 、3C. 、D. 、3【答案】C【解析】解：这组数据中出现次数最多，有4次，这组数据的众数为，最大数据为、最小数据为，极差为，故选：C．根据众数和极差的定义分别进行解答即可．本题主要考查极差与众数，解题的关键是掌握极差最大值最小值、一组数据中出现次数最多的数据叫做众数．7.将抛物线向左平移2个单位长度，再向下平移3个单位长度，则平移后所得到的抛物线解析式是A. B.C. D.【答案】C【解析】解：将抛物线向左平移2个单位长度，再向下平移3个单位长度，平移后所得抛物线解析式为，故选：C．直接根据平移的规律即可求得答案．本题主要考查函数图象的平移，掌握平移的规律是解题的关键，即“左加右减，上加下减”．8.若关于x的一元二次方程有实根，则m的取值范围是A. B. C. 且 D. 且【答案】D【解析】解：关于x的一元二次方程有实根，，并且，且．故选：D．由于x的一元二次方程有实根，那么二次项系数不等于0，并且其判别式是非负数，由此可以建立关于m的不等式组，解不等式组即可求出m的取值范围．本题考查了根的判别式的知识，总结：一元二次方程根的情况与判别式的关系：方程有两个不相等的实数根；方程有两个相等的实数根；方程没有实数根．此题切记不要忽略一元二次方程二次项系数不为零这一隐含条件．9.如图：有一块含有的直角三角板的两个顶点放在直尺的对边上，如果，那么的度数是A. B. C. D.【答案】B【解析】解：，，，，，，故选：B．直接利用平行线的性质进而结合等腰直角三角形的性质得出答案．此题主要考查了平行线的性质以及等腰直角三角形的性质，正确应用平行线的性质是解题关键．10.如图，正五边形ABCDE内接于，若的半径为5，则的长度为A.B.C.D.【答案】B【解析】解：连接OA、OB，五边形ABCDE是正五边形，，的长度，故选：B．连接OA、OB，根据正五边形的性质求出，根据弧长公式计算即可．本题考查的是正多边形的性质、弧长的计算，掌握正多边形的中心角的计算公式、弧长的计算公式是解题的关键．二、填空题（本大题共9小题，共36.0分）11.因式分解：______．【答案】【解析】解：原式．故答案为：．直接利用完全平方公式分解因式得出答案．此题主要考查了公式法分解因式，正确应用公式是解题关键．12.如图，在“”网格中，有3个涂成黑色的小方格若再从余下的6个小方格中随机选取1个涂成黑色，则完成的图案为轴对称图案的概率是______．【答案】【解析】解：如图，可选2个方格完成的图案为轴对称图案的概率．故答案为：．根据轴对称的性质设计出图案即可．本题考查的是利用轴对称设计图案，熟知轴对称的性质是解答此题的关键．13.如图，▱ABCD中，点E在边AD上，以BE为折痕，将向上翻折，点A正好落在CD上的F点，若的周长为8 cm，的周长为20cm，则FC的长为______cm．【答案】6【解析】解：，；的周长为，的周长为 cm，分析可得：的周长的周长．故答案为6．根据折叠的性质，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．本题通过折叠变换考查学生的逻辑思维能力，解决此类问题，应结合题意，最好实际操作图形的折叠，易于找到图形间的关系．14.把直线向上平移m个单位后，与直线的交点在第一象限，则m的取值范围是______．【答案】【解析】解：方法一：直线向上平移m个单位后可得：，联立两直线解析式得：，解得：，即交点坐标为，交点在第一象限，，解得：．故答案为：．方法二：如图所示：把直线向上平移m个单位后，与直线的交点在第一象限，则m的取值范围是．故答案为：．直线向上平移m个单位后可得：，求出直线与直线的交点，再由此点在第一象限可得出m的取值范围．本题考查了一次函数图象与几何变换、两直线的交点坐标，注意第一象限的点的横、纵坐标均大于0．15.某班体育委员对本班学生一周锻炼时间单位：小时进行了统计，绘制了如图所示的折线统计图，则该班这些学生一周锻炼时间的中位数是______小时．【答案】11【解析】解：由统计图可知，一共有：人，该班这些学生一周锻炼时间的中位数是第20个和21个学生对应的数据的平均数，该班这些学生一周锻炼时间的中位数是11，故答案为：11．根据统计图中的数据可以得到一共多少人，然后根据中位数的定义即可求得这组数据的中位数．本题考查折线统计图、中位数，解答本题的关键是明确中位数的定义，利用数形结合的思想解答．16.若是关于字母a，b的二元一次方程的一个解，代数式的值是______．【答案】24【解析】解：把，代入，得，．故答案为：24．把，代入原方程可得的值，把代数式变形为，然后计算．本题考查了公式法分解因式，把作为一个整体是解题的关键，而也需要运用公式变形，以便计算．17.如图，同心圆的半径为6，8，AB为小圆的弦，CD为大圆的弦，且ABCD为矩形，若矩形ABCD面积最大时，矩形ABCD的周长为______．【答案】【解析】解：连接OA，OD，作，，，根据矩形的面积和三角形的面积公式发现：矩形的面积为面积的4倍，、OD的长是定值，当的正弦值最大时，三角形的面积最大，即，则，，，，则矩形ABCD的周长是：．故答案是：．连接OA，OD，作，，，将此题转化成三角形的问题来解决，根据三角函数的定义可以证明三角形的面积，根据这一公式分析面积的最大值的情况，然后熟练应用勾股定理，以及直角三角形斜边上的高等于两条直角边乘积除以斜边求得长方形的长和宽，进一步求其周长．本题考查了垂径定理和矩形的性质，考生应注意熟练运用勾股定理，来求边长和周长．18.如图，在矩形ABCD中，将绕点A按逆时针方向旋转一定角度后，BC的对应边交CD边于点连接、若，，，则结果保留根号．【答案】【解析】解：连接AC，AG，，由旋转可得，，，，，∽，，，，是等腰直角三角形，，设，则，，中，，，解得，舍去，，中，，，故答案为：．先连接AC，AG，，构造直角三角形以及相似三角形，根据∽，可得到，设，则，，中，根据勾股定理可得方程，求得AB 的长以及AC的长，即可得到所求的比值．本题主要考查了旋转的性质，相似三角形的判定与性质，等腰直角三角形的性质，解一元二次方程以及勾股定理的综合应用，解决问题的关键是作辅助线构造直角三角形以及相似三角形，依据相似三角形的对应边成比例，将转化为，并依据直角三角形的勾股定理列方程求解，从而得出矩形的宽AB，这也是本题的难点所在．19.在平面直角坐标系，对于点和，给出如下定义：若，则称点Q为点P的“可控变点”例如：点的“可控变点”为点，点的“可控变点”为点点的“可控变点”坐标为______；若点P在函数的图象上，其“可控变点”Q的纵坐标的取值范围是，实数a的值为______．【答案】【解析】解：根据定义，点的“可控变点”坐标为；依题意，图象上的点P的“可控变点”必在函数的图象上，如图．当时，，此时，抛物线的开口向下，故当时，随x的增大而减小，即：，当时，，，，当时，，抛物线的开口向上，故当时，随x的增大而减小，即：，又，的值是：．故答案为，．直接根据“可控变点”的定义直接得出答案；时，求出x的值，再根据“可控变点”的定义即可解决问题．本题主要考查了二次函数图象上点的坐标特征，解答本题的关键是熟练掌握新定义“可控变点”，解答此题还需要掌握二次函数的性质，此题有一定的难度，属于创新题目，中考常考题型．三、计算题（本大题共1小题，共6.0分）20.先化简，再求值：，其中【答案】解：原式，当时，原式．【解析】先根据分式混合运算顺序和运算法则化简原式，再将x的值代入计算可得．本题主要考查分式的化简求值，解题的关键是熟练掌握分式混合运算顺序和运算法则．四、解答题（本大题共8小题，共78.0分）21.计算：；解不等式，并把解集在数轴上表示出来．【答案】解：原式；，解不等式得：，解不等式得：，不等式组的解集为，在数轴上表示为．【解析】先求出每一部分的值，再代入求出即可；先求出每个不等式的解集，再求出不等式组的解集即可．本题考查了解一元一次不等式组、在数轴上表示不等式组的解集、零指数幂、负整数指数幂、特殊角的三角函数值等知识点，能求出每一部分的值是解的关键，能正确根据不等式的解集得出不等式组的解集是解的关键．22.为了测量白塔的高度AB，在D处用高为米的测角仪 CD，测得塔顶A的仰角为，再向白塔方向前进12米，又测得白塔的顶端A的仰角为，求白塔的高度参考数据，，，，结果保留整数【答案】解：设，在中，，在中，，由题意得，，解得：，故AB米．答：这个电视塔的高度AB为23米．【解析】设，在中表示出CE，在中表示出FE，再由米，可得出关于x的方程，解出即可得出答案．本题考查了解直角三角形的应用，解答本题要求学生能借助仰角构造直角三角形并解直角三角形，难度一般．23.某销售公司年终进行业绩考核，人事部门把考核结果按照A，B，C，D四个等级，绘制成两个不完整的统计图，如图1，图2．参加考试的人数是______，扇形统计图中D部分所对应的圆心角的度数是______，请把条形统计图补充完整；若考核为D等级的人中仅有2位女性，公司领导计划从考核为D等级的人员中选2人交流考核意见，请用树状图或表格法，求所选人员恰为一男一女的概率；为推动公司进一步发展，公司决定计划两年内考核A等级的人数达到30人，求平均每年的增长率精确到，【答案】50【解析】解：参加考试的总人数为人，扇形统计图中D部分所对应的圆心角的度数是，C等级人数为，补全图形如下：故答案为：50、；画树状图为：共有20种等可能的结果数，其中恰好抽到一名男生和一名女生的结果数为12，所以恰好抽到一名男生和一名女生的概率；设增长率是x，根据题意，得：，解得：负值舍去，所以，答：每年的增长率为．由A等级人数及其百分比可得总人数，用乘以D等级人数所占比例可得其圆心角度数，再用总人数减去其他学生人数求得C等级人数即可补全图形；画树状图展示所有20种等可能的结果数，再找出恰好抽到一名男生和一名女生的结果数，然后利用概率公式求解．设增长率是x，根据“两年内考核A等级的人数达到30人”列出关于x的方程，解之即可得．本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式求事件A或B的概率也考查了统计图和一元二次方程．24.如图，已知，是直线AB和某反比例函数的图象的两个交点．求直线AB和反比例函数的解析式；观察图象，直接写出当x满足什么范围时，直线AB在双曲线的下方；反比例函数的图象上是否存在点C，使得的面积等于的面积？如果不存在，说明理由；如果存在，求出满足条件的所有点C的坐标．【答案】解：设反比例函数解析式为，把代入，可得，反比例函数解析式为；把代入，可得，即，，设直线AB的解析式为，把，代入，可得，解得，直线AB的解析式为；由题可得，当x满足：或时，直线AB在双曲线的下方；存在点C．如图所示，延长AO交双曲线于点，点A与点关于原点对称，，的面积等于的面积，此时，点的坐标为；如图，过点作BO的平行线，交双曲线于点，则的面积等于的面积，的面积等于的面积，由可得OB的解析式为，可设直线的解析式为，把代入，可得，解得，直线的解析式为，解方程组，可得；如图，过A作OB的平行线，交双曲线于点，则的面积等于的面积，设直线的解析式为“，把代入，可得“，解得b“，直线的解析式为，解方程组，可得；综上所述，点C的坐标为，，【解析】运用待定系数法，根据，，即可得到直线AB和反比例函数的解析式；根据直线AB在双曲线的下方，即可得到x的取值范围；分三种情况进行讨论：延长AO交双曲线于点，过点作BO的平行线，交双曲线于点，过A作OB的平行线，交双曲线于点，根据使得的面积等于的面积，即可得到点C的坐标为，，本题主要考查了反比例函数与一次函数交点问题，解决问题的关键是求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解．25.如图，是的外接圆，，，过点B的直线l是的切线，点D是直线l上一点，过点D作交CB延长线于点E，连接AD，交于点F，连接BF、CD交于点G．求证： ∽ ；当时，求的值；若CD平分，，连接CF，求线段CF的长．【答案】证明：如图1中，，，是切线，，，，，，∽ ；解：如图2中，∽ ；四边形ACED是矩形，：DE：：2：4，，∽ ，．解：如图3中，，，，易证 ≌ ， ∽ ，：：AC，，设，则，，，，，可得，，，设CF交AB于H．则．【解析】只要证明，即可；首先证明BE：DE：：2：4，由 ∽ ，可得；想办法证明AB垂直平分CF即可解决问题；本题考查相似三角形的判定和性质、圆周角定理、切线的性质、解直角三角形、线段的垂直平分线的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，所以中考常考题型．26.为进一步缓解城市交通压力，湖州推出公共自行车公共自行车在任何一个网店都能实现通租通还，某校学生小明统计了周六校门口停车网点各时段的借、还自行车数，以及停车点整点时刻的自行车总数称为存量情况，表格中时的y的值表示8：00点时的存量，时的y值表示9：00点时的存量以此类推，他发现存量辆与为整数满足如图所示的一个二次函数关系．______，解释m的实际意义：______；求整点时刻的自行车存量y与x之间满足的二次函数关系式；已知10：：00这个时段的还车数比借车数的2倍少4，求此时段的借车数．【答案】13 7：00时自行车的存量【解析】解：，，则m的实际意义：7：00时自行车的存量；故答案为：13，7：00时自行车的存量；由题意得：，设二次函数的关系式为：，把、和分别代入得：，解得：，；当时，，当时，，设10：：00这个时段的借车数为x，则还车数为，根据题意得：，，答：10：：00这个时段的借车数为3辆．根据等量关系式：借车数还车数：00的存量，列式求出m的值，并写出实际意义；先求出9点时自行车的存量，当时所对应的y值，即求出n的值；再设一般式将三点坐标代入求出解析式；先分别计算9：：00和10：：00的自行车的存量，即当和时所对应的y值，设10：：00这个时段的借车数为x，根据上一时段的存量还车数借车数此时段的存量，列式求出x的值即可．本题是二次函数的应用，理解各量的实际意义：还车数、借车数、存量；弄清等量关系式：上一时段的存量还车数借车数此时段的存量，考查了利用待定系数法求二次函数的关系式，并根据图象理解真正意义．27.在正六边形ABCDEF中，N、M为边上的点，BM、AN相交于点P如图1，若点N在边BC上，点M在边DC上，，求证：；如图2，若N为边DC的中点，M在边ED上，，求的值；如图3，若N、M分别为边BC、EF的中点，正六边形ABCDEF的边长为2，请直接写出AP的长．【答案】证明：在正六边形ABCDEF中，，，，≌ ，，，∽ ，，；延长BC，ED交于点H，延长BN交DH于点G，取BG的中点K，连接KC，在正六边形ABCDEF中，，，，，，，，，，，，，≌ ，，，，，四边形MABG是平行四边形，，，即，如图3，过N作，交AB的延长线于H，，，中，，，，，中，，连接FC，延长FC与AN交于G，设FC与BM交于K，易证 ≌ ，，，，，，，，，，，，，，，设，，由得：，，．【解析】先证明 ≌ ，得，再证明 ∽ ，列比例式可得结论；作辅助线，构建等边三角形的三角形的中位线CK，先证明是等边三角形得：，，由 ≌ ，得，，利用四边形MABG是平行四边形，得，所以，即；如图3，作辅助线，构建直角三角形和全等三角形，根据直角三角形的性质得：，，利用勾股定理求，证明 ≌ ，利用和，列比例式可得：，设，，根据得：，可得结论．本题是相似三角形的综合题，考查了正六边形的性质、全等三角形和相似三角形的性质和判定、平行四边形的性质和判定、平行线分线段成比例定理等知识，一般情况下，正多边形的题解答都比较麻烦，熟练掌握正多边形的定义及性质是关键，第三问比较复杂，辅助线的作法是关键．28.如图，直线l：与x轴、y轴分别相交于A、B两点，抛物线经过点B，交x轴正半轴于点C．求该抛物线的函数表达式；已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM、BM，设点M的横坐标为m，的面积为S，求S与m的函数表达式，并求出S的最大值及此时动点M的坐标；将点A绕原点旋转得点，连接、，在旋转过程中，一动点M从点B出发，沿线段以每秒3个单位的速度运动到，再沿线段以每秒1个单位长度的速度运动到C后停止，求点M在整个运动过程中用时最少是多少？【答案】解：将代入，得，点B的坐标为，抛物线经过点B，，得，抛物线的解析式为：；将代入，得，，点C的坐标为，点M是抛物线上的一个动点，并且点M在第一象限内，点M的横坐标为m，，点M的坐标为，将代入，得，点A的坐标，的面积为S，，四边形化简，得，当时，S取得最大值，此时，此时点M的坐标为，即S与m的函数表达式是，S的最大值是，此时动点M的坐标是；如右图所示，取点H的坐标为，连接、，，，，∽ ，，即，，，即点M在整个运动过程中用时最少是秒【解析】根据题意可以求得点B的坐标，从而可以求得抛物线的解析式；根据题意可以求得点A的坐标，然后根据题意和图形可以用含m的代数式表示出S，然后将其化为顶点式，再根据二次函数的性质即可解答本题；根据题意作出点H，然后利用三角形相似和勾股定理、两点之间线段最短即可求得t的最小值．这是一道二次函数综合题，主要考查二次函数的最值、最短路径、三角形相似，待定系数法求二次函数解析式，解答本题的关键是明确题意，找出所求问题需要的条件，作出合适的辅助线，利用数形结合的思想和转化的数学思想解答．。

2018成都二诊理科数学高清(可编辑修改word版)

成都市2015级高中毕业班第二次诊断性检测数学(理_)本试卷分选择题和非选择题两部分。

第I卷(选择题)i至2页，第n卷(非选择题)3至4页，共4页，满分150分，考试时间120分钟。

注意事项：1.答题前，务必将自己的姓名、考籍号填写在答题卡规定的位置上。

2.答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其它答案标号。

3.答非选择题时，必须使用0. 5毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4.所有题目必须在答题卡上作答，在试题卷上答题无效。

5.考试结束后,只将答题卡交回。

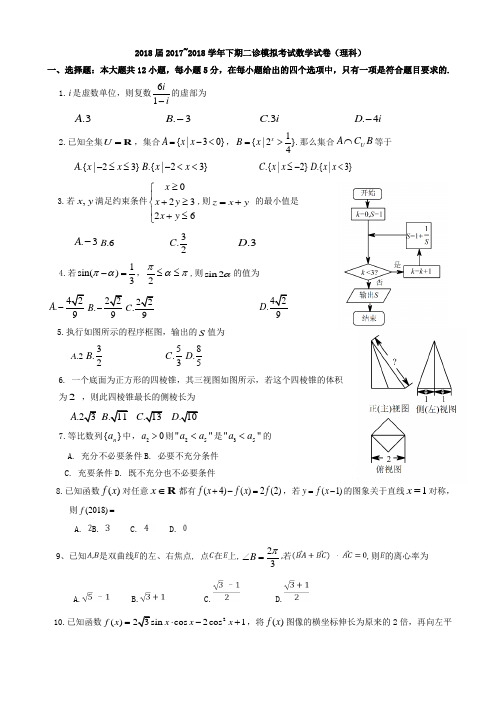
第I卷(选择题，共60分)一、选择题:本大题共12小题,毎小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合P = {x | |x-l|<l} ,Q = U |-l<x<2},则P =(A)(-l,j) (B)(—1,2) (0(1,2) (D)(0,2)2.已知向量a = (2,l),&=(3,4),c=a,2).若(3a~b)#c,则实数i 的值为(A)-8 (B)-6 (0-1 (D)63.若复数z满足(l + i)z=l —2i3,则\z\等于(A)华(B)吾(C)T (D)|4.设等差数列{a H}的前n项和为S B .若S< =20,a5=10,则a16 =(A)-32 (B) 12 (C) 16 (D)325.已知是空间中两条不同的直线，a,芦为空间中两个互相垂直的平面，则下列命题正确的是(A)若znCZa，则m 丄芦(B)若m CZa,n CZp,则m 丄 rt(C)若丄芦，则rn // a(D)若a门资=m，n丄?n，则w丄a6.若a -梦的展开式中含项的系数为160,则实数a的值为(A)2(B)-2 (C)2V2 (D)-2V2数学(理科)“二诊”考试鵬1页(共4页)数学(理科)“二诊”考试题第2页(共4页)7. 已知函数 /(x)=Asin(a*x-|-^)(A >0,<w>0, | <p |<y) 的部分图象如图所示.现将函数/(x)图象上的所有点向右平移j 个单位长度得到函数g(x)的图象，则函数 g(x)的解析式为(A) g(x) = 2sin(2r +-7)(B) g(x) = 2sin(2r+字)44(C) g(x) = 2cos2z(D) gCz) = 2sin(2z _■)8. 若x 为实数，则“”是“ 242 << 3”成立的zx(A)充分不必要条件 (B)必要不充分条件 (C)充要条件(D)既不充分也不必要条件9. 《九章算术》中将底面为长方形，且有一条侧棱与底面垂直的四棱锥称之为“阳马”.现有 —阳马，其正视图和侧视图是如图所示的直角三角形.若该阳马的顶点都在同一个球面上，则该球的体积为(A 呼(C)V6x(D) 24K 10. 执行如图所示的程序框图，若输出的结果为56,则判断框中的条件可以是(A) n < 7?(B)n> 7? (C) n<6? (D)n> 6?11. 已知函数_/Xx) =—■_ 1 —nlnx(m >-0,0^n ^e)在区X间[l ，e]内有唯一零点，则 H 的取值范围为m +1(A )[e d*++1]2 e⑴)[^n ，1] (D)[l,y+ 1]12.已知双曲线C ：^-^C 的两条渐近线分别相交于A ，B 两点.若点A ，B 分别位于第一，四象限，O 为坐标原点.当AP=y PB04-, AAOB 的面积为2b ，则双曲线C 的实轴长为 “、32(A )72=l(a>0,6>0)右支上的一点P ，经过点P 的直线与双曲线(B)琴⑹吾4(D )T(B) 8A /6X 側视图i —H正视图s=Q,a=2,n=\是/输出s/ [结束|第II卷(非选择题，共90分)二、填空题:本大题共4小题，每小题5分，共20分.把答案填在答题卡上.13.已知a= 2^，b= (~^)i，贝!j log2(aZ>) = .2 0. 814.如图是调査某学校髙三年级男女学生是否喜欢篮球运动的等髙条形图，阴影部分的髙表示喜欢该项运动的频率.已知该年级男生女生各500名(假设所有学生都0. 4参加了调査)，现从所有喜欢篮球运动的同学中按分层抽样的方式抽取32人，则抽取的男生人数为15.已知抛物线C：y2=2px(/)>0)的焦点为F,准线Z与x轴的交点为A，P是抛物线C上的点，且PF丄轴.若以AF为直径的圆截直线AP 所得的弦长为2,则实数p的值为.16.已知数列｛a”｝共16项，且ai = 1 ,a8 =毛记关于x的函数f… Or) = yx3—a…x z + (aS — l)x,n6N* .若x =a…+1(l < n < 15)是函数/…(x)的极值点，且曲线=/8(x)在点(ai6,/8(ai6))处的切线的斜率为15.则满足条件的数列的个数为.三、解答题:本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)已知函数/(X)=^3 sin yCOS y — COS2 y +y.(I )求函数/(x)的单调递减区间；(II)若AABC的内角A,B,C所对的边分别为a，b，c，f(M =|,a =73, sinB =2sinC，求c .18.(本小题满分12分)近年来，共享单车已经悄然进人了广大市民的日常生活，并慢慢改变了人们的出行方式.为了更好地服务民众，某共享单车公司在其官方APP中设置了用户评价反馈系统，以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出200条较为详细的评价信息进行统计，对优惠活动好评对优惠活动不满意合计对车辆状况好评10030130对车辆状况不满意403070合计14060200(I )能否在犯错误的概率不超过0.001的醒下认为讎g动好评与车槲鵬评之间有关系? (H )为了回馈用户，公司通过APP向用户随机派送每张面额为0元，1元，2元的三种骑行券.用户每次使用APP扫码用车后，都可获得一张骑行券.用户骑行一次获得1元券，获得2元券的概率分别是y，去，且各次获取骑行券的结果相互独立.若某用户一天使用了两次该公司的共享单车，记该用户当天获得的骑行券面额之和为X，求随机变量X的分布列和数学期望. 参考数据：PGK2彡是) 0.1500.1000. 0500. 0250. 0100. 0050. 001 k 2. 072 2. 706 3. 841 5.024 6. 6357. 87910. 828数学(理科)“二诊”考试题第3页(共4页)…2_ n(ad — be)2 ______参考公式: ，其中n =a +d +c +</ .= U+6)(c+a)(a+c)(6+a)19.(本小»分12分)如图，D是AC的中点，四边形BDEF；^^，平面BDEF丄平面_ABC，ZFBD= 6Cf，AB 丄BC,AB=BC=^2. (I )若点M是线段BF的中点，证明:BF丄平面迦S ；(n )求平面姬与平面BCF所面角wwr.20.(本小题满分12分)工2 y2 已知椭圆C：^+^-=l(a>6>0)的左右焦点分别jo为^，厂2，左顶点为A，离心率为j，点B是楠圆上的动,/9 —1 点，△ABF:的面积的最大值为(1)求楠圆(：的方程；(D )设经过点F.的直线I与楠圆C相交于不同的两点A4，N，线段_ 的中垂线为Z'. 若直线I'与直线I相交于点P，与直线x = 2相交于点Q，求的最小值.21.(本小题满分12分)已知函数/(x) =xlnx +ax + 1，a 6 R .(I )当x>0时，若关于工的不等式/(x) >0恒成立，求a的取值范围;(II)当n 6 N*时，证明:T~^7<ln22 + ln24 + …+ ln2^^<-4f. 2n + 4 2 n n +1请考生在第22.23题中任选一题作答，如果多做，则按所做的第一题计分.作答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑.22.(本小题满分10分)选修4一4:极坐标与参数方程在平面直角坐标系xOy中，曲线C的参数方程为J X==2^C0Sff,其中a为参数，ly = 2sinaa € (0，n).在以坐标原点O为极点，:c轴的正半轴为极轴的极坐标系中，点P的极坐标为(472, j),直线I的极坐标方程为^(^--^)+572 =0.(I )求直线I的直角坐标方程与曲线C的普通方程；(II)若Q是曲线C上的动点，A4为线段PQ的中点.求点M到直线Z的距离的最大值.23.(本小题满分10分)选修4一5:不等式选讲已知函数/(x) = |2x + l|+|x-l| .(I)解不等式/(x)>3；(II)记函数/Gr)的最小值为m.若a，b，c均为正实数，且|a+6 + 2c=/n,求a z+b2+c z的最小值.数学(理科)“二诊”考试题第4页(共4页)。

成都市2018届高中毕业班第二次诊断性检测

成都市2018届高中毕业班第二次诊断性检测数学（理科）第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合，则为（）A ．B ．C ．D ． 2. 已知复数，则在复平面内对应的点在（） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限3. 已知函数的定义域为，为常数.若：对，都有；：是函数的最小值，则是的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件考点：1.常用逻辑用语；2.充分条件与必要条件.4. 如果为各项都大于零的等差数列，公差，则（） A ． B ． C. D ．5. 已知，则等于（） A ．． D6. 已知集合，从这三个集合中各取一个元素构成空间直角坐标系上的坐标，则确定的不同点的个数为（） A ．6 B ．32 C.33 D ．347. 设，则对任意实数，若，则（） A ． B ． C.{}30 103x A x B x x x ⎧+⎫=≤=-≥⎨⎬-⎩⎭，A B []1 3，[)1 3，[)3 -∞，(]3 3-，11z i i=++z ()f x R M p x R ∀∈()f x M ≥q M ()f x p q 128 a a a ，，…，0d ≠1845a a a a >1845a a a a <1845a a a a +<+1845a a a a =24cos 0352παπα⎛⎫+=-<< ⎪⎝⎭，sin sin 3παα⎛⎫++ ⎪⎝⎭43333343{}{}{}5 1 2 1 3 4A B C ===，，，，，()()322log 1f x x x x =+++ a b ，0a b +≥()()0f a f b +≤()()0f a f b +≥()()0f a f b -≤D ．8. 某企业节能降耗技术改造后，在生产某产品过程中记录的产量（吨）与相应的生产能耗（吨）的几组对应数据如下表所示：3 若根据表中数据得出关于的线性回归方程为，则表中的值为（） A ． B ． C. D ．9. 将函数的图象向右平移个周期后，所得图象对应的函数为，则函数的单调递增区间（）A ．B ． C. D ． 10. 已知，，则函数在区间上为增函数的概率是（） A ．B ． C. D ． 11. 若正整数除以正整数后的余数为，则记为，例如.如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图，则输出的等于（）()()0f a f b -≥x y y x 0.70.35y x =+a 3 3.15 3.5 4.52sin 26y x π⎛⎫=+ ⎪⎝⎭14()f x ()f x ()5 1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦，()511 1212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦，()57 2424k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦，()719 2424k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦，{}0 1 2a ∈，，{}1 1 3 5b ∈-，，，()22f x ax bx =-()1 +∞，512131416N m n ()mod N n m =()102mod 4=nA ．B ．21 C.22 D ．2312. 设函数，其中，若有且只有一个整数使得，则的取值范围是（）A ．B ． C. D ．第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上） 13.在二项式的展开式中，若常数项为-10，则． 14.在一个容量为5的样本中，数据均为整数，已测出其平均数为10，但墨水污损了两个数据，其中一个数据的十位数字1未被污损，即9，10，11，1，那么这组数据的方差可能的最大值是．15.如图，抛物线的一条弦经过焦点，取线段的中点，延长至点，使，过点，作轴的垂线，垂足分别为，则的最小值为．20()()31x f x e x ax a =--+1a <0x ()00f x ≤a 23 4e ⎛⎫ ⎪⎝⎭，23 4e ⎡⎫⎪⎢⎣⎭，2 1e ⎛⎫ ⎪⎝⎭，2 1e ⎡⎫⎪⎢⎣⎭，25(ax +a =2s24y x =AB F OB D OA C OA AC =C D y ,E G EG16.在数列中，，（，），则数列的前项和．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17. 如图，在平面四边形中，已知，，，在边上取点，使得，连接，若，.（1）求的值；（2）求的长.18. 某项科研活动共进行了5次试验，其数据如下表所示：特征量第1次第2次第3次第4次第5次555 559 551 563 552601605597599598（1）从5次特征量的试验数据中随机地抽取两个数据，求至少有一个大于600的概率；（2）求特征量关于的线性回归方程；并预测当特征量为570时特征量的值.{}n a 11a =2121n n n a a n -=-2n ≥*n N ∈2{}n a n n n T =ABCD 2A π∠=23B π∠=6AB =AB E 1BE =,EC ED 23CED π∠=EC=sin BCE ∠CD x y y y x x y（附：回归直线的斜率和截距的最小二乘法估计公式分别为，）19. 如图，已知梯形与所在平面垂直，，，，，，，连接.（1）若为边上一点，，求证：平面；（2）求二面角的余弦值.20. 在平面直角坐标系中，已知椭圆（），圆（），若圆的一条切线与椭圆相交于两点. （1）当，时，若点都在坐标轴的正半轴上，求椭圆的方程；（2）若以为直径的圆经过坐标原点，探究之间的等量关系，并说明理由.21. 已知函数，其中.（1）若在上存在极值点，求的取值范围；（2）设，，若存在最大值，记为，则当时，是否存在最大值？若存在，求出其最大值；若不存在，请说明理由.121()()()niii nii x x y y b x x ==--=-∑∑a y bx =-CDEF ADE ∆,AD DE CD DE ⊥⊥////AB CD EF 28AE DE ==3AB =9EF =12CD =,BC BF G AD 13DG DA =//EG BCF E BF C --xOy 2222:1x y E a b+=0a b >>222:O x y r+=0r b <<O :l y kx m =+E ,A B 12k =-1r =,A B E AB O ,,a b r 1()ln f x a x x x=-+0a >()f x (2,)+∞a 1(0,1)x ∈2(1,)x ∈+∞21()()f x f x -()M a 1a e e≤+()M a请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分. 22.选修4-4：坐标系与参数方程在直角坐标系中，曲线的参数方程为，（为参数），直线的参数方程为（为参数），在以坐标原点为极点，轴的正半轴为极轴的极坐标系中，过极点的射线与曲线相交于不同于极点的点，且点的极坐标为，其中.（1）求的值；（2）若射线与直线相交于点，求的值. 23.选修4-5：不等式选讲已知函数. （1）求不等式的解集；（2）若为正实数，且，求的最小值.xOy C 2cos 22sin x y αα=⎧⎨=+⎩αl 2132x y t ⎧=⎪⎪⎨⎪=+⎪⎩t O x O C AA )θ(,)2πθπ∈θOA l B AB ()43f x x x =---3()02f x +≥,,p q r 111432p q r++=32p q r ++成都市2018届高中毕业班第二次诊断性检测数学（理科）试卷答案一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知集合，则为（）A ．B ．C ．D ．【答案】B考点：1.不等式的解法；2.集合的运算. 2. 已知复数，则在复平面内对应的点在（） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限【答案】A 【解析】{}30 103x A x B x x x ⎧+⎫=≤=-≥⎨⎬-⎩⎭，A B []1 3，[)1 3，[)3 -∞，(]3 3-，11z i i=++z试题分析：,该复数对应的点为，在第一象限，故选A.考点：1.复数的运算；2.复数的几何意义.3. 已知函数的定义域为，为常数.若：对，都有；：是函数的最小值，则是的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】B 【解析】试题分析：：对，都有是函数的最小值, 是函数的最小值对，都有,所以是的必要不充分条件，故选B. 考点：1.常用逻辑用语；2.充分条件与必要条件.4. 如果为各项都大于零的等差数列，公差，则（） A ． B ． C. D ．【答案】B考点：等差数列的性质.5. 已知，则等于（） A ．．D【答案】A 【解析】11111(1)(1)22i z i i ii i i -=+=+=+++-11(,)22Z ()f x R M p x R ∀∈()f x M ≥q M ()f x p q x R ∀∈()f x M ≥/⇒M ()f x M ()f x ⇒x R ∀∈()f x M ≥p q 128 a a a ，，…，0d ≠1845a a a a >1845a a a a <1845a a a a +<+1845a a a a =24cos 0352παπα⎛⎫+=-<< ⎪⎝⎭，sin sin 3παα⎛⎫++ ⎪⎝⎭试题分析：因为，所以，故选A. 考点：三角恒等变换与诱导公式.6. 已知集合，从这三个集合中各取一个元素构成空间直角坐标系上的坐标，则确定的不同点的个数为（） A ．6 B ．32 C.33 D ．34 【答案】A 【解析】试题分析：不考虑限定条件确定的不同点的个数为，但集合，中有相同元素1，由5，1，1三个数确定的不同点的个数只有三个，故所求的个数为：个,故选A.考点：1.分类计数原理与分步计数原理；2.排列与组合.7. 设，则对任意实数，若，则（） A ． B ． C. D ．【答案】B考点：函数的奇偶性与单调性.24cos 35πα⎛⎫+= ⎪⎝⎭111sin sin sin sin cos sin 3222πααααααα⎛⎫⎫++=++=+ ⎪⎪⎝⎭⎭22333πππααπα⎡⎤⎛⎫⎛⎫⎛⎫=-=+-=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦{}{}{}5 1 2 1 3 4A B C ===，，，，，11323336C C A =B C 36333-=()()322log 1f x x x x =+++ a b ，0a b +≥()()0f a f b +≤()()0f a f b +≥()()0f a f b -≤()()0f a f b -≥8. 某企业节能降耗技术改造后，在生产某产品过程中记录的产量（吨）与相应的生产能耗（吨）的几组对应数据如下表所示：3 若根据表中数据得出关于的线性回归方程为，则表中的值为（） A ． B ． C. D ．【答案】D 【解析】试题分析：，由回归方程：，解之得,故选D. 考点：线性回归.9. 将函数的图象向右平移个周期后，所得图象对应的函数为，则函数的单调递增区间（）A ．B ． C. D ．【答案】A. 【解析】试题分析：函数的周期，所以，函数的图象向右平移后所得函数的解析式为，由得函数的单调递增区间为,故选A. 考点：1.图象的平移变换；2.三角函数的图象与性质.x y y x 0.70.35y x =+a 3 3.15 3.5 4.5a y bx =- 2.53434560.350.70.744a y x ++++++=-=-⨯4.5a =2sin 26y x π⎛⎫=+ ⎪⎝⎭14()f x ()f x ()5 1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦，()511 1212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦，()57 2424k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦，()719 2424k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦，2sin 26y x π⎛⎫=+ ⎪⎝⎭T π=44T π=2sin 26y x π⎛⎫=+ ⎪⎝⎭4π()2sin 2()2sin(2)463f x x x πππ⎡⎤=-+=-⎢⎥⎣⎦222()232k x k k Z πππππ-≤-≤+∈()f x ()5 1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦，10. 已知，，则函数在区间上为增函数的概率是（）A ．B ． C. D ．【答案】B考点：1.一次函数与二次函数的性质；2.古典概型.【名师点睛】本题考查一次函数与二次函数的性质、古典概型，属中档题；求解古典概型问题的关键是找出样本空间中的基本事件数及所求事件包含的基本事件数，常用方法有列举法、树状图法、列表法等，所求事件包含的基本事件数与样本空间包含的基本事件数的比值就是所求事件的概率.11. 若正整数除以正整数后的余数为，则记为，例如.如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图，则输出的等于（）{}0 1 2a ∈，，{}1 1 3 5b ∈-，，，()22f x ax bx =-()1 +∞，512131416N m n ()mod N n m =()102mod 4=nA ．B ．21 C.22 D ．23【答案】C考点：程序框图.【名师点睛】本题考查程序框图，属中档题；识别运行算法流程图和完善流程图是高考的热点．解答这一类问题，第一，要明确流程图的顺序结构、条件结构和循环结构；第二，要识别运行流程图，理解框图所解决的实际问题；第三，按照题目的要求完成解答．对流程图的考查常与数列和函数等知识相结合，进一步强化框图问题的实际背景．12. 设函数，其中，若有且只有一个整数使得，则的取值范围是（）A ．B ． C. D ．【答案】D【解析】20()()31x f x e x ax a =--+1a <0x ()00f x ≤a 23 4e ⎛⎫ ⎪⎝⎭，23 4e ⎡⎫⎪⎢⎣⎭，2 1e ⎛⎫ ⎪⎝⎭，2 1e ⎡⎫⎪⎢⎣⎭，试题分析：设，，则，∴，，单调递减；，，单调递增，所以处取得最小值，所以，，直线恒过定点且斜率为，所以，∴而，∴的取值范围考点：1.导数与函数的单调性、极值；2.函数与方程、不等式.【名师点睛】本题考查导数与函数的单调性、极值，函数与方程、不等式，属难题；导数在不等式中的应用问题是每年高考的必考内容，主要考查证明不等式、不等式恒成立或不等式恒成立求参数范围等问题，证明不等式可通过构造两个函数的差函数，证明差函数恒大于（或小于）证明，利用导数解决不等式恒成立问题时，首先要构造函数，利用导数研究所构造函数的单调性、最值，进而得到相应的含参不等式，求出范围即可.二、填空题13. -2 14. 32.8 15. 4 16.三、解答题17.解：（1）在中，据正弦定理，有. ∵，，， ∴. （2）由平面几何知识，可知，在中，∵，，()()31x g x e x =-()h x ax a=-()()'32xg x e x =+2 3x ⎛⎫∈-∞- ⎪⎝⎭，()'0g x <()g x 2 3x ⎛⎫∈-+∞ ⎪⎝⎭，()'0g x >()g x 23x =-233e --()()010g a h =-<-=()()1120g h e -=>()h x ax a =-()1 0，a ()()111420e g h a ----=-+≥2e a ≥1a <a 12e ⎡⎫⎪⎢⎣⎭，0021n n +BEC ∆sin sin BE CE BCE B=∠23B π∠=1BE =CE =sin sin 14BE B BCE CE •∠===DEA BCE ∠=∠Rt AED ∆2A π∠=5AE =∴. ∴在中，据余弦定理，有∴18.解：（1）记“至少有一个大于600”为事件.∴. （2），. ∴∵，∴线性回归方程为.当时，∴当时，特征量的估计值为.19.解：（1）如图，作，交于点，连接，作，交于，交于.∵，,cos 14DEA ∠===cos EA ED DEA ===∠CED ∆22212cos 7282()492CD CE DE CE DE CED =+-••∠=+--=7CD =A 23257()110C P A C =-=5555595515635525565x ++++==600y =222221135(5)(3)7(1)(4)(2)300.3(1)3(5)7(4)100b -⨯+⨯+-⨯-+⨯-+-⨯-===-++-++-6000.3556433.2a y bx =-=-⨯=0.3433.2y x =+570x =0.3570433.2604.2y =⨯+=570x =y 604.2//GM CD BC M MF //BH AD GM N DC H //EF CD //GM EF∴，.∵，∴. ∴.∴.∴. ∴四边形为平行四边形，∴.又平面，平面四边形，∴平面.（2）∵平面平面，，平面，∴平面.以为坐标原点，为轴，为轴，为轴建立如图所示的空间直角坐标系.∴.∴，,设平面的法向量.由，得. 取，得.3GN AB ==9HC =////AB GM DC 23NM BM AG HC BC AD ===6NM =9GM GN NM =+=GM //=EF GMFE //GE MF MF ⊂BCF GE ⊄//GEBCF ADE ⊥CDEF AD DE ⊥AD ⊂ADE AD ⊥CDEF D DC x DE y DA z xyzD (0,4,0),(9,4,0),(12,0,0),(3,0,EF C B (9,0,0)EF=(3,4,EB =-EBF 1111(,,)n x y z =1100n EF n EB ⎧•=⎪⎨•=⎪⎩111190340x x y =⎧⎪⎨-+=⎪⎩1y =1(0,3,1)n =同理，，.设平面的法向量.由，得. 取，得.∴. ∵二面角为钝二面角，∴二面角的余弦值为. 20.解：（1）∵直线与.由，，解得∵点都在坐标轴正半轴上，∴∴切线与坐标轴的交点为，. ∴，. ∴椭圆的方程是. （2）设，∵以为直径的圆经过点，∴，即.(3,4,0)FC=-(6,4,FB =--BCF 2222(,,)n x y z =2200n FC n FB ⎧•=⎪⎨•=⎪⎩22222340640x y x y -=⎧⎪⎨--+=⎪⎩24x =2n =121212cos ,n n n n n n •====E BF C --E BF C --26-l O r =12k =-1r =m =,A B 1:2l y x =-+l a =2b =E 224155x y +=11(,)A x y 22(,)B x y AB O 0OA OB •=12120x x y y +=∵点在直线上，∴. ∴ （*）由消去，得. 即显然 ∴由一元二次方程根与系数的关系，得代入（*）式，得. 整理，得.又由（1），有.消去，得 ∴ ∴满足等量关系. 21.解：（1），. 由题意，得，在上有根（不为重根）.即在上有解. ,A B l 1122y kx m y kx m =+⎧⎨=+⎩221212(1)()0k x x mk x x m ++++=2222220y kx m b x a y a b =+⎧⎨+-=⎩y 22222222(2)0b x a k x kmx m a b +++-=222222222()2()0b a k x kma x a m a b +++-=0∆>2122222222122222kma x x b a k a m a bx x b a k ⎧-+=⎪⎪+⎨-⎪=⎪+⎩2222222222222222222222a m a m k a b a b k k m a m b a k m b a k+--++++22222222()0m a b a b a b k +--=222(1)m k r =+2m 2222222(1)()(1)k r a b a b k ++=+222111a b r +=,,a b r 222111a b r +=2'221(1)()1a x ax f x x x x --+=--=(0,)x ∈+∞210x ax -+=(2,)x ∈+∞1a x x=+(2,)x ∈+∞由在上单调递增，得. 检验：当时，在上存在极值点. ∴. （2）若，∵在上满足， ∴在上单调递减，∴.∴不存在最大值.则.∴方程有两个不相等的正实数根，令其为，且不妨设则.在上单调递减，在上调递增，在上单调递减，对，有；对，有，∴.∴ . 将，代入上式，消去得 ∵，∴，. 1y x x =+(2,)x ∈+∞15(,)2x x +∈+∞52a >()f x (2,)x ∈+∞5(,)2a ∈+∞02a <≤2'2(1)()x ax f x x --+=(0,)+∞'()0f x ≤()f x (0,)+∞21()()0f x f x -<21()()f x f x -2a >210x ax -+=,m n 01m n <<<1m n a mn +=⎧⎨=⎩()f x (0,)m (,)m n (,)n +∞1(0,1)x ∀∈1()()f x f m ≥2(1,)x ∀∈+∞2()()f x f n ≤21max [()()]()()f x f x f n f m -=-11()()()(ln )(ln )M a f n f m a n n a m m n m=-=-+--+11ln ()()n a m n m n m=+-+-1a m n n n =+=+1m n=,a m 21111()()ln 2()2[()ln ()]M a n n n n n n n n n n=++-=++-12a e e <≤+11n e n e+≤+1n >据在上单调递增，得. 设，.，. ∴，即在上单调递增.∴ ∴存在最大值为. 22.解：（1）曲线的普通方程为，曲线的极坐标方程为. 化简，得. 由，得∵，∴. （2）射线的极坐标方程为，直线的普通方程为. ∴直线的极坐标方程为.联立，解得. 1y x x=+(1,)x ∈+∞(1,]n e∈11()2()ln 2()h x x x xx x =++-(1,]x e ∈'22211111()2(1)ln 2()2(1)2(1)ln h x x x x x x x x x =-++++--=-(1,]x e ∈'()0h x >()h x (1,]e max 114[()]()2()2()h x h e e e e e e==++-=()M a 4eC 22(2)4x y +-=C 22(cos )(sin 2)4ρθρθ+-=4sin ρθ=ρ=sin θ=(,)2πθπ∈23πθ=OA 23πθ=l 0x +-=l cos sin 0ρθθ+-=23cos sin 0πθρθθ⎧=⎪⎨⎪-=⎩ρ=∴.23.解：（1）根据绝对值的几何意义，得表示点到，两点距离之和.接下来找出到距离之和为4的点.将点向左移动个单位到点，这时有；同理，将点向右移动个单位到点，这时有. ∴，即的解集为. （2）令，由柯西不等式，得即 ∵ ∴. 上述不等式当且仅当，即，，时，取等号. ∴的最小值为. B A AB ρρ=-==333()40222f x x x +=-+--≥3322x x ++-(,0)x 3(,0)2A -3(,0)2B ,A B A 121(2,0)A -114A A A B +=B 121(2,0)B 114B A B B +=33422x x ++-≤3()02f x +≥[2,2]-1a =2a 3a =2222222123123123123111111[()()()]()()a a a a a a a a a a a a ++•++≥•+•+•111()(32)932p q r p q r++++≥111432p q r++=9324p q r ++≥1114323p q r +==14p =38q =34r =32p q r ++94。

2018年高三最新成都市2018届高中毕业班第二次诊断性检测题数学(理科) 精品

成都市2018届高中毕业班第二次诊断性检测题数学（理科）注意事项：全卷满分为150分，完成时间为120分钟. 表示球的半径其中）（）（，率是在一次试验中发生的概如果事件球的体积公式）（）（）（表示球的半径其中相互独立，那么、如果事件）（）（）（球的表面积公式，那么互斥、参考公式：如果事件R P P C k P R V P A B P A P B A P R B A R S B P A P B A P B A kn k k n n --==⋅=⋅=+=+134432ππ第Ⅰ卷（选择题，共60分）一、选择题：本题共有12个小题，每小题5分；在每小题给出的四个选项中，只有一项是符合题目要求的，把正确选项的代号填在机读卡的指定位置上。

必要条件甲是乙的既不充分也不、、甲是乙的充要条件件甲是乙的必要不充分条、条件、甲是乙的充分不必要），那么（乙：，命题甲：是非空集合，命题、已知、D C B A B A B B A B A ≠⊂=⋃1项项或第第、项第、项第、项第、）项为（展开式中，系数最大的）（、65543129D C B A x -32331203、、、、）的最短距离为（么这两个切点在球面上两点，那、两个半平面于的球，该球切二面角的半径为的二面角内，放置一个在、D C B A B A πππ︒2202214150sin 02cos .234-⎪⎭⎫ ⎝⎛-⎪⎩⎪⎨⎧<≤⎪⎭⎫⎝⎛<≤-=、、、、）等于（则，）（，，，）（若的函数，最小正周期为是定义域为）（设、D C B A f x x x x x f R x f ππππ 不存在、、、、）的值等于（、D C B A x x x 210211211lim 521-⎪⎪⎭⎫ ⎝⎛---→156521326132423}{61310753、、、、）项之和等于（则此数列的前，）（）（中，在等差数列、D C B A a a a a a a n =++++1323||.3||||47、、、、）的最小值为（则满足的中点，动点为线段，，其长度为段已知平面内有一固定线、D C B A PO PB PA P AB O AB =-），（、），（、），（、），（、）的解集为（不等式、1211010|log ||log |82121D C B A x x x x ∞+∞++<-9、质点P 在半径为r 的圆周上逆时针作匀角速运动，角速度为1rad / s . 设A 为起点，那么在t 时刻，点P 在x轴上射影点M 的速度为（）A 、rsintB 、－rsintC 、rcostD 、－rcost 1101110024102-<>=-<>>==+=-k k k D k k C k k B k A k kx x x 或或、或、或、、）的值为（只有一个实数根，则的方程若关于、11、如图，A 、B 、C 、D 为湖中4个小岛，准备修建3座桥把这4个小岛连接起来，若不考虑建桥费用等因素，则不同的建桥方案有（）A 、24种B 、28种C 、16种D 、12种不存在、、、、）的最大值为（，则，且若、D C B A y x y x x y 643tan 3tan 2012ππππ-=<≤<第Ⅱ卷（非选择题，共90分）二、填空题：（本大题共4小题，每小题4分，共16分）把答案填在题中横线上。

【高三数学试题精选】2018年高考数学二诊试卷(成都市理科带答案和解释)

2018年高考数学二诊试卷（成都市理科带答案和解释）
5 c 5不等式选讲]
23．已知函数f（x）=4﹣|x|﹣|x﹣3|
（Ⅰ）求不等式f（x+ ）≥0的解集；
（Ⅱ）若p，q，r为正实数，且 + + =4，求3p+2q+r的最小值．
5不等式选讲]
23．（2018 成都模拟）已知函数f（x）=4﹣|x|﹣|x﹣3|
（Ⅰ）求不等式f（x+ ）≥0的解集；
（Ⅱ）若p，q，r为正实数，且 + + =4，求3p+2q+r的最小值．【考点】绝对值三角不等式；绝对值不等式的解法．
【分析】（I）由题意，分类讨论，去掉绝对值，解不等式即可；
（Ⅱ）运用柯西不等式，可3p+2q+r的最小值．
【解答】解（Ⅰ）f（x+ ）≥0，即|x+ |+|x﹣|≤4，
x≤﹣，不等式可化为﹣x﹣﹣x+ ≤4，∴x≥﹣2，∴﹣2≤x≤﹣；
﹣＜x＜，不等式可化为x+ ﹣x+ ≤4恒成立；
x≥ ，不等式可化为x+ +x﹣≤4，∴x≤2，∴ ≤x≤2，
综上所述，不等式的解集为[﹣2，2]；
（Ⅱ）∵（ + + ）（3p+2q+r）≥（1+1+1）2=9， + + =4
∴3p+2q+r≥ ，∴3p+2q+r的最小值为．
【点评】本题考查不等式的解法，考查运用柯西不等式，考查运算和推理能力，属于中档题．
5 c。

四川省成都市2018届高三数学二诊试卷理科含解析

2018年四川省成都市高考数学二诊试卷（理科）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A={x|y=}，B={x||x|≤2}，则A∪B=（）A．[﹣2，2] B．[﹣2，4] C．[0，2]D．[0，4]2．函数f（x）=2x+x﹣2的零点所在区间是（）A．（﹣∞，﹣1）B．（﹣l，0）C．（0，1）D．（1，2）3．复数z=（其中i为虚数单位）的虚部是（）A．﹣1 B．﹣i C．2i D．24．已知某几何体的正视图和侧视图均如图所示，则该几何体的俯视图不可能为（）A． B．C．D．5．将函数f（x）=cos（x+）图象上所有点的横坐标缩短为原来的倍，纵坐标不变，得到函数g（x）的图象，则函数g（x）的一个减区间是（）A．[﹣，] B．[﹣，]C．[﹣，]D．[﹣，]6．某校高三（1）班在一次单元测试中，每位同学的考试分数都在区间[100，128]内，将该班所有同学的考试分数分为七组：[100，118），[118，118），[118，112），[112，116），[116，120），[120，124），[124，128]，绘制出频率分布直方图如图所示，已知分数低于112分的有18人，则分数不低于120分的人数为（）A．10 B．12 C．20 D．407．某微信群中甲、乙、丙、丁、卯五名成员同时抢4个红包，每人最多抢一个，且红包被全部抢光，4个红包中有两个2元，两个3元（红包中金额相同视为相同的红包），则甲乙两人都抢到红包的情况有（）A．35种B．24种C．18种D．9种8．在三棱锥P﹣ABC中，已知PA⊥底面ABC，AB⊥BC，E，F分别是线段PB，PC上的动点．则下列说法错误的是（）A．当AE⊥PB时，△AEF﹣定为直角三角形B．当AF⊥PC时，△AEF﹣定为直角三角形C．当EF∥平面ABC时，△AEF﹣定为直角三角形D．当PC⊥平面AEF时，△AEF﹣定为直角三角形9．已知函数f（x）=，则不等式f（f（x））＜4f（x）+1的解集是（）A．（﹣3，0）B．（﹣，1）C．（0，2）D．（﹣，log32）10．已知抛物线y=x2的焦点为F，经过y轴正半轴上一点N作直线l与抛物线交于A，B两点，且=2（O为坐标原点），点F关于直线OA的对称点为C，则四边形OCAB面积的最小值为（）A．3 B．C．2D．二、填空题：本大题共5小题，每小题5分，共25分．11．已知双曲线=1的右焦点为（3，0），则该双曲线的离心率等于______．12．的展开式中，x2项的系数为______．（用数字作答）13．已知实数x，y满足，则x2+y2﹣2x的取值范围是______．14．执行如图所示的程序框图，输出的S的值为______15．已知函数f（x）=x+sin2x．给出以下四个命题：①∀x＞0，不等式f（x）＜2x恒成立；②∃k∈R，使方程f（x）=k有四个不相等的实数根；③函数f（x）的图象存在无数个对称中心；④若数列{a n}为等差数列，且f（a l）+f（a2）+f（a3）=3π，则a2=π．其中的正确命题有______．（写出所有正确命题的序号）三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．16．在△ABC中，内角A，B，C所对的边分别为a，b，c．已知a=，且b2+c2=3+bc．（I）求角A的大小；（Ⅱ）求bsinC的最大值．17．已知数列{a n}满足a1=1，（n+1）a n=（n﹣1）a n，（n≥2，n∈N*）．﹣1（I）求数列{a n}的通项公式a n；（Ⅱ）设数列{a n}的前n项和为S n．证明：S n＜2．18．某商场举行购物抽奖活动，抽奖箱中放有除编号不同外，其余均相同的20个小球，这20个小球编号的茎叶图如图所示，活动规则如下：从抽奖箱中随机抽取一球，若抽取的小球编号是十位数字为l的奇数，则为一等奖，奖金100元；若抽取的小球编号是十位数字为2的奇数，则为二等奖，奖金50元；若抽取的小球是其余编号则不中奖．现某顾客有放回的抽奖两次，两次抽奖相互独立．（I）求该顾客在两次抽奖中恰有一次中奖的概率；（Ⅱ）记该顾客两次抽奖后的奖金之和为随机变量X，求X的分布列和数学期望．19．如图．在三棱柱ABC﹣A1B1C1中，已知侧棱与底面垂直，∠CAB=90°，且AC=1，AB=2，E为BB1的中点，M为AC上一点，=．（I）证明：CB1∥平面A1EM；（Ⅱ）若二面角C1﹣A1E﹣M的余弦值为，求AA1的长度．20．已知椭圆C：=1（a＞b＞0）的左右焦点分别为F1，F2，抛物线y2=4x与椭圆C有相同的焦点，点P为抛物线与椭圆C在第一象限的交点，且|PF1|=．（I）求椭圆C的方程；（Ⅱ）与抛物线相切于第一象限的直线l，与椭圆交于A，B两点，与x轴交于M点，线段AB的垂直平分线与y轴交于N点，求直线MN斜率的最小值．21．设函数f（x）=lnx．（I）求函数g（x）=x﹣1﹣f（x）的极小值；（Ⅱ）若关于x的不等式mf（x）≥在[1，+∞）上恒成立，求实数m的取值范围；（Ⅲ）已知a∈（0，），试比较f（tana）与﹣cos2a的大小，并说明理由．2018年四川省成都市高考数学二诊试卷（理科）参考答案与试题解析一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A={x|y=}，B={x||x|≤2}，则A∪B=（）A．[﹣2，2] B．[﹣2，4] C．[0，2]D．[0，4]【考点】并集及其运算．【分析】求出集合的等价条件，根据集合的基本运算进行求解即可．【解答】解：A={x|y=}={x|4x﹣x2≥0}={x|0≤x≤4}，B={x||x|≤2}={x|﹣2≤x≤2}，则A∪B={x|﹣2≤x≤4}，故选：B．2．函数f（x）=2x+x﹣2的零点所在区间是（）A．（﹣∞，﹣1）B．（﹣l，0）C．（0，1）D．（1，2）【考点】函数零点的判定定理．【分析】据函数零点的判定定理，判断f（﹣1），f（0），f（1），f（2）的符号，即可求得结论．【解答】解：f（﹣1）=2﹣1+1﹣2=﹣＜0，f（0）=﹣1＜0，f（1）=1＞0，f（2）=4＞0，故有f（0）•f（1）＜0，由零点的存在性定理可知：函数f（x）=2x+x﹣2的零点所在的区间是（0，1）故选：C．3．复数z=（其中i为虚数单位）的虚部是（）A．﹣1 B．﹣i C．2i D．2【考点】复数代数形式的乘除运算．【分析】利用复数的化数形式的乘除运算法则求解．【解答】解：∵z=====1+2i，∴复数z=（其中i为虚数单位）的虚部是2．故选：D．4．已知某几何体的正视图和侧视图均如图所示，则该几何体的俯视图不可能为（）A． B．C．D．【考点】简单空间图形的三视图．【分析】几何体为椎体与柱体的组合体，分四种情况进行判断．【解答】解：由主视图和侧视图可知几何体为椎体与柱体的组合体，（1）若几何体为圆柱与圆锥的组合体，则俯视图为A，（2）若几何体为棱柱与圆锥的组合体，则俯视图为B，（3）若几何体为棱柱与棱锥的组合体，则俯视图为C，（4）若几何体为圆柱与棱锥的组合体，则俯视图为故选：D．5．将函数f（x）=cos（x+）图象上所有点的横坐标缩短为原来的倍，纵坐标不变，得到函数g（x）的图象，则函数g（x）的一个减区间是（）A．[﹣，] B．[﹣，]C．[﹣，]D．[﹣，]【考点】函数y=Asin（ωx+φ）的图象变换．【分析】根据三角函数的图象变换关系求出g（x）的解析式，结合三角函数的单调性进行求解即可．【解答】解：将函数f（x）=cos（x+）图象上所有点的横坐标缩短为原来的倍，纵坐标不变，则y=cos（2x+），即g（x）=cos（2x+），由2kπ≤2x+≤2kπ+π，k∈Z，得kπ﹣≤x≤kπ+，k∈Z，即函数的单调递减区间为[kπ﹣，kπ+]，k∈Z，当k=0时，单调递减区间为[﹣，]，故选：D．6．某校高三（1）班在一次单元测试中，每位同学的考试分数都在区间[100，128]内，将该班所有同学的考试分数分为七组：[100，118），[118，118），[118，112），[112，116），[116，120），[120，124），[124，128]，绘制出频率分布直方图如图所示，已知分数低于112分的有18人，则分数不低于120分的人数为（）A．10 B．12 C．20 D．40【考点】频率分布直方图．【分析】由频率分布直方图求出得分数低于112分的频率，从而求出高三（1）班总人数，再求出分数不低于120分的频率，由此能求出分数不低于120分的人数．【解答】解：由频率分布直方图得分数低于112分的频率为：（0.01+0.18+0.18）×4=0.36，∵分数低于112分的有18人，∴高三（1）班总人数为：n==50，∵分数不低于120分的频率为：（0.18+0.18）×4=0.2，∴分数不低于120分的人数为：50×0.2=10人．故选：A．7．某微信群中甲、乙、丙、丁、卯五名成员同时抢4个红包，每人最多抢一个，且红包被全部抢光，4个红包中有两个2元，两个3元（红包中金额相同视为相同的红包），则甲乙两人都抢到红包的情况有（）A．35种B．24种C．18种D．9种【考点】计数原理的应用．【分析】根据红包的性质进行分类，若甲乙抢的是一个2和一个3元的，若两个和2元或两个3元，根据分类计数原理可得．【解答】解：若甲乙抢的是一个2和一个3元的，剩下2个红包，被剩下的3人中的2个人抢走，有A22A32=12种，若甲乙抢的是两个和2元或两个3元的，剩下2个红包，被剩下的3人中的2个人抢走，有A22C32=6种，根据分类计数原理可得，共有12+6=18种，故选：C．8．在三棱锥P﹣ABC中，已知PA⊥底面ABC，AB⊥BC，E，F分别是线段PB，PC上的动点．则下列说法错误的是（）A．当AE⊥PB时，△AEF﹣定为直角三角形B．当AF⊥PC时，△AEF﹣定为直角三角形C．当EF∥平面ABC时，△AEF﹣定为直角三角形D．当PC⊥平面AEF时，△AEF﹣定为直角三角形【考点】棱锥的结构特征．【分析】A．当AE⊥PB时，又PA⊥底面ABC，AB⊥BC，可得AE⊥BC，利用线面垂直的判定与性质定理可得AE⊥EF，即可判断出正误．B．当AF⊥PC时，无法得出△AEF﹣定为直角三角形，即可判断出正误；C．当EF∥平面ABC时，可得EF∥BC，利用线面垂直的判定与性质定理可得：BC⊥AE，EF⊥AE，即可判断出正误；D．当PC⊥平面AEF时，可得PC⊥AE，由C可知：BC⊥AE利用线面垂直的判定与性质定理即可判断出正误．【解答】解：A．当AE⊥PB时，又PA⊥底面ABC，AB⊥BC，∴AE⊥BC，可得：AE⊥平面PBC，∴AE⊥EF，∴△AEF﹣定为直角三角形，正确．B．当AF⊥PC时，无法得出△AEF﹣定为直角三角形，因此不正确；C．当EF∥平面ABC时，平面PBC∩ABC=BC，可得EF∥BC，∵PA⊥底面ABC，AB⊥BC，∴BC⊥平面PAB，∴BC⊥AE，因此EF⊥AE，则△AEF﹣定为直角三角形，正确；D．当PC⊥平面AEF时，可得PC⊥AE，由C可知：BC⊥AE，∴AE⊥平面PBC，∴AE ⊥EF，因此△AEF﹣定为直角三角形，正确．故选：B．9．已知函数f（x）=，则不等式f（f（x））＜4f（x）+1的解集是（）A．（﹣3，0）B．（﹣，1）C．（0，2）D．（﹣，log32）【考点】分段函数的应用．【分析】根据分段函数的表达式，讨论f（x）的符号，将不等式进行转化求解即可．【解答】解：由3x+1=0得x=﹣，当x＜﹣时，3x+1＜0，则由f（f（x））＜4f（x）+1得f（3x+1））＜4（3x+1）+1，即3（3x+1）+1＜12x+4+1，即9x+4＜12x+5，得x＞﹣，此时不等式无解，当x≥﹣时，当x≥0时，f（x）=3x≥1，则由f（f（x））＜4f（x）+1得＜4•3x+1，设t=3x，则不等式等价为3t＜4t+1，设g（t）=3t﹣4t﹣1，则g（0）=0，g（2）=9﹣8﹣1=0，即g（t）＜0的解为0＜t＜2，即0＜3x＜2，得0≤x＜log32，当﹣≤x＜0时，f（x）=3x+1≥0，则f（f（x））=33x+1，则由f（f（x））＜4f（x）+1得33x+1＜4（3x+1）+1，设t=3x+1，则不等式等价为3t＜4t+1，设g（t）=3t﹣4t﹣1，则g（0）=0，g（2）=9﹣8﹣1=0，即g（t）＜0的解为0＜t＜2，即0＜3x+1＜2，即﹣1＜3x＜1，得﹣＜x＜，此时﹣＜x＜0，综上所述，﹣＜x＜log32．即不等式的解集为（﹣，log32），故选：D10．已知抛物线y=x2的焦点为F，经过y轴正半轴上一点N作直线l与抛物线交于A，B两点，且=2（O为坐标原点），点F关于直线OA的对称点为C，则四边形OCAB面积的最小值为（）A．3 B．C．2D．【考点】抛物线的简单性质．【分析】先设直线AB方程为y=kx+b（b＞0），联立y=x2求解利用=2，求出b，可得直线AB方程为y=kx+2，设d1、d2分别为F到OA、O到AB的距离，利用四边形OCAB的面积S=S△OAC+S△OAB=（OA•d1+AB•d2），可得S关于k的函数，利用导数知识即可求解．【解答】解：不妨设位于第一象限的交点为A（x1，y1）、第二象限的交点为B（x2，y2），则x1＞0，x2＜0．OA的直线方程为y=x=x1x，F点的坐标为（0，）．设直线AB方程为y=kx+b（b＞0），联立y=x2求解，有x2﹣kx﹣b=0∴x1+x2=k，x1x2=﹣b，∴y1y2=b2，∵=2，∴x1x2+y1y2=﹣b+b2=2∵b＞0，∴b=2∴△=k2+8，x1=（k+）①；线段AB=②．设d1、d2分别为F到OA、O到AB的距离．∵C是F关于OA的对称点，∴C到OA的距离=d1．∴四边形OCAB的面积S=S△OAC+S△OAB=（OA•d1+AB•d2）．根据点到直线距离公式，d1=③，d2=④．又线段OA=⑤，∴将①～⑤代入S，有S=（k+17）．由S对k求导，令导函数=0，可得1+=0，解得k=﹣时，S最小，其值为3．故选：A．二、填空题：本大题共5小题，每小题5分，共25分．11．已知双曲线=1的右焦点为（3，0），则该双曲线的离心率等于．【考点】双曲线的简单性质．【分析】利用双曲线=1的右焦点为（3，0），求出|a|，再利用双曲线的定义，即可求出双曲线的离心率．【解答】解：∵双曲线=1的右焦点为（3，0），∴a2+5=9，∴|a|=2，∵c=3，∴双曲线的离心率等于．故答案为：．12．的展开式中，x2项的系数为﹣20．（用数字作答）【考点】二项式定理的应用．【分析】先求出二项式展开式的通项公式，再令x的幂指数等于2，求得r的值，即可求得展开式中的x2项的系数．【解答】解：在的展开式中，它的通项公式为T r+1=•x5﹣r•（﹣1）r，令5﹣r=2，求得r=3，可得x2项的系数为﹣=﹣20，故答案为：﹣20．13．已知实数x，y满足，则x2+y2﹣2x的取值范围是[﹣1，19] ．【考点】简单线性规划．【分析】画出满足条件的平面区域，求出角点的坐标，而（x﹣1）2+y2的几何意义表示平面区域内的点与（1，0）的点距离的平方，求出（x﹣1）2+y2的范围，从而求出x2+y2﹣2x的范围即可．【解答】解：画出满足条件的平面区域，如图示：由，解得A（3，4），x2+y2﹣2x=（x﹣1）2+y2﹣1，而（x﹣1）2+y2的几何意义表示平面区域内的点与（1，0）的点距离的平方，0≤（x﹣1）2+y2≤20，∴﹣1≤（x﹣1）2+y2≤19，故答案为：[﹣1，19]．14．执行如图所示的程序框图，输出的S的值为【考点】程序框图．【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量S的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．【解答】解：模拟执行程序，可得该程序的功能是利用循环结构计算并输出变量S=•tan•tan…tan的值．由于：S=•tan•tan…tan tan=•tan•tan…cot•cot=tan=．故答案为：．15．已知函数f（x）=x+sin2x．给出以下四个命题：①∀x＞0，不等式f（x）＜2x恒成立；②∃k∈R，使方程f（x）=k有四个不相等的实数根；③函数f（x）的图象存在无数个对称中心；④若数列{a n}为等差数列，且f（a l）+f（a2）+f（a3）=3π，则a2=π．其中的正确命题有③④．（写出所有正确命题的序号）【考点】函数的图象．【分析】①用特殊值的方法即可；②③根据函数图象判断；④可用反代的方法判断成立．【解答】解：①当x=时，显然f（x）＞2x，故错误；②根据函的图象易知，方程f（x）=k最多有三个不相等的实数根，故错误；③根据函数的图象易知函数f（x）的图象存在无数个对称中心，故正确；④f（a l）+f（a2）+f（a3）=3π，∴a l+a2+a3=3π，sina l+sina2+sina3=0，解得a2=π，故正确．故答案为：③④．三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．16．在△ABC中，内角A，B，C所对的边分别为a，b，c．已知a=，且b2+c2=3+bc．（I）求角A的大小；（Ⅱ）求bsinC的最大值．【考点】余弦定理；正弦定理．【分析】（I）由余弦定理可得：cosA===，即可得出．（II）由正弦定理可得：可得b=，可得bsinC=2sinBsin=+，根据B∈即可得出．【解答】解：（I）由余弦定理可得：cosA===，∵A∈（0，π），∴A=．（II）由正弦定理可得：，可得b=，bsinC=•sinC=2sinBsin=2sinB=sin2B+=+，∵B∈，∴∈．∴∈．∴bsinC∈．17．已知数列{a n}满足a1=1，（n+1）a n=（n﹣1）a n，（n≥2，n∈N*）．﹣1（I）求数列{a n}的通项公式a n；（Ⅱ）设数列{a n}的前n项和为S n．证明：S n＜2．【考点】数列的求和；数列递推式．【分析】（Ⅰ）依题意，可得a n=••…×××a1=，再验证n=1时是否符合该式即可得到答案，（Ⅱ）先裂项求和，再放缩法证明即可．【解答】解：（Ⅰ）∵a1=1，（n+1）a n=（n﹣1）a n，﹣1∴=，∴=，…，==，==，∴a n=••…×××a1=，又n=1时a1=1，满足上式，∴数列{a n}的通项公式a n=，（Ⅱ）∵a n==2（﹣），∴S n=a1+a2+…+a n=2（1﹣+﹣+…+﹣）=2（1﹣）＜2，问题得以证明．18．某商场举行购物抽奖活动，抽奖箱中放有除编号不同外，其余均相同的20个小球，这20个小球编号的茎叶图如图所示，活动规则如下：从抽奖箱中随机抽取一球，若抽取的小球编号是十位数字为l的奇数，则为一等奖，奖金100元；若抽取的小球编号是十位数字为2的奇数，则为二等奖，奖金50元；若抽取的小球是其余编号则不中奖．现某顾客有放回的抽奖两次，两次抽奖相互独立．（I）求该顾客在两次抽奖中恰有一次中奖的概率；（Ⅱ）记该顾客两次抽奖后的奖金之和为随机变量X，求X的分布列和数学期望．【考点】离散型随机变量的期望与方差；茎叶图；列举法计算基本事件数及事件发生的概率；离散型随机变量及其分布列．【分析】（Ⅰ）设一次抽奖抽中i等奖的概率为P i（i=1，2），没有中奖的概率为P0，由此能求出该顾客两次抽奖中恰有一次中奖的概率．（Ⅱ）X的可能取值为0，50，100，150，200，分别求出相应的概率，由此能求出X的分布列和EX．【解答】解：（Ⅰ）设一次抽奖抽中i等奖的概率为P i（i=1，2），没有中奖的概率为P0，则P1+P2==，即中奖的概率为，∴该顾客两次抽奖中恰有一次中奖的概率为：P==．（Ⅱ）X的可能取值为0，50，100，150，200，P（X=0）=，P（X=50）==，P（X=100）==，P（X=150）==，P（X=200）==，X∴EX==55（元）．19．如图．在三棱柱ABC﹣A1B1C1中，已知侧棱与底面垂直，∠CAB=90°，且AC=1，AB=2，E为BB1的中点，M为AC上一点，=．（I）证明：CB1∥平面A1EM；（Ⅱ）若二面角C1﹣A1E﹣M的余弦值为，求AA1的长度．【考点】二面角的平面角及求法；直线与平面平行的判定．【分析】（I）建立空间直角坐标系，利用向量关系求出F的坐标，根据线面平行的判定定理即可证明证明：CB1∥平面A1EM；（Ⅱ）建立空间直角坐标系，求出平面的法向量，利用向量法进行求解即可．【解答】（I）如图，连接AB1，交A1E于F，连接MF，∵E为BB1的中点，∴建立以A为坐标原点，AB，AC，AA1分别为x，y，z轴的空间直角坐标系如图：设AA1=h，则A（0，0，0），C1（0，1，h），A1（0，0，h），E（2，0，），M（0，，0），B1（2，0，h），设F（x，0，z），则∥，∥，∵=（x，0，z），=（2，0，h），∴①∵=（x，0，z﹣h），=（2，0，﹣），∴=②，由①②得z=h，x=，或F作FT⊥AB，则==，则∴AF=AB1，∵=．∴MF∥CB1，∵MF⊂平面平面A1EM，CB1⊄平面A1EM，∴CB1∥平面A1EM；（Ⅱ）设平面C1A1E的法向量为=（x，y，z），平面MA1E的法向量为=（x，y，z），则，则，令z=1，则x=，y=0，则=（，0，1），由得，令z=1，则x=，y=，即=（，，1）|cos＜，＞|==，得h2=2，即h=，则AA1的长度为．20．已知椭圆C：=1（a＞b＞0）的左右焦点分别为F1，F2，抛物线y2=4x与椭圆C有相同的焦点，点P为抛物线与椭圆C在第一象限的交点，且|PF1|=．（I）求椭圆C的方程；（Ⅱ）与抛物线相切于第一象限的直线l，与椭圆交于A，B两点，与x轴交于M点，线段AB的垂直平分线与y轴交于N点，求直线MN斜率的最小值．【考点】椭圆的简单性质．【分析】（I）求得抛物线的焦点，可得c=1，设P为（，m），由椭圆的焦半径公式可得，|PF1|=a+•=，由椭圆和抛物线的定义可得，2a=++1，解方程可得a=2，由a，b，c的关系，可得b，进而得到椭圆方程；（Ⅱ）设直线l的方程为y=kx+b（k＞0），代入抛物线的方程，由判别式为0，可得kb=1，再由椭圆方程联立，运用韦达定理和判别式大于0，结合中点坐标公式和直线的斜率公式，以及基本不等式即可得到所求最小值．【解答】解：（I）抛物线y2=4x的焦点为（1，0），可得椭圆的c=1，设P为（，m），由椭圆的焦半径公式可得，|PF1|=a+•=，由椭圆和抛物线的定义可得，2a=++1，解得a=2，b==，即有椭圆的方程为+=1；（Ⅱ）设直线l的方程为y=kx+b（k＞0），代入抛物线的方程，可得k2x2+（2kb﹣4）x+b2=0，由相切的条件可得，△=（2kb﹣4）2﹣4k2b2=0，化简可得kb=1，由y=kx+和椭圆方程3x2+4y2=12，可得（3+4k2）x2+8x+﹣12=0，由64﹣4（3+4k2）（﹣12）＞0，可得k＞，设A（x1，y1），B（x2，y2），可得x1+x2=﹣，即有中点坐标为（﹣，），设N（0，n），由=﹣，可得n=﹣，由y=kx+，设y=0，则x=﹣，M（﹣，0），可得直线MN的斜率为k MN==﹣=﹣≥﹣=﹣．当且仅当k=＞时，取得最小值﹣．21．设函数f（x）=lnx．（I）求函数g（x）=x﹣1﹣f（x）的极小值；（Ⅱ）若关于x的不等式mf（x）≥在[1，+∞）上恒成立，求实数m的取值范围；（Ⅲ）已知a∈（0，），试比较f（tana）与﹣cos2a的大小，并说明理由．【考点】利用导数求闭区间上函数的最值；利用导数研究函数的单调性．【分析】（I）求导数，确定函数的单调性，即可求函数g（x）=x﹣1﹣f（x）的极小值；（Ⅱ）mf（x）≥可化为mlnx﹣≥0，构造函数，得出m（x+1）2﹣2x≥0在[1，x0]上恒成立，即可求实数m的取值范围；（Ⅲ）已知a∈（0，），证明＜，分类讨论，即可比较f（tana）与﹣cos2a的大小．【解答】解：（I）函数g（x）=x﹣1﹣f（x）=x﹣1﹣lnx，g′（x）=（x＞0），∴g（x）在（0，1）上单调递减，（1，+∞）上单调递增，∴x=1时，g（x）的极小值为0；（Ⅱ）mf（x）≥可化为mlnx﹣≥0，令h（x）=mlnx﹣（x≥1），则h′（x）=，∵h（1）=0，∴∃x0＞1，h（x）在[1，x0]上单调递增，∴m（x+1）2﹣2x≥0在[1，x0]上恒成立，∴m≥；（Ⅲ）由（Ⅱ）可知x＞1，＞．∵0＜x＜1，∴＞1∴＞，∴＜，令x=t2，可得t＞1，lnt＞，0＜t＜1，lnt＜，∵f（tana）=lntana，﹣cos2a=，∴0＜a＜，0＜tana＜1，f（tana）＜﹣cos2aa=，tana﹣1，f（tana）=﹣cos2a，＜a＜，tana＞1，f（tana）＞﹣cos2a．2018年9月20日。

2018级成都二诊参考答案

藉田
古代吉礼的一种。古代天子、诸侯征用民力耕种的田。相传天子籍田千亩，诸侯百亩。每逢孟春正月，春耕前，由天子率诸侯诸侯亲自执耒耜在籍田上三推或一拨，称为“籍礼”，寓有重视农耕之意。亦指天子示范性的耕作。它是“祈年”(祈求丰收)的礼俗之一。又称“亲耕”。
旧制，宰相以（在）未时归第，是岁大热，特许普夏中（夏季）至午时归私第。淳化三年春，以老衰久病，令留守通判刘昌言奉表求致政（官吏将执政的权柄归还给君主。解除政务职责，辞官退休），中使（内廷的使者，多指宦官）驰传（①驾驭驿站车马疾行；②古代驿站的一种马车。驾四匹中等马）抚问，凡三上表乞骸骨。拜太师，封魏国公。令养疾，七月卒，年七十一。二女皆笄，普妻和氏言愿为尼，太宗再三谕（劝告）之，不能夺（改变）。
1、未读懂题干要求，不能合理分点。题干要求针对三次提问，找出两位受访者每次回答的各自的侧重点。那么应该分三点，针对第一第二第三次提问，分别说张的侧重点是什么，郭的侧重点是什么。但不少同学只分两点，回答张的侧重点有哪些哪些，郭的侧重点有哪些哪些。这Hale Waihona Puke 的回答分点不太合理，回答不够清楚。
2.不返回原文，细读内容，而是仅根据阅读后的大体印象，笼统随意作答。比如不少学生笼统回答说张侧重于政治、宏观、国家层面；郭侧重于经济、微观、企业自身层面。这就是完全没回原文细读，没抓住重点。
第六题问“面对主持人前三个提问，张、郭两位受访者回答的侧重点各有何不同？请结合材料简要分析。”题干限定明确，是面对主持人的“前三个提问”，帮助学生能够迅速锁定答题区间。题干指向清晰，是要求比较两位受访者的回答“侧重点各有何不同”，这里的 “侧重点”要求学生要能理解把握受访者答话的重点，“各”要求学生要分别说到两个人， “不同”二字提醒学生是求异而非求同。所以有的学生在答了二者的不同后又总结列两人的共同处，就是审题不清，画蛇添足。本次二诊，第六题满分6分，学生平均得分1.84分，难度系数0.31，是所有主观题中得分最低的一道题。

2018成都市高新区二诊数学试题答案.docx

2018年九年级第二次诊断性考试试题数学（满分150分，时间：120分钟）第Ⅰ卷A卷（100分）一、选择题（每小题3分，共30分, 在下面每一个小题给出的四个选项中，只有一项是正确的.）1．计算9的结果为（A）A．3B．﹣3C．6D．﹣92．下列运算正确的是（C）A．a+a=a2B．a3÷a=a3C．a2•a=a3D．（a2）3=a53．如图是由六个相同的小正方体搭成的几何体，这个几何体的主视图是（B）A．B．C．D．4．把0.0813写成a×10n（1≤a＜10，n为整数）的形式，则n为（ B ）A．1B．﹣2C．2D．8.135．谜语：干活两腿脚，一腿勤，一腿懒，一脚站，一脚转．打一数学学习用具，谜底为（D）A．量角器B．直尺C．三角板D．圆规6．在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示：成绩/m 1.50 1.60 1.65 1.70 1.75 1.80人数232341则这些运动员成绩的众数、极差分别为（C）A．1.70、0.25B．1.75、3C．1.75、0.30D．1.70、37．将抛物线y=﹣x2向左平移2个单位长度，再向下平移3个单位长度，则平移后所得到的抛物线解析式是（C）A．B．C．D．8．若关于x的一元二次方程（m﹣2）x2﹣2x+1=0有实根，则m的取值范围是（D）A．m＜3B．m≤3C．m＜3且m≠2D．m≤3且m≠29．如图：有一块含有45°的直角三角板的两个顶点放在直尺的对边上，如果∠1=20°，那么∠2的度数是（B）A．30°B．25°C．20°D．15°10．如图，正五边形ABCDE 内接于⊙O ，若⊙O 的半径为5，则的长度为（ B ）A ．πB ．2πC ．5πD ．10π第Ⅱ卷二、填空题（每小题4分，共16分） 11．因式分解：=++49142x x()27+x．12．如图，在“3×3”网格中，有3个涂成黑色的小方格．若再从余下的6个小方格中随机选取1个涂成黑色，则完成的图案为轴对称图案的概率是．13．如图，▱ABCD 中，点E 在边AD 上，以BE 为折痕，将△ABE 向上翻折，点A 正好落在CD 上的F 点，若△FDE 的周长为8 cm ，△FCB 的周长为20cm ，则FC 的长为 6 cm ．14. 把直线y=﹣x +3向上平移m 个单位后，与直线y=2x +4的交点在第一象限，则m 的取值范围是 m ＞1 ．三、解答题（本题共54分） 15. （每小题6分，共12分）（1）计算：()o45cos 2341|21|01--+⎪⎭⎫ ⎝⎛-+--π解：()分分分原式14-12141242221412⋯⋯=⋯⋯-+--=⋯⋯⨯-+-+-=（2）解不等式组()⎪⎩⎪⎨⎧-<-+-≥xx x x 613121，并把解集在数轴上表示出来．解：分分分1212211⋯⋯<≤-∴⋯⋯<⋯⋯-≥x 由②得:x 由①得：x将原不等式组解集在数轴上表示如下：数轴表示……2分16、（本小题6分）先化简，再求值：⎪⎭⎫⎝⎛---÷--225262x x x x ，其中12-=x ．解：()()()()()分分分原式132133223222452322⋯⋯+-=⋯⋯+--⨯---=⋯⋯⎪⎪⎭⎫⎝⎛---÷--=x x x x x x x x x x 分分原式时当1221312212⋯⋯-=⋯⋯+--=-=x17、（本小题8分）为了测量白塔的高度AB ，在D 处用高为1.5米的测角仪 CD ，测得塔顶A 的仰角为42°，再向白塔方向前进12米，又测得白塔的顶端A 的仰角为61°，求白塔的高度AB ．（参考数据sin42°≈0.67，tan42°≈0.90，sin61°≈0.87，tan61°≈1.80，结果保留整数）解：设AE=x ，在Rt △ACE 中，CE==1.1x ，………………………………2分在Rt △AFE 中，FE==0.55x ，………………………………2分由题意得，CF=CE ﹣FE=1.1x ﹣0.55x=12，………………………………2分解得：x=，………………………………1分故AB=AE +BE=+1.5≈23米．答：这个电视塔的高度AB 为23米．………………………………1分18、（本小题8分）某销售公司年终进行业绩考核，人事部门把考核结果按照A ，B ，C ，D 四个等级，绘制成两个不完整的统计图，如图1，图2．（1）参加考试人数是，扇形统计图中D 部分所对应的圆心角的度数是，请把条形统计图补充完整；（2）若考核为A 等级的人中仅有2位女性，公司领导计划从考核为A 等级的人员中选2人交流考核意见，请用树状图或表格法，求所选人员恰为一男一女的概率；（3）为推动公司进一步发展，公司决定计划两年内考核A 等级的人数达到30人，求平均每年的增长率．（精确到0.01，=2.236）解：（1）参加考试的人数是：24÷48%=50人；………………………………1分扇形统计图中D 部分所对应的圆心角的度数是：360°×=36°；…………………………………1分C 等级的人数是：50﹣24﹣15﹣5=6人，补图如下：………………………………1分故答案为：50，36；（2）树状图或表格因为共有20种可能，其中满足一男一女的情况有12种，………………………………2分 ∴P （一男一女）=532012 ；………………………………1分（3）设增长率是x ，依题意列方程得：24（1+x ）2=30，………………………………1分解得：x 1=﹣1+≈0.12，x 2=﹣1﹣（舍去），答：每年增长率为12%．………………………………1分19、（本小题10分）如图，已知A （3，m ），B （﹣2，﹣3）是直线AB 和某反比例函数的图象的两个交点．（1）求直线AB和反比例函数的解析式；（2）观察图象，直接写出当x满足什么范围时，直线AB在双曲线的下方；（3）反比例函数的图象上是否存在点C，使得△OBC的面积等于△OAB的面积？如果不存在，说明理由；如果存在，求出满足条件的所有点C的坐标．解：（1）设反比例函数解析式为y=，把B（﹣2，﹣3）代入，可得k=﹣2×（﹣3）=6，∴反比例函数解析式为y=；………………………………1分把A（3，m）代入y=，可得3m=6，即m=2，∴A（3，2），………………………………1分设直线AB 的解析式为y=ax+b，把A（3，2），B（﹣2，﹣3）代入，可得，解得，∴直线AB 的解析式为y=x﹣1；………………………………1分（2）由题可得，当x满足：x＜﹣2或0＜x＜3时，直线AB在双曲线的下方；…………………2分（3）存在点C．………………………………1分如图所示，延长AO交双曲线于点C1，∵点A与点C1关于原点对称，∴AO=C1O，∴△OBC1的面积等于△OAB的面积，此时，点C1的坐标为（﹣3，﹣2）；………………………………1分如图，过点C 1作BO 的平行线，交双曲线于点C 2，则△OBC 2的面积等于△OBC 1的面积， ∴△OBC 2的面积等于△OAB 的面积，由B （﹣2，﹣3）可得OB 的解析式为y=x ，可设直线C 1C 2的解析式为y=x +b'，把C 1（﹣3，﹣2）代入，可得﹣2=×（﹣3）+b'，………………………………1分解得b'=，∴直线C 1C 2的解析式为y=x +，解方程组，可得C 2（，）；………………………………1分如图，过A 作OB 的平行线，交双曲线于点C 3，则△OBC 3的面积等于△OBA 的面积，设直线AC 3的解析式为y=x +b“，把A （3，2）代入，可得2=×3+b“，解得b“=﹣，∴直线AC 3的解析式为y=x ﹣，解方程组，可得C 3（﹣，﹣）；………………………………1分综上所述，点C 的坐标为（﹣3，﹣2），（，），（﹣，﹣）．20、（本小题10分）如图， ⊙O ABC Rt ∆的外接圆，o90=∠C ，21tan =B ，过点B 的直线l 是 ⊙O 的切线，点D 是直线l 上一点，过点D 作CB DE ⊥交CB 延长线于点E ,连结AD ，交⊙O 于点F ,连结BF 、CD 交于点G.（1）ACB ∆∽BED ∆；（2）当AC AD ⊥时，求CGDG的值；（3）若CD 平分ACB ∠，AC =2，连结CF,求线段CF 的长.（1）分∽分分111⋯⋯∆∆⋯⋯∠=∠⋯⋯∠=∠BED ACB BDE ABC E ACB （2）分分∽分为矩形∽141124:2:1::⋯⋯=⋯⋯∆∆⋯⋯=∴∆∆CG DG GDF GCB BC DE BE ACED BED ACB （3）分分分15581454,5218,442⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯=∴⋯⋯⊥⇒==⇒==⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯===⇒=CF AB CF BC BF BD AB DE BE BC ACB 卷（50分）一、填空题（每小题4分，共20分）21.某班体育委员对本班学生一周锻炼时间（单位：小时）进行了统计，绘制了如图所示的折线统计图，则该班这些学生一周锻炼时间的中位数是 11 小时． 22.若⎩⎨⎧-==21b a 是关于b a ,的二元一次方程7=-+b ay ax 的一个解，代数式1222-++y xy x 的值是 24 ．23.如图，同心圆的半径为6cm ，8cm ，AB 为小圆的弦，CD 为大圆的弦，且ABCD 为矩形，若矩形ABCD 面积最大时，矩形ABCD 的周长为 39.2 cm ．24.如图，在矩形ABCD 中，将∠ABC 绕点A 按逆时针方向旋转一定角度后，BC 的对应边B'C'交CD 边于点G ．连接BB'、CC'．若AD=7，CG=4，AB'=B'G ，则=（结果保留根号）．25.在平面直角坐标系，对于点P （x ，y ）和Q （x ，y′），给出如下定义：若y′=，则称点Q 为点P 的“可控变点”．例如：点（1，2）的“可控变点”为点（1，2），点（﹣1，3）的“可控变点”为点（﹣1，﹣3）．点（﹣5，﹣2）的“可控变点”坐标为 3或﹣；若点P 在函数y=﹣x 2+16（﹣5≤x ≤a ）的图象上，其“可控变点”Q 的纵坐标y′的取值范围是﹣16≤y′≤16，实数a 的取值范围为__≤a ≤4．____________．二、解答题（本题共30分）26、（本小题8分）为进一步缓解城市交通压力，成都大力支持共享单车的推广，并规范共享单车定点停放，某校学生小明统计了周六校门口停车点各时段的借、还自行车数，以及停车点整点时刻的自行车总数（称为存量）情况，表格中x=1时的y 的值表示8：00点时的存量，x=2时的y 值表示9：00点时的存量…以此类推，他发现存量y （辆）与x （x 为整数）满足如图所示的一个二次函数关系．时段 x 还车数借车数存量y 7：00﹣8：00 1 7 5 15 8：00﹣9：002 8 7 n ……………根据所给图表信息，解决下列问题：（1）m=，解释m的实际意义：；（2）求整点时刻的自行车存量y与x之间满足的二次函数关系式；（3）已知10：00﹣11：00这个时段的还车数比借车数的2倍少4，求此时段的借车数．解：（1）m+7﹣5=15，m=13，………………………………1分则m的实际意义：7：00时自行车的存量；………………………………1分故答案为：13，7：00时自行车的存量；（2）由题意得：n=15+8﹣7=16，………………………………1分设二次函数的关系式为：y=ax2+bx+c，把（0，13）、（1，15）和（2，16）分别代入得：，………………………………1分解得：，∴y=﹣x2+x+13；………………………………1分（3）当x=3时，y=﹣×32+×3+13=16，………………………………1分当x=4时，y=﹣×42+×4=13=15，………………………………1分设10：00﹣11：00这个时段的借车数为x，则还车数为2x﹣4，根据题意得：16+2x﹣4﹣x=15，x=3，………………………………1分答：10：00﹣11：00这个时段的借车数为3辆．27、（本小题10分）在正六边形ABCDEF中，N、M为边上的点，BM、AN相交于点P（1）如图1，若点N在边BC上，点M在边DC上，BN=CM，求证：BP•BM=BN•BC；（2）如图2，若N为边DC的中点，M在边ED上，AM∥BN，求的值；（3）如图3，若N、M分别为边BC、EF的中点，正六边形ABCDEF的边长为2，请直接写出AP的长．（1）证明：在正六边形ABCDEF中，AB=BC，∠ABC=∠BCD=120°，………………………………1分∵BN=CM，∴△ABN≌△BCM，∴∠ANB=∠BMC，………………………………1分∵∠PBN=∠CBM，∴△BPN∽△BCM，∴=，∴BP•BM=BN•BC；………………………………1分（2）延长BC，ED交于点H，延长BN交DH于点G，取BG的中点K，连接KC，………………1分在正六边形ABCDEF中，∠BCD=∠CDE=120°，∴∠HCD=∠CDH=60°，∴∠H=60°，∴DC=DH=CH，∵DC=BC，∴CH=BC，∵BK=GK，∴2KC=GH，KC∥DH，………………………………1分∴∠GDN=∠KCN，∵CN=DN，∠DNG=∠CNK，∴△DNG≌△CNK，∴KC=DG，∴DG=DH=DE，∵MG∥AB，AM∥BG，∴四边形MABG是平行四边形，………………………………1分∴MG=AB=ED，∴ME=DG=DE，即=，………………………………1分（3）如图3，过N作NH⊥AB，交AB的延长线于H，………………………………1分∵∠ABC=120°，。

成都市2018级高三二诊数学(理)答案

→
４x１＋２y１＝０
m EC ＝０
,得
令z１＝１,得 m ＝ (
２,
１)．
－１,
→
z１＝０
－y１＋２
m EA ＝０
ìï２y２＝０
→
ï
nDE ＝０
,得 í４
由
令z２＝１,得 n ＝ (
０,
１)．
－１,
４
→
ï x２＋ z２＝０
nDF ＝０
３
î３
由
{
{
{
数学(理科)“二诊”考试题参考答案第
５分
在 Rt△ BMN 中,BM ＝ BN２＋ MN２＝３２＋４２＝５

在 △ ABM 中,∵AB ＝２９ ,∴AM２＋BM２＝２２＋５２＝２９＝AB２
∴AM ⊥ BM
又 AM ⊥ DE ,BM ∩ DE ＝ M ,BM ,
DE ⊂ 平面
BCED ,
７分
∴AM ⊥ 平面 BCED
二、填空题:(每小题５分,共２０分)
１３．－１;
１４．３;
三、解答题:(共７０分)
１
１５． ;
２
１６．
b ＜c ＜ a ．
１７．解:(Ⅰ )由已知及正弦定理,得２s
i
nBc
o
s
C －s
i
nAc
os
C ＝s
i
nCc
osA ．
∴ ２s
i
nBc
o
s
C ＝s
i
nAc
o
s
C ＋cosAs
f(
e
e
∴f(
x )在 [

2018年4月四川省成都市天府新区初2018届初三中考二诊数学试题参考答案

( (
能性相等$其中同时选择去同一个景点的结果有( (
种 $7 同时
选择
去同
一个景
点的
概率
+
( 3
+
* (
!
#*!解#如图$过点 & 作 &( "#$ 于点($过点 % 作 %+ "&( 于点 + $则 &)+$(+%+ +*0B!在 56$#&( 中$= #( + >0 & *0 + )0 !B"$
正
整数
解
的
概
率
为
* )
!
!&!-+
&
( "
!
解
析
设
#
00*
!= 点 # 与点 $
关于原点对称7,# +,$!= $#$% 为等边三
角形7 #$ " ,%,% + 槡( #,!= #, +
槡槡 0. ,
( (
##%,+ #%,+!= ,$ + ,%7 #,$% + ( (
#,%$7 ##$% , #%$, + ##%$ , (
#,%$即 ##$& + ##%,7 ##$% +
( (
#%,+!= #+ + #$#& +3047 $#$& 1 (
(
$+,%7%#+& +,$%& +.7%+ + * .&#!

成都2018届二诊模拟考试数学试卷二(理科)

成都2018届二诊模拟考试数学试卷二(理科)一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合，，则（）A ．B ．C ．D ． 2.若复数（），，且为纯虚数，则在复平面内所对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 3.在等比数列中，已知，，则（） A ．12 B ．18 C ．24 D ．364.已知平面向量，夹角为，且，，则与的夹角是（）A ．B ．C ．D ．5.若曲线（为常数）不存在斜率为负数的切线，则实数的取值范围是（） A ．B ．C ．D ．6.若实数满足不等式，且的最大值为5，则实数的值为（）A ．0B ．-1C ．-2D ．-57.已知是空间中两条不同的直线，是两个不同的平面，且，有下列命题：①若，则；②若，则；③若，且，，则；④若，且，，则，其中真命题的个数是（） A ．0 B ．1 C ．2 D ．3[1,2]A =-2{,}B y x x A =∈A B = [1,4][1,2][1,0]-[0,2]1z a i =+a R ∈21z i =-12z z 1z {}n a 36a =35778a a a ++=5a =a b 3π1a = 12b = 2a b + b 6π56π4π34π2ln y x ax =+a a 1(,)2-+∞1[,)2-+∞(0,)+∞[0,)+∞,x y 22010x y x y y m ++≥⎧⎪+-≤⎨⎪≥⎩x y -m ,m n ,αβ,m n αβ⊂⊂//αβ//m n //αβ//m βl αβ= m l ⊥n l ⊥αβ⊥l αβ= m l ⊥m n ⊥αβ⊥8.已知函数（）的反函数的图象经过点，若函数的定义域为，当时，有，且函数为偶函数，则下列结论正确的是（）A ．B ．C ．D ．9.执行如图所示的程序框图，若输入的分别为1，2，0.3，则输出的结果为（）A ．1.125B ．1.25C ．1.3125D ．1.37510.已知函数（）在上单调递减，则的取值范围是（） A ．B ．C ．D ．()x f x a =0,1a a >≠1)2()g x R [2,2]x ∈-()()g x f x =(2)g x+()(3)g g g π<<()(3)g g g π<<(3)()g g g π<<()(3)g g g π<<,,a bc ()sin(2)2sin cos()f x x x ωϕϕωϕ=+-+0,R ωϕ>∈3(,)2ππω(0,2]1(0,]21[,1]215[,]2411.设双曲线（）的左右焦点分别为，以为直径的圆与双曲线左支的一个交点为，若以（为坐标原点）为直径的圆与相切，则双曲线的离心率为（） ABC12.把平面图形上的所有点在一个平面上的射影构成的图形叫做图形在这个平面上的射影，如图，在三棱锥中，，，，，，将围成三棱锥的四个三角形的面积从小到大依次记为，设面积为的三角形所在的平面为，则面积为的三角形在平面上的射影的面积是（）A ．B ．C ．10D ．30二、填空题（每题5分，满分20分，将答案填在答题纸上）13. 在边长为1的正三角形中，设，则． 14.设实数满足，则的最小值为．15. 已知一个多面体的三视图如图所示：其中正视图与侧视图都是边长为1的等腰直角三角形，俯视图是边长为1的正方形，若该多面体的顶点都在同一个球面上，则该球的表面积为．2222:1x y C a b-=0,0a b >>12,F F 12,F F P 1OF O 2PF C M 'M M A BCD -BD CD ⊥AB DB ⊥AC DC ⊥5AB DB ==4CD =1234,,,S S S S 2S α4S α252ABC 2 3BC BD CA CE == ，AD BE ⋅=x y ，70310350x y x y x y +-≤⎧⎪-+≤⎨⎪--≥⎩2z x y =-16. 设是函数的导数，是函数的导数，若方程有实数解，则称点为函数的拐点，某同学经过探究发现：任何一个三次函数都有拐点，任何一个三次函数都有对称中心，且拐点就是对称中心，设函数，利用上述探究结果计算：．三.解答题(17-21每小题12分, 22或23题10分,共70分.在答题卷上解答,解答应写出文字说明,证明过程或演算步骤.)17．（12分）设各项均为正数的数列{a n }和{b n }满足：对任意n ∈N *，a n ，b n ，a n +1成等差数列，b n ，a n +1，b n +1成等比数列，且a 1=1，b 1=2，a 2=3．（Ⅰ）证明数列{}是等差数列；（Ⅱ）求数列{}前n 项的和．18．（12分）某校的学生记者团由理科组和文科组构成，具体数据如下表所示：()'f x ()f x ()''f x ()'f x ()''0f x =0x ()()00 x f x ，()f x ()()320f x ax bx cx d a =+++≠()32342g x x x x =-++1231910101010g g g g ⎛⎫⎛⎫⎛⎫⎛⎫++++= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭…学校准备从中选出4人到社区举行的大型公益活动进行采访，每选出一名男生，给其所在小组记1分，每选出一名女生则给其所在小组记2分，若要求被选出的4人中理科组、文科组的学生都有．（Ⅰ）求理科组恰好记4分的概率？（Ⅱ）设文科男生被选出的人数为ξ，求随机变量ξ的分布列和数学期望Eξ．19．已知等边△//AB CBCD中，1,BD CD BC ==1所示），现将B 与/B ，C 与/C 重合，将△//AB C向上折起，使得AD =2所示）. （1）若BC 的中点O ，求证：⊥平面BCD 平面AOD ; （2）在线段AC 上是否存在一点E ，使E D B C D 与面成30 角，若存在，求出CE 的长度，若不存在，请说明理由;（3）求三棱锥A BCD -的外接球的表面积.20.已知圆222:2,E x y +=将圆2E按伸缩变换：//2x x y y ⎧=⎪⎨=⎪⎩后得到曲线1E ，（1）求1E 的方程；（2）过直线2x =上的点M 作圆的两条切线，设切点分别是A ，B ，若直线AB 与交于2E 1E BACDC ,D两点，求的取值范围.21.已知函数()sin ln sin g x x x θθ=--在[1,)+∞单调递增，其中(0,)θπ∈ （1）求θ的值；（2）若221()()x f x g x x-=+，当[1,2]x ∈时，试比较()f x 与/1()2f x +的大小关系（其中/()f x 是()f x 的导函数），请写出详细的推理过程；（3）当0x ≥时，1(1)x e x kg x --≥+恒成立，求k 的取值范围.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分. 22.选修4-4：坐标系与参数方程在直角坐标系中，以原点为极点，x 轴的正半轴为极轴建立极坐标系，已知曲线C ：2sin 2cos (0)a a ρθθ=>，又过点(2,4)P --的直线l 的参数方程为224x y ⎧=-+⎪⎪⎨⎪=-⎪⎩(t 为参数)，l 与曲线C 分别交于M ，N.(1)写出曲线C 的平面直角坐标系方程和l 的普通方程； (2)若,,PM MN PN 成等比数列，求a 的值.23．选修4-5：不等式选讲CDAB设函数()f x =1(0)x x a a a++->（1）证明：()2f x ≥；（2）若()35f <，求a 的取值范围.成都2018届二诊模拟考试数学试卷(理科参考答案）一、选择题1-5:DABAD 6-10:CBCDC 11、12：DA13. 在边长为1的正三角形中，设，则．【答案】考点：向量线性运算与数量积的几何运算.14. 设实数满足，则的最小值为．【答案】【解析】ABC 2 3BC BD CA CE == ，AD BE ⋅=14-x y ，70310350x y x y x y +-≤⎧⎪-+≤⎨⎪--≥⎩2z x y =-8试题分析：作出不等式组表示的平面区域如图：根据图形得：当直线经过点时取得最大值，由解得：，∴.考点：线性规划.15. 已知一个多面体的三视图如图所示：其中正视图与侧视图都是边长为1的等腰直角三角形，俯视图是边长为1的正方形，若该多面体的顶点都在同一个球面上，则该球的表面积为．【答案】考点:三视图.【名师点睛】本题考查三视图，属基础题；解三视图相减问题的关键在于根据三视图还原几何体，要掌握常见几何体的三视图，比如三棱柱、三棱锥、圆锥、四棱柱、四棱锥、圆锥、球、圆台以及其组合体，并且要弄明白几何体的尺寸跟三视图尺寸的关系；有时候还可以利70310350x y x y x y +-≤⎧⎪-+≤⎨⎪--≥⎩2z x y =-B z 70310x y x y +-=⎧⎨-+=⎩()5 2B ，max 5228z =⨯-=3π用外部补形法，将几何体补成长方体或者正方体等常见几何体16. 设是函数的导数，是函数的导数，若方程有实数解，则称点为函数的拐点，某同学经过探究发现：任何一个三次函数都有拐点，任何一个三次函数都有对称中心，且拐点就是对称中心，设函数，利用上述探究结果计算：．【答案】考点：1.新定义问题；2.导数的运算；3.函数的对称性.【名师点睛】本题考查新定义问题、导数的运算、函数的对称性，属难题；解决新定义问题首先要对新概念迅速理解，并学以致用，本题注意经过两次求导得到的零点为函数的拐点，也是函数的对称中心，再就是对函数中心对称的性质在掌握，即若函数关于点成中心对称，则三、解答题17．（12分）设各项均为正数的数列{a n }和{b n }满足：对任意n ∈N *，a n ，b n ，a n +1成等差数列，b n ，a n +1，b n +1成等比数列，且a 1=1，b 1=2，a 2=3．（Ⅰ）证明数列{}是等差数列；（Ⅱ）求数列{}前n 项的和．【考点】数列的求和．【分析】（I ）对任意n ∈N *，a n ，b n ，a n +1成等差数列，b n ，a n +1，b n +1成等比数()'f x ()f x ()''f x ()'f x ()''0f x =0x ()()00 x f x ，()f x ()()320f x ax bx cx d a =+++≠()32342g x x x x =-++1231910101010g g g g ⎛⎫⎛⎫⎛⎫⎛⎫++++= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭…76()f x (,)a b (2)()2f a x f x b -+=列，可得2b n=a n+a n+1，=b n•b n+1，a n＞0，a n+1=，代入即可证明．（II）a1=1，b1=2，a2=3．由（I）可得：32=2b2，解得：b2．公差=．可得=×．b n代入=b n•b n+1，a n+1＞0．可得a n+1=，可得=．即可得出．【解答】（I）证明：∵对任意n∈N*，a n，b n，a n+1成等差数列，b n，a n+1，b n+1成等比数列，∴2b n=a n+a n+1，=b n•b n+1，a n＞0，∴a n+1=，∴2b n=+，∴=+．∴数列{}是等差数列．（II）解：a1=1，b1=2，a2=3．由（I）可得：32=2b2，解得：b2=．∴公差d===．=+（n﹣1）=×．∴b n=．∴=b n•b n+1=，a n+1＞0．∴a n+1=，∴n≥2时，a n=．n=1时也成立．∴a n=．n∈N*．∴=．∴数列{}前n项的和=+…+=2=．【点评】本题考查了数列递推关系、等差数列与等比数列的定义通项公式、“裂项求和”方法，考查了推理能力与计算能力，属于中档题．18．（12分）某校的学生记者团由理科组和文科组构成，具体数据如下表所示：学校准备从中选出4人到社区举行的大型公益活动进行采访，每选出一名男生，给其所在小组记1分，每选出一名女生则给其所在小组记2分，若要求被选出的4人中理科组、文科组的学生都有．（Ⅰ）求理科组恰好记4分的概率？（Ⅱ）设文科男生被选出的人数为ξ，求随机变量ξ的分布列和数学期望Eξ．【考点】离散型随机变量的期望与方差；离散型随机变量及其分布列．【分析】（I）要求被选出的4人中理科组、文科组的学生都有共有：．其中“理科组恰好记4分”的选法有两种情况：从理科组中选取2男1女，再从文科组中任选1人，可有方法；另一种是从理科组中选取2女，再从文科组中任选2人，可有方法．根据互斥事件的概率计算公式与古典概型的概率计算公式即可得出．（II）由题意可得ξ=0，1，2，3．P（ξ=0）==，P（ξ=1）==，P（ξ=2）==，P（ξ=4）==，即可得出分布列与数学期望．【解答】解：（I）要求被选出的4人中理科组、文科组的学生都有共有：=424．其中“理科组恰好记4分”的选法有两种情况：从理科组中选取2男1女，再从文科组中任选1人，可有方法；另一种是从理科组中选取2女，再从文科组中任选2人，可有方法．∴P==．（II ）由题意可得ξ=0，1，2，3．P （ξ=0）==，P （ξ=1）==，P （ξ=2）==，P （ξ=4）==，由题意可得ξ=0，1，2，3．其分布列为：）ξ的数学期望Eξ=++=．【点评】本题考查了互斥事件的概率计算公式与古典概型的概率计算公式、随机变量的分布列与数学期望，考查了推理能力与计算能力，属于中档题．19. 解：（1）∵△ABC 为等边三角形，△BCD 为等腰三角形，且O 为中点 ∴,BC AO BC DO ⊥⊥，AO DO O ⋂= ，BC AOD ∴⊥平面，又BC ABC ⊂面∴⊥平面BCD 平面AOD ………………3分（2）（法1）作,AH DO ⊥交DO 的延长线于H ，则平面BCD ⋂平面,AOD HD =则AH BCD ⊥平面，在Rt BCD ∆中，12OD BC ==，在Rt ACO ∆中，AO AC ==AOD ∆中， 222cos 23AD OD AO ADO AD OD +-∠==⋅， DABCOEF Hsin 3ADO ∴∠=，在Rt ADH ∆中sin 1AH AD ADO =∠=，设(0CE x x =≤≤，作EF CH F ⊥于，平面AHC ⊥平面B C D ，,EF BCD EDF ∴⊥∠平面就是E D B C D与面所成的角。

2018年四川省成都市天府新区二诊(5月份)

2018年四川省成都市天府新区中考数学模拟试卷（5月份）一、选择题（本大题共10个小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．（3分）（2016•长春）﹣5的相反数是（）A．B．C．﹣5D．52．（3分）（2013•绍兴）由5个相同的立方体搭成的几何体如图所示，则它的主视图是（）A．B．C．D．3．（3分）（2016•安顺）中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为4 400 000 000人，这个数用科学记数法表示为（）A．44×108B．4.4×109C．4.4×108D．4.4×1010 4．（3分）（2018•成都模拟）在下列二次根式中，x的取值范围是x＞3的是（）A．B．C．D．5．（3分）（2018•成都模拟）下列交通标志中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．6．（3分）（2015•永春县校级自主招生）下列计算正确的是（）A．a•a2=a3B．（a3）2=a5C．a+a2=a3D．a6÷a2=a3 7．（3分）（2018•成都模拟）数据3，4，5，5，5的中位数和众数分别是（）A．4，5B．5，5C．5，4D．5，18．（3分）（2013•德阳）如图，⊙O的直径CD过弦EF的中点G，∠DCF=20°，则∠EOD等于（）A．10°B．20°C．40°D．80°9．（3分）（2018•成都模拟）若关于x的方程无解，则m的值为（）A．m=1B．m=﹣1C．m=2D．m=﹣2 10．（3分）（2018•成都模拟）二次函数y=ax2+bx+c的图象如图所示，则应满足的条件是（）A．a＞0，b＞0，c＞0B．a＜0，b＜0，c＞0C．a＞0，b＜0，c＜0D．a＞0，b＞0，c＜0二、填空题（本大题共4个小题，每小题4分，共16分）11．（4分）（2018•成都模拟）计算：（﹣2018）0=．12．（4分）（2018•成都模拟）在△ABC中，∠C=90°，∠A比∠B大20°．则∠B=．13．（4分）（2018•成都模拟）已知P1（x1，y1），P2（x2，y2）两点都在反比例函数y=﹣的图象上，且x2＜x1＜0，则y1y2（填“＞”或“＜”）14．（4分）（2018•成都模拟）在平行四边形ABCD中，连接AC，按以下步骤作图，分别以A、C为圆心，以大于AC的长为半径画弧，两弧分别相交于点M、N，作直线MN交CD于点E，交AB于点F．若AB=6，BC=4，则△ADE的周长为．三、解答题（本大题共6个小题，共54分．解答应写出必要的文字说明、证明过程或演算步骤）15．（8分）（2018•成都模拟）（1）计算：|﹣2|﹣4sin45°+（3﹣π）0﹣（）﹣2；（2）解不等式组：，并在数轴上表示它的解集．16．（8分）（2018•成都模拟）先化简（1﹣）•，再在1，2，3中选取一个适当的数代入求值．17．（10分）（2017•安顺）随着交通道路的不断完善，带动了旅游业的发展，某市旅游景区有A、B、C、D、E等著名景点，该市旅游部门统计绘制出2017年“五•一”长假期间旅游情况统计图，根据以下信息解答下列问题：（1）2017年“五•一”期间，该市周边景点共接待游客万人，扇形统计图中A景点所对应的圆心角的度数是，并补全条形统计图．（2）根据近几年到该市旅游人数增长趋势，预计2018年“五•一”节将有80万游客选择该市旅游，请估计有多少万人会选择去E景点旅游？（3）甲、乙两个旅行团在A、B、D三个景点中，同时选择去同一景点的概率是多少？请用画树状图或列表法加以说明，并列举所有等可能的结果．18．（8分）（2018•成都模拟）如图，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB=70m，DE=10m，求障碍物B，C两点间的距离（结果精确到0.1m）（参考数据：≈1.414，≈1.732）19．（10分）（2012•重庆）已知：如图，在平面直角坐标系中，一次函数y=ax+b （a≠0）的图象与反比例函数的图象交于一、三象限内的A、B两点，与x轴交于C点，点A的坐标为（2，m），点B的坐标为（n，﹣2），tan∠BOC=．（1）求该反比例函数和一次函数的解析式；（2）在x轴上有一点E（O点除外），使得△BCE与△BCO的面积相等，求出点E的坐标．20．（10分）（2018•成都模拟）已知：BD为⊙O的直径，O为圆心，点A为圆上一点，过点B作⊙O的切线交DA的延长线于点F，点C为⊙O上一点，且AB=AC，连接BC交AD于点E，连接AC．（1）如图1，求证：∠ABF=∠ABC；（2）如图2，点H为⊙O内部一点，连接OH，CH若∠OHC=∠HCA=90°时，求证：CH=DA；（3）在（2）的条件下，若OH=6，⊙O的半径为10，求CE的长．一、填空题（本大题5个小题，每小题4分，共20分）B卷（50分）21．（4分）（2018•成都模拟）如图正方形ABCD一边在以点D为原点的数轴上，以点A为圆心，以AC长为半径画弧，且与数轴相交于点E，则点E所对应的实数是．22．（4分）（2018•成都模拟）已知x1，x2是方程x2﹣x+=0的两根，若实数a 满足a+x1+x2﹣x1x2=2018，则a=．23．（4分）（2018•成都模拟）有五张正面分别标有数0，1，2，3，4，5的不透明卡片，它们除了数字不同外其余全部相同．现将它们背面朝上，洗匀后从中任取一张，将卡片上的数记为a，则使关于x的方程+2=有正整数解的概率为24．（4分）（2018•成都模拟）已知点A是双曲线y=在第一象限上的一动点，连接AO并延长交另一分支于点B，以AB为一边作等边△ABC．随着点A的运动，点C的位置也不断变化，但始终在一个函数的图象上运动，则这个函数的表达式为．25．（4分）（2018•成都模拟）在三角形纸片ABC中，∠A=90°，∠C=30°，AC=10cm，将该纸片沿过点B的直线折叠，使点A落在斜边BC上的一点E处，折痕记为BD（如图1），剪去△CDE后得到双层△BDE（如图2），再沿着过△BDE某顶点的直线将双层三角形剪开，使得展开后的平面图形中有一个是平行四边形，则所得平行四边形的周长为cm．二、解答题（本大题共3个小题，共30分，解答应写出必要的文字说明、证明过程或演算步骤）26．（8分）（2018•成都模拟）某地特色农产品在国际市场上颇具竞争力，其中绿色蔬菜远销日本和韩国等地．上市时，若按市场价格10元/千克在新区收购了2000千克绿色蔬菜存放入冷库中．据预测，绿色蔬菜的市场价格每天每千克将上涨0.5元，但冷库存放这批绿色蔬菜时每天需要支出各种费用合计340元，而且绿色蔬菜在冷库中最多保存110天，同时，平均每天有6千克的绿色蔬菜损坏不能出售．（1）若存放x天后，将这批绿色蔬菜一次性出售，设这批绿色蔬菜的销售总金额为y元，试写出y与x之间的函数关系式．（2）这批绿色蔬菜存放多少天后出售可获得最大利润？最大利润是多少？27．（10分）（2018•成都模拟）如图，在Rt△ABC中，AB=AC，点D为AC延长线上一点，连接BD，过A作AM⊥BD，垂足为M，交BC于点N（1）如图1，若∠ADB=30°，BC=3，求AM的长；（2）如图2，点E在CA的延长线上，且AE=CD，连接EN并延长交BD于点F，求证：EF=FD；（3）在（2）的条件下，当AE=AC时，请求出的值．28．（12分）（2018•成都模拟）如图，在平面直角坐标系xoy中，把抛物线y=x2先向右平移1个单位，再向下平移4个单位，得到抛物线y=（x﹣h）2+k，所得抛物线与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，顶点为M；（1）写出h、k的值以及点A、B的坐标；（2）判断三角形BCM的形状，并计算其面积；（3）点P是抛物线上一动点，在y轴上找点Q．使点A，B，P，Q组成的四边形是平行四边形，直接写出对应的点P的坐标．（不用写过程）（4）点P是抛物线上一动点，连接AP，以AP为一边作正方形APFG，随着点P 的运动，正方形的大小、位置也随之改变．当顶点F或G恰好落在y轴上时，请直接写出对应的点P的坐标．（不写过程）2018年四川省成都市天府新区中考数学模拟试卷（5月份）参考答案与试题解析一、选择题（本大题共10个小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．（3分）（2016•长春）﹣5的相反数是（）A．B．C．﹣5D．5【解答】解：﹣5的相反数是5．故选：D．2．（3分）（2013•绍兴）由5个相同的立方体搭成的几何体如图所示，则它的主视图是（）A．B．C．D．【解答】解：从正面可看到从左往右三列小正方形的个数为：1，1，2．故选：C．3．（3分）（2016•安顺）中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为4 400 000 000人，这个数用科学记数法表示为（）A．44×108B．4.4×109C．4.4×108D．4.4×1010【解答】解：4 400 000 000=4.4×109，故选：B．4．（3分）（2018•成都模拟）在下列二次根式中，x的取值范围是x＞3的是（）A．B．C．D．【解答】解：A、∵是二次根式，∴3﹣x≥0，∴x≤3，故本选项错误；B、∵是二次根式，∴x+3≥0，∴x≥﹣3，故本选项错误；C、∵是二次根式，∴x﹣3≥0，∴x≥3，故本选项错误；D、∵是二次根式，∴≥0，∴x＞3，故本选项正确；故选：D．5．（3分）（2018•成都模拟）下列交通标志中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．【解答】解：A、是轴对称图形，不是中心对称图形，故本选项错误；B、不是轴对称图形，是中心对称图形，故本选项错误；C、不是轴对称图形，也不是中心对称图形，故本选项错误；D、既是轴对称图形又是中心对称图形，故本选项正确．故选：D．6．（3分）（2015•永春县校级自主招生）下列计算正确的是（）A．a•a2=a3B．（a3）2=a5C．a+a2=a3D．a6÷a2=a3【解答】解：A、a•a2=a3，正确；B、应为（a3）2=a3×2=a6，故本选项错误；C、a与a2不是同类项，不能合并，故本选项错误D、应为a6÷a2=a6﹣2=a4，故本选项错误．故选：A．7．（3分）（2018•成都模拟）数据3，4，5，5，5的中位数和众数分别是（）A．4，5B．5，5C．5，4D．5，1【解答】解：数据1，2，3，3，5，5，5中，5出现了3次，出现的次数最多，则众数是5；最中间的数是5，则中位数是5；故选：B．8．（3分）（2013•德阳）如图，⊙O的直径CD过弦EF的中点G，∠DCF=20°，则∠EOD等于（）A．10°B．20°C．40°D．80°【解答】解：∵⊙O的直径CD过弦EF的中点G，∠DCF=20°，∴弧DF=弧DE，且弧的度数是40°，∴∠DOE=40°，故选：C．9．（3分）（2018•成都模拟）若关于x的方程无解，则m的值为（）A．m=1B．m=﹣1C．m=2D．m=﹣2【解答】解：方程去分母得，x+2=m，则x=m﹣2，当分母x+3=0即x=﹣3时，方程无解，所以m﹣2=﹣3即m=﹣1时方程无解，故选：B．10．（3分）（2018•成都模拟）二次函数y=ax2+bx+c的图象如图所示，则应满足的条件是（）A．a＞0，b＞0，c＞0B．a＜0，b＜0，c＞0C．a＞0，b＜0，c＜0D．a＞0，b＞0，c＜0【解答】解：由图象可得，a＞0，b＞0，c＜0，故选：D．二、填空题（本大题共4个小题，每小题4分，共16分）11．（4分）（2018•成都模拟）计算：（﹣2018）0=1．【解答】解：（﹣2018）0=1．故答案为：1．12．（4分）（2018•成都模拟）在△ABC中，∠C=90°，∠A比∠B大20°．则∠B= 35°．【解答】解：∵∠C=90°，∴∠B+∠A=90°①，∵∠A比∠B大20°，∴∠A﹣∠B=20°②，①﹣②得，2∠B=70°，∴∠B=35°．故答案为：35°．13．（4分）（2018•成都模拟）已知P1（x1，y1），P2（x2，y2）两点都在反比例函数y=﹣的图象上，且x2＜x1＜0，则y1＞y2（填“＞”或“＜”）【解答】解：∵P1（x1，y1），P2（x2，y2）两点都在反比例函数y=﹣的图象上，且x2＜x1＜0，∴每个分支上y随x的增大而增大，则y1＞y2．故答案为：＞．14．（4分）（2018•成都模拟）在平行四边形ABCD中，连接AC，按以下步骤作图，分别以A、C为圆心，以大于AC的长为半径画弧，两弧分别相交于点M、N，作直线MN交CD于点E，交AB于点F．若AB=6，BC=4，则△ADE的周长为10．【解答】解：∵四边形ABCD是平行四边形，∴AD=BC=4，CD=AB=6，∵由作法可知，直线MN是线段AC的垂直平分线，∴AE=CE，∴AE+DE=CD=6，∴△ADE的周长=AD+（DE+AE）=4+6=10．故答案为：10．三、解答题（本大题共6个小题，共54分．解答应写出必要的文字说明、证明过程或演算步骤）15．（8分）（2018•成都模拟）（1）计算：|﹣2|﹣4sin45°+（3﹣π）0﹣（）﹣2；（2）解不等式组：，并在数轴上表示它的解集．【解答】解：（1）原式=2﹣4×+1﹣9=2﹣2﹣8=﹣8；（2）解不等式x﹣3（x﹣2）≥4，得：x≤1，解不等式＜，得：x＞﹣1，则不等式组的解集为﹣1＜x≤1，将解集表示在数轴上如下：16．（8分）（2018•成都模拟）先化简（1﹣）•，再在1，2，3中选取一个适当的数代入求值．【解答】解：原式=（﹣）•=•=，∵x﹣1≠0且x﹣3≠0，∴x≠1、x≠3，∴把x=2代入，得：原式==﹣2．17．（10分）（2017•安顺）随着交通道路的不断完善，带动了旅游业的发展，某市旅游景区有A、B、C、D、E等著名景点，该市旅游部门统计绘制出2017年“五•一”长假期间旅游情况统计图，根据以下信息解答下列问题：（1）2017年“五•一”期间，该市周边景点共接待游客50万人，扇形统计图中A景点所对应的圆心角的度数是108°，并补全条形统计图．（2）根据近几年到该市旅游人数增长趋势，预计2018年“五•一”节将有80万游客选择该市旅游，请估计有多少万人会选择去E景点旅游？（3）甲、乙两个旅行团在A、B、D三个景点中，同时选择去同一景点的概率是多少？请用画树状图或列表法加以说明，并列举所有等可能的结果．【解答】解：（1）该市周边景点共接待游客数为：15÷30%=50（万人），A景点所对应的圆心角的度数是：30%×360°=108°，B景点接待游客数为：50×24%=12（万人），补全条形统计图如下：故答案为：50，108°；（2）∵E景点接待游客数所占的百分比为：×100%=12%，∴2018年“五•一”节选择去E景点旅游的人数约为：80×12%=9.6（万人）；（3）画树状图可得：∵共有9种可能出现的结果，这些结果出现的可能性相等，其中同时选择去同一个景点的结果有3种，∴同时选择去同一个景点的概率==．18．（8分）（2018•成都模拟）如图，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB=70m，DE=10m，求障碍物B，C两点间的距离（结果精确到0.1m）（参考数据：≈1.414，≈1.732）【解答】解：如图，过点D作DF⊥AB于点F，过点C作CH⊥DF于点H．则DE=BF=CH=10m，在直角△ADF中，∵AF=70m﹣10m=60m，∠ADF=45°，∴DF=AF=60m，在直角△CDE中，∵DE=10m，∠DCE=30°，∴CE==10（m）∴BC=BE﹣CE=60﹣10≈60﹣17.32≈42.7（m）答：障碍物B，C两点间的距离约为42.7m19．（10分）（2012•重庆）已知：如图，在平面直角坐标系中，一次函数y=ax+b （a≠0）的图象与反比例函数的图象交于一、三象限内的A、B两点，与x轴交于C点，点A的坐标为（2，m），点B的坐标为（n，﹣2），tan∠BOC=．（1）求该反比例函数和一次函数的解析式；（2）在x轴上有一点E（O点除外），使得△BCE与△BCO的面积相等，求出点E的坐标．【解答】解：（1）过B点作BD⊥x轴，垂足为D，∵B（n，﹣2），∴BD=2，在Rt△OBD中，tan∠BOC=，即=，解得OD=5，又∵B点在第三象限，∴B（﹣5，﹣2），将B（﹣5，﹣2）代入y=中，得k=xy=10，∴反比例函数解析式为y=，将A（2，m）代入y=中，得m=5，∴A（2，5），将A（2，5），B（﹣5，﹣2）代入y=ax+b中，得，解得．则一次函数解析式为y=x+3；（2）由y=x+3得C（﹣3，0），即OC=3，=S△BCO，∵S△BCE∴CE=OC=3，∴OE=6，即E（﹣6，0）．20．（10分）（2018•成都模拟）已知：BD为⊙O的直径，O为圆心，点A为圆上一点，过点B作⊙O的切线交DA的延长线于点F，点C为⊙O上一点，且AB=AC，连接BC交AD于点E，连接AC．（1）如图1，求证：∠ABF=∠ABC；（2）如图2，点H为⊙O内部一点，连接OH，CH若∠OHC=∠HCA=90°时，求证：CH=DA；（3）在（2）的条件下，若OH=6，⊙O的半径为10，求CE的长．【解答】解：（1）∵BD为⊙O的直径，∴∠BAD=90°，∴∠D+∠ABD=90°，∵FB是⊙O的切线，∴∠FBD=90°，∴∠FBA+∠ABD=90°，∴∠FBA=∠D，∵AB=AC，∴∠C=∠ABC，∵∠C=∠D，∴∠ABF=∠ABC；（2）如图2，连接OC，∵∠OHC=∠HCA=90°，∴AC∥OH，∴∠ACO=∠COH，∵OB=OC，∴∠OBC=∠OCB，∴∠ABC+∠CBO=∠ACB+∠OCB，即∠ABD=∠ACO，∴∠ABC=∠COH，∵∠H=∠BAD=90°，∴△ABD∽△HOC，∴==2，∴CH=DA；（3）由（2）知，△ABC∽△HOC，∴=2，∵OH=6，⊙O的半径为10，∴AB=2OH=12，BD=20，∴AD==16，在△ABF与△ABE中，，∴△ABF≌△ABE，∴BF=BE，AF=AE，∵∠FBD=∠BAD=90°，∴AB2=AF•AD，∴AF==9，∴AE=AF=9，∴DE=7，BE==15，∵AD，BC交于E，∴AE•DE=BE•CE，∴CE===．一、填空题（本大题5个小题，每小题4分，共20分）B卷（50分）21．（4分）（2018•成都模拟）如图正方形ABCD一边在以点D为原点的数轴上，以点A为圆心，以AC长为半径画弧，且与数轴相交于点E，则点E所对应的实数是1﹣．【解答】解：∵正方形ABCD的边长AD=1，∴AC==，∴AE=AC=，∴DE=AE﹣AD=﹣1，∵点D在原点，点E在原点的左边，∴点E所对应的实数为1﹣，故答案为：1﹣．22．（4分）（2018•成都模拟）已知x1，x2是方程x2﹣x+=0的两根，若实数a 满足a+x1+x2﹣x1x2=2018，则a=2016．【解答】解：根据题意得x1+x2═，x1x2=，∵a+x1+x2﹣x1•x2=2018，∴a+﹣=2018，∴a=2016．故答案为2016．23．（4分）（2018•成都模拟）有五张正面分别标有数0，1，2，3，4，5的不透明卡片，它们除了数字不同外其余全部相同．现将它们背面朝上，洗匀后从中任取一张，将卡片上的数记为a，则使关于x的方程+2=有正整数解的概率为【解答】解：解分式方程得：x=，∵分式方程的解为正整数，∴2﹣a＞0，∴a＜2，∴a=0，1，∵分式方程的解为正整数，当a=1时，x=2不合题意，∴a=0，∴使关于x的分式方程有正整数解的概率为，故答案为：．24．（4分）（2018•成都模拟）已知点A是双曲线y=在第一象限上的一动点，连接AO并延长交另一分支于点B，以AB为一边作等边△ABC．随着点A的运动，点C的位置也不断变化，但始终在一个函数的图象上运动，则这个函数的表达式为y=﹣．【解答】解：设A（a，），∵点A与点B关于原点对称，∴OA=OB，∵△ABC为等边三角形，∴AB⊥OC，OC=AO，∵AO=，∴CO=，过点C作CD⊥x轴于点D，则可得∠AOD=∠OCD（都是∠COD的余角），设点C的坐标为（x，y），则tan∠AOD=tan∠OCD，即=，解得：y=﹣a2x，在Rt△COD中，CD2+OD2=OC2，即y2+x2=3a2+，将y=﹣a2x代入，（a4+1）x2=3×可得：x2=，故x=，y=﹣a2x=﹣a，则xy=﹣3，故可得：y=﹣（x＞0）．故答案为：y=﹣（x＞0）．25．（4分）（2018•成都模拟）在三角形纸片ABC中，∠A=90°，∠C=30°，AC=10cm，将该纸片沿过点B的直线折叠，使点A落在斜边BC上的一点E处，折痕记为BD（如图1），剪去△CDE后得到双层△BDE（如图2），再沿着过△BDE某顶点的直线将双层三角形剪开，使得展开后的平面图形中有一个是平行四边形，则所得平行四边形的周长为或cm．【解答】解：如图1中，∵∠A=90°，∠C=30°，AC=10cm，∴AB=BE=，CB=，设AD=DE=x，在Rt△CDE中，（10﹣x）2=x2+（）2，∴x=，∴DE=，①如图2中，当ED=EF时，沿着直线EF将双层三角形剪开，展开后的平面图形中有一个是平行四边形，此时周长=4×=（cm）．②如图2﹣1中，当FD=FB时，沿着直线DF将双层三角形剪开，展开后的平面图形中有一个是平行四边形，此时周长=4DF=4×=（cm）综上所述，满足条件的平行四边形的周长为cm或cm，故答案为为或．二、解答题（本大题共3个小题，共30分，解答应写出必要的文字说明、证明过程或演算步骤）26．（8分）（2018•成都模拟）某地特色农产品在国际市场上颇具竞争力，其中绿色蔬菜远销日本和韩国等地．上市时，若按市场价格10元/千克在新区收购了2000千克绿色蔬菜存放入冷库中．据预测，绿色蔬菜的市场价格每天每千克将上涨0.5元，但冷库存放这批绿色蔬菜时每天需要支出各种费用合计340元，而且绿色蔬菜在冷库中最多保存110天，同时，平均每天有6千克的绿色蔬菜损坏不能出售．（1）若存放x天后，将这批绿色蔬菜一次性出售，设这批绿色蔬菜的销售总金额为y元，试写出y与x之间的函数关系式．（2）这批绿色蔬菜存放多少天后出售可获得最大利润？最大利润是多少？【解答】解：（1）由题意y与x之间的函数关系式为：y=（10+0.5x）（2000﹣6x），=﹣3x2+940x+20000（1≤x≤110，且x为整数）；（2）设利润为w，由题意得：w=﹣3x2+940x+20000﹣10×2000﹣340x=﹣3（x﹣100）2+30000，∵a=﹣3＜0，∴抛物线开口方向向下，=30000，∴x=100时，w最大100天＜110天．∴存放100天后出售可获得最大利润30000元．27．（10分）（2018•成都模拟）如图，在Rt△ABC中，AB=AC，点D为AC延长线上一点，连接BD，过A作AM⊥BD，垂足为M，交BC于点N（1）如图1，若∠ADB=30°，BC=3，求AM的长；（2）如图2，点E在CA的延长线上，且AE=CD，连接EN并延长交BD于点F，求证：EF=FD；（3）在（2）的条件下，当AE=AC时，请求出的值．【解答】解：（1）在Rt△ABC中，AB=AC，∴△ABC是等腰直角三角形，∵BC=3，∴AB=3．∵∠ADB=30°，∴BD=6，AD=3．根据等面积法可得：AB•AD=AM•BD，∴3×3=6•AM，∴AM=．（2）证明：作AH⊥BC，垂足为H，延长AH交BD于P，连接CP，如图3所示．∵△ABC是等腰直角三角形，∴AH=BH=CH，BP=CP，∠PBC=∠PCB．∵AM⊥BD，AH⊥BC，∴∠BMN=∠AHN=90°，∵∠BNM=∠ANH，∴∠NBM=∠NAH=∠PBH．在△BHP和△AHN中，，∴△BHP≌△AHN（ASA），∴BP=AN，∴CP=AN．∵∠PCB=∠PAM，∴∠MAD=∠PAM+45°=∠PCB+45°=∠PCA，∴∠EAN=∠PCD，在△AEN和△CDP中，，∴△AEN≌△CDP（SAS），∴∠E=∠D，∴EF=DF．（3）过点F作FQ⊥AC于Q，由（2）可得，Q是DE的中点，过N作NR⊥AC 于R，如图4所示．设AE=a，∵AE=AC，∴AC=3a，∴EQ=a，AD=4a，∵NR∥FQ∥AB，∴△ANR∽△FDQ∽△BAD，∴===，∴NR=AR．∵△NRC为等腰直角三角形∴AR+AR=3a，∴AR=a，∴RQ=EQ﹣AE﹣AR=a﹣a﹣a=a．∵NR∥FQ，∴△ENR∽△EFQ，∴===．28．（12分）（2018•成都模拟）如图，在平面直角坐标系xoy中，把抛物线y=x2先向右平移1个单位，再向下平移4个单位，得到抛物线y=（x﹣h）2+k，所得抛物线与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，顶点为M；（1）写出h、k的值以及点A、B的坐标；（2）判断三角形BCM的形状，并计算其面积；（3）点P是抛物线上一动点，在y轴上找点Q．使点A，B，P，Q组成的四边形是平行四边形，直接写出对应的点P的坐标．（不用写过程）（4）点P是抛物线上一动点，连接AP，以AP为一边作正方形APFG，随着点P 的运动，正方形的大小、位置也随之改变．当顶点F或G恰好落在y轴上时，请直接写出对应的点P的坐标．（不写过程）【解答】解：（1）∵抛物线y=x2先向右平移1个单位，再向下平移4个单位，得到抛物线y=（x﹣1）2﹣4，∴h=1，k=﹣4；令y=0，即（x﹣1）2﹣4=0解得x=﹣1或x=3，∴A（﹣1，0），B （3，0），（2）∵令x=0，得y=（0﹣1）2﹣4=﹣3，∴点C的坐标为（0，﹣3），点M的坐标为（1，﹣4）∴BC=3，MC=，BM=2∴BC2+MC2=BM2∴△BMC是直角三角形；∴S=BC•CM=×3×=3；（3）由（1）知，抛物线y=（x﹣1）2﹣4=x2﹣2x﹣3，∵点P是抛物线上一动点，∴设P（p，p2﹣2p﹣3），∵点Q在y轴上，∴设Q（0，m），∵A（﹣1，0），B（3，0），∴AB=4，AB的中点M（1，0）∵点A，B，P，Q组成的四边形是平行四边形，①当AB为边时，AB∥PQ，AB=PQ，∴p2﹣2p﹣3=m，|p|=4，Ⅰ、当p=4时，m=5，∴P（4，5），Ⅱ、当p=﹣4时，m=21，∴P（﹣4，21）②当AB为对角线时，点M是PQ的中点，∴p=2，p2﹣2p﹣3+m=0，∴p=2，m=3，∴P（2，﹣3），∴点P的坐标为（4，5），（﹣4，21）或（2，﹣3），（4）①如图（1），（2）当点G在y轴上时，由△AOG≌△PHA，得PH=OA，得y P=x A=﹣1，∴x2﹣2x﹣3=﹣1，得x=1±，∴P1（1﹣，﹣1），P2（1+，﹣1）②如图（3），当点F在y轴上时，由△AMP≌△FNP，得PM=PN，得y P=x P，则x2﹣2x﹣3=x，得x=，x=故P3（，）或（，）。

四川省成都市2018届高三数学第二次诊断性检测试题文

四川省成都市2018届高三数学第二次诊断性检测试题文第Ⅰ卷（选择题，共60分）一、选择题：本大题共12个小题,每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的。

1.设集合{|11}P x x =-<,{|12}Q x x =-<<,则PQ =( )A ．1(1,)2- B ．(1,2)- C ．(1,2) D ．(0,2)2。

已知向量(2,1)a =，(3,4)b =，(,2)c k =.若(3)//a b c -，则实数的值为（） A ．8- B ．6- C ．1- D ． 3。

若复数满足3(1)12i z i +=-，则z 等于（）A B ．32 C ．124。

设等差数列{}n a 的前项和为n S 。

若420S =,510a =，则16a =( ） A ．32- B ．12 C ．16 D ．325.已知m ，是空间中两条不同的直线,α，β为空间中两个互相垂直的平面，则下列命题正确的是（） A ．若m α⊂,则m β⊥ B ．若m α⊂,n β⊂，则m n ⊥ C ．若m α⊄，m β⊥，则//m α D ．若m αβ=，n m ⊥，则n α⊥6.在平面直角坐标系中,经过点P ）A ．22142x y -= B ．221714x y -= C ．22136x y -= D ．221147y x -= 7.已知函数()sin()f x A x ωϕ=+(0,0,)2A πωϕ>><的部分图象如图所示.现将函数()f x 图象上的所有点向右平移4π个单位长度得到函数()g x 的图象，则函数()g x 的解析式为（ )A ．()2sin(2)4g x x π=+B ．3()2sin(2)4g x x π=+C ．()2cos 2g x x =D ．()2sin(2)4g x x π=-8。

若为实数，则“2222x ≤≤”是“22223x x +≤≤”成立的（） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件9.《九章算术》中将底面为长方形，且有一条侧棱与底面垂直的四棱锥称之为“阳马”。

四川省成都市2018届高三二诊模拟考试数学理科试卷有答案AlUAwl

2018届2017~2018学年下期二诊模拟考试数学试卷（理科）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的. 1.i 是虚数单位，则复数61ii-的虚部为.3A.3B -.3C i.4D i -2.已知全集U =R ，集合{|30}A x x =-<，1{|2}.4x B x =>那么集合U A C B ⋂等于.{|23}A x x -≤≤.{|23}B x x -<< .{|2}C x x ≤-.{|3}D x x <3.若,x y 满足约束条件02326x x y x y ≥⎧⎪+≥⎨⎪+≤⎩,则z x y =+ 的最小值是.3A -.6B3.2C .3D4.若1sin()3πα-=，2παπ≤≤,则sin 2α的值为 42.9A -22.9B -22.9C 42.9D 5.执行如图所示的程序框图，输出的S 值为.2A 3.2B 5.3C 8.5D 6. 一个底面为正方形的四棱锥，其三视图如图所示，若这个四棱锥的体积为2 ，则此四棱锥最长的侧棱长为 .23A .11B .13C .10D7.等比数列{}n a 中，20a >则25""a a <是35""a a <的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件8.已知函数()f x 对任意x ∈R 都有(4)()2(2)f x f x f +-=，若(1)y f x =-的图象关于直线1x =对称，则(2018)f = A. B. C. D.9、已知是双曲线的左、右焦点, 点在上,23B π∠=若,则的离心率为A. B. C. D.10.已知函数2()23sin cos 2cos 1f x x x x =⋅-+，将()f x 图像的横坐标伸长为原来的2倍，再向左平移2π个单位后得到函数()g x ，在区间[0,]π上随机取一个数x ，则()1g x ≥的概率为 1.3A 1.4B 1.5C 1.2D 11.若函数y =f (x )的图象上存在不同的两点,使得函数的图象在这两点处的切线的斜率之和等于常数t ,则称函数y =f (x )为“t 函数”.下列函数中为“2函数”的个数有 ① y =x -x 3 ②y =x +e x ③y =x ln x ④y =x +cos xA.1个B.2 个C.3 个D.4个12、已知向量满足，若，的最大值和最小值分别为，则等于A. B.2 C. D.二、填空题：本大题共4小题，每小题5分，共20分．13、若1()nx x-的展开式中第3项和第5项的二项式系数相等，则展开式中的常数项为．14、已知数列{}n a 的各项都为正数，前n 项和为n S ，若2{log }n a 是公差为1的等差数列，且5=62S ，则2=a15．已知四面体ABCD 的所有棱长都为,O 是该四面体内一点,且点O 到平面ABC 、平面ACD 、平面ABD 、平面BCD 的距离分别为,x ,和y ,则+的最小值是 .16．为抛物线上一点，且在第一象限，过点作垂直该抛物线的准线于点为抛物线的焦点,为坐标原点, 若四边形的四个顶点在同一个圆上,则该圆的方程为．三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17－21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分17．（本小题满分12分）如图，,,a b c 分别是锐角ABC ∆的三个内角A B C ，，的对边，sin cos =2b A a B a +，4sin 5BAC ∠=.（1）求sin C 的值；（2）若点D 在边BC 上,3BD CD =，ABC ∆的面积为14，求AD 的长度.18. （本小题满分12分）2014年9月，国务院发布了《关于深化考试招生制度改革的实施意见》，某地作为高考改革试点地区，从当年秋季新入学的高一学生开始实施，高考不再分文理科，每个考生，英语，语文，数学三科为必考科目，并从物理、化学、生物、政治、历史、地理六个科目中任选三个科目参加高考，物理、化学、生物为自然科学科目，政治、历史、地理为社会科学科目.假设某位考生选考这六个科目的可能性相等. （1）求他所选考的三个科目中，至少有一个自然科学科目的概率；（2）已知该考生选考的三个科目中有一个科目属于社会科学科目，两个科目属于自然科学科目，若该考生所选的社会科学科目考试的成绩获A 等的概率都是0.75，所选的自然科学科目考试的成绩获A 等的概率都是0.8，且所选考的各个科目考试的成绩相互独立，用随机变量X 表示他所选的三个科目中考试成绩获A 等的科目数，求X 的分布列和数学期望.19．（本小题满分12分）如图，在多面体ABCDEF 中，矩形BDEF 所在平面与正方形ABC D 所在平面垂直，点M 为AE 的中点. （1）求证：BM //平面EFC（2）若DE AB =，求直线AE 与平面BDM 所成角的正弦值.20、（本小题满分12分）已知椭圆2222:1(0)x y C a b a b +=>>的离心率为12，过椭圆上顶点和右顶点的直线与圆2212:7O x y +=相切,O 为坐标原点. （1）求椭圆C 的方程；（2）若斜率大于0的直线l 交椭圆C 于A B 、两点（A 在x 轴上方），交x 轴正半轴于P 点,若3PB PA +=0u u u r u u u r，求AOB ∆面积的最大值以及此时直线l 的方程.21.（本小题满分12分）已知a ∈R ，()(1)ln f x ax x =-（1）若2()ln f x x x x ≤--恒成立，求a 的值；（2）若()f x 有两个极值点，，求a 的范围并证明1()4f x >.（二）选考题：共10分．请考生在第22、23题中任选一题作答．如果多做，则按所做的第一题计分．22．选修4－4：坐标系与参数方程在平面直角坐标系中,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线的极坐标方程为2sin 2cos (0)a a ρθθ=>，过点的直线的参数方程为222242x t y t ⎧=-+⎪⎪⎨⎪=-+⎪⎩（t 为参数），直线与曲线相交于两点.(1)写出曲线的直角坐标方程和直线的普通方程； (2)若2PA PB AB ⋅=,求a 的值.23．选修4-5：不等式选讲已知函数()|32|f x x =+. （1）解不等式()4|1|f x x <--（2）若0a >，不等式||()4x a f x --≤恒成立，求实数a 的取值范围．石室中学高2018届2017-2018学年下期二诊模拟考试数学参考答案（理科）一、选择题题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 ACCACCADDDBC13. 20-； 14. 4； 15. 2213+；16. 2215227()()248x y -+-=三、解答题17. 解：（1）由题知sin sin sin cos 2sin B A A B A +=，则sin cos 2B B +=，sin()14B π+=，因B 为锐角，所以4B π=……………………3分，由43sin ,cos 55BAC BAC ∠=∠=得所以72sin sin()10C B BAC =∠+∠=…………………….6分（2）由正弦定理sin 42sin 7BC BAC AB C ∠== 又1sin 142BC AB B ⋅⋅=，282BC AB ⋅=……………….8分解得7,42AB BC ==……………………9分所以32BD =，由余弦定理，2222cos AD AB BD AB BD B =+-⋅⋅，解得5AD =…………………………12分18..(1).记“某位考生选考的三个科目中至少有一个科目是自然科学科目”为事件M ，分 (2)随机变量X 的所有可能取值有0，1，2，3.所以X 的分布列为:19..(1)由题知BDEF ABCD ⊥面面，而BD ED ⊥，BDEF ABCD=BD 面面∩，DE BDEF ⊂面所以DE ABCD 面⊥，以DA ，DC ，DE 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系，设AD=1，则()1,1,0B ，，()0,0,1E ，()1,1,1F ，()0,1,0C ，所以而面EFC 的法向量为()1,1,1m =-u r ，则0MB m ⋅=u u u r u r 即MB m ⊥u u u r u r ，又面MB EFC ⊄，所以//面MB EFC ;……………6分(2)由（1）知所以面BDM 的法向量为()1,1,1n =-r又()1,0,1AE =-u u u r ,所以直线AE 与面BDM 12分 20.解：（1）设切线为0bx ay ab +-=，则，解得224,3a b ==，所以椭圆C 的方程分（2）设直线l 为(0,0)x my n m n =+>>，联立22143x my n x y =+⎧⎪⎨+=⎪⎩，得222(34)63120m y mny n +++-=，设1122(,),(,)A x y B x y ，122634mn y y m -+=+①2122312,34n y y m -=+②由0∆>，可得22340m n -+>…….6分又因为3PB PA +=0u u u r u u u r，可得123y y -=③…………7分由①③解得122239,3434mn mny y m m -==++，代入②22222227312(34)34m n n m m --=++，整理得2223431m n m +=+……….9分212221666()31234313AOBmn m S n y y m m m m∆=⋅-===≤+++………11分当且仅当13103,32m m n m ===即，时，满足0∆>，所以AOB ∆面积的最大值为3,此时直线l 的方程为31032x y =+………12分 21. 解(1)由题:得1ln 0x a x --≥ 令:，，…………………1分所以F ，且．所以当时恒成立，此时在上单调递增，(0,1),()0x F x ∴∈<这与F 矛盾；………………………………..3分当时令，解得，所以在上单调递减，在上单调递增，即，又因为，又F(1)=0 所以………………………..6分(2)1'()ln f x a x a x =+-21''()(0)ax f x x x+=> ①若0a ≥时, 知:'()f x 在(0,)+∞单调递增,不合题… ②若0a <时, 知:'()f x 在1(0,)a -单调递增,在1(,)a-+∞单调递减只需要22111'()ln()20f a a e a e a a a--=-+>∴-<∴<-………………….9分此时知道：()f x 在1(0,)x 单减，12(,)x x 单增，2(,)x +∞单减且易知:1210x x a<<-< 又由1111111'()0ln 0ln 1f x a x a x x ax =⇒+-=∴=- 111111111()(1)ln (1)(1)2f x ax x ax ax ax ax ∴=-=--=--又110ax -<<1()4f x ∴>…………………………………………………12分 22. (1)由=整理得=,∴曲线的直角坐标方程为=,直线的普通方程为=…………………………………………………….4分(2)将直线的参数方程代入曲线的直角坐标方程=中,得, 设两点对应的参数分别为,则有==,……………………………….6分∵=,∴=即=…………………………….8分∴= 即,解得或者(舍去),∴的值为1…………………………………………………………………………….10分23. （1）不等式．当，，解之得；当时，，解之得；当时，，无解．综上，不等式的解集为．…………………… 5分（2）令，则当时，．欲使不等式恒成立，只需，即．又因为，所以，即…………………………….10分。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

天府新区2017-2018学年度下期初三学业质量监测
一、选择题（本大题共10个小题，每小题3分，共30分。

在每小题给出的四个选项中，只有一项是符合题目要求的） 1.5-的相反数是（）（A ）51-
（B ） 5
1
（C ）-5 （D ）5 2．由5个相同的立方体搭成的几何体如图所示，则它的主视图是（）
A ．
B ．
C ．
D ．
3．中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为4400000000人，这个数用科学记数法表示为（） A ．44×108
B ．4.4×109
C ．4.4×108
D ．4.4×1010
4．在下列二次根式中，x 的取值范围是x ＞3的是（） A ．x -3 B ．3+x C ．3-x D ．
31
-x
5．下列交通标志中，既是轴对称图形又是中心对称图形的是（）
A ．
B ．
C ．
D ．
6．下列计算正确的是（）
A ．a•a 2
=a 3
B ．（a 3
）2
=a 5
C ．a+a 2
=a 3
D ．a 6
÷a 2
=a 3
7．数据3，4，5，5，5的中位数和众数分别是（） A ．4，5 B ．5，5 C ．5，4 D ．5，1
8．如图，⊙O 的直径CD 过弦EF 的中点G ，∠DCF =20°，则∠EOD 等于（） A ．10° B ．20° C ．40° D ．80°
9．若关于x 的方程
3
32+=++x m
x x 无解，则m 的值为（）
A ．m =1
B ．m =﹣1
C ．m =2
D ．m =﹣2
10．二次函数y=ax 2
+bx+c 的图象如图所示，则应满足的条件是（） A ．a ＞0，b ＞0，c ＞0 B ．a ＜0，b ＜0，c ＞0 C ．a ＞0，b ＜0，c ＜0 D ．a ＞0，b ＞0，c ＜0
二、填空题（本大题共4个小题，每小题4分，共16分） 11．计算:（-2018）0
= ．
12．在△ABC 中，∠C =90°，∠A 比∠B 大20°,则∠B = ． 13.已知P 1（x 1 ，y 1），P 2（x 2 ，y 2）两点都在反比例函数x
y 3
-=的图象上，且x 2< x 1 < 0，则y 1 ____ y 2.（填“>”或“<”）
14．如图，在平行四边形ABCD 中，连接AC ，按以下步骤作图，分别以A 、C 为圆心，以大于
2
1
AC 的长为半径画弧，两弧分别相交于点M 、N ，作直线MN 交CD 于点E ，交AB 于点F ．若AB =6，BC =4，则△ADE 的周长为．三、解答题（本大题共6个小题，共54分。

解答应写出必要的文字说明、证明过程或演算步骤）
15．（本题满分12分，每小题6分）
（1）计算：|﹣22|﹣4sin45o
+（3﹣π）0
﹣（3
1）-2
；
（2）解不等式组：⎪⎩⎪
⎨⎧-<-≥--3122
14)2(3x x x x ，并在数轴上表示它的解集．
16. （本小题满分6分）
先化简9
6)121(22+--⋅--x x x
x x ,再在1，2，3中选取一个适当的数代入求值．
随着交通道路的不断完善，带动了旅游业的发展，某市旅游景区有A、B、C、D、E等著名景点，该市旅游部门统计绘制出2017年“五·一”长假期间旅游情况统计图，根据以下信息解答下列问题：
（1）2017年“五·一”期间，该市周边景点共接待游客万人，扇形统计图中A景点所对应的圆心角的度数是，并补全条形统计图.
（2）根据近几年到该市旅游人数增长趋势，预计2018年“五·一”节将有80万游客选择该市旅游，请估计有多少万人会选择去E景点旅游？
（3）甲、乙两个旅行团在A、B、D三个景点中，同时选择去同一景点的概率是多少？请用画树状图或列表法加以说明.
如图，大楼AB右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上），已知AB=70m，DE=10m，求障碍物B，C两点间的距离（结果精确到0.1m）（参考数据：2≈1.414，3≈1.732）
如图，在平面直角坐标系中，一次函数y﹦ax+b的图象与反比例函数y﹦k
x
的图象交于一、
三象限内的A，B两点，与x轴交于C点．已知点A的坐标为（2，m），点B的坐标为（n，
﹣2），tan∠BOC﹦1
2．
（1）求该反比例函数和一次函数的表达式；
（2）P是x轴上的点，且△PAC的面积与△BOC的面积相等，求P
20. （本小题满分10分）
已知：BD 为⊙O 的直径，O 为圆心，点A 为圆上一点，过点B 作⊙O 的切线交DA 的延长线于点F ，点C 为⊙O 上一点，且AB=AC ，连接BC 交AD 于点E ，连接AC ．（1）如图1，求证：AB 平分∠FBC ；
（2）如图2，点H 为⊙O 内部一点，连接OH ，CH ；若∠OHC ﹦∠HCA ﹦90°时，求证：CH ﹦2
1
DA ；（3）在（2）的条件下，若OH ﹦3，⊙O 的半径为5，求CE 的长．
一、填空题（本大题5个小题，每小题4分，共20分）
21．如图正方形ABCD 一边在以点D 为原点的数轴上，以点A 为圆心，以AC 长为半径画弧，且与数轴相交于点E ，则点E 所对应的实数是．
22. 已知x 1，x 2是方程03
1
372
=+-x x 的两根，
若实数a 满足20182121=-++x x x x a 则a= ．
23.有五张正面分别标有数0，1，2，3，4, 5的不透明卡片，它们除了数字不同外其余全部相同。

现将它们背面朝上，洗匀后从中任取一张，将卡片上的数记为a ，则使关于x 的方程
x
x ax -=
+--21
221有正整数解的概率为． 24.已知点A 是双曲线x
y 1
=在第一象限上的一动点，连接AO 并延长交另一分支于点B ，以
AB 为一边作等边△ABC ．随着点A 的运动，点C 的位置也不断变化，但始终在一个函数的图
象上运动，则这个函数的表达式为___________．
25．在三角形纸片ABC 中，∠A =90°，∠C =30°，AC =10cm ，将该纸片沿过点B 的直线折叠，使点A 落在斜边BC 上的一点E 处，折痕记为BD （如图1），剪去△CDE 后得到双层△BDE （如图2），再沿着过△BDE 某顶点的直线将双层三角形剪开，使得展开后的平面图形中有一个是平行四边形，则所得平行四边形的周长为 cm ．
二、解答题（本大题共3个小题，共30分，解答应写出必要的文字说明、证明过程或演算步骤）
26．（本小题满分8分）
某地特色农产品在国际市场上颇具竞争力，其中绿色蔬菜远销日本和韩国等地．上市时，若按市场价格10元/千克在新区收购了2000千克绿色蔬菜存放入冷库中．据预测，绿色蔬菜的市场价格每天每千克将上涨0.5元，但冷库存放这批绿色蔬菜时每天需要支出各种费用合计340元，而且绿色蔬菜在冷库中最多保存110天，同时，平均每天有6千克的绿色蔬菜损坏不能出售．
（1）若存放x天后，将这批绿色蔬菜一次性出售，设这批绿色蔬菜的销售总金额为y元，试写出y与x之间的函数关系式．
（2）这批绿色蔬菜存放多少天后出售可获得最大利润？最大利润是多少？
如图，在Rt △ABC 中，AB=AC ，点D 为AC 延长线上一点，连接BD ，过A 作AM ⊥BD ，垂足为
M ，交BC 于点N ．
（1）如图1，若∠ADB =30°，BC =32，求AM 的长；
（2）如图2，点E 在CA 的延长线上，且AE=CD ，连接EN 并延长交BD 于点F ，求证：EF=FD ；（3）在（2）的条件下，当AE =31
AC 时，请求出FN
EN 的值．
如图，在平面直角坐标系xoy中，把抛物线y=x2先向右平移1个单位，再向下平移4个单位，得到抛物线y=（x﹣h）2+k，所得抛物线与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，顶点为M；
（1）写出h、k的值以及点A、B的坐标；
（2）点P是抛物线上一动点，在y轴上找点Q．使点A，B，P，Q组成的四边形是平行四边形，请求出对应的点P的坐标．
（3）点P是抛物线上一动点，连接AP，以AP为一边作正方形APFG，随着点P的运动，正方形的大小、位置也随之改变．当顶点F或G恰好落在y轴上时，请直接写出对应的点P
的坐标．（不写过程）。