土地确权登记中数据七参数坐标转换方法
用七参数法实现坐标转换应用七参数...

第9章GPS测量数据处理9.1概述GPS数据处理过程大致分为GPS测量数据的基线向量解算、GPS基线向量网平差以及GPS网平差或与地面网联合平差等几个阶段。
各阶段数据处理软件可采用随机软件或经正式鉴定的软件,对于高精度的GPS网成果处理也可选用国际著名的GAMIT/GLOBK、BERNESE、GIPSY、GFZ等软件。
数据处理的基本流程如图9-1所示。
9.1.1数据传输大多数的GPS接收机(如ASHTECH,TRIMBLE等型号),采集的数据记录在接收机的内存模块上。
数据传输是用专用电缆将接收机与计算机连接,并在后处理软件的菜单中选择传输数据选项后,便将观测数据传输至计算机。
数据传输的同时进行数据分流,生成四个数据文件:载波相位和伪距观测值文件、星历参数文件、电离层参数和UTC参数文件、测站信息文件。
经数据分流后生成的四个数据文件中,除测站文件外,其余均为二进制数据文件。
为下一步预处理的方便,必须将它们解译成直接识别的文件,将数据文件标准化。
9.1.2预处理GPS 数据预处理的目的是:① 对数据进行平滑滤波检验,剔除粗差;② 统一数据文件格式并将各类数据文件加工成标准化文件(如GPS 卫星轨道方程的标准化,卫星时钟钟差标准化,观测值文件标准化等); ③ 找出整周跳变点并修复观测值(整周跳变的修复见5.3.3); ④ 对观测值进行各种模型改正。
GPS 卫星轨道方程的标准化数据处理中要多次进行卫星位置的计算,而GPS 广播星历每小时有一组独立的星历参数,使得计算工作十分繁杂,需要将卫星轨道方程标准化,以便计算简便,节省内存空间。
GPS 卫星轨道方程标准化一般采用以时间为变量的多项式进行拟合处理。
将已知的多组不同历元的星历参数所对应的卫星位置Pi(t)表达为时间t 的多项式形式:)19()(2210-++++=nin i i i i t a t a t a a t P利用拟合法求解多项式系数。
解出的系数ain 记入标准化星历文件,用它们来计算任一时刻的卫星位置。
用七参数法实现WGS84到北京54的坐标转换

用七参数法实现WGS84到北京54的坐标转换用七参数法实现WGS84到北京54的坐标转换摘要:GPS技术在提供精确定位等方面具有重要价值, 通过GPS采集的坐标数据也日趋广泛,所以实现WGS - 84和BJ - 54坐标的转换有着重要意义。
通过简述了WGS84坐标系、北京54 坐标系的基本情况与空间转换的思想原理,最后详细介绍了利用七参数法在ARCGIS软件中实现WGS84到北京54的坐标转换的过程及方法,证明利用ARCGIS可以得到较高精度的坐标转换。
关键字:WGS84坐标系,北京54 坐标系,七参数,坐标转换1 坐标系概述坐标系是定义坐标如何实现的一套理论方法,包括定义原点、基本平面和坐标轴的指向,同时还包括基本的数学和物理模型,简单来说就是是描述空间位置的一种表达形式,即采用什么方法来表示空间位置。
目前国际上采用的是1984世界大地坐标系,我国通常采用的是1954北京坐标系、1980西安坐标系或地方局部坐标系等参心坐标系。
1.1 1984世界大地坐标系(WGS84)WGS84坐标系是美国国防部研制确定的大地坐标系,是为GPS 全球定位系统使用而建立的坐标系统,也是国际上采用的地心坐标系。
其原点是地球的质心,空间直角坐标系的Z轴指向BIH1984.0定义的协议地球极(CTP)方向,X轴指向BIH1984.0的零度子午面和CTP 赤道的交点,Y轴和Z,X轴构成右手坐标系。
1.2 1954北京坐标系(Beijing54)1954北京坐标系是一个参心大地坐标系,原点是前苏联的普尔科沃,采用了前苏联的克拉索夫斯基椭球体[1]。
1954年北京坐标系虽然是苏联1942年坐标系的延伸,但也还不能说它们完全相同。
2 坐标转换2.1 坐标转换的必要性首先我们先弄清楚三种常用的坐标系统及其表示方法:大地坐标系,即常说的经纬度坐标系,其表示方法为经纬度和高程(B,L,H);空间直角坐标系统,表示为空间直角坐标(X,Y,Z);平面直角坐标系统,表示方法为平面坐标和高程(X,Y,H)。
七参数法的应用原理

七参数法的应用原理1. 什么是七参数法?七参数法是一种用于地理坐标转换的方法。
它可以通过一组七个参数,将一个坐标系统中的点转换到另一个坐标系统中。
这些参数包括平移参数、旋转参数和尺度因子等,用于描述两个坐标系统之间的差异。
七参数法的应用广泛,可以用于测绘、大地坐标系统转换以及地图配准等方面。
2. 七参数法的应用原理七参数法的应用原理基于几何变换的概念。
在地理坐标转换中,我们需要考虑两个坐标系统之间的平移、旋转和尺度变化等因素。
七参数法通过计算这些变化,并用一组参数来表示,从而实现两个坐标系统之间的转换。
2.1 平移参数平移参数描述了两个坐标系统之间的平移差异。
它包括了在水平和垂直方向上的平移量。
通过计算两个坐标系统中某一固定点的坐标差异,可以确定平移参数。
2.2 旋转参数旋转参数描述了两个坐标系统之间的旋转差异。
它可以描述在水平面上的旋转角度。
通过计算两个坐标系统中三个非共线点的旋转角度差异,可以确定旋转参数。
2.3 尺度参数尺度参数描述了两个坐标系统之间的尺度差异。
它可以描述水平和垂直方向上的尺度变化。
通过计算两个坐标系统中一组点的尺度差异,可以确定尺度参数。
2.4 七参数的计算七参数的计算是通过最小二乘法来实现的。
最小二乘法是一种通过最小化残差平方和来拟合数据的方法。
在七参数法中,需要通过最小二乘法来计算平移参数、旋转参数和尺度参数,从而得到最佳拟合的转换结果。
3. 七参数法的应用场景七参数法在地理信息系统、大地测量和地图配准等领域有着广泛的应用。
下面列举了一些常见的应用场景:•地图配准:利用七参数法可以将不同坐标系统的地图配准到同一个坐标系统中,实现地图叠加和分析。
•大地坐标转换:利用七参数法可以将大地坐标系统中的点转换到其他坐标系统中,实现坐标的互通。
•摄影测量:在空间三维重建中,七参数法可以用于相机的姿态精确定位,从而实现精确的模型重建。
•GPS坐标转换:七参数法可以用于将GPS坐标系统中的点转换到其他坐标系统中,实现GPS数据的无缝整合。
施工测量坐标转换中的七参数详谈

施工测量坐标转换中的七参数详谈施工测量中的坐标转换是一种用于将不同坐标系下的坐标相互转换的方法,七参数法是其中一种常用的转换方法。
七参数法是一种通过引入七个参数来描述两个坐标系之间的相对位置和方向关系的转换方法。
在本文中,将详细介绍七参数法的原理和应用。
七参数法的原理主要基于以下几个假设:1.两个坐标系之间的转换关系可以用平移、旋转和尺度变换来描述。
2.被转换的坐标系是刚性的,即在转换过程中保持形状不变。
根据上述假设,七参数法可以通过引入七个参数来描述两个坐标系之间的转换关系,这七个参数分别是:1.平移参数:分别表示在x、y、z方向上的平移量。
2.旋转参数:分别表示沿x、y、z轴方向的旋转角度。
3.尺度参数:表示坐标系之间的尺度变换。
七参数法的转换计算过程主要分为两步:1.参数估计:通过选择一部分已知的控制点,利用最小二乘法估计出七个参数的值。
2.坐标转换:通过估计的参数值,将待转换的坐标点从一个坐标系转换到另一个坐标系。
在实际应用中,七参数法常常用于大地坐标系和工程坐标系之间的转换。
在施工测量中,经常需要在不同坐标系下进行测量,并将测量结果进行转换和比较,以确保测量的精度和一致性。
例如,在两个不同测量网络之间进行坐标转换时,可以使用七参数法来完成。
七参数法在施工测量中具有广泛的应用,主要体现在以下几个方面:1.建筑物变形监测:在建筑物变形监测中,往往需要将监测数据转换到同一参考坐标系下进行分析。
七参数法可以用于将不同测量网络之间的测量数据进行坐标转换,并进行变形分析和监测。
2.地质灾害监测:地质灾害监测中,常常需要将不同测量数据进行对比和分析。
七参数法可以用于将不同时期或不同位置的测量数据进行坐标转换,以实现数据的一致性分析和比较。
3.工程测量:在工程测量中,往往需要将不同测量网络之间的测量数据进行叠加和分析。
七参数法可以用于将不同测量网络之间的坐标数据进行转换,以实现数据的一致性和可比性。
综上所述,七参数法是一种常用的施工测量坐标转换方法,通过引入七个参数来描述两个坐标系之间的相对位置和方向关系。
七参数四参数转化

七参数四参数转化七参数和四参数转化是在大地测量中常用的两种经纬度转换方法,用于将不同坐标参考系下的坐标相互转换。
下面将详细介绍七参数和四参数转化的原理和应用。
1.七参数转化七参数转化是一种常用的大地测量中的坐标转换方法,其基本原理是通过七个参数来描述两个坐标参考系的空间相对关系。
这七个参数包括三个平移参数(dx, dy, dz),三个旋转参数(rx, ry, rz),以及一个尺度因子(s)。
假设我们有一个已知坐标参考系A,以及一个需要转换到的目标坐标参考系B,我们可以通过测量的方式获得A到B之间的七个参数,并利用这些参数将A坐标系下的点转换到B坐标系下的点。
七参数转化的公式如下:Xb = s(Rx * Xa - Ry * Za + Rz * Ya) + dxYb = s(Ry * Xa + Rx * Za - Rz * Xa) + dyZb = s(Rz * Xa + Rx * Ya + Ry * Xa) + dz其中(Xa,Ya,Za)是坐标参考系A中的点的坐标,(Xb,Yb,Zb)是坐标参考系B中的点的坐标。
七参数转化广泛应用于地理信息系统(GIS)、大地测量、导航等领域。
通过七参数转化,可以将不同坐标系统下的点转换到同一坐标系统下,实现数据融合和统一管理。
四参数转化是七参数转化的一种特殊情况,即在七参数转化中忽略了旋转和尺度因子的影响。
四参数转化只考虑了平移因子,即通过三个平移参数(dx, dy, dz)来描述两个坐标参考系的空间相对关系。
四参数转化的公式如下:Xb = Xa + dxYb = Ya + dyZb = Za + dz其中(Xa,Ya,Za)是坐标参考系A中的点的坐标,(Xb,Yb,Zb)是坐标参考系B中的点的坐标。
四参数转化通常应用于简单的坐标系转换,适用于小区域的坐标变换问题。
总结:七参数和四参数转化是大地测量中常用的坐标转换方法,用于将不同坐标参考系下的点的空间位置相互转换。
RTK求解参数(三参、四参、七参)详解

• 投影讲解 四参数+高程拟合
二、三参数转换
• (1)、架设基准站 • 基准站(基准站架设在已知点上,如果基准站架设在未知点上,手簿 软件使用方法和四参数类似,只是在计算参数时选择计算三参数)。 • 架设点必须满足以下要求: • a、高度角在15度以上开阔,无大型遮挡物; • b、无电磁波干扰(200米内没有微波站、雷达站、手机信号站等, 50米内无高压线); • c、位置比较高,用电台作业时,基准站到移动站之间最好无大型遮 挡物,否则差分传播距离迅速缩短; • d、只需一个已知坐标点 (已知点可以是国家坐标系下的坐标,或坐 标系和WGS-84坐标系之间的旋转很小); • e、此方法都适用于客户对坐标精度要求不是很高的情况,随着移动 站离基准站距离的增加,精度越来越低,一般3KM精度能在5CM以内。
空间直角坐标(X,Y,Z)
大地坐标(B,L,H) 投影正算 平面直角坐标(x,y,h) 平面转换 当地平面坐标(x,y)
ቤተ መጻሕፍቲ ባይዱ
RTK简易操作流程
• 以下只是软件的简易操作流程,详细使用步骤请参照接下来的详细说明。此 流程只是我们提供给的一种解决方案,在熟练使用本软件后,可以不依照此 步骤操作。在作业过程中,通常的使用方法为:
• 投影讲解 七参数
四、一步法转换
• 使用要求:至少三个已知坐标点(已知点可以是国家坐标系下的坐标 或自定义坐标系下的坐标,最好三个以上已知点,可以检验已知点的 正确性)。 • 用一步法转换、七参数转换、四参数转换、三参数转换(基准站架设 在未知点)时,仪器和手簿软件操作步骤类似,只是要求的已知点数 据和使用范围不一致。
• 一般的:
• • • • 三参数:要求已知一个国家坐标点,精度随传输距离增加而减少 四参数:要求两个任意坐标点,精度在小范围内可靠 七参数:三个国家坐标点,精度高,对已知点要求严格 一步法:三个任意坐标点,在残差不大的情况下,精度可靠
中海达七参数坐标数据转换方法

中海达七参数坐标数据转换方法1.引言中海达七参数坐标数据转换方法是用于将一个坐标系统的坐标数据转换到另一个坐标系统的方法。
七参数包括三个平移参数、三个旋转参数和一个尺度参数。
在实际应用中,七参数转换常用于地理信息系统(GIS)、测量和导航等领域。
2.数据准备在进行坐标数据转换之前,需要准备两个坐标系的坐标数据。
每个坐标数据包括坐标点的三维坐标(x,y,z)和相应的椭球高(h)。
3.参数计算根据已知的源坐标系和目标坐标系的坐标数据,可以计算七个参数的值。
参数计算可采用多种方法,其中较常用的方法是最小二乘法。
最小二乘法的计算步骤如下:3.1.根据坐标数据,计算相应的坐标系平移中心。
平移中心的计算可以采用几何平均法、最大似然法等方法。
3.2.将源坐标系中的坐标点平移到平移中心。
3.3.计算源坐标系和目标坐标系的旋转矩阵。
旋转矩阵的计算可以采用相似性变换法、最小二乘法等方法。
3.4.计算旋转矩阵的欧拉角。
3.5.根据平移、旋转和尺度的定义,计算平移参数、旋转参数和尺度参数。
3.6.利用最小二乘法求解得到七参数的最优解。
4.坐标数据转换得到七参数的值之后,可以将源坐标系的坐标数据转换到目标坐标系。
转换步骤如下:4.1.将源坐标系的坐标点减去平移中心得到坐标差值。
4.2.根据旋转矩阵将坐标差值旋转到目标坐标系中。
4.3.根据尺度参数对坐标差值进行尺度变换。
4.4.将坐标差值加上目标坐标系的平移中心得到目标坐标系的坐标点。
5.转换精度评估完成坐标数据转换后,需要对转换结果的精度进行评估。
评估方法可以采用坐标残差法、平差误差法等方法。
通过比较转换后的坐标数据与目标坐标数据的差异,可以评估转换结果的精度和可靠性。
6.应用案例中海达七参数坐标数据转换方法已在许多应用案例中得到成功应用。
例如,在陆地测量中,可以将不同基准坐标系的测量数据转换到统一的坐标系统中,以实现数据的一致性和比较。
在导航领域,可以将GPS接收到的坐标数据转换到地理信息系统中使用的坐标系统,以实现位置的准确定位和导航。
两种七参数坐标转换方法

两种七参数坐标转换方法七参数坐标转换方法是一种将不同坐标系之间的坐标进行转换的方法。
常用于地理信息系统(GIS)、大地测量学和空间测量学等领域。
以下介绍两种常见的七参数坐标转换方法:1.七参数最小二乘法:七参数最小二乘法是通过最小化两个坐标系之间的残差平方和来求解七个参数的方法。
假设有两个坐标系A和B,七个参数分别为平移量(ΔX,ΔY,ΔZ)、旋转角度(θX,θY,θZ)和尺度比例(k)。
通过找到最佳的七个参数值,使得在坐标系A和B之间的转换中,两个坐标系之间的差异最小。
2.矩阵变换法:矩阵变换法是将坐标系A和坐标系B之间的转换表示为一个矩阵的乘法运算。
这种方法将七个参数分别表示为一个3×3的旋转矩阵R和一个3×1的平移矩阵T。
具体的转换公式为:```BX=RX*AX+T```其中,BX和AX分别为坐标系B和坐标系A中的坐标值,RX为旋转矩阵,T为平移矩阵。
通过确定旋转矩阵和平移矩阵的数值,可以将坐标系A中的坐标转换为坐标系B中的坐标。
这两种七参数坐标转换方法在实际应用中都有其优缺点。
七参数最小二乘法在计算过程中需要通过迭代方法来找到最优的参数值,计算量较大;而矩阵变换法相对来说计算较为简单。
然而,七参数最小二乘法在处理大数据集时可能会得到更精确的结果。
对于具体的应用场景,可以根据实际需求选择合适的方法。
此外,在实际应用中,还有一些常见的改进七参数坐标转换方法,例如七参数地面控制点法和七参数线性组合法等。
这些方法通过引入更多的控制点或采用线性组合的方式,可以提高坐标转换的精度和稳定性。
总的来说,七参数坐标转换方法是地理信息系统、大地测量学和空间测量学等领域中常用的一种坐标转换方法,通过确定平移量、旋转角度和尺度比例等参数,可以将不同坐标系之间的坐标进行转换。
在实际应用中,可以根据具体需求选择合适的转换方法,并根据实际情况进行适当的改进。
两种七参数坐标转换方法

两种七参数坐标转换方法目前国内所用GNSS (Global Navigation Satellite System)即全球卫星导航系统,已经发展到多星,尤其随着北斗导航系统的逐步完善,正在向CGCS2000 椭球过渡,但还是以WGS-84 坐标系统为主流,即仍以美国GPS 为主,所发布的星历参数也是基于此坐标系统。
WGS-84 坐标系统(World Geodetic System-84,世界大地坐标系-84) 的坐标原点位于地球的质心,Z 轴指向BIH1984.0 定义的协议地球极方向,X 轴指向BIH1984.0的启始子午面和赤道的交点,Y 轴与X 轴和Z 轴构成右手系。
WGS-84 系所采用椭球参数为:长半轴6378137;扁率1:298.257223563。
而我国目前广泛采用的大地测量坐标系有3种:①北京1954 坐标系。
该坐标系采用的参考椭球是克拉索夫斯基椭球,该椭球的主要参数为:长半轴6378245;扁率1:298.3。
②1980 年国家大地坐标系。
该坐标系是参心坐标系,采用地球椭球基本参数为1975 年国际大地测量与地球物理联合会第十六届大会推荐的数据,大地原点设在我国中部的陕西省泾阳县永乐镇,也称西安80 坐标系。
长半轴6378140±5;扁率1:298.257。
③2000 中国大地坐标系。
该坐标系是地心坐标系,与WGS-84 坐标类似。
原点在包括海洋和大气的整个地球的质量中心;定向在1984.0 时与BIH(国际时间局)。
长半轴6378137.0;扁率1:298.257 222 101。
各坐标系之间的转换是工作中的经常遇到的问题,主要的转换方法有三参数、四参数和七参数法,而这三种方法中,七参数是一种空间直角坐标系的转换模型,是基于椭球间的三维转换,精度最高。
如果用七参数法来实现WGS84 坐标系与1980 年国家大地坐标系的转换,求解前必须确定控制网中各点对的距离。
如果两点间距离超过15 公里,必须考虑曲面因素即两种不同坐标系的椭球参数,避免因椭球的差异,导致转换后所得坐标残差过大,精度过低,为了保证精度必须采用七参数法。
七参数空间直角坐标系坐标转换

七参数空间直角坐标系坐标转换七参数空间直角坐标系坐标转换是一种将不同基准下的直角坐标系坐标相互转换的方法。
七参数包括三个平移参数(x、y、z),三个旋转参数(α、β、γ)和一个尺度参数(s)。
这种方法常用于地理信息系统(GIS)、大地测量学、地质学及遥感等领域。
七参数空间直角坐标系坐标转换的原理是通过对源坐标系(即要转换的坐标系)和目标坐标系进行参数化,进而实现坐标系之间的转换。
其中,平移参数表示了源坐标系相对于目标坐标系在三个方向上的平移量,旋转参数表示了源坐标系相对于目标坐标系的旋转角度,尺度参数则表示了两个坐标系之间的尺度差异。
具体来说,七参数空间直角坐标系坐标转换的步骤如下:1.确定源坐标系和目标坐标系,包括它们的基准、坐标原点和坐标轴方向。
2.根据实际测量数据,计算源坐标系和目标坐标系之间的三个平移参数(x、y、z),三个旋转参数(α、β、γ)和一个尺度参数(s)。
这些参数可以通过一系列大地测量或地球物理测量方法得到。
3.根据计算得到的参数,建立转换矩阵。
转换矩阵是一个3×3的矩阵,用于将源坐标系下的点坐标转换为目标坐标系下的点坐标。
4.对于源坐标系中的每一个点,根据转换矩阵进行坐标转换。
具体方法是将源坐标系下的点坐标与转换矩阵相乘,并加上平移参数。
5.得到目标坐标系下的点坐标,完成坐标转换。
需要注意的是,在进行七参数空间直角坐标系坐标转换时,应该尽量选择准确的参数值。
这些参数可以通过现场测量或者前人的实验数据获得。
如果参数值不准确,可能会导致转换结果的偏移或失真。
此外,七参数空间直角坐标系坐标转换通常是一个数学复杂的过程。
为了简化计算,现代的地理信息系统和大地测量软件通常提供了自动化的坐标转换功能,用户只需输入源坐标系和目标坐标系的参数,软件就可以帮助完成坐标转换的计算。
如何使用RTK手簿求坐标转换参数(四参数七参数)

如何使用RTK手簿求坐标转换参数(四参数七参数)手簿:南方H5安卓手簿;软件:工程之星5.01、四参数示例:2000坐标系转地方坐标系准备材料:2个以上的已知点坐标步骤:1.1 打开求转换参数操作:“输入”→“求转换参数”1.2 设置四参数在求转换参数界面首先点击右上角的设置按钮,将“坐标转换方法”改为“一步法”,点击“确定”,则可以开始四参数的设置。
1.3 添加坐标参数“一步法”设置完成后,在求转换参数界面点击“添加”1.4 输入坐标参数平面坐标输入已知点坐标,大地坐标输入RTK测的已知点的坐标。
大地坐标可以点击更多获取方式,里面有“定位获取”和“点库获取”,输入完成以后,点击“确定”,添加完第一个坐标Pt1。
然后以同样的方法输入第二个坐标Pt2,如下图所示:1.5 计算四参数并应用如果Pt1或Pt2不小心输入错误,单击改点可进行编辑或者删除。
坐标输入无误后,点击“计算”即可获得2000坐标系转当地坐标系的四参数,再点击“应用”即可,再进行点测量时,获取的坐标就是当地坐标系了。
需要主要的是,四参数覆盖范围较少,一般推荐使用七参数。
2、七参数示例说明:2000坐标系转地方坐标系准备材料:3个以上的已知点坐标2.1 打开求转换参数操作:“输入”→“求转换参数”2.2 设置七参数在求转换参数界面首先点击右上角的设置按钮,将“坐标转换方法”改为“七参数”,点击“确定”,则可以开始七参数的设置。
2.3 添加坐标参数“七参数”设置完成后,在求转换参数界面点击“添加”2.4 输入坐标参数坐标输入方法同四参数一样,但是需要至少输入3个已知点坐标。
输入完成后点击“计算”即可获得2000坐标系转当地坐标系的七参数,最后点击应用即可。
华测手簿:HCE320、HCE300等;软件:测地通LandStar7七参数1.1 打开参数计算操作:在主界面依次点击“工具”→“参数计算”1.2 设置七参数将计算类型设置为七参数1.3 添加坐标点击左下角“添加”按钮,添加已知点坐标。
农村土地承包经营权确权登记颁证工作中的一种坐标转换方案

农村土地承包经营权确权登记颁证工作中的一种坐标转换方案作者:王清华来源:《西部资源》2018年第06期摘要:现阶段农村土地承包经营权确权登记颁证工作采用的是2000国家大地坐标系,权属调查中的承包地块调查内容包含土地用途、地力等级、利用类型和是否基本农田等信息,这些信息资料需要从当地国土、林业等相关部门收集。
这些信息资料通常多以数据库、电子图件、电子表格等形式存在,其中涉及的坐标系通常为1954年北京坐标系或1980西安坐标系。
如何把收集的资料中的坐标转换成CGCS2000坐标就成为非常紧迫和十分重要的任务。
但是,从2009年开展农村土地承包经营权确权登记颁证工作试点至今,针对这项工作的图件及数据坐标转换的研究较少。
针对此问题,本文从实际应用出发,以山西省某县为例,首先通过对比两种坐标转换方法的转换结果,确定了在县域范围内采用七参数法,接着又提出了一种应用南方CASS及TGO等软件对图件及数据进行坐标转换的方案,并通过实践验证了该方案的正确性和可行性,这种坐标转换方案流程简单,易掌握,可以有效提升工作效率。
本文还对本项工作中涉及坐标转换的关键环节提出了注意事项。
关键词土地承包经营权;坐标转换;CGCS2000;布尔莎模型;四参数;七参数;CASS;TGO引言《农村土地承包经营权确权登记调查规程》(NY/T2537-2014)明确指出,农村土地承包经营权调查采用2000国家大地坐标系(CGCS2000,即China Geodetic CoordinateSystem 2000)。
在农村土地承包经营权确权登记颁证工作中,权属调查是核心环节之一。
权属调查中的承包地块调查内容包含土地用途、地力等级、利用类型和是否基本农田等信息,这些信息资料需要从当地国土、林业等相关部门收集。
这些信息资料通常多以数据库、电子图件、电子表格等形式存在,其中涉及的坐标系通常为1954年北京坐标系或1980西安坐标系。
如何把收集的资料中的坐标转换成CGCS2000坐标就成为非常紧迫和十分重要的任务。
中海达七参数坐标数据转换方法

中海达七参数坐标数据转换方法一、使用数据文件进行七参数计算1、数据文件格式如下。
元宝山,4720024.35,655128.78,457.10,4719990.05,655080.46,457.10成善,4745095.01,622946.72,596.30,4745060.48,622897.74,596.30孟家子,4769755.52,646447.14,358.80,4769721.20,646397.94,358.80点名,源坐标X,源坐标Y,源坐标系大地高或水准高,目标坐标系X,目标坐标系Y,目标坐标系大地高或水准高,文件名为*.dat2、打开软件显示如下,点文件→新建3、设置→地图投影输入中央子午线值(注意选择使用的成果是三度带还是六度带)4、设置→计算七参数将编辑好的数据文件导入后,将源坐标系、目标坐标系椭球和坐标类型选中,点击计算,完成七参数计算。
若点击确定则弹出下面对话框。
若导出生成七参数计算文件,则点击文件中的保存在命名栏内输入文件名和所在国家名,点确定,完成七参数文件存储,下次在用时可直接调用该文件。
二、不同椭球间的坐标转换(一)直角坐标转换1、准备数据文件,文件格式如下元宝山,4718856.506339,408872.658209,457.100000,成善,4745051.426992,377603.848545,596.300000,孟家子,4768856.777635,401966.828513,358.800000,老鹰山,4719694.054295,402204.627001,442.820000,点名,源坐标系X坐标,源坐标系Y坐标,源坐标系大地高或水准高;文件名为*.dat2、打开计算好的七参数文件(文件→打开)3、点击设置→换带计算若为从6度带转换到3度带,则投影前中央经线送6度带值若为3度带转换到3度带,则投影前中央经线送3度带值再输入转换后3度带经线值4、设置源坐标系、目标坐标系,选中坐标类型,选中七参数转换。
写给测绘小白,讲解四参数与七参数坐标转换含义及区别

写给测绘小白,讲解四参数与七参数坐标转换含义及区别坐标转换时RTK技术里不可缺少的重要部分。
不同坐标系,其椭球体的长半径,短半径和扁率是不同的。
比如我们常用的四种坐标系北京54、西安80、WGS84、CGCS2000所对应的椭球体,它们的椭球体参数就各不相同。
而不同空间直角坐标系之间的转换一般通过七参数或者四参数来实现坐标转换。
今天,小编就为大家讲解一下四参数和七参数的含义、区别及转换方法。
1四参数两个不同的二维平面直角坐标系之间转换通常使用四参数模型,四参数适合小范围测区的空间坐标转换,相对于七参数转换的优势在于只需要2个公共已知点就能进行转换,操作简单。
在该模型中有四个未知参数,即:(1)两个坐标平移量(△X,△Y),即两个平面坐标系的坐标原点之间的坐标差值。
(2)平面坐标轴的旋转角度A,通过旋转一个角度,可以使两个坐标系的X和Y轴重合在一起。
(3)尺度因子K,即两个坐标系内的同一段直线的长度比值,实现尺度的比例转换。
通常K值几乎等于1。
四参数的数学含义是:用含有四个参数的方程表示因变量(y)随自变量(x)变化的规律。
举个例子,在珠海既有北京54的平面坐标又有珠海的平面坐标,在这两种坐标之间转换就用到四参数。
四参数的获取需要有两个公共已知点。
2七参数七参数一般采用布尔沙模型法,适合大范围测区的空间坐标转换,转换时需要至少3个公共已知点。
因为有较多的已知点,所以七参数转换的坐标精度要高于四参数转换的坐标精度,但是操作较四参数法复杂。
七参数模型中有七个未知参数,即:(1)三个坐标平移量(△X,△Y,△Z),即两个空间坐标系的坐标原点之间坐标差值。
(2)三个坐标轴的旋转角度(△α,△β,△γ)),通过按顺序旋转三个坐标轴指定角度,可以使两个空间直角坐标系的XYZ轴重合在一起。
(3)尺度因子K,即两个空间坐标系内的同一段直线的长度比值,实现尺度的比例转换。
通常K值几乎等于1。
七参数其涉及到的七个参数为:X平移,Y平移,Z平移,X旋转,Y旋转,Z旋转,尺度变化K。
在测绘过程中如何处理地理空间数据的坐标转换

在测绘过程中如何处理地理空间数据的坐标转换在测绘过程中,坐标转换扮演着至关重要的角色。
地理空间数据的坐标转换可以将不同坐标系统下的数据相互转换,使得这些数据能够在同一个坐标系统中进行分析与应用。
本文将探讨在测绘过程中如何处理地理空间数据的坐标转换,并介绍常用的转换方法与工具。
首先,我们需要了解什么是坐标转换。
坐标转换是指将一个坐标系下的点的坐标转换成另一个坐标系下的点的坐标的过程。
在测绘中,常见的坐标系统包括经纬度坐标系统、平面直角坐标系和高斯-克吕格投影坐标系等。
由于各种不同坐标系统的存在,不同数据的坐标存在差异,因此,在数据使用过程中必须进行坐标转换。
接下来,我们来讨论一下为什么需要进行坐标转换。
首先,不同的测量设备和技术可能使用不同的坐标系统,将它们获得的数据转换到同一个坐标系统中,可以将各种数据进行统一分析与处理。
其次,不同的应用领域对坐标系统的要求也不同,如地理信息系统(GIS)、地形图制作、气象学和环境学等。
在进行这些应用之前,必须将数据转换到相应的坐标系统中。
最后,有些地方会使用不同的坐标系统进行测绘,如国境线,因此,在数据的测绘过程中,坐标转换是十分必要的。
坐标转换的方法有很多种,我们来介绍几种常用的方法。
首先是四参数法,它适用于需要进行平移和旋转的坐标转换。
四参数法使用了平移参数和旋转参数来对坐标进行转换,从而使得数据能够在不同坐标系统下对齐。
其次是七参数法,它适用于需要进行平移、旋转和缩放的坐标转换。
七参数法通常用于将地心坐标系统下的数据转换到大地坐标系统下,或者将不同大地坐标系统之间的数据进行转换。
最后是多项式法,它适用于需要进行高阶拟合的坐标转换。
多项式法通过使用多项式函数来对坐标进行转换,从而实现高精度的转换结果。
除了这些方法,还有一些常用的坐标转换工具可以帮助我们处理地理空间数据的坐标转换。
如ArcGIS软件中的“坐标系统工具”,它提供了各种坐标转换方法和参数设置选项,可以满足不同数据的转换需求。
地籍图斑坐标系统转换方法的探讨

一、引言根据控制点的坐标(至少3个已知点,并且两个坐 经过变换,可等价得到如下公式:在ArcGIS 用中,通过ArcToolBox Data 应a n a g e m e n t T o o l s —P r o j e c t i o n s a n d Transformations—Feature—Project或Raster—Project来实现两个矢量数据或影像数据坐标系之间的数据转换。
首先选择要转换的文件或数据集,如果文件或德清县国土资源局 马宝平 张腊平图1数据集已有坐标系统,将自带显示此坐标系,然后选择转换后的坐标系统,并选择地理变换模板(Geographic Transformation)下拉框中自动加载可用的模板。
如果没有可选项,需要用户自定义。
地理变换模板可通过亦可借助南方Cass9.1平台(图4),利用地物编ArcToolBox—Data Management Tools—Projections辑(A)菜单下的坐标转换模块(红色区域),利用前and Transformations—Create Custom Geographic面求解得到的布尔莎七参数,对已知图斑直接进行坐标Transformation来创建定义需要进行坐标系统转换的类系统转化图形输出。
(如1980西安坐标系统转1954北京坐标系统或方法二:间接的属性坐标系统转换1954北京坐标系统转1980西安坐标系统)。
此方法可对.shp数据文件进行直接转换,方便快捷。
需注意的是,在定义地理转换方法时,ArcGIS软件中提供了10种投影方法。
投影变换大致分为2种,三参数和七参数方法。
GEOCENTRIC_TRANSLATION方法是地心变换,也就是三参数计算出dx、dy、dz,平借助南方Cass9.1平台,通过获取地籍图斑中每一个界址点元素的图形坐标串及其属性数据,新建一个.dat或.txt数据文件,将每一个元素在原始坐标系统中的坐标串数组,经过七参数转换生成新坐标系统下的坐标串数组,附带属性数据生成新的元素,保存在新的图2图3图4Copyright©博看网 . All Rights Reserved.=第i个重合点转换坐标-第i个重合点已知坐标 (i=1,2,3,…,n)空间直角坐标系转换精度评定方法:X残差中误差为: Mx= = = Y残差中误差为:My= = = Z残差中误差为: Mz= =则点位中误差为: MP= 本区域检测点选取3个C级点,17个D级点,通过计算(详见表Mp方法一=± =±6.6mm 国土资源“一张图”及国土资源执法监察系统的建MP方法二=± =±6.8mm设,势必要求多源信息的有效融合,构建统一的综合监因此,求解的布尔莎七参数转换坐标精度完全可满管平台。
七参数转换法推导公式

七参数转换法推导公式七参数转换法是大地测量中常用的一种方法,用于将不同大地坐标系之间的坐标转换为相互对应的坐标。
这种方法基于七个参数的数学模型,通过对观测数据进行处理和计算,得到坐标转换的公式。
七参数转换法的基本思想是,在两个大地坐标系之间建立一个七参数的转换模型,通过对大地测量数据进行观测和处理,计算出这七个参数的具体数值,从而实现坐标的转换。
这七个参数分别是三个平移参数(dx, dy, dz),三个旋转参数(rx, ry, rz),以及一个尺度参数(s)。
平移参数表示两个坐标系之间的平移差别,旋转参数表示两个坐标系之间的旋转差别,尺度参数表示两个坐标系之间的尺度差别。
具体的转换公式如下:X' = X + dx - Y*rz + Z*ry + sY' = Y + X*rz + Z*rx + sZ' = Z - X*ry + Y*rx + s其中,(X, Y, Z)是原始坐标系的坐标,(X', Y', Z')是目标坐标系的坐标。
通过这个公式,可以将原始坐标系的坐标转换为目标坐标系的坐标。
七参数转换法的推导过程比较复杂,需要依据大地测量的理论和观测数据进行数学推导。
这里不再详细介绍推导的具体步骤和过程,只简要说明一下。
需要建立两个大地坐标系之间的联系,确定两个坐标系的原点和坐标轴方向。
然后,在这两个坐标系中选择若干个控制点,测量这些控制点在两个坐标系中的坐标。
接下来,根据测量数据,建立坐标转换的数学模型。
通过对测量数据进行处理和计算,得到七个参数的数值。
将这七个参数代入转换公式,即可实现坐标的转换。
七参数转换法在实际应用中具有广泛的用途。
例如,当需要将GPS 测量得到的坐标转换为地理坐标时,就可以使用七参数转换法。
又或者,在不同的大地坐标系中进行坐标转换时,也可以使用这种方法。
七参数转换法是一种重要的大地测量方法,通过对大地测量数据进行处理和计算,可以实现不同大地坐标系之间的坐标转换。
7参数转换

区域参数在坐标系统转换中的应用探讨陈文波(广西第二测绘院广西柳州545006)【摘要】本文对四参数法和七参数法的坐标转换方法进行分析与探讨,并结合测量作业实例对四参数法和七参数法的坐标转换方法进行验证,最后给出选择方法。
【关键词】GPS WGS84 坐标系统四参数七参数转换参数0 引言在工程测量过程中,经常碰到不同坐标系统间坐标转换的问题。
常见的转换类型有以下两种:①大地坐标(BLH)与平面直角坐标(XYZ)相互转换;②任意两空间坐标系的转换(包括54北京坐标、80西安坐标、地方坐标及WGS84坐标系的相互转换)。
所谓坐标转换的过程就是转换参数的求解过程。
常用的坐标转换方法有四参数法和七参数法。
下面对四参数法和七参数法的坐标转换方法进行分析和探讨,并结合测量作业实例对四参数法和七参数法坐标转换方法进行验证。
1 区域参数坐标转换方法1.1 四参数坐标转换方法(经典2D)图1 平面直角坐标系的转换四参数坐标转换方法是一种降维的坐标转换方法,即由三维空间的坐标转换为二维平面的坐标,避免了由于已知点高程系统不一致而引起的误差。
如图1所示,在两平面直角坐标系之间进行转换,需要有四个转换参数,其中两个平移参数(Δx0,Δy0),一个旋转参数α和一个尺度比因子m ,转换公式如下:以Leica“一步法”为例:这种转换方法是通过将高程与点位分开进行转换。
在平面点位转换中,首先将WGS84地心坐标投影到临时的横轴墨卡托投影,然后通过平移,旋转和尺度变换使之与计算的“真实”投影相符合,高程转换则采用简单的一维高程拟合。
如果54北京坐标和80西安坐标高程的资料不是很好或根本没有,你仍可仅对平面点位进行转换;高程已知的点和平面点位已知的点也不必是同一个点,用这种方法进行转换,能够在只有一个公共点的情况下计算54北京坐标系统、80西安坐标系统和WGS84坐标系统之间的转换参数,具有平面点位的点的数量以及利用它们可计算的平面转换参数的组合如下:表一:经典2D表二:转换中包括高程点的数量直接影响高程转换的类型四参数法不需要已知地方椭球和地图通用模型就可利用最少的点计算出转换参数。
七参数计算步骤
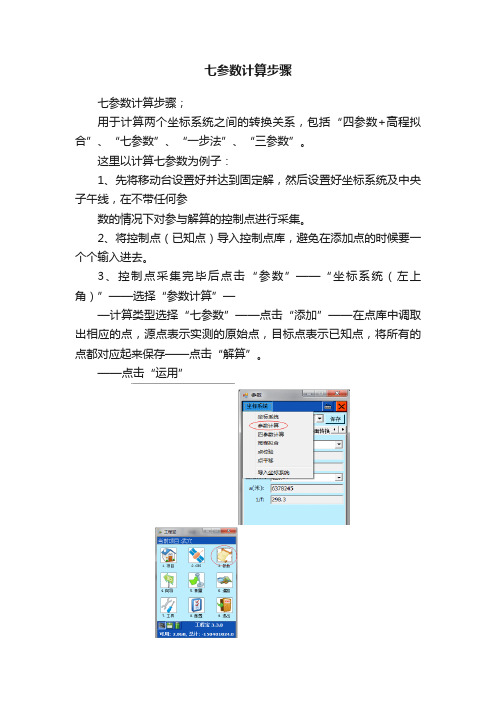
七参数计算步骤
七参数计算步骤;
用于计算两个坐标系统之间的转换关系,包括“四参数+高程拟合”、“七参数”、“一步法”、“三参数”。
这里以计算七参数为例子:
1、先将移动台设置好并达到固定解,然后设置好坐标系统及中央子午线,在不带任何参
数的情况下对参与解算的控制点进行采集。
2、将控制点(已知点)导入控制点库,避免在添加点的时候要一个个输入进去。
3、控制点采集完毕后点击“参数”——“坐标系统(左上角)”——选择“参数计算”—
—计算类型选择“七参数”——点击“添加”——在点库中调取出相应的点,源点表示实测的原始点,目标点表示已知点,将所有的点都对应起来保存——点击“解算”。
——点击“运用”
注:源点表示实测的原始点,目标点表示已知点(两个点是在不同坐标系下的同一个点)。
所有点都添加完毕。
所有点添加完毕后点击“解算”点名前方打钩表示参与解算。
解算完后会出现“七参数结果”——点击“运用”。
拖动滚动条查看平面和高程中误差是否满
足要求(一般在3公分以下)。
如果有个别点不满足要求,将其点名前方钩取消掉不参与解算。
参数运用完后可在“椭球转换”中查看。
然
后将移动台在已知点上检查,看手簿显示坐标是否与控制点坐标吻合。
4、如果移动台接收的差分源发生改变(接收其他基站的信号)移动台需要做点平移进行校正。
测得当前点(控制点)坐标,调取已知点坐标或输入然后点“计算”
dx/dy/dh是当前点与控制点计算出来的差值,点击应用后当前坐标会显示准确坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
土地确权登记中数据七参数坐标转换方法
作者:李俊俊
来源:《经营者》2016年第06期
摘要农村土地承包经营权确权登记颁证工作中,涉及数据坐标转换的事项较多,对确权、颁证过程中土地信息的准确性以及承包经营权的核准均有重要影响。
本文基于上述背景,对农村土地承包经营权确权登记颁证工作中,数据坐标转换工作进行概述,并探讨数据七参数坐标转换方法,以期能为农村土地确权工作提供参考。
关键词农村土地确权颁证七参数坐标转换 ACRGIS
一、开展农村土地确权颁证工作的背景
在确权颁证过程中,要以第二轮土地承包合同以及相应的农村土地承包经营权权属资料为主要依据,同时要结合国土二调成果资料、林权发证资料和图件成果、农村集体土地所有权数据、基本农田划定数据、行政区域勘界资料以及相关基础地理信息资料等。
由于涉及多部门的多类资料且坐标基准和投影方式各不相同,其中包含了1980西安坐标系、1954北京坐标系,而本次确权颁证工作明确了坐标系统为2000国家大地坐标系,选择高斯-克吕格投影,采用标准三度分带。
坐标基准不统一将对数据资料的使用造成极大不便,还会引起不必要的权属纠纷和部门纠纷。
因此,对数据坐标进行转换处理在农村土地确权颁证工作中有重要意义。
以下将从实际数据出发,对数据坐标转换的特点进行简要介绍,希望能提高农村土地确权颁证的工作效率。
二、坐标转换方法
确权颁证工作中大量数据需从80坐标系转换到2000国家大地坐标系,由于采用不一样的椭球基准,因此转换是不严密的转换,一般选用七参数法,即X平移,Y平移,Z平移,X旋转,Y旋转,Z旋转,尺度变化K。
当然,如果区域范围不大,最远点间的距离小于30Km (经验值),就可以使用三参数法,即X平移,Y平移,Z平移,而将X旋转,Y旋转,Z旋转,尺度变化K视为0,三参数只是七参数的一种特例,因此,本文只对七参数转换法进行介绍。
(一)七参数坐标转换原理
两个空间直角坐标系,它们的原点不一致,相应的坐标轴相互不平行,两个坐标轴间除了三个平移参数,还有三个欧勒角,即三个旋转参数,又考虑到两个坐标系的尺度不尽相同,还需设一个尺度变化参数k,总计共有七个参数。
用七参数进行空间直角坐标系转换有布尔莎公式、莫洛琴斯基公式和范式公式等。
下面给出布尔莎七参数公式:
式中的(X0,Y0,Z0)为三个平移参数,(εX,εY,εZ)为三个旋转角参数,m为尺度参数。
(二)七参数求取方法
由于坐标转换的计算复杂,为避免不必要的错误、提高效率,通常采用软件进行计算,采用布尔莎模型进行求解七参数至少需3个同名点。
考虑到确权颁证工作中面对的经常是一个县(区)的资料转换,故应多选取几个同名点,一般10到15个为宜,过少会导致离同名点较远的误差偏大,过多则会因为约束条件太多,导致整体精度不佳。
此外,所选同名点分布要尽量均匀,并留出2~3个不参与七参数计算用于转换参数校核。
以我市红塔区为例,确权颁证项目涉及11个乡(镇)行政区域面积1004平方公里,村(社区居)委会104个,其中:社区94个、村委会10个;村(居)民小组1106个,其中:社区居民小组1035个、村民小组71个、自然村436个。
人口约40.29万人,农户约65670户,二调面积耕地为262934.7亩、二轮承包面积120351亩。
项目中采用七参数坐标转换方法,应用COORD GX参数计算软件,步骤如下:
第一,打开COORD GX软件“工具”菜单中“坐标转换”,在“文件”菜单下对“椭球管理”定义好需要的椭球参数。
分别输入椭球名称、长半径a和扁率1/e的具体参数。
第二,将“投影设置”选为高斯三度带投影,并设定红塔区域所对应的中央子午线经度。
第三,同名点输入,将源坐标和目标坐标类型均选择为平面坐标,椭球分别设置成1980西安和2000国家大地坐标系。
选择“计算七参数”,按软件格式要求分别输入点的源坐标和目标坐标,点击计算。
红塔区本次选取12个同名点,其中参与计算七参数的同名点9个,3个作为校核点。
计算过程中未出现误差超限的点,当然如果出现超限情况应及时将超限点剔除再次计算。
通过计算我们得到(X0、Y0、Z0、εX、εY、εZ、m)7个转换参数。
第四,将剩余3个同名点带入COORD GX软件,用已经求得的七参数进行80坐标到2000大地坐标的转换,得出结果与3个点原有的2000大地坐标进行比较,差值均在厘米以内,满足确权颁证工作的要求。
(三)利用七参数对图件进行转换
第一,打开ARCGIS10.1,在“图层”中将图形窗口的地理空间参考参数设置为“国家2000”坐标系。
第二,在ArcToolbox中选择Create CustomGeographic Transformation工具,在弹出的窗口中,输入一个转换的名字,如xian80 To 2000。
在定义地理转换方法下面,在Method中选择合适的转换方法如 COORDINATE_FRAME,然后输入七参数,即平移参数、旋转角度和比例因子,核实输入无误后,进入下一步。
第三,打开的Projections and Transformations>Feature>Project,在弹出的窗口中输入要转换的数据以及Output Coordinate System,然后输入第一步自定义的地理坐标系如xian80 To 2000,开始转换,转换完成就得到了我们需要的坐标。
三、结束语
目前我国农村土地承包经营权确权登记颁证工作正在循序渐进的开展,对维护农村社会稳定,促进农村土地改革起到了重要作用。
其中,确权登记的数据坐标转换为土地承包经营群确权登记颁证工作提供了数据支持,因此需选择合适的坐标转换方法,并结合地理信息测绘技术,保证土地登记信息数据的准确,提高确权工作的质量和效率。
(作者单位为玉溪市不动产登记中心)
[作者简介:李俊俊(1986—),男,云南玉溪人,本科,助理工程师。
]
参考文献
[1] 刘开红,王萃.浅析农村土地承包经营权确权登记颁证工作中数据坐标转换方法[J].江西测绘,2015(4):23-25.
[2] 崔振龙.浅谈农村土地承包经营权确权登记颁证工作的流程与技术应用[J].城市建设理论研究(电子版),2015(20):1488-1489.
[3] 张爱净.浅谈如何开展农村土地承包经营权确权登记颁证工作[J].农业开发与装备,2015(12):23.。
