奥数五年级秋季班全集
五年级上册秋季奥数培优讲义——5-11-燕尾模型3-讲义-学生
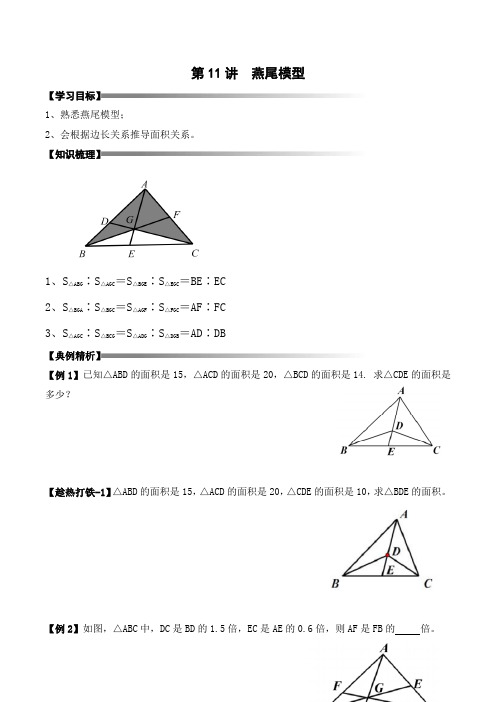
第11讲燕尾模型【学习目标】1、熟悉燕尾模型;2、会根据边长关系推导面积关系。
【知识梳理】1、S△ABG∶S△AGC=S△BGE∶S△EGC=BE∶EC2、S△BGA∶S△BGC=S△AGF∶S△FGC=AF∶FC3、S△AGC∶S△BCG=S△ADG∶S△DGB=AD∶DB【典例精析】【例1】已知△ABD的面积是15,△ACD的面积是20,△BCD的面积是14. 求△CDE的面积是多少?【趁热打铁-1】△ABD的面积是15,△ACD的面积是20,△CDE的面积是10,求△BDE的面积。
【例2】如图,△ABC中,DC是BD的1.5倍,EC是AE的0.6倍,则AF是FB的倍。
【趁热打铁-2】如图,△ABC中,DC是BD的1.5倍,EC是AE的0.6倍,△ABG的面积是5,则△AGC的面积是________。
【例3】如图,已知BD=3DC,EC=AE,BE与AD相交于点O,则△ABC的面积是四边形OECD 的面积倍。
【趁热打铁-3】在△ABD中, BD=1.5DC,AE=3EC,如果OB=3,则OE=。
【例4】如图三角形ABC的面积是120平方厘米,AE=DE,BC=2DC,求阴影部分的面积。
【趁热打铁-4】如图,在三角形ABC中,DC=2BD,点E为AD的中点。
若三角形ABC的面积为120平方厘米,则阴影部分的面积是多少平方厘米?【例5】如图,已知三角形ABC的面积为24平方厘米,AE=ED,BC=1.5BD,求阴影部分的面积。
【趁热打铁-5】如图,三角形ABC的面积为72dm²,BD是DC的2倍,AE=ED,求两个阴影三角形面积和。
【例6】两条线段把三角形分为三个三角形和一个四边形,如图所示,三个三角形的面积分别是3,7,7,则四边形ADPE的面积是多少?【趁热打铁-6】在四边形ABCD中,AB=3BE,AD=3AF,四边形AEOF的面积为12,那么平行四边形BODC的面积为多少?【过关精炼】1、如图,E为AC的中点,BD=2CD,三角形DGC的面积为4,求三角形ABC的面积?2、如图,设定E、F分别是△ABC的边AB、AC上的点,线段CE,BF交于点D,若△CDF,△BCD,△BDE的面积分别为3,7,7,则四边形AEDF的面积是___.3、如图,S△BDF=5cm²,S△CDF=3cm²,S△CEF=4cm²,求△ABC的面积.4、如图,在△ABC中,M是边AB的中点,N是边AC上的三等分点,CM是BN相交于点K.若△BCK的面积等于3,则△ABC的面积等于_____.5、如图所示,在三角形ABC中,D为BC的中点,AE=3CE,AD和BE相交F点,已知三角形ABC 的面积为42平方厘米,求三角形BDF的面积.6、如图,三角形ABC的面积为1,且AD=BD,CE=2BE,那么,四边形DBEF的面积等于____.。
五年级奥数秋季教材

X X X 教育五年级思维奥数教材目录第1讲平均数(1) 1 第2讲平均数(2) 5 第3讲长方形、正方形的周长9第4讲长方形、正方形的面积12 第5讲尾数和余数15 第6讲一般应用题(1)18 第7讲一般应用题(2)22 第8讲周期问题26 第9讲盈亏问题29 第10讲长方体和正方体(1)33 第11讲长方体和正方体(2)37 第12讲倍数问题(1)41 第13讲倍数问题(2)45 第14讲组合图形面积(1)49 第15讲组合图形面积(2)53第1讲平均数(1)一、例题精讲例题1:有4箱水果,已知苹果、梨、橘子平均每箱42个,梨、橘子、桃平均每箱36个,苹果和桃平均每箱37个。
一箱苹果多少个?分析:(1)1箱苹果+1箱梨+1箱橘子=42×3=136(个);(2)1箱桃+1箱梨+1箱橘子=36×3=108(个)(3)1箱苹果+1箱桃=37×2=72(个)由(1)(2)两个等式可知:1箱苹果比1箱桃多126-108=18(个),再根据等式(3)就可以算出:1箱桃有(74-18)÷2=28(个),1箱苹果有28+18=46(个)。
1箱苹果和1箱桃共有多少个:37×2=74(个)1箱苹果比1箱桃多多少个:42×3-36=18(个)1箱苹果有多少个:28+18=46(个)例题2:一次数学测验,全班平均分是91.2分,已知女生有21人,平均每人92分;男生平均每人90.5分。
求这个班男生有多少人?分析:女生每人比全班平均分高92-91.2=0.8(分),而男生每人比全班平均分低91.2-90.5=0.7(分)。
全体女生高出全班平均分0.8×21=16.8(分),应补给每个男生0.7分,16.8里包含有24个0.7,即全班有24个男生。
例题3:某3个数的平均数是2.如果把其中一个数改为4,平均数就变成了3。
被改的数原来是多少?分析:原来三个数的和是2×3=6,后来三个数的和是3×3=9,9比6多出了3.是因为把那个数改成了4。
小学五年级奥数思维训练全集

专题1 平均数(一)专题简析:把几个不相等的数,在总数不变的条件下,通过移多补少,使它们完全相等,求得的相等的数就是平均数。
平均数=总数量÷总份数总数量=平均数×总份数总份数=总数量×平均数例1:有4箱水果,已知苹果、梨、橘子平均每箱42个,梨、橘子、桃平均每箱36个,苹果和桃平均每箱37个。
一箱苹果多少个?分析:①:1箱苹果+1箱梨+1箱橘子=42×3=136(个);②:1箱桃+1箱梨+1箱橘子=36×3=108(个)③:1箱苹果+1箱桃=37×2=74(个)由①、②可知:1箱苹果比1箱桃多126-108=18(个),再根据等式③,用和差关系求出:1箱桃有(74-18)÷2=28(个),1箱苹果有28+18=46(个)。
试一试1:甲、乙、丙、丁四人称体重,乙、丙、丁三人共重120千克,甲、丙、丁三人共重126千克,丙、丁二人的平均体重是40千克。
求四人的平均体重是多少千克?例2:某3个数的平均数是2,如果把其中一个数改为4,平均数就变成了3。
被改的数原来是多少?分析:原来三个数的和是2×3=6,后来三个数的和是3×3=9,9比6多出了3,是因为把那个数改成了4。
因此,原来的数应该是4-3=1。
试一试2:有五个数,平均数是9。
如果把其中的一个数改为1,那么这五个数的平均数为8。
这个改动的数原来是多少?例3:五一班同学数学考试平均成绩91.5分,事后复查发现计算成绩时将一位同学的98分误作89分计算了。
经重新计算,全班的平均成绩是91.7分,五一班有多少名同学?分析:98分比89分多9分。
多算9分就能使全班平均每人的成绩上升91.7-91.5=0.2(分)。
9里面包含有几个0.2,五一班就有几名同学。
试一试3:某班的一次测验,平均成绩是91.3分。
复查时发现把张静的89分误看作97分计算,经重新计算,该班平均成绩是91.1分。
五年级数学奥数课程40讲(精品)

四年级数学奥数培训资料姓名:__________________ 小学四年级奥数举一反三第1讲至第40讲全目录第1讲找规律(一)第2讲找规律(二)第3讲简单推理第4讲应用题(一)第5讲算式谜(一)第6讲算式谜(二)第7讲最优化问题第8讲巧妙求和(一)第9讲变化规律(一)第10讲变化规律第11讲错中求解第12讲简单列举第13讲和倍问题第14讲植树问题第15讲图形问题第16讲巧妙求和第17讲数数图形第18讲数数图形第19讲应用题第20讲速算与巧算第二十一周速算与巧算(二)第二十二周平均数问题第二十三周定义新运算第二十四周差倍问题第二十五周和差问题第二十六周巧算年龄第二十七周较复杂的和差倍问题第二十八周周期问题第二十九周行程问题(一)第三十周用假设法解题第三十一周还原问题第三十二周逻辑推理第三十三周速算与巧算(三)第三十四周行程问题(二)第三十五周容斥原理第三十六周二进制第三十七周应用题(三)第三十八周应用题(四)第三十九周盈亏问题第四十周数学开放题第1讲找规律(一)一、知识要点观察是解决问题的根据。
通过观察,得以揭示出事物的发展和变化规律,在一般情况下,我们可以从以下几个方面来找规律:1.根据每组相邻两个数之间的关系,找出规律,推断出所要填的数;2.根据相隔的每两个数的关系,找出规律,推断出所要填的数;3.要善于从整体上把握数据之间的联系,从而很快找出规律;4.数之间的联系往往可以从不同的角度来理解,只要言之有理,所得出的规律都可以认为是正确的。
二、精讲精练【例题1】先找出下列数排列的规律,并根据规律在括号里填上适当的数。
1,4,7,10,(),16,19【思路导航】在这列数中,相邻的两个数的差都是3,即每一个数加上3都等于后面的数。
根据这一规律,括号里应填的数为:10+3=13或16-3=13。
像上面按照一定的顺序排列的一串数叫做数列。
练习1:先找出下列各列数的排列规律,然后在括号里填上适当的数。
小学五年级奥数思维训练全集

小学五年级奥数思维训练全集第一周平均数(一)专题简析:把几个不相等的数,在总数不变的条件下,通过移多补少,使它们完全相等,求得的相等的数就是平均数。
平均数=总数量÷总份数总数量=平均数×总份数总份数=总数量×平均数例1:有4箱水果,已知苹果、梨、橘子平均每箱42个,梨、橘子、桃平均每箱36个,苹果和桃平均每箱37个。
一箱苹果多少个?分析:①:1箱苹果+1箱梨+1箱橘子=42×3=136(个);②:1箱桃+1箱梨+1箱橘子=36×3=108(个)③:1箱苹果+1箱桃=37×2=74(个)由①、②可知:1箱苹果比1箱桃多126-108=18(个),再根据等式③,用和差关系求出:1箱桃有(74-18)÷2=28(个),1箱苹果有28+18=46(个)。
试一试1:甲、乙、丙、丁四人称体重,乙、丙、丁三人共重120千克,甲、丙、丁三人共重126千克,丙、丁二人的平均体重是40千克。
求四人的平均体重是多少千克?例2:某3个数的平均数是2,如果把其中一个数改为4,平均数就变成了3。
被改的数原来是多少?分析:原来三个数的和是2×3=6,后来三个数的和是3×3=9,9比6多出了3,是因为把那个数改成了4。
因此,原来的数应该是4-3=1.试一试2:有五个数,平均数是9。
如果把其中的一个数改为1,那么这五个数的平均数为8。
这个改动的数原来是多少?例3:五一班同学数学考试平均成绩91。
5分,事后复查发现计算成绩时将一位同学的98分误作89分计算了。
经重新计算,全班的平均成绩是91。
7分,五一班有多少名同学?分析:98分比89分多9分。
多算9分就能使全班平均每人的成绩上升91.7-91。
5=0.2(分)。
9里面包含有几个0.2,五一班就有几名同学。
试一试3:某班的一次测验,平均成绩是91。
3分.复查时发现把张静的89分误看作97分计算,经重新计算,该班平均成绩是91。
秋季班五年级奥数小学奥数各类题型中点突破题目类型大全(可编辑)

帅帅看一本减肥书,第一天看了全书的18还多30页,第二天看了全书的16少4页,还剩全书的35没有看,这本故事书一共有多少页?崔气球给北极熊运蜂窝煤,第一次运了全部的38,第二次运了50块,这时已运来的恰好是没运来的57。
问还有多少块蜂窝煤没有运来?(用方程解法)英国伦敦博物馆保存着一部极其珍贵的文物——纸莎草文书。
现存世界上最古老的方程就出现在这部英国考古学家兰德1858年找到的纸草书上。
经破译,上面都是一些方程,共85个问题。
其中有如下一道著名的求未知数的问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33,这个数为几何?碧空万里,一群大雁在飞翔,迎面又飞来一只小灰雁,它对群雁说:“你们好,百只雁!你们百雁齐飞,好气派!可怜我是孤雁独飞。
”群雁中一只领头的老雁说:“不对!小朋友,我们远远不足100只。
将我们这一群加倍,再加上半群,又加上四分之一群,最后还得请你也凑上,那才一共是100只呢!”请问这群大雁有多少只?列分数系数方程解应用题味多美西饼屋推出一款新蛋糕,第一天卖出了全部的15,第二天卖出了剩下的12,第二天比第一天多卖出40个,那么味多美西饼屋这次共推出新蛋糕多少个?(用方程解法)北京大学为庆祝其建校110周年举行徒步比赛。
甲、乙、丙三名运动员同时从同一个出发点起步后不间断地匀速步行,每分钟乙比甲少走15米,而比丙多走3米。
当乙到达赛程中点折返处时,比甲晚到4分钟,而比丙早到1分钟。
这次徒步比赛全程多少米?在线测试题温馨提示:请在线作答,以便及时反馈孩子的薄弱环节!1.小明看书第一天读了15,第二天比第一天多14,第三天读12页,此时还剩下全书的一半少2页没有看,全书共( )页。
A.175 B.180 C.195 D.2002.工程队修一条路,第一天修了60米,第二天修了全长的18,此时已修的路刚好是没修路的717,这条路全长()米。
A.380 B.360 C.345 D.3303.一个数的23与它的15的差等于26与它的14的和,那么这个数是()A.120B.60C.30D.154.实验小学的校园里,原来柳树的棵数是全校树木总棵数的25,今年又载种了50棵柳树。
秋季五年级第5 讲 电梯和发车小学高年级数学竞赛奥数培训班

秋季五年级第5讲电梯和发车▲关于电梯和发车问题:(整体思路)一列二解三代入。
寻找不变量,根据不变量;列方程,求解问题。
★扶梯问题两个不变量:可见梯、电梯速度不变;★发车问题同向:追及:=⨯发车间距速度差追及时间相向:相遇:=⨯发车间距速度和相遇时间不变量:发车间隔时间t=间隔发车间距车速1.小志与小刚两个孩子在电梯上的行走速度分别为每秒2个台阶和每秒3个台阶,电梯运行后,他俩沿电梯运行方向的相同方向从一楼走上二楼,分别用时28秒和20秒,那么如果小志攀登静止的电梯需要用时多少秒?2.在地铁车站中,从站台到地面架设有向上的自动扶梯.小明想逆行从上到下,如果每秒向下迈2级台阶,那么他走过100级台阶后到达站台;如果每秒向下迈3级台阶,那么走过75级台阶到达站台.自动扶梯有多少级台阶?3.从电车总站每隔一定时间开出一辆电车.甲与乙两人在一条街上反方向步行.甲沿电车发车方向每分钟步行60米,每隔20分钟有一辆电车从后方超过自己;乙每分钟步行80米,每隔10分遇上迎面开来的一辆电车.那么电车总站每隔多少分钟开出一辆电车?4.小红放学后沿着公共汽车的线路以4千米/时的速度往家走,一边走一边数来往的公共汽车.到家时迎面来的公共汽车数了11辆,后面追过的公共汽车数了9辆.如果公共汽车按相等的时间间隔发车,那么公共汽车的平均速度是多少?数学解题能力行程(过程写在笔记本上):1. (2011年“数学解题能力展示”6年级初试)甲、乙、丙三人同时从A 出发去B ,甲、乙到B 后调头回A ,并且调头后速度减少到各自原来速度的一半.甲最先调头,调头后与乙在C 迎面相遇,此时丙已行2010米;甲又行一段后与丙在AB 中点D 迎面相遇;乙调头后也在C 与丙迎面相遇.那么,AB 间路程是 米.2. (2010年“数学解题能力展示”6年级初试)如图,C 、D 为AB 的三等分点。
8点整时甲从A 出发匀速向B 行走,8点12分乙从B 出发匀速向A 行走,再过几分钟丙从B 出发匀速向A 行走;甲、乙在C 点相遇时丙恰好走到D 点,甲、丙8:30相遇时乙恰好到A 。
小学五年级奥数题大全及答案(更新版)

小学五年级奥数题大全及答案五年级奥数1、小数的巧算2、数的整除性3、质数与合数4、约数与倍数5、带余数除法6、中国剩余定理7、奇数与偶数8、周期性问题9、图形的计数10、图形的切拼11、图形与面积12、观察与归纳13、数列的求和14、数列的分组15、相遇问题16、追及问题17、变换和操作18、逻辑推理19、逆推法20、分数问题1.1小数的巧算(一)年级班姓名得分一、填空题1、计算 1.135+3.346+5.557+7.768+9.979=_____.2、计算 1.996+19.97+199.8=_____.3、计算 9.8+99.8+999.8+9999.8+99999.8=_____.4、计算6.11+9.22+8.33+7.44+5.55+4.56+3.67+2.78 +1.89=_____.5、计算1.1+3.3+5.5+7.7+9.9+11.11+13.13+15.15+17.17+19.19=_____.6、计算 2.89⨯4.68+4.68⨯6.11+4.68=_____.7、计算 17.48⨯37-17.48⨯19+17.48⨯82=_____.8、计算 1.25⨯0.32⨯2.5=_____.9、计算 75⨯4.7+15.9⨯25=_____.10、计算 28.67⨯67+32⨯286.7+573.4⨯0.05=_____.二、解答题11、计算 172.4⨯6.2+2724⨯0.3812、计算 0.00...0181⨯0.00 (011)963个0 1028个013、计算12.34+23.45+34.56+45.67+56.78+67.89+78.91+89.12+91.2314、下面有两个小数:a=0.00...0105 b=0.00 (019)1994个0 1996个0求a+b,a-b,a⨯b,a÷b.1.2小数的巧算(二)年级班姓名得分一、真空题1、计算 4.75-9.64+8.25-1.36=_____.2、计算 3.17-2.74+4.7+5.29-0.26+6.3=_____.3、计算 (5.25+0.125+5.75)⨯8=_____.4、计算 34.5⨯8.23-34.5+2.77⨯34.5=_____.5、计算 6.25⨯0.16+264⨯0.0625+5.2⨯6.25+0.625⨯20=_____.6、计算 0.035⨯935+0.035+3⨯0.035+0.07⨯61⨯0.5=_____.7、计算 19.98⨯37-199.8⨯1.9+1998⨯0.82=_____.8、计算 13.5⨯9.9+6.5⨯10.1=_____.9、计算 0.125⨯0.25⨯0.5⨯64=_____.10、计算 11.8⨯43-860⨯0.09=_____.二、解答题11、计算32.14+64.28⨯0.5378⨯0.25+0.5378⨯64.28⨯0.75-8⨯64.28⨯0.125⨯0.537812、计算 0.888⨯125⨯73+999⨯313、计算 1998+199.8+19.98+1.99814、下面有两个小数:a=0.00...0125 b=0.00 (08)1996个0 2000个0试求a+b, a-b, a⨯b, a÷b.2.1数的整除性(一)年级班姓名得分一、填空题1、四位数“3AA1”是9的倍数,那么A=_____.2、在“25□79这个数的□内填上一个数字,使这个数能被11整除,方格内应填_____.3、能同时被2、3、5整除的最大三位数是_____.4、能同时被2、5、7整除的最大五位数是_____.5、1至100以内所有不能被3整除的数的和是_____.6、所有能被3整除的两位数的和是______.7、已知一个五位数□691□能被55整除,所有符合题意的五位数是_____.8、如果六位数1992□□能被105整除,那么它的最后两位数是_____.9、42□28□是99的倍数,这个数除以99所得的商是_____.10、从左向右编号为1至1991号的1991名同学排成一行,从左向右1至11报数,报数为11的同学原地不动,其余同学出列;然后留下的同学再从左向右1至11报数,报数为11的留下,其余同学出列;留下的同学第三次从左向右1至11报数,报到11的同学留下,其余同学出列,那么最后留下的同学中,从左边数第一个人的最初编号是_____号.二、解答题1、173□是个四位数字.数学老师说:“我在这个□中先后填入3个数字,所得到的3个四位数,依次可被9、11、6整除.”问:数学老师先后填入的3个数字的和是多少?12、在1992后面补上三个数字,组成一个七位数,使它们分别能被2、3、5、11整除,这个七位数最小值是多少?13、在“改革”村的黑市上,人们只要有心,总是可以把两张任意的食品票换成3张其他票券,也可以反过来交换.试问,合作社成员瓦夏能否将100张黄油票换成100张香肠票,并且在整个交换过程中刚好出手了1991张票券?14、试找出这样的最小自然数,它可被11整除,它的各位数字之和等于13.2.2数的整除性(二)年级班姓名得分一、填空题1、一个六位数23□56□是88的倍数,这个数除以88所得的商是_____或_____.2、123456789□□,这个十一位数能被36整除,那么这个数的个位上的数最小是_____.3、下面一个1983位数33…3□44…4中间漏写了一个数字(方框),已知这991个 991个个多位数被7整除,那么中间方框内的数字是_____.4、有三个连续的两位数,它们的和也是两位数,并且是11的倍数.这三个数是_____.5、有这样的两位数,它的两个数字之和能被4整除,而且比这个两位数大1的数,它的两个数字之和也能被4整除.所有这样的两位数的和是____.6、一个小于200的自然数,它的每位数字都是奇数,并且它是两个两位数的乘积,那么这个自然数是_____.7、任取一个四位数乘3456,用A表示其积的各位数字之和,用B表示A的各位数字之和,C表示B的各位数字之和,那么C是_____.8、有0、1、4、7、9五个数字,从中选出四个数字组成不同的四位数,如果把其中能被3整除的四位数从小到大排列起来,第五个数的末位数字是_____.9、从0、1、2、4、5、7中,选出四个数,排列成能被2、3、5整除的四位数,其中最大的是_____.10、所有数字都是2且能被66……6整除的最小自然数是_____位数.100个二、解答题11、找出四个互不相同的自然数,使得对于其中任何两个数,它们的和总可以被它们的差整除,如果要求这四个数中最大的数与最小的数的和尽可能的小,那么这四个数里中间两个数的和是多少?12、只修改21475的某一位数字,就可知使修改后的数能被225整除,怎样修改?13、500名士兵排成一列横队.第一次从左到右1、2、3、4、5(1至5)名报数;第二次反过来从右到左1、2、3、4、5、6(1至6)报数,既报1又报6的士兵有多少名?14、试问,能否将由1至100这100个自然数排列在圆周上,使得在任何5个相连的数中,都至少有两个数可被3整除?如果回答:“可以”,则只要举出一种排法;如果回答:“不能”,则需给出说明.3.1质数与合数(一)年级班姓名得分一、填空题1在一位的自然数中,既是奇数又是合数的有_____;既不是合数又不是质数的有_____;既是偶数又是质数的有_____.2、最小的质数与最接近100的质数的乘积是_____.3、两个自然数的和与差的积是41,那么这两个自然数的积是_____.4、在下式样□中分别填入三个质数,使等式成立.□+□+□=505、三个连续自然数的积是1716,这三个自然数是_____、_____、_____.6、找出1992所有的不同质因数,它们的和是_____.7、如果自然数有四个不同的质因数, 那么这样的自然数中最小的是_____.8、9216可写成两个自然数的积,这两个自然数的和最小可以达到_____.9、从一块正方形的木板上锯下宽为3分米的一个木条以后,剩下的面积是108平方分米.木条的面积是_____平方分米.10、今有10个质数:17,23,31,41,53,67,79,83,101,103.如果将它们分成两组,每组五个数,并且每组的五个数之和相等,那么把含有101的这组数从小到大排列,第二个数应是_____.二、解答题11、2,3,5,7,11,…都是质数,也就是说每个数只以1和它本身为约数.已知一个长方形的长和宽都是质数个单位,并且周长是36个单位.问这个长方形的面积至多是多少个平方单位?12、把7、14、20、21、28、30分成两组,每三个数相乘,使两组数的乘积相等.13、学生1430人参加团体操,分成人数相等的若干队,每队人数在100至200之间,问哪几种分法?14、四只同样的瓶子内分别装有一定数量的油,每瓶和其他各瓶分别合称一次,记录千克数如下:8、9、10、11、12、13.已知四只空瓶的重量之和以及油的重量之和均为质数,求最重的两瓶内有多少油?3.2质数与合数(二)年级班姓名得分一、填空题1、在1~100里最小的质数与最大的质数的和是_____.2、小明写了四个小于10的自然数,它们的积是360.已知这四个数中只有一个是合数.这四个数是____、____、____和____.3、把232323的全部质因数的和表示为AB,那么A⨯B⨯AB=_____.4、有三个学生,他们的年龄一个比一个大3岁,他们三个人年龄数的乘积是1620,这三个学生年龄的和是_____.5、两个数的和是107,它们的乘积是1992,这两个数分别是_____和_____.6、如果两个数之和是64,两数的积可以整除4875,那么这两数之差是_____.7、某一个数,与它自己相加、相减、相乘、相除,得到的和、差、积、商之和为256.这个数是_____.8、有10个数:21、22、34、39、44、45、65、76、133和153.把它们编成两组,每组5个数,要求这组5个数的乘积等于那组5个数的乘积.第一组数____________;第二组数是____________.9、有_____个两位数,在它的十位数字与个位数字之间写一个零,得到的三位数能被原两位数整除.10、主人对客人说:“院子里有三个小孩,他们的年龄之积等于72,年龄之和恰好是我家的楼号,楼号你是知道的,你能求出这些孩子的年龄吗?”客人想了一下说:“我还不能确定答案。
2023年五年级秋季奥数材料第八讲统筹规划课件

2、中国海警船对钓鱼岛及其附属岛屿附近海域进行维权巡航执法。海警船每天 行驶 200 千米,每船可载供行驶 14 天的燃料。现有 5 艘船同时从驻地 A 出发,完 成任务后都沿原路返回驻地。为了让其中 3 艘船尽可能向更远的地方巡航,然后 再一起返回,甲、乙两船行到途中 B 处后,仅留足自己返回驻地所需的燃料,将多 余的燃料留给另外 3 艘船使用。其他 3 艘船可行进的最远距离是多少千米?
温馨提示:若选用方式一,每月固定交费 58 元,当主动打出电话月累计时间不超 过 150 分钟,不再额外交费;当超过 150 分钟,超过的部分每分钟加收 0.25 元。 (1)小明的爸爸每月主叫时间约 240 分钟,他选择哪种计费方式合算? (2) 小明的妈妈预算每月移动电话费为 126 元,那么她选择哪种计费方式,可以主 叫通话时间更长?
5、甲、乙两厂生产同一规格的单人课桌和凳子(一张课桌和一条凳子配成 1 套), 甲厂每月 用 16 天生产课桌,用 14 天生产凳子,正好配成 448 套;乙厂每月用 12 天生产课桌,用 18 天生产凳子,正好配成 720 套。现将两厂合并后,合理制定生 产方案使得生产效率最高,那么每月 30 天最多可生产桌凳多少套?
1、如果 4 个矿泉水空瓶可以换 1 瓶矿泉水,现有 15 个矿泉水空瓶,则不花钱最多
可以喝矿泉水____。
A.3 瓶 B.4 瓶
C.5 瓶 D.6 瓶
2、某市有甲种货车和乙种货车,它们的装载量及每辆车的运费如下表所示。现有 待处理的垃圾 28 吨,要求一次运到垃圾处理厂,并且每辆车要满载。
若不考虑总运费,请列举出完成上述运输任务的不同方案,并求出最少运费。
例 2、移动电话有两种计费方式:A.每月租费 22 元,然后按每分钟 0.15 元计费;B. 无月租
秋季班5年级奥数教程(学生版)

五年级上册奥数培训教程班级:姓名:目录1 长方形、正方形的周长第2页2 长方形、正方形的面积第6页3 尾数和余数第10页4 一般应用题(一)第13页5 一般应用题(二)第16页6 一般应用题(三)第19页7 分解质因数(一)第22页8 分解质因数(二)第25页9 数的整除第29页10 最大公约数第34页11 最小公倍数第38页12 最小公倍数(二)第42页13平行四边形第46页14 三角形公式的应用第50页例1 有5张同样大小的纸如下图(a)重叠着,每张纸都是边长6厘米的正方形,重叠的部分为边长的一半,求重叠后图形的周长。
练习一1,下图由8个边长都是2厘米的正方形组成,求这个图形的周长。
例2 一块长方形木板,沿着它的长度不同的两条边各截去4厘米,截掉的面积为192平方厘米。
现在这块木板的周长是多少厘米?练习二1.有一个长方形,如果长减少4米,宽减少2米,面积就比原来减少44平方米,且剩下部分正好是一个正方形。
求这个正方形的周长。
例3 已知下图中,甲是正方形,乙是长方形,整个图形的周长是多少?练习三1.有一张长40厘米,宽30厘米的硬纸板,在四个角上各剪去一个同样大小的正方形后准备做一个长方体纸盒,求被剪后硬纸板的周长。
例4 下图是边长为4厘米的正方形,求正方形中阴影部分的周长。
练习四1,求下面图形的周长(单位:厘米)。
15302,在()里填上“>”、“<”或“=”。
甲的周长()乙的周长例5 如下图,阴影部分是正方形,DF=6厘米,AB=9厘米,求最大的长方形的周长。
练习五1,下面三个正方形的面积相等,剪去阴影部分的面积也相等,求原来正方形的周长发生了什么变化?(单位:厘米)1.下图由1个正方形和2个长方形组成,求这个图形的周长。
30cm2.有两个相同的长方形,长是8厘米,宽是3厘米,如果按下图叠放在一起,这个图形的周长是多少?3.一个长12厘米,宽2厘米的长方形和两个正方形正好拼成下图(1)所示长方形,求所拼长方形的周长。
小学五年级奥数思维训练全集

小学五年级奥数思维训练全集第一周平均数(一)专题简析:把几个不相等的数,在总数不变的条件下,通过移多补少,使它们完全相等,求得的相等的数就是平均数。
平均数=总数量÷总份数总数量=平均数×总份数总份数=总数量×平均数例1:有4箱水果,已知苹果、梨、橘子平均每箱42个,梨、橘子、桃平均每箱36个,苹果和桃平均每箱37个。
一箱苹果多少个?分析:①:1箱苹果+1箱梨+1箱橘子=42×3=136(个);②:1箱桃+1箱梨+1箱橘子=36×3=108(个)③:1箱苹果+1箱桃=37×2=74(个)由①、②可知:1箱苹果比1箱桃多126-108=18(个),再根据等式③,用和差关系求出:1箱桃有(74-18)÷2=28(个),1箱苹果有28+18=46(个).试一试1:甲、乙、丙、丁四人称体重,乙、丙、丁三人共重120千克,甲、丙、丁三人共重126千克,丙、丁二人的平均体重是40千克。
求四人的平均体重是多少千克?例2:某3个数的平均数是2,如果把其中一个数改为4,平均数就变成了3。
被改的数原来是多少?分析:原来三个数的和是2×3=6,后来三个数的和是3×3=9,9比6多出了3,是因为把那个数改成了4。
因此,原来的数应该是4-3=1.试一试2:有五个数,平均数是9.如果把其中的一个数改为1,那么这五个数的平均数为8.这个改动的数原来是多少?例3:五一班同学数学考试平均成绩91。
5分,事后复查发现计算成绩时将一位同学的98分误作89分计算了。
经重新计算,全班的平均成绩是91。
7分,五一班有多少名同学?分析:98分比89分多9分。
多算9分就能使全班平均每人的成绩上升91。
7-91。
5=0。
2(分)。
9里面包含有几个0。
2,五一班就有几名同学。
试一试3:某班的一次测验,平均成绩是91.3分。
复查时发现把张静的89分误看作97分计算,经重新计算,该班平均成绩是91.1分.全班有多少同学?专题二平均数(二)专题简析:平均数=总数量÷总份数总数量=平均数×总份数总份数=总数量×平均数例1:小明前几次数学测验的平均成绩是84分,这次要考100分,才能把平均成绩提高到86分。
秋季五年级同步奥数教材(经典课辅资料)

目录第一讲生活中的负数 (1)第二讲图形的周长 (3)第三讲多边形面积计算(长方形与正方形的面积) (7)第四讲多边形面积计算(三角形与多边形的面积) (10)第五讲平面图形的操作 (14)第六讲小数加减法的简便计算 (17)第七讲找规律(周期问题) (19)第八讲解决问题的策略(用枚举法解决问题) (21)第九讲小数乘法和除法的简便计算 (24)第十讲四则运算速算 (27)第十一讲数学专题(数列计算) (30)第十二讲数学专题(列车过桥问题) (32)第十三讲数学专题(稍复杂的相遇问题) (34)第十四讲数学专题(稍复杂的追及问题) (36)第十五讲数学专题(简单的消去问题) (38)第十六讲数学专题(还原问题) (40)综合能力测试(一) (43)综合能力测试(二) (47)坚其志,苦其心,劳其力,事无大小,必有所成。
-----------------(清)曾国藩第一讲生活中的负数例题精讲例1. 刘翔在第十届世界田径锦标赛半决赛中,110米栏的成绩是13.42秒,当时赛场的风速为每秒-0.4米,你知道这个风速所表示的意思吗?例2. 中国最大的咸水湖——青海湖高于海平面3193米,世界最低最咸的湖——死海低于海平面400米。
想一想青海湖与死海的海拔相差多少米呢?例3. 哈尔滨:零下12℃,漠河:零下30℃(漠河是我国最北边的一个城市)。
海口:零上30℃,你知道海口比哈尔滨和漠河各高多少度吗?哈尔滨和漠河相差的温度呢?同步练习1、今天,在学校跑道上正举行着100米短跑比赛,当时赛场风速为每秒-0.5米,预测一下,选手们在正常发挥状态下,成绩将()①上升一些②与平时相同③下降一些2、小船在静水中的速度是每小时7千米,当它从A港驶向B港时,测得当时的水流速度为每小时+2千米,此时,小船的速度将是多少?3、我国青藏高原的海拔为高于海平面5023米,新疆吐鲁番盆地的艾丁湖底低于海平面越155米,想一想,两者海拔高度相差多少米?4王叔叔与李叔叔年前用相同的资金对不同的项目进行投资,投资股市的王叔叔亏了15万元,投资房地产的李叔叔赚了163万元,此时,王叔叔与李叔叔的资金相差多少万元?5地球表面的最低温度在南极,是-88℃,月球表面的最低气温是-183℃,月球表面气温比南极低多少度?6.赤道温度40℃,北极温度-34℃,南极温度-40℃。
最新秋季五年级奥数第四讲--小数乘除法的简便运算资料

2015年秋季五年级奥数第四讲----小数乘除法的简便计算常用的计算技巧:1、分解凑整法:将一个数适当地分解为n个数,运用乘法的交换律、乘法的结合律或乘法的分配律凑整进行计算。
2、运用商不变的性质:被除数和除数同时扩大或缩小相同的倍数(零除外),商不变。
3、运用积不变的性质:一个因数扩大若干倍(零除外)另一个因数同时缩小相同的倍数,积不变。
4、运用乘除法的性质,改变运算顺序和运算方法。
①一个数除以另一个数的商,再除以第三个数,等于第一个数除以二、三两个数的积;也等于第一个数除以第三个数的商,再除以第二个数。
②两个数的积除以第三个数,等于用任意一个因数除以第三个数,再乘以另一个因数相乘。
5、n个数的和(差)除以一个数,可以用这个数分别去除这n个数(在能除尽的情况下),再求n个商的和。
例1、 2.005×390+20.05×41+200.5×2 训练、0.79×0.46+7.9×0.24+11.4×0.079例2、2424.2424÷242.4 训练、69316.931÷69.31例3、(0.1+0.12+0.123+0.1234)×(0.12+0.123+0.1234+0.12345)-(0.1+0.12+0.123+01234+0.12345)×(0.12+0.123+0.1234)训练、(1+0.23+0.34)×(0.23+0.34+0.45)-(1+0.23+0.34+0.45)×(0.23+0.34)例4、9×1.7+9.1÷1.7-5×1.7+4.5÷1.7训练、17.6×1.3+6.4÷1.3-9.6×1.3+5.3÷1.3例5、(3.6×0.75×1.2)÷(1.5×2.4×0.18) 训练、(7.2×4.5×8.1)÷(1.8×1.5×2.7) 例6、41.2×8.1+11×1.25+537×0.19 训练、18.3×0.25+5.3×2.5+71.3×0.75例7、19.97×19.98-19.96×19.99 训练、20.05×20.12-20.04×20.11例8、2.15×3.8+3.8×5.34-74.9×0.28 训练、4.37×5.1-0.49×3.6+4.73×4.91.(6.4×7.2×4.9)÷(0.8×3.6×7)2.22×17+3.33×4+6.66×92. 2.2+3.4+7.8+2.6 0.999×1.3-0.111×2.73. 3.9×1.1+6.7×1.3 1÷32÷0.05÷0.25÷0.54.0.739×(48.8+20.3+51.2+4.7)×8.88÷7396.25×0.16+264×0.0625+5.2×6.25+0.625×205.0.9÷1.3+130÷90+0.11÷0.13+1.4÷0.9+6÷13 1.25×17.6+36×1.25+2.64×12.56.153.7×0.789-937×0.0789+153.7×0.211-9.37×2.11 1.25×17.6+36÷0.8+2.64×12.57.11×1.1×1.1-1.1×1.1-1.1 3.75×4.23×36-125×0.423×1.88.(12×21×45×10.2)÷(15×4×0.7×51)20.68-(7.21-6.32+3.79)9.(1+0.23+0.34)×(0.23+0.34+0.45)-(1+0.23+0.34+0.45)×(0.23+0.34)10.327×2.8+17.3×28 75×4.67+19.9×2.511.2.5×7.2÷(0.9÷4) 4 .2×0.34÷(1.4×0.34)12.1÷32÷0.05÷0.25÷0.5 0.24×0.125÷0.313.45.3×3.2+578×0.68+12.5×1.2 117.8÷2.3-4.88÷0.2314.16.46×15.1+8.54×15.1-25×14.7 11.1×4÷9×3÷7.4×215.(3.8+3.4×3.8+3.8×5.6)÷(1.9×0.8×0.25)99.99×0.8+11.11×2.8提高练习1.计算: 48.576-(38.576+6.75)2.计算: 12+12.1+12.2+12.3+12.4+……+12.8+12.93.计算: 752×1.25+4.45×12.5+0.035×1254.计算:(1)7×2.4÷2.5 (2)4.8×15.4÷1.6÷0.77 5.计算:(12×21×45×10.2) ÷(15×4×0.7×51) 0.125×160×5000 511×0.71+11×9.29+525×0.29(1+0.43+0.29)×(0.43+0.29+0.87)—(1+0.43+0.29+0.87)×(0.43+0.29)199.9×19.98-199.8×19.97 123456×73.28×*(4-3.2÷0.8)。
小学五年级奥数思维训练全集

小学五年级奥数思维训练全集第一周平均数(一)专题简析:把几个不相等的数,在总数不变的条件下,通过移多补少,使它们完全相等,求得的相等的数就是平均数.平均数=总数量÷总份数总数量=平均数×总份数总份数=总数量×平均数例1:有4箱水果,已知苹果、梨、橘子平均每箱42个,梨、橘子、桃平均每箱36个,苹果和桃平均每箱37个。
一箱苹果多少个?分析:①:1箱苹果+1箱梨+1箱橘子=42×3=136(个);②:1箱桃+1箱梨+1箱橘子=36×3=108(个)③:1箱苹果+1箱桃=37×2=74(个)由①、②可知:1箱苹果比1箱桃多126-108=18(个),再根据等式③,用和差关系求出:1箱桃有(74-18)÷2=28(个),1箱苹果有28+18=46(个).试一试1:甲、乙、丙、丁四人称体重,乙、丙、丁三人共重120千克,甲、丙、丁三人共重126千克,丙、丁二人的平均体重是40千克。
求四人的平均体重是多少千克?例2:某3个数的平均数是2,如果把其中一个数改为4,平均数就变成了3。
被改的数原来是多少?分析:原来三个数的和是2×3=6,后来三个数的和是3×3=9,9比6多出了3,是因为把那个数改成了4.因此,原来的数应该是4-3=1。
试一试2:有五个数,平均数是9.如果把其中的一个数改为1,那么这五个数的平均数为8。
这个改动的数原来是多少?例3:五一班同学数学考试平均成绩91.5分,事后复查发现计算成绩时将一位同学的98分误作89分计算了。
经重新计算,全班的平均成绩是91.7分,五一班有多少名同学?分析:98分比89分多9分。
多算9分就能使全班平均每人的成绩上升91。
7-91.5=0.2(分).9里面包含有几个0.2,五一班就有几名同学.试一试3:某班的一次测验,平均成绩是91。
3分。
复查时发现把张静的89分误看作97分计算,经重新计算,该班平均成绩是91。
小学五年级奥数思维训练全集

小学五年级奥数思维训练全集第一周平均数(一)专题简析:把几个不相等的数,在总数不变的条件下,通过移多补少,使它们完全相等,求得的相等的数就是平均数。
平均数=总数量÷总份数总数量=平均数×总份数总份数=总数量×平均数例1:有4箱水果,已知苹果、梨、橘子平均每箱42个,梨、橘子、桃平均每箱36个,苹果和桃平均每箱37个。
一箱苹果多少个?分析:①:1箱苹果+1箱梨+1箱橘子=42×3=136(个);②:1箱桃+1箱梨+1箱橘子=36×3=108(个)③:1箱苹果+1箱桃=37×2=74(个)由①、②可知:1箱苹果比1箱桃多126-108=18(个),再根据等式③,用和差关系求出:1箱桃有(74-18)÷2=28(个),1箱苹果有28+18=46(个)。
试一试1:甲、乙、丙、丁四人称体重,乙、丙、丁三人共重120千克,甲、丙、丁三人共重126千克,丙、丁二人的平均体重是40千克。
求四人的平均体重是多少千克?例2:某3个数的平均数是2,如果把其中一个数改为4,平均数就变成了3。
被改的数原来是多少?分析:原来三个数的和是2×3=6,后来三个数的和是3×3=9,9比6多出了3,是因为把那个数改成了4。
因此,原来的数应该是4-3=1。
试一试2:有五个数,平均数是9。
如果把其中的一个数改为1,那么这五个数的平均数为8。
这个改动的数原来是多少?例3:五一班同学数学考试平均成绩91.5分,事后复查发现计算成绩时将一位同学的98分误作89分计算了。
经重新计算,全班的平均成绩是91.7分,五一班有多少名同学?分析:98分比89分多9分。
多算9分就能使全班平均每人的成绩上升91.7-91.5=0.2(分)。
9里面包含有几个0.2,五一班就有几名同学。
试一试3:某班的一次测验,平均成绩是91.3分。
复查时发现把张静的89分误看作97分计算,经重新计算,该班平均成绩是91.1分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 讲 找规律 讲义..............................................................................................3 第 1 讲 找规律 课后练习......................................................................................6 第 2 讲 头脑体操 讲义..........................................................................................9 第 2 讲 头脑体操 课后练习................................................................................12........................................................15 第 3 讲 组合图形面积 1 课后练习.....................................................................17 第 4 讲 组合图形面积 2 讲义.............................................................................19 第 4 讲 组合图形面积 2 课后练习.....................................................................22 第 5 讲 组合图形面积 3 讲义.............................................................................24 第 5 讲 组合图形面积 3 课后练习.....................................................................27 第 6 讲 图形面积综合............................................................................................28 第 6 讲 图形面积综合 课后练习 1.....................................................................31 第 6 讲 图形面积综合 课后练习 2.....................................................................36 第 3 讲 数的问题 课后练习................................................................................43 第 4 讲 较复杂的和差倍问题 讲义....................................................................44 第 4 讲 较复杂的和差倍问题 课后练习............................................................47 第 5 讲 一般应用题(一) 讲义........................................................................49 第 5 讲 一般应用题(一) 课后练习................................................................52 第 6 讲 一般应用题 讲义....................................................................................53 第 6 讲 一般应用题(二) 课后练习................................................................55 第 7 讲 小数加减法应用 讲义............................................................................57 第 7 讲 小数加减法应用 课后练习....................................................................59 第 8 讲 小数乘除法应用 讲义............................................................................61 第 8 讲 小数乘除法应用 课后练习....................................................................63 第 9 讲 平均数 讲义............................................................................................64 第 9 讲 平均数 课后练习(1)..........................................................................67 第 9 讲 平均数 课后练习(2)..........................................................................69 第 10 讲 统筹安排 讲义......................................................................................71 第 10 讲 统筹安排 课后练习..............................................................................74
