直角三角形斜边上的中线等于斜边的一半的专题训练
2019年人教版八下数学《18.2 直角三角形斜边上的中线》专项复习资料

2019年人教版八下数学《18.2 直角三角形斜边上的中线》专项复习资料一.选择题(共10小题)1.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是()A.2.5 B.C.D.22.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=7,BC=10,则△EFM的周长是()A.17 B.21 C.24 D.273.如图,在四边形ABCD中,∠BCD=∠BAD=90°,AC,BD相交于点E,点G,H分别是AC,BD的中点,若∠BEC=80°,那么∠GHE等于()A.5°B.10°C.20°D.30°【1】【2】【3】4.如图,∠MON=90°,边长为2的等边三角形ABC的顶点A、B分别在边OM,ON上当B在边ON上运动时,A 随之在边OM上运动,等边三角形的形状保持不变,运动过程中,点C到点O的最大距离为()A.2.4 B.C.D.5.如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点,则DC和EF的大小关系是()A.DC>EF B.DC<EF C.DC=EF D.无法比较6.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则∠ECD=()A.22.5°B.30°C.36°D.45°【4】【5】【6】7.已知:如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,AC=10,BD=8,则MN为()A.3 B.4 C.5 D.68.如果三角形中一边上的中线等于这边的一半,则这个三角形是()A.等腰三角形B.直角三角形C.等边三角形D.等腰直角三角形9.如图,在Rt△ABC中,∠ACB=90°,∠A=60°,过点C的直线与AB交于点D,且将△ABC的面积分成相等的两部分,则∠CDA=()A.30°B.45°C.60°D.75°10.如图,△ABC中,AB、BC、CA的中点分别是E,F,G,AD是高.则下列选项正确的有()个(1)∠EDG=∠EFG;(2)∠B=∠BDE;(3)∠CDG=∠C;(4)∠GFC=∠ADE.A.1 B.2 C.3 D.4【7】【9】【10】二.填空题(共10小题)11.如图,在△ABC中,∠ACB=90°,∠A=60°,AC=a,作斜边AB边中线CD,得到第一个三角形ACD;DE⊥BC 于点E,作Rt△BDE斜边DB上中线EF,得到第二个三角形DEF;依此作下去…则第n个三角形的面积等于.12.如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连接AE,若AE=6.5,AD=5,则AC=;△ABE的周长是.13.把一副三角板如图放置,E是AB的中点,连接CE、DE、CD,F是CD的中点,连接EF.若AB=4,则S△CEF=.【11】【12】【13】14.如图,∠MON=90°,△ABC的顶点A、B分别在OM、ON上,当A点从O点出发沿着OM向右运动时,同时点B在ON上运动,连结OC.若AC=4,BC=3,AB=5,则OC的长度的最大值是.15.如图,在四边形ABCD中,BC⊥AC于点C,BE⊥AD于点E,∠BAC=60°,点G是AB的中点,已知BC=,则GE的长是.16.如图,在△ABC中,∠ACB=90°,AC=8,BC=3,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C 随之在y轴上运动,在运动过程中,点B到原点O的最大距离为.【14】【15】【16】17.如图所示,在平面直角坐标系中,矩形ABCD定点A、B在y轴、x轴上,当B在x轴上运动时,A随之在y 轴运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为.18.一个直角三角形斜边上的中线长为10,周长为48,则此直角三角形的面积为.19.如图,在△ABC中,∠ACB=90°,∠CAB=30°.以AB长为一边作△ABD,且AD=BD,∠ADB=90°,取AB中点E,连DE、CE、CD.则∠EDC=°.20.如图是一副三角尺拼成的四边形ABCD,E为斜边BD中点,则∠ACE=.【17】【19】【20】21.如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM.(1)求证:EF=AC.(2)若∠BAC=45°,求线段AM、DM、BC之间的数量关系.22.如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.(1)证明:DC=DG;(2)若DG=5,EC=2,求DE的长.23.如图所示,四边形ABCD由一个∠ACB=30°的Rt△ABC与等腰Rt△ACD拼成,E为斜边AC的中点,求∠BDE 的大小.24.如图,已知在△ABC中,延长CA到D,使BA=BD,延长BA到E,使CA=CE,设P、M、N分别是BC、AD、AE的中点.求证:△PMN是等腰三角形.25.△ABC中,BE⊥AC,CF⊥AB,D为BC中点,设EB与CF相交于K,N为KA的中点,探索DN和EF的位置关系.26.已知:在△ABC中,∠ABC=90°,点E在直线AB上,ED与直线AC垂直,垂足为D,且点M为EC中点,连接BM,DM.(1)如图1,若点E在线段AB上,探究线段BM与DM及∠BMD与∠BCD所满足的数量关系,并直接写出你得到的结论;(2)如图2,若点E在BA延长线上,你在(1)中得到的结论是否发生变化?写出你的猜想并加以证明;(3)若点E在AB延长线上,请你根据条件画出相应的图形,并直接写出线段BM与DM及∠BMD与∠BCD所满足的数量关系.27.小明在学习矩形这一节时知道“直角三角形斜边上的中线等于斜边的一半”,由此引发他的思考,这个定理的逆命题成立吗?即:如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是否为直角三角形?通过探究,小明发现这个猜想也成立,以下是小明的证明过程:已知:如图1,在△ABC中,点D是AB的中点,连接CD,且CD=AB求证:△ABC为直角三角形证明:由条件可知,AD=BD=CD则∠A=∠DCA,∠B=∠DCB又∵∠A+∠DCA+∠B+∠DCB=180°∴∠DCA+∠DCB=90°爱动脑筋的小明发现用本学期所学知识也能证明这个结论,并想出了图2、图3两种不同的证明思路,请你选择其中一种,把证明过程补充完整:28.引理:如图1所示已知Rt△ABC中,CD是斜边AB上的中线,则CD=AD=DB=AB应用格式为:∵CD是斜边AB上的中线,∴CD=AD=DB=AB如图2所示已知,△ABC中,AC=BC,∠ACB=90°,D为AB的中点,若E在直线AC上任意一点,DF⊥DE,交直线BC于F点.G为EF的中点,延长CG交AB直线于点H.(1)若E在边AC上.①试说明DE=DF;②试说明CG=GH;(本题需要用引理)(2)若AE=3,CH=5.求边AC的长.29.如图,△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.(1)求证:MN⊥DE;(2)连结DM,ME,猜想∠A与∠DME之间的关系,并写出推理过程;(3)若将锐角△ABC变为钝角△ABC,如图,上述(1)(2)中的结论是否都成立?若结论成立,直接回答,不需证明;若结论不成立,说明理由.《直角三角形斜边上的中线》专项提升参考答案与试题解析一.选择题(共10小题)1.(2014•宁波)如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH 的长是()A.2.5 B.C. D.2【解答】解:如图,连接AC、CF,∵正方形ABCD和正方形CEFG中,BC=1,CE=3,∴AC=,CF=3,∠ACD=∠GCF=45°,∴∠ACF=90°,由勾股定理得,AF===2,∵H是AF的中点,∴CH=AF=×2=.故选:B.2.(2015秋•无锡期中)如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=7,BC=10,则△EFM 的周长是()A.17 B.21 C.24 D.27【解答】解:∵CF⊥AB,M为BC的中点,∴MF是Rt△BFC斜边上的中线,∴FM=BC=×10=5,同理可得,ME=BC=×10=5,又∵EF=7,∴△EFM的周长=EF+ME+FM=7+5+5=17.故选A.3.(2015春•威海期末)如图,在四边形ABCD中,∠BCD=∠BAD=90°,AC,BD相交于点E,点G,H分别是AC,BD的中点,若∠BEC=80°,那么∠GHE等于()A.5°B.10°C.20°D.30°【解答】解:连接AH,CH,∵在四边形ABCD中,∠BCD=∠BAD=90°,H是BD的中点,∴AH=CH=BD.∵点G时AC的中点,∴HG是线段AC的垂直平分线,∴∠EGH=90°.∵∠BEC=80°,∴∠GEH=∠BEC=80°,∴∠GHE=90°﹣80°=10°.故选B.4.(2014春•范县期末)如图,∠MON=90°,边长为2的等边三角形ABC的顶点A、B分别在边OM,ON上当B 在边ON上运动时,A随之在边OM上运动,等边三角形的形状保持不变,运动过程中,点C到点O的最大距离为()A.2.4 B.C.D.【解答】解:如图,取AB的中点D,连接CD.∵△ABC是等边三角形,且边长是2,∴BC=AB=2,∵点D是AB边中点,∴BD=AB=1,∴CD===,即CD=;连接OD,OC,有OC≤OD+DC,当O、D、C共线时,OC有最大值,最大值是OD+CD,由(1)得,CD=,又∵△AOB为直角三角形,D为斜边AB的中点,∴OD=AB=1,∴OD+CD=1+,即OC的最大值为1+.故选:C.5.(2016•东明县一模)如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点,则DC和EF 的大小关系是()A.DC>EF B.DC<EF C.DC=EF D.无法比较【解答】解:∵E、F分别为AC、BC的中点,∴EF=AB,在Rt△ABC中,D是AB的中点,∴CD=AB,∴CD=EF,故选:C.6.(2015春•唐山期末)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则∠ECD=()A.22.5° B.30°C.36°D.45°【解答】解:∵∠ACB=90°,∠ACD=3∠BCD,∴∠BCD=90°×=22.5°,∠ACD=90°×=67.5°,∵CD⊥AB,∴∠B=90°﹣22.5°=67.5°,∵E是AB的中点,∠ACB=90°,∴CE=BE,∴∠BCE=∠B=67.5°,∴∠ECD=∠BCE﹣∠BCD=67.5°﹣22.5°=45°,故选D.7.(2015秋•邗江区期中)已知:如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点,AC=10,BD=8,则MN为()A.3 B.4 C.5 D.6【解答】解:连接BM、DM,∵∠ABC=∠ADC=90°,M是AC的中点,∴BM=AC,DM=AC,∴BM=DM=5,又N是BD的中点,∴BN=DN=BD=4,∴MN==3,故选:A.8.(2015春•邵阳县期末)如果三角形中一边上的中线等于这边的一半,则这个三角形是()A.等腰三角形B.直角三角形C.等边三角形D.等腰直角三角形【解答】解:∵三角形中一边上的中线等于这边的一半,∴这个三角形是直角三角形.故选B.9.(2016•保定三模)如图,在Rt△ABC中,∠ACB=90°,∠A=60°,过点C的直线与AB交于点D,且将△ABC的面积分成相等的两部分,则∠CDA=()A.30°B.45°C.60°D.75°【解答】解:如图,∵在Rt△ABC中,∠ACB=90°,∠A=60°,∴AC=AB,又∵过点C的直线与AB交于点D,且将△ABC的面积分成相等的两部分,∴AD=BD∴AC=AD,∵∠A=60°,∴△ADC是等边三角形,∴∠CDA=60°.10.(2014秋•新泰市期末)如图,△ABC中,AB、BC、CA的中点分别是E,F,G,AD是高.则下列选项正确的有()个(1)∠EDG=∠EFG;(2)∠B=∠BDE;(3)∠CDG=∠C;(4)∠GFC=∠ADE.A.1 B.2 C.3 D.4【解答】解:∵AD是高,且E是AB的中点,∴DE=BE=AE,∴∠B=∠BDE,∠EAD=∠ADE,故(2)正确.同理,∠DAG=∠ADG,∠CDG=∠C,则(3)正确,(4)错误;又∵AB、BC、CA的中点分别是E,F,G,∴EF∥AC,FG∥AE,∴四边形AEFG是平行四边形,∴∠EFG=∠EAG=∠EAD+∠DAG=∠ADE+∠ADG=∠EDG.故(1)正确.故选C.二.填空题(共10小题)11.(2012•鞍山)如图,在△ABC中,∠ACB=90°,∠A=60°,AC=a,作斜边AB边中线CD,得到第一个三角形ACD;DE⊥BC于点E,作Rt△BDE斜边DB上中线EF,得到第二个三角形DEF;依此作下去…则第n个三角形的面积等于.【解答】解:∵∠ACB=90°,CD是斜边AB上的中线,∴CD=AD,∵∠A=60°,∴△ACD是等边三角形,同理可得,被分成的第二个、第三个…第n个三角形都是等边三角形,∵CD是AB的中线,EF是DB的中线,…,∴第一个等边三角形的边长CD=DB=AB=AC=a,第二个等边三角形的边长EF=DB=a,…第n个等边三角形的边长为a,所以,第n个三角形的面积=×a×(•a)=.故答案为:.12.(2012秋•义乌市期末)如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连接AE,若AE=6.5,AD=5,则AC= 6.5;△ABE的周长是25.【解答】解:∵AD⊥AB,∴△ABD为直角三角形.又∵点E是BD的中点,∴BD=AE=BE=6.5,∴∠EAB=∠B,∴∠AEC=∠B+∠EAB=2∠B=∠C,即∠AEC=∠C,∴AE=AC=6.5.在Rt△ABD中,AD=5,BD=2AE=2×6.5=13∴AB=12(勾股定理),∴△ABE的周长是AB+AE+BE=12+6.5+6.5=25.故答案分别是:6.5;25.13.(2014•松北区一模)把一副三角板如图放置,E是AB的中点,连接CE、DE、CD,F是CD的中点,连接EF.若AB=4,则S△CEF=.【解答】解:作DG⊥CE于点G.∵AB=4∴CE=BC=AB=2,DE=AB=2,∵∠CED=∠DEB+∠CEB=90°+60°=150°,∴∠DEG=180°﹣150°=30°.在直角△DEG中,DG=DE=×2=1.∴S△CDE=CE•DG=×2×1=1,∵F是CD中点.∴S△CEF=S△CDE=×1=.故答案是:.14.(2015秋•宜兴市校级期中)如图,∠MON=90°,△ABC的顶点A、B分别在OM、ON上,当A点从O点出发沿着OM向右运动时,同时点B在ON上运动,连结OC.若AC=4,BC=3,AB=5,则OC的长度的最大值是5.【解答】解:取AB中点E,连接OE、CE,在直角三角形AOB中,OE=AB,∵AC=4,BC=3,AB=5,∴AC2+BC2=AB2,∴CE=AB,∵OE+CE≥OC,∴OC的最大值为OE+CE,即OC的最大值=AB=5,故答案为5.15.(2014•丹东一模)如图,在四边形ABCD中,BC⊥AC于点C,BE⊥AD于点E,∠BAC=60°,点G是AB的中点,已知BC=,则GE的长是1.【解答】解:设AB=2x,∵BC⊥AC,∠BAC=60°,∴∠ABC=90°﹣60°=30°,∴AC=AB=x,在Rt△ABC中,由勾股定理得,AB2=AC2+BC2,即(2x)2=x2+()2,解得x=1,∴AB=2,∵BE⊥AD,点G是AB的中点,∴GE=AB=x=1.故答案为:1.16.(2014•路南区三模)如图,在△ABC中,∠ACB=90°,AC=8,BC=3,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离为9.【解答】解:作AC的中点D,连接OD、BD.∵OB≤OD+BD,∴当O、D、B三点共线时OB取得最大值,∵BD===5,OD=AD=AC=4,∴点B到原点O的最大距离为5+4=9.故答案是:9.17.(2016•郑州校级模拟)如图所示,在平面直角坐标系中,矩形ABCD定点A、B在y轴、x轴上,当B在x 轴上运动时,A随之在y轴运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为+1.【解答】解:如图,取AB的中点E,连接OD、OE、DE,∵∠MON=90°,AB=2,∴OE=AE=AB=1,∵BC=1,四边形ABCD是矩形,∴AD=BC=1,∴DE===,根据三角形的三边关系,OD<OE+DE,∴当OD过点E是最大,最大值为+1.故答案为:+1.18.(2011秋•诸暨市校级期中)一个直角三角形斜边上的中线长为10,周长为48,则此直角三角形的面积为96.【解答】解:∵直角三角形斜边上的中线长为10,∴斜边的长为20,设两直角边分别为x、y,∵周长为48,∴x+y=48﹣20=28,平方得,x2+2xy+y2=784,根据勾股定理,x2+y2=202=400,∴2xy=784﹣400=384,∴xy=96,即直角三角形的面积为96.故答案为:96.19.(2015秋•南京期中)如图,在△ABC中,∠ACB=90°,∠CAB=30°.以AB长为一边作△ABD,且AD=BD,∠ADB=90°,取AB中点E,连DE、CE、CD.则∠EDC=75°.【解答】解:∵∠ACB=90°,点E是AB中点,∴EC=EA=EB=AB,∴∠ECA=∠CAB=30°,∴∠CEB=60°,∵AD=BD,点E是AB中点,∴DE⊥AB,即∠AED=90°,∴∠DEC=180°﹣90°﹣60°=30°,∵∠ADB=90°,点E是AB中点,∴DE=AB,∴ED=EC,∴∠EDC=75°,故答案为:75.20.(2014秋•鄄城县期中)如图是一副三角尺拼成的四边形ABCD,E为斜边BD中点,则∠ACE=15°.【解答】解:根据直角三角形性质,∵E为斜边BD中点,∴CE=DB,AE=DB,即CE=AE,又根据题意及图知∠ADB=60°,∠CDE=45°,∴∠DEA=∠ADB=60°,∠DEC=90°,∴∠AEC=150°,又CE=AE,∴∠ACE=∠CAE=15°.故答案为:15°.三.解答题(共9小题)21.(2014•锦州)如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM.(1)求证:EF=AC.(2)若∠BAC=45°,求线段AM、DM、BC之间的数量关系.【解答】(1)证明:∵CD=CB,点E为BD的中点,∴CE⊥BD,∵点F为AC的中点,∴EF=AC;(2)解:∵∠BAC=45°,CE⊥BD,∴△AEC是等腰直角三角形,∵点F为AC的中点,∴EF垂直平分AC,∴AM=CM,∵CD=CM+DM=AM+DM,CD=CB,∴BC=AM+DM.22.(2014秋•沧浪区校级期中)如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.(1)证明:DC=DG;(2)若DG=5,EC=2,求DE的长.【解答】(1)证明:∵DE⊥BC,∴∠DEB=90°,∵AD∥BC,∴∠ADE+∠DEB=180°,∴∠ADE=90°,∵G为AF的中点,∴DG=AG,∴∠DAF=∠ADG,∴∠DGC=∠DAF+∠ADG=2∠DAC,∵AD∥BC,∴∠ACB=∠DAC,∵∠ACD=2∠ACB,∴∠DGC=∠DCA,∴DC=DG;(2)解:∵在Rt△DEC中,∠DEC=90°,DG=DC=5,CE=2,∴由勾股定理得:DE==.23.(2014春•海盐县校级期末)如图所示,四边形ABCD由一个∠ACB=30°的Rt△ABC与等腰Rt△ACD拼成,E 为斜边AC的中点,求∠BDE的大小.【解答】解:∵点E是Rt△ABC,Rt△ACD斜边AC的中点,∴BE=DE=AC=CE,DE⊥AC,∴∠ACB=∠EBC,∠BDE=∠EBD,又∵∠ACB=30°,∴∠AEB=∠EBC+∠ECB=30°+30°=60°∴∠BED=∠BEA+∠DEA=60°+90°=150°∴∠BDE=(180°﹣∠BED)=(180°﹣150°)=15°.24.如图,已知在△ABC中,延长CA到D,使BA=BD,延长BA到E,使CA=CE,设P、M、N分别是BC、AD、AE的中点.求证:△PMN是等腰三角形.【解答】证明:连接BM、CN,∵BA=BD,DM=MA,∴BM⊥AD,∴∠BMC=90°,又BP=PC,∴MP=BC,同理,NP=BC,∴MP=NP,∴△PMN是等腰三角形.25.△ABC中,BE⊥AC,CF⊥AB,D为BC中点,设EB与CF相交于K,N为KA的中点,探索DN和EF的关系.【解答】解:∵BE⊥AC,CF⊥AB,D为BC中点,∴DE=DF=BC,连接NE、NF,∵N为KA的中点,∴NE=NF=AK,∴DN垂直平分EF.26.(2012秋•海淀区期末)已知:在△ABC中,∠ABC=90°,点E在直线AB上,ED与直线AC垂直,垂足为D,且点M为EC中点,连接BM,DM.(1)如图1,若点E在线段AB上,探究线段BM与DM及∠BMD与∠BCD所满足的数量关系,并直接写出你得到的结论;(2)如图2,若点E在BA延长线上,你在(1)中得到的结论是否发生变化?写出你的猜想并加以证明;(3)若点E在AB延长线上,请你根据条件画出相应的图形,并直接写出线段BM与DM及∠BMD与∠BCD所满足的数量关系.【解答】解:(1)结论:BM=DM,∠BMD=2∠BCD.理由:∵BM、DM分别是Rt△DEC、Rt△EBC的斜边上的中线,∴BM=DM=CE;又∵BM=MC,∴∠MCB=∠MBC,即∠BME=2∠BCM;同理可得∠DME=2∠DCM;∴∠BME+∠DME=2(∠BCM+∠DCM),即∠BMD=2∠BCD.(2)在(1)中得到的结论仍然成立.即BM=DM,∠BMD=2∠BCD证法一:∵点M是Rt△BEC的斜边EC的中点,∴BM=EC=MC,又点M是Rt△BEC的斜边EC的中点,∴DM=EC=MC,∴BM=DM;∵BM=MC,DM=MC,∴∠CBM=∠BCM,∠DCM=∠CDM,∴∠BMD=∠EMB﹣∠EMD=2∠BCM﹣2∠DCM=2(∠BCM﹣∠DCM)=2∠BCD,即∠BMD=2∠BCD.证法二:∵点M是Rt△BEC的斜边EC的中点,∴BM=EC=ME;又点M是Rt△DEC的斜边EC的中点,∴DM=EC=MC,∴BM=DM;∵BM=ME,DM=MC,∴∠BEC=∠EBM,∠MCD=∠MDC,∴∠BEM+∠MCD=∠BAC=90°﹣∠BCD,∴∠BMD=180°﹣(∠BMC+∠DME),=180°﹣2(∠BEM+∠MCD)=180°﹣2(90°﹣∠BCD)=2∠BCD,即∠BMD=2∠BCD.(3)所画图形如图所示:图1中有BM=DM,∠BMD=2∠BCD;图2中∠BCD不存在,有BM=DM;图3中有BM=DM,∠BMD=360°﹣2∠BCD.解法同(2).27.(2015春•瑶海区期末)小明在学习矩形这一节时知道“直角三角形斜边上的中线等于斜边的一半”,由此引发他的思考,这个定理的逆命题成立吗?即:如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是否为直角三角形?通过探究,小明发现这个猜想也成立,以下是小明的证明过程:已知:如图1,在△ABC中,点D是AB的中点,连接CD,且CD=AB求证:△ABC为直角三角形证明:由条件可知,AD=BD=CD则∠A=∠DCA,∠B=∠DCB又∵∠A+∠DCA+∠B+∠DCB=180°∴∠DCA+∠DCB=90°爱动脑筋的小明发现用本学期所学知识也能证明这个结论,并想出了图2、图3两种不同的证明思路,请你选择其中一种,把证明过程补充完整:【解答】证明:如图2,延长CD至E,使DE=CD,连接AE、BE;又∵AD=DB,∴四边形ACBE是平行四边形,又∵CD=AB,CD=CE,∴四边形ACBE是矩形,∴∠ACB=90°,∴△ABC为直角三角形.28.(2015秋•启东市校级月考)引理:如图1所示已知Rt△ABC中,CD是斜边AB上的中线,则CD=AD=DB=AB 应用格式为:∵CD是斜边AB上的中线,∴CD=AD=DB=AB如图2所示已知,△ABC中,AC=BC,∠ACB=90°,D为AB的中点,若E在直线AC上任意一点,DF⊥DE,交直线BC于F点.G为EF的中点,延长CG交AB直线于点H.(1)若E在边AC上.①试说明DE=DF;②试说明CG=GH;(本题需要用引理)(2)若AE=3,CH=5.求边AC的长.【解答】解:(1)①连接CD,∵∠ACB=90°,D为AB的中点,AC=BC,∴CD=AD=BD,又∵AC=BC,∴CD⊥AB,∴∠EDA+∠EDC=90°,∠DCF=∠DAE=45°,∵DF⊥DE,∴∠EDF=∠EDC+∠CDF=90°,∴∠ADE=∠CDF,在△ADE和△CDF中,,∴△ADE≌△CDF,∴DE=DF.②连接DG,∵∠ACB=90°,G为EF的中点,∴CG=EG=FG,∵∠EDF=90°,G为EF的中点,∴DG=EG=FG,∴CG=DG,∴∠GCD=∠CDG又∵CD⊥AB,∴∠CDH=90°,∴∠GHD+∠GCD=90°,∠HDG+∠GDC=90°,∴∠GHD=∠HDG,∴GH=GD,∴CG=GH.(2)分两种情况:①如图,当E在线段AC上时,∵CG=GH=EG=GF,∴CH=EF=5,∵△ADE≌△CDF,∴AE=CF=3,∴在Rt△ECF中,由勾股定理得:CE==4,∴AC=AE+EC=3+4=7;②如图,当E在线段CA延长线上时,AC=EC﹣AE=4﹣3=1.③E在AC延长线上时,AC=AE﹣CE,AC=3﹣4=﹣1(舍去).综合上述,AC=7或1.29.(2016春•广饶县期末)如图,△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.(1)求证:MN⊥DE;(2)连结DM,ME,猜想∠A与∠DME之间的关系,并写出推理过程;(3)若将锐角△ABC变为钝角△ABC,如图,上述(1)(2)中的结论是否都成立?若结论成立,直接回答,不需证明;若结论不成立,说明理由.【解答】解:(1)如图,连接DM,ME,∵CD、BE分别是AB、AC边上的高,M是BC的中点,∴DM=BC,ME=BC,∴DM=ME又∵N为DE中点,∴MN⊥DE;(2)在△ABC中,∠ABC+∠ACB=180°﹣∠A,∵DM=ME=BM=MC,∴∠BMD+∠CME=(180°﹣2∠ABC)+(180°﹣2∠ACB),=360°﹣2(∠ABC+∠ACB),=360°﹣2(180°﹣∠A),=2∠A,∴∠DME=180°﹣2∠A;(3)结论(1)成立,结论(2)不成立,理由如下:在△ABC中,∠ABC+∠ACB=180°﹣∠A,∵DM=ME=BM=MC,∴∠BME+∠CMD=2∠ACB+2∠ABC,=2(180°﹣∠A),=360°﹣2∠A,∴∠DME=180°﹣(360°﹣2∠A),=2∠A﹣180°.。
直角三角形斜边上的中线等于斜边的一半例题

直角三角形斜边上的中线等于斜边的一半例题全文共四篇示例,供读者参考第一篇示例:在中学数学课堂上,直角三角形是一个非常常见的几何形状。
直角三角形的特点是其中一个角为直角(90度),而其他两个角则为锐角和钝角,另外两条边分别为斜边和两条直角边。
直角三角形的性质十分有趣,其中有一条性质是斜边上的中线等于斜边的一半。
这个性质看似简单,但需要一些几何知识和推理来证明。
让我们来了解一下中线是什么。
在一个三角形中,中线是连接一个角的顶点和对边中点的线段。
对于直角三角形来说,如果我们将斜边一分为二,使之成为等分线,那么这条等分的线段就是斜边上的中线。
接下来,让我们来证明斜边上的中线等于斜边的一半。
假设我们有一个直角三角形ABC,其中角A为直角,AB和AC分别为直角边,BC为斜边。
我们需要证明BD(BC的中线)等于BC的一半。
我们可以得出直角三角形ABC中的角B和角C分别为锐角和钝角。
根据直角三角形的性质,角B和角C的和为90度,即B+C=90度。
又因为直角三角形中,直角边的对边相等,所以AB=AC。
我们可以得出结论:斜边上的中线等于斜边的一半。
在这个例子中,BD等于BC的一半,也就是说斜边BC的中线等于一半的斜边BC。
这个性质在几何学中有许多应用,特别是在解题时。
通过掌握这个性质,我们可以更快地解决直角三角形的问题,提高我们的数学能力和解题速度。
直角三角形斜边上的中线等于斜边的一半是一个十分有趣的几何性质。
通过几何推理和证明,我们可以更深入地理解这个性质,并在实际问题中灵活运用。
希望同学们在学习数学的过程中,能够多多探索,多多实践,不断提升自己的数学水平。
【2000字】第二篇示例:直角三角形是三角形中特殊的一种,其中一个角是直角(即90度角)。
在直角三角形中,斜边是最长的一条边,其余两边分别称为直角边。
而直角三角形斜边上的中线等于斜边的一半,这是一个非常有趣且有趣的几何性质。
考虑一个直角三角形ABC,其中∠C是直角,AB为斜边,AC和BC为直角边。
直角三角形斜边上的中线应用题目

直角三角形斜边上的中线应用题目
直角三角形是一种特殊的三角形,其中一个角为直角(90度角)。
在直角三角形中,斜边是指与直角的两条边不重合的另外那条边。
斜边上的中线是指从斜边中点垂直于斜边的线段。
直角三角形斜边上的中线有很多应用,下面是一些题目:
1. 题目一:
已知一个直角三角形的斜边长为10cm,求斜边上的中线的长度。
解答:
由于直角三角形中,斜边的一半就是中线的长度。
所以,中线的长度为10cm的一半,即5cm。
2. 题目二:
已知一个直角三角形的斜边长为12cm,中线的长度为6cm,求与中线相交的直角三角形两个直角边的长度。
解答:
由于中线是斜边的一半,所以斜边的长度是中线的两倍,即12cm。
因此,直角边的长度可以使用勾股定理求解。
设一个直角边为x,则另一个直角边为12-x。
根据勾股定理,我们可以得到以下方程:
x^2 + (12-x)^2 = 12^2
化简方程后,求解x的值,即可得到另一个直角边的长度。
这些题目是直角三角形斜边上的中线应用题目的一些例子。
通过解答这些题目,我们可以更深入地理解直角三角形的性质和中线的应用。
在解题过程中,可以运用勾股定理和直角三角形的基本性质,加深对数学知识的理解和应用能力。
希望以上内容对您有所帮助,如有其他问题,请随时提问。
直角三角形斜边上的中线性质练习
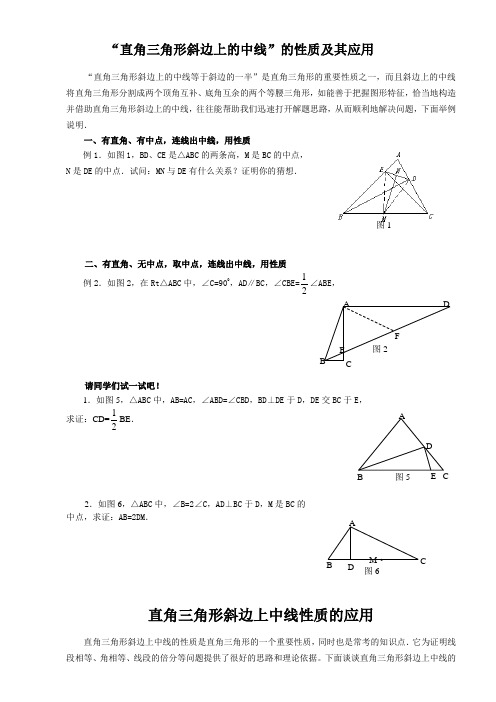
“直角三角形斜边上的中线”的性质及其应用“直角三角形斜边上的中线等于斜边的一半”是直角三角形的重要性质之一,而且斜边上的中线将直角三角形分割成两个顶角互补、底角互余的两个等腰三角形,如能善于把握图形特征,恰当地构造并借助直角三角形斜边上的中线,往往能帮助我们迅速打开解题思路,从而顺利地解决问题,下面举例说明.一、有直角、有中点,连线出中线,用性质例1.如图1,BD 、CE 是△ABC 的两条高,M 是BC 的中点, N 是DE 的中点.试问:MN 与DE 有什么关系?证明你的猜想.二、有直角、无中点,取中点,连线出中线,用性质 例2.如图2,在Rt △ABC 中,∠C=900,AD ∥BC ,∠CBE=12∠ABE ,请同学们试一试吧!1.如图5,△ABC 中,AB=AC ,∠ABD=∠CBD ,BD ⊥DE 于D ,DE 交BC 于E , 求证:CD=12BE .2.如图6,△ABC 中,∠B=2∠C ,AD ⊥BC 于D ,M 是BC 的 中点,求证:AB=2DM .直角三角形斜边上中线性质的应用直角三角形斜边上中线的性质是直角三角形的一个重要性质,同时也是常考的知识点.它为证明线段相等、角相等、线段的倍分等问题提供了很好的思路和理论依据。
下面谈谈直角三角形斜边上中线的图1BADCEF图2B图5ACBD M · 图6性质及应用。
一、直角三角形斜边上中线的性质1、性质:直角三角形斜边上的中线等于斜边的一半.如图1,在Rt △BAC 中,∠BAC=︒90,D 为BC 的中点,则BC 21AD =。
2、性质的拓展:如图1:因为D 为BC 中点,所以BC 21DC BD ==,所以AD=BD=DC=BC21,所以∠1=∠2,∠3=∠4, 因此∠ADB=2∠3=2∠4, ∠ADC=2∠1=2∠2。
因而可得如下几个结论:①直角三角形斜边上的中线将直角三角形分成两个等腰三角形;②分成的两个等腰三角形的腰相等,两个顶角互补、底角互余,并且其中一个等腰三角形的顶角等于另一个等腰三角形底角的2倍. 二、性质的应用 1、求值例1、(2004年江苏省苏州市中考)如图2,CD 是Rt △ABC 斜边AB 上的中线,若CD=4,则AB= .2、证明线段相等例2、(2004年上海市中考)如图4,在△ABC 中,∠BAC=90°,延长BA 到D 点,使AB 21AD =,点E 、F 分别为边BC 、AC 的中点。
矩形--直角三角形斜边上的中线等于斜边的一半

18.2.1(2.1)矩形--直角三角形斜边上的中线等于斜边的一半一.【知识要点】1.直角三角形的性质:直角三角形斜边上的中线等于斜边的一半。
二.【经典例题】1.如图,平行四边形ABCD 的周长是26cm ,对角线AC 与BD 交于点O ,AC ⊥AB ,E 是BC 中点,△AOD 的周长比△AOB 的周长多3cm ,求AE 的长.2. 如图,在△ABE 中,AE ⊥BE,AE=BE,AD ⊥BC 于D,BC 平分∠ABE. (1)求证:BC=2AD; (2)求∠ADE 的度数.3.如图,在△ABC 中,BD ⊥AC 于点D ,CE ⊥AB 于点E ,点M,N 分别是BC,DE 的中点, (1)求证:MN ⊥DE; (2)若∠A=60°,求MNDE的值.4.如图,在△ABC 中,AB=BC ,∠ABC=90°,点E ,F 分别在AB ,AC 上,且AE=EF ,点O ,M分别为 AF ,CE 的中点.求证:(1)12OM CE =;(2)OB =5.如图,△CDE中,∠CDE=135°,CB⊥DE于点B,EA⊥CD于点A,求证:CE .6.如图,∠ACB=∠ADB=90°,AD与BC交于点M,∠AMB=105°,点O为AB的中点连CO,OD,求∠COD的度数.7.如图,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的关系,并证明你的结论.三.【题库】 【A 】【B 】1. 如图 ,在ABC Rt ∆,︒=∠90ACB ,D 、E 、 F 分别是AB 、BC 、CA 的中点,若CD=5,则EF=__________2.如图,在∆ABC 中,∠C=90°,AC=BC,D 点为AB 的中点,PE ⊥AC 于点E ,PF ⊥BC 于点F ,连接DE ,DF ,求证:DE=DF (10分)【C 】1.(本小题共8分)如图,在四边形ABCD 中,∠ABC=∠ADC=90°,M 、N 分别是AC 、BD 的中点 (1)求证:MN ⊥BD.(2)若AC=10 ,BD=8.求MN 的长.2.如图,在RtΔABC中,∠ACB=900,点D、E分别是AB、BC的中点,点F在AC的延长线上,∠FEC=∠B,①CF=DE吗?请说明理由.②若AC=6cm,AB=10cm,求四边形DCFE的面积.3. 如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为.4.如图,△BCD和△BCE中,∠BDC=∠BEC=90°,O为BC的中点,BD,CE交于点A,∠BAC=120°,求证:DE=OE.【D】1. 如图,平行四边形ABCD中,点E是BC边上的一点,且DE=BC,过点A作AF⊥CD于点F,交DE于点G,连结AE、EF.(1)若AE平分∠BAF,求证:BE=GE;(2)若点E是BC边上的中点,求证:∠AEF=2∠EFC.2.如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )①2∠DCF=∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.A. ①②③④B. ①②④C. ①②D. ②③3.(16分)已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.(1)如图1,当点P与点Q重合时,AE与BF的位置关系是,QE与QF的数量关系式;(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.。
直角三角形斜边上的中线-北京习题集-教师版
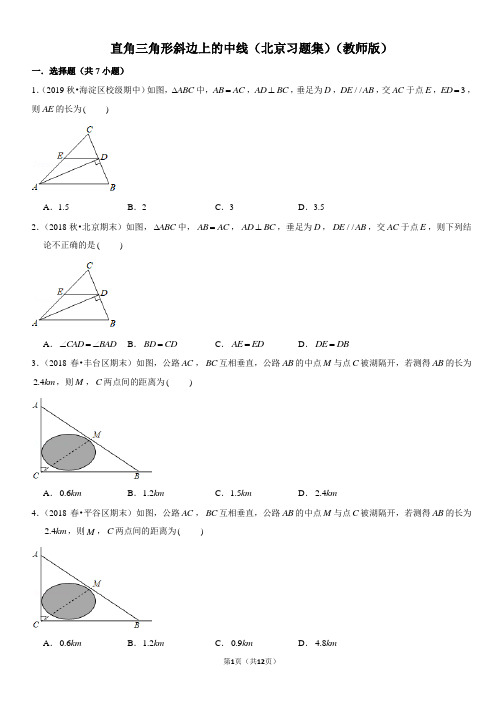
直角三角形斜边上的中线(北京习题集)(教师版)一.选择题(共7小题)1.(2019秋•海淀区校级期中)如图,ABC ∆中,AB AC =,AD BC ⊥,垂足为D ,//DE AB ,交AC 于点E ,3ED =,则AE 的长为( )A .1.5B .2C .3D .3.52.(2018秋•北京期末)如图,ABC ∆中,AB AC =,AD BC ⊥,垂足为D ,//DE AB ,交AC 于点E ,则下列结论不正确的是( )A .CAD BAD ∠=∠B .BD CD =C .AE ED =D .DE DB =3.(2018春•丰台区期末)如图,公路AC ,BC 互相垂直,公路AB 的中点M 与点C 被湖隔开,若测得AB 的长为2.4km ,则M ,C 两点间的距离为( )A .0.6kmB .1.2kmC .1.5kmD .2.4km4.(2018春•平谷区期末)如图,公路AC ,BC 互相垂直,公路AB 的中点M 与点C 被湖隔开,若测得AB 的长为2.4km ,则M ,C 两点间的距离为( )A .0.6kmB .1.2kmC .0.9kmD .4.8km5.(2018春•海淀区期末)如图,在ABC ∆中,90ACB ∠=︒,点D 为AB 的中点,若4AB =,则CD 的长为( )A .2B .3C .4D .56.(2017•昌平区二模)如图,ABC ∆中,90ACB ∠=︒,55B ∠=︒,点D 是斜边AB 的中点,那么ACD ∠的度数为()A .15︒B .25︒C .35︒D .45︒7.(2017春•顺义区校级期中)Rt ABC ∆中,90B ∠=︒,3AB =,4BC =,BD 是AC 边上中线,BH 是AC 边上高,则BD 与BH 的值分别是( ) A .5,2.4B .2.5,7C .2.5,2.5D .2.5,2.4二.填空题(共6小题)8.(2019春•朝阳区期末)笔直的公路AB ,AC ,BC 如图所示,AC ,BC 互相垂直,AB 的中点D 与点C 被建筑物隔开,若测得AC 的长为3km ,BC 的长为4km ,则C ,D 之间的距离为 km .9.(2019春•海淀区校级期中)如图,在ABC ∆中,90ACB ∠=︒,CD 为AB 边上的中线,若A a ∠=,则BCD ∠的度数为 (用含a 的代数式表示)10.(2018秋•石景山区期末)如图,ACB ∆中,5AC =,12BC =,13AB =,点D 是AB 的中点,则CD 的长为 .11.(2019秋•昌平区校级期中)在Rt ABC ∆中,90ACB ∠=︒,如果斜边AB 上的中线4CD cm =,那么斜边AB =cm .12.(2017春•西城区校级期中)在Rt ABC ∆中,90ACB ∠=︒,5AC =,12BC =,点D 是AB 的中点,则CD = .13.(2016春•东城区校级期中)如图,Rt ABC ∆中,90C ∠=︒,D 为AB 中点,CE AB ⊥于E ,5CD =,6BC =,则AC = ,CE = .三.解答题(共2小题)14.(2019•朝阳区模拟)如图,在Rt ABC ∆中,90BAC ∠=︒,AD 是BC 边上的中线,ED BC ⊥于D ,交BA 延长线于点E ,若35E ∠=︒,求BDA ∠的度数.15.(2019秋•平谷区期末)在平面直角坐标系xOy 中,有任意三角形,当这个三角形的一条边上的中线等于这条边的一半时,称这个三角形叫“和谐三角形”,这条边叫“和谐边”,这条中线的长度叫“和谐距离”.(1)已知(2,0)A ,(0,4)B ,(1,2)C ,(4,1)D ,这个点中,能与点O 组成“和谐三角形”的点是 ,“和谐距离”是 ;(2)连接BD ,点M ,N 是BD 上任意两个动点(点M ,N 不重合),点E 是平面内任意一点,EMN ∆是以MN 为“和谐边”的“和谐三角形”,求点E 的横坐标t 的取值范围;(3)已知O 的半径为2,点P 是O 上的一动点,点Q 是平面内任意一点,OPQ ∆是“和谐三角形”,且“和谐距离”是2,请描述出点Q 所在位置.直角三角形斜边上的中线(北京习题集)(教师版)参考答案与试题解析一.选择题(共7小题)1.(2019秋•海淀区校级期中)如图,ABC ∆中,AB AC =,AD BC ⊥,垂足为D ,//DE AB ,交AC 于点E ,3ED =,则AE 的长为( )A .1.5B .2C .3D .3.5【分析】根据等腰三角形的性质,直角三角形的性质解答. 【解答】解:AB AC =,AD BC ⊥,BD CD ∴=, //DE AB , AE CE ∴=,132DE AE AB ∴===, 故选:C .【点评】本题考查的是直角三角形的性质,等腰三角形的性质,平行线的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.2.(2018秋•北京期末)如图,ABC ∆中,AB AC =,AD BC ⊥,垂足为D ,//DE AB ,交AC 于点E ,则下列结论不正确的是( )A .CAD BAD ∠=∠B .BD CD =C .AE ED =D .DE DB =【分析】根据等腰三角形的性质,直角三角形的性质解答. 【解答】解:AB AC =,AD BC ⊥,CAD BAD ∴∠=∠,A 正确,不符合题意; BD CD =,B 正确,不符合题意;//DE AB ,EDA BAD ∴∠=∠, EAD BAD ∠=∠,EAD EDA ∴∠=∠,AE ED ∴=,C 正确,不符合题意;DE 与DB 的关系不确定,D 错误,符合题意;故选:D .【点评】本题考查的是直角三角形的性质,等腰三角形的性质,平行线的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.3.(2018春•丰台区期末)如图,公路AC ,BC 互相垂直,公路AB 的中点M 与点C 被湖隔开,若测得AB 的长为2.4km ,则M ,C 两点间的距离为( )A .0.6kmB .1.2kmC .1.5kmD .2.4km【分析】根据直角三角形斜边上的中线性质得出12CM AB =,代入求出即可. 【解答】解:AC BC ⊥,90ACB ∴∠=︒,M 为AB 的中点,12CM AB ∴=, 2.4AB km =, 1.2CM km ∴=,故选:B .【点评】本考考查了直角三角形斜边上的中线性质,能根据直角三角形斜边上的中线性质得出12CM AB =是解此题的关键.4.(2018春•平谷区期末)如图,公路AC ,BC 互相垂直,公路AB 的中点M 与点C 被湖隔开,若测得AB 的长为2.4km ,则M ,C 两点间的距离为( )A .0.6kmB .1.2kmC .0.9kmD .4.8km 【分析】根据直角三角形斜边上的中线等于斜边的一半,可得11.22MC AB km ==. 【解答】解:在Rt ABC ∆中,90ACB ∠=︒,M 为AB 的中点, 11.22MC AB km ∴==. 故选:B .【点评】本题考查了直角三角形斜边上的中线的性质:在直角三角形中,斜边上的中线等于斜边的一半.理解题意,将实际问题转化为数学问题是解题的关键.5.(2018春•海淀区期末)如图,在ABC ∆中,90ACB ∠=︒,点D 为AB 的中点,若4AB =,则CD 的长为( )A .2B .3C .4D .5【分析】根据直角三角形斜边上中线的性质得出12CD AB =,代入求出即可. 【解答】解:在ABC ∆中,90ACB ∠=︒,点D 为AB 的中点,4AB =, 114222CD AB ∴==⨯=, 故选:A .【点评】本题考查了直角三角形斜边上中线的性质,能根据直角三角形斜边上中线的性质得出12CD AB =是解此题的关键.6.(2017•昌平区二模)如图,ABC ∆中,90ACB ∠=︒,55B ∠=︒,点D 是斜边AB 的中点,那么ACD ∠的度数为()A .15︒B .25︒C .35︒D .45︒【分析】先根据在直角三角形中,斜边上的中线等于斜边的一半,得出CD BD =,进而得到55B DCB ∠=∠=︒,再根据90ACB ∠=︒,即可得出ACD ∠的度数.【解答】解:ABC ∆中,90ACB ∠=︒,点D 是斜边AB 的中点, 12CD BD AB ∴==, 55B DCB ∴∠=∠=︒,又90ACB ∠=︒, 905535ACD ∴∠=︒-︒=︒,故选:C .【点评】本题主要考查了直角三角形斜边上中线的性质,解题时注意:在直角三角形中,斜边上的中线等于斜边的一半.7.(2017春•顺义区校级期中)Rt ABC ∆中,90B ∠=︒,3AB =,4BC =,BD 是AC 边上中线,BH 是AC 边上高,则BD 与BH 的值分别是( ) A .5,2.4B .2.57C .2.5,2.5D .2.5,2.4【分析】根据勾股定理求出AC ,根据直角三角形的性质解答. 【解答】解:Rt ABC ∆中,90B ∠=︒,3AB =,4BC =,225AC AB BC ∴=+=,BD 是AC 边上中线,2.5BD ∴=,1153422BH ⨯⨯=⨯⨯, 解得, 2.4BH =, 故选:D .【点评】本题考查的是直角三角形的性质、勾股定理的应用,掌握直角三角形中,斜边上的中线等于斜边的一半是解题的关键. 二.填空题(共6小题)8.(2019春•朝阳区期末)笔直的公路AB ,AC ,BC 如图所示,AC ,BC 互相垂直,AB 的中点D 与点C 被建筑物隔开,若测得AC 的长为3km ,BC 的长为4km ,则C ,D 之间的距离为52km .【分析】由勾股定理可得5AB =,根据直角三角形斜边中线等于斜边的一半,于是得到结论. 【解答】解:在Rt ABC ∆中,222AB AC CB =+, AC 的长为3km ,BC 的长为4km , 5AB km ∴=,D 点是AB 中点,1522CD AB km ∴==. 故答案为:52. 【点评】本题考查了勾股定理和直角三角形斜边中线的性质,综合了直角三角形的线段求法,是一道很好的问题. 9.(2019春•海淀区校级期中)如图,在ABC ∆中,90ACB ∠=︒,CD 为AB 边上的中线,若A a ∠=,则BCD ∠的度数为 90a ︒- (用含a 的代数式表示)【分析】根据直角三角形的性质求出B ∠,根据直角三角形的斜边上的中线等于斜边的一半得到12CD AB BD ==,根据等腰三角形的性质解答即可. 【解答】解:9090B A a ∠=︒-∠=︒-, 90ACB ∠=︒,CD 为AB 边上的中线,12CD AB BD ∴==, 9090BCD B A a ∴∠=∠=︒-∠=︒-,故答案为:90a ︒-.【点评】本题考查的是直角三角形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键. 10.(2018秋•石景山区期末)如图,ACB ∆中,5AC =,12BC =,13AB =,点D 是AB 的中点,则CD 的长为132.【分析】由三角形ABC 的三边长,利用勾股定理的逆定理判断出三角形为直角三角形,且AB 为斜边,再由D 为斜边上的中点,得到CD 为斜边上的中线,利用直角三角形斜边上的中线等于斜边的一半,即可求出CD 的长. 【解答】解:13AB =,5AC =,12BC =,2213169AB ∴==,2225144169AC BC +=+=,即222AC BC AB +=, ABC ∴∆为以AB 为斜边的直角三角形,又D 为AB 的中点,即CD 为斜边上的中线, 则11322CD AB ==. 故答案为:132. 【点评】此题考查了勾股定理的逆定理,以及直角三角形斜边上的中线性质,熟练掌握定理及性质是解本题的关键. 11.(2019秋•昌平区校级期中)在Rt ABC ∆中,90ACB ∠=︒,如果斜边AB 上的中线4CD cm =,那么斜边AB = 8cm .【分析】根据直角三角形斜边上的中线等于斜边的一半,且已知中线CD 的长,则可直接得出斜边AB 的长度. 【解答】解:在Rt ABC ∆中,斜边AB 上的中线4CD cm =, 28AB CD cm ∴==.故答案为:8.【点评】本题考查了直角三角形的斜边上的中线的性质,属于基础知识的考查,比较简单.12.(2017春•西城区校级期中)在Rt ABC ∆中,90ACB ∠=︒,5AC =,12BC =,点D 是AB 的中点,则CD = 132. 【分析】利用勾股定理求出AB ,再利用直角三角形斜边中线的性质解决问题即可. 【解答】解:如图,在Rt ACB ∆中,90ACB ∠=︒,5AC =,12BC =,222251213AB AC BC ∴=+=+=,AD BD =,11322CD AB ∴==, 故答案为132. 【点评】本题考查直角三角形斜边中线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.13.(2016春•东城区校级期中)如图,Rt ABC ∆中,90C ∠=︒,D 为AB 中点,CE AB ⊥于E ,5CD =,6BC =,则AC = 8 ,CE = .【分析】在直角三角形ABC 中,由CD 为斜边上的中线,得到2AB CD =,求出AB 的长,利用勾股定理求出AC 的长,直角三角形ABC 面积可以由两直角边乘积的一半来求,也可以由斜边乘以斜边上的高来求,根据两直角边与斜边,求出CE 的长即可. 【解答】解:Rt ABC ∆中,90C ∠=︒,D 为AB 上的中点,12CD AB ∴=, 5CD =, 10AB ∴=,由勾股定理得:228AC AB BC =-=,1122ABC S AC BC AB CE ∆==,即AC BC AB CE =, 864.810AC BC CE AB ⨯∴===故答案为:8;4.8【点评】此题考查了勾股定理,直角三角形斜边上的中线,熟练掌握勾股定理是解本题的关键.三.解答题(共2小题)14.(2019•朝阳区模拟)如图,在Rt ABC ∆中,90BAC ∠=︒,AD 是BC 边上的中线,ED BC ⊥于D ,交BA 延长线于点E ,若35E ∠=︒,求BDA ∠的度数.【分析】根据直角三角形的性质得到DA DB =,根据三角形内角和定理计算即可. 【解答】解:35E ∠=︒,ED BC ⊥, 55B ∴∠=︒90BAC ∠=︒,AD 是BC 边上的中线,DA DB ∴=,55B DAB ∴∠=∠=︒,180555570BDA ∴∠=︒-︒-︒=︒.【点评】本题考查的是直角三角形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.15.(2019秋•平谷区期末)在平面直角坐标系xOy 中,有任意三角形,当这个三角形的一条边上的中线等于这条边的一半时,称这个三角形叫“和谐三角形”,这条边叫“和谐边”,这条中线的长度叫“和谐距离”.(1)已知(2,0)A ,(0,4)B ,(1,2)C ,(4,1)D ,这个点中,能与点O 组成“和谐三角形”的点是 A ,B ,“和谐距离”是 ;(2)连接BD ,点M ,N 是BD 上任意两个动点(点M ,N 不重合),点E 是平面内任意一点,EMN ∆是以MN 为“和谐边”的“和谐三角形”,求点E 的横坐标t 的取值范围;(3)已知O 的半径为2,点P 是O 上的一动点,点Q 是平面内任意一点,OPQ ∆是“和谐三角形”,且“和谐距离”是2,请描述出点Q 所在位置.【分析】(1)根据题意利用“和谐三角形”和“和谐距离”求解;(2)根据题意画出图形即可得到结论;(3)根据题意画出图形进行分析即可得到结论.【解答】解:(1)由题意得,当(2,0)A ,(0,4)B 与原点O 构成三角形时,满足圆周角定理,即点A 、B 能与点O 组成“和谐三角形”2AB ==,∴,故答案为:A ,B ;(2)根据题意作图如图1,以BD 为直径,线段BD 的中点为圆心,当点E 在如图的所示的位置时, 求得t 的值为:12t =-或92t =, ∴点E 的横坐标t 的取值范围为:1922t -;(3)如图3,当PQ 为“和谐边”时,点Q 在以点O 为圆心,当OQ 为“和谐边”时,点Q 在以点O 为圆心,4为半径的圆上.【点评】本题考查了直角三角形斜边上的中线,坐标与图形性质,正确的作出图形是解题的关键.。
冲刺2020年数学中考专题练习题:《直角三角形斜边上的中线》

冲刺2020年数学中考专题练习:《直角三角形斜边上的中线》一.选择题1.如图,在Rt△ABC中,CE是斜边AB上的中线,CD⊥AB,若CD=5,CE=6,则△ABC的面积是()A.24 B.25 C.30 D.362.在△ABC中,∠ACB=90°,∠ABC=60°,BD平分∠ABC,P点是BD的中点,若AD=6,则CP的长为()A.3 B.3.5 C.4 D.4.53.如图,△ABC中,AB=AC,AD⊥BC,垂足为D,DE∥AB,交AC于点E,ED=3,则AE的长为()A.1.5 B.2 C. 3 D.3.54.如图,∠MON=90°,已知△ABC中,AC=BC=AB=6,△ABC的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的距离为整数的点有()个.A.5 B.6 C.7 D.85.到直角三角形的三个顶点距离相等的点()A.是该三角形三个内角平分线的交点B.是斜边上的中点C.在直角三角形的外部D.在直角三角形的内部6.如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于点G,CD=AE.若BD=8,CD=5,则△DCG的面积是()A.B.C.D.7.如图,已知A(3,6)、B(0,n)(0<n≤6),作AC⊥AB,交x轴于点C,M为BC 的中点,若P(,0),则PM的最小值为()A.3 B.C.D.8.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,CE是AB边上的中线,AD=3,CE=5,则CD等于()A.3 B.4 C.D.9.已知,在Rt△ABC中,∠ACB=90°,点D,E分别是AB,BC的中点,延长AC到F,使得CF=AC,连接EF.若EF=4,则AB的长为()A.8 B.C.4 D.10.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为()A.B.C.3 D.4二.填空题11.如图,在△ABC中,CD⊥AB于点D,BE⊥AC于点E,F为BC的中点,DE=5,BC =8,则△DEF的周长是.12.已知:如图,四边形ABCD中,∠ABC=∠ADC=90°,AC与BD相交于点O,E、F分别是AC、BD的中点.则∠EFO=.13.如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,CE是AB边上的中线,若AD=3,CE=5,则CD等于.14.如图,△ABC中,AB=AC,以AC为斜边作Rt△ADC,使∠ADC=90°,∠CAD =∠CAB=28°,E、F分别是BC、AC的中点,则∠EDF=.15.如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC 至F,使CF=BC,若EF=13,则线段AB的长为.16.如图,DE是Rt△ABD的斜边AB上的中线,AB=12,在ED上找一点F,使得DF=2,连结AF并延长至C,使得AF=CF,连结CD,CB,则CB长为.三.解答题17.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD 于点F,交CB于点E,且∠EAB=∠DCB.(1)求∠B的度数:(2)求证:BC=3CE.18.在Rt△ABC中,∠ABC=90°,BD为∠ABC的角平分线,F为AC的中点,AE∥BC 交BD的延长线于点E,其中∠FBC=2∠FBD.(1)求∠EDC的度数.(2)求证:BF=AE.19.如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,CD=AE.(1)求证:CG=EG.(2)已知BC=13,CD=5,连结ED,求△EDC的面积.20.如图1,已知锐角△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.(1)求证:MN⊥DE.(2)连结DM,ME,猜想∠A与∠DME之间的关系,并证明猜想.(3)当∠A变为钝角时,如图2,上述(1)(2)中的结论是否都成立,若结论成立,直接回答,不需证明;若结论不成立,说明理由.参考答案一.选择题1.解:∵CE是斜边AB上的中线,∴AB=2CE=2×6=12,∴S△ABC=×CD×AB=×5×12=30,故选:C.2.解:∵∠ACB=90°,∠ABC=60°,∴∠A=30°,∵BD平分∠ABC,∴∠CBD=∠DBA=30°,∴BD=AD,∵AD=6,∴BD=6,∵P点是BD的中点,∴CP=BD=3.故选:A.3.解:∵AB=AC,AD⊥BC,∴BD=CD,∵DE∥AB,∴AE=CE,∴DE=AE=AB=3,故选:C.4.解:如图,取AB的中点D,连接CD.∵AC=BC=AB=6.∵点D是AB边中点,∴BD=AB=3,∴CD==3;连接OD,OC,有OC≤OD+DC,当O、D、C共线时,OC有最大值,最大值是OD+CD,又∵△AOB为直角三角形,D为斜边AB的中点,∴OD=AB=3,∴3﹣3≤OD+CD≤3+3.∴点C到点O的距离为整数的点有5个,故选:A.5.解:∵在直角三角形中,斜边上的中线等于斜边的一半,∴直角三角形斜边的中点到直角三角形的三个顶点距离相等的点,故选:B.6.解:连接DE,∵AD是BC边上的高线,CE是AB边上的中线,∴AE=ED=BE,∵CD=AE.∴ED=CD,∵DG⊥CE于点G,∴EG=GC,∵BD=8,CD=5,∴DE=5,∴AB=10,∴AD=6,过E作EF⊥BC于F,∵△ABC的面积=,∴△BEC的面积=,∵△BED的面积=,∴△EDC的面积=﹣12=,∴△DGC的面积=,故选:D.7.解:如图,作AH⊥y轴于H,CE⊥AH于E,作MN⊥OC于N.则四边形CEHO是矩形,OH=CE=6,∵∠BAC=∠AHB=∠A EC=90°,∴∠ABH+∠HAB=90°,∠HAB+∠EAC=90°,∴∠ABH=∠EAC,∴△AHB∽△CEA,∴=,∴=,∴AE=2BH,设BH=x,则AE=2x,∴OC=HE=3+2x,OB=6﹣x,∴B(0,6﹣x),C(3+2x,0)∵BM=CM,∴M(,),∵P(,0),∴PN=ON﹣OP=﹣=x,∴PM2=PN2+MN2=x2+()2=x2﹣3x+9=(x﹣)2+,∴x=时,PM2有最小值,最小值为,∴PM的最小值为=.故选:D.8.解:∵在Rt△ABC中,∠ACB=90°,CE为AB边上的中线,CE=5,∴AE=CE=5,∵AD=3,∴DE=2,∵CD为AB边上的高,∴在Rt△CDE中,CD==,故选:C.9.解:连接CD,∵点D,E分别是AB,BC的中点,∴DE∥AC,DE=AC.∵延长AC到F,使得CF=AC,∴DE∥CF且DE=CF,∴四边形CDEF是平行四边形.∴CD=EF=4.∵∠ACB=90°,CD为斜边AB中线,∴AB=2CD=8.故选:A.10.解:∵四边形ABCD是正方形,∴∠D CE=90°,OD=OB,∵DF=FE,∴CF=FE=FD,∵EC+EF+CF=18,EC=5,∴EF+FC=13,∴DC==12,∴BC=CD=12,∴BE=BC﹣EC=7,∵OD=OB,DF=FE,∴OF=BE=,故选:A.二.填空题(共6小题)11.解:∵CD⊥AB,F为BC的中点,∴DF=BC=×8=4,∵BE⊥AC,F为BC的中点,∴EF=BC=×8=4,∴△DEF的周长=DE+EF+DF=5+4+4=13.故答案为:13.12.解:连接EB、ED,∵∠ABC=90°,E是AC的中点,∴BE=AC,同理,DE=AC,∴EB=ED,又F是BD的中点,∴EF⊥BD,∴∠EFO=90°,故答案为:90°.13.解:∵在Rt△ABC中,∠ACB=90°,CE为AB边上的中线,CE=5,∴AE=CE=5,∵AD=3,∴DE=2,∵CD为AB边上的高,∴在Rt△CDE中,CD=,故答案为:14.解:∵∠ADC=90°,F是AC的中点,∴DF=AC=AF,∴∠FDA=∠CAD=28°,∴∠DFC=∠FDA+∠CAD=56°,∵E、F分别是BC、AC的中点,∴EF=AB,EF∥AB,∴∠EFC=∠CAB=28°,∴∠EFD=56°+28°=84°,∵AB=AC,∴FE=FD,∴∠EDF=∠DEF=×(180°﹣84°)=48°,故答案为:48°.15.解:∵点D,E分别是边AB,AC的中点,∴DE=BC,DE∥BC,∵CF=BC,∴DE=CF,又DE∥CF,∴四边形DEFC为平行四边形,∴CD=EF=13,∵∠ACB=90°,点D是边AB的中点,∴AB=2CD=26,故答案为:26.16.解:∵DE是Rt△ABD的斜边AB上的中线,∴DE=AB=6,∴EF=DE﹣DF=4,∵AF=CF,AE=EB,∴BC=2EF=8,故答案为:8.三.解答题(共4小题)17.解:(1)∵AE⊥CD,∴∠AFC=∠ACB=90°,∴∠CAF+∠ACF=∠ACF+∠ECF=90°,∴∠ECF=∠CAF,∵∠EAD=∠DCB,∴∠CAD=2∠DCB,∵CD是斜边AB上的中线,∴CD=BD,∴∠B=∠DCB,∴∠CAB=2∠B,∵∠B+∠CAB=90°,∴∠B=30°;(2)∵∠B=∠BAE=∠CAE=30°,∴AE=BE,CE=AE,∴BC=3CE.18.解:(1)∵∠ABC=90°,BD为∠ABC的角平分线,∴∠ABD=∠DBC=45°,∵∠FBC=2∠FBD.∴∠FBD=15°,∠FBC=30°,∵∠ABC=90°,点F是AC中点,∴AF=BF=CF,∴∠C=∠FBC=30°,∴∠EDC=∠C+∠DBC=75°;(2)∵∠C=30°,∠ABC=90°,∴AC=2AB,∴AB=AF=BF,∵AE∥BC,∴∠E=∠DBC=45°=∠ABD,∴AB=AE,∴AE=BF.19.(1)证明:连接DE,在Rt△ADB中,点E是AB的中点,∴DE=AB=AE,∵CD=AE,∴DE=DC,又DG⊥CE,∴CG=E G.(2)解:作EF⊥BC于F,∵BC=13,CD=5,∴BD=13﹣5=8,∵DE=BE,EF⊥BC,∴DF=BF=4,∴EF===3,∴△EDC的面积=×CD×EF=×5×3=7.5.20.(1)证明:如图,连接DM,ME,∵CD、BE分别是AB、AC边上的高,M是BC的中点,∴DM=BC,ME=BC,∴DM=ME,又∵N为DE中点,∴MN⊥DE;(2)在△ABC中,∠ABC+∠ACB=180°﹣∠A,∵DM=ME=BM=MC,∴∠BMD+∠CME=(180°﹣2∠ABC)+(180°﹣2∠ACB),=360°﹣2(∠ABC+∠ACB),=360°﹣2(180°﹣∠A),=2∠A,∴∠DME=180°﹣2∠A;(3)结论(1)成立,结论(2)不成立,理由如下:在△ABC中,∠ABC+∠ACB=180°﹣∠A,∵DM=ME=BM=MC,∴∠BME+∠CMD=2∠ACB+2∠ABC,=2(180°﹣∠A),=360°﹣2∠A,∴∠DME=180°﹣(360°﹣2∠A),=2∠A﹣180°.。
专题13 斜边上的中线问题(解析版)-2021年中考数学二轮复习经典问题专题训练

专题13 斜边上的中线问题【规律总结】直角三角形中遇到斜边上的中点,常联想“斜边上的中线等于斜边的一半”【典例分析】例1.(2021·上海九年级专题练习)一副三角板如图摆放,点F 是45角三角板ABC 的斜边的中点,4AC .当30角三角DEF 的直角顶点绕着点F 旋转时,直角边DF EF ,分别与,AC BC 相交于点.M N ,则CMFN 的面积为____________.【答案】4【分析】连结CF ,证明CFM BFN =,根据12BFC ACB CMFN S SS ==四边形即可求解. 【详解】解:连结CF ,如图,点F 是45角三角板ABC 的斜边的中点,CF BF CF ∴=,平分,,45ACB CF AB B ∠⊥∠=︒,45,2345ACF ∴∠=︒∠+∠=︒1290∠+∠=︒,13∴∠=∠,在CFM △和BFN 中,13MCF B CF BF∠=∠⎧⎪=⎨⎪∠=∠⎩()CFM BFN ASA ∴=,CFM BFNS S ∴=,111444222BFC ACB CMFN S SS ∴===⨯⨯⨯=四边形. 【点睛】 此题考查的知识点有等腰直角三角形,全等三角形的判定与性质等知识点,综合性强,难度较大,是一道难题.例2.(2020·湖北恩施土家族苗族自治州·九年级期中)如图,在等腰直角三角形ABC 中,90C ∠=︒,AC a =,点E 为边AC 上任意一点,点D 为AB 的中点,过点D 作DF DE ⊥交BC 于点F .求证:CE CF +为定值.【答案】证明见解析【分析】连接CD ,证明△CDE△△BDF ,得CE=BF ,进一步证明CE+CF=BC=AC a =,从而得到结论.【详解】 证明:连接CD ,如图,△△ABC 是等腰直角三角形,且D 为AB 的中点,△CD△AB ,CD 平分△ACB ,AD=BD=CD△△DCA=△DCB=△DBC=45°又DE△DF△△EDC+△FDC=90°而△FDC+△FDB=90°△△EDC=△FDB在△CDE 和△BDF 中,DCE DBF CD CDEDC BDF ∠=∠⎧⎪=⎨⎪∠=∠⎩△△CDE△△BDF△CE=BF△BC=AC=a△CE+CF=BE+CF=BC=AC=a ,故:CE CF +为定值.【点睛】此题主要考查了全等三角形的判定与性质以及等腰直角三角形的性质,证明CE=BF 是解答此题的关键.【真题演练】一、填空题1.(2020·哈尔滨市萧红中学八年级月考)如图,在ABC 中,∠B=60°,CD 为AB 边上的高,E 为AC 边的中点,点 F 在BC 边上,∠EDF=60°,若 BF=3,CF=5,则AC 边的长为 .【答案】【分析】如图(见解析),先根据直角三角形的性质、勾股定理得出,4D B F D ==,再根据等边三角形的判定与性质得出4,60DH BDH =∠=︒,然后根据三角形的中位线定理、平行线的性质得出60EHD BDH ∠=∠=︒,从而可得EHD B ∠=∠,BDF HDE ∠=∠,最后根据三角形全等的判定定理与性质得出DE DF ==据此根据直角三角形斜边上的中线等于斜边的一半即可得.【详解】如图,过点D 作DG BC ⊥于点G3,5BF CF ==8BC BF CF ∴=+=在Rt BCD 中,60B ∠=︒,9030BCD B ∠=︒-∠=︒142BD BC ∴== 在Rt BDG 中,60B ∠=︒,9030BDG B ∠=︒-∠=︒12,2BG BD DG ∴====1GF BF BG ∴=-=,DF =取BC 的中点H ,连接DH 、EH142DH BH BC BD ∴==== BDH ∴是等边三角形60BDH ∴∠=︒点E 是AC 边的中点∴EH 是ABC 的中位线//EH AB ∴60EHD BDH ∴∠=∠=︒60EHD B ∴∠=∠=︒又60BDF FDH BDH ∠+∠=∠=︒,60HDE FDH EDF ∠+∠=∠=︒BDF HDE ∴∠=∠在HDE 和BDF 中,EHD B DH DBHDE BDF ∠=∠⎧⎪=⎨⎪∠=∠⎩()HDE BDF ASA ∴≅DE DF ∴==则在Rt ACD △中,12DE AC =,即2AC DE ==故答案为:【点睛】本题考查了直角三角形的性质、等边三角形的判定与性质、三角形全等的判定定理与性质、三角形的中位线定理等知识点,通过作辅助线,构造等边三角形和全等三角形是解题关键.二、解答题2.(2020·庆云县第二中学八年级期中)已知:在ABC 中,AC=BC ,∠ACB=90°,点D 是AB 的中点,点E 是AB 边上一点.(1)直线BF 垂直于CE 于点F ,交CD 于点G (如图1),求证:AE=CG ;(2)直线AH 垂直于CE ,垂足为H ,交CD 的延长线于点M (如图2),求证:BCE CAM ≌.【答案】(1)证明见解析;(2)证明见解析.【分析】(1)运用等腰直角三角形性质,三线合一,可以得到△AEC 和△CGB 一组对应边、一组对应角相等,AC BC =,CAE BCG ∠=∠;然后利用同角的余角相等,证得ACE CBG ∠=∠;两角及其夹边对应相等()ASA 则两三角形全等.(2)运用等腰直角三角形性质,三线合一,可以得到△BCE 和△CAM 一组对应边、一组对应角相等,AC BC =,ACM CBE ∠=∠;然后利用同角的余角相等,证得BEC CMA ∠=∠;两角及其中一角的对边对应相等()AAS 则两三角形全等.【详解】(1)证明:△点D 是AB 中点,AC=BC ,△ACB=90°,△CD△AB ,△ACD=△BCD=45°,△△CAD=△CBD=45°,△△CAE=△BCG ,又△BF△CE ,△△CBG+△BCF=90°,又△△ACE+△BCF=90°,△△ACE=△CBG ,在△AEC 和△CGB 中,CAE BCG AC BCACE CBG ∠=∠⎧⎪=⎨⎪∠=∠⎩△△AEC△△CGB (ASA ),△AE=CG ,(2)证明:△CH△HM ,CD△ED ,△△CMA+△MCH=90°,△BEC+△MCH=90°,△△CMA=△BEC ,又△△ACM=△CBE=45°,在△BCE 和△CAM 中,BEC CMA ACM CBE BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩△△BCE△△CAM (AAS ).【点睛】本题考查全等三角形判定定理,从题中找到对应边、角的信息,灵活运用三角形判定定理是解题关键.3.(2020·张家港市梁丰初级中学八年级期中)已知,∠ABC中,AC=BC,∠ACB=90°,CD为边AB上的中线,若E是线段CA上任意一点,DF∠DE,交直线BC于F点.G为EF的中点,连接CG并延长交直线AB于点H.(1)试说明:①AE=CF;②CG=GD;(2)若AE=6,CH=10,求边AC的长.【答案】(1)理由见详解;(2)AC=14【分析】(1)①由题意易得AD=DC=DB,△A=△B=45°,CD△AB,进而可证△ADE△△CDF,然后根据全等三角形的性质可得;②由直角三角形斜边中线定理可得11,22CG EF DG EF==,进而问题得证;(2)由(1)可得AE=CF=6,由题意易得12DG CH=,则有EF=CH=10,然后根据勾股定理可求解.【详解】解:(1)①AE=CF,理由如下:△AC=BC,△ACB=90°,CD为边AB上的中线,△AD=DC=DB,△A=△B=45°,CD△AB,△△A=△BCD=45°,△DF△DE,△△EDC+△CDF=90°,又△△ADE+△EDC=90°,△△ADE=△CDF,△△ADE△△CDF(ASA),△AE=CF,②CG=GD,理由如下:△△ACB=90°,△EDF=90°,EG=GF,△11,22CG EF DG EF==,△CG=GD;(2)由(1)得:AE=CF=6,CG=GD,12DG EF=,△△GCD=△GDC,△△GCD+△CHD=90°,△GDC+△GDH=90°,△△CHD=△GDH,△GH=GD,△12DG CH=,△CH=10,△CH=EF=10,在Rt△CEF 中,222+=CF CE EF ,即222610CE +=,解得:CE=8,△AC=AE+CE=14.【点睛】本题主要考查等腰三角形的性质与判定、勾股定理及直角三角形斜边中线定理,熟练掌握等腰三角形的性质与判定、勾股定理及直角三角形斜边中线定理是解题的关键.4.(2019·陇东学院附属中学八年级期末)如图在Rt ABC △中,AB AC =,90BAC ∠=︒,O 为BC 的中点.(1)写出点O 到ABC 的三个顶点A 、B 、C 的距离的大小关系.(2)如果点M 、N 分别在线段AB 、AC 上移动,移动中保持AN BM =,请判断OMN 的形状,并证明你的结论.(3)当点M 、N 分别在AB 、AC 上运动时,四边形AMON 的面积是否发生变化?说明理由.【答案】(1)OA OB OC ==;(2)OMN 是等腰直角三角形,证明见解析;(3)四边形AMON 的面积不变,理由见解析【分析】(1)连接OA ,由O 为BC 的中点可得OC OB =,由直角三角形斜边上的中线的性质可得12OA BC =,即可得OA OB OC ==. (2)由(1)不难证明45CAO B ∠=∠=︒,结合已知条件进而证明OAN △OBM ,即可得OM ON =,NOA MOB ∠=∠,即90NOM AOB ∠=∠=︒,所以OMN 是等腰直角三角形.(3)由(2)可得OAN S =OBM S ,进而将四边形AMON 的面积转化为AOB 的面积,AOB 的面积保持不变,故四边形AMON 的面积保持不变.【详解】(1)连接OA ,Rt ABC △中,O 为BC 的中点,∴12OA BC =,OC OB =, ∴122OA OB OB =⨯⨯=, ∴OA OB OC ==.(2)OMN 是等腰直角三角形,证明如下:AB AC =,O 为BC 的中点,∴AO BC ⊥,∴90AOB ∠=︒,OA OB OC ==,∴45CAO B ∠=∠=︒,在OAN 与OBM 中,OA OB CAO B AN BM =⎧⎪∠=∠⎨⎪=⎩,∴OAN △OBM ,∴OM ON =,NOA MOB ∠=∠,∴90NOM AOB ∠=∠=︒,∴OMN 是等腰直角三角形.(3)四边形AMON 的面积保持不变,理由如下:由(2)可得: OAN S =OBM S , ∴OAN AOM OBM AOM AOB AMON S S S S S S =+=+=四边形. AOB 的面积保持不变∴四边形AMON 的面积保持不变.【点睛】本题主要考查直接三角形斜边上中线的性质以及全等三角形的判定与性质,掌握全等三角形的判定与性质定理并灵活运用是解题关键.5.(2020·乌兰察布市·内蒙古凉城县宏远中学八年级月考)已知:三角形ABC 中,∠A =90°,AB =AC ,D 为BC 边的中点,(1)如图①,E ,F 分别是AB ,AC 上的点,且BE =AF ,求证:∠DEF 为等腰直角三角形.(2)如图②,若E ,F 分别为AB ,CA 延长线上的点,仍有BE =AF ,其他条件不变,那么,∠DEF 是否仍为等腰直角三角形?证明你的结论.【答案】(1)见解析;(2)△DEF为等腰直角三角,证明见解析【分析】(1)先连接AD,构造全等三角形:△BED和△AFD.AD是等腰直角三角形ABC底边上的中线,所以有△CAD=△BAD=45°,AD=BD=CD,而△B=△C=45°,所以△B=△DAF,再加上BE=AF,AD=BD,可证出:△BED△△AFD,从而得出DE=DF,△BDE=△ADF,从而得出△EDF=90°,即△DEF是等腰直角三角形;(2)还是证明:△BED△△AFD,主要证△DAF=△DBE(△DBE=180°-45°=135°,△DAF=90°+45°=135°),再结合两组对边对应相等,所以两个三角形全等.【详解】(1)证明:连接AD,△AB=AC,△BAC=90°,D为BC的中点,△AD△BC,BD=AD.△△B=△DAC=45° 又BE=AF,△△BDE△△ADF(SAS).△ED=FD,△BDE=△ADF.△△EDF=△EDA+△ADF=△EDA+△BDE=△BDA=90°.△△DEF为等腰直角三角形.(2)△DEF为等腰直角三角形.证明:若E,F分别是AB,CA延长线上的点,如图所示:连接AD,△AB=AC,△△ABC为等腰三角形,△△BAC=90°,D为BC的中点,△AD=BD,AD△BC(三线合一),△△DAC=△ABD=45°.△△DAF=△DBE=135°.又AF=BE,△△DAF△△DBE(SAS).△FD=ED,△FDA=△EDB.△△EDF=△EDB+△FDB=△FDA+△FDB=△ADB=90°.△△DEF仍为等腰直角三角形.【点睛】本题利用了等腰直角三角形底边上的中线平分顶角,并且等于底边的一半,还利用了全等三角形的判定和性质,及等腰直角三角形的判定.6.(2019·全国九年级专题练习)如图所示,E,F分别是正方形ABCD的边AD,CD上AB=,连DH.求线段DH长度的最小的两个动点,且AE DF=,BE交AF于点H,2值.【答案】DH1【解析】【分析】根据正方形性质可得AB=DA ,△BAD=△ADF=90°,又根据AE=DF ,利用SAS 可证得△ABE△△DAF ,于是△ABE=△DAF ;由于△DAF+△BAH=△ABE+△BAH=90°,从而△AHB=90°,取AB 的中点O ,连接OH 、OD ,则OH=12AB=1,在Rt△AOD 中,根据勾股定理计算出OD 的值;根据三角形的三边关系,可得OH+DH >OD ,于是当O 、D 、H 三点共线时,DH 的长度最小为OD -OH ,据此解答.【详解】解:△四边形ABCD 是正方形,△AB=DA ,△BAD=△ADF=90°,又△AE=DF ,△△ABE△△DAF ,△△ABE=△DAF.△△DAF+△BAH=△ABE+△BAH=90°,△△AHB=90°,取AB 的中点O ,连OH 、OD ,△112OH AB ==,OD ==OHD ∆中有DH OD OH >-,即1DH >.故O、H、D三点共线时DH最小,△DH1.【点睛】本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边的中线等于斜边的一半,勾股定理及三角形三条边的关系,确定出点H的位置是解答本题的关键.。
《直角三角形边上的中线等于斜边的一半》经典练习

《直角三角形边上的中线等于斜边的一半》1、如图所示,BD、CE是三角形ABC的两条高,M、N分别是BC、DE的中点求证:MN⊥DEM C2、如图,四边形ABCD中,∠DAB=∠DCB=90o,点M、N分别是BD、AC的中点。
MN、AC的位置关系如何?证明你的猜想。
DAB3.如图,在△ABC中,AD是高,CE是中线,DC=BE,DF⊥CE,F为垂足,求证:(1)F是CE的中点;(2)∠B=2∠BCE.4、如图△ABC 中,∠B=2∠C,AH 为高,M 是BC 边的中点.求证:AB=2HMMABC5.如图,在四边形ABCD 中,CD ∥AB ,对角线AC 、BD 相交于点O ,AB=CD ,60ACD ∠=︒,点S 、P 、Q 分别是DO 、AO 、BC 的中点.求证:△SPQ 是等边三角形。
P O AB CD 图6-1SQ6、如图甲,在正方形ABCD 和正方形CGEF (CG >BC )中,点B 、C 、G 在同一直线上,M 是AE 的中点,(1)探究线段MD 、MF 的位置及数量关系,并证明;(2)将图甲中的正方形CGEF 绕点C 顺时针旋转,使正方形CGEF 的对角线CE 恰好与正方形ABCD 的边BC 在同一条直线上,原问题中的其他条件不变。
(1)中得到的两个结论是否发生变化?写出你的猜想并加以证明图乙 图甲B A EF7.已知:△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°,点M是CE的中点,连接BM.(1)如图①,点D在AB上,连接DM,并延长DM交BC于点N,可探究得出BD与BM的数量关系为;(2)如图②,点D不在AB上,(1)中的结论还成立吗?如果成立,请证明;如果不成立,说明理由.图①图②A B C D EFM 8.在正方形ABCD 中,点E 、F 分别为BC 和AB 的中点,DE 与CF 交于点M ,连接AM 。
求证:AM=AD。
中考经典题型--“直角三角形斜边上的中线”的性质及其应用
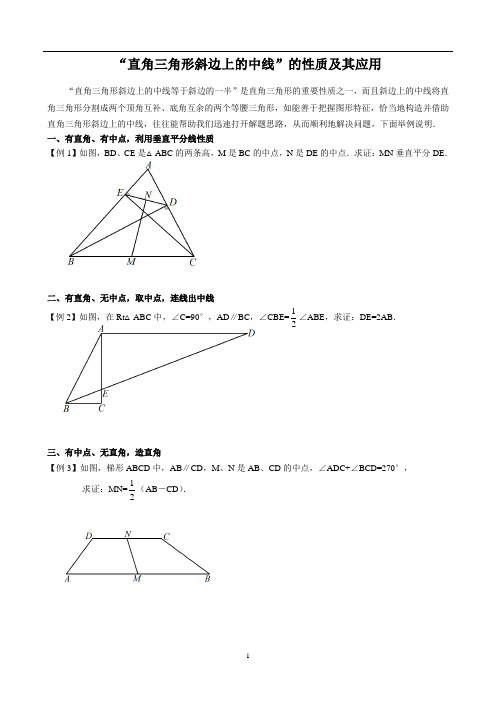
“直角三角形斜边上的中线”的性质及其应用 “直角三角形斜边上的中线等于斜边的一半”是直角三角形的重要性质之一,而且斜边上的中线将直角三角形分割成两个顶角互补、底角互余的两个等腰三角形,如能善于把握图形特征,恰当地构造并借助直角三角形斜边上的中线,往往能帮助我们迅速打开解题思路,从而顺利地解决问题,下面举例说明.一、有直角、有中点,利用垂直平分线性质【例1】如图,BD 、CE 是△ABC 的两条高,M 是BC 的中点,N 是DE 的中点.求证:MN 垂直平分DE .二、有直角、无中点,取中点,连线出中线【例2】如图,在Rt △ABC 中,∠C=90°,AD ∥BC ,∠CBE=21∠ABE ,求证:DE=2AB .三、有中点、无直角,造直角【例3】如图,梯形ABCD 中,AB ∥CD ,M 、N 是AB 、CD 的中点,∠ADC+∠BCD=270°,求证:MN=21(AB -CD ).四、逆用性质解题 【例4】如图,延长矩形ABCD 的边CB 至E ,使CE=CA ,P 是AE 的中点.求证:BP ⊥DP .【习题练习】1、如图,△ABC 中,AB=AC ,∠ABD=∠CBD ,BD ⊥DE 于D ,DE 交BC 于E ,求证:CD=21BE .2、如图,△ABC 中,∠B=2∠C ,AD ⊥BC 于D ,M 是BC 的中点,求证:AB=2DM .3、如图,在四边形ABCD 中,∠DAB=∠DCB=90°,点M 、N 分别是BD 、AC 的中点.确定MN 、AC 的位置关系.直角三角形斜边上中线性质的应用 一、直角三角形斜边上中线的性质 1、性质:直角三角形斜边上的中线等于斜边的一半.如图,在Rt △BAC 中,∠BAC=90°,D 为BC 的中点,则BC 21AD =. 2、性质的拓展:如图:因为D 为BC 中点,所以BC 21DC BD ==, 所以AD=BD=DC=BC 21, 所以∠1=∠2,∠3=∠4,因此∠ADB=2∠1=2∠2,∠ADC=2∠3=2∠4.因而可得如下几个结论:①直角三角形斜边上的中线将直角三角形分成两个等腰三角形;②分成的两个等腰三角形的腰相等,两个顶角互补、底角互余,并且其中一个等腰三角形的顶角等于另一个等腰三角形底角的2倍.二、性质的应用1、21倍关系求值 例1、如图,CD 是Rt △ABC 斜边AB 上的中线,若CD=4,则AB= .2、证明线段相等例2、如图,在△ABC 中,∠BAC=90°,延长BA 到D 点,使AB 21AD =,点E 、F 分别为边BC 、AC 的中点.(1)求证:DF=BE ;(2)过点A 作AG ∥BC ,交DF 于G .求证:AG=DG .3、证明角相等及角的倍分关系例3、已知,如图,在△ABC中,∠BAC 90°,BD、CE分别为AC、AB上的高,F为BC的中点,求证:∠FED=∠FDE.例4、已知:如图,在△ABC中,AD是高,CE是中线。
八年级数学常考点精练(苏科版):专题16 直角三角形斜边上的中线(解析版)

专题16直角三角形斜边上的中线知识点一直角三角形斜边上的中线性质1.直角三角形斜边上的中线等于斜边的_____.【答案】一半【解析】【详解】试题解析:根据在直角三角形中,斜边上的中线等于斜边的一半得解.故答案为一半.2.Rt△ABC中,∠C=90°,D是AB的中点,若AB=10,则CD的长等于_____.【答案】5【解析】【分析】根据直角三角形斜边上的中线等于斜边的一半即可求解.【详解】解:∵Rt△ABC中,∠ACB=90°,D是AB的中点,∴CD=12AB,∵AB=10,∴CD=12×10=5.故答案为5.【点睛】本题考查了直角三角形斜边上的中线的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.3.如图,在Rt ABC△中,斜边AB上的中线5CD ,则AB ________.【答案】10【解析】【分析】根据直角三角形斜边上中线性质得出AB =2CD ,代入求出即可.【详解】解:∵CD 是直角三角形ABC 斜边AB 上的中线,CD =5,∴AB =2CD =10,故答案为:10.【点睛】本题考查了直角三角形斜边上中线性质的应用,注意:直角三角形斜边上的中线等于斜边的一半.4.如图, ABC 中,90ACB ,CD 是AB 边上的中线,且12CD AB ,则AB 的长为______.【答案】8【解析】【分析】根据在直角三角形中,斜边上的中线等于斜边的一半解答.【详解】解:∵∠ACB =90°,D 是AB 边的中点,12CD AB ,∵12CD AB 8AB 故答案为:8.【点睛】本题考查的是直角三角形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.5.若直角三角形斜边上的高是4cm ,斜边上的中线是5m ,则这个直角三角形的面积是_____.【答案】20m 2【解析】【分析】根据直角三角形斜边上的中线等于斜边的一半求出斜边的长,再根据三角形的面积公式列式计算即可得解.【详解】解:∵直角三角形斜边上的中线长是5m∴斜边长为10m∵直角三角形斜边上的高是4m ∴这个直角三角形的面积=12×10×4=20m 2故答案为20m 2【点睛】本题考查直角三角形斜边上中线的性质,熟记直角三角形斜边上的中线等于斜边的一半是解题的关键.6.如图,在Rt ABC 中,90ACB ,点D 是AC 上一点,连接BD ,P 点是BD 的中点,若D A BA ,8AD ,则CP 的长为().A .8B .4C .16D .6【答案】B【解析】【分析】由题意推出BD =AD ,然后在Rt △BCD 中,CP =12BD ,即可推出CP 的长度.【详解】∵D A BA ,∴BD =AD=8,∵P 点是BD 的中点,90ACB∴CP =12BD =4,故选:B .【点睛】本题主要考查等腰三角形的判定和性质、直角三角形斜边上的中线的性质,关键在于根据已知推出BD =AD ,求出BD 的长度.7.如图,AD 是ABC 的角平分线,点E 为AC 的中点,连结DE .若10AB AC ,8BC ,则CDE △的周长为()A .20B .12C .14D .13【答案】C【解析】【分析】根据等腰三角形三线合一的性质可得AD ⊥BC ,CD=BD ,再根据直角三角形斜边上的中线等于斜边的一半可得DE=CE=12AC ,然后根据三角形的周长公式列式计算即可得解.【详解】解:∵AB=AC ,AD 平分∠BAC ,BC=8,∴AD ⊥BC ,CD=BD=12BC=4,∵点E 为AC 的中点,∴DE=CE=12AC=5,∴△CDE 的周长=CD+DE+CE=4+5+5=14.故选:C .【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,熟记性质并准确识图是解题的关键.知识点二斜边上中线分割直角三角形成两个等腰三角形8.如图,在Rt △ABC 中,CD 是斜边AB 上的中线,若∠A =26°,则∠BDC 的度数是()A .26°B .38°C .42°D .52°【答案】D【解析】【分析】根据直角三角形斜边上中线定理得出CD=AD,求出∠DCA=∠A,根据三角形的外角性质求出求出即可.【详解】解:∵∠ACB=90 ,CD是斜边AB上的中线,∴BD=CD=AD,∴∠A=∠DCA=26 ,∴∠BDC=∠A+∠DCA=26 +26 =52 .故选:D.【点睛】本题考查了对三角形的外角性质,直角三角形斜边上的中线性质,等腰三角形性质等知识点的理解和运用,能求出BD=CD=AD和∠DCA的度数是解此题的关键.9.如图,在△ABC中,∠ACB=90°,∠B=40°,D为线段AB的中点,则∠ACD=_____.【答案】50°【解析】【分析】由“直角三角形的两个锐角互余”得到∠A=50°,根据“直角三角形斜边上的中线等于斜边的一半”得到CD=AD,则等边对等角,即∠ACD=∠A=50°.【详解】解:如图,∵在△ABC中,∠ACB=90°,∠B=40°,∴∠A=50°.∵D为线段AB的中点,∴CD=AD,∴∠ACD=∠A=50°.故答案是:50°.【点睛】本题考查了直角三角形的性质.在直角三角形中,斜边上的中线等于斜边的一半.10.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若BC=BD,则∠A=_____度.【答案】30【解析】【分析】根据直角三角形斜边上的中线等于斜边的一半可得CD=BD,再由BC=BD,可得CD=BC=BD,可得△BCD是等边三角形,再根据等边三角形的性质即可求解.【详解】解:∵在Rt△ABC中,∠ACB=90°,D是AB的中点,∴CD=BD,∵BC=BD,∴CD=BC=BD,∴△BCD是等边三角形,∴∠B=60°,∴∠A=30°.故答案为30.【点睛】考查了直角三角形的性质,等边三角形的判定与性质,关键是证明△BCD是等边三角形.11.如图,△ABC中,若∠ACB=90°,∠B=56°,D是AB的中点,则∠ACD=_____°.【答案】34°.【解析】【分析】由∠ACB=90°,D是AB的中点,可得出CD=BD=AD,结合∠B的度数可得出∠BCD的度数,再由∠ACD和∠BCD互余可求出∠ACD的度数.【详解】解:∵∠ACB=90°,D是AB的中点,∴CD=BD=AD=12AB,∴∠BCD=∠B=56°,∴∠ACD=∠ACB﹣∠BCD=90°﹣56°=34°.故答案为34°.【点睛】本题考查了直角三角形斜边上的中线以及等腰三角形的性质,牢记“在直角三角形中,斜边上的中线等于斜边的一半”是解题的关键.12.如图,在Rt△ABC中,∠ACB=90°,将边BC沿斜边上的中线CD折叠到CB′,若∠B=50°,则∠ACB′=______.【答案】10°【解析】【分析】根据三角形内角和定理求出∠A的度数,根据直角三角形的性质分别求出∠BCD、∠DCA的度数,根据翻折变换的性质求出∠B′CD的度数,计算即可.【详解】∵∠ACB=90 ,∠B=50 ,∴∠A=40 ,∵∠ACB=90 ,CD是斜边上的中线,∴CD=BD,CD=AD,∴∠BCD=∠B=50 ,∠DCA=∠A=40 ,由翻折变换的性质可知,∠B′CD=∠BCD=50 ,∴∠ACB′=∠B′CD−∠DCA=10 ,故答案为10 .【点睛】本题考查直角三角形斜边上的中线.知识点三斜边上的中线应用13.如图,公路AC ,BC 互相垂直,公路AB 的中点M 与点C 被湖隔开,若测得AB 的长为5km ,则M ,C 两点间的距离为()A .2kmB .2.5kmC .3kmD .4km【答案】B【解析】【分析】根据直角三角形斜边上的中线等于斜边的一半直接可以得出答案.【详解】∵AC ,BC 互相垂直,ABC 是直角三角形,M ∵是AB 的中点, 1 2.52CM AB ,故选B .【点睛】本题考查了直角三角形斜边上的中线性质,能根据直角三角形斜边上的中线性质得出12CM AB 是解此题的关键.14.如图,有一架梯子斜靠在与地面(OM )垂直的墙(ON )上,在墙角(点O 处)有一只猫紧紧盯住位于梯子(AB )正中间(点P 处)的老鼠,等待与老鼠距离最小时扑捉,把梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图,若梯子A 端沿墙下滑,且梯子B 端沿地面向右滑行.在此滑动过程中,猫与老鼠的距离()A .不变B .变小C .变大D .无法判断【解析】【分析】根据直角三角形斜边的中线等于斜边的一半,即可解答.【详解】如图,连接OP ,由题意可知:点P 为AB 的中点,∠AOB =90 ,在Rt AOB 中,12OP AB ,若梯子A 端沿墙下滑,且梯子B 端沿地面向右滑行.在此滑动过程中,OP 始终等于AB 的一半,故OP 的长不变,即猫与老鼠的距离不变.故选:A【点睛】本题主要考查了直角三角形形斜边中线的性质,解题的关键是熟练掌握直角三角形形斜边中线的性质,并会利用数学建模思想.知识点四共斜边的两个直角三角形的斜边上的中线相等15.如图,四边形ABCD 中,90ACB ADB ,取AB 中点E ,连接DE ,CE ,CD ,则EDC △为______三角形.【答案】等腰【解析】【分析】根据题意结合直角三角形中“斜中半”定理即可推出结论.由题ABC ADB,均为直角三角形,且都以AB为斜边,∵E为AB的中点,∴1122CE AB DE AB CE DE,,,即:EDC为等腰三角形,故答案为:等腰.【点睛】本题考查直角三角形中“斜中半”定理,理解并灵活运用定理是解题关键.16.如图,点C为线段AB的中点,90AMB ANB,则CMN△是_______________三角形.【答案】等腰【解析】【分析】根据直角三角形斜边上的中线等于斜边的一半即可求解.【详解】∵90AMB ANB∴在Rt△ABM中,C是斜边AB上的中点,∴MC=12AB,同理在Rt△ABN中,CN=12AB,∴MC=CN∴CMN△是等腰三角形,故答案为:等腰.【点睛】此题主要考查等腰三角形的判定,解题的关键是熟知直角三角形斜边上的中线等于斜边的一半.三、解答题(共0分)17.如图所示,在△ABC中,CD是AB上的中线,且DA=DB=DC.(1)已知∠A=30°,求∠ACB的度数;(2)已知∠A=40°,求∠ACB的度数;(3)已知∠A=x°,求∠ACB的度数;(4)请你根据解题结果归纳出一个结论.【答案】(1)90°;(2)90°;(3)90°;(4)三角形中,一边上的中线等于这边的一半,那么这边所对的角等于90°.【解析】【分析】(1)(2)(3)利用等腰三角形及三角形内角和定理即可求出答案;(4)三角形中,一边上的中线等于这边的一半,那么这边所对的角等于90°.【详解】解:(1)∵在△ABC中,CD是AB上的中线,且DA=DC,∠A=30°∴∠ACD=30°∵∠CDB是△ACD的外角∴∠CDB=60°∵DB=CD∴∠DCB=∠B=60°∴∠ACB=∠ACD+∠DCB=30°+60°=90°;(2)若∠A=40°,同(1),可知∠ACD=40°,∠CDB=40°+40°=80°∠DCB=12(180°﹣∠CDB)=12(180°﹣80°)=50°∴∠ACB=∠ACD+∠DCB=40°+50°=90°;(3)若∠A=x°,同(1),可知∠ACD=x°,∠CDB=x°+x°=2x°∠DCB=12(180°﹣∠CDB)=12(180°﹣2x°)=90°﹣x°,故∠ACB=∠ACD+∠DCB=x°+90°﹣x°=90°;(4)三角形中,一边上的中线等于这边的一半,那么这边所对的角等于90°.【点睛】此题主要考查直角三角形的性质,解题的关键是熟知直线三角形斜边上的中线的性质.18.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.(1)求证:△MEF是等腰三角形;(2)若∠ABC=50°,∠ACB=60°,求∠EMF的度数.【答案】(1)见解析,(2)40°【解析】【分析】(1)根据直角三角形斜边上的中线等于斜边的一半证明EM=FM即可;(2)根据等腰三角形两底角相等求出∠BMF,∠CME,然后根据平角等于180°列式计算即可求出∠EMF.【详解】(1)证明:∵CF⊥AB,BE⊥AC,M为BC的中点,∴EM=12BC,FM=12BC,∴BM=FM,∴△MEF是等腰三角形;(2)∵BM=FM,∠ABC=50°,∴∠MBF=∠MFB=50°,∴∠BMF=180°﹣2×50°=80°,∵CM=EM,∠ACB=60°,∴∠MCE=∠MEC=60°,∴∠CME=180°﹣2×60°=60°,∴∠EMF=180°﹣∠BMF﹣∠CME=40°.【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形的判定与性质,熟记性质并准确识图是解题的关键.19.如图,已知ABC 的高BD CE 、相交于点O M N ,、分别是BC AO 、的中点,求证:MN 垂直平分DE .(括号中需写本学期新学理由)【答案】见解析【解析】【分析】联结EN DN EM DM 、、、,根据直角三角形斜边中线等于斜边一半可得EN DN EM DM ,,进而判断M N 、在线段DE 的垂直平分线上,即可证明MN 垂直平分DE【详解】证明:联结EN DN EM DM 、、、,∵BD AC ,CE AB ,∴90AEC ADB BEC BDC ,∵M N 、是BC AO 、的中点,∴1111,,,2222EN AO DN AO EM BC DM BC (直角三角形斜边中线等于斜边一半),∴EN DN EM DM ,,∴M N 、在线段DE 的垂直平分线上(垂直平分线的逆定理),∴MN 垂直平分DE .【点睛】本题考查了直角三角形斜边上的中线等于斜边的一半,垂直平分线的判定,掌握以上性质定理是解题的关键.。
直角三角形斜边上的中线专题训练

直角三角形斜边上的中线专题训练LEKIBM standardization office【IBM5AB- LEKIBMK08- LEKIBM2C】CBD直角三角形斜边上的中线班级:_____________ 姓名:_____________1、已知Rt △ABC 中,斜边AB=10cm ,则斜边上的中线的长为______2、如左下图,DE 为△ABC 的中位线,点F 在DE 上,且∠AFB=90°,若AB=5,BC=8,则EF 的长为_____3、如右上图:已知在△ABC 中,∠C=25°,点D 在边BC 上,且∠DAC=90°,AB=12DC . 则∠BAC 的度数为_________4、如图,在Rt △ABC 中,CD 是斜边AB 上的中线,∠CDA=80°,则∠A=_____ ∠B=_____(第4题) (第5题) (第6题)5、如图,△ABC 中,∠C=90°,D 在CB 上,E 为AB 之中点,AD 、CE 相交于F ,且AD=DB .若∠B=20°,则∠DFE=( )A 、40°B 、50°C 、60°D 、70°6、如图,△ABC 中,AB=AC=10,BC=8,AD 平分∠BAC 交BC 于点D ,点E 为AC 的中点,连接DE ,则△CDE 的周长为( ) A 、20 B 、12 C 、14 D 、137、如图,已知△ABC 和△ABD 均为直角三角形,其中∠ACB=∠ADB=90°,E 为AB 的中点,求证:CE=DE .NM EDCBA NMDCBA8、如图所示,BD 、CE 是三角形ABC 的两条高,M 、N 分别是BC 、DE 的中点 求证:MN ⊥DE9、如图,四边形ABCD 中,∠DAB=∠DCB=90°,点M 、N 分别是BD 、AC 的中点。
MN 、AC 的位置关系如何?证明你的猜想10、如图,AB 、CD 交于点E ,AD=AE ,CB=CE ,F 、G 、H 分别是DE 、BE 、AC 的中点(1)求证:AF ⊥DE (2)求证:FH=GH。
直角三角形斜边上的中线等于斜边的一半的专题训练
《直角三角形斜边上的中线等于斜边的一半》的专题训练
1、如图,在锐角三角形ABC 中,AD ⊥BC 于D,E 、F 、G 分别是AC 、AB 、BC 的中点。
求证:四边形DEFG 是等腰梯形。
F E
G D C B A
2、如图所示,BD 、CE 是三角形ABC 的两条高,M 、N 分别是BC 、DE 的中点
求证:MN ⊥DE
N
M E D
C A
3、已知梯形ABCD 中,∠B+∠C =90o ,EF 是两底中点的连线,试说明BC -AD =2EF
梯形ABCD 中,AD ∥BC ,且∠B+∠C=90°,E 、F 分别是两底的中点,连结EF ,若AB=8,CD=6,求EF 的长
F E D
C
B A
4、如图,四边形ABCD 中,∠DAB=∠DCB=90o ,点M 、N 分别是BD 、AC 的中点。
MN 、AC 的位置关系如何?证明你的猜想。
N
M
D C
B A
5、过矩形ABCD 对对角线AC 的中点O 作EF ⊥AC 分别交AB 、DC 于E 、F ,点G 为AE 的中点,若∠AOG =30o
求证:3OG=DC
O F
E D A 6、如图所示;过矩形ABCD 的顶点A 作一直线,交BC 的延长线于点E ,
F 是AE 的中点,连接FC 、FD 。
求证:∠FDA=∠FCB
D
A
F
E
C
B。
中考数学真题解析矩形的性质与判定,直角三角形斜边上的中线等于斜边的一半(含答案)

(2012年1月最新最细)2011全国中考真题解读120考点汇编矩形的性质与判定,直角三角形斜边上的中线等于斜边的一半一、选择题1.(2011•南通)如图,在矩形纸片ABCD中,AB=2cm,点E在BC上,且AE=CE.若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=4cm.考点:翻折变换(折叠问题)。
分析:根据题意推出AB= A'B=2,由AE=CE推出AB1=B1C,即AC=4.解答:解:∵AB=2cm,A'B=AB,,∴A'B=2,∵矩形ABCD,AE=CE,∴∠ABE=∠AB1E=90°,∵AE=CE,∴A'B='B C,∴AC=4.故答案为4.点评:本题主要考察翻折的性质、矩形的性质、等腰三角形的性质,解题的关键在于推出AB= A'B.2.(2011江苏无锡,5,3分)菱形具有而矩形不一定具有的性质是()A.对角线互相垂直B.对角线相等C.对角线互相平分D.对角互补考点:矩形的性质;菱形的性质。
专题:推理填空题。
分析:根据菱形对角线垂直平分的性质及矩形对交线相等平分的性质对各个选项进行分析,从而得到最后的答案.解答:解:A、菱形对角线相互垂直,而矩形的对角线则不垂直;故本选项错误;B、菱形和矩形的对角线都相等;故本选项正确;C、菱形和矩形的对角线都互相平分;故本选项正确;D、菱形对角相等,但不互补;故本选项正确;故选A.点评:此题主要考查了学生对菱形及矩形的性质的理解及运用.菱形和矩形都具有平行四边形的性质,但是菱形的特性是:对角线互相垂直、平分,四条边都相等.3.(2011•宁夏,2,3分)如图,矩形ABCD 的两条对角线相交于点O ,∠AOD=60°,AD=2,则AB 的长是( )A 、2B 、4C 、23D 、43考点:矩形的性质;等边三角形的判定与性质。
分析:本题的关键是本题的关键是利用等边三角形和矩形对角线的性质即锐角三角函数关系求长度.解答:解:∵在矩形ABCD 中,AO=21AC ,DO=21BD ,AC=BD , ∴AO=DO , 又∵∠AOD=60°, ∴∠ADB=60°, ∴∠ABD=30°, ∴AB AD=tan30°, 即AB 2=33, ∴AB=23. 故选C .点评:本题考查了矩形的性质和锐角三角函数关系,具有一定的综合性,难度不大属于基础性题目.4.(2011台湾,29,4分)如图,长方形ABCD 中,E 为BC 中点,作∠AEC 的角平分线交AD 于F 点.若AB =6,AD =16,则FD 的长度为何?( )A .4B .5C .6D .8考点:矩形的性质;角平分线的性质;勾股定理。
关于“直角三角形斜边中线定理”应用2道几何题目解答

直角三角形斜边中线定理:
如果一个三角形是直角三角形,那么这个三角形斜边上的中线等于斜边的一半
一.如图,在四边形ABCD中,BD⊥CD,AC⊥AB,E为BC的中点,
∠EDA=60°,求证:AD=DE证明:根据题意,可得
∠BAC=90°,∠CDB=90°
△BAC、△CDB为直角三角形
又E为BC的中点
∴AE为直角△BAC斜边BC上的中线,BC=2AE
同理,DE直角△CDB斜边BC上的中线,BC=2DE
∴AE=DE,又∠EDA=60°
∴∠EDA=∠EAD=60°
∴△EDA为等边三角形
即:AD=DE
二.如图,在△ABC中,AD⊥CB、BE⊥AC,且相交于O点,N、M是
CO、AB的中点,连接MN、ED,求证:MN是ED的中垂线
证明:连接ME、MD、NE、ND
(注:DE与MN交于P点)
因AD⊥CB、BE⊥AC,可得
EM为直角△AEB斜边AB上的中线,EM=1/2 AB;
MD为直角△ADB斜边AB上的中线,MD=1/2 AB
∴EM=MD
NE为直角△CEO斜边CO上的中线,NE=1/2 CO ND为直角△CDO斜边CO上的中线,ND=1/2 CO ∴NE=ND
又MN=MN
∴△MEN≌△MDN
所以∠EMN=≌∠DMN
又ME=MD,MP=MP
∴△EMP≌△DMP
∴EP=DP
∠EPM =∠DPM = 180°÷2 = 90°
即:MN是ED的中垂线。
《直角三角形斜边上的中线》专题训练

7、如图,已知△ABC和△ABD均为直角三角形,其中∠ACB=∠ADB=90°,E为AB的中点,求证:CE=DE.
8、如图所示,BD、CE是三角形ABC的两条高,M、N分别是BC、DE的中点
求证:MN⊥DE
9、如图,四边形ABCD中,∠DAB=∠DCB=90°,点M、N分别是BD、AC的中点。MN、AC的位置关系如何?证明你的猜想
(第4题) (第5题)(第6题)
5、如图,△ABC中,∠C=90°,D在CB上,E为AB之中点,AD、CE相交于F,且AD=DB.若∠B=20°,则∠DFE=( )
A、40°B、50°C、60°D、70°
6、如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点AC的中点,连接DE,则△CDE的周长为( )
2、如左下图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为_____
3、如右上图:已知在△ABC中,∠C=25°,点D在边BC上,且∠DAC=90°,AB= DC.
则∠BAC的度数为_________
4、如图,在Rt△ABC中,CD是斜边AB上的中线,∠CDA=80°,则∠A=_____ ∠B=_____
若b20则dfe706如图abc中abac10bc8ad平分bac交bc于点ac的中点连接de则cde的周长为137如图已知abc和abd均为直角三角形其中acbadb90ab的中点求证
直角三角形斜边上的中线
班级:_____________ 姓名:_____________
1、已知Rt△ABC中,斜边AB=10cm,则斜边上的中线的长为______
10、如图,AB、CD交于点E,AD=AE,CB=CE,F、G、H分别是DE、BE、AC的中点
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《直角三角形斜边上的中线等于斜边的一半》的专题训练
1、如图,在锐角三角形ABC中,AD⊥BC于D,E、F、G分别是AC、AB、BC的中点。
求证:四边形OEFG是等腰梯形。
B
G D C
2、如图所示,BD、CE是三角形ABC的两条高,M、N分别是BC、DE的中点
求证:MN⊥DE
M C
3、已知梯形ABCD 中,∠B+∠C =90o ,EF 是两底中点的连线,试说明AB -AD =2EF
F
C
B
4、如图,四边形ABCD 中,∠DAB=∠DCB=90o ,点M 、N 分别是BD 、AC 的中点。
MN 、AC 的位置关系如何证明你的猜想。
D B A
5、过矩形ABCD对对角线AC的中点O作EF⊥AC分别交AB、DC于E、F,点G为AE的中点,若∠AOG=30o
求证:3OG=DC
F
E
A
6、如图所示;过矩形ABCD的顶点A作一直线,交BC的延长线于点E,F是AE的中点,连接FC、FD。
求证:∠FDA=∠FCB
A
C
B。
