必修一必修二综合测试 3

合集下载

高中人教版生物必修一必修二必修三综合练习题必修试卷期末试题2(含详细答案,答题卡).doc

高二生物综合试卷学校:___________姓名：___________班级：___________考号：___________一、单选题（本题共6道小题，每小题6分，共36分）1.下面①～⑤是利用显微镜观察时的几个操作步骤，在显微镜下要视野里的标本从图中的甲转为乙，其正确的操作步骤是①转动粗准焦螺旋②调节光圈③转动细准焦螺旋④转动转换器⑤移动标本A. ①→②→③→④B. ④→⑤→③→②C. ②→①→⑤→④D. ⑤→④→②→③2.下列关于组成生物体化学元素的叙述，正确的是A. 组成生物体的化学元素在无机自然界都能找到B. 细胞中的微量元素因含量极少而不如大量元素重要C. 碳元素是最基本元素，原因是其在细胞中含量最多D. 组成人体细胞的化学元素中，含量最多的四种元素是C、H、O、K3.下列哪种物质通过细胞膜的运输方式如下图所示A. H2OB. KC. 甘油D. 氧气4.无花果有红色和黄色之分，如果红色由显性基因（T）控制，现用两种红色无花果进行杂交实验，结果如下图。

该实验亲代的基因型分别是A. TT、TTB. TT、TtC. Tt、TTD. Tt、Tt5.下图表示某高等动物细胞的一个细胞周期中每条染色体上的DNA含量变化曲线。

下列有关说法，不正确的是A. AB段处于细胞分裂的间期B. BC段细胞中存在姐妹染色单体C. CD段表示分裂期的后期D. DE段细胞中出现细胞板6.现代生物进化理论是在达尔文自然选择学说基础上发展起来的，对自然选择学说进行了补充修正。

下列哪项不是现代生物进化理论的内容A. 进化的基本单位是种群，而不是生物个体B. 自然选择是因为生物存在过度繁殖而导致生存斗争来实现的C. 基因频率的改变是生物进化的实质D. 突变和基因重组、自然选择及隔离是物种形成过程中的基本环节三、简答题(每小题2分，共54分）7.下图表示兴奋通过神经骨骼肌接头引起肌肉收缩的部分过程，当乙酰胆碱（Ach）作用于A（Ach受体兼Na＋通道）时，产生动作电位；当兴奋传导至B 时，C（Ca2＋通道）打开，肌质网中Ca2＋释放，引起肌肉收缩。

高一英语必修一必修二综合测试卷(有答案)

高一英语必修一必修二综合测试卷(有答案)第一部分听力 (共两节，满分 20 分)第一节（共 5 小题；每小题 1 分，满分 5 分）听下面 5 段对话。

每段对话后有一个小题，从题中所给的 A、B、C 三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10 秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. What does the man suggest the woman do?A. Go to bed early.B. Work all night.C. Take a nap.2. What is the woman going to do after the meeting?A. Have a talk with Jack.B. Attend a meeting.C. Have coffee with David.3. What is the woman doing now?A. Sitting on the sofa.B. Watching TV.C. Reading a book.4. What is the probable relationship between the speakers?A. Friends.B. Teacher and student.C. Shop assistant and customer.5. What does the man say about the woman's photo?A. It was taken by him.B. It is very beautiful.C. It was in a magazine.第二节（共 15 小题；每小题 1 分，满分 15 分）听下面 5 段对话或独白。

每段对话或独白后有几个小题，从题中所给的 A、B、C 三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题，每小题 5 秒钟；听完后，各个小题将给出 5 秒钟的作答时间。

生物必修一必修二综合试卷及答案

生物必修一必修二综合试卷及答案第Ⅰ卷（选择题，共40分）一、选择题（本大题共20小题，每小题2分，共40分。

每小题有一个选项符合题意。

）1.形成蛋白质分子结构的层次，从小到大依次是A。

①→②→③→④→⑥→⑤B。

①→②→③→④→⑥→⑤C。

②→①→⑥→③→④→⑤D。

②→①→③→⑤→④→⑥2.下列关于细胞学说及其建立，叙述错误的是A。

细胞学说主要是由XXX和XXX提出的B。

细胞学说的重要内容是：动物和植物都是由细胞发育而来C。

细胞学说认为细胞分为真核细胞和原核细胞D。

细胞学说阐明了细胞的统一性和生物体结构的统一性3.右图是用光学显微镜观察某植物细胞的叶绿体实验中的两个视野，要把视野中的物像从甲图转为乙图，下列操作步骤正确的排序是A。

③—⑤—②—①B。

④—③—②—⑤C。

③—①—④—⑤D。

③—⑤—④—①4.下列关于植物细胞内合成ATP的叙述中，错误的是A。

在有氧与缺氧的条件下，细胞质基质中都能形成ATP B。

只要供给二氧化碳，在叶绿体中就能形成ATPC。

绿色植物叶肉细胞无光照时也能合成ATPD。

在线粒体中形成大量ATP需要氧气5.某高等生物基因型为AaBb，经减数分裂能产生四种数量相等的配子。

右图为其体内的某个细胞的状态示意图，下列说法中错误的是A。

图中基因位点1、2、3、4可能分别是A、b、B、bB。

高尔基体、线粒体、核糖体等细胞器与该细胞分裂过程有密切关系C。

该状态下的细胞不发生ATP水解D。

该状态下的细胞中含有同源染色体6.下列关于细胞内元素和化合物的叙述，错误的是A。

组成细胞的化学元素有20多种，其中C是构成细胞的基本元素B。

动物乳汁中的乳糖和植物细胞中的纤维素都属于多糖C。

一切生命活动都离不开蛋白质，蛋白质是生命活动的主要承担者D。

磷脂是所有细胞必不可少的脂质7.生物膜是生物学研究的一个重要领域。

下面对此有关叙述合理的是A。

生物膜是生物体内所有膜结构的统称B。

细胞的各种生物膜功能的差异是由于磷脂分子种类不同造成的C。

铁岭高中高一必修一、必修二综合测试题三

铁岭高中高一必修一、必修二综合测试题三出题人：王铁刚一、选择题（在每小题给出的四个选项中，只有一项是符合要求的.本题共12小题，每小题5分，满分60分）1、已知集合S ={c b a ,,}中的三个元素可构成∆ABC 的三条边长，那么∆ABC 一定不是（） A ．锐角三角形B ．直角三角形C ．钝角三角形D ．等腰三角形2、与直线3450x y ++=关于x 轴对称的直线的方程为（）A ．3450x y -+=B ．0543=-+y xC ．0534=-+y xD ．0534=++y x 3、已知正方体外接球的体积是323π，那么正方体的棱长等于（）A B 3C 3D 34、已知直线⊥l 平面α，直线⊂m 平面β，下列四个命题中正确的是( )（1）m l ⊥⇒βα// （2）m l //⇒⊥βα （3）βα⊥⇒m l // （4）βα//⇒⊥m l A ．（1）与（2） B ．（3）与（4） C ．（2）与（4） D ．（1）与（3）5、某新产品电视投放市场后第一个月销售100台，第二个月销200台，第三个月销售400台，第四个月销售790台，则下列函数模型中能较好地反映销量y 与投放市场的月数x 之间关系的是（）.A.100y x =B.25050100y x x =-+C.502x y =⨯D.2100log 100y x =+ 6、一个圆柱的侧面展开图是一个正方形，这个圆柱的全面积与侧面积的比是（）. A.122ππ+ B.144ππ+ C.12ππ+ D.142ππ+7、设()f x 是奇函数，且在(0,)+∞内是增函数，又(3)0f -=，则()0x f x ⋅<的解集是（） A ．{}|303x x x -<<>或 B ．{}|303x x x <-<<或 C ．{}|33x x x <->或 D ．{}|3003x x x -<<<<或8、已知平面上一点(5,0)M ，若直线上存在点P 使得4PM =，则称直线为“切割型直线”. 下列直线中是“切割型直线”的是（）1AAA 5x=- B 5y=-C3420x y-+=D21y x=+9、设13(),(),()logxaf x ag x xh x x===,a满足2log(1)0aa->,那么当1x>时必有A．()()()h x g x f x<<B．()()()h x f x g x<<C．()()()f xg xh x<<D．()()()f x h xg x<<10、如右图，定圆半径为a，圆心为(,)b c，则直线0ax by c++=与直线10x y+-=的交点在（）A．第一象限B．第二象限C．第三象限D．第四象限11、若x1满足x+2x=4, x2满足x+log2x=4, 则x1+x2=( )A.52B. 3C.72D. 412、下列5个正方体图形中，l是正方体的一条对角线，点M、N、P分别为其所在棱的中点，能得出⊥l面MNP的图形的所有序号正确的是（）.①②③④⑤A. ①④⑤B. ①④③C. ②④⑤D. ①③⑤二、填空题（本题共4小题，每小题5分，满分20分）13、函数y=的奇偶性为 .14、如图，正方体1111ABC D A B C D-的棱长为4，P、Q分别为棱11B C、C上的中点，M在11A D上，且11A M=，过P、Q、M的平面与1DD交于点N，则MN= .15、已知点P是圆2225x y+=上动点，定点(0,1)A，则A P的中点M的轨迹方程是.16、圆台上底半径为5cm，下底半径为10cm，母线AB=20cm，A在上底面上，B在下底面上，从AB中点M拉一条绳子，绕圆台侧面一周到B点，则绳子最短时长为_ ___三、解答题（本题共6小题，满分70分.解答应写出文字说明，证明过程或演算步骤.）17、（本小题满分10分）（1）2lg2lg5lg201+-（）C（2）4160.2532164()8(2011)49----18、（本小题满分12分）已知四棱锥的底面是矩形，侧棱长相等，棱锥的高为4，其俯视图如图所示.（1）作出此四棱锥的主视图和侧视图，并在图中标出相关的数据；（2）求该四棱锥的侧面积S ．19. （本小题满分12分）求经过直线03:1=-+y x l 与直线01:2=--y x l 的交点M ，且分别满足下列条件的直线方程：（1）与直线032=-+y x 平行；（2）与直线032=-+y x 垂直.20、（本小题满分12分）如图，在四棱锥P-ABCD 中，底面ABCD 是正方形，侧棱PD ⊥底面PD =DC ，E 是P C 的中点，作EF ⊥PB 交PB 于点F ．（1）证明 PA //平面EDB ；（2）证明PB ⊥平面EFD ；21（本小题满分12分）已知圆,01046:22=+--+y x y x C 两直线01023:,:21=++=y x l kx y l . （Ⅰ）若1l 与圆C 交于A 、B 两点，求k 的取值范围；（Ⅱ）设A B 的中点为P ，1l 与2l 交点为Q ，求||||OQ OP ⋅的值.22、（本小题满分12分）已知集合M 是满足下列性质的函数()x f 的全体：在定义域内存在0x ，使得()()()0011f x f x f +=+成立。

高中化学必修一必修二综合测试题和解答

高中化学必修一必修二综合测试题和解答专业技术资料分享：高中化学必修一/必修二综合测试题本文为高中化学综合测试题，时间为90分钟，总分为100分。

单项选择题：1.“垃圾是放错了位置的资源”。

生活中废弃的铁锅、铝制易拉罐、铜导线等可以归为一类加以回收，它们属于金属或合金。

2.近日，一批湖南大米中重金属元素镉超标事件被媒体广泛报道。

下列有关镉(Cd)的说法正确的是：原子序数为48.3.下列物质水解的最终产物中含有葡萄糖的是淀粉。

4.可以用来鉴别甲烷和乙烯两种气体的试剂是溴水。

5.下列可用排水法收集的气体是NH3.6.常温下，将铜片投入到稀盐酸中，会产生气体。

7.有NaCl、MgCl2、A1C13三种溶液，只用一种试剂就可以把它们鉴别开来，这种试剂是氨水。

8.下列物质既含离子键又含共价键的是CaCl2.9.在无色透明的强酸性溶液中，能大量共存的一组离子是Cu、SO4ˉ、NO3ˉ+2.10.下列反应的离子方程式书写正确的是铁溶于盐酸中：Fe + 2H+ == Fe2+ + H2↑。

11.下列有机物互为同分异构体的是正丁烷和异丁烷。

本文为高中化学综合测试题，涉及多个知识点，包括化学元素、化学反应、有机物等。

通过选择题的形式，考察学生对这些知识点的掌握情况。

12.下列有机物的说法中错误的是：A。

CH4和Cl2反应可生成CCl4.B。

石油的主要成分是碳氢化合物。

C。

苯能使酸性KMnO4溶液褪色。

D。

乙醇能与金属钠反应。

13.下列有关表示正确的是：A。

CH4的比例模型：四个氢原子围绕着一个碳原子。

B。

HCl的电子式：H:Cl。

C。

S的结构示意图：S。

D。

Fe2(SO4)3的电离方程式：Fe2(SO4)3 → 2Fe3+ + 3SO42-。

14.下列有关离子(或物质)的检验及结论正确的是：A。

用一束光照射区别氢氧化铁胶体和氯化铁溶液，都会出现XXX现象。

B。

向无色溶液中加入BaCl2溶液有白色沉淀出现，则溶液中一定含有SO42-。

必修一综合测试题(必修一、二)

必修一综合测试题说明：1.本试卷分第I、II 两卷，共100分。

考试时间90分钟2.相对原子质量：H：1 C：12 O：16 Na：23 Cl：35.5 N：14 Mn:55第Ⅰ卷（选择题，共50分）一．选择题：（本题包括10小题，每小题2分，共20分，每小题只有一个选项符合题意）1.我国是世界上严重缺碘的地区，全国有约四亿多人缺碘，因此我国政府规定：国内销售的食盐必须加碘。

关于加碘盐的下列叙述中不正确的是（）。

A.加碘食盐开袋后，不宜长期放置后再食用B. 加碘食盐中加入的是单质碘C.加碘食盐中加入的是碘酸钾D.加碘食盐在使用过程中，不宜长时间高温加热2.下列物质保存方法正确的是( )。

A．锂保存在煤油中B．NaOH固体保存在细口试剂瓶中C．Na2O2隔绝空气密封保存D．氢氟酸用玻璃试剂瓶保存3.下列物质属于纯净物的是（）。

A.漂白粉B.盐酸C.氯水D.液氯4.下列变化必须加入氧化剂才能完成的是（）。

A.MnO4-→MnO2B.Fe2＋→Fe3＋C.I2 →I-D.HCO3-→CO32-5.下列溶液中，Cl－的物质的量浓度最大的是（）。

A.100 mL0.5 mol/L AlCl3(aq)B.200 mL0.5 mol/L MgCl2(aq)C.300 mL1 mol/L NaCl(aq)D.400 mL0.5 mol/L BaCl2(aq)6.下列各组离子中，能在溶液中大量共存的是（）。

A.H＋、Na＋、HCO3-、Cl-B.Ba2＋、Na＋、OH-、Cl-C.Ag＋、K＋、NO3-、CO32-D.Cu2＋、Ag＋、Cl-、OH-7.下列反应中，SO2被还原的是（）。

A.SO2＋2NaOH＝Na2SO3＋H2OB.SO2＋Cl2＋2H2O＝H2SO4＋2HClC.SO2＋2H2S＝3S＋2H2OD.SO2＋NO2＝SO3＋NO8.在化学上，常用CaH2作制取氢气的药剂，有关的化学方程式为CaH2+2H2O=Ca(OH)2+2H2↑在这个反应中，H2O的作用是 ( )。

完整word版)高一物理必修一必修二综合测试试卷

完整word版)高一物理必修一必修二综合测试试卷致相等的是（）A.圆周频率B.向心加速度C.角速度D.周期10.一质点做平抛运动，其抛出角度为45°，抛出速度为v，重力加速度为g，下列说法中正确的是（）A.当抛出速度为2v时，其飞行时间为原来的2倍B.当抛出速度为v时，其最大高度为C.当抛出速度为v时，其飞行距离为D.当抛出速度为v时，其落点与抛出点的水平距离为11.一物体在水平面上做匀速圆周运动，下列说法中正确的是（）A.物体所受的向心力与物体的速度方向垂直B.物体所受的向心力与物体的速度方向平行C.物体所受的向心力与物体的速度方向夹角为45°D.物体所受的向心力与物体的速度方向夹角为90°12.一物体做匀变速直线运动，其速度随时间t的变化规律为v=2t+1(m/s)，下列说法中正确的是（）A.物体在t=1s时的速度为3m/sB.物体在t=0.5s时的速度为1.5m/sC.物体在t=2s时的位移为5mD.物体在t=3s时的位移为10m13.一物体做匀变速直线运动，其位移随时间t的变化规律为x=2t2+2t(m)，下列说法中正确的是（）A.物体在t=1s时的位移为4mB.物体在t=2s时的速度为8m/sC.物体在t=1s时的速度为6m/sD.物体在t=3s时的加速度为4m/s214.一个物体从高处自由落下，下列说法中正确的是（）A.物体在下落过程中速度越来越小B.物体在下落过程中加速度越来越小C.物体下落的时间只与物体所在的高度有关D.物体下落的速度只与物体所在的高度有关2015学年第二学期XXX3月阶段性测试高一年级物理学科试题卷考生须知：1.本试题卷分为第Ⅰ卷（客观题）和第Ⅱ卷（主观题）两部分，共4页23小题，满分为100分，考试时间为90分钟。

2.答案请填写在答题卡上，不得在试题卷上作答。

第Ⅰ卷（共42分）一、单项选择题（本大题共14小题，每小题3分，共42分）1.下列单位都属于力学国际单位制的基本单位的是（）A。

必修一必修二综合测试3.

必修一必修二综合测试3第I 卷（选择题共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一个选项是符合题目要求的． 1．集合A={}3<x x ，集合B={}1>x x ，则=（）A ．()(),11,3-∞-⋃B ．()11，-C ．()31，D ．()1，∞- 2．直线l 的倾斜角为45，且经过点P （0，1），则直线l 的方程为（）A ．01=+-y xB ． 01=++y xC ． 01=--y xD ． 01=-+y x3. 用二分法求下图所示函数()x f 的零点时，不可能求出的零点是（）A ． x 1B ． x 2C ． x 3D ． x 44. 已知函数()()⎩⎨⎧∈-⋅==*N n n f n n n f ,10,1 , 则()6f 的值是（）A ． 6B ． 24C ． 120D ． 7205. 棱台上、下底面面积之比为1∶9,则棱台的中截面分棱台成两部分的体积之比是（注：中截面是过棱台高的中点与棱台上，下底面平行的平面） ( )A. 1∶7B.2∶7C. 7∶19D. 5∶ 16 6. 直线01:0=+-y x l ，直线012:1=+-y ax l 与0l 平行，且直线03:2=++by x l 与0l 垂直，则=+b a （） A ．4 B ．3 C ．2 D ．17. 一种计算机病毒专门占据计算机的内存．在刚开机时它占据的内存2KB ，然后每3分钟自身复制一次，复制后所占的内存是原来的2倍，那么开机后经过（）分钟，该病毒占据64MB 的内存．（注：KB MB 1021=）（）A ．39B ．42C ．45D ．488. 设α、β、γ为两两不重合的平面，l 、m 、n 为两两不重合的直线，给出下列四个命题：① 若α⊥γ，β⊥γ，则α∥β；②若m ⊂α，n ⊂α，m ∥β，n ∥β，则α∥β； ③若α∥β，l ⊂α，则l ∥β；④若α∩β=l ，β∩γ=m ，γ∩α=n ，l ∥γ，则m ∥n ．其中真命题的个数是（）A.1B.2C.3D.4 9. 下列三视图所表示的几何体是( )A. 正方体B. 圆锥体C. 正四棱台D. 长方体10．函数2()2(1)2f x x a x =+-+在区间(,6]-∞上递减,则a 的取值范围是（）A.[5,)-+∞B.(,5]-∞-C.(,7]-∞D.[5,)+∞11．如下图，一个正四棱柱的底面棱长为2，高为2，其下底面位于半球的大圆上，上底面四个顶点都在半球面上，则其上底面相邻两顶点间的球面距离为（）A ．2πB ．32πC ．22π D ． 23π 12. 已知函数y =的最大值为M,最小值为m,则mM的值为（）俯视图侧视图正视图A 14B 12第II 卷（非选择题共90分）二、填空题：本大题共4小题，每小题4分，共16分．13.()f x 是定义在R 上的奇函数，(1)2f =，且(1)(5)f x f x +=+，则(12)(3)f f +的值是．14. 已知函数()f x 是定义在［-e ，0）∪（0，e ］上的奇函数，当x ∈［-e ，0）时，()f x ln ()ax x =+-，则当x ∈（0，e ］时，()f x = ．15. 对于任意的两个实数对（a ，b ）和（c ，d ），规定：（a ，b ）=（c ，d ），当且仅当a =c ，b =d ；运算“⊗”为：（a ，b ）⊗（c ，d ）=（ac-bd ，bc+ad ）；运算“⊕”为:（a ，b ）⊕（c ，d ）=（a+c ，b +d ），设p ，q ∈R ，若（1，2）⊗（p ，q ）=（5，0），则（1，2）⊕（p ，q ）=_________ 16. 在平面几何中，有如下结论：三边相等的三角形内任意一点到三边的距离之和为定值.拓展到空间，类比平面几何的上述结论，可得：四个面均为等边三角形的四面体内任意一点_______________________________________．三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤． 17．（本小题满分12分）已知集合{}73|<≤=x x A ，{}102|<<=x x B ，{}a x a x C <<-=5|. (1) 求B A ，()B A C R ；(2) 若()B A C ⊆，求a 的取值范围.18．（本小题满分12分）如右图是古希腊数学家阿基米德的墓碑文，墓碑上刻着一个圆柱，圆柱内有一个内切球，这个球的直径恰好与圆柱的高相等．相传这个图形表达了阿基米德最引以自豪的发现．我们来重温这个伟大发现：（1）求圆柱的体积与球的体积之比；（2）求圆柱的表面积与球的表面积之比．19．（本小题满分12分）已知圆22:(1)(2)25,C x y -+-=直线:(21)(1)740l m x m y m +++--=，（1）求证：直线l 恒过定点；（2）判断直线l 被圆C 截得的弦长何时最长，何时最短？并求截得的弦长最短时，求m的值以及最短长度。

人教版物理必修一必修二综合测试试卷及答案

必修一必修二综合测试一、选择题（每小题有一个或几个正确选项，全部选对的得4分，选不全的得2分，本大题共48分）1．关于摩擦力，下列说法正确的是（）A．受滑动摩擦力的物体可以静止B．两个相互接触的粗糙物体间发生相对滑动时，产生滑动摩擦力C．两个相对静止的物体间的正压力增大，两者之间摩擦力一定增大D．摩擦力的方向与物体的运动方向可以不同，摩擦力可以充当动力，也可以充当阻力2．用3 N的水平恒力, 使在水平面上一质量为2 kg的物体, 从静止开始运动，在2 s内通过的位移是2 m, 则物体的加速度大小和所受摩擦力的大小分别是（）A．0.5 m / s2，2 N B．1 m / s2，1 NC．2 m/ s2，0.5 N D．1.5 m / s2，03．升降机地板上放一个弹簧磅秤，秤上放一质量为m的物体，当秤的示数为0.8mg时，升降机可能作的运动是（）A．加速上升B．加速下降C．减速上升D．减速下降．4．如图所示，把重为20N的物体放在倾角为30的粗糙斜面上处于静止，物体左端与固定在斜面上的与斜面平行的轻弹簧相连接，若物体与斜面间的最大静摩擦力为13N，则关于弹簧的弹力下列说法中错误．．的是（）A. 可以为22N，方向沿斜面向上B. 可以为2N，方向沿斜面向上C. 可以为2N，方向沿斜面向下D. 摩擦力不可能为零5．下列所给的作直线运动物体的位移—时间图象或速度—时间图像中，不可能正确．．．．．反映物体从某点开始运动又重新回到初始位置的图象是（）6．一质点的加速度方向始终与质点的速度方向相同，当加速度逐渐减小的时候，下述情况中可能出现的是（）Ａ．速度和位移均增大，加速度为零时，速度达到最大Ｂ．速度和位移均减小，速度减小得越来越慢Ｃ．速度逐渐减小，位移逐渐增大，速度减为零时，位移达到最大Ｄ．速度先增大，后减小，而位移一直在不断增大7.如图所示，汽车以速度v通过一圆弧式的拱桥顶端时，关于汽车受力的说法正确的是（）A、汽车的向心力就是它所受的重力B、汽车的向心力就是它所受的重力和支持力的合力，方向指向圆心C、汽车受重力、支持力、牵引力、摩擦力和向心力的作用D、以上均不正确8.关于平抛运动下列说法正确的是（）A、因为轨迹是曲线，所以平抛运动是变加速运动B、运动时间由下落高度和初速度共同决定C、水平位移由初速度决定D、运动时间由下落高度决定9.一颗正在绕地球转动的人造卫星，由于受到阻力作用则将会出现（）A、速度变大B、动能增大C、角速度变小D、半径变小10.火星有两颗卫星，分别是火卫I和火卫II，它们的轨道近似为圆，已知火卫I的周期为7小时39分，火卫II的周期为30小时18分，则两颗卫星相比（）A．火卫II距火星表面较近B．火卫II的角速度大C．火卫I的运动速度较大D．火卫I的向心加速度较大11．关于功和能，下列说法正确的是（）A．功有正负，因此功是矢量B ．功是能量转化的量度C ．能量的单位是焦耳，功的单位是瓦特D ．物体发生1m 位移的过程中，作用在物体上大小为1 N 的力对物体做的功一定为1 J12．人造地球卫星可以看起来相对地面静止，就是我们常说的同步卫星。

高一数学必修一必修二综合测试卷(有答案)

高一数学试题四（考试时间：120分钟试卷满分：150分）一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）1. 下列说法正确的是（）A . 经过三点确定一个平面B . 经过一条直线和一个点确定一个平面C . 四边形确定一个平面D . 两两相交且不共点的三条直线确定一个平面2. 下列哪个函数的定义域与函数()15xf x ⎛⎫= ⎪⎝⎭的值域相同（）A . 2y x x =+B . ln 2y x x =-C . 1y x =D . 1y x x=+3. 已知集合12|log 1A x x ⎧⎫=>-⎨⎬⎩⎭，{}|22xB x =>，则A B =（）A . 1,22⎛⎫ ⎪⎝⎭B . 1,2⎛⎫+∞⎪⎝⎭C . ()0,+∞D . ()0,24. 已知圆锥的侧面展开图是一个半圆，则其母线与底面半径之比为（） A . 1B .2C .3D . 25. 已知函数()2f x x x a =++在区间()0,1上有零点，则实数a 的取值范围是（） A . 1,4⎛⎤-∞ ⎥⎝⎦B . 1,4⎛⎫-∞ ⎪⎝⎭C . ()2,0-D . []2,0-6. 函数()()10,1x f x a a a -=>≠的图象恒过点A ，则下列函数中图象不经过点A 的是（）A . 1y x =-B . 2y x =-C . 21xy =-D . ()2log 2y x =7. 正四面体ABCD 中，E ，F 分别为棱AD ，BC 的中点，则异面直线EF 与CD 所成的角为（） A .6π B .4π C . 3π D . 2π8. 已知函数()212log 3y x ax a =-+在[)2,+∞上为减函数，则实数a 的取值范围是（）A . 4a ≤B . 4a ≥C . 4a <-或4a ≥D . 44a -<≤9. 某几何体的三视图如图所示，该几何体表面上的点P 与点Q 在正视图与侧视图上的对应点分别为A ，B ，则在该几何体表面上，从点P 到点Q 的路径中，最短路径的长度为（） A .5B .6 C . 22D .1010. 已知函数()ln 1f x x =-，()223g x x x =-++，用{}min ,m n 表示m ，n 中最小值，设()()(){}min ,h x f x g x =，则函数()h x 的零点个数为（）A . 1B . 2C . 3D . 411. 已知()g x 为偶函数，()h x 为奇函数，且满足()()2x g x h x -=.若存在[]1,1x ∈-，使得不等式()()0m g x h x ⋅+≤有解，则实数m 的最大值为（）A .315-B . 35-C . 1D . -1 12. 无论x ，y ，z 同为三条不同的直线还是同为三个不同的平面，给出下列说法：①若//x y ，//x z ，则//y z ；②若x y ⊥，x z ⊥，则y z ⊥；③若x y ⊥，//y z ，则x z ⊥；④若x 与y 无公共点，y 与z 无公共点，则x 与z 无公共点； ⑤若x ，y ，z 两两相交，则交点可以有一个，三个或无数个.其中说法正确的序号为（） A . ①③B . ①③⑤C . ①③④⑤D . ①④⑤二、填空题（本大题共4小题，每小题5分，共20分） 13. 设函数()()xxf x e aea R -=+∈，若()f x 为奇函数，则a =______.14. 一个正四棱锥的侧棱长与底面边长相等，体积为423，则它的侧面积为______. 15. 已知函数()f x 为定义在[]2,3a -上的偶函数，在[]0,3上单调递减，并且()22522a f m m f m ⎛⎫-- ⎪⎝⎭>-+-，则m 的取值范围是______.16. 正四面体ABCD 的棱长为4，E 为棱BC 的中点，过E 作其外接球的截面，则截面面积的最小值为______.三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤） 17. 如图所示，在正方体1111ABCD A B C D -中，E 、F 分别是AB 和1AA 的中点.求证：CE ，1D F ，DA 交于一点.18. 已知函数()21x ax b f x x +=++是定义域为R 的奇函数. （1）求实数a 和b 的值，判断并证明函数()f x 在()1,+∞上的单调性；（2）已知0k <，且不等式()()22310f t t f k -++-<对任意的t R ∈恒成立，求实数k 的取值范围.19. 食品安全问题越来越引起人们的重视，农药、化肥的滥用对人民群众的健康带来一定的危害，为了给消费者带来放心的蔬菜，某农村合作社每年投入200万元，搭建了甲、乙两个无公害蔬菜大棚，每个大棚至少要投入20万元，其中甲大棚种西红柿，乙大棚种黄瓜，根据以往的种菜经验，发现种西红柿的年收入P 、种黄瓜的年收入Q 与投入a （单位：万元）满足8042P a =+，11204Q a =+.设甲大棚的投入为x （单位：万元），每年两个大棚的总收益为()f x （单位：万元）. （1）求()50f 的值；（2）试问如何安排甲、乙两个大棚的投入，才能使总收益()f x 最大？20. 已知幂函数()()3*p N x x f p -=∈的图象关于y 轴对称，且在()0,+∞上为增函数. （1）求不等式()()22132pp x x +<-的解集；（2）设()()()log 0,1a f x ax g x a a =->≠⎡⎤⎣⎦，是否存在实数a ，使()g x 在区间[]2,3上的最大值为2，若存在，求出a 的值，若不存在，请说明理由.21. 已知函数()11439x xm f x ⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭.（1）当2m =-时，求函数()f x 在(),0-∞上的值域；（2）若对任意[)0,x ∈+∞，总有()6f x ≤成立，求实数m 的取值范围.22. 在菱形ABCD 中，2AB =且60ABC ∠=︒，点M ，N 分别是棱CD ，AD 的中点，将四边形ANMC 沿着AC 转动，使得EF 与MN 重合，形成如图所示多面体，分别取BF ，DE 的中点P ，Q .（1）求证：//PQ 平面ABCD ；（2）若平面AFEC ⊥平面ABCD ，求多面体ABCDFE 的体积.参考答案一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的） 1-5：DBCDC6-10：ABDCC11-12：AB1.【解析】A 选项考查公理2，即三点必须不在同一条直线上，才能确定一个平面；B 选项如果点在直线上，则该直线和这个点不能确定一个平面；C 选项中的四边形有可能是空间四边形，故选D .2.【解析】函数()15xf x ⎛⎫= ⎪⎝⎭的值域为()0,+∞，函数2y x x =+的定义域为R ，函数ln 2y x x =-的定义域为()0,+∞；函数1y x x=+的定义域为()(),00,-∞+∞，函数1y x=的定义域为()(),00,-∞+∞，故选B .3.【解析】由{}12|log 1|02A x x x x ⎧⎫=>-=<<⎨⎬⎩⎭，{}1|22|2xx x x B =⎧⎫>=>⎨⎬⎩⎭，则()0,A B =+∞，故选C .4.【解析】由已知可得2r l ππ=，所以2l r =，故2lr=.故选D . 5.【解析】函数()2f x x x a =++的图象的对称轴为12x =-，故函数在区间()0,1上单调递增，再根据函数()f x 在()0,1上有零点，可得()()00120f a f a =<⎧⎪⎨=+>⎪⎩，解20a -<<，故选C .6.【解析】函数()()10,1x f y ax a a -=>≠=的图象恒过点A ，即10x -=，可得1x =，那么1y =.∴恒过点()1,1A .把1x =，1y =带入各选项，只有A 没有经过A 点.故选A . 7.【解析】略8.【解析】()23g x x ax a =-+，则()230x a a g x x =-+>在[)2,+∞恒成立，且()23g x x ax a =-+在[)2,+∞上为增函数，所以22a≤且()240g a =+>，所以44a -<≤.故选D .9.【解析】由题，几何体如图所示（1）前面和右面组成一面此时222222PQ =+=.（2）前面和上面在一个平面此时223110PQ =+=，2210<，故选C . 10.【解析】作出函数()f x 和()g x 的图象如图，两个图象的下面部分图象，由()2230g x x x =-++=，得1x =-，或3x =，由()ln 10f x x =-=，得x e =或1x e=，∵()0g e >，∴当0x >时，函数()h x 的零点个数为3个，故选C .11.【解析】由()()2xg x h x -=，及()g x 为偶函数，()h x 为奇函数，得()222x xg x -+=，()222x x h x --=.由()()0m g x h x ⋅+≤得224121224141x x x x x x x m ----≤==-+++，∵2141x y =-+为增函数，∴max 231415x ⎛⎫+= ⎪+⎝⎭，故选A . 12.【解析】由平行于同一直线的两直线平行，平行于同一平面的两平面平行，可得①正确；由垂直于同一直线的两直线平行、相交或异面；垂直于同一平面的两平面相交或平行，可得②错误；由垂直于两平行直线中的一条，也垂直于另一条；垂直于两平行平面中的一个，也垂直于另一个，可得③正确；若一条直线与另两条直线无公共点，可得另两条直线可以相交；若一个平面与另两个平面无公共点，可得另两个平面无公共点；可得④错误.若三条直线两两相交，则交点可以有一个或三个，若三个平面两两相交，则交点有无数个.故选B . 二、填空题（本大题共4小题，每小题5分，共20分）13. -1 14. 43 15. 1122m -≤< 16. 4π13.【解析】若函数()x x f x e ae -=+为奇函数，则()()f x f x -=-，即()x x x x ae ae e e --+=-+，即()()10x x e a e -++=对任意的x 恒成立，则10a +=，得1a =-. 14.【解析】设正四棱锥的侧棱长与底面边长相等为2a ，则24ABCD S a =，2222422h PB BO a a a =-=-=，则31442233V a =⨯=，则1a =，则 22142242BC PF a a a S ⎛⎫=⨯⨯⨯=⨯⨯- ⎪⎝⎭侧24343a ==.15.【解析】由题设可得230a -+=，即5a =，故()()22122f m f m m -->-+-可化()()22122f m f m m +>-+，又2113m ≤+≤，21223m m ≤-+≤，故2211222m m m m +<-+⇒<，且12m ≥-.故应填答案1122m -≤<.16.【解析】将四面体ABCD 放置于正方体中，如图所示可得正方体的外接球就是四面体ABCD 的外接球，∵正四面体ABCD 的棱长为4，∴正方体的棱长为22，可得外接球半径R 满足()22322R =⨯，解得6R =.E 为棱BC 的中点，过E 作其外接球的截面，当截面到球心O 的距离最大时，截面圆的面积达最小值，此时球心O 到截面的距离等于正方体棱长的一半，可得截面圆的半径为222r R =-=，得到截面圆的面积最小值为24S r ππ==.三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤） 17.【解析】证明：如图所示，连接1CD 、EF 、1A B ，因为E 、F 分别是AB 和1AA 的中点，所以1//EF A B 且112EF A B =.即：1//EF CD ，且112EF CD =，所以四边形1CD FE 是梯形，所以CE 与1D F 必相交，设交点为P ，则P CE ∈，且1P D F ∈，又CE ⊂平面ABCD ，且1D F ⊂平面11A ADD ，所以P ∈平面ABCD ，且P ∈平面11A ADD ，又平面ABCD平面11A ADD AD =，所以P AD ∈，所以CE 、1D F 、DA 三线交于一点.18.【解析】（1）因为()()f x f x -=-，所以2211x a x ax bx x bx -+--=-+++， ∴0a b ==，()21xf x x =+，任取()12,1,x x ∈+∞，且12x x <，()()1212221211x xf x f x x x -=-++()()()()21122212111x x x x x x --=++， ∵210x x ->，1210x x ->，()()2212110x x ++>，∴()f x 在()1,+∞单调递减.（2）()()2231f t t f k -+<--，()()2231f t t f k -+<-， ∵2232t t -+≥，11k ->，∴2231t t k -+>-，即()211k t >---， ∵t R ∈≤，∴()1,0k ∈-. 19.【解析】（1）由题可知：甲大棚投入50万元，则乙大棚投入150万元，所以()1804250150120277.5450f =+⨯+⨯+=. （2）依题意得202018020020x x x ≥⎧⇒≤≤⎨-≥⎩.故()()142250201804x x f x x =-++≤≤. 令25,65t x ⎡⎤=∈⎣⎦，则()()2211422508228244f x t t t =-++=--+，当82t =，即128x =时，()max 282f x =，所以投入甲大棚128万元，乙大棚72万元时，总收益最大，且最大收益为282万元. 20.【解析】（1）由已知得30p ->且*p N ∈，所以1p =或2p =，当2p =时，()3p f x x -=为奇函数，不合题意，当1p =时，()2f x x =.所以不等式()()22132pp x x +<-变为()()1122132x x +<-，则0132x x ≤+<-，解得213x -≤<. 所以不等式()()22132p p x x +<-的解集为21,3⎡⎫-⎪⎢⎣⎭.（2）()()2log a a g x x x =-，令()2h x x ax =-，由()0h x >得()(),0,x a ∈-∞+∞，因为()g x 在[]2,3上有定义，所以02a <<且1a ≠，所以()2h x x ax =-在[]2,3上为增函数，当12a <<时，()()()max 3log 932a g x g a ==-=，即2390a a +-=，∴3352a -±=，又12a <<， ∴3352a -+=. 当01a <<时，()()()max 2log 422a g x g a ==-=，即2240a a +-=，∴15a =-±，此时解不成立.综上：3352a -+=. 21.【解析】（1）当2m =-时，设13xt ⎛⎫= ⎪⎝⎭，∵(),0x ∈-∞，∴()1,t ∈+∞，∴()()222413t t t y g t -+=-=+=，对称轴1t =，图像开口向上，∴()g t 在()1,t ∈+∞为增函数， ∴()3g t >，∴()f x 的值域为()3,+∞.（2）由题意知，()6f x ≤在[)0,+∞上恒成立，即11239xxm ⎛⎫⎛⎫⋅≤- ⎪ ⎪⎝⎭⎝⎭，∴1233xx m ≤⋅-在[)0,x ∈+∞恒成立，则只需当[)0,x ∈+∞时，min 1233x x m ⎛⎫≤⋅- ⎪⎝⎭，设3xt =，()12h t t t=-，由[)0,x ∈+∞得1t ≥，设121t t ≤<，则()()()()12121212210t t t t h t h t t t -+-=<，所以()h t 在[)1,+∞上递增，()h t 在[)1,+∞上的最小值为()11h =，所以实数m 的取值范围为(],1-∞. 22.【解析】（1）取BE 中点R ，连接PR ，QR ，BD ，由P ，Q 分别是BF ，DE 的中点， ∴//PR EF ，//QR BD ，又∵//EF AC ，∴//PR 平面ABCD ，//QR 平面ABCD ，又∵PR QR R =，∴平面//PQR 平面ABCD ，又∵PQ ⊂平面PQR ， ∴//PQ 平面ABCD .（2）连接AC ，设AC ，BD 交于点O ， ∴BD AC ⊥，又∵平面AFEC ⊥平面ABCD ，平面AFEC平面ABCD AC =，∴BD ⊥平面AFEC .∴多面体ABCDFE 可以分解为四棱锥B ACEF -和四棱锥D ACEF -，菱形ABCD 中，2AB =且60ABC ∠=︒知：2AC =，23BD =，12ACEF ==，设梯形EFAC 的面积为()133244EFAC BD EF AC S =+⋅=， 1332ABCDFE EFAC V S BD =⋅⋅=.。

高中数学必修一必修二综合测试题(含答案)

Q PC'B'A'C BA高中数学必修一必修二综合测试题（时间90分钟，满分150分）姓名___________________ 总分：________________ 一、选择题（本大题共10小题，每小题5分，共50分） 1．下面四个命题：①分别在两个平面内的两直线是异面直线；②若两个平面平行，则其中一个平面内的任何一条直线必平行于另一个平面； ③如果一个平面内的两条直线平行于另一个平面，则这两个平面平行；④如果一个平面内的任何一条直线都平行于另一个平面，则这两个平面平行．其中正确的命题是( )A ．①②B ．②④C ．①③D ．②③ 2．过点(1,3)P -且垂直于直线032=+-y x 的直线方程为（） A ．012=-+y x B ．052=-+y x C ．052=-+y x D ．072=+-y x 3．圆(x －1)2＋y 2＝1的圆心到直线y ＝33x 的距离是( )A ．12B ．32 C ．1 D ．34．设0<a <1，函数f (x )＝log a (a 2x －2a x －2)，则使f (x )<0的x 的取值范围是( )A ．(－∞，0)B ．(0，＋∞)C ．(－∞，log a 3)D ．(log a 3，＋∞)5．设y1＝40.9，y2＝80.48，y3＝(12)-1.5，则( )A ．y3>y1>y2B ．y2>y1>y3C ．y1>y2>y3D ．y1>y3>y26．圆x 2＋y 2－2x ＋4y －20＝0截直线5x －12y ＋c ＝0所得的弦长为8，则c 的值是( ) A ．10 B ．10或－68 C ．5或－34 D ．－68 7．已知0,0ab bc <<，则直线ax by c +=通过（）A ．第一、二、三象限B ．第一、二、四象限C ．第一、三、四象限D ．第二、三、四象限8．正方体ABCD —A 1B 1C 1D 1中，E 、F 分别是AA 1与CC 1的中点，则直线ED 与D 1F 所成角的大小是（）A ．15B ．13 C ．12D 39. 在三棱柱111ABC A B C -中，各棱长相等，侧掕垂直于底面，点D 是侧面11BB C C 的中心，则AD 与平面11BB C C 所成角的大小是 ( )A ．30B ．45C ．60D ．9010．如图:直三棱柱ABC —A 1B 1C 1的体积为V ，点P 、Q 分别在侧棱AA 1 和 CC 1上，AP=C 1Q ，则四棱锥B —APQC 的体积为( ) A ．2V B ．3V C ．4V D ．5V（10题）二、填空题（本大题共4小题，每小题5分，共20分）11．函数f (x )＝⎩⎪⎨⎪⎧log 12x ，x ≥12x ，x <1的值域为________．12．两圆221x y +=和22(4)()25x y a ++-=相切，则实数a 的值为13．已知集合U ＝{2,3,6,8}，A ＝{2,3}，B ＝{2,6,8}，则(∁U A )∩B ＝________.14.过点A (4,0)的直线l 与圆(x －2)2＋y 2＝1有公共点，则直线l 斜率的取值范围为三、解答题（本大题共6小题，共80分）15．(本小题满分10分)如图，在三棱柱ABC －A 1B 1C 1中，△ABC 与△A 1B 1C 1都为正三角形且AA 1⊥面ABC ，F 、F 1分别是AC ，A 1C 1的中点．求证：(1)平面AB 1F 1∥平面C 1BF ； (2)平面AB 1F 1⊥平面ACC 1A 1.（17题）16．(本小题满分12分)(1)定义在(－1,1)上的奇函数f (x )为减函数，且f (1－a )＋f (1－a 2)>0，求实数a 的取值范围．(2)定义在[－2,2]上的偶函数g (x )，当x ≥0时，g (x )为减函数，若g (1－m )<g (m )成立，求m 的取值范围．17．(本小题满分12分)如图，DC⊥平面ABC，EB∥DC，AC＝BC＝EB＝2DC＝2，∠ACB＝120°，P，Q分别为AE，AB的中点．（1）证明：PQ∥平面ACD；（2）求AD与平面ABE所成角的正弦值（17题）18．(本小题满分15分)已知圆C1：x2+y2－2x－4y+m=0，（1）求实数m的取值范围；（2）若直线l：x+2y－4=0与圆C相交于M、N两点，且OM⊥ON，求m的值。

高中物理必修一必修二综合测评(含答案)

高中物理必修一必修二综合测评(时间:90分钟满分:100分)一、单项选择题(本题共7小题,每小题4分,共28分.)1.甲、乙两个小物体,甲的重力是乙的3倍,它们从同一高度处同时自由下落,不考虑空气阻力,则下列说法中正确的是()A.甲比乙先落地B.甲的加速度比乙大C.甲、乙同时落地D.无法确定谁先落地2.下列各图分别表示的是某一物体的运动情况或其所受合外力的情况.其中甲图是某物体的位移—时间图象;乙图是某一物体的速度—时间图象;丙图表示某一物体的加速度—时间图象;丁图表示某一物体所受合外力随时间变化的图象.四幅图中的图线都是直线,从这些图象中可判断出一定质量物体的某些运动特征.下列有关说法中不正确的是()A.甲物体受合外力为零B.乙物体受到的合外力不变C.丙物体的速度一定越来越大D.丁物体的加速度越来越大3．已知靠近地面运转的人造卫星，每天转n圈，如果发射一颗同步卫星，它离地面的高度与地球半径的比值为()A．n B．n2C.n3－1D.3n2－14.如图所示，质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面，其运动的加速度为34g，此物体在斜面上上升的最大高度为h，则在这个过程中物体()A．重力势能增加了34mghB．动能损失了12mgh C．动能损失了mghD．动能损失了32mgh5.如图所示，两个相对的斜面，倾角分别为37°和53°.在顶点把两个小球以同样大小的初速度分别向左、向右水平抛出，小球都落在斜面上. 若不计空气阻力，则A、B两个小球的运动时间之比为()A．1∶1B．4∶3C．16∶9 D．9∶166.一质量为1 kg的质点静止于光滑水平面上，从t＝0时刻开始，受到水平外力F作用，如图所示．下列判断正确的是()A．0～2 s内外力的平均功率是4 WB．第2 s内外力所做的功是4 JC．第2 s末外力的瞬时功率最大D．第1 s末与第2 s末外力的瞬时功率之比为9∶57．如图所示，两颗星组成的双星，在相互之间的万有引力作用下，绕连线上的O点做周期相同的匀速圆周运动．现测得两颗星之间的距离为L，质量之比为m1∶m2＝3∶2，下列说法中正确的是()A．m1、m2做圆周运动的线速度之比为3∶2B．m1、m2做圆周运动的角速度之比为3∶2C．m1做圆周运动的半径为2 5LD．m2做圆周运动的半径为2 5L二、多项选择题(本大题共3小题，每小题5分，共15分．每小题有多个选项是正确的，全选对得5分，少选得3分，选错、多选或不选得0分)8．我国发射的“嫦娥三号”登月探测器靠近月球后，先在月球表面附近的近似圆轨道上绕月运行；然后经过一系列过程，在离月面4 m高处做一次悬停(可认为是相对于月球静止)；最后关闭发动机，探测器自由下落．已知探测器的质量约为1.3×103 kg，地球质量约为月球的81倍，地球半径约为月球的3.7倍，地球表面的重力加速度大小约为9.8 m/s2，则此探测器()A．在着陆前的瞬间，速度大小约为8.9 m/sB．悬停时受到的反冲作用力约为2×103 NC．从离开近月圆轨道到着陆这段时间内，机械能守恒D．在近月圆轨道上运行的线速度小于人造卫星在近地圆轨道上运动的线速度9.如图所示,车内绳AB与绳BC拴住一小球,BC水平,车由原来的静止状态变为向右加速直线运动,小球仍处于图中所示的位置,则()A.AB绳拉力F T1不变,BC绳拉力F T2变大B.AB绳拉力F T1变大,BC绳拉力F T2变小C.AB绳拉力F T1变大,BC绳拉力F T2不变D.AB绳拉力F T1不变,BC绳拉力F T2的大小为(F T1sin θ+ma)10.如图所示，在“嫦娥”探月工程中，设月球半径为R，月球表面的重力加速度为g.飞船在半径为4R的圆形轨道Ⅰ上运动，到达轨道的A点时点火变轨进入椭圆轨道Ⅱ，到达轨道的近月点B时，再次点火进入半径约为R的近月轨道Ⅲ绕月做圆周运动，则()A．飞船在轨道Ⅰ上的运行速率等于12g0RB．飞船在轨道Ⅰ上的运行速率小于在轨道Ⅱ上B处的速率C．飞船在轨道Ⅰ上的加速度大于在轨道Ⅱ上B处的加速度D．飞船在轨道Ⅰ、轨道Ⅲ上运行的周期之比TⅠ∶TⅢ＝4∶1三、非选择题(共57分)11.(8分)某同学用图(a)所示的实验装置测量物块与斜面之间的动摩擦因数.已知打点计时器所用电源的频率为50 Hz,物块下滑过程中所得到的纸带的一部分如图(b)所示,图中标出了五个连续点之间的距离图(a)图(b)(1)物块下滑时的加速度a=m/s2,打C点时物块的速度v=m/s;(2)已知重力加速度大小为g,为求出动摩擦因数,还必须测量的物理量是(填正确答案:标号).A.物块的质量B.斜面的高度C.斜面的倾角12．(8分)利用图甲装置做“验证机械能守恒定律”实验．图甲(1)为验证机械能是否守恒，需要比较重物下落过程中任意两点间的________．A．动能变化量与势能变化量B．速度变化量与势能变化量C．速度变化量与高度变化量(2)(多选)除带夹子的重物、纸带、铁架台(含铁夹)、电磁打点计时器、导线及开关外，在下列器材中，还必须使用的两种器材是________．A．交流电源B．刻度尺C．天平(含砝码)(3)实验中，先接通电源，再释放重物，得到图乙所示的一条纸带．在纸带上选取三个连续打出的点A、B、C，测得它们到起始点O的距离分别为h A、h B、h C.已知当地重力加速度为g，打点计时器打点的周期为T.设重物的质量为m.从打O点到打B点的过程中，重物的重力势能变化量ΔE p＝__________，动能变化量ΔE k＝________．图乙(4)大多数学生的实验结果显示，重力势能的减少量大于动能的增加量，原因是________．A．利用公式v＝gt计算重物速度B．利用公式v＝2gh计算重物速度C．存在空气阻力和摩擦阻力的影响D．没有采用多次实验取平均值的方法(5)某同学想用下述方法研究机械能是否守恒：在纸带上选取多个计数点，测量它们到起始点O的距离h，计算对应计数点的重物速度v，描绘v2h图象，并做如下判断：若图象是一条过原点的直线，则重物下落过程中机械能守恒．请你分析论证该同学的判断依据是否正确．13．(8分)在做“研究平抛运动”的实验中，为了确定小球不同时刻在空中所通过的位置，实验时用了如图所示的装置．先将斜槽轨道的末端调整水平，在一块平整的木板表面钉上白纸和复写纸．将该木板竖直立于水平地面上，使小球从斜槽上紧靠挡板处由静止释放，小球撞到木板并在白纸上留下痕迹A；将木板向远离槽口的方向平移距离x，再使小球从斜槽上紧靠挡板处由静止释放，小球撞在木板上得到痕迹B；将木板再向远离槽口的方向平移距离x，小球再从斜槽上紧靠挡板处由静止释放，再得到痕迹C.若测得木板每次移动距离x＝10.00 cm.A、B间距离y1＝5.02 cm，B、C间距离y2＝14.82 cm(g＝9.80 m/s2).(1)为什么每次都要使小球从斜槽上紧靠挡板处由静止释放？______________________________________________________.(2)根据以上直接测量的物理量来求得小球初速度的表达式为v0＝________________(用题中所给字母表示)．(3)小球初速度的值为v0＝________ m/s.14．(6分)如图所示，半径为R的半球形陶罐，固定在可以绕竖直轴旋转的水平转台上，转台转轴与过陶罐球心O的对称轴OO′重合，转台以一定角速度ω匀速旋转，一质量为m的小物块落入陶罐内，经过一段时间后，小物块随陶罐一起转动且相对罐壁静止，它和O点的连线与OO′之间的夹角θ为45°.已知重力加速度大小为g，小物块与陶罐之间的最大静摩擦力大小为f＝24mg.(1)若小物块受到的摩擦力恰好为零，求此时的角速度ω0；(2)若小物块一直相对陶罐静止，求陶罐旋转的角速度的最大值和最小值．15．(12分)我国将于2022年举办冬奥会，跳台滑雪是其中最具观赏性的项目之一．如图所示，质量m＝60 kg 的运动员从长直助滑道AB的A处由静止开始以加速度a＝3.6 m/s2匀加速滑下，到达助滑道末端B时速度v B ＝24 m/s，A与B的竖直高度差H＝48 m．为了改变运动员的运动方向，在助滑道与起跳台之间用一段弯曲滑道衔接，其中最低点C处附近是一段以O为圆心的圆弧．助滑道末端B与滑道最低点C的高度差h＝5 m，运动员在B、C间运动时阻力做功W＝－1 530 J，取g＝10 m/s2.(1)求运动员在AB段下滑时受到阻力F f的大小；(2)若运动员能够承受的最大压力为其所受重力的6倍，则C点所在圆弧的半径R至少应为多大．16．(15分)如图所示，一轻质弹簧左端固定在足够长的水平轨道左侧，水平轨道的PQ段粗糙，调节其初始长度为l0＝1.5 m，水平轨道右侧连接半径为R＝0.4 m的竖直圆形光滑轨道，可视为质点的滑块将弹簧压缩至A点后由静止释放，经过水平轨道PQ后，恰好能通过圆形轨道的最高点B.已知滑块质量m＝1 kg，与PQ段间的动摩擦因数μ＝0.4，轨道其他部分摩擦不计．g取10 m/s2，求：(1)弹簧压缩至A点时弹簧的弹性势能E p；(2)若每次均从A点由静止释放滑块，同时调节PQ段的长度，为使滑块在进入圆形轨道后能够不脱离轨道而运动，PQ段的长度l应满足什么条件？高中物理必修一必修二综合测评高中物理必修一必修二综合测评（答案）一、单项选择题(本题共7小题,每小题4分,共28分.)1.甲、乙两个小物体,甲的重力是乙的3倍,它们从同一高度处同时自由下落,不考虑空气阻力,则下列说法中正确的是()A.甲比乙先落地B.甲的加速度比乙大C.甲、乙同时落地h=gt2,t=可知,甲、乙同时落地.2.下列各图分别表示的是某一物体的运动情况或其所受合外力的情况.其中甲图是某物体的位移—时间图象;乙图是某一物体的速度—时间图象;丙图表示某一物体的加速度—时间图象;丁图表示某一物体所受合外力随时间变化的图象.四幅图中的图线都是直线,从这些图象中可判断出一定质量物体的某些运动特征.下列有关说法中不正确的是()A.甲物体受合外力为零B.乙物体受到的合外力不变C.丙物体的速度一定越来越大,甲是匀速运动,乙、丙都是匀变速运动,而丁的加速度越来越大;对丙:如果a与v方向反向,速度会越来越小,故选项C错误.3．已知靠近地面运转的人造卫星，每天转n圈，如果发射一颗同步卫星，它离地面的高度与地球半径的比值为()A．n B．n2C.n3－1D.3n2－1解析：设同步卫星离地面的高度为h，地球半径为R.近地卫星的周期为T1＝24 hn，同步卫星的周期为T2＝24 h，则T1∶T2＝1∶n，对于近地卫星有G MmR 2＝m 4π2T 21R ，对于同步卫星有G Mm ′（R ＋h ）2＝m ′4π2T 22(R ＋h )，联立解得h ＝(3n 2－1)R ，故D 正确．答案：D4.如图所示，质量为m 的物体(可视为质点)以某一速度从A 点冲上倾角为30°的固定斜面，其运动的加速度为34g ，此物体在斜面上上升的最大高度为h ，则在这个过程中物体( )A ．重力势能增加了34mghB ．动能损失了12mghC ．动能损失了mghD ．动能损失了32mgh解析：重力做功W G ＝－mgh ，故重力势能增加了mgh ，A 错．物体所受合力F ＝ma ＝34mg ，合力做功W合＝－Fh sin 30°＝－34mg ×2h ＝－32mgh ，由动能定理知，动能损失了32mgh ，B 、C 错，D 正确．答案：D5.如图所示，两个相对的斜面，倾角分别为37°和53°.在顶点把两个小球以同样大小的初速度分别向左、向右水平抛出，小球都落在斜面上. 若不计空气阻力，则A 、B 两个小球的运动时间之比为( )A ．1∶1B ．4∶3C ．16∶9D ．9∶16解析：两小球均做平抛运动，且均落在斜面上，则对于A 球有tan 37°＝y x ＝12gt 2Av 0t A ＝gt A2v 0，解得t A ＝2v 0tan 37°g ，同理对于B 球有t B ＝2v 0tan 53°g ，则t A t B ＝tan 37°tan 53°＝916，故D 正确．答案：D6.一质量为1 kg 的质点静止于光滑水平面上，从t ＝0时刻开始，受到水平外力F 作用，如图所示．下列判断正确的是( )A ．0～2 s 内外力的平均功率是4 WB ．第2 s 内外力所做的功是4 JC ．第2 s 末外力的瞬时功率最大D ．第1 s 末与第2 s 末外力的瞬时功率之比为9∶5 解析：0～1 s 内，质点的加速度a 1＝F 1m ＝31 m/s 2＝3 m/s 2，则质点在0～1 s 内的位移x 1＝12a 1t 21＝12×3×1 m ＝1.5 m ，1 s 末的速度v 1＝a 1t 1＝3×1 m/s ＝3 m/s ，第2 s 内质点的加速度a 2＝F 2m ＝11m/s 2＝1 m/s 2，第2 s 内的位移x 2＝v 1t 2＋12a 2t 22＝3×1 m ＋12×1×1 m ＝3.5 m ，在0～2 s 内外力F 做功的大小W ＝F 1x 1＋F 2x 2＝3×1.5 J ＋1×3.5 J ＝8 J ，可知0～2 s 内外力的平均功率P ＝W t ＝82 W ＝4 W ，故A 正确；第2 s 内外力做功W 2＝F 2x 2＝1×3.5 J ＝3.5 J ，故B 错误；第1 s 末外力的瞬时功率P 1＝F 1v 1＝3×3 W ＝9 W ，第2 s 末的速度v 2＝v 1＋a 2t 2＝3 m/s ＋1×1 m/s ＝4 m/s ，则外力的瞬时功率P 2＝F 2v 2＝1×4 W ＝4 W ，可知第2 s 末外力的瞬时功率不是最大，第1 s 末和第2 s 末外力的瞬时功率之比为9∶4，故C 、D 错误．答案：A7．如图所示，两颗星组成的双星，在相互之间的万有引力作用下，绕连线上的O 点做周期相同的匀速圆周运动．现测得两颗星之间的距离为L ，质量之比为m 1∶m 2＝3∶2，下列说法中正确的是( ) A ．m 1、m 2做圆周运动的线速度之比为3∶2 B ．m 1、m 2做圆周运动的角速度之比为3∶2 C ．m 1做圆周运动的半径为25LD ．m 2做圆周运动的半径为25L解析：根据F 万＝F 向，对m 1得G m 1m 2L 2＝m 1v 21r 1＝m 1r 1ω2，对m 2得G m 1m 2L 2＝m 2v 22r 2＝m 2r 2ω2，又r 1＋r 2＝L ，由以上各式得v 1v 2＝r 1r 2＝m 2m 1＝23，A 错误．由于T 1＝T 2，故ω＝2πT 相同，B 错误．r 1＝25L ，r 2＝35L ，C 正确，D错误．答案：C二、多项选择题(本大题共3小题，每小题5分，共15分．每小题有多个选项是正确的，全选对得5分，少选得3分，选错、多选或不选得0分)8．我国发射的“嫦娥三号”登月探测器靠近月球后，先在月球表面附近的近似圆轨道上绕月运行；然后经过一系列过程，在离月面4 m 高处做一次悬停(可认为是相对于月球静止)；最后关闭发动机，探测器自由下落．已知探测器的质量约为1.3×103 kg ，地球质量约为月球的81倍，地球半径约为月球的3.7倍，地球表面的重力加速度大小约为9.8 m/s 2，则此探测器( )A ．在着陆前的瞬间，速度大小约为8.9 m/sB ．悬停时受到的反冲作用力约为2×103 NC ．从离开近月圆轨道到着陆这段时间内，机械能守恒D ．在近月圆轨道上运行的线速度小于人造卫星在近地圆轨道上运动的线速度解析：在地球表面附近有G M 地m R 2地＝mg 地，在月球表面附近有G M 月mR 2月＝mg 月，可得g 月＝1.656 m/s 2，所以探测器落地的速度为v ＝2g 月h ＝3.64 m/s ，故A 错误；探测器悬停时受到的反冲作用力为F ＝mg 月≈2×103 N ，B 正确；探测器由于在着陆过程中开动了发动机，因此机械能不守恒，C 错误；在靠近星球的轨道上有G MmR 2＝mg ＝m v 2R ，即有v ＝gR ，可知在近月圆轨道上运行的线速度小于人造卫星在近地圆轨道上运行的线速度，故选项D 正确．答案：BD9.如图所示,车内绳AB 与绳BC 拴住一小球,BC 水平,车由原来的静止状态变为向右加速直线运动,小球仍处于图中所示的位置,则( )A.AB 绳拉力F T 1不变,BC 绳拉力F T 2变大B.AB 绳拉力F T 1变大,BC 绳拉力F T 2变小C.AB 绳拉力F T 1变大,BC 绳拉力F T 2不变F T 1不变,BC 绳拉力F T 2的大小为(F T 1sin θ+ma ) 解析:受力分析如图所示,由F T 1cos θ=mg 可知F T 1不变;由F T 2-F T 1sin θ=ma 可知F T 2=F T 1sin θ+ma.10.如图所示，在“嫦娥”探月工程中，设月球半径为R ，月球表面的重力加速度为g .飞船在半径为4R 的圆形轨道Ⅰ上运动，到达轨道的A 点时点火变轨进入椭圆轨道Ⅱ，到达轨道的近月点B 时，再次点火进入半径约为R 的近月轨道Ⅲ绕月做圆周运动，则( )A ．飞船在轨道Ⅰ上的运行速率等于12g 0R B ．飞船在轨道Ⅰ上的运行速率小于在轨道Ⅱ上B 处的速率 C ．飞船在轨道Ⅰ上的加速度大于在轨道Ⅱ上B 处的加速度 D ．飞船在轨道Ⅰ、轨道Ⅲ上运行的周期之比T Ⅰ∶T Ⅲ＝4∶1 解析：根据G Mm （4R ）2＝m v 214R ，得飞船在轨道Ⅰ上的运行速率v 1＝GM4R，又GM ＝g 0R 2，解得v 1＝ g 0R 4＝12g 0R ，故A 正确；根据G Mmr2＝m v 2r ，解得v ＝GMr，飞船在轨道Ⅰ和轨道Ⅲ上的速率关系为v Ⅲ＞v Ⅰ，飞船在轨道Ⅱ上的B 处减速进入轨道Ⅲ，则飞船在轨道Ⅰ上的运行速率小于在轨道Ⅱ上B 处的速率，故B 正确；根据牛顿第二定律，得a ＝G Mm r 2m ＝GMr 2，飞船在轨道Ⅰ上的加速度小于在轨道Ⅱ上B 处的加速度，故C错误；根据G Mmr 2＝mr 4π2T 2，得T ＝4π2r 3GM，飞船在轨道Ⅰ、轨道Ⅲ上运行的轨道半径之比为4∶1，则周期之比为8∶1，故D 错误．答案：AB三、非选择题(共57分)11.(8分)某同学用图(a)所示的实验装置测量物块与斜面之间的动摩擦因数.已知打点计时器所用电源的频率为50 Hz,物块下滑过程中所得到的纸带的一部分如图(b)所示,图中标出了五个连续点之间的距离图(a )图(b )(1)物块下滑时的加速度a= m/s 2,打C 点时物块的速度v= m/s;(2)已知重力加速度大小为g ,为求出动摩擦因数,还必须测量的物理量是 (填正确答案:标号). A.物块的质量 B.斜面的高度.25 1.79 (2)C 1)滑块下滑的加速度a== m/s2解得a=3.25 m/s2v C=== m/s=1.79 m/s.(2)由mg sin θ-μmg cos θ=ma可得μ=tan θ-,故还需要测出斜面的倾角,选项C正确.12．(8分)利用图甲装置做“验证机械能守恒定律”实验．图甲(1)为验证机械能是否守恒，需要比较重物下落过程中任意两点间的________．A．动能变化量与势能变化量B．速度变化量与势能变化量C．速度变化量与高度变化量(2)(多选)除带夹子的重物、纸带、铁架台(含铁夹)、电磁打点计时器、导线及开关外，在下列器材中，还必须使用的两种器材是________．A．交流电源B．刻度尺C．天平(含砝码)(3)实验中，先接通电源，再释放重物，得到图乙所示的一条纸带．在纸带上选取三个连续打出的点A、B、C，测得它们到起始点O的距离分别为h A、h B、h C.已知当地重力加速度为g，打点计时器打点的周期为T.设重物的质量为m.从打O点到打B点的过程中，重物的重力势能变化量ΔE p＝__________，动能变化量ΔE k＝________．图乙(4)大多数学生的实验结果显示，重力势能的减少量大于动能的增加量，原因是________．A．利用公式v＝gt计算重物速度B．利用公式v＝2gh计算重物速度C．存在空气阻力和摩擦阻力的影响D．没有采用多次实验取平均值的方法(5)某同学想用下述方法研究机械能是否守恒：在纸带上选取多个计数点，测量它们到起始点O的距离h，计算对应计数点的重物速度v，描绘v2h图象，并做如下判断：若图象是一条过原点的直线，则重物下落过程中机械能守恒．请你分析论证该同学的判断依据是否正确．解析：(1)在重物下落过程中，若任意两点间重力势能的减少量等于动能的增加量，则重物的机械能守恒，所以A 正确．(2)打点计时器需要交流电源，测量纸带上各点之间的距离需要刻度尺，本实验需要验证的等式为mgh ＝12m v 2，即gh ＝12v 2(或mgh ＝12m v 22－12m v 21，即gh ＝12v 22－12v 21)，所以不需要测量重物的质量，不需要天平． (3)从打O 点到打B 点的过程中，重力势能的变化量ΔE p ＝－mgh B ，动能的变化量ΔE k ＝12m v 2B ＝12m⎝⎛⎭⎫h C －h A 2T 2＝m （h C －h A ）28T 2.(4)重力势能的减少量大于动能的增加量，主要原因是重物在运动过程中存在空气阻力和摩擦阻力，选项C 正确．(5)该同学的判断依据不正确．在重物下落h 的过程中，若阻力f 恒定，根据mgh －fh ＝12m v 2－0⇒v 2＝2()g －fm h ，可知v 2h 图象就是过原点的一条直线．要想通过v 2h 图象的方法验证机械能是否守恒，还必须看图象的斜率是否接近2g .答案：(1)A (2)AB (3)－mgh B m （h C －h A ）28T 2(4)C (5)见解析13．(8分)在做“研究平抛运动”的实验中，为了确定小球不同时刻在空中所通过的位置，实验时用了如图所示的装置．先将斜槽轨道的末端调整水平，在一块平整的木板表面钉上白纸和复写纸．将该木板竖直立于水平地面上，使小球从斜槽上紧靠挡板处由静止释放，小球撞到木板并在白纸上留下痕迹A ；将木板向远离槽口的方向平移距离x ，再使小球从斜槽上紧靠挡板处由静止释放，小球撞在木板上得到痕迹B ；将木板再向远离槽口的方向平移距离x ，小球再从斜槽上紧靠挡板处由静止释放，再得到痕迹C .若测得木板每次移动距离x ＝10.00 cm.A 、B 间距离y 1＝5.02 cm ，B 、C 间距离y 2＝14.82 cm(g ＝9.80 m/s 2).(1)为什么每次都要使小球从斜槽上紧靠挡板处由静止释放？ ______________________________________________________.(2)根据以上直接测量的物理量来求得小球初速度的表达式为v 0＝________________(用题中所给字母表示)．(3)小球初速度的值为v 0＝________ m/s.解析：(1)每次从斜槽上紧靠挡板处由静止释放小球，是为了使小球离开斜槽末端时有相同的初速度． (2)根据平抛运动在水平方向上为匀速直线运动，则小球从A 到B 和从B 到C 运动时间相等，设为T ；竖直方向由匀变速直线运动推论有y2－y1＝gT2，且v0T＝x.解以上两式得：v0＝xgy2－y1.(3)代入数据解得v0＝1.00 m/s.答案：(1)为了保证小球每次做平抛运动的初速度相同(2)xgy2－y1(3)1.0014．(6分)如图所示，半径为R的半球形陶罐，固定在可以绕竖直轴旋转的水平转台上，转台转轴与过陶罐球心O的对称轴OO′重合，转台以一定角速度ω匀速旋转，一质量为m的小物块落入陶罐内，经过一段时间后，小物块随陶罐一起转动且相对罐壁静止，它和O点的连线与OO′之间的夹角θ为45°.已知重力加速度大小为g，小物块与陶罐之间的最大静摩擦力大小为f＝24mg.(1)若小物块受到的摩擦力恰好为零，求此时的角速度ω0；(2)若小物块一直相对陶罐静止，求陶罐旋转的角速度的最大值和最小值．解析：(1)当小物块受到的摩擦力为零，支持力和重力的合力提供向心力，有mg tan θ＝mω20R sin θ，解得ω0＝2g R.(2)当ω＞ω0时，重力和支持力的合力不够提供向心力，当角速度最大时，摩擦力方向沿罐壁切线向下时摩擦力达到最大值，设此时最大角速度为ω1，由牛顿第二定律，得f cos θ＋F N sin θ＝mω21R sin θ，f sin θ＋mg＝F N cos θ，联立以上三式，解得ω1＝32g 2R.当ω＜ω0时，重力和支持力的合力大于所需向心力，摩擦力方向沿罐壁切线向上，当角速度最小时，摩擦力向上达到最大值，设此最小角速度为ω2，由牛顿第二定律，得F N sin θ－f cos θ＝mω22R sin θ，mg＝F N cos θ＋f sin θ，联立解得ω2＝2g 2R.答案：(1) 2gR(2)32g2R2g2R15．(12分)我国将于2022年举办冬奥会，跳台滑雪是其中最具观赏性的项目之一．如图所示，质量m＝60 kg的运动员从长直助滑道AB 的A 处由静止开始以加速度a ＝3.6 m/s 2匀加速滑下，到达助滑道末端B 时速度v B ＝24 m/s ，A 与B 的竖直高度差H ＝48 m ．为了改变运动员的运动方向，在助滑道与起跳台之间用一段弯曲滑道衔接，其中最低点C 处附近是一段以O 为圆心的圆弧．助滑道末端B 与滑道最低点C 的高度差h ＝5 m ，运动员在B 、C 间运动时阻力做功W ＝－1 530 J ，取g ＝10 m/s 2.(1)求运动员在AB 段下滑时受到阻力F f 的大小；(2)若运动员能够承受的最大压力为其所受重力的6倍，则C 点所在圆弧的半径R 至少应为多大．解析：(1)运动员在AB 上做初速度为零的匀加速运动，设AB 的长度为x ，则有v 2B ＝2ax ，① 由牛顿第二定律，有mg Hx －F f ＝ma ，②联立①②式，代入数据，解得F f ＝144 N ．③(2)设运动员到达C 点时的速度为v C ，在由B 到达C 的过程中，由动能定理，有mgh ＋W ＝12m v 2C －12m v 2B ，④设运动员在C 点所受的支持力为F N ，由牛顿第二定律，有 F N －mg ＝m v 2CR，⑤由运动员能够承受的最大压力为其所受重力的6倍，联立④⑤式，代入数据解得R ＝12.5 m. 答案：(1)144 N (2)12.5 m16．(15分)如图所示，一轻质弹簧左端固定在足够长的水平轨道左侧，水平轨道的PQ 段粗糙，调节其初始长度为l 0＝1.5 m ，水平轨道右侧连接半径为R ＝0.4 m 的竖直圆形光滑轨道，可视为质点的滑块将弹簧压缩至A 点后由静止释放，经过水平轨道PQ 后，恰好能通过圆形轨道的最高点B .已知滑块质量m ＝1 kg ，与PQ 段间的动摩擦因数μ＝0.4，轨道其他部分摩擦不计．g 取10 m/s 2，求：(1)弹簧压缩至A 点时弹簧的弹性势能E p ；(2)若每次均从A 点由静止释放滑块，同时调节PQ 段的长度，为使滑块在进入圆形轨道后能够不脱离轨道而运动，PQ 段的长度l 应满足什么条件？解析：(1)设滑块冲上圆形轨道最高点B 时速度为v ，由能量守恒定律，得 E p ＝12m v 2＋2mgR ＋μmgl 0，①滑块在B 点时，重力提供向心力，由牛顿第二定律，得 mg ＝m v 2R，②联立①②式并代入数据，解得E p＝16 J.(2)若要使滑块不脱离轨道，分两种情况讨论：①滑块能够通过B点而不脱离轨道，则应满足l≤1.5 m，③②滑块能够到达圆形轨道，则应满足E p≥μmgl，解得l≤4 m，④滑块到达圆形轨道而又不超过与圆心等高的C点时，如图所示，临界条件取到达C点时速度恰好为零，则有E p≤mgR＋μmgl，解得l≥3 m，⑤联立③④⑤式，可得PQ段长度l应满足的条件是：l≤1.5 m或3 m≤l≤4 m.答案：(1)16 J(2)l≤1.5 m或3 m≤l≤4 m。

高中数学必修一、必修二、必修三测试题

高中数学必修一、必修二、必修三测试卷总分150分时间120分钟命题人：班级：姓名：总分：一、选择题（本题共12小题，共60分）1、已知集合M＝{x|x≥－1}，N＝{x|2－x2≥0}，则M∪N＝( )A、[－，＋∞)B、[－1，]C、[－1，＋∞)D、(－∞，－]∪[－1，＋∞)2、下列函数中，为奇函数的是（）A、 B、 C、 D、3、设，则的大小关系是（）A、 B、 C、 D、4、已知平面，直线，下面的四个命题中，所有正确命题的序号是（）A、①②B、②③C、①④D、②④5、函数的零点是（）A、x=-2B、x=-1C、x=1D、26、圆:与圆:的位置关系是( )A、相交B、外切C、内切D、相离7、执行右图的程序框图，若输入，那么输出的等于（）A、720B、360C、240D、120输出p（第7题）（第8题）8、执行右图程序框图，如果输入的x,t均为2，则输出的S= （）A、4B、5C、6D、79、用随机数表法从100名学生（其中男生25人）中抽取20人进行评估，某男学生被抽中的概率为（）A、 B、 C、 D、10、右图是2010年在惠州市举行的全省运动会上，七位评委为某跳水比赛项目打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为（）A、84，4.84B、84，1.6C、85，1.6D、85，411、已知的单调递减区间是（）A、 B、 C、 D、12、某几何体的三视图如图所示，则该几何体的表面积为( )A. B.＋6 C.＋5 D.＋5二、填空题（本题共4道小题，共20分）13、完成下列进位制之间的转化：14、甲校有3600名学生，乙校有5400名学生，丙校有1800名学生，为统计三个学校的某方面情况，计划采用分层抽样法，抽取一个容量为90的样本，应在甲校抽取人。

15、已知点是圆上一点，则点P到直线的最小距离为。

16、已知球O与边长为的正方形ABCD相切于该正方形的中心P点，PQ为球O 的直径，若线段QA与球O的球面的交点R恰为线段QA的中点，则球O的体积为．三、解答题（本题共6道小题，共70分）17、设集合实数a的取值范围是？18、已知圆心为的圆经过点.（1）求圆的标准方程；（2）若直线过点且被圆截得的线段长为，求直线的方程.19、已知直线：，直线经过（5，-1），且（1）、求直线的方程。

高一物理必修1、2综合测试题(人教版)

高一物理必修一必修二综合测试题一、选择题（本大题共12小题，共44分。

每小题给出的四个选项中，其中1~8只有一个正确选项，每小题3分；9~12有多个选项正确。

全部选对的得5分，选对但不全的得3分，有选错的得0分。

）1．关于能源的说法正确的是：（）A ．在利用能源的过程中，能量在总量上逐渐减少B ．由于自然界的能量守恒，所以不需要节约能源C ．能源耗散说明能量在转化过程中有方向性D ．人类在不断地开发和利用新能源，所以能量可以被创造2．汽车紧急刹车后，停止运动的车轮在水平地面上滑动直至停止，在地面上留下的痕迹称为刹车线。

由刹车线的长短可知汽车刹车前的速度。

已知汽车轮胎与地面之间的动摩擦因数为0.80，测得刹车线长25m 。

汽车在刹车前的瞬间的速度大小为（重力加速度g 取10m/s 2）：（）A ．10m/sB ．20m/sC ．30m/sD ．40m/s3．如图所示为某校学生开展无线电定位“搜狐”比赛，甲、乙两人从O 点同时出发，并同时到达A 点搜到狐狸，两人的搜狐路径已在图中标出，则：（）A ．甲的平均速度大于乙的平均速度B ．两人运动的平均速度相等C ．甲的位移大于乙的位移D ．甲的路程大于乙的路程4．以下说法中正确的是：（）A ．合力的大小一定大于分力的大小B ．合力的大小至少大于一个分力的大小C ．合力的大小可以比两个分力都小，也可以比两个分力都大D ．若两个分力F 1>F 2，则合力大小的变化范围是F 1>F >F 25．两个物体A 和B ，质量分别为m 1和m 2，互相接触放在光滑的水平面上，如图所示，对物体A 施以水平的推力F ，则物体B 受到A 的作用力等于：（）A ．F m m m 211+ B ．F m m m 212+ C ．F D ．F m m 21 6．如图所示，升降机的水平地面上放有重为G 的物体，它受升降机地面的支持力大小为N ，它对升降机地面压力大小为F ，下列说法正确的是：（）A ．当升降机正上升时，N >GB ．当升降机自由下落时，N =0，G =0C ．当物体超重时，升降机的加速度一定向下D ．不管升降机怎样运动，总有F =N7．滑雪运动深受人民群众的喜爱，某滑雪运动员（可视为质点）由坡道进入竖直面内的圆弧形滑道AB ，从滑道的A 点滑行到最低点B 的过程中，由于摩擦力的存在，运动员的速率不变，则运动员沿AB 下滑过程中：（）A ．所受合外力始终为零B ．所受摩擦力大小不变C ．合外力做功一定为零D ．机械能始终保持不变8．已知地球质量为月球质量的81倍，地球半径约为月球半径的4倍。

高一物理必修1、2综合试题及答案

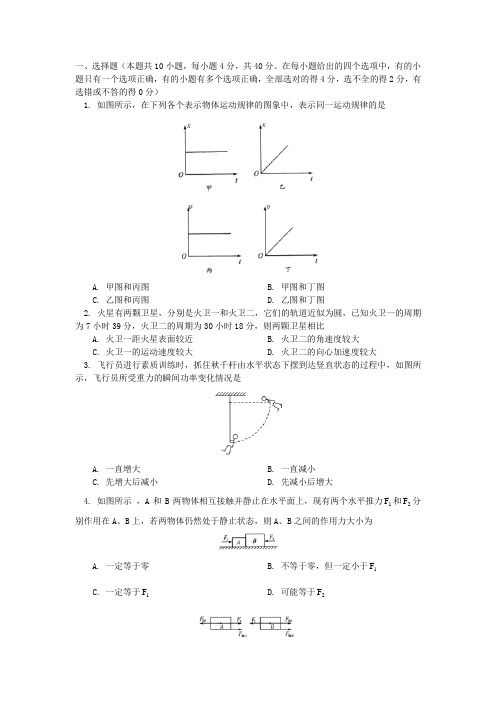
一、选择题（本题共10小题，每小题4分，共40分。

在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确，全部选对的得4分，选不全的得2分，有选错或不答的得0分）1. 如图所示，在下列各个表示物体运动规律的图象中，表示同一运动规律的是A. 甲图和丙图B. 甲图和丁图C. 乙图和丙图D. 乙图和丁图2. 火星有两颗卫星，分别是火卫一和火卫二，它们的轨道近似为圆，已知火卫一的周期为7小时39分，火卫二的周期为30小时18分，则两颗卫星相比A. 火卫一距火星表面较近B. 火卫二的角速度较大C. 火卫一的运动速度较大D. 火卫二的向心加速度较大3. 飞行员进行素质训练时，抓住秋千杆由水平状态下摆到达竖直状态的过程中，如图所示，飞行员所受重力的瞬间功率变化情况是A. 一直增大B. 一直减小C. 先增大后减小D. 先减小后增大4. 如图所示，A 和B 两物体相互接触并静止在水平面上，现有两个水平推力1F 和2F 分别作用在A 、B 上，若两物体仍然处于静止状态，则A 、B 之间的作用力大小为A. 一定等于零B. 不等于零，但一定小于1FC. 一定等于1FD. 可能等于2F5. （经典回放）如图所示，两完全相同的小球质量均为m ，放在竖直挡板和倾角为α的固定斜面间，若缓慢转动挡板至与斜面垂直，此过程中A. A 、B 两球间的弹力逐渐增大B. B 球对挡板的压力逐渐减小C. B 球对斜面的压力逐渐增大D. A 球对斜面的压力逐渐增大6. （经典回放）如图所示，长度相同的三根轻杆构成一个正三角形支架，在A 处固定质量为2m 的小球，B 处固定质量为m 的小球，支架悬挂在O 点，可绕过O 点并与支架所在平面相垂直的固定轴转动，开始时OB 与地面相垂直，放手后开始运动，在不计任何阻力的情况下，下列说法正确的是A. A 球到达最低点时速度为零B. A 球机械能减少量等于B 球机械能增加量C. B 球向左摆动所能达到的最高位置应高于A 球开始运动的高度D. 当支架从左向右回摆时，A 球一定能回到起始高度 7. 对如图所示的皮带传动装置，下列说法中正确的是A. A 轮带动B 轮沿逆时针方向旋转B. B 轮带动A 轮沿逆时针方向旋转C. C 轮带动D 轮沿顺时针方向旋转D. D 轮带动C 轮沿顺时针方向旋转8. 如图所示，在倾角为α的固定光滑斜面上，有一用绳子拴着的长木板，木板上站着一只猫，已知木板的质量是猫的质量的2倍，当绳子突然断开时，猫立即沿着板向上跑，以保持其相对斜面的位置不变，则此时木板沿斜面下滑的加速度为A. αsin 2gB. αsin gC. αsin g 23D. αsin g 29. 如图所示，倾斜的传送带保持静止，一木块从顶端以一定的初速度匀加速下滑到底端，如果让传送带沿图中虚线箭头所示的方向匀速运动，同样的木块从顶端以同样的初速度下滑到底端的过程中，与传送带保持静止时相比A. 木块在没到底端的过程中，摩擦力的冲量变大B. 木块在没到底端的过程中，摩擦力的冲量不变C. 木块在没到底端的过程中，木块克服摩擦力所做的功变大D. 木块在没到底端的过程中，系统产生的内能数值将变大 10. 有一星球的密度与地球的密度相同，但它表面处的重力加速度是地球表面上重力加速度的4倍，则该星球的质量是地球质量的A.41B. 4倍C. 16倍D. 64倍二、实验题（本题共2个小题，共14分，把答案填在相应的横线上） 11. （8分）（2006上海高考）科学探究活动通常包括以下环节：提出问题，作出假设，制定计划，搜集证据，评估交流等。

必修1必修2综合测试题

高一级经济生活、政治生活综合测试本试卷分选择题和非选择题两部分，满分为150分。

考试用时120分钟。

注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名、考生号填写在答题卷上。

2．选择题每小题选出答案后，用2B型铅笔把答题卷上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案；不能答在试题卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卷各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不按以上要求作答的答案无效，不准使用铅笔和涂改液，否则将按考试违规论处。

4．考生必须保持答题卷整洁，不能折叠、撕破、穿孔。

考试结束后，将答题卷交回。

第一部分选择题(共75分)第一部分选择题(共75分)一、选择题I：在每题给出的四个选项中，只有一项是最符合题意的。

本大题共24 小题，每小题2分，共48分。

1．《关于惩治破坏金融秩序犯罪的决定》规定：“明知是伪造的货币而持有、使用、数额较大者，处3年以下有期徒刑或者拘役，并处1万元以上10万元以下的罚金。

”这表明A．纸币是一种等价物B．只有金银货币才能在市场上使用C．纸币也有价值，不允许伪造D．人民币是国家发行的强制使用的价值符号2．在现实生活中，同一晶牌同一质量的商品，有时卖得贵，有时卖得便宜；同一商品在同一时间里，有的商店价格高，有的商店价格低。

对上述现象认识正确的是A．商品价格与价值相背离是绝对的，相符合是暂时的B．等价只是一种观念，理论与实践往往是脱节的C．在商品交换中，等价交换只存在于平均数中，并不存在于每个场合D．商品价值量是由社会必要劳动时间决定的，商品的价格是由销售者决定的3．孔子曾说“不患寡，而患不均”是对当时剥削制度的抨击，但这话若放在当今我国的分配领域来看，则是错误的。

因为它A．违背“社会公平”的原则B．违背“平等互助”的原则C．违背“效率优先”的原则D．违背“等价交换”的原则4．财政政策在促进经济增长方面的功能，主要是通过————来实现的。

高一数学必修一必修二综合测试题(有答案)

高一数学《必修1》《必修2》综合测试题一、选择题（共12小题；每小题5分，共60分）1. 已知全集R U =，集合}32{≤≤-=x x A ，}41{>-<=x x x B 或，则()B C A U ⋃（）A.{}42≤≤-x xB.}43{≥≤x x x 或C.}12{-<≤-x xD.}31{≤≤-x x2. 过点(1,0)且与直线x －2y －2＝0垂直的直线方程是( )A ．x －2y －1＝0B ．x －2y ＋1＝0C ．2x ＋y －2＝0D ．x ＋2y －1＝03. 圆台的一个底面圆周长是另一个底面圆周长的3倍，母线长为3，圆台的侧面积为84π，则圆台较小底面圆的半径为( )A ．3B ．5C ．6D ．74. 已知圆C ：x 2：y 2：4y ：0，直线l 过点P (0,1)，则 ( )A. l 与C 相交B. l 与C 相切C. l 与C 相离D. 以上三个选项均有可能5. 一个几何体的三视图如图所示（单位：m ），则该几何体的体积为（）3mA.π2B.38πC.π3D. 310π6. 已知，则函数的图象不经过（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限7. 若直线2x y -=被圆22()4x a y -+=所截得的弦长为22,则实数a 的值为（） A. 0或4 B. 1或3 C. 2-或6 D. 1-或3 8. 在三棱柱ABCA 1B 1C 1中，各棱长相等，侧棱垂直于底面，点D 是侧面BB 1C 1C 的中心，则AD 与平面BB 1C 1C 所成角的大小是( ) A ．30° B ．45° C ．60° D ．90° 9. 若幂函数)(x f y =是经过点)33,3(，则此函数在定义域上是 ( ) A ．偶函数 B ．奇函数 C ．增函数 D ．减函数 10. 一个多面体的三视图如图所示，则该多面体的表面积为 A.321+ B.318+ C.18 D.21 11.若定义在R 上的偶函数()x f 满足)()2(x f x f =+，且当[]1,0∈x 时，x x f y x x f 3log )(,)(-==则函数的零点个数是（） A ．6个 B ．4个 C ．3个 D ．2个 12. 已知A(3,1)，B(－1,2)，若：ACB 的平分线方程为y ＝x ＋1，则AC 所在的直线方程为( ) A ．y ＝2x ＋4 B ．y ＝12x －3 C ．x －2y －1＝0 D ．3x ＋y ＋1＝001,1a b <<<-x y a b =+二、填空题（共4小题，每小题5分，共20分）13. 若直线1x y +=与圆222(0)x y r r +=>相切，则实数r 的值等于________.14. 在平面直角坐标系中，正三角形ABC 的边BC 所在直线的斜率是0，则AC ，AB 所在直线的斜率之和为________．15. 函数ax x y 22--=()10≤≤x 的最大值是2a ，则实数a 的取值范围是________ ．16.若圆C :x 2+y 2−2ax +b =0上存在两个不同的点A ,B 关于直线x −3y −2=0对称,其中b ∈N ,则圆C 的面积最大时,b = ．三、解答题（共6小题，共70分．解答时应写出必要的文字说明、证明过程或演算步骤）17. (10分)已知f (x )是定义在R 上的奇函数，当x ≥0时，f (x )＝2x －1.(1)求f (3)＋f (－1)；(2)求f (x )的解析式.18. (12分)如图，在三棱锥P ABC 中，PC ⊥底面ABC ，AB ⊥BC ，D ，E 分别是AB ，PB 的中点.(1)求证：DE ∥平面PAC ；(2)求证：AB ⊥PB ．19．(12分)直线l 1过点A (0,1)，l 2过点B (5,0)，如果l 1∥l 2且l 1与l 2的距离为5，求l 1，l 2的方程． 20.（12分）已知圆22:2240C x y mx ny ++++=，直线:10l x my -+=相交于A ：B 两点．：1）若交点为(1,2)A ，求m 及n 的值．：2）若直线l 过点(2,3)：60ACB ∠=︒，求22m n +的值． 21.（12分）已知直线:(1)(23)60m a x a y a -++-+=，:230n x y -+=. （1）当0a =时，直线l 过m 与n 的交点，且它在两坐标轴上的截距相反，求直线l 的方程；（2）若坐标原点O 到直线m 的距离为5，判断m 与n 的位置关系. 22.（12分）(1)圆C 与直线2x ＋y －5＝0切于点(2,1)，且与直线2x ＋y ＋15＝0也相切，求圆C 的方程． (2)已知圆C 和y 轴相切，圆心C 在直线x －3y ＝0上，且被直线y ＝x 截得的弦长为27，求圆C 的方程.高一数学答案一、选择题（共12小题；每小题5分，共60分）. 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 A C D A B A A C D A B C二、填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上13.22 14.0 15.[－1,0] 16.0三、解答题（本大题共6小题，共70分）17.解：(1)∵f (x )是奇函数，∴f (3)＋f (－1)＝f (3)－f (1)＝23－1－2＋1＝6. .................4分(2)设x ＜0，则－x ＞0，∴f (－x )＝2－x －1，∵f (x )为奇函数，∴f (x )＝－f (－x )＝－2－x ＋1，.................8分∴f (x )＝⎩⎪⎨⎪⎧ 2x －1，x ≥0，－2－x ＋1，x ＜0. ........................10分18. 解 (1)证明：因为D ，E 分别是AB ，PB 的中点，所以DE ∥PA.又因为PA ⊂平面PAC ，DE ⊄平面PAC ，所以DE ∥平面PAC. .................6分(2)证明：因为PC ⊥底面ABC ，AB ⊂底面ABC ，所以PC ⊥AB.又因为AB ⊥BC ，PC ∩BC ＝C ，所以AB ⊥平面PBC ，又因为PB ⊂平面PBC ，所以AB ⊥PB. .................6分19．解: 若直线l 1，l 2的斜率都不存在，则l 1的方程为x ＝0，l 2的方程为x ＝5，此时l 1，l 2之间距离为5，符合题意；.................3分若l 1，l 2的斜率均存在，设直线的斜率为k ，由斜截式方程得直线l 1的方程为y ＝kx ＋1，即kx －y ＋1＝0，.................6分由点斜式可得直线l 2的方程为y ＝k (x －5)，即kx －y －5k ＝0，在直线l 1上取点A (0,1)，则点A 到直线l 2的距离d ＝|1＋5k |1＋k2＝5，∴25k 2＋10k ＋1＝25k 2＋25，∴k ＝125. ∴l 1的方程为12x －5y ＋5＝0，l 2的方程为12x －5y －60＝0. .................10分综上知，满足条件的直线方程为l 1：x ＝0，l 2：x ＝5或l 1：12x －5y ＋5＝0，l 2：12x －5y －60＝0. .......12分20.【解析】试题分析：（1）将点()1,2A 代入直线和圆方程，可解得1m =，114n =-．（2）将点()2,3代入直线方程得1m =．又由已知可判断ACB V 是等边三角形．所以有圆心到直线10x y -+=的距离233322d r n ==-，代入解得29n =，从而2210m n +=．试题解析：：1）将点()1,2A 代入直线10x my -+=：∴1210m -+=，解出1m =：再将()1,2A 代入圆2221240x y x ny ++⨯++=： ∴22122440n ++++=，解得114n =-： ∴1m =：114n =-：：2）将点()2,3代入直线10x my -+=：∴2310m -+=，解出1m =：又∵在ACB V 中，CA CB =且60ACB ∠=︒：∴ACB V 是等边三角形．∵圆()()222221230x x y ny nn ++++++-=：即()()22213x y n n +++=-：圆心()1,n --，半径23r n =-：其中圆心到直线10x y -+=的距离222113332211n d r n -++===-+：代入解出29n =：∴2210m n +=：21．（12分）【详解】试题分析：（1）联立360230.x y x y -++=⎧⎨-+=⎩，解得m 与n 的交点为（-21，-9），当直线l 过原点时，直线l 的方程为370x y -=；当直线l 不过原点时，设l 的方程为1x y b b+=-，将（-21，-9）代入得12b =-，解得所求直线方程（2）设原点O 到直线m 的距离为d ，则()()2265123a d a a -+==-++，解得：14a =-或73a =-，分情况根据斜率关系判断两直线的位置关系;试题解析：解：（1）联立360230.x y x y -++=⎧⎨-+=⎩，解得21,9,x y =-⎧⎨=-⎩即m 与n 的交点为（-21，-9）. 当直线l 过原点时，直线l 的方程为370x y -=；当直线l 不过原点时，设l 的方程为1x y b b+=-，将（-21，-9）代入得12b =-，所以直线l 的方程为120x y -+=，故满足条件的直线l 方程为370x y -=或120x y -+=.（2）设原点O 到直线m 的距离为d ，则()()2265123a d a a -+==-++，解得：14a =-或73a =-，当14a =-时，直线m 的方程为250x y --=，此时//m n ；当73a =-时，直线m 的方程为250x y +-=，此时m n ⊥.22.解： (1)设圆C 的方程为(x －a )2＋(y －b )2＝r 2.∵两切线2x ＋y －5＝0与2x ＋y ＋15＝0平行，∴2r ＝|15－(－5)|22＋12＝45，∴r ＝25， ∴|2a ＋b ＋15|22＋1＝r ＝25，即|2a ＋b ＋15|＝10①|2a ＋b －5|22＋1＝r ＝25，即|2a ＋b －5|＝10② 又∵过圆心和切点的直线与过切点的切线垂直，∴b －1a －2＝12③ 由①②③解得⎩⎨⎧ a ＝－2，b ＝－1.∴所求圆C 的方程为(x ＋2)2＋(y ＋1)2＝20.(2)设圆心坐标为(3m ，m )．∵圆C 和y 轴相切，得圆的半径为3|m |，∴圆心到直线y ＝x 的距离为|2m |2＝2|m |.由半径、弦心距、半弦长的关系得9m 2＝7＋2m 2，∴m ＝±1，∴所求圆C 的方程为(x －3)2＋(y －1)2＝9或(x ＋3)2＋(y ＋1)2＝9.。

高中语文必修一必修二必修三综合测试题

高中语文必修一必修二必修三综合测试题人教版高三上学期语文课堂模拟测验一、古文阅读理解本部分旨在检验学生对古代文言文的阅读理解能力。

古文阅读理解模拟题，选自《论语》、《史记》等古代经典著作。

学生需借助古汉语词典等工具，自行理解文本含义。

二、现当代文学鉴赏本部分选取了中国现当代文学中的经典作品，如鲁迅的《呐喊》、巴金的《家》等。

学生需对这些作品进行深入阅读和分析，理解作品所表现的主题、人物形象、艺术手法等。

三、诗歌创作技巧本部分将通过分析古代和现代诗歌的创作技巧，帮助学生了解诗歌的基本创作原则和方法。

学生需根据所选诗歌，分析其韵律、节奏、意象等，理解诗歌的内在情感和精神内涵。

四、文言词汇积累本部分选取古代文言文中的常用词汇，如《古文观止》等，供学生积累和记忆。

学生需通过阅读和注释，理解词汇的含义和用法，提高文言文阅读理解能力。

五、语言表达与应用本部分将通过模拟情境和语境，检验学生的语言表达和应用能力。

学生需运用所学知识，完成短文写作、段落改写、句子翻译等任务，做到表达准确、语言得体、逻辑清晰。

六、传统文化常识本部分将通过历史、文化、地理等方面的知识，检验学生对中国文化的了解和认知。

学生需了解古代文化常识、历史人物、典故等，提高文化素养和人文素质。

七、作文实战演习本部分将通过命题作文、材料作文等形式，检验学生的写作能力和水平。

学生需根据题目要求，结合自身经历和思考，完成一篇结构完整、内容充实、语言流畅的作文。

八、阅读理解专项训练本部分将通过各种类型的文本材料，检验学生的阅读理解和分析能力。

学生需阅读不同领域的文本材料，如文学类文本、社科类文本、科技类文本等，回答问题并完成相关任务。

九、语言表达与应用本部分将通过各种语言表达形式，如口语表达、书面表达等，检验学生的语言表达和应用能力。

学生需根据不同的情境和要求，运用所学知识进行表达，做到表达准确、语言得体、逻辑清晰。

十、名著导读模拟题本部分将选取国内外经典名著作为阅读材料，学生需在深入阅读和理解原著的基础上，回答相关问题并完成相关任务。