第11章组合逻辑电路
第11章 数字电路综合案例

第11章数字电路综合案例内容提要前面的章节介绍了数字电路的基本知识、基本理论、常用器件,以及数字电路分析和设计的基本方法。
本章涉及到复杂数字系统的设计。
数设计对象从译码器、计数器等这些基本逻辑功能电路到了数字钟等综合的数字逻辑系统的设计;设计方法也由采用真值表到求逻辑表达式、画出电路图的方式到通过确定总体方案,采取从局部到整体,用各种中、大规模集成电路来满足要求的数字电路系统的方式。
本章结合数字钟这一实际的案例来介绍数字电路系统的设计方法,进一步提高学生的综合能力和解决实际问题的能力。
基本教学要求1.了解中小规模集成电路的作用及实用方法。
2.了解数字钟电路的原理。
3.掌握综合数字电路系统的设计流程和设计方法。
11.1概述数字系统的设计,采用从整体到局部,再从局部到整理的设计方法。
首先对系统的目标、任务、指标要求等进行分析,确定系统的总体方案;然后把系统的总体方案分成若干功能部件,绘出系统的方框图;之后运用数字电路的分析和设计方法分别进行设计,或者是直接选用集成器件去构成功能部件;最后把这些功能部件连接组合起来,便构成了完整的数字系统,通过对电路的分析和测试修改,完善与优化整个系统。
这是传统的数字系统的设计方法,也是下面要介绍的内容。
随着计算机技术的发展,电子设计自动化EDA成为了现代电子系统设计与仿真的重要手段,对于复杂系统的设计十分有效,尤其是硬件描述语言的使用,使硬件软件化,让数字系统的设计更加方便、高效。
下面以数字钟系统设计为例,介绍综合数字电路系统的设计方法。
数字钟是一种用数字电子技术实现时、分、秒计时的装置,与传统的机械式时钟相比具准确、直观、寿命长等特点。
目前广泛用于个人家庭以及车站、码头、剧场、办公室等公共场所,给人们的生活、学习、工作、娱乐带来极大的方便。
数字钟也是一种典型的数字电路,其中包括了组合逻辑电路和时序逻辑电路。
通过数字钟的设计进一步了解数字系统设计时用到的中小规模集成电路的使用方法,进一步学习与掌握各种组合逻辑电路与时序电路的原理与使用方法。
第11章触发器和时序逻辑电路

第11章 触发器和时序逻辑电路 11章
基本RS触发器图形符号如图11-1b所示,图中 RD S下标的D , D 表示直接输入,非号表示触发信号0时对电路有效,RD 故称 S D 称直接置"1"(直接置位)端, 直接置"0"(直接复位)端, Q 逻辑符号中的小圆圈"○" 表示非号,在 端同样加 "○". 输 入 输 基本RS触发器的逻辑功能表,如下表所示. 出
第11章 触发器和时序逻辑电路 11章
11.1.3. 边沿型JK触发器
边沿触发器是利用电路内部速度差来克服"空翻"现 象的时钟触发器.它的触发方式为边沿触发,通常为下降 沿触发方式,即输入数据仅在时钟脉冲的下降沿这一"瞬 间"起作用.在图11-4b的逻辑符号中,CP输入端用小圆 圈表示低电平有效,而加一三角来表示边沿触发,则CP表 示为下降沿触发. JK触发器是应用最广的基本"记忆"部件,用它可以 组成多种具有其它功能的触发器和数字器件.集成JK触发 器有各种型号和规格,常用的有74HC73A,74HC107A, 74HC76A,等TTL触发器;CC4027,CC4013等CMOS触 发器.
由表11-2可见,R,S全是"1"的输入组合是应当禁止的, 因为当CP=1时,若R=S=1,则导引门G3,G4均输出"0"态, 致使Q==1,当时钟脉冲过去之后,触发器恢复成何种稳态 是随机的.在同步RS触发器中,通常仍设有RD和SD,它们只 允许在时钟脉冲的间歇期内使用,采用负脉冲使触发器置 "1"或置"0",以实现清零或置数,使之具有指定的初始状 态.不用时"悬空",即高电平.R,S端称同步输入端,触 发器的状态由CP脉冲来决定. 同步RS触发器结构简单,但存在两个严重缺点:一是会出 现不确定状态.二是触发器在CP持续期间,当R,S的输入 状态变化时,会造成触发器翻转,造成误动作,导致触发器 的最后状态无法确定.
组合逻辑电路 课后答案
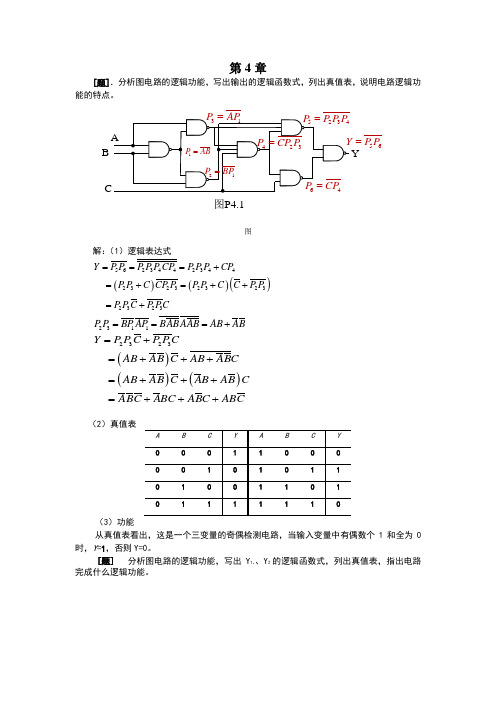
第4章[题].分析图电路的逻辑功能,写出输出的逻辑函数式,列出真值表,说明电路逻辑功能的特点。
图P4.1B YAP 56P P =图解:(1)逻辑表达式()()()5623442344232323232323Y P P P P P CP P P P CP P P C CP P P P C C P P P P C P PC ===+=+=++=+ 2311P P BP AP BABAAB AB AB ===+()()()2323Y P P C P P CAB AB C AB ABC AB AB C AB AB CABC ABC ABC ABC=+=+++=+++=+++(2)真值表(3)功能从真值表看出,这是一个三变量的奇偶检测电路,当输入变量中有偶数个1和全为0时,Y =1,否则Y=0。
[题] 分析图电路的逻辑功能,写出Y 1、、Y 2的逻辑函数式,列出真值表,指出电路完成什么逻辑功能。
图P4.3B1Y 2[解]解: 2Y AB BC AC =++12Y ABC A B C Y ABC A B C AB BC AC ABC ABC ABC ABC =+++=+++++=+++()())由真值表可知:、C 为加数、被加数和低位的进位,Y 1为“和”,Y 2为“进位”。
[题] 图是对十进制数9求补的集成电路CC14561的逻辑图,写出当COMP=1、Z=0、和COMP=0、Z=0时,Y 1~Y 4的逻辑式,列出真值表。
图P4.4[解](1)COMP=1、Z=0时,TG1、TG3、TG5导通,TG2、TG4、TG6关断。
,(2)COMP=0、Z=0时,Y1=A1,Y2=A2,Y3=A3,Y4=A4。
、COMP=1、Z=0时的真值表、Z=0的真值表从略。
[题] 用与非门设计四变量的多数表决电路。
当输入变量A、B、C、D有3个或3个以上为1时输出为1,输入为其他状态时输出为0。
[解] 题的真值表如表所示,逻辑图如图(b)所示。
电工学2第11章组合逻辑电路
分析 逻辑图 设计 功能
已知函数的逻辑图如图所示, 例 : 已知函数的逻辑图如图所示,试求它的逻辑 函数式。 函数式。 从输入端A、 解: 从输入端 、 B开始逐个写出每 开始逐个写出每 个图形符号输出端 的逻辑式,即得: 的逻辑式,即得:
Y = A+ B+ A+ B
Y = A + B + A + B = ( A + B)( A + B) = ( A + B)( A + B)
第11章 组合逻辑电路 11章
脉 冲 信 号 模拟信号:在时间上和 数值上连续的信号。
u
数字信号:在时间上和 数值上不连续的(即离 散的)信号。
u t
数字信号波形(正脉冲) 数字信号波形(正脉冲)
t
模拟信号波形
对模拟信号进行传输、 对模拟信号进行传输、 处理的电子线路称为 模拟电路。 模拟电路。
对数字信号进行传输、 对数字信号进行传输、 处理的电子线路称为 数字电路。 数字电路。
数字电路的分类
按半导体类型可分为: a、按半导体类型可分为: 双极型电路和单极型电路 按半导体类型可分为 b、按电路的集成度可分为: 按电路的集成度可分为: 按电路的集成度可分为 SSI(Small Scale Integrated )电路 数十器件 片) 电路(数十器件 电路 数十器件/片 MSI(Medium Scale Integrated)电路 数百器件 片) 电路(数百器件 电路 数百器件/片 LSI(Large Scale Integrated )电路 数千器件 片) 电路(数千器件 电路 数千器件/片 VLSI (Very Large Scale Integrated )电路 数万器件 片) 电路(数万器件 电路 数万器件/片 ASIC(Application Specific Integrated Circuit,专用集成电路) CPLD(Complex Programmable Logic Device,复杂可编程逻辑器件 ) FPGA(Filed Programmable Gate Array,现场可编程门阵列 ) IP核(Intellectual Property,知识产权) 硬件设计包 SoC(System on a Chip,单片电子系统) CPLD/FPGA—可编程专用IC,或可编程ASIC。 EDA(Electronic Design Automation,电子设计自动化)
组合逻辑电路

⒊ 8-3线优先编码器74LS148
7.2.2 译码器
将给定的二值代码转换为相应的输出信号或另一种形式 二值代码的过程,称为译码。 能实现译码功能的电路称为译码器(Decoder)。译码 是编码的逆过程。 ⒈ 工作原理 为便于分析理解,以2-4线译码器为例。
⒉ 3-8线译码器74LS138
⒊ 译码器应用举例 【例7-6】 试利用74LS138和门电路实现例7-3中要求的 3人多数表决逻辑电路。 解:3人表决逻辑最小项表达式为:
⑵ 现象Ⅱ
⒉ 竞争与冒险的含义 ⑴ 竞争:门电路输入端的两个互补输入信号同时向相反 的逻辑电平跳变的现象称为竞争。 ⑵ 冒险:门电路由于竞争而产生错误输出(尖峰脉冲) 的现象称为竞争-冒险。 对大多数组合逻辑电路来说,竞争现象是不可避免的。 但竞争不一定会产生冒险,而产生冒险必定存在竞争。
⒊ 判断产生竞争-冒险的方法 ⑴ 或(或非)门,在某种条件下形成 时, 会产生竞争现象;与(与非)门,在某种条件下形成 时,会产生竞争现象。 ⑵ 卡诺图中有相邻的卡诺圈相切。
8选1数据选择器74LS151/251
数据选择器应用 【例7-10】 试利用74LS151实现例7-3中要求的3人多 数表决逻辑电路。 解:3人表决逻辑最小项表达式为: Y=
7.2.5 加法器
⒈ 半加器(Half Adder) ⑴ 定义:能够完成两个一位二进制数A和B相加的组 合逻辑电路称为半加器。 ⑵ 真值表:半加器真值表如表7-13,其中S为和, CO为进位。 ⑶ 逻辑表达式:S= =AB;CO=AB ⑷ 逻辑符号:半加器逻辑符号如图7-20所示。
⒉ 全加器(Full Adder)
⑴ 定义:两个一位二进制数A、B与来自低位的进位 CI三者相加的组合逻辑电路称为全加器。
组合逻辑运算

1 1 1
≥1
&
≥1
I2 = I3 = 1 , I1= I0= 0时, Y 1Y 0 = ?
Y1
Y1Y0 = 00
&
当所有的输入都为1时, Y1Y0 = ?
Y0
1
Y1Y0 = 00 无法输出有效编码!
&
结论:普通编码器不能同时输入两个以上 的有效编码信号
总目录 章目录 返回 上一页 下一页
Y0 Y1 Y2 Y3 Y4 Y5 当 S×=1 1或 × 2 S3 × × 1 1 1 1 1 1 S × =0时,译码 1 1 1 × × × × × 器被选通,处于工作状态; 1 1 1 1 1 0 1 1 1 1 1 1 × × × × × 1 0 0 0 0 0 0 1 1 1 1 1 当 S1=01 或1 S 2 S 31=1时,译码 1 0 0 0 0 0 1 1 1 1 0 0 0 1 0 1 1 0 1 1 器处于禁止状态,输出全为1 1 1 0 0 0 1 1 1 1 1 0 1 1 1 0 0 1 0 0 1 1 1 1 0 1 1 0 0 1 0 1 1 1 1 1 1 0 1 0 0 1 1 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1
2. 优先编码器
计算机系统中,经常 有两个或更多输入编码信 号同时有效, 必须根据轻 重缓急,规定好这些外设 允许操作的先后次序,即 优先级别。 识别多个编码请求信号的优先级别,并进行相 应编码的逻辑部件称为优先编码器。
总目录 章目录 返回 上一页 下一页
4/2 线优先编码器:
输入编码信号高电平有效,输出为二进制代码
输出(8421反码)
Y3 Y2 1 1 0 1 0 1 1 0 1 0 1 0 1 0 1 1 1 1 1 1
大学电子电路基础 第十一章

二.触发器的分类
I. 从电路结构不同分 1).基本触发器 2).同步触发器 3).主从触发器 4).边沿触发器 II. 从逻辑功能不同分 1). RS触发器 2). JK触发器 3). T 触发器 4). D 触发器
11.1 基本触发器
11.1.1、 基本RS触发器
1.电路结构与工作原理 (1).电路结构(以与非门构成为例) Q 端、Q 端为两个互补的输出端 ; Q = 1、Q = 0 , 定义为 1 态; RD、SD 端是触发信号引入端。 非号表示“0”触发有效, 脚标“D”表示直接触发 SD 端 是 置 1 端(置位端), RD 端 是 清 0 端(复位端), &
Q
Q ┌
Q ┌
Q ┌ C1 1T
当T触发器的输入控制端为 T=1时,称为T’触发器。
┌
1K C1 1J
CP
T
4.主从JK触发器存在的问题——一次变化现象
例 已知主从JK触发器 J 、 K 的波形如图所示,画出输出 Q 的
波形图(设初始状态为0)。
解:画出输出波形如图示。
CP J K =0
Q
由此看出,主从JK触发器在 CP=1期间,主触发器只变化(翻转)一次,
t D 0 0 设初态Q=0 t
触发器保存下来的状态是CP 作用沿到达时刻的输入状态。 特别注意:当 D 端信号和 CP 作用沿同时跳变时,触发器存 入的是 D 跳变前的状态。
Q
t
触发器的逻辑功能及其描述仿法
本节只讨论有时钟控制的触发器。
有时钟控制的触发器,从功能不同分:
RS 触发器、JK 触发器、T 触发器、 D 触发器等。
n+1 Q = D D=0 0
D = 1 1 D = 0 D=1
数字电路组合逻辑电路

分),如下图。 2)数字电路与数字系统
元
辑
件
符
号
根据前面所述,提出数字电路地概念。数字电路是指以逻辑门为核心元件
连接关系
,以分立元件为辅助元件,根据设计电路所得元件引脚地连接关系组合而成地电路。
逻辑门地输入输出引脚承载地物理量是稳定地电压,只有高,低两种电平,在逻辑上
认为实现了1,0数字地传递。核心电路组合后,我们主要针对电路(函数)输入
形图体现地随时间数据变化地规律,就能找到时序电路地逻辑功能,但在组合电路里,转化为真值表
方法分析电路功能会更好。
8 1.2组合逻辑电路分析
组组合合逻逻辑析辑电电路路分分析 组合逻辑电路设计 电路竞争与冒险 常用组合逻辑电路
3)组合电路分析步骤 要分析逻辑电路功能,就要得到电路地逻辑图,转变为函数,真值表或波形图,然后按照 前面所述去分析其功能。 (1)根据逻辑门组成地电路,确定输入输出变量,从输入端开始,逐级写出每个逻辑门 地逻辑表达式,直到写出所有输出表达式为止。然后利用化简逻辑函数地方法对函数进 行化简,得到最简化地表达式。 (2)根据逻辑表达式列出真值表,根据真值表分析逻辑功能 (3)根据表达式与真值表分析电路地功能确定最后地电路功能,与实践相联系,确定 应用性功能。 该电路实现了或非门地功能。 (4)观察图形,分析电路可能存在地问题 实例1分析如图所示电路,要求: (1)列出逻辑表达式 (2)列真值表 (3)分析逻辑功能 (4)电路使用了几个芯片,哪里不合理?说明原因。
1
第3章
组合逻辑电路分析 组合逻辑电路设计 电路竞争与冒险 常用组合逻辑电路
言宜慢,心宜善
阅 解
推
逻辑 设计
2
组合逻辑电路分析 组合逻辑电路设计 电路竞争与冒险 常用组合逻辑电路
第11章 组合逻辑电路

11.1 数制与编码
11.2 基本逻辑运算 11.3 集成逻辑门电路 11.4 组合逻辑电路
11.5 编码器
11.6 译码器和数字显示
主页面
!
重点:
二进制、十进制、十六进制转换
及8421BCD编码
基本逻辑运算 集成逻辑门电路及应用 组合逻辑电路分析、设计 编码器、译码器功能及应用
=0.9UDD;UOL的理论值为0V,UOL(max)=0.01UDD。所以
CMOS门电路的逻辑摆幅(即高低电平之差)较大,
进制即可。
(4)十六进制转换成二进制
将每一位变成4位二进制数,按位的高低依次排列即可。
(6E.3A5)H=(110 1110.0011 1010 0101)B
(5)十六进制转换成十进制 由“按权相加”法将十六进制数转换为十进制数。 (7A.58)H=7×161+10×160+5×16-1+8×16-2 =112+10+0.3125+0.03125=(122.34375)D
(3)二进制转换成十六进制 用“ 4 位分组”法将二进制数化为十六进制数。 从二进制的小数点开始,分别向左、右按4位分 组,最后不满 4 位的,用 0 补。将每组用对应的十六
进制数代替,就是等值的十六进制数。
(1001101.100111)B=(0100 1101.1001 1100)B=(4D.9C)H 若将二进制数转换为八进制数 ,可将二进制数 分为3位一组,再将每组的3位二进制数转换成一位8
11.1.3 二—十进制码
把若干个0和1按一定规律编排在一起,组成不同的
代码,并赋与每一个代码固定的含义,这叫做编码。 编制代码所遵循的规则叫码制。 BCD码:用二进制代码来表示十进制的0~9十个数。 常见的有8421码、5421码、2421码、余3码、 格雷码等。
《组合逻辑电路》公开课教案

《组合逻辑电路》公开课教案第一章:组合逻辑电路概述1.1 教学目标让学生了解组合逻辑电路的定义和特点使学生掌握组合逻辑电路的基本构成要素培养学生理解组合逻辑电路在数字电路中的应用1.2 教学内容组合逻辑电路的概念组合逻辑电路的特点组合逻辑电路的基本构成要素组合逻辑电路的应用1.3 教学方法采用讲授法,讲解组合逻辑电路的基本概念和特点采用案例分析法,分析组合逻辑电路的应用实例采用互动讨论法,引导学生探讨组合逻辑电路的构成要素1.4 教学准备教案、PPT、教学设备组合逻辑电路的相关案例资料1.5 教学过程1.5.1 导入利用生活中的实例引入组合逻辑电路的概念1.5.2 讲解讲解组合逻辑电路的定义和特点讲解组合逻辑电路的基本构成要素1.5.3 案例分析分析组合逻辑电路的应用实例1.5.4 互动讨论引导学生探讨组合逻辑电路的构成要素第二章:组合逻辑电路的设计方法2.1 教学目标让学生掌握组合逻辑电路的设计方法培养学生运用设计方法解决实际问题的能力2.2 教学内容组合逻辑电路的设计方法组合逻辑电路设计实例2.3 教学方法采用讲授法,讲解组合逻辑电路的设计方法采用案例分析法,分析组合逻辑电路设计实例采用互动讨论法,引导学生探讨设计方法的应用2.4 教学准备教案、PPT、教学设备组合逻辑电路设计的相关案例资料2.5 教学过程2.5.1 导入复习组合逻辑电路的概念,引出设计方法的话题2.5.2 讲解讲解组合逻辑电路的设计方法2.5.3 案例分析分析组合逻辑电路设计实例2.5.4 互动讨论引导学生探讨设计方法的应用第三章:组合逻辑电路的仿真与测试3.1 教学目标让学生掌握组合逻辑电路的仿真与测试方法培养学生运用仿真与测试方法诊断和优化电路的能力3.2 教学内容组合逻辑电路的仿真方法组合逻辑电路的测试方法组合逻辑电路仿真与测试实例3.3 教学方法采用讲授法,讲解组合逻辑电路的仿真与测试方法采用案例分析法,分析组合逻辑电路仿真与测试实例采用互动讨论法,引导学生探讨仿真与测试方法的应用3.4 教学准备教案、PPT、教学设备组合逻辑电路仿真与测试的相关案例资料3.5 教学过程3.5.1 导入复习组合逻辑电路的设计方法,引出仿真与测试的话题3.5.2 讲解讲解组合逻辑电路的仿真方法讲解组合逻辑电路的测试方法3.5.3 案例分析分析组合逻辑电路仿真与测试实例3.5.4 互动讨论引导学生探讨仿真与测试方法的应用第四章:组合逻辑电路的应用实例4.1 教学目标让学生了解组合逻辑电路在实际应用中的典型实例培养学生运用组合逻辑电路解决实际问题的能力4.2 教学内容组合逻辑电路的应用实例4.3 教学方法采用讲授法,讲解组合逻辑电路的应用实例采用案例分析法,分析组合逻辑电路应用实例采用互动讨论法,引导学生探讨应用实例的设计与实现4.4 教学准备教案、PPT、教学设备组合逻辑电路应用实例的相关资料4.5 教学过程4.5.1 导入复习组合逻辑电路的仿真与测试,引出应用实例的话题4.5.2 讲解讲解组合逻辑电路的应用实例4.5第五章:组合逻辑电路的综合设计实例5.1 教学目标让学生掌握组合逻辑电路的综合设计方法培养学生运用综合设计方法解决实际问题的能力5.2 教学内容组合逻辑电路的综合设计方法组合逻辑电路综合设计实例5.3 教学方法采用讲授法,讲解组合逻辑电路的综合设计方法采用案例分析法,分析组合逻辑电路综合设计实例采用互动讨论法,引导学生探讨综合设计方法的应用5.4 教学准备教案、PPT、教学设备组合逻辑电路综合设计的相关案例资料5.5 教学过程5.5.1 导入复习组合逻辑电路的应用实例,引出综合设计的话题5.5.2 讲解讲解组合逻辑电路的综合设计方法5.5.3 案例分析分析组合逻辑电路综合设计实例5.5.4 互动讨论引导学生探讨综合设计方法的应用第六章:组合逻辑电路的优化6.1 教学目标让学生了解组合逻辑电路的优化方法培养学生运用优化方法提高电路性能的能力6.2 教学内容组合逻辑电路的优化方法组合逻辑电路优化实例6.3 教学方法采用讲授法,讲解组合逻辑电路的优化方法采用案例分析法,分析组合逻辑电路优化实例采用互动讨论法,引导学生探讨优化方法的应用6.4 教学准备教案、PPT、教学设备组合逻辑电路优化的相关案例资料6.5 教学过程6.5.1 导入复习组合逻辑电路的综合设计,引出优化的话题6.5.2 讲解讲解组合逻辑电路的优化方法6.5.3 案例分析分析组合逻辑电路优化实例6.5.4 互动讨论引导学生探讨优化方法的应用第七章:组合逻辑电路的troubleshooting 与维护7.1 教学目标让学生掌握组合逻辑电路的troubleshooting 与维护方法培养学生运用troubleshooting 与维护方法解决实际问题的能力7.2 教学内容组合逻辑电路的troubleshooting 方法组合逻辑电路的维护方法组合逻辑电路troubleshooting 与维护实例7.3 教学方法采用讲授法,讲解组合逻辑电路的troubleshooting 与维护方法采用案例分析法,分析组合逻辑电路troubleshooting 与维护实例采用互动讨论法,引导学生探讨troubleshooting 与维护方法的应用7.4 教学准备教案、PPT、教学设备组合逻辑电路troubleshooting 与维护的相关案例资料7.5 教学过程7.5.1 导入复习组合逻辑电路的优化,引出troubleshooting 与维护的话题7.5.2 讲解讲解组合逻辑电路的troubleshooting 方法讲解组合逻辑电路的维护方法7.5.3 案例分析分析组合逻辑电路troubleshooting 与维护实例7.5.4 互动讨论引导学生探讨troubleshooting 与维护方法的应用第八章:组合逻辑电路在现代电路中的应用8.1 教学目标让学生了解组合逻辑电路在现代电路中的应用领域培养学生运用组合逻辑电路解决现代电路问题的能力8.2 教学内容组合逻辑电路在现代电路中的应用领域组合逻辑电路在现代电路中的应用实例8.3 教学方法采用讲授法,讲解组合逻辑电路在现代电路中的应用领域采用案例分析法,分析组合逻辑电路在现代电路中的应用实例采用互动讨论法,引导学生探讨组合逻辑电路在现代电路中的应用8.4 教学准备教案、PPT、教学设备组合逻辑电路在现代电路中的应用领域的相关资料8.5 教学过程8.5.1 导入复习组合逻辑电路的troubleshooting 与维护,引出现代电路应用重点和难点解析1. 教学内容的选取与编排:确保教学内容既能够覆盖组合逻辑电路的基础知识,又能够结合实例深入讲解,使学生能够理解并应用所学知识。
《数字电子技术》详细目录

《数字电子技术》目录第1章数制与编码1.1 数字电路基础知识1.1.1 模拟信号与数字信号1.1.2 数字电路的特点1.2 数制1.2.1 十进制数1.2.2 二进制数1.2.3 八进制数1.2.4 十六进制数1.3 数制转换1.3.1 二进制数与八进制数的相互转换1.3.2 二进制数与十六进制数的相互转换1.3.3 十进制数与任意进制数的相互转换1.4 二进制编码1.4.1 加权二进制码1.4.2 不加权的二进制码1.4.3 字母数字码1.4.4 补码1.5带符号二进制数的加减运算1.5.1 加法运算1.5.2 减法运算第2章逻辑门2.1 基本逻辑门2.1.1 与门2.1.2 或门2.1.3 非门2.2 复合逻辑门2.2.1 与非门2.2.2 或非门2.2.3 异或门2.2.4 同或门2.3 其它逻辑门2.3.1 集电极开路逻辑门2.3.2 集电极开路逻辑门的应用2.3.3 三态逻辑门2.4 集成电路逻辑门2.4.1 概述2.4.2 TTL集成电路逻辑门2.4.3 CMOS集成电路逻辑门2.4.4 集成逻辑门的性能参数2.4.5 TTL与CMOS集成电路的接口*第3章逻辑代数基础3.1 概述3.1.1 逻辑函数的基本概念3.1.2 逻辑函数的表示方法3.2 逻辑代数的运算规则3.2.1 逻辑代数的基本定律3.2.2 逻辑代数的基本公式3.2.3 摩根定理3.2.4 逻辑代数的规则3.3 逻辑函数的代数化简法3.3.1 并项化简法3.3.2 吸收化简法3.3.3 配项化简法3.3.4 消去冗余项法3.4 逻辑函数的标准形式3.4.1 最小项与最大项3.4.2 标准与或表达式3.4.3 标准或与表达式3.4.4 两种标准形式的相互转换3.4.5 逻辑函数表达式与真值表的相互转换3.5 逻辑函数的卡诺图化简法3.5.1 卡诺图3.5.2 与或表达式的卡诺图表示3.5.3 与或表达式的卡诺图化简3.5.4 或与表达式的卡诺图化简3.5.5 含无关项逻辑函数的卡诺图化简3.5.6 多输出逻辑函数的化简*第4章组合逻辑电路4.1 组合逻辑电路的分析4.1.1 组合逻辑电路的定义4.1.2 组合逻辑电路的分析步骤4.1.3 组合逻辑电路的分析举例4.2 组合逻辑电路的设计4.2.1 组合逻辑电路的一般设计步骤4.2.2 组合逻辑电路的设计举例4.3 编码器4.3.1 编码器的概念4.3.2 二进制编码器4.3.3 二-十进制编码器4.3.4 编码器应用举例4.4 译码器4.4.1 译码器的概念4.4.2 二进制译码器4.4.3 二-十进制译码器4.4.4 用译码器实现逻辑函数4.4.5 显示译码器4.4.6 译码器应用举例4.5 数据选择器与数据分配器4.5.1 数据选择器4.5.2 用数据选择器实现逻辑函数4.5.3 数据分配器4.5.4 数据选择器应用举例4.6 加法器4.6.1 半加器4.6.2 全加器4.6.3 多位加法器4.6.4 加法器应用举例4.6.5 加法器构成减法运算电路*4.7 比较器4.7.1 1位数值比较器4.7.2 集成数值比较器4.7.3 集成数值比较器应用举例4.8 码组转换电路4.8.1 BCD码之间的相互转换4.8.2 BCD码与二进制码之间的相互转换4.8.3 格雷码与二进制码之间的相互转换4.9 组合逻辑电路的竞争与冒险4.9.1 冒险现象的识别4.9.2 消除冒险现象的方法第5章触发器5.1 RS触发器5.1.1 基本RS触发器5.1.2 钟控RS触发器5.1.3 RS触发器应用举例5.2 D触发器5.2.1 电平触发D触发器5.2.2 边沿D触发器5.3 JK触发器5.3.1 主从JK触发器5.3.2 边沿JK触发器5.4 不同类型触发器的相互转换5.4.1 概述5.4.2 D触发器转换为JK、T和T'触发器5.4.3 JK触发器转换为D触发器第6章寄存器与计数器6.1 寄存器与移位寄存器6.1.1 寄存器6.1.2 移位寄存器6.1.3移位寄存器应用举例6.2 异步N进制计数器6.2.1 异步n位二进制计数器6.2.2 异步非二进制计数器6.3 同步N进制计数器6.3.1 同步n位二进制计数器6.3.2 同步非二进制计数器6.4 集成计数器6.4.1 集成同步二进制计数器6.4.2 集成同步非二进制计数器6.4.3 集成异步二进制计数器6.4.4 集成异步非二进制计数器6.4.5 集成计数器的扩展6.4.6 集成计数器应用举例第7章时序逻辑电路的分析与设计7.1 概述7.1.1 时序逻辑电路的定义7.1.2 时序逻辑电路的结构7.1.3 时序逻辑电路的分类7.2 时序逻辑电路的分析7.2.1时序逻辑电路的分析步骤7.2.2 同步时序逻辑电路分析举例7.2.3 异步时序逻辑电路分析举例7.3 同步时序逻辑电路的设计7.3.1 同步时序逻辑电路的基本设计步骤7.3.2 同步时序逻辑电路设计举例第8章存储器与可编程器件8.1 存储器概述8.1.1 存储器的分类8.1.2 存储器的相关概念8.1.3 存储器的性能指标8.2 RAM8.2.1 RAM分类与结构8.2.2 SRAM8.2.3 DRAM8.3 ROM8.3.1 ROM分类与结构8.3.2 掩膜ROM8.3.3 可编程ROM8.3.4 可编程ROM的应用8.4 快闪存储器(Flash Memory)8.4.1 快闪存储器的电路结构8.4.2 闪存与其它存储器的比较8.5 存储器的扩展8.5.1 存储器的位扩展法8.5.2 存储器的字扩展法8.6 可编程阵列逻辑8.6.1 PAL的电路结构8.6.2 PAL器件举例8.6.3 PAL器件的应用8.7 通用阵列逻辑8.7.1 GAL的性能特点8.7.2 GAL的电路结构8.7.3 OLMC8.7.4 GAL器件的编程与开发8.8 CPLD、FPGA和在系统编程技术8.8.1 数字可编程器件的发展概况8.8.2数字可编程器件的编程语言8.8.3数字可编程器件的应用实例第9章D/A转换器和A/D转换器9.1 概述9.2 D/A转换器9.2.1 D/A转换器的电路结构9.2.2 二进制权电阻网络D/A转换器9.2.3 倒T型电阻网络D/A转换器9.2.4 D/A转换器的主要技术参数9.2.5 集成D/A转换器及应用举例9.3 A/D转换器9.3.1 A/D转换的一般步骤9.3.2 A/D转换器的种类9.3.3 A/D转换器的主要技术参数9.3.4 集成A/D转换器及应用举例第10章脉冲波形的产生与整形电路10.1 概述10.2 多谐振荡器10.2.1 门电路构成的多谐振荡器10.2.2 采用石英晶体的多谐振荡器10.3 单稳态触发器10.3.1 门电路构成的单稳态触发器10.3.2 集成单稳态触发器10.3.3 单稳态触发器的应用10.4 施密特触发器10.4.1 概述10.4.2 施密特触发器的应用10.5 555定时器及其应用10.5.1 电路组成及工作原理10.5.2 555定时器构成施密特触发器10.5.3 555定时器构成单稳态触发器10.5.4 555定时器构成多谐振荡器第11章数字集成电路简介11.1 TTL门电路11.1.1 TTL与非门电路11.1.2 TTL或非门电路11.1.3 TTL与或非门电路11.1.4 集电极开路门电路与三态门电路11.1.5 肖特基TTL与非门电路11.2 CMOS门电路11.2.1 概述11.2.2 CMOS非门电路11.2.3 CMOS与非门电路11.2.4 CMOS或非门电路11.2.5 CMOS门电路的构成规则11.3 数字集成电路的使用。
数字电路:组合逻辑电路

逻辑代数和普通代数一样,有一套完整的运算规则,包括公理、定理和定律,用它们对逻辑函数式进行处理,可以完成对电路的化简、变换、分析与设计。
一.逻辑代数的基本公式
包括9个定律,其中有的定律与普通代数相似,有的定律与普通代数不同,使用时切勿混淆。
表3.1.1逻辑代数的基本公式
名称
公式1
公式2
表3.2.2三变量全部最小项的真值表
变量
m0
m1
m2
m3
m4
m5
m6
m7
ABC
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
1
0
0
0
0
0
1
0
0
1
0
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
0
0—1律
互补律
重叠律
交换律
结合律
分配律
反演律
吸收律
对合律
表中略为复杂的公式可用其他更简单的公式来证明。
例3.1.1证明吸ຫໍສະໝຸດ 律证:表中的公式还可以用真值表来证明,即检验等式两边函数的真值表是否一致。
例3.1.2用真值表证明反演律 和
证:分别列出两公式等号两边函数的真值表即可得证,见表3.1.2和表3.1.3
本节介绍一种比代数法更简便、直观的化简逻辑函数的方法。它是一种图形法,是由美国工程师卡诺(Karnaugh)发明的,所以称为卡诺图化简法。
组合逻辑电路

电工学
(四)、逻辑函数的化简
20
在对逻辑函数进行化简时,一般是首先把逻辑函数 化为最简与或式,然后再将其转化为其它形式的最简式, 这是由于从最简与或表达式可以方便地转化为其它形式 的最简式。 在对逻辑函数进行化简时,一般是首先把逻辑函数 化为最简与或式,然后再将其转化为其它形式的最简 式,这是由于从最简与或表达式可以方便地转化为其 它形式的最简式。 在对逻辑函数化简时,主要应用前面讨论的逻辑代 数的基本公式和运算规则。
电工学
15
A B
C
F
信息与控制工程学院 电工电子教学与实验中心电工学课程组
电工学
[例8-2] 已知输出逻辑函数F与输入逻辑变量A、B、C 的波形图如下图所示,试列出该函数的真值表,写出函 数表达式,画出逻辑图。
A B
C
16
F
信息与控制工程学院 电工电子教学与实验中心电工学课程组
电工学
解:①根据波形图求真值表
电工学
1
组合逻辑电路
第八章
本章开始我们将介绍数字电路,数字电路与模拟电路是不 同的,它的特点是,输入与输出信号在时间上和大小上都是不 连续的,电子器件工作在非线性状态,数字电路主要研究输出 与输入信号之间的逻辑关系,因此也将其称为逻辑电路。
第一节 逻辑运算与逻辑门
数字逻辑电路中的输入变量和输出变量之间是逻辑关系,因此 在分析与设计数字逻辑电路时,要用到逻辑运算。本节将讨论逻 辑运算的基本规则和定律以及常用的逻辑门。
(2)由真值表可以确定输入信号 在不同状态下输出函数的状态, 如果输入变量和输出函数的1状态 用高电平表示,0状态用低电平表 示,则可以画出输出与输入之间 的波形图(也叫时序图)。
0 0 0 1 1 1 1 0 1 1 0 0 1 1
Multisim14电子系统仿真与设计第11章 Multisim14在数字电路中的应用

Y (A, B,C, D, E) ABCDE ABCDE ABCDE ABCDE ABCDE ABCDE ABCDE ABCDE ABCDE ABCDE ABCDE
11.1.1 逻辑函数的化简
2)打开逻辑转换仪 点击从A到H八个变量上方与之
11.3 A/D与D/A转换电路的分析与设计
11.3.1 A/D转换电路的仿真分析
滑动变阻器R1构成分 压电路,通过改变滑动变 阻器的大小,即可改变输 入模拟信号的大小,ADC 输出的高4位和低4位分别 接1个数码管,显示输入模 拟信号的转换结果。
11.3 A/D与D/A转换电路的分析与设计
11.3.1 A/D转换电路的仿真分析
11.2.4 555定时器仿真与分析
1. 555定时电路的无稳态工作方式的仿真分析
参数说明: Vs:工作电压。 Frequency:工作频率。 Duty:占空比。 C:电容大小。 Cf:反馈电容大小。 R1、R2、RL:电阻,其中 R1、R2不可更改。
11.2.4 555定时器仿真与分析
第11章 Multisim14 在数字电路中的应用
CHINA MACHINE PRESS
11.1 组合逻辑电路的仿真与分析
11.1.1 逻辑函数的化简
例:将下列逻辑表达式化成最简形式:
Y (A, B,C, D, E) ABCDE ACDE ABCD ABDE BCDE ABCDE ABCDE
11.2.4 555定时器仿真与分析
在Multisim14中有专门针对555定时器设计的向导,通过向导可以很方便地 构建555定时器应用电路。
单击菜单“Tools”→“Circuit Wizards”→“555 Timer Wizard”命 令,可启动定时器使用向导。“Type” 下拉列表框中的选项列表可以设定555定 时电路的两种工作方式:无稳态工作方 式和单稳态工作方式。
电工学-组合逻辑电路A

F=A+B+C
A B
>1
A 1F B
>1
F
C
C
(一)复合门电路
3. 与或非门
A
B
F=AB+CD
C
D
第11章11 2
&
F
>1
&
4. 异或门 F=AB+AB
A
=1
F
C
5. 同或门 F=AB+AB
A
=1
F
B
第11章11 3
例:试用与非门来组成非门、与门及或门。
A
&
A
B
F
&
非门
F
A
&
B
A
&
B
&
& 与门 F=AB
模拟电路的地位和作用
1、工作频率很高的信号只能由模拟电路处理。 2、微弱信号的放大,数字电路不能完成。 3、大功率放大电路,只能由模拟电路完成。 4、与物理世界的接口,必须经过一定的模拟信号处理。 5、与传输介质接口(载波传输),主要应用模拟信号。 6、易于实现各种非线性电路,如相乘器等。
完整的电子系统是模拟-数字混合系统,
F
=AB
或门 F=A+B
&
=A+B
F
=AB
第11章11 2
TTL与非门组件就是将若干个与非门电路, 经过集成电路工艺制作在同一芯片上。
+VC 14 13 12 11 10 9 8 74LS00组件含有
两个输入端的与
&
&
非门四个。
74LS00
电工学组合逻辑电路

组
合
信号输入端 A
≥1
逻
信号控制端 B
F
辑
电
路 当 B = 0 时,F = A 门打开
当 B = 1 时,F = 1 门关闭
大连理工大学电气工程系
4
第 12
章 或门还可以起控制门的作用
组
合
信号输入端 A
≥1
逻
信号控制端 B
F
辑
电
路 当 B = 0 时,F = A 门打开
当 B = 1 时,F = 1 门关闭
大连理工大学电气工程系
第 12
章 二、 与门电路
组 合
+U
真值表
逻 辑
AB F
F
00 0
电
路
A
01 0
B
10 0
11 1
A
&
F
B
6
F=A·B A ·0 = 0 A ·1 = A A ·A = A A ·A = 0
与运算 (逻辑乘)
与逻辑和与门
大连理工大学电气工程系
7
第 12
章 与门也可以起控制门的作用
C3
CI CO
Σ CI CO
C2
Σ CI CO
C1
Σ
C0
CI CO
F4
F3
F2
F1
4 位全加器逻辑图
大连理工大学电气工程系
29
第
12
章
12.5 编码器
组 可实现编码功能的组合逻辑电路。
合
逻
辑
控制信息
编码器
二进制代码
电
路
二进制编码器
编码器的分类
普通编码器 二-十进制编码器
组合逻辑电路

第11章组合逻辑电路11.1.1 电路如题图11.1.1所示,A、B是数据输入端、C是控制输入端,试分析在控制端C=0和C=1的情况下,数据输入A、B和输出Y之间的关系。
题图11.1.1解Y A B C A B C A B C+(A+B)C=⋅⋅=当C = 1时,Y =AB,电路起与门作用;当C = 0时,Y= A+B,电路起或门作用。
11.1.2 逻辑电路如题图11.1.2所示,试证明两电路的逻辑功能相同。
题图11.1.2解Y1 =AB A B=A B+AB⋅Y2 =A AB B AB==Y1⋅⋅⋅A AB+BAB=(A+B)(AB)=A B+AB11.1.3 逻辑电路如题图11.1.3所示。
写出Y的逻辑式,画出用与非门实现的逻辑图。
解Y=(A+B)D+(C+D)A=A C A D B D⋅⋅,用与非门实现的逻辑图如题图11.1.3A所示。
题图11.1.3 题图11.1.3A11.1.4 电路如题图11.1.4所示,分析电路的逻辑功能。
解Y A B B C A C=A B+B C+A C=⋅⋅列真值表如题表11.1.4A所示。
当A,B,C三个输入变量中有两个或两个以上为1时,Y=1,否则为0。
11.1.4题图11.1.5 试用异或门设计一个有三个输入端,一个输出端的组合逻辑电路。
其功能为当3个输入信号中有奇数个1时,电路输出为1,否则为0。
解根据题意列真值表如题表11.1.5A所示。
由真值表可得逻辑函数表达式Y=ABC+ABC+ABC+ABC A(B C)+A B C=⊕⊕A B C=⊕⊕电路如题图11.1.5A所示。
题表11.1.5A题图11.1.5A11.1.6 设计一个组合逻辑电路,该电路输入端接收两个二位二进制数A=A2A1,B=B2B1。
当A>B时,输出Y=1,否则Y=0。
解比较两数大小总是从高位开始进行比较,仅当高位相同时才比较低位,而且二进制数只有1或0两种可能的取值,可分别用原变量和反变量表示,所以,可直接写出该逻辑电路的输出函数表达式22222211Y=A B+A B+A B A B()化简得22121211Y=A B+A B B+A A B若用与非门实现Y,则应将上式变成与非表达式2212121122121211Y=A B+A B B+A A B=A B A B B A A B⋅⋅逻辑电路图如题图11.1.6A所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
输出 Y 1 0 0 0 0 0 D0 D1 D2 D3
地址输入端
控制端 数 据 输 入 端 控制端 数 据 输 入 端
输出端
输出端
8选1数据选择器的逻辑表达式:
Y D0 ( A2 A1 A0 ) D1 ( A2 A1 A0 ) D2 ( A2 A1 A0 ) D3 ( A2 A1 A0 ) D4 ( A2 A1 A0 ) D5 ( A2 A1 A0 ) D6 ( A2 A1 A0 ) D7 ( A2 A1 A0 )
8选1数据选择器74LS151
重点内容
例1:试用4选1数据选择器74LS153实现如下逻辑函数的 组合逻辑电路。
Y AB A
解:逻辑函数变形为最小项之和形式
Y AB A AB AB AB m1 m 2 m 3 D0 m 0 D1 m1 D2 m 2 D3 m 3
A A1 74LS153 D0 D 1 D2 D3 S
B
C
A0
1
11.6.4
数据选择器
从多路数据中选择其中所需要的一路数据输出。 例:四选一数据选择器
A0 A1
控制信号 输 入 数 据
D3 D2 D1 D0
S
输出数据
Y
使能端
一、数据选择器(74LS153)的工作原理
数 据 输 入 端
D0 D1 D2 D3 A1 A0 1 1 1 1 1
& ≥1
Y 输出端
地址输入 端 控制端
比较可得: D0=0,D1=1,D2=1,D3=1
Y Y
1 2
74LS153 A1 A0 S
D0 D1 D2 D3
0 1 1 1
A B 0
重点内容
例2 设计一个用3个开关控制灯的逻辑电路,要求任一 个开关都能控制灯的由亮到灭或由灭到亮。
解:设3个开关分别表示为A、B、C,为“0”时表示 开关打开,为“1”时表示开关闭合,Y为“1”表示灯 亮,为“0”表示灯熄,则可写真值表如下
A
B
C
Y
0 0 0 0 1 1 1 1
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
0 1 1 0 1 0 0 1
Y A BC ABC AB C ABC ( A B)C ( AB)C ( AB)C ( AB )C
令A1 A,A0 B,则D0 D3 C,D1 D2 C Y
S
Y [ D0 ( A1 A0 ) D1 ( A1 A0 ) D2 ( A1 A0 ) D3 ( A1 A0 )] S
Y [ D0 ( A1 A0 ) D1 ( A1 A0 ) D2 ( A1 A0 ) D3 ( A1 A0 )] S
功能表 A1 × 0 0 1 1 输入 A0 × 0 1 0 1
