高中数学1.3基本算法语句素材1苏教版必修

合集下载

高中数学必修三之知识讲解_基本算法语句_基础

基本算法语句【学习目标】1、正确理解输入语句、输出语句、赋值语句的结构.2、会写一些简单的程序.3、掌握赋值语句中的“=”号的作用.4、正确理解条件语句和循环语句的概念，并掌握其结构的区别与联系.5、会应用条件语句和循环语句编写程序.【要点梳理】要点一、输入语句在程序中的INPUT语句就是输入语句.这个语句的一般格式是：其中，“提示内容”一般是提示用户输入什么样的信息.功能：可对程序中的变量赋值．要点诠释：①“提示内容”提示用户输入什么样的信息，必须加双引号，提示内容“原原本本”的在计算机屏幕上显示，提示内容与变量之间要用分号隔开；②变量是指程序在运行时其值是可以变化的量；③一个语句可以给多个变量赋值，中间用“，”分隔，但最后的变量的后面不需要；④要求输入的数据必须是常量，而不能是函数、变量或表达式；⑤无计算功能.例如，输入一个学生数学，语文，英语三门课的成绩，可以写成：INPUT “数学，语文，英语”；a，b，c要点二、输出语句在程序中的PRINT语句是输出语句.它的一般格式是：同输入语句一样，表达式前也可以有“提示内容”.功能：可输出表达式的值，计算.要点诠释：①“提示内容”提示用户输出什么样的信息，提示内容必须加双引号，提示内容要用分号和表达式分开；②表达式是指程序要输出的数据，可以是变量、计算公式或系统信息；③一个语句可以输出多个表达式，不同的表达式之间可用“，”分隔；④有计算功能，可以输出常量、变量或表达式的值以及字符.要点三、赋值语句用来表明赋给某一个变量一个具体的确定值的语句.它的一般格式是：赋值语句中的“=”叫做赋值号.功能：先计算出赋值号右边表达式的值，然后把这个值赋给赋值号左边的变量，使该变量的值等于表达式的值.要点诠释：①赋值号的左右两边不能对换，如“A=B”“B=A”的含义运行结果是不同的；②格式中右边“表达式”可以是一个数据、常量和算式，如果“表达式”是一个算式时，赋值语句的作用是先计算出“=”右边表达式的值，然后将该值赋给“=”左边的变量；③赋值号左边只能是变量名字，而不能是表达式，如：2=X 是错误的；④不能利用赋值语句进行代数式的演算(如化简、因式分解等)；⑤对于一个变量可以多次赋值；⑥有计算功能；⑦赋值号与数学中的等号的意义是不同的.赋值号左边的变量如果原来没有值，则执行赋值语句后，获得一个值，如果已有值，则执行该语句后，以赋值号右边表达式的值代替该变量的原值，即将“原值”冲掉.要点四、条件语句算法中的条件结构是由条件语句来表达的，是处理条件分支逻辑结构的算法语句.它的一般格式是：(IF-THEN-ELSE 格式)当计算机执行上述语句时，首先对IF 后的条件进行判断，如果条件符合，就执行THEN 后的语句1，否则执行ELSE 后的语句2.其对应的程序框图为：(如上右图)在某些情况下，也可以只使用IF-THEN 语句：(即IF-THEN 格式)计算机执行这种形式的条件语句时，也是首先对IF 后的条件进行判断，如果条件符合，就执行THEN 后的语句，如果条件不符合，则直接结束该条件语句，转而执行其他语句.其对应的程序框图为：(如上右图)要点诠释：条件语句的作用：在程序执行过程中，根据判断是否满足约定的条件而决定是否需要转换到何处去.需要计算机按条件进行分析、比较、判断，并按判断后的不同情况进行不同的处理.IF 条件 THEN 语句END IF要点五、循环语句算法中的循环结构是由循环语句来实现的.对应于程序框图中的两种循环结构，一般程序设计语言中也有当型(WHILE 型)和直到型(UNTIL 型)两种语句结构.即WHILE 语句和UNTIL 语句.1.WHILE 语句的一般格式是：其中循环体是由计算机反复执行的一组语句构成的.WHLIE 后面的“条件”是用于控制计算机执行循环体或跳出循环体的.当计算机遇到WHILE 语句时，先判断条件的真假，如果条件符合，就执行WHILE 与WEND 之间的循环体；然后再检查上述条件，如果条件仍符合，再次执行循环体，这个过程反复进行，直到某一次条件不符合为止.这时，计算机将不执行循环体，直接跳到WEND 语句后，接着执行WEND 之后的语句.因此，当型循环有时也称为“前测试型”循环.其对应的程序结构框图为：(如上右图)2.UNTIL 语句的一般格式是：其对应的程序结构框图为：(如上右图)直到型循环又称为“后测试型”循环，从UNTIL 型循环结构分析，计算机执行该语句时，先执行一次循环体，然后进行条件的判断，如果条件不满足，继续返回执行循环体，然后再进行条件的判断，这个过程反复进行，直到某一次条件满足时，不再执行循环体，跳到LOOP UNTIL 语句后执行其他语句，是先执行循环体后进行条件判断的循环语句.要点诠释当型循环与直到型循环的区别①当型循环是先判断后执行，直到型循环是先执行后判断；②当型循环用WHILE 语句，直到型循环用UNTIL 语句；③对同一算法来说，当型循环和直到型循环的条件互为反条件．【典型例题】类型一：输入语句、输出语句和赋值语句例1．判断下列输入、输出语句是否正确？为什么？（1）输入语句INPUT a ；b ；cWHILE 条件循环体 WENDDO 循环体 LOOP UNTIL 条件（2）输入语句INPUT x=3（3）输出语句PRINT A=4（4）输出语句PRINT 20，3*2【解析】（1）错，变量之应用“，”隔开；（2）错，INPUT语句中只能是变量而不能是表达；（3）错，PRINT语句中不能用赋值号“=”；（4）对，PRINT语句可以输出常量、变量、表达的值。

高中数学(各版本教材目录)

高中数学各版本新教材目录体系比较第三章统计案例§1 回归分析1.1回归分析1.2相关系数1.3可线性化的回归分析阅读材料高尔顿与回归§2 独立性检验2.1条件概率与独立事件阅读材料概率与法庭2.2独立性检验2.3独立性检验的基本思想2.4独立性检验的应用《数学选修4-1 几何证明选讲》第一章直线、多边形、圆§1 全等与相似§2 圆与直线§3 圆与四边形第二章圆锥曲线§1 截面欣赏§2 直线与球、平面与球的位置关系§3 柱面与平面的截面§4 平面截圆锥面§5 圆锥曲线的几何性质《数学选修4-2 矩阵与变换》第一章平面向量与二阶方阵§1平面向量及向量的运算§2向量的坐标表示及直线的向量方程§3二阶方阵与平面向量的乘法第二章几何变换与矩阵§1几种特殊的矩阵变换§2矩阵变换的性质第三章变换的合成与矩阵乘法§1变换的合成与矩阵乘法§2矩阵乘法的性质第四章逆变换与逆矩阵§1逆变换与逆矩阵§2初等变换与逆矩阵§3二阶行列式与逆矩阵§4可逆矩阵与线性方程组第五章矩阵的特征值与特征向量§1矩阵变换的特征值与特征向量§2特征向量在生态模型中的简单应用《数学选修4-4坐标系与参数方程》第一章坐标系§1 平面直角坐标系§2 极坐标系§3 柱坐标系和球坐标系第二章参数方程§1 参数方程的概念§2 直线和圆锥曲线的参数方程§3 参数方程化成普通方程§4 平摆线和渐开线§5 圆锥曲线的几何性质《数学选修4-5不等式选讲》第一章不等关系与基本不等式§1 不等式的性质§2 含有绝对值的不等式§3 平均值不等式§4 不等式的证明§5 不等式的应用第二章几个重要不等式§1 柯西不等式§2 排序不等式§3 数学归纳法与贝努利不等式。

高中数学必修三知识点推荐

高中数学必修三知识点推荐以下是作者为大家整理的关于《高中数学必修三知识点推荐》的文章，供大家学习参考！第一章算法初步1.1.1 算法的概念1、算法概念：在数学上，现代意义上的“算法”通常是指可以用运算机来解决的某一类问题是程序或步骤，这些程序或步骤必须是明确和有效的，而且能够在有限步之内完成.2. 算法的特点:(1)有限性：一个算法的步骤序列是有限的，必须在有限操作之后停止，不能是无穷的.(2)肯定性：算法中的每一步应当是肯定的并且能有效地实行且得到肯定的结果，而不应当是模棱两可.(3)顺序性与正确性：算法从初始步骤开始，分为若干明确的步骤，每一个步骤只能有一个肯定的后继步骤，前一步是后一步的条件，只有实行完前一步才能进行下一步，并且每一步都准确无误，才能完成问题.(4)不性：求解某一个问题的解法不一定是的，对于一个问题可以有不同的算法.(5)普遍性：很多具体的问题，都可以设计公道的算法去解决，如心算、运算器运算都要经过有限、事先设计好的步骤加以解决.1.1.2 程序框图1、程序框图基本概念：（一）程序构图的概念：程序框图又称流程图，是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形。

一个程序框图包括以下几部分：表示相应操作的程序框；带箭头的流程线；程序框外必要文字说明。

（二）构成程序框的图形符号及其作用程序框名称功能起止框表示一个算法的起始和终止，是任何流程图不可少的。

输入、输出框表示一个算法输入和输出的信息，可用在算法中任何需要输入、输出的位置。

处理框赋值、运算，算法中处理数据需要的算式、公式等分别写在不同的用以处理数据的处理框内。

判定框判定某一条件是否成立，成立时在出口处标明“是”或“Y”；不成立时标明“否”或“N”。

学习这部分知识的时候，要掌控各个图形的形状、作用及使用规则，画程序框图的规则以下：1、使用标准的图形符号。

2、框图一样按从上到下、从左到右的方向画。

3、除判定框外，大多数流程图符号只有一个进入点和一个退出点。

苏教版高中数学目录

苏教版高中数学目录篇一：苏教版高中数学教材目录必修一第一章集合1.1集合的含义及其表示1.2子集、全集、补集1.3交集、并集第二章函数2.1函数的概念和图象2.2指数函数2.3对数函数2.4幂函数2.5函数与方程2.6函数模型及其应用必修二第一章立体几何初步1.1空间几何体1.2点、线、面之间的位置关系1.3空间几何体的表面积和体积第二章平面解析几何初步 2.1直线与方程2.2圆与方程2.3空间直角坐标系必修三第一章算法初步1.1算法的含义1.2流程图1.3基本算法语句1.4算法案例第二章统计2.1抽样方法2.2总体分布的估计2.3总体特征数的估计2.4线性回归方程第三章概率3.1随机事件及其概率3.2古典概型3.3几何概型3.4互斥事件必修四第一章三角函数1.1任意角、弧度1.2任意角的三角函数1.3三角函数的图象与性质第二章平面向量2.1向量的概念与表示2.2向量的线性运算2.3向量的坐标表示2.4向量的数量积2.5向量的应用第三章三角恒等变换3.1两角和与差的三角函数3.2二倍角的三角函数3.3几个三角恒等式必修五第一章解三角形1.1正弦定理1.2余弦定理1.3正弦定理、余弦定理的应用第二章2.1数列2.2等差数列2.3等比数列第三章3.1不等关系3.2一元二次不等式3.3二元一次不等式组与简单线性规划3.4《基本不等式》选修1-1第一章常用逻辑用语1.1命题及其关系1.2充分条件与必要条件1.3简单的逻辑联结词1.4全称量词与存在量词第二章圆锥曲线与方程2.1椭圆2.2双曲线2.3抛物线第三章导数及其应用3.1变化率与导数3.2导数的计算3.3导数在研究函数中的应用3.4生活中的优化问题举例选修1-2第一章统计案例1.1回归分析的基本思想及其初步应用 1.2独立性检验的基本思想及其初步应用第二章推理与证明2.1合情推理与演绎推理2.2直接证明与间接证明第三章数系的扩充与复数的引入3.1数系的扩充和复数的概念3.2复数代数形式的四则运算第四章框图4.1流程图4.2结构图选修2-1第一章常用逻辑用语1.1命题及其关系1.2充分条件与必要条件1.3简单的逻辑联结词1.4全称量词与存在量词第二章圆锥曲线与方程2.1曲线与方程2.2椭圆2.3双曲线2.4抛物线第三章空间向量与立体几何3.1空间向量及其运算3.2立体几何中的向量方法选修2-2第一章导数及其应用1.1变化率与导数1.2导数的计算1.3导数在研究函数中的应用1.4生活中的优化问题举例1.5定积分的概念1.6微积分的基本定理1.7微积分的简单应用第二章推理与证明2.1合情推理与演绎推理2.2直接证明与间接证明2.3数学归纳法第三章数系的扩充与复数的引入3.1数系的扩充和复数的概念3.2复数代数形式的四则运算选修2-3第一章计数原理1.1分类加法技术原理与分步乘法计数原理1.2排列与组合1.3二项式定理第二章随机变量及其分布2.1离散型随机变量及其分布列2.2二项分布及其应用2.3离散型随机变量的均值与方差2.4正态分布第三章统计案例3.1回归分析的基本思想及其初步应用3.2独立性检验的基本思想及其初步应用篇二：苏教版高中数学目录数学1第1章集合1.1集合的含义及其表示1.2子集、全集、补集1.3交集、并集第2章函数概念与基本初等函数Ⅰ2.1函数的概念和图象函数的概念和图象函数的表示方法函数的简单性质映射的概念2.2指数函数分数指数幂指数函数2.3对数函数对数对数函数2.4幂函数2.5函数与方程二次函数与一元二次方程用二分法求方程的近似解 2.6函数模型及其应用数学2第3章立体几何初步3.1空间几何体棱柱、棱锥和棱台圆柱、圆锥、圆台和球中心投影和平行投影直观图画法空间图形的展开图柱、锥、台、球的体积3.2点、线、面之间的位置关系平面的基本性质空间两条直线(来自: 小龙文档网:苏教版高中数学目录)的位置关系直线与平面的位置关系平面与平面的位置关系第4章平面解析几何初步4.1直线与方程直线的斜率直线的方程两条直线的平行与垂直两条直线的交点平面上两点间的距离点到直线的距离 4.2圆与方程圆的方程直线与圆的位置关系圆与圆的位置关系4.3空间直角坐标系空间直角坐标系空间两点间的距离数学3第5章算法初步5.1算法的意义5.2流程图5.3基本算法语句5.4算法案例第6章统计6.1抽样方法6.2总体分布的估计6.3总体特征数的估计6.4线性回归方程第7章概率7.1随机事件及其概率7.2古典概型7.3几何概型7.4互斥事件及其发生的概率数学4第8章三角函数8.1任意角、弧度8.2任意角的三角函数8.3三角函数的图象和性质第9章平面向量9.1向量的概念及表示9.2向量的线性运算9.3向量的坐标表示9.4向量的数量积9.5向量的应用第10章三角恒等变换10.1两角和与差的三角函数10.2二倍角的三角函数10.3几个三角恒等式数学5 第11章解三角形11．1正弦定理11．2余弦定理11．3正弦定理、余弦定理的应用第12章数列12．1等差数列12．2等比数列12．3数列的进一步认识第13章不等式13．1不等关系113．2一元二次不等式13．3二元一次不等式组与简单的线性规2．3双曲线2．4抛物线划问题13．4基本不等式选修系列1 1-1第1章常用逻辑用语1．1命题及其关系1．2简单的逻辑联结词1．3全称量词与存在量词第2章圆锥曲线与方程2．1圆锥曲线2．2椭圆2．3双曲线2．4抛物线2．5圆锥曲线与方程第3章导数及其应用3．1导数的概念3．2导数的运算3．3导数在研究函数中的应用3．4导数在实际生活中的应用1-2第1章统计案例1．1假设检验1．2独立性检验1．3线性回归分析1．4聚类分析第2章推理与证明2．1合情推理与演绎推理2．2直接证明与间接证明2．3公理化思想第3章数系的扩充与复数的引入3．1数系的扩充3．2复数的四则运算3．3复数的几何意义第4章框图4．1流程图5．2结构图选修系列2 2-1第1章常用逻辑用语1．1命题及其关系1．2简单的逻辑连接词1．3全称量词与存在量词第2章圆锥曲线与方程2．1圆锥曲线2．2椭圆2．5圆锥曲线的统一定义2．6曲线与方程第3章空间向量与立体几何3．1空间向量及其运算3．2空间向量的应用2-2第1章导数及其应用1．1导数的概念1．2导数的运算1．3导数在研究函数中的应用1．4导数在实际生活中的应用1．5定积分第2章推理与证明2．1合情推理与演绎推理2．2直接证明与间接证明2．3数学归纳法2．4公理化思想第3章数系的扩充与复数的引入6．1数系的扩充3．2复数的四则运算3．3复数的几何意义2-3第1章计数原理1．1两个基本原理1．2排列1．3组合1．4计数应用题1．5二项式定理第2章概率2．1随机变量及其概率分布2．2超几何分布2．3独立性2．4二项分布2．5离散型随机变量的均值与方差2．6正态分布第3章统计案例3．1假设检验3．2独立性检验3．3线性回归分析4．4聚类分析2篇三：苏教版高中数学目录（苏教版）高中数学目录高中数学必修教材目录必修一必修二必修三必修四必修五高中数学选修教材目录选修1-1选修1-2选修2-1选修2-2选修2-3。

〖高中数学必修苏教版目录〗

高中数学新课标苏教版教材目录数学1第1章集合§1.1集合的含义及其表示§1.2子集、全集、补集§1.3交集、并集第2章函数概念与基本初等函数Ⅰ§2.1函数的概念和图象§函数的概念和图象§函数的表示方法§函数的简单性质§映射的概念§2.2指数函数§分数指数幂§指数函数§2.3对数函数§对数§对数函数§2.4幂函数§2.5函数与方程§二次函数与一元二次方程§用二分法求方程的近似解§2.6函数模型及其应用数学2第3章立体几何初步§3.1空间几何体§棱柱、棱锥和棱台§圆柱、圆锥、圆台和球§中心投影和平行投影§直观图画法§空间图形的展开图§柱、锥、台、球的体积§3.2点、线、面之间的位置关系§平面的基本性质§空间两条直线的位置关系§直线与平面的位置关系§平面与平面的位置关系第4章平面解析几何初步§4.1直线与方程§直线的斜率§直线的方程§两条直线的平行与垂直§两条直线的交点§平面上两点间的距离§点到直线的距离§4.2圆与方程§圆的方程§直线与圆的位置关系§圆与圆的位置关系§4.3空间直角坐标系§空间直角坐标系§空间两点间的距离数学3第5章算法初步§5.1算法的意义§5.2流程图§5.3基本算法语句§5.4算法案例第6章统计§6.1抽样方法§6.2总体分布的估计§6.3总体特征数的估计§6.4线性回归方程第7章概率§7.1随机事件及其概率§7.2古典概型§7.3几何概型§7.4互斥事件及其发生的概率数学4第8章三角函数§8.1任意角、弧度§8.2任意角的三角函数§8.3三角函数的图象和性质第9章平面向量§9.1向量的概念及表示§9.2向量的线性运算§9.3向量的坐标表示§9.4向量的数量积§9.5向量的应用第10章三角恒等变换§10.1两角和与差的三角函数§10.2二倍角的三角函数§10.3几个三角恒等式数学5第11章解三角形§11.1正弦定理§11.2余弦定理§11.3正弦定理、余弦定理的应用第12章数列§12.1等差数列§12.2等比数列§12.3数列的进一步认识第13章不等式§13.1不等关系§13.2一元二次不等式§13.3二元一次不等式组与简单的线性规划问题§13.4基本不等式选修系列11-1第1章常用逻辑用语§1.1命题及其关系§1.2简单的逻辑联结词§1.3全称量词与存在量词第2章圆锥曲线与方程§2.1圆锥曲线§2.2椭圆§2.3双曲线§2.4抛物线§2.5圆锥曲线的共同性质第3章导数及其应用§3.1导数的概念§3.2导数的运算§3.3导数在研究函数中的应用§3.4导数在实际生活中的应用1-2第1章统计案例§1.1独立性检验§1.2线性回归分析第2章推理与证明§2.1合情推理与演绎推理§2.2直接证明与间接证明第3章数系的扩充与复数的引入§3.1数系的扩充§3.2复数的四则运算§3.3复数的几何意义第4章框图§4.1流程图§4.2结构图选修系列22-1第1章常用逻辑用语§1.1命题及其关系§1.2简单的逻辑连接词§1.3全称量词与存在量词第2章圆锥曲线与方程§2.1圆锥曲线§2.2椭圆§2.3双曲线§2.4抛物线§2.5圆锥曲线的统一定义§2.6曲线与方程第3章空间向量与立体几何§3.1空间向量及其运算§3.2空间向量的应用2-2第1章导数及其应用§1.1导数的概念§1.2导数的运算§1.3导数在研究函数中的应用§1.4导数在实际生活中的应用§1.5定积分第2章推理与证明§2.1合情推理与演绎推理§2.2直接证明与间接证明§2.3数学归纳法第3章数系的扩充与复数的引入§3.1数系的扩充§3.2复数的四则运算§3.3复数的几何意义2-3第1章计数原理§1.1两个基本原理§1.2排列§1.3组合§1.4计数应用题§1.5二项式定理第2章概率§2.1随机变量及其概率分布§2.2超几何分布§2.3独立性§2.4二项分布§2.5离散型随机变量的均值与方差§2.6正态分布第3章统计案例§3.1独立性检验§3.2线性回归分析主要编写人员情况主编单墫副主编李善良陈永高主要编写人员数学与应用数学方面：单墫陈永高苏维宜蒋声丁德成洪再吉许道云孙智伟李跃文王晓谦尤建功秦厚荣唐忠明钱定边傅珏生葛福生夏建国孙智伟汪任观数学教育与数学史方面：李善良赵振威葛军徐稼红周焕山朱家生高中数学教师与教研员：仇炳生冯惠愚张乃达祁建新樊亚东石志群董林伟张松年陈光立陆云泉孙旭东于明寇恒清王红兵卫刚单墫 1943年生，南京师范大学数学系教授，博士生导师，享受政府特殊津贴。

苏教版高中数学必修一知识点总结

苏教版高中数学必修一知识点总结【篇一：苏教版高中数学必修一知识点总结】必修一第一章集合与函数概念 1.用字母表示下列集合。

必修1：集合、函数概念与基本初等函数（指、对、幂函数）必修2：立体几何初步、平面解析几何初步。

必修3：算法初步、统计、概率。

必修4：基本初等函数（三角函数）、平面向量、三角恒等变换。

必修5：解三角形、数列、不等式。

以上是每一个高中学生所必须学习的。

上述内容覆盖了高中阶段传统的数学基础知识和基本技能的主要部分，其中包括集合、函数、数列、不等式、解三角形、立体几何初步、平面解析几何初步等。

不同的是在保证打好基础的同时，进一步强调了这些知识的发生、发展过程和实际应用，而不在技巧与难度上做过高的要求。

优秀文档，精彩无限！优质文档，精彩无限！优秀文档，精彩无限！优质文档，精彩无限！引言 1.课程内容：必修课程由5 个模块组成：必修1：集合、函数概念与基本初等函数（指、对、幂函数）必修2：立体几何初步、平面解析几何初步。

必修3：算法初步、统计、概率。

必修4：三角函数、平面向量、三角恒等变换。

必修5：解三角形、数列、不等式。

以上是每一个高中学生所必须学习的。

不同的是在保证打好基础的同时，进一步强调了这些知识的发生、发展过程和实际应用，而不在技巧与难度上做过高的要求。

此外，基础内容还增加了向量、算法、概率、统计等内容。

选修课程有3 个系列：选修系列1：由2 个模块组成。

选修1—1：常用逻辑用语、圆锥曲线与方程、导数及其应用。

选修1—2：统计案例、推理与证明、数系的扩充与复数的引入、框图选修系列2：由3 个模块组成。

选修2—1：常用逻辑用语、圆锥曲线与方程、空间向量与立体几何。

选修2—2：导数及其应用，推理与证明、数系的扩充与复数的引入选修2—3：计数原理、概率，统计案例。

高中数学必修三1.3算法案例-辗转相除法

解：1）先求1734与816的最大公约数
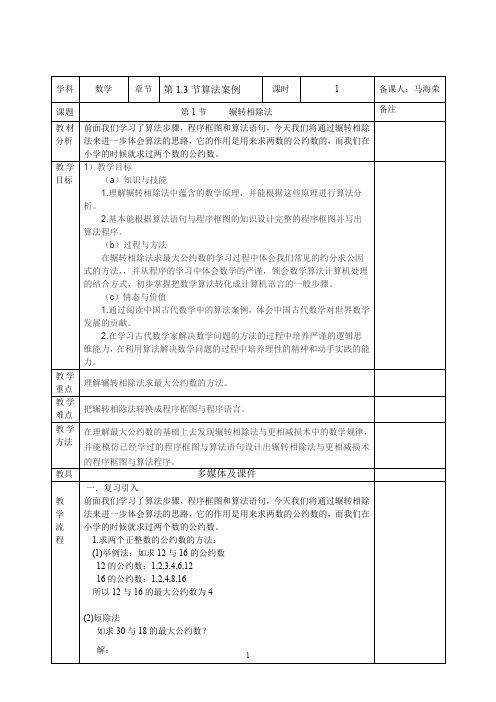
1734=816×2＋102
816=102×8
2）再求102与1343的最大公约数
1343=102×13＋17
102=17×6
所以17为102与1343的最大公约数
所以17为1734、816、1343这三个数的最大公约数
板
书
设
计
第1.3节算法案例-----辗转相除法
............................... ................................... ...............
课后作业
P45练习：1.
P48习题1.3A组：1.
课
后
反
思
1.辗转相除法的思想2.辗转相除法算法框图3.例题讲解
................................ ................................... ...............
............................... ................................... ...............
2.基本能根据算法语句与程序框图的知识设计完整的程序框图并写出算法程序。
（b）过程与方法
在辗转相除法求最大公约数的学习过程中体会我们常见的约分求公因式的方法，，并从程序的学习中体会数学的严谨，领会数学算法计算机处理的结合方式，初步掌握把数学算法转化成计算机语言的一般步骤。
（c）情态与价值
1.通过阅读中国古代数学中的算法案例，体会中国古代数学对世界数学发展的贡献。
PRINT m
END
课堂练习：1.求两数4081与20723的最大公约数.

高中数学必修1、3、4、5知识点归纳及公式大全

必修1数学知识点第一章、集合与函数概念§1.1.1、集合 1、把研究的对象统称为元素，把一些元素组成的总体叫做集合。

集合三要素：确定性、互异性、无序性。

2、只要构成两个集合的元素是一样的，就称这两个集合相等。

3、常见集合：正整数集合：*N 或+N ，整数集合：Z ，有理数集合：Q ，实数集合：R .4、集合的表示方法：列举法、描述法.§1.1.2、集合间的基本关系1、一般地，对于两个集合A 、B ，如果集合A 中任意一个元素都是集合B 中的元素，则称集合A 是集合B 的子集。

记作B A ⊆.2、如果集合B A ⊆，但存在元素B x ∈，且A x ∉，则称集合A 是集合B 的真子集.记作：A B.3、把不含任何元素的集合叫做空集.记作：∅.并规定：空集合是任何集合的子集.4、如果集合A 中含有n 个元素，则集合A 有n2个子集.§1.1.3、集合间的基本运算1、一般地，由所有属于集合A 或集合B 的元素组成的集合，称为集合A 与B 的并集.记作：B A .2、一般地，由属于集合A 且属于集合B 的所有元素组成的集合，称为A 与B 的交集.记作：B A .3、全集、补集？{|,}U C A x x U x U =∈∉且§1.2.1、函数的概念1、设A 、B 是非空的数集，如果按照某种确定的对应关系f ，使对于集合A 中的任意一个数x ，在集合B 中都有惟一确定的数()x f 和它对应，那么就称B A f →:为集合A 到集合B 的一个函数，记作：()A x x f y ∈=,. 2、一个函数的构成要素为：定义域、对应关系、值域.如果两个函数的定义域相同，并且对应关系完全一致，则称这两个函数相等.§1.2.2、函数的表示法1、函数的三种表示方法：解析法、图象法、列表法.§1.3.1、单调性与最大（小）值1、注意函数单调性证明的一般格式：解：设[]b a x x ,,21∈且21x x <，则：()()21x f x f -=…§1.3.2、奇偶性1、一般地，如果对于函数()x f 的定义域内任意一个x ，都有()()x f x f =-，那么就称函数()x f 为偶函数.偶函数图象关于y 轴对称.2、一般地，如果对于函数()x f 的定义域内任意一个x ，都有()()x f x f -=-，那么就称函数()x f 为奇函数.奇函数图象关于原点对称.第二章、基本初等函数（Ⅰ）§2.1.1、指数与指数幂的运算1、一般地，如果a x n=，那么x 叫做a 的n 次方根。

最全高中数学必修三知识点总结归纳(经典版)

最全高中数学必修三知识点总结归纳(经典版)必修三知识点总结归纳（经典版）第一章算法初步1.1.1 算法的概念算法是指可以用计算机来解决的某一类问题的程序或步骤，必须是明确和有效的，而且能够在有限步之内完成。

算法具有有限性、确定性、顺序性与正确性、不唯一性和普遍性等特点。

1.1.2 程序框图程序框图又称流程图，是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形。

一个程序框图包括起止框、输入、输出框、处理框和判断框等部分，需要掌握各个图形的形状、作用及使用规则。

算法的三种基本逻辑结构是顺序结构、条件结构和循环结构。

顺序结构是最简单的算法结构，由若干个依次执行的处理步骤组成，是任何一个算法都离不开的一种基本算法结构。

循环语句循环结构可以通过循环语句来实现。

在程序设计语言中，一般有两种循环结构：当型（WHILE型）和直到型（UNTIL 型），对应于程序框图中的两种循环结构。

下面分别介绍这两种语句结构。

1.WHILE语句WHILE语句的一般格式如下：WHILE 条件循环体WEND当计算机遇到WHILE语句时，先判断条件的真假。

如果条件符合，就执行WHILE与XXX之间的循环体。

然后再检查上述条件，如果条件仍符合，再次执行循环体，这个过程反复进行，直到某一次条件不符合为止。

这时，计算机将不执行循环体，直接跳到WEND语句后，接着执行XXX之后的语句。

因此，当型循环有时也称为“前测试型”循环。

2.UNTIL语句UNTIL语句的一般格式如下：DO循环体LOOP UNTIL 条件当计算机执行该语句时，先执行一次循环体，然后进行条件的判断。

如果条件不满足，继续返回执行循环体，然后再进行条件的判断，这个过程反复进行，直到某一次条件满足时，不再执行循环体，跳到LOOP UNTIL语句后执行其他语句。

因此，直到型循环又称为“后测试型”循环。

注意，是先执行循环体后进行条件判断的循环语句。

辗转相除法与更相减损术1.辗转相除法辗转相除法，也叫欧几里德算法，用于求最大公约数。

灌云县四队中学2013-2014学年高中数学教案：基本算法语句——循环语句 (苏教版必修3)

四队中学教案纸备课时间教学目标重点难点教学课题
（学科：高一数学）
教时 4 计划
教学 3 课时
1．掌握两种循环语句的一般形式，进一步体会算法的基本思想． 2．能够熟练地运用两种循环语句．两种循环语句的形式和特点两种循环语句的形式和特点
教学过程
在本课之前学生已经学习了流程图以及算法设计的三种结构，所以将这个问题的解决留给学生．开始建构数学能不能写出该算法的伪代码呢？用条件语句来表示选择结构．介绍两种循环语句．s ← 1 1．For 循环语句 i ← 1 一般形式： For I From“初值”To“终值”Step“步长” „ i ← i＋1 End For 其中“For”和“End For”之间的步骤“„” s ← 2(s＋1) 称为循环体．若步长为 1， “Step‘步长’ ”可以省略不写．
1
Y
数学运用试设计一个算法，计算 1×3×5×7×„×99． s ← 1 s ← 1 For i From 3 To 99 Step 2 i ← 1 s ← s×i While i≤99 End For s ← s×i Print s i ← i＋2 End End While Print s End
i≤9 2．While 循环语句 N 一般形式：While A 输出 s „ End While 结束其中 A 表示判断执行循环的条件． “While”和 “End While”之间的步骤“„”称为循环体． “While”循环语句的特点是前测试，即先判断，后执行．若初始条件不成立，则循环体的内容一次也不 s ← 1 执行． s ← 1 用 i ← 1 这两种循环语句 i ← 1 可以 While i≤9 写出上述问题的 For I From 1 To 9 Step 1 伪代码： s ← 2(s＋1) s ← 2(s＋1) i ← i＋1 End For Print s i ← i＋1 End While Print s

高中数学基本算法语句——赋值、输入、输出语句苏教版必修三教案

基本算法语句——赋值、输入、输出语句教学目标（1）正确理解赋值语句、输入语句、输出语句的结构；（2）让学生充分地感知、体验应用计算机解决数学问题的方法；（3）通过实例，使学生理解3种基本的算法语句（输入语句、输出语句和赋值语句）的表示方法、结构和用法，能用这三种基本的算法语句表示算法，进一步体会算法的基本思想．教学重点正确理解输入语句、输出语句、赋值语句的作用．教学难点准确写出输入语句、输出语句、赋值语句．教学过程一、问题情境1．问题1：已知我班某学生上学期期末考试语文、数学和英语学科成绩分别为80、100、89，试设计适当的算法求出这名学生三科的平均分．二、学生活动12．怎样将以上算法转换成计算机能理解的语言呢？下面我们将通过伪代码学习基本的算法语句．三、建构数学1．伪代码：伪代码是介于自然语言和计算机语言之间的文字和符号，是表达算法的简单而实用的好方法．为了今后能学好计算机语言，我们在伪代码中将使用一种计算机语言“BASIC语言”的关键词．2．赋值语句：赋值语句是将表达式所代表的值赋给变量的语句．例如：“x y←”表示将y的值赋给x，其中x是一个变量，y是一个与x同类型的变量或表达式．说明：①赋值语句中的赋值号“←”的左右两边不能对换，它将赋值号右边的表达式的值赋给赋值号左边的变量；②赋值语句左边只能是变量名字，而不是表达式，右边表达式可以是一个数据、常量或表达式；③对于一个变量可以多次赋值．例1．写出求23x=时多项式3273511x x x+-+的值的算法．算法1322373511xp x x←←+-+算法223((73)5)11xp x x x←←+-+说明：①以上两种算法，算法1要做6次乘法，算法2只要做3次乘法，由此可见，算法的好坏会影响运算速度；②算法2称为“秦九韶算法”，其算法特点是：通过一次式的反复计算，逐步得出高次多项式的值；对于一个n次多项式，只要做n次乘法和n次加法．附：秦九韶（1202—1261年），字道古，普州安岳（今四川安岳）人．他是我国古代最有成就的数学家之一．著有数学名著《数书九章》（又名数学九章》）．该书共十八卷，分为大衍、天时、田域、测望、赋役、钱谷、营建、军旅、市易等九大类，每类用九个例题全书共八十一题）来阐明各种算法．这部中世纪的数学杰作，许多方面都有创造，而书中最突出的成就是“大衍求一术”和高次方程的数值解法“正负开方术”，是具有世界意义的成就．3．输入、输出语句：输入、输出语句分别用“Input”（或者“Read”）和“Print”来描述数据的输入和输出．（1）输入语句与赋值语句的区别在于：赋值语句可以将一个代数表达式的值赋于一个变量，而输入语句由于要求输入的值只能是具体的常数，不能是函数、变量或表达式，因此输入语句只能将读入的具体数据赋给变量．（2）输出语句的主要作用是：①输出常量、变量的值和系统信息；②输出数值计算的结果．例如：可以将问题1中的算法改进为求任意三门功课的平均值的算法．算法：S1 a←80S2 b←100S3 c←89流程图：流程图：说明：输入语句“Read a ，b ”表示输入的数据依次送给a ，b ；“Print A ”表示输出运算结果A ．四、数学运用 1．例题：例2．“鸡兔同笼”是我国隋朝时期的数学著作《孙子算经》中的一个有趣而具有深远影响的题目：“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？”请你先列出解决这个问题的方程组，并设计一个解二元一次方程组的通用算法，并画出流程图，写出伪代码．解：设有x 只鸡，y 只兔子，则352494x y x y +=⎧⎨+=⎩．设二元一次方程组为1111221222,(0),a x b y c a b a b a x b y c +=⎧-≠⎨+=⎩用消元法解得2112122112211221b c b c x a b a b a c a c y a b a b -⎧=⎪-⎪⎨-⎪=⎪-⎩，因此，只要输入相应的未知数的系数和常数项，就能计算出方程组的解，即可输出,x y 的值．五、回顾小结：1．赋值语句、输入语句、输出语句的结构和作用．六、课外作业：补充：1．将五进制数化为十进制数的方法是“按权展开”，如将(5)1403化为十进制数为321015450535228⨯+⨯+⨯+⨯=．试用输入输出语句、赋值语句表示将五进制数(5)abcd 化为十进制数的算法．2．请用伪代码编写程序，实现三个变量1,2,3A B C ===的值按顺序互换，即A B C A →→→之间的交换．伪代码：Read a ，b ，cA ←(a+b+c)/3 Print AA ←(a+b+c)/3 结束开始输出A 输入a,b,c 开始结束。

高中数学必修三-基本算法语句

基本算法语句知识集结知识元基本算法语句知识讲解1．伪代码（算法语句）【知识点的认识】1．伪代码：一种介于自然语言和计算机语言之间的文字和符号．2．基本算法语句：（1）输入语句：实现算法的输入信息功能．INPUT“提示内容”；变量或INPUY“提示内容1，提示内容2，提示内容3，…”；变量1，变量2，变量3，…说明：①“提示内容”提示用户输入什么样的信息，变量是指程序在运行时其值是可以变化的量．②输入语句要求输入的值只能是具体的常数，不能是函数、变量或表达式．③提示内容与变量之间用分号“；”隔开，若输入多个变量，变量与变量之间用逗号“，”隔开．（2）输出语句：实现算法的输出结果功能．PRINT“提示内容”；表达式说明：①“提示内容”提示用户输入什么样的信息，表达式是指程序要输出的数据．②输出语句可以输出常量、变量或表达式的值及字符．（3）赋值语句：表明赋给某个变量一个具体的确定值的语句．变量＝表达式（其中“＝”为赋值号）说明：①先计算赋值号右边的表达式的值，再把求得的值赋值给左边的变量，使该变量的值等于表达式的值．②赋值号左边只能是变量名字，不能是表达式，且赋值号左右不能对换．③注意赋值号“＝”与数学中等号意义不同，不能用于进行代数式的演算．（4）条件语句：处理条件分支逻辑结构的算法语句．（IF﹣THEN﹣ELSE格式）（IF﹣THEN格式）IF条件THEN IF条件THEN语句1 语句ELSE ENDIF语句2ENDIF说明：①IF﹣THEN﹣ELSE：执行时，先对IF后的条件进行判断，若条件符合，执行语句1，否则执行语句2．②IF﹣THEN：执行时，先对IF后的条件进行判断，若条件符合，执行THEN后的语句，否则结束条件语句，执行其他语句．（5）循环语句：实现算法中的循环结构，分WHILE（当型）和UNTIL（直到型）两种语句．（WHILE语句）（UNTIL语句）WHILE条件DO循环体循环体WEND LOOPUNTIL条件说明：①WHILE语句：前测试型循环．先判断真假，若条件符合执行循环体，再判断条件真假，若仍符合，再次执行，如此反复，直到某次条件不符合为止，跳出循环体，执行WEND之后的语句．②UNTIL语句：先执行，再判断条件是否符合，若不符合，再次执行，再判断，如此反复，直到条件符合为止，跳出循环体，执行循环体外的语句．【命题方向】伪代码知识点的考查常以选择、填空题形式出现，难度不大，属于基础题．掌握各种基本算法语句的定义，了解它们的格式和作用，是正确理解伪代码的关键，也是解此类题的关键．（1）程序运行计算例：根据下列算法语句，当输入x为60时，输出y的值为（）A.25B.30C.31D.61分析：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是计算并输出分段函数y＝的函数值．解答：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是计算并输出分段函数y＝的函数值．当x＝60时，则y＝25+0.6（60﹣50）＝31，故选C．点评：算法是新课程中的新增加的内容，也必然是新高考中的一个热点，应高度重视．程序填空也是重要的考试题型，这种题考试的重点有：①分支的条件②循环的条件③变量的赋值④变量的输出．其中前两点考试的概率更大．此种题型的易忽略点是：不能准确理解流程图的含义而导致错误．（2）程序填空例：阅读如下程序，若输出的结果为，则在程序中横线？处应填入语句为（）A．i≥6 B．i≥7 C．i≤7 D．i≤8．分析：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加并输出变量S的值，要确定进入循环的条件，可模拟程序的运行，用表格对程序运行过程中各变量的值进行分析，不难得到题目要求的结果．解答：程序运行过程中，各变量值如下表所示：S n i是否继续循环循环前0 2 1/第一圈 4 2 是第二圈8 3 是第三圈16 4 是第四圈32 5 是第五圈64 6 是第6圈128 7 是第7圈否即i＝7时退出循环故继续循环的条件应为：i≥7故选B．点评：算法是新课程中的新增加的内容，也必然是新高考中的一个热点，应高度重视．程序填空也是重要的考试题型，这种题考试的重点有：①分支的条件②循环的条件③变量的赋值④变量的输出．其中前两点考试的概率更大．此种题型的易忽略点是：不能准确理解流程图的含义而导致错误．例题精讲算法的基本逻辑结构例1.程序框图符号“”可用于（）A．赋值a=6 B．输出a=5 C．输入a=5 D．判断a=6例2.如图的框图是一古代数学家的一个算法的程序框图，它输出的结果S表示（）A．a0+a1+a2+a3的值B．a3+a2x0+a1x02+a0x03的值C．a0+a1x0+a2x02+a3x03的值D．以上都不对例3.以下是解决数学问题的思维过程的流程图：在此流程图中，①②两条流程线与“推理与证明”中的思维方法匹配正确的是（）A．①-综合法，②-分析法B．①-分析法，②-综合法C．①-综合法，②-反证法D．①-分析法，②-反证法当堂练习单选题练习1.若程序框图如图所示，则该程序运行后输出k的值是（）A．5 B．6 C．7 D．8练习2.如图所示的程序框图的输出值y∈（1，2]，则输入值x∈（）A．[-log23，-1）∪[1，3）B．（-1，-log32]∪[1，2）C．[-log23，-1）∪（1，3]D．（-1，-log32]∪（1，2]按下面的流程图进行计算．若输出的x=202，则输入的正实数x值的个数最多为（）A．2 B．3 C．4 D．5练习4.在如图的程序框图中，若输入m=77，n=33，则输出的n的值是（）A．3 B．7 C．11 D．33练习1.为求3+6+9+…+30的和，补全如图程序“条件”应填___________．练习2.将“杨辉三角”中的数从左到右、从上到下排成一数列：1，1，1，1，2，1，1，3，3，1，1，4，6，4，1，…，如图所示程序框图用来输出此数列的前若干项并求其和，若输入m=4则相应最后的输出S的值是____。

苏教版高中数学必修三-第一章-算法初步1.3.1、2ppt课件

●重点难点重点：输入语句、输出语句、赋值语句．难点：准确写出输入语句、输出语句、赋值语句．引导与合作交流相结合，学生在体会三种语句结构格式的过程中，让学生积极参与，讨论交流，充分挖掘三种算法语句的格式特点及意义，在分析具体问题的过程中总结三种算法语句的思想与特征，突破难点．
由老师引导，学生们自己讨论并总结出什么是输入语句、输出语句和赋值语句，这样比老师直接地将知识传授给他们，学习的效果更佳，同时也锻炼了学生们思考问题的能力和概括能力，激发学习兴趣，通过习题的训练达到强化重点的目的．
§1.3 基本算法语句 1．3.1 1．3.2 赋值语句
输入、输出语句
教师用书独具演示
●三维目标 1．知识与技能：(1)理解输入语句、输出语句、赋值语句的结构．(2)掌握赋值语句中的“←”的作用．
2．过程与方法：(1)让学生充分地感知、体验应用计算机解决数学问题的方法；并能初步操作、模仿．(2)通过模仿、操作、探索的过程，体会算法的基本思想和基本语句的用途． 3．情感、态度和价值观：(1)通过对三种语句的学习、发展有条理的思考、表达的能力、提高逻辑思维能力． (2)通过算法语句的学习，提高思维的有序性，表述的条理性．
其中 x 是一个变量，y 是一个与 x ．
同类型的变量或表达式
输入、输出语句
【问题导思】输入、输出语句与三种基本的逻辑结构有什么关系？
【提示】这三种语句对应流程图中的顺序结构．
用输入语句“ Read a，b ”表示输入的数据依次送给 a，b；用输出语句“ Print x ”表示输出运算结果 x.
写出下面伪代码运行后的结果．
a←3 b←2 c←5 a←a＋b b←b－a c←ab/c Print a，b，c

苏教版高中数学必修三-第一章-算法初步1.3.3ppt课件

用基本算法语句描述如下：
1．本题中，由于分段函数有三个解析式，因此需要两次判断，利用条件结构的嵌套，从而翻译为伪代码时，要利用条件语句的嵌套．
2．条件语句的嵌套，其一般形式为：
x2， x<1，函数 y＝2x－10， 1≤x<10， 3x＋11， x≥10，的函数值，写出伪代码．
1．条件语句的适用范围：用于解决需分情况处理的问题． 2．注意问题：Then 部分和 Else 部分是可选的，语句中的 End If 不能省略． 3．书写格式：“Then”分支和“Else”分支一般缩进书写．
试用伪代码写出任给一个实数，求它的算术平方根的一个算法，并画出流程图．
【解】伪代码如下：
输入的 x 值，计算 y 值的一个算法．
【错解】伪代码如下： Read x If x>0 Then y←1 Print y Else y←0
【错因分析】 (1)伪代码中缺少“End If”语句； (2)“Print y”语句位置错误，致使当 x>0 时正确输出，但当 x＝0 时，则无任何结果输出．
输入 x 的值，输出相应
【解】伪代码如下：
条件语句的实际应用
已知震级是用来表示地震强度的单位，根据震级不同，我们又把地震划分为微震(震级小于 3 级的)、有感地震(震级大于或等于 3 级而小于或等于 4.5 级的)、中强震(震级大于 4.5 级而小于 6 级的)、强震(震级大于或等于 6 级的)，请用语句描述根据震级确定地震的划分层次的算法．
【思路探究】
在划分地震层次时，根据输入的震级范
围不同对应层次不同，这类似于一个分段函数，因此在描述该算法时应用条件语句．
【自主解答】

苏教版高中高二数学必修3《基本算法语句》教案及教学反思

苏教版高中高二数学必修3《基本算法语句》教案及教学反思一、教案设计1.1 教学目标•掌握循环语句的使用方法•掌握条件语句的使用方法•学会使用算法设计解决问题•加深对于计算机基本概念和基本算法的理解1.2 教学重点•循环语句•条件语句•算法设计1.3 教学难点•如何将实际问题转化为计算机可处理的问题•如何编写复杂的算法1.4 教学内容1.循环语句•执行次数确定的循环：“for”语句•执行次数不确定的循环：“while”语句•“while”语句与“for”语句的比较2.条件语句•“if”语句•“if-else”语句•“if-else”嵌套语句•“switch”语句3.算法设计•算法的概念及基本特点•模拟算法•贪心算法•分治算法•动态规划算法•回溯算法1.5 教学过程1.导入：教师先介绍循环语句、条件语句以及算法设计的概念，以“小陈去超市买东西”为例子来引入说解决问题也会用到类似的算法。

2.准备：为了让学生更好的理解，先列举一些常见的算法问题，如不借助任何辅助内存，如何在一列数中找到最大的数？3.实操：让学生分别用for、while来编写求1-100和的程序，并比较for和while的区别。

4.拓展：让学生设计一个命令行界面的计算器，介绍if/else、switch等条件语句的使用方法。

5.总结：在学生练习完这些算法后，教师就应该让学生自行思考算法问题的设计方法，并通过优化算法提高执行效率。

二、教学反思教学效果本节课的教学效果还不错，学生们都能够掌握循环语句和条件语句的使用方法，并在练习中逐渐掌握了算法设计的基本方法和思路。

此外，让学生自主思考算法问题的设计方法也起到了良好的效果，学生们的创造力以及掌握算法的能力都得到了提高。

教学难点本节课的教学难点是如何将实际问题转化为计算机可处理的问题，以及如何编写复杂的算法。

初步策略是通过实际问题的演示，让更多的学生理解为什么要使用算法。

学生反馈通过调查问卷和讨论，学生们发现这节课解释了许多过去难以理解的概念。

数学苏教版必修3名师导航 1.3基本算法语句

5.3 基本算法语句名师导航三点剖析一、赋值语句顾名思义赋值语句就是将表达式所代表的值赋给变量，在伪代码中通常用“←”表示.例如，x ←y 就表示将表达式y 的值赋给变量x ，其中x 是一个变量，而y 则是与x 同类型的变量、表达式或数值.例如，x ←5是指将5赋给变量x ，这里5是一个常数；x ←y+5则表示将表达式y+5的值赋给变量x.当“←”的右边为表达式时，赋值语句包含两项功能：（1）计算表达式的值；（2）将表达式的值赋给左边的变量. 注意:在赋值语句中箭头指向的是变量. 二、输入、输出语句输入、输出语句分别用来实现算法的输入信息、输出结果的功能. 1．输入语句的格式与功能格式：read 变量它表示将输入的数据送给变量，在这里变量的个数可以是多个，它是与所输入的数据的个数对应的，变量之间用逗号隔开.例如: Read a ，b ，c 表示依次输入的数据分别送给变量a ，b ，c. 2．输出语句的格式与功能格式：Print 表达式它表示输出表达式的值，在输出语句中，输出的结果也可以是多个，它们之间也用逗号隔开.例如，Print x 表示输出运算结果x ；Print x ，y ，z 则表示输出运算结果x ，y ，z. 为了更形象地说明赋值语句,输入、输出语句的格式和功能，看下面的一个具体的例子. Read x ，y ，z m ←(x+y+z)/3 n ←3xyz .Print m ，n在上面的算法的伪代码中，第一个语句为输入语句，它表示将输入的数据分别送给了x ，y ，z ，最后一个语句为输出语句，它表示输出了运算结果m ，n ；中间两个语句为赋值语句，它们分别表示将表达式3xyz 3和z y x ++的值赋给变量m ，n. 输入、输出语句和赋值语句一般对应用于算法的顺序结构，算法从上而下按语句的顺序执行这些语句.如图5-21所示.图5-21三、条件语句算法中的选择结构由语句来表达，条件语句的一般格式为If A then B Else C End if 在语句中A表示判断条件，B表示满足条件时执行的操作内容，C则表示不满足条件时执行的内容，End if则表示条件语句的结束.而在表示算法的具体过程中，其格式和对应的框图为：If条件then语句1Else语句2End if对应框图（如图5-22所示）：图5-22在这里，语句1称为“then”的分支，语句2称为“Else”的分支，为了醒目和便于阅读，这些分支一般要缩进书写.例如，下面为一个算法的流程图（如图5-23所示）:图5-23由流程图可知，在此算法的表示过程中用到了选择结构，判断条件为“x≤3”，若x≤3成立，则执行语句“y←2x”，否则执行语句“y←x+1”.因此，上面流程图所表示的算法可用条件语句表示为：Read xIf x≤3 theny←2xElsey←x+1End if在此算法中，虚框内为条件语句，语句“y←2x”为“then”的分支，语句“y←x+1”为“Else”的分支，这两个分支均缩进书写.某些情况下，条件语句中还可以使用If then语句，即If 条件then语句End if它对应的框图为（如图5-24所示）.图5-24例如，使得任意输入的3个整数，按从大到小的顺序输出，其流程图如下（如图5-25所示）：图5-25本算法的伪代码如下：Read a，b，cIf b>a thent←a,a←b,b←tEnd ifIf c>a thent←a,a←c,c←tEnd ifIf c>b thent←b,b←c,c←tEnd ifPrint a，b，c在这个算法中，不存在Else语句.除此之外，条件语句是可以嵌套的，即在条件语句的一个分支中还可以出现条件语句，这种嵌套结构一般用于执行过程中选择结构中还存在选择结构的算法中，其格式为：If 条件1 then语句1Else if 条件2 then语句2……Else if 条件n then 语句n Else语句n+1 End if例如，输入自变量的值，求函数⎪⎩⎪⎨⎧>+=<-=0． x 3，x 0，x 0，0，x 1)(x ，x f 函数值的一个算法的伪代码如下：Read xIf x<0 then y ←1-x Else if x>0 then y ←x+3 Else y ←0 End ifPrint y四、循环语句当算法中存在循环结构时，我们可以用循环语句来实现算法过程.循环语句有两种：一种是“For ”语句；一种是“While ”语句. 1．“For ”语句当循环次数已经确定，则循环结构可用“For ”语句来表示，“For ”语句的一般格式为： For I from “初始值”to “终值”step “步长”…End for 例如，计算1+2+3+…+100值的算法，可表示为 S ←0For I from 1 to 100 step 1 S ←S+Ｉ End for Print S上面算法中，“For ”和“End for ”之间缩进部分称为循环体.因此，用循环语句表示算法时，其格式为：For I from “初始值”to “终值”step “步长” 循环体 End for而且应该注意，循环体要缩进书写. 在循环语句中，当步长为1时可以省略.如计算1+2+3+…+100值的算法，也可表示为 S ←0For I from 1 to 100S←S+IEnd forPrint S2．While语句当循环次数不能确定时，可用while语句来实现循环. while语句的一般格式为：While A…End while具体应用时格式为：在While语句中A表示判断执行循环体的条件，书写时循环体也要缩进书写.例如，寻求满足1+2+3+…+_________>2 008的最小正整数的算法可用While语句表示为S←1I←2While S≤2 008S←S+II←I+1End WhilePrint I算法在执行循环体的过程中，先检验条件S≤2 008是否成立，若条件成立则执行循环体，直到条件不成立时才结束循环.While语句的特点是“前测试”，即先判断再执行，当条件成立时，则执行循环体，然后再检验条件是否成立，若条件仍然成立则继续执行循环体，这个过程反复进行，直到某一次条件不成立为止，这时算法不再执行循环体，而直接转到End While语句后按着执行的先后执行语句.若初始条件不成立，则一次也不执行循环体的内容.任何一种需要重复处理的问题都可以用这种“前测试”循环来实现.问题探究问题1:怎样用伪代码和流程图设计算法来判断N是否为素数？探究：由于素数的特点是它的因数只有1和它的本身，则要判断某个数N是否为素数的方法：将N作为被除数，用2到N各个整数轮流作除数，如果都不能被整除，则N为素数.为了使程序能符合结构化程序设计，这里设计了一个开关W，使初值为0.若N能被某一个整数整除，则使W值为1，否则W值不变.最后根据W的值来确定N是否为素数，若W值为0，则N为素数，否则N为非素数.用伪代码设计算法如下：Begin（算法开始）Read NW←0I←2While I≤N且 W=0If R=0 then W←1Else I←I+1End ifEnd whileIf W=0 then print N，“是素数”Else print N，“不是素数”End ifEnd （算法结束）流程图（如图5-26所示）：图5-26问题2:依次将十个数输入，要求将其中最大的数打印出来.怎样用流程图和伪代码来表示问题的算法？探究：解决这个问题的思路很简单，先选2个数进行比较，去掉小的，留下大的；再取第3个数与留下的数进行比较去掉小的留下大的；继续进行，直到每个数都被比较，最后留下的数就是最大数.但用这种思想写出的算法比较复杂.由于在本算法中某些步骤是重复进行，则可用循环语句来描述此算法.用伪代码设计算法如下：Read Xmax←XFor I from 2 to 10Read XIf X>max thenmax←XEnd ifEnd forPrint maxEnd流程图（如图5-27所示）：图5-27精题精讲例1．写出下列用伪代码描述的算法执行后的结果.（1）算法开始a←2；a←4；a←a+a；输出a的值；算法结束执行结果：（）思路解析本题考查了赋值语句的功能，第一个语句中将2赋给了变量a，此时a的值为2.第二个语句中将4赋给了变量a，此时a值由原来的2变为了4.第三个语句中将a+a的值赋给了变量a，此时a的值为4+4=8.★答案★：8（2）算法开始君子食无求饱，居无求安，敏于事而慎于言，就有道而正焉，可谓好学也已。