CGB-38-70100M;CGB-38-70050M;CGB-38-78050M;CGB-38-78010M;CGB-38-79010M;中文规格书,Datasheet资料
钢号对照
Ni不锈
195
304N
0Cr18Ni8Mn3N
Ni不锈
196
305J1
00Cr19Mn2Ni13
Ni不锈
197
305M
00Cr18Ni11
Ni不锈
198
30CD12
30Cr3MoV
高强钢
199
30CrH-M
30CrMn
结构钢
200
30NCD16
30Ni4CrMo
高强钢
203
316LN
工具钢
13
1.2241Cr1MFra bibliotekV工具钢
15
1.2311
4Cr2Mn1Mo
工具钢
17
1.2316
4Cr15Mo
工具钢
18
1.2323
5Cr2MoV
工具钢
19
1.2328
4Cr2MnMoV
工具钢
20
1.2343
4Cr5MoSiMnV1
工具钢
21
1.2344
4Cr5Mo1V1
工具钢
22
1.2344
4Cr5MoSiV1
结构钢
170
24CrMoV5.5
24CrMoV
结构钢
171
25CrMo4
25CrMo
结构钢
172
25MnCr5
25CrMnS
结构钢
173
27CD4
27CrMnMoSN
结构钢
174
28MnCr5
28CrMnS
结构钢
175
300M
40SiMnCrNi2MoV
高强钢
5v 3.3 1.2 1.5 1.8 2.5V稳压电源芯片大全

编辑 删除
【19楼】 ratrat 积分:164 派别: 等级:-----来自:
谢谢
2009-03-20,12:55:3 3
资料 邮件
回复
引用回复
↑↑
↓↓
编辑 删除
【20楼】 hailing
积分:261 派别: 等级:-----来自:
最好写下静态电流。对于低功耗的设备使用时很重要。我们用317是上面的电阻使用240的,这样就有1.2 5/240=5MA的电流了,对于要求低功耗的设备还是太大了。78系列也有几毫安的电流的。 补充一些:MAX6190 1.25V 5PPM基准 HT7533 3.3V100MA HT7133 3.3V 30MA 78L05 5V 100MA MCP1700 LDO,2.5V SPX3819 3V 1% SPX29032 ADJ 3A 1%
资料 邮件 回复 引用回复 ↑↑ ↓↓
【23楼】 wajlh
make
积分:2115 派别: 等级:-----来自:山东-莱阳
__________________________ 喜欢这里的气氛
2009-03-20,16:14:4 3
资料 邮件 回复 引用回复
↑↑
↓↓
【24楼】 jiongeyes 书册糕 积分:136 派别: 等级:-----来自:潮州,现在广州 单身
mark!
2009-03-23,08:10:3 0
资料 邮件
回复
引用回复
↑↑
↓↓
【31楼】 cgbabc 积分:1036 派别: 等级:-----来自:
MARK!
2009-03-23,11:38:2 3
资料 邮件
回复
引用回复
↑↑
胶囊内镜 ppt课件

ppt课件
13
德国威斯巴登市Horst Schmidt医 院Ell 等于 2001 年 4 月至 10 月,该医院收 治了 65 例慢性胃肠道出血,其中 32 例进行了 完全的传统诊断性检查(包括小肠灌肠造影、 血管造影和闪烁显像以及 PE 和 CE )。 CGB 患 者的平均患病期为29 ± 24 个月(6 - 126);最 低血色素水平为 3.0 - 9.9 g/dl ( 均值 5.9 ± 1.4); 输血17 ± 18 个血单位(0 - 60);每位患 者经历6 ± 7( 1 - 38)次住院治疗,在CE之前 平均做过14 ± 9次诊断性检查。
ppt课件
10
胶囊式内镜有助于诊断隐性胃肠道出血
Lim等,美国胃肠病学会第67届年会
迈阿密大学医学院Lim等对20例原因不明胃 肠道出血病人进行了检查,先做微型无线胶囊内 镜检查,然后再做推进式肠镜检查。进行推进式 肠镜检查时,将一根装备有微型摄像机、长4英 尺的管子通过食管和胃送入小肠上1/3部位。 结果显示,微型无线胶囊内镜检查可发现70% 病人的出血原因,而推进式肠镜检查只能发现4 5%病人的出血原因。
ppt课件
7
组成
小型短焦镜头 彩色照(摄)相机 发白光二极管 两个微型电池 射频发送器 天线。
ppt课件
8
•图象采集过程
–一个如随身听大小 的便携式数据记录 仪。 –照相机可对直径小 至0.1毫米的目标 进行摄影,放大8 倍。 –每秒钟可拍摄80幅 图像,8小时内能 向数据记录仪传送 近6万幅图。 –由工作站专用处理 软件进行数据处理, 得到完整的图象和 数据。 9
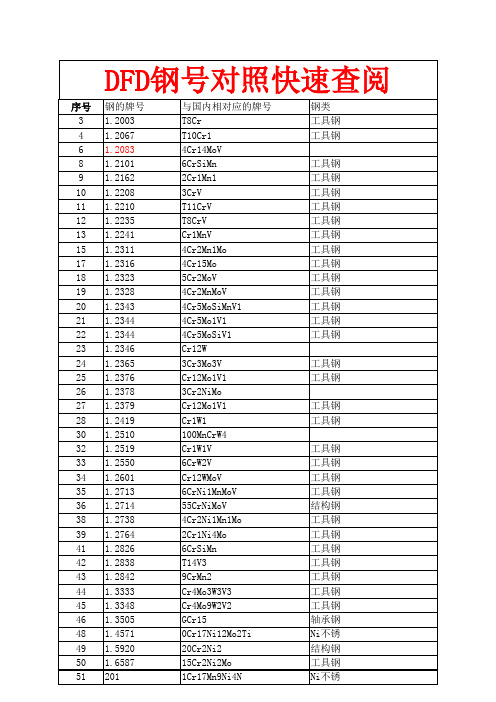
钢号对照表

108 5140 40Cr 结构钢
109 5150 50Cr 结构钢
110 8630 30CrNiMo 结构钢
111 8660 60CrNiMnMo 结构钢
112 8740 40CrNiMo 结构钢
113 9260 60Si2Mn 弹簧钢
10 1.2162 2Cr1Mn1 工具钢
11 1.2208 3CrV 工具钢
12 1.2210 T11CrV 工具钢
13 1.2235 T8CrV 工具钢
14 1.2241 Cr1MnV 工具钢
15 1.2311 40Cr2Mn1Mo 工具钢
16 1.2311 40Cr2MnMo QJ/DT0130023-2006
165 20Cr4 20Cr 结构钢
166 20CrH-M 20CrMn 结构钢
167 20MnCr5 20CrMnS 结构钢
168 20MnCr5H 20MnCrH 结构钢
169 20MoCr4E 20CrMo 结构钢
170 21-4N 5Cr21Mn9Ni4N Ni不锈
183 302HQA 00Cr18Ni9Cu3 QJ/DT0120036-2005
184 302TH 1Cr18Ni9 Ni不锈
185 303Cu Y1Cr18Ni9Cu2 Ni不锈
186 303HCB1 05Cr19Ni8Cu2 QJ/DT02.0212-2008
76 446 0Cr24 Cr不锈
77 631 0Cr17Ni7Al QJ/DT01.20050-2005
78 648 80CrMn 结构钢
79 675 30CrNi3MoV 高强钢
SCALANCE XB004-1LD 6GK5004-1BF00-1AB2 10 100M 工业以太

/bilddb
● to website: CAx-Download-Manager
/cax
● to website: Industry Online Support
https://
EN 60079-0:2009, EN60079-15:2010, II 3 G Ex nA IIC T4 Gc, KEMA 07ATEX0145 X
certificate of suitability
● CCC / for hazardous zone according to GB standard Yes
standards, specifications, approvals / other
certificate of suitability
EN 61000-6-2, EN 61000-6-4
● C-Tick
Yes
● KC approval
Yes
further information / internet-Links
KFE
standards, specifications, approvals / CE
certificate of suitability / CE marking
Yes
standards, specifications, approvals / hazardous environments
standard / for hazardous zone
supply voltage, current consumption, power loss type of voltage / 1 / of the supply voltage ● supply voltage / 1 / rated value ● power loss [W] / 1 / rated value ● supply voltage / 1 / rated value ● consumed current / 1 / maximum ● type of electrical connection / 1 / for power supply ● product component / 1 / fusing at power supply input ● fuse protection type / 1 / at input for supply voltage type of voltage / 2 / of the supply voltage ● supply voltage / 2 / rated value
药芯焊丝牌号对照表
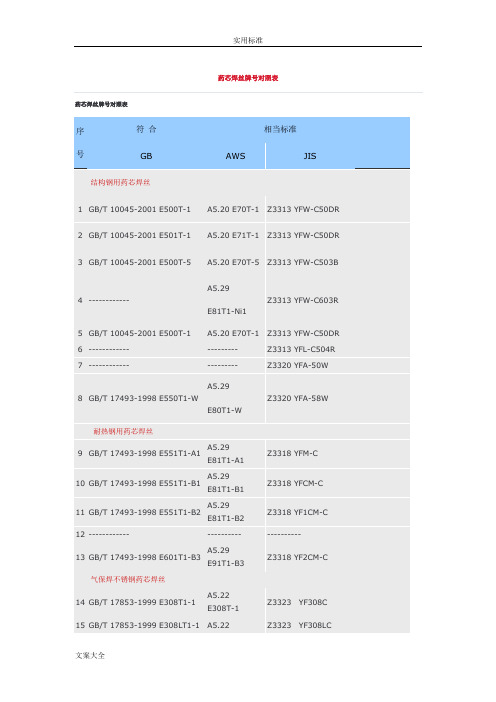
药芯焊丝牌号对照表序号符合相当标准GB AWS JIS 结构钢用药芯焊丝1GB/T 10045-2001 E500T-1A5.20 E70T-1Z3313 YFW-C50DR 2GB/T 10045-2001 E501T-1A5.20 E71T-1 Z3313 YFW-C50DR 3GB/T 10045-2001 E500T-5A5.20 E70T-5Z3313 YFW-C503B 4------------A5.29E81T1-Ni1Z3313 YFW-C603R5GB/T 10045-2001 E500T-1A5.20 E70T-1Z3313 YFW-C50DR 6---------------------Z3313 YFL-C504R 7---------------------Z3320 YFA-50W8GB/T 17493-1998 E550T1-WA5.29E80T1-WZ3320 YFA-58W 耐热钢用药芯焊丝9GB/T 17493-1998 E551T1-A1 A5.29E81T1-A1Z3318 YFM-C10GB/T 17493-1998 E551T1-B1A5.29E81T1-B1Z3318 YFCM-C11GB/T 17493-1998 E551T1-B2A5.29E81T1-B2Z3318 YF1CM-C12--------------------------------13GB/T 17493-1998 E601T1-B3 A5.29E91T1-B3Z3318 YF2CM-C气保焊不锈钢药芯焊丝14GB/T 17853-1999 E308T1-1A5.22E308T-1Z3323YF308C15GB/T 17853-1999 E308LT1-1A5.22Z3323YF308LC序中国钢廉日本神户韩国现代号1------------DW-100F------------2GL-YJ502(Q)DW-100SF-713GL-YJ507(Q)------------------------4GL-YJ602(Q)DW-60------------5------------MX-100SF-70MX6GL-YJ502Ni(Q)------------------------7GL-YJ502CrNiCu(Q)DW-50W SF-70W8GL-YJ602CrNiCu(Q)DW-588SF-80W 耐热钢用药芯焊丝9------------------------------------10------------------------------------11GL-YR302(Q)DW-1CMA------------12------------------------------------13GL-YR402(Q)DW-2CMA------------气保焊不锈钢药芯焊丝14GL-YA102(Q)DW-308------------15GL-YA002(Q)DW-308L SW-308L Cored16GL-YA302(Q)DW-309------------17GL-YA062(Q)DW-309L SW-309L Cored18------------------------------------19GL-YA202(Q)DW-316------------20GL-YA022(Q)DW-316L SW-316L Cored21GL-YA132(Q)DW-347SW-347 Cored22------------DW-410Nb------------23------------DW-430Nb------------不锈钢TIG焊用药芯焊丝24------------------------------------25------------------------------------26------------------------------------27------------------------------------28------------------------------------29------------------------------------30------------------------------------31------------------------------------------------ MAG焊用耐磨堆焊药芯焊丝32------------DWH-250------------33GL-YD350(Q)DWH-350------------34 GL-YD450(Q) DWH-450 ------------35 ------------ DWH-600 ------------36 ------------ DWH-800 ------------37 ------------------------------------埋弧焊用耐磨堆焊药芯焊丝38 ------------G-50/USH-250N ------------39 ------------ G-50/USH-350N ------------40 ------------ G-50/USH-450N ------------41 ------------ G-50/USH-500N ------------42 ------------MF-30/USH-600N ------------气保护药芯焊丝使用说明:碳钢药芯焊丝,执行GB/T10045-2001标准;低合金钢药芯焊丝,执行GB/T17493-1998标准;不锈钢药芯焊丝,执行GB/T17853-1999标准药芯焊丝是上世纪70年代逐步发展起来的,由于它效率高、节能、工艺性能好、质量高、综合成本低(只有手工焊条的1/2,埋弧焊丝的1/3,CO2实芯焊丝的90%)、飞溅少,已成为21世纪新一代焊材。
SL654-2014水利水电工程合理使用年限及耐久设计规范

胶凝材料中含有较大比例的粉煤灰、硅灰、磨细矿渣等矿物 掺合料和混合料,需要采取较低水胶比的混凝土。 2.0. 12 钢筋的混凝土保护层 concrete cover to reinforcemen
上海勘测设计研究院 本标准出版、发行单位:中国水利水电出版社 本标准主要起草人:刘志明 陆忠民柏宝忠李现社
王以仁孙卫岳毛影秋雷兴顺 张政伟刘计山 肖贡元钟源清 汤洪洁管蕾 本标准审查会议负责人:高安泽 本标准体例格式审查人:陈立秋
目次
1 总则- 2 术语…………………………………………………………… 2 3 工程合理使用年限…………………………………………… 4 4 耐久性设计要求……………………………………………… 6
本标准共 4 章和 1 个附录,主要技术内容有:水利水电工程 及其水工建筑物的合理使用年限、水工建筑物耐久性设计要求。
本标准为全文推荐。
本标准批准部门:中华人民共和国水利部 本标准主持机构:水利部水利水电规划设计总院 本标准解释单位:水利部水利水电规划设计总院 本标准主编单位:水利部水利水电规划设计总院
50
50
水库泄洪建筑物
150
100
50
50
50
调(输)水建筑物
100
100
50
30
30
发电建筑物
100
100
30
30
防洪(潮)、供水水闸
100
100
50 _,
工银亚洲分行地址及联系方式
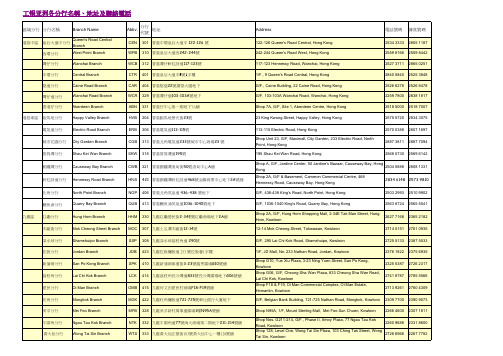
工银亚洲各分行名稱、地址及聯絡電話
區域分行 分行名稱
中小企分 行群區 上環分行 尖沙咀東分行 尖沙咀分行 油麻地分行 太子分行 康寧道分行 將軍澳分行 觀塘分行 新界西區 屯門分行 葵涌分行 葵芳分行 沙咀道分行
Branch Name
Sheung Wan Branch Tsimshatsui East Branch Tsim Sha Tsui Branch Yaumatei Branch Prince Edward Branch Hong Ning Road Branch Tseung Kwan O Branch Kwun Tong Branch Tuen Mun Branch Kwai Chung Branch Kwai Fong Branch Sha Tsui Road Branch
Abbv.
SWB TSE TST YMT PED HNG TKO KWT TMB KCB KFB STR TWC THG TPB YUL TWO SHT
分行 地址 代號
303 香港上環德輔道中317-319號啟德商業大廈地下F舖 302 九龍尖沙咀漆咸道南39號鐵路大廈地下B舖 402 尖沙咀漢口道35至37號地下1-2號舖 305 九龍油麻地彌敦道542號 322 九龍旺角彌敦道777號 317 九龍觀塘康寧道58號 326
Abbv.
CEN WPB WCB CTR CAR WCR ABN HVB ERB CGB SKW CWB HNS NOP QUB HHM MOC SSP JDB SPK LCK OMB MGK MFB NTK WTS
分行 地址 代號
301 香港中環皇后大道中 122-126 號 310 香港皇后大道西242-244號 312 香港灣仔軒尼詩道117-123號 401 香港皇后大道中9號1字樓 404 香港堅道22號廣堅大廈地下 329 香港灣仔道103-103A號地下 331 香港仔中心第一期地下7A舖 304 香港跑馬地景光街23號 306 香港電氣道113-115號 313 香港北角電氣道233號城市中心商場23 號 318 香港筲箕灣道195號 321 香港銅鑼灣渣甸街50號渣甸中心A舖 421 香港銅鑼灣軒尼詩道468號金聯商業中心地下2A號舖 406 香港北角英皇道 436-438 號地下 413 香港鰂魚涌英皇道1036-1040號地下 330 九龍紅磡德民街2-34E號紅磡商場地下2A舖 307 九龍土瓜灣木廠街12-14號 308 九龍深水埗荔枝角道 290號 423 九龍佐敦彌敦道 233 號佐敦薈1字樓 410 九龍新蒲崗寧遠街3-23號越秀廣場G10號舖 414 九龍荔枝角長沙灣道833號長沙灣廣場地下G06號舖 415 九龍何文田愛民村商場F18-F19號舖 422 九龍旺角彌敦道721-725號華比銀行大廈地下 328 九龍美孚新村萬事達廣場1樓N95A號舖 332 九龍牛頭角道77號淘大商場第二期地下211-214號舖 333 九龍黃大仙正德街103號黃大仙中心一樓128號舖
产品计件倍率一览表
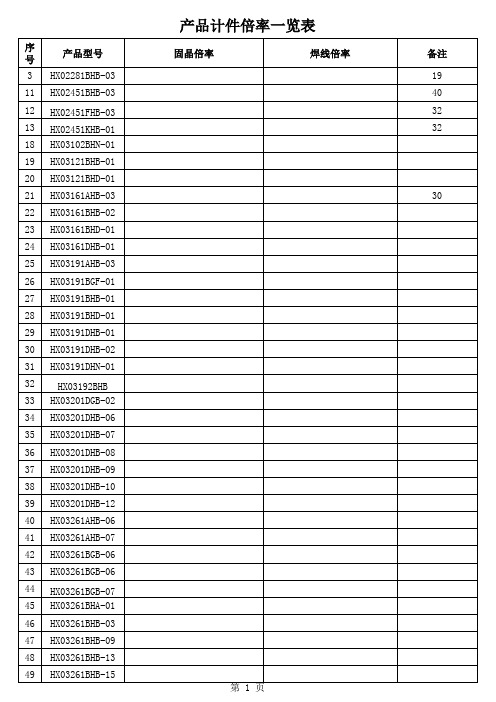
产品计件倍率一览表
序号 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 产品型号 HX04301FHB-01 HX04301FHB-01 HX04301FHB-01 HX04301FHB-06 HX04301FHB-10 HX04301FHB-11 HX04352BHB-01 HX04401AGB-01 HX04401AHB-01 HX04401AHB-02 HX04401AHB-03 HX04401AHB-05 HX04401BGB-01 HX04401BGB-02 HX04401BHB-01 HX04401BHB-01 HX04401BHB-01 HX04401BHB-02 HX04401BHB01BHB-06 HX04401DGB-01 HX04401EHB-01 HX04401EHD-01 HX04402AHB-01 HX04402AHB-01 HX04402BGB-02 HX04402BHB-02 HX04402BHB-02 HX04402BHB-02 HX04402BHB-02 HX04402BHB-02 HX04402BHB-09 HX04402BHB-10 HX04402BHB-11 HX04402BHB-12 第 7 页 固晶倍率 焊线倍率 备注
产品计件倍率一览表
序号 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 产品型号 HX-04402DHB-03 HX04403AGB-01 HX04407BGB-02 HX04471AHB-01 HX04471AHB-02 HX04601AHB-01 HX04601AHB-02 HX04601AHB-03 HX05101AGB HX05101AGB-01 HX05101AHB HX05101AHB-05 HX05101BGB HX05101BGB -03 HX05101BHB HX05101BHB-06 HX05101BHB-07 HX05101BHB-08 HX05101BHN-01 HX05101BSB-01 HX05102BON-01 HX05161AHB-01 HX05161AHB-01 HX05161AHB-01 HX05161AHD-01 HX05161BGB-01 HX05161BHB-01 HX05161BHB-07 HX05161BHB-08 HX05161BHD-01 HX05163AHN-01 HX05201SSB-01 HX05202CHB-02 HX05202EGB-02 HX05202EGB-03 HX05202EHB-02 第 8 页 固晶倍率 焊线倍率 备注
爱普生墨水ID

黑色 ID:T88-E8A-VPD-TJ7Y黄色 ID:37Q-SKF-P8E-K68C红色 ID:NLK-TRS-MGW-CEKG 蓝色 ID:327-SK6-D73-W6DJ M:3XK-BKY-ZW3-STBYC:HHY-HQU-PGT-CAKBY:TV8-TZP-4J7-TJ7MBK:3WW-49Y-DKE-2NVF黑色:MFE-VLS-Q56-DF4E洋红:8RD-V8E-R9U-9PYN黄色:MUD-5KA-F39-TPXZ蓝色:324-4CP-U83-WRKQ黑色:32D-EHN-873-2VLR洋红:8N4-CUN-JPZ-8JYY黄色:TN8-CZQ-KJB-TJ9N蓝色:FCS-RGS-QBS-NEW363C-8CD-DDQ-55DA黑洋红色:8DS-Z8N-CGB-AJGN黑色:CW2-6G4-XEFA青色:HKX-HKZ-5AD-RFAR黄色:F4L-GL8-ZEN-FFLN黑色:S4S-78F-LJD-8P7F红色:3XW-F8X-9T3-S6XM黄色:KHP-DKZ-5GD-FGVZ青色:9LS-S3A-XHZ-8JTJ黑色:SCK-EUE-NR7-SJJF洋红色:JKC-6GS-YA6-VNQG 青色:3XT-S3Y-UH3-4V7Q黄色:KD7-XKT-JA V-GJX5 黑:KHG-YQS-JAX-GA7B红:FQU-TRS-PBX-EFWF黑:3W2-BUN-DLE-2N7R青:KKX-6M8-AAX-EEKZ黄:FW2-AV8-5ZW-ZECG黑色:SC2-2UN-FG7-9P5M黑色:MWL-V64-ZP8-NFW3 Black ID: N48-9AS-Z5E-PFQR Red ID: 3WB-ELM-PHZ-26TQ Yellow ID: T68-ZZC-QJZ-9JRCC yan ID: 3XD-FU6-9S5-4NGY 黑:TFT-W8E-RHD-SPNQ红:KHV-6Q9-EA9-4YXZ黄:RML-NV8-ZA6-JACF青:RK2-GAS-BBX-RALG K:Y4L-V AS-Z3A-GFLFY:TFT-9ZG-KHP-SJHEC:YC4-A6S-PZT-FFWAM:9L8-TUN-HHZ-TPNQ黑37X-EUY-UHB-2T2C蓝32U-EKN-9L5-WV9Y红KD6-GQD-A3X-9ALZ黄HKP-JQP-PGD-LPLG黑:HU9-TQ3-ZGT-6EUG红:FQ3-6GS-P5N-7AFF青:8VL-KZB-CH2-8JPC黄:326-S3X-9K5-L9UF黑sf4-k8f-rju-8pdr黄3xk-e8m-9ua-lnqf青9v4-pzf-fhd-tphq红hkr-yqg-aad-vy8a蓝色KKH-5M8-5GT-TAK2红色MKU-TAS-JGX-RFWA黄色37J-SUX-GD3-KT黑色没找到黄色:T4D-J33-FG2-SJ7F黑色:TCH-285-492-8J9W洋红:JQ3-6GS-5GN-XNLA青色:37V-SGN-UKE-4VJM蓝YQS-NNS-JBT-JE4E红HHR-PQ7-GGD-9EHZ黄NMK-A68-Z3M-EFFA黑TC4-AUA-CDU-TP7M黑色3XW-W9N-9LA-2VEC青色KHX-PQ7-AED-3FH5洋红988-PUN-4JP-9JVC黄色YW2-RFL-J3K-YN4E黑色:SNH-38A-6RD-9P9M黑色:KU9-TKG-NA9-4FSE黄色:HK5-RQZ-EGX-FGGR青色:CQ3-ATS-BGN-XAK3 黑色:3XU-EUF-D2G-2G8N 洋红色:MKL-9GS-JE4-ZNC3 黄色:32U-EUX-UDA-L6WC 青色:8S9-43B-6D2-TP7R黑色:C4F-TNS-JB6-8AM3洋红色:JLC-T6S-Z54-4A4G黄色:TNK-3ZR-6G2-9PXN青色:86D-EZA-FR7-9PTN 黑色:3xk-ehf-88p-2nkr黄色:3XP-EDY-PU3-KGWF 红色:9R4-UUN-HHP-SP7F青色:MQS-GGS-QBS-GF4E 黄色:TF9-S3P-JPB-9P5Q黑色:37X-SK6-DD3-29GF洋红:946-A8F-HJB-9PRJ青色:37D-B9W-ZWA-W9NJ 黄色:HHD-RKP-BA V-GCRQ 黑色:MML-TSS-BA4-QEKC 洋红:NL8-TF4-BBL-REQG 青色:NK8-GL4-ZBL-REFN 黑色 ID:KUA-7QA-YE6-8YW5洋红色 ID:9VX-N8N-NRU-8P9F青色 ID:84U-2ZY-6V2-8JTM黄色 ID:KD7-XK3-CGX-3P7B黑色:SS9-G8Y-CP2-8PPM黄色:TE4-U3C-ND2-9JRF洋红:8S8-SUN-FPB-8PAM青色:KHY-5KE-G3D-SMUA 黑色:SL4-F85-CD2-SJ5R黑色:SZT-UUN-VH7-GJTQ 黄色:KU7-PQB-GEX-LQLZ 蓝色:83T-73N-VP7-9PXC红色:8C8-98F-QPZ-TP6M。
华为光模块的型号命名规则是怎样的?

华为光模块的型号命名规则是怎样的?华为光模块的型号命名规则是怎样的?我们知道光模块的外观会有标签,标签上⾯标记有光模块的型号和具体信息,我们常常通过光模块的标签来区分光模块。
那么光模块的型号命名所代表的含义以及命名的规则是怎么样的呢?本⽂中飞速光纤将给⼤家讲讲华为光模块的型号命名规则。
⼀、华为光模块的分类1、华为GE SFP光模块:GE代表百兆,GE SFP光模块就是封装类型为SFP的百兆光模块。
华为FE SFP光模块:FE代表千兆,华为FE SFP光模块就是封装类型为SFP的千兆光模块。
FE光模块的FE光接⼝⽀持激光器热插拔,可根据⽤户的需要选配合适的激光器,⽀持不同距离的光接⼝。
华为10G SFP+光模块:这种光模块的封装类型是SFP+,且数据速率是10G。
它是⼀种增强型的可热插拔的光模块。
华为QSFP+光模块:这种光模块的数据速率为40G,封装类型为QSFP+,QSFP+光模块有SR4、LR4等多种型号。
华为GBIC光模块:这种光模块的数据速率为10G,封装类型为GBIC。
华为GBIC光模块是早期的光模块,体积相对SFP和SFP+来说较⼤,在⽹络应⽤中的密度不及SFP和SFP+。
华为XENPAK光模块:这种光模块的数据速率是10G,封装类型为XENPAK,并且这种光模块⽀持所有的IEEE 802.3ae定义的光接⼝,但是体积和功耗都⽐较⼤。
华为XFP光模块:这种光模块的数据速率为10G,封装类型为XFP,且密度较⾼。
华为X2光模块:这种光模块的数据速率为10G,封装类型为X2。
X2光模块由XENPAK光模块发展⽽来,⽀持热插拔的输⼊/输出装置,主要⽤于以太⽹X2端⼝的交换机、路由器与⽹络连接的端⼝。
华为光模块型号中字母代表的含义:1、SFP为百兆或千兆光模块,其中分为多模模块和单模模块,在单模模块中⼜分为传输距离为10KM、40KM、80KM等多种型号。
2、XFP为万兆模块,其中也分为多模模块和单模模块两种,单模模块中⼜分为不同传输距离有不同的型号,例如10G表⽰为万兆,XFP光模块就是10G光模块。
北京市第十批自主创新产品目录

4
北京安博维科技发展有限公司
MedInfoUp电子病历系统V2.0
电子信息
5
北京安码科技有限公司
安码网页防篡改系统V1.0
电子信息
6
北京安信通网络技术有限公司
数据库安全扫描系统V2.0
电子信息
7
北京奥美达科技有限公司
具有七种显示模式的高清助视器Eye-C
电子信息
8
北京奥美达科技有限公司
手持式电子助视器AUKEY
电子信息
73
北京市速连科通信设备有限责任公司
T-NET-AL01室外智能机柜控制管理系统V1.0
电子信息
74
北京市太阳能研究所有限公司
太阳能发电综合利用系统
电子信息
75
北京天和正通信息技术有限公司
物联网应用管理平台软件V1.0
电子信息
76
北京天和正通信息技术有限公司
广播发射机自动监控系统V1.0
电子信息
电子信息
39
北京建筑技术发展有限责任公司
集中供热量化管理综合节能技术服务平台
电子信息
40
北京久其软件股份有限公司
基于在线服务模式的数据采集与报送处理应用软件(简称:报表大厅)
电子信息
41
北京久其软件股份有限公司
政府直补一卡(折)通管理信息系统
电子信息
42
北京久其软件股份有限公司
久其OLAP多维分析系统
USDI信息共享交换平台软件V1.0(简称USDI共享交换平台)
电子信息
82
北京天宇数字城市科技有限公司
网格化城市管理平台软件V1.0 (简称:SmartCMP)
电子信息
SMC样本

导线引出方式
DC24V、 12V、 6V、 5V、 3V/AC100V、 110V、 200V、 220V 直接出线式 L形插座式 M形插座式
G: 导线 长300mm L: 带导线 (长300mm) M: 带导线 MN: 不带导线 (长300mm)
++-
DC24V、 12V AC100V、 110V、 200V、 220V
型号/SY7000系列
阀的 型号 流量特性 质量g 1→4/2(P→A/B) 4/2→5/3(A/B→EA/EB) L形、 W形 直接 M形 DIN形 M8 5、 3 4、 2 C[dm3/ 机能 1、 C[dm3/ 出线式 插座式 插座式 接头 (P、EA、EB) (A、 B) b Cv b Cv (s ・ bar)] (s ・ bar)] 单电控 101 104 125 129 2位 4.1 0.23 0.93 3.3 0.33 0.81 双电控 120 125 167 175 接管口径 中封式 3位 中泄式 中压式 63 67 83 101 SY7□20 -□-C8 单电控 1(P) 2位 双电控 通口 C8 ¿8 5、 3 3位 中泄式 (EA、 EB) 快换 通口 接头 中压式 1 8 2位 SY7□20 -□-C10 单电控 双电控 中封式 3位 中泄式 中压式 C10 ¿10 快换 接头 中封式
导线引出方式(D式的场合) 无记号 无指示灯及过电压保护回路 S 带过电压保护回路(无极性式) Z 带指示灯及过电压保护回路(无极性式)
※ 没有DOZ式。 ※ AC 的场合, 用整流器防 止过电压的发生, 故无 S 式。
M8接头
WO: 接头 无电缆
※ LN、 MN式带2个导线插头。 ※ SY3000系列的DIN形插座式参见后附10。 ※ 符合DIN43650C 标准的 DIN 形插座式 [ Y 式 ] 也有。 详见 P.212。 ※ M8接头的接头电缆参见后附12。
海螺系列门窗节点图

4
5
HJ61NC SF49NC
GB19NC
CO36NC
1
2
85窗型材断面
105 31
61
49
38 85
31
27
42.5
边上框 HJ61NC 1664g/m
提升扇 SF49NC 681g/m
扇封盖 IL27NC 180g/m
15
36
43
6
22 120
18
19
下框 TH43NC 1103g/m
盖板 CO36NC 168g/m
4
4+12A+4中空玻璃
1
2 或2a
3
AD30胶条
5
6
STC35×27.5 玻璃垫块
GDE35胶条 ST61NC
6
室内
2a
BR58NC
FR71NC
UP72NC
1
2
单玻GB34NC 双玻GB19NC
3
60系列百页窗节点
3 1 2
室内
STU28×21.5 RP18NC LP61NC
3R58NC
50
88系列推拉窗特点
▲推拉窗中的经典作品,全部采用平面设计,外观平整, 各种配套型材齐全 ▲此型材是仅次于海螺95系列、海螺77系列的高档门窗
▲出材率高、窗形丰富,价格适中 ▲强度高,完全适用于10-25层左右的建筑物
88系列推拉窗节点
7 4 5 86
室内
型钢STU28 21.5 玻璃垫块 GDE35胶条
扇封盖 IL39NC 米比重:206g/m
21
21
19.5
7.5
56
40
65
5
射频功率放大器(黄智伟)1-5章 (4)

第9章 蓝牙功率放大器电路 CGB241采用SLIM-7封装,引脚封装形式如图9.2.1所示, 引脚功能如表9.2.1所示。
图9.2.1 CGB241引脚封装形式
第9章 蓝牙功率放大器电路
第9章 蓝牙功率放大器电路 CGB241内部结构方框图如图9.2.2所示,芯片内部包含有2 级放大器。 CGB241使用微带线(TRL) 匹配的蓝牙PA参考设计应用电路 和印制板图如图9.2.3所示,在印制板图中,VC1和VC2连在一起, VCTR1和VCTR2连接在一起。电路所用元器件的参数如表9.2.2所示。
第9章 蓝牙功率放大器电路 MAX2244/45/46带有闭环模拟功率控制电路, MAX2244/MAX2246功率控制电压为0.5~2 V,MAX2245功率控制 电压为0.9~2.2 V。内部电路自动控制开启/关断期间输出功 率的斜坡上升/下降,以满足蓝牙低寄生发射要求,功率上升 和下降时间为4 μs,功率下降时间为1.8 μs。他们的RF输入 功率为0~4 dB;输出功率为24/24/21 dBm;输入VSWR(RS=50 Ω时)为1.5∶1~2∶1。
第9章 蓝牙功率放大器电路 MAX2240功率放大器要求在RFOUT端口有一个外部匹配网络, 用来优化放大器的输出功率和效率。对于2.45 GHz频段上适宜 的匹配,在RFOUT端口上的负载阻抗大约为15 Ω+ j18 Ω。获 得适宜的50 Ω传输阻抗有很多方法,典型的工作电路中输出 匹配可以串联一根长度为75 Ω∥26°的传输线,或者使用一 根末端开口的传输线与一个长度为65Ω∥ 41°的波导管短路 线并联。并联波导管短路线可以减少输出中的二次谐波。
CGB240采用TSSOP-10封装,引脚封装形式如图9.1.1所示, 引脚功能如表9.1.1所示。
萤石 智能锁 执手系列-DL20系列 CS-DL20C-FS-CgB 使用说明书

目录236782026使用须知产品简介5产品清单首次使用设置锁2931使用锁菜单介绍9操作说明售后服务支持添加到“萤石云视频”维护与保养42附录使用须知. . . . . . . . 萤石智能门锁(以下简称为“锁”)作为高科技产品,安装的好坏直接影响到门锁的正常操作及使用寿命,建议您请有智能锁安装经验的师傅进行安装,并根据产品附件中门板开孔图样板进行开孔,凿支承窝,确认所开凿的孔准确无误,然后严格按照本手册中的步骤进行操作,如果安装后发现锁有任何异常,请及时和当地的经销商或本公司的售后服务部门联系,以便快速解决问题。
如果您的房间正在装修,我们建议您将产品卸下,待装修完成后再把产品重新装上,这样做的目的是:①.避免装修过程中腐蚀性物质或腐蚀性气体腐蚀锁体,影响外观及降低产品使用寿命;②.避免门的油漆未干会影响锁的灵活传动;③.为避免对锁外观面造成腐蚀,请勿使用消毒液等腐蚀性液体擦拭锁外表面。
门锁在恢复出厂设置后会清空所有用户信息,在门锁安装调试完成后,请您尽快将锁恢复出厂设置并重新添加密码、感应卡、指纹等开锁信息。
门锁使用一段时间后,电池电量偏低时,门锁会发出低电压警报,门锁会语音提示电量不足,此时请及时更换电池并注意正负极的安装。
更换电池前请购买质量好的5号电池,因为好的电池使用时间比较长,以确保锁长时间正常使用。
若您要出远门或长期不使用锁,请将机械钥匙随身携带。
指纹较平较细或年龄较小的用户,建议您用大拇指注册指纹,提高指纹采集时的成功率,且同一用户注册2枚以上指纹。
鉴于锁产品本身置于开放环境等特点,我们建议您谨慎注意使用安全,包括妥善保管机械钥匙及感应卡等细小部件、开锁前核查周围环境、定期更新密码及感应卡设置、及时擦除残留指纹等,避免您的开锁信息被非法盗取、复制,造成安全隐患。
支持人脸或指纹识别开锁的电子锁,将涉及您的人脸、指纹信息的处理。
萤石仅为向您提供开锁功能之必要,仅针对您以事先录入方式做出授权的人脸或指纹进行分析比对,您所录入的原始信息及其处理过程均在您自行控制管理的设备本地进行,不会在云端存储。
2024-2025学年湖北省武汉第一初级中学九年级上学期第一次月考数学试题及答案

2024年九年级上学期数学9月同步练习一、选择题(共10小题,每小题3分,共30分)1. 3的相反数是( ) A. 13−B.13C. 3−D. 32. 下列方程一定是一元二次方程是( ) A. 210x -=B. 20++=x x yC. 110x x++= D. 210x x−= 3. 如图有关环保的四个图形中,是中心对称图形的是( )A. B. C. D.4. 一元二次方程2320x x +−=根的情况为( )A. 有两个不相等的实数根B. 有两个相等的实数根C. 没有实数根D. 不能判定5. 某县2020年人均可支配收入为2.36万元,2022年达到2.7万元,若2020年至2022年间每年人均可支配收入的增长率都为x ,则下面所列方程正确的是( ) A. ()22.71 2.36x += B. ()22.361 2.7x += C. ()22.71 2.36x −=D. ()22.361 2.7x −=6. 以下函数的图象的顶点坐标为()2,0的是() A. 223y x =+B. 23(2)y x =−−C. 22(2)y x =−+D. 22y x =−+7. 已知m ,n 是一元二次方程2310x x +−=两个根,则()()11m n ++的值( ) A. 3−B. 3C. 1D. 1−8. 已知二次函数2y ax bx c =++的图象如图所示,则点(),P c b 所在的象限是( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限9. 若24217M x x =−+,2327N x x =++,x 为实数,则M 与N 的大小关系为( )的的A. M N >B. M N <C. M ND. M N 、大小关系与x 的取值有关10. 若点A (﹣3,1y ),B (1,2y ),C (m ,3y )在抛物线y =ax 2+4ax +c 上,且1y <3y <2y ,则m 的取值范围是( ) A. ﹣3<m <1 B. ﹣5<m <﹣1或﹣3<m <1 C. m <﹣3或m >1D. ﹣5<m <﹣3或﹣1<m <1二、填空题(共6小题,每小题3分,共18分)11. 若关于x 的一元二次方程220x x m −+=的一个根为1x =,则m 的值为____. 12. 点()3,4−关于原点对称点为__________.13. 将抛物线21y x =+向右平移2个单位长度,再向上平移3个单位长度,得到抛物线的解析式是__________.14. 如图,在ABC 中,45BAC ∠=°,15C ∠=°,将ABC 绕点A 逆时针旋转α角度()0180α°<<°得到ADE ,若DE AB ∥,则α=______度.15. 已知关于x 的函数()()222020x x x y x x x +≤ = −+>,有下列结论:①函数的图象是轴对称图形;②函数图象上纵坐标为0的点有3个;③满足纵坐标为n 的点,恰好只有两个,则1n =或1−;④点()1,M x m ,()2,N x m 是该函数图象上的两个点,则MN 的最大距离是4.其中正确的结论是__________.(填写序号) 16. 已知二次函数2221y x mx m =−+−(m 为常数),当该二次函数的图象与x 轴交于点A B 、两个点.若线段AB 上有且只有5个点的横坐标为整数,则m 的取值范围是__________.三、解答题(共8小题,72分)17. 解下列方程: (1)221x x −=; (2)2650x x ++=.18. 如图,五边形ABCDE 中,90EAB BCD ∠∠== ,AB BC =,ABC α∠=,AE CD DE +=.的在(1)将ABE 绕点B 顺时针旋转α,画出旋转后的BCM ,并证明D C M 、、三点在一条直线上; (2)求证:△≌△EBD MBD .19. 关于 x 的方程 x 2﹣2(k ﹣1)x +k 2=0 有两个实数根 x 1,x 2. (1)求 k 的取值范围;(2)请问是否存在实数 k ,使得 x 1+x 2=1﹣x 1x 2 成立?若存在,求出 k 的值;若不存在, 说明理由. 20. 抛物线243y x x =−+与x 轴交于A B 、两点,A 在B 左侧,与y 轴交于C 点. (1)C 点坐标为 ,顶点坐标为 ; (2)不等式2430x x −+>的解集是 ; (3)当x 满足23x −≤≤时,y 的取值范围 .21. 如图是由小正方形组成的1010×网格,每个小正方形的顶点叫做格点.、、A B C 三点是格点.仅用无刻度直尺在给定网格中完成画图.(1)在图1中,将线段AB 绕A 点逆时针旋转90°至AE ,设AB 的中点D ,标出D 点旋转后的对应点F ;(2)在图2中,过B 点作AC 的平行线BG ,在BG 上取一点M ,使MAB CAB ∠=∠. 22. 某商店销售一种商品,经市场调查发现:在实际销售中,售价x 为整数,且该商品的月销售量y (件)是售价x (元/件)的一次.函数.,其售价(元/件)、月销售量y (件)月销售利润w (元)的部分对应值如下表:()=×− 月销售利润月销售量售价进价售价x /(元/件) 30 35 月销售量y /件300250月销售利润w /元 4500 5000(1)商品的进价为 元/件,y 关于x 的函数表达式为 ; (2)当该商品的售价是多少元时,月销售利润最大?并求出最大利润;(3)现公司决定每销售1件商品就捐赠m 元利润()10m ≤给“精准扶贫”对象,要求:在售价不低于42元时,每月扣除捐赠后的月销售最大利润为3960元,则m = . 23. 在菱形ABCD 中,60ABC ∠=°,BD 为菱形的一条对角线.(1)如图1,过A 作AE BC ⊥于点E 交BD 于点F ,求证:2FD BF =; (2)在(1)的条件下,若2FE =,则菱形ABCD 面积为 ;(3)如图2,M 为菱形ABCD 外一动.点且CM CB =,连接AM ,DM ,BBBB ,试探究DM BM AM 、、的数量关系,请写出三条线段的数量关系 .(选择其中一种数量关系,并写出其证明过程)24. 如图1,在平面直角坐标系中,已知抛物线()230y ax bx a =+−≠与x 轴交于点()1,0A −,()3,0B ,与y 轴交于点C ,D 是该抛物线上的一动点...(1)C 点坐标 ,该抛物线解析式为 ,顶点为 ;为(2)如图1中,连接AC BD 、,直线AC 交直线BD 于点G ,若45CGB∠=°,求此时D 点坐标; (3)如图2,连接BC ,过D 点作BC 的平行线交该抛物线于点E (不与D 重合),连接CD BE 、,直线CD 与直线BE 交于点P ,求点P 的横坐标.2024年九年级上学期数学9月同步练习一、选择题(共10小题,每小题3分,共30分)1. 3的相反数是( ) A. 13− B.13C. 3−D. 3【答案】C 【解析】【分析】本题考查相反数的定义,熟记相反数的定义是解题的关键. 根据相反数的定义即可直接选择. 【详解】解:3的相反数是3−. 故选:C .2. 下列方程一定是一元二次方程的是( ) A. 210x -= B. 20++=x x yC. 110x x++= D. 210x x−= 【答案】A 【解析】【分析】本题考查了一元二次方程的定义:只含有一个未知数,并且所含未知数的项的最高次数是2的整式方程叫一元二次方程.根据一元二次方程的定义即可解答.【详解】解:方程20++=x x y 含有两个未知数,不是一元二次方程,故选项B 不符合题意; 方程110x x++=和方程210x x −=都不是整式方程,都不是一元二次方程,故选项C 、D 不符合题意; 210x -=符合题意一元二次方程的定义,是一元二次方程,故选项A 符合题意;故选:A .3. 如图有关环保的四个图形中,是中心对称图形的是( )A. B. C. D.【答案】B 【解析】【分析】本题主要考查了中心对称图形,根据中心对称图形的定义判断即可,解题的关键是正确理解中心对称图形的定义:把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形可得答案.【详解】A 、图形绕某一点旋转180°后与原来的图形不重合,所以不是中心对称图形,不符合题意;B 、图形绕某一点旋转180°后与原来的图形重合,所以是中心对称图形,符合题意;C 、图形绕某一点旋转180°后与原来图形不重合,所以不是中心对称图形,不符合题意;D 、图形绕某一点旋转180°后与原来的图形不重合,所以不是中心对称图形,不符合题意;故选:B .4. 一元二次方程2320x x +−=根的情况为( )A. 有两个不相等的实数根B. 有两个相等的实数根C. 没有实数根D. 不能判定【答案】A 【解析】【分析】根据题意,求得2498170b ac ∆=−=+=>,根据一元二次方程根的判别式的意义,即可求解. 【详解】解:∵一元二次方程2320x x +−=中,1,3,2a b c ===−, ∴2498170b ac ∆=−=+=>,∴一元二次方程2320x x +−=有两个不相等的实数根, 故选:A .【点睛】本题考查了一元二次方程的根的判别式的意义,熟练掌握一元二次方程根的判别式的意义是解题的关键.5. 某县2020年人均可支配收入为2.36万元,2022年达到2.7万元,若2020年至2022年间每年人均可支配收入的增长率都为x ,则下面所列方程正确的是( ) A. ()22.71 2.36x += B. ()22.361 2.7x += C. ()22.71 2.36x −= D. ()22.361 2.7x −=【答案】B 【解析】【分析】设2020年至2022年间每年人均可支配收入的增长率都为x ,根据题意列出一元二次方程即可. 【详解】解:设2020年至2022年间每年人均可支配收入的增长率都为x ,根据题意得,()22.361 2.7x +=,故选:B .【点睛】本题考查了一元二次方程的应用,根据题意列出一元二次方程是解题的关键. 6. 以下函数的图象的顶点坐标为()2,0的是()的A. 223y x =+B. 23(2)y x =−−C. 22(2)y x =−+D. 22y x =−+【答案】B 【解析】【分析】本题考查由抛物线的顶点坐标式写出抛物线顶点的坐标,比较容易.因为抛物线()2y a x h k =−+,顶点坐标是(),h k ,根据这个模式求出每个函数的顶点坐标,再比较. 【详解】解:A 、223y x =+的顶点坐标是(0,3),不符合题意; B 、23(2)y x =−−的顶点坐标是(2,0),符合题意; C 、22(2)y x =−+的顶点坐标是()2,0−,不符合题意; D 、22y x =−+的顶点坐标是(0,2),不符合题意. 故选:B .7. 已知m ,n 是一元二次方程2310x x +−=的两个根,则()()11m n ++的值( ) A. 3− B. 3C. 1D. 1−【答案】A 【解析】关系.根据一元二次方程根与系数的关系得出3m n +=−,1mn =−,代入整理后的代数式,即可求解.【详解】解:∵m ,n 是一元二次方程2310x x +−=的两个根, ∴3m n +=−,1mn =−,∴()()1113131mm m n m n =+++=−−+++=−, 故选:A .8. 已知二次函数2y ax bx c =++的图象如图所示,则点(),P c b 所在的象限是( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限【答案】C的【解析】【分析】本题考查二次函数的图象与系数的关系,以及判断点所在象限.首先根据二次函数的图象及性质判断c 和b 的符号,从而得出点(),P c b 所在象限.【详解】解:由图可知二次函数的图象开口向上,对称轴在y 轴右侧,∴0a >,02ba−>, ∴0b <,二次函数的图象与y 轴的交点在原点下方,∴0c <,∴(),P c b 在第三象限,故选:C .9. 若24217M x x =−+,2327N x x =++,x 为实数,则M 与N 的大小关系为( ) A. M N > B. M N <C. M ND. M N 、的大小关系与x 的取值有关【答案】A 【解析】【分析】本题考查了整式的加减,配方法的应用.直接利用整式的加减运算法则结合偶次方的性质得出答案.【详解】解:∵24217M x x =−+,2327N x x =++, ∴()224217327M N x x x x −=−+−++224217327x x x x =−+−−− 2410x x =−+ ()226x =−+,∵()220x −≥, ∴(xx −2)2+6>0, ∴M N >. 故选:A .10. 若点A (﹣3,1y ),B (1,2y ),C (m ,3y )在抛物线y =ax 2+4ax +c 上,且1y <3y <2y ,则m 的取值范围是( ) A. ﹣3<m <1 B. ﹣5<m <﹣1或﹣3<m <1 C. m <﹣3或m >1 D. ﹣5<m <﹣3或﹣1<m <1【答案】D 【解析】【分析】根据二次函数的解析式可得出二次函数的对称轴为x =﹣2,分a <0和a >0两种情况讨论,分别根据图像上点的坐标特征得到关于m 的不等式,然后解不等式即可解答. 【详解】解:抛物线y =ax 2+4ax +c 的对称轴为x =﹣42aa=﹣2, ∵点A (﹣3,y 1),B (1,y 2),C (m ,y 3)在抛物线y =ax 2+4ax +c 上,且y 1<y 3<y 2, ∴当a <0,则|m +2|<1且|m +2|>3,(不存在);当a >0,则1<|m +2|<3,解得﹣5<m <﹣3或﹣1<m <1. 故选:D .【点睛】本题考查了二次函数图像上点的坐标特征、二次函数的性质、解一元一次不等式组,解题的关键是根据二次函数的性质找出关于m 的一元一次不等式.二、填空题(共6小题,每小题3分,共18分)11. 若关于x 的一元二次方程220x x m −+=的一个根为1x =,则m 的值为____. 【答案】1 【解析】【分析】本题主要考查了一元二次方程解的定义,熟知一元二次方程的解是使方程左右两边相等的未知数的值是解题的关键.把1x =代入一元二次方程得到120m −+=,然后解一次方程即可. 【详解】解:把1x =代入方程220x x m −+=得120m −+=, 解得1m =. 故答案为:112. 点()3,4−关于原点对称点为__________. 【答案】(3,−4) 【解析】【分析】本题考查了关于原点对称的点的坐标,熟练掌握两点关于原点对称,横、纵坐标互为相反数是解题关键.根据“两点关于原点对称,则两点的横、纵坐标都是互为相反数”解答即可. 【详解】解:点()3,4−关于原点O 的对称点为()3,4−.故答案为:()3,4−.13. 将抛物线21y x =+向右平移2个单位长度,再向上平移3个单位长度,得到抛物线的解析式是__________.【答案】()224y x =−+【解析】【分析】此题主要考查了函数图象的平移.根据二次函数图象左加右减,上加下减的平移规律进行解答即可.【详解】解:函数21y x =+向右平移2个单位,得:()221y x =−+;再向上平移3个单位,得:()2213y x =−++,即()224y x =−+; 故答案为:()224y x =−+.14. 如图,在ABC 中,45BAC ∠=°,15C ∠=°,将ABC 绕点A 逆时针旋转α角度()0180α°<<°得到ADE ,若DE AB ∥,则α=______度.【答案】60【解析】【分析】本题考查了旋转的性质、平行线的性质.先根据旋转的性质可得15C E ∠=°∠=,再根据平行线的性质可得15BAE E °∠==∠,然后根据角的和差可得60EAC ∠=°,由此即可得.【详解】解:由旋转性质得:15C E ∠=°∠=,DE AB ∥,15BAE E °∴=∠=∠,45BAC ∠=° ,60EAC BAC BAE ∴∠=∠+∠=°,即旋转角为60°,60α∴=°,故答案为:60.的15. 已知关于x 的函数()()222020x x x y x x x +≤ = −+>,有下列结论:①函数的图象是轴对称图形;②函数图象上纵坐标为0的点有3个;③满足纵坐标为n 的点,恰好只有两个,则1n =或1−;④点()1,M x m ,()2,N x m 是该函数图象上的两个点,则MN 的最大距离是4.其中正确的结论是__________.(填写序号)【答案】②③④【解析】【分析】本题考查了二次函数和图象和性质.根据题意画出草图,根据图象求解即可.【详解】解:对于()22211y x x x =+=+−()0x ≤, 顶点坐标为()1,1A −,令0y =,则220x x +=,解得0x =或2x =−,与x 轴的交点坐标为()2,0D −,OO (0,0),对于()22211y x x x =−+=−−+()0x >,顶点坐标为()1,1B , 令0y =,则220x x +=,解得0x =或2x =,与x 轴的交点坐标为()2,0E ,如图,观察图象,①函数的图象是中心对称图形,不是轴对称图形,结论①错误;②函数图象上纵坐标为0的点有点D O E 、、,共3个,结论②正确;③满足纵坐标为n 的点,恰好只有两个,即经过点A 或B 且平行于x 轴两条直线与图象的交点,此时1n =或1−,结论③正确;④点()1,M x m ,()2,N x m 是该函数图象上的两个点,由图象知,当0m =时,则MN 的最大距离即4DE =,结论④正确.故答案为:②③④.16. 已知二次函数2221y x mx m =−+−(m 为常数),当该二次函数的图象与x 轴交于点A B 、两个点.若线段AB 上有且只有5个点的横坐标为整数,则m 的取值范围是__________.【答案】 1.51m −<≤−或3 3.5m ≤<.【解析】【分析】本题考查了二次函数与x 轴的交点问题.先求得二次函数的图象与x 轴的交点坐标,再利用线段AB 上有且只有5个点的横坐标为整数,分两种讨论,分别列不等式组,计算即可求解.【详解】解:令0y =,则22210x mx m −+−=,解得11x =,221x m =−, 不妨设()1,0A ,则()21,0B m −,当点B 在点A 左侧时,由题意得4213m −<−≤−,解得 1.51m −<≤−;当点B 在点A 右侧时,由题意得5216m ≤−<,解得3 3.5m ≤<;综上,m 的取值范围 1.51m −<≤−或3 3.5m ≤<.故答案为: 1.51m −<≤−或3 3.5m ≤<.三、解答题(共8小题,72分)17. 解下列方程:(1)221x x −=;(2)2650x x ++=.【答案】(1)11x =+21x =−(2)11x =−,25x =−.【解析】【分析】本题考查求一元二次方程的解,解一元二次方程的一般方法有配方法、公式法和因式分解法. (1)在方程两边同时加上一次项系数一半的平方,配成完全平方公式,再开平方求解即可;(2)根据因式分解法将方程变为()()150x x ++=,将方程转化为两个一元一次方程求解即可. 【小问1详解】解:221x x −=,配方得:22111x x −+=+,即()212x −=,∴1x −=解得:1x =±∴11x =21x =【小问2详解】解:2650x x ++=, 分解因式得:()()150x x ++=, ∴10x +=或50x +=, 得:11x =−,25x =−.18. 如图,在五边形ABCDE 中,90EAB BCD ∠∠== ,AB BC =,ABC α∠=,AE CD DE +=.(1)将ABE 绕点B 顺时针旋转α,画出旋转后的BCM ,并证明D C M 、、三点在一条直线上; (2)求证:△≌△EBD MBD .【答案】(1)画图见解析,证明见解析(2)见解析【解析】【分析】此题是几何变换综合题,主要考查了全等三角形的判定和性质,旋转的性质,利用旋转构造出全等三角形时解本题的关键.(1)先根据题意画出图形,再由旋转的性质可得90EAB BCM ∠∠==°,由90BCD ∠=°,可得180BCM BCD ∠∠+=°;(2)由旋转的性质可得BM BE =,AE CM =,再由AE CD DE +=可得CM CD DE +=,即:DM DE =,最后通过“SSS ”证明△≌△EBD MBD 即可.【小问1详解】如图所示,将ABE 绕点B 顺时针旋转α,AB BC =,ABC α∠=,90EAB BCM ∠∠°∴,90BCD ∠=° ,180BCM BCD ∠∠∴+=°,∴D C M 、、三点在一条直线上;【小问2详解】将ABE 绕点B 顺时针旋转α,得到ACM △,BCM BAE ∴ ≌,BM BE ∴=,AE CM =,AE CD DE += ,CM CD DE ∴+=,即:DM DE =,BD BD = ,()SSS EBD MBD ∴ ≌;19. 关于 x 的方程 x 2﹣2(k ﹣1)x +k 2=0 有两个实数根 x 1,x 2.(1)求 k 的取值范围;(2)请问是否存在实数 k ,使得 x 1+x 2=1﹣x 1x 2 成立?若存在,求出 k 的值;若不存在, 说明理由.【答案】(1)12k ≤ (2)存在,3k =−【解析】【分析】(1)根据关于 x 的方程 x 2﹣2(k ﹣1)x +k 2=0 有两个实数根,∆≥0,代入计算求出k 的取值范围.(2)根据根与系数的关系,12= x b x a+−,12=c x x a ,根据题意列出等式,求出k 的值,根据k 的值是否在取值范围内做出判断.【小问1详解】解:∵关于 x 的方程 x 2﹣2(k ﹣1)x +k 2=0 有两个实数根根据题意得()22414480k k k ∆=−−=−≥, 解得12k ≤. 【小问2详解】解:存在.根据根与系数关系122()1x x k +=−,212x x k =, ∵x 1+x 2=1﹣x 1x 2,∴2()211k k −=−,解得1231k k =−=,, ∵12k ≤. ∴存在实数k =-3,使得x 1+x 2=1﹣x 1x 2.【点睛】本题考查一元二次方程根的判别式及根与系数的关系,解一元二次方程,要注意根据k 的取值范围来进取舍.20. 抛物线243y x x =−+与x 轴交于A B 、两点,A 在B 左侧,与y 轴交于C 点.(1)C 点坐标为 ,顶点坐标为 ;(2)不等式2430x x −+>的解集是 ;(3)当x 满足23x −≤≤时,y 的取值范围 .【答案】(1)()0,3;()2,1−;(2)1x <或3x >(3)115y −≤≤.【解析】【分析】本题考查了二次函数的性质、抛物线与两坐标轴的交点及不等式组,本题利用数形结合的思想是关键,从图象中读出不等式组的解集和对应y 的取值.(1)配方可得抛物线顶点M 的坐标;将0x =和0y =代入抛物线的解析式可求得点C 的坐标; (2)将0y =代入抛物线的解析式可求得A ,B 的坐标;画出草图,根据图象得出结论;(3)计算得出当23x −≤≤时对应的函数值,根据图象即可写出二次函数y 的取值范围.【小问1详解】解:()224321y x x x =−+=−− ,∴抛物线顶点M 的坐标为()2,1−;把0x =代入243y x x =−+得3y =;C ∴点坐标为(0,3);【小问2详解】解:把0y =代入243y x x =−+得2430x x −+=,解得11x =,23x =,A ∴点坐标为(1,0)、B 点坐标为()3,0,草图,如图所示;2430x x −+>,即0y >,由图象得:当1x <或3x >时,0y >,则2430x x −+>;故答案为:1x <或3x >;【小问3详解】解:由图象得:当2x =−时,()()2242348315y =−−×−+=++=;当2x =时,1y =−最小;当3x =时,0y =;所以y 取值范围:115y −≤≤.21. 如图是由小正方形组成的1010×网格,每个小正方形的顶点叫做格点.、、A B C 三点是格点.仅用无刻度直尺在给定网格中完成画图.(1)在图1中,将线段AB 绕A 点逆时针旋转90°至AE ,设AB 的中点D ,标出D 点旋转后的对应点F ;(2)在图2中,过B 点作AC 的平行线BG ,在BG 上取一点M ,使MAB CAB ∠=∠. 【答案】(1)见解析 (2)见解析【解析】【分析】本题考查作图-旋转变换,平行线的性质,正方形的性质,线段垂直平分线的性质,熟练掌握相关知识点是解答本题的关键.(1)利用全等三角形的性质作出AE ,线段AB 与格线交点即为AB 的中点D ,线段AE 与格线交点即为AE 的中点F ;(2)作平行四边形BCHG ,得到BG AC ∥,作正方形ABRE ,分别取AB 和RE 与格线的交点D 和N ,作射线DN 交BG 于点M ,此时MN 是线段AB 的垂直平分线,则MAB GBA CAB ∠∠∠==. 【小问1详解】解:线段AE ,以及点D 和点F 如图1所示;【小问2详解】解:所作图形如图所示:22. 某商店销售一种商品,经市场调查发现:在实际销售中,售价x 为整数,且该商品的月销售量y (件)是售价x (元/件)的一次.函数.,其售价(元/件)、月销售量y (件)月销售利润w (元)的部分对应值如下表:()=×− 月销售利润月销售量售价进价 售价x /(元/件)30 35 月销售量y /件 300 250 月销售利润w /元 4500 5000(1)商品的进价为 元/件,y 关于x 的函数表达式为 ;(2)当该商品售价是多少元时,月销售利润最大?并求出最大利润;(3)现公司决定每销售1件商品就捐赠m 元利润()10m ≤给“精准扶贫”对象,要求:在售价不低于42元时,每月扣除捐赠后的月销售最大利润为3960元,则m =.【答案】(1)15,10600y x =−+; (2)当该商品的售价是37.5元时,月销售利润最大,最大利润为5062.5元;(3)5【解析】【分析】本题考查了二次函数在实际生活中的应用.(1)根据表中数据可以求出每件进价,设出函数解析式,用待定系数法求函数解析式即可;(2)设该商品的月销售利润为w 元,根据利润=单件利润×销售量列出函数解析式,根据函数的性质求出函数最值;(3)根据总利润=(单件利润m −)×销售量列出函数解析式,再根据42x ≤时,利用函数性质求解即可.【小问1详解】的解:由表中数据知,每件商品进价为30030455300010×−=(元/件), 设一次函数解析式为y kx b =+, 根据题意,得3030035250k b k b += +=, 解得:10600k b =− =, 所以y 与x 的函数表达式为10600y x =−+; 故答案为:15,10600y x =−+; 【小问2详解】解:设该商品的月销售利润为w 元,则()15w x y =−()()1510600x x =−−+2107509000x x =−+−()21037.55062.5x =−−+,∵100−<,∴当37.5x =时,w 最大,最大值为5062.5,∴当该商品的售价是37.5元时,月销售利润最大,最大利润为5062.5元;【小问3详解】解:根据题意得: ()()()2151060010750109000600w x m x x m x m =−−−+=−++−−, 对称轴为直线()7501037.52210m m x ++==−×−, ∵10m ≤,∴37.542.52m +≤, ∵100−<,∴当42x =时,w 取得最大值为3960元,∴()()421510426003960m −−−×+=,解得:5m =.故答案为:5.23. 在菱形ABCD 中,60ABC ∠=°,BD 为菱形的一条对角线.(1)如图1,过A 作AE BC ⊥于点E 交BD 于点F ,求证:2FD BF =;(2)在(1)的条件下,若2FE =,则菱形ABCD 面积为 ;(3)如图2,M 为菱形ABCD 外一动.点且CM CB =,连接AM ,DM ,BBBB ,试探究DM BM AM 、、的数量关系,请写出三条线段的数量关系 .(选择其中一种数量关系,并写出其证明过程)【答案】(1)见解析 (2)(3)DM BM =(答案不唯一),理由见解析 【解析】【分析】(1)利用菱形的性质以及直角三角形的性质求得1122BE AB AD ==,推出ADF EBF ∽,得到2FDAD BF BE==,据此即可证明2FD BF =; (2)同(1)求得ADF EBF ∽,得到2AF AD EF BE==,求得4AF =,6AE =,解直角三角形求得BC AB ==,利用菱形的面积公式即可求解;(3)连接AC ,延长BM 到H ,证明点B M A D 、、、在以点C 为圆心的C 上,利用圆心角与圆周角的关系求得AMD AMH ∠=∠,证明()Rt Rt HL MAN MAG ≌,求得=NM MG ,再证明()Rt Rt HL ANB AGD ≌,求得ABN ADG ∠=∠,BN DG =,然后利用直角三角形的性质即可解决问题.【小问1详解】证明:如图1中,四边形ABCD 是菱形,60ABC ∠=°,AE BC ⊥,30BAE =∴∠°,AB BC AD ==,AD BC ∥, ∴1122BE AB AD ==,∵AD BE ∥,∴ADF EBF ∽, ∴2FD ADBF BE ==,∴2FD BF =;【小问2详解】解:由(1)ADF EBF ∽, ∴2AFADEF BE ==,∵2FE =,∴4AF =,∴6AE =,∵30BAE ∠=°, ∴cos AE BAE AB ∠=,即6cos30AB °=,∴AB =BC AB ==,∴ABCD S BC AE =⋅=菱形;故答案为:;【小问3详解】解:DM BM =,理由如下:连接AC ,延长BM 到H ,∵四边形ABCD 是菱形,60ABC ∠=°,∴ABC 和ACD 都是等边三角形,∴60ACB ACD ∠=∠=°,∵CM CB =,∴CB CM CA CD ===,∴点B M A D 、、、在以点C 为圆心的C 上, ∴1302AMD ACD ∠=∠=°,()1302MAB MBA MCB MCA ∠+∠=∠+∠=°, ∵30MAB M HMA BA ∠+∠=°∠=,∴AMD AMH ∠=∠,如图,过A 作AN BH ⊥点N ,AG DM ⊥于点G ,AMN AMG ∠=∠ ,AN MN ⊥,AG DM ⊥,AN AG ∴=,90MNA MGA ∠=∠=° ,AM AM =,AN AG =,()Rt Rt HL MAN MAG ∴ ≌,NM MG ∴=,90ANB AGD ∠=∠=° ,AN AG =,AB AD =,()Rt Rt HL ANB AGD ∴ ≌,∴ABN ADG ∠=∠,BN DG =,120BMD BAD ∠=∠=° ,60NMG ∴∠=°,30AMN AMG ∴∠=∠=°,()2DM BM MG DG BN MN MN ∴−=+−−==,DM BM ∴=+.【点睛】本题考查菱形的性质,圆心角与圆周角,相似三角形的判定和性质,全等三角形的判定和性质,直角三角形的性质,解直角三角形等知识,正确引出辅助线解决问题是解题的关键.24. 如图1,在平面直角坐标系中,已知抛物线()230y ax bx a =+−≠与x 轴交于点()1,0A −,()3,0B ,与y 轴交于点C ,D 是该抛物线上的一动点...(1)C 点坐标为 ,该抛物线解析式为 ,顶点为 ;(2)如图1中,连接AC BD 、,直线AC 交直线BD 于点G ,若45CGB∠=°,求此时D 点坐标; (3)如图2,连接BC ,过D 点作BC 的平行线交该抛物线于点E (不与D 重合),连接CD BE 、,直线CD 与直线BE 交于点P ,求点P 的横坐标.【答案】(1)()0,3−,223y x x =−−,()1,4−;(2)此时D 点坐标()1,4−或39,24 −; (3)点P 的横坐标为32. 【解析】【分析】(1)当0x =时,求出点C 坐标,然后利用待定系数法求出抛物线解析式,最后配方即可求出顶点坐标; (2)先求出直线AC 解析式为33y x =−−,然后分当G 在直线BC 下方时和当G 在直线BC 下方时两种情况分,由相似三角形的判定与性质即可求解;(3)设()2,23E m m m −−,()2,23D n n n −−,然后求出直线BC 解析式为3y x =−,由DE BC ∥,设直线DE 解析式为y x t =+,联立得223x t x x +=−−,整理得:2330x x t −−−=,根据两根关系可得3m n +=,则()23,4D m m m −−,分别出直线CD 解析式为()13y m x =−−,直线BE 解析式为()133y m x m =+−−,联立得()()13313y m x m y m x =+−− =−−,最后解方程即可求解.【小问1详解】解:由抛物线23y ax bx =+−,当0x =时,=3y −,∴CC (0,−3),∵抛物线与x 轴交于点()1,0A −,()3,0B ,∴309330a b a b −−= +−= ,解得:12a b = =−, ∴抛物线解析式为223y x x =−−,由()222314y x x x =−−=−−,∴顶点坐标为()1,4−,故答案为:()0,3−,223y x x =−−,()1,4−;【小问2详解】解:由(1)得:CC (0,−3),设直线AC 解析式为11y m x n =+, ∴11103m n n −+= =− ,解得:1133m n =− =− , ∴直线AC 解析式为33y x =−−, ∵()3,0B ,CC (0,−3),()1,0A −,∴3OB OC ==,1OA =,∴4AB =,AC 45OBC OCB ∠=∠=°,BC ==, ∴1143622ABC S AB OC =×=××=△, 如图,当G 直线BC 下方时,过G 作GM x ⊥轴于点M ,∵45CGB∠=°, ∴45CGB OBC ∠=∠=°, ∵BAC GAB ∠=∠,∴BAC GAB ∽,∴2258ABC AGB S AC S AB == , ∴658AGB S = , ∴485AGB S =,即14825AB GM ×=, ∴148425GM ××=, ∴245GM =, 当245y =−时,24335x −=−−,解得:35x =, ∴324,55G −,在设BG 解析式为11y k x b =+, ∴11113032455k b k b += +=− ,解得:1126k b = =− , ∴设BG 解析式为26y x =−, ∴22326y x x y x =−− =− ,解得:14x y = =− 或30x y = = (舍去) ∴()1,4D −;如图,当G 在直线BC 上方时,过G 作GN x ⊥轴于点N ,同理∴BAC GBC ∽,∴2259ABC BGC S AC S BC ==, ∴659BGC S = , ∴545BGC S =,即()15425AB GN OC ×+=, ∴()1544325GN ××+=, ∴125GN =, 当125y =时,12335x =−−,解得:95x =−,∴912,55G −, 设BG 解析式为22y k x b =+, ∴22223091255k b k b += −+= ,解得:221232k b =− =, ∴BG 解析式为1322y x =−+, ∴2231322y x x y x =−− =−+ ,解得:3294x y =− =或30x y = = (舍去) ∴39,24D −; 综上可知:此时D 点坐标()1,4−或39,24 −; 【小问3详解】解:如图,设()2,23E m m m −−,()2,23D n n n −−,∵点E 不与D 重合,∴m n ≠且3m ≠,同上理可得:直线BC 解析式为3y x =−,∵DE BC ∥,∴设直线DE 解析式为y x t =+,∴联立得223x t x x +=−−,整理得:2330x x t −−−=,∴根据两根关系可得3m n +=,∴()23,4D m m m −−, 设直线CD 解析式为33y k x =−, ∴()23433m m m k −=−−,解得:31k m =−, ∴直线CD 解析式为()13y m x =−−,同理直线BE 解析式为()133y m x m =+−−,联立得()()13313y m x m y m x =+−− =−−, ∴()()13313m x m m x +−−=−−,∴23mx m =, ∴32x =, ∴点P 的横坐标为32. 【点睛】本题考查了相似三角形的判定与性质,待定系数法求解析式,二次函数和一次函数的性质,一元二次方程根与系数的关系等知识,熟练掌握知识点的应用是解题的关键.。
2022年青岛版九年级数学上册第2章单元检测1(附答案)

第2章单元检测一、填空题:1.如图,A市东偏北60°方向有一旅游景点M,在A市东偏北30°的公路上向前行800米到C处,测得M 位于C的北偏西15°,那么景点M到公路AC的距离MN为米〔结果保存根号〕.【考点】解直角三角形的应用-方向角问题.【专题】压轴题.【分析】过点C作CP⊥AM.根据可求得各角的度数,从而根据三角函数可求得AM和CP的长,再根据面积公式即可求得MN的长.【解答】解:过点C作CP⊥AM.∵AC=800米,∠MAC=30°,∠ACM=180°﹣〔90°﹣30°+15°〕=105°,∴∠AMC=45°,∴CP=PM=400米,AP=400米,∴AM=400+400米,∵AM•PC=AC•MN,∴MN=200+200〔米〕.【点评】解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.2.如图,B、C是河岸边两点,A是对岸岸边一点,测得∠ABC=45°,∠ACB=45°,BC=60 m,那么点A到对岸BC的距离是m.【考点】解直角三角形的应用-方向角问题.【分析】由题意知三角形为直角三角形.可求得AB,AC的长度,再根据面积的两种表示形式可得出A到对岸BC的距离.【解答】解:由题意可得:∠A=180°﹣45°﹣45°=90°,AB=AC=BC×sin45°=30.∵面积S=AB×AC=BC×h,∴h=30.故点A到对岸BC的距离是30米.【点评】此题考查解直角三角形的知识,运用面积的两种表达式是解决此题的关键,要熟练掌握这种解题方法.3.如图,防洪大堤的横断面是梯形,坝高AC=6米,背水坡AB的坡度i=1:2,那么斜坡AB的长为米〔精确到0.1米〕.【考点】解直角三角形的应用-坡度坡角问题.【分析】设出垂直高度,表示出水平宽度,利用勾股定理求解即可.【解答】解:∵背水坡AB的坡度i=1:2,AC=6,∴BC=12.根据勾股定理可得:AB=6≈13.4〔米〕.【点评】此题的关键是熟悉且会灵活应用公式:tanα〔坡度〕=垂直距离:水平距离.综合利用了勾股定理.4.如图小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得1 m杆的影子长为2 m,那么电线杆的高度约为m.〔结果保存两位有效数字,≈1.41,≈1.73〕【考点】解直角三角形的应用-坡度坡角问题;近似数和有效数字.【专题】计算题;压轴题.【分析】先根据CD的长以及坡角求出落在斜坡上的影长在地面上的实际长度,即可知AB的总影长,然后根据1 m杆的影子长为2 m,求解电线杆的高度.【解答】解:作DE⊥BC于E.那么电线杆的高度分3局部进行求解.BC对应的电线杆的高度:根据同一时刻物高与影长成比例,得10÷2=5;在Rt△CDE中,根据30°所对的直角边是斜边的一半,得DE=2.再根据勾股定理,得CE=2;因为DE⊥BC,那么DE对应的电线杆高度和DE相等,CE对应的电线杆高度同样根据:同一时刻物高与影长成比例,是2÷2=.故电线杆的高度是5+2+≈8.7.【点评】注意:影子平行于物体时,影子和物体的实际高度相等;影子垂直于物体时,根据同一时刻物高与影长成比例进行计算.二、选择题〔共2小题,每题3分,总分值6分〕5.如图,小强和小明去测量一座古塔的高度,他们在离古塔60m的A处,用测角仪测得古塔顶的仰角为30°,测角仪高AD=1.5m,那么古塔BE的高为〔〕A.〔20﹣1.5〕m B.〔20【考点】解直角三角形的应用-仰角俯角问题.【分析】作AC⊥BE于点C.那么CE=AD,AC=DE.在直角△ABC中选择适当的三角函数求出BC即可得解.【解答】解:过点A作AC⊥BE于点C.根据题意有:AC=DE=60,CE=AD=1.5.∴BC=AC×tan30°=20.故古塔BE的高为BC+CE=〔20+1.5〕m.应选B.【点评】此题考查仰角的定义,要求学生能借助仰角构造直角三角形并解直角三角形.6.如图是一台54英寸的大背投彩电放置在墙角的俯视图.设∠DAO=α,彩电后背AD平行于前沿BC,且与BC的距离为60cm,假设AO=100cm,那么墙角O到前沿BC的距离OE是〔〕A.〔60+100sinα〕cm B.〔60+100cosα〕cmC.〔60+100tanα〕cm D.以上答案都不对【考点】解直角三角形的应用.【专题】应用题;压轴题.【分析】墙角O到前沿BC的距离OE是O到AD的距离加上AD与BC的距离60cm.【解答】解:根据直角三角形的边角关系,O到AD的距离=100sinacm.∵AD与BC的距离60cm.∴OE=〔60+100sina〕cm.应选A.【点评】此题考查了三角函数定义的应用.三、解答题〔共2小题,总分值6分〕7.如图,河流的两岸MN、PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C、D、E….某人在河岸MN的A处测得∠DAN=38°,然后沿河岸走了120m到达B处,测得∠CBN=70°.求河流的宽度CF.〔结果精确到0.1m,参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,sin70°≈0.94,cos70°≈0.34,tan70°≈2.75〕【考点】解直角三角形的应用.【分析】过点C作CG∥DA交AB于点F,易证四边形AGCD是平行四边形.再在直角△CBF中,利用三角函数求解.【解答】解:过点C作CG∥DA交AB于点G.∵MN∥PQ,CG∥DA,∴四边形AGCD是平行四边形.∴AG=CD=50m,∠CGB=38°.∴GB=AB﹣AG=120﹣50=70〔m〕.∴tan38°==0.78,在Rt△BFC中,tan70°==2.75,∴BF=,∴==0.78,解得:CF≈76.2〔m〕.答:河流的宽是76.2米.【点评】此题主要考查了解直角三角形的应用,不规那么图形可以通过作平行线转化为平行四边形与直角三角形的问题进行解决.8.如图,在测量塔高AB时,选择与塔底在同一水平面的同一直线上的C、D两点,用测角仪器测得塔顶A 的仰角分别是30°和60°,测角仪器高CE=1.5米,CD=30米,求塔高AB.〔保存根号〕【考点】解直角三角形的应用-仰角俯角问题.【专题】应用题.【分析】首先设AF=x.分析图形:根据题意构造直角三角形,此题涉及到两个直角三角形△AGF、△AEF,应利用其公共边AF构造等量关系,借助GE=CD=EF﹣GF=30,构造方程关系式,进而可求出答案.【解答】解:设AF=x;在Rt△AGF中,有GF==x,同理在Rt△AEF中,有EF==x.结合图形可得:GE=CD=EF﹣GF=30即x﹣x=30,解可得:x=15;故AB=15+答:塔高AB为15+米.【点评】此题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.二、能力提升9.如图,某船以每小时36海里的速度向正东方向航行,在点A测得某岛C在北偏东60°方向上,航行半小时后到达点B测得该岛在北偏东30°方向上,该岛周围16海里内有暗礁.〔1〕说明点B是否在暗礁区域内;〔2〕假设继续向东航行有无触礁的危险?请说明理由.【考点】解直角三角形的应用-方向角问题.【专题】应用题.【分析】〔1〕求点B是否在暗礁区域内,其实就是求CB的距离是否大于16,如果大于那么不在暗礁区域内,反之那么在.可通过构造直角三角形来求CB的长,作CD⊥AB于点D,CD是直角三角形ACD和CBD的公共直角边,可先求出CD的长,再求出CB的长;〔2〕此题实际上是问,C到AB的距离即CD是否大于16,如果大于那么无触礁危险,反之那么有,CD的值,〔1〕已经求出,只要进行比较即可.【解答】解:〔1〕作CD⊥AB于点D,设BC为x,在Rt△BCD中∠CBD=60°,∴..在Rt△ACD中∠CAD=30°,∴.∴x=18.∴B点不在暗礁区域内;〔2〕∵,∵,∴假设继续向东航行船有触礁的危险.【点评】此题是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到这个直角三角形中,使问题解决.10.如图,登山缆车行驶线与水平线间的夹角α=30°,β=47度.小明乘缆车上山,从A到B,再从B到D都走了200米〔即AB=BD=200米〕,请根据所给的数据计算缆车垂直上升的距离.〔计算结果保存整数〕.〔以下数据供选用:sin47°≈0.7314,cos47°≈0.6820,tan47°≈1.0724〕.【考点】解直角三角形的应用-仰角俯角问题.【专题】计算题.【分析】此题要求的实际是BC和DF的长度,了AB、BD都是200米,可在Rt△ABC和Rt△BFD中用α、β的正切函数求出BC、DF的长.【解答】解:Rt△ABC中,斜边AB=200米,∠α=30°,BC=AB•sinα=200×sin30°=100〔米〕,Rt△BDF中,斜边BD=200米,∠β=47°,DF=BD•sinβ=200×sin47°≈146〔米〕,因此缆车垂直上升的距离应该是BC+DF=246〔米〕.答:缆车垂直上升了246米.【点评】此题的关键是根据所求的线段和的条件,正确地选用适宜的三角函数进行求解.11.如图,从一块矩形薄板ABCD上裁下一个工件GEHCPD〔阴影局部〕.图中EF∥BC,GH∥AB,∠AEG=11°18′,∠PCF=33°42′,AG=2cm,FC=6cm.求工件GEHCPD的面积.〔参考数据:tan11°18'≈,tan33°42′≈〕【考点】解直角三角形的应用.【专题】计算题.【分析】工件GEHCPD的面积=矩形面积减去其余三个三角形的面积.其余三角形正好等于矩形面积的一半,只需求得矩形边长即可.【解答】解:∵∠AEG=11°18′,AG=2cm∴AE=AG÷tan11°18'≈10那么DF=10∵FC=6cm,∠PCF=33°42′∴PF=FC×tan33°42′≈4那么CD=DF+FC=16,AD=EP+PF=6∵△AGE和△DPF底相等,高加到一起是AD所以是矩形AEFD的一半,同理可得到其余两个三角形是下边矩形的一半.∴工件GEHCPD的面积=矩形面积÷2=6×16÷2=48.【点评】解决此题的关键是根据题意得到所求面积与大矩形的关系.12.如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度i=1:,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A 的仰角为60°.〔1〕求小山的高度;〔2〕求铁架的高度.〔≈1.73,精确到0.1米〕【考点】解直角三角形的应用-仰角俯角问题;解直角三角形的应用-坡度坡角问题.【专题】应用题.【分析】〔1〕过D作DF垂直于坡底的水平线BC于点F,再由斜坡的坡比的概念,可得坡角为30°;解Rt△DFB可得DF即山高;〔2〕首先根据题意分析图形;此题涉及到两个直角三角形Rt△AED与Rt△ACB,解可得AC与BC的大小,再由AC=AE+EC,进而可求出答案.【解答】解:〔1〕如图,过D作DF垂直于坡底的水平线BC于点F.由,斜坡的坡比i=1:,于是tan∠DBC=,∴坡角∠DBC=30°.于是在Rt△DFB中,DF=DBsin30°=25,即小山高为25米.〔2〕设铁架的高AE=x.在Rt△AED中,∠ADE=60°,于是DE=,在Rt△ACB中,∠ABC=45°,∵AC=AE+EC=AE+DF=x+25,又BC=BF+FC=BF+DE=25x,由AC=BC,得x+25=25x.∴x=25≈43.3,即铁架高43.3米.【点评】此题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.13.梅华中学九年级数学课外学习小组某下午实践活动课时,测量朝西教学楼前的旗杆AB的高度.如图,当阳光从正西方向照射过来时,旗杆AB的顶端A的影子落在教学楼前的坪地C处,测得影长CE=2m,DE=4m,BD=20m,DE与地面的夹角α=30度.在同一时刻,测得一根长为1m的直立竹竿的影长恰为4m.根据这些数据求旗杆AB的高度.〔可能用到的数据:≈1.414,≈1.732,结果保存两个有效数字〕【考点】勾股定理的应用.【专题】应用题.【分析】根据题意过点C,E分别作CF⊥AB于点F,EH⊥BD的延长线于H,构造出直角三角形,利用勾股定理解答.【解答】解:如图,过点C,E分别作CF⊥AB于点F,EH⊥BD的延长线于H.在Rt△DEH中,∵DE=4m,∠EDH=30°,∴EH=2m,DH==2m又∵=∴AF=CF=〔EF+CE〕=〔BD+DH+CE〕≈6.2.∴AB=EH+AF≈8.2〔m〕.【点评】此题考查正确运用勾股定理.善于观察题目的信息是解题以及学好数学的关键.三、应用与探究14.高为12米的教学楼ED前有一棵大树AB,如图〔a〕.〔1〕某一时刻测得大树AB、教学楼ED在阳光下的投影长分别是BC=2.5米,DF=7.5米,求大树AB的高度;〔2〕现有皮尺和高为h米的测角仪,请你设计另一种测量大树AB高度的方案,要求:①在图〔b〕中,画出你设计的测量方案示意图,并将应测量的数据标记在图上〔长度用字母m,n …表示,角度用希腊字母α,β…表示〕;②根据你所画出的示意图和标注的数据,求出大树的高度.〔用字母表示〕【考点】相似三角形的应用;解直角三角形的应用.【专题】应用题;方案型.【分析】此题考查了学生学以致用的能力,考查了学生利用数学知识解决实际问题的能力;解此题的关键是利用相似三角形的性质,相似三角形的对应边成比例求解.解题时还要注意认识图形.【解答】解:〔1〕连接AC,EF,那么△ABC∽△EDF,∴,〔2分〕∴AB=4,即大树AB高是4米.〔2〕解法一:①如图〔b〕〔标注m,α,画草图也可给相同的分〕;〔5分〕②在Rt△CMA中,∵AM=CMtanα=mtanα,〔6分〕∴AB=mtanα+h.〔7分〕解法二:①如图〔c〕〔标注m,α,β,画草图也可给相同的分〕;〔5分〕②AMcotα﹣AMcotβ=m,∴AM=,〔6分〕∴AB=.〔7分〕【点评】此题只要是把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程,通过解方程求出树的高度,表达了方程的思想.还要注意学以致用,注意知识的积累.期中试卷〔2〕一、选择题〔共15题,每题3分,共45分〕1.〔3分〕下面所给的交通标志图中是轴对称图形的是〔 〕A .B .C .D .2.〔3分〕三角形一边上的中线把原三角形分成两个〔 〕A .形状相同的三角形B .面积相等的三角形C .直角三角形D .周长相等的三角形3.〔3分〕三条线段a=5,b=3,c 的值为整数,由a 、b 、c 为边可组成三角形〔 〕A .1个B .3个C .5个D .无数个4.〔3分〕多边形每一个内角都等于150°,那么从此多边形一个顶点发出的对角线有〔 〕A .7条B .8条C .9条D .10条5.〔3分〕如图,△ABC 的六个元素,那么下面甲、乙、丙三个三角形中和△ABC 全等的图形是〔 〕A .甲和乙B .乙和丙C .只有乙D .只有丙 6.〔3分〕如图,△ABC 的三边AB ,BC ,CA 长分别是20,30,40,其三条角平分线将△ABC 分为三个三角形,那么S △ABO :S △BCO :S △CAO 等于〔 〕A .1:1:1B .1:2:3C .2:3:4D .3:4:57.〔3分〕小明不小心把一块三角形形状的玻璃打碎成了三块,如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带〔 〕A .①B .②C .③D .①和②8.〔3分〕以下说法正确的选项是〔〕A.周长相等的两个三角形全等B.有两边和其中一边的对角对应相等的两个三角形全等C.面积相等的两个三角形全等D.有两个角和其中一角的对边对应相等的两个三角形全等9.〔3分〕以下条件中,能判定△ABC≌△DEF的是〔〕A.AB=DE,BC=ED,∠A=∠D B.∠A=∠D,∠C=∠F,AC=EFC.∠B=∠E,∠A=∠D,AC=EF D.∠B=∠E,∠A=∠D,AB=DE10.〔3分〕AD是△ABC中BC边上的中线,假设AB=4,AC=6,那么AD的取值范围是〔〕A.AD>1 B.AD<5 C.1<AD<5 D.2<AD<1011.〔3分〕如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么以下结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长等于AB与AC的和;④BF=CF.其中正确的有〔〕A.①②③B.①②③④C.①②D.①12.〔3分〕如图,Rt△ABC中,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,那么以下结论中不正确的选项是〔〕A.∠ACD=∠B B.CH=CE=EF C.AC=AF D.CH=HD13.〔3分〕以下命题正确的选项是〔〕A.两条直角边对应相等的两个直角三角形全等B.一条边和一个锐角对应相等的两个三角形全等C.有两边和其中一边的对角〔此角为钝角〕对应相等的两个三角形全等D.有两条边对应相等的两个直角三角形全等14.〔3分〕将点A〔3,2〕沿x轴向左平移4个单位长度得到点A′,点A′关于y轴对称的点的坐标是〔〕A.〔﹣3,2〕B.〔﹣1,2〕C.〔1,2〕 D.〔1,﹣2〕15.〔3分〕如图,△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD和CE交于O,AO的延长线交BC于F,那么图中全等的直角三角形有〔〕A.3对 B.4对 C.5对 D.6对二、填空题〔共10小题,每题3分,总分值30分〕16.〔3分〕假设一个n边形的边数增加一倍,那么内角和将增加.17.〔3分〕如图,由平面上五个点A、B、C、D、E连接而成,那么∠A+∠B+∠C+∠D+∠E=.18.〔3分〕如图:在△ABC和△FED中,AD=FC,AB=FE,当添加条件时,就可得到△ABC≌△FED.〔只需填写一个即可〕19.〔3分〕在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,假设BC=15,且BD:DC=3:2,那么D到边AB的距离是.20.〔3分〕如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,那么图中有对全等三角形.21.〔3分〕如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,那么AP=.22.〔3分〕如图,从镜子中看到一钟表的时针和分针,此时的实际时刻是.23.〔3分〕如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC与E,那么△ADE的周长等于.24.〔3分〕如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,假设原来点A坐标是〔a,b〕,那么经过第2021变换后所得的A点坐标是.25.〔3分〕如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,使整个涂成黑色的图形成为轴对称图形,这样的白色小方格有个.三、解答题〔共7小题,总分值45分〕26.〔6分〕作图题:〔不写作法,但要保存痕迹〕〔1〕作出下面图形关于直线l的轴对称图形〔图1〕.〔2〕在图2中找出点A,使它到M,N两点的距离相等,并且到OH,OF的距离相等.〔3〕在图3中找到一点M,使它到A、B两点的距离和最小.27.〔4分〕A〔a+b,1〕,B〔﹣2,2a﹣b〕,假设点A,B关于x轴对称,求a,b的值.28.〔6分〕:如图,AB=AE,BC=ED,AF是CD的垂直平分线,求证:∠B=∠E.29.〔6分〕如图,在△ABC中,D是AB上一点,DF交AC于点E,DE=FE,AE=CE,AB与CF有什么位置关系?证明你的结论.30.〔6分〕如图,∠AOB=90°,OM平分∠AOB,将直角三角板的顶点P在射线OM上移动,两直角边分别与OA、OB相交于点C、D,问PC与PD相等吗?试说明理由.31.〔6分〕:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E 三点在同一直线上,连接BD.求证:△BAD≌△CAE.32.〔11分〕如图,点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC 于F,AD交CE于H.〔1〕求证:△BCE≌△ACD;〔2〕求证:FH∥BD.人教版八年级上册期中试卷〔2〕参考答案与试题解析一、选择题〔共15题,每题3分,共45分〕1.〔3分〕下面所给的交通标志图中是轴对称图形的是〔〕A.B.C.D.【考点】轴对称图形.【分析】根据轴对称图形的概念对各选项分析判断后利用排除法求解.【解答】解:A、是轴对称图形,故本选项正确;B、不是轴对称图形,故本选项错误;C、不是轴对称图形,故本选项错误;D、不是轴对称图形,故本选项错误.应选A.【点评】此题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两局部折叠后可重合.2.〔3分〕三角形一边上的中线把原三角形分成两个〔〕A.形状相同的三角形B.面积相等的三角形C.直角三角形D.周长相等的三角形【考点】三角形的角平分线、中线和高.【分析】根据三角形的面积公式以及三角形的中线定义,知三角形的一边上的中线把三角形分成了等底同高的两个三角形,所以它们的面积相等.【解答】解:三角形一边上的中线把原三角形分成两个面积相等的三角形.应选:B.【点评】考查了三角形的中线的概念.构造面积相等的两个三角形时,注意考虑三角形的中线.3.〔3分〕三条线段a=5,b=3,c的值为整数,由a、b、c为边可组成三角形〔〕A.1个 B.3个 C.5个 D.无数个【考点】三角形三边关系.【分析】两边,那么第三边的长度应是大于两边的差而小于两边的和,这样就可求出第三边c的范围,根据c的值为整数,即可确定c的值.从而确定三角形的个数.【解答】解:c的范围是:2<c<8,因而c的值可以是:3、4、5、6、7共5个数,因而由a、b、c为边可组成5个三角形.应选C.【点评】此题需要理解的是如何根据的两条边求第三边的范围.4.〔3分〕多边形每一个内角都等于150°,那么从此多边形一个顶点发出的对角线有〔〕A.7条 B.8条 C.9条 D.10条【考点】多边形内角与外角;多边形的对角线.【分析】多边形的每一个内角都等于150°,多边形的内角与外角互为邻补角,那么每个外角是30度,而任何多边形的外角是360°,那么求得多边形的边数;再根据不相邻的两个顶点之间的连线就是对角线,那么此多边形从一个顶点出发的对角线共有〔n﹣3〕条,即可求得对角线的条数.【解答】解:∵多边形的每一个内角都等于150°,∴每个外角是30°,∴多边形边数是360°÷30°=12,那么此多边形从一个顶点出发的对角线共有12﹣3=9条.应选C.【点评】此题主要考查了多边形的外角和定理,外角求边数的这种方法是需要熟记的内容.多边形从一个顶点出发的对角线共有〔n﹣3〕条.5.〔3分〕如图,△ABC的六个元素,那么下面甲、乙、丙三个三角形中和△ABC全等的图形是〔〕A.甲和乙B.乙和丙C.只有乙D.只有丙【考点】全等三角形的判定.【分析】全等三角形的判定定理有SAS ,ASA ,AAS ,SSS ,根据定理逐个判断即可.【解答】解:图甲不符合三角形全等的判定定理,即图甲和△ABC 不全等;图乙符合SAS 定理,即图乙和△ABC 全等;图丙符合AAS 定理,即图丙和△ABC 全等;应选B .【点评】此题考查了全等三角形的判定的应用,注意:全等三角形的判定定理有SAS ,ASA ,AAS ,SSS .6.〔3分〕如图,△ABC 的三边AB ,BC ,CA 长分别是20,30,40,其三条角平分线将△ABC 分为三个三角形,那么S △ABO :S △BCO :S △CAO 等于〔 〕A .1:1:1B .1:2:3C .2:3:4D .3:4:5【考点】角平分线的性质.【专题】数形结合.【分析】利用角平分线上的一点到角两边的距离相等的性质,可知三个三角形高相等,底分别是20,30,40,所以面积之比就是2:3:4.【解答】解:利用同高不同底的三角形的面积之比就是底之比可知选C .应选C .【点评】此题主要考查了角平分线上的一点到两边的距离相等的性质及三角形的面积公式.做题时应用了三个三角形的高时相等的,这点式非常重要的.7.〔3分〕小明不小心把一块三角形形状的玻璃打碎成了三块,如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带〔 〕A .①B .②C .③D .①和②【考点】全等三角形的应用.【分析】根据全等三角形的判定方法解答即可.【解答】解:带③去可以利用“角边角〞得到全等的三角形.应选C.【点评】此题考查了全等三角形的应用,熟练掌握三角形全等的判定方法是解题的关键.8.〔3分〕以下说法正确的选项是〔〕A.周长相等的两个三角形全等B.有两边和其中一边的对角对应相等的两个三角形全等C.面积相等的两个三角形全等D.有两个角和其中一角的对边对应相等的两个三角形全等【考点】全等三角形的判定.【分析】利用三角形全等的判定方法逐项判断即可.【解答】解:A、周长相等的两个三角形,三组边不一定对应相等,那么这两个三角形不一定全等,故A不正确;B、由条件可知这两个三角形满足的是SSA,可知不能判定其全等,故B不正确;C、只要等底等高的两个三角形面积都是相等的,但是不一定全等,故C不正确;D、由条件可知这两个三角形满足AAS,可判定其全等,故D正确;应选D.【点评】此题主要考查全等三角形的判定,掌握全等三角形的判定方法SSS、SAS、ASA、AAS 和HL是解题关键,注意AAA和SSA不能判定两个三角形全等.9.〔3分〕以下条件中,能判定△ABC≌△DEF的是〔〕A.AB=DE,BC=ED,∠A=∠D B.∠A=∠D,∠C=∠F,AC=EFC.∠B=∠E,∠A=∠D,AC=EF D.∠B=∠E,∠A=∠D,AB=DE【考点】全等三角形的判定.【分析】考查三角形的判定定理,有AAS,SSS,ASA,SAS四种.做题时要按判定全等的方法逐个验证.【解答】解:AB=DE,BC=ED,∠A=∠D,不符合SAS,A不能选;∠A=∠D,∠C=∠F,AC=EF不是对应边,B不能选;∠B=∠E,∠A=∠D,AC=EFAC=EF不是对应边,C不能选;根据三角形全等的判定,当∠B=∠E,∠A=∠D,AB=DE时,△ABC≌△DEF〔ASA〕.应选D.【点评】此题考查了全等三角形的判定;注意要证明两个三角形是否全等,要看对应边和对应角是否对应相等.10.〔3分〕AD是△ABC中BC边上的中线,假设AB=4,AC=6,那么AD的取值范围是〔〕A.AD>1 B.AD<5 C.1<AD<5 D.2<AD<10【考点】三角形三边关系.【分析】此题要倍长中线,再连接,构造新的三角形.根据三角形的三边关系:任意两边之和大于第三边,任意两边之差小于第三边.即可求解.【解答】解:根据题意得:得6﹣4<2AD<6+4,即1<AD<5.应选C.【点评】注意此题中常见的辅助线:倍长中线.11.〔3分〕如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么以下结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长等于AB与AC的和;④BF=CF.其中正确的有〔〕A.①②③B.①②③④C.①②D.①【考点】等腰三角形的判定;角平分线的性质.【分析】由平行线得到角相等,由角平分线得角相等,根据平行线的性质及等腰三角形的判定和性质.【解答】解:∵DE∥BC,∴∠DFB=∠FBC,∠EFC=∠FCB,∵BF是∠ABC的平分线,CF是∠ACB的平分线,∴∠FBC=∠DFB,∠FCE=∠FCB,∵∠DBF=∠DFB,∠EFC=∠ECF,∴△DFB,△FEC都是等腰三角形.∴DF=DB,FE=EC,即有DE=DF+FE=DB+EC,∴△ADE的周长AD+AE+DE=AD+AE+DB+EC=AB+AC.应选A.【点评】此题考查了等腰三角形的性质及角平分线的性质及平行线的性质;题目利用了两直线平行,内错角相等,及等角对等边来判定等腰三角形的;等量代换的利用是解答此题的关键.12.〔3分〕如图,Rt△ABC中,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,那么以下结论中不正确的选项是〔〕A.∠ACD=∠B B.CH=CE=EF C.AC=AF D.CH=HD【考点】角平分线的性质;全等三角形的判定与性质.【分析】根据角的平分线的性质,得CE=EF,两直线平行,内错角相等,得∠AEF=∠CHE,用AAS判定△ACE≌△AEF,由全等三角形的性质,得∠CEH=∠AEF,用等角对等边判定边相等.【解答】解:A、∵∠B和∠ACD都是∠CAB的余角,∴∠ACD=∠B,故正确;B、∵CD⊥AB,EF⊥AB,∴EF∥CD∴∠AEF=∠CHE,∴∠CEH=∠CHE∴CH=CE=EF,故正确;C、∵角平分线AE交CD于H,∴∠CAE=∠BAE,又∵∠ACB=∠AFE=90°,AE=AE,∴△ACE≌△AEF,∴CE=EF,∠CEA=∠AEF,AC=AF,故正确;D、点H不是CD的中点,故错误.应选D.【点评】此题是一道综合性较强的题目,需要同学们把直角三角形的性质和三角形全等的判定等知识结合起来解答.13.〔3分〕以下命题正确的选项是〔〕A.两条直角边对应相等的两个直角三角形全等B.一条边和一个锐角对应相等的两个三角形全等C.有两边和其中一边的对角〔此角为钝角〕对应相等的两个三角形全等D.有两条边对应相等的两个直角三角形全等【考点】命题与定理.【分析】利用全等三角形的判定定理分别对四个命题进行判断后即可确定正确的选项.【解答】解:A、两条直角边对应相等的两个直角三角形全等,正确;B、一条边和一个锐角对应相等的两个三角形全等,错误;C、有两边和其中一边的对角〔此角为钝角〕对应相等的两个三角形全等,错误;D、有两条边对应相等的两个直角三角形全等,错误,应选A.【点评】此题考查了命题与定理的知识,解题的关键是能够熟练掌握全等三角形的判定,难度不大.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1220
Dimensions are shown for
reference purposes only.
Dimensions are in inches over
(millimeters) unless otherwise
specified.
Specifications and availability
subject to change.
Technical support:
Refer to inside back cover.
CG series
CMOS IC Time Delay Relay
•Repeatability to .05%
•Choice of timing modes
– Delay on operate
– Delay on release
– Interval on
•Knob adjustable
•10A output relay with DPDT contacts
•Various models time from 0.5 sec. to 100 min.
File E22575
File LR15734
Contact Data @ 25°C
Arrangements:2 Form C (DPDT).
Material: Silver-cadmium oxide alloy.
Rating:10A @ 30VDC or 277VAC, resistive; 1/2 HP @ 250VAC;
1/3 HP @ 120VAC.
Expected Mechanical Life: 10 million operations.
Expected Electrical Life:
100,000 operations, min., at rated load.
Input Data @ 25C
Voltage: 120VAC and 24VDC.
Power Requirement:AC Types:Typically less than 3 VA.
DC Types:Typically less than 3 W.
Transient Protection: Yes.
Reverse Voltage Protection: Yes.
Initial Dielectric Strength
Between Open Contacts:500V rms, 60 Hz.
Between All Other Conductors:500V rms, 60 Hz.
Environmental Data
Temperature Range:Storage: -40°C to +85°C.
Operating: -10°
C to +55°C.
Mechanical Data
Termination: 8- or 11-pin octal style plug.
Enclosure:Yellow plastic case. Knob adjustable types have dial scale for
reference only.
Sockets:Models with 8-pin base fit either 27E122 or 27E891 (snap-on)
screw terminal sockets. 11-pin types fit either 27E123 or
27E892 (snap-on) screw terminal sockets.
Weight: 8 oz. (227g) approximately.
Timing Modes
Delay on operate – Delay period begins when input voltage is applied. At
the end of the delay period, the relay will operate and will not release until
input voltage is removed. Reset occurs when input voltage is reapplied.
Delay on release – Input voltage must be applied continuously to operate
the internal relay. When the control switch is closed, the relay energizes.
When the control switch is opened, timing begins. When timing is
complete, the relay will de-energize. Time may be reset to zero during
timing by closing the control switch.
Interval on – The relay energizes and timing begins when input voltage is
applied. At the end of the time delay period the relay will de-energize.
Reset is accomplished by removing, then reapplying, the input voltage.
Timing Specifications
Timing Ranges: From 0.5 to 5.0 sec. through 10 to 100 min.
Timing Adjustment: Knob adjustable.
Tolerance (for AC units add ±1/2 cycle 60 Hz.):
Knob Adj. Types:–0, +10% of max. specified at high end of timing range;
+0, –10% of min. specified at low end.
Delta Time (for AC units add ±1 cycle 60 Hz.):±2%, typ.; ±5%, max.
Repeatability (including first cycle of operation):
AC:±0.1%, typ.; ±0.5%, max.; but not less than ±16 ms.
DC:±0.05% typ.; ±0.1% max.; but not less than ±3 ms.
Release Time: 30 ms, typ.; 45 ms, max.
Recycle Time:AC:40 ms, typ.; 60 ms, max.
DC:30 ms, typ.; 45 ms, max.
INPUT
VOLTAGE
ON
OFF
N.O. RELAY
CONTACTS
ON
OFF
TIME
➛➛
CONTROL
SWITCH
ON
OFF
ON
OFF
N.O. RELAY
CONTACTS TIME
➛➛
INPUT
VOLTAGE
ON
OFF
N.O. RELAY
CONTACTS
ON
OFF
TIME
➛➛
Note:DC voltage must be filtered (5% p-p ripple max. at nom. voltage).
AC models will operate on 50 or 60 Hz.
Users should thoroughly review the technical data before selecting a product part
number. It is recommended that user also seek out the pertinent approvals files of
the agencies/laboratories and review them to ensure the product meets the
requirements for a given application.
/
1221Dimensions are shown for reference purposes only.
Dimensions are in inches over (millimeters) unless otherwise specified.
Specifications and availability subject to change.
Technical support:Refer to inside back cover.
/
分销商库存信息:
TYCO
CGB-38-70100M CGB-38-70050M CGB-38-78050M CGB-38-78010M CGB-38-79010M。
