2012年山东省济南市中考数学 试题及答案
初三数学07------12年济南市数学中考试题(二次函数部分)

济南市数学中考试题(二次函数部分)(07年)10.已知2y ax bx =+的图象如图所示,则y ax b =-的图象一定过( ) A .第一、二、三象限 B .第一、二、四象限 C .第二、三、四象限D .第一、三、四象限22.(本小题满分9分)已知:如图,直角梯形ABCD 中,A D B C ∥,90A ∠= ,BC=CD=10,4sin 5C =。
(1)求梯形ABCD 的面积;(2)点E ,F 分别是BC ,CD 上的动点,点E 从点B 出发向点C 运动,点F 从点C 出发向点D 运动,若两点均以每秒1个单位的速度同时出发,连接EF 。
求E F C △面积的最大值,并说明此时E ,F 的位置。
24.(本小题满分9分)已知:如图,在平面直角坐标系中,A B C △是直角三角形,90ACB ∠= ,点A ,C 的坐标分别为A (-3,0),C (1,0),3tan 4B AC ∠=。
(1)求过点A ,B 的直线的函数表达式;(2)在x 轴上找一点D ,连接DB ,使得A D B △与A B C △相似(不包括全等),并求点D 的坐标;(3)在(2)的条件下,如P ,Q 分别是AB 和AD 上的动点,连接PQ ,设AP=DQ=m ,问是否存在这样的m 使得APQ △与AD B △相似,如存在,请求出m 的值;如不存在,请说明理由。
(08年)23.(本小题满分9分)已知:如图,直线343y x =-+与x 轴相交于点A ,与直线3y x =相交于点P . (1)求点P 的坐标.(2)请判断O PA ∆的形状并说明理由.(3)动点E 从原点O 出发,以每秒1个单位的速度沿着O →P →A 的路线向点A 匀速运动(E 不与点O 、A 重合),过点E 分别作EF ⊥x 轴于F ,EB ⊥y 轴于B .设运动t 秒时,矩形EBOF 与△OPA 重叠部分的面积为S .求:① S 与t 之间的函数关系式.② 当t 为何值时,S 最大,并求S 的最大值.ACO Bxy第24题图yxO第10题图F第23题图yOAxPEB24.(本小题满分9分)已知:抛物线2y ax bx c =++(a ≠0),顶点C (1,3-),与x 轴交于A 、B 两点,(10)A -,.(1)求这条抛物线的解析式.(2)如图,以AB 为直径作圆,与抛物线交于点D ,与抛物线对称轴交于点E ,依次连接A 、D 、B 、E ,点P 为线段AB 上一个动点(P 与A 、B 两点不重合),过点P 作PM ⊥AE 于M ,PN ⊥DB 于N ,请判断PM PN BEAD+是否为定值? 若是,请求出此定值;若不是,请说明理由.(3)在(2)的条件下,若点S 是线段EP 上一点,过点S 作FG ⊥EP ,FG 分别与边.AE 、BE 相交于点F 、G(F 与A 、E 不重合,G 与E 、B 不重合),请判断PA EF PBEG=是否成立.若成立,请给出证明;若不成立,请说明理由(09年)24.(本小题满分9分)已知:抛物线()20y a x b x c a =++≠的对称轴为1x =-,与x 轴交于A B ,两点,与y 轴交于点C ,其中()30A -,、()02C -,.(1)求这条抛物线的函数表达式.(2)已知在对称轴上存在一点P ,使得P B C △的周长最小.请求出点P 的坐标.(3)若点D 是线段O C 上的一个动点(不与点O 、点C 重合).过点D 作D E P C ∥交x 轴于点E .连接P D 、P E .设C D 的长为m ,P D E △的面积为S .求S 与m 之间的函数关系式.试说明S 是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.A CxyBO (09年24题第24题图C OxA D P M EB Ny10年第10yxO-1 2 DC MNOABPl10年第24y E xO t /sh /m26(10年)10.二次函数22y x x =--的图象如图所示,则函数值y <0时x 的取值范围是A .x <-1B .x >2C .-1<x <2D .x <-1或x >2 24.(本小题满分9分)如图所示,抛物线223y x x =-++与x 轴交于A 、B 两点,直线BD 的函数表达式为333y x =-+,抛物线的对称轴l 与直线BD 交于点C 、与x 轴交于点E .⑴求A 、B 、C 三个点的坐标.⑵点P 为线段AB 上的一个动点(与点A 、点B 不重合),以点A 为圆心、以AP 为半径的圆弧与线段AC 交于点M ,以点B 为圆心、以BP 为半径的圆弧与线段BC 交于点N ,分别连接AN 、BM 、MN . ①求证:AN=BM .②在点P 运动的过程中,四边形AMNB 的面积有最大值还是有最小值?并求出该最大值或最小值.(11年)13.竖直向上发射的小球的高度h(m)关于运动时间t(s)的函数表达式为h =at 2+bt ,其图象如图所示.若小球在发射后第2s 与第6s 时的高度相等,则下列时刻中小球的高度最高的是第【 】A .3sB .3.5sC .4.2sD .6.5s27.(9分)如图,在矩形OABC 中,点O 为原点,点A 的坐标为(0,8),点C 的坐标为(6,0).抛物线y =- 4 9x 2+bx +c经过点A 、C ,与AB 交于点D . (1)求抛物线的函数解析式;(2)点P 为线段BC 上一个动点(不与点C 重合),点Q 为线段AC 上一个动点,AQ =CP ,连接PQ ,设CP =m ,△CPQ 的面积为S .①求S 关于m 的函数表达式;②当S 最大时,在抛物线y =- 49x 2+bx +c 的对称轴l 上,若存在点F ,使△DFQ 为直角三角形,请直接..写出所有符合条件的点F 的坐标;若不存在,请说明理由.(12年)15.如图,二次函数的图象经过(-2,-1),(1,1)两点,则下列关于此二次函数的说法正确的是( )A .y 的最大值小于0B .当x=0时,y 的值大于1C .当x=-1时,y 的值大于1D .当x=-3时,y 的值小于021.如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax 2+bx .小强骑自行车从拱梁一端O 沿直线匀速穿过拱梁部分的桥面OC ,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC 共需 秒.28.如图1,抛物线y=ax2+bx+3与x 轴相交于点A (-3,0),B (-1,0),与y 轴相交于点C ,⊙O1为△ABC 的外接圆,交抛物线于另一点D . (1)求抛物线的解析式;(2)求cos ∠CAB 的值和⊙O1的半径;(3)如图2,抛物线的顶点为P ,连接BP ,CP ,BD ,M 为弦BD 中点,若点N 在坐标平面内,满足△BMN ∽△BPC ,请直接写出所有符合条件的点N 的坐标.ADBPQOCxy ADBOCx y l备用图。
2012年山东省济南市中考数学试题及答案

【考点】科学记数法—表示较大的数.
PS:双击后Ctrl+A,Ctrl+C然后粘贴到word即可 不能直接提供word版,抱歉。
2题,每小题 3 分,满分 45 分)
1.-12 的绝对值是( A ) A.12 【考点】绝对值. 【专题】 【分析】根据绝对值的定义进行计算. 【解答】解:|-12|=12, 故选 A. 【点评】本题考查了绝对值.一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0 的绝 对值是 0. B.-12 C.
3. 2012 年伦敦奥运会火炬传递路线全长约为 12800 公里, 数字 12800 用科学记数法表示为 ( C ) A.1.28× 3 10 B.12.8× 3 10 C.1.28× 4 10 D.0.128× 5 10
【考点】科学记数法—表示较大的数.
3. 2012 年伦敦奥运会火炬传递路线全长约为 12800 公里, 数字 12800 用科学记数法表示为 ( C ) A.1.28× 3 10 B.12.8× 3 10 C.1.28× 4 10 D.0.128× 5 10
1 12
D.
1 12
2. 如图, 直线 a∥b, 直线 c 与 a, 相交, b ∠1=65° 则∠2= , ( B ) A.115° B.65° C.35° D.25°
【考点】平行线的性质. 【专题】 【分析】由直线 a∥b,∠1=65° ,根据两直线平行,同位角相等, 即可求得∠3 的度数,又由对顶 角相等,即可求得答案. 【解答】解:∵直线 a∥b,∠1=65° , ∴∠3=∠1=65° , ∴∠2=∠3=65° . 故选 B. 【点评】此题考查了平行线的性质.此题比较简单,注意掌握两直线平行,同位角相等定理的应用, 注意数形结合思想的应用.
济南市2012年初三年级学业水平考试

济南市2012年初三年级学业水平考试数 学 试 题第Ⅰ卷(选择题 共45分)一、选择题(本大题共15个小题,每题3分,共45分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
) 1、12-的绝对值是A 、12B 、12-C 、112 D 、112- 2、如图,直线a ∥b ,直线c 与a 、b 相交,∠1=650,则∠2=A 、1150B 、650C 、350D 、250ba3、2012年伦敦奥运会火炬传递路线全长约为12800公里,数字12800用科学记数法表示为A 、1.28×103B 、12.8×103C 、1.28×104D 、0.128×1054、下列事件中是必然事件的是A 、任意买一张电影票,座位号是偶数B 、正常情况下,将水加热到1000C 水会沸腾C 、三角形的内角和是3600D 、打开电视机,正在播动画片 5、下列计算正确的是A 、3x -2x=1B 、a 2+a 2=a 4C 、a 5÷a 5=aD 、a 3·a 2=a 56、下列四个立体图形中,主视图是三角形的是DC BA第6题图7、化简5(2x -3)+4(3-2x)的结果为A 、2x -3B 、2x+9C 、8x -3D 、18x -38、暑假即将来临,小明和小亮每人要从甲、乙、丙三个社区中随机抽取一个社区参加综合实践活动,那么小明和小亮选到同一社区参加综合实践活动的概率为A 、12 B 、13 C 、16 D 、199、如图,在8×4的矩形网格中,每个小正方形的边长都是1,若△ABC 的三个顶点在图中相应的格点上,则tan ∠ACB 的值为A 、13 B 、12 C、2D 、3 CBA第9题图第11题图NMDCBA第13题图O10、下列命题是真命题的是A 、对角线相等的四边形是矩形B 、一组邻边相等的四边形是菱形C 、四个角是直角的四边形是正方形D 、对角线相等的梯形是等腰梯形 11、一次函数y=kx+b 的图象如图所示,则方程kx+b=0的解为A 、x=2B 、y=2C 、x =-1D 、y =-112、已知⊙O 1和⊙O 2的半径是一元二次方程x 2-5x+6=0的两根,若圆心距O 1O 2=5,则⊙O 1和⊙O 2的位置关系是A 、外离B 、外切C 、相交D 、内切13、如图,∠MON=900,矩形ABCD 的顶点A ,B 分别在OM 、ON 上,当B 在边ON 上运动时,A 随之在边OM 上运动,矩形ABCD 的形状保持不变,其中AB=2,BC=1。
2012年济南中考压轴题
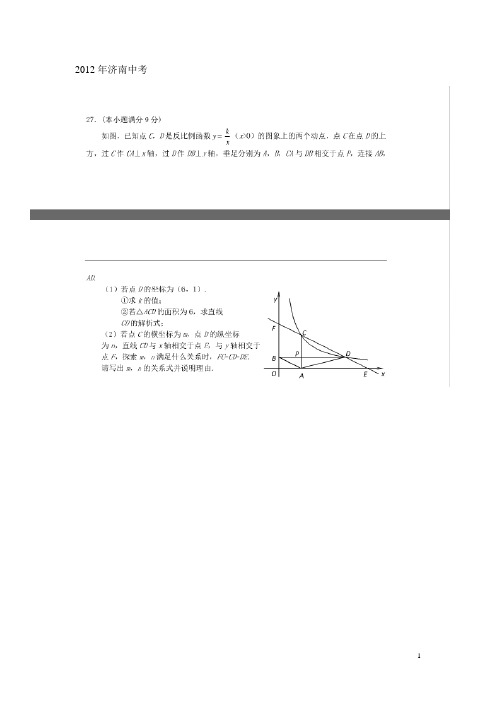
2012年济南中考DEA M NC B2011年:28.(9分)如图,点C为线段AB上任意一点(不与点A、B重合),分别以AC、BC为一腰在AB的同侧作等腰△ACD和△BCE,CA=CD,CB=CE,∠ACD与∠BCE都是锐角,且∠ACD=∠BCE,连接AE交CD于点M,连接BD交CE于点N,AE与BD交于点P,连接CP.(1)求证:△ACE≌△DCB;(2)请你判断△ACM与△DPM的形状有何关系并说明理由;(3)求证:∠APC=∠BPC.已知:抛物线()20y ax bx c a =++≠的对称轴为1x =-,与x 轴交于A B ,两点,与y 轴交于点C ,其中()30A -,、()02C -,.(1)求这条抛物线的函数表达式.(2)已知在对称轴上存在一点P ,使得PBC △的周长最小.请求出点P 的坐标. (3)若点D 是线段OC 上的一个动点(不与点O 、点C 重合).过点D 作DE PC ∥交x 轴于点E .连接PD 、PE .设CD 的长为m ,PDE △的面积为S .求S 与m 之间的函数关系式.试说明S 是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.(第24题图)如图所示,抛物线223y x x =-++与x 轴交于A 、B 两点,直线BD 的函数表达式为y =+l 与直线BD 交于点C 、与x 轴交于点E .⑴求A 、B 、C 三个点的坐标.⑵点P 为线段AB 上的一个动点(与点A 、点B 不重合),以点A 为圆心、以AP 为半径的圆弧与线段AC 交于点M ,以点B 为圆心、以BP 为半径的圆弧与线段BC 交于点N ,分别连接AN 、BM 、MN .①求证:AN =BM .②在点P 运动的过程中,四边形AMNB 的面积有最大值还是有最小值?并求出该最大值或最小值.2008年:24.(本小题满分9分)已知:抛物线2yaxbxc=++(a≠0),顶点C (1,3−),与x轴交于A、B两点,(10)A−,.(1)求这条抛物线的解析式.(2)如图,以AB为直径作圆,与抛物线交于点D,与抛物线对称轴交于点E,依次连接A、D、B、E,点P为线段AB上一个动点(P与A、B两点不重合),过点P 作PM⊥AE于M,PN⊥DB于N,请判断PMPNBEAD+是否为定值? 若是,请求出此定值;若不是,请说明理由.(3)在(2)的条件下,若点S是线段EP上一点,过点S作FG⊥EP ,FG分别与边.AE、BE相交于点F、G(F与A、E 不重合,G与E、B不重合),请判断PAEFPBEG=是否成立.若成立,请给出证明;若不成立,请说明理由.2007年:24.已知:如图,在平面直角坐标系中,△ABC 是直角三角形,∠ACB=90°,点A ,C 的坐标分别为A (-3,0),C (1,0),tan ∠BAC= .(1)求过点A ,B 的直线的函数表达式;(2)在x 轴上找一点D ,连接DB ,使得△ADB 与△ABC 相似(不包括全等),并求点D 的坐标; (3)在(2)的条件下,如P ,Q 分别是AB 和AD 上的动点,连接PQ ,设AP=DQ=m ,问是否存在这样的m ,使得△APQ 与△ADB 相似?如存在,请求出m 的值;如不存在,请说明理由.3 4。
2012年山东济南市中考数学

114.如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是()A.(2,0)B.(-1,1)C.(-2,1)D.(-1,-1)第14题图第15题图15.如图,二次函数的图象经过(-2,-1),(1,1)两点,则下列关于此二次函数的说法正确的是()A.y的最大值小于0B.当x=0时,y的值大于1C.当x=-1时,y的值大于1D.当x=-3时,y的值小于0二、填空题(每小题3分,满分18分)16.分解因式:21a-= .17.计算:2sin30°= .18.不等式组24010xx-<⎧⎨+≥⎩的解集为.19.如图,在Rt△ABC中,∠C=90°,AC=4,将△ABC沿CB向右平移得到△DEF,若平移距离为2,则四边形ABED的面积等于.第19题图第20题图20.如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,以其三边为直径向三角形外作三个半圆,矩形EFGH的各边分别与半圆相切且平行于AB或BC,则矩形EFGH的周长是.21.如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需秒.三、解答题(共7小题,共57分)22.(7分)(1)解不等式324x-≥,并将解集在数轴上表示出来.(2)化简:2121224a a aa a--+÷--.223.(7分)(1)如图1,在□ABCD中,点E,F分别在AB,CD上,AE=CF.求证:DE=BF.(2)如图2,在△ABC中,AB=AC,∠A=40°,BD是∠ABC的平分线,求∠BDC的度数.图1 图224.(8分)冬冬全家周末一起去济南山区参加采摘节,他们采摘了油桃和樱桃两种水果,其中油桃比樱桃多摘了5斤,若采摘油桃和樱桃分别用了80元,且樱桃每斤价格是油桃每斤价格的2倍,问油桃和樱桃每斤各是多少元?25.(8分)济南以“泉水”而闻名,为保护泉水,造福子孙后代,济南市积极开展“节水保泉”活动,宁宁利用课余时间对某小区300户居民的用水情况进行了统计,发现5月份各户居民的用水量均比4月份有所下降,宁宁将5月份户数508010070(1)300户居民5月份节水量的众数,中位数分别是多少米3?(2)扇形统计图中2.5米3对应扇形的圆心角为度;(3)该小区300户居民5月份平均每户节约用水多少米3?3426. (9分)如图1,在菱形ABCD 中,AC =2,BD=,AC ,BD 相交于点O .(1)求边AB 的长;(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD 的顶点A 处,绕点A 左右旋转,其中三角板60°角的两边分别与边BC ,CD 交于点E ,F ,连接EF ,与AC 交于点G . ①判断△AEF 是哪种特殊三角形,并说明理由; ②旋转过程中,当点E 为边BC 的四等分点时 (BE >CE ),求CG 的长.27. (9分)如图,已知双曲线ky x经过点D (6,1),点C 是双曲线第三象限分支上的动点,过C 作CA ⊥x 轴,过D 作DB ⊥y 轴,垂足分别为A ,B ,连接AB ,BC . (1)求k 的值;(2)若△BCD 的面积为12,求直线CD 的函数解析式;(3)判断AB 与CD 的位置关系,并说明理由.28.(9分)如图1,抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1为△ABC的外接圆,交抛物线于另一点D.(1)求抛物线的解析式;(2)求cos∠CAB的值和⊙O1的半径;(3)如图2,抛物线的顶点为P,连接BP,CP,BD,M为弦BD中点,若点N在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点N的坐标.562012年山东济南中考数学参考答案一、选择题(每小题3分,满分45分)二、填空题(每小题3分,满分18分)三、解答题(共7小题,共57分) 22.(1)x ≥2;(2)原式=21a -. 23.(1)证明略;(2)75°.24.油桃每斤8元,樱桃每斤16元. 25.(1)众数是2.5米3,中位数是2.5米3;(2)120;(3)平均每户节约用水2.1 米3. 26.(1)2;(2)①等边三角形,理由略; ②38.27.(1)=6k ;(2)1=22y x -;(3)AB ∥CD ,理由略.28.(1)2=+4+3 y x x ;(2)cos ∠CAB 的值为2,⊙O 1 (3)所有符合条件的点N 的坐标为7319() ()2222--,,,.。
山东省济南市2012年中考数学第一次模拟考试试题

2012年初三年级学业水平考试数 学 模 拟 题 注意事项:1.本试题分第I 卷和第II 卷两部分.第I 卷满分45分;第II 卷满分75分.本试题共10页,满分120分,考试时间为120分钟.2.答卷前,考生务必将自己的某某、某某号、考试科目涂写在答题卡上,并同时将考点、某某、某某号、座号填写在试卷的密封线内.3.第Ⅰ卷为选择题,每小题选出答案后,用2B 铅笔把答题卡上对应题目的正确答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案,答案写在试卷上无效. 4.考试期间,一律不得使用计算器;考试结束,应将本试卷和答题卡一并交回.第Ⅰ卷(选择题 共45分)一、选择题(本大题共15个小题.每小题3分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.-2的倒数是( ) A. 2 B.21212.如图所示的几何体的俯视图是( )A .B .C .D .3.据报道,5月28日参观2010某某世博会的人数达万﹒用科学记数法表示数万是() A .3.56×101B .3.56×104C .3.56×105D .35.6×1044.已知点M (-2,3 )在双曲线xky =上,则下列一定在该双曲线上的是( ) A.(3,-2 ) B.(-2,-3 )C.(2,3 )D.(3,2)5.为估计池塘两岸A 、B 间的距离,晓明在池塘一侧选取了一点P ,测得PA=16m ,PB=12m ,那么AB 间的距离不可能是( ) A.5m B.15mC.20mD.28m6.下列各等式成立的是( )A.752a a a =+ B.236()a a -= C.21(1)(1)a a a -=+- D.222()a b a b +=+7.已知四边形ABCD 是平行四边形,下列结论中不正确的是( )⊥BD 时,它是菱形∠ABC=90°时,它是矩形 D.当AC=BD 时,它是正方形8.某企业1~5月份利润的变化情况图所示,以下说法与图中反映 的信息相符的是( )A .1~2月份利润的增长快于2~3月份分利润的增长B .1~4月份利润的极差与1~5月份利润的极差不同C .1~5月份利润的的众数是130万元D .1~5月份利润的中位数为120万元9.如图,CD 是⊙O 的直径,A B ,是⊙O 上的两点,若20ABD ∠=, 则ADC ∠的度数为( )A .70B .060 C .050 D .04010.某商店进了一批商品,每件商品的进价为a 元.若要获利15%,则每件商品的零售价应为( ) A .15%a 元 B .(1+15%)a 元 C.%151+a元 D .(1-15%)a 元11.如图,CA⊥BE 于A ,AD⊥BF 于D ,下列正确的是( ) A. α的余角只有∠BB. α的邻补角是∠DAC第2题图AB DCO某某: 某某号密 封 线 内 不 要 答 题y–1 13Ox(第15题图)C. ∠ACF 是α的余角D. α与∠ACF 互补 12.如图反映的过程是:小强从家去菜地浇水,又去玉米地除草,然后回菜地和玉米地的距离为a 千米,小强在玉米地除草比在菜地浇水多用的时间为b 分钟,则a ,b 的值分别为( )A .1.1,8B .0.9,3C .1.1,12D .0.9,8 13.不等式组21318x x --⎧⎨->⎩≥的解集在数轴上可表示为( )A .B .C .D .14.关于x 的方程(a -5)x 2-4x -1=0有实数根,则a 满足( ) A .a ≥1 B .a >1且a ≠5 C .a ≥1且a ≠5 D .a ≠515.抛物线c bx x y ++-=2的部分图象如图所示,若0>y ,则x 的取值X 围是( ) A.14<<-x B. 13<<-x C. 4-<x 或1>x D.3-<x 或1>x2012年初三年级学业水平考试数 学 模 拟注意事项:1.第Ⅱ卷共6页.用蓝、黑钢笔或圆珠笔直接答在考试卷上.2.答卷前将密封线内的项目填写清楚.考试期间,一律不得使用计算器.第II 卷(非选择题 共72分)二、填空题(本大题共6个小题.每小题3分,共18分.把答案填在题中横线上) 16.因式分解:4162-a =.17.一组数据2,3,2,3,5的方差是__________. 18.如图,直线l 1∥l 2,则α=度。
2012济南中考数学试题及答案解析

济南市2012年初三年级学业水平考试数 学 试 题第Ⅰ卷(选择题 共45分)一、选择题(本大题共15个小题,每题3分,共45分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
) 1、12-的绝对值是A 、12B 、12-C 、112 D 、112-2、如图,直线a ∥b ,直线c 与a 、b 相交,∠1=650,则∠2=A 、1150B 、650C 、350D 、2503、2012年伦敦奥运会火炬传递路线全长约为12800公里,数字12800用科学记数法表示为A 、1.28×103B 、12.8×103C 、1.28×104D 、0.128×1054、下列事件中是必然事件的是A 、任意买一张电影票,座位号是偶数B 、正常情况下,将水加热到1000C 水会沸腾C 、三角形的内角和是3600D 、打开电视机,正在播动画片 5、下列计算正确的是A 、3x -2x=1B 、a 2+a 2=a 4C 、a 5÷a 5=aD 、a 3·a 2=a 56、下列四个立体图形中,主视图是三角形的是DC BA第6题图7、化简5(2x -3)+4(3-2x)的结果为A 、2x -3B 、2x+9C 、8x -3D 、18x -38、暑假即将来临,小明和小亮每人要从甲、乙、丙三个社区中随机抽取一个社区参加综合实践活动,那么小明和小亮选到同一社区参加综合实践活动的概率为A 、12B 、13 C 、16 D 、199、如图,在8×4的矩形网格中,每个小正方形的边长都是1,若△ABC 的三个顶点在图中相应的格点上,则tan ∠ACB 的值为A 、13 B 、12CD 、3CBA第9题图第11题图NMDCBA第13题图O10、下列命题是真命题的是A 、对角线相等的四边形是矩形B 、一组邻边相等的四边形是菱形C 、四个角是直角的四边形是正方形D 、对角线相等的梯形是等腰梯形 11、一次函数y=kx+b 的图象如图所示,则方程kx+b=0的解为A 、x=2B 、y=2C 、x =-1D 、y =-112、已知⊙O 1和⊙O 2的半径是一元二次方程x 2-5x+6=0的两根,若圆心距O 1O 2=5,则⊙O 1和⊙O 2的位置关系是A 、外离B 、外切C 、相交D 、内切13、如图,∠MON=900,矩形ABCD 的顶点A ,B 分别在OM 、ON 上,当B 在边ON 上运动时,A 随之在边OM 上运动,矩形ABCD 的形状保持不变,其中AB=2,BC=1。
济南中考数学试题及答案

4.有 30 位同学参加数学竞赛,已知他们的分数互不相同,按分数从高到低选 l5 位同 学进入下一轮
比赛.小明同学知道自己的分数后,还需知道哪个统计量,才能判断自己能否进入下一轮比赛?
A.中位数
B.方差
C.众数
D.平均数
5.已知△ABC 如图 2-1 所示。则与△ABC 相似的是图 2-2 中的
6.已知⊙O1 的半径为 3cm,⊙O 2 的半径为 7cm,若⊙O1 和⊙O 2 的公共点不超过 1 个,则两圆的圆心距
A.3
B.4
C.5
D.6
8题 图
9.已知梯形的两条对角线长分别为 6cm、8cm,且对角线相互垂直,梯形的上底长为 3cm,则梯形的下底
长为
A.Байду номын сангаасcm
B. 10cm
C. 13cm
D. 16cm
1
双击获取 文档
2012 济南中考数学试题及答案
一.选择题(本大题共 15 小题,每小题 3 分,共 45 分.在每小题给出的四个选项中,只 有一项是符合题目要求的).
1. 16 的平方根是
A. 2
2. - 1 的绝对值是 2
A.- 1 2
B.2
B. 1 2
C.±2 C.-2
D. 2 D.2
3.图 3-1 是由 5 个大小相同的正方体摆成的立方体图形,它的主视图是图 3-2 中的
不可能为 A.0 cm
B.8 cm
C.4 cm
D.12 cm
7.下列计算正确的是 A.2x+3y=5xy
B.x·x4=x4
C.x·x=2x
D.(x2y)3=x6y3
8. 如图,已知矩形 ABCD 沿着直线 BD 折叠,使点 C 落在 C/处,
2012年山东济南市中区中考数学三模试卷

2012年山东济南市中区中考数学三模试卷
中考数学考什么,这是考生和家长最关心的问题。
以往的中考考题主要体现在对知识点的考查上,强调知识点的覆盖面,对能力的考查没有放在一个突出的位置上。
近几年的中考命题发生了明显的变化,既强调了由知识层面向能力层面的转化,又强调了基础知识与能力并重。
注重在知识的交汇处设计命题,对学生能力的考查也提出了较高的要求。
中考数学重点考查学生的数学思维能力已经成为趋势和共识。
初三学生可利用寒假时间对数学思想方法进行梳理、总结,逐个认识它们的本质特征、思维程序和操作程序。
有针对性地通过典型题目进行训练,能够真正适应中考命题。
12年-山东省济南市中考真题

济南市2012年初三年级学业水平考试数学试题本试题分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷共2页,满分为45分;第Ⅱ卷共6页,满分为75分.本试题共8页,满分为120分.考试时间为120分钟.答题前,请考生务必将自己的姓名、准考证号、座号、考试科目涂写在答题卡上,并同时将考点、姓名、准考证号、座号填写在试卷规定的位置,考试结束后,将本试卷和答题卡一并交回.本考试不允许使用计算器.第Ⅰ卷(选择题 共45分)注意事项:第Ⅰ卷为选择题,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号.答案写在试卷上无效.一、选择题(本大题共15个小题,每小题3分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.12-的绝对值是( ).(A )12 (B )12- (C )112 (D )112- 2.如图,直线a b ∥,直线c 与a ,b 相交,165=∠°,则2=∠( ).(A )115° (B )65°(C )35° (D )25°3.2012年伦敦奥运会火炬传递路线全长约12800公里,数字12800用科学记数法表示为( ).(A )31.2810⨯ (B )312.810⨯(C )41.2810⨯ (D )50.12810⨯4.下列事件中是必然事件的是( ).(A )任意买一张电影票,座位号是偶数(B )正常情况下,将水加热到100℃时水会沸腾(C )三角形的内角和是360°(D )打开电视机,正在播动画片5.下列各式计算正确的...是( ). (A )321x x -= (B )224a a a +=(C )55a a a ÷= (D )325a a a =6.下列四个立体图中,主视图...是三角形的是( ).7.化简()()523432x x -+-的结果为( ).(A )23x - (B )29x +(C )83x - (D )183x -8.暑假即将来临,小明和小亮每人要从甲、乙、丙三个社区中随机选取一个社区参加综合实践活动,那么小明和小亮选到同一社区参加综合实践活动的概率为( ).(A )12 (B )13 (C )16 (D )199.如图,在8×4的矩形网格中,每个小正方形的边长都是1,若ABC △的三个顶点在图中相应的格点上,则tan ACB ∠的值为( ).(A )13 (B )12(C )22 (D )3 10.下列命题是真命题的是( ).(A )对角线相等的四边形是矩形(B )一组邻边相等的四边形是菱形(C )四个角是直角的四边形是正方形(D )对角线相等的梯形是等腰梯形11.一次函数y kx b =+的图象如图所示,则方程0kx b +=的解为( ).(A )2x = (B )2y = (C )1x =- (D )1y =-12.已知1O 和2O 的半径是一元二次方程2560x x -+=的两根,若圆心距125O O =,则1O 和2O 的位置关系是( ). (A )外离 (B )外切 (C )相交 (D )内切13.如图,90MON =∠°,矩形ABCD 的顶点A B ,分别在边OM ON,上,当B 在边ON 上运动时,A 随之在边OM 上运动,矩形ABCD 的形状保持不变,其中2 1.AB BC ==,运动过程中,点D 到点O 的最大距离是( ).(A )21+ (B )5 (C )1455 (D )5214.如图,矩形BCDE 的各边分别平行于x 轴或y 轴,物体甲和物体乙分别由点()20A ,同时出发,沿矩形BCDE 的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是( ).(A )()20, (B )()11-, (C )()21-, (D )()11--,15.如图,二次函数的图象经过()21--,,()11,两点,则下列关于此二次函数的说法正确的是( ).(A )y 的最大值小于0(B )当0x =时,y 的值大于1(C )当1x =-时,y 的值大于1(D )当3x =-时,y 的值小于0济南市2012年初三年级学业水平考试数学试题第Ⅱ卷(非选择题 共75分)注意事项:1.第Ⅱ卷为非选择题,请考生用蓝、黑色钢笔(签字笔)或圆珠笔直接在试卷上作答.2.答卷前,请考生先将考点、姓名、准考证号、座号填写在试卷规定的位置.二、填空题(本大题共6个小题,每小题3分,共18分.把答案填在题中的横线上)16.分解因式:21a -= .17.计算:2sin 3016-=° .18.不等式组210x x <⎧⎨+⎩-40,≥的解集为 . 19.如图,在Rt ABC △中,904C AC ==∠°,,将ABC △沿CB 向右平移得到DEF △,若平移距离为2,则四边形ABED 的面积等于 .20.如图,在Rt ABC △中,9068B AB BC ===∠°,,,以其三边为直径向三角形外作三个半圆,矩形EFGH 的各边分别与半圆相切且平行于AB 或BC ,则矩形EFGH 的周长..是 . 21.如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为2.y ax bx =+小强骑自行车从拱梁一端O 沿直线匀速穿过拱梁部分的桥面OC ,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC 共需 秒.三、解答题(本大题共7个小题,共57分.解答应写出文字说明、证明过程或演算步骤)22.(本小题满分7分)(1)解不等式324x -≥,并将解集在数轴上表示出来.(2)化简:2121.224a a a a a --+÷--23.(本小题满分7分)(1)如图,在ABCD 中,点E F ,分别在AB CD ,上,.AE CF =求证:.DE BF =(2)如图,在ABC △中,40AB AC A BD ==,∠°,是ABC ∠的平分线.求BDC ∠的度数.24.(本小题满分8分)冬冬全家周末一起去南部山区参加采摘节,他们采摘了油桃和樱桃两种水果,其中油桃比樱桃多摘了5斤.若采摘油桃和樱桃分别用了80元钱,且樱桃每斤价格是油桃每斤价格的2倍,问油桃和樱桃每斤各是多少元?25.(本小题满分8分)济南以“泉水”而闻名,为保护泉水,造福子孙后代,济南市积极开展“节水保泉”活动.宁宁利用课余时间对某小区300户居民的用水情况进行了统计,发现5月份各户居民的用水量均比4月份有所下降,宁宁将5月份各户居民节水量统计整理制成如下统计图:(1)300户居民5月份节水量的众数、中位数分别是多少米3?(2)扇形统计图中2.5米3对应扇形的圆心角为____________度;(3)该小区300户居民5月份平均每户节约用水多少米3?26.(本小题满分9)如图1,在菱形ABCD 中,223,AC BD ==,AC BD ,相交于点.O(1)求边AB 的长;(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD 的顶点A 处,绕点A 左右旋转,其中三角板60°角的两边分别与边BC CD ,相交于点E F ,,连接EF 与AC 相交于点.G①判断AEF △是哪一种特殊三角形,并说明理由;②旋转过程中,当点E 为边BC 的四等分点时()BE CE >,求CG 的长.27.(本小题满分9分) 如图,已知双曲线k y x=经过点()61D ,,点C 是双曲线第三象限分支上的动点,过C 作CA x ⊥轴,过D 作DB y ⊥轴,垂足分别为A B ,,连接.AB BC ,(1)求k 的值;(2)若BCD △的面积为12,求直线CD 的解析式;(3)判断AB 与CD 的位置关系,并说明理由.28.(本小题满分9分)如图1,抛物线23y ax bx =++与x 轴相交于点()()3010A B --,,,,与y 轴相交于点C .1O 为ABC △的外接圆,交抛物线于另一点D .(1)求抛物线的解析式;(2)求cos CAB ∠的值和1O 的半径;(3)如图2,抛物线的顶点为P ,连接BP CP BD M ,,,为弦BD 的中点.若点N 在坐标平面内,满足BMN BPC △∽△,请直接写出所有符合条件的点N 的坐标.。
2012年山东省济南市中考数学试卷及答案

2012年山东省济南市中考数学试卷一.选择题(共15小题)1.(2012济南)12-的绝对值是( )A .12B .12-C .112D .112- 故选A .2.(2012济南)如图,直线a ∥b ,直线c 与a ,b 相交,∠1=65°,则∠2=( )A .115°B .65°C .35°D .25°故选B .3.(2012济南)2012年伦敦奥运会火炬传递路线全长约为12800公里,数字12800用科学记数法表示为( )A .1.28×103B .12.8×103C .1.28×104D .0.128×105 故选C .4.(2012济南)下列事件中必然事件的是( )A .任意买一张电影票,座位号是偶数B .正常情况下,将水加热到100℃时水会沸腾C .三角形的内角和是360°D .打开电视机,正在播动画片故选B .5.(2012济南)下列各式计算正确的是( )A .321x x -=B .224a a a +=C .55a a a ÷=D .325a a a ⋅=故选D .6.(2012济南)下面四个立体图形中,主视图是三角形的是( ) A .B .C .D .故选C . 7.(2012济南)化简5(23)4(32)x x -+-结果为( )A .23x -B .29x +C .83x -D .183x - 故选A .8.(2012济南)暑假即将来临,小明和小亮每人要从甲、乙、丙三个社区中随机选取一个社区参加综合实践活动,那么小明和小亮选到同一社区参加实践活动的概率为( )A .12B .13C .16D .19考点:列表法与树状图法。
解答:解:画树状图得:∵共有9种等可能的结果,小明和小亮选到同一社区参加实践活动的有3种情况, ∴小明和小亮选到同一社区参加实践活动的概率为:=.故选B .9.(2012济南)如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC 的三个顶点在图中相应的格点上,则tan ∠ACB 的值为( )A .13B .12C .2D .3故选A .10.(2012济南)下列命题是真命题的是( )A .对角线相等的四边形是矩形B .一组邻边相等的四边形是菱形C .四个角是直角的四边形是正方形D .对角线相等的梯形是等腰梯形故选D . 11.(2012济南)一次函数y kx b =+的图象如图所示,则方程0kx b +=的解为( )A .2x =B .2y =C .1x =-D .1y =-故选C .12.(2012济南)已知⊙O 1和⊙O 2的半径是一元二次方程2560x x -+=的两根,若圆心距O 1O 2=5,则⊙O 1和⊙O 2的位置关系是( )A .外离B .外切C .相交D .内切故选B . 13.(2012济南)如图,∠MON=90°,矩形ABCD 的顶点A .B 分别在边OM ,ON 上,当B 在边ON 上运动时,A 随之在边OM 上运动,矩形ABCD 的形状保持不变,其中AB=2,BC=1,运动过程中,点D 到点O 的最大距离为( )A 1BCD .52考点:直角三角形斜边上的中线;三角形三边关系;勾股定理;矩形的性质。
山东省济南市中考数学试卷及答案

2012年山东省济南市中考数学试卷一.选择题(共15小题)1.(2012济南)-12的绝对值是()A.12 B.-12C.112D.--12考点:绝对值。
解答:解:|﹣12|=12,故选A.2.(2012济南)如图,直线a∥b,直线c与a,b相交,∠1=65°,则∠2=()A.115°B.65°C.35°D.25°考点:平行线的性质。
解答:解:∵直线a∥b,∠1=65°,∴∠3=∠1=65°,∴∠2=∠3=65°.故选B.3.(2012济南)2012年伦敦奥运会火炬传递路线全长约为12800公里,数字12800用科学记数法表示为()A.1.28×103B.12.8×103C.1.28×104D.0.128×105考点:科学记数法—表示较大的数。
解答:解:12 800=1.28×104.故选C.4.(2012济南)下列事件中必然事件的是()A.任意买一张电影票,座位号是偶数B.正常情况下,将水加热到100℃时水会沸腾C.三角形的内角和是360°D.打开电视机,正在播动画片考点:随机事件。
解答:解:A.是随机事件,可能发生也可能不发生,故选项错误;B.必然事件,故选项正确;C.是不可能发生的事件,故选项错误;D.是随机事件,可能发生也可能不发生,故选项错误.故选B.5.(2012济南)下列各式计算正确的是()A、3x-2x=1B、a2+a2=a4C、a5÷a5=aD、a3·a2=a5考点:同底数幂的除法;合并同类项;同底数幂的乘法。
解答:解:A.3x﹣2x=x,本选项错误;B.a2+a2=2a2,本选项错误;C.a5÷a5=a 5﹣5=a0=1,本选项错误;D.a3a2=a3+2=a5,本选项正确;故选D.6.(2012济南)下面四个立体图形中,主视图是三角形的是()A.B.C.D.考点:简单几何体的三视图。
济南市中考试题及答案

济南市中考试题及答案一、语文试题1. 根据题目所给的古诗文,默写以下句子:- 春眠不觉晓,处处闻啼鸟。
- 独在异乡为异客,每逢佳节倍思亲。
2. 阅读下文,回答问题:《济南的春天》济南的春天,是一幅流动的画卷。
柳树抽出嫩绿的新芽,湖面上波光粼粼,小船在水面上轻轻摇曳。
请根据文中描述,描绘济南春天的特点。
答案:济南的春天以柳树的嫩绿、湖面的波光和水面上小船的摇曳为特点,展现了一幅生机勃勃、宁静美好的画面。
3. 作文题目:《我的家乡》要求:不少于600字,描述家乡的自然风光、人文特色等。
答案:略(考生需根据个人家乡的实际情况进行创作)二、数学试题1. 解方程:\[ x^2 - 5x + 6 = 0 \]答案:\[ x = 2 \] 或 \[ x = 3 \]2. 已知一个直角三角形的两条直角边分别为3cm和4cm,求斜边的长度。
答案:根据勾股定理,斜边长度为5cm。
3. 应用题:某工厂生产一批零件,原计划每天生产100个,实际每天生产120个,结果提前5天完成生产任务。
问原计划需要生产多少天?答案:设原计划需要生产x天,则有方程 \( 120 \times (x - 5) = 100x \),解得 \( x = 30 \) 天。
三、英语试题1. 根据题目所给的英文句子,翻译成中文:- "The early bird catches the worm."- "Actions speak louder than words."答案:早起的鸟儿有虫吃。
/ 行动胜于空谈。
2. 阅读理解:文章大意:介绍济南的名胜古迹,如趵突泉、大明湖等。
问题:What is the most famous spring in Jinan?答案:The most famous spring in Jinan is Baotu Spring.3. 书面表达:写一篇关于“我的一天”的短文,不少于80词。
2012年济南市中考数学模拟试题四

2012年济南市中考数学模拟试题四一、选择题:本大题共12个小题.每小题4分;共48分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.12-的绝对值是( )A.2- B.12- C.2 D.122.如图,AD BC ∥,点E 在B D 的延长线上,若155ADE ∠= ,则D B C ∠的度数为( ) A.35B.50C.45D.253.点()53P -,关于原点对称的点的坐标是( ) A.()35-,B.()53--,C.()53-,D.()35-,4.同时抛掷两枚均匀的硬币,则两枚硬币正面都向上的概率是( )A.41 B.21 C.43 D. 15.不等式组1340x x +>⎧⎨-⎩≥的解集用数轴表示为( )6.若分式2362x xx --的值为0,则x 的值为( A)A.0 B.2 C.2- D.0或27.与如图所示的三视图对应的几何体是( )8.如图,D E 与A B C △的边A B A C ,分别相交于D E ,两点,且D E BC ∥.若22cm 3cm cm 3D E BC EC ===,,,则AC 等于( ).A. 1B.34 C.35 D. 29.如图,矩形OABC 的边OA 在x 轴上,O 与原点重合,OA =1,OC =2,点D 的坐标为(2,0),则直线BD 的函数表达式为( )ADECBA BCD xyO A B C DA B CDE A. 2 4B.2 4 C.24 D.2 4A. 2+-=x yB. 42+-=x yC. 3+-=x yD. 42+=x y10.如图,已知AD 是△ABC 的外接圆的直径,AD =13 cm ,5cos 13B =,则AC的长等于( )A .5 cmB .6 cmC .10 cmD .12 cm11.在如图所示的5×5方格中,每个小方格都是边长为1的正方形,△ABC 是格点三角形(即顶点恰好是正方形的顶点),则与△ABC 有一条公共边且全等的所 有格点三角形的个数是( )A. 1B. 2C. 3D. 412.已知二次函数)0(2≠++=a c bx ax y 的图象如图所示,有下列5个结论:①0>abc ;② c a b +<;③ 024>++c b a ;④ b c 32<;⑤)(b am m b a +>+,(1≠m 的实数)其中正确的结论有( ) A. 2个B. 3个C. 4个D. 5二、填空题:本大题共5个小题.每小题3分;共15分.把答案填在题中横线上. 13.分解因式: 2x 2-18= . 14.已知反比例函数5m y x-=的图象在第二、四象限,则m 的取值范围是__________.15.用扇形统计图反映地球上陆地与海洋所占的比例时,“陆地”部分对应的圆心角是108.宇宙中一块陨石落在地球上,落在陆地的概率是_________0.316.若1m <-,则下列函数①()0m y x x=>,②1y mx =-+,③ym x =,④()1y m x =+中,y 的值随x 的值增大而增大的函数是_______________(填上序号即可)17.如图,已知AO B O A O B ∠=,,点E 在O B 边上,四边形AEBF 是矩形.请 你只用无刻度的直尺在图中画出A O B ∠的平分线(请保留画图痕迹).三、解答题:本大题共7个小题.共57分.解答应写出文字说明、证明过程或演算步骤. 18.(本小题满分7分)(1)化简23111aa a a a a -⎛⎫- ⎪-+⎝⎭· (2)解方程:211x x x-=-.ACB (第8题)ADCBABFE O(第17题)19.(本小题满分7分)(1)如图,在一次龙卷风中,一棵大树在离地面若干米处折断倒下,B 为折断处最高点,树顶A 落在离树根C 的12米处,测得∠BAC=300,求BC 的长。
山东省济南市中考数学真题试题(无答案)

济南市2012年初三年级学业水平考试数 学 试 题第Ⅰ卷(选择题 共45分)一、选择题(本大题共15个小题,每题3分,共45分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
) 1、12-的绝对值是A 、12B 、12-C 、112 D 、112- 2、如图,直线a ∥b ,直线c 与a 、b 相交,∠1=650,则∠2=A 、1150B 、650C 、350D 、2503、2012年伦敦奥运会火炬传递路线全长约为12800公里,数字12800用科学记数法表示为A 、1.28×103B 、12.8×103C 、1.28×104D 、0.128×1054、下列事件中是必然事件的是A 、任意买一张电影票,座位号是偶数B 、正常情况下,将水加热到1000C 水会沸腾C 、三角形的内角和是3600D 、打开电视机,正在播动画片 5、下列计算正确的是A 、3x -2x=1B 、a 2+a 2=a 4C 、a 5÷a 5=aD 、a 3·a 2=a 56、下列四个立体图形中,主视图是三角形的是DC BA第6题图7、化简5(2x -3)+4(3-2x)的结果为A 、2x -3B 、2x+9C 、8x -3D 、18x -38、暑假即将来临,小明和小亮每人要从甲、乙、丙三个社区中随机抽取一个社区参加综合实践活动,那么小明和小亮选到同一社区参加综合实践活动的概率为A 、12B 、13C 、16D 、199、如图,在8×4的矩形网格中,每个小正方形的边长都是1,若△ABC 的三个顶点在图中相应的格点上,则tan ∠ACB 的值为baA 、13 B 、12C 、22D 、3CBA第9题图第11题图NMDCBA第13题图O10、下列命题是真命题的是A 、对角线相等的四边形是矩形B 、一组邻边相等的四边形是菱形C 、四个角是直角的四边形是正方形D 、对角线相等的梯形是等腰梯形 11、一次函数y=kx+b 的图象如图所示,则方程kx+b=0的解为A 、x=2B 、y=2C 、x=-1D 、y=-112、已知⊙O 1和⊙O 2的半径是一元二次方程x 2-5x+6=0的两根,若圆心距O 1O 2=5,则⊙O 1和⊙O 2的位置关系是A 、外离B 、外切C 、相交D 、内切13、如图,∠MON=900,矩形ABCD 的顶点A ,B 分别在OM 、ON 上,当B 在边ON 上运动时,A 随之在边OM 上运动,矩形ABCD 的形状保持不变,其中AB=2,BC=1。
20072012年济南中考数学试题(带答案)

2007-2010年济南中考数学试题(带答案)二00七年济南市高中阶段学校招生考试数学试题第I 卷(选择题 共48分)一、选择题:本大题共12个小题.每小题4分;共48分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.4的平方根是( ) A .2 B .4 C .2± D .4± 2.下列各式中计算结果等于62x 的是( ) A .33x x +B .32(2)xC .322x xD .72x x ÷3.已知:如图,AB CD ⊥,垂足为O ,EF 为过点O 的一条直线,则1∠与2∠的关系一定 成立的是( ) A .相等 B .互余 C .互补 D .互为对顶角 4.点(21)P -,关于x 轴的对称点的坐标为( ) A .(21),B .(21)--,C .(21)-,D .(12)-,5.已知一个三角形三个内角度数的比是1:5:6,则其最大内角的度数为( ) A .60B .75C .90D .1206.样本数据3,6,a ,4,2的平均数是5,则这个样本的方差是( ) A .8B .5C .3D.7.下列说法不正确的是( )A .有一个角是直角的菱形是正方形B .两条对角线相等的菱形是正方形C .对角线互相垂直的矩形是正方形D .四条边都相等的四边形是正方形8.计算(021322(1)11(3)(7)9-++-⎛⎫-⨯--- ⎪⎝⎭的结果为( )A .1B .1-C .4D .14-ABCDE F2 1O第3题图x9.已知:如图ABC △的顶点坐标分别为(43)A --,,(03)B -,,(21)C -,,如将B 点向右平移2个单位后再向上平移4个单位到达1B 点,若设ABC △的面积为1S ,1AB C △的面积为2S ,则12S S ,的大小关系为( )A .12S S >B .12S S =C .12S S <D .不能确定10.已知2y ax bx =+的图象如图所示, 则y ax b =-的图象一定过( )A .第一、二、三象限B .第一、二、四象限C .第二、三、四象限D .第一、三、四象限11.已知整式61x -的值是2,2y y -的值是2,则22(557)(457)x y xy x x y xy x +--+-=( ) A .14-或12B .14或12- C .14-或12 D .14或1212.世界上著名的莱布尼茨三角形如图所示:1112 12 13 16 13 14 112 112 14 15 120 130 120 15 16 130 160 160 130 16 17 142 1105 1140 1105 142 17……………………………………………………第12题图则排在第10行从左边数第3个位置上的数是( ) A .1132B .1360C .1495D .1660第II 卷(非选择题 共72分)第10题图注意事项:1.第II 卷共6页.用蓝、黑钢笔或圆珠笔直接答在考试卷上. 2.答卷前将密封线内的项目填写清楚.二、填空题:本大题共5个小题.每小题3分;共15分.把答案填在题中横线上. 13.不等式210x +>的解集是 . 14.分解因式3244y y y -+的结果为 .15.把12500取两个有效数字的近似数用科学记数法表示为 .16.如图,数轴上两点A B ,,在线段AB 上任取一点,则点C 到表示1的点的距离不大于2的概率是 .17.如图所示是某种型号的正六角螺母毛坯的三视图,则它的表面积为 2cm .第17题图三、解答题:本大题共7个小题.共57分.解答应写出文字说明、证明过程或演算步骤. 18.(本小题满分7分) (1)解方程:2233x x x+=--; (2)解方程组:2622x y x y -=⎧⎨+=-⎩ ①②19.(本小题满分7分)(1)已知:如图1,在矩形ABCD 中,AF BE =.求证:DE CF =;(2)已知:如图2,O 的半径为3,弦AB 的长为4.求sin A 的值.20.(本小题满分8分)在一个不透明的盒子中放有四张分别写有数字1,2,3,4的红色卡片和三张分别写有数字1,2,3的蓝色卡片,卡片除颜色和数字外完全相同.B 第19题图1第19题图23- 13第16题图(1)从中任意抽取一张卡片,求该卡片上写有数字1的概率;(2)将3张蓝色卡片取出后放入另外一个不透明的盒子内,然后在两个盒子内各任意抽取一张卡片,以红色卡片上的数字作为十位数,蓝色卡片上的数字作为个位数组成一个两位数,求这个两位数大于22的概率. 21.(本小题满分8分)某校准备组织290名学生进行野外考察活动,行李共有100件.学校计划租用甲、乙两种型号的汽车共8辆,经了解,甲种汽车每辆最多能载40人和10件行李,乙种汽车每辆最多能载30人和20件行李.(1)设租用甲种汽车x 辆,请你帮助学校设计所有可能的租车方案;(2)如果甲、乙两种汽车每辆的租车费用分别为2000元、1800元,请你选择最省钱的一种租车方案.22.(本小题满分9分)已知:如图,直角梯形ABCD 中,AD BC ∥,90A ∠=,10BC CD ==,4sin 5C =. (1)求梯形ABCD 的面积;(2)点E F ,分别是BC CD ,上的动点,点E 从点B 出发向点C 运动,点F 从点C 出发向点D 运动,若两点均以每秒1个单位的速度同时出发,连接EF .求EFC △面积的最大值,并说明此时E F ,的位置.23.(本小题满分9分)已知:如图,O 为平面直角坐标系的原点,半径为1的B 经过点O ,且与x y ,轴分交于点A C ,,点A的坐标为(),AC 的延长线与B 的切线OD 交于点D .(1)求OC 的长和CAO ∠的度数;(2)求过D 点的反比例函数的表达式.24.(本小题满分9分)已知:如图,在平面直角坐标系中,ABC △是直角三角形,90ACB ∠=,点A C ,的坐标分别为(30)A -,,(10)C ,,3tan 4BAC ∠=. (1)求过点A B ,的直线的函数表达式;ADCFBE第22题图x第23题图(2)在x 轴上找一点D ,连接DB ,使得ADB △与ABC △相似(不包括全等),并求点D 的坐标;(3)在(2)的条件下,如P Q ,分别是AB 和AD 上的动点,连接PQ ,设AP DQ m ==,问是否存在这样的m 使得APQ △与ADB △相似,如存在,请求出m 的值;如不存在,请说明理由.济南市2007年高中阶段学校招生考试数学试题参考答案及评分标准一、选择题 1.C 2.D 3.B 4.B 5.C 6.A 7.D8.A 9.B10.C11.C12.B二、填空题 13.12x >-14.2(2)y y -15.41.310⨯16.2317.36)三、解答题 18.(1)解:2233x x x+=-- 去分母得:22(3)x x -=- ·············································································· 1分 解得:4x = ·································································································· 2分 经检验4x =是原方程的根. ············································································ 3分 (2)解法一:2⨯+①②得510x = ·································································· 4分 解得:2x = ·································································································· 5分 将2x =代入①得2y =- ················································································· 6分∴方程组的解为22x y =⎧⎨=-⎩ ·················································································· 7分解法二:由①得26y x =- ③ ······································································· 4分 将③代入②得2(26)2x x +-=-解得:2x = ·································································································· 5分 将2x =代入③得2y =- ················································································· 6分第24题图∴方程组的解为22x y =⎧⎨=-⎩ ·················································································· 7分19.(1)证明:AF BE =,EF EF =,AE BF ∴= ······································· 1分 四边形ABCD 是矩形,90A B ∴==∠∠,AD BC =,DAE CBF ∴△≌△ ············································· 2分 DE CF ∴= ························································ 3分 (2)解:过点O 作OC AB ⊥,垂足为C ,则有AC BC = ····················································· 4分4AB =,2AC ∴= ···················································································· 5分 在Rt AOC △中,OC ==································································ 6分sin 3OC A OA == ·························································································· 7分 20.解:(1)在7张卡片中共有两张卡片写有数字1 ········································· 1分∴从中任意抽取一张卡片,卡片上写有数字1的概率是27······································· 2分 (2或列树状图为:························································· 6分∴这个两位数大于22的概率为712. ·································································· 8分 21.解:(1)由租用甲种汽车x 辆,则租用乙种汽车(8)x -辆 ······························· 1分由题意得:4030(8)2901020(8)100x x x x +-⎧⎨+-⎩≥≥ ··································································· 4分解得:56x ≤≤ ··························································································· 5分即共有2种租车方案:第19题图21 12 3 (11) (12) (13) 2 1 2 3 (21) (22) (23) 3 1 2 3 (31) (32) (33) 4 1 2 3 (41) (42) (43)十位数 个位数第一种是租用甲种汽车5辆,乙种汽车3辆; 第二种是租用甲种汽车6辆,乙种汽车2辆. ······················································ 6分 (2)第一种租车方案的费用为520003180015400⨯+⨯=元; 第二种租车方案的费用为620002180015600⨯+⨯=元 ········································ 7分 ∴第一种租车方案更省费用. ··········································································· 8分 22.解:(1)过点D 作DM BC ⊥,垂足为M ,在Rt DMC △中, 4sin 1085DM CD C ==⨯= ································· 1分6CM ==······················ 2分 1064BM BC CM ∴=-=-=,4AD ∴= ············· 3分 11()(410)85622ABCD S AD BC DM ∴=+=+⨯=梯形············································· 4分 (2)设运动时间为x 秒,则有BE CF x ==,10EC x =- ··································· 5分 过点F 作FN BC ⊥,垂足为N ,在Rt FNC △中,4sin 5FN CF C x == ···························································· 6分21142(10)42255EFC S EC FN x x x x ∴==-⨯=-+△ ············································ 7分 当45225x =-=⎛⎫⨯- ⎪⎝⎭时,22545105EFC S =-⨯+⨯=△即EFC △面积的最大值为10 ··········································································· 8分 此时,点E F ,分别在BC CD ,的中点处 ··························································· 9分 23.解:(1)90AOC =∠,AC ∴是B 的直径,2AC ∴= ······································································· 1分 又点A 的坐标为(,OA ∴=1OC ∴=== ···························································· 2分 1sin 2OC CAO AC ∴==∠,30CAO ∴=∠ ························································· 3分 (2)如图,连接OB ,过点D 作DE x ⊥轴于点E ·············································· 4分 OD 为B 的切线,OB OD ∴⊥,90BOD ∴=∠ ·······································AB OB =,30AOB OAB ∴==∠∠,3090120AOD AOB BOD ∴=+=+=∠∠∠,在AOD △中,1801203030ODA OAD =--==∠∠第22题图A BENM 第23题图OD OA ∴== ························································································· 6分在Rt DOE △中,18012060DOE =-=∠1cos 602OE OD OD ∴===,3sin 602ED OD ==∴点D 的坐标为32⎫⎪⎪⎝⎭, ················································································ 7分设过D 点的反比例函数的表达式为ky x=32k ∴== ······················································································ 8分 4y x∴=··································································································· 9分 24.解:(1)点(30)A -,,(10)C ,4AC ∴=,3tan 434BC BAC AC =⨯=⨯=∠,B 点坐标为(13),·························· 1分 设过点A B ,的直线的函数表达式为y kx b =+,由0(3)3k b k b =⨯-+⎧⎨=+⎩得34k =,94b = ································································ 2分∴直线AB 的函数表达式为3944y x =+ ······························································ 3分 (2)如图1,过点B 作BD AB ⊥,交x 轴于点D , 在Rt ABC △和Rt ADB △中,BAC DAB =∠∠ Rt Rt ABC ADB ∴△∽△,D ∴点为所求 ······················································ 4分 又4tan tan 3ADB ABC ==∠∠, 49tan 334CD BC ADB ∴=÷=÷=∠ ································································ 5分134OD OC CD ∴=+=,1304D ⎛⎫∴ ⎪⎝⎭, ······························································· 6分 (3)这样的m 存在 ························································································ 7分在Rt ABC △中,由勾股定理得5AB = 如图1,当PQ BD ∥时,APQ ABD △∽△第24题图1第24题图2则133413534mm +-=+,解得259m = ···························· 8分如图2,当PQ AD ⊥时,APQ ADB △∽△则133413534mm+-=+,解得12536m = ······························································· 9分济南市2008年高中阶段学校招生考试1.-2的绝对值是( ) A .2B .-2C .12 D .12-2.下列计算正确的是( )A .347a a a +=B .347a a a ⋅=C .347()a a =D .632a a a ÷=3.下面简单几何体的主.视图是( )4.国家游泳中心——“水立方”是2008年北京奥运会标志性建筑物之一,其工程占地面积为62828平方米,将62828用科学记数法表示是(保留三个有效数字) ( ) A .362.810⨯ B .46.2810⨯C .46.282810⨯D .50.6282810⨯ 5.已知ABC ∆在平面直角坐标系中的位置如图所示,将ABC ∆向右平移6个单位,则平移后A 点的坐标是( )A .(2-,1)B .(2,1)C .(2,1-)D .(2-,1-)6.四川省汶川发生大地震后,全国人民“众志成城,抗震救灾”,积极开展捐款捐物献爱心活动.下表是我市某中学初一·八班50名同学捐款情况统计表:根据表中提供的信息,这50名同学捐款数的众数是( ) A .15 B .20 C .30 D .100 7.如图:点A 、B 、C 都在⊙O 上,且点C 在弦AB 所对的优弧上,A .B .C .D . 第5题图OCBA第7题图4 )第11题图若72AOB ∠=︒,则ACB ∠的度数是( ) A .18° B .30° C .36° D .72°8.如果23321133a b x y x y +--与是同类项,那么a 、b 的值分别是( )A .12a b =⎧⎨=⎩B .02a b =⎧⎨=⎩C .21a b =⎧⎨=⎩D .11a b =⎧⎨=⎩9.“迎奥运,我为先”联欢会上,班长准备了若干张相同的卡片,上面写的是联欢会上同学们要回答的问题.联欢会开始后,班长问小明:你能设计一个方案,估计联欢会共准备了多少张卡片?小明用20张空白卡片(与写有问题的卡片相同),和全部写有问题的卡片洗匀,从中随机抽取10张,发现有2张空白卡片,马上正确估计出了写有问题卡片的数目,小明估计的数目是( ) A .60张 B .80张 C .90张 D .110张 10.关于x 的一元二次方程222310x x a --+=的一个根为2,则a 的值是( )A .1BC .D .11.济南市某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资S (吨)与时间t (小时)之间的函数关系如图所示,这批物资从开始调进到全部调出需要的时间是( ) A .4小时 B .小时 C .小时 D .5小时12.如图:等腰直角三角形ABC 位于第一象限,AB=AC=2,直角顶点A 在直线y =x 上,其中A 点的横坐标为1,且两条直角边AB 、AC 分别平行于x 轴、y 轴,若双曲线ky x =(k ≠0)与ABC ∆有交点,则k 的取值范围是( ) A .12k << B .13k ≤≤ C .14k ≤≤ D .14k <≤二、填空题:本大题共5个小题.每小题3分,共15分.把答案填在题中横线上.13.当3,1x y ==时,代数式2()()x y x y y +-+的值是 .14.分解因式:223x x +-= .15.如图,在∆ABC 中,EF 为∆ABC 的中位线,D为BC边上一点(不与B 、C 重合),AD 与EF 交于点O,连接AEBCF O第15题图D。
济南市2012年初三年级学业水平考试数学试题

济南市2012年初三年级学业水平考试数 学 试 题 第Ⅰ卷(选择题 共45分)一、选择题(本大题共15个小题,每题3分,共45分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
) 1、12-的绝对值是A 、12B 、12-C 、112 D 、112- 2、如图,直线a ∥b ,直线c 与a 、b 相交,∠1=650,则∠2=A 、1150B 、650C 、350D 、250ba3、2012年伦敦奥运会火炬传递路线全长约为12800公里,数字12800用科学记数法表示为A 、1.28×103B 、12.8×103C 、1.28×104D 、0.128×1054、下列事件中是必然事件的是A 、任意买一张电影票,座位号是偶数B 、正常情况下,将水加热到1000C 水会沸腾C 、三角形的内角和是3600D 、打开电视机,正在播动画片 5、下列计算正确的是A 、3x -2x=1B 、a 2+a 2=a 4C 、a 5÷a 5=aD 、a 3·a 2=a 56、下列四个立体图形中,主视图是三角形的是DC BA第6题图7、化简5(2x -3)+4(3-2x)的结果为A 、2x -3B 、2x+9C 、8x -3D 、18x -38、暑假即将来临,小明和小亮每人要从甲、乙、丙三个社区中随机抽取一个社区参加综合实践活动,那么小明和小亮选到同一社区参加综合实践活动的概率为A 、12 B 、13 C 、16 D 、199、如图,在8×4的矩形网格中,每个小正方形的边长都是1,若△ABC 的三个顶点在图中相应的格点上,则tan ∠ACB 的值为A 、13 B 、12CD 、3CBA第9题图第11题图NMDCBA第13题图O10、下列命题是真命题的是A 、对角线相等的四边形是矩形B 、一组邻边相等的四边形是菱形C 、四个角是直角的四边形是正方形D 、对角线相等的梯形是等腰梯形 11、一次函数y=kx+b 的图象如图所示,则方程kx+b=0的解为A 、x=2B 、y=2C 、x =-1D 、y =-112、已知⊙O 1和⊙O 2的半径是一元二次方程x 2-5x+6=0的两根,若圆心距O 1O 2=5,则⊙O 1和⊙O 2的位置关系是A 、外离B 、外切C 、相交D 、内切13、如图,∠MON=900,矩形ABCD 的顶点A ,B 分别在OM 、ON 上,当B 在边ON 上运动时,A 随之在边OM 上运动,矩形ABCD 的形状保持不变,其中AB=2,BC=1。
山东省济南市市中区2012年九年级数学学业水平调查考试试题

2012年九年级学业水平调查考试数 学 试 题注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分120分.第Ⅰ卷1至2页,第Ⅱ卷3至8页.考试时间120分钟.2.答第Ⅰ卷前,考生务必将自己的某某、某某号、考试科目用2B 铅笔涂写在答题卡上,并同时将考点、某某、某某号、座号填写在试卷规定的地方.3.选择题选出答案后,用2B 铅笔把答题卡上对应题目的正确答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案,答案写在试卷上无效.4.数学考试不允许使用计算器,考试结束后,应将本试卷和答题卡一并交回.第Ⅰ卷(选择题 共45分)一、选择题(本大题共15个小题,每小题3分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.﹣2012的相反数是( )A. 2012B.﹣2012C.20121D. 20121- 2.如图,已知∠1 = 70º,如果CD ∥BE ,那么∠B 的度数为( )A .70ºB .100ºC .110ºD .120º3.某汽车参展商为了参加第八届中国国际汽车博览会,印制了105000X 宣传彩页.105000这个数字用科学记数法表示为( )A .10.5×104B .1.05×105C .1.05×106D .0.105×1064.估计20的算术平方根的大小在( )5.下列计算正确的是( )A.623a a a =⋅B.1055a a a =+C.2236)3(a a =- D.723)(a a a =⋅第2题图B CED A 1(第7题图)30°(CABP6.若三角形的两边长分别为2和6,则第三边的长可能是( )A .3B .4C .5D .8 7.如图,ABC ∆中,90=∠C ,3=AC ,30=∠B ,点P 是BC 边上的动点,则AP 长不可能...是( ) B. 4.2 C. 5.8 D. 78.若△ABC ∽△DEF , △ABC 与△DEF 的相似比为1∶2,则 △ABC 与△DEF 的周长比为( ) A .1∶4 B .1∶2 C .2∶1D .1∶29.化简41(-4x +8)-3(4-5x )的结果为( ) A.-16x -10 B.-16x -4 C. 56x -40 D. 14x -10 10.不等式组211420x x ->⎧⎨-⎩,≤的解在数轴上表示为( )11.如图,△ABC 中,AB =AC =6,BC =8,AE 平分∠BAC 交BC 于点E ,点D 为AB 的中点,连接DE ,则△BDE 的周长是( )A.75+B. 10C.425+D. 1212.某单位向一所希望小学赠送1080件文具,现用A 、B 两种不同的包装箱进行包装,已知每个B 型包装箱比A 型包装箱多装15件文具,单独使用B 型包装箱比单独使用A 型包装箱可少用12个. 设B 型包装箱每个可以装x 件文具,根据题意列方程为( ) A .1080x =1080x +15-12 B .1080x =1080x +15+121 02A1 02D1 02B1 02CC .1080x =1080x -15+12D .1080x =1080x -15-1213.现定义运算“★”,对于任意实数a 、b ,都有a ★b =23a a b -+,如:4★5=54342+⨯-,若x ★2=6,则实数x 的值是( ) A.4-或1- B.4或1- C.4或2- D.4-或214.如图,菱形ABCD 中,对角线AC 、BD 相交于点O ,M 、N分别是边AB 、AD 的中点,连接OM 、ON 、MN ,则下列叙 述正确的是( )A .△AOM 和△AON 都是等边三角形B .四边形MBON 和四边形MODN 都是菱形C .四边形MBCO 和四边形NDCO 都是等腰梯形D .四边形AMON 与四边形ABCD 是位似图形 15.如图,用围棋子按下面的规律摆图形,则摆第n 个图形需要围棋子的枚数为( ) A .5n B .5n -1 C .6n -1D .2n 2+1第Ⅱ卷(非选择题 共75分)注意事项:1.第Ⅱ卷共6页.用蓝、黑色钢笔或圆珠笔直接答在考试卷上. 2.答卷前将密封线内的项目填写清楚.二、填空题(本大题共6个小题,每小题3分,共18分.把答案填在题中的横线上.)16.实数a ,b 在数轴上对应点的位置如图所示,则||a ||b (填“>”“<”或“=”). 17.分解因式:39a a -= __________ 18.不等式325x +≥的解集是.19.将两个形状相同的三角板放置在一X 矩形纸片上,按图示画线得到四边形ABCD ,则得 分 评卷人ab0 (第16题)n =1 n =2 n =3…DBCA NM O四边形ABCD 的形状是.20.如图,△ABD 与△AEC 都是等边三角形,AB ≠AC .下列结论中,正确的是.①BE =CD ;②∠BOD =60º;③△BOD ∽△COE .21.如图,以Rt △ABC 的三边为斜边分别向外作等腰直角三角形.若斜边AB =3,则图中阴影部分的面积为.三、解答题(本大题共7个小题,共57分.解答应写出文字说明、证明过程或演算步骤.) 22.(本小题满分7分)完成下列各题: (1)化简:21422---x x x(2)计算:1211)2-⎛⎫+- ⎪⎝⎭DCB A第19题图 第12题图第21题图A D EO 第20题图23.(本小题满分7分)完成下列各题: (1)如图,四边形ABCD 中,AB ∥CD ,∠B=∠D ,3 ,6==AB BC ,求四边形ABCD 的周长.(2)已知:如图,在△ABC中,D 为边BC 上的一点,AD 平分∠EDC ,且∠E =∠B ,DE =DC 。
济南市2012年初三年级学业水平考试数学试题

济南市2012年初三年级学业水平考试数 学 试 题 第Ⅰ卷(选择题 共45分)一、选择题(本大题共15个小题,每题3分,共45分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
) 1、12-的绝对值是A 、12B 、12-C 、112 D 、112- 2、如图,直线a ∥b ,直线c 与a 、b 相交,∠1=650,则∠2=A 、1150B 、650C 、350D 、250ba3、2012年伦敦奥运会火炬传递路线全长约为12800公里,数字12800用科学记数法表示为A 、1.28×103B 、12.8×103C 、1.28×104D 、0.128×1054、下列事件中是必然事件的是A 、任意买一张电影票,座位号是偶数B 、正常情况下,将水加热到1000C 水会沸腾C 、三角形的内角和是3600D 、打开电视机,正在播动画片 5、下列计算正确的是A 、3x -2x=1B 、a 2+a 2=a 4C 、a 5÷a 5=aD 、a 3·a 2=a 56、下列四个立体图形中,主视图是三角形的是DC BA第6题图7、化简5(2x -3)+4(3-2x)的结果为A 、2x -3B 、2x+9C 、8x -3D 、18x -38、暑假即将来临,小明和小亮每人要从甲、乙、丙三个社区中随机抽取一个社区参加综合实践活动,那么小明和小亮选到同一社区参加综合实践活动的概率为A 、12 B 、13 C 、16 D 、199、如图,在8×4的矩形网格中,每个小正方形的边长都是1,若△ABC 的三个顶点在图中相应的格点上,则tan ∠ACB 的值为A 、13 B 、12C 、22D 、3CBA第9题图第11题图NMDCBA第13题图O10、下列命题是真命题的是A 、对角线相等的四边形是矩形B 、一组邻边相等的四边形是菱形C 、四个角是直角的四边形是正方形D 、对角线相等的梯形是等腰梯形 11、一次函数y=kx+b 的图象如图所示,则方程kx+b=0的解为A 、x=2B 、y=2C 、x =-1D 、y =-112、已知⊙O 1和⊙O 2的半径是一元二次方程x 2-5x+6=0的两根,若圆心距O 1O 2=5,则⊙O 1和⊙O 2的位置关系是A 、外离B 、外切C 、相交D 、内切13、如图,∠MON=900,矩形ABCD 的顶点A ,B 分别在OM 、ON 上,当B 在边ON 上运动时,A 随之在边OM 上运动,矩形ABCD 的形状保持不变,其中AB=2,BC=1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
济南市2012年初三年级学业水平考试数学试题注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分120分.第Ⅰ卷1至2页,第Ⅱ卷3至8页.考试时间120分钟.2.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用2B铅笔涂写在答题卡上,并同时将考点、姓名、准考证号、座号填写在试卷规定的地方.3.选择题选出答案后,用2B铅笔把答题卡上对应题目的正确答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案,答案写在试卷上无效.4.数学考试不允许使用计算器,考试结束后,应将本试卷和答题卡一并交回.第Ⅰ卷(选择题共45分)一、选择题(本大题共15个小题,每题3分,共45分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1、的绝对值是A、 B、 C、 D、2、如图,直线a∥b,直线c与a、b相交,∠1=650,则∠2=A、1150B、650C、350D、2503、2012年伦敦奥运会火炬传递路线全长约为12800公里,数字12800用科学记数法表示为A、1.28×103B、12.8×103C、1.28×104D、0.128×1054、下列事件中是必然事件的是A、任意买一张电影票,座位号是偶数B、正常情况下,将水加热到1000C水会沸腾C、三角形的内角和是3600 D、打开电视机,正在播动画片5、下列计算正确的是A、3x-2x=1B、a2+a2=a4C、a5÷a5=aD、a3·a2=a56、下列四个立体图形中,主视图是三角形的是7、化简5(2x-3)+4(3-2x)的结果为A、2x-3B、2x+9C、8x-3D、18x-38、暑假即将来临,小明和小亮每人要从甲、乙、丙三个社区中随机抽取一个社区参加综合实践活动,那么小明和小亮选到同一社区参加综合实践活动的概率为A、 B、 C、 D、9、如图,在8×4的矩形网格中,每个小正方形的边长都是1,若△ABC 的三个顶点在图中相应的格点上,则tan∠ACB的值为A、 B、 C、 D、310、下列命题是真命题的是A、对角线相等的四边形是矩形B、一组邻边相等的四边形是菱形C、四个角是直角的四边形是正方形D、对角线相等的梯形是等腰梯形11、一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为A、x=2B、y=2C、x=-1D、y=-112、已知⊙O1和⊙O2的半径是一元二次方程x2-5x+6=0的两根,若圆心距O1O2=5,则⊙O1和⊙O2的位置关系是A、外离B、外切C、相交D、内切13、如图,∠MON=900,矩形ABCD的顶点A,B分别在OM、ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1。
运动过程中,点D到点O的最大距离为A、 B、 C、 D、14、如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别有点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是A、(2,0)B、(-1,1)C、(-2,1)D、(-1,-1)15、如图,二次函数的图象经过(-2,-1),(1,1)两点,则下列关于此二次函数的说法正确的是A、y的最大值小于0B、当x=0时,y的值大于1C、当x=-1时,y的值大于1D、当x=-3时,y的值小于0第Ⅱ卷(非选择题共75分)二、填空题(本大题共6个小题,每题3分,共18分。
把答案填在题中的横线上.)16、分解因式:a2-1= .17、计算:= .18、不等式组的解集为 .19、如图,在R t△ABC中,∠C=900,AC=4,将△ABC沿BC向右平移得到△DEF,若平移的距离为2,则四边形ABED的面积等于.20、如图,在R t△ABC中,∠B=900,AB=6,BC=8,以其三边为直径向三角形外作三个半圆,矩形EFGH的各边分别与半圆相切且平行于AB或BC,则矩形EFGH的周长是 .21、如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式是y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需.三、解答题:(本大题共7个小题,每题57分.共18分。
解答应写出文字说明、证明过程或演算步骤.)22、(本小题满分7分)(1)解不等式,并将解集在数轴上表示出来.(2)化简:.23、(本小题满分7分)(1)如图,在平行四边形ABCD中,点E,F分别在AB,CD上,AE=CF.求证:DE=BF.(2)如图,在△ABC中,AB=A C,∠A=400,BD是∠ABC的平分线. 求∠BDC的度数.24、(本小题满分8分)冬冬全家周末一起去南部山区参加采摘节,它们采摘了油桃和樱桃两种水果,其中油桃比樱桃多摘了5斤,若采摘油桃和樱桃分别用了80元钱,且樱桃每斤价格是油桃每斤价格的2倍,问油桃和樱桃每斤各是多少元?25、(本小题满分8分)济南以“泉水”而闻名,为保护泉水,造福子孙后代,济南市积极开展“节水保泉”活动.宁宁利用课余时间对某小区300户居民的用水情况进行了统计,发现5月份各户居民的用水量均比4月份有所下降,宁宁将5月份各户居民的节水量统计整理制成如下统计图表:1 1.5 2.53节水量(米3)户数508010070(1)300户居民5月份节水量的众数、中位数分别是多少米3?(2)扇形统计图中2.5米3对应扇形的圆心角为度;(3)该小区300户居民5月份平均每户节约用水多少米3?26、(本小题满分9分)如图1,在菱形ABCD中,AC=2,BD=,AC,BD相交于点O.(1)求边AB的长;(2)如图2,将一个足够大的直角三角板600角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板600角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.①判断△AEF是哪一种特殊三角形,并说明理由;②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长.27、(本小题满分9分)如图,已知双曲线经过点D(6,1),点C是双曲线第三象限分支上的动点,过C作C A⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.(1)求k的值;(2)若△BCD的面积为12,求直线CD的解析式;(3)判断AB与CD的位置关系,并说明理由.28、(本小题满分9分)如图1,抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),与y轴相交于点C.⊙O1为△ABC的外接圆,交抛物线与另一点D.(1)求抛物线的解析式;(2)求co s∠CAB的值和⊙O1的半径;(3)如图2,抛物线的顶点为P,连接BP,CP,BD,M为弦BD的中点.若点N在坐标平面内,满足△BM N∽△BPC,请直接写出所有符合条件的点N的坐标.一、选择题(共15小题,每小题3分,满分45分)1.-12的绝对值是( A )A.12 B.-12 C. D.【考点】绝对值.【专题】【分析】根据绝对值的定义进行计算.【解答】解:|-12|=12,故选A.【点评】本题考查了绝对值.一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.2.如图,直线a∥b,直线c与a,b相交,∠1=65°,则∠2=( B )A.115° B.65° C.35° D.25°【考点】平行线的性质.【专题】【分析】由直线a∥b,∠1=65°,根据两直线平行,同位角相等, 即可求得∠3的度数,又由对顶角相等,即可求得答案.【解答】解:∵直线a∥b,∠1=65°,∴∠3=∠1=65°,∴∠2=∠3=65°.故选B.【点评】此题考查了平行线的性质.此题比较简单,注意掌握两直线平行,同位角相等定理的应用,注意数形结合思想的应用.3.2012年伦敦奥运会火炬传递路线全长约为12800公里,数字12800用科学记数法表示为( C )A.1.28×103 B.12.8×103 C.1.28×104 D.0.128×105【考点】科学记数法—表示较大的数.【专题】【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于12800有5位,所以可以确定n=5-1=4.【解答】解:12 800=1.28×104.故选C.【点评】此题考查科学记数法表示较大的数的方法,准确确定n值是关键.4.下列事件中必然事件的是( B )A.任意买一张电影票,座位号是偶数 B.正常情况下,将水加热到100℃时水会沸腾C.三角形的内角和是360° D.打开电视机,正在播动画片【考点】随机事件.【专题】【分析】根据必然事件的定义就是一定发生的事件,即可作出判断.【解答】解:A、是随机事件,可能发生也可能不发生,故选项错误;B、必然事件,故选项正确;C、是不可能发生的事件,故选项错误;D、是随机事件,可能发生也可能不发生,故选项错误.故选B.【点评】考查了随机事件,解决本题需要正确理解必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件.不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.5.下列各式计算正确的是( D )A.3x-2x=1 B.a2+a2=a4 C.a5÷a5=a D.a3•a2=a5【考点】同底数幂的除法;合并同类项;同底数幂的乘法.【专题】【分析】根据合并同类项法则,同底数幂乘除法法则,逐一检验.【解答】解:A、3x-2x=x,本选项错误;B、a2+a2=2a2,本选项错误;C、a5÷a5=a5-5=a0=1,本选项错误;D、a3•a2=a3+2=a5,本选项正确;故选D.【点评】本题考查了同底数幂的乘除法,合并同类项法则.关键是熟练掌握每一个法则.6.下面四个立体图形中,主视图是三角形的是( C )A. B. C. D.【考点】简单几何体的三视图.【专题】【分析】找到立体图形从正面看所得到的图形为三角形即可.【解答】解:A、主视图为长方形,不符合题意;B、主视图为中间有一条竖线的长方形,不符合题意;C、主视图为三角形,符合题意;D、主视图为长方形,不符合题意;故选C.【点评】本题考查了三视图的知识,主视图是从物体的正面看得到的视图.7.化简5(2x-3)+4(3-2x)结果为( A )A.2x-3 B.2x+9 C.8x-3 D.18x-3【考点】考整式的加减.【专题】【分析】首先利用分配律相乘,然后去掉括号,进行合并同类项即可求解【解答】解:原式=10x-15+12-8x=2x-3.故选A.【点评】本题考查了整式的加减,解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.8.暑假即将来临,小明和小亮每人要从甲、乙、丙三个社区中随机选取一个社区参加综合实践活动,那么小明和小亮选到同一社区参加实践活动的概率为( B )A. B. C. D.【考点】列表法与树状图法.【专题】【分析】首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小明和小亮选到同一社区参加实践活动的情况,再利用概率公式即可求得答案.【解答】解:画树状图得:∵共有9种等可能的结果,小明和小亮选到同一社区参加实践活动的有3种情况,∴小明和小亮选到同一社区参加实践活动的概率为:.故选B.【点评】此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.9.如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC 的三个顶点在图中相应的格点上,则tan∠ACB的值为( A )A. B. C. D.3【考点】锐角三角函数的定义.【专题】网格型.【分析】结合图形,根据锐角三角函数的定义即可求解.【解答】解:由图形知:tan∠ACB=,故选A.【点评】本题考查了锐角三角函数的定义,属于基础题,关键是掌握锐角三角函数的定义.10.下列命题是真命题的是( D )A.对角线相等的四边形是矩形 B.一组邻边相等的四边形是菱形C.四个角是直角的四边形是正方形 D.对角线相等的梯形是等腰梯形【考点】命题与定理.【专题】【分析】根据矩形、菱形的判定方法以及定义即可作出判断【解答】解:A、对角线相等的平形四边形是矩形,故选项错误;B、一组邻边相等的平行四边形是菱形,故选项错误;C、四个角是直角的四边形是矩形,故选项错误;D、正确.故选D.【点评】本题考查了真命题的判断,正确掌握定义、定理是关键.11.一次函数y=kx+b的图象如图所示,则方程kx+b=0的解为(C)A.x=2 B.y=2 C.x=-1 D.y=-1【考点】一次函数与一元一次方程.【专题】数形结合.【分析】直接根据函数图象与x轴的交点进行解答即可.【解答】解:∵一次函数y=kx+b的图象与x轴的交点为(-1,0),∴当kx+b=0时,x=-1.故选C.【点评】本题考查的是一次函数与一元一次方程,能根据数形结合求出x 的值是解答此题的关键.12.已知⊙O1和⊙O2的半径是一元二次方程x2-5x+6=0的两根,若圆心距O1O2=5,则⊙O1和⊙O2的位置关系是( B )A.外离 B.外切 C.相交 D.内切【考点】圆与圆的位置关系.【专题】【分析】先根据一元二次方程根与系数的关系,可知圆心距=两圆半径之和,再根据圆与圆的位置关系即可判断.【解答】:解:∵⊙O1和⊙O2的半径是一元二次方程x2-5x+6=0的两根,∴两根之和=5=两圆半径之和,又∵圆心距O1O2=5,∴两圆外切.故选B.【点评】此题综合考查一元二次方程根与系数的关系及两圆的位置关系的判断.圆和圆的位置与两圆的圆心距、半径的数量之间的关系:①两圆外离⇔d>R+r;②两圆外切⇔d=R+r;③两圆相交⇔R-r<d<R+r(R≥r);④两圆内切⇔d=R-r(R>r);⑤两圆内含⇔d<R-r(R>r).13.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON 上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为(A)A. B. C.5 D.【考点】直角三角形斜边上的中线;三角形三边关系;勾股定理;矩形的性质.【专题】代数综合题.【分析】取AB的中点E,连接OE、DE、OD,根据三角形的任意两边之和大于第三边可知当O、D、E三点共线时,点D到点O的距离最大,再根据勾股定理列式求出DE的长,根据直角三角形斜边上的中线等于斜边的一半求出OE的长,两者相加即可得解.【解答】解:如图,取AB的中点E,连接OE、DE、OD,∵OD≤OE+DE,∴当O、D、E三点共线时,点D到点O的距离最大,此时,∵AB=2,BC=1,∴OE=AE=AB=1,DE=,∴OD的最大值为:.故选A.【点评】本题考查了直角三角形斜边上的中线等于斜边的一半得到性质,三角形的三边关系,矩形的性质,勾股定理,根据三角形的三边关系判断出点O、E、D三点共线时,点D到点O的距离最大是解题的关键.14.如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是(D)A.(2,0) B.(-1,1) C.(-2,1) D.(-1,-1)【考点点的坐标.【专题】规律型【分析】利用行程问题中的相遇问题,由于矩形的边长为4和2,物体乙是物体甲的速度的2倍,求得每一次相遇的地点,找出规律即可解答.【解答】解:矩形的边长为4和2,因为物体乙是物体甲的速度的2倍,时间相同,物体甲与物体乙的路程比为1:2,由题意知:①第一次相遇物体甲与物体乙行的路程和为12×1,物体甲行的路程为12×=4,物体乙行的路程为12×=8,在BC边相遇;②第二次相遇物体甲与物体乙行的路程和为12×2,物体甲行的路程为12×2×=8,物体乙行的路程为12×2×=16,在DE边相遇;③第三次相遇物体甲与物体乙行的路程和为12×3,物体甲行的路程为12×3×=12,物体乙行的路程为12×3×=24,在A点相遇;…此时甲乙回到原出发点,则每相遇三次,两点回到出发点,∵2012÷3=670…2,故两个物体运动后的第2012次相遇地点的是:第二次相遇地点,即物体甲行的路程为12×2×=8,物体乙行的路程为12×2×=16,在DE边相遇;此时相遇点的坐标为:(-1,-1),故选:D.【点评】此题主要考查了行程问题中的相遇问题及按比例分配的运用,通过计算发现规律就可以解决问题.15.如图,二次函数的图象经过(-2,-1),(1,1)两点,则下列关于此二次函数的说法正确的是( D )A.y的最大值小于0 B.当x=0时,y的值大于1C.当x=-1时,y的值大于1 D.当x=-3时,y的值小于0【考点】二次函数的图象;二次函数的性质.【专题】【分析】根据图象的对称轴的位置、增减性及开口方向直接 回答.【解答】解:A、由图象知,点(1,1)在图象的对称轴的左边,所以y 的最大值大于1,不小于0;故本选项错误;B、由图象知,当x=0时,y的值就是函数图象与y轴的交点,而图象与y轴的交点在(1,1)点的左边,故y<1;故本选项错误;C、对称轴在(1,1)的右边,在对称轴的左边y随x的增大而增大,∵-1<1,∴x=-1时,y的值小于x=-1时,y的值1,即当x=-1时,y的值小于1;故本选项错误;D、当x=-3时,函数图象上的点在点(-2,-1)的左边,所以y的值小于0;故本选项正确.故选D.【点评】本题主要考查了二次函数图象上点的坐标特征.解答此题时,需熟悉二次函数图象的开口方向、对称轴、与x轴的交点等知识.二、填空题(共6小题,每小题3分,满分18分)16.分解因式:a2-1=(a+1)(a-1).【考点】因式分解-运用公式法.【专题】【分析】符合平方差公式的特征,直接运用平方差公式分解因式.平方差公式:a2-b2=(a+b)(a-b).【解答】解:a2-1=(a+1)(a-1).【点评】本题主要考查平方差公式分解因式,熟记公式是解题的关键.17.计算:2sin30°- =-3 .【考点】实数的运算;特殊角的三角函数值.【专题】【分析】由特殊角的三角函数值与二次根式的化简的知识,即可将原式化简,继而求得答案.【解答】解:2sin30° =2×1 2 -4=1-4=-3.故答案为:-3.【点评】此题考查了实数的混合运算.此题难度不大,注意掌握特殊角的三角函数值与二次根式的化简,注意运算要细心.18.不等式组 2x-4<0 x+1≥0 的解集为-1≤x<2 .【考点】解一元一次不等式组.【专题】【分析】分别求出各不等式的解集,再求出其公共解集即可.【解答】解:,由①得,x<2;由②得,x≥-1,故此不等式组的解集为:-1≤x<2.故答案为:-1≤x<2.【点评】本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.19.如图,在Rt△ABC中,∠C=90°,AC=4,将△ABC沿CB向右平移得到△DEF,若平移距离为2,则四边形ABED的面积等于 8 .【考点】平移的性质;平行四边形的判定与性质.【专题】【分析】根据平移的性质,经过平移,对应点所连的线段平行且相等,可得四边形ABED是平行四边形,再根据平行四边形的面积公式即可求解.【解答】解:∵将△ABC沿CB向右平移得到△DEF,平移距离为2,∴AD∥BE,AD=BE=2,∴四边形ABED是平行四边形,∴四边形ABED的面积=BE×AC=2×4=8.故答案为8.【点评】本题主要考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.20.如图,在Rt△ABC中,∠B=90°,AB=6,BC=8,以其三边为直径向三角形外作三个半圆,矩形EFGH的各边分别与半圆相切且平行于AB或BC,则矩形EFGH的周长是 48 .【考点】切线的性质;勾股定理;矩形的性质.【专题】【分析】首先取AC的中点O,过点O作MN∥EF,PQ∥EH, 由题意可得PQ⊥EF,PQ⊥GH,MN⊥EH,MN⊥FG,PL,KN,OM,OQ分别是各半圆的半径,OL,OK是△ABC的中位线,又由在Rt△ABC中,∠B=90°,AB=6,BC=8,即可求得个线段长,继而求得答案.【解答】解:取AC的中点O,过点O作MN∥EF,PQ∥EH,∵四边形EFGH是矩形,∴EH∥PQ∥FG,EF∥MN∥GH,∠E=∠H=90°,∴PQ⊥EF,PQ⊥GH,MN⊥EH,MN⊥FG,∵AB∥EF,BC∥FG,∴AB∥MN∥GH,BC∥PQ∥FG,∴AL=BL,BK=CK,∴OL=BC=×8=4,OK=AB=×6=3,∵矩形EFGH的各边分别与半圆相切,∴PL=AB=×6=3,KN=BC=×8=4,在Rt△ABC中,,∴OM=OQ=AC=5,∴EH=FG=PQ=PL+OL+OQ=3+4+5=12,EF=GH=MN=OM+OK+NK∴矩形EFGH的周长是:EF+FG+GH+EH=12+12+12+12=48.故答案为:48.【点评】此题考查了切线的性质、矩形的性质,三角形中位线的性质以及勾股定理等知识.此题难度较大,解题的关键是掌握辅助线的作法,注意数形结合思想的应用.21.如图,济南建邦大桥有一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需 36 秒.【考点】二次函数的应用【专题】【分析】10秒时和26秒时拱梁的高度相同,则A,B一定是关于对称轴对称的点,据此即可确定对称轴,则O到对称轴的时间可以求得,进而即可求得OC之间的时间.【解答】解:设在10秒时到达A点,在26秒时到达B,∵10秒时和26秒时拱梁的高度相同,∴A,B关于对称轴对称.则从A到B需要16秒,则从A到D需要8秒.∴从O到D需要10+8=18秒.∴从O到C需要2×18=36秒.故答案是:36.【点评】本题考查了二次函数的应用,注意到A、B关于对称轴对称是解题的关键.三、解答题(共7小题,共57分,解答应写出文字说明,证明过程或演算步骤)22.(1)解不等式3x-2≥4,并将解集在数轴上表示出来.(2)化简:.【考点】分式的乘除法;在数轴上表示不等式的解集;解一元一次不等式.【专题】计算题.【分析】(1)先根据不等式的性质求出不等式的解集,然后在数轴上表示出来即可;(2)先将的分子和分母因式分解,再将除法转化为乘法进行解答.【解答】解:(1)移项得,3x>6,系数化为1得,x>2,在数轴上表示为.(2)原式.【点评】本题考查了解一元一次不等式、在数轴上表示不等式的解集、分式的乘除法,不仅要熟悉不等式的性质,还要熟悉分式的除法法则.23.(1)如图1,在▱ABCD中,点E,F分别在AB,CD上,AE=CF.求证:DE=BF.(2)如图2,在△ABC中,AB=AC,∠A=40°,BD是∠ABC的平分线,求∠BDC的度数.【考点】平行四边形的性质;全等三 角形的判定与性质;等腰三角形的性质.【专题】证明题.【分析】(1)根据四边形ABCD是平行四边形,利用平行四边形的性质得到一对边和一对角的对应相等,在加上已知的一对边的相等,利用“SAS”,证得△ADE≌△CBF,最后根据全等三角形的对应边相等即可得证;(2)首先根据AB=AC,利用等角对等边和已知的∠A的度数求出∠ABC和∠C的度数,再根据已知的BD是∠ABC的平分线,利用角平分线的定义求出∠DBC的度数,最后根据三角形的内角和定理即可求出∠BDC的度数.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD=BC,∠A=∠C,在△ADE和△CBF中,AD=CB,∠A=∠C,AE=CF,∴△ADE≌△CBF(SAS),∴DE=BF;(2)解:∵AB=AC,∠A=40°,∴∠ABC=∠C=(180°-40°)=70°,又BD是∠ABC的平分线,∴∠DBC=∠ABC=35°,∴∠BDC=180°-∠DBC-∠C=75°.【点评】此题考查了平行四边形的性质,等腰三角形的性质,三角形的内角和定理,角平分线的定义以及全等三角形的性质与判定,熟练掌握定理与性质是解本题的关键.24.冬冬全家周末一起去济南山区参加采摘节,他们采摘了油桃和樱桃两种水果,其中油桃比樱桃多摘了5斤,若采摘油桃和樱桃分别用了80元,且樱桃每斤价格是油桃每斤价格的2倍,问油桃和樱桃每斤各是多少元?【考点】分式方程的应用.【专题】【分析】根据樱桃每斤价格是油桃每斤价格的2倍,得出设油桃每斤为x 元,则樱桃每斤是2x元,再利用油桃比樱桃多摘了5斤,采摘油桃和樱桃分别用了80元,得出等式方程求出即可.【解答】解:设油桃每斤为x元,则樱桃每斤是2x元,根据题意得出:,解得:x=8,经检验得出:x=8是原方程的根,则2x=16,答:油桃每斤为8元,则樱桃每斤是16元.【点评】此题主要考查了分式方程的应用,根据已知利用购买两种水果的质量得出等式方程求出是解题关键.25.济南以“泉水”而闻名,为保护泉水,造福子孙后代,济南市积极开展“节水保泉”活动,宁宁利用课余时间对某小区300户居民的用水情况进行了统计,发现5月份各户居民的用水量比4月份有所下降,宁宁将5月份各户居民的节水量统计整理如下统计图表:节水量1 1.5 2.53(米3)户数5080100700(1)300户居民5月份节水量的众数,中位数分别是多少米3?(2)扇形统计图中2.5米3对应扇形的圆心角为 120 度;(3)该小区300户居民5月份平均每户节约用水多少米3?【考点】考点:扇形统计图;统计表;加权平均数;中位数;众数.【专题】【分析】(1)众数是一组数据中出现次数最多的数据;将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数,根据定义可求解;(2)首先计算出节水量2.5米3对应的居名民数所占百分比,再用360°×百分比即可;(3)根据加权平均数公式:若n个数x1,x2,x3,…,x n的权分别是w1,w2,w3,…,w n,则,进行计算即可;【解答】解:(1)数据2.5出现了100次,次数最多,所以节水量的众数是2.5(米3);位置处于中间的数是第150个和第151个,都是2.5,故中位数是2.5米3.(2)×100%×360°=120°;(3)(50×1+80×1.5+2.5×100+3×70)÷300=2.1(米3).【点评】此题主要考查了统计表,扇形统计图,平均数,中位数与众数,关键是看懂统计表,从统计表中获取必要的信息,熟练掌握平均数,中位数与众数的计算方法.26.如图1,在菱形ABCD中,AC=2,BD=2 3 ,AC,BD相交于点O.(1)求边AB的长;(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD 的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.①判断△AEF是哪一种特殊三角形,并说明理由;②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长.【考点】相似三角形的判定与性质;全等三角形的判定与性质;等边三角形的判定与性质;勾股定理;菱形的性质.【专题】几何综合题.【分析】(1)根据菱形的性质,确定△AOB为直角三角形,然后利用勾股定理求出边AB的长度;(2)①本小问为探究型问题.要点是确定一对全等三角形△ABE≌△ACF,得到AE=AF,再根据已知条件∠EAF=60°,可以判定△AEF是等边三角形;②本小问为计算型问题.要点是确定一对相似三角形△CAE∽△CFG,由对应边的比例关系求出CG的长度.解答:【解答】解:(1)∵四边形ABCD是菱形,∴△AOB为直角三角形,且OA=AC=1,OB=BD= 3 .在Rt△AOB中,由勾股定理得:AB=.(2)①△AEF是等边三角形.理由如下:∵由(1)知,菱形边长为2,AC=2,∴△ABC与△ACD均为等边三角形,∴∠BAC=∠BAE+∠CAE=60°,又∠EAF=∠CAF+∠CAE=60°,∴∠BAE=∠CAF.在△ABE与△ACF中,∵∠BAE=∠CAF,AB=AC=2 ,∠EBA=∠FCA=60°,。
