逻辑代数的运算规则doc资料

合集下载

逻辑代数基本公式及定律.

证明：左式 AB AC BC
AB AC (A A)BC
AB AC ABC ABC 添加
添冗余因子
口诀：正负相对, 余全完。（消冗余项）
（8）
( AB ABC) ( AC ABC)
AB AC =右式
4. A · A· B=A · B
（12）
例1： F1 A B C D 0 注意括号
F1 (A B) (C D) 1
注意括号
F1 AC BC AD BD
与或式
（13）
例 2： F2 A B C D E
反号不动
F2 A B C D E
A 0 0 , A 1 A, A A A, A A 0
AA
（1）
二、交换律
A+B=B+A A• B=B • A
三、结合律
A+(B+C)=(A+B)+C=(A+C)+B A• (B • C)=(A • B) • C
四、分配律
A(B+C)=A • B+A • C A+B • C=(A+B)(A+C)
证明：
A· A· B=A
A· A· B = A·(A+B) =A · B
(A+B)=A A· A· B= A· A· A· B= ?
A × A √ A· B A· B × ×
（9）
§ 2.4 逻辑代数的基本定理
2.4.1 代入定理
内容：在任何一个包含变量A的逻辑等式中，若以另外一个逻辑式代替式中所有的变量A，则等式仍然成立。

(完整版)逻辑代数的运算规则

逻辑代数的运算规则逻辑代数的基本定律逻辑代数的三个规则1、代入规则在任一逻辑等式中，如果将等式两边所有出现的某一变量都代之以一个逻辑函数，则此等式仍然成立，这一规则称之为代入规则。

2、反演规则已知一逻辑函数F，求其反函数时，只要将原函数F中所有的原变量变为反变量，反变量变为原变量；“＋”变为“·”,“·”变为“＋”；“0”变为“1”；“1”变为“0”。

这就是逻辑函数的反演规则。

3、对偶规则已知一逻辑函数F，只要将原函数F中所有的“＋”变为“·”,“·”变为“＋”；“0”变为“1”；“1”变为“0”，而变量保持不变、原函数的运算先后顺序保持不变，那么就可以得到一个新函数，这新函数就是对偶函数F'。

其对偶与原函数具有如下特点：1.原函数与对偶函数互为对偶函数；2.任两个相等的函数，其对偶函数也相等。

这两个特点即是逻辑函数的对偶规则。

逻辑运算的常用公式逻辑代数的总结基本逻辑运算：与（或称“积”）---符号（&、?、无、∧、∩）或（或称“和”）---符号（| 、＋、∨、∪）非（或称“反”）---符号（! 、）1、基本运算法则：0-1律：0?A=0 0＋A=11?A=A 1＋A=A同一律：A?A=A A＋A=A互补律：A?A=0 A＋A=0反演律A?B =A＋B A＋B=A?B还原律A =A√⊕⊙？?＋A=02、常用公式交换律：A?B=B?A A+B=B+A结合律：A?(A?B)=(A?B)?C A＋(A＋B)=(A＋B)＋C 分配律：A?(A＋B)=A?B＋A?C A＋(A?B)=(A＋B)?(A＋C) 吸收律：A?(A+B)=AB A+(A?B)=ABA?B+(A?B)=A (A+B)?(A+B)=A。

逻辑代数运算法则

辑【量例，1.3得.3到】的已Y结=知A果B就+C是+CD。 Y Y，求(A+B。C)(C+D)
代
数
Y=AC BC AD BCD
运算
Y AC BC AD
法 3.对偶定理：若两个逻辑表达式相等，则他们的对偶式也相等。则
对偶式就是指：对于任何一个表达式Y，若将其中的“·”
换成“+”， “+”换成“·”，0换成Y1,1换成0，得到一
数字电子技术
逻之辑代数运算法则
主讲教师：谢永超
湖南铁道职业技术
学习导入
逻辑代数有什么法则呢？
本次课主要内容
逻辑代数基本运算规
则
第一点
逻辑代数的基本定律
第二点
逻辑代数的基本定理
第三点
主一、逻辑代数的运算题规则
1.基本公理：
逻（1）1=0 ；0=1 （2）1·1=1；0+0=0
主一、逻辑代数的运算题规则
（4）0 1 律1·A=A ；A+0=A ；0·A=0 ；
（5）互补律 A A 0; AA A+11=1
逻
辑（6）重叠律 A ·A = A ； A + A =A
代
数（7）还原律A A
运算
（8）反演律—摩根定A律B A B; A B A B
法
则证明：反演律—摩根定
个新的表达式。
A B C=(A B) (A+C)
A (B+C) AB+AC
谢谢观看
湖南铁道职业技术学院作品
AB AC ABC ABC
( AB ABC) ( AC ABC)

逻辑代数运算法则

0
0
1
1
0
1
1
1
1
0
1
1
1
1
0
0
主二、逻辑代数的基本定律
题
（1）原变量吸收公式 AABA
逻辑
（2）反变量吸收公式 AABAB
代
数运
（3）冗余律
A B + A C + B C D = A B + A C
算
法
则
证明：
ABACBCABACBC(AA)
ABACABC ABC
(ABAB)C(ACABC)
运算
Y AC BC AD
法 3.对偶定理：若两个逻辑表达式相等，则他们的对偶式也相等。则
对偶式就是指：对于任何一个表达式Y，若将其中的“·”换成“+”， “+”
换成“·”，0换成1,1换成0，得到一个新的表达式 Y 。
A B C = ( A B )( A + C )
A(B+C) AB+AC
湖南铁道职业技术学院作品
谢谢观看
ABAC
主三、逻辑代数的基本定理
题
1.代入定理：在任何一个包含逻辑变量A的逻辑等式中，若以另外一个逻辑表达式代入
式中所有A的位置，则等式依然成立。
逻
辑代
将摩根定理推广为三变量的应用情况：
数
运
AB=A+B
算
法则
现将 B C 代入等式左边B的位置，于是得到
A ( B C ) A ( B C ) A + B + C
数字电子技术之
逻辑代数运算法则
主讲教师：谢永超
湖南铁道职业技术学院作品

(完整版)逻辑代数的基本公式和运算规则

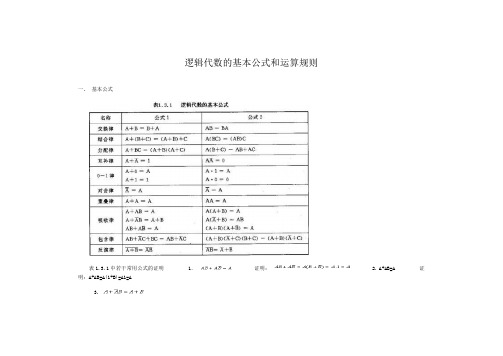
逻辑代数的基本公式和运算规则
一、基本公式
表1.3.1中若干常用公式的证明1．证明： 2. A+AB=A 证明：A+AB=A(1+B)=A1=A
3.
证明：
4.
证明：
推论：
二、运算规则
1．代入定理任何一个含有某变量的等式，如果等式中所有出现此变量的位置均代之以一个逻辑函数式，则此等式依然成立，这称为代入规则。

利用代入规则，反演律能推广到n个变量，即:
2．反演定理对于任意一个逻辑函数式F，若把式中的运算符“.”换成“+”, “+” 换成“.”，常量“0”换成“1”，“1”换成“0”，原变量换成反变量，反变量换成原变量，则得到的结果为。

这个规则叫反演定理运用反演定理时注意两点：① 必须保持原函数的运算次序。

② 不属于单个变量上的非号保留，而非号下面的函数式按反演规则变换。

例如：
其反函数：
3．对偶定理对于任意一个逻辑函数F，若把式中的运算符“.”换成“+”，“+”换成“.”，常量“0”换成“1”，“1”换成“0”，则得到F的对偶式F′。

例如：
其对偶式：
对偶定理：如果两个函数式相等，则它们对应的对偶式也相等。

逻辑代数基本运算规则和基本定律

逻辑代数基本运算规则和基本定律
逻辑代数（又称布尔代数），它是分析设计逻辑电路地数学工具.虽然它和普通代数一样也用字母表示变量，但变量地取值只有“”，“”两种，分别称为逻辑“”和逻辑“”.这里“”和“”并不表示数量地大小，而是表示两种相互对立地逻辑状态.
逻辑代数所表示地是逻辑关系，而不是数量关系.这是它与普通代数地本质区别.
注意：在逻辑代数中，只有加、乘、非运算，没有减、除、移项运算.
、逻辑代数基本运算规则
；；；
；；；；.
、基本定律
交换律
结合律
分配律
―――――注意：普通代数不成立
反演律即摩根定理
可以推广到多变量可以推广到多变量
吸收律。

逻辑代数的基本定律及规则

逻辑代数的基本定律及规则文章来源：互联网作者：佚名发布时间：2012年05月26日浏览次数： 1 次评论：[已关闭] 功能：打印本文一、逻辑代数相等：假定Ｆ、Ｇ都具有ｎ个相同变量的逻辑函数，对于这ｎ个变量中的任意一组输入，如Ｆ和Ｇ都有相同的输出值，则称这两个函数相等。

在实际中，可以通过列真值表来判断。

二、逻辑代数的基本定律：在逻辑代数中，三个基本运算符的运算优先级别依次为：非、与、或。

由此推出10个基本定律如下：1.交换律Ａ＋Ｂ＝Ｂ＋Ａ；Ａ·Ｂ＝Ｂ·Ａ2.结合律Ａ＋（Ｂ＋Ｃ）＝（Ａ＋Ｂ）＋Ｃ；Ａ·（ＢＣ）＝（ＡＢ）·Ｃ3.分配律Ａ·（Ｂ＋Ｃ）＝ＡＢ＋ＡＣ；Ａ＋ＢＣ＝（Ａ＋Ｂ）·（Ａ＋Ｃ）4.0－1律Ａ＋0＝Ａ；Ａ·1＝ＡＡ＋1＝1 ；Ａ·0＝05.互补律Ａ＋＝1 ；Ａ·＝06.重叠律Ａ·Ａ＝Ａ；Ａ＋Ａ＝Ａ7.对合律＝Ａ8.吸收律Ａ＋ＡＢ＝Ａ；Ａ·（Ａ＋Ｂ）＝ＡＡ＋Ｂ＝Ａ＋Ｂ；Ａ·（＋Ｂ）＝ＡＢＡＢ＋Ｂ＝Ｂ；（Ａ＋Ｂ）·（＋Ｂ）＝Ｂ9.反演律＝·；＝＋10.多余项律ＡＢ＋Ｃ＋ＢＣ＝ＡＢ＋Ｃ；(Ａ＋Ｂ）·（＋Ｃ）·（Ｂ＋Ｃ）＝（Ａ＋Ｂ）·（＋Ｃ）上述的定律都可用真值表加以证明，它们都可以用在后面的代数化简中。

三、逻辑代数的基本规则：逻辑代数中有三个基本规则：代入规则、反演规则和对偶规则。

1.代入规则：在任何逻辑代数等式中，如果等式两边所有出现某一变量（如Ａ）的位置都代以一个逻辑函数（如Ｆ），则等式仍成立。

利用代入规则可以扩大定理的应用范围。

例：＝＋，若用Ｆ＝ＡＣ代替Ａ，可得＝＋＋2.反演规则：已知函数Ｆ，欲求其反函数时，只要将Ｆ式中所有的“·”换成“＋”，“＋”换成“·”；“0”换成“1”，“1”换成“0”时，原变量变成反变量，反变量变成原变量，便得到。

逻辑代数的基本定理和规则

2、基本公式的证明 (真值表证明法)
例证明 A A B＝A B
列出等式、右边的函数值的真值表
AB A
00 1 01 1 10 0 11 0
A· B A+AB A+B
0 0+0=0 0 1 0+1=1 1 0 1+0=1 1 0 1+0=1 1
例：试化简下列逻辑函数L=(A + B)(A + B)
解：按照反演规则，得
L (A B) (C D) 1 ( A B)(C D)
3. 对偶规则：
对于任何逻辑函数式，若将其中的与（• ）换成或（+），或（+）换成与（•）；并将1换成0，0换成1；那么，所得的新的函数式就是L的对偶式，记作。 L
例: 逻辑函数 L (A B)(A C)的对偶式为
2.1.1 逻辑代数的基本定律和恒等式
1、基本公式 0、1律：A + 0 = A A + 1 = 1 A ·1 = A A ·0 = 0 互补律：A + A = 1 A ·A = 0 交换律：A + B = B + A A ·B = B ·A 结合律：A + B + C = (A + B) + C A ·B ·C = (A ·B) ·C 分配律：A ( B + C ) = AB + AC A + BC = ( A + B )( A + C )
2.1 逻辑代数的基本定理和规则
逻辑代数又称布尔代数。它是分析和设计现代数字逻辑电路不可缺少的数学工具。逻辑代数有一系列的定律、定理和规则，用于对表达式进行处理，以完成对逻辑电路的化简、变换、分析和设计。逻辑关系指的是事件产生的条件和结果之间的因果关系。在数字电路中往往是将事情的条件作为输入信号，而结果用输出信号表示。条件和结果的两种对立状态分别用逻辑“1” 和“0”表示。

逻辑代数的基本公式和运算规则

逻辑代数的基本公式和
运算规则
-CAL-FENGHAI.-(YICAI)-Company One1
逻辑代数的基本公式和运算规则
一、基本公式
表1.3.1中若干常用公式的证明1．证明： 2. A+AB=A 证明：A+AB=A(1+B)=A1=A
3.
2
证明：
4.
证明：
推论：
二、运算规则1．代入定理任何一个含有某变量的等式，如果等式中所有出现此变量的位置均代之以一个逻辑函数式，则此等式依然成立，这称为代入规则。

这个规则叫反演定理运用反演定理时注意两点：① 必须保持原函数的运算次序。

② 不属于单个变量上的非号保留，而非号下面的函数式按反演规则变换。

例如：
其反函
数：
3．对偶定理对于任意一个逻辑函数F，若把式中的运算符“.”换成“+”，“+”换成“.”，常量“0”换成“1”，“1”换成“0”，则得到F的对偶式F′。

例如：
3
其对偶
式：
对偶定理：如果两个函数式相等，则它们对应的对偶式也相等。

4。

逻辑代数的运算公式和规则

• 若把式其中反的函运数算为符F“.”(A换成B“) •+”A,• C“+”B •换(A成“B.”;C)
•
常量“0”换成“1”，“1”换成“0”；
• 原或变量F换成(反A变量B，) •反(A变量C换)成• B原•变(A量 B C)
那么得到的新函数式称为原函数式F的反函数式。
注：
重叠律反演律还原律合并律吸收律消因律包含律
证明方法
利用真值表
例：用真值表证明反演律
A B AB A+ B A• B A+B
00 1
1
1
1
01 110 Nhomakorabea0
10 1
1
0
0
11 0
0
0
0
A• B= A+B A+ B=AB
利用基本定律
例：证明包含律 AB AC BC AB AC成立
• 函数式中有“”和“⊙”运算符，求反
函数及对偶函数时，要将运算符“”换成 “⊙”， “⊙”换成“”。
公式可推广： AB AC BCDE AB AC
逻辑代数的运算公式和规则
• 三个基本运算规则
• 代入规则：任何一个含有某变量的等式，如果等
式中所有出现此变量的位置均代之以一个逻BC辑替函代数B 式，则此等式依然成立
例： A• B= A+B 利用反演律得 ABC A BC A B C
由此反演律能推广到n个变量：
A1 • A2 • • A n A1 A2 A n A1 A2 A n A1 • A2 • • A n
基本运算规则
•对例于反：任演意F规(一A则、个：B逻、辑C函)数A式BF，做(A如下C处) B理：A • B • C

逻辑代数

逻辑代数逻辑代数（又称布尔代数），它是分析设计逻辑电路的数学工具。

虽然它和普通代数一样也用字母表示变量，但变量的取值只有“0”，“1”两种，分别称为逻辑“0”和逻辑“1”。

这里“0”和“1”并不表示数量的大小，而是表示两种相互对立的逻辑状态。

若定义一种状态为“1”，则另一种状态就为“0”。

例：灯亮用“1”表示、则灯灭就表示为“0”，不考虑灯损坏等其它可能性。

逻辑代数所表示的是逻辑关系（因果关系），而不是数量关系。

这是它与普通代数的本质区别。

1. 基本运算法则一、逻辑代数运算法则从三种基本的逻辑运算关系，我们可以得到以下的基本运算法则（公式1—9）。

0 • 0=01 • 1=10 • 1=0 1 • 0=0公式10 •A=0公式2 1 •A=A 公式3 A •A=A 公式4A •A=0与运算或运算0+0=01+1=10+1=11+0=1公式50 +A=A 公式61+A=1公式7 A +A=A 公式8A+A=1非运算01=10=公式9AA =交换律：结合律：公式11A+B=B+A 公式10A• B=B • A公式13A+(B+C)=(A+B)+C=(A+C)+B 公式12 A• (B • C)=(A • B) • C分配律：公式14A(B+C)=A • B+A • C公式15A+B • C=(A+B)(A+C)（少用）证明：右边=AA+AC+BA+BC=A+AC+BA+BC=A （1+C+B ）+BC=A+BC吸收律：1. 基本运算法则公式16A （A+B ）=A 证明：左边=AA+AB=A+AB=A （1+B ）=A公式17A （A+B ）=AB普通代数不适用！证明：BA B A A A B A A +=++=+)15())((公式DCBC A DC BC A A ++=++被吸收B A B A A +=+公式19（常用）公式18A+AB=A （常用）证明：A+AB=A(1+B)=A•1=A CDAB )F E (D AB CD AB +=+++1. 基本运算法则例：例：1. 基本运算法则公式20AB+AB=A公式21（A+B ）（A+B ）=A（少用）证明：BC)A A (C A AB BCC A AB +++=++CA AB BC A C AB BC A ABC C A AB +=+++=+++=)1()1(推论：CA AB BCDC A AB +=++1C A AB BC C A AB +=++公式22（常用）摩根定律公式23B A AB +=（常用）公式24BA B A ∙=+（常用）记忆：记忆：可以用列真值表的方法证明：A B 00110011A B 00001111AB A+B 00111111A+B A• B 00000011公式25=⊕B A AB或A B =BA ⊕其中：BA B A B A +=⊕是异或函数BA AB B A+=是同或函数用列真值表的方法证明：A B 00110011ABAB10000100B A 11000000A B 1100B A ⊕0011A B其中，吸收律公式16 A （A+B ）= A 公式18 A+AB = A对偶式BA B A A +=+公式19公式20AB+AB=A 公式21(A+B)(A+B)=A对偶关系：将某逻辑表达式中的与（• ）换成或（+），或（+）换成与（• ），得到一个新的逻辑表达式，即为原逻辑式的对偶式。

逻辑代数运算的基本规则

逻辑代数运算的基本规则
1. 嘿，交换律啊，就像你换个顺序排队一样简单呀！比如在逻辑代数里，A+B 就等于 B+A 呢，这不是很直观嘛！就好比你先穿左脚的鞋再穿右脚的鞋，和先穿右脚的鞋再穿左脚的鞋，结果不都是穿好鞋了嘛，真有意思呀！
2. 哇塞，结合律呢，就像是好伙伴永远在一起！比如(A+B)+C 就等于
A+(B+C)呀。

这就好像你和两个好朋友一起玩，不管你们先两两一起玩然后再一起，还是一开始就三个人一起玩，都是一起玩呀，多神奇呀！
3. 分配律呀，这可重要啦！就跟分糖果一样清楚呢！A(B+C) 就等于
AB+AC 呢。

你想呀，把一堆糖果按照不同情况去分，最后得到的不就是该
得的嘛，是不是很妙！
4. 同一律啊，听着就很特别吧！A+0 等于 A，A·1 等于 A，这就好比你自
己还是你自己呀，多直白的道理嘛，太酷啦！
5. 互补律呀，这可真特别呢！就像是有正反两面一样，A+A' 等于 1，A·A' 等于 0 。

这不是跟有白天就有黑夜一样理所当然嘛，真的很奇妙呀！
6. 反演律呢，这真的很有反转的魅力呀！(AB)' 就等于 A'+B' ，(A+B)' 就等于 A'B' 。

就好像一件事情反过来理解，会有不一样的感觉，是不是超有趣呀！
7. 对合律也是很重要的哦！(A')' 等于 A 呀。

这就好像走了一圈又回到原点
一样，这种感觉是不是很神奇呀！
结论：逻辑代数运算的这些基本规则真的是又有趣又好用呀，掌握了它们，就能在逻辑的世界里畅游啦！。

1.2 逻辑代数运算规则

( A C ) ( C+D )
“或非－或非” 表达式
AC CD
“与-或-非”表达式
2、逻辑函数的变换（1）适应器件的情况: 例1 用与非门实现逻辑函数 L1 AC CD 将逻辑函数与或式变换与非-与非表达式方法：将逻辑函数两次求反后用摩根定律
L1 AC CD AC CD ACCD
≥1
≥1 Y
C1
& BC
Y AB B BC BC
逻辑函数的建立及其表示方法
■根据真值表画出波形图
一般方法：将真值表中的变量和函数的对应值分别用高、低电平表示
真值表
AB
L A0 1
0
0
10
00
1 B0
1
1
01 0
L
10 0
1
1
0
11
1
t1
t2
0
00
1
0
1
t3
t4
t5
例:异或函数的几种表达方式
事件发生的条件具备时，事件不会发生；事件发生的条件不具备时，事件发生。这种因果关系称为非逻辑关系。
非逻辑举例
A
NC V
非逻辑举例状态表
A
灯
不通电
亮
通电
灭
3.非运算
非逻辑举例状态表
A
灯
不通电
亮
通电
灭
非逻辑符号
A
1
L
线圈(A)通电- 1 不通电- 0
灯(L)灭 -----0 亮 -----1
A
非逻辑真值表
逻辑函数为： Y F ( A, B,C )
１．与运算
(1) 与逻辑:只有当决定某一事件的条件全部具备时，这一事件才会发生。这种因果关系称为与逻辑关系。

[全]数字电路--逻辑代数的基本运算定律

数字电路--逻辑代数的基本运算定律
逻辑代数的基本定律可以用真值表证明：
分别列出等式两边的真值表，如果等式两边对于变量的可能取值所得的结果相符，就证明该公式是正确的。

如：证明
A +
B ·
C = (A + B) ·(A + C) 成立
逻辑代数中的基本公式只反映了变量之间的逻辑关系，而不是数量之间的关系。

在运算中不能把初等代数的其他运算规律套用到逻辑代数中。

例如，等式两边不允许移项，因为逻辑代数中没有减法和除法。

在进行逻辑运算时，按先算括号、再算乘积、最后算加法的顺序进行，与普通代数是一样的。

最简的与或表达式的条件：在不改变逻辑关系的情况下，首先乘积项的个数最少，在此前提下，其次是每一个乘积项中变量的个数最少。

逻辑函数的化简方法l代数化简法l卡诺图化简法
2．卡诺图化简法
卡诺图—将真值表按一定的规则转换成相应变量的方格图
最小项—在一个有n个变量的逻辑函数中，包括全部n个变量的乘积项（每个变量必须而且只能以原变量或反变量的形式出现一次）。

（1）卡诺图的画法
由卡诺图可以看到，任何两个相邻小方格中的最小项仅有一个变量不同。

因而卡诺图边框的变量取值的填法，每次只改变一个变量的值以实现相邻的最小项只有一个变量不同。

2) 由逻辑表达式画卡诺图
与或式→每个乘积项所包含的最小项填“1”，其余的填“0”。

逻辑代数的公式、定理

C)
A 0 0
分配律：
A
A
(B B
C) C
A (A
B B)
A (A
C C)
1 1
B A.B B.A
00 0 10 0 00 0 11 1
反演律（摩根定律）：
B A B
证明分配率：A+BA=(A+B)(A+C)
证明：
(A+B)(A+C)=AA+AB+AC+BC
分配率 A(B+C)=AB+AC
=A+AB+AC+BC =A(1+B+C)+BC
等幂率AA=A
分配率 A(B+C)=AB+AC
=A+BC
0-1率A+1=1
（4）常用公式
还原律：
A
B
A
B
A
( A B) ( A B ) A
吸收率：
A A
(
A A
B B)
A A
A (A B) A B A A B A B
逻辑代数的公式、定理和规则
1、逻辑代数的公式和定理（1）常量之间的关系
与运算：0 0 0 0 1 0 1 0 0 11 1 或运算：0 0 0 0 1 1 1 0 1 1 1 1
非运算： 1 0
0 1
（2）基本公式
0-1
律：AA
0 A 1 A
A 1 1 A 0 0
互补律： A A 1 A A 0
（3）与非-与非表达式：Y A B AC
（4）或非-或非表达式：Y A B A C （5）与或非表达式：Y AB AC

逻辑代数的三个重要规则

逻辑代数的三个重要规则逻辑代数是一门重要的数学学科，它研究的是逻辑推理和符号运算的关系。

逻辑代数有许多重要的规则，这些规则帮助我们进行逻辑推理和计算，使得逻辑代数成为了现代数学和计算机科学中不可或缺的一部分。

本文将介绍逻辑代数的三个重要规则：合取范式、析取范式和德·摩根定律。

一、合取范式合取范式是逻辑代数中的一个重要规则，它能将一个命题推理问题转化为符号运算问题。

合取范式的基本思想是将命题表示为一系列逻辑与（∧）运算的结果，通过对这些逻辑与的操作得到最终的结果。

合取范式的推理过程是一个逐步求解的过程，通过对命题中的各个子命题进行合取操作，最终得到整个命题的合取范式。

合取范式的推理过程可以帮助我们理清思路，简化复杂的逻辑问题。

二、析取范式析取范式是逻辑代数中的另一个重要规则，它与合取范式相对应。

析取范式的基本思想是将命题表示为一系列逻辑或（∨）运算的结果，通过对这些逻辑或的操作得到最终的结果。

析取范式的推理过程和合取范式类似，也是一个逐步求解的过程，通过对命题中的各个子命题进行析取操作，最终得到整个命题的析取范式。

析取范式的推理过程可以帮助我们对多个条件进行分析，找出其中的共性和差异。

三、德·摩根定律德·摩根定律是逻辑代数中的一个重要规则，它描述了逻辑非（¬）运算和逻辑与（∧）、逻辑或（∨）运算之间的关系。

德·摩根定律的基本思想是将逻辑非运算应用于逻辑与、逻辑或运算，通过对这些运算的操作得到最终的结果。

德·摩根定律可以将复杂的逻辑运算转化为简单的逻辑运算，使得逻辑推理和计算更加简单和高效。

总结：逻辑代数是一门重要的数学学科，它研究的是逻辑推理和符号运算的关系。

逻辑代数的三个重要规则：合取范式、析取范式和德·摩根定律，帮助我们进行逻辑推理和计算，简化复杂的逻辑问题。

合取范式将命题表示为逻辑与运算的结果，析取范式将命题表示为逻辑或运算的结果，德·摩根定律描述了逻辑非运算和逻辑与、逻辑或运算之间的关系。