七下期末测试题

合集下载

七年级下期末真题精选(常考60题29个考点专练)(原卷版)

七年级下期末真题精选（常考60题29个考点专练）一．幂的乘方与积的乘方（共1小题）1．（2022春•嵊州市期末）已知10a＝20，100b＝50，则的值是．二．多项式乘多项式（共1小题）2．（2022春•鄞州区期末）给出如下定义：我们把有序实数对（a，b，c）叫做关于x的二次多项式ax2+bx+c 的特征系数对，把关于x的二次多项式ax2+bx+c叫做有序实数对（a，b，c）的特征多项式．（1）关于x的二次多项式3x2+2x﹣1的特征系数对为；（2）求有序实数对（1，4，4）的特征多项式与有序实数对（1，﹣4，4）的特征多项式的乘积；（3）若有序实数对（p，q，﹣1）的特征多项式与有序实数对（m，n，﹣2）的特征多项式的乘积的结果为2x4+x3﹣10x2﹣x+2，直接写出（4p﹣2q﹣1）（2m﹣n﹣1）的值为．三．完全平方式（共1小题）3．（2022春•普陀区期末）有4张长为a、宽为b（a＞b）的长方形纸片，按如图的方式拼成一个边长为（a+b）的正方形，图中阴影部分的面积为S1，空白部分的面积为S2．若S1＝S2，则a、b满足（）A．2a＝3b B．2a＝5b C．a＝2b D．a＝3b四．整式的除法（共1小题）4．（2022春•北仑区期末）计算：（15x2y﹣10xy2）÷（5xy）＝．五．整式的混合运算（共2小题）5．（2022春•宁波期末）如图，将两张长为a，宽为b的长方形纸片按图1，图2两种方式放置，图1和图2中两张长方形纸片重叠部分分别记为①和②，正方形ABCD中未被这两张长方形纸片覆盖部分用阴影表示，图1和图2中阴影部分的面积分别记为S1和S2．若知道下列条件，仍不能求S1﹣S2值的是（）A．长方形纸片长和宽的差B．长方形纸片的周长和面积C．①和②的面积差D．长方形纸片和①的面积差6．（2022春•宁波期末）已知长方形ABCD，AD＞AB，AD＝10，将两张边长分别为a和b（a＞b）的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为S1，图2中阴影部分的面积为S2．当S2﹣S1＝3b时，AB＝．六．整式的混合运算—化简求值（共1小题）7．（2022春•拱墅区期末）已知（x+a）（x﹣3）的结果中不含x的一次项．（1）求a的值．（2）化简：（a+2）2﹣（1﹣a）（﹣a﹣1），并在（1）的条件下求值．七．因式分解-提公因式法（共2小题）8．（2022春•杭州期末）因式分解：m2﹣mn＝．9．（2022春•乐清市期末）因式分解：m2﹣2m＝．八．因式分解-运用公式法（共3小题）10．（2022春•新昌县期末）因式分解：x2﹣2x+1＝．11．（2022春•嵊州市期末）分解因式：x2+4x+4＝．12．（2022春•诸暨市期末）因式分解：x2﹣9＝．九．提公因式法与公式法的综合运用（共2小题）13．（2022春•钱塘区期末）因式分解：a3﹣9a＝．14．（2022春•宁波期末）分解因式：xy2﹣4x＝．一十．分式的混合运算（共1小题）15．（2022春•上虞区期末）下列运算正确的是（）A．B．C．D．一十一．分式的化简求值（共2小题）16．（2008春•台州校级期末）先化简，再求值：（﹣）•，其中x＝1．17．（2022春•常山县期末）先化简，再求值：；其中a＝，b＝．一十二．二元一次方程的解（共4小题）18．（2022春•宁波期末）若是方程2x+ay＝3的解，则a的值为（）A．1B．﹣1C．7D．﹣719．（2022春•绍兴期末）下列各组数中，是二元一次方程5x﹣y＝2的一个解的是（）A．B．C．D．20．（2022春•椒江区期末）关于x，y的二元一次方程（k﹣2）x﹣（k﹣1）y﹣3k+5＝0，当k取一个确定的值时就得到一个方程，所有这些方程有一个公共解，则这个公共解是（）A．B．C．D．21．（2022春•普陀区期末）写出一个解为的二元一次方程是．一十三．解二元一次方程（共1小题）22．（2022春•慈溪市期末）将方程2x﹣y＝1变形成用x代数式表示y，则y＝．一十四．二元一次方程组的解（共4小题）23．（2022春•慈溪市期末）若关于x，y的方程组的解满足x+y＝2022，则k的值为（）A．2020B．2021C．2022D．202324．（2022春•宁波期末）已知方程组的解是，则方程组的解是（）A．B．C．D．25．（2022春•慈溪市期末）若关于x，y的方程组的解是，则4a2﹣9b2为．26．（2022春•杭州期末）已知是二元一次方程组的解．（1）求a，b的值．（2）求方程组的解．一十五．解二元一次方程组（共1小题）27．（2022春•南浔区期末）已知方程组，则2x+6y的值是．一十六．由实际问题抽象出二元一次方程组（共4小题）28．（2022春•拱墅区期末）我国古代算题：“马四匹，牛六头，共价四十八两（我国古代货币单位）；马三匹，牛五头，共价三十八两．问马、牛各价几何？”设马价x两，牛价y两，可列方程组为（）A．B．C．D．29．（2022春•南阳期末）上学期某班的学生都是双人桌，其中男生与女生同桌，这些女生占全班女生的，本学期该班新转入4个男生后，男女生刚好一样多．设上学期该班有男生x人，女生y人，根据题意可得方程组为（）A．B．C．D．30．（2022春•上虞区期末）《九章算术》是人类科学史上应用数学的“算经之首”，书中记载：今有三人共车，二车空；二人共车，九人步．问：人与车各几何？译文：若3人坐一辆车，则两辆车是空的；若2人坐一辆车，则9人需要步行，问：人与车各多少？设有x辆车，人数为y，根据题意可列方程组为．31．（2022春•定海区期末）中国清代算书《御制数理精蕴》中有这样一题：“马四匹、牛六头，共价四十八两（我国古代货币单位）；马三匹、牛五头，共价三十八两．问马、牛各价几何？”设马每匹x两，牛每头y两，根据题意可列方程组为．一十七．二元一次方程组的应用（共2小题）32．（2022春•婺城区期末）《九章算术》中的算筹图是竖排的，为看图方便，我们把它改为横排，如图1，图2．图中各行从左到右列出的算筹数分别表示未知数x，y的系数与相应的常数项．把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来，就是，在图2所示的算筹图中有一个图形被墨水覆盖了，如果图2所表示的方程组中x的值为3，则被墨水所覆盖的图形为（）A．|B．||C．|||D．||||33．（2022春•上虞区期末）为创建省文明卫生城市，某街道将一公园进行绿化改造．计划种植甲、乙两种花木，甲种花木每棵进价800元，乙种花木每棵进价3000元，共需107万元；每种植一棵甲种花木需人工费30元，每种植一棵乙种花木需人工费80元，共需人工费32000元．（1）求计划种植甲、乙两种花木各多少棵？（2）如果承包植树的老板安排28人同时种植这两种花木，每人每天能种植甲种花木20棵或乙种花木5棵，应分别安排多少人种植甲种花木和乙种花木，才能确保同时完成各自的任务？一十八．解分式方程（共2小题）34．（2022春•常山县期末）解分式方程：+＝1．35．（2022春•余姚市校级期末）解方程（组）（1）（2）．一十九．分式方程的增根（共2小题）36．（2022春•诸暨市期末）若关于x的分式方程有增根，则a＝．37．（2022春•湖州期末）若关于x的分式方程＝+1有增根，则a＝．二十．由实际问题抽象出分式方程（共2小题）38．（2022春•定海区期末）2022年北京冬奥会的吉祥物“冰墩墩”和“雪容融”深受国内外朋友的喜爱，某特许零售店准备购进一批吉祥物销售．已知用300元购进“冰墩墩”的数量与用250元购进“雪容融”数量相同，已知购进“冰墩墩”的单价比“雪容融”的单价多10元，设购进“雪容融”的单价为x元，则列出方程正确的是（）A．B．C．D．39．（2022春•余姚市校级期末）张老师和李老师住在同一个小区，离学校3000米．某天早晨，张老师和李老师分别于7点10分，7点15分离家骑自行车上班，刚好在校门口遇上．已知李老师骑车的速度是张老师的1.2倍，为了求他们各自骑自行车的速度，设张老师骑自行车的速度是x米/分，则可列得方程为（）A．B．C．D．二十一．分式方程的应用（共1小题）40．（2021秋•汉阳区期末）某手机专卖店的一张进货单上有如下信息：A款手机进货单价比B款手机多800元，花38400元购进A款手机的数量与花28800元购进B款手机的数量相同．（1）求A，B两款手机的进货单价分别是多少元？（2）某周末两天销售单上的数据，如表所示：日期A款手机（部）B款手机（部）销售总额（元）星期六5840100星期日6741100求A，B两款手机的销售单价分别是多少元？（3）根据（1）（2）所给的信息，手机专卖店要花费28000元购进A，B两款手机若干部，问有哪几种进货方案？根据计算说明哪种进货方案获得的总利润最高．二十二．同位角、内错角、同旁内角（共1小题）41．（2022春•绍兴期末）如图，直线l1，l2被直线l3所截，则（）A．∠1和∠2是同位角B．∠1和∠2是内错角C．∠1和∠3是同位角D．∠1和∠3是内错角二十三．平行线的性质（共9小题）42．（2022春•南浔区期末）如图1，当光线从空气斜入射到某种透明的液体时发生了折射，满足入射角∠1与折射角∠2的度数比为3：2．如图2，在同一平面上，两条光线同时从空气斜射入这种液体中，两条入射光线与水平液面夹角分别为α，β，在液体中两条折射光线的夹角为γ，则α，β，γ三者之间的数量关系为（）A．B．C．α+β＝γD．α+β+γ＝180°43．（2022春•杭州期末）将一个直角三角板和一把直尺按如图所示的方式摆放，若∠2＝55°，则∠1的度数为（）A．45°B．55°C．25°D．35°44．（2022春•定海区期末）三角板是我们学习数学的好帮手．将一对直角三角板如图放置，点C在FD的延长线上，点B在ED上，AB∥CF，∠F＝∠ACB＝90°，∠E＝45°，∠A＝60°，则∠CBD＝（）A．10°B．15°C．20°D．25°45．（2022春•上虞区期末）生活中常见一种折叠拦道闸，如图1所示．若想求解某些特殊状态下的角度，需将其抽象为几何图形，如图2所示，BA垂直于地面AE于A，CD平行于地面AE，则∠ABC+∠BCD ＝°．46．（2022春•西湖区校级期末）如图a，已知长方形纸带ABCD，将纸带沿EF折叠后，点C、D分别落在H、G的位置，再沿BC折叠成图b，若∠DEF＝72°，则∠GMN＝°．47．（2022春•杭州期末）如图，ABCD为一长条形纸带，AD∥CB，将ABCD沿EF折叠，C、D两点分别与C′、D'对应，若∠1＝2∠2，则∠AEF的度数为．48．（2022春•鄞州区期末）如图，直线a∥b，三角板的直角顶点放在直线b上，若∠1＝65°，则∠2＝．49．（2022春•诸暨市期末）如图，将矩形ABCD折叠，折痕为EF，BC的对应边B'C′与CD交于点M，若∠B′MD＝50°，则∠BEF的度数为．50．（2022春•慈溪市期末）在综合与实践课上，老师让同学们以“两条平行线AB，CD和一块含60°角的直角三角尺EFG（∠EFG＝90°，∠EGF＝60°）”为主题开展数学活动．（1）如图（1），若三角尺的60°角的顶点G放在CD上，若∠2＝2∠1，求∠1的度数；（2）如图（2），小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上，请你探索并说明∠AEF 与∠FGC间的数量关系；（3）如图（3），小亮把三角尺的直角顶点F放在CD上，30°角的顶点E落在AB上．若∠AEG＝α，∠CFG＝β，则∠AEG与∠CFG的数量关系是什么？用含α，β的式子表示（不写理由）．二十四．平行线的判定与性质（共3小题）51．（2022春•襄州区期末）在一次数学活动课上，老师让同学们用两个大小、形状都相同的三角板画平行线AB，CD，贝贝、晶晶、欢欢三位同学的做法如图所示：上述三位同学的做法中，依据“内错角相等，两直线平行”的是（）A．仅贝贝同学B．贝贝和晶晶C．晶晶和欢欢D．贝贝和欢欢52．（2022春•西湖区校级期末）如图，直线MN分别与直线AB，CD相交于点E，F，EG平分∠BEF，交直线CD于点G，若∠MFD＝∠BEF＝58°，射线GP⊥EG于点G，则∠PGF＝°．53．（2022春•鄞州区期末）如图，已知CD平分∠ACB，∠1＝∠2．（1）求证：DE∥AC；（2）若∠3＝30°，∠B＝25°，求∠BDE的度数．二十五．平移的性质（共2小题）54．（2022春•上虞区期末）如图，将△ABC沿BC方向平移1cm得到对应的△A'B'C'．若B'C＝2cm，则BC′的长是（）A．2cm B．3cm C．4cm D．5cm55．（2022春•柯桥区期末）如图：直角△ABC中，AC＝5，BC＝12，AB＝13，则内部五个小直角三角形的周长为．二十六．调查收集数据的过程与方法（共1小题）56．（2021秋•于洪区期末）当前，“低头族”已成为热门话题之一，小颖为了解路边行人边步行边低头看手机的情况，她应采用的收集数据的方式是（）A．对学校的同学发放问卷进行调查B．对在路边行走的学生随机发放问卷进行调查C．对在路边行走的行人随机发放问卷进行调查D．对在图书馆里看书的人发放问卷进行调查二十七．频数与频率（共2小题）57．（2022春•西湖区校级期末）期中考试结束后，老师统计了全班40人的数学成绩，这40个数据共分为6组，第1至第4组的频数分别为10，5，7，6，第5组的频率为0.1，那么第6组的频率是．58．（2022春•兰山区期末）已知一组数据有40个，把它分成六组，第一组到第四组的频数分别是10，5，7，6，第五组的频率是0.2，则第六组的频率是．二十八．扇形统计图（共1小题）59．（2022春•上虞区期末）右图是某种学生快餐（共400g）营养成分扇形统计图，已知其中表示脂肪的扇形的圆心角为36°，维生素和矿物质含量占脂肪的一半，蛋白质含量比碳水化合物多40g．有关这份快餐，下列说法正确的是（）A．表示维生素和矿物质的扇形的圆心角为20°B．脂肪有44g，含量超过10%C．表示碳水化合物的扇形的圆心角为135°D．蛋白质的含量为维生素和矿物质的9倍二十九．折线统计图（共1小题）60．（2022春•乐清市期末）某校开展了“爱阅读”活动，七（1）班统计了1月～6月全班同学的课外阅读数量（单位：本），绘制了折线统计图（如图所示），则下列说法正确的是（）A．6月份阅读数量最大B．阅读数量超过40本的月份共有5个月C．相邻的两个月中，1月到2月的月阅读数量增长最快D．4月份阅读数量为38本。

七年级下学期期末考试数学试卷(带答案)

七年级下学期期末考试数学试卷(带答案)一、选择题（本题共10个小题，每小题3分，共30分）1．下列四个图形中，不是轴对称图形的为（）A． B．C． D．2．在球的体积公式V＝πR3中，下列说法正确的是（）A．V、π、R是变量，为常量B．V、π是变量，R为常量C．V、R是变量，、π为常量D．以上都不对3．下列事件中是不可能事件的是（）A．从一副扑克牌中任抽一张牌恰好是“红桃”B．在装有白球和黑球的袋中摸球，摸出了红球C．2022年大年初一早晨艳阳高照D．从两个班级中任选三名学生，至少有两名学生来自同一个班级4．新型冠状病毒（2019﹣nCoV）是目前已知的第7种可以感染人的冠状病毒，经研究发现，它的单细胞的平均直径约为0.000000203米，该数据用科学记数法表示为（）A．2.03×10﹣8B．2.03×10﹣7C．2.03×10﹣6D．0.203×10﹣65．已知a，b，c分别为三角形的三边长，则化简|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a+b|的结果为（）A．a+b+c B．﹣a+b﹣3c C．a+2b﹣c D．﹣a+b+3c6．等腰三角形的两边长分别为4和8，则这个等腰三角形的周长是（）A．20或16 B．20C．16 D．以上答案均不对7．如图，在△ABC中，∠C＝90°，AD是∠BAC的角平分线，E是边AB上一点，若CD＝6，则DE的长可以是（）A．1 B．3 C．5 D．78．如图，下列条件中，不能判断直线a∥b的是（）A．∠1＝∠3 B．∠2＝∠3 C．∠4＝∠5 D．∠2+∠4＝180°9．已知∠1＝∠2，AC＝AD，要使△ABC≌△AED，还需添加一个条件，那么在以下条件中不能选择的是（）A．AB＝AE B．BC＝ED C．∠C＝∠D D．∠B＝∠E10．已知（x﹣2019）2+（x﹣2021）2＝34，则（x﹣2020）2的值是（）A．4 B．8 C．12 D．16二、填空题（本题共6小题，每小题3分，共18分.）11. 2-的相反数是_____．12. 如图，将三角形ABC沿直线BC平移得到三角形DEF，其中点A与点D是对应点，点B与点E是对应点，点BC=，EC=2，那么线段CF的长是_______．C与点F是对应点．如果513. 已知点P (2a −2，a +5)，点Q (4，5)，且直线PQ ∥y 轴，则点P 的坐标为________．14. 如图a ∥b,∠1＋∠2=75°，则∠3+∠4＝______________.15. 方程组{4x +3y =1,mx +(m −1)y =3的解x 和y 的值相等，则m ＝＿＿＿.16. 已知实数x 满足{5(x +1)≥3x −112x −1≤7−32x ，若S ＝|x ﹣1|+|x+1|的最大值为m ，最小值为n ，则mn ＝_____．三、解答题（本题共9小题，共72分.解答应写出文字说明、证明过程或演算步骤）17．（6分）计算：||﹣+﹣（﹣1）2019．18．（6分）解方程组：．19．（6分）解不等式组．20．（8分）如图，在平面直角坐标系中，有三点A （1，0），B （3，0），C （4，﹣2）．（1）画出三角形ABC ；（2）将三角形ABC 先向左平移4个单位长度，再向上平移3个单位长度，画出平移后的三角形DEF ，并写出D、E、F三点的坐标；（3）求三角形ABC的面积．21．（8分）某体育老师测量了自己任教的甲、乙两班男生的身高，并制作了不完整的统计图表．身高分组频数频率152≤x＜155 3 0.06155≤x＜158 7 0.14158≤x＜161 m0.28161≤x＜164 13 n164≤x＜167 9 0.18167≤x＜170 3 0.06170≤x＜173 1 0.02根据以上统计图表完成下列问题：（1）统计表中m＝，n＝；并将频数分布直方图补充完整；（2）在这次测量中两班男生身高的中位数在什么范围内？22．（8分）实验室需要一批无盖的长方体模型，一张大纸板可以做成长方体的侧面30个，或长方体的底面25个，一个无盖的长方体由4个侧面和一个底面构成．现有26张大纸板，则用多少张做侧面，多少张做底面才可以使得刚好配套，没有剩余？23．（10分）已知，如图，∠CDG＝∠B，AD⊥BC于点D，∠1＝∠2，EF分别交AB、BC于点E、F，试判断EF与BC的位置关系，并说明理由．24．（10分）某业主贷款18920元购进一台机器，生产某种产品．已知产品的成本是每个5元，售价是每个8元，应付的税款和其他费用是售价的10%．若每个月能生产、销售2000个产品．（1）问每个月所获得利润为多少元？（2）问至少几个月后能赚回这台机器的贷款？25．（10分）已知数轴上三点A、O、B表示的数分别为4、0、﹣2，动点P从A点出发，以每秒3个单位的速度沿数轴向左匀速运动．（1）当点P到点A的距离与点P到点B的距离相等时，点P在数轴上表示的数是．（2）另一动点R从点B出发，以每秒2个单位的速度沿数轴向左匀速运动，若点P、R同时出发，问点P运动多长时间追上点R？（3）若点M为AP的中点，点N为PB的中点，点P在运动过程中，线段MN的长度是否发生变化？若发生变化，请你说明理由；若不变，请你画出图形，并求出线段MN的长度．参考答案一、选择题1．选：C．2．选：C．3．选：B．4．选：B．5．选：D．6．选：B．7．选：D．8．选：B．9．选：B．10．选：D．二、填空题11、【答案】√5-212、【答案】313、【答案】（4，8）14、【答案】105°15、【答案】1116、【答案】16三、解答题17．【解答】解：原式＝﹣1﹣2+2+1＝．18．【解答】解：方程组整理得：，①+②得：﹣6y＝6，解得：y＝﹣1，把y＝﹣1代入②得：x﹣2＝1，解得：x＝3，则方程组的解为．19．【解答】解：∵由①得：x≤3，由②得：x＞﹣4，∴不等式组的解集为﹣4＜x≤3．20．【解答】解：（1）如图所示，△ABC即为所求；（2）如图所示，△DEF即为所求；其中D（﹣3，3），E（﹣1，3），F（0，1）；（3）三角形ABC的面积＝×2×2＝2．21．【解答】解：（1）测量的总人数是：3÷0.06＝50（人），则m＝50×0.28＝14，n＝＝0.26．补全频数分布直方图：故答案为14，0.26．（2）观察表格可知中位数在 161≤x＜164范围内．22．【解答】解：设用x张做侧面，y张做底面才可以使得刚好配套，没有剩余，根据题意得：，解得：．答：用20张做侧面，6张做底面才可以使得刚好配套，没有剩余．23．【解答】解：EF与BC的位置关系是垂直关系．证明：∵∠CDG＝∠B（已知），∴DG∥AB（同位角相等，两直线平行），∴∠1＝∠DAB（两直线平行，内错角相等），又∠1＝∠2（已知），∴∠2＝∠DAB（等量代换），∴EF∥AD（同位角相等，两直线平行），∴∠EFB＝∠ADB（两直线平行，同位角相等），又AD⊥BC（已知），∴∠ADB＝90°，∴∠EFB＝∠ADB＝90°，∴EF与BC的位置关系是垂直（垂直的定义）．24．【解答】解：（1）每个月总收入为：2000×8＝16000（元），则应付的税款和其他费用为：16000×10%＝1600（元），利润＝16000﹣2000×5﹣1600＝4400（元），答：每个月所获得利润为4400元；（2）设需要x个月后能赚回这台机器贷款，依题意，得：4400x≥18920，解得：x≥43．答：至少43个月后能赚回这台机器贷款．25．【解答】解：（1）∵A，B表示的数分别为4，﹣2，∴AB＝6，∵PA＝PB，∴点P表示的数是1，故答案为：1；（2）设P点运动x秒追上R点，由题意得：2x+6＝3x 解得：x＝6答：P点运动6秒追上R点．（3）MN的长度不变．①当P点在线段AB上时，如图示：∵M为PA的中点，N为PB的中点∴又∵MN＝MP+NP∴∵AP+BP＝AB，AB＝6∴②当P点在线段AB的延长线上时，如图示：∵MN＝MP﹣NP，AB＝AP﹣BP＝6∴＝．。

七年级下册期末试卷测试卷(含答案解析)

七年级下册期末试卷测试卷（含答案解析）一、选择题1．2的平方根是（）A ．﹣1.414B ．±1.414C ．2D ．2± 2．下列现象属于平移的是（） A ．投篮时的篮球运动B ．随风飘动的树叶在空中的运动C ．刹车时汽车在地面上的滑动D ．冷水加热过程中小气泡变成大气泡 3．在平面直角坐标系中，点P （-3，0）在（） A ．第二象限 B ．第三象限 C ．x 轴上 D ．y 轴上 4．给出以下命题：①对顶角相等；②在同一平面内，垂直于同一条直线的两条直线平行；③相等的角是对顶角；④内错角相等．其中假命题有（）A ．1个B ．2个C ．3个D ．4个 5．将一张边沿互相平行的纸条如图折叠后，若边//AD BC ，则翻折角1∠与2∠一定满足的关系是（）A ．122∠=∠B ．1290∠+∠=︒C ．1230∠-∠=︒D ．213230∠-∠=︒ 6．下列说法中正确的是( )A ．有理数和数轴上的点一一对应B ．0.304精确到十分位是0.30C ．立方根是本身的数只有0D ．平方根是本身的数只有07．如图，//a b ，160∠=︒，则2∠的大小是（）A ．60︒B ．80︒C ．100︒D ．120︒8．在平面直角坐标系中，对于点P （x ，y ），我们把点P’（－y ＋1，x ＋1）叫做点P 的伴随点．已知点A 1的伴随点为A 2，点A 2的伴随点为A 3，点A 3的伴随点为A 4，…，这样依次得到点A 1，A 2，A 3，…，A n ，…．若点A 1的坐标为（a ，b ），则点A 2021的坐标为（） A ．（a ，b ）B ．（－b ＋1，a ＋1）C ．（－a ，－b ＋2）D ．（b －1，－a ＋1）二、填空题 9．已知x ，y ()2120x y --=，则x-y =___________．10．点(,1)a 关于x 轴的对称点的坐标为(5,)b ，则+a b 的值是______．11．如图，在△ABC 中，∠A=50°，∠C=72°，BD 是△ABC 的一条角平分线，求∠ADB=__度．12．如图，已知AB //EF ，∠B =40°，∠E =30°，则∠C -∠D 的度数为________________．13．如图，在长方形纸片ABCD 中，点E 、F 分别在AD 、BC 上，将长方形纸片沿直线EF 折叠后，点D 、C 分别落在点D 1、C 1的位置，如果∠1AED =40°，那么∠EFB 的度数是_____度．14．对于有理数a ，b ，规定一种新运算：a ※b=ab+b ，如2※3=2×3+3=9．下列结论：①（﹣3）※4=﹣8；②若a ※b=b ※a ，则a=b ；③方程（x ﹣4）※3=6的解为x=5；④（a ※b ）※c=a ※（b ※c ）．其中正确的是_____（把所有正确的序号都填上）． 15．若点P （a +3，2a +4）在y 轴上，则点P 到x 轴的距离为________．16．如图，一个点在第一象限及x 轴、y 轴上运动，在第一秒钟，它从原点()0,0运动到()0,1，然后接着按图中箭头所示方向运动，即()()()()0,00,11,11,0→→→，…，且每秒运动一个单位，到()1,1点用时2秒，到()2,2点用时6秒，到()3,3点用时12秒，…，那么第421秒时这个点所在位置的坐标是____．三、解答题17．（133181254（2）3|12|427-+-（3）2(22)3(21)+-+18．已知m +n =2，mn =-15，求下列各式的值．（1）223m mn n ++；（2）2()m n -．19．完成下面的证明：已知：如图， //AB CD ， CD 和BE 相交于点O ， DE 平分CDF ∠，DE 和BE 相交于点E ，2E ∠=∠．求证：22B ∠=∠．证明：2E ∠=∠（已知），//BE DF ∴（______________），CDF ∴∠=∠________（两直线平行，同位角相等）．又//AB CD （已知），B ∴∠=∠______（________）B CDF ∴∠=∠（等量代换）．DE 平分CDF ∠（已知），2CDF ∴∠=∠_______（角平分线的定义）．22B ∴∠=∠（_________）．20．已知在平面直角坐标系中有三点A （﹣2，1）、B （3，1）、C （2，3）．请回答如下问题：（1）在坐标系内描出点A 、B 、C 的位置；（2）求出以A 、B 、C 三点为顶点的三角形的面积；（3）在y 轴上是否存在点P ，使以A 、B 、P 三点为顶点的三角形的面积为10，若存在，请直接写出点P 的坐标；若不存在，请说明理由．21．计算：（1）239(6)27----；（2）﹣12+（﹣2）3×31127()89--⨯-；（3）已知实数a 、b 满足1a -+|b ﹣1|=0，求a 2017+b 2018的值．（4）已知5+1的整数部分为a ，5﹣1的小数部分为b ，求2a+3b 的值．二十二、解答题22．如图，用两个面积为28cm 的小正方形纸片剪拼成一个大的正方形．（1）大正方形的边长是________cm ；（2）请你探究是否能将此大正方形纸片沿着边的方向裁出一个面积为214cm 的长方形纸片，使它的长宽之比为2:1，若能，求出这个长方形纸片的长和宽，若不能，请说明理由．二十三、解答题23．如图1，AB //CD ，点E 、F 分别在AB 、CD 上，点O 在直线AB 、CD 之间，且100EOF ∠=︒．（1）求BEO OFD ∠+∠的值；（2）如图2，直线MN 分别交BEO ∠、OFC ∠的角平分线于点M 、N ，直接写出EMN FNM ∠-∠的值；（3）如图3，EG 在AEO ∠内，AEG m OEG ∠=∠；FH 在DFO ∠内，DFH m OFH ∠=∠，直线MN 分别交EG 、FH 分别于点M 、N ，且50FMN ENM ∠-∠=︒，直接写出m 的值．24．已知直线//AB CD ，M ，N 分别为直线AB ，CD 上的两点且70MND ∠=︒，P 为直线CD 上的一个动点．类似于平面镜成像，点N 关于镜面MP 所成的镜像为点Q ，此时,,NMP QMP NPM QPM MNP MQP ∠=∠∠=∠∠=∠．（1）当点P 在N 右侧时：①若镜像Q 点刚好落在直线AB 上（如图1），判断直线MN 与直线PQ 的位置关系，并说明理由；②若镜像Q 点落在直线AB 与CD 之间（如图2），直接写出BMQ ∠与DPQ ∠之间的数量关系；（2）若镜像PQ CD ⊥，求BMQ ∠的度数．25．问题情境：如图1，AB ∥CD ，∠PAB=130°，∠PCD=120°．求∠APC 度数．小明的思路是：如图2，过P 作PE ∥AB ，通过平行线性质，可得∠APC=50°+60°=110°．(1)如图3，AD ∥BC ，点P 在射线OM 上运动，当点P 在A 、B 两点之间运动时，∠ADP=∠α，∠BCP=∠β．∠CPD 、∠α、∠β之间有何数量关系？请说明理由；(2)在(1)的条件下，如果点P 在A 、B 两点外侧运动时(点P 与点A 、B 、O 三点不重合)，请你直接写出∠CPD 、∠α、∠β间的数量关系．26．如果三角形的两个内角α与β满足290αβ+=︒，那么我们称这样的三角形是“准互余三角形”．（1）如图1，在Rt ABC 中，90ACB ∠=︒，BD 是ABC 的角平分线，求证：ABD △是“准互余三角形”；（2）关于“准互余三角形”，有下列说法：①在ABC 中，若100A ∠=︒，70B ∠=︒，10C ∠=︒，则ABC 是“准互余三角形”； ②若ABC 是“准互余三角形”，90C ∠>︒，60A ∠=︒，则20B ∠=︒；③“准互余三角形”一定是钝角三角形．其中正确的结论是___________（填写所有正确说法的序号）；（3）如图2，B ，C 为直线l 上两点，点A 在直线l 外，且50ABC ∠=︒．若P 是直线l 上一点，且ABP △是“准互余三角形”，请直接写出APB ∠的度数．【参考答案】一、选择题1．D【分析】根据平方根的定义求解即可．【详解】解：2的平方根是故选：D．【点睛】本题考查了平方根的定义．注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．2．C【分析】判断是否是平移现象，要根据平移的性质进行，即图形平移前后的形状和大小没有变化，只是位置发生变化．【详解】解：A. 投篮时的篮球运动，不是沿直线运动，此选项不是平移现象；B解析：C【分析】判断是否是平移现象，要根据平移的性质进行，即图形平移前后的形状和大小没有变化，只是位置发生变化．【详解】解：A. 投篮时的篮球运动，不是沿直线运动，此选项不是平移现象；B. 随风飘动的树叶在空中的运动，在空中不是沿直线运动，此选项不是平移现象；C. 刹车时汽车在地面上的滑动，此选项是平移现象；D. 冷水加热过程中小气泡变成大气泡，大小发生了变化，此选项不是平移现象．故选：C．【点睛】本题考查的知识点是平移的概念，掌握平移的性质是解此题的关键．3．C【分析】根据点的坐标特点判断即可．【详解】解：在平面直角坐标系中，点P（-3，0）在x轴上，故选C．【点睛】此题考查了点的坐标，熟练掌握平面直角坐标系中点的特征是解本题的关键．4．B根据对顶角的性质、平行线的判定和性质进行判断即可．【详解】解：①对顶角相等，是真命题；②在同一平面内，垂直于同一条直线的两条直线平行，是真命题；③相等的角不一定是对顶角，原命题是假命题；④两直线平行，内错角相等，原命题是假命题．故选：B．【点睛】考查了命题与定理的知识，解题的关键是了解对顶角的性质、平行线的判定和性质，难度较小．5．B【分析】根据平行可得出∠DAB+∠CBA=180°，再根据折叠和平角定义可求出1290∠+∠=︒．【详解】解：由翻折可知，∠DAE=21∠，∠CBF=22∠，∵//AD BC,∴∠DAB+∠CBA=180°，∴∠DAE+∠CBF=180°，∠+∠=°，即2122180∴1290∠+∠=︒，故选：B．【点睛】本题考查了平行线的性质和角平分线的性质，解题关键是熟练运用平行线的性质进行推理计算．6．D【分析】根据实数与数轴、精确度、立方根及平方根的概念和性质逐项判断即可．【详解】解：A. 实数和数轴上的点一一对应，原说法错误；B. 0.304精确到十分位是0.3，原说法错误；C. 立方根是本身的数是0、±1，原说法错误；D. 平方根是本身的数只有0，正确，故选：D．【点睛】本题考查了实数与数轴、精确度、立方根及平方根的概念和性质，熟练掌握基础知识是解题关键．7．D【分析】根据同位角相等，两直线平行即可求解．【详解】解：如图：a b，∠1=60°，因为//所以∠3=∠1=60°．因为∠2+∠3=180°，所以∠2=180°-60°=120°．故选：D．【点睛】本题考查的是平行线的判定定理，掌握同位角相等，两直线平行是解题的关键．8．A【分析】据“伴随点”的定义依次求出各点，不难发现，每4个点为一个循环组依次循环，用2021除以4，根据商和余数的情况确定点A2021的坐标即可．【详解】解：观察发现：A1（a，b），A2（解析：A【分析】据“伴随点”的定义依次求出各点，不难发现，每4个点为一个循环组依次循环，用2021除以4，根据商和余数的情况确定点A2021的坐标即可．【详解】解：观察发现：A1（a，b），A2（-b+1，a+1），A3（-a，-b+2），A4（b-1，-a+1），A5（a，b），A6（-b+1，a+1）…∴依此类推，每4个点为一个循环组依次循环，∵2021÷4=505……1，∴点A 2021的坐标与A 1的坐标相同，为（a ，b ），故选：A ．【点睛】本题是对点的变化规律的考查，读懂题目信息，理解“伴随点”的定义并求出每4个点为一个循环组依次循环是解题的关键，也是本题的难点．二、填空题9．-1【分析】根据算术平方根的非负性和平方的非负性即可求出x 和y ，代入求值即可．【详解】解：∵，∴解得：∴x-y=-1故答案为：-1．【点睛】此题考查的是非负性的应用，掌握算术平方解析：-1【分析】根据算术平方根的非负性和平方的非负性即可求出x 和y ，代入求值即可．【详解】解：∵()220y -=()20,20y -≥ ∴10,20x y -=-=解得：1,2x y ==∴x-y =-1故答案为：-1．【点睛】此题考查的是非负性的应用，掌握算术平方根的非负性和平方的非负性是解决此题的关键．10．4【分析】根据横坐标不变，纵坐标相反，确定a,b 的值，计算即可．【详解】∵点关于轴的对称点的坐标为，∴a=5，b= -1，∴a+b= 5-1=4，故答案为：4．【点睛】本题考查了坐解析：4【分析】根据横坐标不变，纵坐标相反，确定a,b的值，计算即可．【详解】∵点(,1)a关于x轴的对称点的坐标为(5,)b，∴a=5，b= -1，∴a+b= 5-1=4，故答案为：4．【点睛】本题考查了坐标系中轴对称问题，熟练掌握轴对称的坐标变化特点是解题的关键．11．101【分析】直接利用三角形内角和定理得出∠ABC的度数，再利用角平分线的性质结合三角形内角和定理得出答案．【详解】∵在△ABC中,∠A=50°,∠C=72°，∴∠ABC=180°−50°解析：101【分析】直接利用三角形内角和定理得出∠ABC的度数，再利用角平分线的性质结合三角形内角和定理得出答案．【详解】∵在△ABC中,∠A=50°,∠C=72°，∴∠ABC=180°−50°−72°=58°，∵BD是△ABC的一条角平分线，∴∠ABD=29°，∴∠ADB=180°−50°−29°=101°.故答案为：101.【点睛】此题考查三角形内角和定理，解题关键在于掌握其定理.12．10°【分析】过点C作CG∥AB，过点D作DH∥EF，根据平行线的性质可得AB∥CG∥DH∥EF，从而可得∠BCG=∠B=40°，∠EDH=∠E=30°，∠DCG=∠CDH，即可求解．【详解】解析：10°【分析】过点C作CG∥AB，过点D作DH∥EF，根据平行线的性质可得AB∥CG∥DH∥EF，从而可得∠BCG=∠B=40°，∠EDH=∠E=30°，∠DCG=∠CDH，即可求解．【详解】解：如图，过点C作CG∥AB，过点D作DH∥EF，∵AB//EF，∴AB∥CG∥DH∥EF，∵∠B=40°，∠E=30°，∴∠BCG=∠B=40°，∠EDH=∠E=30°，∠DCG=∠CDH，∴∠BCD-∠CDE=∠BCG-∠EDH=40°-30°=10°．故答案为：10°．【点睛】本题主要考查了平行线的性质，准确作出辅助线是解题的关键．13．70【分析】先利用折叠的性质得出∠DEF＝∠D1EF，再由利用平角的应用求出∠DEF，最后长方形的性质即可得出结论．【详解】解：如图，由折叠可得∠DEF＝∠D1EF，∵∠AED1＝40°解析：70【分析】先利用折叠的性质得出∠DEF＝∠D1EF，再由利用平角的应用求出∠DEF，最后长方形的性质即可得出结论．【详解】解：如图，由折叠可得∠DEF＝∠D1EF，∵∠AED 1＝40°，∴∠DEF ＝180402︒-︒＝70°， ∵四边形ABCD 是长方形，∴AD ∥BC ，∴∠EFB ＝∠DEF ＝70°．故答案为：70．【点睛】考查了长方形的性质，折叠的性质，关键是利用折叠的性质得出∠DEF ＝∠D 1EF 解答． 14．①③【分析】题目中各式利用已知的新定义公式计算得到结果，即可做出判断．【详解】(−3)※4=−3×4+4=−8，所以①正确；a ※b=ab+b ，b ※a=ab+a ，若 a=b ，两式相等，若解析：①③【分析】题目中各式利用已知的新定义公式计算得到结果，即可做出判断．【详解】(−3)※4=−3×4+4=−8，所以①正确；a ※b=ab+b ，b ※a=ab+a ，若 a=b ，两式相等，若 a≠b ，则两式不相等，所以②错误；方程(x−4) )※3=6化为3(x−4)+3=6，解得x=5，所以③正确；左边=(a ※b) ※c=(a×b+b) )※c=(a×b+b)·c+c=abc+bc+c 右边=a ※（b ※c ）=a ※(b×c+c)=a(b×c+c) +(b×c+c)=abc+ac+bc+c 2两式不相等，所以④错误．综上所述，正确的说法有①③．故答案为①③.【点睛】有理数的混合运算, 解一元一次方程，属于定义新运算专题，解决本题的关键突破口是准确理解新定义．本题主要考查学生综合分析能力、运算能力．15．2【分析】点在y轴上，则横坐标为0，可求得a的值，然后再判断点到x轴的距离即可．【详解】∵点P(a+3，2a+4)在y轴上∴a+3=0，解得：a=－3∴P(0，－2)∴点P到x轴的距离解析：2【分析】点在y轴上，则横坐标为0，可求得a的值，然后再判断点到x轴的距离即可．【详解】∵点P(a+3，2a+4)在y轴上∴a+3=0，解得：a=－3∴P(0，－2)∴点P到x轴的距离为：2故答案为：2【点睛】本题考查坐标点与坐标轴的关系，注意，点到坐标轴的距离一定是非负的．16．【分析】由题目中所给的点运动的特点找出规律，即可解答．【详解】由题意可知这点移动的速度是1个单位长度/每秒，设这点为（x，y）到达（1，0）时用了3秒，到达（2，0）时用了4秒，从（2，19,20解析：()【分析】由题目中所给的点运动的特点找出规律，即可解答．【详解】由题意可知这点移动的速度是1个单位长度/每秒，设这点为（x，y）到达（1，0）时用了3秒，到达（2，0）时用了4秒，从（2，0）到（0，2）有四个单位长度，则到达（0，2）时用了4+4=8秒，到（0，3）时用了9秒；从（0，3）到（3，0）有六个单位长度，则到（3，0）时用9+6=15秒；依此类推到（4，0）用16秒，到（0，4）用16+8=24秒，到（0，5）用25秒，到（6，0）用36秒，到（6，6）时用36+6=42秒…，可得在x 轴上，横坐标为偶数时，所用时间为x 2秒，在y 轴上时，纵坐标为奇数时，所用时间为y 2秒，∵20×20=400∴第421秒时这个点所在位置的坐标为（19，20），故答案为：（19，20）．【点睛】本题主要考查了点的坐标的变化规律，得出运动变化的规律是解决问题的关键．三、解答题17．（1）；（2）；（3）【分析】（1）先化简后计算即可；（2）先化简后计算即可；（3）首先去括号，然后再合并即可．【详解】解：（1）原式（2）原式（3）原式【点睛】此题主要考查了实解析：（1）172；（22；（3）1-【分析】（1）先化简后计算即可；（2）先化简后计算即可；（3）首先去括号，然后再合并即可．【详解】解：（1）原式1112577222=++=+=（2）原式1232=+-=（3）原式231=+=-【点睛】此题主要考查了实数运算，关键是掌握数的开方，正确化简各数．18．（1）-11；（2）68【分析】（1）直接利用完全平方公式将原式变形进而得出答案；（2）直接利用完全平方公式将原式变形进而得出答案．【详解】解：（1）====-11；（2）=解析：（1）-11；（2）68【分析】（1）直接利用完全平方公式将原式变形进而得出答案；（2）直接利用完全平方公式将原式变形进而得出答案．【详解】解：（1）223m mn n ++=222m mn n mn +++=()2m n mn ++=2215-=-11；（2）2()m n -=2()4m n mn +-=()22415-⨯- =464+=68【点睛】此题主要考查了完全平方公式，正确应用完全平方公式是解题关键．19．内错角相等，两直线平行；1；1；两直线平行，同位角相等；2；等量代换．【分析】由可判定，即得出，再根据得出，等量代换得到，再根据角平分线的定义等量代换即可得解．【详解】证明：（已知），（内解析：内错角相等，两直线平行；1；1；两直线平行，同位角相等；2；等量代换．【分析】由2E ∠=∠可判定//BE DF ，即得出1CDF ∠=∠，再根据//AB CD 得出1B ∠=∠，等量代换得到B CDF ∠=∠，再根据角平分线的定义等量代换即可得解．【详解】证明：2∠=∠（已知），EBE DF∴（内错角相等，两直线平行），//CDF∴∠=∠（两直线平行，同位角相等）．1AB CD（已知），又//∴∠=∠（两直线平行，同位角相等），B1∴∠=∠（等量代换）．B CDF∠（已知），DE平分CDF∴∠=∠（角平分线的定义）．22CDF∴∠=∠（等量代换）．B22故答案为：内错角相等，两直线平行；1；1；两直线平行，同位角相等；2；等量代换．【点睛】本题考查了平行线的判定与性质，解题的关键是熟记“内错角相等，两直线平行”、“两直线平行，同位角相等”．20．（1）见解析；（2）S△ABC＝5；（3）存在，P点的坐标为（0，5）或（0，﹣3）．【分析】（1）根据点的坐标，直接描点；（2）根据点的坐标可知，ABx轴，且AB＝3﹣（﹣2）＝5，点C到线解析：（1）见解析；（2）S△ABC＝5；（3）存在，P点的坐标为（0，5）或（0，﹣3）．【分析】（1）根据点的坐标，直接描点；（2）根据点的坐标可知，AB//x轴，且AB＝3﹣（﹣2）＝5，点C到线段AB的距离3﹣1＝2，根据三角形面积公式求解；（3）因为AB＝5，要求ABP的面积为10，只要P点到AB的距离为4即可，又P点在y 轴上，满足题意的P点有两个．【详解】解：（1）描点如图；（2）依题意，得AB//x轴，且AB＝3﹣（﹣2）＝5，∴S△ABC＝1×5×2＝5；2（3）存在；∵AB＝5，S△ABP＝10，∴P点到AB的距离为4，又点P在y轴上，∴P点的坐标为（0，5）或（0，﹣3）．【点睛】本题考查了点的坐标的表示方法，能根据点的坐标表示三角形的底和高并求三角形的面积．21．(1)0；（2）-3；（3）2；（4）.【解析】【分析】直接利用算术平方根以及立方根的定义化简进而得出答案；直接利用有理数的乘方、算术平方根以及立方根的定义化简进而得出答案利用绝对值以及平解析：(1)0；（2）-3；（3）2；（4）35.【解析】【分析】() 1直接利用算术平方根以及立方根的定义化简进而得出答案；()2直接利用有理数的乘方、算术平方根以及立方根的定义化简进而得出答案 ()3利用绝对值以及平方根的非负性质得出a ，b 的值，进而得出答案；()4直接利用253＜的范围进而得出a ，b 的值，即可得出答案．【详解】解：(2319(6)27--3630=-+=；()2331121(2)2789⎛-+-⨯- ⎝111333⎛⎫=--+⨯-=- ⎪⎝⎭； ()3110a b -+-=，1a ∴=，1b =，20172018a b +112=+=；()451+的整数部分为a 51的小数部分为b ， 3a ∴=，52b =，2366a b ∴+=+=【点睛】此题主要考查了估算无理数的大小以及实数运算，正确化简各数是解题关键．二十二、解答题22．（1）4；（2）不能，理由见解析．【分析】（1）根据已知正方形的面积求出大正方形的边长即可；（2）先设未知数根据面积=14（cm2）列方程，求出长方形的边长，将长方形的长与正方形边长比较大小再解析：（1）4；（2）不能，理由见解析．【分析】（1）根据已知正方形的面积求出大正方形的边长即可；（2）先设未知数根据面积=14（cm 2）列方程，求出长方形的边长，将长方形的长与正方形边长比较大小再判断即可．【详解】解：（1）两个正方形面积之和为：2×8=16（cm 2），∴拼成的大正方形的面积=16（cm 2），∴大正方形的边长是4cm ；故答案为：4；（2）设长方形纸片的长为2xcm ，宽为xcm ，则2x •x =14，解得：x =2x ，∴不存在长宽之比为2:1且面积为214cm 的长方形纸片．【点睛】本题考查了算术平方根，能够根据题意列出算式是解此题的关键．二十三、解答题23．（1）；（2）的值为40°；（3）．【分析】（1）过点O 作OG ∥AB ，可得AB ∥OG ∥CD ，利用平行线的性质可求解；（2）过点M 作MK ∥AB ，过点N 作NH ∥CD ，由角平分线的定义可设∠BEM解析：（1）260BEO DFO ∠+∠=︒ ；（2）EMN FNM ∠-∠的值为40°；（3）53．【分析】（1）过点O 作OG ∥AB ，可得AB ∥OG ∥CD ，利用平行线的性质可求解；（2）过点M 作MK ∥A B ，过点N 作NH ∥CD ，由角平分线的定义可设∠BEM =∠OEM =x ，∠CFN =∠OFN =y ，由∠BEO +∠DFO =260°可求x -y =40°，进而求解；（3）设直线FK 与EG 交于点H ，FK 与AB 交于点K ，根据平行线的性质即三角形外角的性质及50FMN ENM ∠-∠=︒，可得50KFD AEG ∠-∠=︒，结合260AEG n OEG DFK n OFK BEO DFO ∠=∠=∠∠+∠=︒，，，可得11180100AEG AEG KFD KFD n n∠+∠+︒-∠-∠=︒，即可得关于n 的方程，计算可求解n 值．【详解】证明：过点O 作OG ∥AB ，∵AB ∥CD ，∴AB ∥OG ∥CD ，∴180180BEO EOG DFO FOG ∠+∠=︒∠+∠=︒，，∴360BEO EOG DFO FOG ∠+∠+∠+∠=︒，即360BEO EOF DFO ∠+∠+∠=︒，∵∠EOF =100°，∴∠260BEO DFO +∠=︒；（2）解：过点M 作MK ∥AB ，过点N 作NH ∥CD ，∵EM 平分∠BEO ，FN 平分∠CFO ，设BEM OEM x CFN OFN y ∠=∠=∠=∠=，，∵260BEO DFO ∠+∠=︒∴21802260BEO DFO x y ∠+∠=+︒-=︒，∴x -y =40°，∵MK ∥AB ，NH ∥CD ，AB ∥CD ，∴AB ∥MK ∥NH ∥CD ，∴EMK BEM x HNF CFN y KMN HNM ∠=∠=∠=∠=∠=∠，，，∴EMN FNM EMK KMN HNM HNF ∠+∠=∠+∠-∠+∠（）x KMN HNM y =+∠-∠-=x -y=40°，故EMN FNM ∠-∠的值为40°；（3）如图，设直线FK 与EG 交于点H ，FK 与AB 交于点K ，∵AB ∥CD ，∴AKF KFD ∠=∠，∵AKF EHK HEK EHK AEG ∠=∠+∠=∠+∠，∴KFD EHK AEG ∠=∠+∠，∵50EHK NMF ENM ∠=∠-∠=︒，∴50KFD AEG ∠=︒+∠，即50KFD AEG ∠-∠=︒，∵AEG n OEG ∠=∠，FK 在∠DFO 内，DFK n OFK ∠=∠． ∴1180180CFO DFK OFK KFD KFD n∠=︒-∠-∠=︒-∠-∠ ， 1AEO AEG OEG AEG AEG n∠=∠+∠=∠+∠， ∵260BEO DFO ∠+∠=︒，∴100AEO CFO ∠+∠=︒， ∴11180100AEG AEG KFD KFD n n∠+∠+︒-∠-∠=︒，即(180)1KFD AEG n ⎛⎫ ⎪⎝∠⎭+-∠︒＝， ∴115080n ⎛⎫ ⎪⨯⎭︒︒⎝+＝，解得53n = ．经检验，符合题意，故答案为：53．【点睛】本题主要考查平行线的性质，角平分线的定义，灵活运用平行线的性质是解题的关键． 24．（1）①，证明见解析，②，（2）或．【分析】(1) ①根据和镜像证出，即可判断直线与直线的位置关系，②过点Q 作QF ∥CD ，根据平行线的性质证即可；(2)过点Q 作QF ∥CD ，根据点P 的位置不同，解析：（1）①//MN PQ ，证明见解析，②70DPQ BMQ ∠∠+=︒，（2）160︒或20︒．【分析】(1) ①根据//AB CD 和镜像证出NMP QPM ∠=∠，即可判断直线MN 与直线PQ 的位置关系，②过点Q 作QF ∥CD ，根据平行线的性质证DPQ BM MQP Q ∠=∠∠+即可；(2)过点Q 作QF ∥CD ，根据点P 的位置不同，分类讨论，依据平行线的性质求解即可．【详解】（1）①//MN PQ ，证明：∵//AB CD ，∴NPM QMP ∠=∠，∵,NMP QMP NPM QPM ∠=∠∠=∠，∴NMP QPM ∠=∠，∴//MN PQ ；②过点Q 作QF ∥CD ，∵//AB CD ，∴////AB CD QF ，∴1BMQ ∠=∠，2QPD ∠=∠，∴DPQ BM MQP Q ∠=∠∠+，∵70MNP MQP ∠=∠=︒，∴70DPQ BMQ ∠∠+=︒；（2）如图，当点P 在N 右侧时，过点Q 作QF ∥CD ，同（1）得，////AB CD QF ，∴180NP FQP Q ∠=∠+︒，FQM BMQ ∠=∠，∵PQ CD ⊥，∴90NPQ ∠=︒，∴90FQP ∠=︒，∵70MND PQM ∠=∠=︒，∴20FQM ∠=︒，∴20BMQ ∠=︒，如图，当点P 在N 左侧时，过点Q 作QF ∥CD ，同（1）得，////AB CD QF ，同理可得，90FQP ∠=︒，∵70MND ∠=︒，∴110MNP PQM ∠=∠=︒，∴20FQM ∠=︒，∵//AB QF ，∴180BM FQM Q ∠=∠+︒，∴160BMQ ∠=︒；综上，BMQ ∠的度数为160︒或20︒．【点睛】本题考查了平行线的性质与判定，解题关键是恰当的作辅助线，熟练利用平行线的性质推导角之间的关系．25．（1），理由见解析；（2）当点P 在B 、O 两点之间时，；当点P在射线AM上时，.【分析】（1）过P作PE∥AD交CD于E，推出AD∥PE∥BC，根据平行线的性质得出∠α=∠DPE，∠β=∠C∠=∠+∠，理由见解析；解析：（1）CPDαβ∠=∠-∠；（2）当点P在B、O两点之间时，CPDαβ∠=∠-∠.当点P在射线AM上时，CPDβα【分析】（1）过P作PE∥AD交CD于E，推出AD∥PE∥BC，根据平行线的性质得出∠α=∠DPE，∠β=∠CPE，即可得出答案；（2）分两种情况：①点P在A、M两点之间，②点P在B、O两点之间，分别画出图形，根据平行线的性质得出∠α=∠DPE，∠β=∠CPE，即可得出结论．【详解】解：(1)∠CPD＝∠α＋∠β，理由如下：如图，过P作PE∥AD交CD于E.∵AD∥BC，∴AD∥PE∥BC，∴∠α＝∠DPE，∠β＝∠CPE，∴∠CPD＝∠DPE＋∠CPE＝∠α＋∠β.(2)当点P在A、M两点之间时，∠CPD＝∠β－∠α.理由：如图，过P作PE∥AD交CD于E.∵AD∥BC，∴AD∥PE∥BC，∴∠α＝∠DPE，∠β＝∠CPE，∴∠CPD＝∠CPE－∠DPE＝∠β－∠α；当点P在B、O两点之间时，∠CPD＝∠α－∠β.理由：如图，过P作PE∥AD交CD于E.∵AD∥BC，∴AD ∥PE ∥BC ，∴∠α＝∠DPE ，∠β＝∠CPE ，∴∠CPD ＝∠DPE －∠CPE ＝∠α－∠β.【点睛】本题考查了平行线的性质的运用，主要考核了学生的推理能力，解决问题的关键是作平行线构造内错角，利用平行线的性质进行推导．解题时注意：问题（2）也可以运用三角形外角性质来解决．26．（1）见解析；（2）①③；（3）∠APB 的度数是10°或20°或40°或110°【分析】（1）由和是的角平分线，证明即可；（2）根据“准互余三角形”的定义逐个判断即可；（3）根据“准互余三角解析：（1）见解析；（2）①③；（3）∠APB 的度数是10°或20°或40°或110°【分析】（1）由90ABC A ∠+∠=︒和BD 是ABC 的角平分线，证明290ABD A ∠+∠=︒即可；（2）根据“准互余三角形”的定义逐个判断即可；（3）根据“准互余三角形”的定义，分类讨论：①2∠A +∠ABC =90°；②∠A +2∠APB =90°；③2∠APB +∠ABC =90°；④2∠A +∠APB =90°，由三角形内角和定理和外角的性质结合“准互余三角形”的定义，即可求出答案．【详解】（1）证明：∵在Rt ABC 中，90ACB ∠=︒，∴90ABC A ∠+∠=︒，∵BD 是ABC ∠的角平分线，∴2ABC ABD ∠=∠，∴290ABD A ∠+∠=︒，∴ABD △是“准互余三角形”；（2）①∵70,10B C ∠=︒∠=︒，∴290B C ∠+∠=︒，∴ABC 是“准互余三角形”，故①正确；②∵60A ∠=︒， 20B ∠=︒，∴210090A B ∠+∠=︒≠︒，∴ABC 不是“准互余三角形”，故②错误；③设三角形的三个内角分别为,,αβγ，且αβγ<<，∵三角形是“准互余三角形”，∴290αβ+=︒或290αβ+=︒，∴90αβ+<︒，∴180()90γαβ=︒-+>︒，∴“准互余三角形”一定是钝角三角形，故③正确；综上所述，①③正确，故答案为：①③；（3）∠APB 的度数是10°或20°或40°或110°；如图①，当2∠A +∠ABC =90°时，△ABP 是“准直角三角形”，∵∠ABC =50°，∴∠A =20°，∴∠APB =110°；如图②，当∠A +2∠APB =90°时，△ABP 是“准直角三角形”，∵∠ABC =50°，∴∠A +∠APB =50°，∴∠APB =40°；如图③，当2∠APB +∠ABC =90°时，△ABP 是“准直角三角形”，∵∠ABC =50°，∴∠APB =20°；如图④，当2∠A +∠APB =90°时，△ABP 是“准直角三角形”，∵∠ABC =50°，∴∠A+∠APB=50°，所以∠A=40°，所以∠APB=10°；综上，∠APB的度数是10°或20°或40°或110°时，ABP△是“准互余三角形”．【点睛】本题是三角形综合题，考查了三角形内角和定理，三角形的外角的性质，解题关键是理解题意，根据三角形内角和定理和三角形的外角的性质，结合新定义进行求解．。

部编版语文七年级下册《期末检测题》附答案

部编版语文七年级下学期期末测试卷学校________ 班级________ 姓名________ 成绩________一、语言积累（24分）1. 下列加点字的读音完全正确的一项是（）A. 殷．红（yīn）字帖．（tiè）诧．异（chà）鲜．为人知（xiǎn）B. 跳跃．（yuè）憎．恶（zèng）颤．抖（chàn）潜．心贯注（qián）C. 销蚀．（shì）贮．藏（zhù）癫．狂（diān）深恶．痛绝（wù）D. 蹒跚．（shān）舷．窗（xián）胆怯．（qiè）九曲．连环（qū）2. 下列词语中没有错别字的一项是（）A. 选聘彷徨锋芒必露妇孺皆知B. 震悚爆炸炯炯目光姗姗来迟C. 竹竿度假荒草萋萋一泄万丈D. 疲惫告磬坚持不懈察言观色3. 下列加点的成语使用恰当的一项是（）A. 在党中央领导下，中国人民万众一心，众志成城．．．．，对打赢疫情防控阻击战充满信心B. 这位著名演唱家的歌声气冲斗牛．．．．，声入九霄，赢得在场观众的阵阵掌声与喝彩C. 见到亲人，在外漂泊多年的他终于忍俊不禁．．．．地流下了泪水D. 他只关心孩子的学习，对于孩子品德上的问题却不以为然．．．．4. 下列句子没有语病的一项是（）A.．．保护并了解我们的传统文化，是每个中国人义不容辞的责任.B.．．成绩的好坏首先取决于能否刻苦学习.C.．．十多年后，班主任李老师音容笑貌仍然常常在我耳边回响.D.．．通过改善交通条件，增设旅游景点，使章丘区旅游发展再上新台阶.5. 下列语法知识有误的一项是（）A. “啊．！清早的．．有这么多人在．晨练”句中加点的词语依次是：叹词、助词、．．．体育公园和．龙盘山公园里竟然连词、副词和介词B. “家喻户晓、苛捐杂税、仙露琼浆、耀武扬威”都是并列短语C. “千钧重负、言外之意、酣然入梦、如释重负”都是偏正短语D. “狐假虎威、兄弟和睦、心有灵犀、波涛澎湃”都是主谓短语6. 下列场合中，文明警示语使用不得体的一项是（）A. “即使饥肠辘辘，也须风度翩翩.”（食堂里）B. “我想有个家！”（垃圾箱旁）C. “外地回来不报告，整个小区找你闹！”（防疫期间的小区）D. “一花一草皆生命，一枝一叶总关情.”（花园旁）7. 下列文学常识表述不正确的一项是（）A. 铭，是古代刻在器物上用来警诫自己或称述功德的文字，后来成为一种文体，一般是用韵的.B. 《阿长与<山海经>》一文选自《朝花夕拾》，原名《旧事重提》，这是部回忆性小说集.C. 《卖油翁》的作者是欧阳修，他是唐宋八大家之一.D. 《回忆鲁迅先生》作者萧红，代表作有《生死场》《呼兰河传》等。

七下期末考试题及参考答案

七下期末考试题及参考答案（时间：120分钟总分：100分）一、积累和运用（17分）1.下列各组词语中，加点字的读音全都正确的一组是()（2分）A．吞噬(shì) 咀嚼(jiáo) 俯瞰（kàn）海市蜃楼(shèn)B．殷红(yān) 震悚(sǒng) 孱头(chán) 忧心忡忡(zhōng)C．炽热(chì) 遨游(áo) 执着(zhuó) 屏息凝神(bǐng)D．修葺(qì) 晌午(xiǎng) 无虞(yú) 心有灵犀(xī)2.下列各组词语中，汉字书写全都正确的一组是（）（2分）A.深宵字帖妇孺皆知天崖海角B.斑斓闲暇姗姗来迟锲而不舍C.漫步严谨以身作责千钩重负D.契约愧怍酣然入梦不期而致3.请从所给的三个词语中，选出一个最符合语境的填写在横线上。

(2分)（1）人生的真谛是在嘈杂喧闹中活出一种________（肃静寂静恬静），让生命在宁静中运转，而不是在焦虑中追赶，正所谓宁静以致远。

（2）梦想成功的青年，面对那此起彼伏、________（惊心动魄险象环生毛骨悚然）的生活海洋，只有带上自信，才能扬帆破浪，从暗夜奔向黎明。

4.经典诗文默写。

（6分）（1）杨花榆荚无才思，。

（韩愈《晚春》）（2）当窗理云鬓，。

（《木兰诗》）（3）不畏浮云遮望眼，。

（王安石《登飞来峰》）（4），夜泊秦淮近酒家。

（杜牧《泊秦淮）（5），濯清涟而不妖。

（周敦颐《爱莲说》）（6）而那过去了的，。

（普希金《假如生活欺骗了你》）5.阅读语段，按要求完成下面的题目。

（3分）①“环球时报”报导，华为CEO任正非接受采访时特别强调“一个国家的强盛，是在小学教师的讲台上完成的”。

②他认为一个国家强大的基础是教育。

③如果不重视教育，我们国家就会重返贫穷。

④在几年前他就自己花钱，请中央党校、中国基础教育课题组的专家做中国农村九年义务教育的状况调查，分析了乡村贫困学生怎么学习，怎么能够保障他们的学习。

七年级下学期期末考试数学试卷(附含答案)

第5题图第9题图七年级下学期期末考试数学试卷(附含答案)一选择题（每小题4分，共40分） 1. 9的平方根是（）A.3±B. 3C. 81D.81± 2.在平在直角坐标系中，点M （3，-2）位于（）A.第一象限B. 第二象限C. 第三象限D. 第四象限 3.下列调查中适合采用全面调查的是（）A.了解凯里市“停课不停学”期间全市七年级学生的听课情况B.了解新冠肺炎疫情期间某校七（1）班学生的每日体温C.了解疫情期间某省生产的所有口罩的合格率D.了解全国各地七年级学生对新冠状病毒相关知识的了解情况 4.下列运动属于平移的是（）A. 荡秋千B. 地球绕太阳转C. 风车的转动D.急刹车时，汽车在地面上的滑动5. 如图，在下列条件中，不能判定AB ∥DF 的是（）A. ∠A+∠AFD=180°B.∠A=∠CFDC. ∠BED=∠EDFD. ∠A=∠BED 6. 已知二元一次方程432=-y x ，用含x 的代数式表示y ，正确的是（） A.342+=x y B. 342-=x y C. 234y x += D. 234yx -= 7. 已知b a >，下列不等式中错误的是（）A. 11+>+b aB. 22->-b aC. b a 22>D. b a 44->-8. 下列命题是真命题的是（）A.若||||b a =，则b a =B.经过直线外一点有且只有一条直线与已知直线平行C.同位角相等D.在同一平面内，如果b a ⊥，c b ⊥，那么c a ⊥ 9.如图，数轴上与40对应的点是（） A.点A B.点B C.点C D.点D 10. 某种服装的进价为200元，出售时标价为300元；由于换季，商店准备对该服装打折销售，但要保持利润不低于20%，那么最多打（）A. 6折B. 7折C. 8折D. 9折二填空题（每小题4分，共32分） 11. 在实数①21，②11，③1415926.3，④16，⑤π，⑥ 2020020002.0（相邻两个2之间依次多一个0）中，无理数有（填写序号）.12. 如图，要在河岸l 上建立一水泵房引水到C 处，做法是：过点C 作CD ⊥l 于点D ，将水泵房建在了D 处.这样做最节省水管长度，其数学道理是 . 13. 已知⎩⎨⎧=-=13y x 是方程7=+y mx 的解，则m .14.如图，直线a ∥b ，点B 在a 上，点A 与点C 在b 上；且AB ⊥BC.若∠1=034，则∠2= .第12题图第14题图15. 将50个数据分成5组列出频数分布表，其中第一组的频数为6，第二组与第五组的频数和为18，第三组的频率为0.2，则第四组的频率为 . 16.一个正数b 有两个不同的平方根1+a 和72-a ，则b a -21的立方根是 . 17.若关于x 的不等式组⎪⎩⎪⎨⎧<->-2210x a x 的所有整数解之和等于9，则a 的取值范围是 .18.在平面直角坐标系中，一蚂蚁从原点O 出发，按向上向右向下向右的方向依次不断移动，每次移动1个单位，移动的路线如图所示。

人教七年级下册数学期末测试题(附答案)

人教七年级下册数学期末测试题（附答案）一、选择题 1．81的算术平方根是（）A ．3B ．﹣3C ．﹣9D ．9 2．下列现象中是平移的是（） A ．翻开书中的每一页纸张 B ．飞碟的快速转动C ．将一张纸沿它的中线折叠D ．电梯的上下移动3．在平面直角坐标系中位于第二象限的点是（）A ．()2,3B ．()2,3-C ．()2,3-D ．()2,3-- 4．下列四个命题：①4±是64的立方根；②5是25的算术平方根；③如果两条直线都与第三条直线平行，那么这两条直线也互相平行；④在平面直角坐标系中，与两坐标轴距离都是2的点有且只有2个．其中真命题有（）个A ．1B ．2C ．3D ．45．如图，直线12//l l ，23216∠+∠=°，则1∠的度数为（）A ．216︒B ．36︒C ．44︒D ．18︒6．下列算式，正确的是（）A ．42±=±B ．42±=C ．382--=-D ．()288-=- 7．如图，AB //CD ，∠EBF ＝2∠ABE ，∠ECF ＝3∠DCE ，设∠ABE ＝α，∠E ＝β，∠F ＝γ，则α，β，γ的数量关系是（）A ．4β﹣α+γ＝360°B ．3β﹣α+γ＝360°C ．4β﹣α﹣γ＝360°D ．3β﹣2α﹣γ＝360°8．在平面直角坐标系xOy 中，对于点P (x ，y )，我们把P 1(y ﹣1，﹣x ﹣1)叫做点P 的友好点，已知点A 1的友好点为A 2，点A 2的友好点为A 3，点A 3的友好点为A 4，这样依次得到各点．若A 2021的坐标为(﹣3，2)，设A 1(x ，y )，则x +y 的值是( )A ．﹣5B ．3C ．﹣1D ．5九、填空题9．364--________．十、填空题10．若点P(a,b)关于y 轴的对称点是P 1 ,而点P 1关于x 轴的对称点是P 2 ,若点P 2的坐标为(-3,4),则a=_____,b=______十一、填空题11．如图，已知AD 是ABC 的角平分线，CE 是ABC 的高，∠BAC =60°，∠BCE =40°，则∠ADB =_____．十二、填空题12．如图，直线m 与∠AOB 的一边射线OB 相交，∠3＝120°，向上平移直线m 得到直线n ，与∠AOB 的另一边射线OA 相交，则∠2－∠1＝_______º．十三、填空题13．如图，在△ABC 中，将∠B 、∠C 按如图所示的方式折叠，点B 、C 均落于边BC 上的点Q 处，MN 、EF 为折痕，若∠A=82°，则∠MQE= _________十四、填空题14．按下面的程序计算：若输入n=100，输出结果是501；若输入n=25，输出结果是631，若开始输入的n 值为正整数，最后输出的结果为656，则开始输入的n 值可以是________．十五、填空题15．已知ABC ∆的面积为16，其中两个顶点的坐标分别是()()7,0,1,0A B -，顶点C 在y 轴上，那么点C 的坐标为 ____________十六、填空题16．如图，点()00,0A ，()11,2A ，()22,0A ，()33,2A -，()44,0A ，……根据这个规律，探究可得点2021A 的坐标是________．十七、解答题17．计算：（1）3840.04--- （2）23(2)279-+-十八、解答题18．求下列各式中x 的值：（1）()2125x -=；（2）381250x -=．十九、解答题19．完成下面的证明．如图，AB ∥CD ，∠B +∠D ＝180°，求证：BE ∥DF ．分析：要证BE ∥DF ，只需证∠1＝∠D ．证明：∵AB ∥CD （已知）∴∠B +∠1＝180°（）∵∠B +∠D ＝180°（已知）∴∠1＝∠D （）∴BE ∥DF （）二十、解答题20．已知：如图，把△ABC 向上平移4个单位长度，再向右平移3个单位长度，得到△A ′B ′C ′，（1）画出△A ′B ′C ′，写出A ′、B ′、C ′的坐标；（2）点P 在y 轴上，且S △BCP =4S △ABC ，直接写出点P 的坐标．二十一、解答题21．任意无理数都是由整数部分和小数部分构成的．已知一个无理数a ，它的整数部分是b ，则它的小数部分可以表示为-a b ．例如：469<<，即263<<，显然6的整数部分是2，小数部分是62-．根据上面的材料，解决下列问题：（1）若11的整数部分是m ，5的整数部分是n ，求5m n -+的值．（2）若714+的整数部分是2x ，小数部分是y ，求142x y -+的值．二十二、解答题22．如图，用两个面积为28cm 的小正方形纸片剪拼成一个大的正方形．（1）大正方形的边长是________cm ；（2）请你探究是否能将此大正方形纸片沿着边的方向裁出一个面积为214cm 的长方形纸片，使它的长宽之比为2:1，若能，求出这个长方形纸片的长和宽，若不能，请说明理由．二十三、解答题23．如图1，把一块含30°的直角三角板ABC的BC边放置于长方形直尺DEFG的EF边上．（1）根据图1填空：∠1＝°，∠2＝°；（2）现把三角板绕B点逆时针旋转n°．①如图2，当n＝25°，且点C恰好落在DG边上时，求∠1、∠2的度数；②当0°＜n＜180°时，是否会存在三角板某一边所在的直线与直尺（有四条边）某一边所在的直线垂直？如果存在，请直接写出所有n的值和对应的那两条垂线；如果不存在，请说明理由．二十四、解答题24．（1）光线从空气中射入水中会产生折射现象，同时光线从水中射入空气中也会产生折射现象，如图1，光线a从空气中射入水中，再从水中射入空气中，形成光线b，根据光学∠=∠∠=∠，请判断光线a与光线b是否平行，并说明理由．知识有12,34（2）光线照射到镜面会产生反射现象，由光学知识，入射光线与镜面的夹角与反射光线与镜面的夹角相等，如图2有一口井，已知入射光线α与水平线OC的夹角为40︒，问如何放置平面镜MN，可使反射光线b正好垂直照射到井底?（即求MN与水平线的夹角）（3）如图3，直线EF上有两点A、C，分别引两条射线AB、CD．105∠=︒，BAFDCF∠=︒，射线AB、CD分别绕A点，C点以1度/秒和3度/秒的速度同时顺时针转65动，设时间为t，在射线CD转动一周的时间内，是否存在某时刻，使得CD与AB平行？若存在，求出所有满足条件的时间t．二十五、解答题AB CD，E、F是AB、CD上的两点，直线l与AB、CD分别交于点25．如图，直线//G、H，点P是直线l上的一个动点（不与点G、H重合），连接PE、PF．（1）当点P 与点E 、F 在一直线上时，GEP EGP ∠=∠，60FHP ∠=︒，则PFD ∠=_____．（2）若点P 与点E 、F 不在一直线上，试探索AEP ∠、EPF ∠、CFP ∠之间的关系，并证明你的结论．【参考答案】一、选择题1．A解析：A【分析】 819=，再计算9的算术平方根即可．【详解】 819=，993=故选A【点睛】 819是解题的关键．2．D【分析】判断是否是平移现象，要根据平移的性质进行，即图形平移前后的形状和大小没有变化，只是位置发生变化．【详解】解：A ：翻开书中的每一页纸张，这是翻折现象；B ：飞碟的快速转动，这是旋转现解析：D【分析】判断是否是平移现象，要根据平移的性质进行，即图形平移前后的形状和大小没有变化，只是位置发生变化．【详解】解：A ：翻开书中的每一页纸张，这是翻折现象；B ：飞碟的快速转动，这是旋转现象；C ：将一张纸沿它的中线折叠，这是轴对称现象；D ：电梯的上下移动这是平移现象．故选：D ．【点睛】本题考查了图形的平移，图形的平移只改变图形的位置，而不改变图形的形状和大小，学生易混淆图形的平移与旋转或翻转而误选．3．B【分析】第二象限的点的横坐标小于0，纵坐标大于0，据此解答即可．【详解】解：根据第二象限的点的坐标的特征：横坐标符号为负，纵坐标符号为正，各选项中只有B （-2，3）符合，故选：B ．【点睛】本题主要考查了平面直角坐标系中各象限的点的坐标的符号特点，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）． 4．B【分析】根据立方根和算术平方根的定义、平行线的性质、点到直线的距离逐项判断即可．【详解】64的立方根是4，故①是假命题； 25的算数平方根是5，故②是真命题；如果两条直线都与第三条直线平行，那么这两条直线也互相平行，故③是真命题；与两坐标轴距离都是2的点有(2，2)、(2，-2)、(-2，2)、(-2，-2)共4点，故④是假命题．故选：B ．【点睛】本题考查命题真、假的判断．正确掌握相关定义、性质与判定是解题关键．5．B【分析】记∠1顶点为A ，∠2顶点为B ，∠3顶点为C ，过点B 作BD ∥l 1，由平行线的性质可得∠3+∠DBC =180°，∠ABD +(180°－∠1)=180°，由此得到∠3+∠2+(180°－∠1)=360°，再结合已知条件即可求出结果．【详解】如图，过点B 作BD ∥l 1，∵12//l l ，∴BD ∥l 1∥l 2，∴∠3+∠DBC =180°，∠ABD +(180°－∠1)=180°，∴∠3+∠DBC+∠ABD+(180°－∠1)=360°，即∠3+∠2+(180°－∠1)=360°，又∵∠2+∠3=216°，∴216°+(180°－∠1)=360°，∴∠1=36°．故选：B．【点睛】本题考查了平行线的性质，正确作出辅助线，熟练掌握平行线性质是解题的关键．6．A【分析】根据平方根、立方根及算术平方根的概念逐一计算即可得答案．【详解】A.42±=±，计算正确，故该选项符合题意，B.42±=±，故该选项计算错误，不符合题意，C.38(2)2--=--=，故该选项计算错误，不符合题意，D.()288-=，故该选项计算错误，不符合题意，故选：A．【点睛】本题考查平方根、立方根、算术平方根的概念，熟练掌握定义是解题关键．7．A【分析】由∠EBF＝2∠ABE，可得∠EBF＝2α．由∠EBF+∠BEC+∠F+∠ECF＝360°，可得∠ECF＝360°﹣（2α+β+γ），那么∠DCE＝13ECF∠．由∠BEC＝∠M+∠DCE，可得∠M＝∠BEC﹣∠DCE．根据AB//CD，得∠ABE＝∠M，进而推断出4β﹣α+γ＝360°．【详解】解：如图，分别延长BE、CD并交于点M．∵AB//CD，∴∠ABE＝∠M．∵∠EBF＝2∠ABE，∠ABE＝α，∴∠EBF＝2α．∵∠EBF+∠BEC+∠F+∠ECF＝360°，∴∠ECF＝360°﹣（2α+β+γ）．又∵∠ECF ＝3∠DCE ，∴∠DCE ＝11(3602)33ECF a βγ︒∠=---．又∵∠BEC ＝∠M +∠DCE ，∴∠M ＝∠BEC ﹣∠DCE ＝β﹣1(3602)3a βγ︒---． ∴β﹣1(3602)3a βγ︒---＝α． ∴4β﹣α+γ＝360°．故选：A ．【点睛】本题考查了平行线的性质，三角形的外角性质，角度的计算，构造辅助线转化角度是解题的关键．8．C【分析】列出部分An 点的坐标，根据坐标的变化找出变化规律，依此规律即可得出结论；根据以上结论和A2021的坐标为(﹣3，2)，找出A1的坐标，由此即可得出x 、y 的值，二者相加即可得出结论．【解析：C【分析】列出部分A n 点的坐标，根据坐标的变化找出变化规律，依此规律即可得出结论；根据以上结论和A 2021的坐标为(﹣3，2)，找出A 1的坐标，由此即可得出x 、y 的值，二者相加即可得出结论．【详解】解：∵A 2021的坐标为(﹣3，2)，根据题意可知：A 2020的坐标为(﹣3，﹣2)，A 2019的坐标为(1，﹣2)，A 2018的坐标为(1，2)，A 2017的坐标为(﹣3，2)，…∴A 4n +1(﹣3，2)，A 4n +2(1，2)，A 4n +3(1，﹣2)，A 4n +4(﹣3，﹣2)(n 为自然数)．∵2021＝505×4•••1，∵A 2021的坐标为(﹣3，2)，∴A 1(﹣3，2)，∴x +y ＝﹣3+2＝﹣1．故选：C ．【点睛】本题考查了规律型中的点的坐标的变化，解决该题型题目时，根据友好点的定义列出部分点的坐标，根据坐标的变化找出变化规律是关键．九、填空题9．2【分析】先求出=4，再求出算术平方根即可．【详解】解：∵=4，∴的算术平方根是2，故答案为：2．【点睛】本题考查了立方根和算术平方根的应用，主要考查学生的计算能力．解析：2【分析】，再求出算术平方根即可．先求出【详解】，解：∵∴2，故答案为：2．【点睛】本题考查了立方根和算术平方根的应用，主要考查学生的计算能力．十、填空题10．a=3 b=-4【分析】先求得P1的坐标,再根据点P1关于x轴的对称点是P,则即可求得a与b的值【详解】由于P1与P2关于x轴对称，P2的坐标为（-3，4），则P1的坐标为（-解析：a=3 b=-4【分析】先求得P1的坐标,再根据点P1关于x轴的对称点是P2,则即可求得a与b的值【详解】由于P1与P2关于x轴对称，P2的坐标为（-3，4），则P1的坐标为（-3，-4），点P（a，b）关于y轴对称的点是P1，则P点的坐标为（3，-4），则a=3，b=-4.【点睛】此题考查关于x轴、y轴对称的点的坐标，难度不大十一、填空题11．100°【分析】根据AD是ABC的角平分线，CE是ABC的高，∠BAC＝60°，可得∠BAD和∠CAD相等，都为30°，∠CEA＝90°，从而求得∠ACE的度数，又因为∠BCE＝40°，∠ADB解析：100°【分析】根据AD是ABC的角平分线，CE是ABC的高，∠BAC＝60°，可得∠BAD和∠CAD相等，都为30°，∠CEA＝90°，从而求得∠ACE的度数，又因为∠BCE＝40°，∠ADB＝∠BCE+∠ACE+∠CAD，从而求得∠ADB的度数．【详解】解：∵AD是ABC的角平分线，∠BAC＝60°．∠BAC＝30°，∴∠BAD＝∠CAD＝12∵CE是ABC的高，∴∠CEA＝90°．∵∠CEA+∠BAC+∠ACE＝180°．∴∠ACE＝30°．∵∠ADB＝∠BCE+∠ACE+∠CAD，∠BCE＝40°．∴∠ADB＝40°+30°+30°＝100°．故答案为：100°．【点睛】本题考查三角形的内角和、角的平分线、三角形的一个外角等于和它不相邻的内角的和，关键是根据具体目中的信息，灵活变化，求出相应的问题的答案．十二、填空题12．60【分析】延长BO交直线n于点C，由平行线的性质得∠ACB=∠1，由邻补角得∠AOC=60°，再由三角形外角的性质可得结论．【详解】解：延长BO交直线n于点C，如图，∵直线m向上平移直解析：60【分析】延长BO交直线n于点C，由平行线的性质得∠ACB=∠1，由邻补角得∠AOC=60°，再由三角形外角的性质可得结论．【详解】解：延长BO交直线n于点C，如图，∵直线m 向上平移直线m 得到直线n ，∴m ∥n ，∴∠ACB =∠1，∵∠3＝120°，∴∠AOC =60°∵∠2=∠ACO +∠AOC =∠1+60°，∴∠2-∠1=60°．故答案为60．【点睛】本题考查了平移的性质，平行线的性质，以及三角形外角的性质，作辅助线构造三角形是解答此题的关键．十三、填空题13．【分析】根据折叠的性质得到，，再根据的度数即可求出的度数，再根据求解即可．【详解】解：∵折叠，∴，，∵，∴，∴．故答案是：．【点睛】本题考查折叠问题，解题的关键是掌握折叠的性质解析：82︒【分析】根据折叠的性质得到B MQN ∠=∠，C EQF ∠=∠，再根据A ∠的度数即可求出MQN EQF ∠+∠的度数，再根据()180MQE MQN EQF ∠=︒-∠+∠求解即可．【详解】解：∵折叠，∴B MQN ∠=∠，C EQF ∠=∠，∵82A ∠=︒，∴1808298MQN EQF B C ∠+∠=∠+∠=︒-︒=︒，∴()1801809882MQE MQN EQF ∠=︒-∠+∠=︒-︒=︒．故答案是：82︒．【点睛】本题考查折叠问题，解题的关键是掌握折叠的性质．十四、填空题14．131或26或5.【解析】试题解析：由题意得，5n+1=656，解得n=131，5n+1=131，解得n=26，5n+1=26，解得n=5.解析：131或26或5.【解析】试题解析：由题意得，5n+1=656，解得n=131，5n+1=131，解得n=26，5n+1=26，解得n=5.十五、填空题15．或【分析】已知，可知AB=8，已知的面积为，即可求出OC 长，得到C 点坐标．【详解】∵∴AB=8∵的面积为∴=16∴OC=4∴点的坐标为(0,4)或(0,-4)故答案为：(0,4)解析：(0,4)或(0,4) -【分析】已知()()7,0,1,0A B -，可知AB=8，已知ABC ∆的面积为16，即可求出OC 长，得到C 点坐标．【详解】∵()()7,0,1,0A B -∴AB=8∵ABC ∆的面积为16 ∴12AB OC ⨯⨯=16 ∴OC=4∴点C 的坐标为(0,4)或(0,-4)故答案为：(0,4)或(0,-4)【点睛】本题考查了直角坐标系中坐标的性质，已知两点坐标可得出两点间距离长度，如果此两点在坐标轴上，求解距离很简单，如果不在坐标轴上，可通过两点间距离公式求解．十六、填空题16．【分析】由图形得出点的横坐标依次是0、1、2、3、4、、，纵坐标依次是0、2、0、、0、2、0、、，四个一循环，继而求得答案．【详解】解：观察图形可知，点的横坐标依次是0、1、2、3、4、解析：()2021,2【分析】由图形得出点的横坐标依次是0、1、2、3、4、⋯、n ，纵坐标依次是0、2、0、2-、0、2、0、2-、⋯，四个一循环，继而求得答案．【详解】解：观察图形可知，点的横坐标依次是0、1、2、3、4、⋯、n ，纵坐标依次是0、2、0、2-、0、2、0、2-、⋯，四个一循环，202145051÷=⋯，故点2021A 坐标是(2021,2)．故答案是：(2021,2)．【点睛】本题考查了规律型：点的坐标，学生的观察图形的能力和理解能力，解此题的关键是根据图形得出规律．十七、解答题17．（1）;（2）．直接利用立方根以及算术平方根的定义化简得出答案．【详解】（1）（2）【点睛】此题主要考查了实数运算，正确化简各数是解题关键．解析：（1） 4.2-;（2）2．【分析】直接利用立方根以及算术平方根的定义化简得出答案．【详解】（1220.2=---4.2=-（2233=+-2=【点睛】此题主要考查了实数运算，正确化简各数是解题关键．十八、解答题18．（1）或；（2）【分析】（1）直接根据求平方根的方法解方程即可；（2）直接根据求立方根的方法解方程即可．【详解】解：（1）∵，∴，∴，∴或；（2）∵，∴，∴．【点睛】本题主解析：（1）6x =或4x =-；（2）52x =（1）直接根据求平方根的方法解方程即可；（2）直接根据求立方根的方法解方程即可．【详解】解：（1）∵()2125x -=，∴15x -=±，∴15x =±，∴6x =或4x =-；（2）∵381250x -=， ∴31258x =， ∴52x =．【点睛】本题主要考查了利用求平方根和求立方根的方法解方程，解题的关键在于能够熟练掌握相关知识进行求解．十九、解答题19．两直线平行，同旁内角互补；同角的补角相等；同位角相等，两直线平行【分析】要证BE ∥DF ，只需证∠1＝∠D ，由AB ∥CD 可知∠B+∠1＝180°，又有∠B+∠D ＝180°，由此即可证得．【详解】解析：两直线平行，同旁内角互补；同角的补角相等；同位角相等，两直线平行【分析】要证BE ∥DF ，只需证∠1＝∠D ，由AB ∥CD 可知∠B +∠1＝180°，又有∠B +∠D ＝180°，由此即可证得．【详解】证明：∵AB ∥CD （已知）∴∠B +∠1＝180°（两直线平行，同旁内角互补）∵∠B +∠D ＝180°（已知）∴∠1＝∠D （同角的补角相等），∴BE ∥DF （同位角相等，两直线平行）故答案为：两直线平行，同旁内角互补；同角的补角相等；同位角相等，两直线平行．【点睛】本题主要考查了平行线的性质与判定，解题的关键在于能够熟练掌握相关知识进行求解．二十、解答题20．（1）作图见解析，A′（1，5），B′（0，2），C′（4，2）；（2）P（0，10）或（0，-12）．【分析】（1）分别作出A，B，C的对应点A′，B′，C′即可解决问题；（2）设P（0，m解析：（1）作图见解析，A′（1，5），B′（0，2），C′（4，2）；（2）P（0，10）或（0，-12）．【分析】（1）分别作出A，B，C的对应点A′，B′，C′即可解决问题；（2）设P（0，m），构建方程解决问题即可．【详解】解：（1）如图，△A′B′C′即为所求，A′（1，5），B′（0，2），C′（4，2）；（2）设P（0，m），由题意：12×4×|m+2|=4×12×4×3，解得m=10或-12，∴P（0，10）或（0，-12）．【点睛】本题考查了坐标与图形的性质，平移变换，三角形的面积等知识，解题的关键是熟练掌握平移变换的性质．二十一、解答题21．（1）0；（2）【分析】（1）仿照题例，可直接求出的整数部分和小数部分，代入计算；（2）先求出的整数部分，再得到的整数部分和小数部分，代入计算．【详解】解：（1）∵，∴，∴的整数部分是解析：（1）0；（2）112 【分析】（1（27【详解】解：（1）∵∴34<， ∴3，即m=3， ∵∴23<<，∴2，即n=2，∴；（2）∵< ∴10711<， ∴710，即2x=10，∴x=5， ∴77103，即3，∴2x y -)532-112．【点睛】本题考查了二次根式的整数和小数部分．看懂题例并熟练运用是解决本题的关键．二十二、解答题22．（1）4；（2）不能，理由见解析．【分析】（1）根据已知正方形的面积求出大正方形的边长即可；（2）先设未知数根据面积=14（cm2）列方程，求出长方形的边长，将长方形的长与正方形边长比较大小再解析：（1）4；（2）不能，理由见解析．【分析】（1）根据已知正方形的面积求出大正方形的边长即可；（2）先设未知数根据面积=14（cm2）列方程，求出长方形的边长，将长方形的长与正方形边长比较大小再判断即可．【详解】解：（1）两个正方形面积之和为：2×8=16（cm2），∴拼成的大正方形的面积=16（cm2），∴大正方形的边长是4cm；故答案为：4；（2）设长方形纸片的长为2xcm，宽为xcm，则2x•x=14，解得：7x ，2x=27>4，∴不存在长宽之比为2:1且面积为214cm的长方形纸片．【点睛】本题考查了算术平方根，能够根据题意列出算式是解此题的关键．二十三、解答题23．（1）120，90；（2）①∠1=120°-n°，∠2=90°+n°；②见解析【分析】（1）根据邻补角的定义和平行线的性质解答；（2）①根据邻补角的定义求出∠ABE，再根据两直线平行，同位角相解析：（1）120，90；（2）①∠1=120°-n°，∠2=90°+n°；②见解析【分析】（1）根据邻补角的定义和平行线的性质解答；（2）①根据邻补角的定义求出∠ABE，再根据两直线平行，同位角相等可得∠1=∠ABE，根据两直线平行，同旁内角互补求出∠BCG，然后根据周角等于360°计算即可得到∠2；②结合图形，分A B、B C、AC三条边与直尺垂直讨论求解．【详解】解：（1）∠1=180°-60°=120°，∠2=90°；故答案为：120，90；（2）①如图2，∵∠ABC=60°，∴∠ABE=180°-60°-n°=120°-n°，∵DG∥EF，∴∠1=∠ABE=120°-n°，∠BCG=180°-∠CBF=180°-n°，∵∠ACB+∠BCG+∠2=360°，∴∠2=360°-∠ACB-∠BCG=360°-90°-（180°-n°）=90°+n°；②当n=30°时，∵∠ABC=60°，∴∠ABF=30°+60°=90°，AB⊥DG（EF）；当n=90°时，∠C=∠CBF=90°，∴BC⊥DG（EF），AC⊥DE（GF）；当n=120°时，∴AB⊥DE（GF）．【点睛】本题考查了平行线角的计算，垂线的定义，主要利用了平行线的性质，直角三角形的性质，读懂题目信息并准确识图是解题的关键．二十四、解答题24．（1）平行，理由见解析；（2）65°；（3）5秒或95秒【分析】（1）根据等角的补角相等求出∠3与∠4的补角相等，再根据内错角相等，两直线平行即可判定a∥b；（2）根据入射光线与镜面的夹角与反解析：（1）平行，理由见解析；（2）65°；（3）5秒或95秒【分析】（1）根据等角的补角相等求出∠3与∠4的补角相等，再根据内错角相等，两直线平行即可判定a∥b；（2）根据入射光线与镜面的夹角与反射光线与镜面的夹角相等可得∠1=∠2，然后根据平角等于180°求出∠1的度数，再加上40°即可得解；（3）分①AB与CD在EF的两侧，分别表示出∠ACD与∠BAC，然后根据两直线平行，内错角相等列式计算即可得解；②CD旋转到与AB都在EF的右侧，分别表示出∠DCF与∠BAC，然后根据两直线平行，同位角相等列式计算即可得解；③CD旋转到与AB都在EF 的左侧，分别表示出∠DCF与∠BAC，然后根据两直线平行，同位角相等列式计算即可得解．【详解】解：（1）平行．理由如下：如图1，∵∠3=∠4，∴∠5=∠6，∵∠1=∠2，∴∠1+∠5=∠2+∠6，∴a∥b(内错角相等，两直线平行）；（2）如图2：∵入射光线与镜面的夹角与反射光线与镜面的夹角相等，∴∠1=∠2，∵入射光线a与水平线OC的夹角为40°，b垂直照射到井底，∴∠1+∠2=180°-40°-90°=50°，∴∠1＝1×50°=25°，2∴MN与水平线的夹角为：25°+40°=65°，即MN与水平线的夹角为65°，可使反射光线b正好垂直照射到井底；（3）存在．如图①，AB与CD在EF的两侧时，∵∠BAF=105°，∠DCF=65°，∴∠ACD=180°-65°-3t°=115°-3t°，∠BAC=105°-t°，要使AB∥CD，则∠ACD=∠BAC，即115-3t=105-t，解得t=5；如图②，CD旋转到与AB都在EF的右侧时，∵∠BAF=105°，∠DCF=65°，∴∠DCF=360°-3t°-65°=295°-3t°，∠BAC=105°-t°，要使AB∥CD，则∠DCF=∠BAC，即295-3t=105-t，解得t=95；如图③，CD旋转到与AB都在EF的左侧时，∵∠BAF=105°，∠DCF=65°，∴∠DCF=3t°-（180°-65°+180°）=3t°-295°，∠BAC=t°-105°，要使AB∥CD，则∠DCF=∠BAC，即3t-295=t-105，解得t=95，此时t＞105，∴此情况不存在．综上所述，t为5秒或95秒时，CD与AB平行．【点睛】本题考查了平行线的判定与性质，光学原理，读懂题意并熟练掌握平行线的判定方法与性质是解题的关键，（3）要注意分情况讨论．二十五、解答题25．（1）120°；（2）∠EPF =∠AEP+∠CFP或∠AEP=∠EPF+∠CFP，证明见详解．【分析】（1）根据题意，当点与点、在一直线上时，作出图形，由AB∥CD，∠FHP=60°，可以推出解析：（1）120°；（2）∠EPF =∠AEP+∠CFP或∠AEP=∠EPF+∠CFP，证明见详解．【分析】（1）根据题意，当点P与点E、F在一直线上时，作出图形，由AB∥CD，∠FHP=60°，可∠=∠=60°，计算∠PFD即可；以推出GEP EGP（2）根据点P是动点，分三种情况讨论：①当点P在AB与CD之间时；②当点P在AB 上方时；③当点P在CD下方时，分别求出∠AEP、∠EPF、∠CFP之间的关系即可．【详解】（1）当点P与点E、F在一直线上时，作图如下，∠=∠，∵AB∥CD，∠FHP=60°，GEP EGP∠=∠=∠FHP=60°，∴GEP EGP∴∠EFD=180°-∠GEP=180°-60°=120°，∴∠PFD=120°，故答案为：120°；（2）满足关系式为∠EPF =∠AEP+∠CFP或∠AEP=∠EPF+∠CFP．证明：根据点P是动点，分三种情况讨论：①当点P在AB与CD之间时，过点P作PQ∥AB，如下图，∵AB∥CD，∴PQ∥AB∥CD，∴∠AEP=∠EPQ，∠CFP=∠FPQ，∴∠EPF=∠EPQ+∠FPQ=∠AEP+∠CFP，即∠EPF =∠AEP+∠CFP；②当点P在AB上方时，如下图所示，∵∠AEP=∠EPF+∠EQP，∵AB∥CD，∴∠CFP=∠EQP，∴∠AEP=∠EPF+∠CFP；③当点P在CD下方时，∵AB∥CD，∴∠AEP=∠EQF，∴∠EQF=∠EPF+∠CFP，∴∠AEP=∠EPF+∠CFP，综上所述，∠AEP、∠EPF、∠CFP之间满足的关系式为：∠EPF =∠AEP+∠CFP或∠AEP=∠EPF+∠CFP，故答案为：∠EPF =∠AEP+∠CFP或∠AEP=∠EPF+∠CFP．【点睛】本题考查了平行线的性质，外角的性质，掌握平行线的性质是解题的关键，注意分情况讨论问题．。

七年级下册语文期末考试卷及答案【必考题】

七年级下册语文期末考试卷及答案【必考题】满分：120分考试时间：120分钟一、语言的积累与运用。

（35分）1、下列词语中加点字的注音完全正确的一项是( )A．投掷．(zhì) 憎．恶(zèng) 糟．糕(zāo)B．震悚．(sǒng) 取缔．(dì) 肿胀．(zhàng)C．侮．辱(wǔ) 晌．午(xiàng) 镶嵌．(qiàn)D．门框．(kuāng) 愧怍．(zuò) 惶．恐(huáng)2、下列各组词语书写全都正确的一项是（）A．遮弊各得其所美不盛收呼朋引伴B．蝉褪人生鼎沸截然不同疲倦不堪C．分岐高枕而卧小心翼翼不求深解D．尴尬众目睽睽花团锦簇油然而生3、下列句子中加点的成语使用不正确的一项是（）A．野鸡多用两只腿跑动，即使能飞起来的也只能飞很短的距离。

当它逃不脱追者时，就把头钻进草堆里，自以为安然无恙．．．．了。

B．红树林深处，简直就是一个海上的世外桃源．．．．，一个神秘的植物天地。

C．生活中正因为有了这种精益求精、锲而不舍．．．．的精神，人才会变得更优秀。

D．每天早晨，他都要一个人跑到花园里，指手画脚．．．．地练动作，抑扬顿挫地背台词。

4、下列句子中没有语病的一项是( )A．经调查，“8·12”天津港爆炸事故原因是瑞海公司违规经营、违规储存危险货物以及安全管理极其混乱造成的。

B．面对叙利亚小难民艾兰伏尸海滩的照片，使欧洲一些国家终于松口，允许更多难民入境。

C．磁州瓷器工艺精湛，具有高雅、时尚、个性的艺术享受，是一种观赏价值极高的艺术品。

D．屠呦呦用青蒿素治疗疟疾的研究，有效降低了疟疾患者的死亡率，为医学发展做出了卓越的贡献。

5、下列各句所使用的修辞手法判断错误的一项是（）A．“我在开花！”它们在笑。

“我在开花！”它们嚷嚷。

（反复、拟人）B．如果说自然的智慧是大海，那么，人类的智慧就只是大海中的一个小水滴。

2022-2023学年部编人教版七年级下册期末考试及答案

2022-2023学年部编人教版七年级下册期
末考试及答案
一、选择题
1.下列中不是色盲的是（）
A．父亲 B．母亲 C．儿子 D．女儿
【答案】D
2.生态系统中，垂直带状分布的现象是由于（）
A．太阳辐射强度不同
B．空气密度有区别
C．地球离太阳的距离远近不同;
D．水平气温分布不规则
【答案】A
二、填空题
1.北限是指阔叶林的最南缘，南限是指针叶林的最北缘，两者之间是、。

2.模拟实验是近年来涌现出的一种实验方法，它是在和实验室中进行的。

【答案】
1、过渡林、针阔混交林
2、计算机、模拟装置
三、解答题
1.简述黄河的重要性及其治理措施
【答案】黄河是我国第二大河流，母亲河之一，也是国家重要的水资源和农业灌溉基地。

近年来，黄河进入生态危机，其主要表现是携带的泥沙下降、水量减少、干支流断流、水质污染等一系列问题。

治理黄河的措施包括涵养和节约水资源，加强河道建设，严格控制黄河上游经济发展和治理黄河流域生态环境等。

2.某地区空气污染严重，你会采取哪些措施进行治理？
【答案】采取治理大气污染的措施，如减少机动车污染排放、控制工业废气排放、推广清洁能源、加强城市绿化建设、进行科学
的城市规划等。

同时，也需要加强公众环保意识的培养，促进人类与自然生态系统更加和谐的发展。

人教版七年级下册语文期末测试卷及答案【A4打印版】

人教版七年级下册语文期末测试卷及答案【A4打印版】满分：120分考试时间：120分钟一、语言的积累与运用。

（35分）1、下列词语中加点字的注音全部正确的一项是（）A．绽．开（dìng）罕．至（hǎn）倜傥．（tǎng）逾．矩（yú）B．感慨．（kǎi）和蔼．（ǎi）惭愧．（kuì）锦簇．（cù）C．确凿．（zuó）油蛉．（líng）收敛．（liǎn）书塾．（shū）D．淋．漓（línɡ）啄．食（zhuó）奥．秘（ào）企．盼（qǐ）2、词语书写完全正确的一项是（）A．朗润小心翼翼各得其所混为一谈B．瘫痪尴尬烂慢蛛丝马迹C．点缀搏学笃志众目睽睽人迹罕至D．荫蔽岐斜祷告恍然大悟3、下列句子中加点词语使用不恰当的一项是（）A．王教授的演讲十分精彩，在场人士听得津津有味．．．．。

B．看到小朋友掉进水缸里，司马光毫不犹豫．．．．地搬起石头砸缸。

C．他站在台上窃窃自语．．．．，向大家介绍自己的新发现。

D．草原的气候变幻莫．．．测．，一会儿烈日当空，一会儿大雨倾盆。

4、下面句子没有语病的一项是（）A．屠呦呦科研团队研究出了用青蒿素治疗疟疾的方法，使全球数亿人受益。

B．针对近来频频发生的校园暴力事件，几个学校的领导进行了深刻反思。

C．家长要让孩子接受“吃苦教育”，以此提高孩子自食其力的能力和独立自主的精神。

D．一堂堂看似普通的体育课，不仅影响青少年的体育价值观，更直接地关系到他们的身体健康。

5、下列语句修辞手法与其他三项不同的是（）A．树尖上顶着一髻儿白花，好像日本看护妇。

B．天儿越晴，水藻越绿，就凭这些绿的精神，水也不忍得冻上。

C．那点薄雪好像忽然害了羞，微微露出点粉色。

D．济南市受不住大雪的，那些小山太秀气。

6、下面一段文字依次填入横线处的语句，衔接最恰当的一组是（）春日踏青，青芜如毯，___________________；夏日听雨，雨声淅沥，___________________；秋日看花，花叶相辉，_____________；冬日观雪，雪意阑珊， ______________。

人教版七年级语文下册期末测试卷(完整版)

人教版七年级语文下册期末测试卷（完整版）满分：120分考试时间：120分钟一、语言的积累与运用。

（35分）1、下列各组词语中注音全部正确的一组是（）A．忏．悔（chàn）迸．溅(bìng) 孱头（càn）久久伫．立（zhù）B．枯槐．（huái）颤．抖（chàn）矜．持（jīn）忍俊不禁．（jīn）C．遗憾．（hàn）猥．琐（wěi）恍．然（huǎng）一摞．一摞．（luó）D．凝．望（níng）服侍．（shì）萋．萋（qī）仙露琼．浆（qíng）2、下列各组词语书写无误的一项是( )A．摧枯拉朽记忆尤新惨绝人寰延续B．苍海桑田风华正茂色彩斑斓镌刻C．天翻地覆恢宏壮丽殚精竭虑缅怀D．从容不迫眼花瞭乱震耳欲聋由衷3、下列加点成语使用有误的一项是（）A．要想取得优异的成绩，我们必须对知识不求甚解．．．．。

B．在众目睽睽．．．．之下，一向害羞的她脸一下子红了。

C．他们夜以继日废寝忘食．．．．地工作，终于按时完成了任务。

D．他小心翼翼．．．．地对爸爸说他想星期六到公园去玩，但还是遭到爸爸的反对。

4、下列句子没有语病的一项是( )A．通过队列比赛，使同学们体会到个人服务集体的重要性，也就更加珍惜集体荣誉。

B．美术小组的每一个同学运用自己最喜欢的色彩，在过去的岁月中创作了优秀的大量的美术作品，来赞美美丽的校园。

C．深受人们喜爱的游泳运动员宁泽涛，被公认是新时代青年的杰出代表。

D．为了发展阳光体育运动，提升学生身体素质，学校加快了校园运动器械和操场改造的速度和规模。

5、对下列句子的修辞手法判断有误的一项是( )A．航母就像汪洋中的一片树叶，在海上起伏行进。

(比喻)B．金戈铁马，气吞万里如虎。

(借代、夸张)C．发动机的咆哮声越来越大，舰载机越来越近了。

(夸张、拟人)D．她已经展开身体，像轻盈的、笔直的箭，“哧”地插进碧波之中，几串白色的气泡拥抱了这位自天而降的仙女，四面水花则悄然不惊。

七年级下期末测试题带答题卡

七年级下册期末考试模拟试题一．选择题每小题2分,共50分1．“人类从何而来”人们一直在探索着;下列有关人类的起源和进化的叙述,正确的是A．人类起源于生理特征与现代人最接近的类人猿B．人类进化过程中一直向着有利于直立行走的方向变异C．能使用工具是人猿分界的标志D．人类不同种族的差异是在不同地域内经过自然选择形成的2．二胎政策全面放开后,洋洋的妈妈想再生一个孩子,一年多来,一直没有怀孕,经检查,原因是输卵管堵塞,输卵管堵塞造成的后果是A．不能产生卵细胞 B．胚胎的发育得不到营养C．精子与卵细胞不能结合D．不能产生雌性激素3．下列关于青春期发育特点的叙述,错误的是A．身高突增 B．性意识开始萌动 C．体重突增 D．男生长胡须、喉结突出属于第一性征4．下列有关人类生殖发育知识的叙述中,错误的是A．胎儿与母体进行物质交换的器官是胎盘和脐带B．正常情况下,人体受精卵形成部位是输卵管C．男、女主要生殖器官分别是睾丸、卵巢D．男性的输精管结扎后,仍具有男性的第二性征,并能产生精子5．探究“馒头在口腔中的变化”,实验设计如图,试管均置于37℃温水中10分钟,以下说法错误的是A．滴加碘液后,①号试管不会变蓝色B．②③对照,可探究“舌的搅拌对馒头的消化作用”C．①②对照,可探究“唾液淀粉酶对淀粉的消化作用”D．①②对照,②号试管为对照组6．维生素和无机盐在人体中血液量虽然很少,却起着“人体运作的润滑剂”和“健康的基石”的作用;下面所列物质与缺乏症,不相符的是A．维生素A——夜盲症 B．钙——骨质疏松症C．维生素B1——坏血病 D．铁——贫血症7．每年5月20日是中国学生数据表明,我国学生营养不良和营养过剩的状况令人担忧;右图表示不同人群每天摄入的食物比例,有关说法正确的是A．水果、蔬菜只为人体提供水和无机盐两类营养B．粮谷类食物中含蛋白质较多C．肥胖患者应该减少粮谷类及肉类的摄入量D．营养不良的原因是水果、蔬菜摄入量较粮谷类少8．如图是某同学做模拟实验,并绘制的肺内气压变化曲线图,下列选项正确的是A．甲图中曲线的AB段与乙图都表示吸气状态B．甲图中曲线的BC段与乙图都表示呼气状态C．甲图中曲线的AB段与丙图都表示呼气状态D．甲图中曲线的BC段与丙图都表示吸气状态9．外界气体进入肺的途径依次是A．鼻→咽→喉→气管→支气管 B．口→鼻→喉→气管→支气管C．咽→口→鼻→喉→支气管 D．支气管→口→喉→鼻→气管10．下列关于胸廓变化与吸气、呼气之间关系的叙述,正确的是A．胸廓扩大导致呼气 B．呼气导致胸廓扩大 C．胸廓扩大导致吸气 D．吸气导致胸廓扩大11．人体的结构与功能高度统一,使得体内复杂多变的生理功能得以实现,下列叙述错误的是A．左心室壁最厚,心肌发达,可以将血液“泵”到全身各处B．肺泡壁和毛细血管壁都由一层上皮细胞构成,利于肺泡与血液进行气体交换C．心房与心室之间、心室与动脉之间、各静脉内都有瓣膜,保证血液不能倒流D．小肠内表面有许多环形皱襞和小肠绒毛,增加了消化和吸收的面积12．在“观察小鱼尾鳍内血液的流动”实验中,血液流动情况如右图所示,下列对血管类型判断正确的是A．①是静脉 B．②是毛细血管C．③是动脉 D．全是毛细血管13．下图曲线表示人体血液中氧气和二氧化碳含量的变化,其中H为上肢动脉;下列能表示该图含义的正确组合是①A曲线代表氧气在血液中的变化②B曲线代表二氧化碳在血液中的变化③B曲线代表氧在血液中的变化④A曲线代表二氧化碳在血液中的变化⑤J表示上肢毛细血管⑥I表示上肢毛细血管A．①②⑥ B．①②⑤ C．③④⑤ D．③④⑥14．下列有关输血和献血的说法中,不正确的是A．O型血的人能输入任何血型的血 B．安全输血应以输同型血为原则C．一次献血200300毫升不影响健康 D．1855周岁的健康公民有无偿献血的义务15．利用显微镜观察人的血细胞涂片,在两种不同的放大倍率下,视野分别为甲和乙,如图所示,下列相关叙述正确的是A．若玻片往左移,则像也会往左移B．若使用相同的光圈和反光镜,则甲比乙亮C．甲中所观察到的细胞,在乙中均可观察到D．若在甲看到模糊的像,则改换成乙就可以看到清晰的像16．人体的每个肾由100多万个肾单位组成,如图为一个肾单位的结构示意图,下列相关叙述正确的是A．2内流动的血液中含有较多的二氧化碳B．6内流动的血液中二氧化碳和代谢废物均较少C．4内有血细胞、葡萄糖、尿素、水和无机盐等D．5肾小管能重吸收全部葡萄糖、大部分水和部分无机盐17． 2017年5月7日,第东营国际金标马拉松大赛在市政府广场鸣枪开赛,比赛中运动员奋力向前、汗流浃背、满脸通红如图 ;上述现象体现了皮肤的哪些功能①保护②排泄③调节体温④感受外界刺激A．①②③ B．②③ C．②④ D．③④18．如图是三种血管示意图,下列叙述不正确的是A．若b为肺部毛细血管,则a内流的是静脉血B．若b为肾小球处毛细血管,则c内流的是动脉血C．若b为肾小管处毛细血管,则c内血液中尿素的含量比a多D．若b为小肠绒毛内的毛细血管,则c内血液中的营养物质比a多19．某学生陶耳垢时,不小心戳坏耳朵中某结构导致耳聋,该结构最可能是A．外耳道 B．鼓膜 C．咽鼓管 D．半规管20．医学临床上的“植物人”通受伤后只有呼吸和心跳、没有意识或意识朦胧、不能自主活动的病人,“植物人”脑部可能没有受到损伤的部位是A．大脑B．小脑 C．脊髓 D．脑干21．济宁公共自行车,为市民出行提供了极大方便,某生骑车遇到红灯信号停车等待时,下列说法错误的是A．遇红灯停车属于复杂反射B．红灯信号形成的物像在视网膜上C．完成红灯停车反射的神经结构是反射弧D．遇红灯停车是人类特有的反射活动22．为了研究甲状腺的功能,科学家利用蝌蚪进行如下表所示的实验：乙组后来加入甲状腺激素,结果又能继续发育;请依据实验判断,正确的是A．甲状腺能分泌甲状腺激素 B．甲状腺激素能提高神经系统的兴奋性C．甲状腺是内分泌腺 D．甲与乙、乙与丙形成对照23．如图为某人手指被蔷薇刺扎到后迅速缩手的反射孤,下列叙述不正确的是A．该反射属于简单的反射B．该人被蔷薇刺扎扎到后的疼痛感觉形成于脊髓C．该反射中,神经冲动传导的方向是：①→③→④→⑤→②D．若某人只是⑤处受损,用针刺一①处,此人有痛觉,无缩手反射24．降低大气中的二氧化碳含量,减轻温室效应带来的不利影响,人类的共同责任,下列做法与此无关的是A．及时清理垃圾,维护环境卫生 B．开发风能、太阳能C．积极植树种草,增大绿化面积 D．倡导节能减排,少开车多步行25．下列关于人对生物圈影响的叙述,错误的是A．科技发展使人类对生物圈的影响与日俱增B．人口膨胀对生物圈的压力越来越大,环境破坏不断加剧C．人类活动造成的环境污染正在影响生物圈其他生物的生存D．人类活动对生物圈的影响都是负面的二．非选择题每空1分,共50分26．衡阳的鱼粉可谓闻名遐滑爽口,鱼肉鲜美细腻,是备受人们青睐的早点之一,吃下一碗鱼粉,其中的主要成分会在你的体内经过下图所示的神奇旅程,最后被消化为可吸收的物质;Ⅰ．图中的曲线甲、乙、丙表示食物中淀粉、脂肪和蛋白质在消化道中各部位依次用A、B、C、D、E表示被消化的程度,请据图回答：1米粉的主要成分是淀粉,能代表淀粉消化过程的是曲线;2鱼肉的主要成分是蛋白质,它的初步消化在图中所示的填字母段完成;3小华同学长期偏食、挑食、爱吃鱼肉,不吃蔬菜水果,导致他牙龈出血,可能是他缺乏;Ⅱ．某中学生物兴趣小组欲探究“米粉在口腔中的变化”,按照如表所示的方案进行了实验,请根据下表回答问题：4为探究“唾液对米粉的消化作用”,选用1号和2号两支试管做对照实验,在A处应加入 ;51号试管中加入碘液后溶液不变蓝,原因是 ;6如选用1、3、4号试管进行试验,所探究的问题是：对淀粉的消化是否有影响27．如图是人体血液循,A、B、C、D表示心脏的四个腔,1~11表示部分动脉、静脉和毛细血管,箭头表示血流方向,请结合所学知识回答问题：1图中肺循环的途径用数字、字母和箭头表示．体循环和肺循环是同时进行的,并在处连通一起,构成一条完整的血液循环路线;2动脉瓣是存在于填标号之间的瓣膜,其作用是防止血液从动脉倒流;3饭后的血管6与11相比,血液中明显增加的是;4某人患有肠炎,在上臂进行静脉注射,药物需经过心脏次才能到达病灶;28．下图是人体部分生理活动示意图,数字表示的是生理过程,请据图回答问题：1A系统表示的是,图中①表示的生理过程是,完成该过程的主要器官是;2C 系统内的液体只能按照一定的方向流动,而不能倒流,其主要原因是心脏内和静脉内都有;3在寒冷的冬天,人的饮水量尽但排尿量却往往比其它季节还要多,其原因是水分由生理过程填数字的排出量大大减少的缘故;4上述各种生理活动之所以能够顺利进行,都有赖于和的调节作用,也依靠各种器官、系统的分工协作;29．如图为人体呼吸系统、消化系统、循环系统和泌尿系统的生理活动示意图,请据图回答：1图中a生理过程叫;2图中1生理过程进行时,膈肌处于填“收缩”或“舒张”状态;3图中心腔A与B之间、C与D之间防止血液倒流的结构是;若从手臂静脉注射药物,则药物经过心脏各腔的先后顺序是用图中字母表示;4当血液流经肺部毛细血管时,血液将变成血;5某肾炎患者尿检时发现尿液中有红细胞和蛋白质,此人肾脏的可能发生了病变;6肺泡壁、小肠绒毛壁以及毛细血管壁等结构的共同特点是：壁很薄,只由构成,这些结构特点都是与其功能相适应的;30．我市中小阳光体育”活动,朝气蓬勃的校园真正成为了青少年健康成长的乐园;下图为人体部分生理活动示意图图中①—⑦表示肾单位的结构,A—C表示生理过程,a表示物质;请据图回答问题：1丰富的的晨练提供了充足的营养,其中面包主要成分是淀粉在消化道内全部被消化分解成a的过程中,参与消化的消化液有 ;a被吸收后进入血液循环,经静脉流回心脏,首先到达心脏的 ;2体育课上,学生跳绳时需要消耗大量的氧气和能量,氧气进入组织细胞后,在细胞的内氧化分解有机物,释放出能量;3学生进行图中B过程时,肋间肌和膈肌处于状态;完成图中C过程的血管类型是 ;4运动过程中产生的代谢废物需及时排出体外,血液流经肾单位时,血液中尿素的流经途径是用图中的序号和箭头表示;5运动会上,参加100米赛跑的运动员听到发令枪响立刻冲出,这一活动属于反射;31．宁津杂技历史源远流长被国家文化部命名为中国民间艺术杂技之乡,草根杂技演员李立秋以其精湛的杂记技艺不仅成为山东我是大明星舞台上闪耀的明星,而且在2015年还登上了央视春晚的舞台;请根据下列图一、图二和所学生物学知识回答下列问题：1李立秋的蹬大缸表演令人震撼,300多斤重的大缸在李立秋的脚上来回翻飞,潇洒自如,李立秋维持身体平衡主要是依靠图二中;2在表演时,杂技演员伴做出各种精巧的动作和优美的造型．这些反射活动的完成主要受图二6内的调节,演员感受音乐刺激的感受器位于图一的中;3表演时要消耗大量的能量,她们常常面红耳赤,大汗淋漓．说明了人体皮肤具有功能;4杂技演员要顺利完成表演,需要运动、神经、循环、消化、呼吸等多个系统密切配合协调活动,这充分体现了的生物学观点;32．实验探究某实验中学环保兴趣小组为探究“废旧电池对水质的影响及防治”,开展了以下研究活动;一查阅资料资料一：废旧电池丢弃到自然界腐烂后,因含汞、铅、铜等有害物质造成水质污染;资料二：满江红为常见的水生蕨类植物,在美化水体景观、净化水质、保持河道生态平衡方面有显着功效;资料三：5号电池比7号电池较大些;二设计实验方案及数据统计A E共5组数据见表A B C D E加无污染河水的体积500毫升500毫升500毫升500毫升500毫升加废电池的数量及型号不加1节5号1节7号1节5号1节5号加满江红的数量不加不加不加10克30克放同样小鱼的数目1条1条1条1条1条小鱼存活的时间10天3天5天6天8天该小组根据上述有关内容,做了如下探究活动,请你结合自己的所学,帮助完成下列问题：1若某成员选择了A实验,那么,他想要探究的问题是作出的假设是,实验变量是;为探究这同一问题还可以选择进行对照实验;2B、E对照实验的变量是 ,E组的鱼比B组的鱼存活天数多说明,满江红在水中的这一作用充分体现了用生物与环境的关系解释;三实验反思3该实验设计中明显的不足之处是;四交流讨论废旧电池不能随意乱丢,应放在指定的容器内,以便集中无害化处理;33．人体各个系统相互联,以完成生命活动．下图是小明同学在参加体育中考时,身体与外界环境之间的部分物质交换示意图,请据图回答问题;1为保证测试时充足的能早晨吃了鸡蛋、牛奶、面包等食物．这些食物中的营养物质在填图中字母系统中被消化吸收;2当营养物质随血液流经一个肾单位时,部分葡萄糖随其他物质滤出形成原尿,这些葡萄糖在被重吸收,回到血液中;3长跑测试时,小明的呼吸加剧,物质①通过肺内的气体交换进入血液循环后,最先进入心脏四腔中的;4听到考官指令后,小明掷出了手中的实心球．完成这一反射活动需依靠相应的反射弧,其感受器位于内耳的中;答题卡26.Ⅰ1 .2 .3 .Ⅱ4 .5 .6 .27.1 , .2 .3 .4 .。

人教版七年级下册数学期末测试卷(含答案解析)

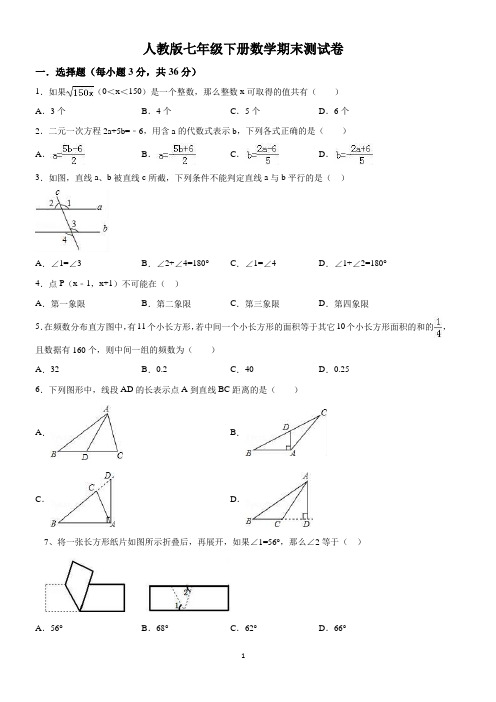
人教版七年级下册数学期末测试卷一．选择题（每小题3分，共36分）1．如果（0＜x＜150）是一个整数，那么整数x可取得的值共有（）A．3个B．4个C．5个D．6个2．二元一次方程2a+5b=﹣6，用含a的代数式表示b，下列各式正确的是（）A．B．C．D．3．如图，直线a、b被直线c所截，下列条件不能判定直线a与b平行的是（）A．∠1=∠3 B．∠2+∠4=180°C．∠1=∠4 D．∠1+∠2=180°4．点P（x﹣1，x+1）不可能在（）A．第一象限B．第二象限C．第三象限D．第四象限5．在频数分布直方图中，有11个小长方形，若中间一个小长方形的面积等于其它10个小长方形面积的和的，且数据有160个，则中间一组的频数为（）A．32 B．0.2 C．40 D．0.256．下列图形中，线段AD的长表示点A到直线BC距离的是（）A．B．C．D．7、将一张长方形纸片如图所示折叠后，再展开，如果∠1=56°，那么∠2等于（）A．56°B．68°C．62°D．66°8、如图，已知AB∥DE，∠ABC=70º，∠CDE=140º，则∠BCD的值为( )A．70ºB．50ºC．40º D.30º9、若a、b均为正整数，且，则a+b的最小值是（）A．3 B．4 C．5 D．610、若+|2a﹣b+1|=0，则（b﹣a）2016的值为（）A．﹣1 B．1 C．52015 D．﹣5201511、若关于x的不等式组只有5个整数解，则a的取值范围（）A．B．C．D．12、. 如图，所有正方形的中心均在坐标原点，且各边与x轴或y轴平行.从内到外，它们的边长依次为2，4，6，8，…，顶点依次用A1，A2，A3，A4，…表示，则顶点A55的坐标是（）A．（13，13）B．（–13，–13）C．（14，14）D．（–14，–14）二、填空题（每小题3分，共18分）13．如图，当剪刀口∠AOB增大21°时，∠COD增大__________度．14．在二元一次方程x+4y=13中，当x=5时，y=__________．15．如图所示，一个机器人从O点出发，向正东方向走3m到达A1点，再向正北方向走6m到达A2点，再向正西方向走9m到达A3点，再向正南方向走12m到达A4点，再向正东方向走15m到达A5点，按如此规律走下去，相对于点O，机器人走到A6时是__________位置．16、已知关于的不等式组只有两个整数解，则的取值范围__________.17、如图，在△ABC中，EF∥BC，∠ACG是△ABC的外角，∠BAC的平分线交BC于点D，记∠ADC=α，∠ACG=β，∠AEF=γ，则：α、β、γ三者间的数量关系式是__________.18、如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2011次运动后，动点P的坐标是__________．三、解答题（共8小题，共66分）19．（6分）计算：20．（6分）解方程组:21．（8分）解不等式组：22．（8分）已知直线AB∥CD．（1）如图1，直接写出∠BME、∠E、∠END的数量关系为；（2）如图2，∠BME与∠CNE的角平分线所在的直线相交于点P，试探究∠P与∠E之间的数量关系，并证明你的结论；（3）如图3，∠ABM=∠MBE，∠CDN=∠NDE，直线MB、ND交于点F，则=．23．（9分）如图，已知四边形ABCD（网格中每个小正方形的边长均为1）.（1）写出点A，B，C，D的坐标；（2）求四边形ABCD的面积.24．（9分）已知关于x，y的方程组的解满足不等式组求满足条件的m的整数值.25．（10分）如图，BE平分∠ABD，DE平分∠BDC，且∠1+∠2=90°．求证：AB∥CD．26．（10分）某中学将组织七年级学生春游一天，由王老师和甲、乙两同学到客车租赁公司洽谈租车事宜．（1）两同学向公司经理了解租车的价格，公司经理对他们说：“公司有45座和60座两种型号的客车可供租用，60座的客车每辆每天的租金比45座的贵100元．”王老师说：“我们学校八年级昨天在这个公司租了5辆45座和2辆60座的客车，一天的租金为1600元，你们能知道45座和60座的客车每辆每天的租金各是多少元吗”甲、乙两同学想了一下，都说知道了价格．聪明的你知道45座和60座的客车每辆每天的租金各是多少元吗？（2）公司经理问：“你们准备怎样租车”，甲同学说：“我的方案是只租用45座的客车，可是会有一辆客车空出30个座位”；乙同学说“我的方案只租用60座客车，正好坐满且比甲同学的方案少用两辆客车”，王老师在﹣旁听了他们的谈话说：“从经济角度考虑，还有别的方案吗”？如果是你，你该如何设计租车方案，并说明理由．参考答案一．选择题（共12小题，满分36分，每小题3分）1．B．2．D．3．D．4．D．5．A．6．D．7、B．8、D 9、B．10、B 11、A 12、C 二．填空题（共6小题，满分24分，每小题4分）13．21度．14．215．（9，12）．16、17、2∠α=∠β+∠γ.18、（2011，2）三解答题19.答案为：20.答案为:x=2,y=–1.5;21．解：解不等式3（x﹣1）＜2x，得：x＜3，解不等式﹣＜1，得：x＞﹣9，则原不等式组的解集为﹣9＜x＜3．22．解：（1）如图1，∵AB∥CD，∴∠END=∠EFB，∵∠EFB是△MEF的外角，∴∠E=∠EFB﹣∠BME=∠END﹣∠BME，故答案为：∠E=∠END﹣∠BME；（2）如图2，∵AB∥CD，∴∠CNP=∠NGB，∵∠NPM是△GPM的外角，∴∠NPM=∠NGB+∠PMA=∠CNP+∠PMA，∵MQ平分∠BME，PN平分∠CNE，∴∠CNE=2∠CNP，∠FME=2∠BMQ=2∠PMA，∵AB∥CD，∴∠MFE=∠CNE=2∠CNP，∵△EFM中，∠E+∠FME+∠MFE=180°，∴∠E+2∠PMA+2∠CNP=180°，即∠E+2（∠PMA+∠CNP）=180°，∴∠E+2∠NPM=180°；（3）如图3，延长AB交DE于G，延长CD交BF于H，∵AB∥CD，∴∠CDG=∠AGE，∵∠ABE是△BEG的外角，∴∠E=∠ABE﹣∠AGE=∠ABE﹣∠CDE，①∵∠ABM=∠MBE，∠CDN=∠NDE，∴∠ABM=∠ABE=∠CHB，∠CDN=∠CDE=∠FDH，∵∠CHB是△DFH的外角，∴∠F=∠CHB﹣∠FDH=∠ABE﹣∠CDE=（∠ABE﹣∠CDE），②由①代入②，可得∠F=∠E，即．故答案为：．23解：（1）由图象可知A（﹣2，1），B（﹣3，﹣2），C（3，﹣2），D（1，2）；（2）S四边形ABCD=S△ABE+S△ADF+S△CDG+S正方形AEGF=0.5×1×3+0.5×1×3+0.5×2×4+3×3=16。

七年级数学下册期末考试题(附答案解析)

七年级数学下册期末考试题（附答案解析）一、单选题1．目前代表华为手机最强芯片的麒麟990处理器采用7nm工艺制程，1nm＝0.0000001cm，则7nm用科学记数法表示为（）A．0.7×10﹣6cm B．0.7×10﹣7cm C．7×10﹣6cm D．7×10﹣7cm2．下列各式，计算结果为a6的是（）A．a2+a4B．a7÷a C．a2•a3D．（a2）43．若a＜b，则下列不等式中正确的是（）A．a﹣3＜b﹣3 B．a﹣b＞0 C．b D．﹣2a＜﹣2b4．不等式2x+3＞1的解集在数轴上表示正确的是（）A．B．C．D．5．下列命题中，可判断为假命题的是（）A．在同一平面内，过一点有且只有一条直线与已知直线垂直B．两条直线被第三条直线所截，同位角相等C．同旁内角互补，两直线平行D．直角三角形两个锐角互余6．如图，在四边形ABCD中，连接BD，下列判断正确的是（）A．若∠1＝∠2，则AB∥CDB．若∠3＝∠4，则AD∥BCC．若∠A+∠ABC＝180°，则AB∥CDD．若∠A＝∠C，∠ABC＝∠ADC，则AB∥CD7．《九章算术》中记载：“今有上禾三秉，益实六斗，当下禾十秉；下禾五秉，益实一斗，当上禾二秉．问上、下禾实一秉各几何？”其大意是：今有上等稻子三捆，若打出来的谷子再加六斗，则相当于十捆下等稻子打出来的谷子；有下等稻子五捆，若打出来的谷子再加一斗，则相当于两捆上等稻子打出来的谷子．问上等、下等稻子每捆打多少斗谷子？设上等稻子每捆打x斗谷子，下等稻子每捆打y斗谷子，根据题意可列方程组为（）A．B．C．D．8．如图，在△ABC中，BC＝7，∠A＝80°，∠B＝70°，把△ABC沿RS的方向平移到△DEF的位置，若CF ＝4，则下列结论中错误的是（）A．DF＝7 B．∠F＝30°C．AB∥DE D．BE＝49．已知a是任何实数，若M＝（2a﹣3）（3a﹣1），N＝2a（a﹣）﹣1，则M、N的大小关系是（）A．M≥NB．M＞NC．M＜ND．M，N的大小由a的取值范围10．如图，四边形ABCD中，AD∥BC，AB⊥BC，AD＝6，BC＝10，DC＝DE，∠CDE＝90°，则△ADE的面积是（）A．4 B．8 C．12 D．1611．若x、y满足2134x yx y=-⎧⎨+≥⎩，则x的最小整数值为（）A．－1 B．1 C．0 D．212．如图1是长方形纸带，∠DEF＝10°，将纸带沿EF折叠成图2，再沿BF折叠成图3，则图3中∠CFE度数是多少( )A ．160°B ．150°C ．120°D ．110°二、填空题 13．已知112x y =⎧⎪⎨=⎪⎩是方程42ax y +=的一个解，那么a =___________． 14．如图，将△ABC 向左平移3cm 得到△DEF ，AB 、DF 交于点G ，如果△ABC 的周长是12cm ，那么△ADG 与△BGF 的周长之和是__．15．如图，C 岛在A 岛的北偏东45°方向，在B 岛的北偏西25°方向，则从C 岛看A ，B 两岛的视角∠ACB ＝________.16．对于实数a ，b ，定义运算“*”：a *b ＝22()()a ab a b ab b a b ⎧-≥⎨-<⎩，例如：4*2，因为4＞2，所以4*2＝42﹣4×2＝8．若x ，y 是二元一次方程组521x y x y +=⎧⎨-=⎩的解，则x *y ＝_____． 17．为了加强学生课外阅读，开阔视野，某学校开展了“书香校园，从我做起”的主题活动学校随机抽取50名学生，对他们一周的课外阅读时间进行调查，结果如图所示，学校将每周课外阅读时间在8小时以上的学生评为“阅读之星”，若学校共有2000人，则获得“阅读之星”的有 ___人．18．在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点.观察图中每一个正方形（实线）四条边上的整点的个数，请你猜测由里向外第n个正方形（实线）四条边上的整点个数共有_______________个.19．如图，点A的坐标为（1，3），点B在x轴上，把△OAB沿x轴向右平移到△ECD，若四边形ABDC的面积为15，则点C的坐标为 ________．20．如图，动点P从坐标原点(0,0)出发，以每秒一个单位长度的速度按图中箭头所示方向运动，第1秒运动到点(1,0)，第2秒运动到点(1,1)，第3秒运动到点(0,1)，第4秒运动到点(0,2)…则第2068秒点P所在位置的坐标是_______________．三、解答题21．计算下列各题：（13；（2）若（2x ﹣1）2＝9，试求x 的值．22．解不等式组()2532113x x +≥⎧⎪+⎨<⎪⎩，并把它的解集在数轴上表示出来．23．为庆祝中国共产党成立100周年，让红色基因、革命薪火代代传承，某校开展以学习“四史”（党史、新中国史、改革开放史、社会主义发展史）为主题的书画展，为了解作品主题分布情况，在学生上交的作品中，随机抽取了若干份进行统计，并根据调查统计结果绘制了统计图表：请结合上述信息完成下列问题：（1）m＝，n＝；（2）请补全频数分布直方图；（3）在扇形统计图中，“新中国史”主题作品份数对应的圆心角是度；（4）若该校共上交书画作品1800份，估计以“党史”为主题的作品有多少份？24．如图，AD∥BE，AB∥CD，点C在直线BE上，连接AC、AE，∠3＝∠4，求证：∠1＝∠225．甲、乙两同学在商店购买中性笔和笔记本，甲要买3支中性笔，2本笔记本需花费19元；乙要买7支中性笔，1本笔记本需花费26元，（1）求中性笔和笔记本的单价；（2）商店新进一种单价为3元的小装饰品，甲、乙两同学非常喜欢，都想购买，但各自付款后，只有甲还剩2元钱，他们看到商店的优惠条件“中性笔每盒10支，整盒买每支可优惠0.5元”后，经商讨两人找到了一种购买方法，如愿以偿，他们是怎样买的？请通过计算说明．26．在综合与实践课上，老师计同学们以“两条平行线AB，CD和一块含60°角的直角三角尺EFG（∠EFG=90°，∠EGF=60°）”为主题开展数学活动．°（1）如图（1），若三角尺的60°角的顶点G放在CD上，若∠2 = 2∠1，求∠1的度数；（2）如图（2），小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上，请你探索并说明∠AEF与∠FGC间的数量关系；（3）如图（3），小亮把三角尺的直角顶点F放在CD上，30°角的顶点E落在AB上．若∠AEG=α，∠CFG=β，则∠AEG与∠CFG的数量关系是什么？用含α，β的式子表示．参考答案与解析：1．【解答】解：7nm＝7×0.0000001cm＝7×10﹣7cm，故选：D．2．【解答】解：A、a2+a4，无法计算，故此选项错误；B、a7÷a＝a6，故此选项正确；C、a2•a3＝a5，故此选项错误；D、（a2）4＝a8，故此选项错误．故选：B．3．【解答】解：A、不等式的两边都减3，不等式的方向不变，故A正确；B、不等式的两边都减b，不等号的方向不变，故B错误；C、不等式的两边都乘以，不等号的方向不变，故C错误；D、不等式的两边都乘以﹣2，不等号的方向改变，故D错误；故选：A．4．【解答】解：2x＞1﹣3，2x＞﹣2，x＞﹣1，故选：D．5．【解答】解：A、在同一平面内，过一点有且只有一条直线与已知直线垂直，正确，是真命题；B、两条平行直线被第三条直线所截，同位角相等，故错误，是假命题；C、同旁内角互补，两直线平行，正确，是真命题；D、直角三角形两个锐角互余，正确，是真命题，故选：B．6．【解答】解：A、根据∠1＝∠2不能推出AB∥CD，故本选项不符合题意；B、根据∠3＝∠4不能推出AD∥BC，故本选项不符合题意；C、根据∠A+∠ABC＝180°能不能推出AB∥CD，故本选项不符合题意；D、根据∠A＝∠C，∠ABC＝∠ADC，可得∠A+∠ADC＝180°，能推出AB∥CD，故本选项符合题意．故选：D．7．【解答】解：设上等稻子每捆打x斗谷子，下等稻子每捆打y斗谷子，根据题意可列方程组为：．故选：C．8．【解答】解：∵把△ABC沿RS的方向平移到△DEF的位置，BC＝7，∠A＝80°，∠B＝70°，∴EF＝BC＝7，CF＝BE＝4，∠F＝∠ACB＝180°﹣∠A﹣∠B＝180°﹣80°﹣70°＝30°，AB∥DE，∴B、C、D正确，A错误，故选：A．9．【解答】解：∵M＝（2a﹣3）（3a﹣1），N＝2a（a﹣）﹣1，∴M﹣N＝（2a﹣3）（3a﹣1）﹣2a（a﹣）+1，＝6a2﹣11a+3﹣2a2+3a+1＝4a2﹣8a+4＝4（a﹣1）2∵（a﹣1）2≥0，∴M﹣N≥0，则M≥N．故选：A．10．【解答】解：过D点作DH⊥BC于H，过E点作EF⊥AD于F，如图，∵AB⊥BC，AD∥BC，∴∠DAB＝∠B＝90°，∵DH⊥BC，∴四边形ABHD为矩形，∴BH＝AD＝6，∴CH＝BC﹣BH＝10﹣6＝4，∵∠ADH＝90°，∴∠FDC +∠CDH ＝90°，∵∠CDE ＝90°，即∠EDF +∠FDC ＝90°，∴∠EDF ＝∠CDH ，在△DEF 和△DCH 中，，∴△DEF ≌△DCH （AAS ），∴EF ＝CH ＝4，∴S △ADE ＝•AD •EF ＝×6×4＝12．故选：C ．11．B【解析】∵2134x y x y =-⎧⎨+≥⎩， ∴1234x y x y +⎧=⎪⎨⎪+≥⎩， ∴3342x x ++≥，解得1≥x ，∴x 的最小整数为1，故选B ．12．B【解析】∵四边形ABCD 为长方形，∴AD ∥BC ，∴∠BFE ＝∠DEF ＝10°．由翻折的性质可知：图2中，∠EFC ＝180°﹣∠BFE ＝170°，∠BFC ＝∠EFC ﹣∠BFE ＝160°， ∴图3中，∠CFE ＝∠BFC ﹣∠BFE ＝150°．故选B ．13．0【解析】∵112xy=⎧⎪⎨=⎪⎩是方程42ax y+=的一个解，∴1422a+⨯=，即：a=0．故答案是：0．14．12【解析】∵△ABC向左平移3cm得到∆DEF，∴AD=FC，∴△ADG与△BGE的周长之和=AD+BF+DF+AB=BC+AC+AB=12，故答案为12；15．70°##70度【解析】连接AB．∵C岛在A岛的北偏东45°方向，在B岛的北偏25°方向，∴∠CAB+∠ABC=180°-（45°+25°）=110°，∵三角形内角和是180°，∴∠ACB=180°-（∠CAB+∠ABC）=180°-110°=70°．故答案为：70°．16．-3【解析】=52=1x yx y+⎧⎨-⎩①②，①+②得：3=6x，∴=2x，代入①得：=3y，∵2＜3，∴原式2=233=69=3⨯---．故答案为：﹣3．17．200【解析】2000×550=200（人），即若学校共有2000人，则获得“阅读之星”的有200人，故答案为：200．18．4n【解析】第1个正方形的整点个数为4=41⨯，第2个正方形的整点个数为8=4⨯2，第3个正方形的整点个数为12=4⨯3，，∴第n个正方形的整点个数为4n，故答案为：4n.19．（6，3）【解析】∵把△OAB沿x轴向右平移到△ECD，∴四边形ABDC是平行四边形，∴AC＝BD，A和C的纵坐标相同，∵四边形ABDC的面积为15，点A的坐标为（1，3），∴3AC＝15，∴AC＝5，∴C（6，3），故答案为：（6，3）．20．(45,43)【解析】由题意分析可得，动点P第8=2×4秒运动到（2，0）动点P第24=4×6秒运动到（4，0）动点P第48=6×8秒运动到（6，0）以此类推，动点P第2n(2n+2)秒运动到（2n，0）∴动点P第2024=44×46秒运动到（44，0）2068-2024=44∴按照运动路线，点P到达（44，0）后，向右一个单位，然后向上43个单位∴第2068秒点P所在位置的坐标是（45，43）故答案为：（45，43）21．（1；（2）2或﹣1．【解析】（1）原式＝4﹣1﹣（3＝4﹣1﹣；（2）根据平方根的意义可得：2x ﹣1＝3或2x ﹣1＝﹣3，解得：x ＝2或x ＝﹣1，即x 的值为2或﹣1．22．10.5x -≤<，图见解析【解析】：解不等式253x +≥，得1x ≥-，解不等式()2113x +<，得0.5x <，则不等式组的解集为10.5x -≤<，将其解集表示在数轴上如下：同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．23．（1）10；28；（2）见解析；（3）144°；（4）216份【解析】（1）由题意得：样本总数=6÷12%=50人，∴m =50×20%=10，∴n %=14÷50=28%，∴n =28，故答案为：10，28；（2）如图（3）由题意得：“新中国史”主题作品份数对应的圆心角=360°×20÷50=144°；（4）由题意得：以“党史”为主题的作品=1800×12%=216（份）答：以“党史”为主题的作品大约有216份．24．见解析【解析】证明：∵AD∥BE，∴∠3=∠DAC，又∵AB∥CD，∴∠4=∠BAE，又∵∠3=∠4，∴∠DAC =∠BAE，∴∠DAC-∠5=∠BAE-∠5，∴∠1=∠2．25．（1）笔记本的单价为5元，单独购买一支笔芯的价格为3元；（2）他们合买笔芯即可如愿以偿，见解析【解析】（1）设笔记本的单价为x元，中性笔单价为y元，依题意，得：2319726x yx y+=⎧⎨+=⎩，解得：53xy=⎧⎨=⎩．答：笔记本的单价为5元，单独购买一支笔芯的价格为3元．（2）他们合买笔芯即可如愿以偿．甲、乙带的总钱数为19+2+26＝47（元）．两人合在一起购买所需费用为：5×（2+1）+（30.5-）×10＝40（元）．∵4740-＝7（元），3×2＝6（元），7＞6，∴他们合在一起购买笔芯，即可如愿以偿．进行解题．26．（1）∠1＝40°；（2）∠AEF＋∠FGC＝90°，理由见详解；（3）α+β＝300°，理由见详解【解析】：（1）∵AB∥CD，∴∠1＝∠EGD，∵∠2＋∠FGE＋∠EGD＝180°，∠2＝2∠1，∴2∠1＋60°＋∠1＝180°，解得∠1＝40°；（2）∠AEF＋∠FGC＝90°，理由如下：如图，过点F作FP∥AB，∵CD∥AB，∴FP∥AB∥CD，∴∠AEF＝∠EFP，∠FGC＝∠GFP，∴∠AEF＋∠FGC＝∠EFP＋∠GFP＝∠EFG，∵∠EFG＝90°，∴∠AEF＋∠FGC＝90°；（3）α+β＝300°．理由如下：∵AB∥CD，∴∠AEF＋∠CFE＝180°，∴∠AEG−∠FEG＋∠CFG−∠EFG＝180°，∵∠FEG＝30°，∠EFG＝90°，∴∠AEG−30°＋∠CFG−90°＝180°，∴∠AEG＋∠CFG＝300°，即：α+β＝300°．。

七年级(下)期末数学试卷(含答案)

七年级（下）期末数学试卷（解析版）一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．根据下列表述，能确定位置的是（）A．东经118°，北纬40°B．江东大桥南C．北偏东30°D．某电影院第2排2．为了了解某校初三年级400名学生的体重情况，从中抽查了50名学生的体重进行统计分析，在这个问题中，总体是（）A．400名学生的体重B．被抽取的50名学生C．400名学生D．被抽取的50名学生的体重3．在平面直角坐标系中，点P（3，﹣x2﹣1）所在的象限是（）A．第一象限 B．第二象限 C．第三象限 D．第四象限4．如果关于x的不等式（a+1）x＞a+1的解集为x＜1，那么a的取值范围是（）A．a＞0 B．a＜0 C．a＞﹣1 D．a＜﹣15．若x、y满足方程组，则x﹣y的值等于（）A．﹣1 B．1 C．2 D．36．如图：AB∥CD，直线MN与AB交于E，过点E作直线HE⊥MN，∠1=130°，则∠2等于（）A．50°B．40°C．30°D．60°7．下列选项中正确的是（）A．27的立方根是±3 B．的平方根是±4C．9的算术平方根是3 D．立方根等于平方根的数是18．甲、乙两种商品原来的单价和为100元，因市场变化，甲商品降价10%，乙商品提价40%，调价后两种商品的单价和比原来的单价和提高了20%、若设甲、乙两种商品原来的单价分别为x元、y元，则下列方程组正确的是（）A．B．C．D．9．如图，木工师傅在一块木板上画两条平行线，方法是：用角尺画木板边缘的两条垂线，这样画的理由有下列4种说法：其中正确的是（）①同位角相等，两直线平行；②内错角相等，两直线平行；③同旁内角互补，两直线平行；④平面内垂直于同一直线的两条直线平行．A．①②③ B．①②④ C．①③④ D．①③10．若关于x的一元一次不等式组有解，则m的取值范围为（）A． B．m≤C．D．m≤二、填空题：本大题共5小题，每小题3分，共15分，把答案填在题中横线上．11．若|x+3|+=0，则x y的值为．12．已知关于x的不等式x﹣a＜1的解集如图所示，则a的值为．13．若方程4x m﹣n﹣5y m+n=6是二元一次方程，则m=，n=．14．如图，两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，AB=6，BC=9，DH=2，平移距离为3，则阴影部分的面积是．15．在平面直角坐标系中，点A1（1，2），A2（2，5），A3（3，10），A4（4，17），…，用你发现的规律确定点A n的坐标为．三、解答题：本大题共7小题，共55分，解答应写出证明过程或演算步骤．16．（1）解方程组：；（2）解不等式组：．17．如图，已知：AD⊥BC于D，EG⊥BC于G，∠E=∠1．求证：AD平分∠BAC．下面是部分推理过程，请你将其补充完整：∵AD⊥BC于D，EG⊥BC于G （已知）∴∠ADC=∠EGC=90°∴AD∥EG．∴∠1=∠2．=∠3（两直线平行，同位角相等）又∵∠E=∠1（已知）∴∠2=∠3．∴AD平分∠BAC．18．甲乙两人解方程组．由于甲看错了方程①中的m的值，得到方程组的解为，乙看错了方程②中的n的值，得到方程组的解为，试求m2+n2+mn 的值．19．某市球类运动协会为了筹备一次大型体育活动，购进了一定数量的体育器材，器材管理员对购买的部分器材进行了统计，图表和图是器材管理员通过采集数据后，绘制的两幅不完整的频率分布表与频数分布直方图．请你根据图表中提供的信息，解答以下问题：频率分布表器材种类频数频率排球20乒乓球拍50 0.50篮球25 0.25足球合计 1（1）填充频率分布表中的空格．（2）在图中，将表示“排球”和“足球”的部分补充完整．（3）若该协会购买这批体育器材时，篮球和足球一共花去950元，且足球每个的价格比篮球多10元，现根据筹备实际需要，准备再采购篮球和足球这两种球共10个（两种球的个数都不能为0），计划资金不超过320元，试问该协会有哪几种购买方案？20．某中学计划从办公用品公司购买A，B两种型号的小黑板．经洽谈，购买一块A型小黑板比购买一块B型小黑板多用20元，且购买5块A型小黑板和4块B型小黑板共需820元．（1）求购买一块A型小黑板、一块B型小黑板各需多少元．（2）根据该中学实际情况，需从公司购买A，B两种型号的小黑板共60块，要求购买A，B两种型号小黑板的总费用不超过5240元．并且购买A型小黑板的数量不小于购买B型小黑板数量的．则该中学从公司购买A，B两种型号的小黑板有哪几种方案？哪种方案的总费用最低？21．我们用[a]表示不大于a的最大整数，例如：[2.5]=2，[3]=3，[﹣2.5]=﹣3；用＜a＞表示大于a的最小整数，例如：＜2.5＞=3，＜4＞=5，＜﹣1.5＞=﹣1．解决下列问题：（1）[﹣4.5]=，＜3.5＞=．（2）若[x]=2，则x的取值范围是；若＜y＞=﹣1，则y的取值范围是．（3）已知x，y满足方程组，求x，y的取值范围．22．如图，已知直线AC∥BD，直线AB、CD不平行，点P在直线AB上，且和点A、B 不重合．（1）如图①，当点P在线段AB上时，若∠PAC=20°，∠PDB=30°，求∠CPD的度数；（2）当点P在A、B两点之间运动时，∠PCA、∠PDB、∠CPD之间满足什么样的等量关系？（直接写出答案）（3）如图②，当点P在线段AB延长线运动时，∠PCA、∠PDB、∠CPD之间满足什么样的等量关系？并说明理由．参考答案与试题解析一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．根据下列表述，能确定位置的是（）A．东经118°，北纬40°B．江东大桥南C．北偏东30°D．某电影院第2排【分析】根据在平面内，要有两个有序数据才能清楚地表示出一个点的位置，即可得答案．【解答】解：在平面内，点的位置是由一对有序实数确定的，只有A能确定一个位置，故选A．【点评】本题考查了在平面内，如何表示一个点的位置的知识点．2．为了了解某校初三年级400名学生的体重情况，从中抽查了50名学生的体重进行统计分析，在这个问题中，总体是（）A．400名学生的体重B．被抽取的50名学生C．400名学生D．被抽取的50名学生的体重【分析】本题考查的是确定总体．解此类题需要注意“考查对象实际应是表示事物某一特征的数据，而非考查的事物．”．我们在区分总体、个体、样本、样本容量这四个概念时，首先找出考查的对象，从而找出总体、个体，再根据被收集数据的这一部分对象找出样本．【解答】解：本题考查的对象是某校初三年级400名学生的体重情况，故总体是400名学生的体重．故选：A．【点评】解题要分清具体问题中的总体、个体与样本，关键是明确考查的对象．总体、个体与样本的考查对象是相同的，所不同的是范围的大小．样本容量是样本中包含的个体的数目，不能带单位．3．在平面直角坐标系中，点P（3，﹣x2﹣1）所在的象限是（）A．第一象限 B．第二象限 C．第三象限 D．第四象限【分析】根据非负数的性质判断出点P的纵坐标是负数，再根据各象限内点的坐标特征解答．【解答】解：∵﹣x2﹣1≤﹣1，∴点P（3，﹣x2﹣1）所在的象限是第四象限．故选D．【点评】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．4．如果关于x的不等式（a+1）x＞a+1的解集为x＜1，那么a的取值范围是（）A．a＞0 B．a＜0 C．a＞﹣1 D．a＜﹣1【分析】本题可对a＞﹣1，与a＜﹣1的情况进行讨论．不等式两边同时除以一个正数不等号方向不变，同时除以一个负数不等号方向改变，据此可解本题．【解答】解：（1）当a＞﹣1时，原不等式变形为：x＞1；（2）当a＜﹣1时，原不等式变形为：x＜1．故选：D．【点评】本题考查了解简单不等式的能力，解答这类题学生往往在解题时不注意同除a+1时是否要改变符号这一点而出错．解不等式要依据不等式的基本性质，在不等式的两边同时加上或减去同一个数或整式，不等号的方向不变．在不等式的两边同时乘以或除以同一个正数，不等号的方向不变；在不等式的两边同时乘以或除以同一个负数，不等号的方向改变．5．若x、y满足方程组，则x﹣y的值等于（）A．﹣1 B．1 C．2 D．3【分析】方程组两方程相减即可求出x﹣y的值．【解答】解：，②﹣①得：2x﹣2y=﹣2，则x﹣y=﹣1，故选：A．【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．6．如图：AB∥CD，直线MN与AB交于E，过点E作直线HE⊥MN，∠1=130°，则∠2等于（）A．50°B．40°C．30°D．60°【分析】先根据平行线的性质及对顶角相等求出∠AEM的度数，再根据垂直的性质求出∠2的度数即可．【解答】解：∵∠1=130°，∴∠3=∠1=130°，∵AB∥CD，∴∠3=∠AEM，∵HE⊥MN，∴∠HEM=90°，∴∠2=∠3﹣∠HEM=130°﹣90°=40°．故选B．【点评】本题涉及到的知识点为：（1）对顶角相等；（2）两直线平行，同位角相等；（3）垂线的定义．7．下列选项中正确的是（）A．27的立方根是±3 B．的平方根是±4C．9的算术平方根是3 D．立方根等于平方根的数是1【分析】A、根据立方根的即可判定；B、根据算术平方根、平方根的定义即可判定；C、根据算术平方根的定义即可判定；D、根据平方根、立方根的定义求解即可判定．【解答】解：A、27的立方根是3，故选项错误；B、的平方根是±2，故选项错误；C、9的算术平方根是3，故选项正确；D、立方根等于平方根的数是1和0，故选项错误．故选C．【点评】本题主要考查了平方根和立方根的性质，并利用此性质解题．平方根的被开数不能是负数，开方的结果必须是非负数；立方根的符号与被开立方的数的符号相同．要注意一个正数的平方根有两个，它们互为相反数．8．甲、乙两种商品原来的单价和为100元，因市场变化，甲商品降价10%，乙商品提价40%，调价后两种商品的单价和比原来的单价和提高了20%、若设甲、乙两种商品原来的单价分别为x元、y元，则下列方程组正确的是（）A．B．C．D．【分析】如果设甲商品原来的单价是x元，乙商品原来的单价是y元，那么根据“甲、乙两种商品原来的单价和为100元”可得出方程为x+y=100；根据“甲商品降价10%，乙商品提价40%，调价后，两种商品的单价之和比原来的单价之和提高了20%”，可得出方程为x（1﹣10%）+y（1+40%）=100（1+20%）．【解答】解：设甲商品原来的单价是x元，乙商品原来的单价是y元．根据题意列方程组：．故选：C．【点评】找到两个等量关系是解决本题的关键，还需注意相对应的原价及相应的百分比得到的新价格．9．如图，木工师傅在一块木板上画两条平行线，方法是：用角尺画木板边缘的两条垂线，这样画的理由有下列4种说法：其中正确的是（）①同位角相等，两直线平行；②内错角相等，两直线平行；③同旁内角互补，两直线平行；④平面内垂直于同一直线的两条直线平行．A．①②③ B．①②④ C．①③④ D．①③【分析】利用同位角相等（都等于90°），同旁内角互补，两条直线平行，或同一平面内，垂直于同一条直线的两条直线平行作答．【解答】解：由图可知，用角尺画木板边缘的两条垂线，这样画的理由：①同位角相等，两直线平行；③同旁内角互补，两直线平行；④平面内垂直于同一直线的两条直线平行．故选C．【点评】本题考查平行线的判定：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行；两条直线都和第三条直线平行，那么这两条直线平行；在同一平面内，如果两条直线同时垂直于同一条直线，那么这两条直线平行．10．若关于x的一元一次不等式组有解，则m的取值范围为（）A． B．m≤C．D．m≤【分析】先求出两个不等式的解集，再根据有解列出不等式组求解即可．【解答】解：，解不等式①得，x＜2m，解不等式②得，x＞2﹣m，∵不等式组有解，∴2m＞2﹣m，∴m＞．故选C．【点评】本题主要考查了一元一次不等式组解集的求法，其简便求法就是用口诀求解．求不等式组解集的口诀：同大取大，同小取小，大小小大中间找，大大小小找不到（无解）．二、填空题：本大题共5小题，每小题3分，共15分，把答案填在题中横线上．11．若|x+3|+=0，则x y的值为9．【分析】直接利用非负数的性质得出x，y的值，进而利用有理数的乘方运算法则求出答案．【解答】解：∵|x+3|+=0，∴x=﹣3，y=2，则x y=（﹣3）2=9．故答案为：9．【点评】此题主要考查了非负数的性质，正确得出x，y的值是解题关键．12．已知关于x的不等式x﹣a＜1的解集如图所示，则a的值为1．【分析】根据在数轴上表示不等式解集的方法得出不等式的解集，再用a表示出不等式的解集，进而可得出a的值．【解答】解：由题意可知，x＜2，∵解不等式x﹣a＜1得，x＜1+a，∴1+a=2，解得a=1．故答案为：1．【点评】本题考查的是解一元一次不等式，熟知不等式的基本性质是解答此题的关键．13．若方程4x m﹣n﹣5y m+n=6是二元一次方程，则m=1，n=0．【分析】根据二元一次方程的定义，可得x和y的指数分别都为1，列关于m、n的方程组，再求出m和n的值，最后代入可得到m n的值．【解答】解：根据二元一次方程的定义，得，解得，故答案为：1，0．【点评】考查了二元一次方程的定义，二元一次方程必须符合以下三个条件：（1）方程中只含有2个未知数；（2）含未知数项的最高次数为一次；（3）方程是整式方程．14．如图，两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，AB=6，BC=9，DH=2，平移距离为3，则阴影部分的面积是15．【分析】根据平移的性质，判断出△HEC∽△ABC，再根据相似三角形的性质列出比例式解答．【解答】14.15解：由平移的性质知，BE=3，DE=AB=6，∴HE=DE﹣DH=6﹣2=4，∴S四边形HDFC =S梯形ABEH=（AB+EH）BE=（6+4）×3=15．故答案为：15．【点评】本题主要利用了平行线截线段对应成比例和平移的基本性质求解，找出阴影部分和三角形面积之间的关系是关键．15．在平面直角坐标系中，点A1（1，2），A2（2，5），A3（3，10），A4（4，17），…，用你发现的规律确定点A n的坐标为（n，n2+1）．【分析】首先观察各点坐标，找出一般规律，然后根据规律确定点A n的坐标．【解答】解：设A n（x，y）．∵当n=1时，A1（1，1），即x=1，y=12+1，当n=2时，A2（2，5），即x=2，y=22+1；当n=3时，A3（3，10），即x=3，y=32+1；当n=4时，A1（4，17），即x=4，y=42+1；…∴当n=n时，x=n，y=n2+1，故答案为：（n，n2+1）．【点评】此题主要考查了点的坐标规律，解决本题的关键在于总结规律．对于寻找规律的题，应通过观察，发现哪些部分没有变化，哪些部分发生了变化，变化的规律是什么．三、解答题：本大题共7小题，共55分，解答应写出证明过程或演算步骤．16．（1）解方程组：；（2）解不等式组：．【分析】（1）先用加减消元法求出x的值，再用代入消元法求出y的值即可；（2）分别求出各不等式的解集，再求出其公共解集即可．【解答】解：（1），①+②×3得，10x=50，解得x=5，把x=5代入②得，10+y=13，解得y=3．故方程组的解为；（2），由①得，x＜3，由②得，x≥﹣2，故方程组的解为：﹣2≤x＜3．【点评】本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．17．如图，已知：AD⊥BC于D，EG⊥BC于G，∠E=∠1．求证：AD平分∠BAC．下面是部分推理过程，请你将其补充完整：∵AD⊥BC于D，EG⊥BC于G （已知）∴∠ADC=∠EGC=90°∴AD∥EG同位角相等，两直线平行．∴∠1=∠2两直线平行，内错角相等．∠E=∠3（两直线平行，同位角相等）又∵∠E=∠1（已知）∴∠2=∠3等量代换．∴AD平分∠BAC角平分线的定义．【分析】根据平行线的判定与性质进行解答即可．【解答】解：∵AD⊥BC于D，EG⊥BC于G （已知）∴∠ADC=∠EGC=90°∴AD∥EG，（同位角相等，两直线平行）．∴∠1=∠2，（两直线平行，内错角相等）．∠E=∠3（两直线平行，同位角相等）又∵∠E=∠1（已知）∴∠2=∠3，（等量代换）．∴AD平分∠BAC．（角平分线的定义）故答案为：同位角相等，两直线平行；两直线平行，内错角相等；∠E；等量代换；角平分线的定义．【点评】本题考查的是平行线的判定与性质，用到的知识点为：同位角相等，两直线平行；两直线平行，内错角相等，同位角相等．18．甲乙两人解方程组．由于甲看错了方程①中的m的值，得到方程组的解为，乙看错了方程②中的n的值，得到方程组的解为，试求m2+n2+mn的值．【分析】根据甲看错了方程①中的m，②没有看错，代入②得到一个方程求出n的值，乙看错了方程②中的n，①没有看错，代入①求出m的值，然后再把m、n的值代入代数式计算即可求解【解答】解：根据题意得，4×（﹣3）﹣b（﹣1）=﹣2，5a+5×4=15，解得m=﹣1，n=10，把m=﹣1，n=10代入代数式，可得：原式=91．【点评】本题考查了二元一次方程的解，根据题意列出方程式解题的关键．19．某市球类运动协会为了筹备一次大型体育活动，购进了一定数量的体育器材，器材管理员对购买的部分器材进行了统计，图表和图是器材管理员通过采集数据后，绘制的两幅不完整的频率分布表与频数分布直方图．请你根据图表中提供的信息，解答以下问题：频率分布表器材种类频数频率排球20乒乓球拍50 0.50篮球25 0.25足球合计 1（1）填充频率分布表中的空格．（2）在图中，将表示“排球”和“足球”的部分补充完整．（3）若该协会购买这批体育器材时，篮球和足球一共花去950元，且足球每个的价格比篮球多10元，现根据筹备实际需要，准备再采购篮球和足球这两种球共10个（两种球的个数都不能为0），计划资金不超过320元，试问该协会有哪几种购买方案？【分析】（1）根据乒乓球的总数为50，频数为0.50，求出体育器材总数，然后减去乒乓球、排球、篮球数目，即可得到足球频数、频率及合计数．（2）根据统计表中的数据，将统计图补充完整即可．（3）列方程求出篮球和足球的单价，再根据单价列出不等式，推知购买方案．【解答】解：（1）50÷0.50=100个；则足球有100﹣20﹣50﹣25=5个；足球频率=0.05；排球频率=0.2；合计为100．故答案为：0.2；5，0.05；100．（2）如图：．（3）设篮球每个x元，足球每个（x+10）元，列方程得，25x+5（x+10）=950，解得x=30，则篮球每个30元，足球每个40元．设再买y个篮球，列不等式得，30y+40（10﹣y）≤320，解得y≥8，由于篮球足球共10个，则篮球8个，足球2个；或篮球9个，足球1个．【点评】本题考查了频数分布表、频数分布直方图及一元一次方程的应用，从图中得到相关信息是解题的关键．20．某中学计划从办公用品公司购买A，B两种型号的小黑板．经洽谈，购买一块A型小黑板比购买一块B型小黑板多用20元，且购买5块A型小黑板和4块B型小黑板共需820元．（1）求购买一块A型小黑板、一块B型小黑板各需多少元．（2）根据该中学实际情况，需从公司购买A，B两种型号的小黑板共60块，要求购买A，B两种型号小黑板的总费用不超过5240元．并且购买A型小黑板的数量不小于购买B型小黑板数量的．则该中学从公司购买A，B两种型号的小黑板有哪几种方案？哪种方案的总费用最低？【分析】（1）设购买一块A型小黑板需要x元，一块B型为y元，根据等量关系：购买一块A型小黑板比买一块B型小黑板多用20元；购买5块A型小黑板和4块B型小黑板共需820元；可列方程组求解．（2）设购买A型小黑板m块，则购买B型小黑板（60﹣m）块，根据需从公司购买A、B 两种型号的小黑板共60块，要求购买A、B两种型号小黑板的总费用不超过5240元．并且购买A型小黑板的数量不小于购买B型小黑板数量的，可列不等式组求解．【解答】解：（1）设一块A型小黑板x元，一块B型小黑板y元．则，解得．答：一块A型小黑板100元，一块B型小黑板80元．（2）设购买A型小黑板m块，则购买B型小黑板（60﹣m）块则，解得20≤m≤22，又∵m为正整数∴m=20，21，22则相应的60﹣m=40，39，38∴共有三种购买方案，分别是方案一：购买A型小黑板20块，购买B型小黑板40块；方案二：购买A型小黑板21块，购买B型小黑板39块；方案三：购买A型小黑板22块，购买B型小黑板38块．方案一费用为100×20+80×40=5200元；方案二费用为100×21+80×39=5220元；方案三费用为100×22+80×38=5240元．∴方案一的总费用最低，即购买A型小黑板20块，购买B型小黑板40块总费用最低，为5200元．【点评】本题考查理解题意的能力，关键根据购买黑板块数不同钱数的不同求出购买黑板的钱数，然后要求购买A、B两种型号小黑板的总费用不超过5240元．并且购买A型小黑板的数量不小于购买B型小黑板数量的，列出不等式组求解．21．我们用[a]表示不大于a的最大整数，例如：[2.5]=2，[3]=3，[﹣2.5]=﹣3；用＜a＞表示大于a的最小整数，例如：＜2.5＞=3，＜4＞=5，＜﹣1.5＞=﹣1．解决下列问题：（1）[﹣4.5]=﹣5，＜3.5＞=4．（2）若[x]=2，则x的取值范围是2≤x＜3；若＜y＞=﹣1，则y的取值范围是﹣2≤y＜﹣1．（3）已知x，y满足方程组，求x，y的取值范围．【分析】（1）根据题目所给信息求解；（2）根据[2.5]=2，[3]=3，[﹣2.5]=﹣3，可得[x]=2中的2≤x＜3，根据＜a＞表示大于a 的最小整数，可得＜y＞=﹣1中，﹣2≤y＜﹣1；（3）先求出[x]和＜y＞的值，然后求出x和y的取值范围．【解答】解：（1）由题意得，[﹣4.5]=﹣5，＜3.5＞=4；（2）∵[x]=2，∴x的取值范围是2≤x＜3；∵＜y＞=﹣1，∴y的取值范围是﹣2≤y＜﹣1；（3）解方程组得：，∴x，y的取值范围分别为﹣1≤x＜0，2≤y＜3．【点评】本题考查了一元一次不等式组的应用，解答本题的关键是读懂题意，根据题目所给的信息进行解答．22．如图，已知直线AC∥BD，直线AB、CD不平行，点P在直线AB上，且和点A、B 不重合．（1）如图①，当点P在线段AB上时，若∠PAC=20°，∠PDB=30°，求∠CPD的度数；（2）当点P在A、B两点之间运动时，∠PCA、∠PDB、∠CPD之间满足什么样的等量关系？（直接写出答案）（3）如图②，当点P在线段AB延长线运动时，∠PCA、∠PDB、∠CPD之间满足什么样的等量关系？并说明理由．【分析】（1）如图①，过P点作PE∥AC交CD于E点，由于AC∥BD，则PE∥BD，根据平行线的性质得∠CPE=∠PCA=20°，∠DPE=∠PDB=30°，所以∠CPD=50°；（2）证明方法与（1）一样；（3）如图②，过P点作PF∥BD交CD于F点，由于AC∥BD，则PF∥AC，根据平行线的性质得∠CPF=∠PCA，∠DPF=∠PDB，所以∠CPD=∠PCA﹣∠PDB．【解答】解：（1）如图①，过P点作PE∥AC交CD于E点，∵AC∥BD∴PE∥BD，∴∠CPE=∠PCA=20°，∠DPE=∠PDB=30°，∴∠CPD=∠CPE+∠DPE=50°；（2）∠CPD=∠PCA+∠PDB（证明方法与（1）一样；（3）∠CPD=∠PCA﹣∠PDB．理由如下：如图②，过P点作PF∥BD交CD于F点，∵AC∥BD，∴PF∥AC，∴∠CPF=∠PCA，∠DPF=∠PDB，∴∠CPD=∠CPF﹣∠DPF=∠PCA﹣∠PDB；【点评】本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．合理添加平行线是解决此题的关键．。

七年级下册语文期末试卷(必考题)

七年级下册语文期末试卷（必考题）满分：120分考试时间：120分钟一、语言的积累与运用。

（35分）1、汉字积累——下列字形和加点字注音全部正确的一项是（）A．中．伤（zhōng）澄澈酝酿．（liàng）咄咄逼人B．缥．缈（piāo）陛下抖擞．（sǒu）人声鼎沸C．忙碌．（lǜ）静谧充沛．（pèi）浑为一谈D．蜷．伏（quán）苛刻笨拙．（zhuó）花枝招绽2、下列各组词语书写无误的一项是( )A．摧枯拉朽记忆尤新惨绝人寰延续B．苍海桑田风华正茂色彩斑斓镌刻C．天翻地覆恢宏壮丽殚精竭虑缅怀D．从容不迫眼花瞭乱震耳欲聋由衷3、下面加点词语运用不正确的一项是（）A．鸟儿将巢安在繁花嫩叶当中，高兴起来了，呼朋引伴．．．．地卖弄清脆的喉咙，唱出宛转的曲子，与轻风流水应和着．B．矮胖老师站在讲台上，双目含笑，右嘴角微微斜翘，胖脸上一副狂妄自大．．．．的表情．C．突然间，我恍然大悟．．．．，有股神奇的感觉在我脑中激荡，我一下子理解了语言文字的奥秘了．D．可我却一直都不知道，她的病已经到了那步田地．后来妹妹告诉我，她常常肝疼得整宿整宿翻来覆去．．．．地睡不了觉．4、下列句子中，没有语病的一项是（）A．随着网络时代的来临，催生了世界大国战略博弈的新格局。

B．未成年学生玩手机的危害应该得到有效引导和管理。

C．我国拟把足球学习情况纳入学生档案，作为学生综合素质评价的参考。

D．通过考古发掘、征集和捐赠，甘肃省博物馆获得历史文物藏品近82 000多件。

5、下列各句修辞手法与其他三项不同的是（）A．树尖上顶着一髻儿白花，好像日本看护妇。

B．那点儿薄雪好像忽然害了羞，微微露出点儿粉色。

C．他们全安静不动地低声地说：“你们放心吧，这儿准保暖和。

”D．一个老城，有山有水，全在蓝天下很暖和安适地睡着，只等春风来把他们唤醒。

6、下列句子组成语段顺序排列正确的一项是（）①窗外的竹子或青山，经过窗子的框框望出，就是一幅画。

七下期末检测题

期末检测题一、选择题（每小题2分，共30分）1、有人说：“隋朝，犹如一颗流星划过历史的夜空，时间虽然短暂却光芒四射。

”请你计算一下，隋朝从建立到最后的灭亡，前后仅经历了：A、36年B、37年C、28年D、29年2、在唐太宗、武则天和唐玄宗三朝治国措施的共同点是重视人才、任用贤能。

下面历史人物中哪些是在唐玄宗时被提拔担任宰相的①房玄龄②杜如晦③魏征④姚崇⑤宋暻A、①②B、③④⑤C、①②③D、④⑤3、下列关于唐朝与少数民族关系叙述正确的是A．文成公主入藏，密切了唐与吐蕃的关系B．唐太宗封粟末靺鞨首领为渤海郡王C. 唐玄宗册封南诏首领为怀仁可汗D．帮助唐朝平定安史之乱的回纥是今天回族的祖先4、我国诗歌创作的黄金时代是A．先秦时期B．唐朝C．秦汉时期D．宋朝5、下列我国古代科技成就中，两项都属于同一个领域的一组是A、《千金方》和《本草纲目》B、《水经注》和《农政全书》C、《缀术》和《天工开物》D、《齐民要术》和《本草纲目》6、下列四幅古代绘画作品中，内容题材与当时社会商业繁荣无关的是7、“赵州桥什么人儿修？玉石栏杆什么人留？什么人骑驴桥上走？什么人推车轧了一道沟？赵州桥鲁班爷修……”这是河北民歌《小放牛》的歌词，它是根据当地民间传说编成的，并广泛流传到今天。

其实，赵州桥并不是鲁班修建的，它的设计和主持建造者是A、祖冲之B、贾思勰C、僧一行D、李春8、梁山好汉黑旋风李逵与兄弟逛街，这条街上有人说书、唱曲、卖饮料、相面算卦、杂耍、表演等等。

请问他们走到了当时被称为什么的地方A、专门制造房瓦的瓦厂B、食客盈门的酒楼C、娱乐兼营商业的瓦子D、好汉比武的擂台9、“起朔漠，并西域，平西夏，灭女真，臣高丽，定南诏，遂下江南，而天下为一，”这一史书记载反映的是下列哪个王朝的兴起？A．宋B．元C．明D．清10、一位生活在元朝的商人，他不可能有的经历是A．去江南贩运棉布B．经运河到杭州游览C．友人送他一部《红楼梦》D．购买景德镇真花瓷器11、“司马光砸缸”的故事，在民间广为流传，司马光后来“臣之精力，尽于此书”，此书是A．《史记》B．《资治通鉴》C．《宋书》D．《二十四史》12、抒发民族英雄戚继光爱国情怀的诗句是A．“人生自古谁无死，留取丹心照汗青”B．“醉里挑灯看剑，梦回吹角连营”C．“封侯非我意，但愿海波平”D．“文臣不爱钱，武臣不惜死，天下太平矣”13、明长城的东西起点是A．临洮和陇西B．鸭绿江和嘉峪关C．余杭和涿郡D．临清和东平14、代表清朝中央政府同达赖共同管理西藏事务的是A、盛京将军B、伊犁将军C、乌理雅苏台D、驻藏大臣15、一首《七子之歌·澳门》唱出了澳门人民渴望回归祖国的强烈心愿。