浙江省2019高考数学课时跟踪检测(十五)大题考法——圆锥曲线中的最值、范围、证明问题

合集下载

专题23 圆锥曲线中的最值、范围问题微点1 圆锥曲线中的最值问题试题及答案

题型四、与面积有关的最值问题
例7．
7．已知点A(−2,0)，B(2,0)，动点M(x,y)满足直线AM与BM的斜率之积为− .记M的轨迹为曲线C.
（1）求C的方程，并说明C是什么曲线；
（2）过坐标原点的直线交C于P，Q两点，点P在第一象限，PE⊥x轴，垂足为E，连结QE并延长交C于点G.
（i）证明：是直角三角形；
最值问题不仅解答题中分量较大，而且客观题中也时常出现．
一、常用方法
解决圆锥曲线中的最值问题，常见的方法有：
（1）函数法：一般需要找出所求几量的函数解析式，要注意自变量的取值范围．求函数的最值时，一般会用到配方法、均值不等式或者函数单调性．
（2）方程法：根据题目中的等量关系建立方程，根据方程的解的条件得出目标量的不等关系，再求出目标量的最值．
题型三、与向量有关的最值问题
例6．
6．如图，已知椭圆C1：＋＝1(a>b>0)的右焦点为F，上顶点为A，P为椭圆C1上任一点，MN是圆C2：x2＋(y－3)2＝1的一条直径，在y轴上截距为3－的直线l与AF平行且与圆C2相切．
(1)求椭圆C1的离心率；
(2)若椭圆C1的短轴长为8，求 · 的最大值．
题型二、与角度有关的最值问题
例5．
5．在平面直角坐标系中，椭圆：的离心率为，焦距为 .
（Ⅰ）求椭圆的方程；
（Ⅱ）如图，动直线：交椭圆于两点，是椭圆上一点，直线的斜率为，且，是线段延长线上一点，且，的半径为，是的两条切线，切点分别为 .求的最大值，并求取得最大值时直线的斜率.
专题23 圆锥曲线中的最值、范围问题微点1 圆锥曲线中的最值问题
专题23圆锥曲线中的最值、范围问题

2019届高三数学备考冲刺140分问题35圆锥曲线中的最值、范围问题(含解析)_9895

问题 35 圆锥曲线中的最值、范围问题一、考情分析与圆锥曲线有关的范围、最值问题 , 各种题型都有 , 既有对圆锥曲线的性质、曲线与方程关系的研究 , 又对最值范围问题有所青睐 , 它能综合应用函数、三角、不等式等有关知识 , 紧紧抓住圆锥曲线的定义进行转化, 充分展现数形结合、函数与方程、化归转化等数学思想在解题中的应用．二、经验分享1. 解决圆锥曲线中的取值范围问题应考虑的五个方面(1) 利用圆锥曲线的几何性质或判别式构造不等关系，从而确定参数的取值范围；(2) 利用已知参数的范围，求新参数的范围，解这类问题的核心是建立两个参数之间的等量关系；(3) 利用隐含的不等关系建立不等式，从而求出参数的取值范围；(4) 利用已知的不等关系构造不等式，从而求出参数的取值范围；(5) 利用求函数的值域的方法将待求量表示为其他变量的函数，求其值域，从而确定参数的取值范围．2. 处理圆锥曲线最值问题的求解方法圆锥曲线中的最值问题类型较多，解法灵活多变，但总体上主要有两种方法：一是利用几何法，即通过利用曲线的定义、几何性质以及平面几何中的定理、性质等进行求解；二是利用代数法，即把要求最值的几何量或代数表达式表示为某个 ( 些 ) 参数的函数 ( 解析式 ) ，然后利用函数方法、不等式方法等进行求解．三、知识拓展1.x 2 y 21 a b0 一点， F 是该椭圆焦点，则b OP a, ac PF a c；已知 P 是椭圆 C ：b 2a 22. 已知 P 是双曲线 C ：x 2y 2 1 a 0, b 0 一点， F 是该椭圆焦点，则 OP a, PFc a ；双曲线a 2b 22b 2.C 的焦点弦的最小值为2a,amin四、题型分析( 一 ) 利用圆锥曲线定义求最值借助圆锥曲线定义将最值问题等价转化为易求、易解、易推理证明的问题来处理．22 【例 1】已知 A(4，0), B(2， 2) 是椭圆xy1 内的两个点 , M 是椭圆上的动点 , 求 MA MB 的最大值259和最小值．【分析】很容易想到联系三角形边的关系, 无论 A、M 、B 三点是否共线,总有 MA MB AB ,故取不到等号 , 利用椭圆定义合理转化可以起到柳暗花明又一村的作用．【解析】由已知得 A(4，0) 是椭圆的右焦点,设左焦点为F( 4，0) 根据椭圆定义得MA MB =2a MF MB 10 MB MF ,因为MB MF FB 2 10 ,所以MB MF [ 2 10, 2 10] ,故MA MB 的最小值和最大值分别为 10 2 10 和10 2 10 .【点评】涉及到椭圆焦点的题目, 应想到椭圆定义转化条件, 使得复杂问题简单化．【小试牛刀】【山东省济宁市2019 届高三第一次模拟】已知双曲线分别为，实轴长为4，渐近线方程为，点N在圆的左、右焦点上，则的最小值为 ( )A．B． 5 C． 6 D． 7 【答案】 B【解析】由题意可得2a＝4，即 a＝ 2，渐近线方程为y＝± x，即有，即 b＝ 1，可得双曲线方程为y2＝ 1，焦点为 F1（，0），F2，（， 0），由双曲线的定义可得1 2 2 |MF | ＝2a+|MF | ＝ 4+|MF | ，由圆 x2+y2﹣ 4y＝ 0 可得圆心 C（0， 2），半径 r ＝ 2，|MN|+|MF 1| ＝ 4+|MN|+|MF 2| ，连接 CF2，交双曲线于 M，圆于 N，可得 |MN|+|MF 2| 取得最小值，且为 |CF 2| 3，则则 |MN|+|MF 1| 的最小值为 4+3﹣ 2＝ 5．故选： B．( 二 ) 单变量最值问题转化为函数最值建立目标函数求解圆锥曲线的范围、最值问题, 是常规方法 , 关键是选择恰当的变量为自变量．【例 2】已知椭圆 C ：x 2y 2 1 a b 0 的两焦点与短轴的一个端点的连线构成等腰直角三角形, 直线a 2b 2x y 1 0 与以椭圆 C 的右焦点为圆心 , 以椭圆的长半轴长为半径的圆相切 .（ 1）求椭圆的方程 .（ 2）设 P 为椭圆上一点 , 若过点 M (2,0) 的直线 l 与椭圆 E 相交于不同的两点 S 和T ,且满足OS OTtOP (O 为坐标原点 ), 求实数 t 的取值范围 .【分析】（1）由题意可得圆的方程为 (xc)2y2a 2, 圆心到直线 x y1 0 的距离 d c 1 a ；2根据椭圆 C : x2y 21(a b 0) 的两焦点与短轴的一个端点的连线构成等腰直角三角形, b=c,a 2b 2a 2b 2c 代入 * 式得 b c 1, 即可得到所求椭圆方程；（Ⅱ）由题意知直线 L 的斜率存在 , 设直线 L方程为 y k (x 2) , 设 p x 0 , y 0 , 将直线方程代入椭圆方程得：1 2k2 x 28k 2 x 8k 22 0 ,根据64k44 1 2k 2 8 k2216k28 0得到 k 21；设 S x 1 , y 1 , T x 2 , y 2 应用韦达定理2x 1 x 28k 22 , x 1x 28k 2 2t 0 的情况 , 确定 t 的不等式 .1 2k 1 2k2 . 讨论当 k=0,【解析】（ 1）由题意：以椭圆 C 的右焦点为圆心 , 以椭圆的长半轴长为半径的圆的方程为( x c) 2 y 2a 2 ,xy1c 1∴圆心到直线 0 的距离 da *2∵椭圆 C : x2y 2 1(a b 0) 的两焦点与短轴的一个端点的连线构成等腰直角三角形, b=c,a 2b 2a 2b 2c 代入 * 式得b c 1 ∴ a 2b 2故所求椭圆方程为x 2 y 2 1.2（Ⅱ）由题意知直线L 的斜率存在,设直线 L 方程为y k( x 2) ,设 p x0 , y0 将直线方程代入椭圆方程得： 1 2k 2 x 2 8k 2 x 8k 2 2 0∴64k 4 4 1 2 2 8k2 2 16k2 8 0k∴ k2 12设 S x1 , y1 , T x2 , y2 则 x1 x2 8k 2, x1 x28k 2 28 分1 2k 2 1 2k 2当 k=0 时 , 直线 l 的方程为 y=0, 此时 t=0, OS OT t OP 成立,故,t=0符合题意. 当 t 0 时tx 0 x 1 x 28 k 21 2 k 24 k得ty 0 y 1 y 2 k ( x1 x 2 4 )1 2 k 21 21 4k∴x0 8k 2 , y0t 1 t 1 2k 22k将上式代入椭圆方程得：32k 4 16k 21 t2 (1 2k 2 ) 2 t 2 (1 2k 2 ) 2整理得： t 2 16k 21 2k 2由 k 2 1 知 0 t 2 42所以 t （2，2）【点评】确定椭圆方程需要两个独立条件, 从题中挖掘关于a、 b、c 的等量关系；直线和椭圆的位置关系问题 , 往往要善于利用韦达定理设而不求, 利用点P在椭圆上和向量式得t f (k) ,进而求函数值域．【小试牛刀】【吉林省吉林市2018 届高三第三次调研】已知椭圆C : x2 y2 3 ，a2 b2 1(a b 0) 的离心率是 2且椭圆经过点0,1 ．（ 1）求椭圆 C 的标准方程；（ 2）若直线 l 1 ： x 2 y 20 与圆 D : x 2 y 2 6x 4 y m 0 相切：（ⅰ）求圆 D 的标准方程；（ⅱ）若直线 l 过定点，，与椭圆 C 交于不同的两点 E, F ，与圆 D 交于不同的两点 M , N ，求 ·23 0EF MN 的取值范围．【解析】(1)椭圆经过点0,1 ，1 1，解得 b 2 1，b 2e3 ,c3 ，2a 23a 24c 2 4 a21 ，解得 a2 4 ∴椭圆 C 的标准方程为 x 2y 2 14(2) (i)圆 D 的标准方程为 x2y 22m , 圆心为 3,2 ，313∵直线 l 1 ： x2y2 0与圆 D 相切，∴圆 D 的半径 r 3 2 225 ,5∴圆 D 的标准方程为 x2y2 25．3（ⅱ）由题可得直线 l 2 的斜率存在 , 设 l 2方程为 y k x3 ,y k x 34k 2 x 2 24k 2 x 36k 2由 { x 2y 2消去 y 整理得 14 0 ，41∵直线 l 2 与椭圆 C 交于不同的两点 E,F ，∴24k224 1 4k236k 2416 1 5k20，解得 0 k 21 ．5设 E x 1 , y 1 , F x 2 , y 2 ,则 x 1x 224k 2 2, x 1x236k 244k 1 4k 2,12221 k 21 5k 2EF1 k2x 1 x 2 24x 1 x 21 k224k4 36k4∴44k2，1 4k 21 4k 21 2又圆 D 的圆心 3,2 到直线 l 2 : kxy 3k 0 的距离 d3k 2 3k2,k 2 1 k 21∴圆 D 截直线 l 2 所得弦长 MN2 r2d22 5k 21 ,k 211 k2 1 5k22 5k 2 11 25k 4EF ·MN 42k 2 82，1 4k 211 4k 2设 t 14k21,9,5则 k 2t 4 1 ,21 25 t 121EF ·MN842150t 2925 ,tt1,912501∵ t，∴ 9 250,16 ，5tt∵ EF ·MN 的取值范围为 0,8 ．( 三 ) 二元变量最值问题转化为二次函数最值利用点在二次曲线上 , 将二元函数的最值问题转化为一元函数的最值问题来处理．【例 2】若点 O 、F 分别为椭圆x 2y 2 1 的中心和左焦点 , 点 P 为椭圆上的任一点 , 则 OP PF 的最大值为43【分析】设点 P （ x ， y ）, 利用平面向量数量积坐标表示 , 将 OP PF 用变量 x ， y 表示 , 借助椭圆方程消元 , 转化为一元函数的最值问题处理．22【解析】设, 则 OP PF =22xyP （ x ， y ）（ x ，y ）（ x 1，y ） x xy , 又点 P 在椭圆上 , 故1, 所以432 x （3 2 2 x 3 1 2 2 ,又- 2≤x≤2,所以当x=2时, 1 x 2 2x 3 x ） 1 x x 2 2 取得最大值为4 4 4 46, 即OP PF的最大值为6, 故答案为： 6．【点评】注意利用“点在椭圆上”这个条件列方程．【小试牛刀】【湖南省益阳市2019 届高三上学期期末】已知定点及抛物线上的动点，则（其中为抛物线的焦点）的最大值为（）A．2 B．C．D．3【答案】 C【解析】方法一：作准线于，则.设倾斜角为，则. 当与相切时，取最大值，由代入抛物线得，，解得或. 故最大值为4，即最大值为 5. 即最大值为. 故选.方法二：作准线于，则，设，，，则，则取最大值，只需取最大值，又表示的斜率，所以取最大值时，直线与抛物线相切，由代入抛物线得，，解得或.故最大值为4，即最大值为 5.即最大值为.故选.( 四 )双参数最值问题该类问题往往有三种类型：①建立两个参数之间的等量关系和不等式关系, 通过整体消元得到参数的取值范围；②建立两个参数的等量关系, 通过分离参数, 借助一边变量的范围, 确定另一个参数的取值范围；③建立两个参数的等量关系, 通过选取一个参数为自变量, 令一个变量为参数（主元思想）, 从而确定参数的取值范围．【例 3】在平面直角坐标系xOy中 , 已知椭圆C：x2y2 1(a＞ b≥1) 的离心率e3 , 且椭圆 C上一点Na 2 b2 2到点 Q（0，3）的距离最大值为 4, 过点M（3,0）的直线交椭圆C于点A、B.（Ⅰ）求椭圆C的方程；（Ⅱ）设 P 为椭圆上一点 , 且满足 OA OB tOP （ O为坐标原点） , 当AB＜ 3 时,求实数t的取值范围. 【分析】第一问 , 先利用离心率列出表达式找到 a 与b的关系,又因为椭圆上的N 点到点Q的距离最大值为4, 利用两点间距离公式列出表达式, 因为N在椭圆上 , 所以x2 4b2 4 y2 , 代入表达式 , 利用配方法求最大值 , 从而求出b2 1,所以 a2 4 ,所以得到椭圆的标准方程；第二问, 先设A, P, B点坐标 , 由题意设出直线 AB方程, 因为直线与椭圆相交, 列出方程组 , 消参韦达定得到两根之和、两根之积, 用坐标表示OA OB tOP 得出x, y,由于点P 在椭圆上,得到一个表达式,再由 | AB | 3,得到一个表达式,2个表达式联立 , 得到t的取值范围 .【解析】（Ⅰ）∵ e2 c2 a2 b2 3 , ∴ a2 4b2 ,a2 a2 4则椭圆方程为x2 y2 1, 即 x2 4 y2 4b2.4b2 b2设 N (x, y), 则NQ ( x 0)2 ( y 3)2 4b2 4 y2 ( y 3)23 y2 6 y 4b2 9 3( y 1)2 4b2 12当 y 1 时,NQ有最大值为4b2 12 4,解得b 21,∴a 24 , 椭圆方程是x 24y 21（Ⅱ）设A( x 1, y 1), B( x 2, y 2 ), P( x, y), AB 方程为yk( x3),y k ( x 3),2 222由整得 (14 0 .x 2y24k )x24k x36k1,4由24k 2k416(9k21)(1 4k 2 )＞0 , 得 k 2＜1.5x 1 x 224k 2 2 , x1x 236k 2 24.1 4k14k∴OA OB (x 1 x 2 , y 1 y 2 )t ( x, y), 则 x1(x 1 x 2 ) 24 k 2 2 ) ,tt (1 4ky1( y 1 y 2 )1k ( x 1 x 2 ) 6k6k 2 .ttt(1 4k )由点 P 在椭圆上 , 得(24 k 2 ) 2 144k 2 4, 化简得 36k 2 t 2 (1 4k 2 ) ①t 2 (1 4k 2 ) 2 t 2 (1 4k 2 )2又由 AB1 k2 x 1 x 2 ＜ 3, 即 (1 k 2 ) ( x 1 x 2 )2 4x 1 x 2 ＜3, 将 x 1 x 2 , x 1 x 2 代入得 (1 k 2 )242 k 44(36k 2 4) ＜3, 化简 , 得 (8k 2 1)(16k 213)＞0,(1 4k 2 ) 21 4k 2则 8k21＞0, k 2＞ 1,∴ 1＜ k 2＜ 1②88 5由① , 得 t 236k 2 9 1 9 ,1 4k2 4k 2联立② , 解得 3＜ t 2＜ 4, ∴ 2＜ t ＜3 或 3＜ t ＜2.【点评】第一问中转化为求二次函数最大值后 , 要注意变量取值范围；第二问利用点 P 在椭圆上 , 和已知向量等式得变量 k, t 的等量关系 , 和变量 k,t 的不等关系联立求参数t的取值范围．222M : x22r 2( r0) , 若椭圆 C :x2y1( a b 0) 的右顶点为圆 M【小试牛刀】已知圆y 2ab的圆心 , 离心率为2. 2（1）求椭圆C的方程；（2）若存在直线l : y kx , 使得直线l与椭圆C分别交于A, B两点 , 与圆M分别交于G, H两点 , 点G在线段 AB 上,且AG BH ,求圆M的半径r的取值范围.【解析】（1）设椭圆的焦距为2c, 因为a2, c 2, c 1, b 1 a 2所以椭圆的方程为 C : x2 y 2 1.2（2）设A( x1, y1), B( x2, y2) ,联立方程得y kxx2 2 y 2 2 0所以 (1 2k2 )x2 2 0x1 x2 0, x1 x221 2k 2则AB (1 k 2 ) 8 8(1 k 2 )1 2k2 1 2k 22k 2 r 2 2k 2又点 M ( 2 ,0) 到直线l的距离d , 则 GH1 k2 1 k 2显然 , 若点H也在线段AB上 , 则由对称性可知 , 直线y kx 就是y轴,与已知矛盾,所以要使AG BH, 只要 AB GH ,所以8(1 k 2 )4( r 22k 21 2k2 1 k 2)22k 2 2(1 k 2 ) 2 2(3k 4 3k 2 1) k 4r 1 k 2 1 2k 2 1 2k 2 2k 4 3k 2 1 2(1 2k 4 3k 2 1 ) 当 k 0 时, r 2 .当 k 0 时, r 2 2(11 1 ) 2(1 1 ) 3, 322k 4 k2又显然 r 2 2(11 1 )2 , 所以 2 r3 . 32k 4 k 2综上 , 圆M的半径r的取值范围是[ 2, 3).圆锥曲线中的最值、范围问题类型较多, 解法灵活多变 , 但总体上主要有两种方法：一是利用几何方法, 即通过利用曲线的定义、几何性质以及平面几何中的定理、性质等进行求解；二是利用代数方法, 即把要求最值的几何量或代数表达式表示为某个( 些 ) 参数的函数 ( 解析式 ), 然后利用函数方法、不等式方法等进行求解．四、迁移运用1．【湖南省浏阳一中、醴陵一中2019 联考】在椭圆上有两个动点，为定点，，则的最小值为 ( )．A． 4 B．C．D． 1【答案】 C【解析】由题意得．设椭圆上一点，则，∴，又，∴当时，取得最小值．故选 C．2．【湖南省怀化市2019 届高三 3 月第一次模拟】过抛物线的焦点作两条互相垂直的弦，，则四边形面积的最小值为（）A． 8 B． 16 C． 32 D． 64【答案】 C【解析】显然焦点的坐标为，所以可设直线的方程为，代入并整理得，所以，，同理可得，所以故选 C.3.【河北省张家口市N，设，2019 期末】已知抛物线，且C：，过点的直线l与抛物线时，则直线MN斜率的取值范围是C交于不同的两点M，A．B．C．D．【答案】 A【解析】设直线l 的方程为将直线 l 的方程与抛物线C的方程联立，则，设点，消去x 得，、，由韦达定理得．．所以，，所以，将式代入韦达定理得x 轴为的角平分线，，，所以，，则，所以，，，所以，．设直线 MN的斜率为 k，则即，所以，，解得或．故选： A．4．【浙江省宁波市 2019 届高三上学期期末】已知椭圆直线交椭圆于点为坐标原点且的离心率，则椭圆长轴长的取值范围是（的取值范围为），A． B ． C ． D ．【答案】 C【解析】联立方程得，设，，则，由，得，∴，化简得，∴，化简得，∵，∴，∵，∴，∴，∴，∴，∴，∴，∴，即椭圆的长轴长的取值范围为，故选 C．5．【江西省红色七校2019 届高三第二次联考】定长为为线段 MN的中点，则点P 到 y 轴距离的最小值为( A．B．1C．D．4 的线段)MN的两端点在抛物线上移动，设点P【答案】 D【解析】由抛物线方程得，准线方程为，设，根据抛物线的定义可知，到轴的距离，当且仅当三点共线时，能取得最小值，此时. 故选 D.6．【四川省泸州市2019 届高三第二次教学质量诊断】已知，若点是抛物线上任意一点，点是圆上任意一点，则的最小值为A．3 B．4C．5D．6【答案】 B【解析】抛物线的焦点，准线：，圆的圆心为，半径，过点作垂直准线，垂足为，由抛物线的定义可知，则，当三点共线时取最小值，．即有取得最小值 4，故选 B．7．【安徽省合肥一中、马鞍山二中等六校教育研究会2019 届高三第二次联考】已知抛物线上一点到焦点的距离为，分别为抛物线与圆上的动点，则的最小值为（）A． B ． C ． D ．【答案】 D【解析】由抛物线焦点在轴上，准线方程，则点到焦点的距离为，则，所以抛物线方程：，设，圆，圆心为，半径为1，则当时，取得最小值，最小值为故选 D.8．【河南省郑州市2019 届高中毕业年级第一次为抛物线上的两个动点，且满足的最小值为A．B．1C．D．2，，（ 1 月 ) 质量预测】抛物线，过弦的中点作该抛物线准线的垂线的焦点为，垂足为，已知点，则【答案】 B【解析】设| AF|＝ a，| BF|＝ b，由抛物线定义，得| AF| ＝| AQ|，| BF|＝| BP|在梯形ABPQ中，∴2| CD|＝|AQ|+|BP|＝ a+b．由余弦定理得，| AB| 2＝a2+b2﹣ 2ab cos60°＝a2+b2﹣ab配方得， | AB| 2＝（a+b）2﹣ 3ab，又∵ ab≤（）2，∴（ a+b）2﹣3ab≥（ a+b） 2 （ a+b） 2 （a+b） 2 得到 | AB| （ a+b）＝| CD|．∴1，即的最小值为1．故选： B．9．已知抛物线y2 8x ,点Q是圆 C : x2 y 2 2x 8 y 13 0 上任意一点 , 记抛物线上任意一点到直线x 2的距离为d , 则PQ d的最小值为（）A． 5 B ． 4 C．3 D．2【答案】 C【解析】如图所示 , 由题意知 , 抛物线y28x的焦点为F (2, 0), 连接PF , 则d PF．将圆 C 化为(x 1)2 ( y 4) 2 4,圆心为C( 1,4半径为r 2 , 则PQ d PQ PF,于是由,PQ PF FQ（当且仅当F ,P,Q三点共线时取得等号）．而FQ为圆 C 上的动点Q到定点 F 的距离,显然当 F ,Q,C 三点共线时取得最小值 , 且为CFr ( 1 2)2 (4 0)2 23,故应选C．10．【福建省龙岩市2019 届高三下学期教学质量检查】已知抛物线为，过点作直线与抛物线交于两点．若以为直径的圆过点【答案】 4 ，则的焦点为，其准线与轴的交点的值为 ________．【解析】假设k 存在，设 AB方程为： y＝ k（ x﹣1），与抛物线 y2＝4x 联立得 k2（ x2﹣2x+1）＝4x，即 k2x2﹣（2k2+4） x+k2＝0设两交点为A（ x2， y2）， B（ x1， y1），∵以为直径的圆过点,∴∠ QBA＝90°，∴（ x1﹣2）（ x1+2）+y12＝0，∴x12+y12＝4，2∴ x1+4x1﹣1＝0（ x1＞0），∴ x12，∵x1x2＝1，∴ x22，∴| AF| ﹣ | BF| ＝（x2+1）﹣（x1+1）＝ 4，故答案为： 411．【辽宁省沈阳市东北育才学校2019 届高三第五次模拟】抛物线的焦点为，设是抛物线上的两个动点，若，则的最大值为____________.【答案】【解析】由是抛物线上的两个动点，得又，所以，在中，由余弦定理得：，又，即，所以，因此的最大值为.故答案为12．【江西省九江市2019 届高三第一次高考模拟】已知抛物线的焦点F，过F 的直线与抛物线交于A，B 两点，则的最小值是______．【答案】18【解析】抛物线y2＝8x 的焦点 F（2，0），， 2），则| |+4| | ＝1+2+4（+2）＝+4 +10，设（1， 1 ），（2A x yB x y FA FB x当直线 AB斜率不存在时，| FA|+4| FB| ＝2+4×2+10＝ 20，当直 AB斜率存在时，设直线AB的方程为 y＝ k（ x﹣2），代入 y2＝8x 得 k2x2﹣（4k2+8） x+4k2＝0，∴＝4，∴ |FA|+4|FB| 4 +10≥210＝ 18，当且仅当 x1＝1时取等号．| FA|+4| FB| 的最小值是18．故答案为： 18．13．【山东省淄博市2018-2019 学年度 3 月高三模拟】已知抛物线：上一点，点是抛物线上的两动点，且，则点到直线的距离的最大值是 __________．【答案】【解析】设直线的方程为，，，联立直线的方程与抛物线方程，则有，即，，因为直线与抛物线方程有两个交点，所以，，，因为，所以，即，，解得或者，化简可得或者因为，所以，，所以直线的方程为，即，故直线过定点，当垂直于直线时，点到直线的距离取得最大值，最大值为，故答案为。

新高考方案二轮-数学(新高考版)大题专攻(二) 第1课时圆锥曲线中的最值、范围、证明问题

(2)已知 O 为坐标原点，M，N 为椭圆上不重合两点，且 M，N 的中点 H
落在直线 y＝12x 上，求△MNO 面积的最大值．
[解题微“点”]
(1)利用―A→G ·―B→G ＝0 及 e＝ 23构建方程组求 a，b，即得椭圆方程；切入点 (2)设出点 M，N 与 H 的坐标，表示出直线 MN 的方程，与椭圆联立，利用弦长公式和点到直线的距离公式表示△MNO 的面积后求最大值障碍点不要漏掉 Δ>0，利用此条件可求参数的取值范围
解：(1)依题意，2c＝6，则 b＝ 9－5＝2，
则双曲线 C：x52－y42＝1，B1(0，－2)，F2(3,0)．
设直线 l：4x＋3y＋m＝0，将 B1(0，－2)代入解得 m＝6，
此时 l：4x＋3y＋6＝0，F2 到 l 的距离为 d＝158.
(2)设双曲线上的点 P(x，y)满足―PB→1 ·―PB→2 ＝－2，即 x2＋y2＝b2－2，又xa22－by22＝1⇒y2＝ba22x2－b2，
[对点训练] (2021·济南三模)已知抛物线C：x2＝4y，过点P(1，－2)作斜率为k(k>0)的直线l1与抛物线C相交于A，B两点． (1)求k的取值范围； (2)过P点且斜率为－k的直线l2与抛物线C相交于M，N两点，求证：直线AM、BN 及y轴围成等腰三角形．
解：(1)由题意设直线 l1 的方程为 y＋2＝k(x－1)，由xy＋2＝24＝y，kx－1，得到：x2－4kx＋4k＋8＝0，由题意知 Δ>0，所以 k2－k－2>0，即 k<－1 或 k>2. 因为 k>0，所以 k 的取值范围为(2，＋∞)．
[提分技巧] 解决范围问题的常用方法
利用待求量的几何意义，确定出极端位置后，利数形结合法

圆锥曲线专题：最值与范围问题的6种常见考法(解析版)

圆锥曲线专题：最值与范围问题的6种常见考法一、圆锥曲线中的最值问题类型较多，解法灵活多变，但总体上主要有两种方法：1、几何法：通过利用曲线的定义、几何性质以及平面几何中的定理、性质等进行求解；2、代数法：把要求最值的几何量或代数表达式表示为某个(些)参数的函数(解析式)，然后利用函数方法、不等式方法等进行求解．二、最值问题的一般解题步骤三、参数取值范围问题1、利用圆锥曲线的几何性质或判别式构造不等关系，从而确定参数的取值范围；2、利用已知参数的范围，求新参数的范围，解这类问题的核心是建立两个参数之间的等量关系；3、利用隐含的不等关系建立不等式，从而求出参数的取值范围；4、利用已知的不等关系构造不等式，从而求出参数的取值范围；5、利用求函数的值域的方法将待求量表示为其他变量的函数，求其值域，从而确定参数的取值范围．题型一距离与长度型最值范围问题【例1】已知椭圆22221(0)x y a b a b+=>>的左、右焦点分别为1F 、2F ，焦距为2，点E 在椭圆上．当线段2EF 的中垂线经过1F 时，恰有21cos EF F ∠．（1）求椭圆的标准方程；（2）直线l 与椭圆相交于A 、B 两点，且||2AB =，P 是以AB 为直径的圆上任意一点，O 为坐标原点，求||OP 的最大值．【答案】（1）2212x y +=；（2）max ||OP 【解析】（1）由焦距为2知1c =，连结1EF ，取2EF 的中点N ，线段2EF 的中垂线经过1F 时，1||22EF c ∴==，221212cos ,.1,F N EF F F N F F ∠∴∴-2122,2EF a EF EF a ∴=-∴=+=∴由所以椭圆方程为2212x y +=；（2）①当l 的斜率不存在时，AB 恰为短轴，此时||1OP =；②当l 的斜率存在时，设:l y kx m =+．联立2212x y y kx m ⎧+=⎪⎨⎪=+⎩，得到222(21)4220k x kmx m +++-=，∴△2216880k m =-+>，122421km x x k -+=+，21222221m x x k -=+．21AB x x =-=2==，化简得2222122k m k +=+．又设M 是弦AB 的中点，121222()221my y k x x m k +=++=+∴()2222222241,,||212121km m k M OM k k k m -+⎛⎫= ⎪⎝⎭+⋅++,∴()()()222222222412141||22212221k k k OM k k k k +++=⋅=++++,令2411k t += ，则244||43(1)(3)4t OM t t t t===-++++∴||1OM =- （仅当t =，又||||||||1OP OM MP OM +=+2k =时取等号）．综上：max ||OP =【变式1-1】已知抛物线21:4C y x =的焦点F 也是椭圆22222:1(0)x y C a b a b+=>>的一个焦点，1C 与2C 的公共弦长为3．（1）求椭圆2C 的方程；（2）过椭圆2C 的右焦点F 作斜率为(0)k k ≠的直线l 与椭圆2C 相交于A ，B 两点，线段AB 的中点为P ，过点P 做垂直于AB 的直线交x 轴于点D ，试求||||DP AB 的取值范围．【答案】（1）22143x y +=；（2）1(0,)4【解析】（1）抛物线21:4C y x =的焦点F 为(1,0)，由题意可得2221c a b =-=①由1C 与2C 关于x 轴对称，可得1C 与2C 的公共点为2,33⎛± ⎝⎭，可得2248193a b +=②由①②解得2a =，b ，即有椭圆2C 的方程为22143x y+=；（2）设:(1)l y k x =-，0k ≠，代入椭圆方程，可得2222(34)84120k x k x k +-+-=，设1(A x ，1)y ，2(B x ，2)y ，则2122834kx x k +=+，212241234k x x k -=+，即有()312122286223434k ky y k x x k k k k -+=+-=-=++，由P 为中点，可得22243()3434k kP k k -++，，又PD 的斜率为1k -，即有222314:3434k k PD y x k k k ⎛⎫--=-- ++⎝⎭，令0y =，可得2234k x k=+，即有22034k D k ⎛⎫⎪+⎝⎭可得2334PD k ==+又AB ==2212(1)34k k +=+，即有DP AB =，由211k +>，可得21011k <<+，即有104<，则有||||DP AB 的取值范围为1(0,)4．【变式1-2】已知曲线C 上任意一点(),P x y2=，（1）求曲线C 的方程；（2）若直线l 与曲线C 在y 轴左､右两侧的交点分别是,Q P ，且0OP OQ ⋅=，求22||OP OQ +的最小值.【答案】（1）2212y x -=；（2）8【解析】（1）设())12,F F ，2=，等价于12122PF PF F F -=<，∴曲线C 为以12,F F 为焦点的双曲线，且实轴长为2，焦距为故曲线C 的方程为：2212y x -=；（2）由题意可得直线OP 的斜率存在且不为0，可设直线OP 的方程为()0y kx k =≠，则直线OQ 的方程为1=-y x k ，由2212y x y kx ⎧-=⎪⎨⎪=⎩，得222222222x k k y k ⎧=⎪⎪-⎨⎪=⎪-⎩，所以()2222221||2k OP x y k+=+=-，同理可得，()2222212121||1212k k OQ k k⎛⎫+ ⎪+⎝⎭==--，所以()()()22222222211111||||22121k k k OP OQ k k -+-++===++()()22222222112222228||||OQ OP OP OQ OP OQOP OQ OP OQ ⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥+=++=++≥+= ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，当且仅当2OP OQ ==时取等号，所以当2OP OQ ==时，22||OP OQ +取得最小值8.【变式1-3】已知抛物线()2:20E x py p =>的焦点为F ，过点F 且倾斜角为3π的直线被E 所截得的弦长为16.（1）求抛物线E 的方程；（2）已知点C 为抛物线上的任意一点，以C 为圆心的圆过点F ，且与直线12y =-相交于,A B两点，求FA FB FC ⋅⋅的取值范围.【答案】（1）24x y =；（2）[)3,+∞【解析】（1）由抛物线方程得：0,2p F ⎛⎫ ⎪⎝⎭，可设过点F 且倾斜角为3π的直线为：2py =+，由222p y x py⎧=+⎪⎨⎪=⎩得：220x p --=，由抛物线焦点弦长公式可得：)12122816y y p x x p p ++=++==，解得：2p =，∴抛物线E 的方程为：24x y =.（2）由（1）知：()0,1F ，准线方程为：1y =-；设AFB θ∠=，圆C 的半径为r ，则2ACB θ∠=，FC CA CB r ===，1133sin 2224AFBSFA FB AB AB θ∴=⋅=⋅=，又2sin AB r θ=，3FA FB r ∴⋅=；由抛物线定义可知：11c CF y =+≥，即1r ≥，333FA FB FC r ∴⋅⋅=≥，即FA FB FC ⋅⋅的取值范围为[)3,+∞.题型二面积型最值范围问题20y -=与圆O 相切．（1）求椭圆C 的标准方程；（2）椭圆C 的上顶点为B ，EF 是圆O 的一条直径，EF不与坐标轴重合，直线BE 、BF 与椭圆C 的另一个交点分别为P 、Q ，求BPQ 的面积的最大值及此时PQ 所在的直线方程．【答案】（1）2219x y +=；（2）()max278BPQ S=，PQ 所在的直线方程为115y x =±+【解析】20y -=与圆O相切，则1b =，由椭圆的离心率223c e a ==，解得：29a =，椭圆的标准方程：2219x y +=；（2）由题意知直线BP ，BQ 的斜率存在且不为0，BP BQ ⊥，不妨设直线BP 的斜率为(0)k k >，则直线:1BP y kx =+．由22119y kx x y =+⎧⎪⎨+=⎪⎩，得22218911991k x k k y k -⎧=⎪⎪+⎨-⎪=⎪+⎩，或01x y =⎧⎨=⎩，所以2221819,9191k k P k k ⎛⎫-- ⎪++⎝⎭.用1k -代替k ，2229189,9k k Q k k ⎛⎫-+ ⎝+⎪⎭则21891k PB k ==+2189BQ k==+，22222111818162(1)22919(9)(19)BPQ k k k S PB BQ k k k k +=⋅=⋅=++++△342221162()162()99829982k k k k k k k k ++==++++，设1k k μ+=，则21621622764829(2)89BPQ S μμμμ∆==≤+-+．当且仅当649μμ=即183k k μ+==时取等号，所以()max278BPQ S=.即21128(()49k k kk-=+-=，1k k -=直线PQ的斜率222222291911191918181010919PQk k k k k k k k k k k k k ---+-⎛⎫++===-= ⎪⎝⎭--++PQ所在的直线方程：1y =+.【变式2-1】在平面直角坐标系xOy 中，ABC 的周长为12，AB ，AC 边的中点分别为()11,0F -和()21,0F ，点M 为BC 边的中点（1）求点M 的轨迹方程；（2）设点M 的轨迹为曲线Γ，直线1MF 与曲线Γ的另一个交点为N ，线段2MF 的中点为E ，记11NF O MF E S S S =+△△，求S 的最大值.【答案】（1）()221043x y y +=≠；（2）max 32S =【解析】（1）依题意有：112F F =，且211211262MF MF F F ++=⨯=，∴121242MF MF F F +=>=，故点M 的轨迹C 是以()11,0F -和()21,0F 为焦点，长轴长为4的椭圆，考虑到三个中点不可共线，故点M 不落在x 上，综上，所求轨迹方程：()221043x y y +=≠.（2）设()11,M x y ，()22,N x y ，显然直线1MF 不与x 轴重合，不妨设直线1MF 的方程为：1x ty =-,与椭圆()221043x y y +=≠方程联立整理得：()2234690t y ty +--=，()()22236363414410t t t ∆=++=+>，112634t y y t +=+，1129034y y t =-<+,11111122NF O S F y y O ==△，112122211112222MF E MF F S S F F y y ==⋅=△△,∴()()1112122111Δ22234NF O MF E S S S y y y y t =+=+=-=⋅=+△△令()2344u t u =+≥，则()S u ϕ====∵4u ≥，∴1104u <≤，当114u =，即0=t 时，∴max 32S =,∴当直线MN x ⊥轴时，∴max 32S =.【变式2-2】已知双曲线()222210x y a a a-=>的右焦点为()2,0F ，过右焦点F 作斜率为正的直线l ，直线l 交双曲线的右支于P ，Q 两点，分别交两条渐近线于,A B 两点，点,A P 在第一象限，O 为原点．（1）求直线l 斜率的取值范围；（2）设OAP △，OBP ，OPQ △的面积分别是OAP S △，OBP S △，OPQS ，求OPQ OAP OBPS S S ⋅△△△的范围．【答案】（1）()1,+∞；（2）).【解析】（1）因为双曲线()222210x y a a a-=>的右焦点为()2,0F ，故2c =，由222c a a =+得22a =，所以双曲线的方程为，22122x y -=，设直线l 的方程为2x ty =+，联立双曲线方程得，()222222121021420Δ0120t x y t y ty t x ty y y ⎧⎧-≠⎪-=⎪⇒-++=⇒>⇒<⎨⎨=+⎪⎪⋅<⎩⎩，解得01t <<，即直线l 的斜率范围为()11,k t=∈+∞；（2）设()11,P x y ，渐近线方程为y x =±，则P 到两条渐近线的距离1d ，2d 满足，22111212x yd d-⋅==而21221AAxy x tx ty yt⎧⎧=⎪⎪=⎪⎪-⇒⎨⎨=+⎪⎪=⎪⎪-⎩⎩，OA==21221BBxy x tx ty yt⎧⎧=⎪⎪=-⎪⎪+⇒⎨⎨=+-⎪⎪=⎪⎪+⎩⎩，OB==所以12122112221OAP OBPS S OA d OB d d dt⋅=⋅⋅⋅=-△△由()2222214202x y t y tyx ty⎧-=⇒-++=⎨=+⎩，12OPQ OFP OFQ P QS S S OF y y=+=-△△△所以，OPQOAP OBPSS S=⋅△△△，∵01t<<，∴)2OPQOAP OBPSS S∈⋅△△△.【变式2-3】已知抛物线()2:20E y px p=>的焦点为F，P为E上的一个动点，11,2⎛⎫⎪⎝⎭Q与F在E的同一侧，且PF PQ+的最小值为54.（1）求E的方程；（2）若A点在y轴正半轴上，点B、C为E上的另外两个不同点，B点在第四象限，且AB，OC互相垂直、平分，求四边形AOBC的面积.（人教A版专题）【答案】（1）2y x=；（2）【解析】（1）作出E的准线l，方程为2px=-，作PR l⊥于R，所以PR PF=，即PR PQ+的最小值为54，因为11,2⎛⎫⎪⎝⎭Q与F在E的同一侧，所以当且仅当P，Q，R三点共线时PR PQ+取得最小值，所以5124p+=，解得0.5p=，所以E的方程为2y x=；（2）因为AB，OC互相垂直、平分，所以四边形AOBC是菱形，所以BC x⊥轴，设点()0,2A a，所以2BC a=，由抛物线对称性知()2,B a a-，()2,C a a，由AO OB =，得2a=a =所以菱形AOBC 的边AO =23h a ==，其面积为3S AO h =⋅==题型三坐标与截距型最值范围问题【例3】已知双曲线C ：()222210,0x y a b a b-=>>过点()，渐近线方程为12y x =±，直线l 是双曲线C 右支的一条切线，且与C 的渐近线交于A ，B 两点．（1）求双曲线C 的方程；（2）设点A ，B 的中点为M ，求点M 到y 轴的距离的最小值．【答案】（1）2214x y -=；（2）2【解析】（1）由题设可知2281112a b b a ⎧-=⎪⎪⎨⎪=⎪⎩，解得21a b =⎧⎨=⎩则C ：2214x y -=．（2）设点M 的横坐标为0M x >当直线l 斜率不存在时，则直线l ：2x =易知点M 到y 轴的距离为2M x =﹔当直线l 斜率存在时，设l ：12y kx m k ⎛⎫=+≠± ⎪⎝⎭，()11,A x y ，()22,B x y ，联立2214x y y kx m ⎧-=⎪⎨⎪=+⎩，整理得()222418440k x kmx m -+++=，()()222264164110k m k m ∆=--+=，整理得2241k m =+联立2204x y y kx m ⎧-=⎪⎨⎪=+⎩，整理得()22241840k x kmx m -++=，则122288841km km k x x k m m+=-=-=--，则12402Mx x kx m +==->，即0km <则222216444Mk x m m==+>，即2M x >∴此时点M 到y 轴的距离大于2；综上所述，点M 到y 轴的最小距离为2．【变式3-1】若直线:l y =22221(0,0)x y a b a b -=>>的一个焦点，且与双曲线的一条渐近线平行.（1）求双曲线的方程；（2）若过点B (0，b )且与x 轴不平行的直线和双曲线相交于不同的两点M ，N ，MN 的垂直平分线为m ，求直线m 与y 轴上的截距的取值范围.【答案】（1）2213x y -=；（2）(4,)+∞.【解析】（1）直线323:33l y =-过x 轴上一点(2,0)，由题意可得2c =，即224a b +=，双曲线的渐近线方程为b y x a=±，由两直线平行的条件可得b a =1a b ==，即有双曲线的方程为2213x y -=.（2）设直线1(0)y kx k =+≠，代入2213x y -=，可得22(13)660k x kx ---=，设1122(,),(,)M x y N x y ，则12122266,1313k x x x x k k +==--，MN 中点为2231,1313kk k ⎛⎫ --⎝⎭，可得MN 的垂直平分线方程为221131313k y x k k k ⎛⎫-=-- ⎪--⎝⎭，令0x =，可得2413y k =-，由223624(13)0k k ∆=+->，解得232k <，又26031k <-，解得231k <，综上可得，2031k <<，即有2413k -的范围是(4,)+∞，可得直线m 与y 轴上的截距的取值范围为(4,)+∞.【变式3-2】已知动圆C 过定点(2,0)A ，且在y 轴上截得的弦长为4，圆心C 的轨迹为曲线Γ.（1）求Γ的方程：（2）过点(1,0)P 的直线l 与F 相交于,M N 两点.设PN MP λ=，若[]2,3λ∈，求l 在y 轴上截距的取值范围.【答案】（1）24y x =；（2）⎡-⎣【解析】（1）设(,)C x y ，圆C 的半径为R ，则()()22222220R x x y =+=-+-整理，得24y x=所以Γ的方程为24y x =.（2）设1122(,),(,)M x y N x y ，又(1,0)P ，由PN MP λ=，得()()22111,1,x y x y λ-=--21211(1)x x y y λλ-=-⎧∴⎨=-⎩①②由②，得12222y y λ=，∵2211224,4y x y x ==∴221x x λ=③联立①､③解得2x λ=，依题意有0λ>(2,N N ∴-或，又(1,0)P ，∴直线l 的方程为())11y x λ-=-，或())11y x λ-=--，当[2,3]k ∈时，l 在y轴上的截距为21λ-或21λ--，21=[2,3]上是递减的，21λ≤≤-，21λ-≤-≤-∴直线l 在y轴上截距的取值范围为⎡--⎣.【变式3-3】已知两个定点A 、B 的坐标分别为()1,0-和()1,0，动点P 满足AP OB PB ⋅=（O 为坐标原点）．（1）求动点P 的轨迹E 的方程；（2）设点(),0C a 为x 轴上一定点，求点C 与轨迹E 上点之间距离的最小值()d a ；(3)过点()0,1F 的直线l 与轨迹E 在x 轴上方部分交于M 、N 两点，线段MN 的垂直平分线与x 轴交于D 点，求D 点横坐标的取值范围．【答案】（1）24y x =；（2）(),22a a d a a ⎧<⎪=⎨≥⎪⎩；（3）()3,+∞【解析】（1）设(),P x y ，()1,AP x y =+，()1,0OB =，()1,PB x y =--，()1101AP OB x y x ⋅=+⨯+⨯=+，B P =AP OB PB ⋅=，则1x +，所以2222121x x x x y ++=-++，即24y x =．（2）设轨迹E ：24y x =上任一点为()00,Q x y ，所以2004y x =，所以()()222200004CQ x a y x a x =-+=-+()()20200220x a x a x =--+≥，令()()()220000220g x x a x a x =--+≥，对称轴为：2a -，当20a -<，即2a <时，()0g x 在区间[)0,∞+单调递增，所以00x =时，()0g x 取得最小值，即2min 2CQ a =，所以min CQ a =，当20a -≥，即2a ≥时，()0g x 在区间[)0,2a -单调递减，在区间[)2,a -+∞单调递增，所以02x a =-时，()0g x 取得最小值，即()22min 2244CQ a a a =--+=-，所以minCQ =，所以(),22a a d a a ⎧<⎪=⎨≥⎪⎩（3）当直线l 的斜率不存在时，此时l ：0x =与轨迹E 不会有两个交点，故不满足题意；当直线l 的斜率存在时，设l ：1y kx =+，()11,M x y 、()22,N x y ，代入24y x =，得2+14y y k =⨯，即2440ky y -+=，所以124y y k +=，124y y k =，121212211242y y y y x x k k k k k--+-+=+==-，因为直线l 与轨迹E 在x 轴上方部分交于M 、N 两点，所以0∆>，得16160k ->，即1k <；又M 、N 两点在x 轴上方，所以120y y +>，120y y >，即40k>，所以0k >，又1k <，所以01k <<，所以MN 中点1212,22x x y y ++⎛⎫⎪⎝⎭，即2212,kk k ⎛⎫- ⎪⎝⎭，所以垂直平分线为22121y x k k k k ⎛⎫-=--+ ⎝⎭，令0y =，得222111152248x k k k ⎛⎫=-+=-+ ⎪⎝⎭，因为01k <<，所以11k >，所以21115248x k ⎛⎫=-+ ⎪⎝⎭在11k >时单调递增，所以22111511522134848k ⎛⎫⎛⎫-+>-+= ⎪ ⎪⎝⎭⎝⎭，即3x >，所以D 点横坐标的取值范围为：()3,+∞.题型四斜率与倾斜角最值范围问题【例4】设12F F 、分别是椭圆2214x y +=的左、右焦点．（1）若P 是该椭圆上的一个动点，求125=4PF PF ⋅-，求点P 的坐标；（2）设过定点(0,2)M 的直线l 与椭圆交于不同的两点A 、B ，且AOB ∠为锐角（其中O 为坐标原点），求直线l 的斜率k 的取值范围．【答案】（1）⎛ ⎝⎭；（2）2,2⎛⎛⎫-⋃ ⎪ ⎪⎝⎭⎝⎭.【解析】（1）由题意知，2,1,a b c ===所以())12,F F ，设(,)(0,0)P m n m n >>，则22125(,),)34PF PF m n m n m n ⋅=-⋅-=+-=-，又2214m n +=，有222214534m n m n ⎧+=⎪⎪⎨⎪+-=-⎪⎩，解得1m n =⎧⎪⎨=⎪⎩，所以P ；（2）显然0x =不满足题意，设直线l 的方程为2y kx =+，设()()1122,,A x y B x y ，，22221(14)1612042x y k x kx y kx ⎧+=⎪⇒+++=⎨⎪=+⎩，22(16)4(41)120k k ∆=-+⨯>，解得234k >，①1212221612,4141k x x x x k k +=-=++，则212121212(2)(2)2()4y y kx kx k x x k x x =++=+++，又AOB ∠为锐角，则cos 0AOB ∠>，即0OA OB ⋅>，12120x x y y +>，所以21212121212(1)2()4x x y y y y k x x k x x +==++++2222212(1)1624(4)40414141k k k k k k k +⋅-=-+=>+++，解得204k <<，②由①②，解得322k -<<或322k <<，所以实数k的取值范围为(2,-.【变式4-1】已知椭圆:Γ22221(0x y a b a b +=>>）的左焦点为F ，其离心率22e =，过点F垂直于x 轴的直线交椭圆Γ于P ，Q两点，PQ （1）求椭圆Γ的方程；（2）若椭圆的下顶点为B ，过点D （2，0）的直线l 与椭圆Γ相交于两个不同的点M ，N ，直线BM ，BN 的斜率分别为12,k k ，求12k k +的取值范围．【答案】（1）2212x y +=；（2）()1211,,2222k k ⎛⎫⎛+∈-∞⋃-⋃+∞⎪ ⎝⎭⎝【解析】（1）由题可知2222222c e a bPQ a a b c⎧==⎪⎪⎪==⎨⎪=+⎪⎪⎩，解得11a b c ⎧=⎪=⎨⎪=⎩.所以椭圆Γ的方程为：2212x y +=.（2）由题可知，直线MN 的斜率存在，则设直线MN 的方程为(2)y k x =-，11(,)M x y ，22(,)N x y .由题可知2212(2)x y y k x ⎧+=⎪⎨⎪=-⎩，整理得2222(21)8820k x k x k +-+-=22222(8)4(21)(81)8(21)0k k k k ∆=--+-=-->，解得22k ⎛∈- ⎝⎭.由韦达定理可得2122821k x x k +=+，21228221k x x k -=+.由（1）知，点(0,1)B -设椭圆上顶点为A ，(0,1)A ∴，12DA k k ≠=-且12DB k k ≠=，∴()()1212121212211111k x k x y y k k x x x x -+-++++=+=+()()()221221228121212228212k k k x x k k k k x x k -⋅-++=+=+-+()242111212,,221212122k k k k k k ⎛⎫⎛=-==-∈+∞⋃-∞⋃ ⎪ +++⎝⎭⎝∴12k k +的取值范围为()11,,2222⎛⎫⎛-∞⋃-⋃+∞ ⎪ ⎝⎭⎝．【变式4-2】）已知椭圆1C 的方程为22143x y +=，双曲线2C 的左、右焦点分别为1C 的左、右顶点，而2C 的左、右顶点分别是1C 的左、右焦点.（1）求双曲线2C 的方程；（2）若直线:2l y kx =+与双曲线2C 恒有两个不同的交点A 和B ，且1OA OB ⋅>（其中O 为原点），求k 的取值范围.【答案】（1）2213y x -=（2）(()1,1-【解析】（1）由题,在椭圆1C 中,焦点坐标为()1,0-和()1,0；左右顶点为()2,0-和()2,0,因为双曲线2C 的左、右焦点分别为1C 的左、右顶点，而2C 的左、右顶点分别是1C 的左、右焦点,所以在双曲线2C 中,设双曲线方程为22221x ya b-=,则221,4a c ==,所以2223b c a =-=,所以双曲线2C 的方程为2213y x -=（2）由（1）联立22213y kx y x =+⎧⎪⎨-=⎪⎩,消去y ,得()223470k x kx -++=①；消去x ,得()2223121230k y y k -+-+=②设()()1122,,,A x y B x y ,则12,x x 为方程①的两根,12,y y 为方程②的两根；21212227123,33k x x y y k k -+⋅=⋅=--，21212227123133k OA OB x x y y k k -+⋅=⋅+⋅=+>--，得23k >或21k <③,又因为方程①中,()22216384k k k ∆=-4⨯7-=-12+>0,得27k <④,③④联立得k的取值范围(()1,1⋃-⋃【变式4-3】已知抛物线2:2(0)C y px p =>的焦点F 到准线的距离为2．（1）求C 的方程;（2）已知O 为坐标原点，点P 在C 上，点Q 满足9PQ QF =，求直线OQ 斜率的最大值.【答案】（1）24y x =；（2）最大值为13.【解析】（1）抛物线2:2(0)C y px p =>的焦点,02p F ⎛⎫⎪⎝⎭，准线方程为2p x =-，由题意，该抛物线焦点到准线的距离为222p p p ⎛⎫--== ⎪⎝⎭，所以该抛物线的方程为24y x =；（2）[方法一]：轨迹方程+基本不等式法设()00,Q x y ，则()00999,9PQ QF x y ==--，所以()00109,10P x y -，由P 在抛物线上可得()()200104109y x =-，即20025910y x +=，据此整理可得点Q 的轨迹方程为229525=-y x ，所以直线OQ 的斜率000220001025925910OQ y y y k y x y ===++，当00y =时，0OQ k =；当00y ≠时，0010925OQ k y y =+，当00y >时，因为0092530y y +≥，此时103OQ k <≤，当且仅当00925y y =，即035y =时，等号成立；当00y <时，0OQ k <；综上，直线OQ 的斜率的最大值为13.[方法二]：【最优解】轨迹方程+数形结合法同方法一得到点Q 的轨迹方程为229525=-y x ．设直线OQ 的方程为y kx =，则当直线OQ 与抛物线229525=-y x 相切时，其斜率k 取到最值．联立2,29,525y kx y x =⎧⎪⎨=-⎪⎩得22290525k x x -+=，其判别式222940525⎛⎫∆=--⨯= ⎪⎝⎭k ，解得13k =±，所以直线OQ 斜率的最大值为13．题型五向量型最值范围问题【例5】在平面直角坐标系xOy 中，已知双曲线221:142x y C -=与椭圆222:142x y C +=，A ，B分别为1C 的左､右顶点，点P 在双曲线1C 上，且位于第一象限.（1）直线OP 与椭圆2C 相交于第一象限内的点M ，设直线PA ，PB ，MA ，MB 的斜率分别为1k ，2k ，3k ，4k ，求1234k k k k +++的值；（2）直线AP 与椭圆2C 相交于点N （异于点A ），求AP AN ⋅的取值范围.【答案】（1）0；（2）()16,+∞【解析】（1）方法1：设直线():0OP y kx k =>，联立22142y kxx y =⎧⎪⎨-=⎪⎩，消y ，得()22124k x -=，所以20120k k >⎧⎨->⎩，解得202k <<，设()()1111,0,0P x y x y >>，则11x y ⎧=⎪⎪⎨⎪=⎪⎩，所以P ⎛⎫.联立22142y kxx y =⎧⎪⎨+=⎪⎩，消y ，得()22124k x +=，设()()2222,0,0M x y x y >>，则22x y ⎧=⎪⎪⎨⎪=⎪⎩，所以M ⎛⎫.因为()2,0A -，()2,0B ，所以211111221112821124224412k y y x y k k k x x x k k-+=+===-+---，222223422222821124224412ky y x y k k k x x x k k ++=+==--+--+，所以1234110k k k k k k ⎛⎫+++=+-= ⎪⎝⎭.方法2设()()1111,0,0P x y x y >>，()()2222,0,0M x y x y >>，因为()2,0A -，()2,0B ，所以11111221112224y y x yk k x x x +=+=-+-，22223422222224y y x yk k x x x +=+=-+-.因为点P 在双曲线1C 上，所以2211142x y -=，所以221142x y -=，所以1121x k k y +=.因为点Q 在椭圆线2C 上，所以2222142x y +=，所以222242x y -=-，所以2342x k k y +=-.因为O ，P ，M 三点共线，所以1212y y x x =，所以121234120x x k k k k y y +++=-=.（2）设直线AP 的方程为2y kx k =+，联立22224y kx k x y =+⎧⎨-=⎩，消y ，得()()22222184210k x k x k -+++=，解得12x =-，2224212k x k +=-，所以点P 的坐标为222424,1212k k k k ⎛⎫+ ⎪--⎝⎭，因为点P 位于第一象限，所以222420124012k k k k ⎧+>⎪⎪-⎨⎪>⎪-⎩，解得202k <<，联立22224y kx k x y =+⎧⎨+=⎩，消y ，得()()22222184210k x k x k +++-=，解得32x =-，2422412kx k -=+，所以点N 的坐标为222244,1212k k k k ⎛⎫- ++⎝⎭，所以()22222224161422444221212121214k k k k kAP AN AP AN k k k k k +⎛⎫⎛⎫+-⋅=⋅=--+⋅= ⎪⎪-+-+-⎝⎭⎝⎭，设21t k =+，则312t <<，所以22161616314(1)48384t tAP AN t t t t t ⋅===---+-⎛⎫-+ ⎪⎝⎭.因为函数3()4f x x x=+在区间31,2⎛⎫⎪⎝⎭上单调递增，所以当312t <<时，3748t t <+<，所以30841t t ⎛⎫<-+< ⎪⎝⎭，所以1616384t t >⎛⎫-+ ⎪⎝⎭，即16AP AN ⋅>，故AP AN ⋅的取值范围为()16,+∞.【变式5-1】已知O为坐标原点，椭圆2222:1(0)x yC a ba b+=>>的离心率为3，且经过点P．（1）求椭圆C的方程；（2）直线l与椭圆C交于A，B两点，直线OA的斜率为1k，直线OB的斜率为2k，且1213k k=-，求OA OB⋅的取值范围．【答案】（1）22193x y+=；（2）[3,0)(0,3]-.【解析】（1）由题意，223611caa b⎧=⎪⎪⎨⎪+=⎪⎩，又222a b c=+，解得3,a b==所以椭圆C为22193x y+=.（2）设()()1122,,,A x yB x y，若直线l的斜率存在，设l为y kx t=+，联立22193y kx tx y=+⎧⎪⎨+=⎪⎩，消去y得：()222136390+++-=k x ktx t，22Δ390k t=+->，则12221226133913ktx xktx xk-⎧+=⎪⎪+⎨-⎪=⎪+⎩，又12k k=121213y yx x=-，故121213=-y y x x且120x x≠，即2390-≠t，则23≠t，又1122,y kx t y kx t=+=+，所以()()()222222222121212221212122691133939313-+++++-+==+=+==---+k t tkx t kx t kt x x ty y t kkk ktx x x x x x tk，整理得222933=+≥t k，则232≥t且Δ0>恒成立．221212121212222122393333133313--⎛⎫⋅=+=-==⋅=⋅=-⎪+⎝⎭t tOA OB x x y y x x x x x xk t t，又232≥t，且23≠t，故2331[3,0)(0,3)⎛⎫-∈-⎪⎝⎭t.当直线l的斜率不存在时，2121,x x y y==-，又12k k=212113-=-yx，又2211193x y+=，解得2192x=则222111233⋅=-==OA OB x y x．综上，OA OB ⋅的取值范围为[3,0)(0,3]-．【变式5-2】已知双曲线22221(00)x y C a b a b-=>>：，的离心率为2，F 为双曲线的右焦点，直线l 过F 与双曲线的右支交于P Q ，两点，且当l 垂直于x 轴时，6PQ =；（1）求双曲线的方程；（2）过点F 且垂直于l 的直线'l 与双曲线交于M N ，两点，求MP NQ MQ NP ⋅⋅+的取值范围．【答案】（1）2213y x -=；（2）(],12-∞-【解析】（1）依题意，2c a =，当l 垂直于x 轴时，226b PQ a==，即23b a =，即223c a a -=，解得1a =，b =2213y x -=；（2）设:2PQ l x my =+，联立双曲线方程2213y x -=，得：()22311290m y my -++=，当0m =时，()()()()2,3,2,3,0,1,0,1P Q M N --，12MP NQ MQ NP ⋅+⋅=-，当0m ≠时，设()()()()11223344,,,,,,,P x y Q x y M x y N x y ，因为直线PQ 与双曲线右支相交，因此1229031y y m =<-，即m ⎛⎫⎛∈⋃ ⎪ ⎝⎭⎝⎭，同理可得234293m y y m =-，依题意()()MP NQ MF FP NF FQ MF NF FP FQ =+⋅+=⋅+⋅⋅，同理可得，()()MQ NP MF FQ NF FP MF NF FP FQ =+⋅+⋅=⋅+⋅，而()212342111FP FQ MF NF m y y y y m ⎛⎫⋅+⋅=+++ ⎪⎝⎭，代入122931y y m =-，234293m y y m =-，()()()()()()222242224222919118163633133103133m m m m m FP FQ MF NF m m m m m m ++-+++⋅+⋅=+==----+--，分离参数得，2429663103m FP FQ MF NF m m ⋅+⋅=---+，因为3333m ⎛⎫⎛∈⋃ ⎪ ⎝⎭⎝⎭，当210,3m ⎛⎫∈ ⎪⎝⎭时，由22110,3m m ⎛⎫+∈+∞ ⎪⎝⎭，()22966,61310FP FQ MF NF m m ⋅+⋅=-∈-∞-⎛⎫+- ⎪⎝⎭，所以()()2,12MP NQ MQ N FP FQ MF NF P ⋅=⋅+⋅∈∞-⋅-+，综上可知，MP NQ MQ NP ⋅⋅+的取值范围为(],12-∞-.【变式5-3】已知抛物线()2:20E x py p =>的焦点为F ，直线4x =分别与x 轴交于点P ，与抛物线E 交于点Q ，且54QF PQ =.（1）求抛物线E 的方程；（2）如图，设点,,A B C 都在抛物线E 上，若ABC 是以AC 为斜边的等腰直角三角形，求AB AC ⋅uu u r uuu r的最小值.【答案】（1）24x y =；（2）32【解析】（1）设点()04,Q y ，由已知000216524py p y y =⎧⎪⎨+=⎪⎩，则8102p p p +=，即24p =.因为0p >，则2p =，所以抛物线E 的方程是24x y =.（2）设点()222312123123,,,,,444x x x A x B x C x x x x ⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，直线AB 的斜率为()0k k >，因为AB BC ⊥，则直线BC 的斜率为1k-.因为AB BC =，则1223x x x x -=-，得()2312x x k x x -=-，①因为22121212444x x x x k x x -+==-，则124x x k +=，即124x k x =-，②因为223223231444x x x x k x x -+-==-，则234x x k +=-，即324x x k =--③将②③代入①，得()2242420x k k x k+--=，即()()322212120k k x k kk-+---=，则()()32211k xk k -=+，所以()()()()22222122··cos 451421AB AC AB AC AB x x k k x k ︒===-+=-+()()()()()2332222411614111k k k k k k k k ⎡⎤-+⎢⎥=-+=++⎢⎥⎣⎦因为212k k +≥，则()22214k k +≥，又()22112k k++≥，则()()3222121k k k +≥+，从而()()3222121kk k +≥+当且仅当1k =时取等号，所以AB AC 的最小值为32.题型六参数型最值范围问题【例6】已知点()()1122,,,M x y N x y 在椭圆222:1(1)xC y a a+=>上，直线,OM ON 的斜率之积是13-，且22212x x a +=.（1）求椭圆C 的方程；（2）若过点()0,2Q 的直线与椭圆C 交于点,A B ，且(1)QB t QA t =>，求t 的取值范围.【答案】（1）2213x y +=；（2）(]1,3【解析】（1）椭圆方程改写为:2222x a y a +=，点()()1122,,,M x y N x y 在椭圆上，有222211a y a x =-，222222a y a x =-，两式相乘，得：()()()222222222241142122122a a a y y a x a x x x x x --==-++，由22212x x a +=，得222212241a y y x x =，由直线,OM ON 的斜率之积是13-，得121213y y x x =-，即222212129y y x x =，∴49a =，23a =，椭圆C 的方程为：2213x y +=.（2）过点()0,2Q 的直线若斜率不存在，则有()0,1A ，()0,1B -，此时3t =；当过点()0,2Q 的直线斜率存在，设直线方程为2y kx =+，由22213y kx x y =+⎧⎪⎨+=⎪⎩，消去y ，得()22131290k x kx +++=，直线与椭圆C 交于点,A B 两点，∴()2221249(13)36360k k k ∆=-⨯⨯+=->，得21k >设()()1122,,,A x y B x y ''''，(1)QB t QA t =>，21x x t '='由韦达定理12122121212(1)13913k x x t x k x x tx k ''''-⎧+==+⎪⎪+⎨⎪⋅+'='=⎪⎩，消去1x '，得()229131441t k t ⎛⎫=+ ⎪⎝⎭+，由21k >，2101k<<，∴()2311641t t <<+，由1t >，解得13t <<，综上，有13t <≤，∴t 的取值范围为(]1,3【变式6-1】已知A 、B 分别是椭圆2222:1(0)x y C a b a b+=>>的左右顶点，O 为坐标原点，=6AB ，点2,3⎛⎫⎪⎝⎭5在椭圆C 上．过点()0,3P -，且与坐标轴不垂直的直线交椭圆C 于M 、N 两个不同的点．（1）求椭圆C 的标准方程；（2）若点B 落在以线段MN 为直径的圆的外部，求直线的斜率k 的取值范围；（3）当直线的倾斜角θ为锐角时，设直线AM 、AN 分别交y 轴于点S 、T ，记PS PO λ=，PT PO μ=，求λμ+的取值范围．【答案】（1）22195x y +=；（2）227,,1,332k ⎛⎫⎛⎫⎛⎫∈-∞-⋃⋃+∞ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭；（3）4,23⎛⎫ ⎪⎝⎭【解析】（1）因为=6AB ，所以=3a ；又点2,3⎛⎫ ⎪⎝⎭5在图像C 上即()22252319b⎛⎫⎪⎝⎭+=，所以b 所以椭圆C 的方程为22195x y +=；（2）由（1）可得()3,0B ，设直线3l y kx =-：，设11(,)M x y 、22(,)N x y ，由22=-3=195y kx x y ⎧⎪⎨+⎪⎩得22(59)54360k x kx +-+=，22(54)436(59)0k k ∆=-⨯⨯+>解得23k >或23k <-①∵点()3,0B 在以线段MN 为直径的圆的外部，则0BM BN ⋅>，又12212254+=5+936=5+9k x x k x x k ⎧⎪⎪⎨⎪⎪⎩②211221212(3,)(3,)(1)3(1)()180BM BN x y x y k x x k x x ⋅=--=+-+++>，解得1k <或72k >由①②得227,,1,332k ⎛⎫⎛⎫⎛⎫∈-∞-⋃⋃+∞ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭（3）设直线3l y kx =-：，又直线的倾斜角θ为锐角，由（2）可知23k >，记11(,)M x y 、22(,)N x y ，所以直线AM 的方程是：()1133y y x x =++，直线AN 的方程是：()2233y y x x =++.令=0x ，解得113+3y y x =，所以点S 坐标为1130,+3y x ⎛⎫ ⎪⎝⎭；同理点T 为2230,+3y x ⎛⎫⎪⎝⎭.所以1130,3+3y PS x ⎛⎫=+ ⎪⎝⎭，2230,3+3y PT x ⎛⎫=+ ⎪⎝⎭，()0,3PO =.由PS PO λ=，PT PO μ=，可得：11333+3y x λ+=，22333+3y x μ+=，所以1212233y yx x λμ+=++++，由（2）得1225495k x x k +=+，1223695x k x =+，所以()()()1212121212122311333338229kx x k x x kx kx x x x x x x λμ--++-+-+=++=+++++()222254231189595254936369595k k k k k k k k ⎛⎫⋅+-- ⎪++⎝⎭=+⎛⎫++ ⎪++⎝⎭21012921k k k +=-⨯+++()()2110291k k +=-⨯++101291k =-⨯++，因为23k >，所以5131,0315k k +><<+，10142,2913k ⎛⎫-⨯+∈ ⎪+⎝⎭，故λμ+的范围是4,23⎛⎫⎪⎝⎭.【变式6-2】设A ，B 为双曲线C ：22221x y a b-=()00a b >>，的左、右顶点，直线l 过右焦点F 且与双曲线C 的右支交于M ，N 两点，当直线l 垂直于x 轴时，AMN 为等腰直角三角形．（1）求双曲线C 的离心率；（2）已知4AB =，若直线AM ，AN 分别交直线1x =于P ，Q 两点，若()0D t ，为x 轴上一动点，当直线l 的倾斜角变化时，若PDQ ∠为锐角，求t 的取值范围．【答案】（1）2；（2）{2t t <-或}4t >【解析】（1）由双曲线C ：22221x y a b-=()00a b >>，可得：右焦点(),0F c ，将x c =代入2222:1(0,0)x y C a b a b -=>>中，2by a=±，当直线l 垂直于x 轴时，AMN 为等腰直角三角形，此时AF FM =，即2b ac a+=，整理得：220a ac b +-=，因为222b c a =-，所以2220a ac c +-=，方程两边同除以2a 得：220e e +-=，解得：2e =或1-（舍去），所以双曲线C 的离心率为2；（2）因为24AB a ==，所以2a =，因为2c e a ==，解得4c =，故22212b c a =-=，所以双曲线的方程为221412x y -=，当直线l 的斜率存在时，设直线l 的方程为：()4y k x =-，与双曲线联立得：()22223816120kxk x k -+--=，设()()1122,,,M x y N x y ，则212283k x x k +=-，212216123k x x k +=-，则()()()221212121244416y y k x x k x x x x =--=-++⎡⎤⎣⎦222221612321633k k k k k ⎛⎫+=-+ ⎪--⎝⎭22363k k -=-，因为直线l 过右焦点F 且与双曲线C 的右支交于,M N 两点，所以22121222816124,433k k x x x x k k ++=>=>--，解得：23k >，直线()11:22y AM y x x =++，则1131,2y P x ⎛⎫ ⎪+⎝⎭，同理可求得：2231,2y Q x ⎛⎫⎪+⎝⎭，所以11,213y D x P t ⎪+⎛⎫=- ⎝⎭，22,213y D x Q t ⎪+⎛⎫=- ⎝⎭，因为PDQ ∠为锐角，所以()()12221192202D y y x Q t x P D t ⋅=+-+>++，即()1122122109224y y x x x t x t +-+++>+，所以22222221203693161216433k k k k t k t k -⨯-++--+++>-所以21290t t +-->即()219t ->，解得2t <-或4t >；当直线l 的斜率不存在时，将4x =代入双曲线可得6y =±，此时不妨设()()4,6,4,6M N -，此时直线:2AM y x =+，点P 坐标为()1,3，同理可得：()1,3Q -，所以()1,3DP t =-，()1,3DQ t =--，因为PDQ ∠为锐角，所以2280DP DQ t t ⋅=-->，解得2t <-或4t >；综上所述，t 的取值范围{2t t <-或}4t >【变式6-3】22122:1y x C a b-=上的动点P 到两焦点的距离之和的最小值为22:2(0)C x py p =>的焦点与双曲线1C 的上顶点重合．（1）求抛物线2C 的方程；（2）过直线:(l y a a =为负常数）上任意一点M 向抛物线2C 引两条切线，切点分别为AB ，坐标原点O 恒在以AB 为直径的圆内，求实数a 的取值范围．【答案】（1）24x y =；（2）40a -<<.【解析】（1）由已知：双曲线焦距为，则长轴长为2，故双曲线的上顶点为(0,1)，即为抛物线焦点.∴抛物线2C 的方程为24x y =；（2）设(,)M m a ，2111(,)4A x x ，2221(,)4B x x ，故直线MA 的方程为211111()42y x x x x -=-，即21142y x x x =-，所以21142a x m x =-，同理可得：22242a x m x =-，∴1x ，2x 是方程242a xm x =-的两个不同的根，则124x x a =，2212121()416OA OB x x x x a a ∴⋅=+=+，由O 恒在以AB 为直径的圆内，240a a ∴+<，即40a -<<．。

第3讲大题专攻——圆锥曲线中的最值、范围、证明问题 2023高考数学二轮复习课件

当t∈(2，3)时，u′＞0，u＝4t3－t4单调递增，
当t∈(3，4)时，u′＜0，u＝4t3－t4单调递减，
所以当
t＝3
时，u
取得最大值，则
S
也取得最大值，最大值为3 4
3.
目录
圆锥曲线中的范围问题
【例2】已知抛物线E：x2＝2py(p＞0)的焦点为F，点P在抛物线E上，点P 的横坐标为2，且|PF|＝2. (1)求抛物线E的标准方程；解法一：依题意得 F0，2p，设 P(2，y0)，则 y0＝2－p2，因为点 P 是抛物线 E 上一点，所以 4＝2p2－2p，即 p2－4p＋4＝0，解得 p＝2.所以抛物线 E 的标准方程为 x2＝4y. 法二：依题意，设 P(2，y0)，代入抛物线 E 的方程 x2＝2py 可得 y0＝2p，由抛物线的定义可得|PF|＝y0＋p2，即 2＝2p＋p2，解得 p＝2.所以抛物线 E 的标准方程为 x2＝4y.
4 1＋k2· k2＋b.
因为x2＝4y，即y＝x42，所以y′＝x2，则抛物线在点A处的切线斜率为
x1 2
，在
点A处的切线方程为y－x421＝x21(x－x1)，即y＝x21x－x421，
目录
同理得抛物线在点B处的切线方程为y＝x22x－x422，
联立得yy＝＝xx2212xx－－xx442212，，则xy＝＝xx114x＋22＝x2－＝b2，k，即P(2k，－b)．
＋ 2，圆心O(0，0)到MN的距离d＝ m22＋1＝1⇒m2＝1.
联立xx＝ 2＋m3yy＋2＝32，⇒(m2＋3)y2＋2 2my－1＝0⇒4y2＋2 2my－1＝0，
|MN|＝
1＋m2·
8m2＋16＝ 4

第1部分板块2 核心考点突破拿高分专题5 第3讲圆锥曲线中的最值、范围、证明问题(大题)

第3讲圆锥曲线中的最值、范围、证明问题(大题)热点一最值问题求圆锥曲线中三角形面积的最值的关键(1)公式意识，把求三角形的面积转化为求距离、求角等； (2)方程思想，即引入参数，寻找关于参数的方程；(3)不等式意识，寻找关于参数的不等式，利用基本不等式等求最值.例1 (2019·邯郸模拟)已知椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点分别为F 1，F 2，P 为E 上的一个动点，且|PF 2|的最大值为2＋3，E 的离心率与椭圆Ω：x 22＋y 28＝1的离心率相等.(1)求E 的方程；(2)直线l 与E 交于M ，N 两点(M ，N 在x 轴的同侧)，当F 1M ∥F 2N 时，求四边形F 1F 2NM 面积的最大值.跟踪演练1 (2019·焦作模拟)已知椭圆C ：x 22＋y 2＝1，点A ⎝⎛⎭⎫1，12，B (1,2). (1)若直线l 1与椭圆C 交于M ，N 两点，且A 为线段MN 的中点，求直线MN 的斜率； (2)若直线l 2：y ＝2x ＋t (t ≠0)与椭圆C 交于P ，Q 两点，求△BPQ 的面积的最大值.圆锥曲线的范围问题的常见解法(1)几何法：若题目中的条件和结论能明显体现几何特征和意义，则考虑利用图形性质来解决； (2)代数法：若题目中的条件和结论能体现一种明确的函数关系或不等关系或已知参数与新参数之间的等量关系等，则可利用这些关系去求参数的范围.例2 (2019·江西九校联考)已知椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的右焦点F (1,0)，A ，B ，C 是椭圆上任意三点，A ，B 关于原点对称且满足k AC ·k BC ＝－12.(1)求椭圆E 的方程；(2)若斜率为k 的直线与圆：x 2＋y 2＝1相切，与椭圆E 相交于不同的两点P ，Q ，求|PQ |≥435时，k 的取值范围.跟踪演练2 (2019·合肥质检)已知抛物线C ：x 2＝2py (p >0)上一点M (m ,9)到其焦点F 的距离为10.(1)求抛物线C 的方程；(2)设过焦点F 的直线l 与抛物线C 交于A ，B 两点，且抛物线在A ，B 两点处的切线分别交x 轴于P ，Q 两点，求|AP |·|BQ |的取值范围.圆锥曲线的证明问题，常表现为证明相等、定值、过定点、点在曲线上等，一般是以直线与圆锥曲线为载体，综合使用圆锥曲线的性质及位置关系进行论证.例3 (2019·南开模拟)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为12，以原点为圆心，以椭圆的短半轴长为半径的圆与直线x －y ＋6＝0相切.(1)求椭圆C 的方程；(2)过椭圆的右焦点F 的直线l 1与椭圆交于A ，B ，过F 与l 1垂直的直线l 2与椭圆交于C ，D ，与l 3：x ＝4交于P ，求证：直线P A ，PF ，PB 的斜率k P A ，k PF ，k PB 成等差数列.跟踪演练3 (2019·深圳调研)在平面直角坐标系xOy 中，椭圆C 的中心在坐标原点O ，其右焦点为F (1,0)，且点⎝⎛⎭⎫1，32在椭圆C 上.(1)求椭圆C 的方程；(2)设椭圆的左、右顶点分别为A ，B ，M 是椭圆上异于A ，B 的任意一点，直线MF 交椭圆C 于另一点N ，直线MB 交直线x ＝4于Q 点，求证：A ，N ，Q 三点在同一条直线上.真题体验(2019·全国Ⅱ，理，21)已知点A (－2,0)，B (2,0)，动点M (x ，y )满足直线AM 与BM 的斜率之积为－12.记M 的轨迹为曲线C .(1)求C 的方程，并说明C 是什么曲线；(2)过坐标原点的直线交C 于P ，Q 两点，点P 在第一象限，PE ⊥x 轴，垂足为E ，连接QE 并延长交C 于点G .①证明：△PQG 是直角三角形； ②求△PQG 面积的最大值.押题预测已知椭圆W ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为22，点P (2a ，3)，F 1，F 2分别是椭圆W 的左、右焦点，△PF 1F 2为等腰三角形. (1)求椭圆W 的方程；(2)过左焦点F 1作直线l 1交椭圆于A ，B 两点，其中A (0,1)，另一条过F 1的直线l 2交椭圆于C ，D 两点(不与A ，B 重合)，且D 点不与点(0，－1)重合.过F 1作x 轴的垂线分别交直线AD ，BC 于E ，G . ①求B 点坐标； ②求证：|EF 1|＝|F 1G |.A 组专题通关1.(2019·吉林调研)已知A ，B 为椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的上、下顶点，|AB |＝2，且离心率为32. (1)求椭圆E 的方程；(2)若点P (x 0，y 0)(x 0≠0)为直线y ＝2上任意一点，P A ，PB 交椭圆于C ，D 两点，求四边形ACBD 面积的最大值.2.已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的短轴长为2，离心率为32.(1)求椭圆C 的标准方程；(2)若过点(－3,0)的直线l 与椭圆C 交于不同的两点M ，N ，O 为坐标原点，求OM →·ON →的取值范围.3.(2019·恩施州质检)已知抛物线C ：y 2＝2px (p >0)的焦点为F ，其准线L ：x ＝－1与x 轴的交点为K ，过点K 的直线l 与抛物线C 交于A ，B 两点. (1)求抛物线C 的方程；(2)点A 关于x 轴的对称点为D ，证明：存在实数t ∈(0,1)，使得KF →＝tKB →＋(1－t )KD →.B 组能力提高4.(2019·泰安质检)已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率e ＝22，且经过点⎝⎛⎭⎫－22，32.(1)求椭圆C 的方程；(2)过点P (－2,0)且不与x 轴重合的直线l 与椭圆C 交于不同的两点A (x 1，y 1)，B (x 2，y 2)，过右焦点F 的直线AF ，BF 分别交椭圆C 于点M ，N ，设AF →＝αFM →，BF →＝βFN →，α，β∈R ，求α＋β的取值范围.5.(2019·六安模拟)设椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)，其中长轴长是短轴长的2倍，过焦点且垂直于x 轴的直线被椭圆截得的弦长为2 3.(1)求椭圆E 的方程；(2)点P 是椭圆E 上动点，且横坐标大于2，点B ，C 在y 轴上，(x －1)2＋y 2＝1内切于△PBC ，试判断点P 的横坐标为何值时△PBC 的面积S 最小.。

圆锥曲线的最值定值范围等经典考题型附答案作业

圆锥曲线的综合应用一、圆锥曲线的最值问题方法1：定义转化法①根据圆锥曲线的定义列方程；②将最值问题转化为距离问题求解．例1、已知点F 是双曲线错误!－错误!＝1的左焦点,定点A 的坐标为（1,4），P 是双曲线右支上的动点，则｜PF ｜＋|P A ｜的最小值为________．方法2：数形结合（切线法）当所求的最值是圆锥曲线上的点到某条直线的距离的最值时:①求与直线平行的圆锥曲线的切线；②求出两平行线的距离即为所求的最值．例2、求椭圆错误!＋y 2＝1上的点到直线y ＝x ＋2错误!的距离的最大值和最小值,并求取得最值时椭圆上点的坐标．方法3:参数法（函数法）① 选取合适的参数表示曲线上点的坐标；②求解关于这个参数的函数最值例3、在平面直角坐标系xOy 中，点P （x ，y ）是椭圆错误!＋y 2＝1上的一个动点，则S ＝x ＋y 的最大值为________．方法4：基本不等式法①将最值用变量表示．②利用基本不等式求得表达式的最值．例4、求椭圆错误!＋y 2＝1内接矩形ABCD 面积的最大值．二、圆锥曲线的范围问题方法1：曲线几何性质法①由几何性质建立关系式；②化简关系式求解．例1、已知双曲线错误!－错误!＝1(a ＞0,b ＞0)的左，右焦点分别为F 1,F 2,点P 在双曲线的右支上，且｜PF 1｜＝4|PF 2｜，则此双曲线中ac 的取值范围是________．方法2：判别式法当直线和圆锥曲线相交、相切和相离时，分别对应着直线和圆锥曲线方程联立消元后得到的一元二次方程的判别式大于零、等于零、小于零①联立曲线方程，消元后求判别式；②根据判别式大于零、小于零或等于零结合曲线性质求解．例2、在平面直角坐标系xOy中，经过点（0,错误!）且斜率为k的直线l与椭圆错误!＋y2＝1有两个不同的交点P和Q。

（1)求k的取值范围;（2）设椭圆与x轴正半轴、y轴正半轴的交点分别为A，B,是否存在常数m，使得向量错误!＋错误!与错误!共线？如果存在，求m值;如果不存在，请说明理由．三、圆锥曲线的定值、定点问题方法1:特殊到一般法根据特殊情况能找到定值（或定点）的问题①根据特殊情况确定出定值或定点；②对确定出来的定值或定点进行一般情况的证明．例1、已知双曲线C：x2－错误!＝1，过圆O:x2＋y2＝2上任意一点作圆的切线l，若l交双曲线于A，B两点，证明：∠AOB的大小为定值．方法2:引进参数法定值、定点是变化中的不变量，引入参数找出与变量与参数没有关系的点（或值)即是定点(或定值）。

2019年高三理科数学高考大题精练：圆锥曲线：范围(最值)问题(附解析)

2019年高三理科数学高考大题精练：圆锥曲线：范围（最值）问题（附解析）精练例题[2019·江南十校]已知椭圆()2222:10x y C a b a b+=>>，B 为其短轴的一个端点，1F ，2F 分别为其左右两个焦点，已知三角形12BF F 121cos 3F BF ∠=．（1）求椭圆C 的方程；（2）若动直线22:0,3l y kx m m k ⎛⎫=+≠≠ ⎪⎝⎭与椭圆C 交于()11,P x y ，()22,Q x y ，M 为线段PQ 的中点，且22123x x +=，求OM PQ ⋅的最大值．【答案】（1）22132x y +=；（2）52．【解析】（1）由2222212222411cos 3233a c c F BF a c a a -∠==⇒=⇒=，222bc =，12121cos sin 3F BF F BF ∠=⇒∠=，结合1222132F BF S a a ===△，22b ⇒=，故椭圆C 的方程为22132x y +=．另解：依题意：12122F BF S cb bc =⨯==△221212212cos 2cos1233F BF b F BF a ∠∠=-=⇒=，解得23a =，22b =，故椭圆C 的方程为22132x y +=．（2）联立()()2222222223263602432032236y kx mk x kmx m Δk m k m x y =+⇒+++-⎧⎨⎩=⇒=+->⇒+>+=．且122632kmx x k -+=+，21223632m x x k -=+；依题意()()()()2222212121222262632333232m km x x x x x x k k--+=⇒+-=⇒-=++，化简得：22322k m +=（∵232k ≠）；设()00,M x y ，由()()22112222012121222120222362233236x y x y y x x y y k x x y x y ⎧⎪⎨+=-⇒-=--⇒==--+=⎪⎩，又00y kx m =+，解得31,2k M m m ⎛⎫- ⎪⎝⎭22222943142k m OM m m +-⇒==， ()()()()()2222222221222222243222111251132432k m m PQ kx x kOM PQ m m m k+-+⎛⎫⎛⎫=+-=+=⇒⋅=-+≤ ⎪⎪⎝⎭⎝⎭+，52OM PQ ⋅≤．当且仅当221132m m -=+，即m =时，OM PQ ⋅的最大值为52．模拟精炼1．[2019·柳州模拟]已知点()1,0F-，直线:4l x=-，P为平面内的动点，过点P作直线l的垂线，垂足为点M，且1122PF PM PF PM⎛⎫⎛⎫-⋅+=⎪ ⎪⎝⎭⎝⎭．（1）求动点P的轨迹C的方程；（2）过点F作直线1l（与x轴不重合）交C轨迹于A，B两点，求三角形面积OAB的取值范围．（O为坐标原点）2．[2019·雷州期末]如图，已知抛物线2:2C y px =和()22:41M x y -+=，过抛线C 上一点()()000,1H x y y ≥作两条直线与M 相切于A 、B 两点，分别交抛物线于E 、F 两点，圆心点M 到抛物线准线的距离为174．（1）求抛物线C 的方程；（2）当AHB ∠的角平分线垂直x 轴时，求直线EF 的斜率；（3）若直线AB 在y 轴上的截距为t ，求t 的最小值．3．[2019·周口调研]已知直线2py x =-与抛物线()2:20C y px p =>交于B ，D 两点，线段BD 的中点为A ，点F 为C 的焦点，且OAF △（O 为坐标原点）的面积为1．（1）求抛物线C 的标准方程；（2）过点()2,2G 作斜率为()2k k ≥的直线l 与C 交于M ，N 两点，直线OM ，ON 分别交直线2y x =+于P ，Q 两点，求PQ 的最大值．答案与解析1．【答案】（1）22143x y +=；（2）30,2⎛⎤⎥⎝⎦．【解析】（1）设动点(),P x y ，则()4,M y -，由11022PF PM PF PM ⎛⎫⎛⎫-+= ⎪⎪⎝⎭⎝⎭，2214PF PM ∴=，即2214PF PM ∴=，()2221144x y x ∴++=+，化简得22143x y +=．（2）由（1）知轨迹C 的方程为22143x y +=，当直线1l 斜率不存在时31,2A ⎛⎫-- ⎪⎝⎭，31,2B ⎛⎫- ⎪⎝⎭，1322OAB S AB OF ∴=⋅=△，当直线1l 斜率存在时，设直线l 方程为()10x my m =-≠，设()11,A x y ，()22,B x y ，由221143x my x y ⎧⎪⎨-+=⎪⎩=，得()2234690m y my +--=．则21441440Δm =+>，122634m y y m +=+，122934y y m -=+，1211122OABS OF y y =⋅-=⨯△=令()211m t t +=>，则OAB S ==△，令()196f t t t =++，则()219f t t'=-，当1t >时，()0f t '>，()196f t t t∴=++在()1,+∞上单调递增，()()116f t f∴>=，32OAB S ∴<△，综上所述，三角形OAB 面积的取值范围是30,2⎛⎤⎥⎝⎦．2．【答案】（1）2y x =；（2）14-；（3）11-．【解析】（1）∵点M 到抛物线准线的距离为17424p +=，∴12p =，即抛物线C 的方程为2y x =．（2）∵当AHB ∠的角平分线垂直x 轴时，点()4,2H ，∴HE HF k k =-，设()11,E x y ，()22,F x y ，∴1212H H H H y y y y x x x x --=---，∴12222212H H H H y y y y y y y y --=---， ∴1224H y y y +=-=-．212122212121114EF y y y y k x x y y y y --====---+．（3）设点()()2,1H m m m ≥，242716HM m m =-+，242715HA m m =-+．以H 为圆心，HA 为半径的圆方程为()()22242715x m y m m m -+-=-+，……①M 方程：()2241x y -+=．……②①-②得：直线AB 的方程为()()()22422442714x m m y m m m m -----=-+．当0x =时，直线AB 在y 轴上的截距()1541t m m m=-≥， ∵t 关于m 的函数在[)1,+∞单调递增，∴min 11t =-． 3．【答案】（1）24y x =；（2）【解析】（1）设()11,B x y ，()22,D x y ，则12121y y x x -=-．由2112y px =，2222y px =两式相减，得()()121212()2y y y y p x x -+=-． ∴12121222x x y y p p y y -+=⋅=-，所以点A 的纵坐标为122y y p +=， ∴OAF △的面积1122pS p =⨯⨯=，解得2p =．故所求抛物线的标准方程为24y x =．（2）直线l 的方程为()22y k x -=-．由方程组()2224y k x y x-=-=⎧⎪⎨⎪⎩，得24880ky y k --+=．设233,4y M y ⎛⎫ ⎪⎝⎭，244,4y N y ⎛⎫ ⎪⎝⎭，则344y y k +=，3488y y k =-．直线OM 的方程为34y x y =，代入2y x =+，解得3324y x y =-，所以33328,44y P y y ⎛⎫⎪--⎝⎭．同理得44428,44y Q y y ⎛⎫⎪--⎝⎭．所以484PQ y =-==-== 因为2k ≥，所以1102k <≤，所以当112k =，即2k =时，PQ 取得最大值。

圆锥曲线中的最值、范围、证明问题

第九节圆锥曲线中的最值、范围、证明问题突破点(一) 圆锥曲线中的最值问题圆锥曲线中的最值问题是高考中的热点问题，常涉及不等式、函数的值域问题，综合性比较强，解法灵活多变，但总体上主要有两种方法：一是利用几何方法，即利用曲线的定义、几何性质以及平面几何中的定理、性质等进行求解；二是利用代数方法，即把要求最值的几何量或代数表达式表示为某个(些)参数的函数(解析式)，然后利用函数方法、不等式方法等进行求解.考点贯通抓高考命题的“形”与“神”利用几何性质求最值[例1] 设P 是椭圆x 225＋y 29＝1上一点，M ，N 分别是两圆：(x ＋4)2＋y 2＝1和(x －4)2＋y 2＝1上的点，则|PM |＋|PN |的最小值、最大值分别为( )A ．9,12B ．8,11C ．8,12D ．10,12[解析] 如图，由椭圆及圆的方程可知两圆圆心分别为椭圆的两个焦点，由椭圆定义知|P A |＋|PB |＝2a ＝10，连接P A ，PB 分别与圆相交于两点，此时|PM |＋|PN |最小，最小值为|P A |＋|PB |－2R ＝8；连接P A ，PB 并延长，分别与圆相交于两点，此时|PM |＋|PN |最大，最大值为|P A |＋|PB |＋2R ＝12，即最小值和最大值分别为8,12.[答案] C[方法技巧]利用曲线的定义、几何性质以及平面几何中的定理、性质等进行求解，也叫做几何法．建立目标函数求最值本节主要包括3个知识点： 1.圆锥曲线中的最值问题； 2.圆锥曲线中的范围问题； 3.圆锥曲线中的几何证明问题.[例2] 已知△ABP 的三个顶点都在抛物线C ：x 2＝4y 上，F 为抛物线C 的焦点，点M 为AB 的中点，PF ＝3FM .(1)若|PF |＝3，求点M 的坐标； (2)求△ABP 面积的最大值．[解] (1)由题意知焦点F (0,1)，准线方程为y ＝－1. 设P (x 0，y 0)，由抛物线定义知|PF |＝y 0＋1，得y 0＝2，所以P (22，2)或P (－22，2)，由PF ＝3FM ，得M ⎝⎛⎭⎫－223，23或M ⎝⎛⎭⎫223，23. (2)设直线AB 的方程为y ＝kx ＋m ，点A (x 1，y 1)，B (x 2，y 2)，P (x 0，y 0)，由⎩⎪⎨⎪⎧y ＝kx ＋m ，x 2＝4y ，得x 2－4kx －4m ＝0. 于是Δ＝16k 2＋16m >0，x 1＋x 2＝4k ，x 1x 2＝－4m ，所以AB 中点M 的坐标为(2k,2k 2＋m )．由PF ＝3FM ，得(－x 0,1－y 0)＝3(2k,2k 2＋m －1)，所以⎩⎪⎨⎪⎧x 0＝－6k ，y 0＝4－6k 2－3m .由x 20＝4y 0得k 2＝－15m ＋415，由Δ>0，k 2≥0，得－13<m ≤43.又因为|AB |＝1＋k 2·(x 1＋x 2)2－4x 1x 2＝41＋k 2·k 2＋m ，点F (0,1)到直线AB 的距离为d ＝|m －1|1＋k 2，所以S △ABP ＝4S △ABF ＝8|m －1|k 2＋m ＝16153m 3－5m 2＋m ＋1. 记f (m )＝3m 3－5m 2＋m ＋1⎝⎛⎭⎫－13<m ≤43，令f ′(m )＝9m 2－10m ＋1＝0，解得m 1＝19，m 2＝1，可得f (m )在⎝⎛⎭⎫－13，19上是增函数，在⎝⎛⎭⎫19，1上是减函数，在⎝⎛⎭⎫1，43上是增函数，又f ⎝⎛⎭⎫19＝256243>f ⎝⎛⎭⎫43＝59.所以当m ＝19时，f (m )取到最大值256243，此时k ＝±5515.所以△ABP 面积的最大值为2565135. [方法技巧](1)当题目中给出的条件有明显的几何特征，考虑用图象性质来求解．(2)当题目中给出的条件和结论的几何特征不明显，则可以建立目标函数，再求这个函数的最值．求函数最值的常用方法有配方法、判别式法、单调性法、三角换元法等．利用基本不等式求最值[例3] 已知椭圆M ：x 2a 2＋y 23＝1(a >0)的一个焦点为F (－1,0)，左、右顶点分别为A ，B .经过点F 的直线l 与椭圆M 交于C ，D 两点．(1)当直线l 的倾斜角为45°时，求线段CD 的长；(2)记△ABD 与△ABC 的面积分别为S 1和S 2，求|S 1－S 2|的最大值． [解] (1)由题意，c ＝1，b 2＝3，所以a 2＝4，所以椭圆M 的方程为x 24＋y 23＝1，易求直线方程为y ＝x ＋1，联立方程，得⎩⎪⎨⎪⎧x 24＋y 23＝1，y ＝x ＋1，消去y ，得7x 2＋8x －8＝0，设C (x 1，y 1)，D (x 2，y 2)，Δ＝288，x 1＋x 2＝－87，x 1x 2＝－87，所以|CD |＝2|x 1－x 2|＝ 2(x 1＋x 2)2－4x 1x 2＝247.(2)当直线l 的斜率不存在时，直线方程为x ＝－1，此时△ABD 与△ABC 面积相等，|S 1－S 2|＝0；当直线l 的斜率存在时，设直线方程为y ＝k (x ＋1)(k ≠0)，联立方程，得⎩⎪⎨⎪⎧x 24＋y 23＝1，y ＝k (x ＋1)，消去y ，得(3＋4k 2)x 2＋8k 2x ＋4k 2－12＝0， Δ>0，且x 1＋x 2＝－8k 23＋4k 2，x 1x 2＝4k 2－123＋4k 2，此时|S 1－S 2|＝2||y 2|－|y 1||＝2|y 2＋y 1|＝2|k (x 2＋1)＋k (x 1＋1)|＝2|k (x 2＋x 1)＋2k |＝12|k |3＋4k 2，因为k ≠0，上式＝123|k |＋4|k |≤1223|k |·4|k |＝12212＝3当且仅当k ＝±32时等号成立，所以|S 1－S 2|的最大值为 3. [方法技巧](1)求最值问题时，一定要注意对特殊情况的讨论．如直线斜率不存在的情况，二次三项式最高次项的系数的讨论等．(2)利用基本不等式求函数的最值时，关键在于将函数变形为两项和或积的形式，然后用基本不等式求出最值．能力练通抓应用体验的“得”与“失”1.[考点一]如图所示，已知直线l ：y ＝kx －2与抛物线C ：x 2＝－2py (p >0)交于A ，B 两点，O 为坐标原点，OA ＋OB ＝(－4，－12)．(1)求直线l 和抛物线C 的方程；(2)抛物线上一动点P 从A 到B 运动时，求△ABP 面积的最大值．解析：(1)由⎩⎪⎨⎪⎧y ＝kx －2，x 2＝－2py ，得x 2＋2pkx －4p ＝0.设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝－2pk ，y 1＋y 2＝k (x 1＋x 2)－4＝－2pk 2－4. 因为OA ＋OB ＝(x 1＋x 2，y 1＋y 2)＝(－2pk ，－2pk 2－4)＝(－4，－12)，所以⎩⎪⎨⎪⎧ －2pk ＝－4，－2pk 2－4＝－12，解得⎩⎪⎨⎪⎧p ＝1，k ＝2.所以直线l 的方程为y ＝2x －2，抛物线C 的方程为x 2＝－2y .(2)设P (x 0，y 0)，依题意，知抛物线过点P 的切线与l 平行时，△ABP 的面积最大，又y ′＝－x ，所以－x 0＝2，故x 0＝－2，y 0＝－12x 20＝－2，所以P (－2，－2)．此时点P 到直线l 的距离d ＝|2×(－2)－(－2)－2|22＋(－1)2＝45＝455.由⎩⎪⎨⎪⎧y ＝2x －2，x 2＝－2y ，得x 2＋4x －4＝0，故x 1＋x 2＝－4，x 1x 2＝－4，所以|AB |＝1＋k 2×(x 1＋x 2)2－4x 1x 2＝1＋22×(－4)2－4×(－4)＝410. 所以△ABP 面积的最大值为410×4552＝8 2.2.[考点二]平面直角坐标系xOy 中，已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为32，左、右焦点分别是F 1，F 2.以F 1为圆心、以3为半径的圆与以F 2为圆心、以1为半径的圆相交，且交点在椭圆C 上．(1)求椭圆C 的方程；(2)设椭圆E ：x 24a 2＋y 24b 2＝1，P 为椭圆C 上任意一点．过点P 的直线y ＝kx ＋m 交椭圆E于A ，B 两点，射线PO 交椭圆E 于点Q .①求|OQ ||OP |的值；②求△ABQ 面积的最大值．解析：(1)由题意知2a ＝4，则a ＝2. 又c a ＝32，a 2－c 2＝b 2，可得b ＝1，所以椭圆C 的方程为x 24＋y 2＝1.(2)由(1)知椭圆E 的方程为x 216＋y 24＝1.①设P (x 0，y 0)，|OQ ||OP |＝λ，由题意知Q (－λx 0，－λy 0)．因为x 204＋y 20＝1，又(－λx 0)216＋(－λy 0)24＝1，即λ24⎝⎛⎭⎫x 204＋y 20＝1，所以λ＝2，即|OQ ||OP |＝2.②设A (x 1，y 1)，B (x 2, y 2)．将y ＝kx ＋m 代入椭圆E 的方程，可得(1＋4k 2)x 2＋8kmx ＋4m 2－16＝0，由Δ>0，可得m 2<4＋16k 2.(*)则有x 1＋x 2＝－8km1＋4k 2，x 1x 2＝4m 2－161＋4k 2.所以|x 1－x 2|＝416k 2＋4－m 21＋4k 2.因为直线y ＝kx ＋m 与y 轴交点的坐标为(0，m )，所以△OAB 的面积S ＝12|m ||x 1－x 2|＝216k 2＋4－m 2|m |1＋4k 2＝2(16k 2＋4－m 2)m 21＋4k 2＝2⎝⎛⎭⎫4－m 21＋4k 2m 21＋4k 2.设m 21＋4k 2＝t .将y ＝kx ＋m 代入椭圆C 的方程，可得(1＋4k 2)x 2＋8kmx ＋4m 2－4＝0，由Δ≥0，可得m 2≤1＋4k 2.(**) 由(*)(**)可知0<t ≤1，因此S ＝2(4－t )t ＝2－t 2＋4t ，故S ≤2 3. 当且仅当t ＝1，即m 2＝1＋4k 2时取得最大值2 3. 由①知，△ABQ 的面积为3S ，所以△ABQ 面积的最大值为6 3.3.[考点三]定圆M ：(x ＋3)2＋y 2＝16，动圆N 过点F (3，0)且与圆M 相切，记圆心N 的轨迹为E .(1)求轨迹E 的方程；(2)设点A ，B ，C 在E 上运动，A 与B 关于原点对称，且|AC |＝|BC |，当△ABC 的面积最小时，求直线AB 的方程．解析：(1)∵F (3，0)在圆M ：(x ＋3)2＋y 2＝16内， ∴圆N 内切于圆M . ∵|NM |＋|NF |＝4>|FM |，∴点N 的轨迹E 为椭圆，且2a ＝4，c ＝3，∴b ＝1， ∴轨迹E 的方程为x 24＋y 2＝1.(2)①当AB 为长轴(或短轴)时，S △ABC ＝12|OC |·|AB |＝2.②当直线AB 的斜率存在且不为0时，设直线AB 的方程为y ＝kx ，A (x A ，y A )，由题意，C 在线段AB 的中垂线上，则OC 的方程为y ＝－1kx .联立方程⎩⎪⎨⎪⎧x 24＋y 2＝1，y ＝kx得，x 2A ＝41＋4k 2，y 2A ＝4k 21＋4k 2，∴|OA |2＝x 2A ＋y 2A ＝4(1＋k 2)1＋4k 2.将上式中的k 替换为－1k ，可得|OC |2＝4(1＋k 2)k 2＋4.∴S △ABC ＝2S △AOC ＝|OA |·|OC |＝4(1＋k 2)1＋4k 2·4(1＋k 2)k 2＋4＝4(1＋k 2)(1＋4k 2)(k 2＋4). ∵(1＋4k 2)(k 2＋4)≤(1＋4k 2)＋(k 2＋4)2＝5(1＋k 2)2，∴S △ABC ≥85，当且仅当1＋4k 2＝k 2＋4，即k ＝±1时等号成立，此时△ABC 面积的最小值是85.∵2>85，∴△ABC 面积的最小值是85，此时直线AB 的方程为y ＝x 或y ＝－x .突破点(二) 圆锥曲线中的范围问题圆锥曲线中的范围问题是高考中的热点问题，常涉及不等式的恒成立问题、函数的值域问题，综合性比较强.解决此类问题常用几何法和判别式法.考点贯通抓高考命题的“形”与“神”利用判别式构造不等关系求范围[例1] 已知A ，B ，C 是椭圆M ：x 2a 2＋y 2b2＝1(a >b >0)上的三点，其中点A 的坐标为(23，0)，BC 过椭圆的中心，且AC ·BC ＝0，|BC |＝2|AC |. (1)求椭圆M 的方程；(2)过点(0，t )的直线l (斜率存在时)与椭圆M 交于两点P ，Q ，设D 为椭圆M 与y 轴负半轴的交点，且|DP |＝|DQ |，求实数t 的取值范围．[解] (1)因为|BC |＝2|AC |且BC 过(0,0)，则|OC |＝|AC |.因为AC ·BC ＝0，所以∠OCA ＝90°，即C (3，3)．又因为a ＝23，设椭圆的方程为x 212＋y 212－c 2＝1，将C 点坐标代入得312＋312－c 2＝1，解得c 2＝8，b 2＝4.所以椭圆的方程为x 212＋y 24＝1.(2)由条件D (0，－2)，当k ＝0时，显然－2<t <2；当k ≠0时，设l ：y ＝kx ＋t ，⎩⎪⎨⎪⎧x 212＋y 24＝1，y ＝kx ＋t ，消去y 得(1＋3k 2)x 2＋6ktx ＋3t 2－12＝0 由Δ>0可得t 2<4＋12k 2，①设P (x 1，y 1)，Q (x 2，y 2)，PQ 中点H (x 0，y 0)，则x 0＝x 1＋x 22＝－3kt1＋3k 2，y 0＝kx 0＋t ＝t1＋3k 2，所以H ⎝⎛⎭⎫－3kt 1＋3k 2，t1＋3k 2，由|DP |＝|DQ |，所以DH ⊥PQ ，即k DH ＝－1k ，所以t1＋3k 2＋2－3kt 1＋3k 2－0＝－1k ，化简得t ＝1＋3k 2，②所以t >1，将②代入①得，1<t <4. 所以t 的范围是(1,4)．综上可得t ∈(1,2)．[方法技巧]圆锥曲线中取值范围问题的五种常用解法(1)利用圆锥曲线的几何性质或判别式构造不等关系，从而确定参数的取值范围． (2)利用已知参数的范围，求新参数的范围，解决这类问题的核心是建立两个参数之间的等量关系．(3)利用隐含的不等关系建立不等式，从而求出参数的取值范围． (4)利用已知的不等关系构造不等式，从而求出参数的取值范围．(5)利用求函数的值域的方法将待求量表示为其他变量的函数，求其值域，从而确定参数的取值范围．利用函数性质求范围[例2] 已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为22，过点M (1,0)的直线l 交椭圆C 于A ，B 两点，|MA |＝λ|MB |，且当直线l 垂直于x 轴时，|AB |＝ 2.(1)求椭圆C 的方程；(2)若λ∈⎣⎡⎦⎤12，2，求弦长|AB |的取值范围．[解] (1)由已知e ＝22，得c a ＝22，又当直线垂直于x 轴时，|AB |＝2，所以椭圆过点⎝⎛⎭⎫1，22，代入椭圆方程得1a 2＋12b2＝1，∵a 2＝b 2＋c 2，联立方程可得a 2＝2，b 2＝1， ∴椭圆C 的方程为x 22＋y 2＝1.(2)当过点M 的直线斜率为0时，点A ，B 分别为椭圆长轴的端点， λ＝|MA ||MB |＝2＋12－1＝3＋22>2或λ＝|MA ||MB |＝2－12＋1＝3－22<12，不符合题意． ∴直线的斜率不能为0.设直线方程为x ＝my ＋1，A (x 1，y 1)，B (x 2，y 2)，将直线方程代入椭圆方程得：(m 2＋2)y 2＋2my －1＝0，由根与系数的关系可得，⎩⎨⎧y 1＋y 2＝－2mm 2＋2①，y 1y 2＝－1m 2＋2②，将①式平方除以②式可得：y 1y 2＋y 2y 1＋2＝－4m 2m 2＋2，由已知|MA |＝λ|MB |可知，y 1y 2＝－λ，∴－λ－1λ＋2＝－4m 2m 2＋2，又知λ∈⎣⎡⎦⎤12，2， ∴－λ－1λ＋2∈⎣⎡⎦⎤－12，0， ∴－12≤－4m 2m 2＋2≤0，解得m 2∈⎣⎡⎦⎤0，27. |AB |2＝(1＋m 2)|y 1－y 2|2＝(1＋m 2)[(y 1＋y 2)2－4y 1y 2]＝8⎝ ⎛⎭⎪⎫m 2＋1m 2＋22＝8⎝⎛⎭⎫1－1m 2＋22， ∵m 2∈⎣⎡⎦⎤0，27， ∴1m 2＋2∈⎣⎡⎦⎤716，12，∴|AB |∈⎣⎡⎦⎤2，928. [方法技巧]利用函数性质解决圆锥曲线中求范围问题的关键是建立求解关于某个变量的函数，通过求这个函数的值域确定目标的取值范围．在建立函数的过程中要根据题目的其他已知条件，把需要的量都用我们选用的变量表示，有时为了运算方便，在建立函数的过程中也可以采用多个变量，只要在最后结果中把多个变量化为单个变量即可，同时要特别注意变量的取值范围．1.[考点一]设F 1，F 2分别是椭圆E ：x 24＋y 2b 2＝1(b >0)的左、右焦点，若P 是该椭圆上的一个动点，且1PF ·2PF 的最大值为1.(1)求椭圆E 的方程；(2)设直线l ：x ＝ky －1与椭圆E 交于不同的两点A ，B ，且∠AOB 为锐角(O 为坐标原点)，求k 的取值范围．解析：(1)易知a ＝2，c ＝4－b 2，b 2<4，所以F 1(－4－b 2，0)，F 2(4－b 2，0)，设P (x ，y )，则1PF ·2PF ＝(－4－b 2－x ，－y )·(4－b 2－x ，－y )＝x 2＋y 2－4＋b 2＝x 2＋b 2－b 2x 24－4＋b 2＝⎝⎛⎭⎫1－b 24x 2＋2b 2－4.因为x ∈[－2,2]，故当x ＝±2，即点P 为椭圆长轴端点时，1PF ·2PF 有最大值1，即1＝⎝⎛⎭⎫1－b24×4＋2b 2－4，解得b 2＝1. 故所求椭圆E 的方程为x 24＋y 2＝1.(2)设A (x 1，y 1)，B (x 2，y 2)，由⎩⎪⎨⎪⎧x ＝ky －1x 24＋y 2＝1得(k 2＋4)y 2－2ky －3＝0，Δ＝(－2k )2＋12(4＋k 2)＝16k 2＋48>0，故y 1＋y 2＝2kk 2＋4，y 1·y 2＝－3k 2＋4.又∠AOB 为锐角，故OA ·OB ＝x 1x 2＋y 1y 2>0，又x 1x 2＝(ky 1－1)(ky 2－1)＝k 2y 1y 2－k (y 1＋y 2)＋1，所以x 1x 2＋y 1y 2＝(1＋k 2)y 1y 2－k (y 1＋y 2)＋1＝(1＋k 2)·－34＋k 2－2k 24＋k 2＋1＝－3－3k 2－2k 2＋4＋k 24＋k 2＝1－4k 24＋k 2>0，所以k 2<14，解得－12<k <12，故k 的取值范围是⎝⎛⎭⎫－12，12. 2.[考点二]已知圆心为H 的圆x 2＋y 2＋2x －15＝0和定点A (1,0)，B 是圆上任意一点，线段AB 的中垂线l 和直线BH 相交于点M ，当点B 在圆上运动时，点M 的轨迹记为曲线C .(1)求C 的方程；(2)过点A 作两条相互垂直的直线分别与曲线C 相交于P ，Q 和E ，F ，求PE ·QF 的取值范围．解析：(1)由x 2＋y 2＋2x －15＝0，得(x ＋1)2＋y 2＝16，所以圆心为H (－1,0)，半径为4.连接MA ，由l 是线段AB 的中垂线，得|MA |＝|MB |，所以|MA |＋|MH |＝|MB |＋|MH |＝|BH |＝4，又|AH |＝2<4.根据椭圆的定义可知，点M 的轨迹是以A ，H 为焦点，4为长轴长的椭圆，所以a 2＝4，c 2＝1，b 2＝3，所求曲线C 的方程为x 24＋y 23＝1.(2)由直线EF 与直线PQ 垂直，可得AP ·AE ＝AQ ·AF ＝0，于是PE ·QF ＝(AE －AP )·(AF －AQ )＝AE ·AF ＋AP ·AQ .①当直线PQ 的斜率不存在时，直线EF 的斜率为零，此时可不妨取P ⎝⎛⎭⎫1，32，Q ⎝⎛⎭⎫1，－32，E (2,0)，F (－2,0)，所以PE ·QF ＝⎝⎛⎭⎫1，－32·⎝⎛⎭⎫－3，32＝－3－94＝－214. ②当直线PQ 的斜率为零时，直线EF 的斜率不存在，同理可得PE ·QF ＝－214. ③当直线PQ 的斜率存在且不为零时，直线EF 的斜率也存在，于是可设直线PQ 的方程为y ＝k (x －1)，P (x P ，y P )，Q (x Q ，y Q )，AP ＝(x P －1，y P )，AQ ＝(x Q －1，y Q )，则直线EF 的方程为y ＝－1k(x －1)．将直线PQ 的方程代入曲线C 的方程，并整理得，(3＋4k 2)x 2－8k 2x ＋4k 2－12＝0，所以x P ＋x Q ＝8k 23＋4k 2，x P ·x Q ＝4k 2－123＋4k 2.于是AP ·AQ ＝(x P －1)(x Q －1)＋y P ·y Q ＝(1＋k 2)[x P x Q －(x P ＋x Q )＋1] ＝(1＋k 2)⎝ ⎛⎭⎪⎫4k 2－123＋4k 2－8k 23＋4k 2＋1＝－9(1＋k 2)3＋4k 2.将上面的k 换成－1k ，可得AE ·AF ＝－9(1＋k 2)4＋3k 2，所以PE ·QF ＝AE ·AF ＋AP ·AQ ＝－9(1＋k 2)⎝⎛⎭⎫13＋4k 2＋14＋3k 2. 令1＋k 2＝t ，则t >1，于是上式化简整理可得，PE ·QF ＝－9t ⎝⎛⎭⎫14t －1＋13t ＋1＝－63t 212t 2＋t －1＝－63494－⎝⎛⎭⎫1t －122. 由t >1，得0<1t <1，所以－214<PE ·QF ≤－367.综合①②③可知，PE ·QF 的取值范围为⎣⎡⎦⎤－214，－367.突破点(三) 圆锥曲线中的几何证明问题圆锥曲线中的几何证明问题多出现在解答题中，难度较大，多涉及线段或角相等以及位置关系的证明等.考点贯通抓高考命题的“形”与“神”圆锥曲线中的几何证明问题[典例] 如图，圆C 与x 轴相切于点T (2,0)，与y 轴正半轴相交于两点M ，N (点M 在点N 的下方)，且|MN |＝3.(1)求圆C 的方程；(2)过点M 任作一条直线与椭圆x 28＋y 24＝1相交于两点A ，B ，连接AN ，BN ，求证：∠ANM ＝∠BNM .[解] (1)设圆C 的半径为r (r >0)，依题意，圆心C 的坐标为(2，r )． ∵|MN |＝3，∴r 2＝⎝⎛⎭⎫322＋22，解得r 2＝254. ∴r ＝52，圆C 的方程为(x －2)2＋⎝⎛⎭⎫y －522＝254. (2)证明：把x ＝0代入方程(x －2)2＋⎝⎛⎭⎫y －522＝254，解得y ＝1或y ＝4，即点M (0,1)，N (0,4)． ①当AB ⊥x 轴时，可知∠ANM ＝∠BNM ＝0.②当AB 与x 轴不垂直时，可设直线AB 的方程为y ＝kx ＋1. 联立方程 ⎩⎪⎨⎪⎧y ＝kx ＋1，x 28＋y 24＝1，消去y 得，(1＋2k 2)x 2＋4kx －6＝0.设直线AB 交椭圆于A (x 1，y 1)，B (x 2，y 2)两点，则x 1＋x 2＝－4k 1＋2k 2，x 1x 2＝－61＋2k 2. ∴k AN ＋k BN ＝y 1－4x 1＋y 2－4x 2＝kx 1－3x 1＋kx 2－3x 2＝2kx 1x 2－3(x 1＋x 2)x 1x 2.若k AN ＋k BN ＝0，则∠ANM ＝∠BNM . ∵2kx 1x 2－3(x 1＋x 2)＝－12k 1＋2k 2＋12k1＋2k 2＝0， ∴∠ANM ＝∠BNM .1．设椭圆C 1：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为32，F 1，F 2是椭圆的两个焦点，M 是椭圆上任意一点，且△MF 1F 2的周长是4＋2 3.(1)求椭圆C 1的方程；(2)设椭圆C 1的左、右顶点分别为A ，B ，过椭圆C 1上的一点D 作x 轴的垂线交x 轴于点E ，若点C 满足AB ⊥BC ，AD ∥OC ，连接AC 交DE 于点P ，求证：PD ＝PE .解析：(1)由e ＝32，知c a ＝32，所以c ＝32a ，因为△MF 1F 2的周长是4＋23，所以2a ＋2c ＝4＋23，所以a ＝2，c ＝3，所以b 2＝a 2－c 2＝1，所以椭圆C 1的方程为：x 24＋y 2＝1.(2)证明：由(1)得A (－2,0)，B (2,0)，设D (x 0，y 0)，所以E (x 0,0)，因为AB ⊥BC ，所以可设C (2，y 1)，所以AD ＝(x 0＋2，y 0)，OC ＝(2，y 1)，由AD ∥OC 可得：(x 0＋2)y 1＝2y 0，即y 1＝2y 0x 0＋2.所以直线AC 的方程为：y 2y 0x 0＋2＝x ＋24. 整理得：y ＝y 02(x 0＋2)(x ＋2)．又点P 在DE 上，将x ＝x 0代入直线AC 的方程可得：y ＝y 02，即点P 的坐标为⎝⎛⎭⎫x 0，y 02，所以P 为DE 的中点，所以PD ＝PE .2．已知点A (－4,0)，直线l ：x ＝－1与x 轴交于点B ，动点M 到A ，B 两点的距离之比为2.(1)求点M 的轨迹C 的方程；(2)设C 与x 轴交于E ，F 两点，P 是直线l 上一点，且点P 不在C 上，直线PE ，PF 分别与C 交于另一点S ，T ，证明：A ，S ，T 三点共线．解析：(1)设点M (x ，y )，依题意，|MA ||MB |＝(x ＋4)2＋y 2(x ＋1)2＋y 2＝2，化简得x 2＋y 2＝4，即轨迹C 的方程为x 2＋y 2＝4. (2)证明：由(1)知曲线C 的方程为x 2＋y 2＝4，令y ＝0得x ＝±2，不妨设E (－2，0)，F (2,0)，如图所示．设P (－1，y 0)，S (x 1，y 1)，T (x 2，y 2)，则直线PE 的方程为y ＝y 0(x ＋2)，由⎩⎪⎨⎪⎧y ＝y 0(x ＋2)，x 2＋y 2＝4得(y 20＋1)x 2＋4y 20x ＋4y 20－4＝0，所以－2x 1＝4y 20－4y 20＋1，即x 1＝2－2y 20y 20＋1，y 1＝4y 0y 20＋1.直线PF 的方程为y ＝－y 03(x －2)，由⎩⎪⎨⎪⎧y ＝－y 03(x －2)，x 2＋y 2＝4得(y 20＋9)x 2－4y 20x ＋4y 20－36＝0，所以2x 2＝4y 20－36y 20＋9，即x 2＝2y 20－18y 20＋9，y 2＝12y 0y 20＋9.所以k AS ＝y 1x 1＋4＝4y 0y 20＋12－2y 20y 20＋1＋4＝2y 0y 20＋3， k AT ＝y 2x 2＋4＝12y 0y 20＋92y 20－18y 20＋9＋4＝2y 0y 20＋3，所以k AS ＝k AT ，所以A ，S ，T 三点共线．[全国卷5年真题集中演练——明规律] 1.(2014·新课标全国卷Ⅰ)已知点A (0，－2)，椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为32，F 是椭圆E 的右焦点，直线AF 的斜率为233，O 为坐标原点．(1)求E 的方程；(2)设过点A 的动直线l 与E 相交于P ，Q 两点．当△OPQ 的面积最大时，求l 的方程．解析：(1)设F (c,0)，由条件知，2c ＝233，得c ＝ 3.又c a ＝32，所以a ＝2，b 2＝a 2－c 2＝1. 故E 的方程为x 24＋y 2＝1.(2)当l ⊥x 轴时不合题意，故设l ：y ＝kx －2，P (x 1，y 1)，Q (x 2，y 2)．将y ＝kx －2代入x 24＋y 2＝1，得(1＋4k 2)x 2－16kx ＋12＝0. 当Δ＝16(4k 2－3)>0，即k 2>34时，x 1,2＝8k ±24k 2－34k 2＋1.从而|PQ |＝k 2＋1|x 1－x 2|＝4k 2＋1·4k 2－34k 2＋1.又点O 到直线PQ 的距离d ＝2k 2＋1. 所以△OPQ 的面积S △OPQ ＝12d ·|PQ |＝44k 2－34k 2＋1.设4k 2－3＝t ，则t >0，S △OPQ ＝4t t 2＋4＝4t ＋4t.因为t ＋4t ≥4，当且仅当t ＝2，即k ＝±72时等号成立，且满足Δ>0.所以，当△OPQ 的面积最大时，l 的方程为y ＝72x －2或y ＝－72x －2. 2．(2013·新课标全国卷Ⅱ)平面直角坐标系xOy 中，过椭圆M ：x 2a 2＋y 2b 2＝1 (a >b >0)右焦点的直线x ＋y －3＝0交M 于A ，B 两点，P 为AB 的中点，且OP 的斜率为12.(1)求M 的方程；(2)C ，D 为M 上的两点，若四边形ACBD 的对角线CD ⊥AB ，求四边形ACBD 面积的最大值．解析：(1)设A (x 1，y 1)，B (x 2，y 2)，P (x 0，y 0)，则x 21a 2＋y 21b 2＝1，x 22a 2＋y 22b 2＝1，y 2－y 1x 2－x 1＝－1，由此可得b 2(x 2＋x 1)a 2(y 2＋y 1)＝－y 2－y 1x 2－x 1＝1.因为x 1＋x 2＝2x 0，y 1＋y 2＝2y 0，y 0x 0＝12，所以a 2＝2b 2.又由题意知，M 的右焦点为(3，0)，故a 2－b 2＝3. 因此a 2＝6，b 2＝3.所以M 的方程为x 26＋y 23＝1.(2)由⎩⎪⎨⎪⎧x ＋y －3＝0，x 26＋y 23＝1，解得⎩⎨⎧x ＝433，y ＝－33，或⎩⎨⎧x ＝0，y ＝ 3.因此|AB |＝463.由题意可设直线CD 的方程为y ＝x ＋n ⎝⎛⎭⎫－533＜n ＜3，设C (x 3，y 3)，D (x 4，y 4)．由⎩⎪⎨⎪⎧y ＝x ＋n ，x 26＋y 23＝1得3x 2＋4nx ＋2n 2－6＝0. 于是x 3,4＝－2n ±2(9－n 2)3.因为直线CD 的斜率为1，所以|CD |＝2|x 4－x 3|＝439－n 2. 由已知，四边形ACBD 的面积S ＝12|CD |·|AB |＝8699－n 2.当n ＝0时，S 取得最大值，最大值为863.所以四边形ACBD 面积的最大值为863.[课时达标检测] 难点增分课时——设计3级训练，考生据自身能力而选一、全员必做题1．已知椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的一个焦点为F 2(1,0)，且该椭圆过定点M ⎝⎛⎭⎫1，22.(1)求椭圆E 的标准方程；(2)设点Q (2,0)，过点F 2作直线l 与椭圆E 交于A ，B 两点，且2F A ＝λ2F B ，λ∈[－2，－1]，以QA ，QB 为邻边作平行四边形QACB ，求对角线QC 长度的最小值．解析：(1)由题易知c ＝1，1a 2＋12b 2＝1，又a 2＝b 2＋c 2，解得b 2＝1，a 2＝2，故椭圆E 的标准方程为x 22＋y 2＝1.(2)设直线l ：x ＝ky ＋1，由⎩⎪⎨⎪⎧x ＝ky ＋1，x 22＋y 2＝1得(k 2＋2)y 2＋2ky －1＝0， Δ＝4k 2＋4(k 2＋2)＝8(k 2＋1)>0.设A (x 1，y 1)，B (x 2，y 2)，则可得y 1＋y 2＝－2k k 2＋2，y 1y 2＝－1k 2＋2.QC ＝QA ＋QB ＝(x 1＋x 2－4，y 1＋y 2)＝⎝ ⎛⎭⎪⎫－4(k 2＋1)k 2＋2，－2k k 2＋2，∴|QC |2＝|QA ＋QB |2＝16－28k 2＋2＋8(k 2＋2)2，由此可知，|QC |2的大小与k 2的取值有关．由2F A ＝λ2F B 可得y 1＝λy 2，λ＝y 1y 2，1λ＝y 2y 1(y 1y 2≠0)．从而λ＋1λ＝y 1y 2＋y 2y 1＝(y 1＋y 2)2－2y 1y 2y 1y 2＝－6k 2－4k 2＋2，由λ∈[－2，－1]得⎝⎛⎭⎫λ＋1λ∈⎣⎡⎦⎤－52，－2，从而－52≤－6k 2－4k 2＋2≤－2，解得0≤k 2≤27. 令t ＝1k 2＋2，则t ∈⎣⎡⎦⎤716，12，∴|QC |2＝8t 2－28t ＋16＝8⎝⎛⎭⎫t －742－172， ∴当t ＝12时，|QC |min ＝2.2.已知点F 为抛物线E ：y 2＝2px (p >0)的焦点，点A (2，m )在抛物线E 上，且|AF |＝3. (1)求抛物线E 的方程；(2)已知点G (－1,0)，延长AF 交抛物线E 于点B ，证明：以点F 为圆心且与直线GA 相切的圆，必与直线GB 相切．解析：(1)由抛物线的定义得|AF |＝2＋p2.因为|AF |＝3，即2＋p2＝3，解得p ＝2，所以抛物线E 的方程为y 2＝4x .(2)证明：设以点F 为圆心且与直线GA 相切的圆的半径为r. 因为点A(2，m)在抛物线E ：y2＝4x 上，所以m ＝±2 2.由抛物线的对称性，不妨设A(2,22)．由A(2,22)，F(1,0)可得直线AF 的方程为 y ＝22(x －1)．由⎩⎨⎧y ＝22x －1，y2＝4x ，得2x2－5x ＋2＝0，解得x ＝2或x ＝12，从而B ⎝⎛⎭⎫12，－2. 又G(－1,0)，故直线GA 的方程为22x －3y ＋22＝0，从而r ＝|22＋22|8＋9＝4 217 .又直线GB 的方程为22x ＋3y ＋22＝0，所以点F 到直线GB 的距离 d ＝|22＋22|8＋9＝4217＝r.这表明以点F 为圆心且与直线GA 相切的圆必与直线GB 相切．3．已知中心在原点，焦点在y 轴上的椭圆C ，其上一点P 到两个焦点F 1，F 2的距离之和为4，离心率为32. (1)求椭圆C 的方程；(2)若直线y ＝kx ＋1与曲线C 交于A ，B 两点，求△OAB 面积的取值范围．解析：(1)设椭圆的标准方程为y 2a 2＋x 2b2＝1(a >b >0)，由条件知，⎩⎪⎨⎪⎧2a ＝4，e ＝c a ＝32，a 2＝b 2＋c 2，解得a ＝2，c ＝3，b ＝1，故椭圆C 的方程为y 24＋x 2＝1.(2)设A (x 1，y 1)，B (x 2，y 2)，由⎩⎪⎨⎪⎧x 2＋y 24＝1，y ＝kx ＋1得(k 2＋4)x 2＋2kx －3＝0，故x 1＋x 2＝－2k k 2＋4，x 1x 2＝－3k 2＋4，设△OAB 的面积为S ，由x 1x 2＝－3k 2＋4<0，知S ＝12×1×|x 1－x 2|＝12(x 1＋x 2)2－4x 1x 2＝2k 2＋3(k 2＋4)2，令k 2＋3＝t ，知t ≥3， ∴S ＝21t ＋1t＋2. 对函数y ＝t ＋1t (t ≥3)，知y ′＝1－1t 2＝t 2－1t 2>0，∴y ＝t ＋1t 在t ∈[3，＋∞)上单调递增，∴t ＋1t ≥103，∴0<1t ＋1t＋2≤316，∴0<S ≤32. 故△OAB 面积的取值范围为⎝⎛⎦⎤0，32. 二、重点选做题1．过离心率为22的椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的右焦点F (1,0)作直线l 与椭圆C 交于不同的两点A ，B ，设|F A |＝λ|FB |，T (2,0)．(1)求椭圆C 的方程；(2)若1≤λ≤2，求△ABT 中AB 边上中线长的取值范围．解析：(1)∵e ＝22，c ＝1，∴a ＝2，b ＝1，即椭圆C 的方程为：x 22＋y 2＝1.(2)①当直线的斜率为0时，显然不成立． ②设直线l ：x ＝my ＋1，A (x 1，y 1)，B (x 2，y 2)，联立⎩⎪⎨⎪⎧x 2＋2y 2－2＝0，x ＝my ＋1得(m 2＋2)y 2＋2my －1＝0，则y 1＋y 2＝－2m m 2＋2，y 1y 2＝－1m 2＋2，由|F A |＝λ|FB |，得y 1＝－λy 2， ∵－λ＋1－λ＝y 1y 2＋y 2y 1，∴－λ＋1－λ＋2＝(y 1＋y 2)2y 1y 2＝－4m 2m 2＋2，∴m 2≤27，又∵AB 边上的中线长为12 |TA ＋TB |＝12(x 1＋x 2－4)2＋(y 1＋y 2)2＝4m 4＋9m 2＋4(m 2＋2)2＝ 2(m 2＋2)2－7m 2＋2＋4∈⎣⎡⎦⎤1，13216.2．如图所示，已知直线l 过点M (4,0)且与抛物线y 2＝2px (p ＞0)交于A ，B 两点，以弦AB 为直径的圆恒过坐标原点O .(1)求抛物线的标准方程；(2)设Q 是直线x ＝－4上任意一点，求证：直线QA ，QM ，QB 的斜率依次成等差数列．解析：(1)设直线l 的方程为x ＝ky ＋4，代入y 2＝2px 得y 2－2kpy －8p ＝0.设A (x 1，y 1)，B (x 2，y 2)，则有y 1＋y 2＝2kp ，y 1y 2＝－8p ，而AB 为直径，O 为圆上一点，所以OA ·OB ＝0，故0＝x 1x 2＋y 1y 2＝(ky 1＋4)(ky 2＋4)－8p ＝k 2y 1y 2＋4k (y 1＋y 2)＋16－8p ，即0＝－8k 2p ＋8k 2p ＋16－8p ，得p ＝2，所以抛物线方程为y 2＝4x .(2)设Q (－4，t )由(1)知y 1＋y 2＝4k ，y 1y 2＝－16，所以y 21＋y 22＝(y 1＋y 2)2－2y 1y 2＝16k 2＋32.因为k QA ＝y 1－t x 1＋4＝y 1－t y 214＋4＝4(y 1－t )y 21＋16，k QB ＝y 2－t x 2＋4＝y 2－t y 224＋4＝4(y 2－t )y 22＋16，k QM ＝t －8，所以k QA ＋k QB ＝4(y 1－t )y 21＋16＋4(y 2－t )y 22＋16＝4×(y 1－t )(y 22＋16)＋(y 2－t )(y 21＋16)(y 21＋16)(y 22＋16)＝4×y 1y 22＋16y 1－ty 22－16t ＋y 2y 21＋16y 2－ty 21－16t y 21y 22＋16(y 21＋y 22)＋16×16＝－t (y 21＋y 22)－32t 8×16＋4(y 21＋y 22)＝－t (16k 2＋32)－32t 8×16＋4(16k 2＋32) ＝－t 4＝2k QM . 所以直线QA ，QM ，QB 的斜率依次成等差数列．三、冲刺满分题1.已知椭圆C ：x 24＋y 2b 2＝1(0<b <2)的离心率为32，与坐标轴不垂直且不过原点的直线l 1与椭圆C 相交于不同的两点A ，B (如图所示)，过AB 的中点M 作垂直于l 1的直线l 2，设l 2与椭圆C 相交于不同的两点C ，D ，且CN ＝12CD . (1)求椭圆C 的方程；(2)设原点O 到直线l 1的距离为d ，求d |MN |的最大值．解析：(1)依题意得，⎩⎪⎨⎪⎧a ＝2，c a ＝32，c 2＝a 2－b 2，解得b 2＝1，所以椭圆C 的方程为x 24＋y 2＝1. (2)设直线l 1：y ＝kx ＋m (k ≠0，m ≠0)，由⎩⎪⎨⎪⎧ x 24＋y 2＝1，y ＝kx ＋m 得(1＋4k 2)x 2＋8kmx ＋4m 2－4＝0，设A (x 1，y 1)，B (x 2，y 2)，则⎩⎪⎨⎪⎧ x 1＋x 2＝－8mk 1＋4k 2，x 1x 2＝4m 2－41＋4k 2.故M ⎝⎛⎭⎫－4mk 1＋4k 2，m 1＋4k 2. l 2：y －m 1＋4k 2＝－1k ⎝⎛⎭⎫x ＋4mk 1＋4k 2，即y ＝－1k x －3m 1＋4k 2.由⎩⎨⎧ y ＝－1k x －3m 1＋4k 2，x 24＋y 2＝1，得⎝⎛⎭⎫1＋4k 2x 2＋24m k (1＋4k 2)x ＋36m 2(1＋4k 2)2－4＝0，设C (x 3，y 3)，D (x 4，y 4)，则x 3＋x 4＝－24mk (1＋4k 2)(k 2＋4)，故N ⎝⎛⎭⎫－12mk (1＋4k 2)(k 2＋4)，－3mk 2(1＋4k 2)(k 2＋4). 故|MN |＝|x M －x N | 1＋1k 2＝4|m |(k 2＋1)k 2＋1(1＋4k 2)(k 2＋4). 又d ＝|m |1＋k 2，所以d |MN |＝(1＋4k 2)(k 2＋4)4(k 2＋1)2. 令t ＝k 2＋1(t >1)，则d |MN |＝4t 2＋9t －94t 2＝－94t 2＋94t ＋1＝－94⎝⎛⎭⎫1t －122＋2516≤2516(当且仅当t ＝2时取等号)，所以d |MN |的最大值为2516. 2．已知椭圆x 2a 2＋y 2b2＝1(a ＞b ＞0)的左、右焦点分别为F 1，F 2，且|F 1F 2|＝6，直线y ＝kx 与椭圆交于A ，B 两点．(1)若△AF 1F 2的周长为16，求椭圆的标准方程；(2)若k ＝24，且A ，B ，F 1，F 2四点共圆，求椭圆离心率e 的值； (3)在(2)的条件下，设P (x 0，y 0)为椭圆上一点，且直线P A 的斜率k 1∈(－2，－1)，试求直线PB 的斜率k 2的取值范围．解析：(1)由题意得c ＝3，根据2a ＋2c ＝16，得a ＝5. 结合a 2＝b 2＋c 2，解得a 2＝25，b 2＝16.所以椭圆的方程为x 225＋y 216＝1. (2)法一：由⎩⎨⎧x 2a 2＋y 2b 2＝1，y ＝24x ，得⎝⎛⎭⎫b 2＋18a 2x 2－a 2b 2＝0. 设A (x 1，y 1)，B (x 2，y 2)．所以x 1＋x 2＝0，x 1x 2＝－a 2b 2b 2＋18a 2，由AB ，F 1F 2互相平分且共圆，易知，AF 2⊥BF 2，因为2F A ＝(x 1－3，y 1)，2F B ＝(x 2－3，y 2)，所以2F A ·2F B ＝(x 1－3)(x 2－3)＋y 1y 2＝⎝⎛⎭⎫1＋18x 1x 2＋9＝0. 即x 1x 2＝－8，所以有－a 2b 2b 2＋18a 2＝－8，结合b 2＋9＝a 2，解得a 2＝12(a 2＝6舍去)，所以离心率e ＝32.(若设A (x 1，y 1)，B (－x 1，－y 1)相应给分) 法二：设A (x 1，y 1)，又AB ，F 1F 2互相平分且共圆，所以AB ，F 1F 2是圆的直径，所以x 21＋y 21＝9，又由椭圆及直线方程综合可得：⎩⎨⎧ x 21＋y 21＝9，y 1＝24x 1，x 21a 2＋y 21b 2＝1.由前两个方程解得x 21＝8，y 21＝1，将其代入第三个方程并结合b 2＝a 2－c 2＝a 2－9，解得a 2＝12，故e ＝32. (3)由(2)的结论知，椭圆方程为x 212＋y 23＝1，由题可设A (x 1，y 1)，B (－x 1，－y 1)，k 1＝y 0－y 1x 0－x 1，k 2＝y 0＋y 1x 0＋x 1，所以k 1k 2＝y 20－y 21x 20－x 21，又y 20－y 21x 20－x 21＝3⎝⎛⎭⎫1－x 2012－3⎝⎛⎭⎫1－x 2112x 20－x 21＝－14，即k 2＝－14k 1，由－2＜k 1＜－1可知，18＜k 2＜14. 即直线PB 的斜率k 2的取值范围是⎝⎛⎭⎫18，14.。

2019高考数学(浙江)二轮复习练习：课时跟踪检测(十六)大题考法——圆锥曲线中的定点、定值、存在性问题

2019年4月课时跟踪检测（十六）大题考法——圆锥曲线中的定点、定值、存在性问题1．(2018·浙江高考名师预测卷二)已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的一个焦点与抛物线y 2＝82x 的焦点相同，F 1，F 2分别为椭圆的左、右焦点．M 为椭圆上任意一点，△MF 1F 2面积的最大值为4 2.(1)求椭圆C 的方程；(2)设椭圆C 上的任意一点N (x 0，y 0)，从原点O 向圆N ：(x －x 0)2＋(y －y 0)2＝3作两条切线，分别交椭圆于A ，B 两点．试探究|OA |2＋|OB |2是否为定值，若是，求出定值；若不是，请说明理由．解：(1)抛物线y 2＝82x 的焦点为(22，0)，由题意可得c ＝2 2.当点M 位于椭圆短轴的端点处时，△MF 1F 2的面积最大，即有12×b ×2c ＝42，解得b ＝2，所以a 2＝b 2＋c 2＝4＋8＝12，故椭圆C 的方程为x 212＋y 24＝1.(2)设直线OA ：y ＝k 1x ，OB ：y ＝k 2x ，A (x 1，y 1)，B (x 2，y 2)，设过原点与圆(x －x 0)2＋(y －y 0)2＝3相切的切线方程为y ＝kx ，则有|kx 0－y 0|1＋k 2＝3，整理得(x 20－3)k 2－2x 0y 0k ＋y 20－3＝0，所以k 1＋k 2＝2x 0y 0x 20－3，k 1k 2＝y 20－3x 20－3.又因为点N 在椭圆上，所以x 2012＋y 204＝1，所以可求得k 1k 2＝y 20－312－3y 20－3＝－13.将y ＝k 1x 代入椭圆方程x 2＋3y 2＝12，得x 21＝121＋3k 21，则y 21＝12k 211＋3k 21.同理可得x 22＝121＋3k 22，y 22＝12k 221＋3k 22，所以|OA |2＋|OB |2＝12(1＋k 21)1＋3k 21＋12(1＋k 22)1＋3k 22＝12(1＋k 21)(1＋3k 22)＋12(1＋k 22)(1＋3k 21)(1＋3k 21)(1＋3k 22)＝16[2＋3(k 21＋k 22)]2＋3(k 21＋k 22)＝16. 所以|OA |2＋|OB |2的值为定值，且为16.2.如图，曲线C 由上半椭圆C 1：y 2a 2＋x 2b 2＝1(a >b >0，y ≥0)和部分抛物线C 2：y ＝－x 2＋1(y ≤0)连接而成，C 1与C 2的公共点为A ，B ，其中C 1的离心率为32. (1)求a ，b 的值；(2)过点B 的直线l 与C 1，C 2分别交于点P ，Q (均异于点A ，B )，是否存在直线l ，使得以P Q 为直径的圆恰好过点A ，若存在，求出直线l 的方程；若不存在，请说明理由．解：(1)在C 2的方程中，令y ＝0，可得x ＝±1，∴A (－1,0)，B (1,0)．又A ，B 两点是上半椭圆C 1的左、右顶点，∴b ＝1.设C 1的半焦距为c ，由c a ＝32及a 2－c 2＝b 2＝1可得a ＝2，∴a ＝2，b ＝1. (2)由(1)知，上半椭圆C 1的方程为y 24＋x 2＝1(y ≥0)．由题易知，直线l 与x 轴不重合也不垂直，设其方程为y ＝k (x －1)(k ≠0)．代入C 1的方程，整理得(k 2＋4)x 2－2k 2x ＋k 2－4＝0.设点P 的坐标为(x P ，y P )，又直线l 经过点B (1,0)，∴x P ＋1＝2k 2k 2＋4，x P ＝k 2－4k 2＋4. 从而y P ＝－8kk 2＋4，∴点P 的坐标为⎝ ⎛⎭⎪⎫k 2－4k 2＋4，－8k k 2＋4. 同理，由⎩⎪⎨⎪⎧y ＝k (x －1)(k ≠0)，y ＝－x 2＋1(y ≤0)得点Q 的坐标为(－k －1，－k 2－2k )．∴AP ―→＝2k k 2＋4(k ，－4)，A Q ―→＝－k (1，k ＋2)．依题意可知AP ⊥A Q ，∴AP ―→·A Q ―→＝0，即－2k 2k 2＋4[k －4(k ＋2)]＝0， ∵k ≠0，∴k －4(k ＋2)＝0，解得k ＝－83. 经检验，k ＝－83符合题意，故直线l 的方程为y ＝－83(x －1)．3.已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为12，右焦点为F ，右顶点为E ，P 为直线x ＝54a 上的任意一点，且(PF ―→＋PE ―→)·EF ―→＝2. (1)求椭圆C 的方程；(2)过F 且垂直于x 轴的直线AB 与椭圆交于A ，B 两点(点A 在第一象限)，动直线l 与椭圆C 交于M ，N 两点，且M ，N 位于直线AB 的两侧，若始终保持∠MAB ＝∠NAB ，求证：直线MN 的斜率为定值．解：(1)设P ⎝⎛⎭⎫54a ，t ，F (c,0)，E (a,0)，则PF ―→＝⎝⎛⎭⎫c －54a ，－t ，PE ―→＝⎝⎛⎭⎫－a 4，－t ，EF ―→＝(c －a,0)，所以(PF ―→＋PE ―→)·EF ―→＝⎝⎛⎭⎫c －32a ，－2t ·()c －a ，0＝2，即⎝⎛⎭⎫c －32a ·(c －a )＝2，又e ＝c a ＝12，所以a ＝2，c ＝1，b ＝3，从而椭圆C 的方程为x 24＋y 23＝1. (2)由(1)知A ⎝⎛⎭⎫1，32，设M (x 1，y 1)，N (x 2，y 2)，设MN 的方程为y ＝kx ＋m ，代入椭圆方程x 24＋y 23＝1，得(4k 2＋3)x 2＋8kmx ＋4m 2－12＝0，所以x 1＋x 2＝－8km4k 2＋3，x 1x 2＝4m 2－124k 2＋3. 又M ，N 是椭圆上位于直线AB 两侧的动点，若始终保持∠MAB ＝∠NAB ，则k AM ＋k AN ＝0，即y 1－32x 1－1＋y 2－32x 2－1＝0， ⎝⎛⎭⎫kx 1＋m －32(x 2－1)＋⎝⎛⎭⎫kx 2＋m －32(x 1－1)＝0，即(2k －1)(2m ＋2k －3)＝0，得k ＝12. 故直线MN 的斜率为定值12. 4．(2018·镇海中学5月模拟)已知抛物线C 1，C 2的方程分别为x 2＝2y ，y 2＝2x .(1)求抛物线C 1和抛物线C 2的公切线l 的方程；(2)过点G (a ，b )(a ，b 为常数)作一条斜率为k 的直线与抛物线C 2：y 2＝2x 交于P ，Q 两点，当弦P Q 的中点恰好为点G 时，试求k 与b 之间的关系．解：(1)由题意可知，直线l 的斜率显然存在，且不等于0，设直线l 的方程为y ＝tx ＋m .联立⎩⎪⎨⎪⎧x 2＝2y ，y ＝tx ＋m ，消去y 并整理得x 2－2tx －2m ＝0，因为直线l 与抛物线C 1相切，所以Δ1＝(－2t )2－4×(－2m )＝0，整理得t 2＋2m ＝0. ①同理，联立⎩⎪⎨⎪⎧ y 2＝2x ，y ＝tx ＋m ，得2tm ＝1. ②由①②，解得⎩⎪⎨⎪⎧t ＝－1，m ＝－12，所以直线l 的方程为y ＝－x －12. (2)由题意知直线P Q 的方程为y －b ＝k (x －a )，即y ＝k (x －a )＋b .联立⎩⎪⎨⎪⎧y 2＝2x ，y ＝k (x －a )＋b ，消去y 得k 2x 2＋(－2k 2a ＋2kb －2)x ＋k 2a 2＋b 2－2kab ＝0，当k ＝0时，直线P Q 与抛物线C 2：y 2＝2x 只有一个交点，故k ≠0，设点P (x 1，y 1)，Q (x 2，y 2)，所以由根与系数的关系得x 1＋x 2＝2k 2a －2kb ＋2k 2，所以x 1＋x 22＝k 2a －kb ＋1k 2. 又y 1＋y 2＝k (x 1－a )＋b ＋k (x 2－a )＋b＝k (x 1＋x 2)－2ka ＋2b ＝2k 2a －2kb ＋2k－2ka ＋2b ＝2k 2a －2kb ＋2－2k 2a ＋2kb k＝2k ，所以y 1＋y 22＝1k . 要满足弦P Q 的中点恰好为点G (a ，b )，根据中点坐标公式可知⎩⎪⎨⎪⎧ x 1＋x 22＝a ，y 1＋y 22＝b ，即⎩⎪⎨⎪⎧ k 2a －kb ＋1k 2＝a ，1k ＝b ，所以kb ＝1.故k 与b 之间的关系是互为倒数．5．已知椭圆C 的中心在原点，焦点在x 轴上，离心率为22，它的一个焦点恰好与抛物线y 2＝4x 的焦点重合．(1)求椭圆C 的方程；(2)设椭圆的上顶点为A ，过点A 作椭圆C 的两条动弦AB ，AC ，若直线AB ，AC 斜率之积为14，直线BC 是否恒过一定点？若经过，求出该定点坐标；若不经过，请说明理由．解：(1)由题意知椭圆的一个焦点为F (1,0)，则c ＝1.由e ＝c a ＝22得a ＝2，所以b ＝1，所以椭圆C 的方程为x 22＋y 2＝1. (2)由(1)知A (0,1)，当直线BC 的斜率不存在时，设BC ：x ＝x 0，设B (x 0，y 0)，则C (x 0，－y 0)，k AB ·k AC ＝y 0－1x 0·－y 0－1x 0＝1－y 20x 20＝12x 20x 20＝12≠14，不合题意．故直线BC 的斜率存在．设直线BC 的方程为y ＝kx ＋m (m ≠1)，并代入椭圆方程，得：(1＋2k 2)x 2＋4kmx ＋2(m 2－1)＝0，① 由Δ＝(4km )2－8(1＋2k 2)(m 2－1)>0，得2k 2－m 2＋1>0. ② 设B (x 1，y 1)，C (x 2，y 2)，则x 1，x 2是方程①的两根，由根与系数的关系得，x 1＋x 2＝－4km 1＋2k 2，x 1x 2＝2(m 2－1)1＋2k 2，由k AB ·k AC ＝y 1－1x 1·y 2－1x 2＝14得： 4y 1y 2－4(y 1＋y 2)＋4＝x 1x 2，即(4k 2－1)x 1x 2＋4k (m －1)(x 1＋x 2)＋4(m －1)2＝0，整理得(m －1)(m －3)＝0，又因为m ≠1，所以m ＝3，此时直线BC 的方程为y ＝kx ＋3.所以直线BC 恒过一定点(0,3)．。

[精品]2019版高考数学二轮复习专题七解析几何专题对点练23圆锥曲线中的最值、范围、证明问题文

=
+
=8. ∴ a=4, ∴b2=a2-c 2=4, e= .
∴ 椭圆 C的标准方程 T( x0, y0)( x0≠0, y0≠0),
则
=1.
M(4,0), N(0,2), ∴ 直线 TN的方程为 y- 2= x, 令 y=0, 得 Q
,
直线 TM的方程为 y= ( x- 4),
如图 , 若△ POQ的重心恰好在圆上 , 求 m的取值范围 .
6. 已知椭圆 C与双曲线 y2-x 2 =1 有共同焦点 , 且离心率为 . (1) 求椭圆 C的标准方程 ; (2) 若 A为椭圆 C的下顶点 , M, N为椭圆 C上异于 A的两点 , 直线 AM与 AN的斜率之积为 1. ① 求证 : 直线 MN恒过定点 , 并求出该定点坐标 ;
(2) 对于 (1) 中求出的抛物线 C, 若点 D( x0,0)
, 记点 B 关于 x 轴的对称点为 E, AE交 x 轴于点 P, 且 AP⊥ BP, 求
证 : 点 P的坐标为 ( -x 0,0), 并求点 P 到直线 AB的距离 d 的取值范围 .
推荐下载
专题对点练 23 答案 1. (1) 解当 l 与 x 轴垂直时 , l 的方程为 x=2, 可得 M的坐标为 (2,2) 或 (2, - 2) . 所以直线 BM的方程为 y=x+1 或 y=-x- 1. (2) 证明当 l 与 x 轴垂直时 , AB为 MN的垂直平分线 , 所以∠ ABM∠= ABN. 当 l 与 x 轴不垂直时 , 设 l 的方程为 y=k( x- 2)( k≠0), M( x1, y1), N( x2 , y2), 则 x1>0, x2>0.
消去 x, 得 y2- 4my-4x0=0. ∵x0≥，∴Δ =16m2 +16x0>0, y1+y2=4m, y1y2=- 4x0, 设 P 的坐标为 =( x1-x P, y1),

(浙江专用)高考数学大二轮复习专题四大题考法课二圆锥曲线中的定点、定值、存在性问题课时跟踪检测

圆锥曲线中的定点、定值、存在性问题[课时跟踪检测]1．(2019·某某九校联考)已知离心率为22的椭圆C ：x 2a 2＋y2b 2＝1(a ＞b＞0)，过椭圆C 上点P (2,1)作两条互相垂直的直线，分别交椭圆于A ，B 两点．(1)求椭圆C 的方程；(2)求证：直线AB 过定点，并求出此定点的坐标．解：(1)依题意有⎩⎪⎨⎪⎧4a 2＋1b 2＝1，c a ＝22，解得⎩⎪⎨⎪⎧a 2＝6，b 2＝3，所以椭圆C 的方程为x 26＋y 23＝1.(2)证明：易知直线AB 的斜率存在，故设直线AB 的方程为y ＝kx ＋m ，由⎩⎪⎨⎪⎧y ＝kx ＋m ，x 26＋y23＝1得(2k 2＋1)x 2＋4mkx ＋2m 2－6＝0.设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝－4mk 2k 2＋1，x 1x 2＝2m 2－62k 2＋1，由P A →·P B →＝0，得(x 1－2)(x 2－2)＋(y 1－1)(y 2－1)＝0，即(x 1－2)(x 2－2)＋(kx 1＋m －1)(kx 2＋m －1)＝0，得(k 2＋1)x 1x 2＋(km －k －2)(x 1＋x 2)＋m 2－2m ＋5＝0，则3m 2＋8mk ＋4k 2－2m －1＝0，即(3m ＋2k ＋1)(m ＋2k －1)＝0，由直线AB 不过点P ，知m ＋2k －1≠0，故3m ＋2k ＋1＝0.所以直线AB 过定点⎝ ⎛⎭⎪⎫23，－13.2．已知抛物线C 1：x 2＝4y 的焦点为F ，过抛物线C 2：y ＝－18x 2＋3上一点M 作抛物线C 2的切线l ，与抛物线C 1交于A ，B 两点．(1)记直线AF ，BF 的斜率分别为k 1，k 2，若k 1·k 2＝－35，求直线l 的方程；(2)是否存在正实数m ，使得对任意点M ，都有|AB |＝m (|AF |＋|BF |)成立？若存在，求出m 的值；若不存在，请说明理由．解：(1)设M (x 0，y 0)，由y ＝－x 28＋3，得y ′＝－x4，则切线l 的斜率为k ＝－x 04. 切线l 的方程为y ＝－x 04(x －x 0)＋y 0＝－x 04x ＋x 204＋y 0＝－x 04x －2y 0＋6＋y 0，即y ＝－x 04x －y 0＋6.与x 2＝4y 联立，消去y 得x 2＋x 0x ＋4y 0－24＝0. 设A (x 1，y 1)，B (x 2，y 2)，则有x 1＋x 2＝－x 0，x 1x 2＝4y 0－24，则y 1＋y 2＝－x 04(x 1＋x 2)－2y 0＋12＝x 204－2y 0＋12＝－4y 0＋18，y 1y 2＝x 21x 2216＝(y 0－6)2，则由k 1·k 2＝y 1－1x 1×y 2－1x 2＝y 1y 2－(y 1＋y 2)＋1x 1x 2＝(y 0－6)2－(－4y 0＋18)＋14y 0－24＝－35，得5y 20－28y 0＋23＝0，解得y 0＝1或y 0＝235.∵x 20＝－8(y 0－3)≥0，∴y 0≤3，故y 0＝1，∴x 0＝±4. 则直线l 的方程为y ＝±x ＋5.(2)由(1)知直线l 的方程为y ＝－x 04x －y 0＋6，且x 1＋x 2＝－x 0，x 1x 2＝4y 0－24，则|AB |＝1＋x 2016|x 1－x 2|＝1＋x 2016·(x 1＋x 2)2－4x 1x 2＝16＋x 204·x 20－4(4y 0－24)，即|AB |＝16－8y 0＋244·－8y 0＋24－16y 0＋96＝23(5－y 0)，而|AF |＋|BF |＝(y 1＋1)＋(y 2＋1)＝－4y 0＋20＝4(5－y 0)，则|AB |＝32(|AF |＋|BF |)，故存在正实数m ＝32，使得对任意点M ，都有|AB |＝32(|AF |＋|BF |)成立． 3．(2019·嵊州高三期末)已知抛物线y 2＝2x ，P (1,0)，M (0，a )，其中a ＞0，过点M 作抛物线的切线，切点为A (不同于原点O )，过点A ，P 作直线交抛物线于点B ，过点M ，P 作直线交抛物线于点C ，D .(1)求证：直线MA ，MP 的斜率之积为定值；(2)若△BCD 的面积为2716，某某数a 的值．解：(1)证明：设A (2m 2,2m )(m ≠0)，则k AM ＝2m －a 2m 2，所以直线AM ：y ＝2m －a 2m 2x ＋a ，即x ＝2m 22m －a ·(y －a )，与抛物线方程联立得y 2－4m 22m －a y ＋4m 2a 2m －a＝0，因为直线AM 与抛物线相切，所以Δ＝16m 4(2m －a )2－16m 2a2m －a ＝0，解得m ＝a ，所以A (2a 2,2a )，所以k MA ·k MP ＝2a －a 2a 2－0·a －00－1＝－12，为定值． (2)易得k CD ＝k MP ＝－a ，所以直线CD ：y ＝－ax ＋a ，即x ＝－1ay ＋1，与抛物线方程联立得y 2＋2ay －2＝0，设C (x 1，y 1)，D (x 2，y 2)， |y 1－y 2|＝4a 2＋8＝22a 2＋1a， |CD |＝1＋1a2·|y 1－y 2|＝2(a 2＋1)·(2a 2＋1)a2，又k AB ＝2a 2a 2－1，所以直线AB ：y ＝2a 2a 2－1(x －1)，即x ＝2a 2－12a y ＋1，与抛物线方程联立得y 2－2a 2－1ay －2＝0，所以y A y B ＝－2，所以y B ＝－1a ，所以B ⎝ ⎛⎭⎪⎫12a2，－1a ，所以点B 到直线CD 的距离d ＝12a＋a a 2＋1，所以S △BCD ＝⎝ ⎛⎭⎪⎫12a ＋a 2a 2＋1a 2＝2716，整理得(2a 2＋1)3a 3＝278，所以2a 2＋1a＝32，解得a ＝2或a ＝－2(舍去)．4.如图，A 为椭圆x 22＋y 2＝1的下顶点，过点A 的直线l 交抛物线x 2＝2py (p ＞0)于B ，C 两点，C 是AB 的中点．(1)求证：点C 的纵坐标是定值；(2)过点C 作与直线l 倾斜角互补的直线l ′交椭圆于M ，N 两点，p 为何值时，△BMN 的面积最大？解：(1)证明：易知A (0，－1)，不妨设B ⎝ ⎛⎭⎪⎫t ，t 22p ，则C ⎝ ⎛⎭⎪⎫t 2，t 2－2p 4p ，代入抛物线方程得⎝ ⎛⎭⎪⎫t 22＝2p ·t 2－2p 4p ，得t 2＝4p ，∴y C ＝4p －2p 4p ＝12，故点C 的纵坐标为定值．(2)∵点C 是AB 的中点，∴S △BMN ＝S △AMN . 设直线l 的斜率为k ，直线l ′的斜率为k ′，则k ＝12－(－1)t2＝3t ，k ′＝－3t，∴直线l ′的方程为y －12＝－3t ⎝ ⎛⎭⎪⎫x －t 2，即y ＝－3t x ＋2，不妨记m ＝－3t ，则l ′：y ＝mx＋2，代入椭圆方程整理得(2m 2＋1)x 2＋8mx ＋6＝0，设M (x 1，y 1)，N (x 2，y 2)，则x 1＋x 2＝－8m 2m 2＋1，x 1x 2＝62m 2＋1，|MN |＝1＋m 2|x 1－x 2|＝22·1＋m 2·2m 2－32m 2＋1，又A 到直线MN 的距离d ＝3m 2＋1，所以S △AMN ＝12·|MN |·d ＝322m 2－32m 2＋1＝322m 2－3＋42m 2－3≤324. 当且仅当2m 2－3＝42m 2－3时取等号，解得m 2＝72，所以t 2＝9m 2＝187，从而p ＝t 24＝914，故当p ＝914时△BMN 的面积最大．5．已知椭圆C 的中心在原点，焦点在x 轴上，离心率为22，它的一个焦点恰好与抛物线y 2＝4x 的焦点重合．(1)求椭圆C 的方程；(2)设椭圆的上顶点为A ，过点A 作椭圆C 的两条动弦AB ，AC ，若直线AB ，AC 斜率之积为14，直线BC 是否恒过一定点？若经过，求出该定点坐标；若不经过，请说明理由．解：(1)由题意知椭圆的一个焦点为F (1,0)，则c ＝1. 由e ＝c a ＝22得a ＝2，所以b ＝1，所以椭圆C 的方程为x 22＋y 2＝1.(2)由(1)知A (0,1)，当直线BC 的斜率不存在时，设BC ：x ＝x 0，设B (x 0，y 0)，则C (x 0，－y 0)， k AB ·k AC ＝y 0－1x 0·－y 0－1x 0＝1－y 2x 20＝12x 20x 20＝12≠14，不合题意．故直线BC 的斜率存在．设直线BC 的方程为y ＝kx ＋m (m ≠1)，并代入椭圆方程，得：(1＋2k 2)x 2＋4kmx ＋2(m 2－1)＝0，① 由Δ＝(4km )2－8(1＋2k 2)(m 2－1)>0，得2k 2－m 2＋1>0.②设B (x 1，y 1)，C (x 2，y 2)，则x 1，x 2是方程①的两根，由根与系数的关系得，x 1＋x 2＝－4km 1＋2k 2，x 1x 2＝2(m 2－1)1＋2k 2，由k AB ·k AC ＝y 1－1x 1·y 2－1x 2＝14得： 4y 1y 2－4(y 1＋y 2)＋4＝x 1x 2，即(4k 2－1)x 1x 2＋4k (m －1)(x 1＋x 2)＋4(m －1)2＝0，整理得(m －1)(m －3)＝0，又因为m ≠1，所以m ＝3，此时直线BC 的方程为y ＝kx ＋3. 所以直线BC 恒过一定点(0,3)．。

全国通用近年高考数学一轮复习高考达标检测(三十九)圆锥曲线的综合问题——最值、范围、证明问题文(2

（全国通用版）2019版高考数学一轮复习高考达标检测（三十九）圆锥曲线的综合问题——最值、范围、证明问题文编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（全国通用版）2019版高考数学一轮复习高考达标检测（三十九）圆锥曲线的综合问题——最值、范围、证明问题文）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（全国通用版）2019版高考数学一轮复习高考达标检测（三十九）圆锥曲线的综合问题——最值、范围、证明问题文的全部内容。

高考达标检测（三十九）圆锥曲线的综合问题——最值、范围、证明问题1．已知A ,B 分别是椭圆C ：错误!＋错误!＝1(a 〉b 〉0)的长轴与短轴的一个端点，F 1,F 2分别是椭圆C 的左、右焦点，D 是椭圆上的一点,△DF 1F 2的周长为6，｜AB |＝错误!。

（1）求椭圆C 的方程；(2)若P 是圆x 2＋y 2＝7上任一点,过点P 作椭圆C 的切线，切点分别为M ,N ，求证：PM ⊥PN 。

解：（1）由△DF 1F 2的周长为6，得2a ＋2c ＝6，由｜AB |＝错误!，得a 2＋b 2＝7，又b 2＋c 2＝a 2，∴a ＝2,b ＝错误!，c ＝1.故椭圆C 的方程为错误!＋错误!＝1。

(2）证明：①当切线PM 的斜率不存在或为零时，此时取P （2，3）,显然直线PN :y ＝错误!与直线PM :x ＝2恰是椭圆的两条切线．由圆及椭圆的对称性，可知PM ⊥PN .②当切线PM ，PN 斜率存在且不为零时，设切线PM 的方程为y ＝k 1x ＋m ， PN 的方程为y ＝k 2x ＋t ,P (x 0,y 0)（x 0≠±2），由错误!消去y ，得（4k 错误!＋3）x 2＋8k 1mx ＋4（m 2－3）＝0,∵PM 与椭圆C 相切，∴Δ＝64k 错误!m 2－16(4k 错误!＋3)(m 2－3)＝0，∴m 2＝4k 21＋3.∵y 0＝k 1x 0＋m ，∴m ＝y 0－k 1x 0,∴(y 0－k 1x 0）2＝4k 错误!＋3。

2019高考数学专项讲解21：解析几何专项4圆锥曲线中的最值和范围问题

线段 AB 上，且 AP PB 〔为常数且 0 〕、
〔1〕求点 P 的轨迹方程 C ，并说明轨迹类型；
〔2〕当 =2 时，直线 l1 与原点 O 的距离为 a ，且直线 l1 与轨迹 C 有公共点，求直线 l1 的 2
斜率 k 的取值范围、
答案：(1)设 P(x , y) 、 A(x0 , 0) 、 B(0 , y0 ) ，那么
km k2 9
1 2
m
k2 9 2k
②
把②代入①式中得
(k 2 9)2 4k 2
(k2
9)
0
，
∴k＞ 3 或 k＜－ 3
∴直线 l 倾斜角 ( ， ) ( ，2 ) 32 2 3
第二十二讲圆锥曲线中的最值和范围问题〔二〕
【例 5】长度为 a 〔 a 0 〕的线段 AB 的两个端点 A 、 B 分别在 x 轴和 y 轴上滑动，点 P 在
AP
PB
x
y
x0 x ( y0 y)
x0
y0
(1 )x 1 y
，由此及 |
AB
|
a
x02
y02
a2
，得
(1 )x2
1
y
2
，即
a2
x2
y2 2
1
a
2 〔*〕
①当 0 1时，方程〔*〕的轨迹是焦点为 (
1 1
a,0)
，长轴长为
1
2
a
的椭圆、
②当 1时，方程〔*〕的轨迹是焦点为 (0,
由①③得:x2+1=－ 2 ，代入⑤得：S△OAB= 3 | k | (k 0)
3k 2 1
3k 2 1
〔2〕因 S△OAB=

2019届高考(浙江)数学(理)二轮专题训练：第1部分专题五第3讲圆锥曲线中的定点、定值和最值问题

1.(2018·重庆高考)如图，椭圆的中心为原点O ，长轴在x 轴上，离心率e ＝22，过左焦点F 1作x 轴的垂线交椭圆于A ，A′两点，|AA′|＝4.(1)求该椭圆的标准方程；(2)取平行于y 轴的直线与椭圆相交于不同的两点P ，P′，过P ，P′作圆心为Q 的圆，使椭圆上的其余点均在圆Q 外．求△PP′Q 的面积S 的最大值，并写出对应的圆Q 的标准方程．解：(1)设该椭圆的方程为x 2a 2＋y 2b 2＝1(a>b>0)，由题意知点A(－c,2)在椭圆上，则－2a 2＋22b2＝1，从而e 2＋4b 2＝1，又e ＝22，故b 2＝41－e 2＝8，从而a 2＝b 21－e2＝16. 故该椭圆的标准方程为x 216＋y28＝1.(2)由椭圆的对称性，可设Q(x 0,0)．又设M(x ，y)是椭圆上任意一点，则|QM|2＝(x －x 0)2＋y 2＝x 2－2x 0x ＋x 2＋8×⎝ ⎛⎭⎪⎫1－x 216＝12(x －2x 0)2－x 20＋8(x ∈[－4,4])．设P(x 1，y 1)，由题意知，点P 是椭圆上到点Q 的距离最小的点，因此，当x ＝x 1时|QM|2取最小值，又x 1∈(－4，4)，从而x 1＝2x 0，且|QP|2＝8－x 20.由对称性知P′(x 1，－y 1)，故|PP′|＝|2y 1|，所以S ＝12|2y 1||x 1－x 0|＝12×28×⎝ ⎛⎭⎪⎫1－x 2116|x 0|＝2－x 220＝ 2 －20－22＋4.故当x 0＝±2时，△PP′Q 的面积S 取得最大值2 2.此时对应的圆Q 的圆心坐标为Q(±2，0)，半径|QP|＝8－x 20＝6，因此，这样的圆有两个，其标准方程分别为(x ＋2)2＋y 2＝6，(x －2)2＋y 2＝6. 2.如图，椭圆C0：x 2a 2＋y 2b 2＝1(a>b>0，a ，b 为常数)，动圆C 1：x 2＋y 2＝t 21，b<t 1<a.点A 1，A 2分别为C 0的左，右顶点，C 1与C 0相交于A ，B ，C ，D 四点．(1)求直线AA 1与直线A 2B 交点M 的轨迹方程；(2)设动圆C 2：x 2＋y 2＝t 22与C 0相交于A′，B′，C′，D′四点，其中b<t 2<a ，t 1≠t 2.若矩形ABCD 与矩形A′B′C′D′的面积相等，证明：t 21＋t 22为定值．解：(1)设 A(x 1，y 1)，B(x 1，－y 1)，又知A 1(－a,0)，A 2(a,0)，则直线A 1A 的方程为y ＝y 1x 1＋a (x ＋a)，①直线A 2B 的方程为y ＝－y 1x 1－a (x －a)．② 由①×②得y 2＝－y 21x 21－a2(x 2－a 2)．③由点A(x 1，y 1)在椭圆C 0上，得x 21a 2＋y 21b 2＝1.从而y 21＝b 2⎝ ⎛⎭⎪⎫1－x 21a ，代入③得x 2a 2－y 2b 2＝1(x<－a ，y<0)．(2)证明：设A′(x 2，y 2)，由矩形ABCD 与矩形A′B′C′D′的面积相等，得4|x 1||y 1|＝4|x 2||y 2|，故x 21y 21＝x 22y 22.因为点A ，A′均在椭圆上，所以b 2x 21⎝ ⎛⎭⎪⎫1－x 21a 2＝b 2x 22⎝ ⎛⎭⎪⎫1－x 22a 2.由t 1≠t 2，知x 1≠x 2，所以x 21＋x 22＝a 2. 从而y 21＋y 22＝b 2，因此t 21＋t 22＝a 2＋b 2为定值．3.(2018·珠海模拟)如图，抛物线的顶点O 在坐标原点，焦点在y 轴负半轴上．过点M(0，－2)作直线l 与抛物线相交于A ，B 两点，且满足OA ＋OB ＝(－4，－12)．(1)求直线l 和抛物线的方程；(2)当抛物线上一动点P 从点A 向点B 运动时，求△ABP 面积的最大值．解：(1)根据题意可设直线l 的方程为y ＝kx －2，抛物线方程为x 2＝－2py(p ＞0)．由⎩⎪⎨⎪⎧y ＝kx －2，x 2＝－2py ，得x 2＋2pkx －4p ＝0.设点A(x 1，y 1)，B(x 2，y 2)，则x 1＋x 2＝－2pk ， y 1＋y 2＝k(x 1＋x 2)－4＝－2pk 2－4，∴OA ＋OB ＝(x 1＋x 2，y 1＋y 2)＝(－2pk ，－2pk 2－4)．∵OA ＋OB ＝(－4，－12)，∴⎩⎪⎨⎪⎧－2pk ＝－4，－2pk 2－4＝－12.解得⎩⎪⎨⎪⎧p ＝1，k ＝2.故直线l 的方程为y ＝2x －2，抛物线方程为x 2＝－2y.(2)据题意，当抛物线过点P 的切线与l 平行时，△APB 的面积最大．设点P(x 0，y 0)，则y′＝－x ，故由－x 0＝2，得x 0＝－2，则y 0＝－12x 20＝－2，故P(－2，－2)．此时点P 到直线l 的距离 d ＝－－－－2|22＋－2＝45＝455.由⎩⎪⎨⎪⎧y ＝2x －2，x 2＝－2y ，得x 2＋4x －4＝0.故|AB|＝1＋k 21＋x 22－4x 1x 2＝1＋22－2－－＝410.故△ABP 的面积的最大值为12×|AB|×d＝12×410×455＝8 2.4．(2018·广东高考)已知抛物线C 的顶点为原点，其焦点F(0，c)(c>0)到直线l ：x －y －2＝0的距离为3 22.设P 为直线l 上的点，过点P 作抛物线C 的两条切线PA ，PB ，其中A ，B 为切点． (1)求抛物线C 的方程；(2)当点P(x 0，y 0)为直线l 上的定点时，求直线AB 的方程； (3)当点P 在直线l 上移动时，求|AF|·|BF|的最小值．解：(1)依题意，设抛物线C 的方程为x 2＝4cy(c>0)，则|0－c －2|2＝3 22，结合c>0，解得c ＝1.所以抛物线C 的方程为x 2＝4y.(2)抛物线C 的方程为x 2＝4y ，即y ＝14x 2，求导得y′＝12x.设A(x 1，y 1)，B(x 2，y 2)⎝ ⎛⎭⎪⎫其中y 1＝x 214，y 2＝x 224，则切线PA ，PB 的斜率分别为12x 1，12x 2. 所以切线PA 的方程为y －y 1＝x 12(x －x 1)，即y ＝x 12x －x 212＋y 1，即x 1x －2y －2y 1＝0.同理，可得切线PB 的方程为x 2x －2y －2y 2＝0.因为切线PA ，PB 均过点P(x 0，y 0)，所以x 1x 0－2y 0－2y 1＝0，x 2x 0－2y 0－2y 2＝0. 所以(x 1，y 1)，(x 2，y 2)为方程x 0x －2y 0－2y ＝0的两组解．所以直线AB 的方程为x 0x －2y 0－2y ＝0.(3)由抛物线定义可知|AF|＝y 1＋1，|BF|＝y 2＋1，所以|AF|·|BF|＝(y 1＋1)(y 2＋1)＝y 1y 2＋(y 1＋y 2)＋1.联立方程⎩⎪⎨⎪⎧x 0x －2y －2y 0＝0，x 2＝4y ，消去x 整理得y 2＋(2y 0－x 20)y ＋y 20＝0，由根与系数的关系可得y 1＋y 2＝x 20－2y 0，y 1y 2＝y 20，所以|AF|·|BF|＝y 1y 2＋(y 1＋y 2)＋1＝y 20＋x 20－2y 0＋1. 又点P(x 0，y 0)在直线l 上，所以x 0＝y 0＋2. 所以y 20＋x 20－2y 0＋1＝2y 20＋2y 0＋5＝2⎝ ⎛⎭⎪⎫y 0＋122＋92.[:所以当y 0＝－12时，|AF|·|BF|取得最小值，且最小值为92.5.如图，经过点P(2,3)，且中心在坐标原点，焦点在x 轴上的椭圆M 的离心率为12.(1)求椭圆M 的方程；(2)若椭圆M 的弦PA ，PB 所在直线分别交x 轴于点C ，D ，且|PC|＝|PD|，求证：直线AB 的斜率为定值．[: 解：设椭圆M 的方程为x 2a 2＋y2b 2＝1(a ＞b ＞0)，则4a 2＋9b 2＝1，且e 2＝a 2－b 2a 2＝14，解得a 2＝16，b 2＝12. 故椭圆M 的方程为x 216＋y212＝1.(2)证明：由题意知，直线PA 的斜率必存在，故设直线PA 的方程为y ＝k(x －2)＋3，A(x A ，y A )，B(x B ，y B )，由|PC|＝|PD|可知，直线PB 的方程为y ＝－k(x －2)＋3.由方程组⎩⎪⎨⎪⎧y ＝－＋3，x 216＋y212＝1，可得(4k 2＋3)x 2－8k(2k －3)x ＋4(2k －3)2－48＝0. ①又方程①有一实根为2，故另一实根为－2－482＋＝－2－244k 2＋3＝2－12k －4k 2＋3，故x A ＝2－12k －4k 2＋3.同理，x B ＝2＋12k －4k 2＋3.所以x A ＋x B ＝2－4k 2＋3，x A ＋x B －4＝－244k 2＋3， x A －x B ＝－48k4k 2＋3.所以直线AB 的斜率k AB ＝y A －y Bx A －x B＝A＋x B －x A －x B＝12，即直线AB 的斜率为定值． 6．已知椭圆C 的中心在坐标原点，焦点在x 轴上，椭圆C 上的点到焦点的距离的最大值为3，最小值为1. (1)求椭圆C 的标准方程；(2)若直线l ：y ＝kx ＋m 与椭圆C 相交于A ，B 两点(A ，B 不是左右顶点)，且以AB 为直径的圆过椭圆C 的右顶点D.求证：直线l 过定点，并求出该定点的坐标．解：(1)由题意设椭圆的标准方程为： x 2a 2＋y2b2＝1(a>b>0)．由已知得a ＋c ＝3，a －c ＝1，所以a ＝2，c ＝1，所以b 2＝a 2－c 2＝3，因此椭圆C 的标准方程为x 24＋y23＝1.(2)证明：设A(x 1，y 1)，B(x 2，y 2)，联立⎩⎪⎨⎪⎧y ＝kx ＋m ，x 24＋y23＝1，得(3＋4k 2)x 2＋8mkx ＋4(m 2－3)＝0，则⎩⎪⎨⎪⎧Δ＝64m 2k 2－＋4k22－，即3＋4k 2－m 2>0，x 1＋x 2＝－8mk 3＋4k2，x 1x 2＝2－3＋4k2.又y 1y 2＝(kx 1＋m)(kx 2＋m) ＝k 2x 1x 2＋mk(x 1＋x 2)＋m 2＝2－4k 23＋4k2.因为以AB 为直径的圆过椭圆的右顶点D(2,0)，所以k AD k BD ＝－1，即y 1x 1－2·y 2x 2－2＝－1.故y 1y 2＋x 1x 2－2(x 1＋x 2)＋4＝0. 即3m 2－4k23＋4k2＋4m 2－33＋4k2＋16mk 3＋4k2＋4＝0. 则7m 2＋16mk ＋4k 2＝0.解得m ＝－2k ，或m ＝－2k 7，且均满足3＋4k 2－m 2>0.当m ＝－2k 时，l 的方程为y ＝k(x －2)，直线过定点(2,0)，与已知矛盾；当m ＝－2k7时，l 的方程为y ＝k ⎝ ⎛⎭⎪⎫x －27，直线过定点⎝ ⎛⎭⎪⎫27，0.[: 所以，直线l 过定点，定点坐标为⎝ ⎛⎭⎪⎫27，0.。

圆锥曲线中的范围、最值问题 (解析版)--高二数学上册常考题专练(人教A版2019选修一)

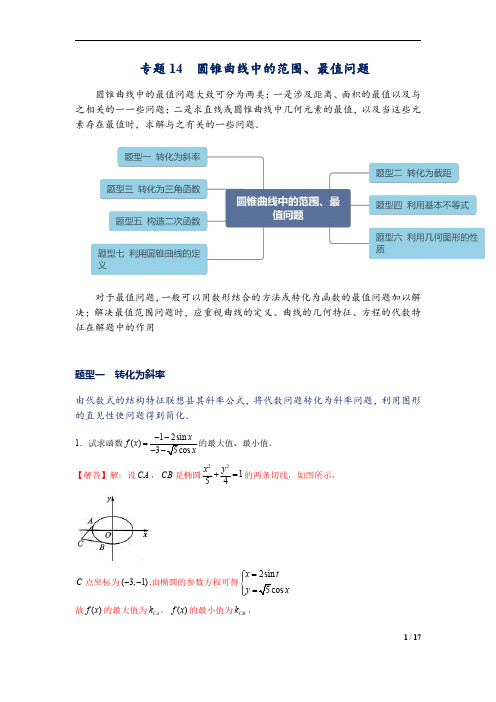
专题14圆锥曲线中的范围、最值问题圆锥曲线中的最值问题大致可分为两类：一是涉及距离、面积的最值以及与之相关的一一些问题；二是求直线或圆锥曲线中几何元素的最值，以及当这些元素存在最值时，求解与之有关的一些问题．对于最值问题，一般可以用数形结合的方法或转化为函数的最值问题加以解决；解决最值范围问题时，应重视曲线的定义、曲线的几何特征、方程的代数特征在解题中的作用题型一转化为斜率由代数式的结构特征联想县其斜率公式，将代数问题转化为斜率问题，利用图形的直见性使问题得到简化．1．试求函数()f x =的最大值、最小值．【解答】解：设CA ，CB 是椭圆22154x y +=的两条切线，如图所示，C 点坐标为(3,1)--,由椭圆的参数方程可得2sin x ty x=⎧⎪⎨=⎪⎩故()f x 的最大值为CA k ，()f x 的最小值为CB k ，设过C 与椭圆22154x y +=相切的切线方程为y kx m =+．由22154y kx mx y =+⎧⎪⎨+=⎪⎩，消去y ，得222(45)105200k x kmx m +++-=，由△0=得m =，所以切线方程为y kx =±因为切线过点(3,1)C --，所以13k -=-所以12k k ==，所以()f x的最大值3()4f x +的最小值为34-．题型二转化为截距利用直线在y 轴上的截距的直观性，可求有关参数的取值范围，进而得到最值．2．已知x ，y 满足2211625x y +，则3z y x =-的最大值为13，最小值为．【解答】解：将所给的函数式改写为3y x z =+，则z 表示直线3y x z =+在y 轴上的截距，x ，y 满足2211625x y +，∴可行域为椭圆2211625x y +=的边界及其内部，画出图形，如图所示，由图可知，z 的最大值，最小值在直线与椭圆相切时取得，联立方程22311625y x z x y =+⎧⎪⎨+=⎪⎩，消去y 得：2216996164000x zx z ++-=，由△0=得：22(96)4169(16400)0z z -⨯⨯-=，解得13z =±，z ∴的最大值为13，最小值为13-，故答案为：13，13-．题型三转化为三角函数3．设A 、B 分别是椭圆22:12y C x+=的左顶点和上顶点，点P 在C 上，则点P 到直线AB 的距离的最大值为()ABCD 【解答】解：椭圆22:12y C x +=的焦点在y轴上，22a =，21b =，可得a=1b =．∴椭圆的左顶点为(1,0)A-，上顶点为B ，则AB 所在直线方程为11x=-0y -=．P 在椭圆22:12y C x +=上，∴设(cos )P θθ，P ∴到直线AB 的距离d =|2cos()4πθ++=，∴点P 到直线AB3=．故选：D ．4．过点(0,)B b -作椭圆22221(0)x y a b a b+=>>的弦，求这些弦长的最大值.【解答】设椭圆上任意一点M 的坐标为(cos ,sin )a b αα则||BM ===因为a>b>0，所以220b a -<①当2210b b a ω-≤<-，即a ≥时，取22sin ,b b a ωα=-得2max ||a BM c==②当2221b b a <--，即b a <<时，取sin 1,α=-得max ||2.BM b =题型四利用基本不等式5．函数3(0,1)xy aa a -=>≠的图象恒过定点A ，若点A 在双曲线221(0,0)x y m n m n-=>>上，则m n -的最大值为()A ．6B ．4C ．2D ．1【解答】解：由题意可知，函数3(0,1)xy a a a -=>≠的图象恒过定点(3,1)A ，又点A 在双曲线221(0,0)x y m n m n-=>>上，∴911(0,0)m n m n-=>>，919()()()10()104n m m n m n m n m n -=--=-+-=，当且仅当9n m m n =时，即2n =，6m =时，等号成立．故选：B ．6．设O 为坐标原点，直线x a =与双曲线2222:1(0,0)x y C a b a b-=>>的两条渐近线分别交于A ，B 两点，若C 的焦距为12，则OAB ∆面积的最大值为()A ．72B ．36C ．18D ．9【解答】解：双曲线22221x y a b-=的渐近线方程为b y x a =±，C 的焦距为12，212c ∴=，即6c =，22236a b c ∴+==，直线x a =与双曲线C 的两条渐近线分别交于A ，B 两点，∴不妨取(,)A a b ，B (,)a b -，OAB ∴∆面积221136||2182222a b S a AB a b ab+=⋅=⋅⋅===，当且仅当a b ==时，等号成立，OAB ∴∆面积的最大值为18．故选：C ．7．设O 为坐标原点，点(1,0)A ，动点P 在抛物线24y x =上，且位于第一象限，M 是线段PA的中点，则直线OM 的斜率的取值范围为()A ．(0，1]B ．(0,1)C ．(1,)+∞D ．[1，)+∞【解答】解：设点P 的坐标为2(4P m ，4)(0)m m >，很明显直线的斜率为正数，则：2221244(2,2),111241242OM m m M m m k m m m m+====+++，当且仅当12m =时等号成立即直线OM 的斜率的取值范围为(0，1]．故选：A ．8．椭圆2222:1(0,0)x y M a b a b+=>>的左、右焦点分别为1F ，2F ，P 为椭圆M 上任一点，且12||||PF PF ⋅最大值取值范围为2[2c ，23]c （其中222)c a b =-，则椭圆M 的离心率的取值范围是()A ．32[32B ．2[2C ．3[3D ．11[,32【解答】解：由题意的定义可得：12||||2PF PF a +=，再由均值不等式可得：2221212||||2||||(()22PF PF aPF PF a +⋅==，12||||PF PF ⋅的最大值为2a ，由题意可得22223c a c 可得21132e ，解得3232e，故选：A ．9．已知函数log (1)1(0a y x a =-+>，且1)a ≠的图象恒过定点A ，若点A 在椭圆221x y m n+=上，则m n +的最小值为()A ．12B ．10C ．9D ．8【解答】解：对于函数log (1)1(0a y x a =-+>，且1)a ≠的图象，令11x -=，求得2x =，1y =，可得它的图象恒过定点(2,1)A ．因为点(2,1)A 在椭圆221(0x y m m n+=>，0n >，)m n ≠上，则411m n +=，则414()(559n m m n m n m n m n +=+⋅+=+++=，当且仅当2m n =时，等号成立，故m n +的最小值为9，故选：C ．10．抛物线2:4E y x =的焦点为F ，E 的准线l 与x 轴交于点A ，M 为E 上的动点．则||||MF MA 的最小值为()A ．1B ．32C ．22D ．12【解答】解：由题意可得焦点(,0)F a ，准线x a =-，过点M 作MH ⊥准线，所以||||cos ||||MF MH AMH MA MA ==∠，因为//HM AF ，所以cos cos ((0,))2AMH MAF MAF π∠=∠∠∈，求cos MAF ∠的最小值等价于求MAF ∠的最大值，设(,)M x y，21tan 144y y MAF y a y x a a a y a∠====+++，所以tan (0MAF ∠∈，1]，所以(0MAF ∠∈，4π．当4MAF π∠=时，cos MAF ∠最小值为22，所以||||MF MA最小值为2．故选：C ．题型五构造二次函数利用解析几何中的代数和识，把问题转化为关于某个变量的二次函数，利用二次函数的有关知识来求最值．11．抛物线22y x =上的点到直线50x ++=距离的最小值是()A ．3B ．85C ．74D ．43【解答】解：因为点P 在抛物线22y x =上，设200(,)2y P y ，则点P到直线50x ++=的距离20220000|5||10||(7|244y y y d +++++===0y R ∈ ，∴当0y =74min d =．故选：C ．12．已知点P 在椭圆22193x y +=上运动，点Q 在圆225(1)8x y -+=上运动，则||PQ 的最小为()A ．2B ．102C ．1024-D ．104【解答】解：设圆225(1)8x y -+=的圆心为A ，则(1,0)A ，设(,)P x y ，则222||(1)AP x y =-+，椭圆22193x y +=，∴2233x y =-，∴22222||2132433x AP x x x x =-++-=-+，[3x ∈-，3]，令22()243h x x x =-+，求导4()203h x x '=-=，解得32x =，()h x ∴在[3-，3)2单调递减，3(,3]2单调递增，()h x ∴在32x =时最小，即2||AP 最小值为52，10||2min AP ∴=，101010||||244min min PQ AP r =-=-=．故选：D ．13．已知抛物线21:4C y x =，过抛物线焦点的直线交抛物线于A ，B 两点，若直线AO ，BO 分别交直线2y x =-于E ，F 两点，则||EF 的最小值()A ．253BC ．12825D【解答】设AB 的方程为1y kx =+代入214y x =，得2440x kx --=，所以124x x k +=，124x x =-，12||x x -=联立1112,84E y x x y y x x x =-⎧⎪⇒=⎨=-⎪⎩；同理可得284F x x =-，所以||EF ==，令43(0)k t t -=≠，34t k +=，||EF =，当0t >时，||EF =，当0t >时，82||5EF =，故||EF故选：D ．14．已知直线l 与抛物线24y x =交于A ，B 两点（点A 在第一象限，点B 在第四象限），与x 轴交于点(,0)M m ，若线段AB 的中点的横坐标为3，则m 的取值范围是()A ．(0，3]B ．(-∞，3]C ．(0，6]D ．(1，6]【解答】解：设1(A x ，1)y ，2(B x ，2)y ，直线方程为(0)x ty m m =+>．联立24x ty m y x=+⎧⎨=⎩，消去x ，得2440y ty m --=，所以124y y t +=．所以21212()242x x t y y m t m +=++=+，因为A 、B 中点横坐标为3，所以126x x +=，故2323m t =-，又0m >，所以m 的取值范围(0，3]．故选：A ．15．P 为双曲线221x y -=左支上任意一点，EF 为圆22:(2)4C x y -+=的任意一条直径，则PE PF ⋅的最小值为()A ．3B ．4C ．5D ．9【解答】解：设(,)P x y ，且1x -，则221x y -=，设直线EF 的方程为2x my =+，222(2)4x my x y =+⎧⎨-+=⎩整理可得：22(1)4m y +=，解得y =设2E +，(2F +，，则2PE PF x ⋅=-，)(2y x ⋅+-，)y -222222244(2)2412(1)311m x y x x x m m=-+--+=--=--++，因为1x -，所以2(1)4x -，所以可得22(1)32435x --⨯-=，当直线的斜率为0时，则设(0,0)E ，(4,0)F ，这时(PE PF x ⋅=- ，)(4y x --，22)(4)241y x x y x x -=--+=-+，与上面类似，综上所述：5PE PF ⋅，故选：C ．16．在过动直线2x y t +=（其中(0,3])t a ∈与定直线2x y a -=的交点Q 的等轴双曲线系：22x y λ-=中，当t 取何值时，λ达到最大值与最小值？【解答】解：由22x y ax y t -=⎧⎨+=⎩得交点22(,)55t a t a Q +-，交点Q 坐标代入双曲线，222222142522()()[3(]552533t a t a a a x y t λ+-=-=-=--+，(0t ∈，3]a ，当43a t =，13max λ=又因为(0t ∈，3]a ，所以445333a aat -<-，所以45||33a a t -；当3t a =时，0min λ=，故43at =，达到最大值，3t a =时，达到最小值．17．已知抛物线2:C y x =，M 为x 轴负半轴上的动点，MA ，MB 为抛物线的切线，A ，B分别为切点，则MA MB的最小值为()A ．14-B ．18-C ．116-D ．12-【解答】解：设切线MA 的方程为x ty m =+，代入抛物线方程得20y ty m --=，由直线与抛物线相切可得△240t m =+=，则2(4t A ，)2t ，2(4t B ，)2t -，将点A 的坐标代入x ty m =+，得24t m =-，2(4t M ∴-，0)，∴2(2t MA MB = ，2)(22t t ，4222111)(2444216t t t t -=-=--，则当212t =，即2t =±时，MA MB 的最小值为116-故选：C ．题型六利用几何图形的性质18．已知过抛物线22(0)y px p =>的焦点且斜率为1的直线交抛物线于A 、B 两点，点R 是含抛物线顶点O 的弧AB 上一点，求RAB ∆的最大面积．【解答】解：设1(A x ，1)y ，2(B x ，2)y ，AB 所在的直线方程为2py x =-，将其代入抛物线22y px =，得22304p x px -+=，∴212123,4p x x p x x +==，12|||4AB x x p ∴=-=，当过R 的直线l 平行于AB 且与抛物线相切时RAB ∆的面积有最大值．设直线l 方程为y x b =+，代入抛物线方程得2220y py pb -+=，由△2480p pb =-=，得2p b =，这时(,)2pR p ，它到AB 的距离为22h p =，RAB ∴∆的最大面积为21||2AB h = ．19．已知平行四边形ABCD 内接于椭圆2222:1(0)x y a b a b Ω+=>>，且AB ，AD 斜率之积的取值范围为43(,54--，则椭圆Ω的离心率的取值范围为()A．1)2B．22C．1(4D ．11(,54【解答】解：设1(A x ，1)y ，2(B x ，2)y ，由平行四边形对角线互相平分可得A 与C ，B 与D 关于原点对称，所以可得2(D x -，2)y -，所以2221121222211212AB ADy y y y y y k k x x x x x x -+-⋅=⋅=-+-，将A ，B 的坐标代入可得22112222222211x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩相减可得22221212220x x y y a b --+=，可得2221222212y y b x x a-=--，由题意可得：224354b a -<-<-，即223445b a <<，可得：2234145c a <-<，解得：5(5c e a =∈，1)2，故选：A ．20．设(,)P x y 是双曲线22154x y -=的右支上的点，则代数式-的最小值为()AB．-C-D3-【解答】解：表示点(,)P x y 到点(0,1)的距离与点(,)P x y 到点2(3,0)F 的距离之差，又双曲线22154x y -=的左右焦点左右焦点分别为1(3,0)F -，2(3,0)F ，根据双曲线定义可得212PF PF a =-，212PA PF PA PF a ∴-=-+，(,)P x y 是双曲线22154x y -=的右支上的点，1122PA PF a AF a ∴-+-+=，故选：B ．21．已知点P 是抛物线24y x =上的一个动点，点P 到点的距离与P 到y 轴的距离之和的最小值为()A ．1B C ．2D ．1【解答】解：抛物线24y x =，抛物线的焦点坐标(1,0)．依题点P 到点A 的距离与点P 到y 轴的距离之和的最小值，就是P 到与P 到该抛物线准线的距离的和减去1．由抛物线的定义，可得则点P 到点A 的距离与P 到该抛物线焦点坐标的距离之和减1，11=．故选：A ．22．已知抛物线2y ax =的焦点为(0,1)，直线1y kx =+与该抛物线相交于A ，B 两点，则线段AB 的最小值为()A ．1B ．2C ．3D ．4【解答】解：由2y ax =，可得21x y a =，则114a =，即14a =，易知直线1y kx =+过该抛物线的焦点(0,1)，因为过焦点的弦中通径最短，所以线段AB 的最小值为14a=，故选：D ．23．已知双曲线22:18x C y -=的左焦点为F ，点M 在双曲线C 的右支上，(0,3)A ，当MAF∆的周长最小时，MAF ∆的面积为()A ．607B ．9C ．37D ．4【解答】解：如图，设C 的右焦点为F '，由题意可得a =，3c =，因为||||2MF MF a '-==，所以||||MF MF '=+，||AF =．MAF ∆的周长为||||||||||||10MA MF AF MA MF AF ''++=+++，即当A ，M ，F '三点共线时，MAF ∆的周长最小，此时直线AF '的方程为3y x =-+，联立方程组22318y x x y =-+⎧⎪⎨-=⎪⎩，解得17y =或1y =-，即此时M 的纵坐标为17，故MAF ∆的面积为111160||||||||6(322277M FF OA FF y ''⋅-⋅=⨯⨯-=．故选：A．题型七利用圆锥曲线的定义24．已知椭圆22143x y +=，F 是椭圆的左焦点，P 是椭圆上一点，若椭圆内一点(1,1)A ，则||||PA PF +的最小值为()A ．3BC12D1【解答】解：由椭圆的方程可得24a =，焦点(1,0)F -，因为A 在椭圆内部，设右焦点F '，则(1,0)F '，则||||||2||2||||413PA PF PA a PF a PA PF ''+=+-+-=-=，当且仅当P ，A ，F '三点共线时取等号，故选：A ．25．已知抛物线2:4C y x =的焦点为F ，设A 和B 是C 上的两点，且M 是线段AB 的中点，若||6AB =，则M 到y 轴的距离的最小值是()A ．2B ．4C ．6D ．8【解答】解：因为C 的方程为24y x =，所以(1,0)F ，过A 作准线1x =-的垂线，垂足为E ，过B 作准线的垂线，垂足为D ，过M 作准线的垂线，垂足为K ，根据抛物线定义可得：||||||||||6AF BF AE BD AB +=+=，则1||(||||)32MK AE BD =+，所以，线段MN 的中点M 到C 的准线1x =-的距离最小值为3，故点M 到y 轴的距离最小值为312-=．故选：A．26．双曲线22:148x y C -=，已知O 是坐标原点，A 是双曲线C 的斜率为正的渐近线与直线233x =的交点，F 是双曲线C 的右焦点，D 是线段OF 的中点，若B 是圆221x y +=上的一点，则ABD ∆的面积的最小值为()A．2-B．33-C ．2D．13-【解答】解：由双曲线22:148x y C -=的方程知24a =，28b =，2a ∴=，b =c ==，所以斜率为正的渐近线方程为y =，与直线233x =的交点A 的坐标为2326((,33，AD点D的坐标为，所以直线AD的方程为y x =--，AD ==点B 是圆221x y +=的动点，当点B 到直线AD 的距离最小时ABD ∆的面积的最小，又点B 到直线AD113=-，所以ABD ∆的面积的最小值为126223(1)232S ==．故选：A ．27．已知M 为抛物线2:4C y x =上一点，过抛物线C 的焦点F 作直线(1)52x m y m +-=-的垂线，垂足为N ，则||||MF MN +的最小值为()A．3B．2-C．2+D．3【解答】解：由题可得抛物线焦点(1,0)F ，准线方程为1x =-，过点M 作MD 与准线垂直，交于点D ，直线(1)52x m y m +-=-整理得(2)5m y y x +=-+，联立2050y y x +=⎧⎨-+=⎩可得32x y =⎧⎨=-⎩，即该直线过定点(3,2)-，设(3,2)P -，连接FP ，取FP 中点E ，则(2,1)E -，||EP =，若FN l ⊥，则N 在以FP 为直径的圆上，该圆方程为(2)2(1)22x y -++=，又由||||MF MD =，得||||||||MF MN MD MN +=+，如图，||||MD MN +的最小值为圆(2)2(1)22x y -++=上的点到准线的距离的最小值，过点E 作ED '与准线1x =-垂直并交于点D '，与圆E 交于点N '，与抛物线交于点M ’，则||D N ''即为||||MD MN +的最小值，即||||MD MN +的最小值为||3ED r '-=．故选：D ．28．已知双曲线2221(0)4x y b b -=>0y -=，右焦点为F ，点M 在双曲线左支上运动，点N 在圆22(3)1x y ++=上运动，则||||MN MF +的最小值为()A ．6B ．7C ．8D ．9【解答】解：由题意双曲线2221(0)4x y b b-=>0y -=，可得2a =，则b =可得双曲线221412x y -=，焦点为(4,0)F ，(4,0)F '-，由双曲线的定义可得||2||4||MF a MF MF =+'=+'，由圆22(3)1x y ++=可得圆心(0,3)C -，半径1r =，||||4||||MN MF MN MF +=++'，连接CF '，交双曲线于M ，圆于N ，可得||||MN MF +取得最小值，且为||5CF '==，则||||MN MF +的最小值为4518+-=．故选：C ．。