《3.4互斥事件》课件1-优质公开课-苏教必修3精品
【高中数学必修3 精品课件】第3章 3.4 互斥事件

6. 学校成立了数学、英语、音乐 3 个课外兴趣 小组,3 个小组分别有 39,32,33 个成员,一 些成员参加了不止 1 个小组,具体情况如 图所示.随机选出一个成员,求: (1)他至少参加 2 个小组的概率; (2)他参加不超过 2 个小组的概率.
mac加速器 mac清理磁盘空间 mac垃圾清理 mac 清理工具
∵A、B、C 两两互斥,
∴P(M)=P(A+B+C)=P(A)+P(B)+P(C)
(6 分)
=1+11000+0 50=1
61 000.
故
1
张奖券的中奖概率为1
61 000.
(7 分)
(3)法一:设“1 张奖券不中特等奖且不中一等奖”为事件 N,则事件 N 与“1 张奖券中特等奖或中一等奖”为对立事件,
[例 2] (12 分)某商场有奖销售中,购满 100 元商品得 1 张 奖券,多购多得.1 000 张奖券为一个开奖单位,设特等奖 1 个, 一等奖 10 个,二等奖 50 个.设 1 张奖券中特等奖、一等奖、二 等奖的事件分别为 A、B、C,求:
(1)事件 A、B、C 的概率; (2)1 张奖券的中奖概率; (3)1 张奖券不中特等奖且不中一等奖的概率. [思路点拨] 明确事件的特征,利用互斥事件或对立事件求解.
4.在某一时期内,一条河流某处的年最高水位在各个范 围内的概率如下表:
年最高水位 (单位:m) [8,10) [10,12) [12,14) [14,16) [16,18)
概率
0.1 0.28 0.38 0.16 0.08
计算在同一时期内,河流这一处的年最高水位在下列范 围内的概率: (1)[10,16)(m); (2)[8,12)(m); (3)水位不低于 14 m.
最新苏教版数学必修三:3.4《互斥事件》ppt课件

栏 目
链
率.
接
分析: 军火库要发生爆炸,只要炸弹炸中一个军火 库即可,因为只投掷了一个炸弹,故炸中第一、第 二、第三军火库的事件是彼此互斥的.
典例 剖析
解析: 设以A、B、C分别表示炸中第一、第二、
第 三 军 火 库 这 三 个 事 件 , 则 P(A) = 0.025 , P(B) =
P(C)=0.1.
P(C)=0.1.
栏
又设D表示军火库爆炸这个事件,则有D=
目 链
接
A∪B∪C,其中A、B、C是互斥事件,因为只投掷
了一个炸弹,不会同时炸中两个以上军火库,
所以P(D)=P(A)+P(B)+P(C)=0.025+0.1+0.1= 0.225.
典例 剖析
规律总结: 对于一个较复杂的事件,一般将其分
解成几个简单的事件,当这些事件彼此互斥时,原事
栏
目
件的概率就是这些事件的概率的和.关键是确定事件
链 接
是否互斥、是否对立.
典例 剖析
变式训练
2.抛掷一骰子,观察出现的点数,设事件 A 为“出现 1
点”,B 为“出现 2 点”,已知 P(A)=P(B)=61,求出现 1 点
栏
或 2 点的概率.
目 链
接
解析: 设事件 C 为“出现 1 点或 2 点”,因为事件 A、B 是
栏
事件,所以 C 与 D 互为对立事件,所以 P(D)=1-P(C)
目
链
=1-12=12.
接
规律总结: (1)“ 互 斥 ” 和 “ 对 立 ” 事 件 很 容 易 搞
混.互斥事件是指两事件不可能同时发生,对立事件
是指互斥的两事件中必有一个发生.
高中数学第三章概率3.4互斥事件课件苏教版必修3

跟踪训练 1
一个射手进行一次射击,试判断下列事件哪些是互斥事件?
解答
哪些是对立事件?
事件A :命中环数大于7环; 事件B :命中环数为10环;
事件C :命中环数小于6环; 事件D :命中环数为6、7、8、9、10环.
A 与C 互斥(不可能同时发生),B 与C 互斥,C 与D 互斥,C 与D 是对立
第3章 概率
3.4 互斥事件
学习目标
1.理解互斥事件、对立事件的概念和实际意义,能根据定义辨 别事件的互斥、对立关系; 2.掌握互斥事件的概率加法计算公式.
内容索引
问题导学
题型探究 当堂训练
问题导学
知识点一
互斥事件
思考
一粒骰子掷一次,记事件A:点数大于4;事件B:点数小于3,
则事件A,B可能在一次试验中同时发生吗?
知识点三
对立事件
思考
在“知识点一思考”中,一次试验里,A,B是否必有一个发生? 你能定义一个事件C,使A,C必有一个发生吗?
答案
不是,比如掷出点数为3,则A,B都不发生,定义C:点数不大 于4,则A,C必有一个发生.
梳理
对立事件及其概率公式:
如果两个互斥事件必有一个发生,那么称这两个事件为对立事件 .事件A
不可能.
答案
梳理
互斥事件的概念: 不能同时发生 的两个事件称为互斥事件.
知识点二
事件A+B
思考
一粒骰子掷一次,A:点数为奇数;事件B:点数大于3,则A, B至少有一个发生包含哪些基本事件?
答案
A,B至少有一个发生包含点数为1,3,4,5,6.
梳理
一般地,事件“A,B至少有一个发生”记为A+B.如果事件A,B互斥, 那么事件A+B发生的概率,等于事件A,B分别发生的概率的和, 即P(A+B)= P(A)+P(B) .一般地,如果事件A1,A2,…,An两两互斥, 那么P(A1+A2+…+An)= P(A1)+P(A2)+…+P(An) .
高中数学必修三 [苏教版]3.4《互斥事件》ppt课件之一
![高中数学必修三 [苏教版]3.4《互斥事件》ppt课件之一](https://img.taocdn.com/s3/m/17a47c53bb68a98271fefab4.png)
《江苏省2009普通高考方案》对必修测
问 试科目等级规定如下:各科满分为100分。 题 100-90分为A等级(优),89-75分为B等 情 级(良),74-60分为C等级(中),59分 境 及其以下为D等级(不通过)。现某班50名
学生参加了某必修科的测试,结果如下:
等级 人数(人)
事件
优
9
A
良
得良?
探
不能同时发生的两个事件称为互斥事件。 如:本例中的事件 A,B,C,D,其中任意两个
索 都是互斥事件。
新
一般地,如果事件A1、A2,…,An 中的
知 任意两个都是互斥事件,就说事件A1、A2,
…,An 彼此互斥。
你能举出生活中一些 彼此互斥的例子吗?
问题2:从这个班任意抽取一位同学,那么这位同学
例3 袋中装有红、黄、白3种颜色的球各一
应 只,从中每次任取1只,有放回的抽取3次,求: 用 (1)3只全是红球的概率; 新 (2)3只颜色全相同的概率; 知 (3)3只颜色不全相同的概率;
(4)3只颜色全不相同的概率。
1、把红桃、黑桃、方块、梅花四张纸牌随机
课 分给甲、乙、丙、丁四个人,每人得一张,
新
知
A、B为互斥事件
A、B为对立事件
根据对立事件的意义,A A 是必然事
探
件,从而 P( A A) P( A) P( A) 1
索
新
由此,我们可以得到一个重要公式:
知
P( A) 1 P( A)
例1 抛掷一颗骰子1次,记“向上的点数是4,
5,6”为事件A,“向上的点数是1,2”为事件B,
欢迎各位同仁莅临指导ຫໍສະໝຸດ 扬子二中 syh 2010.11.2
2017-2018学年高中数学必修3课件:3-4 互斥事件 精品

目标导航
预习导引
1
2
3
预习交流4 (1)袋中装有除颜色外其他均相同的红球和黄球各3个,从中任取2 个球,在下列事件中是对立事件的序号是 . ①恰有1个红球和恰有2个黄球 ②至少有1个红球和全是红球 ③至少有1个红球和至少有1个黄球 ④至少有1个红球和全是黄球 (2)小明、小欣两人下棋,两人下成和棋的概率是0.2,小欣获胜的 概率是0.5,则小欣不输的概率是 . 提示:(1)④ (2)0.7
提示:对互斥事件的理解,也可以从集合的角度去加以认识,如果 A,B是两个互斥事件,反映在集合上是表示A,B这两个事件所含结果 组成的集合彼此互不相交,即如果事件A与B是互斥事件,那么A与B 两事件同时发生的概率为0.
目标导航
预习导引
1
2
3
2.互斥事件的概率计算 如果事件A,B互斥,那么事件A+B发生的概率,等于事件A,B分别发 生的概率的和,即P(A+B)=P(A)+P(B).一般地,如果事件A1,A2,…,An 两两互斥,那么P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An). 预习交流2 某人射击一次,击中环数大于7的概率为0.6,击中环数是6或7或8 的概率为0.3,则该人击中环数大于5的概率是0.6+0.3=0.9对吗?为 什么? 提示:不对.该人“击中环数大于7”与“击中环数是6或7或8”不是互 斥事件,不能用互斥事件的概率加法公式求解.
问题导学
即时检测
一
二
三
解:(1)是互斥事件,不是对立事件. 理由是:从40张扑克牌中任意抽取1张,“抽出红桃”和“抽出黑桃” 是不可能同时发生的,所以是互斥事件.同时,不能保证其中必有一 个发生,这是由于还可能抽出“方块”或者“梅花”,因此,二者不是对 立事件. (2)既是互斥事件,又是对立事件. 理由是:从40张扑克牌中任意抽取1张.“抽出红色牌”与“抽出黑色 牌”两个事件不可能同时发生,且其中必有一个发生,所以它们既是 互斥事件,又是对立事件. (3)不是互斥事件,当然不可能是对立事件. 理由是:从40张扑克牌中任意抽取1张,“抽出的牌点数为5的倍数” 与“抽出的牌点数大于9”这两个事件可能同时发生,如抽得点数为 10,因此,二者不是互斥事件,当然不可能是对立事件.
高中数学3-4互斥事件课件苏教版必修

彼此互斥的,可运用概率的加法公式求解.
解 设事件 C 为“出现 1 点或出现 2 点”,∵事件 A、B 是 互斥事件,由 C=A∪B 可得 1 1 1 P(C)=P(A)+P(B)= + = , 6 6 3 1 ∴出现 1 点或出现 2 点的概率是 . 3
[思路探索]
解 (1) 由于事件 C“至多订一种报”可能只订甲报,即事 件A与事件C有可能同时发生,故A与C不是互斥事件.
(2)事件B“至少订一种报”与事件E“一种报也不订”是不 可能同时发生的,故事件B与事件生会导致事件B一定不发生,
故事件B与事件E是对立事件. (3) 事 件 B“ 至 少 订 一 种 报 ” 中 有 这 些 可 能 : “ 只 订 甲 报”,“只订乙报”,“订甲、乙两种报”.事件 D“不订甲 报”中包括“只订乙报”,所以事件B和D可能同时发生,故B与
追本溯源 互斥事件概率的加法公式必须在各个事件彼此互 斥的前提条件下使用.当直接求其一事件的概率较为复杂时, 可转化去求其对立事件的概率.
法二 设事件 A 为“甲不输”,看作是“乙获胜”的对立事 件, 1 2 ∴P(A)=1- = . 3 3 2 ∴甲不输的概率是 . 3 (14 分) (10 分)
【题后反思】 对立事件是比较重要的事件,利用对立事件
的概率公式求解时,必须准确判断两个事件是对立事件时才能
应用.
【变式3】 据最近中央电视台报道,学生的视力下降是十
误区警示
互斥事件与对立事件不清致误
【示例】 抛掷一枚骰子,向上的一面出现 1 点、2 点、3 点、 1 4 点、5 点、6 点的概率都是 .记事件 A“出现奇数”,事件 B 为 6 “向上的点数不超过 3”,求 P(A+B).
苏教版数学必修3课件3.4互斥事件(第一课时)

50
互斥事件一定不能同时发生,那么是否可以同时不发 生?举例说明.
对立事件:必有一个发生的互斥事件. 事件A的对立事件记为事件 A
对立事件是互斥事件的特殊情形, 对立事件必互 斥,互斥事件不 试说明这种特殊性的表现. 一定对立.
A
A
A I
B
P(A)+P(A)=P(A+A )=1
事件B:抽取一张牌,得到黑桃;
事件C:抽取一张牌,得到方片;
事件D:抽取一张牌,得到梅花. 一般地,如果事件 A1 , A2 , , An中的任何两个都是互 斥的,那么就说事件 A1 , A2 , , An 两两互斥.
试一试:
从装有4只红球、4只白球的黑袋中任意取 出3只球,你能例举两个事件,使它们是互斥事件 吗?不互斥呢?
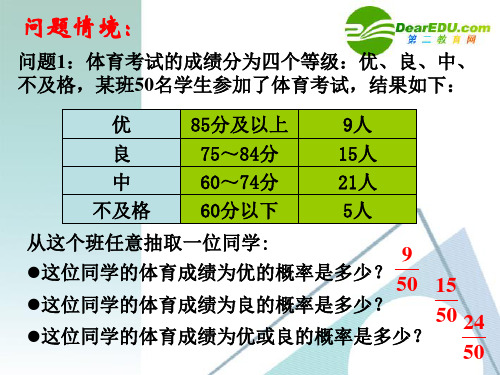
问题情境:
问题1:体育考试的成绩分为四个等级:优、良、中、 不及格,某班50名学生参加了体育考试,结果如下: 及格
优
85分及以上
9人
良 中 不及格
75~84分 60~74分 60分以下
15人 21人 5人
从这个班任意抽取一位同学:
45 这位同学的体育成绩为及格的概率是多少? 50
这位同学的体育成绩为不及格的概率是多少? 5
A9 , A8 或 A7 之一发生, 事件A发生由互斥事件的概率加 . 法公式, 得 P A P A10 A9 A8 A7
10 环 0.12
9环 0.18
8环 0.28
7环 0.32
P A10 P A9 P A8 P A7
例 2 某人射击1 次, 命中7 ~ 10 环的概率如下:
命中环数 概 率
数学:3.4《互斥事件》课件(苏教必修3)

互斥事件及其发生矗概率江苏如东马塘中学张伟锋设问题:」体育考试的成绩分为4个等级;优、良、中、不及格。
某班50名学生参加了体育考试,结果如下:解决问题:体育考试的成绩分为4个等级;优、良、中、不及格。
某班50名学生参加了体育考试,结果如下:体育考试成绩的等级为优、良、中、不及格的事件分别记为A, B, C, D o不能同时发生的两个事件称为互斥事件。
出定义:—不能同时发生的两个事件称为互斥事件。
体育考试成绩的等级为优、良、中、不及格的事件A, B, C, Do事件A、B、C、D其中任意两个都是互斥的。
一般地,如果事件州、A2, A.中的任何两个都是互斥事件,那么就说事件厲、A2, A n 彼此互斥。
强化定义:」判断以下各组中的事件是否是互斥事件?1 •粉笔盒里有红粉笔,绿粉笔,黄粉笔,现从中任取1支:抽得红粉笔”「抽得绿粉笔”,“抽得黄粉笔”;2•—周七天中:周一晴天”周二晴天”,…;周六晴天”周日晴天”。
3•必然事件与不可能事件—军决问题:体育考试的成绩分为4个等级;优、良、中、不及格。
某班50名学生参加了体育考试,结果如下:了解定义:事件A+B表示的含义:即A, B中有至少有一个发生。
说明:本节所研究的和事件“A+B”,只局限于A、B互斥》A、B有一个发生的情形!如果事件A, B是互斥事件,那么事件A+B发生 (即A, B中有一个发生)的概率,等于事件A, B分别发生的概率的和©■即、P (A+B) =P (A) +P (B)■一般地,如果事件A“ A卽…,An彼此互斥,那么事件A4+A2+…+An发生(即A2, A n 中有一个发生)的概率,等于这n个事件分别发生的概率的和,即P (A1+A2+…+AJ —P(A I)4-P(A2)+.…+P(A n)巩固结论:1个盒内放有10个大小相同的小球,其中有7 个红球,2个绿球,1个黄球,从中任取一个球,求:(1)得到红球的概率;(2)得到绿球的概率;(3)得到红球或者绿球的概率。
2019-2020学年苏教版必修三 3.4 互斥事件 课件(38张)

3.口袋内装有一些大小相同的红球、白球和黑球,从中摸出 1
个球,摸出红球的概率是 0.42,摸出白球的概率是 0.28,那么
摸出黑球的概率是( )
A.0.42
B.0.28
C.0.3
D.0.7
解析:选 C.摸出红球、白球、黑球是互斥事件,所以摸出黑球
的概率是 1-0.42-0.28=0.3.
4.若事件 A 和 B 是互斥事件,且 P(A)=0.1,则 P(B) 的取值 范围是________. 解析:由于事件 A 和 B 是互斥事件,则 P(A∪B)=P(A)+P(B) =0.1+P(B),又 0≤P(A∪B)≤1, 所以 0≤0.1+P(B)≤1, 所以 0≤P(B)≤0.9. 答案:[0,0.9]
【解】
题号
理由
结论
“恰有 1 名男生”即为“1 男 1 女”,与“恰 是互斥
(1)
有 2 名男生”不会同时发生
事件
“至少 1 名男生”为“1 男 1 女”和“2 名男 (2) 生”两种结果;“至少 1 名女生”为“1 女 1
男”和“2 名女生”两种结果,可能同时发生
不是互 斥事件
题号
理由
结论
“至少 1 名男生”为“1 男 1 女”和“2 名男 不是互
1.判断(正确的打“√”,错误的打“×”) (1)互斥事件一定对立.( ) (2)对立事件一定互斥.( ) (3)互斥事件不一定对立.( ) (4)事件 A 与 B 的和事件的概率一定大于事件 A 的概率.( ) (5)事件 A 与 B 互斥,则有 P(A)=1-P(B).( )
解析:对立必互斥,互斥不一定对立.所以(2)(3)正确,(1)错; 又当 A∪B=A 时,P(A∪B)=P(A),所以(4)错; 只有 A 与 B 为对立事件,才有 P(A)=1-P(B), 所以(5)错.
高中数学 3.4 互斥事件及其发生的概率课件 苏教版必修3

由以上分析不,概 难率 发必 现须满足如 个下第 基本要: 求
如果事 A,B件 互斥 ,那么事 AB 件 发生的,等 概率 于事A,件 B分别发生的,概 即率的和
PABPAPB
事 A k 两 件 .两互斥
1记"射击 一次 ,至少命 7环中 "的事件 A,那 为么A1当 0,
A9,A8或A7之一发 ,事生 件 A发生 .由互斥事件的概
法公,得 式P A P A 1 0 A 9 A 8 A 7
P A 1 0 P A 9 P A 8 P A 7
0 . 1 0 . 1 2 0 . 2 8 0 . 3 8 0 . 2 9
一般 ,如地 果 A 1,A 事 2,,A 件 n两两 ,则 互斥
P A 1 A 2 A n P A 1 P A 2 P A n .
在 上 面 问 ,如题 果中 "体 将育 成 绩 "记及为格事 件 E,那 么 E与D不 可 能 同,但 时 必 发 有 生 一.个 发
感谢亲观看此幻灯片,此课件部分内容来源于网络, 如有侵权请及时联系我们删除,谢谢配合!
对于本例中A的 ,B,事 C,D 件 ,其中任意两个都 的.是互 一般,地 如果事A1件 ,A2,,An中的任何两个都 事是互 件,就说事A1件 ,A2,,An彼此互. 斥
设A,B为互斥,事 当件 事A件 ,B有一个,发 我生 们把这个 件记A作 B.在上述关于体 成育 绩考 的试 问,题 事中 件 A B就表示"事 优"件 或"良",那么 ,事件 AB发生的概率 多少?呢 从 5人 0 中任1意 个,抽 人 有 5取 种 0 等可能 ,而的 抽方 到法 良的同学9的 15 种 方 ,从 法 而 有 A 事 B发 件生的概
高中数学必修三 3.4《互斥事件》ppt课件

两个互斥事件必有一个发生,则称这两个事件为对立事件。事件A的对立事件
记为
A
对立事件与互斥事 件有何异同?
1、对立事件是相对于两个互斥事件来说的 ;
2、我们可用如图所示的两个图形来 区分:
AB
A、B为互斥事件:
、
为 对 立 事 件
4、在10件产品中,有8件一级品,2件二级
品.从中任取2件,其中至少有1件为二级品
例题选讲:
1、有10张奖券,其中2张有奖,甲、乙先后各抽1张,求: (1)甲中奖的概率 (2)甲乙都中奖的概率 (3)甲乙至少有一人中奖的概率 (4)只有乙中奖的概率 (5)乙中奖的概率。
例题选讲:
1、有朋自远方来,他乘火车、轮船、汽车、 飞机来的概率分别为0.3、0.2、0.1、0.4.求: (1)他乘火车或汽车来到概率; (2)他不乘轮船来的概率;
的概率是多少? 6 37 40 45 52 61 72
1-28/45=17/45
5 26 29 34 41 50 61
5、若以连续两次掷 4
骰子分别得到的点 3
数m,n作为点P的坐 2
标,则点P在圆
1
x2+y2=8外的概率是 *
多少?
8/9
17 20 25 32 41 52 10 13 18 25 34 45 5 8 13 20 29 40 2 5 10 17 26 37 123456
巩固练习
1、判断下列事件是否是互斥事件: 某小组 有3名男生和2名女生,从中任选2两名,
(1)恰有1名男生和恰有2名男生; (2)至少有1名男生和全是男生。 2、袋中有12个小球,分别为4红球、黑球和黄球共5个、黄球和绿球共5个, 从中任取一球,求得到个色球的概率。 3、同时抛掷两颗骰子,求至少有一个5点或6点的概率。 4、抛掷一颗骰子,记A=得到奇数点,B=点数不超过3,求 :P(A+B).
苏教版2017高中数学(必修三)3.4 互斥事件PPT课件

自主预习
目标导航 预习导引 1 2 3
合作探究
1.互斥事件 在一次试验中,不能同时发生的两个事件称为互斥事件.一般地, 如果事件A1,A2,…,An中的任何两个都是互斥事件,那么就说事件 A1,A2,…,An彼此互斥.设A,B为互斥事件,若事件A,B至少有1个发生, 那么我们把这个事件记作A+B. 预习交流1 如何从集合的角度理解互斥事件?
提示:对互斥事件的理解,也可以从集合的角度去加以认识,如果 A,B是两个互斥事件,反映在集合上是表示A,B这两个事件所含结果 组成的集合彼此互不相交,即如果事件A与B是互斥事件,那么A与B 两事件同时发生的概率为0.
自主预习
目标导航 预习导引 1 2 3
合作探究
2.互斥事件的概率计算 如果事件A,B互斥,那么事件A+B发生的概率,等于事件A,B分别发 生的概率的和,即P(A+B)=P(A)+P(B).一般地,如果事件A1,A2,…,An 两两互斥,那么P(A1+A2+…+An)=P(A1)+P(A2)+…+P(An). 预习交流2 某人射击一次,击中环数大于7的概率为0.6,击中环数是6或7或8 的概率为0.3,则该人击中环数大于5的概率是0.6+0.3=0.9对吗?为 什么? 提示:不对.该人“击中环数大于7”与“击中环数是6或7或8”不是互 斥事件,不能用互斥事件的概率加法公式求解.
自主预习
问题导学 即时检测 一 二 三
合作探究
解:(1)是互斥事件,不是对立事件. 理由是:从40张扑克牌中任意抽取1张,“抽出红桃”和“抽出黑桃” 是不可能同时发生的,所以是互斥事件.同时,不能保证其中必有一 个发生,这是由于还可能抽出“方块”或者“梅花”,因此,二者不是对 立事件. (2)既是互斥事件,又是对立事件. 理由是:从40张扑克牌中任意抽取1张.“抽出红色牌”与“抽出黑色 牌”两个事件不可能同时发生,且其中必有一个发生,所以它们既是 互斥事件,又是对立事件. (3)不是互斥事件,当然不可能是对立事件. 理由是:从40张扑克牌中任意抽取1张,“抽出的牌点数为5的倍数” 与“抽出的牌点数大于9”这两个事件可能同时发生,如抽得点数为 10,因此,二者不是互斥事件,当然不可能是对立事件.
【全版】数学必修ⅲ苏教版互斥事件课件8推荐PPT

§3.4 互斥事件
及其
发生的概率
复习提问:
1、求一个事件的概率的基本方法: 进行大量的重复试验,用这个事件发生的频
率近似地作为它的概率.
2、古典概型的事件A发生的概率为:
P(A)= m
n
3、几何概型的事件A发生的概率为:
P(A)
d的测度 D的测度
创设问题: 《江苏省 普通高考方案》对必修测试科目等级
如果事件A,B是互斥事件,那么事件A+B发生(即A,B中有一个发生)的概率,等于事件A,B分别发生的概率的和。
⑵ 求射击一次,命中不足7环的概率。
P( )=推1-广P(:A)
(1)A与B
(2)A与C
(3)A与D
一般地,如果事件A 、A ,…,A 中的任何 如果条件不变,你能自编不同的问题吗?试试看?
例2 某人射击1次,命中7~10环的概率 如下表所示:
命中环数 10环 9环 8环 7环
概率
0.12 0.18 0.28 0.32
⑴ 求射击1次,至少命中7环的概率; ⑵ 求射击一次,命中不足7环的概率。
注:像例2这样,在求某些稍复杂的事件的概率时,通常有两种方法:一是将 所求事件的概率化成一些彼此互斥的事件的概率的和, 二是先去求此事件的对 立事件的概率。
⑴P(求A射1+击A12次+,如…至+:少An命本) 中=例7P环(中A的1)概的+P率(事A;2)件+…A+P、(ABn)、C、D其中任意两个都是互斥的。
一般地,如果事件A1,A2,…,An彼此互斥,那么事件A1+A2+…+An发生(即A1,A2,…,An中有一个发生)的概率,等于这n
个事件分别发生的概率的和,即
返回
高中数学:3.4互斥事件(第一课时)课件 苏教版必修3
P(A) 1 P(A)
回顾小结:
二、在求某些复杂事件(如“至多、至少”的 概率时,通常有两种方法:
1、将所求事件的概率化为若干互斥事件的概 率的和; 2、求此事件的对立事件的概率.
课外作业
课本P108~109习题1~4
直通车相应练习
50
24
50
问题2:由1,2,3,4,5,6六个数字中任取一个数字:
它是2的倍数的概率为多少?
1
它是3的倍数的概率为多少?
21
32
它是2或3的倍数的概率为多少?
3
对比问题1和问题2的异同,谈谈你的看法?
问题1:体育考试的成绩分为四个等级:优、良、中、 不及格,某班50名学生参加了体育考试,结果如下:
A1 A2 An I
事件A1 + A2 + … + An :事件A1、A2 、… 、 An 有一个发生. A1、 A2 、 … 、 An 彼此互斥,则 P(A1 + A2 + … + An )=P(A1) + P(A2) + …+ P(An)
互斥事件一定不能同时发生,那么是否可以同时不发 生?举例说明.
答:从中任选2名,恰好是2名男生或2名女生的
概率为7/15.
练一练
课本P108练习1~3
回顾小结:
一、本节课主要应掌握如下知识: ⑴ 互斥事件、对立事件的概念及它们的关系; ⑵ n 个彼此互斥事件的概率公式:
P(A1 A2 An ) P(A1) P(A2 ) P(An )
⑶ 对立事件的概率之和等于1,即:
答案:(互斥但不对立,不互斥,不互斥, 互斥对立)
例2 某人射击1次, 命中7 ~ 10环的概率如下:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
要 点 导 航 ③从集合角度看,事件A的对立事件是全集中由事件A所含 结果组成的集合的补集.如上图所示.④在一次试验中, 事件A与A只能发生其中之一,并且也必然发生其中之一.
3.对立事件的概率公式:P(A)=1-P(A).
4.对立事件公式使用的前提条件是对立事件,否则 不能使用此公式.当一事件的概率直接求解困难时,可考 虑求其对立事件的概率,即运用间接法求概率.
典 例 剖 析
分析: 利用互斥事件、对立事件的定义. 解析: (1)由于事件C“至多订一种报”中有可能只订 甲报,即事件A与事件 C有可能同时发生,故 A与 C不是互 斥事件. ( 2 ) 事件 B “至少订一种报”与事件 E “一种报也不 订”是不可能同时发生的,故 B 与 E 是互斥事件.由于事 件B发生可导致事件E一定不发生,且事件E发生会导致事 件B一定不发生,故B与E还是对立事件.
P( A1)+P(A2)+„+ 两两互斥,则P(A1+A2+„+An)= _______________ .P(An)
自 主 学 习
必有一个发生 3 .两个互斥事件 _______________ ,则称这两个事件为
对立事件 A ________.事件A的对立事件记为________ .
必然事件 4.对立事件A与A必有一个发生.故A+A为________ .从
例1某县城有甲、乙两种报纸供居民订阅,记事件 A为“只订甲报”,事件B为“至少订一种报”,事件 C为“至多订一种报”,事件D为“不订甲报”,事件
E为“一种报纸也不订”.判断下列每对事件是不是互
斥事件,如果是,再判断它们是不是对立事件. (1)A与C;(2)B与E;(3)B与D;(4)B与C;(5)C与E.
数学· 必修3(苏教版)
第 3章 3.4
概
率
互斥事件
情景切入
掷一枚骰子,观察其向上的点数,设 A=“出现奇数点”,B= 1 1 “出现 2 点”,可知 P(A)= ,P(B)= .如果记 C=“出现奇数点或 2 6 2 点”, 那么如何求 P(C)呢?显然, 这个试验的基本事件空间 Ω={1, 2,3,4,5,6},随机事件 C 包含了 4 个基本事件:1,3,5,2(点), 4 2 即 C={1,3,5,2},则直观可知 P(C)= = . 6 3 2 1 1 如果我们注意到: = + ,即 P(C)=P(A)+P(B),那么求 P(C) 3 2 6 的问题可转化为求 P(A)、P(B),这说明求较复杂事件的概率问题可 转化为求较简单事件的概率,其转化有条件吗?
1.理解互斥事件、对立事件的定义. 2.掌握对立事件的概率计算公式.
自 主 学 习
不能同时发生的 1. _______________ 两个事件称为互斥事件.如果事件 A1,
A2,„,An中任何两个都是互斥事件,就说事件A1,
A2,„,An________ 彼此互斥. 2.设A, B为互斥事件,当事件 A, B中至少有一个发生, 我们把这个事件记作 ________ A+B .它是由事件A或B所包含的 所有基本事件组成的集合.事件A+B发生的概率等于事件 A , B 分 别 发 生 的和 概 率 的 _ _ _ _ _ _ , 即 P(__________________ A+B)=P(A)+P(B).一般地,如果事件A1,A2,„,An
典 例 剖 析 (3)事件B“至少订一种报”中可能只订乙报,即有可能不订甲 报,也就是说事件 B 发生,事件 D 也可能发生,故 B 与 D 不互 斥. (4)事件B“至少订一种报”中有这些可能:“只订甲报”“只 订乙报”“订甲、乙两种报”.事件 C“至多订一种报”中有 这些可能:“什么也不订”“只订甲报”“只订乙报”.由于
要 点 导 航
二、对立事件及概率公式
1.定义:不能同时发生且必有一个发生的两个事件叫 作互为对立事件,事件A的对立事件记作A.
2.对对立事件的理解:①事件A与B对立是指事件
A与事件B在一次试验中有且仅有一个发生.事件A 与事件 B在一次试验中不会同时发生 与B互斥且A+B为必然事件.
1 而P(A+A)=________ .由此我们得到一个重要公式P(A) 1-P(A) . =________ 互斥事件 5.对立事件一定是__ ______,互斥事件未必是 对立事件 ________.,
要 点 导 航
一、互斥事件
1.互斥事件的定义及理解: ( 1) 定义:事件 A与事 件B不可能同时发生.这种不可能同时发生的两个事件叫 做互斥事件 ( 或称为互不相容事件 ) .若 A ∩ B 为不可能事 件,即为A∩B=∅,那么事件A与事件B互斥.(2)对互斥 事件的理解:①A、B互斥是指事件A与事件B在一次试验 中不会同时发生.②如果事件A与B是互斥事件,那么A与
要 点 导 航 5.互斥事件与对立事件的关系:互斥事件和对立事 件有区别又有联系.在一次试验中,两个互斥事件有可能 都不发生,也可能有一个发生;而两个对立的事件则必有
一个发生,但不可能同时发生.所以,两个事件互斥,它
们未必对立;反之,两个事件对立,它们一定互斥.
典 例 剖 析
题型一 互斥事件与对立事件的判断
B两事件同时发生的概率为0.③与集合类比,可用下图表
示.④推广:如果事件A1,A2,„,An.
要 点 导 航
中的任何两个都互斥,就称事件 A 1 , A 2 ,„, A n 彼此互斥, 从集合角度看,n个事件彼此互斥是指各个事件所含结果的 集合彼此不相交.在一次投骰子的试验中,若 C 1 = { 出现 1 点},C2={出现2点},C3={出现3点},C4={出现4点},C5
={出现5点},C6={出现6点}.则事件C1,C2,C3,C4,C5,
C6彼此互斥
要 点 导 航
2.事件A+B:(1)事件A+B表示事件A和B至少有一个
发生(即A发生,或B发生,或A、B都发生)所构成的事件. (2)用集合表示两个事件A和B的A+B,如下图阴影部分 所示:
( 3) 事件 A + B 发生具有三层意思:①事件 A 发生,事件 B 不发 生;②事件A不发生,事件B发生;③事件A和B同时发生. (4)性质:A+B=B+A,(A+B)+C=A+(B+C).
