重庆市第一中学2015届九年级政治下学期期中试题
2023届九年级下学期期中考试化学专题训练(重庆市第一中学)

选择题下列材料中属于复合材料的是()A. 不锈钢B. 陶瓷C. 玻璃钢D. 水泥【答案】C【解析】复合材料是由两种或两种以上不同性质的材料,通过物理或化学的方法,在宏观上组成具有新性能的材料。
A、不锈钢是合金,属于金属材料,故A不正确;B、陶瓷属于无机非金属材料,故B不正确;C、玻璃钢是由玻璃与树脂混合而成的,前者是无机非金属材料,后者是有机高分子合成材料,玻璃钢是复合材料,故C正确;D、水泥是粉状硬性无机胶凝材料,故D不正确。
故选C。
选择题下列选项中物质的名称、俗名、化学式一致的是()A. 二氧化碳冰CO2B. 氢氧化钙熟石灰Ca(OH)2C. 氧化钙石灰石CaOD. 氢氧化钠烧碱Na2O【答案】B【解析】固体二氧化碳俗称干冰,氢氧化钙俗称熟石灰,氧化钙俗称生石灰,氢氧化钠俗称烧碱。
A、固体二氧化碳俗称干冰,其化学式为CO2,故A不正确;B、氢氧化钙俗称熟石灰,化学式为Ca(OH)2,故B正确;C、氧化钙俗称生石灰,化学式为CaO,故C不正确;D、氢氧化钠俗称烧碱,化学式为,故D不正确。
故选B。
选择题下列各组物质中,按酸、碱、盐、氧化物的顺序排列的是()A. HNO3、CaO、MgCl2、SB. NaHCO3、KOH、NaCl、ZnC. HCl、KOH、NH4Cl、COD. H2SO4、NaOH、KCl、O2【答案】C【解析】氧化物是由两种元素组成并且一种元素是氧元素的化合物,酸是电离时生成的阳离子都是氢离子的化合物,碱是电离时生成的阴离子都是氢氧根离子的化合物,盐是由金属离子和酸根离子组成的化合物。
A、HNO3是酸,CaO属于氧化物,MgCl2属于盐,S属于单质,故A不正确;B、NaHCO3属于盐,KOH属于碱,NaCl属于盐,Zn属于单质,故B 不正确;C、HCl属于酸,KOH属于碱,NH4Cl属于盐,CO属于氧化物,故C 正确;D、H2SO4属于酸,NaOH属于碱,KCl属于盐,O2属于单质,故D 不正确。
精品:【全国百强校】重庆市第一中学2015-2016学年高一下学期期中考试数学试题(原卷版)
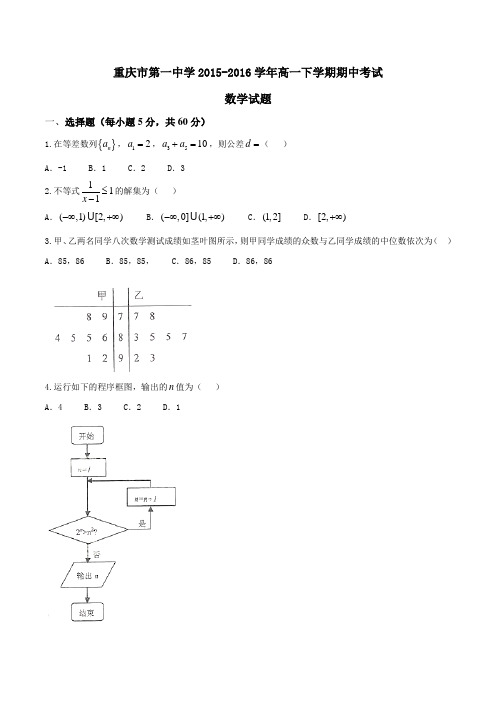
重庆市第一中学2015-2016学年高一下学期期中考试数学试题一、选择题(每小题5分,共60分)1.在等差数列{}n a ,12a =,3510a a +=,则公差d =( )A .-1B .1C .2D .32.不等式111x ≤-的解集为( )A .(,1)[2,)-∞+∞B .(,0](1,)-∞+∞C .(1,2]D .[2,)+∞3.甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为() A .85,86 B .85,85, C .86,85 D .86,864.运行如下的程序框图,输出的n 值为( )A .4B .3C .2D .15.(原创)ABC ∆中,角090C =,若(,1),(2,2)AB t AC ==,则t =( )A .-1B .1C .-3D .3 6.已知21()sin x f x x ⎧-⎪=⎨⎪⎩ 00x x >≤,则下列结论正确的是( ) A .()f x 为偶函数 B .()f x 为增函数 C . ()f x 为周期函数 D .()f x 值域为()1,-+∞7.从向阳小区抽取100户居民进行月用电量调查,为制定阶梯电价提供数据,发现其用电量都在50到350度之间,制作频率分布直方图的工作人员精心大意,位置t 处未标明数据,你认为t =( )A .0.0041B .0.0042C .0.0043D .0.00448.(原创)已知递减的等比数列{}n a 满足22a =,前三项和为7,则12n a a a 取最大值时n =( ) A .2 B .3 C .2或3 D .3或49.(原创)设a 为实数,则下列不等式一定不成立的是( )A .24a a >B .2lg lg a a <C .20a a +≤D .12a a+< 10.锐角ABC ∆三边长分别为,1,2x x x ++,则x 的取值范围是( )A .(1,3)-B .(1,3)C .(3,)+∞D .(1,3)(3,)+∞11.(原创)设G 为ABC ∆的重心,2AG AM =,则( ) A .2136BM BA BC =-+ B .2136BM BA BC =+ C .2136BM BA BC =- D .2136BM BA BC =-- 12.已知函数()(1)f x x m x =+,关于x 的不等式()()f x f x m >+的解集记为T ,若区间11,22T ⎡⎤-⊆⎢⎥⎣⎦,则实数m 的取值范围是( )A. B. C.(-∞ D.13(0,+ 二、填空题(每小题5分,共20分)13.(原创)重庆某教育研究机构对重庆38个区县中学生体重进行调查,按地域把它们分成甲、乙、丙、丁四个组,对应区县个数为4,10,16,8,若用分层抽样抽取9个城市,则丁组应抽取的区县个数为__________.14. ABC ∆中,05,7,120AB AC B ===,则ABC ∆的面积为__________.15.设0,0x y >>,且312()2x y -=,则14x y+的最小值为__________. 16.(原创)对数列{}n a 前n 项和为n S ,0n a >(1,2,n =),121a a ==,且对2n ≥有12()n n a a a a +++1211()n n a a a a -+=+++,则1223341n n S S S S S S S S -++++=__________.三、解答题 (共70分.)17.(10分)已知数列{}n a 前n 项和为212n S n n =-+. (1)求{}n a 的通项公式;(2)求数列{}n a 的前10项和10T .18.(12分)在ABC ∆中,角,,A B C 对边分别为,,a b c ,角34C π=,且sin 2sin cos()B A A B =+. (1)证明:222b a =;(2)若ABC ∆面积为1,求边c 的长.19.(12分)某家父母记录了女儿玥玥的年龄(岁)和身高(单位cm )的数据如下:(1)试求y 关于x 的线性回归方程y bx a =+;(2)试预测玥玥10岁时的身高.(其中,121()()()ni ii n ii x x y y b x x ==--=-∑∑,a y bx =-)20.(12分)直角三角形ABC 中,角,,A B C 对边长分别为,,a b c ,090C ∠=.(1)若三角形面积为2,求斜边长c 最小值;(2)试比较n n a b +与n c *()n N ∈的大小,并说明理由.21.(12分)已知函数9()log (91)()x f x kx k R =++∈是偶函数.(1)求k 的值;(2)若函数94()log (3)3x g x a a =∙-的图象与()f x 的图象有且只有一个公共点,求a 的取值范围. 22. (12分)已知函数{}1:n a a t =,2221()n n n n n S n S a a +=++,1,2,n = (1)设{}n a 为等差数列,且前两项和23S =,求t 的值;(2)若13t =,证明:121n n a n ≤<+。
《抓痒痒》的阅读答案

《抓痒痒》的阅读答案【篇一:《乱挠痒痒的章鱼》阅读目标】txt>包铝小学刘芳瑞阅读目标:1、通过认真欣赏、理解故事内容,激发学生对绘本的阅读兴趣。
2、认真观察画面,培养观察能力,受到美的熏陶。
3、懂得同伴之间要和谐相处,犯错误要及时改正的道理。
4、学习发现每个人身上的优点《乱挠痒痒的章鱼》阅读导引单时间:30分钟出示动画片《海绵宝宝》图片,海绵宝宝有位好朋友叫章鱼哥,它是什么样的?今天我们也来认识一只章鱼。
(激发兴趣)一、看一看(提取封面信息)封面上有()(只填序号)1、章鱼2、小鱼3、水草4、泡泡5、海星6、螃蟹二、数一数猜一猜(预测、想象)数一数章鱼有几条触手?它这八条触手可以干什么?填在泡泡里三、师生共读,指导看图(理解内容,深化认识)1、章鱼挠谁痒痒?它们都高兴吗?2、章鱼把珠母贝的珍珠弄丢了,它是怎么做的??3、题目中的“乱”是什么意思?你喜欢这只章鱼吗?为什么?四、联系实际(联系实际,深化感悟)1、我们周围也有像章鱼一样的人,他们在和同学的相处中,不太注意自己的行为,惹得同学不开心。
在你身上有这样的事吗?请你给大家讲一讲。
2、章鱼在追赶珍珠的过程中发现了自己很多优点,它说的最多的话就是“我从来都不知道自己还能……”其实我们每个人身上都藏着很多闪光点,你也用这句话发现一下自己的优点吧!五、活动拓展(品味语言,发展想象)1、分角色表演这个故事2、续编故事:想象在以后的时光中,章鱼用自己的长处为自己或朋友做了哪些事情呢?可以讲一讲,也可以画一画。
《乱挠痒痒的章鱼》导引单使用分析刘芳瑞阅读课上我先引导学生看封面,并练习看图说话。
这一环节渗透绘本阅读的方法:先看封面。
接下来让学生预测章鱼的八条触手可以干什么。
这个问题既可激发学生的阅读欲望,也可以引导学生阅读的关注点。
接下来师生共读,指导看图。
“章鱼挠谁痒痒了?它们高兴吗?把珠母贝的珍珠弄丢了,它是怎么做的?你喜欢这只章鱼吗?为什么?”这些问题引导学生提取信息,图文结合,思考内容。
2022-2023学年重庆市第一中学高二下学期期中数学试题
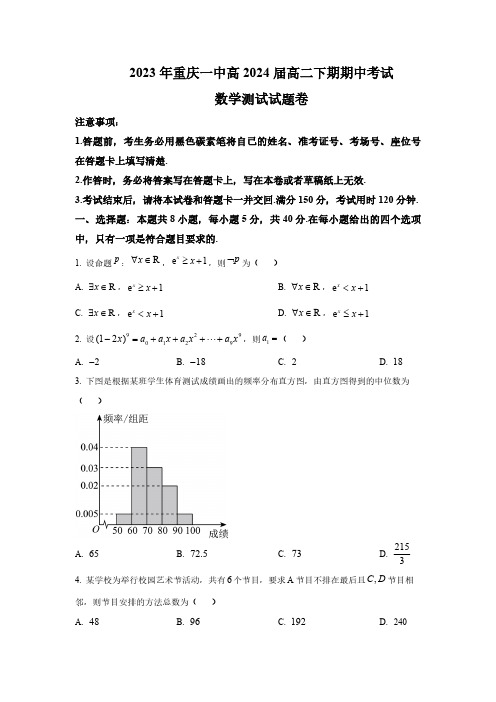
2023年重庆一中高2024届高二下期期中考试数学测试试题卷注意事项:1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚.2.作答时,务必将答案写在答题卡上,写在本卷或者草稿纸上无效.3.考试结束后,请将本试卷和答题卡一并交回.满分150分,考试用时120分钟. 一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设命题:,,则为( )p R x ∀∈e 1xx ≥+p ⌝A. , B. , R x ∃∈e 1x x ≥+R x ∀∈e 1x x <+C. ,D. ,R x ∃∈e 1x x <+R x ∀∈e 1≤+x x 2. 设,则( )9290129(12)x a a x a x a x -=++++ 1a =A. B. C. D.2-18-2183. 下图是根据某班学生体育测试成绩画出的频率分布直方图,由直方图得到的中位数为( )A. B. C.D.6572.57321534. 某学校为举行校园艺术节活动,共有个节目,要求节目不排在最后且节目相6A ,C D 邻,则节目安排的方法总数为( ) A.B.C.D.48961922405. 已知抛物线,直线交该抛物线于两点.若线段的中点坐标为2:4G y x =l ,A B AB ,则直线斜率为()()3,2l A.B.C. D.1214126. 已知函数有两个极值点, 则实数的取值范围是( ) ()2ln f x k x x x =-+k A.B.C.D.1,8⎛⎫-∞ ⎪⎝⎭1,8⎛⎫+∞ ⎪⎝⎭(),1-∞-10,8⎛⎫ ⎪⎝⎭7. 已知,则的最小值是( )0x y >>222x y xy y +-A. B.2+2+C.D.228. 已知随机变量的分布列服从,记X ()~,X B n p ()()(),1f n p P X n P X n ==-+=,在上的最大值为,若正整数满足,则(),f n p 10,2p ⎡⎤∈⎢⎥⎣⎦()F n ,a b 2003a b >>和的大小关系是( )()F a ()F b A. B. ()()F a F b <()()F a F b =C.D. 无法确定()()F a F b >二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9. 下列结论中,所有正确的结论是( )A. 当 0x >2≥B. 若时,a b <a b <C. 若,则 ,0x y z x y z <<++=xz yz >D. 当时,的最小值为 3x >-13y x x =++1-10. 下列说法中,正确的命题有( ) A. 已知随机变量服从正态分布,,则ξ()2N 2,δ(4)0.84P ξ<=(24)0.16P ξ<<=B. 以模型去拟合一组数据时,为了求出回归方程,设,求得线性回归方e kx y c =ln z y =程为,则 的值分别是和0.3 ˆ0.34zx =+,c k 4e C. 8个完全相同的球放入编号为1,2,3的三个空盒中,要求放入后3个盒子均不空且数量均不同,则有12种放法D. 若样本数据的方差为2,则数据,,的方差为129,,,x x x 1132x +2132x +91...,32x +411. 已知某一物品的单件回收费为,根据以往回收经验可得,随机变量0,,2X a =02a <<的分布列如图所示,其中结论正确的是( )X X 0a2 P1214bA 14b =B. 若该物品4件,其中2件单件回收费为2的概率为9256C. 若该物品4件,单件回收费不为0的件数为,则 Y ()2E Y =D. 当时,取得最小值 23a =()D X 12. 小明与小兵两位同学计划去科技博物馆参加活动.小明在如图的街道E 处,小兵在如图的街道F 处,科技博物馆位于如图的G 处,则下列说法正确的是( )A. 小明到科技博物馆选择的最短路径条数为126条B. 小兵到科技博物馆选择的最短路径条数为4条C. 小明到科技博物馆在选择的最短路径中,与到F 处和小兵会合一起到科技博物馆的概率为1021D. 小明与小兵到科技博物馆在选择的最短路径中,两人约定在科技博物馆门口汇合,事件A :小明经过F ;事件B :从F 到科技博物馆两人的路径没有重叠部分(路口除外),则()29P B A =三、填空题:本题共4小题,每小题5分,共20分.13. 一个袋子中装有大小和质地均相同的3个黑球和和2个白球,则从中摸出2个球恰好是1个黑球和1个白球的概率为________.14. 若随机变量,且,则的值是________. (),0.8X B n ()4E X =()1P X =15. 有两个分类变量和,其中一组观测值为如下的列联表:x y 22⨯1y2y 总计1xa10a -102x10a -20a +30 总计103040其中均为大于的整数,则________时,在犯错误的概率不超过0.01的前提,10a a -3=a 下为“和之间有关系”.附: x y ()()()()()22n ad bc K a b c d a c b d -=++++()2P K k ≥ 0.10 0.05 0.025 0.0100.005k 2.706 3.841 5.024 6.6357.87916. 某靶场有两种型号的步枪可供选用,其中甲使用两种型号的步枪的命中率分,A B ,A B 别为.现在两把步枪中各装填3发子弹,甲打算轮流使用两种步枪进行射1,314,A B ,A B 击,若击中标靶,则继续使用该步枪,若未击中标靶,则改用另一把步枪,甲首先使用A 种型号的步枪,若出现连续两次子弹脱靶或者其中某一把步枪的子弹打光耗尽的现象便立刻停止射击,记为射击的次数,则________.X ()5P X ==四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.17. 已知集合和非空集合 {}2870A x x x =-+≤{}121B x m x m =+≤≤-(1)若,求;5m =A B ⋂(2)若“”是“”的必要不充分条件,求实数的取值范围. x A ∈x B ∈m 18. 根据国家统计局统计,我国2018—2022年的新生儿数量如下:年份编号 x 12345年份2018 2019 2020 2021 2022新生儿数量(单位:万人) y 1523 1465 1200 1062 956(1)由表中数据可以看出,可用线性回归模型拟合新生儿数量与年份编号的关系,请y x 用相关系数说明相关关系的强弱;(,则认为与线性相关性很强) r 0.751r ≤≤y x (2)建立关于的回归方程,并预测我国2025年的新生儿数量. y x 参考公式及数据:rn∑i =1x i y i ‒nx ⋅yb n∑i =1x i y i ‒nx ⋅ya y ‒bx ,5∑i =1y i=6206,5∑i =1y i =6206, i ≈1564.19. 已知双曲线,焦点为,其中一条渐近线的倾斜角为()2222:10,0x y C a b a b-=>>12,F F ,点在双曲线上,且.30 M 12MF MF -=(1)求双曲线的标准方程;C (2)若直线交于两点,若,求正实数的值. :l y x m =+C ,A B AOB m 20. 已知正项数列满足:;为数列为的前项{}n a 22111230,3n n n n a a a a a ++--==n T {}n b n 和,,对任意的自然数,恒有. 222b a =-n 23n n T nb n =+(1)求数列的通项公式及其前项和;{}n a n n S(2)证明:数列是等差数列,并求其通项公式.{}n b 21. 在全球抗击新冠肺炎疫情期间,我国医疗物资生产企业加班加点生产口罩、防护服、消毒水等防疫物品,保障抗疫一线医疗物资供应,在国际社会上赢得一片赞誉.我国某口罩生产厂商在加大生产的同时,狠抓质量管理,不定时抽查口罩质量.该厂质检人员从某日生产的口罩中随机抽取了100个,将其质量指标值分成以下五组:,[)100,110,,, ,得到如下频率分布直方图.规定:口[)110,120[)120130,[)130140,[]140,150罩的质量指标值越高,说明该口罩质量越好,其中质量指标值低于130的为二级口罩,质量指标值不低于130的为一级口罩.(1)将上述质量检测的频率视为概率,现从该工厂此类口罩生产线上生产出的大量口罩中,采用随机抽样方法每次抽取1个口罩,抽取8次,记被抽取的8个口罩中一级口罩个数为.若每次抽取的结果是相互独立的,求的方差;ξξ(2)现从样本口罩中利用分层抽样的方法随机抽取8个口罩,再从中抽取3个,记其中一级口罩个数为,求的分布列及数学期望;ηη(3)在2023年“五一”劳动节前,甲、乙两人计划同时在该型号口罩的某网络购物平台上分别参加两店各一个订单“秒杀”抢购,其中每个订单由个该型号口,A B ()2,Nn n n *≥∈罩构成.假定甲、乙两人在 两店订单“秒杀”成功的概率分别为,,记,A B 2πnπ2cosn n甲、乙两人抢购成功的口罩总数量为,求当的数学期望取最大值时正整数X X ()E X n 的值.22. 已知函数. ()()()3211e R ,e 23axx f x x a g x x mx =+∈=-+(1)讨论函数在上的单调性;()f x ()0,∞+(2)若,当时,判断函数的零点个数.()()()h x f x g x =-1,0a m =≥()h x2023年重庆一中高2024届高二下期期中考试数学测试试题卷一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设命题:,,则为( )p R x ∀∈e 1xx ≥+p ⌝A. , B. , R x ∃∈e 1x x ≥+R x ∀∈e 1x x <+C. , D. ,R x ∃∈e 1x x <+R x ∀∈e 1≤+x x 【答案】C2. 设,则( )9290129(12)x a a x a x a x -=++++ 1a =A. B. C. D.2-18-218【答案】B3. 下图是根据某班学生体育测试成绩画出的频率分布直方图,由直方图得到的中位数为( )A. B. C.D.6572.5732153【答案】D4. 某学校为举行校园艺术节活动,共有个节目,要求节目不排在最后且节目相6A ,C D 邻,则节目安排的方法总数为( ) A. B.C.D.4896192240【答案】C5. 已知抛物线,直线交该抛物线于两点.若线段的中点坐标为2:4G y x =l ,A B AB ,则直线斜率为()()3,2l A.B.C. D.121412【答案】C6. 已知函数有两个极值点, 则实数的取值范围是( )()2ln f x k x x x =-+k A. B.C.D.1,8⎛⎫-∞ ⎪⎝⎭1,8⎛⎫+∞ ⎪⎝⎭(),1-∞-10,8⎛⎫ ⎪⎝⎭【答案】D7. 已知,则的最小值是( ) 0x y >>222x y xy y+-A. B.2+2+C. D.22【答案】C8. 已知随机变量的分布列服从,记X ()~,X B n p ()()(),1f n p P X n P X n ==-+=,在上的最大值为,若正整数满足,则(),f n p 10,2p ⎡⎤∈⎢⎥⎣⎦()F n ,a b 2003a b >>和的大小关系是( )()F a ()F b A. B. ()()F a F b <()()F a F b =C. D. 无法确定()()F a F b >【答案】A二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9. 下列结论中,所有正确的结论是( )A. 当 0x >2≥B. 若时,a b <a b <C. 若,则 ,0x y z x y z <<++=xz yz >D. 当时,的最小值为 3x >-13y x x =++1-【答案】AD10. 下列说法中,正确的命题有( ) A. 已知随机变量服从正态分布,,则ξ()2N 2,δ(4)0.84P ξ<=(24)0.16P ξ<<=B. 以模型去拟合一组数据时,为了求出回归方程,设,求得线性回归方e kx y c =ln z y =程为,则 的值分别是和0.3 ˆ0.34zx =+,c k 4e C. 8个完全相同的球放入编号为1,2,3的三个空盒中,要求放入后3个盒子均不空且数量均不同,则有12种放法D. 若样本数据的方差为2,则数据,,的方差为129,,,x x x 1132x +2132x +91...,32x +4【答案】BC11. 已知某一物品的单件回收费为,根据以往回收经验可得,随机变量0,,2X a =02a <<的分布列如图所示,其中结论正确的是( )X X 0a2 P1214bA. 14b =B. 若该物品4件,其中2件单件回收费为2的概率为9256C. 若该物品4件,单件回收费不为0的件数为,则 Y ()2E Y =D 当时,取得最小值 23a =()D X 【答案】ACD12. 小明与小兵两位同学计划去科技博物馆参加活动.小明在如图的街道E 处,小兵在如图的街道F 处,科技博物馆位于如图的G 处,则下列说法正确的是( )A. 小明到科技博物馆选择的最短路径条数为126条B. 小兵到科技博物馆选择的最短路径条数为4条C. 小明到科技博物馆在选择的最短路径中,与到F 处和小兵会合一起到科技博物馆的概率为1021D. 小明与小兵到科技博物馆在选择的最短路径中,两人约定在科技博物馆门口汇合,事件A :小明经过F ;事件B :从F 到科技博物馆两人的路径没有重叠部分(路口除外),则()29P B A =【答案】ACD三、填空题:本题共4小题,每小题5分,共20分.13. 一个袋子中装有大小和质地均相同的3个黑球和和2个白球,则从中摸出2个球恰好是1个黑球和1个白球的概率为________. 【答案】## 350.614. 若随机变量,且,则的值是________. (),0.8X B n ()4E X =()1P X =【答案】## 46250.006415. 有两个分类变量和,其中一组观测值为如下的列联表:x y 22⨯1y2y 总计1xa10a -102x10a -20a +30 总计103040其中均为大于的整数,则________时,在犯错误的概率不超过0.01的前提,10a a -3=a 下为“和之间有关系”.附: x y ()()()()()22n ad bc K a b c d a c b d -=++++()2P K k ≥ 0.10 0.05 0.025 0.0100.005k 2.706 3.841 5.024 6.6357.879【答案】616. 某靶场有两种型号的步枪可供选用,其中甲使用两种型号的步枪的命中率分,A B ,A B 别为.现在两把步枪中各装填3发子弹,甲打算轮流使用两种步枪进行射1,314,A B ,A B 击,若击中标靶,则继续使用该步枪,若未击中标靶,则改用另一把步枪,甲首先使用A 种型号的步枪,若出现连续两次子弹脱靶或者其中某一把步枪的子弹打光耗尽的现象便立刻停止射击,记为射击的次数,则________. X ()5P X ==【答案】772四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.17. 已知集合和非空集合 {}2870A x x x =-+≤{}121B x m x m =+≤≤-(1)若,求;5m =A B ⋂(2)若“”是“”的必要不充分条件,求实数的取值范围. x A ∈x B ∈m 【答案】(1){}67A B x x ⋂=≤≤(2) []2,4【解析】【分析】(1)解集合A 中的不等式,得到集合A ,求出时集合B ,再求; 5m =A B ⋂(2)问题转化为是的真子集,由此列不等式组求出实数m 的取值范围. B A 【小问1详解】不等式解得,则有, 2870x x -+≤17x ≤≤{}17A x x =≤≤当时,,. 5m ={}69B x x =≤≤{}67A B x x ∴⋂=≤≤【小问2详解】因为“”是“”的必要不充分条件,故是的真子集,x A ∈x B ∈B A 则有,由于等号不能同时成立,故,21111217m m m m -≥+⎧⎪+≥⎨⎪-≤⎩24m ≤≤所以实数的取值范围.m []2,418. 根据国家统计局统计,我国2018—2022年的新生儿数量如下:年份编号 x 12345年份2018 2019 2020 2021 2022新生儿数量(单位:万人) y 1523 1465 1200 1062 956(1)由表中数据可以看出,可用线性回归模型拟合新生儿数量与年份编号的关系,请y x 用相关系数说明相关关系的强弱;(,则认为与线性相关性很强) r 0.751r ≤≤y x (2)建立关于的回归方程,并预测我国2025年的新生儿数量. y x 参考公式及数据:rn∑i =1x i y i ‒nx ⋅yb n∑i =1x i y i ‒nx ⋅ya y ‒bx ,5∑i =1y i =6206,5∑i =1y i =6206, i ≈1564.【答案】(1)答案见解析;(2),472.7万人. 153.71702.3y x =-+【解析】【分析】(1)求出相关系数即得解;(2)利用最小二乘法求出关于的回归方程,再预测我国2025年的新生儿数量. y x 【小问1详解】,15370.981564r -=≈≈-,故与的线性相关性很强..0.75r > y x 从而可以用线性回归模型拟合与的关系. y x 【小问2详解】,()51111123453,62061241.2555i i x y y ==++++===⨯=∑.52222222215123455310ii xx =-=++++-⨯=∑故, 51522151537ˆ153.7105i ii ii x y xybxx ==--===--∑∑所以, ()ˆˆ1241.2153.731702.3ay bx =-=--⨯=所以关于的回归方程为,y x 153.71702.3y x =-+将2025年对应的年份编号代入回归方程得 8x =153.781702.3ˆ472.7y=-⨯+=所以我国2025年的新生儿数量约为472.7万人.19. 已知双曲线,焦点为,其中一条渐近线的倾斜角为()2222:10,0x y C a b a b-=>>12,F F ,点在双曲线上,且.30M 12MF MF -=(1)求双曲线的标准方程;C (2)若直线交于两点,若,求正实数的值.:l y x m =+C ,A B AOB m 【答案】(1)2213x y -=(2)2【解析】【分析】(1)利用双曲线的定义和渐近线方程即可求得双曲线的标准方程. (2)联立双曲线和直线方程,利用韦达定理表示出弦长,即可得出答案. 【小问1详解】 由条件知,,2tan 30b a a ==︒=故.1a b ==即双曲线标准方程为.2213x y -=【小问2详解】设,到直线的距离为,()()1122,,,A x y B x y O l h 联立得,2213x y y x m ⎧-=⎪⎨⎪=+⎩2226330x mx m +++=由,解得, ()2223683312240m m m ∆=-+=->22m >又,故,0m>m >而又由,21212333,2m x x m x x ++=-=故弦长,AB ==h 又12AOB S AB h == 解得,, 42280m m --=24m =又,故.m >2m =20. 已知正项数列满足:;为数列为的前项{}n a 22111230,3n n n n a a a a a ++--==n T {}n b n 和,,对任意的自然数,恒有. 222b a =-n 23n n T nb n =+(1)求数列的通项公式及其前项和;{}n a n n S(2)证明:数列是等差数列,并求其通项公式. {}n b 【答案】(1) 1133,322nn n n a S +==⨯-(2)证明见解析, 41n b n =-【解析】【分析】(1)由题目条件可得,即可得是以为首项,公()()1130n n n n a a a a ++-+={}n a 3比为3的等比数列,代入公式即可求得通项公式和前项和;n n S (2)由利用等差中项性质即可得,即可得数列是23n n T nb n =+212n n n b b b --+={}n b ,公差的等差数列,所以.13b =4d =41n b n =-【小问1详解】由题意可知,,且()()1130n n n n a a a a ++-+=0n a >即可得,即 13n n a a +=13n na a += 所以是首项为,公比为3的等比数列, {}n a 13a =所以,即数列的通项公式为111333n n n n a a q--==⨯={}n a ,3N n n a n +=∈由等比数列前项和公式可得; n ()13131331322nn n S +⨯-==⨯--【小问2详解】在中,令得,,又23n n T nb n =+1n =13b =2227b a =-=由得: 23n n T nb n =+()()112131,2n n T n b n n --=-+-≥两式相减得:()1213n n n b nb n b -=--+即 ()()()1213,2n n n b n b n --=--≥⋅⋅⋅⋅⋅⋅①当时,由①可得: 3n ≥()()12323,n n n b n b ---=--⋅⋅⋅⋅⋅⋅② 可得对任意的都成立, ①-②212n n n b b b --+=3n ≥ 故是等差数列,首项是,公差是{}n b 13b =214d b b =-=从而,11(41)n b n b n d +-=-=所以数列的通项公式为{}n b 41,N n b n n +-∈=21. 在全球抗击新冠肺炎疫情期间,我国医疗物资生产企业加班加点生产口罩、防护服、消毒水等防疫物品,保障抗疫一线医疗物资供应,在国际社会上赢得一片赞誉.我国某口罩生产厂商在加大生产的同时,狠抓质量管理,不定时抽查口罩质量.该厂质检人员从某日生产的口罩中随机抽取了100个,将其质量指标值分成以下五组:,[)100,110,,, ,得到如下频率分布直方图.规定:口[)110,120[)120130,[)130140,[]140,150罩的质量指标值越高,说明该口罩质量越好,其中质量指标值低于130的为二级口罩,质量指标值不低于130的为一级口罩.(1)将上述质量检测的频率视为概率,现从该工厂此类口罩生产线上生产出的大量口罩中,采用随机抽样方法每次抽取1个口罩,抽取8次,记被抽取的8个口罩中一级口罩个数为.若每次抽取的结果是相互独立的,求的方差;ξξ(2)现从样本口罩中利用分层抽样的方法随机抽取8个口罩,再从中抽取3个,记其中一级口罩个数为,求的分布列及数学期望;ηη(3)在2023年“五一”劳动节前,甲、乙两人计划同时在该型号口罩的某网络购物平台上分别参加两店各一个订单“秒杀”抢购,其中每个订单由个该型号口,A B ()2,Nn n n *≥∈罩构成.假定甲、乙两人在 两店订单“秒杀”成功的概率分别为,,记,A B 2πnπ2cosn n甲、乙两人抢购成功的口罩总数量为,求当的数学期望取最大值时正整数X X ()E X n 的值.【答案】(1)1.5 (2)分布列见解析,34(3)6 【解析】【分析】(1)由题可知,抽到一级口罩的频率为0.25,且,根据二项分布(8,0.25)B ξ 的方差公式,计算结课;(2)根据题意知,可能的值有,计算对应概率,写出分布列和期望即可; η0,1,2(3)设甲乙抢购成功的订单总量为,由题可知,可能为,计算出对应概率,求Y Y 0,1,2出,结合,化简,最后用导数找出最大值,求解即可. ()E Y X nY =()E Y 【小问1详解】(1)由题知,抽到一级口罩的频率为,则, ()0.020.005100.25+⨯=(8,0.25)B ξ 故. ()(1)80.250.75 1.5D np p ξ=-=⨯⨯=【小问2详解】按分层抽样抽取8个口罩,则其中一级、二级口罩个数分别为,0.2582⨯=,()10.2586-⨯=故可能的取值为0,1,2,η,,,306238C C 5(0)C 14P η===21623815(1)28C C P C η===1262383(2)28C C P C η===的分布列为 η η012P 514 1528 328. 15()0114533228284E η+⨯⨯+⨯==【小问3详解】设甲乙抢购成功的订单总数量为,由题知,可能的取值为0,1,2,Y Y , 2232cos2cos 2cos(0)(1)(11ππππππn n n P Y n n n n n ==--=--+, 22232cos2cos 2cos 4cos(1)(1(1)ππππππππn n n n P Y n n n n n n n ==-+-⋅=+-,32cos(2)ππn P Y n ==所以232332cos2cos 2cos 4cos 2cos ()0(1)1(2ππππππππππn n n n n E X nn n n n n n =⨯--++⨯+-+⨯,2π2cos πn n n=+因为,所以, X nY =22cos()()()2cos ππππn E X nE Y n nn n n==+=+令,设, 11(0,]2t n =∈()2cos f t πt πt =+则,()()E X f t =因为, 1()2sin 2(sin )2f t πππt ππt '=-=-所以当时,;当时,; 10,6t ⎛⎫∈ ⎪⎝⎭()0f t '>11,62t ⎛⎫∈ ⎪⎝⎭()0f t '<所以在上单调递增,在上单调递减, ()f t 10,6⎛⎫ ⎪⎝⎭11,62⎛⎫ ⎪⎝⎭故当,即时,取最大值, 16t =6n =()f t 所以,所以取最大值时,正整数. ()max 1π66f t f ⎛⎫==⎪⎝⎭()E X 6n =22. 已知函数. ()()()3211e R ,e 23axx f x x a g x x mx =+∈=-+(1)讨论函数在上的单调性; ()f x ()0,∞+(2)若,当时,判断函数的零点个数.()()()hx f x g x =-1,0a m =≥()h x 【答案】(1)答案见解析;(2)只有1个零点. 【解析】【分析】(1)求出,再对分和两种情况讨论得解; ()f x 'a 0a ≥a<0(2)求出,再对分三种情况讨论,得到每一种情(),()h x h x 'm 111,,0222m m m =>≤<况下,在上都只有1个零点,综合即得解. ()h x R 【小问1详解】,因为()f x '()e e e 1ax ax axax ax =+=+0x >故当时,在上恒成立,所以函数的增区间为;0a ≥()0f x ¢>()0,∞+()f x ()0,∞+当时,令得,令得, a<0()0f x ¢>1x a<-()0f x '<1x a>-综上当时,的增区间为;当时,的增区间为,减0a ≥()f x ()0,∞+a<0()f x 10,a ⎛⎫-⎪⎝⎭区间为. 1,a ∞⎛⎫-+ ⎪⎝⎭【小问2详解】,定义域为.()()()()32111e 32x h x f x g x x x mx =-=-+-+R()h x '()2e 2e 2x xx x mx x x m =+-=+-令,()e 2xt x x m =+-当时,,故在上单调递增, 12m =()e 1,xt x x =+-()e 10x t x '=+>()t x R 又()00e 010t =+-=故当时, 恒成立,0x >()e 10,xt x x =+->()(e 1)0x h x x x '=+->当时, 恒成立,且0x <()e 10,xt x x =+-<()(e 1)0x h x x x '=+->()00h '=综上,在上单调递增, ()h x R 又,故在上只有1个零点 ()()11010,1023h h =-+=()h x R 当时,在上单调递增,12m >()e 2x t x x m =+-R()()0120,e m t m t m m =-<=-令,则在上恒成立()x φ1e ,2xx x =->()x φ'e 10x =->12x >所以在上单调递增,故,故 ()x φ1,2⎛⎫+∞ ⎪⎝⎭1()()2x φφ>102=->()0t m >所以存在唯一,使得,即 ()10,x m ∈()10t x =()10h x '=当时,,故, 0x <()0t x >()(e 2)0x h x x x k '=+->当时,,故 10x x <<()0t x <()(e 2)0x h x x x k '=+-<当时,,故,1x x >()0t x >()(e 2)0x h x x x k '=+->所以在上单调递增,在上单调递减,在上单调递增 ()h x (),0∞-()10,x ()1,x +∞因为 ()()()()3111010,331e 022m h x h h m m <=-+=-+所以当时,在上只有1个零点, 12m >()h x R当时,在上单调递增102m ≤<()e 2xt x x m =+-R 因为()()10120,1120t m t e m -=->-=--<所以存在唯一,使得,即 ()21,0x ∈-()20t x =()20h x '=当时,,故 2x x <()0t x >()(e 2)0x h x x x k '=+->当时,,故 20x x <<()0t x <()(e 2)0x h x x x k '=+-<当时,,故,0x >()0t x >()(e 2)0x h x x x k '=+->所以在上单调递增,在上单调递减,在上单调递增 ()h x ()2,x -∞()2,0x ()0,∞+因为 ()()111010,10232h h m =-+=-+所以当时,恰有1个零点, ()0,x ∈+∞()h x 当时, (),0x ∈-∞()()()2322222max 111e 32xh x h x x x mx ==-+-+,令,解得:2()h x '22222e 2x x x mx =+-2()0h x '=22e 2x x m +=所以 ()()()222322322222222e 11111e 22e 132223x x x x h x x x x x x x +⎡⎤=-+-⋅+=--++-⎢⎥⎣⎦令,则 ()()()23122e 1,1,03x x x x x x φ=-++-∈-()x φ'()2e 10x x =+≥所以在上单调递增, 故 ()x φ()1,0-()(1)x φφ>-5154154e 10e 3e 33e -=--=-=>所以()20h x <故当时,无零点(),0x ∈-∞()h x 当时,在上只有1个零点 102m ≤<()h x R 综上,当时,函数在上只有1个零点1,0a m =≥()h x R 【点睛】方法点睛:利用导数研究函数的零点问题,常用的方法是:(1)方程法,直接解方程得解;(2)图象法,直接画出函数的图象分析得解;(3)方程+图象法,令()f x 得到,再画出函数的图象分析得解. ()0f x =()()g x h x =(),()g x h x。
重庆市大学城第一中学校2024_2025学年高二政治下学期期中试题

重庆市高校城第一中学校2024-2025学年高二政治下学期期中试题一、选择题(本大题共24小题,每小题2分,共48分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.“红白旧俗该从简,礼轻情重有脸面”“谁言孤老无依靠,天下人帮天下人”……让一面面旧墙体变成美观而又会“说话”的文化墙,是某镇运用乡风文明助推漂亮乡村建设的一个缩影。
让墙壁说“文明话”,表明①文化对人的影响来自于特定的环境和活动②文化墙成为乡村建设新的宣扬阵地和载体③振兴乡村文化是推动农村发展的确定力气④增加群众文化体验是乡村振兴的主要目的A.①②B.①④C.②③D.③④2.2024年,俄罗斯将首次在国家统一考试中进行汉语科目的考试,这将进一步推动中国和俄罗斯之间友好合作关系的发展。
这现象反映出①文化对于政治互信和经济合作起着重要的支撑作用②汉语以其博大精深的特点驾驭了世界语言的主导权③我国综合实力的增加和汉语言文化国际影响力提升④各国文化因不同而精彩,世界文化因差异而多样化A.①②B.①③C.②④D.③④3.每逢遇到重大灾难,社会各界就会纷纷加入到救灾和爱心捐助活动中来,化爱心为行动。
从文化生活角度看,这说明①文化与经济相互影响,文化与政治相互交融②爱心捐助作为精神力气,对社会发挥重要作用③文化作为一种精神力气,可以在实践中转化为物质力气④人们的精神活动离不开物质活动,精神产品离不开物质载体A.①②B.②③C.①④D.③④4.2018年11月6日,国内最长的地铁海底隧道青岛地铁一号线贯穿。
为限制施工风险,施工单位细心组织、创新科技和艰苦鏖战,突破了海底隧道海疆段最难断裂带,获得了多项世界顶尖的科研成果。
这些重大科技成果将极大地推动我国的社会主义现代化建设,提高我国在国际上的地位和竞争力。
这表明:①我国已成为科技全面领先世界的国家②文化越来越成为综合国力竞争的重要因素③科技已成为民族振兴和社会进步的基石④文化越来越成为经济社会发展的重要支撑A.①②B.①③C.②④D.③④5.那鲜红的对联,那成双的“喜”字,那倒贴的“福”字,那前额突出的“老寿星”画……全部这一切都唤起海外游子们浓郁的乡愁。
2014-2015学年七年级下学期政治期末试卷及答案(人教版)及答案

2014-2015学年七年级下学期政治期末试卷及答案(人教版)及答案2014-2015学年七年级政治下册期末测试题及答案一、单项选择题。
(下列各题只有一个答案最符合题意,请把你认为正确答案前的字母填在题后括号内。
每题4分,共60分)1.许多心理学家的实验都证明,愉快的事情令人记忆得最清晰,回忆的细节也多;人对描写美的词的记忆效果最好,这一事实告诉我们CA.爱美之心人皆有之B.人应该活得无忧无虑C.积极的情绪可以产生积极的结果D.不同的情绪会导致不同的结果2.为了专心致志地搞好研究,不少同学凭着毅力放弃了自己迷恋的一些活动,如下棋、玩游戏机等等。
这说明坚强意志对人的行动具有(A)作用。
A.克制B.激励C.阻碍D.推动3.一个人能否努力克服研究、工作、生活中的困难是A A.个人意志是否坚强的最好证明B.人个身体是否健康的最好证明C.智商不高,智力水平低D.情绪不健全,情感不丰富4.“苦难对于天才是一块垫脚石……对于能干的人是一笔财富,对于弱者是一个万丈深渊。
”这说明CA.挫折无处不在,而且人人都会遇到B.挫折是坏事,遇到挫折就像落入万丈深渊C.对于能承受挫折的人来说,挫折可以孕育成功D.挫折给人以身心打击,造成精神痛苦,所以它只有消极作用5.创造成功的记录,最需要的是AA.坚定的信念B.克服依赖心理C.有勇敢的行动D.选准适当的目标6.XXX从小下煤窑做苦工,不到20岁参加了革命,从一个半文盲成长为我国第一代兵工专家。
他之所以能为祖国作出这么大的贡献,就在于他(C)A、个人想出人头地B、人生的好事多磨C、具有良好的心理品质D、为家庭、为家乡争光7.渴望表现自己是(A)A、青少年自尊自信的特点B、敢于干别人不敢干的事情C、与人之间逞强斗胜D、时时处处都要吸引别人注意8.缺少自尊自信,就像一艘搁浅的航船,难以驶向成功的港湾。
这句话的意思是CA.航船需要港湾停泊B.一艘航船容易搁浅C.有成就的人离不开自尊自信D.自卑是人生的第一大敌9.科学家XXX在实验中失败了次,但对蓄电池的发明信心十足,最后终于成功。
重庆万州第二高级中学2015九年级上期中试题--政治

重庆万州第二高级中学2015届九年级政治上学期期中试题(开卷,本卷共四个大题,满分50分,与历史共用90分钟完卷)一、选择题:下列10小题的备选答案中,只有一项是最符合题意的,请选出,并将其字母1、日前,国家发改委发文批复新建郑万铁路项目建议书。
郑万铁路全长785公里,途经平顶山、襄阳、巫山、奉节、云阳等地,是连接重庆万州到的一条客运专线。
A、洛阳B、新郑C、郑州D、郑重2、2014年8月16日至28日,第二届夏季青少年奥林匹克运动会在中国举行。
A、北京B、上海C、沈阳D、南京3、王某身患绝症后,怕自己死后10岁的儿子小强无人照顾,便决定依法将自己遗产的1/3留给父母满足老人的生活需要,另2/3由小强继承并到公证处进行了公证。
王某的行为,是在行使对自己财产的,其财产继承方式是。
A、占有权遗嘱继承B、使用权法定继承C、处分权遗嘱继承D、收益权法定继承4、在重庆市825路公交车上,一名老太太指责身旁的一名农民工影响市容(见右图)。
下列对老太太的言行认识正确的是:①这是不尊重他人的表现②这是在依法行使言论自由权利,无可厚非③这是缺乏包容精神的表现,也损害了自身形象④这不利于社会主义核心价值体系建设A、①②③B、①③④C、②③④D、①②④5、2014年9月底,电影《亲爱的》在全国热映,影片揭露了拐卖儿童的揪心故事,发人深思。
在《亲爱的》即将下线之际,《人民日报》官方微博发布了消息:刑法修正案(九)草案已做出修改——收买被拐卖儿童的行为,若未虐待被买儿童、不阻碍对其解救的,可“从轻、减轻或者免除处罚”,但一律做出犯罪评价。
换句话说,若草案颁布,收买被拐卖儿童,将属犯罪行为。
这说明()A、未成年被拐现象将消失B、未成年人受到了司法保护C、党和国家重视保护未成年人D、被拐卖的儿童都能获救6、入世10余年来,“中国制造”也被一些人打上了低价、低档的标签,在高速发展中逐步暴露出“成长的烦恼”。
“中国制造”所创造的利润,贴牌生产的中国企业最多只能拿到8%,其余的都归外商支配。
2014-2015第一学期九年级期中考试思品试卷及答案

2014~2015学年度第一学期九年级思品期中考试试题满分:50分,考试形式:闭卷一、单项选择题(以下各题都有四个选项,选出其中最符合题意的一项。
每小题1分,共20分)1.“房子大了电话小了,感觉越来越好;假期多了收入高了,工作越来越好……”从歌曲《越来越好》的歌词中,我们可以感受到①社会的发展②人们生活水平的提高③社会的文明进步④我国已是发达国家A.①②③ B.①②④ C.①③④ D.②③④2.“风声雨声读书声,声声入耳;家事国事天下事,事事关心。
”与这句名言表达的意思最接近的是A.不识庐山真面目,只缘身在此山中B.举头望明月,低头思故乡C.天下兴亡,匹夫有责D.大漠孤烟直,长河落日圆3.曾有人问一位哲学家:“一滴水怎样才能不干涸?”哲学家回答说:“把它放到大海里去。
”这表明A.只要生活在社会中,我们就一定能健康成长B.个人的生存和发展离不开社会C.社会的发展需要每个人的积极参与D.个人的力量是渺小的,对社会的发展作用不大4.每个人都要承担一定的责任,责任有主有次,有轻有重。
作为公民,你最重要的责任是A.自觉履行自己的工作职责B.对自己的责任、对家人的责任C.自觉履行宪法和法律规定的义务D.承担国家责任和社会责任5.在生活中,美与丑,是与非,良与莠交织在一起,这就要求我们分清是非,分清是非依据是A.道德和法律要求 B.是否损害自己利益C.个人的兴趣和爱好 D.自己的情感好恶6.南京青奥会期间,有2万多名志愿者为青奥会提供服务。
参与志愿者服务A.有利于发扬个人英雄主义 B.是亲近社会、服务社会的体现C.只有付出,没有回报 D.与我们中学生无关7.当看到青奥会上中国运动员获得奖牌五星红旗升起时,我们无比自豪;从新闻报道中了解到我国人民遭遇重大自然灾害时,我们都无比悲伤。
我们的这些表现源于A.强烈的民族文化认同感 B.我国综合国力的增强C.优秀的传统文化和传统美德 D.非常丰富的非物质文化遗产8.2014年7月13日,第二届《中国汉字听写大会》开播。
-上学期九年级政治第二次月考试题 新人教版-新人教版初中九年级全册政治试题

某某省渑池县直中学2015-2016上学期九年级政治第二次月考试题一、请你选择(共20分)▲单项选择(4小题,每小题2分,共8分)1、2015年12月4日,在首都国际机场,诺贝尔奖获得者、中国科学家屠呦呦出发前往瑞典领奖。
屠呦呦曾说:“在青蒿素发现的过程中,古代文献在研究的最关键时刻给了我灵感”。
对此理解正确的是()A民族文化是民族魂、民族的根B必须完全传承中华民族的传统文化C民族文化源远流长、博大精深D中华文化已经对全世界产生了深远的影响2、2015年9月22 — 29日,国家主席对美国进行成功访问并出席联合国大会,他在演讲中谈友谊,话文明,论合作,谋发展,纵论古今,使“中国热”在美国及联合国持续升温。
下列理解正确的是()A诠释了世界强国的非凡气度和文化自信B有利于对外展示中华文明提升国际地位C能够让美国从新的视角认识到中国的强大D 有助于加强中国在世界各国的领导力3、2015年9月3日,我国在天安门广场上举行了纪念抗日战争胜利70周年大阅兵,2400人军乐团先后合唱了 6首歌曲,在整个仪式的开场时,连续演唱《抗日军政大学校歌》《保卫黄河》《游击队歌》《在太行山上》《强军战歌》等。
演唱这些具有代表性和历史性的歌曲()A有利于增强人们对中华民族传统文化认同感B有利于弘扬艰苦奋斗和热爱祖国的民族精神C有利于提高我军乐团的演唱水平和职业技能D是为了配合纪念活动达到更加震撼的视听效果4、2015年10月23日,首届中蒙博览会在某某呼和浩特开幕。
博览会规模空前,共设32项具体活动,包括投资贸易洽谈、会议论坛、展览展示、文化交流等。
国家主席和蒙古国总统额勒贝格道尔吉分别致贺信。
请为本次博览会选择一个合适的主题是()A中蒙联手剑出鞘,反恐维和护太平B百花齐放文化园,中蒙互奏阳春曲C消除分歧达共识,两国同庆办盛会D同行草原.丝绸之路联结合作.发展走廊▲多项选择(4小题,每题3分,共12分)5、2015年9月4日至7日,中华民族传统文化高峰论坛暨某某省第二届古镇文化与生态文明建设研讨会在某某某某举行。
学年度第一学期期末教学质量监测九年级思想品德试题及答案

2017——2018学年度第一学期期末教学质量监测九年级思想品德试题一、单项选择题(每小题2分,共56分)1、我们不断感受到身边生活的变化,下列是人民生活水平提高的表现的是()①物质生活水平在不断提高②文化生活日益丰富③生活方式也发生了很大的变化④国家实力不断增强A、①②③B、①②④C、①③④D、②③④2、当今世界各国综合国力竞争的主战场与焦点是()A改革开放B科学技术C教育水平D军事力量3.下列描述能表达改革开放以来藏族人民物质生活水平提高的有()①西藏铁路建成通车②有家用电器与汽车③国民生产总值提高④蔬菜市场品种繁多A 、①②B 、②③C、①③D、②④4、积聚着我国最先进的生产力,控制着国民经济命脉的是()A公有制经济B 集体经济C 国有经济D外资经济⒌“干部用的准不准,交给群众审一审;干部用的行不行,交给群众评一评”这是黑龙江省大庆市干部任用的通俗说法。
这种制度主要说明了()A我国公民可以按照自己的好恶来行使政治权利B我国公民依法享有选举权与被选举权C扩大民主监督渠道,有利于增强民主监督实效D我国公民享有广泛的政治权利6.某乡镇政府计划砍伐道路两旁树木,建设一坐玻璃加工厂,实验中学课外研究小组通过调查,这种做法不利于环境保护,危害人民身体健康,他们准备向政府建议,下列哪种方法是不可取的()A张贴大字报,号召村民抵制B通过媒体发表意见C直接向人民代表反映D打直接向政府有关人员反映⒎“物价上涨慢一点,收入增长快一点;就业机会多一点,资源消耗少一点……”这一民谣从根本上反映了()A现阶段我国社会的主要矛盾B经济发展与人口众多的矛盾C东部发达地区与西部落后地区的矛盾D精神文明与物质文明之间的矛盾⒏要解决上题民谣中的问题,必须()①坚持一个中心,两个基本点②集中精力进行社会主义现代化建设③走改革开放的强国之路④坚持四项基本原则A②③④B①②③④C①②③D①③④9.中国特色社会主义进入新时代,我国社会主要矛盾已经转化为人民日益增长的______需要与__________的发展之间的矛盾。
讲练测中考政治二轮复习 专题01 实现中华民族的伟大复兴(测)(含解析)-人教版初中九年级全册政治试

实现中华民族的伟大复兴一、单项选择题1.(2015届某某某某市老僧堂乡中学九年级上学期期末测试思品试卷)中国梦召唤中国力量,中国梦凝聚中国力量,下列有利于汇集中国力量,实现中国梦的行为有()①某某市环卫工人X冲自愿选择到地点最偏僻、条件最艰苦的垃圾填埋场工作,在垃圾填埋事业中实现自己的价值②15岁的李某无照驾驶宝马车,在小区门口暴打一对夫妇,并叫嚣“谁敢打110!”③12岁女孩何玥患有严重疾病,当听说自己的生命只剩三个月时,她决定将自己的器官捐献给需要的人④某某汽运公司的退休职工李金山老人捡到10万元钱,历经周折交还失主A.①②④B.②③④C.①②③D.①③④【答案】D考点:本题考查积极承担社会责任。
2.(2016届某某某某环科园联盟初三上学期期中考试政治试卷)辛亥革命100多年来的历史表明,实现中华民族伟大复兴的中国梦,必须找到引领中国人民前进的正确道路和核心力量。
中国人民付出艰辛努力、找到了实现中华民族伟大复兴的正确道路和核心力量。
这条正确的道路就是,这个核心力量就是()A.中国特色社会主义道路、中国共产党B.党的基本路线、广大人民群众C.中国特色社会主义道路、广大人民群众D.可持续发展道路、中国共产党【答案】A【解析】试题分析:此题旨在考查学生对中国道路和党的认识,主要考查学生对知识的识记能力。
根据教材知识,中国正确的道路是坚持中国特色社会主义道路,核心力量是中国共产党,所以正确答案选A考点:中国特色社会主义道路和中国共产党3.(2015届某某某某市部分学校九年级1月月考政治试卷)中国梦既是国家的梦、民族的梦,又是我们每个人的梦。
实现中国梦,我们要坚持的根本方向是()【答案】D【解析】试题分析:此题旨在考查学生对教材基础知识的掌握。
根据教材知识,其中ABC是我国的指导思想,实现中国梦必须坚持的根本方向是中国特色社会主义道路。
所以正确答案选D考点:中国特色社会主义4.(2016届某某某某环科园联盟初三上学期期中考试政治试卷)总书记谈到“实现中华民族的伟大复兴,就是中华民族近代以来最伟大的梦想。
2015文化期中试题

石嘴山市第一中学3014---2015高二政治期中试卷高二年级王英芳命题一、单项选择题〔此题共25小题,每题2分,共50分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
〕1.我们讲文化生活,这里的“文化”是相对于经济、政治而言的人类全部精神活动及其产品。
以下属于文化现象的是〔〕①物质资料生产方式②“三个代表”重要思想③古代四大发明④十二届全国人大一次会议⑤千年古树⑥园林雕塑A.①③④⑤ B.②③⑥ C.①②③⑥ D.②③④2.台湾果农为提高水果附加值,把冰激凌灌入柿饼中,使之有双重口味,并别出心裁地将其取名为“你柿我的冰激凌”。
由于加入了文化元素,该商品推向市场后受到消费者热捧。
这表达了〔〕A.文化与经济相互交融B.文化创新决定社会实践的发展C.文化总能推动经济的发展D.文化发展要以经济发展为基础3.近年来,随着市场经济的发展和经济发展方式的转变,劳务需求已由体力型向智力型、技能型转变,对素质低、技能差的劳动力需求迅速减少。
可见〔〕A.经济发展是文化发展的基础B.文化有其自身的传承性和相对的独立性C.经济发展对人的文化素质提出越来越高的要求D.人们在社会实践中创造和发展文化4.2013年6月27日-30日,韩国新任总统朴槿惠访华,并在清华大学发表了“韩中心信之旅,共创新20年”为主题的演讲,在此次演讲的开场和结尾,朴槿惠总统都熟练地使用了中文,充分展现了其“中国通”的汉语实力。
汉语成为了拉近两国关系的“秘密武器”这展现出A.文化的趋同有利于推动社会实践的发展B.文化作为软实力会对政治生活产生影响C.语言是文化传播交流的重要途径之一D.中华文化源远流长和博大精深的特征5.经济学家指出,金融危机对中国的影响要小得多,这要归功于中国人的文化传统和消费方式。
中国人保持着勤劳节俭的传统,而且习惯于不借钱不欠债。
这说明( )A.世界观、人生观和价值观是文化的核心B.文化根源于经济,又高于经济C.中华文化是世界上最先进的文化D.文化影响到人的思维方式和行为方式6、韩国某外交官说:“如果外国人对韩国歌手有更多的关注,逐渐地他们就会喜欢上韩国……如果他们喜欢韩国,他们就会购买更多的韩国产品。
中考政治(第2期)时政热点试题06(含解析)-人教版初中九年级全册政治试题

2016年中考政治(第2期)时政热点试题06(含解析)1.中国共产党第十八届五中全会于2015年10月30日在举行。
全会提出,建设社会主义文化强国,必须坚定文化自信,增强文化自觉,加快文化改革发展,坚持中国特色社会主义文化的发展道路.那么,发展中国特色社会主义文化就要①继承和发扬中华民族的传统美德②在实践中不断推进民族文化的创新与发展③继承民族优秀文化,吸收国外一切文化④充分挖掘中华民族的优秀文化遗产A.①②③B.①③④C.②③④D.①②④【答案】D考点:发展先进文化2.强调,中国坚持改革开放不动摇;中国越发展,就越开放,中国开放的大门不可能关闭;改革开放永无止境,只有进行时没有完成时。
如此重视“改革”是因为①改革是社会发展的直接动力,是实现科学发展的政治保证②改革是我国解决当前所有问题的关键,是我国必须长期坚持的一项基本国策③现阶段我国社会主义具体制度还不够完善④我国社会主义制度已经不适应时代的要求,要进行根本的变革A.①②④ B.②③④ C.③ D.①②③【答案】C【解析】试题分析:①说法错误,四项基本原则是实现科学发展的政治保证;②说法错误,发展是解决我国当前所有问题的关键;④说法错误,改革是社会主义制度的自我完善,不是社会主义制度的根本变革。
故应选C。
考点:改革的重要性3.下列能直接体现我国国际地位提高的是A.12月1日,人民币被纳入“特别提款权篮子,成为可自由使用的货币B.目前,我国仍有相当一部分人完全自费就医,享受不到基本医疗保险C.2015年9月18日,我国举行第五届全国道德模X颁奖晩会【答案】D【解析】试题分析:题目要求选出能直接体现我国国际地位提高的事例,选项D属于我国在科技方面取得的成就,且在世界处于领先地位,应入选。
其它三个选项则不是。
考点:世界舞台上的中国4.中国的网购用户持续增加,双十一购物节作为电商“造节”的代表,自天猫创立至今,已经演变成每年网络购物者的狂欢日。
2015年,“双十一”全球狂欢节成交额为912亿元,再创历史新高,各大网店迅速发展,说明A.国家鼓励、支持和引导非公有制经济的发展B.公有制差经济已经控制我事国民经济的命脉【答案】A考点:我国的基本经济制度5.在某某自贸区成立一周年之际,国务院总理李克强在某某调研时说:不论国企民企,还是外资内资,也不论何种身份,何种出身,都将平等对待,一视某某。
重庆市第一中学2015届九年级物理上学期第一次定时作业试题

重庆市第一中学2015届九年级物理上学期第一次定时作业试题(考试时间:与化学共用120分钟 满分:80分)一.选择题(每小题只有一个选项符合题意,每小题3分,共24分) 1.下列温度最接近23℃的是( )A. 让人感觉温暖舒适的室温B. 重庆8月份的平均气温C. 洗热水澡时感觉舒适的水温D. 成年人的体温 2.水无常形,变化万千。
如图1所示的各种自然现象,属于熔化的是( )33.如图2所示,能正确描述石蜡变成蜡汁的过程中温度随时间的变化情况的是( )4.南极是世界上最冷的地方,常年平均气温是–25℃。
如图3所示,一天,企鹅妈妈和小企鹅之间发生了一次有趣的对话,它们的部分说法如下,其中正确的是( )A4.小企鹅:妈妈,这么冷,我都没温度了 B5.企鹅妈妈:不对,是没有内能C6.小企鹅:冰天雪地的,可能连水蒸气都没有吧 D7.企鹅妈妈:呵呵,水蒸气倒肯定有,因为冰是可以升华的呀5.水的比热容较大,人们往往利用它的这一特性为生活、生产服务,下列事例中与它的这一特性无关..的是( ) A8.夏天,在教室里洒水,感觉比较凉快 B9.人们培育秧苗时,傍晚向农田中灌水,以防冻坏秧苗 C10.汽车发动机用循环水冷却 D11.让流动的热水流过散热器取暖6.将装有酒精的金属管固定在桌子上,并用塞子塞紧。
来回快速拉动绕在管上的绳子,过一会儿塞子就跳起来了,如图4所示,则 ( ) A .拉动绳子过程,金属管温度升高,含有的热量增加B .拉动绳子过程,金属管和管内酒精发生热传递,酒精吸热,温度升高,内能增加春天,冰雪消融 夏天,花草叶上的露珠 秋天,山林间大雾弥漫 冬天,霜打枝头A B 图 1 C D 图4图3C .塞子跳起时,管内气体对塞子做功,气体温度升高,其内能增加D .塞子跳起时,管内气体的内能全部转化为塞子的机械能7.取两个完全相同的验电器,分别让它们带上一些电荷,然后用金属棒把它们连接起来,如图5所示。
发现A 张开的角度稍微减小一些,B 张开的角度稍微增大一些,最后两验电器张开角度相同。
重庆市第一中学校2024届高三下学期5月月考测试数学试题(含答案与解析)_6502

重庆第一中学2024届高三下期5月月考试题数 学本试卷满分150分,考试时间120分钟注意事项:1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚.2.作答时,务必将答案写在答题卡上,写在本卷或者草稿纸上无效.3.考试结束后,请将本试卷和答题卡一并交回.满一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 集合{}0,1,2,3A =,{}2log 1B x x =<,则A B ⋂=R ð( )A. {}3B. {}2,3C. {}1,2,3D. {}0,2,32. 已知{}n a 是实数集内的等比数列,满足21a =,681a =,则4a =( ) A. 3B. 3-或3C. 9D. 9-或93. 已知圆锥的轴截面为正三角形,该圆锥的侧面积数值与其体积数值相等,则该圆锥的底面积为( ) A. 3πB. 12πC. 27πD. 48π4. 已知定义在R 上函数()f x 是奇函数,且当0x ≥时,()()2log 3x a f x =++,则()3f -=( ) A. 1B. 1-C. 2D. 2-5. 如图,左车道有2辆汽车,右车道有3辆汽车等待合流,则合流结束时汽车通过顺序共有( )种.A. 10B. 20C. 60D. 1206. 已知正数a ,b 满足111a b+=,则3ab b +的最小值为( ) A. 8B. 9C. 10D. 12的7. 已知直线y x =与函数()ln y x a b =++的图象相切(,a b ∈R ),则e a b +(e 为自然对数的底数)的最小值为( ) A. 0B. 1C. 2D. e8. “四二一广场”是重庆第一中学校文化地标(如图1),广场中心的建筑形似火炬宛若花开,三朵“花瓣”都是拓扑学中的莫比乌斯带(如图2).将莫比乌斯带投影到平面上,会得到无穷大符号“∞”.在平面直角坐标系中,设线段AB 长度为2a (0a >),坐标原点O 为AB 中点且点A ,B 均在x 轴上,若动点P 满足2PA PB a ⨯=,那么点P 的轨迹称为双纽线,其形状也是无穷大符号“∞”(如图3).若1a =,点P 在第一象限且3cos 4POB ∠=,则PA =( )A.12B.C.D. 2二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9. 已知随机变量X 和Y ,下列说法正确是( )A. X 和Y 是分类变量,则2χ值越大,则判断“X 与Y 独立”的把握越大B. 若()()E X E Y =,则()()D X Y D =C. 若1~9,3X B ⎛⎫ ⎪⎝⎭,则()2D X = D. 若()2~0,Y N σ,则()()11P Y P Y <=>-10. 已知中心在原点,焦点在x 轴上的双曲线两个焦点分别为1F ,2F ,过2F线相交于点P,若12PF F =,则双曲线的离心率可能是( )A.B.1+C.1+D.2的的11. 冒泡排序是一种计算机科学领域的较简单的排序算法.其基本思想是:通过对待排序序列{}12,,,n x x x 从左往右,依次对相邻两个元素{}1,k k x x +(1k =,2,L,n 1-)比较大小,若1k k x x +>,则交换两个数的位置,使值较大的元素逐渐从左移向右,就如水底下的气泡一样逐渐向上冒,重复以上过程直到序列中所有数都是按照从小到大排列为止.例如:对于序列{}2,1,4,3进行冒泡排序,首先比较{}2,1,需要交换1次位置,得到新序列{}1,2,4,3,然后比较{}2,4,无需交换位置,最后比较{}4,3,又需要交换1次位置,得到新序列{}1,2,3,4,最终完成了冒泡排序.同样地,序列{}1,4,2,3需要依次交换{}4,2,{}4,3完成冒泡排序.因此,{}2,1,4,3和{}1,4,2,3均是交换2次的序列.现在对任一个包含n 个不等实数的序列进行冒泡排序(3n ≥),设在冒泡排序中序列需要交换的最大次数为n a ,只需要交换1次的序列个数为n b ,只需要交换2次的序列个数为n c ,则下列说法正确的有( ) A. ()12n n n a -=B. 1n b n =-C. 11n n c c n +=+-D. 222n n n c --=三、填空题:本题共3小题,每小题5分,共15分.12. 已知复数z 的共轭复数是z ,若20242i i z z z ⋅=⋅+,则z =___________. 13. 已知()()cos 2sin f x x x ϕ=++的最大值为3,则tan2ϕ=___________.14. 如图,已知棱长均为4正四棱锥P -ABCD 中,M 和N 分别为棱AB 、PC 的中点,过M 和N 可以作平面α使得//PB α,则平面α截正四棱锥P -ABCD 所得的截面面积为___________.四、解答题:共77分.解答应写出文字说明、证明过程或演算步骤.15. 已知ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且1cos 2a C cb -=. (1)求A 的大小;的(2)若sin 3sin C B =,BC 边上的中线AD,求ABC 的面积.16. 在一种新能源产品的客户调查活动中发现,某小区10位客户有4人是该产品的潜在用户,小刘负责这10人的联系工作,他先随机选择其中5人安排在上午联系,剩余5人下午联系. (1)设上午联系的这5人中有ξ个潜在用户,求的ξ分布列与期望;(2)小刘逐一依次联系,直至确定所有潜在用户为止,求小刘6次内即可确定所有潜在用户的概率. 17. 如图,直三棱柱111ABC A B C -侧棱长为2,2AC =,AB BC =,D ,E ,F 分别为11A B ,1BB ,BC 的中点.(1)证明:平面DEF ⊥平面11ACC A ;(2)若直线DE 与平面ABC 所成的角大小为π4,求二面角A DE F --的余弦值. 18. 已知()2,0F -,()3,0A ,直线l :92x =-,动点P 到l 的距离为d ,满足32PF d =,设点P 的轨迹为C ,过点F 作直线1l ,交C 于G ,H 两点,过点F 作与1l 垂直的直线2l ,直线l 与2l 交于点K ,连接AG ,AH ,分别交直线l 于M ,N 两点. (1)求C 的方程; (2)证明:KN KM =;(3)记GMK ,HNK 的面积分别为1S ,2S ,四边形AGKH 的面积为3S ,求312S S S +的范围.19. 函数极限是现代数学中非常重要的概念,函数()f x 在0x x =处的极限定义如下:0∀ε>,存在正数δ,当00x x δ<-<时,均有()f x A ε-<,则称()f x 在0x x =处的极限为A ,记为()lim f x A =,例如:()2f x x =在1x =处的极限为2,理由是:0∀ε>,存在正数2εδ=,当01x δ<-<时,均有222122x x εε-=-<⨯=,所以()lim 22x =.已知函数()()2e g x a x=-,的()(]()()ln ,0,e ,e,xx h x x g x x ∞⎧∈⎪=⎨⎪∈+⎩,(0a >,e 为自然对数的底数).(1)证明:()g x 在e x =处的极限为e a ;(2)若21e=a ,()()12h x h x =,12x x <,求1112x x x ⋅的最大值; (3)若()e lim x A f x →=,用函数极限的定义证明:()()()elim e x f x x g A a →+=+. 参考答案一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 集合{}0,1,2,3A =,{}2log 1B x x =<,则A B ⋂=R ð( )A. {}3B. {}2,3C. {}1,2,3D. {}0,2,3【答案】D 【解析】【分析】解对数不等式求出集合B ,然后由集合的补集运算和交集运算可得. 【详解】由2log 1x <解得()0,2B =,所以(][),02,B ∞∞=-⋃+R ð, 所以{}0,2,3A B ⋂=R ð. 故选:D2. 已知{}n a 是实数集内的等比数列,满足21a =,681a =,则4a =( ) A. 3 B. 3-或3C. 9D. 9-或9【答案】C 【解析】【分析】由等比中项的性质即可求解.【详解】由等比中项可得,242681a a a ==,又22420a a q q ==>, 于是49a =. 故选:C.3. 已知圆锥的轴截面为正三角形,该圆锥的侧面积数值与其体积数值相等,则该圆锥的底面积为( ) A. 3π B. 12πC. 27πD. 48π【答案】B 【解析】【分析】由轴截面正三角形可得2,l r h ==,进而由圆锥的侧面积数值与其体积数值相等可求半径,从而可得圆锥的底面积. 【详解】几何体如图所示:因为轴截面PAB 是正三角形,所以2,l r h ==.圆锥的侧面积等于2π2πrl r =,圆锥的体积等于231π3r h r =,由圆锥的侧面积数值与其体积数值相等,得232ππr r =,得r =. 故圆锥的底面积为2π12πr =. 故选:B.4. 已知定义在R 上的函数()f x 是奇函数,且当0x ≥时,()()2log 3x a f x =++,则()3f -=( ) A. 1 B. 1-C. 2D. 2-【答案】B 【解析】【分析】定义在R 上的函数()f x 是奇函数,所以()00f =,由此可得a 的值,进而由()3f 可得()3f -的值.【详解】因为()f x 是定义在R 上的奇函数,所以()2log 003a f =+=, 解得2log 3a =-,则()()22log 3lo 3g f x x =+-,()222log log 1o 3632l g f ===-,所以()()331f f -=-=-. 故选:B.5. 如图,左车道有2辆汽车,右车道有3辆汽车等待合流,则合流结束时汽车通过顺序共有( )种.A. 10B. 20C. 60D. 120【答案】A 【解析】【分析】合流结束时5辆车需要5个位置,第一步从5个位置选2个位置安排左边的2辆汽车,第二步剩下3个位置安排右边的3辆汽车,从而由分步乘法计数原理可得结果. 【详解】设左车辆汽车依次为12,A A ,右车辆汽车依次为123,,B B B ,则通过顺序的种数等价于将12,A A 安排在5个顺序中的某两个位置(保持12,A A 前后顺序不变),123,,B B B 安排在其余3个位置(保持123,,B B B 前后顺序不变),123,,B B B ,所以,合流结束时汽车通过顺序共有2353C C 10=. 故选:A.6. 已知正数a ,b 满足111a b+=,则3ab b +的最小值为( ) A. 8 B. 9C. 10D. 12【答案】B 【解析】【分析】将111a b +=变形为ab a b =+,代入3ab b +,再通过常数代换和基本不等式可得. 【详解】因为111a b+=,所以ab a b =+,所以()114344559b a ab b a b a b a b a b ⎛⎫+=+=++=++≥+= ⎪⎝⎭,当且仅当33,2a b ==时,等号成立,所以3ab b +的最小值为9.故选:B7. 已知直线y x =与函数()ln y x a b =++的图象相切(,a b ∈R ),则e a b +(e 为自然对数的底数)的最小值为( ) A. 0 B. 1 C. 2 D. e【答案】C 【解析】【分析】设切点为()00,Q x y ,根据切点在切线和曲线上,以及切点处的导数等于切线斜率,联立求解可得1a b +=,则e e 1a a b a +=-+,构造函数()e 1xf x x =-+,利用导数求最小值即可.【详解】设直线y x =与函数()ln y x a b =++的图象相切于点()00,Q x y ,则()0000ln y x y x a b =⎧⎨=++⎩,所以()00ln x a b x ++=,又()1ln x a b x a '⎡⎤++=⎣⎦+,所以011x a =+,即01x a +=,所以0ln1b x +=,即0b x =,所以1a b +=,所以e e 1a a b a +=-+, 令()e 1xf x x =-+,则()e 1xf x '=-,当0x <时,()0f x '<,()f x 在(),0∞-上单调递减; 当0x >时,()0f x '>,()f x 在()0,∞+上单调递增. 所以,当0x =时,()f x 取得最小值()()min 02f x f ==, 所以e a b +的最小值为2. 故选:C8. “四二一广场”是重庆第一中学校文化地标(如图1),广场中心的建筑形似火炬宛若花开,三朵“花瓣”都是拓扑学中的莫比乌斯带(如图2).将莫比乌斯带投影到平面上,会得到无穷大符号“∞”.在平面直角坐标系中,设线段AB 长度为2a (0a >),坐标原点O 为AB 中点且点A ,B 均在x 轴上,若动点P 满足2PA PB a ⨯=,那么点P 的轨迹称为双纽线,其形状也是无穷大符号“∞”(如图3).若1a =,点P 在第一象限且3cos 4POB ∠=,则PA =( ) 的A.12B.C.D. 2【答案】C 【解析】【分析】设(),P x y ,根据双纽线的定义求出点P 的轨迹方程,设,OP r POB θ=∠=,则()cos ,sin P r r q q ,代入方程求出OP ,再在POB 中,利用余弦定理求出PB ,即可得解.【详解】()()1,0,1,0A B -,设(),P x y , 由双纽线的定义得1PA PB ⨯=,1=,化简得()()222222x y x y +=-,显然1OB =,设,OP r POB θ=∠=,则()cos ,sin P r r q q , 代入方程()()222222x y x y +=-,得()422222cos sin 2cos 2r r r θθθ=-=,所以()22912cos 222cos 1221164r θθ⎛⎫==-=⨯⨯-= ⎪⎝⎭,由余弦定理得22211312cos 1214242PB OP OB OP OB POB =+-∠=+-⨯⨯⨯=,所以PB =,所以1PA PB==. 故选:C.【点睛】方法点睛:求动点的轨迹方程有如下几种方法:(1)直译法:直接将条件翻译成等式,整理化简后即得动点的轨迹方程;(2)定义法:如果能确定动点的轨迹满足某种已知曲线的定义,则可利用曲线的定义写出方程;(3)相关点法:用动点Q 的坐标x 、y 表示相关点P 的坐标0x 、0y ,然后代入点P 的坐标()00,x y 所满足的曲线方程,整理化简可得出动点Q 的轨迹方程;(4)参数法:当动点坐标x 、y 之间的直接关系难以找到时,往往先寻找x 、y 与某一参数t 得到方程,即为动点的轨迹方程;(5)交轨法:将两动曲线方程中的参数消去,得到不含参数的方程,即为两动曲线交点的轨迹方程.二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9. 已知随机变量X 和Y ,下列说法正确的是( )A. X 和Y 是分类变量,则2χ值越大,则判断“X 与Y 独立”的把握越大B. 若()()E X E Y =,则()()D X Y D =C. 若1~9,3X B ⎛⎫ ⎪⎝⎭,则()2D X = D. 若()2~0,Y N σ,则()()11P Y P Y <=>-【答案】CD 【解析】【分析】根据2χ的意义可判断A ;根据平均数与方差的意义可判断B ;由二项分布的方差公式求解可判断C ;由正态分布的对称性可判断D .【详解】对于A ,2χ值越大,X 和Y 有关系的可能性就越大,则“X 与Y 独立”的把握越小,A 错误; 对于B ,平均数相等,数据的分散程度不一定相等,即方差不一定相等,B 错误; 对于C ,若1~9,3X B ⎛⎫ ⎪⎝⎭,则()129233D X =⨯⨯=,C 正确; 对于D ,若()2~0,Y N σ,则由正态分布的对称性可知()()11P Y P Y <=>-,D 正确.故选:CD10. 已知中心在原点,焦点在x 轴上的双曲线两个焦点分别为1F ,2F ,过2F线相交于点P ,若12PF F =,则双曲线的离心率可能是( )A.B.1+C.1+D.2【答案】AD 【解析】【分析】根据题意,分双曲线的渐近线的斜率ba <和b a>2PF x =,结合余弦定理和双曲线的定义,求得x 的值,进而求得双曲线的离心率,得到答案.【详解】由题意,可得122F F c =,因为12PF F =,则1PF =,设2PF x =,①若双曲线的渐近线的斜率b a <,则2e =<,如图(1)所示,因为过2F 112π3PF F ∠=, 由余弦定理得2222π12422cos3c c x c x =+-⨯⋅⋅,整理得22280x cx c +-=,解得2x c =或4x c =-(舍去),所以1221)a PF PF c =-=-,可得1)a c =-,所以离心率为2c e a ===<,满足题意,所以A 正确;②若双曲线的渐近线的斜率b a >2e =>,如图(1)所示,因为过2F 11π3PF F ∠=, 由余弦定理得222π12422cos3c c x c x =+-⨯⋅⋅,整理得22280x cx c --=,解得4x c =或2x c =-(舍去),所以122(4a PF PF c =-=-,可得(2a c =,所以离心率为22c e a ===+>,满足题意,所以C 正确, 故选:AD.11. 冒泡排序是一种计算机科学领域的较简单的排序算法.其基本思想是:通过对待排序序列{}12,,,n x x x 从左往右,依次对相邻两个元素{}1,k k x x +(1k =,2,L,n 1-)比较大小,若1k k x x +>,则交换两个数的位置,使值较大的元素逐渐从左移向右,就如水底下的气泡一样逐渐向上冒,重复以上过程直到序列中所有数都是按照从小到大排列为止.例如:对于序列{}2,1,4,3进行冒泡排序,首先比较{}2,1,需要交换1次位置,得到新序列{}1,2,4,3,然后比较{}2,4,无需交换位置,最后比较{}4,3,又需要交换1次位置,得到新序列{}1,2,3,4,最终完成了冒泡排序.同样地,序列{}1,4,2,3需要依次交换{}4,2,{}4,3完成冒泡排序.因此,{}2,1,4,3和{}1,4,2,3均是交换2次的序列.现在对任一个包含n 个不等实数的序列进行冒泡排序(3n ≥),设在冒泡排序中序列需要交换的最大次数为n a ,只需要交换1次的序列个数为n b ,只需要交换2次的序列个数为n c ,则下列说法正确的有( ) A. ()12n n n a -=B. 1n b n =-C. 11n n c c n +=+-D. 222n n n c --=【答案】ABD 【解析】【分析】根据题意,不妨设序列的n 个元素为1,2,3,,n ,再根据等差数列前n 项和公式即可判断A ;得出只要交换1次的序列的特征即可判断B ;确定元素1n +在新序列的位置,再分类讨论即可判断C ;结合C 选项,利用累加法即可判断D.【详解】不妨设序列的n 个元素为1,2,3,,n , 对于A ,交换次数最多的序列为{},1,,2,1n n - , 将元素n 冒泡到最右侧,需交换n 1-次, 将元素n 1-冒泡到最右侧,需交换2n -次,L故共需要()()()()()1111122122n n n n n n -+---+-+++== ,故A 正确;对于B ,只要交换1次的序列是将{}1,2,3,,n 中的任意相邻两个数字调换位置的序列,故有n 1-个这样的序列,即1n b n =-,故B 正确;对于C ,当n 个元素的序列顺序确定后,将元素1n +添加进原序列, 使得新序列(共1n +个元素)交换次数也是2, 则元素1n +在新序列的位置只能是最后三个位置, 若元素1n +在新序列的最后一个位置,则不会增加交换次数,故原序列交换次数为2(这样的序列有n c 个), 若元素1n +在新序列的倒数第二个位置,则会增加1次交换,故原序列交换次数为1(这样的序列有1n b n =-个), 若元素1n +在新序列的倒数第三个位置,则会增加2次交换,故原序列交换次数为0(这样的序列有1个), 因此111n n n c c n c n +=+-+=+,故C 错误; 对于D ,考虑3n =时,则序列有{}{}{}{}{}{}1,2,3,1,3,2,2,1,3,2,3,1,3,1,2,3,2,1共6种情况, 交换次数分别为0,1,1,2,2,3,故需要交换2次的序列有{}{}2,3,1,3,1,2共2个,因此32c =, 由C 知1n n c c n +=+,则()()()123121341n n n c c n c n n c n --=+-=+-+-==++++-()()()2122234122n n n n n +---=++++-==,故D 正确. 故选:ABD.【点睛】关键点点睛:在解根数列新定义相关的题目时,理解新定义是解决本题的关键.三、填空题:本题共3小题,每小题5分,共15分.12. 已知复数z 的共轭复数是z ,若20242i i z z z ⋅=⋅+,则z =___________. 【答案】i - 【解析】【分析】设i z a b =+,代入条件中,根据复数相等列方程组求解可得.【详解】设i,,z a b a b =+∈R ,则i z a b =-, 因为()50620244i i 1==,所以()()()2i i i i 1a b a b a b +=+-+,整理得2222i 1b a a b -+=++,所以221220a b b a ⎧++=-⎨=⎩,解得0,1a b ==-,所以i z =-.故答案为:i -13. 已知()()cos 2sin f x x x ϕ=++的最大值为3,则tan 2ϕ=___________.【答案】1- 【解析】【分析】先写出()f x 的展开式,然后利用辅助角公式求最大值,进而得sin 1ϕ=-,从而可得结果. 【详解】()()()cos 2sin cos cos sin 2sin f x x x x x ϕϕϕ=++=+-, 由辅助角公式可得()f x3=,化简得954sin ϕ-=,即sin 1ϕ=-,解得π2π,Z 2k k ϕ=-∈, 所以,()4tanta n 24n ta 1k k ϕππ⎛⎫⎛⎫π-=-=-∈Z ⎪ ⎪⎝⎝⎭=⎭. 故答案为:1-.14. 如图,已知棱长均为4的正四棱锥P -ABCD 中,M 和N 分别为棱AB 、PC 的中点,过M 和N 可以作平面α使得//PB α,则平面α截正四棱锥P -ABCD 所得的截面面积为___________.【答案】【解析】【分析】取AP 中点为E ,取BC 中点为F ,易证明//PB 平面EMFN ,再通过取四等分点G ,可证明截的面就是五边形GEMFN ,最后通过证明四边形EMFN 是矩形,再来计算截面的面积即可.【详解】取AP 中点为E ,取BC 中点为F ,连结四点可得四边形EMFN , 结合题意可知//,//EM PB NF PB ,所以//EM NF ,同理://,//EN AC MF AC ,所以//EN MF ,即四边形EMFN 是平行四边形, 因为//,EM PB EM ⊂平面EMFN , PB ⊄平面EMFN ,所以//PB 平面EMFN , 设MF BD H = ,可得14HB BD =,再在PD 上取点G ,满足14PG PD =,此时//HG PB ,所以//////HG PB EM NF ,可得截面五边形GEMFN , 由正四棱锥可知:PO ⊥平面ABCD ,且MF ⊂平面ABCD ,所以PO MF ⊥,又因为BD MF ⊥,BD PO O = ,BD ⊂平面PBD ,PO ⊂平面PBD ,所以MF ⊥平面PBD , 又因为PB ⊂平面PBD ,所以MF PB ⊥,又因为//NF PB ,所以MF NF ⊥,从而可得四边形EMFN 是矩形,由正四棱锥所有棱长均为4,可知12MF AC ==122EM PB ==,所以四边形EMFN 的面积为2MF EM ⋅==, 再由14HB BD =,//HG PB ,可知:334HG PB ==又因为2EM =,所以三角形EMG 的面积为()32⨯-=12,所以截面五边形GEMFN 的面积为+=故答案为:四、解答题:共77分.解答应写出文字说明、证明过程或演算步骤.15. 已知ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且1cos 2a C cb -=. (1)求A 的大小;(2)若sin 3sin C B =,BC 边上的中线AD ,求ABC 的面积. 【答案】(1)2π3;(2) 【解析】【分析】(1)利用正弦定理边化角,结合sin sin cos cos sin B A C A C =+化简可得;(2)根据正弦定理角化边,由()12AD AB AC =+平方可得2b =,6c =,再由面积公式可得. 【小问1详解】由正弦定理边化角得1sin cos sin sin 2A C CB -=, 又()sin sin sin cos cos sin B A C A C A C =+=+,所以1sin cos sin sin cos cos sin 2-=+A C C A C A C ,即1sin cos sin 2C A C -=,因为()0,π,sin 0C C ∈>,所以1cos 2A =-,因为()0,πA ∈,所以2π3A =. 【小问2详解】由sin 3sin C B =得3c b =,因为()12AD AB AC =+,AD =, 所以()()2222117244AB AC AB AC c b bc =++⋅=+- , 所以2229328b b b +-=,即2b =,所以6c =,所以11sin 2622ABC S bc A ==⨯⨯= 16. 在一种新能源产品的客户调查活动中发现,某小区10位客户有4人是该产品的潜在用户,小刘负责这10人的联系工作,他先随机选择其中5人安排在上午联系,剩余5人下午联系.(1)设上午联系的这5人中有ξ个潜在用户,求的ξ分布列与期望;(2)小刘逐一依次联系,直至确定所有潜在用户为止,求小刘6次内即可确定所有潜在用户概率. 【答案】(1)分布列见详解,()2E ξ=(2)43630【解析】【分析】(1)根据超几何分布的概率公式求出相应概率,即可得分布列,再由期望公式可得期望; (2)6次内确定所有潜在用户有:前4次抽到的全是潜在用户;前4次抽到3个潜在用户,第5次抽到一个潜在用户;前5次抽到3个潜在用户,第6次抽到一个潜在用户,共三种情况,根据组合知识结合古典概型概率公式可得. 【小问1详解】由题知,ξ服从超几何分布,可能取值有0,1,2,3,4,所以()()()504132646464555101010C C C C C C 15100,1,2C 42C 21C 21P P P ξξξ=========, ()()23146464551010C C C C 513,4C 21C 42P P ξξ======.得分布列为:ξ 01 2 3 4P142 521 1021 521 142所以()1510510123424221212142E ξ=⨯+⨯+⨯+⨯+⨯=. 【小问2详解】记确定所有潜在用户所需要的联系次数为X ,则()()()343544456101010C C C 1114,5,6C 210C 63C 21P X P X P X =========. 所以,6次内即可确定所有潜在用户的概率为111432106321630++=. 17. 如图,直三棱柱111ABC A B C -的侧棱长为2,2AC =,AB BC =,D ,E ,F 分别为11A B ,1BB ,BC 的中点.的(1)证明:平面DEF ⊥平面11ACC A ; (2)若直线DE 与平面ABC 所成的角大小为π4,求二面角A DE F --的余弦值. 【答案】(1)证明见解析(2 【解析】【分析】(1)取AC 的中点O ,连接OB ,以点O 为原点建立空间直角坐标系,证明两个平面的法向量垂直即可;(2)建立空间直角坐标系,求出相关点的坐标,利用向量法求解即可. 【小问1详解】取AC 的中点O ,连接OB , 因为AB BC =,所以OB AC ⊥,如图,以点O 为原点,OA OB 所在直线为,x y 轴,在平面11ACC A 内过O 作垂线为z 轴, 建立空间直角坐标系,设OB b =, 则()11,,2,0,,1,,,02222b b D E b F ⎛⎫⎛⎫-⎪ ⎪⎝⎭⎝⎭,故()1,,1,1,0,222b DE DF ⎛⎫=-=- ⎪⎝⎭,设平面DEF 的法向量为(),,n x y z =,则有102220b n DE x y z n DF x z ⎧⋅=+-=⎪⎨⎪⋅=-=⎩,令2x =,则1,0z y ==, 所以()2,0,1n =,因为y 轴⊥平面11ACC A ,则可取平面11ACC A 的法向量为()0,1,0m =,则0n m ⋅= ,所以n m ⊥ ,所以平面DEF ⊥平面11ACC A ; 【小问2详解】 因为z 轴⊥平面ABC ,则可取平面ABC 的法向量为()0,0,1p =, 因为直线DE 与平面ABC 所成的角大小为π4,所以πcos ,sin4DE p DE p DE p⋅====b =,则()()12,,1,0,02D E A ⎛⎫-- ⎪ ⎪⎝⎭,故111,222DE AD ⎛⎫⎛⎫=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,设平面ADE 的法向量为()111,,q x y z =,则有1111111021202q DE x y z q AD x y z ⎧⋅=+-=⎪⎪⎨⎪⋅=+=⎪⎩,令1x =111,0y z ==,所以()q =,所以cos ,n q n q n q ⋅===,由图可知二面角A DE F --锐二面角, 所以二面角A DE F --18. 已知()2,0F -,()3,0A ,直线l :92x =-,动点P 到l 的距离为d ,满足32PF d =,设点P 的轨迹为C ,过点F 作直线1l ,交C 于G ,H 两点,过点F 作与1l 垂直的直线2l ,直线l 与2l 交于点K ,连接AG ,AH ,分别交直线l 于M ,N 两点. (1)求C 的方程; (2)证明:KN KM =;(3)记GMK ,HNK 的面积分别为1S ,2S ,四边形AGKH 的面积为3S ,求312S S S +的范围.【答案】(1)22195x y +=(2)证明见解析 (3)2,23⎛⎤ ⎥⎝⎦【解析】【分析】(1)利用坐标公式代入32PF d =得到C 的轨迹方程22195x y +=;(2)利用方程组思想,先求出交点1122(,),,()G x y H x y 满足的韦达定理,再利用这两个坐标写直线方程去求出交点()11159,223y M x ⎛⎫-- ⎪ ⎪-⎝⎭和()22159,223y N x ⎛⎫-- ⎪ ⎪-⎝⎭,最后利用韦达定理去证明2MN K y y y +=,即可; (3)利用所求的坐标去表示()312=AMN S S S S -+ ,然后把312S S S +转化到韦达定理上来,可得到32221+31S m ⎛⎫= ⎪+⎝⎭,然后求出取值范围即可.小问1详解】为【由()2229329242PF d x y x ⎡⎤=⇒++=+⎣⎦,得到:()22294443681x x y x x +++=++, 即:22225945195x y x y +=⇒+=,所以C 的方程为22195x y +=; 【小问2详解】 证明:要证KN KM =,即证明K 为MN 的中点,如图:易知:1l 的斜率不为0,可设直线方程111222,(,),(,),l x my G x y H x y =-: 联立:221952x y x my ⎧+=⎪⎨⎪=-⎩,消元得:()225920250m y my +--=, 得到()222Δ=400100599009000m m m ++=+>,则1212222025,5959m y y y y m m -+==++, 可得AG 方程为()1133y y x x =--,令92x =-,得到()111523y y x =--, 所以()11159,223y M x ⎛⎫-- ⎪ ⎪-⎝⎭,同理:()22159,223y N x ⎛⎫-- ⎪ ⎪-⎝⎭,即()()121212121515152323255M N y y y y y y x x my my ⎛⎫+=--=-+ ⎪----⎝⎭()()221212221212222520252515155959=52520252525255959m m my y y y m m m m m y y m y y m m m m -⎛⎫-⎛⎫ ⎪-+++=-=- ⎪ ⎪ ⎪--++ ⎪⎝⎭-+++⎝⎭, 直线()22l y m x =-+:,令92x =-,得到52K m y =, 所以有2M N K y y y +=,而M N K x x x ==,所以K 为MN 的中点,即KN KM =;【小问3详解】由()12121219191922224S S MK x NK x MN x x ⎛⎫⎛⎫+=+++=++ ⎪ ⎪⎝⎭⎝⎭, ()()3121219=322AMN S S S S MN S S ⎛⎫-+=+-+ ⎪⎝⎭ , 得:()()312121212193151522=11119594MN S S S x x m y y MN x x ⎛⎫+ ⎪⎝⎭-=-=-+++++++ ()2221559112031559m m m m m +=-=-+++ ()22222262322==1+313131m m m m m ++⎛⎫= ⎪+++⎝⎭, 因为22221+,2313m ⎛⎫⎛⎤∈ ⎪ ⎥+⎝⎭⎝⎦,所以3122,23S S S ⎛⎤∈ ⎥+⎝⎦. 【点睛】方法点睛:利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下:(1)设直线方程,设交点坐标为()()1122,,,x y x y ;(2)联立直线与圆锥曲线的方程,得到关于x (或y )的一元二次方程,注意∆的判断;(3)列出韦达定理;(4)将所求问题或题中的关系转化为12x x +、12x x (或12y y +、12y y )的形式;(5)代入韦达定理求解.19. 函数极限是现代数学中非常重要的概念,函数()f x 在0x x =处的极限定义如下:0∀ε>,存在正数δ,当00x x δ<-<时,均有()f x A ε-<,则称()f x 在0x x =处的极限为A ,记为()lim f x A =,例如:()2f x x =在1x =处的极限为2,理由是:0∀ε>,存在正数2εδ=,当01x δ<-<时,均有222122x x εε-=-<⨯=,所以()lim 22x =.已知函数()()2e g x a x =-,()(]()()ln ,0,e ,e,x x h x x g x x ∞⎧∈⎪=⎨⎪∈+⎩,(0a >,e 为自然对数的底数).(1)证明:()g x 在e x =处的极限为e a ;(2)若21e =a ,()()12h x h x =,12x x <,求1112x x x ⋅的最大值; (3)若()e lim x A f x →=,用函数极限的定义证明:()()()elim e x f x x g A a →+=+. 【答案】(1)证明见解析(2)2ee e +(3)证明见解析【解析】【分析】(1)要使得()e g x a ε-<,即e x a ε-<,再根据题意即可得证;(2)利用导数求出函数的单调区间,令()()12h x h x m ==,确定m 的范围,再将1112,x x x 分别用m 表示,构造函数,利用导数求出最大值即可;(3)有()e lim x f x A →=结合(1),对任意正数ε,取122εεε==,112212,,δδδδδδδ≤⎧=⎨>⎩,0∀ε>,当0e x δ<-<时,有()()()()()()()e e f x g x A a f x A g x a +-+=-+-,即可得证.【小问1详解】要使得()e g x a ε-<,即()2e e a x a ε--<,即()e a x ε-<,即e x a ε-<,所以0∀ε>,存在整数a εδ=,当0e x δ<-<时,均有()()e e e g x a a x a x a a εε-=-=⋅-<⋅=,所以()elim e x g x a →=; 【小问2详解】 当0e x <≤时,()ln x h x x =,则()21ln 0x h x x '-=≥, 所以函数()h x 在(]0,e 上单调递增, 当e x >时,()()()221212e e e eh x g x x x ==-=-单调递减,因为()()12h x h x =,12x x <,所以120e x x <<<,令()()12h x h x m ==,因为()()1e e eh g ==,0x →时,()h x ∞→-,x →+∞时,()h x ∞→-, 所以1,e m ∞⎛⎫∈- ⎪⎝⎭,由()1h x m =,得11ln x m x =,得11ln x mx =,得()111e e x mx m x ==,得111e x m x =, 由()2h x m =,得222e e x m =-, 所以()11212e 2e e x m x x m ⋅=-, 令()()2e 2e e m p m m =-,1,e m ∞⎛⎫∈- ⎪⎝⎭, 则()()12e e e m p m m +=--',令()0p m '=,得21e m =-, 当21e m <-时,()0p m '>,当211e em -<<时,()0p m '<, 所以函数()p m 在2,1e ∞⎛⎫-- ⎪⎝⎭上单调递增,在211,ee ⎛⎫- ⎪⎝⎭上单调递减, 所以()2ee max21e e p m p +⎛⎫=-= ⎪⎝⎭, 即1112x x x ⋅的最大值为2e e e +;【小问3详解】 因为()elim x f x A →=, 所以10ε∀>,存在正数1δ,当10e x δ<-<时,均有()1f x A ε-<;由(1)知()elim e x g x a →=, 即20ε∀>,存在正数2δ,当20e x δ<-<时,均有()2e f x a ε-<,对任意正数ε,取122εεε==,112212,,δδδδδδδ≤⎧=⎨>⎩, 0∀ε>,当0e x δ<-<时, 有()()()()()()()e e f x g x A a f x A g x a +-+=-+-()()12e f x A g x a εεε≤-+-=+=,所以()()()elim e x f x g x A a →+=+. 【点睛】方法点睛:导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等式恒成立问题,注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理.。
广西桂林市第一中学2024_2025年高一政治上学期期中检测试卷含解析

桂林市第一中学2024~2024学年度上学期期中质量检测高一政治试卷一.单项选择题(共30题,每题2分,共计60分。
请把答案填入相应答题卡中。
)1.2017年8月8日,四川九寨沟发生7.0级地震,牵动着全国人民的心。
大家通过挚友圈表达着对灾区的祝愿和关切,传递着“一方有难,八方支援”的理念。
志愿者捐款捐物,为灾区人民做好后勤保障。
这里捐赠的救灾物品( )A. 是商品因为有运用价值B. 不是商品因为不是劳动产品C. 是商品因为进行交换D. 不是商品因为不用于交换【答案】D【解析】本题考查商品的含义。
商品是用于交换的劳动产品,凡商品必需满意两个条件:一是劳动产品,二是用于交换,二者缺一不行,这里捐赠的救灾物品不是商品,因为没有用于交换,D 正确且符合题意;A C观点错误;B观点正确但理由错误,故本题答案选D。
2. 2011年10月19日第20届金鸡百花电影节开幕式在合肥实行。
门票定价有几百元到几千元不等的不同档次,张楠花了600元在黄牛手里买了一张标价是500元的票。
这里的600元、500元分别执行的货币职能是()。
A. 价值尺度商品流通B. 支付手段价值尺度C. 流通手段价值尺度D. 价值尺度流通手段【答案】C【解析】试题分析:“张楠花了600元在黄牛手里买了一张标价是500元的票”,标价500元表示商品的价格是500元,属于价值尺度职能;花了600元进行了购买行为,600元在这里是属于流通手段职能;故C符合,解除A、B、D。
考点:本题考查货币的基本职能。
3.假如在一年里全社会用现金支付的销售商品总量为5000亿件,平均价格水平为8元,在这一年里货币平均周转5次。
那么,这一年里货币发行量应为亿元。
假如这一年实际发行了16000亿元纸币,这时的1元钱相当于元购买力,这会引起。
A. 8000,0.5,通货膨胀 B. 4000,0.2,购买力降低C. 16000,2,纸币升值D. 2000,3,购买力提高【解析】本题考查流通中所需货币量、通货膨胀。
2022-2023学年重庆市第一中学九年级下学期期中考试物理试题

2022-2023学年重庆市第一中学九年级下学期期中考试物理试题1.下列认识中,最接近实际的是()A.人的正常体温约为38℃B.一部普通智能手机的质量约为2kgC.家用电冰箱的额定功率约为1000WD.声音在空气中的传播速度约为340m/s2.如图所示的光现象中是由于光的反射形成的是()A.海市蜃楼B.水中倒影C.月食形成D.雨后彩虹3.生活处处有物理,留心观察皆学问,对以下现象解释正确的是()A.冬天草叶上有一层霜,霜是凝固形成的B.打开冰箱门时,常会看见门前冒“白气”,这是液化现象C.放在衣橱里的樟脑丸时间久了会变小,是因为樟脑丸汽化了D.洗澡时卫生间镜子上布满水珠,这些水珠是水蒸气液化时吸热形成的4.如图所示现象中涉及的物理知识错误的是()A.如图甲,电流周围存在磁场是由奥斯特第一个发现的B.如图乙,电动机的工作过程将电能主要转化为机械能C.如图丙,导体在磁场中沿任何方向运动,闭合回路中都会产生感应电流D.如图丁,滑动变阻器的滑片向左滑动,电磁铁的磁性会增强,吸引的铁钉会增加5.青少年科技创新大赛的获奖作品-5G高铁轨道螺丝警报器,设计了检测螺丝松动的报警方案,如图所示,其主要的科学原理是:螺丝(其电阻不计)连接在电路中,当螺丝松动时,它会与下端的导线分离而断开,此时报警灯工亮起而发出警报,及时提醒工人修理。
下列符合题意的电路图是()A.B.C.D.6.图是北京2022年冬奥会冰球比赛中的情景,下列说法不正确的是(不计空气阻力)()A.冰球被击出后,由于具有惯性会继续向前运动B.用力击球时,球杆对球的力与球对球杆的力是一对相互作用力C.冰球在冰面上静止时受到的重力和冰面对冰球的支持力是一对平衡力D.被击出的冰球在水平冰面上最终会停下来说明力是维持物体运动的原因7.如图所示,电源电压保持不变,闭合开关S,当滑动变阻器滑片P向右滑动过程中,下列说法正确的是()A.电流表A 2的示数变大B.电压表V的示数变大C.电压表V的示数与电流表A 1的示数的比值变大D.电压表V的示数与电流表A 2的示数的乘积变大8.如图甲所示,A、B两正方体静置在水平地面上,已知A的密度ρA=2×103kg/m3,A的边长L A=10cm。
【全国百强校】重庆市第一中学2015-2016学年高二下学期期中考试理数试题(解析版)

重庆市第一中学2015-2016学年高二下学期期中考试理数试题一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(原创)已知集合{}x y x M ==,{}2x y y N ==,则下列说法正确的是( )A .),0(+∞=MB .N M =C .{}1,0=N MD .∅=N M 【答案】B考点:集合运算.【易错点晴】本题主要考查集合之间的运算,属于容易题. 本题容易错的地方: 容易把集合中的元素弄错,集合M 中的元素为x ,就是求函数y =的定义域;集合N 中的元素为y ,就是求函数2y x =的值域. 用描述法表示集合时,竖线前的部分表示这个集合的元素是什么,初学者容易弄错,请同学们引起重视. 2.在ABC ∆中,已知π32=∠A ,7=BC ,5=AC ,则=AB ( ) A .3 B .23 C .8 D .38 【答案】A 【解析】试题分析:利用余弦定理有,2222cos BC AC AB AC AB A =+-,令(0),AB x x =>解方程有3x =(负值舍去),即3,AB =选A.考点:1.余弦定理;2.一元二次方程的解. 3.在104)1(xx -的展开式中,常数项为( ) A .90- B .90 C .45- D .45 【答案】D 【解析】试题分析:通项为101051101041()(1)r rr r r r r T C x C x x--+=-=-,令1050,2r r -==,故常数项为231045T C ==,选D.考点:二项式定理.4.已知b a ,均为正实数,则)4)(1(ab b a ++的最小值为( ) A .3 B .7 C .8 D .9 【答案】D 【解析】试题分析:144()()559a b ab b a ab ++=++≥+=,当4ab ab=,2ab =(,a b 为正数)等号成立,故最小值为9,选D. 考点:基本不等式.5.已知随机变量ξ服从正态分布)4,2(N ,且8.0)4(=<ξP ,则=<<)20(ξP ( )A .6.0B .4.0C .3.0D .2.0 【答案】C考点:正态分布.6.某校在半期考试中要考察六个学科,已知语文考试必须安排在首场,且数学与英语不能相邻, 则这六个学科总共有( )种不同的考试顺序A .36B .48C .72D .112 【答案】C 【解析】试题分析:先排语文,有1种排法,再排除了数学和英语外的3科,全排列有336A =种,把数学和英语插在这3科的空中有2412A =种排法,利用分步乘法计数原理,共有161272⨯⨯=种排法.故选C. 考点:1.排列的应用;2.相邻问题和不相邻问题.7.(原创)集合{}y x A ,,1=,{}y x B 2,,12=,若B A =,则实数x 的取值集合为( ) A .⎭⎬⎫⎩⎨⎧21 B .⎭⎬⎫⎩⎨⎧-21,21 C .⎭⎬⎫⎩⎨⎧21,0 D .⎭⎬⎫⎩⎨⎧-21,21,0 【答案】A 【解析】试题分析:由集合中元素的互异性有21,1,1,21x y x y ≠≠≠≠,若2,2x x y y ==有0x =或1,0y =不符合,舍去;所以22,x y y x ==,解得11,24x y ==(0x y ==舍去).所以选A. 考点:集合相等的条件.8.已知双曲线的方程为)0,0(12222>>=-b a by a x ,它的一个顶点到一条渐近线的距离为d ,已知c d 32≥(c 为双曲线的半焦距长),则双曲线的离心率的取值范围为( ) A .]2,26[B .]3,26[C .]3,2(D .),3[]26,1(+∞ 【答案】B考点:1.双曲线的几何性质;2.点到直线距离公式. 9.下列说法中正确的是( )A .“若12=x ,则1=x 或1-=x ”的否命题为“若12≠x ,则1≠x 或1-≠x ”B .已知命题“q p ∧”为假命题,则命题“q p ∨”也是假命题C .设U 为全集,集合B A ,满足A B C B A C U U )()(=,则必有∅==B AD .设λ为实数,“]1,1[-∈∃x ,满足λ≤-21x ”的充分不必要条件为“1≥λ” 【答案】D 【解析】试题分析:对于选项A,原命题的否命题为“若21,x ≠则1x ≠且1x ≠-”,A 错;对于B,当命题“p q ∧”为假命题时,则命题p 、q 中至少有一个为假,所以“q p ∨”可能为真命题, B 错;对于C, 反例:{}{}1,2,3,1U A B ===, 则()()U U C A B C B A φ==,C 错;对于D, 若命题“[]1,1,x ∃∈-满足λ≤”为真, 则min λ≥,所以0λ≥,而01,10λλλλ≥≠>≥≥⇒≥,故选项D 是真命题,选D.考点:1.否命题的书写;2.简单复合命题真假的判断;3.充分条件与必要条件.10.如下图,已知AC AB ,是圆的两条弦,过B 作圆的切线与AC 的延长线相交于D .过点C 作BD 的 平行线与AB 相交于点E ,3=AE ,1=BE ,则BC 的长为( )A .2B .3C .2D .23【答案】C考点:1.切割线定理;2.相似三角形. 11.在ABC ∆中,已知BC A tan 2tan 1tan 1=+,则B cos 的最小值为( ) A .32 B .42 C .31 D .21 【答案】D【解析】 试题分析:由112tan tan tan A C B +=有cos cos 2cos sin sin sin A C B A C B+=,通分化简有2sin 2sin sin cos B A C B =,由正弦定理有22cos b ac B =,由余弦定理有222cos 2a c b B ac +-=①,化简得2221()2b a c =+,代入①有2221cos 442a c ac B ac ac +=≥=,所以cos B 的最小值为12,选D.考点:1.正弦定理;2.余弦定理;3.重要不等式(222a c ac +≥).【思路点晴】本题主要考查利用重要不等式: 222a c ac +≥求cos B 的最小值,属于中档题. 由已知等式112tan tan tan A C B +=,切化弦,得cos cos 2cos sin sin sin A C BA C B+=,通分,利用两角和的正弦公式及在三角形中,sin()sin A C B +=,化简得2sin 2sin sin cos B A C B =,由正、余弦定理化简得2221()2b ac =+,代入2221cos 442a c ac B ac ac +=≥=.本题考查的公式比较多,技巧性比较强,平时要多加练习.12.(原创)函数13)(23+--=x x x x f 在0x x =处取得极大值,设0x m ≠,且)()(0m f x f =, 则=-0x m ( )A .3B .32C .33D .63 【答案】B考点:1.用导数求极值;2.求一元二次方程的根.【方法点晴】本题主要考查利用导数求极值,属于中档题. 先求出函数32()31f x x x x =--+的导数,求出导数值为零的点,判断出01x =为函数()f x 的极大值点, 由0()()f x f m =,这里采用分解因式,计算量要小很多,由25(203m m -+=求m 的值时,另外本题采用分解因式求出m 的值,用求根公式求出m 也可以.第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题,每题5分,满分20分.)13.在以原点O 为极点,x 轴正半轴为极轴的极坐标系中,已知两点)32,2(πA ,)6,3(πB ,则AOB ∆的面积为 . 【答案】3考点:1.极坐标的意义;2.三角形面积的计算.14.在10瓶饮料中,其中有3瓶已过了保质期,从这10瓶饮料中任取3瓶,则至少取到一瓶已过保 质期饮料的概率为 . 【答案】1724【解析】试题分析:用间接法,“至少取到一瓶已过保质期饮料”的对立事件是“取出的3瓶都没有过保质期”,其概率是37310724C C =,故至少取到一瓶已过保质期的概率为71712424-=. 考点:1.用古典概型求概率;2.对立事件的概率加法公式.15.如右图所示,网格纸上每个小正方形的边长为1,粗线画出的是某四面体的三视图,则该四面 体的表面积为 .【答案】考点:1.三视图的识别;2.表面积的计算.【方法点晴】本题主要考查了由三视图求该几何体的表面积,属于中档题. 由俯视图知底面为等腰三角形,且顶点在底面的投影落在底面的一个顶点处,说明有一条侧棱垂直于底面.再由正视图,画出直观图如上图,PB ⊥平面ABC ,证明AC PD ⊥的目的是求PD 的长,计算PAC ∆的面积.本题中由三视图还原出直观图是关键,考查了空间想象能力.16.集合B A ,满足条件∅≠B A ,{}5,4,3,2,1=B A ,当B A ≠时,我们将),(B A 和),(A B 视 为两个不同的集合对,则满足条件的集合对),(B A 共有 个. 【答案】211 【解析】试题分析:因为∅≠B A ,{}5,4,3,2,1=B A ,所以集合,A B 都是{}1,2,3,4,5的非空子集.①当集合A 中含有一个元素时,不妨设{}5A =,则{}1,2,3,4,5B =,此时集合对(,)A B 有155C =种;②当集合A 中含有二个元素时,不妨设{}4,5A =,则集合{}1,2,3,4B =,或{}1,2,3,5B =,或{}1,2,3,4,5B =,此时集合对(,)A B 有25330C ⨯=种;③当集合A 中含有三个元素时,不妨设{}3,4,5A =,则{}1,2,3B =,或{}1,2,4B =,或{}1,2,5B =,或{}1,2,3,4B =,或{}1,2,3,5B =,或{}1,2,4,5B =,或{}1,2,3,4,5B =,此时集合对(,)A B 有35770C ⨯=种;④当集合A 中含有四个元素时,不妨设{}2,3,4,5A =,则集合B 至少含有两个元素,且有一个元素为1,此时集合对(,)A B 有4123454444()75C C C C C ⨯+++=种;当集合A 中含有吴个元素时, 此时集合对(,)A B 有555(21)31C ⨯-=个.故共有530707531211++++=. 考点:1.集合的运算性质;2.组合数的计算公式;3.分类讨论.【方法点晴】本题主要考查集合的运算性质以及分类讨论等,属于难题. 先由已知条件: ∅≠B A ,{}5,4,3,2,1=B A ,得到集合,A B 都是{}1,2,3,4,5的非空子集. 故对集合A 中元素的个数分情况讨论,共五种情况.每种情况要做到不重不漏,若可能种数比较多时,用组合数写出来比较好.本题用到了分类讨论的思想, 推理能力与计算能力.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分12分)已知集合{}1≤-=a x x A ,{}0452≤+-=x x x B . (1)当1=a 时,求B A ;(2)已知“A x ∈”是“B x ∈”的充分条件,求实数a 的取值范围. 【答案】(1)[]0,4;(2)[]2,3a ∈.(2)11111+≤≤-⇔≤-≤-⇔≤-a x a a x a x ,且]4,1[=B 由已知B A ⊆,画出数轴分析知:41≤+a 且11≥-a ,解得]3,2[∈a .考点:1.一元二次不等式的解法;2.集合的运算;3.充分条件的理解.18.(本小题满分12分)小明在某社交网络的朋友圈中,向在线的甲、乙、丙随机发放红包,每次 发放1个,甲、乙、丙每人每次抢到红包的概率均为31. (1)若小明发放1元的红包2个,求甲最多抢到1个红包的概率;(2)若小明共发放3个红包,第一次发放5元,第二次发放5元,第三次发放10元,记甲抢到红包的总 金额为ξ元,求ξ的分布列和数学期望. 【答案】(1)89;(2)分布列见解析,数学期望为203.(2)ξ的所有可能值为20,15,10,5,0278)32()0(3===ξP ;27832)3231()5(12=⨯⨯⨯==C P ξ 27631)32(32)31()10(22=⨯+⨯==ξP ;27431)3231()15(12=⨯⨯⨯==C P ξ 271)31()20(3===ξP ,故ξ的分布列: 期望3202712027152710275270=⨯+⨯+⨯+⨯+⨯=ξE 考点:1.概率计算公式;2.数学期望的计算.19.(本小题满分12分)已知ABC P -为正三棱锥,底面边长为2,设D 为PB 的中点,且PC AD ⊥, 如右图所示.(1)求证:⊥PC 平面PAB ;(2)求二面角B AC D --的平面角的余弦值.【答案】(1)证明见解析;.试题解析:(1)以AB 中点O 为原点,OC 为x 轴,OA 为y 轴建立如图坐标系,各点坐标如下:)0,1,0(A ,)0,1,0(-B ,)0,0,3(C ,由于点P 在ABC ∆中的射影为ABC ∆的中心,故可设),0,33(h P ,故),0,332(h -=,而)0,2,0(-= 00)()2(00332=⨯-+-⨯+⨯=⋅h AB PC ,所以AB PC ⊥,而AD PC ⊥ 因为AD AB ,为平面PAB 中的两条相交直线,所以⊥PC 平面PAB(2)由中点公式知)2,21,63(hD -,由0=⋅PC AD 知:02131),0,332()2,23,63(2=-=-⋅-h h h ,解得32=h 设平面ACD 的法向量为),,(z y x =,由上面的计算知)66,23,63(-= )0,1,3(-=AC ,由0=⋅及0=⋅知:⎪⎩⎪⎨⎧=-=+-030662363y x z y x ,解得)8,6,2(=, 显然平面ABC 的法向量为)1,0,0(=b 设所求二面角的平面角为θ,则322728cos =θ考点:1.线面垂直的证明;2.空间直角坐标系的建立;3.向量夹角的计算.20.(原创)(本小题满分12分)已知椭圆)0(1:2222>>=+b a by a x C 的左右焦点分别为21,F F ,点P 在椭圆上,且0211=⋅F F PF ,421=F F ,551=PF . (1)求椭圆C 的标准方程;(2)经过点)0,3(P 的直线l 和椭圆C 交于B A ,两个不同的点,设AB 的中点为),(00y x Q ,求00y x +的 取值范围.【答案】(1)22+15x y =;(2)73⎫⎪⎪⎭.试题解析:(1)由242=⇒=c c ,由勾股定理5591651221212=+=+=F F PF PF ,由椭圆定义55255955221=⇒=+=+=a PF PF a ,从而122=-=c a b , 故椭圆方程为1522=+y x考点:1.求椭圆的方程;2.韦达定理;3.利用函数性质求范围.【易错点晴】本题主要考查椭圆的方程,以及直线与椭圆相交时求交点弦中点横纵坐标和的范围,属于中档题. (1)很容易,大部分学生会做;(2)中,注意直线方程的特殊情况:与x 轴重合,在求22153351030m tu m t t -==+-+,注意5t m =-的取值范围,由对勾函数图象可以看出单调性,求出u 的范围来.本题在求u 的范围时,计算量大,容易算错.21.(原创)(本小题满分12分)已知函数x x x f ln 2)(=. (1)求函数)(x f 的单调区间;(2)经过点)2,0(-作函数)(x f 图象的切线,求该切线的方程; (3)当),1(+∞∈x 时)1()(2-<x x f λ恒成立,求常数λ的取值范围.【答案】(1)增区间为1(,)e +∞,减区间为1(0,)e;(2)22y x =-;(3)[)1,λ∈+∞.试题解析:(1)2ln 2)('+=x x f ,令0)('>x f 得增区间),1(+∞e ,令0)('<x f 得减区间)1,0(e(2)设切点的坐标为)ln 2,(000x x x ,设切线的斜率为k ,一方面0)2(ln 2000---=x x x k ,另一方面2ln 2)('00+==x x f k ,从而有2ln 22ln 20000+=+x x x x ,化简得10=x从而切点坐标为)0,1(,所以切线方程为22-=x y(3)由已知)1(ln 2)1(ln 22xx x x x x -<⇔-<λλ在),1(+∞∈x 时恒成立 构造)1(ln 2)(xx x x g --=λ,则0)(<x g 在),1(+∞∈x 时恒成立 由0)2(<g 即0232ln 2<-λ得必要条件0>λ 2222)11(2)('xx x x x x g λλλ-+-=+-=,记λλ-+-=x x x h 2)(2,判别式244λ-=∆ 若1≥λ,则0≤∆,且)(x h 开口向下,故0)(≤x h 恒成立,此时0)('≤x g 恒成立, 从而)(x g 在),1(+∞上单调递减,故0)1()(=<f x g ,符合题意若10<<λ,则0>∆,此时0)(=x h 有两个实数根21,x x ,不妨设21x x <,由韦达定理01,022121>=>=+x x x x λ,故21,x x 均为正数,且211x x <<从而0)(=x h 在),1(+∞上有唯一的实数根2x ,结合图象知:当),1(2x x ∈时0)(>x h ,即)(0)('x g x g ⇒>在),1(2x x ∈时单调递增, 故当),1(2x x ∈时0)1()(=>g x g ,不符合题意 综上:λ的取值范围为),1[+∞考点:1.求函数的单调区间;2.导数的几何意义;3.利用导数求函数的范围.【易错点晴】本题主要考查利用导数求函数的单调区间,切线斜率以及求函数范围,属于难题. 在(1)中,求函数的单调区间一定要注意定义域;在(2)中,根据斜率的两种计算方法: 已知直线上两点坐标和导数的几何意义,列出等式,算出0x 的值;(3)由已知得到12ln ()x x xλ<-对于(1,)x ∈+∞恒成立,构造函数1()2ln ()g x x x xλ=--,分类讨论,求出λ的值.请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.解答时请写清题号.22.(原创)(本小题满分10分)选修4—1:几何证明选讲如下图所示,设P 为圆O 外的点,过点P 作圆O 的切线PA ,切点为A ,过点P 作圆O 的割线PBC , 与圆交于C B ,两点,OP AH ⊥,垂足为H . (1)求证:PCO PHB ∆∆~;(2)已知圆O 的半径为1, 3=PA ,26=PB ,求四边形BCOH 的面积.【答案】(1)证明见解析; 【解析】(2)由勾股定理2=PO ,由切线长定理PC PB PA ⋅=2知:6263=⇒=PC PC , 在POC ∆中410sin 462cos 222=⇒=⋅-+=C CP CO PO CP CO C 所以415sin 21=⋅⋅=∆C PC OC S OCP 由PCO PHB ∆∆~,相似比为46=PO PB ,面积比为83)46(2=从而四边形BCOH 的面积1532585==∆OCP S S 考点:1.勾股定理;2.切割线定理;3.相似三角形的证明. 23.(本小题满分10分)选修4-4:极坐标与参数方程在直角坐标系xOy 中,直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧+-=+=ta y t x 211231(其中参数R t ∈,a 为常数),在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线C 的方程为)4cos(22πθρ+=.(1)求曲线C 的普通方程;(2)已知直线l 与曲线C 相交于B A ,两点,且5=AB ,求常数a 的值. 【答案】(1) 02222=+-+y x y x ;(2)1a =±. 【解析】试题分析:(1)先把曲线C 利用两角和的余弦公式展开,再利用cos ,sin x y ρθρθ==化成普通方程;(2)联立直线l 的参数方程和曲线C 的普通方程,由参数t 的含义,得出12AB t t =-,求出a .试题解析:(1)θθπθπθπθρsin 2cos 2)4sin sin 4cos(cos 22)4cos(22-=-=+=故y x y x 22sin 2cos 2222-=+⇒-=θρθρρ 所以曲线C 的普通方程为:02222=+-+y x y x(2)将曲线C 的方程变形为2)1()1(22=++-y x 与直线l 的参数方程联立得:022)21(432222=-++⇒=++a at t t a t 首先3802<⇒>∆a由韦达定理2,22121-=-=+a t t a t t 由参数t 的含义知:5)2(44)(222122121=--=-+=-=a a t t t t t t AB即153822=⇒=-a a ,满足382<a ,故1±=a 综上常数a 的值为1±考点:1.极坐标方程化为普通方程;2.韦达定理. 24.(本小题满分10分)选修4-5:不等式选讲 已知函数a x x x x f +++-=12)(2.(1)当2=a 时,求)(x f 的最小值;(2)当]1,32[∈x 时,x x f ≤)(恒成立,求a 的取值范围. 【答案】(1)3;(2)]31,1[--∈a .(2)由于a x x x f ++-=1)(,当]1,32[∈x 时x a x x x f ≤++-=1)(恒成立,变形为012)(≤+-+=x a x x g 在]1,32[∈x 时恒成立,即0)(max ≤x g 当0≥+a x 时112)(++-=+-+=a x x a x x g ,此时)(x g 单调递减 当0<+a x 时1312)(+--=+---=a x x a x x g ,此时)(x g 仍单调递减由于)(x g 图象连续,故)(x g 在R 上单调递减,03132)32()(max ≤-+==a g x g 变形为313231≤+≤-a ,解得]31,1[--∈a考点:1.绝对值三角不等式;2.恒成立的等价转化.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆市第一中学2015届九年级政治下学期期中试题
(开卷本卷共四个大题,满分50分,与历史学科共用90分钟)
一、选择题:下列各题的备选答案中,只有一项
....是最符合题意的,请选出,并将其字母符号填入答题卷相应的方框中。
(本大题共10小题,每小题2分,共20分)
1.2014年12月11日晚,从泰国曼谷飞往中国南京的某航班上,两名中国游客因提供热水及找零问题与亚航空姐发生冲突,出现了中国乘客“用开水泼空姐”事件,进而导致航班返航。
这两名游客的行为警示我们
①要我行我素,张扬个性
②要遵纪守法,宽以待人
③和谐的生活需要相互尊重、理解
④要增强文明、责任意识,维护自身和国家形象
A.①②③
B.①②④
C.①③④
D.②③④
2.近年来,公平已成为社会的共同期盼和呼声,引起党和政府的高度重视。
下列举措体现公平要求的是
①完善城乡最低生活保障制度
②加大教育资源向中西部和农村倾斜
③建立和完善城乡居民大病保险制度
④改革收入分配制度,实现均等分配
A.①②③
B.①②④
C.①③④
D.②③④
3.下列侵犯公民人身权利的行为中,对应不正确的是
A.小明因妒忌而诬陷小辉在考试中作弊——名誉权
B.商家未经本人同意使用明星的照片做广告——肖像权
C.同学给长得胖的小刘起了“小肥猪”的外号——姓名权
D.农民工张某为了讨薪,绑架了老板——人身自由权
4.2014年11月1日第十二届全国人大常委会第十一次会议表决通过了关于修改《中华人民共和国行政诉讼法》的决定。
这说明
A.全国人大具有重大事项决定权
B.法律面前人人平等
C.我国建立了以宪法为核心的权利保障体系
D.法律是由国家制定或认可的特殊行为规范
5.右侧漫画告诉我们
①法律保护公民的合法财产所有权
②要增强法律意识,懂得依法维权
③法律是保护公民合法权益的有力武器
④法律保护公民的所有财产
A.①②③
B.①③④
C.②③④
D.①②④
6.3月30日是全国第20个中小学生安全教育日,今年的活动主题是“我安全,我健康,我快乐”。
下列行为能体现这一主题的是
A.看到路边某酒店发生大火,立即冲进酒店救火
B.在寝室里面私拉乱接电线
C.暑假,和小伙伴偷偷到河里游泳
D.不在楼梯或狭窄的通道嬉戏打闹
7.2014年12月20日是澳门回归祖国15周年纪念日。
15年来,澳门经济实现跨越式发展,GDP 从60亿美元增长为500多亿美元,失业率从6.3%降至1.8%。
这表明
A.民族区域自治制度符合我国国情
B.我国已经跨越社会主义初级阶段
C.社会主义制度发挥了巨大的优越性
D.“一国两制”方针具有强大的生命力
8.中考前夕,小明复习思想品德课本时,喜欢用一些文字、符号、图示和表格等来表述相关知识间的联系。
下列表述错误的一项是
特殊保护
全面建成小康社会 基本实现现代化
D.刑法+民法+婚姻法+…… = 宪法
9.右侧漫画中的行为
A.能杜绝浪费现象发生
B.不利于我国经济持续快速发展
C.体现的是一种理性消费观念
D.说明人民生活水平显著提高
10.当今世界拥有60多亿人口,200多个国家和地区,2500多个民族,5000多种语言,不同国家和民族的特色文化交相辉映,构成了多姿多彩的人类文明。
我们青少年应该
A.努力消除文化差异,使世界更加和谐统一
B.珍视本民族文化,漠视、歧视其他民族的文化
C.多吸收发达国家的文化,少吸收落后地区的文化
D.以平等的态度与其他国家和民族的人民友好交往
二、简答题(本大题共3小题,每小题4分,共12分)
11.下面是九年级学生小明读初中以来的生活片段。
片段一:初一进校不久,小明因不认真做清洁和室友发生了争执。
事后,小明深感愧疚,主动道歉,
室友原谅了他。
片段二:初二时,小明和同桌组成了学习小组。
两人互相帮助,共同进步。
片段三:初三开学后,小明加入了校学生会组织的社区服务队。
利用课余时间打扫社区卫生,看望孤寡老人。
请运用所学知识,与小明一起感悟生活,逐片段谈谈你的收获。
(4分)
12.观察右侧漫画,据此回答下列问题。
(1)请点评漫画中经营者的言行。
(2分)
(2)面对经营者的托词,漫画中的就餐者应该
怎么办?(2分)
13. 2014年度最具影响力的十大“科技创新人物”之一曲道奎,带领团队创造了中国机器人发展史
上的88项第一,研发的机器人遍布全球15个国家。
他们用满满的自信,书写着中国机器人发展的新篇章。
(1)从曲道奎及其团队的经历来看,取得成功需要具备哪些意识和精神?(2分 列出两种即可)
(2)我们应如何向曲道奎等学习,培养自己的创新能力?(2分)
三、分析说明题(本大题共2小题,每小题6分,共12分)
14.霾,席卷中国多个省市,天地变色,引起公愤。
人,历数霾的万千罪状。
霾,感觉异常委屈,开始了自己的诉说……
【诉说一】我是你们请来的,是你们为我提供了良好的生存条件。
(1)请举例说明我们为霾提供了哪些“良好的生存条件”。
(2分 举出两例)
【诉说二】新修订的《环境保护法》中的有些规定,对我威胁很大,实在让我忧心忡忡。
(2)请联系下图中的相关规定,谈谈《环境保护法》的这一规定为何会使霾忧心忡忡。
(2分)
【诉说三】听说你们向我宣战了。
那就让我们决一死战吧!
(
3)请从国家的角度为打赢这场“呼吸保卫战”出谋划策。
(2分)
15.回望2014,与中国外交有关的热词扑面而来:
【关键词】主场外交
70多位外国元首和政府首脑先后到访,52个国家和地区的政、商、学界人士出席博鳌亚洲论坛,1800多位中外企业家聚首夏季达沃斯……除了这些“保留节目”,2014年中国开展的另外两场“主场外交”尤其引人关注,即5月举行的亚信上海峰会和11月举行的APEC北京会议。
【关键词】千里驰援
2014年12月5日晚,由中方独立运营管理的中国援助利比里亚埃博拉诊疗中心正式开始收治埃博拉疑似患者。
2014年12月4日,马尔代夫首都马累海水淡化处理厂发生火宅导致水荒后,中方第一时间派民航客机、军用运输机千里驰援,将一批批饮用水运抵马累,并派遣装备海水淡化设备的海军长兴岛船前往执行紧急供水任务。
(1)上述材料说明了什么?(2分)
(2)请结合教材知识,谈谈我国为什么积极发展同其他国家的友好关系。
(2分)
(3)为推动建设持久和平、共同繁荣的和谐世界,我们青少年应当承担怎样的责任?(2分)
四、活动探究题(共6分)
16.我市某中学九年级同学准备在国家宪法日这天在校园里举办“学习宪法,依法治国”为主题的法制宣传活动。
(1)在准备阶段,同学们研究学习了《中共中央关于全面推进依法治国若干重大问题的决定》,张
二
(2)小明听说这个活动后,感到很疑惑:宪法离我们学生的生活太远了,干嘛要去学习呢?请你运用所学知识帮他答疑解惑。
(2分)
(3)请你就“如何做一个依法治国的践行者”向全校同学提出倡议。
(2分)。
