轴对称图形专项练习题60
初二数学轴对称练习题及答案

初二数学轴对称练习题及答案轴对称是初中数学中的一个重要概念,它在几何图形的研究中具有广泛的应用。
本文将为大家提供一些初二数学轴对称的练习题及答案,帮助同学们更好地理解和掌握这个知识点。
1. 练习题一在平面上,画出图形ABC,其中AB=3 cm,BC=4 cm,AC=5 cm。
找出图形的对称中心,并标出。
解答:首先,根据给定条件画出图形ABC。
由题目可知,三角形ABC是一个直角三角形,其中∠ABC=90°。
以边AC为轴,将三角形沿中点F对折,使得点B和B'重合。
连接BB',则BB'即为轴对称线,其交点F即为图形ABC的对称中心。
2. 练习题二如图所示,J、K、L、M是矩形ABCD的四个顶点,N是JL的中点,P是KN的中点,连接BM和CP,交于点O。
证明:BO=OC。
解答:根据题目所给条件,我们可以先证明三角形MBN与三角形PCO全等。
首先,由矩形ABCD的性质可知,AD∥BC,故∠NBC=∠BAN=90°。
其次,由题目可知,N是JL的中点,所以NJ=NL,结合矩形的性质可得∠NJL=∠NLF=90°,因此NFBJ是一个矩形。
同理,NEDK也是一个矩形。
由于FB=EK,NJ=NL,所以根据余角定理可知∠NBF=∠NEK。
再根据SSS全等定理,得到三角形MBN与三角形PCO全等,因此MB=PC。
又因为M和P分别是BC和KN的中点,故MB=BC/2,PC=KN/2。
所以BC/2=KN/2,即BC=KN。
由于BO和OC分别是BM和CP的中线,所以BO=BM/2,OC=CP/2。
综上所述,BO=OC。
3. 练习题三已知矩形EFGH中,AB=8 cm,BC=6 cm。
在边AB和BC上分别取两个等分点D和I,并连接DI。
求证:DI垂直于FG。
解答:根据题目中所给条件,我们可以先证明三角形GBD与三角形ACI全等。
首先,由矩形EFGH的性质可知,EF∥GH,所以∠FGB=∠AGH=90°。
三年级下册轴对称、平移练习(图题30题)
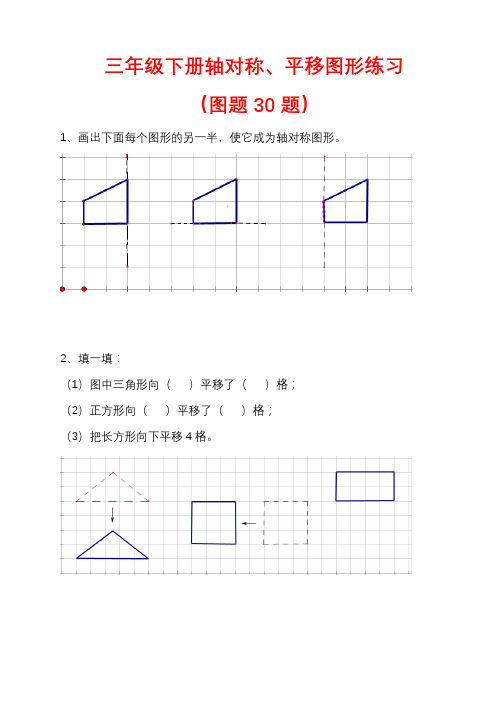
三年级下册轴对称、平移图形练习(图题30题)1、画出下面每个图形的另一半,使它成为轴对称图形。
2、填一填:(1)图中三角形向()平移了()格;(2)正方形向()平移了()格;(3)把长方形向下平移4格。
3、画出下面每个图形的另一半,使它成为一个轴对称图形,再把左边的图形向上平移5格。
4、画一画,填一填:(1)图1向()平移了()格。
(2)画出图2向右平移6格后的图形。
5、画一画,填一填:(1)画出小船图向左平移8格的图形。
(2)画出图1和图2的另一半,使它成为一个轴对称图形。
(3)图3向()移动了()格。
6、画一画,填一填:(1)图3向()平移了()格。
(2)请画出图2向左平移10格后的图形。
(3)请画出图1的另一半,使它成为一个轴对称图形。
7、画一画,填一填:(1)把方格纸上左边的三角形向右平移6格。
(2)画出方格纸右边图形的另一半,使它成为一个轴对称图形。
8、填一填,画一画:(1)小船向()平移了()格。
(2)画出把小树图向右平移6格的图形。
9、填一填,画一画:(1)在下图中,火箭向()平移了()格。
(2)画出图中三角形向右平移4格后的图形。
10、画出下列每个图形的另一半,使它成为一个轴对称图形。
三角形向()平移了()格。
11、看图填一填:(1)金鱼图向()平移了()格;(2)“十”字向()平移了()格;(3)盒子图向()平移了()格;(4)箭头图向()平移了()格。
12、看图填一填:(1)小房子向()平移了()格;(2)直角三角形向()平移了()格;(3)三角形向()平移了()格。
13、按要求画一画:(1)将图①向右平移8格;(2)将图②先向左平移3格,再向上平移6格。
14、按要求画一画:(1)将图①向右平移6格;(2)将图②向左平移7格;(3)将图③向上平移8格。
15、看图画一画:(1)将图①向右平移6格;(2)将图②先向左平移2格,再向上平移4格。
16、按要求画一画:(1)将图①向右平移6格;(2)将图②先向下平移3格,再向左平移7格。
轴对称练习题(含答案)

轴对称练习题(含答案)一.选择题1.下列图形中,是轴对称图形的是()A.B.C.D.2.如图,在△ABC中,D,E是BC边上两点,且满足AB=BE,AC=CD,若∠B=α,∠C=β,则∠DAE的度数为()A.B.C.D.3.如图,等腰△ABC的周长为21,底边BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为()A.13 B.16 C.8 D.104.点A(4,﹣2)关于x轴的对称点的坐标为()A.( 4,2 )B.(﹣4,2)C.(﹣4,﹣2)D.(﹣2,4)5.已知一个等腰三角形一内角的度数为80°,则这个等腰三角形顶角的度数为()A.100°B.80°C.50°或80°D.20°或80°6.若等腰△ABC中有一个内角为40°,则这个等腰三角形的一个底角的度数为()A.40°B.100°C.40°或100°D.40°或70°7.在△ABC中,∠A=30°,∠B=70°,直线将△ABC分成两个三角形,如果其中一个三角形是等腰三角形,这样的直线有()条.A.5 B.7 C.9 D.108.如图,Rt△ACB中,∠ACB=90°,∠A=60°,CD、CE分别是△ABC的高和中线,下列说法错误的是()A.AD=ABB.S△CEB =S△ACEC.AC、BC的垂直平分线都经过ED.图中只有一个等腰三角形9.如图,a∥b,△ABC的顶点A在直线a上,AC=BC,∠1=50°,∠2=20°,则∠C的度数为()A.70°B.30°C.40°D.55°10.对于问题:如图1,已知∠AOB,只用直尺和圆规判断∠AOB是否为直角?小意同学的方法如图2:在OA、OB上分别取C、D,以点C为圆心,CD长为半径画弧,交OB的反向延长线于点E,若测量得OE=OD,则∠AOB=90°.则小意同学判断的依据是()A.等角对等边B.线段中垂线上的点到线段两段距离相等C.垂线段最短D.等腰三角形“三线合一”11.如图,在△ABC中,∠CDE=64°,∠A=28°,DE垂直平分BC;则∠ABD=()A.100°B.128°C.108°D.98°12.如图,AB∥CD,点E在AD上,且CD=DE,∠C=75°,则∠A的大小为()A.35°B.30°C.28°D.26°二.填空题13.在平面直角坐标系中,点M(a,b)与点N(3,﹣1)关于x轴对称,则b a的值是.14.已知一个等腰三角形腰上的高与底边的夹角为37°,则这个等腰三角形的顶角等于度.15.如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线交BC于M,交AB于E,AC 的垂直平分线交BC于N,交AC于F,若MN=2,则NF=.16.如图,BC的垂直平分线分别交AB、BC于点D和点E,连接CD,AC=DC,∠B=25°,则∠ACD的度数是.三.解答题17.如图,△ABC中,AE=BE,∠AED=∠ABC.(1)求证:BD平分∠ABC;(2)若AB=CB,∠AED=4∠EAD,求∠C的度数.18.如图,AD⊥BC于D,且DC=AB+BD,若∠C=26°,求∠BAC的度数.19.已知:方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).(1)请以y轴为对称轴,画出与△ABC对称的△A1B1C1,并直接写出点A1、B1、C1的坐标;(2)△ABC的面积是;(3)点P(a+1,b﹣1)与点C关于x轴对称,则a=,b=.20.如图,已知AB =A 1B ,A 1B 1=A 1A 2,A 2B 2=A 2A 3,A 3B 3=A 3A 4…. (1)若∠A 4=9°,则∠BAA 4的度数为 ; (2)若∠BAA 4=α,则∠B n ﹣1A n A n ﹣1的度数为 ; (3)过A 做AC ∥A 3B 2,若∠BAC =100°,求∠B 3A 4A 3的度数.参考答案一.选择题1.解:A、不是轴对称图形,故此选项错误;B、不是轴对称图形,故此选项错误;C、是轴对称图形,故此选项正确;D、不是轴对称图形,故此选项错误;故选:C.2.解:∵BE=BA,∴∠BAE=∠BEA,∴α=180°﹣2∠BAE,①∵CD=CA,∴∠CAD=∠CDA,∴β=180°﹣2∠CAD,②①+②得:α+β=360°﹣2(∠BAE+∠CAD)∴α+β=360°﹣2[(∠BAD+∠DAE)+(∠DAE+∠CAE)] =360°﹣2[(∠BAD+∠DAE+∠CAD)+∠DAE]=360°﹣2(∠BAC+∠DAE),∵∠BAC=180°﹣(α+β),∴α+β=360°﹣2[180°﹣(α+β)+∠DAE]∴α+β=2∠DAE,∴∠DAE=(α+β),故选:A.3.解:∵△ABC是等腰三角形,底边BC=5,周长为21,∴AC=AB=8,又∵DE是AB的垂直平分线,∴AE=BE,∴△BEC的周长=BE+CE+CB=AE+CE+BC=AC+CB=13,∴△BEC的周长为13.故选:A.4.解:点A(4,﹣2)关于x轴的对称点为(4,2).故选:A.5.解:(1)若等腰三角形一个底角为80°,顶角为180°﹣80°﹣80°=20°;(2)等腰三角形的顶角为80°.因此这个等腰三角形的顶角的度数为20°或80°.故选:D.6.解:当40°的角为等腰三角形的顶角时,底角的度数==70°;当40°的角为等腰三角形的底角时,其底角为40°,故它的底角的度数是70°或40°.故选:D.7.解:如图:∴最多画9条,故选:C.8.解:∵∠ACB=90°,AD⊥AB,∠A=60°,∴∠ACD=∠B=30°,∴AC=,AD=AC,∴AD=AB;故A正确;∵CE是△ABC的中线,∴S△BCE =S△ACE,故B正确,∵CE=AE=BE=AB,∴AC、BC的垂直平分线都经过E,故C正确;∴△ACE和△BCE是等腰三角形,故D错误;故选:D.9.解:延长AB交直线b于E,∵a∥b,∴∠3=∠1=50°,∴∠ABC=∠2+∠3=20°+50°=70°,∵CA=CB,∴∠BAC=∠ABC=70°,∴∠C=180°﹣70°﹣70°=40°,故选:C.10.解:由作图可知,CE=CD,∵OE=OD,∴CO⊥ED(等腰三角形的三线合一),∴∠AOB=90°.故选:D.11.解:∵DE垂直平分BC,∴BD=DC,∴∠BDE=∠CDE=64°,∴∠ADB=180°﹣64°﹣64°=52°,∵∠A=28°,∴∠ABD=180°﹣28°﹣52°=100°.故选:A.12.解:∵CD=DE,∴∠DEC=∠C=75°,∴∠D=180°﹣∠C﹣∠DEC=180°﹣75°﹣75°=30°,∵AB∥CD,∴∠A=∠D=30°;故选:B.二.填空题(共4小题)13.解:∵点M(a,b)与点N(3,﹣1)关于x轴对称,∴a=3,b=1,∴b a=1,故答案为:1.14.解:如图(1)顶角是钝角时,∵等腰三角形腰上的高与底边的夹角为37°,∴∠OCB=37°,∵OC⊥OB,∴∠ABC=90°﹣37°=53°,∴∠BAC=180°﹣53°﹣53°=74°,即△ABC为锐角三角形,顶角是钝角这种情况不成立;(2)顶角是锐角时,∠B=90°﹣37°=53°,∠A=180°﹣2×53°=74°.因此,顶角为74°.故答案为:74.15.解:∵在△ABC中,AB=AC,∠A=120°,∴∠C=∠B=(180°﹣∠A)=30°,连接AN,AM,∵AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,∴BM=AM,CN=AN,∴∠MAB=∠B=30°,∠C=∠NAC=30°,∴∠AMN=∠B+∠MAB=60°,∠ANM=∠C+∠NAC=60°,∴AM=AN,∴△AMN是等边三角形,∵MN=2,∴AN=2=CN,在Rt△NFC中,∠C=30°,∠NFC=90°,CN=2,∴NF=CN=1,故答案为:1.16.解:∵BC的垂直平分线分别交AB、BC于点D和点E,∴CD=BD,∵∠B=25°,∴∠DCB=∠B=25°.∵∠ADC是△BCD的外角,∴∠ADC=∠B+∠DCB=25°+25°=50°.∵AC=DC,∴∠CAD=∠ADC=50°,∴∠ACD=180°﹣∠CAD﹣∠ADC=180°﹣50°﹣50°=80°.故答案为:80°.三.解答题(共4小题)17.(1)证明:∵∠AED=∠ABC,∠AED=∠ABE+∠EAB,∠ABC=∠ABE+∠DBC,∵AE=BE,∴∠EAB=∠ABE,∴∠DBC=∠ABE,∴BD平分∠ABC;(2)设∠EAD=x,则∠AED=4x,∵∠AED=∠ABE+∠EAB,∠EAB=∠ABE,BD平分∠ABC,∴∠BAE=2x,∠ABC=4x,∴∠BAC=3x,∵AB=CB,∴∠BAC=∠C,∴∠C=3x,∵∠ABC+∠BAC+∠C﹣180°,∴4x+3x+3x=180°,解得,x=18°,∴∠C=3x=54°,即∠C的度数是54°.18.解:截取DE=BD,连接AE,如右图所示,∵DC=AB+BD,BD=DE,∴AB=CE,∵AD⊥BE,∴∠ADB=∠ADE=90°,在△ADB和△ADE中,,∴△ADB≌△ADE(SAS),∴AB=AE,∠B=∠AED,∴AE=CE,∴∠EAC=∠C,∵∠C=26°,∠AED=∠EAC+∠C,∴∠AED=52°,∴∠B=52°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣52°﹣26°=102°,即∠BAC的度数是102°.19.解:(1)如图所示,△A1B1C1即为所求;A 1(﹣1,﹣4)、B1(﹣5,﹣4)、C1(﹣4,﹣1);(2)△ABC的面积是×4×3=6,故答案为:6;(3)∵点P(a+1,b﹣1)与点C(4,﹣1)关于x轴对称,∴a+1=4、b﹣1=1,解得:a=3、b=2,故答案为:3、2.20.解:(1)∵AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4….,∴∠B 2A 3A 2=2∠A 4=18°, ∴∠B 1A 2A 1=2∠B 2A 3A 2=36°, ∴∠BAA 4=∠BA 1A =2∠B 1A 2A 1=72°;(2)∵AB =A 1B ,∴∠BAA 4=BA 1A =α, ∵A 1B 1=A 1A 2,A 2B 2=A 2A 3,A 3B 3=A 3A 4…. ∴∠B 1A 2A 1=∠BA 1A =α; 同理可得,∠B 2A 3A 2=α,∠B 3A 4A 3=α, 以此类推,∠B n ﹣1A n A n ﹣1=,故答案为:72°,; (3)设∠B 3A 4A 3=x °, ∵A 3B 3=A 3A 4,∴∠A 3B 3A 4=∠A 4,∴∠B 2A 3A 2=2x °,同理,∠BAA 4=8x °, ∵AC ∥A 3B 2,∴∠A 4AC =∠A 4,∴8x +2x =100,∴x =10,∴∠B 3A 4A 3的度数为10°.。
轴对称练习题及答案

轴对称练习题及答案一、选择题1. 以下哪个图形是轴对称图形?A. 圆形B. 三角形C. 正方形D. 五边形2. 轴对称图形的对称轴与图形的对称点之间的关系是:A. 垂直B. 平行C. 相交D. 重合3. 一个轴对称图形的对称点到对称轴的距离是:A. 相等B. 不相等C. 有时相等有时不相等D. 无法确定4. 如果一个图形关于x轴对称,那么它的对称点的坐标关系是:A. (x,y)和(x,-y)B. (x,y)和(-x,y)C. (x,y)和(-x,-y)D. (x,y)和(y,x)5. 一个点关于y轴的对称点的坐标是:A. (-x,y)B. (x,-y)C. (-y,x)D. (y,-x)二、填空题1. 轴对称图形的对称轴是图形中所有对称点的________。
2. 如果一个图形关于y轴对称,那么它的对称点的坐标关系是(x,y)和________。
3. 一个图形关于原点对称,那么它的对称点的坐标关系是(x,y)和________。
三、解答题1. 已知点A(3,4),求点A关于x轴的对称点的坐标。
2. 已知点B(-2,-3),求点B关于y轴的对称点的坐标。
3. 已知点C(1,-1),求点C关于原点的对称点的坐标。
四、判断题1. 所有矩形都是轴对称图形。
()2. 所有等腰三角形都是轴对称图形。
()3. 所有等边三角形都是轴对称图形。
()4. 所有平行四边形都是轴对称图形。
()五、综合题1. 给出一个等腰梯形的上底长为4cm,下底长为8cm,高为3cm,求等腰梯形的对称轴。
2. 如果一个矩形的长为10cm,宽为6cm,求矩形关于x轴对称后,新的矩形的长和宽。
3. 已知一个正方形的边长为5cm,求正方形关于y轴对称后,新正方形的边长。
答案:一、选择题1. A2. D3. A4. A5. A二、填空题1. 连线中点2. (-x,y)3. (-x,-y)三、解答题1. 点A关于x轴的对称点的坐标为(3,-4)。
轴对称图形练习题(带答案)

轴对称图形一、选择题1.下列命题中:①两个全等三角形合在一起是一个轴对称图形;②等腰三角形的对称轴是底边上的中线;③等边三角形一边上的高就是这边的垂直平分线;④一条线段可以看着是以它的垂直平分线为对称轴的轴对称图形. 正确的说法有( )个 A .1个 B .2个 C .3个 D .4个 2.下列图形中:①平行四边形;②有一个角是30°的直角三角形;③长方形;④等腰三角形. 其中是轴对称图形有( )个 A .1个 B .2个 C .3个 D .4个 3.已知∠AOB =30°,点P 在∠AOB 的内部,P 1与P 关于OA 对称,P 2与P 关于OB 对称,则△P 1OP 2是 ( )A .含30°角的直角三角形;B .顶角是30的等腰三角形;C .等边三角形D .等腰直角三角形.4.如图:等边三角形ABC 中,BD =CE ,AD 与BE 相交于点P ,则 ∠APE 的度数是 ( ) A .45° B .55° C .60° D .75° 5. 等腰梯形两底长为4cm 和10cm ,面积为21cm 2,则 这个梯形较小的底角是( )度. A .45° B .30° C .60° D .90° 6.已知点P 在线段AB 的中垂线上,点Q 在线段AB 的中垂线外,则 ( ) A .PA+PB >QA+QB B .PA+PB <QA+QB D .PA+PB =QA+QB D .不能确定7.已知△ABC 与△A 1B 1C 1关于直线MN 对称,且BC 与B 1C 1交与直线MN 上一点O , 则 ( ) A .点O 是BC 的中点 B .点O 是B 1C 1的中点 C .线段OA 与OA 1关于直线MN 对称 D .以上都不对 8.如图:已知∠AOP=∠BOP=15°,PC ∥OA ,PD ⊥OA ,若PC=4,则PD=( ) A .4 B .3 C .2 D .19.∠AOB 的平分线上一点P 到OA 的距离为5,Q 是OB 上任一点,则 ( )A .PQ >5B .PQ≥5C .PQ <5D .PQ≤510.等腰三角形的周长为15cm ,其中一边长为3cm .则该等腰三角形的底长为 ( ) A .3cm 或5cm B .3cm 或7cm C .3cm D .5cm 二.填空题11.线段轴是对称图形,它有_______条对称轴. 12.等腰△ABC 中,若∠A=30°,则∠B=________.13.在Rt △ABC 中,∠C=90°,AD 平分∠BAC 交BC 于D ,若CD=4,则点D 到AB 的距离是__________. 14.等腰△ABC 中,AB=AC=10,∠A=30°,则腰AB 上的高等于___________.AP A ECBD15.如图:等腰梯形ABCD 中,AD ∥BC ,AB=6,AD=5,BC=8,且AB ∥DE ,则△DEC 的周长是____________. 16.等腰梯形的腰长为2,上、下底之和为10且有一底角为60°,则它的两底长分别为____________.17.若D 为△ABC 的边BC 上一点,且AD=BD ,AB=AC=CD , 则∠BAC=____________. 18.△ABC 中,AB 、AC 的垂直平分线分别交BC 于点E 、F ,若∠BAC=115°,则 ∠EAF=___________. 三.解答题19.如图:已知∠AOB 和C 、D 两点,求作一点P ,使PC=PD ,且P 到∠AOB 两边的距离相等.20.如图:AD 为△ABC 的高,∠B=2∠C ,用轴对称图形说明:CD=AB+BD .21.有一本书折了其中一页的一角,如图:测得AD=30cm,BE=20cm , ∠BEG=60°,求折痕EF 的长.22.如图:△ABC 中,AB=AC=5,AB 的垂直平分线DE 交AB 、AC 于E 、D ,① 若△BCD 的周长为8,求BC 的长;② 若BC=4,求△BCD 的周长.23.等边△ABC 中,点P 在△ABC 内,点Q 在△ABC 外,且∠ABP=∠ACQ ,BP=CQ ,问 △APQ 是什么形状的三角形?试说明你的结论.。
中考数学复习《轴对称》专项练习题-带含有答案
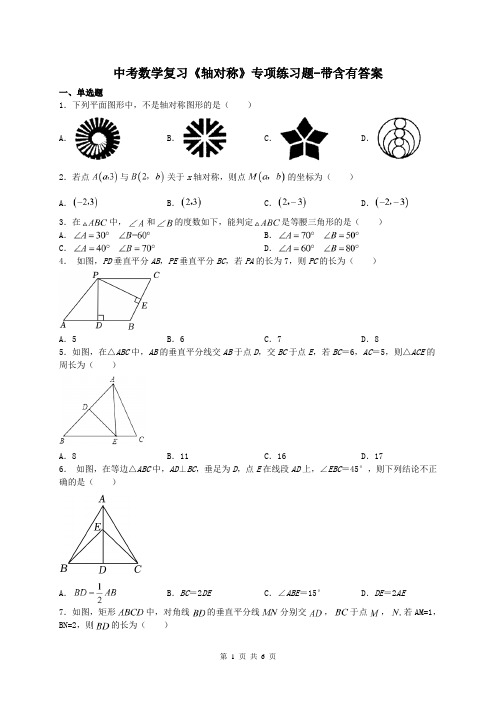
中考数学复习《轴对称》专项练习题-带含有答案一、单选题1.下列平面图形中,不是轴对称图形的是()A.B.C.D.2.若点与关于x轴对称,则点的坐标为()A.B.C.D.3.在中,和的度数如下,能判定是等腰三角形的是()A.B.C.D.4.如图,PD垂直平分AB,PE垂直平分BC,若PA的长为7,则PC的长为()A.5 B.6 C.7 D.85.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若BC=6,AC=5,则△ACE的周长为()A.8 B.11 C.16 D.176.如图,在等边△ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则下列结论不正确的是()A.B.BC=2DE C.∠ABE=15°D.DE=2AE7.如图,矩形中,对角线的垂直平分线分别交,于点,若AM=1,BN=2,则的长为()A.B.C.D.8.如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM、MC下列结论:①DF=DN;②ABE≌△MBN;③△CMN 是等腰三角形;④AE=CN;,其中正确的结论个数是()A.1个B.2个C.3个D.4个二、填空题9.如图,在△ABC中,AB=AC,AD⊥BC于点D,若BC=6,则CD=.10.已知等腰三角形ABC,其中两边,满足,则ABC的周长为.11.在中,点D为斜边上的一点,若为等腰三角形,那么的度数为.12.如图,在中AB=AC,∠A=120°,AB的垂直平分线分别交,于D,E,BE=3,则的长为.13.如图,在中,∠ACB=90°,∠A=30°,将绕点C逆时针旋转得到,点M是的中点,点N是的中点,连接,若,则线段的最大值是.三、解答题14.如图,在正方形网格上的一个△ABC.(其中点A. B. C均在网格上)①作△ABC关于直线MN的轴对称图形△A′B′C′;②以P点为一个顶点作一个与△ABC全等的△EPF(规定点P与点B对应,另两顶点都在图中网格交点处).③在MN上画出点Q,使得QA+QC最小。
轴对称图形的练习题

轴对称图形的练习题轴对称图形的练习题轴对称图形是数学中一个有趣且常见的概念。
它们在几何形状的研究中起着重要的作用。
通过练习轴对称图形的题目,我们可以更好地理解轴对称性质以及如何判断一个图形是否具有轴对称性。
本文将给出一些有趣的练习题,帮助读者巩固对轴对称图形的理解。
练习题1:判断轴对称图形首先,让我们来判断一些常见的图形是否具有轴对称性。
请仔细观察下面的图形,并在心中判断它们是否具有轴对称性。
然后,将你的答案写下来。
1. 一个圆2. 一个正方形3. 一个长方形4. 一个等边三角形5. 一个五角星答案:1. 一个圆:具有轴对称性。
无论从哪个方向旋转180度,都可以得到与原图形完全相同的图形。
2. 一个正方形:具有轴对称性。
以正方形的中心为轴,将正方形旋转180度,可以得到与原图形完全相同的图形。
3. 一个长方形:不具有轴对称性。
无论从哪个方向旋转180度,都无法得到与原图形完全相同的图形。
4. 一个等边三角形:具有轴对称性。
以三角形的中线为轴,将三角形旋转180度,可以得到与原图形完全相同的图形。
5. 一个五角星:不具有轴对称性。
无论从哪个方向旋转180度,都无法得到与原图形完全相同的图形。
练习题2:找出轴对称图形的轴线现在,让我们来找出一些具有轴对称性的图形的轴线。
请仔细观察下面的图形,并在心中想象它们的轴线。
然后,将你的答案写下来。
1. 一个心形2. 一个蝴蝶形状3. 一个字母“X”4. 一个字母“H”5. 一个字母“O”答案:1. 一个心形:具有轴对称性。
心形的轴线位于心形的中心,将心形沿轴线旋转180度,可以得到与原图形完全相同的图形。
2. 一个蝴蝶形状:具有轴对称性。
蝴蝶形状的轴线位于蝴蝶的中心,将蝴蝶形状沿轴线旋转180度,可以得到与原图形完全相同的图形。
3. 一个字母“X”:具有轴对称性。
字母“X”的轴线位于字母“X”的中心,将字母“X”沿轴线旋转180度,可以得到与原图形完全相同的图形。
轴对称练习题

轴对称练习题Standardization of sany group #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#ED CABI轴对称练习题一、选择题1.下列说法错误的是 ( )A .关于某条直线对称的两个三角形一定全等;B .轴对称图形至少有一条对称轴C .全等三角形一定能关于某条直线对称;D .角是关于它的平分线对称的图形 2.如图,其中是轴对称图形的是( )3.如图所示的图案中,是轴对称图形且有两条对称轴的是( )二、填空题4.把一个图形沿某一条直线_________,如果它能够与另一个图形________,•那么就说这两个图形关于这条直线____________.5.如果一个图形沿某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做__________. 6.观察图中的两个图案,是轴对称图形的是__________,它有________条对称轴.7.如图,△ABC 与△AED 关于直线1对称,若AB=2cm ,∠C=95°,则AE=____,•∠D=___度.8.坐标平面内,点A 和B 关于x 轴对称,若点A 到x轴的距离是3cm ,则点B到x•轴的距离是__________.三、解答题9.上图中的图形都是轴对称图形,请你试着画出它们的对称轴.10.如图,△ABC与△ADE关于直线MN对称.BC与DE的交点F在直线MN上.•①指出两个三角形中的对称点;②指出图中相等的线段和角;③图中还有对称的三角形吗EDCABMNF四、探究题11.如图,把一张纸片对折后,用笔尖在纸上扎出图(3)所示的图案,•将纸打开后铺平,观察你所得的图案.位于折痕两侧的部分有什么关系•与同伴交流你的想法.。
轴对称图形专题练习含答案

轴对称图形专题练习练习一一、填空题1、如果一个图形沿着一条直线折叠,直线两旁的部分(),这个图形就叫做(),这条直线就是它的()2、把一个图形沿着某一条直线折叠,如果它能够与()重合,那么就说这两个图形关于这条直线对称,这条直线叫做()3、经过线段中点并且()这条线段的直线,叫做这条线段的()二、选择题1、下面所示的交通标志,是轴对称图形的是()A、B、C、D、2、正方形,长方形,三角形,梯形,平行四边形中,一定是轴对称图形的有()A、5个B、4个C、3个D、2个3、下列说法中,不正确的是()A、等边三角形是轴对称图形B、若两个图形的对应点的连线都被同一条直线垂直平分,则这两个图形关于这条直线对称C、直线MN是线段AB的垂直平分线,若点P使PA=PB,则点P在MN上,若PA≠PB,则P不在MN上D、等腰三角形的对称轴是它的中线三、解决问题如图,BD垂直平分线段AC,AE⊥BC,垂足为E,AE交BD于P,PE=3cm,求点P 到AB的距离练习二一、选择题1、下列说法错误的是()A、关于某直线对称的两个图形一定能完全重合B、全等的两个三角形一定关于某直线对称C、轴对称图形的对称轴至少有一条D、线段是轴对称图形2、轴对称图形的对称轴是()A、直线B、线段C、射线D、以上都有可能3、下面各组点关于y轴对称的是()A、(0,10)与(0,-10)B、(-3,-2)与(3,-2)C、(-3,-2)与(3,2)D、(-3,-2)与(-3,2)二、作图题1、如图所示,作出△ABC关于直线l的对称△A'B'C'。
2、如图,已知点M、N和∠AOB,求作一点P,使P到点M、N的距离相等,且到∠AOB的两边的距离相等AMN参考答案练习一一、填空题1、能够互相重合,轴对称图形,对称轴2、另一个图形,对称轴3、垂直于,垂直平分线二、选择题1、D2、D3、D三、解决问题∵BD垂直平分线段AC∴BD为AC的中垂线∴AB=AC过点P做PF⊥AB,垂足为F。
轴对称图形及性质专项练习30题(有答案)ok
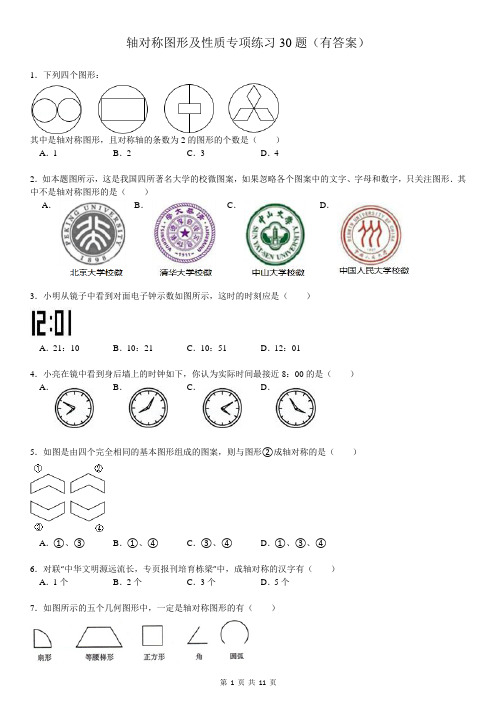
25.如图,点P在∠AOB内,点M,N分别是点P关于AO,BO的对称点,若△PEF的周长是30cm,求MN的长.
26.如图,△ABC和△A′B′C′关于直线m对称.
轴对称图形及性质专项练习30题(有答案)
1.下列四个图形:
其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
A.
1
B.
2
C.
3
D.
4
2.如本题图所示,这是我国四所著名大学的校微图案,如果忽略各个图案中的文字、字母和数字,只关注图形.其中不是轴对称图形的是( )
A.
B.
C.
D.
3.小明从镜子中看到对面电子钟示数如图所示,这时的时刻应是( )
∴对称轴的条数为2的图形的个数是3;
故选:C
2.解:根据轴对称图形的概念可得:A、B和C选项中的图案是轴对称图形,D选项中的图案不是轴对称图形,
故选D
3.解:根据镜面对称的性质,题中所显示的时刻与10:51成轴对称,
所以此时实际时刻为10:51.
故选C
4.解:根据平面镜成像原理可知,镜中的像与原图象之间实际上只是进行了左右对换,由轴对称知识可知,只要将其进行左可翻折,即可得到原图象,实际时间为8点的时针关于过12时、6时的直线的对称点是4点,那么8点的时钟在镜子中看来应该是4点的样子,则应该在C和D选项中选择,D更接近8点.
A.
2种
B.
3种
C.
4种
D.
5种
13.下列说法错误的是( )
A.
线段是轴对称图形,它的对称轴是线段的垂直平分线
轴对称(练习题)

轴对称(练习题)轴对称(练习题)一、填空题1.下列图形中,是轴对称图形的为()2.在下列四个图案中既是轴对称图形,又是中心对称图形的是()3.点P(1,2)关于y轴对称点的坐标是().A.(-1,2) B.(1,-2) C.(1,2) D.(-1,-2)4.下列图形中,既是轴对称图形,又是中心对称图形的个数是()①等边三角形;②矩形;③等腰梯形;④菱形;⑤正八边形;⑥圆.A.2 B.3 C.4 D.55.若等腰三角形的周长为26cm,一边为11cm,则腰长为()A.11cmB.7.5cm C.11cm 或7.5cm D.以上都不对6.等腰三角形的两边分别为6,13,则它的周长为()A.25 B.25或32 C.32 D.197.下列命题中,真命题的是( )A.相等的两个角是对顶角B.若a>b,则a>bC.两条直线被第三条直线所截,内错角相等D.等腰三角形的两个底角相等8.墙上有一面镜子,镜子对面的墙上有一个数字式电子钟。
如果在镜子里看到该电子钟的时间显示如图所示,那么它的实际时间是()A.12∶51 B.15∶21 C.15∶51 D.12∶219.如图,直线1表示石家庄的太平河,点P表示朱河村,点Q表示黄庄村,欲在太平河1上修建一个水泵站(记为点M),分别向两村供水,现有如下四种修建水泵站供水管道的方案,图中实线表示修建的管道,则修建的管道最短的方案是()10.如图,在△ABC内有一点D,且DA=DB=DC,若∠DAB=20°,∠DAC=30°,则∠BDC的度数为( )A.100° B.80° C.70° D.50°11.等腰三角形中有一个内角等于40°,其余两个内角的度数为( )A.40°,100°B.70°,70°C.40°,100°或70°,70°D.60°,80°12.如图,在△ABC中,AB=AC,AE=BE,∠BAE=40°,且AE=AF,则∠FEC等于()A.10° B.15° C.20° D.25°13.将△ABC三个顶点横坐标都乘以-1,纵坐标不变,则所得图形与原图形的关系是A、关于x轴对称B、关于y轴对称C、关于原点对称D、不存在对称关系14.如图,△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,则∠BDC的度数为()A.72°B.36°C.60°D.82°15.已知点P关于x轴的对称点为(a,-2),关于y轴的对称点为(1,b),那么点P的坐标为()A. (a, -b)B.(b, -a)C. (-2,1)D. (-1,2)16.等腰三角形一腰上的高与另一腰的夹角是35°,则顶角的度数是()A.55° B.125° C.125°或55° D.35°或145°17.(2014•潍坊)如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD 先沿x轴翻折,再向左平移1个单位”为一次变换,如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为()A.(﹣2012,2)B.(﹣2012,﹣2)C.(﹣2013,﹣2)D.(﹣2013,2)18.如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下结论不成立的是()A.AD=BEB.AP=BQC.DE=DPD.PQ∥AE二、填空题19.已知一个等腰三角形两内角的度数之比1∶4,则这个三角形顶角为度20.若1|2|0ab-+-=,则以,a b为边长的等腰三角形的周长为___________.21.如图,在△ABC中,AB=AC,D、E分别是AB、AC的中点,M、N为BC上的点,连接DN、EM.若AB=10cm,BC=12cm,MN=6cm,则图中阴影部分的面积为_________cm2.22.如图,在等边△ABC中,AB=6,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM、MN,则BM+MN的最小值是 .23.点P(3,-5)关于x轴对称的点的坐标是.24.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB,若EC=1,则EF= 。
(完整版)小学三年级轴对称图形专题练习

小学三年级数学轴对称图形专项练习一、填空。
1、如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是(),折痕所在的直线叫做()。
2、圆的对称轴有()条,半圆形的对称轴有()条。
3、在对称图形中,对称轴两侧相对的点到对称轴的()相等。
4、()三角形有三条对称轴,()三角形有一条对称轴。
5、正方形有()条对称轴,长方形有()条对称轴,等腰梯形有()条对称轴。
6、如果把一个图形沿着一条直线折过来,直线两侧部分能够完全重合,那么这个图形就叫做___________,这条直线叫做________.7、对称轴_______连结两个对称点之间的线段.8、宋体的汉字“王”、“中”、“田”等都是轴对称图形,•请再写出三个这样的汉字:_________.9、长方形有_____条对称轴,正方形有_____条对称轴,圆有_____条对称轴.10、如图是一种常见的图案,这个图案有_____条对称轴,请在图上画出对称轴.11、右图是从镜中看到的一串数字,这串数字应为. 12、下列图形中是轴对称图形的在括号里画“√”。
二、选择题。
1、下列英文字母中,是轴对称图形的是()A、S B 、H C、P D、Q2、下列各种图形中,不是轴对称图形的是()3、下图是一些国家的国旗,其中是轴对称图形的有()A、4个B、3个C、2个D、1个4、下列图形中:角、线段、直角三角形、等边三角形、长方形,其中一定是轴对称图形的有()A、2个B、3个C、4个D、5个5、下列图形中,对称轴最多的是()。
A、等边三角形 B 、正方形 C 、圆 D、长方形6、下面不是轴对称图形的是()。
A、长方形B、平行四边形C、圆D、半圆7、要使大小两个圆有无数条对称轴,应采用第()种画法。
AB、c8、图中的图形中是常见的安全标记,其中是轴对称图形的是 ( )9、找出下面图形中是轴对称图形,并且有两条对称轴的是()A.B.C.D.三、操作题:1、下列图形是轴对称图形吗?如果是,分别画出它们的对称轴。
轴对称图形练习题及答案

轴对称图形练习题及答案轴对称图形练习题及答案在数学学科中,轴对称图形是一种非常重要的概念。
轴对称图形是指可以通过某条直线将图形分成两个完全相同的部分的图形。
轴对称图形不仅在几何学中有广泛的应用,也常常出现在生活中的各个方面。
下面,我们来看一些轴对称图形的练习题及答案。
练习题一:请画出下列图形的轴对称线,并判断图形是否具有轴对称性。
1. 正方形2. 长方形3. 五角星4. 圆形5. 三角形答案一:1. 正方形:具有四条轴对称线,分别是连接对角线的两条线和连接中点的两条线。
因此,正方形具有轴对称性。
2. 长方形:具有两条轴对称线,分别是连接对角线的线。
因此,长方形具有轴对称性。
3. 五角星:具有五条轴对称线,分别是连接对角线的线。
因此,五角星具有轴对称性。
4. 圆形:具有无数条轴对称线,因为圆形的任意直径都可以作为轴对称线。
因此,圆形具有轴对称性。
5. 三角形:具有零条或一条轴对称线。
如果三角形的三条边相等,则具有三条轴对称线,分别是连接各边中点的线。
如果三角形的三条边不相等,则没有轴对称线。
因此,三角形可能具有轴对称性,也可能不具有轴对称性。
练习题二:请找出下列图形的轴对称图形,并画出轴对称线。
1. 矩形2. 正五边形3. 椭圆4. 等腰梯形5. 菱形答案二:1. 矩形的轴对称图形是自身,因为矩形具有四条轴对称线,分别是连接对角线的两条线和连接中点的两条线。
2. 正五边形的轴对称图形是自身,因为正五边形具有五条轴对称线,分别是连接对角线的线。
3. 椭圆的轴对称图形是自身,因为椭圆具有无数条轴对称线,因为椭圆的任意直径都可以作为轴对称线。
4. 等腰梯形的轴对称图形是自身,因为等腰梯形具有一条轴对称线,即连接两个底边中点的线。
5. 菱形的轴对称图形是自身,因为菱形具有两条轴对称线,分别是连接对角线的两条线。
通过以上练习题,我们可以更好地理解和掌握轴对称图形的概念和性质。
轴对称图形在几何学中有着广泛的应用,例如在设计中常常使用轴对称图形来增加美感和平衡感。
