全等三角形2
专题02 全等三角形(专题详解)(解析版)

专题02 全等三角形专题详解专题02 全等三角形专题详解 (1)12.1 全等三角形 (2)知识框架 (2)一、基础知识点 (2)知识点1 全等形的概念及性质 (2)知识点2 全等形的定义和表示方法 (2)知识点3 全等三角形的性质与拓展 (2)知识点4 全等变换的保形性 (2)12.2三角形全等的判定 (3)知识框架 (3)一、基础知识点 (3)知识点1 全等三角形判定条件 (3)二、典型题型 (4)题型1 全等三角形的判定 (4)三、添加辅助线方法 (5)方法1 关于中点的辅助线 (5)方法2 作垂线构造全等求点的坐标 (12)方法3 截长补短法(往往需证2次全等) (14)12.3角平分线的性质 (17)知识框架 (17)一、基础知识点 (17)知识点1 角平分线的性质 (17)知识点2 角平分线的判定 (17)知识点3 三角形的内心和旁心 (17)二、典型题型 (17)题型1 角平分线的性质和定义的应用 (17)题型2 三角形内心的应用 (18)三、添加辅助线方法 (20)方法1 角平分线上的点向两边作垂线 (20)方法2 过边上的点向两边作垂线 (22)方法3 过平分线上的点作一条边平行线构造等腰三角形 (24)方法4 利用角平分线的性质,在角两边截长补短 (25)12.1 全等三角形知识框架一、基础知识点知识点1 全等形的概念及性质1)全等形:能够完全重合的两个图形2)全等形的性质:①形状相同;②大小相同注:①全等图形与其所在的位置无关(只要通过平移、旋转、翻折后能够使两个图形完成重合即可)。
对称图形要求更苛刻些。
②因两图形完全相等,故图形所有对应条件都相同(例:周长、面积、对应角角度等皆相等)知识点2 全等形的定义和表示方法1)全等三角形:能够完全重合的三角形(长得完全一样的三角形)2)表示方法:①△ABC≌△DEF(读作:三角形ABC全等于三角形DEF)②顶点需要一一对应(即长得一样的在描述中至于同等地位)③从书写中,我们根据一一对应的关系,可得:a.点A与点D为对应顶点,点B与点E为对应顶点,点C与点F为对应顶点;b.∠A与∠D为对应角,∠B与∠E为对应角,∠C与∠F为对应角;c.AB与DE为对应边,AC与DF为对应边,BC与EF为对应边。
2022年人教版八年级上册数学第十二章全等三角形第2节 第3课时判定三角形全等ASA,AAS)

基基础础巩巩固固
能力提升
核心素养
-10-
第3课时 利用两角一边判定三角形全等(ASA,AAS)
8.如图,课间小明拿着老师的等腰三角板玩,不小心掉到两张 凳子之间(凳子与地面垂直).已知DC=a,CE=b,则两张凳子 的高度之和为 a+b .
基基础础巩巩固固
能力提升
核心素养
-11-
第3课时 利用两角一边判定三角形全等(ASA,AAS)
∴△ABC≌△DCB(ASA),∴AB=DC.
基基础础巩巩固固
能力提升
核心素养
-5-
第3课时 利用两角一边判定三角形全等(ASA,AAS)
知识点2 三角形全等的判定方法(AAS) 4.如图,在△ABC中,∠C=90°,D是AB上的一点,DM⊥AB,且DM =AC,过点M作ME∥BC交AB于点E,则△ACB≌△MDE , 判定依据是 AAS(答案不唯一) .(用字母表示)
-8-
第3课时 利用两角一边判定三角形全等(ASA,AAS)
解:∵AB∥DE,∴∠ABC=∠DEF.
∠ABC=∠DEF, 在△ABC 和△DEF 中, ∠A=∠D,
AC=DF,
∴△ABC≌△DEF(AAS),
∴BC=EF,∴EC=BF=3 m,
∴FC=10-3-3=4(m).
基基础础巩巩固固
能力提升
第3课时 利用两角一边判定三角形全 等(ASA,AAS)
第3课时 利用两角一边判定三角形全等(ASA,AAS)
限时:15分钟
知识点1 三角形全等的判定方法(ASA)
1.如图,已知∠1=∠2,则不一定能使△ABC≌△ABD的条件
是( B )
A.AC=AD
B.BC=BDC.∠C=∠来自 D.∠3=∠4第1题图
全等三角形 2

2. 能够重合的两个三角形 叫做全等三角形。 全等于 3.“全等”用符号“ ≌ ”来表示,读作 “ ” 4.全等三角形的 对应边 和 对应角 分别相等 5.书写全等式时要求把对应字母放在对应的位置上 6.哪些图形的 运动可以得到全等图形?
作业:
(1)课本第4页第1及第2题
(2)完成习题上的其他题目
4.请指出下列全等三角形中相等的边和相等角
1、 △ ABE ≌ △ ACF 2、 △ BCE ≌ △ CBF
3、 △ BOF ≌ △ COE
通过这节课的学习,你有 什么收获?
Hale Waihona Puke 课 堂 小 结1.能够重合的两个图形叫做 全等形 。
对应顶点 其中:互相重合的顶点叫做___ 对应边 互相重合的边叫做____ 对应角 互相重合的角叫做___
结论:平移,翻折,旋转前后 全等 的图形__。
惠高杨庆凡制作
A
能否记作 ∆ABC≌ ∆DEF?
D
B
F
C
E
应该记作:∆ABC≌ ∆DFE 原因:A与D、B与F、C与E对应。对应 顶点要写在对应位置上。
惠高杨庆凡制作
全等三角形的对应边相等 全等三角形的对应角相等
全等三角形的周长相等; 全等三角形的面积相等。
惠高杨庆凡制作
A
D
O B A
1、若△AOC≌△BOD,对应 边是 ,对应角是 ; C
2、若△ABD≌△ACD,对应边 是 ,对应角是 ;
B 3、若△ABC≌△CDA,对应 边是 ,对应角是 ; A
D
C D
从以上你能总结出找全等三角 形的对应边,对应角的规律吗?
B
C
寻找对应元素的规律
(1)有公共边的,公共边是对应边; (2)有公共角的,公共角是对应角; (3)有对顶角的,对顶角是对应角;
全等三角形判定(二)

例01.如图,已知:21∠=∠,43∠=∠. 求证:BCD ADC ∆≅∆.分析:ADC ∆与BCD ∆的对应边是DC 与DC ,AD 与BC ,AC 与BD . 对应角是1∠与2∠,ADC ∠与BCD ∠,DAC ∠与CBD ∠. 由条件已有一对应边DC 与DC ,和一对应角1∠和2∠相等,只需证明BCD ADC ∠=∠,就可以证明两三角形全等.证明:21∠=∠,43∠=∠(已知),∴ 4231∠+∠=∠+∠. 即BCD ADC ∠=∠ 在ADC ∆与BCD ∆中,⎪⎩⎪⎨⎧∠=∠=∠=∠)(12)()(已知公共边已证CD DC BCD ADC ∴ )(ASA BCD ADC ∆≅∆例02.已知:如图,21∠=∠,C B ∠=∠. 求证:COD BOE ∆≅∆.分析:欲证COD BOE ∆≅∆,已有两组条件,即C B ∠=∠和COD BOE ∠=∠. 因此,必须再具备一组对应边相等这一条件. BE 和CD 是在BOE ∆和COD ∆中,但直接证明CE BE =比较困难. 若证OE 和OD 相等或OB 和OC 相等,可以分别转化到证明AOD AOE ∆≅∆和AOC AOB ∆≅∆. 由已知条件,不难证出这两对三角形分别全等.证明:∵ 21∠=∠(已知),DOC EOB ∠=∠(对顶角相等), ∴ DOC EOB ∠+∠=∠+∠21. 即 AOC AOB ∠=∠. 在AOB ∆与AOC ∆中,⎪⎩⎪⎨⎧=∠=∠∠=∠)()()(公共边已证已知AO AO AOC AOB C B ∴ )(AAS AOC AOB ∆≅∆. ∴CO BO =在EOB ∆与COD ∆中⎪⎩⎪⎨⎧∠=∠=∠=∠)()()(已知已证对顶角相等C B CO BO COD EOB∴ COD BOE ∆≅∆(ASA )例03.如图,已知:AB 与CD 相交于点O ,且OD OC BD AC =,//,E 、F 为AB 上两点,且BF AE =.求证:DOF COE ∆≅∆.分析:欲证DOF COE ∆≅∆,已具备了两个条件,OD OC =和DOF COE ∠=∠. 所以只需证另一对角相等或证明OF OE =,即可. 证明另一对角相等,比较困难. 所以就证明OF OE =. 因为有BF AE =. 要证OF OE =只需证OB OA =即可. 由已知条件容易证得BOD AOC ∆≅∆,从而证明OB OA =.证明:∵BD AC //(已知)∴B A ∠=∠(两直线平行,内错角相等) 在AOC ∆与BOD ∆中,⎪⎩⎪⎨⎧=∠=∠∠=∠)()()(已知对顶角相等已证OD OC BOD AOC B A ∴)(AAS BOD AOC ∆≅∆∴BO AO =(全等三角形的对应边相等) ∵BF AE =(已知), ∴BF BO AE AO -=-. 即OF OE =在COE ∆与DOF ∆中,⎪⎩⎪⎨⎧=∠=∠=)()()(已证对顶角相等已知OE OE DOE COE DO CO ∴)(SAS DOF COE ∆≅∆例04.如图,已知:CE BD ACE ABD DAE BAC =∠=∠∠=∠,,. 求证:AE AD =.分析:欲证相等的两条线段AD ,AE 分别在ABD ∆和ACE ∆中,由于CE BD =,ACE ABD ∠=∠,所以只需再证CAE BAD ∠=∠即可,这由已知条件DAE BAC ∠=∠容易得到.证明:∵DAE BAC ∠=∠(已知) ∴DAC DAE DAC BAC ∠-∠=∠-∠ 即CAE BAD ∠=∠ 在ABD ∆与ACE ∆中,⎪⎩⎪⎨⎧∠=∠∠=∠=)()()(已证已知已知CAE BAD ACE ABD CE BD ∴)(AAS ACE ABD ∆≅∆∴AE AD =(全等三角形的对应边相等)例05.已知:(如图)21,∠=∠∠=∠D A . 求证:DO AD =分析:要证DO AD =,只要证DOC AOB ∆≅∆即可,在AOB ∆和DOC ∆中,已知D A ∠=∠,DOC AOB ∆=∆,只要再证一边对应相等即可,根据已知可得DCB ABC ∆≅∆,从而可证DC AB =,进而可证DO AO =,思路即为:DO AO =⇐DOC AOB ∆≅∆⇐DC AB =⇐DCB ABC ∆≅∆⇐“AAS ”证明:在ABC ∆和DCB ∆中⎪⎩⎪⎨⎧=∠=∠∠=∠)()()(21公共边已知已知CB BC D A ∴)(AAS DCB ABC ∆≅∆∴DC AB =(全等三角形的对应边相等)在AOB ∆和DOC ∆中⎪⎩⎪⎨⎧=∠=∠∠=∠)()()(已证已知对顶角相等DC AB D A DOC AOB ∴ )(AAS DOC AOB ∆≅∆∴ DO AO =(全等三角形的对应边相等)例06.求证:三角形的一边的两端到这边的中线或中线的延长线的距离相等.分析:这是一道了题,必须先根据题意画出图形,再结合题意写出已知,求证,再证明.已知:AD 是ABC ∆的中线. 如图,且AD CF ⊥于F ,AD BE ⊥的延长线于E , 求证:CF BE =证明:∵AD 为ABC ∆的中线(已知) ∴ CD BD =(中线定义)∵ AD BE ⊥ AD CF ⊥(已知)∴ ︒=∠=∠90CFD BED (等于定义) 在BED ∆与CFD ∆中⎪⎩⎪⎨⎧=∠=∠∠=∠)()(21)(已证对顶角相等已知CD BD CFD BED ∴CFD BED ∆≅∆(AAS )∴CF BE =(全等三角形对应边相等)说明 本题还可利用面积相等来证明,提示,过A 作BC AN ⊥于N ,希同学们自己来证明.例07.已知:如图,BC AD CD AB //,//, 求证:CD AB =.分析:因为四边形,我只学过三角形的有关知识,因此只要连结四边形的对角线从而把四边形的总是转化为三角形的总是来解决.证明:连结AC∵BC AD CD AB //,//(已知)∴43,21∠=∠∠=∠(两直线平行内错角相等)在ABC ∆和CDA ∆中⎪⎩⎪⎨⎧∠=∠=∠=∠)(43)()(21已证公共边已知CA AC∴ )(ASA CDA ABC ∆≅∆∴CD AB =(全等三角形的对应边相等)例08.已知:如图,AO CO DO BO ==,求证:OF OE =证明:在BOC ∆和DOA ∆中⎪⎩⎪⎨⎧=∠=∠=)()()(已知对顶角相等已知OA OC DOA BOC DO BO ∴ )(SAS DOA BOC ∆≅∆∴ D B ∠=∠(全等三角形的对应角相等) 在BOE ∆和DOF ∆中⎪⎩⎪⎨⎧∠=∠=∠=∠)()()(对顶角相等已知已证DOF BOE DO BO D B ∴)(ASA DOF BOE ∆≅∆∴OF OE =(全等三角形的对应边相等)说明 找到题目中的隐性条件并加以应用是关键.例09.如图,在ABC ∆和DBC ∆中,43,21∠=∠∠=∠,P 是BC 上任意一点, 求证:PD PA =.证明:在ABC ∆和DBC ∆中,⎪⎩⎪⎨⎧∠=∠=∠=∠)(43)()(21已知公共边已知BC BC ∴ )(ASA DBC ABC ∆=∆∴ DB AB =(全等三角形对应边相等) 在ABP ∆和DBP ∆中,⎪⎩⎪⎨⎧=∠=∠=)()(21)(公共边已知已证BP BP DB AB ∴ )(SAS DBP ABP ∆≅∆∴ PD PA =(全等三角形对应边相等)说明:本题也可通过DBC ABC ∆≅∆,得到DC AC =,从而证DCP ACP ∆≅∆,得到PD PA =.选择题(1)已知ABC Rt ∆与C B A Rt '''∆,︒=∠90C ,︒='∠90C ,B A '∠=∠.B A AB ''=.那么下列结论正确的是( )(A )C A AC ''= (B )C B BC ''= (C )C B AC ''= (D )以上答案都不对(2)在ABC ∆和C B A '''∆,甲:B A AB ''=;乙:C B BC ''=;丙:C A AC ''=;丁:A A '∠=∠;戊:B B '∠=∠;己:C C '∠=∠,则不能保证ABC ∆≌C B A '''∆成立的条件为( )(A )丙、丁、己 (B )甲、丙、戊 (C )甲、乙、戊 (D )乙、戊、己 (3)如图,已知ABD ∆和ACE ∆均为等边三角形,那么ADC ∆≌ABE ∆的根据是( )(A )ASA (B )SAS(C )AAS (D )以上都不对(4)如图,C 是BE 上一点,CD AB =,D A ∠=∠,E BCA ∠=∠,那么( )(A )ECD B ∠=∠ (B )C 是BE 的中点 (C )CD AB //(D )以上结论都正确参考答案:(1)C (2)B (3)B (4)D填空题(1)如图,已知:21∠=∠,D C ∠=∠. 求证:AD AC =.证明:在ACB ∆与ADB ∆中,⎪⎩⎪⎨⎧=∠=∠∠=∠) _______()()(21AB D C 已知已知 ∴ACB ∆≌ADB ∆( ) ∴AD AC =(2)如图,已知:BC AB ⊥,DC AD ⊥,垂足分别为B ,D .21∠=∠. 求证:AD AB =.证明:在ABC ∆与ADC ∆中,⎪⎩⎪⎨⎧=∠=∠∠=∠) ()(21)(AC AC ADC ABC ∴ ABC ∆≌ADC ∆( ) ∴AD AB =( )(3)如图,已知:CE AE =,C A ∠=∠.求证:ADE ∆≌CEB ∆.证明:在AED ∆与CEB ∆中,⎪⎩⎪⎨⎧==∠=∠) _____(______)()(已知CE AE C A ∴ AED ∆≌CEB ∆(ASA )(4)如图,已知:C B ∠=∠,AD AE =.求证:AEC ∆≌ADB ∆.证明:在AEC ∆与ADB ∆中,⎪⎩⎪⎨⎧=∠=∠∠=∠) ()()(AE AE C B A A 已知 ∴AEC ∆≌ADB ∆( )参考答案:(1)AB ;公共边;AAS ;全等三角形的对应边相等(2)垂直定义;已知;公共边;AAS ;全等三角形的对应边相等. (3)已知:AED ∠;CEB ∠;对顶角相等 (4)公共角;已知;AAS证明题1.如图,已知,21∠=∠,DCB ABC ∠=∠. 求证:DC AB =.2.如图,已知:E D ∠=∠,AM EM CN DN ===. 求证:点B 是线段AC 的中点.3.如图,已知:21∠=∠,AE AD =. 求证:OC OB =.4.如图,已知:在ABC ∆中,AD 是BAC ∠的平分线,AB DE ⊥于E ,AC DF ⊥于C ,求证:AF AE =.5.如图,已知:E 在AC 上,21∠=∠,43∠=∠. 求证:DE BE =.6.如图,已知:BC AD //,21∠=∠,43∠=∠,直线DC 过E 点交AD 于D ,交BC 于C .求证:AB BC AD =+.7.求证:三角形一边的两个端点到这边上的中线的距离相等. 8.如图,已知:DE AB =,直线AE ,BD 相交于点C ,︒=∠+∠180D B ,DE AF //,交BD 于F .求证:CD CF =.9.如图,已知:AB 与CD 相交于点O ,O 是AB ,CD 的中点,过点O 引直线EF 分别与AD ,BC 相交于E 、F 两点.求证:BF AE =.参考答案:1.证:由DCB ABC =∠,21∠=∠,可得ACB DBC ∠=∠.易证ABC ∆≌DCB ∆,∴ DC AB =2.证:易证DNB ∆≌EMB ∆,∴ EB DB =,由此可证:EA DC =.因此,可证DCB ∆≌EAB ∆.∴BC AB =,∴B 是AC 的中点.3.易证ABE ∆≌ACD ∆,∴C B ∠=∠,AC AB =,又∵AE AD =,∴CE BD =.由此可证BOD ∆≌COE ∆,∴OC OB =4.︒=∠=∠90AFD AED ,FAD EAD ∠=∠,AD AD =,∴AFD AED ∆≅∆,∴AF AE =.5.∵ 21∠=∠,AC AC =,43∠=∠,∴ABC ∆≌ADC ∆,∴AD AB =,又∵21∠=∠,AE AE =,∴ADE ABE ∆≅∆,∴DE BE =6.在AB 上取一点F ,使BF BC =,又∵43∠=∠,EB EB =,∴EC B EFB ∆≅∆,∴C EFB ∠=∠,又∵BC AD //,由此可推出D EFA ∠=∠.可证AFE ADE ∆≅∆,∴AF AD =,∴BC AD AB +=.7.已知:如图,AD 为ABC ∆的中线,AD BF ⊥于F ,AD CE ⊥于E . 求证:CE BF =.证:︒=∠=∠90BFD CED ,BDF CDE ∠=∠,BD CD =,∴ BFD CED ∆≅∆,∴ CE BF =8.证:∵ DE AF //, ∴AFC D ∠=∠,又∵︒=∠+∠180AFB AFC ,︒=∠+∠180D B ,∴ AFB B ∠=∠∴ DE AF AB ==,∴ 可证ECD ACF ∆≅∆,∴CD CF =9.证:BO AO =,BOC AOD ∠=∠,CO DO =,∴B O C A O D ∆≅∆,∴B A ∠=∠.而BOF AOE ∠=∠,BO AO =,∴BOF AOE ∆≅∆,∴ BF AE =能力:1、如图1,已知:AD 平分∠BAC ,AB=AC ,连接BD ,CD ,并延长相交AC 、AB 于F 、E 点.则图形中有( )对全等三角形.A 、2B 、3C 、4D 、5答案:C.2、如图2,已知:∠1=∠2,AB=DC ,图中全等三角形的对数是( )A 、0B 、1C 、2D 、3答案:A3、如图3,已知:△ABC 中,DF=FE ,BD=CE ,AF ⊥BC 于F ,则此图中全等三角形共有( )A 、5对B 、4对C 、3对 D2对答案:C.1、如图4,已知:在△ABC 中,AD 是BC 边上的高,AD=BD ,DE=DC ,延长BE 交AC 于F ,求证:BF 是△ABC 中边上的高. 图1 A B B 、E F D C AD B O C 1 2 图2 图3 D FE C AF C D B E 图4提示:关键证明△ADC ≌△BFC2、如图5,已知:∠D=∠E ,DN=EM ,AM=CN ,求证:点B 是线段AC 的中点.提示:欲证点B 是线段AC 的中点,只需证AB =BC.选择AB 、BC 所在的两个三角形,然后证这两个三角形△AMB ≌△CNB.由条件可得△EMB ≌△DNB ,所以得到∠EMB =∠DNB ,MB =NB由此易证△AMB ≌△CNB.3、如图6,已知:AB=CD ,∠A=∠D.求证:∠ABC=∠DCB提示:欲证∠ABC=∠DCB ,选择这两个角所在的三角形,只需证△ABC ≌△DBC由条件可知△ADC ≌△DAB ,所以得到∠DAC =∠ADB ,BD =AC ,加之条件利用边角边公理可证△ABC ≌△DBC4、如图7,已知:在△ABC 中,∠ACB=090,AC=BC ,AE 是BC 边上的中线过C 作CF ⊥AE ,垂足为F ,过B 作BD ⊥BC 交CF 的延长线于点D.(1)求证:AE=CD.(2)AC=12cm ,求BD 的长.提示:欲证AE=CD ,只需证△ACE ≌△CBD 由条件可知∠CAE =∠BCD (同角的余角相等)加之其它两个条件易证得结论.由E 是BC 的中点,EC =BE又BD =EC ,BC =AC 知BD =6 cm5、如图8,已知:在△ABC 中,AB=AC ,∠A=90,BD 平分∠ABC 交AC 于D ,CE ⊥BD 交BD 的延长线于E ,求证:BD=2CE提示:本题的关键是从结论BD=2CE 出发,想到构造线段CF =2CE ,再证BD =CFA M N E C DB 图5 A D BC 图6 O E ┛ ┓ ┏D A CF 图7 B A E C D 图8 F。
全等三角形判定二边角边

全等三角形的定义和
02
性质
全等三角形的定义
01
两个三角形,如果它们的对应边 和对应角都相等,则这两个三角 形全等。
02
全等三角形是几何中一个重要的 概念,它在证明定理、解决几何 问题等方面有广泛应用。
全等三角形的性质
全等三角形的对应边 相等,对应角相等。
全等三角形的对应边 上的中线、高、角平 分线也相等。
定理证明
01
第四步,根据全等三角形的性质,由于$Delta ABD cong Delta A'B'D'$,所以$BD = B'D'$。
02
第五步,根据SAS全等定理,由于$AC = A'C'$,$CD = C'D'$,$angle ACD = angle A'C'D'$,所以$Delta ACD cong Delta A'C'D'$。
定理证明
第一步,由已知条件可知,$AB = A'B'$,$AC = A'C'$,$angle BAC = angle B'A'C'$。
第二步,根据SAS全等定理,作辅助线AD,使得$angle BAD = angle B'A'D'$,并 连接BD和CD。
第三步,根据SAS全等定理,由于$AB = A'B'$,$AD = A'D'$,$angle BAD = angle B'A'D'$,所以$Delta ABD cong Delta A'B'D'$。
全等三角形的周长、 面积、高、中线、角 平分线等都相等。
全等三角形(二)

练4-1.如图,在△ABC中,AC = BC,AD = CE,BE⊥CE于点E,AD⊥CE于点D.求证:∠ACB = 90 .
练4-2.已知:如图,BE⊥CD,BE = DE,BC = DA.求证:(1)△BEC≌△DEA; (2)DF⊥BC.
拓展题:
1.如图,点A在DE上,点F在AB上,且AC = CE,AB = 3,∠DAF =∠ACE =∠DCB.求DE的长.
练3-1.如图,AE⊥EC于E,AF⊥FB于F,小明想要利用HL判定△ AEC≌△ AFB,那么他需要添加的条件可以是____________.
练3-2.如图,AD⊥BC,AC = AB.若BD =13,那么BC = __________.
例4.如图,AD为△ABC的高,E为AC上一点,BE交AD于点F,且有BF = AC,FD = CD.求证:BE⊥AC.
全等三角形(二)
【知识点一】全等三角形的判定(二)
思考:小明不小心打碎一块三角形模具,他应该带哪块去商店配一个与原来一样的?
全等三角形判定3:
两角和它们的夹边分別相等的两个三角形全等.简写成“角边角”或“ASA” .
例. 中, B= E, C= F,BC=EF,求证: .
三角形全等的书写方法:五行法
思考:判定两个直角三角形全等的方法有哪些呢?
练习:判断下列直角三角形的全等判定方法是否正确,正确请写出原因。
(1)两条直角边对应相等. ( )
(2)斜边和一锐角对应相等. ( )
(3)斜边和一直角边对应相等. ( )
(4)两锐角相等. ( )
例3.如图,AC⊥BC,BD⊥AD,AC=BD.求证:△ABC≌△BAD.
八年级上册数学三角形全等证明之二次全等(含答案)
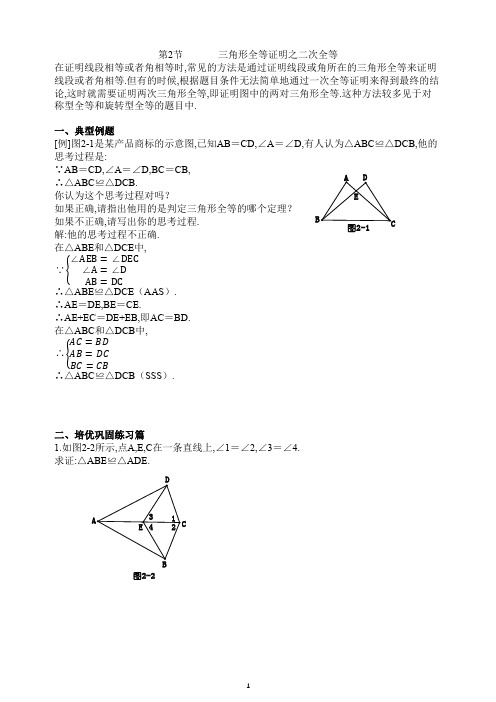
第2节 三角形全等证明之二次全等在证明线段相等或者角相等时,常见的方法是通过证明线段或角所在的三角形全等来证明线段或者角相等.但有的时候,根据题目条件无法简单地通过一次全等证明来得到最终的结论,这时就需要证明两次三角形全等,即证明图中的两对三角形全等.这种方法较多见于对称型全等和旋转型全等的题目中.一、典型例题[例]图2-1是某产品商标的示意图,已知AB =CD,∠A =∠D,有人认为△ABC ≌△DCB,他的思考过程是:∵AB =CD,∠A =∠D,BC =CB,∴△ABC ≌△DCB.你认为这个思考过程对吗?如果正确,请指出他用的是判定三角形全等的哪个定理?如果不正确,请写出你的思考过程.解:他的思考过程不正确.在△ABE 和△DCE 中,∵{∠AEB =∠DEC∠A =∠D AB =DC∴△ABE ≌△DCE (AAS ).∴AE =DE,BE =CE.∴AE+EC =DE+EB,即AC =BD.在△ABC 和△DCB 中,∴{AC =BDAB =DC BC =CB∴△ABC ≌△DCB (SSS ).二、培优巩固练习篇1.如图2-2所示,点A,E,C 在一条直线上,∠1=∠2,∠3=∠4.求证:△ABE ≌△ADE.图2-2图2-12.如图2-3所示,点A,E,F,C 在一条直线上,AE =CF,分别过点E,F 作DE ⊥ AC,BF ⊥AC,连接AB,CD,且AB ∥CD,连接BD 交AC 于点C.求证:△DEG ≌△BFG.3.如图2-4所示,AB =AC,DB =DC,F 是AD 延长线上的一点.求证:BF =CF.4.如图2-5所示,AE 是∠BAC 的角平分线,EB ⊥AB 于点B,EC ⊥AC 于点C,点D 是AE 上一点.求证:BD =CD.5.如图2-6所示,DE ⊥AC,BF ⊥AC,AD =BC,DE =BF.求证:AB ∥DC.图2-3C图2-4图2-5图2-66.如图2-7所示,点E,F 在BD 上,且AB =CD,BF =DE,AE =CF.求证:AO =CO.7.如图2-8所示,AB 之间有一条河.想要测量AB 的长,但无法过河接近点A,于是在AB 外任取一点D,在AB 的延长线上任取一点E,连接ED 和BD,并延长BD 到点G,使DG =DB,延长ED 到点F,使DF =DE,连接FG,并延长FG 到点H,使点H,D,A 在一条直线上,则HG =AB.试说明这种测量方法的原理.8.如图2-9所示,在Rt △ABC 和Rt △ADE 中,∠ABC =∠ADE =90°,BC 与DE 相交于点F,且AB =AD,AC =AE,连接CD,EB.求证:(1)∠CAD =∠EAB;(2)CF =EFDH图2-8图2-99.如图2-10所示,在等边△ABC 内取一点D,使DA =DB,在△ABC 外取一点E,使∠DBE =∠DBC,且BE =BA,则∠BED =_______°.10.如图2-11所示,∠BAC 是钝角,AB =AC,点D,E 分别在AB,AC 上,且CD =BE.试说明:∠ADC =∠AEB.一个同学的解法是这样的: 在△ACD 和△ABE 中, ∵{AB =AC BE =CD ∠BAE =∠CAD ∴△ABE ≌△ACD.∴∠ADC =∠AEB.这种解法遭到了其他同学的质疑.理由是错在不能用“SSA ”判定三角形全等.请你给出正确的解法.图2-10CB AC B答案解析1.证明:在△DEC和△BEC中,{∠1=∠2 EC=EC ∠3=∠4∴△DEC≌△BEC(ASA).∴DE=BE.∵∠3=∠4,∴∠DEA=∠BEA.在△ABE和△ADE中,{AE=AE∠AEB=∠AEDBE=DE∴△ABE≌△ADE(SAS).2.证明:∵DE⊥AC,BF⊥AC, ∴∠AFB=90°=∠CED. ∵AE=CF,∴AE+EF=CF+FE,即AF=CE.∵AB∥CD,∴∠A=∠C.在△ABF和△CDE中,{∠A=∠C AF=CE∠AFB=∠CED ∴△ABF≌△CDE(ASA).∴DE=BF.在△BFG和△DEG中,{∠BFG=∠DEG ∠BGF=∠DGE BF=DE∴△BFG≌△DEG(AAS).3.证明:在△ABD和△ACD中,{AB=AC BD=CD AD=AD∴△ABD≌△ACD(SSS).∴∠BAD=∠CAD.在△BAF和△CAF中,{AB=AC∠BAF=∠CAF AF=AF∴△BAF≌△CAF(SAS).∴BF=CF.4.证明:∵AE是∠BAC的角平分线, ∴∠CAE=∠BAE. ∵EB⊥AB,EC⊥AC, ∴∠ECA=∠EBA=90°.在△CAE和△BAE中,{∠CAE=∠BAE ∠ECA=∠EBA AE=AE∴△CAE≌△BAE(AAS).∴AC=AB.在△CAD和△BAD中,{AC=AB ∠CAD=∠BAD AD=AD∴△CAD≌△BAD(SAS).∴BD=CD.5.证明:∵DE ⊥AC,BF ⊥AC, ∴∠AED =∠CFB =90°, ∠AFB =∠CED =90°, 在Rt △ADE 和Rt △CBF 中,∵{AD =CB DE =BF ∴Rt △ADE ≌Rt △CBF (HL ).∴AE =CF.∴AE+EF =CF+FE,即AF =CE.在△AFB 和△CED 中,∵{AF =CE∠AFB =∠CED DE =BF∴△AFB ≌△CED (SAS ). ∴∠BAF =∠DCE.∴AB ∥DC.∴AO =CO.6.证明:∵BF =DE, ∴BF-EF =DE-FE,即BE =DF. 在△ABE 和△CDF 中, {AB =CDAE =CF BE =DF∴△ABE ≌△CDF (SSS ).∴∠B =∠D.在△AOB 和△COD 中,{∠AOB =∠COD∠B =∠D AB =CD∴△AOB ≌△COD (AAS )7.解:在△BED 和△GFD 中,{DB =DG∠BDE =∠GDF DE =DF∴△BED ≌△GFD (SAS ).∴∠EBD =∠FGD.∴∠ABD =∠HGD.在△ABD 和△HGD 中,{∠ABD =∠HGDBD =GD∠BDA =∠GDH∴△ABD ≌△HGD (ASA ).∴HG =AB.8.证明:(1)在Rt △ABC 和Rt △ADE 中,{AC =AE AB =AD ∴Rt △ABC ≌Rt △ADE (HL ).∴∠BAC =∠DAE.∴∠BAC-∠DAB =∠DAE-∠DAB,即∠CAD =∠EAB.(2)在△ACD 与△AEB 中, {AC =AE∠CAD =∠EAB AD =AB∴△ACD ≌△AEB (SAS ).∴CD =BE,∠ACD =∠AEB.∵Rt △ABC ≌Rt △ADE (HL ), ∴∠ACB =∠AED.∴∠ACB-∠ACD =∠AED-∠AEB,即∠DCF =∠BEF.又∵∠DFC =∠BFE, ∴△DFC ≌△BFE (AAS ).∴CF =EF.9.解:如图2所示,连接CD.∵△ABC是等边三角形, ∴AB=BC=CA.∵BE=BA,BA=BC, ∴BE=BC.在△BDC和△BDE中,{BD=BD∠DBE=∠DBC BE=BC∴△BDC≌△BDE(SAS). ∴∠BED=∠BCD.在△BCD和△ACD中,{BC=AC BD=AD CD=CD∴△BCD≌△ACD(SSS).∴∠BCD=∠ACD=30°.∴∠BED=30°.10.证明:因为∠BAC是钝角,故过点B,C分别作CA,BA的垂线,垂足分别为点F, G,如图3所示.在△ABF和△ACG中,{∠F=∠G=90°∠FAB=∠GACAC=AB∴△ABF≌△ACG(AAS).∴BF=CG.在Rt△BEF和Rt△CDG中,{BF=CGBE=CD∴Rt△BEF≌Rt△CDG(HL).∴∠ADC=∠AEBEDC BA。
数学人教版八年级上册12.2三角形全等的判定定理2(SAS).2 三角形全等的判定

A
A
B 图一 在图一中, ∠A 是AB和AC的夹角, 符合图一的条件,它可称为 “两边夹角”。
C
B
图二
C
符合图二的条件, 通常 说成“两边和其中一边的对角”
探索边角边
已知△ABC,画一个△A′B′C′使A B =A′B′,A C =A′ C ′, ∠A =∠A′。
画法: 1.画 ∠DA′ E= ∠A; ′ 2.在射线A D上截取A′ B′ =AB,在射线A′ E上截 取A ′C ′=AC; C C′ 3. 连接B ′C′.
补充题:
例1 如图AC与BD相交于点O, 已知OA=OC,OB=OD,说明 △AOB≌△COD的理由。 A B
O
D C C D
例2 如图,AC=BD, ∠CAB= ∠DBA,你能判断 BC=AD吗?说明理由。
A B 归纳:判定两条线段相等或二个角相等可以通 过从它们所在的两个三角形全等而得到。
课堂小结:
A B A′ B′ D
思考: ① △A′ B′ C′ 与 △ABC 全等吗?如何验正? 思考: ②这两个三角形全等是满足哪三个条件? 结论:两边及夹角对应相等的两个三角形全等
三角形全等判定方法2
两边和它们的夹角对应相等的两个三角形全
等。(可以简写成“边角边”或“ SAS ” )
用符号语言表达为:
A D
B
1
那么量出ED的长,就是A、B的 距离.为什么?【要求学生写出 理由即证明过程】
C
2
E
D
例2:点E、F在AC上,AD//BC,AD=CB,AE=CF
求证(1)△AFD≌△CEB
A 分析:证三角形全等的三个条件 边 AD = CB (已知) 角 ∠A=∠ 边 C AF = CE E F C D
全等三角形(2)

《数学思维与能力训练》辅导讲义姓名 辅导时间全 等 三 角 形 (2)【知识要点】1、能够完全重合的两个图形叫做全等形,两个三角形重合后,互相重合的顶点叫做对应顶点,互相重合的边叫做对应边,互相重合的角叫做对应角,全等用符号“≌”表示,全等三角形对应边相等,对应角相等。
判断两个三角形全等的定理有:① 边角边(SAS )② 角边角(ASA )③ 角角边(AAS )④ 边边边(SSS )⑤ 斜边直角边(HL )2、全等三角形的对应边、对应角、对应中线、对应角平分线、对应高等对应线段或角全都相等,所以可利用三角形全等证明某些等式成立,如线段相等、角相等等。
【拓展探究】[例题1]如图所示,在ΔABC 中,∠C = 90°,∠A = 30°,分别以AB 、AC 为边在ΔABC 外侧作正ΔABE 和正ΔACD ,DE 与AB 相交于F ,求证:EF = FDF A E B C D[例题2]如图所示,ΔABC 中,∠ACB = 90°,AD ⊥AB ,AD = AB ,BE ⊥DC ,AF ⊥AC ,求证:CF 平分∠ACB[例题3]如图所示,ΔABC 中,若AB = 6,AC = 4,求BC 边上的中线AD 长的范围DC A FB E A CD B〖小试牛刀〗1、如图所示,AD 、A 1D 1 分别是ΔABC 和ΔA 1B 1C 1 的中线,已知AB = A 1B 1,AC = A 1C 1,AD = A 1D 1,求证:ΔABC ≌ ΔA 1B 1C 12、如图所示,AB = AD ,BC = DC ,E 、F 在AC 上,AC 与BD 交于P 点,请找出图中共有多少对全等三角形,并简述全等的理由。
B DC A E P F A B CD3、如图所示,在∠AOB 的OA 边上取两点P 和S ,再在OB 边上取两点Q 和T ,使OQ = OP ,OT = OS ,PT 与QS 相交于点C ,求证:OC 平分∠AOB4、(1) 如图所示,A 、B 、C 三点在一直线上,分别以AB 、BC 为边在AC 同侧作等边ΔABD 和等边ΔBCE ,AE 交BD 于点F ,DC 交BE 于点G ,求证:AE = DC ,BF = BG(2) 如图所示,如果A 、B 、C 不在同一直线上,那么这时AE = DC ,BF = BG 是否仍然成立?如果成立,请加以证明;如果不成立,请说明理由。
三角形全等的判定 (2)

一、全等三角形
1.什么是全等三角形?一个三角形经过 哪些变化可以得到它的全等形?
能够完全重合的两个三角形叫做全等三角形。 一个三角形经过平移、翻折、旋转可以得到 它的全等形。
2:全等三角形有哪些性质?
(1)全等三角形的对应边相等、对应角相等。
(2)全等三角形的周长相等、面积相等。
(3)全等三角形的对应边上的对应中线、角平分线、 高线分别相等。
练习
6:如图,已知,AB∥DE,AB=DE,AF=DC。请问图中有那几对全
等三角形?请任选一对给予证明。
E
答: △ABC≌△DEF
A
F
B
证明:∵ AB∥DE
∴ ∠A=∠D
C
D
∵ AF=DC ∴ AF+FC=DC+FC
∴ AC=DF
在△ABC和△DEF中
AC=DF
∠A=∠D
AB=DE
∴ △ABC≌△DEF (SAS)
谢谢观赏
You made my day!
我们,还在路上……
∵BM是△ABC的角平分线,点P
在BM上,
A
ND
M
PF
∴PD=PE
B
E
C
(角平分线上的点到这个角的两边距离相等).
同理,PE=PF.
∴PD=PE=PF.
即点P到三边AB、BC、CA的距离相等
3.如图,已知△ABC的外角∠CBD和∠BCE的平 分线相交于点F,
求证:点F在∠DAE的平分线上.
证明:过点F作FG⊥AE于G,
E
证明:
A
∵ △ABC和△ECD都是等边三角形
∴ AC=BC DC=EC
∠BCA=∠DCE=60°
全等三角形的性质2

八年级数学暑期辅导全等三角形性质教学目标:1.理解全等形和全等三角形的概念,并能准确的表示全等三角形,找出对应边和对应角2.掌握全等形的三种变换:平移、翻折和旋转3.掌握三角形全等及其性质,能用符号正确地表示两个三角形全等,运用全等三角形的性质灵活解决相关问题4.学生通过观察、发现生活中的全等形和实际操作中获得全等三角形的体验在探索和运用全等三角形性质的过程中感受到数学的乐趣。
教学重难点:重点:全等三角形的概念和性质;难点:找全等三角形的对应边、对应角。
掌握几种常见的全等三角形类型教学过程:一、三角形相关知识点回顾知识点1.三角形的概念:1、由直线上的三条线段组成的图形叫三角形2、三角形的基本元素:三角形有条边个顶点个内角三角形的分类:按边可分为三角形和三角形,按角可分为三角形三角形三角形【注意:等边三角形属于特殊的三角形,锐角三角形和钝角三角形有时称为三角形】知识点2.三角形的性质:1、三角形的内角和是三角形的任意一个外角和它不相交两个内角的和三角形的一个外角任意一个和它不相邻的内角2、三角形任意两边之和第三边,任意两边之差第三边3、三角形具有性注意:1、三角形的外角是指三角形一边和另一边的组成的角,三角形的外角和是2、三角形三边关系定理是确定三条线段是否构成三角形和判断限度间不等关系的主要依据1、角平分线:三角形的三条角平分线都在三角形部且交于一点,这些是三角形的心它到得距离相等2、中线:三角形的三条中线都在三角形部,且交于一点3、高线:不同三角形的三条高线位置不同,锐角三角形三条高都连三角形直角三角形有一条高线在部,另两条河重合,钝角三角形有一条高线在三角形部,两条在三角形部4、中位线:连接三角形任意两边的线段叫做三角形的中位线。
定理:三角形的中位线第三边且等于第三边的【注意:三角形的平分线、中线、高线、中位线都是且都有条】二、知识点梳理1.全等形的概念:能够完全重合的两个图形叫做全等形.2.全等形的性质:(1)形状相同.(2)大小相等.3.全等三角形的概念:能够完全重合的两个三角形叫做全等三角形.4.全等三角形的表示:(1)两个全等的三角形重合时:重合的顶点叫做对应顶点;重合的边叫做对应边;重合的角叫做对应角.(2)如图,和全等,记作.通常对应顶点字母写在对应位置上.5.对应顶点,对应边,对应角:对应顶点,对应边,对应角定义两个全等三角形重合在一起,重合的顶点叫对应顶点,重合的边叫对应边,重合的角叫对应角.注意:在写两个三角形全等时,通常把对应顶点的字母写在对应位置上,这样容易找出对应边、对应角.如下图,△ABC与△DEF全等,记作△ABC≌△DEF,其中点A和点D,点B和点E,点C和点F是对应顶点;AB和DE,BC和EF,AC和DF是对应边;∠A和∠D,∠B和∠E,∠C 和∠F是对应角.找对应边、对应角的方法(重点)(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边;(2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角;(3)有公共边的,公共边是对应边;(4)有公共角的,公共角是对应角;(5)有对顶角的,对顶角一定是对应角;(6)两个全等三角形中一对最长的边(或最大的角)是对应边(或角),一对最短的边(或最小的角)是对应边(或角),等等.6.全等三角形的性质:(1)全等三角形的对应边相等;全等三角形的对应角相等.(2)全等三角形的周长、面积相等.7.全等变换:只改变位置,不改变形状和大小的图形变换.平移、翻折(对称)、旋转变换都是全等变换.8.全等三角形基本图形翻折:找到中心线经此翻折后能互相重合的两个三角形,易发现其对应元素旋转:两个三角形绕某一定点旋转一定角度能够重合时,易于找到对应元素将两个三角形沿某一直线推移能重合时也可找到对应元素三、常考点分析考点一、全等形和全等三角形的概念例1 下列每组中的两个图形,是全等图形的为()A. B.C.D.总结归纳:是不是全等形,既要看形状是否相同,还要看大小是否相等.同类练习:如图,在5个条形方格图中,图中由实线围成的图形与①全等的有______________.类型二、全等三角形的对应边,对应角例2 如图,△ABN≌△ACM,∠B和∠C是对应角,AB与AC是对应边,写出其他对应边和对应角.总结归纳:全等三角形对应角所对的边是对应边;全等三角形对应边所对的角是对应角.全等,记作 ,其中点A 和点 ,点B 和点 ,点 和点D 是对应点, 边AB 和 , 和ED ,AC 和 是对应边;例4 分别写出下列三组全等三角形的对应点和对应边: 分析:注意问题:1、把两个全等的三角形重合在一起,重合的顶点叫做对应顶点;重合的边叫 做对应边;重合的叫做对应角。
《全等三角形2》 精品教案

当我们在日常办公时,经常会遇到一些不太好编辑和制作的资料。
这些资料因为用的比较少,所以在全网范围内,都不易被找到。
您看到的资料,制作于2021年,是根据最新版课本编辑而成。
我们集合了衡中、洋思、毛毯厂等知名学校的多位名师,进行集体创作,将日常教学中的一些珍贵资料,融合以后进行再制作,形成了本套作品。
本套作品是集合了多位教学大咖的创作经验,经过创作、审核、优化、发布等环节,最终形成了本作品。
本作品为珍贵资源,如果您现在不用,请您收藏一下吧。
因为下次再搜索到我的机会不多哦!12.1 全等三角形教学目标知识与技能通过实例理解全等形的概念和特征,并能识别图形的全等.②知道全等三角形的有关概念,能正确地找出对应顶点、对应边、对应角;掌握全等三角形对应边相等,对应角相等的性质.③能运用性质进行简单的推理和计算,解决一些实际问题.过程与方法通过两个重合的三角形变换其中一个的位置,使它们呈现各种不同位置的活动,让学生从中了解并体会图形变换的思想,逐步培养学生动态的研究几何图形的意识.情感态度价值观培养学生的观察能力、动手操作能力和自主学习能力,发展学生的空间观念。
教学重点掌握全等三角形对应边相等、对应角相等的性质教学难点理解全等三角形边、角之间的对应关系.教学准备复写纸、剪刀、半透明的纸、多媒体课件(几个重要片断中使用).教学过程(师生活动)设计理念问题情境1.展现生活中的大量图片或录像片断。
丰富的图形容易引起学生的注意,使他们能很快地投入到学习的情境中.它反映了现实生活中存在着大量的全等图形.2.学生讨论:(1)从上面的片断中你有什么感受?(2)你能再举出生活中的一些类似例子吗?教师明晰,建立模型观察下列图案,指出这些图案中中形状与大小相同的图形问题:你还能举出生活中一些实际例子吗?这些形状、大小相同的图形放在一起能够完全重合。
能够完全重合的两个图形叫做全等形能够完全重合的两个三角形叫做全等三角形通过构图,为学生理解全等三角形的有关概念奠定基础.解析、应用与拓广1.学生用半透明的纸描绘下图中左边的△ABC,然后按要求在三个图中依次操作.体验“平移、翻折、旋转前后的两个图形全等”.你发现变换前后的两个三角形有什么关系?结论:一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,即平移、翻折、旋转前后的图形全等。
八年级数学全等三角形2

[单选,A1型题]患者男,34岁。较长距离步行后,感下肢疼痛,肌肉抽搐,休息后症状消失,再走一段路后症状又出现。平时有右足发凉、怕冷及麻木感。检查:右足背动脉较左侧搏动减弱。应考虑为()A.静脉血栓形成B.血栓性静脉炎C.动静脉瘘D.雷诺综合征E.血栓闭塞性脉管炎 [判断题]施工单位可在工程正式开工后,将企业资质、施工方案、开工报告一并提交监理单位进行审核。()A.正确B.错误 [单选,A1型题]下列需要急则治其标的病证是()A.突然神昏脉微B.大便干燥C.气虚乏力D.阴虚内热E.久咳虚喘 [单选,A1型题]中毒的主要机理有()A.局部刺激、腐蚀作用B.缺氧C.麻醉作用D.抑制酶的活力E.以上都是 [多选]MEN2A的临床表现包括()。A.甲状腺髓样癌B.嗜铬细胞瘤C.甲状旁腺肿瘤D.类马凡体型E.多发性黏膜神经瘤 [单选]如何切入动态锁定模式。()A、shift键↑+photo↓B、shift键↑+waypoint键↑C、waypoint键↑D、shift键↑+waypoint键↓ [单选,A1型题]WHO给健康下的定义是()A.无病就是健康B.身体各器官结构完好,功能正常C.没有疾病,身体又不虚弱D.身体、心理和社会适应的完好状态,而不仅仅是没有疾病和虚弱E.身体强壮,精神饱满 [单选]行李室考核制度规定:应在当班期间完成的工作任务不完成,推给别人者,扣当月绩效工资的()。A.25%-35%B.10%-20%C.30%-40%D.5% [问答题,简答题]什么叫稀土选矿?常用稀土选矿方式有哪些? [单选]茶叶加工道德根源于()A.先天的人性B.阶级斗争C.经济关系D.生存需要工 [单选]发生车种代用装车时,应采取保证()的相应措施。A、车辆安全B、货物数量C、货物质量D、货物安全 [单选,A1型题]下列除哪项外皆可面见青色:()A.虚证B.痛证C.寒证D.惊风E.瘀血 [单选]未成年人的保护包括()。A、家庭保护、学校保护、社会保护B、幼儿园保护、父母保护C、教师保护、保育员保护D、公共场所保护 [问答题,案例分析题]女性,30岁。主诉:发热伴咽痛2天急诊就诊。请针对该案例,说明问诊内容与技巧。 [问答题,简答题]离心泵如何停用? [判断题]进一步简政放权,就是要深化行政审批制度改革,最大限度减少中央政府对微观事务的管理A.正确B.错误 [单选]船舶搁浅后轮机部应首先检查()的工作情况。A.轴系B.主机C.离合器D.发电机 [单选]()是信托的对象物或信托的客体,也是信托关系得以创立的载体。A.信托主体B.信托行为C.信托财产D.信托目的 [单选,A2型题,A1/A2型题]肺结核患者咳痰带血,最恰当的处理是()A.可待因0.03gB.垂体后叶素5~10UC.6-氨基己酸4~6gD.10%葡萄糖酸钙10mlE.安静休息,避免紧张情绪 [单选]()是实施美育的重要途径,对于培养德、智、体等方面全面发展的社会主义事业的建设者和接班人,塑造完美的人格,提高全民族的素质,具有不可替代的作用。A.环境教育B.历史教育C.艺术教育D.科学教育 [填空题]质量文化的功能包括()、()和辐射功能。 [单选,A1型题]列腺电切(TURP)术中及术后常见的并发症有()A.TURP综合征B.术后出血C.膀胱穿孔D.尿失禁E.以上都是 [单选,A2型题,A1/A2型题]鼻息肉的主要浸润细胞是()。A.中性粒细胞B.淋巴细胞C.嗜酸性粒细胞D.浆细胞E.肥大细胞 [单选]下列儿科用药中,属于慢惊及久病、气虚者忌服的是()A.小儿咽扁颗粒B.牛黄抱龙丸C.小儿热速清口服液D.琥珀抱龙丸E.小儿肺热咳喘口服液 [填空题]根据卵黄的多少与分布不同,可将动物的卵细胞分为()、()、()、()。 [多选]国际物流运作,生产企业依赖()完成跨国运输。A.国际外贸企业B.船承运人C.邮政快递D.报关行E.码头 [单选,A1型题]中医认为维生素D缺乏性佝偻病的病位主要在()A.脾B.脾肾C.肺D.肺脾E.肺肾 [单选]卫星通信中,监视和控制卫星轨道位置及姿态的是()A.地球站分系统B.跟踪遥测指令分系统C.监控管理分系统 [单选,A2型题,A1/A2型题]以下主诉描述正确的是()A.月经停闭3年B.月经过多5天C.痛经3年D.每次月经期间及月经以后发热,五心烦热,口干咽燥1年E.小产3次 [名词解释]收货人 [单选]心肌脂肪变性最常累及的部位是:A.左心室前壁B.左心室后壁C.右心室前壁D.右心室后壁E.左心室乳头肌 [单选]内燃机是热机的一种,它是()。A.在气缸内燃烧并利用某中间工质对外做功的动力机械B.在气缸内进行二次能量转换并利用某中间工质对外做功的动力机械C.在气缸内燃烧并利用燃烧产物对外做功的动力机械D.在气缸内燃烧并利用燃烧产物对外做功的往复式动力机械 [单选,A型题]测定机体对白喉棒状杆菌的免疫力可在前臂皮内注射()A.白喉毒素B.白喉类毒素C.加热灭活的白喉毒素D.加热灭活的白喉棒状杆菌E.白喉抗毒素 [判断题]加氢气密试验的压力应等于操作压力。A.正确B.错误 [单选]杆头与地面平等击球产生()。A、弹道变高B、弹道变低C、弹道平行D、标准弹道 [单选]为了对计算机信息系统的安全威胁有更全面、更深刻的认识,信息应用系统安全威胁的分类方法一般用()3种"综合分类"方法。A.高、中、低B.对象的价值、实施的手段、影响(结果)C.按风险性质、按风险结果、按风险源D.自然事件、人为事件、系统薄弱环节 [单选]信托财产的处分,分为事实上的处分和法律上的处分。其中,事实上的处分是指()。A.消费信托财产B.转让信托财产C.赠予信托财产D.对信托财产设立抵押 [多选]保险待遇的计算依据为()A.职工原工资B.职工工龄C.保险费的交纳D.国家宏观政策 [单选]超声心动图检查以下哪项可确诊感染性心内膜炎()A.二尖瓣瓣叶有增生粘连B.左房、左室扩大C.瓣膜上可探测到赘生物D.二尖瓣有反流E.主动脉根部扩张 [多选]对于安装工程施工图预算,可采用()编制单位工程施工图预算。ABCD
八年级数学全等三角形2

三角形全等的判定2(sk)

1.若AB=AC,则添加什么条件可得 A △ABD≌ △ACD?
△ABD≌ △ACD
D B S S A S AD=AD ∠BAD= ∠CAD AB=AC BD=CD
C
2.如图:己知AD ∥BC, AF=CE,AD=BC,E、 F都在直线AC上,试说明∠D=∠B。
A E F B D
C
P36~P37
除了SSS外,还有其他情况吗?继续探索三角形全 等的条件.
当两个三角形满足六个条件中的三个时,有四种 情况:
(1) 三个角 (2) 三条边 (3) 两边一角 (4) 两角一边
不能! SSS ?
三角形全等的判定 (2)
继续探讨三角形全等的条件: 两边一角
思考:已知一个三角形的两条边和一个角,那么这两条边 与这一个角的位置上有几种可能性呢? A A
两边和它们的夹角分别相等的两个三角形全等.
可以简写成 “边角边” 或“ SAS ”
用 数学语言表述:
证明: 在△ABC与△DEF 中
A
﹛
AB= DE , (已知) ∠B= ∠E, (已知) BC=EF, (已知)
B D
C
∴ △ABC≌ △DEF(SAS)
E F
已知:AE= AD ,AB=AC,求 △ABE≌ △ACD 证明: 在△ABE与△ACD 中
图一 在图一中, ∠A 是AB和AC的夹角, 符合图一的条件,它 可称为“两边夹角”。
B
C
B
图二
C
符合图二的条件, 通常 说成“两边和其中一边的对角”
动手剪一剪
• 条件:三角形一边为20cm,一边为15cm, 其中有一个角为45°。
探索边边角
两边及其中一边的对角对应相等的两个三角形全等吗? 已知:AC=20cm,BC=15cm, ∠A=45 °.
2.2三角形全等的判定(二)SAS (2)

想象比知识更重要。 ——爱因斯坦
语文
小魔方站作品 盗版必究
湖北鸿鹄志文化传媒有限公司——《名师测控》助您成功
谢谢您下载使用!
更多精彩内容,微信扫描二维码获取 扫描二维码获取更多资源
湖北鸿鹄志文化传媒有限公司——《名师测控》助您成功
湖北鸿鹄志文化传媒有限公司——助您成功
湖北鸿鹄志文化传媒有限公司——助您成功
湖北鸿鹄志文化传媒有限公司——《名师测控》助您成功
湖北鸿鹄志文化传媒有限公司——《名师测控》助您成功
上海 2006 高考 理科 状元-武亦 文
武亦文 格致中学理科班学生 班级职务:学习委员 高考志愿:复旦经济 高考成绩:语文127分 数学142分 英语144分
物理145分 综合27分 总分585分
北京市文科状元 阳光女孩--何旋
湖北鸿鹄志文化传媒有限公司——《名师测控》助您成功
来自北京二中,高考成绩672分,还有20 分加分。“何旋给人最深的印象就是她 的笑声,远远的就能听见她的笑声。” 班主任吴京梅说,何旋是个阳光女孩。 “她是学校的摄影记者,非常外向,如 果加上20分的加分,她的成绩应该是 692。”吴老师说,何旋考出好成绩的秘 诀是心态好。“她很自信,也很有爱心。 考试结束后,她还问我怎么给边远地区 的学校捐书”。
湖北鸿鹄志文化传媒有限公司——助您成功
湖北鸿鹄志文化传媒有限公司——《名师测控》助您成功
“用好课堂40分钟最重要。我的经验是,哪怕 是再简单的内容,仔细听和不上心,效果肯 定是不一样的。对于课堂上老师讲解的内容, 有的同学觉得很简单,听讲就不会很认真, 但老师讲解往往是由浅入深的,开始不认真, 后来就很难听懂了;即使能听懂,中间也可 能出现一些知识盲区。高考试题考的大多是 基础知识,正就是很多同学眼里很简单的内 容。”常方舟告诉记者,其实自己对竞赛试 题类偏难的题目并不擅长,高考出色的原因 正在于试题多为基础题,对上了自己的“口 味”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【例2】如图,在 ABC 中, B 2C , BAC 的平分线 AD 交 BC 与 D .求证:
AB BD AC .
【例3】如图,在 △ABC 中, AD BC 于 D , B 2C .求证: AB BD CD .
A
C
D
B
【例4】如图,在 ABC 中, BAC 120 , AD BC 于 D ,且 AB BD DC ,那么 C 的 度数是_______.
△ANF ,得到 AB AN , 通过“ AAS ”证明 △ABF ≌ BF NF CF △FCE ,得到 NE CE . 再通过“ HL ”证明 △FNE ≌
A
求证: ABC 是等腰三角形.
B C
D
【例7】如图, ABC 中, AB AC , A 108 , BD 平分 ABC 交 AC 于 D 点.求证:
BC AC CD .
【例8】已知等腰 ABC , A 100 , ABC 的平分线交 AC 于 D ,求证 BD AD BC .
B AFD 通过“ SAS ”证明 △ABD ≌ △AFD , BD FD ,
∵ B 2C AFD C FDC
DF FC BD , ∴ FDC C ,
∴ AB BD AC . 3. 【解析】 延长 DB 到点 E 使得 DE CD , 连接 AE , 易证 AD 为线段 CE 的垂直平分线, ∴ AC AB ,∴ C E ,∵ ABC 2 C ∴ ABC 2E ∴ E BAE ∴ AB BE
1 1 ∵ ADB 90 BDC ,∴ ADB BDC 90 2 2
A
A
B C
D
E
则 2ADB BDC 180 , 即 ADC ADB 180 ∵ ADB ADE 180 , ∴ ACD ≌ AED AAS ∴ ABC 是等腰三角形. 7.【解析】在 BC 上截取 BE BA ,连结 DE . 通过“ SAS ”证明 △ABD ≌ △EBD ,到 A BED 108 再通过导角,推出 △CDE 为等腰三角形 CD CE . ∴ ADC ADE , ∴ AE AC ,∴ AB AC
全等三角形辅助线(二)
知识回顾
一、全等三角形的性质
全等三角形, 对应角相等, 对应边相等, 对应边上的中线相等, 对应边上的高相等, 对应角的角平分线相等,周长相等,面积相等.
二、全等的性质和判定
(1)全等三角形的判定方法:
SSS 、 SAS 、 ASA 、 AAS 、 HL Rt△
(2)全等三角形的图形变换形式: 平移、对称、旋转 (3)由全等可得到的相关定理: ①角平分线定理 ②等腰、等边三角形性质和判定 ③垂直平分线定理
A
B
D
C
A
【例5】如图,在 ABC 中, AB AC , D 是 ABC 外的一点,且
ABD 60 , ACD 60 .
求证: BD Dห้องสมุดไป่ตู้ AB .
B C D
1 【例6】如图,已知 ABD ACD 60 ,且 ADB 90 BDC . 2
BOE COD 60 ∴ BOC 120 ,
通 过 “
S A ” S 证 明
△BOE ≌ △BOF
,
OE OF , BOE BOF 60
△DOC , 再 通 过 “ ASA ” 证 明 △FOC ≌
CF CD , OF OD
∴ BC BE CD , OE OD 解法二:过 O 作 OH AB 于 H , O 作 ON AC 于 N ∵ A 60 , BD 、 CE 分别平分 ABC 和 ACB
A
CD DE DB BE DB AB
也可以,延长 DB 至 E ,使 BE BA,连接
AE .易证 ABC 2E ,所以 C E ,进
C D B E
而 △ACE 是等腰三角形, 根据等腰三角形的三 线合一性质可知 CD DE DB BE DB AB .
B C D E
8.【解析】在 BC 上截取 BE BA ,连结 DE ;在 BC 上截取 BM BD , 连结 DM 通过“ SAS ”证明 △ABD ≌ △EBD ,到 A BED 110 , DA DE
ABC C 40
2 20 , BDM BMD 80 DEM ,
C MDC 40 , DE DM MC
∴ BD AD BC
EF ,过 F 点作 FN AE 于 9.【解析】取 BC 中点 F ,连接 AF 、
N
依题可知:通过“ SAS ”证明 △ABF ≌ △ADM ,得到
BAF DAM
∵ BAE 2DAM
∴ BAF EAF
知识讲解
常见辅助线的作法有以下几种: (1)遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题, 思维模式是全等变换中的“对称” . (2)遇到三角形的中点或中线,倍长中线或倍长类中线,使延长线段与原中线长相等, 构造“ 8 ”字形全等三角形,利用的思维模式是全等变换中的“旋转” . (3)遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,或者沿着角平分线翻 折, 利用的思维模式是三角形全等变换中的“对称” ,所考知识点常常是角平分线的性质 定理 或逆定理.
O 为三条内角角平分线的交点
∴ OH ON , HON EOD 120 , HOE NOD
△NOD 再通过“ ASA ”证明 △HOE ≌
∴ OE OD 【答案】 (1) BC BE CD (2) OE OD 2.【解析】在 AC 上截取 AB AF ,连接 DF
(4)过图形上某一点作特定的平行线,构造全等三角形, 利用的思维模式是全等变换中的“平移” . (5)截长补短,适合于证明线段的和、差、倍、分等类的题目. 具体做法是在某条线段端点处截取一条线段与特定线段相等, 或是将某条线段延长, 使之与特定线段相等,再利用三角形全等的有关性质加以说明.
常见辅助线模型:
C C E A E D A E B “角平分线+垂直”模型 D A B “角平分线+斜交”模型 C D
B
“角平分线+平行”模型
A A O B
A F
B
D
C
B
D E
C
D
C E “倍长中线”模型
“8字形”中心对称全等模型
“倍长类中线”模型
等边对等角模型
等角对等边模型
等腰三角形三线合一模型
30°
等边三角形三条高线
4.【解析】已知条件“ AB BD DC ” ,为了构造与之相关的 条件,将 ABD 沿 AD 翻折,点 B 落在点 E , 在 CD 上截取一点 E , 使得 DE DB , 连接 AE , 易证
AB AE EC ,因此设 C EAC x ,
B D E C A
则 AEB B 2x , ∵ B C 60 , ∴
x 2x 6 ,∴ 0 x 20 .
【答案】 20 . 5.【解析】延长 BD 至 E ,使 BE AB ,连接 AE, CE . ∵ ABE 60 , BE AB ∴ ABE 为等边三角形. ∴ AEB ACD 60 , AE AB AC . ∴ ACE AEC , DCE DEC , DC DE ∴ AB BE BD DE BD DC ,故原题得证. 6.【解析】延长 BD 到 E ,使得 BE AB ,连结 AE . ∵ ABD ACD 60 , BE AB ∴ ABE 是等边三角形, AEB 60 ,AE AB ∴ AEB ACD
等腰直角三角形斜边高线
截长补短常见模型
【例1】(2006 年北京中考题)已知 ABC 中, A 60 , BD 、 CE 分别平分 ABC 和
ACB , BD 、 CE 交于点 O .
(1)判断 BE 、 CD 、 BC 的数量关系,并加以证明.
OD 的数量关系,并加以证明 (2)判断 OE 、
【例9】如图.已知正方形 ABCD 中, M 为 CD 的中点, E 为 MC 上一 点,且 BAE 2DAM . 求证: AE BC CE .
1.【解析】解法一:在 BC 上截取 BF BE ,连接 OF ∵ A 60 , BD 、 CE 分别平分 ABC 和 ACB
