2年级奥数第二讲学
二年级奥数:巧妙填数数阵图练习题含答案

第二讲:数字游戏—填图与拆数【有话要说】填数是一种既有趣,又能锻炼头脑、发展智力的趣味活动。
它不仅可以提高你的运算能力,而且能促使你积极地去思考问题,解决问题。
填数这类题目的题型比较多,解答时除了口算要熟练外,更重要的是要会分析、推理。
有的题目答案不止一种,要多尝试,要尽量运用发散思维、求异思维,把各种可能的答案想出来。
【经典例题】例1:把1、3、5、7、9、11、13七个数填入右图中的七个圆圈内,使每条直线上三个数的和都等于21.思路导航:这道题可以这样想:1+3+5+7+9+11+13=49,21+21+21=63,63-49=14,由于计算三条直线上三个数时,中间圆圈里的数多算了两次,就多出了14,正好7+7=14,说明中间圆圈里应该填“7”,21-7=14,把另外六个数两个两个分组,使每组两个数的和都等于14; 1+13=3+11=5+9=14,也就是首尾配对。
例2:如图:在空格中填入不同的数,使每一横行、竖行、 斜行的三个数的和等于15.思路导航:因为每一横行、竖行、斜行三个数的和都等于15,我们可以先填一行中只有一个空格的数,如:4+(9)+2=15,竖行6+(7)+2=15,斜行6+(5)+4=15,根据填出的数再填只有一个空格的数。
6 42375645213解:例3:把1、2、3、4、5、6这六个数填入右图的圆内,使每个大圆的四个数的和都等于13。
思路导航:先确定图形中央的两个数分别填几,可以这样想,先求六个数的和与两个大圆上八个数的和:1+2+3+4+5+6=21,13+13=26,26-21=5,这个5就是中央两个圆的数的和,1+4=5,2+3=5,就是说中央两个小圆里可以填1和4,也可以填2和3,中央填1和4,13-5=8,左边填3和5,右边填2和6,中央填2和3行不行呢?剩下的数有1、4、5、6任意两个数的和都不是8,所以无法填出,因此,中央只能填1和4. 解:例4:由图中三个圆圈两两相交形成七个部分,分别填上1~7七个自然数,在一些部分中,自然数3、5、7三个数已填好,请填上其余各数,使每个圆圈中四个数的和都是15.思路导航:5462137524675381图中空着四个部分要填入四个数:1、2、4、6,可以看出中心部分属三个圆圈公共部分,关键要确定中心填哪个数,我们用拆数的方法来确定。
小学二年级奥数培训教材-小学数学二年级奥数培训资料

小学二年级奥数辅导讲座目录第一章:算一算第一讲巧填竖式(二)第二讲简便运算(一)第三讲简便运算(二)第四讲简单数的分解用第五讲数的读写单元练习(一)(另附)第二章:实践与应用(一)第一讲应用题(一)第二讲应用题(二)第三讲应用题(三)单元练习(二)(另附)第三章:合理推算第一讲简单推理(一)第二讲简单推理(二)第三讲简单推理(三)第四讲合理安排单元练习(三)(另附)第四章:趣味数学与游戏第一讲巧填数第二讲数学游戏第三讲杂题单元练习(四)(另附)第五章:实践与应用(二)第一讲余数的妙用(二)第二讲年龄问题第三讲间隔趣谈(三)第四讲画画凑凑第五讲排队问题单元练习(五)(另附)第六章:认识时间第一讲时钟问题(一)第二讲时钟问题(二)单元练习(六)(另附)综合练习(一)(另附)综合练习(二)(另附)第一章算一算第一讲巧填竖式(二)【专题导引】“算式谜”是一种常见的猜谜游戏。
通常是给出一个式子,但式子中却含有一些用汉字、字母等表示的特定的数字。
要求我们根据一定的法则和逻辑推理的方法,找到要填的数字。
解答这类题目,要分析算式的特点,运用加、减的运算法则来安排每一个数。
一个算式中填几个数时,要选好先填什么,再填什么,选准“突破口”,其他就好填了。
【典型例题】【例1】在下面竖式中的空白处填入适当的数,使算式成立。
□4+79□【试一试】1、在下面竖式中的空白处填入适当的数,使算式成立。
8□+4□02、在下面竖式中的空白处填入适当的数,使算式成立。
□3+□90【例2】在下面竖式中的空白处填入适当的数,使算式成立。
6□-9□2【试一试】1、在下面竖式中的空白处填入适当的数,使算式成立。
5□-7□12、在下面竖式中的空白处填入适当的数,使算式成立。
□7-□49【例3】在下面竖式中的空白处填入适当的数,使算式成立。
□□+□□191【试一试】1、在下面空白处填入适当的数,有哪几种填法?□□+□□1492、在下边的算式里,空格里的四个数字总和是()。
二年级奥数培优专题第二讲 数 学 游 戏

二年级奥数培优专题第二讲数学游戏【专题导引】小朋友都很喜欢做游戏,数学中也有很多游戏。
通过数学游戏,不仅能培养我们把实际问题数学化的能力,而且还能培养我们学习数学的兴趣。
在这些游戏中,要是拿到最后一个者获胜,首先要决定谁先拿,如果把物品总数除以两个每次取物品个数的和,没有余数,就让对方先拿,自己拿的个数必须和对方拿的个数合起来是两人每次取的和。
【典型例题】【例1】小花和小民一起做游戏,他们把20粒棋子放在桌面上,然后轮流拿,每人每次只能拿1粒,取到最后一粒的一方胜出,你能找到必胜的方法吗?【试一试】1、桌面上有20根火柴,小林和小英轮流拿,每人每次只能拿1根,谁拿到最后一根,谁就获胜,小英怎样才能保证必胜?2、两个同学一起做游戏,他们把14粒棋子放在桌面上,然后轮流拿,每人每次只能拿1粒,谁拿到最后一粒,谁就获胜,你能找到必胜的方法吗?【例2】桌上有20粒棋子,由甲、乙两人轮流拿,每人每次只能拿2根,拿到最后一根的人获胜。
问该怎样拿才能保证获胜?【试一试】1、小林和小英一起做取物游戏,他们把16根火柴放在桌上,然后轮流拿,规定每人每次只能拿2根,谁拿到最后一根,谁就获胜,小林怎样才能保证必胜?2、报21,两人轮流数,从1开始,,每人每次只能报2个数,谁先报到21谁就获胜,问怎样报才能取胜?【例3】桌上有21根火柴,小邱和小红两人轮流取,每人每次取1根或2根。
谁取到最后一根谁就获胜。
小红该怎样取才能保证获胜?【试一试】1、小东和小华一起做游戏,他们把18粒棋子放在桌上,然后轮流拿,每人每次只能拿1粒或者2粒,谁拿到最后一粒谁就获胜,你能让小东保证获胜吗?2、绕口令:“车上放着一个盆,盆里放着一个瓶,砰砰砰,砰砰砰,瓶碰盆,盆碰瓶。
不是瓶碰了盆,就是盆碰了瓶。
”两人轮流着说,每人每次只说一字,最后一个字谁说谁就胜,该怎样说才能保证获胜?【例4】桌上有20根火柴,小邱和小红轮流拿,每人每次只能拿1根或2根,谁拿到最后一根,谁就获胜,这次小红该怎样拿才能保证获胜呢?【试一试】1、小东和小华做游戏,他们把19粒棋子放在桌上,然后轮流拿,每人每次能拿1粒或者2粒,谁拿到最后一粒,谁就获胜。
二年级奥数教案

二年级奥数教案教案一:寻找数字规律教学目标:通过寻找数字规律,培养学生的逻辑思维能力。
教学内容:1. 数列的概念2. 数字规律的找寻教学步骤:1. 导入新知识:通过举例子,引出数列的概念,如1,2,3,4…可以组成一个数列。
2. 引导学生发现数字规律:给出一个数列,让学生观察并找出其中的规律,如2,4,6,8,...3. 学生探索:让学生自己创造数列,并找出其中的数字规律。
4. 总结归纳:引导学生总结数字规律的方法和技巧。
5. 练习巩固:布置一些练习题,让学生运用所学方法进行练习。
教学评价:1. 观察学生的学习情况,看他们是否能够找出数字规律。
2. 对学生的练习结果进行评价,看他们是否能够熟练运用所学方法。
教案二:数的大小比较教学目标:通过比较数的大小,掌握比较符号的使用。
教学内容:1. 比较符号的概念2. 数的大小比较教学步骤:1. 导入新知识:通过游戏,让学生体验比大小的乐趣,学习比较符号的含义。
2. 通过示例讲解比较符号的使用方法:如“>”表示大于,“<”表示小于。
3. 给出一些演示题,让学生运用比较符号进行比较。
4. 引导学生思考:如何快速确定两个数的大小。
5. 练习巩固:布置一些练习题,让学生独立完成。
6. 复习和总结:回顾所学内容,再次巩固比较符号的使用。
教学评价:1. 观察学生的识别比较符号的能力。
2. 评价学生练习的结果,看他们是否能正确运用比较符号进行比较。
教案三:解决逻辑问题教学目标:通过解决逻辑问题,培养学生的思维能力和逻辑推理能力。
教学内容:1. 逻辑问题的特点2. 解决逻辑问题的方法和策略教学步骤:1. 导入新知识:通过一个有趣的问题引入逻辑问题的概念,激发学生的兴趣。
2. 解决示例问题:给出一个逻辑问题,引导学生进行分析和推理,找出正确答案。
3. 学生探索:让学生自己设计逻辑问题,并带领同学进行解答。
4. 总结归纳:引导学生总结解决逻辑问题的方法和策略。
5. 练习巩固:布置一些逻辑问题,让学生独立解答。
奥数班二年级 第2讲 简单数的分解

一共: 2 + 2 + 1 + 1 = 6种
答:有6种不同的分拆方式。
9
练习3 1.把4拆成几个数相加的形式,有多少种不同的分拆方式?
2个数:
3个数:
4个数:
1 + 3 1 + 1 + 2 1 + 1 + 1+ 1
2+2
一共: 2 + 1 + 1 = 4种
答:有4种不同的分拆方式。
10
【课堂精炼】 1.把8拆成两个数相加的形式,有多少种不同的分拆方式?
妈妈:
答:妈妈先吃1块,再把剩下的平均分给3个孩子。
16
Thanks
二年级奥数班
第二讲 简单数的分解
【典型例题】
【典型例题】 例1:五个连续自然数的和是30,这五个数中最中间的数是( 6 ),最 小的数是( 4 ),最大的数是( 8 )。
中间数 = 和 ÷ 个数 4 5 6 7 8 中间数: 30 ÷ 5 = 6
3
练习1 1.小明用5天时间做了25道数学题,他每天都比前一天多做一道,这五 天里,小明最后一天做几道题?
9= 1 + 8 =2 + 7 =3 + 6 =4 + 5
答:共有4种不同的分拆方法。
6
练习2 1.把10拆分成两个个不同的数相加的形式(0除外),共有多少种不同 的分拆方法?
10= 1 + 9 =2 + 8 =3 + 7 =4 + 6
答:共有4种不同的分拆方法。
7
练习2 2.把24分拆成两个不同的数相乘的形式,问由这样的两个数组成的算 式有多少个?
中间数: 25 ÷ 5 = 5道
二年级下册数学奥数练习-时 钟 问 题(二) 全国通用(无答案)

第二讲时钟问题(二)【专题导引】小朋友,我们已经认识了时间,时间的用处可多了,我们的日常生活、学习、工作都离不开时间。
关于时间的数学问题有很多,下面我们就一起来研究有关时间的趣题。
这组与时间有关的趣题,不仅与时间的知识有关,还与平均分、间隔等数学问题有关系。
小朋友要注意,当你所学的数学知识越来越多时,你还要学会综合运用所学知识解决问题的本领。
【典型例题】【例1】1路车每隔5分钟开一班,从上午8时到9时,1路车一共开了多少班?【试一试】1、张阿姨白天每两小时喝一杯水,从上午9时到下午3时,她共喝了几杯水?2、摇头风扇每10秒钟转一次方向,那么1分钟内风扇共转过多少次方向?【例2】时钟敲5下,用8秒钟,敲10下用几秒?【试一试】1、锯一根粗细均匀的木料,每锯一次要4分钟,锯成6段,一共需要多少分钟?2、时钟12秒敲7下,敲8下需要多少时间?【例3】钟面上有12个数,你能在钟面上画一条线,把钟面平均分成两部分,使每一部分数的个数相等,和也相等吗?【试一试】1、钟面上有12个数,你能画两条线将钟面分成三部分,使每部分的数相加的和相等吗?2、如果要把钟面分成六部分,使每一部分数的个数相等,和也相等,应该怎样分?【例4】54路车每隔20分钟开一班,爷爷想搭8:30的一班车到水果批发市场,现在是8:38分,他要等几分钟,才可搭乘下一班汽车?【试一试】1、二年级小朋友去春游,到车站时是8:55分。
如果汽车要在9:05到,小朋友还要等候多长时间?2、汽车每隔10分钟开出一班,哥哥想搭9时15分的一班车,到达车站时,已是9时18分,他要等多少分钟,才可以搭乘下一班汽车?【例5】小兰的钟停了,电视显示3点时,爷爷跟电视对钟,由于爷爷年老眼花,把时针和分针颠倒了,妈妈下班回家,见钟才3点钟,大吃一惊。
请你帮小兰妈妈想一想,现在应该是几点?【试一试】1、小明家的钟停了,电台广播2点时,奶奶跟电台对表,由于年老眼花把时针与分针颠倒了,小明放学回家见钟才2点整,大吃一惊,请你帮助想一想,现在应该是几点钟?2、张爷爷的手表停了,下午电台广播1点时,他跟着电台对表,不小心把时针和分针颠倒了,等他午睡醒来,发现手表还是1点。
奥数 二年级 讲义 小二教案 第讲精英班教师版单位量的概念
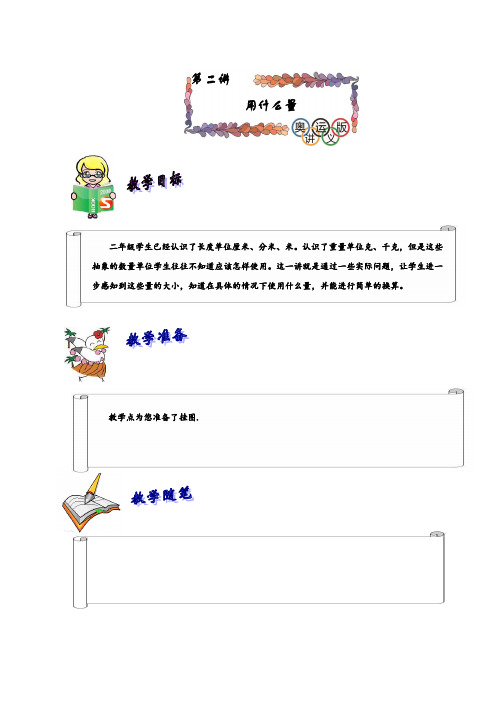
第二讲用什么量二年级学生已经认识了长度单位厘米、分米、米。
认识了重量单位克、千克,但是这些抽象的数量单位学生往往不知道应该怎样使用。
这一讲就是通过一些实际问题,让学生进一步感知到这些量的大小,知道在具体的情况下使用什么量,并能进行简单的换算。
教学点为您准备了挂图.同学们,我们已经认识了长度单位厘米、分米、米.拿出你的尺子,找出1厘米、2厘米……可以发现10厘米长是1分米,还可以发现10分米是1米.我们还认识了重量单位克和千克,知道了1千克=1000克,认识了时间单位时、分、秒.那么你知道什么时候用什么单位?当我们手里没有尺子、秤或钟表时,又用什么来测量呢?今天这节课我们就一起来学习这些知识. 例1李志一个人量两棵树之间的距离,他把卷尺的开头一段系在一棵树上,正好50厘米的刻度对着这棵树,在另一棵树的刻度是15米.这两棵树的距离是多少?【分析】列式:15米=1500厘米,1500厘米-50厘米=1450厘米=14米5分米;这两棵树的距离是14米5分米.动手动脑测量小能手1. 用手势比画一下,1厘米、1分米、1米分别有多长? 2. 找一找身边哪些物体的重量是用“克”做单位的,哪些物体的重量是用“千克”做单位的?3. 闭上眼睛感受一下一分钟有多长?比一比一分钟谁写的字多?我就是李志我来做小明与小青拿了一个开头断了一截的卷尺量一根木材的长度,木材的一端在2米的刻度上,另一端在6【分析】列式:6米8分米-2米=4米8分米,这根木材长4米8分米.例2观察下面的尺子,算一算红、蓝条各长多少厘米?0厘米蓝色红色1457454150140130120110100908070605040302010【分析】量物体长度的一般方法是从“0”刻度开始量起,但如果不用“0”刻度对着物体的一端,这种量法不能直接看出所量长度,必须通过计算才知道,其算法为:最后的刻度数减去起点的刻度数就等于实际长度.(1)红色纸条是从20厘米开始量,到54厘米为止.那么红色纸条的长度是:542034-=(厘米).2()蓝色纸条是从74厘米开始量,到145厘米为止.那么蓝色纸条的长度是:1457471-=(厘米).[铺垫]把两根长都是450毫米的铁条焊接为一根,焊接点(如图)用去50毫米.焊接后铁条长多少毫米?[分析]生活实践中常常把两条绳子、两根铁条连(焊接)为一条,像这样的问题,我们把它称做接头问题.这里两根铁条一共长是450+450=900 (毫米),现在焊在一起,重叠部分长度是50毫米,所以焊接后的铁条长是90050850-= (毫米).[拓展]把三根长都是32厘米的铁条,焊为一根,焊头部分长是4厘米,焊接后铁条长是多少厘米? [分析]3232324488++--=(厘米),焊接后铁条长是88厘米.例3教室的门高多少厘米?(图中3把尺均为100厘米长)50毫米【分析】注意到每把尺子都是100厘米,上、下两把尺子接起来还不够,故门高有200多厘米,关键要算出第3把尺子中间的厘米数.多的厘米数是从25刻度到75刻度.应为752550-= (厘米).20050250+= (厘米).所以门高250厘米.例4明明生日的时候,妈妈送给他一份礼物,并用漂亮的彩带包装好.算一算,下图的彩带长多少厘米?(不计算打结的长度)20cm30cm40cm【分析】先观察前后缠绕的这部分绳子,总长是:30+30+20+20=100厘米,或302402140⨯+⨯=厘米.这里要引导学生去思考为什么有2个30厘米,有2个40厘米.要考虑到我们看不见的部分.再观察左右缠绕的这部分,总长是:40+40+20+20=120厘米,或402202120⨯+⨯=厘米.上下的绳子长度相同,下面我们看不见也是40,左边和右边的长度也相同,左边看不见也应该是20.这样就有两个40厘米和两个20厘米.不计算打结的部分,这根绳子的总长就是100+120=220厘米.例5把三条大小相同的铁环连在一起(如图),拉紧后是多少? 加油【分析】 三个铁环连在一起的总长是:12+12+12=36 (厘米),现环环相扣,连在一起,重叠部分长度为:1+1+1+1=4 (厘米),拉紧后的长为:36432-= (厘米).[拓展] 把两个大小相同的铁环连在一起(如图),拉紧后的总长为20厘米,问一个铁环长为多少厘米?[分析] 两个铁环如果不连一起一共长20+2+2=24(厘米),那么一个铁环就长24212÷=(厘米). 例6 同样大小的小正方体积木排队,排了两种队形: (1) 这两种队形各用了多少块积木?(2) 这两种队形都是长方体,它们的表面谁大?【分析】 1()要求每一个长方体有多少积木,可以用乘法计算,也可以数一数有多少块.3412⨯=(块),2612⨯= (块).2()关于长方体的表面大小,也可以数一数长方体表面的格子数,看谁多.但是要注意与桌面在一起的那个面也应该数一数,但是看不见,怎样才能数出来呢?其实我们看到的格字数和没有看到的格子数正好同样多,所以只要数看得见的格子数,然后再做相同加数的和,就可以知道表面有多少格子数了.格子多的表面就大.第一个长方体的表面看得见的格子数: 344319⨯++=(格). 所以一共有19+19=38 (格).第二个长方体的表面看得见的格子数:266220⨯++=(格),所以一共有20+20=40 (格).[拓展] 算一算,图(1)、图(2)、图(3)的表面各有多少个方格?[分析] 图1:前后各有6块,左右各有3块,上下各有2块.一共有62322222⨯+⨯+⨯=个小方格.76254310254310图2:看的见的有11块,看不见的有4+4+3=11(块).一共有11+11=22个小方格.图3:前后各有6块,左右各有3块,上下各有3块.一共有62323224⨯+⨯+⨯=个小方格.或这样想看的见的有12块,看不见的有6+3+3=12(块).一共有12+12=24个小方格.[拓展]1个方盒长40厘米、宽12厘米、高20厘米,能否放入2个棱长为11厘米的正方体?[分析]可以放,如果把这两个正方体上下叠在一起,那么高就有22厘米,这样超出了方盒的高,因此放不进去.如果把这两个正方体摆成一排,这样长就是11+11=22厘米,宽和高不变都是11厘米,这样就可以把这两个正方体放入到这个长方体的盒子里面.例7十五的月亮圆又圆.根据天文学家的观察,每逢一个月的农历十五日.月亮最圆.请你根据几个月形,推算日期,填在图下的方框内.【分析】观察这个图我们发现月亮从三月三号开始慢慢变大,到三月十五变圆,然后又慢慢变小.从第一次变化到第二次变化经过了6天,从第二次变化到第三次变化经过了6天,按这种规律推算,从第三次变化到第四次变化也要经过6天,15+6=21,第四次变化的时间是三月二十一日.从第四次变化到第五次变化也要经过6天,21+6=27,第五次变化的时间是三月二十七日.[拓展]小刚每天早晨起床后就把昨天的日历撕掉.今年八月份的一天下午他们全家开车到外地旅游,过了三天回家,小刚一连撕掉了三张日历.这3张日历上的3个日期加起来是60,小刚他们是几号出发去旅游的?[分析]三个日期是连续的自然数,最大的不超过31.而且它们的和要等于60,所以第二天的日期是÷=,从而第一天是19,第三天是21.小刚他们是8月19日去旅游的.60320[拓展]如果3张日历上的3个日期加起来是62,那么小刚他们是几号出发去旅游的?[分析]三天分别是8月30日,8月31日,9月1日.小刚他们是8月30日去旅游的.例8小华要称1粒米的重量,天平自带的砝码只有1克,2克,4克,8克,16克,32克,64克各一个.(1)1粒米远远没有1克,小华该怎么办?(2)小华要称100克的米,天平应放哪几个砝码?【分析】 (1)小华可以用1克的砝码去称1克米,天平平衡的时候,再去数一数有几粒米,就可以说多少粒米是1克.如果数出有10粒米.这10粒米就是1克的米,也就是1克,一粒米就是0.1克(2)先使用大的砝码64克,再考虑加哪几个?100=64+32+4,应放64克,32克,4克的砝码.[拓展] 称一称,只有1克,2克,4克,8克,16克,32克,64克砝码各1个的天平能称出88克,55克的物体吗?[分析] 164+16+8=88() ,所以称88克的物体要用64克、16克、8千克的砝码. (2) 32+16+4+2+1=55,所以称55克的物体要用32克、16克、4克、2克、1克的砝码.[拓展] 已知同样大小的木块比冰块轻.铁块比冰块重,铜块与木块的重量之和与冰块与铁块的重量之和同样多,四种物品谁最重?[分析] 因为铜块与木块的重量之和与铁块与冰块的重量之和同样多,木块又比冰块轻,所以铜块就比铁块重.又因为铁块比冰块重,当然也比木块重,所以铜块最重.铜块重量>铁块重量>冰块重量>木块重量例9 如图,第一只壶里的茶只有一半,小华倒出了5大杯,第二只壶里的茶是一满壶,小明倒出了15小杯.已知3小杯的茶与2大杯的茶同样多,现在问你哪个壶大?【分析】 我们可以按以下三个步骤来思考:(1)第二只壶满壶茶倒出15小杯,而每3小杯可以倒满2大杯,所以第二只壶可以装茶10大杯.(2)第一只壶的一半倒出了5大杯,那么满壶茶可以倒出10大杯. (3)由(1)(2)、可知,两个茶壶一样大.木块铜块铁块[铺垫]第一只茶壶能装10大杯水,第二只茶壶可以装15小杯水.已知5大杯水与9小杯水同样多,哪个茶壶大?[分析]因为5大杯水与9小杯水同样多,那么10大杯水就等于18小杯的水,而现在只有15小杯的水,10大杯水和15小杯水比较,10大杯水要多一些,所以第一个茶壶大.例10有9个乒乓球,但有一个轻些,其余一样重.现在给你一个天平,能2次称出哪个乒乓球轻些吗?【分析】可以用2次就称出哪个乒乓球轻一些.先把9个乒乓球分成3份,每3个一份.先把其中的两份拿来称一次,如果天平左右平衡,说明这两份中的三个乒乓球一样重,轻的那个就在另外第三份里面.如果这两堆乒乓球不一样重,那么天平高出的一端里面的乒乓球就有一个轻的.这样第一次就能称出轻的乒乓球在哪三个里面.然后再把轻的这一份中的三个乒乓球分成三份每份1个.第二次称时天平左右盘里各放一个,如果天平平衡,说明这两个一样重,这样就检测出另外第三个是轻的那一个.如果天平不保持平衡,那么就检测出高的那一端里面的乒乓球就是轻的那个.第一次称:第二次称:试试看练习二1.人自己用卷尺测量自己的身高,用脚踩着卷尺的开头一端,正好踩去1分米长,在头顶的刻度是1米40厘米,李玲的身高是多少?【答案】1分米=10厘米,1米40厘米-10厘米=1米30厘米,李玲的身高是1米30厘米.2.天平有5个砝码,1克,3克,9克,20克,27克各1个,你能称出50克,60克吗?应怎样称出这两种重量?【答案】3+20+27=50(克),1+3+9+20+27=60(克),称50克重量的时候放3克、20克、27克的砝码,称60克重量的时候再加上1克和9克.3.数一数,每个图形的表面有几个小方格?比比谁的表面大?【答案】第一个图形表面有18个小方格,第二个图形表面有24个方格,第三个图形表面有18个小方格,比一比第二个图形表面大.4.把四个大小相同的铁环连在一起(如图),拉紧后长是多少?【答案】1616161644452+++---=(厘米),拉紧后长52厘米.羽毛球于1873年起源于英格兰格拉斯哥郡的巴德明顿(minBad ton),1988年被列为汉城奥运会表演项目,后于1992年开始成为奥运会正式比赛项目,共设男、女单打和双打4块金牌.1996年亚特兰大奥运会又增设了混合双打,使奥运会羽毛球项目的金牌总数增至5枚.2008年北京奥运会羽毛球比赛将于2008年8月9日至17日在北京工业大学体育馆举行.国际奥委会把参加奥运会羽毛球比赛的选手限定在172人之内,每个项目根据世界排名选出单打前38名、双打和混合双打各16对选手直接参赛.但每个项目中至少包括五大洲的各1名选手或1对选手参加.这些选手必须在该洲世界排名领先.如果在世界排名中仍没有某洲的选手,则由在积分期间最近一次该洲锦标赛冠军参加.奥运会东道主拥有不少于两名选手参赛的权利.每个国家或地区在1个项目中最多有3个席位,多出的席位依次让给排名列后的国家和地区选手.羽毛球场地呈长方形,长13.4米,单打场地宽5.18米,双打场地宽6.10米.奥运会羽毛球赛用球需经过世界羽联批准.奥运会羽毛球赛馆需将700个适合比赛的三种速度的球储存于安全的仓库中.球拍由参赛运动员自备,由于不符合规定的球拍并未给球员带来明显的有利,因而裁判员对运动员的球拍并不做严格检查.2006年5月,羽毛球世界联合会在日本东京举行的年度代表大会上决定实行21分的新赛制,北京奥运会也将采用这一赛制.21分赛制对于调动运动员积极性、减少运动员受伤,以及改进电视转播效率等比原来的15分制有更大优势.王亚南睡三角床许多科学家、文学家的成才之路就是从小刻苦读书.王亚南小时候胸有大志,酷爱读书.他在读中学时,为了争取更多的时间读书,特意把自己睡的木板床的一条腿锯短半尺,成为三脚床.每天读到深夜,疲劳时上床去睡一觉后,迷糊中一翻身,床向短脚方向倾斜过去,他一下子被惊醒过来,便立刻下床,伏案夜读.天天如此,从未间断.结果他年年都取得优异的成绩,被誉为班内的三杰之一.他由于少年时勤奋刻苦读书,后来,终于成为我国杰出的经济学家.读书有很多好处,也许我们容易看到这一点,但读书真正的目的是充实我们的人生,改变我们的命运.唯有珍惜时间、勤奋刻苦读书,获取尽可能多的知识,才能实现理想,实现人生的价值.1.知识改变命运.2.读书是人生成功的重要起点.。
最新二年级奥数第二讲练习“移多补少”

二年级奥数“移多补少”第一关轻装上阵★级1、甲筐比乙筐多10棵白菜,从甲筐拿几棵到乙筐,甲乙两筐的白菜棵数同样多?2、小明有16个贝壳,小红有12个贝壳.小明给小红岞个贝壳,两人贝壳个数就会同样多?3、二(1)班第一队有28人,第二队有36人,怎样调整,两队人数同样多?4、肖肖有8根小棒,肖肖给飞飞2根后两人小棒数一样多,飞飞原来有几根小棒?5、芳芳有16根小棒,强强有8根小棒,芳芳给强强几根小棒,两人的小棒根数相等?第二关勇往直前★★级1、哥哥有22张邮票,他给弟弟4张后,两人的邮票同样多,弟弟原来有几张邮票?2、小白兔有15个萝卜,小黑兔有18个萝卜。
妈妈又买7个萝卜,怎么分,才能让两只小兔的萝卜同样多?3、一班有35个同学,二班有32个同学。
开学以后,又新转来5个新同学,怎样分才能使两个班的人数相等?第三关★★★:挑战自我1、小芳有15多花,她给小明3朵后,两人的花就同样多。
小明原来有多少朵花?2、甲、乙两筐都有一些西瓜,从甲筐中取出4个放入乙筐后,甲筐的西瓜还比乙筐多3个。
甲筐原来比乙筐多几个西瓜?3、甲、乙两筐都有一些西瓜,从甲筐中取出6个放入乙筐后,甲筐的西瓜还比乙筐少2个。
甲筐原来比乙筐多几个西瓜?4、一个两层文具盒,共放了12枝铅笔,从上层拿出2枝放到下层,两层铅笔的枝数就同样多,原来下层有多少枝铅笔?5、红盒子里有52个玻璃球,蓝盒子里有34个玻璃球,每次从多的盒子里取出3个放到少的盒子里,拿几次才能使两个盒子里的玻璃球的个数相等?6、书架的上层有25本书,下层有27本书,爸爸又买回10本书,怎样放才能使书架上、下两层的书同样多?7、甲、已两筐各有西瓜20个,从甲筐取几个放入乙筐中后,乙筐就比甲筐多8个,甲筐现有多少个西瓜?11、两筐水果共50千克,如果从第一筐取出6千克放入第二筐中,那么第一筐还比第二筐多2千克,两筐原有水果各多少千克?12、甲、乙两筐共有苹果91千克,从甲筐里取出4千克放到乙筐里,结果甲筐的苹果比乙筐少3千克,求甲、乙两筐原来各有苹果多少千克练习卷1、一年(1)班有40个学生,一年(2)班有43个学生.开学后又转来5 ,怎样分才能使两个班的人数相等?2、小明有27本书。
二年级下册数学试题奥数思维训练第二讲迷宫探险解析版全国通用

第二讲迷宫探险迷宫游戏是一种开发学生智力的活动,迷宫的设计很巧妙,也很有趣味性.在这节课中,老师引导学生来玩走迷宫的游戏,可以考验他们的眼力,锻炼耐力,提高孩子的想象力.前半节课我们通过一些简单的迷宫游戏,让学生来找破解迷宫的方法,一般情况下可采用倒走的方法,就是从出口处开始,倒着走到入口,这样可以避免误入死胡同.后半节课我们通过一些数字迷宫游戏来锻炼学生的计算能力和观察能力,提高难度,不断升华,让学生在活动中有所获.数学乐园圣诞老爷爷要送礼物给小企鹅,可是他必须先通过这个图形迷宫才可以,怎么办呢?聪明的小朋友们,请你顺着○的路线画线,和圣诞老爷爷一起把礼物送给小企鹅吧.小淘气玩了半天的足球,该回家了.你能帮他找到一条回家的路吗?画一画吧!图形迷宫神秘的迷宫,你敢走吗?聪明的小朋友们,我们一起来走一走吧.如下图,从A 走到B ,途中必须按照白、灰、白、灰……的格子前进,不可以直走或横走,只能斜着走,小朋友们想一想,可以怎样走?画一画吧!【教学思路】在这个迷宫图里,首先老师要引导学生理解题目的意思.走的时候开始要走一个白格子,再走一个黑格子,这样不断重复.走的顺序不能直走,也不能横走,只能斜着走.一般情况下,我们可以从B 点倒着走回到A 点,然后再检验是否正确.汤姆和杰瑞在迷宫里玩儿捉迷藏的游戏,小猫汤姆要捉到老鼠杰瑞,你来帮帮它吧.告诉你们一个小窍门:先从出口处倒回来找到进口,这样就容易多了.【教学思路】让学生从出口走到进口,再从进口走到出口验证一下,这个迷宫图就轻松解决了.答案如右上.要从迷宫的起点走到终点,应该从A、B、C哪个门出去呢?【教学思路】本题迷宫比较复杂,我们可以分别从A、B、C 三个出口往起点倒走,我们发现A 和B出口都走不到起点去,无法走通.只有C出口可以走通,所以只能从C出口出去.如下图:请帮小文找出一条参观花展的通道,要求能看到所有的花,但不能走交叉重复的路线,也不能走入白格.该选A、B、C、D哪个入口?【教学思路】让学生从每个入口都走一走,只有D点不重复走能看见所有的花.如下:迷宫里放有一些小鱼.小猫能往上、下、左、右四个方向走,请问小猫一共能吃到几条鱼?【教学思路】先引导学生整体观察,小猫能往上、下、左、右四个方向来走,小猫往上走时,可吃到2条小鱼;往下走,可吃到1条小鱼;往左走,可吃到5条小鱼;往右走,可吃到2条小鱼.一共能吃到的小鱼:2+1+5+2=10(条).所以小猫一共能吃到10条小鱼.数字迷宫如下图.从A开始按“1-9-8-5”的顺序走,你能在半分钟内走出迷宫吗?【教学思路】从A点起,按“1-9-8-5”的顺序试,答案如上.小乌龟迷了路,请你按照先倒数、再顺数的顺序帮它找到回家的路.请用线连一连.【教学思路】学生首先要弄清楚小乌龟走的路线,先是倒数,从20数到1,然后再顺数,从1数到20.通过试画我们可以找到答案.如下图,按箭头所指,从2开始,到5为止,选择一条不重复的路线,使经过的数的和最大,该怎么走?【教学思路】只有右下的“10”不能走到,有两种路线可以走,如上图.附加题(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)仔细观察下图的数字迷宫.请你由入口进去,按经过的数与运算符号计算,到出口时,其最后结果必须是1,走时可上,可下,可横,但不能返回.你选择怎样的一条线路呢?【教学思路】这道题主要是培养学生快速口算的能力,由于口算过程比较多,老师可以帮助学生一起来找,此题的路线不唯一.下面的火柴棍游戏中,如果规定火柴棍头尾相接才能走通,那么怎样才能从A到达B?【教学思路】首先让学生理解火柴棍头尾相接才能走通的意思,老师可以通过画图举例来演示.理解了题意,这道题也就容易解答了.练习二1.小兔子想吃萝卜,请你帮它找到路线.【答案】2.如下图,哈哈要通知小老鼠参加新年联欢会,你看应该怎么走才能找到小老鼠?【答案】3.如下图,赛车手小狗如何很快走出迷宫?【答案】4.请你从入口开始,按“快一乐一学一数一学”的顺序走到出口,要求只能横走、竖走,不能斜走,也不能走重复的路.【答案不唯一】5.右下图的方格里分别有数字1,9,9,7.请你从起点开始,按“1—9—9—7—1—9—9—7……”顺序走到终点,不能斜走,也不能向上走,更不能跳格.请仔细观察后,选择正确的走法.【答案】小公主被一个可怕的妖怪捉走了,关到了下图出口处的城堡里,国王非常难过,可是想了很多办法,还是没救出公主,后来,国王许下诺言,如果谁能救出美丽的公主,就把公主嫁给那个勇士,有一个猎人很勇敢,要来试一试。
二年级下册数学奥数习题:年龄问题-全国通用

第二讲年龄问题【专题导引】小朋友,今年你8岁,明年你几岁?妈妈今年34岁,比你大26岁,明年妈妈比你大多少岁呢?这一讲我们就讨论和年龄有关的数学问题。
在解答年龄问题时,要记住:每过一年,每人年龄都要长大一岁。
今年两个差几岁,再过几年,两人还相差几岁,这个差是不会变的。
【典型例题】【例1】今年明明比哥哥小3岁,5年后明明比哥哥小几岁?【试一试】1、今年晶晶比妹妹大2岁,10年后晶晶读初中了,那时晶晶比妹妹大几岁?2、妈妈在26岁时生下儿子小光,当小光8岁时,妈妈比小光大几岁?【例2】敏敏7岁,妈妈34岁,敏敏8岁时,妈妈几岁?【试一试】1、玲玲9岁,哥哥12岁,玲玲12岁时,哥哥几岁?2、爸爸36岁,儿子10岁,爸爸30岁时,儿子几岁?【例3】小宝宝今年2岁,她比妈妈小25岁,6年前妈妈几岁?6年后妈妈几岁?【试一试】1、妈妈今年30岁,女儿比妈妈小24岁,3年后女儿几岁?3年前女儿几岁?2、小红今年10岁,比爸爸小26岁,5年前爸爸比小红大几岁?5年后爸爸多少岁?【例4】程程今年6岁,程程5年后的年龄与洋洋今年的年龄相等,洋洋今年几岁?【试一试】1、李明今年10岁,8年后的年龄与哥哥今年的年龄相等,哥哥今年多少岁?2、姐姐4年前的年龄和妹妹今年年龄相等,姐姐今年25岁,妹妹今年多少岁?【例5】弟弟今年7岁,弟弟4年后的年龄与哥哥2年前的年龄相等,问哥哥今年多少岁?【试一试】1、姐姐今年10岁,姐姐3年前的年龄与妹妹2年后的年龄相等,问妹妹今年多少岁?2、哥哥2年前与弟弟2年后的年龄相等,弟弟今年8岁,哥哥今年几岁?【例6】妈妈今年30岁,女儿今年2岁,几年以后母女俩的年龄之和是60岁?【试一试】1、小华今年18岁,小冬今年12岁,几年后他们俩的年龄之和是50岁?2、今年小丽3岁,小强9岁,当两人的岁数和是30岁时,小丽和小强各是多少岁?【※例7】女儿今年4岁,妈妈今年28岁,妈妈的年龄是女儿的7倍,几年以后,妈妈的年龄正好是女儿的5倍?【※试一试】1、小强今年6岁,爸爸今年30岁,爸爸的年龄是小强的5倍,几年后,爸爸的年龄正好是小强的几倍?2、妈妈今年29岁,女儿今年5岁,几年后,妈妈的年龄是女儿的4倍?课外作业家长签名:_____________1、妈妈在24岁时生下女儿灵儿,当妈妈30岁时,妈妈比灵儿大几岁?2、小红3岁,妈妈30岁,妈妈32岁时,小红几岁?3、爷爷今年70岁,他有三个孙子,大孙子20岁,二孙子15岁,三孙子才5岁。
奥数讲座(2年级-下)(15讲)

二年级奥数讲座(二)目录第一讲机智与顿悟第二讲数数与计数第三讲速算与巧算第四讲数与形相映第五讲一笔画问题第六讲七座桥问题第七讲数字游戏问题(一)第八讲数字游戏问题(二)第九讲整数的分拆第十讲枚举法第十一讲找规律法第十二讲逆序推理法第十三讲画图显示法第十四讲等量代换法第十五讲等式加减法第一讲机智与顿悟数学需要踏实与严谨,也含有机智与顿悟.例1 在美国把5月2日写成5/2,而在英国把5月2日写成2/5.问在一年之中,在两国的写法中,符号相同的有多少天?解:一年中两国符号相同的日子共有12天.它们是:一月一日 1/1 七月七日 7/7二月二日 2/2 八月八日 8/8三月三日 3/3 九月九日 9/9四月四日 4/4 十月十日 10/10五月五日 5/5 十一月十一日 11/11六月六日 6/6 十二月十二日 12/12注意由差异应当想到统一,有差异就必须有统一,仔细想一想这道题就会有所领悟.例2 有一个老妈妈,她有三个男孩,每个男孩又都有一个妹妹,问这一家共有几口人?解:全家共有5口人.妹妹的年龄最小,她是每一个男孩的妹妹.如果你列出算式:1个妈妈+3个男孩+3个妹妹=7口人那就错了.为什么呢?请你想一想.例3 小明给了小刚2支铅笔,他们俩的铅笔数就一样多了,问小明比小刚多几支铅笔?解:小明比小刚多4支铅笔.注意,可不是多2支;如果只多2支的话,小明给小刚后,小刚就反而比小明多2支,不会一样多了.例4 小公共汽车正向前跑着,售票员对车内的人数数了一遍,便说道,车里没买票的人数是买票的人数的2倍.你知道车上买了票的乘客最少有几人吗?解:最少1人.因为售票员和司机是永远不必买票的,这是题目的“隐含条件”.有时发现“隐含条件”会使解题形势豁然开朗.例5 大家都知道:一般说来,几个数的和要比它们的积小,如2+3+4比2×3×4小.那么请你回答:0、1、2、3、4、5、6、7、8、9这几个数相加的和大还是相乘的积大?解:和大.注意:“0”是个很有特点的数.①0加到任何数上仍等于这个数本身;②0乘以任何数时积都等于0;把它们写出来就是:0+1+2+3+4+5+6+7+8+9=450×1×2×3×4×5×6×7×8×9=0所以,应当重视特例.例6 两个数的和比其中一个数大17,比另一个数大15,你知道这两个数都是几?你由此想到一般关系式吗?解:这两个数就是17和15.因为它们的和比15大17,又比17大15.由一个特例联想、推广到一般,是数学思维的特点之一.此题可能引起你如下联想:和-15=17,那么和=15+17.一般和=一个数+另一个加数,或写成:和-一个加数=另一个加数,或写成:被减数-减数=差,也可写成:被减数-差=减数.以上这些都是你从课本上学过的内容,这里不过是把它们联想到一起罢了.学数学要注意联想,学会联想才能融会贯通.例7 小明和小英一同去买本,小明买的是作文本,小英买的是数学本.已知小英买的数学本的本数是小明买的作文本的2倍.又知一本作文本的价钱却是一本数学本的价钱的2倍,请问他俩谁用的钱多?解:他俩花的钱一样多.可以这样想:因为作文本的价钱是数学本的2倍,所以把买作文本的钱用来买数学本,同样多的钱所买到的本数应该是作文本的2倍,这刚好与题意相符.可见两人花的钱一样多.结论是隐含着的,推理就是要把它明明白白地想通,写出来的推理过程就叫“证明”,这是同学们现在就可以知道的.例8 中午放学的时候,还在下雨,大家都盼着晴天.小明对小英说:“已经连续三天下雨了,你说再过36小时会出太阳吗?”小朋友你说呢?解:不会出太阳.因为从中午起再过36个小时正好是半夜.而阴雨天和夜里是不会出太阳的.注意:解题的第一要义是首先明确“问什么”,而且要紧紧抓住“问什么”?“问什么”是思考目标,这就好比小朋友走着来上学,学校是你走路的目的,试想,如果你走路没有目标,结果会怎样?本题迷惑人的地方就是想用阴天下雨把你的注意力从应当思考的目标引开,给你的思维活动造成干扰.学会删繁就简,抓住目标,将会大大地提高你的解题效率.例9 一位画家想订做一个像框,用来装进他的立体画.他画了一张像框的尺寸图拿给你看(右图),请你帮他算算,需要多长的材料才能做好?(画家说,材料粗细要求一样,形状尺寸一定要按图示加工,拐角部分都要做成直角).解:不管多长的材料,像框也无法做成.从每一部分来说,这个图看来是合理的,但从整体上看,这个图是“荒谬的”、“失调的”.用一句普通的话说,就是“有点不对劲的”.请你注意,对现实生活觉得有点不对劲的感觉是创造性的起因.习题一1.如右图所示,若每个圆圈里都有五只蚂蚁,问右图中一共应有多少只蚂蚁?2.一个课外小组活动日,老师进教室一看,来参加活动的学生只占教室里全体人数的一半.老师很生气.你知道这天共来了多少学生吗?3.小林和小蓉两人口袋里各有10元钱.两人去书店买书.买完书后发现,小林花去的钱正好和小蓉剩下的钱数一样多.请问,现在他们两人一共还有多少钱?4.满满一杯牛奶,小明先喝了半杯;然后添水加满,之后再喝去半杯;再一次添水加满,最后把它全部喝完.请问小明一共喝了多少杯牛奶多少杯水?5.小黄和小兰想买同一本书.小黄缺一分钱,小兰缺4角2分钱.若用他俩的钱合买这本书,钱还是不够.请问这本书的价钱是多少?他俩各有多少钱?6.一个骑自行车的人以每小时10公里的速度从一个城镇出发去一个村庄;与此同时,另一个人步行,以每小时5公里的速度从那个村庄出发去那个城镇.经过一小时后他们相遇.问这时谁离城镇较远,是骑车的人还是步行的人?7.有人去买葱,他问多少钱一斤.卖葱的说:“1角钱1斤.”买葱的说:“我要都买了.不过要切开称.从中间切断,葱叶那段每斤2分,葱白那部分每斤8分.你卖不卖?”卖葱的一想:“8分+2分就是1角”.他就同意全部卖了.但是卖后一算账,发现赔了不少钱.小朋友,你知道为什么吗?8.一天鲍勃用赛车送海伦回家.汽车在快车道上急驶.鲍勃看到前面有辆大卡车.灵机一动,突然向海伦提出了一个巧妙的问题.鲍勃说:“海伦,你看!前面那辆大卡车开得多快!但是我们可以超过它.假定现在我们在它后面正好是1500米,它以每分钟1000米的速度前进,而我用每分钟1100米的速度追赶它,我们这样一直开下去,到时候肯定会从后面撞上它.但是,海伦,请你告诉我,在相撞前一分钟,我们与它相距多少米?”聪明的海伦略加思考立刻回答了鲍勃的问题.小朋友,你也能回答吗?9.小明家附近有个梯形公园,公园中有4棵树排成了一行,如图所示.小明每天放学回家都要到公园里去玩一会儿.有一天,他玩着玩着突然想出了一个问题:“能不能把公园分成大小和形状都相同的4块,而且每一块上保留一棵树?”回到家以后,他又和爸爸妈妈一块儿讨论,终于像小明想的那样分好了,小明非常高兴.小朋友,你也回家与爸爸妈妈讨论讨论,看能不能分好?10.小莉在少年宫学画油画.一天,他找到了一块中间有个圆孔的纸板.他想把这块板分成两块,重新组合成一块调色板,如下图,小朋友看该怎么切才好呢?注意:回顾由第9题到第10题的解题思路,这里有一个克服“思维定势”的问题.在做第9题时,你可能费了很大劲,把大梯形这样划分,那样划分,试来试去,最终得到了满意的结果.做完了第9题后这种思考问题的方式方法就可能深深地在你的头脑中扎根了.当你着手解第10题时,你可能还是沿着原来的思路,按原来的思维方式处理面临的新问题,这种情况心理学上就叫做“思维定势”.思维定势不利于创造性的发挥,从这个意义上讲,有人说学习的最大障碍是头脑中已有的东西,是有一定道理的,你在做第10题时,对此大概也有体会了吧!今后要以此为训.对本讲其它各题,在你做完以后也希望你做一些回顾和总结,以便发现些更有价值的东西,使自己变得更聪明起来.习题一解答1.解:一共只有5只蚂蚁.如右图所示,每一个圆圈里都有五只蚂蚁.2.解:只来了一名学生.教室里共有两人,另一个人是老师,所以说学生占教室里全体人数的一半.3.解:他们两人此时一共还有10元.如下图所示.4.解:小明共喝了一杯牛奶和一杯水.因为原来就有一杯牛奶,最后喝光了;后来又加了两次水,每次半杯,合起来是一杯水,最后也喝光了.5.解:这本书的价钱就是4角2分钱.小黄有4角1分钱(所以买书还差1分),小兰1分钱都没有,所以他若买这本书,还差4角2分钱;小兰若是有1分钱的话,他俩的钱合起来也就够买这本书了.6.解:相遇后,两人就在一处了,此时二人离城自然一样远.7.解:按照买葱人的说法,葱叶那段每斤2分,葱白那段每斤8分,合起来确是1角.但是这样合起来后是2斤卖1角,不再是一斤1角钱,所以卖葱的人赔了钱.8.解:相撞前一分钟赛车落后卡车100米.海伦思考的窍门是倒着想.鲍勃的赛车比卡车每分钟快100米(即1100米-1000米=100米),所以碰车前的1分钟它们相距100米.9.解:划分方法如右图所示.每一块都是个小梯形,四个小梯形大小相等,形状相同.小梯形和大梯形之间是大小不等、形状相似.10.解:方法不止一种.①从中切下一条,倒换个位置放进去.(见图)②在需要开孔的位上开一个小圆孔,把切下的部分填到中间的孔中去.(见图)第二讲数数与计数从数数与计数中,可以发现重要的算术运算定律.例1 数一数,下面图形中有多少个点?解:方法1:从上到下一行一行地数,见下图.点的总数是:5+5+5+5=5×4.方法2:从左至右一列一列地数,见下图.点的总数是:4+4+4+4+4=4×5.因为不论人们怎样数,点数的多少都是一定的,不会因为数数的方法不同而变化.所以应有下列等式成立:5×4=4×5从这个等式中,我们不难发现这样的事实:两个数相乘,乘数和被乘数互相交换,积不变.这就是乘法交换律.正因为这样,在两个数相乘时,以后我们也可以不再区分哪个是乘数,哪个是被乘数,把两个数都叫做“因数”,因此,乘法交换律也可以换个说法:两个数相乘,交换因数的位置,积不变.如果用字母a、b表示两个因数,那么乘法交换律可以表示成下面的形式:a×b=b×a.方法3:分成两块数,见右图.前一块4行,每行3个点,共3×4个点.后一块4行,每行2个点,共2×4个点.两块的总点数=3×4+2×4.因为不论人们怎样数,原图中总的点数的多少都是一定的,不会因为数数的方法不同而变化.所以应有下列等式成立:3×4+2×4=5×4.仔细观察图和等式,不难发现其中三个数的关系:3+2=5所以上面的等式可以写成:3×4+2×4=(3+2)×4也可以把这个等式调过头来写成:(3+2)×4=3×4+2×4.这就是乘法对加法的分配律.如果用字母a、b、c代表三个数,那么乘法对加法的分配律可以表示成下面的形式:(a+b)×c=a×c+b×c分配律的意思是说:两个数相加之和再乘以第三数的积等于第一个数与第三个数的积加上第二个数与第三个数的积之和.进一步再看,分配律是否也适用于括号中是减法运算的情况呢?请看下面的例子:计算(3-2)×4和3×4-2×4.解:(3-2)×4=1×4=43×4-2×4=12-8=4.两式的计算结果都是4,从而可知:(3-2)×4=3×4-2×4这就是说,这个分配律也适用于一个数与另一个数的差与第三个数相乘的情况.如果用字母a、b、c(假设a>b)表示三个数,那么上述事实可以表示如下:(a-b)×c=a×c-b×c.正因为这个分配律对括号中的“+”和“-”号都成立,于是,通常人们就简称它为乘法分配律.例2 数一数,下左图中的大长方体是由多少个小长方体组成的?解:方法1:从上至下一层一层地数,见上右图.第一层4×2个第二层4×2个第三层4×2个三层小长方体的总个数(4×2)×3个.方法2:从左至右一排一排地数,见下图.第一排2×3个第二排2×3个第三排2×3个第四排2×3个四排小长方体的总个数为(2×3)×4.若把括号中的2×3看成是一个因数,就可以运用乘法交换律,写成下面的形式:4×(2×3).因为不论人们怎样数,原图中小长方体的总个数是一定的,不会因为数数的方法不同而变化.把两种方法连起来看,应有下列等式成立:(4×2)×3=4×(2×3).这就是说在三个数相乘的运算中,改变相乘的顺序,所得的积相同.或是说,三个数相乘,先把前两个数相乘再乘以第三个数,或者先把后两个数相乘,再去乘第一个数,积不变,这就是乘法结合律.如果用字母a、b、c表示三个数,那么乘法结合律可以表示如下:(a×b)×c=a×(b×c).巧妙地运用乘法交换律、分配律和结合律,可使得运算变得简洁、迅速.从数数与计数中,还可以发现巧妙的计算公式.例3 数一数,下图中有多少个点?解:方法1:从上至下一层一层地数,见下图.总点数=1+2+3+4+5+6+7+8+9=45.方法2:补上一个同样的三角形点群(但要上下颠倒放置)和原有的那个三角形点群共同拼成一个长方形点群,则显然有下式成立(见下图):三角形点数=长方形点数÷2因三角形点数=1+2+3+4+5+6+7+8+9而长方形点数=10×9=(1+9)×9代入上面的文字公式可得:1+2+3+4+5+6+7+8+9=(1+9)×9÷2=45.进一步把两种方法联系起来看:方法1是老老实实地直接数数.方法2可以叫做“拼补法”.经拼补后,三角形点群变成了长方形点群,而长方形点群的点数就可以用乘法算式计算出来了.即1+2+3+4+5+6+7+8+9=(1+9)×9÷2.这样从算法方面讲,拼补法的作用是把一个较复杂的连加算式变成了一个较简单的乘除算式了.这种方法在700多年前的中国的古算书上就出现了.习题二下列各题至少用两种方法数数与计数.1.数一数,下图中有多少个点?2.数一数,下图中的三角形点群有多少个点?3.数一数,下图中有多少个小正方形?4.数一数,下图中共有多少个小三角形?习题二解答1.解:方法1:从上至下一行一行地数,共4行每行5个点,得5×4=20.方法2:分成两个三角形后再数,见下图.得:(1+2+3+4)×2=20.发现一个等式:1+2+3+4=(1+4)×4÷2.2.解:方法1:从上至下一行一行地数,再相加,得:1+2+3+4+5+6+7+8+9+10=55.方法2:用拼补法,如图所示:11×10÷2=55.发现一个等式:1+2+3+4+5+6+7+8+9+10=(1+10)×10÷2.3.解:方法1:从上至下一层一层地数,得:5×4=20.方法2:做阶梯形切割,分两部分数,见右图.(1+2+3+4)×2=20.发现一个等式:1+2+3+4=(1+4)×4÷2.4:解:方法1:从上至下一层一层地数(图略)得:20×10=200.方法2:分成两个三角形来数:(1+3+5+7+9+11+13+15+17+19)×2=200.发现一个等式:1+3+5+7+9+11+13+15+17+19第三讲速算与巧算利用上一讲得到的乘法运算定律和等差数列求和公式,可以使计算变得巧妙而迅速.例1 2×4×5×25×54=(2×5)×(4×25)×54 (利用了交换=10×100×54 律和结合律)=54000例2 54×125×16×8×625=54×(125×8)×(625×16)(利用了=54×1000×10000 交换律和结合律)=540000000例3 5×64×25×125 将64分解为2、4、8=5×(2×4×8)×25×125 的连乘积是关键一=(5×2)×(4×25)×(8×125)步.=10×100×1000=1000000例5 37×48×625=37×(3×16)×625 注意37×3=111=(37×3)×(16×625)=111×10000=1110000例6 27×25+13×25 逆用乘法分配律,=(27+13)×25 这样做叫提公因数=40×25=1000例7 123×23+123+123×76 注意123=123×1;再=123×23+123×1+123×76 提公因数123=123×(23×1+76)=123×100=12300例8 81+991×9 把81改写(叫分解因=9×9+991×9 数)为9×9是为了下=(9+991)×9 一步提出公因数9=1000×9=9000例9 111×99=111×(100-1)=111×100-111=11100-111=10989例10 23×57-48×23+23=23×(57-48+1)=23×10=230例11 求1+2+3+…+24+25的和.解:此题是求自然数列前25项的和.方法1:利用上一讲得出的公式和=(首项+末项)×项数÷21+2+3+…+24+25=(1+25)×25÷2=26×25÷2=325方法2:把两个和式头尾相加(注意此法多么巧妙!)想一想,这种头尾相加的巧妙求和方法和前面的“拼补法”有联系吗?例12 求8+16+24+32+…+792+800的和.解:可先提公因数8+16+24+32+…+792+800=8×(1+2+3+4+…+99+100)=8×(1+100)×100÷2=8×5050=40400例13 某剧院有25排座位,后一排都比前一排多2个座位,最后一排有70个座位,问这个剧院一共有多少个座位?解:由题意可知,若把剧院座位数按第1排、第2排、第3排、…、第25排的顺序写出来,必是一个等差数列.那么第1排有多少个座位呢?因为:第2排比第1排多2个座位,2=2×1第3排就比第1排多4个座位,4=2×2第4排就比第1排多6个座位,6=2×3这样,第25排就比第1排多48个座位,48=2×24.所以第1排的座位数是:70-48=22.再按等差数列求和公式计算剧院的总座位数:和=(22+70)×25÷2=92×25÷2=1150.习题三计算下列各题:1.4×135×252.38×25×63.124×254.132476×1115.35×53+47×356.53×46+71×54+82×547.①11×11 ②111×111③1111×1111 ④11111×11111⑤111111111×1111111118.①12×14 ②13×17③15×17 ④17×18⑤19×15 ⑥16×129.①11×11 ②12×12③13×13 ④14×14⑤15×15 ⑥16×16⑦17×17 ⑧18×18⑨19×1910.计算下列各题,并牢记答案,以备后用.①15×15 ②25×25③35×35 ④45×45⑤55×55 ⑥65×65⑦75×75 ⑧85×85⑨95×9511.求1+2+3+…+(n-1)+n之和,并牢记结果.12.求下列各题之和.把四道题联系起来看,你能发现具有规律性的东西吗?①1+2+3+…+10②1+2+3+…+100③1+2+3+…+1000④1+2+3+…+1000013.求下表中所有数的和.你能想出多少种不同的计算方法?习题三解答1.解:4×135×25=(4×25)×135=100×135=13500.2.解:38×25×6=19×2×25×2×3=19×(2×25×2)×3=19×100×3=1900×3=5700.3.解:124×25=(124÷4)×(25×4)=31×100=3100.4.解:132476×111=132476×(100+10+1)=13247600+1324760+132476=14704836.或用错位相加的方法:5.解:35×53+47×35=35×(53+47)=35×100=3500.6.解:53×46+71×54+82×54=(54-1)×46+71×54+82×54=54×46-46+71×54+82×54=54×(46+71+82)-46=54×199-46=54×(200-1)-46=54×200-54-46=10800-100=10700.7.解:①11×11=121②111×111=12321③1111×1111=1234321④11111×11111=123454321⑤111111111×111111111=12345678987654321.8.解:①12×14=12×(10+4)=12×10+12×4=12×10+(10+2)×4=12×10+10×4+2×4 多次运用乘法分配=(12+4)×10+2×4 律(或提公因数)=160+8=168②13×17=13×(10+7)=13×10+13×7 多次运用乘法分配=13×10+(10+3)×7 律(或提公因数)=13×10+10×7+3×7=(13+7)×10+3×7=200+21=221发现规律:求十几乘以十几的积的速算方法是:用一个数加上另一个数的个位数,乘以10(即接着添个“0”),再加上它们个位数字的积.用这个方法计算下列各题:③15×17=(15+7)×10+5×7=220+35=255④17×18=(17+8)×10+7×8=250+56=306⑤19×15=240+45=285⑥16×12=180+12=192.9.解:作为十几乘以十几的特例,以下各小题的结果请牢牢记住:10.解:①15×15 注意矩形框中=15×(10+5)式子=15×10+15×5=15×10+(10+5)×5=15×10+10×5+5×5=(15+5)×10+5×5==225②25×25=25×(20+5)=25×20+25×5=25×20+(20+5)×5=25×20+20×5+5×5=(25+5)×20+5×5 注意矩形框中= 式子=625发现规律:几十五的自乘积就是十位数字和十位数字加1的积,再在其后写上25.如15×15的积就是1×2再写上25得225.25×25的积就是2×3再写上25得625.用这个方法写出其他各题的答案如下:③35×35=3×4×100+25=1225④45×45=4×5×100+25=2025⑤55×55=5×6×100+25=3025⑥65×65=6×7×100+25=4225⑦75×75=7×8×100+25=5625⑧85×85=8×9×100+25=7225⑨95×95=9×10×100+25=9025要牢记以上方法和结果.要知道,孤立的一道题不好记,但有规律的一整套的东西反而容易记住!11.解:有的同学问:“n是几?”老师告诉你:“n就是末项,你说是几就是几”.用头尾相加法求,自然数列的前n项之和.12.解:请注意规律性的东西.①1+2+3+…+10=(1+10)×10÷2=55②1+2+3+…+100=(1+100)×100÷2=5050③1+2+3+…+1000=(1+1000)×1000÷2=500500④1+2+3+…+10000=(1+10000)×10000÷2=50005000.13.解:方法1:仔细观察不难发现把每列(或每行)的10个数相加之和按顺序排列起来构成一个等差数列,它就是:55,65,75,85,95,105,115,125,135,145∴总和=(55+145)×10÷2=1000.方法2:首先各行都按第一行计数,得10行10列数字方阵的所有数之和为55×10=550.但第二行比第一行多10,第三行比第一行多20,…,第十行比第一行多90.总计共多:10+20+30+40+50+60+70+80+90=450.所以原题数字方阵的所有数相加之和为:550+450=1000.方法3:仔细观察可发现,若以数字10所在的对角线为分界线,将该数字方阵折叠之后,它就变成下述的三角形阵(多么巧妙!)20 20 20 20 20 20 20 20 20 1020 20 20 20 20 20 20 20 1020 20 20 20 20 20 20 1020 20 20 20 20 20 1020 20 20 20 20 1020 20 20 20 1020 20 20 1020 20 1020 1010总和=20×(1+2+3+4+5+6+7+8+9+10)-100=20×55-100=1000.方法4:找规律,先从简单情况开始可见原来数字方阵的所有数的和=10×10×10=1000.看!方法多么简捷;数学多么微妙!第四讲数与形相映形和数的密切关系,在古代就被人们注意到了.古希腊人发现的形数就是非常有趣的例子.例1 最初的数和最简的图相对应.这是古希腊人的观点,他们说一切几何图形都是由数产生的.例2 我国在春秋战国时代就有了“洛图”(见下图).图中也是用“圆点”表示数,而且还区分了偶数和奇数,偶数用实心点表示,奇数用空心点表示.你能把这张图用自然数写出来吗?见下图所示,这个图又叫九宫图.例3 古希腊数学家毕达哥拉斯发现了“形数”的奥秘.比如他把1,3,6,10,15,…叫做三角形数.因为用圆点按这些数可以堆垒成三角形,见下图.毕达哥拉斯还从圆点的堆垒规律,发现每一个三角形数,都可以写成从1开始的n 个自然数之和,最大的自然数就是三角形底边圆点的个数.第一个数:1=1第二个数:3=1+2第三个数:6=1+2+3第四个数:10=1+2+3+4第五个数:15=1+2+3+4+5…第n个数:1+2+3+4+5+…+n指定的三角形数.比如第100个三角形数是:例4 毕达哥拉斯还发现了四角形数,见下图.因为用圆点按四角形数可以堆垒成正方形,因此它们最受毕达哥拉斯及其弟子推崇.第一个数:1=12=1第二个数:4=22=1+3第三个数:9=32=1+3+5第四个数:16=42=1+3+5+7第五个数:25=52=1+3+5+7+9…第n个数:n2=1+3+5+9+…+(2n-1).四角形数(又叫正方形数)可以表示成自然数的平方,也可以表示成从1开始的几个连续奇数之和.奇数的个数就等于正方形的一条边上的点数.例5 类似地,还有四面体数见下图.仔细观察可发现,四面体的每一层的圆点个数都是三角形数.因此四面体数可由几个三角形数相加得到:第一个数:1第二个数:4=1+3第三个数:10=1+3+6第四个数:20=1+3+6+10第五个数:35=1+3+6+10+15.例6 五面体数,见下图.仔细观察可以发现,五面体的每一层的圆点个数都是四角形数,因此五面体数可由几个四角形数相加得到:第一个数:1=1第二个数:5=1+4第三个数:14=1+4+9第四个数:30=1+4+9+16第五个数:55=1+4+9+16+25.例7 按不同的方法对图中的点进行数数与计数,可以得出一系列等式,进而可猜想到一个重要的公式.由此可以使人体会到数与形之间的耐人导味的微妙关系.方法1:先算空心点,再算实心点:22+2×2+1.方法2:把点图看作一个整体来算32.因为点数不会因计数方法不同而变,所以得出:22+2×2+1=32.方法1:先算空心点,再算实心点:32+2×3+1.方法2:把点图看成一个整体来算:42.因为点数不会因计数方法不同而变,所以得出:32+2×3+1=42.方法1:先算空心点,再算实心点:42+2×4+1.方法2:把点图看成一个整体来算52.因为点数不会因计数方法不同而变,所以得出:42+2×4+1=52.把上面的几个等式连起来看,进一步联想下去,可以猜到一个一般的公式:22+2×2+1=3232+2×3+1=4242+2×4+1=52…n2+2×n+1=(n+1)2.利用这个公式,也可用于速算与巧算.如:92+2×9+1=(9+1)2=102=100992+2×99+1=(99+1)2=1002=10000.习题四1.第25个三角形数是几?2.第50个三角形数是几?3.第1000个三角形数是几?4.三角形数的奇偶性是很有规律的,想一想,这是为什么?5.观察下列图形,你能发现什么?6.第99个与第100个三角形数的和等于多少?7.每一个四角形数(或叫正方形数)(除1外)都能拆成两个三角形数吗?比如,100是哪两个三角形数的和?8.第8个三角形数恰是第6个四角形数,因为你还能试着找到一个这样的例子吗?(这事比较困难)9.请你试着画一画五角形数和六角形数的图形.并试着把第n个五(六)角形数拆成以1为首页、有n项的等差数列之和的形式.10.写出前10个四面体数.11.写出前10个五面体数.12.按不同的方法对下图中的点进行数数与计数,得出一系列等式,进而猜想出一个公式来,从中体会数与形之间的微妙关系.如:因为点数不会因计数方法不同而变,所以得出:请你照此继续做下去.(可参考本讲例7)13.模仿例7,用不同的方法分别对下两图中的点进行数数与计数,先得出一系列等式,进而猜想出一个重要的公式.习题四解答1.解:1+2+3+…+25=(1+25)×25÷2=325.2.解:1+2+3+…+50=(1+50)×50÷2=1275.3.解:1+2+3+…+1000=(1+1000)×1000÷2=500500.4.解:观察前几个三角形数的构成,就可以发现其中的规律:第1个数=1…奇数;第2个数=第1个数+2…奇数+偶数=奇数;第3个数=第2个数+3…奇数+奇数=偶数;第4个数=第3个数+4…偶数+偶数=偶数;第5个数=第4个数+5…偶数+奇数=奇数.5.解:相邻的两个三角形之和是一个四角形数(或叫正方形数),或是说,一个四角形数,可以拆成两个三角形数之和.或者根据第6题,=第100个四角形数=100×100=10000.7.解:能拆.100=55+45.8.解:寻找这样的例子比较困难.有人找到第49个三角形数是第35个四角形数,因为:(49+1)×49÷2=1225=352.9.解:五角形数如下图所示:第一个数:1=l第二个数:5=1+4第三个数:12=1+4+7第四个数:22=1+4+7+10第五个数:35=1+4+7+10+13 六角形数如下图所示:第一个数 1=1第二个数 6=1+5第三个数 15=1+5+9第四个数 28=1+5+9+13第五个数 45=1+5+9+13+17.第五讲一笔画问题一天,小明做完作业正在休息,收音机中播放着轻松、悦耳的音乐.他拿了支笔,信手在纸上写了“中”、“日”、“田”几个字.突然,他脑子里闪出一个念头,这几个字都能一笔写出来吗?他试着写了写,“中”和“日”可以一笔写成(没有重复的笔划),但写到“田”字,试来试去也没有成功.下面是他写的字样.(见下图)这可真有意思!由此他又联想到一些简单的图形,哪个能一笔画成,哪个不能一笔画成呢?下面是他试着画的图样.(见下图)经过反复试画,小明得到了初步结论:图中的(1)、(3)、(5)能一笔画成;(2)、(4)、(6)不能一笔画成.真奇怪!小明发现,简单的笔画少的图不一定能一笔画得出来.而复杂的笔画多的图有时反倒能够一笔画出来,这其中隐藏着什么奥秘呢?小明进一步又提出了如下问题:如果说一个图形是否能一笔画出不决定于图的复杂程度,那么这事又决定于什么呢?能不能找到一条判定法则,依据这条法则,对于一个图形,不论复杂与否,也不用试画,就能知道是不是能一笔画成?。
小学 奥数 数学课本 二年级 打印版

99+98+97+96+95=97×5=485
(2)9+99+999=10+100+1000-3
=1110-3=1107
5.解:(1)5+6+7+8&5+10+15+20+25+30+35
=20×7=140
(3)9+18+27+36+45+54
=(9+54)×3=63×3=189
第一讲速算与巧算 一、“凑整”先算
1.计算:(1)24+44+56 (2)53+36+47 解:(1)24+44+56=24+(44+56) =24+100=124 这样想:因为44+56=100是个整百的数,所以先把它们的 和算出来. (2)53+36+47=53+47+36 =(53+47)+36=100+36=136 这样想:因为53+47=100是个整百的数,所以先把+47带 着符号搬家,搬到+36前面;然后再把53+47的和算出来. 2.计算:(1)96+15 (2)52+69 解:(1)96+15=96+(4+11) =(96+4)+11=100+11=111 这样想:把15分拆成15=4+11,这是因为96+4=100,可凑 整先算. (2)52+69=(21+31)+69 =21+(31+69)=21+100=121 这样想:因为69+31=100,所以把52分拆成21与31之和, 再把31+69=100凑整先算. 3.计算:(1)63+18+19 (2)28+28+28 解:(1)63+18+19 =60+2+1+18+19 =60+(2+18)+(1+19) =60+20+20=100 这样想:将63分拆成63=60+2+1就是因为2+18和1+19可以 凑整先算. (2)28+28+28 =(28+2)+(28+2)+(28+2)-6 =30+30+30-6=90-6=84 这样想:因为28+2=30可凑整,但最后要把多加的三个2 减去. 二、改变运算顺序:在只有“+”、“-”号的混合算式中,运 算顺序可改变 计算:(1)45-18+19 (2)45+18-19 解:(1)45-18+19=45+19-18 =45+(19-18)=45+1=46 这样想:把+19带着符号搬家,搬到-18的前面.然后先算 19-18=1. (2)45+18-19=45+(18-19) =45-1=44 这样想:加18减19的结果就等于减1.
二年级下册数学试题-奥数思维训练:第二讲 迷宫探险(解析版)全国通用

第二讲迷宫探险数学乐园圣诞老爷爷要送礼物给小企鹅,可是他必须先通过这个图形迷宫才可以,怎么办呢?聪明的小朋友们,请你顺着○的路线画线,和圣诞老爷爷一起把礼物送给小企鹅吧.小淘气玩了半天的足球,该回家了.你能帮他找到一条回家的路吗?画一画吧!迷宫游戏是一种开发学生智力的活动,迷宫的设计很巧妙,也很有趣味性.在这节课中,老师引导学生来玩走迷宫的游戏,可以考验他们的眼力,锻炼耐力,提高孩子的想象力.前半节课我们通过一些简单的迷宫游戏,让学生来找破解迷宫的方法,一般情况下可采用倒走的方法,就是从出口处开始,倒着走到入口,这样可以避免误入死胡同.后半节课我们通过一些数字迷宫游戏来锻炼学生的计算能力和观察能力,提高难度,不断升华,让学生在活动中有所获.图形迷宫神秘的迷宫,你敢走吗?聪明的小朋友们,我们一起来走一走吧.如下图,从A走到B,途中必须按照白、灰、白、灰……的格子前进,不可以直走或横走,只能斜着走,小朋友们想一想,可以怎样走?画一画吧!【教学思路】在这个迷宫图里,首先老师要引导学生理解题目的意思.走的时候开始要走一个白格子,再走一个黑格子,这样不断重复.走的顺序不能直走,也不能横走,只能斜着走.一般情况下,我们可以从B点倒着走回到A点,然后再检验是否正确.汤姆和杰瑞在迷宫里玩儿捉迷藏的游戏,小猫汤姆要捉到老鼠杰瑞,你来帮帮它吧.告诉你们一个小窍门:先从出口处倒回来找到进口,这样就容易多了.【教学思路】让学生从出口走到进口,再从进口走到出口验证一下,这个迷宫图就轻松解决了.答案如右上.要从迷宫的起点走到终点,应该从A 、B 、C 哪个门出去呢?【教学思路】本题迷宫比较复杂,我们可以分别从A、B、C 三个出口往起点倒走,我们发现A 和B出口都走不到起点去,无法走通.只有C出口可以走通,所以只能从C出口出去.如下图:请帮小文找出一条参观花展的通道,要求能看到所有的花,但不能走交叉重复的路线,也不能走入白格.该选A、B、C、D哪个入口?【教学思路】让学生从每个入口都走一走,只有D点不重复走能看见所有的花.如下:迷宫里放有一些小鱼.小猫能往上、下、左、右四个方向走,请问小猫一共能吃到几条鱼?【教学思路】先引导学生整体观察,小猫能往上、下、左、右四个方向来走,小猫往上走时,可吃到2条小鱼;往下走,可吃到1条小鱼;往左走,可吃到5条小鱼;往右走,可吃到2条小鱼.一共能吃到的小鱼:2+1+5+2=10(条).所以小猫一共能吃到10条小鱼.数字迷宫如下图.从A开始按“1-9-8-5”的顺序走,你能在半分钟内走出迷宫吗?【教学思路】从A点起,按“1-9-8-5”的顺序试,答案如上.小乌龟迷了路,请你按照先倒数、再顺数的顺序帮它找到回家的路.请用线连一连.【教学思路】学生首先要弄清楚小乌龟走的路线,先是倒数,从20数到1,然后再顺数,从1数到20.通过试画我们可以找到答案.如下图,按箭头所指,从2开始,到5为止,选择一条不重复的路线,使经过的数的和最大,该怎么走?【教学思路】只有右下的“10”不能走到,有两种路线可以走,如上图.附加题(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)仔细观察下图的数字迷宫.请你由入口进去,按经过的数与运算符号计算,到出口时,其最后结果必须是1,走时可上,可下,可横,但不能返回.你选择怎样的一条线路呢?【教学思路】这道题主要是培养学生快速口算的能力,由于口算过程比较多,老师可以帮助学生一起来找,此题的路线不唯一.下面的火柴棍游戏中,如果规定火柴棍头尾相接才能走通,那么怎样才能从A到达B?【教学思路】首先让学生理解火柴棍头尾相接才能走通的意思,老师可以通过画图举例来演示.理解了题意,这道题也就容易解答了.练习二1.小兔子想吃萝卜,请你帮它找到路线.【答案】2.如下图,哈哈要通知小老鼠参加新年联欢会,你看应该怎么走才能找到小老鼠?【答案】3. 如下图,赛车手小狗如何很快走出迷宫?【答案】4.请你从入口开始,按“快一乐一学一数一学”的顺序走到出口,要求只能横走、竖走,不能斜走,也不能走重复的路.【答案不唯一】5.右下图的方格里分别有数字1,9,9,7.请你从起点开始,按“1—9—9—7—1—9—9—7……”顺序走到终点,不能斜走,也不能向上走,更不能跳格.请仔细观察后,选择正确的走法.【答案】小公主被一个可怕的妖怪捉走了,关到了下图出口处的城堡里,国王非常难过,可是想了很多办法,还是没救出公主,后来,国王许下诺言,如果谁能救出美丽的公主,就把公主嫁给那个勇士,有一个猎人很勇敢,要来试一试。
高斯小学奥数二年级(上)第02讲 奇与偶的应用

第二讲 奇与偶的应用前续知识点:二年级第一讲;XX 模块第X 讲 后续知识点:X 年级第X 讲;XX 模块第X 讲小高萱萱小高,你在看什么书啊?萱萱萱萱小高小高把里面的人物换成相应红字标明的人物.【提示】每换一次座位,奇偶性都会发生变化,有什么变化规律?灰鼠贝贝、恐龙维维和小象佳佳这三只小动物排成一排传气球,每次只传给与自己相邻的伙伴.开始气球在恐龙维维的手中,传了10次之后,气球在谁的手中呢?在下面横线上填一填:奇数:个位为 的整数;偶数:个位为 的整数. 奇数+奇数= 数;偶数+偶数= 数;奇数+偶数= 数; 奇数-奇数= 数;偶数-偶数= 数;奇数-偶数= 数.有三个座位让小狗来挑,它开始坐在1号座位,然后每次都换到相邻的座位。
换了9次座位后,小狗在几号座位?例题11 2 3练习1【提示】把偶数看成“0”,把奇数看成“1”.算式8597394658++++的结果是奇数还是偶数?对于多个数相加,结果的奇偶性由 数的个数决定.(1)偶数个偶数之和是 数; (2)奇数个偶数之和是 数; (3)奇数个奇数之和是 数; (4)偶数个奇数之和是 数.【提示】任意多个偶数相加的结果是奇数还是偶数?甜甜有一盒糖,共50块.甜甜每天吃4块糖,过了若干天后,盒子里会不会只剩3块糖?小山后的桃树结了100个桃子.小猴每天摘2个桃子吃,过了若干天后,树上会不会只剩1个桃子?例题3算式1011121314151617181920++++++++++的结果是奇数还是偶数?例题2练习2 练习3利用奇数与偶数的分类及其特殊性质,可以简便地求解一些与整数有关的问题.我们把这种通过分析整数的奇偶性来解决问题的方法称为奇偶分析法.【提示】分别从行或列入手,根据要求的摆放方法算出总数的奇偶性,与实际的总数比较看奇偶性是否一样.练习4 你能把7枚棋子放到下面的方格中,每格只放1枚,使每行、每列中的棋子总数都是奇数个吗?如果能,请填出来;如果不能,说明理由.如果是6枚棋子呢?你能把7颗豆子放到下面的方格中,每格只放1颗,使每行、每列中的豆子总数都是偶数个吗?如果能,请填出来;如果不能,说明理由.如果是6颗豆子呢?例题4【提示】1个杯子经过翻动后,杯口朝上变成杯底朝上,可能翻动的下数有什么规律?如下图所示,9个小方格中分别放上9枚硬币.(1) 若取出4枚硬币后,使每横行和每竖列中剩下奇数枚硬币,怎么取? (2) 若取出3枚硬币后,使每横行和每竖列中剩下偶数枚硬币,怎么取?【提示】动手操作并适当调整.课堂内外例题6桌上有7个茶杯,全部是杯口朝上,每次翻动4个茶杯,称为一次翻动.你能不能经过多次翻动,使这7个茶杯的杯底全部朝上?如果能,需要翻动几次?如果不能,请说明理由.例题5奇数和偶数的故事话说大灰狼想吃羊,可是办法已穷尽,只好再去学艺.一个月后,他总算是学会了一点数学知识,于是,便化装成一位教授的模样去抓羊了.大灰狼来到羊群中大声嚷嚷:“我是羊羊教育局派来考察教育的专家,有一道题想考考你们,答对者有重奖!”羊小笨以为有好吃的,第一个迫不及待地说:“大叔,有好吃的奖品吗?”只见这位头戴眼镜、两鬓斑白的教授严厉地说:“请先回答下列问题:我有一本书,中间掉了一张,其正反两面页码之和是21,请问掉的是哪一张?”羊小笨目瞪口呆,刚叫了一声“啊”就被大灰狼关了起来.如此这番,大灰狼又接连抓了三只羊.直到这时,羊儿们才发现,原来那教授竟然是大灰狼!大家决定派羊小聪来解题并救出羊小笨他们.羊小聪一听题,心中窃喜,哈哈,这也太小儿科了吧,羊小笨他们有救了.于是,便对大灰狼说:“如果我答对了,你要把羊小笨他们放了.”大灰狼心想,这可是我好不容易才学来的本领,哪就那么容易被你破了:“好!快解题吧!”羊小聪想了想回答道:“这两页的页码应该是10和11.可是,如果是掉一张纸,正面页码应该是奇数,反面页码才是偶数.因此,10、11根本不可能在一张纸上,若掉的话,应该掉两张纸,所以,教授你出错题了!”“我怎么能输给一只小羊呢?呜……”大灰狼很无奈,只好放了羊儿们,并送给羊小聪10万元的大奖.这真是“偷鸡不成蚀把米,竹篮打水一场空”.作业1.小美蛙、奇奇猫和壮壮鼠从左往右按顺序排成一排,熊猫博士把一顶帽子给壮壮鼠戴上了,相邻的小动物之间可以抢帽子.帽子被抢了7次之后,在哪个小动物的头顶上?++++的结果是奇数还是偶数?2.算式29384958773.小兔子拔了60根胡萝卜,每天吃2根,过了若干天后,还剩1根胡萝卜,可能吗?4.你能把5枚金币放到下面的方格中,且每格只放1枚,使每行、每列中的金币总数都是偶数个吗?如果能,请填出来.如果不能,请说明理由.5.田田有7顶帽子,全部帽口朝下,每次翻动2顶帽子,称为一次翻动.她能不能经过多次翻动,使这7顶帽子的帽口全部朝上?如果能,需要翻动几次?如果不能,请说明理由.第二讲 奇与偶的应用1. 例题1答案:2号详解:如图所示:“√”代表小狗.开始时小狗在1号座位,换1次后,她只能到2号座位;再换1次后,小狗可能在1号座位或3号座位;再换1次后,小狗又只能到2号座位……得出变化规律是换奇数次之后,小狗总是坐在2号座位上.所以换到第9次之后,小狗最后坐在2号座位上.2. 例题2答案:奇数详解:用“1、0法”,把偶数看成“0”,奇数看成“1”,算式中,有5个奇数,也就是5个“1”,共6个偶数,也就是6个“0”,5个“1”和6个“0”相加的结果是“5”,是奇数.所以这个算式的结果是奇数.3. 例题3答案:不会详解:小猴每天摘2个桃子,不管几天后,小猴摘的桃子总数都是偶数.任意多个偶数相加的结果都是偶数,100是偶数,根据“-=偶数偶数偶数”,树上剩下的桃子数应该是偶数.1不是偶数,所以树上不会只剩1个桃子.4. 例题4答案:7颗豆子不能;6颗豆子能详解:从行入手,如果每行的豆子数都是偶数,一共3行,3个偶数相加的结果是偶数,方格中的豆子总数应该是偶数.7不是偶数,所以不能够摆放出来.6是偶数,可以摆放出来,如下图所示,摆放方法不唯一.①开始: ②③换1次: 换2次: 换3次: 换4次: 换5次:?? ……5. 例题5答案:不能详解:我们把1个杯子由上到下(由下到上)的翻动称作翻动1下.把1个杯子经过翻动后,杯口朝上变成杯底朝上,可能翻动1下、3下、5下……也就需要奇数下.共有7个杯子,每个杯子都需要翻动奇数下才能杯底朝上.那么根据7个奇数相加的和是奇数,得出要使这7个茶杯的杯底全部朝上,一共需要翻动奇数下.而实际的操作是每次翻动4个杯子,也就是每次翻动4下,那么不管翻动多少次,444+++=偶数,杯子一共被翻动偶数下.即按照“每次翻动4个茶杯”这个操作,杯子一共要被翻动偶数下才能完成.因为“奇数≠偶数”,所以不能经过多次翻动,使这7个茶杯的杯底全部朝上.6. 例题6答案:如图所示:详解:动手操作一下,答案不唯一.7.练习1答案:恐龙维维简答:开始气球在恐龙维维的手中,找规律得出传偶数次之后,气球总是在恐龙维维手中.所以传了10次之后,气球在恐龙维维手中.8.练习2答案:奇数简答:用“1、0法”,把偶数看成“0”,奇数看成“1”,算式中,有3个奇数,也就是3个“1”,共2个偶数,也就是2个“0”,3个“1”和2个“0”相加的结果是“3”,是奇数.所以这个算式的结果是奇数.9.练习3答案:不会简答:甜甜每天吃4块糖,不管几天后,田田吃的糖总数都是偶数.50是偶数,根据“-=偶数偶数偶数”,盒子里剩下的糖数应该是偶数.3不是偶数,所以盒子里不会只剩3块糖.10.练习4答案:7枚棋子不能,6枚棋子能简答:从行入手,如果每行的棋子数都是奇数,一共4行,4个奇数相加的结果是偶数,方格中的(1)(2)豆子总数应该是偶数.7不是偶数,所以不能够摆放出来.6是偶数,可以摆放出来,如下图所示,摆放方法不唯一.11.作业1答案:奇奇猫根据表格发现:帽子被抢奇数次都会落到奇奇猫头上,而7次是奇数次,所以应该在奇奇猫头上.12.作业2答案:奇数简答:用“1、0法”,把偶数看成“0”,奇数看成“1”,算式中,有3个奇数,也就是3个“1”,共2个偶数,也就是2个“0”,3个“1”和2个“0”相加的结果是“3”,是奇数.所以这个算式的结果是奇数.13.作业3答案:不对简答:因为“-=偶数偶数偶数”,则不管吃多少天,剩下的胡萝卜根数都是偶数,所以结果还剩1根胡萝卜是不对的.14.作业4答案:5枚不能简答:要使每列的金币数和都为偶数,一共2列,则+=偶数偶数偶数;另一个要求是每行的金币数都为偶数,一共4行,+++=偶数偶数偶数偶数偶数.而一共有5枚棋子,为奇数.则5枚棋子既不能满足行的要求,也不能满足列的要求.15.作业5答案:不能简答:我们把1顶帽子由下到上(由上到下)的翻动称作翻动1下.把1顶帽子经过翻动后,帽口朝下变成帽口朝上,可能翻动1下、3下、5下……也就需要奇数下.共有7顶帽子,每顶帽子都需要翻动奇数下才能帽口朝上.那么根据7个奇数相加的和是奇数,得出要使这7顶帽子的帽口全部朝上,一共需要翻动奇数下.而实际的操作是每次翻动2顶帽子,也就是每次翻动2下,那么不管翻动多少次,222+++=偶数,帽子一共被翻动偶数下.即按照“每次翻动2顶帽子”这个操作,帽子一共要被翻动偶数下才能完成.因为“奇数≠偶数”,所以不能经过多次翻动,使这7顶帽子的帽口全部朝上.。
二年级下册奥数教材含试卷

二年级奥数教材含试卷目录第一章:算一算第一讲巧填竖式(二)第二讲简便运算(一)第三讲简便运算(二)第四讲简单数的分解用第五讲数的读写单元练习(一)(另附)第二章:实践与应用(一)第一讲应用题(一)第二讲应用题(二)第三讲应用题(三)单元练习(二)(另附)第三章:合理推算第一讲简单推理(一)第二讲简单推理(二)第三讲简单推理(三)第四讲合理安排单元练习(三)(另附)第四章:趣味数学与游戏第一讲巧填数第二讲数学游戏第三讲杂题单元练习(四)(另附)第五章:实践与应用(二)第一讲余数的妙用(二)第二讲年龄问题第三讲间隔趣谈(三)第四讲画画凑凑第五讲排队问题单元练习(五)(另附)第六章:认识时间第一讲时钟问题(一)第二讲时钟问题(二)单元练习(六)(另附)综合练习(一)(另附)综合练习(二)(另附)第一章算一算第一讲巧填竖式(二)【专题导引】“算式谜”是一种常见的猜谜游戏。
通常是给出一个式子,但式子中却含有一些用汉字、字母等表示的特定的数字。
要求我们根据一定的法则和逻辑推理的方法,找到要填的数字。
解答这类题目,要分析算式的特点,运用加、减的运算法则来安排每一个数。
一个算式中填几个数时,要选好先填什么,再填什么,选准“突破口”,其他就好填了。
【典型例题】【例1】在下面竖式中的空白处填入适当的数,使算式成立。
□4+79□【试一试】在下面竖式中的空白处填入适当的数,使算式成立。
8□+4□0□3+□90【例2】在下面竖式中的空白处填入适当的数,使算式成立。
6□-9□25□-7□1□7-□49□□+□□【试一试】191+□□1492、在下边的算式里,空格里的四个数字总和是()。
□□+□□175【例4】在下面算式的空格里填上数字,使竖式成立。
□81+□5□□94□【试一试】在□里填上适当的数,使算式成立。
【例5】请计算下面竖式中的字母各代表多少?【试一试】下面竖式中的汉字和字母各代表多少?车卒马兵卒马=()车=()卒=()【例6】下面竖式中的□、○、△各代表一个数字,你能求出来吗?【试一试】下面各竖式中的图形和字母分别代表什么数字?【※例7】请你猜一猜,每个算式中的汉字各表示几?【※试一试】下面竖式中的汉字各代表多少?课外作业□3+□902、□4-□773、请猜一猜,竖式中的汉字各代表几?学生+生学6 64、在下面竖式中的空白处填入适当的数,使算式成立。
小学二升三年级奥数教程讲义

目录◆第一讲加减法的巧算(一) (5)◆第二讲加减法的巧算(二) (12)◆第三讲配对求和 (14)◆第四讲找简单的数列规律 (18)◆第五讲数图形 (20)◆第六讲填数游戏 (26)◆第七讲推理 (30)◆第八讲移多补少与求平均数 (35)◆第九讲盈亏问题 (42)◆第十讲等量代换 (51)第一讲加减法的巧算森林王国的歌舞比赛进行得既紧张又激烈。
选手们为争夺冠军,都在舞台上发挥着自己的最好水平。
台下的工作人员小熊和小白兔正在统计着最后的得分。
由于他们对每个选手分数的及时通报,台下的观众频频为选手取得的好成绩而热烈鼓掌,同时,观众也带着更浓厚的兴趣边看边猜测谁能拿到冠军。
观众的情绪也影响着两位分数统计者。
只见分数一到小白兔手中,就像变魔术般地得出了答案。
等小熊满头大汗地算出来时,小白兔已欣赏了一阵比赛,结果每次小熊算得结果和小白兔是一样的。
小熊不禁问:“白兔弟弟,你这么快就算出了答案,有什么决窍吗”小白兔说:“比如2号选手是93、95、98、96、88、89、87、91、93、91,去掉最高分98,去掉最低分87,剩下的都接近90为基准数,超过90的表示成90+‘零头数’,不足90的表示成90-‘零头数’。
于是(93+95+96+88+89+91+93+91)÷8=90+(3+5+6―2―1+1+3+1)÷8=90+2=92。
你可以试一试。
”小熊照着小白兔说的去做,果然既快又对。
这下小熊明白了,掌握了速算的技巧,在工作和生活中的作用很大。
它不仅可以节省运算时间,更主要的是提高了我们的工作效率。
我们在进行速算时,要根据题目的具体情况灵活运用有关定律和法则,选择合理的方法。
下面介绍在整数加减法运算中常用的几种速算方法。
例题与方法第一题:巧算下面各题① 36+87+64 ②99+136+101 ③ 1361+972+639+28解答:①式=(36+64)+87=100+87=187②式=(99+101)+136=200+136=336③式=(1361+639)+(972+28)=2000+1000=3000第二题:拆数补数① 188+873 ②548+996 ③9898+203解答:①式=(188+12)+(873-12)(熟练之后,此步可略)=200+861=1061②式=(548-4)+(996+4)=544+1000=1544③式=(9898+102)+(203-102)=10000+101=10101第三题:减法中的巧算① 300-73-27 ② -10解答:①式= 300-(73+ 27)=300-100=200②式=1000-(90+80+20+10)=1000-200=800第四题:巧算① 4723-(723+189)② 2356-159-256解答:①式=4723-723-189=4000-189=3811②式=2356-256-159=2100-159=1941第五题:巧算① 506-397 ②323-189 ③467+997 解答:①式=500+6-400+3(把多减的 3再加上)=109②式=323-200+11(把多减的11再加上)=123+11=134③式=467+1000-3(把多加的3再减去)=1464例1计算:(1)2458+503 (2)574+798例2.计算:(1)956-597 (2)3475-308例3 用简便方法计算:(1)783+25+175 (2)2803+(2178+5497)+4722例4. 计算: 999+99+9练习与思考。
奥数 二年级 讲义 小二教案 第二讲 有余数除法

本节课主要内容:在二年级春季学习的周期问题中我们将应用到有余数的除法的相关知识点,因此在这节课中,我们将来学习有余数的除法.1、理解有余数除法的意义,明白余数要比除数小的道理.2、会用竖式计算有余数的除法.3、会利用有余数的除法解决一些实际问题.个鬼脸应该是哪个?第52你能看出下面这些鬼脸的排列规律吗?请你想一想,.5个图案为一组循环排列的【教学思路】仔细观察这些图案可以发现,它们是按照下面这个个图案是5组的第22221222÷5=4……2,个可以排成这样的4组,还余下个.所以第.图案,应该是,分别可以摆几个?15131、用12根、根、根小棒摆①用12根摆:想:口三四十②用13根摆:想:口诀三四十二13-12=1③用15根摆:想:口诀三四十二15-12=3【教学思路】通过这个题的学习让学生来认识有余数的除法,以及余数的写法.(1)12根小棒每4根摆成一个,想三四十二,正好可以摆成3个.列式:12÷4=3(个),想三四十二,13-12=1(根)这样摆成342()13根小棒每根摆成一个个后还余下了1根.列式:13÷4=3(个)……1(根)(3)15根小棒每4根摆成一个,想三四十二,15-12=3(根)这样摆成3个后还余下了3根.列式:15÷4=3(个)……3(根)总结:13÷4=3……1和15÷4=3……3都是有余数的除法算式,在这两个有余数的除法算式中:13和15是被除数,4和4是除数,3和3是商,最后余下的部分1和3就是余. 数.2、计算下面各题?【教学思路】通过这个题让学生学会计算带余数的除法,答案如下:(1)余数是1的算式是:22÷7;37÷4;(2)余数是3的算式是:48÷9;33÷5;(3)没有余数的是:27÷8;36÷6;48÷8;49÷73、在有余数的除法算式中,比较余数和除数的大小,你发现了什么?整数除法较容易,余数除法不简单;整数除法余数“0,”余数除法有剩余;余数定比除数小,这个要求要记牢.【教学思路】把刚才的这些有余数的除法算式放在一起让学生进行观察.使学生明确被除数÷除数=商……余数,余数要比除数小,整数除法也有余数,余数为“0”,“0”也是余数,只是在整除当中我们不写出来.对于这个概念一定要弄清.有余数的除法在我们的生活中有什么用途呢?在一个有余数除法的算式里,.被除数、除数、商、余数之间有什么关系呢?今天这节课我们就一起来研究余数问题下面算式中的被除数不知道,你能算出来吗?(1)( )÷3=2 (1)(2)( )÷2=4 (1)(3)( )÷9=2 (6)【教学思路】在整数除法中,被除数=除数×商,那么有余数的除法中的被除数=除数×商+余数.(1)被除数是2×3+1=7,在括号里填上7.(2)被除数是2×4+1=9,在括号里填上9.(3)被除数是2×9+6=24,在括号里填上24.根据下面的要求写数.在1~90的自然数中:(1)除以9,没有余数的有哪些数?(2)除以9,余数是1的有哪些数?(3)除以9,余数是8的有哪些数?【教学思路】这道题我们只要先找出除以9没有余数的,就可以写出其他的数了.根据被除数=除数×商+余数,只需要在这个数的基础上加上余数就可以了.(1)除以9,没有余数的有:9,18,27,36,45,54,63,72,81,90(2)除以9,余数是1的有:10,19,28,37,46,55,64,73,82.在(1)基础上每个数加1. (3)除以9,余数是8的有: 17,26,35,44,53,62,71,80,89. 在(1)基础上每个数加8..求下列有余数除法算式中的除数2 ……)=4(1)30÷(1 ……)=62)25÷((2……)=93)47÷((-余数)÷商通过这个题的学习,我们发现在有余数的除法中:除数=(被除数求有余数除法计算里的除数,我们可以分两步计算,先用被除数减去余数,再用差除以商,【教学思路】 .具体答案如下:其结果就是所要求的除数2 =4……÷( 7 ))(30-2)÷4=7,所以30(11 …… 4 )=625-1)÷6=4,所以25÷(2()(2……)=99=5,所以47÷( 5 )(3(47-2)÷巩固练习在下面的()里填上适当的数.(1)86÷9=( 9)……( 5 )(2)(55)÷8=6 (7)(3)74÷( 8)=9 (2)(4)56÷6=(9 ) (2)【教学思路】这道题是有余数除法中数量关系的综合应用,学生应该根据题目来判断是求什么,怎样求.把下面□里面的数补充完整.进一步巩固有余数除法中各部分之间的数量这道题引导学生学习用竖式计算有余数除法,【教学思路】关系,具体分析如下:56+3=59. ,那么被除数就是余数是31)想七八五十六,所以除数是7.(42+2=44.,那么被除数是想余数是2(2)7+3=38.=5×=除数×商+余数,所以被除数)(3 被除数,,又因为余数要比除数小,所以被除数只能是61)想六九五十四,所以商肯定是6(461-54=7.余数是. )里填上合适的数按要求在(. )里最小能填几下面(. 里最大能填几)下面(4 ……)=3()÷()……(()÷8=78)÷()=5……())÷5=9……((【教学思路】这道题主要要考虑到余数要比除数小,具体分析如下:3+4=19. ×5,被除数=5 (1)要使()里填的数最小.除数应该是5+8=53. =9×9)里填的数最小.除数应该是,被除数(2)要使(7+7=63. ×,被除数=87 (3)要使()里填的数最大.余数应该是9+4=49.×=54. 4()要使()里填的数最大余数应该是,被除数“奥”、“数”分别代表一个数,请你将所有满足下列等式的“奥”、“数”所代表的数分别列出.【教学思路】因为除数是6,余数要比除数小,所以“数”的情况有6种:0、1、2、3、4、5.在这里要特别引导学生理解的是“0”也是余数.当“数”=0时,“奥”=6×7+0=42;当“数”=1时,“奥”=6×7+1=43;当“数”=2时,“奥”=6×7+2=44;当“数”=3时,“奥”=6×7+3=45;当“数”=4时,“奥”=6×7+4=46;当“数”=5时,“奥”=6×7+5=47.拓展与提高几个动物小朋友围坐在一起玩扑克牌,按照小猫、小狗、小猴、小猪的顺序发牌,你能不能算出来第39张牌发给了谁?【教学思路】每发一圈需要4张牌,39÷4=9……3,就是说39张牌可以发9圈,余下3张,最后l张应发给排在第3个的小猴.附加题(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)在算式( )÷8=3……( )中被除数最大是几?最小是几?【教学思路】这是一道有余数的除法算式,余数最大时,被除数最大;余数最小时,被除数最小.因为除数是8,所以余数最大就是7,余数最小是0(没有余数).( 31)÷8=3……(7 ),(24)÷8=3.找出下面图形的排列规律,根据规律算出第16个图形是什么?【教学思路】⑴这一排图形是一个△,两个○,这样三个图形为一个组,不断重复出现的.先算16个图形里面有几组这样的图形,16÷3=5(组)……1(个),余数是1,这一个图形是第6组的第一个,应该是△.⑵这一排图形是一个○,一个△,两个□,这样四个图形为一个组,不断重复出现的.先算16个图形里面有几组这样的图形,16÷4=4(组),没有余数,那么第16个图形是第4组的第四个,应该是□.有一筐苹果,如果每个小朋友拿4个会剩下1个,如果每个小朋友拿5个会剩下2个,那么这筐苹果至少有多少个?【教学思路】每个小朋友拿4个会剩下1个,被4除余1的数有:l,5,9,13,17,21,…每个小朋友拿5个会剩下2个,被5除余2的数有:2,7,12,17,22,…两个条件都满足的数最小的是17.所以这筐苹果至少有17个..在()里填上适当的数1.3 ……7 )=6÷9=2……6 45÷( ( 24 )6 ……)=6 97=6……2 60÷( ( 44 )÷2 ……)=9……5 74÷(8 ( 69 )÷8=89+8=89)×9 )+6=30 (8×( 3.2.把数分类81.45,;被9除没有余数的有:24,56,48,648【答案】(1)被除没有余数的有:,,289,;被9除有余数的有:23238除有余数的有:27,54,,28,49,632()被16.,49.在□里填上合适的数字3.5;7=8)61÷……3……)541)÷6=6……;(247÷8=57;(1【答案】(14=3……÷或……÷)(23=6204()÷……;5174=41134. 玲玲是卫生小组长,她带领8个同学一起擦教室里的38张课桌,平均每人擦多少张课桌,余下的要玲玲自己擦,那么玲玲共擦多少张桌子才能完成任务?【答案】这道题要求平均每人擦多少张课桌要用除法计算.不过应该有9个同学在劳动.列式:38÷9=4(张)……2(张)平均每个人要擦4张桌子,余下的玲玲来擦,所以玲玲要擦4+2=6(张)桌子.5. 松鼠妈妈给松鼠宝宝分松子,最少要拿出多少个,才能把100个松子刚好平均分给8个宝宝?【答案】100÷8=12(个)……4(个),最少要拿出4个,才能把100个松子刚好平均分给8个宝宝.文物失窃2008年1月1日上午,黑猫警长接到紧急报案:云龙博物馆的青铜方鼎被盗!青铜方鼎是一件战国时期的著名出土文物,重3千克,四周刻有各种图案,是一件价值连城的稀世之宝.这可是一件重大的文物失窃案!警长放下电话,带领猴侦探火速赶到博物馆.他们先察看了周围环境:博物馆坐落在云龙山南麓,东靠云龙村;四面高墙环绕,墙上架设了电网,看上去防范还是周密的;意外的是,东墙外有一个洞口.然后,他们来到值班室,找守卫人员斑马了解情况.斑马对警长说:“昨晚我值班,凌晨4时青铜方鼎还在展厅内.4时后,我不知不觉睡着了.6时醒来,发现文物被盗.”警长听完斑马的讲述,经过分析,断定此案是附近村里了解情况的人所为.于是,警长和猴侦探来到云龙村.向村长说明来意,并请村长协助破案.警长问:“村长先生,本村居民中有谁擅长挖洞?”村长回答:“本村共有12户居民,每户的情况我都了如指掌.他们当中只有土豚、田鼠和山兔三户会挖洞,其他人都不擅长此道.”“请村长把这三户的当家人请来,好吗?”警长十分客气地对村长说.“好!请警长稍等片刻.”村长边说边走出门去.不一会儿,土豚、田鼠、山兔三人跟在村长身后来了,村长一一向警长作了介绍.警长不动声色地逐一看了看三人的脸色,问道:“三位先生今天起得早吗?都干了些什么事?”土豚见警长发问,赶忙站起来,慢吞吞地说:“我有6个孩子.今天早晨4时我到山脚下采萝卜,直到6时,采回20个萝卜.因为6个孩子的食量不同,所以我把20个萝卜整个整个地分成数量都不相同的6份.每个孩子各自吃了一份,吃得可香呢!”土豚说完,田鼠、山兔接着说.他们俩的情况与土豚相似,都是从早晨4时至6时到山上为孩子采食.不同的是,田鼠采回28个山果,整个整个地分成数量都不相同的7份,分给7个孩子;山兔采回36棵甜菜,整棵整棵地分成数量都不相同的8份,分给8个孩子.结果在土豚家的床下搜出了失窃的青铜方鼎.黑猫警长命令猴侦探到土豚家搜查听完三人的讲述,文物犯土豚被依法拘留.青铜方鼎又在博物馆展厅里出现了,向中外参观者展示了中华民族光辉灿烂的古代文明.小朋友,你能说出确定土豚为重大嫌疑犯的依据吗?。
二年级下册数学试题-奥数思维训练:第二讲 迷宫探险(解析版)全国通用

第二讲迷宫探险【精品】数学乐园圣诞老爷爷要送礼物给小企鹅,可是他必须先通过这个图形迷宫才可以,怎么办呢?聪明的小朋友们,请你顺着○的路线画线,和圣诞老爷爷一起把礼物送给小企鹅吧.小淘气玩了半天的足球,该回家了.你能帮他找到一条回家的路吗?画一画吧!迷宫游戏是一种开发学生智力的活动,迷宫的设计很巧妙,也很有趣味性.在这节课中,老师引导学生来玩走迷宫的游戏,可以考验他们的眼力,锻炼耐力,提高孩子的想象力.前半节课我们通过一些简单的迷宫游戏,让学生来找破解迷宫的方法,一般情况下可采用倒走的方法,就是从出口处开始,倒着走到入口,这样可以避免误入死胡同.后半节课我们通过一些数字迷宫游戏来锻炼学生的计算能力和观察能力,提高难度,不断升华,让学生在活动中有所获.图形迷宫神秘的迷宫,你敢走吗?聪明的小朋友们,我们一起来走一走吧.如下图,从A走到B,途中必须按照白、灰、白、灰……的格子前进,不可以直走或横走,只能斜着走,小朋友们想一想,可以怎样走?画一画吧!【教学思路】在这个迷宫图里,首先老师要引导学生理解题目的意思.走的时候开始要走一个白格子,再走一个黑格子,这样不断重复.走的顺序不能直走,也不能横走,只能斜着走.一般情况下,我们可以从B点倒着走回到A点,然后再检验是否正确.汤姆和杰瑞在迷宫里玩儿捉迷藏的游戏,小猫汤姆要捉到老鼠杰瑞,你来帮帮它吧.告诉你们一个小窍门:先从出口处倒回来找到进口,这样就容易多了.【教学思路】让学生从出口走到进口,再从进口走到出口验证一下,这个迷宫图就轻松解决了.答案如右上.要从迷宫的起点走到终点,应该从A、B、C哪个门出去呢?【教学思路】本题迷宫比较复杂,我们可以分别从A、B、C 三个出口往起点倒走,我们发现A 和B出口都走不到起点去,无法走通.只有C出口可以走通,所以只能从C出口出去.如下图:请帮小文找出一条参观花展的通道,要求能看到所有的花,但不能走交叉重复的路线,也不能走入白格.该选A、B、C、D哪个入口?【教学思路】让学生从每个入口都走一走,只有D点不重复走能看见所有的花.如下:迷宫里放有一些小鱼.小猫能往上、下、左、右四个方向走,请问小猫一共能吃到几条鱼?【教学思路】先引导学生整体观察,小猫能往上、下、左、右四个方向来走,小猫往上走时,可吃到2条小鱼;往下走,可吃到1条小鱼;往左走,可吃到5条小鱼;往右走,可吃到2条小鱼.一共能吃到的小鱼:2+1+5+2=10(条).所以小猫一共能吃到10条小鱼.数字迷宫如下图.从A开始按“1-9-8-5”的顺序走,你能在半分钟内走出迷宫吗?【教学思路】从A点起,按“1-9-8-5”的顺序试,答案如上.小乌龟迷了路,请你按照先倒数、再顺数的顺序帮它找到回家的路.请用线连一连.【教学思路】学生首先要弄清楚小乌龟走的路线,先是倒数,从20数到1,然后再顺数,从1数到20.通过试画我们可以找到答案.如下图,按箭头所指,从2开始,到5为止,选择一条不重复的路线,使经过的数的和最大,该怎么走?【教学思路】只有右下的“10”不能走到,有两种路线可以走,如上图.附加题(老师可根据自己的课堂进度灵活处理讲义内容,附加题仅供老师参考使用.)仔细观察下图的数字迷宫.请你由入口进去,按经过的数与运算符号计算,到出口时,其最后结果必须是1,走时可上,可下,可横,但不能返回.你选择怎样的一条线路呢?【教学思路】这道题主要是培养学生快速口算的能力,由于口算过程比较多,老师可以帮助学生一起来找,此题的路线不唯一.下面的火柴棍游戏中,如果规定火柴棍头尾相接才能走通,那么怎样才能从A到达B?【教学思路】首先让学生理解火柴棍头尾相接才能走通的意思,老师可以通过画图举例来演示.理解了题意,这道题也就容易解答了.练习二1.小兔子想吃萝卜,请你帮它找到路线.【答案】2.如下图,哈哈要通知小老鼠参加新年联欢会,你看应该怎么走才能找到小老鼠?【答案】3.如下图,赛车手小狗如何很快走出迷宫?【答案】4.请你从入口开始,按“快一乐一学一数一学”的顺序走到出口,要求只能横走、竖走,不能斜走,也不能走重复的路.【答案不唯一】5.右下图的方格里分别有数字1,9,9,7.请你从起点开始,按“1—9—9—7—1—9—9—7……”顺序走到终点,不能斜走,也不能向上走,更不能跳格.请仔细观察后,选择正确的走法.【答案】小公主被一个可怕的妖怪捉走了,关到了下图出口处的城堡里,国王非常难过,可是想了很多办法,还是没救出公主,后来,国王许下诺言,如果谁能救出美丽的公主,就把公主嫁给那个勇士,有一个猎人很勇敢,要来试一试。
高斯小学奥数含答案二年级(下)第02讲 天平上的数学

第二讲天平上的数学前续知识点:二年级第一讲;XX模块第X讲后续知识点:X年级第X讲;XX模块第X讲把里面的人物换成相应红字标明的人物.阿瓜,还是你来玩吧! 卡莉娅,别怕,我来帮你!你们都太重了……哇!我们两个才和你一样重啊!阿瓜,我也想玩!嘿嘿,我们也一样重哦!那阿瓜和阿呆谁重呢?卡莉娅小高 阿瓜卡莉娅小山羊阿瓜卡莉娅和小山羊(小山羊在卡莉娅的衣袋里)阿呆卡莉娅和小山羊阿呆萱萱 萱萱小山羊阿瓜阿呆- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 1只大灰狼的体重等于2只小羊的体重,1只小羊的体重等于4只大白兔的体重,那么1只大灰狼的体重等于几只大白兔的体重呢?这是一个简单的推理题,需要小朋友根据已知条件,有条理、有次序地思考,充分利用每次得出的结论,作为后一步推理的依据.那么,在这里,小羊是做什么用的呢?天平上的数学,实际上是最基本的等量代换,重点是找出中间量,然后用标数法或是写出等量关系式进行分析推理.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题1在括号里填上合适的数,使天平保持平衡.【提示】把第2个天平上的桃子换成草莓吧!练习1在括号里填上合适的数,使天平保持平衡.例题2在括号里填上合适的数,使天平保持平衡.()只()个()个【提示】2个苹果=4个梨,那么1个苹果=()个梨.练习2在括号里填上合适的数,使天平保持平衡.()个- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 等量代换的类型有很多,前面两个例题都是直接在物体的数量之间进行等量代换,还有一种类型是根据等量代换求出某一物体的具体量.在解决这类题目时,首先是仔细观察题中给出的条件,然后利用等量代换的思想把未知的量换成已知的量.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题3如图所示,1只小鸭子的重量是100克,那么1辆玩具汽车的重量是多少克?【提示】根据小鸭子的重量,算算1个皮球的重量是多少克?练习31只小狗重8千克,1只小猫重多少千克?- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 如果我们找不到中间量,我们可以通过观察比较,找出两个对象之间的差异,去相同,比不同.当对象较多时,我们可以先两两进行比较,一步一步地解决问题.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题4观察下图电子秤上的数,1个乒乓球重多少克?126克132克【提示】去相同,比不同!练习4观察下图电子秤上的数,1只小猫重多少千克?9千克12千克例题5小猴子在架子上放了茶壶、热水瓶和水杯.如图所示,回答问题.我知道每层容器盛水总量相等.每个水杯盛水1千克.(1)一个茶壶能倒满几杯水?(2)每个茶壶盛水多少千克?每个热水瓶盛水多少千克?(3)每一层的水重多少千克?【提示】去掉架子上都相同的容器!例题6观察下图的三个天平,回答问题.(1)1个芒果换几个樱桃?(2)1个樱桃换几个花生?(3)1个桃子换几个花生?【提示】观察前两个天平,找出中间量——桃子,得到芒果和樱桃的关系.课堂内外比重量聪明的小朋友们,想一想,这四个小动物中,体重最重的是谁?最轻的是谁?作业1.在括号里填上合适的数,使天平保持平衡.2.在括号里填上合适的数,使天平保持平衡.3.如图所示,1只小公鸡的重量是1千克,那么1只小兔子的重量是几千克?()只()个4.观察下图电子秤上的数,1个梨重几克?2个苹果重几克?60克90克5.淘淘在三层玩具箱里摆放了玩具飞机、玩具枪和玩具汽车.如图所示,回答问题.我知道每层的玩具总价格正好相等,每架小飞机的价格是5元.(1)每个玩具枪的价格是几元钱?每辆小汽车的价格是几元钱?(2)每层箱子里的玩具总价格是多少元钱?第二讲 天平上的数学1.例题1 答案:8详解:如图所示,桃子既和草莓有数量关系,又和苹果有数量关系,那么桃子就是“中间量”.由前两个天平可以得出:1个桃子=4个草莓,4416⨯=,4个桃子=16个草莓,2个苹果=4个桃子,也就是2个苹果=16个草莓,计算可得1628÷=,1个苹果=8个草莓. 2.例题2 答案:4详解:2个苹果=4个梨,422÷=,那么1个苹果=2个梨.先把第2个天平上的苹果换成梨,得出天平左边有8个梨,右边有1个菠萝和2个梨;然后把天平两边同时去掉2个梨,得出1个菠萝=6个梨;把第3个天平上的菠萝换成梨,天平左边有8个梨,根据“1个苹果=2个梨”,824÷=,得出8个梨=4个苹果. 3.例题3 答案:600详解:1只小鸭子的重量是100克,3只小鸭子的重量是3100300⨯=(克),根据“2个皮球=3只小鸭子”,3002150÷=(克),得出1个皮球的重量是150克,那么4个皮球的重量是4150600⨯=(克).所以1辆玩具汽车的重量是600克. 4.例题4 答案:3详解:两个电子秤上相同的部分是都有1个足球、2个乒乓球、3个羽毛球,不同的部分是右边的电子秤比左边的多2个乒乓球,1321266-=(克),2个乒乓球的重量是6克,623÷=(克),1个乒乓球的重量是3克. 5.例题5答案:(1)2;(2)2,4;(3)9详解:先把架子上三层都相同的部分去掉,每层去掉3个水杯,如图所示.比较第一层和第二层,分别去掉1个茶壶,得出1个热水瓶=2个茶壶;比较第一层和第三层,分别去掉一个热水瓶,得出1个茶壶=2个水杯,那么一个茶壶能倒满2杯水.根据“每个水杯盛水1千克”,每个茶壶盛水122⨯=(千克),每个热水瓶盛水224⨯=(千克).每一层的水重459+=(千克).6.例题6答案:(1)2;(2)4;(3)16÷=(个),1个芒果=2个樱桃;把第3详解:把第2个天平上的桃子换成芒果,得到2个芒果=4个樱桃,422个天平上的桃子和芒果都换成樱桃,天平左边有4个樱桃,右边有3个樱桃和4个花生,两边同时去掉3个樱桃,得到1个樱桃=4个花生;4416⨯=(个),4个樱桃=16个花生,再根据“1个桃子=4个樱桃”,得到1个桃子=16个花生.7.练习1答案:4简答:小公鸡既和小乌龟有关系,又和小狐狸有关系,那么小公鸡就是“中间量”.由前两个天平得出:1只小公⨯=,2只小公鸡=4只小乌龟,也就是1只小狐狸=4只小乌龟.鸡=2只小乌龟,2248.练习2答案:6简答:把第2个天平上的“□”换成“△”,得出1个“○”=4个“△”;把第3个天平上的“○”和“□”都换成“△”,得出1个“○”+1个“□”=6个“△”.9.练习3答案:1简答:1只小狗重8千克,根据“1只小狗=2只小兔”,824÷=(千克),得出1只小兔重4千克.再根据“1÷=(千克),得出1只小猫重1千克.只小兔=4只小猫”,44110.练习4答案:1简答:右边的电子秤比左边的多3只小猫,1293-=(千克),3只小猫重3千克,331÷=(千克),1只小猫重1千克.11.作业1答案:2简答:根据题意得出中间量是草莓,由前两个天平可以得出:1个苹果=4个草莓,2个草莓=1个香蕉,计算得出1个苹果=2个香蕉.12.作业2答案:6简答:根据题意得出小青蛙是中间量,由前两个天平得出:1只乌龟=2只青蛙,2只青蛙=4只小鸭子,所以1只青蛙=2只小鸭子,1只乌龟=4只鸭子,然后计算出1只乌龟+1只青蛙=426+=(只)鸭子.13.作业3答案:6简答:根据题意得出小狗是中间量,由右边的天平得出1只小狗=3只小公鸡,已知1只小公鸡的重量是1千克,所以1只小狗的重量是3千克;由左边的天平得出1只小兔子=2只小狗,所以1只小兔子的重量是6千克.14.作业4答案:15;45简答:比较两个电子称得出右边电子称上的水果比左边电子称上的水果多了2个梨,并且计算得出右边电子称的示数比左边电子称的示数多30克,所以得出1个梨重30215÷=(克);由左边电子称得出2个苹果+1个梨=60(克),计算得出2个苹果重601545-=(克).15.作业5答案:(1)10;30.(2)65简答:根据每层玩具总价格相等,先把每层都有的3架飞机去掉,再比较上层和下层的玩具,去掉都有的1辆汽车和1个手枪,得出1个手枪=2架飞机=2510⨯=(元);再比较中层和下层的玩具,得出1辆汽车=3个手枪=31030⨯=(元).最后把任意一层的所有玩具价格相加,例如把上层箱子的所有玩具价格相加:⨯+⨯+=(元).532103065。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二讲数数与计数(一)
数学需要观察.大数学家欧拉就特别强调观察对于数学发现的重要作用,认为“观察是一件极为重要的事”.本讲数数与计数的学习有助于培养同学们的观察能力.在这里请大家记住,观察不只是用眼睛看,还要用脑子想,要充分发挥想像力.
例1 数一数,图2-1和图2-2中各有多少黑方块和白方块?
解:仔细观察图2-1
再仔细观察图2-2,
再一种方法是:
例2 图2-3所示砖墙是由正六边形的特型砖砌成,中间有个“雪花”状的墙洞,问需要几块正六边形的砖才能把它补好?
例3将8个小立方块组成如图2-5所示的“丁”字型,再将表面都涂成红色,然后就把小立方块分开,问:
(1)3面被涂成红色的小立方块有多少个?
(2)4面被涂成红色的小立方块有多少个?
(3)5面被涂成红色的小立方块有多少个?
例4如图2-7所示,一个大长方体的表面上都涂上红色,然后切成18个小立方体(切线如图中虚线所示).在这些切成的小立方体中,问:]
(1)1面涂成红色的有几个?
(2)2面涂成红色的有几个?
(3)3面涂成红色的有几个?
习题二
1.如图2-8所示,数一数,需要多少块砖才能把坏了的墙补好?
2.图2-9所示的墙洞,用1号和2号两种特型砖能补好吗?若能补好,共需几块?
3.图2-10所示为一块地板,它是由1号、2号和3号三种不同图案的瓷砖拼成.问这三种瓷砖各用了多少块?
4.如图2-11所示,一个木制的正方体,棱长为3寸,它的六个面都被涂成了红色.如果沿着图中画出的线切成棱长为1寸的小正方体.
求:(1)3面涂成红色的有多少块?
(2)2面涂成红色的有多少块?
(3)1面涂成红色的有多少块?
(4)各面都没有涂色的有多少块?
(5)切成的小正方体共有多少块?
5.图2-12所示为棱长4寸的正方体木块,将它的表面全染成蓝色,然后锯成棱长为1寸的小正方体.
问:(1)有3面被染成蓝色的多少块?
(2)有2面被染成蓝色的多少块?
(3)有1面被染成蓝色的多少块?
(4)各面都没有被染色的多少块?
(5)锯成的小正方体木块共有多少块?
6.图2-13所示为一个由小正方体堆成的“塔”.如果把它的外表面(包括底面)全部涂成绿色,那么当把“塔”完全拆开时,3面被涂成绿色的小正方体有多少块?
7.图2-14中的小狗与小猫的身体的外形是用绳子分别围成的,你知道哪一条绳子长吗?(仔细观察,想办法比较出
来).。
