方程求根实验报告
大学数学实验报告----迭代(一)——方程求解

Do M n , n, 2, 100
运行结果:
M n_Integer : Module y, k , m 2; k m ^ n 1 ;
x Mod k, n ;
Print n, " ", PrimeQ n , " ", x, "
", GCD m, n
Do M n , n, 2, 100
2 True 0 2 3 True 1 1 4 False 0 2 5 True 1 1 6 False 2 2 7 True 1 1 8 False 0 2 9 False 4 1 10 False 2 2 11 True 1 1 12 False 8 2 13 True 1 1 14 False 2 2 15 False 4 1 16 False 0 2 17 True 1 1 18 False 14 2 19 True 1 1 20 False 8 2 21 False 4 1 22 False 2 2 23 True 1 1 24 False 8 2 25 False 16 1 26 False 2 2 27 False 13 1 28 False 8 2 29 True 1 1 30 False 2 2 31 True 1 1 32 False 0 2 33 False 4 1 34 False 2 2 35 False 9 1 36 False 32 2 37 True 1 1 38 False 2 2 39 False 4 1 40 False 8 2
99 False 3 27 100 False 1 67 Null2
m=4 时
输入程序:
M n_Integer : Module y, k , m 4; k m ^ n 1 ; x Mod k, n ; Print n, " ", PrimeQ n , " ", GCD m, n , " ", x Do M n , n, 2, 100
数值计算实验报告

本科实验报告课程名称:计算机数值方法实验项目:方程求根、线性方程组的直接解法、线性方程组的迭代解法、代数插值实验地点:专业班级:学生姓名:指导教师:实验一方程求根}五、实验结果与分析二分法实验结果迭代法实验结果结果分析:本题目求根区间为[1,2],精度满足|x*-x n|<0.5×10-5,故二分法用公式|x*-x n|<(b-a)/ 2n,可求得二分次数并输出每次结果。
对迭代法首先要求建立迭代格式。
迭代格式经计算已输入程序之中,故直接给初值便可利用迭代法求出精度下的解。
六、讨论、心得每次的实验都是对已学过的理论知识的一种实战。
通过本次实验,我将二分法与迭代法的思路清晰化并且将其变成计算机设计语言编写出来,运用到了实际解决问题上感觉很好。
我自认为本次跟其他同学比较的优点在于我在二分法实现的时候首先利用换底公式将需要的二分次输输出,如此便很清晰明了的知道接下来每一步的意思。
迭代法给我的感觉便是高度的便捷简化,仅用几行代码便可以同样解决问题。
相比较二分法来说,我更喜欢迭代的思路。
实验二线性方程组的直接解法for(k=n-2;k>=0;k--){sum=0;for(j=k+1;j<n;j++)sum=sum+a[k][j]*x[j];x[k]=(b[k]-sum)/a[k][k];}for(i=0;i<n;i++)printf("x[%d]=%f ",i,x[i]); printf("\n"); //输出解向量x}五、实验结果与分析结果结果分析:如上图所示,输入线性方程组元数n=3,则会要求输入3*3的系数矩阵A与向量b构成的增广矩阵。
根据算法需要将系数矩阵A消元成上三角矩阵。
随后根据矩阵乘法公式变形做对应的回代。
六、讨论、心得本次实验在编写时候感觉还好,感觉将思路变成了程序设计语言,得以实现题目的要求。
但是在运行以及结果分析的时候,感觉到了本实验的一些不足之处:就是我的实验虽然可以实现不同的元数的线性方程组求解,但是缺少了分析初始条件——主元素不能为零。
方程求根 实验报告

实验一方程求根一、实验目的用各种方法求任意实函数方程f(x)=0在自变量区间[a,b]上,或某一点附近的实根。
并比较方法的优劣。
二、实验方法(1)二分法对方程f(x)=0在[a,b]内求根。
将所给区间等分,在分点x=(b-a)/2判断是否f(x)=0,若是,则有根x=(b-a)/2.否则,继续判断是否f(a)·f(x)<0,若是,则令b=x,否则令a=x。
重复此过程直至求出方程f(x)=0在[a,b]中的近似根为止。
(2)迭代法将方程f(x)=0等价变换为x=h(x)形式,并建立相应的迭代公式Xk+1=h(Xk)。
(3)牛顿法若已知方程f(X)=0的一个近似根X0,则函数f(X)在点X0附近可用一阶泰勒多项式P1= f (X0) + f’ (X0) (X-X0)来近似,因此方程f(X)=0可近似表示为f(X0)+ f’ (X0) (X-X0)=0.设f’ (X0)≠0,则X= X0- f (X0)/ f’ (X0),取X作为原方程新的近似根X1,然后将X1作为X0带入上式,迭代公示为:X k+1=X k - f (X k)/ f’ (X k)。
三、实验内容在区间[0,1]上用二分法求方程的近似根,要求误差不超过0.5×10^3。
取初值X0=0,用迭代公式X k+1=(2-e^k)/10,(k=0,1,2,…)求方程e^x+10x-2=0的近似根。
要求误差不超过0.5×10^3。
取初值X0=0,用牛顿迭代法求方程e^x+10x-2=0的近似根。
要求误差不超过0.5×10^3。
四、实验程序1.二分法function x=agui_bisect(fname,a,b,e)fa=feval(fname,a);fb=feval(fname,b);if fa*fb>0 error('两端函数值为同号');endk=0x=(a+b)/2while(b-a)>(2*e)fx=feval(fname,x);if fa*fx<0b=x;fb=fx;elsea=x;fa=fx;endk=k+1x=(a+b)/2end2.迭代法function x=agui_iterative(fname,x0,e)N=100;x=x0;x0=x+2*e;k=0;while abs(x0-x)>e & k<Nk=k+1x0=x;x=feval(fname,x0);disp(x)endif k==N warning('已达最大迭代次数');end3.牛顿法function x=agui_newton(fname,dfname,x0,e)N=100;x=x0;x0=x+2*e;k=0;while abs(x0-x)>e&k<Nk=k+1x0=x;x=x0-feval(fname,x0)/feval(dfname,x0);disp(x)endif k==N warning('已达最大迭代次数');end五、实验结果1.二分法2.迭代法3.牛顿法六、结果分析二分法要循环10次,迭代法要迭代4次,牛顿法要迭代3次才能达到精度为0.5×1^-3的要求,由此可知:二分法方法简单,编程容易,且对函数f(x)的性质要求不高,但其收缩速度较慢,计算量大,因此常被用于精度不高的近似根,或为迭代法求初值。
计算方法-方程求根实验
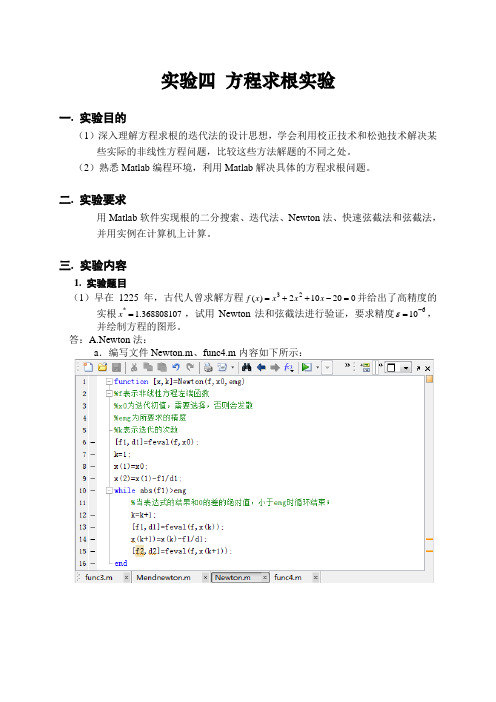
实验四 方程求根实验一. 实验目的(1)深入理解方程求根的迭代法的设计思想,学会利用校正技术和松弛技术解决某些实际的非线性方程问题,比较这些方法解题的不同之处。
(2)熟悉Matlab 编程环境,利用Matlab 解决具体的方程求根问题。
二. 实验要求用Matlab 软件实现根的二分搜索、迭代法、Newton 法、快速弦截法和弦截法,并用实例在计算机上计算。
三. 实验内容1. 实验题目(1)早在1225年,古代人曾求解方程020102)(23=-++=x x x x f 并给出了高精度的实根368808107.1*=x ,试用Newton 法和弦截法进行验证,要求精度610-=ε,并绘制方程的图形。
答:A.Newton 法:a .编写文件Newton.m 、func4.m 内容如下所示:b.运行,如下所示A为矩阵,由上面可知,对于初值为5,运行7次即可得到所需的精度,验证结果为古人给出的解释正确的;c.作图,编写下面的文件photo1.m.然后运行即可:注意下面中的x矩阵即为刚才计算出来的x系列,k为迭代的次数:a.编写文件Chord.m内容如下所示:b.运行结果如下所示:由上表可知,在精度为10^-6时有7位有效数字,古人的结果还是正确的c.作图,在上面运行后,即运行newton法时写的photo1.m文件即可出现图像:可以看到图中两条曲线基本重合; (2)取5.00=x ,用迭代法求方程x e x -=的根,然后用Aitken 方法加速,要求精度为结果有4为有效数字。
答:a. 编写文件func7.m 和Aiken.m ,内容如下所示:b .运行:具有四位有效数字 (3)用快速弦截法求解方程01)(=-=x xe x f ,要求精度为610-=ε,取6.05.010==x x ,作为开始值,并绘制1)(-=x xe x f 的图形。
答:对照可知,书本后面的程序已经正确,运行即可:下面为快速弦截法的主程序文件:函数文件如下:运行如下:作图,编写下面的文件:运行该文件就可以y=x*exp(x)-1函数和插值函数的图:可以看到两条直线基本重合在一起了,扩大图片可以看到两条直线是不重合的:2. 设计思想要求针对上述题目,详细分析每种算法的设计思想。
Newton迭代法求方程的根

《计算方法》实验报告一一、上机实验的问题和要求:用Newton 法求方程:x 7-28x 4+14=0在(0.1,1.9)中的近似值(初始近似值取为区间端点,迭代6次或误差小于0.00001)。
二、程序设计的基本思想,原理和算法描述:(包括程序的结构,数据结构,输入/输出设计,符号名说明等) Newton 迭代法的公式和使用条件:设函数在有限区间[a ,b]上二阶导数存在,且满足条件:1. )(a f )(b f <0;2. )(,,x f 在区间[a ,b]上不变号;3. )(,x f ≠0;4.)(,)(c f c f ≤,其中c 是a ,b 中使min ()(,a f ,)(,b f )达到的一个。
则对任意的初始近似值x0∈[a ,b],由Newton 迭代过程 x k+1=ψ(x k )=x k -)()(,kk x f x f ,k=0,1,2,…所生成的迭代序列{x k }平方收敛于方程f (x )=0在区间[a ,b]上的唯一解α。
设计思路:此程序比较简单,在设计时先把)(x f 和)(,x f 的表达式用c 语言表示出来,然后在经过一个while 循环做迭代,求出迭代后的解:x k+1=ψ(x k )=x k -)()(,kk x f x f ,当x k+1- x k 的绝对值小于0.00001时,循环终止。
循环结束时,方程的近似解已求出。
三、源程序及注释:#include "stdio.h" #include "math.h" main() {double x,x0=5,f,df; 给x0赋一个初值,程序使满足进入循环的条件 printf(" Please input x,x=[0.1,1.9]:\n x="); 输入一个端点a 或b scanf("%lf",&x);df=7*pow(x,6)-28*4*pow(x,3); 算出)(,x fwhile(fabs(x-x0)>=0.00001&&df!=0) 在迭代中如果|x-x0|<0.00001或)(,x f =0,则停止迭代 {x0=x; 迭代计算:x k+1=ψ(x k )=x k -)()(,kk x f x fx=x-(pow(x,7)-28*pow(x,4)+14)/(7*pow(x,6)-28*4*pow(x,3)); df=7*pow(x,6)-28*4*pow(x,3); }printf("\n The root is %lf",x); 打印出计算结果 getch(); }四、运行输出结果:输入x=0.1时的解 输入x=0.4时的解 输入x=1.9时的解五、调试和运行程序过程中产生的问题及采取的措施:调试程序时会报错,运行时一开始运行结果不正确,得不到理想结果,只有经过反复检查语言彻底消除错误。
MATL新编计算方法迭代法牛顿法二分法实验报告

M A T L新编计算方法迭代法牛顿法二分法实验报告 Prepared on 22 November 2020姓名 实验报告成绩评语:指导教师(签名)年 月 日说明:指导教师评分后,实验报告交院(系)办公室保存。
实验一 方程求根一、 实验目的用各种方法求任意实函数方程0)(=x f 在自变量区间[a ,b]上,或某一点附近的实根。
并比较方法的优劣。
二、 实验原理(1)、二分法对方程0)(=x f 在[a ,b]内求根。
将所给区间二分,在分点2a b x -=判断是否0)(=x f ;若是,则有根2ab x -=。
否则,继续判断是否0)()(<•x f a f ,若是,则令x b =,否则令x a =。
否则令x a =。
重复此过程直至求出方程0)(=x f 在[a,b]中的近似根为止。
(2)、迭代法将方程0)(=x f 等价变换为x =ψ(x )形式,并建立相应的迭代公式=+1k x ψ(x )。
(3)、牛顿法若已知方程 的一个近似根0x ,则函数在点0x 附近可用一阶泰勒多项式))((')()(0001x x x f x f x p -+=来近似,因此方程0)(=x f 可近似表示为+)(0x f 0))(('0=-x x x f 设0)('0≠x f ,则=x -0x )(')(00x f x f 。
取x 作为原方程新的近似根1x ,然后将1x 作为0x 代入上式。
迭代公式为:=+1k x -0x )(')(k k x f x f 。
三、 实验设备:MATLAB 软件四、 结果预测 (1)11x = (2)5x = (3)2x =0,09052五、 实验内容(1)、在区间[0,1]上用二分法求方程0210=-+x e x 的近似根,要求误差不超过3105.0-⨯。
(2)、取初值00=x ,用迭代公式=+1k x -0x )(')(k k x f x f ,求方程0210=-+x e x 的近似根。
西安交通大学数学实验报告(MATLAB求解开普勒方程和方程求根)

实验报告(五)完成人:L.W.Yohann注:本次实验主要学习了用MATLAB求解开普勒方程和方程求根的问题,了解学习了用fzero命令、二分法、Newton迭代法、一般迭代法求解方程,以及学习了非线性方程组的求解问题,完成后,小组对第90页的上级练习题进行了程序编辑和运行。
1.绘图并观察函数零点的分布.解:在编辑窗口输入:f=inline('x-0.5*sin(x)-1');fplot(f,[0,1])grid存盘后运行得2. 利用fzero 命令求解方程.解:在编辑窗口输入:f=inline('x-0.5*sin(x)-1');c=fzero(f,[1,2])存盘后运行得c =1.49873. 用二分法求解方程.求解(1)方程x^2-2=0在(0,2)内的近似根;(2)圆x^2+y^2=2与曲线y=e^-x 的两个交点;(3)方程∫t 21+t 2x 0dt =12的近似根. (1)解:在编辑窗口输入:00.10.20.30.40.50.60.70.80.91-1-0.9-0.8-0.7-0.6-0.5-0.4-0.3f=inline('x^2-2');x1=0;x2=2;while abs(x1-x2)>10^(-5)x3=(x1+x2)/2;if f(x3)==0break;elseif f(x1)*f(x3)>0x1=x3;else f(x2)*f(x3)>0;x2=x3;endendx0=x3存盘后运行得x0 =1.4142(2)解:在编辑窗口输入:f=inline('(x^2)*exp(2*x)+1-2*exp(2*x)');x1=0;x2=2;x5=-2;x6=0;while abs(x1-x2)>10^(-5)x3=(x1+x2)/2;if f(x3)==0break;elseif f(x1)*f(x3)>0x1=x3;else f(x2)*f(x3)>0;x2=x3;endendwhile abs(x5-x6)>10^(-5)x7=(x5+x6)/2;if f(x7)==0break;elseif f(x5)*f(x7)>0x5=x7;else f(x6)*f(x7)>0;x6=x7;endendx0=x3x4=x7存盘后运行得x0 =1.3922x4 =-0.3203(3)解:在编辑窗口输入:clear;clc;syms t xf1=(t^2)/(1+t^2);f2=int(f1,t,0,x);%¼ÆËã²»¶¨»ý·Öf=inline('x - atan(x)-0.5');x1=-5;x2=5;while abs(x1-x2)>10^(-5)x3=(x1+x2)/2;if f(x3)==0break;elseif f(x1)*f(x3)>0x1=x3;else f(x2)*f(x3)>0;x2=x3;endendx0=x3存盘后运行得x0 =1.47504.用Newton迭代法求解方程求解:x=0.5sinx+1的近似根;解:在编辑窗口输入:f=inline('x-0.5*sin(x)-1');df=inline('1-0.5*cos(x)');d2f=inline('0.5*sin(x)');a=1;b=2;dlt=1.0e-5;if f(a)*d2f(a)>0x0=a;elsex0=b;endm=min(abs(df(a)),abs(df(b)));k=0;while abs(f(x0))>m*dltk=k+1;x1=x0-f(x0)/df(x0);x0=x1;fprintf('k=%d x=%.5f\n',k,x0); end存盘后运行得k=1 x=1.54858k=2 x=1.49933k=3 x=1.498705.求解非线性方程组.试求非线性方程组{2x12−x1x2−5x1+1=0x1+3lgx1−x22=0的解,初值如下:(1)x0=[1.4,−1.5](2)x0=[3.7,2.7]解:在编辑窗口输入:function f=group5(x)f=[2*x(1)^2-x(1)*x(2)-5*x(1)+1;x(1)+3*log10(x(1))-x(2)^2];(1):输入:[f,fval]=fsolve('group2',[1.4,-1.5]) 运行得f =1.4589 -1.3968fval =1.0e-011 *0.0759-0.6178(2):输入:[f,fval]=fsolve('group2',[3.7,2.7])运行得f =3.4874 2.2616fval =1.0e-006 *0.0059-0.20126.解决实际问题.为了在海岛I与某城市C之间铺设一条地下光缆,每千米光缆铺设成本在水下部分使C1万元,在地下部分使C2万元,为使得该光缆的总成本最低,光缆的转折点P(海岸线上)应该取在何处?如果实际测得海岛I与城市C之间的水平距离l=30km,海岛距海岸线垂直距离h1=15km,城市距海岸线垂直距离h=10km,C1=3000万元/km,C2=1500万元/km,求P点的坐标(误差<10−3km).解:在编辑窗口输入:f=inline('(3000*x)/(x^2 + 225)^(1/2) + (750*(2*x - 60))/((x - 30)^2 + 100)^(1/2)'); x1=5;x2=10;while abs(x1-x2)>10^(-3)x3=(x1+x2)/2;if f(x3)==0break;elseif f(x1)*f(x3)>0x1=x3;else f(x2)*f(x3)>0;x2=x3;endendfprintf('x=%.5f',x3) 存盘后运行得x=7.69104>>。
第二次实验报告(非线性方程求根)

班级: 学号: 姓名: 成绩:实验2 非线性方程的数值解法实验1实验目的1)进一步熟练掌握求解非线性方程的牛顿迭代法和弦截法。
2)根据牛顿迭代法和弦截法的原理,编写程序求解非线性方程,提高编程解决问题的能力。
2 实验内容(1)用牛顿法和割线法求下列方程的根x^2-e^x=0;x*e^x-1=0;(23实验原理(1)牛顿迭代公式:1()/'()k k k k x x f x f x +=- 双点弦法公式:111()()()()k k k k k k k f x x x x x f x f x +--=--- (2)令2()f x x A =-,再用牛顿法求根。
4实验步骤1)根据牛顿迭代法,双点弦法的算法编写相应的求根函数;2)用牛顿迭代法和双点弦法分别对方程进行求解;5 程序设计牛顿迭代法x0=1.0;N=100;k=0;eps=5e-6;delta=1e-6;while(1)x1=x0-fc1(x0)/fc2(x0);k=k+1;if k>Ndisp('Newton method failed')breakendif(abs(x1-x0)<delta || abs(fc1(x1))<delta) break;endx0=x1;endfprintf('%f',x0)fprintf('%f',abs(fc1(x1)))双点弦法function cutline(x0,x1)N=100;k=0;delta=5e-8;while(1)(abs(x1-x0)>=delta)c=x1;x1=cutnext(x0,x1);x0=c;k=k+1;if k>Ndisp('Cutline method failed')break;endif(abs(x1-x0)<delta || abs(fc1(x1))<delta) break;endendfprintf('%10f\n',x1);function y=cutnext(a,b)y=b-fc(b)/(fc(b)-fc(a))*(b-a);1)原函数function fc1=fc1(x)fc1=x^2-exp(x);end导函数function fc2=fc2(x)fc2=2*x-exp(x);end2)原函数导函数3)原函数导函数6实验结果及分析注:牛顿迭代法由于设置delta=1e-6,所以算出的误差e<1.0*10^-6;割线法由于设置delta=5e-8,所以误差e<5.0*10^-8.7总结。
计算方法上机2 方程求根

实验报告名称方程求根班级:学号:姓名:成绩:1实验目的(1)通过对二分法与牛顿迭代法做编程练习和上机运算,进一步体会二分法和牛顿法的不同。
(2)编写割线迭代法的程序,求非线性方程的解,并与牛顿迭代法作比较。
2 实验内容求方程f(x)=x^3+x^2-3*x-3在1.5附近的根。
3实验步骤二分法算法给定区间(a,b),并设f(a)与f(b)符号相反,取ε为根的容许误差,δ为|f(x)|的容许误差。
①令c=(a+b)/2.②如果(c-a)<ε或|f(c)|<δ,则输出c,结束;否则执行③。
③如果f(a)*f(c)>0,则a=c;否则令b=c,重复①②③。
牛顿迭代法算法给定初始值x0,ε为根的容许误差,η为|f(x)|的容许误差,N为迭代次数的容许值。
①如果f(x0)’=0或迭代次数大于N,则算法失败,结束;否则执行②。
②计算x1=x0-f(x0)/f(x0)’.③令x0=x1,转向①。
4 程序设计二分法c语言程序设计:#include <stdio.h>#include <math.h>#define eps 5e-6#define delta 1e-6float Bisection(float a,float b,float(*f)(float)){float c, fc,fa=(*f)(a),fb=(*f)(b);int n=1;printf("二分次数\t\tc\t\tf(c)\n");while(1){if(fa*fb>0){printf("不能用二分法求解");break;}c=(a+b)/2,fc=(*f)(c);if(fabs(fc)<delta)break;else if(fa*fc<0){ b=c;fb=fc;}else{a=c;fa=fc;}if(b-a<eps)break;printf("%d\t\t%f\t\t%f\n",n++,c,fc);}return c;}float f(float x){return x*x*x+x*x-3*x-3;}void main(){float a=1,b=2;float x;x=Bisection(a,b,f);printf("\n方程的根是:%f",x);}牛顿法c语言程序设计:#include<stdio.h>#include<math.h>#define N 100#define eps 1e-6#define eta 1e-8float Newton(float(*f)(float),float(*f1)(float),float x0) {float x1,d;int k=0;do{x1=x0-(*f)(x0)/(*f1)(x0);if(k++>N||fabs((*f1)(x1))<eps){printf("\n Newton迭代散发");break;}d=fabs(x1)<1?x1-x0:(x1-x0)/x1;x0=x1;printf("x(%d)=%f\t",k,x0);}while(fabs(d)>eps&&fabs((*f)(x1))>eta);return x1;float f(float x){return x*x*x+x*x-3*x-3;}float f1(float x){return 3.0*x*x+2*x-3;}void main(){float x0,y0;printf("请输入迭代值x0\n");scanf("%f",&x0);printf("x(0)=%f\n",x0);y0=Newton(f,f1,x0);printf("方程的根为:%f\n",y0);}5实验结果及分析二分法的输出结果:牛顿法的输出结果:实验分析:上面程序取三个不同初值,得到同样的结果,但迭代次数不同,初值越接近所求的根,迭代次数越少。
(完整word版)数值分析报告-二分法和牛顿法方程求根(word文档良心出品)

《数值分析》实验报告一**: **学号: PB********实验一一、实验名称方程求根二、实验目的与要求:通过对二分法和牛顿法作编程练习和上机运算,进一步体会它们在方程求根中的不同特点;比较二者的计算速度和计算精度。
三、实验内容:通过对二分法和牛顿迭代法作编程练习和上机运算,进一步体会它们在方程求根中的不同特点 。
(一)二分法算法:给定区间[a,b],并设f (a )与f (b )符号相反,取δ为根的容许误差,ε为值的容许误差。
(1)令c=(a+b)/2(2)如果(c-a)< δ或)(c f <ε,则输出c ,结束;否则执行(3)(3)如果f(a)f(c)<0,则令)()(,c f b f c b ←←;否则,则令)()(,c f a f c a ←←,重复(1),(2),(3)。
(二)牛顿迭代法:给定初值0x ,ε为根的容许误差,η为)(x f 的容许误差,N 为迭代次数的容许值。
(1)如果)(x f <η或迭代次数大于N ,则算法结束;否则执行(2)。
(2)计算)('/)(0001x f x f x x -=(3)若 < 或 < ,则输出 ,程序结束;否则执行(4)。
(4)令 = ,转向(1)。
四、实验题目与程序设计1、二分法3.1.1、用二分法求方程a. f(x)= x x tan 1--在区间[0,π/2]上的根,c. f(x)=6cos 22-++-x e x x 在区间[1,3]上的根。
源程序:3.1.1.a#include<stdio.h>#include<math.h>void main(){float a,b;double c,y,z;printf("plese input two number a and b:\n");scanf("%f%f",&a,&b);c=(a+b)/2;y=1/c-tan(c);printf("a=%f,b=%f,b-a=%f,c=%f,f(c)=%f\n",a,b,b-a,c,y);while(fabs(b-a)>0.00001|| fabs(y)>0.00001){z=1/a-tan(a);if(z*y<0)b=c;elsea=c;c=(a+b)/2;y=1/c-tan(c);printf("a=%f,b=%f,b-a=%f,c=%f,f(c)=%f\n",a,b,b-a,c,y);}x x 01-ε)(1x f ηx 1x 0x 1}输入0 1.5707563( /2~1.5705563)得到下表:由上表可以看出刚开始时f(c)取值幅度很大,但是经过一段历程之后,幅度变得平缓甚至基本接近与零,我们认为,x=0.8603是方程的根,结果与实际想要得到的值相当接近。
(完整word版)数值分析报告-二分法和牛顿法方程求根(word文档良心出品)

《数值分析》实验报告一**: **学号: PB********实验一一、实验名称方程求根二、实验目的与要求:通过对二分法和牛顿法作编程练习和上机运算,进一步体会它们在方程求根中的不同特点;比较二者的计算速度和计算精度。
三、实验内容:通过对二分法和牛顿迭代法作编程练习和上机运算,进一步体会它们在方程求根中的不同特点 。
(一)二分法算法:给定区间[a,b],并设f (a )与f (b )符号相反,取δ为根的容许误差,ε为值的容许误差。
(1)令c=(a+b)/2(2)如果(c-a)< δ或)(c f <ε,则输出c ,结束;否则执行(3)(3)如果f(a)f(c)<0,则令)()(,c f b f c b ←←;否则,则令)()(,c f a f c a ←←,重复(1),(2),(3)。
(二)牛顿迭代法:给定初值0x ,ε为根的容许误差,η为)(x f 的容许误差,N 为迭代次数的容许值。
(1)如果)(x f <η或迭代次数大于N ,则算法结束;否则执行(2)。
(2)计算)('/)(0001x f x f x x -=(3)若 < 或 < ,则输出 ,程序结束;否则执行(4)。
(4)令 = ,转向(1)。
四、实验题目与程序设计1、二分法3.1.1、用二分法求方程a. f(x)= x x tan 1--在区间[0,π/2]上的根,c. f(x)=6cos 22-++-x e x x 在区间[1,3]上的根。
源程序:3.1.1.a#include<stdio.h>#include<math.h>void main(){float a,b;double c,y,z;printf("plese input two number a and b:\n");scanf("%f%f",&a,&b);c=(a+b)/2;y=1/c-tan(c);printf("a=%f,b=%f,b-a=%f,c=%f,f(c)=%f\n",a,b,b-a,c,y);while(fabs(b-a)>0.00001|| fabs(y)>0.00001){z=1/a-tan(a);if(z*y<0)b=c;elsea=c;c=(a+b)/2;y=1/c-tan(c);printf("a=%f,b=%f,b-a=%f,c=%f,f(c)=%f\n",a,b,b-a,c,y);}x x 01-ε)(1x f ηx 1x 0x 1}输入0 1.5707563( /2~1.5705563)得到下表:由上表可以看出刚开始时f(c)取值幅度很大,但是经过一段历程之后,幅度变得平缓甚至基本接近与零,我们认为,x=0.8603是方程的根,结果与实际想要得到的值相当接近。
计算方法第二章方程求根上机报告

实验报告名称班级:学号:姓名:成绩:1实验目的1)通过对二分法与牛顿迭代法作编程练习与上级运算,进一步体会二分法与牛顿迭代法的不同特点。
2)编写割线迭代法的程序,求非线性迭代法的解,并与牛顿迭代法。
2 实验内容用牛顿法和割线法求下列方程的根x^2-e^x=0;x*e^x-1=0;lgx+x-2=0;3实验步骤1)根据二分法和牛顿迭代法,割线法的算法编写相应的求根函数;2)将题中所给参数带入二分法函数,确定大致区间;3)用牛顿迭代法和割线法分别对方程进行求解;3 程序设计牛顿迭代法x0=1.0;N=100;k=0;eps=5e-6;delta=1e-6;while(1)x1=x0-fc1(x0)/fc2(x0);k=k+1;if k>Ndisp('Newmethod failed')breakendif(abs(x1-x0)<delta || abs(fc1(x1))<delta)break;endx0=x1; %²»ÄÜ·ÅÔÚabs(x1-x0)Ç°endfprintf('%f',x0)fprintf(' %f ', abs(fc1(x1)) )割线法function cutline(x0,x1)N=100;k=0;delta=5e-8;while(1)while(abs(x1-x0)>=delta)c=x1;x1=cutnext(x0,x1);x0=c; %x0 x1µÝÍƵõ½x1 x2 ÈÔÈ»±£´æÔÚx0 x1 endk=k+1;if k>Ndisp('Cutline method failed')break;endif(abs(x1-x0)<delta || abs(fc1(x1))<delta)break;endendfprintf('%.10f\n',x1);function y=cutnext(a,b)y=b-fc(b)/(fc(b)-fc(a))*(b-a);1)原函数function fc1=fc1(x)fc1=x^2-exp(x);end导函数function fc2=fc2(x)fc2=2*x-exp(x);end2)原函数function fc1=fc1(x)fc1=x*exp(x)-1;end导数function fc2=fc2(x)fc2=(x+1)*exp(x);end3)原函数function fc1=fc1(x)fc1=log10(x)+x-2;end导函数function fc2=fc2(x)fc2=1/x/log(10)+1;end4实验结果及分析1)牛顿法结果-0.7034722378割线法结果-0.70346742252)牛顿法结果0.5671435302割线法结果0.56714329043)牛顿法结果1.7553985566割线法结果1.7555794993牛顿迭代法由于设置delta=1e-6,所以算出的误差e<1.0*10^-5; 割线法由于设置delta=5e-8,所以误差e<1.0*10^-7;5总结编程时由于将迭代的代码x0=x1放在if(abs(x1-x0)<delta || abs(fc1(x1))<delta)break;end之前导致程序没有执行就跳出,通过Debug发现了问题,将x0=x1;放到了循环体内部的最后一行,程序得以成功的运行。
实验四非线性方程求根

《数值分析》课程设计实验报告实验四 非线性方程求根一、问题提出设方程3()310f x x x =--=有三个实根**121.8793,0.34727,x x ==- *3 1.53209x =-现采用下面六种不同计算格式,求 f(x)=0的根*1x 或*2x 1、 231x x x+= 2、 313x x -=3、 x =4、 213x x =-5、 x =6、 32131()31x x x x x --=-- 二、实验步骤#include "stdio.h"#include<math.h>main(){float x0=1.8793;printf("初值是%f\n",x0);/*输出x0*/float x1,x2,x3;x1=x0;int i;for(i=1;i<21;i++){x2=(3*x1+1)/(x1*x1);//第一种迭代方式 //x2=(x1*x1*x1-1)/3;//第二种迭代方式//x2=pow(3*x1+1,1.0/3);//第三种迭代方式//x2=1/(x1*x1-3);//第四种迭代方式//x2=sqrt(3+1/x1);//第五种迭代方式//x2=x1-(1/3.0)*((x1*x1*x1-3*x1-1)/(x1*x1-1));//第六种迭代方式x3=x2-x1;printf("第%d 次迭代值为%f,相邻两次迭代值差值为%f\n",i,x2,x3);/*输出x2*/x1=x2;if(x3<0)x3=-x3;if(x3<0.000001)//误差精度break;} } 当迭代格式为231x x x +=时,实验结果为由相邻两次迭代值差值结果可知,迭代过程处于发散状态。
当迭代格式为313x x -=,实验结果为由相邻两次迭代值差值结果可知,迭代过程前8次处于发散状态,第8次之后处于收敛状态,并且经过16次迭代,得到非线性方程的一个根。
matlab计算方法实验报告1(方程求根)

计算方法实验报告(1)学生姓名杨贤邦学号指导教师吴明芬实验时间2014.3.26地点综合实验楼大楼203实验题目非线性方程求根实验目的●掌握Matlab编程方法;●掌握非线性方程的数值求根方法及Matlab或C实现;实验内容●Matlab常用命令;●二分求根法及其Matlab实现●Newton求根法或割线法及其Matlab实现●题目由同学从学习材料中任意选两题算法分析与二分法:function x=method2(fname,a,b,e)fa=feval(fname,a);fb=feval(fname,b);if fa*fb>0error('两个函数值同号');endk=0x=(a+b)/2while(b-a)>eif k>3000error('已运行3000次,请检查是否为死循环(e太小或e为负数)');end fx=feval(fname,(b+a)/2);if fx*fa>0a=(b+a)/2;fa=fx;elseb=(b+a)/2;endk=k+1x=(b+a)/2end割线法:function x=gexianfa(fname,x0,x1,e)k=0;x=x1;while abs(x-x0)>eif k>3000error('已迭代3000次,请检查是否收敛或e太小');end源程序fx0=feval(fname,x0);fx1=feval(fname,x1);cache=x1;k=k+1x=x1-fx1/(fx1-fx0)*(x1-x0)x0=x1;x1=x;end实验结果与分析分别用二分法和割线法计算x3-15x2+42x+8=0在区间[3,5]的一个根,且误差不超过10-8割线法:k=1x=3.89655172413793k=2x=3.99315350368514k=3x=4.00007427733589k=4x=3.99999994899663k=5x=3.99999999999962k=6x=4.00000000000000ans=4.00000000000000二分法:k=1x=3.50000000000000k=2x=3.75000000000000k=3x=3.87500000000000k=4x=3.93750000000000k=5x=3.96875000000000k=6x=3.98437500000000k=7x=3.99218750000000k=8x=3.99609375000000k=9x=3.99804687500000k=10x=3.99902343750000k=11x=3.99951171875000k=12x=3.99975585937500k=13x=3.99987792968750k=14x=3.99993896484375k=15x=3.99996948242188k=16x=3.99998474121094k=17x=3.99999237060547k=18x=3.99999618530273k=19x=3.99999809265137k=20x=3.99999904632568k=21x=3.99999952316284k=22x=3.99999976158142k=23x=3.99999988079071k=24x=3.99999994039536k=25x=3.99999997019768k=26x=3.99999998509884k=27x=3.99999999254942k=28x=3.99999999627471ans=3.99999999627471从上面的计算结果很直观的体现了二分法的的效率真的很低,割线法只需要迭代6次就可以得出结果,而二分法却需要运行28次其它Matlab遇到死循环就出现程序假死的情况,想关都关不掉,真的很烦。
计算数值方法实验报告_太原理工大学

计算数值方法实验报告学院:计算机与软件学院专业:计算机与科学技术班级:计算机学号:11姓名:某某太原理工大学学生实验报告分析:雅克比迭代公式简单,每迭代一次只须计算一次矩阵和向量的乘法。
在计算机运算时需要两组存储单元,以存放x(k)及x(k+1)。
实验地点综合楼六层606室指导教师王峥学院名称 计算机科学与技术 专业班级 计算机 学号 11 学生姓名 某某 实验日期 2011-6-20成绩课程名称数值计算方法实验题目实验四 最小二乘法拟合多项式一、课题名称(1)了解矩阵特征值与特征向量问题解法,掌握幂法。
(2)加深对矩阵特征值与特征向量问题求解方法的认识,掌握算法。
(3)会进行误差分析。
二、目的和意义学习使用最小二乘法拟合多项式 三、计算公式幂法:由已知的非零向量x0和矩阵A 的乘幂构造向量序列{xn}以计算矩阵A 的按模最大特征值及其特征向量的方法,称为幂法。
迭代公式:1max(),1,2,...k k k k kk k y Axm y k y x m结果可取111kk km y x或四、结构程序设计#include <iostream> #include <cmath> const int N(3);using namespace std;void matrixx(double A[N][N],double x[N],double y[N]) {cin>>x;while(1){int choice=3;cout<<"请您选择使用哪种插值法计算:"<<endl;cout<<" (0):退出"<<endl;cout<<" (1):Lagrange"<<endl;cout<<" (2):Newton"<<endl;cout<<"输入你的选择:";cin>>choice;//取得用户的选择项if(choice==2){cout<<"你选择了牛顿插值计算方法,其结果为:";y=Newton(x,count);break;//调用相应的处理函数}if(choice==1){cout<<"你选择了拉格朗日插值计算方法,其结果为:";y=lagrange(x,count);break;//调用相应的处理函数}if(choice==0)break;system("cls");cout<<"输入错误!!!!"<<endl;}cout<<x<<" , "<<y<<endl;//输出最终结果}五、结果讨论和分析分析:拉格朗日插值的优点是插值多项式特别容易建立,缺点是增加节点是原有多项式不能利用,必须重新建立,即所有基函数都要重新计算,这就造成计算量的浪费。
方程求根

贵州师范大学数学与计算机科学学院学生实验报告课程名称: 数值分析 班级: 实验日期: 学 号: 姓名: 指导教师:实验成绩:一、实验名称实验四:方程求根二、实验目的及要求1. 要求学生能够用Newton 迭代法求方程的根2. 要求学生能够找出Newton 迭代法的收敛域三、实验环境每人一台微机,要求安装Windows2000或Windows XP 操作系统,Matlab 软件四、实验内容题1 求解下列方程:1) Newton 迭代法求解的第一个方程0523=--x x2) 无求根公式的五次方程0245=--x x3) 超越方程0tan =-x x要求:1) 先用图象法求初始近似,再用Newton 迭代法加工,计算结果达到5位有效数字.2) 设计一个程序找出Newton 迭代的收敛域(注:方程1)必须写实验报告)五、算法描述及实验步骤输入 '0(),(),,,f x f x x M ε;输出 方程()0f x =在0x 附近的根或失败信息; 步1 0dv ⇐;步2 对1,2,3.....,k M =执行步3——步5;步3 若'()0f x =则2dv ⇐,退出循环;否则:010'0()()f x x x f x ⇐-; 步4 1001;e x x x x ⇐-⇐;步5 若e ε≤则1dv ⇐,退出循环;步6 若1dv ⇐则输出1x ,否则若0dv ⇐则输出“迭代M 次失败”,否则输出“奇异”;六、调试过程及实验结果1输入:syms x y;x=-5:0.1:5;ezplot('x^3-2*x-5',x)hold onezplot('x',x)ezplot(‘0’,x)grid on结果如图1>> x0=2.2;tol=0.00005;M=50;>>x=Newton('x^3-2*x-5','3*x^2-2',x0,tol,M)x =2.09462输入:syms x y;x=-5:0.1:5;ezplot('x^5-4*x-2',x)hold onezplot('x',x)ezplot(‘0’,x)grid on结果如图2:>> x0=1.5;tol=0.00005;M=50;>>x=Newton('x^5-4*x-2','5*x^4-4',x0,tol,M)x =1.5185>> x0=-5;tol=0.00005;M=100;>>x=Newton('x^5-4*x-2','5*x^4-4',x0,tol,M)x =-1.2436>> x0=0;tol=0.00005;M=100;>> x=Newton('x^5-4*x-2','5*x^4-4',x0,tol,M)x =-0.5085>> x0=-pi/5;tol=0.00005;M=200; 3syms x y;x=-4*pi:0.1:4*pi;ezplot('tan(x)',x)hold onezplot('x',x)ezplot('0',x)grid on结果如图3;有无数的结果都是互为相反数>>x=Newton('x-tan(x)','-tan(x)^2',x0,tol,M)x =-9.3105e-005>> x0=pi/5;tol=0.00005;M=200;>>x=Newton('x-tan(x)','-tan(x)^2',x0,tol,M)x =9.3105e-005>> x0=-pi/2;tol=0.00005;M=200;>>x=Newton('x-tan(x)','-tan(x)^2',x0,tol,M)x =-1.5708>> x0=pi/2;tol=0.00005;M=200;>> x=Newton('x-tan(x)','-tan(x)^2',x0,tol,M)x =1.5708七、总结1、在应用Newton 程序时,第三个程序当去取一定初值时都迭代不出来,我取M 到了200次结果还是一样,不知道是什么原因;2、画图中出现很多问题,怎么加网格,怎么样连续画几个函数图在一个平面上;3、由于tan()y x =与y x =的交点很多,无法用程序表现出来;4、无法编写出Newton 迭代法的收敛域;图3八、附录(源程序清单)function x=Newton(f,df,x0,tol,M)dv=0;for k=1:Mif feval(df,x0)==0dv=2;breakelsex1=x0-feval(f,x0)/feval(df,x0);ende=abs(x1-x0);x0=x1;if e<=toldv=1;breakendendif dv==1x=x1;elseif dv==0x=['迭代',num2str(M),'次失败'];elsex='奇异'endsyms x y; x=-5:0.1:5;ezplot('x^3-2*x-5',x)hold onezplot('x',x)ezplot(‘0’,x)grid onsyms x y;x=-5:0.1:5;ezplot('x^5-4*x-2',x)hold onezplot('x',x)ezplot(‘0’,x)grid onsyms x y;x=-4*pi:0.1:4*pi;ezplot('tan(x)',x)hold onezplot('x',x)ezplot('0',x) grid on。
计算数值实验报告

本科实验报告课程名称:计算数值方法实验地址:综合楼五层506 室专业班级:计科1002学号:14 学生姓名:xxx指导教师:王峥2012 年6月20太原理工大学学生实验报告学院名称计算机科学与技术专业班级计科 1002 学号14学生姓名xxx 实验日期成绩课程名称计算数值方法实验题目实验一方程求根一、课题名称方程求根:熟习使用、迭代法、牛顿法、割线法等方法对给定的方程进行根的求解。
选择上述方法中的两种方法求方程:二分法f(x)=x3+4x2-10=0在[1,2]内的一个实根,且要求知足精度 |x *-x n|< × 10-5迭代法:用迭代公式x=f(x)进行迭代计算,直到知足|x * -x n|< × 10-5为止。
二分法:设 f (x)在 [a,b] 上连续,且 f ( a1)*f (x1)<0, 记( a2,b2)=(x1,b1)带入计算式进行计算直到 |x * -x n|< ×10-5为止。
二、目的和意义(1)认识非线性方程求根的常有方法,如二分法、迭代法、牛顿法、割线法。
(2)加深对方程求根方法的认识,掌握算法。
会进行偏差剖析,并能对不同方法进行比较。
三、计算公式( 1)迭代法1).第一对给定的计算公式进行变形使其能够迭代或许找出相应迭代速度较快的式子。
2).带入求好的式子到循环中去比方:xk 1( xk)( k0,1, 2,L )( 2)二分法:f(x)在区间(x,y)上连续1) . 先找到 a、 b 属于区间( x, y),使 f(a),f(b)异号,说明在区间(a,b)内一定有零点,而后求f[(a+b)/2],2) . 假如 f[(a+b)/2]=0,该点就是零点,假如 f[(a+b)/2]<0,则在区间((a+b)/2,b)内有零点,反之在(a,(a+b)/2)内有零点带入 1)中持续。
四、主要仪器设施Vc++ C-free CodeBlocks五、结构程序设计迭代法 :#include<>#include<>main(){int i;double xn[15],y,x1,x2,m ;printf("请输入 x1,x2 的值: \n" );scanf("%lf%lf",&x1,&x2);printf("请输入精度要求:\n" );scanf("%lf",&m);printf(" n xn\n");i=0;do{xn[0]=(x1+x2)/2 ;xn[i+1]= sqrt(10/(4+xn[i]));1 2 3 x1 14 0.3 10 15 59.14 3 1 x1 59.17 4 2 1 5 x15.2916.130 1 2 x2 46.78 8 7 2 10 x20 1 2 x2 811.2 9 5 2 x3 1 4 8 3 6 x3 2 4 1 x3 131 2 1 1 x4 2 12 6 11 20 x41 x1 72 1 x2 51 2 1 xn 1 51 2 x n 5追赶法:用来求对角方程组;将系数矩阵 A 转变为 A=L*U, L 为一般下 n-1 对角矩阵, U 为单位上 n-1 对角矩阵,而后经过程组 l*y=b,u*x=y, 来求解 x.计算数值实验报告、主要仪器设施c++ C-free CodeBlocks、结构程序设计Gauss消元法:#include <iostream>#include <cmath>using namespace std;int main(){int n,i,j,k;double a[100][100],b[100],o;cout<<" 输入未知数个数:"<<endl;cin>>n;cout<<" 输入数列 :"<<endl;for (i=1;i<=n;i++)for (j=1;j<=n+1;j++)cin>>a[i][j];for (i=1;i<=n;i++)for (j=i+1;j<=n;j++)if (fabs(a[j][i])>1e-7){o=a[i][i]/a[j][i];for (k=i;k<=n+1;k++)a[j][k]=a[j][k]*o-a[i][k];}for (i=n;i>0;i--){b[i]=a[i][n+1]/a[i][i];for (j=i-1;j>0;j--)a[j][n+1]=a[j][n+1]-b[i]*a[j][i];}cout<<" 解得 :"<<endl;for (i=1;i<=n;i++) cout<<b[i]<<endl;lf\n",i,d[i]);}、结果议论和剖析消元法:列主元素消元法:计算数值实验报告解法:追赶法:议论从消元过程能够看出,关于 n 阶线性方程组,只需各步主元素不为零,经过n-1 步消元,就能够获得一个等价的系数三角形阵的方程组,而后再利用回代过程可求得原方程组的解.因为列主元素法相像且优于完整主元素法因此省略消元过程相当于分解 A 为单位下三角阵 L 与上三角阵 U 的乘积,解方程组 Ly=b 回代过程就是解方程组 Ux=y。
实验四 非线性方程的求根

ek 1 ek
p
e xk 3xk 2 x* xk x
1 * 2
1 ,故该迭代函数是线性收敛的。 2
6
利用 Matlab 编程计算: (取初值为 0.2;精度为 10 )
程序功能:线性迭代函数求根 clear,clc x0=0.2%定义初值 e=10^-6;%定义精度为 10 的-6 次方 N=500;%最大迭代次数 k=0;%迭代次数 while k<N
end k x1
得到结果为:
初值 迭代次数 k=65 迭代结果
x0 =0.200
结果检验:
x1 =2.0844 + 2.7330i
将迭代结果 x1 代入原方程 x 2 3 x 2 e x 0 ,在 Matlab 命令窗口输入: abs(x1^2-3*x1+2-exp(x1)),得到 5.1676e-006,结果非常接近 0,比较可靠。
6
。
(1)请自行设计一种线性收敛的迭代法求方程的根,输出迭代初值、各次迭代值及迭 代次数。 (2)用牛顿迭代法求方程的根,输出迭代初值、各次迭代值及迭代次数,并与(1)的 结果比较。 (3)用 MATLAB 内部函数 solve 直接求出方程的所有根,并与(1) 、 (2)的结果进行 比较。 B题 求方程 x 3 x 1 0 在 x =1.5 附近的根。
3 xk xk 1 ,编写程序进行实验,分别取 x0 0 , 2 3xk 1
(1)对牛顿迭代公式: x k 1 x k
x0 1.5 迭代 10 次,观察比较其计算值,并分析原因。
(2)用 MATLAB 内部函数 solve 直接求出方程的所有根,并与(1)的结果进行比较。 C题 公元 1225 年,Lenardo 宣布他求得方程
【免费下载】数值计算方法 方程求根

计ห้องสมุดไป่ตู้方法实习报告
9.用艾特肯算法求方程 f(x)=x^3+4*x^2+10=0 在区间[1,2]内的根 的近似值(取 X0=1.5,g(x)= 10 ,精确到|Xk+1-Xk|<=10^-5,
x4
并与第 2,3,6 题的相应结果进行比较。
function guest(tolerance) k=0; x0=1.5; y0=sqrt(10/(x0+4)); z0=sqrt(10/(y0+4)); while(abs(z0-y0)>tolerance); x1=x0-(y0-x0)^2/(z0-2*y0+x0); y1=sqrt(10/(x1+4)); z1=sqrt(10/(y1+4)); z0=z1; y0=y1; k=k+1; end disp(z0); disp(k);
运行结果
1.36523 1
5
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力根通保据过护生管高产线中工敷资艺设料高技试中术卷资,配料不置试仅技卷可术要以是求解指,决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资,配料而置试且时卷可,调保需控障要试各在验类最;管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下,安与要全过加,度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高;试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中,核资或对料者定试对值卷某,弯些审扁异核度常与固高校定中对盒资图位料纸置试,.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置,弯高尤曲中其半资要径料避标试免高卷错等调误,试高要方中求案资技,料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高,术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术,管以术来架及避等系免多统不项启必方动要式方高,案中为;资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资,管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装,工置合作调理并试利且技用进术管行,线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确:指灵在导活分。。线对对盒于于处调差,试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷,术调应问试采题技用,术金作是属为指隔调发板试电进人机行员一隔,变开需压处要器理在组;事在同前发一掌生线握内槽图部内 纸故,资障强料时电、,回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资,料料线试试缆卷卷敷试切设验除完报从毕告而,与采要相用进关高行技中检术资查资料和料试检,卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
方程求根二分法

实验项目 非线性方程求解方法 理论内容 非线性方程求根的二分法 实验室名称 文理馆 203
实验日期 2016.09.02 授课日期 2016.09.02 微机编号 E1
实验目的及要求:
1、 使学生掌握非线性方程求解二分法的基本理论。 2、使学生借助于计算机这一高效计算工具和本课程中的基本数值计算方法
}
3
public class Demo02 { public static void main(String[] args) { double temp = 1.0; double y = (double) 1.0; double a = 1; double b = 2; for (int i = 2; i < 300; i++) { y = (a + b) / ((double) 2.0); temp = Math.sin(y)-y*y/2; System.out.print(a + "|"); System.out.print(y + "|"); System.out.print(b + "\n"); if (temp < 0) { b = y; } else { a = y; } if (b - a <= 5*Math.pow(0.1, 6)) { System.out.println(y); break; } } }
解,虽然我们得到了最终结果但是这种方法所体现时间复杂度非常的高,计算量庞大,在计算误差
精确度位数比较高时,我们需对二分法进行改进。
实验报告评分标准
评分项目
满分 得分
评分项目
实验步骤及程序 10
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
~
*
~
f &# ( xk )
取 x 作为原方程的新的近似跟 xk+1,即令 xk 1 xk 三.实验仪器设备及操作步骤
(k=0,1,2...)
二分法: 算法:给定区间[a,b],并设 f(a)与 f(b)符号相反,取ε为根的容许误差,δ为 |f(x)|的容许误差。
牛顿迭代法求解: VB表示
Private Sub Command1_Click() Dim x0!, x!, eps!, k
x0 = Val(InputBox("x0=", "输入初始值", 0.5)) eps = Val(InputBox("eps=", "牛顿迭代法求根", 0.000005))
材料科学与工程实验教学中心
实验报告
课 程 名 称 计算机在材料中的应用 实 验 名 称 方程求根 专 班 学 姓 业 无机非金属材料工程 级 材料 1103 号 XX 名 XXX
实 验 日 期 2013/11/01
南京工业大学材料科学与工程学院
材料科学与工程实验教学中心实验报告
一. 实验目的 (1) 通过对二分法与牛顿迭代法作编程练习与上机运算,进一步体力会 二分法与牛顿迭代法的不同特点; (2) 别写割线迭代法的程序,求非线性方程的解,并与牛顿迭代法作比 较。 二.实验原理(方法) 在求方程近似根的方法中,最直观、最简单的方法是二分法。 设函数 f(x)在[a,b]上连续,严格单调,且 f(a)f(b)<0,则[a,b]为 f(x)=0 的一 个有根区间,二分法的基本思想是用对分区间的方法根据分点处函数 f(x)值的符 号逐步将有根区间缩小,使在足够小的区间内方程有且仅有一个根。 为叙述方便起见,a0=a,b0=b。用中点 x0=( a0,b0)/2 将区间[a0,b0]分成两 个小的区间:[a0,x0]和[x0, b0]。计算 f(x0),若 f(x0)=0,则 x0 为 f(x)=0 的根, 计 算 结 束 。 否 则 f(a0)f(x0)<0 与 f(b0)f(x0)<0 两 式 中 有 且 仅 有 一 式 成 立 。 若 f(a0)f(x0)<0,令 a1=a0,b1=x0;若 f(b0)f(x0)<0,令 a1=x0,b1=b0;不论哪种情 况均有 f(a1)f(b1)<0,于是[a1,b1]为新的有根区间,
(b a ) ,则 | xk x | 。
*
用迭代法求方程 f(x)=0 的根时,首先要把它写成等价形式 x=φ(x) 构造迭代函数的一条重要途径,是用近似方程来代替原方程去求根。因此如 果能将非线性方程 f=(0)用线性方程来近似代替,那么求近似根问题就很容易解 决,而且十分方便。牛顿法就是把非线性方程线性化的一种方法。 设 xk 是 f(x)=0 的一个近似跟, ,把 f(x)在 xk 处作一届泰勒展开,即 f(x)≈f(xk)+f'(xk)(x-xk) 于是我们得到近似方程 f(xk)+f'(xk)(x-xk)=0 设 f'(xk)≠0,则式*的解为
牛顿迭代法的 N-S 图及程序设计 定义函数 f(x)=…
定义迭代函数Φ(x)=… 读入数据 x0,eps x= Φ(x0), k=1 |x-x0|>=eps 输出 k, x k=k+1 x0=x x= Φ(x0) 结束
五.实验结果分析及结论(算例及结果) 二分法: 二分次数 1 2 3 4 5 6 7 8 9 10 c 1.500000 1.250000 1.375000 1.312500 1.343750 1.359375 1.367188 1.363281 1.365234 1.364258 f(c) 2.375000 -1.796875 0.162109 -0.848389 -0.350983 -0.096409 0.032356 -0.032150 0.000072 -0.016047
x = x0 - f(x0) / p(x0) k=1
Print Do While Abs(x - x0) >= eps Print "k=" & k, "x=" & x, "f(x)=" & f(x)
x0 = x k=k+1 x = x0 - f(x0) / p(x0) Loop
End Sub Function f(ByVal x!) As Single f = 3 * x - Sin(x) - Cos(x) End Function Function p(ByVal x!) As Single p = 3 - Cos(x) + Sin(x) End Function
x x ②计算
1
0
f ' ( x0 ) 。
f ( x0 )
③若|x1-x0|<ε或|f(x1)<η则输出 x1,程序结束;否则执行④。 ④令 x0=x1,转向①。 四.实验数据及处理(N-S 图和程序) 二分法求解: VB表示 Private Sub Command1_Click() Dim a As Single, b As Single, eps As Single, x As Single, k As Integer
1 2 3
令 c=(a+b)/2. 如果(c-a)<ε或|f(c)|<δ,则输出 c,结束;否则执行③ 如果 f(a)f(c)>0,则令 a=c;否则令 b=c,重复①②③
牛顿迭代法: 给定初始值 x0,ε为根的容许误差,η为|f(x)|容许误差,N 为迭代次数的容 许值 ①如果 f'(x0)=0 或迭代次数大于 N,则算法失败,结束;否则执行②。
x = (a + b) / 2 k=1 Print
Do While Abs(b - a) >= eps And Abs(f(x)) >= eps If (f(x) * f(b)) > 0 Then b=x Else a=x End If
Print "k=" & k, "a=" & a, "x=" & x, "b=" & b
方程的根为 1.365231
牛顿迭代法: 当 x0=1.5 时 x(0)=1.500000 x(1)=1.777778 x(2)=1.733361 x(3)=1.732052 x(4)=1.732051
方程的根为 1.732051 六.思考题 _____________________________________________________________________ _____________________________________________________________________ _____________________________________________________________________ _____________________________________________________________________ _____________________________________________________________________ _____________________________________________________________________ _____________________________________________________________________
[a 0 , b0] [a1 , b1]
,且[a1,b1]
的长度为[a0,b0]长度的一半。对此新的有根区间[a1,b1]可施行同样的手续,于是 得到一系列有根区间
[a0 , b0] [a1 ,b1] [a 2 ,b2]... [a k , bk ]
其中每一个区间的长度都是前一个区间长度的一半,最后一个区间的长度为
b a
k
k
1
2
k
(b a )
如果取最有一个区间[ak,bk]的中点 xk 误差估计式
a b
k
k
2
作为 f(x)=0 的根的近似值,则有
| X K X |
*
1 1 (bK a k ) k 1 (b a ) 2 2 1
对于所给精度ε,若取 k 使得 牛顿迭代法
2
k 1
11 12 13 14 15 16 17 18
1.364746 1.364990 1.365112 1.365173 1.365204 1.365219 1.365227 1.365231
-0.007989 -0.003959 -0.001944 -0.000936 -0.000432 -0.000180 -0.000054 0.000009
a = Val(Text1.Text) b = Val(Text2.Text) eps = Val(Text3.Text)
' ' '
a = Val(InputBox("a=", "输入左边界", 0)) b = Val(InputBox("b=", "输入右边界", 1)) eps = Val(InputBox("eps=", "二分法求根", 0.000005))
x = (a + b) / 2: k = k + 1
Loop
End Sub Function f(ByVal x As Single) As Single f=x^3-x^2-2*x+1 End Function 二分法的N-S图及程序设计
