华东师范大学版 初中数学 八年级上册 一课一练 课堂精练 同步练习册_77
华东师范大学版 初中数学 八年级上册 一课一练 课堂精练 同步练习册_19
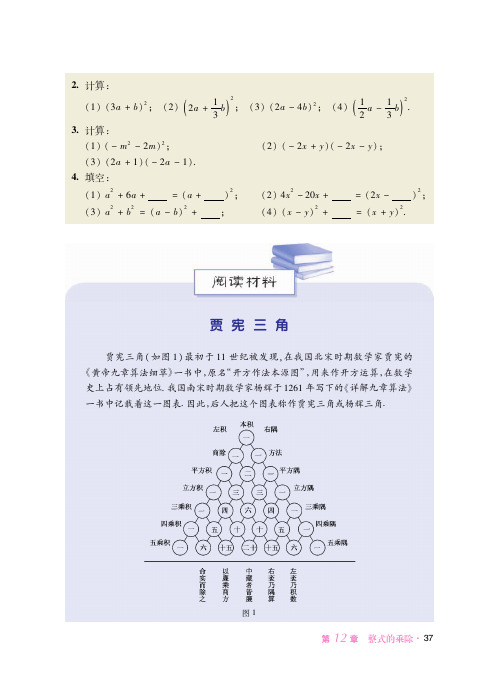
贾宪三角!!贾宪三角"如图/#最初于//世纪被发现&在我国北宋时期数学家贾宪的,黄帝九章算法细草-一书中&原名(开方作法本源图)&用来作开方运算&在数学史上占有领先地位!我国南宋时期数学家杨辉于/":/年写下的,详解九章算法-一书中记载着这一图表!因此&后人把这个图表称作贾宪三角或杨辉三角!图/第 章!整式的乘除 #'"!!在欧洲&贾宪三角则被人们称为(帕斯卡三角)&这是因为法国数学家帕斯卡于/:#1年发表了此(三角)&这比我国已经迟了近:00年!其实&数学史上有不少人各自独立地绘制过类似图表&如/1"5年阿拉伯的阿尔+卡西&/#"5年德国的阿皮亚纳斯&/#11年德国的施蒂费尔&/#1#年法国的薛贝尔等!贾宪三角在历史上被不同时代的人绘制出来&有着不同的应用指向!贾宪将它应用于开方运算&注重增乘方法&并把这种方法推向求高次方根$帕斯卡关心数字三角阵的性质探讨&并把这种性质推广到组合数的性质上$施蒂费尔则注重二项展开式系数间的关系$还有我国元代数学家朱世杰于/2世纪巧妙地利用贾宪三角得出了一系列级数求和的重要公式&并且利用这些公式求出许多更为复杂的级数之和&这在当时世界上也处于领先水平!与我们现在的学习联系最紧密的是二项式乘方展开式的系数规律!如图"&在贾宪三角中&第三行的三个数"/&"&/#恰好对应着两数和的平方""')#"的展开式""'"")')"的系数!类似地&通过计算可以发现!第四行的四个数"/&2&2&/#恰好对应着两数和的立方""')#2的展开式"2'2"")'2")"')2的系数&第五行的五个数"/&1&:&1&/#恰好对应着两数和的四次方""')#1的展开式"1'1"2)':"")"'1")2')1的系数&等等!由此可见&贾宪三角可以看作是对两数和平方公式的推广!""')#0****""')#/****""')#"****""')#2**** ""')#1**** ""')##**** ""')#:****!!//!!//!!"!!//!!2!!2!!//!!1!!:!!1!!//!!#!!/0!!/0!!#!!/ /!!:!!/#!!"0!!/#!!:!!/图"贾宪三角告诉了我们二项式乘方展开式的系数规律&你发现其中的字母及字母指数的排列规律了吗%请你试着写出""')## ""')#:与""')#5的展开式!#(" 第 章!整式的乘除。
华东师范大学版 初中数学 八年级上册 一课一练 课堂精练 同步练习册_2

槡 槡 然后得知 的平方根是 /00 #/0
/00
% /00 #%/0!
! 例 # 将下列各数开平方
/ 14!!!!!!!!" "1#!
因为 所以 槡 因此 的 ! 解 /
5" #14
14 #5 14
平方根为 槡% 14 #%5!
! 例 $ 用计算器求下列各数的算术平方根(
精确到 "/# #"4'!!!!""# 1189/"
0!0/# !
! 说明 用计算器求一个正数的算术平方根!只需直 接按书写顺序按键即可!
! 解 "/# 在计算器上依次键入
槡$ # " 4 7 ! 显示结果为 "2!所以 #"4 的算术平方根为
槡#"4 #"2! ""# 在计算器上依次键入
2
14 9/
!
$"用计算器计算
槡 / :534;58959 1 !! 2 18""#
080/ !
%"下列说法正确吗 为什么 如果不正确请予以改正!
的平方根是 槡 / /:
1!!!!! " "# #%#!
第 章 "$ !数的开方
概括
一个正数如果有平方根"那么必定有两个它们互 为相反数!显然如果我们知道了这两个平方根中的一 个那么立即可以得到另一个!
正数 " 的正的平方根叫做 " 的算术平方根记作 槡"读作 根号 "另一个平方根是它的相反数即 槡. "!因此正数 " 的平方根可以记作 槡3 "其中 " 称为 被开方数!
华东师范大学版 初中数学 八年级上册 一课一练 课堂精练 同步练习册_63

直角三角形 '((((((' ' 勾勾股股(((定定理理的'逆'定''理'' '((((((' 应用 (! 反证法
二 要点
/8本章研究了揭示直角三角形三边之间关系的勾股定理和勾股 定理的逆定理!勾股定理是一个著名的几何定理在西方也被称为毕 达哥拉斯定理早在几千年以前我国古代劳动人民就已经发现并开 始应用勾股定理了!勾股定理有几百种证明方法本章主要介绍的是 我国古代数学家赵爽的证明方法这种方法利用直角三角形的面积与 正方形的面积的关系数形结合直观简洁体现了我国古代几何学 的思想方法!
三边长分别为 /
0" '1" 01 0" $1" 0 (1 (0
%"一"架 三"8边# 米长长之的比梯为子/]靠/]在槡"一!座建筑物上梯子的底部离建筑物 085 米如果梯 子的顶部滑下 081 米梯子的底部向外滑出多远
第 章 "*!& !勾股定理
Байду номын сангаас
第 1 题
第 章 !勾股定理"*!%
A组
!"求下列各图形着色部分的面积 / 着色部分是正方形!" 着色部分是长方形!2 着色部分是半圆!
第 / 题
#"如图以 U-*:;<的三边为斜边分别向外作三个等腰直角三角形试探索这三 个等腰直角三角形的面积之间的关系!
第 " 题
$"试判断由下列三边围成的三角形是否是直角三角形
"8如果知道了直角三角形任意两边的长度那么应用勾股定理可 以计算出第三边的长度如果知道了一个三角形三边的长也可以利 用勾股定理的逆定理判断这个三角形是否是直角三角形!勾股定理可 以解决直角三角形中的许多问题在现实生活中有许多重要应用!
华东师范大学版 初中数学 八年级上册 一课一练 课堂精练 同步练习册zhch_50

" # // 5 4 2 /" / 9 /0 /" 5 9 " // /0 " 4 : 1 4 // # /" 2 9 1 /0 /" 5 9 : 5 / 9 // 5 # 2 4 // 1 " 4 : # 9 2 9 /"!
!!一 知识结构
利用数据分析解决简单实际问题的过程
提出问题 '1 收集数据 '1 整理和描述数据 '1 分析数据 '1 回答问题
(((
(''''(''''(
频数 ''' 频率 统计图表
二 要点
/8通过解决一些简单的实际问题我们了解到在现实生活中有 许多问题应当先做调查研究收集数据再通过分析作出判断!
第 5 题
)"小明投掷一个普通的正方体骰子 10 次已知他掷得奇数的次数是 求 /# 掷得 偶数的次数!他掷得奇数的频率高还是掷得偶数的频率高 如果再掷 10 次此 结论会改变吗
C组
*"利用图B C提供的某公司的一些信息回答后面的问题!
!!!!!
B "0/0 年和 "0// 年总支出图
A组
!"如果你想了解自己花在看电视上的时间在全班同学中属于多的还是少的该怎 么办呢 请说明你的计划!
#"已知全班共有 10 名学生他们上学有的步行有的骑车还有的乘车根据以下 已知信息完成整个统计表!
上学方式
步!行
骑!车
乘!车
正字法记录
正正正
频!数
4
频!率
பைடு நூலகம்
10a
华东师范大学版 初中数学 八年级上册 一课一练 课堂精练 同步练习册_27

13.1 !命题ห้องสมุดไป่ตู้定理与证明
!!!"命题
我们已经学过一些图形的特性!例如( "/# 三角形的内角和等于 /90O' ""# 如果两个角是对顶角!那么这两个角相等' "2# 两直线平行!同位角相等' "1# 直角都相等! 它们都是判断某一件事情的语句!像这样表示判断 的语句叫做命题" P*,P,&F-F,G# ! 许多命题是由条件和结论两部分组成的!条件是已 知事项'结论是由已知事项推出的事项!这样的命题通常 可写成% 如果++!那么++& 的形式!用% 如果& 开始的 部分就是条件!而用%那么&开始的部分就是结论! 例如!在命题""#中!%两个角是对顶角&是条件!%这 两个角相等& 是结论!有的命题的条件与结论不十分明 显!若将它写成% 如果++!那么++& 的形式!则容易分 清它的条件与结论!例如!命题" 1 # 可写成% 如果两个角 都是直角!那么这两个角相等&! ! 例 ! 把命题%三个角都相等的三角形是等边三 角形&改写成%如果++!那么++&的形式!并分别指出 该命题的条件与结论! ! 解 这个命题可以写成%如果一个三角形的三 个角都相等!那么这个三角形是等边三角形&!该命题的 条件是%一个三角形的三个角都相等&!结论是%这个三 角形是等边三角形&! 根据已学过的知识!可以判断前面所列举的命题都 是正确的!也就是说!如果条件成立!那么结论一定成立! 像这样的命题!称为真命题!
华东师大版八年级上册初中数学全册作业设计一课一练(课时练)

11.1.1平方根一、选择题1、9的平方根是()A、±3B、±C、3D、﹣32、25的算术平方根是()A、5B、-5C、±5D、3、的平方根是()A、±4B、4C、±2D、 24、以下叙述中错误的是()A、± =±0.5B、=0.5C、0和1的平方根是它们本身D、负数没有平方根5、的平方根是()A、﹣2B、2C、±2D、 46、下列说法正确的是()A、﹣81的平方根是±9B、任何数的平方是非负数,因而任何数的平方根也是非负C、任何一个非负数的平方根都不大于这个数D、2是4的平方根7、a﹣1与3﹣2a是某正数的两个平方根,则实数a的值是()A、4B、C、2D、﹣28、下列说法不正确的是()A、是2的平方根B、是2的平方根C、2的平方根是D、2的算术平方根是9、下列各数中没有平方根的是()A、0B、﹣82C、D、﹣(﹣3)10、求一个正数的算术平方根,有些数可以直接求得,如,有些数则不能直接求得,如.但可以利用计算器求得,还可以通过一组数的内在联系,运用规律求得.请同学们观察下表:n 0.09 9 900 90000 …0.3 3 30 300 …运用你发现的规律解决问题,已知≈1.435,则≈()A、14.35B、1.435C、0.1435D、143.511、己知一个表面积为12dm2的正方体,则这个正方体的棱长为()A、1dmB、dmC、dmD、3dm12、若=0,则(x+y)2015等于()A、﹣1B、1C、32014D、﹣3201413、用计算器求2014的算术平方根时,下列四个键中,必须按的键是()A、B、C、D、14、有一列数如下排列,,,,,…,则第2015个数是()A、B、C、D、15、若a2=4,b2=9,且ab<0,则a-b的值为()A、-2B、±5C、5D、-5二、填空题16、如果a ,b分别是9的两个平方根,那ab=________.17、平方根节是数学爱好者的节目,这一天的月份和日期的数字正好是当年年份最后两位数字的算术平方根,例如2009年的3月3日,2016年的4月4日.请你写出本世纪内你喜欢的一个平方根(题中所举例子除外).________年________月________日.18、在草稿纸上计算:①;②;③;④,观察你计算的结果,用你发现的规律直接写出下面式子的值:=________.三、解答题19、计算.(1).(2)20、计算:(1)=________,=________,=________,=________,=________,(2)根据计算结果,回答:一定等于a吗?你发现其中的规律了吗?请你用自己的语言描述出来.(3)利用你总结的规律,计算:.21、已知2a+1的平方根是±3,5a+2b﹣2的算术平方根是4,求:3a﹣4b的平方根.22、如图,在长和宽分别是a、b的长方纸片的四个角都剪去一个边长为x的正方形,当a=8,b=6,且剪去部分的面积等于剩余部分的面积的时,求正方形的边长x的值.23、如图①,是由5个边长是1的正方形组成的“十”字形.把图②中的4个浅色直角三角形对应剪拼到4个深色直角三角形的位置从而得到图③,试求:图①图②图③(1)图②中1个浅色直角三角形的面积;(2)图③中大正方形的边长.答案解析一、1、【答案】A 【解析】9的平方根是:± =±3.【考点】平方根2、【答案】C 【解析】∵(5)2=25,∴25的算术平方根是5.【考点】算术平方根3、【答案】C 【解析】=4,± =±2,【考点】平方根,算术平方根4、【答案】C 【解析】∵0.52=0.25,∴A,B正确;0的平方根是它的本身,但1的平方根是±1,C错;D正确.【考点】平方根,算术平方根5、【答案】C 【解析】=4,则4的平方根是.【考点】平方根6、【答案】D 【解析】A:﹣81是负数,由于负数没有平方根,故A选项错误;B:任何数的平方为非负数,正确;但只有非负数才有平方根,且平方根有正负之分(0的平方根为0).故选项B错误;C:任何一个非负数的平方根都不大于这个数,不一定正确,如:当0<a<1时,a>a2,故选项错误;D:2的平方是4,所以2是4的平方根,故选项正确.【考点】平方根7、【答案】C 【解析】∵a﹣1与3﹣2a是某正数的两个平方根,∴a﹣1+3﹣2a=0,解得a=2.【考点】平方根,一元一次方程的应用8、【答案】C 【解析】2的平方根为± ,所以A,B都正确;是2的算术平方根,故C不正确;所以说法不正确的是C.【考点】平方根,算术平方根9、【答案】B 【解析】A.0的平方根是0,故错误;B.﹣82=﹣64<0,没有平方根,故正确;C.有平方根,故错误;D.﹣(﹣3)=3,有平方根,故错误.【考点】平方根10、【答案】A 【解析】根据表格的规律:,,可知≈1.435,则≈14.35.【考点】算术平方根,计算器—数的开方11、【答案】B 【解析】因为正方体的表面积公式:s=6a2,可得6a2=12,解得a= .【考点】平方根12、【答案】A 【解析】表示的是(x-1)的算术平方根,是非负数;也是非负数,∴,=0,∴x=1,y=﹣2,∴=(1﹣2)2015=﹣1.【考点】平方的非负性,二次根式的非负性13、【答案】C 【解析】表示求正弦;表示求余弦;表示求平方根;求的是次幂. 【考点】计算器—数的开方14、【答案】D 【解析】观察可以发现:第一个数字是;第二个数字是;第三个数字是;第四个数字是;…;可得第2015个数即是,故选D.【考点】平方根15、【答案】B 【解析】∵a2=4,b2=9,∴a=±2,b=±3,∵ab<0,∴a=2,则b=-3,a=-2,b=3,则a-b的值为:2-(-3)=5或-2-3=-5.【考点】平方根二、16、【答案】﹣9 【解析】∵9的平方根为±3,∴ab=﹣3×3=﹣9.【考点】平方根17、【答案】2036;6;6 【解析】2036年6月6日中,62=36,符合题意.【考点】算术平方根18、【答案】210 【解析】=1,=1+2,=1+2+3,=1+2+3+4,… =1+2+3+4+…+20=210.【考点】算术平方根三、19、【解析】(1)中,其前面的符号保持不变;(2)任何不为0的实数的0次幂为1;;.【解】(1)原式=4+13+5=22.(2)原式=1-1+2=2.【考点】算术平方根,实数的运算20、【解析】(1)=,=0.7,=0,=6,= .(2)中根据算术的平方根的定义可知,结果是一个正数,但a不一定是正数,所以需要去分类讨论;(3)在计算时需要注意括号里3.14﹣π的正负性,并利用(2)中得到的结论去做.【解】(1);0.7;0;6;(2)解:分类讨论:当时,;当时,;当时,;综上所述:= ;(3)解:利用(2)中得到的规律,可得原式=|3.14﹣π|=π﹣3.14.【考点】算术平方根21、【解析】根据已知得出2a+1=9,5a+2b﹣2=16,求出a ,b ,代入求出即可.【解】根据题意得:2a+1= =9,5a+2b﹣2=16,即a=4,b=﹣1,∴3a﹣4b=16,∴3a﹣4b的平方根是± =±4.答:3a﹣4b的平方根是±4.【考点】平方根,算术平方根22、【解析】根据题意列出等式4x2= (ab﹣4x2),把8和6代入得出4x2= (8×6﹣4x2),求出即可.【解】剪去部分的面积等于剩余部分的面积的,∴4x2= (ab﹣4x2),∴4x2= (8×6﹣4x2),∴12x2=48﹣4x2,∴x2=3,∵x表示边长,不能为负数,∴x= .【考点】平方根,算术平方根23、【解析】(1)根据直角三角形的面积公式计算即可;(2)根据图中得出大正方形的面积等于5个小正方形的面积之和.【解】(1)图②中1个浅色直角三角形的面积.(2)大正方形的面积等于5个小正方形的面积之和=5,∴图③中大正方形的边长为.【考点】算术平方根11.1.2 立方根一、选择题1、64的立方根是()A、4B、±4C、8D、±82、若a是的平方根,则=()A、﹣3B、C、或D、3或﹣33、如果一个有理数的平方根和立方根相同,那么这个数是()A、±1B、0C、1D、0和14、用计算器计算某个运算式,若正确的按键顺序是,则此运算式应是()A、43B、34C、D、5、下列语句正确的是()A、如果一个数的立方根是这个数的本身,那么这个数一定是零B、一个数的立方根不是正数就是负数C、负数没有立方根D、一个数的立方根与这个数同号,零的立方根是零6、下列命题中正确的是()①0.027的立方根是0.3;②不可能是负数;③如果a是b的立方根,那么ab≥0;④一个数的平方根与其立方根相同,则这个数是1.A、①③B、②④C、①④D、③④7、已知x没有平方根,且|x|=125,则x的立方根为()A、25B、﹣25C、±5D、﹣58、下列计算或说法:①±3都是27的立方根;②=a;③的立方根是2;④=±3,其中正确的个数是()A、1个B、2个C、3个D、4个9、若,则x和y的关系是()A、x=y=0B、x和y互为相反数C、x和y相等D、不能确定10、下列说法中,正确的是()A、一个数的立方根有两个,它们互为相反数B、负数没有立方根C、如果一个数有立方根,那么它一定有平方根D、一个数的立方根的符号与被开方数的符号相同11、若a2=36,b3=8,则a+b的值是()A、8或﹣4B、+8或﹣8C、﹣8或﹣4D、+4或﹣412、﹣a2的立方根的值一定为()A、非正数B、负数C、正数D、非负数13、下列说法正确的是()A、﹣0.064的立方根是0.4B、﹣9的平方根是±3C、16的立方根是D、0.01的立方根是0.00000114、将一个大的正方体木块锯成n个同样大小的小正方体木块,其中n的取值不可能的是()A、216B、343C、25D、6415、若是m+n+3的算术平方根,是m+2n的立方根,则B-A的立方根是()A、1B、-1C、0D、无法确定二、填空题16、若一个数的立方根就是它本身,则这个数是________.17、已知1.53=3.375,则=________.18、若一个偶数的立方根比2大,平方根比4小,则这个数一定是________.19、在数集上定义运算a﹡b ,规则是:当a≥b时,a﹡b=b3;当a<b时,a﹡b=b2.根据这个规则,方程4﹡x=64的解是________.三、解答题20、求下列各式的值:(1).(2);(3)21、某居民生活小区需要建一个大型的球形储水罐,需储水13.5立方米,那么这个球罐的半径r为多少米(球的体积V= ,π取3.14,结果精确到0.1米)?22、已知2a﹣1的平方根是±3,3a+b+9的立方根是3,求2(a+b)的平方根.23、我们知道a+b=0时,a3+b3=0也成立,若将a看成a3的立方根,b看成b3的立方根,我们能否得出这样的结论:若两个数的立方根互为相反数,则这两个数也互为相反数.(1)试举一个例子来判断上述猜测结论是否成立;(2)若与互为相反数,求的值.24、数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:39.众人十分惊奇,忙问计算的奥妙.你知道怎样迅速准确的计算出结果吗?请你按下面的问题试一试:(1)103=1000,1003=1000000,你能确定59319的立方根是几位数吗?答:________位数.(2)由59319的个位数是9,你能确定59319的立方根的个位数是几吗?答:________(3)如果划去59319后面的三位319得到数59,而33=27,43=64,由此你能确定59319的立方根的十位数是几吗?答:________.因此59319的立方根是________.(4)现在换一个数185193,你能按这种方法说出它的立方根吗?答:①它的立方根是________位数,②它的立方根的个位数是________,③它的立方根的十位数是________,④185193的立方根是________.答案一、1、【答案】A 【解析】∵43=64,∴64的立方根等于4.【考点】立方根2、【答案】C 【解析】∵,∴a=±3,∴= ,或= .【考点】平方根,立方根3、【答案】B 【解析】0的平方根和立方根相同.【考点】立方根4、【答案】C 【解析】根据符号可知,求的是4的立方根,选C.【考点】立方根,计算器—数的开方5、【答案】D 【解析】A:0,-1,1的立方根都是它们本身;B:0的立方根是0;C:负数有立方根;D正确.【考点】立方根6、【答案】A 【解析】①0.33=0.027,故说法正确;②当a<0时,是负数,故说法错误;③如果a是b的立方根,a ,b同号,∴ab≥0,故说法正确;④一个数的平方根与其立方根相同,则这个数是0,故说法错误.所以①③正确.【考点】平方根,立方根7、【答案】D 【解析】由题意得,x为负数,又∵|x|=125,∴x=﹣125,故可得x的立方根为:﹣5.【考点】立方根8、【答案】B 【解析】∵33=27,,∴3是27的立方根,①错误;②=a正确,表示a3的立方根是a ,正确;③的立方根是,错误;④=±3,正确;故②④正确.【考点】立方根9、【答案】B 【解析】∵,∴,等式两同时立方得,x=﹣y ,即x、y 互为相反数,故选B.【考点】立方根,等式的性质10、【答案】D 【解析】A.一个数的立方根只有1个,故选项错误;B.负数有立方根,故选项错误;C.一个负数有立方根,负数没有平方根,故选项错误;D.一个数的立方根的符号与被开方数的符号相同是正确的,故选项正确.【考点】立方根11、【答案】A 【解析】a2=36,得a=6或a=﹣6;b3=8,得b=2;故a+b=8或﹣4.【考点】平方根,立方根12、【答案】A 【解析】﹣a2是一个非正数,则它的立方根的值一定为非正数,故选A.【考点】立方根13、【答案】C 【解析】A、﹣0.064的立方根是﹣0.4,故本选项错误;B、﹣9没有平方根,故本选项错误;C、16的立方根是,故本选项正确;D、0.000000000000000001的立方根是0.000001,故本选项错误;故选C.【考点】立方根14、【答案】C 【解析】,,不是整数,,不可能是C.【考点】立方根15、【答案】B 【解析】∵是m+n+3的算术平方根,∴m-n=2,∵是m+2n的立方根,∴m-2n+3=3.∴解得∴,,∴B-A=-1.【考点】算术平方根,立方根,二元一次方程组二、16、【答案】±1,0 【解析】∵立方根是它本身有3个,分别是±1,0.【考点】立方根18、【答案】﹣150 【解析】∵1.53=3.375,∴(150)3=3375000,∴=-150.【考点】立方根19、【答案】10,12,14 【解析】∵2的立方是8,4的平方是16,所以符合题意的偶数是10,12,14.【考点】平方根,立方根20、【答案】4或8 【解析】∵当a≥b时,a﹡b=b3;当a<b时,a﹡b=b2.∴4﹡x=64,当4≥x ,∴x3=64,∴x=4,当4<x ,∴x2=64,∴x=8.故答案为:4或8.【考点】平方根,立方根三、21、【解析】根据立方根的定义求解即可.【解】(1);(2);(3).【考点】立方根22、【解析】利用球体的体积公式和立方根的定义计算即可.【解】根据球的体积公式,得=13.5,解得r≈1.5.故这个球罐的半径r为1.5米.【考点】立方根23、【解析】根据平方根的定义求出a的值,再根据立方根的定义求出b的值,最后计算2(a+b)的值,即可解答.【解】由已知得,2a﹣1=9解得:a=5,又3a+b+9=27,b=3,2(a+b)=2×(3+5)=16,∴2(a+b)的平方根是:± =±4.【考点】平方根,立方根24、【解析】(1)题是一个开放题,举一个符合题意的即可;(2)运用(1)的结论可得1﹣2x与3x﹣5互为相反数,即而算出x的值即可.【解】(1)解:∵3+(﹣3)=0,而且33=27,(﹣3)3=﹣27,有27﹣27=0,∴结论成立;∴“若两个数的立方根互为相反数,则这两个数也互为相反数”是成立的.(2)由(1)验证的结果知,1﹣2x+3x﹣5=0,∴x=4,∴=1﹣2=﹣1.【考点】平方根,立方根,解一元一次方程25、【解析】(1)103=1000,1003=1000000,则59319的立方根是2位数;(2)由59319的个位数是9,因为93=729,则59319的立方根的个位数是9.(3)如果划去59319后面的三位319得到数59,而33=27,43=64,由此你能确定59319的立方根的十位数是几3.因此59319的立方根是39.(4)∵103=1000,1003=1000000,1000<185193<1000000,∴185193的立方根是一个两位数,∵185193的最后一位是3,∴它的立方根的个位数是7,185193去掉后3位,得到185,∵53<185<63,∴立方根的十位数是5,则立方根一定是:57.【答案】(1)2(2)9(3)3;39(4)2;7;5;57【考点】立方根11.2实数一、选择题(共15题)1.在实数0、π、227、2、9-中,无理数的个数有()A. 1个B.2个C.3个D. 4个答案:B解析:π、2是无理数了.2.估计11的值在()A.在1和2之间B.在2和3之间C.在3和4之间D.在4和5之间答案:C解析:∵9<11<16,∴9<11<16,从而有3<11<4.3.﹣64的立方根与81的平方根之和是()A.﹣7 B.﹣1或﹣7 C.﹣13或5 D.5答案:B解析:﹣64的立方根为﹣4,81的平方根±3,则﹣64的立方根与81的平方根之和为﹣1或﹣7.4.如图,数轴上A,B两点表示的数分别为﹣1和3,点B关于点A的对称点为C,则点C所表示的数为()A.23-B.13-C.23-D.13答案:A解析:设点C表示的数是x,∵A,B两点表示的数分别为﹣13C,B两点关于点A对称,∴(1)3(1)x--=-,解得x=23-5.化简3|﹣π得()A3B3C.23D32π答案:B30,∴3|336.有下列说法:①被开方数开方开不尽的数是无理数;②无理数是无限不循环小数;③无理数包括正无理数、零、负无理数;④无理数都可以用数轴上的点来表示.其中正确的说法的个数是( )A . 1B . 2C . 3D . 4 答案:C解析:①被开方数开方开不尽的数是无理数,正确;②无理数是无限不循环小数,正确;③0是有理数,不是无理数,则命题错误;④无理数都可以用数轴上的点来表示,正确.7.若0<x <1,则x ,x2,x ,1x 中,最小的数是( ) A . x B .x C .1xD . x2 答案:B 解析:可采用特殊值,令14x =,0<14<1,则x2=116,x =12,1x =4,则x2<x <x <1x . 8.若2的整数部分为a ,小数部分为b ,则a ﹣b 的值为( )A . 2B . 2C . 2﹣2D . 2+2答案:C解析:∵0<2<1,,∴1a =,21b =-,则1(21)22a b -=--=-.9.|63||26|-+-的值为( )A . 5B . 526-C . 1D .261- 答案:C解析:原式=3﹣6+6﹣2=1.10.如图,数轴上的A 、B 、C 、D 四点中,与数3-表示的点最接近的是( )A .点AB .点BC .点CD .点D 答案:B3 1.732,∴3 1.732,∵点A 、B 、C 、D 表示的数分别为﹣3、﹣2、﹣1、2,∴与数3-表示的点最接近的是点B.11.已知下列结论:①在数轴上的点只能表示无理数;②任何一个无理数都能用数轴上的点表示;③实数与数轴上的点一一对应;④有理数有无限个,无理数有限个,其中正确的结论是( )A . ①②B . ②③C . ③④D . ②③④ 答案:B解析:①数轴上的点既能表示无理数,又能表示有理数,故①错误;②任何一个无理数都能用数轴上的点表示,故②正确;③实数与数轴上的点一一对应,故③正确;④有理数有无限个,无理数无限个,故④错误.12. 有一个数值转换器原理如图,当输入的x的值为256时,输出的y的值为()A. 16 B.2C.3D.8答案:A解析:x=256,第一次运算,256=16,第二次运算,16=4,第三次运算,4=2,第四次运算,2,输出2.13.如图,矩形OABC的边OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,则这个点表示的实数是()A.3B.8C.5D. 2.5答案:C解析:25 2.5825C.14. 任意实数a,可用[a]表示不超过a的最大整数,如[4]=43,现对72进行如下操作:72→72→8→2,这样对72只需进行3次操作后变为1.类似地:对数字900进行了n次操作后变为1,那么n的值为()A. 3 B.4 C. 5 D. 6答案:C解析:900→第一次900→第二次30→第三次5→第四次2,即对数字900进行了4次操作后变为1.15. 将1236m,n)表示第m排从左向右第n个数,则(6,5)与(13,6)表示的两数之积是()A 6B .6C 2D 3答案:B 解析:6,5)表示第6排从左向右第5613,6)表示第13排从左向右第6个数,可以看出奇数排最中间的一个数都是1,第13排是奇数排,最中间的也就是这排的第7个数是1,那么第66,则(6,5)与(13,6)表示的两数之积是6.二、填空题(共5题)1622之间的无理数 . 3 2.5解析:设此无理数为x 222x <2,∴2<x2<4,∴符合条件的无理数可3 2.517.下列各数:32514-327-,1.414,3π-,3.12122,9- 3.161661666…(每两个1之间依次多1个6)中,无理数有 个,有理数有 个,负数有 个,整数有 个.答案:3|5|4|2 解析:无理数有:323π-,3.161661666…;有理数有: 514-327- 1.414,3.12122,9-数有:514-327-,3π-,9327-,918.在数轴上表示3 52的相反数是 ,绝对值是 . 32552 解析:在数轴上表示3-|33-=52的相反数是(52)-=2552,∴52|52.19.若a1=1,23a4=2,…,按此规律在a1到a2014中,共有无理数 个. 答案:1970解析:∵12=1,22=4,32=9,42=16,…,442=1936,452=2025,∴a1到a2014中,共有44个有理数,则无理数有2014﹣44=1970.20.有下列说法:①任何无理数都是无限小数;②有理数与数轴上的点一一对应;③在1和34个; ④2π是分数,它是有理数.⑤近似数7.30所表示的准确数a 的范围是:7.295≤a <7.305.其中正确的有 (填序号).答案:①⑤解析:①任何无理数都是无限小数,正确;②实数与数轴上的点一一对应,错误;③在1和3之间的无理数有无数个,错误;④ 是分数,它是无理理数,错误.⑤近似数7.30所表示的准确数a 的范围是:7.295≤a <7.305,正确.三、解答题(共5题)21.计算:(111|3|()(20153-0--+.答案:-1解析:原式3311-=-;(2)1.43≈=).答案:-2.7解析:原式3 3.162 1.43 2.7≈-+-⨯=-.分析:根据实数的运算法则运算即可.22.有一组实数:202π,13,0.1010010001…(两个1之间依次多个0); (1)将他们分类,填在相应括号内;有理数{ }无理数{ }答案:2,0132π,0.1010010001…(两个1之间依次多个0)解析:(1)将他们分类,填在相应括号内,如下:有理数{2,013}无理数{2,π,2π,0.1010010001…(两个1之间依次多个0)}(2)选出2个有理数和2个无理数,用+,﹣,x,÷中三个不同的运算符号列成一个算式,(可以添括号),使得运算结果为正整数.答案:π×2π﹣0+2=4.(本题答案不唯一)解析:选出2个有理数为:2,0;选出2个无理数为:π,2π;则π×2π﹣0+2=4.(本题答案不唯一).23.已知实数x和﹣1.41分别与数轴上的A、B两点对应.(1)直接写出A、B两点之间的距离(用含x的代数式表示).答案:|x+1.41|解析:∵实数x和﹣1.41分别与数轴上的A、B两点对应,∴A、B两点之间的距离为:|x+1.41|.(2)求出当x=3﹣1.41时,A、B两点之间的距离(结果精确到0.01).答案:1.73解析:当x=3﹣1.41时,A、B两点之间的距离为:|x+1.41|=|3﹣1.41+1.41|=3≈1.73.(3)若x=3,请你写出大于﹣1.41,且小于x的所有整数,以及2个无理数?答案:±4解析:∵3 1.73,∴大于﹣1.4131,0,1.21224. 如图,4×4方格中每个小正方形的边长都为1.(1)直接写出图1中正方形ABCD的面积及边长;答案:5解析:(1)四边形ABCD的面积是21341252-⨯⨯⨯=5(2)在图2的4×4方格中,画一个面积为8的格点正方形(四个顶点都在方格的顶点上);并把图(2)中的数轴补充完整,然后用圆规在数轴上表示实数.答案:如图:解析:如图:在数轴上表示实数8,25.阅读下面的文字,解答问题:2221221479 273,7272).请解答:(15a13的整数部分为b,求a+b的值;答案:5解析:(1)根据题意得:a=2,b=3,则a+b=2+3=5.(2)已知:3,其中x是整数,且0<y<1,求x﹣y的相反数.3解析:∵x为整数,3,且0<y<1,∴x=11,31,则x﹣y的相反数为﹣(x﹣y)=﹣12.12.1幂的运算一.相信你的选择(每题3分,共12分)1.化简(-x)3·(-x)2的结果正确的是( )A.-x 6B.x 6C.x 5D.-x 52.下列运算中,正确的是( )A.x 2·x 3=x 6B.(a b)3=a 3b 3C.3a +2a =5a 2D.(x ³)²= x 5 3.))((22a ax x a x ++-的计算结果是( )A.3232a ax x -+B.33a x -C.3232a x a x -+D.322222a a ax x -++4.计算(32)2003×1.52002×(-1)2004的结果是( ) A.32 B.23 C.-32 D.-23 二.试试你的身手(每题4分,共28分)1计算:(-3x ²y )(32xy ²)=2计算:(-x ²y) 5 =3计算:32(2)(12)________.a a a -⋅-+=4卫星绕地球运动的是7.9×10³米/秒,则卫星绕地球运行2×10²秒走过的路程是5若 36,272,m n ==则243m n +=6.用边长为 1cm 的小正方形搭如下的塔状图形,则第 n 次所搭图形的周长是____cm 。
华东师范大学版 初中数学 八年级上册 一课一练 课堂精练 同步练习册_60

第章!勾股定理 **)"一般认为这个定理是毕达哥拉斯"^V -Q)X ,*)&#学派首先证明的&因而称为毕达哥拉斯定理!勾股定理曾引起很多人的兴趣&人们对这个定理的证明找到了很多方法!/410年卢米斯"Z A <AT ,,%F &#专门编辑了一本证明勾股定理的小册子///,毕氏命题-&收集了这个著名定理的250种证明&其中包括大画家达+芬奇和美国第"0任总统詹姆士+阿+加菲尔德"_)%+&B ;*)%Y )*M F +H W &/92//99/#的证法!美丽的勾股树!!你可能去过森林公园&看到过许许多多千姿百态的植物!可是你是否见过如下的勾股树呢%你知道这是如何画出来的吗%仔细观察&你就会发现那一个个细小的部分正是我们学过的勾股图&它们一个接着一个连在一起&构成了多么奇妙美丽的勾股树.动手画画看&相信你也能画出其他形态的勾股树!*!," 第 章!勾股定理!勾股定理的应用勾股定理能解决直角三角形的许多问题!因此在现实生活和数学中有着广泛的应用!!如图/18"8/!一圆柱体的底面周长为"0$%!高:;为1$%!;<是上底面的直径!一只蚂蚁从点:出发!沿着圆柱的侧面爬行到点<!试求出爬行的最短路程!"精确到0!0/$%#图*$+!+*!蚂蚁实际上是在圆柱的半个侧面内爬行!如果将这半个侧面展开"如图/18"8"#!得到长方形:;<>!根据%两点之间!线段最短&!所求的最短路程就是这一展开图///长方形:;<>的对角线:<之长!图*$+!+!!如图/18"8"!在U -*:;<中!;<7底面周长的一半7/0$%!由勾股定理!可得:<#:;"';<槡"#1"'/0槡"#槡//:%/0!55"$%#!答(爬行的最短路程约为/0!55$%!。
新课程课堂同步练习册八年级上册华东师大版数学答案

《新课程课堂同步练习册·数学(华东版八年级上)》参考答案 第12章 数的开方§12.1平方根与立方根(一)一、 1.B 2.A 3.B二、1. ±7 2. ±2, 3.-1; 4.0三、1.从左至右依次为: ±3,±4,±5, ±6,±7,±8,±9,±10,±11,±12,±13,±14,±15. 2.(1)±25 (2)±0.01 (3)45± (4)29±(5)±100 (6) ±23.(1)±0.2 (2)±3 (3)79±(4) 17±4.(1)a >-2 (2)a =-2 (3)a <-2. §12.1平方根与立方根(二) 一、1.D 2.A 3.C二、1. 14±,142.(1)25.53 (2)4.11 4. 0或1.三、1.(1)80 (2)1.5 (3)114(4)3;2.(1)-9 (2) 12±(3)4 (4)-53.(1)2.83 (2)28.09(3)-5.34 (4)±0.47.4. 正方形铁皮原边长为5cm . §12.1平方根与立方根(三) 一、1.D 2.A 3.C二、,-3 2. 6,-343 3.-4 4. 0,1,-1. 三、1.(1)0.4 (2)-8 (3)56( 4)112- (5)-2 (6)100;2.(1)19.09(2)2.652(3)-2.098(4)-0.9016;3. 63.0cm 2;4.计算得:0.5151,5.151,51.51,515.1,得出规律:当被开方数的小数点向左(右)每移动2位,它的平方根的小数点就向左(右)移动1位.5151.§12.2实数(一) 一、1.B 2.C二、1. 略 2. ≥12-.三、1.(1)√(2)×(3)√(4)×(5)×(6)×(7)√(8)×;2.有理数集合中的数是:13,3.1415,2-5,0,⋅⋅43.6,0.8π,0.1010010001…; 3.A 点对应的数是-3,B 点对应的数是-1.5,C D E 点对应的数是π.§12.2实数(二)一、 1.C 2.B 3.B二、1. (11(2)2-3. 5 .三、1.(1)(2)--(3)1+;2.(1)7.01 (2)-1.41 (3)2.743.略4. 7第13章 整式的乘除§13.1幂的运算 (一)一、1.C 2.B 3.D 二、1.1010 2. 6 ,8 3. 9三、1.(1)10a (2)9a (3)6a (4)10()x y + (5)82x (6)51n b +2.可进行1410次运算3. 2 §13.1幂的运算(二) 一、1.D 2.B 3.C二、1.10m ,18x 2.14x 3.62y ;4. 2三、1.(1)9a (2)21x (3)215a (4)123a (5)0 (6) 23n a + 2.b >a >c §13.1幂的运算(三) 一、1. C 2.D 3.A 二、1. 4109x y ,96318a b c 2. 44m ,54a b 3. 216三、1.(1) 3327x y (2)464x y (3) 85a (4)927a2. (1) 1- (2) 3 3.x =5 4.52 §13.1幂的运算(四) 一、1.C 2.A 3.B二、1.8a ,2a 2. y ,5y 3.22x y ,5x -三、1.(1)3a (2)3m (3) 5x - (4) 4x (5)1 (6) 4y 2. 12x y ==§13.2 整式的乘法(一) 一、1.B 2.D 二、1.232x y 2.-5412x y z 3.5312x y -三、1.(1)1254a b (2)-23x y (3)-4044a b (4)-18628a b c (5)10()x y - (6)3.6⨯17102. 2.37⨯710 3. 11,,23a b c ==-=-§13.2整式的乘法(二)一、1.B 2.C二、1.263m n mn -,4362x x -+ 2.1832a b -2723a b ,33a b +3. 3223122a b a b ab -+,32232212812x y x y x y --三、1.(1)2155x xy - (2)3222612a b a b -+ (3) 3223423x y x y xy -+(4) 42241827m n m n - (5)222322a b a b - (6)222x y xy + 2. 12x =-3.提示:n (2n +1)-2n (n -1)=2n ²+n -2n ²+2n =3n .§13.2整式的乘法(三) 一、1.B 2.D 3.C二、1.22124m mn n -- 2.22276x xy y -+ 3.-6三、 1.(1)221x x +- (2)249x - (3)2456x x -- (4)22672m mn n -+-(5)48x + (6)2278x y + 2. -3§13.2整式的乘法(四) 一、1.D 2.B 3.C二、1.-2 2. 2 3.2(123)x cm - ,233cm 三、1. 化简得252x x --,多项式的值为14-2.(1)x =5 (2)6x <3.(1)①2710x x ++②2710x x -+③2310x x --④2310x x +-(2)2()x a b x ab +++ (3)①21128x x ++ ②26m m +-§13.3 乘法公式(一) 一、1.C 2.B二、1.22925a b -,229x y -; 2.2249b a -,224x y -; 3. 22()()a b a b a b +-=-三、1.(1)229a b - (2)22161y x -(3) x 2-9y 2 (4) x 2-4 (5) 2mn (6) 5x -92.(1) 44a -, 8 (2)25x -, -26 §13.3乘法公式(二) 一、1.A 2.D 3.C二、1. 5 2. 1 ,89993.3x y +三、1.(1)2125y - (2)29y (3)2121a a +- (4)81x - (5)9999 (6)8359992.1282 §13.3乘法公式(三) 一、1.A 2.D 3.A二、1.2244m mn n -+,2244x xy y -+ 2.224493a ab b ++,2214a ab b -+3.222()2a b a ab b -=-+ 三、1.(1)2961m m ++ (2)21424x x -+(3)229124x xy y ++(4) 224129x xy y ---(5)9604 (6) 121042.(1) 23x -,6 (2) 22a b -,21 3.1528§13.3乘法公式(四) 一、1.B 2.C二、1.924x -,2441a a ++;2.6±;3. 6x ±或4814x三、1.(1)42242x x y y -+ (2)31x -+ (3)2319a a -+ (4)8xy 2(1)2 (2)3 §13.4整式的除法(一) 一、1.D 2.B 3.B二、1.42x ,5xy - 2. 34mn ,25()x y - 3. 4 ,3三、1.(1) 2x (2)4m - (3) 224x y (4) 54ab 2.225a b -,-1 ;3. 45.410⨯倍§13.4整式的除法(二) 一、1.C 2.C 3.C二、1.32a b - 2.24x -+ 3. 4m -2n 三、1.(1)2322x xy -(2)222m n mn - (3)2351m m -+ (4)23212ab b -+-2.(1)2ab -,1 (2) xy -,5 3.2,4x y ==- ,-24 §13.4整式的除法(三) 一、1.B 2.C二、1.27510⋅⨯ 2.221510x y xy - 3.(464)a b ab ++cm 三、1.(1) 23()x y + (2) -b (3)5463x y -(4)22x - 2.14x ≤-3. 429156x x x -+ §13.4整式的除法(四) 一、1.C 2.B 3.A 二、1.2233ab b -+- 2.-5 3.18,4三、1.(1)422a b a b +(2)2322x x --+(3)123y x -(4) 261a b -2.(1) 任一单项式与它前面的单项式的商都为2x - (2)10512x - §13.5因式分解(一) 一、1.D 2.B二、1. ab 2.a (a -2) ,3xy (4x -1) 3.-12三、1.(1)a (a +2b ) (2)3ab(b-2a-3) (3)(x -2) (6-x ) (4)3x (a +b )(a +b -2y )(5)2x 2(x -5)(6)x (x +4) 2. (1)220 (2) 2.732§13.5因式分解(二)一、1.A 2.A 3.D二、1.-(x -2y )2,3 (a -4)2 ;2.②③④⑤; 3.(x -3) 三、1.(1)(x +2y )(x -2y ) (2)(9+m)(9-m) (3)(m -5)2 (4)(3a+4b)2(5)3(x +4)(x -4) (6)(x +y )2(x -y )2 (7)(x -2)2 (8)(2a -3b )22. (1)2000 (2) 59853.∵4x 2-4x +2= 4x 2-4x +1+1=(2x-1)2+1>0, ∴ 4x 2-4x +2的值恒为正数.第14章 勾股定理§14.1 勾股定理(一) 一、1.B 2.D二、1.(1)13 (2)12 (3)24 (4)63 2. 2 3. 1三、1.30cm 2 2.28米 3.AB=§14.1 勾股定理(二) 一、1.B 2.D 3.D 二、1. a ²+c ²=b ² 2.1360 3.5三、1. 略 2. 169 cm 2 3.36 §14.1 勾股定理(三)一、1.C 2.B 3.C 二、1. 6.93 2. 3.2 3. 5三、1. 1米 2. 2.2米 3.(略) §14.1 勾股定理(四)一、1.B 2.C 3.B二、1.22`1 2. 10三、1. 提示:利用勾股定理的逆定理检验2.(1)面积为12.5,周长为1851320+++ (2)∠BCD 不是直角3.∵a 2+b 2=(n 2-1)2+(2n)2 =n 4-2n 2+1+4n 2 =n 4+2n 2+1=(n 2+1)2 ∴ a 2+b 2=c 2 ∴ △ABC 是直角三角形 §14.2 勾股定理的应用(一) 一、1.A 2.D二、三、1. BF=12,AD=13,ED=2.6 2.略; 3. 10. §14.2 勾股定理的应用(二) 一、1. 12≤a ≤13 2.815 3. 150二、1. 34海里 2. 因为小汽车的速度为72千米/时 ,所以小汽车超速 3.996.9m 2第15章 平移与旋转§15.1平移(一)一、1.D 2.C 3.B二、1.B B '的方向 线段B B '的距离(答案不唯一) 2.形状 大小 位置 3.2cm 三、1.略 2.图略 §15.1平移(二)一、1.D 2.D 3.C二、1.A , Q 2. 72° 3. 7,7三、1.CF=4cm CD=3cm DF=3 cm EF=2 cm 2.图略3.(1)图略(2)重叠部分的面积与原长方形ABCD 面积的41§15.1平移(三) 一、1.D 2.C二、1. 13㎝ 2.B B ' ,C C ',D D ';B A '',D C '' ,CD ,不能 3.相等,相等三、1.图略 ;2.(1)相等,理由如下:由题意可知,AB ∥CD ,AD ∥BC ,所以∠DAC=∠BCA ,∠BAC=∠ACD ,所以∠B=∠D 3.4个 ,9个 §15.2旋转(一) 一、1.D 2.C二、1.中心 ,方向 ,角度 2.180°3.点C,∠ACD(答案不唯一)的度数,D 、E ,EC ,∠DCE 三、1.(1)点A , 60° (2)AC 边上的中点(3)等边三角形 2.能 ,点A , 120° 3.(1)垂直 (2)13㎝2§15.2旋转(二) 一、1.C 2.D 3.B二、1.中心,角度,距离 2.点B ,点C ,BC 边的中点3. 4,△ABO 与△CDO 、△ADO 与△CBO 、△ABC 与△CDA 、△ABD 与△CDB4.60 三、1.略 2.略 §15.2旋转(三)一、1.C 2.D 3.B 二、1.略 2.120 3.2π三、1.(1)点D (2)正方形 , 64 (3)30C DC '∠= ,CDA '∠=60° 2.略 §15.2旋转(四) 一、1.B 2.C二、1.轴对称,平移,旋转 2.B , D ,旋转3.线段的中点 , 180°,对角线的交点, 90°,180°,270°,圆心 ,任何度数4. 4.5 三、1.图略 2.CG=CE ,理由如下:由题意可知,DE=BF=BG ,∵四边形ABCD 是正方形,∴BC=CD=AD=AB ,∵CG=BC-BG ,CE=CD-DE ,∴CG=CE §15.3中心对称(一) 一、1.B 2.D二、1. A ,B 2.略 3. HINO XZ, BC HIM OU X , HI OX三、1.图略 2.能,对称中心是点C ,对应线段有:DC 与CE ,AD 与EF ,AB 与GF ,BC与GC ;对应角有:∠D 与∠E ,∠A 与∠F ,∠B 与∠G ,∠DCB 与∠GCB3.图略4.图略§15.3中心对称(二) 一、1.A 2.B二、1.OA=OD ,OB=OC 2.2㎝ , 1.5㎝ 3.关于点O 成中心对称 三、1.图略; 2.图略; 3.图略 , 成中心对称 ; 4. 图略§15.4图形的全等 一、1.C 2.B二、1.12; 2.55; 3.120 , 4 ; 4.①②③④三、1.(1)△ADE ≌△ABC ,对应边有:AB 与AD , BC 与DE , AC 与AE ,对应角有:∠BAC 与∠DAE ,∠B 与∠D ,∠C 与∠E (2)∠C=30° ∠B=110° ∠BAE=100° 2.(1)AC=BD AO=OB OC=OD (2)∠D=32° (3)AC ∥BD ,∵AO=OB ,CO=OD , ∴ △AOC 与△BOD 是关于点O 成中心对称的, ∵AC ∥BD. 3.CD=3㎝第16章 平行四边形§16.1平行四边形的性质(一) 一、1.D 2.B 3.B二、1.110,70,110 2.120,60 3.115° 三、1. ∠A=50°,∠B=130°,∠C=50°,∠D=130°;2. ∠ADE=30°,∠EDF=60°,∠FDC=30°.3. AE ⊥BE,∵∠DAB+∠ABC=180°,∴12∠DAB+12∠ABC=90°,即∠EAB+∠ABE=90,∴∠AEB=90°,即AE⊥BE§16.1平行四边形的性质(二)一、1.D 2.C二、1.2cm 2.16 3.5,7三、1. 21cm 2. 8cm;3.8cm§16.1平行四边形的性质(三)一、1.B 2.D二、1.10 2.40° 3.7.三、1. 24cm; 2. 略; 3.略§16.1平行四边形的性质(四)一、1.B 2.B二、1.55 2.3 3.100°,80°三、1.16 2. 略§16.2矩形、菱形与正方形的性质(一)一、1.C 2.A 3.B二、1.7 2.28 3.90,45三、1. 2cm; 2. 5cm 3.45°§16.2矩形、菱形与正方形的性质(二)一、1.A 2.B二、1.32 cm 2.60°,120°, 60°,120° 3.30 4.5三、1. 8cm;2. 面积24cm2,周长20cm3.60°,120°,60°,120°.§16.2矩形、菱形与正方形的性质(三)一、1.C 2.B二、1.22.5° 2.67.5三、1.15°;2. 提示:因为四边形EFOG为矩形,所以EF=OG,只要说明EG=GB即可.§16.2矩形、菱形与正方形的性质(四)一、1.D 2.B二、1.4cm 2.5cm 3.1 4.12三、1.20cm 2.150° 3.(1)提示:∠FBC=∠BCE=45°(2)AE=DF,理由略. §16.3 梯形的性质(一)一、1.D 2.C二、1. 60 2.10 3. 26 4.110三、1. 60°,120°, 60°,120°;2. 24cm§16.3 梯形的性质(二)一、1.B 2.B二、1.6 2.9 3. 5<a<13三、1.(1)等边三角形,理由略 (2)25; 2. 108°,72°,108°,72°;3.(1)略(2)∠A=108°,∠B=72°,∠C=72°,∠ADC=108°4.∵CE∥BD,AE∥DC,∴四边形BECD是平行四边形,∴DB=CE,又∵梯形ABCD 是等腰梯形,∴AC=BD,∴AC=CE,即三角形CAE是等腰三角形5.2(10cm。
华东师范大学版 初中数学 八年级上册 一课一练 课堂精练 同步练习册_75
第 章 !数据的收集与表示"*$)
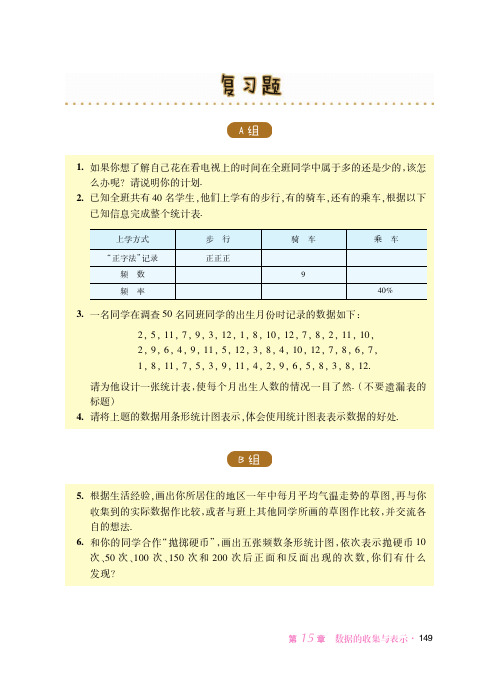
("如图是某市场调查公司调查 B C D E Z ? Y等各大手机品牌占我国智能 手机市场份额情况得到的统计图! / 图中最大的扇形表示!!!!手机占我国智能手机市场份额的 !!!!a这个扇形的圆心角为!!!!O精确到 /O! " 你从图中还能得到哪些信息
A组Βιβλιοθήκη !"如果你想了解自己花在看电视上的时间在全班同学中属于多的还是少的该怎 么办呢 请说明你的计划!
#"已知全班共有 10 名学生他们上学有的步行有的骑车还有的乘车根据以下 已知信息完成整个统计表!
上学方式
步!行
骑!车
乘!车
正字法记录
正正正
频!数
4
频!率
10a
$"一名同学在调查 #0 名同班同学的出生月份时记录的数据如下
C "0// 年总支出的分配图
第 4 题
/ "0// 年管理费支出的金额是多少 保险费支出的金额是多少 " "0// 年的总支出比 "0/0 年增加多少 增加百分之几
第 章 "*%, !数据的收集与表示
第 5 题
)"小明投掷一个普通的正方体骰子 10 次已知他掷得奇数的次数是 求 /# 掷得 偶数的次数!他掷得奇数的频率高还是掷得偶数的频率高 如果再掷 10 次此 结论会改变吗
C组
*"利用图B C提供的某公司的一些信息回答后面的问题!
!!!!!
华东师范大学版 初中数学 八年级上册 一课一练 课堂精练 同步练习册zhch_3
08/ $%
第 : 题
第 章 !数的开方"'
11.2 !实数
练!习
!"完成下列表格
被开方数 .:1 ."5 .9 ./
0
/
9
"5
:1
立方根
#"求下列各数的立方根
/ #/"!!!!!" .080"5!!!!!2 ./:"1#!
$"用计算器计算
槡 槡 / 2 : 9#4 !! " 2 /58#5: !!
槡 精确到 2 2 #8:4/
/ 08/"#!!
" .:"15!!
%"用计算器计算精确到 080/
2 5"4!
槡 / /:894 !!
槡 " 2 : 94" !
&"/ 槡/0在哪两个相邻的整数之间
" 2
2下8/列&四个槡/结0 论&中28"正正确确的吗是!!!
槡 槡 B828/# & /0 &28/: !!!!!!!C828/: & /0 &28/5 '"如D8图28/在5 做&浮槡力/0实&验2时8/9小!华!用一根细线将E8一28正/9方&体铁槡/块0 &28/4
形!容易知道!这个大正方形的面积是 "!所以大正方形
华东师范大学版 初中数学 八年级上册 一课一练 课堂精练 同步练习册_64
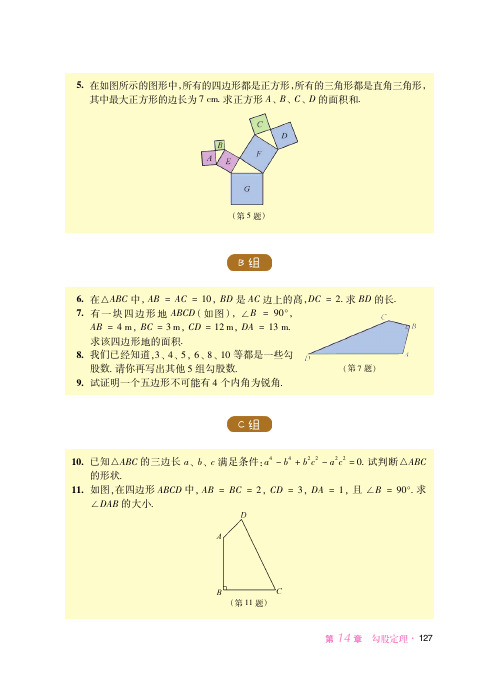
" ) 3
"1 .)1 J)" 3" ."" 3" 70!
*:;<
的形状!
如图 在四边形 中 且 求 !!"
:;<> :; #;< #" <> #2 >:#/ +; #40O!
+>:;的大小!
ห้องสมุดไป่ตู้
第 题 //
第 章 !勾股定理"*!'
如图 在五边形 中 的面积是 !#"
第 题 /2
第 章 "*!( !勾股定理
:; #1 % ;<#2 % <> #/" % >:#/2 %!
求该四边形地的面积! )"我们已经知道2 1 # : 9 /0 等都是一些勾
股数!请你再写出其他 # 组勾股数! *"试证明一个五边形不可能有 1 个内角为锐角!
第 5 题
C组
已知 的三边长 满足条件 试判断 !+" *:;<
&"在如图所示的图形中所有的四边形都是正方形所有的三角形都是直角三角形 其中最大正方形的边长为 5 $%!求正方形 : ; < >的面积和!
第 # 题
B组
在 中 是 边上的高 求 的长 '" *:;< :; #:< #/0 ;> :<
>< #"! ;> !
有 (" 一块四边形地 :;<> 如图 +; #40O
:;<>? +; #+? #40O :; ## $% *:;<
华东师范大学版 初中数学 八年级上册 一课一练 课堂精练 同步练习册zhch_6
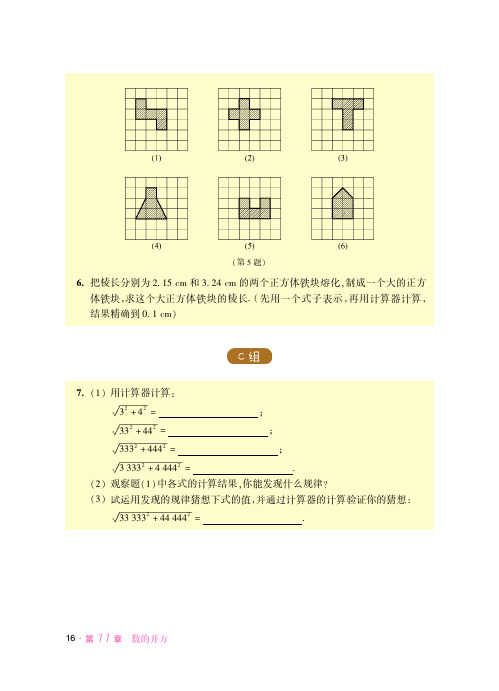
从中你能发现什么
规律$ 若指数为任
意 的 正 整 数 0) 1!
等于什么 "0*"1
$
根据幂的意义填空(
"/# "2 /"1 #"" /" /"# /"" /" /" /"#
#""!!# '
""# #2 /#1 #
!
##"!!# '
"2# "2 *"1 #
!
#""!!# !
概括
! "0*"1 #" "*"*+*"# " "*"*+*"#
0个
1个
!!利用这个法 则!可直接求出 同底数幂的积!
可得
#"*"*+*" #"0'1 !
个 " 0'1#
为正整数 "0*"1 #"0'1"0) 1
#!
这就是说!同底数幂相乘!底数不变!指数相加! ! 例 ! 计算(
"/# /02 //01 '!!!!!!""# "*"2 '
"2# "*"2 *"# !
" 观察题/中各式的计算结果你能发现什么规律 2 试运用发现的规律猜想下式的值并通过计算器的计算验证你的猜想
槡22 222" J11 111" 7!!!!!!!!!!!
华东师大版八年级数学上册同步练习题及答案

12.1.1 平方根(第一课时)◆随堂检测1、若x 2= a ,则 叫 的平方根,如16的平方根是 ,972的平方根是 2、3±表示 的平方根,12-表示12的 3、196的平方根有 个,它们的和为 4、下列说法是否正确说明理由 (1)0没有平方根; (2)—1的平方根是1±; (3)64的平方根是8; (4)5是25的平方根; (5)636±= 5、求下列各数的平方根(1)100 (2))8()2(-⨯- (3) (4)49151◆典例分析例 若42-m 与13-m 是同一个数的平方根,试确定m 的值◆课下作业●拓展提高一、选择1、如果一个数的平方根是a+3和2a-15,那么这个数是( )A 、49B 、441C 、7或21D 、49或441 2、2)2(-的平方根是( )A 、4B 、2C 、-2D 、2± 二、填空3、若5x+4的平方根为1±,则x=4、若m —4没有平方根,则|m —5|=5、已知12-a 的平方根是4±,3a+b-1的平方根是4±,则a+2b 的平方根是 三、解答题6、a 的两个平方根是方程3x+2y=2的一组解 (1) 求a 的值 (2)2a 的平方根7、已知1-x +∣x+y-2∣=0 求x-y 的值● 体验中考1、(09河南)若实数x ,y 满足2-x +2)3(y -=0,则代数式2x xy -的值为2、(08咸阳)在小于或等于100的非负整数中,其平方根是整数的共有 个3、(08荆门)下列说法正确的是( )A 、64的平方根是8B 、-1 的平方根是1±C 、-8是64的平方根D 、2)1(-没有平方根12.1.1平方根(第二课时)◆随堂检测1、259的算术平方根是 ;___ __ 2、一个数的算术平方根是9,则这个数的平方根是3x 的取值范围是 ,若a ≥0 4、下列叙述错误的是( )A 、-4是16的平方根B 、17是2(17)-的算术平方根 C 、164的算术平方根是18 D 、的算术平方根是◆典例分析例:已知△ABC 的三边分别为a 、b 、c 且a 、b |4|0b -=,求c 的取值范围 分析:根据非负数的性质求a 、b 的值,再由三角形三边关系确定c 的范围◆课下作业●拓展提高一、选择12=,则2(2)m +的平方根为( )A 、16B 、16±C 、4±D 、2±2 )A 、4B 、4±C 、2D 、2± 二、填空3、如果一个数的算术平方根等于它的平方根,那么这个数是42(4)y +=0,则xy =三、解答题5、若a 是2(2)-的平方根,b 2a +2b 的值6、已知a b-1是400●体验中考1.(2009年山东潍坊)一个自然数的算术平方根为,则和这个自然数相邻的下一个自然数是()A.B.C.D.2、(08的整数部分是;若<b,(a、b为连续整数),则a= ,b=3、(08年广州)如图,实数a、b在数轴上的位置,化简 =4、(08年随州)小明家装修用了大小相同的正方形瓷砖共66块铺成米2的房间,小明想知道每块瓷砖的规格,请你帮助算一算.12.1.2 立方根◆随堂检测1、若一个数的立方等于 —5,则这个数叫做—5的 ,用符号表示为 ,—64的立方根是 ,125的立方根是 ; 的立方根是 —5.2、如果3x =216,则x = . 如果3x =64, 则x = .3、当x 为 时,.4、下列语句正确的是( )A 、64的立方根是2B 、3-的立方根是27C 、278的立方根是32± D 、2)1(-立方根是1- 典例分析例 若338x 51x 2+-=-,求2x 的值.◆课下作业●拓展提高一、选择1、若22)6(-=a ,33)6(-=b ,则a+b 的所有可能值是( )A 、0B 、12-C 、0或12-D 、0或12或12- 2、若式子3112a a -+-有意义,则a 的取值范围为( )A 、21≥aB 、1≤aC 、121≤≤a D 、以上均不对 二、填空3、64的立方根的平方根是4、若162=x ,则(—4+x )的立方根为 三、解答题5、求下列各式中的x 的值(1)1253)2(-x =343 (2)64631)1(3-=-x6、已知:43=a ,且03)12(2=-++-c c b ,求333c b a ++的值●体验中考1、(09宁波)实数8的立方根是2、(08泰州市)已知0≠a ,a ,b 互为相反数,则下列各组数中,不是互为相反数的一组是( )A 、3a 与3bB 、a +2与b +2C 、2a 与2b -D 、3a 与3b3、(08益阳市)一个正方体的水晶砖,体积为100 cm 3,它的棱长大约在( ) A 、4~5cm 之间 B 、5~6cm 之间 C 、6~7 cm 之间D 、7~8cm 之间实数与数轴◆随堂检测1、下列各数:23,722-,327-,414.1,3π-,12122.3,9-,••9641.3中,无理数有 个,有理数有 个,负数有 个,整数有 个. 2、33-的相反数是 ,|33-|=57-的相反数是 ,21-的绝对值=3、设3对应数轴上的点A ,5对应数轴上的点B ,则A 、B 间的距离为4、若实数a<b<0,则|a| |b|;大于17小于35的整数是 ; 比较大小:3 5 5、下列说法中,正确的是( )A .实数包括有理数,0和无理数B .无限小数是无理数C .有理数是有限小数D .数轴上的点表示实数.◆典例分析例: 设a 、b 是有理数,并且a 、b 满足等式2522-=++b b a ,求a+b 的平方根◆课下作业●拓展提高一、选择1、 如图,数轴上表示1,2的对应点分别为A 、B ,点B 关于点A 的对称点为C ,则点C 表示的实数为 ( )A .2-1B .1-2C .2-2D .2-22、设a 是实数,则|a|-a 的值( )A .可以是负数B .不可能是负数C .必是正数D .可以是整数也可以是负数二、填空3、写出一个3和4之间的无理数CAB4、下列实数1907,3π-,0,49-,21,31-,…(每两个1之间的0的个数逐次加1)中,设有m 个有理数,n 个无理数,则n m = 三、解答题5、比较下列实数的大小(1)|8-| 和3 (2)52- 和9.0- (3)215-和876、设m 是13的整数部分,n 是13的小数部分,求m-n 的值.● 体验中考2.(2011年青岛二中模拟)如图,数轴上两点表示的数分别为和, 点B 关于点A 的对称点为C ,则点C 所表示的数为( ) A . B .C .D .3.(2011年湖南长沙)已知实数a在数轴上的位置如图所示,则化简|1|a -的结果为( )A .1B .1-C .12a -D .21a -3、(2011年江苏连云港)实数a b ,在数轴上对应点的位置如图所示, 则必有( )A .0a b +>B .0a b -<C .0ab >D .0ab< 4、(2011年浙江省杭州市模2)如图,数轴上点A 所表示的数的倒数是( )A. 2-B. 2C. 12D. 12-§ 幂的运算(第46题图)a 0 (第8题图)1. 同底数幂的乘法试一试(1) 23×24=( )×( )=2();(2) 53×54=5(); (3) a 3·a 4=a ().概 括:a m ·a n =( )( )= =a n m +.可得 a m ·a n =a n m +这就是说,同底数幂相乘, .例1计算:(1) 103×104; (2) a ·a 3; (3) a ·a 3·a 5.练习1. 判断下列计算是否正确,并简要说明理由.(1) a ·a2=a 2;(2) a +a 2=a 3;(3)a 3·a 3=a 9;(4)a 3+a 3=a 6.2. 计算:(1) 102×105; (2) a 3·a 7; (3) x ·x 5·x 7.3.填空:(1)ma 叫做a 的m 次幂,其中a 叫幂的________,m 叫幂的________;(2)写出一个以幂的形式表示的数,使它的底数为c ,指数为3,这个数为________; (3)4)2(-表示________,42-表示________;(4)根据乘方的意义,3a =________,4a =________,因此43a a⋅=)()()(+同底数幂的乘法练习题1.计算: (1)=⋅64a a(2)=⋅5b b(3)=⋅⋅32m m m (4)=⋅⋅⋅953c c c c(5)=⋅⋅p n ma a a (6)=-⋅12m t t (7)=⋅+q qn 1(8)=-+⋅⋅112p p n n n2.计算:(1)=-⋅23b b (2)=-⋅3)(a a(3)=--⋅32)()(y y (4)=--⋅43)()(a a(5)=-⋅2433 (6)=--⋅67)5()5((7)=--⋅32)()(q q n(8)=--⋅24)()(m m(9)=-32 (10)=--⋅54)2()2((11)=--⋅69)(b b(12)=--⋅)()(33a a3.下面的计算对不对如果不对,应怎样改正(1)523632=⨯; (2)633a a a =+;(3)nnny y y 22=⨯; (4)22m m m =⋅;(5)422)()(a a a =-⋅-; (6)1243a a a =⋅;(7)334)4(=-; (8)6327777=⨯⨯;(9)42-=-a ; (10)32n n n =+. 4.选择题: (1)22+m a可以写成( ).A .12+m aB .22a am+ C .22a a m ⋅ D .12+⋅m a a(2)下列式子正确的是( ).A .4334⨯= B .443)3(=- C .4433=- D .3443= (3)下列计算正确的是( ).A .44a a a =⋅ B .844a a a =+C .4442a a a =+D .1644a a a=⋅2. 幂的乘方根据乘方的意义及同底数幂的乘法填空:(1)(23)2=×=2();(2)(32)3=×=3();(3)(a3)4=×××=a().概括(a m)n=(n个)=(n个)=a mn可得(a m)n=a mn(m、n为正整数).这就是说,幂的乘方,.例2计算:(1)(103)5;(2)(b3)4.练习1. 判断下列计算是否正确,并简要说明理由.(1)(a3)5=a8;(2) a5·a5=a15;(3)(a2)3·a4=a9.2. 计算:(1)(22)2;(2)(y2)5;(3)(x4)3;( 4)(y3)2·(y2)3.3、计算:(1)x·(x2)3(2)(x m)n·(x n)m (3)(y4)5-(y5)4(4)(m3)4+m10m2+m·m3·m8 (5)[(a-b)n] 2 [(b-a)n-1] 2(6)[(a-b)n] 2 [(b-a)n-1] 2 (7)(m3)4+m10m2+m·m3·m8幂的乘方一、基础练习1、幂的乘方,底数_______,指数____.(a m)n= ___(其中m、n都是正整数)2、计算:(1)(23)2=_____;(2)(-22)3=______;(3)-(-a3)2=______;(4)(-x2)3=_______。
华东师范大学版 初中数学 八年级上册 一课一练 课堂精练 同步练习册_73
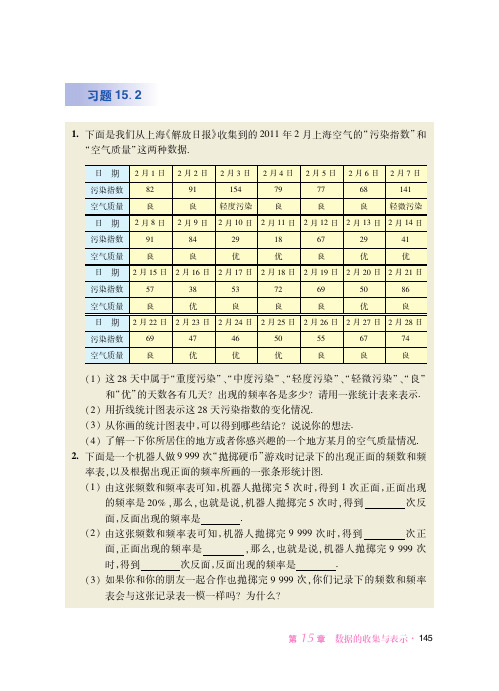
/ #90 14!1a
次 : 000
" 490 14!5a
次 4 444
# 00: #0!/a
第 " 题
$"现在有些学校试行了分班制就是将年级中学习成绩比较接近的同学分在同一
个班上课A就学校的这种做法校学生会对全校每名同学做了调查发现有 " 名
同学投赞同票)名同学投反对票还有 3名同学弃权!如果全校共有 J 名同学
习题 !! !
!"下面是我们从上海解放日报收集到的 "0// 年 " 月上海空气的污染指数和 空气质量这两种数据!
日!期 " 月 / 日 " 月 " 日 " 月 2 日 " 月 1 日 " 月 # 日 " 月 : 日 " 月 5 日
污染指数 9"
4/
/#1
54
55
:9
/1/
空气质量 良 良 轻度污染 良 良 良 轻微污染
污染指数 #5
29
#2
5"
:4
#0
9:
空气质量 良 优 良 良 良 优 良
日!期 " 月 "" 日 " 月 "2 日 " 月 "1 日 " 月 "# 日 " 月 ": 日 " 月 "5 日 " 月 "9 日
华东师范大学版 初中数学 八年级上册 一课一练 课堂精练 同步练习册_67
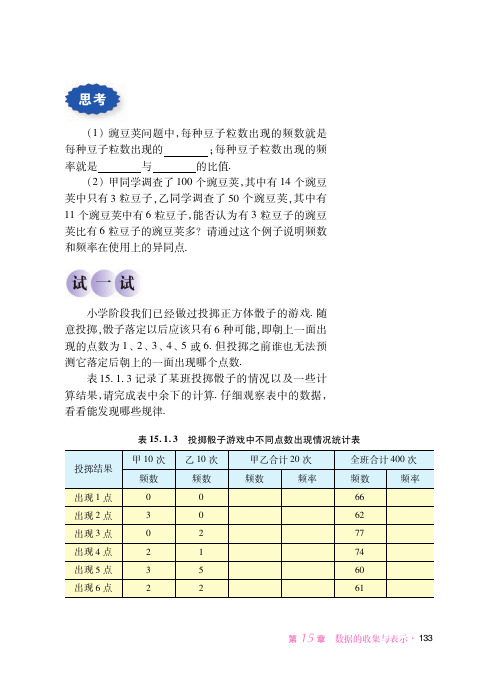
/ 豌豆荚问题中每种豆子粒数出现的频数就是 每种豆子粒数出现的!!!!每种豆子粒数出现的频 率就是!!!!与!!!!的比值!
" 甲同学调查了 /00 个豌豆荚其中有 /1 个豌豆 荚中只有 2 粒豆子乙同学调查了 #0 个豌豆荚其中有 // 个豌豆荚中有 : 粒豆子能否认为有 2 粒豆子的豌豆 荚比有: 粒豆子的豌豆荚多 请通过这个例子说明频数 和频率在使用上的异同点!
投掷结果
出现 / 点 出现 " 点 出现 2 点 出现 1 点 出现 # 点 出现 : 点
表 !&,!,$-投掷骰子游戏中不同点数出现情况统计表
甲 /0 次 乙 /0 次 甲乙合计 "0 次
全班合计 100 次
频数 频数 频数 频率 频数 频率
0
0
::
2
0
:"
ห้องสมุดไป่ตู้
0
"
55
"
/
51
2
#
:0
"
"
:/
第 章 !数据的收集与表示"*##
小学阶段我们已经做过投掷正方体骰子的游戏!随 意投掷骰子落定以后应该只有 : 种可能即朝上一面出 现的点数为 / " 2 1 # 或 :!但投掷之前谁也无法预 测它落定后朝上的一面出现哪个点数!
表 /#!/!2 记录了某班投掷骰子的情况以及一些计 算结果请完成表中余下的计算!仔细观察表中的数据 看看能发现哪些规律!
谁是《红楼梦》的作者
!!我国有一部古典文学名著 , 红楼梦- & 虽然书的 封面上通常都印有曹雪芹和高鹗两位作家的名字&但 是&它的作者究竟是谁&现在还是一个谜A一些专家正 在试图用数学方法揭开这个谜A
华东师范大学版 初中数学 八年级上册 一课一练 课堂精练 同步练习册_62
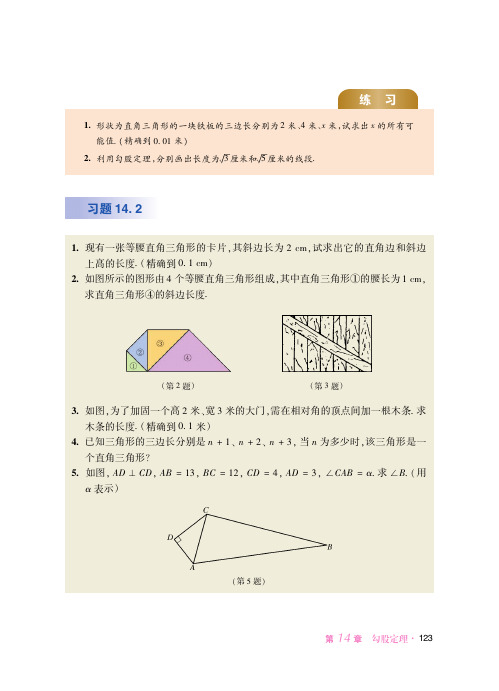
!"形状为直角三角形的一块铁板的三边长分别为" 米1 米-米试求出 -的所有可 能值!精确到 0!0/ 米
#"利用勾股定理分别画出长度为槡2 厘米和槡# 厘米的线段!
习题 !!
!"现有一张等腰直角三角形的卡片其斜边长为 " $%试求出它的直角边和斜边 上高的长度!精确到 0!/ $%
如图 求 用 &" :>, <> :;#/2 ;<#/" <> #1 :> #2 +<:;#! +;! 表示
第 # 题
第 章 !勾股定理"*!#
勾股定理的“无字证明”
!!在勾股定理的学习过程中我们已经学会了运用以下图形验证著名的勾股定理!
这种根据图形直观推论或验证数学规律和公式的方法简称为无字证明! 对于勾股定理我们还可以找到一些用于无字证明的图形如下列各图! 你会用这些图形验证勾股定理吗
第 章 "*!$ !勾股定理
#"如图所示的图形由1 个等腰直角三角形组成其中直角三角形的腰长为/ $% 求直角三角形的斜边长度!第 " 题!!!第 2 题
$"如图为了加固一个高 " 米宽 2 米的大门需在相对角的顶点间加一根木条!求 木条的长度!精确到 08/ 米
%"已知三角形的三边长分别是 1 '/ 1 '" 1 '2 当 1 为多少时该三角形是一 个直角三角形
!!!!!!!!!
!!!!!!
现在请你和大家一起查阅课本和其他有关书籍或上网查询各种相应的资 料相信你一定能够找到更多有趣的图形验证勾股定理!
实际上你还可以发现 无字证明 也可以用于验证数与代数图形与几何 等领域中的许多数学公式和规律! 无字证明 体现了数形结合的思想方法展 示了数学美!
华东师范大学版 初中数学 八年级上册 一课一练 课堂精练 同步练习册_7

记
-#/&代入(
) 得 #
-
'-
."&
( ) # /
'/
."
#2&
再将 2 代入( ) #-J- 得 K"&
继续上述过程&得
( ) # 2
'2
."
#"8222*&
( ) # "8222
'"8222
."
#"8"29*&
( ) # "8"29
'"8"29
."Leabharlann #"8"2:*&
**
数学上可以证明&计算步骤越多&得到的数值就越靠近 槡#! 如果要求精确到 0800/&那么就可得到 槡# % "8"2:!
!!一 知识结构 二 要点
/8掌握平方根算术平方根立方根的意义是学习本章的关键!在 研究时要抓住平方根立方根与平方立方之间的关系例如可以 通过平方立方运算来寻求平方根立方根并可以用来验证开平方 开立方的正确性!
"8在实数范围内任意一个正数有两个平方根它们互为相反数 0 的平方根是 0负数没有平方根!任意一个实数有且仅有一个立方根 正数的立方根为正数0 的立方根是 0负数的立方根为负数!
如果使用计算器&你不妨按照下面的按键顺序试试看!
/ 7 " # K BG& J BG& # K " 7 7 7 7 **
后面的 7 键按的次数越多&数值就越精确&到一定时候&由于计算器显示位数
华东师范大学版 初中数学 八年级上册 一课一练 课堂精练 同步练习册_65

!!!"数据有用吗
你喜欢看球赛吗 有没有注意过解说员是怎样点评 一场球赛的
解说员常常在比赛间隙对双方的表现评价一番比 如领先的队为什么能取得优势落后的队输在哪里教 练是否应该调整比赛策略等等!
通常在比赛开始之前解说员都会准备一些双方球 队的数据资料比如每位队员的身高体重年龄以及球 队以往的战绩等!另外还会准备一份用于记录本场比赛 攻守情况的统计表格!表 /#!/!/ 是 "0/0 "0// 年赛季 DCB总决赛第三场比赛后公布的比赛统计表!
/5 `":
罚篮命中率
9:a
:#a
进攻篮板
/1
"0
防守篮板
/:
/#
快攻
2 `2
1 `1
扣篮
"
2
第 章 "*#, !数据的收集与表示
从表中的数据 看 新 疆 队 最 终 为 什 么能够战胜广东队
表 !&,!,!-#+!+ #+!! 年赛季 ./0总决赛第三场比赛统计表
新疆
广东
最终得分 二分球
//9 20 `15
9# "" `25Βιβλιοθήκη 二分球命中率:1a
#4a
三分球
// `"1
9 `2"
!!三!分!球命中率
1:a
"#a
罚篮
"# `"4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结思论考与
"8大任多意与一估片计叶值子接真近实A的长宽比通常并不等于估计值但 思考/8是否可以利用叶子的长宽比对植物进行分类
"8这种方法可以用于解决其他分类问题吗
报告人Leabharlann 第 章 !数据的收集与表示"*%#
数学实验附图
方格图
22222222 33223332233223332233223332233223332233 33223332233223332233223332233223332233 33223332233223332233223332233223332233 33223332233223332233223332233223332233 33223332233223332233223332233223332233 33223332233223332233223332233223332233 33223332233223332233223332233223332233 33223332233223332233223332233223332233
22222222
222222222 332233322332233322332233223332233223332233 332233322332233322332233223332233223332233 332233322332233322332233223332233223332233 332233322332233322332233223332233223332233 332233322332233322332233223332233223332233 332233322332233322332233223332233223332233 332233322332233322332233223332233223332233 332233322332233322332233223332233223332233 332233322332233322332233223332233223332233
宽 #A# 9 5A" 9A# 5A: 4
4
5 :A2 /"A#
计算求出每片叶子的长宽比再计算平均数保留两位小数的 结果是 /A55A 作图将 /0 片叶子的长宽比绘制成如下统计图发现数据点在 /A55 附近波动A
数处据理
/0 片绿萝叶子的长宽比统计图
结论/8绿萝叶子的长宽比大约为 /A55A
研究问题 了解绿萝叶子的长宽比!
选择一株绿萝亲自测量其中 /0 片叶
子的长和宽!
数据来源
注 /8将右图中长方形的长和宽当作叶子
的长和宽
"8尽量选择大小有差异的叶子!
绿萝叶子的长和宽统计表单位12
数记据录
编号 / " 2 1 # 长 /0A# /1 /2A" /2A# /2
: 5 9 4 /0 /9 /:A# // /"A# /4A#
222222222
"*%$数学实验附图
