大学物理练习题3
大学物理综合练习(三)

《大学物理》综合练习(三)——气体动理论与热力学班级学号: 姓 名: 日 期: 一、选择题(把正确答案的序号填入括号内)1.若气体分子的速率分布曲线如图所示, 其中a 、b 两部分面积相等,则图中0v 为 (A)最概然速率p v v =0; (B)平均速率v v =0; (C)方均根速率20v v =;(D)速率大于和小于0v 的分子数各占一半。
2.一定质量的理想气体,从状态),(V p A 然速率之比Ap Bp v v /为(A)2; (B)3; (C)1; (D)π/2。
[ ]3.如图所示的两条曲线分别表示在相同温度下,氢气和氧气分子的速率分布曲线,则氧分子和氢分子最概然速率之比22/pH po v v 为 (A)2/1; (B)4/1; (C)8/1; (D)1。
[ ]4.容器中装有温度为273K 、压强为1atm 的氧气,假设容器的绝对温度加倍,因此分子被分离为原子,试问氧原子的方均根速率为氧分子的方均根速率的多少倍? (A)2; (B)1; (C)2/1; (D)2。
[ ]5.一容器内盛有一摩尔的氢气和一摩尔的氦气,其混合后的稳恒温度为127℃,则混合气体的算术平均速率为 (A))12(54+ππR; (B))12(5200+πR;f (v )p o 2 p H 22(C)πR15200; (D) π310400R。
[ ]6.气体的温度升高时,麦克斯韦速率分布函数曲线的变化是 (A)曲线下的面积增大,最概然速率增大; (B)曲线下的面积不变,最概然速率增大; (C)曲线下的面积减小,最概然速率增大; (D)曲线下的面积不变,最概然速率减小。
[ ]7.一容器装着一定量的某种气体,下述几种说法哪一种对? (A) 容器内各部分压强相等,这状态一定是平衡态; (B) 容器内各部分温度相等,这状态一定是平衡态;(C) 容器内各部分压强相等,且各部分密度也相同,这状态一定是平衡态。
[ ]8.图中表示在不同条件下理想气体的体积密度ρ随压强变化的五种曲线,试问哪个图准确地描述了等温条件下一定质量的气体的密度随压强的变化?[ ]9.理想气体作一循环过程acba ,其中ba 为等压过程,acb 为半圆弧, a c p p 2=。
北航《大学物理(上)》在线作业三

B. 250 K
C. 300 K
D. 350 K
-----------------选择:C
9. 容器内有11 kg二氧化碳和2 kg氢气(两种气体均视为刚性分子的理想气体),已知混合气体的内能是8.1×106 J.则混合气体的温度()
A. 273 K
B. 300 K
C. 373 K
D. 400 K
-----------------选择:B
10. 下列关于惯性的说法中正确的是()
A. 物体只有静止或做匀速直线运动时才有惯性
B. 物体只有受外力作用时才有惯性
C. 物体的运动速度大时惯性大
D. 物体在任何情况下都有惯性
-----------------选择:D
北航《大学物理(上)》在线作业三
单选题 判断题 多选题
一、单选题(共 15 道试题,共 60 分。)
1. 已知水星的半径是地球半径的0.4倍,质量为地球的0.04倍。设在地球上的重力加速度为g,则水星表面上的重力加速度为()
A. 0.1g
B. 0.25g
C. 4g
D. 多普勒效应已在科学研究、工程技术、交通管理、医疗诊断等各方面有着十分广泛的应用
-----------------选择:ABD
4. 关于分子动理论,下述说法正确的是 [ ]
A. 分子是组成物质的最小微粒
B. 物质是由大量分子组成的
C. 分子永不停息地做无规则运动
D. 分子间有相互作用的引力或斥力
7. 车厢内有一乘客竖直上跳,仍落回原地,列车这时作怎样的运动[ ]
A. 转弯
B. 匀速直线运动
大学物理学 习题三 三大守恒定律

习题三 三大守恒定律院 系: 班 级:_____________ 姓 名:___________ 班级个人序号:______1.质量为m 的质点,以不变速率v 沿图中正三角形ABC 的水平光滑轨道运动.质点越过A 角时,轨道作用于质点的冲量的大小为[ C ](A) mv . (B)mv . (C) mv . (D) 2mv .2.对功的概念有以下几种说法: [ C ](1) 保守力作正功时,系统内相应的势能增加. (2) 质点运动经一闭合路径,保守力对质点作的功为零.(3) 作用力和反作用力大小相等、方向相反,所以两者所作功的代数和必为零. 在上述说法中:(A) (1)、(2)是正确的. (B) (2)、(3)是正确的.(C)只有(2)是正确的.(D)只有(3)是正确的.3. A 、B 两条船质量都为M ,首尾相靠且都静止在平静的湖面上,如图所示.A 、B 两船上各有一质量均为m 的人,A 船上的人以相对于A 船的速率u 跳到B 船上,B 船上的人再以相对于B 船的相同速率u 跳到A 船上. 取如图所示x 坐标,设A 、B 船所获得的速度分别为v A 、v B ,下述结论中哪一个是正确的? [ C ] (A) v A = 0,v B = 0. (B) v A = 0,v B > 0. (C) v A < 0,v B > 0. (D) v A < 0,v B = 0. (E) v A > 0,v B > 0.4. 一人造地球卫星到地球中心O 的最大距离和最小距离分别是R A 和R B .设卫星对应的角动量分别是L A 、L B ,动能分别是E KA 、E KB ,则应有 [ E ](A) L B > L A ,E KA > E KB . (B) L B > L A ,E KA = E KB . (C) L B = L A ,E KA = E KB . (D) L B < L A ,E KA = E KB . (E) L B = L A ,E KA < E KB .5.物体在恒力F 作用下作直线运动,在时间t 1内速度由0增加到v ,在时间t 2内速度由v 增加到2 v ,设F 在t 1内作的功是W 1,冲量是I 1,在t 2内作的功是W 2,冲量是I 2.那么,[ C ](A) W 1 = W 2,I 2 > I 1. (B) W 1 = W 2,I 2 < I 1. (C) W 1 < W 2,I 2 = I 1. (D) W 1 > W 2,I 2 = I 1.6.质量分别为m A 和m B (m A >m B )、速度分别为A v 和B v(v A > v B )的两质点A 和B ,受到相 同的冲量作用,则[C ](A) A 的动量增量的绝对值比B 的小. (B) A 的动量增量的绝对值比B 的大. (C) A 、B 的动量增量相等.(D) A 、B 的速度增量相等.x237.一质点在如图所示的坐标平面内作圆周运动,有一力)(0j y i x F F+=作用在质点上.在该质点从坐标原点运动到(0,2R )位置过程中,力F对它所作的功为[ B ](A) 20R F . (B) 202R F .(C) 203R F . (D) 204R F .8.质量为20 g 的子弹沿X 轴正向以 500 m/s 的速率射入一木块后,与木块一起仍沿X 轴正向以50 m/s 的速率前进,在此过程中木块所受冲量的大小为 [ C ](A) 7 N·s . (B) 8 N·s . (C) 9 N·s . (D) 10N·s .9.如图所示,圆锥摆的摆球质量为m ,速率为v ,圆半径为R ,当摆球在轨道上运动半周时,摆球所受重力冲量的大小为 [ C ](A) 2m v . (B) 22)/()2(v v R mg m π+(C) v /Rmg π. (D) 0.10.质量为m =0.5 kg 的质点,在Oxy 坐标平面内运动,其运动方程为x =5t ,y =0.5t 2(SI ),从t =2 s 到t =4 s 这段时间内,外力对质点作的功为 [ B ](A) 1.5 J . (B) 3 J . (C) 4.5 J .(D) -1.5 J .二、填空题1. 质量为0.05 kg 的小块物体,置于一光滑水平桌面上.有一绳一端连接此物,另一端穿过桌面中心的小孔(如图所示).该物体原以3 rad/s 的角速度在距孔0.2 m 的圆周上转动.今将绳从小孔缓慢往下拉,使该物体之转动半径减为0.1 m .则物体的角速度ω=_____________________.12 rad/s2. 如图所示,轻弹簧的一端固定在倾角为α的光滑斜面的底端E ,另一端与质量为m 的物体C 相连, O 点为弹簧原长处,A 的平衡位置, x 0点沿斜面向上缓慢移动了2x 0距离而到达B ____________________. 2 mg x 0 sin α3.湖面上有一小船静止不动,船上有一打渔人质量为60 kg .如果他在船上向船头走了4.0米,但相对于湖底只移动了 3.0米,(水对船的阻力略去不计),则小船的质量为____________________. 180 kg4. 如图所示,钢球A 和B质量相等,正被绳牵着以4 rad/s 的角速度绕竖直轴转动,二球与轴的距离都为r 1=15 cm .现在把轴上环C 下移,使得两球离轴的距离缩减为r 2=5 cm .则钢球的角速度__________. 36 rad/s参考解:系统对竖直轴的角动量守恒.rad/s 36/22210==r r ωω5.二质点的质量各为m 1,m 2.当它们之间的距离由a 缩短到b 时,它们之间万有引力所做的功为____________.)11(21ba m Gm --6.某质点在力F =(4+5x )i(SI)的作用下沿x 轴作直线运动,在从x =0移动到x =10 m 的过程中,力F 所做的功为__________.290 J7.两块并排的木块A和B,质量分别为2m 和m ,静止地放置在光滑的水平面上,一子弹水平地穿过两木块,设子弹穿过两木块所用的时间均为∆t ,木块对子弹的阻力为恒力F ,则子弹穿出木块B 后,木块B 的速度大小为______________________.4 1.33F t F t3m m∆∆或8.地球的质量为m ,太阳的质量为M ,地心与日心的距离为R ,引力常量为G ,则地球绕太阳作圆周运动的轨道角动量为L =_______________.GMR m9.一块木料质量为45 kg ,以 8 km/h 的恒速向下游漂动,一只10 kg 的天鹅以 8 km/h 的速率向上游飞动,它企图降落在这块木料上面.但在立足尚未稳时,它就又以相对于木料为2 km/h 的速率离开木料,向上游飞去.忽略水的摩擦,所有速率均为水平速率,则木料的末速度为________ km/h .5.46 (5.4—5.5均可) 三、计算题1. 一小球在弹簧的作用下振动(如图所示),弹力F = - kx ,而位移x = A cos ωt ,其中k 、A 、ω 都是常量。
大学物理练习题3((角)动量与能量守恒定律)

大学物理练习题3:“力学—(角)动量与能量守恒定律”一、填空题1、一个质量为10kg 的物体以4m/s 的速度落到砂地后经0.1s 停下来,则在这一过程中物体对砂地的平均作用力大小为 。
2、t F x 430+=(式中x F 的单位为N ,t 的单位为s )的合外力作用在质量为kg m 10=的物体上,则:(1)在开始s 2内,力x F 的冲量大小为: ;(2)若物体的初速度1110-⋅=s m v ,方向与x F 相同,则当力x F 的冲量s N I ⋅=300时,物体的速度大小为: 。
3、一质量为kg 1、长为m 0.1的均匀细棒,支点在棒的上端点,开始时棒自由悬挂。
现以100N 的力打击它的下端点,打击时间为0.02s 时。
若打击前棒是静止的,则打击时棒的角动量大小变化为 ,打击后瞬间棒的角速度为 。
4、某质点最初静止,受到外力作用后开始运动,该力的冲量是100.4-⋅⋅s m kg ,同时间内该力作功4.00J ,则该质点的质量是 ,力撤走后其速率为 。
5、设一质量为kg 1的小球,沿x 轴正向运动,其运动方程为122-=t x ,则在时间s t 11=到s t 32=内,合外力对小球的功为 ;合外力对小球作用的冲量大小为 。
6、一个力F 作用在质量为 1.0 kg 的质点上,使之沿x 轴运动。
已知在此力作用下质点的运动学方程为3243t t t x +-= (SI)。
则在0到4 s 的时间间隔内,力F 的冲量大小I = ,力F 对质点所作的功W = 。
7、设作用在质量为 2 kg 上的物体上的力x F x 6=(式中x F 的单位为N ,x 的单位为m )。
若物体由静止出发沿直线运动,则物体从0=x 运动到m x 2=过程中该力作的功=W ,m x 2=时物体的速率=v 。
8、已知质量kg 2=m 物体在一光滑路面上作直线运动,且0=t 时,0=x ,0=ν。
若该物体受力为x F 43+=(式中F 的单位为N ,x 的单位为m ),则该物体速率ν随 x 的函数关系=)(x ν ;物体从0=x 运动到2=x m 过程中该力作的功=W 。
大学物理测试题及答案3
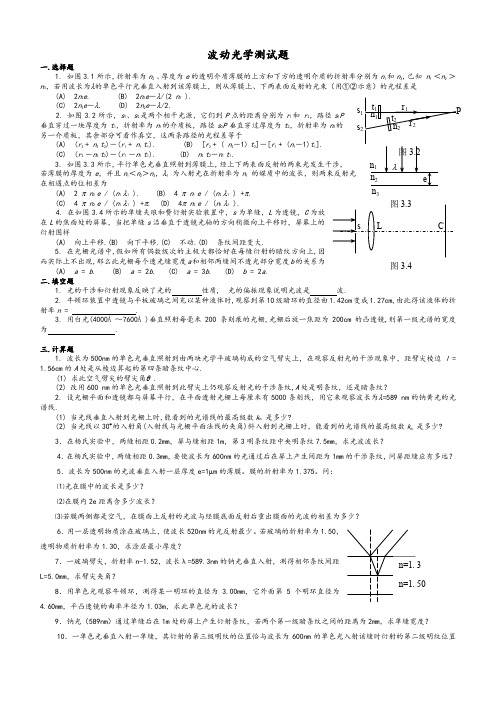
波动光学测试题一.选择题1. 如图3.1所示,折射率为n 2 、厚度为e 的透明介质薄膜的上方和下方的透明介质的折射率分别为n 1和n 3,已知 n 1 <n 2 >n 3,若用波长为λ的单色平行光垂直入射到该薄膜上,则从薄膜上、下两表面反射的光束(用①②示意)的光程差是(A) 2n 2e . (B) 2n 2e -λ/(2 n 2 ).(C) 2n 2e -λ. (D) 2n 2e -λ/2. 2. 如图3.2所示,s 1、s 2是两个相干光源,它们到P 点的距离分别为r 1和 r 2,路径s 1P 垂直穿过一块厚度为t 1,折射率为n 1的介质板,路径s 2P 垂直穿过厚度为t 2,折射率为n 2的另一介质板,其余部分可看作真空,这两条路径的光程差等于 (A) (r 2 + n 2 t 2)-(r 1 + n 1 t 1). (B) [r 2 + ( n 2-1) t 2]-[r 1 + (n 1-1)t 1]. (C) (r 2 -n 2 t 2)-(r 1 -n 1 t 1). (D) n 2 t 2-n 1 t 1.3. 如图3.3所示,平行单色光垂直照射到薄膜上,经上下两表面反射的两束光发生干涉,若薄膜的厚度为e ,并且n 1<n 2>n 3,λ1 为入射光在折射率为n 1 的媒质中的波长,则两束反射光在相遇点的位相差为 (A) 2 π n 2 e / (n 1 λ1 ). (B) 4 π n 1 e / (n 2 λ1 ) +π.(C) 4 π n 2 e / (n 1 λ1 ) +π. (D) 4π n 2 e / (n 1 λ1 ). 4. 在如图3.4所示的单缝夫琅和费衍射实验装置中,s 为单缝,L 为透镜,C 为放在L 的焦面处的屏幕,当把单缝s 沿垂直于透镜光轴的方向稍微向上平移时,屏幕上的衍射图样(A) 向上平移.(B) 向下平移.(C) 不动.(D) 条纹间距变大.5. 在光栅光谱中,假如所有偶数级次的主极大都恰好在每缝衍射的暗纹方向上,因而实际上不出现,那么此光栅每个透光缝宽度a 和相邻两缝间不透光部分宽度b 的关系为 (A) a = b . (B) a = 2b . (C) a = 3b . (D) b = 2a .二.填空题1. 光的干涉和衍射现象反映了光的 性质, 光的偏振现象说明光波是 波.2. 牛顿环装置中透镜与平板玻璃之间充以某种液体时,观察到第10级暗环的直径由1.42cm 变成1.27cm,由此得该液体的折射率n = .3. 用白光(4000Å~7600Å)垂直照射每毫米200条刻痕的光栅,光栅后放一焦距为200cm 的凸透镜,则第一级光谱的宽度为 .三.计算题1. 波长为500nm 的单色光垂直照射到由两块光学平玻璃构成的空气劈尖上,在观察反射光的干涉现象中,距劈尖棱边 l =1.56cm 的A 处是从棱边算起的第四条暗条纹中心.(1) 求此空气劈尖的劈尖角θ .(2) 改用600 nm 的单色光垂直照射到此劈尖上仍观察反射光的干涉条纹,A 处是明条纹,还是暗条纹?2. 设光栅平面和透镜都与屏幕平行,在平面透射光栅上每厘米有5000条刻线,用它来观察波长为λ=589 nm 的钠黄光的光谱线.(1) 当光线垂直入射到光栅上时,能看到的光谱线的最高级数k m 是多少?(2) 当光线以30︒的入射角(入射线与光栅平面法线的夹角)斜入射到光栅上时,能看到的光谱线的最高级数k m 是多少?3.在杨氏实验中,两缝相距0.2mm ,屏与缝相距1m ,第3明条纹距中央明条纹7.5mm ,求光波波长?4.在杨氏实验中,两缝相距0.3mm ,要使波长为600nm 的光通过后在屏上产生间距为1mm 的干涉条纹,问屏距缝应有多远?5.波长为500nm 的光波垂直入射一层厚度e=1μm 的薄膜。
大学物理练习题3动量与能量守恒定律

大学物理练习题3:“力学—(角)动量与能量守恒定律”一、填空题1、一个质量为10kg 的物体以4m/s 的速度落到砂地后经停下来,则在这一过程中物体对砂地的平均作用力大小为 。
2、t F x 430+=(式中x F 的单位为N ,t 的单位为s )的合外力作用在质量为kg m 10=的物体上,则:(1)在开始s 2内,力x F 的冲量大小为: ;(2)若物体的初速度1110-⋅=s m v ,方向与x F 相同,则当力x F 的冲量s N I ⋅=300时,物体的速度大小为: 。
3、一质量为kg 1、长为m 0.1的均匀细棒,支点在棒的上端点,开始时棒自由悬挂。
现以100N 的力打击它的下端点,打击时间为时。
若打击前棒是静止的,则打击时棒的角动量大小变化为 ,打击后瞬间棒的角速度为 。
4、某质点最初静止,受到外力作用后开始运动,该力的冲量是100.4-⋅⋅s m kg ,同时间内该力作功,则该质点的质量是 ,力撤走后其速率为 。
5、设一质量为kg 1的小球,沿x 轴正向运动,其运动方程为122-=t x ,则在时间s t 11=到s t 32=内,合外力对小球的功为 ;合外力对小球作用的冲量大小为 。
6、一个力F ϖ作用在质量为 1.0 kg 的质点上,使之沿x 轴运动。
已知在此力作用下质点的运动学方程为3243t t t x +-= (SI)。
则在0到4 s 的时间间隔内,力F ϖ的冲量大小I = ,力F ϖ对质点所作的功W = 。
7、设作用在质量为 2 kg 上的物体上的力x F x 6=(式中x F 的单位为N ,x 的单位为m )。
若物体由静止出发沿直线运动,则物体从0=x 运动到m x 2=过程中该力作的功=W ,m x 2=时物体的速率=v 。
8、已知质量kg 2=m 物体在一光滑路面上作直线运动,且0=t 时,0=x ,0=ν。
若该物体受力为x F 43+=(式中F 的单位为N ,x 的单位为m ),则该物体速率ν随 x 的函数关系=)(x ν ;物体从0=x 运动到2=x m 过程中该力作的功=W 。
3大学物理习题_静电场

。
12.两个同心球面的半径分别为 R1 和 R2 ,各自带有电荷 Q1 和 Q2 ,则两球面的电势差
为
。
13.如图,在带电量为+2q 的点电荷电场中,取图中 P 点处为电势零点,则 M 点的电势为_
__________。
14.如图所示电量为 q 的试验电荷, 在电量为 Q
R
·Q d
·a q
3 大学物理习题_静电场
(A)大小不变,方向改变;
(B)大小改变,方向不变;
(C)大小和方向都不变;
(D)大小和方向都改变。
3.下列几种说法中哪一个是正确的?
(A)电场中某点场强的方向,就是将点电荷放在该点所受电场力的方向;
(B)在以点电荷为中心的球面上,由该点电荷所产生的场强处处相同;
(C)场强方向可由
E
F
定义给出,其中
量等于:
q
(A) ;
6 0
(B) q ; 12 0
a
d
A·q
q
(C) ;
24 0
q
(D) 。
48 0
b
c
图
7.下列说法正确的是
(A)闭合曲面上各点的电场强度都为零,曲面内一定没有电荷;
(B)闭合曲面上各点的电场强度都为零,曲面内电荷代数和必定为零;
(C)闭合曲面的电通量为零时,曲面上各点的电场强度必定为零;
意路径移动到b 点,外力所作的功__________;电场力所作的功____________。
16.平行板电容器的电容随两极板距离的增大而___________(填增大或减小)。
17.平行板电容器两极板间的距离为 d ,两极板的面积均为 S ,极板间为真空,则该平行板
大学物理期末试题练习题3

一、填空题1、狭义相对论的两条基本原理是____________原理和相对性原理.2、在洛伦兹变换和伽利略变换中,哪一种变换导致了时间延缓现象:______________.3、某观察者看到一把米尺沿其长度方向作匀速直线运动,此时米尺的动能是它静止能量的四分之一,则米尺相对观察者的速率为_________,观察者测得米尺的长度为_______m .4、光速不变原理指的是光在所有介质中的传播速度相等,这种说法是否正确?答 ,并说明理由: .5、、已知某μ子静止时的寿命为2.20×10—8s ,若相对于μ子作匀速直线运动的观察者测得其寿命为2.75×10-8s,则观察者相对于μ子的运动速度大小为 .6、、根据狭义相对论质能关系,一对正负电子相撞湮灭后释放出的总能量为 .已知正电子和负电子的质量均为9.1×10—31kg .7、一列平面简谐波的波函数为)3ππ22πcos(2.0+-=x t y ,式中各物理量的单位均为国际单位制.那么这列波的波速为u =________m/s . 8、、平面简谐波的表达式0.05cos(2π4ππ)(SI)y t x =-+,则x =0。
25m 处的P 点相位比x =0处的O 点相位落后 .9、两相干波源S 1和S 2同相位且振幅均为A ,则S 1和S 2连线中点处的振幅为________.10、酒吧门口的大喇叭发出频率为750 Hz 的噪声,一辆警车以50m/s 驶向酒吧.空气中声速为340 m/s ,则车上的警长听到该声音的频率是__________Hz (至少保留三位有效数字),比喇叭固有频率的音调更________(填“高”或“低”). 11、某个简谐振动的振幅为A ,振动总能量为E 。
若将其振幅变为错误!A ,则振动总能量会变为________. 12、若一列入射波的波函数为)ππ2cos(5.0x t y +=,在原点处发生了反射,反射点为一固定端.那么反射波的波函数为y =_______________________.13、渡轮以20m/s 的速度驶离岸边,渡轮上有人用小提琴演奏频率为1300 Hz 的音符,站在岸上的观察者听到的频率是_________Hz (保留四位有效数字,空气中声速为340 m/s ).14、质点做简谐振动,振动方程)SI )(2π3πcos(06.0-=t x .质点在t =2s 时的相位为 。
大学物理习题课3-7(1)

道上滑行。若物体 A 以恒定的速率 v 向
左滑行,当α= 60° 时,物体B的速度为
多少?
y
•B
l
0
•A v x
额外习题
解:建立坐标系如图,则物体A的速度为:
vAvx
dxi dt
vi
物体B的速度为:
dy vB vy dt j
y •B
l
0
•A v x
额外习题
x2 y2 l2
2xdx2ydy0 dt dt
该题要先对m1,m2进行受力分析,同 时要确定物体的运动方向和加速度的
方向,有题意可见,m1,m2都向下加
T
速运动,与m1相连的绳向下运动,与
m2相连的绳子向上运动,确定正方向。
a1牵连
f T
a2相对
m1 g
m2 g
• 5.因绳子质量不计,所
以环受到的摩擦力在数
值上等于张力T,设环对 T
地加速度为 a 2 ,取向下 为正;物体对地加速度
(D)
(C) aA<0, aB>0; (D) aA<0, aB=0;
对滑块A、B进行受力分析
A:F拉F弹-f摩 0 B:F弹 f摩
2.体重、身高相同的甲乙两人,分别用双手握住跨过无摩擦轻
滑轮的绳子各一端,他们由初速为零向上爬,经过一定时间,
甲相对绳子速率是乙相对绳子速率的两倍,则到达顶点的情况
是: (A)甲先到达 ;
y
dy x dx tg(v)
dt y dt vtg600 3v
dy vB dt j 3vj
•B
l
0
•A v x
额外习题
例 速5度已为知v0抛(如体图运)动,求
大学物理(上)习题3

习题3一、单项选择题1.下列说法哪一项正确?( )。
A 、加速度恒定不变时,物体运动方向也不变B 、平均速率等于平均速度的大小C 、不管加速度如何,平均速率表达式总可以写成 ()221/υυυ+=D 、运动物体速率不变时,速度可以变化2. 质量为0.10kg 的质点,由静止开始沿曲线3=5/3+2 SI r t i j ()()运动,则在t =0到t =2s 时间内,作用在该质点上的合外力所做的功为( )。
A 、5/4JB 、20JC 、40JD 、75/4J3.力矩的功就是力所做的功的一部分。
以上说法( )。
A 、正确 B 、错误C 、不确定D 、无意义二、判断题1.一定量给定理想气体内能只是温度的函数,与热力学温度成反比。
()2.内力的冲量=0,内力不能改变质点系的动量。
()3.第一类永动机是存在的。
()4.惯性是物体保持自己原有运动状态不变的性质。
()5. 标量是既有大小也有方向的物理量。
()6.圆周运动是位矢的大小始终不变的一般曲线运动。
()7.绝热膨胀过程,温度降低;绝热压缩过程,温度升高。
()三、填空题1. 质点系的动量定理是_________。
2. 机械振动指物体在其平衡位置附近, _________随时间t 的周期性变化。
3. 振动状态在空间的传播过程叫做_________。
4. 理想气体的比热容比只与分子的_________有关,与气体的温度无关。
5. 确定一个物体的空间位置所需要的独立坐标数目叫_________。
6. 一瓶氦气和一瓶氮气密度相同,分子平均平动动能同,且均处于平衡态,则它们的压强关系_________。
四、简答题1. 保守力的特点是什么?2. 什么是质点的角动量守恒定律?3. 牛顿第一定律正确说明平衡状态是什么?4. 什么是平行轴定理?5. 什么是简谐波?6. 什么是准静态过程?习题3答案一、单项选择题二、判断题(注:T表示正确,F表示错误)三、填空题四、简答题1、(1)保守力沿闭合路径一周所做的功为零,(2)保守力作功与过程无关,与参考系的选取无关。
大学物理练习题3

大学物理练习题3练习题第一章质点运动学一、选择题[] 1. 以下陈述是正确的:(a)质点沿x轴运动,若加速度a<0,则质点必做减速运动;(b)在曲线运动中,质点的加速度必定不为零;(c)当粒子在抛射体中移动时,其at和an不断变化,所以a也在变化;(d)如果一个粒子的加速度是一个恒定的矢量,那么它的轨迹必须是一条直线。
[] 2. 对于沿曲线移动的物体,以下陈述是正确的:(a)切向加速度不得为零;(b)法向加速度必不为零(拐点处除外);(c)由于速度沿切线方向,法向部分速度必须为零,因此法向加速度必须为零;(d)若物体做匀速率运动,其总加速度必为零;(e)如果物体的加速度a是一个恒定的矢量,它必须以匀速运动;[] 3. 以下哪项陈述是正确的:(a)质点做匀速率圆周运动时,其加速度是恒定的;(b)匀速圆周运动的切向加速度必须等于零;(c)质点做变速率圆周运动时,其加速度方向与速度方向处处垂直;(d)质点做变速圆周运动时,其切向加速度方向总与速度方向相同。
[] 4. 粒子在曲线中移动。
在时间t,粒子的势能向量是r,t到(t+δt),时间上的位移是?r、距离是δs。
矢量大小的变化是δr(或δ|r)。
那么必须有:(a)?r??s??r(b) ??Rsr、当δDr当t→ 0? ds?博士(c)?rsr,当δt→0时有dr?dr?ds(d) ??Rsr、当δDr当t→ 0? ds?博士[]5.一质点做曲线运动,则下列各式正确的是:drdsdtdt??[] 6. 粒子在曲线中移动。
在时间t,粒子的速度是V,速度是V,平均速度是V,平均速度是(a)?r??s;(b)?r??r;(c)dr?ds;(d)v、必须有:v?v(b)(a)v?v,??v?v(d)(c)v?v,??v?v,v?v??v?v,v?v[] 7. 粒子沿轨道呈曲线运动,速度逐渐降低。
下图中的哪个数字正确地表示粒子的添加速度?一[]8.一运动质点在某瞬时位于失经r(x,y)的端点处,其速度大小为(a) drdt(b)?drdt(c)drdt(d)?drdt[]9.质点沿半径为r的圆周做变速运动,在任一时刻质点加速度的大小为(其中v 表示任意时刻的速率):dv?2.v2?2.dvvdvv(a)(b);(c)(d)dtrdtrdtr[]10.质点做曲线运动,r表示位置矢量,v表示速度,v表示速率,a表示加速度,s221/2表示距离,at表示切向加速度。
大学物理作业(三)答案

班级___ ___学号____ ____姓名____ _____成绩______________ 一、填空题1. 一旋转齿轮的角加速度β=4at 3-3bt 2 ,式中a 、b 均为恒量,若齿轮具有初角速度为ω0,则任意时刻t的角速度 ,转过的角度为 .2. 质量为m ,半径为R 的均质圆盘,平放在水平桌面上,它与桌面的滑动摩擦系数为μ,试问圆盘绕中心轴转动所受摩擦力矩为 。
3. 一长为L 质量为m 的均质细杆,两端附着质量分别为m 1和m 2的小球,且m 1>m 2 ,两小球直径d 1 、d 2都远小于L ,此杆可绕通过中心并垂直于细杆的轴在竖直平面内转动,则它对该轴的转动惯量为 , 若将它由水平位置自静止释放,则它在开始时刻的角加速度为多大: 。
4. 质量为m ,半径为r 的均质圆盘,绕通过其中心且与盘垂直的固定轴以角速度ω匀速转动,则对其转轴来说,它的动量为____________,角动量为__________.三、计算题:1. 固定在一起的两个同轴均匀圆柱体可绕其光滑的水平对称轴OO ’转动,设大小圆柱的半径分别为R 和r ,质量分别为M 和m ,绕在两柱体上的细绳分别与物体m 1和物体m 2 相连,m 1和m 2则挂在圆柱体的两侧,如图所示,设R =0.20m ,r =0.10m ,m =4kg ,M =10kg ,m 1=m 2=2kg ,求柱体转动时的角加速度及两侧绳中的张力. 解:设1a ,2a 和β分别为1m ,2m 和柱体的加速度及角加速度,方向如图(如图b).题2-26(a)图 题2-26(b)图(1) 1m ,2m 和柱体的运动方程如下:2222a m g m T =- ①1111a m T g m =- ②12T R T r I α''-= ③rRO ’Om 2m 1式中 112221,,,T T T T a r a R αα''==== 而 222121mr MR I += 由上式求得122212222220.220.129.811100.2040.1020.2020.10226.13rad s Rm rm gI m R m r β--=++⨯-⨯=⨯⨯⨯+⨯⨯+⨯+⨯=⋅(2)由①式 22220.10 6.1329.820.8T m r m g α=+=⨯⨯+⨯=N 由②式11129.820.2. 6.1317.1T m g m R α=-=⨯-⨯⨯=N2. 计算题3-13图所示系统中物体的加速度.设滑轮为质量均匀分布的圆柱体,其质量为M ,半径为r ,在绳与轮缘的摩擦力作用下旋转,忽略桌面与物体间的摩擦,设1m =50kg ,2m =200 kg,M =15 kg, r =0.1 m解: 分别以1m ,2m 滑轮为研究对象,受力图如图(b)所示.对1m ,2m 运用牛顿定律,有a m T g m 222=- ① a m T 11= ②对滑轮运用转动定律,有α)21(212Mr r T r T =- ③又, αr a = ④联立以上4个方程,得 2212s m 6.721520058.92002-⋅=++⨯=++=M m m g m a题3-13(a)图 题3-13(b)图3. 如图质量为M ,长为L 的均匀直杆可绕O 轴在竖直平面内无摩擦地转动,开始时杆处于自由下垂位置,一质量为m 的弹性小球水平飞来与杆下端发生完全弹性碰撞,若M >3m ,且碰撞后,杆上摆的最大角度为θ=30,则求:(A)小球的初速度v 0,(B)碰撞过程中杆给小球的冲量. (教材)解: (1)设小球的初速度为0v ,棒经小球碰撞后得到的初角速度为ω,而小球的速度变为v ,按题意,小球和棒作弹性碰撞,所以碰撞时遵从角动量守恒定律和机械能守恒定律,可列式:mvl I l mv +=ω0 ①2220212121mv I mv +=ω ② 上两式中231Ml I =,碰撞过程极为短暂,可认为棒没有显著的角位移;碰撞后,棒从竖直位置上摆到最大角度o30=θ,按机械能守恒定律可列式:)30cos 1(2212︒-=lMg I ω ③ 由③式得 2121)231(3)30cos 1(⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡︒-=l g I Mgl ω 由①式 mlI v v ω-=0 ④ 由②式 mI v v 2202ω-= ⑤所以 22001)(2ωωmv ml I v -=-求得glmM m m Ml ml I l v +-=+=+=31232(6)311(2)1(220ωω(2)相碰时小球受到的冲量为 ⎰-=∆=0d mv mv mv t F由①式求得 ωωMl l I mv mv t F 31d 0-=-=-=⎰gl M 6)32(6--=负号说明所受冲量的方向与初速度方向相反.m v MOL。
《大学物理》作业3

《大学物理》作业 No. 3环路定理 电势班级 ____________ 学号 ___________ 姓名 ____________ 成绩 ________说明:字母为黑体者表示矢量一、选择题1.关于静电场中某点电势值的正负,下列说法中正确的是: [ ] (A) 电势值的正负取决于置于该点的试验电荷的正负;(B) 电势值的正负取决于电场力对试验电荷作功的正负;(C) 电势值的正负取决于电势零点的选取;(D) 电势值的正负取决于产生电场的电荷的正负。
2. 真空中一半径为R 的球面均匀带电Q ,在球心O 处有一带电量为q 的点电荷,如图所示。
设无穷远处为电势零点,则在球内离球心O 距离为r 的P 点处电势为: [ ] (A)rq 04πε (B))(410RQ r q +πε (C)r Q q 04πε+ (D))(410RqQ r q -+πε 3. 在带电量为-Q 的点电荷A 的静电场中,将另一带电量为q 的点电荷B 从a 点移到b 点,a 、b 两点距离点电荷A 的距离分别为r 1和r 2,如图所示。
则在电荷移动过程中电场力做的功为 [ ] (A))11(4210r r Q --πε; (B) )11(4210r r qQ -πε; (C))11(4210r r qQ --πε; (D) )(4120r r qQ--πε。
4.以下说法中正确的是[ ] (A) 沿着电力线移动负电荷,负电荷的电势能是增加的;(B) 场强弱的地方电位一定低,电位高的地方场强一定强; (C) 等势面上各点的场强大小一定相等;(D) 初速度为零的点电荷, 仅在电场力作用下,总是从高电位处向低电位运动; (E) 场强处处相同的电场中,各点的电位也处处相同.二、填空题 1.电量分别为q 1, q 2, q 3的三个点电荷位于一圆的直径上, 两个在圆周上,一个在圆心.如图所示. 设无穷远处为电势零点,圆半径为R ,则b 点处的电势U = .-• • • q 1 q 2q 3 RO b2.如图所示,在场强为E 的均匀电场中,A 、B 两点间距离为d ,AB 连线方向与E 的夹角为α. 从A 点经任意路径到B 点的场强线积分l E d ⎰⋅AB= .3.如图所示, BCD 是以O 点为圆心,以R 为半径的半圆弧,在A 点有一电量为-q 的点电荷,O 点有一电量为+q 的点电荷. 线段BA = R .现将一单位正电荷从B 点沿半圆弧轨道 BCD 移到D 点,则电场力所作的功为 .三、计算题1.电量q 均匀分布在长为l 2的细杆上,求: (1)在杆延长线上与杆较近端距为a 处的电势; (2)在杆中垂线上与杆距为a 处的电势。
大学物理练习题第三章 动量守恒定律和能量守恒定律

大学物理练习题第三章动量守恒定律和能量守恒定律一、选择题1. 质量m=2kg的质点在力F⃗=12ti⃗ (SI)的作用下,从静止出发沿X轴正方向作直线运动,求它在3秒末的动量( )A. −54i⃗ kg∙m/sB. 54i⃗ kg∙m/sC.−27i⃗ kg∙m/sD. 27i⃗ kg∙m/s2. 一个质点同时在几个力作用下的位移为:∆r⃗=4i⃗−5j⃗+6k⃗⃗ (SI)其中一个力为恒力F⃗=−3i⃗−5j⃗+9k⃗⃗,则此力在该位移过程中所作的功为( )A. 67JB. 91JC. 17JD. -67J3. 对质点组有以下几种说法①质点组总动量的改变与内力无关②质点组总动能的改变与内力无关③质点组机械能的改变与保守内力无关在上述说法中( )A. 只有①是正确的B. ①、③是正确的C. ①、②是正确的D. ②、是正确的4. 质点系的内力可以改变( )A. 系统的总质量B. 系统的总动量C. 系统的总动能D. 系统的总角动量5. 质量为m的质点在外力作用下,其运动方程为r⃗=Acosωti⃗+bsinωtj⃗其中A,B,ω都是正的常数,则在t1=0到t2=π(2ω)⁄这段时间内所作的功( )A.mω2(A2+B2)2⁄B. mω2(A2+B2)C. mω2(A2−B2)2⁄D.mω2(B2−A2)2⁄6. 如图,一劲度系数为k的轻弹簧水平放置,左端固定,右端与桌面上一质量为m的木块相连,用一水平力F向右拉木块而使其处于静止状态。
若木块与桌面间的静摩擦系数为μ,弹簧的弹性势能为E,则下列关系中正确的是( )A. E=(F−μmg)22kB.E=(F+μmg)22kC. E=F22kD. (F−μmg)22k ≤E≤(F+μmg)22k二、填空题1. 设作用在质量为M=1kg的物体上的力F=6t+3 (SI)。
如果物体在这个力的作用下,由静止开始沿直线运动,在0到2.0s的时间间隔内,这个力作用在物体上的冲量大小I= 。
大学物理习题及答案3

一 选择题 (共69分)1. (本题 3分)(4468) 一定量某理想气体按pV 2=恒量的规律膨胀,则膨胀后理想气体的温度 (A) 将升高. (B) 将降低.(C) 不变. (D)升高还是降低,不能确定. [ ]2. (本题 3分)(4552) 若室内生起炉子后温度从15℃升高到27℃,而室内气压不变,则此时室内的分子数减少了(A)0.500. (B) 400.(C) 900. (D) 2100. [ ]3. (本题 3分)(4304) 两个相同的容器,一个盛氢气,一个盛氦气(均视为刚性分子理想气体),开始时它们的压强和温度都相等,现将6 J 热量传给氦气,使之升高到一定温度.若使氢气也升高同样温度,则应向氢气传递热量 (A) 12 J . (B) 10 J .(C) 6 J . (D) 5 J . [ ]4. (本题 3分)(4014) 温度、压强相同的氦气和氧气,它们分子的平均动能ε和平均平动动能w 有如下关系:(A) ε和w 都相等. (B) ε相等,而w 不相等. (C) w 相等,而ε不相等.(D) ε和w 都不相等. [ ]5. (本题 3分)(4651) 下列各式中哪一式表示气体分子的平均平动动能?(式中M 为气体的质量,m 为气体分子质量,N 为气体分子总数目,n 为气体分子数密度,N A 为阿伏加得罗常量)(A) pV M m23. (B)pV M M mol 23. (C) npV 23. (D) pV N MM A 23mol . [ ]6. (本题 3分)(5335) 若在某个过程中,一定量的理想气体的内能E随压强p 的变化关系为一直线(其延长线过E -p 图的原点),则该过程为(A) 等温过程. (B) 等压过程.(C) 等体过程. (D) 绝热过程. []p7. (本题 3分)(4665) 假定氧气的热力学渭度提高一倍,氧分子全部离解为氧原子,则这些氧原子的平均速率是原来氧分子平均速率的 (A) 4倍. (B) 2倍.(C) 2倍. (D) 21倍. [ ]下列各图所示的速率分布曲线,哪一图中的两条曲线能是同一温度下氮气和氦气的分子速率分布曲线?[]vv(B(A(D(C9. (本题 3分)(5603)已知分子总数为N,它们的速率分布函数为f(v),则速率分布在v1~v2区间内的分子的平均速率为(A) ∫21d)(vvvvv f.(B) ∫21d)(vvvvv f/∫21d)(vvvvf.(C) ∫21d)(vvvvv fN.(D) ∫21d)(vvvvv f/N.[]10. (本题 3分)(4133)关于可逆过程和不可逆过程的判断:(1) 可逆热力学过程一定是准静态过程.(2) 准静态过程一定是可逆过程.(3) 不可逆过程就是不能向相反方向进行的过程.(4) 凡有摩擦的过程,一定是不可逆过程.以上四种判断,其中正确的是(A) (1)、(2)、(3).(B) (1)、(2)、(4).(C)(2)、(4).(D)(1)、(4).[]11. (本题 3分)(4674)置于容器内的气体,如果气体内各处压强相等,或气体内各处温度相同,则这两种情况下气体的状态(A) 一定都是平衡态.(B) 不一定都是平衡态.(C) 前者一定是平衡态,后者一定不是平衡态.(D) 后者一定是平衡态,前者一定不是平衡态.[]理想气体向真空作绝热膨胀.(A) 膨胀后,温度不变,压强减小. (B) 膨胀后,温度降低,压强减小. (C) 膨胀后,温度升高,压强减小.(D) 膨胀后,温度不变,压强不变. [ ]13. (本题 3分)(4579) 对于理想气体系统来说,在下列过程中,哪个过程系统所吸收的热量、内能的增量和对外作的功三者均为负值?(A) 等体降压过程. (B) 等温膨胀过程.(C) 绝热膨胀过程. (D) 等压压缩过程. [ ]14. (本题 3分)(4679) 一物质系统从外界吸收一定的热量,则 (A) 系统的温度一定升高. (B) 系统的温度一定降低.(C) 系统的温度一定保持不变. (D) 系统的温度可能升高,也可能降低或保持不变.[ ]15. (本题 3分)(4310) 一定量的理想气体,其状态改变在p -T 图上沿着一条直线从平衡态a 到平衡态b (如图).(A) 这是一个膨胀过程.(B) 这是一个等体过程.(C) 这是一个压缩过程.(D) 数据不足,不能判断这是那种过程. []1216. (本题 3分)(4122) 如果卡诺热机的循环曲线所包围的面积从图中的abcda 增大为da c b a ′′,那么循环abcda 与da c b a ′′所作的净功和热机效率变化情况是:(A) 净功增大,效率提高.(B) 净功增大,效率降低.(C) 净功和效率都不变.(D) 净功增大,效率不变. [ ]c ′d T 2ab b ′c T 1Op两个卡诺热机的循环曲线如图所示,一个工作在温度为T 1 与T 3的两个热源之间,另一个工作在温度为T 2 与T 3的两个热源之间,已知这两个循环曲线所包围的面积相等.由此可知:(A ) 两个热机的效率一定相等.(B ) 两个热机从高温热源所吸收的热量一定相等.(C ) 两个热机向低温热源所放出的热量一定相等.(D ) 两个热机吸收的热量与放出的热量(绝对值)的差值一定相等. [ ]T 1 T 2T 3 T 3V p O18. (本题 3分)(5342) 一定量的理想气体,起始温度为T ,体积为V 0.后经历绝热过程,体积变为2 V 0.再经过等压过程,温度回升到起始温度.最后再经过等温过程,回到起始状态.则在此循环过程中(A) 气体从外界净吸的热量为负值. (B) 气体对外界净作的功为正值. (C) 气体从外界净吸的热量为正值.(D) 气体内能减少. [ ]19. (本题 3分)(4125) 有人设计一台卡诺热机(可逆的).每循环一次可从 400 K 的高温热源吸热1800 J ,向 300 K 的低温热源放热 800 J .同时对外作功1000 J ,这样的设计是 (A) 可以的,符合热力学第一定律. (B) 可以的,符合热力学第二定律. (C) 不行的,卡诺循环所作的功不能大于向低温热源放出的热量.(D) 不行的,这个热机的效率超过理论值. [ ]20. (本题 3分)(5074) 理想气体卡诺循环过程的两条绝热线下的面积大小(图中阴影部分)分别为S 1和S 2,则二者的大小关系是: (A) S 1 > S 2. (B) S 1 = S 2.(C) S 1 < S 2. (D) 无法确定. [ ]21. (本题 3分)(4135) 根据热力学第二定律可知:(A) 功可以全部转换为热,但热不能全部转换为功.(B) 热可以从高温物体传到低温物体,但不能从低温物体传到高温物体 (C) 不可逆过程就是不能向相反方向进行的过程.(D) 一切自发过程都是不可逆的. [ ]设有以下一些过程:(1) 两种不同气体在等温下互相混合.(2) 理想气体在定体下降温.(3) 液体在等温下汽化.(4) 理想气体在等温下压缩.(5) 理想气体绝热自由膨胀.在这些过程中,使系统的熵增加的过程是:(A) (1)、(2)、(3). (B) (2)、(3)、(4).(C) (3)、(4)、(5). (D) (1)、(3)、(5). []23. (本题 3分)(4340)气缸中有一定量的氮气(视为刚性分子理想气体),经过绝热压缩,使其压强变为原来的2倍,问气体分子的平均速率变为原来的几倍?(A) 22/5.(B) 22/7.(C) 21/5.(D) 21/7.[]二填空题 (共77分)24. (本题 3分)(4153)下面给出理想气体的几种状态变化的关系,指出它们各表示什么过程.(1) p d V= (M / M mol)R d T表示____________________过程.(2) V d p= (M / M mol)R d T表示____________________过程.(3) p d V+V d p= 0 表示____________________过程.25. (本题 4分)(4307)分子物理学是研究________________________________________________ __________的学科.它应用的基本方法是_________________方法.26. (本题 5分)(4016)三个容器内分别贮有1 mol氦(He)、 1 mol氢(H2)和1 mol氨(NH3)(均视为刚性分子的理想气体).若它们的温度都升高1 K,则三种气体的内能的增加值分别为:(普适气体常量R=8.31 J·mol−1·K−1)氦:△E=___________________;氢:△E=___________________;氨:△E=____________________.1 mol 氧气(视为刚性双原子分子的理想气体)贮于一氧气瓶中,温度为27℃,这瓶氧气的内能为________________J ;分子的平均平动动能为____________J;分子的平均总动能为_____________________J.(摩尔气体常量 R = 8.31 J ·mol -1·K -1 玻尔兹曼常量 k = 1.38×10-23J·K -1)28. (本题 3分)(5061) 分子热运动自由度为i 的一定量刚性分子理想气体,当其体积为V 、压强为p 时,其内能E =______________________.29. (本题 3分)(4655) 有两瓶气体,一瓶是氦气,另一瓶是氢气(均视为刚性分子理想气体),若它们的压强、体积、温度均相同,则氢气的内能是氦气的________倍.30. (本题 3分)(4283) 当理想气体处于平衡态时,若气体分子速率分布函数为f (v ),则分子速率处于最概然速率v p 至∞范围内的概率△N / N =________________.31. (本题 4分)(4459) 已知f (v )为麦克斯韦速率分布函数,N 为总分子数,则(1) 速率v > 100 m ·s -1的分子数占总分子数的百分比的表达式为_________; (2) 速率v > 100 m ·s -1的分子数的表达式为__________________.32. (本题 5分)(4037) 已知f (v )为麦克斯韦速率分布函数,v p 为分子的最概然速率.则()∫p f v v v 0d表示___________________________________________;速率v >v p 的分子的平均速率表达式为______________________.33. (本题 3分)(4082) 在p −V 图上(1) 系统的某一平衡态用_____________来表示; (2) 系统的某一平衡过程用________________来表示; (3) 系统的某一平衡循环过程用__________________来表示;一定量的理想气体处于热动平衡状态时,此热力学系统的不随时间变化的三个宏观量是__________________________________,而随时间不断变化的微观量是____________________________________________________________________.35. (本题 3分)(4578) 如图所示,已知图中画不同斜线的两部分的面积分别为S 1和S 2,那么(1) 如果气体的膨胀过程为a ─1─b ,则气体对外做功W =________; (2) 如果气体进行a ─2─b ─1─a 的循环过程,则它对外做功W =_______________.36. (本题 5分)(4676)设在某一过程中,系统由状态A 变为状态B ,如果__________________________________________________________________________________________________________________________,则该过程称为可逆过程;如果_____________________________________________________________________则该过程称为不可逆过程.37. (本题 3分)(4147) 同一种理想气体的定压摩尔热容C p 大于定体摩尔热容C V ,其原因是_______________________________________________________.38. (本题 3分)(4688) 刚性双原子分子的理想气体在等压下膨胀所作的功为W ,则传递给气体的热量为__________.39. (本题 5分)(4472) 一定量理想气体,从A 状态 (2p 1,V 1)经历如图所示的直线过程变到B 状态(2p 1,V 2),则AB 过程中系统作功W =_________;内能改变∆E =_________.p 112气体经历如图所示的一个循环过程,在这个循环中,外界传给气体的净热量是___________.23)41. (本题 5分)(4137)热力学第二定律的克劳修斯叙述是:___________________________________;开尔文叙述是________________________________________________________.42. (本题 3分)(4141)从统计的意义来解释, 不可逆过程实质上是一个________________________ __________________________的转变过程, 一切实际过程都向着_____________ _____________________________的方向进行.43. (本题 4分)(4713)给定的理想气体(比热容比γ为已知),从标准状态(p0、V、T)开始,作绝热膨胀,体积增大到三倍,膨胀后的温度T=____________,压强p=__________.三计算题 (共78分)44. (本题10分)(4070)容积为20.0 L(升)的瓶子以速率v=200 m·s−1匀速运动,瓶子中充有质量为100g的氦气.设瓶子突然停止,且气体的全部定向运动动能都变为气体分子热运动的动能,瓶子与外界没有热量交换,求热平衡后氦气的温度、压强、内能及氦气分子的平均动能各增加多少?(摩尔气体常量R=8.31 J·mol-1·K−1,玻尔兹曼常量k=1.38×10-23 J·K−1)45. (本题10分)(4155)有1 mol刚性多原子分子的理想气体,原来的压强为1.0 atm,温度为27℃,若经过一绝热过程,使其压强增加到16 atm.试求:(1) 气体内能的增量;(2) 在该过程中气体所作的功;(3) 终态时,气体的分子数密度.( 1 atm= 1.013×105 Pa,玻尔兹曼常量k=1.38×10-23 J·K-1,普适气体常量R=8.31 J·mol-1·K-1 )一定量的某种理想气体,开始时处于压强、体积、温度分别为p0=1.2×106Pa,V0=8.31×10-3m3,T0 =300 K的初态,后经过一等体过程,温度升高到T1 =450 K,再经过一等温过程,压强降到p = p0的末态.已知该理想气体的等压摩尔热容与等体摩尔热容之比Cp / CV=5/3.求:(1) 该理想气体的等压摩尔热容Cp 和等体摩尔热容CV.(2) 气体从始态变到末态的全过程中从外界吸收的热量.(普适气体常量R = 8.31 J·mol-1·K-1)47. (本题10分)(4587)一定量的理想气体,由状态a经b到达c.(如图,abc为一直线)求此过程中(1) 气体对外作的功;(2) 气体内能的增量;(3) 气体吸收的热量.(1 atm=1.013×105 Pa)48. (本题 5分)(4591)一卡诺循环的热机,高温热源温度是 400 K.每一循环从此热源吸进 100 J 热量并向一低温热源放出80 J热量.求:(1) 低温热源温度;(2) 这循环的热机效率.49. (本题10分)(4097)1 mol理想气体在T1 = 400 K的高温热源与T2 = 300 K的低温热源间作卡诺循环(可逆的),在400 K的等温线上起始体积为V1= 0.001 m3,终止体积为V2 = 0.005 m3,试求此气体在每一循环中(1) 从高温热源吸收的热量Q1(2) 气体所作的净功W(3) 气体传给低温热源的热量Q250. (本题 5分)(4703)以氢(视为刚性分子的理想气体)为工作物质进行卡诺循环,如果在绝热膨胀时末态的压强p2是初态压强p1的一半,求循环的效率.1 mol双原子分子理想气体作如图的可逆循环过程,其中1-2为直线,2-3为绝热线,3-1为等温线.已知T2 =2T1,V3=8V1试求:(1) 各过程的功,内能增量和传递的热量;(用T1和已知常量表示)(2) 此循环的效率η.(注:循环效率η=W/Q1,W为整个循环过程中气体对外所作净功,Q1为循环过程中气体吸收的热量)p12352. (本题10分)(4118)一定量的理想气体经历如图所示的循环过程,A→B和C→D是等压过程,B→C和D→A是绝热过程.已知:TC = 300 K,TB= 400K.试求:此循环的效率.(提示:循环效率的定义式η=1-Q2 /Q1,Q1为循环中气体吸收的热量,Q2为循环中气体放出的热量)A BCDO Vp一选择题 (共69分)1. (本题 3分)(4468)(B)2. (本题 3分)(4552)(B)3. (本题 3分)(4304)(B)4. (本题 3分)(4014)(C)5. (本题 3分)(4651)(A)6. (本题 3分)(5335)(C)7. (本题 3分)(4665)(B)8. (本题 3分)(4559)(B)9. (本题 3分)(5603)(B)10. (本题 3分)(4133)(D)11. (本题 3分)(4674)(B)12. (本题 3分)(4146)(A)13. (本题 3分)(4579)(D)14. (本题 3分)(4679)(D)15. (本题 3分)(4310)(C)16. (本题 3分)(4122)(D)17. (本题 3分)(4121)(D)18. (本题 3分)(5342)(A)(D)20. (本题 3分)(5074) (B)21. (本题 3分)(4135) (D)22. (本题 3分)(5073) (D)23. (本题 3分)(4340) (D)二 填空题 (共77分)24. (本题 3分)(4153) 等压 1分 等体 1分 等温 1分25. (本题 4分)(4307) 物质热现象和热运动规律 2分统计 2分26. (本题 5分)(4016) 12.5 J 2分20.8 J 2分24.9 J 1分27. (本题 5分)(4017) 6.23×10 32分6.21×10 − 212分1.035×10 − 21 1分28. (本题 3分)(5061) ipV 213分29. (本题 3分)(4655) 5 / 3 3分30. (本题 3分)(4283)∫∞pf v v v d )( 3分31. (本题 4分)(4459) (1) ∫∞100d )(v v f 2分 (2)∫∞100d )(v v Nf 2分速率区间0 ~ v p 的分子数占总分子数的百分率; 3分∫∫∞∞=ppf f v v vv v v v v d )(d )( 2分33. (本题 3分)(4082) 一个点。
大学物理练习题3((角)动量与能量守恒定律)

大学物理练习题3((角)动量与能量守恒定律)大学物理练习题3:“力学―(角)动量与能量守恒定律”一、填空一、一个质量为10kg的物体以4m/s的速度落到砂地后经0.1s停下来,则在这一过程中物体对砂地的平均作用力大小为。
2、外汇?30? 4T的组合外力(其中FX以N为单位,t以s为单位)作用在M的质量上?在10kg物体上,则:(1)在前2S内,力FX的冲量为:;(2)如果物体的初始速度V1?10米?s1.如果方向与FX相同,力FX的冲量I?300n?S、对象的速度为:。
3.一根质量为1kg、长度为1.0m的均匀细杆,支点位于杆的上端,杆在开始时自由悬挂。
现在用100N的力撞击其下端,撞击时间为0.02s。
如果杆在撞击前是静止的,杆的角动量变为,撞击后杆的角速度为。
4、某质点最初静止,受到外力作用后开始运动,该力的冲量是4.00kg?m?s?1,同时间内该力作功4.00j,则该质点的质量是,力撤走后其速率为。
5、设一质量为1kg的小球,沿x轴正向运动,其运动方程为x?2t2?1,则在时间t1?1s到t2?3s内,合外力对小球的功为;合外力对小球作用的冲量大小为。
? 6.力F作用在质量为1.0kg的粒子上,使其沿x轴移动。
粒子在这个力下的运动是已知的?学方程为x?3t?4t?t(si)。
则在0到4s的时间间隔内,力f的冲量大小i=,23? 力F对质点w=所做的功。
7、设作用在质量为2kg上的物体上的力fx?6x(式中fx的单位为n,x的单位为m)。
若物体由静止出发沿直线运动,则物体从x?0运动到x?2m过程中该力作的功W十、物体在2m v?下的速度?。
8、已知质量m?2kg物体在一光滑路面上作直线运动,且t?0时,x?0,ν?0。
若该物体受力为f?3?4x(式中f的单位为n,x的单位为m),则该物体速率ν随x的函数关系ν(x)来自x的物体?0比x?该力在2MW?过程中所做的功?。
??9、一质量为10kg的物体,在t=0时,物体静止于原点,在作用力f?(3?4x)i作用下,无摩第1页,共7页?擦地运动,则物体运动到3米处,在这段路程中力f所做的功为。
大学物理(一)课外练习题3

大学物理(一)课外练习题31. mol 4的多原子分子理想气体,当温度为T 时,其内能为( )。
A . KT 12B . KT 10C . RT 12D . RT 102. 若理想气体的压强为p ,温度为T ,体积为V ,一个分子的质量为m ,k 为玻尔兹曼常量,R 为普适气体常量,则该理想气体的分子数为( )。
A . RB . kT pVC . R 3D . RTpV 3. 关于温度的意义,有下列几种说法:(1)气体的温度是分子平均平动动能的量度。
(2)气体的温度是大量气体分子热运动的集体表现,具有统计意义。
(3)从微观上看,气体的温度表示每个气体分子的冷热程度。
(4)温度的高低反映物质内部分子运动剧烈程度的不同。
这些说法中正确的是( )。
A . (1)、(2) 、(4)B . (1)、(2) 、(3)C . (2)、(3) 、(4)D . (1)、(3) 、(4)4. 一个容器内贮有1mol 氧气和1mol 氦气,若两种气体各自对器壁产生的压强分别为1p 和2p ,则两者的大小关系是( )。
A . 12>p pB . 12<p pC . 12=p pD . 不确定的5.两个体积不等的容器,分别储有氦气和氧气,若它们的压强相同,温度相同,则下列各量中相同的是( )。
A .单位体积中的分子数B .单位体积中的气体内能C .单位体积中的气体质量D .容器中的分子总数6.两个体积相等的容器中,分别储有氦气和氢气。
以1E 和2E 分别表示氦气和氢气的内能,若它们的压强相同,则( )。
A .21E E =B .21E E >C .21E E <D .无法确定7. 一瓶氢气和一瓶氧气密度相同,分子平均平动动能相同,而且它们都处于平衡状态,则它们( )。
A .温度相同、压强相同B .温度、压强都不相同C .温度相同,但氢气的压强大于氧气的压强D .温度相同,但氢气的压强小于氧气的压强8. 如图所示,设某热力学系统经历一个由→→C D E 的过程,其中,AB 是一条曲线,E 、C 该曲线上。
大学物理习题3第三篇

制作:石永锋 制作:
15、一带正电荷的物体M,靠近一原不带电的金属导体 ,N 、一带正电荷的物体 ,靠近一原不带电的金属导体N, 的左端感生出负电荷,右端感生出正电荷.若将N的左端接地 的左端接地, 的左端感生出负电荷, 右端感生出正电荷. 若将 的左端接地 , 如图所示, 如图所示,则 (A) N上有负电荷入地. 上有负电荷入地. 上有负电荷入地 (B) N上有正电荷入地. 上有正电荷入地. 上有正电荷入地 (C) N上的电荷不动. 上的电荷不动. 上的电荷不动 (D) N上所有电荷都入地. 上所有电荷都入地. 上所有电荷都入地
O x
v E
第三篇
静电场总复习
4
浙江理工大学理学院物理系
制作:石永锋 制作:
5、有一边长为 的正方形平面,在其中垂线上距中心 点a/2 、有一边长为a的正方形平面 在其中垂线上距中心O点 的正方形平面, 有一电荷为q的正点电荷 如图所示, 的正点电荷, 处 , 有一电荷为 的正点电荷 ,如图所示 , 则通过该平面的电 场强度通量为
第三篇
静电场总复习
17
浙江理工大学理学院物理系
制作:石永锋 制作:
18、半径分别为R和r的两个金属球,相距很远.用一根细长导 、半径分别为 和 的两个金属球,相距很远. 的两个金属球 线将两球连接在一起并使它们带电.在忽略导线的影响下, 线将两球连接在一起并使它们带电.在忽略导线的影响下,两球 表面的电荷面密度之比σR /σr为 表面的电荷面密度之比σ σ (A) R / r . (C) r2 / R2. (B) R2 / r2. (D) r / R .
浙江理工大学理学院物理系
制作:石永锋 制作:
一、选择题
1、如图所示,在坐标 ,0)处放置一点电荷 ,在坐标 ,0) 、如图所示,在坐标(a, 处放置一点电荷 处放置一点电荷+q,在坐标(-a, 处放置另一点电荷- . 点是 轴上的一点,坐标为(x, . 点是x轴上的一点 处放置另一点电荷 - q.P点是 轴上的一点, 坐标为 , 0).当 x>>a时,该点场强的大小为: 时 该点场强的大小为:
大学物理习题及解答3

二、填空题: 填空题: 1、半径为r=1.5m的飞轮,初角速度ω0=10rad/s,角加速 度 β = -5rad/s2,若初始时刻角位移为零,则在t= 4s 时角位移再次为零,而此时边缘上点的线速度v= −15m/ s 。 2β(∆θ ) = ω 2 −ω 2
t 0
2βθ = ωt −ω0
2 2
v 3v ω= = 2 l 2l 3
v
l
m
1 2 2 2 I = 2m⋅ l + m⋅ l = ml 3 3 3
O 2m
2 2 3v L = Iω = ml ⋅ = mvl 3 2l
大学物理
刘凌虹
4、如图所示 , 用三根长为 的细杆 ,(忽略杆的质量 、 如图所示,用三根长为l 的细杆, 忽略杆的质量 忽略杆的质量) 将三个质量均为m的质点连接起来 并与转轴O相连 的质点连接起来, 将三个质量均为 的质点连接起来 , 并与转轴 相连 若系统以角速度ω绕垂直于杆的 轴转动, 绕垂直于杆的O轴转动 接,若系统以角速度 绕垂直于杆的 轴转动,则中间 2 一个质点的角动量为________, 一个质点的角动量为 L = 4mωl 系统的总角动量为 , 2 L总 =14mωl。 如考虑杆的质量 , 若每根杆的质量为 , __________。如考虑杆的质量, 若每根杆的质量为M, 则此系统绕轴O的总转动惯量为 的总转动惯量为____________, 总转2 则此系统绕轴 的总转动惯量为 , I = (9M +14m)l 1 2 动动能为_____________________。 2 动动能为 E = (9M +14m)l。 ω
2 2 L = m(ω ⋅ 2l) ⋅ 2l = 4mωl
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学物理练习题
三、刚体力学
1. 有一半径为R 的圆形平板平放在水平桌面上,平板与水平桌面的摩擦系数为μ,若平板绕通过其中心且垂直板面的固定轴以角速度ω0开始旋转,它将在旋转几圈后停止?(已知圆形平板的转动惯量22
1
mR J =,其中m 为圆形平板的质量)
4. 质量为m ,长为L 的棒,中心固定,可在水平内自由转动,另有一子弹,质量也是m ,以速度v 0垂直射入棒端。
求:
(1) 子弹和棒的末角速度多大? (2) 中心轴所受冲量的大小和方向。
6. 如图,一长为l 的均质杆自水平放置的初始位置平动自由下落,落下h 距离时与一竖直固定板的顶部发生完全弹性碰撞,杆上碰撞点在距质心C 为l /4处,求碰撞后瞬间的质
心速率和杆的角速度。
8. 如图示,质量为m 1的物体可在倾角为θ的光滑斜面上滑动。
m 1的一边系有倔强系数为k 的弹簧,另一边系有不可伸长的轻绳,绳绕过转动惯量为I ,半径为r 的小轮与质量为m 2(>m 1)的物体相连。
开始时用外力托住m 2使弹簧保持原长,然后撤去外力,求m 2由静止下落h 距离时的速率及m 2下降的最大距离。
10. 如图示,一根长L ,质量为M 的直尺置于水平光滑桌面上,可在其上自由运动,现一质量为m 的橡皮小球以速率v 向直尺运动,在距尺质心为d 处两者作弹性碰撞。
(a ) 试确定碰撞中系统守恒的量是哪些?
(b ) 为使小球碰撞后静止,其质量m 应为多少?
11. 如图示,一长为L ,质量为m 的均匀细棒,一端悬挂在o 点上,可绕水平轴在竖直面内无摩擦地转动,在同一悬挂点,有长为l 的轻绳悬挂一小球,质量也为m ,当小球悬线偏离铅垂方向某一角度由静止释放,小球在悬点正下方与静止细棒发生弹性碰撞,
若碰撞后
计算题6图
计算题9图
k m 1
θ
I
m 2
计算题8图
计算题10图
小球刚好静止,试求绳长l 应为多少?
12. 如图所示,长为l 的轻杆,两端各固定质量分别为m 和2m 的小球,杆可绕水平光滑固
定轴O 在竖直面内转动,转轴O 距两端分别为
31l 和3
2
l .轻杆原来静止在竖直位置.今有一质量为m 的小球,以水平速度0v
与杆下端小球m 作对心碰撞,碰后以02
1v 的速度返回,
试求碰撞后轻杆所获得的角速度.
13 在半径为R 的具有光滑竖直固定中心轴的水平圆盘上,有一人静止站立在距转轴为
R 2
1
处,人的质量是圆盘质量的1/10.开始时盘载人对地以角速度ω0匀速转动,现在此人垂直圆盘半径相对于盘以速率v 沿与盘转动相反方向
作圆周运动,如图所示. 已知圆盘对中心轴的转动惯量为2
2
1MR .求:
(1) 圆盘对地的角速度. (2) 欲使圆盘对地静止,人应沿着R 2
1圆周对圆盘的速度v
的大小及方向?
计算题11图
m
m
021v 0v。
