正弦稳态电路的功率、 复功率 、最大功率传输共28页文档
电路原理3章 正弦交流电路的功率

UI cos [1 cos 2t] UI sin sin2t
Q UI sin 单位:乏 (var)
Q UI sin I 2 X
感性电路: Q > 0
容性电路: Q < 0
I
U
+
U X U
UR _
R jX
+ U_ R _+U X
视在功率、无功功率、平均功率关系:
电感在一个周期内吸收的平均功率 为:
P 1
T
pdt
1
T
UI sin 2tdt 0
T0
T0
电感是储能元件,不消耗能量,但是在某一
时间段内,它从外部电路吸收功率。
电感瞬时功率的最大值,定义为电感的无功
功率QL:
电感无功功率:QL UI
I2 XL
U2
XL
单位:乏 (var)
3.7.1.3 电容元件的功率
(1) 视在功率(apparent power)
•
Ii
一端口网络电压有效值与
电流有效值的乘积
Z
S UI 单位:伏安 (VA)
+
•
U
u
-
无 源 网 络
S UI Z I 2
注: SN=UN IN 称为发电机、变压器 等供
电设备的额定视在功率,表示其容量。
(2) 无功功率(reactive power)
并联电容器是电网中用得最多的一种无功功 率补偿设备,目前国内外电力系统中90%的无 功补偿设备是并联电容器。
可以串电容吗?
串联电容器补偿,现在主要应用于超高 压、大容量的输电线路上,例如,山西大同 至北京的500kV输电电线路全长300km,加装 了串联电容补偿后,电网线损降低,电压质 量改善,电网运行的稳定性得到加强,而且 输电能力提高30%以上。
《电路分析基础》正弦稳态最大功率传递定理

Pmax
U
2 oc
4 Req
21.472 42
57.62mW
X
求当RL、CL为何值时,负载可得到最大功率?
PLmax ?
Zs
解:当ZL Zs* 5 j5时,负载获得
最大功率。
RL CL
U
s
亦即
YL
1 ZL
1 Zs*
1 5 j5 1 j 1 5 j5 50 10 10
因为 YL
1 RL
j CL
所以: 1 1 RL 10
RL 10
X
解(续)
Zs
I
UL
U
s
ZL
X
最大功率传输定理
PL I 2RL
Rs RL
U
2 s
2 Xs XL
2 RL
欲使PL最大,首先应使分母最小。
对RL来说,当电抗之和 Xs XL 0,
即 XL Xs 时,分母 最小。
对PL求导,确定使PL为最大值的RL值。
dPL dRL
Rs RL 2 2 Rs RL Rs RL 4
CL
1, 10
CL 0.1F
PL max
Us2 4Rs
102 45
5W
X
例题2 电路如图所示,已知 Us 240 V,R 10k,
XC 5k ,XL 20k 求负载获得最大功率的条件
及负载得到的最大功率。
jX C
jX L
解:将负载移去,求剩下的单
口网络的戴维南等效电路。
Uoc
Us R R jXC
PL
Rs
|
Z
Us2 | Z | cos
| cos 2 Xs
|
正弦稳态电路的复功率

返回 上页 下页
解2
I1
10
0
10
5 j15 j25 5
j15 A
8.77
105.3
A
I2 Is I1 14.94 34.5 A
S1吸
I2 1
Z1
8.772
(10
j25)V
A
(769
j1923)V
A
S2吸
I
Z2
2
2
14.942
(5
j15)V
A
(1
116
j3
348
)V
A
S发 I1Z1 IS* 10 8.77 105.3 (10 j25)V A
(1885 j1 423) V A
返回 上页 下页
9-5 复功率
1. 复功率
为了用相量U和I来计算功率,引入“复功率”
+ I
U_
负 载
定义:S UI* 单位 V A
S UI(u i ) UIφ S
也可表示为
UIcos jUIsin P jQ
S UI* ZI I* ZI2 (R jX)I2 RI2 jXI2
或
S
UI*
U
_
U 10 Z 236 37.1 V
I1 10W I2
j25W
S发 236 37.1 10V A (1882 j1424) V A
S1吸
U
Y2 * 1
2362 (10
1
j25
)*
VA(768j Nhomakorabea920)V
A
S2吸
U
Y2 * 2
(1113
j3 345)
V
A
电路第9章 正弦稳态电路的分析

I 1 Y G jC j G jB Y y U L
§9-1
阻抗和导纳
Y—复导纳;|Y| —复导纳的模;y—
导纳角; G —电导(导纳的实部);
B —电纳(导纳的虚部);
| Y | G 2 B 2 转换关系: 或 B y arctan G
I
相量图:选电压为参考向量,
u 0
y
IG
.
IB U
I I G2 I B2 I G2 (I C I L )2
注意
RLC并联电路会出现分电流大于总电流的现象
§9-1
阻抗和导纳
+ I R U -
等效电路
IR
1 jC eq
I B
(3)wC<1/wL,B<0,y<0,电路为感性,电流落后电压;
1 Y 0.0128 50.20 Z 78.150.20 0.0082 j0.0098 S 1
R’
L’
1 1 1 0.102mH R 122 L 0.0098 G 0.0082
§9-1
阻抗和导纳
① 一端口N0的阻抗或导纳是由其内部的参数、
y
IG
I
.
U
.
I I I I (I L IC )
2 G 2 B 2 G
2
IC .
IL
§9-1
阻抗和导纳
I
+
IR
R
j Leg
等效电路
I B
U -
(4)wC=1/wL,B=0,j y =0,电路为电阻性, 电流与电压同相。
I
C
IL
I IG
7.3 正弦稳态电路的功率

cos t ω无源网络(1cos2φ+第一种分解形式()()cos cos 2p t UI φt φω=+-⎡⎤⎣⎦UI cos j 恒定分量UI cos (2ωt -j )为正弦分量ωtiOu p (t )∙p 有时为正,有时为负;∙p >0,电路吸收功率;∙p <0,电路发出功率;ωtOp(2)平均功率(有功功率)P第 2 页第二种分解形式:()()cos 1+cos2sin sin 2p t UI φt UI tωj ω=+UI cos j (1+cos2ωt )≥0为不可逆分量UI sin j sin2ωt 为可逆分量ωto能量在电源和一端口之间来回交换(3)无功功率Q可逆分量的最大值定义为无功功率sin Q UI φ=单位:var (乏)Q >0,表示网络吸收无功功率Q <0,表示网络发出无功功率无功功率第 4 页有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)(4)R 、L 、C 元件及阻抗Z 的有功功率和无功功率P R =UI cos j =UI cos0︒=UI =I 2R =U 2/R Q R =UI sin j =UI sin0︒=0P L =UI cos j =UI cos90︒=0Q L =UI sin j =UI sin90︒=UI=I 2X LP C =UI cos j =UI cos(-90︒)=0Q C =UI sin j =UI sin (-90︒)= -UI=I 2X Cu i R+-i u C+-i u L+-电感的无功功率>0吸收无功电容的无功功率<0发出无功第 5 页u i Z+-P Z =UI cos j Q Z =UI sin j 2L L 2C C 00Q I X Q I X ⎧=>⎪⎨=<⎪⎩=I |Z|I cos j =I 2|Z|cos j =I 2R =I |Z |I sin j =I 2|Z |sin j =I 2X=I 2(X L +X C )=Q L +Q C发出无功吸收无功电感和电容具有无功互相补偿的作用第 6 页以感性负载为例R cos P UI U I j ==G cos P UI φUI ==jIUBI GI X sin Q UI U Ij ==Bsin Q UI φUI ==RX +_+_+_U RU XU I GB+_GI IBI U jIURU XU XU 电压的无功分量RU 电压的有功分量GI 电流的有功分量BI 电流的无功分量(3)电压、电流三角形第8 页R P U I =GP UI =X Q U I=BQ UI =jSPQj⎥Z ⎪RX相似三角形jII GI BjUU RU XRX +_+_+_U RU XU I GB+_GI I BI U P =I 2RQ =I 2XRX +_+_+_U RU XU I第9 页3、复功率*S UI= U I负载+_定义:()u iS UI j j =∠- *S UI = 也可表示为:**()S UI U UY ==j P Q =+cos j sin UI φUI φ=+UI φS φ=∠=∠2ZI=有功功率无功功率视在功率*ZII = ***2UU Y Y U == 复数第10 页有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)()R L C P P Q Q Q =∑⎧⎨=+∑⎩总总视在功率不守恒=+j S P Q 总总总()R L C j P Q Q =++∑∑()RL C j P Q Q ⎡⎤=++∑⎣⎦=S ∑ =S S∑ 总复功率守恒无功功率守恒有功功率守恒=S S∑总第11 页求电流源发出的复功率o o 100 236(37.1)VU Z =∠⨯=∠- 例题解法1()()o10j25//5j1523.6(37.1)Z =+-=∠-W()*o o 236(37.1)100 1.88j1.42 kVAS UI ==∠-⨯∠=- +_U 10∠0oA10W j25W5W -j15W第12 页o o 100 236(37.1)VU Z =∠⨯=∠- 解法2()()o10j25//5j1523.6(37.1)Z =+-=∠-W23610 2.36 kVAS UI ==⨯≈+_U 10∠0oA10W j25W5W -j15W()o 2.36(37.1) 1.88j1.42 kVAS =∠-=- 第13 页21I Z =+_+ A_= 8.77* AW V+_D I30⨯4、功率因数的提高设备容量S (额定)向负载送多少有功由负载的阻抗角决定。
第九章 正弦稳态电路的分析

1 1 Y = = −53.13°S = (0.024 − j0.032)S (感 ) 性 eq Zeq 25
9-2
电路的相量图
分析阻抗(导纳) 分析阻抗(导纳)串、并联电路时,可以利用相关的 并联电路时, 电压和电流相量在复平面上组成的电路的相量图。 电压和电流相量在复平面上组成的电路的相量图。 1. 并联电路相量图的画法 并联电路相量图的画法 ① 参考电路并联部分的电压相量。 参考电路并联部分的电压相量。 根据支路的VCR确定各并联支路的电流相量与电压相 ② 根据支路的 确定各并联支路的电流相量与电压相 量之间的夹角。 量之间的夹角。 根据结点上的KCL方程,用相量平移求和法则,画出结点 方程, ③ 根据结点上的 方程 用相量平移求和法则, 上各支路电流相量组成的多边形。 上各支路电流相量组成的多边形。
R = G2GB2 , +
−B X = G2+B2
1 | Y |= , φZ = −φY |Z|
已知:R=15Ω, L=12mH, C=5µF, u =100 2cos(5000t) 例9-1 已知 试求:(1)电路中的电流 i, (瞬时表达式)和各元件的 电路中的电流 瞬时表达式) 试求 电压相量; 电路的等效导纳和并联等效电路 电路的等效导纳和并联等效电路。 电压相量;(2)电路的等效导纳和并联等效电路。 jω L R L R • + • - + UL + + uR - + uL - + + + uS C
第二种分解方法
第一种分解方法: p(t) =UI[cosϕ + cos(2ωt −ϕ)] 第一种分解方法: p UIcosϕ 恒定分量 恒定分量 u i
O
正弦稳态电路分析PPT课件

2
解法二: 采用阻抗Z计算;
·IS
+ 1
U·
2 Z 2 (1 j)(2 j) 2 3 j
1 j 2 j
3
_ j1
-j1
3 j 1 ()
Z
•
U
ZIS
(3
3j 1)50 3
(15
j 5)(V ) 3
P IS 2 Re[Z ] 52 3 75(W )
3 32 (1/ 3)2
75(W )
Q UIS sin φ
152 (5 / 3)2 5
1/ 3 32 (1/ 3)2
8.3(Var)
S UIS 152 (5 / 3)2 5 75.5(VA) cos φ 0.993
第6章 正弦稳态电路分析
例:如图电路中,已知 is 5 2 sin 2(t A ),求电源提供的P、
+
U·S_
·I1
5
j5
3 -j4
解:U s 100V I1 2 45( A) I2 253.1( A)
P1 I12R1 ( 2)2 5 10(W)
或: P1 USI1 cos φ1=10 2 cos 45 10(W)
P2
I
2 2
R2
22
3
12(W)
或: P2 USI2 cos φ2=10 2 cos 53.1 12(W)
例:电路如图,已知 us (t) 10 2 sin 5(t V) ,求电阻R1,R2
消耗的功率,并分析功率关系。
·I2
+ uS(t)_
R1 5 R2 3 L 1H C 0.05F
+
正弦稳态电路的最大功率传输
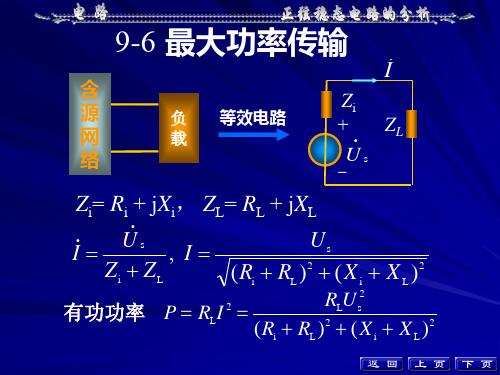
P
RLU
2 s
(Ri RL )2 ( X i X L )2
①若ZL= RL + jXL可任意改变
PPmax(RiRL4UURRsLs2i)2
(a)先设 RL 不变,XL 改变
显然,当Xi + XL=0,即XL =-Xi时,P 获得最大值。
(b)再讨论 RL 改变时,P 的最大值。
最佳
当RL= Ri 时,P 获得最大值
当
RL
1 (CRL )2
5
CRL2
5
1 (CRL )2
CRL11μ0FΩ 获最大功率
I 10 0 A 1A 10
Pmax I 2Ri 1 5W 5W
返回 上页 下页
50H I
5
+
RL
10 0o V
_
ZL
1 Y
1
RL
jCRL
1
RL
(CRL
)
2
j
1
CRL2 (CRL
)
2
当
RL
1 (CRL )2
负载获得的功率为
P
(Ri
RLU
2 s
RL )2
X2 i
模匹配
令
dP 0 dRL
获得最大功率条件为
RL
Ri2
X
2 i
Zi
返回 上页 下页
例6-1电路如图。求:1.RL=5时其消耗的功率;
2.RL=?能获得最大功率,并求最大功率;
3.在RL两端并联一电容,问RL和C为多大时能与
内阻抗最佳匹配,并求最大功率。 50H
返回 上页 下页
I 10 0 A 0.766 22.5 A 5 j5 7.07
正弦稳态电路的分析

+
U
-
+ UR R L +U - L C
+ UC -
U L
U
UC
U R
I
8.2 简单正弦稳态电路的分析、相量图
4、R-L-C并联交流电路
(1)电流、电压的关系 I IR I IL C
U
R
L
C
I I R I L IC 1 1 U( j C ) R j L
k 1
n
Gk j Bk
k 1 k 1
Yk Ik I Y
8.2 简单正弦稳态电路的分析、相量图
例1:写出下列电路阻抗和导纳的表达式。
R L1 C L2 R1 C1 R2 C2
(a)
Z R j L1 1 Y Z 1 1 j C j L2 Y
(b)
1 j C1 R1 1 Y 1 R2 1 j C 2
五、 功率因数(Power Factor)的提高
六、复功率(Complex Power)----VA
8.3
正弦稳态电路中的功率
8.3
正弦稳态电路中的功率
Power in Sinusoidal Steady State
一、瞬时功率(Instantaneous Power)----W
i
设 :u i 2U costV 2 I cos( t ) A
(2)RLC串联电路的复数阻抗
I
+
U
-
+ UR R L +U - L
C + UC -
Z R j X L X C
8.2 简单正弦稳态电路的分析、相量图
电路分析基础-7正弦稳态功率的计算-精选文档

上 页
下 页
7.2.2 无功功率 Q (reactive power)
Q UIsin φ
def
单位:var (乏)。
P UI cos 单位:W
单位:var Q UI si n
S UI 单位:VA
Q P tan
S P Q
2 2
S
P
Q
功率三角形
上 页 下 页
7.2.4-6 R、L、C元件的有功功率和无功功率 i + u i + u i + u C L R
2 2 P UI cos UI cos 0 UI I RU / R
X
P UI cos U I R
U R
I G
P UI cos φ UI G
U
+
U
I G
G
IB
_
B
I B
I
Q UI sin φ UI B
为 的有功分量 称 I I G 为 的无功分量 称 I I
B
上 页
下 页
例
+
U _
三表法测线圈参数。 已知 f =50Hz,且测得U=50V, I=1A,P=30W。 I * A * W 方法一 解 R V S UI 50 1 50 V A Z LΒιβλιοθήκη 吸收无功为正 吸收无功为负
2 2 2 2
S P Q IR X I Z
2 2
正弦稳态电路的分析

第九章正弦稳态电路的分析本章内容1.阻抗和导纳的概念2.阻抗的串并联及电路的相量图3.正弦稳态电路的分析4.瞬时功率、有功功率、无功功率、视在功率、复功率及最大输出功率5.串联和并联谐振本章重点:正弦量的向量正表示; 正弦电路中的阻抗和导纳;正弦电路的分析串联谐振的谐振条件及特征; 并联谐振的谐振条件及特征本章重点:正弦电路参数的分析及最大功率输出的分析§9-1 阻抗和导纳阻抗和导纳是正弦电流电路分析的重要内容一、阻抗在无源的线性网络中,端口的电压相量与电流相量的比值定义为该一端口的阻抗(复阻抗),用Z表示。
式中:•U=U∠ϕu•I=I∠ϕI阻抗的模:Z= U/I,阻抗角:ϕZ= ϕu-ϕi 阻抗的代数式: Z=R+jX式中:R—电阻 X—电抗1.若网络N 0内只含单一元件,则单一元件的复阻抗(1)电阻的复阻抗:Z R =R(2)电感的复阻抗:Z L =ωj L=jX L X L =ωL —感抗 (3)电容的复阻抗:Z C =cj ω1=c jω1-=jX C X C =cω1-—容抗 2.若网络N 0内为RLC 串联,则阻抗为(1)阻抗:Z=•U /•I = R+ωj L+cj ω1=R+j(ωL-Cω1)=R+jx=Z ϕ∠Z可见:阻抗Z 的实部为电阻R (R=Z cos ϕZ ),阻抗Z 的虚部为电抗X (X= R=Z sin ϕZ ),三者构成阻抗三角形 (2) 阻抗的模:Z =22)(C L X X R -+=22X R +=U/I (3)阻抗角:ϕZ =arctanR X X C L -=RX=ϕu -ϕi X 〉0 ωL>C ω1电路呈电感性 X<0 ωL<Cω1电路呈电容性X=0 电路呈电阻性一、 导纳:复阻抗的倒数定义为复导纳(电流相量与对应端口的电流相量的比值),用Y 表示 Y=Z 1=••UI =)(u i U Iϕϕ-∠=Y Y ϕ∠导纳的模: Y =U I导纳角: Y ϕ=u i ϕϕ- 导纳的代数式: Y=G+JB式中:G —电导 B —电纳1.若网络N 0内只含单一元件,则单一元件的复阻抗 (1) 电阻的复导纳:Y R =G=1/R (2) 电感的复导纳:Y L =Lj ω1=L jω1- =jB L B L =Lω1-—感纳 (3)电容的复导纳:Z C ==ωj C =jB C B C =ωC —容纳2.若网络N 0内为RLC 并联,则导纳为(1)导纳Y=••UI基尔霍夫电流定律的相量形式:∑•I =0•I =•I R +•I L +•I C =⎥⎦⎤⎢⎣⎡-+)1(1L C j R ωω•U =G+j(B C +B L )•UY=R 1+L j ω1+ωj C=R1+)1(L C j ωω-=G+jB可见:导纳Y 的实部为电导G (G=Y cos ϕY ),导纳Y 的虚部为电纳B (B= Y sin ϕY ),三者构成导纳三角形 (2)导纳的模:Y =22)(L C B B G -+=22B G +=I/U (3)阻抗角:ϕY =arctanG B B L C -=GB=ϕi -ϕu B 〉0 ωC>L ω1电路呈电容性 B<0 ωC<Lω1电路呈电感性B=0 电路呈电阻性二、阻抗和导纳相互转换(自学)§9-2 阻抗(导纳)串联和并联阻抗的串并联与电阻的串并联的计算规则相同,只是要把电阻换成阻抗。
正弦稳态电路的分析

一、阻抗 1. 一端口的阻抗 不含独立电源N0 ,当它在正弦电源激励下处于稳 不含独立电源N 态时,端口的电压、电流都是同频率的正弦量, 态时,端口的电压、电流都是同频率的正弦量,即 u = 2U cos(ωt +ϕ ) U = U∠ϕ →ɺ
u u
9-1 阻抗与导纳
0
i = 2I cos(ωt +ϕi ) I = I∠ϕi →ɺ 则它的端电压相量与端电流相量的比 阻抗Z 值定义为该一端口N 值定义为该一端口N0的(复)阻抗Z,即
ɺ 解: 选择 U'作为参考相量
ɺ IR
ɺ U'
α =45°
ɺ IC
∵ωL = 200×0.25 = 50Ω= R ∴IR = IL 由几何关系得: 由几何关系得:
ɺ IL
ɺ US ɺ UC
ɺ ɺ ɺ IC = I R + I L ɺ ɺ ɺ US = U′ +UC
UC =US =100V, U′ =100 2V U′ ∴IR = IL = = 2 2A , IC = 2IR = 4A , R IC 1 UC ∴ = ,C= = 2×10−4 F = 200µF ωC IC ωUC
def
R jX
|Z|——阻抗 的模; ϕ Z ——阻抗角; 阻抗Z的模 阻抗角; 阻抗 的模; 阻抗角 R——等效电阻;X——等效电抗。 等效电阻; 等效电抗。 等效电阻 等效电抗 为实数, 称为感性阻抗, (R为实数,X>0称为感性阻抗,X<0称 为实数 X>0称为感性阻抗 X<0称
ɺ U U Z === = ∠(ϕu −ϕi ) =| Z | ∠ϕZ = R + jX ɺ I I
第九章 正弦稳态电路的分析
正弦稳态电路的功率

率为
PL
100 100 100
2
100
25W
可见,采用共轭匹配网络,负载获得的
平均功率将大大增加。
3 设计一个由电感和 电容构成的网络来满 足共轭匹配条件,以 使负载获最大功率。
上图网络是可满足上述条件的一种方案。
由LC匹配网络和负载形成网络的输入
阻抗: Zab
1000 36.9 800 j600 VA
S S~ 1000 VA
P Re[ S~] 800 W Q Im[ S~] 600 Var
由于 Z 36.9
所以 pf cosZ cos(36.9) 0.8(导前)
例18 感性负载接在U=220V,f=50Hz
的交流电源上,其平均功率P=1.1KW,功
率因数pf=0.5,欲并联电容使负载的功
率因数提高到0.8(滞后),求电容。
解:负载电流有效值:
P
1.1103
I
10A
U pf 220 0.5
I' I
U C
IC
感性 负载
感性负载的阻抗角: Z arccos 0.5 60 设电压相量为: U 2200 V
则负载电流相量: I 10 60 A
、S、pf。
解:设端口电压相量 为: U 1000 V
-j14
+
U 16
-
j16
网络的等效阻抗:
Z j14 16 j16 j14 8 j8 16 j16
8 j6 10 36.9
因此
I1
U Z
1000 10 36.9
1036.9 A
故:
S~
U S
*
I1
1000
10
稳态功率

例: 图(a)表示电压源向一个电感性负载供电的电路 模型,试用并联电容的方法来提高负载的功率因数。
解:图(a)电路中的电流为
100 U I S I 2 53 . 1 A 1 Z 3 j4
其相量图如图(d)所示。单口网络吸收的平均功率为
P UI cos φ 10 2 cos(53.1 ) 12W
p(t ) u (t )i(t )
在单口网络工作于正弦稳态的情况下。端口电压和电流是
相同频率的正弦电压和电流,即
u (t ) U m cos(t u ) 2U cos(t u ) i (t ) I m cos(t i ) 2 I cos(t i )
则电感和电容的瞬时能量分别为
1 2 1 2 1 Li LI m sin 2 (t u ) LI 2 1 cos 2(t u ) 2 2 2 1 1 1 2 2 2 wC Cu CU m cos (t u ) CU 2 1 cos 2(t u ) 2 2 2 wL
比直流电路中复杂些,需要引入一些新的概念。
正弦稳态单口网络的瞬时功率、平均功率、视
在功率和功率因数。正弦稳态单口网络向可变负载
传输最大功率的问题以及非正弦稳态平均功率的计
算。三相电路等。
§11-1 瞬时功率和平均功率
一、瞬时功率和平均功率
图示单口网络,在端口电压和电流
采用关联参考方向的条件下,它吸收的 功率为
P cos UI
功率因数cos 之值与单口网络电压与电流间的相位差密切 相关,故称 =u–i为功率因数角。
当单口网络呈现纯电阻时, 功率因数角为零以及功率因数 cos =1,功率利用程度最高。当单口网络等效为一个电阻与电 感或电容连接时,即单口呈现电感性或电容性时,功率因数角 = 090以及功率因数cos < 1,以致于P<UI。为了提高电能 的利用效率,电力部门采用各种措施力求提高功率因数。
