浙江高考数学二轮讲义:专题四第3讲 空间向量与立体几何 Word版含解析
2024版高考数学二轮总复习第1篇核心专题提升多维突破专题4立体几何第3讲空间向量与空间角课件

角)
考查.
真题研究·悟高考
1. (2023·全国乙卷理科)已知△ABC为等腰直角三角形,AB为斜边, △ABD为等边三角形,若二面角C-AB-D为150°,则直线CD与平面 ABC所成角的正切值为( C )
A.15
B.
2 5
C.
3 5
D.25
【解析】 如图,取AB的中点E,连接CE,DE,
则根据题意易得 AB⊥CE,AB⊥DE,∴二面角 C-AB-D 的平面角
【解析】 (1)连接BD,因为PD⊥底面ABCD,且AM⊂平面ABCD, 则AM⊥PD,又AM⊥PB,PB∩PD=P,PB,PD⊂平面PBD, 所以AM⊥平面PBD,又BD⊂平面PBD,则AM⊥BD, 所以Rt△DAB∽Rt△ABM, 则AADB=BBMA , 所以12BC2=1,解得 BC= 2.
(1)证明:B2C2∥A2D2; (2)点P在棱BB1上,当二面角P-A2C2-D2为 150°时,求B2P.
【解析】 (1)证明:根据题意建系如图,则有:
B2(0,2,2),C2(0,0,3),A2(2,2,1),D2(2,0,2),
→
→
∴B2C2=(0,-2,1),A2D2=(0,-2,1),
∵EF=DA, ∴F(- 2,0, 2), ∴D→A=(- 2,0, 2),A→B=(0, 2,- 2), → AF=(- 2,0,0), 设平面DAB与平面ABF的一个法向量分别为n1=(x1,y1,z1),n2= (x2,y2,z2),
则-2y12-x1+2z12=z10=,0, 令 x1=1,解得 y1=z1=1, -2y22-x2=20z,2=0, 令y2=1,解得x2=0,z2=1, 故n1=(1,1,1),n2=(0,1,1), 设二面角D-AB-F的平面角为θ,
高三数学二轮复习 第一篇 专题4 第3课时空间向量与立体几何课件 理

(1)证明:A→S=(x-2,y-2,z),B→S=(x,y-2,z),D→S =(x-1,y,z),
由|A→S|=|B→S|得 x-22+y-22+z2= x2+y-22+z2,
故 x=1. 由|D→S|=1 得 y2+z2=1.① 又由|B→S|=2 得 x2+(y-2)2+z2=4, 即 y2+z2-4y+1=0,②
联立①②得y=12,
z=
3 2.
于是 S1,12, 23,A→S=-1,-32, 23, B→S=1,-32, 23,D→S=0,12, 23. 因为D→S·A→S=0,D→S·B→S=0,故 DS⊥AS,DS⊥BS,
又 AS∩BS=S,所以 SD⊥平面 SAB.
(2)设平面 SBC 的法向量 a=(m,n,p), 则 a⊥B→S,a⊥C→B,a·B→S=0,a·C→B=0. 又B→S=1,-32, 23,C→B=(0,2,0),
2.运用空间向量坐标运算求空间角的一般步骤为: (1)建立恰当的空间直角坐标系; (2)求出相关点的坐标; (3)写出向量坐标; (4)结合公式进行论证、计算; (5)转化为几何结论.
2.如图,在四棱锥 P-ABCD 中,PA ⊥面 ABCD,AB⊥BC,AB⊥AD,且 PA =AB=BC=12AD=1.
解析: 如图,以 D 为坐标原点,线段 DA 的长为单位 长,射线 DA 为 x 轴的正半轴建立空间直角坐标系 D-xyz.
(1)证明:依题意有 Q(1,1,0),C(0,0,1),P(0,2,0). 则D→Q=(1,1,0),D→C=(0,0,1),P→Q=(1,-1,0). 所以P→Q·D→Q=0,P→Q·D→C=0. 即 PQ⊥DQ,PQ⊥DC. 又 DQ∩DC=D,所以 PQ⊥平面 DCQ. 又 PQ⊂平面 PQC,所以平面 PQC⊥平面 DCQ.
高考专题-- 立体几何与空间向量-浙江高三数学三轮复习---精校解析Word版

立体几何与空间向量1. 立体图形的截面问题高考对用一平面去截一立体图形所得平面图形的考查实质上对学生空间想象能力及对平面基本定理及线面平行与面面平行的性质定理的考查。
考生往往对这一类型的题感到吃力,实质上高中阶段对作截面的方法无非有如下两种:一种是利有平面的基本定理:一个就是一条直线上有两点在一平面内则这条直线上所在的点都在这平面内和两平面相交有且仅有一条通过该公共点的直线(即交线)(注意该定理地应用如证明诸线共点的方法:先证明其中两线相交,再证明此交点在第三条直线上即转化为此点为两平面的公共点而第三条直线是两平的交线则依据定理知交点在第三条直线;诸点共线:即证明此诸点都是某两平面的共公点即这此点转化为在两平的交线上)据这两种定理要做两平面的交线可在两平面内通过空间想象分别取两组直线分别相交,则其交点必为两平面的公共点,并且两交点的连线即为两平的交线.另一种方法就是依据线面平行及面面平行的性质定理,去寻找线面平行及面面平行关系,然后根据性质作出交线。
一般情况下这两种方法要结合应用.例1.已知正三棱柱111ABC A B C 的底面边长是10,高是12,过底面一边AB ,作与底面ABC 成060角的截面面积是___________________。
【答案】点评:判断截面的形状,应该将现有截面进行延伸,必须找出与整个几何体表面的截线.2.三视图高考对三视图的要求是:(1)理解简单空间图形 (柱、锥、台、球的简易组合) 的含义,了解中心投影的含义,掌握平行投影的含义;(2)理解三视图和直观图间的关系,掌握三视图所表示的空间几何体.会用斜二测法画出它们的直观图.从学生反馈情况看,主要错误是不能正确视图,还原几何体.突破这一瓶颈的有效途径,一是熟悉规则,二是多做一些练习.例2.【2017课标II ,理4】如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )90πB.63πC.42πD.36π【答案】B【解析】点评:在由三视图还原为空间几何体的实际形状时,要从三个视图综合考虑,根据三视图的规则,空间几何体的可见轮廓线在三视图中为实线,不可见轮廓线在三视图中为虚线。
浙江专用2020高考数学二轮复习专题四立体几何第3讲空间向量与立体几何课件1

(2)线面夹角
设直线 l 与平面 α 的夹角为 θ0≤θ≤π2,
则 sin θ=||aa|·|μμ||=|cos〈a,μ〉|.
(3)面面夹角 设平面 α、β 的夹角为 θ0≤θ≤π2, 则|cos θ|=||μμ|·|υυ||=|cos〈μ,υ〉|.
[典型例题] (1)如图,在直三棱柱 ADE BCF 中,平面 ABFE 和平面 ABCD 都是正方形且互相垂直,M 为 AB 的中点,O 为 DF 的中点.运用向 量方法证明: ①OM∥平面 BCF; 州诊断考试)如图,在四棱锥 P-ABCD 中,PA⊥平面 ABCD, PA=AB=AD=2,四边形 ABCD 满足 AB⊥AD,BC∥AD 且 BC=4, 点 M 为 PC 的中点,点 E 为 BC 边上的动点,且BEEC=λ. (1)求证:平面 ADM⊥平面 PBC; (2)是否存在实数 λ,使得二面角 P-DE-B 的余弦值为 22?若存在,试求出实数 λ 的值; 若不存在,说明理由.
l∥α⇔a⊥μ⇔a·μ=0⇔a1a2+b1b2+c1c2=0.
(2)线面垂直 l⊥α⇔a∥μ⇔a=kμ⇔a1=ka2,b1=kb2,c1=kc2.
(3)面面平行 α∥β⇔μ∥υ⇔μ=λυ⇔a2=λa3,b2=λb3,c2=λc3. (4)面面垂直 α⊥β⇔μ⊥υ⇔μ·υ=0⇔a2a3+b2b3+c2c3=0.
(2)如图,在平面 BEC 内,过 B 作 BQ∥EC, 因为 BE⊥CE,所以 BQ⊥BE, 又因为 AB⊥平面 BEC,所以 AB⊥BE,AB⊥BQ, 以 B 为原点,BE、BQ、BA 所在直线分别为 x,y,z 轴,建立空间 直角坐标系,则 A(0,0,2),B(0,0,0),E(2,0,0),F(2,2,1),G(1,0,0),G→F= (1,2,1),平面 ABE 的法向量 n=(0,1,0), 设 GF 与平面 ABE 所成的角为 θ,
高考数学二轮复习专题四立体几何第三讲空间向量与立体几何课件理

考点(kǎo diǎn)一 向量法证明线面平行、垂直关 系
(1)因为E→F=-12A→B,所以E→F∥A→B, 即 EF∥AB. 又 AB⊂平面 PAB,EF⊄平面 PAB, 所以 EF∥平面 PAB. (2)因为A→P·D→C=(0,0,1)·(1,0,0)=0, A→D·D→C=(0,2,0)·(1,0,0)=0, 所以A→P⊥D→C,A→D⊥D→C, 即 AP⊥DC,AD⊥DC.
第三页,共五十二页。
考情分析 明确 方向 (míngquè)
年份 卷 考查角度及命题位置
命题分析及学科素养
面面垂直的证明及二 Ⅰ卷
面角的求解·T18 线面垂直证明及二面 Ⅱ卷 角的求解·T19
命题分析 高考中此部分命题较为稳定,以解答 题的形式考查空间平行关系和垂直 关系的证明,空间几何体表面积和体 积的计算,异面直线所成的角、线面
则 sin θ=|cos〈n,a〉|=||nn|·|aa||.
12/8/2021
第十七页,共五十二页。
考点二
小
向量(xiàngliàng)法求空间角大
3.向量法求二面角 求出二面角 α-l-β 的两个半平面 α 与 β 的法向量 n1,n2,若二 面角 α-l-β 所成的角 θ 为锐角,则 cos θ=|cos〈n1,n2〉|=||nn11|·|nn22||; 若二面角 α-l-β 所成的角 θ 为钝角,则 cos θ=-|cos〈n1,n2〉 |=-||nn11|·|nn22||.
12/8/2021
第十六页,共五十二页。
考点二
小
向量(xiàngliàng)法求空间角大
[悟通——方法结论]
1.向量法求异面直线所成的角
若异面直线 a,b 的方向向量分别为 a,b,异面直线所成的角
2019届高三理科数学第二轮专题复习配套文档专题四 第3讲立体几何中的向量方法

第3讲立体几何中的向量方法[真题再现]1.(2018·课标Ⅰ)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF为折痕把△DFC使点C到达点P的位置,且PF⊥BF。
(1)证明:平面PEF⊥平面ABFD;(2)求DP与平面ABFD所成角的正弦值.[解](1)证明:由已知可得BF⊥PF,BF⊥EF,所以BF⊥平面PEF.又BF⊂平面ABFD,所以平面PEF⊥平面ABFD。
(2)解:如图,作PH⊥EF,垂足为H.由(1)得,PH⊥平面ABFD。
以H为坐标原点,错误!的方向为y轴正方向,|错误!|为单位长,建立如图所示的空间直角坐标系H.xyz.由(1)可得,DE⊥PE.又DP=2,DE=1,所以PE=错误!.又PF=1,EF=2,所以PE⊥PF.所以PH=错误!,EH=错误!.则H(0,0,0),P错误!,D错误!,错误!=错误!,错误!=错误!.又错误!为平面ABFD的法向量,设DP与平面ABFD所成角为θ,则sin θ=错误!=错误!=错误!。
所以DP与平面ABFD所成角的正弦值为错误!.2.(2018·课标Ⅱ)如图,在三棱锥P-ABC中,AB=BC=22,P A=PB=PC=AC=4,O为AC的中点.(1)证明:PO⊥平面ABC;(2)若点M在棱BC上,且二面角M。
P A-C为30°,求PC与平面P AM所成角的正弦值[解](1)证明:因为P A=PC=AC=4,O为AC的中点,所以OP⊥AC,且OP=2错误!.如图,连接OB.因为AB=BC=错误!AC,所以△ABC为等腰直角三角形,且OB ⊥AC,OB=错误!AC=2。
由OP2+OB2=PB2知PO⊥OB.由OP⊥OB,OP⊥AC,OB∩AC=O,得PO⊥平面ABC.(2)解:如图,以O为坐标原点,错误!的方向为x轴正方向,建立空间直角坐标系O。
xyz。
由已知得O(0,0,0),B(2,0,0),A(0,-2,0),C(0,2,0),P(0,0,2错误!),错误!=(0,2,2错误!).取平面P AC的一个法向量错误!=(2,0,0).设M (a ,2-a,0)(0≤a ≤2),则错误!=(a ,4-a,0).设平面P AM 的法向量为n =(x ,y ,z ).由AP ,→·n =0,错误!·n =0得错误!可取y =错误!a ,得平面P AM 的一个法向量为n =(错误!(a -4),错误!a ,-a ),所以cos 错误!,n =错误!。
2021高考数学重难点03 空间向量与立体几何(解析版)

求点到平面的距离问题:采用等体积法.
求几何体的表面积体积问题:应注意巧妙选取底面积与高.
对于二面角问题应采用建立立体坐标系去求.但是坐标系要注意采用左手系务必要标记 准确对应点以及法向量对应的坐标.
【常见题型限时检测】(建议用时:35 分钟) 一、单选题
1.(2020·全国高三专题练习(理))已知三棱锥 O-ABC,点 M,N 分别为 AB,OC 的中
3 2
3
,故 A 错误;
对于 B,由于 A1B1 平面 ABC1D1 ,故 B1 到平面 ABC1D1 的距离即点 E 到平面 ABC1D1 的
距离,
连接 B1C 交 BC1 于 G ,可得 B1G 平面 ABC1D1 ,而 B1G 2 ,∴点 E 到平面 ABC1D1 的距离为
2 ,故 B 错误; 对于 C,三棱锥 E ABC1 的外接球即四棱锥 E ABC1D1 的外接球, ∵ ABC1D1 为矩形,且 AB 2 , BC1 2 2 , EA EB EC1 ED1 5 ,四棱锥 E ABC1D1 的高为 2 ,
设四棱锥 E ABC1D1 的外接球的半径为 R ,则 R2 (
3)2 (
2
R)2
,解得
R
5
2 4
.
S 4 (5 2 )2 25
∴三棱锥的外接球的表面积
4
2 ,故 C 错误;
对于 D,连接 DC1 ,取 DC1 的中点 H ,连接 DB1 交 EC 于 K ,连接 CH , HK ,
∵ EB1 DC ,∴ CKH 是直线 CE 与平面 ADB1 所成的角,在直角三角形 CKH 中,
13
则 B1(0,
3 ,2),F(1,0,1),E ( 2 ,
2023年高考数学二轮复习第一部分专题攻略专题四立体几何第三讲立体几何

第三讲立体几何——大题备考【命题规律】立体几何大题一般为两问:第一问通常是线、面关系的证明;第二问通常跟角有关,一般是求线面角或二面角,有时与距离、几何体的体积有关.微专题1线面角保分题[2022·辽宁沈阳二模]如图,在四棱锥P-ABCD中,底面ABCD是正方形,P A⊥平面ABCD,P A=2AB=4,点M是P A的中点.(1)求证:BD⊥CM;(2)求直线PC与平面MCD所成角的正弦值.提分题例1 [2022·全国乙卷]如图,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E 为AC的中点.(1)证明:平面BED⊥平面ACD;(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求CF与平面ABD所成的角的正弦值.听课笔记:【技法领悟】利用空间向量求线面角的答题模板巩固训练1[2022·山东泰安一模]如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2AD=2,P A⊥平面ABCD,E为PD中点.(1)若P A=1,求证:AE⊥平面PCD;(2)当直线PC与平面ACE所成角最大时,求三棱锥E-ABC的体积.微专题2二面角保分题[2022·山东临沂二模]如图,AB是圆柱底面圆O的直径,AA1、CC1为圆柱的母线,四边形ABCD是底面圆O的内接等腰梯形,且AB=AA1=2BC=2CD,E、F分别为A1D、C1C的中点.(1)证明:EF∥平面ABCD;(2)求平面OEF与平面BCC1夹角的余弦值.提分题例2 [2022·湖南岳阳三模]如图,在四棱锥P-ABCD中,底面ABCD是菱形,F是PD 的中点.(1)证明:PB∥平面AFC;(2)若直线P A⊥平面ABCD,AC=AP=2,且P A与平面AFC所成的角正弦值为√21,求7锐二面角F-AC-D的余弦值.听课笔记:AD,现例3 [2022·山东日照二模]如图,等腰梯形ABCD中,AD∥BC,AB=BC=CD=12以AC为折痕把△ABC折起,使点B到达点P的位置,且P A⊥CD.(1)证明:平面APC⊥平面ADC;(2)若M为PD上一点,且三棱锥D-ACM的体积是三棱锥P-ACM体积的2倍,求二面角P-AC-M的余弦值.听课笔记:【技法领悟】利用空间向量求二面角的答题模板巩固训练21.[2022·广东韶关二模]如图,在四棱锥P-ABCD中,底面ABCD为矩形,点S是边AB 的中点.AB=2,AD=4,P A=PD=2√2.(1)若O是侧棱PC的中点,求证:SO∥平面P AD;(2)若二面角P-AD-B的大小为2π,求直线PD与平面PBC所成角的正弦值.32.[2022·河北保定一模]如图,在等腰梯形ABCD中,AD∥BC,AD=AB=CD=1,∠BCD =60°,现将DAC沿AC折起至P AC,使得PB=√2.(1)证明:AB⊥PC;(2)求二面角A-PC-B的余弦值.微专题3探索性问题提分题例4 [2022·山东聊城三模]已知四边形ABCD为平行四边形,E为CD的中点,AB=4,△ADE为等边三角形,将三角形ADE沿AE折起,使点D到达点P的位置,且平面APE⊥平面ABCE.(1)求证:AP⊥BE;(2)试判断在线段PB上是否存在点F,使得平面AEF与平面AEP的夹角为45°.若存在,试确定点F的位置;若不存在,请说明理由.听课笔记:【技法领悟】1.通常假设问题中的数学对象存在或结论成立,再在这个前提下进行推理,如果能推出与条件吻合的数据或事实,说明假设成立,并可进一步证明;否则假设不成立.2.探索线段上是否存在满足条件的点时,一定注意三点共线的条件的应用.巩固训练3[2022·湖南岳阳一模]如图,在三棱锥S-ABC中,SA=SB=SC,BC⊥AC.(1)证明:平面SAB⊥平面ABC;(2)若BC=SC,SC⊥SA,试问在线段SC上是否存在点D,使直线BD与平面SAB所成的角为60°,若存在,请求出D点的位置;若不存在,请说明理由.第三讲 立体几何微专题1 线面角保分题解析:(1)证明:如图,连接AC ,∵四边形ABCD 是正方形,∴AC ⊥BD .又P A ⊥平面ABCD ,BD ⊂平面ABCD ,∴P A ⊥BD , ∵P A ,AC ⊂平面P AC ,P A∩AC =A , ∴BD ⊥平面P AC , 又CM ⊂平面P AC , ∴BD ⊥CM .(2)易知AB ,AD ,AP 两两垂直,以点A 为原点,建立如图所示的空间直角坐标系A - xyz . ∵P A =2AB =4,∴A (0,0,0),P (0,0,4),M (0,0,2),C (2,2,0),D (0,2,0), ∴MC ⃗⃗⃗⃗⃗⃗ =(2,2,-2),MD ⃗⃗⃗⃗⃗⃗ =(0,2,-2),PC ⃗⃗⃗⃗ =(2,2,-4). 设平面MCD 的法向量为n =(x ,y ,z ),则{n ·MC⃗⃗⃗⃗⃗⃗ =2x +2y −2z =0n ·MD ⃗⃗⃗⃗⃗⃗ =2y −2z =0,令y =1,得n =(0,1,1).设直线PC 与平面MCD 所成角为θ,由图可知0<θ<π2,则sin θ=|cos 〈n ,PC ⃗⃗⃗⃗ 〉|=|n·PC ⃗⃗⃗⃗⃗||n ||PC ⃗⃗⃗⃗⃗|=√12+12×√22+22+(−4)2=√36.即直线PC 与平面MCD 所成角的正弦值为√36.提分题[例1]解析:(1)证明:∵AD=CD,∠ADB=∠BDC,BD=BD,∴△ABD≌△CBD,∴AB=CB.∵E为AC的中点,∴DE⊥AC,BE⊥AC.∵DE∩BE=E,DE,BE⊂平面BED,∴AC⊥平面BED.∵AC⊂平面ACD,∴平面BED⊥平面ACD.(2)如图,连接EF.由(1)知AC⊥平面BED.又∵EF⊂平面BED,∴EF⊥AC.AC·EF.∴S△AFC=12当EF⊥BD时,EF的长最小,此时△AFC的面积最小.由(1)知AB=CB=2.又∵∠ACB=60°,∴△ABC是边长为2的正三角形,∴BE=√3.∵AD⊥CD,∴DE=1,∴DE2+BE2=BD2,∴DE⊥BE.以点E为坐标原点,直线EA,EB,ED分别为x轴、y轴、z轴建立空间直角坐标系,则E(0,0,0),A(1,0,0),B(0,√3,0),C(-1,0,0),D(0,0,1),⃗⃗⃗⃗⃗ =(-1,√3,0),AD⃗⃗⃗⃗⃗ =(-1,0,1),DB⃗⃗⃗⃗⃗ =(0,√3,-1),ED⃗⃗⃗⃗⃗ =(0,0,1),EC⃗⃗⃗⃗ =(-∴AB1,0,0).设DF⃗⃗⃗⃗⃗ =λDB ⃗⃗⃗⃗⃗ (0≤λ≤1), 则EF ⃗⃗⃗⃗ =ED ⃗⃗⃗⃗⃗ +DF ⃗⃗⃗⃗⃗ =ED ⃗⃗⃗⃗⃗ +λDB ⃗⃗⃗⃗⃗ =(0,0,1)+λ(0,√3,-1)=(0,√3λ,1-λ). ∵EF ⊥DB ,∴EF⃗⃗⃗⃗ ·DB ⃗⃗⃗⃗⃗ =(0,√3λ,1-λ)·(0,√3,-1)=4λ-1=0, ∴λ=14,∴EF ⃗⃗⃗⃗ =(0,√34,34),∴CF ⃗⃗⃗⃗ =EF ⃗⃗⃗⃗ −EC ⃗⃗⃗⃗ =(0,√34,34)-(-1,0,0)=(1,√34,34).设平面ABD 的法向量为n =(x ,y ,z ), 则{n ·AB⃗⃗⃗⃗⃗ =0,n ·AD⃗⃗⃗⃗⃗ =0,即{−x +√3y =0,−x +z =0.取y =1,则x =√3,z =√3,∴n =(√3,1,√3).设当△AFC 的面积最小时,CF 与平面ABD 所成的角为θ,则sin θ=|cos 〈n ,CF ⃗⃗⃗⃗ 〉|=|n·CF ⃗⃗⃗⃗⃗||n ||CF ⃗⃗⃗⃗⃗ |=|√3×1+1×√34+√3×34|√3+1+3× √1+316+916=4√37. 故当△AFC 的面积最小时,CF 与平面ABD 所成的角的正弦值为4√37. [巩固训练1]解析:(1)证明:∵P A ⊥平面ABCD ,CD ⊂平面ABCD ,∴P A ⊥CD , ∵四边形ABCD 为矩形,∴AD ⊥CD ,又AD∩P A =A ,AD 、P A ⊂平面P AD ,∴CD ⊥平面P AD , ∵AE ⊂平面P AD ,∴AE ⊥CD ,在△P AD 中,P A =AD ,E 为PD 的中点,∴AE ⊥PD , 而PD∩CD =D ,PD 、CD ⊂平面PCD , ∴AE ⊥平面PCD .(2)以A 为坐标原点,分别以AB 、AD 、AP 所在直线为x 、y 、z 轴建立空间直角坐标系, 设AP =a (a >0),则C (2,1,0),P (0,0,a ),E (0,12,a2), ∴AC⃗⃗⃗⃗⃗ =(2,1,0),AE ⃗⃗⃗⃗⃗ =(0,12,a2),PC ⃗⃗⃗⃗ =(2,1,-a ), 设平面ACE 的一个法向量为n =(x ,y ,z ), 则{n ·AC ⃗⃗⃗⃗⃗ =2x +y =0n ·AE⃗⃗⃗⃗⃗ =12y +a 2z =0,取y =-a ,可得n =(a2,-a ,-1).设直线PC 与平面ACE 所成角为θ,则sin θ=|cos 〈n ,PC ⃗⃗⃗⃗ 〉|=|n·FC ⃗⃗⃗⃗⃗||n ||FC ⃗⃗⃗⃗⃗|=√54a 2+1·√5+a 2=√29+20a2+5a ≤27,当且仅当a =√2时等号成立.即当AP =√2时,直线PC 与平面ACE 所成角最大, 此时三棱锥E - ABC 的体积V =13×12×2×1×√22=√26.微专题2 二面角保分题解析:(1)证明:取AD 的中点M ,连接EM 、MC ,∵E 为A 1D 的中点,F 为CC 1的中点,∴EM ∥AA 1,EM =12AA 1,又CF ∥AA 1,CF =12AA 1,∴EM ∥CF ,EM =CF ,∴四边形EMCF 为平行四边形,∴EF ∥CM , 又EF ⊄平面ABCD ,CM ⊂平面ABCD , ∴EF ∥平面ABCD .(2)设AB =AA 1=2BC =2CD =4,∵AC ⊥BC ,∴AC =2√3.由题意知CA 、CB 、CC 1两两垂直,故以C 为坐标原点,分别以CA 、CB 、CC 1所在直线为x 、y 、z 轴建立空间直角坐标系.则A 1(2√3,0,4)、O (√3,1,0)、F (0,0,2)、C (0,0,0)、D (√3,-1,0), ∴A 1D 的中点E 的坐标为(3√32,-12,2), ∴OF⃗⃗⃗⃗⃗ =(-√3,-1,2),EF ⃗⃗⃗⃗ =(-3√32,12,0), 设平面OEF 的一个法向量为n =(x ,y ,z ),则{n ·OF ⃗⃗⃗⃗⃗ =0n ·EF ⃗⃗⃗⃗ =0,即{−√3x −y +2z =0−3√32x +12y =0,即{√3x +y −2z =03√3x −y =0, 令x =√3,得n =(√3,9,6), ∵AC ⊥BC ,AC ⊥CC 1,BC ∩CC 1=C , ∴AC ⊥平面BCC 1,∴平面BCC 1的一个法向量为CA ⃗⃗⃗⃗⃗ =(2√3,0,0),cos 〈n ,CA ⃗⃗⃗⃗⃗ 〉=n·CA ⃗⃗⃗⃗⃗|n |·|CA ⃗⃗⃗⃗⃗|=√3+81+36·2√3=√1020, ∴平面OEF 与平面BCC 1夹角的余弦值为√1020. 提分题[例2] 解析:(1)证明:连接BD 交AC 于O , 易证O 为BD 中点,又F 是PD 的中点, 所以OF ∥PB ,又OF ⊂平面AFC ,且PB 不在平面AFC 内, 故PB ∥平面AFC .(2)取PC 中点为Q ,以O 为坐标原点,OB 为x 轴,OC 为y 轴,OQ 为z 轴建立空间直角坐标系,设OB =m ,则A (0,-1,0),B (m ,0,0),C (0,1,0),P (0,-1,2),D (-m ,0,0)⇒F (-m2,-12,1),AP ⃗⃗⃗⃗⃗ =(0,0,2),OF ⃗⃗⃗⃗⃗ =(-m 2,-12,1),OC⃗⃗⃗⃗⃗ =(0,1,0), 设平面AFC 的法向量为n =(x ,y ,z ),由{n ⊥OF ⃗⃗⃗⃗⃗ n ⊥OC ⃗⃗⃗⃗⃗ ⇒{−m2x −12y +z =0y =0,令x =2,有n =(2,0,m ),由P A 与平面AFC 所成的角正弦值为√217⇒√217=|AP ⃗⃗⃗⃗⃗ ·n||AP⃗⃗⃗⃗⃗ |·|n|=2√4+m 2⇒m =√3, 平面ACD 的法向量为m =(0,0,1),则锐二面角F - AC - D 的余弦值为 |m·n ||m |·|n |=√3√7=√217. [例3] 解析:(1)证明:在梯形ABCD 中取AD 中点N ,连接CN , 则由BC 平行且等于AN 知ABCN 为平行四边形,所以CN =AB , 由CN =12AD 知C 点在以AD 为直径的圆上,所以AC ⊥CD . 又AP ⊥CD ,AP∩AC =A, AP ,AC ⊂平面P AC , ∴CD ⊥平面P AC , 又CD ⊂平面ADC , ∴平面APC ⊥平面ADC .(2)取AC 中点O ,连接PO ,由AP =PC ,可知PO ⊥AC ,再由平面P AC ⊥平面ACD ,AC 为两面交线,所以PO ⊥平面ACD ,以O 为原点,OA 为x 轴,过O 且与OA 垂直的直线为y 轴,OP 为z 轴建立空间直角坐标系,令AB =2,则A (√3,0,0),C (-√3,0,0),P (0,0,1),D (-√3,2,0), 由V P - ACM ∶V D - ACM =1∶2,得PM ⃗⃗⃗⃗⃗⃗ =13PD ⃗⃗⃗⃗⃗ , 所以OM⃗⃗⃗⃗⃗⃗ =OP ⃗⃗⃗⃗⃗ +PM ⃗⃗⃗⃗⃗⃗ =OP ⃗⃗⃗⃗⃗ +13PD ⃗⃗⃗⃗⃗ =(-√33,23,23), 设平面ACM 的法向量为n =(x ,y ,z ),则由{n ·OM ⃗⃗⃗⃗⃗⃗ =0n ·OA ⃗⃗⃗⃗⃗ =0得{−√33x +23y +23z =0√3x =0, 取z =-1得x =0,y =1,所以n =(0,1,-1),而平面P AC 的法向量m =(0,1,0),所以cos 〈n ,m 〉=m·n |m ||n |=√22. 又因为二面角P - AC - M 为锐二面角,所以其余弦值为√22. [巩固训练2]1.解析:(1)证明:取线段PD 的中点H ,连接OH 、HA ,如图,在△PCD 中,O 、H 分别是PC 、PD 的中点,所以OH ∥CD 且OH =12CD , 所以OH ∥AS 且OH =AS ,所以四边形ASOH 是平行四边形,所以SO ∥AH , 又AH ⊂平面P AD ,SO ⊄平面P AD ,所以SO ∥平面P AD .(2)取线段AD 、BC 的中点E 、F ,连结PE 、EF .由点E 是线段AD 的中点,P A =PD 可得PE ⊥AD ,又EF ⊥AD ,所以∠PEF 是二面角P - AD - B 的平面角,即∠PEF =23π,以E 为原点,EA ⃗⃗⃗⃗⃗ 、EF ⃗⃗⃗⃗ 方向分别为x 轴、y 轴正方向,建立如图所示坐标系,在△P AD 中,AD =4,P A =PD =2√2知:PE =2,所以P (0,-1,√3),D (-2,0,0),B (2,2,0),C (-2,2,0),所以PD⃗⃗⃗⃗⃗ =(-2,1,-√3),PB ⃗⃗⃗⃗⃗ =(2,3,-√3),PC ⃗⃗⃗⃗ =(-2,3,-√3), 设平面PBC 的法向量n =(x ,y ,z ),则{n ·PB ⃗⃗⃗⃗⃗=0n ·PC⃗⃗⃗⃗ =0,即{2x +3y −√3z =0−2x +3y −√3z =0,可取n =(0,1,√3),设直线PD 与平面PBC 所成角为θ, 则sin θ=|cos 〈PD⃗⃗⃗⃗⃗ ,n 〉|=2·2√2=√24,所以直线PD 与平面PBC 所成角的正弦值为√24.2.解析:(1)证明:在等腰梯形ABCD 中,过A 作AE ⊥BC 于E ,过D 作DF ⊥BC 于F ,因为在等腰梯形ABCD 中,AD ∥BC ,AD =AB =CD =1,∠BCD =60°,所以BE =CF =12CD =12,AE =DF =√12−(12)2=√32,所以AC =BD =√(32)2+(√32)2=√3,BC =2,所以BD 2+CD 2=BC 2,所以BD ⊥CD ,同理AB ⊥AC , 又因为AP =AB =1,PB =√2, ∴AP 2+AB 2=PB 2,∴AB ⊥AP 又AC∩AP =A ,AC ,AP ⊂平面ACP , 所以AB ⊥平面ACP , 因为PC ⊂平面ACP , 所以AB ⊥PC .(2)取AC 的中点为M ,BC 的中点为N ,则MN ∥AB , 因为AB ⊥平面ACP ,所以MN ⊥平面ACP ,因为AC ,PM ⊂平面ACP ,所以MN ⊥AC ,MN ⊥PM , 因为P A =PC ,AC 的中点为M ,所以PM ⊥AC , 所以MN ,MC ,MP 两两垂直,所以以M 为原点,以MN 所在直线为x 轴,以MC 所在直线为y 轴,以MP 所在直线为z 轴建立空间直角坐标系,则A (0,-√32,0),B (1,-√32,0),C (0,√32,0),P (0,0,12), PC⃗⃗⃗⃗ =(0,√32,-12),PB ⃗⃗⃗⃗⃗ =(1,-√32,-12), 平面APC 的一个法向量为m =AB ⃗⃗⃗⃗⃗ =(1,0,0), 设平面PBC 的一个法向量为n =(x ,y ,z ),则 {n ·PC⃗⃗⃗⃗ =√32y −12z =0n ·PB ⃗⃗⃗⃗⃗ =x −√32y −12z =0,令y =1,则n =(√3,1,√3),所以cos 〈m ,n 〉=m·n |m ||n |=√31×√7=√217, 因为二面角A - PC - B 为锐角, 所以二面角A - PC - B 的余弦值为√217.微专题3 探索性问题提分题[例4] 解析:(1)证明:因为四边形ABCD 为平行四边形,且△ADE 为等边三角形, 所以∠BCE =120°,又E 为CD 的中点,所以CE =ED =DA =CB ,即△BCE 为等腰三角形, 所以∠CEB =30°.所以∠AEB =180°-∠AED -∠BEC =90°, 即BE ⊥AE .又因为平面AEP ⊥平面ABCE ,平面APE ∩平面ABCE =AE ,BE ⊂平面ABCE , 所以BE ⊥平面APE ,又AP ⊂平面APE ,所以BE ⊥AP .(2)取AE 的中点O ,连接PO ,由于△APE 为正三角形,则PO ⊥AE , 又平面APE ⊥平面ABCE ,平面APE ∩平面ABCE =AE ,PO ⊂平面EAP , 所以PO ⊥平面ABCE ,PO =√3,BE =2√3, 取AB 的中点G ,则OG ∥BE , 由(1)得BE ⊥AE ,所以OG ⊥AE ,以点O 为原点,分别以OA ,OG ,OP 所在的直线为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系O - xyz ,则O (0,0,0),A (1,0,0),B (-1,2√3,0),P (0,0,√3),E (-1,0,0), 则EA ⃗⃗⃗⃗⃗ =(2,0,0),EB ⃗⃗⃗⃗⃗ =(0,2√3,0),PB ⃗⃗⃗⃗⃗ =(-1,2√3,-√3),EP ⃗⃗⃗⃗ =(1,0,√3), 假设存在点F ,使平面AEF 与平面AEP 的夹角为45°, 设PF⃗⃗⃗⃗ =λPB ⃗⃗⃗⃗⃗ =(-λ,2√3λ,-√3λ),λ∈[0,1], 则EF ⃗⃗⃗⃗ =EP ⃗⃗⃗⃗ +PF ⃗⃗⃗⃗ =(1,0,√3)+(-λ,2√3λ,-√3λ)=(1-λ,2√3λ,√3−√3λ), 设平面AEF 的法向量为m =(x ,y ,z ),由{EF ⃗⃗⃗⃗·m =0EA ⃗⃗⃗⃗⃗ ·m =0得{(1−λ)x +2√3λy +(√3,-√3λ)z =02x =0, 取z =2λ,得m =(0,λ-1,2λ); 由(1)知EB⃗⃗⃗⃗⃗ 为平面AEP 的一个法向量,于是,cos 45°=|cos 〈m ,EB ⃗⃗⃗⃗⃗ 〉|=|m·EB ⃗⃗⃗⃗⃗||m |·|EB⃗⃗⃗⃗⃗ |=2√3|λ−1|2√3·√5λ2−2λ+1=√22,解得λ=13或λ=-1(舍去),所以存在点F ,且当点F 为线段PB 的靠近点P 的三等分点时,平面AEF 与平面AEP 的夹角为45°.[巩固训练3]解析:(1)证明:取AB 的中点E ,连接SE ,CE ,∵SA =SB ,∴SE ⊥AB , ∵BC ⊥AC ,∴三角形ACB 为直角三角形,∴BE =EC , 又BS =SC ,∴△SEC ≌△SEB ,∴∠SEB =∠SEC =90°, ∴SE ⊥EC ,又SE ⊥AB ,AB∩CE =E ,∴SE ⊥平面ABC . 又SE ⊂平面SAB ,∴平面SAB ⊥平面ABC .(2)以E 为坐标原点,平行AC 的直线为x 轴,平行BC 的直线为y 轴,ES 为z 轴建立空间直角坐标系,如图,不妨设SA =SB =SC =2,SC ⊥SA ,则AC =2√2,BC =SC =2知EC =2√3,SE =1,则A (-√2,1,0),B (√2,-1,0),C (√2,1,0),E (0,0,0),S (0,0,1),∴AB⃗⃗⃗⃗⃗ =(2√2,-2,0),SA ⃗⃗⃗⃗ =(-√2,1,-1), 设D (x ,y ,z ),CD ⃗⃗⃗⃗⃗ =λCS ⃗⃗⃗⃗ (0≤λ≤1),则(x -√2,y -1,z )=λ(-√2,-1,1), ∴D (√2−√2λ,1-λ,λ),BD⃗⃗⃗⃗⃗ =(-√2λ,2-λ,λ). 设平面SAB 的一个法向量为n =(x 1,y 1,z 1),则{n ·AB ⃗⃗⃗⃗⃗ =2√2x 1−2y 1=0n ·SA ⃗⃗⃗⃗ =−√2x 1+y 1−z 1=0,取x 1=1,得n =(1,√2,0),sin 60°=|n·BD ⃗⃗⃗⃗⃗⃗ ||n ||BD⃗⃗⃗⃗⃗⃗ |,则√2−2√2λ|√3×√2λ2+(2−λ)2+λ2=√32, 得λ2+7λ+1=0,又∵0≤λ≤1,方程无解,∴不存在点D ,使直线BD 与平面SAB 所成的角为60°.。
高考数学大二轮复习专题3立体几何第3讲空间向量与立体几何课件(理科)

利用空间向量求空间角
考情调研
考向分析
本考点为高考中的必考内容,涉及用向量
法计算空间异面直线所成角、直线和平面
所成角、二面角及空间距离等内容,考查 1.利用空间向量求线线角、线面角、二面角.
热点是空间角的求解.题型以解答题为主, 2.由空间角的大小求参数值或线段长
要求有较强的运算能力,广泛应用函数与
的建立及空间向量坐标的运算能力及应用能力,有
时也以探索论证题的形式出现.
[题组练透] 1.如图所示,正三棱柱(底面为正三角形的直三棱柱)ABC-A1B1C1 的所有棱长都为 2, D 为 CC1 的中点.求证:AB1⊥平面 A1BD.
证明:取 BC 的中点 O,连接 AO. 因为△ABC 为正三角形, 所以 AO⊥BC. 因为在正三棱柱 ABC-A1B1C1 中,平面 ABC⊥平面 BCC1B1, 且平面 ABC∩平面 BCC1B1=BC, 所以 AO⊥平面 BCC1B1. 取 B1C1 的中点 O1,以 O 为原点,分别以 OB,OO1, OA 所在直线为 x 轴,y 轴,z 轴建立空间直角坐标系,如图所示,
则 B(1,0,0),D(-1,1,0),A1(0,2, 3),A(0,0, 3),B1(1,2,0). 设平面 A1BD 的法向量为 n=(x,y,z),B→A1=(-1,2, 3),B→D=(-2,1,0). 因为 n⊥B→A1,n⊥B→D, 故nn··BB→→DA1==00,, 即- -x2+ x+2yy+ =0,3z=0, 令 x=1,则 y=2,z=- 3, 故 n=(1,2,- 3)为平面 A1BD 的一个法向量, 而A→B1=(1,2,- 3),所以A→B1=n,所以A→B1∥n, 故 AB1⊥平面 A1BD.
n·A→B=0 由n·A→M=0
全国高考数学二轮复习专题四立体几何与空间向量第3讲立体几何中的向量方法课件理

解
由题意知
M-1,2,
22,C(2,4,0),M→C=3,2,-
22.
设直线MC与平面BDP所成的角为α,则 sin α=|cos〈n,M→C〉|=||nn|·|MM→→CC||=296.
所以直线
MC
与平面
BDP
所成角的正弦值为2 9
6 .
解答
2.(2018·全国Ⅲ)如图,边长为2的正方形ABCD所 在的平面与半圆弧CD 所在平面垂直,M是 CD上异 于C,D的点. (1)证明:平面AMD⊥平面BMC;
跟踪演练2 如图,在四面体ABCD中,BA= BC,∠BAD=∠BCD=90°. (1)证明:BD⊥AC;
证明
(2)若∠ABD=60°,BA=2,四面体ABCD的体积为2,求二面角B-AC -D的余弦值.
解答
热点三 利用空间向量求解存在探索性问题
存在探索性问题的基本特征是要判断在某些确定条件下的某一数学对 象(数值、图形、函数等)是否存在或某一结论是否成立.解决这类问题 的基本策略是先假设题中的数学对象存在(或结论成立)或暂且认可其 中的一部分结论,然后在这个前提下进行逻辑推理,若由此导出矛盾, 则否定假设;否则,给出肯定结论.
解答
真题押题精练
真题体验 1.(2017·北京)如图,在四棱锥P—ABCD中,底 面ABCD为正方形,平面PAD⊥平面ABCD,点 M在线段PB上,PD∥平面MAC,PA=PD= 6, AB=4. (1)求证:M为PB的中点;
证明
(2)求二面角B—PD—A的大小;
解答
(3)求直线MC与平面BDP所成角的正弦值.
(3)二面角 设 α-a-β 的平面角为 θ(0≤θ≤π), 则|cos θ|=||μμ|·|vv||=|cos〈μ,v〉|.
《创新设计》2022高考数学(浙江专用理科)二轮专题精练:专题四 立体几何4-3 Word版含解析

第3讲 立体几何中的向量方法(建议用时:60分钟) 一、选择题1.已知平面ABC ,点M 是空间任意一点,点M 满足条件OM→=34OA →+18OB →+18OC →,则直线AM( ).A .与平面ABC 平行B .是平面ABC 的斜线 C .是平面ABC 的垂线D .在平面ABC 内解析 由已知得M ,A ,B ,C 四点共面,所以AM 在平面ABC 内,选D. 答案 D2.如图,正方体ABCD -A 1B 1C 1D 1的棱长为a ,M ,N 分别为A 1B 和AC 上的点,A 1M =AN =2a3,则MN 与平面BB 1C 1C 的位置关系是 ( ).A .相交B .平行C .垂直D .不能确定解析 MN →=MB →+BC →+CN →=23A 1B →+BC →+23CA → =23(A 1B 1→+B 1B →)+BC →+23(CD →+DA →) =23B 1B →+BC →+23DA →, 又CD →是平面BB 1C 1C 的一个法向量,且MN →·CD →=23B 1B →+BC →+23DA →·CD →=0,∴MN →⊥CD →,又MN ⊄面BB 1C 1C ,∴MN ∥平面BB 1C 1C . 答案 B3.如图,四棱锥S -ABCD 的底面为正方形,SD ⊥底面ABCD ,则下列结论中不正确的是 ( ).A .AC ⊥SB B .AB ∥平面SCDC .SA 与平面SBD 所成的角等于SC 与平面SBD 所成的角 D .AB 与SC 所成的角等于DC 与SA 所成的角解析 选项A 正确,由于SD 垂直于底面ABCD ,而AC ⊂平面ABCD ,所以AC ⊥SD ;再由四边形ABCD 为正方形,所以AC ⊥BD ;而BD 与SD 相交,所以,AC ⊥平面SBD ,AC ⊥SB . 选项B 正确,由于AB ∥CD ,而CD ⊂平面SCD ,AB ⊄平面SCD ,所以AB ∥平面SCD . 选项C 正确,设AC 与BD 的交点为O ,易知SA 与平面SBD 所成的角就是∠ASO ,SC 与平面SBD 所成的角就是∠CSO ,易知这两个角相等.选项D 错误,AB 与SC 所成的角等于∠SCD ,而DC 与SA 所成的角是∠SAB ,这两个角不相等. 答案 D4.已知正三棱柱ABC -A 1B 1C 1的侧棱长与底面边长相等,则AB 1与侧面ACC 1A 1所成角的正弦等于 ( ).A.64B.104C.22D.32解析 如图所示建立空间直角坐标系,设正三棱柱的棱长为2,O (0,0,0),B (3,0,0),A (0,-1,0),B 1(3,0,2),则AB 1→=(3,1,2),则BO →=(-3,0,0)为侧面ACC 1A 1的法向量,由sin θ=|AB 1→·BO →||AB1→||BO →|=64.答案 A5.(2022·新课标全国Ⅱ卷)直三棱柱ABC -A 1B 1C 1中,∠BCA =90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC =CA =CC 1,则BM 与AN 所成角的余弦值为 ( ). A.110 B.25 C.3010D.22解析 法一 由于∠BCA =90°,三棱柱为直三棱柱,且BC =CA =CC 1,可将三棱柱补成正方体.建立如图(1)所示空间直角坐标系.设正方体棱长为2,则可得A (0,0,0),B (2,2,0),M (1,1,2),N (0,1,2),∴BM→=(1,1,2)-(2,2,0)=(-1,-1,2),AN →=(0,1,2).∴cos 〈BM →,AN →〉=BM →·AN →|BM →||AN →|=-1+4(-1)2+(-1)2+22×02+12+22=36×5=3010. 法二 如图(2),取BC 的中点D ,连接MN ,ND ,AD ,由于MN 綉12B 1C 1綉BD ,因此有ND 綉BM ,则ND 与NA 所成角即为异面直线BM 与AN 所成角.设BC =2,则BM =ND =6,AN =5,AD =5,因此cos ∠AND =ND 2+NA 2-AD 22ND ·NA =3010.答案 C6.如图,点P 是单位正方体ABCD -A 1B 1C 1D 1中异于A 的一个顶点,则AP →·AB→的值为( ).A .0B .1C .0或1D .任意实数 解析 AP→可为下列7个向量:AB →,AC →,AD →,AA 1→,AB 1→,AC 1→,AD 1→. 其中一个与AB →重合,AP →·AB →=|AB →|2=1; AD →,AD 1→,AA 1→与AB →垂直, 这时AP →·AB→=0; AC →,AB 1→与AB →的夹角为45°, 这时AP →·AB→=2×1×cos π4=1, 最终AC 1→·AB →=3×1×cos ∠BAC 1=3×13=1,故选C. 答案 C7.(2021·浙江卷)如图,已知△ABC ,D 是AB 的中点,沿直线CD 将△ACD 翻折成△A ′CD ,。
新(浙江专用)高考数学二轮专题突破 专题四 立体几何与空间向量 第3讲 立体几何中的向量方法 理

第3讲立体几何中的向量方法1.(2014·课标全国Ⅱ)直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为( )A.110B.25C.3010D.222.(2015·浙江)如图,在三棱柱ABCA1B1C1中,∠BAC=90°,AB=AC=2,A1A=4,A1在底面ABC的射影为BC的中点,D是B1C1的中点.(1)证明:A1D⊥平面A1BC;(2)求二面角A1BDB1的平面角的余弦值.以空间几何体为载体考查空间角是高考命题的重点,与空间线面关系的证明相结合,热点为二面角的求解,均以解答的形式进行考查,难度主要体现在建立空间直角坐标系和准确计算上.热点一利用向量证明平行与垂直设直线l的方向向量为a=(a1,b1,c1),平面α、β的法向量分别为μ=(a2,b2,c2),v=(a3,b3,c3)则有:(1)线面平行l∥α⇔a⊥μ⇔a·μ=0⇔a1a2+b1b2+c1c2=0.(2)线面垂直l⊥α⇔a∥μ⇔a=kμ⇔a1=ka2,b1=kb2,c1=kc2.(3)面面平行α∥β⇔μ∥v⇔μ=λv⇔a2=λa3,b2=λb3,c2=λc3.(4)面面垂直α⊥β⇔μ⊥v⇔μ·v=0⇔a2a3+b2b3+c2c3=0.例1 如图,在直三棱柱ADE—BCF中,面ABFE和面ABCD都是正方形且互相垂直,M为AB的中点,O为DF的中点.运用向量方法证明:(1)OM∥平面BCF;(2)平面MDF⊥平面EFCD.思维升华用向量知识证明立体几何问题,仍然离不开立体几何中的定理.如要证明线面平行,只需要证明平面外的一条直线和平面内的一条直线平行,即化归为证明线线平行,用向量方法证明直线a∥b,只需证明向量a=λb(λ∈R)即可.若用直线的方向向量与平面的法向量垂直来证明线面平行,仍需强调直线在平面外.跟踪演练1 如图所示,已知直三棱柱ABC —A 1B 1C 1中,△ABC 为等腰直角三角形,∠BAC =90°,且AB =AA 1,D 、E 、F 分别为B 1A 、C 1C 、BC 的中点.求证:(1)DE ∥平面ABC ; (2)B 1F ⊥平面AEF .热点二 利用空间向量求空间角设直线l ,m 的方向向量分别为a =(a 1,b 1,c 1),b =(a 2,b 2,c 2).平面α,β的法向量分别为μ=(a 3,b 3,c 3),v =(a 4,b 4,c 4)(以下相同). (1)线线夹角设l ,m 的夹角为θ(0≤θ≤π2),则cos θ=|a ·b ||a ||b |=|a 1a 2+b 1b 2+c 1c 2|a 21+b 21+c 21a 22+b 22+c 22.(2)线面夹角设直线l 与平面α的夹角为θ(0≤θ≤π2),则sin θ=|a ·μ||a ||μ|=|cos 〈a ,μ〉|.(3)面面夹角设平面α、β的夹角为θ(0≤θ<π), 则|cos θ|=|μ·v ||μ||v |=|cos 〈μ,v 〉|.例2 (2015·安徽)如图所示,在多面体A 1B 1D 1DCBA 中,四边形AA 1B 1B ,ADD 1A 1,ABCD 均为正方形,E 为B 1D 1的中点,过A 1,D ,E 的平面交CD 1于F . (1)证明:EF ∥B 1C ;(2)求二面角E A 1D B 1的余弦值.思维升华(1)运用空间向量坐标运算求空间角的一般步骤:①建立恰当的空间直角坐标系;②求出相关点的坐标;③写出向量坐标;④结合公式进行论证、计算;⑤转化为几何结论.(2)求空间角注意:①两条异面直线所成的角α不一定是直线的方向向量的夹角β,即cos α=|cos β|.②两平面的法向量的夹角不一定是所求的二面角,有可能为两法向量夹角的补角.③直线和平面所成的角的正弦值等于平面法向量与直线方向向量夹角的余弦值的绝对值,即注意函数名称的变化.跟踪演练2 如图,已知⊙O的直径AB=3,点C为⊙O上异于A,B的一点,VC⊥平面ABC,且VC=2,点M为线段VB的中点.(1)求证:BC⊥平面VAC;(2)若AC=1,求二面角M-VA-C的余弦值.热点三利用空间向量求解探索性问题存在探索性问题的基本特征是要判断在某些确定条件下的某一数学对象(数值、图形、函数等)是否存在或某一结论是否成立.解决这类问题的基本策略是先假设题中的数学对象存在(或结论成立)或暂且认可其中的一部分结论,然后在这个前提下进行逻辑推理,若由此导出矛盾,则否定假设;否则,给出肯定结论.例3 (2015·宁波二模)如图,三棱柱ABC -A 1B 1C 1的侧棱AA 1,底面ABC ,∠ACB =90°,E 是棱CC 1上的动点,F 是AB 的中点,AC =1,BC =2,AA 1=4. (1)当E 是棱CC 1的中点时,求证:CF ∥平面AEB 1;(2)在棱CC 1上是否存在点E ,使得二面角A -EB 1-B 的余弦值是21717?若存在,求CE 的长;若不存在,请说明理由.思维升华 空间向量最适合于解决这类立体几何中的探索性问题,它无需进行复杂的作图、论证、推理,只需通过坐标运算进行判断.解题时,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标是否有解,是否有规定范围内的解”等,所以为使问题的解决更简单、有效,应善于运用这一方法.跟踪演练3 如图所示,四边形ABCD 是边长为1的正方形,MD ⊥平面ABCD ,NB ⊥平面ABCD ,且MD =NB =1,E 为BC 的中点.(1)求异面直线NE 与AM 所成角的余弦值;(2)在线段AN 上是否存在点S ,使得ES ⊥平面AMN ?若存在,求线段AS 的长;若不存在,请说明理由.如图,五面体中,四边形ABCD 是矩形,AB ∥EF ,AD ⊥平面ABEF ,且AD =1,AB =12EF =22,AF =BE =2,P 、Q 分别为AE 、BD 的中点.(1)求证:PQ ∥平面BCE ;(2)求二面角A -DF -E 的余弦值.提醒:完成作业专题四第3讲二轮专题强化练专题四第3讲 立体几何中的向量方法A 组 专题通关1.已知平面ABC ,点M 是空间任意一点,点M 满足条件OM →=34OA →+18OB →+18OC →,则直线AM ( )A .与平面ABC 平行B .是平面ABC 的斜线 C .是平面ABC 的垂线D .在平面ABC 内2.如图,点P 是单位正方体ABCD -A 1B 1C 1D 1中异于A 的一个顶点,则AP →·AB →的值为( ) A .0 B .1 C .0或1 D .任意实数3.如图所示,正方体ABCD -A 1B 1C 1D 1的棱长为a ,M 、N 分别为A 1B 和AC 上的点,A 1M =AN =23a ,则MN 与平面BB 1C 1C 的位置关系是( ) A .相交 B .平行 C .垂直D .不能确定4.如图,三棱锥A -BCD 的棱长全相等,E 为AD 的中点,则直线CE 与BD 所成角的余弦值为( )A.36B.32C.336D.125.已知正三棱柱ABC -A 1B 1C 1的侧棱长与底面边长相等,则AB 1与侧面ACC 1A 1所成角的正弦值等于( ) A.64 B.104 C.22D.326.在棱长为1的正方体ABCD -A 1B 1C 1D 1中,M ,N 分别为A 1B 1,BB 1的中点,那么直线AM 与CN 所成角的余弦值为________.7.在一直角坐标系中,已知A (-1,6),B (3,-8),现沿x 轴将坐标平面折成60°的二面角,则折叠后A 、B 两点间的距离为________.8.已知ABCD -A 1B 1C 1D 1为正方体,①(A 1A →+A 1D 1→+A 1B 1→)2=3A 1B 1→2;②A 1C →·(A 1B 1→-A 1A →)=0;③向量AD 1→与向量A 1B →的夹角是60°;④正方体ABCD -A 1B 1C 1D 1的体积为|AB →·AA 1→·AD →|.其中正确命题的序号是________.9.如图,在底面是矩形的四棱锥P —ABCD 中,PA ⊥底面ABCD ,E ,F 分别是PC ,PD 的中点,PA =AB =1,BC =2. (1)求证:EF ∥平面PAB ; (2)求证:平面PAD ⊥平面PDC .10.(2015·重庆)如图,三棱锥PABC 中,PC ⊥平面ABC ,PC =3,∠ACB =π2.D ,E 分别为线段AB ,BC 上的点,且CD =DE =2,CE =2EB =2. (1)证明:DE ⊥平面PCD ; (2)求二面角APDC 的余弦值.B 组 能力提高11.设A ,B ,C ,D 是空间不共面的四个点,且满足AB →·AC →=0,AD →·AC →=0,AD →·AB →=0,则△BCD 的形状是( ) A .钝角三角形 B .直角三角形 C .锐角三角形D .无法确定12.(2015·温州质检)如图所示,在矩形ABCD 中,点E ,F 分别在线段AB ,AD 上,AE =EB =AF =23FD =4.沿直线EF 将△AEF 翻折成△A ′EF ,使平面A ′EF ⊥平面BEF ,则二面角A ′-FD -C 的余弦值为________.13.已知正方体ABCD -A 1B 1C 1D 1的棱长为1,E 、F 分别为BB 1、CD 的中点,则点F 到平面A 1D 1E 的距离为______________.14.(2015·浙江名校联考)如图,AB 为圆O 的直径,点E 、F 在圆O 上,AB ∥EF ,矩形ABCD所在的平面与圆O所在的平面互相垂直.已知AB=2,EF=1.(1)求证:平面DAF⊥平面CBF;(2)求直线AB与平面CBF所成角的大小;(3)当AD的长为何值时,平面DFC与平面FCB所成的锐二面角的大小为60°?学生用书答案精析第3讲 立体几何中的向量方法 高考真题体验1.C [方法一 补成正方体,利用向量的方法求异面直线所成的角. 由于∠BCA =90°,三棱柱为直三棱柱,且BC =CA =CC 1, 可将三棱柱补成正方体.建立如图(1)所示空间直角坐标系.设正方体棱长为2,则可得A (0,0,0),B (2,2,0),M (1,1,2),N (0,1,2), ∴BM →=(-1,-1,2), AN →=(0,1,2).∴cos〈BM →,AN →〉=BM →·AN →|BM →||AN →|=-1+4-12+-12+22×02+12+22=36×5=3010.方法二 通过平行关系找出两异面直线的夹角,再根据余弦定理求解.如图(2),取BC 的中点D ,连接MN ,ND ,AD ,由于MN 綊12B 1C 1綊BD ,因此有ND 綊BM ,则ND 与NA 所成的角即为异面直线BM 与AN 所成的角.设BC =2,则BM =ND =6,AN =5,AD =5,因此cos∠AND =ND 2+NA 2-AD 22ND ·NA =3010.]2.(1)证明 设E 为BC 的中点,由题意得A 1E ⊥平面ABC ,所以A 1E ⊥AE . 因为AB =AC ,所以AE ⊥BC .故AE ⊥平面A 1BC .由D ,E 分别为B 1C 1,BC 的中点,得DE ∥B 1B 且DE =B 1B ,从而DE ∥A 1A 且DE =A 1A ,所以A 1AED 为平行四边形. 故A 1D ∥AE .又因为AE ⊥平面A 1BC ,所以A 1D ⊥平面A 1BC .(2)解 以CB 的中点E 为原点,分别以射线EA ,EB ,EA 1为x ,y ,z 轴的正半轴,建立空间直角坐标系Exyz ,如图所示. 由题意知各点坐标如下:A 1(0,0,14),B (0,2,0),D (-2,0,14),B 1(-2,2,14).因此A 1B →=(0,2,-14),BD →=(-2,-2,14),DB 1→=(0,2,0).设平面A 1BD 的法向量为m =(x 1,y 1,z 1),平面B 1BD 的法向量为n =(x 2,y 2,z 2). 由⎩⎪⎨⎪⎧ m ·A 1B →=0,m ·BD →=0,即⎩⎨⎧2y 1-14z 1=0,-2x 1-2y 1+14z 1=0,可取m =(0,7,1). 由⎩⎪⎨⎪⎧n ·DB 1→=0,n ·BD →=0,即⎩⎨⎧2y 2=0,-2x 2-2y 2+14z 2=0,可取n =(7,0,1).于是 |cos 〈m ,n 〉|=|m ·n ||m |·|n |=18.由题意可知,所求二面角的平面角是钝角,故二面角A 1BDB 1的平面角的余弦值为-18.热点分类突破例1 证明 方法一 由题意,得AB ,AD ,AE 两两垂直,以A 为原点建立如图所示的空间直角坐标系.设正方形边长为1,则A (0,0,0),B (1,0,0),C (1,1,0),D (0,1,0), F (1,0,1),M ⎝ ⎛⎭⎪⎫12,0,0,O ⎝ ⎛⎭⎪⎫12,12,12. (1)OM →=⎝ ⎛⎭⎪⎫0,-12,-12,BA →=(-1,0,0),∴OM →·BA →=0, ∴OM →⊥BA →. ∵棱柱ADE —BCF 是直三棱柱, ∴AB ⊥平面BCF ,∴BA →是平面BCF 的一个法向量, 且OM ⊄平面BCF , ∴OM ∥平面BCF .(2)设平面MDF 与平面EFCD 的一个法向量分别为n 1=(x 1,y 1,z 1),n 2=(x 2,y 2,z 2).∵DF →=(1,-1,1),DM →=⎝ ⎛⎭⎪⎫12,-1,0,DC →=(1,0,0),CF →=(0,-1,1),由⎩⎪⎨⎪⎧n 1·DF →=0,n 1·DM →=0.得⎩⎪⎨⎪⎧x 1-y 1+z 1=0,12x 1-y 1=0,解得⎩⎪⎨⎪⎧y 1=12x 1,z 1=-12x 1,令x 1=1,则n 1=⎝ ⎛⎭⎪⎫1,12,-12.同理可得n 2=(0,1,1).∵n 1·n 2=0,∴平面MDF ⊥平面EFCD . 方法二 (1)OM →=OF →+FB →+BM →=12DF →-BF →+12BA →=12(DB →+BF →)-BF →+12BA →=-12BD →-12BF →+12BA → =-12(BC →+BA →)-12BF →+12BA →=-12BC →-12BF →.∴向量OM →与向量BF →,BC →共面, 又OM ⊄平面BCF ,∴OM ∥平面BCF . (2)由题意知,BF ,BC ,BA 两两垂直, ∵CD →=BA →,FC →=BC →-BF →,∴OM →·CD →=⎝ ⎛⎭⎪⎫-12BC →-12BF →·BA →=0,OM →·FC →=⎝ ⎛⎭⎪⎫-12BC →-12BF →·(BC →-BF →)=-12BC →2+12BF →2=0.∴OM ⊥CD ,OM ⊥FC ,又CD ∩FC =C , ∴OM ⊥平面EFCD .又OM ⊂平面MDF ,∴平面MDF ⊥平面EFCD .跟踪演练1 证明 (1)如图建立空间直角坐标系A -xyz , 令AB =AA 1=4,则A (0,0,0),E (0,4,2),F (2,2,0),B (4,0,0),B 1(4,0,4).取AB 中点为N ,连接CN , 则N (2,0,0),C (0,4,0),D (2,0,2),∴DE →=(-2,4,0), NC →=(-2,4,0),∴DE →=NC →,∴DE ∥NC ,又∵NC ⊂平面ABC ,DE ⊄平面ABC . 故DE ∥平面ABC .(2)B 1F →=(-2,2,-4),EF →=(2,-2,-2),AF →=(2,2,0).B 1F →·EF →=(-2)×2+2×(-2)+(-4)×(-2)=0, B 1F →·AF →=(-2)×2+2×2+(-4)×0=0.∴B 1F →⊥EF →,B 1F →⊥AF →, 即B 1F ⊥EF ,B 1F ⊥AF ,又∵AF ∩FE =F ,∴B 1F ⊥平面AEF .例2 (1)证明 由正方形的性质可知A 1B 1∥AB ∥DC ,且A 1B 1=AB =DC ,所以四边形A 1B 1CD 为平行四边形,从而B 1C ∥A 1D ,又A 1D ⊂面A 1DE ,B 1C ⊄面A 1DE ,于是B 1C ∥面A 1DE .又B 1C ⊂面B 1CD 1.面A 1DE ∩面B 1CD 1=EF ,所以EF ∥B 1C .(2)解 因为四边形AA 1B 1B ,ADD 1A 1,ABCD 均为正方形,所以AA 1⊥AB ,AA 1⊥AD ,AB ⊥AD 且AA 1=AB =AD .以A 为原点,分别以AB →,AD →,AA 1→为x轴,y 轴和z 轴单位正向量建立如图所示的空间直角坐标系,可得点的坐标A (0,0,0),B (1,0,0),D (0,1,0),A 1(0,0,1),B 1(1,0,1),D 1(0,1,1),而E 点为B 1D 1的中点,所以E 点的坐标为⎝ ⎛⎭⎪⎫12,12,1.设面A 1DE 的法向量n 1=(r 1,s 1,t 1),而该面上向量A 1E →=⎝ ⎛⎭⎪⎫12,12,0,A 1D →=(0,1,-1),由n 1⊥A 1E →.n 1⊥A 1D →得r 1,s 1,t 1应满足的方程组⎩⎪⎨⎪⎧12r 1+12s 1=0,s 1-t 1=0,(-1,1,1)为其一组解, 所以可取n 1=(-1,1,1).设面A 1B 1CD 的法向量n 2=(r 2,s 2,t 2),而该面上向量A 1B 1→=(1,0,0),A 1D →=(0,1,-1),由此同理可得n 2=(0,1,1).所以结合图形知二面角E A 1D B 1的余弦值为|n 1·n 2||n 1|·|n 2|=23×2=63.跟踪演练2 (1)证明 因为VC ⊥平面ABC ,BC ⊂平面ABC ,所以VC ⊥BC .又点C 为圆O 上一点,且AB 为直径, 所以AC ⊥BC . 又VC ∩AC =C , 所以BC ⊥平面VAC .(2)解 由(1)得BC ⊥VC ,VC ⊥AC ,AC ⊥BC ,以C 为坐标原点,AC ,BC ,VC 所在的直线分别为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系,则C (0,0,0),A (1,0,0),V (0,0,2),B (0,22,0),故CB →=(0,22,0),VA →=(1,0,-2),AB →=(-1,22,0).设平面VAM 的法向量为n =(x ,y ,z ),由⎩⎪⎨⎪⎧n ·VA →=0,n ·AB →=0,得⎩⎨⎧x -2z =0,-x +22y =0,令y =2,得x =4,z =2,所以n =(4,2,2)是平面VAM 的一个法向量. 又BC ⊥平面VAC ,所以CB →=(0,22,0)是平面VAC 的一个法向量. 从而cos 〈CB →,n 〉=CB →·n |CB →|·|n |=422×16+2+4=1111,故二面角M -VA -C 的余弦值为1111. 例3 (1)证明 取AB 1的中点G , 连接EG ,FG .∵F 、G 分别是AB 、AB 1的中点, ∴FG ∥BB 1,FG =12BB 1.又∵B 1B ∥C 1C ,EC =12CC 1,BB 1=CC 1,∴FG ∥EC ,FG =EC ,∴四边形FGEC 是平行四边形, ∴CF ∥EG .∵CF ⊄平面AEB 1,EG ⊂平面AEB 1,∴CF ∥平面AEB 1.(2)解 假设这样的点E 存在.以C 为坐标原点,CA ,CB ,CC 1所在直线为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系C -xyz .则C (0,0,0),A (1,0,0),B 1(0,2,4).设E (0,0,m )(0≤m ≤4),平面AEB 1的法向量为n 1=(x ,y ,z ), 由AB 1→=(-1,2,4),AE →=(-1,0,m ),AB 1→⊥n 1,AE →⊥n 1,得⎩⎪⎨⎪⎧-x +2y +4z =0,-x +mz =0,令z =2,则n 1=(2m ,m -4,2), ∵CA ⊥平面C 1CBB 1,∴CA →是平面EBB 1的一个法向量,则平面EBB 1的一个法向量为n 2=CA →=(1,0,0). ∵二面角A -EB 1-B 的平面角的余弦值为21717,∴21717=|cos 〈n 1,n 2〉|=|n 1·n 2||n 1||n 2|=2m4m 2+m -42+4, 解得m =1(满足0≤m ≤4),∴在棱CC 1上存在点E 符合题意,此时CE =1.跟踪演练3 解 (1)如图,以D 为坐标原点,DA ,DC ,DM 所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系,则D (0,0,0), A (1,0,0), M (0,0,1), C (0,1,0),B (1,1,0),N (1,1,1),E (12,1,0),所以NE →=(-12,0,-1),AM →=(-1,0,1).因为|cos 〈NE →,AM →〉|=|NE →·AM →||NE →|×|AM →|=1252×2=1010,所以异面直线NE 与AM 所成角的余弦值为1010. (2)假设在线段AN 上存在点S , 使得ES ⊥平面AMN . 因为AN →=(0,1,1),可设AS →=λAN →=(0,λ,λ)(0≤λ≤1), 又EA →=(12,-1,0),所以ES →=EA →+AS →=(12,λ-1,λ).由ES ⊥平面AMN , 得⎩⎪⎨⎪⎧ES →·AM →=0,ES →·AN →=0,即⎩⎪⎨⎪⎧-12+λ=0,λ-1+λ=0,故λ=12,此时AS →=(0,12,12),|AS →|=22.经检验,当AS =22时,ES ⊥平面AMN . 故线段AN 上存在点S , 使得ES ⊥平面AMN ,此时AS =22. 高考押题精练(1)证明 连接AC ,∵四边形ABCD 是矩形,且Q 为BD 的中点, ∴Q 为AC 的中点,又在△AEC 中,P 为AE 的中点, ∴PQ ∥EC ,∵EC ⊂面BCE ,PQ ⊄面BCE , ∴PQ ∥平面BCE .(2)解 如图,取EF 的中点M ,则AF ⊥AM ,以A 为坐标原点,以AM ,AF ,AD 所在直线分别为x ,y ,z 轴建立空间直角坐标系.则A (0,0,0),D (0,0,1),M (2,0,0),F (0,2,0). 可得AM →=(2,0,0),MF →=(-2,2,0), DF →=(0,2,-1).设平面DEF 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·MF →=0,n ·DF →=0.故⎩⎪⎨⎪⎧-2x +2y =0,2y -z =0,即⎩⎪⎨⎪⎧x -y =0,2y -z =0.令x =1,则y =1,z =2,故n =(1,1,2)是平面DEF 的一个法向量. ∵AM ⊥面ADF ,∴AM →为平面ADF 的一个法向量. ∴cos〈n ,AM →〉=n ·AM →|n |·|AM →|=2×1+0×1+0×26×2=66. 由图可知所求二面角为锐角, ∴二面角A -DF -E 的余弦值为66二轮专题强化练答案精析第3讲 立体几何中的向量方法1.D [由已知得M 、A 、B 、C 四点共面.所以AM 在平面ABC 内,选D.]2.C [AP →可为下列7个向量:AB →,AC →,AD →,AA 1→,AB →1,AC →1,AD →1,其中一个与AB →重合,AP →·AB →=|AB →|2=1;AD →,AD →1,AA →1与AB →垂直,这时AP →·AB →=0;AC →,AB →1与AB →的夹角为45°,这时AP →·AB →=2×1× cos π4=1,最后AC →1·AB →=3×1× cos ∠BAC 1=3×13=1,故选C.] 3.B [分别以C 1B 1、C 1D 1、C 1C 所在直线为x ,y ,z 轴,建立空间直角坐标系,如图所示.∵A 1M =AN =23a , ∴M ⎝ ⎛⎭⎪⎫a ,23a ,a 3, N ⎝ ⎛⎭⎪⎫23a ,23a ,a , ∴MN →=⎝ ⎛⎭⎪⎫-a 3,0,23a . 又C 1(0,0,0),D 1(0,a,0),∴C 1D 1→=(0,a,0),∴MN →·C 1D 1→=0,∴MN →⊥C 1D 1→.∵C 1D 1→是平面BB 1C 1C 的法向量,且MN ⊄平面BB 1C 1C ,∴MN ∥平面BB 1C 1C .]4.A [设AB =1,则CE →·BD →=(AE →-AC →)·(AD →-AB →)=12AD →2-12AD →·AB →-AC →·AD →+AC →·AB → =12-12cos 60°-cos 60°+cos 60°=14.∴cos 〈CE →,BD →〉=CE →·BD →|CE →||BD →| =1432=36.选A.] 5.A[如图所示建立空间直角坐标系,设正三棱柱的棱长为2,O (0,0,0),B (3,0,0),A (0,-1,0),B 1(3,0,2),则AB 1→=(3,1,2),则BO →=(-3,0,0)为侧面ACC 1A 1的法向量,由sin θ=|AB 1→·BO →||AB 1→||BO →|=64.] 6.25解析 以D 点为坐标原点,分别以DA ,DC ,DD 1所在直线为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系,则A (1,0,0),M (1,12,1),C (0,1,0),N (1,1,12). 所以AM →=(0,12,1),CN →=(1,0,12). 故AM →·CN →=0×1+12×0+1×12=12, |AM →|=02+122+12=52, |CN →|= 12+02+122=52, 所以cos 〈AM →,CN →〉=AM →·CN →|AM →||CN →|=1252×52=25. 7.217解析 如图为折叠后的图形,其中作AC ⊥CD ,BD ⊥CD ,则AC =6,BD =8,CD =4,两异面直线AC 、BD 所成的角为60°,故由AB →=AC →+CD →+DB →,得|AB →|2=|AC →+CD →+DB →|2=68,∴|AB →|=217.8.①②解析 设正方体的棱长为1,①中(A 1A →+A 1D 1→+A 1B 1→)2=A 1C →2=3A 1B 1→2=3,故①正确;②中A 1B 1→-A 1A →=AB 1→,由于AB 1⊥A 1C ,故②正确;③中A 1B 与AD 1两异面直线所成的角为60°,但AD 1→与A 1B→的夹角为120°,故③不正确;④中|AB →·AA 1→·AD →|=0.故④也不正确.9.证明 (1)以A 为原点,AB 所在直线为x 轴,AD 所在直线为y 轴,AP 所在直线为z 轴,建立如图所示的空间直角坐标系,则A (0,0,0),B (1,0,0),C (1,2,0),D (0,2,0),P (0,0,1),∵E ,F 分别是PC ,PD 的中点,∴E ⎝ ⎛⎭⎪⎫12,1,12,F ⎝ ⎛⎭⎪⎫0,1,12, EF →=⎝ ⎛⎭⎪⎫-12,0,0,AB →=(1,0,0). ∵EF →=-12AB →,∴EF →∥AB →, 即EF ∥AB ,又AB ⊂平面PAB ,EF ⊄平面PAB ,∴EF ∥平面PAB .(2)由(1)可知PB →=(1,0,-1), PD →=(0,2,-1),AP →=(0,0,1), AD →=(0,2,0), DC →=(1,0,0),∵AP →·DC →=(0,0,1)·(1,0,0)=0, AD →·DC →=(0,2,0)·(1,0,0)=0,∴AP →⊥DC →,AD →⊥DC →,即AP ⊥DC ,AD ⊥DC .又AP ∩AD =A ,∴DC ⊥平面PAD .∵DC ⊂平面PDC ,∴平面PAD ⊥平面PDC .10.(1)证明 由PC ⊥平面ABC ,DE ⊂平面ABC ,故PC ⊥DE .由CE =2,CD =DE =2得△CDE 为等腰直角三角形,故CD ⊥DE . 由PC ∩CD =C ,DE 垂直于平面PCD 内两条相交直线,故DE ⊥平面PCD .(2)解 由(1)知,△CDE 为等腰直角三角形,∠DCE =π4,如图,过D 作DF 垂直CE 于F ,易知DF =FC =FE =1,又已知EB =1,故FB =2.由∠ACB =π2得DF ∥AC ,DF AC =FB BC =23, 故AC =32DF =32. 以C 为坐标原点,分别以CA →,CB →,CP →的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系,则C (0,0,0),P (0,0,3),A ⎝ ⎛⎭⎪⎫32,0,0,E (0,2,0),D (1,1,0),ED →=(1,-1,0),DP →=(-1,-1,3),DA →=⎝ ⎛⎭⎪⎫12,-1,0. 设平面PAD 的法向量为n 1=(x 1,y 1,z 1),由n 1·DP →=0,n 1·DA →=0,得⎩⎪⎨⎪⎧ -x 1-y 1+3z 1=0,12x 1-y 1=0,故可取n 1=(2,1,1).由(1)可知DE ⊥平面PCD ,故平面PCD 的法向量n 2可取为ED →,即n 2=(1,-1,0).从而法向量n 1,n 2的夹角的余弦值为cos 〈n 1,n 2〉=n 1·n 2|n 1|·|n 2|=36, 故所求二面角APDC 的余弦值为36. 11.C [BC →·BD →=(AC →-AB →)·(AD →-AB →)=AC →·AD →-AC →·AB →-AB →·AD →+AB →2=AB →2>0.同理DB →·DC →>0,CB →·CD →>0. 故△BCD 为锐角三角形.]12.33解析 取线段EF 的中点H ,连接A ′H .∵A ′E =A ′F ,H 是EF 的中点,∴A ′H ⊥EF .又∵平面A ′EF ⊥平面BEF ,∴A ′H ⊥平面BEF .如图,可建立空间直角坐标系A -xyz ,则A ′(2,2,22),C (10,8,0),F (4,0,0),D (10,0,0),故FA →′=(-2,2,22),FD →=(6,0,0).设n =(x ,y ,z )为平面A ′FD 的一个法向量,∴⎩⎨⎧ -2x +2y +22z =0,6x =0.取z =2,则n =(0,-2,2).又平面BEF 的一个法向量m =(0,0,1),故cos 〈n ,m 〉=n ·m |n |·|m |=33, ∴二面角的余弦值为33. 13.3510解析 以A 为坐标原点,AB 、AD 、AA 1所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,如图所示,则A 1(0,0,1),E (1,0,12),F (12,1,0),D 1(0,1,1).∴A 1E →=(1,0,-12),A 1D 1→=(0,1,0).设平面A 1D 1E 的一个法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧ n ·A 1E →=0,n ·A 1D 1→=0,即⎩⎪⎨⎪⎧x -12z =0,y =0.令z =2,则x =1.∴n =(1,0,2).又A 1F →=(12,1,-1),∴点F 到平面A 1D 1E 的距离为d =|A 1F →·n ||n |=|12-2|5=3510.14.(1)证明 ∵平面ABCD ⊥平面ABEF ,CB ⊥AB ,平面ABCD ∩平面ABEF =AB ,∴CB ⊥平面ABEF .∵AF ⊂平面ABEF ,∴AF ⊥CB .又AB 为圆O 的直径,∴AF ⊥BF ,又BF ∩CB =B ,∴AF ⊥平面CBF .∵AF ⊂平面DAF ,∴平面DAF ⊥平面CBF .(2)解 由(1)知AF ⊥平面CBF ,∴FB 为AB 在平面CBF 内的射影,因此,∠ABF 为直线AB 与平面CBF 所成的角.∵AB ∥EF ,∴四边形ABEF 为等腰梯形,过点F 作FH ⊥AB ,交AB 于H .已知AB =2,EF =1,则AH =AB -EF 2=12. 在Rt △AFB 中,根据射影定理得AF 2=AH ·AB ,∴AF =1,sin ∠ABF =AF AB =12,∴∠ABF =30°. ∴直线AB 与平面CBF 所成角的大小为30°.(3)解 设EF 中点为G ,以O 为坐标原点,OA →、OG →、AD →方向分别为x 轴、y轴、z 轴正方向建立空间直角坐标系(如图).设AD =t (t >0),则点D 的坐标为(1,0,t ),C (-1,0,t ).又A (1,0,0),B (-1,0,0),F (12,32,0), ∴CD →=(2,0,0),FD →=(12,-32,t ). 设平面DCF 的法向量为n 1=(x ,y ,z ),则n 1·CD →=0,n 1·FD →=0.即⎩⎪⎨⎪⎧ 2x =0,x 2-32y +tz =0,令z =3, 解得x =0,y =2t ,∴n 1=(0,2t ,3).由(1)可知AF ⊥平面CBF ,取平面CBF 的一个法向量为n 2=AF →=(-12,32,0),依题意,n 1与n 2的夹角为60°.∴cos 60°=|n 1·n 2||n 1|·|n 2|, 即12=3t 4t 2+3×1, 解得t =64, 因此,当AD 的长为64时,平面DFC 与平面FBC 所成的锐二面角的大小为60°.。
2020浙江高考数学二轮专题强化训练:专题四第3讲空间向量与立体几何Word版含解析
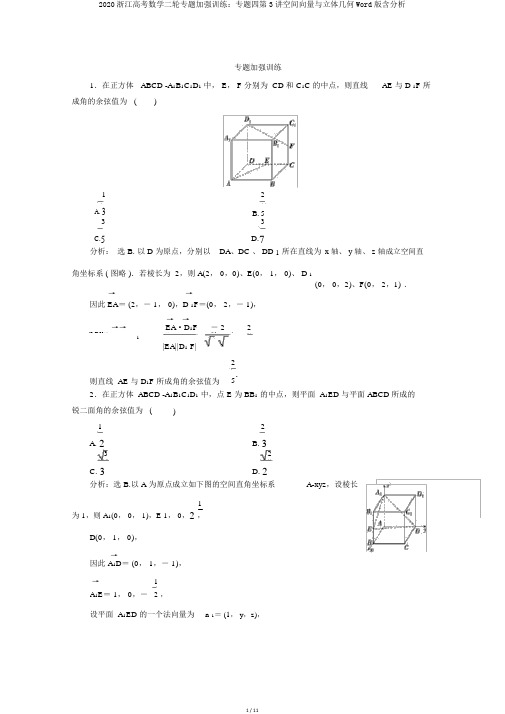
专题加强训练1.在正方体 ABCD -A 1B 1C 1D 1 中, E , F 分别为 CD 和 C 1C 的中点,则直线 AE 与 D 1F 所成角的余弦值为 ()1 B.2 A.3 5 33 C.5D.7分析: 选 B. 以 D 为原点,分别以 DA 、DC 、 DD 1 所在直线为 x 轴、 y 轴、 z 轴成立空间直角坐标系 ( 图略 ).若棱长为 2,则 A(2, 0,0)、E(0, 1, 0)、 D 1.(0, 0,2)、F(0, 2,1) → →因此 EA = (2,- 1, 0),D 1F =(0, 2,- 1),→ → - 22→→EA ·D 1Fcos 〈EA ,D F 〉=→ →=5·5=-5.1|EA||D 1 F|2则直线 AE 与 D 1F 所成角的余弦值为 5.2.在正方体 ABCD -A 1B 1C 1D 1 中,点 E 为 BB 1 的中点,则平面 A 1ED 与平面 ABCD 所成的 锐二面角的余弦值为 ()1 2 A. 2 B. 3 3 2 C. 3D. 2分析:选 B.以 A 为原点成立如下图的空间直角坐标系A-xyz ,设棱长1为 1,则 A 1(0, 0, 1),E 1, 0,2 ,D(0, 1, 0),→因此 A 1D = (0, 1,- 1),→1A 1E = 1, 0,- 2 ,设平面 A 1ED 的一个法向量为n 1= (1, y ,z),y- z= 0,y= 2,则1 因此1-2z= 0,z= 2.因此 n1= (1, 2, 2).因为平面 ABCD 的一个法向量为n2= (0, 0, 1),因此 cos〈 n 1, n2〉= 2 =2.3×1 32即所成的锐二面角的余弦值为3.3.(2019 浙·江省十校联合体期末联考)在三棱锥 O-ABC 中,已知 OA, OB,OC 两两垂直且相等,点P、 Q 分别是线段BC 和 OA 上的动点,且知足1 1BP≤ BC, AQ≥ AO ,则 PQ 和2 2OB 所成角的余弦的取值范围是()A. 2, 1 B.3, 1 2 3C. 3 2 5D.2 2 53 , 5 2,5分析:选 B.依据题意,以O 为原点,成立如下图的空间直角坐标→系,不如设 OA= OB=OC= 2, OB= (2,0, 0),设1 1P(x,y,0),Q(0,0,z) ,因为 BP≤2BC,AQ≥2AO,因此 1≤ x≤ 2,→ →0≤ y≤→→ →OB·PQ 1 且 x+ y= 2,0≤ z≤ 1,PQ= (- x, x- 2,z), |cos〈OB, PQ〉 |=→ →|OB|·|PQ| - x= 2 2,2x - 4x+4+ z→→ 3当 x= 1, z= 1 时, |cos〈 OB, PQ〉|= 3 ;→→ 2 5当 x= 2, z= 1 时, |cos〈 OB, PQ〉|= 5 ;→→当 x= 2, z= 0 时, |cos〈 OB, PQ〉 |=1.→ → 2当 x= 1, z=0 时, |cos〈 OB,PQ〉 |= 2 ,联合四个选项可知PQ 和 OB 所成角的余弦的3.取值范围是3, 1π,AB = AC =4.(2019 宁·波市镇海中学高考模拟 )在直三棱柱 A 1 B 1C 1- ABC 中,∠ BAC = 2AA 1=1,已知 G 和 E 分别为 A 1B 1 和 CC 1 的中点, D 与 F 分别为线段 AC 和 AB 上的动点 (不包 括端点 ),若 GD ⊥ EF ,则线段 DF 的长度的取值范围为 ()5 B. 5A.5 , 1 5 , 1C. 2 5,1D.2 5,155分析: 选 A. 成立如下图的空间直角坐标系,则A(0, 0, 0),1 1E 0,1,2 ,G 2,0, 1 , F( x ,0, 0), D(0, y , 0),因为 GD ⊥ EF ,因此 x + 2y - 1= 0,DF = x 2+ y 2=5 y -2 2 + 1,5 51由 x = 1- 2y>0,得 y<2,2 时,线段 DF1,因此当 y = 长度的最小值是5 5当 y = 0 时,线段 DF 长度的最大值是1 而不包含端点,故 y = 0 不可以取,应选 A.5.已知直三棱柱 ABC-A 1 B 1 C 1 中,∠ ABC = 120 °,AB = 2,BC =CC 1 =1,则异面直线 AB 1与 BC 1 所成角的余弦值为 ()315 A. 2 B. 5103 C. 5D. 3分析: 选 C.如下图,将直三棱柱 ABC-A 1B 1C 1 补成直四棱柱 ABCD -A 1B 1C 1D 1,连结 AD 1 ,B 1D 1,则 AD 1∥BC 1,因此 ∠ B 1AD 1或其补角为异面直线AB 1 与 BC 1 所成的角.因为 ∠ ABC = 120°,AB = 2, BC = CC 1= 1,因此 AB 1= 5, AD 1= 2.在 △ B 1D 1C 1 中, ∠B 1C 1D 1= 60°,B 1C 1= 1,D 1C 1=2,因此 B 1D 1= 12+22-2× 1× 2×cos 60°= 3,因此 cos ∠B 1 1 5+ 2- 3 = 10,选择 C.AD = 2× 5× 2 56.(2019 杭·州市学军中学高考数学模拟 )如图,在二面角 A-CD-B 中, BC ⊥ CD , BC =CD = 2,点 A 在直线 AD 上运动,知足 AD ⊥ CD ,AB =3.现将平面 ADC 沿着 CD 进行翻折,在翻折的过程中,线段 AD 长的取值范围是 ________.→ → → → 分析: 由题意得 AD ⊥ DC , DC ⊥CB ,设平面 ADC 沿着 CD 进行翻折过程中,二面角→ →A-CD-B 的夹角为 θ,则〈 DA , CB 〉= θ,→→→→ → 2 → 2 →2 →2 →→→→→→因为 AB = AD +DC + CB ,因此平方得 AB =AD +DC + CB + 2AD ·DC + 2CB ·AD + 2DC ·CB ,设 AD =x ,因为 BC =CD = 2, AB = 3,因此 9= x 2+ 4+ 4- 4xcos θ,x 2- 1即 x 2- 4xcos θ- 1= 0,即 cos θ= 4x .x 2- 1因为- 1≤ cos θ≤ 1,因此- 1≤ ≤1,4xx 2 -1≤ 4xx 2- 4x - 1≤0即 ,即,x 2- 1≥ - 4x x 2+ 4x - 1≥ 0 则 2- 5≤ x ≤ 2+ 5,x ≥ - 2+ 5或 x ≤ - 2- 5.因为 x>0,因此 5- 2≤ x ≤ 5+ 2,即 AD 的取值范围是 [ 5- 2, 5+ 2]. 答案: [ 5- 2, 5+ 2]7.(2019 ·州市高考模拟台 )如图,在棱长为 2 的正四周体 A-BCD 中, E 、 F 分别为直线 AB 、 CD 上的动点,且 |EF |=3.若记 EF 中点 P 的轨迹为 L ,则 |L|等于 ________. (注: |L|表示 L 的测度,在此题, L 为曲线、平 面图形、空间几何体时, |L|分别对应长度、面积、体积 )分析:如图,当 E 为 AB 中点时, F 分别在 C ,D 处,知足 |EF|= 3, 此时 EF 的中点 P 在 EC ,ED 的中点 P 1 2的地点上;当 F 为CD 中点,P时, E 分别在 A ,B 处,知足 |EF|= 3,此时 EF 的中点 P 在 BF ,AF 的中点 P 3,P 4 的地点上,连结 P 1P 2, P 3P 4 订交于点 O ,则四点 P 1, P 2,1 1P3, P4共圆,圆心为O,圆的半径为2,则 EF 中点 P 的轨迹 L 为以 O 为圆心,以2为半径的1圆,其测度 |L|= 2π×2=π.答案:π8.(2019 金·丽衢十二校联考)如图,在三棱锥D-ABC 中,已知 AB= 2,→ →c2AC·BD =- 3,设 AD=a,BC= b,CD = c,则的最小值为 ________.ab+ 1→→→分析:设 AD = a,CB= b,DC=c,因为 AB= 2,因此 |a+ b+ c|2= 4? a2→→+ b2+ c2+ 2(a·b+ b·c+ c·a)= 4,又因为 AC·BD=- 3,因此 ( a+ c) ·(- b-c) =- 3? a·b+b·c+ c·a + c2= 3,因此 a2+ b2+ c2+ 2(3- c2)= 4? c2= a2+ b2+ 2,因此a2+ b2+ 2 2ab+ 2≥= 2,当且仅当 a ab+1 ab+ 1= b 时,等号成立,即c2的最小值是 2. ab+1答案: 29.(2019 宁·波诺丁汉大学附中高三期中考试 )如图,矩形 ABCD 中,AB= 1,BC= 3,将△ ABD 沿对角线 BD 向上翻折,若翻折过程中 AC长度在210,213内变化,则点A 所形成的运动轨迹的长度为________.分析:过 A 作 AE⊥ BD,垂足为 E,连结 CE, A′E.因为矩形 ABCD 中, AB =1, BC=3,因此 AE=3, CE=72 2.3因此 A 点的轨迹为以 E 为圆心,以2为半径的圆弧.∠ A′EA 为二面角 A-BD -A′的平面角.以 E 为原点,以 EB, EA′所在直线为 x 轴, y 轴成立如下图空间直角坐标系E-xyz,设∠ A′EA=θ,则A3 3θ ,C3θ2 sin -1,-2,0,0,2 cos ,因此 AC=3 3sin2θ=5+ 3cos θ1+( cos θ+ 1)2+4 2,410≤5+ 3cos θ13≤ 因此 222 , 解得 0≤ cos θ1≤ 2,因此 60°≤ θ≤ 90°,因此 A 点轨迹的圆心角为 30°,因此 A 点轨迹的长度为π 3 3π6· =12 .2答案: 3π1210.(2019 宁·波十校联考模拟 )如图,在四棱锥 P-ABCD 中,∠BAD = 120°, AB = AD = 2,△ BCD 是等边三角形, E 是 BP 的中点, AC 与 BD 交于点 O ,且 OP ⊥平面 ABCD .(1)求证: PD ∥平面 ACE ;(2)当 OP = 1 时,求直线 PA 与平面 ACE 所成角的正弦值.解: (1) 证明: 因为在四棱锥 P-ABCD 中,∠BAD = 120°,AB =AD = 2,△BCD 是等边三角形,因此 △ ABC ≌△ ACD ,因为 E 是 BP 中点, AC 与 BD 交于点 O ,因此 O 是 BD 中点,连结OE ,则 OE ∥PD ,因为 PD ?平面 ACE , OE? 平面 ACE ,因此 PD ∥ 平面 ACE.(2)因为 BD ⊥AC , PO ⊥平面 ABCD ,以 O 为原点, OB , OC , OP 所在直线为坐标轴成立空间直角坐标系,则 P(0, 0, 1),A(0,- 1, 0), B( 3, 0, 0), C(0, 3, 0),E 23, 0,12 ,→31→31→EA = - 2 ,- 1,- 2 ,EC = -2, 3,- 2 , PA = (0,- 1,- 1),设平面 ACE 的一个法向量 n = (x , y ,z) ,→ n ·EA = 3x +2y + z = 0则,取 x = 1,得 n = (1, 0,- 3), →n ·EC = 3x - 6y + z = 0设直线 PA 与平面 ACE 所成角为 θ,→3 6则 sin θ=|n ·PA|→ =2 2 = 4 ,|n| ·|PA|因此直线 PA 与平面 ACE 所成角的正弦值为64.11.(2019 浙·江暨阳 4 月联考卷 )在四棱锥 P - ABCD 中, PC ⊥平面 ABCD , BC ∥ AD , BC ⊥ AB , PB = AD =2, AB = BC =1, E 为棱PD 上的点.1(1)若 PE = 3PD ,求证: PB ∥平面 ACE ;(2)若 E 是 PD 的中点,求直线 PB 与平面 ACE 所成角的正弦值.解: (1) 证明: 过 A 作 Az ⊥平面 ABCD ,以 A 为原点,如图成立直角坐标系,由题意解得, PC =→3),C(1, 1,3,因此 B(1, 0, 0), P(1, 1, 3),因此 BP = (0, 1, 0), D (0,2, 0),→ 1 →2 4 2 3设 E(x , y , z),由 PE = 3PD ,得 E(3, 3,3 ), 设平面 ACE 的法向量为 n = (x , y , z),→nAC =x + y = 0则→ 24 2,取 z = 1,得 n = ( 3,- 3, 1),3nAE = 3x + 3y + 3 z = 0→因此 BP ·n = 0,因为 PB?平面 ACE ,因此 PB ∥ 平面 ACE.(2)过 A 作 Az ⊥ 平面 ABCD ,以 A 为原点,如图成立直角坐标系,由题意解得 PC = 3,因此 B(1 ,0, 0), P(1, 1, 3), A(0, 0,0),→1 3 3 因此 BP = (0, 1, 3), C(1,1, 0), D(0, 2, 0),因此 E( 2, 2,2 ), → → 1 33AC = (1, 1, 0), AE = (2, 2, 2 ), 设平面 ACE 的法向量为 n = (x , y , z),→nAC =x + y = 0则→ 1 3,3nAE =2x + 2y + 2 z =0取 z =2,得 n = ( 3,- 3, 2),因此直线 PB 与平面 ACE 所成角的正弦值:→3 = 30 θ |BP ·n| =sin = →2 10 20 .|BP||n|12.(2019 嵊·州市第二次高考适应性考试 ) 如图,在直三棱柱ABC-A B C 中,底面 ABC 为边长为 2 的正三角形, D 是棱 A C的 1 11 1 1中点, CC 1= h(h>0).(1)证明: BC 1∥平面 AB 1D ;(2)若直线 BC 1 与平面 ABB 1A 1 所成角的大小为π,求 h 的值.6解: (1) 证明: 连结 A 1B 交 AB 1 于 E ,连结 DE ,则 DE 是 △ A 1BC 1 的中位线.因此 DE ∥ BC 1.又 DE ? 平面 AB 1D , BC 1?平面 AB 1D ,故 BC 1∥平面 AB 1D .(2)以 AB 的中点 O 为坐标原点, OB ,OC 所在直线分别为x 轴,y 轴成立空间直角坐标系,如下图,则B(1, 0, 0), C 1 (0, 3, h).易得平面 ABB 1A 1 的一个法向量为n = (0, 1, 0).→又BC 1= (- 1, 3, h).→ 因此 sinπ→|BC 1·n|.= |cos 〈 BC 1, n 〉 |=→6|BC 1|·|n|3 1即= ,解得 h = 2 2. h 2+ 4213.(2019 温·州十五校联考 )已知菱形 ABCD 中,对角线 AC 与 BD 订交于一点 O ,∠ BAD = 60°,将△ BDC 沿着 BD 折起得△ BDC ′,连接 AC ′.(1)求证:平面 AOC ′⊥平面 ABD ;(2)若点 C ′在平面 ABD 上的投影恰巧是△ ABD 的重心,求直线CD 与底面 ADC ′所成角的正弦值.解: (1) 证明: 因为 C ′O ⊥BD , AO ⊥ BD , C ′O ∩ AO =O ,因此BD ⊥ 平面 C ′OA ,又因为BD? 平面 ABD ,因此平面 AOC ′⊥平面 ABD .(2)如图建系 O- xyz ,令 AB = a ,则31A 2 a , 0, 0 ,B 0, 2a , 0 ,1D 0,- 2a , 0 ,C ′ 3 66 a ,0, 3 a ,→ → 3 a , 1a , 0 ,平面 ADC ′的法向量为 m = 1,- 3, 2 ,设直线 CD 因此 DC =AB = -2 22与底面 ADC ′所成角为 θ,则→ 3a6 →|DC ·m|sin θ= |cos 〈 DC ,m 〉 |= →= 3 = 3,|DC||m|a ·2故直线CD 与底面ADC ′所成角的正弦值为6 3 .14.(2019 宝·鸡市质量检测(一 ))如图,四棱锥P-ABCD 的底面ABCD 为矩形, PA⊥平面ABCD ,点 E 是PD 的中点,点 F 是PC 的中点.(1)证明: PB∥平面 AEC;(2)若底面 ABCD 为正方形,研究在什么条件下,二面角 C-AF-D 的大小为 60°?解:易知 AD, AB, AP 两两垂直,成立如下图的空间直角坐标系 A-xyz,设 AB=2a, AD = 2b, AP= 2c,则 A(0,0, 0), B(2a,0,0),C(2a, 2b,0) ,D (0, 2b, 0),P(0 ,0, 2c).设 AC ∩BD = O,连结OE,则O(a, b, 0),又 E 是PD 的中点,因此E(0, b, c) .→→(1)证明:因为 PB= (2a, 0,- 2c), EO= (a, 0,- c),→→→ →因此 PB=2EO,因此 PB ∥EO,即 PB∥ EO.因为 PB?平面 AEC, EO? 平面 AEC ,因此 PB∥平面 AEC.(2)因为四边形 ABCD 为正方形,因此 a= b, A(0, 0, 0), B(2a, 0, 0), C(2a, 2a,0) ,D (0,2a, 0), P(0 ,0, 2c), E(0,a, c), F(a, a, c),因为 z 轴 ? 平面 CAF ,因此设平面 CAF 的一个法向量为→n= (x, 1, 0),而 AC= (2a, 2a,0),→因此 AC·n= 2ax+ 2a= 0,得 x=- 1,因此 n= (- 1,1, 0).因为 y 轴 ? 平面 DAF ,因此设平面 DAF 的一个法向量为→m= (1,0,z),而 AF= (a,a,c),→ a因此 AF ·m=a+ cz= 0,得 z=-c,a因此 m= (1, 0,-c) ∥m′= (c, 0,- a).2020浙江高考数学二轮专题加强训练:专题四第3讲空间向量与立体几何Word 版含分析 11 / 11|n ·m ′| c1 cos 60°== 2( a 2+ c 2) = ,得 a = c. |n||m ′|2 故当 AP 与正方形 ABCD 的边长相等时,二面角 C-AF -D 的大小为 60°.。
高三理科数学二轮复习讲义:模块二 专题四 立体几何 高考解答题专讲(四) 空间向量与立体几何 Word版含解

专题四立体几何高考解答题专讲(四)空间向量与立体几何一、向量法证明空间位置关系设直线l,m的方向向量分别为a=(a1,b1,c1),b=(a2,b2,c2),平面α、β的法向量分别为μ=(a3,b3,c3),v=(a4,b4,c4),(μ、v≠0).(1)线面平行l∥α⇔a⊥μ⇔a·μ=0⇔a1a3+b1b3+c1c3=0.(2)线面垂直l⊥α⇔a∥μ⇔a=kμ⇔a1=ka3,b1=kb3,c1=kc3.(3)面面平行α∥β⇔μ∥v⇔μ=λv⇔a3=λa4,b3=λb4,c3=λc4.(4)面面垂直α⊥β⇔μ⊥v⇔μ·v=0⇔a3a4+b3b4+c3c4=0.[证明] (1)以B 为坐标原点,BA ,BC ,BB 1所在的直线分别为x 轴、y 轴、z 轴建立空间直角坐标系,如图所示,则B (0,0,0),D (0,2,2),B 1(0,0,4),C (0,2,0)设BA =a ,则A (a,0,0),所以BA →=(a,0,0),BD →=(0,2,2),B 1D →=(0,2,-2), B 1D →·BA →=0,B 1D →·BD →=0+4-4=0, 即B 1D ⊥BA ,B 1D ⊥BD .又BA ∩BD =B ,BA ,BD ⊂平面ABD , 因此B 1D ⊥平面ABD .(2)由(1)知,E (0,0,3),G ⎝ ⎛⎭⎪⎫a 2,1,4,F (0,1,4),则EG →=⎝ ⎛⎭⎪⎫a 2,1,1,EF →=(0,1,1),B 1D →·EG →=0+2-2=0,B 1D →·EF →=0+2-2=0, 即B 1D ⊥EG ,B 1D ⊥EF .又EG ∩EF =E ,EG ,EF ⊂平面EGF , 因此B 1D ⊥平面EGF .结合(1)可知平面EGF ∥平面ABD .[探究追问] 本例用几何方法如何证明?谈谈你对两种方法的认识.[证明](1)∵AB ⊥平面BCC 1B 1,B 1D ⊂平面BCC 1B 1, ∴AB ⊥B 1D .在矩形BCC 1B 1中,D 为CC 1的中点,且DC =BC =DC 1=2,∴∠BDC =∠B 1DC 1=45°,∴∠BDB 1=90°,即B 1D ⊥BD . 又∵AB ∩BD =B . ∴B 1D ⊥平面ABD .(2)取BB 1的中点H ,则HC 1∥BD . ∵B 1E =1,B 1H =2,∴E 为B 1H 的中点. ∵F 为B 1C 1的中点,∴EF ∥HC 1.∴EF∥BD.∵EF⊄平面ABD,BD⊂平面ABD,∴EF∥平面ABD.又G为A1C1的中点,∴GF∥A1B1∥AB,∵GF⊄平面ABD,AB⊂平面ABD,∴GF∥平面ABD.又∵GF∩EF=F.∴平面EGF∥平面ABD.向量法证明平行与垂直的4个步骤(1)建立空间直角坐标系,建系时,要尽可能地利用载体中的垂直关系.(2)建立空间图形与空间向量之间的关系,用空间向量表示出问题中所涉及的点、直线、平面的要素.(3)通过空间向量的运算求出平面向量或法向量,再研究平行、垂直关系.(4)根据运算结果解释相关问题.[对点训练]1.(2017·福州质检)如图,在四棱锥P-ABCD中,P A⊥平面ABCD,底面ABCD是菱形,P A=AB=2,∠BAD=60°,E是P A的中点.(1)求证:直线PC ∥平面BDE ; (2)求证:BD ⊥PC .[证明]设AC ∩BD =O .因为∠BAD =60°,AB =2,底面ABCD 为菱形,所以BO =1,AO =CO =3,AC ⊥BD.如图,以O 为坐标原点,以OB ,OC 所在直线分别为x 轴,y 轴,过点O 且平行于P A 的直线为z 轴,建立空间直角坐标系O -xyz ,则P (0,-3,2),A (0,-3,0),B (1,0,0),C (0,3,0),D (-1,0,0),E (0,-3,1).(1)设平面BDE 的法向量为n 1=(x 1,y 1,z 1),因为BE →=(-1,-3,1),BD →=(-2,0,0),由⎩⎨⎧n 1·BD →=0,n 1·BE →=0,得⎩⎪⎨⎪⎧-2x 1=0,-x 1-3y 1+z 1=0,令z 1=3,得y 1=1,所以n 1=(0,1,3).又PC →=(0,23,-2),所以PC →·n 1=0+23-23=0, 即PC →⊥n 1,又PC ⊄平面BDE , 所以PC ∥平面BDE .(2)因为PC →=(0,23,-2),BD →=(-2,0,0), 所以PC →·BD →=0. 故BD ⊥PC .二、向量法求直线与平面所成的角[解](1)证明:设AD 的中点为O ,连接OB ,OP .∵△P AD 是以AD 为斜边的等腰直角三角形,∴OP ⊥AD . ∵BC =12AD =OD ,且BC ∥OD , ∴四边形BCDO 为平行四边形, 又∵CD ⊥AD ,∴OB ⊥AD , ∵OP ∩OB =O ,∴AD ⊥平面OPB .过点O 在平面POB 内作OB 的垂线OM ,交PB 于M ,以O 为原点,OB 所在直线为x 轴,OD 所在直线为y 轴,OM 所在直线为z 轴,建立空间直角坐标系,如图.设CD =1,则有A (0,-1,0),B (1,0,0),C (1,1,0),D (0,1,0). 设P (x,0,z )(z >0),由PC =2,OP =1,得⎩⎪⎨⎪⎧(x -1)2+1+z 2=4,x 2+z 2=1,得x =-12,z =32. 即点P ⎝ ⎛⎭⎪⎫-12,0,32,而E 为PD 的中点,∴E ⎝ ⎛⎭⎪⎫-14,12,34.设平面P AB 的法向量为n =(x 1,y 1,z 1), ∵AP →=⎝ ⎛⎭⎪⎫-12,1,32,AB →=(1,1,0),∴⎩⎨⎧-12x 1+y 1+32z 1=0,x 1+y 1=0,⇒⎩⎪⎨⎪⎧x 1=-y 1,z 1=-3y 1,取y 1=-1,得n =(1,-1,3).而CE →=⎝ ⎛⎭⎪⎫-54,-12,34,则CE →·n =0,而CE ⊄平面P AB ,∴CE∥平面P AB .(2)设平面PBC 的法向量为m =(x 2,y 2,z 2), ∵BC →=(0,1,0),BP →=⎝ ⎛⎭⎪⎫-32,0,32,∴⎩⎨⎧y 2=0,-32x 2+32z 2=0,取x 2=1,得m =(1,0,3),设直线CE 与平面PBC 所成角为θ. 则sin θ=|cos 〈m ,CE →〉|=|CE →·m ||CE →|·|m |=28,故直线CE 与平面PBC 所成角的正弦值为28.求直线与平面所成角应注意的两点(1)准确求出平面的法向量.(2)直线和平面所成的角的正弦值等于直线的方向向量与平面法向量夹角的余弦值的绝对值,即注意函数名称的变化.[对点训练]2.如图,在底面为正三角形的三棱柱ABC -A 1B 1C 1中,AA 1⊥平面ABC,A1B⊥B1C,AB=4,M为AB的中点,P为B1C上任意一点.(1)求证:MP⊥A1B;(2)若P为B1C的中点,求直线MP与平面AB1C所成角的正弦值.[解](1)证明:如图,连接CM,B1M,∵△ABC为正三角形,M为AB的中点,∴CM⊥AB.∵AA1⊥平面ABC,CM⊂平面ABC,∴AA1⊥CM.∵AB⊂平面ABB1A1,AA1⊂平面ABB1A1,AB∩AA1=A,∴CM⊥平面ABB1A1.∵A1B⊂平面ABB1A1,∴CM⊥A1B.又A1B⊥B1C,B1C⊂平面B1CM,CM⊂平面B1CM,B1C∩CM=C ,∴A 1B ⊥平面B 1CM .∵MP ⊂平面B 1CM ,∴MP ⊥A 1B .(2)取BC 的中点O ,连接OA ,OP ,易知OA ,OP ,OB 两两垂直,故以O 为原点,OA ,OB ,OP 所在直线分别为x ,y ,z 轴建立如图所示的空间直角坐标系,设AA 1=h ,则A (23,0,0),B (0,2,0),C (0,-2,0),M (3,1,0),A 1(23,0,h ),B 1(0,2,h ),CA →=(23,2,0).由A 1B ⊥B 1C 得A 1B →·B 1C →=0,即(-23,2,-h )·(0,-4,-h )=-8+h 2=0,得h =22,则B 1(0,2,22),P (0,0,2),CB 1→=(0,4,22).设平面AB 1C 的法向量为n =(x ,y ,z ),则⎩⎨⎧n ⊥CA →,n ⊥CB 1→,即⎩⎨⎧n ·CA →=0,n ·CB 1→=0,⎩⎪⎨⎪⎧23x +2y =0,4y +22z =0,取x =2,得y =-6,z =23,∴n =(2,-6,23)为平面AB 1C 的一个法向量.又MP →=(-3,-1,2),设直线MP 与平面AB 1C 所成的角为θ, ∴sin θ=|n ·MP →||n |·|MP →|=|-6+6+26|2+6+12×3+1+2=55.∴直线MP 与平面AB 1C 所成角的正弦值为55.三、向量法求二面角[解](1)证明:∵∠BAP=∠CDP=90°,∴AB⊥AP,CD⊥DP.又AB∥CD,∴AB⊥DP,AP∩DP=P,AP,DP⊂平面P AD,∴AB⊥平面P AD.又AB⊂平面P AB,∴平面P AB⊥平面P AD.(2)取AD,BC的中点分别为E,F,连接PE和EF. ∵P A=PD,∴PE⊥AD.又由(1)知AB⊥平面P AD,PE⊂平面P AD,∴AB ⊥PE .又AB ∩AD =A ,AB ,AD ⊂平面ABCD , ∴PE ⊥平面ABCD .又AB ∥CD ,AB =CD ,AB ⊥AD ,所以四边形ABCD 为矩形, ∴PE ,AE ,EF 两两垂直,以E 为原点,EA 为x 轴,EF 为y 轴,EP 为z 轴,建立如图所示空间直角坐标系E -xyz.设P A =PD =AB =CD =a (a >0),则AD =2a ,PE =22a ,于是E (0,0,0),A ⎝ ⎛⎭⎪⎫22a ,0,0,P ⎝ ⎛⎭⎪⎫0,0,22a ,B ⎝ ⎛⎭⎪⎫22a ,a ,0,C ⎝ ⎛⎭⎪⎫-22a ,a ,0, PB →=⎝ ⎛⎭⎪⎫22a ,a ,-22a ,P A →=⎝ ⎛⎭⎪⎫22a ,0,-22a , PC →=⎝⎛⎭⎪⎫-22a ,a ,-22a .设平面P AB 的法向量为m =(x 1,y 1,z 1),则⎩⎨⎧PB →·m =0,P A →·m =0,即⎩⎨⎧22ax 1+ay 1-22az 1=0,22ax 1-22az 1=0,取x 1=1,则z 1=1,y 1=0,于是m =(1,0,1). 设平面PBC 的法向量为n =(x 2,y 2,z 2),则⎩⎨⎧PB →·n =0,PC →·n =0,即⎩⎨⎧22ax 2+ay 2-22az 2=0,-22ax 2+ay 2-22az 2=0,取z 2=2,则x 2=0,y 2=1,即n =(0,1,2). 设二面角A -PB -C 的平面角为θ, ∴|cos θ|=⎪⎪⎪⎪⎪⎪m ·n |m |·|n |=33, 又由题可知,θ为钝角,∴二面角A -PB -C 的余弦值为-33.求二面角的易错点一是求两个平面的法向量出错,应注意点的坐标的求解的准确性;二是公式用错,把二面角的向量公式与线面角的向量公式搞混,导致结果出错.[对点训练]3.(2017·石家庄高三二检)如图,在三棱柱ABC -DEF 中,侧面ABED 是边长为2的菱形,且∠ABE =π3,BC =212.四棱锥F -ABED 的体积为2,点F 在平面ABED 内的正投影为点G ,且点G 在AE 上,点M 在线段CF 上,且CM =14CF .(1)证明:直线GM ∥平面DEF ; (2)求二面角M -AB -F 的余弦值.[解](1)证明:因为四棱锥F -ABED 的体积为2,所以V F -ABED =13×34×4×2×FG =2,所以FG = 3.又BC =EF =212,所以EG =32,即点G 是靠近点A 的四等分点. 过点G 作GK ∥AD 交DE 于点K ,连接FK ,如图1所示,所以GK =34AD =34CF . 又MF =34CF ,所以MF =GK 且MF ∥GK , 所以四边形MFKG 为平行四边形,所以GM ∥FK ,又FK ⊂平面DEF ,所以直线GM ∥平面DEF . (2)连接BD ,设AE ,BD 的交点为O ,OB 所在直线为x 轴,OE 所在直线为y 轴,过点O 作平面ABED 的垂线为z 轴,建立空间直角坐标系,如图2所示,则A (0,-1,0),B (3,0,0),F ⎝ ⎛⎭⎪⎫0,-12,3,M ⎝ ⎛⎭⎪⎫334,-54,3, BA →=(-3,-1,0),BM →=⎝ ⎛⎭⎪⎫-34,-54,3,BF →=⎝⎛⎭⎪⎫-3,-12,3. 设平面ABM ,ABF 的法向量分别为m ,n ,则⎩⎨⎧m ·BA →=0,m ·BM →=0,得m =(1,-3,-1),⎩⎨⎧n ·BA →=0,n ·BF →=0,得n =⎝ ⎛⎭⎪⎫1,-3,12, 所以cos 〈m ,n 〉=m ·n |m ||n |=78585,故二面角M -AB -F 的余弦值为78585.热点课题16 向量法解决探索性问题[感悟体验](2017·北京朝阳区检测)如图,正方形ADEF 与梯形ABCD 所在平面互相垂直,已知AB ∥CD ,AD ⊥CD ,AB =AD =12CD .(1)求平面BDF 与平面CDE 所成锐二面角的余弦值;(2)线段EC 上是否存在点M ,使得平面BDM ⊥平面BDF ?若存在,求出EMEC 的值;若不存在,说明理由.[解](1)因为平面ADEF ⊥平面ABCD ,平面ADEF ∩平面ABCD =AD ,CD ⊥AD ,CD ⊂平面ABCD ,所以CD ⊥平面ADEF ,又DE ⊂平面ADEF ,故CD ⊥ED .而四边形ADEF 为正方形,所以AD ⊥DE ,又AD ⊥CD ,所以AD ,DE ,DC 两两垂直.以D 为原点,DA ,DC ,DE 所在直线分别为x 轴、y 轴、z 轴,建立空间直角坐标系D -xyz ,如图所示.设AD =1,则D (0,0,0),A (1,0,0),B (1,1,0),F (1,0,1),C (0,2,0),E (0,0,1),易知平面CDE 的一个法向量DA →=(1,0,0). 设平面BDF 的一个法向量n =(x ,y ,z ),则⎩⎨⎧n ·DB →=0,n ·DF →=0,即⎩⎪⎨⎪⎧x +y =0,x +z =0, 令x =1,则y =z =-1,所以n =(1,-1,-1). 设平面BDF 与平面CDE 所成锐二面角的大小为θ, 则cos θ=|cos 〈DA →,n 〉|=13=33.所以平面BDF 与平面CDE 所成锐二面角的余弦值为33. (2)假设存在点M 满足题意.若M 与C 重合,则易知平面BDM (C )的一个法向量m 0=(0,0,1),由(1)知平面BDF 的一个法向量n =(1,-1,-1),又m 0·n =-1≠0,则此时平面BDF 与平面BDM 不垂直.若M 与C 不重合,设EMEC =λ(0≤λ<1,则M (0,2λ,1-λ), 设平面BDM 的一个法向量m =(x 0,y 0,z 0),则⎩⎨⎧m ·DB →=0,m ·DM →=0,即⎩⎪⎨⎪⎧x 0+y 0=0,2λy 0+(1-λ)z 0=0,令x 0=1,则y 0=-1,z 0=2λ1-λ,所以m =⎝ ⎛⎭⎪⎫1,-1,2λ1-λ,又平面BDF ⊥平面BDM ,则m ·n =0,即1+1-2λ1-λ=0, 所以λ=12∈[0,1).所以线段EC 上存在点M 使得平面BDF ⊥平面BDM ,且EM EC =12.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3讲 空间向量与立体几何利用空间向量证明平行、垂直及求空间角[核心提炼]1.利用直线的方向向量与平面的法向量证明空间平行、垂直设直线l 的方向向量为a =(a 1,b 1,c 1),平面α、β的法向量分别为μ=(a 2,b 2,c 2),υ=(a 3,b 3,c 3),则有:(1)线面平行l ∥α⇔a ⊥μ⇔a·μ=0⇔a 1a 2+b 1b 2+c 1c 2=0. (2)线面垂直l ⊥α⇔a ∥μ⇔a =k μ⇔a 1=ka 2,b 1=kb 2,c 1=kc 2. (3)面面平行α∥β⇔μ∥υ⇔μ=λυ⇔a 2=λa 3,b 2=λb 3,c 2=λc 3.(4)面面垂直α⊥β⇔μ⊥υ⇔μ·υ=0⇔a 2a 3+b 2b 3+c 2c 3=0.2.利用直线的方向向量与平面的法向量求空间角设直线l ,m 的方向向量分别为a =(a 1,b 1,c 1),b =(a 2,b 2,c 2).平面α,β的法向量分别为μ=(a 3,b 3,c 3),υ=(a 4,b 4,c 4)(以下相同).(1)线线夹角设l ,m 的夹角为θ⎝⎛⎭⎫0≤θ≤π2,则cos θ=|a·b ||a||b|=|a 1a 2+b 1b 2+c 1c 2|a 21+b 21+c 21a 22+b 22+c 22. (2)线面夹角设直线l 与平面α的夹角为θ⎝⎛⎭⎫0≤θ≤π2,则sin θ=|a·μ||a||μ|=|cos 〈a ,μ〉|.(3)面面夹角设平面α、β的夹角为θ⎝⎛⎭⎫0≤θ≤π2,则|cos θ|=|μ·υ||μ||υ|=|cos 〈μ,υ〉|. [典型例题](1)如图,在直三棱柱ADEBCF 中,平面ABFE 和平面ABCD都是正方形且互相垂直,M 为AB 的中点,O 为DF 的中点.运用向量方法证明:①OM ∥平面BCF ; ②平面MDF ⊥平面EFCD .(2)(·高考浙江卷)如图,已知多面体ABCA 1B 1C 1,A 1A ,B 1B ,C 1C 均垂直于平面ABC ,∠ABC =120°,A 1A =4,C 1C =1,AB =BC =B 1B =2.①证明:AB 1⊥平面A 1B 1C 1;②求直线AC 1与平面ABB 1所成的角的正弦值.【解】 (1)证明:由题意知,AB ,AD ,AE 两两垂直,以A 为原点建立如图所示的空间直角坐标系.设正方形边长为1,则A (0,0,0),B (1,0,0),C (1,1,0),D (0,1,0),F (1,0,1),M ⎝⎛⎭⎫12,0,0,O ⎝⎛⎭⎫12,12,12. ①OM →=⎝⎛⎭⎫0,-12,-12,BA →=(-1,0,0), 所以OM →·BA →=0,所以OM →⊥BA →. 因为棱柱ADEBCF 是直三棱柱,所以AB ⊥平面BCF ,所以BA →是平面BCF 的一个法向量,又OM ⊄平面BCF ,所以OM ∥平面BCF .②设平面MDF 与平面EFCD 的法向量分别为n 1=(x 1,y 1,z 1),n 2=(x 2,y 2,z 2). 因为DF →=(1,-1,1),DM →=⎝⎛⎭⎫12,-1,0,DC →=(1,0,0), 由n 1·DF →=n 1·DM →=0,得⎩⎪⎨⎪⎧x 1-y 1+z 1=0,12x 1-y 1=0,解得⎩⎨⎧y 1=12x 1,z 1=-12x 1,令x 1=1,则n 1=⎝⎛⎭⎫1,12,-12. 同理可得n 2=(0,1,1).因为n 1·n 2=0,所以平面MDF ⊥平面EFCD .(2)①证明:如图,以AC 的中点O 为原点,分别以射线OB ,OC 为x ,y 轴的正半轴,建立空间直角坐标系O -xyz .由题意知各点坐标如下:A (0,-3,0),B (1,0,0),A 1(0,-3,4),B 1(1,0,2),C 1(0,3,1). 因此AB 1→=(1,3,2),A 1B 1→=(1,3,-2). A 1C 1→=(0,23,-3). 由AB 1→·A 1B 1→=0得AB 1⊥A 1B 1. 由AB 1→·A 1C 1→=0得AB 1⊥A 1C 1. 所以AB 1⊥平面A 1B 1C 1.②设直线AC 1与平面ABB 1所成的角为θ.由①可知AC 1→=(0,23,1),AB →=(1,3,0),BB 1→=(0,0,2).设平面ABB 1的法向量n =(x ,y ,z ).由⎩⎪⎨⎪⎧n ·AB →=0,n ·BB 1→=0,即⎩⎪⎨⎪⎧x +3y =0,2z =0,可取n =(-3,1,0).所以sin θ=|cosAC 1→,n|=|AC 1→·n ||AC 1→|·|n |=3913.因此,直线AC1与平面ABB1所成的角的正弦值是3913.(1)利用空间向量证明平行与垂直的步骤①建立空间直角坐标系,建系时,要尽可能地利用载体中的垂直关系.②建立空间图形与空间向量之间的关系,用空间向量表示出问题中所涉及的点、直线、平面的要素.③通过空间向量的运算研究平行、垂直关系.④根据运算结果解释相关问题.(2)运用空间向量求空间角的一般步骤①建立恰当的空间直角坐标系;②求出相关点的坐标;③写出向量坐标;④结合公式进行论证、计算;⑤转化为几何结论.(3)求空间角的注意点①两条异面直线所成的角α不一定是直线的方向向量的夹角β,即cos α=|cos β|.②所求的二面角不一定是两平面的法向量的夹角,有可能为两法向量夹角的补角.[对点训练]1.(·绍兴市柯桥区高三期中考试)如图,在几何体ABCDE中,四边形ABCD是矩形,AB⊥平面BCE,BE⊥CE,AB=BE=EC=2,G,F分别是线段BE,DC的中点.(1)求证:GF∥平面ADE;(2)求GF与平面ABE所成角的正切值.解:(1)证明:如图,取AE的中点H,连接HG,HD,又G是BE的中点,所以GH∥AB,且GH=12AB,又F是CD中点,所以DF=12CD,由四边形ABCD是矩形得,AB∥CD,AB=CD,所以GH∥DF,且GH=DF.所以四边形HGFD是平行四边形,所以GF∥DH,又DH⊂平面ADE,GF⊄平面ADE,所以GF∥平面ADE.(2)如图,在平面BEC 内,过B 作BQ ∥EC , 因为BE ⊥CE ,所以BQ ⊥BE ,又因为AB ⊥平面BEC ,所以AB ⊥BE ,AB ⊥BQ ,以B 为原点,BE 、BQ 、BA 所在直线分别为x ,y ,z 轴,建立空间直角坐标系,则A (0,0,2),B (0,0,0),E (2,0,0),F (2,2,1),G (1,0,0),GF →=(1,2,1),平面ABE 的法向量n =(0,1,0),设GF 与平面ABE 所成的角为θ, 则sin θ=|GF →·n ||GF →|·|n |=26,所以cos θ=1-⎝⎛⎭⎫262=26,所以tan θ=sin θcos θ=2626= 2.所以GF 与平面ABE 所成角的正切值为 2.2.(·宁波市镇海中学高考模拟)在边长为3的正三角形ABC 中,E 、F 、P 分别是AB 、AC 、BC 边上的点,满足AE ∶EB =CF ∶F A =CP ∶PB =1∶2.如图(1)将△AEF 沿EF 折起到△A 1EF 的位置,使二面角A 1EF B 成直二面角,连接A 1B 、A 1P (如图(2)).(1)求证:A 1E ⊥平面BEP ; (2)求二面角B -A 1P E 的余弦值.解:(1)证明:在图(1)中,取BE 的中点D ,连接DF , 因为AE ∶EB =CF ∶F A =1∶2,所以AF =AD =2, 而∠A =60°,所以△ADF 为正三角形. 又AE =DE =1,所以EF ⊥AD . 在图(2)中,A 1E ⊥EF ,BE ⊥EF ,所以∠A 1EB 为二面角A 1EF B 的一个平面角,由题设条件知此二面角为直二面角,所以A 1E ⊥平面BEP .(2)分别以EB 、EF 、EA 1所在直线为x 、y 、z 轴建立空间直角坐标系, 则E (0,0,0),B (2,0,0),P (1,3,0),A 1(0,0,1),EA 1→=(0,0,1),EP →=(1,3,0),BA 1→=(-2,0,1),BP →=(-1,3,0). 设平面EA 1P 的法向量为m =(x ,y ,z ), 则⎩⎪⎨⎪⎧m ·EA 1→=z =0m ·EP →=x +3y =0,取y =-1,得m =(3,-1,0); 设平面BA 1P 的法向量为n =(x ′,y ′,z ′),则⎩⎪⎨⎪⎧n ·BA 1→=-2x ′+z ′=0n ·BP →=-x ′+3y ′=0,取y ′=1,得n =(3,1,23).所以cos 〈m ,n 〉=m ·n |m ||n |=3×3-1×12×4=14,所以二面角B -A 1P E 的余弦值为14.立体几何中的探索性问题[核心提炼]探索性问题主要考两类问题 (1)条件探索型问题; (2)存在探索型问题.探索性问题求解思路为利用空间向量的坐标运算,建立目标函数或目标方程,将问题转化为代数问题解决.[典型例题](·浙江高考冲刺卷)如图所示的几何体ABCDE 中,EA ⊥平面ABC ,EA ∥DC ,AB ⊥AC ,EA =AB =AC =2DC ,M 是线段BD 上的动点.(1)当M 是BD 的中点时,求证:BC ⊥平面AME ;(2)是否存在点M ,使得直线BD 与平面AMC 所成的角为60°,若存在,确定点M 的位置;若不存在,请说明理由.【解】 (1)证明:因为EA ⊥平面ABC ,AB ⊥AC ,所以直线AB ,AC ,AE 两两垂直,以A 为原点,以AB ,AC ,AE 所在直线为坐标轴建立如图空间直角坐标系A -xyz ,设CD =1,则AB =AC =AE =2,所以A (0,0,0),B (2,0,0),C (0,2,0),D (0,2,1),E (0,0,2),因为M 是BD 中点,所以M ⎝⎛⎭⎫1,1,12, 所以AE →=(0,0,2),AM →=⎝⎛⎭⎫1,1,12, BC →=(-2,2,0),所以AE →·BC →=0,AM →·BC →=0, 所以AE ⊥BC ,AM ⊥BC ,又AM ⊂平面AME ,AE ⊂平面AME ,AE ∩AM =A , 所以BC ⊥平面AME .(2)由(1)得,BD →=(-2,2,1),AC →=(0,2,0),AB →=(2,0,0), 设BM →=λBD →=(-2λ,2λ,λ)(0<λ<1),则AM →=AB →+BM →=(2-2λ,2λ,λ), 设平面AMC 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·AC →=0n ·AM →=0,所以⎩⎪⎨⎪⎧2y =0(2-2λ)x +2λy +zλ=0,令x =1得n =⎝⎛⎭⎫1,0,2-2λ,所以cos 〈BD →,n〉=BD →·n |BD →||n |=-2λ3× 1+⎝⎛⎭⎫2-2λ2=-235λ2-8λ+4,令235λ2-8λ+4=sin 60°=32,得5λ2-8λ+9227=0,Δ=64-4×5×9227<0,所以方程无解,所以BD 上不存在点M ,使得直线BD 与平面AMC 所成的角为60°.利用空间向量巧解探索性问题(1)空间向量最适合于解决立体几何中的探索性问题,它无需进行复杂的作图、论证、推理,只需通过坐标运算进行判断.(2)解题时,把要成立的结论当作条件,据此列方程或方程组,把“是否存在”问题转化为“点的坐标是否有解,是否有规定范围内的解”等,所以为使问题的解决更简单、有效,应善于运用这一方法解题.[对点训练](·衢州诊断考试)如图,在四棱锥P -ABCD 中,P A ⊥平面ABCD ,P A =AB =AD =2,四边形ABCD 满足AB ⊥AD ,BC ∥AD 且BC =4,点M 为PC 的中点,点E 为BC 边上的动点,且BE EC=λ.(1)求证:平面ADM ⊥平面PBC ;(2)是否存在实数λ,使得二面角P -DE -B 的余弦值为22?若存在,试求出实数λ的值;若不存在,说明理由.解:(1)证明:取PB 的中点N ,连接MN 、AN , 因为M 是PC 的中点,所以MN ∥BC ,MN =12BC =2,又BC ∥AD ,所以MN ∥AD ,MN =AD , 所以四边形ADMN 为平行四边形,因为AP ⊥AD ,AB ⊥AD ,所以AD ⊥平面P AB ,所以AD ⊥AN ,所以AN ⊥MN ,因为AP =AB ,所以AN ⊥PB ,所以AN ⊥平面PBC , 因为AN ⊂平面ADM ,所以平面ADM ⊥平面PBC .(2)法一:存在实数λ=1,使得二面角P -DE -B 的余弦值为22. 因为λ=1,所以点E 为BC 边的中点, 所以DE ∥AB , 所以DE ⊥平面P AD ,所以∠PDA 为二面角P -DE -B 的一个平面角. 在等腰Rt △PDA 中,∠PDA =π4,所以二面角P -DE -B 的余弦值为22. 法二:存在符合条件的λ.以A 为原点,建立如图所示的空间直角坐标系A -xyz . 设E (2,t ,0),P (0,0,2),D (0,2,0),B (2,0,0), 从而PD →=(0,2,-2),DE →=(2,t -2,0), 设平面PDE 的法向量为n 1=(x ,y ,z ), 则⎩⎪⎨⎪⎧n 1·PD →=0n 1·DE →=0,即⎩⎪⎨⎪⎧2y -2z =02x +(t -2)y =0,令y =z =2,解得x =2-t , 所以n 1=(2-t ,2,2),又平面DEB 即为平面xAy ,故其一个法向量为n 2=(0,0,1), 则|cos 〈n 1,n 2〉|=|n 1·n 2||n 1|·|n 2|=2(2-t )2+4+4=22, 解得t =2,可知λ=1.立体几何中的动态问题[核心提炼]立体几何中的动态问题主要包括:空间动点轨迹的判断,求轨迹的长度及动角的范围等;求解方法一般根据圆锥曲线的定义判断动点轨迹是什么样的曲线;利用空间向量的坐标运算求轨迹的长度等.[典型例题](1)(·金华十校高考模拟)在正方体ABCD -A 1B 1C 1D 1中,点M 、N 分别是直线CD 、AB 上的动点,点P 是△A 1C 1D 内的动点(不包括边界),记直线D 1P 与MN 所成角为θ,若θ的最小值为π3,则点P 的轨迹是( )A .圆的一部分B .椭圆的一部分C .抛物线的一部分D .双曲线的一部分(2)(·浙江名校协作体高三联考)已知平面ABCD ⊥平面ADEF ,AB ⊥AD ,CD ⊥AD ,且AB =1,AD =CD =2.ADEF 是正方形,在正方形ADEF 内部有一点M ,满足MB ,MC 与平面ADEF 所成的角相等,则点M 的轨迹长度为( )A.43B.163C.49π D.83π 【解析】 (1)把MN 平移到平面A 1B 1C 1D 1中,直线D 1P 与MN 所成角为θ,直线D 1P 与MN 所成角的最小值是直线D 1P 与平面A 1B 1C 1D 1所成角,即原问题转化为:直线D 1P 与平面A 1B 1C 1D 1所成角为π3,点P在平面A 1B 1C 1D 1的投影为圆的一部分,因为点P 是△A 1C 1D 内的动点(不包括边界), 所以点P 的轨迹是椭圆的一部分.故选B.(2)根据题意,以D 为原点,分别以DA ,DC ,DE 所在直线为x ,y ,z 轴,建立空间直角坐标系D xyz ,如图1所示,则B (2,1,0),C (0,2,0),设M (x ,0,z ),易知直线MB ,MC 与平面ADEF 所成的角分别为∠AMB ,∠DMC ,均为锐角,且∠AMB =∠DMC ,所以sin ∠AMB =sin ∠DMC ⇒AB MB =CD MC,即2MB =MC ,因此2(2-x )2+12+z 2=x 2+22+z 2,整理得⎝⎛⎭⎫x -832+z 2=169,由此可得,点M 在正方形ADEF 内的轨迹是以点O ⎝⎛⎭⎫83,0,0为圆心, 半径为43的圆弧M 1M 2,如图2所示,易知圆心角∠M 1OM 2=π3,所以lM 1M 2=π3×43=49π.故选C.【答案】 (1)B (2)C求解立体几何中的轨迹问题时,首先要探究点的轨迹的形成过程,同时还要注意动点的性质以及点、线、面之间的位置关系,若动点的性质满足解析几何中圆锥曲线的定义,也可借助定义求出轨迹.[对点训练](·杭州市高考二模)在等腰直角△ABC 中,AB ⊥AC ,BC =2,M 为BC 中点,N 为AC 中点,D 为BC 边上一个动点,△ABD 沿AD 翻折使BD ⊥DC ,点A 在面BCD 上的投影为点O ,当点D 在BC 上运动时,以下说法错误的是( )A .线段NO 为定长B .|CO |∈[1,2)C .∠AMO +∠ADB >180°D .点O 的轨迹是圆弧解析:选C.如图所示,对于A ,△AOC 为直角三角形,ON 为斜边AC 上的中线,ON =12AC 为定长,即A 正确;对于B ,D 在M 时,AO=1,CO =1,所以|CO |∈[1,2),即正确;对于D ,由A 可知,点O 的轨迹是圆弧,即D 正确,故选C.立体几何中的最值(范围)问题[核心提炼]求解立体几何中的最值问题,需要先确定最值的主体,确定题目中描述的相关变量,然后根据所求,确定是利用几何方法求解,还是转化为代数(特别是函数)问题求解.利用几何方法求解时,往往利用几何体的结构特征将问题转化为平面几何中的问题进行求解,如求几何体表面距离的问题.利用代数法求解时,要合理选择参数,利用几何体中的相关运算构造目标函数,再根据条件确定参数的取值范围,从而确定目标函数的值域,即可利用函数最值的求解方法求得结果.[典型例题](1)(·宁波十校联考)如图,平面P AB ⊥平面α,AB ⊂α,且△P AB 为正三角形,点D 是平面α内的动点,ABCD 是菱形,点O 为AB 中点,AC 与OD 交于点Q ,l ⊂α,且l ⊥AB ,则PQ 与l 所成角的正切值的最小值为( )A.-3+372B. 3+372C. 7D .3(2)(·温州高考模拟)如图,在三棱锥A -BCD 中,平面ABC ⊥平面BCD ,△BAC 与BCD 均为等腰直角三角形,且∠BAC =∠BCD =90°,BC =2,点P 是线段AB 上的动点,若线段CD 上存在点Q ,使得直线PQ 与AC 成30°的角,则线段P A 长的取值范围是( )A.⎝⎛⎭⎫0,22 B.⎣⎡⎦⎤0,63 C.⎝⎛⎭⎫22,2 D.⎝⎛⎭⎫63,2【解析】 (1)如图,不妨以CD 在AB 前侧为例.以O 为原点,分别以OB 、OP 所在直线为y 、z 轴建立空间直角坐标系,设AB =2,∠OAD =θ(0<θ<π),则P (0,0,3),D (2sin θ,-1+2cos θ,0), 所以Q ⎝⎛⎭⎫23sin θ,23cos θ-13,0, 所以QP →=⎝⎛⎭⎫-23sin θ,13-23cos θ,3, 设α内与AB 垂直的向量n =(1,0,0),PQ 与l 所成角为φ,则cos φ=⎪⎪⎪⎪⎪⎪⎪⎪QP →·n |QP →||n |=⎪⎪⎪⎪⎪⎪-23sin θ329-49cos θ=sin θ8-cos θ=1-cos 2θ8-cos θ.令t =cos θ(-1<t <1),则s =1-t 28-t ,s ′=t 2-16t +1(8-t )2, 令s ′=0,得t =8-37,所以当t =8-37时,s 有最大值为16-67. 则cos φ有最大值为16-67,此时sin φ取最小值为67-15.所以正切值的最小值为67-1516-6 7=3+372.故选B. (2)以C 为原点,CD 为x 轴,CB 为y 轴,过C 作平面BCD 的垂线为z 轴,建立空间直角坐标系,则A (0,1,1),B (0,2,0),C (0,0,0),设Q (q ,0,0),AP →=λAB →=(0,λ,-λ),则PQ →=CQ →-CP →=CQ →-(CA →+AP →)=(q ,0,0)-(0,1,1)-(0,λ,-λ)=(q ,-1-λ,λ-1),因为直线PQ 与AC 成30°的角,所以cos 30°=|CA →·PQ →||CA →|·|PQ →|=22·q 2+(1+λ)2+(λ-1)2 =2q 2+2λ2+2=32,所以q 2+2λ2+2=83,所以q 2=23-2λ2∈[0,4],所以⎩⎨⎧23-2λ2≥023-2λ2≤4,解得0≤λ≤33,所以|AP →|=2λ∈⎣⎡⎦⎤0,63, 所以线段P A 长的取值范围是⎣⎡⎦⎤0,63. 故选B.【答案】 (1)B (2)B用向量法解决立体几何中的最值问题,不仅简捷,更减少了思维量.用变量表示动点的坐标,然后依题意用向量法求其有关几何量,构建有关函数,从而用代数方法即可求其最值.[对点训练]1.(·浙江省五校联考二模)如图,棱长为4的正方体ABCD -A 1B 1C 1D 1,点A 在平面α内,平面ABCD 与平面α所成的二面角为30°,则顶点C 1到平面α的距离的最大值是( )A .2(2+2)B .2(3+2)C .2(3+1)D .2(2+1)解析:选B.如图所示,作C 1O ⊥α,交ABCD 于O ,交α于E ,由题得O 在AC 上,则C 1E 为所求,∠AOE =30°, 由题意,设CO =x ,则AO =42-x , C 1O =16+x 2,OE =12OA =22-12x ,所以C 1E =16+x 2+22-12x ,令y =16+x 2+22-12x ,则y ′=x16+x 2-12=0,可得x =43, 所以x =43,顶点C 1到平面α的距离的最大值是2(3+2). 2.(·温州十五校联合体期末考试)在正四面体P -ABC 中,点M 是棱PC 的中点,点N 是线段AB 上一动点,且AN →=λAB →,设异面直线NM 与AC 所成角为α,当13≤λ≤23时,则cos α的取值范围是________.解析:设点P 到平面ABC 的射影为点O ,以AO 所在直线为y 轴,OP 所在直线为z 轴,过点O 作BC 的平行线为x 轴,建立空间直角坐标系,如图.设正四面体的棱长为43,则有A (0,-4,0),B (23,2,0),C (-23,2,0),P (0,0,42),M (-3,1,22).由AN →=λAB →,得N (23λ,6λ-4,0).从而有NM →=(-3-23λ,5-6λ,22),AC →=(-23,6,0). 所以cos α=|NM →·AC →||NM →||AC →|=3-2λ24λ2-4λ+3,设3-2λ=t ,则53≤t ≤73.则cos α=12t 2t 2-4t +6=126⎝⎛⎭⎫1t 2-4·1t +1,因为13<37≤1t ≤35,所以51938≤cos α≤71938. 答案:⎣⎡⎦⎤51938,71938专题强化训练1.在正方体ABCD -A 1B 1C 1D 1中,E ,F 分别为CD 和C 1C 的中点,则直线AE 与D 1F 所成角的余弦值为( )A.13 B.25 C.35D.37解析:选B.以D 为原点,分别以DA 、DC 、DD 1所在直线为x 轴、y 轴、z 轴建立空间直角坐标系(图略).若棱长为2,则A (2,0,0)、E (0,1,0)、D 1(0,0,2)、F (0,2,1).所以EA →=(2,-1,0),D 1F →=(0,2,-1), cos 〈EA →,D 1F →〉=EA →·D 1F →|EA →||D 1F →|=-25·5=-25.则直线AE 与D 1F 所成角的余弦值为25.2.在正方体ABCD -A 1B 1C 1D 1中,点E 为BB 1的中点,则平面A 1ED 与平面ABCD 所成的锐二面角的余弦值为( )A.12B.23C.33D.22解析:选B.以A 为原点建立如图所示的空间直角坐标系A -xyz ,设棱长为1,则A 1(0,0,1),E ⎝⎛⎭⎫1,0,12, D (0,1,0),所以A 1D →=(0,1,-1), A 1E →=⎝⎛⎭⎫1,0,-12, 设平面A 1ED 的一个法向量为n 1=(1,y ,z ),则⎩⎪⎨⎪⎧y -z =0,1-12z =0,所以⎩⎪⎨⎪⎧y =2,z =2.所以n 1=(1,2,2).因为平面ABCD 的一个法向量为n 2=(0,0,1), 所以cos 〈n 1,n 2〉=23×1=23.即所成的锐二面角的余弦值为23.3.(·浙江省十校联合体期末联考)在三棱锥O -ABC 中,已知OA ,OB ,OC 两两垂直且相等,点P 、Q 分别是线段BC 和OA 上的动点,且满足BP ≤12BC ,AQ ≥12AO ,则PQ 和OB 所成角的余弦的取值范围是( )A.⎣⎡⎦⎤22,1B.⎣⎡⎦⎤33,1C.⎣⎡⎦⎤33,255D.⎣⎡⎦⎤22,255解析:选B.根据题意,以O 为原点,建立如图所示的空间直角坐标系,不妨设OA =OB =OC =2,OB →=(2,0,0),设P (x ,y ,0),Q (0,0,z ),因为BP ≤12BC ,AQ ≥12AO ,所以1≤x ≤2,0≤y ≤1且x +y =2,0≤z ≤1,PQ →=(-x ,x -2,z ),|cos 〈OB →,PQ →〉|=⎪⎪⎪⎪⎪⎪⎪⎪OB →·PQ →|OB→|·|PQ →|=⎪⎪⎪⎪⎪⎪⎪⎪-x 2x 2-4x +4+z 2, 当x =1,z =1时,|cos 〈OB →,PQ →〉|=33;当x =2,z =1时,|cos 〈OB →,PQ →〉|=255;当x =2,z =0时,|cos 〈OB →,PQ →〉|=1.当x =1,z =0时,|cos 〈OB →,PQ →〉|=22,结合四个选项可知PQ 和OB 所成角的余弦的取值范围是⎣⎡⎦⎤33,1.4.(·宁波市镇海中学高考模拟)在直三棱柱A 1B 1C 1ABC 中,∠BAC =π2,AB =AC =AA 1=1,已知G 和E 分别为A 1B 1和CC 1的中点,D 与F 分别为线段AC 和AB 上的动点(不包括端点),若GD ⊥EF ,则线段DF 的长度的取值范围为( )A.⎣⎡⎭⎫55,1B.⎣⎡⎦⎤55,1C.⎝⎛⎭⎫255,1D.⎣⎡⎭⎫255,1解析:选 A.建立如图所示的空间直角坐标系,则A (0,0,0),E ⎝⎛⎭⎫0,1,12,G ⎝⎛⎭⎫12,0,1,F (x ,0,0),D (0,y ,0), 由于GD ⊥EF ,所以x +2y -1=0, DF =x 2+y 2=5⎝⎛⎭⎫y -252+15, 由x =1-2y >0,得y <12,所以当y =25时,线段DF 长度的最小值是15,当y =0时,线段DF 长度的最大值是1而不包括端点,故y =0不能取,故选A. 5.已知直三棱柱ABC -A 1B 1C 1中,∠ABC =120°,AB =2,BC =CC 1=1,则异面直线AB 1与BC 1所成角的余弦值为( )A.32B.155C.105D.33解析:选C.如图所示,将直三棱柱ABC -A 1B 1C 1补成直四棱柱ABCD -A 1B 1C 1D 1,连接AD 1,B 1D 1,则AD 1∥BC 1,所以∠B 1AD 1或其补角为异面直线AB 1与BC 1所成的角.因为∠ABC =120°,AB =2,BC =CC 1=1,所以AB 1=5,AD 1= 2.在△B 1D 1C 1中,∠B 1C 1D 1=60°,B 1C 1=1,D 1C 1=2,所以B 1D 1=12+22-2×1×2×cos 60°=3,所以cos ∠B 1AD 1=5+2-32×5×2=105,选择C.6.(·杭州市学军中学高考数学模拟)如图,在二面角A -CD -B 中,BC ⊥CD ,BC =CD =2,点A 在直线AD 上运动,满足AD ⊥CD ,AB =3.现将平面ADC 沿着CD 进行翻折,在翻折的过程中,线段AD 长的取值范围是________.解析:由题意得AD →⊥DC →,DC →⊥CB →,设平面ADC 沿着CD 进行翻折过程中,二面角A -CD -B 的夹角为θ,则〈DA →,CB →〉=θ,因为AB →=AD →+DC →+CB →,所以平方得AB →2=AD →2+DC →2+CB →2+2AD →·DC →+2CB →·AD →+2DC →·CB →,设AD =x ,因为BC =CD =2,AB =3, 所以9=x 2+4+4-4x cos θ,即x 2-4x cos θ-1=0,即cos θ=x 2-14x .因为-1≤cos θ≤1,所以-1≤x 2-14x≤1,即⎩⎪⎨⎪⎧x 2-1≤4x x 2-1≥-4x ,即⎩⎪⎨⎪⎧x 2-4x -1≤0x 2+4x -1≥0,则⎩⎪⎨⎪⎧2-5≤x ≤2+5,x ≥-2+5或x ≤-2- 5.因为x >0,所以5-2≤x ≤5+2, 即AD 的取值范围是[5-2,5+2]. 答案:[5-2,5+2]7.(·台州市高考模拟)如图,在棱长为2的正四面体A -BCD 中,E 、F 分别为直线AB 、CD 上的动点,且|EF |= 3.若记EF 中点P 的轨迹为L ,则|L |等于________.(注:|L |表示L 的测度,在本题,L 为曲线、平面图形、空间几何体时,|L |分别对应长度、面积、体积)解析:如图,当E 为AB 中点时,F 分别在C ,D 处,满足|EF |=3,此时EF 的中点P 在EC ,ED 的中点P 1,P 2的位置上;当F 为CD 中点时,E 分别在A ,B 处,满足|EF |=3,此时EF 的中点P 在BF ,AF 的中点P 3,P 4的位置上,连接P 1P 2,P 3P 4相交于点O ,则四点P 1,P 2,P 3,P 4共圆,圆心为O ,圆的半径为12,则EF 中点P 的轨迹L 为以O 为圆心,以12为半径的圆,其测度|L |=2π×12=π.答案:π8.(·金丽衢十二校联考)如图,在三棱锥D -ABC 中,已知AB =2,AC →·BD →=-3,设AD =a ,BC =b ,CD =c ,则c 2ab +1的最小值为________.解析:设AD →=a ,CB →=b ,DC →=c ,因为AB =2,所以|a +b +c |2=4⇒a 2+b 2+c 2+2(a ·b +b ·c +c ·a )=4,又因为AC →·BD →=-3,所以(a +c )·(-b -c )=-3⇒a ·b +b ·c +c ·a +c 2=3,所以a 2+b 2+c 2+2(3-c 2)=4⇒c 2=a 2+b 2+2,所以a 2+b 2+2ab +1≥2ab +2ab +1=2,当且仅当a=b 时,等号成立,即c 2ab +1的最小值是2.答案:29.(·宁波诺丁汉大学附中高三期中考试)如图,矩形ABCD 中,AB =1,BC =3,将△ABD 沿对角线BD 向上翻折,若翻折过程中AC 长度在⎣⎡⎦⎤102,132内变化,则点A 所形成的运动轨迹的长度为________.解析:过A 作AE ⊥BD ,垂足为E ,连接CE ,A ′E . 因为矩形ABCD 中,AB =1,BC =3, 所以AE =32,CE =72. 所以A 点的轨迹为以E 为圆心,以32为半径的圆弧.∠A ′EA 为二面角A -BD -A ′的平面角. 以E 为原点,以EB ,EA ′所在直线为x 轴,y 轴建立如图所示空间直角坐标系E -xyz ,设∠A ′EA =θ,则A ⎝⎛⎭⎫0,32cos θ,32sin θ,C ⎝⎛⎭⎫-1,-32,0,所以AC =1+34(cos θ+1)2+34sin 2θ=5+3cos θ2, 所以102≤ 5+3cos θ2≤132, 解得0≤cos θ≤12,所以60°≤θ≤90°,所以A 点轨迹的圆心角为30°, 所以A 点轨迹的长度为π6·32=3π12.答案:312π 10.(·宁波十校联考模拟)如图,在四棱锥P -ABCD 中,∠BAD =120°,AB =AD =2,△BCD 是等边三角形,E 是BP 的中点,AC 与BD 交于点O ,且OP ⊥平面ABCD .(1)求证:PD ∥平面ACE ;(2)当OP =1时,求直线P A 与平面ACE 所成角的正弦值. 解:(1)证明:因为在四棱锥P -ABCD 中,∠BAD =120°,AB =AD =2,△BCD 是等边三角形,所以△ABC ≌△ACD ,因为E 是BP 中点,AC 与BD 交于点O ,所以O 是BD 中点,连接OE ,则OE ∥PD ,因为PD ⊄平面ACE ,OE ⊂平面ACE ,所以PD ∥平面ACE .(2)因为BD ⊥AC ,PO ⊥平面ABCD ,以O 为原点,OB ,OC ,OP 所在直线为坐标轴建立空间直角坐标系,则P (0,0,1),A (0,-1,0),B (3,0,0),C (0,3,0),E ⎝⎛⎭⎫32,0,12, EA →=⎝⎛⎭⎫-32,-1,-12,EC →=⎝⎛⎭⎫-32,3,-12,P A →=(0,-1,-1),设平面ACE 的一个法向量n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·EA →=3x +2y +z =0n ·EC →=3x -6y +z =0,取x =1,得n =(1,0,-3), 设直线P A 与平面ACE 所成角为θ,则sin θ=|n ·P A →||n |·|P A →|=322=64, 所以直线P A 与平面ACE 所成角的正弦值为64. 11.(·浙江暨阳联考卷)在四棱锥P -ABCD 中,PC ⊥平面ABCD ,BC ∥AD ,BC ⊥AB ,PB =AD =2,AB =BC =1,E 为棱PD 上的点.(1)若PE =13PD ,求证:PB ∥平面ACE ; (2)若E 是PD 的中点,求直线PB 与平面ACE 所成角的正弦值.解:(1)证明:过A 作Az ⊥平面ABCD ,以A 为原点,如图建立直角坐标系,由题意解得,PC =3,所以B (1,0,0),P (1,1,3),所以BP →=(0,1,3),C (1,1,0),D (0,2,0),设E (x ,y ,z ),由PE →=13PD →,得E (23,43,233), 设平面ACE 的法向量为n =(x ,y ,z ),则⎩⎨⎧n AC →=x +y =0n AE →=23x +43y +233z =0,取z =1,得n =(3,-3,1),所以BP →·n =0,因为PB ⊄平面ACE ,所以PB ∥平面ACE .(2)过A 作Az ⊥平面ABCD ,以A 为原点,如图建立直角坐标系,由题意解得PC =3,所以B (1,0,0),P (1,1,3),A (0,0,0),所以BP →=(0,1,3),C (1,1,0),D (0,2,0),所以E (12,32,32), AC →=(1,1,0),AE →=(12,32,32), 设平面ACE 的法向量为n =(x ,y ,z ),则⎩⎨⎧n AC→=x +y =0n AE →=12x +32y +32z =0, 取z =2,得n =(3,-3,2),所以直线PB 与平面ACE 所成角的正弦值:sin θ=|BP →·n ||BP →||n |=3210=3020. 12.(·嵊州市第二次高考适应性考试)如图,在直三棱柱ABC -A 1B 1C 1中,底面ABC 为边长为2的正三角形,D 是棱A 1C 1的中点,CC 1=h (h >0).(1)证明:BC 1∥平面AB 1D ;(2)若直线BC 1与平面ABB 1A 1所成角的大小为π6,求h 的值. 解:(1)证明:连接A 1B 交AB 1于E ,连接DE ,则DE 是△A 1BC 1的中位线.所以DE ∥BC 1.又DE ⊂平面AB 1D ,BC 1⊄平面AB 1D ,故BC 1∥平面AB 1D .(2)以AB 的中点O 为坐标原点,OB ,OC 所在直线分别为x 轴,y 轴建立空间直角坐标系,如图所示,则B (1,0,0),C 1(0,3,h ).易得平面ABB 1A 1的一个法向量为n =(0,1,0).又BC 1→=(-1,3,h ).所以sin π6=|cos 〈BC 1→,n 〉|=|BC 1→·n ||BC 1→|·|n |. 即3h 2+4=12,解得h =2 2. 13.(·温州十五校联考)已知菱形ABCD 中,对角线AC 与BD 相交于一点O ,∠BAD =60°,将△BDC 沿着BD 折起得△BDC ′,连接AC ′.(1)求证:平面AOC ′⊥平面ABD ;(2)若点C ′在平面ABD 上的投影恰好是△ABD 的重心,求直线CD 与底面ADC ′所成角的正弦值.解:(1)证明:因为C ′O ⊥BD ,AO ⊥BD ,C ′O ∩AO =O ,所以BD ⊥平面C ′OA ,又因为BD ⊂平面ABD ,所以平面AOC ′⊥平面ABD .(2)如图建系O -xyz ,令AB =a ,则 A ⎝⎛⎭⎫32a ,0,0,B ⎝⎛⎭⎫0,12a ,0, D ⎝⎛⎭⎫0,-12a ,0, C ′⎝⎛⎭⎫36a ,0,63a , 所以DC →=AB →=⎝⎛⎭⎫-32a ,12a ,0,平面ADC ′的法向量为m =⎝⎛⎭⎫1,-3,22,设直线CD 与底面ADC ′所成角为θ,则sin θ=|cos 〈DC →,m 〉|=|DC →·m ||DC →||m |=3a a ·32=63, 故直线CD 与底面ADC ′所成角的正弦值为63. 14.(·宝鸡市质量检测(一))如图,四棱锥P -ABCD 的底面ABCD 为矩形,P A ⊥平面ABCD ,点E 是PD 的中点,点F 是PC 的中点.(1)证明:PB ∥平面AEC ;(2)若底面ABCD 为正方形,探究在什么条件下,二面角C -AF -D 的大小为60°?解:易知AD ,AB ,AP 两两垂直,建立如图所示的空间直角坐标系A -xyz ,设AB =2a ,AD =2b ,AP =2c ,则A (0,0,0),B (2a ,0,0),C (2a ,2b ,0),D (0,2b ,0),P (0,0,2c ).设AC ∩BD =O ,连接OE ,则O (a, b ,0),又E 是PD 的中点,所以E (0,b ,c ).(1)证明:因为PB →=(2a ,0,-2c ),EO →=(a ,0,-c ),所以PB →=2EO →,所以PB →∥EO →,即PB ∥EO .因为PB ⊄平面AEC ,EO ⊂平面AEC ,所以PB ∥平面AEC .(2)因为四边形ABCD 为正方形,所以a =b ,A (0,0,0),B (2a ,0,0),C (2a ,2a ,0),D (0,2a ,0),P (0,0,2c ),E (0,a ,c ),F (a ,a ,c ),因为z 轴⊂平面CAF ,所以设平面CAF 的一个法向量为n =(x ,1,0),而AC →=(2a ,2a ,0),所以AC →·n =2ax +2a =0,得x =-1,所以n =(-1,1,0).因为y 轴⊂平面DAF ,所以设平面DAF 的一个法向量为m =(1,0,z ),而AF →=(a ,a ,c ),所以AF →·m =a +cz =0,得z =-a c, 所以m =(1,0,-a c)∥m ′=(c ,0,-a ). cos 60°=|n ·m ′||n ||m ′|=c 2(a 2+c 2)=12,得a =c . 故当AP 与正方形ABCD 的边长相等时,二面角C -AF -D 的大小为60°.。
