作图计算题(带答案)
2019年一级注册建筑师《建筑技术设计[作图题]》试题及答案(卷一)
![2019年一级注册建筑师《建筑技术设计[作图题]》试题及答案(卷一)](https://img.taocdn.com/s3/m/09819fd1856a561252d36fdb.png)
2019年一级注册建筑师《建筑技术设计[作图题]》试题及答案(卷一)城市住宅(1)设计任务在我国的中南部地区,某住宅区内一场地新建9层住宅,总面积14200m2,共计144套住宅(详见总平面图1-55)。
(2)设计要求拟建住宅可以为一栋或多栋组合,朝向为南北向或南偏东≤45°或南偏西≤45°。
拟建住宅与原有住宅日照间距为33m。
住宅单元要求布置电梯和楼梯。
每层共16套住宅,其中10套两室户型,6套三室户型。
户型采用单元组合形式,每个单元可为两个户型或多个户型组合。
每套户型包括主卧、次卧、客厅、卫生间、厨房等房间和空间,各空间开间、面积要求等见表1-17。
每个空间都要求自然通风(包括卫生间),每套户型要求两个主要居住空间为南向或南偏东≤45°或南偏西≤45°,并能看见湖面。
每个户型要求有一个为南北向或为南偏东≤45°或南偏西≤45°的阳台。
(3)图纸要求1)总平面图a)画出住宅总平面图,标明间距、尺寸及层数。
b)在场地内布置能停30辆机动车的停车场。
c)画出场地与道路的连接方式。
2)标准层平面图a)用单线画出标准层组合平面图及楼电梯间位置。
在图中表示开间、进深轴线尺寸、标准户型编号并填写表1-18。
b)组合图中不同户型均要求画出完整的户型,其余相同的可用轮廓线。
c)标出户型面积。
3)户(套)型平面图a)用双线画出户型组合平面图中所有户型平面图。
b)画出墙、门、窗,标出各房间主要开间及进深轴线尺寸和总尺寸,标明各个房间名称、面积、户内面积、标准户型编号并填写表1-19。
参考答案:作图提示见图1-56~图1-62及表1-20~表1-23。
1)房间内容、房间面积与总建筑面积(允许浮动±5%)符合任务书要求。
2)根据题中提示,朝向可为南偏东≤45°或南偏西≤45°。
正确确定建筑物及设施的位置(图1-59、图1-62)。
机械制图-作图题-210题(答案)

1.已知点A距H面为12,距V面为15,距W面为10,点B在点A的左方5,后方10,上方8,试作A、B两点的三面投影。
答案:X ZY HY WO XZYYOa aabbb2.作平面四边形ABCD的投影。
答案:ab da'b'c'd'3.完成下列各形体的投影。
答案:4.完成下列各形体的投影。
5.根据给出的视图,补画第三视图(或视图所缺的图线)。
答案:6.根据给出的视图,补画第三视图(或视图所缺的图线)。
答案:7.在指定位置将主视图画成全剖视图8.在指定位置将主视图画成剖视图。
答案:9.补全螺栓连接图中所缺的图线。
答案:10.已知两平板齿轮啮合,m1=m2=4mm,z1=20,z2=35,分别计算其齿顶圆、分度圆、齿根圆直径,并画出其啮合图(比例1:2)。
答案:11.作水平线AB 的三面投影。
已知点A 距H 面为15,距V 面为5,距W 面为10,AB 与V 面夹角为30°,实长为30,点B 在点A 的左前方。
答案:aa ab bb XY HY HZO12.已知直线为AC 为正平线,试补全平行四边形ABCD 的水平投影。
答案:adacd cb13.根据已知视图补画第三视图或视图中所缺的图线。
14.根据已知视图补画第三视图或视图中所缺的图线。
答案:15.在指定位置将主视图画成全剖视图。
答案:16.在指定位置画出剖面图(键槽深3mm)。
17.改正双头螺柱连接中的错误画法。
答案:18.画出齿轮的两个视图,已知m=3mm,z=20,写出主要计算式。
答案:d=mz=3╳20=60mmda=m(z+2)=66mmdf=m(z-2.5)=52.5mm19.在平面ABC内作一条水平线,使其到H面的距离为10mm。
答案:20.根据给出的视图,补画第三视图或视图中所缺的图线。
答案:21.根据给出的视图,补画第三视图或视图中所缺的图线。
22.在指定位置将主视图画成剖视图。
23.补画视图中的缺线。
土建类专业知识作图计算题(有答案)
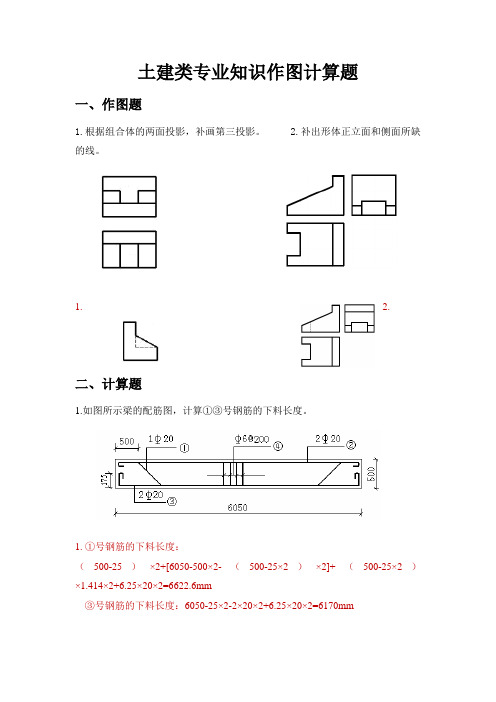
土建类专业知识作图计算题一、作图题1.根据组合体的两面投影,补画第三投影。
2.补出形体正立面和侧面所缺的线。
1. 2.二、计算题1.如图所示梁的配筋图,计算①③号钢筋的下料长度。
1. ①号钢筋的下料长度:(500-25)×2+[6050-500×2-(500-25×2)×2]+(500-25×2)×1.414×2+6.25×20×2=6622.6mm③号钢筋的下料长度:6050-25×2-2×20×2+6.25×20×2=6170mm2.二层混和结构住宅楼的主体结构由砌块墙、安装模板、浇梁板混凝土3个施工 过程组成,它们的流水节拍均取3d,设安装模板后要绑扎钢筋2d 才能浇梁板混凝土,梁板浇筑完成后要养护4d,试计算施工工期。
2.流水步距K =t=3d 求施工段数:段53432321=++=++=∑K Z KZ n m 计算工期 d )(z K )n m j (T 3823135211=+⨯-+⨯=+⋅-+⋅=∑3.某轴心受压柱,截面尺寸为b×h=400×400mm ,轴向力设计值为N=2500kN,计算长度l o =4.4m ,混凝土强度等级为C35(c f =16.7N/mm 2),柱内配置A /s =1964 mm 2的4根HRB400的纵向受力钢筋(/y f =360N/mm 2),试校核此柱是否安全。
3.确定稳定系数ϕb l o =4004400=11 查表ϕ=0.965 验算配筋率ρ=bhA s /×100%=4004001964⨯×100%=1.228% 0.5%<1.228%<3%,符合要求确定柱承载力设计值N=0.9ϕ(c f A+/y f A /s )=0.9×0.965×(16.7×400×400+1964×360)= 2934696.24N=2934.69624kN>2500 Kn经校核此柱安全。
2021年人教版小学数学三年级上册第七单元专项—《作图题》【含答案】

2021年人教版小学数学三年级上册第七单元专项—《作图题》1.画一画。
下面方格纸上每小格的边长按1厘米计算,在方格中画一个长是5厘米宽是2厘米的长方形;再画一个边长是3厘米的正方形。
2.请你在方格纸上画3个不同形状的四边形。
3.请用彩色描边这些图形的边线。
4.画一个边长为2厘米的正方形和一个周长为10厘米的长方形。
5.用4个长3厘米、宽1厘米的长方形拼不同的长方形,拼成的哪种形状的图形周长最短,请你画出来。
6.按要求画一画。
(每个小正方形的边长为1厘米)(1)在下面的方格纸上画一个长6厘米、宽4厘米的长方形。
(2)在下面的方格纸上画一个周长为16厘米的正方形。
7.下面的方格纸中,每个小方格的边长都是1厘米,按要求画图。
(1)宽2厘米,长是宽的3倍的长方形。
(2)和上面长方形周长相等的正方形。
8.下面每个方格的边长是1厘米。
在方格纸上画一个周长是14厘米的长方形,并在这个长方形中画一个最大的正方形。
9.在下面的方格纸上画一个长1分米,宽20毫米的长方形。
10.在方格中分别画1个长方形和1个正方形,使它们的周长都是20厘米。
(小正方形边长看作1厘米)11.下面是一张方格纸,每个小方格的边长是1厘米,请在这张方格纸上画出所有周长是12厘米的长方形。
(边长是整厘米数)12.在下面方格纸上画一个周长是16厘米的正方形,再画一个周长是24厘米的长方形(每个小方格的边长为1厘米)。
13.在边长为1厘米的方格纸上,画周长都是16厘米的长方形,有几种画法,试一试。
14.下面每个方格表示边长1厘米的正方形,在下面的格子图中画周长是20厘米的长方形和正方形各一个。
15.下面每个小方格都是边长1厘米的小正方形,请在下图中画一个周长18厘米的长方形和一个周长24厘米的正方形。
答案1.见详解【分析】每小格的边长按1厘米计算,则长方形的长画5个小格,宽画2个小格即可;再画一个边长是3厘米的正方形,则正方形的四条边都画3个小格即可。
奥数-16画图法解应用题+答案

画图法解应用题苏联教育家苏霍姆林斯基曾经说过:“如果哪个学生学会了画应用题,我就可以有把握地说,他一定能学会解应用题。
”可见,画图对于小学数学解决问题的重要性。
在解答一些应用题时,用作图法可以把题目的数量关系揭示出来,以其形象、直观的特点,使题意一目了然,对解答条件隐蔽,复杂疑难应用题,能起到化难为易,化繁为简的作用,从而有助于快速找到解题的途径,有效地提高学生的自我学习能力和创新能力,使学生学会学习。
作图法解应用题中,常见的数学图有以下几种:一、线段图线段图是由几条线段组合在一起,用来表示应用题中的数量关系,帮助人们分析题意,解答问题的一种平面图形。
线段图在小学数学应用题学习中它可以帮助学生轻松地解答复杂关系的应用题,强化数量关系的表述训练,能根据数量关系有序地进行解题演练。
举例:欢欢和喵喵共有25个本子,如果欢欢用去了3个本子,喵喵买回2个本子,那么她们的本子就一样多了,你知道她们原来各有本子多少个吗?列式计算:喵喵 (25-3-2)÷2=10(本) 欢欢 25-10=15(本)二、树形图在解答应用题时,我们常常采用枚举法把所有符合题目条件的对象一一列举出来。
我们采用画树形图的方法,借助树的分叉特征构造出的树形图可以对数学问题中有可能出现的多种可能逐一例举出来,不仅形象直观,而且有条理又不易重复或遗漏,使人一目了然,有助于作出正确的判断。
举例:一个口袋中装有红、白、绿三只小球,另一只口袋中装有红、白两只小球。
现从两只口袋中各取一只小球,求两只小球颜色一样的概率是多少?从图中可以看出,两只小球颜色搭配的可能性共6种,而两只小球颜色一样的可能性只有(红-红),(白-白)共2种,所以两只小球颜色一样的概率为三分之一。
三、集合图在数学中,经常用平面上封闭曲线的内部代表集合,以及用以表示集合之间的关系,这样的图形称之为“集合图”。
举例:参加跳绳的有6人,参加踢毽子的有7人,两项都参加的有3人,这个组共有几人?6+7-3=10(人)四、情景图把复杂的数学问题用简单的图画表示,把情景再现出来,让人有身临其境的感觉,便于学生理解和分析应用题。
作图计算题(带答案)

作图计算题(带答案)⼀、作图计算题1.图⽰机构,由曲柄1、连杆2、摇杆3及机架6组成铰链四杆机构,轮1′与曲柄1固接,其轴⼼为B,轮4分别与轮1′和轮5相切,轮5活套于轴D上。
各相切轮之间作纯滚动。
试⽤速度瞬⼼法确定曲柄1与轮5的⾓速⽐ω1/ω5。
2.画出图⽰油泵机构的运动简图,计算其⾃由度,并作出所有速度瞬⼼。
3. 如图所⽰正切机构,尺⼨及瞬时位置如图,且构件1的⾓速度ω1=6rad/s ,⾓加速度α1=0,请完成:(1)并标明所有的瞬⼼。
(2)求构件3的瞬时速度和加速度(提⽰:建议先求构件3的位移,然后求1阶和2阶导数求速度和加速度)。
(1). 并标明所有的瞬⼼。
(2). 求构件3?======60cos sin 8.0cos 4.0tan 4.0111211211t tt dt dv a t dt dsv t s ωωωωωωω4. 已知主动件4的⾓速度及⾓加速度,写出求出构件2的⾓速度及⾓加速度度⽮量⽅程。
(仅要求列出向量⽅程,指明各项向量的⼤⼩和⽅向)写出nBCBC C nB B BCC B a a a a av v v ++=++=ττ⽮量5. 在题图机构中,已知曲柄AB 的等⾓速度ω1为常数,转向如图所⽰,⽤相对运动图解法求构件3的ω3⾓速度(仅要求列出向量⽅程,指明各项的⼤⼩和⽅向)3B23B2B B v v v =+6. 在图试铰链四杆机构中,已知L AB =10mm ,L BC =50mm ,L CD =30mm 。
请完成:(1)要是机构为曲柄摇杆机构时,L AD 的范围;(2)若L AD =40mm ,⽤作图法求当L AB 杆主动件时的摇杆的两个极限位置;(3)若L AD =40mm ,⽤作图法求当L AB 杆主动件时的最⼩传动⾓γmin 。
BD50103010503010+≤+>>++AD AD L L 或50301010503010+≤+>>++AD AD L L7. 图⽰⽤铰链四杆机构作为加热炉炉门的启闭机构。
六年级数学作图题练习试题集

六年级数学作图题练习试题答案及解析1.如图,以校门为观测点,根据下面提供的信息完成图示.(1)校门正北40米处是一个小花园.(2)实验楼在校门北偏西50°,离校门80米.(3)学生宿舍在校门东南方向,与正南成35°夹角,离校门100米.【答案】【解析】(1)根据图上距离=实际距离×比例尺,求出校门到小花园的图上距离,然后在图上标出它的位置.(2)根据图上距离=实际距离×比例尺,求出实验楼到校门的图上距离,然后在图上标出它的位置.(3)同理,求出行驶宿舍到校门的图上距离,然后根据方向和距离确定其位置.解:(1)40×=0.01(米)=1(厘米);(2)80×=0.02(米)=2(厘米);(3)100×=0.025(米)=2.5(厘米);作图如下:【点评】此题考查的目的是理解掌握比例尺的意义及应用,并且能够根据方向和距离确定物体的位置.2.按要求作图.用3种不同的方法,把正方形的面积四等分.【答案】【解析】把正方形的面积四等分,即分成面积、形状都相同的4部分,根据正方形的对称性作图即可.解:如图:【点评】本题考查图形划分的方法,要明确正方形是轴对称和中心对称图形.3.分别画出下列图形的所有对称轴。
【答案】图略【解析】思路分析:这是关于轴对称图形的知识,比较简单。
名师详解:正方形有四条对称轴,扇形有一条对称轴。
易错提示:此题要将正方形的对称轴画全,不要遗漏。
4.先在长方形中涂色表示与的乘积,再完成下面的填空.×= .【答案】.【解析】首先把这个长方形看作单位“1”,平均分成5份,涂其中的3份,再把看作单位“1”,平均分成3份,画斜线表示它的即可,根据分数乘法的计算法则计算.解:作图如下:×=故答案为:.【点评】此题考查的目的是理解一个数乘分数的意义,掌握分数乘法的计算法则,关键是确定单位“1”.5.画出一个周长是12.56cm的圆.【答案】【解析】要画出圆,必须求出半径;根据圆的周长计算公式“c=2πr”,得出r=c÷π÷2,代入数值,求出半径,然后画圆即可.解:12.56÷3.14÷2=2(厘米);作图如下:【点评】此题考查了画圆的方法,解决的关键是先求出半径,根据圆的周长、半径的关系,求出半径画圆即可.6.画图。
场地设计(作图题)题库(139道)

场地设计(作图题)1、设计条件1.如图,拟在某自然坡地内平整出大小为16m×20m的场地一块,场地内标高为50m。
2.高于场地部分拟设置1:1放坡,低于场地部分采用挡土墙。
——[简答题]正确答案:解题要点1.掌握场地护坡的概念。
2.掌握填方、挖方及挡土墙概念。
作图提示1.由于护坡1:1,所以A点沿垂直(竖向)方向至58m等高线的距离为58-50=8m。
同理求出其他各等高线上1:1处点,连接绘制护坡线。
2.从场地零点开始沿低于场地部分均为挡土墙。
答案解析:2、设计条件1.如图,拟在某自然坡地内平整出大小为16m×20m的场地一块,场地内标高为50m。
2.高于场地部分拟设置1:1放坡,低于场地部分采用挡土墙。
——[简答题]正确答案:D答案解析:3、设计条件1.如图,拟在某自然坡地内平整出大小为16m×20m的场地一块,场地内标高为50m。
2.高于场地部分拟设置1:1放坡,低于场地部分采用挡土墙。
——[简答题]正确答案:B答案解析:4、设计条件1.如图,拟在某自然坡地内平整出大小为16m×20m的场地一块,场地内标高为50m。
2.高于场地部分拟设置1:1放坡,低于场地部分采用挡土墙。
——[简答题]正确答案:C参考评分标准答案解析:5、设计条件1.某城市拟建一座综合性展览馆,用地南侧为城市公园,用地范围见图。
2.综合性展览馆包括:展览厅、序厅、库房、餐厅、办公楼、旅馆、过街楼、中心广场、卸货广场、停车场。
各项目层数及尺寸见下图。
当地日照间距系数1.2。
3.规划及设计要求:用地红线后退15m范围内不能安排建筑物及展场,作为绿化带。
——[简答题]正确答案:解题要点1.场地设计的主要任务是:(1)进行合理的功能分区,包括主次、动静、内外、先后、洁污等空间的功能分区:(2)选择建筑与设施的最佳位置,即根据建筑朝向、间距、采光、通风、景观及建筑规模等确定建筑物的落位;(3)布置顺畅便捷的道路。
2020年中考数学一轮复习:尺规作图专项练习题(解析版)

中考一轮复习:尺规作图专项练习题1.请用直尺、圆规作图,不写作法,但要保留作图痕迹.已知:∠α,直线l及l上两点A,B.求作:Rt△ABC,使点C在直线l的上方,且∠ABC=90°,∠BAC=∠α.2.如图,在△ABC中,点D是AB边上的一点.(1)请用尺规作图法,在△ABC内,求作∠ADE,使∠ADE=∠B,DE交AC于E;(不要求写作法,保留作图痕迹)(2)在(1)的条件下,若=2,求的值.3.已知:AC是▱ABCD的对角线.(1)用直尺和圆规作出线段AC的垂直平分线,与AD相交于点E,连接CE.(保留作图痕迹,不写作法);(2)在(1)的条件下,若AB=3,BC=5,求△DCE的周长.4.如图,已知等腰△ABC顶角∠A=36°.(1)在AC上作一点D,使AD=BD(要求:尺规作图,保留作图痕迹,不必写作法和证明,最后用黑色墨水笔加墨);(2)求证:△BCD是等腰三角形.5.如图,AB为⊙O的直径,点C在⊙O上.(1)尺规作图:作∠BAC的平分线,与⊙O交于点D;连接OD,交BC于点E(不写作法,只保留作图痕迹,且用黑色墨水笔将作图痕迹加黑);(2)探究OE与AC的位置及数量关系,并证明你的结论.6.如图,在Rt△ABC中,∠ACB=90°,AC=2,BC=3.(1)尺规作图:不写作法,保留作图痕迹.①作∠ACB的平分线,交斜边AB于点D;②过点D作BC的垂线,垂足为点E.(2)在(1)作出的图形中,求DE的长.7.在5×3的方格纸中,△ABC的三个顶点都在格点上.(1)在图1中画出线段BD,使BD∥AC,其中D是格点;(2)在图2中画出线段BE,使BE⊥AC,其中E是格点.8.【阅读理解】用10cm×20cm的矩形瓷砖,可拼得一些长度不同但宽度均为20cm的图案.已知长度为10cm、20cm、30cm的所有图案如下:【尝试操作】如图,将小方格的边长看作10cm,请在方格纸中画出长度为40cm的所有图案.【归纳发现】观察以上结果,探究图案个数与图案长度之间的关系,将下表补充完整.图案的长度10cm20cm30cm40cm50cm60cm 所有不同图案的个数1239.如图,在△ABC中,AB=AC,AD是BC边上的高.请用尺规作图法,求作△ABC的外接圆.(保留作图痕迹,不写作法)10.已知:∠AOB.求作:∠A′O′B′,使得∠A′O′B′=∠AOB.作法:①以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;③以点C′为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D′;④过点D′画射线O′B′,则∠A′O′B′=∠AOB.根据上面的作法,完成以下问题:(1)使用直尺和圆规,作出∠A′O′B′(请保留作图痕迹).(2)完成下面证明∠A′O′B′=∠AOB的过程(注:括号里填写推理的依据).证明:由作法可知O′C′=OC,O′D′=OD,D′C′=,∴△C′O′D′≌△COD()∴∠A′O′B′=∠AOB.()11.如图,点M和点N在∠AOB内部.(1)请你作出点P,使点P到点M和点N的距离相等,且到∠AOB两边的距离也相等(保留作图痕迹,不写作法);(2)请说明作图理由.12.按要求解答下列各题:(1)如图①,求作一点P,使点P到∠ABC的两边的距离相等,且在△ABC的边AC 上.(用直尺和圆规作图,保留作图痕迹,不写作法和证明);(2)如图②,B、C表示两个港口,港口C在港口B的正东方向上.海上有一小岛A在港口B的北偏东60°方向上,且在港口C的北偏西45°方向上.测得AB=40海里,求小岛A与港口C之间的距离.(结果可保留根号)13.尺规作图(只保留作图痕迹,不要求写出作法):如图,已知△ABC,请根据“SAS”基本事实作出△DEF,使△DEF≌△ABC.14.如图,⊙O的直径AB=10,弦AC=8,连接BC.(1)尺规作图:作弦CD,使CD=BC(点D不与B重合),连接AD;(保留作图痕迹,不写作法)(2)在(1)所作的图中,求四边形ABCD的周长.15.如图,四边形ABCD是矩形.(1)用尺规作线段AC的垂直平分线,交AB于点E,交CD于点F(不写作法,保留作图痕迹);(2)若BC=4,∠BAC=30°,求BE的长.16.已知:在△ABC中,AB=AC.(1)求作:△ABC的外接圆.(要求:尺规作图,保留作图痕迹,不写作法)(2)若△ABC的外接圆的圆心O到BC边的距离为4,BC=6,则S⊙O=.17.如图,AD是△ABC的角平分线.(1)作线段AD的垂直平分线EF,分别交AB、AC于点E、F;(用直尺和圆规作图,标明字母,保留作图痕迹,不写作法.)(2)连接DE、DF,四边形AEDF是形.(直接写出答案)18.如图,△ABC中,∠C=90°,AC=4,BC=8.(1)用直尺和圆规作AB的垂直平分线;(保留作图痕迹,不要求写作法)(2)若(1)中所作的垂直平分线交BC于点D,求BD的长.19.尺规作图(只保留作图痕迹,不要求写出作法).如图,已知∠α和线段a,求作△ABC,使∠A=∠α,∠C=90°,AB=a.20.如图,在四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).(1)在图1中,画出△ABD的BD边上的中线;(2)在图2中,若BA=BD,画出△ABD的AD边上的高.21.已知:如图,∠ABC,射线BC上一点D.求作:等腰△PBD,使线段BD为等腰△PBD的底边,点P在∠ABC内部,且点P到∠ABC两边的距离相等.22.图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、B、C、D、E、F均在格点上.在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.(1)在图①中以线段AB为边画一个△ABM,使其面积为6.(2)在图②中以线段CD为边画一个△CDN,使其面积为6.(3)在图③中以线段EF为边画一个四边形EFGH,使其面积为9,且∠EFG=90°.23.图①,图②均为4×4的正方形网格,每个小正方形的顶点称为格点.在图①中已画出线段AB,在图②中已画出线段CD,其中A、B、C、D均为格点,按下列要求画图:(1)在图①中,以AB为对角线画一个菱形AEBF,且E,F为格点;(2)在图②中,以CD为对角线画一个对边不相等的四边形CGDH,且G,H为格点,∠CGD=∠CHD=90°.24.在6×6的方格纸中,点A,B,C都在格点上,按要求画图:(1)在图1中找一个格点D,使以点A,B,C,D为顶点的四边形是平行四边形.(2)在图2中仅用无刻度的直尺,把线段AB三等分(保留画图痕迹,不写画法).25.如图,在7×5的方格纸ABCD中,请按要求画图,且所画格点三角形与格点四边形的顶点均不与点A,B,C,D重合.(1)在图1中画一个格点△EFG,使点E,F,G分别落在边AB,BC,CD上,且∠EFG =90°.(2)在图2中画一个格点四边形MNPQ,使点M,N,P,Q分别落在边AB,BC,CD,DA上,且MP=NQ.中考一轮复习:尺规作图专项练习题参考答案与试题解析1.请用直尺、圆规作图,不写作法,但要保留作图痕迹.已知:∠α,直线l及l上两点A,B.求作:Rt△ABC,使点C在直线l的上方,且∠ABC=90°,∠BAC=∠α.【分析】先作∠DAB=α,再过B点作BE⊥AB,则AD与BE的交点为C点.【解答】解:如图,△ABC为所作.2.如图,在△ABC中,点D是AB边上的一点.(1)请用尺规作图法,在△ABC内,求作∠ADE,使∠ADE=∠B,DE交AC于E;(不要求写作法,保留作图痕迹)(2)在(1)的条件下,若=2,求的值.【分析】(1)利用基本作图(作一个角等于已知角)作出∠ADE=∠B;(2)先利用作法得到∠ADE=∠B,则可判断DE∥BC,然后根据平行线分线段成比例定理求解.【解答】解:(1)如图,∠ADE为所作;(2)∵∠ADE=∠B∴DE∥BC,∴==2.3.已知:AC是▱ABCD的对角线.(1)用直尺和圆规作出线段AC的垂直平分线,与AD相交于点E,连接CE.(保留作图痕迹,不写作法);(2)在(1)的条件下,若AB=3,BC=5,求△DCE的周长.【分析】(1)利用基本作图作AC的垂直平分线得到E点;(2)利用平行四边形的性质得到AD=BC=5,CD=AB=3,再根据线段垂直平分线上的性质得到EA=EC,然后利用等线段代换计算△DCE的周长.【解答】解:(1)如图,CE为所作;(2)∵四边形ABCD为平行四边形,∴AD=BC=5,CD=AB=3,∵点E在线段AC的垂直平分线上,∴EA=EC,∴△DCE的周长=CE+DE+CD=EA+DE+CD=AD+CD=5+3=8.4.如图,已知等腰△ABC顶角∠A=36°.(1)在AC上作一点D,使AD=BD(要求:尺规作图,保留作图痕迹,不必写作法和证明,最后用黑色墨水笔加墨);(2)求证:△BCD是等腰三角形.【分析】(1)作AB的垂直平分线交AC于D;(2)利用等腰三角形的性质和三角形内角和计算出∠ABC=∠C=72°,再利用DA=DB得到∠ABD=∠A=36°,所以∠BDC=72°,从而可判断△BCD是等腰三角形.【解答】(1)解:如图,点D为所作;(2)证明:∵AB=AC,∴∠ABC=∠C=(180°﹣36°)=72°,∵DA=DB,∴∠ABD=∠A=36°,∴∠BDC=∠A+∠ABD=36°+36°=72°,∴∠BDC=∠C,∴△BCD是等腰三角形.5.如图,AB为⊙O的直径,点C在⊙O上.(1)尺规作图:作∠BAC的平分线,与⊙O交于点D;连接OD,交BC于点E(不写作法,只保留作图痕迹,且用黑色墨水笔将作图痕迹加黑);(2)探究OE与AC的位置及数量关系,并证明你的结论.【分析】(1)利用基本作图作AD平分∠BAC,然后连接OD得到点E;(2)由AD平分∠BAC得到∠BAD=∠BAC,由圆周角定理得到∠BAD=∠BOD,则∠BOD=∠BAC,再证明OE为△ABC的中位线,从而得到OE∥AC,OE=AC.【解答】解:(1)如图所示;(2)OE∥AC,OE=AC.理由如下:∵AD平分∠BAC,∴∠BAD=∠BAC,∵∠BAD=∠BOD,∴∠BOD=∠BAC,∴OE∥AC,∵OA=OB,∴OE为△ABC的中位线,∴OE∥AC,OE=AC.6.如图,在Rt△ABC中,∠ACB=90°,AC=2,BC=3.(1)尺规作图:不写作法,保留作图痕迹.①作∠ACB的平分线,交斜边AB于点D;②过点D作BC的垂线,垂足为点E.(2)在(1)作出的图形中,求DE的长.【分析】(1)利用基本作图,先画出CD平分∠ACB,然后作DE⊥BC于E;(2)利用CD平分∠ACB得到∠BCD=45°,再判断△CDE为等腰直角三角形,所以DE=CE,然后证明△BDE∽△BAC,从而利用相似比计算出DE.【解答】解:(1)如图,DE为所作;(2)∵CD平分∠ACB,∴∠BCD=∠ACB=45°,∵DE⊥BC,∴△CDE为等腰直角三角形,∴DE=CE,∵DE∥AC,∴△BDE∽△BAC,∴=,即=,∴DE=.7.在5×3的方格纸中,△ABC的三个顶点都在格点上.(1)在图1中画出线段BD,使BD∥AC,其中D是格点;(2)在图2中画出线段BE,使BE⊥AC,其中E是格点.【分析】(1)将线段AC沿着AB方向平移2个单位,即可得到线段BD;(2)利用2×3的长方形的对角线,即可得到线段BE⊥AC.【解答】解:(1)如图所示,线段BD即为所求;(2)如图所示,线段BE即为所求.8.【阅读理解】用10cm×20cm的矩形瓷砖,可拼得一些长度不同但宽度均为20cm的图案.已知长度为10cm、20cm、30cm的所有图案如下:【尝试操作】如图,将小方格的边长看作10cm,请在方格纸中画出长度为40cm的所有图案.【归纳发现】观察以上结果,探究图案个数与图案长度之间的关系,将下表补充完整.图案的长度10cm20cm30cm40cm50cm60cm 所有不同图案的个数1235813【分析】根据已知条件作图可知40cm时,所有图案个数5个;猜想得到结论;【解答】解:如图根据作图可知40cm时,所有图案个数5个50cm时,所有图案个数8个;60cm时,所有图案个数13个;故答案为5,8,13;9.如图,在△ABC中,AB=AC,AD是BC边上的高.请用尺规作图法,求作△ABC的外接圆.(保留作图痕迹,不写作法)【分析】作线段AB的垂直平分线,交AD于点O,以O为圆心,OB为半径作⊙O,⊙O 即为所求.【解答】解:如图所示:⊙O即为所求.10.已知:∠AOB.求作:∠A′O′B′,使得∠A′O′B′=∠AOB.作法:①以O为圆心,任意长为半径画弧,分别交OA,OB于点C,D;②画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;③以点C′为圆心,CD长为半径画弧,与第②步中所画的弧相交于点D′;④过点D′画射线O′B′,则∠A′O′B′=∠AOB.根据上面的作法,完成以下问题:(1)使用直尺和圆规,作出∠A′O′B′(请保留作图痕迹).(2)完成下面证明∠A′O′B′=∠AOB的过程(注:括号里填写推理的依据).证明:由作法可知O′C′=OC,O′D′=OD,D′C′=DC,∴△C′O′D′≌△COD(SSS)∴∠A′O′B′=∠AOB.(全等三角形的对应角相等)【分析】(1)根据题意作出图形即可;(2)根据全等三角形的判定和性质即可得到结论.【解答】解:(1)如图所示,∠A′O′B′即为所求;(2)证明:由作法可知O′C′=OC,O′D′=OD,D′C′=DC,∴△C′O′D′≌△COD(SSS)∴∠A′O′B′=∠AOB.(全等三角形的对应角相等)故答案为:DC,SSS,全等三角形的对应角相等.11.如图,点M和点N在∠AOB内部.(1)请你作出点P,使点P到点M和点N的距离相等,且到∠AOB两边的距离也相等(保留作图痕迹,不写作法);(2)请说明作图理由.【分析】(1)根据角平分线的作法、线段垂直平分线的作法作图;(2)根据角平分线的性质、线段垂直平分线的性质解答.【解答】解:(1)如图,点P到点M和点N的距离相等,且到∠AOB两边的距离也相等;(2)理由:角的平分线上的点到角的两边的距离相等、垂直平分线上的点到线段两端点的距离相等.12.按要求解答下列各题:(1)如图①,求作一点P,使点P到∠ABC的两边的距离相等,且在△ABC的边AC 上.(用直尺和圆规作图,保留作图痕迹,不写作法和证明);(2)如图②,B、C表示两个港口,港口C在港口B的正东方向上.海上有一小岛A在港口B的北偏东60°方向上,且在港口C的北偏西45°方向上.测得AB=40海里,求小岛A与港口C之间的距离.(结果可保留根号)【分析】(1)利用尺规作∠BAC的角平分线交AC于点P,点P即为所求.(2)作AD⊥BC于D.解直角三角形求出AD,再利用等腰直角三角形的性质即可解决问题.【解答】解:(1)如图,点P即为所求.(2)作AD⊥BC于D.在Rt△ABD中,∵AB=40海里,∠ABD=30°,∴AD=AB=20(海里),∵∠ACD=45°,∴AC=AD=20(海里).答:小岛A与港口C之间的距离为20海里.13.尺规作图(只保留作图痕迹,不要求写出作法):如图,已知△ABC,请根据“SAS”基本事实作出△DEF,使△DEF≌△ABC.【分析】先作一个∠D=∠A,然后在∠D的两边分别截取ED=BA,DF=AC,连接EF 即可得到△DEF;【解答】解:如图,△DEF即为所求.14.如图,⊙O的直径AB=10,弦AC=8,连接BC.(1)尺规作图:作弦CD,使CD=BC(点D不与B重合),连接AD;(保留作图痕迹,不写作法)(2)在(1)所作的图中,求四边形ABCD的周长.【分析】(1)以C为圆心,CB为半径画弧,交⊙O于D,线段CD即为所求.(2)连接BD,OC交于点E,设OE=x,构建方程求出x即可解决问题.【解答】解:(1)如图,线段CD即为所求.(2)连接BD,OC交于点E,设OE=x.∵AB是直径,∴∠ACB=90°,∴BC===6,∵BC=CD,∴=,∴OC⊥BD于E.∴BE=DE,∵BE2=BC2﹣EC2=OB2﹣OE2,∴62﹣(5﹣x)2=52﹣x2,解得x=,∵BE=DE,BO=OA,∴AD=2OE=,∴四边形ABCD的周长=6+6+10+=.15.如图,四边形ABCD是矩形.(1)用尺规作线段AC的垂直平分线,交AB于点E,交CD于点F(不写作法,保留作图痕迹);(2)若BC=4,∠BAC=30°,求BE的长.【分析】(1)根据线段的垂直平分线的作图解答即可;(2)利用含30°的直角三角形的性质解答即可.【解答】解:(1)如图所示:(2)∵四边形ABCD是矩形,EF是线段AC的垂直平分线,∴AE=EC,∠CAB=∠ACE=30°,∴∠ACB=60°,∴∠ECB=30°,∵BC=4,∴BE=.16.已知:在△ABC中,AB=AC.(1)求作:△ABC的外接圆.(要求:尺规作图,保留作图痕迹,不写作法)(2)若△ABC的外接圆的圆心O到BC边的距离为4,BC=6,则S⊙O=25π.【分析】(1)作线段AB,BC的垂直平分线,两线交于点O,以O为圆心,OB为半径作⊙O,⊙O即为所求.(2)在Rt△OBE中,利用勾股定理求出OB即可解决问题.【解答】解:(1)如图⊙O即为所求.(2)设线段BC的垂直平分线交BC于点E.由题意OE=4,BE=EC=3,在Rt△OBE中,OB==5,∴S圆O=π•52=25π.故答案为25π.17.如图,AD是△ABC的角平分线.(1)作线段AD的垂直平分线EF,分别交AB、AC于点E、F;(用直尺和圆规作图,标明字母,保留作图痕迹,不写作法.)(2)连接DE、DF,四边形AEDF是菱形.(直接写出答案)【分析】(1)利用尺规作线段AD的垂直平分线即可.(2)根据四边相等的四边形是菱形即可证明.【解答】解:(1)如图,直线EF即为所求.(2)∵AD平分∠BAC,∴∠BAD=∠CAD,∵∠AOE=∠AOF=90°,AO=AO,∴△AOE≌△AOF(ASA),∴AE=AF,∵EF垂直平分线段AD,∴EA=ED,F A=FD,∴EA=ED=DF=AF,∴四边形AEDF是菱形.故答案为菱.18.如图,△ABC中,∠C=90°,AC=4,BC=8.(1)用直尺和圆规作AB的垂直平分线;(保留作图痕迹,不要求写作法)(2)若(1)中所作的垂直平分线交BC于点D,求BD的长.【分析】(1)分别以A,B为圆心,大于AB为半径画弧,两弧交于点M,N,作直线MN即可.(2)设AD=BD=x,在Rt△ACD中,利用勾股定理构建方程即可解决问题.【解答】解:(1)如图直线MN即为所求.(2)∵MN垂直平分线段AB,∴DA=DB,设DA=DB=x,在Rt△ACD中,∵AD2=AC2+CD2,∴x2=42+(8﹣x)2,解得x=5,∴BD=5.19.尺规作图(只保留作图痕迹,不要求写出作法).如图,已知∠α和线段a,求作△ABC,使∠A=∠α,∠C=90°,AB=a.【分析】根据作一个角等于已知角,线段截取以及垂线的尺规作法即可求出答案.【解答】解:如图所示,△ABC为所求作20.如图,在四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).(1)在图1中,画出△ABD的BD边上的中线;(2)在图2中,若BA=BD,画出△ABD的AD边上的高.【分析】(1)连接EC,利用平行四边形的判定和性质解答即可;(2)连接EC,ED,F A,利用三角形重心的性质解答即可.【解答】解:(1)如图1所示,AF即为所求:(2)如图2所示,BH即为所求.21.已知:如图,∠ABC,射线BC上一点D.求作:等腰△PBD,使线段BD为等腰△PBD的底边,点P在∠ABC内部,且点P到∠ABC两边的距离相等.【分析】根据角平分线的性质、线段的垂直平分线的性质即可解决问题.【解答】解:∵点P到∠ABC两边的距离相等,∴点P在∠ABC的平分线上;∵线段BD为等腰△PBD的底边,∴PB=PD,∴点P在线段BD的垂直平分线上,∴点P是∠ABC的平分线与线段BD的垂直平分线的交点,如图所示:22.图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、B、C、D、E、F均在格点上.在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.(1)在图①中以线段AB为边画一个△ABM,使其面积为6.(2)在图②中以线段CD为边画一个△CDN,使其面积为6.(3)在图③中以线段EF为边画一个四边形EFGH,使其面积为9,且∠EFG=90°.【分析】(1)直接利用三角形的面积的计算方法得出符合题意的图形;(2)直接利用三角形面积求法得出答案;(3)根据矩形函数三角形的面积的求法进而得出答案.【解答】解:(1)如图①所示,△ABM即为所求;(2)如图②所示,△CDN即为所求;(3)如图③所示,四边形EFGH即为所求;23.图①,图②均为4×4的正方形网格,每个小正方形的顶点称为格点.在图①中已画出线段AB,在图②中已画出线段CD,其中A、B、C、D均为格点,按下列要求画图:(1)在图①中,以AB为对角线画一个菱形AEBF,且E,F为格点;(2)在图②中,以CD为对角线画一个对边不相等的四边形CGDH,且G,H为格点,∠CGD=∠CHD=90°.【分析】(1)根据菱形的定义画出图形即可(答案不唯一).(2)利用数形结合的思想解决问题即可.【解答】解:(1)如图,菱形AEBF即为所求.(2)如图,四边形CGDH即为所求.24.在6×6的方格纸中,点A,B,C都在格点上,按要求画图:(1)在图1中找一个格点D,使以点A,B,C,D为顶点的四边形是平行四边形.(2)在图2中仅用无刻度的直尺,把线段AB三等分(保留画图痕迹,不写画法).【分析】(1)由勾股定理得:CD=AB=CD'=,BD=AC=BD''=,AD'=BC=AD''=;画出图形即可;(2)根据平行线分线段成比例定理画出图形即可.【解答】解:(1)由勾股定理得:CD=AB=CD'=,BD=AC=BD''=,AD'=BC=AD''=;画出图形如图1所示;(2)如图2所示.25.如图,在7×5的方格纸ABCD中,请按要求画图,且所画格点三角形与格点四边形的顶点均不与点A,B,C,D重合.(1)在图1中画一个格点△EFG,使点E,F,G分别落在边AB,BC,CD上,且∠EFG =90°.(2)在图2中画一个格点四边形MNPQ,使点M,N,P,Q分别落在边AB,BC,CD,DA上,且MP=NQ.【分析】(1)利用数形结合的思想构造全等三角形或等腰直角三角形解决问题即可.(2)如图3中,构造矩形即可解决问题.如图4中,构造MP=NQ=5即可.【解答】解:(1)满足条件的△EFG,如图1,2所示.(2)满足条件的四边形MNPQ如图所示.。
专题 尺规作图与计算(解析版)
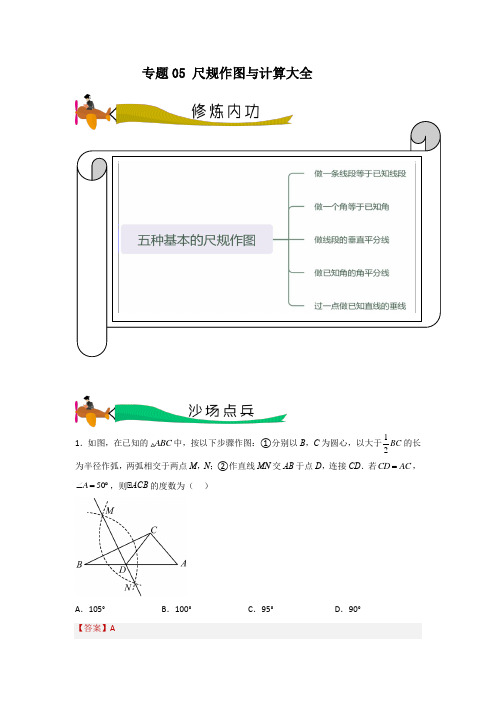
专题05 尺规作图与计算大全1.如图,在已知的ABC中,按以下步骤作图:①分别以B,C为圆心,以大于12BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD AC=,50A∠=︒,则∠ACB的度数为()A.105°B.100°C.95°D.90°【答案】A【分析】根据作图,得到DB =DC ,根据CD =AC ,∠A =50°,利用三角形内角和定理,三角形外角性质计算求解即可.【详解】∠MN 是BC 的垂直平分线,∠DB =DC ,∠∠B =∠DCB ,∠CD =AC ,∠A =50°,∠∠CDA =50°=∠B +∠DCB ,∠ACD =180°-50°-50°=80°,∠∠B =∠DCB =25°,∠ACD =80°,∠∠ACB =∠DCB +∠ACD =80°+25°=105°,故选:A .【我思故我在】本题考查了线段的垂直平分线,等腰三角形的判定和性质,三角形外角性质,熟练掌握线段垂直平分线,灵活运用三角形外角性质是解题的关键.2.如图,在ABC 中,AB AC =,40A ∠=︒,点D ,P 分别是图中所作直线和射线与AB ,CD 的交点,根据图中尺规作图的痕迹推断,以下结论错误的是( )A .AD CD =B .ABP CBP ∠=∠C .115BPC ∠=︒D .PBC ACD ∠=∠【答案】D【分析】根据角平分线的定义和垂直平分线的性质判断A 、B ,再根据等腰三角形的性质和三角形的内角定理判断C 、D .【详解】解:根据图中尺规作图可知,AC 的垂直平分线交AB 于D BP ,平分ABC ∠, ∠AD CD =,ABP CBP ∠=∠;选项A 、B 正确;∠40A ∠=︒,∠40ACD A ∠=∠=︒,∠40A ∠=︒,AB AC =,∠70ABC ACB ∠=∠=︒,∠35ABP CBP ∠=∠=︒,∠PBC ACD ∠≠∠选项D 错误;704030,BCP ACB ACD ∠=∠-∠=︒-︒=︒ ∠180115CB BPC BCP P ∠=︒-∠=∠-︒,选项C 正确.故选:D .【我思故我在】本题考查了基本作图,垂直平分线的性质,角平分线的定义,等腰三角形的性质,熟练掌握相关的知识是解题的关键.3.如图,已知AB ∥CD ,小妍同学进行以下尺规作图:①以点A 为圆心,AC 长为半径作弧,交射线AB 于点E ;②以点E 为圆心,小于线段CE 的长为半径作弧,与射线CE 交于点M ,N ;③分别以点M ,N 为圆心,大于12MN 的长为半径作弧,交于点F ,直线EF 交CD 于点G .若CGE α∠=,则A ∠的度数可以用α表示为( )A .90α︒-B .1902α︒-C .1804︒-αD .2α 【答案】D 【分析】由作图可知:AC =AE ,CE ∠CE ,所以∠ACE =∠AEC ,∠CEG =90°,则∠CGE +∠ECG =90°,所以∠ECG =90°-α,再根据平行线的性质得∠AEC =∠ECG =90°-α,即可由三角形内角和定理求解.【详解】解:由作图可知:AC =AE ,CE ∠CE ,∠∠ACE =∠AEC ,∠CEG =90°,∠∠CGE +∠ECG =90°,∠∠ECG =90°-α,∠AB∥CD,∠∠ACE=∠AEC=∠ECG=90°-α,∠∠A=180°-∠ACE-∠AEC=180°-2∠AEC=180°-2(90°-α)=2α,故D正确.故选:D.【我思故我在】本题考查作线段等于已知线段,经过上点作直线的垂线,平行线的性质,等腰三角形的性质,三角形内角和定理,熟练掌握尺规基本作图和三角形内角和定理是解题的关键.4.已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作PQ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交PQ于点M,N;(3)连接OM,MN.根据以上作图过程及所作图形,下列结论中错误的是()A.∠COM=∠COD B.若OM=MN,则∠AOB=20°C.MN∠CD D.MN=3CD【答案】D【分析】由作图知CM=CD=DN,再利用圆周角定理、圆心角定理逐一判断可得.【详解】解:由作图知CM=CD=DN,∠∠COM=∠COD,故A选项正确;5.如图,在平行四边形ABCD 中,以点A 为圆心,AB 长为半径画弧交AD 于点F ,再分别以点B 、F 为圆心,大于12BF 的相同长为半径画弧,两弧交于点P ,连接AP 并延长交BC 于点E ,连接EF .根据以上尺规作图的过程,小明得到下列结论:①AE 平分DAB ∠ ②ABF ∆是等边三角形 ③EF CD = ④AB BE =,其中,结论正确的有( )个A .1B .2C .3D .4 【答案】C【分析】由作图可知,AE 平分∠BAD ,证明四边形ABCD 是菱形,可得结论.【详解】解:由作图可知,AE 平分∠BAD ,故①正确, ∠∠BAE =∠EAD ,∠四边形ABCD 是平行四边形,∠CB ∠AD ,AB =CD ,∠∠AEB =∠EAD ,∠∠BAE =∠BEA ,∠AB =BE ,故④正确,∠AF =AB ,∠BE =AF ,∠BE ∠AF ,∠四边形ABEF 是平行四边形,∠AB =AF ,∠四边形ABEF 是菱形,∠AB =EF ,∠EF =CD ,故③正确.无法判断∠ABF 是等边三角形,故选:C .【我思故我在】本题考查作图一复杂作图,平行四边形的性质,菱形的判定和性质等知识,解题的关键是读懂图象信息,灵活运用所学知识解决问题.6.如图,ABC 中,若80BAC ∠=︒,70ACB ∠=︒,根据图中尺规作图的痕迹推断,以下结论错误的是( )A .40BAQ ∠=︒B .12DE BD =C .AF AC =D .25EQF ∠=︒直角三角形的性质等知识,解题的关键是读懂图象信息.7.如图,在平行四边形ABCD上,尺规作图:以点A为圆心,AB的长为半径画弧交AD于点F,分别以点B、F为圆心,以大于12BF的长为半径画弧交于点P,作射线AP交BC于点E,连接EF.若12BF=,10AB=,则线段AE的长为()A.18B.17C.16D.14相关知识点,掌握特殊四边形的判定方法及重要图形的尺规作图是解决本题的关键. 8.如图,在ABC 中,90,60C BAC ∠=︒∠=︒,用尺规作图,作BAC ∠的平分线交BC 于点D ,则下列说法中:①若连接,PM PN ,则AMP ANP ≌;②60ADC ∠=︒;③点D 在AB 的中垂线上;④:1:3DAC ABC S S =.其中正确的个数是( )A .1B .2C .3D .4于点O,连结BE、OC.下列结论中,不一定成立的是()【答案】A【分析】由图可知,AD平分∠BAC,EF垂直平分AB.根据等腰三角形的性质以及线段垂直平分线的判定与性质对各选项进行判断即可.【详解】解:由图可知,AD平分∠BAC,EF垂直平分AB.∠AB=AC,AD平分∠BAC,∠AD垂直平分BC,∠OB=OC,∠EF垂直平分AB,∠OA=OB,BE=AE,∠OA=OC,故选项C结论成立;∠BE=AE,EF垂直平分AB,∠EF平分∠AEB,故选项B结论成立;∠BE=AE,AB=AC,∠AB=AC=AE+EC=BE+EC,故选项D结论成立;当∠BAC=45°时,AE∠BE,故选项A不一定成立.故选:A.【我思故我在】本题考查了等腰三角形三线合一的性质,线段垂直平分线的判定与性质,熟练掌握相关定理是解题的关键.10.小明在研究矩形的时候,利用直尺和圆规作出了如图的图形,依据尺规作图的痕迹,可∠的度数为()知αA.56B.68C.28D.34【答案】A【分析】由尺规作图可知,EF是AC的垂直平分线,AE是∠DAC的角平分线,即可求出∠AFE 和∠EAF的度数,然后利用三角形内角和定理求解.【详解】解:如图所示,11.如图,已知∠ABC,∠ACB=90°,BC=3,AC=4,小红按如下步骤作图:AC的长为半径在AC两边作弧,交于两点M、N;①分别以A、C为圆心,以大于12②连接MN,分别交AB、AC于点D、O;③过C作CE∥AB交MN于点E,连接AE、CD.则四边形ADCE的周长为()A.10B.20C.12D.2412.如图,在Rt ABC △中,90ACB ∠=︒.按以下步骤作图:①以点C 为圆心,适当长为半径画弧,分别交AC ,CB 于点N ,M ;②分别以M ,N 为圆心,大于12MN 的长为半径画弧,两弧在ACB ∠内交于点G ;③作射线CG .若4AC =,D 为AC 边的中点,E 为射线CG 上一动点,则AE DE +的最小值为( )A .3B .C .D .5 【详解】ACB ∠=1ACA ∴△是等腰直角三角形,CG AA ∴⊥∴A 1为点连接A 1D ,交AC 13.如图,在ABCD 中,以点A 为圆心,以适当长度为半径作弧分别交AB AD 、于点E 、F ,再分别以点E 、F 为圆心,大于EF 一半的长度为半径作弧,两弧交于一点H ,连接AH 并延长交DC 于点G ,若5,4AB AD ==,则CG 的长为( )A .1B .2C .3D .4 【答案】A【分析】根据作图过程可得AG 平分∠DAB ,再根据角平分线的定义和平行四边形的性质可证明∠DAG =∠DGA ,进而得到AD =DG =4,即可求出CG .【详解】解:根据作图的方法可得AG 平分DAB ∠,∠DAG BAG ∠=∠,∠四边形ABCD 是平行四边形,∠CD AB ∥,5CD AB ==,∠DGA BAG ∠=∠, ∠DAG DGA ∠=∠,∠4AD DG ==,∠541CG CD DG =-=-=,故选:A .【我思故我在】此题主要考查了平行四边形的性质、角平分线的作法、等角对等边;熟记平行四边形的性质是解决问题的关键.14.如图,在矩形ABCD 中,连接AC ,以点A 为圆心,小于AD 的长为半径画弧,分别交AD ,AC 于点E ,F ,分别以点E ,F 为圆心,大于12EF 的长为半径画弧,两弧在∠DAC 内交于点G ,作射线AG ,交DC 于点H .若AD =6,AB =8,则△AHC 的面积为( )A .24B .30C .15D .915.如图,在Rt∠ABC中,∠C=90°,首先以顶点B为圆心,适当长为半径作弧,在边BC、BA上截取BE、BD;然后分别以点D、E为圆心,大于12DE为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G.若CG=4,P为边AB上一动点,则GP的最小值为()A.2B.4C.8D.无法确定【答案】B【分析】根据角平分线的性质定理以及垂线段最短解决问题即可.【详解】解:过点G作GP'∠AB于点P',由尺规作图步骤可得,BG平分∠ABC,∠∠C=90°,GP'∠AB,CG =4,∠GC=GP'=4,∠P为边AB上一动点,∠GP GP'≥,∠GP的最小值为4.故选:B.【我思故我在】本题考查了垂线段最短,角平分线的性质定理等知识,熟记垂线段最短是解题的关键.16.如图,小明在以∠A为顶角的等腰三角形ABC中用圆规和直尺作图,作出过点A的射线交BC于点D,然后又作出一条直线与AB交于点E,连接DE,若∠BED的面积为4,则∠ABC 的面积为()A.1B.4C.12D.1617.如图,在ABCD中,AD AB,按以下步骤作图:(1)以点A为圆心,AB的长为半径作弧,交AD于点E;(2)分别以点B、E为圆心,大于12BE的长为半径作弧,两弧在∠BAD的内部交于点G,连接AG并延长交BC于点F.若AB=5,BE=6,则AF的长是()A.4B.6C.8D.10【我思故我在】此题考查了角平分线的作图,菱形的判定定理及性质定理,勾股定理,正确理解角平分线的作图是解题的关键.18.如图,在∠ABCD中,以点C为圆心,适当长度为半径作弧,分别交CD、BC于点F、G,再分别以点F、G为圆心,大于12FG长为半径作弧,两弧交于点H,作射线CH交AD于点E,连接BE,若DE=5,AE=3,BE=4,则CE的长为()A.B.C.D.8【我思故我在】本题考查了作角平分线,角平分线的意义和平行四边形的性质、勾股定理和勾股定理的逆定理,掌握以上知识是解题的关键.19.如图,已知ABCD 的顶点()6,0A -,()14,8C ,点B 在x 轴正半轴上,点D 在y 轴正半轴上,以顶点A 为圆心,适当长为半径画弧,分别交AB 、AD 于点E 、F ,再分别以点E 、F 为圆心,大于12EF 的长为半径画弧,两弧交于点M ,作射线CM 交边CD 于点G .则G 的坐标为( )A .()4,8B .()6,8C .()8,8D .()10,8∠G的坐标为(10,8),故选:D.【我思故我在】本题考查尺规作图-作角平分线、平行四边形的性质、平行线的性质、等角对等边、勾股定理、坐标与图形,熟练掌握相关知识的联系与运用是解答的关键.。
基本平面图形综合测试(作图、计算)(含答案)

学生做题前请先回答以下问题问题1:与平行有关的两个基本事实是什么?问题2:与垂直有关的两个基本事实是什么?问题3:常见的几何语言书写:问题4:在直线l上的任取一点A,截取AB=4cm,再截取BC=5cm.求AC的长.(根据题意画图求解)基本平面图形综合测试(作图、计算)一、单选题(共10道,每道10分)1.如图,为了解决A,B,C,D四个小区的缺水问题,市政府准备投资修建一个水厂E,使之到A,B,C,D 四个小区的距离之和最小,则水厂E应建在( )A.线段AC的中点B.线段BD的中点C.线段AC与线段BD的交点D.直线AB与直线CD的交点答案:C解题思路:试题难度:三颗星知识点:两点之间线段最短2.如图,已知线段AB,用尺规作图(保留作图痕迹):延长线段AB到点C,使BC=2AB.下列尺规作图正确的是( )A.线段BC即为所求B.线段BC即为所求C.线段AC即为所求D.线段BC即为所求答案:A解题思路:试题难度:三颗星知识点:尺规作图3.按照下列要求作图:①作线段AB;②作射线DA;③作直线AC.其中符合要求的是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:几何作图4.如图,已知四点A,B,C,D,按要求作图:①作射线AB,反向延长AB到点E,使EA=AB;②连接CE,过点D作直线DF∥CE交射线AB于点F;③过点D作射线AB的垂线交AB于点P,正确的是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:几何作图5.已知线段AB=16cm,点C在直线AB上,AC=3BC,则BC的长为( )A.32cm或4cmB.32cm或16cmC.cm或cmD.4cm或8cm答案:D解题思路:试题难度:三颗星知识点:线段的计算6.已知∠AOB=60°,∠AOC=4∠BOC,则∠AOC的度数为( )A.12°或20°B.12°或48°C.48°或80°D.20°或80°答案:C解题思路:试题难度:三颗星知识点:角度的计算7.在直线上任取一点A,截取AB=8cm,再截取AC=20cm,则AB的中点D与点C之间的距离为( )A.16cm或6cmB.16cm或24cmC.6cm或14cmD.14cm或24cm答案:B解题思路:试题难度:三颗星知识点:中点8.已知∠AOB=80°,∠BOC=30°,OM平分∠AOB,ON平分∠AOC,则∠MON的度数为( )A.15°B.15°或55°C.30°或110°D.30°或55°答案:A解题思路:试题难度:三颗星知识点:角平分线9.已知三点在同一条直线上,且,分别为线段的中点,则的长为( )A.16B.25C.16或25D.16或7答案:A解题思路:试题难度:三颗星知识点:中点的六种表示10.已知∠AOB=20°,∠AOC=4∠AOB,且∠BOC<∠AOC,OD平分∠AOB,OM平分∠AOC,则∠MOD 的度数为( )A.30°或50°B.20°或60°C.30°D.50°答案:C解题思路:试题难度:三颗星知识点:角度的计算。
大题第二讲尺规作图练习
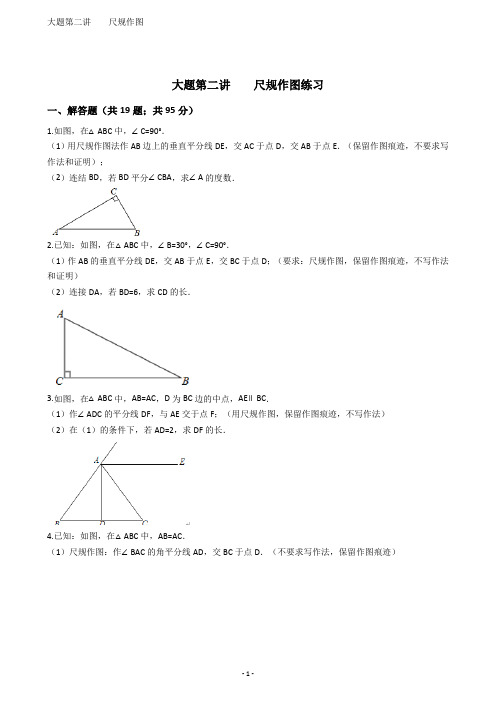
大题第二讲尺规作图练习一、解答题(共19题;共95分)1.如图,在△ABC中,∠C=90°.(1)用尺规作图法作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);(2)连结BD,若BD平分∠CBA,求∠A的度数.2.已知:如图,在△ABC中,∠B=30°,∠C=90°.(1)作AB的垂直平分线DE,交AB于点E,交BC于点D;(要求:尺规作图,保留作图痕迹,不写作法和证明)(2)连接DA,若BD=6,求CD的长.3.如图,在△ABC中,AB=AC,D为BC边的中点,AE∥BC.(1)作∠ADC的平分线DF,与AE交于点F;(用尺规作图,保留作图痕迹,不写作法)(2)在(1)的条件下,若AD=2,求DF的长.4.已知:如图,在△ABC中,AB=AC.(1)尺规作图:作∠BAC的角平分线AD,交BC于点D.(不要求写作法,保留作图痕迹)(2)延长AD至E点,使DE=AD,连接BE、CE.求证:四边形ABEC是菱形.5.如图的斜边AB=5,cosA=(1)用尺规作图作线段AC的垂直平分线(保留作图痕迹,不要求写作法、证明);(2)若直线与AB,AC分别相交于D,E两点,求DE的长6.如图,在△ABC中,已知∠CDB=110°,∠ABD=30°.(1)请用直尺和圆规在图中直接作出∠A的平分线AE交BD于E;(不写作法,保留作图痕迹)(2)在(1)的条件下,求出∠AED的度数.7.如图,△ABC中,AB=AC=6,BC=4,∠A=40°.(1)用尺规作出边AB的中垂线交AB于点D,交AC于点E(不写作法,保留作图痕迹,并在图中表明字母)(2)连接BE,求△EBC的周长和∠EBC的度数.8.如图,在△ABC中,AB=AC,∠ABC=72°,(1)用直尺和圆规作∠ABC的平分线BD,交AC于点D.(保留作图痕迹,不要求写作法)(2)在(1)中作出∠ABC的平分线后,求∠BDC的度数.9.如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.实验与操作:根据要求进行尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法)(1)作∠DAC的平分线AM;(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE,CF.猜想并证明:判断四边形AECF的形状并加以证明.10.如图,BD是矩形ABCD的一条对角线.(1)作BD的垂直平分线EF,分别交AD,BC于点E,F,垂足为点O(要求用尺规作图,保留作图痕迹,不要求写作法)(2)在(1)中,连接BE和DF,求证:四边形DEBF是菱形.11.作图题:(要求保留作图痕迹,不写作法)(1)作△ABC中BC边上的垂直平分线EF(交AC于点E,交BC于点F);(2)连结BE,若AC=10,AB=6,求△ABE的周长.12.如图,△ABC是等腰三角形,AB=BC,点D为BC的中点.(1)用圆规和没有刻度的直尺作图,并保留作图痕迹:①过点B作AC的平行线BP;②过点D作BP的垂线,分别交AC,BP,BQ于点E,F,G.(2)在(1)所作的图中,连接BE,CF.求证:四边形BFCE是平行四边形.13.尺规作图:(用圆规和直尺作图,不写过程,但要保留作图痕迹)已知:如图,直线AB与直线BC相交于点B,点D是直线BC上一点.求作:点E,使直线DE∥AB,且使线段BE长度最短.14.如图,在△ABC中,AB=AC,∠CAB=30°.(1)用直尺和圆规作AC边上的高线BD交AC于点D(保留作图痕迹,不要求写作法);(2)在(1)中作出AC边上的高线BD后,求∠DBC的度数.15.已知:△ABC.(1)尺规作图(保留作图痕迹,不写作法):作AB的垂直平分线MN,使MN交AC于D;(2)连BD,若AC=5cm,BC=4cm,求△BDC的周长。
物理(作图题、计算题、问答题)

作图题1、三个完全相同的烧杯装有质量相等的三种液体,其中甲杯装纯水,乙杯装硫酸,丙杯装汽油.请在图11中画出其他两种液面的合理位置.(已知:ρ硫酸>ρ水>ρ汽油)2、神力小BB 做单手虎卧撑.若把他的脚趾看作支点O ,请在图12中画出: (1)小BB 的重力G (重心在A 点)和重力G 对应的力臂l 2; (2)地面对手掌竖直向上的支撑力F ;3、小明用弹簧测力计测量不同数量钩码的重力,得到如下表所示的实验数据.(1)根据测量数据在图13的甲中描点,把这些点连起来表示出物质的重力与质量的关系; (2)在图13乙中用箭头标出测量0.2 kg 钩码时弹簧测力计指针所在的位置;4、如图5所示,重为G 的木箱A 静止在斜面上,请作出木箱受到重力的示意图.(图5)甲 图13 乙甲 乙 丙图11图12AO5、图6是安装在安全文明小区进出口的栏杆示意图,当在A 处施加一个压力F 时,可将栏杆拉起通行。
请在图中画出此时压力F 的力臂L 1和重力G 的力臂L 2。
(图6)6、一个站在地面上的工人利用滑轮组将重物G 提起来,请在图7中画出滑轮组的绕线(图7)7、一个重为10N 的小球,放在水平桌面上(如图10),请画出小球受到的重力。
8、请在图11中画出力F 的力臂。
9、在图12中用线代表绳子,将两个滑轮连成省力的滑轮组,要求人用力往下拉绳使重物升起。
10、一个被按到水里的乒乓球放手后迅速上浮,图8中已画出F浮,请在图中补充画出球所受重力的示意图.图8G图10图11图12F浮计算题1、一辆车空载时自身质量为2.8t,额定载重货物的最大质量为3.6t,轮子与水平地面的总接触面积是0.2m2,求:(已知泥沙的密度为2.4×103 kg/m3;g取10N/kg)(1)空载时,此车的重力;(2)空载时,此车对水平地面的压强;(3)此车不能超载,它最多能装多少立方米的泥沙.2、工人用滑轮组(如图14示)经过10s将重200N的货物从地面提到4m高的二楼工场,所用的拉力是80N,求:(1)此过程的有用功;(2)此过程的总功;图14 (3)工人做功的功率.3、如图示的容器,高h=20cm,底面积S=1.0×10-2m2,容积V=4.0×10-3m3,当此容器盛满水时,问:(1)水对容器底的压强是多少?(2)水对容器底的压力是多少?(3)水受到的重力是多少?(g=10N/Kg)4、如图所示,小明通过动滑轮用200N的力在10s内把重为150N的物体升高4m,求:(1)小明做功是多少?(3)使用动滑轮的机械效率是多少?(g=10N/kg)5、一辆车空载时自身质量为2.8t ,额定载重货物的最大质量为3.6t ,轮子与水平地面的总接触面积是0.2m 2,求:(已知泥沙的密度为2.4×103 kg /m 3;g 取10N /kg ) (1)空载时,此车的重力;(2)空载时,此车对水平地面的压强;(3)此车不能超载,它最多能装多少立方米的泥沙.6、小黄同学用图13所示的滑轮组经过10s 将一个重200N 的重物提高 1m ,所用的拉力是80N ,求: (1)小黄所做的有用功;(2)拉力做功的功率;7、“大洋一号”是我国第一艘现代化的综合性远洋科学考察船,船的质量为5.6×103t 。
透镜作图题含答案

透镜作图题含答案1.请绘制下列图中凸透镜的折射光线方向图。
2.请绘制下列图中凹透镜的折射光线方向图。
3.请完成下列透镜的光路图。
4.请在下列图中适当位置绘制合适的透镜。
5.请绘制下列图中凸透镜的入射光线或折射光线方向图。
6.请绘制下列图中凹透镜的折射光线或入射光线方向图。
7.请在下列方框内绘制合适的透镜,并确定其位置。
8.请在下列方框内绘制合适的透镜,并确定其位置。
9.(1)如图所示,L1为入射光线,L2为出射光线。
请在图中添加一个合理的光学器件。
2)请在图中完成光线从左边射向凸透镜折射后,再向凹透镜折射后的光路。
3)一条光线与凸透镜主光轴夹角为60度,斜向上入射到放在主光轴上方的平面镜上,如图所示,入射光线与镜面夹角为30度。
请完成光路图。
10.请在图10中完成物体AB经凸透镜成像的光路图。
11.请完成图11中的光路图。
12.如图12所示,请绘制入射光线经过凸透镜后的折射光线。
13.如图13所示是照相机的原理图,A'B'是AB的像。
请绘制图中与入射光线对应的折射光线,并确定凸透镜一侧焦点的位置,用字母F表示。
14.请绘制图14中光线经过透镜折射后的光线。
15.根据图15中经透镜折射后的光线绘制入射光线。
16.我国古代的“千里眼”是富有想象力的神话,随着科学技术的飞速发展,天文望远镜已将神话变成现实。
图8中天文望远镜是由两个透镜组成的,请绘制两条入射光线经过两个透镜的光路(其中F1是透镜L1的焦点,F2是透镜L2的焦点)。
量为1000kg,求岩石的密度和质量。
6、一块铁块的质量为20kg,体积为0.04m3,求它的密度。
7、一根木棒的质量为0.3kg,长度为20cm,直径为2cm,求它的密度。
8、一种物质的质量为2.5kg,体积为0.0025m3,求它的密度。
9、有一块金属的质量为500g,体积为100cm3,求它的密度。
10、一种液体的密度为0.9g/cm3,用一个100cm3的瓶子装了80g的液体,求瓶子中剩余的液体体积。
初中物理专题复习:机械与人计算题,实验题,作图题(有答案和解析) (1)

绝密★启用前初中物理试机械与人计算题、实验题、作图题考试范围:xxx;考试时间:100分钟;命题人:xxx题号一二三总分得分注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第Ⅰ卷(选择题)请点击修改第I卷的文字说明评卷人得分一.作图题(共6小题)1.要用滑轮组将陷在泥中的汽车拉出来,试在图中画出最省力的绕绳方法。
2.如图所示,轻质杠杆的A点挂一重物G,绳受的拉力为F2,O为杠杆的支点。
请在杠杆的端点B处画出使杠杆保持静止的最小的力F l的示意图,并作出F2的力臂l2。
3.如图,在杠杆AB上挂了一个重为G 的物体。
为使杠杆在图中的位置静止。
请在杠杆上画出最小动力。
4.小华借助滑轮组提升重物,请画出最省力的绕线方法。
5.如图是静止在水平地面上的拉杆旅行箱的示意图,O是轮子的转轴,O′是箱体的重心。
以O为支点,画出力F的力臂和箱体所受重力的示意图。
6.右图是一个杠杆式简易起吊机,它上面装了一个定滑轮可以改变拉绳的方向,杠杆OBA可绕O点转动。
在图上画出动力臂L1和阻力F2的示意图。
第Ⅱ卷(非选择题)请点击修改第Ⅱ卷的文字说明评卷人得分二.实验探究题(共13小题)7.某同学用如图所示的实验装置测量滑轮组的机械效率,相关数据记录在如表中。
实验次数钩码重/N钩码上升的高度/m绳端的拉力/N绳端移动的距离/m140.10 1.80.3260.10 2.50.3360.15 2.5(1)实验中,使用滑轮组提升重物时,应竖直向上拉动弹簧测力计。
(2)第三次实验中,绳端移动的距离为m,滑轮组的机械效率为。
(3)分析实验数据发现,同一滑轮组提升重物的重力变大时,滑轮组的机械效率将(选填“变大”“变小”或“不变”)8.在探究“物体动能的大小与哪些因素有关”的实验中,如图所示,让同一铁球从斜面的不同高度由静止释放,撞击同一木块。
请回答下列问题:(1)该实验的目的是研究(选填“铁球”或“木块”)的动能大小与的关系。
三年级奥数题及答案:作图题

三年级奥数题及答案:作图题。
以下这道三年级奥数题主要考查平行四边形、三角形和梯形的面积的计算方法的灵活应用,关键是先确定出计算这几个图形的面积所需要的主要线段的长度,进而完成画图.在下面的方格图里分别画一个平行四边形、三角形和梯形,使它们的面积都是8厘米.(每个方格都是边长1厘米的正方形).考点:画指定面积的长方形、正方形、三角形;平行四边形的特征及性质;梯形的特征及分类.专题:作图题.分析:平行四边形、三角形和梯形的面积都已知,且都相等,于是可以分别确定出平行四边形的底和高、三角形的底和高以及梯形的上底、下底和高的值,进而就可以在方格图中画出这几个图形.解答:解:因为S平行四边形=S三角形=S梯形=8平方厘米,平行四边形的底和高为4厘米和2厘米,三角形的底和高为8厘米和2厘米,梯形的上底、下底和高为3厘米、5厘米和2厘米,于是可以画出这几个图形:。
初中数学旋转作图专题训练含答案

初中数学旋转作图专题训练含答案姓名:__________ 班级:__________考号:__________一、作图题(共20题)1、如图,在一个10×10的正方形DEFG网格中有一个△ABC。
①在网格中画出△ABC向下平移3个单位得到的△A1B1C1。
②在网格中画出△ABC绕C点逆时针方向旋转90°得到的△A2B2C。
③若以EF所在的直线为x轴,ED所在的直线为y轴建立直角坐标系,写出A1、A2两点的坐标。
2、如图,△ABC的顶点坐标分别为A(4,6),B(2,3),C(5,2)。
如果将△ABC 绕C点顺时针旋转90°,得到△A1B1 C。
(1)请在图中画出△A1B1 C;(2)请作出△A1B1C的外接圆(尺规作图,要求保留作图痕迹,不必写出作法);(3)在图中已画好的格点上,是否存在点D,使得=,请写出符合条件的所有D 点的坐标(C点除外)。
(原创)3、如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.ΔABO 的三个顶点A,B,O都在格点上.(1)画出ΔABO绕点O逆时针旋转900后得到的三角形Δ;(2)根据所画的图找出点和点的坐标.4、 ,如图,在由边长为的小正方形组成的方格纸中,有两个全等的三角形,即和.请你指出在方格纸内如何运用平移、旋转变换,将重合到上;5、已知△ABC在平面直角坐标系中的位置如图所示。
⑴分别写出图中点A和点C的坐标;⑵画出△ABC绕点A按逆时针方向旋转90°后的△AB′C′;⑶在⑵的条件下,求点C旋转到点C′所经过的路线长(结果保留π)6、如右图,在网格图中建立平面直角坐标系,的顶点坐标为、、.(1)若将向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的;顺时针方(2)画出绕C1向旋转900后得到的;(3)与是中心对称图形,请写出对称中心的坐标:;并计算的面积: .(4)在坐标轴上是否存在P点,使得△PAB与△CAB的面积相等,若有,则求出点P的坐标.7、在网格纸上按以下要求作图,不用写作法:(1)作出“小旗子”向右平移6格后的图案.(2)作出“小旗子”绕O 点按逆时针方向旋转90°后的图案.8、 如下图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点, △ABC 的顶点均在格点上.(1)画出将△ABC 向右平移2个单位后得到的△A 1B 1C 1,再画出将△A 1B 1C 1绕点B 1按逆时针方向旋转90°后所得到的△A 2B 1C 2;(2)求线段B 1C 1旋转到B 1C 2的过程中,点C 1所经过的路径长.9、 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一个△ABC 和一点O ,△ABC 的顶点与点O 均与小正方形的顶点重合.(1)在方格纸中,将△ABC 向下平移6个单位长度得到△A 1B 1C 1,请画△A 1B 1C 1. (2)在方格纸中,将△ABC 绕点O 旋转180°得到△A 2B 2C 2,请画△A 2B 2C 2.10、每个小方格都是边长为1个单位长度,正方形ABCD在坐标系中的位置如图所示.(1)画出正方形ABCD关于原点中心对称的图形;(2)画出正方形ABCD绕点D点顺时针方向旋转90°后的图形;(3)求出正方形ABCD的点B绕点D点顺时针方向旋转90°后经过的路线.11、如图,在方格纸中每个小正方形的边长均为1个单位,△ABC的三个顶点都在小方格的顶点上.(1)在图中作出将△ABC向右平移5个单位后的图形△A1B1C1;(2)在图中作出△ABC以C为旋转中心,沿顺时针方向旋转90°后的图形△A2B2 C.12、已知△ABC在平面直角坐标系中的位置如图所示.(1)分别写出图中点A和点C的坐标;(2)画出△ABC绕点C按顺时针方向旋转90°后的△A′B′C′;(3)求点A旋转到点A′所经过的路线长(结果保留π).13、在如图的方格纸中,每个小方格都是边长为1个单位的正方形,的三个顶点都在格点上(每个小方格的顶点叫格点).(1)画出向下平移4个单位后的,并直接写出在平移过程中扫过的面积;(2)画出绕点顺时针旋转后的,并直接写出点旋转到所经过的路线长.14、如图,在平面直角坐标系中,和关于点成中心对称。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、作图计算题
1.图示机构,由曲柄1、连杆2、摇杆3及机架6组成铰链四杆机构,轮1′与曲柄
1固接,其轴心为B,轮4分别与轮1′和轮5相切,轮5活套于轴D上。
各相切轮之间作纯滚动。
试用速度瞬心法确定曲柄1与轮5的角速比ω1/ω5。
2.画出图示油泵机构的运动简图,计算其自由度,并作出所有速度瞬心。
3. 如图所示正切机构,尺寸及瞬时位置如图,且构件1的角速度ω1=6rad/s ,角加速
度α1=0,请完成:(1)并标明所有的瞬心。
(2)求构件3的瞬时速度和加速度(提示:建议先求构件3的位移,然后求1阶和2阶导数求速度和加速度)。
(1). 并标明所有的瞬心。
(2). 求构件3︒
===
=
==60cos sin 8.0cos 4.0tan 4.01112
1
1211t t
t dt dv a t dt ds
v t s ωωωωωωω
4. 已知主动件4的角速度及角加速度,写出求出构件2的角速度及角加速度度矢量
方程。
(仅要求列出向量方程,指明各项向量的大小和方向)
写出
n
BC
BC C n
B B BC
C B a a a a a
v v v ++=++=ττ
矢量
5. 在题图机构中,已知曲柄AB 的等角速度ω1为常数,转向如图所示,用相对运动图
解法求构件3的ω3角速度(仅要求列出向量方程,指明各项的大小和方向)
3B23B2
B B v v v =+
6. 在图试铰链四杆机构中,已知L AB =10mm ,L BC =50mm ,L CD =30mm 。
请完成:(1)要是机构
为曲柄摇杆机构时,L AD 的范围;(2)若L AD =40mm ,用作图法求当L AB 杆主动件时的摇杆的两个极限位置;(3)若L AD =40mm ,用作图法求当L AB 杆主动件时的最小传动角γmin 。
B
D
50
103010503010+≤+>>++AD AD L L 或
50
301010503010+≤+>>++AD AD L L
7. 图示用铰链四杆机构作为加热炉炉门的启闭机构。
炉门上两铰链的位置已知,炉
门打开后成水平位置时,要求炉门的外边朝上,固定铰链装在xy 轴线上,其相互位置的尺寸如图上所示。
试设计此机构。
解:
根据连杆的两位置实际此四杆机构;做出垂直平分线。
根据条件找到正确位置的,
写出答案,LAB=69;LCD=117.5;LAD=98.5
8. 偏置曲柄滑块机构如图所示,e =20mm ,l AB =40mm ,l BC =100mm 。
请完成:(1)画出滑
块的两个极限位置;(2)准确计算(不要在图上测量)出极位夹角θ和行程速比系数K 。
13
.126
.1118026.1118026.1153.7076.81arccos arccos =-+=︒
=︒-︒=⎪⎪⎭
⎫ ⎝⎛--⎪⎪⎭⎫
⎝⎛
+=K l
l e
l l e AB
BC AB
BC θ
9. 用图解法设计图示用于控制装置的摇杆滑块机构,要求摇杆和滑块满足三组对应
位置α1=600
时S 1=80mm ,α2=900
时S 2=60mm ,α3=1200
时S 3=40mm ,偏距e =20。
确定摇杆上转动副的位置以及摇杆和连杆的长度。
10. 在图示的偏心为0
的凸轮机构上标出理论廓线、基圆半径、最大位移、推程运动
角、远休止角、回程运动角、近休止角、图示位置压力角。
(10分)
11. 图(a )和图(b )分别为滚子对心直动从动件盘形凸轮机构和滚子偏置直动从动
件盘形凸轮机构,已知:R =100mm ,OA =20mm ,e =10mm ,r T =10mm ,试用图解法确定;当凸轮自图示位置(从动件最低位置)顺时针方向回转90°时两机构的压力角及从动件的位移值。
(15分)
图(a ) 图(b )
解:略
12. 在图示的轮系中,各齿轮齿数分别为Z 1 =17,Z 2 =Z 2' =17,Z 3=51,Z 4 =52,齿轮1
的转速为120r/min 。
试求其它个齿轮和转臂H 的转速。
=
=-=---
=--1433141,03
17*1752
*17i n n n n n n n n n H H
H H
13. 图示为纺织机中的差动轮系,设已知各齿轮的齿数Z 1 =30、Z 2 =25、Z 3 =Z 4 =24、
Z 5=18、Z 6 =121;齿轮1的转速n 1 =200r/min ,系杆H 的转速n H =316 r/ min ,且转向相同。
试求各齿轮的转速,并在图中标出各轮的转动方向。
min
r/ 3.295., (18)
2430121
2425316316200)1(665
316
42261=⨯⨯⨯⨯=---=--n n z z z z z z n n n n H H
14. 在图示复合轮系中,已知各齿轮齿数Z 1=36、Z 2=60、Z 3=23、Z 4=49、Z 4' =69 、Z 5 =31、
Z 6=131、Z 7=94、Z 8=36、Z 9 =167,主动齿轮1的转速n 1 =3000 r/ min ,试求行星
架H 的转速n H 和其它各齿轮的转速。
105
05.29109.8449
7774677443
14
241=⇒-=--=⇒-=--=⇒=H H H n z z
n n n n z z
n n n n z z z z n n
15. 某铣床的转盘行星减速装置如图所示。
已知各齿轮的齿数分别为Z 1=Z 2=17,Z 3=51,
试求当手柄转90度,转盘H 和齿轮2转过的角度及方向。
写出轮系的传动比关系:
2
331z z
n n n n h h -=--,其中n 3=0,;
解出他们之间的数字关系,转盘H 转过的角度:22.5度
16. 在图示轮系中,各齿轮的齿数为Z 1=20、Z 2=40、Z '2=Z 3=30、Z 4=90,齿轮1的转速
n 1=300r/min 。
求出其它各齿轮和系杆H 的转速,并标出转动方向。
解:略
4
1
3
2 2' H
17.在图示的凸轮机构中,高副的摩擦角φ=15o,转动副的摩擦圆和高副接触的法线如
图中细线所示,凸轮在驱动力矩M1推动下顺时针转动,工作阻力P r=50N。
请完成:(1)画出凸轮和从动件的受力图;(2)图解法运动副反力和平衡力矩M1。
18.图示楔块机构中,已知:γ=β=60°,Q
=1000N,各接触面摩擦系数f=0.15。
如Q为有效阻力,试求所需的驱动力F。
解:首先对图所示的构件2,进行受力分析,画出地面及物体1对2的作用力;
对图所示的构件1,进行受力分析,画出地面及物体2对1的作用力;
写出它们之间的数字关系。
19.图示为一夹紧机构。
设已知夹紧力Q=1KN,楔块斜角α=6o, l BC=100mm,l CD=300mm。
各移动副摩擦系数为f=0.1,忽略转动副摩擦。
请完成:(1)画出斜块1、2的受力图;(2)图解法计算驱动力P的大小和各移动副中约束反力的大小。
解:图示为一夹紧机构。
设已知夹紧力Q=1KN,楔块斜角α=6o,摩擦系数为 f=0.1,L BC =100mm,L CD =300mm。
忽略铰链处的摩擦,请完成:
a、画出两斜块1、2的受力图
b、图解法求AB杆的受力
c、计算加紧时需用驱动力P的大小。
20.图示为一双滑块机构,已知主动力P=100N,移动副的摩擦角φ=15,转动副的摩擦
圆如图中细线圆所示。
忽略惯性力和重力,用图解法求工作阻力Q。
⎪⎪⎩⎪⎪⎨
⎧-=---=--'214
241
1331z z z z n n n n z z n n n n h
h h
h。
