最新整理2019年二模18题解析
2019年全国大联考高考物理二模试卷(新课标ⅲ卷)解析版

B.两个过程中外力做功之比W'1:W'2=1:4
C.两个过程中外力之比F1:F2=1:1
D.两个过程中流过金属杆的电荷量相同
7.(6分)图1是2018年12月3日广州半程马拉松赛中两位选手参赛的某一情形,假设甲、乙两人起跑时都做匀加速直线运动,到达某一速度后都各自做匀速直线运动,且跑到终点。他们的速度﹣时间图象如图2所示,则下列说法正确的是( )
A.小滑块在C点处的动能为
B.小滑块在C点处的机械能为8mgR
C.在C点处轨道对小滑块的压力大小为
D.小滑块能通过最高点,且最高点轨道对小滑块的压力为3mg
二、非选择题:本卷包括必考题和选考题两部分.第22~25题为必考题,每个试题考生都必须作答.第33~34题为选考题,考生根据要求作答.(一)必考题(共47分)
A.1:1B.2:1C.3:2D.3:5
5.(6分)如图所示中的L1和L2称为地月连线中的拉格朗日点L1和拉格朗日点L2.在L1点处的物体可与月球同步绕地球转动。在L2点处附近的飞行器无法保持静止平衡,但可在地球引力和月球引力共同作用下围绕L2点绕行,且处于动态平衡状态。我国中继星鹊桥就是绕L2点转动的卫星,嫦娥四号在月球背面工作时所发出的信号通过鹊桥卫星传回地面,若鹊桥卫星与月球、地球两天体中心距离分别为R1、R2,信号传播速度为c。则( )
(2)某次实验中得到了如图2所示的一条纸带,打点计时器的打点时间间隔为0.02s,图中相邻两计数点之间还有四个点未画出。由该纸带可求得小车此次运动的加速度大小为a=m/s2。
(3)他们根据每次实验的纸带计算出每次实验的加速度值以及计算出了每次实验中加速度的倒数,实验数据如表所示,请根据表中的实验数据在图3所示的 坐标中作出 图象。
精品解析:2019年辽宁省锦州市中考二模语文试题(解析版)

辽宁省锦州市2019届九年级第二次模拟语文试题1.选出下列词语中加点字音、形完全正确的一项()A. 嘹.亮(liáo)狼藉.(jí)聆.听(líng)井然有绪.(xù)B. 拮据.(jū)猝.然(cù)违.背(wéi)别具.匠心(jù)C. 坎坷.(kē)胚.芽(pēi)束缚.(fù)潜.移默化(qián)D. 暴噪.(zào)隐匿.(nì)拯.救(zhěng)络绎不绝.(jué)【答案】B【解析】【详解】A项,井然有序。
C项,坎坷(kě)。
D项,暴躁。
2.下列词语中没有错别字的一项是()A. 阔绰喧闹不知所措地大物博B. 嬉戏决窍家喻户晓不屑置辩C. 狼藉渺茫一代天娇冥思苦想D. 分歧葱笼金碧辉煌因地治宜【答案】A【解析】【详解】B项,诀窍。
C项,一代天骄。
D项,葱茏,因地制宜。
3.选出填入下面语段横线处的词语最恰当的一项()梦想与奋斗______________。
年轻人最不该在能奋斗的时候选择______________。
与时代同向同行,以奋斗筑梦圆梦,用脚步______________的青春,定会______________出灿烂的光华。
请记住:幸福是奋斗出来的!A. 一脉相承享受丈量绽放B. 相辅相成悠闲衡量闪耀C. 一脉相承清闲衡量闪耀D. 相辅相成安逸丈量绽放【答案】D【解析】【详解】试题分析:(1)一脉相承:比喻某种思想、行为或学说之间有继承关系。
相辅相成:相互补充,相互促成。
第一空,要填写的是“梦想与奋斗”的关系,显然不能是“一脉相承”,应该选用“相辅相成”。
可排除A项和C项。
(2)悠闲:从容闲适而无所牵挂。
安逸:安闲舒适。
“悠闲”“安逸”多用于生活的状态,“悠闲”偏向于静,“安逸”偏向于动。
第二空,故选择“安逸”更恰当。
(3)衡量:指量度物体的重量和容积。
丈量:是测量的意思。
上海市宝山区2019届高三英语二模试题(含解析)

上海市宝山区2019届高三英语二模试题(含解析)Ⅱ. Grammar and VocabularyDirections:After reading the passage below, fill in the blanks to make the passage coherent and grammatically correct. For the blanks with a given word, fill in each blank with the proper form of the given word; for the other blanks, use one word that best fits each blank.Curiosity is part of human nature. Children are famous for wanting answers____1____ tons of questions. People keep reading or watching ____2____ they want to find out what happens. But curiosity also provides many practical benefits.Learning is easiest if you have a genuine desire for knowledge. Curiosity can create that desire when you have a question.Many of history greatest discoveries ____3____(make)by curious people. People wondered ____4____ processes worked or how certain tasks could be done more effectively. Thanks to their curiosity, people now know far more about the world and have useful technology ____5____(help)them.Even if you don’t p lan to be an inventor of researcher, curiosity can still help you in the classroom. If you develop the joy of learning, classes will become more fun. And you’ll excel because you will be fully engaged in the process of learning. Even if you’re no longer a student, curiosity will make you better ____6____(inform)and thus a more capable worker.What do you do if you’re not already curious? Fortunately, curiosity is a skill that can be improved. If you act like you’re curious, you’ll quickly start to actually feel curious. Often, the more you learn about a topic the ____7____(interesting)it becomes.As you learn about a topic, gather information from as many sources as possible. Read a variety of books, watch or listen to lectures and ask questions. Don’t always get your information from the same source. Instead, learn to appreciate facts that different people know and the different opinions ____8____ they express.Ask a lot of questions, Remember, everyone knows ____9____ that you don’t. Findout what that is, and ask about it. This lets you learn something and makes the other person happy by letting them show off their knowledge.In the classroom or out of it, ____10____(develop)curiosity is sure to be worthwhile.【答案】1. to 2. because3. were made4. how5. to help6. informed7. more interesting8. that/which9. something10. developing【解析】这是一篇说明文。
2019年中考数学二模试卷(含解析)

2019年中考数学二模试卷一、选择题(每小题4分,共48分)1.(4分)在实数﹣2,|﹣2|,(﹣2)0,0中,最大的数是()A.﹣2B.|﹣2|C.(﹣2)0D.02.(4分)据《经济日报》2018年5月21日报道:目前,世界集成电路生产技术水平最高已达到7nm(1nm=10﹣9m),主流生产线的技术水平为14~28nm,中国大陆集成电路生产技术水平最高为28nm.将28nm用科学记数法可表示为()A.28×10﹣9m B.2.8×10﹣8m C.28×109m D.2.8×108m 3.(4分)如图,它是由5个完全相同的小正方体搭建的几何体,若将最右边的小正方体拿走,则下列结论正确的是()A.主视图不变B.左视图不变C.俯视图不变D.三视图都不变4.(4分)如图,若直线MN∥PQ,∠ACB的顶点C在直线MN与PQ之间,若∠ACB=60°,∠CFQ=35°,则∠CEN的度数为()A.35°B.25°C.30°D.45°5.(4分)下列几道题目是小明同学在黑板上完成的作业,他做错的题目有()①a3÷a﹣1=a2②(2a3)2=4a5③(ab2)3=a3b6④2﹣5=⑤(a+b)2=a2+b2A.2道B.3道C.4道D.5道6.(4分)在一次数学测试后,随机抽取九年级(3)班5名学生的成绩(单位:分)如下:80、98、98、83、91,关于这组数据的说法错误的是()A.众数是98B.平均数是90C.中位数是91D.方差是56 7.(4分)若二次函数y=x2﹣2x+m的图象与x轴有两个交点,则实数m的取值范围是()A.m≥1B.m≤1C.m>1D.m<18.(4分)如图,AC是矩形ABCD的一条对角线,E是AC中点,连接BE,再分别以A,D为圆心,大于的长为半径作弧,两弧相交于点F,连接EF交AD于点G.若AB =3,BC=4,则四边形ABEG的周长为()A.8B.8.5C.9D.9.59.(4分)点P的坐标是(m,n),从﹣5,﹣3,0,4,7这五个数中任取一个数作为m的值,再从余下的四个数中任取一个数作为n的值,则点P(m,n)在平面直角坐标系中第四象限内的概率是()A.B.C.D.10.(4分)如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2x,y+1),则y关于x的函数关系为()A.y=x B.y=﹣2x﹣1C.y=2x﹣1D.y=1﹣2x 11.(4分)如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=,则△ABC移动的距离是()A.B.C.D.﹣12.(4分)如图,在直角坐标系中,已知点A(﹣3,0),B(0,4),对△OAB连续作旋转变换,依次得到△1,△2,△3,△4,…,则△2019的直角顶点的坐标为()A.(8076,0)B.(8064,0)C.(8076,)D.(8064,)二、填空题(每小题4分,共24分)13.(4分)分解因式:a3b+2a2b2+ab3=.14.(4分)如图,在▱ABCD中,点E在BC边上,且AE⊥BC于点E,ED平分∠CDA,若BE:EC=1:2,则∠BCD的度数为.15.(4分)如图,等边三角形△ABC的边长为4,以BC为直径的半圆O交AB于点D,交AC于点E,阴影部分的面积是.16.(4分)新定义:[a,b]为一次函数y=ax+b(a≠0,a,b为实数)的“关联数”.若“关联数”[2,m+1]的一次函数是正比例函数,则关于x的方程+=1的解为.17.(4分)若函数y=与y=x+2图象的一个交点坐标为(a,b),则﹣的值是.18.(4分)如图①,在正方形ABCD中,点E是AB的中点,点P是对角线AC上一动点,设PC的长度为x,PE与PB的长度和为y,图②是y关于x的函数图象,则图象上最低点H的坐标为.三、解答题(7小题,共78分)19.(8分)先化简,再求值:(x﹣1﹣)÷,其中x是方程x2+2x=0的解.20.(10分)为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:(1)求样本容量及表格中m、n的值;(2)请补全统计图;(3)被调查的60个喜欢球类同学中有3人最喜欢足球,若该校有3000名学生,请估计该校最喜欢足球的人数.21.(10分)如图,AB为⊙O的直径,ED切⊙O于点C,AD交⊙O于点F,连接AC,BF,且BF∥CD.(1)求证:AC平分∠BAD;(2)若⊙O的半径为,AF=2,求CD的长度.22.(12分)如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线交⊙A于点F,连接AF,BF,DF.(1)求证:△ABC≌△ABF;(2)填空:①当∠CAB=°时,四边形ADFE为菱形;②在①的条件下,BC=cm时,四边形ADFE的面积是6cm2.23.(12分)数学兴趣小组几名同学到某商场调查发现,一种纯牛奶进价为每箱40元,厂家要求售价在40~70元之间,若以每箱70元销售平均每天销售30箱,价格每降低1元平均每天可多销售3箱.老师要求根据以上资料,解答下列问题,你能做到吗?(1)写出平均每天销售量y(箱)与每箱售价x(元)之间的函数关系;(2)写出平均每天销售利润W(元)与每箱售价x(元)之间的函数关系;(3)现该商场要保证每天盈利900元,同时又要使顾客得到实惠,那么每箱售价为多少元?(4)你认为每天赢利900元,是牛奶销售中的最大利润吗?为什么?24.(12分)定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.理解:(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.求证:BD是四边形ABCD的“相似对角线”;(3)如图3,已知FH是四边形EFGH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2,求FH的长.25.(14分)如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B 的坐标为(1,0).抛物线y=﹣x2+bx+c经过A、B两点.(1)求抛物线的解析式;(2)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB 于点E,使PE=DE.①求点P的坐标;②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.2019年中考数学二模试卷参考答案与试题解析一、选择题(每小题4分,共48分)1.【解答】解:∵|﹣2|=2,(﹣2)0=1,∵﹣2<0<1<2,∴最大的数是|﹣2|,故选:B.2.【解答】解:28nm=28×10﹣9m=2.8×10﹣8m.故选:B.3.【解答】解:根据三视图的定义,若将最右边的小正方体拿走,俯视图、主视图都发生变化,左视图不变.故选:B.4.【解答】解:如图作CK∥MN,∵MN∥PQ,MN∥CK,∴PQ∥CK,∴∠CEN=∠ACK,∠FCK=∠CFQ,∴∠ACB=∠CEN+∠CFQ,∴60°=∠CEN+35°,∴∠CEN=25°,故选:B.5.【解答】解:①a3÷a﹣1=a4,故此选项错误;②(2a3)2=4a6,故此选项错误;③(ab2)3=a3b6,故此选项错误;④2﹣5=,正确;⑤(a+b)2=a2+2ab+b2,故此选项错误;则错误的一共有4道.故选:C.6.【解答】解:98出现的次数最多,∴这组数据的众数是98,A说法正确;=(80+98+98+83+91)=90,B说法正确;这组数据的中位数是91,C说法正确;S2=[(80﹣90)2+(98﹣90)2+(98﹣90)2+(83﹣90)2+(91﹣90)2]=×278=55.6,D说法错误;故选:D.7.【解答】解:由题意可知:△=4﹣4m>0,∴m<1,故选:D.8.【解答】解:连接ED,如图,由作法得F A=FD,∵AC是矩形ABCD的一条对角线,E是AC中点,∴B、E、D共线,EA=ED,∴EF垂直平分AD,∴AG=DG=AD=BC=×4=2,∵G为AD的中,E为BD的中点,∴GE为△ABD的中位线,∴GE=AB=,在Rt△ABC中,AC==5,∴BE=,∴四边形ABEG的周长=3+++2=9.故选:C.9.【解答】解:画树状图为:共有20种等可能的结果数,其中点P(m,n)在平面直角坐标系中第四象限内的结果数为4,所以点P(m,n)在平面直角坐标系中第四象限内的概率为=,故选:B.10.【解答】解:由题意可得出:P点在第二象限的角平分线上,∵点P的坐标为(2x,y+1),∴2x=﹣(y+1),∴y=﹣2x﹣1.故选:B.11.【解答】解:∵△ABC沿BC边平移到△DEF的位置,∴AB∥DE,∴△ABC∽△HEC,∴=()2=,∴EC:BC=1:,∵BC=,∴EC=,∴BE=BC﹣EC=﹣.故选:D.12.【解答】解:∵点A(﹣3,0)、B(0,4),∴AB==5,由图可知,每三个三角形为一个循环组依次循环,一个循环组前进的长度为:4+5+3=12,∵2019÷3=673,∴△2019的直角顶点是第673个循环组的最后一个三角形的直角顶点,∵673×12=8076,∴△2019的直角顶点的坐标为(8076,0).故选:A.二、填空题(每小题4分,共24分)13.【解答】解:a3b+2a2b2+ab3=ab(a2+2ab+b2)=ab(a+b)2.故答案为:ab(a+b)2.14.【解答】解:∵四边形ABCD是平行四边形,∴AB=CD,AD∥BC,AB∥CD,∴∠ADE=∠CED,∠B+∠BCD=180°,∵ED平分∠CDA,∴∠ADE=∠CDE,∴∠CED=∠CDE,∴CD=EC,∴AB=EC,∵BE:EC=1:2,∴BE:AB=1:2,即BE=AB,∵AE⊥BC,∴∠AEB=90°,∴∠BAE=30°,∴∠B=60°,∴∠BCD=120°;故答案为:120°.15.【解答】解:连接OD、DE、OE,∵△ABC为等边三角形,∴∠B=∠C=60°,∴∠BOD=60°,∠COE=60°,∴∠DOE=60°,即△DOE为等边三角形,∵∠A=∠ODB=60°,∴OD∥AE,同理,OE∥OD,∴四边形ADOE为菱形,∴阴影部分的面积=2×﹣=2,故答案为:2,16.【解答】解:根据关联数”[2,m+1]的一次函数是正比例函数,得到m+1=0,即m=﹣1,则方程为﹣1=1,即x﹣1=,解得:x=,经检验是分式方程的解.故答案为:17.【解答】解:∵函数y=与y=x+2图象的一个交点坐标为(a,b),∴b=,b=a+2,∴ab=3,b﹣a=2,∴﹣==.故答案为:.18.【解答】解:如图,连接PD.∵B、D关于AC对称,∴PB=PD,∴PB+PE=PD+PE,∴当D、P、E共线时,PE+PB的值最小,观察图象可知,当点P与A重合时,PE+PB=9,∴AE=EB=3,AD=AB=6,在Rt△AED中,DE==3,∴PB+PE的最小值为3,∴点H的纵坐标为3,∵AE∥CD,∴==2,∵AC=6,∴PC=×=4,∴点H的横坐标为4,∴H(4,3).故答案为(4,3).三、解答题(7小题,共78分)19.【解答】解:原式=•=•=,解方程x2+2x=0得:x1=﹣2,x2=0,由题意得:x≠﹣2,所以x=0.把x=0代入=,原式==﹣1.20.【解答】解:(1)样本容量为:12÷0.1=120,m=60÷120=0.5,n=120×0.15=18;(2)如图所示:;(3)学校喜欢球类人有:3000×0.5×=75(人).答:估计该校最喜欢足球的人数为75.21.【解答】解:(1)如图,连接OC,交BF于点H,∵ED切⊙O于点C,∴OC⊥DE,∵AB为⊙O的直径,∴BF⊥AD,∵BF∥CD,∴ED⊥AD,∴OC∥AD,∴∠OCA=∠CAD,∵OC=OA,∴∠OCA=∠OAC,∴∠OAC=∠CAD,∴AC平分∠BAD;(2)∵⊙O的半径为,AF=2,∠AFB=90°,∴BF=,由(1)知,∠D=∠HFD=∠OCD=90°,∴四边形HFDC为矩形,∴OC⊥BF,∴CD=HF=BF=4.22.【解答】(1)证明:∵EF∥AB,∴∠E=∠CAB,∠EF A=∠F AB,∵∠E=∠EF A,∴∠F AB=∠CAB,在△ABC和△ABF中,,∴△ABC≌△ABF;(2)当∠CAB=60°时,四边形ADFE为菱形.证明:∵∠CAB=60°,∴∠F AB=∠CAB=∠CAB=60°,∴EF=AD=AE,∴四边形ADFE是菱形.故答案为60.(3)解:∵四边形AEFD是菱形,设边长为a,∠AEF=∠CAB=60°,∴△AEF、△AFD都是等边三角形,由题意:2×a2=6,∴a2=12,∵a>0,∴a=2,∴AC=AE=2,在RT△ACB中,∠ACB=90°,AC=2,∠CAB=60°,∴∠ABC=30°,∴AB=2AC=4,BC==6.故答案为6.23.【解答】接:(1)y=30+3(70﹣x)=﹣3x+240;(2)w=(x﹣40)(﹣3x+240)=﹣3x2+360﹣9600;(3)当w=900时,(x﹣40)(﹣3x+240)=900整理得:x2﹣120x+3500=0∴x1=50,x2=70,∵要使顾客得到实惠,∴x=70舍去∴每箱价格定为50元;(4)由w=(x﹣40)(﹣3x+240)=﹣3x2+360﹣9600得w=﹣3(x﹣60)2+1200w最大=1200(元)∴赢利900元不是销售的最大利润.24.【解答】解:(1)由图1知,AB=,BC=2,∠ABC=90°,AC=5,∵四边形ABCD是以AC为“相似对角线”的四边形,①当∠ACD=90°时,△ACD∽△ABC或△ACD∽△CBA,∴=或=2,∴CD=10或CD=2.5同理:当∠CAD=90°时,AD=2.5或AD=10,(2)证明:∵∠ABC=80°,BD平分∠ABC,∴∠ABD=∠DBC=40°,∴∠A+∠ADB=140°∵∠ADC=140°,∴∠BDC+∠ADB=140°,∴∠A=∠BDC,∴△ABD∽△DBC,∴BD是四边形ABCD的“相似对角线”;(3)如图3,∵FH是四边形EFGH的“相似对角线”,∴△EFH与△HFG相似,∵∠EFH=∠HFG,∴△FEH∽△FHG,∴,∴FH2=FE•FG,过点E作EQ⊥FG于Q,∴EQ=FE•sin60°=FE,∵FG×EQ=2,∴FG×FE=2,∴FG•FE=8,∴FH2=FE•FG=8,∴FH=2.25.【解答】解:(1)∵B(1,0),∴OB=1,∵OC=2OB=2,∴C(﹣2,0),Rt△ABC中,tan∠ABC=2,∴,∴,∴AC=6,∴A(﹣2,6),把A(﹣2,6)和B(1,0)代入y=﹣x2+bx+c得:,解得:,∴抛物线的解析式为:y=﹣x2﹣3x+4;(2)①∵A(﹣2,6),B(1,0),易得AB的解析式为:y=﹣2x+2,设P(x,﹣x2﹣3x+4),则E(x,﹣2x+2),∵PE=DE,∴﹣x2﹣3x+4﹣(﹣2x+2)=(﹣2x+2),x=1(舍)或﹣1,∴P(﹣1,6);②∵M在直线PD上,且P(﹣1,6),设M(﹣1,y),∴AM2=(﹣1+2)2+(y﹣6)2=1+(y﹣6)2,BM2=(1+1)2+y2=4+y2,AB2=(1+2)2+62=45,分三种情况:i)当∠AMB=90°时,有AM2+BM2=AB2,∴1+(y﹣6)2+4+y2=45,解得:y=3,∴M(﹣1,3+)或(﹣1,3﹣);ii)当∠ABM=90°时,有AB2+BM2=AM2,∴45+4+y2=1+(y﹣6)2,y=﹣1,∴M(﹣1,﹣1),iii)当∠BAM=90°时,有AM2+AB2=BM2,∴1+(y﹣6)2+45=4+y2,y=,∴M(﹣1,);综上所述,点M的坐标为:∴M(﹣1,3+)或(﹣1,3﹣)或(﹣1,﹣1)或(﹣1,).。
上海市2019年中考数学真题与模拟题分类 专题18 图形的变化之解答题(2)(39道题)(解析版)(1)

专题18 图形的变化之解答题(2)参考答案与试题解析一.解答题(共39小题)1.(2019•宝山区一模)已知:如图,在△ABC中,AB=AC,点E、F在边BC上,∠EAF=∠B.求证:BF•CE=AB2.【答案】证明:∵∠AEC=∠B+∠BAE=∠EAF+∠BAE=∠BAF,又∵AB=AC,∴∠B=∠C,∴△ABF∽△ECA,∴AB:CE=BF:AC,∴BF•EC=AB•AC=AB2.【点睛】此题考查了相似三角形的判定与性质.注意证得△ABF∽△ECA是解此题的关键.2.(2019•青浦区二模)如图,在△ABC中,∠C=90°,AB的垂直平分线分别交边BC、AB于点D、E,联结AD.(1)如果∠CAD:∠DAB=1:2,求∠CAD的度数;(2)如果AC=1,tan∠B,求∠CAD的正弦值.【答案】解:(1)∵∠CAD:∠DAB=1:2∴∠DAB=2∠CAD在Rt△ABC中,∠CAD+∠DAB+∠DBA=90°∵DE垂直平分AB交边BC、AB于点D、E∴∠DAB=∠DBA∴∠CAD+∠DAB+∠DBA=∠CAD+2∠CAD+2∠CAD=90°解得,∠CAD=18°(2)在Rt△ABC中,AC=1,tan∠B,∴BC=2由勾股定理得,AB∵DE垂直平分AB交边BC、AB于点D、E∴BE=AE∵∠DAE=∠DBE∴在Rt△ADE中tan∠B=tan∠DAE∴DE∴由勾股定理得AD∴cos∠CAD∴sin∠CAD则∠CAD的正弦值为【点睛】本题主要是应用三角函数定义来解直角三角形,关键要运用锐角三角函数的概念及比正弦和余弦的基本关系进行解题.3.(2019•青浦区二模)如图,一座古塔AH的高为33米,AH⊥直线l,某校九年级数学兴趣小组为了测得该古塔塔刹AB的高,在直线l上选取了点D,在D处测得点A的仰角为26.6°,测得点B的仰角为22.8°,求该古塔塔刹AB的高.(精确到0.1米)【参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.5,sin22.8°=0.39,cos22.8°=092,tan22.8°=0.42】【答案】解:∵AH⊥直线l,∴∠AHD=90°,在Rt△ADH中,tan∠ADH,∴DH,在Rt△BDH中,tan∠BDH,∴DH,∴,解得:AB≈5.3m,答:该古塔塔刹AB的高为5.3m.【点睛】本题考查了解直角三角形的应用﹣仰角俯角问题,正确的解直角三角形是解题的关键.4.(2019•浦东新区二模)如图1,一辆吊车工作时的吊臂AB最长为20米,吊臂与水平线的夹角∠ABC最大为70°,旋转中心点B离地面的距离BD为2米.(1)如图2,求这辆吊车工作时点A离地面的最大距离AH(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75);(2)一天,王师傅接到紧急通知,要求将这辆吊车立即开到40千米远的某工地,因此王师傅以每小时比平时快20千米的速度匀速行驶,结果提前20分钟到达,求这次王师傅所开的吊车速度.【答案】解:(1)根据题意,得AB=20,∠ABC=70°,CH=BD=2,在Rt△ACB中,∵∠ACB=90°,∴AC=AB•sin70°=20×0.94=18.8,∴AH=20.8.答:这辆吊车工作时点A离地面的最大距离AH为20.8米;(2)设这次王师傅所开的吊车的速度为每小时x千米,由题意,得,解得,x1=60,x2=﹣40,经检验:x1=60,x2=﹣40都是原方程的解,但x2=﹣40符合题意,舍去,答:这次王师傅所开的吊车的速度为每小时60千米.【点睛】本题是解直角三角形与分式方程应用的综合题,主要考查了解直角三角形,列分式方程解应用题,(1)题的关键是解直角三角形求出AC,(2)小题的关键是找出等量关系列出分式方程.5.(2019•长宁区二模)如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,点D是边AC的中点,CF ⊥BD,垂足为点F,延长CF与边AB交于点E.求:(1)∠ACE的正切值;(2)线段AE的长.【答案】解:(1)∵∠ACB=90°,∴∠ACE+∠BCE=90°,又∵CF⊥BD,∴∠CFB=90°,∴∠BCE+∠CBD=90°,∴∠ACE=∠CBD,∵AC=4且D是AC的中点,∴CD=2,又∵BC=3,在Rt△BCD中,∠BCD=90°.∴tan∠BCD,∴tan∠ACE=tan∠CBD;(2)过点E作EH⊥AC,垂足为点H,在Rt△EHA中,∠EHA=90°,∴tan A,∵BC=3,AC=4,在Rt△ABC中,∠ACB=90°,∴tan A,∴,设EH=3k,AH=4k,∵AE2=EH2+AH2,∴AE=5k,在Rt△CEH中,∠CHE=90°,∴tan∠ECA,∴CH k,∴AC=AH+CH k=4,解得:k,∴AE.【点睛】此题考查了解直角三角形,涉及的知识有:勾股定理,锐角三角函数定义,熟练掌握各自的性质是解本题的关键.6.(2019•闵行区二模)如图,在△ABC中,AB=AC,BC=10,cos∠,点D是边BC的中点,点E在边AC上,且,AD与BE相交于点F.求:(1)边AB的长;(2)的值.【答案】解:(1)∵AB=AC,点D是边BC的中点,∴AD⊥BC,BD=DC BC=5,在Rt△ABD中,cos∠ABC,∴AB=13;(2)过点E作EH∥BC,交AD与点H,∵EH∥BC,,∴,∵BD=CD,∴,∵EH∥BC,∴.【点睛】本题考查的是等腰三角形的性质、解直角三角形、平行线分线段成比例定理,掌握等腰三角形的三线合一、余弦的定义是解题的关键.7.(2019•金山区二模)已知:如图,在Rt△ABC中,∠ACB=90°,D是边AB的中点,CE=CB,CD=5,sin∠.求:(1)BC的长.(2)tan E的值.【答案】解:(1)∵在Rt△ABC中,∠ACB=90,D是边AB的中点;∴CD AB,∵CD=5,∴AB=10,∵sin∠ABC,∴AC=6∴;(2)作EH⊥BC,垂足为H,∴∠EHC=∠EHB=90°∵D是边AB的中点,∴BD=CD AB,∠DCB=∠ABC,∵∠ACB=90°,∴∠EHC=∠ACB,∴△EHC∽△ACB,∴由BC=8,CE=CB得CE=8,∠CBE=∠CEB,∴解得EH,CH,BH=8∴tan∠CBE3,即tan E=3.【点睛】本题考查了解直角三角形,熟练运用直角三角函以及三角形相似是解题的关键.8.(2019•徐汇区二模)如图,已知⊙O的弦AB长为8,延长AB至C,且BC AB,tan C.求:(1)⊙O的半径;(2)点C到直线AO的距离.【答案】解:(1)过O作OD⊥AB于D,则∠ODC=90°,∵OD过O,∴AD=BD,∵AB=8,∴AD=BD=4,∵BC AB,∴BC=4,∴DC=4+4=8,∵tan C,∴OD=4,在Rt△ODA中,由勾股定理得:OA4,即⊙O的半径是4;(2)过C作CE⊥AO于E,则S△AOC,即,解得:CE=6,即点C到直线AO的距离是6.【点睛】本题考查了垂径定理,三角形的面积公式,勾股定理,解直角三角形等知识点,能求出AD、OD的长度是解此题的关键.9.(2019•包头模拟)如图,已知:Rt△ABC中,∠ACB=90°,点E为AB上一点,AC=AE=3,BC=4,过点A作AB的垂线交射线EC于点D,延长BC交AD于点F.(1)求CF的长;(2)求∠D的正切值.【答案】解:(1)∵∠ACB=90°,∴∠ACF=∠ACB=90°,∠B+∠BAC=90°,∵AD⊥AB,∴∠BAC+∠CAF=90°,∴∠B=∠CAF,∴△ABC∽△F AC,∴,即,解得CF;(2)如图,过点C作CH⊥AB于点H,∵AC=3,BC=4,∴AB=5,则CH,∴AH,EH=AE﹣AH,∴tan D=tan∠ECH.【点睛】本题主要考查解直角三角形与相似三角形的判定和性质,解题的关键是添加辅助线构造与∠D 相等的角,并熟练掌握相似三角形的判定与性质、勾股定理等知识点.10.(2019•黄浦区一模)如图,P点是某海域内的一座灯塔的位置,船A停泊在灯塔P的南偏东53°方向(本题参考数据sin53°≈0.80,cos53°的50海里处,船B位于船A的正西方向且与灯塔P相距海里.≈0.60,tan53°≈1.33.)(1)试问船B在灯塔P的什么方向?(2)求两船相距多少海里?(结果保留根号)【答案】解:(1)过P作PC⊥AB交AB于C,在Rt△APC中,∠C=90°,∠APC=53°,AP=50海里,∴PC=AP•cos53°=50×0.60=30海里,在Rt△PBC中,∵PB=20,PC=30,∴cos∠BPC,∴∠BPC=30°,∴船B在灯塔P的南偏东30°的方向上;(2)∵AC=AP•sin53°=50×0.8=40海里,BC PB=10,∴AB=AC﹣BC=(40﹣10)海里,答:两船相距(40﹣10)海里.【点睛】本题考查了解直角三角形的应用,解答本题的关键是理解方位角的定义,能利用三角函数值计算有关线段,难度一般.11.(2019•东阳市模拟)安装在屋顶的太阳能热水器的横截面示意图如图所示.已知集热管AE与支架BF 所在直线相交于水箱横截面⊙O的圆心O,⊙O的半径为0.2米,AO与屋面AB的夹角为32°,与铅垂线OD的夹角为40°,BF⊥AB,垂足为B,OD⊥AD,垂足为D,AB=2米.(1)求支架BF的长;(2)求屋面AB的坡度.(参考数据:tan18°,tan32°,tan40°)【答案】解::(1)∵∠OAC=32°,OB⊥AD,∴tan∠OAB tan32°,∵AB=2m,∴,∴OB=1.24m,∵⊙O的半径为0.2m,∴BF=1.04m;(2)∵∠AOD=40°,OD⊥AD,∴∠OAD=50°,∵∠OAC=32°∴∠CAD=18°,∴AB的坡度为tan18°,【点睛】本题主要考查了解直角三角形的应用,解答本题的关键是求出角的度数,利用三角函数的知识即可求解,难度一般.12.(2019•松江区一模)如图,已知△ABC中,∠ACB=90°,D是边AB的中点,P是边AC上一动点,BP与CD相交于点E.(1)如果BC=6,AC=8,且P为AC的中点,求线段BE的长;(2)联结PD,如果PD⊥AB,且CE=2,ED=3,求cos A的值;(3)联结PD,如果BP2=2CD2,且CE=2,ED=3,求线段PD的长.【答案】解:(1)∵P为AC的中点,AC=8,∴CP=4,∵∠ACB=90°,BC=6,∴BP=2,∵D是边AB的中点,P为AC的中点,∴点E是△ABC的重心,∴BE BP;(2)如图1,过点B作BF∥CA交CD的延长线于点F,∴,∵BD=DA,∴FD=DC,BF=AC,∵CE=2,ED=3,则CD=5,∴EF=8,∴,∴,∴,设CP=k,则P A=3k,∵PD⊥AB,D是边AB的中点,∴P A=PB=3k∴BC=2k,∴AB=2k,∵AC=4k,∴cos A;(3)∵∠ACB=90°,D是边AB的中点,∴CD=BD AB,∵PB2=2CD2,∴BP2=2CD•CD=BD•AB,∵∠PBD=∠ABP,∴△PBD∽△ABP,∴∠BPD=∠A,∵∠A=∠DCA,∴∠DPE=∠DCP,∵∠PDE=∠CDP,∴△DPE∽△DCP,∴PD2=DE•DC,∵DE=3,DC=5,∴PD.【点睛】本题考查了相似三角形的判定和性质,直角三角形的性质,正确的作出辅助线是解题的关键.13.(2019•松江区一模)如图,已知△ABC中,AB=AC=5,cos A.求底边BC的长.【答案】解:过点B作BD⊥AC,垂足为点D,在Rt△ABD中,cos A,∵cos A,AB=5,∴AD=AB•cos A=53,∴BD4,∵AC=AB=5,∴DC=2,∴BC2.【点睛】本题考查了解直角三角形,勾股定理,等腰三角形的性质,正确的作出辅助线是解题的关键.14.(2019•靖江市一模)2018年首届“进博会”期间,上海对周边道路进行限速行驶.道路AB段为监测区,C、D为监测点(如图).已知C、D、B在同一条直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°.(1)求道路AB段的长;(精确到1米)(2)如果AB段限速为60千米/时,一辆车通过AB段的时间为90秒,请判断该车是否超速,并说明理由.(参考数据:sin35°≈0.57358,cos35°≈0.8195,tan35°≈0.7)【答案】解:(1)∵AC⊥BC,∴∠C=90°,∵tan∠ADC2,∵CD=400,∴AC=800,在Rt△ABC中,∵∠ABC=35°,AC=800,∴AB1395 米;(2)∵AB=1395,∴该车的速度55.8km/h<60千米/时,故没有超速.【点睛】此题主要考查了解直角三角形的应用,关键是掌握三角函数定义.15.(2019•松江区一模)某数学社团成员想利用所学的知识测量某广告牌的宽度(图中线段MN的长),直线MN垂直于地面,垂足为点P.在地面A处测得点M的仰角为58°、点N的仰角为45°,在B处测得点M的仰角为31°,AB=5米,且A、B、P三点在一直线上.请根据以上数据求广告牌的宽MN的长.(参考数据:sin58°=0.85,cos58°=0.53,tan58°=1.60,sin31°=0.52,cos31°=0.86,tan31°=0.60.)【答案】解:在Rt△APN中,∠NAP=45°,∴P A=PN,在Rt△APM中,tan∠MAP,设P A=PN=x,∵∠MAP=58°,∴MP=AP•tan∠MAP=1.6x,在Rt△BPM中,tan∠MBP,∵∠MBP=31°,AB=5,∴0.6,∴x=3,∴MN=MP﹣NP=0.6x=1.8(米),答:广告牌的宽MN的长为1.8米.【点睛】此题主要考查了解直角三角形的应用﹣仰角俯角问题,根据已知直角三角形得出AP的长是解题关键.16.(2019•濉溪县二模)如图1是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转,如图2,从侧面看,立柱DE高1.8米,踏板静止时踏板连杆与DE上的线段AB重合,BE长为0.2米,当踏板连杆绕着点A旋转到AC处时,测得∠CAB=37°,此时点C距离地面的高度CF为0.45米,求AB和AD的长(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)【答案】解:过点C作CG⊥AB于G,则四边形CFEG是矩形,∴EG=CF=0.45,设AD=x,∴AE=1.8﹣x,∴AC=AB=AE﹣BE=1.6﹣x,AG=AE﹣CF=1.35﹣x,在Rt△ACG中,∠AGC=90°,∠CAG=37°,cos∠CAG0.8,解得:x=0.35,∴AD=0.35米,AB=1.25米,答:AB和AD的长分别为1.25米,0.35米.【点睛】此题主要考查了解直角三角形的应用,熟练应用锐角三角函数关系是解题关键.17.(2019•随县模拟)如图是某品牌自行车的最新车型实物图和简化图,它在轻量化设计、刹车、车篮和座位上都做了升级.A为后胎中心,经测量车轮半径AD为30cm,中轴轴心C到地面的距离CF为30cm,座位高度最低刻度为155cm,此时车架中立管BC长为54cm,且∠BCA=71°.(参考数据:sin71°≈0.95,cos71°≈0.33,tan71°≈2.88)(1)求车座B到地面的高度(结果精确到1cm);(2)根据经验,当车座B'到地面的距离B'E'为90cm时,身高175cm的人骑车比较舒适,此时车架中立管BC拉长的长度BB'应是多少?(结果精确到1cm)【答案】解:(1)设AC于BE交于H,∵AD⊥l,CF⊥l,HE⊥l,∴AD∥CF∥HE,∵AD=30cm,CF=30cm,∴AD=CF,∴四边形ADFC是平行四边形,∵∠ADF=90°,∴四边形ADFC是矩形,∴HE=AD=30cm,∵BC长为54cm,且∠BCA=71°,∴BH=BC•sin71°=51.3cm,∴BE=BH+EH=BH+AD=51.3+30≈81cm;答:车座B到地面的高度是81cm;(2)如图所示,B'E'=96.8cm,设B'E'与AC交于点H',则有B'H'∥BH,∴△B'H'C∽△BHC,得.即,∴B'C=63cm.故BB'=B'C﹣BC=63﹣54=9(cm).∴车架中立管BC拉长的长度BB'应是9cm.【点睛】本题考查了相似三角形的应用、切线的性质解解直角三角形的应用,解题的难点在于从实际问题中抽象出数学问题,难度较大.18.(2019•徐汇区校级一模)如图,某小区A栋楼在B栋楼的南侧,两楼高度均为90m,楼间距为MN.春分日正午,太阳光线与水平面所成的角为55.7°,A栋楼在B栋楼墙面上的影高为DM;冬至日正午,太阳光线与水平面所成的角为30°,A栋楼在B栋楼墙面上的影高为CM.已知CD=44.5m.(1)求楼间距MN;(2)若B号楼共30层,每层高均为3m,则点C位于第几层?(参考数据:tan30°≈0.58,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)【答案】解:(1)过点P作PE∥MN,交B栋楼与点E,则四边形PEMN为矩形.∴EP=MN由题意知:∠EPD=55.7°∠EPC=30°.在Rt△ECP中,EC=tan∠EPC×EP=tan30°×EP EP≈0.58EP,在Rt△EDP中,ED=tan∠EPD×EP=tan55.7°×EP≈1.47EP,∵CD=ED﹣EC,∴1.47EP﹣0.58EP=44.5∴EP=MN=50(m)答:楼间距MN为50m.(2)∵EC=0.58EP=0.58×50=29(m)∴CM=90﹣29=61(m)∵61÷3≈20.3≈21(层)答:点C位于第21层.【点睛】本题考查了解直角三角形的应用.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.19.(2019•浦东新区一模)“雪龙”号考察船在某海域进行科考活动,在点A处测得小岛C在它的东北方向上,它沿南偏东37°方向航行2海里到达点B处,又测得小岛C在它的北偏东23°方向上(如图所示),求“雪龙”号考察船在点B处与小岛C之间的距离.(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40, 1.4, 1.7)【答案】解:过点A作AM⊥BC,垂足为M.由题意知:AB=2海里,∠NAC=∠CAE=45°,∠SAB=37°,∠DBC=23°,∵∠SAB=37°,DB∥AS,∴∠DBA=37°,∠EAB=90°﹣∠SAB=53°.∴∠ABC=∠ABD+∠DBC=37°+23°=60°,∠CAB=∠EAB+∠CAE=53°+45°=98°.∴∠C=180°﹣∠CAB﹣∠ABC=180°﹣98°﹣60°=22°.在Rt△AMB中,∵AB=2海里,∠ABC=60°,∴BM=1海里,AM海里.在Rt△AMC中,tan C,∴CM 4.25(海里)∴CB=CM+BM=4.25+1=5.25(海里)答:“雪龙”号考察船在点B处与小岛C之间的距离为5.25海里.【点睛】本题主要考查了解直角三角形的应用﹣方向角问题.解决本题的关键是作垂线构造直角三角形,利用直角三角形的边角间关系求解.20.(2019•宝山区一模)地铁10号线某站点出口横截面平面图如图所示,电梯AB的两端分别距顶部9.9米和2.4米,在距电梯起点A端6米的P处,用1.5米的测角仪测得电梯终端B处的仰角为14°,求电梯AB的坡度与长度.参考数据:sin14°≈0.24,tan14°≈0.25,cos14°≈0.97.【答案】解:作BC⊥P A交P A的延长线于点C,作QD∥PC交BC于点D,由题意可得,BC=9.9﹣2.4=7.5米,QP=DC=1.5米,∠BQD=14°,则BD=BC﹣DC=7.5﹣1.5=6米,∵tan∠BQD,∴tan14°,即0.25,解得,ED=18,∴AC=ED=18,∵BC=7.5,∴tan∠BAC,即电梯AB的坡度是5:12,∵BC=7.5,AC=18,∠BCA=90°,∴AB.19.5,即电梯AB的坡度是5:12,长度是19.5米.【点睛】本题考查解直角三角形的应用﹣仰角俯角问题、坡度坡角问题,解答本题的关键是明确题意,利用锐角三角函数和数形结合的思想解答.21.(2019•青浦区一模)如图,在港口A的南偏东37°方向的海面上,有一巡逻艇B,A、B相距20海里,这时在巡逻艇的正北方向及港口A的北偏东67°方向上,有一渔船C发生故障.得知这一情况后,巡逻艇以25海里/小时的速度前往救援,问巡逻艇能否在1小时内到达渔船C处?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin67°,cos67°,tan67°)【答案】解:过点A作AH⊥BC,垂足为点H.由题意,得∠ACH=67°,∠B=37°,AB=20.在Rt△ABH中,∵sin B,∴AH=AB•sin∠B=20×sin37°≈12,∵cos B,∴BH=AB•cos∠B=20×cos37°≈16,在Rt△ACH中,∵tan∠ACH∠,∴CH5,∵BC=BH+CH,∴BC≈16+5=21.∵21÷25<1,所以,巡逻艇能在1小时内到达渔船C处.【点睛】本题考查了解直角三角形的应用,解答本题的关键是将一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.22.(2019•寿光市模拟)某学生为测量一棵大树AH及其树叶部分AB的高度,将测角仪放在F处测得大树顶端A的仰角为30°,放在G处测得大树顶端A的仰角为60°,树叶部分下端B的仰角为45°,已知点F、G与大树底部H共线,点F、G相距15米,测角仪高度为1.5米.求该树的高度AH和树叶部分的高度AB.【答案】解:由题意可得,∠AEC=30°,∠ADC=60°,∠BDC=45°,CH=DG=EF=1.5米,FG=ED=15米,∵∠ADC=∠AED+∠EAD,∴∠EAD=30°,∴∠EAD=∠AED,∴ED=AD,∴AD=15米,∵∠ADC=60°,∠ACD=90°,∴∠DAC=30°,∴DC米,AC米,∴AH=AC+CH米,∵∠BDC=45°,∠BCD=90°,∴∠DBC=45°,∴∠BDC=∠DBC,∴BC=CD米,∴AB=AC﹣BC米,即AH米,AB米.【点睛】本题考查解直角三角形的应用﹣仰角俯角问题,解答本题的关键是明确题意,利用特殊角的三角函数和数形结合的思想解答.23.(2019•静安区一模)计算:【答案】解:原式=3﹣2.【点睛】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.24.(2019•射阳县一模)“滑块铰链”是一种用于连接窗扇和窗框,使窗户能够开启和关闭的连杆式活动链接装置(如图1).图2是“滑块铰链”的平面示意图,滑轨MN安装在窗框上,悬臂DE安装在窗扇上,支点B、C、D始终在一条直线上,已知托臂AC=20厘米,托臂BD=40厘米,支点C,D之间的距离是10厘米,张角∠CAB=60°.(1)求支点D到滑轨MN的距离(精确到1厘米);(2)将滑块A向左侧移动到A′,(在移动过程中,托臂长度不变,即AC=A′C′,BC=BC′)当张角∠C′A'B=45°时,求滑块A向左侧移动的距离(精确到1厘米).(备用数据: 1.41, 1.73,2.45, 2.65)【答案】解:(1)过C作CG⊥AB于G,过D作DH⊥AB于H,∵AC=20,∠CAB=60°,∴AG AC=10,CG AG=10,∵BC=BD﹣CD=30,∵CG⊥AB,DH⊥AB,∴CG∥DH,∴△BCG∽△BDH,∴,∴,∴DH23(厘米);∴支点D到滑轨MN的距离为23厘米;(2)过C′作C′S⊥MN于S,∵A′C′=AC=20,∠C′A′S=45°,∴A′S=C′S=10,∴BS10,∴A′B=1010,∵BG10,∴AB=10+10,∴AA′=A′B﹣AB≈6(厘米),∴滑块A向左侧移动的距离是6厘米.【点睛】本题考查解直角三角形,勾股定理、相似三角形的判定和性质,解题的关键是理解题意,灵活运用所学知识解决问题.25.(2019•闵行区一模)如图,某公园内有一座古塔AB,在塔的北面有一栋建筑物,某日上午9时太阳光线与水平面的夹角为32°,此时塔在建筑物的墙上留下了高3米的影子CD.中午12时太阳光线与地面的夹角为45°,此时塔尖A在地面上的影子E与墙角C的距离为15米(B、E、C在一条直线上),求塔AB的高度.(结果精确到0.01米)参考数据:sin32°≈0.5299,cos32°≈0.8480,tan32°≈0.6249, 1.4142.【答案】解:过点D作DH⊥AB,垂足为点H,由题意,得HB=CD=3,EC=15,HD=BC,∠ABC=∠AHD=90°,∠ADH=32°,设AB=x,则AH=x﹣3,在Rt△ABE中,由∠AEB=45°,得tan∠AEB=tan45°.∴EB=AB=x.∴HD=BC=BE+EC=x+15,在Rt△AHD中,由∠AHD=90°,得tan∠ADH,即得tan32°,解得:x32.99∴塔高AB约为32.99米.【点睛】本题考查的是解直角三角形的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.26.(2019•嘉定区一模)计算:2|1﹣sin60°|.【答案】解:2|1﹣sin60°|=2(1)=2=2=2.【点睛】本题考查了特殊角三角函数值、实数的混合运算;熟记特殊角三角函数值是解题关键.27.(2019•无锡一模)某小区开展了“行车安全,方便居民”的活动,对地下车库作了改进.如图,这小区原地下车库的入口处有斜坡AC长为13米,它的坡度为i=1:2.4,AB⊥BC,为了居民行车安全,现将斜坡的坡角改为13°,即∠ADC=13°(此时点B、C、D在同一直线上).(1)求这个车库的高度AB;(2)求斜坡改进后的起点D与原起点C的距离(结果精确到0.1米).(参考数据:sin13°≈0.225,cos13°≈0.974,tan13°≈0.231,cot13°≈4.331)【答案】解:(1)由题意,得:∠ABC=90°,i=1:2.4,在Rt△ABC中,i,设AB=5x,则BC=12x,∴AB2+BC2=AC2,∴AC=13x,∵AC=13,∴x=1,∴AB=5,答:这个车库的高度AB为5米;(2)由(1)得:BC=12,在Rt△ABD中,cot∠ADC,∵∠ADC=13°,AB=5,∴DB=5cot13°≈21.655(m),∴DC=DB﹣BC=21.655﹣12=9.655≈9.7(米),答:斜坡改进后的起点D与原起点C的距离为9.7米.【点睛】本题考查的是解直角三角形的应用﹣坡度坡角问题,掌握坡度的概念、熟记锐角三角函数的定义是解题的关键.28.(2019•虹口区一模)计算:【答案】解:原式=3+2.【点睛】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.29.(2019•金山区一模)计算:cos245°tan260°﹣cot45°•sin30°.【答案】解:原式=()2()2﹣11+3=2.【点睛】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.30.(2019•长宁区一模)计算:60°.【答案】解:原式()2().【点睛】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.31.(2019•崇明区一模)计算:cos245°cot30°•sin60°.【答案】解:原式=()2.【点睛】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.32.(2019•普陀区一模)如图,小山的一个横断面是梯形BCDE,EB∥DC,其中斜坡DE的坡长为13米,坡度i=1:2.4,小山上有一座铁塔AB,在山坡的坡顶E处测得铁塔顶端A的仰角为45°,在与山坡的坡底D相距5米的F处测得铁塔顶端A的仰角为31°(点F、D、C在一直线上),求铁塔AB的高度.(参考数值:sin31°≈0.52,cos31°≈0.86,tan31°≈0.6)【答案】解:延长AB交DC于G,过E作EH⊥CD于H,则四边形EHGB是矩形,∵斜坡DE的坡长为13米,坡度i=1:2.4,∴设EH=5x,DH=12x,∵EH2+DH2=DE2,∴(5x)2+(12x)2=132,∴x=1,∴EH=5,DH=12,∵EB∥DC,∴∠ABE=∠AGH=90°,∵∠AEB=45°,∴AB=BE,∴HG=AB,∴FG=5+12+AB,AG=AB+5,∵∠F=31°,∴tan F=tan31°0.6,∴AB=13米,答:铁塔AB的高度是13米.【点睛】本题考查了解直角三角形的应用﹣仰角俯角问题,解直角三角形的应用﹣坡度坡角问题,矩形的性质,掌握的作出辅助线是解题的关键.33.(2019•长宁区一模)如图,小明站在江边某瞭望台DE的顶端D处,测得江面上的渔船A的俯角为40°.若瞭望台DE垂直于江面,它的高度为3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,cot40°≈1.19)(1)求瞭望台DE的顶端D到江面AB的距离;(2)求渔船A到迎水坡BC的底端B的距离.(结果保留一位小数)【答案】解:(1)延长DE交AB于点F,过点C作CG⊥AB,垂足为点G,由题意可知CE=GF=2,CG=EF在Rt△BCG中,∠BGC=90°,∴i,设CG=4k,BG=3k,则BC5k=10,∴k=2,∴BG=6,∴CG=EF=8,∵DE=3,∴DF=DE+EF=3+8=11(米),答:瞭望台DE的顶端D到江面AB的距离为11米;(2)由题意得∠A=40°,在Rt△ADF中,∠DF A=90°,∴cot A,∴ 1.19,∴AF≈11×1.19=13.09(m),∴AB=AF﹣BG﹣GF=5.09≈5.1(米),答:渔船A到迎水坡BC的底端B的距离为5.1米.【点睛】此题主要考查了解直角三角形的应用,正确掌握锐角三角函数关系是解题关键.34.(2019•黄浦区一模)计算:2cos245°tan45°.【答案】解:原式=2×()21=21=11=46.【点睛】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.35.(2019•宝山区一模)计算:sin30°tan30°+cos60°cot30°.【答案】解:原式.【点睛】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.36.(2019•金山区一模)如图,已知某水库大坝的横断面是梯形ABCD,坝顶宽AD是6米,坝高24米,背水坡AB的坡度为1:3,迎水坡CD的坡度为1:2.求(1)背水坡AB的长度.(2)坝底BC的长度.【答案】解:(1)分别过点A、D作AM⊥BC,DN⊥BC,垂足分别为点M、N,根据题意,可知AM=DN=24(米),MN=AD=6(米),在Rt△ABM中,∵,∴BM=72(米),∵AB2=AM2+BM2,∴AB24(米),答:背水坡AB的长度为24米;(2)在Rt△DNC中,,∴CN=48(米),∴BC=72+6+48=126(米),答:坝底BC的长度为126米.【点睛】此题考查了坡度坡角问题.此题难度适中,注意构造直角三角形,并借助于解直角三角形的知识求解是关键.37.(2019•普陀区一模)计算:4sin45°+cos230°.【答案】解:原式=4()2=22().【点睛】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键.38.(2019•杨浦区一模)如图,AD是△ABC的中线,tan B,cos C,AC.求:(1)BC的长;(2)∠ADC的正弦值.【答案】解:(1)如图,作AH⊥BC于H.在Rt△ACH中,∵cos C,AC,∴CH=1,AH1,在Rt△ABH中,∵tan B,∴BH=5,∴BC=BH+CH=6.(2)∵BD=CD,∴CD=3,DH=2,AD在Rt△ADH中,sin∠ADH.∴∠ADC的正弦值为.【点睛】本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考中考常考题型.39.(2019•杨浦区三模)如图,已知某船向正东方向航行,在点A处测得某岛C在其北偏东60°方向上,前进8海里处到达点B处,测得岛C在其北偏东30°方向上.已知岛C周围6海里内有一暗礁,问:如果该船继续向东航行,有无触礁危险?请说明你的理由.【答案】解:作CD⊥AB于点D,由题意可知,∠CAB=30°,∠CBD=60°,∴∠ACB=30°,在Rt△BCD中,∵∠BDC=90°,∠CBD=60°,∴∠BCD=30°,∴∠ACB=∠BCD.∴△CDB∽△ADC.∴∵AB=CB=8∴BD=4,AD=12.。
天津市2019年中考数学二模试卷(解析版)

2019年天津市中考数学二模试卷一.选择题(共12小题,满分36分,每小题3分)1.与2的积为1的数是()A.2B.C.﹣2D.2.3tan60°的值为()A.B.C.D.33.下列图形中,中心对称图形有()A.1个B.2个C.3个D.4个4.中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划“一带一路”地区覆盖总人口44亿,这个数用科学记数法表示为()A.44×108B.4.4×109C.4.4×108D.4.4×10105.如图是一个空心圆柱体,其俯视图是()A.B.C.D.6.估计的值在()A.2和3之间B.3和4之间C.4和5之间D.5和6之间7.计算A.0结果是()B.1C.﹣1D.x8.如图,A,B的坐标分别为(2,0),(0,1),将线段AB平移至A1B1,连接BB1,AA1,则四边形ABB1A1的面积为()A.29.对于反比例函数y=B.3C.4,下列说法不正确的是()D.5A.y随x的增大而增大B.它的图象在第二、四象限C.当k=2时,它的图象经过点(5,﹣1)D.它的图象关于原点对称10.要组织一次篮球比赛,赛制为主客场形式(每两队之间都需在主客场各赛一场),计划安排30场比赛,设邀请x个球队参加比赛,根据题意可列方程为()A.x(x﹣1)=30B.x(x+1)=30C.=30D.=3011.如图,将两张长为5,宽为1的矩形纸条交叉,让两个矩形对角线交点重合,且使重叠部分成为一个菱形.当两张纸条垂直时,菱形周长的最小值是4,把一个矩形绕两个矩形重合的对角线交点旋转一定角度,在旋转过程中,得出所有重叠部分为菱形的四边形中,周长的最大值是()A.8B.10C.10.4D.1212.对于抛物线y=﹣(x+2)2+3,下列结论中正确结论的个数为()①抛物线的开口向下;②对称轴是直线x=﹣2;③图象不经过第一象限;④当x>2时,y随x的增大而减小.A.4B.3C.2D.1二.填空题(共6小题,满分18分,每小题3分)13.计算:(﹣a2b)2=.14.计算:=.15.口袋内装有除颜色外完全相同的红球、白球和黑球共10个,从中摸出一球,摸出红球的概率是0.2,摸出白球的概率是0.5,那么黑球的个数是个.16.已知一次函数y=kx+2k+3(k≠0),不论k为何值,该函数的图象都经过点A,则点A的坐标为.17.如图,四边形A BCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于点G,F两点,若M,N分别是DG,CE的中点,则MN的长是.18.如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.(Ⅰ)AB的长度等于(Ⅱ)请你在图中找到一个点P,使得AB是∠P AC的角平分线请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)三.解答题(共7小题,满分66分)19.(8分)解不等式组,并在数轴上表示其解集.20.(8分)某校260名学生参加植树活动,活动结束后学校随机调查了部分学生每人的植树棵数,并绘制成如下的统计图①和统计图②.请根据相关信息,解答下列问题:(Ⅰ)本次接受调查的学生人数为,图①中m的值为;(Ⅱ)求本次调查获取的样本数据的众数和中位数;(Ⅲ)求本次调查获取的样本数据的平均数,并根据样本数据,估计这260名学生共植树多少棵.21.(10分)如图,已知AB是⊙O的直径,PC切⊙O于点P,过A作直线AC⊥PC交⊙O于另一点D,连接P A、PB.(1)求证:AP平分∠CAB;(2)若P是直径AB上方半圆弧上一动点,⊙O的半径为2,则①当弦AP的长是时,以A,O,P,C为顶点的四边形是正方形;②当的长度是时,以A,D,O,P为顶点的四边形是菱形.22.(10分)如图,“人字梯”放在水平地面上,梯子的两边相等(AB=AC),当梯子的一边AB 与梯子两底端的连线BC的夹角α为60°时,BC的长为2米,若将α调整为65°时,求梯子顶端A上升的高度.(参考数据:sin65°≈0.91,cos65°=0.42,tan65°≈2.41,精确到0.1m)=1.73,结果23.(10分)A城有肥料200吨,B城有肥料300吨.现要把这些肥料全部运往C,D两乡,从A 城往C,D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C,D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.设从A城调往C乡肥料x吨(Ⅰ)根据题意,填写下表:调入地数量/吨调出地AB总计C Dx240260(Ⅱ)给出完成此项调运任务最节省费用的调运方案及所需费用,并说明理由.24.(10分)已知直线l经过A(6,0)和B(0,12)两点,且与直线y=x交于点C,点P(m,0)在x轴上运动.(1)求直线l的解析式;(2)过点P作l的平行线交直线y=x于点D,当m=3时,求△PCD的面积;(3)是否存在点△P,使得PCA成为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.25.(10分)已知抛物线y=﹣x2﹣x+2与x轴交于点A,B两点,交y轴于C点,抛物线的对称轴与x轴交于H点,分别以OC、OA为边作矩形AECO.(1)求直线AC的解析式;(2)如图2,P为直线AC上方抛物线上的任意一点,在对称轴上有一动点M,当四边形AOCP 面积最大时,求|PM﹣OM|的值.(3)如图△3,将AOC沿直线AC翻折得△ACD,再将△ACD沿着直线AC平移得△A'C′D'.使得点A′、C'在直线AC上,是否存在这样的点△D′,使得A′ED′为直角三角形?若存在,请求出点D′的坐标;若不存在,请说明理由.2019年天津市中考数学二模试卷参考答案与试题解析一.选择题(共12小题,满分36分,每小题3分)1.与2的积为1的数是()A.2B.C.﹣2D.【分析】根据有理数的乘法分别计算每个数与2的积即可得出答案.【解答】解:A.2×2=4≠1,不符合题意;B.×2=1,符合题意;C.﹣2×2=﹣4≠1,不符合题意;D.﹣×2=﹣1,不符合题意;故选:B.【点评】本题主要考查有理数的乘法,解题的关键是掌握有理数的乘法法则.2.3tan60°的值为()A.B.C.D.3【分析】把tan60的数值代入即可求解.【解答】解:3tan60°=3×=3.故选:D.【点评】本题考查了特殊角的三角函数值,正确记忆特殊角的三角函数值是关键.3.下列图形中,中心对称图形有()A.1个B.2个C.3个D.4个【分析】根据中心对称图形的概念求解.【解答】解:第一个图形是中心对称图形;第二个图形不是中心对称图形;第三个图形是中心对称图形;第四个图形不是中心对称图形.故共2个中心对称图形.故选:B.【点评】此题主要考查了中心对称图形与轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.4.中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划“一带一路”地区覆盖总人口44亿,这个数用科学记数法表示为()A.44×108B.4.4×109C.4.4×108D.4.4×1010【分析】用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,据此判断即可.【解答】解:44亿=4.4×109.故选:B.【点评】此题主要考查了用科学记数法表示较大的数,一般形式为a×10n,其中1≤|a|<10,确定a与n的值是解题的关键.5.如图是一个空心圆柱体,其俯视图是()A.B.C.D.【分析】根据从上边看得到的图形是俯视图,可得答案.【解答】解:该空心圆柱体的俯视图是故选:D.【点评】本题考查了简单几何体的三视图,从上边看得到的图形是俯视图.6.估计的值在()A.2和3之间【分析】直接得出【解答】解:∵B.3和4之间C.4和5之间D.5和6之间的取值范围进而得出答案.,∴故选:C.,【点评】此题主要考查了估算无理数的大小,正确得出的取值范围是解题关键.7.计算A.0结果是()B.1C.﹣1D.x【分析】由于是同分母的分式的加减,直接把分子相减即可求解.【解答】解:==﹣1.故选:C.【点评】此题主要考查了分式的加减,解题时首先判定分母是否相同,然后利用分式加减的法则计算即可求解.8.如图,A,B的坐标分别为(2,0),(0,1),将线段AB平移至A1B1,连接BB1,AA1,则四边形ABB1A1的面积为()A.2B.3C.4D.5【分析】先利用点A平移都A1、B点得到B1得到平移的规律,于是可求出a、b的值,然后利用四边形的面积解答即可.【解答】解:如图:由A,B的坐标分别为(2,0),(0,1),平移后得到(3,b),(a,2),2+1=3,0+1=a,1+1=2,0+1=b,可得:a=1,b=1,所以四边形ABB1A1的面积=,故选:B.【点评】此题主要考查图形的平移及平移特征.在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.9.对于反比例函数y=,下列说法不正确的是()A.y随x的增大而增大B.它的图象在第二、四象限C.当k=2时,它的图象经过点(5,﹣1)D.它的图象关于原点对称【分析】利用反比例函数的性质用排除法解答.【解答】解:A、反比例函数y=,因为﹣k2﹣1<0,根据反比例函数的性质它的图象分布在第二、四象限,在每个象限内,y随x的增大而减小,故本选项错误.B、反比例函数y=,因为﹣k2﹣1<0,根据反比例函数的性质它的图象分布在第二、四象限,故本选项正确;C、当k=2时,y=﹣,把点(5,﹣1)代入反比例函数y=中成立,故本选项正确;D、反比例函数y=中﹣k2﹣1<0根据反比例函数的性质它的图象分布在第一、三象限,是关于原点对称,故本选项正确;故选:A.【点评】本题考查了反比例函数的性质:①、当k>0时,图象分别位于第一、三象限;当k<0时,图象分别位于第二、四象限.②、当k>0时,在同一个象限内,y随x的增大而减小;当k<0时,在同一个象限,y随x的增大而增大.10.要组织一次篮球比赛,赛制为主客场形式(每两队之间都需在主客场各赛一场),计划安排30场比赛,设邀请x个球队参加比赛,根据题意可列方程为()A.x(x﹣1)=30B.x(x+1)=30C.=30D.=30【分析】由于每两队之间都需在主客场各赛一场,即每个队都要与其余队比赛一场.等量关系为:球队的个数×(球队的个数﹣1)=30,把相关数值代入即可.【解答】解:设邀请x个球队参加比赛,根据题意可列方程为:x(x﹣1)=30.故选:A.【点评】本题考查了由实际问题抽象出一元二次方程,解决本题的关键是读懂题意,得到总场数的等量关系.11.如图,将两张长为5,宽为1的矩形纸条交叉,让两个矩形对角线交点重合,且使重叠部分成为一个菱形.当两张纸条垂直时,菱形周长的最小值是4,把一个矩形绕两个矩形重合的对角线交点旋转一定角度,在旋转过程中,得出所有重叠部分为菱形的四边形中,周长的最大值是()A.8B.10C.10.4D.12【分析】由矩形和菱形的性质可得AE=EC,∠B=90°,由勾股定理可求AE的长,即可求四边形AECF的周长.【解答】解:如图所示,此时菱形的周长最大,∵四边形AECF是菱形∴AE=CF=EC=AF,在△Rt ABE中,AE2=AB2+BE2,∴AE2=1+(5﹣AE)2,∴AE=2.6∴菱形AECF的周长=2.6×4=10.4故选:C.【点评】本题考查了旋转的性质,菱形的性质,矩形的性质,勾股定理,熟练运用勾股定理求线段的长度是本题的关键.12.对于抛物线y=﹣(x+2)2+3,下列结论中正确结论的个数为()①抛物线的开口向下;②对称轴是直线x=﹣2;③图象不经过第一象限;④当x>2时,y随x的增大而减小.A.4B.3C.2D.1【分析】根据抛物线的解析式可求得其开口方向、对称轴,则可判断①、②,由解析式可求得抛物线的顶点坐标及与x轴的交点坐标,则可判断③;利用抛物线的对称轴及开口方向可判断④;则可求得答案.【解答】解:∵y=﹣(x+2)2+3,∴抛物线开口向下、对称轴为直线x=﹣2,顶点坐标为(﹣2,3),故①、②都正确;在y=﹣(x+2)2+3中,令y=0可求得x=﹣2+<0,或x=﹣2﹣<0,∴抛物线图象不经过第一象限,故③正确;∵抛物线开口向下,对称轴为x=﹣2,∴当x>﹣2时,y随x的增大而减小,∴当x>2时,y随x的增大而减小,故④正确;综上可知正确的结论有4个,故选:A.【点评】本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x﹣h)2+k中,对称轴为x=h,顶点坐标为(h,k).二.填空题(共6小题,满分18分,每小题3分)13.计算:(﹣a2b)2=a4b2.【分析】直接利用积的乘方运算法则计算得出答案.【解答】解:(﹣a2b)2=a4b2.故答案为:a4b2.【点评】此题主要考查了积的乘方运算,正确掌握运算法则是解题关键.14.计算:=2.【分析】先把分子中的二次根式化为最简二次根式,然后合并后进行二次根式的除法运算.【解答】解:原式===2.故答案为2.【点评】本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,在进行二次根式的乘除运算,然后合并同类二次根式.15.口袋内装有除颜色外完全相同的红球、白球和黑球共10个,从中摸出一球,摸出红球的概率是0.2,摸出白球的概率是0.5,那么黑球的个数是3个.【分析】根据题意可以求得摸得黑球的概率,从而可以求得摸得黑球的个数,本题得以解决.【解答】解:由题意可得,摸出黑球个数是:10×(1﹣0.2﹣0.5)=3个,故答案为:3.【点评】本题考查概率公式,解答本题的关键是明确题意,利用概率的知识解答.16.已知一次函数y=kx+2k+3(k≠0),不论k为何值,该函数的图象都经过点A,则点A的坐标为(﹣2,3).【分析】当k=0时,得出y=3,把y=3,k=1代入解析式得出x即可.【解答】解:∵一次函数y=kx+2k+3(k≠0),不论k为何值,该函数的图象都经过点A,∴当k=0时,y=3,把y=3,k=1代入y=kx+2k+3中,可得:x=﹣2,所以点A的坐标为(﹣2,3),故答案为:(﹣2,3),【点评】此题考查一次函数图象与系数的关系,关键是当k=0时,得出y=3.17.如图,四边形A BCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于点G,F两点,若M,N分别是DG,CE的中点,则MN的长是.【分析】作辅助线,构建矩形MHPK和直角三角形NMH,利用平行线分线段成比例定理或中位线定理得:MK=FK=1,NP=3,PF=2,利用勾股定理可得MN的长.【解答】解:过M作MK⊥CD于K,过N作NP⊥CD于P,过M作MH⊥PN于H,则MK∥EF∥NP,∵∠MKP=∠MHP=∠HPK=90°,∴四边形MHPK是矩形,∴MK=PH,MH=KP,∵NP∥EF,N是EC的中点,∴=1,==∴PF=FC=BE=2,NP=EF=3,同理得:FK=DK=1,∵四边形ABCD为正方形,∴∠BDC=45°,∴△MKD是等腰直角三角形,∴MK=DK=1,NH=NP﹣HP=3﹣1=2,∴MH=2+1=3,在△Rt MNH中,由勾股定理得:MN=故答案为:.=;【点评】本题考查了正方形的性质、等腰直角三角形的性质和判定、直角三角形的性质、勾股定理、平行线的性质等知识;本题的关键是构造直角三角形MNH,根据勾股定理计算.18.如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.(Ⅰ)AB的长度等于2(Ⅱ)请你在图中找到一个点P,使得AB是∠P AC的角平分线请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)【分析】(I)直接利用勾股定理即可得出答案;(II)直接利用网格结合平行线的性质分析得出答案.【解答】解:(I)AB==2;故答案为:2;(II)如图所示:AP即为所求.【点评】此题主要考查了应用设计与作图,正确应用网格是解题关键.三.解答题(共7小题,满分66分)19.(8分)解不等式组,并在数轴上表示其解集.【分析】分别解两个不等式,找出其解集的公共部分即不等式组的解集,再把不等式组的解集在数轴上表示出来即可.【解答】解:解不等式①,得:x<3,解不等式②,得:x>﹣1,则不等式组的解集为﹣1<x<3,将不等式的解集表示在数轴上如下:【点评】本题考查解一元一次不等式组和在数轴上表示不等式的解集,正确掌握解不等式组的方法是解决本题的关键.20.(8分)某校260名学生参加植树活动,活动结束后学校随机调查了部分学生每人的植树棵数,并绘制成如下的统计图①和统计图②.请根据相关信息,解答下列问题:(Ⅰ)本次接受调查的学生人数为20,图①中m的值为20;(Ⅱ)求本次调查获取的样本数据的众数和中位数;(Ⅲ)求本次调查获取的样本数据的平均数,并根据样本数据,估计这260名学生共植树多少棵.【分析】(Ⅰ)由棵数为5的人数除以占的百分比求出调查学生总数,进而确定出m的值即可;(Ⅱ)根据条形统计图中的数据确定出众数与中位数即可;(Ⅲ)求出本次调查获取的样本数据的平均数,并根据样本数据,估计出这260名学生共植树的棵数即可.【解答】解:(Ⅰ)根据题意得:8÷40%=20,m%==20%,即m=20,故答案为:20;20;(Ⅱ)本次调查获取的样本数据的众数和中位数分别为都为5棵;(Ⅲ)根据题意得:4×20%+5×40%+6×30%+7×10%=0.8+2+1.8+0.7=5.3(棵),)则 260×5.3=1378(棵),即估计这 260 名学生共植树 1378 棵.【点评】此题考查了条形统计图,扇形统计图,中位数,以及众数,弄清题中的数据是解本题的关键.21.(10 分)如图,已知 AB 是⊙O 的直径,PC 切⊙O 于点 P ,过 A 作直线 AC ⊥PC 交⊙O 于另一点 D ,连接 P A 、PB .(1)求证:AP 平分∠CAB ;(2)若 P 是直径 AB 上方半圆弧上一动点,⊙O 的半径为 2,则①当弦 AP 的长是 2时,以 A ,O ,P ,C 为顶点的四边形是正方形;②当 的长度是 π 或 π 时,以 A ,D ,O ,P 为顶点的四边形是菱形.【分析】(1)利用切线的性质得 OP ⊥PC ,再证明 AC ∥OP 得到∠1=∠3,加上∠2=∠3,所以∠1=∠2;(2 ①当∠AOP =90°,根据正方形的判定方法得到四边形 A OPC 为正方形,从而得到 AP =2 ;②根据菱形的判定方法,当 AD =AP =OP =OD 时,四边形 ADOP 为菱形,所以△AOP 和△AOD为等边三角形,然后根据弧长公式计算的长度.当 AD =DP =PO =OA 时,四边形 ADPO 为菱形,△AOD 和△DOP 为等边三角形,则∠AOP =120°,根据弧长公式计算的长度.【解答】(1)证明:∵PC 切⊙O 于点 P ,∴OP ⊥PC ,∵AC ⊥PC ,∴AC ∥OP ,∴∠1=∠3,∵OP =OA ,∴∠2=∠3,∴∠1=∠2,∴AP 平分∠CAB ;(2)解:①当∠AOP =90°,四边形 AOPC 为矩形,而 OA =OP ,此时矩形 AOPC 为正方形,AP=OP=2;②当AD=AP=OP=OD时,四边形ADOP为菱形,△AOP和△AOD为等边三角形,则∠AOP=60°,的长度==π.当AD=DP=PO=OA时,四边形ADPO为菱形,△AOD和△DOP为等边三角形,则∠AOP=120°,故答案为2的长度=,π或π.=π.【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了正方形和菱形的判定.22.(10分)如图,“人字梯”放在水平地面上,梯子的两边相等(AB=AC),当梯子的一边AB 与梯子两底端的连线BC的夹角α为60°时,BC的长为2米,若将α调整为65°时,求梯子顶端A上升的高度.(参考数据:sin65°≈0.91,cos65°=0.42,tan65°≈2.41,精确到0.1m)=1.73,结果【分析】先由等腰三角形的一个60°的角,确定梯子AB的长,在直角三角形ABD和A1B1D1中,利用锐角三角函数计算AD、A1D11的长,求差得结论.【解答】解:如图1,由题意可得:∠B=∠C=△60°,则ABC是等边三角形,∴BC=AB=AC=2m,在△Rt ABD中,AD=2sin60°==≈1.73m;如图2,由题意可得:∠B1=∠C1=65°,A1B1=AB=2m,在△Rt A1B1D1中,A1D1=2sin65°≈2×0.91=1.82m;∴A1D1﹣AD=1.82﹣1.73=0.09≈0.1(m)答:梯子顶端A上升的高度约为0.1m.【点评】本题考查了解直角三角形的应用.掌握直角三角形的边角间关系是解决本题的关键.23.(10分)A城有肥料200吨,B城有肥料300吨.现要把这些肥料全部运往C,D两乡,从A 城往C,D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C,D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.设从A城调往C乡肥料x吨(Ⅰ)根据题意,填写下表:调入地数量/吨调出地C DAB总计x240﹣x240200﹣x60+x260(Ⅱ)给出完成此项调运任务最节省费用的调运方案及所需费用,并说明理由.【分析】(Ⅰ)A城运往C乡的肥料量为x吨,则运往D乡的肥料量为(200﹣x)吨;B城运往C、D乡的肥料量分别为(240﹣x)吨和(60+x)吨,由此填表即可;(Ⅱ)设总费用为y元,根据表格列出y与x的关系式,根据一次函数的增减性可求.【解答】解:(Ⅰ)根据题意,填写下表如下:=(Ⅱ)设总费用为 y 元根据题意得:y =20x +25(200﹣x )+15(240﹣x )+24(60+x )=4x+10040(0≤x ≤200)∵k =4>0,∴y 随 x 的增大而增大∴x =0 时,y 最小 10040 答:从 A 城运往 C 乡 0 吨,运往 D 乡 200 吨;从 B 城运往 C 乡 240 吨,运往 D 乡 60 吨,此时总运费最少,总运费最小值是 10040 元.【点评】本题主要考查了一次函数应用,根据已知得出 A 城和 B 城运往各地的肥料吨数是解题关键.24.(10 分)已知直线 l 经过 A (6,0)和 B (0,12)两点,且与直线 y =x 交于点 C ,点 P (m ,0)在 x 轴上运动.(1)求直线 l 的解析式;(2)过点 P 作 l 的平行线交直线 y =x 于点 D ,当 m =3 时,求△PCD 的面积;(3)是否存在点 △P ,使得 PCA 成为等腰三角形?若存在,请直接写出所有符合条件的点 P 的坐标;若不存在,请说明理由.【分析】(1)由 A 、B 两点的坐标,利用待定系数法即可求得直线 l 的解析式;(2)联立直线 l 和直线 y =x ,可求得 C 点坐标,由条件可求得直线 PD 的解析式,同理可求得 D点坐标,则可分别求得△POD 和△POC 的面积,则可求得△PCD 的面积;(3)由 P 、A 、C 的坐标,可分别表示出 P A 、PC 和 AC 的长,由等腰三角形的性质可得到关于m 的方程,则可求得 m 的值,则可求得 P 的坐标.【解答】解:(1)设直线 l 解析式为 y =kx +b ,△S POD = ×3×2=3,S △S PCD =S把 A 、B 两点坐标代入可得∴直线 l 解析式为 y =﹣2x +12; ,解得 ,(2)解方程组 ,可得 ,∴C 点坐标为(4,4),设 PD 解析式为 y =﹣2x +n ,把 P (3,0)代入可得 0=﹣6+n ,解得 n =6,∴直线 PD 解析式为 y =﹣2x +6,解方程组 ,可得 ,∴D 点坐标为(2,2),∴ △POC= ×3×4=6,∴ △POC ﹣ △S POD =6﹣3=3; (3)∵A (6,0),C (4,4),P (m ,0),∴P A 2=(m ﹣6)2=m 2﹣12m +36,PC 2=(m ﹣4)2+42=m 2﹣8m +32,AC 2=(6﹣4)2+42=20,当△P AC 为等腰三角形时,则有 P A =PC 、P A =AC 或 PC =AC 三种情况,①当 P A =PC 时,则 P A 2=PC 2,即 m 2﹣12m +36=m 2﹣8m +32,解得 m =1,此时 P 点坐标为(1,0);②当 P A =AC 时,则 P A 2=AC 2,即 m 2﹣12m +36=20,解得 m =6+2或 m =6﹣2 ,此时 P 点坐标为(6+2,0)或(6﹣2 ,0);③当 PC =AC 时,则 PC 2=AC 2,即 m 2﹣8m +32=20,解得 m =2 或 m =6,当 m =6 时,P 与 A重合,舍去,此时 P 点坐标为(2,0);综上可知存在满足条件的点 P ,其坐标为(1,0)或(6+2,0)或(6﹣2 ,0)或(2,0).【点评】本题为一次函数的综合应用,涉及待定系数法、函数图象的交点、三角形的面积、等腰三角形的性质、勾股定理、分类讨论思想及方程思想等知识.在(1)中注意待定系数法的应用,在(2)中求得 C 、D 的坐标是解题的关键,在(3)中用 P 点坐标分别表示出 P A 、PC 的长是解题的关键,注意分情况讨论.本题考查知识点较多,综合性较强,难度适中.25.(10 分)已知抛物线 y =﹣ x 2﹣ x +2 与 x 轴交于点 A ,B 两点,交 y 轴于 C 点,抛物线的对称轴与 x 轴交于 H 点,分别以 OC 、OA 为边作矩形 AECO .(1)求直线 AC 的解析式;(2)如图 2,P 为直线 AC 上方抛物线上的任意一点,在对称轴上有一动点 M ,当四边形 AOCP面积最大时,求|PM﹣OM|的值.(3)如图△3,将AOC沿直线AC翻折得△ACD,再将△ACD沿着直线AC平移得△A'C′D'.使得点A′、C'在直线AC上,是否存在这样的点△D′,使得A′ED′为直角三角形?若存在,请求出点D′的坐标;若不存在,请说明理由.【分析】(1)令x=0,则y=2,令y=0,则x=2或﹣6,求出点A、B、C坐标,即可求解;(2)连接OP′交对称轴于点M,此时,|PM﹣OM|有最大值,即可求解;(3)存在;分A′D′⊥A′E、A′D′⊥ED′、ED′⊥A′E,三种情况求解即可.【解答】解:(1)令x=0,则y=2,令y=0,则x=2或﹣6,则:点A、B、C坐标分别为(﹣6,0)、(2,0)、(0,2),函数对称轴为:x=﹣2,顶点坐标为(﹣2,),C点坐标为(0,2),则过点C的直线表达式为:y=kx+2,将点A坐标代入上式,解得:k=,则:直线AC的表达式为:y=x+2;(2)如图,过点P作x轴的垂线交AC于点H,四边形AOCP面积=△AOC的面积+△ACP的面积,四边形AOCP面积最大时,只需要△ACP的面积最大即可,|设:点P坐标为(m,﹣m2﹣m+2),则点G坐标为(m,m+2),△S ACP=PG•OA=•(﹣m2﹣m+2﹣m﹣2)•6=﹣m2﹣3m,当m=﹣3时,上式取得最大值,则点P坐标为(﹣3,),在抛物线上取点P关于对称轴的对称点P′(﹣1,),连接OP′交对称轴于点M,此时,PM ﹣OM|有最大值,直线OP′的表达式为:y=﹣x,当x=﹣2时,y=5,即:点M坐标为(﹣2,5),∴|PM﹣OM|=OP′=(3)存在;;∵AE=CD,∠AEC=∠ADC=90°,∠EMA=∠DMC,∴△EAM≌△DCM(AAS),∴EM=DM,AM=MC,设:EM=a,则:MC=6﹣a,在△Rt DCM中,由勾股定理得:MC2=DC2+MD2,即:(6﹣a)2=22+a2,解得:a=,则:MC=,过点D作x轴的垂线交x轴于点N,交EC于点P,在△Rt DMC中,DP•MC=MD•DC,即:DP×则:DP=,HC==,=×2,即:点D的坐标为(﹣,);设:△ACD沿着直线AC平移了m个单位,则:点A′坐标(﹣6+,),点D′坐标为(﹣+,+),而点E坐标为(﹣6,2),则:直线A′D′表达式的k值为:,则:直线A′E表达式的k值为:,则:直线E′D表达式的k值为:,根据两条直线垂直,其表达式中k值的乘值为﹣1,可知:当A′D′⊥A′E时,=﹣,解得:m=,D'坐标为:(0,4),当A′D′⊥ED′时,=﹣,解得:m=﹣,D'坐标为:(﹣,)同理,当ED′⊥A′E时,点D的坐标为:(﹣0.6,3.8),则:D'标为:(0,4)或(﹣,)或(﹣0.6,3.8).【点评】本题考查的是二次函数知识综合运用,涉及到一次函数、图形平移、解直角三角形等知识,其中(3)中图形是本题难点,其核心是确定平移后A′、D′的坐标,本题难度较大.。
2019上海数学初三二模第18题汇编
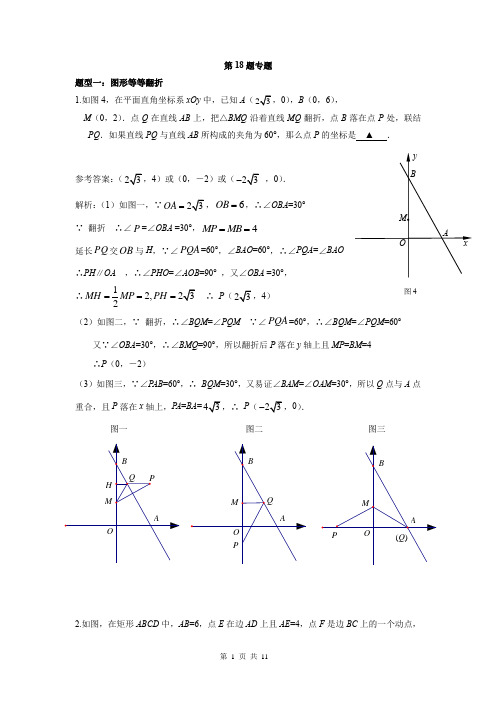
第18题专题题型一:图形等等翻折1.如图4,在平面直角坐标系xOy 中,已知A (23,0),B (0,6),M (0,2).点Q 在直线AB 上,把△BMQ 沿着直线MQ 翻折,点B 落在点P 处,联结PQ .如果直线PQ 与直线AB 所构成的夹角为60°,那么点P 的坐标是 ▲ .参考答案:(23,4)或(0,-2)或(23- ,0). 解析:(1)如图一,∵23OA =,6OB =,∴∠OBA =30° ∵ 翻折 ∴∠P =∠OBA =30°,4MP MB ==延长PQ 交OB 与H ,∵∠PQA =60°,∠BAO =60°,∴∠PQA =∠BAO ∴PH ∥OA ,∴∠PHO =∠AOB =90° ,又∠OBA =30°, ∴12,232MH MP PH === ∴ P (23,4) (2)如图二,∵ 翻折,∴∠BQM =∠PQM ∵∠PQA =60°,∴∠BQM =∠PQM =60°又∵∠OBA =30°,∴∠BMQ =90°,所以翻折后P 落在y 轴上且MP =BM =4 ∴P (0,-2)(3)如图三,∵∠P AB =60°,∴ BQM =30°,又易证∠BAM =∠OAM =30°,所以Q 点与A 点重合,且P 落在x 轴上,P A =BA =43,∴ P (23-,0).图一 图二 图三2.如图,在矩形ABCD 中,AB =6,点E 在边AD 上且AE =4,点F 是边BC 上的一个动点,yQ 图4ABOM xQ﹒PQ ABO MP(Q )ABOMH PQMOB A将四边形ABFE 沿EF 翻折,A 、B 的对应点A 1、B 1与点C 在同一直线上,A 1B 1与边AD 交于点G ,如果DG =3,那么BF 的长为 ▲ .参考答案:658-解析:易证1EGA CGD △∽△,∴11AG A E GD DC=,∴12A E =,∴ EG =25 ∴BC =AD =725+,设BF =x ,则1,725FB x FC x ==+- 易证1FCB CGD △∽△,∴1FB FCDC GC=,GC =35,∴1658FB =-,即658FB =-3.如图,在△ABC 中,AB = AC = 5,25BC = ,D 为边AC 上一点(点D 与点A 、C 不重合).将△ABC 沿直线BD 翻折,使点A 落在点E 处,联结CE .如果CE // AB ,那么AD ︰CD =_____参考答案:5:6解析:过A 作AH ⊥BC ,∵AC =AB ,∴ BH=5,过C 作CF ⊥AB ,5cos 5BF BH ABC BC AB ===∠,∴ BF =2,AF =3,C F=4,∵CE // AB ,∴四边形ABCE 为梯形,又因为翻折,所以AB =BE ,所以BE =AC ,所以梯形ABCE 为等腰梯形,所以OA =OB ,C第18题图ABDEABC(第18题图)OE =OC ,过O 作OP ⊥AB ,所以AP =52,因为OP ∥CF ,所以AO AP AC AF =,所以AO =256,OC =OE =56,因为CE // AB ,∴ EC COAB AO=,∴ EC =1,因为翻折,所以DAB DEB =∠∠,又因为CE // AB ,所以DAB ECD =∠∠,所以DEB ECD =∠∠,又∠EDC =∠EDC ,所以△DEO ∽△DCO ,所以56ED EO DC EC ==,又ED =AD ,所以AD :DC =5:6题型二:图形等等旋转4.如图4,在ABC △中,已知AB AC =,30BAC ∠=︒,将ABC △绕着点A 逆时针旋转30︒,记点C 的对应点为点D ,AD 、BC 的延长线相交于点E .如果线段DE 的长为2,那么边AB 的长为 . 参考答案.62+解析:如图,过点D 作DH ⊥CE ,∵AB AC =,30BAC ∠=︒∴ ∠ABC =∠ACB =75°,∵ 旋转,∴ ∠CAD =30°,∠ACD =∠ADC =75° ∴∠DCH =30°,∠DEC =45°,∵DE =2,∴ DH =HE =1,∴ CD =2,CH =3 ∴ CE =3+1,∵ ∠E =∠E ,∠DCH =∠CAD =30°,∴ △CDE ∽△ACE ∴CD DEAC CE=,∴ AC =62+,∴ AB =62+BOEDABCH5.如图,在Rt △ABC 中,∠ACB =90°,AB =6,cosB =23,先将△ACB 绕着顶点C 顺时针旋转90°,然后再将旋转后的三角形进行放大或缩小得到△A'CB'(点A'、C 、B'的对应点分别是点A 、C 、B ),联结A'A 、B'B ,如果△AA'B 和△AA'B'相似,那么A C '的长是 ▲ .参考答案:355-解析:∵∠ACB =90°,AB =6,cosB =23,∴ BC =4,AC =25,∵因为旋转,∴ 1=ABC B ∠∠又∵△AA'B 和△AA'B'相似,∴11BAA CAA =∠∠,过B 作BD ∥AC ,延长1AA 交BD 于点D ,则∠D =1CAA ∠,∴∠D =1BAA ∠,∴ BD =AB =6,因为BD ∥AC ,所以11BA BD AC A C= 即64=25ACAC-,∴AC =355-6.如图3,在ABC ∆中,5==AC AB ,8=BC ,将ABC ∆绕着点C 旋转,点B A 、的对应点分别是点'A 、'B ,若点'B 恰好在线段'AA 的延长线上,则'AA 的长等于 ▲ .参考答案:145解析:过A 作AE ⊥BC ,所以BE =4,AE =3,因为旋转,所以'8,'5B C BC AC A C ===='B B=∠∠,过C作'CH AA ⊥,3sin 'sin '5CH B B CB ===,所以245CH =,所以2275AH AC CH =-=,所以'145AA =ACBB C D B 1A 1A图3BCH A'B'ABCE7.如图3,在ABC ∆中,90ACB ∠=︒,3sin 5B =,将ABC ∆绕顶点C 顺时针旋转,得到11A B C ∆ ,点A 、B 分别与点1A 、1B 对应,边11A B 分别交边AB 、BC 于点D 、E ,如果点E 是边11A B 的中点,那么1BDB C= ▲ . 【参考答案】35.因为在ABC ∆中,90ACB ∠=︒,3sin 5B =, 所以设3AC x =,则5AB x =;4BC x =因为11A B C ∆由将ABC ∆绕顶点C 顺时针旋转得到, 所以1190ACB ∠=︒,1B B ∠=∠ 又因为点E 是边11A B 的中点, 所以1111115222A EB E CE A B AB x ===== 所以11CEB B ∠=∠;所以1CEB B ∠=∠;所以1//BD B C ;所以11BDB B ∠=∠; 所以1BDB B ∠=∠ 所以542DE BE x x ==-所以15432552x xBD BEB C CEx -===.8.如图,已知Rt △ABC 中,∠ACB=90°,AC =8,BC =6.将△ABC 绕点B 旋转得到△DBE ,点A 的对应点D 落在射线BC 上.直线AC 交DE 于点F ,那么CF 的长为________.【参考答案】3.根据题意得:22228610BD AB AC BC ==+=+=;1064DC DB BC \=-=-=Q 旋转,所以=A D 行,又Q 90ACBDCF ??o\ ACB V ∽DCF V \43DC AC CF BC ==, 3CF \=.9.如图5,矩形ABCD ,AD =a ,将矩形ABCD 绕着顶点B 顺时针旋转,得到矩形EBGF ,顶点A 、D 、C 分别与点E 、F 、G 对应(点D 与点F 不重合).如果点D 、E 、F 在同一条直线上,那么线段DF 的长是 ▲ .(用含a 的代数式表示)【参考答案】2a .根据题意,由旋转得到90BEF DAB ??o矩形对角线BD BF = 所以BDF V 是一个等腰三角形所以DE EF a ==(等腰三角形三线合一) 所以2DF a =.10.如图7,AD 是△的中线,点E 在边AB 上,且DE ⊥AD ,将△BDE 绕着点D 旋转,使得点B 与点C 重合,点E 落在点F 处,联结AF 交BC 于点G ,如果52AE BE ,那么GFAB的值等于 ▲ .【参考答案】1063.ABC E 图7联结AF ;因为CFD △由BDE ∆绕点D 旋转得到 所以BDE BDE ∆∆≌ 所以DE FD =;B DCF ∠=∠;27CF AB = 所以//AB CF所以27FG AG =;所以29FG AF =在ADE ∆和ADF ∆中90AD AD ADE ADF DE FD o=⎧⎪∠=∠=⎨⎪=⎩;得到ADE ADF ∆∆≌ 所以AE AF =设5AE x =;则5AF x =;7AB x =;109xFG = 所以1063FG AB =.题型三:其他题型:11.我们把满足某种条件的所有点组成的图形,叫做符合这个条件的点的轨迹.如图6,在Rt △ABC 中,∠C =90°,AC =8,BC =12,动点P 从点A 开始沿射线AC 方向以1个单位/秒的速度向点C 运动,动点Q 从点C 开始沿射线CB 方向以2个单位/秒的速度向点B 运动,P 、Q 两点分别从点A 、C 同时出发,当其中一点到达端点时,另一点也随之停止运动,在整个运动过程中,线段PQ 的中点M 运动的轨迹长为 .参考答案:35CBAP QM 图6G E DB解析:当t =0时,M 在AC 中点处,即1M 处,当t=6时,Q 运动到B ,此时P 在线段AC 上,且AP=6,CP=2,M 在BP 中点处,即2M 处,过2M 作2M H AC ⊥,交AC 于H ,则26M H =,HP=1,∴ 1HM =3,∴221221()()35M M M H HM =+=,即轨迹长为3512.如图3,点M 的坐标为)2,3(,点P 从原点O 出发,以每秒1个单位的速度沿y 轴向上移动,同时过点P 的直线l 也随之上下平移,且直线l 与直线x y -=平行,如果点M 关于直线l 的对称点落在坐标轴上,如果点P 的移动时间为t 秒,那么t 的值可以是 .参考答案:3或2(任意一个都可以)解析:设M 关于直线l 的对称点为点N ,直线l 与x 轴交于点P ,与y 轴交于点F ,易知45?FPO PFO ==∠∠(1)当对称点落在x 轴上时,直线l 垂直平分线段MN ,所以45?MNP PN PM ==∠, ∴45?NMP =∠,∴=90?NPM ∠,∴ P (3,0),∴ OF =OP =3,所以t=3(2)当对称点落在y 轴上时,直线l 垂直平分线段MN ,所以45?,FN=FM MNF =∠ ∴45?NMF =∠,∴ =90?NFM ∠,∴ F (0,2),所以OF =2,所以t =213.如图,在矩形ABCD 中,过点A 的圆O 交边AB 于点E ,交边AD 于点F ,已知AD =5,AE =2,AF =4.如果以点D 为圆心,r 为半径的圆D 与圆O 有两个公共点,那么r 的取值范围是 ▲ .参考答案:105105r -<<+解析:过O 作OH ⊥AD ,OG ⊥AB ,∴AH =2,AG =1,易知四边形AGOH 为矩形,所以OH =1,所以AO =5,易知HD =3,所以OD =10,连接OD 并延长DO ,交圆O 于点P ,Q ,所以PD=105-,DQ=10+5,所以105105r -<<+OFPl N MOPFl NMABCDE F (第18题图)14.定义:如果P是圆O所在平面内的一点,Q是射线OP上一点,且线段OP、OQ的比例中项等于圆O的半径,那么我们称点P与点Q为这个圆的一对反演点。
2019年深圳二模语文答案详解

2019年深圳市高三年级第二次调研考试语文答案(一)论述类文本阅读(本题共3小题,9分)1.答案:B。
解析:A项错误,“荒腔走板的解读”虽然只是“随之出现”,但并不是因“提倡多元解读”而造成的,真正的原因是后文所说的“未能正确理解西方‘接受美学’中的‘读者中心论’”。
B项正确,原文提到“读者接受有其时代局限性和主观任意性”“单个读者的接受理解还不能等于作品的全部”,又提到“只有代代相承的接受链才有望接近于作品本身”,综合以上可知。
C项错误,原文表述是“召唤读者去言明,并希望读者完全按照文本召唤”。
D项错误,“以便从中挑选正确的理解”并非作者本意,“多元理解”反对“唯一标准答案”,更好理解作品则需要通过“代代相承”的接受链、以及多种理解的互补来实现,这些都等同于“挑选正确的理解”。
2.答案:D。
解析:A项正确。
文章以真正理解作品为出发点,这是其“写作动机”,并指出了多元解读中“混淆事物根本属性与它的附属功能”“读者决定论”等误区,也阐述了“避免纯主观、任意理解的心理主义陷阱”“多元解读与文本制约是同时发生”等原则。
B项正确,文章先从正面说明接受美学“没有接受者的积极参与,一部文学作品的历史生命是不可想象的”,接着将“斧头—石头”的关系与“作品—废纸”的关系进行类比,批驳了那些片面夸大读者作用的观点。
C项正确,由原文“作品的‘召唤结构’的‘空白’,既为阅读提供了想象的自由,又为阅读提供了基本的限制。
正如鲁迅所言……”可推断。
D项错误,原文“历史上错误的‘读者决定论’不止出现过一次。
李白、杜甫的诗歌曾经不入流……然而,一切‘假哈姆雷特’都动摇不了经典文本的地位”。
引用李、杜诗歌的例子,意在为了说明“读者决定论”之类的错误在历史上并不少见,读者虽然无法起到决定作用,但根据前文,读者的主观理解对作品阐释有着重要作用,对经典文本的地位也必然产生影响,没有读者的推崇也就不存在经典文本的地位。
3.答案:C。
解析:A项正确,根据原文“多元解读与文本制约是同时发生的”,“作品的‘召唤结构’的‘空白’,既为阅读提供了想象的自由,又为阅读提供了基本的限制”可以推断。
2019年上海初三数学二模18题专题讲解

杨浦区18.如图,在矩形ABCD中,过点A的圆O交边AB于点E,交边AD于点F,已知AD=5,AE=2,AF=4.如果以点D为圆心,r为半径的圆D 与圆O有两个公共点,那么r的取值范围是______.18.【答案】√10-√5<r<√10+√5【解析】解:如图,连接EF,∵四边形ABCD是矩形,∴∠BAC=90°,则EF是⊙O的直径,取EF的中点O,连接OD,作OG⊥AF,则点G是AF的中点,∴GF=AF=2,∴OG是△AEF的中位数,∴OG=AE=1,∴OF==,OD==,∵圆D与圆O有两个公共点,∴-<r<+,黄浦区如图,在△ABC中,∠ACB=90°,sin B=35,将△ABC绕顶点C顺时针旋转,得到△A1B1C,点A、B分别与点A1、B1对应,边A1B1分别交边AB、BC于点D、E,如果点E是边A1B1的中点,那么BDB1C=______.18.【答案】351.解:∵∠ACB=90°,sinB==,∴设AC=3x,AB=5x,∴BC==4x,∵将△ABC绕顶点C顺时针旋转,得到△A1B1C,∴CB1=BC=4x,A1B1=5x,∠ACB=∠A1CB1,∵点E是A1B1的中点,∴CE=A1B1=2.5x=B1E,∴BE=BC-CE=1.5x,∵∠B=∠B1,∠CEB1=∠BED∴△CEB1∽△DEB∴=18.如图,在Rt△ABC中,∠ACB=90°,AB=6,cos B=,先将△ACB绕着顶点C顺时针旋转90°,然后再将旋转后的三角形进行放大或缩小得到△A′CB′(点A′、C、B′的对应点分别是点A、C、B),连接A′A、B′B,如果△AA′B和△AA′B′相似,那么A′C的长是3﹣5 .【解答】解:由题意当点A′在线段BC上且AA′平分∠BAC时,△AA′B和△AA′B′相似,作A′H⊥AB于H.在Rt△ABC中,∵cos B==,AB=6,∴BC=4,AC==2,∵∠A′AH=∠A′AC,∠AHA′=∠ACA′=90°,AA′=AA′,∴△AA′H≌△AA′C(AAS),∴A′C=A′H,AC=AH=2,设A′C=A′H=x,在Rt△A′BH中,(4﹣x)2=x2+(6﹣2)2,∴x=3﹣5,∴A′C=3﹣518.如图,在△ABC中,AB = AC = 5,25BC ,D为边AC上一点(点D与点A、C不重合).将△ABC沿直线BD翻折,使点A落在点E处,联结CE.如果CE // AB,那么AD︰CD = ▲.普陀区18.如图7,AD 是△的中线,点E 在边AB 上,且DE ⊥AD ,将△BDE 绕着点D 旋转,使得点B 与点C 重合,点E 落在点F 处,联结AF 交BC 于点G ,如果52AE BE ,那么GFAB 的值等于 ▲ .ABC18.如图,在△ABC中,AB=AC=5,BC=8,将△ABC绕着点C 旋转,点A、B的对应点分别是点A'、B',若点B'恰好在线段AA'的延长线上,则AA'的长等于______.18.【答案】145【解析】解:如图,过点C作CF⊥AA'于点F,∵旋转∴AC=A'C=5,AB=A'B'=5,BC=B'C=8∵CF⊥AA',∴AF=A'F在Rt△AFC中,AC2=AF2+CF2,在Rt△CFB'中,B'C2=B'F2+CF2,∴B'C2-AC2=B'F2-AF2,∴64-25=(8+AF)2-AF2,∴AF=∴AA'=18 .如图4,在平面直角坐标系x O yA ( 23 ,0 ),点Q 在直线AB 上,把BMQ 沿着直线MQ 翻折,点B 落在点P 处,联结PQ,如果直线PQ 与直线A B 所构成的夹角为60°,那么点P 的坐标是奉贤区金山区18.一个正多边形的对称轴共有10条,且该正多边形的半径等于4,那么该正多边形的边长等于______.崇明区18.如图,在△ABC中,已知AB=AC,∠BAC=30°,将△ABC绕着点A逆时针旋转30°,记点C的对应点为点D,AD、BC的延长线相交于点E.如果线段DE的长为√2,那么边AB的长为______.18.【答案】√6+√2【解析】解:如图,作DF⊥BE于F,CH⊥AD于H,∵将△ABC绕着点A逆时针旋转30°,记点C的对应点为点D,AD、BC的延长线相交于点E,∴AD=AC=AB,∠CAD=∠BAC=30°,∴∠ACB=∠ACD=∠ADC=75°,∴∠DCE=30°,∠E=45°,∵DE=,∴DF=EF=1,CF=,∴CE=+1,∴CH=HE=,AH=,∴AD=AH+HE-DE=,∴AB=.松江区18.如图,已知Rt△ABC中,∠ACB=90°,AC=8,BC=6.将△ABC绕点B 旋转得到△DBE,点A的对应点D落在射线BC上.直线AC交DE于点F,那么CF的长为______.18.【答案】3【解析】解:∵如图,已知Rt△ABC中,∠ACB=90°,AC=8,BC=6.∴AB=,tan∠A=,∵将△ABC绕点B旋转得到△DBE,点A的对应点D落在射线BC上,直线AC交DE于点F,∴BD=AB=10,∠D=∠A,∴CD=BD-BC=10-6=4,在Rt△FCD中,∠DCF=90°,∴tanD=,即,∴CF=3.嘉定宝山区18.如图,点M的坐标为(3,2),动点P从点O出发,沿y轴以每秒1个单位的速度向上移动,且过点P的直线l:y=-x+b也随之移动,若点M关于l的对称点落在坐标轴上,设点P的移动时间为t,则t的值是______.18.【答案】2或3【解析】解:如图,过点M作MF⊥直线l,交y轴于点F,交x轴于点E,则点E、F为点M在坐标轴上的对称点,过点M作MD⊥x轴于点D,则OD=3,MD=2.由直线l:y=-x+b可知∠PDO=∠OPD=45°,∴∠MED=∠OEF=45°,则△MDE与△OEF均为等腰直角三角形,∴DE=MD=2,OE=OF=1,∴E(1,0),F(0,-1).∵M(3,2),F(0,-1),∴线段MF中点坐标为(,).直线y=-x+b过点(,),则=-+b,解得:b=2,∴t=2.∵M(3,2),E(1,0),∴线段ME中点坐标为(2,1).直线y=-x+b过点(2,1),则1=-2+b,解得:b=3,∴t=3.故点M关于l的对称点,当t=2时,落在y轴上,当t=3时,落在x轴上.虹口区青浦区18.(3分)我们把满足某种条件的所有点组成的图形,叫做符合这个条件的点的轨迹,如图,在Rt△ABC中,∠C=90°,AC=8,BC=12,动点P从点A开始沿射线AC方向以1个单位秒的速度向点C运动,动点Q从点C开始沿射线CB方向以2个单位/秒的速度向点运动,P、Q两点分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,在整个运动过程中,线段PQ的中点M运动的轨迹长为.【解答】解:以C为原点,以AC所在直线为x轴,建立平面直角坐标系:依题意,可知0≤t≤6,当t=0时,点M1的坐标为(4,0);当t=6时,点M2的坐标为(1,6),设直线M1M2的解析式为y=kx+b,∴,解得:,∴直线M1M2的解析式为y=﹣2x+8.设动点运动的时间为t秒,则有点Q(0,2t),P(8﹣t,0),∴在运动过程中,线段PQ中点M3的坐标为(,t),把x=代入y=﹣2x+8,得y=﹣2×+8=t,∴点M3在M1M2直线上,过点M2作M2N⊥x轴于点N,则M2N=6,M1N=3,∴M1M2=3,∴线段PQ中点M所经过的路径长为3个单位长度.浦东新区解。
2019年中考数学二模试卷(含解析)

2019年中考数学二模试卷一、选择题(本大题共8小题,每小题3分,共24分,在每小题所给出的四个选项中,只有一个选项是正确的,请将正确选项的字母代号填涂在答题卡相应位置上)1.(3分)下列四个数,表示无理数的是()A.sin30°B.πC.D.2.(3分)下列四种标志图案中,既是轴对称图形又是中心对称图形的是()A.B.C.D.3.(3分)下列各式正确的是()A.6a2﹣5a2=a2B.(2a)2=2a2C.﹣2(a﹣1)=﹣2a+1D.(a+b)2=a2+b24.(3分)如图所示,直线a、b、c、d的位置如图所示,若∠1=125°,∠2=125°,∠3=135°,则∠4的度数为()A.45°B.55°C.60°D.65°5.(3分)某工艺品厂草编车间共有16名工人,为了了解每个工人的日均生产能力,随机调查了某天每个工人的生产件数,获得数据如下表:则这一天16名工人生产件数的众数和中位数分别是()A.5件、11件B.12件、11件C.11件、12件D.15件、14件6.(3分)如图,▱ABCD的周长为22m,对角线AC、BD交于点O,过点O与AC垂直的直线交边AD于点E,则△CDE的周长为()A.8cm B.9cm C.10cm D.11cm7.(3分)一个圆锥的主视图是边长为6cm的正三角形,则这个圆锥的侧面积等于()A.36 πcm2B.24πcm2C.18πcm2D.12 πcm28.(3分)如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF ⊥AB交AC于点G,反比例函数y=(x>0)经过线段DC的中点E,若BD=4,则AG的长为()A.B.+2C.2+1D.+1二、填空题(本大题共有8小题,每小题3分,共24分不需写出解答过程,请将答案直接写在答题卡相应位置上)9.(3分)要使有意义,则实数x的取值范围是.10.(3分)若x=﹣1是关于x的方程2x+3m﹣7=0的解,则m的值为.11.(3分)青盐铁路(青岛一盐城),是我国“八纵八横”高速铁路网中第一纵“沿海通道”的一部分,全长428.752千米.数据428.752千米用科学记数法表示为米.12.(3分)在一个不透明的盒子中装有红、白两种除颜色外完全相同的球,其中有a个白球和3个红球,若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在20%左右,则a的值约为.13.(3分)边长为a、b的长方形,它的周长为14,面积为10,则a2b+ab2的值为.14.(3分)如图,CE、BF分别是△ABC的高线,连接EF,EF=6,BC=10,D、G分别是EF、BC的中点,则DG的长为.15.(3分)如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=1.将边BA绕点B顺时针旋转90°得线段BD,再将边CA绕点C顺时针旋转90°得线段CE,连接DE,则图中阴影部分的面积是.16.(3分)如图,已知△ABC中,∠BAC=120°,AB=AC=2.D为BC边一点,且BD:DC=1:2.以D为一个点作等边△DEF,且DE=DC连接AE,将等边△DEF绕点D旋转一周,在整个旋转过程中,当AE取得最大值时AF的长为.三、解答题(本大题共有11小题,共102分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)17.(6分)解不等式,并把它的解集在数轴上表示出来:18.(6分)先化简,再求值:(x﹣3)2+2(x﹣2)(x+7)﹣(x+2)(x﹣2),其中x2+2x﹣3=0.19.(8分)已知关于x方程x2﹣6x+m+4=0有两个实数根x1,x2(1)求m的取值范围;(2)若x1=2x2,求m的值.20.(8分)某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项,现随机抽查了m名学生,并将其结果绘制成如下不完整的条形图和扇形图,请结合以上信息解答下列问题:(1)求m的值;(2)请补全上面的条形统计图;(3)在图2中,“乒乓球”所对应扇形的圆心角的度数为多少度?(4)已知该校共有1200名学生,请你估计该校约有多少名学生最喜爱足球活动?21.(8分)“2019大洋湾盐城马拉松”的赛事共有三项:A,“全程马拉松”、B,“半程马拉松”、C.“迷你健身跑”,小明和小刚参与了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组.(1)小明被分配到“迷你健身跑”项目组的概率为;(2)求小明和小刚被分配到不同项目组的概率.22.(10分)如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC,对角线AC、BD交于点O,AO=BO,DE平分∠ADC交BC于点E,连接OE.(1)求证:四边形ABCD是矩形;(2)若AB=2,求△OEC的面积.23.(10分)某公司研发生产的560件新产品需要精加工后才能投放市场.现由甲、乙两个工厂来加工生产,已知甲工厂每天加工生产的新产品件数是乙工厂每天加工生产新产品件数的1.5倍,并且加工生产240件新产品甲工厂比乙工厂少用4天.(1)求甲、乙两个工厂每天分别可加工生产多少件新产品?(2)若甲工厂每天的加工生产成本为2.8万元,乙工厂每天的加工生产成本为2.4万元要使这批新产品的加工生产总成本不超过60万元,至少应安排甲工厂加工生产多少天?24.(10分)如图,以AB为直径作半圆O,点C是半圆上一点,∠ABC的平分线交⊙O于E,D为BE延长线上一点,且DE=FE.(1)求证:AD为⊙O切线;(2)若AB=20,tan∠EBA=,求BC的长.25.(10分)甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线OBCDA 表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:(1)当轿车刚到乙地时,此时货车距离乙地千米;(2)当轿车与货车相遇时,求此时x的值;(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.26.(12分)【操作发现】如图(1),在△OAB和△OCD中,OA=OB,OC=OD,∠AOB =∠COD=45°,连接AC,BD交于点M.①AC与BD之间的数量关系为;②∠AMB的度数为;【类比探究】如图(2),在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC,交BD的延长线于点M.请计算的值及∠AMB的度数;【实际应用】如图(3),是一个由两个都含有30°角的大小不同的直角三角板ABC、DCE 组成的图形,其中∠ACB=∠DCE=90°,∠A=∠D=30°且D、E、B在同一直线上,CE=1,BC=,求点A、D之间的距离.27.(14分)如图,二次函数y=ax2﹣3ax+c的图象与x轴交于点A、B,与y轴交于点C直线y=﹣x+4经过点B、C.(1)求抛物线的表达式;(2)过点A的直线交抛物线于点M,交直线BC于点N.①点N位于x轴上方时,是否存在这样的点M,使得AM:NM=5:3?若存在,求出点M的坐标;若不存在,请说明理由.②连接AC,当直线AM与直线BC的夹角∠ANB等于∠ACB的2倍时,请求出点M的横坐标.2019年江苏省盐城市建湖县中考数学二模试卷参考答案与试题解析一、选择题(本大题共8小题,每小题3分,共24分,在每小题所给出的四个选项中,只有一个选项是正确的,请将正确选项的字母代号填涂在答题卡相应位置上)1.(3分)下列四个数,表示无理数的是()A.sin30°B.πC.D.【分析】无限不循环小数叫做无理数,根据无理数的定义逐个排除即可.【解答】解:A、sin30°=,不是无理数,故本选项不符合题意;B、π是无限不循环小数,是无理数,符合题意;C、=4,不是无理数,故本选项不符合题意;D.=﹣2,不是无理数,故本选项不符合题意;故选:B.【点评】本题考查了无理数,正确理解无理数的意义是解题的关键.2.(3分)下列四种标志图案中,既是轴对称图形又是中心对称图形的是()A.B.C.D.【分析】根据轴对称图形与中心对称图形的概念判断即可.【解答】解:A、不是轴对称图形,是中心对称图形;B、是轴对称图形,是中心对称图形;C、不是轴对称图形,是中心对称图形;D、不是轴对称图形,不是中心对称图形.故选:B.【点评】本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.3.(3分)下列各式正确的是()A.6a2﹣5a2=a2B.(2a)2=2a2C.﹣2(a﹣1)=﹣2a+1D.(a+b)2=a2+b2【分析】根据合并同类项法则、积的乘方、单项式乘多项式法则及完全平方公式逐一判断即可得.【解答】解:A.6a2﹣5a2=a2,正确;B.(2a)2=4a2,错误;C.﹣2(a﹣1)=﹣2a+2,错误;D.(a+b)2=a2+2ab+b2,错误;故选:A.【点评】本题主要考查幂的乘方与积的乘方,解题的关键是掌握合并同类项法则、积的乘方、单项式乘多项式法则及完全平方公式.4.(3分)如图所示,直线a、b、c、d的位置如图所示,若∠1=125°,∠2=125°,∠3=135°,则∠4的度数为()A.45°B.55°C.60°D.65°【分析】先依据同位角相等,判定a∥b,再根据平行线的性质,即可得出∠4=45°.【解答】解:如图所示,∵∠1=125°,∠2=125°,∴a∥b,∴∠4=∠5,又∵∠3=135°,∴∠5=45°,∴∠4=45°,故选:A.【点评】本题考查了平行线的判定和性质的应用,能求出a∥b是解此题的关键.5.(3分)某工艺品厂草编车间共有16名工人,为了了解每个工人的日均生产能力,随机调查了某天每个工人的生产件数,获得数据如下表:则这一天16名工人生产件数的众数和中位数分别是()A.5件、11件B.12件、11件C.11件、12件D.15件、14件【分析】根据众数和中位数的概念求解可得.【解答】解:这组数据的众数为11件,中位数为=12(件),故选:C.【点评】此题考查了众数与中位数,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),众数是一组数据中出现次数最多的数.6.(3分)如图,▱ABCD的周长为22m,对角线AC、BD交于点O,过点O与AC垂直的直线交边AD于点E,则△CDE的周长为()A.8cm B.9cm C.10cm D.11cm【分析】由平行四边形的性质可得AB=CD,AD=BC,AO=CO,可得AD+CD=11cm,由线段垂直平分线的性质可得AE=CE,即可求△CDE的周长=CE+DE+CD=AE+DE+CD=AD+CD=11cm.【解答】解:∵四边形ABCD是平行四边形∴AB=CD,AD=BC,AO=CO,又∵EO⊥AC,∴AE=CE,∵▱ABCD的周长为22cm,∴2(AD+CD)=22cm∴AD+CD=11cm∴△CDE的周长=CE+DE+CD=AE+DE+CD=AD+CD=11cm故选:D.【点评】本题考查了平行四边形的性质,线段垂直平分线的性质,熟练运用平行四边形的性质是本题的关键.7.(3分)一个圆锥的主视图是边长为6cm的正三角形,则这个圆锥的侧面积等于()A.36 πcm2B.24πcm2C.18πcm2D.12 πcm2【分析】根据视图的意义得到圆锥的母线长为6cm,底面圆的半径为3cm,然后根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式求解.【解答】解:根据题意得圆锥的母线长为6cm,底面圆的半径为3cm,所以这个圆锥的侧面积=×6×2π×3=18π(cm2).故选:C.【点评】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.8.(3分)如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF ⊥AB交AC于点G,反比例函数y=(x>0)经过线段DC的中点E,若BD=4,则AG的长为()A.B.+2C.2+1D.+1【分析】过E作y轴和x的垂线EM,EN,证明四边形MENO是矩形,设E(b,a),根据反比例函数图象上点的坐标特点可得ab=,进而可计算出CO长,根据三角函数可得∠DCO=30°,再根据菱形的性质可得∠DAB=∠DCB=2∠DCO=60°,∠1=30°,AO=CO=2,然后利用勾股定理计算出DG长,进而可得AG长.【解答】解:过E作y轴和x的垂线EM,EN,设E(b,a),∵反比例函数y=(x>0)经过点E,∴ab=,∵四边形ABCD是菱形,∴BD⊥AC,DO=BD=2,∵EN⊥x,EM⊥y,∴四边形MENO是矩形,∴ME∥x,EN∥y,∵E为CD的中点,∴DO•CO=4,∴CO=2,∴tan∠DCO==.∴∠DCO=30°,∵四边形ABCD是菱形,∴∠DAB=∠DCB=2∠DCO=60°,∠1=30°,AO=CO=2,∵DF⊥AB,∴∠2=30°,∴DG=AG,设DG=r,则AG=r,GO=2﹣r,∵AD=AB,∠DAB=60°,∴△ABD是等边三角形,∴∠ADB=60°,∴∠3=30°,在Rt△DOG中,DG2=GO2+DO2,∴r2=(2﹣r)2+22,解得:r=,∴AG=.故选:A.【点评】此题主要考查了反比例函数和菱形的综合运用,关键是掌握菱形的性质:菱形对角线互相垂直平分,且平分每一组对角,反比例函数图象上的点横纵坐标之积=k二、填空题(本大题共有8小题,每小题3分,共24分不需写出解答过程,请将答案直接写在答题卡相应位置上)9.(3分)要使有意义,则实数x的取值范围是x≥﹣1.【分析】根据二次根式的性质可以得到x﹣1是非负数,由此即可求解.【解答】解:依题意得x+1≥0,∴x≥﹣1.故答案为:x≥﹣1.【点评】此题主要考查了二次根式有意义的条件,根据被开方数是非负数即可解决问题.10.(3分)若x=﹣1是关于x的方程2x+3m﹣7=0的解,则m的值为3.【分析】使方程左右两边的值相等的未知数的值是该方程的解.将方程的解代入方程可得关于m的一元一次方程,从而可求出m的值.【解答】解:根据题意得:2×(﹣1)+3m﹣7=0解得:m=3,故答案为:3.【点评】本题考查了一元一次方程的解的定义.已知条件中涉及到方程的解,把方程的解代入原方程,转化为关于m字母系数的方程进行求解,注意细心.11.(3分)青盐铁路(青岛一盐城),是我国“八纵八横”高速铁路网中第一纵“沿海通道”的一部分,全长428.752千米.数据428.752千米用科学记数法表示为 4.28752×105米.【分析】用科学记数法表示较大的数时,一般形式为a×10﹣n,其中1≤|a|<10,n为整数,据此判断即可.【解答】解:428.752千米=428752米=4.28752×105米.故答案为:4.28752×105.【点评】此题主要考查了用科学记数法表示较大的数,一般形式为a×10﹣n,其中1≤|a|<10,确定a与n的值是解题的关键.12.(3分)在一个不透明的盒子中装有红、白两种除颜色外完全相同的球,其中有a个白球和3个红球,若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在20%左右,则a的值约为12.【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从摸到红球的频率稳定在20%左右得到比例关系,列出方程求解即可.【解答】解:由题意可得,×100%=20%,解得a=12.经检验:a=12是原分式方程的解,所以a的值约为12,故答案为:12.【点评】本题利用了用大量试验得到的频率可以估计事件的概率.关键是根据红球的频率得到相应的等量关系.13.(3分)边长为a、b的长方形,它的周长为14,面积为10,则a2b+ab2的值为70.【分析】先把所给式子提取公因式ab,再整理为与题意相关的式子,代入求值即可.【解答】解:根据题意得:a+b=7,ab=10,则a2b+ab2=ab(a+b)=70.故答案为70.【点评】本题既考查了对因式分解方法的掌握,又考查了代数式求值的方法,同时还隐含了数学整体思想和正确运算的能力.14.(3分)如图,CE、BF分别是△ABC的高线,连接EF,EF=6,BC=10,D、G分别是EF、BC的中点,则DG的长为4.【分析】连接EG、FG,根据直角三角形的性质得到EG=FG=BC=5,根据等腰三角形的性质求出ED,根据勾股定理计算,得到答案.【解答】解:连接EG、FG,∵CE,BF分别是△ABC的高线,∴∠BEC=90°,∠BFC=90°,∵G是BC的中点,∴EG=FG=BC=5,∵D是EF的中点,∴ED=EF=3,GD⊥EF,由勾股定理得,DG==4,故答案为:4.【点评】本题考查的是直角三角形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.15.(3分)如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=1.将边BA绕点B顺时针旋转90°得线段BD,再将边CA绕点C顺时针旋转90°得线段CE,连接DE,则图中阴影部分的面积是﹣.【分析】作EF⊥CD于F,根据勾股定理骑车AC,根据旋转变换的性质求出EF,根据扇形面积公式、三角形的面积公式计算,得到答案.【解答】解:作EF⊥CD于F,由旋转变换的性质可知,EF=BC=1,CD=CB+BD=4,由勾股定理得,CA===,则图中阴影部分的面积=△ABC的面积+扇形ABD的面积+△ECD的面积﹣扇形ACE的面积=×1×3++﹣=﹣,故答案为:﹣.【点评】本题考查的是扇形面积计算、旋转变换的性质,掌握扇形面积公式:S=是解题的关键.16.(3分)如图,已知△ABC中,∠BAC=120°,AB=AC=2.D为BC边一点,且BD:DC=1:2.以D为一个点作等边△DEF,且DE=DC连接AE,将等边△DEF绕点D旋转一周,在整个旋转过程中,当AE取得最大值时AF的长为2.【分析】点E,F在以D为圆心,DC为半径的圆上,当A,D,E在同一直线上时AE 取最大值,过点A作AH⊥BC交BC于H,通过解直角三角形求出DH,BH,CH的长度,∠ADH的度数,证明四边形DEFC是菱形,△ACF为直角三角形,通过勾股定理可求出AF的长度.【解答】解:如图,点E,F在以D为圆心,DC为半径的圆上,当A,D,E在同一直线上时AE取最大值,过点A作AH⊥BC交BC于H,∴∠BAC=120°,AB=AC=2,∴∠B=∠ACB=30°,BH=CH,∴在Rt△ABH中,AH=AB=,BH=AH=3,∴BC=2BH=6,∵BD:DC=1:2,∴BD=2,CD=4,∴DH=BH﹣BD=1,在Rt△ADH中,AH=,DH=1,∴tan∠DAH==,∴∠DAH=30°,∠ADH=60°,∵△DEF是等边三角形,∴∠E=60°,DE=EF=DC,∵∠ADC=∠E=60°,∴DC∥EF,∵DC=EF,∴四边形DEFC为平行四边形,又∵DE=DC,∴平行四边形DEFC为菱形,∴FC=DC=4,∠DCF=∠E=60°,∴∠ACF=ACB+∠DCF=90°,在Rt△ACF中,AF===2,故答案为:2.【点评】本题考查了等腰三角形的性质,解直角三角形,勾股定理,菱形的判定与性质等,解题关键是能够确定AE取最大值时的位置.三、解答题(本大题共有11小题,共102分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)17.(6分)解不等式,并把它的解集在数轴上表示出来:【分析】先去分母,然后去括号,再移项、合并同类项,系数化为1即可,再用数轴表示解集.【解答】解:去分母得3(2+x)≤2(2x﹣1)+6,去括号得6+3x≤4x﹣2+6,移项得3x﹣4x≤﹣2+6﹣6,合并得﹣x≤﹣2,系数化为1得,x≥2,用数轴表示为:【点评】本题考查了解一元一次不等式:根据不等式的性质解一元一次不等式,基本操作方法与解一元一次方程基本相同,都有如下步骤:①去分母;②去括号;③移项;④合并同类项;⑤化系数为1.也考查了在数轴上表示不等式的解集.18.(6分)先化简,再求值:(x﹣3)2+2(x﹣2)(x+7)﹣(x+2)(x﹣2),其中x2+2x﹣3=0.【分析】原式利用完全平方公式,平方差公式,以及多项式乘以多项式法则计算,去括号合并得到最简结果,求出方程的解得到x的值,代入计算即可求出值.【解答】解:原式=x2﹣6x+9+2x2+10x﹣28﹣x2+4=4x﹣15,由x2+2x﹣3=0,即(x﹣1)(x+3)=0,得到x=1或x=﹣3,当x=1时,原式=4﹣15=﹣11;当x=﹣3时,原式=﹣12﹣15=﹣27.【点评】此题考查了整式的混合运算﹣化简求值,熟练掌握运算法则是解本题的关键.19.(8分)已知关于x方程x2﹣6x+m+4=0有两个实数根x1,x2(1)求m的取值范围;(2)若x1=2x2,求m的值.【分析】(1)根据方程的系数结合根的判别式△≥0,即可得出关于m的一元一次不等式,解之即可得出m的取值范围;(2)根据根与系数的关系可得出x1+x2=6,x1x2=m+4,结合x1=2x2可求出x1,x2的值,再将其代入x1x2=m+4中可求出m的值.【解答】解:(1)∵关于x方程x2﹣6x+m+4=0有两个实数根,∴△=(﹣6)2﹣4×1×(m+4)≥0,解得:m≤5.(2)∵关于x方程x2﹣6x+m+4=0有两个实数根x1,x2,∴x1+x2=6,x1x2=m+4.又∵x1=2x2,∴x2=2,x1=4,∴4×2=m+4,∴m=4.【点评】本题考查了根与系数的关系以及根的判别式,解题的关键是:(1)牢记“当△≥0时,方程有实数根”;(2)根据根与系数的关系结合x1=2x2,求出x1,x2的值.20.(8分)某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项,现随机抽查了m名学生,并将其结果绘制成如下不完整的条形图和扇形图,请结合以上信息解答下列问题:(1)求m的值;(2)请补全上面的条形统计图;(3)在图2中,“乒乓球”所对应扇形的圆心角的度数为多少度?(4)已知该校共有1200名学生,请你估计该校约有多少名学生最喜爱足球活动?【分析】(1)根据排球人数及其所占百分比可得总人数;(2)求得“足球“的人数=150×20%=30人,补全上面的条形统计图即可;(3)360°×乒乓球”所占的百分比即可得到结论;(4)用总人数乘以样本中足球所占的百分比.【解答】解:(1)m=21÷14%=150;(2)足球的人数为150×20%=30,补全图形如下:(3)在图2中,“乒乓球”所对应扇形的圆心角的度数为360°×=36°;(4)估计该校最喜爱足球活动的学生约有1200×20%=240人.【点评】本题考查扇形统计图、条形统计图、用样本估计总体.一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.21.(8分)“2019大洋湾盐城马拉松”的赛事共有三项:A,“全程马拉松”、B,“半程马拉松”、C.“迷你健身跑”,小明和小刚参与了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组.(1)小明被分配到“迷你健身跑”项目组的概率为;(2)求小明和小刚被分配到不同项目组的概率.【分析】(1)利用概率公式直接计算即可;(2)先画树状图展示所有9种等可能的结果数,再找出其中小明和小刚被分配到不同项目组的结果数,然后根据概率公式计算.【解答】解:(1)∵共有A,B,C三项赛事,∴小明被分配到“迷你健身跑”项目组的概率是,故答案为:;(2)画树状图为:共有9种等可能的结果数,其中小明和小刚被分配到不同项目组的结果数为6,所以小明和小刚被分配到不同项目组的概率=.【点评】本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B 的概率.22.(10分)如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC,对角线AC、BD交于点O,AO=BO,DE平分∠ADC交BC于点E,连接OE.(1)求证:四边形ABCD是矩形;(2)若AB=2,求△OEC的面积.【分析】(1)证出∠BAD=∠BCD,得出四边形ABCD是平行四边形,得出OA=OC,OB=OD,证出AC=BD,即可解决问题;(2)作OF⊥BC于F.求出EC、OF即可解决问题;【解答】(1)证明:∵AD∥BC,∴∠ABC+∠BAD=180°,∠ADC+∠BCD=180°,∵∠ABC=∠ADC,∴∠BAD=∠BCD,∴四边形ABCD是平行四边形,∴OA=OC,OB=OD,∵OA=OB,∴AC=BD,∴四边形ABCD是矩形.(2)解:作OF⊥BC于F,如图所示.∵四边形ABCD是矩形,∴CD=AB=2,∠BCD=90°,AO=CO,BO=DO,AC=BD,∴AO=BO=CO=DO,∴BF=FC,∴OF=CD=1,∵DE平分∠ADC,∠ADC=90°,∴∠EDC=45°,在Rt△EDC中,EC=CD=2,∴△OEC的面积=•EC•OF=1.【点评】本题考查矩形的性质、三角形的面积、三角形中位线定理等知识,解题的关键是学会添加常用辅助线,构造三角形中位线解决问题,属于中考常考题型.23.(10分)某公司研发生产的560件新产品需要精加工后才能投放市场.现由甲、乙两个工厂来加工生产,已知甲工厂每天加工生产的新产品件数是乙工厂每天加工生产新产品件数的1.5倍,并且加工生产240件新产品甲工厂比乙工厂少用4天.(1)求甲、乙两个工厂每天分别可加工生产多少件新产品?(2)若甲工厂每天的加工生产成本为2.8万元,乙工厂每天的加工生产成本为2.4万元要使这批新产品的加工生产总成本不超过60万元,至少应安排甲工厂加工生产多少天?【分析】(1)设乙工厂每天可加工生产x件新产品,则甲工厂每天可加工生产1.5x件新产品,根据题意列出方程,求出方程的解即可得到结果;(2)设甲工厂加工生产y天,根据题意列出不等式,求出不等式的解集即可得到结果.【解答】解:(1)设乙工厂每天可加工生产x件新产品,则甲工厂每天可加工生产1.5x 件新产品,根据题意得:+4=,去分母得:240+6x=360,解得:x=20,经检验x=20是分式方程的解,且符合题意,∴1.5x=30,则甲、乙两个工厂每天分别可加工生产30件、20件新产品;(2)设甲工厂加工生产y天,根据题意得:2.8y+2.4×≤60,解得:y≥9,则少应安排甲工厂加工生产9天.【点评】此题考查了分式方程的应用,以及一元一次不等式的应用,弄清题意是解本题的关键.24.(10分)如图,以AB为直径作半圆O,点C是半圆上一点,∠ABC的平分线交⊙O于E,D为BE延长线上一点,且DE=FE.(1)求证:AD为⊙O切线;(2)若AB=20,tan∠EBA=,求BC的长.【分析】(1)先利用角平分线定义、圆周角定理证明∠4=∠2,再利用AB为直径得到∠2+∠BAE=90°,则∠4+∠BAE=90°,然后根据切线的判定方法得到AD为⊙O切线;(2)解:根据圆周角定理得到∠ACB=90°,设AE=3k,BE=4k,则AB=5k=20,求得AE=12,BE=16,连接OE交AC于点G,如图,解直角三角形即可得到结论.【解答】(1)证明:∵BE平分∠ABC,∴∠1=∠2,∵AB为直径,∴AE⊥BD,∵DE=FE,∴∠3=∠4,∵∠1=∠3,∴∠4=∠2,∵AB为直径,∴∠AEB=90°,∵∠2+∠BAE=90°∴∠4+∠BAE=90°,即∠BAD=90°,∴AD⊥AB,∴AD为⊙O切线;(2)解:∵AB为直径,∴∠ACB=90°,在Rt△ABC中,∵tan∠EBA=,∴设AE=3k,BE=4k,则AB=5k=20,∴AE=12,BE=16,连接OE交AC于点G,如图,∵∠1=∠2,∴=,∴OE⊥AC,∵∠3=∠2,∴tan∠EBA=tan∠3=,∴设AG=4x,EG=3x,∴AE=5x=12,∴x=,∴AG=,∵OG∥BC,∴AC=2AG=,∴BC==.【点评】本题考查了切线的判定与性质:经过半径的外端且垂直于这条半径的直线是圆的切线;圆的切线垂直于经过切点的半径.判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”;有切线时,常常“遇到切点连圆心得半径”.也考查了圆周角定理、垂径定理和解直角三角形.25.(10分)甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线OBCDA 表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:(1)当轿车刚到乙地时,此时货车距离乙地30千米;(2)当轿车与货车相遇时,求此时x的值;(3)在两车行驶过程中,当轿车与货车相距20千米时,求x的值.【分析】(1)根据图象可知货车5小时行驶300千米,由此求出货车的速度为60千米/时,再根据图象得出货车出发后4.5小时轿车到达乙地,由此求出轿车到达乙地时,货车行驶的路程为270千米,而甲、乙两地相距300千米,则此时货车距乙地的路程为:300﹣270=30千米;(2)先求出线段CD对应的函数关系式,再根据两直线的交点即可解答;(3)分两种情形列出方程即可解决问题.【解答】解:(1)根据图象信息:货车的速度V货=,∵轿车到达乙地的时间为货车出发后4.5小时,∴轿车到达乙地时,货车行驶的路程为:4.5×60=270(千米),此时,货车距乙地的路程为:300﹣270=30(千米).所以轿车到达乙地后,货车距乙地30千米.故答案为:30;(2)设CD段函数解析式为y=kx+b(k≠0)(2.5≤x≤4.5).∵C(2.5,80),D(4.5,300)在其图象上,,解得,∴CD段函数解析式:y=110x﹣195(2.5≤x≤4.5);易得OA:y=60x,,解得,∴当x=3.9时,轿车与货车相遇;(3)当x=2.5时,y货=150,两车相距=150﹣80=70>20,由题意60x﹣(110x﹣195)=20或110x﹣195﹣60x=20,解得x=3.5或4.3小时.答:在两车行驶过程中,当轿车与货车相距20千米时,x的值为3.5或4.3小时.【点评】本题考查了一次函数的应用,对一次函数图象的意义的理解,待定系数法求一次函数的解析式的运用,行程问题中路程=速度×时间的运用,本题有一定难度,其中求出货车与轿车的速度是解题的关键.26.(12分)【操作发现】如图(1),在△OAB和△OCD中,OA=OB,OC=OD,∠AOB =∠COD=45°,连接AC,BD交于点M.①AC与BD之间的数量关系为AC=BD;②∠AMB的度数为45°;【类比探究】如图(2),在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC,交BD的延长线于点M.请计算的值及∠AMB的度数;【实际应用】如图(3),是一个由两个都含有30°角的大小不同的直角三角板ABC、DCE 组成的图形,其中∠ACB=∠DCE=90°,∠A=∠D=30°且D、E、B在同一直线上,CE=1,BC=,求点A、D之间的距离.【分析】【操作发现】如图(1),证明△COA≌△DOB(SAS),即可解决问题.【类比探究】如图(2),证明△COA∽△ODB,可得==,∠MAK=∠OBK,已解决可解决问题.【实际应用】分两种情形解直角三角形求出BE,再利用相似三角形的性质解决问题即可.【解答】解:【操作发现】如图(1)中,设OA交BD于K.。
上海市徐汇区2019届高三英语二模试题(含解析)

5。
A。 A soccer game。B. A bicycle race.
C. A swimming game.D. A Marathon running race.
【答案】A
【解析】
【分析】
W: What? The visiting team scored the first goal?
Questions are based on the following passage。
11.
A。 Many people like to eat dog meat。B。 The world is too competitive。
C. Dogs are unhappy with their existence。D. Dogs enjoy their life with people。
1。
A. At an airport.B。 In the hotel。C。 At a bus stop.D. In a subway station.
【答案】A
【解析】
【分析】
M: How much should I pay for the overweight?
W: The charge for extra baggage is calculated by 1.5% of the standard ticket fare for economy class。
上海市徐汇区2019届高三英语二模试题(含解析)
考生注意:
1. 考试时间120分钟,试卷满分140分.
2. 本考试设试卷和答题纸两部分。所有答題必须涂(选择题)或写(非选择题)在答题纸上,做在试卷上一律不得分。
3。 答題前,务必在答題纸上填写准考证号和姓名,并将核对后的条形码貼在指定位置上,在答題纸反面清楚地填写姓名。
2019届中考物理二模试卷(解析版)(IV).docx

2019 届中考物理二模试卷(解析版)(IV)一、选择题(本题包括8 个小题,每小题 3 分,共 24 分.下列每小题给出的四个选项中有一个或几个选项是正确的,漏选得 2 分,错选得0 分)1.( 3 分)小明同学帮妈妈做饭时根据观察到的现象,进行了解释,其中正确的是()A.切肉时先磨刀,是为了减小受力面积,增大压力B.高压锅做饭时熟得快,是因为气压增大,水的沸点升高C.茶壶的壶嘴与壶身构成连通器,水面总是相平的D.电饭锅用三角插头和三孔插座,是为了防止锅体漏电造成触电事故考点:沸点及沸点与气压的关系;连通器原理;插座的构造与工作方式.专题:汽化和液化、升华和凝华;电与热、生活用电;压强、液体的压强.分析:A、磨刀,刀刃会变薄,减小了受力面积,从而增大压强;B、高压锅通过增大锅内气压的办法来提高水的沸点,从而缩短煮饭时间;C、上端开口、底部连通的容器叫连通器,在连通器中装入同种液体,液体不流动时,液面是相平的;D、三孔插座上有接地线,使用三脚插头和三孔插座可以将用电器的金属外壳接地,防止因漏电而造成触电事故.解答:解: A、磨刀将刀刃磨薄,切肉时受力面积比较小,压强比较大,但压力不会改变,所以 A 是错误的;B、高压锅是通过增大锅内气体压强的办法来提高水的沸点,从而缩短加热时间的,所以 B 是正确的;C、茶壶的壶嘴与壶身构成连通器,在水不流动时,水面总是相平的,所以 C 是正确的;D、电饭锅用三孔插座和三脚插头,可把电饭锅的外壳接地,可防止漏电而造成触电事故,所以D是正确的.故选 BCD.点评:此题考查了增大压强的办法、沸点和气压的关系、连通器的应用、安全用电的常识等,是一道综合题;联系生活实际来考查物理知识,是现在中考考查知识一个很重要的方式,需要掌握其方法.2.( 3 分)下列关于声音的说法不正确的是()A.“响鼓也要重锤敲”说明声音是由振动产生的,且振幅越大响度越大B.“震耳欲聋”指声音的音调高,可能导致人失去听力C.“闻其声知其人”意思是可以根据音色来判断说话者D.“隔墙有耳”说明了固体能传声考点:声音的传播条件;声音的产生;响度与振幅的关系;音色.专题:应用题;声现象.分析:( 1)声音是由物体的振动产生的,响度指声音的强弱,是由物体振动的振动决定的;(2)音调指声音的高低,是由物体振动的频率决定的;(3)音色是指声音的特色,通过音色能辨别物体,不同乐器、不同发声体的材料和结构不同,产生的音色会不同,我们是靠音色来辨别乐器的种类和不同人的声音;(4)声音可以通过固体、液体和气体传播,不能在真空中传播.解答:解: A、“响鼓也要重锤敲”说明声音是由振动产生的,且振幅越大响度越大,该选项说法正确,不符合题意;B、“震耳欲聋”指声音的响度大,可能导致人失去听力,该选项说法不正确,符合题意;C、不同人声音的音色不同,“闻其声知其人”意思是可以根据音色来判断说话者,该选项说法正确,不符合题意;D、“隔墙有耳”说明了固体能传声,该选项说法正确,不符合题意.故选 B.点评:本题考查了声学的相关知识,属于基础内容的考查,比较简单,属于识记性内容.3.( 3 分)下列关于光的现象的说法中正确的是()A.我国古代使用的铜镜能成正立放大的实像B.激光准直利用了光的折射性质C.老花镜的焦距可以在太阳光下用刻度尺粗略测出D.照相机照相时在底片上成倒立放大的虚像考点:凸透镜成像的应用;光直线传播的应用;平面镜成像的特点、原理、现象及其实验方案.分析:铜镜相当于平面镜,物体在平面镜中成正立、等大的虚像.激光准直是利用光的直线传播的原理.根据凸透镜的焦点和焦距的定义进行判断.凸透镜成像时,u>2f ,成倒立、缩小的实像,应用于照相机和摄像机.解答:解: A、铜镜成正立、等大的虚像.不符合题意.B、激光准直是利用光的直线传播的原理.不符合题意.C、老花镜是凸透镜,凸透镜正对太阳光,太阳光平行于主光轴,太阳光经凸透镜折射后,在地面上形成最小最亮的点,这点是凸透镜的焦距,用刻度尺测量凸透镜到焦点的距离是凸透镜的焦距.符合题意.D、照相机照相时在底片上成倒立缩小的实像.不符合题意.故选 C.点评:光的直线传播、光的反射、光的折射是光学中三条重要规律,生活中应用也很广泛,可以搜寻生活中有关事例.4.( 3 分)对下列设备的工作原理解释错误的是()A.验钞器﹣﹣红外线使钞票上的荧光物质发光B.移动电话﹣﹣利用电磁波传播信息C.通信光缆是使光信号在光导纤维的内壁多次反射D.核电站﹣﹣核能转化为电能考点:紫外线;电磁波的传播;光纤通信;核电站发电过程中的能量转化.专题:应用题;其他综合题.分析:( 1)红外线的热效应比较强,穿透力比较强,能制成热谱仪,制成红外线夜视仪;红外线可以用来遥控,制成电视遥控器.紫外线化学效应强,能杀菌,制成消毒灯;紫外线能合成维生素 D,促使钙的吸收;紫外线能使荧光物质发光,制成验钞机来验钞.(2)广播、电视和移动通信都是利用电磁波来传递信息的.(3)光纤通信是利用激光从光纤的一端射入,在内壁上多次反射后在另一端放射出来,然后在接收端,检测器收到光信号后把它变换成电信号,经解调后恢复原信息.(4)核电站的核心是核反应堆,它以铀为燃粒,在裂变过程中释放出核能,再通过热交换器变为高温高压的蒸汽,然后利用蒸汽去驱动蒸汽轮机,蒸汽轮机的旋转带动发电机发电.解答:解: A、紫外线可以使荧光物质发光,钞票上某些位置用荧光物质印上标记,在紫外线下照射下识别这些标记,从而辨别钞票的真伪.故错误.B、手机属于移动电话,它既是电磁波发射台也是电磁波接受台,所以是利用电磁波来传递信息的;故正确.C、激光在传输过程中,从光导纤维的一端射入后,在光导纤维内壁上要发生多次反射,并从另一端射出,这样就把它携带的信息传到远方.故正确.D、根据核电站的发电过程可知,核能发电的能量传递和转化过程是:核能→水和蒸汽的内能→发电机转子的机械能→电能;故正确.故选 A.点评:此题考查了紫外线的应用、电磁波的应用、光纤通信、核电站的能量转化,是一道基础题.5.( 3 分)下列说法中,错误的是()A.自行车、汽车的轮胎上刻有凹凸不平的花纹是为了增大摩擦B.拦河坝筑成上窄下宽是因为水的压强随深度增加而增大C.人造地球卫星在绕地球从近地点向远地点运行的过程中,势能转化为动能D.举重运动员手举杠铃不动,手对杠铃没有做功考点:增大或减小摩擦的方法;液体的压强的特点;力是否做功的判断;动能和势能的转化与守恒.专题:重力、弹力、摩擦力;压强、液体的压强;功、功率、机械效率;机械能及其转化.分析:A、增大摩擦的方法:从压力大小和接触面的粗糙程度考虑,增大压力,增大接触面的粗糙程度,用滑动代替滚动摩擦力.B、根据液体内部的压强特点(液体内部的压强随深度的增加而增大)分析此选项;C、根据影响动能和重力势能大小的因素来分析动能和重力势能的变化,找到转化的方向.D、做功的两个必要因素:一是作用在物体上的力;二是物体在力的方向上通过的距离;二者缺一不可.解答:解:A、车胎上制有凹凸花纹,是在压力一定时,通过增大接触面的粗糙程度增大摩擦,故 A 正确;B、因为液体的压强随深度的增加而增大,为了水坝能承受更大的水压,水坝做成上窄下宽的形状;故 B 正确;C、当卫星从近地点向远地点运动时,所处高度增加,重力势能增加,但运动的速度减小,动能减小.正是动能转化为了重力势能,故 C 错误;D、因为做功需要对物体施力,并且物体要在力的方向上移动距离,而在运动员举着杠铃不动的过程中,杠铃没有移动距离,所以此过程不做功,故D正确.故选 C.点评:此题考查了增大或减小摩擦的方法、液体压强的特点、力是否做功的判断、动能和势能的转化与守恒等知识点,是一道综合性较强的题目.6.( 3 分)早上,一杯香浓的豆浆可以让我们精力充沛.电动豆浆机在工作过程中,转动的)叶轮将豆子打磨研碎,加热体将豆浆加热至煮熟.下面说法中正确的是(A.通电后叶轮转动,电动机将机械能转化为电能B.从开始加热到豆浆煮熟的过程中,豆浆的内能不变C.煮好的豆浆香气四溢的原因是分子在不停地做无规则运动D.喝刚刚煮好的豆浆时,在它表面吹气可以加快豆浆的蒸发,使它凉得快些考点:分子的运动;影响蒸发快慢的因素;直流电动机的构造和工作过程;内能的概念.专题:汽化和液化、升华和凝华;分子热运动、内能;电动机、磁生电.分析:掌握电动机和发电机的区别,热量、温度与内能的关系,扩散现象,六种物态变化的吸热和放热情况是解决此题的关键.解答:解: A、通电后叶轮转动,是电动机将电能转化为机械能,故 A 错误;B、从开始加热到豆浆煮熟,豆浆的温度升高,内能增加,故 B 错误;C、煮好的豆浆温度很高,香气分子无规则运动的速度加剧,所以“香气四溢”,故C正确;D、在刚煮好的豆浆表面吹气,加快豆浆表面上的空气流动,可以使蒸发加快,液体蒸发是吸热的,所以豆浆会凉的快些,故 D 正确;故选 CD.点评:物理来源于生活,又应用于生活.同学们只要留心观察,善于思考,会发现生活中处处都有物理知识.7.( 3 分)小红对如图所示的两个探究实验进行比较后有了以下几点认识,其中正确的是()A.甲实验是发电机的原理,乙实验是电动机的原理B.甲实验是用来探究磁场对电流的作用的实验装置,乙实验是用来探究磁能否生电的实验装置C.实验时,甲中导体 ab 相当于电路中的电源,乙中导体 ab 相当于电路中的用电器D.甲实验中机械能转化为电能,乙实验中电能转化为机械能考点:直流电动机的原理;发电机的构造和原理.专题:应用题;电动机、磁生电.分析:先弄清两个探究实验所研究的是什么,再对题中四个选项进行判断.解答:解:( 1)甲实验有电源,闭合电路时,导体ab 有电流,受磁场的作用而运动,所以甲实验是研究磁场对电流有力的作用,是电能转化为机械能,是电动机的制作原理;( 2)乙实验有电流表是显示电流中有无电流的,所以是研究电磁感应的,因为导体运动起来产生电,所以是将机械能转化为电能,是发电机的制作原理.故ACD错误,B正确.故选 B.点评:题中两个实验是比较容易混淆的,在区分时先要看看有无电源,有电源就是研究磁场对电流作用力的实验,无电源就是研究电磁感应的实验.当然也可以从能的转化上进行判断.8.( 3 分)如图所示的电路,电阻R1=10Ω,闭合开关S,电流表A1的示数为0.3A ,电流表A2的示数为0.5A .下列说法正确的是()A.通过电阻 R2的电流为 0.2A C.阻 R1消耗的电功率为 3W B.电阻 R2的阻值为15ΩD.电源电压为3V考点:欧姆定律的应用;并联电路的电流规律;并联电路的电压规律;电功率的计算.专题:计算题;电路和欧姆定律;电能和电功率.分析:由电路图可知,两电阻并联,电流表A1测 R1支路的电流, A2测干路电流;根据并联电路的电压特点和欧姆定律求出电源的电压,根据并联电路的电流特点求出通过R 的电2流,再根据欧姆定律求出R2的阻值,根据P=UI 求出电阻 R1消耗的电功率.解答:解:由电路图可知,两电阻并联,电流表A1测 R1支路的电流, A2测干路电流;∵并联电路中各支路两端的电压相等,∴根据欧姆定律可得,电源的电压:U=U2=U1=I 1R1=0.3A×10 Ω =3V,故 D 正确;∵并联电路中干路电流等于各支路电流之和,∴通过2R 的电流:I 2=I ﹣ I 1=0.5A﹣ 0.3A=0.2A ,故 A 正确;电阻 R2的阻值:R2= ==15Ω,故 B 正确;电阻 R1消耗的电功率:P1=U1I 1=3V×0.3A=0.9W,故C 不正确.故选 ABD.点评:本题考查了并联电路的特点和欧姆定律、电功率的计算,是一道基础题目.二、填空题(每空 1 分,共 26 分)9.( 2 分)“五一”期间,小明和家人在“二一九”公园游玩,在河中边划船嬉戏边欣赏美景,别有一番情趣.船桨向后划水,船向前运动,说明了物体间力的作用是相互的,小船在河中行驶时,坐在船上的小明相对河岸是运动(选填“静止”或“运动”的)考点:力作用的相互性;运动和静止的相对性.专题:运动和力.分析:( 1)力是物体对物体的作用,物体间力的作用是相互的;(2)判断物体的运动和静止,首先确定被研究的物体,被研究的物体和参照物之间发生了位置是改变,被研究的物体是运动的,否则是静止的.解答:解:( 1)船桨向后划水,对水施加力的作用,由于物体间力的作用是相互的,因此水就会对船桨施加向前的反作用力,船向前运动;(2)小船在河中行驶时,坐在船上的小明相对河岸的位置不断发生变化,小明是运动的.故答案为:物体间力的作用是相互的;运动.点评:( 1)力的作用是相互的,一个物体是受力物体,同时也是施力物体;(2)由参照物判断物体的运动和静止,主要看被研究的物体和参照物之间是否发生了位置的变化.10.( 3 分)有报道说:台湾一家厂商发明了一种“手机自生能”技术,每摇手机一分钟可通话两分钟.如果将手机每秒摇﹣次,相当于将 200g 的重物举高 10cm.则根据报道可知,每摇一次可以获得的电能为 0.2 J,这种获得电能的过程是把机械能转化为电能,该手机使用时的功率约为 0.1 W.(取 g=10N/kg )考点:功的计算;功率的计算.专题:功、功率、机械效率.分析:每秒摇一次相当于将200g 的重物举高10cm,根据公式W=Gh可求产生的电能,还知道每摇一分钟可通话两分钟,根据公式P=可求该手机通话时的功率.解答:解:每摇一次可以获得电能:W=Gh=mgh=0.2kg×10N/kg×0 .1m=0.2J ;通过机械运动得到了电能,因此该过程将机械能转化为电能;该手机使用时的功率:P===0.1W.故答案为0.2 ;机械; 0.1 .解题过程点评:本题考查功和电功率的计算,关键是理解每摇一分钟可通话两分钟的含义,中还要注意单位的换算.11.( 2 分)“可燃冰”作为新型能源,有着巨大的开发、使用潜力,同等条件下,“可燃冰”完全燃烧放出的热量达到煤气的数十倍,说明“可燃冰”的热值很大;以10 倍的87出热量为 4.2 ×10 焦)考点:燃料的热值.专题:比热容、热机、热值.分析:( 1) 1kg 某种燃料完全燃烧放出的热量,叫这种燃料的热值;(2)利用 Q放=mq求出 1kg 煤气完全燃烧放出的热量,“可燃冰”完全燃烧放出的热量达到煤气的 10 倍,据此求 1kg“可燃冰”完全燃烧放出的热量.解答:解:( 1)在同等条件下,包含质量相同,“可燃冰”完全燃烧放出的热量达到煤气的数十倍,说明“可燃冰”的热值很大;( 2) 1kg 煤气完全燃烧放出的热量:77Q放 =mq=1kg×4.2 ×l0 J/kg=4 .2 ×l0 J,78Q放′=Q 放×10=4.2 ×l0 J×10=4.2 ×l0 J;8故答案为:热值; 4.2 ×l0.点评:本题考查了学生对燃料的热值、燃料完全燃烧放热公式掌握和运用,难度不大,是一道基础题.12.( 2 分)少数青少年由于沉迷于网络而过度用眼,使来自远方物体的光线聚焦在视网膜前方(选填“前方”或“后方”)导致了近视,应佩戴凹透镜加以矫正.考点:近视眼的成因与矫正办法.专题:透镜及其应用.分析:近视眼是因为晶状体太厚或眼球太长,像成在视网膜的前方;远视眼是因为晶状体太薄或眼球太短,像成在视网膜的后方.解答:解:少数青少年由于沉迷于网络而过度用眼,使来自远方物体的光线聚焦在视网膜前方,导致近视,应佩戴凹透镜进行矫正.故答案为:前方;凹透.点评:掌握近视眼和远视眼的成因和如何矫正.13.( 3 分)哈大高铁列车驶入鞍山西站过程中,撤去动力,不能立刻停止,这是因为列车具有惯性,此时安全线内的压强比安全线外的压强小(选填“大”、“小”或“相等”);驶出鞍山西站过程中,列车的动能逐渐增大.考点:惯性;流体压强与流速的关系;动能和势能的大小变化.专题:运动和力;气体的压强、流体压强与流速的关系;机械能及其转化.分析:① 惯性是一切物体保持原来运动状态不变的性质;②流体流速越大的位置压强越小,据此来对第二个空进行分析;③动能的大小与物体的质量和速度有关,质量越大、速度越大,物体的动能越大.解答:解:①列车进站过程中,撤去动力,不能立刻停止,这是因为列车具有惯性,仍要保持原来的运动状态;②列车附近空气流速大,压强小,当人靠近时,会形成一个向列车方向的压强差,将人压向列车发生危险;③列车驶出车站过程中,质量不变,速度增大,因此其动能增大.故答案为:惯性;小;增大.点评:本题主要考查了三个力学中的基本知识点:惯性的相关现象、流体压强与流速的关系、动能大小的影响因素,有一定的综合性,都是我们应该熟练把握的知识.14.( 4 分)小明同学喜欢摄影.一天清晨,他用照相机对同一片树叶拍了两张清晰的照片.如图甲和乙所示,小明拍摄这两张照片时相机镜头焦距相同,那么拍摄乙照片时树叶与相机距离大一些.树叶上露珠下面的叶脉看起来比较大,这是因为圆形的露珠相当于凸透镜,通过露珠而形成的虚像(选填“虚”或“实”).过一会儿,小明再次回到这里看这片树叶,发现露珠不见了,露珠不见的原因是汽化.考点:凸透镜成像的应用;汽化及汽化吸热的特点.专题:透镜及其应用;汽化和液化、升华和凝华.分析:( 1)照相机是利用凸透镜成倒立、缩小的实像,凸透镜成实像时,物距减小,像距增大,像变大.(2)水珠是凸透镜,物距小于一倍焦距时,凸透镜成正立、放大的虚像.(3)物质从液态变成气态的过程是汽化.解答:解:(1)用照相机照相时,树叶成清晰倒立、缩小的实像,甲的实像大于乙的实像,所以甲的物距小于乙的物距,所以拍摄乙照片时树叶与照相机距离大一些.(2)水珠的中间比边缘厚,是一个水凸透镜,树叶在水凸透镜的一倍焦距以内,成正立、放大的虚像.(3)水珠变成水蒸气,物质从液态变成气态,这是汽化现象.故答案为:乙;凸透镜;虚;汽化.点评:此题通过给水珠照相、通过水珠看树叶的叶脉、水珠不见了,通过这些生活中的现象,考查了凸透镜成像的情况,是一个好题.15.( 3 分)奥斯特发现了了电和磁的联系,导致了电生磁发电机之后,法拉第发现了的发明.电磁感应现象,进一步揭示考点:电磁感应.专题:电动机、磁生电.分析:( 1)奥斯特发现了通电导体周围存在磁场;( 2)法拉第发现了电磁感应现象,电磁感应现象就是发电机的原理.解答:解:奥斯特发现了电生磁之后,法拉第发现了电磁感应现象,进一步提示了电和磁的联系,导致了发电机的发明.故答案为:电生磁;电磁感应;发电机.点评:本题考查了电与磁的关系、电磁感应现象的应用及其发现者,属于基本知识.16.( 4 分)如图所示,一瓶标有500mL的矿泉水,装满水后放在水平桌面上静止不动,若塑料瓶的质量为50g,瓶与桌面的接触面积是10cm2,则桌面对瓶的支持力为 5.5N,瓶对桌面的压强是5500 Pa,把水倒满一个高10cm的纸杯,杯底受到的水的压强是1000 Pa,如果砸瓶侧壁不同高度的地方用锥子扎出上、下两个小孔,打开瓶盖,可以观察到水从下(选填“上”或“下”)孔流出的水喷得较急.(取g=10N/kg)考点:压强的大小及其计算;液体的压强的特点;液体的压强的计算.专题:计算题;压强、液体的压强.分析:( 1)根据密度公式求出矿泉水瓶内水的质量,利用G=mg求出矿泉水瓶的总重力,矿泉水瓶子放在水平桌面上时静止处于平衡状态,受到重力和支持力是一对平衡力二者大小相等,矿泉水瓶对桌面的压力和总重力相等,根据压强公式求出瓶对桌面的压强( 2)水倒满高10cm的纸杯,水的深度是10cm,根据液体压强的计算公式p=ρ液 gh 就可以计算出杯底受到的水的压强;(3)液体内部存在压强,由于液体的压强随深度的增加而增大,故会看到下孔流出的水喷得最急或喷得远一些.解答:解:( 1)矿泉水平内水的体积:3V=500L=500cm,由ρ =可得,水的质量:m水 =ρ V=1g/cm3×500cm3=0.5kg ,瓶子的总重力:G=G瓶 +G 水=( m瓶+m水) g=( 0.05kg+0.5kg)× 10N/kg=5.5N,∵矿泉水瓶放在水平桌面上静止不动,受到的支持力和重力是一对平衡力,∴F支持 =G=5.5N,瓶对桌面的压强:p====5500Pa;( 2)水倒满一个高10cm的纸杯,杯底受到的水的压强为:33(3)由于液体内部存在压强,且压强随深度的增加而增大,故会观察到水从两个小孔流出来,其中下孔流出的水喷得最急或喷得远一些.故答案为: 5.5 ; 5500; 1000;下.点评:本题考查重力的计算、二力平衡的知识、液体压强的特点和计算,容易出错的是在计算瓶子的重力时容易忽略水的重力,在解题时还要注意单位的换算.17.( 3 分)如图所示是我国引进改造的“瓦良格”号航空母舰,满载排水量为 6.4 ×10 4吨,则满载时受到的浮力为 6.4 ×10 8N(取 g=10N/kg );假如“瓦良格”号航母从海上驶入长江后,受到的浮力不变;停在甲板上的飞机飞离航母时,航母所受浮力减小.(选填“增大”、“减小”或“不变”)考点:阿基米德原理;物体的浮沉条件及其应用.专题:应用题.分析:( 1)航空母舰的排水量是指满载时排开水的质量,根据阿基米德原理求航空母舰满载时受到的浮力;(2)当航空母舰由海上驶入长江后,都是漂浮,根据漂浮条件分析航空母舰受到浮力的变化情况;(3)航母处于漂浮状态,浮力变化决定于重力的变化.解答:解:( 1)满载时受到的浮力:F 浮 =G排 =m排 g=6.4 ×10 7kg×10N/kg=6.4 ×10 8N;(2)当航空母舰由海上驶入长江后,都是漂浮,船受到的浮力: F 浮 =G,∵航空母舰受到的重力不变,∴航空母舰受到的浮力不变;(3)飞机飞离航母前后,航母都处于漂浮状态,浮力始终等于重力,当飞机飞离航母时,航母总重减小,所以浮力相应减小.故答案为: 6.4 ×10 8;不变;减少.点评:本题考查了学生对阿基米德原理、物体的漂浮条件的掌握和运用,关键是浮力公式的应用,本题的难点是由海上进入长江后浮力不变,因为船始终漂浮,这也是最容易出错的地方.三、作图题(本题包括 3 个小题,共8 分)18.(2 分)如图所示,OO′是凸透镜的主光轴,A′B′是蜡烛AB通过凸透镜成的像,试在图中画出光线AC经凸透镜后的折射光线,并用作图的方法找出右侧焦点的位置.考点:透镜的光路图.专题:作图题;压轴题.分析:由于 A′B′是蜡烛AB 通过凸透镜成的像,由此可以画出入射光线AC经过凸透镜折射后的折射光线.由 A 点发出的平行于主光轴的入射光线经过凸透镜折射后要过A′点,同时其折射光线还要经过凸透镜的焦点,由此可以确定其焦点位置.解答:解:连接 CA′,就是入射光线AC经凸透镜后的折射光线;过 A 点画出平行于凸透镜主光轴的入射光线AD,连接 DA′,交主光轴于F 点,则点就是凸透镜的焦点.如图所示:F 点评:实像都是由物体发出的光线经过折射后形成的,利用两者的对应关系是解决此题的关键.19.( 3 分)如图所示,轻质杠杆图中作出重物 G作用在杠杆上的力AO在力 F1、 G作用下处于平衡状态,L1为 F1的力臂,请在F2的示意图及其力臂 L2和力 F1的示意图.。
2019年浙江省杭州市高考数学二模试卷答案解析

2019年省市高考数学二模试卷(理科)答案解析一.选择题(共10小题)1.设集合A={x|x>1},B={x|x2≤4},则A∩B=()A.(1,2)B.(1,2]C.(0,2]D.(1,+∞)【解答】解:B={x|﹣2≤x≤2};∴A∩B=(1,2].故选:B.2.已知复数z=1+i(i是虚数单位),则=()A.i B.﹣i C.1+i D.1﹣i【解答】解:∵z=1+i,∴===i.故选:A.3.二项式的展开式的常数项为()A.20B.﹣20C.160D.﹣160【解答】解:二项式(2x﹣)6的展开式的通项公式为T r+1=•(﹣1)r•26﹣r•x6﹣2r,令6﹣2r=0,求得r=3,可得展开式中的常数项是﹣8•=﹣160,故选:D.4.设a,b∈R,则“a>b”是“a|a|>b|b|”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件【解答】解:若a>b,①a>b≥0,不等式a|a|>b|b|等价为a•a>b•b,此时成立.②0>a>b,不等式a|a|>b|b|等价为﹣a•a>﹣b•b,即a2<b2,此时成立.③a≥0>b,不等式a|a|>b|b|等价为a•a>﹣b•b,即a2>﹣b2,此时成立,即充分性成立.若a|a|>b|b|,①当a>0,b>0时,a|a|>b|b|去掉绝对值得,(a﹣b)(a+b)>0,因为a+b>0,所以a﹣b>0,即a>b.②当a>0,b<0时,a>b.③当a<0,b<0时,a|a|>b|b|去掉绝对值得,(a﹣b)(a+b)<0,因为a+b<0,所以a﹣b>0,即a>b.即必要性成立,综上“a>b”是“a|a|>b|b|”的充要条件,故选:C.5.《九章算术》卷五商功中有如下问题:今有刍甍(音meng,底面为矩形的屋脊状的几何体),下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何.已知该刍甍的三视图如图所示,则此刍甍的体积等于()A.3B.5C.6D.12【解答】解:由三视图还原原几何体如图:沿上棱两端向底面作垂面,且使垂面与上棱垂直,则将几何体分成两个四棱锥和1个直三棱柱,则三棱柱的体积V1=×3×1×2=3,四棱锥的体积V2=×1×3×1=1,由三视图可知两个四棱锥大小相等,∴此刍甍的体积V=V1+2V2=5(立方丈),故选:B.6.函数y=(x﹣1)2(x﹣2)e x(其中e为自然对数的底数)的图象可能是()A.B.C.D.【解答】解:当x→+∞,f(x)→+∞,排除C,D,由f(x)=0得x=2或x=1,且当1<x<2时,f(x)<0,排除B,故选:A.7.已知a≠c,随机变量ξ,η的分布列如表所示.ξ123P a b cη123P c b a命题p:Eξ=Eη,命题q:Dξ=Dη,则()A.p真q真B.p真q假C.p假q真D.p假q假【解答】解:依题意Eξ=a+2b+3c,Eη=c+2b+3a,Eξ﹣Eη=2c﹣2a,a≠c,故Eξ﹣Eη≠0,即p为假命题.E(ξ2)=a+4b+9c,所以D(ξ)=E(ξ2)﹣E2(ξ)=a+4b+9c﹣(a+2b+3c)2.同理:D(η)=c+4b+9a﹣(c+2b+3a)2,∴D(ξ)﹣D(η)=a+4b+9c﹣(a+2b+3c)2﹣c+4b+9a﹣(c+2b+3a)2=8(c﹣a)+(2a ﹣2c)(4a+4b+4c)因为a+b+c=1,所以D(ξ)﹣D(η)=8(c﹣a)﹣8(c﹣a)=0,即D(ξ)=D(η),故q真.综上p假q真,故选:C.8.设函数,则函数y=f(f(x))()A.是偶函数也是周期函数B.是偶函数但不是周期函数C.不是偶函数是周期函数D.既不是偶函数也不是周期函数【解答】解:根据题意,f(x)==,则有f(﹣x)=f(x),即函数f(x)为偶函数,则f(f(﹣x))=f(f(x)),即函数y =f(f(x))为偶函数;又由f(x)==,当x<﹣1时,f(x)=2﹣2x+1,有﹣<f(x)<,当﹣1≤x≤1时,f(x)=﹣,当x>1时,f(x)=2﹣()x﹣1,有﹣<f(x)<,综合可得:﹣<f(x)<,则f(f(x))=﹣,其函数值为常数,y=f(f(x))为周期函数;故y=f(f(x))为偶函数且是周期函数;故选:A.9.已知数列{a n}满足2a n≤a n﹣1+a n+1(n∈N*,n≥2),则()A.a5≤4a2﹣3a1B.a2+a7≤a3+a6C.3(a7﹣a6)≥a6﹣a3D.a2+a3≥a6+a7【解答】解:∵2a n≤a n﹣1+a n+1(n∈N*,n≥2),∴a n﹣a n﹣1≤a n+1﹣a n,∴a4﹣a3≤a5﹣a4≤a6﹣a5≤a7﹣a6,∴a6﹣a3=a6﹣a5+a5﹣a4+a4﹣a3≤3(a7﹣a6),即3(a7﹣a6)≥a6﹣a3,故选:C.10.已知椭圆,直线x+y=1与椭圆Γ交于M,N两点,以线段MN为直径的圆经过原点.若椭圆Γ的离心率不大于,则a的取值围为()A.B.C.D.【解答】解:椭圆,直线x+y=1与椭圆Γ交于M,N两点,可得a>1,由x+y=1联立椭圆方程可得(a2+b2)x2﹣2a2x+a2﹣a2b2=0,设M(x1,y1),N(x2,y2),可得x1+x2=,x1x2=,线段MN为直径的圆经过原点,可得OM⊥ON,即有x1x2+y1y2=0,可得x1x2+(1﹣x1)(1﹣x2)=0,化为2x1x2+1﹣(x1+x2)=0,则2•+1﹣=0,化为a2+b2=2a2b2,由e≤,可得1﹣≤,即b2≥a2,可得≥a2,即有2a2﹣1≤4,解得a≤,可得1<a≤,故选:D.二.填空题(共7小题)11.双曲线的焦距为;渐近线方程为y=.【解答】解:由题知,a2=4,b2=1,故c2=a2+b2=5,∴双曲线的焦距为:,渐近线方程为:.故答案为:;.12.设函数,若,则实数a=,f(f(2))=.【解答】解:函数,若,可得,解得a=;f(2)==﹣.f(f(2))=f(﹣)===.故答案为:;.13.在△ABC中,角A,B,C所对的边分别为a,b,c,已知,则sin C=;当a=2,2sin A=sin C时,则b=或2.【解答】解:因为cos2C=1﹣2sin2C=﹣,与0<C<π,所以解得:sin C=.当a=2,2sin A=sin C时,由正弦定理,解得:c==4.由cos2C=2cos2C﹣1=﹣,与0<C<π得cos C=±.由余弦定理c2=a2+b2﹣2ab cos C,得b2±b﹣12=0,解得b=,或b=2.故答案为:,或2.14.设实数x,y满足不等式组则x+2y的最小值是5;设d=x2+y2,则d的最小值等于10.【解答】解:依题意作出实数x,y满足不等式组可行性区域如图,目标函数z=x+2y在点(3,1)处取到最小值:5.d=x2+y2,由图形可知,A到原点的距离最小,则d的最小值等于:10故答案为:5;10.15.已知集合A={1,3,5},B={0,2,4},分别从A,B中各取2个不同的数,能组成不同的能被3整除的四位偶数的个数是32(用数字作答).【解答】解:若A选1,3,则B中只能选0,2,若个位是0,则有A=6,若个位是4,则有C A=4种,此时有6+4=10种,若A选1,5,则B中只能选4,2,此时偶数有C A=12种,若A选3,5,则B中只能选0,4,若个位是0,则有A=6,若个位是4,则有C A=4种,此时有6+4=10种,综上共有10+12+10=32种,故答案为:32.16.已知向量,平面向量满足,则的最小值等于20.【解答】解:向量,平面向量满足,可得22+•=10+•=||,可得•=||﹣10,则=2﹣4•=||2﹣4||+40=(||﹣2)2+20,当||=2,可得的最小值为20.故答案为:20.17.如图,已知矩形ABCD,,AD=1,AF⊥平面ABC,且AF=3.E为线段DC 上一点,沿直线AE将△DAE翻折成△D'AE,M为BD'的中点,则三棱锥M﹣BCF体积的最小值是.【解答】解:选固定点E,可知D′在圆上运动,现E在线段DC上运动,且AD′=1,∴D′的运动轨迹为以A为球心,半径为AD′=1的球面的一部分,∵S△BCF===,∴求三棱锥M﹣BCF体积的最小值只需求M到面BCF的距离d1的最小值,即求D′到面BCF的距离d的最小值,过A作BF的垂线,垂足为H,当D′为AH与球面的交点G时,D′到面BCF的距离最小,此时点E在DC上,d=AF﹣1=,d1==,∴三棱锥M﹣BCF体积的最小值为:V min=S△BCF×d1=.故答案为:.三.解答题(共5小题)18.已知函数.(1)求函数f(x)的单调递增区间;(2)当时,求函数f(x)的值域.【解答】(本题满分为14分)解:(1)∵=2sin(2x﹣)+1,…5分∴2kπ﹣≤2x﹣≤2kπ+,k∈Z,解得:kπ﹣≤x≤kπ+,k∈Z,∴函数f(x)的单调递增区间为:[kπ﹣,kπ+],k∈Z,…9分(2)因为,∴2x﹣∈[﹣,],∴sin(2x﹣)∈[﹣1,],∴函数f(x)的值域为:[﹣1,2].…14分19.如图,四边形ABCD为矩形,平面ABEF⊥平面ABCD,EF∥AB,∠BAF=90°,AD =2,AB=AF=1,点P在线段DF上.(1)证明:AF⊥平面ABCD.(2)若二面角DF﹣AP﹣C的余弦值为,求PF的长度.【解答】(I)证明:∵∠BAF=90°,∴AB⊥AF.又平面ABEF⊥平面ABCD,平面ABEF∩平面ABCD=AB,AF⊂平面ABEF,∴AF⊥平面ABCD.(II)解:以A为原点,以AB,AD,AF为坐标轴建立空间坐标系,如图所示,则B(1,0,0),C(1,2,0),D(0,2,0),∵AB⊥平面ADF,∴=(1,0,0)为平面ADF的一个法向量,设=λ,则P(0,2λ,1﹣λ),∴=(0,2λ,1﹣λ),=(1,2,0).设平面APC的法向量为=(x,y,z),则,∴,令y=1可得=(﹣2,1,),∴|cos<>|=||=||=,解得λ=,∴PF=.20.设等差数列{a n}前n项和为A n,等比数列{b n}前n项和为B n.若B n+3=8B n+7,a1=b2,a4=b4.(1)求b n和A n;(2)求数列{b n﹣A n}的最小项.【解答】解:(1)等差数列{a n}的公差设为d,等比数列的公比设为q,B n+3=8B n+7,可得b1+b2+b3+(b4+…+b n+3)=b1+b2+b3+q3B n=8B n+7,则q3=8,b1+b2+b3=7,解得q=2,b1=1,则b n=2n﹣1;a1=b2=2,a4=b4=8,可得d==2,A n=2n+•2•n(n﹣1)=n2+n;(2)设c n=b n﹣A n=2n﹣1﹣n2﹣n,c n+1﹣c n=2n﹣(n+1)2﹣n﹣1﹣(2n﹣1﹣n2﹣n)=2n﹣1﹣2(n+1),当n≤4时,c n+1<c n;当n≥5时,c n+1>c n,可得数列{b n﹣A n}的最小项为c5=﹣14.21.如图,已知P(1,1)为抛物线y=x2上一点,斜率分别为k,﹣k(k>2)的直线P A,PB分别交抛物线于点A,B(不与点P重合).(1)证明:直线AB的斜率为定值;(2)若△ABP的切圆半径为,(i)求△ABP的周长(用k表示);(ii)求直线AB的方程.【解答】证明:(1)设直线P A的方程为y=k(x﹣1)+1,与抛物线联立可得x2﹣kx+k ﹣1=0,易知A(k﹣1,(k﹣1)2),B(﹣k﹣1,(k+1)2),∴直线AB的斜率k AB==﹣2为定值.(2)由(1)可得直线AB的方程为y=﹣2(x﹣k+1)+(k﹣1)2,∴点P到直线AB的距离d=,|AP|=•(k﹣2),|BP|=(k+2),|AB|=2k,(i)△ABP的周长l=2k+2k,(ii)设△ABP的切圆半径为r,则r=﹣,即r===﹣,即﹣=﹣,解得k=5,∴直线AB的方程为y=﹣2x+24.22.已知函数f(x)=(x﹣1)e x.(1)求函数f(x)的单调递增区间;(2)若方程f(x)=ax+b(a,b∈R)有非负实数解,求a2+4b的最小值.【解答】解:(1)由f(x)=(x﹣1)e x,的f′(x)=xe x,由f′(x)=xe x>0,得x>0,∴函数f(x)的单调递增区间为(0,+∞);(2)设g(x)=(x﹣1)e x﹣ax﹣b,则g′(x)=xe x﹣a.当a≤0时,g′(x)≥0在[0,+∞)上恒成立,可得g(x)在[0,+∞)上单调递增,∴g(0)=﹣1﹣b≤0,得b≥﹣1,故a2+4b≥﹣4;当a>0时,存在x0>0,使g′(x0)=0,即,且g(x)在[0,x0]上单调递减,在[x0,+∞)上单调递增.∴≤0,解得.因此,.设h(x)=x2e2x﹣4(x2﹣x+1)e x,则h′(x)=2(x2+x)e x(e x﹣2).∴h(x)在[0,ln2]上单调递减,在[ln2,+∞)上单调递增.∴h(ln2)<h(0)=﹣4,h(x)≥h(ln2)=﹣4ln22+8ln2﹣8.∴当a=2ln2,b=﹣2ln22+2ln2﹣2时,a2+4b取到最小值﹣4(ln2﹣1)2﹣4,此时方程f(x)=ax+b有非负实数解ln2.综上所述,a2+4b的最小值为﹣4(ln2﹣1)2﹣4.。
解析―——2019年深圳二模语文简版答案2019.4.18

2019年深圳市高三年级第二次调研考试语文答案(简版)(一)论述类文本阅读1.B【解析】本题考查难度中等,考查分析文章内容的能力,能力层级为C级。
A项强加因果,由原文“然而,众多匪夷所思的‘多元解读’也随之出现,这类荒腔走板的解读”来看,该项将转折关系说成了因果关系。
C项曲解文意,由原文“文本‘空白’中存在某种意向,召唤读者去言明,并希望读者完全按照文本召唤,实现文本解读的一切潜在可能”来看,应该是按照文本召唤,实现文本阅读,而不是按照“自己的理解进行个性化解读”。
D 项“以便从中挑选正确的理解”于文无据。
2.D【解析】本题考查难度中等,考查分析文章论点、论据、论证的能力,能力层级为C级。
由原文最后一段来看,列举李白、杜甫的遭遇是为了论证“历史上错误的‘读者决定论’不止出现过一次”的观点,D项论证“论证经典文本的地位不受读者影响的观点”说法错误。
3.C【解析】本题考查难度中等,考查评价文本中作者的观点态度和合理推断的能力,能力层级为C级。
由原文“读者所推见的人物,却并不一定和作者设想的相同……”来看,C项“读者在理解人物形象时应该做到以作者设想为主”说法错误。
(二)实用类文本阅读(本题共3小题,12分)4. C【解析】本题考查难度中等,考查分析概括材料内容的能力。
能力层级为C级。
结合材料“人口和劳动力的过度集中导致了地价上涨、环境恶化、生活成本增加等问题”,而“东京的人口密度要比首尔低得多”说明人口增长的空间较大,C项“意味着其人口增长的空间比较小”颠倒是非。
5. C【解析】本题考查难度中等,考查分析概括材料内容要点的能力,能力层级为C 级。
A项强加因果,“使得大城市污染更少”的原因是“大城市控制污染的能力更强”,而不是“大城市具有更明显的聚集效应和规模效应”。
B项从材料一来看,主要介绍了大城市与中小城镇的土地利用率,并没有说明特大城市与大城市的比较,故该项中“特大城市要明显大于大城市”的说法于文无据。
2018-2019学年高中毕业班第二次统测数学(理科)试题参考答案

高三数学(理科)试题答案 第 1 页 共 6 页2019届高中毕业班第二次统一检测题理科数学参考答案及评分标准一、选择题13. 2114. ()10102024-写不扣分 15.120 16.)+∞三、解答题(17)(本小题满分12分)解:(1)在ΔABC 中,cos 0,B <所以ππ2B <<,所以sin 7B ==, 由正弦定理可得,sinsin AC BC B A =7sin A=,得sin A =…………4分 又因为A B <,所以π0,2A ⎛⎫∈⎪⎝⎭,所以π3A = …………6分 (2)()()sin sin sin sin cos cos sin C A B A B A B A B π=-+=+=+⎡⎤⎣⎦1172⎛⎫=-+= ⎪⎝⎭ …………9分 11sin 8722ABC S AC BC C ∆==⨯⨯= …………12分 (18)(本小题满分12分)解:(1)取BS 的中点O ,连接CO AO ,,因为ΔSBC 是等边三角形,所以BS CO ⊥,又,BS AC AC CO C ⊥=,所以BS AOC ⊥面.又AO AOC ⊂面,所以BS AO ⊥. …………3分 又O 是BS 的中点,所以AB AS = …………4分高三数学(理科)试题答案 第 2 页 共 6 页(2)设2BS =,依题意可得1AO OS ==,OC =,2CA CS ==.因为222AO OC AC +=,所以AO OC ⊥.又由(1)知,,OS OA OS OC ⊥⊥,如图以O 为原点,,,OS OC OA 分别为x 轴,y 轴,z 轴的正方向建立空间直角坐标系 …………6分 则()0,0,1A ,()1,0,0S,()C ,()1,0,0B -,()AD BC ==,()1,0,1AS =-,设面ASD 的一个法向量为()1111,,n x y z =,则110AS n AD n ⎧=⎪⎨=⎪⎩,即111100x z x -=⎧⎪⎨=⎪⎩,得方程的一组解为1111x y z ⎧=⎪=-⎨⎪=⎩,即(13,n =- …………8分()1,0,1CDBA ==,()SC =-,设面SDC 的一个法向量为()2222,,n x y z =,则220SC n CD n ⎧=⎪⎨=⎪⎩,即222200x x z ⎧-+=⎪⎨+=⎪⎩,得方程的一组解为2221x y z ⎧=⎪=⎨⎪=⎩,即(23,1,n =…………10分1212121cos ,77n n n n n n ===- …………11分所以二面角A SD C --的余弦值为17. …………12分(19)(本小题满分12分)12514x x k =+21211kx k=+=+223165214k AB d k-=+ ,t =则220,16t t k >=9t t14,高三数学(理科)试题答案 第 4 页 共 6 页(20)(本小题满分12分)解:(1) 设“顾客投掷一次硬币,该次投掷‘顾客胜利’”为事件A ,则()344445216C C P A +== 所以顾客投掷一次硬币,该次投掷“顾客胜利”的概率为516. …………3分 (2)方案一:设顾客参加的3次投掷活动中“顾客胜利”次数为X ,获得代金券数目为Y ,则53,16XB ⎛⎫⎪⎝⎭,132Y X =, 2111515332323216216EY E X EX ⎛⎫===⨯⨯= ⎪⨯⎝⎭ …………6分 方案二:设顾客每买一件产品获得的代金券金额为ξ,则()31113310164096P ξ⎛⎫===⎪⎝⎭, 22133151135111815551616164096P C ξ⨯⨯⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭, 2233151131125825111616164096P C ξ⨯⨯⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭, 333331535125516164096P C ξ⨯⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭…………8分 (以上概率的值无需化简)323333311135111311251351330165516111651616E ξ⨯⨯⨯⨯⨯⎛⎫=⨯+⨯+⨯+⨯= ⎪⎝⎭ …………10分 因为231512021616EY E ξ==<⨯ 所以统计的角度来分析,小翁该采取哪种奖励方案二. …………12分高三数学(理科)试题答案 第 5 页 共 6 页(21)(本小题满分12分)解:(1)()2ln 12'x a f x x -=, …………1分 因为()f x 在()0+∞,上单调递减,所以()'0f x ≤,得ln 10x a --≤ 令()ln 1h x x a =--,则()max 0h x ≤ …………2分 ()'h x =,当016x <<时,()'0h x >,()h x 单调递增;当16x >时,()'0h x <,()h x 单调递减,所以当16x =时,()h x 取得最大值()16ln163h a =+-由ln1630a +-≤得34ln 2a ≤- …………4分 (2)()1'g x x=,依题意有1211x x =-,化简整理得122x x -=,因为12x x ≠,所以2= ① …………6分()14122x x =,当且仅当12x x =时,等号成立成立,即()14124x x ≥,即12256x x ≥,又因为12x x ≠,所以12256x x > …………8分()()()121212ln ln ln g x g x x x x x +=+=,结合①式得 ()()()1212ln g x g x x x +=-,令12x x t =,则256t > 由(1)可知()ln 1h x x a =-在()16,+∞上单调递减,所以ln y t =在()16,+∞上单调递增, …………10分 所以当256t >时,ln ln 25688ln 2y t =>=- 即()()1288ln 2g x g x +>- …………12分高三数学(理科)试题答案 第 6 页 共 6 页(22)(本小题满分10分)解:(1)将C 的参数方程化为普通方程得()(2214x y -+=,将c o s ,s i n x y ρθρθ==代入,并化简得C的极坐标方程为2cos ρθθ=+. 2l 的极坐标方程为()πR 3θαρ=+∈ …………4分 (2)依题意可得()2cos ,A ααα+,即4sin ,6A παα⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭πππ2cos ,333B ααα⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,即π4cos ,3B αα⎛⎫+ ⎪⎝⎭ππ4sin 4cos 63OA OB ααα⎛⎫⎛⎫+=++=+ ⎪ ⎪⎝⎭⎝⎭ …………8分因为π02α<<,所以ππ5π336α<+<,当πππ,326αα+==即时,OA OB +取得最大值 …………10分(23)(本小题满分10分)解:(1)不等式()2f x >,即|2||22|2x x -+->. 可得22222x x x ≥⎧⎨-+->⎩,或122222x x x <<⎧⎨-+->⎩或12222x x x ≤⎧⎨--+>⎩ …………3分解得223x x <>或,所以不等式的解集为2|23x x x ⎧⎫<>⎨⎬⎩⎭或. …………5分 (2)()2211f x x a x x a x x =-+-=-+-+- ()11x a x x ≥---+-11a x =-+-1a ≥-当且仅当1x =时,两处等号同时成立, …………8分 所以12a -≥,解得1a ≤-或3a ≥ 实数a 的取值范围是(][),13,-∞-+∞ …………10分。
[精品]2019届高三数学二模试题(含解析)
![[精品]2019届高三数学二模试题(含解析)](https://img.taocdn.com/s3/m/3367bbbd6294dd88d1d26b0f.png)
2019高考数学二模试卷一、填空题:(本大题共14小题,每小题5分,共70分)1.已知全集U=Z ,集合A={x|0<x <5,x ∈U},B={x|x ≤1,X ∈U},则A ∩(∁U B )= .2.若复数z 的共轭复数满足,则复数z 的虚部是 .3.双曲线的准线方程是 .4.某校共有学生1800人,现从中随机抽取一个50人的样本,以估计该校学生的身体状况,测得样本身高小于195cm 的频率分布直方图如图,由此估计该校身高不小于175的人数是 .5.命题“∀x >2,都有x 2>2”的否定是 . 6.如图中流程图的运行结果是 .7.口袋中有大小相同的5个小球,小球上分别标有数字1,1,2,2,4,一次从中取出两个小球,则取出的两个小球上所标数字之积为4的概率是 .8.已知等差数列{a n }的前n 项和为S n ,a 4=10,S 4=28,数列的前n 项和为T n ,则T 2017= .9.将函数y=sinxcosx 的图象向右平移m (m >0)个单位,所得曲线的对称轴与函数的图象的对称轴重合,则实数m 的最小值为 .10.如图,在△ABC 中,D 为BC 的中点,E 为AD 的中点,直线BE 与边AC 交于点F ,若AD=BC=6,则= .11.已知直线l1:x﹣2y=0的倾斜角为α,倾斜角为2α的直线l2与圆M:x2+y2+2x﹣2y+F=0交于A、C两点,其中A(﹣1,0)、B、D在圆M上,且位于直线l2的两侧,则四边形ABCD的面积的最大值是.12.已知四面体ABCD的底面BCD是边长为2的等边三角形,AB=AC=3,则当棱AD长为时,四面体ABCD的体积最大.13.已知函数f(x),g(x)是定义在R上的一个奇函数和偶函数,且f(x﹣1)+g(x﹣1)=2x,则函数f(x)= .14.已知b≥a>0,若存在实数x,y满足0≤x≤a,0≤y≤b,(x﹣a)2+(y﹣b)2=x2+b2=a2+y2,则的最大值为.二、解答题:本大题共6小题,共90分.解答应写出必要的文字说明或推理、验算过程.15.已知△ABC的外接圆半径为1,角A,B,C的对应边分别为a,b,c,若sinB=acosC.,(1)求的值;(2)若M为边BC的中点,,求角B的大小.16.如图,在三棱柱ABC﹣A1B1C1中,侧面A1ABB1是菱形,侧面C1CBB1是矩形.(1)D是棱B1C1上一点,AC1∥平面A1BD,求证:D为B1C1的中点;(2)若A1B⊥AC1,求证:平面A1ABB1⊥平面C1CBB1.17.已知椭圆C:的离心率为,焦距为2,直线y=kx(x≠0)与椭圆C交于A,B两点,M为其右准线与x轴的交点,直线AM,BM分别与椭圆C交于A1,B1两点,记直线A1B1的斜率为k1(1)求椭圆C的方程;(2)是否存在常数λ,使得k1=λk恒成立?若存在,求出λ的值;若不存在,请说明理由.18.数列{a n}满足,n=1,2,3,….(1)求a3,a4,并求数列{a n}的通项公式;(2)设b n=,记F(m,n)=,求证:m<n,F(m,n)<4对任意的;(3)设S k=a1+a3+a5+…+a2k﹣1,T k=a2+a4+a6+…+a2k,W k=,求使W k>1的所有k的值,并说明理由.19.某冰淇淋店要派车到100千米外的冷饮加工厂原料,再加工成冰淇淋后售出,已知汽车每小时的运行成本F(单位:元)与其自重m(包括车子、驾驶员及所载货物等的质量,单位:千克)和车速v(单位:千米/小时)之间满足关系式:.在运输途中,每千克冷饮每小时的冷藏费为10元,每千克冷饮经过冰淇淋店再加工后,可获利100元.若汽车重量(包括驾驶员等,不含货物)为1.3吨,最大载重为1吨.汽车来回的速度为v(单位:千米/小时),且最大车速为80千米,一次进货x千克,而且冰淇淋供不应求.(1)求冰淇淋店进一次货,经加工售卖后所得净利润w与车速v和进货量x之间的关系式;(2)每次至少进货多少千克,才能使得销售后不会亏本(净利润w≥0)?(3)当一次进货量x与车速v分别为多少时,能使得冰淇淋店有最大净利润?并求出最大值.(提示:)20.已知函数(e为自然对数的底数,m∈R).(1)求函数f(x)的单调区间和极值;(2)当时,求证:∀x>0,f(x)<x2lnx恒成立;(3)讨论关于x的方程|lnx|=f(x)的根的个数,并证明你的结论.2017年高考熟中模拟卷B.选修4-2:矩阵与变换21.已知矩阵M对应的变换将点(﹣5,﹣7)变换为(2,1),其逆矩阵M﹣1有特征值﹣1,对应的一个特征向量为,求矩阵M.C.选修4-4:坐标系与参数方程22.在平面直角坐标系xoy中,以O为极点,x轴的正半轴为极轴,取相同的单位长度,建立极坐标系,已知曲线C1的参数方程为,(,α为参数),曲线C2的极坐标方程为,求曲线C1与曲线C2的交点的直角坐标.【必做题】第22题、第23题,每题10分共计20分.请答题卡的指定区域内作答解答应写出文字说明、证明过程或演算步骤.23.在英国的某一娱乐节目中,有一种过关游戏,规则如下:转动图中转盘(一个圆盘四等分,在每块区域内分别标有数字1,2,3,4),由转盘停止时指针所指数字决定是否过关.在闯n关时,转n次,当次转得数字之和大于n2时,算闯关成功,并继续闯关,否则停止闯关,闯过第一关能获得10欧元,之后每多闯一关,奖金翻倍.假设每个参与者都会持续闯关到不能过关为止,并且转盘每次转出结果相互独立.(1)求某人参加一次游戏,恰好获得10欧元的概率;(2)某人参加一次游戏,获得奖金X欧元,求X的概率分布和数学期望.24.(1)证明:;(2)证明:;(3)证明:.2017年江苏省苏州市常熟中学高考数学二模试卷参考答案与试题解析一、填空题:(本大题共14小题,每小题5分,共70分)1.已知全集U=Z,集合A={x|0<x<5,x∈U},B={x|x≤1,X∈U},则A∩(∁U B)= {2,3,4} .【考点】1H:交、并、补集的混合运算.【分析】根据集合的基本运算进行求解即可.【解答】解:A={x|0<x<5,x∈U}={1,2,3,4},B={x|x≤1,X∈U},则∁U B={x|x>1,X∈U}={2,3,4,5,…},则A∩(∁U B)={2,3,4},故答案为:{2,3,4}2.若复数z的共轭复数满足,则复数z的虚部是 3 .【考点】A5:复数代数形式的乘除运算.【分析】利用复数的运算法则、共轭复数与虚部的定义即可得出.【解答】解:∵,∴﹣i••i=﹣i(3+4i),∴=4﹣3i.∴z=4+3i.∴复数z的虚部是3.故答案为:3.3.双曲线的准线方程是y=.【考点】KC:双曲线的简单性质.【分析】直接利用双曲线方程求解双曲线的准线方程即可.【解答】解:双曲线,可得a=1,b=,c=2,双曲线的准线方程为:y=±.故答案为:y=.4.某校共有学生1800人,现从中随机抽取一个50人的样本,以估计该校学生的身体状况,测得样本身高小于195cm的频率分布直方图如图,由此估计该校身高不小于175的人数是288 .【考点】B8:频率分布直方图.【分析】由频率分布直方图得样本身高不小于175cm的频率,由此能估计该校身高不小于175cm的人数.【解答】解:由频率分布直方图得样本身高不小于175cm的频率为:(0.012+0.004)×10=0.16,∴估计该校身高不小于175cm的人数是:1800×0.16=288.故答案为:288.5.命题“∀x>2,都有x2>2”的否定是∃x0>2,x02≤2 .【考点】2J:命题的否定.【分析】直接利用全称命题的否定是特称命题写出结果即可.【解答】解:命题“∀x>2,x2>2”是全称命题,其否定是:∃x0>2,x02≤2.故答案为:∃x0>2,x02≤2.6.如图中流程图的运行结果是 6 .【考点】EF:程序框图.【分析】根据程序框图进行模拟计算即可.【解答】解:第一次,S=1,i=2,S>10不成立,第二次,S=1+2=3,i=3,S>10不成立,第三次,S=3+3=6,i=4,S>10不成立第四次,S=6+4=10,i=5,S>10不成立第五次,S=10+5=15,i=6,S>10成立,输出i=6,故答案为:67.口袋中有大小相同的5个小球,小球上分别标有数字1,1,2,2,4,一次从中取出两个小球,则取出的两个小球上所标数字之积为4的概率是.【考点】CB:古典概型及其概率计算公式.【分析】先求出基本事件总数n=,再由列举法求出取出的两个小球上所标数字之积包含的基本事件个数,由此能求出取出的两个小球上所标数字之积为4的概率.【解答】解:∵口袋中有大小相同的5个小球,小球上分别标有数字1,1,2,2,4,一次从中取出两个小球,基本事件总数n=,取出的两个小球上所标数字之积包含的基本事件有:(1,4),(1,4),(2,2),共3个,∴取出的两个小球上所标数字之积为4的概率p=.故答案为:.8.已知等差数列{a n}的前n项和为S n,a4=10,S4=28,数列的前n项和为T n,则T2017=.【考点】8E:数列的求和.【分析】利用已知条件求出等差数列的前n项和,化简所求的通项公式,然后求和即可.【解答】解:等差数列{a n}的前n项和为S n,a4=10,S4=28,可得a1+a4=14,解得a1=4,10=4+3d,解得d=2,S n=4n+=n2+3n,==,T n=+…+=,则T 2017==.故答案为:.9.将函数y=sinxcosx 的图象向右平移m (m >0)个单位,所得曲线的对称轴与函数的图象的对称轴重合,则实数m 的最小值为.【考点】HJ :函数y=Asin (ωx+φ)的图象变换.【分析】首先化简被平移函数的解析式,得到对称轴的表达式以及函数的图象的对称轴,利用对称轴重合得到m 的值.【解答】解:将函数y=sinxcosx=sin2x 的图象向右平移m (m >0)个单位,所得曲线的对称轴与函数的图象的对称轴重合,即2(x ﹣m )=k,得到x=,k ∈Z ;,得到x=,k 1∈Z ;由题意x==,k ,k 1∈Z所以实数m 的最小值为;故答案为:.10.如图,在△ABC 中,D 为BC 的中点,E 为AD 的中点,直线BE 与边AC 交于点F ,若AD=BC=6,则=﹣18 .【考点】9V :向量在几何中的应用.【分析】建立坐标系,设∠ADC=α,求出各点坐标,代入向量的数量积运算公式计算即可. 【解答】解:以BC 为x 轴,以BC 的中垂线为y 轴建立平面直角坐标系,设∠ADC=α,则A (6cos α,6sin α),E (3cos α,3sin α),C (3,0),B (﹣3,0),设F(a,b),则,解得a=4cosα+1,b=4sinα,∴=(﹣3﹣6cosα,﹣6sinα),=(4cosα﹣2,4sinα),∴=(﹣3﹣6cosα)(4cosα﹣2)﹣24sin2α=﹣24cos2α+6﹣24sin2α=6﹣24=﹣18.故答案为:﹣18.11.已知直线l1:x﹣2y=0的倾斜角为α,倾斜角为2α的直线l2与圆M:x2+y2+2x﹣2y+F=0交于A、C两点,其中A(﹣1,0)、B、D在圆M上,且位于直线l2的两侧,则四边形ABCD的面积的最大值是.【考点】J9:直线与圆的位置关系.【分析】由已知求出tanα,得到直线l2的斜率,进一步求得方程,由A在圆上求得F,得到圆的方程,求出圆心坐标和半径,利用垂径定理求得|AC|的长度,然后结合圆与直线的位置关系图象,将ABCD的面积看成两个三角形△ABC和△ACD的面积之和,分析可得当BD为AC的垂直平分线时,四边形ABCD的面积最大.【解答】解:直线l1:x﹣2y=0的倾斜角为α,则tanα=,∴直线l2的斜率k=tan2α=.则直线l2的方程为y﹣0=(x+1),即4x﹣3y+4=0.又A(﹣1,0)在圆上,∴(﹣1)2﹣2+F=0,得F=1,∴圆的方程为x2+y2+2x﹣2y+1=0,化为标准方程:(x+1)2+(y﹣1)2=1,圆心(﹣1,1),半径r=1.直线l2与圆M相交于A,C两点,由点到直线的距离公式得弦心距d=,由勾股定理得半弦长=,弦长|AC|=2×=.又B,D两点在圆上,并且位于直线l2的两侧,四边形ABCD的面积可以看成是两个三角形△ABC和△ACD的面积之和,如图所示,当BD为弦AC的垂直平分线时(即为直径时),两三角形的面积之和最大,即四边形ABCD的面积最大,最大面积为:S=|AC|×|BE|+|AC|×|DE|=|AC|×|BD|=××2=,故答案为:.12.已知四面体ABCD的底面BCD是边长为2的等边三角形,AB=AC=3,则当棱AD长为时,四面体ABCD 的体积最大.【考点】LF:棱柱、棱锥、棱台的体积.【分析】当体积最大时,平面ABC与底面BCD垂足,利用勾股定理计算AD.【解答】解:取BC的中点E,连结AE,DE,∵AB=AC,BD=CD,∴BC⊥AE,BC⊥DE,∴∠AED为二面角A﹣BC﹣D的平面角,∴A到平面BCD的距离d=AE•sin∠AED,显然当∠AED=90°时,四面体体积最大.此时,AE==2,DE==,∴AD==.故答案为:.13.已知函数f(x),g(x)是定义在R上的一个奇函数和偶函数,且f(x﹣1)+g(x﹣1)=2x,则函数f(x)= 2x﹣2﹣x.【考点】3L:函数奇偶性的性质.【分析】根据题意,由于f(x﹣1)+g(x﹣1)=2x,则f(x)+g(x)=2x+1,同理可得f(﹣x)+g(﹣x)=2﹣x+1,利用函数的奇偶性可得﹣f(x)+g(x)=2﹣x+1,②,联立①②可得f(x)=(2x+1﹣2﹣x+1),对其变形可得答案.【解答】解:根据题意,f(x﹣1)+g(x﹣1)=2x,则f(x)+g(x)=2x+1,①,进而有f(﹣x)+g(﹣x)=2﹣x+1,又由函数f(x),g(x)是定义在R上的一个奇函数和偶函数,则有f(﹣x)+g(﹣x)=﹣f(x)+g(x),即有﹣f(x)+g(x)=2﹣x+1,②,联立①②可得:f(x)=(2x+1﹣2﹣x+1)=2x﹣2﹣x,即f(x)=2x﹣2﹣x,故答案为:2x﹣2﹣x14.已知b≥a>0,若存在实数x,y满足0≤x≤a,0≤y≤b,(x﹣a)2+(y﹣b)2=x2+b2=a2+y2,则的最大值为.【考点】R3:不等式的基本性质.【分析】设A(0,b),B(x,0),C(a,b﹣y),由x﹣a)2+(y﹣b)2=x2+b2=a2+y2得△ABC为等边△,设△ABC边长为m,∠OAB=θ,(0)过C作CH⊥x轴与H,则∠ACH=θ﹣,a=mcos(),b=mcosθ即可求解.【解答】解:如图设A(0,b),B(x,0),C(a,b﹣y)∵(x﹣a)2+(y﹣b)2=x2+b2=a2+y2∴△ABC为等边△,设△ABC边长为m,∠OAB=θ,(0)过C作CH⊥x轴与H,则∠ACH=θ﹣,∴b=mcosθ∴∴当θ=0时,故答案为:二、解答题:本大题共6小题,共90分.解答应写出必要的文字说明或推理、验算过程.15.已知△ABC的外接圆半径为1,角A,B,C的对应边分别为a,b,c,若sinB=acosC.,(1)求的值;(2)若M为边BC的中点,,求角B的大小.【考点】HT:三角形中的几何计算.【分析】(1)由△ABC的外接圆半径为1,及正弦定理得a=2RsinA=2sinA,⇒sinAcosC﹣cosAsinCsin(A﹣C)=0,即可得a=c,即可.(2)由得⇔⇒⇒b=,即可得cosB=.【解答】解:(1)由△ABC的外接圆半径为1,及正弦定理得a=2RsinA=2sinA,∴sinB=acosC变形为:sin(A+C)=2sinAcosC⇒sinAcosC﹣cosAsinC=0sin(A﹣C)=0,∵A﹣C∈(﹣π,π),∴A﹣C=0,∴a=c,∴的值为1(2)∵M为边BC的中点,∴∴⇔又∵,a=c∴⇒⇒b=∴cosB=,∵B∈(0,π),∴角B的大小为.16.如图,在三棱柱ABC﹣A1B1C1中,侧面A1ABB1是菱形,侧面C1CBB1是矩形.(1)D是棱B1C1上一点,AC1∥平面A1BD,求证:D为B1C1的中点;(2)若A1B⊥AC1,求证:平面A1ABB1⊥平面C1CBB1.【考点】LY:平面与平面垂直的判定.【分析】(1)连结AB1交A1B于E,连结DE,由AC1∥平面A1BD可得AC1∥DE,由E为AB1的中点即可得出D是B1C1的中点;(2)证明A1B⊥平面AB1C1,得出A1B⊥B1C1,再结合B1C1⊥BB1得出B1C1⊥平面A1ABB1,于是平面A1ABB1⊥平面C1CBB1.【解答】证明:(1)连结AB1交A1B于E,连结DE.∵AC1∥平面A1BD,AC1⊂平面AB1C1,平面AB1C1∩平面A1BD=DE,∴AC1∥DE,∵侧面A1ABB1是菱形,∴E是AB1的中点,∴D是B1C1的中点.(2)∵侧面A1ABB1是菱形,∴AB1⊥A1B,又A1B⊥AC1,AB1∩AC1=A,AB1⊂平面AB1C1,AC1⊂平面AB1C1,∴A1B⊥平面AB1C1,又B1C1⊂平面AB1C1,∴A1B⊥B1C1,∵侧面C1CBB1是矩形,∴B1C1⊥BB1,又BB1∩A1B=B,BB1⊂平面A1ABB1,A1B⊂平面A1ABB1,∴B1C1⊥平面A1ABB1.∵B1C1⊂平面C1CBB1,∴平面A1ABB1⊥平面C1CBB1.17.已知椭圆C:的离心率为,焦距为2,直线y=kx(x≠0)与椭圆C交于A,B两点,M为其右准线与x轴的交点,直线AM,BM分别与椭圆C交于A1,B1两点,记直线A1B1的斜率为k1(1)求椭圆C的方程;(2)是否存在常数λ,使得k1=λk恒成立?若存在,求出λ的值;若不存在,请说明理由.【考点】KL:直线与椭圆的位置关系.【分析】(1)由题意c=1,根据椭圆的离心率,即可求得a的值,b2=a2﹣c2=1,即可求得椭圆方程;(2)根据椭圆的准线方程,即可求得AM的方程,代入椭圆方程,利用韦达定理即可求得A1及B1,k1==﹣3k,存在λ=﹣3,使得k1=λk恒成立.【解答】解:(1)由椭圆的焦距2c=2,则c=1,双曲线的离心率e==,则a=,则b2=a2﹣c2=1,∴椭圆的标准方程:;(2)设A(x0,y0),则2y02=2﹣y02,则B(﹣x0,﹣y0),k=,右准线方程x=2,则M(2,0),直线AM的方程为y=(x﹣2),,整理得:(x0﹣2)2x2+2y02(x﹣2)2﹣2(x0﹣2)2=0,该方程两个根为x0,,∴x0•===•x0,则=, =(﹣2)=,则A1(,),同理可得B1(,﹣),则k1==﹣3k,即存在λ=﹣3,使得k1=λk恒成立.18.数列{a n}满足,n=1,2,3,….(1)求a3,a4,并求数列{a n}的通项公式;(2)设b n=,记F(m,n)=,求证:m<n,F(m,n)<4对任意的;(3)设S k=a1+a3+a5+…+a2k﹣1,T k=a2+a4+a6+…+a2k,W k=,求使W k>1的所有k的值,并说明理由.【考点】8E:数列的求和;8H:数列递推式.【分析】(1)a3=a1+4=4,a4=2a2=4.当n=2k,k∈N*时,a2k+2=2a2k,可得数列{a2k}是首项与公比都为2的等比数列.当n=2k﹣1,k∈N*时,a2k+1=a2k﹣1+4,∴数列{a2k﹣1}是首项为0,公差为4的等差数列.利用等差数列与等比数列的通项公式即可得出.(2)b n==,设数列{b n}的前n项和为A n,利用错位相减法可得A n=4﹣<4.根据b n≥0,可得F(m,n)≤A n,F(m,n)<4.(3)S k=a1+a3+a5+…+a2k﹣1=2k(k﹣1),T k=a2+a4+a6+…+a2k=2k+1﹣2.W k==,对k分类讨论即可得出.【解答】(1)解:a3=a1+4=4,a4=2a2=4.当n=2k,k∈N*时,a2k+2=2a2k,∴数列{a2k}是首项与公比都为2的等比数列.∴.即n=2k,k∈N*时,a n=.当n=2k﹣1,k∈N*时,a2k+1=a2k﹣1+4,∴数列{a2k﹣1}是首项为0,公差为4的等差数列.∴a2k﹣1=4(k﹣1).即n=2k﹣1,k∈N*时,a n=2n﹣2.综上可得:a3=4,a4=4.a n=,k∈N*.(2)证明:b n==,设数列{b n}的前n项和为A n,则A n=0+1+++…+,A n=++…++,∴=1++…+﹣=﹣,∴A n=4﹣<4.∵b n≥0,∴F(m,n)≤A n,故对任意的m<n,F(m,n)<4.(3)解:S k=a1+a3+a5+…+a2k﹣1==2k(k﹣1),T k=a2+a4+a6+…+a2k==2k+1﹣2.W k==,∴W1=0,W2=1,W3=>1,W4=>1,W5=>1,W6=<1.k≥6时,W k+1﹣W k=﹣=<0,∴当k≥6时,W k+1<W k.∴当k≥6时,W k+1≤W6<1.综上可得:使W k>1的所有k的值为3,4,5.19.某冰淇淋店要派车到100千米外的冷饮加工厂原料,再加工成冰淇淋后售出,已知汽车每小时的运行成本F(单位:元)与其自重m(包括车子、驾驶员及所载货物等的质量,单位:千克)和车速v(单位:千米/小时)之间满足关系式:.在运输途中,每千克冷饮每小时的冷藏费为10元,每千克冷饮经过冰淇淋店再加工后,可获利100元.若汽车重量(包括驾驶员等,不含货物)为1.3吨,最大载重为1吨.汽车来回的速度为v(单位:千米/小时),且最大车速为80千米,一次进货x千克,而且冰淇淋供不应求.(1)求冰淇淋店进一次货,经加工售卖后所得净利润w与车速v和进货量x之间的关系式;(2)每次至少进货多少千克,才能使得销售后不会亏本(净利润w≥0)?(3)当一次进货量x与车速v分别为多少时,能使得冰淇淋店有最大净利润?并求出最大值.(提示:)【考点】7G:基本不等式在最值问题中的应用.【分析】(1)用总收入减去来回两次的运行成本和冷藏成本即可;(2)利用基本不等式得出W的最大值,令其最大值大于或等于零解出x,再验证车速是否符合条件即可;(3)利用导数判断W的最大值函数的单调性,即可得出W的最大值,再验证车速即可.【解答】解:(1)汽车来回一次的运行成本为×1300v2×+×v2×=v,冷藏成本为10x×=,∴W=100x﹣v﹣.(2)∵v+≥2=5•,∴W≤100x﹣5•,当且仅当v=即v=40•时取等号.令100x﹣5•≥0,得2≥,解得x≥,当x=时,v=40•=20∈(0,80],∴每次至少进货千克,才可能使销售后不会亏本.(3)由(2)可知W≤100x﹣5•=5(2x﹣•),x∈[,1000],设f(x)=2x﹣•,则f′(x)=2﹣(•+)=2﹣(+),∵x∈[,1000],∴ =∈[,2],∵函数y=x+在[,2]上单调递增,∴当=2时, +取得最大值,∴f′(x)≥2﹣>0,∴f(x)在[,1000]上单调递增,∴当x=1000时,f(x)取得最大值f已知函数(e为自然对数的底数,m∈R).(1)求函数f(x)的单调区间和极值;(2)当时,求证:∀x>0,f(x)<x2lnx恒成立;(3)讨论关于x的方程|lnx|=f(x)的根的个数,并证明你的结论.【考点】6D:利用导数研究函数的极值;52:函数零点的判定定理;6B:利用导数研究函数的单调性.【分析】(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值;(2)设g(x)=x2lnx,求出函数的导数,根据函数的单调性证明即可;(3)设F(x)=f(x)﹣|lnx|,通过讨论m的范围,求出函数的单调区间,根据单调性判断函数的零点即方程根的个数.【解答】解:(1)f′(x)=,由f′(x)=0得x=1,x<1时,f′(x)>0,x>1时,f′(x)<0,∴f(x)在(﹣∞,1]递增,在递减,在[,+∞)递增,当且仅当x=时,g(x)min=﹣;∴f(x)≤﹣≤g(x),两等号不同时取,故∀x>0,f(x)<x2lnx恒成立;(3)设F(x)=f(x)﹣|lnx|,∴F(x)=f(x)﹣lnx,x≥1,∵f(x),﹣lnx都在递增,∴F(x)在(0,1]递增,∵F(1)=+m,∴m≤﹣时,∀0<x<1,F(x)<F(1)≤0,∴F(x)在(0,1)无零点,当m>﹣时,F(1)>0,∀0<x<1,F(x)<<+m+lnx,显然∈(0,1),∴F()<+m+ln=0,∵F(x)的图象不间断,∴F(x)在(0,1)恰有1个零点,综上,m=﹣时,方程|lnx|=f(x)恰有1个实根,m<﹣时,方程|lnx|=f(x)无实根,m>﹣时,方程|lnx|=f(x)有2个不同的实根.2017年高考熟中模拟卷B.选修4-2:矩阵与变换21.已知矩阵M对应的变换将点(﹣5,﹣7)变换为(2,1),其逆矩阵M﹣1有特征值﹣1,对应的一个特征向量为,求矩阵M.【考点】OU:特征向量的意义.【分析】根据矩阵的变换求得M=,利用矩阵的特征向量及特征值的关系,利用矩阵的乘法,即可求得M的逆矩阵,即可求得矩阵M.【解答】解:由题意可知:M=,M﹣1=,∴M﹣1=,设M﹣1=,则=,=,则,解得:,则M﹣1=,det(M﹣1)=﹣20+18=﹣2,则M=.∴矩阵M=.C.选修4-4:坐标系与参数方程22.在平面直角坐标系xoy中,以O为极点,x轴的正半轴为极轴,取相同的单位长度,建立极坐标系,已知曲线C1的参数方程为,(,α为参数),曲线C2的极坐标方程为,求曲线C1与曲线C2的交点的直角坐标.【考点】Q4:简单曲线的极坐标方程.【分析】求出曲线C1的普通方程和曲线C2的直角坐标方程,两方程联立,能求出曲线C1与曲线C2的交点的直角坐标.【解答】解:∵曲线C1的参数方程为,(,α为参数),∴曲线C1的普通方程为y=1﹣2x2,x∈,∵曲线C2的极坐标方程为,∴曲线C2的直角坐标方程为y=﹣,两方程联立:,得2﹣x﹣=0,解得,,∵x∈,∴,y=﹣,∴曲线C1与曲线C2的交点的直角坐标为().【必做题】第22题、第23题,每题10分共计20分.请答题卡的指定区域内作答解答应写出文字说明、证明过程或演算步骤.23.在英国的某一娱乐节目中,有一种过关游戏,规则如下:转动图中转盘(一个圆盘四等分,在每块区域内分别标有数字1,2,3,4),由转盘停止时指针所指数字决定是否过关.在闯n关时,转n次,当次转得数字之和大于n2时,算闯关成功,并继续闯关,否则停止闯关,闯过第一关能获得10欧元,之后每多闯一关,奖金翻倍.假设每个参与者都会持续闯关到不能过关为止,并且转盘每次转出结果相互独立.(1)求某人参加一次游戏,恰好获得10欧元的概率;(2)某人参加一次游戏,获得奖金X欧元,求X的概率分布和数学期望.【考点】CH:离散型随机变量的期望与方差;CG:离散型随机变量及其分布列.【分析】(1)记“某人参加一次游戏,恰好获得10欧元”为事件A,由题意他只闯过了第一关,没有过第二关,由此求出所求的概率;(2)根据题意知X的所有可能取值,计算对应的概率,写出随机变量X的概率分布,计算数学期望值.【解答】解:(1)记“某人参加一次游戏,恰好获得10欧元”为事件A,由题意知,他只闯过了第一关,没有过第二关,因此,他第一关转得了2、3、4中的一个,第二关转得了(1,1),(1,2),(1,3),(2,1),(2,2)中的一个,∴所求的概率为P(A)=×(5×)=;(2)根据题意,X的所有可能取值为0,10,20,40;计算P(X=0)=,P(X=10)=,P(X=20)=××=,P(X=40)=××=,∴X的概率分布为:数学期望为:E(X)=0×+10×+20×+40×=.24.(1)证明:;(2)证明:;(3)证明:.【考点】D5:组合及组合数公式.【分析】(1)利用组合数的计算公式可得:(k+1)=(k+1)•=.(2)由(1)可得: =,左边==(﹣1)k+1=,即可证明.(3)==+.由(2)可知:==.设f(n)=,则f(1)=1,=f(n﹣1).可得f(n)﹣f(n﹣1)=.利用累加求和方法即可得出.【解答】证明:(1)(k+1)=(k+1)•==(n+1).精品试卷(2)由(1)可得: =,∴左边==(﹣1)k+1= = =右边.∴.(3)==+由(2)可知: ==.设f(n)=,则f(1)=1, =f(n﹣1).∴f(n)﹣f(n﹣1)=.∴n≥2时,f(n)=f(1)+f(2)﹣f(1)+…+f(n)﹣f(n﹣1)=1++…+.n=1时也成立.∴f(n)=1++…+.n∈N*.即:.。
2019年浙江省高考全真二模数学试题解析卷

2 3
(2
x
6
)
[ 6
,
3 2
]sin(2
x
6
)
[1,1]
g
(
x)
[0,
4]
,故本题选
D.
【点睛】本题考查了正弦型函数的平移、以及闭区间上正弦型函数的最值问题,正确求出平移后的函数解析式, 是解题的关键.
6.设 a 0 , b 0 ,则“ lg(ab) 0 ”是“ lg(a b) 0 ”的( )
题的关键.
7.已知二次函数 f (x) x2 bx a 的部分图象如图所示,则函数 g(x) ex f '(x) 的零点所在区间为( )
A. (1, 0)
B. (0,1)
C. (1, 2)
D. (2,3)
【答案】B
【解析】
由函数 f(x)的图象可知,0<f(0)=a<1,f(1)=1-b+a=0,所以 1<b<2.
)
5
A. [2,1)
B.
2 3
,1
C.
2,
2 3
D.
2,
2 3
【答案】D 【解析】
【分析】
由 BC CA CA AB ,可以得到 CA (BC BA) 0 ,利用平面向量加法的几何意义,可以构造平行四边形
又 f′(x)=2x-b,所以 g(x)=ex+2x-b,所以 g′(x)=ex+2>0,所以 g(x)在 R 上单调递增,
又 g(0)=1-b<0,g(1)=e+2-b>0,
根据函数的零点存在性定理可知,函数 g(x)的零点所在的区间是(0,1),
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年上海市中考二模18题集合
一.填空题(共16小题)
1.(黄浦)如图,在△ABC中,∠ACB=90°,sin B=,将△ABC绕顶点C顺时针旋转,得到△A1B1C,点A、B分别与点A1、B1对应,边A1B1分别交边AB、BC于点D、E,如果点E是边A1B1的中点,那么=.
2.(金山)一个正多边形的对称轴共有10条,且该正多边形的半径等于4,那么该正多边形的边长等于.
3.(浦东)定义:如果P是圆O所在平面内的一点,Q是射线OP上一点,且线段OP、OQ 的比例中项等于圆O的半径,那么我们称点P与点Q为这个圆的一对反演点.已知点M、N为圆O的一对反演点,且点M、N到圆心O的距离分别为4和9,那么圆O上任意一点到点M、N的距离之比=.
4.(崇明)如图,在△ABC中,已知AB=AC,∠BAC=30°,将△ABC绕着点A逆时针旋转30°,记点C的对应点为点D,AD、BC的延长线相交于点E.如果线段DE的长为,那么边AB的长为.(2015中考18变型)
5.(宝山)如图,点M的坐标为(3,2),动点P从点O出发,沿y轴以每秒1个单位的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,若点M关于l的对称点落在坐标轴上,设点P的移动时间为t,则t的值是.
6.(长宁)如图,在△ABC中,AB=AC=5,BC=8,将△ABC绕着点C旋转,点A、B的对应点分别是点A'、B',若点B'恰好在线段AA'的延长线上,则AA'的长等于.
7.(闵行)如图,在△ABC中,AB=AC=5,BC=2,D为边AC上一点(点D与点A、C不重合).将△ABD沿直线BD翻折,使点A落在点E处,连接CE.如果CE∥AB,那么AD:CD=.
8.(静安)如图,在平面直角坐标系xOy中,已知A(2,0),B(0,6),M(0,2).点Q在直线AB上,把△BMQ沿着直线MQ翻折,点B落在点P处,联结PQ.如果直线PQ与直线AB所构成的夹角为60°,那么点P的坐标是.
9.(虹口)如图,在矩形ABCD中,AB=6,点E在边AD上且AE=4,点F是边BC上的一个动点,将四边形ABFE沿EF翻折,A、B的对应点A1、B1与点C在同一直线上,A1B1与边AD交于点G,如果DG=3,那么BF的长为.
10.(松江)如图,已知Rt△ABC中,∠ACB=90°,AC=8,BC=6.将△ABC绕点B旋转得到△DBE,点A的对应点D落在射线BC上.直线AC交DE于点F,那么CF的长为.
11.(奉贤)如图,矩形ABCD,AD=a,将矩形ABCD绕着顶点B顺时针旋转,得到矩形EBGF,顶点A、D、C分别与点E、F、G对应(点D与点F不重合).如果点D、E、F 在同一条直线上,那么线段DF的长是.(用含a的代数式表示)
12.(徐汇)如图,在Rt△ABC中,∠ACB=90°,AB=6,cos B=,先将△ACB绕着顶点C顺时针旋转90°,然后再将旋转后的三角形进行放大或缩小得到△A′CB′(点A′、
C、B′的对应点分别是点A、C、B),连接A′A、B′B,如果△AA′B和△AA′B′相
似,那么A′C的长是.
13.(杨浦)如图,在矩形ABCD中,过点A的圆O交边AB于点E,交边AD于点F,已知AD=5,AE=2,AF=4.如果以点D为圆心,r为半径的圆D与圆O有两个公共点,那么r的取值范围是.
14.(青浦)我们把满足某种条件的所有点组成的图形,叫做符合这个条件的点的轨迹,如图,在Rt△ABC中,∠C=90°,AC=8,BC=12,动点P从点A开始沿射线AC方向以1个单位秒的速度向点C运动,动点Q从点C开始沿射线CB方向以2个单位/秒的速度向点运动,P、Q两点分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,在整个运动过程中,线段PQ的中点M运动的轨迹长为.
15.(普陀)如图,AD是△ABC的中线,点E在边AB上,且DE⊥AD,将△BDE绕着点D 旋转,使得点B与点C重合,点E落在点F处,连接AF交BC于点G,如果,那么的值等于.。
