2008年全国硕士研究生入学统一考试农学门类联考数学真题及详解【圣才出品】

合集下载

考研数一08真题

考研数一08真题2008年考研数学一真题中，试题主要分为两个部分：选择题和填空题。

选择题部分包括20道选择题，填空题部分包括10道填空题。

本文将以试题题号为标记逐一解析各道题目。

选择题部分解析：题目1：设A是n阶方阵，且满足A^2 = A，则下列结论正确的是（）A. A = 0B. A = E（单位矩阵）C. A是对称方阵D. A的秩为1这道题目考察了对方阵幂运算的理解。

根据A^2 = A，我们可以发现A作为方阵必然有两种可能：A是零矩阵或者A是单位矩阵。

因此，选项B“A = E”为正确答案。

题目2：设f(x) = x^3 - 3x，则f'(x)的零点的个数是（）A. 0B. 1C. 2D. 3这道题目考察了对函数的导数与零点的关系的理解。

f'(x)是f(x)的导函数，即f'(x) = 3x^2 - 3。

根据函数导数存在零点的性质，当f'(x) = 0时，f(x)存在极值点或转折点。

解方程3x^2 - 3 = 0，得到x = ±1。

因此，f'(x)的零点有2个，选项C“2”为正确答案。

填空题部分解析：题目1：若a是方程x^4 - x^3 - x + 1 = 0的一个实根，则a^3 - a^2 -a + 1的值等于________。

这道题目考察了对方程实根的运算。

首先，我们可以将方程x^4 -x^3 - x + 1 = 0进行变形，得到x(x^3 - x^2 - 1) + 1 = 0。

因为a是方程的一个实根，所以该式等于0，即a(a^3 - a^2 - 1) = -1。

因此，a^3 - a^2 -a + 1 = (-1)/a，即填空的值为-1/a。

题目2：设f(x) = (cosx + sinx)^2，g(x) = (cosx - sinx)^2，则f(x) -g(x)的最小值是________。

这道题目考察了对函数最小值的求解。

我们先展开f(x)与g(x)：f(x) = cos^2 x + 2sinx cosx + sin^2 xg(x) = cos^2 x - 2sinx cosx + sin^2 x再计算f(x) - g(x)：f(x) - g(x) = 4sinx cosx则f(x) - g(x)的值不为负数，且取最小值0，因此填空的答案为0。

2008年全国硕士研究生入学统一考试数学二真题答案

全国硕士研究生入学统一考试数学二试题答案速查：一、选择题二、填空题三、解答题（15）16（16）2222(1)[ln(1)1]d y t t dx =+++（17）21416π+（18）19ln 24+ （19）1()()2x xf x e e -=+（20）略（21）最大值为72，最小值为6 （22）（Ⅰ）略；（Ⅱ）10,(1)n a x n a≠=+；（Ⅲ）0,(0,1,0,,0)(1,0,,0)T Ta x k ==+L L ，其中k 为任意常数（23）（Ⅰ）略；（Ⅱ）1100011001P AP --⎛⎫ ⎪= ⎪ ⎪⎝⎭一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内. (1)【答案】()D【解析】()()()()()()22221212494f x x x x xx x x x x x '=--+-+-=-+令()0f x '=，则可得()f x '零点的个数为3. （2）【答案】()C【解析】()()()()aa a xf x dx xdf x af a f x dx '==-⎰⎰⎰，其中()af a 是矩形面积，0()af x dx⎰为曲边梯形的面积，所以0()axf x dx '⎰为曲边三角形的面积。

（3）【答案】()D【解析】由123cos 2sin 2xy C e C x C x =++可知其特征根为12,31,2i λλ==±.故对应的特征方程为 2(1)(2)(2)(1)(4)i i λλλλλ-+-=-+，即32440λλλ-+-=所以所求微分方程为440y y y y ''''''-+-=, 选()D . （4）【答案】()A【解析】()f x 的间断点为1,0x =，而0lim ()0x f x →+=，故0x =是可去间断点；1lim ()sin1x f x →+=，1lim ()sin1x f x →+=-，故1x =是跳跃间断点故选()A 。

2008年全国硕士研究生入学统一考试数学三真题及答案

2008年全国硕士研究生入学统一考试数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（1）设函数()f x 在区间[1,1]-上连续，则0x =是函数0()()xf t dtg x x=⎰的（）()A 跳跃间断点. ()B 可去间断点. ()C 无穷间断点.()D 振荡间断点.【答案】()B【考点】可去间断点，积分上限函数及其导数【难易度】★★ 【详解】解析：()()0()lim ()limlim 0xx x x f t dt g x f x f x→→→===⎰，所以0x =是函数()g x 的可去间断点.（2）如图，曲线方程为()y f x =，函数()f x 在区间[0,]a 上有连续导数，则定积分'()axf x dx ⎰等于（）()A 曲边梯形ABCD 面积.()B 梯形ABCD 面积.()C 曲边三角形ACD 面积.()D 三角形ACD 面积.【答案】()C【考点】定积分的分部积分法，定积分的几何应用—平面图形的面积【难易度】★★ 【详解】解析：()()()()aa a xf x dx xdf x af a f x dx '==-⎰⎰⎰，其中()af a 是矩形面积，0()af x dx ⎰为曲边梯形的面积，所以0()axf x dx '⎰为曲边三角形ACD 的面积.（3）已知24(,)x y f x y e+=则 ( )()A (0,0),(0,0)x y f f ''都存在 ()B (0,0)x f '存在，(0,0)y f '不存在()C(0,0)x f '不存在，(0,0)y f '存在 ()D (0,0),(0,0)x y f f ''都不存在【答案】()C【考点】多元函数的偏导数【难易度】★★★ 【详解】解析：2400011(0,0)limlim 00xx x x x ee f x x +→→--'==-- 00011lim lim 100xx x x e e x x →+→+--==--，001lim 10x x e x -→--=-- 000011lim lim 00xx x x e e x x -→+→---≠--，所以偏导数不存在. 24200011(0,0)limlim 000y y y y y ee f y y +→→--'===-- 所以偏导数存在。

2008考研数一真题及解析

(x2 y2 )dxdy
x2 y2 4
2 x2 y2 4
1
2
d
2 r3dr 4 。
20
0
（高斯公式）
P d
yd z Qd zd x Rd xd
y
P x
Q y
R z
d xd
ydz；
P cos Q cos R cos
d S=
P Q R x y z
dx d ydz 。
(13) 设 A 为 2 阶矩阵，1,2 为线性无关的 2 维列向量，A1 0, A2 21 2 ，则 A 的非零特征值为
第 4 页共 13 页
.
【答案】1
【详解】
A(1,
2
)
(
A1
,
A
2
)
(0,
21
2
)
(1
,2
)
0 0
2 1
,记
P
(1
,2
)
，
B
0 0
2 1
，
则 AP PB ，因为1,2 线性无关，所以 P 可逆. 从而 B P1AP ，即 A 与 B 相似。
2
由| E B |
( 1) 0 ，得 0 及 1为 B 的特征值，
二、填空题：9-14 小题，每小题 4 分，共 24 分，请将答案写在答题纸指定位置上.
(9) 微分方程 xy y 0 满足条件 y 1 1的解是 y .
【答案】1 x
【详解】由 dy y ，两端积分得 ln y ln x ln | C | ，所以 1 C x ，又 y(1) 1 ，所以 y 1 。
【答案】 B
D 若 f (xn ) 单调，则xn 收敛.

2008年考研农学门类联考《数学》真题及详解【圣才出品】

2008 年考研农学门类联考《数学》真题及详解
一、选择题（1～8 小题，每小题 4 分，共 32 分。下列每题给出的四个选项中，只有
一个选项符合题目要求。）
1．设函数
f
(x)
sin x 1
x2 1
，则（
）。
A．x＝－1 为可去间断点，x＝1 为无穷间断点
B．x＝－1 为无穷间断点，x＝1 为可去间断点
D． ex f (1 ex )dx
【答案】D
【
解
析
】
dy df (1 ex ) f (1 ex )(1 ex )dx ex f (1 ex )dx 。
3．设函数 f (x) 连续， F (x)
0 x2
f (t)dt
，则 F (x) ＝（
）。
A． f (x2 )
B． f (x2 )
C． 2xf (x2 )
由期望和方差的性质可得
二、填空题（9～14 小题，每小题 4 分，共 24 分。）
9．函数 f (x) ex ex 2 的极小值为______。
【答案】－2
【解析】令 f (x) ex e 0 可得 x＝1， f (x) ex , f (1) e 0 ，根据
6 / 15
极值的第二充分条件可得 x＝1 为函数 f (x) ex ex 2 的极小值点，极小值为 f (1) 2 。
lim
x1
sin(x 1) x 1
lim x1
1 x 1
1 2
所以 x＝1 为可去间断点。
2．设函数 f (x) 可微，则 y f (1 ex ) 的微分 dy ＝（）。
A． (1 ex ) f (1 ex )dx
B． (1 ex ) f (1 ex )dx

2008考研数二真题及解析

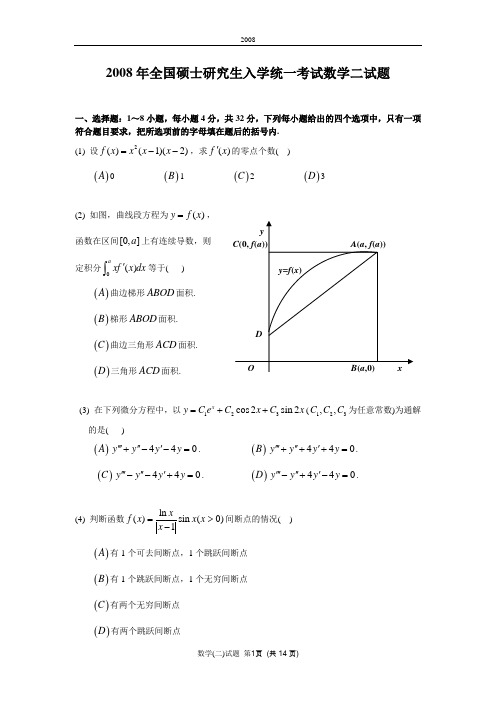
2008年全国硕士研究生入学统一考试数学二试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内. (1) 设2()(1)(2)f x x x x =--，求()f x '的零点个数( )()A 0()B 1 ()C 2()D 3(2) 如图，曲线段方程为()y f x =，函数在区间[0,]a 上有连续导数，则定积分()axf x dx '⎰等于( )()A 曲边梯形ABOD 面积.()B 梯形ABOD 面积. ()C 曲边三角形ACD 面积.()D 三角形ACD 面积.(3) 在下列微分方程中，以123cos2sin 2x y C e C x C x =++(123,,C C C 为任意常数)为通解的是( )()A 440y y y y ''''''+--=. ()B 440y y y y ''''''+++=. ()C 440y y y y ''''''--+=.()D 440y y y y ''''''-+-=.(4) 判断函数ln ()sin (0)1xf x x x x =>-间断点的情况( ) ()A 有1个可去间断点，1个跳跃间断点 ()B 有1个跳跃间断点，1个无穷间断点 ()C 有两个无穷间断点 ()D 有两个跳跃间断点yC (0, f (a )) A (a , f (a ))y =f (x )O B (a ,0) xD(5) 设函数()f x 在(,)-∞+∞内单调有界，{}n x 为数列，下列命题正确的是( )()A 若{}n x 收敛，则{}()n f x 收敛. ()B 若{}n x 单调，则{}()n f x 收敛. ()C 若{}()n f x 收敛，则{}n x 收敛.()D 若{}()n f x 单调，则{}n x 收敛.(6) 设函数f 连续. 若()()2222,uvD f x y F u v dxdy x y+=+⎰⎰，其中区域uv D 为图中阴影部分，则Fu∂=∂( ) ()A ()2vf u()B ()2vf u u ()C ()vf u()D ()v f u u(7) 设A 为n 阶非零矩阵，E 为n 阶单位矩阵. 若3A O =，则( )()A E A -不可逆，E A +不可逆.()B E A -不可逆，E A +可逆. ()C E A -可逆，E A +可逆.()D E A -可逆，E A +不可逆.(8) 设1221A ⎛⎫=⎪⎝⎭，则在实数域上与A 合同的矩阵为( ) ()A 2112-⎛⎫⎪-⎝⎭.()B 2112-⎛⎫⎪-⎝⎭.()C 2112⎛⎫ ⎪⎝⎭.()D 1221-⎛⎫⎪-⎝⎭.二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸指定位置上. (9) ()f x 连续，21cos(sin )lim1(1)()x x x e f x →-=-，则(0)f =(10) 微分方程2()0xy x e dx xdy -+-=的通解是y =O xvx 2+y 2=u 2 x 2+y 2=1 D uvy(11) 曲线()()sin ln xy y x x +-=在点()0,1处的切线方程为 . (12) 求函数23()(5)f x x x =-的拐点______________. (13) 已知xyy z x ⎛⎫=⎪⎝⎭，则(1,2)_______z x ∂=∂. (14) 矩阵A 的特征值是,2,3λ，其中λ未知，且248A =-，则λ=_______.三、解答题：15－23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)求极限()40sin sin sin sin limx x x x x →-⎡⎤⎣⎦.(16) (本题满分10分)设函数()y y x =由参数方程20()ln(1)t x x t y u du =⎧⎪⎨=+⎪⎩⎰确定，其中()x t 是初值问题 020|0xt dx te dtx -=⎧-=⎪⎨⎪=⎩的解. 求22d y dx .(17)(本题满分9分)计算212arcsin 1x x dx x-⎰(18)(本题满分11分)计算{}max ,1,Dxy dxdy ⎰⎰其中{(,)02,02}D x y x y =≤≤≤≤(19)(本题满分11分)设()f x 是区间[0,)+∞上具有连续导数的单调增加函数，且(0)1f =. 对于任意的[0,)t ∈+∞，直线0,x x t ==，曲线()y f x =以及x 轴所围成曲边梯形绕x 轴旋转一周生成一旋转体. 若该旋转体的侧面面积在数值上等于其体积的2倍，求函数()f x 的表达式.(20)(本题满分11分)(I) 证明积分中值定理：若函数()f x 在闭区间[,]a b 上连续，则至少存在一点[,]a b η∈，使得()()()baf x dx f b a η=-⎰；(II) 若函数()x ϕ具有二阶导数，且满足，32(2)(1),(2)()x dx ϕϕϕϕ>>⎰，则至少存在一点(1,3)ξ∈，()0ϕξ''<使得.(21)(本题满分11分)求函数222u x y z =++在约束条件22z x y =+和4x y z ++=下的最大和最小值.(22)(本题满分12分)设n 元线性方程组Ax b =，其中2221212n n a a a A a a ⨯⎛⎫ ⎪⎪= ⎪⎪⎝⎭ ，12n x x x x ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭ ，100b ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭(I) 证明行列式()1nA n a =+(II) 当a 为何值时，该方程组有唯一解，并求1x (III) 当a 为何值时，该方程组有无穷多解，并求通解(23)(本题满分10分)设A 为3阶矩阵，12,αα为A 的分别属于特征值1,1-的特征向量，向量3α满足323A ααα=+，(I) 证明123,,ααα线性无关； (II) 令()123,,P ααα=，求1P AP -2008年全国硕士研究生入学统一考试数学二试题解析一、选择题 (1)【答案】D【详解】因为(0)(1)(2)0f f f ===，由罗尔定理知至少有1(0,1)ξ∈，2(1,2)ξ∈使12()()0f f ξξ''==，所以()f x '至少有两个零点. 由于()f x '是三次多项式，三次方程()0f x '=的实根不是三个就是一个，故D 正确.(2)【答案】C 【详解】00()()()()()()aa a aaxf x dx xdf x xf x f x dx af a f x dx '==-=-⎰⎰⎰⎰其中()af a 是矩形ABOC 面积，0()af x dx ⎰为曲边梯形ABOD 的面积，所以0()axf x dx '⎰为曲边三角形的面积．(3)【答案】D【详解】由微分方程的通解中含有xe 、cos 2x 、sin 2x 知齐次线性方程所对应的特征方程有根1,2r r i ==±，所以特征方程为(1)(2)(2)0r r i r i --+=，即32440r r r -+-=. 故以已知函数为通解的微分方程是440y y y ''''''-+-=(4) 【答案】A【详解】0,1x x ==时()f x 无定义，故0,1x x ==是函数的间断点因为 000ln 11lim ()lim lim lim csc |1|csc cot x x x x x xf x x x x x++++→→→→=⋅=-- 200sin lim lim 0cos cos x x x xx x x++→→=-=-=同理 0lim ()0x f x -→= 又 1111ln 1lim ()lim lim sin lim sin1sin11x x x x x f x x x x ++++→→→→⎛⎫=⋅== ⎪-⎝⎭ 111ln lim ()lim lim sin sin11x x x xf x x x --+→→→=⋅=--所以 0x =是可去间断点，1x =是跳跃间断点.(5)【答案】B【详解】因为()f x 在(,)-∞+∞内单调有界，且{}n x 单调. 所以{()}n f x 单调且有界. 故{()}n f x 一定存在极限.(6)【答案】A【详解】用极坐标得 ()()222()22211,()vu uf r r Df u v F u v dudv dv rdr v f r dr u v +===+⎰⎰⎰⎰⎰所以()2Fvf u u∂=∂(7) 【答案】C【详解】23()()E A E A A E A E -++=-=，23()()E A E A A E A E +-+=+= 故,E A E A -+均可逆．(8) 【答案】D 【详解】记1221D -⎛⎫=⎪-⎝⎭，则()2121421E D λλλλ--==---，又()2121421E A λλλλ---==---- 所以A 和D 有相同的特征多项式，所以A 和D 有相同的特征值.又A 和D 为同阶实对称矩阵，所以A 和D 相似．由于实对称矩阵相似必合同，故D 正确.二、填空题 (9)【答案】2【详解】222220001cos[()]2sin [()2]2sin [()2]()lim lim lim ()[()2]4(1)()x x x x xf x xf x xf x f x x f x xf x e f x →→→-⋅==⋅- 011lim ()(0)122x f x f →=== 所以 (0)2f =(10)【答案】()xx eC --+【详解】微分方程()20xy x e dx xdy -+-=可变形为x dy yxe dx x--= 所以 111()dx dx xx x x x y e xe e dx C x xe dx C x e C x ----⎡⎤⎛⎫⎰⎰=+=⋅+=-+⎢⎥ ⎪⎝⎭⎣⎦⎰⎰(11)【答案】1y x =+【详解】设(,)sin()ln()F x y xy y x x =+--，则1cos()11cos()x y y xy F dy y x dx F x xy y x--'-=-=-'+-，将(0)1y =代入得01x dy dx==，所以切线方程为10y x -=-，即1y x =+(12)【答案】(1,6)-- 【详解】53235y xx =-⇒23131351010(2)333x y x x x -+'=-= ⇒134343101010(1)999x y x x x--+''=+= 1x =-时，0y ''=；0x =时，y ''不存在在1x =-左右近旁y ''异号，在0x =左右近旁0y ''>，且(1)6y -=- 故曲线的拐点为(1,6)--(13)【答案】2(ln 21)2- 【详解】设,y xu v x y==，则v z u = 所以121()ln v v z z u z v y vu u u x u x v x x y-∂∂∂∂∂=⋅+⋅=-+⋅∂∂∂∂∂ 2ln 11ln x yv vy u y y u uxy x y x ⎛⎫⎛⎫⎛⎫=-+=⋅-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭ 所以(1,2)2(ln 21)2z x ∂=-∂(14)【答案】-1【详解】||236A λλ =⨯⨯=3|2|2||A A = 32648λ∴⨯=- 1λ⇒=-三、解答题 (15)【详解】方法一：4300[sin sin(sin )]sin sin sin(sin )limlim x x x x x x x x x→→--= 22220001sin cos cos(sin )cos 1cos(sin )12lim lim lim 3336x x x xx x x x x x x →→→--==== 方法二：331sin ()6x x x o x =-+ 331sin(sin )sin sin (sin )6x x x o x =-+4444400[sin sin(sin )]sin sin (sin )1lim lim 66x x x x xx o x x x x →→⎡⎤-∴ =+=⎢⎥⎣⎦(16)【详解】方法一：由20x dx te dt--=得2x e dx tdt =，积分并由条件0t x =得21x e t =+，即2l n (1)x t =+所以 2222ln(1)2(1)ln(1)21dydy t tdt t t dxt dx dt t +⋅===+++222222[(1)ln(1)]2ln(1)221dt t d y d dy t t tdt dx t dx dx dx dt t ++++⎛⎫=== ⎪⎝⎭+ 22(1)[ln(1)1]t t =+++方法二：由20x dx te dt--=得2x e dx tdt =，积分并由条件0t x =得21x e t =+，即2l n (1)x t =+所以 2222ln(1)2(1)ln(1)21x dydy t tdt t t e x dxt dx dt t +⋅===++=+所以 22(1)x d ye x dx=+(17)【详解】方法一：由于221arcsin lim 1x x x x-→=+∞-，故212arcsin 1x x dx x-⎰是反常积分.令arcsin x t =，有sin x t =，[0,2)t π∈22122222000arcsin sin cos 2cos sin ()cos 221x x t t t t t dx tdt t tdt dt t x πππ===--⎰⎰⎰⎰2222220001sin 21sin 2sin 2441644tt t td t tdt πππππ=-=-+⎰⎰ 222011cos 2168164t πππ=-=+ 方法二：212arcsin 1x x dx x -⎰1221(arcsin )2x d x =⎰ 121122220001(arcsin )(arcsin )(arcsin )28x x x x dx x x dx π=-=-⎰⎰令arcsin x t =，有sin x t =，[0,2)t π∈12222200011(arcsin )sin 2cos 224x x dx t tdt t d t ππ==-⎰⎰⎰ 222200111(cos 2)cos 242164t t t tdt πππ=-+=-⎰故，原式21164π=+(18)【详解】曲线1xy =将区域分成两个区域1D 和23D D +，为了便于计算继续对区域分割，最后为()max ,1Dxy dxdy ⎰⎰123D D D xydxdy dxdy dxdy =++⎰⎰⎰⎰⎰⎰112222211102211x xdx dy dx dy dx xydy =++⎰⎰⎰⎰⎰⎰1512ln 2ln 24=++-19ln 24=+(19)【详解】旋转体的体积2()tV f x dx π=⎰，侧面积202()1()tS f x f x dx π'=+⎰，由题O 0.5 2 xD 1D 3 D 2设条件知220()()1()ttf x dx f x f x dx '=+⎰⎰上式两端对t 求导得 22()()1()f t f t f t '=+，即 21y y '=- 由分离变量法解得 21l n (1)y y t C +-=+，即 21t y y C e +-=将(0)1y =代入知1C =，故21t y y e +-=，1()2tt y e e -=+ 于是所求函数为 1()()2tt y f x e e -==+(20)【详解】(I) 设M 与m 是连续函数()f x 在[,]a b 上的最大值与最小值，即()m f x M ≤≤ [,]x a b ∈由定积分性质，有 ()()()bam b a f x dx M b a -≤≤-⎰，即 ()baf x dx m M b a≤≤-⎰由连续函数介值定理，至少存在一点[,]a b η∈，使得 ()()b af x dx f b aη=-⎰即()()()baf x dx f b a η=-⎰(II) 由(I)的结论可知至少存在一点[2,3]η∈，使 32()()(32)()x dx ϕϕηϕη=-=⎰又由32(2)()()x d x ϕϕϕη>=⎰，知 23η<≤对()x ϕ在[1,2][2,]η上分别应用拉格朗日中值定理，并注意到(1)(2)ϕϕ<，()(2)ϕηϕ<得 1(2)(1)()021ϕϕϕξ-'=>- 112ξ<<2()(2)()02ϕηϕϕξη-'=<- 123ξη<<≤在12[,]ξξ上对导函数()x ϕ'应用拉格朗日中值定理，有2121()()()0ϕξϕξϕξξξ''-''=<- 12(,)(1,3)ξξξ∈⊂(21)【详解】方法一：作拉格朗日函数22222(,,,,)()(4)F x y z x y z x y z x y z λμλμ=++++-+++-令 2222022020040x y z F x x F y y F z F x y z F x y z λμλμλμλμ'=++=⎧⎪'=++=⎪⎪'=-+=⎨⎪'=+-=⎪'=++-=⎪⎩解方程组得111222(,,)(1,1,2),(,,)(2,2,8)x y z x y z ==-- 故所求的最大值为72，最小值为6.方法二：问题可转化为求2242242u x y x x y y =++++在224x y x y +++=条件下的最值设44222222(,,)2(4)F x y u x y x y x y x y x y λλ==++++++++-令 323222442(12)0442(12)040x y F x xy x x F y x y y y F x y x y λλλ'⎧=++++=⎪'=++++=⎨⎪'=+++-=⎩解得1122(,)(1,1),(,)(2,2)x y x y ==--，代入22z x y =+，得122,8z z == 故所求的最大值为72，最小值为6.(22)【详解】(I)证法一：2222122212132101221221122aa a a a a a a a A r ar aaa a =-=121301240134(1)2(1)3231(1)0n n n a a an a a n a r ar a n a nnn a n--+-=⋅⋅⋅=++证法二：记||n D A =，下面用数学归纳法证明(1)nn D n a =+．当1n =时，12D a =，结论成立．当2n =时，2222132a D a a a==，结论成立．假设结论对小于n 的情况成立．将n D 按第1行展开得2212102121212n n a a a a D aD a a-=-21221222(1)(1)n n n n n aD a D ana a n a n a ---- =-=--=+故 ||(1)n A n a =+证法三：记||n D A =，将其按第一列展开得 2122n n n D aD a D --=-，所以 211212()n n n n n n D aD aD a D a D aD ------=-=-222321()()n n n n a D aD a D aD a ---=-==-=即 12122()2n n n n n n n n D a aD a a a aD a a D ----=+=++=++2121(2)(1)n n n n n a a D n a a D --==-+=-+ 1(1)2(1)n n n n a a a n a -=-+⋅=+(II)因为方程组有唯一解，所以由Ax B =知0A ≠，又(1)nA n a =+，故0a ≠．由克莱姆法则，将n D 的第1列换成b ，得行列式为2221122(1)(1)112102121221122n n n nn n a aa a a a a a D na a a a a --⨯-⨯-===所以 11(1)n n D nx D n a-==+(III)方程组有无穷多解，由0A =，有0a =，则方程组为12101101001000n n x x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭此时方程组系数矩阵的秩和增广矩阵的秩均为1n -，所以方程组有无穷多解，其通解为 ()()10000100,TTk k + 为任意常数．(23)【详解】(I)证法一：假设123,,ααα线性相关．因为12,αα分别属于不同特征值的特征向量，故12,αα线性无关，则3α可由12,αα线性表出，不妨设31122l l ααα=+，其中12,l l 不全为零(若12,l l 同时为0，则3α为0，由323A ααα=+可知20α=，而特征向量都是非0向量，矛盾)11,A αα=-22A αα=∴32321122A l l αααααα=+=++，又311221122()A A l l l l ααααα=+=-+ ∴112221122l l l l ααααα-+=++，整理得：11220l αα+=则12,αα线性相关，矛盾. 所以，123,,ααα线性无关.证法二：设存在数123,,k k k ，使得1122330k k k ααα++= (1)用A 左乘(1)的两边并由11,A αα=-22A αα=得1123233()0k k k k ααα-+++= (2)(1)—(2)得 113220k k αα-= (3) 因为12,αα是A 的属于不同特征值的特征向量，所以12,αα线性无关，从而130k k ==，代入(1)得220k α=，又由于20α≠，所以20k =，故123,,ααα线性无关.(II) 记123(,,)P ααα=，则P 可逆，123123(,,)(,,)AP A A A A αααααα==1223(,,)αααα=-+123100(,,)011001ααα-⎛⎫ ⎪= ⎪ ⎪⎝⎭100011001P -⎛⎫ ⎪= ⎪ ⎪⎝⎭所以 1100011001P AP --⎛⎫ ⎪= ⎪ ⎪⎝⎭.。

2008年考研数学数学一真题答案解析

2008年考研数学一试题分析、详解和评注一、选择题：(本题共8小题，每小题4分，共32分. 每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内) （1）设函数2()ln(2)x f x t dt =+ò，则()f x ¢的零点个数为【】(A) 0. (B) 1. (C) 2. (D) 3．【答案】应选(B). 【详解】22()ln(2)22ln(2)f x x x x x ¢=+×=+．显然()f x ¢在区间(,)-¥+¥上连续，且(1)(1)(2ln3)(2ln3)0f f ¢¢-·=-·<，由零点定理，知()f x ¢至少有一个零点．又2224()2ln(2)02x f x x x¢¢=++>+，恒大于零，所以()f x ¢在(,)-¥+¥上是单调递增的．又因为(0)0f ¢=，根据其单调性可知，()f x ¢至多有一个零点．故()f x ¢有且只有一个零点．故应选(B). （2）函数(,)arctanxf x y y=在点(0,1)处的梯度等于【】(A) i (B) i -. (C) j . (D) j-【答案】应选(A). 【详解】因为222211f y y x x x y y ¶==¶++．222221xf x y x y x y y -¶-==¶++．所以(0,1)1fx ¶=¶，(0,1)0f y ¶=¶，于是(0,1)(,)i grad f x y =.故应选(A). （3）在下列微分方程中，以123cos 2sin 2xy C e C x C x =++（123,,C C C 为任意的常数）为通解的是【】(A) 440y y y y ¢¢¢¢¢¢+--=. (B) 440y y y y ¢¢¢¢¢¢+++=. (C) 440y y y y ¢¢¢¢¢¢--+=. (D) 440y y y y ¢¢¢¢¢¢-+-=.【答案】应选(D). 【详解】由123cos 2sin 2xy C e C x C x =++，可知其特征根为11l =，2,32i l =±，故对应的特征值方程为，故对应的特征值方程为2(1)(2)(2)(1)(4)i i l l l l l -+-=-+3244l l l =+-- l l l 3244=-+-所以所求微分方程为440y y y y ¢¢¢¢¢¢-+-=．应选(D). （4）设函数()f x 在(,)-¥+¥内单调有界，{}n x 为数列，下列命题正确的是【】．(A) 若{}n x 收敛，则{()}n f x 收敛收敛 (B) 若{}n x 单调，则{()}n f x 收敛收敛 (C) 若{()}n f x 收敛，则{}n x 收敛. (D) 若{()}n f x 单调，则{}n x 收敛. 【答案】应选(B). 【详解】若{}n x 单调，则由函数()f x 在(,)-¥+¥内单调有界知，若{()}n f x 单调有界，因此若{()}nf x 收敛．故应选(B). （5）设A 为n 阶非零矩阵，E 为n 阶单位矩阵．若30A =，则【】则下列结论正确的是：则下列结论正确的是：(A) E A -不可逆，则E A +不可逆. (B) E A -不可逆，则E A +可逆. (C) E A -可逆，则E A +可逆. (D) E A -可逆，则E A +不可逆. 【答案】应选(C). 【详解】故应选(C). 23()()E A E A A E A E -++=-=，23()()E A E A A E A E +-+=+=．故E A -，E A +均可逆．故应选(C). （6）设A 为3阶实对称矩阵，如果二次曲面方程()1x xyz A y z æöç÷=ç÷ç÷èø在正交变换下的标准方程的图形如图，则A 的正特征值个数为【】(A) 0. (B) 1. (C) 2. (D) 3.【答案】应选(B). 【详解】此二次曲面为旋转双叶双曲面，此曲面的标准方程为222221x y za c+-=．故A 的正特征值个数为1．故应选(B). （7）设随机变量,X Y 独立同分布且X 的分布函数为()F x ，则max {,}Z X Y =的分布函数为【】(A) 2()F x . (B) ()()F x F y . (C) 21[1()]F x --. (D) [1()][1()]F x F y --. 【答案】应选(A)．【详解】(){}()max{,}F z P Z z P X Y z =£=£()()2()()()P X z P Y z F z F z F z =££==．故应选(A)．（8）设随机变量XN (0,1), (1,4)YN , 且相关系数1XY r =，则【】(A) {21}1P Y X =--= (B) {21}1P Y X =-= (C) {21}1P Y X =-+= (D) {21}1P Y X =+= 【答案】应选【答案】应选 (D)．【详解】用排除法．设Y aX b =+．由1XY r =，知X ，Y 正相关，得0a >．排除（A ）和（C ）．由(0,1)XN ，(1,4)Y N ，得，得0,1,()EX EY E aX b aEX b ==+=+．10a b =´+，1b =．从而排除(B).故应选故应选(D)．二、填空题：(9－14小题，每小题4分，共24分. 把答案填在题中横线上.) （9）微分方程0xy y ¢+=满足条件(1)1y =的解是y = . 【答案】应填1yx =．【详解】由dy ydx x=-，得dy dx y x =-．两边积分，得ln ||ln ||y x C =-+．代入条件(1)1y =，得0C =．所以1y x=．（10）曲线sin()ln()xy y x x +-=在点(0,1)的切线方程为的切线方程为 . 【答案】应填1y x =+．【详解】设(,)sin()ln()F x y xy y x x =+--，则，则1(,)cos()1x F x y y xy y x -=+--，1(,)cos()x F x y x xy y x=+-，(0,1)1x F =-，(0,1)1y F =．于是斜率(0,1)1(0,1)x y F k F ¢=-=¢．故所求得切线方程为1y x =+．（11）已知幂级数(2)nn n a x ¥=+å在0x =处收敛，在4x =-处发散，则幂级数0(2)nn n a x ¥=-å的收敛域为的收敛域为. 【答案】 (1,5]．【详解】由题意，知(2)nnn a x ¥=+å的收敛域为(4,0]-，则0nnna x ¥=å的收敛域为(2,2]-．所以(2)nn n a x ¥=-å的收敛域为(1,5]．(12)设曲面S是224z x y=--的上侧，则2xydydz xdzdx x dxdy S++=òò.【答案】 4p ．【详解】作辅助面1:0z S =取下侧．则由高斯公式，有取下侧．则由高斯公式，有2xydydz xdzdx x dxdy S++òò122xydydz xdzdx x dxdy xydydz xdzdx x dxdy åå=++-++òòòò2224x y ydV x dxdy W+£=+òòòòò．2222410()2x y x y dxdy +£=++òòd r rdr p q p p 22200116424=·==òò． (13) 设A 为2阶矩阵，12,a a 为线性无关的2维列向量，10A a =，2122A a a a =+．则A 的非零特征值为___________. 【答案】应填1．【详解】根据题设条件，得1212121202(,)(,)(0,2)(,)01A A A a a a a a a a a æö==+=ç÷èø．记12(,)P a a =，因12,a a 线性无关，故12(,)P a a =是可逆矩阵．因此是可逆矩阵．因此0201AP P æö=ç÷èø，从而10201P AP -æö=ç÷èø．记0201B æö=ç÷èø，则A 与B 相似，从而有相同的特征值．相同的特征值．因为2||(1)01E B l l l l l --==--，0l =，1l =．故A 的非零特征值为1．(14) 设随机变量X 服从参数为1的泊松分布，则{}2P X EX==____________．【答案】应填12e. 【详解】因为X 服从参数为1的泊松分布，所以1EX DX ==．从而由22()DX EX EX =-得22EX =．故{}{}22P X EX P X ====12e．三、解答题：(15－23小题，共94分. ) (15)(本题满分10分)求极限[]40sin sin(sin )sin lim x x x x x®- 【详解1】[]40sin sin(sin)sin lim x x x x x®-[]30sin sin(sin )lim x x x x®-= ＝20cos cos(sin )cos lim 3x x x x x®-201cos(sin )lim 3x x x®-= 0sin(sin )cos lim 6x x x x ®=(或2201(sin )2lim 3x x x ®=，或22201sin (sin )2lim 3x x o x x®+=)16=．【详解2】[]40sin sin(sin)sin lim x x x x x®-[]40sin sin(sin )sin lim sin x x x xx®-= ＝30sin lim t t t t ®-201cos lim 3t t t ®-=2202lim 3t tt ®=（或0sin lim 6t t t ®=） 16=．（16）(本题满分9分)计算曲线积分2sin 22(1)Lxdx x ydy +-ò，其中L 是曲线sin y x =上从(0,0)到(,0)p的一段．的一段．【详解1】按曲线积分的计算公式直接计算．】按曲线积分的计算公式直接计算．2sin 22(1)Lxdx x ydy +-ò20[sin 22(1)sin cos ]xdx x x x dx p=+-ò20sin 2x xdx p=ò200cos 2cos 22x x x xdx pp=-+ò20cos 22x xdx pp =-+ò2sin 2sin 2222x x xdx p pp=-+-ò22p =-．【详解2】添加辅助线，按照Green 公式进行计算．公式进行计算．设1L 为x 轴上从点(,0)p 到(0,0)的直线段．D 是1L 与L 围成的区域围成的区域12sin 22(1)L Lxdx x ydy ++-ò2(2(1)sin 2D x y x dxdy x y éù¶-¶=--êú¶¶ëûòò4Dxydxdy =-òòsin 004xxydydx p=-òò22sin x xdxp=-ò(1cos 2)x x dx p=--ò20cos 22xx xdx pp=-+ò2sin 2sin 2222x x xdx p pp =-+-ò22p =-．因为12sin 22(1)sin 20L xdx x ydyxdx p+-==òò故2sin 22(1)Lxdx x ydy +-ò22p =-【详解3】令2sin 22(1)LI xdx x ydy=+-ò212sin 222LLxdx ydy x ydy I I=-+=+ò对于1I，记sin 2,2P x Q y==-．因为P P y x ¶¶==¶¶，故1I 与积分路径无关．与积分路径无关．1sin 20I xdxp==ò．对于2I ，222222sin cos sin 2LI x ydyx x xdxx xdx pp===òòò200cos 2cos 22x x x xdx pp=-+ò2cos 22x xdx pp =-+ò2sin 2sin 2222x x xdx p pp =-+-ò22p =-．故2sin 22(1)Lxdx x ydy +-ò22p =-17（本题满分11分）已知曲线22220,:35,x y z C x y z ì+-=í++=î求C 上距离xoy 面最远的点和最近的点．的点．【详解1】点(,,)x y z 到xoy 面的距离为||z ，故求C 上距离xoy 面最远的点和最近的点的坐标等价于求函数2H z =在条件22220,x y z +-=35x y z ++=下的最大值点和最小值点．点．构造拉格朗日函数构造拉格朗日函数2222(,,,,)(2)(35)L x y z z x y z x y z l m l m =++-+++-，由222220,20,220,43.,350xy zL x L y L z z x y z x y z l m l m l m ¢=+=ìï¢=+=ïï¢=-++-=++==íïïïî 得x y =，从而22220,23 5.x z x z -=+=ìíî解得5,5,5.x y z ==-ìï=-íïî或1.1,1,z x y =ì=ï=íïî根据几何意义，曲线C 上存在距离xoy 面最远的点和最近的点，故所求点依次为(5,5,5)--和(1,1,1)．【详解2】点(,,)x y z 到xoy 面的距离为||z ，故求C 上距离xoy 面最远的点和最近的点的坐标等价于求函数22H x y =+在条件2225203x y x y +-æö+-=ç÷èø下的最大值点和最小值点．值点．构造拉格朗日函数构造拉格朗日函数222222(,,,)(5)9L x y z x y x yx y l l æö=+++-+-ç÷èø，由222520.422(5)0,9422(5)0,93xy L x x x y L y x x y y y y x l l ìæö¢=+-+-=ïç÷èøïïïæö¢=+-+-=+-íç÷èøæö+-=ç÷èøïïïïî得x y =，从而2222(25)09x x --=．解得解得5,5,5.x y z ==-ìï=-íïî或1.1,1,z x y =ì=ï=íïî 根据几何意义，曲线C 上存在距离xoy 面最远的点和最近的点，故所求点依次为(5,5,5)--和(1,1,1)．【详解3】由22220x y z +-=得2cos ,2sin .x z y z q q ì=ïí=ïî 代入35x y z ++=，得，得532(cos sin )z q q =++所以只要求()z z q =的最值．的最值．令()252(sin cos )()032(cos sin )z q q q q q -+¢==++，得cos sin q q =，解得5,44p p q =．从而．从而5,5,5.x y z ==-ìï=-íïî或1.1,1,z x y =ì=ï=íïî 根据几何意义，曲线C 上存在距离xoy 面最远的点和最近的点，故所求点依次为(5,5,5)--和(1,1,1)．（18）(本题满分10分)设()f x 是连续函数，是连续函数，（I ）利用定义证明函数0()()xF x f t dt =ò可导，且()()F x f x ¢=；（II ）当()f x 是以2为周期的周期函数时，为周期的周期函数时，证明函数证明函数2()2()()xG x f t dt xf t dt=-òò也是以2为周期的周期函数．为周期的周期函数．（I ）【证明】000()()()()()lim lim x xxx x f t dt f t dtF x x F x F x xx+D D ®D ®-+D -¢==D D òò0()lim x xxx f t dtx+D D ®=D ò00()lim lim ()()x x f x f f x x x x D ®D ®D ===D【注】不能利用L ’Hospital 法则得到0()()lim lim x xxx x f t dt f x x xx+D D ®D ®+D =D D ò．(II) 【证法1】根据题设，有】根据题设，有2220(2)2()(2)()(2)()x G x f t dt x f t dt f x f t dt +¢éù¢+=-+=+-êúëûòòò， 22000()2()()2()()xG x f t dt x f t dt f x f t dt ¢éù¢=-=-êúëûòòò．当()f x 是以2为周期的周期函数时，(2)()f x f x +=．从而从而 (2)()G x G x ¢¢+=．因而．因而(2)()G x G x C +-=．取0x =得，(02)(0)0C G G =+-=，故，故 (2)()0G x G x +-=．即2()2()()xG x f t dt xf t dt=-òò是以2为周期的周期函数．为周期的周期函数．【证法2】根据题设，有】根据题设，有2200(2)2()(2)()x G x f t dt x f t dt ++=-+òò，222222()()()2()x f t dt x f t dt x f t dt f t dt +=+--òòòò．对于22()x f t dt +ò，作换元2tu =+，并注意到(2)()f u f u +=，则有，则有22()(2)()()x xxxf t dt f u du f u du f t dt +=+==òòòò，因而因而 222()()0x xf t dt xf t dt +-=òò．于是于是200(2)2()()()xG x f t dt xf t dt G x +=-=òò．即20()2()()xG x f t dt xf t dt =-òò是以2为周期的周期函数为周期的周期函数【证法3】根据题设，有】根据题设，有2200(2)2()(2)()x G x f t dt x f t dt ++=-+òò，2222()2()()2()xx xf t dt f t dt xf t dt f t dt +=+--òòòò2222()()2()2()xx xf t dt xf t dt f t dt f t dt +=-+-òòòò()22()2()()x xG x f t dt f t dt +=+-òò．当()f x 是以2为周期的周期函数时，必有为周期的周期函数时，必有22()()x xf t dt f t dt +=òò．事实上事实上22(())(2)()0x d f t dt f x f x dx+=+-=ò，所以所以22()x f t dt C +ºò．取0x =得，02222()()C f t dt f t dt +º=òò．所以所以200(2)2()()()xG x f t dt xf t dt G x +=-=òò．即20()2()()xG x f t dt xf t dt =-òò是以2为周期的周期函数为周期的周期函数(19)(本题满分11分)将函数2()1(0)f x x x p =-££展开成余弦级数，并求级数11(1)n n n -¥=-å的和．的和．【详解】将()f x 作偶周期延拓，则有0,1,2,n b n ==．0a =22(1)d x x pp-ò2213p æö=-ç÷èø． 02()cos n a f x nxdx p p =ò2002cos cos nxdx x nxdx pp p p éù=-êúëûòò 220cos x nxdxp pp éù=-êúëûò202sin 2sin x nxx nx dxn npppéù-=-êúëûò1222(1)n n p p--=124(1)n n--=．所以2101221()1cos (1)143cos 2n n n n a f x x n a nx nx p -¥¥===-=+=--+åå，0x p ££．令x=0x=0，有，有n n f n p 2121(1)(0)143-¥=-=-+å又(0)1f =，所以n n n p 1221(1)12-¥=-=å．（20）(本题满分10分)设,a b 为3维列向量，矩阵T T A aa bb =+，其中,T Ta b 分别是,a b 得转置．证明：得转置．证明：（I ）秩()2r A £；（II ）若,a b 线性相关，则秩()2r A <．【详解】（I ）【证法1】()()()()()()2TTTTr A r r r r r aa bb aa bb a b =+£+£+£．【证法2】因为T TA aa bb =+，A 为33´矩阵，所以()3r A £．因为,a b 为3维列向量，所以存在向量0x ¹，使得，使得0,0TTa xb x ==于是于是 0TTA x aa x bb x =+= 所以0Ax =有非零解，从而()2r A £．【证法3】因为TT A aa bb =+，所以A 为33´矩阵．矩阵．又因为()00TTTT A a aa bb abb æöç÷=+=ç÷ç÷èø，所以|||0|00T TaA abb ==故 ()2r A £．（II ）【证法】由,a b线性相关，不妨设k a b=．于是()2()()(1)()12TTTr A r rk ra ab b b b b=+=+££<．(21) (本题满分12分)．设n 元线性方程组Ax b =，其中，其中2222212121212a a a a a A a a a a æöç÷ç÷ç÷=ç÷ç÷ç÷ç÷èø，12n x x x xæöç÷ç÷=ç÷ç÷èø，b 100æöç÷ç÷=ç÷ç÷èø．（I ）证明行列式||(1)nA n a =+；（II ）当a 为何值时，该方程组有惟一解，并求1x ．（III ）当a 为何值时，该方程组有无穷多解，并求其通解．为何值时，该方程组有无穷多解，并求其通解．【详解】（I ）【证法1】数学归纳法．记2222212121||212n na aa aaD A aa aa ==以下用数学归纳法证明(1)nn D n a =+．当1n =时，12D a =，结论成立．，结论成立．当2n =时，2222132a D a a a==，结论成立．，结论成立．假设结论对小于n 的情况成立．将n D 按第一行展开得按第一行展开得nn n aa aaD aD aa aa 2212211021212212--=-2122n n aD a D --=-1222(1)n n anaa n a--=--(1)nn a =+故(1)nA n a=+．【注】本题（1）也可用递推法．由2122n n n D aDa D --==-得，2211221()()n n nnn n n D aDa D aD aD aD a ------=-==-=．于是(1)nn D n a =+（I ）【证法2】消元法．记2222212121||212na aa aaA aa aa =22122213121212212na a aa r ar aa aa -3222221301240123321212na a ar ara aaa aa -=n n n a a an r ar n n a n n a n1213012401130111----+(1)nn a =+．（II ）【详解】当0a ¹时，方程组系数行列式0n D ¹，故方程组有惟一解．由克莱姆法则，将n D 得第一列换成b ，得行列式为，得行列式为22211222211121021212121212122n n nn aa a a aaaaD na a a a a aa aa ---===所以，11(1)n n D ax Dn a -==+．（III ）【详解】【详解】当0a =时，方程组为时，方程组为12101101001000n n x x x x -æöæöæöç÷ç÷ç÷ç÷ç÷ç÷ç÷=ç÷ç÷ç÷ç÷ç÷ç÷ç÷ç÷ç÷èøèøèø 此时方程组系数矩阵得秩和增广矩阵得秩均为1n -，所以方程组有无穷多组解，其通解为，所以方程组有无穷多组解，其通解为()()01100TTx k =+，其中k 为任意常数．为任意常数．(22) (本题满分11分)设随机变量X 与Y 相互独立，X 的概率密度为1()(1,0,1)3P X i i ===-，Y 的概率密度为密度为1,01,()0,Yy f y 其它其它..£<ì=íî记Z X Y =+．（I ）求102P Z X æö£=ç÷èø；（II ）求Z 的概率密度)(z f Z . （I ）【详解】解法1．1100221110.222P Z X P X Y X P Y X P Y æöæö£==+£=ç÷ç÷èøèøæöæö=£==£=ç÷ç÷èøèø解法2．()()1,0120201,0112.022P X Y X P Z XP X P Y X P Y P X æö+£=ç÷æöèø£==ç÷=èøæö£=ç÷æöèø==£=ç÷=èø（II ）解法1．Z z P Z z P X Y z P F (){}{} =P{X+Y z,X=-1}+P{X+Y z,X=0}+P{X+Y z,X=1} =P{Y z+1,X=-1}+P{Y z,X=0}+P{Y z-1,X=1} =P{Y z+1}P{X=-1}+P{Y z}P{X=0}+P{Y z-1}P{X=1}1=[{Y z+1}P{Y 3=£=+£££££££££££+£Y Y Y z z Y Y Y F z F z F z f z F z z f z f z f z 'z}P{Y z-1}]1=[(1)()(1)]3 ()()1,12;1(1)()(1)330,.其它+£+++-=ì-<<ï=+++-=éùíëûïî解法2．11()()()1,12;1(1)()(1)330,.Z Y i Y Y Y f z P X i f z i z f z f z f z =-==-ì-<<ï=+++-=éùíëûïîå其它（23）(本题满分11分)设n X X X 21,是来自总体2(,)N m s 的简单随机样本，记å==ni i X n X 11，2211()1ni i S X X n ==--å，221TX S n=-．（1）证明T 是m 2的无偏估计量；的无偏估计量；（2）当m s 0,1==时，求.DT . 【详解1】（1）首先T 是统计量．其次是统计量．其次221()()E T E X ES n=-222222111()()D X EX ES nn ns m s =+-=+-2m =对一切,m s 成立．因此T 是2ˆm 的无偏估计量．的无偏估计量．【详解2】（1）首先T 是统计量．其次是统计量．其次()()22111111n ni j k i j k n T X X X X n n n n n =¹=-=---åå，()()1n j k j kn ET E X EX n ¹=-å2m =，对一切,m s 成立．因此T 是2ˆm 的无偏估计量．的无偏估计量．（2）解法2．根据题意，有(0,1)nXN ，22(1)nXc ，22(1)(1)n Sn c --．于是2()2D nX =，()2(1)2(1)D n Sn -=-．所以221()D T D XS n æö=-ç÷èø()()()22222112()(1)11D nX D n Snn n n n =+-=--。

2008年全国硕士研究生入学统一考试数学一试题解析

2008年全国硕士研究生入学统一考试数学一试题解析一、选择题 (1)【答案】B【详解】2()[ln(2)]2f x x x '=+⋅，(0)0f '=，即0x =是()f x '的一个零点又2224()2ln(2)02x f x x x''=++>+，从而()f x '单调增加（(,)x ∈-∞+∞）所以()f x '只有一个零点.(2)【答案】A【详解】因为2211x yf x y '=+，2221y x y f x y-'=+，所以(0,1)1x f '=，(0,1)0y f '= 所以 (0,1)10f =⋅+⋅=grad i j i(3)【答案】D【详解】由微分方程的通解中含有x e 、cos 2x 、sin 2x 知齐次线性方程所对应的特征方程有根1,2r r i ==±，所以特征方程为(1)(2)(2)0r r i r i --+=，即32440r r r -+-=. 故以已知函数为通解的微分方程是440y y y y ''''''-+-=(4)【答案】B【详解】因为()f x 在(,)-∞+∞内单调有界，且{}n x 单调. 所以{()}n f x 单调且有界. 故{()}n f x 一定存在极限(5)【答案】C【详解】23()()E A E A A E A E -++=-=，23()()E A E A A E A E +-+=+= 故,E A E A -+均可逆．(6)【答案】B【详解】图示的二次曲面为双叶双曲面，其方程为2222221x y z a b c'''--=，即二次型的标准型为222222x y z f a b c'''=--，而标准型的系数即为A 的特征值.(7)【答案】A【详解】()(){}{}()()()()()2max ,Z F z P Z z P X Y z P X z P Y z F z F z F z =≤=≤=≤≤==(8)【答案】D【详解】用排除法. 设Y aX b =+，由1XY ρ=，知道,X Y 正相关，得0a >，排除()A 、()C 由~(0,1),~(1,4)X N Y N ，得0,1,EX EY ==所以 ()()E Y E aX b aEX b =+=+=01,a b ⨯+= 所以1b =. 排除()B . 故选择()D二、填空题 (9) 【答案】1x 【详解】由dy y dx x -=，两端积分得1ln ln y x C -=+，所以1C x y=，又(1)1y =，所以1y x =.(10) 【答案】1y x =+【详解】设(,)sin()ln()F x y xy y x x =+--，则1cos()11cos()x y y xy F dy y x dx F x xy y x--'-=-=-'+-，将(0)1y =代入得01x dydx ==，所以切线方程为10y x -=-，即1y x =+(11)【答案】(1,5]【详解】幂级数(2)nn n a x ∞=+∑的收敛区间以2x =-为中心，因为该级数在0x =处收敛，在4x =-处发散，所以其收敛半径为2，收敛域为(4,0]-，即222x -<+≤时级数收敛，亦即nn n a t∞=∑的收敛半径为2，收敛域为(2,2]-. 则(3)nn n a x ∞=-∑的收敛半径为2，由232x-<-≤得15x <≤，即幂级数0(3)nn n a x ∞=-∑的收敛域为(1,5](12)【答案】4π【详解】加221:0(4)z x y ∑=+≤的下侧，记∑与1∑所围空间区域为Ω，则2xydydz xdzdx x dxdy ∑++⎰⎰ 1122xydydz xdzdx x dxdy xydydz xdzdx x dxdy ∑+∑∑=++-++⎰⎰⎰⎰2222222441()0()2x y x y ydxdydz x dxdy x y dxdy Ω+≤+≤=--=++⎰⎰⎰⎰⎰⎰⎰ 22300142d r dr πθπ==⎰⎰(13)【答案】1【详解】1212121202(,)(,)(0,2)(,)01A A A αααααααα⎛⎫==+=⎪⎝⎭记12(,)P αα=，0201B ⎛⎫=⎪⎝⎭，则AP PB = 因为12,αα线性无关，所以P 可逆. 从而1B P AP -=，即A 与B 相似. 由2||(1)001E B λλλλλ--==-=-，得0λ=及1λ=为B 的特征值.又相似矩阵有相同的特征值，故A 的非零特征值为1.(14)【答案】12e【详解】由22()DX EX EX =-，得22()EX DX EX =+，又因为X 服从参数为1的泊松分布，所以1DX EX ==，所以2112EX =+=，所以 {}21111222P X e e --===！三、解答题(15) 【详解】方法一：4300[sin sin(sin )]sin sin sin(sin )limlim x x x x x x x x x→→--= 22220001sin cos cos(sin )cos 1cos(sin )12lim lim lim 3336x x x xx x x x x x x →→→--==== 方法二：331sin ()6x x x o x =-+ 331sin(sin )sin sin (sin )6x x x o x =-+4444400[sin sin(sin )]sin sin (sin )1lim lim 66x x x x xx o x x x x →→⎡⎤-∴ =+=⎢⎥⎣⎦ (16) 【详解】方法一：（直接取x 为参数将对坐标的曲线积分化成定积分计算）22202220000sin 22(1)[sin 22(1)sin cos ]sin 21cos 2cos 2sin 2sin 222222Lxdx x ydyx x x x dx x xdxx x x x xdx x xdx ππππππππ+-=+-⋅==-+=-+-=-⎰⎰⎰⎰⎰方法二：（添加x 轴上的直线段用格林公式化成二重积分计算）取1L 为x 轴上从点(,0)π到点(0,0)的一段，D 是由L 与1L 围成的区域112220sin 2000022000sin 22(1)sin 22(1)sin 22(1)14sin 24cos 22sin 21(1cos 2)sin 2sin 22222LL L L xDxdx x ydyxdx x ydy xdx x ydyxydxdy xdx dx xydy x x xdx x x x x dx x xdx πππππππππ++-=+--+-=--=--=-=--=-+-=-⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰方法三：（将其拆成2sin 222LLxdx ydy x ydy -+⎰⎰，前者与路径无关，选择沿x 轴上的直线段积分，后者化成定积分计算）2212sin 22(1)sin 222LLLxdx x ydy xdx ydy x ydy I I +-=-+=+⎰⎰⎰对于1I ，因为0P Qy x∂∂==∂∂，故曲线积分与路径无关，取(0,0)到(,0)π的直线段积分10sin 20I xdx π==⎰22222002200022122sin cos sin 2cos 221111cos 22cos 2sin 222221111sin 2cos 22222LI x ydy x x xdx x xdx x d x x x x xdx xd xx x x ππππππππππ====-=-+=-+⎡⎤=-++=-⎢⎥⎣⎦⎰⎰⎰⎰⎰⎰所以，原式212π=-(17) 【详解】点(,,)x y z 到xOy 面的距离为||z ，故求C 上距离xOy 面的最远点和最近点的坐标，等价于求函数2H z =在条件22220x y z +-=与35x y z ++=下的最大值点和最小值点.令 2222(,,,,)(2)(35)L x y z z x y z x y zλμλμ=++-+++- 所以 22220(1)20(2)2430(3)20(4)35(5)xy zL x L y L z z x y z x y z λμλμλμ'=+=⎧⎪'=+=⎪⎪'=-+=⎨⎪+-=⎪++=⎪⎩ 由(1)(2)得x y =，代入(4)(5)有 220235x z x z ⎧-=⎨+=⎩，解得555x y z =-⎧⎪=-⎨⎪=⎩或111x y z =⎧⎪=⎨⎪=⎩(18)【详解】(I) 对任意的x ，由于f 是连续函数，所以0000()()()()limlim x xxx x f t dt f t dtF x x F x xx+→→-+-=⎰⎰0()()limlimlim ()x x xx x x f t dt f xf xxξξ+→→→===⎰ ，其中ξ介于x 与x x +之间由于0lim ()()x f f x ξ→=，可知函数()F x 在x 处可导，且()()F x f x '=.(II)方法一：要证明()G x 以2为周期，即要证明对任意的x ，都有(2)()G x G x +=，()(2)()H x G x G x =+-，则()()()()()()()()22222()2(2)22(2)2()0x x H x f t dt x f t dt f t dt x f t dtf x f t dt f x f t dt +'''=-+--=+--+=⎰⎰⎰⎰⎰⎰又因为 ()()()22(0)(2)(0)2200H G G f t dt f t dt =-=--=⎰⎰所以 ()0H x =，即(2)()G x G x +=方法二：由于f 是以2为周期的连续函数，所以对任意的x ，有()()()()222(2)()2(2)2x x G x G x f t dt x f t dt f t dt x f t dt ++-=-+-+⎰⎰⎰⎰()()()()22202002x x f t dt f t dt f t dt f t dt +⎡⎤=+--⎢⎥⎣⎦⎰⎰⎰⎰ ()()()()000222[2]0x x xf t dt f u du f t f t dt ⎡⎤=-++=+-=⎢⎥⎣⎦⎰⎰⎰即()G x 是以2为周期的周期函数.(19)【详解】由于 220022(1)23a x dx πππ=-=-⎰212024(1)cos (1)1,2,n n a x nxdx n nππ+=-=- =⎰所以 210211(1)()cos 14cos 023n n n n a f x a nx nx x n ππ+∞∞==-=+=-+ ≤≤∑∑ 令0x =，有 2121(1)(0)143n n f n π+∞=-=-+ ∑ 又(0)1f =，所以 1221(1)12n n n π+∞=- =∑(20)【详解】(I) ()()()()()()2TTTTr A r r r r r ααββααββαβ=+≤+≤+≤(II) 由于,αβ线性相关，不妨设k αβ=. 于是()2()()(1)()12T T T r A r r k r ααβββββ=+=+≤≤<(21)【详解】(I)证法一：2222122212132101221221122aa a a a a aa aA r ar aaa a =-=121301240134(1)2(1)3231(1)0n n n a a a n a a n ar ar a n a nnn a n--+-=⋅⋅⋅=++ 证法二：记||n D A =，下面用数学归纳法证明(1)n n D n a =+．当1n =时，12D a =，结论成立．当2n =时，2222132a D a a a==，结论成立．假设结论对小于n 的情况成立．将n D 按第1行展开得2212102121212n n a a a aD aD a a-=-21221222(1)(1)n n n n n aD a D ana a n a n a ---- =-=--=+故 ||(1)nA n a =+证法三：记||n D A =，将其按第一列展开得 2122n n n D aD a D --=-，所以 211212()n n n n n n D aD aD a D a D aD ------=-=-222321()()n n n n a D aD a D aD a ---=-==-=即 12122()2n n n n n n n n D a aD a a a aD a a D ----=+=++=++2121(2)(1)n n n n n a a D n a a D --==-+=-+1(1)2(1)n n n n a a a n a -=-+⋅=+(II)因为方程组有唯一解，所以由Ax B =知0A ≠，又(1)nA n a =+，故0a ≠．由克莱姆法则，将n D 的第1列换成b ，得行列式为2221122(1)(1)112102121221122n n n nn n a aa a a aa aD na a a a a --⨯-⨯-===所以 11(1)n n D nx D n a-==+ (III)方程组有无穷多解，由0A =，有0a =，则方程组为12101101001000n n x x x x -⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪=⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 此时方程组系数矩阵的秩和增广矩阵的秩均为1n -，所以方程组有无穷多解，其通解为()()10000100,TTk k +为任意常数．(22)【详解】(I) 1201(0,)11112(0)(0)()122(0)22P X Y P Z X P X Y X P Y dy P X =≤≤==+≤===≤===⎰ (II) (){}{}Z F z P Z z P X Y z =≤=+≤{,1}{,0}{,1}P X Y z X P X Y z X P X Y z X =+≤=-++≤=++≤={1,1}{,0}{1,1}P Y z X P Y z X P Y z X =≤+=-+≤=+≤-= {1}{1}{}{0}{1}{1}P Y z P X P Y z P X P Y z P X =≤+=-+≤=+≤-=[]1{1}{}{1}3P Y z P Y z P Y z =≤++≤+≤- []1(1)()(1)3Y Y Y F z F z F z =+++- 所以 []1()(1)()(1)3Z Y Y Y f z f z f z f z =+++-1,1230,z ⎧-≤<⎪=⎨⎪⎩其它(23) 【详解】 (I) 因为2(,)XN μσ，所以2(,)XN nσμ，从而2,E X DX nσμ= =．因为 221()()E T E X S n =-221()E X E S n =- 221()()DX E X E S n =+-222211n nσμσμ=+-=所以，T 是2μ的无偏估计(II)方法一：22()()D T ET ET =-，()0E T =，22()1E S σ==所以2()D T ET =442222()S E X X S n n=-⋅+4224221()()()()E X E X E S E S n n=-+ 因为(0,1)X N ，所以1(0,)X N n，有10,E X D X n ==，()221E X DX E X n=+=所以2242222()()()()()E X D X E X D D X E X ⎡⎤=+=++⎣⎦2221()D D X n⎡⎤=+⎣⎦2221132n n n⎛⎫=⋅+= ⎪⎝⎭ ()2422222()1ES E S DS ES DS ⎡⎤==+=+⎢⎥⎣⎦因为2222(1)(1)(1)n S W n S n χσ-==--，所以2(1)DW n =-，又因为22(1)DW n DS =-，所以22(1)DS n =-,所以4211(1)1n ES n n +=+=-- 所以 2223211111n ET n n n n n +=-⋅⋅+⋅-2(1)n n =-. 方法二：当0,1μσ==时221()()D T D X S n=- (注意X 和2S 独立)222222221111(1)(1)DX DS D D n S n nn n ⎡⎤=+=+⋅-⎣⎦- 222111222(1)(1)(1)n n n n n n =⋅+⋅⋅-=--。

2008年考研数学一【试题版】【无水印】

2008年全国硕士研究生入学统一考试数学(一)试卷一、选择题(1-8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1)设函数20()ln(2)x f x t dt =+⎰则()f x '的零点个数 (A)0 (B)1(C)2(D)3(2)函数(,)arctan x f x y y=在点(0,1)处的梯度等于 (A)i(B)-i(C)j(D)-j(3)在下列微分方程中,以123cos 2sin 2x y C e C x C x =++(123,,C C C 为任意常数)为通解的是 (A)440y y y y ''''''+--= (B)440y y y y ''''''+++= (C)440y y y y ''''''--+=(D)440y y y y ''''''-+-=(4)设函数()f x 在(,)-∞+∞内单调有界,{}n x 为数列,下列命题正确的是(A)若{}n x 收敛,则{}()n f x 收敛(B)若{}n x 单调,则{}()n f x 收敛 (C)若{}()n f x 收敛,则{}n x 收敛(D)若{}()n f x 单调,则{}n x 收敛(5)设A 为n 阶非零矩阵,E 为n 阶单位矩阵. 若30=A ,则 (A)-E A 不可逆,+E A 不可逆(B)-E A 不可逆,+E A 可逆 (C)-E A 可逆,+E A 可逆(D)-E A 可逆,+E A 不可逆(6)设A 为3阶实对称矩阵,如果二次曲面方程(,,)1x x y z y z ⎛⎫ ⎪= ⎪ ⎪⎝⎭A 在正交变换下的标准方程的图形如图,则A的正特征值个数为 (A)0 (B)1 (C)2 (D)3(7)设随机变量,X Y 独立同分布且X 分布函数为()F x ,则{}max ,Z X Y =分布函数为(A)()2F x(B) ()()F x F y (C) ()211F x --⎡⎤⎣⎦(D) ()()11F x F y --⎡⎤⎡⎤⎣⎦⎣⎦(8)设随机变量()~0,1X N ,()~1,4Y N 且相关系数1XY ρ=,则 (A){}211P Y X =--= (B){}211P Y X =-= (C){}211P Y X =-+=(D){}211P Y X =+=二、填空题(9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.)(9)微分方程0xy y '+=满足条件()11y =的解是y = . (10)曲线()()sin ln xy y x x +-=在点()0,1处的切线方程为 . (11)已知幂级数()02nn n a x ∞=+∑在0x =处收敛,在4x =-处发散,则幂级数()03nn n a x ∞=-∑的收敛域为 .(12)设曲面∑是z =的上侧,则2xydydz xdzdx x dxdy ∑++=⎰⎰. (13)设A 为2阶矩阵,12,αα为线性无关的2维列向量,12120,2==+A αA ααα,则A 的非零特征值为 .(14)设随机变量X 服从参数为1的泊松分布,则{}2P X EX == .三、解答题(15－23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.) (15)(本题满分10分)求极限()40sin sin sin sin lim x x x x x →-⎡⎤⎣⎦.(16)(本题满分10分)计算曲线积分()2sin 221L xdx x ydy +-⎰,其中L 是曲线sin y x =上从点()0,0到点(),0π的一段.(17)(本题满分10分)已知曲线22220:35x y z C x y z ⎧+-=⎨++=⎩,求曲线C 距离XOY 面最远的点和最近的点.(18)(本题满分10分) 设()f x 是连续函数,(1)利用定义证明函数()()0xF x f t dt =⎰可导,且()()F x f x '=.(2)当()f x 是以2为周期的周期函数时,证明函数()22()()xG x f t dt x f t dt =-⎰⎰也是以2为周期的周期函数.(19)(本题满分10分)()21(0)f x x x π=-≤≤,用余弦级数展开,并求()1211n n n-∞=-∑的和.(20)(本题满分11分)T T =+A ααββ,T α为α的转置,T β为β的转置.证明:(1)()2r ≤A . (2)若,αβ线性相关,则()2r <A .(21)(本题满分11分)设矩阵2221212n na a aa a ⨯⎛⎫⎪⎪= ⎪⎪⎝⎭A ,现矩阵A 满足方程=AX B ,其中()1,,T n x x =X ,()1,0,,0=B ,(1)求证()1n n a =+A .(2)a 为何值,方程组有唯一解,求1x . (3)a 为何值,方程组有无穷多解,求通解.(22)(本题满分11分)设随机变量X 与Y 相互独立,X 的概率分布为{}()11,0,13P X i i ===-,Y 的概率密度为()1010Y y f y ≤≤⎧=⎨⎩其它,记Z X Y =+, (1)求102P Z X ⎧⎫≤=⎨⎬⎩⎭. (2)求Z 的概率密度.(23)(本题满分11分)设12,,,n X X X 是总体为2(,)N μσ的简单随机样本.记11n i i X X n ==∑,2211()1n i i S X X n ==--∑,221T X S n=- (1)证明T 是2μ的无偏估计量. (2)当0,1μσ==时 ,求DT .。

2008年全国硕士研究生入学统一考试数学一试题及答案详解

2008年全国硕士研究生入学统一考试数学一试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内. （1）设函数2()ln(2)x f x t dt =+ò，则()f x ¢的零点个数（） ()A 0()B 1 ()C 2 ()D 3解：()B .分析：22()ln(2)22ln(2)f x x x x x ¢=+?+2224()2ln(2)02xf x x xⅱ=++>+，恒大于0，所以()f x ¢在(,)-??上是单调递增的. 又因为(0)0f ¢=，根据其单调性可知()f x ¢只有一个零点. （2）函数(,)arctanxf x y y=在点(0,1)处的梯度等于（） ()A i()B -i ()C j ()D -j解；()A .分析：由 222222111,(0,1) 1.11x x y yyf f x x y x y y y =====+++ 22222,(0,1)0.1y y x y xf f x x y y--===++所以(0,1)10.gradf i j i =??（3）在下列微分方程中，以123cos 2sin 2x y C e C x C x =++（123,,C C C 为任意常数）为通解的是（）()A 440y y y y ⅱⅱⅱ+--=. ()B 440y y y y ⅱⅱⅱ+++=. ()C 440y y y y ⅱⅱⅱ--+=.()D 440y y y y ⅱⅱⅱ-+-=. 解：()D .分析；由123cos 2sin 2x y C e C x C x =++可知其特征根为12,31,2i l l ==?.故对应的特征方程为 2(1)(2)(2)(1)(4)i i l l l l l -+-=-+32324444l l l lll =+--=-+-所以所求微分方程为440y y y y ⅱⅱⅱ-+-=, 选()D . （4）设函数()f x 在(,)-??内单调有界，{}n x 为数列，下列命题正确的是（）()A 若{}n x 收敛，则{}()n f x 收敛. ()B 若{}n x 单调，则{}()n f x 收敛.()C 若{}()n f x 收敛，则{}n x 收敛.()D 若{}()n f x 单调，则{}n x 收敛.解：()B分析：若{}n x 单调，则由()f x 在(,)-??内单调有界知，{}()n f x 单调有界，因此{}()n f x 收敛,应选()B .（5）设A 为n 阶非零矩阵，E 为n 阶单位矩阵. 若30A =，则（）()A ()1,4Y N :不可逆，E A +不可逆.()B E A -不可逆，E A +可逆.()C E A -可逆，E A +可逆.()D E A -可逆，E A +不可逆.解：选()C分析：23()()E A E A A E A E -++=-=，23()()E A E A A E A E +-+=+= 故,E A E A -+均可逆。

考研资料数三2008年真题.doc

2008年全国硕士研究生入学统一考试xyzsakura 数学三试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内.（1）设函数()f x 在区间[1,1]-上连续，则0x =是函数0()()xf t dtg x x=⎰的（）()A 跳跃间断点. ()B 可去间断点.()C 无穷间断点.()D 振荡间断点.（2）曲线段方程为()y f x =，函数()f x 在区间[0,]a 上有连续的导数，则定积分()at af x dx ⎰等于（）()A 曲边梯形ABCD 面积. ()B 梯形ABCD 面积.()C 曲边三角形ACD 面积.()D 三角形ACD 面积.（3）已知(,)f x y =，则（A ）(0,0)x f '，(0,0)y f '都存在（B ）(0,0)x f '不存在，(0,0)y f '存在（C ）(0,0)x f '不存在，(0,0)y f '不存在（D ）(0,0)x f '，(0,0)y f '都不存在（4）设函数f连续，若22(,)uvD f u v =，其中uv D 为图中阴影部分，则Fu∂=∂（）（A ）2()vf u （B ）2()v f u u （C ）()vf u （D ）()vf u u（5）设A 为阶非0矩阵E 为阶单位矩阵若30A =，则（）()A E A -不可逆，E A +不可逆.()B E A -不可逆，E A +可逆.()C E A -可逆，E A +可逆.()D E A -可逆，E A +不可逆.（6）设1221A ⎛⎫=⎪⎝⎭则在实数域上域与A 合同矩阵为（）()A 2112-⎛⎫ ⎪-⎝⎭.()B 2112-⎛⎫ ⎪-⎝⎭.()C 2112⎛⎫⎪⎝⎭.()D 1221-⎛⎫⎪-⎝⎭.（7）随机变量,X Y 独立同分布且X 分布函数为()F x ，则{}max ,Z X Y =分布函数为（）()A ()2F x .()B ()()F x F y .()C ()211F x --⎡⎤⎣⎦.()D ()()11F x F y --⎡⎤⎡⎤⎣⎦⎣⎦.（8）随机变量()~0,1X N ，()~1,4Y N 且相关系数1XY ρ=，则（）()A {}211P Y X =--=. ()B {}211P Y X =-=. ()C {}211P Y X =-+=.()D {}211P Y X =+=.二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.（9）设函数21,()2,x x cf x x c x ⎧+≤⎪=⎨>⎪⎩在(,)-∞+∞内连续，则c = .（10）设341()1x x f x x x ++=+，则2()______f x dx =⎰.（11）设22{(,)1}D x y x y =+≤，则2()Dx y dxdy -=⎰⎰ . （12）微分方程0xy y '+=满足条件(1)1y =的解y = .（13）设3阶矩阵A 的特征值为1，2，2，E 为3阶单位矩阵，则14_____A E --=. （14）设随机变量X 服从参数为1的泊松分布，则{}2P X EX == .三、解答题：15－23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15) （本题满分10分）求极限201sin limln x x x x→. (16) （本题满分10分）设(,)z z x y =是由方程()22x y z x y z ϕ+-=++所确定的函数，其中ϕ具有2阶导数且1ϕ'≠-时.（1）求dz （2）记()1,z z u x y x y x y ⎛⎫∂∂=- ⎪-∂∂⎝⎭，求u x ∂∂. (17) （本题满分11分）计算max(,1),Dxy dxdy ⎰⎰其中{(,)02,02}D x y x y =≤≤≤≤.(18) （本题满分10分）设()f x 是周期为2的连续函数，（1）证明对任意实数t ，有()()22t tf x dx f x dx +=⎰⎰；（2）证明()()()202xt t G x f t f s ds dt +⎡⎤=-⎢⎥⎣⎦⎰⎰是周期为2的周期函数．(19) （本题满分10分）设银行存款的年利率为0.05r =，并依年复利计算，某基金会希望通过存款A 万元，实现第一年提取19万元，第二年提取28万元，…，第n 年提取（10+9n ）万元，并能按此规律一直提取下去，问A 至少应为多少万元？ (20) （本题满分12分）设矩阵2221212n na a a A a a ⨯⎛⎫⎪⎪= ⎪⎪⎝⎭OO O ，现矩阵A 满足方程AX B =，其中()1,,Tn X x x =L ，()1,0,,0B =L ，（1）求证()1nA n a =+;（2）a 为何值，方程组有唯一解; （3）a 为何值，方程组有无穷多解. （21）（本题满分10分）设A 为3阶矩阵，12,a a 为A 的分别属于特征值1,1-特征向量，向量3a 满足323Aa a a =+，证明（1）123,,a a a 线性无关；（2）令()123,,P a a a =，求1P AP -.（22）（本题满分11分）设随机变量X 与Y 相互独立，X 的概率分布为{}()11,0,13P X i i ===-，Y 的概率密度为()1010Y y f y ≤≤⎧=⎨⎩其它，记Z X Y =+（1）求102P Z X ⎧⎫≤=⎨⎬⎩⎭；（2）求Z 的概率密度．（23）（本题满分11分）12,,,n X X X L 是总体为2(,)N μσ的简单随机样本.记11ni i X X n ==∑，2211()1n ii S X X n ==--∑，221T X S n =-. （1）证 T 是2μ的无偏估计量. （2）当0,1μσ==时，求DT .2008年考研数学（三）真题解析一、选择题 (1)【答案】B【详解】 ()()0()lim ()limlim 0xx x x f t dt g x f x f x→→→===⎰，所以0x =是函数()g x 的可去间断点． (2)【答案】C 【详解】00()()()()()()aa a aaxf x dx xdf x xf x f x dx af a f x dx '==-=-⎰⎰⎰⎰其中()af a 是矩形ABOC 面积，0()af x dx ⎰为曲边梯形ABOD 的面积，所以0()axf x dx '⎰为曲边三角形的面积．(3)【答案】B【详解】000(,0)(0,0)11(0,0)lim lim lim 0xx x x x f x f e f x xx→→→---'===- 0011lim lim 1xx x x e e x x ++→→--==，0011lim lim 1xx x x e e x x---→→--==- 故(0,0)x f '不存在．220000(0,)(0,0)11(0,0)lim limlim lim 00y y y y y y f y f e y f y yyy →→→→---'=====- 所以(0,0)y f '存在．故选B . (4)【答案】A【详解】用极坐标得 ()222()2011,()vu uf r r Df u v F u v dv rdr v f r dr +===⎰⎰⎰所以()2Fvf u u∂=∂. (5)【答案】C【详解】23()()E A E A A E A E -++=-=，23()()E A E A A E A E +-+=+=. 故,E A E A -+均可逆． (6)【答案】D【详解】记1221D -⎛⎫= ⎪-⎝⎭，则()2121421E D λλλλ--==---又()2121421E A λλλλ---==----，所以A 和D 有相同的特征多项式，所以A 和D 有相同的特征值.又A 和D 为同阶实对称矩阵，所以A 和D 相似．由于实对称矩阵相似必合同，故D 正确. (7)【答案】A【详解】()(){}{}()()()()()2max ,Z Z Z Z F z P Z z P X Y z P X z P Y z F z F z F z =≤=≤=≤≤==.(8)【答案】D【详解】用排除法. 设Y aX b =+，由1XY ρ=，知道,X Y 正相关，得0a >，排除()A 、()C 由~(0,1),~(1,4)X N Y N ，得0,1,EX EY ==所以 ()()E Y E aX b aEX b =+=+01,a b =⨯+= 所以1b =. 排除()B . 故选择()D . 二、填空题 (9)【答案】1【详解】由题设知||0c x ≥≥，所以22,()1,2,x x c f x x c x c x x c >⎧⎪=+-≤≤⎨⎪-<-⎩因为 ()22lim lim(1)1x cx cf x x c --→→=+=+，()22lim lim x cx cf x x c++→→== 又因为()f x 在(,)-∞+∞内连续，()f x 必在x c =处连续所以 ()()lim lim ()x c x cf x f x f c +-→→==，即2211c c c+=⇒=. (10)【答案】1ln 32【详解】222111112x xx x f x x x x x x ++⎛⎫+== ⎪⎝⎭⎛⎫++- ⎪⎝⎭，令1t x x =+，得()22t f t t =- 所以()()()22222111ln 2ln 6ln 2ln 32222x f x dx dx x x ==-=-=-⎰⎰. (11)【答案】4π【详解】()22221()2DDDx y dxdy x dxdy x y dxdy -=+⎰⎰⎰⎰⎰⎰利用函数奇偶性21200124d r rdr ππθ==⎰⎰.(12)【答案】1y x= 【详解】由dy ydx x-=，两端积分得1ln ln y x C -=+，所以1x C y =+，又(1)1y =，所以1y x=. (13)【答案】3【详解】A 的特征值为1,2,2，所以1A -的特征值为1,12,12，所以14A E --的特征值为4113⨯-=，41211⨯-=，41211⨯-= 所以143113B E --=⨯⨯=. (14)【答案】112e - 【详解】由22()DX EX EX =-，得22()EX DX EX =+，又因为X 服从参数为1的泊松分布，所以1DX EX ==，所以2112EX =+=，所以 {}21111222P X e e --===！.三、解答题(15) 【详解】方法一：22001sin 1sin limln lim ln 11x x x x x x x x →→⎛⎫=+- ⎪⎝⎭32000sin cos 1sin 1limlim lim 366x x x x x x x x x x →→→--===-=-方法二：2230001sin cos sin cos sin lim ln lim lim 2sin 2x x x x x x x x x xx x x x x→→→--=洛必达法则 20sin 1lim 66x x x x →-=-洛必达法则 (16) 【详解】(I) ()()22xdx ydy dz x y z dx dy dz ϕ'+-=++⋅++()()()122dz x dx y dy ϕϕϕ'''⇒+=-++-+()()221x dx y dydz ϕϕϕ''-++-+⇒='+()1ϕ'≠-Q(II) 由上一问可知22,11z x z yx y ϕϕϕϕ''∂-+∂-+==''∂+∂+，所以 ()11221222,()()1111z z x y y x u x y x y x y x y x y ϕϕϕϕϕϕ''∂∂-+-+-+=-=-=⋅=''''-∂∂-++-++所以 ()()()()223322(1)2(1)2(12)2(12)11111x z u x x x x ϕϕϕϕϕϕϕϕϕϕϕϕ'-∂''+''-+'''''''∂++-++∂==-=-=-∂''''++++. (17) 【详解】曲线1xy =将区域分成两个区域1D 和23D D +，为了便于计算继续对区域分割，最后为()max ,1Dxy dxdy ⎰⎰123D D D xydxdy dxdy dxdy =++⎰⎰⎰⎰⎰⎰112222211102211x xdx dy dx dy dx xydy =++⎰⎰⎰⎰⎰⎰1512ln 2ln 24=++- 19ln 24=+ (18) 【详解】方法一：(I) 由积分的性质知对任意的实数t ，()()()()20222t t ttf x dx f x dx f x dx f x dx ++=++⎰⎰⎰⎰令2x u =+，则()()()()222t tttf x dx f u du f u du f x dx +=+==-⎰⎰⎰⎰所以()()()()()222t tttf x dx f x dx f x dx f x dx f x dx +=+-=⎰⎰⎰⎰⎰(II) 由(1)知，对任意的t 有()()222t f x dx f x dx +=⎰⎰，记()2a f x dx =⎰，则()0()2xG x f u du ax =-⎰. 所以，对任意的x ，()()2(2)()2(2)2x xG x G x f u du a x f u du ax ++-=-+-+⎰⎰()()22022220x xf u du a f u du a +=-=-=⎰⎰所以()G x 是周期为2的周期函数.方法二：(I) 设2()()t tF t f x dx +=⎰，由于()(2)()0F t f t f t '=+-=，所以()F t 为常数，从而有()(0)F t F =. 而2(0)()F f x dx =⎰，所以2()()F t f x dx =⎰，即22()()t tf x dx f x dx +=⎰⎰.(II) 由(I)知，对任意的t 有()()222t f x dx f x dx +=⎰⎰，记()2a f x dx =⎰，则()0()2xG x f u du ax =-⎰ ， ()20(2)2(2)x G x f u du a x ++=-+⎰由于对任意x ，()(2)2(2)2()G x f x a f x a '+=+-=-，()()2()G x f x a '=- 所以 ()(2)()0G x G x '+-=，从而 (2)()G x G x +-是常数即有 (2)()(2)(0)0G x G x G G +-=-= 所以()G x 是周期为2的周期函数.(19) 【详解】方法一：设n A 为用于第n 年提取(109)n +万元的贴现值，则(1)(109)nn A r n -=++故 1111110919102009(1)(1)(1)(1)n n n n nn n n n n n n nA A r r r r ∞∞∞∞∞=====+===+=+++++∑∑∑∑∑ 设 1()(1,1)nn S x nx x ∞==∈-∑因为 21()()()(1,1)1(1)nn x x S x x x x x x x ∞=''=== ∈---∑ 所以 11()()4201 1.05S S r ==+(万元) 故 20094203980A =+⨯=(万元)，即至少应存入3980万元.方法二：设第t 年取款后的余款是t y ，由题意知t y 满足方程1(10.05)(109)t t y y t -=+-+，即 11.05(109)t t y y t --=-+ (1)(1)对应的齐次方程 11.050t t y y --=的通解为 (1.05)tt y C = 设(1)的通解为 *t y at b =+，代入(1)解得 180a =，3980b = 所以(1)的通解为 (1.05)1803980tt y C t =++由0y A =，0t y ≥得 3980A C =+ 0C ≥ 故A 至少为3980万元．(20) 【详解】(I)证法一：222212212121321122122112221301240134(1)2(1)3231(1)0n n n a a aa a a a a a A r ar a aa aa a an a a n a r ar a n a nnn a n-=-=-+-=⋅⋅⋅=++OOLO OO O OO OO OO O K O O OO O证法二：记||n D A =，下面用数学归纳法证明(1)nn D n a =+．当1n =时，222212212121321122122112221301240134(1)2(1)3231(1)0n n n a a aa a a a a a A r ar a aa aa a an a a n a r ar a n a nnn a n-=-=-+-=⋅⋅⋅=++OOLO OO O OO OO OO O K O O OO O12D a =，结论成立．当2n =时，2222132a D a a a==，结论成立．假设结论对小于n 的情况成立．将n D 按第1行展开得221221221210212121222(1)(1)n n n n nn n a a a a D aD a aaD a D ana a n a n a -----=-=-=--=+O OO OO故 ||(1)nA n a =+证法三：记||n D A =，将其按第一列展开得 2122n n n D aD a D --=-，所以 211212()n n n n n n D aD aD a D a D aD ------=-=-222321()()n n n n a D aD a D aD a ---=-==-=L即 12122()2n n n n n n n n D a aD a a a aD a a D ----=+=++=++2121(2)(1)n n n n n a a D n a a D --==-+=-+L1(1)2(1)n n n n a a a n a -=-+⋅=+(II) 因为方程组有唯一解，所以由Ax B =知0A ≠，又(1)nA n a =+，故0a ≠．由克莱姆法则，将n D 的第1列换成b ，得行列式为2221122(1)(1)112102*********n n n nn n a a a aa a a a D na a a a a --⨯-⨯-===O O OO O OO O OO OO所以 11(1)n n D nx D n a-==+ (III) 方程组有无穷多解，由0A =，有0a =，则方程组为12101101001000n n x x x x -⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭M O O M此时方程组系数矩阵的秩和增广矩阵的秩均为1n -，所以方程组有无穷多解，其通解为()()10000100,TTk k +LL为任意常数．(21)【详解】(I)证法一：假设123,,ααα线性相关．因为12,αα分别属于不同特征值的特征向量，故12,αα线性无关，则3α可由12,αα线性表出，不妨设31122l l ααα=+，其中12,l l 不全为零(若12,l l 同时为0，则3α为0，由323A ααα=+可知20α=，而特征向量都是非0向量，矛盾)Q 11,A αα=-22A αα=∴32321122A l l αααααα=+=++，又311221122()A A l l l l ααααα=+=-+ ∴112221122l l l l ααααα-+=++，整理得：11220l αα+=则12,αα线性相关，矛盾. 所以，123,,ααα线性无关.证法二：设存在数123,,k k k ，使得1122330k k k ααα++= (1)用A 左乘(1)的两边并由11,A αα=-22A αα=得1123233()0k k k k ααα-+++= (2)(1)—(2)得 113220k k αα-= (3) 因为12,αα是A 的属于不同特征值的特征向量，所以12,αα线性无关，从而130k k ==，代入(1)得220k α=，又由于20α≠，所以20k =，故123,,ααα线性无关.(II) 记123(,,)P ααα=，则P 可逆，123123(,,)(,,)AP A A A A αααααα==1223(,,)αααα=-+123100(,,)011001ααα-⎛⎫ ⎪= ⎪ ⎪⎝⎭100011001P -⎛⎫ ⎪= ⎪ ⎪⎝⎭所以 1100011001P AP --⎛⎫ ⎪= ⎪ ⎪⎝⎭.(22)【详解】(I) 1201(0,)11112(0)(0)()122(0)22P X Y P Z X P X Y X P Y dy P X =≤≤==+≤===≤===⎰ (II) (){}{}Z F z P Z z P X Y z =≤=+≤{,1}{,0}{,1}P X Y z X P X Y z X P X Y z X =+≤=-++≤=++≤= {1,1}{,0}{1,1}P Y z X P Y z X P Y z X =≤+=-+≤=+≤-= {1}{1}{}{0}{1}{1}P Y z P X P Y z P X P Y z P X =≤+=-+≤=+≤-=[]1{1}{}{1}3P Y z P Y z P Y z =≤++≤+≤- []1(1)()(1)3Y Y Y F z F z F z =+++- 所以 []1()(1)()(1)3Z Y Y Y f z f z f z f z =+++-1,1230,z ⎧-≤<⎪=⎨⎪⎩其它(23) 【详解】(I) 因为2(,)X N μσ:，所以2(,)X N nσμ:，从而2,E X D X nσμ= =．因为 221()()E T E X S n =-221()E X E S n =- 221()()DX E X E S n =+-222211n nσμσμ=+-=所以，T 是2μ的无偏估计(II)方法一：22()()D T ET ET =-，()0E T =，22()1E S σ==所以2()D T ET =442222()S E X X S n n=-⋅+4224221()()()()E X E X E S E S n n=-+因为(0,1)X N :，所以1(0,)X N n:，有10,E X DX n ==，()221E X DX E X n=+=所以2242222()()()()()E X D X E X D D X E X⎡⎤=+=++⎣⎦2221()D D X n⎡⎤=+⎣⎦2221132n n n ⎛⎫=⋅+= ⎪⎝⎭()2422222()1ES E S DS ES DS ⎡⎤==+=+⎢⎥⎣⎦因为2222(1)(1)(1)n S W n S n χσ-==--:，所以2(1)DW n =-，又因为22(1)DW n DS =-，所以22(1)DS n =-,所以4211(1)1n ES n n +=+=--所以 2223211111n ET n n n n n +=-⋅⋅+⋅-2(1)n n =-. 方法二：当0,1μσ==时221()()D T D X S n=- (注意X 和2S 独立)222222221111(1)(1)DX DS DD n S n nn n ⎡⎤=+=+⋅-⎣⎦-精品文档。

2008年全国考研数学一真题及答案.doc

2008年考研数学一真题一、选择题（18小题，每小题4分，共32分。

下列每题给出的四个选项中，只有一个选项是符合题目要求的。

）(1)设函数,则的零点个数为(A)0 (B)1(C)2 (D)3【答案】B。

【解析】且，则是唯一的零点综上所述，本题正确答案是B。

【考点】高等数学—一元函数积分学—积分上限的函数及其导数(2)函数在点处的梯度等于(A)(B)(C)(D)【答案】A。

【解析】所以综上所述，本题正确答案是A。

【考点】高等数学—多元函数微分学—方向导数和梯度(3)在下列微分方程中，以为任意常数为通解的是(A)(B)(C)(D)【答案】D。

【解析】由通解表达式可知其特征根为可见其对应特征方程为故对应微分方程为综上所述，本题正确答案是D。

【考点】高等数学—常微分方程—高于二阶的某些常系数齐次线性微分方程(4)设函数在内单调有界，为数列，下列命题正确的是(A)若收敛，则收敛(B)若单调，则收敛(C)若收敛，则收敛(D)若单调，则收敛【答案】B。

【解析】【方法一】由于单调，单调有界，则数列单调有界，根据单调有界准则知数列收敛。

【方法二】排除法：若取,,则显然单调，收敛，但，为偶数为奇数，显然不收敛，排除A。

若取,显然收敛且单调，但不收敛，排除C和D。

综上所述，本题正确答案是B。

【考点】高等数学—函数、极限、连续—函数的有界性、单调性、周期性和奇偶性，极限存在的两个准则：单调有界准则和夹逼准则(5)设为阶非零矩阵，为阶单位矩阵，若,则(A)不可逆，不可逆(B)不可逆，可逆(C)可逆，可逆(D)可逆，不可逆【答案】C。

【解析】因为所以可知可逆，可逆综上所述，本题正确答案是C。

【考点】线性代数—矩阵—矩阵的概念和性质，矩阵可逆的充分必要条件(6)设为3阶实对称矩阵，如果二次曲面方程在正交变换下的标准方程的图形如右图所示，则的正特征值的个数为(A)(B)1(C)2 (D)3【答案】B。

【解析】所给图形为双叶双曲线，标准方程为二次型正交变换化为标准形时，其平方项的系数就是的特征值，可知的正特征值的个数为1综上所述，本题正确答案是B。

2008年数四考研数学真题及解析

2008年全国硕士研究生入学统一考试数学四试题解析一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内. （1）设0a b <<，则()10lim nnnn ab--→+（）()A a .()B 1a -. ()C b .()D 1b -.（2）设函数()f x 在区间[1,1]-上连续，则0x =是函数0()()x f t dt g x x=⎰的（）()A 跳跃间断点. ()B 可去间断点. ()C 无穷.()D 振荡.（3）设()f x 是连续奇函数，()g x 是连续偶函数，区域{(,)01,D x y x y =≤≤≤则正确的（）()A ()()0Df yg x dxdy =⎰⎰.()B ()()0D f x g y d x d y =⎰⎰.()C [()()]0Df xg y dxdy +=⎰⎰.()D [()()]0Df yg x dxdy +=⎰⎰.（4）曲线方程为()y f x =函数在区间[0,]a 上有连续导数，则定积分'0()axf x dx ⎰（）()A 曲边梯形ABCD 面积.()B 梯形ABCD 面积.()C 曲边三角形ACD 面积.()D 三角形ACD 面积.（5）设A 为n 阶非零矩阵，E 为n 阶单位矩阵. 若30A =，则（）()A E A -不可逆，E A +不可逆.()B E A -不可逆，E A +可逆.()C E A -可逆，E A +可逆.()D E A -可逆，E A +不可逆.（6）设1221A ⎛⎫=⎪⎝⎭，则在实数域上与A 合同的矩阵为（） ()A 2112-⎛⎫⎪-⎝⎭ ()B 2112-⎛⎫ ⎪-⎝⎭ ()C 2112⎛⎫ ⎪⎝⎭()D 1221-⎛⎫⎪-⎝⎭. （7）随机变量,X Y 独立同分布且X 的分布函数为()F x ，则{}max ,Z X Y =的分布函数为（）()A ()2F x .()B ()()F x F y .()C ()211F x --⎡⎤⎣⎦.()D ()()11F x F y --⎡⎤⎡⎤⎣⎦⎣⎦.（8）随机变量()0,1X N ，()1,4Y N 且相关系数1XY ρ=，则（）()A {}211P Y X =--=. ()B {}211P Y X =-=. ()C {}211P Y X =-+=.()D {}211P Y X =+=.二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.（9）设函数21,()2,x x cf x x c x ⎧+≤⎪=⎨>⎪⎩在(,)-∞+∞内连续，则c = .（10）已知函数()f x 连续且0()lim2x f x x→=，则曲线()y f x =上对应0x =处切线方程为 . （11）2113ln y dx x xdy =⎰⎰ .（12）微分方程2()0x y x e dx xdy -+-=通解是y = .（13）设3阶矩阵A 的特征值互不相同，若行列式0A =，则A 的秩为 . （14）设随机变量X 服从参数为1的泊松分布，则{}2P X EX == .三、解答题：15－23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)（本题满分10分）求极限201sin limln x x x x→. (16) （本题满分10分）设()()1f x t t x dt =-⎰，01x <<，求()f x 的极值、单调区间和凹凸区间.(17)（本题满分10分）求函数222u x y z =++在在约束条件22z x y =+和4x y z ++=下的最大和最小值. (18)（本题满分10分）设(),z z x y =是由方程()22x y z x y z ϕ+-=++所确定的函数，其中ϕ具有2阶导数且1ϕ'≠-时，求(1)dz（2）记()1,z z u x y x y x y ⎛⎫∂∂=- ⎪-∂∂⎝⎭，求u x ∂∂.(19)（本题满分10分）()f x 是周期为2的连续函数，（1）证明对任意实数都有()()22t tf x dx f x dx +=⎰⎰（2）证明()()()202xt t g x f t f s ds dt +⎡⎤=-⎢⎥⎣⎦⎰⎰是周期为2的周期函数．（20）（本题满分11分）设矩阵2221212n na a a A a a ⨯⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭ ，现矩阵A 满足方程AX B =，其中()1,,T n X x x = ，()1,0,,0B = ，（1）求证()1nA n a =+（2）a 为何值，方程组有唯一解（3）a 为何值，方程组有无穷多解(21)（本题满分11分）设A 为3阶矩阵，12,αα为A 的分别属于特征值1,1-特征向量，向量3α满足323A ααα=+，证明（1）123,,ααα线性无关；（2）令()123,,P ααα=，求1P AP -.（22）（本题满分9分）设随机变量X 与Y 相互独立，X 概率分布为{}()11,0,13P X i i ===-，Y 概率密度为()1010Y y f y ≤≤⎧=⎨⎩其它，记Z X Y =+（1）求102P Z X ⎧⎫≤=⎨⎬⎩⎭（2）求Z 的概率密度（23）（本题满分9分）设某企业生产线上产品合格率为0.96，不合格产品中只有34产品可进行再加工且再加工的合格率为0.8，其余均为废品，每件合格品获利80元，每件废品亏损20元，为保证该企业每天平均利润不低于2万元，问企业每天至少生产多少产品？.文 - 汉语汉字编辑词条文，wen，从玄从爻。

2008年全国硕士研究生入学统一考试数学一试题

2008年全国硕士研究生入学统一考试数学一试题一、选择题：1～8小题，每小题4分，共32分，下列每小题给出的四个选项中，只有一项符合题目要求，把所选项前的字母填在题后的括号内. （1）设函数2()ln(2)x f x t dt =+⎰则()f x '的零点个数（）()A 0.()B 1. ()C 2.()D 3.（2）函数(,)arctanxf x y y=在点(0,1)处的梯度等于（） ()A i .()B i -. ()C j .()D j -.（3）在下列微分方程中，从123cos2sin 2x y C e C x C x =++（123,,C C C 为任意常数）为通解的是（）()A 440y y y y ''''''+--=.()B 440y y y y ''''''+++=.()C 440y y y y ''''''--+=.()D 440y y y y ''''''-+-=.（4）设函数()f x 在(,)-∞+∞内单调有界，{}n x 为数列，下列命题正确的是（）()A 若{}n x 收敛，则{}()n f x 收敛. ()B 若{}n x 单调，则{}()n f x 收敛.()C 若{}()n f x 收敛，则{}n x 收敛.()D 若{}()n f x 单调，则{}n x 收敛.（5）设A 为n 阶非零矩阵E 为n 阶单位矩阵若30A =，则（）()A E A -不可逆，E A +不可逆.()B E A -不可逆，E A +可逆.()C E A -可逆，E A +可逆.()D E A -可逆，E A +不可逆.（6）设A 为3阶非零矩阵，如果二次曲面方程(,,)1x x y z A y z ⎛⎫ ⎪= ⎪ ⎪⎝⎭在正交变换下的标准方程的图形如图，则A 的正特征值个数（）()A 0.()B 1.()C 2.()D 3.（7）随机变量,X Y 独立同分布且X 分布函数为()F X ，则{}max ,Z X Y =分布函数为（）()A ()2F X .()B ()()F X F Y .()C ()211F X --⎡⎤⎣⎦.()D ()()11F X F Y --⎡⎤⎡⎤⎣⎦⎣⎦.（8）随机变量()0,1XN ，()1,4YN 且相关系数1XY ρ=，则（）()A {}211P Y X =--=. ()B {}211P Y X =-=. ()C {}211P Y X =-+=.()D {}211P Y X =+=.二、填空题：9-14小题，每小题4分，共24分，请将答案写在答题纸指定位置上.（9）微分方程0xy y '+=满足条件()11y =的解是y = . （10）曲线()()sin ln xy y x x +-=在点()0,1处的切线方程为 .（11）已知幂级数()02nn n a x ∞=+∑在0x =处收敛，在4x =-处发散，则幂级数()03nn n a x ∞=-∑的收敛域为 . （12）设曲面∑是z =的上侧，则2xydydz xdzdx x dxdy ∑++=⎰⎰ .（13）设A 为2阶矩阵，12,a a 为线性无关的2维列向量，12120,2Aa Aa a a ==+，则A 的非零特征值为 .（14）设随机变量X 服从参数为1的泊松分布，则{}2P X EX == .三、解答题：15－23小题，共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)（本题满分10分）求极限()40sin sin sin sin lim x x x x x →-⎡⎤⎣⎦.(16)（本题满分12分）计算曲线积分()2sin 221Lxdx x ydy +-⎰，其中L 是曲线sin y x =上从点()0,0到点(),0π的一段.(17)（本题满分12分）已知曲线22220:35x y z C x y z ⎧+-=⎨++=⎩，求C 点距离XOY 面最远点和最近的点.(18)（本题满分12分）函数()f x 连续，()()0xF x f t dt =⎰，证明()F x 可导，且()()F x f x '=.(19)（本题满分12分）()21f x x =-，用余弦级数展开，并求()1211n n n +∞=-∑的和(20)（本题满分9分）T T A ααββ=+，T α为α的转置，T β为β的转置（1）证()2r A ≤；（2）若,αβ线性相关，则()2r A <. （21）（本题满分9分）设矩阵2221212n na a aA a a ⨯⎛⎫⎪⎪= ⎪⎪⎝⎭，现矩阵A 满足方程AX B =，其中()1,,Tn X x x =，()1,0,,0B =，（1）求证()1nA n a =+（2）a 为何值，方程组有唯一解，求1x （3）a 为何值，方程组有无穷多解，求通解（22）（本题满分9分）设随机变量X 与Y 相互独立，X 概率分布为{}()11,0,13P X i i ===-，概率密度为()1010Y y f y ≤≤⎧=⎨⎩其它，记Z X Y =+（1）求102P Z X ⎧⎫≤=⎨⎬⎩⎭（2）求Z 的概率密度．（23）（本题满分9分）12,,,n x x x 是总体为2(,)N μσ的简单随机样本.记11ni i x x n ==∑，2211()1n ii S x x n ==--∑，221T x S n =- （1）证 T 是2μ的无偏估计量.（2）当0,1μσ==时，求DT . .。

2008-2011年全国硕士研究生入学统一考试数学一真题

2008年全国硕士研究生入学统一考试数学(一)试卷一、选择题(1-8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1)设函数2()ln(2)x f x t dt =+⎰则()f x '的零点个数(A)0 (B)1(C)2(D)3(2)函数(,)arctan xf x y y=在点(0,1)处的梯度等于 (A)i (B)-i(C)j(D)-j(3)在下列微分方程中,以123cos 2sin 2xy C e C x C x =++(123,,C C C 为任意常数)为通解的是(A)440y y y y ''''''+--= (B)440y y y y ''''''+++= (C)440y y y y ''''''--+=(D)440y y y y ''''''-+-=(4)设函数()f x 在(,)-∞+∞内单调有界,{}n x 为数列,下列命题正确的是 (A)若{}n x 收敛,则{}()n f x 收敛 (B)若{}n x 单调,则{}()n f x 收敛 (C)若{}()n f x 收敛,则{}n x 收敛(D)若{}()n f x 单调,则{}n x 收敛(5)设A 为n 阶非零矩阵,E 为n 阶单位矩阵. 若30=A ,则 (A)-E A 不可逆,+E A 不可逆 (B)-E A 不可逆,+E A 可逆(C)-E A 可逆,+E A 可逆 (D)-E A 可逆,+E A 不可逆 (6)设A 为3阶实对称矩阵,如果二次曲面方程(,,)1x x y z y z ⎛⎫ ⎪= ⎪ ⎪⎝⎭A 在正交变换下的标准方程的图形如图,则A 的正特征值个数为(A)0 (B)1 (C)2 (D)3(7)设随机变量,X Y 独立同分布且X 分布函数为()F x ,则{}max ,Z X Y =分布函数为(A)()2Fx(B) ()()F x F y(C) ()211F x --⎡⎤⎣⎦(D) ()()11F x F y --⎡⎤⎡⎤⎣⎦⎣⎦(8)设随机变量()~0,1X N ,()~1,4Y N 且相关系数1XY ρ=,则 (A){}211P Y X =--= (B){}211P Y X =-= (C){}211P Y X =-+=(D){}211P Y X =+=二、填空题(9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.) (9)微分方程0xy y '+=满足条件()11y =的解是y = . (10)曲线()()sin ln xy y x x +-=在点()0,1处的切线方程为 . (11)已知幂级数()02nn n a x ∞=+∑在0x =处收敛,在4x =-处发散,则幂级数()03nn n a x ∞=-∑的收敛域为 .(12)设曲面∑是z =的上侧,则2xydydz xdzdx x dxdy ∑++=⎰⎰ . (13)设A 为2阶矩阵,12,αα为线性无关的2维列向量,12120,2==+A αA ααα,则A 的非零特征值为 .(14)设随机变量X 服从参数为1的泊松分布,则{}2P X EX == .三、解答题(15－23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.)(15)(本题满分10分)求极限()40sin sin sin sin lim x x x x x →-⎡⎤⎣⎦. (16)(本题满分10分)计算曲线积分()2sin 221Lxdx x ydy +-⎰,其中L 是曲线sin y x =上从点()0,0到点(),0π的一段.(17)(本题满分10分)已知曲线22220:35x y z C x y z ⎧+-=⎨++=⎩,求曲线C 距离XOY 面最远的点和最近的点.(18)(本题满分10分) 设()f x 是连续函数, (1)利用定义证明函数()()0xF x f t dt =⎰可导,且()()F x f x '=.(2)当()f x 是以2为周期的周期函数时,证明函数()22()()xG x f t dt x f t dt =-⎰⎰也是以2为周期的周期函数.(19)(本题满分10分)()21(0)f x x x π=-≤≤,用余弦级数展开,并求()1211n n n -∞=-∑的和.(20)(本题满分11分)T T =+A ααββ,T α为α的转置,T β为β的转置.证明:(1)()2r ≤A .(2)若,αβ线性相关,则()2r <A . (21)(本题满分11分)设矩阵2221212n na a a a a ⨯⎛⎫⎪⎪= ⎪⎪⎝⎭A OO O ,现矩阵A 满足方程=AX B ,其中()1,,Tn x x =X L ,()1,0,,0=B L ,(1)求证()1nn a =+A .(2)a 为何值,方程组有唯一解,求1x . (3)a 为何值,方程组有无穷多解,求通解. (22)(本题满分11分)设随机变量X 与Y 相互独立,X 的概率分布为{}()11,0,13P X i i ===-,Y 的概率密度为()1010Y y f y ≤≤⎧=⎨⎩其它,记Z X Y =+,(1)求102P Z X ⎧⎫≤=⎨⎬⎩⎭. (2)求Z 的概率密度.(23)(本题满分11分)设12,,,n X X X L 是总体为2(,)N μσ的简单随机样本.记11n i i X X n ==∑,2211()1n ii S X X n ==--∑,221T X S n=- (1)证明T 是2μ的无偏估计量.(2)当0,1μσ==时 ,求DT .2009年全国硕士研究生入学统一考试数学(一)试卷一、选择题(1-8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1)当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-等价无穷小,则(A)11,6a b ==- (B)11,6a b ==(C)11,6a b =-=-(D)11,6a b =-=(2)如图,正方形(){},1,1x y x y ≤≤被其对角线划分为四个区域()1,2,3,4k D k =,cos kk D I y xdxdy =⎰⎰,则{}14max k k I ≤≤=(A)1I(B)2I (C)3I(D)4I(3)设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为1 ()f x-20 2 3-1O(A)(B)(C)(D)(4)设有两个数列{}{},n n a b ,若lim 0n n a →∞=,则(A)当1nn b∞=∑收敛时,1n nn a b∞=∑收敛. (B)当1nn b∞=∑发散时,1n nn a b∞=∑发散.(C)当1nn b∞=∑收敛时,221n nn a b∞=∑收敛. (D)当1nn b∞=∑发散时,221n nn a b∞=∑发散.(5)设123,,ααα是3维向量空间3R 的一组基,则由基12311,,23ααα到基122331,,+++αααααα的过渡矩阵为(A)101220033⎛⎫ ⎪ ⎪ ⎪⎝⎭(B)120023103⎛⎫⎪⎪ ⎪⎝⎭(C)111246111246111246⎛⎫- ⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭(D)111222111444111666⎛⎫-⎪ ⎪ ⎪- ⎪ ⎪ ⎪- ⎪⎝⎭(6)设,A B 均为2阶矩阵,**,A B 分别为,A B 的伴随矩阵,若2,3==A B ,则分块矩阵O A B O ⎛⎫⎪⎝⎭的伴随矩阵为(A)**32O B A O ⎛⎫ ⎪⎝⎭(B)**23OB A O ⎛⎫⎪⎝⎭(C)**32O A BO ⎛⎫ ⎪⎝⎭(D)**23O A BO ⎛⎫⎪⎝⎭(7)设随机变量X 的分布函数为()()10.30.72x F x x -⎛⎫=Φ+Φ ⎪⎝⎭,其中()x Φ为标准正态分布函数,则EX =(A)0(B)0.3(C)0.7(D)1(8)设随机变量X 与Y 相互独立,且X 服从标准正态分布()0,1N ,Y 的概率分布为{}{}1012P Y P Y ====,记()Z F z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为(A)0(B)1(C)2 (D)3二、填空题(9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.)(9)设函数(),f u v 具有二阶连续偏导数,(),z f x xy =,则2zx y∂=∂∂ . (10)若二阶常系数线性齐次微分方程0y ay by '''++=的通解为()12e xy C C x =+,则非齐次方程y ay by x '''++=满足条件()()02,00y y '==的解为y = .(11)已知曲线(2:0L y x x =≤≤,则Lxds =⎰ .(12)设(){}222,,1x y z xy z Ω=++≤,则2z dxdydz Ω=⎰⎰⎰ .(13)若3维列向量,αβ满足2T=αβ,其中T α为α的转置,则矩阵Tβα的非零特征值为 .(14)设12,,,m X X X L 为来自二项分布总体(),B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差.若2X kS +为2np 的无偏估计量,则k = .三、解答题(15－23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.)(15)(本题满分9分)求二元函数()22(,)2ln f x y x y y y =++的极值. (16)(本题满分9分)设n a 为曲线ny x =与()11,2,.....n y x n +==所围成区域的面积,记122111,n n n n S a S a ∞∞-====∑∑,求1S 与2S 的值.(17)(本题满分11分)椭球面1S 是椭圆22143x y +=绕x 轴旋转而成,圆锥面2S 是过点()4,0且与椭圆22143x y +=相切的直线绕x 轴旋转而成. (1)求1S 及2S 的方程. (2)求1S 与2S 之间的立体体积.(18)(本题满分11分)(1)证明拉格朗日中值定理:若函数()f x 在[],a b 上连续,在(,)a b 可导,则存在(),a b ξ∈,使得()()()()f b f a f b a ξ'-=-.(2)证明:若函数()f x 在0x =处连续,在()()0,0δδ>内可导,且()0lim x f x A +→'=,则()0f +'存在,且()0f A +'=.(19)(本题满分10分) 计算曲面积分()32222xdydz ydzdx zdxdyI xy z++=∑++⎰⎰Ò,其中∑是曲面222224x y z ++=的外侧.(20)(本题满分11分)设111111042--⎛⎫⎪=- ⎪ ⎪--⎝⎭A ,1112-⎛⎫ ⎪= ⎪ ⎪-⎝⎭ξ (1)求满足21=A ξξ的2ξ.231=A ξξ的所有向量2ξ,3ξ.(2)对(1)中的任意向量2ξ,3ξ证明123,,ξξξ无关. (21)(本题满分11分)设二次型()()2221231231323,,122f x x x ax ax a x x x x x =++-+-.(1)求二次型f 的矩阵的所有特征值;(2)若二次型f 的规范形为2212y y +,求a 的值.(22)(本题满分11分)袋中有1个红色球,2个黑色球与3个白球,现有回放地从袋中取两次,每次取一球,以,,X Y Z 分别表示两次取球所取得的红球、黑球与白球的个数.(1)求{}10p X Z ==.(2)求二维随机变量(),X Y 概率分布. (23)(本题满分11 分)设总体X 的概率密度为2,0()0,x xe x f x λλ-⎧>=⎨⎩其他,其中参数(0)λλ>未知,1X ,2X ,…n X 是来自总体X 的简单随机样本.(1)求参数λ的矩估计量. (2)求参数λ的最大似然估计量.2010年全国硕士研究生入学统一考试数学(一)试卷一、选择题(1-8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)(1)极限2lim ()()xx x x a x b →∞⎡⎤⎢⎥-+⎣⎦= (A)1(B)e(C)e a b -(D)e b a -(2)设函数(,)z z x y =由方程(,)0y zF x x=确定,其中F 为可微函数,且20,F '≠则z z xy x y∂∂+∂∂= (A)x (B)z (C)x -(D)z -(3)设,m n 为正整数,则反常积分⎰的收敛性(A)仅与m 取值有关 (B)仅与n 取值有关(C)与,m n 取值都有关(D)与,m n 取值都无关(4)2211lim()()nnx i j nn i n j →∞==++∑∑=(A)121(1)(1)xdx dy x y ++⎰⎰(B)11(1)(1)xdx dy x y ++⎰⎰(C)11001(1)(1)dx dy x y ++⎰⎰ (D)112001(1)(1)dx dy x y ++⎰⎰(5)设A 为m n ⨯型矩阵,B 为n m ⨯型矩阵,若,=AB E 则 (A)秩(),m =A 秩()m =B (B)秩(),m =A 秩()n =B(C)秩(),n =A 秩()m =B(D)秩(),n =A 秩()n =B(6)设A 为4阶对称矩阵,且20,+=A A 若A 的秩为3,则A 相似于(A)1110⎛⎫ ⎪⎪ ⎪ ⎪⎝⎭(B)1110⎛⎫⎪⎪ ⎪- ⎪⎝⎭(C)1110⎛⎫⎪- ⎪ ⎪- ⎪⎝⎭(D)1110-⎛⎫⎪- ⎪ ⎪- ⎪⎝⎭ (7)设随机变量X 的分布函数()F x =00101,21e 2x x x x -<≤≤->则{1}P X == (A)0 (B)1(C)11e 2--(D)11e --(8)设1()f x 为标准正态分布的概率密度2,()f x 为[1,3]-上均匀分布的概率密度,()f x =12()()af x bf x 0x x ≤> (0,0)a b >> 为概率密度,则,a b 应满足(A)234a b += (B)324a b +=(C)1a b +=(D)2a b +=二、填空题(9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.)(9)设20e ,ln(1),ttx y u du -==+⎰求220t d ydx == .(10)2π⎰= .(11)已知曲线L 的方程为1{[1,1]},y x x =-∈-起点是(1,0),-终点是(1,0), 则曲线积分2Lxydx x dy +⎰= .(12)设22{(,,)|1},x y z x y z Ω=+≤≤则Ω的形心的竖坐标z = .(13)设123(1,2,1,0),(1,1,0,2),(2,1,1,),T T Tα=-==ααα若由123,,ααα形成的向量空间的维数是2,则α= .(14)设随机变量X 概率分布为{}(0,1,2,),!CP X k k k ===L 则2EX = . 三、解答题(15－23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.)(15)(本题满分10分)求微分方程322e xy y y x '''-+=的通解. (16)(本题满分10分) 求函数221()()e xt f x x t dt -=-⎰的单调区间与极值.(17)(本题满分10分) (1)比较1ln [ln(1)]nt t dt +⎰与1ln (1,2,)n t t dt n =⎰L 的大小,说明理由.(2)记1ln [ln(1)](1,2,),n n u t t dt n =+=⎰L 求极限lim .n x u →∞(18)(本题满分10分)求幂级数121(1)21n nn x n -∞=--∑的收敛域及和函数. (19)(本题满分10分)设P 为椭球面222:1S x y z yz ++-=上的动点,若S 在点P 的切平面与xoy 面垂直,求P 点的轨迹,C并计算曲面积分,I ∑=其中∑是椭球面S 位于曲线C 上方的部分.(20)(本题满分11分)设11010,1,111a λλλ⎛⎫⎛⎫ ⎪ ⎪=-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭A b 已知线性方程组=A x b 存在两个不同的解.(1)求,.a λ(2)求方程组=A x b 的通解.(21)(本题满分11分)设二次型123(,,)T f x x x =A x x 在正交变换x y =Q 下的标准形为2212,y y +且Q 的第三列为.T (1)求.A(2)证明+A E 为正定矩阵,其中E 为3阶单位矩阵. (22)(本题满分11分) 设二维随机变量()X Y +的概率密度为2222(,)e ,,,x xy y f x y A x y -+-=-∞<<∞-∞<<∞求常数及A 条件概率密度|(|).Y X f y x(23)(本题满分11 分) 设总体X其中(0,1)θ∈未知,以i N 来表示来自总体X 的简单随机样本(样本容量为n )中等于i 的个数(1,2,3),i =试求常数123,,,a a a 使31i i i T a N ==∑为θ的无偏估计量,并求T 的方差.2011年全国硕士研究生入学统一考试数学(一)试卷一、选择题(1-8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)1、曲线432)4()3()2)(1(----=x x x x x y 的拐点是（） A （1，0） B （2，0） C （3，0） D （4，0） 2、设数列{}n a 单调减少，且0lim =∞→n n a 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

lim
x 1
sin(x 1) x2 1
所以 x＝－1 为无穷间断点；
lim
x 1
sin(x 1) x2 1
lim
x 1
sin(x 1) (x 1)(x 1)
lim
x 1
sin(x 1) x 1
lim
x 1
1 x 1
1 2
所以 x＝1 为可去间断点．
2．设函数 f (x) 可微，则 y f (1 ex ) 的微分 dy ＝（）.
【解析】令 f (x) ex e 0 可得 x＝1. f (x) ex , f (1) e 0 ，根据极值的第二充分条件可得 x＝1 为函数 f (x) ex ex 2 的极小值点，极小值为 f (1) 2 .
10． 2 e x (1 x)dx ＝____. 2
【答案】 2e2 2 【解析】
0
1 x
dy f (x, y)dx dx 2 f (x, y)dy
0
2 y2
2 0
5．设 1，，2 3 为 3 维列向量，矩阵 A (1，，2，，3 2) B (，2 1 2 3 ). 若行列式|A|＝3，则行列式|B|＝（）.
A．6 B．3 C．－3 D．－6 【答案】D 【解析】根据行列式的性质有
3．设函数 f (x) 连续， F (x)
0 x2
f
(t)dt
，则 F (x)
＝（
）.
A． f (x2 )
B． f (x2 )
C． 2xf (x2 )
D． 2xf (x2 )
【答案】C
0
【解析】由于 F (x) x2 f (t)dt ，则
F(x) ( 0 f (t)dt) ( x2 f (t)dt) f (x2 ) (x2 ) 2xf (x2 )
x2
0
1
0
4．设函数 f (x, y) 连续，交换二次积分次序得 dy f (x, y)dx ＝（）.
0
2 y2
0
1 x
A． dx 2 f (x, y)dy
2
0
B．
0
0
dx
2
1 x
f
(x, y)dy
2
2
1 x
C． dx 2 f (x, y)dy
0
0
2
0
D．
dx
0
1 x
f (x, y)dy
6 / 14
圣才电子书

十万种考研考证电子书、题库视频学习平台
11．曲线 sin（xy）＋1n（y－x）＝x 在点（0，1）处的切线方程是____. 【答案】y＝x＋1 【解析】方程 sin（xy）＋1n（y－x）＝x 两边对 x 求导得
【答案】D
【解析】X 服从参数为 n，p 的二项分布，因此
E( X ) np, D( X ) np(1 p)
由期望和方差的性质可得
二、填空题：9～14 小题，每小题 4 分，共 24 分．请将答案写在题目中的横线上． 9．函数 f (x) ex ex 2 的极小值为____. 【答案】－2
【答案】C
【解析】ABD 三项，由于
根据线性相关的定义可知，这三项是线性相关的. C 项，可以根据定义证明它是线性无关的. 设整理得由于向量组 1，，2 3 线性无关，所以
此线性方程组的系数矩阵
由于
4 / 14
圣才电子书

十万种考研考证电子书、题库视频学习平台
所以方程组
只有零解，即
由线性无关的定义可性无关.
7．设 A1，A，2 A3 为 3 个随机事件，下列结论中正确的是（）. A．若 A1，A，2 A3 相互独立，则 A1，A，2 A3 两两独立 B．若 A1，A，2 A3 两两独立，则 A1，A，2 A3 相互独立 C．若 P( A1 A2 A3 ) P( A1)P( A2 )P( A3 ) ，则 A1，A，2 A3 相互独立 D．若 A1 与 A2 独立， A2 与 A3 独立，则 A1 与 A3 独立【答案】A 【解析】若 A1，A，2 A3 相互独立，由相互独立的性质可知
1．设函数 f (x) x2 1 ，则（）. A．x＝－1 为可去间断点，x＝1 为无穷间断点
B．x＝－1 为无穷间断点，x＝1 为可去间断点
C．x＝－1 和 x＝1 均为可去间断点
D．x＝－1 和 x＝1 均为无穷间断点
【答案】B
f (x) sin(x 1)
【解析】函数
x2 1 在点 x＝±1 没有定义，而
圣才电子书
十万种考研考证电子书、题库视频学习平

台
2008 年全国硕士研究生入学统一考试农学门类联考数学真题及详解
一、选择题：1～8 小题，每小题 4 分，共 32 分．下列每题给出的四个选项中，只有
一个选项是符合题目要求的，请将所选项前的字母填在括号内．
sin x 1
A． (1 ex ) f (1 ex )dx B． (1 ex ) f (1 ex )dx C． ex f (1 ex )dx D． ex f (1 ex )dx
1 / 14
圣才电子书

【答案】D
十万种考研考证电子书、题库视频学习平台
【解析】 dy df (1 ex ) f (1 ex )(1 ex )dx ex f (1 ex )dx ．
由此可得 A1，A，2 A3 两两独立.
8．设随机变量 X 服从参数为 n，p 的二项分布，则（）.
A． E(2X 1) 2np B． E(2X +1) 4np
5 / 14
圣才电子书
十万种考研考证电子书、题库视频学习平

C．
D(2X
1)
2np(1
台
p)
D． D(2X 1) 4np(1 p)
2
【答案】A
【解析】积分区域 D 如下图所示.由于
D {(x, y) | 0 y 1, 2 y 2 x 0} {(x, y) | -2 x 0, 0 y 1 x } 2
所以
2 / 14
圣才电子书
十万种考研考证电子书、题库视频学习平

台
1
0
6．已知向量组 1，，2 3 线性无关，则下列向量组中线性无关的是（）. A． 1 22，2，2 3 3 1
3 / 14
圣才电子书
十万种考研考证电子书、题库视频学习平

台
B． 1 22，， 22 3 3 1
C． 21 2，， 2 23 3 1
D． 1 2，，22 23 3 1