广东省汕头市潮南区12-13学年度八年级数学第一学期期末试卷新人教版

合集下载

2012—2013学年八年级上册数学期末试卷

2012—2013学年八年级上册数学期末试卷2012-2013学年八年级上册数学期末试卷一、选择题(本大题共6小题，每小题3分，共18分)1.在3.14、、、、pi;这五个数中，无理数有 ( )A.0个B.1个C.2个D.3个2.下列交通标识中，是轴对称图形的是 ( )3.点M(-3，2)关于轴对称的点的坐标为 ( )A.(-3，-2)B.(3，-2)C.(3，2)D.(-3，2)4.下列计算正确的是 ( )A.x2bull;x2=2x4B.(-2a)3= -8a3C.(a3)2=a5D. m3÷m3=m5.下列关系中，不是的函数的是 ( )A. ( )B.C.D.6.在长方形ABCD中，AB=2，BC=1，动点P从点B出发，沿路线Brarr;Crarr;D做匀速运动，那么△ABP的面积S与点P运动的路程x之间的函数图象大致为 ( )二、填空题(本大题共8小题，每小题3分，共24分)7.已知木星的质量约是a×1024吨，地球的质量约是3a×1021吨，则木星的质量约是地球质量的___________倍.(结果取整数)8.若一个正数的两个平方根分别为，则这个正数是 ;9.分解因式：。

10.已知，则 .11.已知a、b均为实数且，则a2+b2=12.在函数中，自变量的取值范围是 .13如图:已知AE∥BF, ang;E=ang;F,要使△ADE≌△BCF,可添加的条件是_____________(写一个即可).14. 如图OA、AB分别表示甲、乙两名同学运动的一次函数图象，图中s和t分别表示运动路程和时间，已知甲的速度比乙快，下列说法：①射线BA表示甲的路程与时间的函数关系;②甲的速度比乙快1.5米/秒;③甲让乙先跑12米;④8 秒钟后，甲超过了乙，其中正确的说法是 (填上正确序号)。

(第13题图) ( 第14题图)三、(本大题共4小题，每小题6分，共24分)15、先化简，再求值: ，其中16、已知是正比例函数，且函数图象经过第一、三象限，求的值17、如图所示，要在街道旁修建一个奶站，向居民A,B 提供牛奶，奶站应建在什么地方，才能使从A,B到它的距离之和最短?(在图中作出奶站的位置点P，不要求写作法和证明。

2023-2024学年广东省汕头市潮南区八年级(上)期末数学试卷+答案解析

2023-2024学年广东省汕头市潮南区八年级（上）期末数学试卷一、选择题：本题共10小题，每小题3分，共30分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.当时，下列分式没有意义的是( )A. B. C. D.2.七巧板是我国的一种传统智力玩具，下列用七巧板拼成的图形是轴对称图形的是( )A. B. C. D.3.下列计算正确的是( )A. B. C. D.4.一个多边形的内角和是外角和的2倍，则这个多边形的边数为( )A. 4B. 5C. 6D. 75.已知点关于y轴的对称点N的坐标是，则的值为( )A. 10B. 25C.D. 326.如图，在中，，，BD平分交AC于点D，，交BC于点E，则的度数是( )A.B.C.D.7.若与的乘积中不含x的一次项，则实数m的值为( )A. B. 2 C. 0 D. 18.如图，已知在中，CD是AB边上的高线，BE平分，交CD于点E，，，则的面积等于( )A. 8B. 6C. 5D. 49.若，则代数式的值是( )A. B. 2 C. D. 410.如图，等边中，D为AC中点，点P、Q分别为AB、AD上的点，且，，在BD上有一动点E，则的最小值为( )A. 7B. 8C. 10D. 12二、填空题：本题共5小题，每小题3分，共15分。

11.原子很小，1个氧原子的直径大约为，将用科学记数法表示为__________.12.已知，则代数式的值为______.13.一个三角形的两边长分别是3和8，第三边为奇数，那么第三边长是______.14.如图，在中，DE是BC的垂直平分线，若，，则的周长是______.15.若分式方程有增根，则实数a的值是______.三、计算题：本大题共1小题，共6分。

16.解方程：四、解答题：本题共9小题，共69分。

解答应写出文字说明，证明过程或演算步骤。

17.本小题6分计算：18.本小题6分计算：19.本小题6分如图、在平面直角坐标系中，的三个顶点的坐标分别为，，，画出关于y轴对称的，并写出点，，的坐标.20.本小题7分如图，BE是的角平分线，在AB上取点D，使求证：；若，，求的度数.21.本小题7分接种疫苗是阻断新冠病毒传播的有效途径，针对疫苗急需问题，某制药厂紧急批量生产，计划每天生产疫苗16万剂，但受某些因素影响，有10名工人不能按时到厂.为了应对疫情，回厂的工人加班生产，由原来每天工作8小时增加到10小时，每人每小时完成的工作量不变，这样每天只能生产疫苗15万剂.求该厂当前参加生产的工人有多少人？生产4天后，未到的工人同时到岗加入生产，每天生产时间仍为10小时.若上级分配给该厂共760万剂的生产任务，问该厂共需要多少天才能完成任务？22.本小题7分校园内有一块四边形的草坪造型，课外活动小组实地测量，并记录数据，根据造型画如图的四边形ABCD，其中米，米，求证：≌；求草坪造型的面积．23.本小题10分八年级课外兴趣小组活动时，老师提出了如下问题：将因式分解.【观察】经过小组合作交流，小明得到了如下的解决方法：解法一：原式解法二：原式【感悟】对项数较多的多项式无法直接进行因式分解时，我们可以将多项式分为若干组，再利用提公因式法、公式法达到因式分解的目的，这就是因式分解的分组分解法.分组分解法在代数式的化简、求值及方程、函数等学习中起着重要的作用温馨提示：因式分解一定要分解到不能再分解为止【类比】请用分组分解法将因式分解；【挑战】请用分组分解法将因式分解；若，，请用分组分解法先将因式分解，再求值.24.本小题10分如图，已知：在中，，，将一块足够大的直角三角尺按如图放置，顶点P在线段AB上滑动，三角尺的直角边PM始终经过点C，并且与CB的夹角，斜边PN交AC于点当时，判断的形状，并说明理由；点P在滑动时，当AP长为多少时，与全等，并说明理由；点P在滑动时，的形状可以是等腰三角形吗？若可以，请直接写出夹角的大小；若不可以，请说明理由．25.本小题10分在等边的顶点A，C处各有一只蜗牛，它们同时出发，分别以相同的速度由A向B和由C向A爬行，经过t分钟后，它们分别爬行到D，E处，请问：如图1，爬行过程中，CD和BE的数量关系是______；如图2，当蜗牛们分别爬行到线段AB，CA的延长线上的D，E处时，若EB的延长线与CD交于点Q，其他条件不变，蜗牛爬行过程中的大小将会保持不变，请你证明：；如图3，如果将原题中“由C向A爬行”改为“沿着线段BC的延长线爬行，连接DE交AC于F”，其他条件不变，求证：答案和解析1.【答案】D【解析】解：A、当时，分式有意义，本选项不符合题意；B、当时，，分式有意义，本选项不符合题意；C、当时，分式有意义，本选项不符合题意；D、当时，，分式无意义，本选项符合题意；故选：根据分式无意义的条件是分母等于零判断即可．本题考查的是分式无意义的条件，熟记分式无意义的条件是分母等于零是解题的关键．2.【答案】D【解析】解：A、不是轴对称图形，不符合题意，B、不是轴对称图形，不符合题意，C、不是轴对称图形，不符合题意，D、是轴对称图形，符合题意，故选：根据轴对称图形的定义去逐一判断即可．本题考查了轴对称图形的定义，正确理解定义是解题的关键．3.【答案】B【解析】解：，此选项计算错误，故此选项不符合题意；B.，此选项计算正确，故此选项符合题意；C.，此选项计算错误，故此选项不符合题意；D.，此选项计算错误，故此选项不符合题意；故选：A.根据幂的乘方法则进行计算，然后判断即可；B.根据同底数幂相乘法则进行计算，然后判断即可；C.根据同底数幂相除法则进行计算，然后判断即可；D.根据积的乘方法则进行计算，然后判断即可．本题主要考查了整式的有关运算，解题关键是熟练掌握同底数幂相乘除法则、幂的乘方法则和积的乘方法则．4.【答案】C【解析】本题考查了多边形的内角与外角，熟记内角和公式和外角和定理并列出方程是解题的关键．根据多边形的内角和定理，求边数的问题就可以转化为解方程的问题来解决．设这个多边形是n边形，内角和是，这样就得到一个关于n的方程，从而求出边数n的值．解：根据多边形的外角和是，n边形的内角和是设这个多边形是n边形，根据题意得，解得，即这个多边形为六边形．故选：5.【答案】B【解析】【分析】直接利用关于y轴对称点的性质，得出关于a，b的方程组进而得出答案。

2012-2013人教版八年级上学期数学期末试卷

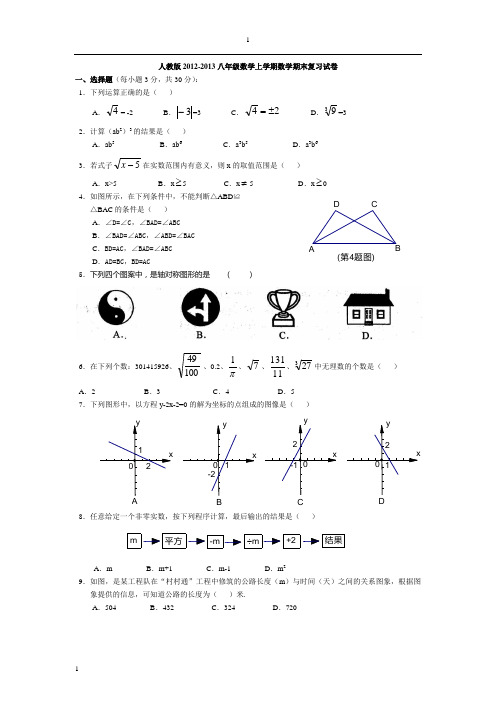
人教版2012-2013八年级数学上学期数学期末复习试卷一、选择题（每小题3分，共30分）： 1．下列运算正确的是（）A ．4= -2 B ．3-=3 C ．24±= D ．39=32．计算（ab 2）3的结果是（）A ．ab 5B ．ab 6C ．a 3b 5D ．a 3b 6 3．若式子5-x 在实数范围内有意义，则x 的取值范围是（）A ．x>5B ．x ≥5C ．x ≠5D ．x ≥0 4．如图所示，在下列条件中，不能判断△ABD ≌△BAC 的条件是（）A ．∠D=∠C ，∠BAD=∠ABCB ．∠BAD=∠ABC ，∠ABD=∠BAC C ．BD=AC ，∠BAD=∠ABCD ．AD=BC ，BD=AC5．下列四个图案中，是轴对称图形的是（）6．在下列个数：301415926、10049、0.2、π1、7、11131、327中无理数的个数是（）A ．2B ．3C ．4D ．5 7．下列图形中，以方程y-2x-2=0的解为坐标的点组成的图像是（）8．任意给定一个非零实数，按下列程序计算，最后输出的结果是（）A ．mB ．m+1C ．m-1D ．m 29．如图，是某工程队在“村村通”工程中修筑的公路长度（m ）与时间（天）之间的关系图象，根据图象提供的信息，可知道公路的长度为（）米.A ．504B ．432C ．324D ．720(第4题图)D CBACB结果+2m10．如图，在平面直角坐标系中，平行四边形ABCD 的顶点A 、B 、D 的坐标分别为（0，0）、（5，0）、（2，3），则顶点C 的坐标为（）A ．（3，7）B ．（5，3）C ．（7，3）D ．（8，2）二、填空题（每小题3分，共18分）： 11．若x -2+y 2=0，那么x+y= .12．若某数的平方根为a+3和2a-15，则a= . 13．等腰三角形的一个外角是80°，则其底角是 .14．如图，已知：在同一平面内将△ABC 绕B 点旋转到△A /BC /的位置时，AA /∥BC ，∠ABC=70°，∠CBC /为 .15．如图，已知函数y=2x+b 和y=ax-3的图象交于点P （-2，-5），则根据图象可得不等式2x+b>ax-3的解集是 .16．如图，在△ABC 中，∠C=25°，AD ⊥BC ，垂足为D ，且AB+BD=CD ，则∠BAC 的度数是 . 三、解答题（本大题8个小题，共72分）：17．（10分）计算与化简：（1）化简：)1(18--π0)12(21214-+-；（2）计算：（x-8y ）（x-y ）.18（15分，每小题5分）（1）分解因式6xy 2-9x 2y-y 3（2） 4x-16x 3 (3) 4a(b-a)-b 2(第10题图)(第14题图)AC /CBA /(第15题图)CBD A(第16题图)19．（7分）先化简，再求值：（10分）(1)先化简，再求值：2[()(2)8]2x y y x y x x+-+-÷，其中x＝－2 .20．（10分）如图，（1）画出△ABC 关于Y 轴的对称图形△A 1B 1C 1（ 2）请计算△ABC 的面积（3）直接写出△ABC 关于X 轴对称的三角形△A 2B 2C 2的各点坐标。

2012 一 2013 学年度上期八年级期末教学质量监测数学试卷

2012~2013 学年度上期八年级期末教学质量监测数学试卷(全卷共六个大题，满分 100 分， 90 分钟完卷）一、选择题（共 10 个小题，每小题 3 分，共 30 分）每小题下面都有代号为 A 、 B 、 C 、D 四个答案选项，其中只有一个选项是正确的，请把正确选项的代号填在题后的括号内，填写正确记 3 分，不填、填错或填出的代号超过一个均记0分。

1. 无理数）A . B.C. D. 2. 点 A （1,23）关于y 轴对称点 A ′的坐标是（） A.1(,2)3- B . 1(2,)3 C.1(,2)3- D . 1(2,)3-3. 下列图形是轴对称图形的有（）A . 1 个B . 2 个C . 3 个D . 4 个4. 下列计算正确的是（）A . 235a a a += B. 632a a a ÷= C . 22431x x -= D. ()326328x yx y -=-5. 下列条件中，不能判定三角形全等的是（）A. 有三边对应相等B. 有两边及夹角对应相等C. 有两角及一边对应相等D. 有两边及一角对应相等6. 按下列程序计算，最后输出的答案是（）A . 3aB . 21a +C . 2aD . a7. 如图： AB 是线段 CD 的垂直平分线，则图中全等三角形的对数有（）A.2对B.3 对C.4 对D.5 对8. 关于一次函数23y x =-，下列结论正确的是（）A. 图像经过点（一 3 , 3 )B. 图像经过第二、四象限C. 当32x >时，y > 0 D. y 随 x 的增大而减小 9. 如图：在△ABC 中，∠C = 90°, AC = BC , AD 平分∠BAC 交边 BC于点 D , DE ⊥AB 于 E ，若 △DEB 的周长为 10cm ，则 AB 的长为（）A . 8cmB . 10cmC . 12cmD . 20cm10. 已知等式()()()222252510ax bx ax bx c ax bx +-+++=++，那么c 的值为（）. A . 5 B . 25 C . 125 D . 225二、填空题（本大题共 8 个小题，每小题 3 分，共 24 分），请将答案直接写在题中横线上。

2012--2013学年八年级上学期期末数学试卷

2012--2013学年八年级上学期期末数学试卷2012－2013八年级第一学期数学期末综合练习（时间：90分钟满分：100分）班级姓名一、选择题（每小题3分，共24分，每小题给出的四个选项中，只有一个选项是正确的.）1．4的平方根是（）A. -2B. 2C. ±2D. 2±2．全球可被人类利用的淡水总量仅占地球上总水量的0.00003，因此珍惜水、保护水，是我们每一位公民义不容辞的责任．其中数字0.00003用科学记数法表示为A ．4103-⨯ B ．5103-⨯ C ．4103.0-⨯D ．5103.0-⨯3. 下列计算正确的是 A ．325xx x += B ．44xx x ÷= C ．325xx x ⋅=题号 1 2 3 4 5 6 7 8 选项那么k 的值是A ．3B ．6C ．12D ．415 二、填空题（每小题3分，共12分） 9. 函数2-=x x y 中自变量x 的取值范围是___________. 10. 如图，已知函数y ax b =+和y kx =的图象交于点P,则根据图象可得，关于y ax b y kx=+⎧⎨=⎩的二元一次方程组的解是___________. 11. 在2011,,4,3,2,1 中，共有个无理数. 12. 已知n是正整数，111222(,),(,),,(,),n n n P x y P x y P x y 是反比例函数k y x=图象上的一列点，其中 121,2,,,n x x x n ===．记112A x y =，223Ax y =，1n n n A x y +=，，若1A a =（a 是非零常数），则A 1·A 2·…·A n 的值是___________（用含a 和n 的代数式表示）．三、解答题（共64分）13．分解因式：33ax y axy - 14．分解因式：22882n mn m +- 15．计算：0119(π4)22----- 16．计算：29631aa --+17．解方程：423532=-+-xx x18．计算：2)2()3)(2()2)(2(y x y x y x y x y x ---+--+19．已知210x x +-=，求222(1)(1)(1)121x x x x x x x --÷+---+的值．20．某学校准备组织部分学生到少年宫参加活动，陈老师从少年宫带回来两条信息：信息一：按原来报名参加的人数，共需要交费用320元，如果参加的人数能够增加到原来人数的2倍，就可以享受优惠，此时只需交费用480元；信息二：如果能享受优惠，那么参加活动的每位同学平均分摊的费用比原来少4元．根据以上信息，原来报名参加的学生有多少人？ 21．设22113-=a，22235-=a，22357-=a……（1）写出na （n 为大于0的自然数）的表达式；（2）探究na 是否为8的倍数，并用文字语言表述你所获得的结论；（3）若一个数的算术平方根是一个自然数，则这个数是“完全平方数”，试找出1a ，2a ，3a ，……，na 这一列数中从小到大排列的前4个完全平方数；并说出当n 满足什么条件时, na 为完全平方数(不必说明理由).22．如图，已知A(n ，-2)，B(1，4)是一次函数b kx y +=的图象和反比例函数y=x m 的图象的两个交点，直线 (1)求反比例函数和一次函数的关系式； (2)求△AO B 的面积；(3)求不等式0<-+xm b kx 的解集(直接写出答案)．23．某蒜薹生产基地喜获丰收收蒜薹200吨。

12-13第一学期期末八年级试题

2012～2013学年度第一学期期末考试八年级数学试题亲爱的同学，你好！本学期即将结束，今天是展示你才华的时候了，只要你仔细审题、认真答题，把平常的水平发挥出来，你就会有出色的表现！可要注意喽，本试卷分卷Ⅰ和卷Ⅱ两部分，收卷时只收卷Ⅱ，卷Ⅰ由学生自己保留．不使用计算器．卷Ⅰ（共40分）一、选一选，比比谁细心（本大题共15小题，每小题2分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的，把这个正确的选项序号涂在答题卡上）． 1．在下列各组图形中，可能是全等图形的一组是2．5的相反数是A ．5C ．5D ．都不对3．根据下列已知条件，能唯一画出△ABC 的是A ．AB ＝3，BC ＝4，CA ＝8 B ．AB ＝4，BC ＝3，∠A ＝30° C ．∠A ＝60°，∠B ＝45°，AB ＝4D ．∠C ＝90°，AB ＝64．已知△ABC 的三条边的长度及三个角的度数如图所示，则下面甲、乙、丙三个三角形中与△ABC 不一定全等的图形是A ．甲B ．乙C ．丙D ．都不对A B CD（第1题图）（第4题图）（第7题图）5．如图是一个轴对称图形，在给出的四条虚线a 、b 、c 、d 中对称轴是直线 A ．a B ．b C ．c D ．d 6．如图，△ABO 是关于x 轴对称的轴对称图形，点A 的坐标为（1，－2），则点B 的坐标为 A ．（1， 2） B ．（1，－2） C ．（－1， 2） D ．（－1，－2）7．如图，以数轴的单位长为边作一个正方形，以数轴的原点为圆心，正方形的对角线长为半径画孤，交数轴于点A ，则点A 表示的数是A ．1B ． 1.4 C8．小明一出校门先加速行驶，然后匀速行驶一段后，在距家门不远的地方开始减速，而最后停下，下面哪一副图可以近似地刻画出以上情况速度速度速度速度9. 如图，小明根据某个一次函数关系式填写了如图的表格:其中有一格不慎被墨汁遮住了,想想看，该空格里原来填的数是A ．1B ．2C ．3D ．410．如图△ABC ，下列推理错误的是A ．因为∠A=∠B=∠C ，所以△ABC 是等边三角形B ．因为AB=AC ，且∠B=∠C ，所以△ABC 是等边三角形 C ．因为∠A=60°，∠B=60°，所以△ABC 是等边三角形D ．因为AB=AC ，且∠B=60°，所以△ABC 是等边三角形xDBFAEC （第5题图）11．如图，∠B=∠D=90°，BC=DC ，∠1=40°，则∠2=A ．40°B ．50°C ．90°D ．都不对12．如图是用直尺和圆规作一个角等于已知角的示意图，则说明A O B A O B '''=∠∠的依据是A ．“边角边”B ．“角角边”C ．“角边角”D ．“边边边” 13．下列各式中，相等关系一定成立的是A.(x-y)2=(y-x)2B.(x+6)(x-6)=x 2-6C.(x+y)2=x 2+y 2D.6(x-2)+x(2-x)=(x-2)(x-6)14. 如图一次函数b ax y +=1和d cx y +=2在同一坐标系内的图象，则⎩⎨⎧+=+=d cx y b ax y 的解⎩⎨⎧==ny m x 中A ．m>0,n>0B ．m>0,n<0C ． m<0,n>0D ．m<0,n<015. 如图，已知函数y ＝3x ＋b 和y ＝ax －3的图象交于点P(－2，－5)，则根据图象可得不等式3x ＋b ＞ax －3的解集是 A ．x ＞0 B ．x ＜0 C ．x ＞-2 D ．x ＜-2（第15题图）（第14题图）（第11题图）AOCBDA 'O 'C 'B 'D '（第12题图）C（第10题图）二、填一填，看看谁仔细（本大题共5小题，每小题2分，共10分，把最简答案填在卷Ⅱ的相应位置）． 16．计算()=-020022003 .17. 如图，△ABC 与△A ′B ′C ′关于直线l 对称，则∠B ＝ °.18．如图，△ABC 中，∠C ＝90°，∠A ＝30°，AB 的垂直平分线交AC 于D ，交AB 于E ，CD ＝2，则AC ＝． 19．已知一个正数的平方根是3x -2和5x +10，则这个数是 .20．下表，填在各正方形中的四个数之间都有相同的规律，根据此规律，m 的值是 .CB（第17题图）l （第20题图）2012～2013学年度第一学期期末考试八年级数学试题卷II （共60分）二、填一填，看看谁仔细（本大题共5小题，每小题2分，共10分，把卷Ⅰ填空题的最简答案填在下面的横线上）．16． . 17． . 18． . 19． . 20． .6小题，共60分，解答应写出文字说明，说理过程或演算步骤）21．计算（每个4分，共16分）：（1）5853--+（2）)1)(1(2-+-a a a（3）()⎪⎭⎫ ⎝⎛-∙-÷a b a ba 21)2(52234（4）分解因式：244x x --22．（本题满分6分）化简求值：2223)(4)84(y x xy y x xy --÷+ 其中 x =－2 y =523．（本题满分8分）如图，△ABC 中，AB=AC ，D 为BC 边的中点，F 为CA 的延长线上一点，过点F 作FG ⊥BC 于G 点，并交AB 于E 点，求证：△AEF 是等腰三角形．24．（本题满分10分）在△ABC 中，若AD 是∠BAC 的角平分线，点E 和点F 分别在AB 和AC上，且DE ⊥AB ，垂足为E ，DF ⊥AC ，垂足为F ，如图（1），则可以得到以下两个结论：①∠AED+∠AFD=180°；②DE=DF ．那么在△ABC 中，仍然有条件“AD 是∠BAC 的角平分线，点E 和点F ，分别在AB 和AC 上”，请探究以下两个问题：（1）若∠AED+∠AFD=180°（如图（2）），则DE 与DF 是否仍相等？若仍相等，请证明；否则请举出反例．（2）若DE=DF ，则∠AED+∠AFD=180°是否成立？请你做出判断，并加以说明。

2012-2013学年新人教版八年级上期末数学试卷

八年级上期末数学试卷一、选择题（每题3分，共30分）1、下列运算不正确．．．的是 ( ) A 、 x 2·x 3 = x 5 B 、 (x 2)3= x 6 C 、 x 3+x 3=2x 6 D 、 (-2x)3=-8x 3 2、下列式子中，从左到右的变形是因式分解的是 ( )．A ．(x －1)(x －2)＝x 2－3x ＋2B ．x 2－3x ＋2＝(x －1)(x －2)C ．x 2＋4x ＋4＝x(x 一4)＋4D ．x 2＋y 2＝(x ＋y)(x —y) 3、下列各组的两项不是同类项的是（）A 、2ax 2与 3x 2B 、－1 和 3C 、2x 2y 和－2y xD 、8xy 和－8xy4．已知等腰三角形两边长是8cm 和4cm ，那么它的周长是（）A.12cmB.16cmC.16cm 或20cmD.20cm5．如图，羊字象征吉祥和美好，下图的图案与羊有关，其中是轴对称图形的有 ( )A ．1个B ．4个C ．3个D ．2个 6．已知点（-4，y 1），（2，y 2）都在直线y=- 12x+2上，则y 1、 y 2大小关系是( )（A ）y 1 >y 2 （B ）y 1 =y 2 （C ）y 1 <y 2 （D ）不能比较7．如图：如图，l 1反映了某公司的销售收入与销售量的关系，l 2反映了该公司产品的销售成本与销售量的关系，当该公司赢利（收入大于成本）时，销售量（）A 小于3吨B 大于3吨C 小于4吨D 大于4吨(第7题) (第8题) (第9题)8．如图，C 、E 和B 、D 、F 分别在∠GAH 的两边上，且AB = BC = CD = DE = EF ，若∠A =18°，则∠GEF 的度数是（） A ．108° B ．100°C ．90°D ．80°ED CA B H F GCDE9．如图，在△ABC 中，AB=AC ，BD=BC ，AD=DE=EB ，则∠A 是（） A 、30° B 、45° C 、60° D 、20°10．如图，是在同一坐标系内作出的一次函数y 1、y 2的图象l 1、l 2，设y 1＝k 1x＋b 1，y 2＝k 2x ＋b 2，则方程组⎩⎨⎧y 1＝k 1x ＋b 1y 2＝k 2x ＋b 2的解是_______.A 、⎩⎨⎧x ＝－2y ＝2B 、⎩⎨⎧x ＝－2y ＝3C 、⎩⎨⎧x ＝－3y ＝3D 、⎩⎨⎧x ＝－3y ＝4二、填空：（每题3分，共30分）11.函数y=2x 向左平移3个单位所得到的函数为再向下平移5个单位得到的函数为 .12．若1242+-kx x 是完全平方式，则k=_____________ 13.已知函数1)1(2+-=m x m y 是一次函数，则m=__________． 14．教育储蓄的月利率为0.22%，现存入1000元，则本息和y （元）与所存月数 x 之间的函数关系式是 . 15．因式分解4x 2-9y 2=____．16．已知5=+b a ，1922=+b a ，则ab =__________，__________)(2=-b a17．在函数y=13x +中，自变量x 的取值范围是 18．对于实数a ，b ，c ，d ，规定一种运算a b c d=ad-bc ，那么当(1)(2)(3)(1)x x x x ++--=27时，则x= ．19.函数y=kx+b （k ≠0）的图象平行于直线y=2x+3，且交y 轴于点（0，-1），•则其解析式是_________ ．20．列几何图形中：①长方形 ② 等腰直角三角形③圆 ④等边三角形。

广东省汕头市潮南区2023-2024学年八年级上学期期末数学试题解析版

广东省惠州市2023-2024学年九年级上学期期末数学试题第Ⅰ卷10小题，每小题3分，满分30分）1．中国古代著作《九章算术》在世界数学史上首次正式引入负数．如果盈利90元记作+90元，那么亏本60元记作（）A．−60元B．−70元C．+60元D．+70元2．第19届亚运会将于2023年9月23日至2023年10月8日在杭州举行，亚奥理事会45个成员全部报名参赛，参赛运动员人数超过12000名，是史上规模最大、项目最多、覆盖面最广的一届亚运会．数据12000用科学记数法表示为（）A．0.12×105B．1.2×104C．1.2×105D．12×1033．下列图标中是中心对称图形的是（）．A．B．C．D．4．如果将抛物线y=2(x−1)2向左平移2个单位，再向下平移2个单位后所得新抛物线的表达式是（）A．y=2(x−3)2−2B．y=2(x−3)2+2C．y=2(x+1)2−2D．y=2(x+1)2+25．如图，小明在A时测得某树的影长为8m，B时又测得该树的影长为2m，若两次日照的光线互相垂直，则树的高度为（）A．2m B．4m C．6m D．8m 6．如图，已知菱形ABCD的周长为20，对角线AC=6，则菱形ABCD的面积为（）A．15B．24C．25D．487．正比例函数y＝2x与反比例函数y=kx的图象有一个交点为（1，2)，则另一个交点的坐标为（）A．（-1，-2）B．（-1，2）C．（1，-2）D．（1，2）8．如图，四边形ABCD内接于⊙O，若∠BOD=100°，则∠DCB等于（）A．90°B．100°C．130°D．140°9．某小区计划在一块长32m、宽20m的长方形空地上修建三条同样宽的道路（如图），剩余的空地上种植草坪，使草坪的面积为570m2．设道路的宽为xm，则下面所列方程正确的是（）A．32×20−3x2=570B．(32−x)(20−x)=570C．(32−2x)(20−x)=570D．3x2=57010．如图，矩形ABCD中，AB=2，BC=4，P为矩形边上的一个动点，运动路线是A→B→C→D→A，设P点经过的路程为x，以A，P，B为顶点的三角形面积为y，则选项图象能大致反映y与x的函数关系的是（）A ．B ．C ．D ．6题，每小题3分，共18分）11．已知a ，b 互为相反数，c ，d 互为倒数，那么“2023cd −a −b ”的值为．12．森林防火报警电话是12119，关于“1，2，1，1，9”这五个数字组成的数据，中位数是． 13．如图，将直尺与30°角的三角尺叠放在一起，若 ∠1=40° ，则 ∠2= .14．在平面直角坐标系中，若点P(5+m ，−2+m)在第一象限，则m 的取值范围为． 15．广大党员群众积极参加公益活动，据统计某市今年第一批志愿者为10万人次，第三批志愿者为12.1万人次．如果第二批、第三批志愿者人次的增长率相同，则这个增长率是．16．如图所示，四边形ABCD 是矩形，以BC 为直径作半圆与AD 相切于点E ，再以点A 为圆心，线段AB 长为半径作弧，与AD 交于点E ．若AB =√2，则阴影部分的面积为．（结果保留π）（本题共3小题，每题7分，共21分）17．计算：√9−√12⋅√8+(12)−1−(π−√3)0．18．先化简，再求值：x 2−4x+4x 2−x÷(1−1x−1)；其中x =√2．19．如图，已知△ABC ，∠C =90°，AC =BC ，BE 是△ABC 的角平分线，ED ⊥AB 于点D ，证明：△ADE的周长等于AB 的长．（本题共3小题，每小题9分，共27分）20．如图，DB是▱ABCD的对角线．（1）尺规作图：作对角线BD的垂直平分线，分别交于AD，BC，BD于E，F，O；（不写作法，保留作图痕迹）（2）连接BE，DF，试判断四边形DEBF的形状，并说明理由．21．如图，三个可以自由转动的转盘，每个转盘被分成面积相等的几个扇形，并涂上图中所示的颜色小强和小亮用转盘A和转盘B做一个转盘游戏：同时转动两个转盘，若其中一个转出红色，另一个转出蓝色即可配成紫色，则小强获胜；若两个转盘转出的颜色相同，则小亮获胜；在其他情况下，小强和小亮不分胜负.（1）用画树状图或列表的方法表示此游戏所有可能出现的结果；（2）小强说，此游戏不公平请你说明理由；（3）请你在转盘C的空白处，涂上适当颜色，使得用转盘C替换转盘B后，使游戏对小强和小亮是公平的（在空白处填写表示颜色的文字即可，不要求说明理由，只需给出一种结果即可）.22．为促进青少年体育运动的发展，某教育集团需要购买一批篮球和足球，已知一个篮球比一个足球的单价高30元，买两个篮球和三个足球一共需要510元.（1）求篮球和足球的单价；（2）根据实际需要，集团决定购买篮球和足球共100个，其中篮球购买的数量不少于40个，若购买篮球x个，学校购买这批篮球和足球的总费用为y（元），求y与x之间的函数关系式；（3）在（2）的条件下，由于集团可用于购买这批篮球和足球的资金最多为 10500 元，求购买篮球和足球各多少个时，能使总费用 y 最小，并求出 y 的最小值.（本题共2题，每题12分，共24分）23．如图，在⊙O 中，直径AB ⊥CD ，垂足为E ，点M 在OC 上，AM 的延长线交⊙O 于点G ，交过C 的直线于F ，∠1=∠2（即：∠BCF =∠BCD ），连接CB 与DG 交于点N ．（1）求证：CF 是⊙O 的切线；（2）求证：CM CN =AC CD；（3）若点M 是OC 的中点，⊙O 的半径长为4，EO =1，求BN 的长．24．如图，抛物线y =x 2+bx +c 与x 轴交于A 、B 两点，与y 轴交于点C ，OA =OC =3，顶点为D ．（1）求此函数的关系式；（2）在AC 下方的抛物线上有一点N ，过点N 作直线l ∥y 轴，交AC 于点M ，当点N 坐标为多少时，线段MN 的长度最大？最大是多少？（3）在对称轴上有一点K ，在抛物线上有一点L ，若使A ，B ，K ，L 为顶点形成平行四边形，求出K ，L 点的坐标．答案解析部分1．【答案】A【知识点】用正数、负数表示相反意义的量【解析】【解答】解：如果盈利90元记作+90元，那么亏本60元记作-60元.故答案为：A.【分析】根据正负数表示具有相反意义的量可求解.2．【答案】B【知识点】科学记数法表示大于10的数【解析】【解答】解：12000=1.2×104.故答案为：B.【分析】科学记数法是指，任何一个绝对值大于或等于1的数可以写成a×10n的形式，其中，n=整数位数-1.根据科学记数法的意义即可求解.3．【答案】C【知识点】中心对称及中心对称图形【解析】【解答】解：A、是轴对称图形，此选项不符合题意；B、是轴对称图形，此选项不符合题意；C、既是轴对称图形又是中心对称图形，此选项符合题意；D、既不是轴对称图形，又不是中心对称图形，此选项不符合题意.故答案为：C.【分析】在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形；根据定义并结合图形即可判断求解.4．【答案】C【知识点】二次函数图象的几何变换【解析】【解答】解：∵抛物线y=2(x-1)2向左平移2个单位，在向下平移2个单位，∴新抛物线的表达式为：y´=2(x-1+2)2+2=2（x+1）2+2.故答案为：C.【分析】根据抛物线的平移规律“左加右减、上加下减”即可求解.5．【答案】B【知识点】相似三角形的应用【解析】【解答】解：根据题意，作△EFC，树高为CD，且△ECF=90°，ED=2m，FD=8m；∵△E+△F=90°，△E+△ECD=90°，∴△ECD=△F，又∠CDE=∠FDC∴△EDC△△CDF，∴EDDC=DCFD，即DC2=ED•FD=2×8=16，解得CD=4m（负值舍去）．故答案为：B．【分析】如图，证明△EDC△△CDF，利用相似三角形对应边成比例即可求解. 6．【答案】B【知识点】勾股定理；菱形的性质【解析】【解答】解：∵菱形ABCD的周长为20，∴AB=14×20=5，AC△BD，AO=CO，BO=OD，∵菱形的对角线AC=6，∴AO=12AC=3，在Rt△AOB中，OB=√AB2−OA2=√52−32=4，∴BD=2BO=8，∴S菱形ABCD=12AC·BD=12×6×8=24.故答案为：B.【分析】根据菱形的性质“菱形的四条边都相等、对角线互相垂直平分”可求得AB、AO的值，在Rt△AOB中，用勾股定理可求得OB的值，然后根据菱形的面积等于两对角线乘积的一半可求解. 7．【答案】A【知识点】反比例函数图象的对称性；反比例函数与一次函数的交点问题【解析】【解答】解：∵反比例函数是中心对称图形，正比例函数与反比例函数的图象的两个交点关于原点对称，∵一个交点的坐标为(1，2)，∴它的另一个交点的坐标是(−1，−2)，故答案为：A.【分析】根据反比例函数图象的对称性可得：正比例函数与反比例函数图象的两个交点关于原点对称，据此不难得到另一个交点的坐标.8．【答案】C【知识点】圆周角定理；圆内接四边形的性质【解析】【解答】解：∵∠BOD=100°，∴∠BAD=12∠BOD=50°；∵∠BAD+∠BCD=180°，∴∠BCD=180°−∠BAD=180°−50°=130°；故答案为：C．【分析】先利用圆周角的性质求出∠BAD=12∠BOD=50°，再利用圆内接四边形的性质求出∠BCD=180°−∠BAD=180°−50°=130°即可。

人教版八年级数学上册期末模拟试卷含答案(广东汕头联考卷)

人教版八年级（上）期末数学试卷一、选择题（每题3分，共30分）1．（3分）若三角形的两边长分别为3和5，则其周长c的取值范围是（）A．6＜c＜15B．6＜c＜16C．11＜c＜13D．10＜c＜16 2．（3分）如图，在△ABC中，∠A＝80°，∠B＝40°．D、E分别是AB，AC上的点，且DE∥BC，则∠AED的度数是（）A．40°B．60°C．80°D．120°3．（3分）计算（﹣3x2）•2x3的结果是（）A．﹣5x6B．﹣6x6C．﹣5x5D．﹣6x54．（3分）不改变代数式a2﹣（2a+b+c）的值，把它括号前的符号变为相反的符号，应为（）A．a2+（﹣2a+b+c）B．a2+（﹣2a﹣b﹣c）C．a2+（﹣2a）+b+c D．a2﹣（﹣2a﹣b﹣c）5．（3分）分式可变形为（）A．B．﹣C．D．﹣6．（3分）下面是四位同学解方程过程中去分母的一步，其中正确的是（）A．2+x＝x﹣1B．2﹣x＝1C．2+x＝1﹣x D．2﹣x＝x﹣1 7．（3分）如图，已知AC＝FE，BC＝DE，点A、D、B、F在一条直线上，要利用“SSS”证明△ABC≌△FDE，还可以添加的一个条件是（）A．AD＝FB B．DE＝BD C．BF＝DB D．以上都不对8．（3分）如图，在CD上求一点P，使它到边OA，OB的距离相等，则点P是（）A．线段CD的中点B．CD与过点O作CD的垂线的交点C．CD与∠AOB的平分线的交点D．以上均不对9．（3分）在平面直角坐标系中，点A（a，﹣5）与点B（1，b）关于x轴对称，则a﹣b的值为（）A．﹣4B．4C．﹣6D．610．（3分）如图，在∠ECF的两边上有点B，A，D，BC＝BD＝DA，且∠ADF＝75°，则∠ECF的度数为（）A．15°B．20°C．25°D．30°二、填空题（本大题7题，每小题4分，共28分）11．（4分）（﹣2a2）3÷a2＝．12．（4分）如图，在△ABC中，D是BC延长线上一点，∠A＝68°，∠B＝65°，则∠ACD ＝．13．（4分）如图，BC＝EF，AC∥DF，请你添加一个适当的条件，使得△ABC≌△DEF，．（只需填一个答案即可）14．（4分）方程的解x＝．15．（4分）已知ab＝﹣3，a+b＝5，则10+a2b+ab2＝．16．（4分）关于x的分式方程的解为正数，则m的取值范围是．17．（4分）如图，∠AOB＝30°，点P是∠AOB内任意一点，且OP＝7，点E和点F分别是射线OA和射线OB上的动点，则△PEF周长的最小值是．三、解答题（一）（本大题3题，每小题6分，共18分）18．（6分）计算：（2x﹣1）2﹣x（4x﹣1）19．（6分）先化简，再求值：，其中a＝﹣1．20．（6分）如图，已知△ABC中，∠BAC＝23°，∠BCA＝125°．（1）尺规作图：作AC的垂直平分线，交BC的延长线于点D；（不写作法，保留作图痕迹）（2）连接AD，求∠BAD的度数．四、解答题（二）（本大题3题，每小题8分，共24分）21．（8分）如图，已知△ABC≌△DEF，BG、EH分别是△ABC和△DEF的中线，求证：BG＝EH．22．（8分）如图，△ABC中，AE＝BE，∠AED＝∠ABC．（1）求证：BD平分∠ABC；（2）若AB＝CB，∠AED＝4∠EAD，求∠C的度数．23．（8分）某商家用1000元购进一批多肉盆栽，很快售完，接着又用了1600元购进第二批多肉盆栽，且数量是第一批的1.2倍，已知第一批盆栽的单价比第二批的单价少3元，问这两批多肉盆栽的单价各是多少元？五、解答题（三）（本大题2题，每小题10分，共20分）24．（10分）如图，在△ABC中，∠ACB＝90°，AC＝BC，D为BC边的中点，BE⊥AB交AD的延长线于点E，CF平分∠ACB交AD于点F，连接CE．求证：（1）点D是EF的中点；（2）△CEF是等腰三角形．25．（10分）已知△ABC中，∠B＝60°，点D是AB边上的动点，过点D作DE∥BC交AC于点E，将△ADE沿DE折叠，点A对应点为F点．（1）如图1，当点F恰好落在BC边上，求证：△BDF是等边三角形；（2）如图2，当点F恰好落在△ABC内，且DF的延长线恰好经过点C，CF＝EF，求∠A的大小；（3）如图3，当点F恰好落在△ABC外，DF交BC于点G，连接BF，若BF⊥AB，AB ＝9，求BG的长．人教版八年级（上）期末数学试卷参考答案与试题解析一、选择题（每题3分，共30分）1．【分析】根据三角形的第三边大于任意两边之差，而小于任意两边之和进行求解．【解答】解：设三角形的第三边为a，由三角形三边关系定理得：5﹣3＜a＜5+3，即2＜a＜8．∴这个三角形的周长C的取值范围是：5+3+2＜c＜5+3+8，∴10＜c＜16．故选：D．2．【分析】根据两直线平行（DE∥BC），同位角相等（∠ADE＝∠B）可以求得△ADE的内角∠ADE＝40°；然后在△ADE中利用三角形内角和定理即可求得∠AED的度数．【解答】解：∵DE∥BC（已知），∠B＝40°（已知），∴∠ADE＝∠B＝40°（两直线平行，同位角相等）；又∵∠A＝80°，∴在△ADE中，∠AED＝180°﹣∠A﹣∠ADE＝60°（三角形内角和定理）；故选：B．3．【分析】根据单项式乘以单项式法则求出即可．【解答】解：（﹣3x2）•2x3＝﹣6x5，故选：D．4．【分析】括号前的“﹣”号变成“+”号，括号里各项变号即可．【解答】解：原式＝a2+（﹣2a﹣b﹣c）．故选：B．5．【分析】根据分式的性质，分子分母都乘以﹣1，分式的值不变，可得答案．【解答】解：分式的分子分母都乘以﹣1，得﹣，故选：D．6．【分析】去分母根据的是等式的性质2，方程的两边乘以最简公分母，即可将分式方程转化为整式方程．【解答】解：方程的两边同乘（x﹣1），得2﹣x＝x﹣1．故选：D．7．【分析】由题意AC＝FE，BC＝DE，根据SSS即可解决问题．【解答】解：∵AC＝EF，BC＝DE，∴要根据SSS证明△ABC≌△FDE，∴需要添加AD＝BF即可．故选：A．8．【分析】利用角平分线的性质得到点P在∠AOB的平分线上，从而可对各选项进行判断．【解答】解：∵点P到边OA，OB的距离相等，∴点P在∠AOB的平分线上，∴点P为CD与∠AOB的平分线的交点．故选：C．9．【分析】根据关于x轴对称点的坐标特点：横坐标不变，纵坐标互为相反数可得a＝1，b ＝5，然后可得a﹣b的值．【解答】解：∵点A（a，﹣5）与点B（1，b）关于x轴对称，∴a＝1，b＝5，∴a﹣b＝1﹣5＝﹣4，故选：A．10．【分析】根据等腰三角形的性质以及三角形外角和内角的关系，逐步推出∠ECF的度数．【解答】解：∵BC＝BD＝DA，∴∠C＝∠BDC，∠ABD＝∠BAD，∵∠ABD＝∠C+∠BDC，∠ADF＝75°，∴3∠ECF＝75°，∴∠ECF＝25°．故选：C．二、填空题（本大题7题，每小题4分，共28分）11．【分析】直接利用积的乘方运算法则化简，再利用整式的除法运算法则计算得出答案．【解答】解：原式＝﹣8a6÷a2＝﹣8a4．故答案为：﹣8a4．12．【分析】根据三角形的一个外角等于和它不相邻的两个内角的和计算．【解答】解：∵∠ACD是△ABC的一个外角，∴∠ACD＝∠A+∠B＝68°+65°＝133°，故答案为：133°．13．【分析】根据全等三角形的判定方法解决问题即可．【解答】解：∵AC∥DF，∴∠ACB＝∠F，∵BC＝EF，∴添加AC＝DF或∠A＝∠D或∠B＝∠DEF即可证明△ABC≌△DEF，故答案为AC＝DF或∠A＝∠D或∠B＝∠DEF．14．【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．【解答】解：去分母得：x2﹣2x﹣x2+4＝3x+6，解得：x＝﹣，经检验x＝﹣是分式方程的解，故答案为：﹣15．【分析】直接提取公因式ab，将原式变形进而求出答案．【解答】解：∵ab＝﹣3，a+b＝5，∴10+a2b+ab2＝10+ab（b+a）＝10﹣3×5＝﹣5．故答案为：﹣5．16．【分析】方程两边同乘以x﹣1，化为整数方程，求得x，再列不等式得出m的取值范围．【解答】解：方程两边同乘以x﹣1，得，m﹣3＝x﹣1，解得x＝m﹣2，∵分式方程的解为正数，∴x＝m﹣2＞0且x﹣1≠0，即m﹣2＞0且m﹣2﹣1≠0，∴m＞2且m≠3，故答案为m＞2且m≠3．17．【分析】设点P关于OA的对称点为C，关于OB的对称点为D，当点F、E在CD上时，△PEF的周长最小．【解答】解：分别作点P关于OA、OB的对称点C、D，连接CD，分别交OA、OB于点E、F，连接OP、OC、OD、PE、PF．∵点P关于OA的对称点为C，关于OB的对称点为D，∴PE＝CE，OP＝OC，∠COA＝∠POA；∵点P关于OB的对称点为D，∴PF＝DF，OP＝OD，∠DOB＝∠POB，∴OC＝OD＝OP＝5cm，∠COD＝∠COA+∠POA+∠POB+∠DOB＝2∠POA+2∠POB＝2∠AOB＝60°，∴△COD是等边三角形，∴CD＝OC＝OD＝7cm．∴△PEF的周长的最小值＝PE+EF+PF＝CE+EF+DF≥CD＝7．故答案为7．三、解答题（一）（本大题3题，每小题6分，共18分）18．【分析】根据完全平方公式和单项式乘以多项式的法则计算即可．【解答】解：（2x﹣1）2﹣x（4x﹣1）＝4x2﹣4x+1﹣4x2+x＝﹣3x+1．19．【分析】首先计算括号里面分式的减法，然后再计算括号外的除法，化简后，再把a的值代入即可．【解答】解：原式＝（﹣），＝，＝•，＝﹣，当a＝﹣1时，原式＝﹣2．20．【分析】（1）直接利用线段垂直平分线的作法得出AC的垂直平分线，进而得出答案；（2）利用线段垂直平分线的性质得出AD＝DC，进而得出∠ACD＝∠CAD＝55°，即可得出答案．【解答】解：（1）如图所示：D点即为所求；（2）∵∠BCA＝125°，∴∠ACD＝55°，∵ED垂直平分线AC，∴DC＝AD，∴∠ACD＝∠CAD＝55°，∵∠BAC＝23°，∴∠BAD＝23°+55°＝78°．四、解答题（二）（本大题3题，每小题8分，共24分）21．【分析】根据全等三角形的性质得到BC＝EF，AC＝DF，∠C＝∠F，证明△BCG≌△EFH，根据全等三角形的性质证明结论．【解答】证明：∵△ABC≌△DEF，∴BC＝EF，AC＝DF，∠C＝∠F，∵BG、EH分别是△ABC和△DEF的中线，∴CG＝AC，FH＝DF，∴CG＝FH，在△BCG和△EFH中，，∴△BCG≌△EFH（SAS）∴BG＝EH．22．【分析】（1）要证明BD平分∠ABC，只要证明∠DBC＝∠ABE即可，根据题目中的条件和三角形外角和内角的关系，可以证明∠DBC＝∠ABE，从而可以证明结论成立；（2）根据（1）中的结论和题意，利用三角形内角和可以求得∠C的度数．【解答】（1）证明：∵∠AED＝∠ABC，∠AED＝∠ABE+∠EAB，∠ABC＝∠ABE+∠DBC，∴∠EAB＝∠DBC，∵AE＝BE，∴∠EAB＝∠ABE，∴∠DBC＝∠ABE，∴BD平分∠ABC；（2）设∠EAD＝x，则∠AED＝4x，∵∠AED＝∠ABE+∠EAB，∠EAB＝∠ABE，BD平分∠ABC，∴∠BAE＝2x，∠ABC＝4x，∴∠BAC＝3x，∵AB＝CB，∴∠BAC＝∠C，∴∠C＝3x，∵∠ABC+∠BAC+∠C﹣180°，∴4x+3x+3x＝180°，解得，x＝18°，∴∠C＝3x＝54°，即∠C的度数是54°．23．【分析】首先设第一批单价为x元，则第二批单价为（x+3）元，根据题意可得等量关系：进一批的数量×1.2＝第二批的数量，根据等量关系列出方程，再解即可．【解答】解：设第一批单价为x元，则第二批单价为（x+3）元，由题意得：×1.2＝，解得：x＝9，经检验：x＝9是分式方程的解，x+3＝9+3＝12，答：第一批单价为9元，则第二批单价为12元．五、解答题（三）（本大题2题，每小题10分，共20分）24．【分析】（1）根据ASA证明△CDF≌△BDE，即可得出DF＝DE；（2）由（1）中的全等得：CF＝BE，判定△ACF≌△CBE，得到∠CAF＝∠BCE，根据三角形外角的性质和等腰三角形的判定可得结论．【解答】证明：（1）∵∠ACB＝90°，AC＝BC，∴∠ABC＝45°，∵EB⊥AB，∴∠ABE＝90°，∴∠CBE＝45°，∵CF平分∠ACB，∴∠DCF＝45°＝∠CBE，在△CDF和△BDE中，∵，∴△CDF≌△BDE（ASA），∴DF＝DE，∴点D是EF的中点；（2）由（1）知△CDF≌△BDE，∴CF＝BE，在△ACF和△CBE中，∵，∴△ACF≌△CBE（SAS），∴∠CAF＝∠BCE，∵∠CFE＝∠CAF+∠ACF，∠ECF＝∠BCF+∠BCE，∠ACF＝∠BCF，∴∠CFE＝∠ECF，∴EC＝EF，∴△CEF是等腰三角形．25．【分析】（1）利用平行线的性质得出∠ADE＝60°，再利用翻折变换的性质得出∠ADE ＝∠EDF＝60°，进而得出∠BDF＝60°，即可得出结论；（2）由折叠的性质得出∠ADE＝∠FDE＝60°，∠A＝∠DFE，得出∠ADC＝120°，由等腰三角形的性质得出∠FEC＝∠FCE，设∠FEC＝∠FCE＝x，由三角形的外角性质得出∠A＝∠DFE＝∠FEC+∠FCE＝2x，在△ADC中，由三角形内角和定理得出方程，解方程即可；（3）同（1）得出△BDG是等边三角形，∠ADE＝∠B＝60°，得出BG＝BD，由折叠的性质得出AD＝FD，由直角三角形的性质得出FD＝2BD，得出AD＝2BD，由已知得出2BD+BD＝9，求出BD＝3，即可得出BG＝BD＝3．【解答】（1）证明：如图1，∵∠B＝60°，DE∥BC，∴∠ADE＝∠B＝60°，∵△ADE沿DE折叠，点A对应点为F点，∴∠ADE＝∠FDE＝60°，∴∠BDF＝60°，∴∠DFB＝60°＝∠B＝∠BDF，∴△BDF是等边三角形；（2）解：∵∠B＝60°，DE∥BC，∴∠ADE＝∠B＝60°，∵△ADE沿DE折叠，点A对应点为F点，∴∠ADE＝∠FDE＝60°，∠A＝∠DFE，∴∠ADC＝120°，∵CF＝EF，∴∠FEC＝∠FCE，设∠FEC＝∠FCE＝x，则∠A＝∠DFE＝∠FEC+∠FCE＝2x，在△ADC中，∠A+∠ACD+∠ADC＝180°，即2x+x+120°＝180°，解得：x＝20°，∴∠A＝2x＝40°；（3）解：同（1）得：∠BDF＝60°，△BDG是等边三角形，∠ADE＝∠B＝60°，∴BG＝BD，由折叠的性质得：AD＝FD，∵BF⊥AB，∴∠BFD＝90°﹣60°＝30°，∴FD＝2BD，∴AD＝2BD，∵AD+BD＝AB，∴2BD+BD＝9，∴BD＝3，∴BG＝BD＝3．。

广东省汕头市八年级上学期数学期末考试试卷

广东省汕头市八年级上学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共10分)1. （1分）点（3，2）关于x轴的对称点为A . （3，﹣2）B . （﹣3，2）C . （﹣3，﹣2）D . （2，﹣3）2. （1分） (2016八上·江津期中) 若一个三角形的两边长分别是3和4，则第三边的长可能是（）A . 1B . 2C . 7D . 83. （1分）(2019·桂林模拟) 计算(﹣x5)7+(﹣x7)5的结果是（）A . ﹣2x12B . ﹣2x35C . ﹣2x70D . 04. （1分） (2017八上·哈尔滨月考) 根据分式的基本性质，分式可变形为（）A .B . -C . -D .5. （1分）如图，在△ABC中，AC= ，∠ABC=45°，∠BAC=15°，将△ACB沿直线AC翻折至△ABC所在的平面内，得△ACD.过点A作AE，使∠DAE=∠DAC，与CD的延长线交于点E，连接BE，则线段BE的长为（）A .B . 3C .D . 46. （1分）一个多边形的内角和是外角和的2倍，则这个多边形是（）A . 四边形B . 五边形C . 六边形D . 八边形7. （1分）一个等腰三角形的两边长分别是4和9，则它的周长为（）A . 17B . 20C . 22D . 17或228. （1分） (2017八上·哈尔滨月考) 下列运算正确的是（）A . (a+b)(a-b)=a2-b2B . a2·a3=a6C . (a+b)2=a2+b2D . a10÷a2=a59. （1分）如图，在△ABC中，∠B=90°，AB=4，∠BAC的角平分线AD交BC于点D，BD=3，则点D到AC的距离是（）A . 2B . 3C . 4D . 510. （1分）下列运算正确的有（）A . 5ab﹣ab=4B . 3﹣=3C . +=D . a6÷a3=a3二、填空题 (共10题；共10分)11. （1分）(2019·岳阳模拟) 分解因式：a3b-2a2b+ab=________．12. （1分） (2019八下·张家港期末) 当 ________时，分式的值为0.13. （1分）(2018·柳州) 如图，，若，则 ________ ．14. （1分） (2019八上·常州期末) 如图，在等边中，D、E分别是边AB、AC上的点，且，则 ________15. （1分） (2020七下·定兴期末) 利用因式分解计算 ________．16. （1分） (2015七上·市北期末) “x平方的3倍与﹣5的差”用代数式表示为：________．当x=﹣1时，代数式的值为________．17. （1分） (2018八上·无锡期中) 如图，在△ABC中，AB=AC．以点C为圆心，以CB长为半径作圆弧，交AC的延长线于点D，连结BD．若∠A=28°，则∠CDB的大小为________°．18. （1分） (2018八上·江汉期末) 已知，点E是△ABC的内角∠ABC与外角∠ACD的角平分线交点，∠A＝50°，则∠E＝________°.19. （1分）若关于x的方程=+1无解，则a的值是________ ．20. （1分）(2018·牡丹江模拟) 如图，等腰直角三角形直角边长为1，，以它的斜边上的高为腰，做第一个等腰直角三角形，其面积为S1；再以所做的第一个等腰直角三角形的斜边上的高为腰，做第二个等腰直角三角形；……以此类推，这样所做的第7个等腰直角三角形的面积S7=________．三、解答题 (共8题；共14分)21. （3分）(2017·赤峰) （﹣）÷ ，其中a=2017°+（﹣）﹣1+ tan30°．22. （2分）(2020·上海模拟) 解方程：23. （1分） (2019八上·黄石港期中)（1）如图1，已知△ABC，请画出△ABC关于直线AC对称的三角形.（2）如图2，△ABC与△DEF关于直线l对称，请作出直线l（请保留作图痕迹）（3）如图3，在矩形ABCD中，已知点E，F分别在AD和AB上，请在边BC上作出点G，在边CD作出点H，使得四边形EFGH的周长最小.24. （1分） (2018九上·渝中期末) 如图，直线AB∥CD ， EF平分∠AEG ，∠DFH＝13°，∠H＝21°，求∠EFG的度数．25. （1分） (2016八上·望江期中) 如图，A，D，F，B在同一直线上，AD=BF，AE=BC，且AE∥BC．求证：EF∥CD．26. （2分） (2015八下·深圳期中) 如图，在△ABC中，AB=BC，CD⊥AB于点D，CD=BD，BE平分∠ABC，点H 是BC边的中点，连接DH，交BE于点G，连接CG．（1）求证：△ADC≌△FDB；（2）求证：CE= BF；（3）判断△ECG的形状，并证明你的结论；（4）猜想BG与CE的数量关系，并证明你的结论．27. （2分） (2017八下·普陀期中) 温度通常有两种表示方法：华氏度（单位：℉）与摄氏度（单位：℃），已知华氏度数y与摄氏度数x之间是一次函数关系，如表列出了部分华氏度与摄氏度之间的对应关系：摄氏度数x（℃）…0…35…100…华氏度数y（℉）…32…95…212…（1）选用表格中给出的数据，求y关于x的函数解析式（不需要写出该函数的定义域）；（2）已知某天的最低气温是﹣5℃，求与之对应的华氏度数．28. （2分）(2017·赤壁模拟) 如图，在△ABC中，AB=AC，以AB为直径作半圆⊙O，交BC于点D，连接AD，过点D作DE⊥AC，垂足为点E，交AB的延长线于点F．（1）求证：EF是⊙0的切线．（2）如果⊙0的半径为5，sin∠ADE= ，求BF的长．参考答案一、单选题 (共10题；共10分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共10题；共10分)11-1、12-1、13-1、14-1、15-1、16-1、17-1、18-1、19-1、20-1、三、解答题 (共8题；共14分)21-1、22-1、23-1、23-2、23-3、24-1、25-1、26-1、26-2、26-3、26-4、27-1、27-2、28-1、28-2、。

广东省汕头市八年级(上)期末数学试卷

A. 10
B. 6
C. 5
D. 3
二、填空题（本大题共 6 小题，共 24.0 分）
第 1 页，共 12 页
11. 分解因式：a2-4b2=
．
12. 正十边形一个内角度数为
．
13. 若 m+n=1，mn=2，则 1m+1n 的值为
．
14. 已知实数 x，y 满足|x-4|+（y-8）2=0，则以 x，y 的值为两边长的等腰三角形的周长
8.【答案】A
【解析】
解：∵△ABC 中，AB=AC， ∴∠B=∠C， ∵∠A=40°，
∴∠B=
=70°，
故选：A．利用等腰三角形的性质和三角形的内角和定理求得∠B 的度数即可．本题考查了等腰三角形的性质，属于基础题，比较简单．
9.【答案】C
【解析】
解：∵在△ABC 和△ADC 中
，
∴△ABC➴△ADC（SSS）， ∴∠BAC=∠DAC，∠BCA=∠DCA，
是
．
15. 如图，已知 BC=EC，∠BCE=∠ACD，要使△ABC➴△DEC，则应添加的一个条件为．（答案不唯一，只需填一个）
16. 如图，已知△ABC 是等边三角形，点 B、C、D、E 在同一直线上，且 CG=CD，DF=DE，则∠E= 度．
三、计算题（本大题共 1 小题，共 5.0 分） 17. 解分式方程：2x2−4+xx−2=1．
2.【答案】B
【解析】
解：∵三角形三个内角度数的比为 2：3：4，
∴三个内角分别是 180°× =40°，180°× =60°，180°× =80°．
所以该三角形是锐角三角形．故选：B．根据三角形的内角和定理和三个内角的度数比，即可求得三个内角的度数，再根据三个内角的度数进一步判断三角形的形状．三角形按边分类：不等边三角形和等腰三角形（等边三角形）；三角形按角分类：锐角三角形，钝角三角形，直角三角形．

汕头市八年级(上)期末数学试卷含答案

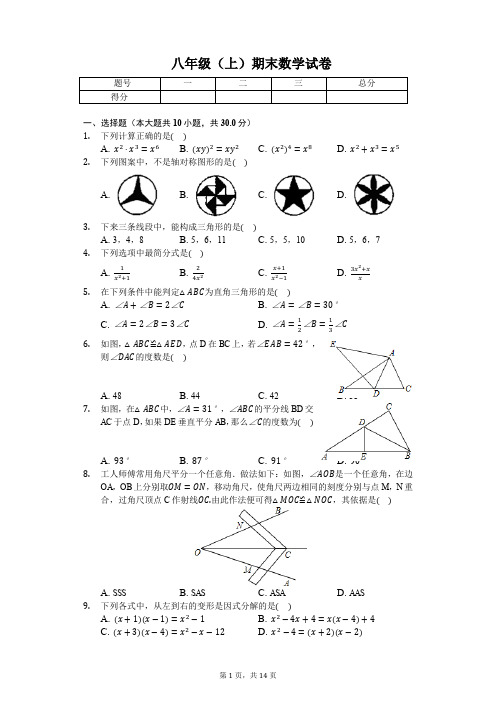
八年级（上）期末数学试卷一、选择题（本大题共10小题，共30.0分）1.下列计算正确的是A. B. C. D.2.下列图案中，不是轴对称图形的是A. B. C. D.3.下来三条线段中，能构成三角形的是A. 3，4，8B. 5，6，11C. 5，5，10D. 5，6，74.下列选项中最简分式是A. B. C. D.5.在下列条件中能判定为直角三角形的是A. B.C. D.6.如图， ≌ ，点D在BC上，若，则的度数是A. 48B. 44C. 42D. 387.如图，在中，，的平分线BD交AC于点D，如果DE垂直平分AB，那么的度数为A. B. C. D.8.工人师傅常用角尺平分一个任意角．做法如下：如图，是一个任意角，在边OA，OB上分别取，移动角尺，使角尺两边相同的刻度分别与点M，N重合，过角尺顶点C作射线由此作法便可得 ≌ ，其依据是A. SSSB. SASC. ASAD. AAS9.下列各式中，从左到右的变形是因式分解的是A. B.C. D.10.对于两个不相等的实数a、b，我们规定符号表示a、b中的较小的值，如，按照这个规定，方程的解为A. 1B. 2C. 1或2D. 1或二、填空题（本大题共6小题，共24.0分）11.当______，分式的的值为零．12.已知三角形的两边为2和5，则第三边x的取值范围是______ ．13.分式，，的最简公分母是______．14.光的速度约为，以太阳系以外距离地球最近的一颗恒星比邻星发出的光，需要4年的时间才能到达地球．若一年以计算，则这颗恒星到地球的距离是______km．15.如图，，，，，垂足分别是点D，E，，，则DE的长是___________．16.如图，，点、、在射线ON上，点、，在射线OM上，，，均为等边三角形，从左起第1个等边三角形的边长记，第2个等边三角形的边长记为，以此类推，若，则______，______．三、解答题（本大题共9小题，共66.0分）17.先化简，再求值：，其中，．18.一个多边形内角和的度数比外角和的度数的4倍多180度，求多边形的边数．19.如图，BD平分交AC于点D，于E，于F，，若，求DF的长．20.先化简再求值：，其中21.如图，中，尺规作图：作AC的垂直平分线，交AC于点D，交BC于点E；连接AE，求证：．22.山地自行车越来越受中学生的喜爱．一网店经营的一个型号山地自行车，今年一月份销售额为30000元，二月份每辆车售价比一月份每辆车售价降价100元，若销售的数量与上一月销售的数量相同，则销售额是27000元．求二月份每辆车售价是多少元？为了促销，三月份每辆车售价比二月份每辆车售价降低了销售，网店仍可获利，求每辆山地自行车的进价是多少元？23.特殊两位数乘法的速算--如果两个两位数的十位数字相同，个位数字相加为10，那么能立即说出这两个两位数的乘积．如果这两个两位数分别写作AB和即十位数字为A，个位数字分别为B、C，，，那么它们的乘积是一个4位数，前两位数字是A和的乘积，后两位数字就是B和C的乘积．如：，．请你直接写出的值；设这两个两位数的十位数字为，个位数字分别为y和，通过计算验证这两个两位数的乘积为．______．24.如图，在中，，，点D在线段BC上运动不与B、C重合，连接AD，作，DE交线段AC于E．当时，________，________；点D从B 向C运动时，逐渐变________填“大”或“小”；当DC等于多少时， ≌ ，请说明理由；在点D的运动过程中，的形状可以是等腰三角形吗？若可以，请直接写出的度数．若不可以，请说明理由．25.如图1，是边长为8的等边三角形，下点D，于点E求证：；若点F是AD的中点，点P是BC边上的动点，连接PE，PF，如图2所示，求的最小值及此时BP的长；在的条件下，连接EF，若，当取最小值时，的面积是______．答案和解析1.【答案】C【解析】解：A、，故原题计算错误；B、，故原题计算错误；C、，故原题计算正确；D、和不是同类项，故原题计算错误；故选：C．根据同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加；积的乘方法则：把每一个因式分别乘方，再把所得的幂相乘；幂的乘方法则：底数不变，指数相乘；合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变进行计算即可．此题主要考查了同底数幂的乘法、积的乘方、幂的乘方、合并同类项，关键是掌握计算法则．2.【答案】B【解析】解：A、是轴对称图形，不合题意；B、不是轴对称图形，符合题意；C、是轴对称图形，不合题意；D、是轴对称图形，不合题意．故选：B．根据轴对称图形的概念作答．此题主要考查了轴对称图形的概念：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．3.【答案】D【解析】解：根据三角形任意两边的和大于第三边，得A，，不能组成三角形；B，，不能组成三角形；C，，不能够组成三角形；D，，能组成三角形．故选：D．根据三角形的三边关系进行分析判断．本题考查了能够组成三角形三边的条件：用两条较短的线段相加，如果大于最长的那条线段就能够组成三角形．4.【答案】A【解析】解：A、是最简分式；B、，不是最简分式；C、，不是最简分式；D、，不是最简分式；故选：A．最简分式的标准是分子，分母中不含有公因式，不能再约分．判断的方法是把分子、分母分解因式，并且观察有无互为相反数的因式，这样的因式可以通过符号变化化为相同的因式从而进行约分．题考查了最简分式，分式的化简过程，首先要把分子分母分解因式，互为相反数的因式是比较易忽视的问题．在解题中一定要引起注意．5.【答案】D【解析】解：A、，而，则，不能确定为直角三角形，所以A选项错误；B、，而，则，所以B选项错误；C、，而，则，所以C选项错误；D、，而，则，所以D选项正确．故选D．根据三角形内角和定理和各选项中的条件计算出的内角，然后根据直角三角形的判定方法进行判断．本题考查了三角形内角和定理：三角形内角和是也考查了直角三角形的定义．6.【答案】C【解析】解： ≌ ，，．故选：C．直接利用全等三角形的性质得出对应角相等进而得出答案．此题主要考查了全等三角形的性质，正确得出对应角是解题关键．7.【答案】B【解析】解：在中，，DE垂直平分AB，，的平分线BD交AC于点D，，，故选：B．根据垂直平分线和角平分线的性质解答即可．此题考查线段垂直平分线的问题，关键是根据垂直平分线和角平分线的性质解答．8.【答案】A【解析】解：在和中，≌ ，，故选：A．由作图过程可得，，再加上公共边可利用SSS定理判定≌ ．此题主要考查了全等三角形的判定，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．9.【答案】D【解析】解：A、，是整式乘法运算，故此选项错误；B、，不是分解因式，故此选项错误；C、，是整式乘法运算，故此选项错误；D、，故此选项正确；故选：D．直接利用因式分解的意义分析得出答案．此题主要考查了因式分解的意义，正确把握相关定义是解题关键．10.【答案】B【解析】解：当时，方程化简得：，去分母得：，即，经检验是分式方程的解；当时，方程化简得：，去分母得：，即，不符合题意，舍去，则方程的解为，故选：B．根据题中的新定义化简已知等式，求出解即可．此题考查了解分式方程，弄清题中的新定义是解本题的关键．11.【答案】2【解析】解：由分式的值为零，得且．解得，故答案为：2．根据分式的值为零的条件可以求出x的值．本题考查了分式值为零的条件，若分式的值为零，需同时具备两个条件：分子为0；分母不为这两个条件缺一不可．12.【答案】【解析】解：依题意得：，即．三角形的任意两边的和大于第三边，已知两边，则第三边的长度应是大于两边的差而小于两边的和，这样就可求出第三边长的范围．此类求三角形第三边的范围的题，实际上就是根据三角形三边关系定理列出不等式，然后解不等式即可．13.【答案】【解析】解：分式，，的分母分别是2x、、4xy，故最简公分母是．故答案为．确定最简公分母的方法是：取各分母系数的最小公倍数；凡单独出现的字母连同它的指数作为最简公分母的一个因式；同底数幂取次数最高的，得到的因式的积就是最简公分母．本题考查了最简公分母，通分的关键是准确求出各个分式中分母的最简公分母，确定最简公分母的方法一定要掌握．14.【答案】【解析】解：依题意，这颗恒星到地球的距离为，，．根据题意列出算式，再根据单项式的运算法则进行计算．本题考查了根据实际问题列算式的能力，科学记数法相乘可以运用单项式相乘的法则进行计算．15.【答案】2【解析】【分析】根据条件可以得出，进而得出 ≌ ，就可以得出，就可以求出DE的值．本题考查全等三角形的判定和性质、熟练掌握全等三角形的判定和性质是解决问题的关键，学会正确寻找全等三角形，属于中考常考题型．【解析】解：，，，．，．在和中，，≌ ，，．故选答案为2．16.【答案】6【解析】解：是等边三角形，，，，，，，，，同理，，，，，，，，，，故答案为：6，．由等边三角形的性质得出，易证，，则，，推出，，同理，，，，则，，，，，即可得出结果．本题考查了等边三角形的性质、等腰三角形的判定与性质、含角直角三角形的性质等知识；熟练掌握等边三角形的性质、等腰三角形的性质、含角直角三角形的性质找出规律是解题的关键．17.【答案】解：原式，当，时，原式．【解析】根据完全平方公式、单项式乘多项式的法则把原式进行化简，代入已知数据计算即可．本题考查的是单项式乘多项式，掌握完全平方公式、单项式乘多项式的法则是解题的关键．18.【答案】解：设多边形的边数为x多边形的外角和是，内角和的度数比外角和的度数的4倍多180度，可得方程解得．多边形的边数为11．【解析】根据多边形的外角和是可得出内角和为，再根据内角和公式可以求得多边形的边数．本题主要考查的是多边形的外角和是以及多边形的内角和公式，掌握公式是解题的关键．19.【答案】解：，，，，平分，，，．【解析】首先利用三角形的面积公式求出DE，再利用角平分线的性质定理解决问题即可．本题考查角平分线的性质，三角形的面积等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．20.【答案】解：原式，当时，原式．【解析】先根据分式的混合运算顺序和运算法则化简原式，再将x的值代入计算可得．本题主要考查分式的化简求值，解题的关键是熟练掌握分式的混合运算顺序和运算法则．21.【答案】解：如图所示：直线DE即为AC的垂直平分线；证明：直线DE为AC的垂直平分线，，，，又，，．【解析】依据垂直平分线的作法，即可得到直线DE即为AC的垂直平分线；依据垂直平分线的性质，即可得到，进而得出，根据，即可得到．本题主要考查了基本作图，解题时注意运用：线段垂直平分线上任意一点，到线段两端点的距离相等．22.【答案】解：设二月份每辆车售价为x元，则一月份每辆车售价为元，根据题意得：，解得：，经检验，是原分式方程的解．答：二月份每辆车售价是900元．设每辆山地自行车的进价为y元，根据题意得：，解得：．答：每辆山地自行车的进价是600元．【解析】设二月份每辆车售价为x元，则一月份每辆车售价为元，根据数量总价单价，即可得出关于x的分式方程，解之经检验后即可得出结论；设每辆山地自行车的进价为y元，根据利润售价进价，即可得出关于y的一元一次方程，解之即可得出结论．本题考查了分式方程的应用以及一元一次方程的应用，解题的关键是：找准等量关系，正确列出分式方程；找准等量关系，正确列出一元一次方程．23.【答案】9999000009【解析】解：和87满足题中的条件，即十位数都是8，，且个位数字分别是3和7，之和为10，那么它们的乘积是一个4位数，前两位数字是8和9的乘积，后两位数字就是3和7的乘积，因而，答案为：7221；这两个两位数的十位数字为，个位数字分别为y和z，则由题知，因而有：得证；．故答案是：9999000009．根据“前两位数字是A和的乘积，后两位数字就是B和C的乘积”进行计算；这两个两位数的十位数字为，个位数字分别为y和z，则由题知，利用多项式乘多项式的计算法则解答；利用，，找出规律解答．考查单项式乘多项式．掌握规律是解题的难点，需要学生具备一定的分析能力．24.【答案】解：，115，小；当时， ≌ ，理由：，，又，，，又，≌ ；当的度数为或时，的形状是等腰三角形，理由：时，，，，，，的形状是等腰三角形；当的度数为时，，，，，的形状是等腰三角形．【解析】【分析】此题主要考查了等腰三角形的性质以及全等三角形的判定等知识，熟练地应用等腰三角形的性质是解决问题的关键．根据以及，即可得出，进而求出的度数，当时，利用，，求出，再利用，即可得出 ≌ ，当的度数为或时，的形状是等腰三角形．【解答】解：，，逐渐变小；故答案为：，，小；见答案；见答案．25.【答案】【解析】证明：如图1中，是等边三角形，，，，，，，，，．解：如图2中，延长DF到H，使得，连接EF，连接EH交BC于点P，此时的值最小．，，，，，，在中，，，，，，，，，，，，的最小值，，．解：如图2中，，，是等边三角形，，，，．解直角三角形求出BE，AE即可判断．如图2中，延长DF到H，使得，连接EF，连接EH交BC于点P，此时的值最小．证明，解直角三角形求出EH即可解决问题．证明是等边三角形，求出PE，EF即可解决问题．本题属于三角形综合题，考查了等边三角形的判定和性质，解直角三角形，轴对称最短问题等知识，解题的关键是学会两条轴对称解决最短问题，属于中考常考题型．。