2012年高考第一轮复习数学:7.6 直线与圆的位置关系
直线与圆的位置关系知识点及例题

直线与圆的位置关系知识点及例题Prepared on 22 November 2020直线与圆的位置关系一、知识点梳理1、直线与圆的位置关系:图形名称相离相切相交判定d>r d=r d<r交点个数无1个2个例1、下列判断正确的是()①直线上一点到圆心的距离大于半径,则直线与圆相离;②直线上一点到圆心的距离等于半径,则直线与圆相切;③直线上一点到圆心的距离小于半径,•则直线与圆相交.A.①②③ B.①② C.②③ D.③例2、过圆上一点可以作圆的______条切线;过圆外一点可以作圆的_____条切线;•过圆内一点的圆的切线______.例3、以三角形一边为直径的圆恰好与另一边相切,则此三角形是_______.例4、下列直线是圆的切线的是()A.与圆有公共点的直线 B.到圆心的距离等于半径的直线C.垂直于圆的半径的直线 D.过圆直径外端点的直线例5.如图所示,Rt△ABC中,∠ACB=90°,CA=6,CB=8,以C为圆心,r为半径作⊙C,当r为多少时,⊙C与AB相切2、切线的判定:(1)根据切线的定义判定:即与圆有一个公共点的直线是圆的切线.(2)根据圆心到直线的距离来判定:即与圆心的距离等于半径的直线是圆的切线. (3)根据切线的判定定理来判定:即经过半径的外端并且垂直于这条半径的直线是圆的切线.判定切线时常用的辅助线作法:(1)若直线与圆有公共点时,辅助线的作法是“连结圆心和公共点”,再证明直线和半径垂直.(2)当直线与圆并没有明确有公共点时,辅助线的作法是“过圆心向直线作垂线”再证明圆心到直线的距离等于圆的半径.例6、判断下列命题是否正确(1)经过半径的外端的直线是圆的切线(2)垂直于半径的直线是圆的切线;(3)过直径的外端并且垂直于这条直径的直线是圆的切线;(4)和圆有一个公共点的直线是圆的切线;(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.例7.OA平分∠BOC,P是OA上任一点(O除外),若以P为圆心的⊙P与OC相离,•那么⊙P与OB的位置关系是()A.相离 B.相切 C.相交 D.相交或相切例8、如图所示,在直角坐标系中,⊙M的圆心坐标为(m,0),半径为2,•如果⊙M与y轴所在直线相切,那么m=______,如果⊙M与y轴所在直线相交,那么m•的取值范围是_______.例9、如图,AB为⊙O的直径,弦CD⊥AB于点M,过点B作BE∥CD,交AC•的延长线于点E,连结BC.(1)求证:BE为⊙O的切线;(2)如果CD=6,tan∠BCD=12,求⊙O的直径.例10、如图,已知:△ABC内接于⊙O,点D在OC的延长线上,sinB=12,∠D=30°.(1)求证:AD是⊙O的切线;(2)若AC=6,求AD的长.例11、如图,P为⊙O外一点,PO交⊙O于C,过⊙O上一点A作弦AB⊥PO于E,若∠EAC=∠CAP,求证:PA是⊙O的切线.3、切线的性质:1、经过切点的半径垂直于圆的切线,经过切点垂直于切线的直线必经过圆心对于切线的性质可分解为:过圆心、过切点、垂直于切线这三个条件中任意两个作为条件,就可以推出第三个作为结论4、切线长定理:切线长定义:经过圆外一点作圆的切线,这点和切点之间的线段的长叫做这点到圆的切线长切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这点和圆心的连线平分两条切线的夹角.例12、如图1,PA、PB是⊙O的两条切线、A、B为切点。
高考数学第一轮知识点总复习 第四节 直线与圆的位置关系

∵|PC|= 112 1 22 5 r 6
∴点P恒在圆C内,∴直线 与l 圆C恒交于两点.
(2)由(1)及平面几何知识知,当l 垂直于PC时,直线l 被圆C截得的弦
长最小,又 kPC
2 1 1 1
1 2
,
k,l
1 kPC
2
∴所求直线 l的方程为y-1=2(x-1),即2x-y-1=0.
题型二 圆与圆的位置关系
2k 6 5 2
3
由点C到直线AB的距离公式 k2 12 ,得k= . 4
l
又直线 的斜率不存在时也满足题意,此时方程为x=0.
3
当k=4
时,直线
l
的方程为3x-4y+20=0.
∴所求直线的方程为x=0或3x-4y+20=0. 方法二:设所求直线的斜率为k,
则直线l的方程为y-5=kx,即y=kx+5,
【例】求过A(3,5)且与圆C: x2 -4yx2-4y+7=0相切的直线方程.
错解 设所求直线 的l 斜率为k,方程为y-5=k(x-3),
即kx-y+5-3k=0,已知圆C的圆心(2,2),r=1.
则圆心到 l的距离为
2k 2 5 ,3即k |1k-3|=
1 k2
, 1 k2
4
∴ k-26k+9= k+2 1,解得k= 3.
∵A到l的距离为 5 ,2
∴所求圆B的直径
即 r2 2.
2r
2
5
2 r,1 2
2
r r 又|OB|=|OA|- 2 , 2
2
1
由 OA与x轴正半轴成45°角,∴B(2,2).
∴所求圆的标准方程为 (x2)2 ( y.2)2 2
一轮复习直线与圆、圆与圆的位置关系

高中数学会考复习训练27直线与圆、圆与圆的位置关系 知识点一、直线与圆的位置关系(圆心到直线的距离为d ,圆的半径为r )二、圆与圆的位置关系(⊙O 1、⊙O 2半径r 1、r 2,d =|O 1O 2|)课前小测1.(教材习题改编)圆(x -1)2+(y +2)2=6与直线2x +y -5=0的位置关系是( ) A .相切 B .相交但直线不过圆心 C .相交过圆心 D .相离2.(2013·银川质检)由直线y =x +1上的一点向圆x 2+y 2-6x +8=0引切线,则切线长的最小值为( )A.7 B .2 2 C .3D.23.直线x -y +1=0与圆x 2+y 2=r 2相交于A ,B 两点,且AB 的长为2,则圆的半径为( ) A.322B.62C .1D .24.(教材习题改编)若圆x 2+y 2=1与直线y =kx +2没有公共点,则实数k 的取值范围是________.5.已知两圆C1:x2+y2-2x+10y-24=0,C2:x2+y2+2x+2y-8=0,则两圆公共弦所在的直线方程是____________.例题[例1]()A.l与C相交B.l与C相切C.l与C相离 D.以上三个选项均有可能[例2]0与圆x2+y2=4相交于A、B两点,则弦AB的长等于()A.33B.2 3 C. 3 D.1(2)(2012·天津高考)设m,n∈R,若直线(m+1)x+(n+1)y-2=0与圆(x-1)2+(y-1)2=1相切,则m+n的取值范围是()A.[1-3,1+ 3 ] B.(-∞,1- 3 ]∪[1+3,+∞)C.[2-22,2+2 2 ] D.(-∞,2-2 2 ]∪[2+22,+∞)[例3](1)(2012·的位置关系为() A.内切B.相交C.外切D.相离(2)设两圆C 1、C 2都和两坐标轴相切,且都过点(4,1),则两圆心的距离|C 1C 2|=________.课后作业一、选择题1.直线2x -y =0与圆C :(x -2)2+(y +1)2=9相交于A ,B 两点,则△ABC (C 为圆心)的面积等于( )A .25B .2 3C .4 3D .452.若直线3x +y +2n =0与圆x 2+y 2=n 2相切,其中n ∈N *,则n 的值为( ) A .1 B .2 C .4 D .1或23.若实数x ,y 满足(x +5)2+(y -12)2=142,则x 2+y 2的最小值是( ) A .2 B .1 C. 3 D.24.(2011·高考江西卷)若曲线C 1:x 2+y 2-2x =0与曲线C 2:y (y -mx -m )=0有四个不同的交点,则实数m 的取值范围是( )A .(-33,33)B .(-33,0)∪(0,33)C .[-33,33]D .(-∞,-33)∪(33,+∞)5.在直线y =2x +1上有一点P ,过点P 且垂直于直线4x +3y -3=0的直线与圆x 2+y 2-2x =0有公共点,则点P 的横坐标取值范围是( )A .(-∞,-1)∪(1,+∞)B .(-1,1)C .[-125,-25]D .(-125,-25)二、填空题 6.(2012·金华质检)若过点A (a ,a )可作圆x 2+y 2-2ax +a 2+2a -3=0的两条切线,则实数a 的取值范围为________.7.已知圆C 1:x 2+y 2-6x -7=0与圆C 2:x 2+y 2-6y -27=0相交于A 、B 两点,则线段AB 的中垂线方程为________.8.过原点O 作圆x 2+y 2-6x -8y +20=0的两条切线,设切点分别为P 、Q ,则线段PQ 的长为________.三、解答题9.已知圆C :x 2+y 2-4x -6y +12=0,点A (3,5). (1)求过点A 的圆的切线方程;(2)O 点是坐标原点,连结OA ,OC ,求△AOC 的面积S .10. (2011·高考陕西卷)如图,设P 是圆x 2+y 2=25上的动点,点D 是P 在x 轴上的投影,M 为PD 上一点且|MD |=45|PD |.(1)当P 在圆上运动时,求点M 的轨迹C 的方程;(2)求过点(3,0)且斜率为45的直线被C 所截线段的长度.11.(探究选做)已知两个圆C 1:x 2+y 2=4,C 2:x 2+y 2-2x -4y +4=0,直线l :x +2y =0,求经过C 1和C 2的交点且和l 相切的圆的方程.。
2012届高考数学(理科)一轮复习课件(人教版)第10单元第62讲 直线与圆锥曲线的位置关系

b x0 a y0
2
.
12
(2)运用类比的方法可以推出:已知AB是双曲 2 y x 线 - 2 =1的弦,弦AB的中点为M( , ), b x b a 则 x =⑫____________.已知抛物线 k AB y a y 2 x, =2px(p>0)的弦AB的中点为M( ),则y = y p ⑬____________. k AB
x
2
1的 交 点 个 数
5
4
2
8
1.直线与圆锥曲线的位置关系的判定 (1)直线与椭圆的位置关系的判定方法 将直线方程与椭圆方程联立,消去一个未 知数,得到一个一元二次方程,若 >0, 相交 则直线与椭圆①____________;若 =0, 相切 则直线与椭圆②____________;若 <0, 则直线与椭圆③____________. 相离
9
(2)直线与双曲线的位置关系的判定方法:
将直线方程与双曲线方程联立消去y(或 x),得到一个一元方程 ax 2 bx c 0 2 a y b y c 0 ). (或
(ⅰ)若a 0,当 >0时,直线与双曲线④ 相交 ____________;当 =0时,直线与双 相切 曲线⑤____________;当 <0时,直 相离 线与双曲线⑥____________.
评析
求直线被二次曲线截得的弦长,通常是将
直 线 与 二 次 曲 线 方 程 联 立 , 得 到 关 于 x ( 或 y )的 一 元 二 次 方程,然后利用韦达定理及弦长公式求解.
23
素材2 解析
本 例 中 将 “以 A B 为 直 径 的 圆 恰 好 过 抛 物 线
高一数学-直线与圆的方程——直线与圆的位置关系(带答案)

专题二 直线与圆的位置关系教学目标:直线和圆的位置关系的判断 教学重难点:直线和圆的位置关系的应用 教学过程:第一部分 知识点回顾考点一:直线与圆的位置关系的判断:直线:0l Ax By C ++=和圆()()222C :x a y b r -+-=()0r >有相交、相离、相切。
可从代数和几何两个方面来判断: (1)代数方法判断直线与圆方程联立所得方程组的解的情况:由⎩⎨⎧=-+-=++222)()(0r b y a x C By Ax ,消元得到一元二次方程,计算判别式∆, ①0∆>⇔相交;②0∆<⇔相离;③0∆=⇔相切; (2)几何方法如果直线l 和圆C 的方程分别为:0=++C By Ax ,222)()(r b y a x =-+-. 可以用圆心),(b a C 到直线的距离=d 22||Aa Bb C A B+++与圆C 的半径r 的大小关系来判断直线与圆的位置关系:①d r <⇔相交;②d r >⇔相离;③d r =⇔相切。
提醒:判断直线与圆的位置关系一般用几何方法较简捷。
例1 直线x sin θ+y cos θ=2+sin θ与圆(x -1)2+y 2=4的位置关系是( )A .相离B .相切C .相交D .以上都有可能答案 B 解析 圆心到直线的距离d =|sin θ-2-sin θ|sin 2θ+cos 2θ所以直线与圆相切. 例2 已知直线l 过点(-2,0),当直线l 与圆x 2+y 2=2x 有两个交点时,其斜率k 的取值范围是( )A .(-22,22)B .(-2,2)C .(-24,24)D .(-18,18)答案C 设l 的方程y =k (x +2),即kx -y +2k =0.圆心为(1,0).由已知有|k +2k |k 2+1<1,∴-24<k <24.例3 圆(x -3)2+(y -3)2=9上到直线3x +4y -11=0的距离为1的点有几个?解:圆(x -3)2+(y -3)2=9的圆心为O 1(3,3),半径r =3, 设圆心O 1(3,3)到直线3x +4y -11=0的距离为d ,则d =22|334311|2334⨯+⨯-=<+如图1,在圆心O 1的同侧,与直线3x +4y -11=0平行且距离为1的直线l 1与圆有两个交点,这两个交点符合题意,又r -d =3-2=1,所以与直线3x +4y -11=0平行的圆的切线的两个切点中有一个切点也符合题意. 所以符合题意的点共有3个。
高中数学一轮复习直线与圆的位置关系

有公共点,则实数a的取值范围是(
A.[-3,-1] C.[-3,1]
)
B.[-1,3] D.(-∞,-3]∪[1,+∞)
【解析】 (1)∵x2+y2=2 的圆心(0,0)到直线 y=kx+1 的距离 |0-0+1| 1 d= = ≤1.又∵r= 2, 2 2 1+k 1+k ∴0<d<r.∴直线与圆相交但直线不过圆心. (2)由题意知,圆心为(a,0),半径 r= 2. 若直线与圆有公共点,则圆心到直线的距离小于或等于半径, |a-0+1| 即 ≤ 2,∴|a+1|≤2.∴-3≤a≤1,故选 C. 2
又直线 l 的斜率不存在时,也满足题意, 此时方程为 x=0. ∴所求直线的方程为 3x-4y+20=0 或 x=0. 解法二: 设所求直线的斜率为 k, 则直线的方程为 y-5=kx, 即 y=kx+5,
y=kx+5, 联立直线与圆的方程 2 2 x +y +4x-12y+24=0,
消去 y,得(1+k )x +(4-2k)x-11=0,① 设方程①的两根为 x1,x2,
y2+4x-12y+24=0. (1)若直线 l 过 P 且被圆 C 截得的线 段长为 4 3,求 l 的方程; (2)求过 P 点的圆 C 的弦的中点的 轨迹方程. 【思路分析】 (1)根据弦长求法,求
直线方程中的参数; (2)由垂直关系 找等量关系.
【解析】
(1)解法一:如图所示,AB=4
3 ,D是AB的 中
解:方法一
(1)证明
消去 y 得(k2+1)x2-(2-4k)x-7=0,
因为 Δ=(2-4k)2+28(k2+1)>0, 所以不论 k 为何实数,直线 l 和圆 C 总有两个交点.
|k+2| 方法二 (1)证明 圆心 C(1,-1)到直线 l 的距离 d= 2, 1+k k2+4k+4 11k2-4k+8 圆 C 的半径 R=2 3,R2-d2=12- ,而 2 = 2 1+k 1+k 在 S=11k2-4k+8 中,Δ=(-4)2-4×11×8<0,
2012届高考数学(文)一轮复习课件:8-4第四节 直线与圆、圆与圆的位置关系(北师大版)

理几何问题的思想.
现解答题,难度中等.
第八章
平面解析几何
北 师 大 版 数 学 文
第八章
平面解析几何
北 师 大 版 数 学 文
1.直线与圆的位置关系
相离、相切、相交. (1)直线与圆的位置关系有三种:
判断直线与圆的位置关系常见的有两种方法:
①代数法:利用判别式Δ
第八章
平面解析几何
北 师 大 版 数 学 文
程.
[思路分析] 本题求解的关键是由“圆C1 与圆C2 交于A,
B两点且这两点平分圆C2的周长”得到|C1C2|2+r22=r12.
第八章
平面解析几何
北 师 大 版 数 学 文
[听课记录]
(1)由已知,圆 C1 的圆心为(an,-an+1),半
径为 r1= an2+an+12+1,圆 C2 的圆心为(-1,-1),半径为 r2=2. 又圆 C1 与圆 C2 交于 A,B 两点且这两点平分圆 C2 的周 长,所以|C1C2|2+r22=r12,所以(an+1)2+(-an+1+1)2+4= an +an+12+1,所以
|-1+2-a| 由 = 2,得|a-1|=2,即 a=-1,或 a=3. 2 ∴直线方程为 x+y+1=0,或 x+y-3=0. 综上,圆的切线方程为 y=(2+ 6)x,或 y=(2- 6)x, 或 x+y+1=0,或 x+y-3=0.
第八章
平面解析几何
北 师 大 版 数 学 文
(2)由|PO|=|PM|,得x12+y12=(x1+1)2+(y1-2)2-2⇒2x1 -4y1+3=0.
第八章
平面解析几何
北 师 大 版 数 学 文
第八章
平面解析几何
北 师 大 版 数 学 文
高考一轮复习直线与圆、圆与圆的位置关系

圆O2的方程.
2 例4 已知以点C(t, )(t∈R,t≠0)为圆心的圆与x轴 t
交于点O、A,与y轴交于点O、B,其中O为原点.
(1)求证:△AOB的面积为定值; (2)设直线2x+y-4=0与圆C交于点M、N,若|OM|=|ON| 求圆C的方程; (3)在(2)的条件下,设P、Q分别是直线l:x+y+2=0和圆 C上的动点,求|PB|+|PQ|的最小值及此时点P的坐标.
直线与圆、圆与圆 的位置关系
一、直线与圆的位置关系
1.常用研究方法 ①判别式法;
②考查圆心到直线的距离与半径的大小关系.
2.直线Ax+By+C=0与圆(x-a) +(y-b) =r 的位置关系有 | Aa Bb C | 三种: 若d 2 2 A B
2 2 2
则d____r⇔相切⇔Δ____0; = =
d____r⇔相交⇔Δ____0; < < < d____r⇔相离⇔Δ____0; >
3.直线和圆相切
(1)过圆上一点的圆的切线方程:圆(x-a) +(y-b) =r 的以P( x0,y0)为切点的切线方程是______________________. (x0-a)(x-a)+(y0-b)(y-b)=r (2)一般地,圆x +y +Dx+Ey+F=0的以点P(x0,y0)为切点的
例2 已知点P(0,5)及圆C:x +y 3 +4x-12y+24=0. (1)若直线l过点P且被圆C截得的线段长为4 ,
求l的方程;
(2)求过P点的圆C的弦的中点的轨迹方程.
高考数学一轮复习第八章第二节第1课时系统知识__圆的方程直线与圆的位置关系圆与圆的位置关系讲义含解析

第二节圆与方程第1课时系统知识——圆的方程、直线与圆的位置关系、圆与圆的位置关系1.圆的定义及方程点M(x0,y0),圆的标准方程(x-a)2+(y-b)2=r2.[提醒] 不要把形如x2+y2+Dx+Ey+F=0的结构都认为是圆,一定要先判断D2+E2-4F的符号,只有大于0时才表示圆.[谨记常用结论]若x2+y2+Dx+Ey+F=0表示圆,则有:当F=0时,圆过原点.当D=0,E≠0时,圆心在y轴上;当D≠0,E=0时,圆心在x轴上.当D=F=0,E≠0时,圆与x轴相切于原点;E=F=0,D≠0时,圆与y轴相切于原点.当D2=E2=4F时,圆与两坐标轴相切.[小题练通]1.[人教A版教材P124A组T4]圆C的圆心在x轴上,并且过点A(-1,1)和B(1,3),则圆C的方程为____________.答案:(x-2)2+y2=102.[教材改编题]经过点(1,0),且圆心是两直线x=1与x+y=2的交点的圆的方程为________________.答案:(x -1)2+(y -1)2=13.[教材改编题]圆心为(1,1)且过原点的圆的方程是________. 答案:(x -1)2+(y -1)2=24.[易错题]已知圆的方程为x 2+y 2+ax +2y +a 2=0,一定点为A (1,2),要使过定点A 的圆的切线有两条,则a 的取值范围是________.答案:⎝ ⎛⎭⎪⎫-233,2335.若坐标原点在圆(x -m )2+(y +m )2=4的内部,则实数m 的取值范围是________. 答案:(-2,2)6.在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为________________. 答案:x 2+y 2-2x =01.直线与圆的位置关系(半径r ,圆心到直线的距离为d )2.圆的切线(1)过圆上一点的圆的切线①过圆x 2+y 2=r 2上一点M (x 0,y 0)的切线方程是x 0x +y 0y =r 2.②过圆(x -a )2+(y -b )2=r 2上一点M (x 0,y 0)的切线方程是(x 0-a )(x -a )+(y 0-b )(y -b )=r 2.(2)过圆外一点的圆的切线过圆外一点M (x 0,y 0)的圆的切线求法:可用点斜式设出方程,利用圆心到直线的距离等于半径求出斜率k ,从而得切线方程;若求出的k 值只有一个,则说明另一条直线的斜率不存在,其方程为x =x 0.(3)切线长①从圆x 2+y 2+Dx +Ey +F =0(D 2+E 2-4F >0)外一点M (x 0,y 0)引圆的两条切线,切线长为 x 20+y 20+Dx 0+Ey 0+F .②两切点弦长:利用等面积法,切线长a 与半径r 的积的2倍等于点M 与圆心的距离d 与两切点弦长b 的积,即b =2ard.[提醒] 过一点求圆的切线方程时,要先判断点与圆的位置关系,以便确定切线的条数. 3.圆的弦问题直线和圆相交,求被圆截得的弦长通常有两种方法:(1)几何法:因为半弦长L2、弦心距d 、半径r 构成直角三角形,所以由勾股定理得L =2r 2-d 2.(2)代数法:若直线y =kx +b 与圆有两交点A (x 1,y 1),B (x 2,y 2),则有: |AB |=1+k 2|x 1-x 2|= 1+1k2|y 1-y 2|.[谨记常用结论]过直线Ax +By +C =0和圆x 2+y 2+Dx +Ey +F =D 2+E 2-4F >交点的圆系方程为x 2+y 2+Dx +Ey +F +λAx +By +C =0.,[小题练通]1.[教材改编题]若直线x -y +1=0与圆(x -a )2+y 2=2有公共点,则实数a 的取值范围是( )A .[-3,-1]B .[-1,3]C .[-3,1]D .(-∞,-3]∪[1,+∞)答案:C2.[教材改编题]直线y =ax +1与圆x 2+y 2-2x -3=0的位置关系是( ) A .相切 B .相交C .相离D .随a 的变化而变化解析:选B ∵直线y =ax +1恒过定点(0,1),又点(0,1)在圆(x -1)2+y 2=4的内部,故直线与圆相交.3.[教材改编题]已知点M (a ,b )在圆O :x 2+y 2=1外,则直线ax +by =1与圆O 的位置关系是________.解析:由题意知点M 在圆外,则a 2+b 2>1,圆心到直线的距离d =1a 2+b 2<1,故直线与圆相交.答案:相交4.[易错题]过点(2,3)且与圆(x -1)2+y 2=1相切的直线的方程为________________. 解析:当切线的斜率存在时,设圆的切线方程为y =k (x -2)+3,由圆心(1,0)到切线的距离为1,得k =43,所以切线方程为4x -3y +1=0;当切线的斜率不存在时,易知直线x=2是圆的切线,所以所求的直线方程为4x -3y +1=0或x =2.答案:x =2或4x -3y +1=05.以M (1,0)为圆心,且与直线x -y +3=0相切的圆的方程是________. 答案:(x -1)2+y 2=86.直线y =x +1与圆x 2+y 2+2y -3=0交于A ,B 两点,则|AB |=________. 解析:由x 2+y 2+2y -3=0,得x 2+(y +1)2=4.∴圆心C (0,-1),半径r =2.圆心C (0,-1)到直线x -y +1=0的距离d =|1+1|2=2,∴|AB |=2r 2-d 2=24-2=2 2. 答案:2 2圆与圆的位置关系(两圆半径为r 1,r 2,d =|O 1O 2|)[提醒] 涉及两圆相切时,没特别说明,务必要分内切和外切两种情况进行讨论.[谨记常用结论]圆C 1:x 2+y 2+D 1x +E 1y +F 1=0与C 2:x 2+y 2+D 2x +E 2y +F 2=0相交时:将两圆方程直接作差,得到两圆公共弦所在直线方程; 两圆圆心的连线垂直平分公共弦;x 2+y 2+D 1x +E 1y +F 1+λx 2+y 2+D 2x +E 2y +F 2=0表示过两圆交点的圆系方程不包括C 2[小题练通]1.[人教A 版教材P133A 组T9]圆x 2+y 2-4=0与圆x 2+y 2-4x +4y -12=0的公共弦的长为________.答案:2 22.[教材改编题]若圆x 2+y 2=1与圆(x +4)2+(y -a )2=25相切,则实数a =________.答案:±25或03.[教材改编题]圆x2+y2=r2与圆(x-3)2+(y+1)2=r2外切,则半径r=________.解析:由题意,得2r=32+-2,所以r=10 2.答案:10 24.[易错题]若两圆x2+y2=m和x2+y2+6x-8y-11=0有公共点,则实数m的取值范围是________.答案:[1,121]5.若圆C1:x2+y2=1与圆C2:x2+y2-6x-8y+m=0外切,则m=( )A.21 B.19C.9 D.-11解析:选C 圆C1的圆心为C1(0,0),半径r1=1,因为圆C2的方程可化为(x-3)2+(y -4)2=25-m,所以圆C2的圆心为C2(3,4),半径r2=25-m(m<25).从而|C1C2|=32+42=5.由两圆外切得|C1C2|=r1+r2,即1+25-m=5,解得m=9,故选C.6.与圆C1:x2+y2-6x+4y+12=0,C2:x2+y2-14x-2y+14=0都相切的直线有( ) A.1条 B.2条C.3条 D.4条解析:选A 两圆分别化为标准形式为C1:(x-3)2+(y+2)2=1,C2:(x-7)2+(y-1)2=36,则两圆圆心距|C1C2|=7-32+[1--2]2=5,等于两圆半径差,故两圆内切.所以它们只有一条公切线.故选A.。
高三数学第一轮复习:圆的方程及直线与圆的位置关系知识精讲

高三数学第一轮复习:圆的方程及直线与圆的位置关系知识精讲【本讲主要内容】圆的方程及直线与圆的位置关系圆的标准方程、圆的一般方程、圆的参数方程、直线和圆的位置关系【知识掌握】 【知识点精析】1. 圆的标准方程:()()222x a y b r -+-=,方程表示圆心为(),C a b ,半径为r 的圆。
2. 圆的一般方程:022=++++F Ey Dx y x⑴当0422>-+F E D 时,表示圆心为,22D E ⎛⎫-- ⎪⎝⎭,的圆; ⑵当2240D E F +-=时,表示一个点,22D E ⎛⎫-- ⎪⎝⎭; ⑶当0422<-+F E D 时,它不表示任何图形。
3. 圆的标准方程与一般方程的比较:圆的标准方程的优点在于它明确地指出了圆心和半径,而一般方程突出了方程形式上的特点:①2x 和2y 的系数相同,都不等于0;②没有xy 这样的二次项。
二元二次方程220Ax Bxy Cy Dx Ey F +++++=表示圆的充要条件是:①2x 和2y 的系数相等且不为零,即0A C =≠;②没有xy 项,即0B =;③0422>-+F E D ,其中①、②是二元二次方程表示圆的必要条件,但不是充分条件。
说明:圆的标准方程和一般方程均含有三个参变量,因此必须有三个独立条件才能确定一个圆;求圆的方程的主要方法为待定系数法。
4. 圆的参数方程:在取定的坐标系中,如果曲线上任意一点的坐标,x y 都是某个变数t 的函数,即()()x f t y g t =⎧⎪⎨=⎪⎩()*,并且对于t 的每一个允许值,由方程组()*所确定的点(),M x y 都在这条曲线上,那么方程组()*就叫做这条曲线的参数方程,联系,x y 之间关系的变数叫做参变数,简称参数。
cos sin x a r y b r θθ=+⎧⎨=+⎩()θ为参数表示圆心为()a ,b ,半径为r 的圆。
5. 直线与圆的位置关系: ⑴点与圆的位置关系:若圆()()222x a y b r -+-=,那么点()000,P x y 在⎪⎪⎩⎪⎪⎨⎧>-+-⇔<-+-⇔=-+-⇔220202202022020)()()()()()(r b y a x r b y a x r b y a x 圆外圆内圆上⑵直线与圆的位置关系:直线与圆的位置关系有三种:相离、相切、相交。
高考数学一轮复习直线与圆、圆与圆的位置关系

4.(易错)过点P(2,4)作圆(x-1)2+(y-1)2=1的切线,则切线方程
为(
)
A.3x+4y-4=0
B.4x-3y+4=0
C.x=2或4x-3y+4=0
D.y=4或3x+4y-4=0
答案:C
解析:当斜率不存在时,x=2与圆相切;当斜率存在时,设切线方程为y-4=
k−1+4−2k
所以满足条件的点P的个数为3.
故选C.
题后师说
判断直线与圆的位置关系的两种方法
巩固训练1
(1)[2023·江西赣州模拟]直线y=kx-k与圆(x-2)2+y2=3的位置关系
是(
)
A.相离
B.相交
C.相切
D.与k取值有关
答案:C
解析:∵直线y=kx-k恒过定点(1,0),且该点在圆内,
∴直线与圆相交,
故选B.
(2)[2023·河南郑州二中模拟]若曲线y= 1 − x 2 与直线y=x+b恒有一
b= 2 或b∈[-1,1)
个公共点,则b的取值范围是_________________.
解析:如图:
y= 1 − x 2 是圆心在原点,半径为1的圆的x轴的上半部分,与x,y轴交于B,C,
A三点,
A(0,1),B(-1,0),C(1,0),当直线y=x+b 与圆相切于D点时,满足题意,
a)(x-a)+(y0-b)(y-b)=r2.
(3)过圆x2+y2=r2外一点M(x0,y0)作圆的两条切线,则两切点所在直
线方程为x0x+y0y=r2.
2.直线被圆截得的弦长的求法
(1)几何法:运用弦心距d、半径r和弦长的一半构成的直角三角形,
计算弦长|AB|=2 r 2 − d2 .
高考数学一轮复习---直线与圆、圆与圆的位置关系知识点与题型复习
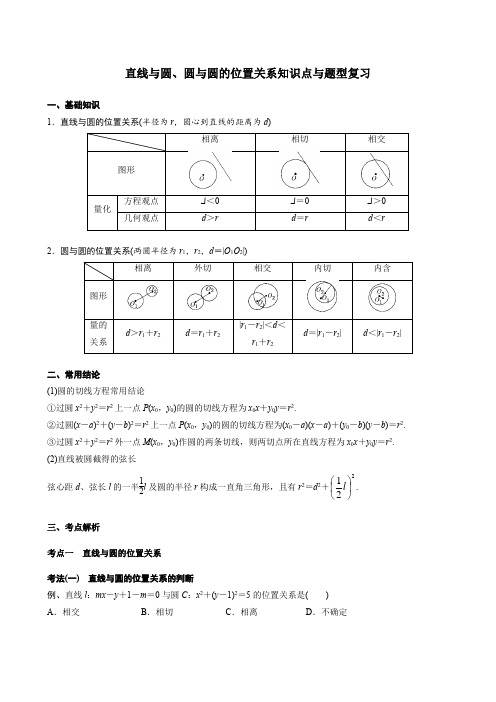
直线与圆、圆与圆的位置关系知识点与题型复习一、基础知识1.直线与圆的位置关系(半径为r ,圆心到直线的距离为d )Δ<0 Δ=0 Δ>02.圆与圆的位置关系(两圆半径为r 1,r 2,d =|O 1O 2|)|r -r |<d <二、常用结论(1)圆的切线方程常用结论①过圆x 2+y 2=r 2上一点P (x 0,y 0)的圆的切线方程为x 0x +y 0y =r 2.②过圆(x -a )2+(y -b )2=r 2上一点P (x 0,y 0)的圆的切线方程为(x 0-a )(x -a )+(y 0-b )(y -b )=r 2. ③过圆x 2+y 2=r 2外一点M (x 0,y 0)作圆的两条切线,则两切点所在直线方程为x 0x +y 0y =r 2. (2)直线被圆截得的弦长弦心距d 、弦长l 的一半12l 及圆的半径r 构成一直角三角形,且有r 2=d 2+221⎪⎭⎫⎝⎛l .三、考点解析考点一 直线与圆的位置关系 考法(一) 直线与圆的位置关系的判断例、直线l :mx -y +1-m =0与圆C :x 2+(y -1)2=5的位置关系是( ) A .相交 B .相切 C .相离 D .不确定[解题技法]判断直线与圆的位置关系的常见方法: (1)几何法:利用d 与r 的关系.(2)代数法:联立方程组,消元得一元二次方程之后利用Δ判断.(3)点与圆的位置关系法:若直线恒过定点且定点在圆内,可判断直线与圆相交.考法(二) 直线与圆相切的问题例、(1)过点P (2,4)作圆(x -1)2+(y -1)2=1的切线,则切线方程为( )A .3x +4y -4=0B .4x -3y +4=0C .x =2或4x -3y +4=0D .y =4或3x +4y -4=0 (2)已知圆C :x 2+y 2-2x -4y +1=0上存在两点关于直线l :x +my +1=0对称,经过点M (m ,m )作圆C 的切线,切点为P ,则|MP |=________.考法(三) 弦长问题例、(1)若a 2+b 2=2c 2(c ≠0),则直线ax +by +c =0被圆x 2+y 2=1所截得的弦长为( ) A.12 B .1 C.22D.2 (2)设直线y =x +2a 与圆C :x 2+y 2-2ay -2=0相交于A ,B 两点,若|AB |=23,则圆C 的面积为( ) A .4π B .2π C .9π D .22π跟踪练习:1.已知圆的方程是x 2+y 2=1,则经过圆上一点M ⎪⎪⎭⎫⎝⎛2222,的切线方程是________. 2.若直线kx -y +2=0与圆x 2+y 2-2x -3=0没有公共点,则实数k 的取值范围是________.3.设直线y =kx +1与圆x 2+y 2+2x -my =0相交于A ,B 两点,若点A ,B 关于直线l :x +y =0对称,则|AB |=________.考点二 圆与圆的位置关系例、已知圆M :x 2+y 2-2ay =0(a >0)截直线x +y =0所得线段的长度是22,则圆M 与圆N :(x -1)2+(y -1)2=1的位置关系是( )A .内切B .相交C .外切D .相离变式练习:1.若圆C 1:x 2+y 2=1与圆C 2:x 2+y 2-6x -8y +m =0外切,则m =( )A .21B .19C .9D .-112.(变结论)若本例两圆的方程不变,则两圆的公共弦长为________.[解题技法]几何法判断圆与圆的位置关系的3步骤: (1)确定两圆的圆心坐标和半径长;(2)利用平面内两点间的距离公式求出圆心距d ,求r 1+r 2,|r 1-r 2|; (3)比较d ,r 1+r 2,|r 1-r 2|的大小,写出结论.课后作业1.若直线2x +y +a =0与圆x 2+y 2+2x -4y =0相切,则a 的值为( ) A .±5 B .±5 C .3 D .±32.与圆C 1:x 2+y 2-6x +4y +12=0,C 2:x 2+y 2-14x -2y +14=0都相切的直线有( ) A .1条 B .2条 C .3条 D .4条3.直线y =kx +3被圆(x -2)2+(y -3)2=4截得的弦长为23,则直线的倾斜角为( ) A.π6或5π6 B .-π3或π3 C .-π6或π6 D.π64.过点(3,1)作圆(x -1)2+y 2=r 2的切线有且只有一条,则该切线的方程为( ) A .2x +y -5=0 B .2x +y -7=0 C .x -2y -5=0 D .x -2y -7=05.若圆x 2+y 2+2x -6y +6=0上有且仅有三个点到直线x +ay +1=0的距离为1,则实数a 的值为( ) A .±1 B .±24 C .± 2 D .±326.过点P (1,-2)作圆C :(x -1)2+y 2=1的两条切线,切点分别为A ,B ,则AB 所在直线的方程为( ) A .y =-34 B .y =-12 C .y =-32 D .y =-147.在平面直角坐标系xOy 中,直线x +2y -3=0被圆(x -2)2+(y +1)2=4截得的弦长为________. 8.若P (2,1)为圆(x -1)2+y 2=25的弦AB 的中点,则直线AB 的方程为________. 9.过点P (-3,1),Q (a,0)的光线经x 轴反射后与圆x 2+y 2=1相切,则a 的值为________.10.点P 在圆C 1:x 2+y 2-8x -4y +11=0上,点Q 在圆C 2:x 2+y 2+4x +2y +1=0上,则|P Q |的最小值是________.11.已知圆C 1:x 2+y 2-2x -6y -1=0和圆C 2:x 2+y 2-10x -12y +45=0. (1)求证:圆C 1和圆C 2相交;(2)求圆C 1和圆C 2的公共弦所在直线的方程和公共弦长.12.已知圆C 经过点A (2,-1),和直线x +y =1相切,且圆心在直线y =-2x 上. (1)求圆C 的方程;(2)已知直线l 经过原点,并且被圆C 截得的弦长为2,求直线l 的方程.提高练习1.过圆x 2+y 2=1上一点作圆的切线,与x 轴、y 轴的正半轴相交于A ,B 两点,则|AB |的最小值为( ) A. 2 B.3 C .2 D .32.在平面直角坐标系xOy 中,A 为直线l :y =2x 上在第一象限内的点,B (5,0),以AB 为直径的圆C 与直线l 交于另一点D .若AB ―→·CD ―→=0,则点A 的横坐标为________. 3.已知圆C :x 2+(y -a )2=4,点A (1,0).(1)当过点A 的圆C 的切线存在时,求实数a 的取值范围; (2)设AM ,AN 为圆C 的两条切线,M ,N 为切点,当|MN |=455时,求MN 所在直线的方程.。
高考数学一轮总复习教学课件第八章 平面解析几何第4节 直线与圆、圆与圆的位置关系

2.直线3x+4y-5=0与圆x2+y2=1的位置关系是(
A.相交
√
C.相离
D.无法判断
)
B.相切
解析:圆心(0,0)到直线3x+4y-5=0的距离 d=
与圆相切.故选B.
|-|
,所以直线
=1=r
+
3.直线x-y+3=0被圆(x+2)2+(y-2)2=2截得的弦长等于(
A.
B.
C.2
)
D.
√
解析:圆心(-2,2)到直线 x-y+3=0 的距离 d= ,圆的半径 r= ,
解直角三角形得,半弦长为 ,所以弦长等于 .故选 D.
4.圆O1:(x-1)2+y2=1与圆O2:x2+(y+2)2=4的位置关系是(
A.外离
B.外切
C.相交
D.内切
故选C.
判断直线与圆的位置关系常见的方法:
(1)几何法:利用d与r的关系.
(2)代数法:联立方程组,消元得一元二次方程之后利用Δ判断.
(3)点与圆的位置关系法:若直线恒过定点且定点在圆内,可判断直
线与圆相交;若点在圆上,直线与圆可能相切,也可能相交.
上述方法中最常用的是几何法,点与圆的位置关系法更适用于动直
A.x-2y+3=0
B.2x+y-4=0
√
D.2x-y-4=0
C.x+2y-5=0
)
解析:圆心为O(0,0),kOP=2,故切线的斜率为
y-2=- (x-1) ,即x+2y-5=0.故选C.
2012年高三理科数学第一轮复习直线与圆(4)直线与圆、圆与圆的位置关系
2012年高三理科数学第一轮复习直线与圆( 4)直线与圆、圆与圆的位置关系理解直线与圆、圆与圆的位置关系。
命题规律直线与圆的位置关系,特别是弦长问题,多以选择填空出现。
考点解读|1•点与圆的位置关系2 2 2已知点(x0, y0)和圆(x a) (y b) r :当(x o a)2(y o b)2r2时,点在圆外;当(X o a)2(y。
b)2r2时,点在圆上;当(X o a)2 (y o b)2 r2时,点在圆内•2. 直线和圆的位置关系(其中,d表示圆心到直线的距离;表示联立直线和圆的方程消去y或x所得到的一元二次方程的判别式,r为圆的半径•)3•圆和圆的位置关系(其中,d表示圆心距,表示联立圆和圆的方程消去y或x所得到的一元二次方程的判别式,R和r为两圆的半径•)4. 圆的切线①切线条数点在圆外 两条;点在圆上 一条;点在圆内 ------------------ 无 ②求切线方程的方法及注意点 (i) 点在圆外如定点 Px 0,y 0,圆:x a 2 y b 2 r 2,[ X ) a? y 0 b? r 2] 第一步:设切线I 方程y y 0 k x x 0 第二步:通过d rk ,从而得到切线方程特别注意:以上解题步骤仅对 k 存在有效,当k 不存在时,应补上 一一千万不要漏了! (ii) 点在圆上5. 圆系2 2x y D 2xE 2yF 2 0。
当1时,①式变为一直线方程:(D^! D 2)x (E 1 E 2)y (F 1 F 2) 0 ②若两圆相交,则方程②是它们的公共弦所在直线的方程; 若两圆相切,则方程②表示它们的一条公切线方程• 考点突破例1:已知圆 :'+ ; " ^,求过点 ":与圆门相切的切线.思路点拨:圆的切线从切线的性质出发去求解。
例题精讲:•••点"^1-不在圆二上,1)若点x 0, y 0在圆 x 2 r 2上,则切线方程为 2x )x y °yr2)若点x o , y o 在圆22y b r 上,则切线方程为x 0 a xY 0 b y b r 2由上述分析,我们知道: 点与圆的位置关系,得出切线的条数过一定点求某圆的切线方程, 非常重要的第一步就是判断③求切线长:利用基本图形,AP CP④求切点坐标:利用两个关系列出两个方程r 2ACk AC AP k AP1CPr 2过两个已知圆x 2D i XE i yF i 2 2x yD 2XE ?yF 20的交点的圆 系方程为:x 2y 2E 』F 1(x 22y D 2x E 2y F 2)0( 1)方程①是一个圆系方程,这些圆的圆心都在两圆的连心线上, 圆系方程代表的圆不包含•••切线 的直线方程可设为'解题反思:上述解题过程容易漏解斜率不存在的情况,要注意补回漏掉的解.例2.已知圆x 2+y 2=8内一点P (-1 , 2),过点P 的直线I 的倾斜角为 ,直线I 交圆于A 、B 两点•(1) 当=・时,求AB 的长;4(2) 当弦AB 被点P 平分时,求直线I 的方程• 思路点拨:用数形结合的方法去分析。
2012届高考数学(理科)一轮复习课件(人教版)第14单元第77讲 直线与圆的位置关系

6. 圆 的 切 线 的 性 质 圆的切线垂直过切点的半径. 推 论 1: 经 过 圆 心 且 垂 直 于 切 线 的 直 线 必 经 过 ⑩ ______ . 推 论 2: 经 过 切 点 且 垂 直 于 切 线 的 直 线 必经过 ________ .
7. 弦 切 角 定 理 弦切角等于它所夹的弧所对的 ____ .
2
① ②
7 2 7
21
. 21 ,
因 为 x y 2 y 2< 9, 即 y< 所以x y 2y 2 7
7 2
,所以y
2 2 1, 2 1.
21 2 9
从 而 DE BC BD EC 9 x y
评 析 :本 题 为 了 方 便 表 示 , 除 设 D B x 外 , 又 引 入 变 量 C E y, 使 各 线 段 长 的 关 系 的 表示更加清晰与简捷,在几何问题中, 这也是常用的做法.
因 为 A B 是 圆 O的 直 径 , 所 以 A E B A D B 9 0 . 因 为 A F C 9 0 , 所 以 A、 F 、 C 、 E 四 点 共 圆 , 所 以 B C B E B F B A .① 同 理 , B、 F 、 C 、 D四 点 共 圆 , 所 以 A C D A F A B .② ① ② 得 A C A D B C B E B F A B A F A B, 即 AC AD BC BE AB .
3. 圆 内 接 四 边 形 的 判 定
1 如 果 一 个 四 边 形 的 一 组 对 角 互 补 , 那 么
这 个 四 边 形 ⑥ __________ 圆 .
2如 果 一 个 四 边 形 的 一 个 外 角 等 于 它 的 内 角
7.6 直线、圆的位置关系

(2)如图所示,由平面几何垂径定理知 如图所示,
m2 r2-d2=12,即5=1. 5 得 m= ± 2 5 ,
直线被圆截得的弦长为2. ∴当m=±2 5 时,直线被圆截得的弦长为2. (3)如图所示,由于交点处两条半径互相垂直, 如图所示,由于交点处两条半径互相垂直, ∴弦与过弦两端的半径组成等腰直角三角形, 弦与过弦两端的半径组成等腰直角三角形, ∴d= 2 r ,即 m = 2 ⋅ 5 , 2 5 2 5 2 解得m 解得m=± . 2 故当m 故当m=± 5 2 时,直线与圆在两交 2 点处的两条半径互相垂直. 点处的两条半径互相垂直.
3×0 − 2 3 +1 = 1, 因此弦长为 2 R 2 − d 2 = 2 4 − 1 = 2 3.
+2x+2y 2=0与圆 与圆C 4.圆C1:x2+y2+2x+2y-2=0与圆C2:x2+y2-4x-2y+1=0
的公切线有且仅有 A.1条 A.1条 解析 B.2条 B.2条 C.3条 C.3条
探究提高
判断直线与圆的位置关系可以看成它们
构成的方程组有无实数解, 构成的方程组有无实数解,也可以根据圆心到直线 的距离与半径长的关系进行判断. 的距离与半径长的关系进行判断. 求圆的弦长有多种方法: 求圆的弦长有多种方法:一是直接求出直线与圆的 交点坐标,再利用两点间的距离公式得出;二是不 交点坐标,再利用两点间的距离公式得出; 求交点坐标,利用一元二次方程根与系数的关系得 求交点坐标, 出,即设直线的斜率为k,直线与圆联立消去y后所 即设直线的斜率为k 直线与圆联立消去y
3 ×1 + m
3 +1 ∴ m= - 3 3 或 3 .
= 3, 即 3 + m = 2 3.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.6 直线与圆的位置关系●知识梳理 直线和圆1.直线和圆位置关系的判定方法一是方程的观点,即把圆的方程和直线的方程联立成方程组,利用判别式Δ来讨论位置关系.①Δ>0,直线和圆相交. ②Δ=0,直线和圆相切. ③Δ<0,直线和圆相离.方法二是几何的观点,即把圆心到直线的距离d 和半径R 的大小加以比较. ①d <R ,直线和圆相交. ②d =R ,直线和圆相切. ③d >R ,直线和圆相离.2.直线和圆相切,这类问题主要是求圆的切线方程.求圆的切线方程主要可分为已知斜率k 或已知直线上一点两种情况,而已知直线上一点又可分为已知圆上一点和圆外一点两种情况.3.直线和圆相交,这类问题主要是求弦长以及弦的中点问题. ●点击双基1.(2005年北京海淀区期末练习题)设m >0,则直线2(x +y )+1+m =0与圆x 2+y 2=m 的位置关系为A.相切B.相交C.相切或相离D.相交或相切解析:圆心到直线的距离为d =21m+,圆半径为m . ∵d -r =21m+-m =21(m -2m +1)=21(m -1)2≥0,∴直线与圆的位置关系是相切或相离.答案:C2.圆x 2+y 2-4x +4y +6=0截直线x -y -5=0所得的弦长等于 A.6 B.225 C.1 D.5 解析:圆心到直线的距离为22,半径为2,弦长为222)22()2(-=6. 答案:A3.(2004年全国卷Ⅲ,4)圆x 2+y 2-4x =0在点P (1,3)处的切线方程为 A.x +3y -2=0 B.x +3y -4=0 C.x -3y +4=0 D.x -3y +2=0 解法一:x 2+y 2-4x =0 y =kx -k +3⇒x 2-4x +(kx -k +3)2=0.该二次方程应有两相等实根,即Δ=0,解得k =33. ∴y -3=33(x -1),即x -3y +2=0. 解法二:∵点(1,3)在圆x 2+y 2-4x =0上, ∴点P 为切点,从而圆心与P 的连线应与切线垂直. 又∵圆心为(2,0),∴1230--²k =-1. 解得k =33,∴切线方程为x -3y +2=0. 答案:D4.(2004年上海,理8)圆心在直线2x -y -7=0上的圆C 与y 轴交于两点A (0,-4)、B (0,-2),则圆C 的方程为____________.解析:∵圆C 与y 轴交于A (0,-4),B (0,-2), ∴由垂径定理得圆心在y =-3这条直线上. 又已知圆心在直线2x -y -7=0上,y =-3,2x -y -7=0.∴圆心为(2,-3),半径r =|AC |=22)]4(3[2---+=5. ∴所求圆C 的方程为(x -2)2+(y +3)2=5. 答案:(x -2)2+(y +3)2=55.若直线y =x +k 与曲线x =21y -恰有一个公共点,则k 的取值范围是___________. 解析:利用数形结合. 答案:-1<k ≤1或k =-2●典例剖析【例1】 已知圆x 2+y 2+x -6y +m =0和直线x +2y -3=0交于P 、Q 两点,且OP ⊥OQ (O 为坐标原点),求该圆的圆心坐标及半径.剖析:由于OP ⊥OQ ,所以k OP ²k OQ =-1,问题可解.解:将x =3-2y 代入方程x 2+y 2+x -6y +m =0,得5y 2-20y +12+m =0. 设P (x 1,y 1)、Q (x 2,y 2),则y 1、y 2满足条件y 1+y 2=4,y 1y 2=512m+. ∵OP ⊥OQ ,∴x 1x 2+y 1y 2=0. 而x 1=3-2y 1,x 2=3-2y 2,∴联立 解得x =2,∴x 1x 2=9-6(y 1+y 2)+4y 1y 2. ∴m =3,此时Δ>0,圆心坐标为(-21,3),半径r =25. 评述:在解答中,我们采用了对直线与圆的交点“设而不求”的解法技巧,但必须注意这样的交点是否存在,这可由判别式大于零帮助考虑.【例2】 求经过两圆(x +3)2+y 2=13和x 2+(y +3)2=37的交点,且圆心在直线x -y -4=0上的圆的方程.剖析:根据已知,可通过解方程组 (x +3)2+y 2=13,x 2+(y +3)2=37由圆心在直线x -y -4=0上,三个独立条件,用待定系数法求出圆的方程;也可根据已知,设所求圆的方程为(x +3)2+y 2-13+λ[x 2+(y +3)2-37]=0,再由圆心在直线x -y -4=0上,定出参数λ,得圆方程.解:因为所求的圆经过两圆(x +3)2+y 2=13和x 2+(y +3)2=37的交点, 所以设所求圆的方程为(x +3)2+y 2-13+λ[x 2+(y +3)2-37]=0.展开、配方、整理,得(x +λ+13)2+(y +λλ+13)2=λλ++1284+22)1()1(9λλ++. 圆心为(-λ+13,-λλ+13),代入方程x -y -4=0,得λ=-7. 故所求圆的方程为(x +21)2+(y +27)2= 289.评述:圆C 1:x 2+y 2+D 1x +E 1y +F 1=0,圆C 2:x 2+y 2+D 2x +E 2y +F 2=0,若圆C 1、C 2相交,那么过两圆公共点的圆系方程为(x 2+y 2+D 1x +E 1y +F 1)+λ(x 2+y 2+D 2x +E 2y +F 2)=0(λ∈R 且λ≠-1).它表示除圆C 2以外的所有经过两圆C 1、C 2公共点的圆.特别提示在过两圆公共点的图象方程中,若λ=-1,可得两圆公共弦所在的直线方程. 【例3】 已知圆C :(x -1)2+(y -2)2=25,直线l :(2m +1)x +(m +1)y -7m -4=0(m ∈R ).(1)证明:不论m 取什么实数,直线l 与圆恒交于两点; (2)求直线被圆C 截得的弦长最小时l 的方程.剖析:直线过定点,而该定点在圆内,此题便可解得. (1)证明:l 的方程(x +y -4)+m (2x +y -7)=0. 2x +y -7=0, x =3, x +y -4=0, y =1,即l 恒过定点A (3,1).∵圆心C (1,2),|AC |=5<5(半径), ∴点A 在圆C 内,从而直线l 恒与圆C 相交于两点. (2)解:弦长最小时,l ⊥AC ,由k AC =-21, ∴l 的方程为2x -y -5=0.评述:若定点A 在圆外,要使直线与圆相交则需要什么条件呢?得圆上两点,∵m ∈R ,∴得思考讨论求直线过定点,你还有别的办法吗?●闯关训练 夯实基础1.若圆(x -3)2+(y +5)2=r 2上有且只有两个点到直线4x -3y =2的距离等于1,则半径r 的范围是A.(4,6)B.[4,6)C.(4,6]D.[4,6] 解析:数形结合法解. 答案:A2.(2003年春季北京)已知直线ax +by +c =0(ab c ≠0)与圆x 2+y 2=1相切,则三条边长分别为|a |、|b |、|c |的三角形A.是锐角三角形B.是直角三角形C.是钝角三角形D.不存在解析:由题意得22|00|b a c b a ++⋅+⋅=1,即c 2=a 2+b 2,∴由|a |、|b |、|c |构成的三角形为直角三角形.答案:B3.(2005年春季北京,11)若圆x 2+y 2+mx -41=0与直线y =-1相切,且其圆心在y 轴的左侧,则m 的值为____________.解析:圆方程配方得(x +2m )2+y 2=412+m ,圆心为(-2m,0).由条件知-2m<0,即m >0.又圆与直线y =-1相切,则0-(-1)=412+m ,即m 2=3,∴m =3.答案:34.(2004年福建,13)直线x +2y =0被曲线x 2+y 2-6x -2y -15=0所截得的弦长等于____________.解析:由x 2+y 2-6x -2y -15=0,得(x -3)2+(y -1)2=25. 知圆心为(3,1),r =5.由点(3,1)到直线x +2y =0的距离d =5|23|+=5.可得21弦长为25,弦长为45. 答案:455.自点A (-3,3)发出的光线l 射到x 轴上,被x 轴反射,其反射光线所在的直线与圆x 2+y 2-4x -4y +7=0相切,求光线l 所在直线的方程.解:圆(x -2)2+(y -2)2=1关于x 轴的对称方程是(x -2)2+(y +2)2=1.设l 方程为y -3=k (x +3),由于对称圆心(2,-2)到l 距离为圆的半径1,从而可得k 1=-43,k 2=-34.故所求l 的方程是3x +4y -3=0或4x +3y +3=0. 6.已知M (x 0,y 0)是圆x 2+y 2=r 2(r >0)内异于圆心的一点,则直线x 0x +y 0y =r 2与此圆有何种位置关系?分析:比较圆心到直线的距离与圆半径的大小.解:圆心O (0,0)到直线x 0x +y 0y =r 2的距离为d =20202y x r +.∵P (x 0,y 0)在圆内,∴220y x +<r . 则有d >r ,故直线和圆相离. 培养能力7.方程ax 2+ay 2-4(a -1)x +4y =0表示圆,求a 的取值范围,并求出其中半径最小的圆的方程.解:(1)∵a ≠0时,方程为[x -a a )1(2-]2+(y +a 2)2=22)22(4a a a +-,由于a 2-2a +2>0恒成立,∴a ≠0且a ∈R 时方程表示圆.(2)r 2=4²2222a a a +-=4[2(a 1-21)2+21],∴a =2时,r min 2=2.此时圆的方程为(x -1)2+(y -1)2=2. 8.(文)求经过点A (-2,-4),且与直线l :x +3y -26=0相切于(8,6)的圆的方程. 解:设圆为x 2+y 2+Dx +Ey +F =0,依题意有方程组 3D -E =-36, 2D +4E -F =20, 8D +6E +F =-100. D =-11, E =3,F =-30.∴圆的方程为x 2+y 2-11x +3y -30=0.(理)已知点P 是圆x 2+y 2=4上一动点,定点Q (4,0). (1)求线段PQ 中点的轨迹方程;(2)设∠POQ 的平分线交PQ 于R ,求R 点的轨迹方程. 解:(1)设PQ 中点M (x ,y ),则P (2x -4,2y ),代入圆的方程得(x -2)2+y 2=1. (2)设R (x ,y ),由||||RQ PR =||||OQ OP =21, 设P (m ,n ),则有∴m =243-x , n =23y ,代入x 2+y 2=4中,得 (x -34)2+y 2=916(y ≠0). 探究创新9.已知点P 到两个定点M (-1,0)、N (1,0)距离的比为2,点N 到直线PM 的距离为1,求直线PN 的方程.解:设点P 的坐标为(x ,y ),由题设有||||PN PM =2,即22)1(y x ++=2²22)1(y x +-, 整理得x 2+y 2-6x +1=0.①因为点N 到PM 的距离为1,|MN |=2, 所以∠PMN =30°,直线PM 的斜率为±33. 直线PM 的方程为y =±33(x +1).②将②代入①整理得x 2-4x +1=0. 解得x 1=2+3,x 2=2-3.代入②得点P 的坐标为(2+3,1+3)或(2-3,-1+3);(2+3,-1-3)或(2-3,1-3).直线PN 的方程为y =x -1或y =-x +1. ●思悟小结1.直线和圆的位置关系有且仅有三种:相离、相切、相交.判定方法有两个:几何法,比较圆心到直线的距离与圆的半径间的大小;代数法,看直线与圆的方程联立所得方程组的解的个数.2.解决直线与圆的位置关系的有关问题,往往充分利用平面几何中圆的性质使问题简化. ●教师下载中心 教学点睛1.有关直线和圆的位置关系,一般要用圆心到直线的距离与半径的大小来确定.2.当直线和圆相切时,求切线方程一般要用圆心到直线的距离等于半径,求切线长一般要用切线、半径及圆外点与圆心连线构成的直角三角形;与圆相交时,弦长的计算也要用弦心距、半径及弦长的一半构成的直角三角形.3.有关圆的问题,注意圆心、半径及平面几何知识的应用.4.在确定点与圆、直线与圆、圆与圆的位置关系时,经常要用到距离,因此,两点间的距离公式、点到直线的距离公式等应熟练掌握,灵活运用.拓展题例【例1】 已知圆的方程为x 2+y 2+ax +2y +a 2=0,一定点为A (1,2),要使过定点A (1,2)作圆的切线有两条,求a 的取值范围.解:将圆的方程配方得(x +2a )2+(y +1)2=4342a -,圆心C 的坐标为(-2a ,-1),半径r =4342a -,条件是4-3a 2>0,过点A (1,2)所作圆的切线有两条,则点A 必在圆外,即22)12()21(+++a >4342a -.化简得a 2+a +9>0. 4-3a 2>0, a 2+a +9>0,-332<a <332,a ∈R .∴-332<a <332. 故a 的取值范围是(-332,332). 【例2】 已知⊙O 方程为x 2+y 2=4,定点A (4,0),求过点A 且和⊙O 相切的动圆圆心的轨迹.剖析:两圆外切,连心线长等于两圆半径之和,两圆内切,连心线长等于两圆半径之差,由此可得到动圆圆心在运动中所应满足的几何条件,然后将这个几何条件坐标化,即得到它的轨迹方程.解法一:设动圆圆心为P (x ,y ),因为动圆过定点A ,所以|P A |即动圆半径. 当动圆P 与⊙O 外切时,|PO |=|P A |+2; 当动圆P 与⊙O 内切时,|PO |=|P A |-2. 综合这两种情况,得||PO |-|P A ||=2. 将此关系式坐标化,得|22y x +-22)4(y x +-|=2.化简可得(x -2)2-32y =1.解法二:由解法一可得动点P 满足几何关系 ||OP |-|P A ||=2,即P 点到两定点O 、A 的距离差的绝对值为定值2,所以P 点轨迹是以O 、A 为焦点,2为实轴长的双曲线,中心在OA 中点(2,0),实半轴长a =1,半焦距c =2,虚半轴长b =22a c -=3,所以轨迹方程为(x -2)2-32y =1.由 解之得。
