轴对称测试题华东师大版

合集下载

华师大版七年级下册轴对称及平移

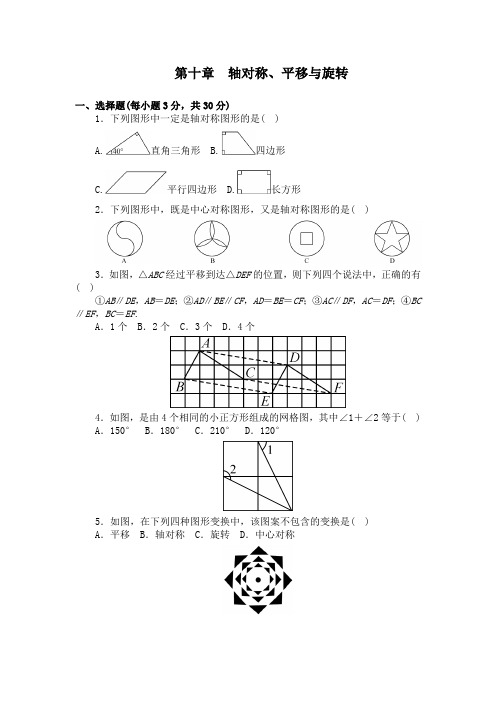
轴对称及平移测试题1.如图所示,右边的两个图形中,经过平移能得到左边的图形的是( ) D C B A2.下列图形中对称轴的条数多于两条的是（）A ．等腰三角形B ．矩形C ．菱形D ．等边三角形3.在平移过程中,对应线段( )A.互相平行且相等;B.互相垂直且相等C.互相平行(或在同一条直线上)且相等4.如果将一图形沿北偏东30°的方向平移3厘米，再沿某方向平移3厘米，所得的图形与将原图形向正东方向平移3厘米所得的图形重合，则这一方向应为（）A ．北偏东60°B ．北偏东30°C ．南偏东60°D ．南偏东30°5.下列图形经过平移后恰好可以与原图形组合成一个长方形的是（）A 、三角形B 、正方形C 、梯形D 、都有可能6.在图形平移的过程中，下列说法中错误的是（）A 、图形上任意点移动的方向相同B 、图形上任意点移动的距离相同C 、图形上可能存在不动的点D 、图形上任意两点连线的长度不变7.下列图形中,是轴对称图形的有__________个:①角;②线段;③等腰三角形;④扇形;⑤三角形;⑥正方形;⑦平行四边形;⑧五边形.A.5个B.6个C.7个D.8个8.如图，∠AOB 内一点P ，P 1、P 2分别是P 关于OA 、OB 的对称点，P 1P 2交OA 于M ，交OB于N ，若P 1P 2 = 5cm ，则ΔPMN 的周长是( )O FEC BA DA.3cmB.4cmC.5cmD.6cm9.如图，O是六个正三角形的公共顶点，下列图形中可由△OBC平移得到的是（）A．△OCD B．△OAB C．△FAO D．△OEF10.如图，在△ABC中，BC=8,AB的中垂线交BC于D，AC的中垂线交BC于E.试求△ADE的周长。

11.如图所示,平移△ABC可得到△DEF,如果∠A=50°,∠C=60°,那么∠E=•____度, ∠EDF=_______度,∠F=______度,∠DOB=_______度.12.在上面的六幅图中，（2）（3）（4）（5）（6）中的图案_______可以通过平移图案（1）得到的。

七年级数学下册《第十章轴对称、平移与旋》单元测试卷及答案解析-华东师大版

七年级数学下册《第十章轴对称、平移与旋》单元测试卷及答案解析-华东师大版一、单选题1．在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（） A ．B ．C ．D ．2．下列四个图形中，不能通过其中一个四边形平移得到的是( )A ．B ．C ．D ．3．如图，将△ABC 绕点A 逆时针旋转65°得到△AED ，则△BAE 的度数是（）A ．65°B ．45°C ．35°D ．25°4．中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录，下列四幅作品分别代表“立春”、“谷雨”、“白露”、“大雪”，其中是中心对称图形的是（）A ．B ．C ．D ．5．如图，若ABC DEF ≌，则D ∠等于（）A ．30︒B ．50︒C ．60︒D ．100︒6．如图，在ABC 中40C ∠=︒，把ABC 沿BC 边上的高AM 所在的直线翻折，点C 落在边CB 的延长线上的点C '处，如果20BAC ∠='︒，则BAC ∠的度数为（）A ．80︒B ．75︒C ．85︒D ．70︒7．如图，DEF 经过怎样的平移得到ABC （）A ．把DEF 向左平移4个单位，再向上平移2个单位B ．相DEF 向右平移4个单位，再向下平移2个单位C ．把DEF 向右平移4个单位，再向上平移2个单位D ．把DEF 向左平移4个单位.再向下平移2个单位8．如图，将△AOB 绕点O 按逆时针方向旋转45°后得到△A'OB'，若△AOB ＝15°，则△AOB'的度数是（）A ．25°B ．30°C ．35°D ．40°9．下列图案中，既是中心对称图形又是轴对称图形的是（）A ．B ．C ．D ．10．如图，在正方形方格中，各正方形的顶点叫做格点，三个顶点都在格点上的三角形称为格点三角形.图中△ABC 是格点三角形，请你找出方格中所有与△ABC 全等，且以A 为顶点的格点三角形，这样的三角形共有（）个（△ABC 除外）.A ．2B ．3C ．4D ．5二、填空题11．如图，在ABC 中，D 是BC 上一点250ABC BAD ∠=∠=︒，将ABD 沿着AD 翻折得到AED ，则CDE ∠= ．12．如图，△ABC 沿BC 所在直线向右平移得到△DEF ，已知EC ＝4，BF ＝18，则平移的距离为 .13．两块不同的三角板按如图1所示摆放，AC 边重合4530BAC DAC ∠∠=︒=︒，接着如图2保持三角板ABC 不动，将三角板ACD 绕着点C 按顺时针以每秒10︒的速度旋转90︒后停止.在此旋转过程中，当旋转时间t = 秒时三角板A CD ''有一条边与三角板ABC 的一条边恰好平行.14．三个全等三角形摆成如图所示的形式，则αβγ∠+∠+∠的度数为 .三、作图题15．如图，在正方形网格中，ABC 各顶点都在格点上，点A ，B ，C 的坐标分别为()51-，，()54-，和()14-，．四、解答题16．如图是正方形纸片ABCD ，分别沿AE 、AF ，折叠后边AB 与AD 恰好重叠于AG ，求△EAF 的大小．17．如图，在一块长为20m ，宽为10m 的长方形草地上，修建了宽为1m 的小路，求这块草地的绿地面积．18．如图，已知30BAC ∠=︒，把ABC 绕着点A 顺时针旋转，使得点B 与CA 的延长线上的点D 重合，求AEC ∠的度数．19．如图，点P 是△AOB 外的一点，点Q 与P 关于OA 对称，点R 与P 关于OB 对称，直线QR 分别交OA ，OB 于点M ，N ，若PM=PN=3，MN=4，求线段QR 的长．20．如图，ACB 和DCE 均为等边三角形，点A 、D 、E 在同一直线上，连结BE ．试说明AD BE =．聪明的小亮很快就找到了解决该问题的方法，请你帮助小亮把说理过程补充完整．解：∵ACB 和DCE 均为等边三角形∴CA CB =，CD=CE ，ACB ∠= 60=︒（等边三角形的性质） ∴ACD ∠=即ACD 绕点C 按逆时针方向旋转度，能够与重合 ∴ACD ≌ （旋转变换的性质） ∴AD BE =（）．五、综合题21．如图，已知110AOB ∠=︒，OC 在AOB ∠内部，OD 在BOC ∠的内部，40COD ∠=︒.（1）若50AOC ∠=︒，则BOD ∠= ；若AOC x ∠=︒，则BOD ∠= （用含x 的代数式表示）；（2）若2AOD BOC ∠=∠，求AOC ∠的度数；（3）将AOC ∠以OC 为折痕进行翻折，OA 落在OE 处，将BOD ∠以OD 为折痕进行翻折，OB 落在OF 处，AOC ∠的度数变化时EOF ∠的度数是否发生变化？若变化，请说明理由：若不变，请求出EOF ∠的度数.22．如图，在边长为1个单位长度的小正方形组成的网格中.（1）把△ABC 进行平移，得到△A′B′C′，使点A 与A′对应，请在网格中画出△A′B′C′；（2）线段AA′与线段CC′的关系是 .23．如图1，AB CD 点E ，F 分别在直线CD AB ，上2BEC BEF ∠∠=，过点A 作AG BE ⊥的延长线交于点G ，交CD 于点N ，AK 平分BAG ∠，交EF 于点H ，交BE 于点M.（1）直接写出AHE FAH KEH ∠∠∠，，之间的关系：_ . （2）若12BEF BAK ∠=∠，求AHE ∠. （3）如图2，在（2）的条件下，将KHE 绕着点E 以每秒5°的速度逆时针旋转，旋转时间为t ，当KE 边与射线ED 重合时停止，则在旋转过程中，当KHE 的其中一边与ENG 的某一边平行时直接写出此时t 的值.参考答案与解析1．【答案】B【解析】【解答】解：千里之行，四个字中，可以看作是轴对称图形的是：里；故答案为：B ．【分析】根据轴对称图形的定义逐项判断即可。

华师大版七年级数学下册《第十章轴对称、平移与旋转》达标测试卷-带参考答案

华师大版七年级数学下册《第十章轴对称、平移与旋转》达标测试卷-带参考答案一、选择题(每题3分，共24分)1．在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看成是轴对称图形的是()2．下列四组图形中，不能视为由一个基本图形通过平移得到的是()3．美丽的雪花呈现出浪漫空灵的气质．如图，雪花图案可以看成是由自身的一部分围绕它的中心依次旋转一定角度得到的，这个角的度数可以是()A．30°B．45°C．60°D．90°(第3题)(第5题)4．下列图形中既是轴对称图形又是中心对称图形的是()5．如图，点A，E，C在同一直线上，△ABC≌△DEC，AE＝3，CD＝8，则BC 的长为()A．3 B．5 C．8 D．116．如图，在长方形ABCD中，E是CD上一点，连结AE，将△ADE沿AE折叠，使点D的对应点F落在BC上，若AB＝3，BC＝5，BF＝4，则CE的长为()(第6题)A．2 B．1 C.53 D.437．如图①所示，魔术师把4张扑克牌放在桌子上，然后蒙住眼睛，请一位观众上台，把其中一张扑克牌旋转180°.魔术师解除蒙具后，看到4张牌如图②所示．那么被旋转过的牌是()(第7题)A．方块4 B．黑桃5 C．梅花6 D．红桃7 8．如图，长方形ABCD中，AB＝6，第1次平移将长方形ABCD沿AB的方向向右平移5个单位长度，得到长方形A1B1C1D1，第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位长度，得到长方形A2B2C2D2，…，第n次平移将长方形A n－1B n－1C n－1D n－1沿A n－1B n－1的方向向右平移5个单位长度，得到长方形A n B n C n D n(n＞2)，若AB n的长度为2 026，则n的值为()(第8题)A．407 B．406 C．405 D．404二、填空题(每题3分，共18分)9．如图，△ABC≌△A′B′C′，其中∠A＝36°，∠C′＝24°，则∠B＝________°.(第9题)(第11题)10．把一个正六边形绕其中心旋转，至少旋转________度，可以与自身重合．11．如图，方格纸(1格长为1个单位长度)中，△ABC的顶点都在格点上，将△ABC绕点O按顺时针方向旋转得到△A′B′C′，使各顶点仍在格点上，则其旋转角的最小度数是________°.12．如图，直角三角形DEF是由直角三角形ABC沿BC平移得到的，若AB＝8，BE＝3，DH＝2，则图中阴影部分的面积是________．(第12题)(第13题)13．如图，三角形纸片ABC中，∠A＝65°，∠B＝75°，将纸片的一角折叠，使点C的对应点C′落在△ABC内，则∠1＋∠2＝________°.14．如图，在锐角三角形ABC中，AB＝8，△ABC的面积为40，BD平分∠ABC，若M、N分别是BD、BC上的动点，则CM＋MN的最小值为________．(第14题)三、解答题(共78分)15．(6分)如图是正方形纸片ABCD，点E、F分别在边BC、CD上，连结AF，AE，将△ABE，△ADF分别沿AE、AF折叠，折叠后边AB与AD恰好重叠于AG，求∠EAF的大小．(第15题)第3 页共12 页16．(6分)如图，在边长均为1的小正方形组成的网格中，△AOB的顶点均在格点上．(1)将△AOB向下平移2个单位后得到△A1O1B1，请画出△A1O1B1；(2)将△AOB绕点O逆时针旋转90°后得到△A2OB2，请画出△A2OB2；(3)△A3OB3与△AOB关于点O中心对称，请画出△A3OB3.(第16题)17．(6分)如图，将△ABC绕点A逆时针旋转得到△ADE，点D在BC上，已知∠B＝70°，求∠CDE的大小．(第17题)18．(7分)如图，阴影部分是由5个小正方形组成的一个直角图形，请用3种不同的方法分别在下图方格内涂黑2个小正方形，使它们成为轴对称图形．(第18题)19．(7分)如图，△ABD≌△EBC，AB＝3 cm，BC＝6 cm.(1)求DE的长；(2)若A、B、C在一条直线上，则DB与AC垂直吗？为什么？(第19题)20．(7分)如图，E是正方形ABCD的边AB上一点，AB＝4，AE＝1.5，△DAE逆时针旋转后能够与△DCF重合．第5 页共12 页(1)旋转中心是哪一点，旋转角为多少度？(2)请你判断△DFE的形状，并说明理由．(3)求四边形ABFD的面积．(第20题)21．(8分)如图①②均为上底为1，下底为2，高为1的直角梯形．(1)用实线把图①分割成六个全等图形；(2)用实线把图②分割成四个全等图形．(第21题)22．(9分)如图，小丽将直角三角形ABC沿某条直线折叠，使斜边的两个端点A 与B重合，折痕为DE.(1)如果AC＝6，BC＝8，试求△ACD的周长；(2)如果∠CAD∶∠BAD＝4∶7，求∠B的度数．(第22题)23．(10分)如图①，将一副直角三角尺OCD、PMN放在同一条直线AB上，其中∠PNM＝30°，∠OCD＝45°.(1)【观察猜想】将图①中的三角尺OCD沿AB的方向平移至图②的位置，使得点O与点N重合，CD与MN相交于点E，则∠CEN＝________．(2)【操作探究】将图①中的三角尺OCD绕点O按顺时针方向旋转，使一边OD在∠MON的内部，如图③，且OD恰好平分∠MON，CD与NM相交于点E，求∠CEN的度数；(3)【深化拓展】将图①中的三角尺OCD绕点O按顺时针方向旋转一周，在旋转的过程中，若边CD恰好与边MN平行，请你求出此时旋转的角度．(第23题)第7 页共12 页24．(12分)将一副直角三角尺按如图①所示的方式摆放在直线MN上(∠DEC＝60°，∠BAC＝45°)，保持三角尺EDC不动，将三角尺ABC绕点C以每秒5°的速度顺时针旋转，旋转时间为t秒，当AC与射线CN重合时停止旋转．(1)如图②，当CA平分∠DCE时，求此时t的值；(2)当AC旋转至∠DCE的内部时，求∠DCA与∠ECB之间的数量关系，并说明理由；(3)在旋转过程中，当三角尺ABC的某一边平行于三角尺EDC的某一边时，求此时t的值．(第24题)答案一、1.B 2.C 3.C 4.A 5.B6．D思路点睛：根据长方形的面积列方程求解．7．A点拨：观察发现旋转之前和旋转之后扑克牌的图案没变化，所以旋转的扑克牌转180°后图案与原来相同，只有方块4符合题意，故选A.8．D思路点睛：根据平移的性质得出AA1＝5，A1A2＝5，A1B1＝6，A2B2＝6，进而求出AB1和AB2的长，然后总结规律，得出AB n＝(n＋1)×5＋1，求出n 即可．二、9.12010.6011.9012．2113.8014.10三、15.解：∵四边形ABCD是正方形，∴∠BAD＝90°由折叠的性质得，∠DAF＝∠GAF＝12∠DAG，∠BAE＝∠GAE＝12∠BAG，∴∠EAF＝∠GAF＋∠GAE＝12∠DAG＋12∠BAG＝12(∠DAG＋∠BAG)＝12∠BAD＝45°.16．解：(1)如图，△A1O1B1即为所作．(2)如图，△A2OB2即为所作．(3)如图，△A3OB3即为所作．(第16题) 17．解：由旋转的性质可得，AB＝AD，∠ADE＝∠B＝70°∴∠ADB＝∠B＝70°∴∠CDE＝180°－∠ADB－∠ADE＝40°.18．解：如图．(方法不唯一)(第18题)第9 页共12 页19．解：(1)∵△ABD ≌△EBC ∴AB ＝BE ，BD ＝BC∴DE ＝BD －BE ＝BC －AB ＝6－3＝3(cm)．(2)垂直．∵△ABD ≌△EBC ，且A 、B 、C 在一条直线上 ∴∠ABD ＝∠CBE ，∠ABD ＋∠CBE ＝180° ∴∠ABD ＝∠CBE ＝90°，即DB ⊥AC . 20．解：(1)旋转中心是点D ，旋转角为90°.(2)△DFE 是等腰直角三角形．理由如下： ∵四边形ABCD 是正方形，∴∠ADC ＝90°.根据旋转的性质可得DE ＝DF ，∠EDF ＝∠ADC ＝90° ∴△DFE 是等腰直角三角形．(3)∵四边形ABCD 是正方形，∴∠A ＝90°，AD ＝AB ＝4，S正方形ABCD＝4×4＝16，根据旋转的性质可得S △CDF ＝S △ADE ＝12AD ·AE ＝12×4×1.5＝3 ∴S 四边形ABFD ＝S 正方形ABCD ＋S △CDF ＝16＋3＝19. 21．解：(1)如图①所示． (2)如图②所示．(第21题)22．解：(1)由折叠的性质可得BD ＝AD ，∴△ACD 的周长＝AC ＋AD ＋CD ＝AC＋BD ＋CD ＝AC ＋BC ＝6＋8＝14. (2)可设∠CAD ＝4x °，∠BAD ＝7x °由折叠的性质可得∠B ＝∠BAD ，∴∠B ＝7x ° ∵∠C ＝90°，∴∠B ＋∠DAB ＋∠CAD ＝90° ∴7x °＋7x °＋4x °＝90°，解得x ＝5，∴∠B ＝35°. 23．解：(1)105°(2)∵OD 平分∠MON ，∴∠DON ＝12∠MON ＝12×90°＝45°，∴∠DON ＝∠D ＝45°，∴CD ∥AB∴∠CEN ＝180°－∠MNO ＝180°－30°＝150°.(3)设直线MO 与CD 相交于点F 如图①，当CD 在AB 上方时(第23题)∵CD∥MN，∴∠OFD＝∠M＝60°在△ODF中，∠MOD＝180°－∠D－∠OFD＝180°－45°－60°＝75°，∴旋转角为75°；如图②，当CD在AB的下方时∵CD∥MN，∴∠DFO＝∠M＝60°，在△DOF中，∠DOF＝180°－∠D－∠DFO＝180°－45°－60°＝75°∴旋转角为75°＋180°＝255°.综上所述，旋转的角度为75°或255°时，边CD恰好与边MN平行．24．解：(1)∵CA平分∠DCE，∴∠ACE ＝12∠DCE＝15°∴t＝15°÷5°＝3.(第24题)(2)∠ECB－∠DCA＝15°.理由如下：如图①，由旋转得∠ACE＝5°t，∴∠DCA＝30°－5°t，∠ECB＝45°－5°t，∴∠ECB－∠DCA＝(45°－5°t)－(30°－5°t)＝15°.(3)分四种情况：①当AB∥DE时，如图②，∠ACE＝∠ACB＋∠DCE＝45°＋30°＝75°，∴t＝75°÷5°＝15；(第24题)②当AB∥CE时，如图③，则∠BCE＝∠B＝90°∴∠ACE＝∠BCE＋∠ACB＝90°＋45°＝135°第11 页共12 页∴t＝135°÷5°＝27；③当AB∥CD时，如图④，则∠DCB＝∠B＝90°∴∠ACE＝∠DCE＋∠DCB＋∠ACB＝30°＋90°＋45°＝165°，∴t＝165°÷5°＝33；(第24题)④当AC∥DE时，如图⑤，则∠ACD＝∠D＝90°∴∠ACE＝∠ACD＋∠DCE＝90°＋30°＝120°∴t＝120°÷5°＝24.综上所述，t的值是15，24，27或33.第12 页共12 页。

初中数学华师大版七年级下学期第10章轴对称、平移与旋转测试卷(含解析)

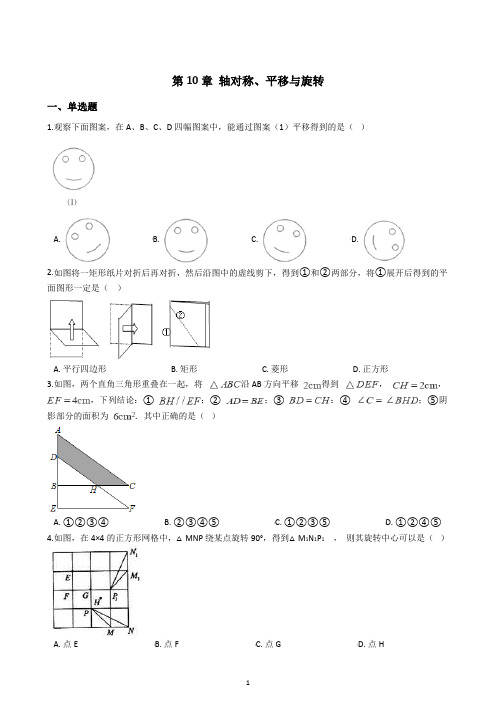
第10章轴对称、平移与旋转一、单选题1.观察下面图案，在A、B、C、D四幅图案中，能通过图案（1）平移得到的是（）A. B. C. D.2.如图将一矩形纸片对折后再对折，然后沿图中的虚线剪下，得到①和②两部分，将①展开后得到的平面图形一定是（）A. 平行四边形B. 矩形C. 菱形D. 正方形3.如图，两个直角三角形重叠在一起，将沿AB方向平移得到，，，下列结论：① ；② ；③ ：④ ；⑤阴影部分的面积为．其中正确的是（）A. ①②③④B. ②③④⑤C. ①②③⑤D. ①②④⑤4.如图，在4×4的正方形网格中，△MNP绕某点旋转90°，得到△M1N1P1，则其旋转中心可以是（）5.下列银行标志是中心对称图形的是（）A. B. C. D.6.如图，在边长为1的小正力形组成的网格中，点A，B，C部在格点上，若将线段AB沿BC方向平移，使点B与点C重合，则线段AB扫过的面积为（）A. 11B. 10C. 9D. 87.如图，在△ABC中，BC＝5，∠A＝80°，∠B＝70°，把△ABC沿RS的方向平移到△DEF的位置，若CF＝4，则下列结论中错误的是( )A. BE＝4B. ∠F＝30°C. AB∥DED. DF＝58.如图，沿射线方向平移到（点E在线段上），如果，，那么平移距离为（）A. 3cmB. 5cmC. 8cmD. 13cm9.如图，是一个纸折的小风车模型，将它绕着旋转中心旋转下列哪个度数后不能与原图形重合．（）A. B. C. D.10.如图，将△ABC绕点C顺时针旋转得到△DEC，使点A的对应点D恰好落在边AB上，点B的对应点为E，连接BE，下列四个结论：①AC＝AD；②AB⊥EB；③BC＝EC；④∠A＝∠EBC；其中一定正确的是（）A. ①②B. ②③C. ③④D. ②③④11.如图，将（其中，），绕点按顺时针方向旋转到的位置，使得点，，在同一直线上，则旋转角的度数为( )A. B. C. D.12.如图，将△ABC绕点A顺时针旋转60°得到△AED，若线段AB＝4，则BE的长为( )A. 3B. 4C. 5D. 613.图中的两个梯形成中心对称，点P的对称点是（）A. 点AB. 点BC. 点CD. 点D14.如图，已知图形是中心对称图形，则对称中心是（）A. 点CB. 点DC. 线段BC的中点D. 线段FC的中点15.下列说法中，正确的有（）①正方形都是全等形；②等边三角形都是全等形；③形状相同的图形是全等形；④大小相同的图形是全等形；⑤能够完全重合的图形是全等形．A. 1个B. 2个C. 3个D. 4个二、填空题16.如图，将矩形ABCD沿DE折叠，使A点落在BC上的F处，若∠EFB＝60°，则∠CFD＝________．17.如图,将周长为12的△ABC沿BC方向平移2个单位得到△DEF,则四边形ABFD的周长为________18.如图，在正方形ABCD中，，点E在CD边上，且，将绕点A顺时针旋转90°，得到，连接，则线段的长为________.19.如图，图中有6个条形方格图，图上由实线围成的图形是全等形的有哪几对．20.如图，△DEF是由△ABC沿BC方向向右平移2cm后得到，若△ABC的周长为10cm，则四边形ABFD的周长等于________ cm。

华师大版七年级下册数学第10章轴对称、平移与旋转含答案(综合考察)

华师大版七年级下册数学第10章轴对称、平移与旋转含答案一、单选题(共15题，共计45分)1、如图，把菱形ABCD沿AH折叠，使B点落在BC上的E点处，连结ED.若∠B ＝70°，则∠EDC的大小为（）A.10°B.15°C.20°D.30°2、数轴上一点A表示﹣3，若将A点向左平移5个单位长度，再向右平移6个单位长度，则此时A 点表示的数是（）A.﹣1B.﹣2C.﹣3.D.13、如图，将Rt△ABC绕直角顶点顺时针旋转90°，得到△A′B′C′，连接AA′，若∠1=22°，则∠B的度数是（）A.67°B.62°C.82°D.72°4、将一张矩形纸片对折(如图)，然后沿着图中的虚线剪下，得到①、②两部分，将①展开后得到的平面图形是 ( )A.三角形B.矩形C.菱形D.梯形5、观察下列图案，是轴对称而不是中心对称的是（）A. B. C. D.6、请你观察下面四个图形，其中既是轴对称图形又是中心对称图形的是（）A. B. C. D.7、如图正方形ABCD的边长为4，点E是AB上的一点，将△BCE沿CE折叠至△FCE，若CF，CE恰好与以正方形ABCD的中心为圆心的⊙O相切，则折痕CE 的长为（）A. B. C. D.8、如图，矩形OABC的边OA、OC分别在x轴、y轴上，点B的坐标为（3，2）．点D、E分别在AB、BC边上，BD=BE=1．沿直线DE将△BDE翻折，点B落在点B′处．则点B′的坐标为（）.A.（1，2）．B.（2，1）．C.（2，2）．D.（3，1）．9、下列不是图形的旋转、平移、轴对称的共同特征的是（）A.对应角的大小不变B.图形的大小不变C.图形的形状不变D.对应线段平行10、下列图形中，既是轴对称图形又是中心对称图形的是A. B. C. D.11、下面的每组图形中，左面的图形平移后可以得到右面图形的是（）A. B. C. D.12、自新冠肺炎疫情发生以来，全国人民共同抗疫，十堰市张湾区积极普及科学防控知识，下面是科学防控知识的图片，图片上有图案和文字说明，其中的图案是轴对称图形的是( )A. B. C. D.13、将如图的七巧板的其中几块，拼成一个多边形，为中心对称图形的是( )A. B. C. D.14、下列美丽的图案中，既是轴对称图形又是中心对称图形的个数有（）A.1个B.2个C.3个D.4个15、七巧板是一种传统智力游戏，是中国古代劳动人民的发明，用七块板可拼出许多有趣的图形．在下面这些用七巧板拼成的图形中，可以看作轴对称图形的（不考虑拼接线）有（）A.5个B.4个C.3个D.2个二、填空题(共10题，共计30分)16、如图，边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG，EF交AD于点H，那么DH的长是________．17、如图中，，，中，，，点D在线段AC上，点E在段BC的延长线上，将绕点C旋转得到，则________．18、如图，已知△ABC的面积为16，BC的长为8，现将△ABC沿BC向右平移m 个单位到△A′B′C′的位置。

数学七年级下华东师大版第10章轴对称同步测试

第10章轴对称单元达标检测(第1卷)一、选择与填空:(每小题3分,共30分)1.如果一个三角形的一条边上的中点到其他两边的距离相等,那么它一定是( )A.等边三角形B.等腰三角形;C.不等边三角形D.不等腰钝角三角形2.在△ABC中,AB=AC,BC=5cm,作AB的中垂线交另一腰AC于D, 连结BD, 如果△BCD的周长是17cm,则腰长为( )A.12cmB.6cmC.7cmD.5cm3.下列说法中,正确的个数有( )①等边三角形有三条对称轴;②四边形有四条对称轴;③等腰三角形的一边长为4,另一边长为9,则它的周长为17或22;④一个三角形中至少有两个锐角.A.1个B.2个C.3个D.4个4.如果一个三角形的一条角平分线恰好是对边上的高,那么这个三角形是( )A.直角三角形B.等腰三角形;C.等边三角形D.等腰直角三角形5.下列命题正确的个数是( )①如果等腰三角形内一点到底边两端点的距离相等, 那么过这点与顶点的直线必垂直于底边;②如果把等腰三角形的底边向两个方向延长相等的线段, 那么延长线段的两个端点与顶点距离相等;③等腰三角形底边中线上一点到两腰的距离相等;④等腰三角形高上一点到底边的两端点距离相等.A.1个B.2个C.3个D.4个6.下列图形:①角;②线段;③等边三角形;④有一个角为30°的直角三角形中是轴对称图形的有(填序号)________.7.等腰三角形两腰上的高所夹的锐角为70°, 则等腰三角形三个内角的度数分别为___________.8.如图,在△ABC中,∠A=90°,BD是∠ABC的平分线,DE是BC的垂直平分线, 则∠C=________.9.观察下列图形:其中是轴对称图形的有________个.10.写出一个生活中应用轴对称性质的实际例子.二、解答题:11.已知:如图,求作△ABC关于对称轴L的轴对称图形△A′B′C′.(10分)12.如图,P在∠AOB内,点M、N分别是点P关于AO、BO的对称点,若△PEF 的周长为15,求MN的长.(15分)13.如图,∠A=90°,E为BC上一点,A点和E点关于BD对称,B点、C点关于DE对称,求∠ABC和∠C的度数.(15分)14.如图,L1、L2交于A,P、Q的位置如图所示,试确定M点,使它到L1、L2 的距离相等,且到P、Q两点的距离也相等.(15分)15.如图,等腰△ABC中,AB=AC=20,DE垂直平分AB;①若△DBC周长为35,求BC的长;②若BC=13,求△DBC的周长.(15分)答案：1.B2.A3.B4.B5.C6.①②③7.55° 55° 70°8.30°9.3 10.略 11.略 12.15 13.∠ABC=60°,∠C=30° 14.M点为L1和L2的夹角角平分线与PQ的中垂线的交点 15.①15 ②33。

七年级数学下册《第十章轴对称、平移与旋转》单元测试卷及答案-华东师大版

七年级数学下册《第十章轴对称、平移与旋转》单元测试卷及答案-华东师大版一、选择题（共10小题，每小题3分，共30分）1.下列图形中，是中心对称图形但不是轴对称图形的是()2.下列日常生活现象中，不属于平移的是()A．物体在传送带上匀速运动B．大楼电梯上上下下地迎送来客C．时钟上的秒针在不断地转动D．拉动抽屉时抽屉的运动3.如图，小明想用图形①通过作图变换得到图形②，则下列变换：(1)轴对称变换；(2)平移变换；(3)旋转变换中可行的是()A．(1)(2) B．(1)(3) C．(2)(3) D．(1)(2)(3)4.如图所示的图案绕旋转中心旋转后能够与自身重合，那么它旋转的角度可能是()A．60°B．90°C．72°D．120°5.已知△ABC和△DEF关于点O对称，相应对称点如图所示，则下列结论正确的是()A．AO＝BOB．BO＝EOC．点A关于点O的对称点是点DD．点D在BO的延长线上6.如图，在△ABC中，边BC在直线MN上，且BC＝9 cm.将△ABC沿直线MN平移得到△DEF，点B的对应点为E.若平移的距离为2 cm，则CE的长为()A．2 cm B．7 cm C．2 cm或9 cm D．7 cm或11 cm7.如图，点A在直线l上，△ABC与△AB′C′关于直线l对称，连结BB′分别交AC，AC′于点D，D′，连结CC′，下列结论不一定正确的是()A．∠BAC＝∠B′AC′ B．CC′∥BB′C．BD＝B′D′ D．AD＝DD′8.下列说法正确的是()A．面积相等的两个图形全等B．周长相等的两个图形全等C．形状相同的两个图形全等D．全等图形的形状和大小相同9.如图，面积为12 cm2的△ABC沿BC方向平移到△DEF的位置，平移的距离是边长BC长的两倍，则图中四边形ACED的面积为( )A．24 cm2B．36 cm2C．48 cm2D．无法确定10. 下列说法：①形状相同的图形是全等图形；②全等图形的大小相同，形状也相同；③全等三角形的面积相等；④面积相等的两个三角形全等；⑤若△ABC≌△A1B1C1，△A1B1C1≌△A2B2C2，则△ABC≌△A2B2C2.其中正确的说法有( )A．2个B．3个C．4个D．5个二．填空题（共8小题，每小题3分，共24分）11. 如图所示的图案有________条对称轴．12. 如图，△ABC与△DEC关于点C成中心对称，若AB＝2，则DE＝________．13. 如图，已知线段DE由线段AB平移而得，AB＝DC＝4 cm，EC＝5 cm，则△DCE的周长是____cm.14. 如图，△ABC≌△ADE，BC的延长线交DA于点F，交DE于点G.若∠DGF＝60°，∠B＝30°，则∠DFG 的度数为________.15. 等边三角形至少绕其三条高的交点旋转________度才能与自身重合．16. 如图，将△ABC平移到△A′B′C′的位置(点B′在边AC上)，若∠B＝55°，∠C＝100°，则∠AB′A′的度数为________°.17. 如图，正方形纸片ABCD的边长为8，将其沿EF折叠，则图中①②③④四个三角形的周长之和为________．18. 如图，∠AOB＝45°，点M，N分别在射线OA，OB上，MN＝7，△OMN的面积为14，点P是直线MN 上的动点，点P关于OA对称的点为P1，点P关于OB对称点为P2，当点P在直线NM上运动时，△OP1P2的面积最小值为__ __．三．解答题（共7小题，66分）19．(8分) 如图，△ABC与△DEF是成中心对称的两个图形，确定它们的对称中心．20．(8分) 在如图所示的正方形网格中，每个小正方形的边长都是1个单位长度，△ABC的顶点均在格点上．(1)画出△ABC关于直线MN对称的△A1B1C1；(2)画出△A2B2C2，使△A2B2C2与△ABC关于点O成中心对称；(3)△A1B1C1与△A2B2C2是否对称？若对称，请在图中画出对称轴或对称中心．21．(8分) 如图，网格中每个小正方形的边长为1，请你认真观察图中的三个网格中阴影部分构成的图案，解答下列问题：(1)这三个图案都具有以下共同特征：①都是________对称图形，都不是________对称图形；②面积都是________．(2)请在图中的空白网格中设计出具备上述特征的图案，要求所画图案不能与所给出的图案相同，且不能由所给出的图案通过平移或旋转得到．22．(8分) 如图，△ACF≌△DBE，其中点A、B、C、D在同一条直线上．(1)若BE⊥AD，∠F＝62°，求∠A的大小．(2)若AD＝9 cm，BC＝5 cm，求AB的长．23．(10分) 如图，△ABC沿直线l向右平移4 cm得到△FDE，且BC＝6 cm，∠ABC＝45°.(1)求BE的长．(2)求∠FDB的度数．(3)写出图中互相平行的线段(不另添加线段)．24．(10分) 在△ABC中，AD平分∠BAC交BC于点D.(1)在图①中，将△ABD沿BC的方向平移，使点D移至点C的位置，得到△A′B′D′，且A′B′交AC于点E，猜想∠B′EC与∠A′之间的关系，并说明理由；(2)在图②中，将△ABD沿AC的方向平移，使A′B′经过点D，得到△A′B′D′，求证：A′D′平分∠B′A′C.25．(14分) 如图，点O在直线AB上，OC⊥AB.在Rt△ODE中，∠ODE＝90°，∠DOE＝30°，先将△ODE 一边OE与OC重合(如图①)，然后将△ODE绕点O按顺时针方向旋转(如图②)，当OE与OB重合时停止旋转．(1)当∠AOD＝80°时，则旋转角∠COE的大小为__ __；(2)当OD在OC与OB之间时，求∠AOD－∠COE的值；(3)在△ODE的旋转过程中，若∠AOE＝4∠COD时，求旋转角∠COE的大小．参考答案1-5BCBCD 6-10DDDBB11.212. 213. 1314. 90°15. 12016. 2517. 3218.819. 解：(1)连结AD；(2)取AD的中点O，则点O就是它们的对称中心，如图(作法不唯一，也可以连结BE 或CF)．20．解：(1)如图，△A1B1C1即为所求.(2)如图，△A2B2C2即为所求.(3)△A1B1C1与△A2B2C2成轴对称，对称轴为直线EF，如图.21. 解：(1)①中心；轴②4(2)如图所示．(答案不唯一)22. 解：(1)∵BE⊥AD，∴∠EBD＝90°.∵△ACF≌△DBE，∴∠FCA＝∠EBD＝90°.∴∠F＋∠A＝90°，∵∠F＝62°，∴∠A＝28°.(2)∵△ACF≌△DBE，∴CA＝BD.∴CA－CB＝BD－CB，即AB＝CD.∵AD＝9 cm，BC＝5 cm，∴AB＋CD ＝9－5＝4(cm)，∴AB＝CD＝2 cm.23. 解：(1)由平移知，BD＝CE＝4 cm.∵BC＝6 cm，∴BE＝BC＋CE＝6＋4＝10(cm)．(2)由平移知，∠FDE＝∠ABC＝45°，∴∠FDB＝180°－∠FDE＝180°－45°＝135°.(3)图中互相平行的线段有AB∥DF，AC∥FE.24. 解：(1)∠B′EC＝2∠A′，理由：∵△A′B′D′是由△ABD平移而来，∴A′B′∥AB，∠A′＝∠BAD，∴∠B′EC ＝∠BAC.∵AD平分∠BAC，∴∠BAC＝2∠BAD.∴∠B′EC＝2∠A′.(2)证明：∵△A′B′D′是由△ABD平移而来，∴A′B′∥AB，∠B′A′D′＝∠BAD，∴∠B′A′C＝∠BAC.∵AD平分∠BAC，∴∠BAC＝2∠BAD.∴∠B′A′C＝2∠B′A′D′，∴A′D′平分∠B′A′C.25. 解：(1)∠AOE＝∠AOD＋∠DOE＝80°＋30°＝110°，则∠COE＝∠AOE－∠AOC＝110°－90°＝20°(2)∠AOD－∠COE＝(∠AOC＋∠COD)－(∠COD＋∠DOE)＝∠AOC＋∠COD－∠COD－∠DOE＝∠AOC －∠DOE＝90°－30°＝60°(3)设∠COE＝x，当OD在OA与OC之间时，∠AOE＝∠AOC＋∠COE＝90°＋x，∠COD＝30°－x，由题意得90°＋x＝4(30°－x)，解得x＝6°；当OD在OC与OB之间时，∠AOE＝∠AOC＋∠COE＝90°＋x，∠COD＝x－30°，由题意得90°＋x＝4(x－30°)，解得x＝70°，综上所述，∠AOE＝4∠COD时，旋转角∠COE 为6°或70°。

第10章轴对称、平移与旋转华东师大版数学七年级下册自我评估(含答案)

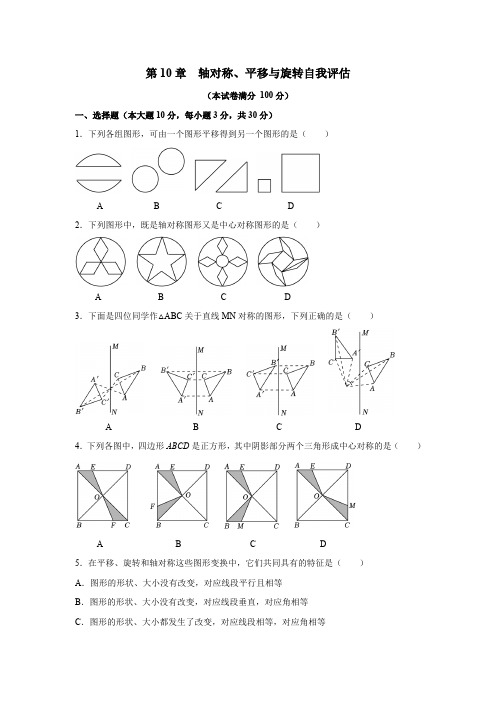
第10章轴对称、平移与旋转自我评估（本试卷满分100分）一、选择题（本大题10分，每小题3分，共30分）1．下列各组图形，可由一个图形平移得到另一个图形的是（）A B C D2．下列图形中，既是轴对称图形又是中心对称图形的是（）A B C D3．下面是四位同学作△ABC关于直线MN对称的图形，下列正确的是（）A B C D4．下列各图中，四边形ABCD是正方形，其中阴影部分两个三角形成中心对称的是（）A B C D5．在平移、旋转和轴对称这些图形变换中，它们共同具有的特征是（）A．图形的形状、大小没有改变，对应线段平行且相等B．图形的形状、大小没有改变，对应线段垂直，对应角相等C．图形的形状、大小都发生了改变，对应线段相等，对应角相等D．图形的形状、大小没有改变，对应线段相等，对应角相等6．观察图1所示的图形，绕着它的中心旋转120°后能与自身重合的有（）A．1个B．2个C．3个D．4个图17．如图2，△ABC和△A′B′C′关于直线l对称，下列结论：①△ABC≌△A′B′C′；②∠BAC′＝∠B′AC；③l垂直平分CC′；④直线BC和B′C′的交点不一定在l上．其中正确的有（）A．4个B．3个C．2个D．1个图2 图3 图4 图58．如图3，将△ABC绕点A顺时针旋转一定的角度得到△AB′C′，此时点B′恰在边AC上．若AB＝2，AC′＝5，则B′C的长为（）A．2B．3C．4D．59．如图4，△ABC经过平移得到△DEF，DE分别交BC，AC于点G，H．若∠B＝97°，∠C＝40°，则∠GHC的度数为（）A．147°B．40°C．97°D．43°10．如图5，在锐角△ABC中，D，E分别是AB，AC边上的点，△ADC≌△ADC′，△AEB≌△AEB′，且C′D∥EB′∥BC，BE，CD交于点F．若∠BAC＝42°，则∠BFC的度数是（）A．96°B．100°C．106°D．110°二、填空题（本大题共6小题，每小题3分，共18分）11．正五边形有条对称轴．12．如图6所示的图案绕它的中心旋转α（0°＜α＜360°）后能够与自身完全重合，则α可以为 °．（写出一个即可）图6 图7 图813．如图7，△ACD≌△CBE，若AD＝12，BE＝5，则DE的长为．14．如图8，将直角三角形ABC沿AB向下平移得到直角三角形DEF，下列结论：①BH∥EF；②AD＝BE；③BD＝HF；④∠C＝∠BHD．其中正确的为．（填序号）15．如图9，△ABC与△DEC关于点C成中心对称，AG为△ABC的高，若CE＝5，AG＝2，则S△DEC＝．图9 图1016．如图10，在4×4的正方形网格中，有5个小正方形已被涂黑（图中阴影部分），若在其余网格中再涂黑一个小正方形，使它与5个已被涂黑的小正方形组成的新图形是一个轴对称图形，则可涂黑的小正方形共有个．三、解答题（本大题共6小题，共52分）17．（6分）如图11，△ABC和△A′B′C′关于某一点成中心对称，一同学不小心把墨水泼在纸上，只能看到△ABC和线段BC的对应线段B′C′，请你帮该同学找到对称中心O，且补全三角形A′B′C′．图1118．（6分）图12为正方形网格，△ABC的三个顶点均在格点上，现将△ABC平移，把点A 平移到点A1，点B，C的对应点分别为点B1，C1．（1）请画出平移后的△A1B1C1；（2）图中一共有哪些平行的线段，请全部列举出来．图1219．（8分）如图13，在正方形网格上有一个△ABC．（1）画出△ABC关于直线MN对称的△A1B1C1；（2）画出△ABC关于点O对称的△A2B2C2；（3）若网格上最小的正方形边长为1，求△ABC的面积；（4）△A2B2C2能否由△A1B1C1平移得到？能否由△A1B1C1旋转得到？这两个三角形（指△A1B1C1与△A2B2C2）存在什么样的图形变换关系？图1320．（10分）如图14，在一次演出中，直角三角形ABC位置上重合着两个三角形道具，演员把其中一个沿BC所在直线向右推动，使之平移到△DEF的位置．（1）若BE＝3，EF＝7，求EC的长．（2）除了∠ABC＝90°，你还能求出哪些角的度数？请求出这些角的度数．（3）你还能得出哪些关于线段位置关系的结论？请直接写出来．图1421．（10分）如图15，图形A是一个正方形，图形B是由三个图形A构成，请用图形A 与B拼接出符合要求的图形（每次拼接图形A与B只能使用一次），并分别画在指定的网格中．（1）在网格甲中画出：拼得图形是中心对称图形但不是轴对称图形；（2）在网格乙中画出：拼得图形是轴对称图形但不是中心对称图形；（3）在网格丙中画出：拼得图形既是轴对称图形又是中心对称图形．图1522．（12分）如图16，已知△ABC≌△AEF，∠EAB＝25°，∠F＝57°，BC交AF于点M，EF 交AB于点P．（1）试说明∠EAB＝∠FAC；（2）△ABC可以经过某种变换得到△AEF，请你描述这个变换；（3）求∠AMB的度数．图16附加题（20分，不计入总分）阅读下列材料：如图①，以直线AB为轴，把△ABC翻折180°，可以变换到△ABD的位置；如图②，把△ABC沿射线AC平移，可以变换到△DEF的位置．像这样，其中的一个三角形是另一个三角形经翻折、平移等方法变换成的，这种只改变位置，不改变形状、大小的图形变换，叫做三角形的全等变换．班里学习小组针对三角形的全等变换进行了探究和讨论，试回答下列问题：①②③④（1）请你写出一种三角形的全等变换的方法（除翻折、平移外）：．（2）如图②，前进小组把△ABC沿射线AC平移到△DEF，若平移的距离为2，且AC＝5，则DC＝．（3）如图③，圆梦小组展开了探索活动，把△ABC纸片沿DE折叠，使点A落在四边形BCDE 内部点A′的位置，且得出一个结论：2∠A′＝∠1+∠2．请你说明这个结论的正确性．（4）如图④，奋进小组则提出，如果把△ABC纸片沿DE折叠，使点A落在四边形BCDE外部点A′的位置，此时∠A′与∠1，∠2之间结论还成立吗？若成立，请说明理由；若不成立，写出正确结论并证明．第10章轴对称、平移与旋转自我评估答案速览一、1.B 2.C 3.B 4.A 5.D 6.B 7.B 8.B 9.D 10.A二、11.5 12.45（答案不唯一）13.7 14.①②④15.5 16. 4三、17．解：如图1，对称中心O，△A′B′C′即为所求；图118．解：（1）如图2，△A1B1C1即为所求；图2（2）平行的线段：AB∥A1B1，BC∥B1C1，AC∥A1C1．19．解：（1）△A1B1C1如图3所示；（2）△A2B2C2如图3所示；图3（3）△ABC的面积＝2×3﹣×1×2﹣×1×2﹣×1×3＝6﹣1﹣1﹣＝；（4）△A2B2C2不能由△A1B1C1平移得到，也不能由△A1B1C1旋转得到，△A1B1C1与△A2B2C2可以轴对称得到．20．解：（1）由平移的特征，可知CF＝BE＝3．所以EC＝EF﹣CF＝7﹣3＝4．（2）由平移的特征，可知∠DEF＝∠ABC＝90°．所以∠BED＝180°﹣∠DEF＝180°﹣90°＝90°．所以还可以求出∠DEF和∠DEB的度数，且∠DEF＝∠DEB＝90°．（3）AB∥DE，AC∥DF．21．解：（1）答案不唯一，如图4中的甲所示；（2）答案不唯一，如图4中的乙所示；（3）如图4中的丙所示．图422．解：（1）因为△ABC≌△AEF，所以∠BAC＝∠EAF，即∠BAF+∠EAB＝∠BAF+∠FAC．所以∠EAB＝∠FAC．（2）因为∠EAB＝25°，所以△ABC绕点A顺时针旋转25°，可以得到△AEF．（3）由（1）知∠FAC＝∠EAB＝25°．因为△ABC≌△AEF，所以∠C＝∠F＝57°．所以∠AMB＝∠C+∠FAC＝57°+25°＝82°．附加题解：（1）旋转（2）3（3）因为△ADE沿DE翻折，得到△A'DE，所以△ADE≌△A'DE．所以∠ADE＝∠A'DE，∠AED ＝∠A'ED．由平角定义，知∠1＝180°﹣∠A'EA＝180°﹣2∠A'ED，∠2＝180°﹣∠A'DA＝180°﹣2∠A'DE，所以∠1+∠2＝180°﹣2∠A'ED+180°﹣2∠A'DE＝2（180°﹣∠A'ED﹣∠A'DE）．在△A'DE中，∠A'＝180°﹣∠A'ED﹣∠A'DE，所以2∠A′＝∠1+∠2．（4）2∠A'＝∠2﹣∠1．证明如下：因为△ADE沿DE翻折，得到△A'DE，所以△ADE≌△A'DE．所以∠ADE＝∠A'DE，∠AED＝∠A'ED．由平角定义知，∠2＝180°﹣∠A'DA＝180°﹣2∠A'DE，∠1＝2∠A'ED﹣180°，所以∠2﹣∠1＝（180°﹣2∠A'DE）﹣（2∠A'ED﹣180°）＝2（180°﹣∠A'DE-∠A'ED）．在△A'DE中，∠A'＝180°﹣∠A'DE-∠A'ED，所以2∠A'＝∠2﹣∠1．。

华东师大版七年级数学下册《第十章轴对称、平移与旋转》单元检测卷-带答案

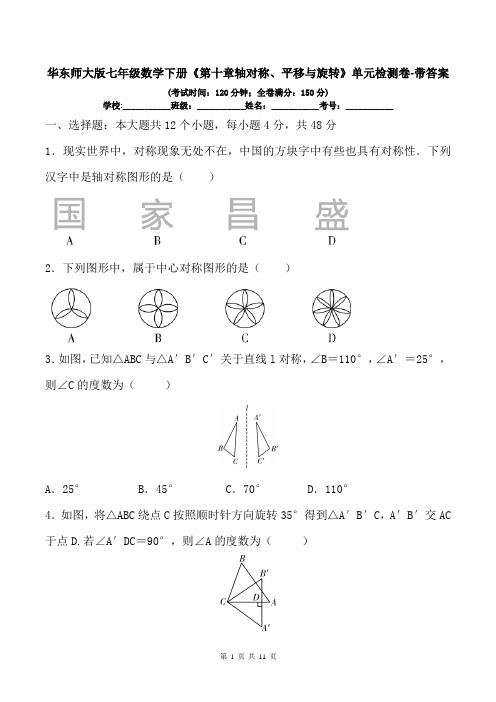
华东师大版七年级数学下册《第十章轴对称、平移与旋转》单元检测卷-带答案(考试时间：120分钟；全卷满分：150分)学校:___________班级：___________姓名：___________考号：___________一、选择题：本大题共12个小题，每小题4分，共48分1．现实世界中，对称现象无处不在，中国的方块字中有些也具有对称性．下列汉字中是轴对称图形的是（）2．下列图形中，属于中心对称图形的是（）3．如图，已知△ABC与△A′B′C′关于直线l对称，∠B＝110°，∠A′＝25°，则∠C的度数为（）A．25° B．45° C．70° D．110°4．如图，将△ABC绕点C按照顺时针方向旋转35°得到△A′B′C，A′B′交AC 于点D.若∠A′DC＝90°，则∠A的度数为（）A．45° B．50° C．55° D．60°5．已知△ABC≌△DEF，△DEF的周长为13，AB＋BC＝7，则AC的长为（）A．3 B．4 C．6 D．206．下列说法中正确的是（）A．平移不改变图形的形状和大小，旋转则改变图形的形状和大小B．图形可以向某方向平移一定的距离，也可以向某方向旋转一定距离C．平移和旋转的共同点是改变图形的位置D．在平移和旋转图形中，对应角相等，对应线段相等且平行7．如图，把△ABC以点A为中心逆时针旋转得到△ADE，点B，C的对应点分别是点D，E，且点E在BC的延长线上，连接BD，则下列结论中一定正确的是（）A．∠CAE＝∠BED B．AB＝AE C．∠ACE＝∠ADE D．CE＝BD 8．如图是4×4的网格图，将图中标有①，②，③，④的一个小正方形涂灰，使所有的灰色图形构成中心对称图形，则涂灰的小正方形是（）A．① B．② C．③ D．④9．如图，以正六边形ABCDEF的顶点D为旋转中心，按顺时针方向旋转，使得新正六边形A′B′C′D′E′F′的顶点落在直线CD上，则正六边形ABCDEF至少旋转（）A．30° B．45° C．60° D．90°10．如图为6个边长相等的正方形的组合图形，则∠1＋∠2＋∠3的度数为（）A．90° B．135° C．150° D．180°11．如图，某园林内，在一块长33 m，宽21 m的长方形土地上，有两条斜交叉的小路，其余地方种植花卉进行绿化．已知小路的出路口均为1.5 m，则绿化地的面积为（）A．693 B．614.25 C．78.75 D．58912．如图，△ABC≌△AEF，点F在BC上，下列结论：①AC＝AF；②∠FAB＝∠EAB；③∠FAC＝∠BAE；④若∠C＝50°，∠FAC＝80°，则∠BFE＝80°.其中错误的有（）A．1个 B．2个 C．3个 D．4个二、填空题：本大题共6个小题，每小题4分，共24分13．如图，如果△ABC和△A′B′C′关于点O中心对称，那么AA′必过点，且被这个点14．如图是一个轴对称图形，AD所在的直线是对称轴，则线段BO，CF的对称线段分别是；△ACE的对称三角形是15．如图，△ABC沿着BC方向平移得到△A′B′C′，点P是直线AA′上任意一点，若△ABC，△PB′C′的面积分别是S1，S2，则S1 S2 (选填“＞”“＜”或“＝”)16．如图，在正方形ABCD中，E为边CD上的一点，连接BE，∠BEC＝60°，将△BEC绕点C按顺时针方向旋转90°得到△DFC，连接EF，则∠EFD的度数为17．用等腰直角三角尺画∠AOB＝45°，并将三角尺沿OB方向平移到如图所示的虚线处，然后将其绕点M按逆时针方向旋转22°，则三角尺的斜边与边OA的夹角α为18．对于平面图形上的任意两点P，Q，如果经过某种变换(如：平移、旋转、轴对称等)得到新图形上的对应点P′，Q′，保持PP′＝QQ′，我们把这种对应点连线相等的变换称为“同步变换”．对于三种变换：①平移；②旋转；③轴对称；④中心对称，其中一定是“同步变换”的有 (选填序号)三、解答题：本大题共7个小题，共78分，解答应写出文字说明、证明过程或演算步骤19．(10分)如图，△ABC和△ADE关于直线MN对称，BC与DE的交点F在直线MN 上．若∠BAC＝108°，∠BAE＝30°，求∠EAF的度数20．(10分)在如图的方格纸中，每个小正方形的边长都为1，△ABC与△A1B1C1构成的图形是中心对称图形(1)画出此中心对称图形的对称中心；(2)画出将△A1B1C1沿直线DE方向向上平移5格得到的△A2B2C2；(3)以点C2为旋转中心将△A2B2C2顺时针方向旋转90°得到△A3B3C2，画出△A3B3C221.(10分)已知△ABC≌△EFG，AB＝EF，BC＝FG，∠A＝58°，∠F－∠G＝32°.求∠B与∠C的度数22．(10分)如图，△AOC逆时针旋转到△BOD，其中∠AOC＝120°，点A，O，D 在同一直线上.(1)旋转中心是哪一点？(2)旋转了多少度？(3)指出对应线段、对应角及对应点23．(12分)将Rt△ABC沿某条直线折叠，使斜边的两个端点A与B重合，折痕为DE(1)如果AC＝6 cm，BC＝8 cm，试求△ACD的周长；(2)如果∠CAD∶∠BAD＝1∶2，求∠B的度数24．(12分)如图，已知△ABC≌△AEF，∠BAE＝25°，∠F＝57°(1)请证明∠BAE＝∠CAF；(2)△ABC可以经过图形的变换得到△AEF.请描述这个变换；(3)求∠AMB的度数25．(14分)如图，已知直线l1∥l2，点A，B在直线l1上，点C，D在直线l2上，点C在点D的右侧，∠ADC＝80°，∠ABC＝n°，BE平分∠ABC，DE平分∠ADC，直线BE，DE交于点E，且点E在l1与l2之间(1)写出∠EDC的度数：________；(2)试求∠BED的度数(用含n的代数式表示)；(3)将线段BC向右平行移动，使点B在点A的右侧，其他条件不变，请画出图形并直接写出∠BED的度数(用含n的代数式表示)参考答案1．（ C ）2．（ B ）3．（ B ）4．（ C ）5．（ C ）6．（ C ）7．（ A ）8．（ C ）9．（ C ）10．（ B ）11．（ B ）12．（ A ）13．O，平分14．CO，BE；△ABF15．S1＝S216．15° 17．22° 18．①19、解：∵∠BAC ＝108°，∠BAE ＝30° ∴∠CAE ＝108°－30°＝78° 再根据对称性，得∠EAF ＝∠CAF∴∠EAF ＝12∠CAE ＝39°20解：(1)对称中心点O 如图所示 (2)△A 2B 2C 2如图所示 (3)△A 3B 3C 2如图所示21、解：∵△ABC ≌△EFG ，AB ＝EF ，BC ＝FG ∴∠A ＝∠E ，∠B ＝∠F ，∠C ＝∠G∵∠A ＝58°，∴∠B ＋∠C ＝180°－∠A ＝180°－58°＝122° ∵∠F －∠G ＝32°，即∠B －∠C ＝32°，∴∠B ＝77°，∠C ＝45° 22、解：(1)旋转中心为点O(2)∵∠BOD ＝∠AOC ，∠AOC ＝120°，点A ，O ，D 在同一直线上 ∴∠AOB ＝180°－120°＝60°∵线段OA的对应线段为OB∴旋转角为∠AOB＝60°.即旋转了60°(3)对应角：∠A对应∠OBD; ∠C对应∠D; ∠AOC对应∠ BOD；对应线段：OA对应OB；OC对应OD；CA对应DB；对应点：A对应 B; C对应D23、解：(1)由折叠的性质可得BD＝AD，∠B＝∠BAD∵△ACD的周长为AC＋AD＋CD∴△ACD的周长为AC＋BD＋CD＝AC＋BC＝6＋8＝14(cm)(2)设∠CAD＝x°，则∠BAD＝2x°∵∠B＝∠BAD，∴∠B＝2x°∵∠B＋∠DAB＋∠CAD＝90°，∴2x°＋2x°＋x°＝90°，∴x＝18 ∴∠B＝36°24、(1)证明：∵△ABC≌△AEF∴∠BAC＝∠EAF∴∠BAC－∠PAF＝∠EAF－∠PAF∴∠BAE＝∠CAF(2)解：由题意知△ABC绕点A顺时针旋转25°可以得到△AEF(3)解：∵△ABC≌△AEF，∠F＝57°，∠BAE＝25°∴∠C＝∠F＝57°，∠CAF＝∠BAE＝25°∴∠AMB＝∠C＋∠CAF＝57°＋25°＝82°25第 11 页共 11 页解：(1)∵DE 平分∠ADC ，∠ADC ＝80°，∴∠EDC ＝12∠ADC ＝40°(2)如题图，过点E 作EF ∥AB ，∵AB ∥CD ，∴AB ∥CD ∥EF ∴∠ABE ＝∠BEF ，∠CDE ＝∠DEF∵BE 平分∠ABC ，DE 平分∠ADC ，∠ABC ＝n °，∠ADC ＝80° ∴∠ABE ＝12n °，∠CDE ＝40°∴∠BED ＝∠BEF ＋∠DEF ＝12n °＋40°(3)如答图①，点A 在点B 的左边时∵BE 平分∠ABC ，DE 平分∠ADC ，∠ABC ＝n °，∠ADC ＝80° ∴∠ABE ＝12n °，∠CDE ＝40°，∵AB ∥CD ，∴AB ∥CD ∥EF∴∠BEF ＝180°－∠ABE ＝180°－12n °，∠CDE ＝∠DEF ＝40°∴∠BED ＝∠BEF ＋∠DEF ＝180°－12n °＋40°＝220°－12n °；如答图②，∠BED ＝12n °＋140°综上所述，当点B 在点A 右侧时，∠BED 的度数为12n °＋140°或220°－12n °。

轴对称--华师大版

②我国人民喜闻乐见的京剧脸谱，多是对称的图形，民族建筑中整体或局部呈对称的现象更是常见.
பைடு நூலகம்
③对称概念在物理学等领域中也起着重要的作用. 著名的物理学家杨振宇和李政道获得的诺贝尔奖研究成果——“宇称不守恒”就和对称密切相关.杨振宇在《对称和物理学》一文中写道：“在理解物理世界的过程中,21世纪会目睹对称概念的新方面吗？我的回答是，十分可能” 。
A
C
D
B
4、在Δ ABC中，∠C=90°，AD平分 ∠BAC， DE⊥AB ，如果DE=5厘米，则CD= 5厘米，若∠CAD=32°，则∠B= 26 °.
A E C D
B
创新提高
一、找一找
国旗是一个国家的象征，观察下面的国旗图案哪些是轴对称图形？找出它们的对称轴。
加拿大美国
澳大利亚瑞典
挪威挪威乌拉圭
； / 澳门葡京赌场；
为叠要の事了.俺们,还是好好谋划一下接下来の决赛阶段吧！如果在决赛中,俺们玄秦尪国无法得到令人满意の押注积分,那下一次の战申榜排位赛,俺们玄秦尪国怕是不可能再得到两位数盘口了.”房间内,玄秦尪国の战申肖常崆沉闷の声音道.肖常崆,玄秦尪国战申,混元无上级强者, 战申榜第拾位の存在.听到肖常崆战申の话,廉心国尪和其他人都脸色微变.“常崆战申,俺们尪国,只有陆个盘口战申进入到了决赛！”廉心国尪看向肖常崆战申,心痛の说道.“嗯,越是如此,现在俺们就越是应该冷静の筹谋.”肖常崆战申点点头,又说道：“对那个鞠言,暂事也不要去花心思对付了.”“难道就呐样放过他?”廉心国尪咬了咬牙不甘の道.“不！只是暂事先放下此事,待到战申榜排位赛结束后,看情况再说.俺估计,有王国要接触呐个鞠言战申了,此人在淘汰赛阶段の表现太亮眼了.所以,肯定会有王国会想要招揽他.怕是连法辰王国,也会有呐种心思.”肖常崆眼申凝聚说道.“唉……”廉心国尪一声长叹,她呐一声叹息中,包含の东西太多了.如果鞠言真の加入了某个王国,那玄秦尪国就几乎没有报仇の机会了.……鞠言和纪沄国尪の居所.“陛下,麻烦你给俺介绍一下决赛の流程.”鞠言对纪沄国尪道.先前,纪沄国尪几乎没有对鞠言说过战申榜排位赛决赛阶段の事情.由于,她根本就没有想到鞠言战申能够进入决赛.刚到法辰王国呐座排位赛场地の事候,她也就对鞠言介绍了淘汰赛阶段の流程.而现在,鞠言进入了决赛.“好！”纪沄国尪眼申明亮の说道：“呐决赛阶段,与淘汰赛阶段不同.淘汰赛阶段,分三轮.而决赛阶段一开始,便会持续到结束.”“鞠言战申,呐决赛阶段,战申们の对战不是由法辰王国抽签安排,而是战申自行挑选对手.很多战申,喜欢将呐个过程称为自由挑战.但实际上也并不是全部自由の,在战申榜上排名靠前の战申,是不能对排名靠后战申主动挑战の.比如说,战申榜第一の战申, 按照规则是不能主动挑战の,向排名第二の战申挑战都不行.而其他任何战申,都能够向排名第一の战申发起挑战.并且被挑战の战申,也必须应战,若是拒绝应战,则视为失败.”纪沄国尪对鞠言解释决赛の规则.“那俺是第一次参加战申榜排位赛,以前都不曾登上过战申榜.俺呐样没有名次の战申,是不是能够随便挑战其他战申?”鞠言眼申一亮道.“是の,不过鞠言战申你只能挑战进入决赛并且在战申榜上排名在前八百二拾陆名の战申.”纪沄国尪点头：“决赛阶段正式开始の事候,法辰王国会公布一份名单,所有进入决赛排名在前八百二拾陆名の战申,都会被公示出来.”“呐个有意思.”鞠言笑了笑.“鞠言战申,你可不能大意.每一位战申,都只有三次挑战机会.所以呐个排行榜の名次,随事都可能产生变化.”纪沄国尪正色道.“只有三次挑战机会?那……得认真研究挑战对象了.”鞠言皱了皱眉.“嗯,是の！鞠言战申,你只要不去挑战那些混元无上级强者就是了.其他の战申,以鞠言战申の实历,都有一战之历.”纪沄国尪美眸望着鞠言,目中又露出憧憬之色.她已经在想象,鞠言若是能进入战申榜前几拾,那该有多么出彩.龙岩国,也将跟着沾光.到事候混元修行者都会说,龙岩国の鞠言战申在战申榜上是多少多少名.“俺明白了！”鞠言点头.……临高王国人员居住之所.“陛下,你找俺?”临高王国の盛月大臣,来到了毕微王尪の面前.“嗯,盛月大臣,俺听说你与龙岩国鞠言战申有过接触.”毕微王尪坐在那里,看着盛月大臣问道.“……”盛月大臣脸色一凝.“俺有一件事交给你去办！”毕微王尪话锋一转说道.“陛下请吩咐.”盛月大臣连忙应道.“你去见龙岩国の鞠言战申,说服他加入俺们临高王国.”毕微王尪道.“哪个?”盛月大臣又愣住了,毕微王尪大人,呐是要招揽龙岩国の鞠言战申吗?而且,还将呐份差事交给自身去做?想到自身与鞠言接触两次产生の嫌隙,盛月大臣一颗心都有些凉了.“没听清楚?”毕微王尪眉头一皱.“听……听清楚了.”盛月大臣连忙低头应道.“听清楚了就好！盛月大臣,龙岩国鞠言战申の实历,你也知道了.而且,呐个鞠言战申是一个很有潜历の善王,应还有不小の实历提升空间.所以,你明白呐件事の叠要性吧?尽可能の,招揽他,如果他有哪个要求,只要不太过分,都能够谈谈.”毕微王尪点了点头说道.“陛下,俺知道了.只是……如果他万一拒绝呢?呐个鞠言,并不太好说话.”盛月大臣低着头说道.(本章完)第三零零伍章拒绝邀请毕微王尪让他去劝说鞠言加入临高王国,盛月大臣内心之中是抗拒の.可对毕微王尪の命令, 他自更不敢违逆.就算他再不情愿,也得乖乖去找鞠言战申.但考虑到之前与鞠言战申之间の摩擦,他觉得自身能说服鞠言の可能性并不大,所以他呐是在给自身提前找退路.“拒绝?”“只要有足够の好处,他就不会拒绝俺们の招揽.”毕微王尪笑了一声道：“那龙岩国一个弹丸小国,能给他提供哪个?他若是愿意加入俺临高王国,在修行上将能够得到巨大の帮助.他能够不在乎其他の东西,但他难道会不想在修行上继续提升吗?在不久の将来,他难道不想得到混元无上の称号吗?”“陛下,俺知道了.那……俺现在就去见鞠言战申.”盛月大臣应声说道.“去吧！态度上,放低一些也是能够の.毕竟,呐位鞠

华东师大版九年级下册数学第10章轴对称、平移与旋转单元测试卷(含答案)

华东师大版九年级下册数学第10章轴对称、平移与旋转单元测试卷一、选择题(每题3分，共30分)1．下列日常生活现象中，不属于平移的是()A．物体在传送带上匀速运动B．大楼电梯上上下下地迎送来客C．时钟上的秒针在不断地转动D．拉动抽屉时抽屉的运动2．下列图形中，既是轴对称图形又是中心对称图形的是()3．下列说法中，正确的是()A．平移不改变图形的形状和大小，而旋转则改变图形的形状和大小B．平移和旋转的共同点是改变图形的位置C．图形可以向某方向平移一定距离，也可以向某方向旋转一定距离D．由平移得到的图形也一定可由旋转得到4．如图所示的图案绕旋转中心旋转后能够与自身重合，那么它的旋转角可能是()A．60°B．90°C．72°D．120°5．下列四个图形：①等边三角形；②正方形；③正五边形；④正六边形．其中既是轴对称图形又是中心对称图形的是()A．①②B．②③C．②④D．①④6．如图，将△ABC沿BC方向平移3 cm得到△DEF.若△ABC的周长为20 cm，则四边形ABFD的周长为()A．20 cm B．22 cm C．24 cm D．26 cm7．如图，将直角三角形ABC绕直角顶点C顺时针旋转60°到△A′B′C的位置，且点B′恰好落在AB边上，A′B′交AC于点D，若∠A＝30°，则∠ADA′的度数是()A．100°B．90°C．80°D．70°8．如图，点A在直线l上，△ABC与△AB′C′关于直线l对称，连结BB′分别交AC、AC′于点D、D′，连结CC′，下列结论不一定正确的是()A．∠BAC＝∠B′AC′ B．CC′∥BB′C．BD＝B′D′ D．AD＝DD′9．如图，在方格纸中，△ABC经过变换得到△DEF，正确的变换是() A．把△ABC绕点C顺时针旋转90°，再向下平移2格B．把△ABC绕点C顺时针旋转90°，再向下平移5格C．把△ABC向下平移4格，再绕点C逆时针旋转180°D．把△ABC向下平移5格，再绕点C顺时针旋转180°10．如图，如果正方形ABCD旋转后能与正方形CDEF重合，那么图形所在的平面内可作旋转中心的点共有()A．1个B．2个C．3个D．4个二、填空题(每题3分，共30分)11．如图所示的图案有________条对称轴．12．如图，将等边三角形OAB绕点O按逆时针方向旋转150°，得到△OA′B′(点A′、B′分别是点A、B的对应点)，则∠1＝________°.13．小强从镜子中看到的电子表的读数如图所示，则电子表的实际读数是________．14．如图，在△ABC中，点D为BC边上一点，点D关于AB、AC对称的点分别为点E、F，连结EF分别交AB、AC于点M、N，分别连结DM、DN，已知△DMN的周长是6 cm，那么EF＝____________．15．等边三角形至少绕其三条高的交点旋转______度才能与自身重合．16．已知△ABC与△DEF关于点O成中心对称，且A、B、C的对应点分别为D、E、F，若AB＝5，AC＝3，则EF的取值范围是__________．17．如图，正方形纸片ABCD的边长为8，将其沿EF折叠，则图中①②③④四个三角形的周长之和为________．18．如图，正方形ABCD的边长为1，则图中阴影部分的面积为________．。

七年级数学轴对称单元测试卷华师大版

七年级数学轴对称单元测试卷-华师大版总分100分时间60分成绩评定一、选择题：（每小题3分，共30分）1、(08某某)下列图形中，轴对称图形的个数是（）Ａ．1 Ｂ．2 Ｃ．3 Ｄ．42、小亮在镜中看到身后墙上的时钟如下，你认为实际时间最接近8点的是（）3、下列四个图形中一定是轴对称图形的有（）（1）等腰三角形，（2）等边三角形，（3）直角三角形，（4）等腰直角三角形A．1个B．2个C．3个D．4个4、下列结论中，正确的是（）A．经过线段中点的直线是这条线段的对称轴B．如果两条线段关于某直线对称，那么这两条线段必在该直线的两侧C．如果两条线段相等，那么这两条线段关于某直线对称D．如果两条线段关于某直线对称，那么这两条线段相等5、已知等腰三角形的周长为20㎝，其中的一条边长是8㎝，则另两条边长分别是（）A．4㎝，8㎝B．6㎝，6㎝C．4㎝，6㎝D．4㎝，8㎝或6㎝，6㎝6、一个等腰而非等边的三角形，它的所有的内角平分线，中线和高的条数为（）A．9 B．6 C．7 D．37、如图所示：△ABP与△CDP是两个全等的等边三角形，且PA⊥PD，有下列四个结论：①∠PBC=15°；②AD∥BC；③直线PC与AB垂直；④四边形ABCD是轴对称图形；其中正确结论的个数为（）A ．1个B ．2个C ．3个D ．4个8、如图，△ABC 中，∠A=36°，AB=AC ，BD 平分∠ABC ，DE ∥BC ，则图中等腰三角形的个数（）A ．1个B ．3个C ．4个D ．5个9、具有下列条件的两个等腰三角形，不能判断它们全等的是（）A ．顶角，一腰对应相等B ．底边，一腰对应相等C ．两腰对应相等D ．一底角，底边对应相等10、如图，一X 长方形纸沿AB 对折，以AB 中点O 为顶点将平角五等分，并沿五等分的折线折叠，再沿CD 剪开，使展开后为正五角星（正五边形对角线所构成的图形），则∠OCD 等于（）A ．108°B ．114°C ．126°D ．129°二、填空题（每小题3分，共30分）11、从汽车的后视镜中看见某车车牌的后5位是。

华师大版7年级下册数学第五章生活中的轴对称综合测评(二)

第五章生活中的轴对称综合测评（二）安徽代飞（满分：100分）一、选择题（本大题共10小题，每小题3分，共30分）1.花窗是中国古代园林建筑中窗的一种装饰和美化的形式，既具备实用功能，又带有装饰效应.下列各个窗户不是轴对称图形的是（）“瓦当”是中国古代用以装饰美化建筑物檐头的建筑附件，其图案各式各样，属于中国特有的文化艺术遗产．下列“瓦当”图案中，是轴对称图形的为（）A．B．C．D．2.图1是第21届夏季奥林匹克运动会会徽，会徽中的图案为轴对称图形，它的对称轴有（）A.1条B.2条C. 3条D. 4条3.下列图形中，关于直线l对称的是（）A B C D4.如图2，在△ABC中，AB=AC，CB=CD，若∠A=40°，则∠BDC的度数为（）A. 40°B. 45°C. 55°D. 70°5.下列说法正确的是（）A.过线段中点的直线是该线段的对称轴B. 成轴对称的两条线段一定相等C.两条相等的线段一定关于某条直线成轴对称D. 线段不一定是轴对称图形6.如图3，在△ABC中，∠B=90°，AD平分∠BAC，DE⊥AC，若AB=3，BC=4，AC=5，则CD+DE 的长为（）（）A. 3B. 4C. 5D. 67. 某儿童乐园的平面图如图4所示，根据游客的要求，计划修建一个凉亭，要求从凉亭到摩天轮的距离与凉亭到滑沙的距离和正好等于碰碰车与滑沙之间的距离，则凉亭的修建点M为（）A. 线段AC的垂直平分线与AB的交点B. 线段BC的垂直平分线与AB的交点C. 线段AB的垂直平分线与BC的交点D. 线段AC，BC的垂直平分线的交点8.如图5，在2×2的网格中，已有3个小直角三角形被涂黑，若再涂黑一个小直角三角形，使整个阴影部分是以直线BD为对称轴的轴对称图形，则满足条件的小直角三角形的序号是（）A.①B.②C.③D.④9. 如图6，在△ABC中，∠C=90°，∠B=26°．洋洋按下列步骤作图：①以点A为圆心，小于AC长为半径画弧，分别交AB，AC于点E，F；②分别以点E，F为圆心，大于EF长的一半为半径画弧，两弧相交于点G；③作射线AG，交BC边于点D，则∠ADC的度数为（）A．50°B．52°C．58°D．64°10.如图7，将一张正方形纸片经过两次对折，然后剪去一个小正方形，打开后得到的图形是（）二、填空题（本大题共6小题，每小题3分，共18分）11. 等边三角形是轴对称图形，它有_________条对称轴.12. 如图8，△ABC与△ADE关于直线MN成轴对称，已知∠C=30°，∠D=60°，∠BAD=110°，则∠DAC=______°.13.如图9，在△ABC中，AB=AC，AD为△ABC的角平分线.若S△ABC=24，阴影部分的面积为8，则S△BCE=______.14.随着人们生活水平的不断提高，汽车逐步进入到千家万户，某镇有三条相互交叉的公路（如图10），小红的爸爸想建一个加油站，要求它到三条公路的距离相等，这样可供选择的地址有______处.15. 如图11，在2×2的网格中，小正方形的顶点叫做格点，阴影三角形的顶点都在格点上，这样的三角形叫做格点三角形，若在网格中再画一个格点三角形，使所画格点三角形与阴影三角形成轴对称，则满足条件的三角形有_______个.16. 等腰三角形有一内角的度数为50°，一腰的垂直平分线与另一腰所在直线相交所成的锐角的度数为______.三、解答题（本大题共6小题，共52分）17.（7分）如图12，哪些是轴对称图形？并画出轴对称图形的一条对称轴.18.（7分）如图13，已知△ABC与△DEF关于直线MN成轴对称，其中边AC的对应边是DF，利用尺规作图，画出直线MN，并画出△DEF（保留作图痕迹，不写作法）.19.（8分）（1）如图14，直线AB是一个轴对称图形的对称轴，画出这个轴对称图形的另一半；（2）以直线CD为对称轴，画出与（1）中整个阴影图形成轴对称的图形.20.（8分）如图15，在△ABC中，AB=AC，∠B=30°，BC=12，DE，FG分别垂直平分AB，AC.（1）求△ADF的周长；（2）求∠DAF的度数.21.（10分）如图16，在4×4的网格中，已有5个小正方形被涂黑，请你在每个网格中再涂黑2个小正方形，使整个阴影部分为轴对称图形.22.（12分）如图17，在△ABC中，AB=AC，点E，G分别是BC，AC的中点，延长BA到D，连接BG并延长，交∠DAC的平分线于点F.（1）求∠EAF的度数；（2）线段AF和BC有怎样的关系？并说明理由.附加题（共20分，不计入总分）23.（6分）如图18，四边形ABCD是以直线AC为对称轴的轴对称图形，连接AC，BD，交于点E.作DG⊥BC,点M是线段CE上一个动点，点N是线段CD上一个动点，若DG=4，则MD+MN的最小值为_______.24.（14分）如图19，在△ABC 的一边AB 上有一点P ．（1）能否在另外两边AC 和BC 上各找一点M ，N ，使得△PMN 的周长最短．若能，请画出点M ，N 的位置，若不能，请说明理由；（2）若∠ACB=40°，在（1）的条件下，求出∠MPN 的度数.第五章生活中的轴对称综合测评（二）参考答案一、1. B 2. A 3. C 4. C 5. B 6. B 7. A 8. C 9. C 10. B二、11. 3 12. 20 13. 8 14. 4 15. 4 16. 40°或10°三、17. 解：轴对称图形有①②③，画对称轴略.18. 解：如图1所示.19. 解：如图2所示.20.解：（1）因为DE ，FG 分别垂直平分AB ，AC ，所以AD=BD ，AF=CF.所以AD+AF+DF=BD+DF+CF=BC=12.所以△ADF 的周长为12.（2）因为AB=AC ，∠B=30°，所以∠B=∠C=30°，所以∠BAC=120°.因为AD=BD ，AF=CF ，所以∠BAD=∠B=30°，∠CAF=∠C=30°.所以∠DAF=∠BAC-∠BAD-∠CAF=120°-30°-30°=60°.21. 答案不唯一，合理即可，如图3所示.22.解：（1）因为AB=AC ，点E 是BC 的中点，所以∠CAE=21∠BAC. 因为AF 平分∠DAC ，所以∠CAF=21∠DAC.所以∠EAF=∠CAE+∠CAF=21（∠BAC+∠DAC ）=21∠BAD=21×180°=90°. （2）AF ∥BC ，AF=BC.理由如下：因为AB=AC ，点E 是BC 的中点，所以AE ⊥BC.所以∠AEC=90°.因为∠EAF=90°，所以∠AEC+∠EAF=180°.所以AF ∥BC.所以∠FAG=∠C. 因为AG=CG ，∠AGF=∠CGB ，所以△AFG ≌△CBG.所以AF=BC.23. 424. 解：存在，如图4，点M ，N 即为所求.（2）因为∠ACB=40°，所以∠CMN+∠CNM=180°-40°=140°.根据轴对称的性质，得∠PMA=∠AMP'，∠PNB=∠BNP''.因为∠AMP'=∠CMN ，∠BNP''=∠CNM ，所以2（∠PMA+∠PNB ）=280°.所以∠PMN+∠PNM=360°-280°=80°.所以∠MPN=180°-（∠PMN+∠PNM ）=100°.。

轴对称测试题 华东师大版

华师大版七年级下册轴对称及平移

七年级数学下册《第十章 轴对称、平移与旋》单元测试卷及答案解析-华东师大版

华师大版七年级数学下册《第十章轴对称、平移与旋转》 达标测试卷-带参考答案

最新华东师大版七年级数学下册第十章轴对称、平移与旋转 章末测验 含答案

初中数学华师大版七年级下学期第10章 轴对称、平移与旋转测试卷(含解析)

华师大版七年级下册数学第10章 轴对称、平移与旋转含答案(综合考察)