地大 Matlab机械原理第二次作业2-好学长不留名

合集下载

Matlab运动仿真在机械原理课程设计中的应用

The Apply of Motion Simulation of Linkage Mechanism Base on SimMechanics During Mechanical Principle Course Designing
WANG Jun-Feng， TIAN Li-Ping （Dept. of Mechnicle Engineering,Luoyang Institude of Science and Technology ， Luoyang Henan 471023， China） Abstract： In the process of the mechanical principle course designing mechanical product development, it usually takes the kinematic simu lation to simulate the movement progress and analyse its parameters for the options and identifications of the programmes.Base on establish ment of Four Bar Mechanism ,this paper realize the movement analysis of the linkage mechanism through the SimMechanics model in Matlab and change traditional graphical methods, offer a experience to improve mechanical principle course designing. Key words: mechanical principle， linkage mechanism； motion simulation； simmechnics

MATLAB大作业

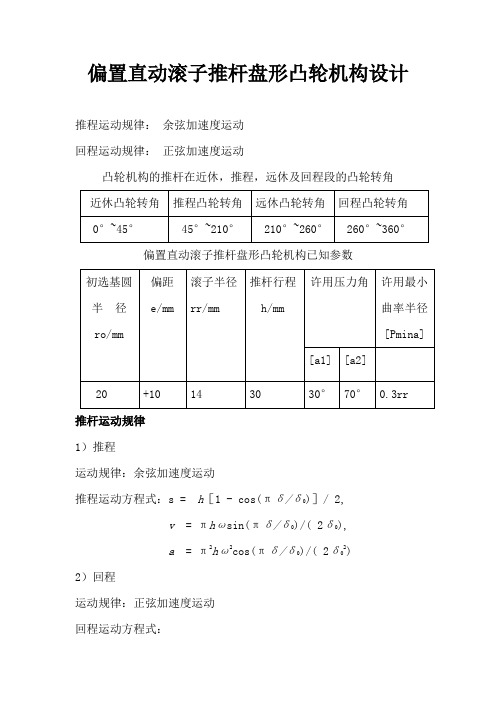
偏置直动滚子推杆盘形凸轮机构设计推程运动规律：余弦加速度运动回程运动规律：正弦加速度运动凸轮机构的推杆在近休，推程，远休及回程段的凸轮转角偏置直动滚子推杆盘形凸轮机构已知参数推杆运动规律1）推程运动规律：余弦加速度运动推程运动方程式：s = h［1 - cos(πδ/δ0)］/ 2,v= πhωsin(πδ/δ0)/( 2δ0),a= π2hω2cos(πδ/δ0)/( 2δ02)2）回程运动规律：正弦加速度运动回程运动方程式：s = h [1-(δ/δ0’)+sin(2πδ/δ0’)/(2π) v = hω [cos(2πδ/δ0’-1)]/δ0’a = -2πhω2sin(2πδ/δ0’)/(δ0’2)滚子中心坐标：x=(s+s0)sinδ+ecosδy=(s+s0)cosδ-ecosδ其中s0=r02−e2实际轮廓曲线坐标：x′=x−r r cosθy′=y−r r sinθ其中sinθdxdδ(dδ)2+(dδ)2cosθ=−dydδ(dδ)2+(dδ)2计算压力角：α=tan−1dsdδ−er02−e2+s计算曲率半径：ρ=dxdδ2+dydδ2 3dδ∙2dδ2−dδ∙2dδ2计算程序符号的表示含义：r0 初选基圆半径x 理论轮廓曲线的x坐标y 理论轮廓曲线的y坐标X 实际轮廓曲线的x坐标Y 实际轮廓曲线的x坐标p 曲率半径s 推杆位移rr 滚子半径 a 压力角paamin 许用最小曲率半径pamin 实际曲率半径的最小值a1max 回程前压力角的最大值a2max 回程后压力角的最大值e 偏距h 推杆行程a1 推程许用压力角a2 回程程许用压力角dar0 每次修正r0所加的长度N 计算点数k1 近休角k2 推程角k3 远休角k4 回程角kamin 实际曲率半径最小值所对应的角度k1max 回程前压力角的最大值所对应的角度k2max 回程后压力角的最大值所对应的角度子程序1计算最大压力角：function [amax,kmax]=yalijiao1(a,N1,b)amax=0;kmax=0;amax=max(a);for i=1:N1if a(i)==amaxkmax=i*b;endendend子程序2计算最小曲率半径：function [pamin,kamin]=qulv(p,b,N)pamin=0;kamin=0;for i=1:N-1p(i)=abs(p(i));endpamin=min(p);for i=1:N-1pamin=min(p)if p(i)==paminkamin=i*b;endendend子程序3计算回程前的压力角及修正r0：function [A,r0]=haha(r0,rr,e,h,a1,dar0,N,k1,k2,k3,k4)N1=(k1+k2)/360*N;eta=pi/180;%化为弧度while(1)s0=(r0^2-e^2)^(1/2);syms k s dk ds d2k d2sn1=k1/360*N;k11=linspace(0,k1,n1);s1=k11./k11.*0;x1=e.*cos(k11.*pi/180)+(s0+s1).*sin(k11.*pi/180);y1=(s0+s1).*cos(k11.*pi/180)-e.*sin(k11.*pi/180);n2=k2/360*N;k22=linspace(k1,k1+k2,n2);s2=(h/2).*(1-cos(pi.*(k22-k1)/k2));x2=e.*cos(k22.*pi/180)+(s0+s2).*sin(k22.*pi/180);y2=(s0+s2).*cos(k22.*pi/180)-e.*sin(k22.*pi/180);x=[x1,x2];y=[y1,y2];k=[k11,k22];s=[s1,s2];dx=diff(x)./diff(k);dk=k(1:end-1);dy=diff(y)./diff(k);dk=k(1:end-1);ds=diff(s)./diff(k);dk=k(1:end-1);ds(N1)=0;for i=1:N1f(i)=(ds(i)-e)/(sqrt(r0^2-e^2)+s(i));a(i)=atan(f(i));%计算a压力角A(i)=abs(a(i))/eta;if A(i)>a1r0=r0+dar0;break;endendif i==N1break;endendend子程序4计算回程后的压力角及修正r0：function [A,r0]=hahaha(r0,rr,e,h,a2,dar0,N,k1,k2,k3,k4) N2=(k3+k4)/360*N;b=360/N;eta=pi/180;%化为弧度while(1)s0=(r0^2-e^2)^(1/2);syms k s dk ds d2k d2sn3=k3/360*N;k33=linspace(k1+k2,k1+k2+k3,n3);s3=k33./k33.*h;x3=e*cos(k33*pi/180)+(s0+h).*sin(k33*pi/180);y3=(s0+h).*cos(k33*pi/180)-e*sin(k33*pi/180);n4=k4/360*N;k44=linspace(k1+k2+k3,k1+k2+k3+k4,n4+1);s4=h.*(1-(k44-k1-k2-k3)./k4+sin(2*pi.*(k44-k1-k2-k3)./k4)/(2*pi));x4=e.*cos(k44*pi/180)+(s0+s4).*sin(k44*pi/180);y4=(s0+s4).*cos(k44*pi/180)-e*sin(k44*pi/180);x=[x3,x4];y=[y3,y4];k=[k33,k44];s=[s3,s4];dx=diff(x)./diff(k);dk=k(1:end-1);dy=diff(y)./diff(k);dk=k(1:end-1);ds=diff(s)./diff(k);dk=k(1:end-1);ds(N2)=0;for i=1:N2f(i)=(ds(i)-e)/(sqrt(r0^2-e^2)+s(i));a(i)=atan(f(i));%计算a压力角A(i)=abs(a(i))/eta;if A(i)>a2r0=r0+dar0;break;endendif i==N2break;endendend子程序5计算曲率半径，并修正r0，计算理论轮廓曲线坐标和实际轮廓曲线的坐标及曲率半径，拖杆位移：function [x,y,X,Y,p,s,r0]=qulvvv(r0,rr,e,h,paamin,dar0,N,k1,k2,k3,k4)eta=pi/180;%化为弧度i=1;while(1)s0=(r0^2-e^2)^(1/2);syms k s dk ds d2k d2sn1=k1/360*N;k11=linspace(0,k1,n1);s1=k11./k11.*0;x1=e.*cos(k11.*pi/180)+(s0+s1).*sin(k11.*pi/180);y1=(s0+s1).*cos(k11.*pi/180)-e.*sin(k11.*pi/180);n2=k2/360*N;k22=linspace(k1,k1+k2,n2);s2=(h/2).*(1-cos(pi.*(k22-k1)/k2));x2=e.*cos(k22.*pi/180)+(s0+s2).*sin(k22.*pi/180);y2=(s0+s2).*cos(k22.*pi/180)-e.*sin(k22.*pi/180);n3=k3/360*N;k33=linspace(k1+k2,k1+k2+k3,n3);s3=k33./k33.*h;x3=e*cos(k33*pi/180)+(s0+h).*sin(k33*pi/180);y3=(s0+h).*cos(k33*pi/180)-e*sin(k33*pi/180);n4=k4/360*N;k44=linspace(k1+k2+k3,k1+k2+k3+k4,n4);s4=h.*(1-(k44-k1-k2-k3)./k4+sin(2*pi.*(k44-k1-k2-k3)./k4)/(2*pi));x4=e.*cos(k44*pi/180)+(s0+s4).*sin(k44*pi/180);y4=(s0+s4).*cos(k44*pi/180)-e*sin(k44*pi/180);x=[x1,x2,x3,x4];y=[y1,y2,y3,y4];k=[k11,k22,k33,k44];s=[s1,s2,s3,s4];dx=diff(x)./diff(k);dk=k(1:end-1);dy=diff(y)./diff(k);dk=k(1:end-1);ds=diff(s)./diff(k);dk=k(1:end-1);d2x=diff(dx)./diff(dk);d2y=diff(dy)./diff(dk);d2y(N)=0;dy(N)=0;dx(N)=0;d2x(N)=0;while(1)p(i)=(dx(i)^2+dy(i)^2)^(3/2)/(dx(i)*d2y(i)-dy(i)*d2x(i));%计算曲率半径pp(i)=abs(p(i))if pp(i)-rr<paaminr0=r0+dar0;i=1;break;elsefor ii=1:Nsino(ii)=dx(ii)/(dx(ii)^2+dy(ii)^2)^0.5;coso(ii)=(-1)*dy(ii)/(dx(ii)^2+dy(ii)^2)^0.5;X(ii)=x(ii)-rr*coso(ii); %定义实际轮廓线的X座标Y(ii)=y(ii)-rr*sino(ii); %定义实际轮廓线的Y座endendi=i+1;if i==Nbreak;endendif i==Nbreak;endendend主程序function[r0,x,y,X,Y,p,s,a,pamin,kamin,a1max,k1max,a2max,k2max]=zuizhong(r0,rr,e,h,a1,a2,paamin,dar0 ,N,k1,k2,k3,k4)N1=(k1+k2)/360*N;N2=(k3+k4)/360*N;b=360/N;eta=pi/180;%化为弧度a11=0;a22=0;s=0;pamin=0;kamin=0;a1max=0;k1max=0;a2max=0; k2max=0;while(1)while(1)[a11,r0]=haha(r0,rr,e,h,a1,dar0,N,k1,k2,k3,k4);%计算符合推程许可压力角的修正的r0r1=r0;[a22,r0]=hahaha(r0,rr,e,h,a2,dar0,N,k1,k2,k3,k4);%计算符合回程许可压力角的修正的r0r2=r0;if r0~=r1break;else[x,y,X,Y,p,s,r0]=qulvvv(r0,rr,e,h,paamin,dar0,N,k1,k2,k3,k4);%计算满足最小许可曲率半径条件的修正的r0，计算实际轮廓曲线坐标和理论轮廓曲线坐标，及曲率半径r3=r0;if r0~=r2break;endendif r0==r3break;endendif r0==r3break;endend[paminkamin]=qulv(p,b,N);[a1max k1max]=yalijiao1(a11,N1,b);[a2max k2max]=yalijiao1(a22,N2,b);a=[a11 a22];figure(1);plot(x,y);hold on;t=linspace(0,2*pi,N);x=r0*cos(t);y=r0*sin(t);plot(0,0,'*',x,y,X,Y);title('凸轮的理论轮廓曲线');axis([-70,70,-70,70]);axis square;end只需输入[r0,x,y,X,Y,p,s,a,pamin,kamin,a1max,k1max,a2max,k2max]=zuizhong(20,14,10,30,40,70,4.2,1,72 ,45,165,50,100)即可得到所需图形和数据。

机械原理习题全解

c ∈ [340 , 600 )
c ∈ [600 ,860 ]
c ∈ [140 , 240 ]
非最短杆， 240 ≤ c ≤ 600 （2）c非最短杆，）非最短杆 c ∈ [240 , 340 240 + 600 ≥ c + 500 也非最长杆 c > 600 为最长杆，（3）c为最长杆，）为最长杆 c ∈ [860 ,1340 240 + c ≥ 600 + 500 且满足安装条件 c ≤ 600 + 240 + 500 综合以上结果，综合以上结果，得：c ∈ 140,1340
习题集 3-1
P34在∞ P24
P13
P12
P23
P12 P23 P14 P34 P13
P14
P12 P14 P23 P34 P24
作业: 作业习题集 3-1
P13在∞
P12 P23
作业: 作业习题集 3-1
P13
P34在∞
P14 P23 P24 P12 P14 P23 P34 P24
P12 P12 P23 P14 P34 P13
作业: 习题集 2-2 作业
解：
5 4 3 2 1
n=4 pl = 4 ph = 2 F’ = 1 F= 3n- (2pl+ph) - F’ = 1 机构自由度数=机构原动件数机构自由度数机构原动件数所以，机构具有确定的运动。所以，机构具有确定的运动。
作业: 习题集 2-2 作业
4 3 2 1 5
a +e αmax = arcsin( ) b
a +e γ min = −αmax = − arcsin( ) 2 2 b

机械原理课程设计matlab程序及成果图

Wjr_main.m%1.输入已知数据clear;l2=0.1605;%AB的长度单位ml4=0.6914;%CD的长度单位ml5=0.2074;%DE的长度单位ml1=0.370;%AC的长度单位ml1p=0.6572;%CF的长度单位momg2=8.378;af2=0;hd=pi/180;du=180/pi;%2.调用子函数abc.m计算牛头刨机构位移，角速度，角加速度for n1=1:689;tt2(n1)=-0.4488+(n1-1)*hd;ll=[l2,l4,l5,l1,l1p];[tt,omg,af]=abc(tt2(n1),omg2,af2,ll);s4(n1)=tt(1);tt4(n1)=tt(2);tt5(n1)=tt(3);sE(n1)=tt(4);v34(n1)=omg(1);omg4(n1)=omg(2);omg5(n1)=omg(3);vE(n1)=omg(4);a3(n1)=af(1);af4(n1)=af(2);af5(n1)=af(3);aE(n1)=af(4);end%3.位移，角速度，角加速度figure(1);n1=1:689;t=(n1-1)*pi/180;subplot(2,2,1); %绘角位移及位移线图plot(t,tt4*du,'r-.');grid on;hold on;axis auto;[haxes,hline1,hine2]=plotyy(t,tt5*du,t,sE);grid on;hold on;xlabel('时间/份');axes(haxes(1));ylabel('角位移/\circ');axes(haxes(2));ylabel('位移/m');hold on;grid on;text(1.15,-0.65,'tt_4');text(3.4,0.27,'tt_5');text(2.25,-0.15,'s_E');subplot(2,2,2); %绘角速度及速度线图plot(t,omg4,'r-.');grid on;hold on;axis auto;[haxes,hline1,hline2]=plotyy(t,omg5,t,vE); grid on;hold on;xlabel('时间/份')axes(haxes(1));ylabel('角速度/rad\cdots^{-1}')axes(haxes(2));ylabel('速度/m\cdots^{-1}')hold on;grid on;text(3.1,0.35,'\omg_4')text(2.1,0.1,'\omg_5')text(5.5,0.45,'v_E')subplot(2,2,3); %绘角加速度和加速度图plot(t,af4,'r-.');grid on;hold on;axis auto;[haxes,hline1,hline2]=plotyy(t,af5,t,aE); grid on;hold on;xlabel('时间/份')axes(haxes(1));ylabel('角加速度/rad\cdots^{-2}')axes(haxes(2));ylabel('加速度/m\cdots^{-2}')hold on;text(1.5,0.3,'\af_4')text(3.5,0.51,'\af_5')text(1.5,-0.11,'a_E')wjr_abc.mfunction[tt,omg,af]=abc(tt2,omg2,af2,ll)l2=ll(1);l4=ll(2);l5=ll(3);l1=ll(4);l1p=ll(5);%1.计算角位移和线位移s4=sqrt((l2*cos(tt2))*(l2*cos(tt2))+(l1+l2*sin(tt2))*(l1+l2*sin(tt2))); tt4=acos((l2*cos(tt2))/s4);tt5=asin((l1p-l4*sin(tt4))/l5);sE=l4*cos(tt4)+l5*cos(tt5);tt(1)=s4;tt(2)=tt4;tt(3)=tt5;%2.计算角速度和线速度A=[cos(tt4),-s4*sin(tt4),0,0; %速度分析矩阵之从动件位置参数矩阵sin(tt4),s4*cos(tt4),0,0;0,-l4*sin(tt4),-l5*sin(tt5),-1;0,l4*cos(tt4),l5*cos(tt5),0];B=[-l2*sin(tt2); %原动件位置参数矩阵l2*cos(tt2);0;0];omg=A\(omg2*B);v34=omg(1);omg4=omg(2);omg5=omg(3);vE=omg(4);%计算角加速度和加速度A=[cos(tt4),-s4*sin(tt4),0,0; %速度分析矩阵之从动件位置参数sin(tt4),s4*cos(tt4),0,0;0,-l4*sin(tt4),-l5*sin(tt5),-1;0,l4*cos(tt4),l5*cos(tt5),0];At=[-omg4*sin(tt4),-v34*sin(tt4)-s4*omg4*cos(tt4),0,0;omg4*cos(tt4),v34*cos(tt4)-s4*omg4*sin(tt4),0,0;0,-l4*omg4*cos(tt4),-l5*omg5*cos(tt5),0;0,-l4*omg4*sin(tt4),-l5*omg5*sin(tt5),0];Bt=[-l2*omg2*cos(tt2);-l2*omg2*sin(tt2);0;0];af=A\(-At*omg+omg2*Bt);a34=af(1);af4=af(2);af5=af(3);aE=af(4);wjr_force.m%1.输入已知数据clear;l2=0.1605;%AB的长度单位ml4=0.6914;%CD的长度单位ml5=0.2074;%DE的长度单位ml1=0.370;%AC的长度单位ml1p=0.6572;%CF的长度单位momg2=8.378;%单位rad/shd=pi/180;du=180/pi;H=0.6;%行程单位msEmax=0.5046; sEmin=0.0954;%单位mJs4=0.9; Js5=0.015;%单位kgm^2g=9.8;%单位m/s^2m4=22; m5=3; m6=52;%kgG4=196; G5=29.4; G6=509.6;%单位NFc=1400;%2.机构运动分析% 位移及角位移for n1=1:689;tt2(n1)=-0.4488+(n1-1)*hd;s4(n1)=sqrt((l2*cos(tt2(n1)))*(l2*cos(tt2(n1)))+(l1+l2*sin(tt2(n1)))*(l1+l2 *sin(tt2(n1))));tt4(n1)=acos((l2*cos(tt2(n1)))/s4(n1));tt5(n1)=asin((l1p-l4*sin(tt4(n1)))/l5);sE(n1)=l4*cos(tt4(n1))+l5*cos(tt5(n1));end%2.计算角速度和线速度for n1=1:689;A=[cos(tt4(n1)),-s4(n1)*sin(tt4(n1)),0,0; %速度分析矩阵之从动件位置参数sin(tt4(n1)),s4(n1)*cos(tt4(n1)),0,0;0,-l4*sin(tt4(n1)),-l5*sin(tt5(n1)),-1;0,l4*cos(tt4(n1)),l5*cos(tt5(n1)),0];B=[-l2*sin(tt2(n1)); %原动件位置参数矩阵l2*cos(tt2(n1));0;0];omg=A\(omg2*B);v34(n1)=omg(1);omg4(n1)=omg(2);omg5(n1)=omg(3);vE(n1)=omg(4);%计算角加速度和加速度A=[cos(tt4(n1)),-s4(n1)*sin(tt4(n1)),0,0; %速度分析矩阵之从动件位置参数sin(tt4(n1)),s4(n1)*cos(tt4(n1)),0,0;0,-l4*sin(tt4(n1)),-l5*sin(tt5(n1)),-1;0,l4*cos(tt4(n1)),l5*cos(tt5(n1)),0];At=[-omg4(n1)*sin(tt4(n1)),-v34(n1)*sin(tt4(n1))-s4(n1)*omg4(n1)*cos(tt4(n1)),0,0;omg4(n1)*cos(tt4(n1)),v34(n1)*cos(tt4(n1))-s4(n1)*omg4(n1)*sin(tt4(n1 )),0,0;0,-l4*omg4(n1)*cos(tt4(n1)),-l5*omg5(n1)*cos(tt5(n1)),0;0,-l4*omg4(n1)*sin(tt4(n1)),-l5*omg5(n1)*sin(tt5(n1)),0];Bt=[-l2*omg2*cos(tt2(n1));-l2*omg2*sin(tt2(n1));0;0];af=A\(-At*omg+omg2*Bt);a34(n1)=af(1);af4(n1)=af(2);af5(n1)=af(3);aE(n1)=af(4);end%3.机构的力平衡计算for n1=1:689;%计算各铰链点坐标xa=0;ya=l1;xb(n1)=l2*cos(tt2(n1));yb(n1)=l1+l2*sin(tt2(n1));xc=0;yc=0;xd(n1)=l4*cos(tt4(n1));yd(n1)=l4*sin(tt4(n1));xe(n1)=sE(n1);ye=l1p;%计算各质心坐标xs4(n1)=(xc+xd(n1))/2;ys4(n1)=(yc+yd(n1))/2;xs5(n1)=(xd(n1)+xe(n1))/2;ys5(n1)=(yd(n1)+ye)/2;xs6=0.15;%各质心点加速度as4x(n1)=-l4*(af4(n1)*sin(tt4(n1))+omg4(n1)^2*cos(tt4(n1)))/2;as4y(n1)=l4*(af4(n1)*cos(tt4(n1))-omg4(n1)^2*sin(tt4(n1)))/2;adx=-l4*(af4(n1)*sin(tt4(n1))+omg4(n1)^2*cos(tt4(n1)));ady=l4*(af4(n1)*cos(tt4(n1))-omg4(n1)^2*sin(tt4(n1)));as5x(n1)=adx+l5*(af5(n1)*sin(tt5(n1))+omg5(n1)^2*cos(tt5(n1)))/2; as5y(n1)=ady+l5*(af5(n1)*cos(tt5(n1))-omg5(n1)^2*sin(tt5(n1)))/2; as6(n1)=aE(n1);%惯性力及惯性力矩F4x(n1)=-m4*as4x(n1);F4y(n1)=-m4*as4y(n1);F5x(n1)=-m5*as5x(n1);F5y(n1)=-m5*as5y(n1);F6(n1)=-m6*as6(n1);M4(n1)=-Js4*af4(n1);M5(n1)=-Js5*af5(n1);%未知力系数矩阵xya=zeros(15);xya(1,2)=-1;xya(1,4)=-1;xya(2,3)=-1;xya(2,5)=-1;xya(3,1)=1;xya(3,4)=yb(n1)-ya;xya(3,5)=xa-xb(n1);xya(4,4)=1;xya(4,6)=-1;xya(5,5)=1;xya(5,7)=-1;xya(6,6)=cos(tt4(n1));xya(6,7)=sin(tt4(n1));xya(7,6)=1; xya(7,8)=-1;xya(7,10)=-1;xya(8,7)=1;xya(8,9)=-1;xya(8,11)=-1;xya(9,6)=ys4(n1)-yb(n1);xya(9,7)=xb(n1)-xs4(n1);xya(9,8)=yc-ys4(n1); xya(9,9)=xs4(n1)-xc;xya(9,10)=yd(n1)-ys4(n1);xya(9,11)=xs4(n1)-xd(n1);xya(10,10)=1;xya(10,12)=-1;xya(11,11)=1;xya(11,13)=-1;xya(12,10)=ys5(n1)-yd(n1); xya(12,11)=xd(n1)-xs5(n1);xya(12,12)=ye-ys4(n1);xya(12,13)=xs5(n1)-xe(n1);xya(13,12)=1;xya(14,13)=1;xya(14,14)=-1;xya(15,13)=xs6;xya(15,15)=1;%已知力矩阵if vE(n1)<0&sE(n1)>=(sEmin+0.05*H)&sE(n1)<=(sEmax-0.05*H)D=[0;0;0;0;0;0;-F4x(n1);-F4y(n1)+G4;-M4(n1);-F5x(n1);-F4y(n1)+G5;-M5( n1);-Fc-F6(n1);G6;0;];elseD=[0;0;0;0;0;0;-F4x(n1);-F4y(n1)+G4;-M4(n1);-F5x(n1);-F4y(n1)+G5;-M5( n1);-F6(n1);G6;0;];end%未知力矩阵FR=inv(xya)*D;M2(n1)=FR(1);FR12x(n1)=FR(2);FR12y(n1)=FR(3);FR45x(n1)=FR(10);FR45y(n1)=FR(11);FR16(n1)=FR(14);M6(n1)=FR(15);end%4.输出力的分析图figure(2);n1=1:689;t=(n1-1)*2*pi/360;subplot(2,2,1); %绘平衡力矩图plot(t,M2);grid on;hold on;axis auto;title('平衡力矩M_2')xlabel('时间/份');ylabel('力矩/N\cdotm');hold on;grid on;text(3.8,880,'M_2');subplot(2,2,2); %绘A处x方向约束反力即FR12x plot(t,FR12x,'-');grid on;hold on;axis auto;title('转动副A处约束反力')xlabel('时间/份');ylabel('力/N');hold on;grid on;text(1.1,5000,'F_R_1_2_x')plot(t,FR12y,'r-.'); %绘A处y方向约束反力即FR12y grid on;hold on;text(1.1,-3000,'F_R_1_2_y')subplot(2,2,3); %绘移动副FR16plot(t,-FR16);grid on;hold on;axis auto;title('移动副6约束反力F_R_1_6')xlabel('时间/份')ylabel('力/N')grid on;hold on;text(1.5,3100,'F_R_1_6')subplot(2,2,4); %绘转动副D处约束反力plot(t,FR45x,'-');grid on;hold on;axis auto;title('转动副D处约束反力')xlabel('时间/份')ylabel('力/N')grid on;hold on;text(1.1,-900,'F_R_4_5_x')plot(t,FR45y,'r-.');grid on;hold on;text(1.1,-3700,'F_R_4_5_y')。

机械原理matlab编程

机械原理（Matlab绘图）专业班级学号姓名：图一：导杆的角位移曲线和刨刀的位移曲线x1=linspace(0,2*pi,100);l1=100;l3=360;l4=200;l6=200；y=336;w1=2*pi;x3=atan((l6+l1*sin(x1))./(l1*cos(x1)));for i = 1 : 100;if x3(i)<0x3(i)=x3(i)+pi;endendS3=l1*cos(x1)./cos(x3);V23=(-1)*w1*l1*sin(x1-x3);w3=w1*l1*cos(x1-x3)./S3;a23=w3.^2.*S3-w1.^2*l1*cos(x1-x3);A3=(w1.^2.*l1.*sin(x3-x1)-2.*w3.*V23)./S3;x4= atan((y-l3*sin(x3))./l4);Se=l3*cos(x3)+l4*cos(x4);w4=(-1)*w3.*l3.*cos(x3)./(l4.*cos(x4));Ve=(-1)*w3.*l3.*sin(x3-x4)./cos(x4);A4=(x3.^2.*l3.*sin(w3)+x4.^2.*l4.*sin(x4)-A3.*l3.*cos(x3))./(l4.*cos(x4)); ae=(-1)*(A3.*l3.*sin(x3-x4)+w3.^2.*l3.*cos(x3-x4)-w4.^2.*l4)./cos(x4); plotyy(180*x1./pi,180*x3./pi,180*x1./pi,Se/1000);xlabel('x1/(°)'),ylabel('x3(°)');title('导杆的角位移曲线和刨刀的位移曲线');text(150,108,'x3');text(200,60,'Se');grid on;plotedit on;图二：导杆的角速度曲线和刨刀的速度曲线x1=linspace(0,2*pi,100);l1=100;l3=360;l4=200;l6=200;y=336;w1=2*pi;x3=atan((l6+l1*sin(x1))./(l1*cos(x1)));for i = 1 : 100;if x3(i)<0x3(i)=x3(i)+pi;endendS3=l1*cos(x1)./cos(x3);V23=(-1)*w1*l1*sin(x1-x3);w3=w1*l1*cos(x1-x3)./S3;a23=w3.^2.*S3-w1.^2*l1*cos(x1-x3);A3=(w1.^2.*l1.*sin(x3-x1)-2.*w3.*V23)./S3;x4= atan((y-l3*sin(x3))./l4);Se=l3*cos(x3)+l4*cos(x4);w4=(-1)*w3.*l3.*cos(x3)./(l4.*cos(x4));Ve=(-1)*w3.*l3.*sin(x3-x4)./cos(x4);A4=(x3.^2.*l3.*sin(w3)+x4.^2.*l4.*sin(x4)-A3.*l3.*cos(x3))./(l4.*cos(x4)); ae=(-1)*(A3.*l3.*sin(x3-x4)+w3.^2.*l3.*cos(x3-x4)-w4.^2.*l4)./cos(x4); plotyy(180*x1./pi,w3,180*x1./pi,Ve/1000);xlabel('x1/(°)'),ylabel('w3(rad/s)');title('导杆的角速度曲线和刨刀的速度曲线');grid on;text(100,-5,'Ve');text(100,1.8,'w3');axis([0 400 -7 4]);plotedit on;图三：导杆的角加速度曲线和刨刀的加速度曲线x1=linspace(0,2*pi,100);l1=100;l3=360;l4=200;l6=200;y=336;w1=2*pi;x3=atan((l6+l1*sin(x1))./(l1*cos(x1)));for i = 1 : 100;if x3(i)<0x3(i)=x3(i)+pi;endendS3=l1*cos(x1)./cos(x3);V23=(-1)*w1*l1*sin(x1-x3);w3=w1*l1*cos(x1-x3)./S3;a23=w3.^2.*S3-w1.^2*l1*cos(x1-x3);A3=(w1.^2.*l1.*sin(x3-x1)-2.*w3.*V23)./S3;x4= atan((y-l3*sin(x3))./l4);Se=l3*cos(x3)+l4*cos(x4);w4=(-1)*w3.*l3.*cos(x3)./(l4.*cos(x4));Ve=(-1)*w3.*l3.*sin(x3-x4)./cos(x4);A4=(x3.^2.*l3.*sin(w3)+x4.^2.*l4.*sin(x4)-A3.*l3.*cos(x3))./(l4.*cos(x4)); ae=(-1)*(A3.*l3.*sin(x3-x4)+w3.^2.*l3.*cos(x3-x4)-w4.^2.*l4)./cos(x4); plotyy(180*x1./pi,A3,180*x1./pi,ae/1000);xlabel('x1/(°)'),ylabel('A3(rad/s^2)'),grid;title('导杆的角加速度曲线和刨刀的加速度曲线');text(250,25,'ae');text(300,50,'A3');plotedit on;图四：凸轮从动件位移曲线h=20;F1=2*pi/3;F2=pi/2;i=1;for x=0:0.01:2*pi;if x>=0&x<=2*pi/3;S(i)=h*(1-cos(pi*x./F1))./2;elseif x>=2*pi/3&x<=pi;S(i)=h;elseif x>=pi&x<=5*pi/4;S(i)=h-2*h*(x-pi).^2./(F2.^2);elseif x>=5*pi/4 &x<=3*pi/2;S(i)= 2*h*(F2-x+pi).^2./(F2.^2); elseif x>=3*pi/2 &x<=2*pi;S(i)=0;endi=i+1;x=0:0.01:2*pi;plot(x,S);title('从动件位移曲线');axis([0 7 0 25]);xlabel('x/(rad)');ylabel('S/(mm)');grid on;图五：凸轮的理论轮廓曲线和实际轮廓曲线e=10;Rt=10;Rb=25;w=2*pi;F1=2*pi/3;F2=pi/2;i=1;for f=0:0.01:2*pi;if f>=0&f<=2*pi/3;S(i)=h*(1-cos(pi*f./F1))./2;elseif f>=2*pi/3&f<=pi;S(i)=h;elseif f>=pi&f<=5*pi/4;S(i)=h-2*h*(f-pi).^2./(F2.^2);elseif f>=5*pi/4 &f<=3*pi/2;S(i)= 2*h*(F2-f+pi).^2./(F2.^2);elseif f>=3*pi/2 &f<=2*pi;S(i)=0;endi=i+1;endf=0:0.01:2*pi;s0=sqrt((Rb.^2)-(e.^2));x =e*cos(f)+(s0+S).*sin(f);y =(s0+S).*cos(f)-e*sin(f);d1=e*(-1).*sin(f).*w+(s0+S).*cos(f).*w;d2=(s0+S).*sin(f).*(-1).*w-e*cos(f).*w;x1=x+Rt*d2./sqrt((d1.^2)+(d2.^2));y1=y-Rt*d1./sqrt((d1.^2)+(d2.^2));plot(x,y,'k-',x1,y1,'k-.');title('凸轮的理论轮廓曲线和实际轮廓曲线'); text(-10,-30,'实际轮廓曲线');text(-10,-40,'理论轮廓曲线');axis([-40 50 -55 40 ]);hold on;plot(0,0);text(0,-3,'O');。

matelab作业2参考答案

matelab作业2参考答案Matlab作业2参考答案Matlab作业2是一项综合性的任务，要求学生运用Matlab编程语言解决一系列数学问题。

本文将为大家提供一份参考答案，帮助学生更好地理解和完成这项作业。

首先，我们将讨论作业的第一个问题，即给定一个矩阵A，求解其特征值和特征向量。

在Matlab中，可以使用eig函数来实现这一功能。

例如，假设我们有一个3×3的矩阵A，可以按照以下方式计算其特征值和特征向量：```A = [1 2 3; 4 5 6; 7 8 9];[eigenvectors, eigenvalues] = eig(A);```在上述代码中，变量eigenvectors将存储A的特征向量，而变量eigenvalues 将存储A的特征值。

通过打印这两个变量的值，我们可以得到矩阵A的特征值和特征向量。

接下来，我们将探讨作业的第二个问题，即求解线性方程组。

假设我们有一个3×3的系数矩阵A和一个3×1的常数向量b，我们需要求解方程组Ax=b。

在Matlab中，可以使用backslash运算符来求解线性方程组。

例如，假设我们有以下方程组：```A = [1 2 3; 4 5 6; 7 8 9];b = [10; 20; 30];x = A \ b;```在上述代码中，变量x将存储方程组的解。

通过打印变量x的值，我们可以得到方程组的解。

此外，作业的第三个问题要求学生使用Matlab绘制函数图像。

在Matlab中，可以使用plot函数来实现这一功能。

例如，假设我们要绘制函数y=sin(x)，其中x的取值范围为0到2π，可以按照以下方式绘制函数图像：```x = 0:0.1:2*pi;y = sin(x);plot(x, y);```在上述代码中，变量x将存储x的取值范围，变量y将存储对应的函数值。

通过调用plot函数，我们可以将函数y=sin(x)的图像绘制出来。

机械原理matlab课程设计

机械原理matlab课程设计一、教学目标本课程的学习目标主要包括知识目标、技能目标和情感态度价值观目标。

知识目标要求学生掌握机械原理的基本概念、理论和方法；技能目标要求学生能够运用MATLAB软件进行机械系统仿真和分析；情感态度价值观目标要求学生培养创新意识、团队合作精神和自主学习能力。

通过本课程的学习，学生将能够：1.描述和解释机械原理的基本概念和理论。

2.使用MATLAB软件进行机械系统仿真和分析。

3.提出问题、解决问题并开展创新设计。

4.能够进行团队合作，共同完成项目任务。

二、教学内容教学内容将根据课程目标进行选择和，确保内容的科学性和系统性。

教学大纲将明确教学内容的安排和进度，指出教材的章节和列举内容。

主要内容包括：1.机械原理的基本概念和理论，包括力学、动力学、运动学等方面。

2.MATLAB软件的基本操作和功能，包括矩阵运算、绘图、编程等。

3.机械系统仿真的方法和技巧，包括模型建立、参数调整、结果分析等。

4.机械系统设计案例分析，包括机器人的运动控制、机构的优化设计等。

三、教学方法为了激发学生的学习兴趣和主动性，将采用多种教学方法。

包括讲授法、讨论法、案例分析法和实验法等。

1.讲授法：通过教师的讲解和演示，向学生传授基本概念和理论知识。

2.讨论法：学生进行小组讨论，促进学生之间的交流和思维碰撞。

3.案例分析法：通过分析实际案例，引导学生运用所学知识解决实际问题。

4.实验法：安排实验课程，让学生亲自动手进行实验操作和数据分析。

四、教学资源为了支持教学内容和教学方法的实施，将选择和准备适当的教学资源。

包括教材、参考书、多媒体资料和实验设备等。

1.教材：选择权威、实用的教材，作为学生学习的主要参考资料。

2.参考书：推荐一些相关的参考书籍，供学生深入学习和拓展知识。

3.多媒体资料：制作精美的PPT、教学视频等多媒体资料，增强课堂教学的趣味性和效果。

4.实验设备：准备必要的实验设备，让学生能够进行实际操作和验证。

机械原理matlab作业

1．在图示的铰链四杆机构中，AB 为主动杆，以s rad /47.10=ω匀角速度逆时针旋转，各杆长度分别为mm l mm l mm l mm l 80,100,120,404321====，连杆点F 的位置是FE ⊥BC ，BE 长mm S 60=，EF 长mm T 10=，选取直角坐标系如图所示。

求当曲柄1与x 轴正向夹角为 360~01=ϕ时，连杆2和摇杆3所转过的角度2ϕ、3ϕ以及它们的角速度和角加速度2ω、3ω、2α、3α，并求出连杆点F 的各位置坐标、速度和加速度。

规定ϕ角从轴x 正向测量时，逆时针为正，反之为负。

y机械原理作业撰写要求机械原理电算分析是机械原理课程学习的重要环节，是检验学生综合素质与实践能力培养的手段。

1、作业内容顺序作业内容顺序一般为：题目、数学模型、程序设计、计算结果和附件M 文件。

2、作业格式要求作业格式要求见摸板，纸张大小一律使用A4复印纸。

3. 书写规定 3.1公式公式号按顺序编号，如（2）表示第2个公式。

公式应采用公式编辑器输入，选择默认格式，公式号右对齐，公式调整至基本居中。

3.2 插表每个表格均应有标题（由表序和表名组成），如第一个插表的序号为“表1”。

表格统一用三线表，表序与表名之间空一格，表名中不允许使用标点符号，表名后不加标点。

标题置于表上，要求用5号字(包括表中的内容)。

3.3 插图插图应与文字紧密配合，文图相符，内容正确。

图题置于图的下方，要求用5号字。

插图应采用AutoCAD 绘制，然后拷贝粘贴到Word 文档，以利于以后编辑。

3.4物理量的名称、符号和计量单位物理量的名称、符号和计量单位应统一按照机械原理教科书的规定书写，某一量的名称、符号和计量单位应与教科书的规定相一致。

4. 排版要求4.1正文字体要求、每部分标题左顶边、小三宋体加粗。

正文文字用宋体小四号汉字和四号“Times New Roman”英文字体，每自然段首行缩进2个字符。

（完整版）MATLAB作业2参考答案

（完整版）MATLAB作业2参考答案MATLAB 作业⼆参考答案1、试求出如下极限。

【求解】极限问题可以由下⾯语句直接求解。

>> syms x; f=(x+2)A(x+2)*(x+3)A(x+3)/(x+5F(2*x+5); limit(f,x,i nf) ans = exp(-5) >> syms x yfa=(x A 2*y+x*y A 3)/(x+y)A 3; limit(limit(fa,x,-1),y,2) ans = -6>> fc=(1-cos(xA2+yA2))*exp(xA2+yA2)/(xA2+yA2); limit(limit(fc,x,O),y,O) ans = 02、试求出下⾯函数的导数。

(1) y(x) . xsinx 、1e x , (2) atan yIn(x 2 y 2)x【求解】由求导函数diff() 可以直接得出如下结果，其中 (2)为隐函数，故需要⽤隐函数求导公式得出导数。

>> syms x;f=sqrt(x*si n( x)*sqrt(1-exp(x))); simple(diff(f)) ans =1/2/(x*s in (x)*(1-exp(x))A(1/2))A(1/2)*(si n(x)*(1-exp(x))A(1/2)+ x*cos(x)*(1-exp(x))A(1/2)-1/2*x*sin (x)/(1-exp(x))A(1/2)*exp(x)) >> syms x,y; f=ata n(y /x)_log(xA2+yA2); f1=simple(-diff(f,x)/diff(f,y)) f1 =(y+2*x)/(x-2*y)2 23、假设U cos 1 J *，试验证⼀———。

\y x y y x【求解】证明⼆者相等亦可以由⼆者之差为零来证明，故由下⾯的语句直接证明。

>> syms x y; u=acos(x/y); diff(diff(u,x),y)-diff(diff(u,y),x) ans =(1) limx (x 2)x 2(x 3)x3(x 5)2x 52..x y lim y 21(x xy 3y)3H xy2Xos2Xe2o o2xyt 2x2f2f2f4、假设 f (x, y) e dt ，试求 22 2y x x yy【求解】由下⾯的命令可以得出所需结果。

matlab机电系统仿真大作业

曲柄滑块机构运动学仿真1、设计任务描述通过分析求解曲柄滑块机构动力学方程，编写matlab 程序并建立Simulink 模型，由已知的连杆长度和曲柄输入角速度或角加速度求解滑块位移与时间的关系，滑块速度和时间的关系，连杆转角和时间的关系以及滑块位移和滑块速度与加速度之间的关系，从而实现运动学仿真目的。

2、系统结构简图与矢量模型下图所示是只有一个自由度的曲柄滑块机构，连杆与长度已知图2-1 曲柄滑块机构简图设每一连杆（包括固定杆件）均由一位移矢量表示，下图给出了该机构各个杆件之间的矢量关系图2-2 曲柄滑块机构的矢量环3．匀角速度输入时系统仿真3.1 系统动力学方程系统为匀角速度输入的时候，其输入为输出为；(1) 曲柄滑块机构闭环位移矢量方程为:(2) 曲柄滑块机构的位置方程(3) 曲柄滑块机构的运动学方程通过对位置方程进行求导，可得由于系统的输出是与，为了便于建立A*x=B 形式的矩阵，使x=[ ],将运动学方程两边进行整理，得到将上述方程的v1 与w3 提取出来，即可建立运动学方程的矩阵形式3.2 M 函数编写与Simulink 仿真模型建立3.2.1 滑块速度与时间的变化情况以及滑块位移与时间的变化情况仿真的基本思路：已知输入w2 与，由运动学方程求出w3 和v1，再通过积分，即可求出与r1。

(1) 编写Matlab 函数求解运动学方程将该机构的运动学方程的矩阵形式用M 函数compv(u)来表示。

设r2=15mm，r3=55mm，r1(0)=70mm，。

其中各个零时刻的初始值可以在Simulink 模型的积分器初始值里设置M 函数如下：function [x]=compv(u) %u(1)=w2%u(2)=sita2%u(3)=sita3 r2=15; r3=55;a=[r3*sin(u(3)) 1;-r3*cos(u(3)) 0]; b=[-r2*u(1)*sin(u(2));r2*u(1)*cos(u(2))]; x=inv(a)*b;2) 建立Simulink 模型M 函数创建完毕后，根据之前的运动学方程建立Simulink 模型，如下图：图3-1 Simulink 模型同时不要忘记设置r1 初始值70，如下图：图3-2 r1 初始值设置设置输入角速度为150rad/s ，运行时间为0.1s ，点击运行，即可从示波器中得到速度和时间以及位移和时间的图像3.2.2 滑块位移和滑块速度之间的图像为了得到滑块位移和滑块速度之间的图像，需要通过to workspace 模块将simulink 里位移和时间的数据传递到Matlab 的工作区中，从而在M 文件中再次利用，从Simulink 模块传递到工作区的数据的名称是simout。

Matlab在机械设计中的应用大作业

Matlab在机械设计中的应⽤⼤作业Matlab在机械设计中的应⽤⼤作业1、试⽤解析综合法设计⼀个曲柄摇杆机构。

已知机构⾏程速度变化系数 1.25k=，摇杆CD的长度3250mml=，摆⾓30ψ=，要求机构的最⼩传动⾓minγ≥40。

确定曲柄摇杆机构各构件杆长调⽤函数的编制：function f=funct(x)k=1.25;theta=pi*(k-1)/(k+1);yg=250;pis=pi/6gamin=2*pi/9f1=(x(2)+x(1))^2+(x(2)-x(1))^2-2*(x(2)+x(1))*(x(2)-x(1))*cos(theta)-(2*yg*sin(pis/2))^2; f2=yg^2+x(3)^2-2*yg*x(3)*cos(x(4))-(x(2)-x(1))^2;f3=yg^2 +x(3)^2-2*yg*x(3)*cos(x(4)+pis)-(x(2)+x(1))^2;f4=yg^2+x(2)^2-2*yg*x(2)*cos(gamin)-(x(3)-x(1))^2;f=[f1;f2;f3;f4];主函数：>> x0=[50 120 200 0.5];>> k=1.25;>> theta=pi*(k-1)/(k+1);>> yg=250;>> gamin=2*pi/9;>> x=fsolve(@funct,x0)求解结果：Equation solved.fsolve completed because the vector of funct values is near zeroas measured by the default value of the funct tolerance, andthe problem appears regular as measured by the gradient.x =62.9934 105.9045 245.0702 0.17242、四连杆机构如图1 所⽰，已知各构件的尺⼨L1, L2, L3, L4及原动件1的⾓位移θ1和等⾓速度ω1，求构件2和3的⾓位移θ 2 ,θ3，⾓速度ω2,ω3，⾓加速度ε2,ε3。

MATLAB-第二次实验课课堂作业

M A T L A B-第二次实验课课堂作业(4学时)(共4页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--MATLAB 第二次实验课课堂作业（4学时）注：1）此课堂作业作为本课程结业成绩的重要依据，请同学们认真、独立完成，不得抄袭。

2）请在授课教师规定的时间内完成；3）完成作业后，请以word格式保存，文件名为：学号+姓名1.请完成如下4小题：1) 在区间[0,1]s上生成均匀分布的长度为20的向量A。

2) 请生成均值为、方差为的5阶正态分布随机矩阵B。

2) 生成长度为100的单位阶跃序列，阶跃点n0＝25。

用离散信号图示。

3）幅度为1V，频率为5Hz的正弦信号和（0，）的白噪声信号的叠加。

信号长1秒。

设采样频率为100Hz。

将正弦信号和白噪声信号表示在一张图形框，不同坐标系内。

另起一个图形框对叠加信号作图。

要求: 1. 给出1和2 小题的矩阵A 和B2. 给出3和4小题中的2组图形3. 给出你的程序内容2. 已知y=conv(x,h)能够完成输入信号x（n）与系统单位样值响应h（n）的卷积操作，得到输出信号y（n）。

请通过调用子函数y=conv(x,h)，编制一个程序 [y ny ]=conv1(x,h,nx,nh)，其中ny是y （n）第一个样值的n值， nx是x（n）第一个样值的n值， nh是h（n）第一个样值的n值.完成: 1）若 x（n）=[3 1 21 5 2 ] ,nx =-1; h（n）=[1 1 3 ] ,nh=-2 ,则y（n）和ny为多少？请用你编制的函数conv1完成。

2）给出conv1的程序内容解1）程序clc;clear;closeA=linspace(0,1,20)A=Columns 1 through 11Columns 12 through 202）程序clc;clear;close allB=+sqrt*randn(5)B =c3)程序内容Clc;clear;close all N=100;n0=25;u=ones(1,N);u(1,1:n0)=0;stem(0:N-1,u) 4)00.51-1-0.8-0.6-0.4-0.20.20.40.60.8100.51-0.25-0.2-0.15-0.1-0.050.050.10.150.200.10.20.30.40.50.60.70.80.91-1.5-1-0.50.511.5程序 clc;clear;close allts=0;te=1;fs=100 ;f1=5;t=ts:1/fs:te;y1=sin(2*pi*f1*t);y2=sqrt*randn(size(t));subplot(1,2,1);plot(t,y1);subplot(1,2,2);plot(t,y2);figure(2)plot(t,y1+y2)2.1)y =3 4 31 29 70 17 6ny =-32) function [y,ny]=conv1(x,nx,h,nh)y =conv(x,h);ny=nx+nh;。

matlab 机械原理

机电控制系统仿真结课论文Matlab 在机械原理中的简单应用摘要：Matlab 是可视化的面向科学计算的优秀科技应用软件，将Matlab 引入机械原理课程学习中，利用其丰富的库函数、编程简单及可视化功能强等优点，来解决机械原理课程学习中的问题，可提高学习效率与学习的极性，学习效果明显。

关键词：Matlab机械原理运动分析引言：Matlab是美国MathWorks公司开发的一套高性能的数值计算和可视化软件，其应用范围涵盖了当今几乎所有的工业应用与科学研究领域，它集数值分析、矩阵运算、信号处理和图形显示于一体，其丰富的库函数和各种专用工具箱，将使用者从繁琐的底层编程中解放出来；它对科学计算结果迅捷而准确的可视化能力，有助于使用者化抽象思维为形象思维，更好地理解概念、发现规律。

机械原理是机械类专业的一门技术基础课，机构的运动分析是其很重要的一章内容。

目前在学习过程中，对机构进行运动分析的方法主要有图解法和解析法两种[1]。

图解法需要列出矢量方程式、作图求解，存在结果出错多、准确性差、作图过程繁琐等问题；解析法需要针对给定机构建立模型、求导得出速度方程和加速度方程、再编程求解，受编程能力限制，编程时易出错、程序调试时间较长；这都在一定程度上影响了学习该部分内容的兴趣和积极性。

由于以上原因，在学习中引入matlab 中的simulink 和simmechanics 工具箱，机械原理课程学习中利用Matlab语言，对学习内容做适当调整，使我们观地领会和理解课程中的内容和实时处理结果。

利用其建模直观简便、我们上手快等特点，激发我们的学习兴趣，提高了学习的自主性。

一、基于Matlab 的四连杆机构运动分析1.建立数学模型四连杆机构如图1 所示，已知各构件的尺寸L 1,L2,L3,L4及原动件1的角位移θ1和等角速度ω1，求构件2和3的角位移θ2,θ3，角速度ω2,ω3，角加速度ε2,ε3。

为了对机构进行运动分析，先如图1 建立一直角坐标系，并将各构件表示为杆矢。

机械优化大作业-MATLAB复合型法

机床主轴机构优化设计机床主轴是机床中重要的零件之一，一般多为支撑空心阶梯轴。

为了便于使用材料力学进行结构分析，常常将阶梯轴简化成以当量直径表示的等截面轴。

如图0.1所示是一个已经简化处理的专用机床双主轴的力学模型。

从机床主轴制造成本较低和加工精度较高的要求出发，需要考虑主轴的自重和外身段挠度这样两个重要因素。

对于专用机床来说，并不追求过高的加工精度。

因此选取零件自身重量轻为设计目标，将主轴的刚度作为约束条件。

一、设计变量和目标函数当主轴的材料选定之后，与主轴重量设计方案有关设计变量主轴的外径D、孔径d、两支承跨度l、和外伸段长度a，如图0.1所示。

由于机床主轴的孔径主要取决于待加工棒料的直径，不能作为设计变量处理。

因此，设计变量为机床主轴重量最轻优化设计目标函数为二、约束条件1.刚度性条件机床的加工质量在很大程度上取决于主轴的刚度，主轴刚度是一个很重要的性能指标。

因此，要求主轴悬臂端挠度不超过给定的变形量y 0 。

根据材料力学可知，主轴悬臂端挠度为）（）（）（44231232d x E 3x x Fx 64EJ 3a l Fa y -+=+=π式中，）（44d -D 64J π=是空心主轴的惯性矩；E=2.1x105MPa 是主轴的弹性模量；F 是作用主轴外伸端的力。

整理得到主轴刚度的约束条件为0d x E 3x x Fx 64X g 442312301≥-+-=）（）（）（πy2.设计边界条件三个设计变量的边界约束条件为max min l l l ≤≤max min D D D ≤≤maxmin a a a ≤≤3.具体算例已知某机床主轴悬臂端受到的切削力F=15000N ，主轴内径d=30mm ，悬臂端许用挠度y 0=0.05mm 。

要求主轴两支承跨度mm lmm 650300≤≤，外径mm D mm 14060≤≤，悬臂长度mm a mm 15090≤≤。

建立优化的数学模型)30)((7854.0)(22231++=x x x X fTT a D l x x x X ],,[],,[321==0)30()(7009.91)(..44231231≥-+⨯-=x x x x X g t s01300/)(12≥-=x X g0650/1)(13≥-=x X g0160/)(24≥-=x X g0140/1)(25≥-=x X g0190/)(36≥-=x X g0150/1)(37≥-=x X g4.基于matlab 程序的复合形法实现优化（1）算法原理复合形法来源于无约束优化问题的单纯形法，通过构造复合形来求得最优解，新的复合形通过替换旧的复合形中的坏点（目标函数最大或次大的点）得到，替换方式仍是单纯性法中的反应、压缩、扩展这几个基本方法。

机械原理课程设计Matlab编程

/*Matlab程序*/l1 = 59.1000;l2 = 263.9000;l3=120;l4=266.83;l5=180;l6=45;x2=170;y2=132.7289;w1=9.4248;N=42:10:402;ay=119:10:479a=2*l1*l3*sin(N/180*pi);b=2*l3*(l1*cos(N/180*pi)-l4);c=l2^2-l1^2-l3^2-l4^2+2*l1*l4*cos(N/180*pi);jiao3=2*atan((a- sqrt(a.^2+b.^2-c.^2))./ (b-c))/pi*180+77g=2*l1*l2*sin(N/180*pi);h=2*l2*(l1*cos(N/180*pi)-l4);m=l1^2+l2^2+l4^2-l3^2-2*l1*l4*cos(N/180*pi);jiao2=2*atan((g- sqrt(g.^2+h.^2-m.^2))./ (h-m))/pi*180+77lof=-sqrt(l6^2-x2^2-l5^2+2*l5*x2*cos((180+jiao3)/180*pi)+l5^2*sin(j iao3/180*pi).^2)+y2-l5* sin((180+jiao3)/180*pi)j12=N-(jiao2-77);j32=jiao3-jiao2;j13=(N-(jiao3-77));j23=(jiao2-jiao3);w3=(w1*l1*sin(j12/180*pi))./ (l3*sin(j32/180*pi))w2=(-1*w1*l1*sin(j13/180*pi))./(l2*sin(j23/180*pi))a3=(w1^2*l1*cos(j12/180*pi)+w2.^2*l2-(w3.^2).*(l3*cos(j32/180*pi)) )./ (l3*sin(j32/180*pi))a2=(-w1^2*l1*cos(j13/180*pi)-(w2.^2).*(l2*cos(j23/180*pi))+l3*w3.^ 2)./ (l3*sin(j23/180*pi))jiao4=acos((x2-l5*cos((180+jiao3)/180*pi))/l6)/pi*180w4=((-l5*sin((pi+jiao3)/180*pi)).*w3)./ (l6*sin(jiao4/180*pi))vof=((l5*sin((180+jiao3-jiao4)/180*pi)).*w3).* sin(jiao4/180*pi)aof=(l6*w4.^2+(l5*w3.^2).*(cos((180+jiao3-jiao4)/180*pi))+l5*a3.*si n((180+jiao3-jiao4)/180*pi))./sin(jiao4/180*pi)作图程序：/*F点的位移*/plot(N+77,lof,'-xk')xlabel('AB杆的角度'),ylabel('F点的位移/(mm)')title('F点的位移曲线图')text(100, 171.3339,'初始值= 171.3339')text(425, 171.3339,'最高值= 180')/*F点的速度*/plot(N+77,vof,'-xk')text(100,-285,'初始值= -347.0624')text(390,-430,'终点值= -347.0624')xlabel('AB杆的角度'),ylabel('F点的速度/(mm/s)')title('F点的速度曲线图')/*F点的加速度*/plot(N+77,aof,'-xk')xlabel('AB杆的角度'),ylabel('F点的加速度/(mm/s^2)')title('F点的加速度曲线图')text(100, 1.0e+004 *-0.9848,'初始值= 1.0e+004 *（-0.9048）') text(350, 1.0e+004 *-0.9048,'终点值= 1.0e+004 *（-0.9048）')/*结果*/ay =Columns 1 through 20119 129 139 149 159 169 179 189 199 209 219 229 239 249 259 269 279 289 299 309Columns 21 through 37319 329 339 349 359 369 379 389 399 409 419 429 439 449 459 469 479jiao3 =Columns 1 through 12152.7283 155.6055 159.2201 163.3851 167.9364 172.7308 177.6411 182.5508 187.3495 191.9295 196.1844 200.0109Columns 13 through 24203.3123 206.0053 208.0272 209.3409 209.9360 209.8245 209.0330 207.5944 205.5410 202.9003 199.6946 195.9435Columns 25 through 36191.6697 186.9095 181.7262 176.2288 170.5899 165.0593 159.9573 155.6378 152.4212 150.5209 150.0024 150.7929Column 37152.7283jiao2 =Columns 1 through 1297.9329 96.9493 96.1177 95.4427 94.9235 94.5564 94.3364 94.2587 94.3188 94.5127 94.8367 95.2869Columns 13 through 2495.8585 96.5454 97.3393 98.2294 99.2013 100.2373 101.3154 102.4095 103.4889 104.5187 105.4597 106.2696Columns 25 through 36106.9048 107.3227 107.4861 107.3682 106.9579 106.2651 105.3223 104.1834 102.9167 101.5959 100.2898 99.0551Column 3797.9329lof =Columns 1 through 12171.3339 162.4831 151.6215 139.2662 125.7535 111.3249 96.2283 80.8029 65.5172 50.9387 37.6489 26.1414Columns 13 through 2416.7408 9.5650 4.5415 1.4741 0.1412 0.3882 2.1781 5.5874 10.7654 17.8808 27.0707 38.3902Columns 25 through 3651.7607 66.9223 83.4132 100.6062 117.8015 134.3068 149.4275 162.3850 172.2940 178.3195 179.9923 177.4473Column 37171.3339w3 =Columns 1 through 122.0420 2.88413.54184.0289 4.3651 4.5686 4.6533 4.6279 4.4965 4.2598 3.9173 3.4690Columns 13 through 242.9187 2.2766 1.5612 0.7980 0.0174 -0.7506 -1.4803 -2.1528 -2.7570 -3.2875 -3.7434 -4.1259Columns 25 through 36-4.4354 -4.6697 -4.8213 -4.8744 -4.8021 -4.5650 -4.1167 -3.4196 -2.4746 -1.3428 -0.1370 1.0209Column 372.0420w2 =Columns 1 through 12-1.4343 -1.1068 -0.8180 -0.5658 -0.3428 -0.1403 0.0504 0.2372 0.4268 0.6248 0.8348 1.0577Columns 13 through 241.2907 1.5265 1.7527 1.95262.1078 2.20042.2158 2.1438 1.9799 1.7238 1.3800 0.9564Columns 25 through 360.4649 -0.0783 -0.6512 -1.2249 -1.7619 -2.2168 -2.5411 -2.6940 -2.6601 -2.4610 -2.1504 -1.7915Column 37-1.4343a3 =Columns 1 through 1252.5560 41.5031 31.2310 22.2213 14.4470 7.6608 1.5603 -4.1325 -9.6312 -15.0579 -20.4136 -25.5519Columns 13 through 24-30.1734 -33.8717 -36.2458 -37.0535 -36.3289 -34.3895 -31.7205 -28.8042 -25.9756 -23.3519 -20.8311 -18.1297Columns 25 through 36-14.8311 -10.4321 -4.3902 3.8075 14.5130 27.6704 42.4330 56.8069 67.8232 72.7326 70.6513 63.0454Column 3752.5560a2 =Columns 1 through 1242.6168 37.6998 32.7111 28.4933 25.3433 23.2851 22.2337 22.0665 22.6383 23.7616 25.1694 26.4765Columns 13 through 2427.1651 26.6283 24.2896 19.7685 13.0154 4.3334 -5.7233 -16.5098 -27.4206 -37.9407 -47.6216 -56.0112Columns 25 through 36-62.5725 -66.6194 -67.2958 -63.6367 -54.7645 -40.2872 -20.8999 1.0456 21.6515 36.8894 44.6857 45.7784Column 3742.6168jiao4 =Columns 1 through 1277.1498 82.2481 87.8236 93.1653 97.6943 100.9570 102.6405 102.6068 100.9154 97.8068 93.6522 88.8959Columns 13 through 2484.0113 79.4692 75.7071 73.0882 71.8537 72.0875 73.7150 76.5391 80.2895 84.6612 89.3256 93.9195Columns 25 through 3698.0213 101.1380 102.7329 102.3311 99.6946 94.9908 88.8525 82.3019 76.5687 72.8043 71.7241 73.3615Column 3777.1498w4 =Columns 1 through 12-3.4249 -4.2204 -4.2959 -3.7606 -2.7325 -1.3398 0.2606 1.8815 3.3352 4.4720 5.1962 5.4568Columns 13 through 245.2293 4.5113 3.3352 1.7918 0.0401 -1.7169 -3.2847 -4.5255 -5.3698 -5.7983 -5.8117 -5.4089Columns 25 through 36-4.5802 -3.3225 -1.6778 0.2193 2.1277 3.7480 4.7881 4.9961 4.2100 2.4944 0.2607 -1.8728Column 37-3.4249vof =Columns 1 through 12-347.0624 -492.8494 -603.7818 -681.3764 -732.8054 -766.8573 -789.4516 -800.4475 -793.1801 -757.7000 -686.9200 -582.3864Columns 13 through 24-455.6459 -323.7142 -201.3442 -95.0327 -1.9924 86.4566 179.8406 284.1862 399.4460 519.0511 631.6416 724.6701Columns 25 through 36788.9608 822.4766 830.9271 823.5243 805.0980 769.5568 700.9268 584.3674 420.0967 225.6063 22.9226 -171.8563Column 37-347.0624aof =1.0e+004 *Columns 1 through 12-0.9048 -0.6847 -0.5221 -0.4123 -0.3300 -0.2449 -0.1309 0.0224 0.2041 0.3874 0.5412 0.6412Columns 13 through 240.6754 0.6479 0.5799 0.5058 0.4597 0.4593 0.4981 0.5531 0.5991 0.6163 0.5913 0.5159Columns 25 through 360.3871 0.2120 0.0106 -0.1886 -0.3676 -0.5349 -0.7184 -0.9361 -1.1628 -1.3170 -1.3111 -1.1438Column 37-0.9048。

Matlab机械原理第二次作业

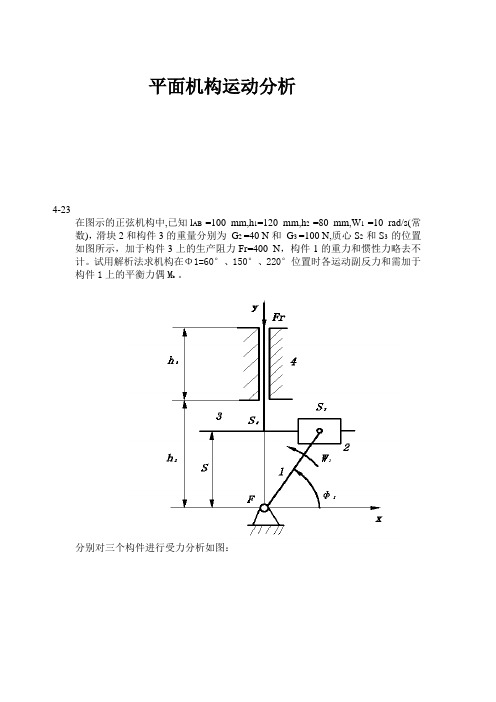
平面机构运动分析4-23在图示的正弦机构中,已知l AB =100 mm,h1=120 mm,h2 =80 mm,W1 =10 rad/s(常数)，滑块2和构件3的重量分别为G2 =40 N和G3 =100 N,质心S2 和S3 的位置如图所示，加于构件3上的生产阻力Fr=400 N，构件1的重力和惯性力略去不计。

试用解析法求机构在Φ1=60°、150°、220°位置时各运动副反力和需加于构件1上的平衡力偶M b 。

分别对三个构件进行受力分析如图：构件3受力图构件2受力图构件1受力图（1）滑块2：V S2 =L AB W1 ①a s2 = L AB W12②构件3：S=L AB sinΦ1 ③V3 =L AB W1 COSΦ1 ④a3 =-L AB W12 sinΦ1 ⑤(2)确定惯性力：F12=m2a s2=(G2/g)L AB W12 ⑥F13=m3a3=(G3/g)L AB W12sinΦ1 ⑦(3)各构件的平衡方程：构件3：∑Fy=0,F R23 =Fr-F13∑Fx=0,F R4’=F R4∑M S3 =0,F R4=F R23L A cosΦ1/h2构件2：∑Fx=0,F R12x=F12cosΦ1∑Fy=0,F R12y=F R32-F12sinΦ1构件1：∑Fx=0,F R41x=F R12x∑Fy=0,F R41y=F R12y∑M A =0,M b =F R32L AB cosΦ1总共有八个方程，八个未知数。

归纳出一元八次方程矩阵：1 0 0 0 0 0 0 0 F R23 Fr-F130 1 -1 0 0 0 0 0 F R4’ 0-L AB COSΦ1/h2 0 1 0 0 0 0 0 F R4 00 0 0 1 0 0 0 0 F R12x = F12cosΦ1 -1 0 0 0 1 0 0 0 F R12y -F12 sinΦ1 0 0 0 -1 0 1 0 0 F R41x 00 0 0 0 -1 0 1 0 F R41y 0-L AB COSΦ1 0 0 0 0 0 0 1 Mb 0AX=B进而可得：X=A\B。

机械原理大作业凸轮结构设计

机械原理大作业(二) 作业名称：机械原理设计题目：凸轮机构设计院系: 机电工程学院班级：设计者:学号:指导教师：丁刚陈明设计时间:哈尔滨工业大学机械设计1、设计题目如图所示直动从动件盘形凸轮机构，根据其原始参数设计该凸轮。

表一:凸轮机构原始参数序号升程(mm) 升程运动角(º)升程运动规律升程许用压力角（º)回程运动角（º)回程运动规律回程许用压力角(º)远休止角(º）近休止角（º)１2 ８0 1５０正弦加速度30 １０0 正弦加速度60 ６0 50２、凸轮推杆运动规律(1)推杆升程运动方程S=ｈ［φ/Φ0-siｎ（２πφ/Φ0)]V＝hω1／Φ０[１-ｃos(2πφ/Φ0）]a=2πhω１2sin(2πφ／Φ0)/Φ02式中:h=1５0，Φ0=5π／6,0<=φ<=Φ０,ω1=1(为方便计算)(2)推杆回程运动方程S=h[1-T/Φ１＋sin(2πＴ/Φ1)/２π]V= -hω１/Φ1[1-coｓ(2πT/Φ1)]ａ＝－２πhω12sin(２πT／Φ1)／Φ1２式中:h=150,Φ１=5π/9，７π/６<＝φ<=3１π／18,T=φ-7π/6３、运动线图及凸轮线图运动线图:用Ｍatlａｂ编程所得源程序如下:t=0:pi/５00:2*pｉ;ｗ1=1;h=150;lｅng=ｌeｎgｔh(ｔ);ｆor m=1:leng;if ｔ(m)＜=5*ｐi/6S(ｍ) = h*(t(m)/(5*pｉ/６)-sin（2*pi*t(m)/(5＊ｐi/6））/(2＊ｐi）);v(m)=h*w1*(1-cos（2*ｐi＊ｔ(m)／(5*pi/6)）)/(５*ｐi/6)；a(m)＝２*ｈ*w1＊w1*ｓin(２*pi*t（m)/(5＊pi/6)）/((5＊pｉ/6)*(5*pｉ/6))；% 求退程位移,速度,加速度elseｉｆt（m)＜=7*pｉ/6Ｓ(m）=h;v（m)=0;a(m)=０；% 求远休止位移，速度，加速度elｓｅif ｔ(ｍ)<=31*pi/１8T(m)＝t(m)-２1＊pi／18;S(m)=ｈ*(1-T(ｍ)／(5*pi/９)＋sｉｎ(2*pi＊T(m)/(5*pｉ／9）)/(2*pi）);v（ｍ)=－h/(5*pi/９）*(１-ｃos(2*pi*T（m)/(5*pi/９）))；a(m)=-２*pi＊h／(5*pi/9）＾2*sin(2＊pi＊Ｔ(m）/（5*pｉ/9));％求回程位移,速度，加速度elｓｅＳ（m)=0;v(m)=0;a(m)=０;% 求近休止位移，速度,加速度endend推杆位移图推杆速度图推杆加速度图4、确定凸轮基圆半径与偏距在凸轮机构得ds/dφ-s线图里再作斜直线Ｄt dｔ与升程得［ｄs/dφ-s(φ)］曲线相切并使与纵坐标夹角为升程许用压力角[α],则D t d t线得右下方为选择凸轮轴心得许用区。

机械原理课程设计用MATLAB做

机械原理课程设计用MATLAB做一、教学目标本课程旨在通过MATLAB软件的应用，让学生掌握机械原理的基本知识和技能，培养学生的创新意识和实践能力。

知识目标：使学生了解机械原理的基本概念、原理和应用，掌握MATLAB在机械原理分析中的基本使用方法。

技能目标：通过案例分析和实践操作，培养学生运用机械原理知识和MATLAB 软件解决实际问题的能力。

情感态度价值观目标：激发学生对机械原理和MATLAB软件应用的兴趣，培养学生的团队协作精神和自主学习能力。

二、教学内容本课程的教学内容主要包括机械原理的基本概念、机构和机器的设计与分析方法，以及MATLAB在机械原理分析中的应用。

教学大纲安排如下：1.机械原理概述：介绍机械原理的基本概念、研究对象和内容。

2.机构分析：讲解各种机构的工作原理和特性，包括齿轮机构、连杆机构等。

3.机器的设计与分析：介绍机器的设计方法和步骤，以及在不同工作条件下机器的性能分析。

4.MATLAB在机械原理分析中的应用：讲解MATLAB软件的基本使用方法，以及如何利用MATLAB进行机械原理分析和设计。

三、教学方法为了提高教学效果，本课程将采用多种教学方法相结合的方式，包括讲授法、案例分析法、实验法和讨论法。

1.讲授法：通过讲解机械原理的基本概念和理论知识，使学生掌握基本原理和方法。

2.案例分析法：通过分析实际案例，让学生了解机械原理在工程中的应用，培养学生的实践能力。

3.实验法：让学生动手操作，利用MATLAB软件进行机械原理分析和设计，提高学生的实际操作能力。

4.讨论法：学生进行分组讨论，培养学生的团队协作精神和批判性思维。

四、教学资源为了支持本课程的教学内容和教学方法，我们将准备以下教学资源：1.教材：《机械原理》，提供机械原理的基本知识和理论。

2.参考书：《MATLAB教程》，介绍MATLAB软件的基本使用方法。

3.多媒体资料：包括教学PPT、视频教程等，辅助学生理解和掌握知识。

昆明理工大学MATLAB实验指导书(第二次实验)

************************ MATLAB上机指导书************************昆明理工大学机电学院彭用新2015年3月实验三符号计算一、操作部分：在命令窗口执行命令完成以下运算，记录运算结果。

1.findsym：帮助我们获取系统定义的自变量f= sym('sin(a*x+b*y)'); findsym(f)2.numden（获取分子分母）, sym2poly,（获取多项式时系数）poly2sym（根据多项式系数获得符号表达式）[n,d]=numden(sym('x*x+y')+sym('y^2'))p=sym('2*x^3+3*x^2+4'); sym2poly(p)x=[2,3,0,4]; poly2sym(x)3. collect ：合并同类项；expand：展开多项式；horner: 分解成嵌套形式；factor：因式分解；simplify: 对表达式化简syms x y; collect(x^2*y+y*x-x^2-2*x)collect((x+y)*(x^2+y^2+1), y)syms x y; expand((x-2)*(x-4))syms x;horner(x^3-6*x^2+11*x-6)syms x;factor(x^3-6*x^2+11*x-6)syms x;simplify((x^2+5*x+6)/(x+2))4. finverse ：求得符号函数的反函数。

syms x y; finverse(1/tan(x))f= x^2+y; finverse(f,y)finverse(f)pose 求符号函数的复合函数syms x y; f = 1/(1 + x^2); g = sin(y); compose(f,g)6. subs :表达式替换。

syms a b;subs(a+b,a,4)subs(a+b,4)subs(cos(a)+sin(b),{a,b},{sym('alpha'),2}) subs('x^2+2*y',{'x','y'},{3,4})7.极限：limitsyms x t;limit(sin(x)/x)limit((x-2)/(x^2-4),2)limit((1+2*t/x)^(3*x),x,inf)limit(1/x,x,0,'right')8. 微分：diffsyms a b c x;f=sym('a*x^2+b*x+c')diff(f)diff(f,2)diff(f,a)diff(f,a,2)9. 积分：intsyms a b c xf=sym('a*x^2+b*x+c')int(f)int(f,x,0,2)int(f,a)int(int(f,a),x)10级数：symsum,taylorsyms ksymsum(1/k,k,1,inf)symsum(1/(k*(k+1)),k,1,inf)syms xtaylor(sin(x),x,10)subs(ans,x,pi/2)11.solve 解符号方程式f=sym('a*x^2+b*x+c');solve(f)f1=sym('x+y+z-10=0');f2=sym('x-y+z=0');f3=sym('2*x-y-z+4=0');solve(f1,f2,f3);[x,y,z]=solve(f1,f2,f3)12解微分符号方程式：dsolve,Dy代表dy/dt, D2y代表d2y/dt2 。

用MATLAB解线性二次型最优控制问题答案课件

曲线优化
通过调整控制变量，可以最小化代价函数，从而找到最优轨迹曲线。
解的物理意义
物理背景
线性二次型最优控制问题的解具有明确的物理意义，它反映了系统状态的最优演化过程。
控制策略
解中的控制变量表示在给定时间内系统状态的最优调整策略，使得系统状态按照最优轨迹演化。
应用价值
解的物理意义有助于理解最优控制问题在实际系统中的应用，例如在航天器轨道优化、经济系统调控等领域具有重要价值。
lqr函数
用于求解线性二次型最优控制问题，返回最优控制策略和最优性能指标。
fmincon函数
用于求解带约束的最小化问题，可以用于求解具有状态和控制约束的线性二次型最优控制问题。
quadprog函数
用于求解带约束的二次型优化问题，可以用于求解具有性能指标约束的线性二次型最优控制问题。
MATLAB求解线性二次型最优控制问题的示例
结果分析对求解结果进行分析，包括最优控制策略、最优性能指标等。
编写MATLAB代码使用MATLAB编程语言，编写求解线性二次型最优控制问题的代码，包括定义变量、设置参数、编写求解函数等。
运行求解运行MATLAB代码，调用求解函数，对线性二次型最优控制问题进行求解。
MATLAB求解线性二次型最优控制问题的函数
航天器轨道优化实例
在航天领域，线性二次型最优控制问题被广泛应用于航天器轨道优化中。例如，在卫星轨道的设计和优化中，通过线性二次型最优控制算法，可以优化卫星的轨道参数，提高卫星的观测精度和运行效率。
在太空探索任务中，线性二次型最优控制问题同样发挥着重要的作用，例如火星探测器的着陆轨迹规划和姿态控制等。
表达式的形式
通常是一个多项式或分式，其分母和分子包含了决策变量和控制变量的幂次。