基于DSP的C程序实验报告_快速傅立叶变换(FFT)算法
DSP实验一--FFT

数字信号处理实验实验1 快速傅里叶变换FFT 算法实验一、实验目的:1、加深对离散信号的DFT 的理解和FFT 算法的运用。
2、学会用mtalab 求解信号的频谱图。
3、学会用DSP 硬件进行频谱分析。
二、实验设备计算机,ccs3.3软件,DSP CPU 挂箱,DSP 仿真器,导线三、实验原理N 点序列的DFT 和IDFT 变换定义式如下:10[][]N kn N n X k x n W-==∑, 101[][]N kn N k x n X k W N --==∑ 利用旋转因子2j nk knN N W e π-=具有周期性,可以得到快速算法(FFT )。
在MATLAB 中,可以用函数X=fft (x ,N )和x=ifft (X ,N )计算N 点序列的DFT 正、反变换。
四、实验内容:1、利用MATLAB 编程完成计算,绘出下式时域图形,并用FFT 求取其傅里叶变换画出相应的频谱图,并分析、说明实验结果。
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);采样频率fs=100Hz ,采样点数为128点。
2、运行ccs 软件,对给定的语音信号进行采集,并应用DSP 挂箱分析该信号的频谱。
相应的实验步骤(1)安装仿真器TDS510驱动(位置在f 盘根目录下).(2)仿真器参数设置打开setup ccstudio 从Familly 中查找C55xx 系列,然后选择C5509 TDS510并将其拖到到左侧窗口。
右键C5509打开属性装载仿真器的配置参数CCstudio_v3.3//cc//bin/TDS510.cgf.(3)打开ccs3.3链接仿真器与电脑点击Debug —connect ;打开已建立的项目点击project—open—fft.pjt;装载编译好的程序fft.out,file--load program—fft.out。
在k++处设置断点,观察采集到的语音信号。
DSP-FFT快速傅立叶计算实验

《DSP原理及应用》课程实验报告学生姓名:所在班级:电信1001指导教师:记分及评价:项目满分5分得分一、实验名称实验5:FFT快速傅立叶计算二、任务及要求【基本部分】3分把教材7-13FFT快速傅立叶计算的程序补充完整,进行仿真实验。
【发挥部分】2分把exam5-1中的sian1或sian2数据调用进来进行快速傅立叶计算。
三、实验程序(原理图)#include "fcomplex.h"void fft(complex *X, unsigned int M, complex *W, unsigned int SCALE){complex temp; /* 复变量临时存储器 */complex U; /* 旋转因子W^k */unsigned int i,j;unsigned int id; /* 蝶形运算中下位节点的序号 */unsigned int N=1<<M; /* FFT 的点数*/unsigned int L; /* FFT 的级序号 */unsigned int LE; /* L级子FFT的点数 */unsigned int LE1; /* L级子FFT蝶形运算的个数 */float scale;scale = 0.5;for (L=1; L<=M; L++){LE=1<<L;LE1=LE>>1;U.re = 1.0;U.im = 0.;for (j=0; j<LE1;j++){for(i=j; i<N; i+=LE) /* 进行蝶形计算 */{id=i+LE1;temp.re = (X[id].re* U.re - X[id].im* U.im)*scale; temp.im = (X[id].im* U.re + X[id].re* U.im)*scale;X[id].re = X[i].re*scale - temp.re;X[id].im = X[i].im*scale - temp.im;X[i].re = X[i].re*scale + temp.re;X[i].im = X[i].im*scale + temp.im;}/* 递推计算W^k */temp.re = U.re* W[L-1].re - U.im* W[L-1].im;U.im = U.re* W[L-1].im + U.im* W[L-1].re;U.re = temp.re;}}}/*fft_test.c - Example to test FFT*/#include <math.h>#include "fcomplex.h"extern void bit_rev(complex *, unsigned int); /*位反转函数声明*/ extern void fft(complex *, unsigned int, complex *, unsigned int); extern void generator(float *, unsigned int);/* fft函数声明 */#define N 128 /* FFT的数据个数 */#define M 7 /* M=log2(N) */#define PI 3.1415926complex X[N]; /* 说明输入信号数组,为复数 */complex W[M]; /* 说明旋转因子数组e^(-j2PI/N),为复数 */ complex temp; /* 说明临时复数变量 */float xin[N];float spectrum[N]; /* 说明功率谱信号数组,为实数 */float re1[N],im1[N]; /* 说明临时变量数组,为实数 */void main(){unsigned int i,L,LE,LE1;/* ------------------------------------------------------------- */ /* 产生旋转因子表 */for (L=1; L<=M; L++){LE=1<<L; /* 子FFT中的点数LE=2^L */LE1=LE>>1; /* 子FFT中的蝶形运算数目*/W[L-1].re = cos(PI/LE1);W[L-1].im = -sin(PI/LE1);}/* ------------------------------------------------------------- */ generator(xin,N);for (;;){/* --------------------------------------------------------- */for (i=0; i<N; i++){/* 构造输入信号样本 */X[i].re =xin[i];X[i].im = 0;/* 复制到参考缓冲器 */re1[i] = X[i].re;im1[i] = X[i].im;}/* 启动 FFT */bit_rev(X,M); /* 以倒位次序排列X[] */fft(X,M,W,1); /* 执行 FFT *//* 计算功率谱,验证FFT结果 */for (i=0; i<N; i++){temp.re = X[i].re*X[i].re;temp.im = X[i].im*X[i].im;spectrum[i] = (temp.re + temp.im)*4;}}}四、仿真及结果分析五、硬件验证无六、小结这次的实验使我理解FFT快速傅立叶计算,同时对傅里叶计算以及CCS应用有更加深的理解,在设计FFT快速傅立叶计算的初期我有很多问题都不太清楚,通过老师和同学的指导,最终使我明白了如何实现FFT快速傅立叶计算。
(完整word版)基于DSP的快速傅立叶变换(FFT)的实现(汇编语言)

快速傅立叶变换(FFT )的实现一、实验目的1.了解FFT 的原理及算法;2.了解DSP 中FFT 的设计及编程方法;3.熟悉FFT 的调试方法;二、实验原理FFT 是一种高效实现离散付立叶变换的算法,把信号从时域变换到频域,在频域分析处理信息。
对于长度为N 的有限长序列x (n ),它的离散傅里叶变换为:(2/)j N nk N W e π-=,称为旋转因子,或蝶形因子。
在x (n )为复数序列的情况下,计算X (k ):对某个k 值,需要N 次复数乘法、(N -1)次复数加法;对所有N 个k 值,需要2N 次复数乘法和N (N -1)次复数加法。
对于N 相当大时(如1024)来说,直接计算它的DFT 所作的计算量是很大的,FFT 的基本思想在于: 利用2()j nk N N W e π-=的周期性即:k N k N N W W +=对称性:/2k k N N N W W +=-将原有的N 点序列分成两个较短的序列,这些序列的DFT 可以很简单的组合起来得到原序列的DFT 。
按时间抽取的FFT ——DIT FFT 信号流图如图5.1所示:图5.1 时间抽取的FFT —DIT FFT 信号流图FFT 算法主要分为以下四步。
第一步 输入数据的组合和位倒序∑=-=10)()(N n nk N W n x k X把输入序列作位倒序是为了在整个运算最后的输出中得到的序列是自然顺序。
第二步 实现N 点复数FFT第一级蝶形运算;第二级蝶形运算;第三级至log2N 级蝶形运算;FFT 运算中的旋转因子N W 是一个复数,可表示:为了实现旋转因子N W 的运算,在存储空间分别建立正弦表和余弦表,每个表对应从0度到180度,采用循环寻址来对正弦表和余弦表进行寻址。
第三步 功率谱的计算X (k )是由实部()R X k 和虚部()I X k 组成的复数:()()()R I X k X k jX k =+;计算功率谱时只需将FFT 变换好的数据,按照实部()R X k 和虚部()I X k 求它们的平方和,然后对平方和进行开平方运算。
基于DSP的快速傅里叶变换

基于DSP的快速傅里叶变换1.简介快速傅氏变换(FFT),是离散傅氏变换的快速算法,是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法进行改进获得的。
FFT是一种高效实现离散傅里叶变换(DFT)的快速算法,是数字信号处理中最为重要的工具之一,它在声学,语音,电信和信号处理等领域有着广泛的应用。
DSP是专门用来处理数字信号的处理器,用它来进行FFT信号处理可以大大缩短运算时间,从而保证系统有较好的实时性。
2.系统设计2.1 DSP采用TMS320F28335为核心的DSP开发板。
TMS320F28335可以用来做数字信号处理和一些简单的控制应用,其核心具有如下几个特点:(1)32位浮点处理器,高性能,高速度;(2)最高时钟频率150MHz,时钟周期6.67ns;(3)低功耗设计,核心电压1.9V,I/O电压3.3V;(4)哈佛总线架构;(5)快速中断响应和处理;(6)高效代码;(7)片内:RAM 34K FLASH 256K;(8)3个32为CPU定时器;(9)16通道12位AD转换:80ns快速转换时间,0~3V输入范围;(10)提供1路2.048V外部精准参考电压,ADCINA1~ADCINA8设计有信号预处理电路;(11)12路PWM输出信号;(12)4路CAP捕获信号;(13)2个QEP正交编码器输入通道;(14)1个SPI同步串口,2个SCI异步串口,1个CAN口,1个2I C口,1个McBSP同步串口,6通道DMA。
2.2 集成开发环境CCS3.3CCS(Code Composer Studio)是美国德州仪器公司(Texas Instrument,TI)出品的代码开发和调试套件,可用于DSP(数字信号处理器)和MCU(微处理器)的开发和调试。
CCS提供环境配置、源程序编辑、编译连接、跟踪分析等各个环节,以加速软件开发进程,提高工作效率。
它把软、硬件开发工具集成在其中,使程序的编写、汇编、软硬件仿真和调试等开发工作在同一的环境中进行,给DSP开发工作带来极大的方便。
快速傅立叶变换(FFT)的实现(DSP实验报告)

快速傅立叶变换(FFT )的实现一、实验目的在数字信号处理系统中,FFT 作为一个非常重要的工具经常使用,甚至成为DSP 运算能力的一个考核因素。
FFT 是一种高效实现离散付氏变换的算法。
离散付氏变换的目的是把信号由时域变换到频域,从而可以在频域分析处理信息,得到的结果再由付氏逆变换到时域。
本实验的目的在于学习FFT 算法,及其在TMS320C54X 上的实现,并通过编程掌握C54X 的存储器管理、辅助寄存器的使用、位倒序寻址方式等技巧,同时练习使用CCS 的探针和图形工具。
另外在BIOS 子目录下是一个使用DSP/BIOS 工具实现FFT 的程序。
通过该程序,你可以使用DSP/BIOS 提供的分析工具评估FFT 代码执行情况。
二、实验原理1)基 2 按时间抽取FFT 算法对于有限长离散数字信号{x[n]} ,0 ≤n ≤-1 N,其离散谱{x[k]} 可以由离散付氏变换(DFT)求得。
DFT 的定义为:X(k) x[n]e N k 0,1,...,N 1 n0可以方便的把它改写为如下形式:N1nkX(k) x[n]W n N k k 0,1,..., N 1n0不难看出,WN 是周期性的,且周期为N,即( n mN )(k lN ) nkm,l 0, 1, 2...W N W NWN 的周期性是DFT 的关键性质之一。
为了强调起见,常用表达式WN 取代W 以便明确其周期是N。
2) 实数FFT 运算对于离散傅立叶变换( DFT)的数字计算,FFT 是一种有效的方法。
一般假定输入序列是复数。
当实际输入是实数时,利用对称性质可以使计算DFT 非常有效。
一个优化的实数FFT 算法是一个组合以后的算法。
原始的2N 个点的实输入序列组合成一个N 点的复序列,之后对复序列进行N 点的FFT 运算,最后再由N 点的复数输出拆散成2N 点的复数序列,这2N点的复数序列与原始的2N点的实数输入序列的DFT 输出一致。
DSP实验手册 实验九 快速傅立叶变换(FFT)

实验九快速傅立叶变换(FFT)一. 实验目的:1.熟悉CCS集成开发环境2.熟悉SEED-DTK5416实验环境3.加深对DFT算法原理和基本性质的理解4.熟悉FFT的算法原理和FFT子程序的算法流程和应用5.学习用FFT对连续信号和时域信号进行频谱分析的方法6.了解DSP处理FFT算法的特殊寻址方式二. 实验内容:1. DSP初始化;2. A/D采样;3. FFT的位倒序程序;4. FFT的蝶形运算程序;5.求功率谱的程序;6.串口发送与接收。
三. 实验背景知识:1. DFT算法的原理2. FFT快速算法的基本原理3. FFT位倒序的实现四. 实验程序功能与结构说明:在数字滤波器实验中,主要包含以下文件:1. Dtk-fft.c:这是实验的主程序,包含了系统的初始化,主要是异步串口的初始化、MCBSP的初始化、以及系统时钟的设置;完成与SEED-MMI5402系统的异步通讯、信号的采集与FFT的运算及功率谱的计算程序。
2. dec5416.c:对SEED-DEC5416各项资源的操作的函数集,主要包含了对UART 的操作的各个函数,对CODEC的各个控制函数。
以及对系统各项的初始化函数。
3. rfft1024.asm:1024点的FFT函数。
4. rftt512.asm:512点的FFT函数。
5. rfft256.asm:256点的FFT函数。
6. cbrev.asm:位倒序函数。
7. sqrt.asm:开方函数。
8. iircas5.asm:IIR滤波器函数。
9. fltoq15.asm:浮点数到Q15定点数的转换;10.b oot.asm:C环境的引导程序。
11.m emory.asm:包含了对FLASH的各项操作、程序空间MEMORY。
12.s ysreg.asm:包含了对DSP的各项控制,像中断的设置、系统时钟设置,及13.对各寄存器的操作。
14.u art.asm:对异步串口的寄存器的读与写。
DSP实验报告(二)

DSP实验报告(二)实验二应用FFT对信号进行频谱分析一、实验目的1、在理论学习的基础上,通过本次实验,加深对快速傅里叶变换的理解,熟悉FFT算法及其程序的编写。
2、熟悉应用FFT对典型信号进行频谱分析的方法。
3、了解应用FFT进行信号频谱分析过程中可能出现的问题,以便在实际中正确应用FFT。
二、实验原理与方法①一个连续信号的频谱可以用它的傅立叶变换表示为+ Xa(jW)=-jWtx(t)edtòa-如果对该信号进行理想采样,可以得到采样序列x(n)=xa(nT)同样可以对该序列进行z变换,其中T为采样周期X(z)=+ x(n)z-n+ -令z为ejw,则序列的傅立叶变换X(ejw)=x(n)ejwn-其中ω为数字频率,它和模拟域频率的关系为w=WT=W/fs式中的是采样频率。
上式说明数字频率是模拟频率对采样率的归一化。
同模拟域的情况相似。
数字频率代表了序列值变化的速率,而序列的傅立叶变换称为序列的频谱。
序列的傅立叶变换和对应的采样信号频谱具有下式的对应关系。
1X(e)=Tjw+ - w-2pXa(j)T即序列的频谱是采样信号频谱的周期延拓。
从式可以看出,只要分析采样序列的谱,就可以得到相应的连续信号的频谱。
注意:这里的信号必须是带限信号,采样也必须满足Nyquist定理。
在各种信号序列中,有限长序列在数字信号处理中占有很重要的地位。
无限长的序列也往往可以用有限长序列来逼近。
有限长的序列可以使用离散傅立叶变换。
当序列的长度是N时,定义离散傅立叶变换为:X(k)=DFT[x(n)]=其中W=e2pj-NN-1n=0WNkn它的反变换定义为:1x(n)=IDFT[X(k)]=N根据式和,则有N-1n=0X(k)WNknX(z)|z=Wnk=NN-1n=0x(n)WNnk=DFT[x(n)]j2pN可以得到X(k)2pk的点,就NN是将单位圆进行N等分以后第k个点。
所以,X(k)是z变换在单位圆上的等距采样,或者说是序列傅立叶变换的等距采样。
DSP的FFT实现设计报告

DSP的FFT实现设计报告一、引言快速傅里叶变换(Fast Fourier Transform, FFT)是一种用于计算离散傅里叶变换(Discrete Fourier Transform, DFT)的快速算法。
FFT广泛应用于信号处理、图像处理、通信等领域。
本报告旨在介绍FFT的实现设计,探讨其原理、算法和优化方法。
二、FFT的原理傅里叶变换是信号处理中的重要工具,可以将一个信号在频域中进行分解。
离散傅里叶变换是对离散信号进行傅里叶变换的离散采样版本。
FFT是一种高效的离散傅里叶变换算法,通过利用输入序列的对称性和分治策略来减少计算量。
三、FFT的算法FFT的算法有多种变种,其中最为常见的是Cooley-Tukey算法。
Cooley-Tukey算法基于分治策略,将一个长度为N的DFT分解为两个长度为N/2的DFT,并通过旋转因子进行合并。
算法的关键步骤包括:分解、旋转因子计算、合并。
四、FFT的优化1.选择合适的长度和分解策略:对于长度为2^k的序列,可以直接使用蝶形操作进行计算,提高效率。
对于长度不是2的幂的序列,可以通过增加0元素的方式填充到2的幂次方长度,再进行计算。
2.使用查表法计算旋转因子:由于旋转因子具有周期性和对称性,可以将旋转因子的计算结果预先存储在一个查找表中,提高运算速度。
3.使用位翻转法重新排列输入序列:FFT的关键步骤是将输入序列重新排列成位翻转的顺序,这样可以实现更高效的计算。
位翻转法可以通过二进制位运算实现,减少乘法和除法的运算量。
4.使用并行计算:FFT的计算过程中存在大量的矩阵乘法运算,可以通过并行计算的方式提高计算效率,如使用SIMD指令来同时计算多个数据。
五、实现设计基于以上原理和优化方法,我们设计了一个基于C语言的FFT算法实现。
主要步骤包括:1.输入信号预处理:将输入信号重排列成位翻转的顺序。
如果输入序列长度不是2的幂次方,则填充0元素。
2.计算旋转因子:通过查表法计算旋转因子。
快速傅里叶变换(含详细实验过程分析)

[实验2] 快速傅里叶变换 (FFT) 实现一、实验目的1、掌握FFT 算法和卷积运算的基本原理;2、掌握用C 语言编写DSP 程序的方法;3、了解利用FFT 算法在数字信号处理中的应用。
二、实验设备 1. 一台装有CCS 软件的计算机; 2. DSP 实验箱的TMS320C5410主控板; 3. DSP 硬件仿真器。
三、实验原理 (一)快速傅里叶变换傅里叶变换是一种将信号从时域变换到频域的变换形式,是信号处理的重要分析工具。
离散傅里叶变换(DFT )是傅里叶变换在离散系统中的表示形式。
但是DFT 的计算量非常大, FFT 就是DFT 的一种快速算法, FFT 将DFT 的N 2 步运算减少至 ( N/2 )log 2N 步。
离散信号x(n)的傅里叶变换可以表示为∑=-=10][)(N N nk N W n x k X , Nj N e W /2π-=式中的W N 称为蝶形因子,利用它的对称性和周期性可以减少运算量。
一般而言,FFT 算法分为时间抽取(DIT )和频率抽取(DIF )两大类。
两者的区别是蝶形因子出现的位置不同,前者中蝶形因子出现在输入端,后者中出现在输出端。
本实验以时间抽取方法为例。
时间抽取FFT 是将N 点输入序列x(n) 按照偶数项和奇数项分解为偶序列和奇序列。
偶序列为:x(0), x(2), x(4),…, x(N-2);奇序列为:x(1), x(3), x(5),…, x(N-1)。
这样x(n) 的N 点DFT 可写成:()()∑++∑=-=+-=12/0)12(12/02122)(N n kn NN n nkNW n x Wn x k X考虑到W N 的性质,即2/)2//(22/)2(2][N N j N j N W e e W ===--ππ因此有:()()∑++∑=-=-=12/02/12/02/122)(N n nkN k NN n nkN W n x WWn x k X或者写成:()()12()kN X k X k W X k =+由于X 1(k) 与X 2(k) 的周期为N/2,并且利用W N 的对称性和周期性,即:k N N k N W W -=+2/可得:()()12(/2)kN X k N X k W X k +=-对X 1(k) 与X 2(k)继续以同样的方式分解下去,就可以使一个N 点的DFT 最终用一组2点的DFT 来计算。
基于DSP的C程序实验报告------快速傅立叶变换(FFT)算法

计算公式如下:
X m1 ( p)
Xm
W
r N
X m (q)
X m1 ( p) X m WNr X m (q)
(3)在FFT运算中,旋转因子WmN=cos(2πm/N)-jsin(2πm/N),求正弦和余弦函数值的
二.FFT 的基本结构: FFT信号流图如下:
x(0)
X3(0) N/4点
X1(0)
X(0)
x(4)
DFT X3(1)
X1(1)
X(1)
x(2)
N/4点
X4(0)
W
0 N
2
X1(2)
X(2)
x(6)
DFT
X4(1)
W
1 N
2
X1(3)
X(3)
x(1)
N/4点
X2(0)
W
0 N
X(4)
x(5)
DFT
X2(1)
/************** following code FFT *******************/ /*说明: 基2fft算法,蝶形运算为核心 */ for ( L=1;L<=7;L++ ) { /* for(1) */
b=1; i=L-1; while ( i>0 ) {
b=b*2; i--; } /* b= 2^(L-1) */
图1
图2
图3 3.清除显示:在以上打开的窗口中单击鼠标右键,选择弹出式菜单中“Clear Display”功 能。 4.设置断点:在程序FFT.c 中有注释“break point”的语句上设置软件断点。
快速傅立叶变换(FFT)算法-DSP实验

快速傅立叶变换(FFT)算法实验摘要:FFT(Fast Fourier Transformation),即为快速傅里叶变换,是离散傅里叶变换的快速算法,它是根据离散傅里叶变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法进行改进获得的。
这种算法大大减少了变换中的运算量,使得其在数字信号处理中有了广泛的运用。
本实验主要要求掌握在CCS环境下用窗函数法设计FFT快速傅里叶的原理和方法;并且熟悉FFT快速傅里叶特性;以及通过本次试验了解各种窗函数对快速傅里叶特性的影响等。
引言:快速傅里叶变换FFT是离散傅里叶变换DFT的一种快速算法。
起初DFT的计算在数字信号处理中就非常有用,但由于计算量太大,即使采用计算机也很难对问题进行实时处理,所以并没有得到真正的运用。
1965年J.W.库利和T.W.图基提出快速傅里叶变换,采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少,特别是被变换的抽样点数N越多,FFT算法计算量的节省就越显著。
从此,对快速傅里叶变换(FFT)算法的研究便不断深入,数字信号处理这门新兴学科也随FFT的出现和发展而迅速发展。
根据对序列分解与选取方法的不同而产生了FFT的多种算法,基本算法是基2DIT和基2DIF。
FFT 的出现,使信号分析从时域分析向频域分析成为可能,极大地推动了信号分析在各领域的实际应用。
FFT在离散傅里叶反变换、线性卷积和线性相关等方面也有重要应用。
一、 实验原理:FFT 并不是一种新的变换,它是离散傅立叶变换(DFT )的一种快速算法。
由于我们在计算DFT 时一次复数乘法需用四次实数乘法和二次实数加法;一次复数加法则需二次实数加法。
每运算一个X (k )需要4N 次复数乘法及2N+2(N-1)=2(2N-1)次实数加法。
所以整个DFT 运算总共需要4N^2次实数乘法和N*2(2N-1)=2N(2N-1)次实数加法。
如此一来,计算时乘法次数和加法次数都是和N^2成正比的,当N 很大时,运算量是可观的,因而需要改进对DFT 的算法减少运算速度。
数字信号处理_快速傅里叶变换FFT实验报告

数字信号处理_快速傅里叶变换FFT实验报告快速傅里叶变换(FFT)实验报告1. 引言数字信号处理是一门研究如何对数字信号进行处理、分析和提取信息的学科。
傅里叶变换是数字信号处理中常用的一种方法,可以将信号从时域转换到频域。
而快速傅里叶变换(FFT)是一种高效的计算傅里叶变换的算法,广泛应用于信号处理、图像处理、通信等领域。
2. 实验目的本实验旨在通过编写程序实现快速傅里叶变换算法,并对不同信号进行频谱分析。
3. 实验原理快速傅里叶变换是一种基于分治策略的算法,通过将一个N点离散傅里叶变换(DFT)分解为多个较小规模的DFT,从而实现高效的计算。
具体步骤如下: - 如果N=1,直接计算DFT;- 如果N>1,将输入序列分为偶数和奇数两部分,分别计算两部分的DFT;- 将两部分的DFT合并为整体的DFT。
4. 实验步骤此处以C语言为例,给出实验的具体步骤:(1) 定义输入信号数组和输出频谱数组;(2) 实现快速傅里叶变换算法的函数,输入参数为输入信号数组和输出频谱数组;(3) 在主函数中调用快速傅里叶变换函数,得到输出频谱数组;(4) 对输出频谱数组进行可视化处理,如绘制频谱图。
5. 实验结果与分析为了验证快速傅里叶变换算法的正确性和有效性,我们设计了以下实验:(1) 生成一个正弦信号,频率为100Hz,采样频率为1000Hz,时长为1秒;(2) 对生成的正弦信号进行快速傅里叶变换,并绘制频谱图;(3) 生成一个方波信号,频率为200Hz,采样频率为1000Hz,时长为1秒;(4) 对生成的方波信号进行快速傅里叶变换,并绘制频谱图。
实验结果显示,对于正弦信号,频谱图中存在一个峰值,位于100Hz处,且幅度较大;对于方波信号,频谱图中存在多个峰值,分别位于200Hz的奇数倍处,且幅度较小。
这与我们的预期相符,说明快速傅里叶变换算法能够正确地提取信号的频谱信息。
6. 实验总结通过本次实验,我们成功实现了快速傅里叶变换算法,并对不同信号进行了频谱分析。
基于DSP的FFT实现设计报告

DSP课程设计姓名:学号:日期:一、实验目的1.加深对DFT算法原理和基本性质的理解;2.熟悉FFT的算法原理和FFT子程序的算法流程和应用;3.学习用FFT对连续信号和时域信号进行频谱分析的方法;4.学习DSP中FFT的设计和编程思想;5.学习使用CCS的波形观察器观察波形和频谱情况;二、实验内容用DSP汇编语言及C语言进行编程,实现FFT运算、对输入信号进行频谱分析。
三、实验原理快速傅里叶变换FFT旋转因子W N有如下的特性。
对称性:W N k+N/2=-W N k(2)周期性:W N n(N-k)=W N k(N-n)=W N-nk (3)利用这些特性,既可以使DFT中有些项合并,减少了乘法积项,又可以将长序列的DFT分解成几个短序列的DFT。
FFT就是利用了旋转因子的对称性和周期性来减少运算量的。
FFT的算法是将长序列的DFT分解成短序列的DFT。
例如:N为偶数时,先将N点的DFT分解为两个N/2点的DFT,使复数乘法减少一半:再将每个N/2点的DFT分解成N/4点的DFT,使复数乘又减少一半,继续进行分解可以大大减少计算量。
最小变换的点数称为基数,对于基数为2的FFT 算法,它的最小变换是2点DFT 。
一般而言,FFT 算法分为按时间抽取的FFT (DIT FFT )和按频率抽取的FFT (DIF FFT )两大类。
DIF FFT 算法是在时域内将每一级输入序列依次按奇/偶分成2个短序列进行计算。
而DIF FFT 算法是在频域内将每一级输入序列依次奇/偶分成2个短序列进行计算。
两者的区别是旋转因子出现的位置不同,得算法是一样的。
在DIF FFT 算法中,旋转因子W N 出现在输入端,而在DIF FFT 算法中它出现在输入端。
假定序列x(n)的点数N 是2的幂,按照DIF FFT 算法可将其分为偶序列和奇序列。
偶序列:x(2r)=x 1(r) 奇序列:x(2r+1)=x 2(r)其中:r=0,1,2,…,N/2-1,则x(n)的DFT 表示为式中,X 1 (k)和X 2(k)分别为X 1(r)和X 2(r)的N/2的DFT 。
dsp实验报告4
一、实验目的1、加深对DFT算法原理和基本性质的理解;2、熟悉FFT算法原理和FFT子程序的应用;3、学习用FFT对连续信号和时域信号进行谱分析的方法,了解可能出现的分析误差及其原因,以便在实际中正确应用FFT。
二、实验内容1.构建本次实验的软硬件环境系统;2.了解实验的硬件原理;3.掌握基2FFT(蝶型)运算的原理;4.调试并分析示例程序;5.撰写实验报告,实验报告包括:2FFT算法的基本原理,画出程序流程图,详细分析2FFT算法子程序,给出该段代码的详细注释。
三、实验步骤及结果1、复习DFT的定义、性质和用DFT作谱分析的有关内容;2、复习FFT算法原理与编程思想,并对照DIT-FFT运算流程图和程序框图,了解本实验提供的FFT子程序;3、阅读本实验所提供的样例子程序;4、运行CCS软件,对样例程序进行跟踪,分析结果;记录必要的参数。
实验截图:四、实验程序及流程图:蝶形算法计算公式:X(K) = X’(K) + X’(K+B) WKN ,X(K+B) = X’(K) - X’(K+B) WKN程序注释:void fft(double pr[], double pi[], int n, int k, double fr[], double fi[], int l, int il){int it,m,is,i,j,nv,l0;double p,q,s,vr,vi,poddr,poddi;for(it=0;it<=n-1;m=it++){is=0;for(i=0;i<=k-1;i++){j=m/2;is=2*is+(m-2*j);m=j;}fr[it]=pr[is];fi[it]=pi[is];}//-------------------该程序段的作用是另倒序存放pr[0]=1.0;pi[0]=0.0;p=6.283185306/n;pr[1]=cos(p);pi[1]=-sin(p);if (l)pi[1]=-pi[1];for(i=2;i<=n-1;i++){p=pr[i-1]*pr[1];q=pi[i-1]*pi[1];s=(pr[i-1]+pi[i-1])*(pr[1]+pi[1]);pr=p-q;pi=s-p-q;}计算WKN *X2(k),其中X2(k)是偶数部分,将其转换成c语言的形式r存实数部分,i 存虚数部分。
实验七快速傅立叶变换(FFT)算法的DSP实现(C语言)

实验七快速傅⽴叶变换(FFT)算法的DSP实现(C语⾔)实验七快速傅⽴叶变换(FFT )算法的DSP 实现(C 语⾔)⼀、实验⽬的1.掌握FFT 算法的基本思想。
2.掌握利⽤ CCS 软件中的dsplib 库进⾏fft 算法的程序设计⼆、实验环境1.奔腾IV 计算机2.Code Composer Studio (CCS)软件三、实验原理1.FFT 算法的基本思想对于序列 x[n](0≤n ≤N-1),其频谱为:X(k)=DFT[x(n)]=∑-=10)(N n kn N Wn x (0≤n ≤N-1),其中:旋转因⼦---=-N j N e W π2在x[n]为复数序列的情况下,完全可以直接运算N 点DFT 需要(N-1)2次复数乘法和N (N-1)次复数加法。
因此,对于⼀些相当⼤的N 值来说,直接计算它的DFT 所需计算量很⼤。
FFT (快速傅⽴叶变换)的基本思想为:将原来的N 点序列最终分成分成两点为⼀组序列,并将这些序列的DFT 通过蝶形运算(见下图)组合起来得到原序列的DFT 。
N 点FFT 仅需 N N 2log 2次复数乘法和N N 2log 次复数加法。
图1 8点FFT 运算流图2. ccs 软件中dsplib (信号处理库)简介TMS320C54X 系列函数库(DSPLIB )是对C 语⾔编程可调⽤优化的DSP 函数库,它含有50个通⽤⽬的的信号处理程序,全部由汇编语⾔编写,并可由C 语⾔调⽤,⽅便C 语⾔与汇编语⾔混合编程。
这些程序⽤在计算强度⼤、执⾏速度重要的实时运算中。
通过使⽤这些程序,可以取得较⽤C 语⾔编写的相关程序快的多的运⾏速度,另外通过使⽤现成的程序可以使开发速度⼤⼤加快。
DSPLIB 可进⾏的运算有:FFT 运算、滤波与卷积运算、⾃适应滤波运算、相关运算、数学函数运算、三⾓函数运算、矩阵运算等。
dsplib 位于C:\ti\c5400\dsplib其⽤户⼿册为:TMS320C54x dsp library programer's reference.pdf三、实验内容1.信号x(n)是2个频率分别为1kHz 和2kHz 余弦信号的合成,取样频率为fs=16000Hz,采⽤FFT 对该信号进⾏频域分析。
基于DSP的FFT实现

基于DSP的FFT实现基于数字信号处理(DSP)的快速傅里叶变换(FFT)是一种高效的信号处理算法,可以将时域信号转换为频域信号。
FFT广泛应用于音频处理、图像处理、通信系统等领域。
FFT算法的核心思想是将N个采样点的离散信号转化为具有N个频域分量的频谱信号。
它通过分治思想,将原始信号分解为两个较小的子问题,并连续进行分解,直到问题规模减小到可以直接求解的程度。
FFT算法的基本步骤如下:1.将N个采样点按照时间顺序排列,作为输入信号。
2.如果N为奇数,将输入信号补零为N+1个点。
3.将输入信号拆分为两个子问题,每个子问题的规模为N/24.对每个子问题递归地应用FFT算法,得到子问题的频域分量。
5.组合子问题的频域分量,得到原始信号的频谱。
6.对频谱进行后处理,如频谱幅值计算、频率估计等。
FFT算法通过递归实现,其中最重要的步骤是蝶形运算。
蝶形运算是FFT算法的核心操作,通过对复数运算的重复应用,将输入信号转换为频域分量。
FFT算法的性能优于传统的傅里叶变换算法,这得益于其时间复杂度的优化。
传统的傅里叶变换算法的时间复杂度为O(N^2),而FFT算法通过分治思想,将时间复杂度优化为O(NlogN)。
这使得FFT算法在大规模信号处理中具有巨大的优势。
在实际应用中,FFT算法可以通过硬件加速来进一步提高性能。
现代DSP芯片内置了专门的FFT硬件,可以实现FFT算法的加速计算。
这些硬件加速器通过并行计算、流水线操作等技术,大幅提升了FFT算法的运行速度。
除了FFT算法之外,还有一些改进的算法可用于实现高效的傅里叶变换。
例如快速哈特利变换(FHT)算法、快速余弦变换(DCT)算法等。
这些算法在一些特定的应用场景下,具有更高的性能和更低的复杂度。
总之,基于DSP的FFT实现是一种高效的信号处理算法,广泛应用于各个领域。
它通过分治思想和蝶形运算,将时域信号转化为频域信号,实现了信号处理的高速计算和高质量结果。
基于DSP的FFT实现设计报告

DSP课程设计:学号:日期:一、实验目的1.加深对DFT算法原理和基本性质的理解;2.熟悉FFT的算法原理和FFT子程序的算法流程和应用;3.学习用FFT对连续信号和时域信号进行频谱分析的方法;4.学习DSP中FFT的设计和编程思想;5.学习使用CCS的波形观察器观察波形和频谱情况;二、实验容用DSP汇编语言及C语言进行编程,实现FFT运算、对输入信号进行频谱分析。
三、实验原理快速傅里叶变换FFT旋转因子W N有如下的特性。
对称性:W N k+N/2=-W N k(2)周期性:W N n(N-k)=W N k(N-n)=W N-nk (3)利用这些特性,既可以使DFT中有些项合并,减少了乘法积项,又可以将长序列的DFT分解成几个短序列的DFT。
FFT就是利用了旋转因子的对称性和周期性来减少运算量的。
FFT的算法是将长序列的DFT分解成短序列的DFT。
例如:N为偶数时,先将N点的DFT分解为两个N/2点的DFT,使复数乘法减少一半:再将每个N/2点的DFT分解成N/4点的DFT,使复数乘又减少一半,继续进行分解可以大大减少计算量。
最小变换的点数称为基数,对于基数为2的FFT算法,它的最小变换是2点DFT。
一般而言,FFT算法分为按时间抽取的FFT(DIT FFT)和按频率抽取的FFT(DIF FFT)两大类。
DIF FFT算法是在时域将每一级输入序列依次按奇/偶分成2个短序列进行计算。
而DIF FFT算法是在频域将每一级输入序列依次奇/偶分成2个短序列进行计算。
两者的区别是旋转因子出现的位置不同,得算法是一样的。
在DIF FFT 算法中,旋转因子W N 出现在输入端,而在DIF FFT 算法中它出现在输入端。
假定序列x(n)的点数N 是2的幂,按照DIF FFT 算法可将其分为偶序列和奇序列。
偶序列:x(2r)=x 1(r) 奇序列:x(2r+1)=x 2(r)其中:r=0,1,2,…,N/2-1,则x(n)的DFT 表示为式中,X 1 (k)和X 2(k)分别为X 1(r)和X 2(r)的N/2的DFT 。
DSP的FFT实现设计报告

DSP的FFT实现设计报告FFT是一种在数字信号处理和图像处理中广泛使用的算法,用于将时域信号转换为频域信号。
在本实现设计报告中,我将详细介绍FFT算法的原理、实现方法以及相关的优化技术。
一、算法原理FFT算法是基于Cooley-Tukey的快速傅立叶变换算法。
它的基本思想是将DFT的计算复杂度从O(n^2)降低到O(nlogn),通过将输入信号分解为奇数偶数项的和,然后分别对偶数项和奇数项计算DFT,并重组结果来得到最终的频域信号。
具体来说,FFT算法可以被分为两个主要步骤:分解和合并。
1.分解:首先将N点的输入序列拆分为两个N/2点的子序列,一个子序列包含所有的奇数项,另一个子序列包含所有的偶数项。
然后,递归地将每个子序列继续拆分,直到子序列长度为1为止。
2.合并:最后,通过按照正确顺序合并每个子序列的结果来得到完整的频域信号。
合并的过程也是递归进行的,但是在合并过程中需要进行频率乘法和加法运算。
二、实现方法FFT算法的实现可以使用多种编程语言,例如C、C++、Python等。
以下是一种C语言实现FFT的基本步骤:1.定义数组存储输入和输出信号,以及临时变量。
2.将输入信号重排为按位反转的顺序。
3.循环执行分解步骤,将输入信号拆分为奇数和偶数子序列。
4.递归调用FFT函数,计算子序列的DFT。
5.循环执行合并步骤,将子序列的结果按正确顺序合并。
6.返回最终的频域信号。
三、优化技术为了提高FFT算法的性能,可以采用一些优化技术。
以下是一些常用的优化技术:1.采用蝶形算法:蝶形算法是FFT算法中最关键的部分,它通过乘法和加法操作对频域信号进行重组。
通过合理地安排计算次序和共享计算结果,可以减少计算量和存储开销。
2.使用快速乘法技术:快速乘法技术可以减少频率乘法的运算次数和复杂度。
例如,可以使用快速傅立叶变换算法中的旋转因子来实现复数乘法运算。
3.使用并行计算:FFT算法中的许多计算步骤可以并行执行,利用多核处理器或图形处理器的并行计算能力可以显著加速计算过程。
快速傅立叶变换(FFT)算法实验

实验二快速傅立叶变换(FFT)算法实验一.实验目的1.加深对DFT算法原理和基本性质的理解;2.熟悉FFT算法原理和FFT子程序的应用;3.学习用FFT对连续信号和时域信号进行谱分析的方法,了解可能出现的分析误差及其原因,以便在实际中正确应用FFT。
二.For personal use only in study and research; not for commercial use三.四.实验设备计算机,CCS 2.0 版软件,实验箱,DSP仿真器,短接块,导线。
五.基本原理1.For personal use only in study and research; not for commercial use2.3.离散傅立叶变换DFT的定义:将时域的采样变换成频域的周期性离散函数,频域的采样也可以变换成时域的周期性离散函数,这样的变换称为离散傅立叶变换,简称DFT。
4.FFT是DFT的一种快速算法,将DFT的N2步运算减少为(N/2)log2N步,极大的提高了运算的速度。
5.旋转因子的变化规律。
6.蝶形运算规律。
7.基2FFT算法。
六.实验步骤1.复习DFT的定义、性质和用DFT作谱分析的有关内容;2.复习FFT算法原理与编程思想,并对照DIT-FFT运算流程图和程序框图,了解本实验提供的FFT子程序;3.阅读本实验所提供的样例子程序;4.运行CCS软件,对样例程序进行跟踪,分析结果;记录必要的参数。
5.填写实验报告。
6.提供样例程序实验操作说明1)实验前的准备“语音处理单元”的拨码开关设置:在信号源单元中,设置左路信号源产生低频正弦波信号,右路产生高频正弦波信号。
实验箱上电,用示波器分别观测OUT1和OUT2输出的模拟信号,并调节电位器直至低频正弦波信号为100Hz/1V左右;高频正弦波信号为6KHz/1V左右;将S3中的拨码开关2打到ON,用示波器观测OUT1输出的混叠信号波形。
用导线连接“信号源单元”中2号孔接口OUT1和语音处理单元中的2号孔接口“IN”;正确完成计算机、DSP仿真器和实验箱的连接后,系统上电.2)实验过程启动CCS 2.0,用Project/Open打开“ExpFFT01.pjt”工程文件;双击“ExpFFT01.pjt”及“Source”可查看各源程序;加载“ExpFFT01.out”;至断点处停止;用View / Graph / Time/Frequency打开一个图形观察窗口;设置该观察图形窗口变量及参数;采用双踪观察在启始地址分别为0x3000h和0x3080h,长度为128的单元中数值的变化,数值类型为16位有符号整型变量,这两段存储单元中分别存放的是经A/D转换后的输入信号和对该信号进行FFT变换后的结果;单击“Animate”运行程序,或按F10运行;调整观察窗口并观察变换结果;单击“Halt”暂停程序运行,关闭窗口,本实验结束;实验结果:在CCS2.0环境,同步观察输入信号波形及其FFT变换结果;七.思考题1.对于不同的N,幅频特性会相同吗?为什么?2.FFT进行谱分析,可以应用的什么方面?八.实验报告要求1.简述实验原理及目的;2.结合实验中所给定典型序列幅频特性曲线,与理论结果比较,并分析说明误差产生的原因以及用FFT作谱分析时有关参数的选择方法。
基于DSP的快速傅里叶变换算法

摘要采用高级C语言实现FFT算法。
利用DSP芯片特有的哈佛结构和专门的FFT指令。
在DSP上能够更快速的实现FFT。
从而促进DSP芯片的发展,同时加快基于DSP数字信号处理的速度。
通过对FFT的算法进行研究,从基础深入研究和学习,掌握FFT算法的关键。
研究DSP芯片如何加快蝶形计算以及如何有效地码位倒置的输出颠倒过来。
熟悉旋转因子的生成。
通过学习DSP芯片的工作原理,分析DSP控制的算法,在DSP芯片上实现快速傅里叶变换算法的设计。
通过对DSP开发环境的学习,掌握CCS的简单调试和软件仿真。
在CCS开发环境中观察正弦波输入波形、输出波形、PC机FFT 计算处理后的仿真波形图。
比较仿真图,验证设计和程序的正确性。
表明利用DSP 控制器特有的反序间接寻址使FFT的实现更加方便。
关键词:DSP;FFT;旋转因子AbstractUsing advanced C language to realize FFT algorithm. Using digital signal processor (DSP) endemic harvard structure and special FFT instructions. In more quickly on DSP can realize FFT. In order to promote the development of digital signal processor (DSP) based on DSP, accelerate the speed of digital signal processing.Base on the study of FFT, from basic research and study, the key to mastering FFT algorithm. Research on how to accelerate DSP and wing how effectively yards of a output upside down. Familiar with the rotation factor production. Through studying the working principle of DSP, analyzes the algorithm, realized the design of FFT algorithm in DSP. Based on studying DSP development environment, CCS simple commissioning and software simulation. CCS development environment in observing sine wave, the output waveform input, PC FFT calculation of wave graph with simulation. Comparative simulation diagram, verify the correctness of design and program. Use DSP controller that peculiar sequence indirect addressing the realization of FFT make more convenient.Key words:DSP; FFT; Rotation目录第1章概述 0课题研究的背景及意义 0本文主要研究内容 (1)第2章快速傅里叶变换及其算法 (3)快速傅里叶变换的原理 (3)快速傅里叶变换算法 (6)本章小结 (13)第3章软件设计 (14)算法设计和程序编写 (14)算法设计流程 (14)CCS开发环境的使用及软件仿真 (18)本章小结 (23)第4章DSP芯片的原理和FFT在DSP上的实现 (25)DSP芯片的原理、特点和结构 (25)FFT算法在DSP上的实现 (30)本章小结 (31)结论 (32)参考文献 (33)致谢 (34)附录 (35)第1章概述课题研究的背景及意义课题背景近十多年来数字信号处理技术同数字计算机、大规模集成电路等,有了突飞猛进的发展,日新月异,已经成为一门具有强大生命力的技术科学。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录一.引言二.实验原理三.FFT基本结构(1)信号流图(2)软件程序流图四.实验程序五.调试过程与步骤六.实验结果七.结果分析八.遇到的问题及解决办法九.实验体会实验题目:快速傅立叶变换(FFT)算法一.引言众所周知,FFT 是离散傅立叶变换(DFT)的一种快速算法。
由于计算DFT 时一次复数乘法需用四次实数乘法和二次实数加法;一次复数加法则需二次实数加法。
每运算一个X(k)需要4N 次复数乘法及2N+2(N-1)=2(2N-1)次实数加法。
所以整个DFT运算总共需要4N^2 次实数乘法和N*2(2N-1)=2N(2N-1)次实数加法。
如此一来,计算时乘法次数和加法次数都是和N^2 成正比的,当N 很大时,运算量是可观的,因而需要改进对DFT 的算法提高运算速度。
我们观察DFT的系数特性,可发现其对称性和周期性,我们可以将DFT 运算中有些项合并。
因此,FFT就孕育而生了。
二.实验原理1.FFT 的原理和参数生成公式:我们先设序列长度为N=2^L,L 为整数。
将N=2^L 的序列x(n)(n=0,1,……,N-1),按N的奇偶分成两组,也就是说我们将一个N 点的DFT 分解成两个N/2 点的DFT,他们又重新组合成一个如下式所表达的N 点DFT:我们称这样的RFFT 优化算法是包装算法:首先2N 点实数的连续输入称为“进包”。
其次N 点的FFT 被连续运行。
最后作为结果产生的N 点的合成输出是“打开”成为最初的与DFT 相符合的2N 点输入。
三.FFT 的基本结构: 1.FFT 信号流图如下:整个过程共有log2N 次,每次分组间隔为2^(L-1)----------------1=<L<=log2N(1)如上图第一次蝶形运算间隔为一,如第一个和第二个,第三个和第四个,以此类推;第二次间隔为二,如第一个和第三个,第二个和第四个等(2)基本运算单元以下面的蝶形运算为主:计算公式如下:)()()()(11q X W X p X q X W X p X m rNm m m rN m m -=+=++(3)在FFT 运算中,旋转因子WmN=cos(2πm/N)-jsin(2πm/N),求正弦和余弦函数值的计算量是很大的。
)/2sin()/2cos(2N R j N R eW NRj r N πππ-==-(4)本程序采用的输入信号为:1024*sin(2*pi*3*t),采样频率为1024X (0)X (1)X (2)X (3)X (4)X (5)X (6)X (7)x (0)x (4)x (2)x (6)x (1)x (5)x (3)x (7)2.程序流程图:四.实验程序#include "DSP281x_Device.h" // DSP281x Headerfi le Include File#include "DSP281x_Examples.h" // DSP281x Examples Include File#include "f2812a.h"#include"math.h"#define PI 3.1415926#define SAMPLENUMBER 128void InitForFFT();void MakeWave();/oid FFT(float dataR[SAMPLENUMBER],float dataI[SAMPLE NUMBER]);int INPUT[SAMPLENUMBER],DATA[SAMPLENUMBER];float fWaveR[SAMPLENUMBER],fWaveI[SAMPLENUMBER],w[SAMPLENU MBER];float sin_tab[SAMPLENUMBER],cos_tab[SAMPLENUMBER];void FFT(float dataR[SAMPLENUMBER],float dataI[SAMPLENUM BER]){int x0,x1,x2,x3,x4,x5,x6,xx;int i,j,k,b,p,L;float TR,TI,temp;/********** following code invert sequence *********** */for ( i=0;i<SAMPLENUMBER;i++ ){x0=x1=x2=x3=x4=x5=x6=0;x0=i&0x01; x1=(i/2)&0x01; x2=(i/4)&0x01; x3=(i/8)&0x01;x 4=(i/16)&0x01; x5=(i/32)&0x01; x6=(i/64)&0x01;xx=x0*64+x1*32+x2*16+x3*8+x4*4+x5*2+x6;dataI[xx]=dataR[i];}for ( i=0;i<SAMPLENUMBER;i++ ){dataR[i]=dataI[i]; dataI[i]=0;}/************** following code FFT *******************/ for ( L=1;L<=7;L++ ){ /* for(1) */b=1; i=L-1;while ( i>0 ){b=b*2; i--;} /* b= 2^(L-1) */for ( j=0;j<=b-1;j++ ) /* for (2) */{p=1; i=7-L;while ( i>0 ) /* p=pow(2,7-L)*j; */{p=p*2; i--;}p=p*j;for ( k=j;k<128;k=k+2*b ) /* for (3) */{TR=dataR[k]; TI=dataI[k]; temp=dataR[k+b];dataR[k]=dataR[k]+dataR[k+b]*cos_tab[p]+dataI[k+b]*sin_tab[ p];dataI[k]=dataI[k]-dataR[k+b]*sin_tab[p]+dataI[k+b]*cos_tab[ p];dataR[k+b]=TR-dataR[k+b]*cos_tab[p]-dataI[k+b]*sin_tab[p]; dataI[k+b]=TI+temp*sin_tab[p]-dataI[k+b]*cos_tab[p];} /* END for (3) */} /* END for (2) */} /* END for (1) */for ( i=0;i<SAMPLENUMBER/2;i++ ){w[i]=sqrt(dataR[i]*dataR[i]+dataI[i]*dataI[i]);}} /* END FFT */main(){int i;InitForFFT();MakeWave();for ( i=0;i<SAMPLENUMBER;i++ ){fWaveR[i]=INPUT[i];fWaveI[i]=0.0f;w[i]=0.0f;}FFT(fWaveR,fWaveI);for ( i=0;i<SAMPLENUMBER;i++ ) {DATA[i]=w[i];}while ( 1 ); // break point}void InitForFFT(){int i;for ( i=0;i<SAMPLENUMBER;i++ ) {sin_tab[i]=sin(PI*2*i/SAMPLENUMBER);cos_tab[i]=cos(PI*2*i/SAMPLENUMBER);}}void MakeWave(){int i;for ( i=0;i<SAMPLENUMBER;i++ ){INPUT[i]=sin(PI*2*i/SAMPLENUMBER*3)*1024;}}五.调试过程与步骤1.编译并下载程序。
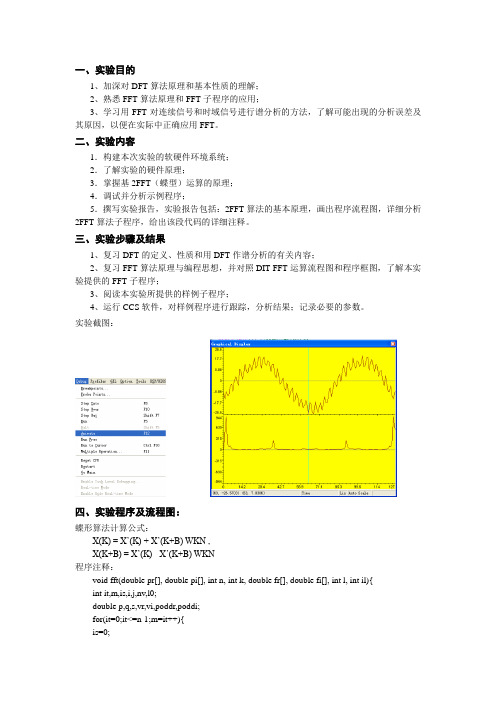
2.打开观察窗口:*选择菜单View->Graph->Time/Frequency…进行如下图所示设置。
图1图2图33.清除显示:在以上打开的窗口中单击鼠标右键,选择弹出式菜单中“Clear Display”功能。
4.设置断点:在程序FFT.c 中有注释“break point”的语句上设置软件断点。
图45.运行并观察结果。
⑴选择“Debug”菜单的“Animate”项,或按Alt+F5 键运行程序。
⑵观察“Test Wave”窗口中时域图形;图5⑶在“Test Wave”窗口中点击右键,选择属性,更改图形显示为FFT。
观察频域图形。
图6⑷观察“FFT”窗口中的由CCS 计算出的正弦波的FFT。
图7六. 实验结果通过观察频域和时域图,程序计算出了测试波形的功率谱,与CCS 计算的FFT 结果相近。
七. 结果分析(1)观察图6和图7,可以看到二者波形相似,但横纵坐标均不相同,纵坐标大约是二倍的关系,横坐标大约为142倍。
(2)观察图8,因为两个频率比较相近,因此出现了前两个频谱交叠的现象。
八.遇到的问题及解决办法S启动失败经过检查,并没有发现什么问题,一时间无从下手,将USB 插头换了一个插口后问题解决,可能原因是电脑的USB插口老化接触不良造成的。
2. 程序编译过程中产生了错误经过检查,工程中缺少(.cmd)文件,添加后编译成功。
3. 未能出现想要的图像经过仔细检查,浏览了程序后,发现断点设置有些问题,改正后问题解决,显示正确图像。
九.实验体会1.本次试验详细的介绍了FFT的特点和原理,以及设计方法,通过实验充分展示了FFT快速傅里叶变换相比于普通的算法的明显优点。
2.通过本次试验,我想我们已经熟练的掌握了FFT快速傅里叶变换的方法,在今后的学习中,可以熟练地运用这一方法解决实际的问题,这对于我们来说至本次实验带给我们的最好的礼物。
3.实验中我们遇到了不少的问题,但我们经过细致的检查,一一解决了问题,我想这说明了两个问题:(1)做实验时不够细心,导致问题百出,这个问题我想必须注意。
(2)类比能力很差,之前的做实验过程中部分步骤做过,相关问题也出现过,但没有好好吸取教训。
4.经过本次试验,我想我收获很多,首先是对于FFT的理解以及应用,再者对于个人能力的提高有很大帮助。
