第三章电阻电路的一般分析
电路原理与电机控制第3章电路的一般分析方法

1
2 - 22V+ 3
3Ω
I
8A 1Ω 1Ω
25A
4
U1 = –9.43V U4 = 2.5V
U3 = 22V
I = –2.36 A
17
• 例2. 列写下图含VCCS电路的节点电压方程。
• 解: (1) 先把受控源当作独立
源列方程;
IS1
1 R2
+ UR2 _
1
R1
1 R2
1 R1
25
I
4
U3–U2 = 22
解得
U1 = –11.93V U2 = –2.5V
U3 = 19.5V I = –2.36 A
16
• 解二:以节点②为参考节点,即U2=0
节点电压方程如下
(1 3
1 4
)U1
1 4
U3
11
4Ω 3A
U3 (1 1)U4 17
U3 = 22
解得:
1
I1 2A
2 1
I2 +U –
2
+
2
3
I
3
用节点电压表示受控源的控制量为:
2I2 –
U U1 U2 1 U1 U2
3
3
I2
U1 2
3
3 24
1
5
U1 U 2
2 0
解之:
U1
20 7
V,
U2
16 7
V
3 3
所求电流为:I
15
• 例1. 电路如图所示,求节点电压U1、U2、U3。
第三章 电阻电路的一般分析

第三章电阻电路的一般分析电路的一般分析是指方程分析法,它是以电路元件的约束特性(VCR)和电路的拓扑约束特性(KCL,KVL)为依据,建立以支路电流或回路电流,或结点电压为变量的回路方程组,从中解出所要求的电流、电压、功率等。
方程分析法的特点是:(1)具有普遍适用性,即无论线性和非线性电路都适用;(2)具有系统性,表现在不改变电路结构,应用KCL,KVL,元件的VCR建立电路变量方程,方程的建立有一套固定不变的步骤和格式,便于编程和用计算机计算。
本章的重点是会用观察电路的方法,熟练运用支路法、回路法和结点电压法的“方程通式”写出支路电流方程、回路方程和结点电压方程,并加以求解。
3-1 在一下两种情况下,画出图示电路的图,并说明其节点数和支路数(1)每个元件作为一条支路处理;(2)电压源(独立或受控)和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理。
解:(1)每个元件作为一条支路处理时,图(a)和(b)所示电路的图分别为题解3-1图(a1)和(b1)。
图(a1)中节点数6b==n,支路数11图(b1)中节点数7=bn,支路数12=(2)电压源和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理时,图(a)和图(b)所示电路的图分别为题解图(a2)和(b2)。
图(a2)中节点数4b=n,支路数8=图(b2)中节点数15b=n,支路数9=3-2指出题3-1中两种情况下,KCL,KVL独立方程数各为多少?解:题3-1中的图(a)电路,在两种情况下,独立的KCL方程数分别为(1)51==4n1--1=6-1-=n (2)3独立的KVL方程数分别为(1)61=84+--n+=1b1=111b (2)5+6+--n=图(b)电路在两种情况下,独立的KCL方程数为(1)61=5-=1n-7n (2)41=1-=-独立的KVL方程数分别为(1)6+1=95b1-n+=-=1271b (2)51=-n++-3-3对题图(a)和(b)所示G,各画出4个不同的树,树支数各为多少?解:一个连通图G 的树T 是这样定义的:(1) T 包含G 的全部结点和部分支路;(2) T 本身是连通的且又不包含回路。
第03章电阻电路的一般分析

例3 列支路电流法方程。
a
解:
I1 7
+ 70V
–
I2
1+
5U
_
7 I3 11 +
U 2-
节点a: –I1–I2+I3=0 回路1: 7I1–11I2 - 70 +5U =0 回路2: 11I2+7I3 - 5U =0 增补方程:
b
U=7I3
(1-18)
§3.4 网孔电流法
网孔电流——假想每个网孔中有一个网孔电流。方向可 任意假设。
(1-22)
理想电流源(恒流源)支路的处理
①若恒流源支路仅有一个网孔电流穿过,则该网孔电 流= ± 该恒流源电流(同方向取+,否则取-)。 ②非上述情况时:设恒流源两端电压,当作恒压源列方 程。然后增补恒流源电流与网孔电流的关系方程。
例2 列网孔电流方程。
R1
R2 im2 I3s
+ im1 I5s
第三章
电阻电路的一般分析
重点: 1.支路电流法; 2. 网孔电流法; 3.回路电流法; 4.节点电压法。
对于简单电路,通过电阻串、并联关系或 Y—△等效变换关系即可求解。如:
i总 R
R
R i=?
+
-u
2R
2R
2R 2R
i总
i总
u 2R
+
- u 2R
111 u i i总 2 2 2 16R
例4 列网孔电流方程。
解:网孔电流方向如图所示。 (R1 + R3)i1-R3i3=-U2
+
U1 _
R1
iS
R3 i1
+
第3章(学1)

1 -1 0 0
0 -1 1 0
0 0 1 -1
0 1 0 -1
图的结点和支路的关联性质
3. 降阶矩阵:
把Aa的任一行划掉,余下的(n-1) b矩阵用A表示, 并称为降阶矩阵。
-1 -1 1 0 0 0 0 0 -1 -1 0 1 1 0 0 1 1 0 0 1 0 0 -1 -1
A =
二. 基本回路矩阵
3. 割集矩阵元素 设有向图的结点数为 n,支路数为 b,则该图 的独立割集数为(n-1)。对每个割集编号,并指定 一个割集方向。可得割集矩阵为一个(n-1) b的矩 阵,用Q表示。 Q 的行对应割集,列对应支路,它的任一元素定义为: 1 表示支路k与割集j关联并方向一致。
qjk=
-1 表示支路k与回路j关联并方向相反。 0 表示支路k与割集j无关
回路2:–u3 + u4 – u5 = 0
回路3: u1 + u5 + u6 = 0
(3)
4 3
+ u – S
独立回路:独立方程所对应的回路。
2
支路电流的方程如下: i1 + i2 – i6 =0 – i2 + i3 + i4 =0 – i4 – i5 + i6 =0
R2 i2 1 i3
R4 i4
支路电流法的未知数是各支路电流;网孔(回 路)电流法的待求量是网孔(回路)电流。 假设网孔(回路)中有网孔(回路)电流存在, 各支路电流用网孔(回路)电流的代数和求得。 网孔电流法仅适用于平面网络。回路电流法不 仅适用于平面网络,也适用于立体网络。网孔 电流法是回路电流法的特例。
回路电流法:以回路电流为未知量列写电路方程分析电路 的方法。
电路分析基础第3章

R11im1+ R12 im2 = us11
R21im1 + R22im2 = uS22
R11=R1+R2 R22=R2+R3 R12=R21=R2 自阻
YANGTZE NORMAL UNIVERSITY 自阻总是正
R1 i1
a
R3
网孔1所有电阻之和
网孔2所有电阻之和
互阻 网孔1、2的公共电阻
i2 R2 + im1 + uS 1 uS2 – – b
us + 2
YANGTZE NORMAL UNIVERSITY
R1
L1
L2
R2
us -
+
L
1
i2
4 3
i4
R2
5
2
i5
C
1 3
4
5
R1
i2 i4 i5
有向图
返回
YANGTZE NORMAL UNIVERSITY
§3-2 KCL和KVL的独立方程数
1、KCL的独立方程数
2
1 1 4 3 5 2 3
YANGTZE NORMAL UNIVERSITY
电路分析基础
1
YANGTZE NORMAL UNIVERSITY
第三章 电阻电路的一般分析
重点:
支路电流法
网孔电流法 回路电流法 节点电压法
YANGTZE NORMAL UNIVERSITY
目的:找出求解线性电路的一般分析方法 。 对象:含独立源、受控源的电阻网络的直流稳态解。 (可推广应用于其他类型电路的稳态分析中) 应用:主要用于复杂的线性电路的求解。 基础: 电路的连接关系—KCL,KVL定律 元件特性(约束)(对电阻电路,即欧姆定律) 相互独 立
电路原理第三章 电阻电路的一般分析

例3.
I1 7 + 70V –
求支路电流(电路中含有受控源)
a I2 1 I3
解 11 + U _ 2
节点a:–I1–I2+I3=0
7I1–11I2=70-2U 11I2+7I3= 2U
7
+
2U
_ b
增补方程:U=7I3
利用支路电流与受控 电源控制量的关系
得 I1=8/3A; I2=14/3A; I3=22/3A;
6 4
+ 2 + 3 + 4 =0
上述四个方程并不相互独立,可由任意三个推 出另一个,即只有三个是相互独立的。
结论
n个结点的电路, 独立的KCL方程为n-1个。
独立方程对应的节点称为独立节点。
2.KVL的独立方程数 KVL的独立方程数=基本回路数=b-(n-1)
结 论
n个结点、b条支路的电路, 独立的 KCL和KVL方程数为:
例
图示为电路的图,画出三种可能的树及其对应的基 本回路。 1
4
8 3
5
6 7 2
5 8 6 7
4 8 3 6
4 8 2 3
3.2 KCL和KVL的独立方程数
1.KCL的独立方程数
2 1 1 4 3 5 2 3 2 3 4 1 1
i1 i4 i6 0 i1 i2 i3 0 i 2 i5 i 6 0 i3 i4 i5 0
整理得:
(R1+R2) im1 – R2 im2 = us1- uS2 -R2im1 + (R2+R3) im2 = uS2-us3 R11=R1+R2 R22=R2+R3 R11im1+ R12 im2 = us11 R21im1 + R22im2 = uS22
第3章 电阻电路的一般分析

解2. I1 7 + 70V –
a
增补方程:I2=6A 11 由于I2已知,故只列写两个方程。 a:–I1+I3=6 7
I2
1 6A b
I3
避开电流源支路取回路: 1: 7I1+7I3=70
返 回 上 页 下 页
例6.
I1 7
+ 70V –
列写支路电流方程(电路中含有受控源)。 a
I2 1 + 5U _ b 11 2 I3 + 7 U _ 解
返 回
支路、结点、路径、回路和网孔的概念。 (1)连通图 图G的任意两结点间至少有一条路径 时,称图G为连通图。非连通图至少 存在两个分离部分。
(2) 子图
若图G1中所有支路和结点都是图G中 的支路和结点,则称G1是G的子图。
返 回
上 页
下 页
(3)树 (Tree)
T是连通图G的一个子图, 并满足条件:
依据:
KCL、KVL以及元件的VCR。
方法: 根据列方程时所选变量不同,可分为支路电流法、
网孔电流法、回路电流法和结点电压法。
返 回 上 页 下 页
对于线性电阻电路,电路方程是一组线性代数方程。
例1
3
I1 R1 uS1 + –
a I2 I3
R2 + – b 2 独立? R3 求I1、I2和I3?
1 uS2
独立回路=2,选为网孔。
+ –
R3
i1 il 1 i3 il 2 i2 il 2 il 1
uS2
b
回路1:R1 il1-R2(il2- il1) +uS2-uS1=0 回路2:R2(il2- il1)+ R3 il2 -uS2=0 自电阻 (R1+ R2) il1 -R2 il2 = uS1-uS2
电阻电路一般分析习题

第三章电阻电路的一般分析习题一、填空题。
1、对于n个节点b条支路的连通图,其树支数为.二、计算题。
1.求图1所示电路的电压U和受控源发出的功率。
解:独立回路的选择以及回路绕行方向如图2所示,列回路电流方程为:/“=4A,/2=2A(6+3+3)∕11+3×∕zi+3×∕z2=3,单连支回路数为解:用结点法求出U=32V,1=1.6ΛEA"人心一、+、,50-15/U—151 ..受控源的电流为-------- + -------- =4A10 4受控源发出的功率为-151X4=96W2.用回路法求图2所示电路的电流I。
6QI1 ----- 1—即有I=I 13=-1.25A(2+2+2)/—2×5—2x4=—u ∣ M 1=2×(5-7)1 1 1∖l , 11. 11. , ti. ------- +一÷—)v.—v>—匕=/<——-R i +R2 R. ---------- R 1l R.2R 13 5 R 1V+(—+—+—)⅛-—½=0R3叫&-R5 --v 1--v,+(—+—+—)½=e+以RJ1.&&R 凡K求得:I 13—=-1.25A123.图3所示电路,用回路法求I 。
图3ς-=i∩ςτ+z n-'n-'m=i n-z rκ+l nι-【=力-力-力£⅛+oι=⅛t+z∕-7-⅛-ι=f∕-z∕ε+7-o=t z-1+7-=力z z-,zε5Ω图9I l=lΛ-2∕,+10∕2-∕3=5(∕X-2∕1-∕2+3∕3=-10U x=I(I3-I2)z1 1 1、〃1rr w s∙1(R+R+y+0)U川—v U“2=⅛+-7-_/u ZH+(,+,)U〃2=仇KI KAκ5补充方程,=-上」R∖+R?14 .列出图14所示电路的结点电压方程(其中④为参考结点)(RR+丁+B)Unl-KU la=i si+ι∖∣+0Kyι∖∣∕∖4^⅛^+⅛+⅛^2=^R∣+R215 .电路如图15所示,求:(1)以4为参考结点,列写结点1、2、3的结点方程。
天津商业大学 大二电路第三章

二、有向图和无向图 有向图:对每条支路都规定了参考方向 的图,也称定向图(directed graph) 支路参考方向:有向图中支路参考方 向通常是支路电流参考方向,也是与其 关联的支路电压参考方向。 无向图:支路无方向的图。
is i1 i3 i4
(a)无向图 图3-2 有向图的概念 (b)有向图
(流入为正)
(3)选择(b-n+1)个独立回路,规定回路 绕向,列出KVL方程,此处选择3个网孔作为 u1 u 2 u3 0 独 (沿回路方向 u3 u 4 u5 0 电压降为正) 立回路,则有: u 2 u4 u6 0
R i R i R i u 0 将支路电流表示的支路电压表达式代入:
is Rs + Us -
R1 i1 i4 R4 i5
(a)
R2 R3 i2 i3 R5
(b) 图3-1 图的概念 (c)
1.
2.
3.
说明:结点与支路各为一个整体 支路必须交于结点,止于结点; 结点不依赖于支路存在(允许孤立结点); 串联支路可视为一条支路。 例:
图3-1(a)电路中,有5结点、7支路(b) ;也可 视为4结点6支路(c) 。
i2
i5
§3-2 KCL和KVL的独立方程数
①
一、KCL的独立方程数
i6
i1
独立方程 ② i 在一组方程中,若任 i i 一个方程无法由其它方程 ④ 得到,这些方程线性无关, 图3-3 KCL独立方程 则称这些线性无关的方程是独立方程。 由此可见,所谓独立方程,只在方程 组中有意义。 对于给定的电路,能够列出多少个独立 方程呢?
1 1 2 2 3 3 S1
R3i3 R4 i4 R5 i5 R5 i S 5 0 R2 i2 R4 i4 R6 i6 0
第6讲 第三章 电阻电路的一般分析(一)

2. 独立方程的列写
1.从电路的n个结点பைடு நூலகம்任意选择n-1个结点列写KCL方程 2.选择基本回路列写b-(n-1)个KVL方程
n=4 b=6
当一条支路仅含电流源而不存 在与之并联的电阻时,无法将 支路电压以支路电流表示
元件VCR
KCL
求解
KVL
3. 支路电流方程的列写步骤
• 标定各支路电流(电压)的参考方向; • 从电路的n个结点中任意选择n-1个结点列写KCL方程 • 选择基本回路,结合元件的特性方程列写b-(n-1)个KVL方程 求解上述方程,得到b个支路电流; • 进一步计算支路电压和进行其它分析 需要注意的是: 支路电流法列写的是 KCL和KVL方程,所以方程列写 方便、直观,但方程数较多,宜于利用计算机求解。人工 计算时,适用于支路数不多的电路。 若将支路的电流用支路电压表示,然后带入KCL方程,连 同支路电压的KVL方程,可以得到以支路电压为变量的b个方程 ——支路电压法
第六讲 电阻电路的一般分析 (一)
• 知识点:
1. 电路的图 2. KCL和KVL的独立方程数 3. 支路电流法、网孔电流法
• 教学目标:
1. 了解电路分析中一些常用的名词 2. 掌握KCL和KVL的独立方程数及其在电路求解中的应用 3. 理解支路电流法、网孔电流法进行电路分析的一般思路
1
电路的图
-I1-I2+I3=0 7I1-11I2+35I3=70 11I2-28I3=0
支路电流法特点: • 支路电流法是最基本的方法,在方程数目不多的情况下可以 使用,由于支路电流法需要同时列写KCL和KVL方程,方程 数较多,且规律性不强,手工求解比较繁琐,也不便于计算 机编程求解。
网孔电流法
第三章--电阻电路的一般分析

i1 R1 ① R3 i3
i2
us+1
-
imu1sR2+2
im2
+ us3
-
-
(1)标出网孔电流的参考方向;
②
(2)以各自的网孔电流方向为绕行方向,
列KVL方程; 注意:im1和im2都流过R2!
孔1: R1 im1+R2 im1-R2im2 = us1 -us2 孔2:-R2 im1+R2 im2 +R3 im2 = us2-us3
3
③
4
5
④6
4个方程相加结果为0,不是相互独立的。
把任意3个方程相加起来,必得另一个方程。
相差一个符号,原因是各电流在结点① ② ③若
是流入(出),则在结点④就是流出(入) 。
2019年9月13日星期
9
五
上述4个方程中,任意3个是独立的。
对具有n个结点的电路,独立的KCL方程为任意 的(n-1)个 。 与独立方程对应的结点叫做独立结点。
现在介绍有关 “图论”的初步知识, 目的是研究电路的连 接性质,并讨论电路 方程的独立性问题。
因为KCL和KVL与元件的性质无关, 所以讨论电路方程的独立性问题时,可以用一
个简单的线段来表示电路元件。
2019年9月13日星期
3
五
用线段代替元件,称支路。 线段的端点称结点 。
这样得到的几何结构图称为 图形,或“图(Graph)”。
二、 KVL的独立方程数 与KVL的独立方程对应的回路称独立回路。
因此,要列出KVL的独立方程组,首先要找出与之 对应的独立回路组。
有时,寻找独立回路组不是一件容易的事。利用 “树”的概念会有助于寻找一个图的独立回路组。
第3章 电阻电路的一般分析答案
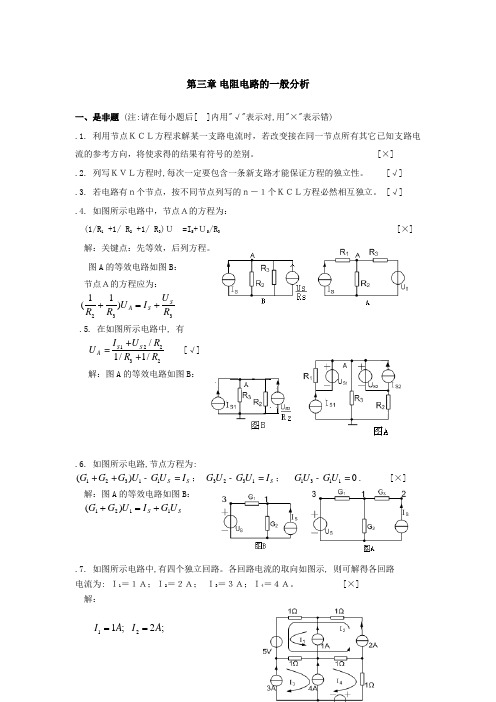
第三章 电阻电路的一般分析一、是非题 (注:请在每小题后[ ]内用"√"表示对,用"×"表示错).1. 利用节点KCL方程求解某一支路电流时,若改变接在同一节点所有其它已知支路电流的参考方向,将使求得的结果有符号的差别。
[×] .2. 列写KVL方程时,每次一定要包含一条新支路才能保证方程的独立性。
[√] .3. 若电路有n个节点,按不同节点列写的n-1个KCL方程必然相互独立。
[√] .4. 如图所示电路中,节点A的方程为: (1/R 1 +1/ R 2 +1/ R 3)U =I S +US /R 3 [×]解:关键点:先等效,后列方程。
图A 的等效电路如图B :节点A的方程应为: 332)11(R U I U R R S S A +=+ .5. 在如图所示电路中, 有 12232/1/1/S S A I U R U R R +=+ [√]解:图A 的等效电路如图B :.6. 如图所示电路,节点方程为:12311()S S G G G U GU I ++-=; 3231S G U G U I -=; 13110GU GU -=. [×]解:图A 的等效电路如图B :S S U G I U G G 1121)(+=+.7. 如图所示电路中,有四个独立回路。
各回路电流的取向如图示, 则可解得各回路 电流为: I1=1A;I2=2A; I3=3A;I4=4A。
[×] 解:;11A I = ;22A I =;33A I = ;7344A I =+=二、选择题(注:在每小题的备选答案中选择适合的答案编号填入该题空白处,多选或不选按选错论).1.对如图所示电路,下列各式求支路电流正确的是 C_。
(A) 12112E E I R R -=+; (B) 222E I R =(C) AB L LUI R =.2. 若网络有b 条支路、n 个节点,其独立KCL方程有_C_个,独立KVL方程有_D__个,共计为_A_个方程。
第三章DIANLU

–
解
KCL方程: i1 + i2 - i3 - i4=0 i3 + i4 - i5 + i6=0
(1) (2)
R4 i4 i1 R1 uS + – a
+ 3 R3
u2
i3
– b i6 i5 + u 4 –
KVL方程: R1i1- R2i2= uS R2i2+ R3i3 +R5i5= 0 R3i3- R4i4= µ u2 (3) (4) (5)
i3 R3
R4
i4 3
R1
i1 R6
4
R5
i5 i6
+
uS –
2 i2 1 R1 R2
i3 R3 i1
+ R5
R4
(1) 标定各支路电流、电压的参考方向 i4 3 u1 =R1i1, u2 =R2i2, u3 =R3i3, u4 =R4i4, u5 =R5i5, u6 =–uS + R6i6 (b=6,6个方程,关联参考方向) (1)
例4. 列写下图所示含受控源电路的支路电流方程。 R4 u2 + – i4 方程列写分两步: 3 i3 i R 3 b 6 a (1) 先将受控源看作独立源 i1 R1 uS + i2 + R5 c R2 u2 2 1 – i5 + u 4 – 列方程;
i1 (2) 将控制量用未知量表示,
im2
回路1 : R11 R1 R5 R4 回路2 : R22 R2 R6 R5 回路3 : R33 R4 R6 R3
互阻:两个网孔的共有电阻
R12 R21 R5 R13 R31 R4 R23 R32 R6
第三章电阻电路的一般分析

第三章电阻电路的一般分析本章内容:1.电路的图及KCL和KVL独立方程数 2.支路分析法3.网孔分析法4.回路电流法5.结点分析法本章重点:主要学习电阻电路的方程建立及一般分析方法(支路分析法、网孔分析法、节点分析法、回路分析法。
其中,支路分析法是最基本的方法)。
本章难点:独立回路数的确定, 回路分析法及节点分析法.§3-1 电路的图本节介绍有关图论的初步知识,学习应用图的方法选择电路方程的独立变量一、电路的图(G)数学上的图:是边(支路)和顶点(结点)的集合,每一条边都连到相应的顶点上,边是抽象的线段,当移去边时,顶点保留,当移去顶点时,应将顶点所连的支路移走。
1.电路的图(连通图G):是将支路画成的抽象线段形成的节点和支路的集合,结点相对于数学图的顶点,支路相当于数学图中的边。
支路是实体。
KVL和KCL 与元件的性质无关,故可用图讨论其方程。
2.无向图:画出的没有方向的图为无向图3.有向图:画出的有方向的图为有向图4.连通图:任意两个结点之间至少有一条支路或路径时的图为连通图。
二、电路的图的画法(有几种,其中简便的画法)1.一般将电阻和电压源串联的组合,电阻和电流源并联的组合看成一条支路, 将流过同一个电流的每一个分支看成一条支路。
如(b)2.指定电流和电压的参考方向,一般选关联参考方向。
如图(c)(a) (b) (c)§3-2 KCL和KVL的独立方程数一、KCL的独立方程数(n个结点电路,KCL的独立方程是n-1个)将电路的有向图,结点和支路加以编号,如下图,对结点①②③④列写KCL 方程有由于每条支路与两个结点相联,其电流从一个节点流出,从另一个结点流入,一正,一负(从表达式可见),将上面4个方程相加,等式两边为0,说明4个方程不是独立的;将上面3个方程相加,等式两边不为0,说明3个方程是独立的。
可见,n个结点电路,n-1个结点的KCL方程是独立的一、KVL的独立方程数(b条支路,n个结点,KVL为b-(n-1)个)KVL的独立方程数等于独立回路数独立回路数等于基本回路数,回路与支路的方向无关,以无向图讨论。
电路原理 第三章

第三章电阻电路的一般分析一、教学基本要求电路的一般分析是指方程分析法,是以电路元件的约束特性(VCR)和电路的拓补约束特性(KCL、KVL)为依据,建立以支路电流或回路电流或结点电压为变量的电路方程组,解出所求的电压、电流和功率。
方程分析法的特点是:(1)具有普遍适用性,即无论线性和非线性电路都适用;(2)具有系统性,表现在不改变电路结构,应用KCL,KVL,元件的VCR建立电路变量方程,方程的建立有一套固定不变的步骤和格式,便于编程和用计算机计算。
本章学习的内容有:电路的图,KCL和KVL的独立方程数,支路电流法,网孔电流法,回路电流法,结点电压法。
本章内容以基尔霍夫定律为基础。
介绍的支路电流法、回路电流法和节点电压法适用于所有线性电路问题的分析,在后面章节中都要用到。
内容重点:会用观察电路的方法,熟练应用支路电流法,回路电流法,结点电压法的“方程通式”写出支路电流方程,回路电流方程,结点电压方程,并求解。
预习知识:线性代数方程的求解难点:1. 独立回路的确定2. 正确理解每一种方法的依据3. 含独立电流源和受控电流源的电路的回路电流方程的列写4. 含独立电压源和受控电压源的电路的结点电压方程的列写二、学时安排总学时:6三、教学内容§3-1 电路的图1. 网络图论图论是拓扑学的一个分支,是富有趣味和应用极为广泛的一门学科。
图论的概念由瑞士数学家欧拉最早提出,欧拉在1736年发表的论文《依据几何位置的解题方法》中应用图的方法讨论了各尼斯堡七桥难题,见图3.1a和b所示。
图3.1 a 哥尼斯堡七桥 b 对应的图19~20世纪,图论主要研究一些游戏问题和古老的难题,如哈密顿图及四色问题。
1847年,基尔霍夫首先用图论来分析电网络,如今在电工领域,图论被用于网络分析和综合、通讯网络与开关网络的设计、集成电路布局及故障诊断、计算机结构设计及编译技术等等。
2. 电路的图电路的图是用以表示电路几何结构的图形,图中的支路和结点与电路的支路和结点一一对应,如图3.2所示,所以电路的图是点线的集合。
第三章 电阻电路的一般分析

例
I1
+ US1
①
+
-
(
U S1 U S 2 1 1 1 U n1 IS3 R1 R2 R3 R1 R2 U S1 U S 2 IS3 R1 R2 U n1 1 1 1 R1 R2 R3
)
-
R1
R2
R3
IS3
对n=2的电路有
U n1
GU I G
I1 I l 1 I 2 I l1 I l 2 I3 Il2
据KVL得
R1 I1 R2 I 2 U S1 U S 2 R I R I U 3 3 S2 2 2
(不可解)
回路电流法比支路电流法求解的方程数少(n1)即只有(b-n+1)个。
由于有受控源,100=R12 ≠R21 = –1350 !
例2.求uA 、iB
a iB 4Ω
6A
b + 20V
-
6Ω
iC
+ u A-
c
3Ω
2 uA
d
- 2Ω 6iB +
a
b
c
o
解:回路取lbodb(2uA) 、 labdoa(iB) 、 lbcdb (iC), lacdoa(6A) labdoa 7iB +3×6=6iB -20 lbcdb 8iC+2×6 = 20
其系数规律为:
R11 ─自电阻,回路l1的所有电阻之和(恒正)(R22…Rmm 同);
R12 、R21 ─互电阻,回路1、2的公有电阻“代数和”,Il1 、 Il2在互电阻上同方向时取正;反之取负。无受控源时相 等.
US11 ─ 回 路 l1 沿 Il1 方 向 上 电 压 源 电 位 升 的 代 数 和 (US22…USmm 同)。
电路分析基础第五版第3章

b
增补方程:U=7I3
解得: I1=-28.3A I2=-46.7A I3=-18.3A
注意 有受控源的电路,方程列写分两步:
① 先将受控源看作独立源列方程;
②将控制量用未知量表示,并代入①中所列的方 程,消去中间变量。
§3-4 网孔电流法
结点a: –I1–I2+I3=0
(2) b–( n–1)=2个KVL方程:
7I1–11I2=70-U
a
11I2+7I3= U 增补方程:I2=6A
I1 7 I2 11
+ 70V
1 6A + U
2
I3 7
解得:
–
-
I1=2A I2=6A I3=8A
b 设电流源 电压
a
解2
I1 7 I2 11
共2b个独立方程。
e
图
有向图
1. KCL的独立方程数
2
1
2
1 43
3
6
5
4
1
i1i4i6 0
2 i1i2i30 3 i2i5i6 0
4 i3i4i50
结论
1 + 2 + 3 + 4 =0
n个节点的电路, 独立的KCL方程为n-1个。
2. KVL的独立方程数
2
1
2
对网孔列KVL方程:
明确 ①对应一个图有很多的树
②树支的数目是一定的 连支数:
bt n1
b lbb tb(n 1 )
②回路(Loop)
L是连通图的一个子图,构成一 条闭合路径,并满足:(1)连通,
3 第 三 章 电阻电路的一般分析

重点掌握
1. 图论有关概念、独立结点、独立回路。 图论有关概念、独立结点、独立回路。 2. 电路三大分析法: 电路三大分析法: 支路电流法 结点电压法 回路电流法(含网孔电流法) 回路电流法(含网孔电流法)
★§3.1 ★§
一、概念 i1 R1 R2 + uS – ② i2
支路与结点的移去: 支路与结点的移去:支路必须 终止在结点上, 终止在结点上,移去支路不意 味着移去结点,但移去结点必 味着移去结点, 须移去与之相连的所有支路, 须移去与之相连的所有支路, 因此可以存在孤立结点 孤立结点。 因此可以存在孤立结点。
6. 回路(loop): 回路 : 由支路所构成的一条闭合路径。 由支路所构成的一条闭合路径。 该闭合路径中与每个结点相关联 的支路数为2。 的支路数为 。 7. 网孔(mesh):平面 网孔( : 图中的自然孔。 图中的自然孔。孔内区 域中不再含有任何支路 和结点。 和结点。 1 ②
i −i −i = 0
− i 2 + i 3 + i4 = 0 − i4 + i 5 − i 6 = 0 u1 + u2 + u3 = 0 − u3 + u4 + u5 = 0 − u2 − u4 + u6 = 0 u1 = R1 i1 − uS 1 u2 = R2 i2 u3 = R3 i3 u4 = R4 i4 u5 = R5 i5 + R5 i S 5 u6 = R6 i6
② ① ③
树支
④
连支
9.单连支回路(基本回路):只有一个连支 单连支回路(基本回路 只有一个连支 单连支回路 的回路。 个单连支回路. 的回路。有(b-n+1)个单连支回路 个单连支回路
3第三章电阻电路的一般分析

b 1 a 2 3 5
树支
7 8 e
选树 连支
6 9 d
图G
2 3 4
5
8
4
2 8 5 4
独立回路 l=5 3
例题:
该图可写出多少个独立的KCL、 KVL方程;该图具有多少个独立 的电流变量和电压变量。 答:该图共有5个结点,10条支路。 独立结点数为5-1=4个;独立回路数为10-4=6个。 所以可写出4个独立KCL方程,6个独立KVL方程。 该图中数支数为4个,连支数为6个。
US2=6V
-
根据回路电流和支路电流的关系
I1=IⅠ=6A ;I2=IⅡ=-2A ; I3=IⅠ+IⅡ=4A
2.电路如图所示,应用网孔分析法求网孔电流 及支路电流I。 0.5I _
6Ω +
解:(1) 选定网孔电流I1、
I I1 I2 2Ω 5Ω
I2的参考方向如图所示。
(2) 列网孔方程:
49
+ _
三、支路电流法解题步骤: (1)确定支路(电流)数b和节点数n b=6,n=4 (2)列出独立的KCL方程(n-1)=3个 R1 a : I 1 + I5 = I2 b: I2 = I3+ I4 I1 c: I3 + I6 = I1 + U 1 (3)列出独立的KVL方程 b-(n-1)=3=(网孔数) R2 b R3 a
(6 2) I1 2I 2 49
(3) 解方程组, 得
补充方程
2I1 (2 5) I 2 0.5I
I I1 I 2
I1 6.5 A, I 2 1.5 A, I 5 A
3.E1=1V,E3=6V,IS=6A,R1=3,R2=2, R3=1,R4=4,求网孔电流。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
网孔2 - R2il1+ (R2 +R3) il2 =uS2
R11il1 + R il 2 = usl1 12 一般形式: 一般形式: R21il1 + R22il 2 = usl 2
你能比较出什么规律吗? 你能比较出什么规律吗?
网孔电流法分析( 网孔电流法分析(续)
i1 R i2 R2 1 + il1 + uS1 b il2 uS2 – –
即两个网孔共有电阻之和, 即两个网孔共有电阻之和, 当两个网孔电流流过相关支 路方向相同时, 路方向相同时,互电阻取正 否则为负号。可见, 号;否则为负号。可见,当 网孔电流均取顺(或逆) 网孔电流均取顺(或逆)时 针方向时,互电阻均为负。 针方向时,互电阻均为负。
(R1+ R ) i -R2il2=uS1-uS2 - R2il1+ (R2 +R3) il2 =uS2
–I1+I3=6 7I1+7I3=70
I1 7Ω + 70V –
b
含受控源的情况
a 7Ω + 70V – I1 I2 11Ω + I3 1 U 7Ω + 2 _ 5U _ b
先将受控源看作独立源列方程; ① 先将受控源看作独立源列方程; 将控制量用未知量表示,并代入①中所列的方程, ② 将控制量用未知量表示,并代入①中所列的方程,消去 中间变量。 中间变量。
树
1 5
3
5、树支:构成树的支路 树支: 连支: 6、连支:属于图而不属于树的支路 树支数: t 树支数: b 连支数: 连支数:
= n −1
bl = b − bt = b − n +1
问题:你还能画出哪些不同的树。 问题:你还能画出哪些不同的树。
基本回路
1 5 2 6 4 3
观察:图的任意一个树,加入一个连支后, 观察:图的任意一个树,加入一个连支后,就形成一 个回路,且此回路除所加连支外均由树支组成, 个回路,且此回路除所加连支外均由树支组成, 基本回路。 这种回路称为单连支回路或基本回路 这种回路称为单连支回路或基本回路。 基本回路数: 基本回路数: l
网孔电流法分析( 网孔电流法分析(续)
i1 R i2 R2 1 + il1 + uS1 b il2 uS2 – – i3 R3
网孔1
整理得: 整理得:
R11il1 + R12il 2 = usl1 R i + R i = u 21 l1 22 l 2 sl 2
(R1+ R2) il1-R2il2=uS1-uS2
R11il1 + R12il 2 = usl1 一般形式: 一般形式: R21il1 + R22il 2 = usl 2
uslk:网孔 在网孔电流方向的 网孔k在网孔电流方向的
电压升之和。 电压升之和。
网孔电流法的一般形式
个网孔的电路, 对于具有 l 个网孔的电路,有:
R11il1 + R12il 2 +L+ R1lill = usl1 R i + R i +L+ R i = u 21 l1 22 l 2 2l ll sl 2 L Rl1il1 + Rl2il 2 +L+ Rllill = usll
2b法示例 2b法示例
支路的VCR: : 支路的 网孔的KVL: : 网孔的
u1 = −uS1 + Ri1 1 u2 = R2i2 u3 = R3i3 u4 = R4i4 u5 = R5i5 + R5iS 5
电路的图
u1 + u2 + u3 = 0 −u3 + u4 + u5 = 0 −u2 − u4 + u6 = 0
1 1 −1 i1 0 7 −11 0 i2 = 64 0 11 7 i 6 3
i1 = 6A i2 = −2A i3 = 4A
P V = 420W 70 PV = −12W 6
求各元件的电流和电压
网孔电流法分析
i1 R i2 R2 1 + il1 + uS1 uS2 b il2 – – i3 R3 网孔数为2 网孔数为 2 。 选图示 的两个网孔电流, 的两个网孔电流,支路电 流可表示为: 流可表示为:
i1 = il1
i3 = il 2
i2 = il 2 − il1
列写的方程 网孔1: 网孔 : R1 il1-R2(il2-il1) +uS2-uS1=0 网孔2: R2(il2- il1)+ R3 il2 -uS2=0 网孔 :
问题:KCL、KVL方程中哪些是相互独立的呢? 问题:KCL、KVL方程中哪些是相互独立的呢? 方程中哪些是相互独立的呢
本章方法的适用性与基础
线性电路的一般分析方法 • 普遍性:对任何线性电路都适用。 普遍性:对任何线性电路都适用。 • 系统性:计算方法有规律可循。 系统性:计算方法有规律可循。 方法的基础 • 电路的连接关系—KCL,KVL定律。 电路的连接关系— 定律。 定律 • 元件的电压、电流关系特性VCR。 元件的电压、电流关系特性VCR。 VCR 复杂电路的一般分析法就是根据KCL、KVL及 复杂电路的一般分析法就是根据 及 元件的VCR列方程、解方程。 VCR列方程 元件的VCR列方程、解方程。
方程列写方便、直观,但方程数较多。 方法的特点 :方程列写方便、直观,但方程数较多。
网孔电流法
以沿网孔连续流动的假想电流为未知量列 写电路方程分析电路的方法称网孔电流法。 写电路方程分析电路的方法称网孔电流法。它仅 适用于平面电路。 适用于平面电路。 基本思想 为减少未知量(方程)的个数, 为减少未知量 (方程 )的个数 , 假想每个回 路中有一个回路电流。 路中有一个回路电流 。 各支路电流可用回路电 流的线性组合表示,来求得电路的解。 流的线性组合表示,来求得电路的解。
Ri1 + R2i2 + R3i3 = uS1 1 −R3i3 + R4i4 + R5i5 = −R5iS 5 −R2i2 − R4i4 + R6i6 = 0
网孔的KVL可由电路图直接得到,你能办到吗? 可由电路图直接得到,你能办到吗? 网孔的 可由电路图直接得到
求各支路电流及各电源发出的功率
a I1 + 70V – 7Ω I2 11Ω 1 + 2 6V – b I3 7Ω
a I1 7Ω + 70V – I2 11Ω 6A I3 7Ω
b
两种求解方法
a I1 7Ω I2 11Ω + 1 6A + 2 70V U – _ b 设电流 源电压 I3 7Ω
–I1–I2+I3=0 7I1–11I2=70-U 11I2+7I3= U I2=6A
a I2 11Ω 6A I3 7Ω
1 5 2 6 4 3
重要结论:任意(n 1)个结点上可以 (n重要结论:任意(n-1)个结点上可以 得出(n 1)个独立的KCL方程 (n- 个独立的KCL方程。 得出(n-1)个独立的KCL方程。
2b法 2b法
1 5 2 6 4 3
电路的图中有n个结点,b条支路,求每个支路的电流 电路的图中有 个结点, 条支路, 个结点 条支路 电压。共计2b个所求量。 电压。共计 个所求量。 个所求量
①②③的 ①②③的KCL: :
u6 = R6i6
−i1 + i2 + i6 = 0 −i2 + i3 + i4 = 0 −i4 + i5 − i6 = 0
支路1 支路 支路5 支路
或
支路电流法
支路的VCR: : 支路的
u1 = −uS1 + Ri1 1 u2 = R2i2 u3 = R3i3 u4 = R4i4 u5 = R5i5 + R5iS 5 u6 = R6i6
–I1–I2+I3=0 7I1–11I2=70-5U 11I2+7I3= 5U U=7I3 增补方程
支路电流法的一般步骤
①标定各支路电流(电压)的参考方向; 标定各支路电流(电压)的参考方向; 个结点, 方程; ②选定(n–1)个结点,列写其 选定 个结点 列写其KCL方程; 方程 个独立回路, ③选定b–(n–1)个独立回路,指定回路绕行方向, 选定b–(n–1)个独立回路 指定回路绕行方向, 结合KVL和支路方程列写; 结合 和支路方程列写; 和支路方程列写 个支路电流; ④求解上述方程,得到 个支路电流; 求解上述方程,得到b个支路电流 ⑤进一步计算支路电压和进行其它分析。 进一步计算支路电压和进行其它分析。
第三章 电阻电路的一般分析
目的:求解电路中各元件的电流、电压。 目的:求解电路中各元件的电流、电压。
1、电路中有8个元件,需要求解16个未知量的值。 电路中有8个元件,需要求解16个未知量的值。 16个未知量的值 观察:电压源电压已知、电流源电流已知、 2、观察:电压源电压已知、电流源电流已知、电 流源电压等于电阻R 电压、 流源电压等于电阻R2电压、电压流电流等于电阻 电流。故需要求解12未知量的值, 12未知量的值 R1电流。故需要求解12未知量的值,即每个电阻 的电压与电流。 的电压与电流。 由欧姆定律, 3、由欧姆定律,只需要求解每个电阻的电流即可 求电压亦可),故只需要求解6个未知量。 ),故只需要求解 (求电压亦可),故只需要求解6个未知量。 根据KCL KVL列方程即可求解 KCL、 列方程即可求解。 4、根据KCL、KVL列方程即可求解。
重要结论:平面图的全部网孔是一 重要结论: 组独立的KVL方程。 KVL方程 组独立的KVL方程。
问题: 问题: 1、哪个是平面图。 、哪个是平面图。 2、画出每个图的树。 、画出每个图的树。 3、每个图的基本回路有几个,分别是 、每个图的基本回路有几个, 什么? 什么?
