六年级下册数学用比例解决问题练习题(含答案)

用比例解决问题六年级下册数学同步练习人教版(含答案)

第四单元：比例第7课时：用比例解决问题班级：姓名: 等级:【基础训练】一、选择题1．甲有图书120本，乙有图书60本，甲给乙（）本后，乙的图书与甲的图书比是4∶5。

A．20 B．40 C．602．一块长方形的耕地（如图），已知其中三小块长方形的面积分别是15km2、16km2和20km2，则阴影部分的面积是（）km2A．19 B．12 C．11 D．213．一个玻璃瓶内原有一些盐水，盐与盐水的质量比为1∶12，加入15克盐后，盐与盐水的质量比为1∶9。

瓶内原有盐水（）克。

A．480 B．440 C．360 D．3004．如下图：一辆汽车早上8：00从A地出发，以平均每小时60千米的速度行驶，11：30到达目的地．目的地应该是（）．A．甲城B．乙城C．丙城5．下面的问题，还需要确定一个信息才能解决，是（）B．玫瑰、三种花总数的比是1：3C．三种花的数量是百合的6倍D．玫瑰的数量是百合的二、填空题6．一个三角形中三个内角的度数的比是2∶3∶7，它最大内角的度数是( )，这是一个( )三角形。

7．某小学五、六年级参加数学竞赛的人数比是8∶7，六年级获奖人数是五年级获奖人数的37，两个年级各有50名同学未获奖，六年级有( )名同学获奖。

8．甲、乙两人从武汉长江大桥的两端出发，相向而行，乙先走556.8米，然后甲从桥的另外一端开始出发。

已知甲、乙两人的速度是3∶2，甲、乙相遇时所走的路程是2∶3，问武汉长江大桥全长( )米。

9．已知平行四边形ABCD周长为80厘米，以BC为底时，高为21厘米．以CD为底时高为27厘米，那么平行四边形的面积为（）平方厘米．10．甲、乙、丙三人进行200米赛跑，当甲到达终点时，乙离终点还有20米，丙离终点还有25米，如果甲、乙、丙赛跑时的速度都不变，那么，当乙到达终点时，丙离终点还有( )米。

三、判断题11．时间和速度成反比例．( )12．变速自行车蹬同样的圈数时，前后轮齿数比的比值越大，自行车走得越远。

人教版六年级数学下册总复习：用比例解决问题专项训练

小学数学试卷2021年04月23日一、解答题（共30题；共175分）1.淘气想测量电线杆的高，量得电线杆在平地上的影子长为5.4米，同时把2米长的竹竿直立在地上，量得影子长为1.8米，电线杆的高度是多少？（用比例解）2.在比例尺是1：6000000的地图上，量得两地之间的距离是12厘米，如果一辆汽车行完全程用7.2时，这辆汽车平均每时行多少千米？3.（1）一辆汽车，每百千米耗油8L。

照这样计算，王叔叔驾驶该汽车从甲地出发去相距80km的乙地，需要用多少升油？（2）一辆汽车，每百千米耗油8L。

照这样计算，王叔叔驾驶该汽车从甲地出发去乙地，共耗油6.4L。

甲地与乙地相距多少千米？4.（1）王叔叔骑车从A地去B地，前10分钟行驶了2800m。

照这样的速度，他从A地到B地一共用了30分钟。

A，B两地相距多少米？（2）王叔叔骑车从A地去B地一共用了30分钟，每分钟行驶280m，返回时每分钟行驶300m。

王叔叔从B地返回A地用了多少分钟？5.用比例的方法解答问题。

（1）李阿姨购买了售价为1.5元/个的A品牌口罩60个，如果这笔钱用来购买售价为1.2元/个的B品牌口罩，可以购买多少个？（2）甲、乙两个圆柱形量杯的容积相等，从里面量，甲量杯的底面半径是5cm，高是12cm，乙量杯的高是15cm。

乙量杯的底面积是多少？6.用比例的方法解答问题。

（1）同学们为了布置教室去商店购买彩带，买了12m，一共花了18元。

如果还要买16m，那么还需多少元？（2）李叔叔需要用36m铁丝。

他采用取样的方式对家中的一捆铁丝进行测量。

先从中截取了2m长的一段，测得它的质量为150g，再测得整捆铁丝重3kg。

这捆铁丝够用吗？7.在比例尺是1：25000的地图上，量得甲、乙两地之间的距离是20cm。

在比例尺为1：20000的地图上，甲、乙两地的距离应画多长？8.南京长江大桥全长约6700m，在一幅比例尺是1：10000的地图上应画多少厘米？9.一个工程队铺一段铁路，实际工作效率与原计划工作效率的比是6：5，实际工作90天，原计划需要工作多少天？10.在一幅地图上，相距72km的A、B两地间的距离是6cm。

【精品】小学六年级数学比例测试题含答案及知识点

【精品】小学六年级数学比例测试题含答案及知识点一、比例1．一个零件的高是4mm，在图纸上的高是2cm．这幅图纸的比例尺是（）A. 1：5B. 5：1C. 1：2D. 2：1【答案】 B【解析】【解答】解：2cm=20mm，比例尺：20：4=5：1。

故答案为：B。

【分析】把2cm换算成mm，然后写出图上距离与实际距离的比并化成后项是1的比就是这幅图的比例尺。

2．把一个长8m，宽6m的长方形画在作业本上，选择比例尺比较合适的是（）。

A. 1：10B. 1：100C. 1：10000【答案】 B【解析】【解答】解：8m=800cm，A、800×=80（cm），不合适；B、800×=8（cm），合适；C、800×=0.08（cm），不合适。

故答案为：B。

【分析】把实际的长度换算成厘米，然后用实际长度乘比例尺，求出图上长度，根据实际情况选择合适的比例尺即可。

3．实验小学新建一个长方形游泳池，长50米，宽30米。

选用比例尺（）画出的平面图最大。

A. 1∶1000B. 1∶1500C. 1∶500【答案】 C【解析】【解答】解：50米=5000厘米，30米=3000厘米，选用1：1000比例尺，在平面图中画出的长是5000÷1000=5厘米，宽是3000÷1000=3厘米，面积是5×3=15平方厘米；选用1：1500比例尺，在平面图中画出的长是5000÷1500≈3.3厘米，宽是3000÷1500=2厘米，面积是 3.3×2=6.6平方厘米；选用1：500比例尺，在平面图中画出的长是5000÷500=10厘米，宽是3000÷500=6厘米，面积是10×6=60平方厘米。

故答案为：C。

【分析】图上距离和实际距离的比叫做这幅图的比例尺，根据比例尺可以求出这个长方形的游泳池的平面图的长和宽，再根据长方形的面积=长×宽计算出面积即可。

六年级数学用比例解决问题试题

六年级数学用比例解决问题试题1.甲乙丙三人共同生产100个零件，甲完成了三成，乙和丙完成的数量比是2:5，乙和丙各完成多少个?【答案】乙完成20个，丙完成50个。

【解析】现已知乙丙完成的数量之比，只要找到他们两个完成的总数，就很容易“按比例分配”了。

解：100×（1-）=70（个），2+5=7，70×=20（个），70×=50（个）答：乙完成20个，丙完成50个。

【考点】比的应用。

2.某工厂采用最新技术，每天用料14吨，这样原来7天的用料，现在可用10天，原来每天用料几吨？【答案】20吨【解析】先求出木料的总量，再用这个总量除以原来使用的天数即可。

解：14×10=140（吨）140÷7=20（吨）答：原来每天用料20吨。

3.师徒两人加工一种零件．用同样的时间，徒弟可以加工3个，师傅可以加工5个。

如果两人共同加工200个这样的零件，师傅、徒弟分别要加工多少个？【答案】师傅加工125个，徒弟加工75个【解析】根据“用同样的时间，徒弟可以加工3个，师傅可以加工5个，”知道徒弟和师傅的工作效率的比是3：5，由此知道徒弟的工作效率是两人工作效率的和的，再根据在时间一定时，工作量与工作效率成正比例，即徒弟的工作量是两人工作量和的，进而解决问题。

解：他们的效率之比是3：5。

徒弟加工零件的个数：200×=200×=75（个）师傅加工零件的个数：200-75=125（个）答：师傅加工125个，徒弟加工75个。

4.某俱乐部男、女会员的人数之比是，分为甲、乙、丙三组．已知甲、乙、丙三组的人数比是，甲组中男、女会员的人数之比是，乙组中男、女会员的人数之比是．求丙组中男、女会员人数之比．【答案】5:9【解析】以总人数为1，则甲组男会员人数为，女会员为，乙组男会员为，女会员为；丙组男会员为，女会员为；所以，丙组中男、女会员人数之比为．5.一班和二班的人数之比是，如果将一班的名同学调到二班去，则一班和二班的人数比变为．求原来两班的人数．【答案】48 42【解析】原来一班的人数为两班总人数的，调班后一班的人数是两班人数的，调班前后一班人数的比值为，所以一班原来的人数为人，二班原来的人数为人.6.甲本月收入的钱数是乙收入的，甲本月支出的钱数是乙支出的，甲节余240元，乙节余480元．甲本月收入多少元？【答案】600【解析】甲、乙本月收入的比是，分别节余240元和480元，支出的钱数之比是．如果乙节余480元，甲节余元，那么两人支出的钱数之比也是，现在甲只节余240元，多支出了60元，结果支出的钱数之比从变成了(即)，所以这60元就对应份，那么甲支出了元，所以甲本月收入为元．7.甲、乙两车分别从、两地同时相向开出，甲车速度是千米／小时，乙车速度是千米／小时，当甲车驶过、距离的多千米时与乙车相遇，、两地相距（）千米．【答案】225【解析】在相同的时间内，两车行驶的路程比等于两车的速度之比，由于两车的速度之比等于，那么、距离的多千米即是、距离的，所以千米的距离相当于全程的，全程的距离为(千米)．8.甲、乙、丙三个数，已知，，求。

六年级下册数学—14用比例解决问题(有解释)

【详解】解：设这堆煤现在可以烧x天。
（3－0.6）x＝3×96
2.4x÷2.4＝288÷2.4
x＝120
答：这堆煤现在可以烧120天。
【点睛】本题考查了用反比例解决问题，积一定是反比例关系。
6．444千米
【分析】设A、B两城相距x千米，根据路程÷时间＝速度（一定），列出正比例算式，解答即可。
【详解】解：设A、B两城相距x千米。
（3）在（2）成立的基础上，若圆柱的底面半径为10厘米，则放入7块铁块后，容器内有水多少毫升？
40．学校图书馆有科技书、文艺书和故事书，其中科技书与文艺书的比是4∶9，科技书与故事书的比是2∶3，故事书有900本，文艺书有多少本？
41．某部队行军演习，4小时走了22.4km，照这样的速度又走了6小时，一共走了多少km？（用比例知识来解）
34．机械厂工人8小时加工440个机器零件，照这样计算，要加工1100个需要多少小时。
35．某车队往四川运送一批救灾物资。原计划每小时行60千米，6.5小时到达，实际每小时行了78千米。照这样计算，行完全程需要多少小时？（用比例解）
36．生产一批零件，计划20天完成任务，由于实际每天比原计划多生产150个，结果提前5天完成任务，这批零件有多少个？（列方程解）
37．学校发起“圆贫困地区孩子一个读书梦”爱心捐书公益活动，短短一周时间，就收到了同学们捐赠的大量书籍。学校决定将书打包后邮寄，现要求每包内装书的本数相同，用这批书的打包了14份还多42本，剩下的书连同第一次余下的刚好又打包了11份。这批书共有多少本？
38．大华把3米长的竹竿直立在地上，测得它的影子长是1.5米，同时测得一棵树影子长3.8米，求这棵树的高？
（4）解：设需要药液，需要水；
50x＝816－x

人教版六年级下册数学比例练习(含答案)

4 比例1.当减数是被减数的47时,差与减数的比是( )A.4：7B.3：7C.4：3D.3：4 2.甲、乙两人进行百米赛跑,当甲到达终点时,乙在甲后面20米处。

如果两人的速度不变,要使甲、乙两人同时到达终点,甲的起跑线应后移( )米。

A.10B.15C.20D.253.右边的图形是左图按一定的比例缩小得到的,则x=( )。

（单位：cm ）A.7.5B.5C.4.84.下面的叙述有一句是错误的,它是( )。

A.2的倍数可能是质数,也可能是合数,但一定是偶数B.任何自然数（0除外）的倒数都不大于1C.正方形的边长和面积不成比例D.用数对()1,x 表示位置,它一定不在第四行5.下面说法错误的是( )。

A.一条直线长6厘米B.钟面上2时整,分针和时针成锐角C.圆的周长与它的半径成正比例D.经过两点,可以画1条线段 6.下列各项中,( )中的两种量成正比例。

A.路程一定,时间和速度B.正方体的表面积与它的棱长C.差一定,被减数和减数D.45x y = 7.下面说法正确的是( )。

A.小明的位置用数对表示为()4,5,他后面的同学用数对表示为()5,5B.4x y =,则x 和y 成正比例C.在1-,2,23-,12-中,最接近0的是1-8.小明为了知道粗细均匀的50kg 铁丝有多长,就剪下5m 长的一段称重是100g 。

50kg铁丝的长度是( )m 。

A.10B.250C.1000D.2500 9.如果143a b （a ,b 不等于0）,那么a 与b 成_____比例。

10.在比例里,两个外项的积是18,其中一个内项是0.5,另一个内项是(_____)。

11.装修一个正方形的客厅,用边长是0.5米的方砖铺地,正好需要144块。

如果改用边长是0.6米的方砖铺地,那么需要(____)块。

12.一个三角形的底是12cm,它的高与面积成(____)比例关系。

13.高一定,圆柱的体积与(____)成正比例；三角形的面积一定,它的底与高成(____)比例。

六年级数学下册《解比例》练习题(附答案解析)

六年级数学下册《解比例》练习题(附答案解析)学校:___________姓名：___________班级：___________一、选择题1．如果1118和12m相等，则m 等于（）。

A ．223 B ．323 C ．173 D ．3332．在下面各比中，与0.5∶0.6的比值相等的比是（）。

A ．15∶16 B ．12∶35 C ．25∶263．3：8＝15：x ，x ＝（）A ．30B ．40C ．504．用2，3，6，9组成的比例中，正确的是（）。

A ．2396：＝：B ．2:36:9=C ．3269：＝：5．全班人数一定，出勤人数和出勤率（）。

A ．成正比例关系B ．成反比例关系C ．不成比例D ．无法确定6．大于47而小于67的分数有（）个。

A ．1B ．2C ．无数7．下列各数中，（）不能与2、8、10组成比例。

A ．58 B ．85 C ．52 D ．40二、填空题8．在一个比例里，两个外项分别是18和2.4，其中一个内项是1.5，另一个内项是()。

9．57ba =、a 与b 成( )比例关系。

10．在比例里，两个外项的积是5，其中一个内项是0.25，另一个内项是( )。

11．如果7a ＝9b （a 和b 都不等于0），那么a∶b ＝( )∶( )。

三、其他计算12．应用比例的基本性质，判断下面各组中的两个比能否组成比例。

如果能，把组成的比例写出来。

（1）560:7和720:9（2）0.45:0.3和1.5:1（3）11:416和11:636（4）30.6:8和4:0.55四、解方程或比例13．解方程。

（3x－0.5）∶（4x＋3）＝4∶9五、解答题14．给一间房子铺地砖，每块地砖的面积和所需地砖的数量如下：（1）每块地砖的面积和所需地砖数量有什么关系？（2）若每块地砖的面积是0.5平方米，需要多少块地砖？参考答案与解析：1．A【解析】略2．B【分析】此题可先算出原式中比的比值，再算出A、B、C中比的比值，即可选出正确答案。

六年级数学下册《用比例解决问题》练习题及答案解析

六年级数学下册《用比例解决问题》练习题及答案解析学校:___________姓名：___________班级：_____________一、选择题1．一条2厘米的线段，选用下面比例尺（）画出的平面图最大。

A．1∶200B．1∶5000C．1∶1D．2∶12．老师买了同样数目的田格本、横线本和练习本。

他发给每个同学1个田格本、3个横线本和5个练习本。

这时横线本还剩24个，那么田格本和练习本共剩了（）个。

A．48B．50C．54D．563．把一个圆柱削成一个最大的圆锥，削去的体积是48立方分米，圆柱的体积是（）立方分米。

A．144B．24C．724．一幅地图的比例尺是1∶1000000，下列说法不正确的是（）。

A．这是一个数值比例尺B．说明要把实际距离缩小为11000000后，再画在图纸上C．图上距离相当于实际距离的1 1000000D．图上1厘米相当于实际1000000米5．下列各数中，（）不能与2、8、10组成比例。

A．58B．85C．52D．406．甲乙两个容积相同的瓶子分别装满盐水，已知甲瓶中盐、水的比是2∶3，乙瓶中盐、水的比是3∶5，现在把甲、乙两瓶水混合在一起，则混合盐水中，盐与盐水的比是（）。

A．519B．521C．524D．31807．一个水池有甲乙两个水管。

单独开甲管，2小时可以把空池注满；单独开乙管，3小时可以把空池注满。

如果同时打开甲乙两管，（）小时可以把空池注满。

A．1B．15C．115D．58．希望小学合唱队共有队员108人，则（）一定不是男队员和女队员人数的比。

A．5∶4B．7∶5C．8∶7D．19∶17 9．表示x和y成正比例关系的式子是()．A．x＋y＝9B．y＝1.5x C．＝0D．xy＋1＝510．学校把560棵树的种植任务，按照六年级三个班的人数分配给各班。

一班有47人，二班有45人，三班有48人。

二班应种树（）。

A．192棵B．188棵C．180棵11．在一幅地图上，用20厘米的线段表示50千米的实际距离，那么这幅地图的比例尺是（）。

苏教版数学六年级下册专项～比例解决问题【含答案】

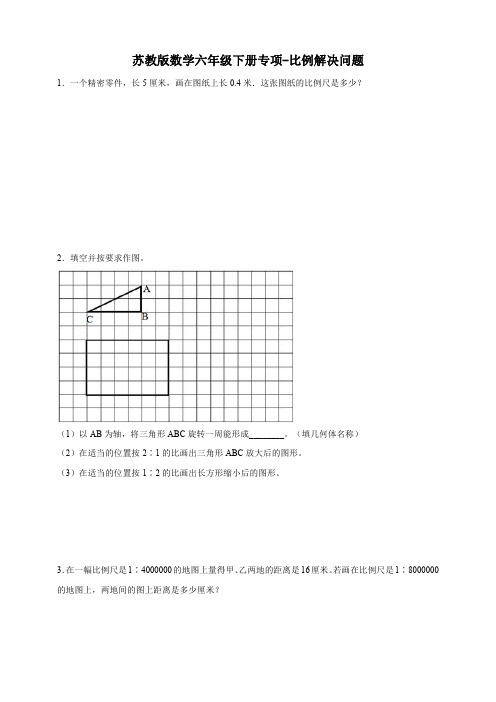
苏教版数学六年级下册专项-比例解决问题1．一个精密零件，长5厘米，画在图纸上长0.4米．这张图纸的比例尺是多少？2．填空并按要求作图。

（1）以AB为轴，将三角形ABC旋转一周能形成________。

（填几何体名称）（2）在适当的位置按2∶1的比画出三角形ABC放大后的图形。

（3）在适当的位置按1∶2的比画出长方形缩小后的图形。

3．在一幅比例尺是1∶4000000的地图上量得甲、乙两地的距离是16厘米。

若画在比例尺是1∶8000000的地图上，两地间的图上距离是多少厘米？4．画一画，填一填。

（1）按3∶1的比画出图形A放大后得到的图形B。

（2）按1∶2的比画出图形B缩小后得到的图形C。

我发现：放大或缩小前后的图形（）变了，但（）没有变，而且图形各部分长度是按一定的比变化的。

5．在一张比例尺是1∶150的建筑图纸上，量得一座大楼的长是6分米，这座大楼的实际长与宽的比是3∶1，这座大楼的实际宽是多少米？6．下图中小平行四边形按比放大后得到大平行四边形，求大平行四边形的高。

（单位：分米）12．根据图中提供的信息，完成下列问题。

（1）自来水厂要从水库取水，取水管道怎样铺最短，请在图中画出来。

（2）自来水厂到城区的送水管道经测算最短是2000米，请你测算：自来水厂到水库的取水管道最短需多少米？13．在一幅地图上，用5厘米长的线段表示实际距离100千米，这幅地图的比例尺是多少？如果甲市至乙市的铁路线路长150千米，那么这段铁路线路在这幅地图上的长度是多少厘米？14．江苏省云龙湖景区杏花坞广场是人们夏天避暑纳凉的佳处。

广场绿地面积与铺装面积的比是6∶5，其中铺装面积共5000平方米，绿地面积有多少平方米？15．甲乙两城相距150千米，在一幅地图上量得甲乙两城之间的距离是5厘米，同时在这幅地图上量得乙丙两城之间的距离是8厘米。

乙丙两城之间的实际距离是多少千米？20．下图中A点是游乐场所在的位置，B点是电影院所在的位置，两地实际距离相距2千米。

用比例解决问题习题(有答案)-数学六年级下第四章比例3.比例的应用人教版

第四章比例3.比例的应用用比例解决问题测试题一、填空．1．两种（）的量，一种量变化，另一种量（），如果这两种量中（）的两个数的（）一定，这两种量就叫做成正比例的量，它们的关系叫做（），关系式是（）．2．两种（）的量，一种量变化，另一种量（），如果这两种量中（）的两个数的（）一定，这两种量就叫做成反比例的量，它们的关系叫做（），关系式是（）．二、下面每题中的两种量是否成比例？如果成比例，成什么比例关系？1.速度一定，路程和时间。

（）2.单价一定，总价和数量。

（）3.学生总人数一定，每行站的人数和站的行数。

（）4.铺地面积一定，方砖面积与所需块数。

（）5.货车的载重量一定，运送货物的总量和辆数。

（）6.小华每天读课外书20页，读书总页数和天数成（）比例关系。

7.长方形的面积一定，长和宽成（）比例关系。

8.李玲的体重与她的年龄（）比例关系。

三、判断．1．一个因数不变，积与另一个因数成正比例．（）2．长方形的长一定，宽和面积成正比例．（）3．大米的总量一定，吃掉的和剩下的成反比例．（）4．圆的半径和周长成正比例．（）5．分数的分子一定，分数值和分母成反比例．（）6．铺地面积一定，方砖的边长和所需块数成反比例．（）7．铺地面积一定，方砖面积和所需块数成反比例．（）8．除数一定，被除数和商成正比例．（）四、选择．1．把一堆化肥装入麻袋，麻袋的数量和每袋化肥的重量．（）A．成正比例B．成反比例C．不成比例2．和一定，加数和另一个加数．（）A．成正比例B．成反比例C．不成比例3．在汽车每次运货吨数，运货次数和运货的总吨数这三种量中，成正比例关系是（），成反比例关系是（）．A．汽车每次运货吨数一定，运货次数和运货总吨数．B．汽车运货次数一定，每次运货的吨数和运货总吨数．C．汽车运货总吨数一定，每次运货的吨数和运货的次数．五、根据条件说出数量关系，并判断成什么比例。

1、食堂买3桶油用了780元，照这样计算，买10桶油需要多少元？因为（）一定，相关联的两种量是（）和（）得数量关系式：所以（）和（）成（）比例关系。

【一课一练】人教版小学数学六年级下册第四单元《比例)》-第8课时用比例解决问题-附答案

第8课时用比例解决问题1．分数1931的分子、分母同时加上一个数后，结果等于34，所加的这个数是。

2．我国发射的科学实验人造卫星，在空中绕地球运行6周需要10.6小时，运行15周要用小时。

3．一桶油，第一次倒出全桶油的16，第二次比第一次多倒出30千克，这时已经倒出的油与剩下的油的比是7：5，这桶油共千克。

4．在比例尺是1∶500000的地图上，量得A、B两地的距离是6cm，两地的实际距离是米？5．一个长方形长与宽的比是5∶3，已知长是2cm，宽是？6．地铁施工队要搅拌40吨的混凝土，水泥、沙子和石子的比是2∶3∶5．需要水泥吨,沙子吨,石子吨.7．把一根长2米，横截面是5平方厘米的钢材，按照2∶3分成两段．每段的体积是多少？1段立方分米、2段立方分米（按1、2段的顺序填写）8．右图中的长方形被两条线段分成4个小长方形，如果图形A、B、C的面积分别为2cm2、4cm2、6cm2，那么阴影部分的面积是大长方形面积的（填分数）9．早上8时，欣宇在操场上量得1.2 m长的标杆的影长是1.8 m.那么此时影长21 m的教学楼的实际高度是m.10．一个圆柱与一个圆锥的底面积相等，体积的比是6：1．如果圆锥的高是8.4厘米，那么圆柱的高是厘米．如果圆柱的高是8.4厘米，那么圆锥的高是厘米．◆基础知识达标11．甲、乙两车从A、B两地同时出发相向而行，结果甲车在距离B地40%处与乙车相遇。

若甲车行全程用5小时，则乙车行全程要用小时。

12．相同质量的冰和水的体积之比是10：9。

有27ml水，结成冰后的体积是mL。

13．把左边的三角形按一定的比缩小后得到右边的三角形，求未知数x．(单位：cm)14．甲乙两堆化肥重量比是5∶3，乙堆化肥重9.6吨，甲堆化肥重吨．15．一种农药，由药粉和水按照1：400混合而成的。

2.5千克药粉，应加水千克。

16．淘气和笑笑收集的邮票张数的比是3∶5。

淘气收集了36 张邮票，笑笑收集的邮票有张？17．大小齿龄的齿数比是7：4，大齿轮有56个齿，则小齿轮有个齿。

六年级数学用比例解决问题练习

六年级数学用比例解决问题练习学校：姓名：用比例知识解决下面问题：1、用边长40厘米的方砖给教室铺地，需要432块，如果用边长60厘米的方砖铺地，需要多少块方砖？解答：由于铺地面积不变，所以两种方砖的面积成比例。

设用60厘米边长的方砖需要x块，则有：40×40×432=60×60×x解得：x=192，所以需要192块60厘米边长的方砖。

2、一辆客车3小时行135千米，照这样计算，如果行315千米，需要多少小时？解答：客车的行驶速度不变，所以行驶时间与行驶距离成反比例。

设需要的时间为x，则有：3×135=315×x解得：x=1.35，所以需要1.35小时。

3、一种农药，用药液和水按1:1500配制而成。

如果只有3千克的药液，应加水多少千克？解答：药液和水的重量成比例。

设应加水x千克，则有：3:1500=x:(3+x)解得：x=4497，所以应加4497千克水。

4、运一批药品，每箱装36瓶，需要40只箱子，如果每箱装24瓶，需要多少只箱子？解答：药品的总瓶数不变，所以需要的箱子数与每箱装瓶数成反比例。

设需要的箱子数为x，则有：36×40=24×x解得：x=60，所以需要60只箱子。

5、一块长方形地长120米，宽90米。

把它画在比例尺是1:1000的图纸上，长和宽各应画多少厘米？解答：地的长度和宽度与图纸上的长度和宽度成比例。

设地在图纸上的长度为x厘米，则有：120:1000=x:1解得：x=12，所以地在图纸上的长度为12厘米。

同理可得，地在图纸上的宽度为9厘米。

6、在一幅比例尺是1:的地图上，量得甲乙两地的距离是12厘米，甲乙两地的实际距离是多少千米？解答：地图上的长度与实际长度成比例。

设甲乙两地的实际距离为x千米，则有：1:=12:x解得：x=420，所以甲乙两地的实际距离为420千米。

7、___用24元买了6本笔记本，___也想买几本，可是他妈妈只给他16元，他最多可以买到多少本笔记本？解答：笔记本的数量与钱数成正比例。

六年级下册数学2017-2018学年第二学期练习题第4单元比例用比例解决问题含答案)

6.北京到长沙的铁路长大约是1600km 。

一列由北京开往长沙的高铁，9:00出发，11:30到达郑州。

北京到郑州的铁路长大约是700km 。

按照这样的平均速度，从北京到长沙6个小时能到吗？7.一列货车前往灾区运送救灾物资，2小时行驶了30km 。

从出发地点到灾区有90km ，按照这样的速度，全程需要多少小时？8.小林读一本文学名著，如果每天读30页，8天可以读完。

小林想6天读完，那么平均每天要读多少页？9.小明家用收割机割小麦。

如果每小时收割0.3公顷，40小时能完成任务。

（1）现在想用30小时收割完，那么每小时应收割多少公顷？（2）每公顷产小麦8t ，这块地共产小麦多少吨？（3）你能提出其他的数学问题并解答吗？10.一辆运货汽车从甲地到乙地，平均每小时行72km ，10小时到达。

回来时空车原路返回，每小时可行90km 。

多长时间能够返回原地？11.小平的姐姐在上大学，妈妈每个月（按30天算）按每天10元的标准给她一笔零花钱。

（1）如果姐姐每天花6元，一个月的零花钱够用多少天？（2）如果姐姐每天花15元，你能提出数学问题并解答吗？12.小东家的客厅是正方形的，用边长0.6m 的方砖铺地，正好需要100块。

如果改用边长0.5m 的方砖铺地，需要多少块？第4单元比例用比例解决问题练习题（答案） 1. 下面哪个图形是图形A 按2:1放大后得到的图形？2. 自己选定比例画图形，把三角形A放大后得到三角形B，再把三角形B缩小后得到三角形C。

（1）哪些三角形可以由A放大后得到？（2）哪些三角形可以由B缩小后得到？（3）*观察三角形A和B，它们的面积有什么变化？面积与边长是按相同的比变化的吗？解：（1）三角形B和三角形C可以由三角形A放大后得到。

（2）三角形A和三角形C可以由三角形B缩小后得到。

（3）三角形B的面积是三角形A的面积的16倍。

面积与边长不是按相同的比变化的。

3. 小兰的身高1.5m，她的影长是2.4m，如果同一时间、同一地点测得一棵树的影子长4m，这棵树有多高？解：设这棵树高x m。

小学六年级解比例练习题及答案

小学六年级解比例练习题及答案精品文档小学六年级解比例练习题及答案解比例: x:10=: 0.4:x=1.2: =:=:x0.8:4=x:81.25:0.25=x:1.6x: =6:2.8:4.2= .8:4.2=x:9.60(6?4,2.4?x34?12,x?45== 5:x=18:2?x,15?131112?45,2536?x :x=3:1=0.612,1.5x人教版小学六年级比和比例单元测试一、想一想，填一填。

1、如果5a=4b，那么a?b=?如果a?0.5=8?0.2，那么a=2、?=24?1.5?3,?3.43、一个数与它的倒数成比例。

4、大圆的直径是4厘米，小圆的直径是2厘米，大圆和小圆面积最简单的整数比是。

5、白兔与灰兔只数的比是7?6,白兔56只,灰兔6、三角形的面积一定，它的底和高成比例。

1 / 8精品文档17、在一个比例中，两个外项互为倒数，其中一个内项是，则另一个内项是。

8、右边的比例尺表示图上1厘米相当于地面实际距离千米，把它改写成数值比例尺是?。

9、每台电视机的价格一定，购买电视机的台数和钱数成比例。

10、一幢楼的模型高度是7厘米，模型高度与实际高度的比是1?400，楼房的实际高度是米。

二、请你来当小裁判。

1、把一个比的前项扩大2倍，后项缩小2倍，这个比的比值不变。

2、由2、3、4、5四个数，可以组成比例。

3、汽车的速度一定，所行路程和时间成正比例。

4、每小时织布米数一定，织布总米数和时间成反比例。

5、圆的半径和它的面积成正比例。

三、选择正确答案的序号填在括号内。

1、一个长4cm，宽2cm的长方形按4?1放大，得到的图形的面积是cm。

A、3B、72C、128112、与 ? 能组成比例的是。

62 / 8精品文档111111 A、? 、 ?、 ?6432233、如果y=x，x和y比例。

A、成正B、成反C、不成只。

4、全班人数一定，出勤人数和出勤率比例。

A、成正B、成反C、不成5、铺地的面积一定，砖块的面积和用砖的块数。

苏教版数学六年级下册专项～解比例计算题【含答案】

参考答案：
1．x＝
8 7
；x＝5；x＝
9 5
【分析】（1）把原式化简为 70%x＝ 4 ，再根据等式的性质，在方程两边同时除以 70%即可； 5
（2）根据比例的基本性质，把比例式化为乘积式 0.9x＝2×2.25，再根据等式的性质，在方程两边同
时除以 0.9 即可；
（3）根据等式的性质，先在方程两边同时加上 1 x，再同时减去 2 ，最后再同时除以 1 即可。
解：40%x＝5＋15
40%x＝20
x＝20÷40%
x＝50
（1－25%）x＝36
解：0.75x＝36
x＝36÷0.75
x＝48
1 7
∶x＝
9 14
∶
3 2
解： 9 x＝ 1 × 3 14 7 2
9 x＝ 3 14 14
x＝ 3 ÷ 9 14 14
x＝
3 14
×
14 9
x＝
1 3
4．x＝0.6；x＝20；x＝130
6∶x＝
1 5
∶
1 2
15．解方程。
7＝ x 12 72
0.75∶x＝3∶28
21 16
∶
5 18
＝
27 20
∶x
16．求未知数。
x∶
1 4
＝4∶
4 3
x ＝ 25 6 30
4 3
∶x＝0.75∶1.8
17．解比例。 25∶7＝x∶35
（x＋2）∶2＝21∶6
3＝ x 8 64
18．解方程。 12 : x 2.4 : 1 6 13x 9.9
3x＝1.5
x＝1.5÷3
x＝0.5
x－60%x＝48

六年级下册解比例练习题及答案

六年级下册解比例练习题及答案解比例: x:10=: 0.4:x=1.2: =:=:x0.8:4=x:81.25:0.25=x:1.6x: =6:2.8:4.2= .8:4.2=x:9.60．6∶4＝2.4∶x34∶12＝x∶45== 5:x=18:2∶x＝15∶131112∶45＝2536∶x :x=3:1= 0.612＝1.5x六年级数学下册解比例班级______姓名______一、填空题。

1．判断两个比能不能组成比例，要看。

2．18：6＝24：＝÷3＝%。

3．甲数是乙数的1.5倍，用最简单的整数比表示：。

34．在一个比例中，两个内项的积是最小的合数，一个外项是4，另一个外项是。

5．在一个比例里，两个外项互为倒数，其中一个内项是4.5，另一个内项是。

6．在一个比例中，两个外项的积是最大的两位数，其中一个内项是33，另一个内项是。

7．在比例3：12＝6：24中，如果将第一个比的后项加6，第二个比的前项应，比例才能成立。

8．在比例尺是1：2000000的地图上，量得甲地到乙地的距离是7厘米，实际距离是千米。

二、判断题。

1．两个比可以组成一个比例。

2．任意两圆各自的周长和直径的比才都可以组成比例。

3．在一张地图上，4厘米表示实际距离200米，这幅地图的比例尺是1：50。

4．x：16＝7：6，求x的值叫做解比例。

5．在比例里，两个外项的积与两个内项积的差是0。

6．在比例尺是8：1的图纸上，2厘米的红段表示零件实际长16厘米。

三、计算题。

1．解比例。

12141＝1：:?:2372．依照条件列比例，再解比例。

1最小的质数与最大的一位数的比等于2与x的比。

最小的两位数与最大的两位数的比等于3与x的比。

最小的质数与最小的合数的比等于分子是1的最大真分数与x的比。

四、应用题。

1．在比例尺是1：6000000的中国地图上，量得上海到南京的铁路长是5厘米，一列火车从南京开往上海用了8小时，求火车的速度。

六年级比例练习题及答案

六年级比例练习题及答案1. 小明每天骑自行车上学，他每小时骑行12公里。

如果他一共需要骑行2个小时，他总共要骑行多远？答案：小明总共要骑行24公里。

2. 一桶果汁中有3升，小红将桶里的果汁倒进了三个杯子中。

如果每个杯子都装满，每个杯子里有多少升果汁？答案：每个杯子里有1升果汁。

3. 校园里有500名学生，其中男生和女生的比例是3:5。

校园里有多少名男生？答案：校园里有150名男生。

4. 玩具店一套积木由240块积木组成，其中红色积木的数量是黄色积木数量的2倍，绿色积木的数量是红色积木数量的3倍。

红色积木和绿色积木的数量加起来是多少？答案：红色积木有80块，绿色积木有240块，红色积木和绿色积木的数量加起来是320块。

5. 某项工程耗时15天，甲组和乙组合作完成。

如果甲组每天完成工程量的1/3，乙组每天完成工程量的2/3，甲组需要多少天完成该工程？答案：甲组需要45天完成该工程。

6. 一辆车以每小时70公里的速度行驶，需要行驶700公里才能到达目的地。

车辆行驶多久才能到达目的地？答案：车辆需要行驶10小时才能到达目的地。

7. 小明用了120元去超市购买文具。

如果他买了笔和纸张，而纸张的价格是笔的价格的2倍。

他用了多少钱买了笔？答案：小明用了80元买了笔。

8. 一辆火车以每小时80公里的速度行驶，经过5个小时后行驶了多远？答案：火车行驶了400公里。

9. 甲组和乙组共同完成一个工程，两组所用的时间比是3:5。

如果甲组耗时15天，那么乙组耗时多久？答案：乙组耗时25天。

10. 某公司的员工总数是120人，其中男性员工的数量是女性员工数量的3倍，那么公司中女性员工有多少人？答案：公司中女性员工有30人。

总结：通过上述六年级比例练习题，我们可以看到比例概念在日常生活中的应用。

了解和掌握比例的概念对于解决实际问题非常重要。

通过练习题的答案，我们可以巩固对比例的理解，并提高解决问题的能力。

希望同学们通过这些练习题的训练，能够更好地应用比例知识解决实际问题。

六年级下册比例练习题答案

六年级下册比例练习题答案1. 题目：张三将一只铅笔分成了3段，第一段占全长的1/4，第二段占全长的2/5，第三段剩下的长度为6厘米。

求这只铅笔的全长。

解答：设这只铅笔的全长为x厘米。

根据题意，题目中已经给出了铅笔的三段长度比例关系：第一段:x/4，第二段：2x/5，第三段:6厘米。

根据比例关系，我们可以得到以下等式：x/4 + 2x/5 + 6 = x将上述等式进行整理和计算，可得：5x + 8x + 120 = 20x13x + 120 = 20x120 = 7xx = 17.14（保留两位小数）所以，这只铅笔的全长约为17.14厘米。

2. 题目：某商品原价200元，由于促销活动，打了8折后，又再打了5折，最后的价格是多少？解答：首先，我们需要计算打8折后的价格。

打8折表示原价的80%。

所以，打8折后的价格为：200 * 0.8 = 160元。

然后，我们需要计算再打5折后的价格。

打5折表示原价的50%。

所以，再打5折后的价格为：160 * 0.5 = 80元。

所以，最后的价格是80元。

3. 题目：某车间有40名工人，其中男工人占总人数的3/5，女工人有多少名？解答：根据题意，男工人占总人数的3/5，那么女工人占总人数的2/5。

假设女工人的人数为x。

根据比例关系，我们可以得到以下等式：2x = 40解方程可得：x = 20所以，女工人有20名。

4. 题目：小明拿了长方形纸片的1/5，小红拿了剩下的3/10，如果纸片的长度是25厘米，小红拿了多少厘米？解答：首先，我们需要计算小明拿走的部分。

纸片的长度的1/5表示小明拿走的长度为：25 * 1/5 = 5厘米。

然后，我们需要计算剩余纸片的长度。

剩余纸片的长度为：25 - 5 = 20厘米。

最后，我们根据小红拿走的比例计算小红拿走的长度。

剩下的3/10表示小红拿走的长度为：20 * 3/10 = 6厘米。

所以，小红拿走了6厘米。

5. 题目：某地一天的白天时间为12小时，黄昏时间为2小时，黑夜时间为剩下的时间的1/3，求黑夜时间。

六年级下册比例试卷【含答案】

六年级下册比例试卷【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 下列哪种比例关系可以用正比例表示？A. 路程与时间B. 速度与时间C. 路程与速度D. 成本与数量2. 如果 a:b = c:d，那么 a 与 c 的关系是？A. a = cB. a > cC. a < cD. 无法确定3. 下列哪个比例关系可以用反比例表示？A. 工作量与人数B. 工作效率与人数C. 工作量与工作效率D. 工作时间与工作效率4. 已知 x:y = 3:4，如果 x 增加 3，y 增加 4，那么新的比例关系是？A. x:y = 6:8B. x:y = 3:4C. x:y = 6:7D. x:y = 7:85. 下列哪个选项不是比例的基本性质？A. 两内项之积等于两外项之积B. 两外项之积等于两内项之积C. 两内项之和等于两外项之和D. 两外项之和等于两内项之和二、判断题（每题1分，共5分）1. 如果 a:b = c:d，那么 a + b = c + d。

（）2. 在比例中，两个外项的乘积等于两个内项的乘积。

（）3. 速度和时间成正比例关系。

（）4. 如果两个相关联的量的乘积一定，那么它们成反比例关系。

（）5. 比例中的项可以是任何数值。

（）三、填空题（每题1分，共5分）1. 如果 a:b = 2:3，那么 2a = __b。

2. 已知 x:y = 4:5，如果 x = 8，那么 y = __。

3. 如果 a:b = c:d，那么 a/c = __。

4. 在比例中，两个外项的乘积等于两个内项的乘积，这个性质叫做比例的 __ 性。

5. 如果两个相关联的量的乘积一定，那么它们成 __ 比例关系。

四、简答题（每题2分，共10分）1. 请简述比例的基本性质。

2. 请解释正比例和反比例的区别。

3. 请举例说明比例在实际生活中的应用。

4. 请解释比例尺的意义。

5. 请解释如何解比例方程。

五、应用题（每题2分，共10分）1. 甲、乙两人分别有 120 元和 150 元，如果甲给乙 30 元，那么他们的钱数比是多少？2. 一辆汽车行驶 240 千米用了 3 小时，求这辆汽车的速度。