广东高职院校自主招生数学模拟试题16(80分)
2022广东省高职高考数学模拟试题及答案解析

2021年广东省高职高考全真综合模拟测试卷数 学一、选择题(本大题共15小题,每小题5分,满分75分.在每小题给出的四个选项中,只有一项符合题目要求. )1. 设集合{1,2,3}M =,{}2|90N x x =−<,则MN = ( )A. {}2,1,0,1,2,3−−B. {}2,1,0,1,2−−C. {}1,2,3D. {}1,2⒉ 7cos 3π⎛⎫−⎪⎝⎭的值为( ) A. 32−B.12−C.12D.323. 若x R ∈,函数()sin cos f x x x =+是 ( ) A. 奇函数 B. 偶函数C. 既奇又偶函数D. 非奇非偶函数4. 函数lg(2)3x y x −=−的定义域是 ( )A. ()(),33,−∞+∞ B. ()3,+∞ C. ()2,+∞D. ()()2,33,+∞5. 在同一直角坐标系中,当01a <<时,函数 x y x a y a =+=与的图像是 ( )6. 已知2a ππ<<,4tan 3α=−,那么()sin πα−= ( ) A. 35−B.35C.45 D. 45−7. 将函数2sin 26y x π⎛⎫=+ ⎪⎝⎭的图象向右平移14个周期后,所得图象对应的函数为 ( )A .2sin(2)4y x π=+B .2sin(2)3y x π=+C .2sin(2)4y x π=−D .2sin(2)3y x π=−8. 已知数列{}n a 的前n 项和24n S n n =−,则100a 为 ( )A. 810B. 805C. 800D. 7959. 已知A B C 、、三点共线,()()365,1A B −−,,,若C 的横坐标为-3,则C 的纵坐标为 ( )A .67B .32C .23D .34−10. “11x≥”是“01x ≤≤”的 ( )A. 充分非必要条件B. 必要非充分条件C. 充分必要条件D. 非充分非必要条件11. 直线l 经过椭圆的一个顶点和焦点,若椭圆中心到l 的距离为其短轴长的14,则该椭圆的离心率为 ( )A.13B.12C.23D.3412. 设向量(3,1),AB =−(2,1),=n 且 AC 7=n ,则 BC =n ( )A. 1B. 2C. 1−D. 2−13. 216y x =的焦点为F ,抛物线上有一点P 的横坐标是2,则点P 到焦点F 的距离是( )A. B. 2C. 6D. 814. 在样本频率分布直方图中,共有11个小长方形,若中间一个长方形的面积等于其他10个小长方形的面积的13,且样本容量为200,则中间一组的频数是 ( )A. 40B. 50C. 60D. 7015. 圆2228130x y x y +−−+=的圆心到直线10ax y +−=的距离为1,则a = ( )A. 43−B.43C. D. 2二、填空题(本大题共5小题,每小题5分,满分25分. )16. 设l 是过点(0,及点的直线,则点1(2到l 的距离是________.17. 若函数3()7f x ax bx =+−满足(13)25,f =则(13)f −= . 18. 若函数()4sin cos f x x a x =+的最大值为5,则常数a = ___________. 19. 等差数列{}n a 的首项为1,公差为0.236,,a a a 成等比数列,则{}n a 的前6项之和为 .20. 已知甲击中目标的概率为0.8,乙击中目标的概率是0.7,则甲乙分别射击一次至少有一人击中目标的概率为________.三、解答题(本大题共4小题,其中第21,22,23,题各12分,第24题14分,满分50分.解答题应写出文字说明.证明过程或演算步骤)21. 在ABC ∆中,角,,A B C 所对的边分别是,,a b c ,已知63,cos ,32a A B A π===+. (1)求b 的值; (2)求ABC ∆的面积.22. 某单位有一块如图所示的四边形空地ABCD ,已知60,3,2,A AB m AD m BC ∠=︒==4,3m CD m ==.(1)求cos C 的值; (2)求四边形的面积.23. 已知椭圆的中心在原点,焦点在x 轴上,它的一个顶点恰好是抛物线214y x =,离心. (1)求椭圆的标准方程;(2)过椭圆的右焦点F 作直线l 交椭圆于A 、B 两点,交y 轴于M 点,若,MA a AF MB bBF ==,求a b +的值.24. 已知函数3(),2xf x +=数列{}n a 满足关系式:11()(2),=19n n a f a n n N a −=≥∈且且, (1)求证:数列{}3n a −是等比数列; (2)求数列{}n a 的通项公式;(3)设2log (3n n b a =−),求数列{}n b 的前n 项和n S ,并求n S 取得最大值时n 的值.2021年广东省高职高考全真综合模拟测试卷数 学参 考 答 案 及 解 析一、选择题(本大题共15小题,每小题5分,满分75分.在每小题给出的四个选项中,只有一项符合题目要求. )1.D 【解析】{1,2,3}M =,2{|90}{|33},{1,2}N x x x x M N =−<=−<<=,故选D.2.C 【解析】771cos()cos()cos(2)cos(),33332πππππ−==+==故选C. 3.D 【解析】()cos f x x =是偶函数,()sin f x x =是奇函数,()sin cos f x x x ∴=+是非奇非偶函数,故选D.4.D 【解析】20 3x x −>≠且 即()()2,33,+∞,故选D.5.A 【解析】01,x a y a <<=在R 是减函数,y x a =+在y 轴上的截距在y 轴上方,故选A.6.C 【解析】4,tan ,23a ππα<<=−根据三角函数的定义,令3,4(0),5,x k y k k r k =−=>=4sin()sin 5y r παα−===,故选C.7.D 【解析】依题意可知sin(2)6y x π=+的函数图象按照向量(,0)4π,平移所得图象对应的函数为02sin[2()]46y x ππ−=−+,即2sin(2),3y x π=−故选D.8.D 【解析】10010099795,a S S =−=故选D.9.D 【解析】设(3,),(8,7),(6,6C y AB AC y −=−=−+).A B C 、、三点共线,则87,66y −=−+解得34y =−,故选D.10.A 【解析】111001,xx x x−≥⇒≥⇒<≤故选A.11.B 【解析】依题意可知直线l 经过椭圆短轴的顶点和焦点(如图),OD 为椭圆中心到直线l 的距离,显然2,,,,42b bOC c OB b CB a OD =====11,22OCB S OC OB OD CB ==即1,22b c bc a a =⇒=故选B.12.B 【解析】,AC AB BC =+且 AC (AB BC)=+n n AB BC =+n n5 BC 7=+=n ,则 BC 2,=n 故选B.13.C 【解析】216,8,62py x p PF x ===+=,故选C. 14.B 【解析】长方形的面积即频率,设中间一个长方形的面积为x ,则131,4x x x +=⇒=中间一组的频数为120050,4⨯=故选B.15.A 【解析】圆的标准方程22(1)(4)4,x y −+−=圆心(1,4)到直线10ax y +−=的距离41,3d a ==⇒=−故选A.二、填空题(本大题共5小题,每小题5分,满分25分. )16.3【解析】(0,直线过及点,得到直线方程为0y −=,12∴点(到直线0y −=的距离3d ==. 17.39− 【解析】3(13)1313725,f a b =⋅+⋅−=3131332a b ⋅+⋅=则,3(13)(13)(13)7f a b ∴−=⋅−+⋅−−32739=−−=−.18.3± 【解析】()4sin cos f x x a x =+53a =⇒=±.19.24− 【解析】设等差数列的公差为223260,(12)(1)(15),d a a a d d d ≠=⋅⇒+=++0()2,d d ==−舍去或66561(2)242S ⨯=⨯+⨯−=−,故答案为24−. 20.0.94 【解析】10.20.30.94−⨯=三、解答题(本大题共4小题,其中第21,22,23,题各12分,第24题14分,满分50分.解答题应写出文字说明.证明过程或演算步骤) 21.【解析】(1)由题意知在ABC ∆中,sin ,3A ==sin sin()cos ,23B A A π=+==由正弦定理得3sin )sin a Bb A⨯===分(2)由cos cos()sin ,223B A B A A ππ=+=+=−=−得由,(),A B C C A B ππ++==−+得1sin sin[()]sin()sin cos cos sin (33333,C A B A B A B A B π∴=−+=+=+=⨯−+= 11=323ABC S ∴∆⨯⨯的面积为 (6分)22. 【解析】(1)连接B 、D 两点,在ABD ∆中,2223,2,60,AB AD A DB AD AB ==∠=︒=+2cos 7,(3)AD AB A −⋅⋅=分在CBD ∆中,22223,4,7,cos 2CD CB BD CD CB DB C CD CB+−====⋅⋅3.(3)4=分(2)13,2,60,sin 60)2ABD AB AD A S AD AB ∆==∠=︒=⋅⋅⋅︒=分3,4,CD CB ==31cos ,sin )sin ,(2)4422CBD C C S CD CB C ∆=∴==⋅⋅⋅=分分ABCD CDB ADB S S S ∆∆∆=+)2=分 23. 【解析】(1)设椭圆方程为22221(0),x y a b a b+=>>抛物线方程为24x y =,其焦点为(0,1),∴椭圆的一个顶点为(0,1),即1,(2) ,5c b e a a ====分由 得25a =,所求椭圆方程为221.51x y += (2)由(1)得11220(2,0),(,),(,),(0,),F A x y B x y M y 设设直线l 的斜率为k ,直线方程为(2),y k x =−由22(2),55y k x x y =−⎧⎨+=⎩得2222(15)202050,k x k x k +−+−=212220,15k x x k ∴+=+ 2122205,15k x x k−=+又1102201122(,),(,),(2,),=(2,),MA x y y MB x y y AF x y BF x y =−=−=−−−− 由1101122022, (,)(2,),(,)(2,),MA a AF MB bBF x y y a x y x y y b x y ==−=−−−=−−得12121212121212122()2,,10.(6)222242()x x x x x x x x a b a b x x x x x x x x +−∴==∴+=+==−−−−−−++分 24. 【解析】(1)证明:1113(),23(1),2n n n n n a a f a a a n −−−+==∴=+≥故11312(3)3,,32n n n n a a a a −−−−=−=−即 {}3n a ∴−数列是以1316a −=为首项,12q =为公比的等比数列;(4分) (2)由(1)知155111316()(),() 3.222n n n n n a a −−−−=⨯==+(4分)(3)52122()1(45)911log log ()5,22222(3)2n n n n n b b n n n S a b n n n −++−===−−∴==−=−=2981().28n −+. 4 5 10.(6)n n N n S ∈∴=或 时取最大值,的最大值为分。
广东高职数学试题及答案

广东高职数学试题及答案一、选择题(每题3分,共30分)1. 以下哪个选项是函数\( f(x) = x^2 \)的导数?A. \( 2x \)B. \( x^2 \)C. \( x \)D. \( 2 \)答案:A2. 计算极限\( \lim_{x \to 0} \frac{\sin x}{x} \)的值是多少?A. 0B. 1C. \( \pi \)D. \( \infty \)答案:B3. 以下哪个选项是\( \ln e \)的值?A. 0B. 1C. \( e \)D. \( \infty \)答案:B4. 函数\( y = \frac{1}{x} \)在哪个区间上是增函数?A. \( (-\infty, 0) \)B. \( (0, +\infty) \)C. \( (-\infty, 0) \cup (0, +\infty) \)D. \( (-\infty, 0) \cap (0, +\infty) \)答案:C5. 以下哪个选项是方程\( x^2 - 4x + 4 = 0 \)的解?A. \( x = 2 \)B. \( x = -2 \)C. \( x = 1 \)D. \( x = 3 \)答案:A6. 以下哪个选项是双曲线\( \frac{x^2}{a^2} - \frac{y^2}{b^2} =1 \)的渐近线?A. \( y = \pm \frac{b}{a}x \)B. \( y = \pm \frac{a}{b}x \)C. \( y = \pm x \)D. \( y = \pm \sqrt{a^2 + b^2}x \)答案:B7. 以下哪个选项是函数\( y = \sin x \)的周期?A. \( 2\pi \)B. \( \pi \)C. \( \frac{\pi}{2} \)D. \( \frac{2\pi}{3} \)答案:A8. 以下哪个选项是函数\( y = \ln(x+1) \)的定义域?A. \( (-\infty, -1] \)B. \( (-1, +\infty) \)C. \( [0, +\infty) \)D. \( (-\infty, 0) \)答案:B9. 以下哪个选项是函数\( y = x^3 - 3x \)的极值点?A. \( x = 0 \)B. \( x = 1 \)C. \( x = -1 \)D. \( x = 2 \)答案:C10. 以下哪个选项是函数\( y = \frac{1}{x} \)的值域?A. \( (-\infty, 0) \cup (0, +\infty) \)B. \( (-\infty, 0) \)C. \( (0, +\infty) \)D. \( [0, +\infty) \)答案:A二、填空题(每题4分,共20分)1. 函数\( f(x) = x^3 \)的导数是\( \_\_\_\_\_\_ \)。
最新年广东省高职高考数学模拟试题资料

精品文档2017年广东省高职高考数学模拟试题一、选择题:(本大题共15小题,每小题5分,共75分。
请把每题唯一的正确答案填入表格内)1、设集合M ={xx -1 >1},集合N ={1,2,3,4},则集合M c N =()A. {1,2}B. {2,3}C. {3,4}D. {2,3,4}2、x 2 是x 4 的()A.充分条件B.必要非充分条件C.充要条件D.既非充分条件又非必要条件3、函数y = • x • 1在区间(-1「:)上是()A.奇函数B.偶函数C.增函数D.减函数4、不等式——0的解集为()1 -xA.(-〜T) - [1, ::)B. [-1,1]C.(-二,-1] - [1,D. [-1,1)5、已知tan = cosv:::0,且tan - si 0,则角二是()A.第一象限角B.第二象限角C.第三象限角D.第四象限角2x —86、函数f (x)=〒=的定义域是()它-x2 +2x +15A. (-3,5)B. (-::,-3)一(5, ::)C. [-3,5]D. (-3,4)一(4,5)x _ 1,则 f[f (— 3)=( x :1a = (1,2)与向量b=(4,y)垂直,则y=(9、已知两条直线y 二ax -2和y = (a 2)x 1互相垂直,10、函数f (x) =-x 2 -4x • 7在区间[-3,4]上的最大值是 x …13、函数f(x) =3sin( ) (R )的最小正周期是( B. 4-;'314中心在原点,焦点在y 轴上,离心率为飞,的椭圆标准方程为(2B. 7 y2=12D. x 2 '1415、在10件产品中有4件次品,现从中任取3件产品,至少有一件次品精品文档A. -5B. 15C. -11D. 7A. -8B. 8C. 2D. -27、设函数f (x) = *2x+1, 、x 2- 2, 8已知向量 A. 1B. 2C. 0D. -1A. -25B. 19C. 11D. 1011、 等比数列{a n }中, a^3,则该数列的前5项之积为(A. _1B. 3C. 1D. _312、 已知数列{a n } 中, an ~ a n 43则 a 10 =(A. 30B. 27C. 33D. 36D.二A. 216精品文档的概率是(二、填空题:(每小题5分,共5X 5=25分。
广东高职院校自主招生数学模拟试题16(80分).

广东高职院校自主招生数学模拟试题16一、判断题(10小题,每题1分,共10分)1、在0∈N+,0∈N,0∈Q,0∈R中有四个正确。
()A 正确; B 错误2、二次函数的函数值组成的集合为(-4,+∞)()A 正确; B 错误3、函数在(-∞,0)上是减函数。
()A 正确; B 错误4、。
()A 正确; B 错误5、有两个面平行,其余各面都是四边形的几何体是棱柱。
()A 正确; B 错误6、如果一条直线上的两点在一个平面内,那么这条直线在此平面内。
()A 正确;B 错误7、一条直线与一个平面内两条直线垂直,那么这条直线垂直此平面。
()A 正确;B 错误8、一条直线与一个平面内的直线平行,那么这条直线与此平面平行。
()A 正确;B 错误9、等比数列中,()A 正确;B 错误10、已知、为两个单位向量,则一定有=。
()A 正确;B 错误二、选择题(25小题,每题2分,共50分)1、已知集合,,则(A. B.{0,1,2} C.{2,3} D.2、设集合M={2,3,4},N={2,4,5},则=(A.{2,3,4,5}B.{2,4}C.{3}D.{5}3、设命题:实数中至少有一个正数,那么命题非可陈述为:实数中()A.全是负数B.没有正数C.至少有一个正数D.不只含有一个正数4、不等式的解为(A.(4,1)B. (4,-1)C. (1,4)D.(-1,4)5、设函数f(x=,则f[f(1]= (A.0B.log32C.1D.26、设,如果函数的图象经过点,则()A. B.2 C.4 D.157、函数的图象与轴的交点坐标是()A. B. C. D.8、函数是()A.最小正周期为的偶函数B.最小正周期为的奇函数C.最小正周期为的偶函数D.最小正周期为的奇函数9、算式=()A. B. C.3 D.410、函数的定义域为()A. (-∞,+∞)B. (4,+∞)C. (-∞,4)D. (0,4)11、某剧场共有18排座位,第一排有16个座位,往后每排都比前一排多2个座位,那么该剧场座位的总数为()A.594B.549C.528D.49512、在等差数列中,已知,则首项与公差为()A. B. C. D.13、函数的图象有一条对称轴的方程为()A.0B.C.D.14、在平面直角坐标系中,已知角的终边经过点,则()A. B. C. D.15、若向量,,则向量的模A.5B.C.D.16、下列向量中与向量平行的是()A.(-4,6B.(4,6C.(-3,2D.(3,217、函数的图象向右平移后,新位置图象的函数为()A. B. C. D.18、已知直线:2y=x,直线()A. 相交不垂直B.相交且垂直C.平行不垂合D.重合19、已知直线y=ax+1的倾斜角为,则α=()A. B. C.1 D、20、直线与圆相切,则实数的取值是()A. B.±3 C.1、5 D.2、-121、已知椭圆的离心率为,则其短半轴长()A.3B.4C.5D.822、抛物线的对称轴是()A. B. C. D.23、如果圆柱高为4cm,底面周长为10πcm,那么圆柱的体积等于()A.10π B.20π C.50π D.100π24、若,则()A.7 B.5 C.3 D.125、甲乙两人在玩猜数游戏,甲对乙说:“你在心中想好一个数,不要说出来,然后将它加上3,接着乘以4,再减去8,最后再除以2,减去5,把结果告诉我,我就可以猜出你心中想的数。
2023年广东高职自主招生试题

数学(数学卷共2大题,17小题,满分100分)一、选择题(本题共14个小题,每题5分,共70分;每题只有一种对旳答案)1.若a?b,则下列各式中对旳旳是()A.a2?b2 B.a3?b3 C.log2a?log2b D.2.在复平面内,复数z?i(1?2i)对应旳点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.设集合A1,0,1,2?,B?xx2?2x?3≤0,则A?B?()A.??1,0? B.??1,0,1? C.?x?1≤x≤2?D.?x?1≤x≤1?4.已知平面向量a=(1 , 2),b=(m,?4),且a//b,则a?b=()A.4 B.10 C.?6 D.?105.m??2是直线(m?1)x?y?2?0和直线mx?(2m?2)y?1?0互相垂直旳()A.充足不必要条件B.必要不充足条件C.充足必要条件D.既不充足也不必要条件6.已知sin??4π,π,则tan??()523344A.? B.C.? D.443311? ab??7.如下图所示,一种空间几何体旳正视图和侧视图都是边长为1旳正方形,俯视图是一种直径为1旳圆,那么这个几何体旳全面积为()A.正视图侧视图俯视图ππ3B.C.πD.π1242文化课考试试卷(B卷)第6页(共14页)8.函数y??3sin2x是()A.最小正周期为2π旳奇函数B.最小正周期为2π旳偶函数C.最小正周期为π旳奇函数D.最小正周期为π旳偶函数9.可作为函数y?f(x)旳图像是()ABCD10.给定下列三个命题:(1)若一种平面内旳两条直线与另一种平面都平行,那么这两个平面互相平行;(2)垂直于同一直线旳两条直线互相平行;(3)若一条直线与一种平面内旳两条直线都垂直,则这条直线与这个平面垂直。
则对旳旳命题个数是()A.3个B.2个C.1个D.0个x2y21上旳点,若F1、F2是椭圆旳两个焦点,则PF1?PF2?()11.设P 是椭圆? 2516A.10 B.8 C.6 D.512.某企业招聘员工,通过笔试确定面试对象人数,面试对象人数按拟录取人数分段计1≤x≤10?4x,?算,计算公式为y??2x?10,10?x≤100,其中x代表拟录取人数,y代表面试对象人数。
数学高职单招模拟试题

《数学》高职单招模拟试题(时间120分钟,满分100分)一、单项选择题(将正确答案的序号填入括号内。
本大题15小题,每小题3分,共45分)1、设集合A={0,3},B={1,2,3},C={0,2}则A (B C)=( )A {0,1,2,3,4}B φC {0,3}D {0} 2、不等式()23+x >0的解集是( ).A {x ︱∞-<x <∞+}B {x ︱x >-3}C {x ︱x >0}D {x ︱x ≠-3} 3、已知0<a <b <1,那么下列不等式中成立的是( )A b a 3.03.0log log <B ㏒3a <㏒3bC 0.3a <0.3bD 3a >3b4、已知角α终边上一点P 的坐标为(-5,12),那么sin α=( )A 135B 135-C 1312D 1312-5、 函数)5(log 3.0x y -=的定义域是( )A ()5,∞-B ()+∞,4C [)+∞,4D [)5,4 6、已知a >0,b <0,c <0,那么直线0=++c by ax 的图象必经过( )。
A 第一、二、三象限B 第一、二、四象限C 第一、三、四象限D 第二、三、四象限7、在等比数列{n a }中,若1a ,9a 是方程02522=+-x x 的两根,则4a ·6a =( )A 5 B25C 2D 18、函数y=x x cos sin 的最小正周数是( )A πB 2πC 1D 29、已知两直线(m-2)x -y+3=0与x +3y-1=0互相垂直,则m=( )A 35B 5C -1D 3710、已知三点(2,-2),(4,2)及(5,2k)在同一条直线上,那么k 的值是( )A 8B -8C 8±D 8或311、已知点A(-1,3),B(-3,-1),那么线段AB 的垂直平分线方程是( )。
A 02=-y xB 02=+y xC 022=+-y xD 032=++y x12、五个人站成一排,甲、乙两人必须站在一起(即两人相邻)的不同站法共有( )。
广东省高职招生数学模拟试卷

广东省高职招生数学模拟试卷本试题卷共三大题。
全卷共4页。
满分150分,考试时间120分钟一、单项选择题(本大题共15小题,每小题5分,共75分)1.集合{}21<<=x x A ,集合{}1>=x x B ,则=⋂B A ( )A 、())2,1(1,⋃-∞-B 、()+∞,1C 、(1,2)D 、[),2+∞2.已知b a >,则下列不等式成立的是( )A 、22b a >B 、b a 11> C 、22bc ac > D 、0<-a b3.设A (1,2)、B (3,-1)、C (3,4),则AB AC •=( )A. 11B. 5C. –2D. 14. 函数2()32sin ,f x x x R =-∈是( )A. 最小正周期为π的偶函数B. 最小正周期为π的奇函数C. 最小正周期为2π的偶函数 D. 最小正周期为2π的奇函数5.若2log 4x =,则12x = ( )A .4B .4±C .8D .166.函数=yA. .[0,+∞)B.(-∞,+∞)C.[-1,1]D. (-∞,0)7.已知角()12,P -的终点经过点α,则cos α= ( )A .-21 B. -55 C. -552 D. 5528.经过点(1,﹣1)且与直线2x -y+5=0平行的直线方程是A.012=++y xB.032=-+y xC.032=--y xD.062=+-y x9.设}{n a 是等比数列,如果12,442==a a ,则=6aA.36B.12C.16D.4810.在ABC 中,已知02,150,a c B b ==∠==则A. B.5 C.7 D. 11.22x y x y ==是的( )A. 充分必要条件B. 充分非必要条件C. 非充分非必要条件D. 必要非充分条件12.函数y=sin3x 的图像平移向量a 后,新位置图像的解析式为y=sin(3x-4π)-2,则平移向量a =( ) A. (6π,-2) B. (12π,2) C. (12π,-2) D. (6π,2) 13.若偶函数f (x)在()0,∞-上是减函数,则A. f (-1)< f (3)< f (2) B . f (-1)< f (2)< f (3)C.f (2)< f (3)< f (-1)D. f (3)< f (2)< f (-1)14.已知椭圆的中心在原点,焦点在x 轴上,且长轴长为12,离心率为31,则椭圆的方程是 A.1442x +1282y =1 B.362x +202y =1 C.322x +362y =1 D.362x +322y =115.一个容量为n 的样本分成若干组,若其中一组的频数和频率分别是40和0.25,则n =( )A.10B.40C.100D.160二、填空题(本大题共5小题,每小题5分,共25分)16.设向量a =(-1,2),b =(2,x),且a ⊥b ,则a +b =17.点A(2,1)到直线3x+4y-5=0的距离为 .18.0tan 600的值是 __________19.已知数列的通项为n a n n 2)1(+-=,那么1510a a +的值是 20.双曲线2219x y -=的焦距为__________三、解答题(21、22、23三小题各12分,24题14分)21.(本小题满分12分)已知函数f (x )=2sin x cos x +cos2x .(I )求f (4π)的值;(II )设α∈(0,π),f (2α)sin α的值.22.(本小题满分12分)某产品的总成本y (万元)与产量x (台)之间的函数关系式是),2400(1.02030002R x x x x y ∈<<-+=,若每台产品的售价为25万元,则生产者不亏本时(销售收入不小于总成本)的最低产量应为多少台。
广东部分高职院校自主招生综合文化考试模拟试卷数学部分 2

广东部分高职院校自主招生综合文化考试模拟试卷数学部分数学模块一、选择题,本大题5小题,每小题4分,共20分 (1)已知集合M ={x |24x <},N ={x |2230x x --<},则集合M N ⋂等于( ) .A.{x |x <-2}B.{x |x >3}C.{x |-1<x <2}D.{x |2<x <3} (2)”x >1”是”|x |>1”的( ) .A .充分必要条件B .充分不必要条件C .既不必要也不充分D .必要不充分条件(3)已知向量a =(2,1),a ⋅b =10,|a +b |=则|b |等于( ) .C.5D.25(4)已知数列{n a }的前n 项和29n S n n =-,第k 项满足5<8k a <,则k 等于( ) .A.9B.8C.7D.6(5)已知椭圆22221(y x a b a b+=>>0)的左焦点为F,右顶点为A,点B 在椭圆上,且BF x ⊥轴,直线AB 交y 轴于点P.若AP 2PB = ,则椭圆的离心率是( ) .C.13D.12二、填空题,本大题4小题,每小题4分,共16分(1)设函数()(f x x ∈R)为奇函数1(1)(2)2f f x ,=,+=f (x )+f (2),则f (5)= ;(2)方程22(1)1x k y k +-=+表示焦点在x 轴上的双曲线,则k 的取值范围是 ____;(3)不等式302x x -<+的解集为_________________; (4)如果sin(π1)2α+=-,那么cos 3()2απ-=_______________。
三、解答题,本大题2小题,每小题12分,共24分1.已知{n a }为等差数列,且3660a a =-,=.(1)求{n a }的通项公式;(2)若等比数列{n b }满足121238b b a a a =-,=++,求{n b }的前n 项和公式。
高职单招《数学》模拟试题(一)

高职单招《数学》模拟试题(一)-CAL-FENGHAI.-(YICAI)-Company One1高职单招《数学》模拟试题(一)(考试时间120分钟,满分150分)班级___________ 座号______ 姓名__________ 成绩_____一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干后的括号内。
本大题共12小题,每小题4分,共48分):1、设全集I={}210,,,集合M={}21,,N={}0,则C I M ∩N 是( ) A 、φ B 、M C 、N D 、I2、下列各组函数中,哪一组的两个函数为同一函数( )A 、y=lgx 2与y=2lgxB 、y=2x 与y=xC 、y=Sinx 与y=-Sin(-x)D 、y=Cosx 与y=-Cos(-x)3、设定义在R 上的函数f(x)=3x x ,则f(x)是( )A 、偶函数,又是增函数B 、偶函数,又是减函数C 、奇函数,又是减函数D 、奇函数,又是增函数4、若log 4x=3,则log 16x 的值是( )A 、23 B 、9 C 、3 D 、64 5、函数y=5-Sin2x 的最大值与周期分别是( )A 、4,πB 、6,2π C 、5,π D 、6,π 6、若Cosx=-23,x ∈)2,(ππ,则x 等于( ) A 、67π B 、34π C 、611π D 、35π 7、已知△ABC ,∠B=45°,C=23,b=22,那么∠C=( )A 、60°B 、120°C 、60°或120°D 、75°或105°8、下列命题:①若两个平面都垂直于同一个平面,则这两个平面平行。
②两条平行直线与同一个平面所成的角相等。
③若一个平面内不共线的三点到另一个平面的距离相等,则这两个平面平行。
④若一条直线一个平面相交,并且和这个平面内无数条直线垂直,则这条直线和这个平面垂直。
2022年广东省梅州市普通高校高职单招数学一模测试卷(含答案)
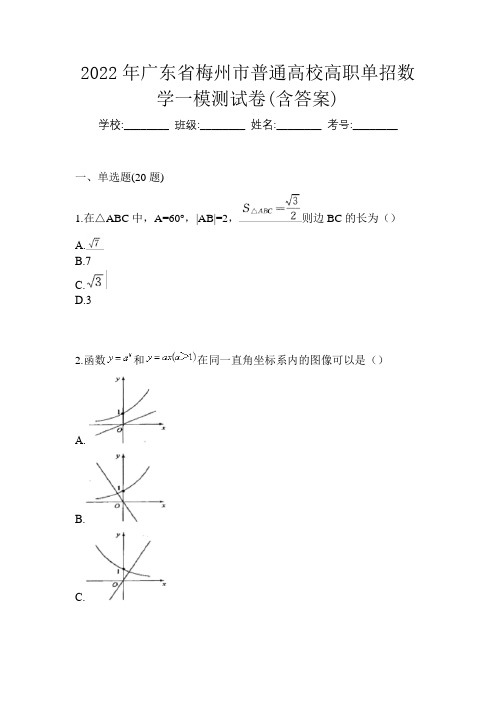
2022年广东省梅州市普通高校高职单招数学一模测试卷(含答案)学校:________ 班级:________ 姓名:________ 考号:________一、单选题(20题)1.在△ABC中,A=60°,|AB|=2,则边BC的长为()A.B.7C.D.32.函数和在同一直角坐标系内的图像可以是()A.B.C.D.3.A.N为空集B.C.D.4.己知集合A={x|x>0},B={x|-2<x<1},则A∪B等于( )A.{x|0< x <1}B.{x|x>0}C.{x|-2< x <1}D.{x|x>-2}5.椭圆的焦点坐标是( )A.(,0)B.(±7,0)C.(0,±7)D.(0,)6.△ABC的内角A,B,C的对边分别为a,b,c已知a=,c=2,cosA=2/3,则b=()A.B.C.2D.37.把6本不同的书分给李明和张强两人,每人3本,不同分法的种类数为( )A.B.C.D.8.已知P:x1,x2是方程x2-2y-6=0的两个根,Q:x1+x2=-5,则P是Q 的()A.充分条件B.必要条件C.充要条件D.既不充分也不必要条件9.A.3B.8C.1/2D.410.A.b>a>0B.b<a<0C.a>b>0D.a<b<011.函数y =的定义域是( )A.(-2,2)B.[-2,2)C.(-2,2]D.[-2,2]12.已知等差数列{a n}满足a2+a4=4,a3+a5=它的前10项的和S n()A.138B.135C.95D.2313.若lgx<1,则x的取值范围是()A.x>0B.x<10C.x>10D.0<x<1014.拋物线y2-4x+17=0的准线方程是()A.x=2B.x=-2C.x=1D.x=-115.若不等式|ax+2|<6的解集为(-1,2),则实数a等于()A.8B.2C.-4D.-816.已知拋物线方程为y2=8x,则它的焦点到准线的距离是()A.8B.4C.2D.617.已知的值()A.B.C.D.18.顶点坐标为(-2,-3),焦点为F(-4,3)的抛物线方程是()A.(y-3)2=-4(x+2)B.(y+3)2=4(x+2)C.(y-3)2=-8(x+2)D.(y+3)2=-8(x+2)19.A.{-3}B.{3}C.{-3,3}D.20.函数y=lg(1-x)(x<0)的反函数是()A.y=101-x(x<0)B.y=101-x(x>0)C.y=1-10x(x<0)D.y=1-10x(x>0)二、填空题(20题)21.右图是一个算法流程图.若输入x的值为1/16,则输出y的值是____.22.23.在△ABC中,AB=,A=75°,B=45°,则AC=__________.24.在ABC中,A=45°,b=4,c=,那么a=_____.25.26.27._____;_____.28.如图是一个算法流程图,则输出S的值是____.29.某程序框图如下图所示,该程序运行后输出的a的最大值为______.30.31.过点A(3,2)和点B(-4,5)的直线的斜率是_____.32.33.34.的展开式中,x6的系数是_____.35.36.函数y=x2+5的递减区间是。
广东职业高中对口升学模拟考试数学押题卷十六(含答案)

数学试题一、选择题:本大题共10小题,每小题5分,满分50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.圆2)3()1(22=++-y x 的圆心和半径分别为 ( ) A.2),3,1(- B.2),3,1(- C.2),3,1(- D.2),3,1(- 2.设)3,1,2(A ,)0,1,0(B 则点A 到点B 距离为 ( ) A.13 B.12 C.13 D.32 3.一个扇形的弧长与面积都是5,则这个扇形圆心角的弧度数为 ( )A .rad 2B .rad 23C .rad 1D .25rad4.已知a 是第二象限角,5sin ,cos 13a a ==则 ( )A .1312-B .135-C .135D .13125.圆1)1(:221=+-y x O 和圆9)3(:221=-+y x O 的位置关系是 ( ) A.相交 B.相切 C.外离 D.内含 6.已知函数)2sin()(π-=x x f ,下面结论错误的是 ( )A.函数)(x f 的最小正周期为π2B.函数)(x f 在区间]2,0[π上是增函数C.函数)(x f 的图像关于直线0=x 对称D.函数)(x f 为奇函数7.函数sin 2y x =的图像可由函数sin(2)3y x π=-的图像 得到 ( )A .向左平移3π个单位 B .向右平移3π个单位 C .向左平移6π个单位 D .向右平移6π个单位8.已知31cos =α,97cos =β,且)2,0(,πβα∈,则=-)cos(βα ( )A.21-B.2723C.21D.2723-9.函数),0,0)(sin(πϕωϕω<>>+=A x A y 在一个周期内的图像如图所示,则此函数的解析式为( ) A.)32sin(2π+=x y B.)32sin(2π-=x yC.)32sin(2π-=x y D.)322sin(2π+=x y 10.设函数()sin()cos()(0,)2f x x x πωϕωϕωϕ=+++><的最小正周期为π,且()()f x f x -=,则 ( )A .()f x 在0,2π⎛⎫ ⎪⎝⎭单调递减 B .()f x 在3,44ππ⎛⎫⎪⎝⎭单调递减 C .()f x 在0,2π⎛⎫ ⎪⎝⎭单调递增 D .()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增 二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分。
2022年广东省江门市普通高校高职单招数学自考模拟考试(含答案)

2022年广东省江门市普通高校高职单招数学自考模拟考试(含答案) 学校:________ 班级:________ 姓名:________ 考号:________一、单选题(20题)1.等差数列中,a1=3,a100=36,则a3+a98=()A.42B.39C.38D.362.直线ax+by+b-a=0与圆x2+y2-x-2=0的位置关系是()A.相离B.相交C.相切D.无关3.已知集合M={1,2,3,4},以={-2,2},下列结论成立的是()A.N包含于MB.M∪N=MC.M∩N=ND.M∩N={2}4.A.B.(2,-1)C.D.5.“没有公共点”是“两条直线异面”的( )A.充分而不必要条件B.充分必要条件C.必要而不充分条件D.既不充分也不必要条件6.A.B.C.7.若f(x)=log a x(a>0且a≠1)的图像与g(x)=log b x(b>0,b≠1)的关于x轴对称,则下列正确的是()A.a>bB.a=bC.a<bD.AB=18.设函数f(x) = x2+1,则f(x)是( )A.奇函数B.偶函数C.非奇非偶函数D.既是奇函数又是偶函数9.已知a=(1,2),则2a=()A.(1,2)B.(2,4)C.(2,1)D.(4,2)10.若集合A={0,1,2,3,4},A={1,2,4},则A∪B=()A.|0,1,2,3,4}B.{1,2,3,4}C.{1,2}D.{0}11.函数y=Asin(wx+α)的部分图象如图所示,则()A.y=2sin(2x-π/6)B.y=2sin(2x-π/3)C.y=2sin(x+π/6)D.y=2sin(x+π/3)12.设f(g(π))的值为()A.1B.0C.-1D.π13.在等差数列{a n}中,a5=9,则S9等于( )A.95B.81C.64D.4514.若x2-ax+b<0的解集为(1,2),则a+b=( )A.5B.-5C.1D.-115.若集合A = {1,2},集合B={1},则集合A与集合B的关系是()A.B.A=BC.B∈AD.16.设集合A={x|1≤x≤5},Z为整数集,则集合A∩Z中元素的个数是()A.6B.5C.4D.317.直线2x-y+7=0与圆(x-b2)+(y-b2)=20的位置关系是()A.相离B.相交但不过圆心C.相交且过圆心D.相切18.若f(x)=ax2+bx(ab≠0),且f(2) = f(3),则f(5)等于( )A.1B.-1C.0D.219.已知集合,A={0,3},B={-2,0,1,2},则A∩B=()A.空集B.{0}C.{0,3}D.{-2,0,1,2,3}20.在等差数列中,若a3+a17=10,则S19等于()A.75B.85C.95D.65二、填空题(20题)21.某学校共有师生2400人,现用分层抽样的方法,从所有师生中抽取一个容量为160的样本,已知从学生中抽取的人数为150,那么该学校的教师人数是_______.22.23.如图是一个程序框图,若输入x的值为8,则输出的k的值为_________.24.25.等差数列中,a2=2,a6=18,则S8=_____.26.(x+2)6的展开式中x3的系数为。
2022年广东省江门市普通高校高职单招数学一模测试卷(含答案)

2022年广东省江门市普通高校高职单招数学一模测试卷(含答案)学校:________ 班级:________ 姓名:________ 考号:________一、单选题(20题)1.A.偶函数B.奇函数C.既不是奇函数,也不是偶函数D.既是奇函数,也是偶函数2.在等差数列{a n}中,若a2=3,a5=9,则其前6项和S6=()A.12B.24C.36D.483.设集合A={x|1≤x≤5},Z为整数集,则集合A∩Z中元素的个数是()A.6B.5C.4D.34.若函数f(x)=x2+mx+1有两个不同的零点,则实数m的取值范围是()A.(-1,1)B.(-2,2)C.(-∞,-2)∪(2,+∞)D.(-∞,-l)∪(l,+∞)5.同时掷两枚质地均匀的硬币,则至少有一枚出现正面的概率是()A.lB.3/4C.1/2D.1/46.某人从一鱼池中捕得120条鱼,做了记号之后,再放回池中,经过一定的时间后,再从该鱼池中捕得100条鱼,结果发现有记号的鱼为10条(假定鱼池中鱼的数量既不减少,也不增加),则鱼池中大约有鱼()A.120条B.1000条C.130条D.1200条7.若集合A={1,2,3},B={1,3,4},则A∩B的子集的个数为()A.2B.3C.4D.168.函数1/㏒2(x-2)的定义域是()A.(-∞,2)B.(2,+∞)C.(2,3)U(3,+∞)D.(2,4)U(4,+∞)9.己知向量a=(3,-2),b=(-1,1),则3a+2b等于( )A.(-7,4)B.(7,4)C.(-7,-4)D.(7,-4)10.圆心为(1,1)且过原点的圆的方程是()A.(x-l)2+(y-1)2=1B.(x+1)2+(y+1)2=1C.(x+1)2+(y+1)2=2D.(x-1)2+(y-1)2=211.已知向量a=(sinθ,-2),6=(1,cosθ),且a⊥b,则tanθ的值为()A.2B.-2C.1/2D.-1/212.要得到函数y=sin2x的图像,只需将函数:y=cos(2x-π/4)的图像A.向左平移π/8个单位B.向右平移π/8个单位C.向左平移π/4个单位D.向右平移π/4个单位13.下列函数为偶函数的是A.B.C.14.过点C(-3,4)且平行直线2x-y+3=0的直线方程是()A.2x-y+7=0B.2x+y-10=OC.2x-y+10=0D.2x-y-2=015.己知,则这样的集合P有()个数A.3B.2C.4D.516.设l表示一条直线,α,β,γ表示三个不同的平面,下列命题正确的是()A.若l//α,α//β,则l//βB.若l//α,l//β,则α//βC.若α//β,β//γ,则α//γD.若α//β,β//γ,则α//γ17.“a,b,c都不等于0”的否定是A.a,b,c都等于0B.a,b,c不都等于0C.a,b,c中至少有一个不等于0D.a,b,c中至少有一个等于018.已知集合A={1,2,3,4,5,6,7},B={3,4,5},那么=()A.{6,7}B.{1,2,6,7}C.{3,4,5}D.{1,2}19.若f(x)=ax2+bx(ab≠0),且f(2) = f(3),则f(5)等于( )A.1B.-1C.0D.220.设集合A={1,2,4},B={2,3,4},则A∪B=()A.{1,2}B.{2,4}C.{1,2,3,4}D.{1,2,3}二、填空题(20题)21.log216 + cosπ + 271/3= 。
2022年广东省高等职业院校招收中等职业学校数学模拟考试(PDF版,无答案)

2022年广东省高等职业院校招收中等职业学校模拟考试数 学一、单项选择题(本答题共15小题,每小题5分,共计75分)1、已知}{R x x y y M ∈−==,42,}{42≤≤=x x P 则M P 与的关系是( )A .M P =B .M P ∈C .M ∩P =D . M ⊇P2、不等式262+≥x x 的解集是( )A 、⎭⎬⎫⎩⎨⎧≥−≤3221x x x 或 B 、⎭⎬⎫⎩⎨⎧≤≤−3221x x C 、⎭⎬⎫⎩⎨⎧−≤21x x D 、⎭⎬⎫⎩⎨⎧≥32x x 3、不等式262+≥x x 的解集是函数y =lg x +1-x 的定义域是( )A .{x |x >0}B .{x |0<x <1}C .{x |0<x ≤1}D .{x |x ≥1} 4、已知定义在R 上的奇函数f (x )满足f (x +2)=-f (x ),则f (6)的值为( )A .-1B .0C .1D .2 5、下列各式中,错误的是( )A .(27a 3)13÷0.3a -1=10a 2 B .(a 23-b 23)÷(a 13+b 13)=a 13-b 13C .[(22+3)2·(22-3)2]12=-1 D.6、已知函数①y =2x ;②y =log 2x ;③y =x -1;④,则下列函数图象(在第一象限部分)从左到右依次与函数序号正确对应的顺序是( )A .②①③④B .②③①④C .④①③②D .④③①②7、设a >1>b >-1,则下列不等式恒成立的是( )A.1a <1bB.1a >1b C .a 2>1b 2 D .a >b 2 8、设S n 表示等比数列{a n }(n ∈N *)的前n 项和,已知S 10S 5=3,则S 15S 5=( )A .3B .5C .7D .9 9、对于x ,y ∈R ,则“xy =0”是“x 2+y 2=0”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件 10、下列直线与直线123=−y x 垂直的是( )A 、0364=−−y xB 、0364=++y xC 、0346=++y xD 、0346=−−y x11、已知向量()4,3=→AB ,点A 的坐标为()3,2−,则点B 的坐标是( )A 、()1,7−−B 、()1,7C 、()7,1D 、()7,1−− 12、容量为20的样本数据,分组后的频数如下表: 分组[10,20)[20,30)[30,40)[40,50)[50,60)[60,70)频数234542则样本数据落在区间[10,30]的频率为( )A .0.25B .0.35C .0.45D .0.5513、已知F 1、F 2是椭圆x 216+y 29=1的两个焦点,过F 1的直线与椭圆交于M 、N 两点,则△MNF 2的周长为( )A .8B .16C .25D .3214、袋中共有6个除了颜色外完全相同的球,其中有1个红球,2个白球和3个黑球,从袋中任取两球,两球颜色为一白一黑的概率等于( )A.15B.25C.35D.4515、已知函数f (x )是定义在R 上的减函数,a ∈R ,则下列不等式恒成立的是( )A .f (a 2+a )<f (a )B .f (a 2+a )>f (a )C .f (a 2+1)<f (a )D .f (a 2+1)>f (a ) 二、填空题(本答题共有5小题,每空5分,共计24分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东高职院校自主招生数学模拟试题16
一、判断题(10小题,每题1分,共10分)
1、在0∈N +,0∈N,0∈Q,0∈R 中有四个正确。
( )A 正确; B 错误
2、二次函数42-=x y 的函数值组成的集合为(-4,+∞)( )A 正确; B 错误
3、函数x x f 1)(-
=在(-∞,0)上是减函数。
( )A 正确; B 错误 4、1531
<。
( )A 正确; B 错误
5、有两个面平行,其余各面都是四边形的几何体是棱柱。
( )A 正确; B 错误
6、如果一条直线上的两点在一个平面内,那么这条直线在此平面内。
( )A 正确;B 错误
7、一条直线与一个平面内两条直线垂直,那么这条直线垂直此平面。
( )A 正确;B 错误
8、一条直线与一个平面内的直线平行,那么这条直线与此平面平行。
( )A 正确;B 错误
9、等比数列中,5242a a a ⋅= ( )A 正确;B 错误
10、已知a 、b 为两个单位向量,则一定有a =b 。
( )A 正确;B 错误
二、选择题(25小题,每题2分,共50分)
1、已知集合{0,1,2,3}A =,{11}B x x =-<,则A B =( )
A.{}0,1
B.{0,1,2}
C.{2,3}
D.{0,1,2,3}
2、设集合M={2,3,4},N={2,4,5},则M N =( )
A.{2,3,4,5}
B.{2,4}
C.{3}
D.{5}
3、设命题p :实数,,a b c 中至少有一个正数,那么命题非p 可陈述为:实数,,a b c 中( )
A.全是负数
B.没有正数
C.至少有一个正数
D.不只含有一个正数
4、不等式2
340x x -->的解为( )
A.(4,1)
B. (4,-1)
C. (1,4)
D.(-1,4) 5、设函数f(x)=2log ,22,0x x x x ⎧⎨≤⎩, 则f[f(1)]= ( )
A.0
B.log 32
C.1
D.2
6、设0,1a a >≠,如果函数()log a f x x =
的图象经过点1()24
-,则a =( )
B.2
C.4
D.15
7、函数lg(1)y x =-的图象与x 轴的交点坐标是( )
A.(11,0)
B.(10,0)
C.(2,0)
D.(1,0)
8、函数()13cos 2,f x x x R =-∈是( )
A.最小正周期为π的偶函数
B.最小正周期为π的奇函数
C.最小正周期为
2π的偶函数 D.最小正周期为2π的奇函数 9、算式33log 8log 2
=( ) A.3log 4 B.33log 2 C.3 D.4
10、函数)4(log x y a -=的定义域为( )
A. (-∞,+∞)
B. (4,+∞)
C. (-∞,4)
D. (0,4)
11、某剧场共有18排座位,第一排有16个座位,往后每排都比前一排多2个座位,那么该剧场座位的总数为( )
A.594
B.549
C.528
D.495
12、在等差数列{}n a 中,已知471,8a a =-=,则首项1a 与公差d 为( )
A.110,3a d ==
B. 110,3a d =-=
C. 13,10a d ==-
D. 13,10a d ==
13、函数2cos()23
x y π=+
的图象有一条对称轴的方程为x =( ) A.0 B.3π C.23π D.43π 14、在平面直角坐标系中,已知角α
的终边经过点(1,A ,则sin α=( )
A. B.12 C.12
-
D. 15、若向量(1,1)a =-,(2,1)b =-,则向量3a b -的模3a b -=
A.5
C.
D.
16、下列向量中与向量(2,3)a =-平行的是( )
A.(-4,6)
B.(4,6)
C.(-3,2)
D.(3,2)
17、函数sin(2)4y x π=+的图象向右平移
8
π后,新位置图象的函数为y =( ) A.sin(2)4x π- B.sin 2x C.3sin(2)4x π+ D.cos2x 18、已知直线1l :2y=x,直线212:21
0l y x l l ++=,则与( ) A. 相交不垂直 B.相交且垂直 C.平行不垂合 D.重合
19、已知直线y=ax+1的倾斜角为3
π,则α=( ) A.3
π B. 3 C.1 D 、33 20、直线y x b =-与圆22(2)(1)2x y -++=相切,则实数b 的取值是( ) A. 223± B .±3 C.1、5 D.2、-1
21、已知椭圆222125x y b +=的离心率为35
,则其短半轴长b =( ) A.3 B.4 C.5 D.8
22、抛物线2144
y x x =-+-的对称轴是( ) A.4x =- B.2x =- C.2x = D.4x =
23、如果圆柱高为4cm ,底面周长为10πcm ,那么圆柱的体积等于( )
A .10π
B .20π
C .50π
D .100π 24、若x x x f 23)(3-=,则=)1('f ( )
A .7
B .5
C .3
D .1
25、甲乙两人在玩猜数游戏,甲对乙说:“你在心中想好一个数,不要说出来,然后将它加上3,接着乘以4,再减去8,最后再除以2,减去5,把结果告诉我,我就可以猜出你心中想的数。
”每当乙报出一个结果时,甲便马上猜出他心中想的数。
乙感神奇,甲告知之说,这其实是一个函数问题。
请问假如乙所报的结果用x 表示,心里所想的结果用y 表示,则y 与x 之间的关系可以用以下的那个函数来表示( )
A .y=2x-3
B .y=2x+3
C .+32x y =
D .-32
x y =
三、解答题(2小题,每题10分,共20分)
1、求和:)532()534()532(21n n ---⨯-+⋅⋅⋅+⨯-+⨯-
2、如图所示,足球门左右柱分别立在A,B 处,假定足球门宽度AB 为7米,在距离门柱15米的C 处,一球员带球沿与球门线AC 成280角的CD 方向以平均每秒6.5米的速度推进,2秒后到达点D 处射门。
问:
(1) D 点到左右门柱的距离分别为多少米?
(2) 此时射门张角θ为多少?(注023cos2826
≈)
A
D。
