数字信号处理实验 第4章
《数字信号处理—理论与实践》课件第4章

4. 围线积分法(留数法) 留数法是求Z反变换的一种有用的方法。 根据复变函数 理论, 若
X (z) x(n)z n , Rx | z | Rx n
第 4 章 Z变换
则
式中, c是X(z)的收敛域中的一条逆时针方向环绕原点的闭 合积分围线。
直接计算围线积分比较麻烦, 一般采用留数定理求解。 按照留数定理, 若函数F(z)=X(z)zn-1在围线c上连续, 在c内 有K个极点zk, 而在围线外部有M个极点zm(M和K都取有限 值), 则有
第 4 章 Z变换
2. 一般X(z)是z的有理分式, 可以表示为X(z)=B(z)/A(z), B(z)、 A(z) 都是z的实系数多项式, 并且没有公因式。 记住了 常用序列的Z变换, 就可以将X(z)表示成简单项之和的形式, 而后求取其中的每一项Z反变换(可以查表), 然后把求得的 每一项部分分式相加, 就得到所求的x(n), 即若
第 4 章 Z变换
(1) X(z)的收敛域为|z|>Rx-, x(n)必为因果序列, 此时 应将X(z)展开为z的负幂级数, 为此X(z)的分子、 分母应按照 z的降幂排列(或z-1升幂);
(2) X(z)的收敛域为|z|<Rx+, x(n)必为左边序列, 此时 应将X(z)展开为z的正幂级数, 为此X(z)的分子、 分母应按照 z的升幂排列(或z-1降幂)。
1. 只在有限长度n1≤n≤n2内序列x(n)才具有非零值, 而在此 区间外x(n)=0, 即
第 4 章 Z变换
x(n), n1≤n≤n2 x(n)= 0, 其他
这类序列称为有限长序列。 有限长序列的Z变换为
n2
X (z) x(n) zn nn1
数字信号处理DSP第4章

k 0,1, , N 1
2
13
4.2 按时间抽取(DIT)的基2–FFT算法
将系数统一为 WNk 2 WN2k ,则可得
x[0]
N 4点
x[4]
DFT
G[0]
X [0]
G[1]
X [1]
x[2]
N 4点
WN0
x[6]
DFT
WN2
G[2]
1 G[3]
1
X [2] X [3]
x[1]
N 4点
X m1[i] WNr X m1[ j] , X m1[i] WNr X m1[ j]
m 1, 2 ,
每一个蝶形需要一次复数乘法和两次复数加法。
17
4.2 按时间抽取(DIT)的基2–FFT算法
N点的DIT-FFT计算量为
复数乘法:
1
N 2
log2
N
N 2
复数加法:
2
N 2
log2
N
N
例: 如果每次复数乘法需要100us,每次复数加法需要20us,来 计算N=1024点DFT,则需要
12
4.2 按时间抽取(DIT)的基2–FFT算法
同理
( N 4)1
( N 4)1
G[k] DFT[g[r]]
g[2l]WN2lk2
g[2l 1]WN(22l1)k
l 0
l 0
( N 4)1
( N 4)1
g[2l]WNlk 4 WNk 2
g[2l 1]WNlk 4 ,
l 0
l 0
k 0,1,
(3) WN0 WN4 WN8 WN12 WN16 WN20 WN24 WN28
或 WN4i i 0,1, 2, 3, 4, 5, 6, 7 (dm 1)
数字信号处理EXPIV型教学实验系统实验四常规实验exp4_常规

第四章常规实验指导实验一常用指令实验一、实验目的1、了解DSP开发系统的组成和结构;2、熟悉DSP开发系统的连接;3、熟悉CCS的开发界面;4、熟悉C54X系列的寻址系统;5、熟悉常用C54X系列指令的用法。
二、实验设备计算机,CCS 2.0版软件,DSP仿真器,实验箱。
三、实验步骤与内容1、系统连接进行DSP实验之前,先必须连接好仿真器、实验箱及计算机,连接方法如下所示:2、上电复位在硬件安装完成后,确认安装正确、各实验部件及电源连接正常后,接通仿真器电源,启动计算机,此时,仿真器上的“红色小灯”应点亮,否则DSP开发系统有问题。
3、运行CCS程序待计算机启动成功后,实验箱后面220V输入电源开关置“ON”,实验箱上电,启动CCS,此时仿真器上的“绿色小灯”应点亮,并且CCS正常启动,表明系统连接正常;否则仿真器的连接、JTAG接口或CCS相关设置存在问题,掉电,检查仿真器的连接、JTAG 接口连接,或检查CCS相关设置是否正确。
注:如在此出现问题,可能是系统没有正常复位或连接错误,应重新检查系统硬件并复位;也可能是软件安装或设置有问题,应尝试调整软件系统设置,具体仿真器和仿真软件CCS的应用方法参见第三章。
●成功运行程序后,首先应熟悉CCS的用户界面●学会CCS环境下程序编写、调试、编译、装载,学习如何使用观察窗口等。
4、修改样例程序,尝试DSP其他的指令。
注:实验系统连接及CCS相关设置是以后所有实验的基础,在以下实验中这部分内容将不再复述。
5、填写实验报告。
6、样例程序实验操作说明仿真口选择开关K9拨到右侧,即仿真器选择连接右边的CPU:CPU2;启动CCS 2.0,在Project Open菜单打开exp01_cpu2目录下面的工程文件“exp01.pjt”注意:实验程序所在的目录不能包含中文,目录不能过深,如果想重新编译程序,去掉所有文件的只读属性。
用下拉菜单中Project/Open,打开“exp01.pjt”,双击“Source”,可查看源程序在File Load Program菜单下加载exp01_cpu2\debug目录下的exp01.out文件:加载完毕,单击“Run”运行程序;实验结果:可见指示灯D1定频率闪烁;单击“Halt”暂停程序运行,则指示灯停止闪烁,如再单击“Run”,则指示灯D1又开始闪烁;注:指示灯D1在CPLD单元的右上方关闭所有窗口,本实验完毕。
数字信号处理实验报告 (实验四)

实验四 离散时间信号的DTFT一、实验目的1. 运用MA TLAB 计算离散时间系统的频率响应。
2. 运用MA TLAB 验证离散时间傅立叶变换的性质。
二、实验原理(一)、计算离散时间系统的DTFT已知一个离散时间系统∑∑==-=-Nk k N k k k n x b k n y a 00)()(,可以用MATLAB 函数frequz 非常方便地在给定的L 个离散频率点l ωω=处进行计算。
由于)(ωj e H 是ω的连续函数,需要尽可能大地选取L 的值(因为严格说,在MA TLAB 中不使用symbolic 工具箱是不能分析模拟信号的,但是当采样时间间隔充分小的时候,可产生平滑的图形),以使得命令plot 产生的图形和真实离散时间傅立叶变换的图形尽可能一致。
在MA TLAB 中,freqz 计算出序列{M b b b ,,,10 }和{N a a a ,,,10 }的L 点离散傅立叶变换,然后对其离散傅立叶变换值相除得到L l eH l j ,,2,1),( =ω。
为了更加方便快速地运算,应将L 的值选为2的幂,如256或者512。
例3.1 运用MA TLAB 画出以下系统的频率响应。
y(n)-0.6y(n-1)=2x(n)+x(n-1)程序: clf;w=-4*pi:8*pi/511:4*pi;num=[2 1];den=[1 -0.6];h=freqz(num,den,w);subplot(2,1,1)plot(w/pi,real(h));gridtitle(‘H(e^{j\omega}的实部’))xlabel(‘\omega/ \pi ’);ylabel(‘振幅’);subplot(2,1,1)plot(w/pi,imag(h));gridtitle(‘H(e^{j\omega}的虚部’))xlabel(‘\omega/ \pi ’);ylabel(‘振幅’);(二)、离散时间傅立叶变换DTFT 的性质。
数字信号处理课后答案+第4章(高西全丁美玉第三版)

6*. 按照下面的IDFT算法编写MATLAB语言 IFFT程 序, 其中的FFT部分不用写出清单, 可调用fft函数。 并分 别对单位脉冲序列、 矩形序列、 三角序列和正弦序列进行 FFT和IFFT变换, 验证所编程序。
解: 为了使用灵活方便, 将本题所给算法公式作为函 数编写ifft46.m如下: %函数ifft46.m %按照所给算法公式计算IFET function xn=ifft46(Xk, N) Xk=conj(Xk); %对Xk取复共轭 xn=conj(fft(Xk, N))/N; %按照所给算法公式计算IFFT 分别对单位脉冲序列、 长度为8的矩形序列和三角序列 进行FFT, 并调用函数ifft46计算IFFT变换, 验证函数 ifft46的程序ex406.m如下:
快速卷积时, 需要计算一次N点FFT(考虑到H(k)= DFT[h(n)]已计算好存入内存)、 N次频域复数乘法和 一次N点IFFT。 所以, 计算1024点快速卷积的计算时间Tc 约为
Fs <
1024 = 15 625 次 /秒 65536 × 10−6
Fs 15625 = = 7.8125 kHz 2 2
1 x ( n) = IDFT[ X ( k )] = [DFT[ X * ( k )]]* N
%程序ex406.m %调用fft函数计算IDFT x1n=1; %输入单位脉冲序列x1n x2n=[1 1 1 1 1 1 1 1]; %输入矩形序列向量x2n x3n=[1 2 3 4 4 3 2 1]; %输入三角序列序列向量x3n N=8; X1k=fft(x1n, N); X2k=fft(x2n, N); X3k=fft(x3n, N); %计算x1n的N点DFT %计算x2n的N点DFT %计算x3n的N点DFT
数字信号处理 第04章 正交变换

给定:
x(n), n = 1, 2, , N
DST
定义: X s (k) =
∑ 2 N
nkπ
x(n) sin( )
N +1 n=1
N +1
k = 1, 2, , N
反变换: x(n) =
∑ 2
N +1
N k =1
X
s
(k
)
sin(
nkπ )
N +1
n = 1, 2, , N
y = Ax 3. 反变换: x = A−1 y = AT y
不需要求逆,特别有利于硬件实现
性质2:展开系数是信号在基向量上的
准确投影 ϕ2
α2
α3
ϕ3
x
α1
ϕ1
非正交基的情况下,“基向量”称为“标架 (Frame)”, 这时,展开系数不是准确投影。
性质3:正交变换保证变换前后信号的能量不变,
此性质又称为“保范(数)变换”。
2N
DCT 反变换
一阶马尔可夫过程(Markov-1):语音和图象处 理中常用的数学模型。一个随机信号 ,若其 pdf满足如下关系
p[ X (tn+1) ≤ xn+1 X (tn ) = xn , X ( tn−1) = xn−1, , X ( t0 ) = x0 ]
= p[ X (tn+1) ≤ xn+1 X (tn ) = xn ], X (tn ) X (n)
即为正交变换,或保范(数)变换
AN×N 实际上是正交矩阵, AT = A−1
(二)、正交变换的性质:
性质1:正交变换的基向量即是其对偶基
北京邮电大学数字信号处理第4章答案

习题解答4.1 根据给定的模拟滤波器的幅度响应平方,确定模拟滤波器的系统函数 H(s)。
(1) 261|()|164H j Ω=+Ω(2) 2222216(25)|()|(49)(36)H j -ΩΩ=+Ω+Ω分析:在模拟滤波器设计中,由各种逼近方法确定了幅度响应,通过下列步骤求出滤波器的系统函数H(s)。
更进一步,通过脉冲响应不变法或双线性变换法,可以得到数字滤波器的传输函数 H(z)。
(1)考虑s j =Ω,将幅度响应表达式整理为s 为变量的表达式,求 ()()a a H s H s - 表达式的零极点;(2)为了系统稳定,选择左半平面的极点构成 H(s);(3)如果没有特殊要求,可以选择取 ()()a a H s H s -以虚轴为对称轴的对称零点的任意一半(应是共轭对)作为 H a (s) 的零点。
但如果要求是最小相位延时滤波器,则应取左半平面零点作为 H a (s) 的零点。
(4)对比()a H s 和()a H j Ω 的低频特性或高频特性,从而确定增益常数K 0。
解:(1)由于2)(Ωj H a 是非负有理函数,它在Ωj 轴上的零点是偶次的,所以满足幅度平方函数的条件,先求2321()()()164()22H s H s H j a a as s -=Ω=+-Ω=-其极点为0.50.250.4330.50.250.433j j --±±我们选出左半平面极点s=0.5和 0.250.433j -± 为)(s H a 的极点,并设增益常数为0K ,则得)(s H a 为:002()(0.5)(0.250.433)(0.250.433)(0.5)(0.50.25)K K H s a s s j s j s s s ==++-+++++ 按着()a H s 和()a H j Ω的低频特性或高频特性的对比可以确定增益常数。
在这里我们采用低频特性,即由00()|()|a s a H s H j =Ω==Ω的条件可得增益常数0K 为:018K =最后得到)(s H a 为:21()8(0.5)(0.50.25)H s a s s s =+++(2)由于2)(Ωj H a 是非负有理函数,它在Ωj 轴上的零点是偶次的,所以满足幅度平方函数的条件,得)36)(49()25(16222)()()(222s s s s j aH s a H s a H --+=-=ΩΩ=- 其极点为:6,7±=±=s s其零点为:5j s ±=(皆为二阶,位于虚轴上)j Ω虚轴上的零点或极点一定是二阶的,其中一半(应为共轭对)属于 H a (s)。
《数字信号处理》第四章 相关分析

对函数两边同时作傅立叶变换有:
F
r12( )
r12 (
)e j2f
d
x1
(t
)
x2
(t
)dtej2f d
x1
(t
)
x2
(t
)ej2f d dt
第二节 相关函数的性质
这是由于:
① r(τ)完全由它的能量谱或功率谱P(f )来决定; ② P(f ) =∣X(f )∣2
具有相同的振幅谱而不同相位谱的信号,可以 有相同的自相关函数。
第一节 相关
相关函数r(τ)存在的条件是:
信号x1(t)和x2(t)是绝对可积函数。
即:
x12
(t)dt
,
或
x(t)dt
x 2 2
(t)dt
与自相关函数相对应,如果参与相关的两个信号是
不同的信号,则其相关函数称为互相关函数。
第一节 相关
t
min
xe2 (t)
x
2
(t
)dt
1
x(t
)
y(t
)dt
2
x
2
(t
)dt
y2 (t)dt
若令
xy
x(t) y(t)dt
x2 (t)dt y2 (t)dt
则相对误差可表示为
min
1
(t
)dt
数字信号处理实验报告_第四章

数字信号处理实验四专业:电子信息工程学号:20101560063 姓名:任子翔Q4.2使用修改后的程序P3.1,计算并画出当时的传输函数的因果线性时不变离散时间系统的频率响应。
他表示那种类型的滤波器?解:%程序P3.1clf;w=0:8*pi/511:pi;num=[0.15,0,-0.15]; den=[1,-0.5,0.7];h=freqz(num,den,w);%plot the DTFTsubplot(2,1,1);plot(w/pi,real(h));grid;title('H(e^{j\omega})的实部'); xlabel('\omega/\pi');ylabel('振幅');subplot(2,1,2)plot(w/pi,imag(h));grid;title('H(e^{j\omega})的虚部'); xlabel('\omega/\pi'); ylabel('振幅');pausesubplot(2,1,1);plot(w/pi,abs(h));grid;title('|H(e^{j\omega})|幅度谱'); xlabel('\omega/\pi');ylabel('振幅');subplot(2,1,2)plot(w/pi,angle(h));grid;title('相位谱[H(e^{j\omega})]'); xlabel('\omega/\pi');ylabel('以弧度为单位的相位谱');Q4.3对下面的传输函数重做习题Q4.2:这两题中给出的两个滤波器之间的区别是什么?你将选择哪个滤波器来滤波,为什么?解:%程序P3.1clf;w=0:8*pi/511:pi;num=[0.15,0,-0.15]; den=[0.7,-0.5,1];h=freqz(num,den,w);%plot the DTFTsubplot(2,1,1);plot(w/pi,real(h));grid;title('H(e^{j\omega})的实部'); xlabel('\omega/\pi');ylabel('振幅');subplot(2,1,2)plot(w/pi,imag(h));grid;title('H(e^{j\omega})的虚部'); xlabel('\omega/\pi'); ylabel('振幅');pausesubplot(2,1,1);plot(w/pi,abs(h));grid;title('|H(e^{j\omega})|幅度谱'); xlabel('\omega/\pi');ylabel('振幅');subplot(2,1,2)plot(w/pi,angle(h));grid;title('相位谱[H(e^{j\omega})]'); xlabel('\omega/\pi');ylabel('以弧度为单位的相位谱');这题中的滤波器的幅度响应较Q4.2的更为尖锐,Q4.7用程序 P4. 1计算并画出近似理想低通滤波器的冲激响应。
数字信号处理实验报告4
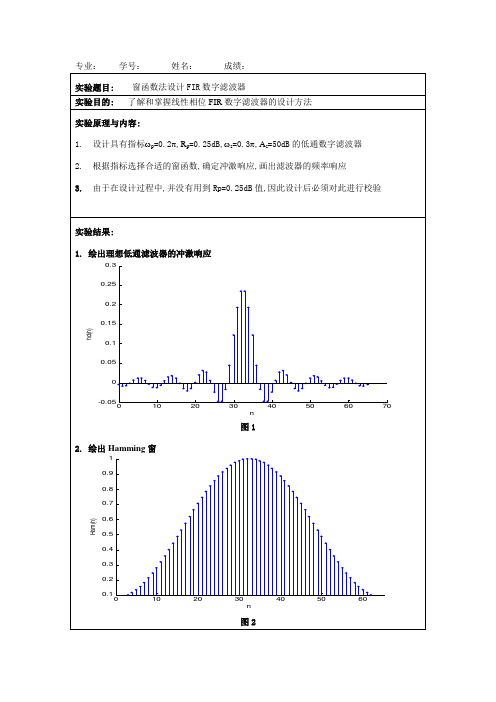
专业: 学号: 姓名: 成绩: 实验题目: 窗函数法设计FIR 数字滤波器实验目的: 了解和掌握线性相位FIR 数字滤波器的设计方法实验原理与内容:1. 设计具有指标ωp =0.2π,R p =0.25dB,ωs =0.3π,A s =50dB 的低通数字滤波器2. 根据指标选择合适的窗函数,确定冲激响应,画出滤波器的频率响应3. 由于在设计过程中,并没有用到Rp=0.25dB 值,因此设计后必须对此进行校验实验结果:1. 绘出理想低通滤波器的冲激响应图12. 绘出Hamming 窗图2010203040506070-0.0500.050.10.150.20.250.3n h d (n )01020304050600.10.20.30.40.50.60.70.80.91n H a m (n )3. 绘出加窗后的滤波器冲激响应图34. 绘出该滤波器的幅频响应图4010203040506070-0.0500.050.10.150.20.250.3Actual Impulse Responsen h (n )00.20.31-100-90-80-70-60-50-40-30-20-10010Magnitude Response in dB w/pi 20l g |H g (w )|思考题:1如果没有给定h(n)的长度N,而是给定了通带边缘截止频率ωc和阻带临界频率ωp,以及相应的衰减,你能根据这些条件用窗函数法设计线性相位FIR低通滤波器吗?2窗函数的傅式变换W(e jω)的主瓣和旁瓣分别决定了H(e jω)的什么特性?程序附录:function hd=ideal_lp(wc,N)alpha=(N-1)/2;n=0:N-1;m=n-alpha+eps;hd=sin(wc*m)./(pi*m);function [db,mag,pha,grd,w]=freqz_m(b,a)[H,w]=freqz(b,a,1000,'whole');H=(H(1:501))';w=(w(1:501))';mag=abs(H);pha=angle(H);db=20*log10((mag+eps)/max(mag));grd=grpdelay(b,a,w);clcwp=0.2*pi;ws=0.3*pi;tr_width=ws-wp;M=ceil(6.6*pi/tr_width);N=0:M-1;wc=(4*ws+6*wp)/10;w_ham=(hamming(M))';hd=ideal_lp(wc,M);h=hd.*w_ham;[db,mag,pha,grd,w]=freqz_m(h,1);delta_w=2*pi/1000;subplot(2,2,1)stem(N,hd,'.');xlabel('n');ylabel('hd(n)');subplot(2,2,2)stem(N,w_ham,'.');axis([0 M-1 0.1 1])xlabel('n');ylabel('Ham(n)');subplot(2,2,3)stem(N,h,'.')title('Actual Impulse Response');xlabel('n');ylabel('h(n)');subplot(2,2,4)plot(w/pi,db)axis([0 1 -100 10])title('Magnitude Response in dB')xlabel('w/pi');ylabel('20lg|Hg(w)|');gridset(gca,'XTickMode','manual','XTick',[0,0.2,0.3 1]) Rp=-(min(db(1:1:wp/delta_w+1)))As=-round(max(db(ws/delta_w+1:1:501)))function hd=ideal_lp(wc,N)alpha=(N-1)/2;n=0:N-1;m=n-alpha+eps;hd=sin(wc*m)./(pi*m);。
数字信号处理-答案第四章

y
l 1
m
( n) ,然后对它求一次 N 点
DFT , 即可计算 X ( z )在单位圆上的 N点抽样 (b)若:N M,可将x ( n)补零 到N点, 即 x ( n) x0 ( n ) 0 则:X (e
j 2 k N
0 n M 1 M n N 1
令 X 1 (k0 , n1 , n0 )
n2 0
x(n , n , n )W
2 1 0 1 ' 1
2
n2 k 0 3
,
k0 0,1,2
X 1' (k0 , n1 , n0 ) X 1 (k0 , n1 , n0 )W6n1k 0 X 2 (k0 , k1 , n0 )
n1 0
2 . 已知X (k ),Y (k )是两个N点实序列x(n), y(n)的DFT值, 今需要从 X (k ),Y (k )求x(n), y (n)值, 为了提高运算效率, 试用一个N点IFFT 运算一次完成。
解 : 依据题意 : x ( n ) X ( k ); y ( n ) Y ( k ) 取序列 Z ( k ) X ( k ) jY ( k ) 对Z ( k )作N点IFFT可得序列 z ( n ). 又根据DFT性质: IDFT [ X(k) jY(k) ] IDFT( [ X( k ) ] jIDFT [Y(k) ] x ( n) jy(n) 由原题可知: x(n),y(n) 都是实序列, 再根据 z(n) x ( n) jy(n) 可得:x(n) Re[ z(n) ] y(n) Im[z(n) ] 综上所述,构造序列 Z(k) X(k) jY(k)可用一次 N点IFFT完成计算x(n),y(n) 值的过程。
数字信号处理第4章部分习题详解
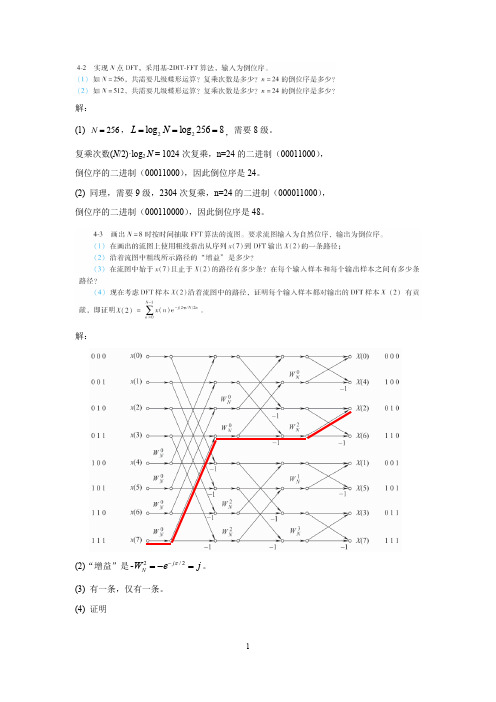
)( 2 k1 k0 ) n1k0 ( 2 n 2 n3 级间旋转因子 W16 。 W16
4
22 n1 2n2 n3 23 n0
0000 1000 0100 1100 0010 1010 0110 1110 0001 1001 0101 1101 0011 1011 0111 1111 x(0) x(8) x(4) -j x(12) x(2) x(10) x(6) -j x(14) x(1) x(9) x(5) -j x(13) x(3) x(11) x(7) x(15) -j -1 -1 -1 -1 -1 -1 -1 -1
nk X (k ) x(n)WN n 0 N 1
1
1
n3 0 n2 0 1
x(n n n n )W
n1 0 1 n0 0 1 0 1 2 3 0 1 2 3
1
1
1
( 23 n0 2 2 n1 2 n2 n3 )( 23 k3 2 2 k 2 2 k1 k0 ) 16
3
n1 0
3
3 n1 ( 4 k1 k 0 ) x(n0 n1 )W4n0 k 0 W16 n 0 0
n1k0 X 1 (n1k0 ) W16 W4n1k1 X 2 (k1k0 ) n1 0
n1 k 0 其中 W16 是级间旋转因子。
n3 0 n 2 0 1 1
n1 0
1 n3 ( 2 2 k 2 2 k1 k 0 ) x(n0n1n2n3 )W2n0 k 0 W4n1k 0 W2n1k1 W8n2 ( 2 k1 k 0 ) W2n2 k 2 W16 W2n3 k3 n 0 0
数字信号处理第4章 相关与谱分析

17
由DTFT的性质,时域上两个序列相乘,在频 域上是两个序列的离散时间傅里叶变换的卷积,即 加窗后序列x1(n)的频谱函数为:
18
图4.1.2矩形窗频谱函数的幅度频谱
19
图4.1.3用矩形窗函数截断余弦序列后的频谱
20
前后序列的频谱存在差异。这种差异对频谱分 ①频谱泄漏。无限长序列加矩形窗截断后,在 矩形窗频谱函数的作用下,使得X(ejω)出现了较大 的频谱扩展和向两边的波动,通常称之为频谱泄漏
1
对信号作频谱分析,实际上就是计算信号的傅 里叶变换,获得信号的频谱函数或频谱图。对于非 周期连续信号,其傅里叶变换是连续非周期函数; 对于周期的连续时间信号,其傅里叶分析是无穷级 数;离散时间序列的傅里叶变换是w的连续周期函 数。无论哪一种变换,都不便于用计算机计算。
2
一、用DFT对连续时间信号进行谱分析的原理和 公式推导 设xa(t) 为连续时间信号,对xa(t)以时间间隔T 进行采样,得到离散时间信号即序列x(n)。分别用 Xa(jΩ)和X(ejω)表示xa(t)和x(n)经过傅里叶变换后的 频谱函数,有:
3
由连续时间信号的傅里叶逆变换得: 因为x(n)是xa(t)
4
令ω=ΩT-2πk,则有
又由IDTFT的定义知:
5
对比上两式可得离散时间信号x(n)与连续时间 信号xa(t)的频谱函数关系为:
6
如果连续时间信号的频谱是有限带宽且最高角 频率为Ωc,同时抽样过程满足取样定理,即Ωs≥2Ω c,那么当时,
7
另一方面,设x(n)是有限长序列,长度为L, 其N点的DFT记为X(k)。 X(k)是X(ejω)在[0,2π)区间上的N个等间隔 采样点,即:
8
由频域取样定理知,当N≥L时,X(ejω)完全可 由X(k)确定,此时有:
数字信号处理第四章作业

求线性卷积,并比较它们的运算量。
k
(b) z k ak , k=0,1„,N-1.a 为实数, a 0 。 (c) (a)和(b)两者都行。 (d) (a)和(b)都不行,即线性调频 z 变换不能计算 H(z)在 z 为实数时的取样。 10. (第四章习题 13)设对列长 N=64 及列长 L=48 的两序列用(1)直接计算法,(2)快速卷积法
数字信号处理第四章作业数字信号处理数字信号处理试卷数字信号处理第三版数字信号处理pdf数字信号处理期末试卷matlab数字信号处理数字信号处理教程数字信号处理实验报告数字信号处理第四版
数字信号处理第四章作业
1. ( 第四章习题 1) 如果一台通用计算机的速度为平均每次复乘需要 100us,每次复加需要 20us, 今用来计算 N=1024 点的 DFT[x(n)],问直接运算需要长时间, 用 FFT 运算需多少时间? 2. (第四章习题 2)把 16 点序列 x(0) x(1) „x(15)排成反序序列。 3. (第四章习题 4)试用基-2 按时间抽取与按频率抽取法分别作出 N=16 时的信号流图。 4. (第四章习题 5)试画出 4 点按时间抽取的 FFT 算法流程图,要求利用本书图 4-8 的蝶形, 具有反序的输入序列,自然顺序的输出序列,并且表示成“原位”计算。 5. (第四章习题 6)重排题 5 的流图,使它仍然符合“原位”计算,但要有自然顺序输入,反 序输出。 6. (第四章习题 8)推导 N=16 时,基-4FFT 公式,并画出流图,就运算量的多少(不计 i, j 的运算量)与基-2 情况作比较。 7. (第四章习题 9)画出 8 点分裂基 L 型运算流图,计算其复数乘法次数,并与基 -2 和基-4 法 进行比较。 8. (第四章习题 10)已知 X(k)和 Y(k)分别是两个 N 点实序列 x(n)和 y(n)的 DFT 为提高运算效 率,试设计用一次 N 点 IFFT 来从 x(k)和 y(k)求 x(n)和 y(n)。 9. (第四章习题 12)在下列说法中选择正确的结论。线性调频 z 变换可以用来计算一个有限长 序列 h(n)在 z 平面实 z 轴上诸点{zk}的 z 变换 H(z) ,使 (a) z k a , k=0,1„,N-1.a 为实数, a 1 。
《数字信号处理》 第4章

右图为描述倒位序的树状图(N=8)
5 倒位序的实现
对照表
变址功能
产生倒序数的十进制运算规律 N=2M,用M位二进制数表示,则从左至右的十进制权值为:
N 1 4
x1(2l)WNk22l
N 1 4
x1(2l
1)WNk22l1
r0
l0
l0
N1
N1
4
4
x3(l)WN kl4WN k2 x4(l)WN kl4
l0
l0
X 3(k) W N k2X 4(k),k0 ,1 ,
,N 1 2
式中
N1 4
N1 4
X3(k)DFTx3(l) x3(l)WN kl4 X4(k)DFTx4(l) x4(l)WN kl4
47线性调频变换chirp变换算法471算法原理已知序列xn0nn1是有限长序列其z变换为为适应z可沿z平面更一般的路径取值就沿z平面上的一段螺线作等分角的采样z的这些采样点zk为因此有其中a决定起始采样点z0的位置a0表示z0的矢量半径长度通常取a010表示z0的相角0表示两相邻采样点之间的角度差w0一般为正值表示螺线的伸展率图471线性调频变换在平面的螺线采样当mn即时各采样点zk就均匀等间隔地分布在单位圆上这就是求序列的dft
N
W N k(N n)W N (N k)nW N kn,
W
2 N
1
N
k
WN 2
WNk
利用这些特性,使DFT运算中有些项可以合并,并且可以 将长序列的DFT分解为几个短序列的DFT,以减少DFT的运算 次数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a2 1/ 3, a3 0,
b0 编1/写6M, ATLAb1B程 1序/ 如2,下(取Nb=2 321点/ 2作, 图): b3 1/ 6
a=[1,0,1/3,0];
b=[1/6,1/2,1/2,1/6];
N=32;
n=0:N-1;
hn=impz(b,a,n);
%求时域单位冲激响应
gn=dstep(b,a,n);
2.dstep 功能:求解数字系统的阶跃响应。 调用格式:
[h,t]=dstep(b,a);求解数字系统的阶跃响应h, 取样点数为缺省值。
[h,t]=dstep(b,a,n);求解数字系统的阶跃响应h, 取样点数由n确定。
dstep(b,a);在当前窗口用stairs(t,h)函数出图。
3.filter 功能:对数字系统的输入信号进行滤波处理。 调用格式:
4.filtic 功能:为filter函数选择初始条件。 调用格式:
z=filtic(b,a,y,x);求给定输入x和y时的初始状态。 z=filtic(b,a,y);求x=0,给定输入y时的初始状态。 其中,矢量x和y分别表示过去的输入和输出: x=[x(-1),x(-2),…,x(-N)] y=[y(-1),y(-2),…,y(-N)]
同时,图4-1显示了系统时域分析方法和z变换域分析 法的关系。如果已知系统的冲激响应h(n),则对它进行z变 换即可求得系统函数H(z);反之,知道了系统函数H(z), 对其进行z逆变换,即可求得系统的冲激响应h(n)。
图4-1 离散LSI系统响应与激励的关系
2.用impz和dstep子函数求解离散系统的单位冲 激响应和阶跃响应
二、实验涉及的MATLAB子函数
1.impz 功能:求解数字系统的冲激响应。 调用格式:
[h,t]=impz(b,a);求解数字系统的冲激响应h, 取样点数为缺省值。
[h,t]=impz(b,a,n);求解数字系统的冲激响应h, 取样点数由n确定。
impz(b,a);在当前窗口用stem(t,h)函数出图。
在MATLAB语言中,求解系统单位冲激响应和阶跃响 应的最简单的方法是使用MATLAB提供的impz和dstep子函 数。
下面举例说明使用impz和dstep子函数求解系统单位冲 激响应和阶跃响应的方法。
例4-1 已知一个因果系统的差分方程为
6y(n)+2y(n-2)=x(n)+3x(n-1)+3x(n-2)+x(n-3)
a k z k
k0
b0 b1z1 b2z2 bmzm 1 a1z1 a 2z2 a kzk
(4-2)
系统函数H(z)反映了系统响应与激励间的关系。一旦 上式中的bm和ak的数据确定了,则系统的性质也就确定了。 其中特别注意:a0必须进行归一化处理,即a0=1。
对于复杂信号激励下的线性系统,可以将激励信号在 时域中分解为单位脉冲序列或单位阶跃序列,把这些单元 激励信号分别加于系统求其响应,然后把这些响应叠加, 即可得到复杂信号加于系统的零状态响应。因此,求解系 统的冲激响应和阶跃响应尤为重要。由图4-1可以看出一个 离散LSI系统响应与激励的关系。
曲线
title(系统的单位阶跃响应);
ylabel(g(n));xlabel(n); axis([0,N,-1.1*min(gn),1.1*max(gn)]); 系统的单位冲激响应和阶跃响应如图4-2所示。
图4-2 例4-1系统的单位冲激响应和阶跃响应
例4-2 已知一个系统函数公式
0.1321 0.3963 z2 0.3963 z4 0.1321 z6 H(z) 1 0.34319 z2 0.60439 z4 0.20407 z6
%求时域单位阶跃响应
subplot(1,2,1),stem(n,hn,k);%显示冲激响应
曲线
title(系统的单位冲激响应);
ylabel(h(n));xlabel(n);
axis([0,N,-1.1*min(hn),1.1*max(hn)]);
subplot(1,2,2),stem(n,gn,k);%显示阶跃响应
实验4 离散系统的冲激响应和 阶跃响应
1.1 市场与市场营销 1.2 我国汽车市场的发展与现状 复习思考题
一、实验目的
(1)加深对离散线性移不变(LSI)系统基本理论的理解, 明确差分方程与系统函数之间的关系。
(2)初步了解用MATLAB语言进行离散时间系统研究的 基本方法。
(3)掌握求解离散时间系统冲激响应和阶跃响应程序的 编写方法,了解常用子函数。
y=filter(b,a,x);对于由矢量a、b定义的数字系统, 当输入信号为x时,对x中的数据进行滤波,结果放于y中, 长度取max(na,nb)。
[y,zf]=filter(b,a,x);除得到结果矢量y外,还 得到x的最终状态矢量zf。
y=filter(b,a,x,zi);可在zi中指定x的初始状态。
满足初始条件y(-1)=0,x(-1)=0,求系统的单位冲
激响应和阶跃响应。
解 将y(n)项的系数a0进行归一化,得到
y(n) 1 y(n 2) 3
1
1
1
1
x(n) x(n1) x(n 2) x(n 3)
6
2
2
6
分析上式可知,这是一个3阶系统,列出其bm和ak系数:
a0 1,
a1 0,
说明:以上子函数中的b和a,分别表示系统函数H(z)
中由对应的分子项和分母项系数所构成的数组。如式(4-2) 所示,H(z)按z-1(或z)的降幂排列。在列写b和a系数向量时, 两个系数的长度必须相等,它们的同次幂系数排在同样的 位置上,缺项的系数赋值为0。
在MATLAB信号处理工具箱中,许多用于多项式处理 的函数,都采用以上的方法来处理分子项和分母项系数所 构成的数组。在后面的实验中不再说明。
三、实验原理 1.离散LSI系统的响应与激励
由离散时间系统的时域和频域分析方法可知,一个线 性移不变离散系统可以用线性常系数差分方程表示:
N
M
ak y(n k) bmx(n m) (4-1)
k0
m0
也可以用系统函数来表示:
M
H (z)
Y (z) X(z)
b(z) a(z)
bmzm
m0 N
