2019 高三联合模拟考试 文科
2019届高考全国统一招生语文模拟试卷5套(含解析)

2019年全国高校招生统一考试模拟试卷语文注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷 阅读题一、现代文阅读(35分)(一)论述类文本阅读(本题共3小题,9分) 阅读下面的文字,完成1-3题。
“音象”,是对中国文学中声音之象的泛称,是指文学(诗歌)作品在音乐或格律的参与下形成的声音效果,以及由声音效果产生的形象体验。
与之相对,“诗象”用于指称依靠文字内容而产生的主体想象和认知。
“音象”与“诗象”是构成文学“意象”的基石,充分剖析作为“意象”重要维度的“音象”,有助于全面认知“意象”概念。
魏晋之前,“音象”主要以“乐象”为存在形态,到了唐代,建构在音律或格律基础上的整体音响效果及形象体验,是“音象”存在形态之一。
就此种“音象”而言,音乐或格律的运用会使作品形成一种独特的氛围或气质,从而在整体上营造出与众不同的声音效果。
对入乐性作品来说,这种整体效果主要借助音乐的曲调、节奏、旋律来实现;对不入乐作品来说,则主要以语辞的韵律性和音乐性来体现。
配乐而歌是中国古代音乐文学的最典型形态,对唐代而言,以齐言歌诗和杂言曲辞最具代表性。
来看王维的《送元二使安西》:“渭城朝雨浥清尘,客舍青青柳色新。
劝君更尽一杯酒,西出阳关无故人。
”据考证,该诗配乐歌唱之事实是确定无疑的。
王维诗的立意在送别,故此可以推断与之相配的音乐也应当以感伤的基调为主,即便是先有辞,然后才根据意境产生了曲,但音乐由回环的旋律而产生的“三叠”的唱法,对诗意的升华无疑是有重要作用的,从而使渭城清雨与阳关漫道、绿柳垂杨与大漠孤烟的形象对比更为突出,惜别之情跃然纸上。
山东省济南市2019届高三模拟考试语文试题及答案

山东省济南市2019年高三模拟考试语文试题注意事项:1.答卷前,考生务必将自己的姓名、考号和座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,用0.5毫米的黑色签字笔将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将答题卡交回。
一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1~3题。
与古文运动的先驱者相比较,我们就能明白为什么“文起八代之衰”的重担会历史地落到韩愈的肩上。
韩愈大大超越了他的先驱者,主要表现在以下几方面:首先,他善于展开文学争鸣。
西魏的宇文泰和苏绰,隋代的杨坚和李谔,曾依靠帝王之尊,将相之权,采用严厉的行政措施,来反对艳丽浮靡的“今文”,推行《尚书》式的“古文”,并且强制规定“自是之后,文笔皆依此体”(《周书·苏绰传》)。
但效果极差,嗣响无闻,终于失败。
韩愈则不同。
他不依靠行政手段,而是在当时的百家争鸣中摆事实,讲道理,深刻地剖析了“古文”与“今文”的功过是非。
是非明则方向定,人们容易接受,乐于响应。
因此在他的周围自然团结了一大批作家及“古文”爱好者,为古文运动的胜利创造了条件。
其次,对六朝文学采取了正确的态度。
对于六朝文学,先驱者常是采用简单的一概骂倒、全盘否定的态度,甚至连屈原的优秀辞赋,也被他们斥为“亡国之音”而不顾(柳冕《谢杜相公论房杜二相书》),但谩骂攻不倒骈文。
韩愈则不然,他在批判的同时,对六朝文学并不全盘否定,对骈文有益的成分加以吸取,以便作为营养,用来壮大“古文”的新肌体。
他虽自称是“非三代两汉之书不敢观”,但这只是口号标榜,实际并非如此。
他对六朝文学是熟悉而精通的,如他对唐初的骈文典范——王勃《滕王阁序》,称赏备至。
他自己的文章如《进学解》《原毁》等,也自然地融骈入散,产生了良好的艺术效果。
山东中学联盟再次,善于理论与实践相结合。
2019年河南省五市高三模拟考试文科综合能力测试

★2019年3月22日2019年河南省五市高三模拟考试文科综合能力测试本试卷分第I卷(选择题)和第II卷(非选择题)两部分,第I卷1至6页,第II卷7至10页。
满分300分。
考试时间150分钟。
考试结束后答题卡和答题纸一并交回。
第I卷注意事项:1.答第I卷前,考生务必将自己的姓名、考号、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试卷上。
3.本卷共35小题,每小题4分,共140分。
在每题给出的四个选项中,只有一项是最符合题目要求的。
保护生物多样性非常重要。
读图1,回答1-2题。
1.从图中可以看出,野骆驼①曾生活在暖温带落叶阔叶林区②分布范围由亚热带季风区扩展至西北干旱区③文献记载区主要在温带草原区和温带荒漠区④目前主要分布在宁夏和内蒙古交界地区A.①③B.②③C.①④D.②④2.影响野骆驼分布区变化的主要因素包括I①草原开垦②过度放牧③大量捕杀④种群退化A:①③④ B.②③④ C.①②④ D.①②③表1是某年我国四个省(区)煤、铁、石油、盐产量占全国总产量比例(%)表。
读表回答3--4题。
3.表中①、②、③、④代表的矿产依次是A.石油、盐、煤、铁B.盐、石油、铁、煤C.煤、盐、铁、石油D.铁、煤、盐、石油4.表中的M省(区)可能是A.山西B.安徽C.山东D.新疆图2是亚洲东部某区域两个时刻的等压线图(单位:百帕)。
读图回答5-7题。
5在图2甲中A处等压线的数值可能为A .1004或1006 B.1006或1008 C.1008或1010 D.1004或10086.在图2乙中,青岛市的风向最可能是A.西南风B.偏北风C.西北风D.偏南风7.在这6个小时中,风力明显加大的是A.台湾岛B.北部湾C.黄河口D.辽东半岛图3所示为台湾省东北海岸“野柳公园”内著名的“女王头”象形石,其“玉颈”逐年变细,预计15年后将面临“断头”危险。
江西省九校2019届高三联合考试文科综合试卷
2019年江西省高三联合考试文综试卷(文科)注意事项:1本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分300分.考试时间为150分钟.2本试卷分试题卷和答题卷,第Ⅰ卷(选择题)的答案应填在答题卷卷首相应的空格内,做在第Ⅰ卷的无效.3答题前,考生务必将自己的姓名、准考证号填涂在答题卡相应的位置。
第Ⅰ卷一、选择题:本题共35小题,每小题4分,共140分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
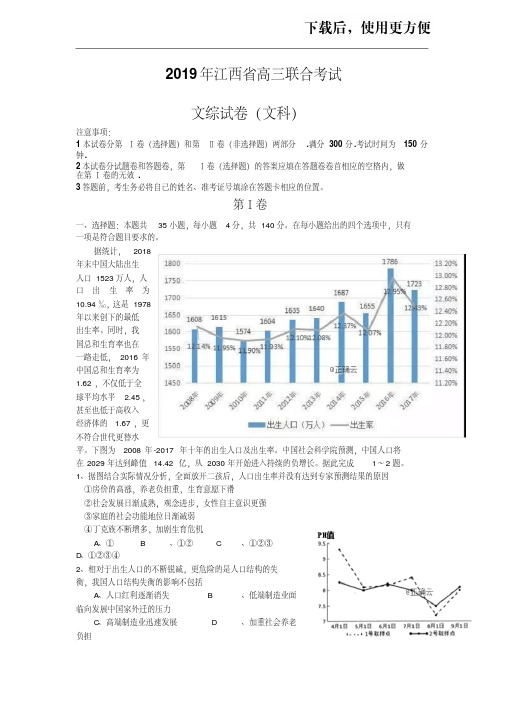
据统计,2018年末中国大陆出生人口1523万人,人口出生率为10.94‰,这是1978年以来创下的最低出生率。
同时,我国总和生育率也在一路走低,2016年中国总和生育率为1.62,不仅低于全球平均水平 2.45,甚至也低于高收入经济体的 1.67,更不符合世代更替水平。
下图为2008年-2017年十年的出生人口及出生率。
中国社会科学院预测,中国人口将在2029年达到峰值14.42亿,从2030年开始进入持续的负增长。
据此完成1~2题。
1、据图结合实际情况分析,全面放开二孩后,人口出生率并没有达到专家预测结果的原因①房价的高涨,养老负担重,生育意愿下滑②社会发展日渐成熟,观念进步,女性自主意识更强③家庭的社会功能地位日渐减弱④丁克族不断增多,加剧生育危机A、①B、①②C、①②③D、①②③④2、相对于出生人口的不断锐减,更危险的是人口结构的失衡,我国人口结构失衡的影响不包括A、人口红利逐渐消失B、低端制造业面临向发展中国家外迁的压力C、高端制造业迅速发展D、加重社会养老负担双河洞位于我国贵州省,双河洞结构复杂,水洞、旱洞并存,是世界最长的白云岩洞穴(白云岩是一种浅海相沉积碳酸盐岩)。
白云岩溶蚀和堆积的双向转化过程对洞穴水的酸碱度(PH值)变化反应灵敏。
某科考队多次进入双河洞内取样,收集洞穴水并检测酸碱度。
下图示意两个取样点收集到的洞穴水酸碱度变化图。
完成3~4题。
3.推断双河洞的形成过程是A. 地壳下沉一海洋侵蚀一地壳抬升一流水沉积B. 地壳下沉一海洋沉积一地壳抬升一流水侵蚀C. 地壳抬升一流水侵蚀一地壳下沉一海洋沉积D. 地壳抬升一海洋沉积一地壳下沉一流水侵蚀4.据图推测科考队考查期间洞内最为干燥的时间是A. 4月1日B. 5月1日C. 8月1日D. 9月1日读长江中游某支流某河段分布图(下左图)和该河段河水水位年变化曲线图(下右图),据此完成5~6题。
2019届高三第三次模拟考试卷+文综(三)+Word版含答案

2019届高三第三次模拟考试卷文科综合能力测试(三)注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷(选择题)本卷共35个小题,每小题4分,共140分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
“物联网”是在“互联网”的基础上,将其用户端延伸和扩展到任何物品与物品之间,进行信息交换和通信的一种网络概念。
“物联网”需要通过射额识别(RFID )、红外感应器、全球定位系统、激光扫描器等信息传感设备,按约定的协议,把任何物品与互联网相连接,进行信息交换和通信,实现智能化识别、定位、跟踪、监控和管理。
据此完成1~2题。
1.据材料推断物联网的特点( )①全面感知 ②人工分拣 ③智能处理 ④可靠传递 ⑤人工投递A .①②④B .①③④C .②③⑤D .③④⑤ 2.上海成为我国目前物联网产业链布局最完整的地区,最主要的原因是( )A .优越的地理位置B .先进的技术和大量的劳动力C .便捷的交通D .产业基础好和技术革新能力强 798艺术区是北京现代艺术的标志,其前身为建国初期外国援建的国营798厂等电子工业老厂区。
21世纪初,相关企业整合重组外迁后,青年艺术家和文化创意企业陆续进入该区,成规模地租用和改造空置厂房,逐渐将其发展成为画廊、艺术中心、设计公司、餐饮酒吧等各种空间聚合体。
据此完成3~5题。
3.推断原有企业整合重组的好处是( )A .推动体制改革以释放企业活力B .提高技术水平以增强竞争力C .提高当地第三产业比重以优化产业结构D .适应城市化扩张带来的用地类型转变4.798艺术区初期吸引有关艺术家及企业入驻的主要因素是( )A .集聚效应B .工业基础C .市场D .地价 5.为实现798艺术区可持续发展,不列措施最合理的是( )A .加大环保投入,促进绿色生产B .发展多元化产业,着力创造产值C .转变管理方式,激发创新机制D .实施工业复兴,引进重化工业植被覆盖度指某一地域植被垂直投影面积与该地域面积之比。
2019年全国普通高等学校招生统一考前模拟文科数学试题(全国Ⅲ卷)Word版含解析

2019年全国普通高等学校招生统一考前模拟文科数学试题(全国Ⅲ卷)一、选择题1.设集合{0,2,4,6,8,10},{4,8}A B ==,则A B ð=(A ){48},(B ){026},, (C ){02610},,, (D ){0246810},,,,, 【答案】C【解析】试题分析:由补集的概念,得C {0,2,6,10}A B =,故选C . 【考点】集合的补集运算. 2.若43i z =+,则||zz = (A )1 (B )1- (C )43i 55+ (D )43i 55-【答案】D【解析】试题分析:43i ||55z z ==-,故选D . 【考点】1、复数的运算;2、共轭复数;3、复数的模.3.已知向量1(2BA =uu v,1),2BC =uu u v 则ABC ∠=(A )300(B ) 450(C )600(D )1200【答案】A【解析】试题分析:由题意,得112222cos 112||||BA BC ABC BA BC ⨯⋅∠===⨯,所以30ABC ∠=︒,故选A .【考点】向量夹角公式.4.某旅游城市为向游客介绍本地的气温情况,绘制了一年中月平均最高气温和平均最低气温的雷达图。
图中A 点表示十月的平均最高气温约为150C ,B 点表示四月的平均最低气温约为50C 。
下面叙述不正确的是(A )各月的平均最低气温都在00C 以上 (B )七月的平均温差比一月的平均温差大(C )三月和十一月的平均最高气温基本相同(D )平均气温高于200C 的月份有5个 【答案】D【解析】试题分析:由图可知0C ︒均在虚线框内,所以各月的平均最低气温都在0℃以上,A 正确;由图可在七月的平均温差大于7.5C ︒,而一月的平均温差小于7.5C ︒,所以七月的平均温差比一月的平均温差大,B 正确;由图可知三月和十一月的平均最高气温都大约在5C ︒,基本相同,C 正确;由图可知平均最高气温高于20℃的月份有3个或2个,所以不正确.故选D . 【考点】1、平均数;2、统计图5.小敏打开计算机时,忘记了开机密码的前两位,只记得第一位是,M I N ,中的一个字母,第二位是1,2,3,4,5中的一个数字,则小敏输入一次密码能够成功开机的概率是 (A )815 (B )18 (C )115 (D )130【答案】C【解析】试题分析:开机密码的可能有(,1),(,2),(,3),(,4),(,5),(,1),(,2),(,3),(,4),(,5)M M M M M I I I I I ,(,1),(,2),(,3),(,4),(,5)N N N N N ,共15种可能,所以小敏输入一次密码能够成功开机的概率是115,故选C .【考点】古典概型. 6.若tan 13θ=,则cos 2θ=( ) (A )45-(B )15-(C )15 (D )45【答案】D【解析】试题分析:2222222211()cos sin 1tan 43cos 2cos sin 1tan 51()3θθθθθθθ---====+++. 【考点】1、同角三角函数间的基本关系;2、二倍角. 7.已知4213332,3,25a b c ===,则(A )b a c << (B )a b c << (C )b c a << (D )c a b << 【答案】A【解析】试题分析:因为423324a ==,1233255c ==,又函数23y x =在[0,)+∞上是增函数,所以222333345<<,即b a c <<,故选A .【考点】幂函数的单调性.8.执行下图的程序框图,如果输入的a=4,b=6,那么输出的n=(A )3 (B )4 (C )5 (D )6 【答案】B【解析】试题分析:第一次循环,得2,4,6,6,1a b a s n =====;第二次循环,得2,6,4,10a b a s =-===,2n =;第三次循环,得2,4,6,16,3a b a s n =====;第四次循环,得2,6,4,2016,4a b a s n =-===>=,退出循环,输出4n =,故选B .【考点】程序框图. 9.在ABC △中,π4B =,BC 边上的高等于13BC ,则sin A = (A )310(B(C(D【答案】D【解析】试题分析:设BC 边上的高线为AD ,则3,2B C A D D C A D ==,所以AC .由正弦定理,知sin sin AC BC B A =3sin AD A =,解得sin A =,故选D .【考点】正弦定理.10.如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为(A)18+(B)54+(C )90 (D )81【答案】B【解析】试题分析:由三视图该几何体是以侧视图为底面的斜四棱柱,所以该几何体的表面积2362332354S =⨯⨯+⨯⨯+⨯⨯=+,故选B .【考点】空间几何体的三视图及表面积.11.在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥,6AB =,8BC =,13AA =,则V 的最大值是(A )4π (B )92π (C )6π (D )323π【答案】B【解析】试题分析:要使球的体积V 最大,必须球的半径R 最大.由题意知球的与直三棱柱的上下底面都相切时,球的半径取得最大值32,此时球的体积为334439()3322R πππ==,故选B . 【考点】1、三棱柱的内切球;2、球的体积.12.已知O 为坐标原点,F 是椭圆C :22221(0)x y a b a b+=>>的左焦点,A ,B 分别为C 的左,右顶点.P 为C 上一点,且PF x ⊥轴.过点A 的直线l 与线段PF 交于点M ,与y 轴交于点E.若直线BM 经过OE 的中点,则C 的离心率为(A )13 (B )12 (C )23 (D )34【答案】A【解析】试题分析:由题意设直线l 的方程为()y k x a =+,分别令x c =-与0x =得点||()FM k a c =-,||OE ka =,由OBECBM ∆∆,得1||||2||||OE OB FM BC =,即2(c)ka a k a a c=-+,整理,得13c a =,所以椭圆离心率为13e =,故选A . 【考点】椭圆方程与几何性质.二、填空题13.若,x y 满足约束条件210,210,1,x y x y x -+≥⎧⎪--≤⎨⎪≤⎩则235z x y =+-的最大值为_____________.【答案】10-【解析】试题分析:作出不等式组满足的平面区域,如图所示,由图知当目标函数235z x y =+-经过点(1,1)A --时取得最小值,即min 2(1)3(1)510z =⨯-+⨯--=-.【考点】简单的线性规划问题.14.函数sin y x x =的图像可由函数2sin y x =的图像至少向右平移_____________个单位长度得到. 【答案】3π【解析】试题分析:因为sin 2sin()3y x x x π=-=-,所以函数sin y x x =的的图像可由函数2sin y x =的图像至少向右平移3π个单位长度得到. 【考点】1、三角函数图象的平移变换;2、两角差的正弦函数.15.已知直线l :60x +=与圆2212x y +=交于,A B 两点,过,A B 分别作l 的垂线与x 轴交于,C D 两点,则||CD =_____________. 【答案】4【解析】试题分析:由60x +=,得6x =-,代入圆的方程,并整理,得260y -+=,解得12y y ==120,3x x ==-,所以||AB ==l 的倾斜角为30︒,由平面几何知识知在梯形ABDC 中,||||4cos30AB CD ==︒.【考点】直线与圆的位置关系.16.已知()f x 为偶函数,当0x ≤ 时,1()x f x e x --=-,则曲线()y f x =在点(1,2)处的切线方程式_____________________________. 【答案】2y x =【解析】试题分析:当0x >时,0x -<,则1()x f x e x --=+.又因为()f x 为偶函数,所以1()()x f x f x e x -=-=+,所以1()1x f x e -'=+,则切线斜率为(1)2f '=,所以切线方程为22(1)y x -=-,即2y x =.【考点】1、函数的奇偶性;2、解析式;3、导数的几何意义.三、解答题17.已知各项都为正数的数列{}n a 满足11a =,211(21)20n n n n a a a a ++---=.(Ⅰ)求23,a a ;(Ⅱ)求{}n a 的通项公式. 【答案】(Ⅰ)41,2132==a a ;(Ⅱ)121-=n n a . 【解析】试题分析:(Ⅰ)将11a =代入递推公式求得2a ,将2a 的值代入递推公式可求得3a ;(Ⅱ)将已知的递推公式进行因式分解,然后由定义可判断数列{}n a 为等比数列,由此可求得数列{}n a 的通项公式. 试题解析:(Ⅰ)由题意得41,2132==a a . (Ⅱ)由02)12(112=---++n n n n a a a a 得)1()1(21+=++n n n n a a a a .因为{}n a 的各项都为正数,所以211=+n n a a . 故{}n a 是首项为1,公比为21的等比数列,因此121-=n n a . 【考点】1、数列的递推公式;2、等比数列的通项公式.18.下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图(Ⅰ)由折线图看出,可用线性回归模型拟合y 与t 的关系,请用相关系数加以说明; (Ⅱ)建立y 关于t 的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量. 附注: 参考数据:719.32ii y==∑,7140.17i i i t y ==∑0.55=,7≈2.646.参考公式:相关系数()()niit t y y r --=∑ 回归方程y a bt =+ 中斜率和截距的最小二乘估计公式分别为:121()()()nii i nii tt y y b tt ==--=-∑∑,=.a y bt -【答案】(Ⅰ)0.99r ≈,说明y 与t 的线性相关程度相当高,从而可以用线性回归模型拟合y 与t 的关系;(Ⅱ)1.82亿吨【解析】试题分析:(Ⅰ)根据相关系数r 公式求出相关数据后,然后代入公式即可求得r 的值,最后根据其值大小回答即可;(Ⅱ)利用最小二乘法的原理提供的回归方程,准确求得相关数据即可建立y 关于t 的回归方程,然后作预测. 试题解析:(Ⅰ)由折线图中数据和附注中参考数据得4=t ,28)(712=-∑=i i t t ,55.0)(712=-∑=i iy y ,89.232.9417.40))((717171=⨯-=-=--∑∑∑===i i i i i i i iy t y t y y t t,99.0646.2255.089.2≈⨯⨯≈r .因为y 与t 的相关系数近似为0.99,说明y 与t 的线性相关程度相当高,从而可以用线性回归模型拟合y 与t 的关系.(Ⅱ)由331.1732.9≈=y 及(Ⅰ)得103.02889.2)())((ˆ71271≈=---=∑∑==i ii i ity y t tb , 92.04103.0331.1ˆˆ≈⨯-≈-=t b y a. 所以,y 关于t 的回归方程为:t y10.092.0ˆ+=. 将2016年对应的9=t 代入回归方程得:82.1910.092.0ˆ=⨯+=y. 所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨.【考点】线性相关与线性回归方程的求法与应用. 19.如图,四棱锥P ABC -中,PA ⊥平面ABCD ,ADBC ,3AB AD AC ===,4PA BC ==,M 为线段AD 上一点,2AM MD =,N 为PC 的中点.(Ⅰ)证明MN平面PAB ;(Ⅱ)求四面体N BCM -的体积. 【答案】(Ⅰ)见解析;【解析】试题分析:(Ⅰ)取PB 的中点T ,然后结合条件中的数据证明四边形AMNT 为平行四边形,从而得到MNAT ,由此结合线面平行的判断定理可证;(Ⅱ)由条件可知四面体N-BCM 的高,即点N 到底面的距离为棱PA 的一半,由此可顺利求得结果. 试题解析:(Ⅰ)由已知得232==AD AM ,取BP 的中点T ,连接TN AT ,,由N 为PC 中点知BC TN //,221==BC TN . 又BC AD //,故TN 平行且等于AM ,四边形AMNT 为平行四边形,于是AT MN //. 因为⊂AT 平面PAB ,⊄MN 平面PAB ,所以//MN 平面PAB .(Ⅱ)因为⊥PA 平面ABCD ,N 为PC 的中点, 所以N 到平面ABCD 的距离为PA 21. 取BC 的中点E ,连结AE .由3==AC AB 得BC AE ⊥,522=-=BE AB AE .由BC AM ∥得M 到BC 的距离为5,故525421=⨯⨯=∆BCM S . 所以四面体BCM N -的体积354231=⨯⨯=∆-PA S V BCM BCM N . 【考点】1、直线与平面间的平行与垂直关系;2、三棱锥的体积.20.已知抛物线C :22y x =的焦点为F ,平行于x 轴的两条直线12,l l 分别交C 于A B ,两点,交C 的准线于P Q ,两点.(Ⅰ)若F 在线段AB 上,R 是PQ 的中点,证明ARFQ ;(Ⅱ)若PQF ∆的面积是ABF ∆的面积的两倍,求AB 中点的轨迹方程. 【答案】(Ⅰ)见解析;(Ⅱ)12-=x y .【解析】试题分析:(Ⅰ)设出与x 轴垂直的两条直线,然后得出,,,,A B P Q R 的坐标,然后通过证明直线AR 与直线FQ 的斜率相等即可证明结果了;(Ⅱ)设直线l 与x 轴的交点坐标1(,0)D x ,利用面积可求得1x ,设出AB 的中点(,)E x y ,根据AB 与x 轴是否垂直分两种情况结合AB DE k k =求解. 试题解析:由题设)0,21(F .设b y l a y l ==:,:21,则0≠ab ,且)2,21(),,21(),,21(),,2(),0,2(22b a R b Q a P b b B a A +---. 记过B A ,两点的直线为l ,则l 的方程为0)(2=++-ab y b a x .(Ⅰ)由于F 在线段AB 上,故01=+ab . 记AR 的斜率为1k ,FQ 的斜率为2k ,则222111k b aaba ab a b a a b a k =-=-==--=+-=. 所以FQ AR ∥.(Ⅱ)设l 与x 轴的交点为)0,(1x D , 则2,2121211b a S x a b FD a b S PQF ABF -=--=-=∆∆. 由题设可得221211ba x ab -=--,所以01=x (舍去),11=x . 设满足条件的AB 的中点为),(y x E . 当AB 与x 轴不垂直时,由DE AB k k =可得)1(12≠-=+x x yb a . 而y ba =+2,所以)1(12≠-=x x y . 当AB 与x 轴垂直时,E 与D 重合.所以,所求轨迹方程为12-=x y . 【考点】1、抛物线定义与几何性质;2、直线与抛物线位置关系;3、轨迹求法. 21.设函数()ln 1f x x x =-+. (Ⅰ)讨论()f x 的单调性;(Ⅱ)证明当(1,)x ∈+∞时,11ln x x x-<<; (Ⅲ)设1c >,证明当(0,1)x ∈时,1(1)xc x c +->.【答案】(Ⅰ)当01x <<时,()f x 单调递增;当1x >时,()f x 单调递减;(Ⅱ)见解析;(Ⅲ)见解析. 【解析】试题分析:(Ⅰ)首先求出导函数()f x ',然后通过解不等式()0f x '>或()0f x '<可确定函数()f x 的单调性(Ⅱ)左端不等式可利用(Ⅰ)的结论证明,右端将左端的x 换为1x即可证明;(Ⅲ)变形所证不等式,构造新函数,然后通过利用导数研究函数的单调性来处理.试题解析:(Ⅰ)由题设,()f x 的定义域为(0,)+∞,'1()1f x x=-,令'()0f x =,解得1x =. 当01x <<时,'()0f x >,()f x 单调递增;当1x >时,'()0f x <,()f x 单调递减.(Ⅱ)由(Ⅰ)知,()f x 在1x =处取得最大值,最大值为(1)0f =.所以当1x ≠时,ln 1x x <-.故当(1,)x ∈+∞时,ln 1x x <-,11ln 1x x <-,即11ln x x x-<<. (Ⅲ)由题设1c >,设()1(1)x g x c x c =+--,则'()1ln x g x c c c =--,令'()0g x =, 解得01lnln ln c c x c -=. 当0x x <时,'()0g x >,()g x 单调递增;当0x x >时,'()0g x <,()g x 单调递减. 由(Ⅱ)知,11ln c c c-<<,故001x <<,又(0)(1)0g g ==,故当01x <<时,()0g x >. 所以当(0,1)x ∈时,1(1)x c x c +->.【考点】1、利用导数研究函数的单调性;2、不等式的证明与解法.22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线1C的参数方程为()sin x y θθθ⎧=⎪⎨=⎪⎩为参数,以坐标原点为极点,以x 轴的正半轴为极轴,,建立极坐标系,曲线2C的极坐标方程为sin()4ρθπ+=(Ⅰ)写出1C 的普通方程和2C 的直角坐标方程;(Ⅱ)设点P 在1C 上,点Q 在2C 上,求|PQ|的最小值及此时P 的直角坐标.【答案】(Ⅰ)1C 的普通方程为2213x y +=,2C 的直角坐标方程为40x y +-=;(Ⅱ)31(,)22. 【解析】试题分析:(Ⅰ)利用同角三角函数基本关系中的平方关系化曲线C 1的参数方程普通方程,利用公式cos x ρθ=与sin y ρθ=代入曲线C 2的极坐标方程即可;(Ⅱ)利用参数方程表示出点P 的坐标,然后利用点到直线的距离公式建立||()PQ d α=的三角函数表达式,然后求出最值与相应的点P 坐标即可.试题解析:(Ⅰ)1C 的普通方程为2213x y +=,2C 的直角坐标方程为40x y +-=. (Ⅱ)由题意,可设点P的直角坐标为,sin )αα,因为2C 是直线,所以||PQ 的最小值, 即为P 到2C 的距离()d α的最小值,()sin()2|3d παα==+-.当且仅当2()6k k Z παπ=+∈时,()d αP 的直角坐标为31(,)22. 【考点】1、椭圆的参数方程;2、直线的极坐标方程.23.选修4-5:不等式选讲已知函数()|2|f x x a a =-+(Ⅰ)当a=2时,求不等式()6f x ≤的解集;(Ⅱ)设函数()|21|,g x x =-当x ∈R 时,()()3f x g x +≥,求a 的取值范围.【答案】(Ⅰ){|13}x x -≤≤;(Ⅱ)[2,)+∞.【解析】试题分析:(Ⅰ)利用等价不等式|()|()h x a a h x a ≤⇔-≤≤,进而通过解不等式可求得;(Ⅱ)根据条件可首先将问题转化求解()()f x g x +的最小值,此最值可利用三角形不等式求得,再根据恒成立的意义建立简单的关于a 的不等式求解即可.试题解析:(Ⅰ)当2a =时,()|22|2f x x =-+.解不等式|22|26x -+≤,得13x -≤≤.因此,()6f x ≤的解集为{|13}x x -≤≤.(Ⅱ)当x R ∈时,()()|2||12|f x g x x a a x +=-++-|212|x a x a ≥-+-+|1|a a =-+, 当12x =时等号成立, 所以当x R ∈时,()()3f x g x +≥等价于|1|3a a -+≥. ①当1a ≤时,①等价于13a a -+≥,无解.当1a >时,①等价于13a a -+≥,解得2a ≥.所以a 的取值范围是[2,)+∞.【考点】1、绝对值不等式的解法;2、三角形绝对值不等式的应用.。
2019届高三联合模拟考试文科数学试题

3
2
所以
且
,所以 0
.
2
4 22
3
因为函数 f( x)在区间 0,2 内恰好取得一次最大值 2,结合函数的图像可知
2
2
且5
2
1
,所以
2
4
5
1
,所以
4
4
2
. 故选 B.
3
12.【答案】 A
【解析】 f ( x) a(1 ln x) x ,令 f ( x) 0 ,
得 a(1 ln x) x 0 , a
x ( x 0, x 1).
13.【答案】 3 2
【解析】 根据 PF FQ , PQ 8 ,得 F 是 PQ 的中点, 且 PF 4 . 过 P 作 PM l 于点 M , 则由抛物线的定义,得 PM PF 4 , 所以 QPM 60 ,即直线 PQ 的倾斜角为 60 .
【解析】满足约束条件
x y10 x y 0 的可行域如下图所示: x 2y 4 0
【解析】复数 z
=
,根据共轭复数的概念得到,
1i 2
D.
z 的共轭复数为:
1
1 i .故答案为
22
3.【答案】 A
【解析】: A
平均数为 27
4. 【答案】 B
r 【解析】: | a
5.【答案】 D
由茎叶图知,乙组数据的中位数为
33 36 32 ,故选 A. 3
rr
r
rr
2b |2 | a |2 4 |b |2 4a b 4 4
b
2
43
23
所以 2R sin B
sin 60 0
, 所以 R
.
3
2019届高三联合模拟考试文科数学试题

7.元朝著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有
一壶酒,携着游春走,遇店添一倍,逢友饮一斗,店友经四处,
没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图
所示,即最终输出的 ,则一开始输入的 的值为()
A. B. C. D.
8.在 中, 所对的边分别为 , ,
,且满足 ,则该三角形的
东北师大附中重庆一中2019届高三联合模拟考试
吉大附中长春十一高中数学(文)科试题
吉林一中松原实验高中
本试卷共23题,共150分,共4页,考试时间120分钟.
注意事项:
1.答题前,考生先将自己的考场、姓名、班级填写清楚,将条形码准确粘贴在条形码区域内.
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字迹工整、笔迹清楚.
由 ,得 ,所以 ,则曲线 的直角坐标方程为 .······5分
( )由( )易得曲线 的极坐标方程为 ,则射线 与曲线 的交点的极径为 ,······7分
射线 与曲线 的交点的极径 满足 ,
解得 .······9分
所以 .······10分
23.【解析】( )当 时, ,
解得 , ;
当 时, ,
解得 , ;
所以当 时, ,所以 在 上没有零点.·10分
当 时,函数 在 上单调递增,
又 , ,
所以 在 上只有1个零点.······11分
综上可知,当 时 ,函数 有且仅有1个零点.······12分
22.【解析】( )由 ,得 .所以曲线 是以(1,0)为圆心,
1为半径的圆,所以曲线 的参数方程为 ( 为参数).····2分
综上,当 时,函数 的单调递增区间是 ;
