湖北省宜昌市部分示范高中教学协作体2018_2019学年高二日语下学期期中试题
湖北省宜昌市部分示范高中教学协作体高二下学期期中考试语文试题.doc

湖北省宜昌市部分示范高中教学协作体高二下学期期中考试语文试题 下列加点字的注音完全正确的一项是()A、  央浼(miǎn)寒砧(zhēn)  一撮毛(zuǒ)载欣载奔(zài)B、出岫(xiù)蕴藉(jiè)框架(kuàng)数见不鲜(shuò)C、拱券(quàn)箭镞(zú)混沌(dùn)锱铢必较(zī)D、讥诮(xiào)筵席(yàn)憎恶(zēng)舸舰弥津(gě)  【答案解析】B(A央浼měiC拱券xuànD讥诮qiào筵席yán) 2下列词语中没有错别字的一组是()A、拔擢盘桓喧阗模棱两可B、孤骛通霄晦朔兴高采烈C、殒首联袂希冀陈词滥调D、尺牍熟稔酒撰哀声叹气 【答案解析】A(B孤鹜通宵C陨首D酒馔唉声叹气) 3在下列各句中,加点的成语使用恰当的一项是()A、期待已久的《华尔街2:金钱永无眠》终于上映了,观众们拍手称快,既被电影史诗般的气质所征服,又对演员的演技赞不绝口。
B、这部轻喜剧逗得大家哈哈大笑,人们所有的烦恼都涣然冰释了。
C、《诗经》中的《卫风•氓》是一首以弃妇为题材的诗歌。
该诗将弃妇遭弃的黍离之悲写得淋漓尽致,感人至深。
D、该产品的试用效果非常好,相信它大量投产后将深孚众望,公司一定会凭借产品的优异品质在激烈的市场竞争中取得骄人业绩。
 【答案解析】D深孚众望:孚:使人信服、信任、相信。
在群众中享有威望,使大家信服。
(拍手称快:多指正义得到伸张或事情的结局使人感到满意。
涣然冰释:像冰块消融流散一样。
形容误会、疑虑、隔阂等一下子完全消除。
黍离之悲:指对国家残破,今不如昔的哀叹。
【精编文档】湖北省宜昌市部分示范高中教学协作体2018-2019学年高二数学下学期期中试卷理.doc

宜昌市部分示范高中教学协作体2019年春期中联考高二(理科)数学(全卷满分:150分 考试用时:120分钟)第Ⅰ卷(选择题 共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题所给出的四个选项中,只有一项是符合题目要求的.1.命题“02000,sin 1x x R x x e ∃∈++<”的否定是( )A .02000,sin 1x x R x x e ∃∈++>B .02000,sin 1x x R x x e ∃∈++≥C .2,sin 1x x R x x e ∀∈++>D .2,sin 1x x R x x e ∀∈++≥2.抛物线24x y =的准线方程为( ) A. 1=xB. 1-=xC. 1=y D . 1-=y3.函数x x x f -=ln )(的单调递增区间是( )A . )1,(-∞B . )(1,0C . ),0(+∞D . ),1(+∞4.如图,已知正方体1111D C B A ABCD -,若11z y x BD ++=,则x y z ++的值为( ) A .3 B .1 C .-1D .-35.0>⋅n m 是方程122=-ny m x 表示双曲线的( ) A.充分不必要条件 B.必要不充分条件 C. 充要条件D.既不充分也不必要条件6.1(2)0x e x dx +⎰ =( )A. 1B. 1-eC. eD. 1+e7.若双曲线)0(19222>=-a x a y 的一条渐近线与直线x y 31=垂直,则此双曲线的实轴长为( ) A . 2 B . 4 C . 18 D . 368.函数y =x ex 3(其中e 为自然对数的底数)的大致图像是( )A B C D9.在三棱锥ABC S -中,,,SA AC AB AC AB ==⊥ABC SA 平面⊥,D 为BC 的中点,则异面直线AB 与SD 所成角的余弦值为( ) A.55B.66 C.630D.530 10.对于函数xxx f ln )(=,下列说法正确的有( )①)(x f 在e x =处取得极大值e1;②)(x f 有两个不同的零点;③)3()()4(f f f <<π.A.0个B.3个C.2个D.1个11.已知双曲线2222:1(0,0)x y C a b a b-=>>的两条渐近线均与圆22650x y x +-+=相切,且双曲线的右焦点为该圆的圆心,则C 的离心率为( )A B C D 12.已知函数⎩⎨⎧≤->=0,30,ln )(x kx x x x f 的图像上有两对关于y 轴对称的点,则实数k 的取值范围是( )A. ()0,2e -B. ⎪⎭⎫⎝⎛-0,212-e C. ()0,e -D.()0,22e -第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分,共20分.请将正确答案填写在答题卡相应的位置上.13.曲线x x f sin )(=在点))0(,0(f 处的切线的倾斜角为 . 14.已知()7,5,3A -,()3,3,1-B ,且2=,则C 点的坐标为 . 15.已知M 为抛物线28y x =上的一点,F 为抛物线的焦点,若120MFO ∠=︒,(2,0)N -(O 为坐标原点),则△MNF 的面积为 .16.一边长为2的正方形纸板,在纸板的四角截去四个边长均为x 的小正方形,然后做成一个无盖方盒.方盒的容积的最大值为 .三、解答题:本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤.17.(本小题满分10分)已知函数R x x x f ∈+-=,121)(2 .(1)求函数)(x f 的图象在点(2,-1)处的切线方程; (2)求函数)(x f 的图象与直线1-=y 所围成的封闭图形的面积.18.(本小题满分12分)如图,在长方体1111D C B A ABCD -中,2,11===AB AD AA ,点E 是11D C 的中点.(1)求证:BCE DE 平面⊥; (2)求二面角C EB A --的大小.19.(本小题满分12分)已知椭圆的焦点在x 轴上,焦距为4,并且经过点),(2325-. (1)求该椭圆的标准方程;(2)该椭圆上是否存在一点,它到直线l :010=--y x 的距离最小?最小距离是多少?20.(本小题满分12分)如图,已知直三棱柱111C B A ABC - 中,,AC AB ⊥11,4,3AC C B AC AB ⊥==. (1)求1AA 的长;(2)若1=BP ,求直线1AA 与平面PC A 1所成角的余弦值.21.(本小题满分12分)已知直线l 与抛物线x y 22=交于B ,A (异于坐标原点O )两点.(1)若直线l 的方程为2-=x y ,求证:OB OA ⊥;(2)若OB OA ⊥,则直线l 是否恒过定点?若恒过定点,求出定点坐标;若不过定点,请说明理由.22.(本小题满分12分)设函数)0,,(21ln )(2≠∈++=c R c b bx x x c x f ,且1=x 为)(x f 的极值点.(1)若1=x 为)(x f 的极大值点,求)(x f 的单调区间(用c 表示);(2)若0)( x f 恰有两解,求实数c 的取值范围.宜昌市部分示范高中教学协作体2019年春期中联考高二(理科)数学参考答案一、选择题二、填空题 13.4π 14. )2,4,1(- 15. 38 16. 2716 三、解答题17.解:(1)由题意 x x f -=')( ...........1分所求切线的斜率2)2(-='=f k ...........3分所求切线方程为 )2(21--=+x y 即032=-+y x ..........5分(2)由⎪⎩⎪⎨⎧-=+-=11212y x y 解答 22=-=x x 或 ............6分所以所求的面积为[]31622)261(1)(2-23=-+-=+=⎰x x dx x f S . .........10分18.解:(1)建立如图所示的空间直角坐标系, 则D (0,0,0),E (0,1,1),B (1,2,0),C (0,2,0),DE =(0,1,1),BE =(-1,-1,1),BC =(-1,0,0)................2分因为0,0DE BE DE BC ⋅=⋅=,所以,DE BE DE BC ⊥⊥. (4)分则DE ⊥BE ,DE ⊥BC . 因为BE ⊂平面BCE ,BC ⊂平面BCE ,BE ∩BC =B , 所以DE ⊥平面BCE ................6分()()z y x n AEB ,,2=的法向量为设平面000n AB y x y z n BE ⎧⋅==⎧⎪⎨⎨--+=⋅=⎩⎪⎩则即 ()1,0,1AEB n ∴=平面的一个法向量为.............8分(),0,1,1.DE BCE DE BCE ⊥∴=平面是平面的一个法向量1cos ,2n DE n DE n DE⋅<>== (11)分.1200的大小为由图形可得二面角C EB A -- ...............12分19.解(1)由题意 设椭圆的方程为)0(12222>>=+b a by a x则⎪⎪⎩⎪⎪⎨⎧+==+-+++==2222210249)225(49)225(22c b a a c ..........3分6,10==∴b a (4)分161022=+y x 所求椭圆的标准方程为 .............5分2=+-n y x m 的方程为)设直线( ⎪⎩⎪⎨⎧=+-=+0161022n y x y x 由305108,22=-++n nx x y 得消去 (7)分4,0±==∆n 解得由 . ............9分的距离最近,与椭圆的交点到时,直线由图像可知,当l m n 4-=间的距离与直线直线l m 232410=+-=d.23最小距离是∴ ...............12分20.解(1)以A 为坐标原点,建立如图所示的空间直角坐标系 设AA 1=t (t>0),)0,0,3(),0,4,0(),,0,3(),,4,0(11B C t B t C),4,3(),,4,0(11t B t AC --==.........2分11B C AC ⊥1120160AC B C t ∴⋅=∴-= .............4分.4,41的长为即AA t =∴ ...............5分 (2)由(1)知)4,4,0(),3,0,3(04,0111-=-==A A ),(.....................6分 ),,(A 1z y x PC =的法向量为设平面⎪⎩⎪⎨⎧=-==-=⋅∴04403311z y A n z x A )1,1,1(,1==x 得令 (8)分 33344,cos 1=>=< (10)分 .36AA 11所成角的余弦值为与平面直线PC A ∴ .................12分21.解:(1)证明:由⎩⎨⎧=-=xy x y 222得x 2-6x+4=0,解得x=3±5 ........2分不妨取A(3-5,1-5), B(3+5,1+5), ...........3分 ∴0=⋅, ∴OA ⊥OB. .............5分(2)显然直线l 的斜率不为0,设直线l 的方程为x=ty+m(m ≠0),A(x 1,y 1),B(x 2,y 2),由⎩⎨⎧=+=xy m ty x 22消去x 得y 2-2ty-2m=0, ...................7分 ∴y 1y 2=-2m,x 1x 2=222221y y ⋅=m 2, ....................8分 由OA ⊥OB,得⋅=x 1x 2+y 1y 2=m 2-2m=0,∴m=2, .............10分直线l 的方程为x=ty+2,∴直线l 恒过定点,且定点坐标为(2,0) ..............12分22.解 f ′(x)=c x +x +b =x 2+bx +c x .因为f ′(1)=0,所以b +c +1=0,f ′(x)=()()x c x x --1 且c ≠1 (1)分(1)因为x =1为f(x)的极大值点,所以c >1. .............2分当0<x <1时,f ′(x)>0;当1<x <c 时,f ′(x)<0; 当x >c 时,f ′(x)>0. ..............4分 所以f(x)的单调递增区间为(0,1),(c ,+∞);单调递减区间为(1,c). ..... ........5分(2)①若c <0,则f(x)在(0,1)上单调递减,在(1,+∞)上单调递增.若f(x)=0恰有两解,则f(1)<0,即12+b<0.所以-12<c<0. ..............7分②若0<c<1,则f(x)极大值=f(c)=clnc+12c2+bc,f(x)极小值=f(1)=12+b.因为b=-1-c,所以f(x)极大值=clnc+c22+c(-1-c)=clnc-c-c22<0.f(x)极小值=-12-c<0,从而f(x)=0只有一解. .............9分③若c>1,则f(x)极小值=clnc+c22+c(-1-c)=clnc-c-c22<0.f(x)极大值=-12-c<0,则f(x)=0只有一解. ..............11分综上,使f(x)=0恰有两解的c的取值范围为(-1 2,0). ...............12分。
2018~2019学年湖北省宜昌市部分示范高中教学协作体高二下学期期中联考化学试卷及答案

绝密★启用前湖北省宜昌市部分示范高中教学协作体2018∽2019学年高二年级下学期期中联考化学试题(全卷满分:100分 考试用时:90分钟)可能用到的相对原子质量:H -1,C -12,N -14,O -16,Na -23,Cl -35.5第Ⅰ卷 (选择题,共48分)一、选择题(本题共16小题,每小题3分,共48分)【其中11-16有两组题,请考生根据自己所学教材《选修3》、《选修5》选择一组进行必答】1. 化学与生活密切相关。
下列说法错误的是A. 明矾电离出的Al 3+具有吸附性,可用作净水剂B. 漂白粉可用于生活用水的消毒C. 电热水器用镁棒防止内胆腐蚀,原理是牺牲阳极的阴极保护法D. 碳酸钠可用于去除餐具的油污2. 反应2()()C s H O g +2()()CO g H g +在一可变容积的密闭容器中进行,下列条件的改变对其反应速率几乎无影响的是 ①增加C 的量②将容器的体积缩小一半③保持体积不变,充入N 2使体系压强增大④保持压强不变,充入N 2使容器体积变大A. ①④B. ②③C. ① ③D. ②④ 3. 盐MN 溶于水存在如图过程,下列有关说法中不正确的是A.该过程可表示MN 的水解过程B.相同条件下结合H +的能力N ->OH -C.该过程使溶液中的c(OH -)>c(H +)D. 溶液中存在c(HN)=c(OH -)-c(H +)4. 反应Ⅰ:CaSO 4(s)+ CO(g)CaO(s)+SO 2(g)+CO 2(g) ΔH =+218.4 kJ·mol -1 反应Ⅱ:CaSO 4(s)+4CO(g)CaS(s)+4CO 2(g) ΔH =-175.6 kJ·mol -1 假设某温度下,反应Ⅰ的速率(v 1)大于反应Ⅱ的速率(v 2),则下列反应过程能量变化示意图正确的是5. 下列关于电解质溶液的判断正确的是A.100℃时,NaCl 溶液的pH<7,则溶液呈酸性B.将pH=4的 CH 3COOH 溶液加水稀释,溶液中所有离子的浓度均减小C.常温下,CH 3COOH 分子可能存在于pH>7的碱性溶液中D. 向氨水中加入盐酸至中性,溶液中432()()()c NH c OH c NH H O +-一定增大 6. N A 代表阿伏加德罗常数的值。
湖北省宜昌市部分示范高中教学协作体2018-2019学年高

宜昌市部分示范高中教学协作体2019年春期中联考高二(理科)数学命题人:曹炼忠 审题人:梁环义 (全卷满分:150分 考试用时:120分钟)第Ⅰ卷(选择题 共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题所给出的四个选项中,只有一项是符合题目要求的.1.命题“02000,sin 1x x R x x e ∃∈++<错误!未找到引用源。
”的否定是( )A .02000,sin 1x x R x x e∃∈++>错误!未找到引用源。
B .02000,sin 1x x R x x e∃∈++≥错误!未找到引用源。
C .2,sin 1xx R x x e ∀∈++>错误!未找到引用源。
D .2,sin 1xx R x x e ∀∈++≥错误!未找到引用源。
2.抛物线24x y =的准线方程为( ) A. 1=xB. 1-=xC. 1=yD. 1-=y3.函数x x x f -=ln )(的单调递增区间是( ) A . )1,(-∞ B . )(1,0C . ),0(+∞D .),1(+∞4.如图,已知正方体1111D C B A ABCD -,若 11z y x BD ++=,则x y z ++的值为( ) A .3 B .1 C .-1D .-35.0>⋅n m 是方程1=-nm 表示双曲线的( ) A.充分不必要条件 B.必要不充分条件 C. 充要条件D.既不充分也不必要条件6.1(2)0xe x dx +⎰ =( )A. 1B. 1-eC. eD. 1+e7.若双曲线)0(19222>=-a x a y 的一条渐近线与直线x y 31=垂直,则此双曲线的实轴长为( ) A . 2B . 4C . 18D . 368.函数y =x ex 3(其中e 为自然对数的底数)的大致图像是( )A B C D9.在三棱锥ABC S -中,,,SA AC AB AC AB ==⊥ABC SA 平面⊥,D 为BC 的中点,则异面直线AB 与SD 所成角的余弦值为( ) A.55 B.66 C.630 D.530 10.对于函数xxx f ln )(=,下列说法正确的有( ) ①)(x f 在e x =处取得极大值e1;②)(x f 有两个不同的零点;③)3()()4(f f f <<π.A.0个B.3个C.2个D.1个11.已知双曲线22:1(0,0)C a b a b-=>>的两条渐近线均与圆22650x y x +-+=相切,且双曲线的右焦点为该圆的圆心,则C 的离心率为( )A .5B .2C .2 D .312.已知函数⎩⎨⎧≤->=0,30,ln )(x kx x x x f 的图像上有两对关于y 轴对称的点,则实数k 的取值范围是( )A. ()0,2e - B. ⎪⎭⎫⎝⎛-0,212-e C. ()0,e - D.()0,22e -第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分,共20分.请将正确答案填写在答题卡相应的位置上.13.曲线x x f sin )(=在点))0(,0(f 处的切线的倾斜角为 . 14.已知()7,5,3A -,()3,3,1-B ,且2=,则C 点的坐标为 . 15.已知M 为抛物线28y x =上的一点,F 为抛物线的焦点,若120MFO ∠=︒,(2,0)N -(O 为坐标原点),则△MNF 的面积为 .16.一边长为2的正方形纸板,在纸板的四角截去四个边长均为x 的小正方形,然后做成一个无盖方盒.方盒的容积的最大值为 .三、解答题:本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤.17.(本小题满分10分)已知函数R x x x f ∈+-=,121)(2. (1)求函数)(x f 的图象在点(2,-1)处的切线方程;(2)求函数)(x f 的图象与直线1-=y 所围成的封闭图形的面积.18.(本小题满分12分)如图,在长方体1111D C B A ABCD -中,2,11===AB AD AA ,点E 是11D C 的中点.(1)求证:BCE DE 平面⊥; (2)求二面角C EB A --的大小.19.(本小题满分12分)已知椭圆的焦点在x 轴上,焦距为4,并且经过点),(2325-. (1)求该椭圆的标准方程;(2)该椭圆上是否存在一点,它到直线l :010=--y x 的距离最小?最小距离是多少?20.(本小题满分12分)如图,已知直三棱柱111C B A ABC - 中,,AC AB ⊥11,4,3AC C B AC AB ⊥==. (1)求1AA 的长;(2)若1=BP ,求直线1AA 与平面PC A 1所成角的余弦值.21.(本小题满分12分)已知直线l 与抛物线x y 22=交于B ,A (异于坐标原点O )两点. (1)若直线l 的方程为2-=x y ,求证:OB OA ⊥;(2)若OB OA ⊥,则直线l 是否恒过定点?若恒过定点,求出定点坐标;若不过定点,请说明理由.22.(本小题满分12分)设函数)0,,(21ln )(2≠∈++=c R c b bx x x c x f ,且1=x 为)(x f 的极值点.(1)若1=x 为)(x f 的极大值点,求)(x f 的单调区间(用c 表示); (2)若0)(=x f 恰有两解,求实数c 的取值范围.宜昌市部分示范高中教学协作体2019年春期中联考高二(理科)数学参考答案一、选择题二、填空题 13.4π 14. )2,4,1(- 15. 38 16. 2716 三、解答题17.解:(1)由题意 x x f -=')( ...........1分 所求切线的斜率2)2(-='=f k ...........3分 所求切线方程为 )2(21--=+x y 即032=-+y x ..........5分(2)由⎪⎩⎪⎨⎧-=+-=11212y x y 解答 22=-=x x 或 (6)分所以所求的面积为[]31622)261(1)(2-23=-+-=+=⎰x x dx x f S . .........10分18.解:(1)建立如图所示的空间直角坐标系, 则D (0,0,0),E (0,1,1),B (1,2,0), C (0,2,0),DE =(0,1,1),BE =(-1,-1,1),BC =(-1,0,0)................2分因为0,0DE BE DE BC ⋅=⋅=,所以,DE BE DE BC ⊥⊥. ...............4分则DE ⊥BE ,DE ⊥BC . 因为BE ⊂平面BCE ,BC ⊂平面BCE ,BE ∩BC =B , 所以DE ⊥平面BCE ................6分()()z y x n AEB ,,2=的法向量为设平面0000n AB y x y z n BE ⎧⋅==⎧⎪⎨⎨--+=⋅=⎩⎪⎩则即 ()1,0,1AEB n ∴=平面的一个法向量为.............8分(),0,1,1.DE BCE DE BCE ⊥∴=平面是平面的一个法向量1cos ,2n DE n DE n DE⋅<>==...............11分 .1200的大小为由图形可得二面角C EB A --...............12分19.解(1)由题意 设椭圆的方程为)0(12222>>=+b a by a x则⎪⎪⎩⎪⎪⎨⎧+==+-+++==2222210249)225(49)225(22c b a a c ..........3分6,10==∴b a ............4分161022=+yx 所求椭圆的标准方程为 .............5分2=+-n y x m 的方程为)设直线(⎪⎩⎪⎨⎧=+-=+161022n y x y x 由305108,22=-++n nx x y 得消去 ...........7分4,0±==∆n 解得由 . ............9分的距离最近,与椭圆的交点到时,直线由图像可知,当l m n 4-=间的距离与直线直线l m 232410=+-=d.23最小距离是∴ ...............12分20.解(1)以A 为坐标原点,建立如图所示的空间直角坐标系 设AA 1=t (t>0),)0,0,3(),0,4,0(),,0,3(),,4,0(11B C t B t C),4,3(),,4,0(11t C B t AC --==.........2分11B C AC ⊥1120160AC B C t ∴⋅=∴-= .............4分.4,41的长为即AA t =∴ ...............5分(2)由(1)知)4,4,0(),3,0,3(04,0111-=-==A A ),(.....................6分),,(A 1z y x n PC =的法向量为设平面⎪⎩⎪⎨⎧=-==-=⋅∴04403311z y A n z x P A n)1,1,1(,1==x 得令 ....................8分33344,cos 1=>=< ....................10分.36AA 11所成角的余弦值为与平面直线PC A ∴ .................12分21.解:(1)证明:由⎩⎨⎧=-=xy x y 222得x 2-6x+4=0,解得x=3±5 ........2分不妨取A(3-5,1-5), B(3+5,1+5), ...........3分 ∴0=⋅, ∴OA ⊥OB. .............5分 (2)显然直线l 的斜率不为0,设直线l 的方程为x=ty+m(m ≠0),A(x 1,y 1),B(x 2,y 2), 由⎩⎨⎧=+=xy mty x 22消去x 得y 2-2ty-2m=0, ...................7分∴y 1y 2=-2m, x 1x 2=222221y y ⋅=m 2, ....................8分 由OA ⊥OB,得OB OA ⋅=x 1x 2+y 1y 2=m 2-2m=0,∴m=2, .............10分直线l 的方程为x=ty+2,∴直线l 恒过定点,且定点坐标为(2,0) ..............12分 22.解 f ′(x)=c x +x +b =x 2+bx +cx .因为f ′(1)=0,所以b +c +1=0,f ′(x)=()()xc x x --1 且c ≠1 .........1分(1)因为x =1为f(x)的极大值点,所以c >1. .............2分 当0<x <1时,f ′(x)>0;当1<x <c 时,f ′(x)<0;当x >c 时,f ′(x)>0. ..............4分 所以f(x)的单调递增区间为(0,1),(c ,+∞);单调递减区间为(1,c). ..... ........5分 (2)①若c <0,则f(x)在(0,1)上单调递减, 在(1,+∞)上单调递增.若f(x)=0恰有两解,则f(1)<0,即12+b <0.所以-12<c <0. ..............7分 ②若0<c <1,则f(x)极大值=f(c)=clnc +12c 2+bc ,f(x)极小值=f(1)=12+b.因为b =-1-c ,所以f(x)极大值=clnc +c 22+c(-1-c)=clnc -c -c22<0.f(x)极小值=-12-c <0,从而f(x)=0只有一解. .............9分③若c >1,则f(x)极小值=clnc +c22+c(-1-c)=clnc -c -c 22<0. f(x)极大值=-12-c <0,则f(x)=0只有一解. ..............11分 综上,使f(x)=0恰有两解的c 的取值范围为(-12,0). ...............12分。
湖北省宜昌市部分示范高中教学协作体2018-2019学年高二下学期期中考试数学(理)试卷Word版含答案

骤.
17.( 本小题满分 10 分 ) 已知函数 f (x)
1 x2 1, x R . 2
( 1)求函数 f ( x) 的图象在点( 2,-1 )处的切线方程;
( 2)求函数 f ( x) 的图象与直线 y 1 所围成的封闭图形的面积 .
-3-
B. 必要不充分条件
C. 充要条件
D. 既不充分也不必要条件
-1-
6. 1 (ex 2x)dx = (
)
0
A. 1
B. e 1
C. e
D. e 1
7. 若双曲线
y2 a2
x2 9
1(a 0) 的一条渐近线与直线
y
1 x 垂直 , 则此双曲线的实轴长为 3
()
A. 2
B. 4
C. 18
D. 36
8. 函数 y
)
A. x0 R, x0 2 sin x0 ex0 1
B. x0 R, x0 2 sin x0 ex0 1
C. x R, x2 sin x ex 1
D. x R, x2 sin x ex 1
2. 抛物线 x2 4 y 的准线方程为(
)
A. x 1
B. x 1
C. y 1
D. y 1
3. 函数 f ( x) ln x x 的单调递增区间是 ( )
ห้องสมุดไป่ตู้
ln x
, 下列说法正确的有 (
)
x
① f ( x) 在 x e 处取得极大值 1 ;② f ( x) 有两个不同的零点;③ e
A.0 个
B.3 个
C.2 个
D. 30 5
f (4) f ( ) f (3) .
D.1 个
湖北省宜昌市教学协作体2018-2019学年高二数学下学期期中试卷理【word版】.doc

宜昌市部分示范高中教学协作体2019年春期中联考高二(理科)数学(全卷满分:150分 考试用时:120分钟)第Ⅰ卷(选择题 共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题所给出的四个选项中,只有一项是符合题目要求的.1.命题“02000,sin 1x x R x x e ∃∈++<”的否定是( )A .02000,sin 1x x R x x e ∃∈++>B .02000,sin 1x x R x x e ∃∈++≥C .2,sin 1x x R x x e ∀∈++>D .2,sin 1x x R x x e ∀∈++≥2.抛物线24x y =的准线方程为( ) A. 1=xB. 1-=xC. 1=y D . 1-=y3.函数x x x f -=ln )(的单调递增区间是( )A . )1,(-∞B . )(1,0C . ),0(+∞D . ),1(+∞4.如图,已知正方体1111D C B A ABCD -,若11AA z y x BD ++=,则x y z ++的值为( ) A .3 B .1 C .-1D .-35.0>⋅n m 是方程122=-ny m x 表示双曲线的( )A.充分不必要条件B.必要不充分条件C. 充要条件D.既不充分也不必要条件6.1(2)0x e x dx +⎰ =( )A. 1B. 1-eC. eD. 1+e7.若双曲线)0(19222>=-a x a y 的一条渐近线与直线x y 31=垂直,则此双曲线的实轴长为( ) A . 2 B . 4 C . 18 D . 368.函数y =x ex 3(其中e 为自然对数的底数)的大致图像是( )A B C D9.在三棱锥ABC S -中,,,SA AC AB AC AB ==⊥ABC SA 平面⊥,D 为BC 的中点,则异面直线AB 与SD 所成角的余弦值为( ) A.55 B.66 C.630 D.530 10.对于函数xxx f ln )(=,下列说法正确的有( ) ①)(x f 在e x =处取得极大值e1;②)(x f 有两个不同的零点;③)3()()4(f f f <<π.A.0个B.3个C.2个D.1个11.已知双曲线2222:1(0,0)x y C a b a b-=>>的两条渐近线均与圆22650x y x +-+=相切,且双曲线的右焦点为该圆的圆心,则C 的离心率为( )A .5B .2C .2D .312.已知函数⎩⎨⎧≤->=0,30,ln )(x kx x x x f 的图像上有两对关于y 轴对称的点,则实数k 的取值范围是( )A. ()0,2e -B. ⎪⎭⎫⎝⎛-0,212-e C. ()0,e -D.()0,22e -第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分,共20分.请将正确答案填写在答题卡相应的位置上.13.曲线x x f sin )(=在点))0(,0(f 处的切线的倾斜角为 . 14.已知()7,5,3A -,()3,3,1-B ,且CB AB 2=,则C 点的坐标为 . 15.已知M 为抛物线28y x =上的一点,F 为抛物线的焦点,若120MFO ∠=︒,(2,0)N -(O 为坐标原点),则△MNF 的面积为 .16.一边长为2的正方形纸板,在纸板的四角截去四个边长均为x 的小正方形,然后做成一个无盖方盒.方盒的容积的最大值为 .三、解答题:本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤.17.(本小题满分10分)已知函数R x x x f ∈+-=,121)(2 .(1)求函数)(x f 的图象在点(2,-1)处的切线方程; (2)求函数)(x f 的图象与直线1-=y 所围成的封闭图形的面积.18.(本小题满分12分)如图,在长方体1111D C B A ABCD -中,2,11===AB AD AA ,点E是11D C 的中点.(1)求证:BCE DE 平面⊥; (2)求二面角C EB A --的大小.19.(本小题满分12分)已知椭圆的焦点在x 轴上,焦距为4,并且经过点),(2325-. (1)求该椭圆的标准方程;(2)该椭圆上是否存在一点,它到直线l :010=--y x 的距离最小?最小距离是多少?20.(本小题满分12分)如图,已知直三棱柱111C B A ABC - 中,,AC AB ⊥11,4,3AC C B AC AB ⊥==. (1)求1AA 的长;(2)若1=BP ,求直线1AA 与平面PC A 1所成角的余弦值.21.(本小题满分12分)已知直线l 与抛物线x y 22=交于B ,A (异于坐标原点O )两点. (1)若直线l 的方程为2-=x y ,求证:OB OA ⊥;(2)若OB OA ⊥,则直线l 是否恒过定点?若恒过定点,求出定点坐标;若不过定点,请说明理由.22.(本小题满分12分)设函数)0,,(21ln )(2≠∈++=c R c b bx x x c x f ,且1=x 为)(x f 的极值点.(1)若1=x 为)(x f 的极大值点,求)(x f 的单调区间(用c 表示); (2)若0)(=x f 恰有两解,求实数c 的取值范围.宜昌市部分示范高中教学协作体2019年春期中联考高二(理科)数学参考答案一、选择题二、填空题 13.4π 14. )2,4,1(- 15. 38 16. 2716 三、解答题17.解:(1)由题意 x x f -=')( ...........1分 所求切线的斜率2)2(-='=f k ...........3分 所求切线方程为 )2(21--=+x y 即032=-+y x ..........5分(2)由⎪⎩⎪⎨⎧-=+-=11212y x y 解答 22=-=x x 或 ............6分所以所求的面积为[]31622)261(1)(2-23=-+-=+=⎰x x dx x f S . .........10分18.解:(1)建立如图所示的空间直角坐标系, 则D (0,0,0),E (0,1,1),B (1,2,0),C (0,2,0),DE =(0,1,1),BE =(-1,-1,1),BC =(-1,0,0)................2分因为0,0DE BE DE BC ⋅=⋅=,所以,DE BE DE BC ⊥⊥................4分则DE ⊥BE ,DE ⊥BC . 因为BE ⊂平面BCE ,BC ⊂平面BCE ,BE ∩BC =B , 所以DE ⊥平面BCE ................6分()()z y x AEB ,,2=的法向量为设平面000n AB y x y z n BE ⎧⋅==⎧⎪⎨⎨--+=⋅=⎩⎪⎩则即 ()1,0,1A E B n ∴=平面的一个法向量为 .............8分(),0,1,1.DE BCE DE BCE ⊥∴=平面是平面的一个法向量1cos ,2n DE n DE n DE⋅<>==...............11分 .1200的大小为由图形可得二面角C EB A -- ...............12分19.解(1)由题意 设椭圆的方程为)0(12222>>=+b a by a x则⎪⎪⎩⎪⎪⎨⎧+==+-+++==2222210249)225(49)225(22c b a a c ..........3分6,10==∴b a ............4分161022=+y x 所求椭圆的标准方程为 .............5分2=+-n y x m 的方程为)设直线(⎪⎩⎪⎨⎧=+-=+0161022n y x y x 由305108,22=-++n nx x y 得消去 ...........7分4,0±==∆n 解得由 . ............9分的距离最近,与椭圆的交点到时,直线由图像可知,当l m n 4-=间的距离与直线直线l m 232410=+-=d.23最小距离是∴ ...............12分20.解(1)以A 为坐标原点,建立如图所示的空间直角坐标系 设AA 1=t (t>0),)0,0,3(),0,4,0(),,0,3(),,4,0(11B C t B t C),4,3(),,4,0(11t B t AC --==.........2分11B C AC ⊥1120160AC B C t ∴⋅=∴-= .............4分.4,41的长为即AA t =∴ ...............5分(2)由(1)知)4,4,0(),3,0,3(04,0111-=-==C A P A AA ),(.....................6分),,(A 1z y x n PC =的法向量为设平面⎪⎩⎪⎨⎧=-==-=⋅∴04403311z y A n z x A)1,1,1(,1==x 得令 ....................8分33344,cos 1=>=<n AA ....................10分.36AA 11所成角的余弦值为与平面直线PC A ∴ .................12分21.解:(1)证明:由⎩⎨⎧=-=xy x y 222得x 2-6x+4=0,解得x=3±5 ........2分不妨取A(3-5,1-5), B(3+5,1+5), ...........3分 ∴0=⋅, ∴OA ⊥OB. .............5分 (2)显然直线l 的斜率不为0,设直线l 的方程为x=ty+m(m≠0),A(x 1,y 1),B(x 2,y 2),由⎩⎨⎧=+=xy m ty x 22消去x 得y 2-2ty-2m=0, ...................7分 ∴y 1y 2=-2m, x 1x 2=222221y y ⋅=m 2, ....................8分由OA ⊥OB,得⋅=x 1x 2+y 1y 2=m 2-2m=0,∴m=2, .............10分 直线l 的方程为x=ty+2,∴直线l 恒过定点,且定点坐标为(2,0) ..............12分 22.解 f′(x)=cx +x +b =x 2+bx +c x . 因为f′(1)=0,所以b +c +1=0,f′(x)=()()xc x x --1 且c≠1 .........1分(1)因为x =1为f(x)的极大值点,所以c >1. .............2分 当0<x <1时,f′(x)>0;当1<x <c 时,f′(x)<0;当x >c 时,f′(x)>0. ..............4分 所以f(x)的单调递增区间为(0,1),(c ,+∞);单调递减区间为(1,c). ..... ........5分 (2)①若c <0,则f(x)在(0,1)上单调递减, 在(1,+∞)上单调递增. 若f(x)=0恰有两解,则f(1)<0,即12+b<0.所以-12<c<0. ..............7分②若0<c<1,则f(x)极大值=f(c)=clnc+12c2+bc,f(x)极小值=f(1)=12+b.因为b=-1-c,所以f(x)极大值=clnc+c22+c(-1-c)=clnc-c-c22<0.f(x)极小值=-12-c<0,从而f(x)=0只有一解. .............9分③若c>1,则f(x)极小值=clnc+c22+c(-1-c)=clnc-c-c22<0.f(x)极大值=-12-c<0,则f(x)=0只有一解. ..............11分综上,使f(x)=0恰有两解的c的取值范围为(-12,0). ...............12分- 11 -。
【精编】湖北省宜昌市教学协作体2018-2019学年高二历史下学期期中试卷.doc

宜昌市部分示范高中教学协作体2019年春期中联考高二历史(全卷满分:100 分考试用时:90 分钟)一、选择题(共24小题,每小题2分,共48分) 1.西周初年兼并无数,封建制度遂发生大变革。
分封同宗以树屏藩,授土勋旧以拓疆域。
材料表明“封建制度”()A. 有助于消除地方与中央的矛盾B. 推动了西周政治文化的传播C. 是西周稳固统治的的重要途径D. 加速了“大一统”局面的形成2.中国古代,“天”被尊为最高神。
秦汉以后,以“天子”自居的皇帝举行祭天大典,表明自己“承天”而“子民”,官员、百姓则祭拜自己的祖先。
这反映了秦汉以后( )A.君主专制缘于宗教权威B.政治统治借助于人伦秩序C.皇权至上促成祖先崇拜D.祭天活动强化了宗法制度3.北魏均田制实行后,文献中出现了“庄园”一词,被指圈占的成片土地。
唐代均田制实行后,“庄园”一词的使用更普遍。
这反映了均田制实行后( ) A.井田制得以恢复B.不存在土地私有现象C.仍存在土地集中现象D.庄园由中央集中管理4.《隋都城图》题记:“畦分棋布,闾巷皆中绳墨,坊有墉(墙),墉有门,逋亡奸伪无所容足。
而朝廷官寺、民居市区不复相参,亦一代之精制也。
”由此可见,隋都城的设计重在( )A.打破市坊的空间界限B.便利居民的交通出行C.加强官府的严格控制D.促进城市的商业活动5.宋人诗云:“小麦青青大麦黄,原头日出天色凉。
妇姑相呼有忙事,舍后煮茧门前香。
缫车嘈嘈似风雨,茧厚丝长无断缕。
今年那暇织绢着,明日西门卖丝去。
”诗中反映了( )A.手工产品质量低下 B.农业生产规模庞大C.农民家庭生活闲适D.农户经营方式多样6.据《书林藻鉴》卷九记载:“(宋四家)蔡胜在度,苏胜在趣,黄胜在韵,米胜在姿。
”下列关于图中书法艺术的表述,正确的是( )A.反映当时复杂的社会矛盾B.体现当时书法艺术丰富多样C.表现文人强烈的爱国情怀D.标志着书法艺术的全面成熟7.费正清在《中国:传统与变迁》中指出:“理学并不仅仅是对前秦和两汉儒学的继承和发展。
【精编文档】湖北省宜昌市部分示范高中教学协作体2018-2019学年高二数学下学期期中试卷文.doc

宜昌市部分示范高中教学协作体2019年春期中联考高二(文科)数学(全卷满分:150分 考试用时:120分钟)第Ⅰ卷(选择题 共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题所给出的四个选项中,只有一项是符合题目要求的. 1. 抛物线24x y =的准线方程为( ) A. 1=x B. 1-=xC. 1=yD.1-=y2.设f (x )=x ln x ,若f ′(x 0)=2,则x 0的值为( ) A .e 2 B .ln 22C.e D .ln 23. 函数x x x f -=cos )(在()π,0上的单调性是( )A. 先增后减B. 先减后增C.增函数D.减函数4.函数31()43f x x x m =--在[]3,0上的最大值为4,则m 的值为( )A.7B.-4C.-3D.45.直线y =kx -k +1与椭圆x 29+y 24=1的位置关系为( )A .相切B .相交C .相离D .不确定6. 双曲线x 24-y 212=1的焦点到渐近线的距离为( )A .2 3B .2C . 3D .17.函数f(x)的定义域为开区间(a ,b),导函数f ′(x)在(a ,b)内的图象如下图所示,则函数f(x)在开区间(a ,b)内有极小值点( ) A .1个 B .2个 C .3个 D .4个8.函数y =x ex 3(其中e 为自然对数的底数)的大致图像是( )A B C D 9. 已知双曲线C 的离心率为2,焦点为F 1,F 2,点A 在C 上.若|F 1A |=2|F 2A |,则cos ∠AF 2F 1=( ) A.14B.13C.24D.2310. 对于函数xxx f ln )(=,下列说法正确的有( )①)(x f 在e x =处取得极大值e1;②)(x f 有两个不同的零点; ③)3()()4(f f f <<π.A.0个B.3个C.2个D.1个11. 已知椭圆22221(0)x y a b a b+=>>左焦点为F ,右顶点为A ,点B在椭圆上,且BF x ⊥轴,直线AB 交y 轴于点P ,若3APPB=,则椭圆的离心率是( )A. C.12 D.1312. 已知函数ln ,0()3,0x x f x kx x >⎧=⎨-≤⎩的图像上有两对关于y 轴对称的点,则实数k 的取值范围是( )A. ()0,e -B. ⎪⎭⎫⎝⎛-0,212-e C. ()0,2e - D.()0,22e -第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分,共20分.请将正确答案填写在答题卡相应的位置上.13. 曲线x x f sin )(=在点))0(,0(f 处的切线方程为 .14. 如右图在圆C :(x +3)2+y 2=100内有一点A (3,0).Q 为圆C 上一点,AQ 的垂直平分线与C ,Q 的连线交于点M ,则点M 的轨迹方程 .15. 设斜率为2的直线l 过抛物线y 2=ax (a ≠0)的焦点F ,且和y 轴交于点A ,若△OAF (O 为坐标原点)的面积为4,则a 的值 .16. 一边长为2的正方形纸板,在纸板的四角截去四个边长均为 x的小正方形,然后做成一个无盖方盒.方盒的容积的最大值为 .三、解答题:本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤.17.(本小题满分10分)已知函数f(x)=x3+ax2+bx+5,曲线y=f(x)在点P(1,f(1))处的切线方程为y =3x+1.(1)求a,b的值;(2)求y=f(x)在[-3,1]上的最大值.18.(本小题满分12分)已知双曲线C:22221(00)x ya ba b-=>>、的离心率为3,且a2c=33.(1)求双曲线C的方程;(2)已知直线x-y+m=0与双曲线C交于不同的两点A,B,且线段AB的中点在圆x2+y2=5上,求m的值.19.(本小题满分12分) 设函数f(x)=e x -k2x 2-x.(1)若k =0,求f(x)的最小值; (2)若k =1,讨论函数f(x)的单调性.20.(本小题满分12分)已知椭圆的焦点在x 轴上,焦距为4,并且经过点),(23-25. (1)求该椭圆的标准方程;(2)该椭圆上是否存在一点,它到直线l :010-=-y x 的距离最小?最小距离是多少?21.(本小题满分12分)已知直线l 与抛物线x y 22=交于B ,A (异于坐标原点O )两点. (1)若直线l 的方程为2-=x y ,求证:OB OA ⊥;(2)若OB OA ⊥,则直线l 是否恒过定点?若恒过定点,求出定点坐标;若不过定点,请说明理由.22.(本小题满分12分) 设函数f(x)=ln kx x+,k ∈R.(1)若曲线y=f(x)在点(e,f(e))处的切线与直线x-2=0垂直,求f(x)的单调递减区间和极值;(2)若对任意1212120,()()x x f x f x x x >>-<-恒成立,求k 的取值范围.宜昌市部分示范高中教学协作体2019年春期中联考高二文科数学参考答案 命题人:张海燕 审题人:向显运 (全卷满分:150分 考试用时:120分钟)一、选择题(每小题5分,共60分)二、填空题(每小题5分,共20分)13. y=x 14. 1162522=+y x 15. 8± 16. 2716 三.解答题(共70分)17.解:(1)依题意可知点P (1,f (1))为切点,代入切线方程y =3x +1可得,f (1)=3×1+1=4,∴f (1)=1+a +b +5=4,即a +b =-2, (1)分又由f (x )=x 3+ax 2+bx +5得, 又f ′(x )=3x 2+2ax +b ,而由切线y =3x +1的斜率可知f ′(1)=3,........................3分∴3+2a +b =3,即2a +b =0,由220a b a b +=-⎧⎨+=⎩,解得24a b =⎧⎨=-⎩∴a =2,b =-4........................5分(2)由(1)知f(x)=x3+2x2-4x+5,f′(x)=3x2+4x-4=(3x-2)(x+2),令f′(x)=0,得x=23或x=-2. (6)分当x变化时,f(x),f′(x)的变化情况如下表:........................8分∴f(x)的极大值为f(-2)=13,极小值为f⎝⎛⎭⎪⎫23=27........................9分又f(-3)=8,f(1)=4,∴f(x)在[-3,1]上的最大值为13 ............10分18.(1)由题意得2acca⎧=⎪⎪⎨⎪=⎪⎩解得1ac=⎧⎪⎨=⎪⎩所以b2=c2-a2=2.所以双曲线C的方程为x2-y22=1.............5分(2)设A,B两点的坐标分别为(x1,y1),(x2,y2),线段AB的中点为M(x0,y)..........6分由22012x y m y x -+=⎧⎪⎨-=⎪⎩得x 2-2mx -m 2-2=0(判别式Δ>0).所以x 0=x 1+x 22=m ,y 0=x 0+m =2m . ..........9分因为点M (x 0,y 0)在圆x 2+y 2=5上, 所以m 2+(2m )2=5.故m =±1............12分19.解:(1)k =0时,f (x )=e x -x ,f ′(x )=e x -1.........1分当x ∈(-∞,0)时,f ′(x )<0;当x ∈(0,+∞)时,f ′(x )>0,所以f (x )在(-∞,0)上单调递减,在(0,+∞)上单调递增,故f (x )的最小值为f (0)=1...........5分(2)若k =1,则f (x )=e x -12x 2-x ,定义域为R...........6分∴f ′(x )=e x-x -1,令g (x )=e x-x -1, 则g ′(x )=e x -1,由g ′(x )≥0得x ≥0,所以g (x )在[0,+∞)上单调递增, 由g ′(x )<0得x <0,所以g (x )在(-∞,0)上单调递减,∴g (x )min =g (0)=0,即f ′(x )min =0,故f ′(x )≥0............11分 所以f (x )在R 上单调递增...............12分20.解(1)由题意 设椭圆的方程为)0(12222>>=+b a by a x则⎪⎪⎩⎪⎪⎨⎧+==+-+++==2222210249)225(49)225(22c b a a c ..........3分6,10==∴b a ............4分所求椭圆的标准方程为161022=+y x .............5分2m ()设直线的方程为0x y n -+=...................6分 ⎪⎩⎪⎨⎧=+-=+0161022n y x y x 由0305108,22=-++n nx x y 得消去 4,0±==∆n 解得由 .............9分的距离最近,与椭圆的交点到时,直线由图像可知,当l m n 4-=间的距离与直线直线l m 232410=+-=d.23最小距离是∴ (12)21.解:(1)证明:由⎩⎨⎧=-=xy x y 222得x 2-6x+4=0,解得x=3分 不妨取), ...........3分 ∴·=0, ∴OA ⊥OB. .............5分(2)显然直线l 的斜率不为0,设直线l 的方程为x=ty+m(m ≠0),A(x 1,y 1),B(x 2,y 2),由⎩⎨⎧=+=xy m ty x 22消去x 得y 2-2ty-2m=0, ...................7分 ∴y 1y 2=-2m, x 1x 2=222221y y ⋅=m 2, ....................8分 由OA ⊥OB,得⋅=x 1x 2+y 1y 2=m 2-2m=0,∴m=2, . (10)分直线l 的方程为x=ty+2,∴直线l 恒过定点,且定点坐标为(2,0)..............12分22.解:(1)由f (x )=ln k x x +知x>0,f'(x )=21k x x-(x>0),因为曲线y=f (x )在点(e,f (e))处的切线与直线x=2垂直,所以f'(e)=0,即210k e e-=,解得k=e,.............2分 所以f'(x)=221e x e x x x--=(x>0). 当0<x<e 时,f'(x)<0,f(x)单调递减;当x>e 时,f'(x)>0,f(x)单调递增..............4分所以当x=e 时,f(x)取得极小值,极小值为f(e)=ln e+1=2...........5分 综上,f(x)的单调递减区间为(0,e),极小值为2,无极大值..........6分(2)因为对任意x 1>x 2>0,f(x 1)-f(x 2)<x 1-x 2恒成立,所以f(x 1)-x 1<f(x 2)-x 2对任意x 1>x 2>0恒成立..........7分令g(x)=f(x)-x=ln x k x+-x(x>0), 则g(x)在(0,+∞)上单调递减所以g'(x)=21k x x--1≤0在(0,+∞)上恒成立,..........9分 所以k ≥-x 2+x=-211()24x --+在(0,+∞)上恒成立. 令h(x)=211()24x --+,则k ≥h(x)max =14,..........11分所以k 的取值范围是,+∞...........12分。
湖北省宜昌市教学协作体2018-2019高二下学期期中考试化学试卷

宜昌市部分示范高中教学协作体2019年春期中联考高二化学注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔在答题卡上填写自己的准考证号、姓名、试室号和座位号。
用2B 型铅笔把答题卡上试室号、座位号对应的信息点涂黑。
2.选择题每小题选出答案后,用2B 型铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.考生必须保持答题卡整洁。
考试结束后,将试卷和答题卡一并交回。
可能用到的相对原子质量:H -1,C -12,N -14,O -16,Na -23,Cl -35.5第Ⅰ卷 (选择题,共48分) 一、选择题(本题共16小题,每小题3分,共48分)【其中11-16有两组题,请考生根据自己所学教材《选修3》、《选修5》选择一组进行必答】1. 化学与生活密切相关。
下列说法错误的是A. 明矾电离出的Al 3+具有吸附性,可用作净水剂B. 漂白粉可用于生活用水的消毒C. 电热水器用镁棒防止内胆腐蚀,原理是牺牲阳极的阴极保护法D. 碳酸钠可用于去除餐具的油污 2. 反应2()()C s H O g +2()()CO g H g +在一可变容积的密闭容器中进行,下列条件的改变对其反应速率几乎无影响的是①增加C 的量②将容器的体积缩小一半③保持体积不变,充入N 2使体系压强增大 ④保持压强不变,充入N 2使容器体积变大A. ①④B. ②③C. ① ③D. ②④3. 盐MN 溶于水存在如图过程,下列有关说法中不正确的是A.该过程可表示MN 的水解过程B.相同条件下结合H +的能力N ->OH -C.该过程使溶液中的c(OH -)>c(H +) D. 溶液中存在c(HN)=c(OH -)-c(H +) 4. 反应Ⅰ:CaSO 4(s)+ CO(g) CaO(s)+SO 2(g)+CO 2(g) ΔH =+218.4 kJ·mol -1反应Ⅱ:CaSO 4(s)+4CO(g) CaS(s)+4CO 2(g) ΔH =-175.6 kJ·mol -1假设某温度下,反应Ⅰ的速率(v 1)大于反应Ⅱ的速率(v 2),则下列反应过程能量变化示意图正确的是5. 下列关于电解质溶液的判断正确的是A.100℃时,NaCl 溶液的pH<7,则溶液呈酸性B.将pH=4的 CH 3COOH 溶液加水稀释,溶液中所有离子的浓度均减小C.常温下,CH 3COOH 分子可能存在于pH>7的碱性溶液中D. 向氨水中加入盐酸至中性,溶液中432()()()c NH c OH c NH H O +-一定增大6. N A 代表阿伏加德罗常数的值。
2018-2019学年湖北省宜昌市部分示范高中教学协作体高二下学期期中考试数学(理)试卷

2018-2019学年湖北省宜昌市部分示范高中教学协作体高二下学期期中考试数学(理)试卷(全卷满分:150分 考试用时:120分钟)第Ⅰ卷(选择题 共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题所给出的四个选项中,只有一项是符合题目要求的. 1.命题“02000,sin 1x x R x x e ∃∈++<”的否定是( )A .02000,sin 1x x R x x e∃∈++>B .02000,sin 1x x R x x e ∃∈++≥ C .2,sin 1xx R x x e ∀∈++>D .2,sin 1xx R x x e ∀∈++≥2.抛物线24x y =的准线方程为( ) A. 1=xB. 1-=xC. 1=yD. 1-=y3.函数x x x f -=ln )(的单调递增区间是( ) A . )1,(-∞ B . )(1,0C . ),0(+∞D . ),1(+∞4.已知正方体1111D C B A ABCD -,若 11AA z y x BD ++=,则x y z ++的值为( )A .3B .1C .-1D .-35.0>⋅n m 是方程122=-ny m x 表示双曲线的( )A.充分不必要条件B.必要不充分条件C. 充要条件D.既不充分也不必要条件6.1(2)0xe x dx +⎰ =( )A. 1B. 1-eC. eD. 1+e7.若双曲线)0(19222>=-a x a y 的一条渐近线与直线x y 31=垂直,则此双曲线的实轴长为( )A . 2B . 4C . 18D . 368.函数y =x ex 3(其中e 为自然对数的底数)的大致图像是( )A B C D9.在三棱锥ABC S -中,,,SA AC AB AC AB ==⊥ABC SA 平面⊥,D 为BC 的中点,则异面直线AB 与SD 所成角的余弦值为( ) A.55 B.66 C.630 D.530 10.对于函数xxx f ln )(=,下列说法正确的有( ) ①)(x f 在e x =处取得极大值e1;②)(x f 有两个不同的零点;③)3()()4(f f f <<π.A.0个B.3个C.2个D.1个11.已知双曲线2222:1(0,0)x y C a b a b-=>>的两条渐近线均与圆22650x y x +-+=相切,且双曲线的右焦点为该圆的圆心,则C 的离心率为( )A B C D 12.已知函数⎩⎨⎧≤->=0,30,ln )(x kx x x x f 的图像上有两对关于y 轴对称的点,则实数 的取值范围是( )A. ()0,2e - B. ⎪⎭⎫⎝⎛-0,212-e C. ()0,e - D.()0,22e -第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分,共20分.请将正确答案填写在答题卡相应的位置上.13.曲线x x f sin )(=在点))0(,0(f 处的切线的倾斜角为 .14.已知()7,5,3A -,()3,3,1-B ,且2=,则C 点的坐标为 . 15.已知M 为抛物线28y x =上的一点,F 为抛物线的焦点,若120MFO ∠=︒,(2,0)N -(O 为坐标原点),则△MNF 的面积为 .16.一边长为2的正方形纸板,在纸板的四角截去四个边长均为x 的小正方形,然后做成一个无盖方盒.方盒的容积的最大值为 .三、解答题:本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤.17.(本小题满分10分)已知函数R x x x f ∈+-=,121)(2. (1)求函数)(x f 的图象在点(2,-1)处的切线方程;(2)求函数)(x f 的图象与直线1-=y 所围成的封闭图形的面积.18.(本小题满分12分)在长方体1111D C B A ABCD -中,2,11===AB AD AA ,点E 是11D C 的中点.(1)求证:BCE DE 平面⊥; (2)求二面角C EB A --的大小.19.(本小题满分12分)已知椭圆的焦点在x 轴上,焦距为4,并且经过点),(2325-. (1)求该椭圆的标准方程;(2)该椭圆上是否存在一点,它到直线l :010=--y x 的距离最小?最小距离是多少?20.(本小题满分12分)已知直三棱柱111C B A ABC - 中,,AC AB ⊥11,4,3AC C B AC AB ⊥==. (1)求1AA 的长;(2)若1=BP ,求直线1AA 与平面PC A 1所成角的余弦值.21.(本小题满分12分)已知直线l 与抛物线x y 22=交于B ,A (异于坐标原点O )两点. (1)若直线l 的方程为2-=x y ,求证:OB OA ⊥;(2)若OB OA ⊥,则直线l 是否恒过定点?若恒过定点,求出定点坐标;若不过定点,请说明理由.22.(本小题满分12分)设函数)0,,(21ln )(2≠∈++=c R c b bx x x c x f ,且1=x 为)(x f 的极值点.(1)若1=x 为)(x f 的极大值点,求)(x f 的单调区间(用c 表示); (2)若0)(=x f 恰有两解,求实数c 的取值范围.宜昌市部分示范高中教学协作体2019年春期中联考高二(理 )数学参考答案二、填空题 13.4π14. )2,4,1(- 15. 38 16.2716 三、解答题17.解:(1)由题意 x x f -=')( ...........1分 所求切线的斜率2)2(-='=f k ...........3分所求切线方程为)2(21--=+x y 即032=-+y x ..........5分(2)由⎪⎩⎪⎨⎧-=+-=11212y x y 解答 22=-=x x 或 ............6分 所以所求的面积为[]31622)261(1)(2-23=-+-=+=⎰x x dx x f S . .........10分 18.解:(1)建立如图所示的空间直角坐标系, 则D (0,0,0),E (0,1,1),B (1,2,0), C (0,2,0),DE =(0,1,1),BE =(-1,-1,1),BC =(-1,0,0)................2分因为0,0DE BE DE BC ⋅=⋅=,所以,DEBE DE BC ⊥⊥................4分则DE ⊥BE ,DE ⊥BC . 因为BE ⊂平面BCE ,BC ⊂平面BCE ,BE ∩BC =B , 所以DE ⊥平面BCE . ...............6分()()z y x n AEB ,,2=的法向量为设平面0000n AB y x y z n BE ⎧⋅==⎧⎪⎨⎨--+=⋅=⎩⎪⎩则即 ()1,0,1AEB n ∴=平面的一个法向量为.............8分(),0,1,1.DE BCE DE BCE ⊥∴=平面是平面的一个法向量1cos ,2n DE n DE n DE⋅<>==...............11分 .1200的大小为由图形可得二面角C EB A --...............12分19.解(1)由题意 设椭圆的方程为)0(12222>>=+b a by a x则⎪⎪⎩⎪⎪⎨⎧+==+-+++==2222210249)225(49)225(22c b a a c ..........3分6,10==∴b a ............4分161022=+y x 所求椭圆的标准方程为 .............5分2=+-n y x m 的方程为)设直线(⎪⎩⎪⎨⎧=+-=+161022n y x y x 由305108,22=-++n nx x y 得消去 ...........7分 4,0±==∆n 解得由 ...........9分 的距离最近,与椭圆的交点到时,直线由图像可知,当l m n 4-=间的距离与直线直线l m .23最小距离是∴ ...............12分20.解(1)以A 为坐标原点,建立如图所示的空间直角坐标系 设AA 1=t (t>0), )0,0,3(),0,4,0(),,0,3(),,4,0(11B C t B t C),4,3(),,4,0(11t B t AC --==.........2分11B C AC ⊥ 112160AC B C t ∴⋅=∴-= .............4分 .4,41的长为即AA t = ...............5分(2)由(1)知 )4,4,0(),3,0,3(04,0111-=-==A A AA ),(.....................6分),,(A 1z y x n PC =的法向量为设平面 ⎪⎩⎪⎨⎧=-==-=⋅∴04403311z y A n z x A )1,1,1(,1==n x 得令 ....................8分 33344,cos 1=>=<AA ....................10分.36AA 11所成角的余弦值为与平面直线PC A ∴ .................12分 21.解:(1)证明:由⎩⎨⎧=-=xy x y 222得x 2-6x+4=0,解得x=3±5 ........2分不妨取A(3-5,1-5), B(3+5,1+5), ...........3分∴0=⋅, ∴OA ⊥OB. .............5分(2)显然直线l 的斜率不为0,设直线l 的方程为x=ty+m(m ≠0),A(x 1,y 1),B(x 2,y 2),由⎩⎨⎧=+=xy m ty x 22消去x 得y 2-2ty-2m=0, ...................7分 ∴y 1y 2=-2m, x 1x 2=222221y y ⋅=m 2, ....................8分由OA ⊥OB,得⋅=x 1x 2+y 1y 2=m 2-2m=0,∴m=2, .............10分直线l 的方程为x=ty+2,∴直线l 恒过定点,且定点坐标为(2,0) ..............12分 22.解 f ′(x)=cx +x +b =x 2+bx +c x .因为f ′(1)=0,所以b +c +1=0,f ′(x)=()()xc x x --1 且c ≠1 .........1分(1)因为x =1为f(x)的极大值点,所以c >1. .............2分 当0<x <1时,f ′(x)>0;当1<x <c 时,f ′(x)<0;当x >c 时,f ′(x)>0. ..............4分 所以f(x)的单调递增区间为(0,1),(c ,+∞);单调递减区间为(1,c). .... .......5分 (2)①若c <0,则f(x)在(0,1)上单调递减, 在(1,+∞)上单调递增.若f(x)=0恰有两解,则f(1)<0,即12+b <0.所以-12<c <0. ..............7分 ②若0<c <1,则f(x)极大值=f(c)=clnc +12c 2+bc ,f(x)极小值=f(1)=12+b.因为b =-1-c ,所以f(x)极大值=clnc +c 22+c(-1-c)=clnc -c -c22<0.f(x)极小值=-12-c <0,从而f(x)=0只有一解. .............9分③若c >1,则f(x)极小值=clnc +c22+c(-1-c)=clnc -c -c22<0.f(x)极大值=-12-c <0,则f(x)=0只有一解. ..............11分综上,使f(x)=0恰有两解的c 的取值范围为(-12,0). ...............12分。
湖北省部分重点中学2018-2019学年高二下学期期中考试英语试卷 Word版含答案

2019年5月湖北省部分重点中学2018-2019学年度高二下学期期中考试英语试卷第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What is the man’s hometown?A. Los Angeles.B. Boston.C. New York.2. What’s worrying the woman?A. It is hard to rent a stereo.B. They haven’t enough money to buy a stereo.C.There is no red stereo for rent.3. What are the speakers talking about?A. A concertB. singer.C. A film4. How much did the man’s wife pay for her coat?A.$120B. $240C. $4805. What does the woman suggest the man to do?A. Give up the exams.B. Prepare the papers in advance.C. Drop one course this semester第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6、7题。
2018-2019学年湖北省宜昌市部分示范高中教学协作体高二下学期期中联考地理试题 解析版
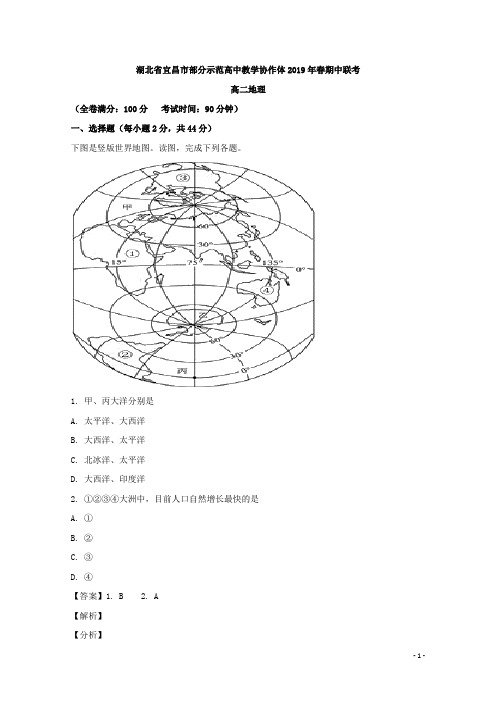
湖北省宜昌市部分示范高中教学协作体2019年春期中联考高二地理(全卷满分:100分考试时间:90分钟)一、选择题(每小题2分,共44分)下图是竖版世界地图。
读图,完成下列各题。
1. 甲、丙大洋分别是A. 太平洋、大西洋B. 大西洋、太平洋C. 北冰洋、太平洋D. 大西洋、印度洋2. ①②③④大洲中,目前人口自然增长最快的是A. ①B. ②C. ③D. ④【答案】1. B 2. A【解析】【分析】本题考查海陆分布和世界人口增长。
【1题详解】据海陆轮廓和相对位置可知,甲大洋为大西洋,丙大洋为太平洋。
B正确。
【2题详解】据海陆轮廓和相对位置可知,①为非洲,②为南美洲,③为北美洲,④为大洋洲。
这四大洲中,目前非洲人口自然增长最快,A正确。
【点睛】本题主要考查获取和解读地理信息的能力,全面获取信息进行概括即可,难度一般。
读图,完成下列各题。
3. 夏季炎热多雨,冬季寒冷干燥的气候分布在图中A. A处B. C处C. E处D. B处4. B处的传统民居是A. 帐篷B. 高脚屋C. 窑洞D. 厚墙、小窗5. 一艘货轮在D地的某港口装船外运,装船的货物最有可能是A. 小麦B. 石油C. 大米D. 煤【答案】3. A 4. B 5. B【解析】【分析】考查亚洲的气候分布状况,聚落与自然环境的关系。
【3题详解】A 地处我国秦岭、淮河以北的东部季风区,是典型的温带季风气候.冬季盛行偏北风,受极地大陆气团影响,寒冷干燥;夏季盛行偏南风,受极地海洋气团或热带海洋气团影响,炎热多雨.A 正确。
【4题详解】B 处位于热带雨林地区,高脚屋利于通风散热,适应这里湿热的气候,B 正确。
帐篷是游牧民族的传统民居,窑洞主要分布在黄土高原地区,高寒地区或沙漠地区传统民居厚墙、小窗利于保温或防晒。
故选B 。
【5题详解】D 处为阿拉伯半岛,它的沿岸蕴藏着丰富的石油和天然气资源.故装船的货物最有可能是石油,B 正确。
【点睛】亚洲面积广大,地跨寒、温、热三带,且地形复杂多样,除温带海洋性气候外,世界上的各种气候在亚洲都有分布。
2018-2019学年湖北省宜昌市教学协作体高二下学期期中考试历史试卷

2018-2019学年湖北省宜昌市教学协作体高二下学期期中考试高二历史★祝考试顺利★注意事项:1、答题前,请先将自己的姓名、准考证号用0.5毫米黑色签字笔填写在试题卷和答题卡上的相应位置,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B铅笔将答题卡上试卷类型A后的方框涂黑。
2、选择题的作答:每个小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非选择题答题区域的答案一律无效。
3、主观题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域的答案一律无效。
如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。
答案用0.5毫米黑色签字笔写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非选修题答题区域的答案一律无效。
5、保持卡面清洁,不折叠,不破损,不得使用涂改液、胶带纸、修正带等。
6、考试结束后,请将本试题卷、答题卡、草稿纸一并依序排列上交。
一、选择题(共24小题,每小题2分,共48分) 1.西周初年兼并无数,封建制度遂发生大变革。
分封同宗以树屏藩,授土勋旧以拓疆域。
材料表明“封建制度”()A. 有助于消除地方与中央的矛盾B. 推动了西周政治文化的传播C. 是西周稳固统治的的重要途径D. 加速了“大一统”局面的形成2.中国古代,“天”被尊为最高神。
秦汉以后,以“天子”自居的皇帝举行祭天大典,表明自己“承天”而“子民”,官员、百姓则祭拜自己的祖先。
这反映了秦汉以后( )A.君主专制缘于宗教权威B.政治统治借助于人伦秩序C.皇权至上促成祖先崇拜D.祭天活动强化了宗法制度3.北魏均田制实行后,文献中出现了“庄园”一词,被指圈占的成片土地。
唐代均田制实行后,“庄园”一词的使用更普遍。
这反映了均田制实行后( )A.井田制得以恢复B.不存在土地私有现象C.仍存在土地集中现象D.庄园由中央集中管理4.《隋都城图》题记:“畦分棋布,闾巷皆中绳墨,坊有墉(墙),墉有门,逋亡奸伪无所容足。
湖北省宜昌市部分示范高中教学协作体2018_2019学年高二生物下学期期中试题20190604025

宜昌市部分示范高中教学协作体年春期中联考高二生物(卷面满分:分考试用时:分钟)一、选择题 (第题每题分,第题每题分,共分) 、组成和的核苷酸种类有().种.种.种.种、真核生物染色体遗传信息的传递与表达过程,在细胞质中进行的是()、基因控制生物体性状的方式是 ()•通过控制酶的合成来控制代谢过程,进而控制生物体 性状 •通过控制蛋白质的结构直接控制生物体的性状 •基因通过控制激素的合成控制生物体的性状 .包括和两种方式、右图中①和②表示发生在常染色体上的变异。
①和②所示的变异类型分别属于 () •基因重组和染色体易位•染色体易位和染色体易位 •染色体易位和基因重组•基因重组和基因重组、把普通小麦(体细胞有个染色体组 )的花粉和一部分体细胞,通过组织培养,分别培育为两种小麦植株,它们分别是()•单倍体、二倍体•三倍体、六倍体.单倍体、六倍体•复制 •转录 .翻译.转录和翻译w ? V.倍体、单倍体、通过对细胞有丝分裂中期或减数第一次分裂时期的观察,发现一些染色体异常的细胞,如图、、、,它们依次属于().三体、染色体片段重复、三倍体、染色体片段缺失.三倍体、染色体片段缺失、三体、染色体片段重复.三倍体、染色体片刻重复、三体、染色体片段缺失.染色体片段缺失、三体、染色体片段重复,三倍体、下列关于基因突变特点的说法正确的是( ).生物在个体发育的特定时期才可发生突变.基因突变是生物变异的根本来源,无论是低等还是高等生物都可能发生突变.自然状态下的突变是不定向的,而人工诱变多是定向的.虽然自发突变频率很低,但对生物的生存往往是有利的、在一个果蝇种群中基因型为的个体占,的个体占,的个体占。
基因和基因的基因频率分别是( ).、.、.、.、、用紫外线照射红色细菌的培养液,几天后出现了一个白色菌落,把这个白色菌落转移培养,长出的菌落全是白色的,这种变异是( ).染色体变异.基因重组.人工诱变.自然突变、根据现代生物进化理论,下列观点中正确的是.人工培育的新物种只能生活在人工环境中.生物进化的实质是种群基因型频率的改变.隔离是新物种形成的必要条件,隔离包括地理隔离和生殖隔离.物种的形成可以不经过隔离、下列有关生物体遗传物质的叙述,正确的是.豌豆的遗传物质主要是.酵母菌的遗传物质主要分布在染色体上.噬菌体的遗传物质含有硫元素.的遗传物质水解产生种脱氧核苷酸、早在年,科学家们启动了人类基因组计划,截至年,人类基因组的测序任务已顺利完成;我国遗传科学家率先绘制了世界上第一张水稻基因遗传图,为水稻基因组计划作出了重要贡献。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖北省宜昌市部分示范高中教学协作体2018-2019学年高二日语下学
期期中试题
答题注意事项:
1.本试卷满分150 分;考试用时120分钟。
2.本试卷分两卷,第一卷听力(共30分),第二卷笔试(共120分)。
3.所有答题均答在答题卡上,不按要求答卷不得分。
第一部分:听力(共两节,满分30分)
第一节----听下面7段录音,每段录音后有1道小题,从题中所给的A B C三个选项中选出最佳选项。
(共7题:每小题2分,满分14分)
1. 女の人は何を作りましたか。
A.すき焼き
B.ケーキ
C.ご飯
2. 2人はどこに行きますか。
A.映画館へ行きます
B.海か山のある所へ行きます
C.プールへ行きます
3. 昨日男の人はどこへ行きましたか。
A.学校
B.病院
C.居酒屋
4. 男の人は新しい店のとこが気に入らないのですか。
A.味
B.人が多いです
C.値段
5.男の人はこれからどうしますか。
A.帰ります
B.女の人の家に入ります
C.別の人に家へ行きます
6.宿題は何曜日までですか。
A.火曜日
B.金曜日
C.木曜日
7. 女の人はいつも何時ごろ寝ますか。
A. 12時
B.9時
C.11時
第二节------听下面4段录音,每段录音后有2道小题,从题中所给的A B C三个选项中选出最佳选项。
(共8题:每小题2分,满分16分)
8. 男の人はいつも何時ごろ家に帰りますか。
A.8時
B.7時
C.10時
9.会議はどのぐらいかかりますか。
A.1時間
B.2時間
C.3時間
10. 女の人は何を食べたいですか。
A.焼きそば
B. ラーメン
C.ケーキ
11. 今日は誰が料理を作りますか。
A.男の人の奥さん
B. 女の人
C.男の人
12. 大学までどのぐらいかかりますか
A.45分
B.1時間
C.1時間半
13. 時間が一番長いのは何ですか。
A. 電車
B.バス
C.地下鉄
14. 最初に入れたのは何ですか。
A.肉
B. 醤油
C.塩
15. 入れないのは何ですか。
A.醤油
B. 砂糖
C.野菜
第二部分:笔试(满分120分)
一、请写出下列日文汉字对应的假名。
(10分)
空港研究絵本経済習慣
教師日記豊作通勤握手
二、请写出下列外来语的中文意思。
(10分)
アルバイトチケットインターネットマフラーダンススピーチクラスエスカレーターデザインコピー
三、选择题。
(30分)
16.静かなところ()住みたいです。
A.に
B.を
C.は
D.と
17.すみません。
ビール()ください。
A.に
B.を
C.が
D.は
18.あなたの家は駅()遠いです。
A.が
B.と
C.で
D.から
19.妹はこれから教師に()たいと思っています。
